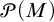1 Introduction
Throughout this paper, we shall work in
![]() $\mathsf {ZF}$
(i.e., the Zermelo–Fraenkel set theory without the axiom of choice).
$\mathsf {ZF}$
(i.e., the Zermelo–Fraenkel set theory without the axiom of choice).
In [Reference Cantor1], Cantor proves that, for all sets M, there are no bijections between M and
![]() $\operatorname {\mathrm {\mathscr {P}}}(M)$
, and since there is an injection from M into
$\operatorname {\mathrm {\mathscr {P}}}(M)$
, and since there is an injection from M into
![]() $\operatorname {\mathrm {\mathscr {P}}}(M)$
, it follows that there are no injections from
$\operatorname {\mathrm {\mathscr {P}}}(M)$
, it follows that there are no injections from
![]() $\operatorname {\mathrm {\mathscr {P}}}(M)$
into M. In [Reference Specker12], Specker proves a generalization of Cantor’s theorem, which states that, for all infinite sets M, there are no injections from
$\operatorname {\mathrm {\mathscr {P}}}(M)$
into M. In [Reference Specker12], Specker proves a generalization of Cantor’s theorem, which states that, for all infinite sets M, there are no injections from
![]() $\operatorname {\mathrm {\mathscr {P}}}(M)$
into
$\operatorname {\mathrm {\mathscr {P}}}(M)$
into
![]() $M^2$
. In [Reference Forster2], Forster proves another generalization of Cantor’s theorem, which states that, for all infinite sets M, there are no finite-to-one functions from
$M^2$
. In [Reference Forster2], Forster proves another generalization of Cantor’s theorem, which states that, for all infinite sets M, there are no finite-to-one functions from
![]() $\operatorname {\mathrm {\mathscr {P}}}(M)$
to M. In [Reference Shen8–Reference Shen10], several further generalizations of these results are proved, among which are the following:
$\operatorname {\mathrm {\mathscr {P}}}(M)$
to M. In [Reference Shen8–Reference Shen10], several further generalizations of these results are proved, among which are the following:
-
(i) For all infinite sets M and all
 $n\in \omega $
, there are no finite-to-one functions from
$n\in \omega $
, there are no finite-to-one functions from
 $\operatorname {\mathrm {\mathscr {P}}}(M)$
to
$\operatorname {\mathrm {\mathscr {P}}}(M)$
to
 $M^n$
or to
$M^n$
or to
 $[M]^n$
.
$[M]^n$
. -
(ii) For all infinite sets M, there are no finite-to-one functions from
 $\operatorname {\mathrm {\mathscr {P}}}(M)$
to
$\operatorname {\mathrm {\mathscr {P}}}(M)$
to
 $\omega \times M$
.
$\omega \times M$
. -
(iii) For all infinite sets M and all sets N, if there is a finite-to-one function from N to M, then there are no surjections from N onto
 $\operatorname {\mathrm {\mathscr {P}}}(M)$
.
$\operatorname {\mathrm {\mathscr {P}}}(M)$
.
For a set M, let
![]() $\operatorname {\mathrm {fin}}(M)$
denote the set of all finite subsets of M. Although it can be proved in
$\operatorname {\mathrm {fin}}(M)$
denote the set of all finite subsets of M. Although it can be proved in
![]() $\mathsf {ZF}$
that, for all infinite sets M, there are no injections from
$\mathsf {ZF}$
that, for all infinite sets M, there are no injections from
![]() $\operatorname {\mathrm {\mathscr {P}}}(M)$
into
$\operatorname {\mathrm {\mathscr {P}}}(M)$
into
![]() $\operatorname {\mathrm {fin}}(M)$
(cf. [Reference Halbeisen and Shelah5, Theorem 3]), the existence of an infinite set A such that there is a finite-to-one function from
$\operatorname {\mathrm {fin}}(M)$
(cf. [Reference Halbeisen and Shelah5, Theorem 3]), the existence of an infinite set A such that there is a finite-to-one function from
![]() $\operatorname {\mathrm {\mathscr {P}}}(A)$
to
$\operatorname {\mathrm {\mathscr {P}}}(A)$
to
![]() $\operatorname {\mathrm {fin}}(A)$
and such that there is a surjection from
$\operatorname {\mathrm {fin}}(A)$
and such that there is a surjection from
![]() $\operatorname {\mathrm {fin}}(A)$
onto
$\operatorname {\mathrm {fin}}(A)$
onto
![]() $\operatorname {\mathrm {\mathscr {P}}}(A)$
is consistent with
$\operatorname {\mathrm {\mathscr {P}}}(A)$
is consistent with
![]() $\mathsf {ZF}$
(cf. [Reference Shen8, Remark 3.10] and [Reference Halbeisen and Shelah5, Theorem 1]). Now it is natural to ask whether the existence of an infinite set A such that there is a surjection from
$\mathsf {ZF}$
(cf. [Reference Shen8, Remark 3.10] and [Reference Halbeisen and Shelah5, Theorem 1]). Now it is natural to ask whether the existence of an infinite set A such that there is a surjection from
![]() $A^2$
onto
$A^2$
onto
![]() $\operatorname {\mathrm {\mathscr {P}}}(A)$
or from
$\operatorname {\mathrm {\mathscr {P}}}(A)$
or from
![]() $[A]^2$
onto
$[A]^2$
onto
![]() $\operatorname {\mathrm {\mathscr {P}}}(A)$
is consistent with
$\operatorname {\mathrm {\mathscr {P}}}(A)$
is consistent with
![]() $\mathsf {ZF}$
, and these questions are originally asked in [Reference Truss13] and in [Reference Halbeisen4] respectively. In [Reference Shen and Yuan11, Question 5.6], it is asked whether the existence of an infinite set A such that there is a surjection from
$\mathsf {ZF}$
, and these questions are originally asked in [Reference Truss13] and in [Reference Halbeisen4] respectively. In [Reference Shen and Yuan11, Question 5.6], it is asked whether the existence of an infinite set A such that there is a surjection from
![]() $\omega \times A$
onto
$\omega \times A$
onto
![]() $\operatorname {\mathrm {\mathscr {P}}}(A)$
is consistent with
$\operatorname {\mathrm {\mathscr {P}}}(A)$
is consistent with
![]() $\mathsf {ZF}$
, and it is noted there that an affirmative answer to this question would yield affirmative answers to the above two questions. In this paper, we give a negative answer to this question; that is, we prove in
$\mathsf {ZF}$
, and it is noted there that an affirmative answer to this question would yield affirmative answers to the above two questions. In this paper, we give a negative answer to this question; that is, we prove in
![]() $\mathsf {ZF}$
that, for all infinite sets M, there are no surjections from
$\mathsf {ZF}$
that, for all infinite sets M, there are no surjections from
![]() $\omega \times M$
onto
$\omega \times M$
onto
![]() $\operatorname {\mathrm {\mathscr {P}}}(M)$
. We also obtain some related results.
$\operatorname {\mathrm {\mathscr {P}}}(M)$
. We also obtain some related results.
2 Preliminaries
In this section, we indicate briefly our use of some terminology and notation. For a function f, we use
![]() $\operatorname {\mathrm {dom}}(f)$
for the domain of f,
$\operatorname {\mathrm {dom}}(f)$
for the domain of f,
![]() $\operatorname {\mathrm {ran}}(f)$
for the range of f,
$\operatorname {\mathrm {ran}}(f)$
for the range of f,
![]() $f[A]$
for the image of A under f,
$f[A]$
for the image of A under f,
![]() $f^{-1}[A]$
for the inverse image of A under f, and
$f^{-1}[A]$
for the inverse image of A under f, and
![]() $f{\upharpoonright } A$
for the restriction of f to A. For functions f and g, we use
$f{\upharpoonright } A$
for the restriction of f to A. For functions f and g, we use
![]() $g\circ f$
for the composition of g and f. We write
$g\circ f$
for the composition of g and f. We write
![]() $f:A\to B$
to express that f is a function from A to B, and
$f:A\to B$
to express that f is a function from A to B, and
![]() $f:A\twoheadrightarrow B$
to express that f is a function from A onto B.
$f:A\twoheadrightarrow B$
to express that f is a function from A onto B.
Definition 2.1. Let
![]() $A,B$
be arbitrary sets.
$A,B$
be arbitrary sets.
-
(1)
 $A\preccurlyeq B$
means that there exists an injection from A into B.
$A\preccurlyeq B$
means that there exists an injection from A into B. -
(2)
 $A\preccurlyeq ^\ast B$
means that there exists a surjection from a subset of B onto A.
$A\preccurlyeq ^\ast B$
means that there exists a surjection from a subset of B onto A. -
(3)
 $\operatorname {\mathrm {fin}}(A)$
denotes the set of all finite subsets of A.
$\operatorname {\mathrm {fin}}(A)$
denotes the set of all finite subsets of A. -
(4)
 $\operatorname {\mathrm {\mathscr {P}_{\infty }}}(A)$
denotes the set of all infinite subsets of A.
$\operatorname {\mathrm {\mathscr {P}_{\infty }}}(A)$
denotes the set of all infinite subsets of A.
Clearly, if
![]() $A\preccurlyeq B$
then
$A\preccurlyeq B$
then
![]() $A\preccurlyeq ^\ast B$
, and if
$A\preccurlyeq ^\ast B$
, and if
![]() $A\preccurlyeq ^\ast B$
then
$A\preccurlyeq ^\ast B$
then
![]() $\operatorname {\mathrm {\mathscr {P}}}(A)\preccurlyeq \operatorname {\mathrm {\mathscr {P}}}(B)$
and
$\operatorname {\mathrm {\mathscr {P}}}(A)\preccurlyeq \operatorname {\mathrm {\mathscr {P}}}(B)$
and
![]() $\operatorname {\mathrm {\mathscr {P}_{\infty }}}(A)\preccurlyeq \operatorname {\mathrm {\mathscr {P}_{\infty }}}(B)$
.
$\operatorname {\mathrm {\mathscr {P}_{\infty }}}(A)\preccurlyeq \operatorname {\mathrm {\mathscr {P}_{\infty }}}(B)$
.
Fact 2.2.
![]() $\omega _1\preccurlyeq ^\ast \operatorname {\mathrm {\mathscr {P}}}(\omega )$
.
$\omega _1\preccurlyeq ^\ast \operatorname {\mathrm {\mathscr {P}}}(\omega )$
.
Proof Cf. [Reference Halbeisen3, Theorem 5.11].
In the sequel, we shall frequently use expressions like “one can explicitly define” in our formulations, which is illustrated by the following example.
Theorem 2.3 (Cantor–Bernstein)
From injections
![]() $f:A\to B$
and
$f:A\to B$
and
![]() $g:B\to A$
, one can explicitly define a bijection
$g:B\to A$
, one can explicitly define a bijection
![]() $h:A\to B$
.
$h:A\to B$
.
Proof Cf. [Reference Levy7, III.2.8].
Formally, Theorem 2.3 states that in
![]() $\mathsf {ZF}$
one can define a class function H without free variables such that, whenever f is an injection from A into B and g is an injection from B into A,
$\mathsf {ZF}$
one can define a class function H without free variables such that, whenever f is an injection from A into B and g is an injection from B into A,
![]() $H(f,g)$
is defined and is a bijection between A and B.
$H(f,g)$
is defined and is a bijection between A and B.
We say that a set M is Dedekind infinite if there exists a bijection between M and a proper subset of M; otherwise M is Dedekind finite. It is well-known that M is Dedekind infinite if and only if there exists an injection from
![]() $\omega $
into M. We say that a set M is power Dedekind infinite if the power set of M is Dedekind infinite; otherwise M is power Dedekind finite. Recall Kuratowski’s celebrated theorem:
$\omega $
into M. We say that a set M is power Dedekind infinite if the power set of M is Dedekind infinite; otherwise M is power Dedekind finite. Recall Kuratowski’s celebrated theorem:
Theorem 2.4 (Kuratowski)
A set M is power Dedekind infinite if and only if there exists a surjection from M onto
![]() $\omega $
.
$\omega $
.
Proof Cf. [Reference Halbeisen3, Proposition 5.4].
3 The main theorem
In this section, we prove our main theorem, which states that, for all infinite sets M, there are no surjections from
![]() $\omega \times M$
onto
$\omega \times M$
onto
![]() $\operatorname {\mathrm {\mathscr {P}}}(M)$
. We first recall some well-known results.
$\operatorname {\mathrm {\mathscr {P}}}(M)$
. We first recall some well-known results.
Theorem 3.1 (Cantor)
From a function
![]() $f:M\to \operatorname {\mathrm {\mathscr {P}}}(M)$
, one can explicitly define an
$f:M\to \operatorname {\mathrm {\mathscr {P}}}(M)$
, one can explicitly define an
![]() $A\in \operatorname {\mathrm {\mathscr {P}}}(M)\setminus \operatorname {\mathrm {ran}}(f)$
.
$A\in \operatorname {\mathrm {\mathscr {P}}}(M)\setminus \operatorname {\mathrm {ran}}(f)$
.
Proof It suffices to take
![]() $A=\{x\in \operatorname {\mathrm {dom}}(f)\mid x\notin f(x)\}$
.
$A=\{x\in \operatorname {\mathrm {dom}}(f)\mid x\notin f(x)\}$
.
Lemma 3.2. For any infinite ordinal
![]() $\alpha $
, one can explicitly define an injection
$\alpha $
, one can explicitly define an injection
![]() $f:\alpha \times \alpha \to \alpha $
.
$f:\alpha \times \alpha \to \alpha $
.
Proof Cf. [Reference Specker12, 2.1] or [Reference Levy7, IV.2.24].
Lemma 3.3. For any infinite ordinal
![]() $\alpha $
, one can explicitly define an injection
$\alpha $
, one can explicitly define an injection
![]() $f:\operatorname {\mathrm {fin}}(\alpha )\to \alpha $
.
$f:\operatorname {\mathrm {fin}}(\alpha )\to \alpha $
.
Proof Cf. [Reference Halbeisen3, Theorem 5.19].
Lemma 3.4. For any infinite ordinal
![]() $\alpha $
, one can explicitly define a bijection
$\alpha $
, one can explicitly define a bijection
![]() $f:\omega ^\alpha \to \alpha $
.
$f:\omega ^\alpha \to \alpha $
.
Proof Let
![]() $\alpha $
be an infinite ordinal. Let
$\alpha $
be an infinite ordinal. Let
and let r be the right lexicographic ordering of
![]() $\exp (\omega ,\alpha )$
. It is easy to verify that r well-orders
$\exp (\omega ,\alpha )$
. It is easy to verify that r well-orders
![]() $\exp (\omega ,\alpha )$
and the order type of
$\exp (\omega ,\alpha )$
and the order type of
![]() $\langle \exp (\omega ,\alpha ),r\rangle $
is
$\langle \exp (\omega ,\alpha ),r\rangle $
is
![]() $\omega ^\alpha $
(cf. [Reference Levy7, IV.2.10]). Let g be the unique isomorphism of
$\omega ^\alpha $
(cf. [Reference Levy7, IV.2.10]). Let g be the unique isomorphism of
![]() $\langle \omega ^\alpha ,\in \rangle $
onto
$\langle \omega ^\alpha ,\in \rangle $
onto
![]() $\langle \exp (\omega ,\alpha ),r\rangle $
. Let h be the function on
$\langle \exp (\omega ,\alpha ),r\rangle $
. Let h be the function on
![]() $\exp (\omega ,\alpha )$
defined by
$\exp (\omega ,\alpha )$
defined by
Then h is an injection from
![]() $\exp (\omega ,\alpha )$
into
$\exp (\omega ,\alpha )$
into
![]() $\operatorname {\mathrm {fin}}(\alpha \times \omega )$
. By Lemmas 3.2 and 3.3, we can explicitly define an injection
$\operatorname {\mathrm {fin}}(\alpha \times \omega )$
. By Lemmas 3.2 and 3.3, we can explicitly define an injection
![]() $p:\operatorname {\mathrm {fin}}(\alpha \times \omega )\to \alpha $
. Therefore,
$p:\operatorname {\mathrm {fin}}(\alpha \times \omega )\to \alpha $
. Therefore,
![]() $p\circ h\circ g$
is an injection from
$p\circ h\circ g$
is an injection from
![]() $\omega ^\alpha $
into
$\omega ^\alpha $
into
![]() $\alpha $
. Now, since the function that maps each
$\alpha $
. Now, since the function that maps each
![]() $\gamma <\alpha $
to
$\gamma <\alpha $
to
![]() $\omega ^\gamma $
is an injection from
$\omega ^\gamma $
is an injection from
![]() $\alpha $
into
$\alpha $
into
![]() $\omega ^\alpha $
, it follows from Theorem 2.3 that we can explicitly define a bijection
$\omega ^\alpha $
, it follows from Theorem 2.3 that we can explicitly define a bijection
![]() $f:\omega ^\alpha \to \alpha $
.
$f:\omega ^\alpha \to \alpha $
.
Fact 3.5. If
![]() $A=B\cup C$
is a set of ordinals which is of order type
$A=B\cup C$
is a set of ordinals which is of order type
![]() $\omega ^\delta $
, then B or C has order type
$\omega ^\delta $
, then B or C has order type
![]() $\omega ^\delta $
.
$\omega ^\delta $
.
Proof Cf. [Reference Levy7, IV.2.22(vii)].
The key step of our proof is the following lemma.
Lemma 3.6. From a surjection
![]() $f:\omega \times M\twoheadrightarrow \alpha $
, where
$f:\omega \times M\twoheadrightarrow \alpha $
, where
![]() $\alpha $
is an uncountable ordinal, one can explicitly define a surjection from M onto
$\alpha $
is an uncountable ordinal, one can explicitly define a surjection from M onto
![]() $\alpha $
.
$\alpha $
.
Proof Let
![]() $\alpha $
be an uncountable ordinal and let f be a surjection from
$\alpha $
be an uncountable ordinal and let f be a surjection from
![]() $\omega \times M$
onto
$\omega \times M$
onto
![]() $\alpha $
. For each
$\alpha $
. For each
![]() $n\in \omega $
, let
$n\in \omega $
, let
![]() $A_n=f[\{n\}\times M]$
, let
$A_n=f[\{n\}\times M]$
, let
![]() $\delta _n$
be the order type of
$\delta _n$
be the order type of
![]() $A_n$
, and let
$A_n$
, and let
![]() $g_n$
be the unique isomorphism of
$g_n$
be the unique isomorphism of
![]() $\delta _n$
onto
$\delta _n$
onto
![]() $A_n$
. Let
$A_n$
. Let
![]() $\delta =\bigcup _{n\in \omega }\delta _n$
and let g be the function on
$\delta =\bigcup _{n\in \omega }\delta _n$
and let g be the function on
![]() $\omega \times \delta $
defined by
$\omega \times \delta $
defined by
 $$ \begin{align*} g(n,\gamma)= \begin{cases} g_n(\gamma), & \text{if }\gamma<\delta_n,\\ 0, & \text{otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*} g(n,\gamma)= \begin{cases} g_n(\gamma), & \text{if }\gamma<\delta_n,\\ 0, & \text{otherwise.} \end{cases} \end{align*} $$
Then g is a surjection from
![]() $\omega \times \delta $
onto
$\omega \times \delta $
onto
![]() $\alpha $
, which implies that
$\alpha $
, which implies that
![]() $\delta $
is also an uncountable ordinal. Hence, it follows from Lemma 3.2 that we can explicitly define a surjection from
$\delta $
is also an uncountable ordinal. Hence, it follows from Lemma 3.2 that we can explicitly define a surjection from
![]() $\delta $
onto
$\delta $
onto
![]() $\alpha $
. So it suffices to explicitly define a surjection from M onto
$\alpha $
. So it suffices to explicitly define a surjection from M onto
![]() $\delta $
. We consider the following two cases:
$\delta $
. We consider the following two cases:
Case 1. There exists an
![]() $n\in \omega $
such that
$n\in \omega $
such that
![]() $\delta _n=\delta $
. Let
$\delta _n=\delta $
. Let
![]() $n_0$
be the least natural number such that
$n_0$
be the least natural number such that
![]() $\delta _{n_0}=\delta $
. Then the function that maps each
$\delta _{n_0}=\delta $
. Then the function that maps each
![]() $x\in M$
to
$x\in M$
to
![]() $g_{n_0}^{-1}(f(n_0,x))$
is a surjection of M onto
$g_{n_0}^{-1}(f(n_0,x))$
is a surjection of M onto
![]() $\delta $
.
$\delta $
.
Case 2. If we are not in Case 1, then, since
![]() $\delta =\bigcup _{n\in \omega }\delta _n$
,
$\delta =\bigcup _{n\in \omega }\delta _n$
,
![]() $\delta $
is a limit ordinal. Since
$\delta $
is a limit ordinal. Since
![]() $\delta>\omega $
, without loss of generality, assume that
$\delta>\omega $
, without loss of generality, assume that
![]() $\delta _n$
is infinite for all
$\delta _n$
is infinite for all
![]() $n\in \omega $
. For each
$n\in \omega $
. For each
![]() $n\in \omega $
, let
$n\in \omega $
, let
![]() $\beta _n=\omega ^{\delta _n}$
. By Lemma 3.4, for each
$\beta _n=\omega ^{\delta _n}$
. By Lemma 3.4, for each
![]() $n\in \omega $
, we can explicitly define a bijection
$n\in \omega $
, we can explicitly define a bijection
![]() $p_n:\beta _n\to \delta _n$
. For each
$p_n:\beta _n\to \delta _n$
. For each
![]() $n\in \omega $
, let
$n\in \omega $
, let
![]() $h_n$
be the function on M defined by
$h_n$
be the function on M defined by
![]() $h_n(x)=p_n^{-1}(g_n^{-1}(f(n,x)))$
. Then, for any
$h_n(x)=p_n^{-1}(g_n^{-1}(f(n,x)))$
. Then, for any
![]() $n\in \omega $
,
$n\in \omega $
,
![]() $h_n$
is a surjection from M onto
$h_n$
is a surjection from M onto
![]() $\beta _n$
. Let
$\beta _n$
. Let
![]() $\beta =\omega ^\delta $
. Clearly,
$\beta =\omega ^\delta $
. Clearly,
![]() $\beta =\bigcup _{n\in \omega }\beta _n$
. By Lemma 3.4, it suffices to explicitly define a surjection
$\beta =\bigcup _{n\in \omega }\beta _n$
. By Lemma 3.4, it suffices to explicitly define a surjection
![]() $h:M\twoheadrightarrow \beta $
.
$h:M\twoheadrightarrow \beta $
.
We first define by recursion two sequences
![]() $\langle B_n\rangle _{n\in \omega }$
and
$\langle B_n\rangle _{n\in \omega }$
and
![]() $\langle q_n\rangle _{n\in \omega }$
as follows. Let
$\langle q_n\rangle _{n\in \omega }$
as follows. Let
![]() $B_0=M$
. Let
$B_0=M$
. Let
![]() $n\in \omega $
and assume that
$n\in \omega $
and assume that
![]() $B_n\subseteq M$
has been defined so that
$B_n\subseteq M$
has been defined so that
We define a subset
![]() $B_{n+1}$
of
$B_{n+1}$
of
![]() $B_n$
and a surjection
$B_n$
and a surjection
![]() $q_n:B_n\setminus B_{n+1}\twoheadrightarrow \beta _n$
as follows. Since
$q_n:B_n\setminus B_{n+1}\twoheadrightarrow \beta _n$
as follows. Since
![]() $\beta _n<\beta $
, by (1), there is a least
$\beta _n<\beta $
, by (1), there is a least
![]() $k\in \omega $
such that
$k\in \omega $
such that
![]() $\beta _n<\beta _k$
and
$\beta _n<\beta _k$
and
![]() $h_k[B_n]$
has order type
$h_k[B_n]$
has order type
![]() $\beta _k$
. Let t be the unique isomorphism of
$\beta _k$
. Let t be the unique isomorphism of
![]() $h_k[B_n]$
onto
$h_k[B_n]$
onto
![]() $\beta _k$
, and let
$\beta _k$
, and let
Since
![]() $\beta _k=\omega ^{\delta _k}$
is closed under ordinal addition, it follows that
$\beta _k=\omega ^{\delta _k}$
is closed under ordinal addition, it follows that
![]() $\beta _n\cdot 2<\beta _k$
. Now, if (1) holds with
$\beta _n\cdot 2<\beta _k$
. Now, if (1) holds with
![]() $B_n$
replaced by D, we define
$B_n$
replaced by D, we define
![]() $B_{n+1}=D$
and let
$B_{n+1}=D$
and let
![]() $q_n$
be the function on
$q_n$
be the function on
![]() $B_n\setminus D$
defined by
$B_n\setminus D$
defined by
 $$ \begin{align*} q_n(x)= \begin{cases} \text{the unique }\gamma<\beta_n\text{ such that }t(h_k(x))=\beta_n+\gamma, & \text{if }t(h_k(x))<\beta_n\cdot2,\\ 0, & \text{otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*} q_n(x)= \begin{cases} \text{the unique }\gamma<\beta_n\text{ such that }t(h_k(x))=\beta_n+\gamma, & \text{if }t(h_k(x))<\beta_n\cdot2,\\ 0, & \text{otherwise.} \end{cases} \end{align*} $$
Otherwise, it follows from (1) and Fact 3.5 that (1) holds with
![]() $B_n$
replaced by
$B_n$
replaced by
![]() $B_n\setminus D$
, and then we define
$B_n\setminus D$
, and then we define
![]() $B_{n+1}=B_n\setminus D$
and let
$B_{n+1}=B_n\setminus D$
and let
![]() $q_n$
be the function on D defined by
$q_n$
be the function on D defined by
![]() $q_n(x)=t(h_k(x))$
. Clearly, in either case,
$q_n(x)=t(h_k(x))$
. Clearly, in either case,
![]() $B_{n+1}\subseteq B_n$
, (1) holds with
$B_{n+1}\subseteq B_n$
, (1) holds with
![]() $B_n$
replaced by
$B_n$
replaced by
![]() $B_{n+1}$
, and
$B_{n+1}$
, and
![]() $q_n$
is a surjection from
$q_n$
is a surjection from
![]() $B_n\setminus B_{n+1}$
onto
$B_n\setminus B_{n+1}$
onto
![]() $\beta _n$
. Now, it suffices to define
$\beta _n$
. Now, it suffices to define
![]() $h=\bigcup _{n\in \omega }q_n\cup (\bigcap _{n\in \omega }B_n\times \{0\})$
.
$h=\bigcup _{n\in \omega }q_n\cup (\bigcap _{n\in \omega }B_n\times \{0\})$
.
Lemma 3.7. For all infinite sets M and all sets N, if there is a finite-to-one function from N to M, then there are no surjections from N onto
![]() $\operatorname {\mathrm {\mathscr {P}}}(M)$
.
$\operatorname {\mathrm {\mathscr {P}}}(M)$
.
Proof Cf. [Reference Shen8, Theorem 5.3].
Now we are ready to prove our main theorem.
Theorem 3.8. For all infinite sets M, there are no surjections from
![]() $\omega \times M$
onto
$\omega \times M$
onto
![]() $\operatorname {\mathrm {\mathscr {P}}}(M)$
.
$\operatorname {\mathrm {\mathscr {P}}}(M)$
.
Proof Assume towards a contradiction that there exist an infinite set M and a surjection
![]() $\Phi :\omega \times M\twoheadrightarrow \operatorname {\mathrm {\mathscr {P}}}(M)$
. We first prove that M is power Dedekind infinite. Let
$\Phi :\omega \times M\twoheadrightarrow \operatorname {\mathrm {\mathscr {P}}}(M)$
. We first prove that M is power Dedekind infinite. Let
![]() $\Psi $
be the restriction of
$\Psi $
be the restriction of
![]() $\Phi $
to the set
$\Phi $
to the set
![]() $\{(n,x)\in \omega \times M\mid \Phi (n,x)=\Phi (k,x)\text { for no }k<n\}$
. Clearly,
$\{(n,x)\in \omega \times M\mid \Phi (n,x)=\Phi (k,x)\text { for no }k<n\}$
. Clearly,
![]() $\Psi $
is a surjection from a subset of
$\Psi $
is a surjection from a subset of
![]() $\omega \times M$
onto
$\omega \times M$
onto
![]() $\operatorname {\mathrm {\mathscr {P}}}(M)$
such that, for all
$\operatorname {\mathrm {\mathscr {P}}}(M)$
such that, for all
![]() $x\in M$
,
$x\in M$
,
![]() $\Psi {\upharpoonright }(\omega \times \{x\})$
is injective. If M is power Dedekind finite, then
$\Psi {\upharpoonright }(\omega \times \{x\})$
is injective. If M is power Dedekind finite, then
![]() $\operatorname {\mathrm {dom}}(\Psi )\cap (\omega \times \{x\})$
is finite for all
$\operatorname {\mathrm {dom}}(\Psi )\cap (\omega \times \{x\})$
is finite for all
![]() $x\in M$
, and thus there exists a finite-to-one function from
$x\in M$
, and thus there exists a finite-to-one function from
![]() $\operatorname {\mathrm {dom}}(\Psi )$
to M, contradicting Lemma 3.7. Hence, M is power Dedekind infinite.
$\operatorname {\mathrm {dom}}(\Psi )$
to M, contradicting Lemma 3.7. Hence, M is power Dedekind infinite.
Now, it follows from Theorem 2.4 that
![]() $\omega \preccurlyeq ^\ast M$
, and thus, by Fact 2.2,
$\omega \preccurlyeq ^\ast M$
, and thus, by Fact 2.2,
![]() $\omega _1\preccurlyeq ^\ast \operatorname {\mathrm {\mathscr {P}}}(\omega )\preccurlyeq \operatorname {\mathrm {\mathscr {P}}}(M)\preccurlyeq ^\ast \omega \times M$
, which implies that
$\omega _1\preccurlyeq ^\ast \operatorname {\mathrm {\mathscr {P}}}(\omega )\preccurlyeq \operatorname {\mathrm {\mathscr {P}}}(M)\preccurlyeq ^\ast \omega \times M$
, which implies that
![]() $\omega _1\preccurlyeq ^\ast M$
by Lemma 3.6 and hence
$\omega _1\preccurlyeq ^\ast M$
by Lemma 3.6 and hence
![]() $\omega _1\preccurlyeq \operatorname {\mathrm {\mathscr {P}}}(M)$
. Let h be an injection from
$\omega _1\preccurlyeq \operatorname {\mathrm {\mathscr {P}}}(M)$
. Let h be an injection from
![]() $\omega _1$
into
$\omega _1$
into
![]() $\operatorname {\mathrm {\mathscr {P}}}(M)$
. In what follows, we get a contradiction by constructing by recursion an injection H from
$\operatorname {\mathrm {\mathscr {P}}}(M)$
. In what follows, we get a contradiction by constructing by recursion an injection H from
![]() $\mathrm {Ord}$
(the class of all ordinals) into
$\mathrm {Ord}$
(the class of all ordinals) into
![]() $\operatorname {\mathrm {\mathscr {P}}}(M)$
.
$\operatorname {\mathrm {\mathscr {P}}}(M)$
.
For
![]() $\gamma <\omega _1$
, we take
$\gamma <\omega _1$
, we take
![]() $H(\gamma )=h(\gamma )$
. Now, we assume that
$H(\gamma )=h(\gamma )$
. Now, we assume that
![]() $\alpha $
is an uncountable ordinal and that
$\alpha $
is an uncountable ordinal and that
![]() $H{\upharpoonright }\alpha $
is an injection from
$H{\upharpoonright }\alpha $
is an injection from
![]() $\alpha $
into
$\alpha $
into
![]() $\operatorname {\mathrm {\mathscr {P}}}(M)$
. Then
$\operatorname {\mathrm {\mathscr {P}}}(M)$
. Then
![]() $(H{\upharpoonright }\alpha )^{-1}\circ \Phi $
is a surjection from a subset of
$(H{\upharpoonright }\alpha )^{-1}\circ \Phi $
is a surjection from a subset of
![]() $\omega \times M$
onto
$\omega \times M$
onto
![]() $\alpha $
and hence can be extended by zero to a surjection
$\alpha $
and hence can be extended by zero to a surjection
![]() $f:\omega \times M\twoheadrightarrow \alpha $
. By Lemma 3.6, f explicitly provides a surjection
$f:\omega \times M\twoheadrightarrow \alpha $
. By Lemma 3.6, f explicitly provides a surjection
![]() $g:M\twoheadrightarrow \alpha $
. Since
$g:M\twoheadrightarrow \alpha $
. Since
![]() $(H{\upharpoonright }\alpha )\circ g$
is a surjection from M onto
$(H{\upharpoonright }\alpha )\circ g$
is a surjection from M onto
![]() $H[\alpha ]$
, it follows from Theorem 3.1 that we can explicitly define an
$H[\alpha ]$
, it follows from Theorem 3.1 that we can explicitly define an
![]() $H(\alpha )\in \operatorname {\mathrm {\mathscr {P}}}(M)\setminus H[\alpha ]$
from
$H(\alpha )\in \operatorname {\mathrm {\mathscr {P}}}(M)\setminus H[\alpha ]$
from
![]() $H{\upharpoonright }\alpha $
(and
$H{\upharpoonright }\alpha $
(and
![]() $\Phi $
).
$\Phi $
).
4 A further generalization
In [Reference Kirmayer6], Kirmayer proves that, for all infinite sets M, there are no surjections from M onto
![]() $\operatorname {\mathrm {\mathscr {P}_{\infty }}}(M)$
. In this section, we generalize this result by showing that, for all infinite sets M, there are no surjections from
$\operatorname {\mathrm {\mathscr {P}_{\infty }}}(M)$
. In this section, we generalize this result by showing that, for all infinite sets M, there are no surjections from
![]() $\omega \times M$
onto
$\omega \times M$
onto
![]() $\operatorname {\mathrm {\mathscr {P}_{\infty }}}(M)$
, which is also a generalization of Theorem 3.8. The proof is similar to that of Theorem 3.8, but first we have to prove that Lemma 3.7 holds with
$\operatorname {\mathrm {\mathscr {P}_{\infty }}}(M)$
, which is also a generalization of Theorem 3.8. The proof is similar to that of Theorem 3.8, but first we have to prove that Lemma 3.7 holds with
![]() $\operatorname {\mathrm {\mathscr {P}}}(M)$
replaced by
$\operatorname {\mathrm {\mathscr {P}}}(M)$
replaced by
![]() $\operatorname {\mathrm {\mathscr {P}_{\infty }}}(M)$
.
$\operatorname {\mathrm {\mathscr {P}_{\infty }}}(M)$
.
Lemma 4.1. For any infinite ordinal
![]() $\alpha $
, one can explicitly define an injection
$\alpha $
, one can explicitly define an injection
![]() $f:\operatorname {\mathrm {\mathscr {P}}}(\alpha )\to \operatorname {\mathrm {\mathscr {P}_{\infty }}}(\alpha )$
.
$f:\operatorname {\mathrm {\mathscr {P}}}(\alpha )\to \operatorname {\mathrm {\mathscr {P}_{\infty }}}(\alpha )$
.
Proof By Lemma 3.2, we can explicitly define an injection
![]() $p:\alpha \times \alpha \to \alpha $
. Let f be the function on
$p:\alpha \times \alpha \to \alpha $
. Let f be the function on
![]() $\operatorname {\mathrm {\mathscr {P}}}(\alpha )$
defined by
$\operatorname {\mathrm {\mathscr {P}}}(\alpha )$
defined by
 $$ \begin{align*} f(A)= \begin{cases} p[A\times\{0\}], & \text{if }A\text{ is infinite,}\\ p[(\alpha\setminus A)\times\{1\}], & \text{otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*} f(A)= \begin{cases} p[A\times\{0\}], & \text{if }A\text{ is infinite,}\\ p[(\alpha\setminus A)\times\{1\}], & \text{otherwise.} \end{cases} \end{align*} $$
Then it is easy to see that f is an injection from
![]() $\operatorname {\mathrm {\mathscr {P}}}(\alpha )$
into
$\operatorname {\mathrm {\mathscr {P}}}(\alpha )$
into
![]() $\operatorname {\mathrm {\mathscr {P}_{\infty }}}(\alpha )$
.
$\operatorname {\mathrm {\mathscr {P}_{\infty }}}(\alpha )$
.
Lemma 4.2. From a set M, a finite-to-one function
![]() $f:N\to M$
, and a surjection
$f:N\to M$
, and a surjection
![]() $g:N\twoheadrightarrow \alpha $
, where
$g:N\twoheadrightarrow \alpha $
, where
![]() $\alpha $
is an infinite ordinal, one can explicitly define a surjection
$\alpha $
is an infinite ordinal, one can explicitly define a surjection
![]() $h:M\twoheadrightarrow \alpha $
.
$h:M\twoheadrightarrow \alpha $
.
Proof Cf. [Reference Shen8, Lemma 5.2].
Lemma 4.3. For all infinite sets M and all sets N, if there is a finite-to-one function from N to M, then there are no surjections from N onto
![]() $\operatorname {\mathrm {\mathscr {P}_{\infty }}}(M)$
.
$\operatorname {\mathrm {\mathscr {P}_{\infty }}}(M)$
.
Proof Assume towards a contradiction that there exist an infinite set M and a set N such that there exist a finite-to-one function
![]() $f:N\to M$
and a surjection
$f:N\to M$
and a surjection
![]() $\Phi :N\twoheadrightarrow \operatorname {\mathrm {\mathscr {P}_{\infty }}}(M)$
. Clearly, the function that maps each cofinite subset A of M to the cardinality of
$\Phi :N\twoheadrightarrow \operatorname {\mathrm {\mathscr {P}_{\infty }}}(M)$
. Clearly, the function that maps each cofinite subset A of M to the cardinality of
![]() $M\setminus A$
is a surjection from a subset of
$M\setminus A$
is a surjection from a subset of
![]() $\operatorname {\mathrm {\mathscr {P}_{\infty }}}(M)$
onto
$\operatorname {\mathrm {\mathscr {P}_{\infty }}}(M)$
onto
![]() $\omega $
, and hence
$\omega $
, and hence
![]() $\omega \preccurlyeq ^\ast \operatorname {\mathrm {\mathscr {P}_{\infty }}}(M)\preccurlyeq ^\ast N$
, which implies that
$\omega \preccurlyeq ^\ast \operatorname {\mathrm {\mathscr {P}_{\infty }}}(M)\preccurlyeq ^\ast N$
, which implies that
![]() $\omega \preccurlyeq ^\ast M$
by Lemma 4.2. Thus
$\omega \preccurlyeq ^\ast M$
by Lemma 4.2. Thus
![]() $\omega \preccurlyeq \operatorname {\mathrm {\mathscr {P}_{\infty }}}(\omega )\preccurlyeq \operatorname {\mathrm {\mathscr {P}_{\infty }}}(M)$
. Let h be an injection from
$\omega \preccurlyeq \operatorname {\mathrm {\mathscr {P}_{\infty }}}(\omega )\preccurlyeq \operatorname {\mathrm {\mathscr {P}_{\infty }}}(M)$
. Let h be an injection from
![]() $\omega $
into
$\omega $
into
![]() $\operatorname {\mathrm {\mathscr {P}_{\infty }}}(M)$
. In what follows, we get a contradiction by constructing by recursion an injection H from
$\operatorname {\mathrm {\mathscr {P}_{\infty }}}(M)$
. In what follows, we get a contradiction by constructing by recursion an injection H from
![]() $\mathrm {Ord}$
into
$\mathrm {Ord}$
into
![]() $\operatorname {\mathrm {\mathscr {P}_{\infty }}}(M)$
.
$\operatorname {\mathrm {\mathscr {P}_{\infty }}}(M)$
.
For
![]() $n\in \omega $
, we take
$n\in \omega $
, we take
![]() $H(n)=h(n)$
. Now, we assume that
$H(n)=h(n)$
. Now, we assume that
![]() $\alpha $
is an infinite ordinal and that
$\alpha $
is an infinite ordinal and that
![]() $H{\upharpoonright }\alpha $
is an injection from
$H{\upharpoonright }\alpha $
is an injection from
![]() $\alpha $
into
$\alpha $
into
![]() $\operatorname {\mathrm {\mathscr {P}_{\infty }}}(M)$
. Then
$\operatorname {\mathrm {\mathscr {P}_{\infty }}}(M)$
. Then
![]() $(H{\upharpoonright }\alpha )^{-1}\circ \Phi $
is a surjection from a subset of N onto
$(H{\upharpoonright }\alpha )^{-1}\circ \Phi $
is a surjection from a subset of N onto
![]() $\alpha $
and hence can be extended by zero to a surjection
$\alpha $
and hence can be extended by zero to a surjection
![]() $g:N\twoheadrightarrow \alpha $
. By Lemma 4.2, from M, f, and g, we can explicitly define a surjection
$g:N\twoheadrightarrow \alpha $
. By Lemma 4.2, from M, f, and g, we can explicitly define a surjection
![]() $p:M\twoheadrightarrow \alpha $
. Then the function q on
$p:M\twoheadrightarrow \alpha $
. Then the function q on
![]() $\operatorname {\mathrm {\mathscr {P}_{\infty }}}(\alpha )$
defined by
$\operatorname {\mathrm {\mathscr {P}_{\infty }}}(\alpha )$
defined by
![]() $q(A)=p^{-1}[A]$
is an injection from
$q(A)=p^{-1}[A]$
is an injection from
![]() $\operatorname {\mathrm {\mathscr {P}_{\infty }}}(\alpha )$
into
$\operatorname {\mathrm {\mathscr {P}_{\infty }}}(\alpha )$
into
![]() $\operatorname {\mathrm {\mathscr {P}_{\infty }}}(M)$
, and thus it follows from Lemma 4.1 that we can explicitly define an injection
$\operatorname {\mathrm {\mathscr {P}_{\infty }}}(M)$
, and thus it follows from Lemma 4.1 that we can explicitly define an injection
![]() $t:\operatorname {\mathrm {\mathscr {P}}}(\alpha )\to \operatorname {\mathrm {\mathscr {P}_{\infty }}}(M)$
. Then
$t:\operatorname {\mathrm {\mathscr {P}}}(\alpha )\to \operatorname {\mathrm {\mathscr {P}_{\infty }}}(M)$
. Then
![]() $t^{-1}\circ (H{\upharpoonright }\alpha )$
is a bijection between a subset of
$t^{-1}\circ (H{\upharpoonright }\alpha )$
is a bijection between a subset of
![]() $\alpha $
and
$\alpha $
and
![]() $t^{-1}[H[\alpha ]]$
, and thus can be extended by zero to a function
$t^{-1}[H[\alpha ]]$
, and thus can be extended by zero to a function
![]() $u:\alpha \to \operatorname {\mathrm {\mathscr {P}}}(\alpha )$
. By Theorem 3.1, we can explicitly define a
$u:\alpha \to \operatorname {\mathrm {\mathscr {P}}}(\alpha )$
. By Theorem 3.1, we can explicitly define a
![]() $B\in \operatorname {\mathrm {\mathscr {P}}}(\alpha )\setminus \operatorname {\mathrm {ran}}(u)$
. Since
$B\in \operatorname {\mathrm {\mathscr {P}}}(\alpha )\setminus \operatorname {\mathrm {ran}}(u)$
. Since
![]() $t^{-1}[H[\alpha ]]\subseteq \operatorname {\mathrm {ran}}(u)$
, it follows that
$t^{-1}[H[\alpha ]]\subseteq \operatorname {\mathrm {ran}}(u)$
, it follows that
![]() $B\notin t^{-1}[H[\alpha ]]$
, which implies that
$B\notin t^{-1}[H[\alpha ]]$
, which implies that
![]() $t(B)\notin H[\alpha ]$
. Now, it suffices to define
$t(B)\notin H[\alpha ]$
. Now, it suffices to define
![]() $H(\alpha )=t(B)$
.
$H(\alpha )=t(B)$
.
We are now in a position to prove the result mentioned at the beginning of this section.
Theorem 4.4. For all infinite sets M, there are no surjections from
![]() $\omega \times M$
onto
$\omega \times M$
onto
![]() $\operatorname {\mathrm {\mathscr {P}_{\infty }}}(M)$
.
$\operatorname {\mathrm {\mathscr {P}_{\infty }}}(M)$
.
Proof We proceed along the lines of the proof of Theorem 3.8. Assume towards a contradiction that there exist an infinite set M and a surjection
![]() $\Phi :\omega \times M\twoheadrightarrow \operatorname {\mathrm {\mathscr {P}_{\infty }}}(M)$
. We first prove that M is power Dedekind infinite. Let
$\Phi :\omega \times M\twoheadrightarrow \operatorname {\mathrm {\mathscr {P}_{\infty }}}(M)$
. We first prove that M is power Dedekind infinite. Let
![]() $\Psi $
be the restriction of
$\Psi $
be the restriction of
![]() $\Phi $
to the set
$\Phi $
to the set
![]() $\{(n,x)\in \omega \times M\mid \Phi (n,x)=\Phi (k,x)\text { for no }k<n\}$
. Clearly,
$\{(n,x)\in \omega \times M\mid \Phi (n,x)=\Phi (k,x)\text { for no }k<n\}$
. Clearly,
![]() $\Psi $
is a surjection from a subset of
$\Psi $
is a surjection from a subset of
![]() $\omega \times M$
onto
$\omega \times M$
onto
![]() $\operatorname {\mathrm {\mathscr {P}_{\infty }}}(M)$
such that, for all
$\operatorname {\mathrm {\mathscr {P}_{\infty }}}(M)$
such that, for all
![]() $x\in M$
,
$x\in M$
,
![]() $\Psi {\upharpoonright }(\omega \times \{x\})$
is injective. If M is power Dedekind finite, then
$\Psi {\upharpoonright }(\omega \times \{x\})$
is injective. If M is power Dedekind finite, then
![]() $\operatorname {\mathrm {dom}}(\Psi )\cap (\omega \times \{x\})$
is finite for all
$\operatorname {\mathrm {dom}}(\Psi )\cap (\omega \times \{x\})$
is finite for all
![]() $x\in M$
, and thus there exists a finite-to-one function from
$x\in M$
, and thus there exists a finite-to-one function from
![]() $\operatorname {\mathrm {dom}}(\Psi )$
to M, contradicting Lemma 4.3. Hence, M is power Dedekind infinite.
$\operatorname {\mathrm {dom}}(\Psi )$
to M, contradicting Lemma 4.3. Hence, M is power Dedekind infinite.
Now, it follows from Theorem 2.4 that
![]() $\omega \preccurlyeq ^\ast M$
, and thus, by Fact 2.2 and Lemma 4.1,
$\omega \preccurlyeq ^\ast M$
, and thus, by Fact 2.2 and Lemma 4.1,
![]() $\omega _1\preccurlyeq ^\ast \operatorname {\mathrm {\mathscr {P}}}(\omega )\preccurlyeq \operatorname {\mathrm {\mathscr {P}_{\infty }}}(\omega )\preccurlyeq \operatorname {\mathrm {\mathscr {P}_{\infty }}}(M)\preccurlyeq ^\ast \omega \times M$
, which implies that
$\omega _1\preccurlyeq ^\ast \operatorname {\mathrm {\mathscr {P}}}(\omega )\preccurlyeq \operatorname {\mathrm {\mathscr {P}_{\infty }}}(\omega )\preccurlyeq \operatorname {\mathrm {\mathscr {P}_{\infty }}}(M)\preccurlyeq ^\ast \omega \times M$
, which implies that
![]() $\omega _1\preccurlyeq ^\ast M$
by Lemma 3.6 and hence
$\omega _1\preccurlyeq ^\ast M$
by Lemma 3.6 and hence
![]() $\omega _1\preccurlyeq \operatorname {\mathrm {\mathscr {P}_{\infty }}}(\omega _1)\preccurlyeq \operatorname {\mathrm {\mathscr {P}_{\infty }}}(M)$
. Let h be an injection from
$\omega _1\preccurlyeq \operatorname {\mathrm {\mathscr {P}_{\infty }}}(\omega _1)\preccurlyeq \operatorname {\mathrm {\mathscr {P}_{\infty }}}(M)$
. Let h be an injection from
![]() $\omega _1$
into
$\omega _1$
into
![]() $\operatorname {\mathrm {\mathscr {P}_{\infty }}}(M)$
. In what follows, we get a contradiction by constructing by recursion an injection H from
$\operatorname {\mathrm {\mathscr {P}_{\infty }}}(M)$
. In what follows, we get a contradiction by constructing by recursion an injection H from
![]() $\mathrm {Ord}$
into
$\mathrm {Ord}$
into
![]() $\operatorname {\mathrm {\mathscr {P}_{\infty }}}(M)$
.
$\operatorname {\mathrm {\mathscr {P}_{\infty }}}(M)$
.
For
![]() $\gamma <\omega _1$
, we take
$\gamma <\omega _1$
, we take
![]() $H(\gamma )=h(\gamma )$
. Now, we assume that
$H(\gamma )=h(\gamma )$
. Now, we assume that
![]() $\alpha $
is an uncountable ordinal and that
$\alpha $
is an uncountable ordinal and that
![]() $H{\upharpoonright }\alpha $
is an injection from
$H{\upharpoonright }\alpha $
is an injection from
![]() $\alpha $
into
$\alpha $
into
![]() $\operatorname {\mathrm {\mathscr {P}_{\infty }}}(M)$
. Then
$\operatorname {\mathrm {\mathscr {P}_{\infty }}}(M)$
. Then
![]() $(H{\upharpoonright }\alpha )^{-1}\circ \Phi $
is a surjection from a subset of
$(H{\upharpoonright }\alpha )^{-1}\circ \Phi $
is a surjection from a subset of
![]() $\omega \times M$
onto
$\omega \times M$
onto
![]() $\alpha $
and hence can be extended by zero to a surjection
$\alpha $
and hence can be extended by zero to a surjection
![]() $f:\omega \times M\twoheadrightarrow \alpha $
. By Lemma 3.6, f explicitly provides a surjection
$f:\omega \times M\twoheadrightarrow \alpha $
. By Lemma 3.6, f explicitly provides a surjection
![]() $g:M\twoheadrightarrow \alpha $
. Then the function q on
$g:M\twoheadrightarrow \alpha $
. Then the function q on
![]() $\operatorname {\mathrm {\mathscr {P}_{\infty }}}(\alpha )$
defined by
$\operatorname {\mathrm {\mathscr {P}_{\infty }}}(\alpha )$
defined by
![]() $q(A)=g^{-1}[A]$
is an injection from
$q(A)=g^{-1}[A]$
is an injection from
![]() $\operatorname {\mathrm {\mathscr {P}_{\infty }}}(\alpha )$
into
$\operatorname {\mathrm {\mathscr {P}_{\infty }}}(\alpha )$
into
![]() $\operatorname {\mathrm {\mathscr {P}_{\infty }}}(M)$
, and thus it follows from Lemma 4.1 that we can explicitly define an injection
$\operatorname {\mathrm {\mathscr {P}_{\infty }}}(M)$
, and thus it follows from Lemma 4.1 that we can explicitly define an injection
![]() $t:\operatorname {\mathrm {\mathscr {P}}}(\alpha )\to \operatorname {\mathrm {\mathscr {P}_{\infty }}}(M)$
. Then
$t:\operatorname {\mathrm {\mathscr {P}}}(\alpha )\to \operatorname {\mathrm {\mathscr {P}_{\infty }}}(M)$
. Then
![]() $t^{-1}\circ (H{\upharpoonright }\alpha )$
is a bijection between a subset of
$t^{-1}\circ (H{\upharpoonright }\alpha )$
is a bijection between a subset of
![]() $\alpha $
and
$\alpha $
and
![]() $t^{-1}[H[\alpha ]]$
, and thus can be extended by zero to a function
$t^{-1}[H[\alpha ]]$
, and thus can be extended by zero to a function
![]() $u:\alpha \to \operatorname {\mathrm {\mathscr {P}}}(\alpha )$
. By Theorem 3.1, we can explicitly define a
$u:\alpha \to \operatorname {\mathrm {\mathscr {P}}}(\alpha )$
. By Theorem 3.1, we can explicitly define a
![]() $B\in \operatorname {\mathrm {\mathscr {P}}}(\alpha )\setminus \operatorname {\mathrm {ran}}(u)$
. Since
$B\in \operatorname {\mathrm {\mathscr {P}}}(\alpha )\setminus \operatorname {\mathrm {ran}}(u)$
. Since
![]() $t^{-1}[H[\alpha ]]\subseteq \operatorname {\mathrm {ran}}(u)$
, it follows that
$t^{-1}[H[\alpha ]]\subseteq \operatorname {\mathrm {ran}}(u)$
, it follows that
![]() $B\notin t^{-1}[H[\alpha ]]$
, which implies that
$B\notin t^{-1}[H[\alpha ]]$
, which implies that
![]() $t(B)\notin H[\alpha ]$
. Now, it suffices to define
$t(B)\notin H[\alpha ]$
. Now, it suffices to define
![]() $H(\alpha )=t(B)$
.
$H(\alpha )=t(B)$
.
Using the method presented here, we can also show that the statements (i)–(iii) in Section 1 hold with
![]() $\operatorname {\mathrm {\mathscr {P}}}(M)$
replaced by
$\operatorname {\mathrm {\mathscr {P}}}(M)$
replaced by
![]() $\operatorname {\mathrm {\mathscr {P}_{\infty }}}(M)$
(Lemma 4.3 is just the statement (iii) for
$\operatorname {\mathrm {\mathscr {P}_{\infty }}}(M)$
(Lemma 4.3 is just the statement (iii) for
![]() $\operatorname {\mathrm {\mathscr {P}_{\infty }}}(M)$
). We shall omit the details.
$\operatorname {\mathrm {\mathscr {P}_{\infty }}}(M)$
). We shall omit the details.
The questions whether the existence of an infinite set A such that there is a surjection from
![]() $A^2$
onto
$A^2$
onto
![]() $\operatorname {\mathrm {\mathscr {P}}}(A)$
or from
$\operatorname {\mathrm {\mathscr {P}}}(A)$
or from
![]() $[A]^2$
onto
$[A]^2$
onto
![]() $\operatorname {\mathrm {\mathscr {P}}}(A)$
is consistent with
$\operatorname {\mathrm {\mathscr {P}}}(A)$
is consistent with
![]() $\mathsf {ZF}$
are still open.
$\mathsf {ZF}$
are still open.
Acknowledgements
We would like to give thanks to an anonymous referee for catching some errors and making useful suggestions. Peng was partially supported by NSFC No. 11901562 and the Hundred Talents Program of the Chinese Academy of Sciences. Shen was partially supported by NSFC No. 12101466.