INTRODUCTION
The resistive stresses generated during glacier sliding tend to slow down ice motion and therefore favor glacier growth and stability (van der Veen and Whillans, Reference van der Veen and Whillans1989). Many processes govern this resistance to sliding (Clarke, Reference Clarke2005). Given the inherent spatial limitations associated with borehole or other direct access to the subglacial environment, geophysical methods such as seismology often provide the most feasible avenue of investigation at the glacier synoptic scale (Podolskiy and Walter, Reference Podolskiy and Walter2016; Aster and Winberry, Reference Aster and Winberry2017). Although a wide variety of naturally occurring phenomena may generate seismic waves in glaciers, basal stick-slip shear motion is particularly informative of glacier sliding processes (Zoet and others, Reference Zoet, Anandakrishnan, Alley, Nyblade and Wiens2012; Winberry and others, Reference Winberry, Anandakrishnan, Wiens and Alley2013; Allstadt and Malone, Reference Allstadt and Malone2014; Helmstetter and others, Reference Helmstetter, Nicolas, Comon and Gay2015; Barcheck and others, Reference Barcheck, Tulaczyk, Schwartz, Walter and Winberry2018). However, despite the commonplace occurrence of this type of seismicity, several basic questions remain concerning its underlying mechanical origin.
Shearing motion that is sufficiently fast to generate seismic waves requires a rapid loss of strength along a sliding interface. Such a strength loss may occur when a sliding interface experiences less friction at greater amounts of sliding or sliding rate. Sliding interfaces are said to have velocity weakening friction. The degree to which rate-weakening occurs is quantified through the parameter (Rice and Ruina, Reference Rice and Ruina1983),
where f ss(v) denotes the steady-state friction coefficient f ss is a function of the sliding velocity v. The exact nature of sliding interfaces in glacial materials has been scrutinized by numerous laboratory studies which have examined the sliding of both clean and debris-laden ice in contact with ice, rock and till (Table 1). These studies, however, have generally failed to reproduce the rate-weakening friction necessary to explain basal seismicity under temperate sliding conditions (Fig. 1).
Table 1. Table of laboratory friction studies

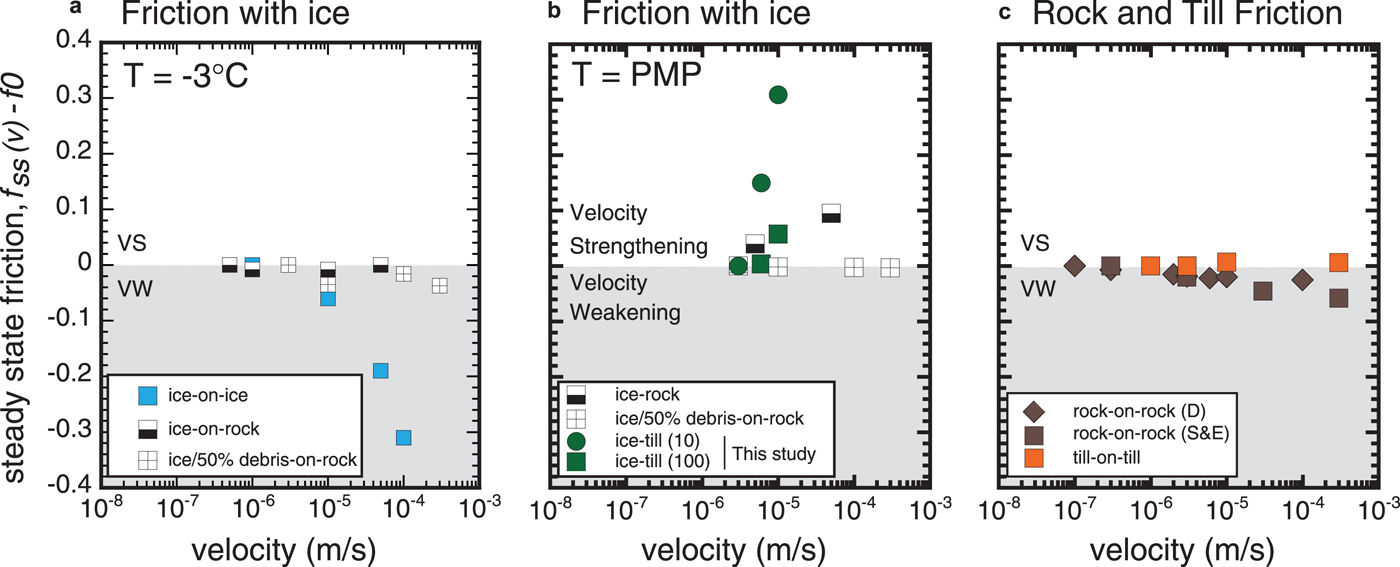
Fig. 1. A review of published and newly conducted laboratory friction experiments on glacial materials. (A) Experiments conducted at −3C involving ice,(B) experiments conducted at the pressure-melting point involving ice, and (C) experiments involving rock and till only. The data sources used in this figure are listed in Table 1.
We focus on temperate sliding conditions, i.e., glaciers with basal ice that is at the pressure-melting point (PMP). Such conditions characterize most fast flowing glaciers and ice streams (Clarke, Reference Clarke2005). Fast flowing glaciers that rest on water-saturated sediment may have basal ice that infiltrates some distance into the sediment. This region of ice infiltration is referred to as a frozen fringe. Perturbations to the basal thermal state are expected to alter the thickness of this fringe while maintaining an ice–water interface at the PMP (Rempel, Reference Rempel2008). For this reason, temperate conditions are expected to prevail along the basal sliding interface of fast flowing glaciers and ice streams, a prediction which is readily confirmed using direct borehole observation (Kamb, Reference Kamb, Alley and Bindschadler2001).
Numerous studies report basal shear seismicity along temperate glacier beds. Location accuracy varies substantially between studies and is sometimes not reported at all. One such high-resolution study by Canassy and others (Reference Canassy, Röösli and Walter2016) estimates a seismicity location accuracy of 2.5–5.1 m. This study was able to achieve particularly high accuracy because of a coincident tomographically-derived velocity model. A typical temperature gradient 0.02°C/m (Kamb, Reference Kamb, Alley and Bindschadler2001) then suggests that these events could have spanned a region with a temperature difference of about 0.05–0.10°C from the temperate glacier bed. Other studies with lower quality velocity models have found somewhat lower accuracy. In Greenland, Roeoesli and others (Reference Roeoesli, Helmstetter, Walter and Kissling2016) estimate seismicity location accuracy of 25 m, and on Antarctic ice streams, Anandakrishnan and Bentley (Reference Anandakrishnan and Bentley1993) and Smith and others (Reference Smith, Smith, White, Brisbourne and Pritchard2015) estimate seismicity location accuracy of 10 and 37 m, respectively. We interpret these observations to be consistent with shear seismicity occurring under temperate conditions.
Temperate conditions, however, pose a paradox in terms of basal shear seismicity. Despite the above-described occurrence of seismicity in this environment, we are aware of no laboratory study to date that has found rate-weakening behavior in material combinations that involve water ice at its PMP sliding against sediments. Till-on-till, ice-on-till and ice-on-ice sliding, for example, have been shown to exhibit rate-strengthening friction under temperate conditions (Barnes and others, Reference Barnes, Tabor and Walker1971; Oksanen and Keinonen, Reference Oksanen and Keinonen1982; McCarthy and others, Reference McCarthy, Savage and Nettles2017). Rock-on-rock sliding, however, commonly exhibits rate-weakening behavior (see reviews by Marone (Reference Marone1998); Scholz (Reference Scholz1998); Dieterich (Reference Dieterich and Schubert2007)).
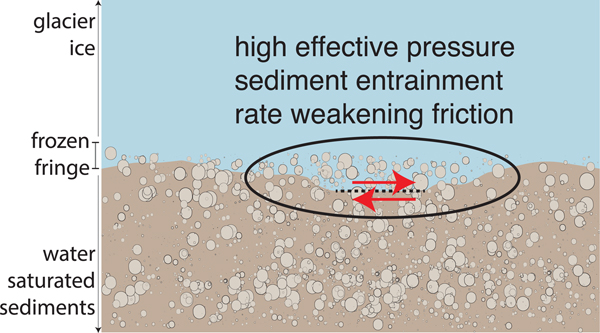
We therefore propose the ‘entrainment-seismicity hypothesis’ that shear seismicity along temperate glacier beds is caused by the sliding of ice with entrained debris against underlying sediments or bedrock. This hypothesis is illustrated schematically in Figure 2. The main goal of this study is to evaluate the ‘entrainment-seismicity hypothesis’ as well as several competing hypotheses.
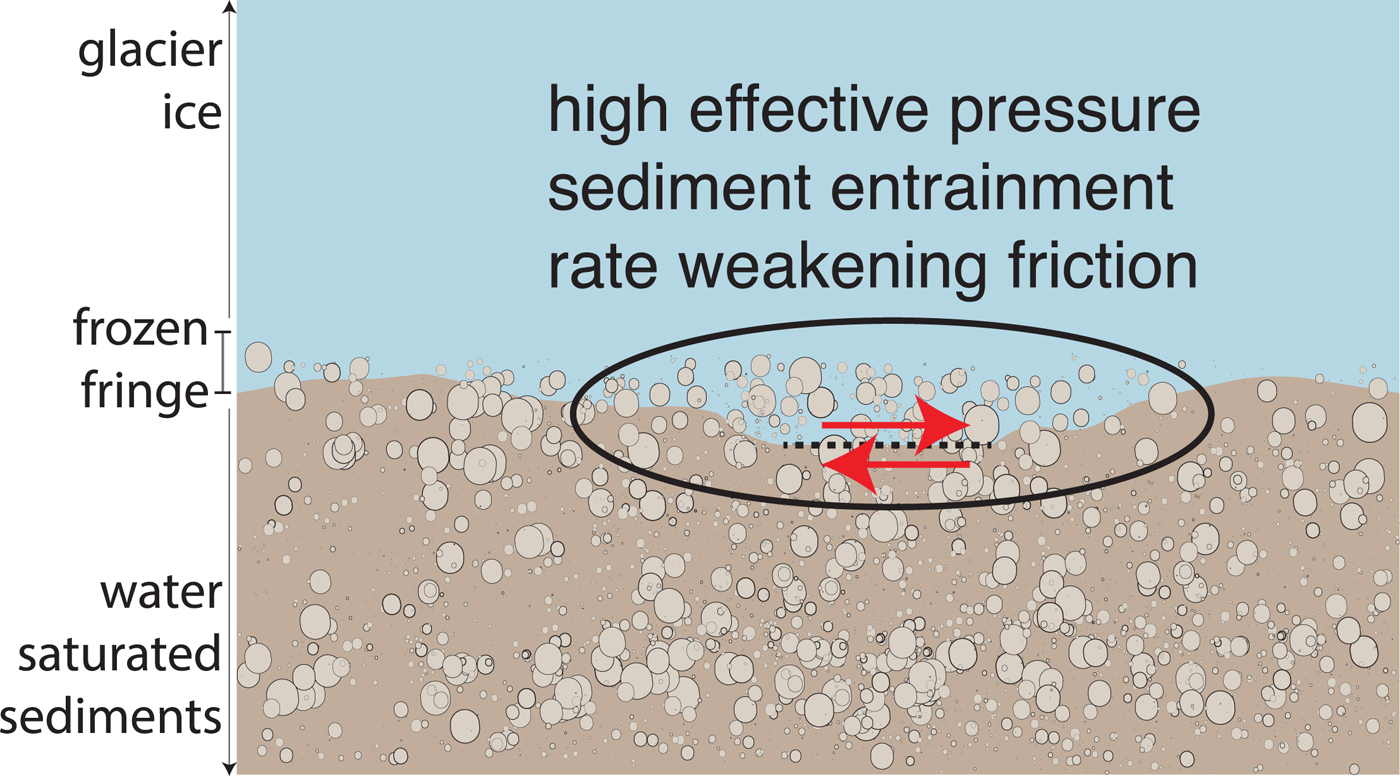
Fig. 2. Basal shear seismicity in temperate glaciers is expected to be caused by rock-on-rock friction as entrained sediments slide across the underlying water saturated sediments or bedrock. The red arrows indicate relative motion and the black oval indicates a region with locally elevated effective pressure and therefore locally thickened frozen fringe.
Under some circumstances, moderately rate strengthening friction may also be able to generate rapid weakening. In particular, rapid shearing motion due to sliding instability is possible between elastically dissimilar solids when (a −b) is smaller than a threshold value (Rice and others, Reference Rice, Lapusta and Ranjith2001). While such a mechanism may permit shear seismicity in the sliding of ice with high debris content-on-rock (a −b ≈ 0.0005), it seems unlikely to explain other material pairs shown in Figure 1 which have much stronger velocity strengthening (a−b as large as 0.131). We discuss this point, as well as other competing hypotheses, in the subsection titled Competing hypotheses.
This paper is organized as follows. We first use laboratory experiments to evaluate the possibility that ice-on-till friction is rate-weakening at the PMP, a competing hypothesis. Then, in order to better understand the conditions under which entrainment and seismicity may co-occur, we develop simple physical models of these processes. These models confirm that seismicity and sediment entrainment are both expected to occur at high effective pressures relative to certain thresholds. We conclude by discussing additional competing hypotheses, the relationship between basal shear seismicity and bed shear stress, and the role of sediment entrainment in the stagnation of the Whillans Ice Stream (WIS). Available data at the present time support the ‘entrainment-seismicity hypothesis’ over competing hypotheses regarding the origin of subglacial shear slip seismicity along temperate glacier beds. This result suggests that basal shear seismicity may be used to infer subglacial geomorphic activity.
LABORATORY SLIDING EXPERIMENTS
The frequent synchronous occurrence of both glacial till (Alley and others, Reference Alley, Blankenship, Bentley and Rooney1986) and basal shear seismicity (Anandakrishnan and Bentley, Reference Anandakrishnan and Bentley1993) beneath fast-flowing temperate-bed glaciers prompts us to investigate frictional sliding between ice and till. In this section, we describe an exploratory study of velocity stepping tests designed to specifically explore the rate behavior of an ice–till interface at temperate conditions. Although the healing process has been investigated for temperate ice slid over till (Zoet and Iverson, Reference Zoet and Iverson2018), to our knowledge no laboratory experiments on the transient friction response have been reported with this pairing of materials.
Experimental methods
A direct shear apparatus was used to slide a 10 cm × 10 cm × 3 cm block of temperate ice over a 10 × 10 × 1 cm thick layer of saturated till for a total displacement of ~1 cm (Fig. 3). The device was housed in a cold room that was held at 0 ± 0.5°C. The apparatus consisted of a modified version of a shear box produced by ELE International and was sufficiently stiff to perform velocity stepping experiments. Weights hung from a lever arm applied a vertical load to the top of the sample chamber, which could expand or contract during shear to accommodate sample dilation or contraction. A load cell oriented perpendicular to vertical motion measured shear stress, and two linear variable displacement transducers recorded horizontal displacement of the sample chamber and vertical displacement of the top platen. A bronze porous plate was placed at the base of the sample chamber to allow melt water to drain from the till.
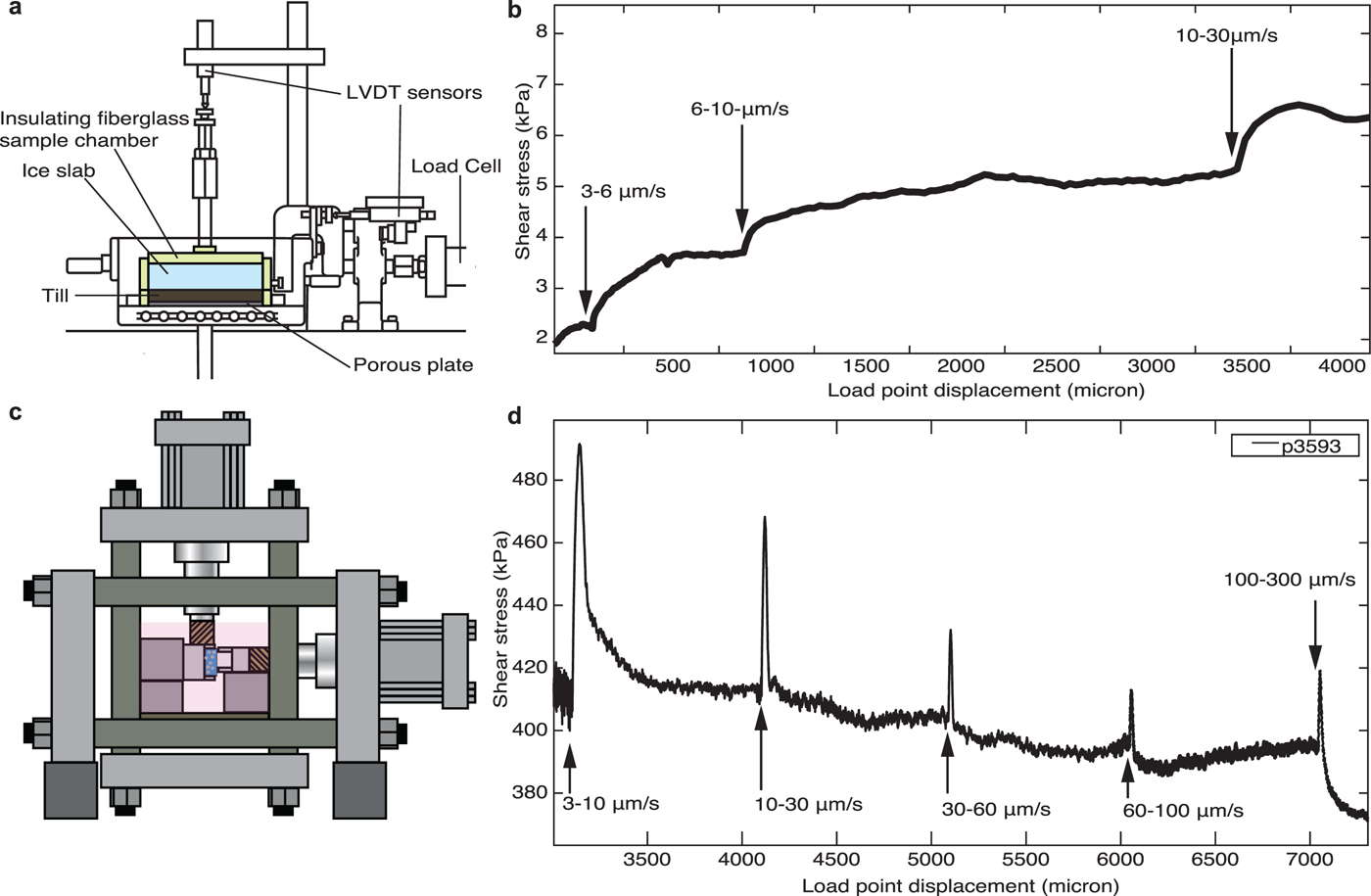
Fig. 3. Diagrams of our experimental apparatus (A and C) and representative sliding histories during velocity stepping experiments (B and D). The sliding velocities are annotated throughout each shear stress-versus-slip plot. The two experiments show increasing (B) and decreasing (D) friction as a function of sliding velocity. These experiments have ice-on-till at the pressure melting point (A and B) and ice with 50% debris content-on-rock at −3°C by Zoet and others (Reference Zoet2013) (C and D). The two apparatus used correspond to the ELE direct shear mechanism (A) and a biaxial testing apparatus with double-direct shear configuration (C). In both cases, the sample is shown in blue, but note that the test specimen in (A) is 10 cm long whereas the specimen in (C) is 7 cm long.
We used till from the Ozaukee member of the Kewaunee formation in all experiments. This unit is comprised of approximately 13% sand, 47% silt and 40% clay. The lithology is 50–63% illite, and ~20% kaolinite plus chlorite (Acomb and others, Reference Acomb, Mickelson and Evenson1982). Grains larger than 1/10 the minimum sample chamber dimension were removed from the sample in order to avoid any length scale effects. The ice sample was constructed from deionized (DI) water that was frozen, crushed and sieved to obtain a mixture of randomly oriented grains with diameters ranging from 2 to 6 mm. Ice grains were then layered in the sample chamber, void space was filled with DI water and the assemblage was frozen. The till was allowed to reach thermal equilibrium in the cold room, and a GEC (brand name) temperature probe with greater than 0.01° C temperature accuracy was embedded ~1 cm into the bottom surface of the ice block to ensure that temperatures reached the PMP prior to shear.
Once ice and till reached the PMP, the temperature probe was removed, the sample chamber was placed in the direct shear apparatus and the horizontal driving ram was immediately engaged to initiate shearing. This immediate shearing and the short duration of the experiments prevented the growth of a frozen fringe layer at the base of the ice block. Minimal melting occurred over the ~10 min duration of each experiment. The short duration and visual inspection of the sample following the experiment ensured that debris-free ice was slid over the till unit, thereby elucidating the rate-strengthening effect for the end member case of clean, temperate ice sliding over saturated till.
Two experiments were conducted, one at an applied normal stress of 10 kPa and another at 100 kPa. An example time series of the resulting shear stress evolution is shown in Figure 3a. Three velocity steps of 3–6, 6–10 and 10–30 μm/s were imposed in each experiment. Sliding was initiated at 3 μm/s. Once the measured shear stress reached a steady state, the velocity was increased.
Experimental results
In both experiments, all velocity steps resulted in an increase in frictional resistance in response to a sudden change in sliding rate (Fig. 1). The frictional resistance to increased sliding rate at 10 kPa normal stress (Fig. 3a). A 3–6, 6–10 and 10–30 μm/s , increase in slip speed resulted in a−b values of 0.145, 0.137, 0.110 at 10 kPa normal stress, and a−b values of 0.001, 0.015, 0.052 at 100 kPa, respectively. All a−b values are positive, indicating that debris-free temperate ice slid over a saturated till leads to a rate-strengthening behavior in response to a sudden increase in slip speed.
The degree of strengthening compared to other systems is also demonstrated in Figure 1, which shows steady-state friction as a function of velocity, normalized by a low-velocity reference point. Only those systems plotting within the gray region display rate-weakening behavior. The details of our experimental measurements are listed side-by-side with several previous studies in Table 1. For comparison, results from a rate weakening biaxial test by Zoet and others (Reference Zoet2013) are shown in Figs 3c and d.
SIMPLE MODELS OF SEISMICITY AND ENTRAINMENT
We now present simplified models of basal sliding, seismicity and sediment entrainment. The purpose of these simulations is to test the ‘entrainment-seismicity hypothesis’ by verifying whether it is possible for seismicity to happen at the same time as sediment entrainment. We find that this is indeed the case because both sediment entrainment and seismicity require high effective pressure N ≡ p i −p w, with ice pressure p i and water pressure p w. Specifically, if effective pressures are too low then frictional weakening never becomes sufficiently pronounced to create stick-slip seismicity. Similarly, if effective pressures are too low then ice will not penetrate into the underlying sediments and sliding will occur with debris-free ice sliding along the water-saturated substrate.
The simple models that we present here are consistent with sediment entrainment being a necessary but not sufficient condition for subglacial seismicity. Entrainment, under the ‘entrainment-seismicity hypothesis’, is necessary insofar as it results in a rate-weakening, rock-on-rock interface. We begin this section by describing an additional necessary condition for seismicity.
Seismicity and frictional sliding
We begin by describing a simple model of frictional sliding to quantify the conditions under which stick-slip motion is expected to occur. We make use of rate-and-state friction as a constitutive law for the basal sliding interface. This type of sliding law is commonly used to model stick-slip behavior (Scholz, Reference Scholz1998; Marone, Reference Marone1998; Dieterich, Reference Dieterich and Schubert2007). Rate-and-state friction describes two phenomena associated with the friction coefficient f, defined as the ratio of shear stress τ to effective pressure N. These two behaviors, described elsewhere in detail (Rice and others, Reference Rice, Lapusta and Ranjith2001), consist of a rate-dependent transient during a step in loading velocity followed by a subsequent evolution to a steady state. So-called rate-weakening materials have a steady-state friction coefficient that is a decreasing function of loading rate. Importantly, rate-weakening materials are conditionally stable, meaning that they may exhibit stick-slip motion if certain additional criteria are met. Specifically, seismicity occurs when the effective pressure exceeds a critical value (Rice and others, Reference Rice, Lapusta and Ranjith2001),
for seismogenic patch rigidity k, rate-weakening parameter b−a (Eqn (1)) and state evolution distance L. These parameters are discussed in detail by Lipovsky and Dunham (Reference Lipovsky and Dunham2016) and Lipovsky and Dunham (Reference Lipovsky and Dunham2017). As an example of typical values, we note that if k = 10 MPa/m, b−a = 0.01 and ![]() $L=10\; {\rm \mu {m}}$, then seismicity is expected to be possible only when the effective pressure is greater than 10 kPa. We note that the state evolution distance L is often inferred to vary with the size of the sliding region; our choice of a relatively small value in this example calculation is typical of ~ meter-scale sliding regions (Lipovsky and Dunham, Reference Lipovsky and Dunham2016). Lastly, we note that dynamic variations in normal stress (Linker and Dieterich, Reference Linker and Dieterich1992; Selvadurai and others, Reference Selvadurai, Selvadurai and Suvorov2018) and stiffness (Leeman and others, Reference Leeman, Scuderi, Marone and Saffer2015) are both neglected here in order to focus on the most basic relationship between friction and entrainment.
$L=10\; {\rm \mu {m}}$, then seismicity is expected to be possible only when the effective pressure is greater than 10 kPa. We note that the state evolution distance L is often inferred to vary with the size of the sliding region; our choice of a relatively small value in this example calculation is typical of ~ meter-scale sliding regions (Lipovsky and Dunham, Reference Lipovsky and Dunham2016). Lastly, we note that dynamic variations in normal stress (Linker and Dieterich, Reference Linker and Dieterich1992; Selvadurai and others, Reference Selvadurai, Selvadurai and Suvorov2018) and stiffness (Leeman and others, Reference Leeman, Scuderi, Marone and Saffer2015) are both neglected here in order to focus on the most basic relationship between friction and entrainment.
Sediment entrainment
We next turn to a simple model of sediment entrainment. The way in which sediments are entrained depends on the forces exerted on the sediments, the heat fluxes into and out of the sediment, and water flow through the sediments. In the subglacial environment, the overburden weight of the overlying ice presses the ice against the underlying till sediments. The water pressure resists some of the weight of the ice but the difference in pressures (i.e. the effective pressure N) causes the ice to conform to the shape of the sediments. Locally, this requires very high curvature on the sediment grain scale, leading to curvature-induced premelting (Rempel and others, Reference Rempel, Wettlaufer and Worster2001, Reference Rempel, Wettlaufer and Worster2004; Dash and others, Reference Dash, Rempel and Wettlaufer2006). When the effective pressure is large enough, the ice can infiltrate into the sediments and form a partially frozen region known as a frozen fringe (O'Neill and Miller, Reference O'Neill and Miller1985). Thus, similar to the frictional onset of stick-slip, sediment entrainment is expected to occur at high effective pressure (Rempel, Reference Rempel2007, Reference Rempel2008, Reference Rempel2009a,Reference Rempelb). The critical effective pressure for ice to infiltrate into a granular substrate is approximated by (Meyer and others, Reference Meyer, Downey and Rempel2018a),
for surface energy γ ≈ 0.035 J/m2 and subglacial sediment grain size r. For the clay-rich tills found on the Siple Coast ice streams, micron-scale grain sizes give an estimate of the critical effective pressure to be in the range of several tens of kPa, for example, 70 kPa for 1 μm grains or 7 kPa for 10 μm grains. In this way, glaciers entrain large quantities of sediment, which are expected to affect the rate and character of their sliding as well as the occurrence of basal seismicity.
The effect of debris content
As the fraction of entrained debris increases, we expect that the frictional properties of the ice–bed interface will begin to resemble those of rock-on-rock friction. This transition occurs at roughly 50% ice volume fraction (Moore, Reference Moore2014) but also depends on grain size (Emerson and Rempel, Reference Emerson and Rempel2007). Eqn (3) is therefore consistent with the notion that high effective pressure is a requirement for stick-slip motion. In particular Eqn (3) states that effective pressures must be great enough to entrain debris along the interface.
As a caveat, we note that frictional resistance may transition before the condition of Eqn (3). Even without fully encapsulating obstacles, for example, ice could drag the top layer of particles against their lower neighbors. Since this behavior would still require enough conformity between the ice and particle surfaces, it ought to nevertheless involve some sort of threshold-like transition. Because our main goal is to capture the existence of such a transition, we retain the condition given by Eqn (3).
The effect of the viscous flow of ice
To ellucidate the role of viscous flow in the overlying ice, we present a simplified model that incorporates the coupled effects of viscoelasticity and frictional sliding in Appendix A. This approach is a simplification of other viscoelastic models that resolve the basal earthquake cycle (Goldberg and others, Reference Goldberg, Schoof and Sergienko2014). The most important result is that viscous deformation overwhelms stick-slip motion when the Maxwell time is much less than the earthquake recurrence time. This behavior is an extension of the elastic case, where stick-slip motion occurs when weakening exceeds the increase in elastic stress per unit slip (Rice and Ruina, Reference Rice and Ruina1983). For the viscoelastic case, this occurs when
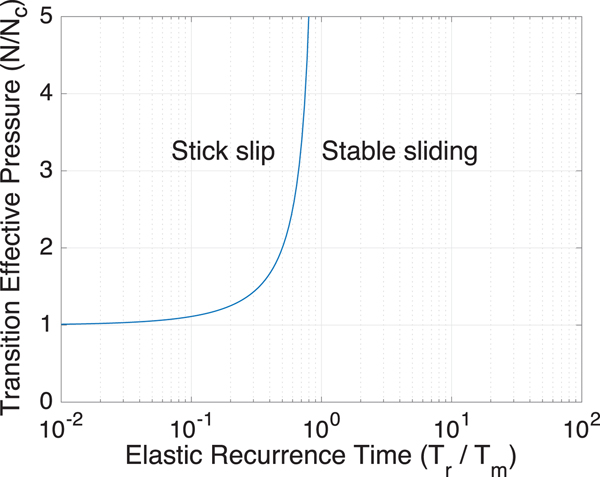
where T m ≡ μ/k is the Maxwell time with linear ice viscosity μ, T r is a time scale that is proportional to the stick-slip recurrence time of an equivalent elastic system (i.e., with μ → ∞), and we have used N c from Eqn (2). We note that the results discussed in this section only strictly pertain to the linear, near-stable conditions considered in Appendix A. We currently have ongoing work in this area that will examine the full non-linear system. However, based on prior experience (Lipovsky and Dunham, Reference Lipovsky and Dunham2016, Reference Lipovsky and Dunham2017), we nevertheless expect the linear problem to yield useful insights.
Equation (4) emphasizes that viscous effects become important as the recurrence time approaches the Maxwell time (Fig. 4). Stick-slip events are not expected to occur when the stick-slip recurrence time is greater than the Maxwell time. This condition could alternatively be written in terms of a critical value of any system parameter. In terms of a critical sliding velocity,
Equations (4) and (5) are different ways of stating the same idea: that the stick-slip instability vanishes at a critical point of the underlying dynamical system. These two expressions are connected because the recurrence time scales inversely with the loading rate T r ~ 1/v 0, so that at low loading rates v 0, viscous stabilization occurs. These findings are also consistent with more detailed continuum models of stick-slip cycles in viscoelastic media (Allison and Dunham, Reference Allison and Dunham2018).
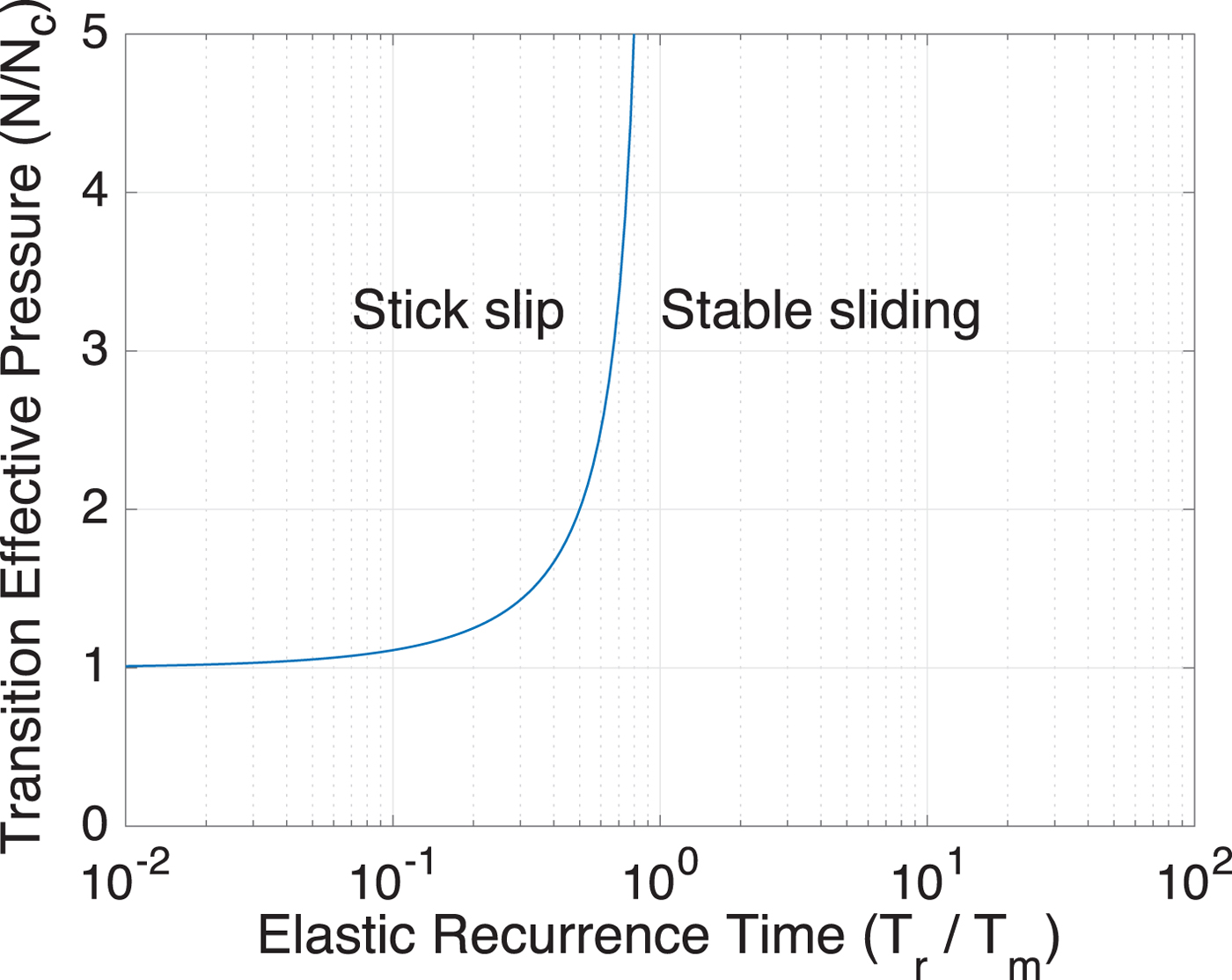
Fig. 4. Under a viscoelastic ice rheology, stick-slip motion cannot occur when the stick-slip recurrence time of the equivalent elastic system T r is equal to the Maxwell viscoelastic relaxation time. As this condition is approached, the effective pressure required for stick-slip motion diverges.
Our analysis predicts that effective pressures may become sufficiently large that viscous deformation overwhelms stick-slip motion. This occurs because the recurrence time depends on effective pressure but the Maxwell time does not. As a result, seismicity may be extinguished in the deep interior of ice sheets. This prediction may be tested by future ice sheet seismicity location studies.
In Figure 5, we show how viscosity the seismically tenable stress for hard and soft beds. This figure shows that viscous flow is particularly important for glaciers resting on bedrock with high shear modulus as opposed to glaciers resting on sediment with lower shear modulus. In each of these figures, seismicity is expected to occur due to stick-slip motion for all conditions represented by points above the blue curves. We note that seismicity generally occurs at high shear stresses, consistent with earlier results connecting glacier bed shear stress to glacier bed seismicity (Alley and others, Reference Alley, Anandakrishnan, Bentley and Lord1994).
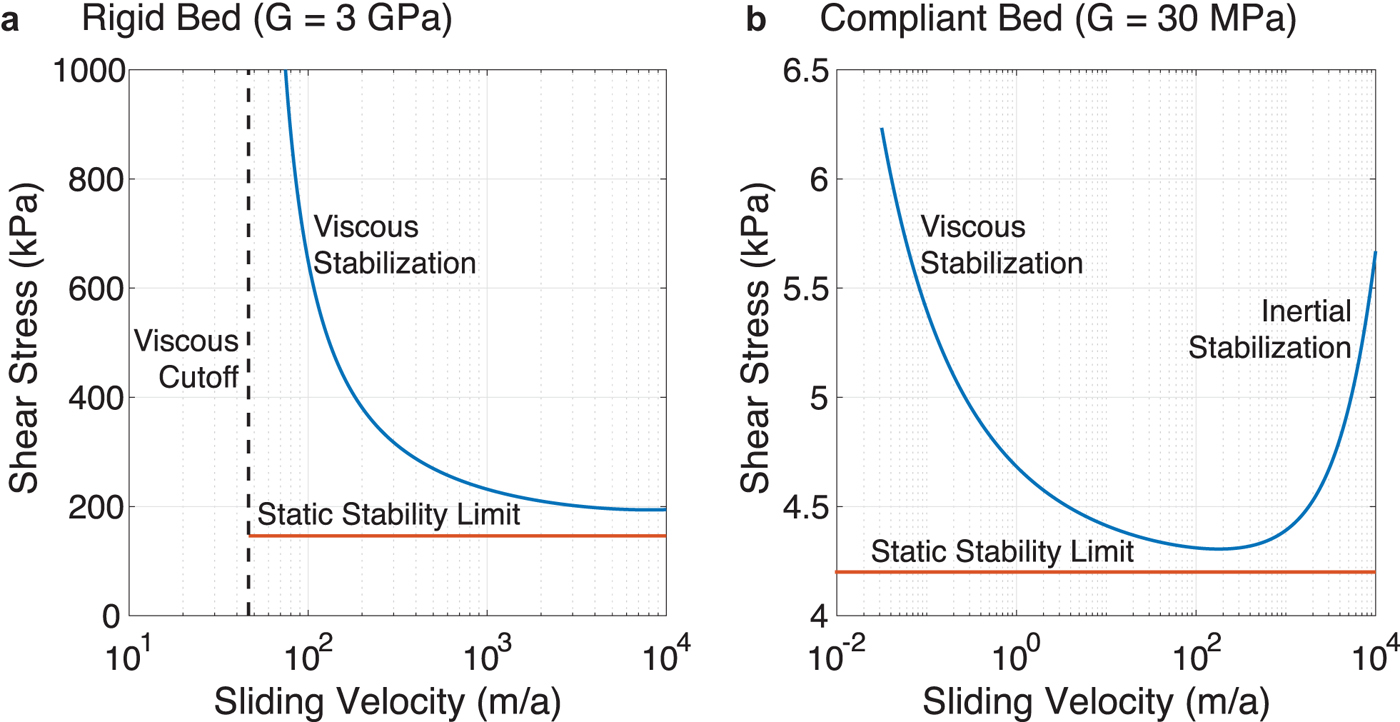
Fig. 5. Stability diagrams where stick-slip seismicity occurs at conditions represented by points above the blue curves. The blue lines denote neutral stability curves; they follow values where shear stress τ = f N takes critical value. The two panels show the cases of hard (A) and soft (B) beds.
Viscous flow imposes another necessary condition for seismicity. Specifically, Eqn (4) (or, equivalently, Eqn (5)) must be satisfied. Figure 5 shows that this condition poses a more severe limitation when the glacier bed has a shear modulus typical of unbroken bedrock. In this case, a glaciologically uncommon (Morlighem and others, Reference Morlighem, Seroussi, Larour and Rignot2013; Meyer and others, Reference Meyer, Downey and Rempel2018a) combination of high bed shear stress ( >200 kPa) and high sliding velocities ( >2 km a −1) are required to cause basal seismicity. We revisit implications of this finding in the Discussion section.
DISCUSSION
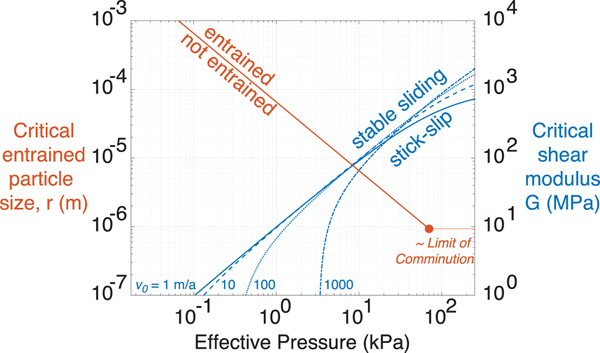
Our central hypothesis is that sediment entrainment is responsible for subglacial shear slip seismicity. Using the models derived in the previous section, we illustrate the necessary conditions for stick-slip motion and sediment entrainment in Figure 6. This figure illustrates that the effective pressure limitation of seismicity is expected to be much more common than effective pressure limitation of sediment entrainment. Specifically, entrainment of some grain size is possible at any N, with only the smallest entrained grain size varying. Seismicity, in contrast, is inhibited at low effective pressures.
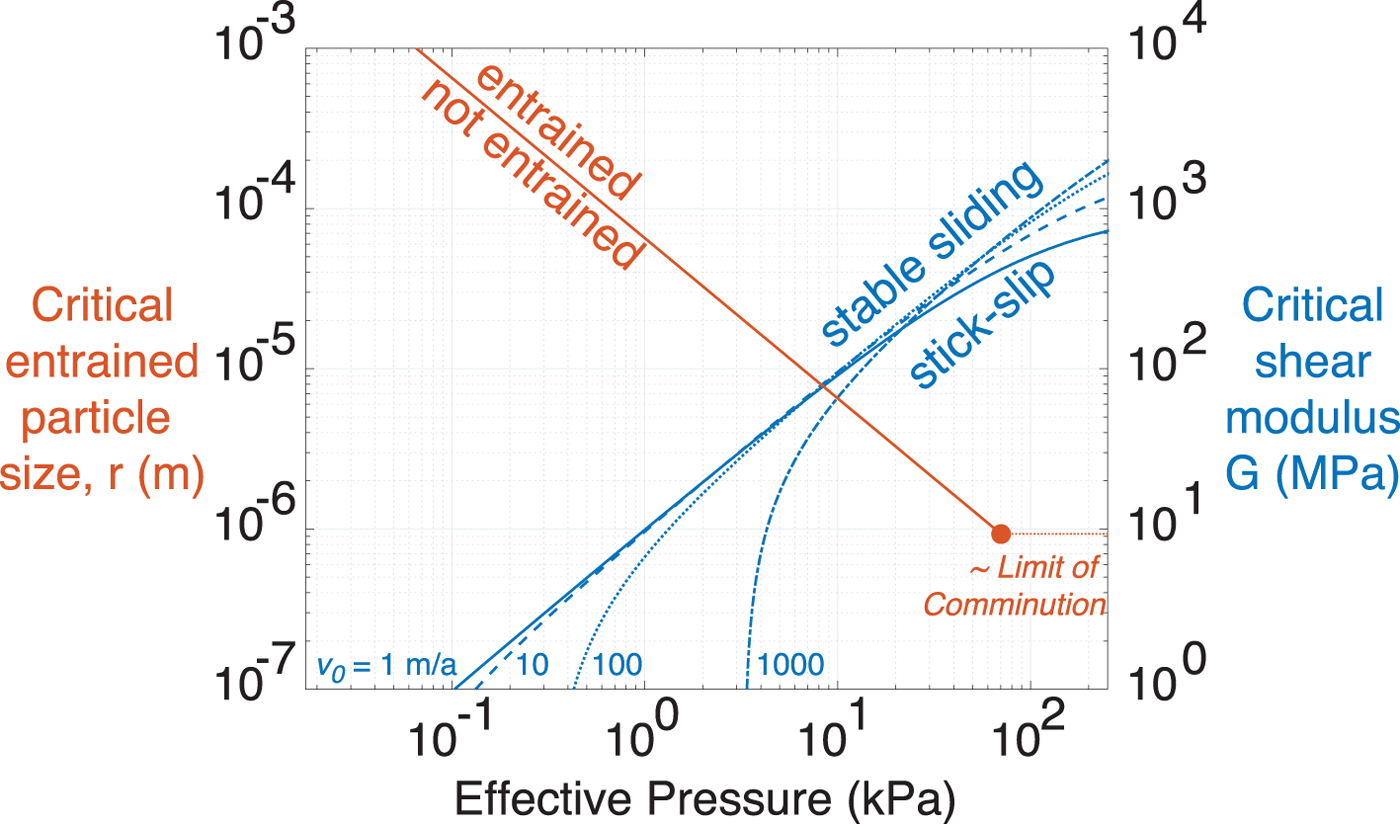
Fig. 6. Basal stick-slip seismicity requires sufficiently high effective pressure (N > N c) so as to entrain almost all grain sizes down to the micron scale. The comminution limit is on the order of 1 μm (Sammis and Ben-Zion, Reference Sammis and Ben-Zion2008; Meyer and others, Reference Meyer, Downey and Rempel2018a).
Before continuing on to discuss several testable predictions of our proposed relationship between sediment entrainment and basal seismicity, we first discuss several competing hypotheses.
Competing hypotheses
Ice-on-ice friction
One competing hypothesis holds that subglacial shear seismicity in temperate glaciers could be caused by ice-on-ice friction. This alternative hypothesis is problematic, however, for several reasons. Foremost among these reasons is that, to our knowledge, the preliminary body of work reporting on laboratory friction experiments in an ice–ice configuration, at the PMP, has yet to observe rate-weakening behavior. Although Kennedy and others (Reference Kennedy, Schulson and Jones2000) and Maeno and Arakawa (Reference Maeno and Arakawa2004) report rate-weakening at temperatures as warm as −3°C and −10°C, such cold temperatures are unlikely to be representative of behavior at the PMP (Barnes and others, Reference Barnes, Tabor and Walker1971).
It is furthermore difficult to invoke ice-on-ice friction for the reason that deformation in the subglacial environment is typically thought to be localized to a narrow sliding plane at the interface between ice (perhaps with entrained sediments) and the underlying bedrock or sediments. Such behavior was demonstrated experimentally by Zoet and Iverson (Reference Zoet and Iverson2018). Glacier thrust faulting is a possible exception to this statement which we discuss later. With regards to basal sliding, however, borehole observations consistently have shown that deformation in the subglacial environment of fast flowing, temperate bed glaciers is narrowly localized along the ice–sediment interface (Blake and others, Reference Blake, Fischer, Bentley and Clarke1994; Kamb, Reference Kamb, Alley and Bindschadler2001). This localization is expected because high water pressures lower frictional strength at the ice–sediment interface but not within the ice.
Glacier thrust faulting is thought to sometimes occur along a sliding interface located entirely within the ice. This phenomenon was reviewed by Moore and others (Reference Moore, Iverson and Cohen2010), who concluded that the 1983 surge of the Variegated Glacier constitutes the only known case of unambiguous thrust faulting. From this assessment, it would not appear as if glacier thrust faulting is a sufficiently pervasive phenomenon to describe the widespread occurrence of subglacial shear seismicity. Furthermore, many thrust faults are identified by the presence of entrained basal debris, thus suggesting that sediment entrainment may play a role in these structures as well (Lovell and others, Reference Lovell2015). Even if such fractures were somehow formed between ice surfaces near the PMP, we would expect them to sinter and heal (Hosler and others, Reference Hosler, Jensen and Goldshlak1957).
Particle ploughing and cavitation
Particle ploughing (Tulaczyk and others, Reference Tulaczyk, Scherer and Clark2001; Moore and Iverson, Reference Moore and Iverson2002; Thomason and Iverson, Reference Thomason and Iverson2008; Iverson, Reference Iverson2010) and cavitation (Schoof, Reference Schoof2005; Zoet and Iverson, Reference Zoet and Iverson2015, Reference Zoet and Iverson2016) both give rise to rate-weakening behavior. While it seems plausible that the transmission of contact forces during particle ploughing could largely be an elastic process that is relevant to glacier stick-slip seismicity, this seems unlikely to be the case for cavitation, a mostly viscous process. The effect of particle ploughing, however, was probably minimized in our experiment by removing clasts larger than 1/10 of the smallest specimen diameter. Experiments on larger samples would clarify the potential seismogenic role for particle ploughing.
Thermal weakening due to shear heating
Shear heating can weaken frictional interfaces when sliding occurs at high enough velocity and for a long enough duration to cause the formation of a lubricating water layer (Barnes and others, Reference Barnes, Tabor and Walker1971; Kennedy and others, Reference Kennedy, Schulson and Jones2000; Rice, Reference Rice2006; Rempel and Rice, Reference Rempel and Rice2006; Viesca and Garagash, Reference Viesca and Garagash2015). Such an explanation in fact appears as an early proposed mechanism for glacier stick-slip motion (Robin, Reference Robin1976). Ice-on-rock friction experiments show that substantial weakening requires that the bulk solid temperature be below the PMP. At the PMP, shear heating does not appear to cause weakening but instead results in a net strengthening of the interface (Barnes and others, Reference Barnes, Tabor and Walker1971), perhaps due to the enlargement of asperity contact areas. Given our focus on temperate conditions at the PMP, this line of reasoning seems to preclude a significant role for shear heating as a mechanism for generating rate-weakening behavior.
Elastic bimaterial instability
Rice and others (Reference Rice, Lapusta and Ranjith2001) demonstrated that mildly rate strengthening friction may be unstable to perturbations due to an elastic coupling between sliding and effective pressure. This result probably does not apply to our experiments because of the large a − b values measured, particularly at 10 kPa effective stress (a − b = 0.131). Bimaterial instability could, however, conceivably destabilize the moderately rate strengthening friction measured by Zoet and others (Reference Zoet2013) in the sliding of debris-laden ice against rock (a − b ≈ 0.0005). Quantifying this effect, however, requires knowledge of parameters measured under variable normal stress and such parameters were not measured by Zoet and others (Reference Zoet2013). In lieu of such measurements, we simply note here that the potentially unstable, moderately strengthening friction measured by Zoet and others (Reference Zoet2013) is consistent with the ‘entrainment-seismicity hypothesis’ in so far as it suggests that seismicity is possible when debris-laden ice slides against rock. Furthermore, the measurements made by Zoet and others (Reference Zoet2013) may reflect a transitional case between rate strengthening and weakening behavior, as their 50% weight fraction debris is lower than the 50% volume fraction where rock-on-rock friction is expected to dominate the rheological response (Moore, Reference Moore2014).
Sediment entrainment and deceleration of the Whillans Ice Stream (WIS)
We expect our analysis of glacier sliding seismicity to be generally applicable to any glacier and ice sheet. However, given the richness of observations from the Siple Coast region of Antarctica, we now discuss our results in the context of the Siple Coast ice streams. We specifically focus on the Whillans Ice Stream, a fast flowing ice stream that is currently undergoing a decades-long deceleration (Beem and others, Reference Beem2014), while simultaneously suffering large-scale stick-slip motion (Bindschadler and others, Reference Bindschadler, King, Alley, Anandakrishnan and Padman2003; Wiens and others, Reference Wiens, Anandakrishnan, Winberry and King2008; Winberry and others, Reference Winberry, Anandakrishnan, Wiens, Alley and Christianson2011; Pratt and others, Reference Pratt, Winberry, Wiens, Anandakrishnan and Alley2014).
Lipovsky and Dunham (Reference Lipovsky and Dunham2017) found that spatially heterogeneous rate-strengthening and rate-weakening friction were required in order to match GPS observations of individual slip events on the WIS. In particular, the central part of the WIS was found to be rate-strengthening while the margins were rate-weakening. In terms of the proposed relationship between seismicity and sediment entrainment, we reinterpret the findings of Lipovsky and Dunham (Reference Lipovsky and Dunham2017) to suggest that sediment entrainment is currently taking place in the margins of the WIS. Lipovsky and Dunham (Reference Lipovsky and Dunham2017) estimate subglacial effective pressure to be 28 kPa. This number is consistent with direct hydraulic head measurements (Kamb, Reference Kamb, Alley and Bindschadler2001), although the latter show a wide variation. Using this estimate of effective pressure and Eqn (3) suggests that under present conditions, grain sizes as small as 2.5 μm may be entrained.
We propose WIS stagnation is being driven by the growth of a frozen fringe in the ice stream margins. This hypothesis is consistent with declining water pressure, as originally proposed by Alley and others (Reference Alley, Anandakrishnan, Bentley and Lord1994) and plausibly related to the subglacial hydrology in the vicinity of active shear margins (Meyer and others, Reference Meyer, Yehya, Minchew and Rice2018b; Meyer and Minchew, Reference Meyer and Minchew2018). The growth of a frozen fringe is expected to ultimately decelerate ice flow by creating a large anchor of frozen sediments with extreme resistance to sliding (Meyer and others, Reference Meyer, Downey and Rempel2018a). While we do not model this entire process here, in the next section we examine several simplified simulations that illustrate the mechanics of fringe growth.
Fringe thickness simulations
To test the idea that sediment entrainment is linked to the increased basal seismicity and attendant slowing of the WIS, we ran a series of simulations of transient frozen fringe growth under conditions similar to WIS (Fig. 7). The numerical calculations underlying our simulations are described by Rempel (Reference Rempel2007, Reference Rempel2008). The inputs into the simulations are the effective pressure N, the geothermal heat flux Q g, the conductive heat flux into the overlying ice Q b and the frictional heat generated at the basal interface Q f. The basal melt rate ![]() $\dot {m}$ is then
$\dot {m}$ is then
where ρi is the ice density, ![]() ${\cal L}$ is the latent heat. The frictional heat Q f is given as
${\cal L}$ is the latent heat. The frictional heat Q f is given as
with the coefficient of friction f 0 and the sliding velocity W s. Consistent with the observed slowing of WIS (Beem and others, Reference Beem2014), we prescribe a sliding velocity that starts at 750 m a−1 and slows to 250 a−1 over 100 years (Fig. 7a). This translates into the frictional heat fluxes given in Figure 7d for the different values of the effective pressure. We choose the conductive loss Q b = 0.45 W m−2 so that when we compile the heat fluxes into the melt rate by Eqn (6) there is a transition from net melting to net freezing as WIS slows.
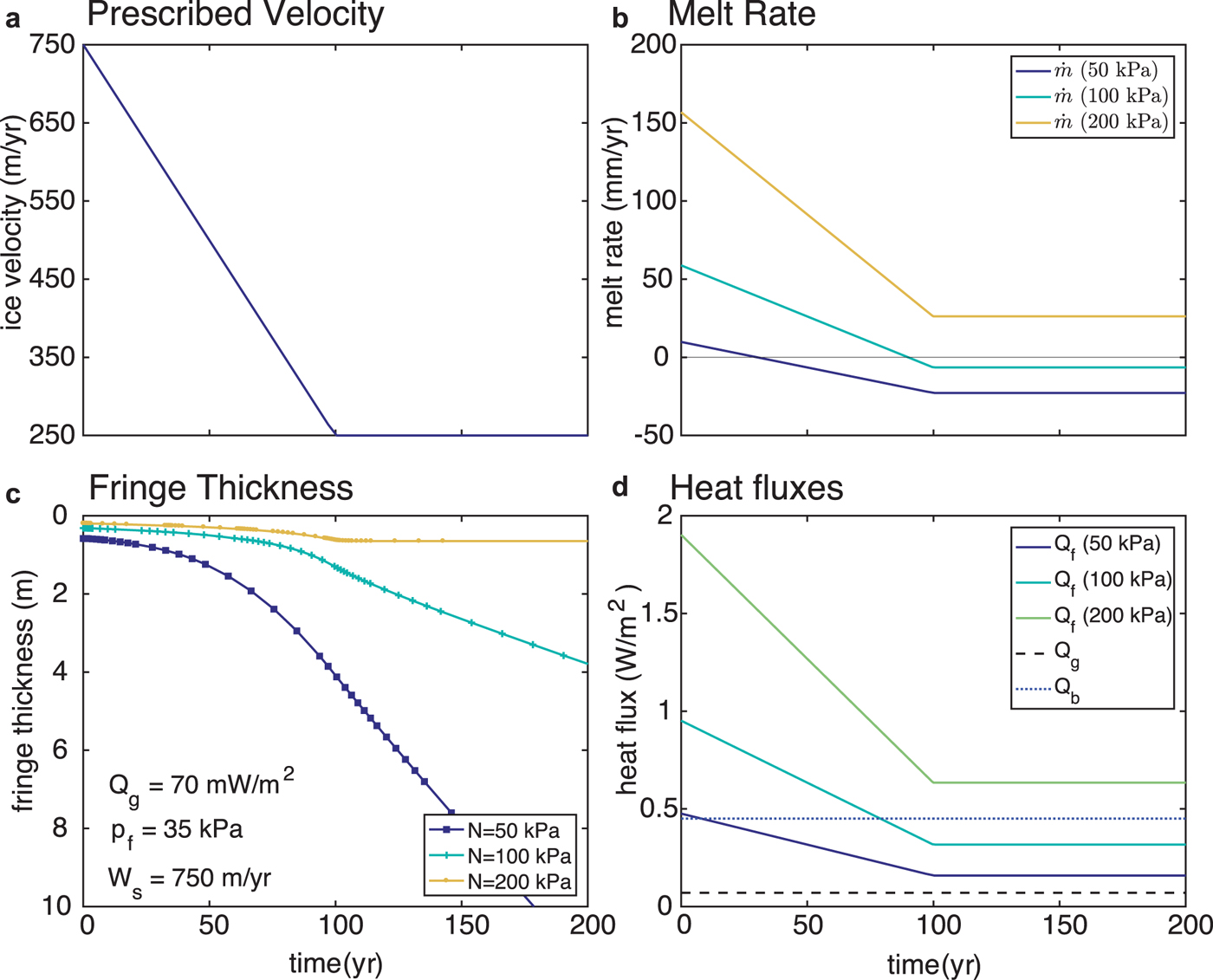
Fig. 7. Transient fringe evolution at the Whillans Ice Stream (WIS): (A) prescribed ice sliding velocity showing the WIS slowdown, (B) basal melt rate for three values of the effective pressure, (C) fringe thickness as a function of time for three effective pressures. Only the largest effective pressure approaches a steady state and the other two grow with time, (D) prescribed heat fluxes with variation in velocity and effective pressure.
As shown in Meyer and others (Reference Meyer, Downey and Rempel2018a), the fringe thickness is determined by the magnitude of the effective pressure and the sign of the melt rate. When the melt rate is positive (i.e. melting) there is always a steady-state fringe thickness for any effective pressure greater than the critical pressure to form a fringe (i.e. Eqn (3)). When the melt rate is negative (i.e. freezing), however, there is not always a steady state and the fringe may grow with time and without bound. These two possibilities are shown in Figure 7c. For the largest effective pressure N = 200 kPa, the melt rate never drops below zero and therefore the fringe grows to a new steady state during the WIS slowdown, which is inconsistent. In the other two cases, however, the melt rate becomes negative and the fringe grows precipitously with time. As the fringe grows, the resistance to sliding must also grow. Thus, it is consistent that the fringe beneath WIS has grown during the slowdown.
The interpretation of active seismic observations
Seismic wave impedance z = ρic, the product of density and wave speed, has been found to be correlated with basal seismicity on the Rutford (Smith, Reference Smith1997, Reference Smith2006) and WIS (Luthra and others, Reference Luthra, Anandakrishnan, Winberry, Alley and Holschuh2016). Impedance variations have historically been inferred to be related to porosity (Blankenship and others, Reference Blankenship, Bentley, Rooney and Alley1986). However, as noted by Smith (Reference Smith1997), in some cases variations in entrained debris may cause similar impedance variations. In light of the proposed connection between rate-weakening friction and entrained debris, we find this line of reasoning to provide a compelling explanation of the relationship between impedance variations and basal seismicity. We note that in cases of high data quality, seismological investigations using amplitude variation with offset may be able to directly resolve the apparent ambiguity between basal debris and low porosity till (Luthra and others, Reference Luthra, Anandakrishnan, Winberry, Alley and Holschuh2016).
CONCLUSIONS
Here, we propose the hypothesis that sediment entrainment is a necessary but not sufficient condition for subglacial shear seismicity in temperate beds of glaciers and ice sheets. We have provided support for this hypothesis using laboratory experiments and simple models. We note that effective pressure and viscous flow impose additional necessary conditions for the occurrence of seismicity. A corollary of our hypothesis is that basal shear seismicity may be used to image active geomorphic processes as well as the processes that govern the strength of the ice–bed interface.
ACKNOWLEDGEMENTS
BPL was funded by a fellowship from the Department of Earth and Planetary Sciences at Harvard University. DDH was funded by the Wisconsin Alumni Research Foundation. CRM and AWR were funded by NSF-1603907. CM was funded by NSF-1245871.
APPENDIX A. STABILITY ANALYSIS
A.1. Governing equations
We examine the sliding displacement D near a small, potentially seismogenic region of the bed. The approximate momentum balance is (Mitsui and Hirahara, Reference Mitsui and Hirahara2001),
where τD is the driving stress, k = αG/R is the elastic stiffness of a bedrock obstacle of dimension R with shear modulus G, and α is a geometrical parameter of order unity (Lipovsky and Dunham, Reference Lipovsky and Dunham2016). The radiation damping parameter η ≡ G/(2c) for shear wave speed c. Viscous displacements D μ follow
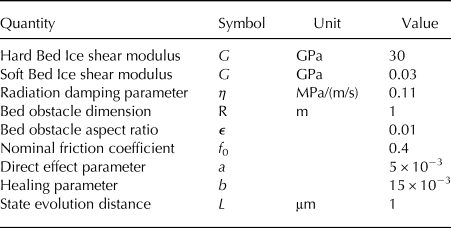
The parameters that are held fixed in our analysis are listed in Table 2. The linearized effective viscosity μ is chosen to reflect flow around a bedrock obstacle of characteristic dimension R (Kamb, Reference Kamb1970; Meyer and others, Reference Meyer, Downey and Rempel2018a). For reference sliding rate v 0 this results in a strain rate ~v 0/R and then
where ε is the bedrock bump aspect ratio.
Table 2. Table of parameters
The basal shear stress τB is set by rate and state friction,
Here, a measures the instantaneous shear strength increase upon an increase of the sliding velocity V , N is the effective pressure, L is the state evolution distance and τss is the steady-state friction coefficient,
with state evolution parameter b. The parameters used in this formulation of basal sliding are discussed extensively by Lipovsky and Dunham (Reference Lipovsky and Dunham2017).
A.2. Linearization and stability
We linearize the four governing equations (Eqns (A1–A4) about a reference state of steady sliding at velocity v 0 and bed shear stress τ0 = N f 0. We examine solutions that are harmonic in time with complex frequency s. Following classical methods (Rice and others, Reference Rice, Lapusta and Ranjith2001), we then seek unstable, stick-slip type behavior in the form of solutions s with positive real part.
The linearized form of the rate and state friction law is then
Perturbed shear stresses and displacements are denoted with a prefixed delta symbol. The linearized momentum balance for the shear stress perturbation is
Eliminating reference to the perturbed quantities then gives the dispersion relation
 $$\eqalign{0=\;& s^{3} \left({\displaystyle {aN }\over {v_0}}+ \eta \right)\cr & +s^2 \left({\displaystyle {N (a-b)} \over{L}} + {\displaystyle {a k N} \over {\mu v_0}} + {\displaystyle {\eta k} \over {\mu }} + k + {\displaystyle {\eta v_0} \over {L}} \right) \cr & +s \left({\displaystyle{k N (a-b)}\over{L \mu }}+ {\displaystyle{k^2} \over {2 \mu}} + {\displaystyle {\eta k v_0} \over{ L \mu}} + {\displaystyle{k v_0} \over{L}}\right) \cr & +{\displaystyle {k^2 v_0} \over {2 L \mu }}}$$
$$\eqalign{0=\;& s^{3} \left({\displaystyle {aN }\over {v_0}}+ \eta \right)\cr & +s^2 \left({\displaystyle {N (a-b)} \over{L}} + {\displaystyle {a k N} \over {\mu v_0}} + {\displaystyle {\eta k} \over {\mu }} + k + {\displaystyle {\eta v_0} \over {L}} \right) \cr & +s \left({\displaystyle{k N (a-b)}\over{L \mu }}+ {\displaystyle{k^2} \over {2 \mu}} + {\displaystyle {\eta k v_0} \over{ L \mu}} + {\displaystyle{k v_0} \over{L}}\right) \cr & +{\displaystyle {k^2 v_0} \over {2 L \mu }}}$$Basal seismicity occurs when solutions s to the dispersion relation have positive real part. This occurs when
When η, ~ μ → ∞, we recover the quasi-static elastic limit,
Including the effect of radiation damping recovers the limit from Lipovsky and Dunham (Reference Lipovsky and Dunham2016),
Neglecting radiation damping but keeping viscosity
This condition can then be rearranged to give Eqn (4) in the main text. Following Lipovsky and Dunham (Reference Lipovsky and Dunham2017), the stick-slip recurrence time is proportional to
which is different from the time scale T c defined by Lipovsky and Dunham (Reference Lipovsky and Dunham2017) by a factor of ![]() $\sqrt {a/(b-a)}$, a difference that we attribute to the approximate nature of the simplified model presented here. Despite this difference, we nevertheless expect the ratio of the Maxwell time and the recurrence time to be the non-dimensional parameter governing the suppression of seismicity due to viscous flow.
$\sqrt {a/(b-a)}$, a difference that we attribute to the approximate nature of the simplified model presented here. Despite this difference, we nevertheless expect the ratio of the Maxwell time and the recurrence time to be the non-dimensional parameter governing the suppression of seismicity due to viscous flow.
Including viscoelastic and radiation damping effects gives the full stability condition: