1. Introduction
Internal waves are a fascinating phenomenon, ubiquitous in the ocean and characterized by the oscillation of the invisible surfaces of constant densities of a stratified water column. Internal waves carry a significant fraction of ocean kinetic energy and are an important intermediary in transferring energy and momentum to smaller scales where they are dissipated. There is renewed theoretical interest in investigating the internal waves in the ocean due to recent developments in our ability to perform high-resolution numerical modelling, with internal waves permitting global ocean simulations (Arbic et al. Reference Arbic, Chassignet, Pascual, Tintoré and Verron2018) and regional numerical models (Pan et al. Reference Pan, Arbic, Nelson, Menemenlis, Peltier, Xu and Li2020).
The wave turbulence kinetic equation has been used extensively to describe processes of spectral energy transfers between internal waves, see Müller et al. (Reference Müller, Holloway, Henyey and Pomphrey1986) and Polzin & Lvov (Reference Polzin and Lvov2011) for reviews. Early on, special types of resonant three-wave triads characterized by extreme scale separations were identified to play an important role in these spectral energy transfers (McComas & Bretherton Reference McComas and Bretherton1977; McComas & Müller Reference McComas and Müller1981a), yet the details and delicate counterbalance of the nonlinear transfers remain an enigma. An important feature of the internal wave kinetic equation is that it diverges for almost all spectral power-law indices in the internal wave spectrum (Lvov et al. Reference Lvov, Polzin, Tabak and Yokoyama2010). This is a mathematical manifestation of the lack of locality in internal wave interactions: nonlinear transfers have significant contributions under extreme scale-separated conditions. The weighting of these extreme scale-separated interactions with spectral power-law assumptions results in divergent integrals. Our goal is to understand and characterize this nonlinear transfer process in this extreme scale-separated limit.
An alternative approach to the wave turbulence kinetic equation is proposed in Henyey, Wright & Flatté (Reference Henyey, Wright and Flatté1986), where ray-tracing (or eikonal) techniques are used to describe spectral energy transfers. In this paradigm, the energy cascade is assessed as a net drift ![]() $\langle \dot {\boldsymbol {p}} \rangle$ of wave packets toward high wavenumber, where
$\langle \dot {\boldsymbol {p}} \rangle$ of wave packets toward high wavenumber, where ![]() ${\boldsymbol {p}}$ is the momentum of a wave and
${\boldsymbol {p}}$ is the momentum of a wave and ![]() $\langle \dots \rangle$ represents an ensemble average. Such studies (Henyey et al. Reference Henyey, Wright and Flatté1986; Sun & Kunze Reference Sun and Kunze1999b; Ijichi & Hibiya Reference Ijichi and Hibiya2017) provide metrics of the net drift rate at a high-wavenumber gate, beyond which waves are considered to ‘break’. These numerical simulations are conducted in a ‘kitchen sink’ manner in which scale separations in vertical and horizontal wavenumber are viewed as tuneable parameters to arrive at downscale transport estimates that align with observations. The alignment requires that the background have similar scales as the wave packet and creates a thematic issue for an asymptotic theory such as ray tracing. A further issue is that a rigorous description of this ensemble average transport
$\langle \dots \rangle$ represents an ensemble average. Such studies (Henyey et al. Reference Henyey, Wright and Flatté1986; Sun & Kunze Reference Sun and Kunze1999b; Ijichi & Hibiya Reference Ijichi and Hibiya2017) provide metrics of the net drift rate at a high-wavenumber gate, beyond which waves are considered to ‘break’. These numerical simulations are conducted in a ‘kitchen sink’ manner in which scale separations in vertical and horizontal wavenumber are viewed as tuneable parameters to arrive at downscale transport estimates that align with observations. The alignment requires that the background have similar scales as the wave packet and creates a thematic issue for an asymptotic theory such as ray tracing. A further issue is that a rigorous description of this ensemble average transport ![]() $\langle \dot {{\boldsymbol {p}}} \rangle$ is an open question that we address here.
$\langle \dot {{\boldsymbol {p}}} \rangle$ is an open question that we address here.
Motivation for our efforts comes from a comparison with the empirical metrics of ocean mixing referred to as ‘fine-scale parameterizations’ (Gregg Reference Gregg1989; Polzin, Toole & Schmitt Reference Polzin, Toole and Schmitt1995); see Polzin et al. (Reference Polzin, Naveira Garabato, Sloyan, Huussen and Waterman2014) for a review and McComas (Reference McComas1977), McComas & Müller (Reference McComas and Müller1981b), Polzin & Lvov (Reference Polzin and Lvov2017) and Dematteis, Polzin & Lvov (Reference Dematteis, Polzin and Lvov2022) for descriptions of the pivotal role that extreme scale-separated interactions play in interpreting the oceanic internal wave spectrum. The most glaring incompatibility of wave turbulence and ray tracing is presented in § 4: if the mean-drift rate in vertical wavenumber is identified as the corresponding gradient of diffusivity as derived from the kinetic equation, then the predicted downscale energy transport is an order of magnitude larger than that supported by the observations. This method parallels assessments for downscale energy transport in ray-tracing numerics (Henyey et al. Reference Henyey, Wright and Flatté1986; Sun & Kunze Reference Sun and Kunze1999b; Ijichi & Hibiya Reference Ijichi and Hibiya2017), but is similarly ten times larger than those numerical results. This disparity has led us to a systematic examination and physical interpretation of the assumptions within both kinetic equation and ray-path approaches to pinpoint the multiple junctures that might underpin a systematic difference between observation and theory concerning extreme scale-separated interactions.
Despite claims by McComas & Bretherton (Reference McComas and Bretherton1977) and Nazarenko, Newell & Galtier (Reference Nazarenko, Newell and Galtier2001) that ray tracing should reduce to the resonant manifold, our understanding is that the kinetic equation and ray tracing differ on fundamental levels. The wave kinetic equation represents the internal wave field as a system of amplitude-modulated waves having constant wavenumber and frequency linked through a dispersion relation. Ray tracing represents a wave packet as a frequency-modulated system with variations in wavenumber linked to the conservation of an Eulerian phase function. The Fokker–Plank equation derived in the ray-tracing approach additionally represents the average drift of wave packets towards high wavenumbers. The role of resonances and off-resonant interactions in the mean drift and dispersion about that mean drift are also different (Polzin & Lvov Reference Polzin and Lvov2023), as are the concepts of resonance broadening (Polzin & Lvov Reference Polzin and Lvov2017) and bandwidth (Cohen & Lee Reference Cohen and Lee1990) that are important metrics of finite-amplitude effects in weakly nonlinear systems.
Our efforts have direct parallels with Kraichnan's 1959 and 1965 studies (Kraichnan Reference Kraichnan1959, Reference Kraichnan1965) of isotropic homogeneous turbulence using field theoretic techniques. Kraichnan's 1959 study was an Eulerian-based approach that yielded a ![]() $k^{-3/2}$ spectrum at high Reynolds number, distinct from Kolmogorov's
$k^{-3/2}$ spectrum at high Reynolds number, distinct from Kolmogorov's ![]() $k^{-5/3}$ inertial subrange based upon dimensional analysis. (Here the k represents the magnitude of the wavenumber.) This Eulerian description was labelled the ‘direct interaction approximation’ (DIA) and extant data were not sufficient to assess the theoretical prediction. Kraichnan (Reference Kraichnan1965) subsequently understood that the quasi-uniform translation associated with coherent advection at the largest scales ( aka sweeping). This sweeping effect was creating an artefact wherein the correlation time scale was proportional to the root-mean-square Doppler shift rather than a more intuitive notion that energy transfers between scales depended upon the rate of strain. In 1965, Kraichnan subsequently presented a Lagrangian description (the abridged Lagrangian history DIA) that isolated the pressure and viscous terms responsible for fluid parcel deformation. The Lagrangian picture resulted in a
$k^{-5/3}$ inertial subrange based upon dimensional analysis. (Here the k represents the magnitude of the wavenumber.) This Eulerian description was labelled the ‘direct interaction approximation’ (DIA) and extant data were not sufficient to assess the theoretical prediction. Kraichnan (Reference Kraichnan1965) subsequently understood that the quasi-uniform translation associated with coherent advection at the largest scales ( aka sweeping). This sweeping effect was creating an artefact wherein the correlation time scale was proportional to the root-mean-square Doppler shift rather than a more intuitive notion that energy transfers between scales depended upon the rate of strain. In 1965, Kraichnan subsequently presented a Lagrangian description (the abridged Lagrangian history DIA) that isolated the pressure and viscous terms responsible for fluid parcel deformation. The Lagrangian picture resulted in a ![]() $-5/3$ power law and Kolmogorov constant (1.77) quite close to that provided by a summary of atmospheric field data (1.56) (Högström Reference Högström1996). The analogy to Kraichnan is that the plane wave formulation corresponds to an Eulerian coordinate system and the Lagrangian coordinate system corresponds to a wave packet formulation in which statistics are accumulated along ray paths.
$-5/3$ power law and Kolmogorov constant (1.77) quite close to that provided by a summary of atmospheric field data (1.56) (Högström Reference Högström1996). The analogy to Kraichnan is that the plane wave formulation corresponds to an Eulerian coordinate system and the Lagrangian coordinate system corresponds to a wave packet formulation in which statistics are accumulated along ray paths.
Similar issues about Doppler shifting arise for internal waves (Holloway Reference Holloway1980, Reference Holloway1982), Rossby waves (Holloway & Hendershott Reference Holloway and Hendershott1977; Nazarenko Reference Nazarenko2011) and in magneto-hydrodynamics (Nazarenko et al. Reference Nazarenko, Newell and Galtier2001). Wave problems are potentially more complicated, in part because the Doppler shifting can be intrinsically related to extreme scale-separated interactions, and due to a multiplicity of time scales introduced through resonant interactions absent in three-dimensional (3-D) turbulence. In wave turbulence one assumes an expansion in terms of small nonlinearity and an assumption about multiple time scales to assess the evolution of amplitude-modulated plane waves. Implicit is a long interaction time scale for third order and a short decorrelation time scale with regards to the higher orders (Newell Reference Newell1968). Reduction of the DIA to the resonant manifold happens as the correlation time scale is small relative to an interaction time scale, and triple correlations associated with nonlinear coupling can be related to the product of two double correlations. Extreme scale-separated wave problems can also be treated with ray-tracing methods, in which the statistics of frequency-modulated wave packets are accumulated along ray characteristics rather than Lagrangian trajectories. Ray tracing is an extremely attractive route to deal with sweeping as the dynamics of ray tracing is grounded in the explicit representation of variations in Doppler shifting. It is understood that there are ray method parallels to the interaction and correlation time scales of wave turbulence and the DIA, (McComas & Bretherton Reference McComas and Bretherton1977; Nazarenko et al. Reference Nazarenko, Newell and Galtier2001). However, the time scale definitions for ray methods have not been sufficiently developed for a detailed comparison of the two strategies for assessing the effects of Doppler shifting. In particular, what has been missing is the identification of the interaction time scale. Here, we provide a derivation of a generalized transport equation for the evolution of an ensemble of wave packets. This generalized transport equation contains a term representing the ensemble mean drift of wave packets in the spectral domain. This mean drift relates to the interaction time scale and can be directly compared with a correlation time scale relating to dispersion about that mean drift. Having accomplished this, we arrive at the understanding that the resonant bandwidths of weakly nonlinear interactions in the two systems, the DIA kinetic equation and from ray methods, are different; that resonant and non-resonant interactions express themselves differently in the correlation time scale than previously understood; and that spectral transports can be significantly altered by the mean-drift term.
We demonstrate here that it is this simple difference in coordinate systems that leads to the celebrated Garrett and Munk (GM) spectrum of the oceanic internal wave field supporting a net downscale transport. Details of this spectral model are presented in Appendix A. The 3-D action spectrum for the GM spectrum is independent of vertical wavenumber, so that in an Eulerian description there is no vertical wavenumber action gradient to support the diffusion of action regardless of how the vertical component of the diffusivity tensor is defined. In a ray description, the mean drift of wave packets to a high wavenumber can be explicitly represented in an ensemble transport equation and an estimate of the action (energy) available for mixing can be obtained by the counting of wave packets past a sufficiently high-wavenumber gate (e.g. Henyey et al. Reference Henyey, Wright and Flatté1986).
This paper is organized as follows. Hamiltonian structures and the derivation of the transport equations from them are the focal points of §§ 2 and 3. We review the Hamiltonian structure in § 2.1. In § 2.2 we present a derivation for internal waves that leads to a Fokker–Planck equation. In § 3 we refine the Hamiltonian structure; extracting only those extreme scale-separated interactions in order to derive the Liouville equation (§ 3.1) and its subsequent Fokker–Planck equation (§ 3.2.4). Subsequent to these theoretical developments, we present estimates of energy transport to mixing scales and demonstrate the mismatch between theory and observations in § 4. We end in § 5 by discussing this contradiction in light of our derivations. The reader who is primarily interested in the disparity between observations and theory is advised to read § 4 and use the equation references to navigate §§ 2 and 3.
2. Background
2.1. Hamiltonian structure and field variables
The equations of motion satisfied by an incompressible stratified rotating flow in hydrostatic balance are
 \begin{equation} \left.\begin{gathered} \frac{\partial}{\partial t}\frac{\partial z}{\partial \rho} + \boldsymbol{\nabla}\,\boldsymbol{\cdot}\,\left(\frac{\partial z}{\partial \rho} \boldsymbol{u} \right) = 0 , \\ \frac{\partial \boldsymbol{u}}{\partial t} +f \boldsymbol{u}^\perp{+} \boldsymbol{u} \,\boldsymbol{\cdot}\, \boldsymbol{\nabla} \boldsymbol{u} + \frac{\boldsymbol{\nabla} M}{\rho} = 0 ,\\ \frac{\partial M}{\partial \rho} - g z = 0 . \end{gathered}\right\}\end{equation}
\begin{equation} \left.\begin{gathered} \frac{\partial}{\partial t}\frac{\partial z}{\partial \rho} + \boldsymbol{\nabla}\,\boldsymbol{\cdot}\,\left(\frac{\partial z}{\partial \rho} \boldsymbol{u} \right) = 0 , \\ \frac{\partial \boldsymbol{u}}{\partial t} +f \boldsymbol{u}^\perp{+} \boldsymbol{u} \,\boldsymbol{\cdot}\, \boldsymbol{\nabla} \boldsymbol{u} + \frac{\boldsymbol{\nabla} M}{\rho} = 0 ,\\ \frac{\partial M}{\partial \rho} - g z = 0 . \end{gathered}\right\}\end{equation}
These equations result from mass conservation, horizontal momentum conservation and hydrostatic balance. The equations are written in isopycnal coordinates with the density ![]() $\rho$ replacing the height
$\rho$ replacing the height ![]() $z$ in its role as an independent vertical variable. Here,
$z$ in its role as an independent vertical variable. Here, ![]() ${\boldsymbol {u}} = (u,v)$ is the horizontal component of the velocity field,
${\boldsymbol {u}} = (u,v)$ is the horizontal component of the velocity field, ![]() ${\boldsymbol {u}}^{\perp } = (-v, u)$,
${\boldsymbol {u}}^{\perp } = (-v, u)$, ![]() $\boldsymbol {\nabla } = (\partial /\partial x, \partial /\partial y)$ is the gradient operator along isopycnals,
$\boldsymbol {\nabla } = (\partial /\partial x, \partial /\partial y)$ is the gradient operator along isopycnals, ![]() $M$ is the Montgomery potential
$M$ is the Montgomery potential
with pressure ![]() $P$, gravity
$P$, gravity ![]() $g$ and Coriolis parameter
$g$ and Coriolis parameter ![]() $f$. The hydrostatic approximation is used since it is an accurate approximation for long internal waves. Investigation of the non-hydrostatic effects is outside of the scope of present paper.
$f$. The hydrostatic approximation is used since it is an accurate approximation for long internal waves. Investigation of the non-hydrostatic effects is outside of the scope of present paper.
Here, we follow Lvov & Tabak (Reference Lvov and Tabak2004) and take (2.1) and decompose the flow into a potential and a divergence-free part
where
The expression for potential vorticity in these coordinates is (Haynes & McIntyre Reference Haynes and McIntyre1987)
where ![]() $\varPi = ({\rho }/{g})\partial ^2 M/\partial \rho ^2 = \rho \partial z/\partial \rho$ is a normalized differential layer thickness. Since potential vorticity is conserved along particle trajectories
$\varPi = ({\rho }/{g})\partial ^2 M/\partial \rho ^2 = \rho \partial z/\partial \rho$ is a normalized differential layer thickness. Since potential vorticity is conserved along particle trajectories
The advection of potential vorticity in (2.6) takes place exclusively along isopycnal surfaces. Therefore, an initial distribution of potential vorticity which is constant on isopycnals, although varying across them, will remain constant. Hence, we shall utilize the following assumption:
where we redefined ![]() $\varPi \to \varPi _{0}+\varPi$ to split the potential
$\varPi \to \varPi _{0}+\varPi$ to split the potential ![]() $\varPi$ into its equilibrium value
$\varPi$ into its equilibrium value ![]() $\varPi _{0} \equiv - g / N^2$ and deviation from it. Stratification
$\varPi _{0} \equiv - g / N^2$ and deviation from it. Stratification ![]() $N^2$ is permitted to vary with density
$N^2$ is permitted to vary with density ![]() $\rho$, but is constant along isopycnals. This effectively decouples the internal wave field from lower-frequency flows such as fronts and mesoscale eddies, which are the subject of their own wave turbulence literature (e.g. Müller Reference Müller1976; Kafiabad et al. Reference Kafiabad, Savva, Miles and Vanneste2019). Such internal wave–mean flow interactions can be a significant regional source of internal wave energy (Polzin Reference Polzin2010) and may be a key issue in determining the regional character of the internal wave field (Polzin & Lvov Reference Polzin and Lvov2011).
$\rho$, but is constant along isopycnals. This effectively decouples the internal wave field from lower-frequency flows such as fronts and mesoscale eddies, which are the subject of their own wave turbulence literature (e.g. Müller Reference Müller1976; Kafiabad et al. Reference Kafiabad, Savva, Miles and Vanneste2019). Such internal wave–mean flow interactions can be a significant regional source of internal wave energy (Polzin Reference Polzin2010) and may be a key issue in determining the regional character of the internal wave field (Polzin & Lvov Reference Polzin and Lvov2011).
The primitive equations of motion (2.1) under the assumption (2.7) can be written as a pair of canonical Hamiltonian equations
where ![]() $\phi$ is the isopycnal velocity potential, and the Hamiltonian is the sum of kinetic and potential energies
$\phi$ is the isopycnal velocity potential, and the Hamiltonian is the sum of kinetic and potential energies
 \begin{align} {\mathcal{H}} &=
\frac{1}{2}\int {\rm d}\kern0.7pt {\boldsymbol{x}}\,{\rm d}\rho
\left[ \left( \varPi_{0}(\rho)+\varPi({\boldsymbol{x}},
\rho) \right) \left|\boldsymbol{\nabla}
\phi({\boldsymbol{x}},\rho) + \frac{f}{\varPi_{0}}
\boldsymbol{\nabla}^{{\perp}}\varDelta^{{-}1}
\varPi(\boldsymbol{x}, \rho) \right|^2\right.\nonumber\\
&\quad \left. -\,g \left|\int^{\rho} {\rm d}\hat{\rho}
\,\frac{\varPi({\boldsymbol{x}},\hat{\rho})}{\hat{\rho}}
\right|^2 \right], \end{align}
\begin{align} {\mathcal{H}} &=
\frac{1}{2}\int {\rm d}\kern0.7pt {\boldsymbol{x}}\,{\rm d}\rho
\left[ \left( \varPi_{0}(\rho)+\varPi({\boldsymbol{x}},
\rho) \right) \left|\boldsymbol{\nabla}
\phi({\boldsymbol{x}},\rho) + \frac{f}{\varPi_{0}}
\boldsymbol{\nabla}^{{\perp}}\varDelta^{{-}1}
\varPi(\boldsymbol{x}, \rho) \right|^2\right.\nonumber\\
&\quad \left. -\,g \left|\int^{\rho} {\rm d}\hat{\rho}
\,\frac{\varPi({\boldsymbol{x}},\hat{\rho})}{\hat{\rho}}
\right|^2 \right], \end{align}
with ![]() $\boldsymbol {\nabla }^{\perp }=(-\partial / \partial y, \partial / \partial x)$, where
$\boldsymbol {\nabla }^{\perp }=(-\partial / \partial y, \partial / \partial x)$, where ![]() $\varDelta ^{-1}$ is the inverse Laplacian and
$\varDelta ^{-1}$ is the inverse Laplacian and ![]() $\hat {\rho }$ represents a variable of integration.
$\hat {\rho }$ represents a variable of integration.
Our intent is to build a perturbation theory around analytical solutions to the linearized primitive equations as plane waves proportional to ![]() $\exp ({\textrm {i} [{\boldsymbol {r}} \boldsymbol {\cdot } {\boldsymbol {p}} - \sigma t]})$. We therefore transition to the Fourier space
$\exp ({\textrm {i} [{\boldsymbol {r}} \boldsymbol {\cdot } {\boldsymbol {p}} - \sigma t]})$. We therefore transition to the Fourier space
 \begin{equation} \left.\begin{gathered} \varPi(x, y, \rho) = \frac{1}{(2 {\rm \pi})^{3/2}}\int \varPi_{\boldsymbol{p}} \, {\rm e}^{ {\rm i} {\boldsymbol{r}} \,\boldsymbol{\cdot}\, {\boldsymbol{p}}} \,{\rm d} {\boldsymbol{p}},\quad \phi(x, y, \rho) = \frac{1}{(2 {\rm \pi})^{3/2}}\int \phi_{\boldsymbol{p}} \,{\rm e}^{ {\rm i} {\boldsymbol{r}} \,\boldsymbol{\cdot}\, \boldsymbol{p}} \,{\rm d}{\boldsymbol{p}}, \\ {\boldsymbol{p}}=( {\boldsymbol{k}},m), \quad {\boldsymbol{k}}=( k, l), \quad {\boldsymbol{r}}=(x, y, \rho) , \end{gathered}\right\}\end{equation}
\begin{equation} \left.\begin{gathered} \varPi(x, y, \rho) = \frac{1}{(2 {\rm \pi})^{3/2}}\int \varPi_{\boldsymbol{p}} \, {\rm e}^{ {\rm i} {\boldsymbol{r}} \,\boldsymbol{\cdot}\, {\boldsymbol{p}}} \,{\rm d} {\boldsymbol{p}},\quad \phi(x, y, \rho) = \frac{1}{(2 {\rm \pi})^{3/2}}\int \phi_{\boldsymbol{p}} \,{\rm e}^{ {\rm i} {\boldsymbol{r}} \,\boldsymbol{\cdot}\, \boldsymbol{p}} \,{\rm d}{\boldsymbol{p}}, \\ {\boldsymbol{p}}=( {\boldsymbol{k}},m), \quad {\boldsymbol{k}}=( k, l), \quad {\boldsymbol{r}}=(x, y, \rho) , \end{gathered}\right\}\end{equation}
and introduce a complex field variable ![]() $a_{\boldsymbol {p}}$ through the canonical transformation
$a_{\boldsymbol {p}}$ through the canonical transformation
Wave frequency ![]() $\sigma _{\boldsymbol {p}}$ is restricted to be positive. We ignore variations in density as they multiply horizontal momentum, replacing
$\sigma _{\boldsymbol {p}}$ is restricted to be positive. We ignore variations in density as they multiply horizontal momentum, replacing ![]() $\rho$ by a reference density
$\rho$ by a reference density ![]() $\rho _0$ (the Boussinesq approximation) and arrive at a linear dispersion frequency
$\rho _0$ (the Boussinesq approximation) and arrive at a linear dispersion frequency ![]() $\sigma$ given by
$\sigma$ given by
 \begin{equation} \sigma_{\boldsymbol{p}}=\sqrt{ f^2 + \frac{g^2}{\rho_0^2 N^2} \frac{|\boldsymbol{k}|^2 }{m^2}} . \end{equation}
\begin{equation} \sigma_{\boldsymbol{p}}=\sqrt{ f^2 + \frac{g^2}{\rho_0^2 N^2} \frac{|\boldsymbol{k}|^2 }{m^2}} . \end{equation}The equations of motion (2.1) adopt the canonical form
with Hamiltonian
 \begin{align} {\mathcal{H}} &= \int {\rm d}\boldsymbol{p} \, \sigma_{\boldsymbol{p}} |a_{\boldsymbol{p}}|^2+ \int {\rm d}{\boldsymbol{p}} \,{\rm d} {\boldsymbol{p}_{\boldsymbol{1}}}\,{\rm d} {\boldsymbol{p}_{\boldsymbol{2}}} \big(\delta_{\boldsymbol{p}+\boldsymbol{p}_1+\boldsymbol{p}_2} (U_{\boldsymbol{p},\boldsymbol{p}_1, \boldsymbol{p}_2} a_{\boldsymbol{p}}^{{\ast}} a_{\boldsymbol{p}_1}^{{\ast}} a_{\boldsymbol{p}_2}^{{\ast}} + \mathrm{c.c.})\nonumber\\ &\quad +\, \delta_{-\boldsymbol{p}+\boldsymbol{p}_1+\boldsymbol{p}_2} (V_{\boldsymbol{p}_1,\boldsymbol{p}_2}^{\boldsymbol{p}} a_{\boldsymbol{p}}^{{\ast}} a_{\boldsymbol{p}_1} a_{\boldsymbol{p}_2} + \mathrm{c.c.}) \big) . \end{align}
\begin{align} {\mathcal{H}} &= \int {\rm d}\boldsymbol{p} \, \sigma_{\boldsymbol{p}} |a_{\boldsymbol{p}}|^2+ \int {\rm d}{\boldsymbol{p}} \,{\rm d} {\boldsymbol{p}_{\boldsymbol{1}}}\,{\rm d} {\boldsymbol{p}_{\boldsymbol{2}}} \big(\delta_{\boldsymbol{p}+\boldsymbol{p}_1+\boldsymbol{p}_2} (U_{\boldsymbol{p},\boldsymbol{p}_1, \boldsymbol{p}_2} a_{\boldsymbol{p}}^{{\ast}} a_{\boldsymbol{p}_1}^{{\ast}} a_{\boldsymbol{p}_2}^{{\ast}} + \mathrm{c.c.})\nonumber\\ &\quad +\, \delta_{-\boldsymbol{p}+\boldsymbol{p}_1+\boldsymbol{p}_2} (V_{\boldsymbol{p}_1,\boldsymbol{p}_2}^{\boldsymbol{p}} a_{\boldsymbol{p}}^{{\ast}} a_{\boldsymbol{p}_1} a_{\boldsymbol{p}_2} + \mathrm{c.c.}) \big) . \end{align}
Here, ![]() $V_{\boldsymbol {p}_1,\boldsymbol {p}_2}$ and
$V_{\boldsymbol {p}_1,\boldsymbol {p}_2}$ and ![]() $U_{\boldsymbol {p}_1,\boldsymbol {p}_2}$ are the interaction cross-sections that define the strength of nonlinear interactions between wavenumbers
$U_{\boldsymbol {p}_1,\boldsymbol {p}_2}$ are the interaction cross-sections that define the strength of nonlinear interactions between wavenumbers ![]() ${\boldsymbol {p}}$,
${\boldsymbol {p}}$, ![]() ${\boldsymbol {p}_{\boldsymbol {1}}}$ and
${\boldsymbol {p}_{\boldsymbol {1}}}$ and ![]() ${\boldsymbol {p}_{\boldsymbol {2}}}$ Lvov & Tabak (Reference Lvov and Tabak2001); c.c. denotes the complex conjugate. Implicit in the canonical transformation (2.11a,b), Hamilton's equation (2.13) and Hamiltonian (2.14) is a time dependence of
${\boldsymbol {p}_{\boldsymbol {2}}}$ Lvov & Tabak (Reference Lvov and Tabak2001); c.c. denotes the complex conjugate. Implicit in the canonical transformation (2.11a,b), Hamilton's equation (2.13) and Hamiltonian (2.14) is a time dependence of ![]() $\textrm {e}^{-\textrm {i} \sigma t}$. The
$\textrm {e}^{-\textrm {i} \sigma t}$. The ![]() $U$ elements have a time dependence of
$U$ elements have a time dependence of ![]() $\exp ({\textrm {i}(\sigma _{{\boldsymbol {p}}_1} + \sigma _{{\boldsymbol {p}}_2} + \sigma _{{\boldsymbol {p}}_3})t})$ with
$\exp ({\textrm {i}(\sigma _{{\boldsymbol {p}}_1} + \sigma _{{\boldsymbol {p}}_2} + \sigma _{{\boldsymbol {p}}_3})t})$ with ![]() $\sigma _{{\boldsymbol {p}}} > 0$. They describe the creation of three waves out of nothing and therefore will not appear in the kinetic equation (2.16). Indeed, the
$\sigma _{{\boldsymbol {p}}} > 0$. They describe the creation of three waves out of nothing and therefore will not appear in the kinetic equation (2.16). Indeed, the ![]() $U$ terms are therefore non-resonant and can be excluded from the Hamiltonian by appropriate near-identity canonical transformation (Zakharov, Lvov & Falkovich Reference Zakharov, Lvov and Falkovich1992).
$U$ terms are therefore non-resonant and can be excluded from the Hamiltonian by appropriate near-identity canonical transformation (Zakharov, Lvov & Falkovich Reference Zakharov, Lvov and Falkovich1992).
This is the standard form of the Hamiltonian of a system dominated by three-wave interactions (Zakharov et al. Reference Zakharov, Lvov and Falkovich1992). Calculations of interaction coefficients are tedious but straightforward tasks, completed in Lvov & Tabak (Reference Lvov and Tabak2004) and Lvov et al. (Reference Lvov, Polzin, Tabak and Yokoyama2010). We stress that the field equation (2.13) with the three-wave Hamiltonian ((2.12), (2.14)) is equivalent to the primitive equations of motion for internal waves (2.1) under the following assumptions: potential vorticity is constant along isopycnals and is given by (2.7) and the Boussinesq approximation is made.
2.2. Wave turbulence theory
In wave turbulence theory, one proposes a perturbation expansion in the amplitude of the nonlinearity, yielding linear waves at the leading order. Wave amplitudes are modulated by the nonlinear interactions, and the modulation is statistically described by a kinetic equation (Zakharov et al. Reference Zakharov, Lvov and Falkovich1992; Nazarenko Reference Nazarenko2011) for the wave-action spectral density ![]() $n_{\boldsymbol {p}}$ defined by
$n_{\boldsymbol {p}}$ defined by
Here, ![]() $\langle \dots \rangle$ denotes an ensemble averaging, i.e. averaging over many realizations of the random wave field. Application to the internal wave problem is presented in § 2b of Lvov et al. (Reference Lvov, Polzin, Tabak and Yokoyama2010).
$\langle \dots \rangle$ denotes an ensemble averaging, i.e. averaging over many realizations of the random wave field. Application to the internal wave problem is presented in § 2b of Lvov et al. (Reference Lvov, Polzin, Tabak and Yokoyama2010).
2.2.1. Generalized (broadened) kinetic equation
In the limit of small nonlinearity, one develops a perturbation expansion in the nonlinearity strength, which leads, under certain assumptions, to the wave turbulence kinetic equation. The derivation of the resonant kinetic equation is well understood and studied, see Zakharov et al. (Reference Zakharov, Lvov and Falkovich1992) and Nazarenko (Reference Nazarenko2011). Taking non-resonant interactions leads to a different version of the kinetic equation with the frequency delta functions being replaced by a Lorentzian, see Lvov et al. (Reference Lvov, Lvov, Newell and Zakharov1997) and Lvov, Polzin & Yokoyama (Reference Lvov, Polzin and Yokoyama2012). This derivation also hinges on the assessment that fourth-order cumulants are a subleading term compared with the product of two double correlators (Deng & Hani Reference Deng and Hani2023). For the three-wave Hamiltonian (2.14), the kinetic equation is (2.16), describing general internal waves interacting in both rotating and non-rotating environments
 \begin{align} \frac{\partial}{\partial
t} n_{{\boldsymbol{p}}} &= \int \int {\rm
d}{\boldsymbol{p}}_1 \,{\rm d}{\boldsymbol{p}}_2 \big(
|V_{{\boldsymbol{p}}_1,{\boldsymbol{p}}_2}^{{\boldsymbol{p}}}|^2\delta(\kern1pt {\boldsymbol{p}}-{\boldsymbol{p}}_1-{\boldsymbol{p}}_2){\mathcal{L}}
(\Delta \sigma_{p12}, \varGamma_{p12})
[n_{{\boldsymbol{p}}_1}n_{{\boldsymbol{p}}_2}-n_{{\boldsymbol{p}}}[n_{{\boldsymbol{p}}_1}+n_{{\boldsymbol{p}}_2}]]\nonumber\\
&\quad-
|V_{{\boldsymbol{p}}_2,{\boldsymbol{p}}}^{{\boldsymbol{p}}_1}
|^2
\delta(\kern1pt {\boldsymbol{p}}-{\boldsymbol{p}}_1+{\boldsymbol{p}}_2)
{\mathcal{L}}(\Delta \sigma_{12p}, \varGamma_{p12})
[n_{{\boldsymbol{p}}_2}n_{{\boldsymbol{p}}}-n_{{\boldsymbol{p}}_1}[n_{{\boldsymbol{p}}_2}+n_{{\boldsymbol{p}}}]]\nonumber\\
&\quad
-\,|V_{{\boldsymbol{p}},{\boldsymbol{p}}_1}^{{\boldsymbol{p}}_2}
|^2
\delta(\kern1pt {\boldsymbol{p}}+{\boldsymbol{p}}_1-{\boldsymbol{p}}_2){\mathcal{L}}(\Delta
\sigma_{2p1},
\varGamma_{p12})[n_{{\boldsymbol{p}}}n_{{\boldsymbol{p}}_1}-n_{{\boldsymbol{p}}_2}[n_{{\boldsymbol{p}}}+n_{{\boldsymbol{p}}_1}]]
\big) , \end{align}
\begin{align} \frac{\partial}{\partial
t} n_{{\boldsymbol{p}}} &= \int \int {\rm
d}{\boldsymbol{p}}_1 \,{\rm d}{\boldsymbol{p}}_2 \big(
|V_{{\boldsymbol{p}}_1,{\boldsymbol{p}}_2}^{{\boldsymbol{p}}}|^2\delta(\kern1pt {\boldsymbol{p}}-{\boldsymbol{p}}_1-{\boldsymbol{p}}_2){\mathcal{L}}
(\Delta \sigma_{p12}, \varGamma_{p12})
[n_{{\boldsymbol{p}}_1}n_{{\boldsymbol{p}}_2}-n_{{\boldsymbol{p}}}[n_{{\boldsymbol{p}}_1}+n_{{\boldsymbol{p}}_2}]]\nonumber\\
&\quad-
|V_{{\boldsymbol{p}}_2,{\boldsymbol{p}}}^{{\boldsymbol{p}}_1}
|^2
\delta(\kern1pt {\boldsymbol{p}}-{\boldsymbol{p}}_1+{\boldsymbol{p}}_2)
{\mathcal{L}}(\Delta \sigma_{12p}, \varGamma_{p12})
[n_{{\boldsymbol{p}}_2}n_{{\boldsymbol{p}}}-n_{{\boldsymbol{p}}_1}[n_{{\boldsymbol{p}}_2}+n_{{\boldsymbol{p}}}]]\nonumber\\
&\quad
-\,|V_{{\boldsymbol{p}},{\boldsymbol{p}}_1}^{{\boldsymbol{p}}_2}
|^2
\delta(\kern1pt {\boldsymbol{p}}+{\boldsymbol{p}}_1-{\boldsymbol{p}}_2){\mathcal{L}}(\Delta
\sigma_{2p1},
\varGamma_{p12})[n_{{\boldsymbol{p}}}n_{{\boldsymbol{p}}_1}-n_{{\boldsymbol{p}}_2}[n_{{\boldsymbol{p}}}+n_{{\boldsymbol{p}}_1}]]
\big) , \end{align}
where Lorentzian ![]() $\mathcal {L}$ is given by
$\mathcal {L}$ is given by ![]() ${\mathcal {L}} = {\varGamma _{p12}}/({(\Delta \sigma )^2 + \varGamma _{p12}^2})$ and
${\mathcal {L}} = {\varGamma _{p12}}/({(\Delta \sigma )^2 + \varGamma _{p12}^2})$ and ![]() $\Delta \sigma _{p12}=\sigma _p-\sigma _{p_1}-\sigma _{p_2}$ represents the distance from the resonant surface. The resonant manifold is defined by
$\Delta \sigma _{p12}=\sigma _p-\sigma _{p_1}-\sigma _{p_2}$ represents the distance from the resonant surface. The resonant manifold is defined by
 \begin{equation}
\left.\begin{gathered}
\sigma = \sigma_1 + \sigma_2 ; \quad \boldsymbol{p} =
\boldsymbol{p}_1 + \boldsymbol{p}_2,\\ \sigma = \sigma_1 -
\sigma_2 ; \quad \boldsymbol{p} = \boldsymbol{p}_1-
\boldsymbol{p}_2,\\ \sigma = \sigma_2 - \sigma_1 ; \quad
\boldsymbol{p} = \boldsymbol{p}_2-
\boldsymbol{p}_1, \end{gathered}\right\}
\end{equation}
\begin{equation}
\left.\begin{gathered}
\sigma = \sigma_1 + \sigma_2 ; \quad \boldsymbol{p} =
\boldsymbol{p}_1 + \boldsymbol{p}_2,\\ \sigma = \sigma_1 -
\sigma_2 ; \quad \boldsymbol{p} = \boldsymbol{p}_1-
\boldsymbol{p}_2,\\ \sigma = \sigma_2 - \sigma_1 ; \quad
\boldsymbol{p} = \boldsymbol{p}_2-
\boldsymbol{p}_1, \end{gathered}\right\}
\end{equation}
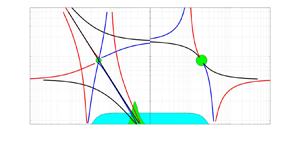
and appears in figure 1. In wave turbulence theory of internal waves the importance of special extreme scale-separated triads was recognized in McComas & Bretherton (Reference McComas and Bretherton1977). These extreme scale-separated limits are called induced diffusion(ID), elastic scattering (ES) and parametric subharmonic instability (PSI). For an explanation of these triads see also McComas & Müller (Reference McComas and Müller1981a).

Figure 1. The resonant manifold (2.17) in the situation where the three horizontal wavevectors are either parallel or anti-parallel, plotted in a vertical wavenumber–frequency space, for a wave at the centre of the green circle. With rotation, extreme scale separations in horizontal wavenumber lead to the extreme scale-separated triads mentioned in the introduction. These triads are Bragg scattering (also called elastic scattering, or ES, and a phase velocity equals ground velocity resonance condition, called induced diffusion, or ID, being located at the Coriolis frequency ![]() $f$. This study focuses on the latter class, with scale separation in both horizontal and vertical wavenumbers. Near-resonant ID conditions are depicted in green, bandwidth-limited non-resonant ID forcing in cyan. The third type of extreme scale separated triads, called parametric subharmonic instability, or PSI, does not play a role in this manuscript.
$f$. This study focuses on the latter class, with scale separation in both horizontal and vertical wavenumbers. Near-resonant ID conditions are depicted in green, bandwidth-limited non-resonant ID forcing in cyan. The third type of extreme scale separated triads, called parametric subharmonic instability, or PSI, does not play a role in this manuscript.
The total resonance width associated with a specific triad is given by ![]() $\varGamma _{p12} = \gamma _p + \gamma _1 +\gamma _2$ and the equation for the individual resonance widths is given by
$\varGamma _{p12} = \gamma _p + \gamma _1 +\gamma _2$ and the equation for the individual resonance widths is given by
 \begin{align} \gamma_p &= \displaystyle
\int \int {\rm d}{\boldsymbol{p}}_1\,{\rm
d}{\boldsymbol{p}}_2\big(
|V_{{\boldsymbol{p}}_1,{\boldsymbol{p}}_2}^{{\boldsymbol{p}}}
|^2 \delta(\kern1pt {\boldsymbol{p}}-{\boldsymbol{p}}_{1}-{\boldsymbol{p}}_2)
{\mathcal{L}} (\sigma-\sigma_1-\sigma_2)
[n_{{\boldsymbol{p}}_1}+n_{{\boldsymbol{p}}_2}]
\nonumber\\ &\quad +
|V_{{\boldsymbol{p}}_2,{\boldsymbol{p}}}^{{\boldsymbol{p}}_1}
|^2 \delta(\kern1pt {\boldsymbol{p}}-{\boldsymbol{p}}_1+{\boldsymbol{p}}_2){\mathcal{L}}(\sigma-\sigma_1+\sigma_2)
[n_{{\boldsymbol{p}}_2}-n_{{\boldsymbol{p}}_1}] \nonumber\\
&\quad +\,
|V_{{\boldsymbol{p}},{\boldsymbol{p}}_1}^{{\boldsymbol{p}}_2}
|^2 \delta(\kern1pt {\boldsymbol{p}}+{\boldsymbol{p}}_1-{\boldsymbol{p}}_2){\mathcal{L}}(\sigma+\sigma_1-\sigma_2)
[n_{{\boldsymbol{p}}_1}-n_{{\boldsymbol{p}}_2}]\big).
\end{align}
\begin{align} \gamma_p &= \displaystyle
\int \int {\rm d}{\boldsymbol{p}}_1\,{\rm
d}{\boldsymbol{p}}_2\big(
|V_{{\boldsymbol{p}}_1,{\boldsymbol{p}}_2}^{{\boldsymbol{p}}}
|^2 \delta(\kern1pt {\boldsymbol{p}}-{\boldsymbol{p}}_{1}-{\boldsymbol{p}}_2)
{\mathcal{L}} (\sigma-\sigma_1-\sigma_2)
[n_{{\boldsymbol{p}}_1}+n_{{\boldsymbol{p}}_2}]
\nonumber\\ &\quad +
|V_{{\boldsymbol{p}}_2,{\boldsymbol{p}}}^{{\boldsymbol{p}}_1}
|^2 \delta(\kern1pt {\boldsymbol{p}}-{\boldsymbol{p}}_1+{\boldsymbol{p}}_2){\mathcal{L}}(\sigma-\sigma_1+\sigma_2)
[n_{{\boldsymbol{p}}_2}-n_{{\boldsymbol{p}}_1}] \nonumber\\
&\quad +\,
|V_{{\boldsymbol{p}},{\boldsymbol{p}}_1}^{{\boldsymbol{p}}_2}
|^2 \delta(\kern1pt {\boldsymbol{p}}+{\boldsymbol{p}}_1-{\boldsymbol{p}}_2){\mathcal{L}}(\sigma+\sigma_1-\sigma_2)
[n_{{\boldsymbol{p}}_1}-n_{{\boldsymbol{p}}_2}]\big).
\end{align}
Physically, this ![]() $\gamma _p$ represents the fast time scale of decay of a narrow perturbation to the otherwise stationary spectrum (Lvov et al. Reference Lvov, Lvov, Newell and Zakharov1997; Polzin & Lvov Reference Polzin and Lvov2017). It coincides with Langevin rates estimated by Pomphrey, Meiss & Watson (Reference Pomphrey, Meiss and Watson1980) and the decay rate of the McComas (Reference McComas1977) spike experiments. The replacement of the frequency-conserving delta function by the Lorentzian takes into account not only resonant but also near-resonant and non-resonant interactions. Non-resonant interactions appear as a result of the Lorentzian decaying slowly. The role of the non-resonant interactions have to be investigated separately for each particular problem.
$\gamma _p$ represents the fast time scale of decay of a narrow perturbation to the otherwise stationary spectrum (Lvov et al. Reference Lvov, Lvov, Newell and Zakharov1997; Polzin & Lvov Reference Polzin and Lvov2017). It coincides with Langevin rates estimated by Pomphrey, Meiss & Watson (Reference Pomphrey, Meiss and Watson1980) and the decay rate of the McComas (Reference McComas1977) spike experiments. The replacement of the frequency-conserving delta function by the Lorentzian takes into account not only resonant but also near-resonant and non-resonant interactions. Non-resonant interactions appear as a result of the Lorentzian decaying slowly. The role of the non-resonant interactions have to be investigated separately for each particular problem.
2.2.2. Bandwidth estimates
The broadened kinetic equation provides access to a time scale as the inverse of the bandwidth ![]() $\gamma _{p}$ (2.18).
$\gamma _{p}$ (2.18).
Considered in isolation from other interactions and in the resonant limit, the extreme scale-separated ID mechanism gives rise to (Polzin & Lvov Reference Polzin and Lvov2017)
where ![]() $k$ is horizontal wavenumber magnitude,
$k$ is horizontal wavenumber magnitude, ![]() $e_o$ is the total energy density in the GM model and
$e_o$ is the total energy density in the GM model and ![]() $m_{\ast }$ is the vertical wavenumber bandwidth parameter; see Appendix A. In the context of a broadened kinetic equation,
$m_{\ast }$ is the vertical wavenumber bandwidth parameter; see Appendix A. In the context of a broadened kinetic equation, ![]() $\gamma _p^{ID}$ represents the decay of a spike introduced into an otherwise smooth spectrum (Lvov et al. Reference Lvov, Lvov, Newell and Zakharov1997) and is identified as such by McComas & Müller (Reference McComas and Müller1981a) in the numerical experiments of McComas (Reference McComas1977). The associated time scale is far smaller than a wave period and at loggerheads with the intent of having (2.16) describe the slow time evolution of the spectral density.
$\gamma _p^{ID}$ represents the decay of a spike introduced into an otherwise smooth spectrum (Lvov et al. Reference Lvov, Lvov, Newell and Zakharov1997) and is identified as such by McComas & Müller (Reference McComas and Müller1981a) in the numerical experiments of McComas (Reference McComas1977). The associated time scale is far smaller than a wave period and at loggerheads with the intent of having (2.16) describe the slow time evolution of the spectral density.
At finite, but yet small-amplitude, analysis of (2.18) reveals that the bandwidth is composed of both resonant ![]() $\gamma _{res}$ and non-resonant terms
$\gamma _{res}$ and non-resonant terms
 \begin{equation} \left.\begin{gathered} \text{resonant:} \ \gamma_{res} = \frac{2}{\rm \pi} \frac{k e_0 m_{{\ast}}}{N} \big(\frac{\sigma}{f}\big)^2 \\ \text{non-resonant:} \ \frac{2}{\rm \pi} \frac{k^2 e_0}{f^2} \,\gamma_{res} \end{gathered}\right\}. \end{equation}
\begin{equation} \left.\begin{gathered} \text{resonant:} \ \gamma_{res} = \frac{2}{\rm \pi} \frac{k e_0 m_{{\ast}}}{N} \big(\frac{\sigma}{f}\big)^2 \\ \text{non-resonant:} \ \frac{2}{\rm \pi} \frac{k^2 e_0}{f^2} \,\gamma_{res} \end{gathered}\right\}. \end{equation}The non-resonant contributions come from vertical scales that are larger than those of the high-frequency wave and come from the tails of the Lorentzian admitting non-resonant interactions with the highly energetic near-inertial wave field.
The non-resonant contributions increase at a greater rate with respect to increasing amplitude than resonant contributions. At realistic oceanic amplitudes, numerical evaluation (Polzin & Lvov Reference Polzin and Lvov2017) demonstrates that ![]() $\gamma _p^{ID}$ is proportional to the root-mean-square (r.m.s.) Doppler shift. The difficulty of placing a physical interpretation on such a short time decay time scale (2.19) and suspicion that the broadened kinetic equation would suffer from the Galilean invariance that plagued Kraichnan's 1959 DIA model for 3-D turbulence led to scepticism and extensive commentary in the literature (Holloway Reference Holloway1980, Reference Holloway1982). Addressing these issues required development of a broadened kinetic equation, which in turn required waiting for the derivation in canonical coordinates presented at the beginning of this section.
$\gamma _p^{ID}$ is proportional to the root-mean-square (r.m.s.) Doppler shift. The difficulty of placing a physical interpretation on such a short time decay time scale (2.19) and suspicion that the broadened kinetic equation would suffer from the Galilean invariance that plagued Kraichnan's 1959 DIA model for 3-D turbulence led to scepticism and extensive commentary in the literature (Holloway Reference Holloway1980, Reference Holloway1982). Addressing these issues required development of a broadened kinetic equation, which in turn required waiting for the derivation in canonical coordinates presented at the beginning of this section.
2.2.3. Fokker–Planck diffusion limit
Following McComas & Bretherton (Reference McComas and Bretherton1977) for the resonant kinetic equation, we start from (2.16) and pick off the interactions having ![]() ${\boldsymbol {p}}$ nearly parallel to
${\boldsymbol {p}}$ nearly parallel to ![]() ${\boldsymbol {p}}_1$ with
${\boldsymbol {p}}_1$ with ![]() ${\boldsymbol {p}}_2$ small, or nearly parallel to
${\boldsymbol {p}}_2$ small, or nearly parallel to ![]() ${\boldsymbol {p}}_2$ with
${\boldsymbol {p}}_2$ with ![]() ${\boldsymbol {p}}_1$ small, which selects the ID class triads. For a sufficiently red spectrum, this permits discarding of the small
${\boldsymbol {p}}_1$ small, which selects the ID class triads. For a sufficiently red spectrum, this permits discarding of the small ![]() $n_{\boldsymbol {p}} n_{\boldsymbol {p} 1}$ (
$n_{\boldsymbol {p}} n_{\boldsymbol {p} 1}$ (![]() $n_{\boldsymbol {p}} n_{\boldsymbol {p} 2}$, respectively) terms. We then rewrite (2.16) as
$n_{\boldsymbol {p}} n_{\boldsymbol {p} 2}$, respectively) terms. We then rewrite (2.16) as
where we introduced
and expanded the difference ![]() $( {\mathcal {B}}({\boldsymbol {p}})-{\mathcal {B}}({\boldsymbol {p}}+{\boldsymbol {q}}))$ in a Taylor series using
$( {\mathcal {B}}({\boldsymbol {p}})-{\mathcal {B}}({\boldsymbol {p}}+{\boldsymbol {q}}))$ in a Taylor series using ![]() ${\boldsymbol {q}}$ to represent the small difference in wavenumber between the two high-frequency waves. Expanding the difference
${\boldsymbol {q}}$ to represent the small difference in wavenumber between the two high-frequency waves. Expanding the difference ![]() $n_{{\boldsymbol {p}}_1}-n_{\boldsymbol {p}}$ for small
$n_{{\boldsymbol {p}}_1}-n_{\boldsymbol {p}}$ for small ![]() ${\boldsymbol {q}}$ gives
${\boldsymbol {q}}$ gives
Combining (2.21) with (2.23) we obtain
or
 \begin{equation} \left.\begin{gathered} \frac{\partial n_{{\boldsymbol{p}}}}{\partial t} = \frac{\partial}{\partial p_i} D_{ij}(\kern1pt {\boldsymbol{p}},{\boldsymbol{q}}) \frac{\partial}{\partial p_j} n_{{\boldsymbol{p}}},\\ D_{ij}(\kern1pt {\boldsymbol{p}},{\boldsymbol{q}}) = 8{\rm \pi} \int {\rm d} {\boldsymbol{q}} \left(q_i q_j\right) |V_{{\boldsymbol{p}}_1,{\boldsymbol{q}}}^{{\boldsymbol{p}}}|^2 n_q \delta_{{{\boldsymbol{p}} - {\boldsymbol{p}}_1-{\boldsymbol{q}}}} {\mathcal{L}}({\sigma_{{\boldsymbol{p}}} -\sigma_{{{\boldsymbol{p}}_1}}-\sigma_{{{\boldsymbol{q}}}}}) \,{\rm d} {\boldsymbol{p}}_{1}. \end{gathered}\right\}\end{equation}
\begin{equation} \left.\begin{gathered} \frac{\partial n_{{\boldsymbol{p}}}}{\partial t} = \frac{\partial}{\partial p_i} D_{ij}(\kern1pt {\boldsymbol{p}},{\boldsymbol{q}}) \frac{\partial}{\partial p_j} n_{{\boldsymbol{p}}},\\ D_{ij}(\kern1pt {\boldsymbol{p}},{\boldsymbol{q}}) = 8{\rm \pi} \int {\rm d} {\boldsymbol{q}} \left(q_i q_j\right) |V_{{\boldsymbol{p}}_1,{\boldsymbol{q}}}^{{\boldsymbol{p}}}|^2 n_q \delta_{{{\boldsymbol{p}} - {\boldsymbol{p}}_1-{\boldsymbol{q}}}} {\mathcal{L}}({\sigma_{{\boldsymbol{p}}} -\sigma_{{{\boldsymbol{p}}_1}}-\sigma_{{{\boldsymbol{q}}}}}) \,{\rm d} {\boldsymbol{p}}_{1}. \end{gathered}\right\}\end{equation}This is a Fokker–Planck diffusion equation describing the diffusion of wave action in the system dominated by non-local-in-wavenumber interactions. Comparison between the Fokker–Planck equation (2.25) obtained here, and the similar Fokker–Planck equation (obtained using Wentzel–Kramers–Brillouin (WKB) theory (§ 3.2.4 below) will lead to critical insights into the spectral energy transfers in internal wave systems and ultimately to the parametrization of the energy supply to internal wave breaking processes.
Extended versions of the Garrett and Munk model (Appendix A) can then be inserted into (2.25) to arrive at families of stationary states (e.g. McComas & Müller Reference McComas and Müller1981b; Polzin & Lvov Reference Polzin and Lvov2011; Dematteis et al. Reference Dematteis, Polzin and Lvov2022) and estimate downscale transport. We will require transport estimates the vertical–vertical component of the diffusivity tensor, ![]() $D_{33}$. For the Garrett and Munk model (GM76),
$D_{33}$. For the Garrett and Munk model (GM76),
Here, ![]() $k$ is horizontal wavenumber magnitude,
$k$ is horizontal wavenumber magnitude, ![]() $e_0$ is the total energy,
$e_0$ is the total energy, ![]() $m_{\ast }$ is a bandwidth parameter and
$m_{\ast }$ is a bandwidth parameter and ![]() $N$ is buoyancy frequency.
$N$ is buoyancy frequency.
3. Wave–wave interactions in the scale-separated limit
In our previous studies Lvov et al. (Reference Lvov, Polzin, Tabak and Yokoyama2010) we have seen that, under a scale-invariant assumption, the integrals in the kinetic equation tend to diverge for small or large wavenumbers or both. Therefore the interactions via extreme scale separations play an important role in energy exchanges in internal waves. In this section, we are going to develop a rigorous formalism based on WKB techniques to study such interactions.
3.1. The primitive equations and Hamiltonian structure
3.1.1. Reynolds decomposition and Hamiltonian structure
To study interactions between long and short waves we start at (2.8a,b) and make a Reynolds decomposition in wave amplitude
Here, the large-amplitude waves are represented with ![]() $\varPi, \varPhi, \varPsi$ and small-amplitude waves are given by
$\varPi, \varPhi, \varPsi$ and small-amplitude waves are given by ![]() $\phi '$,
$\phi '$, ![]() ${\rm \pi} '$ and
${\rm \pi} '$ and ![]() $\psi '$. Given the potentials
$\psi '$. Given the potentials ![]() $\varPhi$ and
$\varPhi$ and ![]() $\phi$, the corresponding velocities are
$\phi$, the corresponding velocities are
To simplify the presentation, we will utilize the non-rotating approximation (![]() $\kern0.7pt f=0$) in which
$\kern0.7pt f=0$) in which ![]() $(\boldsymbol {\nabla }^{\perp } \varPsi, \boldsymbol {\nabla }^{\perp } \psi ) \rightarrow 0$. The case of rotating ocean
$(\boldsymbol {\nabla }^{\perp } \varPsi, \boldsymbol {\nabla }^{\perp } \psi ) \rightarrow 0$. The case of rotating ocean ![]() $f\ne 0$ is presented in Appendix.
$f\ne 0$ is presented in Appendix.
We substitute the Reynolds decomposition (3.1a–c) into the equations of motion (2.1). We then make an assumption that the large scales ![]() $\varPi$ and
$\varPi$ and ![]() $\varPhi$ exactly satisfy the primitive equations of motion. In other words, gradient operator applied to the inertial waves with no horizontal structure will return zero, thus these inertial waves are exact analytical solutions of the primitive Boussinesq equations (2.1). For the application of oceanic internal waves, this assumption is realized if the large-scale waves are a collection of inertial waves having frequency
$\varPhi$ exactly satisfy the primitive equations of motion. In other words, gradient operator applied to the inertial waves with no horizontal structure will return zero, thus these inertial waves are exact analytical solutions of the primitive Boussinesq equations (2.1). For the application of oceanic internal waves, this assumption is realized if the large-scale waves are a collection of inertial waves having frequency ![]() $\sigma =f$: inertial waves do not have horizontal structure and thus a superposition of inertial waves exactly satisfies the primitive equations of motion. We then subtract equations for the large-amplitude waves. The result is given by
$\sigma =f$: inertial waves do not have horizontal structure and thus a superposition of inertial waves exactly satisfies the primitive equations of motion. We then subtract equations for the large-amplitude waves. The result is given by
 \begin{equation} \left.\begin{gathered}
\dot{\rm \pi}' +
\boldsymbol{\nabla}\,\boldsymbol{\cdot}\,((\varPi_{0}+
\varPi+{\rm \pi}') \boldsymbol{\nabla} \varPhi)+
\boldsymbol{\nabla}({\rm \pi}'\varPhi)=0, \\
\dot{\phi}'+\frac{|\boldsymbol{\nabla}\phi'|^2}{2}+\boldsymbol{\nabla}\phi'
\,\boldsymbol{\cdot}\, \boldsymbol{\nabla}\varPhi +
\frac{g}{\rho_0^2} \int\int {\rm d}\rho' \,{\rm
d}\rho^{\prime\prime} \,{\rm \pi}'=0.
\end{gathered}\right\}\end{equation}
\begin{equation} \left.\begin{gathered}
\dot{\rm \pi}' +
\boldsymbol{\nabla}\,\boldsymbol{\cdot}\,((\varPi_{0}+
\varPi+{\rm \pi}') \boldsymbol{\nabla} \varPhi)+
\boldsymbol{\nabla}({\rm \pi}'\varPhi)=0, \\
\dot{\phi}'+\frac{|\boldsymbol{\nabla}\phi'|^2}{2}+\boldsymbol{\nabla}\phi'
\,\boldsymbol{\cdot}\, \boldsymbol{\nabla}\varPhi +
\frac{g}{\rho_0^2} \int\int {\rm d}\rho' \,{\rm
d}\rho^{\prime\prime} \,{\rm \pi}'=0.
\end{gathered}\right\}\end{equation}
In these equations, ![]() $\varPi$ and
$\varPi$ and ![]() $\varPhi$ are given time–space-dependent functions representing the large-amplitude waves.
$\varPhi$ are given time–space-dependent functions representing the large-amplitude waves.
These equations are also Hamilton's equations,
with the time-dependent Hamiltonian given by (this Hamiltonian may be obtained by substituting (3.1a–c) to (2.9))
There are two types of terms here – those that will ultimately describe a sea of interacting small-scale waves and those that will describe the influence of large-amplitude large-scale waves on the small-scale waves. In our previous efforts (Lvov & Tabak Reference Lvov and Tabak2001, Reference Lvov and Tabak2004; Lvov et al. Reference Lvov, Polzin, Tabak and Yokoyama2010; Polzin & Lvov Reference Polzin and Lvov2011, Reference Polzin and Lvov2017) these terms are comingled. Comparing (2.9) and (3.5), we see that (3.5) contains additional terms ![]() $\varPi |\boldsymbol {\nabla } \phi ' |^2$ and
$\varPi |\boldsymbol {\nabla } \phi ' |^2$ and ![]() ${\rm \pi} '\boldsymbol {\nabla }\phi '\boldsymbol {\cdot }\boldsymbol {\nabla }\varPhi$ that are explicit representations of what will be scale-separated interactions. The term
${\rm \pi} '\boldsymbol {\nabla }\phi '\boldsymbol {\cdot }\boldsymbol {\nabla }\varPhi$ that are explicit representations of what will be scale-separated interactions. The term ![]() ${\rm \pi} '\boldsymbol {\nabla }\phi '\boldsymbol {\cdot }\boldsymbol {\nabla }\varPhi$ describes the advection of the small-scale internal field by the given large-scale large-amplitude field. The term
${\rm \pi} '\boldsymbol {\nabla }\phi '\boldsymbol {\cdot }\boldsymbol {\nabla }\varPhi$ describes the advection of the small-scale internal field by the given large-scale large-amplitude field. The term ![]() $\varPi |\boldsymbol {\nabla } \phi ' |^2$ represents a coupling of small scales to large through changes in the stratification by the large-scale wave. The term
$\varPi |\boldsymbol {\nabla } \phi ' |^2$ represents a coupling of small scales to large through changes in the stratification by the large-scale wave. The term ![]() ${\rm \pi} ' |\boldsymbol {\nabla } \phi ' |^2$ will represent interactions local in wavenumber.
${\rm \pi} ' |\boldsymbol {\nabla } \phi ' |^2$ will represent interactions local in wavenumber.
We now express the space-dependent variables ![]() ${\rm \pi} ^{\prime }({\boldsymbol {r}}),\varPi ({\boldsymbol {r}}),\phi ^{\prime }({\boldsymbol {r}})$ and
${\rm \pi} ^{\prime }({\boldsymbol {r}}),\varPi ({\boldsymbol {r}}),\phi ^{\prime }({\boldsymbol {r}})$ and ![]() $\varPhi ({\boldsymbol {r}})$ in terms of their Fourier images
$\varPhi ({\boldsymbol {r}})$ in terms of their Fourier images ![]() ${\rm \pi} ^{\prime }({\boldsymbol {p}}),\varPi ({\boldsymbol {p}}),\phi ^{\prime }({\boldsymbol {p}})$ via (2.10), make the Boussinesq approximation
${\rm \pi} ^{\prime }({\boldsymbol {p}}),\varPi ({\boldsymbol {p}}),\phi ^{\prime }({\boldsymbol {p}})$ via (2.10), make the Boussinesq approximation ![]() ${\varPi }/{\rho }\simeq {\varPi }/{\rho _0}$ and use
${\varPi }/{\rho }\simeq {\varPi }/{\rho _0}$ and use ![]() $\int \textrm {d} {\boldsymbol {p}} \,\textrm {e}^{\textrm {i} {\boldsymbol {p}}\boldsymbol {\cdot } {\boldsymbol {r}}} =(2{\rm \pi} )^3 \delta ({\boldsymbol {p}})$ to obtain
$\int \textrm {d} {\boldsymbol {p}} \,\textrm {e}^{\textrm {i} {\boldsymbol {p}}\boldsymbol {\cdot } {\boldsymbol {r}}} =(2{\rm \pi} )^3 \delta ({\boldsymbol {p}})$ to obtain
 \begin{gather} \left.\begin{gathered}
{\mathcal{H}} = {\mathcal{H}}_{linear}
+{\mathcal{H}}_{nonlinear},\\ {\mathcal{H}}_{linear} =
\frac{1}{2}\int {\rm d} {\boldsymbol{p}} \Big( \varPi_{0}
|{\boldsymbol{k}}|^2 |\phi'_{{\boldsymbol{p}}}|^2-
\frac{g}{\rho_0^2}\frac{| \phi'_{{\boldsymbol{p}}}
|^2}{m^2}\Big), \\ {\mathcal{H}}_{nonlinear} =
{\mathcal{H}}_{local}+ {\mathcal{H}}_{sweeping} +
{\mathcal{H}}_{density}, \end{gathered}\right\}
\end{gather}
\begin{gather} \left.\begin{gathered}
{\mathcal{H}} = {\mathcal{H}}_{linear}
+{\mathcal{H}}_{nonlinear},\\ {\mathcal{H}}_{linear} =
\frac{1}{2}\int {\rm d} {\boldsymbol{p}} \Big( \varPi_{0}
|{\boldsymbol{k}}|^2 |\phi'_{{\boldsymbol{p}}}|^2-
\frac{g}{\rho_0^2}\frac{| \phi'_{{\boldsymbol{p}}}
|^2}{m^2}\Big), \\ {\mathcal{H}}_{nonlinear} =
{\mathcal{H}}_{local}+ {\mathcal{H}}_{sweeping} +
{\mathcal{H}}_{density}, \end{gathered}\right\}
\end{gather} \begin{gather} \left.\begin{gathered} {\mathcal{H}}_{\textit{local}} ={-} {\frac{\textbf{1}}{\textbf{2}(\textbf{2}\boldsymbol{\rm \pi})^{{\textbf{3}}/{\textbf{2}}}}} \int {\rm d} {\boldsymbol{p}}_1 \,{\rm d} {\boldsymbol{p}}_2 \,{\rm d} {\boldsymbol{p}}_3 \delta(\kern1pt {\boldsymbol{p}}_1+{\boldsymbol{p}}_2+{\boldsymbol{p}}_3) {\boldsymbol{k}}_2 \,\boldsymbol{\cdot}\, {\boldsymbol{k}}_3 {\rm \pi}'_{{\boldsymbol{p}}_1} \phi'_{{\boldsymbol{p}}_2} \phi'_{{\boldsymbol{p}}_3}, \\ {\mathcal{H}}_{sweeping} ={-} {\frac{\textbf{1}}{\textbf{2}(\textbf{2}\boldsymbol{\rm \pi})^{{\textbf{3}}/{\textbf{2}}}}} \int {\rm d} {\boldsymbol{p}}_1\,{\rm d} {\boldsymbol{p}}_2 \,{\rm d} {\boldsymbol{p}}_3 \delta(\kern1pt {\boldsymbol{p}}_1+{\boldsymbol{p}}_2+{\boldsymbol{p}}_3) 2 {\boldsymbol{k}}_1\,\boldsymbol{\cdot}\,{\boldsymbol{k}}_2 \varPhi_{{\boldsymbol{p}}_1} \phi'_{{\boldsymbol{p}}_2} {\rm \pi}'_{{\boldsymbol{p}}_3}, \\ {\mathcal{H}}_{density} ={-}{\frac{\textbf{1}}{\textbf{2}(\textbf{2}\boldsymbol{\rm \pi})^{{\textbf{3}}/{\textbf{2}}}}} \int {\rm d} {\boldsymbol{p}}_1 \,{\rm d} {\boldsymbol{p}}_2 \,{\rm d} {\boldsymbol{p}}_3 \delta(\kern1pt {\boldsymbol{p}}_1+{\boldsymbol{p}}_2+{\boldsymbol{p}}_3) {\boldsymbol{k}}_2\,\boldsymbol{\cdot}\,{\boldsymbol{k}}_3 \varPi_{{\boldsymbol{p}}_1} \phi'_{{\boldsymbol{p}}_2} \phi'_{{\boldsymbol{p}}_3}. \end{gathered}\right\}\end{gather}
\begin{gather} \left.\begin{gathered} {\mathcal{H}}_{\textit{local}} ={-} {\frac{\textbf{1}}{\textbf{2}(\textbf{2}\boldsymbol{\rm \pi})^{{\textbf{3}}/{\textbf{2}}}}} \int {\rm d} {\boldsymbol{p}}_1 \,{\rm d} {\boldsymbol{p}}_2 \,{\rm d} {\boldsymbol{p}}_3 \delta(\kern1pt {\boldsymbol{p}}_1+{\boldsymbol{p}}_2+{\boldsymbol{p}}_3) {\boldsymbol{k}}_2 \,\boldsymbol{\cdot}\, {\boldsymbol{k}}_3 {\rm \pi}'_{{\boldsymbol{p}}_1} \phi'_{{\boldsymbol{p}}_2} \phi'_{{\boldsymbol{p}}_3}, \\ {\mathcal{H}}_{sweeping} ={-} {\frac{\textbf{1}}{\textbf{2}(\textbf{2}\boldsymbol{\rm \pi})^{{\textbf{3}}/{\textbf{2}}}}} \int {\rm d} {\boldsymbol{p}}_1\,{\rm d} {\boldsymbol{p}}_2 \,{\rm d} {\boldsymbol{p}}_3 \delta(\kern1pt {\boldsymbol{p}}_1+{\boldsymbol{p}}_2+{\boldsymbol{p}}_3) 2 {\boldsymbol{k}}_1\,\boldsymbol{\cdot}\,{\boldsymbol{k}}_2 \varPhi_{{\boldsymbol{p}}_1} \phi'_{{\boldsymbol{p}}_2} {\rm \pi}'_{{\boldsymbol{p}}_3}, \\ {\mathcal{H}}_{density} ={-}{\frac{\textbf{1}}{\textbf{2}(\textbf{2}\boldsymbol{\rm \pi})^{{\textbf{3}}/{\textbf{2}}}}} \int {\rm d} {\boldsymbol{p}}_1 \,{\rm d} {\boldsymbol{p}}_2 \,{\rm d} {\boldsymbol{p}}_3 \delta(\kern1pt {\boldsymbol{p}}_1+{\boldsymbol{p}}_2+{\boldsymbol{p}}_3) {\boldsymbol{k}}_2\,\boldsymbol{\cdot}\,{\boldsymbol{k}}_3 \varPi_{{\boldsymbol{p}}_1} \phi'_{{\boldsymbol{p}}_2} \phi'_{{\boldsymbol{p}}_3}. \end{gathered}\right\}\end{gather}
The Hamiltonian ![]() ${\mathcal {H}}_{nonlinear}$ is the sum of three terms:
${\mathcal {H}}_{nonlinear}$ is the sum of three terms:
(i)
 ${\mathcal {H}}_{local}$ represents small amplitudes interacting with small amplitudes. We will call this term ‘local’ interactions in anticipation of making a scale separation between large-amplitude large-scale and small-amplitude small-scale waves in §§ 3.1.2 and 3.1.3;
${\mathcal {H}}_{local}$ represents small amplitudes interacting with small amplitudes. We will call this term ‘local’ interactions in anticipation of making a scale separation between large-amplitude large-scale and small-amplitude small-scale waves in §§ 3.1.2 and 3.1.3;(ii)
 ${\mathcal {H}}_{density}$ is the term that describes the variations of stratification that small-amplitude waves experience due to the compression and rarefication of isopycnals associated with the large-amplitude waves. We will refer to this term as a density term;
${\mathcal {H}}_{density}$ is the term that describes the variations of stratification that small-amplitude waves experience due to the compression and rarefication of isopycnals associated with the large-amplitude waves. We will refer to this term as a density term;(iii)
 ${\mathcal {H}}_{sweeping}$ is the term that describes the advection (sweeping) of small-amplitude waves by large-amplitude waves. In the future, we refer to this term as a sweeping term.
${\mathcal {H}}_{sweeping}$ is the term that describes the advection (sweeping) of small-amplitude waves by large-amplitude waves. In the future, we refer to this term as a sweeping term.
The main focus of this manuscript is to investigate how the density and sweeping terms affect the overall spectral energy density.
3.1.2. Sweeping Hamiltonian
Following the traditional wave turbulence approach, we make a transformation to the wave-action variables that represent wave amplitude and phase
We substitute (3.8a,b) into ![]() ${\mathcal {H}}_{sweeping}$ of (3.7), and obtain
${\mathcal {H}}_{sweeping}$ of (3.7), and obtain
 \begin{align}
{\mathcal{H}}_{sweeping}&={-}
{\frac{\textbf{1}}{\textbf{2}(\textbf{2}\boldsymbol{\rm \pi})^{{\textbf{3}}/{\textbf{2}}}}}
\int {\rm d} {\boldsymbol{p}}_1 \,{\rm d}
{\boldsymbol{p}}_2 \,{\rm d} {\boldsymbol{p}}_3
\delta(\kern1pt
{\boldsymbol{p}}_1+{\boldsymbol{p}}_2+{\boldsymbol{p}}_3) 2
{\boldsymbol{k}}_1\,\boldsymbol{\cdot}\,{\boldsymbol{k}}_2
\varPhi_{{\boldsymbol{p}}_1} \frac{{\rm i}N
\sqrt{\sigma_{{\boldsymbol{p}}_2}}}{\sqrt{2
g}|{\boldsymbol{k}}_2|} \frac{\sqrt{g}
|{\boldsymbol{k}}_3|}{\sqrt{2\sigma_{{\boldsymbol{p}}_3}}N}\nonumber\\
&\quad
\times\big(a_{{\boldsymbol{p}}_2}-a^*_{-{\boldsymbol{p}}_2}\big)
\big(a _{{\boldsymbol{p}}_3}+
a^*_{-{\boldsymbol{p}}_3}\big) .
\end{align}
\begin{align}
{\mathcal{H}}_{sweeping}&={-}
{\frac{\textbf{1}}{\textbf{2}(\textbf{2}\boldsymbol{\rm \pi})^{{\textbf{3}}/{\textbf{2}}}}}
\int {\rm d} {\boldsymbol{p}}_1 \,{\rm d}
{\boldsymbol{p}}_2 \,{\rm d} {\boldsymbol{p}}_3
\delta(\kern1pt
{\boldsymbol{p}}_1+{\boldsymbol{p}}_2+{\boldsymbol{p}}_3) 2
{\boldsymbol{k}}_1\,\boldsymbol{\cdot}\,{\boldsymbol{k}}_2
\varPhi_{{\boldsymbol{p}}_1} \frac{{\rm i}N
\sqrt{\sigma_{{\boldsymbol{p}}_2}}}{\sqrt{2
g}|{\boldsymbol{k}}_2|} \frac{\sqrt{g}
|{\boldsymbol{k}}_3|}{\sqrt{2\sigma_{{\boldsymbol{p}}_3}}N}\nonumber\\
&\quad
\times\big(a_{{\boldsymbol{p}}_2}-a^*_{-{\boldsymbol{p}}_2}\big)
\big(a _{{\boldsymbol{p}}_3}+
a^*_{-{\boldsymbol{p}}_3}\big) .
\end{align}The next step is algebraically trivial but conceptually fundamental. We invoke an extreme scale-separated limit in which the two small-amplitude waves have similar frequency and horizontal wavenumber magnitude. No condition is required on the vertical wavenumber. This conditioning retains both the ID and Bragg scattering (ES) branches of the resonant manifold; see figure 1.
In this scale-separated limit of the internal wave problem, ![]() $\sigma _{{\boldsymbol {p}}_2} \cong \sigma _{{\boldsymbol {p}}_3}$ and
$\sigma _{{\boldsymbol {p}}_2} \cong \sigma _{{\boldsymbol {p}}_3}$ and ![]() $|{\boldsymbol {k}}_2| \cong |{\boldsymbol {k}}_3|$. Beyond the obvious algebraic simplifications, upon expanding the brackets, we find terms of the type
$|{\boldsymbol {k}}_2| \cong |{\boldsymbol {k}}_3|$. Beyond the obvious algebraic simplifications, upon expanding the brackets, we find terms of the type ![]() $a_{{\boldsymbol {p}}_2}a_{{\boldsymbol {p}}_3}$,
$a_{{\boldsymbol {p}}_2}a_{{\boldsymbol {p}}_3}$, ![]() $a^*_{-{\boldsymbol {p}}_2}a^*_{-{\boldsymbol {p}}_3}$ and
$a^*_{-{\boldsymbol {p}}_2}a^*_{-{\boldsymbol {p}}_3}$ and ![]() $a_{{\boldsymbol {p}}_2}a^*_{-{\boldsymbol {p}}_3}$,
$a_{{\boldsymbol {p}}_2}a^*_{-{\boldsymbol {p}}_3}$, ![]() $a^*_{-{\boldsymbol {p}}_2}a_{-{\boldsymbol {p}}_3}$. In what follows, we neglect the
$a^*_{-{\boldsymbol {p}}_2}a_{-{\boldsymbol {p}}_3}$. In what follows, we neglect the ![]() $a_{{\boldsymbol {p}}_2}a_{{\boldsymbol {p}}_3}$ and
$a_{{\boldsymbol {p}}_2}a_{{\boldsymbol {p}}_3}$ and ![]() $a^*_{-{\boldsymbol {p}}_2}a^*_{-{\boldsymbol {p}}_3}$ terms and retain the
$a^*_{-{\boldsymbol {p}}_2}a^*_{-{\boldsymbol {p}}_3}$ terms and retain the ![]() $a_{{\boldsymbol {p}}_2}a^*_{-{\boldsymbol {p}}_3}$,
$a_{{\boldsymbol {p}}_2}a^*_{-{\boldsymbol {p}}_3}$, ![]() $a^*_{-{\boldsymbol {p}}_2}a_{-{\boldsymbol {p}}_3}$ terms, since the former terms are non-resonant, while the latter may be in the resonance for some wavenumbers. The discarded terms lead to a process when one lower-frequency wave decays into two high-frequency waves and thus the frequencies do not sum to zero. Such decay is a non-resonant process, so we can remove these terms at the onset.
$a^*_{-{\boldsymbol {p}}_2}a_{-{\boldsymbol {p}}_3}$ terms, since the former terms are non-resonant, while the latter may be in the resonance for some wavenumbers. The discarded terms lead to a process when one lower-frequency wave decays into two high-frequency waves and thus the frequencies do not sum to zero. Such decay is a non-resonant process, so we can remove these terms at the onset.
After relabelling subscripts, in which ![]() $2\to 1$ and
$2\to 1$ and ![]() $3\to 2$, we obtain
$3\to 2$, we obtain
 \begin{equation} \left.\begin{gathered} {\mathcal{H}}_{sweeping} =\int {\rm d} {\boldsymbol{p}}_1 \,{\rm d} {\boldsymbol{p}}_2 \,A_{sweeping}(\kern1pt {\boldsymbol{p}}_1, {\boldsymbol{p}}_2) a_{{\boldsymbol{p}}_1}a^*_{{\boldsymbol{p}}_2},\\ {\rm with}\\ A_{sweeping}(\kern1pt {\boldsymbol{p}}_1, {\boldsymbol{p}}_2) ={-}\frac{1}{2}{\rm i} \left({{\boldsymbol{k}}_1-{\boldsymbol{k}}_2}\right){\cdot}\left( {\boldsymbol{k}}_1+{\boldsymbol{k}}_2\right) \varPhi_{{\boldsymbol{p}}_1-{\boldsymbol{p}}_2} . \end{gathered}\right\}\end{equation}
\begin{equation} \left.\begin{gathered} {\mathcal{H}}_{sweeping} =\int {\rm d} {\boldsymbol{p}}_1 \,{\rm d} {\boldsymbol{p}}_2 \,A_{sweeping}(\kern1pt {\boldsymbol{p}}_1, {\boldsymbol{p}}_2) a_{{\boldsymbol{p}}_1}a^*_{{\boldsymbol{p}}_2},\\ {\rm with}\\ A_{sweeping}(\kern1pt {\boldsymbol{p}}_1, {\boldsymbol{p}}_2) ={-}\frac{1}{2}{\rm i} \left({{\boldsymbol{k}}_1-{\boldsymbol{k}}_2}\right){\cdot}\left( {\boldsymbol{k}}_1+{\boldsymbol{k}}_2\right) \varPhi_{{\boldsymbol{p}}_1-{\boldsymbol{p}}_2} . \end{gathered}\right\}\end{equation}
In the limit of large vertical background scales, (3.10) describes a quasi-coherent translation of small-scale small-amplitude waves by the large-scale background. At ![]() $1/2$ the vertical scale of
$1/2$ the vertical scale of ![]() ${\boldsymbol {p}}_1$ and
${\boldsymbol {p}}_1$ and ![]() ${\boldsymbol {p}}_2$, (3.10) describes a Bragg scattering process. This is distinct from ‘local’ interactions as the large-amplitude wave has a much larger horizontal scale.
${\boldsymbol {p}}_2$, (3.10) describes a Bragg scattering process. This is distinct from ‘local’ interactions as the large-amplitude wave has a much larger horizontal scale.
3.1.3. Density Hamiltonian
We now can repeat the same steps for the density Hamiltonian. We substitute (3.8a,b) into the ![]() ${\mathcal {H}}_{density}$ of (3.7), use
${\mathcal {H}}_{density}$ of (3.7), use ![]() $\sigma _{{\boldsymbol {p}}_2} \cong \sigma _{{\boldsymbol {p}}_3}$ and
$\sigma _{{\boldsymbol {p}}_2} \cong \sigma _{{\boldsymbol {p}}_3}$ and ![]() $|{\boldsymbol {k}}_2| \cong |{\boldsymbol {k}}_3|$, relabel subscripts and obtain
$|{\boldsymbol {k}}_2| \cong |{\boldsymbol {k}}_3|$, relabel subscripts and obtain
 \begin{equation} \left.\begin{gathered} {\mathcal{H}}_{density} =\int {\rm d} {\boldsymbol{p}}_1 \,{\rm d} {\boldsymbol{p}}_2 \,A_{density}(\kern1pt {\boldsymbol{p}}_1, {\boldsymbol{p}}_2) a_{{\boldsymbol{p}}_1}a^*_{{\boldsymbol{p}}_2}, \\ {\rm with}\\ A_{density}(\kern1pt {\boldsymbol{p}}_1, {\boldsymbol{p}}_2) = \frac{1}{2 \varPi_{0}} \varPi_{{\boldsymbol{p}}_2-{\boldsymbol{p}}_1} \sqrt{ \sigma_{{\boldsymbol{p}}_1}\sigma_{{\boldsymbol{p}}_2}} . \end{gathered}\right\} \end{equation}
\begin{equation} \left.\begin{gathered} {\mathcal{H}}_{density} =\int {\rm d} {\boldsymbol{p}}_1 \,{\rm d} {\boldsymbol{p}}_2 \,A_{density}(\kern1pt {\boldsymbol{p}}_1, {\boldsymbol{p}}_2) a_{{\boldsymbol{p}}_1}a^*_{{\boldsymbol{p}}_2}, \\ {\rm with}\\ A_{density}(\kern1pt {\boldsymbol{p}}_1, {\boldsymbol{p}}_2) = \frac{1}{2 \varPi_{0}} \varPi_{{\boldsymbol{p}}_2-{\boldsymbol{p}}_1} \sqrt{ \sigma_{{\boldsymbol{p}}_1}\sigma_{{\boldsymbol{p}}_2}} . \end{gathered}\right\} \end{equation}
In the limit of large vertical background scales, (3.11) describes the modulation of the background stratification. At ![]() $1/2$ the vertical scale of
$1/2$ the vertical scale of ![]() ${\boldsymbol {p}}_1$ and
${\boldsymbol {p}}_1$ and ![]() ${\boldsymbol {p}}_2$, (3.11) describes a Bragg scattering process. This is distinct from ‘local’ interactions as the large-amplitude wave has a much larger horizontal scale.
${\boldsymbol {p}}_2$, (3.11) describes a Bragg scattering process. This is distinct from ‘local’ interactions as the large-amplitude wave has a much larger horizontal scale.
3.1.4. Quadratic Hamiltonian for inhomogeneous wave turbulence
Let us neglect the local interaction term ![]() ${\mathcal {H}}_{local}$ in Hamiltonian (3.7). Then the Hamiltonian (3.7) of small-amplitude small horizontal scale internal waves
${\mathcal {H}}_{local}$ in Hamiltonian (3.7). Then the Hamiltonian (3.7) of small-amplitude small horizontal scale internal waves ![]() $a_{\boldsymbol {p}}$ superimposed into a field of large-amplitude large horizontal scale internal waves given by space–time-dependent
$a_{\boldsymbol {p}}$ superimposed into a field of large-amplitude large horizontal scale internal waves given by space–time-dependent ![]() $\varPi$ and
$\varPi$ and ![]() $\varPhi$ are given by a form that is quadratic in the small-scale variables
$\varPhi$ are given by a form that is quadratic in the small-scale variables ![]() $a_{{\boldsymbol {p}}}$
$a_{{\boldsymbol {p}}}$
 \begin{equation} \left.\begin{gathered} {\mathcal{H}} =\int {\rm d} {\boldsymbol{p}}_1 \,{\rm d} {\boldsymbol{p}}_2 \,A(\kern1pt {\boldsymbol{p}}_1, {\boldsymbol{p}}_2) a_{{\boldsymbol{p}}_1}a^*_{{\boldsymbol{p}}_2}, \\ {\rm with} \\ A(\kern1pt {\boldsymbol{p}}_1,{\boldsymbol{p}}_2)= \sigma_{{\boldsymbol{p}}} \delta(\kern1pt {\boldsymbol{p}}_1-{\boldsymbol{p}}_2) + A_{sweeping}(\kern1pt {\boldsymbol{p}}_1, {\boldsymbol{p}}_2)+ A_{density }(\kern1pt {\boldsymbol{p}}_1, {\boldsymbol{p}}_2), \end{gathered}\right\} \end{equation}
\begin{equation} \left.\begin{gathered} {\mathcal{H}} =\int {\rm d} {\boldsymbol{p}}_1 \,{\rm d} {\boldsymbol{p}}_2 \,A(\kern1pt {\boldsymbol{p}}_1, {\boldsymbol{p}}_2) a_{{\boldsymbol{p}}_1}a^*_{{\boldsymbol{p}}_2}, \\ {\rm with} \\ A(\kern1pt {\boldsymbol{p}}_1,{\boldsymbol{p}}_2)= \sigma_{{\boldsymbol{p}}} \delta(\kern1pt {\boldsymbol{p}}_1-{\boldsymbol{p}}_2) + A_{sweeping}(\kern1pt {\boldsymbol{p}}_1, {\boldsymbol{p}}_2)+ A_{density }(\kern1pt {\boldsymbol{p}}_1, {\boldsymbol{p}}_2), \end{gathered}\right\} \end{equation}
where ![]() $A_{sweeping}({\boldsymbol {p}}_1, {\boldsymbol {p}}_2)$ and
$A_{sweeping}({\boldsymbol {p}}_1, {\boldsymbol {p}}_2)$ and ![]() $A_{density }({\boldsymbol {p}}_1, {\boldsymbol {p}}_2)$ are given in (3.10) and (3.11). The
$A_{density }({\boldsymbol {p}}_1, {\boldsymbol {p}}_2)$ are given in (3.10) and (3.11). The ![]() $A({\boldsymbol {p}}_1,{\boldsymbol {p}}_2)$ are time dependent and depend upon the phases of the external field.
$A({\boldsymbol {p}}_1,{\boldsymbol {p}}_2)$ are time dependent and depend upon the phases of the external field.
3.2. Wentzel–Kramers–Brillouin approach
At this point, we have a three-wave Hamiltonian (3.12) with one large-amplitude large horizontal scale wave interacting with two smaller-amplitude smaller horizontal scale waves that have similar frequencies. Below, we assume a nearly resonant paradigm and perform algebraic manipulations that take into account the ID portion of the resonant manifold.
3.2.1. The wave packet transport equation
In the spatially homogeneous wave turbulence of § 2.2 we used wave-action density ![]() $n_{\boldsymbol {p}}$ and a linear dispersion relation
$n_{\boldsymbol {p}}$ and a linear dispersion relation ![]() $\sigma _{\boldsymbol {p}}$, both being a function of a wavenumber
$\sigma _{\boldsymbol {p}}$, both being a function of a wavenumber ![]() ${\boldsymbol {p}}$. In the case when there is a slowly varying large-scale background, i.e. a system where spatial inhomogeneity is present, the properties of wave action and the dispersion relation will depend on the position in space. Then it makes sense to introduce an additional parameter, a position vector
${\boldsymbol {p}}$. In the case when there is a slowly varying large-scale background, i.e. a system where spatial inhomogeneity is present, the properties of wave action and the dispersion relation will depend on the position in space. Then it makes sense to introduce an additional parameter, a position vector ![]() ${\boldsymbol {r}}$ in wave action and linear dispersion relation. The theory for this spatial dependence is developed in Gershgorin, Lvov & Nazarenko (Reference Gershgorin, Lvov and Nazarenko2009) using a Gabor transform to represent the envelope structure describing the spatial localization and carrier frequency. The leading-order balance in Gershgorin et al. (Reference Gershgorin, Lvov and Nazarenko2009) leads to action and phase conservation along ray paths. The balance on the envelope scale implies phase modulation, for which we direct the reader to the appendix of Cohen & Lee (Reference Cohen and Lee1990) for clarity. Associated with the envelope structure is a residual circulation (Bühler & McIntyre Reference Bühler and McIntyre2005). The potential for the wave packet to interact with its envelope structure is possible (Bühler & McIntyre Reference Bühler and McIntyre2005; Dosser & Sutherland Reference Dosser and Sutherland2011) but would require a modification of the uniform potential vorticity statement (2.7). It is at this stage that one might also want to consider the potential for nonlinear wave steepening effects associated with
${\boldsymbol {r}}$ in wave action and linear dispersion relation. The theory for this spatial dependence is developed in Gershgorin, Lvov & Nazarenko (Reference Gershgorin, Lvov and Nazarenko2009) using a Gabor transform to represent the envelope structure describing the spatial localization and carrier frequency. The leading-order balance in Gershgorin et al. (Reference Gershgorin, Lvov and Nazarenko2009) leads to action and phase conservation along ray paths. The balance on the envelope scale implies phase modulation, for which we direct the reader to the appendix of Cohen & Lee (Reference Cohen and Lee1990) for clarity. Associated with the envelope structure is a residual circulation (Bühler & McIntyre Reference Bühler and McIntyre2005). The potential for the wave packet to interact with its envelope structure is possible (Bühler & McIntyre Reference Bühler and McIntyre2005; Dosser & Sutherland Reference Dosser and Sutherland2011) but would require a modification of the uniform potential vorticity statement (2.7). It is at this stage that one might also want to consider the potential for nonlinear wave steepening effects associated with ![]() ${\mathcal {H}}_{local}$ to counter the dispersion of ray characteristics as a precursor to the description of the solitary wave dynamics.
${\mathcal {H}}_{local}$ to counter the dispersion of ray characteristics as a precursor to the description of the solitary wave dynamics.
The familiar statement of action conservation that we are after is obtained in Gershgorin et al. (Reference Gershgorin, Lvov and Nazarenko2009) by assuming the scale of the envelope structure is large in comparison with the inverse wavenumber of the small-scale wave, i.e. the wave packet contains many oscillations. The result required here can be obtained more simply by using a Wigner transform alone to define the space–time-dependent wave-action spectral density
in which the transform variable ![]() ${\boldsymbol {q}}$ is the difference between two large wavenumbers
${\boldsymbol {q}}$ is the difference between two large wavenumbers ![]() ${\boldsymbol {p}}_1$ and
${\boldsymbol {p}}_1$ and ![]() ${\boldsymbol {p}}_2$,
${\boldsymbol {p}}_2$, ![]() ${\boldsymbol {q}}={\boldsymbol {p}}_1-{\boldsymbol {p}}_2$ and the field variables
${\boldsymbol {q}}={\boldsymbol {p}}_1-{\boldsymbol {p}}_2$ and the field variables ![]() $a$ are evaluated at
$a$ are evaluated at ![]() ${\boldsymbol {p}} \pm {\boldsymbol {q}}/2$. We similarly introduce the space-dependent intrinsic frequency
${\boldsymbol {p}} \pm {\boldsymbol {q}}/2$. We similarly introduce the space-dependent intrinsic frequency ![]() $\omega _{{\boldsymbol {p}},{\boldsymbol {r}}}$
$\omega _{{\boldsymbol {p}},{\boldsymbol {r}}}$
This is a generalization of our ‘traditional’ wave action (2.15) which allows for slow variations of the background. It will incorporate the large vertical scale contributions of ![]() ${\mathcal {H}}_{sweeping}$ and
${\mathcal {H}}_{sweeping}$ and ![]() ${\mathcal {H}}_{density}$.
${\mathcal {H}}_{density}$.
To derive the transport equation, we take definition (3.13), differentiate it with respect to time, use Hamilton's equation of motion (2.13), with the Hamiltonian (3.12). The spatial dependence is then made explicit by representing ![]() $A({\boldsymbol {p}}_1,{\boldsymbol {p}}_2)$ and
$A({\boldsymbol {p}}_1,{\boldsymbol {p}}_2)$ and ![]() $a({\boldsymbol {p}}_1)a^{\ast }({\boldsymbol {p}}_2)$ with their corresponding Fourier transforms. After an inspired change of variables (Lvov & Rubenchik Reference Lvov and Rubenchik1977; Gershgorin et al. Reference Gershgorin, Lvov and Nazarenko2009) that maps the ID portion of the resonant manifold, one obtains an intermediary expression
$a({\boldsymbol {p}}_1)a^{\ast }({\boldsymbol {p}}_2)$ with their corresponding Fourier transforms. After an inspired change of variables (Lvov & Rubenchik Reference Lvov and Rubenchik1977; Gershgorin et al. Reference Gershgorin, Lvov and Nazarenko2009) that maps the ID portion of the resonant manifold, one obtains an intermediary expression
 \begin{align} {\rm i} \frac{\partial
n_{{\boldsymbol{p}},{\boldsymbol{r}}}}{\partial t} &= \int
\frac{{\rm d}{\boldsymbol{r}}^{\prime}\,{\rm
d}{\boldsymbol{r}}^{\prime\prime}}{(2{\rm \pi})^6} {\rm
d}q^{\prime}\,{\rm d}q^{\prime\prime} \exp({{\rm
i}q^{\prime}\,\boldsymbol{\cdot}\,({\boldsymbol{r}}-{\boldsymbol{r}}^{\prime})
+ {\rm i}q^{\prime\prime}\,\boldsymbol{\cdot}\,
({\boldsymbol{r}}-{\boldsymbol{r}}^{\prime\prime}) })
\nonumber\\ &\quad
\times[\omega_{{\boldsymbol{p}}+{q^{\prime\prime}}/{2}}({\boldsymbol{r}}^{\prime})
n_{{\boldsymbol{p}}-{q^{\prime}}/{2}}
({\boldsymbol{r}}^{\prime\prime}) -
\omega_{{\boldsymbol{p}}-{q^{\prime\prime}}/{2}}({\boldsymbol{r}}^{\prime})
n_{{\boldsymbol{p}}+{q^{\prime}}/{2}}({\boldsymbol{r}}^{\prime\prime})
].
\end{align}
\begin{align} {\rm i} \frac{\partial
n_{{\boldsymbol{p}},{\boldsymbol{r}}}}{\partial t} &= \int
\frac{{\rm d}{\boldsymbol{r}}^{\prime}\,{\rm
d}{\boldsymbol{r}}^{\prime\prime}}{(2{\rm \pi})^6} {\rm
d}q^{\prime}\,{\rm d}q^{\prime\prime} \exp({{\rm
i}q^{\prime}\,\boldsymbol{\cdot}\,({\boldsymbol{r}}-{\boldsymbol{r}}^{\prime})
+ {\rm i}q^{\prime\prime}\,\boldsymbol{\cdot}\,
({\boldsymbol{r}}-{\boldsymbol{r}}^{\prime\prime}) })
\nonumber\\ &\quad
\times[\omega_{{\boldsymbol{p}}+{q^{\prime\prime}}/{2}}({\boldsymbol{r}}^{\prime})
n_{{\boldsymbol{p}}-{q^{\prime}}/{2}}
({\boldsymbol{r}}^{\prime\prime}) -
\omega_{{\boldsymbol{p}}-{q^{\prime\prime}}/{2}}({\boldsymbol{r}}^{\prime})
n_{{\boldsymbol{p}}+{q^{\prime}}/{2}}({\boldsymbol{r}}^{\prime\prime})
].
\end{align}
After expanding ![]() $\omega$ and
$\omega$ and ![]() $n$ in Taylor series with respect to
$n$ in Taylor series with respect to ![]() ${\boldsymbol {p}}$ and truncating higher-order terms, one ultimately arrives at the action balance
${\boldsymbol {p}}$ and truncating higher-order terms, one ultimately arrives at the action balance
or alternately
Integration of (3.17) over wavenumber provides a connection to the space–time variational formulations found in Witham (Reference Witham1974, Chapters 11.7 and 14). The Bragg scattering process residing in the scale-separated Hamiltonian (3.10) has been eliminated by using the Wigner transform and Taylor series expansion that serendipitously exploits the symmetries associated with the ID resonance.
3.2.2. Application for internal waves
We now take the expression for ![]() $A_{{\boldsymbol {p}}_1, {\boldsymbol {p}}_2}$ from (3.12) and substitute it into (3.14) for the space-dependent linear dispersion relation. The result is given by
$A_{{\boldsymbol {p}}_1, {\boldsymbol {p}}_2}$ from (3.12) and substitute it into (3.14) for the space-dependent linear dispersion relation. The result is given by
where ![]() ${\boldsymbol {p}}=({\boldsymbol {k}},m)$ is the wavevector,
${\boldsymbol {p}}=({\boldsymbol {k}},m)$ is the wavevector, ![]() ${\mathcal {U}}({\boldsymbol {r}})$ is the time-dependent horizontal velocity of the external large-scale wave field and
${\mathcal {U}}({\boldsymbol {r}})$ is the time-dependent horizontal velocity of the external large-scale wave field and ![]() $\varPi ({\boldsymbol {r}})$ is the time-dependent stratification of the external wave field. Here, the
$\varPi ({\boldsymbol {r}})$ is the time-dependent stratification of the external wave field. Here, the ![]() $\sigma _{{\boldsymbol {p}}}$ term was produced by the term proportional to
$\sigma _{{\boldsymbol {p}}}$ term was produced by the term proportional to ![]() $\delta ({\boldsymbol {p}}_1-{\boldsymbol {p}}_2)$,
$\delta ({\boldsymbol {p}}_1-{\boldsymbol {p}}_2)$, ![]() ${\boldsymbol {k}}\boldsymbol {\cdot }{\mathcal {U}}$ comes from the sweeping term in the Hamiltonian and
${\boldsymbol {k}}\boldsymbol {\cdot }{\mathcal {U}}$ comes from the sweeping term in the Hamiltonian and ![]() $\sigma _{{\boldsymbol {p}}} \varPi / 2 \varPi _0$ comes from density term in the Hamiltonian. The frequency
$\sigma _{{\boldsymbol {p}}} \varPi / 2 \varPi _0$ comes from density term in the Hamiltonian. The frequency ![]() $\sigma _{{\boldsymbol {p}}}$ is given by (2.12) using
$\sigma _{{\boldsymbol {p}}}$ is given by (2.12) using ![]() $f=0$. For a high-frequency wave in a rotating ocean,
$f=0$. For a high-frequency wave in a rotating ocean, ![]() $\mathcal {U}$ is replaced by
$\mathcal {U}$ is replaced by ![]() $\boldsymbol {\nabla } \varPhi + \boldsymbol {\nabla }^{\perp } \varPsi$. The derivation for
$\boldsymbol {\nabla } \varPhi + \boldsymbol {\nabla }^{\perp } \varPsi$. The derivation for ![]() $f \ne 0$ appears in the Appendix.
$f \ne 0$ appears in the Appendix.
3.2.3. The ray-path wave packet transport equation
The transport equation (3.16) or its alternative formulation (3.17) with the space–time-dependent linear dispersion relationship (3.18) is a fundamental result expressing wave-action conservation that provides the basis for the analyses to follow.
The action balance (3.16) can be simply solved by the method of characteristics. The characteristics of (3.16), also called rays, are defined by
Equations (3.19a,b) imply that wave-action spectral density is conserved along these characteristics
This is the classical representation for the conservation of action spectral density along ray trajectories. A derivation for a general Hamiltonian set is presented in Gershgorin et al. (Reference Gershgorin, Lvov and Nazarenko2009), here, the derivation is specifically for internal waves in the scale-separated limit. Integration over wavenumber provides the space–time result presented in Witham (Reference Witham1974). This result often appears as an analogy to Liouville's theorem for the conservation of the phase volume of particles without justification. Note that it is the balance of first-order terms in a Taylor series expansion of (3.15).
3.2.4. An ensemble path transport equation
In what follows we derive a combined advective–diffusive transport equation for the action balance (3.16) by generalizing an approach found in Nazarenko et al. (Reference Nazarenko, Newell and Galtier2001). There are strong parallels here to the discussion of Taylor (Reference Taylor1921) that appears in the appendix of McComas & Bretherton (Reference McComas and Bretherton1977): the illuminating analogy with particle dispersion in Taylor (Reference Taylor1921) is to substitute wavenumber ![]() ${\boldsymbol {p}}$ for the Lagrangian particle position
${\boldsymbol {p}}$ for the Lagrangian particle position ![]() ${\boldsymbol {r}}$ and obtain a quantitative approach for discussing the migration and dispersion of wave packets in the spectral domain following ray trajectories. Having said this, it should be intuitively obvious that, since particle dispersion in
${\boldsymbol {r}}$ and obtain a quantitative approach for discussing the migration and dispersion of wave packets in the spectral domain following ray trajectories. Having said this, it should be intuitively obvious that, since particle dispersion in ![]() ${\boldsymbol {r}}$ has little to do with resonance, neither should the issue of dispersion of
${\boldsymbol {r}}$ has little to do with resonance, neither should the issue of dispersion of ![]() ${\boldsymbol {p}}$ in phase space be intrinsically tied to resonance! Yet, an emphasis on the resonant paradigm is the interpretive context pursued in McComas & Bretherton (Reference McComas and Bretherton1977) and Nazarenko et al. (Reference Nazarenko, Newell and Galtier2001). A second key departure is that our motivation stems from the fact that the GM76 spectrum is a no-flux solution to the Fokker–Planck equation (2.25). We acknowledge the oceanographic literature in this regard and so are focused upon the issue of a mean drift of wave packets to high wavenumber that is accessible in ray-tracing simulations (e.g. Henyey et al. Reference Henyey, Wright and Flatté1986) but not explicitly represented in (2.25). To underscore the distinction, the existence of a mean drift implies relative dispersion (e.g. Bennett Reference Bennett1984) rather than the issue of absolute dispersion addressed in Taylor (Reference Taylor1921).
${\boldsymbol {p}}$ in phase space be intrinsically tied to resonance! Yet, an emphasis on the resonant paradigm is the interpretive context pursued in McComas & Bretherton (Reference McComas and Bretherton1977) and Nazarenko et al. (Reference Nazarenko, Newell and Galtier2001). A second key departure is that our motivation stems from the fact that the GM76 spectrum is a no-flux solution to the Fokker–Planck equation (2.25). We acknowledge the oceanographic literature in this regard and so are focused upon the issue of a mean drift of wave packets to high wavenumber that is accessible in ray-tracing simulations (e.g. Henyey et al. Reference Henyey, Wright and Flatté1986) but not explicitly represented in (2.25). To underscore the distinction, the existence of a mean drift implies relative dispersion (e.g. Bennett Reference Bennett1984) rather than the issue of absolute dispersion addressed in Taylor (Reference Taylor1921).
The very first step in our derivation is to specify a wave packet ensemble mean drift and departures from the mean drift. This decomposition is an improvement on the arguments presented in McComas & Bretherton (Reference McComas and Bretherton1977), Nazarenko et al. (Reference Nazarenko, Newell and Galtier2001) and Lanchon & Cortet (Reference Lanchon and Cortet2023). Our limited knowledge of the ray literature does not permit us to comment on the originality of our interpretation. It is, however, crucial in understanding intrinsic differences between the kinetic equation and ray theory. Given the nature of our understanding, the issue assuredly carries over to other physical problems such as the interaction of near-inertial waves with lower-frequency flows, (e.g. Young & Jelloul Reference Young and Jelloul1997; Kafiabad et al. Reference Kafiabad, Savva, Miles and Vanneste2019; Dong, Bühler & Smith Reference Dong, Bühler and Smith2020) surface gravity wave interaction with lower-frequency flows (Villas Bôas & Young Reference Villas Bôas and Young2020) and Rossby wave–Rossby wave interactions (Nazarenko Reference Nazarenko2011).
We represent the wave action of a single wave packet as a sum of a spatially homogeneous part ![]() $\bar {n}$ and small ‘wiggles’
$\bar {n}$ and small ‘wiggles’ ![]() $\tilde {n}$
$\tilde {n}$
and acknowledge the presence of a mean drift in the spectral domain by adding zero
in which ![]() $\langle \dots \rangle$ is an ensemble average for a system with spatially homogenous statistics, so that
$\langle \dots \rangle$ is an ensemble average for a system with spatially homogenous statistics, so that ![]() $\langle \dots \rangle$ is independent of
$\langle \dots \rangle$ is independent of ![]() ${\boldsymbol {r}}$. The mean drift arises due to inhomogeneities of the ray-path statistics in the spectral domain. Please note that the dimensions of
${\boldsymbol {r}}$. The mean drift arises due to inhomogeneities of the ray-path statistics in the spectral domain. Please note that the dimensions of ![]() $\bar {n}_{{\boldsymbol {p}}}$ and
$\bar {n}_{{\boldsymbol {p}}}$ and ![]() $n_{{\boldsymbol {p}}}$ are different.
$n_{{\boldsymbol {p}}}$ are different.
Starting from the flux form of the action balance (3.17), we substitute (3.21a–c), (3.22) and invoke an ensemble average and integrate over ![]() ${\boldsymbol {r}}$ to obtain
${\boldsymbol {r}}$ to obtain
Closure of this equation depends upon writing ![]() $n_{{\boldsymbol {p}},{\boldsymbol {r}}}$ in terms of
$n_{{\boldsymbol {p}},{\boldsymbol {r}}}$ in terms of ![]() $n_{{\boldsymbol {p}}}$. At this juncture, we invoke that property that wave-action spectral density does not change along trajectories
$n_{{\boldsymbol {p}}}$. At this juncture, we invoke that property that wave-action spectral density does not change along trajectories
 \begin{align} n_{{\boldsymbol{p}},{\boldsymbol{r}}} &\equiv n(\kern1pt {\boldsymbol{p}}(t),{\boldsymbol{r}}(t),t) = n(\kern1pt {\boldsymbol{p}}(t-T),{\boldsymbol{r}}(t-T),t-T) \nonumber\\ & = \bar{n}\left[{\boldsymbol{p}}(t) - \int_{t-T}^t \dot{p}(t')\,{\rm d} t'; t-T\right] \nonumber\\ &\quad + \tilde{n}\left[{\boldsymbol{p}}(t) - \int_{t-T}^t \dot{p}(t')\,{\rm d} t'; {\boldsymbol{r}}(t) - \int_{t-\tau}^t \dot{{\boldsymbol{r}}} (t') \,{\rm d} t'; t-T\right]. \end{align}
\begin{align} n_{{\boldsymbol{p}},{\boldsymbol{r}}} &\equiv n(\kern1pt {\boldsymbol{p}}(t),{\boldsymbol{r}}(t),t) = n(\kern1pt {\boldsymbol{p}}(t-T),{\boldsymbol{r}}(t-T),t-T) \nonumber\\ & = \bar{n}\left[{\boldsymbol{p}}(t) - \int_{t-T}^t \dot{p}(t')\,{\rm d} t'; t-T\right] \nonumber\\ &\quad + \tilde{n}\left[{\boldsymbol{p}}(t) - \int_{t-T}^t \dot{p}(t')\,{\rm d} t'; {\boldsymbol{r}}(t) - \int_{t-\tau}^t \dot{{\boldsymbol{r}}} (t') \,{\rm d} t'; t-T\right]. \end{align}
We then execute a Taylor series expansion of ![]() $\bar {n}$
$\bar {n}$
substitute, add zero once again and, using the definition of ensemble averaging ![]() $\langle \dots \rangle$,
$\langle \dots \rangle$,
and
 \begin{align} &\left\langle \boldsymbol{\nabla}_{{\boldsymbol{p}}} \left[\kern0.7pt \dot{{\boldsymbol{p}}} - \left\langle \kern0.7pt\dot{{\boldsymbol{p}}} \right\rangle\right] \int_{t-\tau}^t \left\langle \kern0.7pt\dot{{\boldsymbol{p}}} \right\rangle {\rm d}t' \,\boldsymbol{\cdot}\,\boldsymbol{\nabla}_{{\boldsymbol{p}}} \bar{n} (\kern1pt {\boldsymbol{p}}(t), t-\tau) \right\rangle \nonumber\\ &\quad \cong \boldsymbol{\nabla}_{{\boldsymbol{p}}} \left\langle \kern0.7pt\dot{{\boldsymbol{p}}} - \left\langle \kern0.7pt\dot{{\boldsymbol{p}}} \right\rangle \right\rangle \int_{t-\tau}^t\left\langle \kern0.7pt\dot{{\boldsymbol{p}}} \right\rangle {\rm d}t' \,\boldsymbol{\cdot}\,\boldsymbol{\nabla}_{{\boldsymbol{p}}} \left\langle \bar{n} (\kern1pt {\boldsymbol{p}}(t), t-\tau) \right\rangle\nonumber\\ &\quad = 0, \end{align}
\begin{align} &\left\langle \boldsymbol{\nabla}_{{\boldsymbol{p}}} \left[\kern0.7pt \dot{{\boldsymbol{p}}} - \left\langle \kern0.7pt\dot{{\boldsymbol{p}}} \right\rangle\right] \int_{t-\tau}^t \left\langle \kern0.7pt\dot{{\boldsymbol{p}}} \right\rangle {\rm d}t' \,\boldsymbol{\cdot}\,\boldsymbol{\nabla}_{{\boldsymbol{p}}} \bar{n} (\kern1pt {\boldsymbol{p}}(t), t-\tau) \right\rangle \nonumber\\ &\quad \cong \boldsymbol{\nabla}_{{\boldsymbol{p}}} \left\langle \kern0.7pt\dot{{\boldsymbol{p}}} - \left\langle \kern0.7pt\dot{{\boldsymbol{p}}} \right\rangle \right\rangle \int_{t-\tau}^t\left\langle \kern0.7pt\dot{{\boldsymbol{p}}} \right\rangle {\rm d}t' \,\boldsymbol{\cdot}\,\boldsymbol{\nabla}_{{\boldsymbol{p}}} \left\langle \bar{n} (\kern1pt {\boldsymbol{p}}(t), t-\tau) \right\rangle\nonumber\\ &\quad = 0, \end{align}
as ![]() $\langle \dot {{\boldsymbol {p}}} - \langle \dot {{\boldsymbol {p}}} \rangle \rangle \equiv 0$ and neglecting an initial transient term
$\langle \dot {{\boldsymbol {p}}} - \langle \dot {{\boldsymbol {p}}} \rangle \rangle \equiv 0$ and neglecting an initial transient term
so that (3.23) becomes
We introduce the auto-lag covariance matrix
The final result is then
Convergence of the time integral, in which one can replace the lower limit of integration by ![]() $-\infty$, is the hallmark of a Markov approximation which we investigate further in Polzin & Lvov (Reference Polzin and Lvov2023). This equation encapsulates our fundamental theoretical result: the transport equation changes from diffusion (2.25) to an expression that involves both advection and diffusion in the spectral domain. Instead of being a no-flux stationary state, the GM76 spectrum, for which
$-\infty$, is the hallmark of a Markov approximation which we investigate further in Polzin & Lvov (Reference Polzin and Lvov2023). This equation encapsulates our fundamental theoretical result: the transport equation changes from diffusion (2.25) to an expression that involves both advection and diffusion in the spectral domain. Instead of being a no-flux stationary state, the GM76 spectrum, for which ![]() $\langle n_{\boldsymbol {p}} \rangle \propto m^0$, now supports a downscale action flux.
$\langle n_{\boldsymbol {p}} \rangle \propto m^0$, now supports a downscale action flux.
Our decomposition of wavenumber tendency into mean drift and dispersion about that mean drift provides a concrete mathematical interpretation for an interaction time scale ![]() $\tau _i$
$\tau _i$
and correlation time scale ![]() $\tau _c$:
$\tau _c$:
Intuitive notions of the interplay between ![]() $\tau _i$ and
$\tau _i$ and ![]() $\tau _c$ are discussed in Müller et al. (Reference Müller, Holloway, Henyey and Pomphrey1986) and in Nazarenko et al. (Reference Nazarenko, Newell and Galtier2001) using expressions for
$\tau _c$ are discussed in Müller et al. (Reference Müller, Holloway, Henyey and Pomphrey1986) and in Nazarenko et al. (Reference Nazarenko, Newell and Galtier2001) using expressions for ![]() ${\mathcal {C}}_{ij}$ (3.30) in which the ensemble mean drift has not been subtracted. The sentiment in Müller et al. (Reference Müller, Holloway, Henyey and Pomphrey1986) is that a separation between
${\mathcal {C}}_{ij}$ (3.30) in which the ensemble mean drift has not been subtracted. The sentiment in Müller et al. (Reference Müller, Holloway, Henyey and Pomphrey1986) is that a separation between ![]() $\tau _c$ and
$\tau _c$ and ![]() $\tau _i$ is problematic for the oceanic internal wave field. Numerical ray-tracing results (Henyey & Pomphrey Reference Henyey and Pomphrey1983; Henyey, Pomphrey & Meiss Reference Henyey, Pomphrey and Meiss1984) do not elucidate why this might be. Our decomposition of wavenumber tendency into mean drift and dispersion about that mean drift, the revised Fokker–Planck (3.31) and revised covariance matrix (3.30) provide a concrete mathematical interpretation for such judgements about
$\tau _i$ is problematic for the oceanic internal wave field. Numerical ray-tracing results (Henyey & Pomphrey Reference Henyey and Pomphrey1983; Henyey, Pomphrey & Meiss Reference Henyey, Pomphrey and Meiss1984) do not elucidate why this might be. Our decomposition of wavenumber tendency into mean drift and dispersion about that mean drift, the revised Fokker–Planck (3.31) and revised covariance matrix (3.30) provide a concrete mathematical interpretation for such judgements about ![]() $\tau _i$ and
$\tau _i$ and ![]() $\tau _c$.
$\tau _c$.
Having summoned the analogy between particle dispersion Taylor (Reference Taylor1921) and dispersion of wave packets in wavenumber, we are led to a degree of scepticism concerning the McComas & Bretherton (Reference McComas and Bretherton1977) and Nazarenko et al. (Reference Nazarenko, Newell and Galtier2001) interpretation that ray tracing should collapse onto the Fokker–Planck equation and diffusivity derived from the resonant kinetic equation (2.25). Convergence of the time-lagged auto-covariance (3.33) relates a finite diffusivity to the product of a covariance and correlation time scale. If one casts this as a resonant process, the covariance will be infinitely small and the correlation time scale infinitely long, thus leading to an inconsistency between interaction and correlation time scales in the resonant limit. Introducing a broadened kinetic equation (2.2.1) with finite bandwidth (2.19) might naively be considered progress. However, that bandwidth represents a spike decay rate rather than a correlation time scale and is not a resolution. As one runs to the finite amplitude of the weakly nonlinear problem, the resonant bandwidth becomes the r.m.s. Doppler shift (Polzin & Lvov Reference Polzin and Lvov2017). This is aphysical.
We find through numerical experimentation in Polzin & Lvov (Reference Polzin and Lvov2023) that the mean drift ![]() $\langle \dot {{\boldsymbol {p}}} \rangle$ is a resonant process and dispersion about the mean drift
$\langle \dot {{\boldsymbol {p}}} \rangle$ is a resonant process and dispersion about the mean drift ![]() ${\mathcal {C}}_{ij}$ is non-resonant. The latter should not come as a surprise once one appreciates the direct analogy between particle dispersion and ray tracing originally suggested in McComas & Bretherton (Reference McComas and Bretherton1977): particle dispersion in turbulence has nothing to do with the concept of resonance. The moments
${\mathcal {C}}_{ij}$ is non-resonant. The latter should not come as a surprise once one appreciates the direct analogy between particle dispersion and ray tracing originally suggested in McComas & Bretherton (Reference McComas and Bretherton1977): particle dispersion in turbulence has nothing to do with the concept of resonance. The moments ![]() $\langle \dot {{\boldsymbol {p}}} \rangle$ and
$\langle \dot {{\boldsymbol {p}}} \rangle$ and ![]() ${\mathcal {C}}_{ij}$, and changes in the structure and scaling of the resonant bandwidth, are the signature differences of ray theory vs the kinetic equation, paralleling differences between Eulerian (Kraichnan Reference Kraichnan1959) and Lagrangian (Kraichnan Reference Kraichnan1965) representations of 3-D turbulence. These differences are rooted in the distinctions between amplitude-modulated and frequency-modulated signals.
${\mathcal {C}}_{ij}$, and changes in the structure and scaling of the resonant bandwidth, are the signature differences of ray theory vs the kinetic equation, paralleling differences between Eulerian (Kraichnan Reference Kraichnan1959) and Lagrangian (Kraichnan Reference Kraichnan1965) representations of 3-D turbulence. These differences are rooted in the distinctions between amplitude-modulated and frequency-modulated signals.
4. Energy transport in oceanic internal waves
In Polzin & Lvov (Reference Polzin and Lvov2011, Reference Polzin and Lvov2017) we note the tension between an apparent pattern match between observed spectral power laws being in apparent agreement with stationary states of the Fokker–Planck equation derived from the kinetic equation (2.16)
and this result being inconsistent with what is observationally understood about the energy sources and sinks. Those stationary states come from asserting a balance only in vertical wavenumber, for which there are two families: no-flux states for which ![]() $n({\boldsymbol {p}}) \propto k^{-x}m^{-y}$ with
$n({\boldsymbol {p}}) \propto k^{-x}m^{-y}$ with ![]() $y=0$ and constant-flux states for which a linear relationship between
$y=0$ and constant-flux states for which a linear relationship between ![]() $x$ and
$x$ and ![]() $y$ is attained. Both families are oceanographically relevant Polzin & Lvov (Reference Polzin and Lvov2011) and, more to the point, the Garrett and Munk model (GM76) is a member of the no-flux family. This no-flux result is attained simply because that spectrum (
$y$ is attained. Both families are oceanographically relevant Polzin & Lvov (Reference Polzin and Lvov2011) and, more to the point, the Garrett and Munk model (GM76) is a member of the no-flux family. This no-flux result is attained simply because that spectrum (![]() $(x,y)=(4,0)$) has no gradients in action in vertical wavenumber.
$(x,y)=(4,0)$) has no gradients in action in vertical wavenumber.
The ray-path perspective (3.31) moves away from this interpretation so that the downscale transport contains an advection contribution of ![]() $\langle \dot {m} \rangle \langle n_{{\boldsymbol {p}}} \rangle$ in addition to the diffusive transport
$\langle \dot {m} \rangle \langle n_{{\boldsymbol {p}}} \rangle$ in addition to the diffusive transport ![]() $D_{33} \partial _m n_{{\boldsymbol {p}}}$. An extensive oceanographic literature on passive tracer dispersion provides a basis for further insight. Here, it is understood that spatially inhomogeneous turbulence will result in a mean drift of either particles (Davis Reference Davis1991) or tracer centre of mass (Armi Reference Armi1979; Ledwell, Watson & Law Reference Ledwell, Watson and Law1998) at a rate proportional to the spatial gradient of the diffusivity. Here, we accept this identification, so that from (2.26) we have
$D_{33} \partial _m n_{{\boldsymbol {p}}}$. An extensive oceanographic literature on passive tracer dispersion provides a basis for further insight. Here, it is understood that spatially inhomogeneous turbulence will result in a mean drift of either particles (Davis Reference Davis1991) or tracer centre of mass (Armi Reference Armi1979; Ledwell, Watson & Law Reference Ledwell, Watson and Law1998) at a rate proportional to the spatial gradient of the diffusivity. Here, we accept this identification, so that from (2.26) we have
Including a factor of two to account for the two-sided spectral representation of ![]() $e(\sigma,m)$, the downscale energy transport is
$e(\sigma,m)$, the downscale energy transport is
 \begin{align} \mathcal{P} = 2 \int_f^N
\langle \dot{m} \rangle e(m,\sigma) \,{\rm d}\sigma = 2
\Big( \frac{2}{\rm \pi} \Big)^2 \left( \frac{e_0
m_{{\ast}}}{N} \right)^2 f
\log\Big(\frac{N}{f}\Big)\cong 1.0\times10^{{-}8}\ [{\rm
W} \ {\rm
kg}^{{-}1}],\end{align}
\begin{align} \mathcal{P} = 2 \int_f^N
\langle \dot{m} \rangle e(m,\sigma) \,{\rm d}\sigma = 2
\Big( \frac{2}{\rm \pi} \Big)^2 \left( \frac{e_0
m_{{\ast}}}{N} \right)^2 f
\log\Big(\frac{N}{f}\Big)\cong 1.0\times10^{{-}8}\ [{\rm
W} \ {\rm
kg}^{{-}1}],\end{align}
which, apart from the prefactor of ![]() $1.0\times 10^{-8}$ being an order of magnitude too large, is virtually identical to the fine-scale parameterization; see Polzin et al. (Reference Polzin, Naveira Garabato, Sloyan, Huussen and Waterman2014), their (27) and (40). In Polzin & Lvov (Reference Polzin and Lvov2023) we demonstrate through a path integral closure that, indeed,
$1.0\times 10^{-8}$ being an order of magnitude too large, is virtually identical to the fine-scale parameterization; see Polzin et al. (Reference Polzin, Naveira Garabato, Sloyan, Huussen and Waterman2014), their (27) and (40). In Polzin & Lvov (Reference Polzin and Lvov2023) we demonstrate through a path integral closure that, indeed, ![]() $\langle \dot {m} \rangle = \partial _m D$ for the 1-D representation of high-frequency internal waves interacting with inertial waves. We further demonstrate that both are consistent with simple scale-invariant ray-tracing numerical simulations that treat the interaction as a 1-D problem.
$\langle \dot {m} \rangle = \partial _m D$ for the 1-D representation of high-frequency internal waves interacting with inertial waves. We further demonstrate that both are consistent with simple scale-invariant ray-tracing numerical simulations that treat the interaction as a 1-D problem.
We believe that this 1-D treatment is a reasonable representation of extreme scale-separated interactions. The 1-D version of (2.25), (4.1), dates to the dawn of modern oceanography and is supported by basic scale analysis (McComas & Bretherton Reference McComas and Bretherton1977; Sun & Kunze Reference Sun and Kunze1999a). It is underpinned by the integrable singularity of the inertial peak in the internal wave frequency spectrum and the lack of horizontal velocity gradients in that peak that is encoded in the dispersion relation. While near-inertial motions are very energetic, they are also are also the most linear part of the internal wave field. In the absence of horizontal wave gradients, nonlinearity vanishes, and thus a superposition of inertial motions is an exact solution of the primitive equations describing the evolution of the large-scale background assumed in § 3.1.1. Such an inertial wave representation is used in Polzin & Lvov (Reference Polzin and Lvov2023) to numerically validate (2.26) and (4.2).
A modern analysis of local and extreme scale-separated interactions in a non-rotating context (Dematteis et al. Reference Dematteis, Polzin and Lvov2022) assigns an energy transport associated with horizontal and diagonal terms of the diffusivity tensor that is an order of magnitude smaller than the fine-scale parameterization, two orders of magnitude smaller than (4.3). These non-vertical transports are likely overestimates in a rotating paradigm due to the vanishing of horizontal velocity gradients at the inertial peak.
Thus, our interpretation is that the advective transport arises in association with variations in the dispersion of wave packets in phase space in a manner that parallels the behaviour of passive tracers. The kinetic equation and ray tracing differ in that the trajectory of a wave packet in phase space returns significantly different information about the statistical inhomogeneity of phase space than is represented in the kinetic equation.
The result (4.3) stands in dramatic contrast with numerical results concerning the more general problem of high-frequency internal wave packets refracting in a background sea of internal waves (e.g. Henyey et al. Reference Henyey, Wright and Flatté1986; Sun & Kunze Reference Sun and Kunze1999b; Ijichi & Hibiya Reference Ijichi and Hibiya2017). This contention has required a systematic examination and physical interpretation of the assumptions within both the kinetic equation(§ 2.2) and ray-path (§ 3.2) approaches to pinpoint the multiple junctures which might underpin a systematic difference between observation and theory concerning extreme scale-separated interactions that are presented above in (4.3).
To date, we have identified three potential soft spots that could resolve the contradiction with general ray-tracing metrics.
The first is that both the ray tracing and kinetic equation discard a coupling between leading-order processes that leads to a subtractive cancellation of these leading orders. These leading orders are provided by the ID mechanism and the Bragg scattering mechanism, in which the phase locking introduced by ID is damped by Bragg scattering. Both are part of an extreme scale-separated Hamiltonian (3.10); Bragg scattering is discarded in a Taylor series expansion about the ID resonance (3.15) that produces the action conservation statement (3.16). Representation of this damping process can be defined by bundling eight distinct triads from the resonant manifold; the standard three-wave kinetic equation is a perturbation expansion in wave amplitude limited to one triad through a ‘random phase’ approximation to obtain (2.16). This coupling is pursued in the companion manuscript (Polzin & Lvov Reference Polzin and Lvov2023), where we argue that these new physics are the route through which the ocean resolves the contradiction.
The second is that there is the potential for finite-amplitude effects in which interactions, both resonant and non-resonant, represent a stochastic forcing in phase space on a short time scale that disrupts the phase velocity–group velocity resonance on a long time scale. This requires assessment of the resonant bandwidth, which differs between Eulerian (kinetic equation, (2.18)) and ray coordinates, in combination with the amplitude and decorrelation time scales of that forcing. This is investigated more fully in Polzin & Lvov (Reference Polzin and Lvov2023). Our opinion is that (4.3) and associated scaling is a fundamental metric that should be recoverable by kitchen sink efforts as a small-amplitude limit of wave turbulence and using a scale separation that aligns with the assumptions underpinning ray tracing. We offer the opinion that this is how the kitchen sink numerics of ray tracing resolves the contradiction.
The third is that extant efforts at ray tracing of the high-frequency internal wave packets refracting in a background sea of internal waves (Henyey et al. Reference Henyey, Wright and Flatté1986; Sun & Kunze Reference Sun and Kunze1999b; Ijichi & Hibiya Reference Ijichi and Hibiya2017) cannot be relied upon as a robust arbiter of this contradiction. Ray tracing is an asymptotic method requiring a scale separation in horizontal wavenumber (3.1.2) in addition to the spatial averaging implied in the envelope structure (3.2.1 Gershgorin et al. Reference Gershgorin, Lvov and Nazarenko2009). The ray-tracing numerical studies acknowledge none of this and regard scale separation as a tuneable parameter. They consistently document sensitivity to the specification of the scale separation and consistently find that the observed fine-scale metric of energy sourced to turbulent dissipation (Polzin et al. Reference Polzin, Naveira Garabato, Sloyan, Huussen and Waterman2014) requires a scale equivalence, i.e. requires the small parameter of an asymptotic expansion to be ![]() $\sim O(1)$. This is the hallmark of interactions represented as
$\sim O(1)$. This is the hallmark of interactions represented as ![]() ${\mathcal {H}}_{local}$ (3.7) that are spectrally local in wavenumber and need to be treated by other methods (Dematteis & Lvov Reference Dematteis and Lvov2021; Dematteis et al. Reference Dematteis, Polzin and Lvov2022). The kitchen sink numerics will additionally suffer from the issue that the background is not a solution of the equations of motion.
${\mathcal {H}}_{local}$ (3.7) that are spectrally local in wavenumber and need to be treated by other methods (Dematteis & Lvov Reference Dematteis and Lvov2021; Dematteis et al. Reference Dematteis, Polzin and Lvov2022). The kitchen sink numerics will additionally suffer from the issue that the background is not a solution of the equations of motion.
5. Conclusions
We have presented two distinct derivations of transport equations for the refraction of high-frequency internal waves in inertial wave shear. One derivation results from ‘standard’ wave turbulence techniques with the addition of near-resonant interactions and describes the wave field as a system of amplitude-modulated waves. This kinetic equation-based derivation results in a Fokker–Plank equation which returns an estimate of no net downscale transport in vertical wavenumber for the canonical spectrum of oceanic internal waves referred to as the Garrett–Munk spectrum and small transports associated with horizontal and off-diagonal elements (Dematteis et al. Reference Dematteis, Polzin and Lvov2022). The second derivation is based on ray-tracing techniques in the WKB limit. Here the ensemble-averaged transport equation (3.31) contains a mean-drift term that is absent from the Fokker–Plank equation derived from the kinetic equation (2.25). This term leads to a prediction of ocean dissipation (4.3) an order of magnitude greater than supported by ocean observations.
The disparity of these results can be interpreted from an analogy between ray characteristics and Lagrangian paths. Recognizing this distinction improves earlier derivations of the ray-path transport equation in McComas & Bretherton (Reference McComas and Bretherton1977) and Nazarenko et al. (Reference Nazarenko, Newell and Galtier2001): it provides a rigorous basis for the intuitive characterization of the transport of energy to dissipation invoked in Henyey et al. (Reference Henyey, Wright and Flatté1986), Sun & Kunze (Reference Sun and Kunze1999b) and Ijichi & Hibiya (Reference Ijichi and Hibiya2017). We arrived at this rigorous result by adding zero and explicitly invoking an ensemble average.
Holloway (Reference Holloway1980, Reference Holloway1982) argue that internal wave interactions might not be sufficiently weak for wave turbulence theory to be valid. That commentary is directed at inferences about the decay rate of narrowband perturbations to the spectrum being much larger than the internal wave frequency (Müller et al. Reference Müller, Holloway, Henyey and Pomphrey1986). This is inconsistent with the express intent that the kinetic equation describes the slow evolution of the wave spectrum. In Polzin & Lvov (Reference Polzin and Lvov2017) we identify this decay rate as the small-amplitude limit of the resonant bandwidth ![]() $\varGamma$ (2.18). However, the differences in our two Fokker–Planck equations do not hinge upon this issue. We have demonstrated in Polzin & Lvov (Reference Polzin and Lvov2017) that, at finite amplitude, the bandwidth is proportional to the r.m.s. Doppler shift. This denotes a degenerate state in which the bandwidth describes the quasi-coherent translation of small-scale waves, i.e. sweeping, rather than their interaction. In the WKB-based derivation, we operate upon the Hamiltonian with a Wigner transform that integrates over that narrow band perturbation and its nearly resonant decay partners in an extreme scale-separated limit. This removes the apparent discrepancy and arrives at different notions of bandwidth and the role of off-resonant interactions (Polzin & Lvov Reference Polzin and Lvov2017). We investigate these issues in greater detail in Polzin & Lvov (Reference Polzin and Lvov2023).
$\varGamma$ (2.18). However, the differences in our two Fokker–Planck equations do not hinge upon this issue. We have demonstrated in Polzin & Lvov (Reference Polzin and Lvov2017) that, at finite amplitude, the bandwidth is proportional to the r.m.s. Doppler shift. This denotes a degenerate state in which the bandwidth describes the quasi-coherent translation of small-scale waves, i.e. sweeping, rather than their interaction. In the WKB-based derivation, we operate upon the Hamiltonian with a Wigner transform that integrates over that narrow band perturbation and its nearly resonant decay partners in an extreme scale-separated limit. This removes the apparent discrepancy and arrives at different notions of bandwidth and the role of off-resonant interactions (Polzin & Lvov Reference Polzin and Lvov2017). We investigate these issues in greater detail in Polzin & Lvov (Reference Polzin and Lvov2023).
As we look back over the landscape of this endeavour, what we have is a well-established metric for ocean mixing known as fine-scale parameterization (Polzin et al. Reference Polzin, Naveira Garabato, Sloyan, Huussen and Waterman2014). At best, the fine-scale parameterization is underpinned by a heuristic description as an advective spectral closure (Polzin Reference Polzin2004) in the context of an energy transport equation that eschews action conservation in which energy transport in horizontal wavenumber keeps pace with that in vertical wavenumber. This interpretation contrasts with the pivotal role that ID was perceived to play in determining downscale transports in vertical wavenumber only. A possible resolution can be found in recent characterizations of the internal wave kinetic equation (Dematteis & Lvov Reference Dematteis and Lvov2021; Dematteis et al. Reference Dematteis, Polzin and Lvov2022) that coincide in magnitude and scaling with the description of transports encapsulated within the fine-scale parameterization. That work emphasizes the importance of local interactions.
The heart of our manuscript is a novel derivation that is an inspired addition of zero to an action balance that permits us to deal with inhomogeneities of dispersive tendencies in phase space. These inhomogeneities give rise to the leading-order transport terms in our system. Adding zero is simplistic, but yet is grounded in deep physical insight into this problem. Our work exposes a major lack of conceptual understanding of extreme scale-separated interactions in the existing literature.
To conclude, here we have derived a transport equation (3.29) based upon a packet ensemble that contains an advective transport term. When the advective transport term is evaluated in a rotating context, it gives rise to a transport estimate (4.3) that is an order of magnitude greater than the fine-scale parameterization. This inconsistency will be analysed in Polzin & Lvov (Reference Polzin and Lvov2023), where we suggest that the fourth-order cumulants, which are subleading to the product of two two-point correlators of inhomogeneous wave turbulence, are playing a significant role in the spatially inhomogeneous ray coordinate system.
Funding
Y.L. gratefully acknowledges the support of the National Science Foundation Division of Mathematical Sciences award 2009418. K.P. gratefully acknowledges support from the Office of Naval Research (Grant N000141712852) and Woods Hole Oceanographic Institution's Investment in Science Program for this project.
Declaration of interests
The authors report no conflict of interest.
Appendix A. The Garrett and Munk spectrum
We utilize what is referred to as GM76, the 1976 version of the Garrett and Munk model. We refer the reader to Garrett & Munk (Reference Garrett and Munk1972) and Garrett & Munk (Reference Garrett and Munk1979) for historical perspectives and to Müller et al. (Reference Müller, Holloway, Henyey and Pomphrey1986); Polzin & Lvov (Reference Polzin and Lvov2011) for reviews. The Garrett and Munk models treat the energy spectrum ![]() $e(\sigma,m)$ as separable in vertical wavenumber
$e(\sigma,m)$ as separable in vertical wavenumber ![]() $m$ and frequency
$m$ and frequency ![]() $\sigma$ with the potential for variable high-wavenumber/high-frequency power-law regimes and vertical wavenumber bandwidth. The two-sided Garrett and Munk 1976 model is
$\sigma$ with the potential for variable high-wavenumber/high-frequency power-law regimes and vertical wavenumber bandwidth. The two-sided Garrett and Munk 1976 model is
in which vertical wavenumber ![]() $m$ can be both positive and negative, frequency
$m$ can be both positive and negative, frequency ![]() $\sigma$ is positive,
$\sigma$ is positive, ![]() $f$ is the Coriolis parameter and
$f$ is the Coriolis parameter and ![]() $m_{\ast }=4{\rm \pi} /b$ with thermocline scale height
$m_{\ast }=4{\rm \pi} /b$ with thermocline scale height ![]() $b=1300$ m the vertical wavenumber bandwidth. The vertical wavenumber bandwidth
$b=1300$ m the vertical wavenumber bandwidth. The vertical wavenumber bandwidth ![]() $m_{\ast }$ implicitly scales with buoyancy as
$m_{\ast }$ implicitly scales with buoyancy as ![]() $m_{\ast } \rightarrow m_{\ast } N/N_0$, in which
$m_{\ast } \rightarrow m_{\ast } N/N_0$, in which ![]() $N$ is the buoyancy frequency and
$N$ is the buoyancy frequency and ![]() $N_0=3$ cph is a thermocline reference value. The total energy
$N_0=3$ cph is a thermocline reference value. The total energy ![]() $e_0$ is obtained by integrating over vertical wavenumber and frequency and then summing both sides of the vertical wavenumber spectrum. One uses linear kinematics and the dispersion relation to convert from energy density to wave-action density and spectral density in frequency to spectral density in horizontal wavenumber.
$e_0$ is obtained by integrating over vertical wavenumber and frequency and then summing both sides of the vertical wavenumber spectrum. One uses linear kinematics and the dispersion relation to convert from energy density to wave-action density and spectral density in frequency to spectral density in horizontal wavenumber.
Appendix B. Rotations included
We now repeat all the calculations with rotations included. We start from the primitive equations (2.1), decompose the velocity using (2.3) and then use the expression for potential vorticity (2.5) to obtain
 \begin{equation} \left.\begin{gathered}
\varPi_t + \boldsymbol{\nabla}\,\boldsymbol{\cdot}\,
\Big(\varPi \Big(\boldsymbol{\nabla} \phi +
\boldsymbol{\nabla}^{{\perp}} \varDelta^{{-}1}
\Big(\frac{f}{\varPi_{0}}
\varPi-f\Big)\Big)\Big)=0,\\ \phi_t + \frac{1}{2}
\Big|\boldsymbol{\nabla}\phi+
\boldsymbol{\nabla}^{{\perp}}\varDelta^{{-}1}
\Big(\frac{f}{\varPi_{0}}\varPi-f\Big) \Big|^2\\ +\,
\varDelta^{{-}1} \boldsymbol{\nabla}
\,\boldsymbol{\cdot}\,\Big[ \frac{f}{\varPi_{0}}\varPi
\Big(\boldsymbol{\nabla}^{{\perp}}\phi -
\boldsymbol{\nabla}\varDelta^{{-}1}\Big(\frac{f}{\varPi_{0}}\varPi-f\Big)\Big)
\Big] \\ + \,\frac{g}{\rho} \int^{\rho}\int^{\rho_2}
\frac{(\varPi-\varPi_{0})} {\rho_1} \, {\rm
d}\rho_1 \, {\rm d}\rho_2 = 0 .
\end{gathered}\right\}\end{equation}
\begin{equation} \left.\begin{gathered}
\varPi_t + \boldsymbol{\nabla}\,\boldsymbol{\cdot}\,
\Big(\varPi \Big(\boldsymbol{\nabla} \phi +
\boldsymbol{\nabla}^{{\perp}} \varDelta^{{-}1}
\Big(\frac{f}{\varPi_{0}}
\varPi-f\Big)\Big)\Big)=0,\\ \phi_t + \frac{1}{2}
\Big|\boldsymbol{\nabla}\phi+
\boldsymbol{\nabla}^{{\perp}}\varDelta^{{-}1}
\Big(\frac{f}{\varPi_{0}}\varPi-f\Big) \Big|^2\\ +\,
\varDelta^{{-}1} \boldsymbol{\nabla}
\,\boldsymbol{\cdot}\,\Big[ \frac{f}{\varPi_{0}}\varPi
\Big(\boldsymbol{\nabla}^{{\perp}}\phi -
\boldsymbol{\nabla}\varDelta^{{-}1}\Big(\frac{f}{\varPi_{0}}\varPi-f\Big)\Big)
\Big] \\ + \,\frac{g}{\rho} \int^{\rho}\int^{\rho_2}
\frac{(\varPi-\varPi_{0})} {\rho_1} \, {\rm
d}\rho_1 \, {\rm d}\rho_2 = 0 .
\end{gathered}\right\}\end{equation}
We now substitute the Reynolds decomposition (3.1a–c) into (B1). In doing so, we use the fact that potential vorticity is assumed to be conserved on isopycnals
Here, we denote by ![]() $\varPsi +\psi '$ the divergence-free part of the velocity field
$\varPsi +\psi '$ the divergence-free part of the velocity field
Then
 \begin{equation} \left.\begin{gathered}
\dot{\rm \pi}'+ \boldsymbol{\nabla}\,\boldsymbol{\cdot}\, \Big(
(\varPi_{0} + \varPi + {\rm \pi}') \Big(\boldsymbol{\nabla}
\phi' + \boldsymbol{\nabla}^{{\perp}}
\Big(\varDelta^{{-}1}\Big(\frac{f {\rm \pi}'}{\varPi_{0}}
\Big)\Big) \Big)\Big)\\
+\,\boldsymbol{\nabla}\,\boldsymbol{\cdot}\,\Big({\rm \pi}'\Big(\boldsymbol{\nabla}\varPhi+\boldsymbol{\nabla}^\perp
\Big(\varDelta^{{-}1}\Big(\frac{f\varPi}{\varPi_{0}}\Big)\Big)\Big)\Big)=
0 , \\ \dot{\phi}' + \frac{1}{2}
\Big|\boldsymbol{\nabla}\phi'+
\boldsymbol{\nabla}^{{\perp}}
\Big(\varDelta^{{-}1}\Big(\frac{f {\rm \pi}'}{\varPi_{0}}
\Big) \Big|^2 \\
+\,\varDelta^{{-}1}\boldsymbol{\nabla}\,\boldsymbol{\cdot}\,\Big(\frac{f}{\varPi_{0}}
(\varPi_{0}+\varPi+{\rm \pi}')\Big(\boldsymbol{\nabla}^\perp\phi'-\boldsymbol{\nabla}
\Big(\varDelta^{{-}1}\Big(\frac{f
{\rm \pi}'}{\varPi_{0}}\Big)\Big)\Big)\\
+\,\varDelta^{{-}1}\,\boldsymbol{\cdot}\,\boldsymbol{\nabla}\Big(\frac{f
{\rm \pi}'}{\varPi_{0}}
\Big(\boldsymbol{\nabla}^\perp\varPhi-\boldsymbol{\nabla}
\Big(\varDelta^{{-}1}\Big(\frac{f
\varPi}{\varPi_{0}}\Big)\Big)\Big)\Big) \\ + \,
\Big(\boldsymbol{\nabla}\phi'+\boldsymbol{\nabla}^\perp
\Big(\varDelta^{{-}1}\Big(\frac{f
{\rm \pi}'}{\varPi_{0}}\Big)\Big)\,\boldsymbol{\cdot}\,
\Big(\boldsymbol{\nabla}\varPhi+\boldsymbol{\nabla}^\perp\Big(\varDelta^{{-}1}\Big(\frac{f
\varPi}{\varPi_{0}}\Big)\Big)\Big)\\ +\,
\frac{g}{\rho} \int^{\rho}\int^{\rho_2} \frac{{\rm \pi}'}{\rho}
\, {\rm d}\rho_1 \, {\rm d}\rho_2 = 0 .
\end{gathered}\right\}\end{equation}
\begin{equation} \left.\begin{gathered}
\dot{\rm \pi}'+ \boldsymbol{\nabla}\,\boldsymbol{\cdot}\, \Big(
(\varPi_{0} + \varPi + {\rm \pi}') \Big(\boldsymbol{\nabla}
\phi' + \boldsymbol{\nabla}^{{\perp}}
\Big(\varDelta^{{-}1}\Big(\frac{f {\rm \pi}'}{\varPi_{0}}
\Big)\Big) \Big)\Big)\\
+\,\boldsymbol{\nabla}\,\boldsymbol{\cdot}\,\Big({\rm \pi}'\Big(\boldsymbol{\nabla}\varPhi+\boldsymbol{\nabla}^\perp
\Big(\varDelta^{{-}1}\Big(\frac{f\varPi}{\varPi_{0}}\Big)\Big)\Big)\Big)=
0 , \\ \dot{\phi}' + \frac{1}{2}
\Big|\boldsymbol{\nabla}\phi'+
\boldsymbol{\nabla}^{{\perp}}
\Big(\varDelta^{{-}1}\Big(\frac{f {\rm \pi}'}{\varPi_{0}}
\Big) \Big|^2 \\
+\,\varDelta^{{-}1}\boldsymbol{\nabla}\,\boldsymbol{\cdot}\,\Big(\frac{f}{\varPi_{0}}
(\varPi_{0}+\varPi+{\rm \pi}')\Big(\boldsymbol{\nabla}^\perp\phi'-\boldsymbol{\nabla}
\Big(\varDelta^{{-}1}\Big(\frac{f
{\rm \pi}'}{\varPi_{0}}\Big)\Big)\Big)\\
+\,\varDelta^{{-}1}\,\boldsymbol{\cdot}\,\boldsymbol{\nabla}\Big(\frac{f
{\rm \pi}'}{\varPi_{0}}
\Big(\boldsymbol{\nabla}^\perp\varPhi-\boldsymbol{\nabla}
\Big(\varDelta^{{-}1}\Big(\frac{f
\varPi}{\varPi_{0}}\Big)\Big)\Big)\Big) \\ + \,
\Big(\boldsymbol{\nabla}\phi'+\boldsymbol{\nabla}^\perp
\Big(\varDelta^{{-}1}\Big(\frac{f
{\rm \pi}'}{\varPi_{0}}\Big)\Big)\,\boldsymbol{\cdot}\,
\Big(\boldsymbol{\nabla}\varPhi+\boldsymbol{\nabla}^\perp\Big(\varDelta^{{-}1}\Big(\frac{f
\varPi}{\varPi_{0}}\Big)\Big)\Big)\\ +\,
\frac{g}{\rho} \int^{\rho}\int^{\rho_2} \frac{{\rm \pi}'}{\rho}
\, {\rm d}\rho_1 \, {\rm d}\rho_2 = 0 .
\end{gathered}\right\}\end{equation}
Remarkably, these equations are indeed Hamiltonian, with the Hamiltonian given by
 \begin{align} {\mathcal{H}} &=
\frac{1}{2}\int \Big[ (\varPi_{0}+\varPi + {\rm \pi}')
\Big|\boldsymbol{\nabla} \phi'+
\boldsymbol{\nabla}^{{\perp}}\varDelta^{{-}1} \Big(\frac{f
{\rm \pi}'}{\varPi_{0}} \Big)\Big|^2 - g \Big|\int^{\rho}
\frac{{\rm \pi}'}{\rho_1} \, {\rm d}\rho_1\Big|^2
\nonumber\\ &\quad
+\,2{\rm \pi}'\Big(\boldsymbol{\nabla}\phi'+\boldsymbol{\nabla}^\perp
\varDelta^{{-}1} \Big(\frac{f
{\rm \pi}'}{\varPi_{0}}\Big)\Big)\,\boldsymbol{\cdot}\,
\Big(\boldsymbol{\nabla}\varPhi+\boldsymbol{\nabla}^\perp\varDelta^{{-}1}\Big(\frac{f
\varPi}{\varPi_{0}}\Big)\Big)\Big]{\rm
d}{\boldsymbol{r}} .
\end{align}
\begin{align} {\mathcal{H}} &=
\frac{1}{2}\int \Big[ (\varPi_{0}+\varPi + {\rm \pi}')
\Big|\boldsymbol{\nabla} \phi'+
\boldsymbol{\nabla}^{{\perp}}\varDelta^{{-}1} \Big(\frac{f
{\rm \pi}'}{\varPi_{0}} \Big)\Big|^2 - g \Big|\int^{\rho}
\frac{{\rm \pi}'}{\rho_1} \, {\rm d}\rho_1\Big|^2
\nonumber\\ &\quad
+\,2{\rm \pi}'\Big(\boldsymbol{\nabla}\phi'+\boldsymbol{\nabla}^\perp
\varDelta^{{-}1} \Big(\frac{f
{\rm \pi}'}{\varPi_{0}}\Big)\Big)\,\boldsymbol{\cdot}\,
\Big(\boldsymbol{\nabla}\varPhi+\boldsymbol{\nabla}^\perp\varDelta^{{-}1}\Big(\frac{f
\varPi}{\varPi_{0}}\Big)\Big)\Big]{\rm
d}{\boldsymbol{r}} .
\end{align}Please compare this with (3.5).
We now can rewrite the Hamiltonian (B5) in the following form:
 \begin{align} \left.\begin{gathered}
{\mathcal{H}} = {\mathcal{H}}_{linear}
+{\mathcal{H}}_{nonlinear},\\ {\mathcal{H}}_{linear} =
\frac{1}{2}\int \Big[ \varPi_{0}\Big|\boldsymbol{\nabla}
\phi'+
\boldsymbol{\nabla}^{{\perp}}\varDelta^{{-}1}\Big(\frac{f
{\rm \pi}'}{\varPi_{0}} \Big) \Big|^2 -g
\Big|\int^{\rho}\frac{{\rm \pi}'}{\rho} \, {\rm
d}\rho_1\Big|^2\Big]{\rm d}{\boldsymbol{r}},\\
{\mathcal{H}}_{nonlinear} = {\mathcal{H}}_{local}+
{\mathcal{H}}_{sweeping} + {\mathcal{H}}_{density},\\
{\mathcal{H}}_{local} = \frac{1}{2}\int {\rm \pi}'
\Big|\boldsymbol{\nabla} \phi'+
\boldsymbol{\nabla}^{{\perp}}\Big(\varDelta^{{-}1}\frac{f
{\rm \pi}'}{\varPi_{0}} \Big) \Big|^2 \,{\rm
d}{\boldsymbol{r}}, \\ {\mathcal{H}}_{density} =
\frac{1}{2}\int \varPi \Big|\boldsymbol{\nabla}\phi'+
\boldsymbol{\nabla}^{{\perp}}\Big(\varDelta^{{-}1}\frac{f
{\rm \pi}'}{\varPi_{0}} \Big)\Big|^2 \,{\rm
d}{\boldsymbol{r}}, \\ {\mathcal{H}}_{sweeping} =
\int
{\rm \pi}'\Big(\boldsymbol{\nabla}\phi'+\boldsymbol{\nabla}^\perp
\Big(\varDelta^{{-}1}\frac{f {\rm \pi}'}{\varPi_{0}}
\Big)\Big)\,\boldsymbol{\cdot}\,
\Big(\boldsymbol{\nabla}\varPhi+\boldsymbol{\nabla}^\perp
\Big(\varDelta^{{-}1}\frac{f
\varPi}{\varPi_{0}}\Big)\Big) {\rm
d}{\boldsymbol{r}}. \end{gathered}\right\}
\end{align}
\begin{align} \left.\begin{gathered}
{\mathcal{H}} = {\mathcal{H}}_{linear}
+{\mathcal{H}}_{nonlinear},\\ {\mathcal{H}}_{linear} =
\frac{1}{2}\int \Big[ \varPi_{0}\Big|\boldsymbol{\nabla}
\phi'+
\boldsymbol{\nabla}^{{\perp}}\varDelta^{{-}1}\Big(\frac{f
{\rm \pi}'}{\varPi_{0}} \Big) \Big|^2 -g
\Big|\int^{\rho}\frac{{\rm \pi}'}{\rho} \, {\rm
d}\rho_1\Big|^2\Big]{\rm d}{\boldsymbol{r}},\\
{\mathcal{H}}_{nonlinear} = {\mathcal{H}}_{local}+
{\mathcal{H}}_{sweeping} + {\mathcal{H}}_{density},\\
{\mathcal{H}}_{local} = \frac{1}{2}\int {\rm \pi}'
\Big|\boldsymbol{\nabla} \phi'+
\boldsymbol{\nabla}^{{\perp}}\Big(\varDelta^{{-}1}\frac{f
{\rm \pi}'}{\varPi_{0}} \Big) \Big|^2 \,{\rm
d}{\boldsymbol{r}}, \\ {\mathcal{H}}_{density} =
\frac{1}{2}\int \varPi \Big|\boldsymbol{\nabla}\phi'+
\boldsymbol{\nabla}^{{\perp}}\Big(\varDelta^{{-}1}\frac{f
{\rm \pi}'}{\varPi_{0}} \Big)\Big|^2 \,{\rm
d}{\boldsymbol{r}}, \\ {\mathcal{H}}_{sweeping} =
\int
{\rm \pi}'\Big(\boldsymbol{\nabla}\phi'+\boldsymbol{\nabla}^\perp
\Big(\varDelta^{{-}1}\frac{f {\rm \pi}'}{\varPi_{0}}
\Big)\Big)\,\boldsymbol{\cdot}\,
\Big(\boldsymbol{\nabla}\varPhi+\boldsymbol{\nabla}^\perp
\Big(\varDelta^{{-}1}\frac{f
\varPi}{\varPi_{0}}\Big)\Big) {\rm
d}{\boldsymbol{r}}. \end{gathered}\right\}
\end{align}Making the Fourier transformation and making the Boussinesq approximation allows us to rewrite this in the form that generalizes (3.7)
 \begin{align} \left.\begin{gathered}
{\mathcal{H}} = {\mathcal{H}}_{linear}
+{\mathcal{H}}_{nonlinear},\\ {\mathcal{H}}_{linear} =
\frac{1}{2}\int {\rm d}{\boldsymbol{p}} \Big( \varPi_{0}
k^2 |\phi'_{{\boldsymbol{p}}}|^2 +
\Big(\frac{f^2}{k^2\varPi_{0}} -\frac{g}{\rho_0^2 m^2}
\Big)|\varPi_{{\boldsymbol{p}}}|^2 \Big),\\
{\mathcal{H}}_{nonlinear} = {\mathcal{H}}_{local}+
{\mathcal{H}}_{sweeping} + {\mathcal{H}}_{density}, \\
{\mathcal{H}}_{local} = \frac{1}{2}{
\frac{1}{(2{\rm \pi})^{3/2}}} \int {\rm d}
{\boldsymbol{p}}_1\,{\rm d} {\boldsymbol{p}}_2\,{\rm d}
{\boldsymbol{p}}_3
\delta(\kern1pt {\boldsymbol{p}}_1+{\boldsymbol{p}}_2+{\boldsymbol{p}}_3)\\
\times\Big(
-{\boldsymbol{k}}_2\,\boldsymbol{\cdot}\,{\boldsymbol{k}}_3
{\rm \pi}'_{{\boldsymbol{p}}_1}
\phi'_{{\boldsymbol{p}}_2}\phi'_{{\boldsymbol{p}}_3}
-\Big(\frac{f}{\varPi_{0}}\Big)^2
\frac{{\boldsymbol{k}}_2\,\boldsymbol{\cdot}\,{\boldsymbol{k}}_3}{k_2^2
k_3^2}
{\rm \pi}'_{{\boldsymbol{p}}_1}{\rm \pi}'_{{\boldsymbol{p}}_2}{\rm \pi}'_{{\boldsymbol{p}}_3}
-2 \frac{f}{\varPi_{0}}
\frac{{\boldsymbol{k}}_2\,\boldsymbol{\cdot}\,{\boldsymbol{k}}_3^{{\perp}}}{k_3^2}{\rm \pi}'_{{\boldsymbol{p}}_1}\phi'_{{\boldsymbol{p}}_2}{\rm \pi}'_{{\boldsymbol{p}}_3}\Big),\\
{\mathcal{H}}_{density} = \frac{1}{2} {
\frac{1}{(2{\rm \pi})^{3/2}}} \int {\rm d} {\boldsymbol{p}}_1
\,{\rm d} {\boldsymbol{p}}_2 \,{\rm d} {\boldsymbol{p}}_3
\delta(\kern1pt {\boldsymbol{p}}_1+{\boldsymbol{p}}_2+{\boldsymbol{p}}_3)\Big(\vphantom{\frac{f}{\varPi_{0}}}
-{\boldsymbol{k}}_2\,\boldsymbol{\cdot}\,{\boldsymbol{k}}_3
\varPi_{{\boldsymbol{p}}_1}
\phi'_{{\boldsymbol{p}}_2}\phi'_{{\boldsymbol{p}}_3}
\\ - \Big(\frac{f}{\varPi_{0}}\Big)^2
\frac{{\boldsymbol{k}}_2\,\boldsymbol{\cdot}\,{\boldsymbol{k}}_3}{k_2^2
k_3^2}
\varPi_{{\boldsymbol{p}}_1}{\rm \pi}'_{{\boldsymbol{p}}_2}{\rm \pi}'_{{\boldsymbol{p}}_3}
+2 \frac{f}{\varPi_{0}}
\frac{{\boldsymbol{k}}_2\,\boldsymbol{\cdot}\,{\boldsymbol{k}}_3^{{\perp}}}{k_3^2}\varPi_{{\boldsymbol{p}}_1}\phi'_{{\boldsymbol{p}}_2}{\rm \pi}'_{{\boldsymbol{p}}_3}\Big),\\
{\mathcal{H}}_{sweeping} = {\frac{1}{(2{\rm \pi})^{3/2}}} \int
{\rm d} {\boldsymbol{p}}_1\,{\rm d} {\boldsymbol{p}}_2
\,{\rm d} {\boldsymbol{p}}_3
\delta(\kern1pt {\boldsymbol{p}}_1+{\boldsymbol{p}}_2+{\boldsymbol{p}}_3)\times
\Big(\vphantom{\frac{f}{\varPi_{0}}}
-{\boldsymbol{k}}_2\,\boldsymbol{\cdot}\,{\boldsymbol{k}}_3
{\rm \pi}'_{{\boldsymbol{p}}_1}
\phi'_{{\boldsymbol{p}}_2}\varPhi_{{\boldsymbol{p}}_3}\\
+\,\frac{f}{\varPi_{0}}
\frac{{\boldsymbol{k}}_2\,\boldsymbol{\cdot}\,{\boldsymbol{k}}_3^\perp}{
k_3^2} {\rm \pi}'_{{\boldsymbol{p}}_1}
\phi'_{{\boldsymbol{p}}_2}\varPi_{{\boldsymbol{p}}_3} +
\frac{f}{\varPi_{0}}\frac{{\boldsymbol{k}}_2^\perp\,\boldsymbol{\cdot}\,{\boldsymbol{k}}_3}{k_2^2}{\rm \pi}_{{\boldsymbol{p}}_1}'{\rm \pi}'_{{\boldsymbol{p}}_2}\varPhi_{{\boldsymbol{p}}_3}
- \Big(\frac{f}{\varPi_{0}}\Big)^2
\frac{{\boldsymbol{k}}_2\,\boldsymbol{\cdot}\,{\boldsymbol{k}}_3}{k_2^2
k_3^2}{\rm \pi}'_{{\boldsymbol{p}}_1}{\rm \pi}'_{{\boldsymbol{p}}_2}\varPi_{{\boldsymbol{p}}_3}\Big).
\end{gathered}\right\}\end{align}
\begin{align} \left.\begin{gathered}
{\mathcal{H}} = {\mathcal{H}}_{linear}
+{\mathcal{H}}_{nonlinear},\\ {\mathcal{H}}_{linear} =
\frac{1}{2}\int {\rm d}{\boldsymbol{p}} \Big( \varPi_{0}
k^2 |\phi'_{{\boldsymbol{p}}}|^2 +
\Big(\frac{f^2}{k^2\varPi_{0}} -\frac{g}{\rho_0^2 m^2}
\Big)|\varPi_{{\boldsymbol{p}}}|^2 \Big),\\
{\mathcal{H}}_{nonlinear} = {\mathcal{H}}_{local}+
{\mathcal{H}}_{sweeping} + {\mathcal{H}}_{density}, \\
{\mathcal{H}}_{local} = \frac{1}{2}{
\frac{1}{(2{\rm \pi})^{3/2}}} \int {\rm d}
{\boldsymbol{p}}_1\,{\rm d} {\boldsymbol{p}}_2\,{\rm d}
{\boldsymbol{p}}_3
\delta(\kern1pt {\boldsymbol{p}}_1+{\boldsymbol{p}}_2+{\boldsymbol{p}}_3)\\
\times\Big(
-{\boldsymbol{k}}_2\,\boldsymbol{\cdot}\,{\boldsymbol{k}}_3
{\rm \pi}'_{{\boldsymbol{p}}_1}
\phi'_{{\boldsymbol{p}}_2}\phi'_{{\boldsymbol{p}}_3}
-\Big(\frac{f}{\varPi_{0}}\Big)^2
\frac{{\boldsymbol{k}}_2\,\boldsymbol{\cdot}\,{\boldsymbol{k}}_3}{k_2^2
k_3^2}
{\rm \pi}'_{{\boldsymbol{p}}_1}{\rm \pi}'_{{\boldsymbol{p}}_2}{\rm \pi}'_{{\boldsymbol{p}}_3}
-2 \frac{f}{\varPi_{0}}
\frac{{\boldsymbol{k}}_2\,\boldsymbol{\cdot}\,{\boldsymbol{k}}_3^{{\perp}}}{k_3^2}{\rm \pi}'_{{\boldsymbol{p}}_1}\phi'_{{\boldsymbol{p}}_2}{\rm \pi}'_{{\boldsymbol{p}}_3}\Big),\\
{\mathcal{H}}_{density} = \frac{1}{2} {
\frac{1}{(2{\rm \pi})^{3/2}}} \int {\rm d} {\boldsymbol{p}}_1
\,{\rm d} {\boldsymbol{p}}_2 \,{\rm d} {\boldsymbol{p}}_3
\delta(\kern1pt {\boldsymbol{p}}_1+{\boldsymbol{p}}_2+{\boldsymbol{p}}_3)\Big(\vphantom{\frac{f}{\varPi_{0}}}
-{\boldsymbol{k}}_2\,\boldsymbol{\cdot}\,{\boldsymbol{k}}_3
\varPi_{{\boldsymbol{p}}_1}
\phi'_{{\boldsymbol{p}}_2}\phi'_{{\boldsymbol{p}}_3}
\\ - \Big(\frac{f}{\varPi_{0}}\Big)^2
\frac{{\boldsymbol{k}}_2\,\boldsymbol{\cdot}\,{\boldsymbol{k}}_3}{k_2^2
k_3^2}
\varPi_{{\boldsymbol{p}}_1}{\rm \pi}'_{{\boldsymbol{p}}_2}{\rm \pi}'_{{\boldsymbol{p}}_3}
+2 \frac{f}{\varPi_{0}}
\frac{{\boldsymbol{k}}_2\,\boldsymbol{\cdot}\,{\boldsymbol{k}}_3^{{\perp}}}{k_3^2}\varPi_{{\boldsymbol{p}}_1}\phi'_{{\boldsymbol{p}}_2}{\rm \pi}'_{{\boldsymbol{p}}_3}\Big),\\
{\mathcal{H}}_{sweeping} = {\frac{1}{(2{\rm \pi})^{3/2}}} \int
{\rm d} {\boldsymbol{p}}_1\,{\rm d} {\boldsymbol{p}}_2
\,{\rm d} {\boldsymbol{p}}_3
\delta(\kern1pt {\boldsymbol{p}}_1+{\boldsymbol{p}}_2+{\boldsymbol{p}}_3)\times
\Big(\vphantom{\frac{f}{\varPi_{0}}}
-{\boldsymbol{k}}_2\,\boldsymbol{\cdot}\,{\boldsymbol{k}}_3
{\rm \pi}'_{{\boldsymbol{p}}_1}
\phi'_{{\boldsymbol{p}}_2}\varPhi_{{\boldsymbol{p}}_3}\\
+\,\frac{f}{\varPi_{0}}
\frac{{\boldsymbol{k}}_2\,\boldsymbol{\cdot}\,{\boldsymbol{k}}_3^\perp}{
k_3^2} {\rm \pi}'_{{\boldsymbol{p}}_1}
\phi'_{{\boldsymbol{p}}_2}\varPi_{{\boldsymbol{p}}_3} +
\frac{f}{\varPi_{0}}\frac{{\boldsymbol{k}}_2^\perp\,\boldsymbol{\cdot}\,{\boldsymbol{k}}_3}{k_2^2}{\rm \pi}_{{\boldsymbol{p}}_1}'{\rm \pi}'_{{\boldsymbol{p}}_2}\varPhi_{{\boldsymbol{p}}_3}
- \Big(\frac{f}{\varPi_{0}}\Big)^2
\frac{{\boldsymbol{k}}_2\,\boldsymbol{\cdot}\,{\boldsymbol{k}}_3}{k_2^2
k_3^2}{\rm \pi}'_{{\boldsymbol{p}}_1}{\rm \pi}'_{{\boldsymbol{p}}_2}\varPi_{{\boldsymbol{p}}_3}\Big).
\end{gathered}\right\}\end{align}
The next step is to substitute formulas for ![]() $\varPi _{\boldsymbol {q}}$ and
$\varPi _{\boldsymbol {q}}$ and ![]() $\varPhi _{\boldsymbol {q}}$ from (2.11a,b), and to perform the steps and approximations that are developed in §§ 3.1, 3.2. Results are the generalization of (3.12) and (3.10) and (3.11)
$\varPhi _{\boldsymbol {q}}$ from (2.11a,b), and to perform the steps and approximations that are developed in §§ 3.1, 3.2. Results are the generalization of (3.12) and (3.10) and (3.11)
 \begin{align} \left.\begin{gathered}
{\mathcal{H}} =\int {\rm d}{\boldsymbol{p}}_1\,{\rm d}
{\boldsymbol{p}}_2 \,A^f(\kern1pt {\boldsymbol{p}}_1,
{\boldsymbol{p}}_2)
a_{{\boldsymbol{p}}_1}a^*_{{\boldsymbol{p}}_2},\quad {\rm
with}\\
A^f(\kern1pt {\boldsymbol{p}}_1,{\boldsymbol{p}}_2)=\omega_{{\boldsymbol{p}}_1}\delta(\kern1pt {\boldsymbol{p}}_1-{\boldsymbol{p}}_2)
+ A_{sweeping}(\kern1pt {\boldsymbol{p}}_1,
{\boldsymbol{p}}_2)+A_{density }^f(\kern1pt {\boldsymbol{p}}_1,
{\boldsymbol{p}}_2), \\ A_{sweeping}^f(\kern1pt {\boldsymbol{p}}_1,
{\boldsymbol{p}}_2)=\frac{1}{(2{\rm \pi})^{3/2}}
\Big(\frac{1}{2}{\rm i}
({{\boldsymbol{k}}_1-{\boldsymbol{k}}_2})\,\boldsymbol{\cdot}\,(
{\boldsymbol{k}}_1+{\boldsymbol{k}}_2)\\
+\, \frac{f}{\varPi_{0}}
{\boldsymbol{k}}_1\,\boldsymbol{\cdot}\,{\boldsymbol{k}}_2^\perp\Big(\frac{1}{k_2^2}
- \frac{1}{k_1^2}\Big) \frac{g k_1
k_2}{2\sqrt{\omega_1\omega_2}N^2}\Big)\varPhi_{{\boldsymbol{p}}_2-{\boldsymbol{p}}_1}\\
+\biggl(\frac{-{\rm i}\dfrac{f}{\varPi_{0}}
{\boldsymbol{k}}_1^\perp\,\boldsymbol{\cdot}\,{\boldsymbol{k}}_2}{|{\boldsymbol{k}}_2-{\boldsymbol{k}}_1|^2}
-\Big(\frac{f}{\varPi_{0}}\Big)^2
\frac{({\boldsymbol{k}}_2-{\boldsymbol{k}}_1)}{({{\boldsymbol{k}}_1-{\boldsymbol{k}}_2})^2}\,\boldsymbol{\cdot}\,\Big(\frac{{\boldsymbol{k}}_2}{k_2^2}+\frac{{\boldsymbol{k}}_1}{k_1^2}\Big)
\frac{g k_1 k_2} {2\sqrt{\omega_1\omega_2}N^2}
\biggr)\varPi_{{\boldsymbol{p}}_2-{\boldsymbol{p}}_1}, \\
A_{density}^f(\kern1pt {\boldsymbol{p}}_1, {\boldsymbol{p}}_2) =
\frac{1}{(2{\rm \pi})^{3/2}} \Big( \frac{N^2}{2~g} \sqrt{
\omega_{{\boldsymbol{p}}_1}\omega_{{\boldsymbol{p}}_2}}
\frac{{\boldsymbol{k}}_2\,\boldsymbol{\cdot}\,{\boldsymbol{k}}_3}{k_2
k_3} +\frac{{\rm i}}{2}\frac{g}{N^2} \frac{f^2}{ \varPi_0^2
\sqrt{
\omega_{{\boldsymbol{p}}_1}\omega_{{\boldsymbol{p}}_2}}}
\Big) \varPi_{{\boldsymbol{p}}_1-{\boldsymbol{p}}_2}.
\end{gathered}\right\} \end{align}
\begin{align} \left.\begin{gathered}
{\mathcal{H}} =\int {\rm d}{\boldsymbol{p}}_1\,{\rm d}
{\boldsymbol{p}}_2 \,A^f(\kern1pt {\boldsymbol{p}}_1,
{\boldsymbol{p}}_2)
a_{{\boldsymbol{p}}_1}a^*_{{\boldsymbol{p}}_2},\quad {\rm
with}\\
A^f(\kern1pt {\boldsymbol{p}}_1,{\boldsymbol{p}}_2)=\omega_{{\boldsymbol{p}}_1}\delta(\kern1pt {\boldsymbol{p}}_1-{\boldsymbol{p}}_2)
+ A_{sweeping}(\kern1pt {\boldsymbol{p}}_1,
{\boldsymbol{p}}_2)+A_{density }^f(\kern1pt {\boldsymbol{p}}_1,
{\boldsymbol{p}}_2), \\ A_{sweeping}^f(\kern1pt {\boldsymbol{p}}_1,
{\boldsymbol{p}}_2)=\frac{1}{(2{\rm \pi})^{3/2}}
\Big(\frac{1}{2}{\rm i}
({{\boldsymbol{k}}_1-{\boldsymbol{k}}_2})\,\boldsymbol{\cdot}\,(
{\boldsymbol{k}}_1+{\boldsymbol{k}}_2)\\
+\, \frac{f}{\varPi_{0}}
{\boldsymbol{k}}_1\,\boldsymbol{\cdot}\,{\boldsymbol{k}}_2^\perp\Big(\frac{1}{k_2^2}
- \frac{1}{k_1^2}\Big) \frac{g k_1
k_2}{2\sqrt{\omega_1\omega_2}N^2}\Big)\varPhi_{{\boldsymbol{p}}_2-{\boldsymbol{p}}_1}\\
+\biggl(\frac{-{\rm i}\dfrac{f}{\varPi_{0}}
{\boldsymbol{k}}_1^\perp\,\boldsymbol{\cdot}\,{\boldsymbol{k}}_2}{|{\boldsymbol{k}}_2-{\boldsymbol{k}}_1|^2}
-\Big(\frac{f}{\varPi_{0}}\Big)^2
\frac{({\boldsymbol{k}}_2-{\boldsymbol{k}}_1)}{({{\boldsymbol{k}}_1-{\boldsymbol{k}}_2})^2}\,\boldsymbol{\cdot}\,\Big(\frac{{\boldsymbol{k}}_2}{k_2^2}+\frac{{\boldsymbol{k}}_1}{k_1^2}\Big)
\frac{g k_1 k_2} {2\sqrt{\omega_1\omega_2}N^2}
\biggr)\varPi_{{\boldsymbol{p}}_2-{\boldsymbol{p}}_1}, \\
A_{density}^f(\kern1pt {\boldsymbol{p}}_1, {\boldsymbol{p}}_2) =
\frac{1}{(2{\rm \pi})^{3/2}} \Big( \frac{N^2}{2~g} \sqrt{
\omega_{{\boldsymbol{p}}_1}\omega_{{\boldsymbol{p}}_2}}
\frac{{\boldsymbol{k}}_2\,\boldsymbol{\cdot}\,{\boldsymbol{k}}_3}{k_2
k_3} +\frac{{\rm i}}{2}\frac{g}{N^2} \frac{f^2}{ \varPi_0^2
\sqrt{
\omega_{{\boldsymbol{p}}_1}\omega_{{\boldsymbol{p}}_2}}}
\Big) \varPi_{{\boldsymbol{p}}_1-{\boldsymbol{p}}_2}.
\end{gathered}\right\} \end{align}
Using these equations and repeating steps above and discarding terms proportional to ![]() $q^2$ leads to
$q^2$ leads to
 \begin{align} \omega(\kern1pt {\boldsymbol{p}},{\boldsymbol{r}})&= \sigma_{{\boldsymbol{p}}} -{\boldsymbol{k}}\,\boldsymbol{\cdot}\,\boldsymbol{\nabla}\varPhi({\boldsymbol{r}},t)- \frac{f}{\varPi_{0}}{\boldsymbol{k}}\,\boldsymbol{\cdot}\,\boldsymbol{\nabla}^\perp\varDelta^{{-}1}\varPi({\boldsymbol{r}},t) \nonumber\\ &\quad +\frac{N^2}{2 g}\varPi({\boldsymbol{r}},t)\sigma_{\boldsymbol{p}} +\frac{f^2 g }{\varPi_0^2\omega_p N^2}\varPi({\boldsymbol{r}},t) \nonumber\\ &\quad +\frac{f^2 g}{2\omega_{\boldsymbol{p}} \varPi_0^2 N^2}\int \cos({2\theta_{{\boldsymbol{q}}{\boldsymbol{p}}}})\varPi({\boldsymbol{q}},t) {\rm e}^{{\rm i} {\boldsymbol{r}}\,\boldsymbol{\cdot}\, {\boldsymbol{q}}}\,{\rm d} q. \end{align}
\begin{align} \omega(\kern1pt {\boldsymbol{p}},{\boldsymbol{r}})&= \sigma_{{\boldsymbol{p}}} -{\boldsymbol{k}}\,\boldsymbol{\cdot}\,\boldsymbol{\nabla}\varPhi({\boldsymbol{r}},t)- \frac{f}{\varPi_{0}}{\boldsymbol{k}}\,\boldsymbol{\cdot}\,\boldsymbol{\nabla}^\perp\varDelta^{{-}1}\varPi({\boldsymbol{r}},t) \nonumber\\ &\quad +\frac{N^2}{2 g}\varPi({\boldsymbol{r}},t)\sigma_{\boldsymbol{p}} +\frac{f^2 g }{\varPi_0^2\omega_p N^2}\varPi({\boldsymbol{r}},t) \nonumber\\ &\quad +\frac{f^2 g}{2\omega_{\boldsymbol{p}} \varPi_0^2 N^2}\int \cos({2\theta_{{\boldsymbol{q}}{\boldsymbol{p}}}})\varPi({\boldsymbol{q}},t) {\rm e}^{{\rm i} {\boldsymbol{r}}\,\boldsymbol{\cdot}\, {\boldsymbol{q}}}\,{\rm d} q. \end{align}
Here, ![]() $\theta _{{\boldsymbol {q}}{\boldsymbol {p}}}$ is an angle between the horizontal part of wave vector
$\theta _{{\boldsymbol {q}}{\boldsymbol {p}}}$ is an angle between the horizontal part of wave vector ![]() ${\boldsymbol {q}} = {\boldsymbol {p}}_1 - {\boldsymbol {p}}_2$ (3.13) and the horizontal part of
${\boldsymbol {q}} = {\boldsymbol {p}}_1 - {\boldsymbol {p}}_2$ (3.13) and the horizontal part of ![]() ${\boldsymbol {p}}$, that is
${\boldsymbol {p}}$, that is ![]() ${\boldsymbol {k}}$, with the sign defined using the right-hand rule going from
${\boldsymbol {k}}$, with the sign defined using the right-hand rule going from ![]() $q$ TO
$q$ TO ![]() $p$. The Eulerian frequency
$p$. The Eulerian frequency ![]() $\sigma _{{\boldsymbol {p}}}$ is given by (2.12). Note that the first line is simply
$\sigma _{{\boldsymbol {p}}}$ is given by (2.12). Note that the first line is simply ![]() $\sigma _{{\boldsymbol {p}}}-{\boldsymbol {k}}\boldsymbol {\cdot }{\mathcal {U}}$, the second line is the density term that we have considered above and the third line is the contribution from a rotating ocean. Equation (3.18), which is lines one and two of (B9) with
$\sigma _{{\boldsymbol {p}}}-{\boldsymbol {k}}\boldsymbol {\cdot }{\mathcal {U}}$, the second line is the density term that we have considered above and the third line is the contribution from a rotating ocean. Equation (3.18), which is lines one and two of (B9) with ![]() $\mathcal {U} = \boldsymbol {\nabla }\varPhi$, applies to a non-rotating ocean. In a rotating ocean, a wave whose frequency is high enough not to be impacted by rotation is described using lines one and two.
$\mathcal {U} = \boldsymbol {\nabla }\varPhi$, applies to a non-rotating ocean. In a rotating ocean, a wave whose frequency is high enough not to be impacted by rotation is described using lines one and two.