Article contents
Vlasov–Maxwell equations with spin effects
Published online by Cambridge University Press: 27 April 2023
Abstract
We present a numerical method to solve the Vlasov–Maxwell equations for spin-1/2 particles, in a semiclassical approximation where the orbital motion is treated classically while the spin variable is fully quantum. Unlike the spinless case, the phase-space distribution function is a $2\times 2$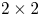 matrix, which can also be represented, in the Pauli basis, as one scalar function $f_0$
matrix, which can also be represented, in the Pauli basis, as one scalar function $f_0$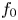 and one three-component vector function $\boldsymbol f$
and one three-component vector function $\boldsymbol f$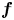 . The relationship between this ‘vectorial’ representation and the fully scalar representation on an extended phase space first proposed by Brodin et al. (Phys. Rev. Lett., vol. 101, 2008, p. 245002) is analysed in detail. By means of suitable approximations and symmetries, the vectorial spin-Vlasov–Maxwell model can be reduced to two-dimensions in the phase space, which is amenable to numerical solutions using a high-order grid-based Eulerian method. The vectorial model enjoys a Poisson structure that paves the way to accurate Hamiltonian split-time integrators. As an example, we study the stimulated Raman scattering of an electromagnetic wave interacting with an underdense plasma, and compare the results with those obtained earlier with the scalar spin-Vlasov–Maxwell model and a particle-in-cell code.
. The relationship between this ‘vectorial’ representation and the fully scalar representation on an extended phase space first proposed by Brodin et al. (Phys. Rev. Lett., vol. 101, 2008, p. 245002) is analysed in detail. By means of suitable approximations and symmetries, the vectorial spin-Vlasov–Maxwell model can be reduced to two-dimensions in the phase space, which is amenable to numerical solutions using a high-order grid-based Eulerian method. The vectorial model enjoys a Poisson structure that paves the way to accurate Hamiltonian split-time integrators. As an example, we study the stimulated Raman scattering of an electromagnetic wave interacting with an underdense plasma, and compare the results with those obtained earlier with the scalar spin-Vlasov–Maxwell model and a particle-in-cell code.
- Type
- Research Article
- Information
- Copyright
- Copyright © The Author(s), 2023. Published by Cambridge University Press
References
- 1
- Cited by



