Stellarator–mirror fusion–fission hybrid – a fast route to clean and safe nuclear energy

Abstract

The multiple-recycle fuel cycle for uranium-238 considered here, if practically realized, can bring revolutionary changes in nuclear energy. A full use of uranium-238 implies a practically infinite resource for power generation. Besides the energy, the fuel cycle net output is only fission products, which are co-products rather than waste. For the same amount of energy produced, the amount of fission products is two orders of magnitude less compared with the amount of spent nuclear fuel generated in currently exploited nuclear energy production scenarios. Using the simplest isotope balance model, key features of the multiple-recycle fuel cycle for uranium-238 are investigated. The repetition of this cycle results in smooth transformation of the initial fuel to ‘stationary’ fuel without strong variations in the fractional isotope content. Deficit of delayed neutrons is a threat of the fuel cycle considered as well as other fuel cycles that use plutonium. It has a dramatic impact on reactor controllability and safety. A solution to this threat could be a subcritical nuclear reactor with an external neutron source. In this paper, use of a stellarator–mirror (SM) fusion–fission hybrid for the multiple-recycle fuel cycle for uranium-238 is analysed. A summary of the experimental and theoretical studies on the SM hybrid is given. Preliminary results for principal design of a SM hybrid nuclear reactor for the multiple-recycle fuel cycle for uranium-238 are presented.

1. Introduction

For about 70 years, nuclear power generation has used mainly the uranium-235 isotope, the concentration of which in natural uranium is only 0.7 %. The remainder is uranium-238. Only about half the uranium-235 enters the fuel after enrichment. The rest remains in depleted uranium. Furthermore, slightly more than half of the uranium-235 burns out in the fuel. In aggregate, only 0.2 % of the mined uranium is used, while the rest is turned into waste. The major part of the waste is depleted uranium. It is usually stored at the site of production of nuclear fuel in the form of hexafluoride which is toxic. The rest of the waste is spent nuclear fuel which is buried in short- and long-term storage facilities.

Note here that the energy gain in fission reactions is almost the same, around 200 MeV, for all fissile isotopes, and they can in principle be burned with an energy output similar to that of uranium-235. The present inefficient use of uranium can be much improved with fast reactors, which are also able to burn the fissionable isotopes which arise from neutron irradiation of uranium-238.

The rate of uranium burning depends on fast reactor type. As an illustration, a travelling wave reactor burns up to 30 % of uranium-238 (Gilleland, Petroski & Weaver 2016).

The idea of full burning of fissile isotopes in the same reactor is not new (Feinberg & Kunegin 1958). The project Integral Fast Reactor (Chang 1989) is of special interest, in particular because of its closing for safety reasons (see https://en.wikipedia.org/wiki/Integral_fast_reactor). Some different approaches with multiple-recycle fuel cycles for fast reactors, which could provide radically higher aggregate combustion percentages, should be mentioned here (Orlov et al. 2005; Moiseenko et al. 2012; Ternovykha et al. 2017; Moiseenko & Chernitskiy 2019). In cyclic reprocessing, after the burning sequence, fuel is unloaded from the reactor, fission products are removed, the corresponding amount of depleted uranium is added and finally new fuel is made from this mixture.

If the start-up fuel has a certain isotopic composition (Moiseenko et al. 2012), the cycles become repeating (periodic). In such a fuel cycle, depleted uranium is burned while for other isotopes, owing to nuclear transformations, the supply rate and the diminution rate appear to be equal which keeps their amount constant. The net output is fission products. They can be considered as co-products, not waste, because they contain some elements of commercial value. These elements could be extracted after the radioactivity of the fission products has decreased to acceptable values.

As only uranium-238 is consumed, the fuel resources could serve worldwide energy production in the range of 100 000 years. The fuel cycle scenario seems consistent with nuclear non-proliferation, since the fuel isotope mixture in all stages has an insufficient fraction of plutonium-239.

So far, critical fast reactors have not reached widespread use. One reason is that fast reactors have a dramatically reduced self-stabilization. In addition, the portion of delayed neutrons in a fast reactor is lower than in light water reactors if the main component in it responsible for fission is plutonium. This implies that a critical fast reactor is less controlled and less resistant against accidents.

Subcritical systems could solve this problem. We propose the stellarator–mirror (SM) hybrid (Moiseenko, Noack & Ågren 2010) as a practical subcritical fast reactor system. The device is aimed at steady-state operation. In a subcritical system, neutron reactions are controlled by an external neutron source (in our case by a plasma neutron generator), which substantially increases safety and also provides more flexibility in control. From a safety point of view, these externally generated neutrons essentially replace the actions of delayed neutrons and can drastically improve reactor safety.

The multiple-recycle fuel cycle realization with the SM hybrid is considered here. The paper is composed as follows. In the next section, using a simple environment-independent model, the basic properties of the uranium-238 multiple-recycle fuel cycle for fast reactors are examined. In § 3 the state of the art in research on the SM fission–fusion hybrid concept is presented. In § 4 the first MCNPX (https://mcnp.lanl.gov/) calculations for the nuclear part of the SM hybrid that burns uranium-238 are presented. Section 5 gives a summary and proposals for future research.

2. Multiple-recycle fuel cycle for fast reactors

Irradiation of uranium-238 by neutrons causes a chain of nuclear transformations which is displayed in figure 1 (see e.g. Waltar & Reynolds 1981). The chain is generated and sustained due to neutron capture and beta-decay reactions. To analyse possibilities given by the multiple-recycle fuel cycle, we introduce a simple zero-dimensional isotope balance model. The nuclear reactions are described by the following equation:

(2.1)\begin{equation}\frac{{\textrm{d}{N_i}}}{{\textrm{d}t}} =- {\sigma _{c,i}}\varPhi {N_i} - {\sigma _{f,i}}\varPhi {N_i} - {\varLambda _i}{N_i} + {\varLambda _l}{N_l} + {\sigma _{c,m}}\varPhi {N_m} + {I_i}.\end{equation}

Here N_i is the isotope normalized content, index i enumerates isotopes, σ denotes cross-sections, indices f and c denote fission and neutron capture, ${\varLambda _i} = \ln 2/{T_{1/2,i}}$ is the decay rate of i type nucleus, T _1/2,i is the half-life, $\varPhi$ is the scalar neutron flux and I is the fuel supply (sink) rate. Indices l and m have values that correspond to processes displayed in figure 1. The chosen cross-sections (see Moiseenko et al. 2012) are representative for a fast reactor. The fission product quantity is enumerated by the number of source nuclei:

(2.2)\begin{equation}\frac{{\textrm{d}{N_0}}}{{\textrm{d}t}} = \mathop \sum \limits_i {\sigma _{f,i}}\varPhi {N_i} - {I_0}.\end{equation}

Figure 1. Scheme of ²³⁸U transformations under neutron irradiation.

Note that in the calculations, beta-decays of ²³⁹U to ²³⁹Np and ²⁴³Pu to ²⁴³Am are assumed as immediate. Thus, ²³⁹U and ²⁴³Pu are not considered. For two isotopes, ²⁴¹Am and ²⁴³Am, on which the nuclear chain ends, the neutron capture processes are blocked.

The calculations were performed for fixed neutron flux $\varPhi$ = 0.0005 barn⁻¹ day⁻¹ with periods of 600 days. At the end of each period a part the fission products (70 %) is substituted with the corresponding quantity of ²³⁸U. Also, the effective neutron multiplication factor, k _eff, the ratio of neutron production and loss rates, is calculated.

The solution of the system of (2.1) and (2.2) depends on initial conditions. The choice of the initial fuel is discussed below. Nevertheless, all the solutions converge to the same periodic process in which the initial fuel for each cycle is identical. The fuel content is shown in table 1.

Table 1. Fuel content at the beginning of the ‘periodic’ cycle.

It is worthwhile to start from such a fuel and make the fuel cycle periodic from the very beginning (Moiseenko et al. 2012). However, a multi-component fuel could be complicated to manufacture. The possibility of starting with uranium–plutonium fuel seems to be more practical. The isotopic content of plutonium is optional, but in this particular case it is chosen as representative for spent nuclear fuel. Using the modelling, the initial fuel is suggested which minimizes k _eff variation at the initial stage. Its content is given in table 2.

Table 2. Initial fuel content.

With this start-up fuel, the time evolution of fuel components is displayed in figure 2 for first, fifth and twentieth time periods (k = 1, k = 5, k = 20). These time dependences do not show complex behaviours.

Figure 2. Time evolution of k _eff, fission products (FP), ²³⁸U, ²³⁹Np and ²³⁹Pu (left-hand column) and ²⁴⁰Pu, ²⁴¹Pu, ²⁴²Pu, ²⁴¹Am and ²⁴³Am (right-hand column) for first, fifth and twentieth time periods (k = 1, k = 5, k = 20). Curves for k = 5 and k = 20 of FP fully overlap and are given in black colour.

As seen in the figure, the fission products grow in time. They quickly reach the quasi-stationary periodic regime. This also applies to the ²³⁸U content which gradually decreases with time during each period. The behaviour of ²³⁹Np becomes rapidly repeating, growing from zero. The ²³⁹Pu content slightly increases during the first five periods and then stays unchanged. Concentrations of remaining plutonium isotopes are initially larger than the ‘stationary’ values, and they slowly decrease from period to period. Characteristic times of the decrease are larger for greater isotope number. Isotope ²⁴¹Am needs more than 20 periods to approach its ‘equilibrium’ fraction. Because of high initial concentration of the parent isotope, ²⁴²Pu, the ²⁴³Am amount slowly ramps up and reaches a value 1.6 times larger than the ‘stationary’ one at the twentieth period. After this its concentration slowly decreases. The calculations in this section disregard environment effects such as neutron capture by the coolant, and the computed value of neutron multiplication factor k _eff can, therefore, exceed unity. The k _eff variation is small: overall change is within 2 %. It is larger within a period than between different periods. The computed value of k _eff ≥ 1.45 gives some margin to avoid a very large reactor size.

The given analysis of the multiple-recycle fuel cycle with only ²³⁸U net consumption suggests that it has a potential for practical usage. Repetition of cycles results in smooth transformation of the initial fuel to ‘stationary’ fuel without strong variations. The fractions of minor actinides are small, and there is no accumulation due to their fission. The k _eff values and variations seem to be within acceptable ranges. There is an option of not full but only partial extraction of fission products.

3. Stellarator–mirror hybrid

In the SM hybrid, fusion neutrons are generated in a deuterium–tritium plasma, confined magnetically in a stellarator-type system (figure 3). The plasma contains a warm electron component, and the majority of deuterium ions are in thermal equilibrium with electrons. The stellarator offers a relatively good confinement for such a warm Maxwellian plasma. Considering the stellarator's inferior ability to confine high-energy ions, it is proposed in Moiseenko et al. (2010) to integrate it with a rectilinear magnetic trap (mirror) with lower field. Hot minority tritium ions are sustained inside the linear magnetic trap plasma by radio-frequency heating (see e.g. Moiseenko & Ågren 2007) or neutral beam injection (NBI).

Figure 3. Sketch of SM hybrid.

The hot ions have mostly perpendicular to the steady magnetic field kinetic energies. Because of the trapping effect, the hot (sloshing) ions’ motion is restricted to the mirror part of the device. The containment of hot sloshing ions and, therefore, contraction of the neutron production zone to the mirror part are favourable, as they make it sufficient to only have the mirror part surrounded with a fission mantle (see figure 3). The main process that determines the fast ion energy loss under the conditions considered is the electron drag. This can be found from estimates and confirmed by kinetic calculations (Moiseenko & Ågren 2013). The electron drag does not change the ion guiding centre trajectory. It also does not change the pitch angle of the hot ions and, therefore, does not cause de-trapping of the ions. The change of the pitch angle is induced by ion–ion collisions, but their frequency is much less than that of the electron drag. Radial diffusion comes into play only at the stage when the ion energy almost totally lost. The features of this system are the following:

• • With sufficient subcriticality (k _eff ≤ 0.95) the system widens the safety and operational margins associated with delayed neutrons by more than one order of magnitude. The controllability of the system strongly increases and the negative consequences of accidents are strongly mitigated.

• • The SM plasma system may provide steady-state operation of the hybrid reactor (for a year or more). Since stellarator-based systems can operate regimes without disruptive magnetohydrodynamic events, such as edge-localized modes and major disruptions, there is a possibility of providing stable operation with power tuning option.

• • The design and operation of all plasma device systems are facilitated with a localization of the neutron emission at the mirror part. The pumping ports, diagnostics windows and other necessary equipment could be placed at the stellarator part where neutron flux is lower by orders of magnitude.

• • Since the fusion neuron flux is by an order of magnitude lower than the fission neutron flux, in a wide range of the machine parameters, a high electric efficiency is possible.

• • A net production of tritium can be provided at the site. The tritium content is also low in a fusion–fission device.

• • There is no need for uranium enrichment, and this reduces the costs of fuel.

• • At a power plant scale, the plasma part is compact enough with a size comparable to that of existing fusion devices.

• • An experimental device could be built at a small scale for a proof-of-principle purpose, and even under these conditions it may have a positive power output.

Both theoretical and experimental studies have been made in support of the SM hybrid concept. The experiments were performed on the Uragan-2M stellarator-type device (Bykov et al. 1990). The distinctive feature of Uragan-2M is that it is equipped with separate magnetic coils which create a purely toroidal magnetic field. Besides this, Uragan-2M has a helical winding of a torsatron type. If one of the 16 toroidal field coils is switched off, an embedded mirror with lower magnetic field is created at the place of the coil with a mirror ratio around 1.5.

One key question concerning the SM system is whether it could have magnetic surfaces. Theoretical calculations (Kotenko, Moiseenko & Ågren 2012) found nested magnetic surfaces and the conditions for their existence. Guided by these calculations, the magnetic surfaces were measured in experiments (Lesnyakov et al. 2013). Studies of the magnetohydrodynamic aspects for plasma confinement in the SM hybrid are planned.

Using MCNPX calculations, the principal design of the nuclear reactor part of the SM hybrid has been developed (Chernitskiy et al. 2014). The reactor has a compact toroidal shape (with a 1.6 m outer radius and a 4 m length) surrounding the mirror part of the SM plasma machine. A schematic is shown in figure 4. Its major parts, moving from the axis in the radial direction, are the inner through-opening for the plasma column, the first wall, the LBE (lead–bismuth eutectic) buffer, the metal fuel-loaded LBE-cooled active zone, the core extension zone (filled by LBE) and the reflector. Fuel for the fission component is assumed to be produced by separating uranium and fission products from spent nuclear fuel. Actual fuel material is an alloy (TRU–10Zr) consisting of transuranic elements with 10 wt% zirconium. The active zone size is chosen using MCNPX calculations to achieve an effective neutron multiplication factor k _eff ≈ 0.95. For this reactor, the calculated power multiplication factor, the ratio of fission power to fusion power, is 65. There are only 5 tons of transuranic elements in the fuel. This suggests that a nuclear plant operated at full capacity will need to be refuelled every 1–2 years.

Figure 4. Sketch of fission mantle of SM hybrid.

The parameters of the whole SM machine are determined using power balance calculations. They were made first with the assumption that in plasma the tritium distribution function is anisotropic Maxwellian (Moiseenko et al. 2010). Kinetic calculations for the tritium distribution function improved the accuracy of the results (Moiseenko & Ågren 2013) although they are only slightly different. A summary of the machine parameters is given in table 3. They are calculated using the results of kinetic code calculations along with the stellarator scaling ISS04. Table 3 compares the results of old and new calculations. Newly calculated parameters are for the uranium-238 SM hybrid that fit well to the reactor part presented below. The listed plasma parameters are already achieved in other fusion devices.

Table 3. The SM hybrid parameters for the case of spent nuclear fuel incineration (Moiseenko et al. 2021) and uranium-238 burning (newly calculated). The values for DRACON-based SM hybrid are given in parentheses.

Further Uragan-2M experiments in the SM regime have shown the possibility of background plasma production and confinement (Moiseenko et al. 2017) in the SM hybrid regime. A discharge was initiated by a radio-frequency pulse of a crankshaft antenna which is placed far away from the embedded mirror location. The discharge start-up was successful, as plasma was produced with a density of (1–3) × 10¹² cm⁻³. The OV and CV lines showed up in the discharge. Their intense emission, especially that of the CV line, indicates an electron temperature of at least 100 eV. The parameter values of the SM discharge are lower, but compatible with those of regular discharges in the stellarator regime. The decrease of the parameter values could be explained by the fact that the minor plasma radius in the SM regime is approximately 1.3 times smaller than in the regular regime.

An experiment to generate sloshing ions in an embedded mirror was carried out on the Uragan-2M. The magnetic beach approach (see e.g. Moiseenko & Ågren 2007) was employed. A compressional Alfvén wave was launched with a two-strap (W7-X-like) antenna (Moiseenko et al. 2020) operated in monopole phasing. In this experiment, the embedded mirror is created near the antenna location. It is expected that on the way to the embedded mirror, at a lower magnetic field, the wave reaches the ion cyclotron layer and heats the sloshing (trapped) ions. A neutral particle analyser is used to detect them. An intense flux of charge-exchange neutrals is observed. The measured energy distribution (Moiseenko et al. 2021) fits well to Maxwellian with a perpendicular temperature of 800 eV.

Theoretical analysis was performed (Moiseenko et al. 2016) for the trapped particle confinement in the Uragan-2M embedded mirror. The mirror had a serious flaw, a curved magnetic axis. Calculated drift surfaces were not closed; hence, there was no radial confinement. Such a situation cannot happen if the embedded mirror have a straight magnetic axis. Unfortunately, this cannot be realized in Uragan-2M in a simple way. Meanwhile, the radial electric field can improve the situation substantially. It causes particle drift in the poloidal direction which competes with the vertical magnetic drift. Above a certain value of the electric field, mean drift surfaces become closed, and particle confinement improves. This value can be obtained from the estimate $e\varphi \sim \mu \Delta B$, where φ is the electric potential, μ is the magnetic moment and ΔB is the variation of the magnetic field across the confinement volume. To establish the electric potential in the plasma column, a very small amount of lost ions is sufficient. The electric potential seems to be small enough and only slightly perturbs the diffusive character of confinement of the bulk plasma.

A candidate for the magnetic confinement device for the SM hybrid is the DRACON magnetic trap system (see figure 5). The stellarator-type DRACON device (see Moiseenko et al. (2016) and references therein) consists of two rectilinear regions and two curvilinear elements (known as CREL), which interconnect the rectilinear parts and whose parameters are chosen so as to keep the Pfirsch–Schlueter currents within the CREL and to prevent them from penetrating into the rectilinear sections. This feature is essential when the rectilinear parts are long and much less important if they are short, as in our case. In order to improve plasma confinement, the magnetic field in the CRELs is higher than the field in the rectilinear parts. So, in fact the rectilinear parts represent two mirror traps, which are closed by the CRELs. Fusion reactions in such a device can be realized in the mirror parts, which confine the hot ion component (tritium) with high perpendicular energy. Unlike the classical DRACON version, the SM device needs one short rather than two longer mirrors. A comparative numerical analysis of collisionless losses occurring in the magnetic trap part of the single-mirror DRACON (Moiseenko et al. 2016) leads to a conclusion about the possibility for high-energy tritium ions to be fairly well confined in the mirror magnetic trap area.

Figure 5. Sketch of DRACON version of SM hybrid.

4. Subcritical nuclear reactor

The fuel used in above-described multi-reprocessing fuel cycle has k _eff smaller than that of a pure plutonium fuel. This is because the main component of this fuel is a fertile isotope, ²³⁸U. This fact has strong impact on reactor design since all the reactor materials except fissile ones are neutron absorbers. A mixture consisting of 25 % fuel and 75 % LBE has k _eff less than unity. Thus, usage of liquid metal cooling of fuel is likely impossible. Gas (helium) cooling is an opportunity in this case.

For preliminary calculations for the nuclear reactor part of the SM hybrid, the proportions of a reactor for spent nuclear fuel incineration (Chernitskiy et al. 2014) were chosen as a prototype. As in previous calculations, the reactor functional blocks are modelled by a homogeneous mixture of the elements of which they consist. Instead of LBE, helium is used. Also, the fuel is considered to be metallic. The following weight fractions were used for the homogenized fission blanket: fuel material, 55.55 %; structure/cladding, 38.79 %; coolant, 0.81 % (assuming that coolant pressure will be 100 atm). A buffer is put between the first wall and the fission blanket in order to increase the neutron flux in the core due to the reaction ²⁰⁷Pb(n,2n)²⁰⁶Pb which has a large cross-section for incident neutron energies above 7 MeV. Also, the buffer has another important purpose to reduce the flow of fission neutrons from the reactor core to the first wall and the vacuum chamber. The homogenized fission blanket mass density is 5.017 g cm⁻³. All other parts of the reactor are kept with similar material contents as in Chernitskiy et al. (2014). The first wall is made of HT-9 steel. The axial reflectors on both sides are modelled by a homogeneous mixture of HT-9 steel and LBE coolant with volume fractions of 70 % and 30 %, respectively. The LBE is assumed to be a mixture of 44.5 wt% lead and 55.5 wt% bismuth with mass density of 10.17 g cm⁻³. The radial reflector in the model is a homogeneous mixture of HT-9 steel and Li17Pb83 (20 % enriched ⁶Li) with volume fractions of 70 % and 30 %, respectively. This mixture is aimed at tritium breeding from the reaction with ⁶Li(n,T)⁴He. A shield is used to reduce the neutron and gamma loads of the SM magnetic coils needed for plasma confinement. The shield contains a 60:40 vol% mixture of the stainless steel alloy S30467 type 304B7 with water.

The parameters varied for MCNPX calculations are the reactor dimensions. The result of the calculations, for a reactor with k _eff = 0.956, is shown in figure 6. Because of less reactive fuel, the reactor sizes increased roughly twice as compared with the reactor in Chernitskiy et al. (2014). The estimated thermal power is about 1.3 (2.6 for the DRACON case) GW_th which corresponds to 0.4 (0.8) GW_e of electric power.

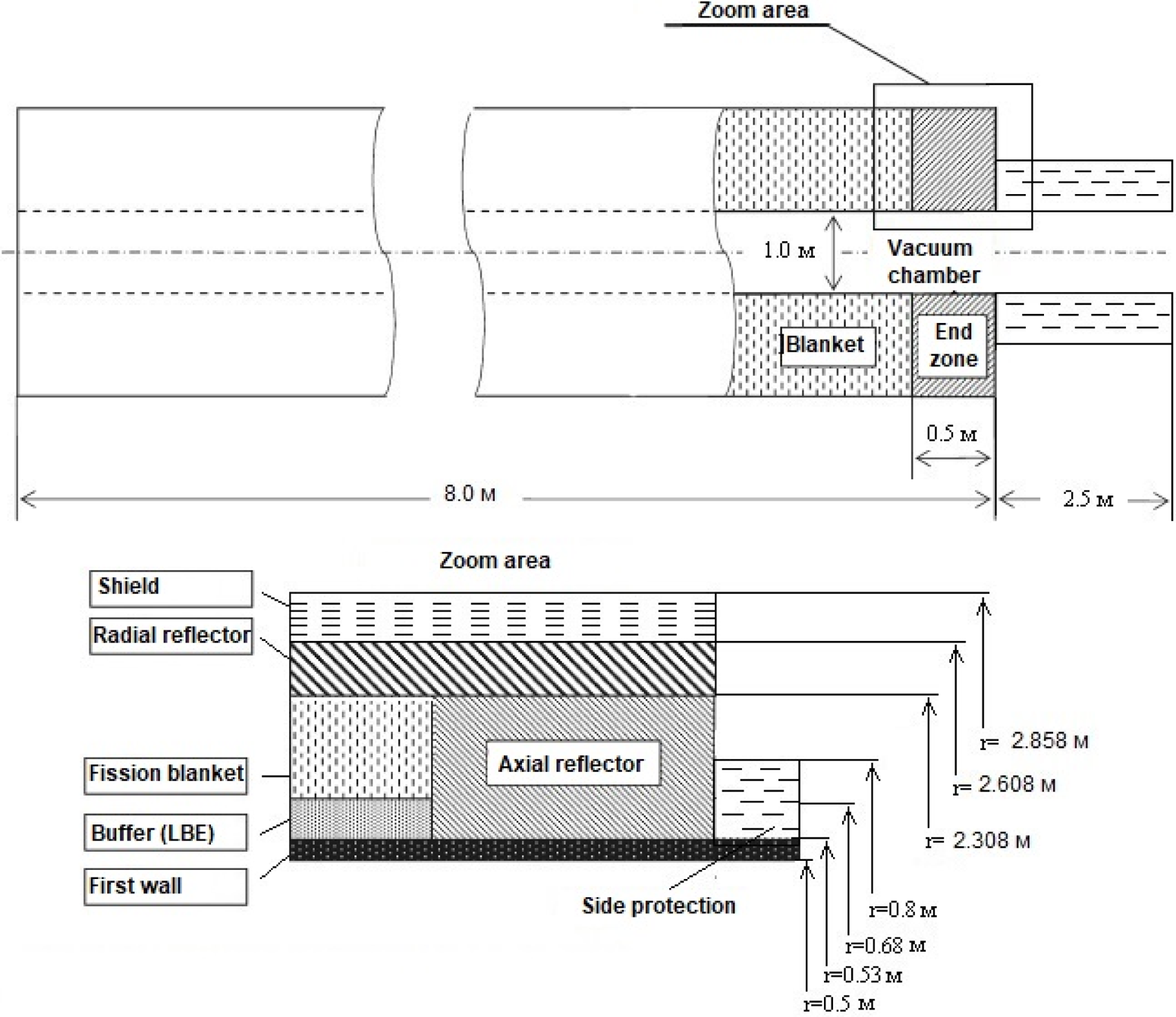
Figure 6. Reactor part of SM hybrid for multiple-recycle fuel cycle.

5. Summary and future plans

The multiple-recycle fuel cycle for uranium-238 considered here, if practically realized, can bring revolutionary changes in nuclear energy. Potentially full usage of uranium-238 makes nuclear energy fuel resources practically infinite. Besides the energy, the fuel cycle principal output is only fission products which are co-products rather than waste. For the same amount of energy produced, the amount of fission products is two orders of magnitude less than the amount of spent nuclear fuel produced within currently exploited nuclear energy production scenarios.

Using the simplest isotope balance model, the key features of the multiple-recycle fuel cycle for uranium-238 are investigated. The repetition of this cycle results in smooth transformation of the initial fuel to ‘stationary’ fuel without strong variations. There is no accumulation of minor actinides due to their fission. The k _eff values and variations are in the frame of acceptability. There is a possibility of not full but only partial extraction of fission products after each cycle. The start-up fuel can be composed of uranium-238 and plutonium. The percentage of plutonium is set to minimize the k _eff variation.

In the start-up fuel the percentage of the plutonium-239 isotope in whole plutonium content is 64 %. During cycling this percentage increases, but does not exceed 76 %. These concentrations are far away from the 93 % required for weapons-grade plutonium. So, in contrast to light water reactors, weapons-grade plutonium can never be produced within the fuel cycle considered.

A problem of the fuel cycle considered as well as other fuel cycles using plutonium is the deficit of delayed neutrons. A solution of this problem is the use of a subcritical nuclear reactor with an external neutron source, i.e. a fusion–fission hybrid system. Here, usage of the SM fusion–fission hybrid for the multiple-recycle fuel cycle for uranium-238 has been analysed. A summary of the experimental and theoretical studies on the SM hybrid is given.

The preliminary results for principal design of the SM hybrid nuclear reactor for multiple-recycle fuel cycle for uranium-238 are presented. The reactor has a design similar to that of a reactor for incineration of spent nuclear fuel (Chernitskiy et al. 2014). The difference is that instead of LBE, gas cooling is used. Also, the reactor is bigger, 13 m in length and 2.86 m in outer radius, and more powerful, about 1.3 (2.6 for the DRACON case) GW_th. The SM hybrid fusion neutron flux should also be proportionally increased for this machine. This is not a problem since fusion neutron generation efficiency increases with the size of the plasma part.

The proposal formulated needs experimental studies, but to build a large SM hybrid machine, substantial investments are necessary. A reasonable first step is to build a compact less costly machine aimed at demonstration of incineration of spent nuclear fuel (Moiseenko et al. 2021). This facilitates developments and improvements of SM hybrid related technologies, including the technologies for closed fuel cycles. A cost estimate for this machine is €0.5 billion. With such a device, there is an important possibility of irradiating by neutrons the multiple-recycle uranium-238-based fuel, which could be added to the reactor active zone in a minor amount, and to study its recycling. The compact SM hybrid experiment will make a basis for a large SM hybrid experimental machine.