1. Introduction
Good confinement of energetic particles (EP) including fusion alpha particles is crucial to improve the burning plasma performance and reduce the wall loading of plasma facing materials in the next generation magnetic confinement fusion devices, such as ITER and CFETR (Tomabechi et al. Reference Tomabechi, Gilleland, Sokolov, Toschi and Team1991; Fasoli et al. Reference Fasoli, Gormenzano, Berk, Breizman, Briguglio, Darrow, Gorelenkov, Heidbrink, Jaun and Konovalov2007; Ding et al. Reference Ding, Pitts, Borodin, Carpentier, Ding, Gong, Guo, Kirschner, Kocan and Li2015; Chen & Zonca Reference Chen and Zonca2016; Wan et al. Reference Wan, Li, Liu, Wang, Chan, Chen, Duan, Fu and Gao2017). Shear Alfvén wave (SAW) instabilities, including Alfvén eigenmodes (Cheng, Chen & Chance Reference Cheng, Chen and Chance1985) (AEs) and EP continuum modes (Chen Reference Chen1994), can be resonantly excited by the expansion free energy associated with the non-uniform EP distribution, since EPs have similar characteristic frequencies as those of SAW in typical reactor parameter regimes (Fasoli et al. Reference Fasoli, Gormenzano, Berk, Breizman, Briguglio, Darrow, Gorelenkov, Heidbrink, Jaun and Konovalov2007). Even finite amplitude SAW instabilities may cause significant anomalous EP loss and performance degradation (Zonca et al. Reference Zonca, Chen, Briguglio, Fogaccia, Vlad and Wang2015; Chen & Zonca Reference Chen and Zonca2016), it is, thus, necessary to have in-depth understanding of the spectrum of SAW, which depends crucially on the nonlinear dynamics of SAW.
There are two possible routes for the nonlinear evolution of EP-driven SAW instability: nonlinear wave–particle phase space dynamics (Berk & Breizman Reference Berk and Breizman1990; Todo et al. Reference Todo, Sato, Watanabe, Watanabe and Horiuchi1995; Zhu, Fu & Ma Reference Zhu, Fu and Ma2013; Zonca et al. Reference Zonca, Chen, Briguglio, Fogaccia, Vlad and Wang2015; Wang et al. Reference Wang, Wang, Briguglio, Qiu, Vlad and Zonca2019) and nonlinear wave–wave interactions (Sagdeev & Galeev Reference Sagdeev and Galeev1969; Hahm & Chen Reference Hahm and Chen1995; Chen & Zonca Reference Chen and Zonca2013), among which, three-wave parametric decay instability is one of the most fundamental nonlinear wave–wave interactions (Sagdeev & Galeev Reference Sagdeev and Galeev1969). Considering the optimal steady state operation scenario of reactors with full non-inductive current drive (Huang et al. Reference Huang, Garofalo, Qian, Gong, Ding, Varela, Chen, Guo, Li and Wu2020), as a specific branch of SAW, the reversed shear Alfvén eigenmode (RSAE) (an alternative name is Alfvén cascades) exists close to the flux surface of $q_{\min }$![]() (Berk et al. Reference Berk, Borba, Breizman, Pinches and Sharapov2001), and can be preferentially excited by fusion produced alpha particles in the core plasmas (Wang et al. Reference Wang, Qiu, Zonca, Briguglio, Fogaccia, Vlad and Wang2018). Here, $q_{\min }$
(Berk et al. Reference Berk, Borba, Breizman, Pinches and Sharapov2001), and can be preferentially excited by fusion produced alpha particles in the core plasmas (Wang et al. Reference Wang, Qiu, Zonca, Briguglio, Fogaccia, Vlad and Wang2018). Here, $q_{\min }$![]() is the off-axis minimum of the safety factor $q$
is the off-axis minimum of the safety factor $q$![]() . Thus, the investigation of the parametric decay process of RSAE has a significant implication for EP transport and overall performance of burning plasmas.
. Thus, the investigation of the parametric decay process of RSAE has a significant implication for EP transport and overall performance of burning plasmas.
The excitation of geodesic acoustic mode (GAM) (Winsor, Johnson & Dawson Reference Winsor, Johnson and Dawson1968; Zonca & Chen Reference Zonca and Chen2008; Qiu, Chen & Zonca Reference Qiu, Chen and Zonca2018a; Conway, Smolyakov & Ido Reference Conway, Smolyakov and Ido2022) by RSAE has been investigated analytically using nonlinear gyrokinetic theory (Wang et al. Reference Wang, Wang, Wei and Qiu2022), where a pump RSAE spontaneously decays into a GAM with toroidally symmetric and poloidally near symmetric mode structures, and a daughter kinetic RSAE (KRSAE) with the same toroidal and poloidal mode numbers as those of the pump RSAE, with the frequency and wavevector matching condition satisfied. It is found that, the resonant parametric decay process can occur if the pump RSAE drive can overcome the threshold due to KRSAE and GAM dissipation caused by, e.g. electron and ion Landau damping, respectively. The excited GAM can transfer energy to thermal ions by ion Landau damping. Thus, the investigated process, besides its apparent effects on RSAE nonlinear saturation, also provides a route to collisionless fuel ion heating, i.e. alpha channelling (Fisch & Herrmann Reference Fisch and Herrmann1994; Qiu et al. Reference Qiu, Chen, Zonca and Chen2018b). Note that, for a given $q$![]() -profile, RSAE frequency lies between toroidal Alfvén eigenmode (TAE) (Cheng et al. Reference Cheng, Chen and Chance1985) and beta-induced Alfvén eigenmode (Heidbrink et al. Reference Heidbrink, Strait, Chu and Turnbull1993) frequency range, depending on the respective $|nq_{\min }-m|$
-profile, RSAE frequency lies between toroidal Alfvén eigenmode (TAE) (Cheng et al. Reference Cheng, Chen and Chance1985) and beta-induced Alfvén eigenmode (Heidbrink et al. Reference Heidbrink, Strait, Chu and Turnbull1993) frequency range, depending on the respective $|nq_{\min }-m|$![]() value. The present channel, is more effective for RSAEs in the TAE frequency range, to have the frequency and (radial) wavenumber matching conditions satisfied. Here, $n/m$
value. The present channel, is more effective for RSAEs in the TAE frequency range, to have the frequency and (radial) wavenumber matching conditions satisfied. Here, $n/m$![]() are the toroidal/poloidal mode numbers of the torus.
are the toroidal/poloidal mode numbers of the torus.
Since RSAE is radially localized around the SAW continuum accumulation point induced by the reversed shear magnetic configuration, with the eigenmode structure and frequency determined by plasma non-uniformities, it is natural to expect that, the plasma non-uniformities will also affect the RSAE nonlinear processes, such as the excitation of GAM of interest here. Consistent with the system non-uniformities, the kinetic dispersiveness that determines the radial propagation of both GAM and KRSAE, leading to the GAM/KRSAE sampling of the non-uniformity, may also be important in the nonlinear process (Rosenbluth Reference Rosenbluth1972), and determine the power deposition by Landau damping of the excited sidebands, that may have a direct consequence on the performance of the burning plasmas. This motivates the present study on the system non-uniformity on the nonlinear excitation of GAM by RSAE.
The rest of the paper is organized as follows. In § 2, the model equations describing the parametric decay process of the pump RSAE into a GAM and a KRSAE are given. In § 3, the effects of kinetic dispersiveness on the parametric decay process are investigated. It is found that, when finite group velocities of both GAM and KRSAE are taken into account, the parametric decay process is a convective instability for typical tokamak parameters. In § 4, the effects of non-uniformities, including non-uniform KRSAE and GAM continuum frequencies and the finite radial extent of pump RSAE, on the parametric decay process are investigated. It is found that, the non-uniformity of KRSAE continuum frequency, $\omega _K(r)$![]() , plays a dominant role in rendering the parametric decay process into a quasiexponentially growing absolute instability by trapping the coupled KRSAE and GAM wave packets between the turning points induced by the non-uniformity of $\omega _K(r)$
, plays a dominant role in rendering the parametric decay process into a quasiexponentially growing absolute instability by trapping the coupled KRSAE and GAM wave packets between the turning points induced by the non-uniformity of $\omega _K(r)$![]() . The GAM continuum, on the other hand, contributes on the time scale comparable to or shorter than the trapping time due to the non-uniformity of $\omega _K(r)$
. The GAM continuum, on the other hand, contributes on the time scale comparable to or shorter than the trapping time due to the non-uniformity of $\omega _K(r)$![]() , and quantitatively modifies the GAM excitation process. Finally, summary and discussions are given in § 5.
, and quantitatively modifies the GAM excitation process. Finally, summary and discussions are given in § 5.
2. Theoretical model
In this work, we will investigate the linear growth stage of the excitation of GAM by the pump RSAE, with emphases on the effects of plasma non-uniformities, such as non-uniform KRSAE and GAM continuum frequencies and the finite spatial extent of the pump RSAE (which is also determined by the RSAE continuum), on the parametric decay process. By ‘linear growth stage’, we mean the feedback of GAM and KRSAE onto the pump RSAE are systematically neglected, which, can become important as the sidebands amplitudes become comparable to the pump RSAE amplitude, and lead to, potentially, complex nonlinear dynamics (Wei, Chen & Qiu Reference Wei, Chen and Qiu2022) as well as ballistic mode propagation in the form of solitons (Guo, Chen & Zonca Reference Guo, Chen and Zonca2009; Chen & Zonca Reference Chen and Zonca2016; Chen et al. Reference Chen, Wei, Wei and Qiu2022). These effects, however, are beyond the scope of present work and focus on the effects of system non-uniformity, and will be investigated in the future.
Since the involved wave frequencies are much smaller than those of the compressional Alfvén wave and $\beta \ll 1$![]() is considered, the scalar potential $\delta \phi$
is considered, the scalar potential $\delta \phi$![]() and parallel component of vector potential $\delta A_\parallel$
and parallel component of vector potential $\delta A_\parallel$![]() are taken as the field variables for investigating the parametric decay process of the pump RSAE $(\boldsymbol {\varOmega }_0 \equiv (\omega _0, \boldsymbol {k}_0))$
are taken as the field variables for investigating the parametric decay process of the pump RSAE $(\boldsymbol {\varOmega }_0 \equiv (\omega _0, \boldsymbol {k}_0))$![]() into a GAM $(\boldsymbol {\varOmega }_G \equiv (\omega _G, \boldsymbol {k}_G))$
into a GAM $(\boldsymbol {\varOmega }_G \equiv (\omega _G, \boldsymbol {k}_G))$![]() and a KRSAE $(\boldsymbol {\varOmega }_K \equiv (\omega _K, \boldsymbol {k}_K))$
and a KRSAE $(\boldsymbol {\varOmega }_K \equiv (\omega _K, \boldsymbol {k}_K))$![]() , with $\beta$
, with $\beta$![]() being the ratio of plasma thermal to magnetic pressure. It is convenient to define $\delta \psi =\omega \delta A_\parallel /(ck_\parallel )$
being the ratio of plasma thermal to magnetic pressure. It is convenient to define $\delta \psi =\omega \delta A_\parallel /(ck_\parallel )$![]() as an alternative field variable for RSAE and KRSAE, where the ideal MHD limit, i.e. vanishing parallel electric field, can be recovered by taking $\delta \psi =\delta \phi$
as an alternative field variable for RSAE and KRSAE, where the ideal MHD limit, i.e. vanishing parallel electric field, can be recovered by taking $\delta \psi =\delta \phi$![]() (Chen & Hasegawa Reference Chen and Hasegawa1991). The total scalar potential perturbation contains $\delta \phi = \delta \phi _0+\delta \phi _K+\delta \phi _G$
(Chen & Hasegawa Reference Chen and Hasegawa1991). The total scalar potential perturbation contains $\delta \phi = \delta \phi _0+\delta \phi _K+\delta \phi _G$![]() , with the subscripts $0$
, with the subscripts $0$![]() , $K$
, $K$![]() and $G$
and $G$![]() denoting the pump RSAE, KRSAE and GAM, respectively. Considering single-$n$
denoting the pump RSAE, KRSAE and GAM, respectively. Considering single-$n$![]() RSAE/KRSAE with one dominant poloidal model number $m$
RSAE/KRSAE with one dominant poloidal model number $m$![]() , the perturbations of RSAE, KRSAE and GAM in straight-field-line ($r,\vartheta, \varphi$
, the perturbations of RSAE, KRSAE and GAM in straight-field-line ($r,\vartheta, \varphi$![]() ) flux coordinate can be expressed as
) flux coordinate can be expressed as
Here, $\phi$![]() is the amplitude of the mode, $\hat {k}_G$
is the amplitude of the mode, $\hat {k}_G$![]() is the radial envelope due to GAM modulation. We note that, the frequency and wavenumber matching conditions, $\boldsymbol {\varOmega }_0=\boldsymbol {\varOmega }_K+\boldsymbol {\varOmega }_G$
is the radial envelope due to GAM modulation. We note that, the frequency and wavenumber matching conditions, $\boldsymbol {\varOmega }_0=\boldsymbol {\varOmega }_K+\boldsymbol {\varOmega }_G$![]() , are applied implicitly.
, are applied implicitly.
The coupled GAM and KRSAE nonlinear equations can be derived by substituting the non-adiabatic particle responses into the field equations of GAM and KRSAE determined by nonlinear gyrokinetic vorticity equation (Chen & Hasegawa Reference Chen and Hasegawa1991) and charge quasineutrality condition, as
while the non-adiabatic particle responses to KRSAE and GAM are derived from the nonlinear gyrokinetic equation (Frieman & Chen Reference Frieman and Chen1982). Equations (2.4) and (2.5) are the nonlinear equations of KRSAE and GAM, respectively. In (2.4), $\mathcal {E}_K \equiv 1-\varGamma _K -k_{K,\parallel }^2 v_A^2 \sigma _K b_K/\omega _K^2 + \varDelta _K$![]() is the WKB dispersion relation of KRSAE, with $\varGamma _k\equiv \langle {\rm J}_k^2 F_0/n_0\rangle$
is the WKB dispersion relation of KRSAE, with $\varGamma _k\equiv \langle {\rm J}_k^2 F_0/n_0\rangle$![]() , $v_A=B_0/\sqrt {4{\rm \pi} n_0 m_i}$
, $v_A=B_0/\sqrt {4{\rm \pi} n_0 m_i}$![]() being the Alfvén speed, $\langle \cdots \rangle$
being the Alfvén speed, $\langle \cdots \rangle$![]() denoting velocity space integration, ${\rm J}_k={\rm J}_{\rm 0}(k_\bot \rho _i)$
denoting velocity space integration, ${\rm J}_k={\rm J}_{\rm 0}(k_\bot \rho _i)$![]() being the Bessel function of zero index accounting for finite Larmor radius (FLR) effects, $\rho _i$
being the Bessel function of zero index accounting for finite Larmor radius (FLR) effects, $\rho _i$![]() being the ion Larmor radius, $b_k= k_\bot ^2 \rho _i^2 /2$
being the ion Larmor radius, $b_k= k_\bot ^2 \rho _i^2 /2$![]() , $\sigma _k\equiv \delta \psi _k/\delta \phi _k=1+\tau -\tau \varGamma _k$
, $\sigma _k\equiv \delta \psi _k/\delta \phi _k=1+\tau -\tau \varGamma _k$![]() , $\tau = T_e/T_i$
, $\tau = T_e/T_i$![]() , and $\sigma _k \neq 1$
, and $\sigma _k \neq 1$![]() corresponding to deviation from ideal MHD limit due to FLR effects. Furthermore, $\varDelta _K$
corresponding to deviation from ideal MHD limit due to FLR effects. Furthermore, $\varDelta _K$![]() represents the kinetic compression of both thermal and EP, and the KRSAE eigenmode equation can be derived by accounting for the curvature of $q$
represents the kinetic compression of both thermal and EP, and the KRSAE eigenmode equation can be derived by accounting for the curvature of $q$![]() at $q_{\min }$
at $q_{\min }$![]() . Note that, in the present work focusing on the ‘linear growth stage’ of the parametric decay process, a finite amplitude pump RSAE is adopted as the initial condition, while its linear excitation by, e.g. EPs, is not considered here. The nonlinear coupling coefficient, $A_K= \varGamma _0-\varGamma _G- \sigma _0 \omega _K (1-\varGamma _K)/(\sigma _K \omega _0)$
. Note that, in the present work focusing on the ‘linear growth stage’ of the parametric decay process, a finite amplitude pump RSAE is adopted as the initial condition, while its linear excitation by, e.g. EPs, is not considered here. The nonlinear coupling coefficient, $A_K= \varGamma _0-\varGamma _G- \sigma _0 \omega _K (1-\varGamma _K)/(\sigma _K \omega _0)$![]() , contains the contribution from both Reynold stress due to ion nonlinearity as well as finite parallel electric field due to nonlinear electron response to KRSAE. In (2.5), $\mathcal {E}_G\equiv \langle (1-{\rm J}_G^2)F_0/n_0\rangle -(T_i/(n_0 e^2)) \overline {\langle e\omega _d ({\rm J}_G \delta H_{G,i}^L -\delta H_{G,e}^L)/\omega _G\rangle }/\overline {\delta \phi _G}$
, contains the contribution from both Reynold stress due to ion nonlinearity as well as finite parallel electric field due to nonlinear electron response to KRSAE. In (2.5), $\mathcal {E}_G\equiv \langle (1-{\rm J}_G^2)F_0/n_0\rangle -(T_i/(n_0 e^2)) \overline {\langle e\omega _d ({\rm J}_G \delta H_{G,i}^L -\delta H_{G,e}^L)/\omega _G\rangle }/\overline {\delta \phi _G}$![]() is the WKB dispersion relation of GAM, with $\overline {(\cdots )}\equiv \int {\rm d}\vartheta (\cdots )/(2{\rm \pi} )$
is the WKB dispersion relation of GAM, with $\overline {(\cdots )}\equiv \int {\rm d}\vartheta (\cdots )/(2{\rm \pi} )$![]() denoting surface averaging, $\omega _d$
denoting surface averaging, $\omega _d$![]() being the magnetic drift frequency and $\delta H$
being the magnetic drift frequency and $\delta H$![]() being the non-adiabatic particle response. The nonlinear coupling coefficient, $A_G\equiv \varGamma _K-\varGamma _0 -(b_0-b_k) k_\parallel ^2 v_A^2 \sigma _0 \sigma _K^*/(\omega _0 \omega _K)$
being the non-adiabatic particle response. The nonlinear coupling coefficient, $A_G\equiv \varGamma _K-\varGamma _0 -(b_0-b_k) k_\parallel ^2 v_A^2 \sigma _0 \sigma _K^*/(\omega _0 \omega _K)$![]() , contains the contribution from the nonlinear Reynolds and Maxwell stresses (Chen & Zonca Reference Chen and Zonca2012), respectively. Interested readers may refer to Wang et al. (Reference Wang, Wang, Wei and Qiu2022) for the detailed derivations and the underlying assumptions of (2.4) and (2.5).
, contains the contribution from the nonlinear Reynolds and Maxwell stresses (Chen & Zonca Reference Chen and Zonca2012), respectively. Interested readers may refer to Wang et al. (Reference Wang, Wang, Wei and Qiu2022) for the detailed derivations and the underlying assumptions of (2.4) and (2.5).
Defining $E_G\equiv \partial _r \delta \phi _G$![]() and adopting the lowest-order KRSAE/GAM dispersion relation, we can obtain the following coupled nonlinear equations:
and adopting the lowest-order KRSAE/GAM dispersion relation, we can obtain the following coupled nonlinear equations:
where $\delta \hat {\phi }_K={\rm i}\sqrt {A_G/A_K} \delta \phi _K$![]() and $\delta \hat {\phi }_0= \delta \phi _0$
and $\delta \hat {\phi }_0= \delta \phi _0$![]() $\sqrt {A_G A_K} ck_{0,\vartheta }/B_0$
$\sqrt {A_G A_K} ck_{0,\vartheta }/B_0$![]() are normalized KRSAE and pump RSAE amplitudes, respectively. The kinetic dispersiveness term of GAM, $\propto C_G$
are normalized KRSAE and pump RSAE amplitudes, respectively. The kinetic dispersiveness term of GAM, $\propto C_G$![]() , comes from FLR and finite orbit width effects, and can be obtained from (9) of Qiu, Chen & Zonca (Reference Qiu, Chen and Zonca2009). On the other hand, $C_K\simeq 3/4 +\tau$
, comes from FLR and finite orbit width effects, and can be obtained from (9) of Qiu, Chen & Zonca (Reference Qiu, Chen and Zonca2009). On the other hand, $C_K\simeq 3/4 +\tau$![]() , with terms proportional to $3/4$
, with terms proportional to $3/4$![]() and $\tau$
and $\tau$![]() represent, respectively, FLR correction to plasma inertial and finite parallel electric field (Chen & Zonca Reference Chen and Zonca1995). Here $\gamma _K$
represent, respectively, FLR correction to plasma inertial and finite parallel electric field (Chen & Zonca Reference Chen and Zonca1995). Here $\gamma _K$![]() and $\gamma _G$
and $\gamma _G$![]() represent the dissipation rates of KRSAE and GAM due to electron and ion contributions to Landau damping, and may determine the threshold of the parametric decay instability. Equations (2.6) and (2.7) are the governing equations describing the parametric decay process of the pump RSAE into the KRSAE and GAM sideband, and will be solved numerically in this work to investigate the effect of plasma non-uniformities as well as kinetic dispersiveness on the nonlinear process. Fourier spectral method for spatial discretization is used in solving (2.6) and (2.7), by changing into a set of ordinary differential equations, which are then solved using MATLAB.
represent the dissipation rates of KRSAE and GAM due to electron and ion contributions to Landau damping, and may determine the threshold of the parametric decay instability. Equations (2.6) and (2.7) are the governing equations describing the parametric decay process of the pump RSAE into the KRSAE and GAM sideband, and will be solved numerically in this work to investigate the effect of plasma non-uniformities as well as kinetic dispersiveness on the nonlinear process. Fourier spectral method for spatial discretization is used in solving (2.6) and (2.7), by changing into a set of ordinary differential equations, which are then solved using MATLAB.
3. The convective/absolute property of the excitation of GAM by RSAE
First, we investigate the effects of finite group velocities due to the kinetic dispersiveness of GAM and KRSAE on the excitation of GAM by a localized pump RSAE. Only the finite radial extent of the pump RSAE, $L_P$![]() , is taken into account, while the non-uniformities associated with $\omega _K(r)$
, is taken into account, while the non-uniformities associated with $\omega _K(r)$![]() and $\omega _G(r)$
and $\omega _G(r)$![]() are neglected by assuming $L_K=L_G=\infty$
are neglected by assuming $L_K=L_G=\infty$![]() , where $L_G$
, where $L_G$![]() and $L_K$
and $L_K$![]() are, respectively, the scale length of GAM and KRSAE continuum frequencies. This simplification is valid in that, the pump RSAE radial eigenmode structure is determined by the RSAE continuum structure, and one naturally has $L_K\sim L_G\gg L_P$
are, respectively, the scale length of GAM and KRSAE continuum frequencies. This simplification is valid in that, the pump RSAE radial eigenmode structure is determined by the RSAE continuum structure, and one naturally has $L_K\sim L_G\gg L_P$![]() , and the effects of $\omega _K(r)$
, and the effects of $\omega _K(r)$![]() and $\omega _G(r)$
and $\omega _G(r)$![]() non-uniformity can be neglected when the considered time scale is shorter than $L_K/V_K$
non-uniformity can be neglected when the considered time scale is shorter than $L_K/V_K$![]() , i.e. before the wave packet propagates and experience the non-uniformity associated with continuum, with $V_K$
, i.e. before the wave packet propagates and experience the non-uniformity associated with continuum, with $V_K$![]() being the characteristic linear KRSAE group velocity, which will be introduced following equation (3.2).
being the characteristic linear KRSAE group velocity, which will be introduced following equation (3.2).
In order to give some insights of the parametric decay process, (2.6) and (2.7) can be reduced to the following form by using temporal and spatial scale expansion of $\delta \hat {\phi }_{K^*}$![]() and $E_G$
and $E_G$![]() , i.e. $\partial _t\simeq \partial _\eta -{\rm i}\omega$
, i.e. $\partial _t\simeq \partial _\eta -{\rm i}\omega$![]() , and $\partial _r\simeq \partial _{\xi }+{\rm i}k_r$
, and $\partial _r\simeq \partial _{\xi }+{\rm i}k_r$![]() , with $|\partial _\eta | \ll |\omega |$
, with $|\partial _\eta | \ll |\omega |$![]() and $|\partial _{\xi }|\ll |k_r|$
and $|\partial _{\xi }|\ll |k_r|$![]() ,
,
Here $V_G=C_G \omega _G^2 \rho _i^2 \hat {k}_r/\hat {\omega }$![]() and $V_K=C_K \omega _K^2\rho _i^2 \hat {k}_r/(\hat {\omega }-\omega _0)$
and $V_K=C_K \omega _K^2\rho _i^2 \hat {k}_r/(\hat {\omega }-\omega _0)$![]() , with $\hat {\omega }$
, with $\hat {\omega }$![]() and $\hat {k}_r$
and $\hat {k}_r$![]() being the frequency and radial wavenumber of GAM determined by the frequency and wavenumber matching conditions of the parametric decay process,
being the frequency and radial wavenumber of GAM determined by the frequency and wavenumber matching conditions of the parametric decay process,
If the finite linear group velocities of GAM and KRSAE are neglected, we can obtain the parametric dispersion relation (Wang et al. Reference Wang, Wang, Wei and Qiu2022),
The threshold condition on pump RSAE amplitude for the parametric decay process can be estimated from $\gamma _G \gamma _K=\hat {k}_r^2 \delta \hat {\phi }_0^2/4$![]() , i.e. nonlinear drive balances the threshold induced by the KRSAE/GAM dissipations.
, i.e. nonlinear drive balances the threshold induced by the KRSAE/GAM dissipations.
When finite group velocities are taken into account, (3.1) and (3.2) are in the standard form of parametric instability discussed in Rosenbluth (Reference Rosenbluth1972), and the mode spatiotemporal evolution is given by (14) of Qiu, Chen & Zonca (Reference Qiu, Chen and Zonca2014). It is known that the instability is a convective amplification process for $V_K V_G >0$![]() , i.e. the nonlinearly excited KRSAE and GAM couple together, and propagate away from the initial position with finite group velocity given by $(V_K+V_G)/2$
, i.e. the nonlinearly excited KRSAE and GAM couple together, and propagate away from the initial position with finite group velocity given by $(V_K+V_G)/2$![]() (Rosenbluth Reference Rosenbluth1972; Qiu et al. Reference Qiu, Chen and Zonca2014) and increasing amplitudes as the temporal growth dominates the radial propagation. For $V_K V_G<0$
(Rosenbluth Reference Rosenbluth1972; Qiu et al. Reference Qiu, Chen and Zonca2014) and increasing amplitudes as the temporal growth dominates the radial propagation. For $V_K V_G<0$![]() , on the other hand, the parametric instability is an absolute instability. To show this in detail, (2.6) and (2.7) are solved numerically. Here, the pump RSAE is localized around the region $r_0=0$
, on the other hand, the parametric instability is an absolute instability. To show this in detail, (2.6) and (2.7) are solved numerically. Here, the pump RSAE is localized around the region $r_0=0$![]() , as shown by the dashed line in figure 1(a), while the KRSAE and GAM are initially loaded at $r_0$
, as shown by the dashed line in figure 1(a), while the KRSAE and GAM are initially loaded at $r_0$![]() with amplitudes much smaller than that of the pump. The sign of $V_KV_G$
with amplitudes much smaller than that of the pump. The sign of $V_KV_G$![]() is determined by the sign of $C_KC_G$
is determined by the sign of $C_KC_G$![]() for the coupled KRSAE and GAM that satisfy the matching condition, as can be seen from their definitions. The fixed $C_K=2$
for the coupled KRSAE and GAM that satisfy the matching condition, as can be seen from their definitions. The fixed $C_K=2$![]() is adopted as a typical parameter, while the sign of $C_G$
is adopted as a typical parameter, while the sign of $C_G$![]() can be changed to investigate the absolute/convective property of the parametric decay instability. As shown in figure 1, for $C_G=1$
can be changed to investigate the absolute/convective property of the parametric decay instability. As shown in figure 1, for $C_G=1$![]() , GAM and KRSAE are coupled together and propagate out of the pump RSAE localized region in the same direction. The amplitude of GAM at the $r_0$
, GAM and KRSAE are coupled together and propagate out of the pump RSAE localized region in the same direction. The amplitude of GAM at the $r_0$![]() decreases with time, exhibiting the typical feature of convective instability. On the other hand, for $C_G=-1$
decreases with time, exhibiting the typical feature of convective instability. On the other hand, for $C_G=-1$![]() , the amplitude of GAM at $r_0$
, the amplitude of GAM at $r_0$![]() keeps growing exponentially, showing the characteristics of an absolute instability.
keeps growing exponentially, showing the characteristics of an absolute instability.

Figure 1. The snapshot of mode structures for $C_G=1$![]() (a,b), and $C_G=-1$
(a,b), and $C_G=-1$![]() (d,e). The GAM amplitude at $r_0$
(d,e). The GAM amplitude at $r_0$![]() versus time for $C_G= 1$
versus time for $C_G= 1$![]() (c) and $C_G=-1$
(c) and $C_G=-1$![]() ( f). The amplitudes of GAM and KRSAE are on the left-hand $y$
( f). The amplitudes of GAM and KRSAE are on the left-hand $y$![]() -axis, the amplitude of RSAE on the right-hand $y$
-axis, the amplitude of RSAE on the right-hand $y$![]() -axis for (a,b,d,e).
-axis for (a,b,d,e).
Note that, $C_K\simeq 3/4+\tau$![]() is positive, while $C_G$
is positive, while $C_G$![]() is positive for typical plasma parameters, as discussed in great detail in Zonca & Chen (Reference Zonca and Chen2008), and $C_G<0$
is positive for typical plasma parameters, as discussed in great detail in Zonca & Chen (Reference Zonca and Chen2008), and $C_G<0$![]() is only assumed artificially here to demonstrate the absolute/convective property of the nonlinear process. Thus, for typical tokamak parameters, the local parametric decay process of the pump RSAE into a GAM and a KRSAE is a convective instability. The generated KRSAE and GAM couple together and propagate out of the unstable region before they can reach sufficiently large amplitude to effectively regulate/suppress Alfvén turbulence. Thus, this process appears to have less interest for improving global confinement performance, which motivates the present investigation of the non-uniform effects associated with GAM and KRSAE continua.
is only assumed artificially here to demonstrate the absolute/convective property of the nonlinear process. Thus, for typical tokamak parameters, the local parametric decay process of the pump RSAE into a GAM and a KRSAE is a convective instability. The generated KRSAE and GAM couple together and propagate out of the unstable region before they can reach sufficiently large amplitude to effectively regulate/suppress Alfvén turbulence. Thus, this process appears to have less interest for improving global confinement performance, which motivates the present investigation of the non-uniform effects associated with GAM and KRSAE continua.
4. Absolute instability of parametric decay process in non-uniform plasma
When spatial scales $|r-r_0| \simeq L_G, L_K$![]() are considered, the non-uniformity of $\omega _K(r)$
are considered, the non-uniformity of $\omega _K(r)$![]() , $\omega _G(r)$
, $\omega _G(r)$![]() and the spatial extent of the pump RSAE must all be taken into account. In particular, the spatial variation of magnetic shear, which correlates with the non-uniform SAW continuum, is mandatory for RSAE formation in realistic tokamak scenario. As will be shown in the following subsections, we construct a representative $\omega _K(r)$
and the spatial extent of the pump RSAE must all be taken into account. In particular, the spatial variation of magnetic shear, which correlates with the non-uniform SAW continuum, is mandatory for RSAE formation in realistic tokamak scenario. As will be shown in the following subsections, we construct a representative $\omega _K(r)$![]() continuum profile as shown in figure 2(a), which is typical for the reversed magnetic shear region, and discuss four scenarios with different combinations of uniform versus non-uniform $\omega _G(r)$
continuum profile as shown in figure 2(a), which is typical for the reversed magnetic shear region, and discuss four scenarios with different combinations of uniform versus non-uniform $\omega _G(r)$![]() profile and radial structure of the pump RSAE. In all the following numerical cases, as shown in figure 2(a), $\omega _K(r)$
profile and radial structure of the pump RSAE. In all the following numerical cases, as shown in figure 2(a), $\omega _K(r)$![]() is symmetric about the origin $r_0$
is symmetric about the origin $r_0$![]() which corresponds to the SAW continuum accumulational point induced by reversed magnetic shear, $\omega _0=0.8 \omega _{K0}$
which corresponds to the SAW continuum accumulational point induced by reversed magnetic shear, $\omega _0=0.8 \omega _{K0}$![]() , with $\omega _{K0}$
, with $\omega _{K0}$![]() being the KRSAE continuum accumulation frequency at $r_0$
being the KRSAE continuum accumulation frequency at $r_0$![]() , $C_G=1$
, $C_G=1$![]() and $C_K=2$
and $C_K=2$![]() are adopted in all the following cases.Footnote 1 Meanwhile, $\omega _G(r)$
are adopted in all the following cases.Footnote 1 Meanwhile, $\omega _G(r)$![]() profile and the pump RSAE structure $\delta \hat {\phi }_0$
profile and the pump RSAE structure $\delta \hat {\phi }_0$![]() are shown in figure 2(b,c), respectively, where the solid curves therein correspond to the ‘non-uniform case’ discussed below and the dashed lines refer to the ‘uniform case’.
are shown in figure 2(b,c), respectively, where the solid curves therein correspond to the ‘non-uniform case’ discussed below and the dashed lines refer to the ‘uniform case’.
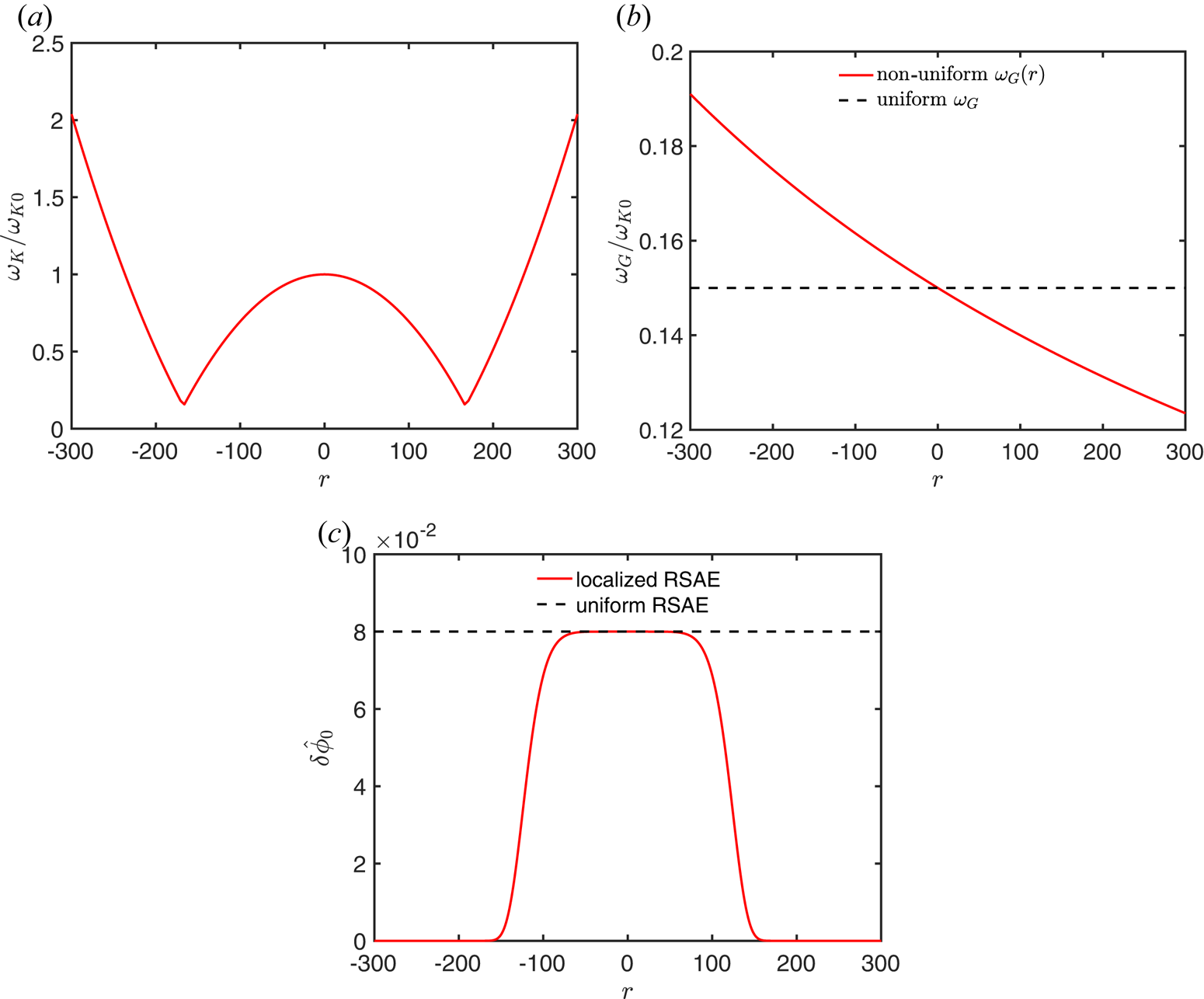
Figure 2. The continua of KRSAE (a) and GAM (b). The normalized mode structure of the pump RSAE (c).
4.1. Uniform $\omega _G$ and uniform pump RSAE
and uniform pump RSAE
In this subsection we investigate the effect of the non-uniform $\omega _K(r)$![]() on the parametric decay process, neglecting the non-uniformity of $\omega _G(r)$
on the parametric decay process, neglecting the non-uniformity of $\omega _G(r)$![]() and the spatial structure of the pump RSAE amplitude. The key parameters include $\omega _G=0.15 \omega _{K0}$
and the spatial structure of the pump RSAE amplitude. The key parameters include $\omega _G=0.15 \omega _{K0}$![]() as shown by the dashed line in figure 2(b), and a uniform amplitude pump RSAE as shown by the dashed line in figure 2(c), and the small KRSAE and GAM initial perturbations are located at $r_0$
as shown by the dashed line in figure 2(b), and a uniform amplitude pump RSAE as shown by the dashed line in figure 2(c), and the small KRSAE and GAM initial perturbations are located at $r_0$![]() , as shown in figure 3(a). The KRSAE frequency satisfy the matching condition, and is given by $\omega _K=\omega _0+\omega _G=0.95 \omega _{K0}$
, as shown in figure 3(a). The KRSAE frequency satisfy the matching condition, and is given by $\omega _K=\omega _0+\omega _G=0.95 \omega _{K0}$![]() . As can be estimated from figure 2(a), $\omega _K$
. As can be estimated from figure 2(a), $\omega _K$![]() intersects with the KRSAE continuum at $r\simeq \pm 240$
intersects with the KRSAE continuum at $r\simeq \pm 240$![]() , forming a pair of turning points, as shown by the vertical dashed lines in figure 3.
, forming a pair of turning points, as shown by the vertical dashed lines in figure 3.

Figure 3. Snapshots of mode structures of GAM and KRSAE at six different times with a uniform pump RSAE.
The coupled nonlinear equations (2.6) and (2.7) with the above given parameters are solved numerically as an initial value problem, and the obtained mode structures of KRSAE and GAM at six different times are shown in figure 3. It is found that, the coupled GAM and KRSAE wave packets propagate away from the original position. As the coupled KRSAE/GAM reaches the turning points by KRSAE continuum, majority of propagating wave energy will be bounced back, and then propagate inward, reach the turning points on the other side, completing a full ‘bouncing period’ of wave packets. Thus, the wave packets are effectively trapped by non-uniform $\omega _{K}(r)$![]() structure.
structure.
The logarithm of the GAM amplitude at $r_0$![]() is shown by the solid curve in figure 4. The amplitude of GAM at $r_0$
is shown by the solid curve in figure 4. The amplitude of GAM at $r_0$![]() firstly decays in time interval of 0–600, indicating the parametric decay process is indeed a convective instability during this time interval, as shown in § 3. Then the amplitude of GAM at $r_0$
firstly decays in time interval of 0–600, indicating the parametric decay process is indeed a convective instability during this time interval, as shown in § 3. Then the amplitude of GAM at $r_0$![]() increases quasiexponentially, after the wave packet is reflected by the turning points, demonstrating that the non-uniform $\omega _K(r)$
increases quasiexponentially, after the wave packet is reflected by the turning points, demonstrating that the non-uniform $\omega _K(r)$![]() structure renders the convective instability into a quasiexponentially growing absolute instability in the longer time scale.
structure renders the convective instability into a quasiexponentially growing absolute instability in the longer time scale.

Figure 4. Logarithm of $E_G$![]() versus $t$
versus $t$![]() with a uniform pump RSAE. The solid curve represents the result with uniform $\omega _G$
with a uniform pump RSAE. The solid curve represents the result with uniform $\omega _G$![]() , while the dashed curve represents the result with non-uniform $\omega _G(r)$
, while the dashed curve represents the result with non-uniform $\omega _G(r)$![]() .
.
4.2. Uniform $\omega _G$ with localized pump RSAE
with localized pump RSAE
In order to investigate the effect of the finite spatial extent of RSAE on the parametric decay process, the coupled equations (2.6) and (2.7) are solved numerically with a uniform $\omega _G$![]() and a localized pump RSAE, while other parameters are the same as those adopted in § 4.1.
and a localized pump RSAE, while other parameters are the same as those adopted in § 4.1.
The evolution of GAM and KRSAE mode structures are shown in figure 5. Firstly, the coupled wave packet propagates away from the origin. When the coupled wave packet propagates out of the pump RSAE localized region, GAM and KRSAE are decoupled from each other, as can be clearly seen from (2.6) and (2.7) by turning off the nonlinear coupling due to finite pump amplitude. As a result, KRSAE and GAM mode packets separate in regions with vanishing pump RSAE amplitude, as KRSAE linear group velocity is much larger than that of GAM, as can be seen in figure 5(b). When KRSAE reaches the turning points due to non-uniform $\omega _K(r)$![]() , KRSAE will be reflected, and couple with GAM again as the KRSAE reaches the pump RSAE localization region. The coupled KRSAE and GAM wave packets will propagate towards and through the origin with increasing amplitude, until they will decouple again when they propagate away the pump RSAE localized region on the other side. The KRSAE with larger linear group velocity will reach and be reflected by the turning point caused by non-uniform $\omega _K(r)$
, KRSAE will be reflected, and couple with GAM again as the KRSAE reaches the pump RSAE localization region. The coupled KRSAE and GAM wave packets will propagate towards and through the origin with increasing amplitude, until they will decouple again when they propagate away the pump RSAE localized region on the other side. The KRSAE with larger linear group velocity will reach and be reflected by the turning point caused by non-uniform $\omega _K(r)$![]() on the other side, completing a full bounce period due to non-uniform $\omega _K(r)$
on the other side, completing a full bounce period due to non-uniform $\omega _K(r)$![]() , similar to the case shown in § 4.1. We note that GAM, with the linear group velocity much smaller than KRSAE, even though it can propagate outside of the pump RSAE localization region ($r\sim \pm 150$
, similar to the case shown in § 4.1. We note that GAM, with the linear group velocity much smaller than KRSAE, even though it can propagate outside of the pump RSAE localization region ($r\sim \pm 150$![]() in figure 5), it will be heavily damped before reaching the turning points, as a finite damping is present, depositing majority of its energy in the tokamak centre.
in figure 5), it will be heavily damped before reaching the turning points, as a finite damping is present, depositing majority of its energy in the tokamak centre.

Figure 5. Snapshots of mode structures of GAM and KRSAE at four different times with a localized pump RSAE.
The amplitude of GAM at $r_0$![]() is shown by the solid line in figure 6. It is shown that, the amplitude of GAM at $r_0$
is shown by the solid line in figure 6. It is shown that, the amplitude of GAM at $r_0$![]() decreases in the time interval of 0–1800, and grows exponentially after the wave packet is reflected by the turning points, similar to the case with uniform pump RSAE amplitude, as shown by the solid curve in figure 4. By comparing the solid lines in figure 6 with those in figure 4, we can conclude that, while the non-uniform $\omega _K(r)$
decreases in the time interval of 0–1800, and grows exponentially after the wave packet is reflected by the turning points, similar to the case with uniform pump RSAE amplitude, as shown by the solid curve in figure 4. By comparing the solid lines in figure 6 with those in figure 4, we can conclude that, while the non-uniform $\omega _K(r)$![]() plays a dominant role in rendering the parametric decay process into a quasiexponentially growing absolute instability, the overall growth rate of GAM in the case with localized pump RSAE is significantly lower than that with uniform pump RSAE, suggesting the importance of system non-uniformity in qualitatively and quantitatively understanding the GAM excitation in the long time scales.
plays a dominant role in rendering the parametric decay process into a quasiexponentially growing absolute instability, the overall growth rate of GAM in the case with localized pump RSAE is significantly lower than that with uniform pump RSAE, suggesting the importance of system non-uniformity in qualitatively and quantitatively understanding the GAM excitation in the long time scales.

Figure 6. Logarithm of $E_G$![]() versus $t$
versus $t$![]() with a localized pump RSAE. The solid curves represent the results with uniform $\omega _G(r)$
with a localized pump RSAE. The solid curves represent the results with uniform $\omega _G(r)$![]() , while the dashed curves represent the results with non-uniform $\omega _G$
, while the dashed curves represent the results with non-uniform $\omega _G$![]() .
.
4.3. Non-uniform $\omega _G$ and uniform pump RSAE
and uniform pump RSAE
In order to investigate the effect of non-uniform $\omega _G(r)$![]() on the parametric decay process, a case similar to that adopted in § 4.1 but with non-uniform $\omega _G(r)$
on the parametric decay process, a case similar to that adopted in § 4.1 but with non-uniform $\omega _G(r)$![]() , as shown by the solid line in figure 2(b), is carried out. Due to the non-uniformity of $\omega _G(r)$
, as shown by the solid line in figure 2(b), is carried out. Due to the non-uniformity of $\omega _G(r)$![]() , one readily finds that the excited GAM has a larger frequency and $k_r$
, one readily finds that the excited GAM has a larger frequency and $k_r$![]() in the region $r<0$
in the region $r<0$![]() than that in the region $r>0$
than that in the region $r>0$![]() , which may cause larger growth rate of GAM and KRSAE in the region $r<0$
, which may cause larger growth rate of GAM and KRSAE in the region $r<0$![]() , as indicated by (3.5).
, as indicated by (3.5).
The obtained mode structures of GAM and KRSAE at six different times are shown in figure 7. It shows that, as anticipated, the mode structures propagating on both sides are not symmetric due to the non-uniformity of $\omega _G(r)$![]() . The wave packet initially propagating towards the $r<0$
. The wave packet initially propagating towards the $r<0$![]() region has larger $k_r$
region has larger $k_r$![]() and, consequently, larger growth rate, as shown in figure 7(b). Due to larger group velocity, KRSAE in the region $r<0$
and, consequently, larger growth rate, as shown in figure 7(b). Due to larger group velocity, KRSAE in the region $r<0$![]() reaches the turning point earlier than that in the region $r>0$
reaches the turning point earlier than that in the region $r>0$![]() . Note that, as the wave approaches the turning point, $k_r \rightarrow 0$
. Note that, as the wave approaches the turning point, $k_r \rightarrow 0$![]() and thus the KRSAE/GAM growth rate $\gamma \rightarrow 0$
and thus the KRSAE/GAM growth rate $\gamma \rightarrow 0$![]() consequently, and the wave amplitude on the $r>0$
consequently, and the wave amplitude on the $r>0$![]() sideband may outgrow that on the $r<0$
sideband may outgrow that on the $r<0$![]() side as shown in figure 7(d), due to the larger initial group velocity on the $r<0$
side as shown in figure 7(d), due to the larger initial group velocity on the $r<0$![]() side. Also consistent with the larger initial $k_r$
side. Also consistent with the larger initial $k_r$![]() , the wave packet is firstly reflected by the turning point on the $r<0$
, the wave packet is firstly reflected by the turning point on the $r<0$![]() side, as shown in figure 7(e, f). Except for the asymmetry induced by $\omega _G(r)$
side, as shown in figure 7(e, f). Except for the asymmetry induced by $\omega _G(r)$![]() , the evolution of the mode structures of GAM and KRSAE is similar to that described in § 4.1, i.e. the wave packet is trapped between the turning points due to non-uniform $\omega _K(r)$
, the evolution of the mode structures of GAM and KRSAE is similar to that described in § 4.1, i.e. the wave packet is trapped between the turning points due to non-uniform $\omega _K(r)$![]() .
.

Figure 7. Snapshots of mode structures of GAM and KRSAE at six different times with a uniform pump RSAE.
The logarithm of GAM amplitude at $r_0$![]() is shown by the dashed line in figure 4. It shows that GAM amplitude at $r_0$
is shown by the dashed line in figure 4. It shows that GAM amplitude at $r_0$![]() evolves similarly with that in uniform $\omega _G$
evolves similarly with that in uniform $\omega _G$![]() case, suggesting that $\omega _K(r)$
case, suggesting that $\omega _K(r)$![]() plays a dominate role on rendering the convective instability into a quasiexponentially absolute instability, while the non-uniform $\omega _G$
plays a dominate role on rendering the convective instability into a quasiexponentially absolute instability, while the non-uniform $\omega _G$![]() plays a relatively minor role on quantitatively changing the profile to be asymmetric between the two sides of $r_0$
plays a relatively minor role on quantitatively changing the profile to be asymmetric between the two sides of $r_0$![]() .
.
4.4. Non-uniform $\omega _G$ and localized pump RSAE
and localized pump RSAE
In real physical processes, non-uniformities of $\omega _K(r)$![]() and $\omega _G(r)$
and $\omega _G(r)$![]() and the finite spatial extent of pump RSAE exist simultaneously. A numerical case containing all the non-uniformities is carried out in this subsection. The pump RSAE is assumed to be localized around $r_0$
and the finite spatial extent of pump RSAE exist simultaneously. A numerical case containing all the non-uniformities is carried out in this subsection. The pump RSAE is assumed to be localized around $r_0$![]() as shown in figure 2(c). The non-uniform $\omega _G(r)$
as shown in figure 2(c). The non-uniform $\omega _G(r)$![]() is the solid line shown in figure 2(b).
is the solid line shown in figure 2(b).
The mode structures of KRSAE and GAM at six different times are shown in figure 8, and the observed phenomena can be understood based on the knowledge obtained from previous cases which delineate each effect separately. Similar to the case in § 4.3, the modes propagating on both sides of $r_0$![]() are not symmetric due to larger $k_r$
are not symmetric due to larger $k_r$![]() and consequently, larger growth rate and propagation speed on the $r<0$
and consequently, larger growth rate and propagation speed on the $r<0$![]() side, as a result of the $\omega _G(r)$
side, as a result of the $\omega _G(r)$![]() non-uniformity. The major difference with that observed in § 4.3 comes from the localized RSAE pump, which causes the KRSAE and GAM decoupling and stopping growth as they propagate out of RSAE localization. Thus, the vanishing $k_r$
non-uniformity. The major difference with that observed in § 4.3 comes from the localized RSAE pump, which causes the KRSAE and GAM decoupling and stopping growth as they propagate out of RSAE localization. Thus, the vanishing $k_r$![]() as the KRSAE approaching the turning point, and the resulting longer time of the mode propagating near and reflecting by the turning point, will not cause the mode structure on the $r>0$
as the KRSAE approaching the turning point, and the resulting longer time of the mode propagating near and reflecting by the turning point, will not cause the mode structure on the $r>0$![]() side outgrowing that on $r<0$
side outgrowing that on $r<0$![]() side, as is in the case with uniform pump RSAE. Thus, the mode structure on the $r<0$
side, as is in the case with uniform pump RSAE. Thus, the mode structure on the $r<0$![]() side, always has a much larger amplitude, as shown by figure 8. This may have a direct consequence on RSAE/GAM dissipation induced power deposition to thermal plasmas, noting the anomalous heating rate is typically proportional to the mode intensity. The anomalous thermal ion heating induced by GAM collisionless damping tends to be accumulated in the plasma core region, which may be beneficial for effective power transfer from EP to thermal ions. Finally the evolution of GAM amplitude at $r_0$
side, always has a much larger amplitude, as shown by figure 8. This may have a direct consequence on RSAE/GAM dissipation induced power deposition to thermal plasmas, noting the anomalous heating rate is typically proportional to the mode intensity. The anomalous thermal ion heating induced by GAM collisionless damping tends to be accumulated in the plasma core region, which may be beneficial for effective power transfer from EP to thermal ions. Finally the evolution of GAM amplitude at $r_0$![]() is shown by the dashed curve of figure 6, which is, qualitatively similar to the case with uniform $\omega _G$
is shown by the dashed curve of figure 6, which is, qualitatively similar to the case with uniform $\omega _G$![]() and localized RSAE pump, confirming the dominant role played by the $\omega _K(r)$
and localized RSAE pump, confirming the dominant role played by the $\omega _K(r)$![]() continuum in qualitatively changing the nonlinear process into the quasiexponentially growing absolute instability.
continuum in qualitatively changing the nonlinear process into the quasiexponentially growing absolute instability.

Figure 8. Snapshots of mode structures of GAM and KRSAE at six different times with a localized pump RSAE.
5. Conclusions and discussions
In this paper, nonlinear excitation of GAM by RSAE is investigated numerically in non-uniform plasmas, accounting for the finite linear group velocities of KRSAE and GAM sidebands due to kinetic dispersiveness, non-uniformities of both KRSAE and GAM continuum frequency and finite radial extent of the pump RSAE. This nonlinear decay channel of RSAE was originally proposed and analysed in Wang et al. (Reference Wang, Wang, Wei and Qiu2022), due to the potential important roles of RSAE nonlinear dynamics in reactor burning plasmas with advanced reversed shear configuration and core localized fusion alpha particles. This channel may lead to RSAE nonlinear saturation, as well as thermal plasma heating due to KRSAE/GAM Landau damping, and is expected to directly affect the sustained burning of fusion plasmas. This present investigated process, while very sensitive to plasma parameters, may have a comparable cross-section with other dominant nonlinear mode coupling channels, e.g. zero-frequency zonal structure generation (Wei et al. Reference Wei, Wang, Chen and Qiu2021; Wang et al. Reference Wang, Wang, Wei and Qiu2022).
For a typical tokamak parameter with $C_G$![]() and $C_K$
and $C_K$![]() being both positive, the nonlinearly excited GAM and KRSAE satisfying the frequency and wavevector matching conditions propagate radially in the same direction, so the parametric decay of the pump RSAE into a KRSAE and a GAM is a convective amplification process, which motivates the inclusion of system non-uniformity in the analyses. There are three spatial scales involved, $L_P$
being both positive, the nonlinearly excited GAM and KRSAE satisfying the frequency and wavevector matching conditions propagate radially in the same direction, so the parametric decay of the pump RSAE into a KRSAE and a GAM is a convective amplification process, which motivates the inclusion of system non-uniformity in the analyses. There are three spatial scales involved, $L_P$![]() , $L_G$
, $L_G$![]() and $L_K$
and $L_K$![]() , corresponding, respectively, to the characteristic scales of pump RSAE width, GAM and SAW continuum variation, and one typically has $L_P\ll L_G\sim L_K$
, corresponding, respectively, to the characteristic scales of pump RSAE width, GAM and SAW continuum variation, and one typically has $L_P\ll L_G\sim L_K$![]() . Since $\omega _K(r)$
. Since $\omega _K(r)$![]() is crucial for RSAE existence, it is always kept in the analysis, while cases with different combinations of pump RSAE radial structure and $\omega _G(r)$
is crucial for RSAE existence, it is always kept in the analysis, while cases with different combinations of pump RSAE radial structure and $\omega _G(r)$![]() non-uniformity are studied to investigate their respective effects on GAM excitaion. It is found that, when the non-uniformity of $\omega _K(r)$
non-uniformity are studied to investigate their respective effects on GAM excitaion. It is found that, when the non-uniformity of $\omega _K(r)$![]() is considered, KRSAE, as well as GAM, will be trapped between the turning points caused by non-uniform $\omega _K(r)$
is considered, KRSAE, as well as GAM, will be trapped between the turning points caused by non-uniform $\omega _K(r)$![]() , and the parametric decay process is rendered into a quasiexponentially growing absolute instability. The non-uniformity of $\omega _G(r)$
, and the parametric decay process is rendered into a quasiexponentially growing absolute instability. The non-uniformity of $\omega _G(r)$![]() continuum introduces asymmetries between outward and inward propagating mode amplitudes before the modes reach the turning points induced by the non-uniform $\omega _K(r)$
continuum introduces asymmetries between outward and inward propagating mode amplitudes before the modes reach the turning points induced by the non-uniform $\omega _K(r)$![]() . The radial extent of the pump RSAE can effectively reduce the overall growth rate of the nonlinearly excited GAM. These numerical investigations suggest that kinetic dispersiveness and plasma non-uniformities must be accounted for to correctly capture the property of the parametric decay process and quantitatively assess the power deposition and anomalous plasma heating due to KRSAE and GAM Landau damping. When all the three major non-uniformities as well as kinetic dispersiveness are taken into account, it is found that, the nonlinearly excited KRSAE/GAM have much larger amplitudes in the $r< r_0$
. The radial extent of the pump RSAE can effectively reduce the overall growth rate of the nonlinearly excited GAM. These numerical investigations suggest that kinetic dispersiveness and plasma non-uniformities must be accounted for to correctly capture the property of the parametric decay process and quantitatively assess the power deposition and anomalous plasma heating due to KRSAE and GAM Landau damping. When all the three major non-uniformities as well as kinetic dispersiveness are taken into account, it is found that, the nonlinearly excited KRSAE/GAM have much larger amplitudes in the $r< r_0$![]() region, which corresponds to a radial inner region with respect to $q_{\min }$
region, which corresponds to a radial inner region with respect to $q_{\min }$![]() . Thus, this nonlinear decay channel of fusion-alpha-particle-driven RSAE, is expected to deposit fusion alpha particle power in the tokamak centre, and directly contributes to the sustained burning of fusion reactors.
. Thus, this nonlinear decay channel of fusion-alpha-particle-driven RSAE, is expected to deposit fusion alpha particle power in the tokamak centre, and directly contributes to the sustained burning of fusion reactors.
In the present study, the KRSAE/GAM sidebands dissipation rates, $\gamma _G$![]() and $\gamma _K$
and $\gamma _K$![]() , are systematically taken as zero, to focus on the global property of the nonlinear process, i.e. the propagation of the coupled KRSAE/GAM wave packets between the two turning points induced by $\omega _K(r)$
, are systematically taken as zero, to focus on the global property of the nonlinear process, i.e. the propagation of the coupled KRSAE/GAM wave packets between the two turning points induced by $\omega _K(r)$![]() continuum. We note that, $\gamma _G$
continuum. We note that, $\gamma _G$![]() and $\gamma _K$
and $\gamma _K$![]() are crucial for the ‘alpha channelling’ process, as they not only determine the threshold of the spontaneous decay process, but also determine the rate of thermal plasma heating. In fact, the former requires $\gamma _G$
are crucial for the ‘alpha channelling’ process, as they not only determine the threshold of the spontaneous decay process, but also determine the rate of thermal plasma heating. In fact, the former requires $\gamma _G$![]() and $\gamma _K$
and $\gamma _K$![]() to be small to have the decay process occur, while the latter, requires $\gamma _G$
to be small to have the decay process occur, while the latter, requires $\gamma _G$![]() and $\gamma _K$
and $\gamma _K$![]() to be big to have efficient power transfer to thermal plasmas via GAM/KRSAE Landau damping. Thus, to find the optimized operation regime for efficient collisionless fuel ion heating, more in-depth numerical investigations with realistic geometry are needed, and will be carried out in a future publication.
to be big to have efficient power transfer to thermal plasmas via GAM/KRSAE Landau damping. Thus, to find the optimized operation regime for efficient collisionless fuel ion heating, more in-depth numerical investigations with realistic geometry are needed, and will be carried out in a future publication.
As a final remark, the present analysis adopts RSAE as a paradigm case, and is general and can be applied to other AEs, e.g. the nonlinear decay of toroidal Alfvén eigenmodes (Cheng et al. Reference Cheng, Chen and Chance1985) into its corresponding kinetic counterpart, kinetic TAE (Mett & Mahajan Reference Mett and Mahajan1992; Berk, Mett & Lindberg Reference Berk, Mett and Lindberg1993) and GAM (Qiu et al. Reference Qiu, Chen, Zonca and Chen2018b), with the continuum structure consistently changed but the essential physics of distant continuum coupling and wave trapping are the same. The present analysis, however, is of particular importance, as we have addressed, due to the relevance of RSAE in the centre of future reactors (Wang et al. Reference Wang, Qiu, Zonca, Briguglio, Fogaccia, Vlad and Wang2018; Huang et al. Reference Huang, Garofalo, Qian, Gong, Ding, Varela, Chen, Guo, Li and Wu2020).
Acknowledgements
This work is supported by the National Key R&D Program of China under grant nos. 2019YFE03020003 and 2017YFE0301900, the National Science Foundation of China under grant nos. 11875233 and Users of Excellence program of Hefei Science Center CAS under contract no. 2021HSC-UE016.
Editor P. Catto thanks the referees for their advice in evaluating this article.
Declaration of interests
The authors report no conflict of interest.


























