1 Introduction
The flow of a film or drop over a solid surface is ubiquitous in industry and science, with applications in microfluidics, ink-jet printing, coatings and crop spraying, to name a few (Bonn et al.
Reference Bonn, Eggers, Indekeu, Meunier and Rolley2009). A prerequisite for understanding such phenomena is an accurate model of the contact line – the curve defined by the edge of the drop where the free surface meets the solid surface. For the drop to move, the contact line must also move. This seemingly obvious and innocuous statement hides a conundrum: moving the contact line while respecting the no-slip boundary condition leads to a divergence of the shear stress, or equivalently the dissipation rate. Research on this problem, though far from over, has proved to be a rich source of insights, as well as new physics and mathematics.
For a drop on a smooth homogeneous surface spreading due to capillarity, the motion of the contact line is largely understood (see, for example, Snoeijer & Andreotti Reference Snoeijer, Andreotti, Davis and Moin2013). The same cannot be said about inertia-dominated spreading, as occurs when a drop is subjected to vibrations or impacts a solid surface at speed. Moreover, most spreading applications must contend with contact line pinning – an effect epitomized by a drop tenaciously clinging to a windshield even when the car is in motion. Pinning is caused by microscopic irregularities that act as energy barriers hindering the motion of a drop, and are present on even the smoothest looking surfaces, such as glass (Good Reference Good1992; Mistura & Pierno Reference Mistura and Pierno2017). In the quasistatic limit, pinning manifests as hysteresis in the relationship between contact line speed and the contact angle. Inertia-dominated spreading on a regular surface is currently poorly understood – partly because of the difficulty in disentangling pinning and inertia. In this issue, Sartori et al. (Reference Sartori, Guglielmin, Ferraro, Filippi, Zaltron, Pierno and Mistura2019) investigate the motion of a drop induced by vibrations on a surface with very low hysteresis, shedding needed light on this regime.
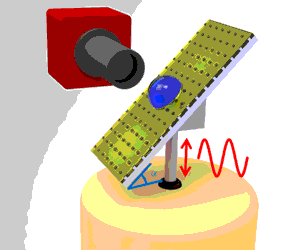
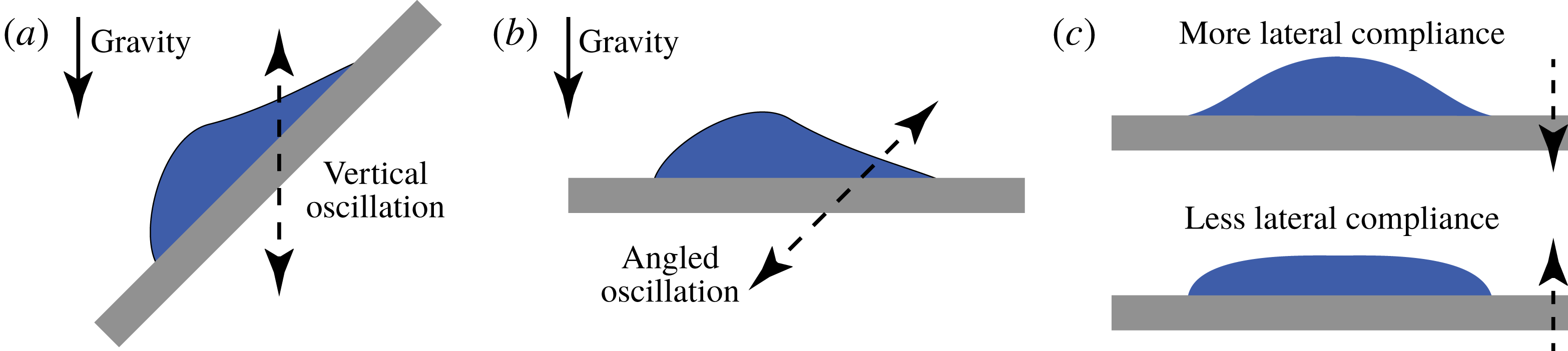
Figure 1. (a) Experimental configuration in climbing-drop experiments. A drop rests on an inclined substrate undergoing harmonic oscillations along the vertical axis. The drop moves rightwards on the substrate. (b) Alternative experimental configuration where gravity plays no role but the drop still moves rightwards. (c) Schematic indicating that the drop is more susceptible to sideways oscillations during the down stroke of the oscillation.
2 Overview
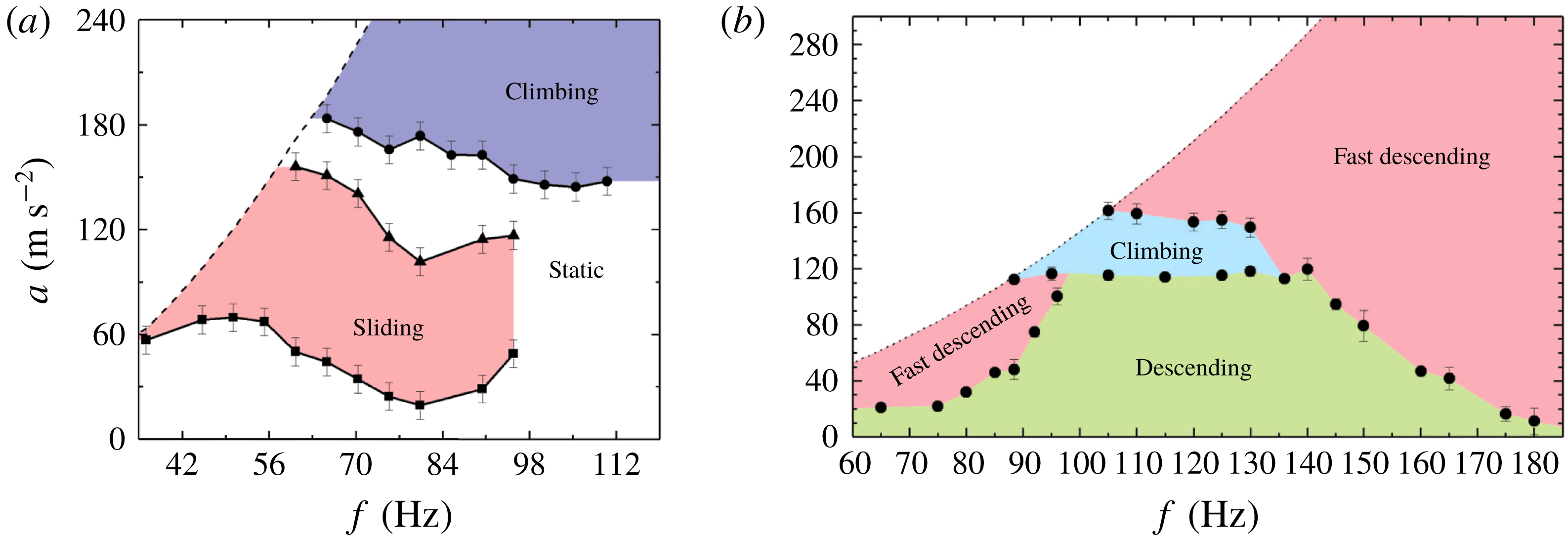
Since the work of Daniel, Chaudhury & de Gennes (Reference Daniel, Chaudhury and de Gennes2005), it is known that drops can be moved across a surface with vibrations. (We omit from this discussion the surface acoustic wave technique, which also employs vibrations but with much higher frequencies.) They showed how a drop on a horizontal substrate vibrated in the horizontal direction with an anharmonic waveform will cause the drop to translate. Daniel et al. (Reference Daniel, Chaudhury and de Gennes2005) ascribed the movement to a ratchet-like response of the contact line in the presence of pinning. Brunet, Eggers & Deegan (Reference Brunet, Eggers and Deegan2007) discovered that a drop will climb up an inclined substrate oscillated vertically with a sufficiently large harmonic amplitude. In their experiment, a drop of silicone oil was placed on an inclined plate of polymethylmethacrylate (PMMA) and vibrated in the vertical direction, as illustrated in figure 1(a). Initially the drop was pinned by the surface. Several thresholds for qualitatively different responses were observed as the amplitude of vibration was increased. Above the first threshold the drop moves down the plate. Above the next threshold the drop stops moving. Above yet a higher threshold the drop moves up the plate. This last regime was found to persist up to the highest accelerations obtainable with their apparatus. A typical phase diagram of this behaviour is shown in figure 2(a). Additional experiments by Brunet, Eggers & Deegan (Reference Brunet, Eggers and Deegan2009) and Sartori et al. (Reference Sartori, Quagliati, Varagnolo, Pierno, Mistura, Magaletti and Casciola2015) confirmed these results and extended them to other liquids.
While the ability of drops to climb may appear paradoxical at first glance, the experiments of Brunet et al. (Reference Brunet, Eggers and Deegan2007) show that gravity is a confounding factor and the problem is better understood by configuring experiments as shown in figure 1(b), where the effect of gravity is nullified. In this configuration, drops are pinned at the lower accelerations, while above a threshold they de-pin and move to the right. Noblin, Kofman & Celestini (Reference Noblin, Kofman and Celestini2009) showed that the problem is better conceptualized by decomposing the angled vibrations into vertical and horizontal components, with a phase difference that can be tuned to vary the mean speed of the drop from positive to negative. As shown in figure 1(c), the vertical oscillations alternately make the drop tall or flat, depending on the direction of the acceleration; superimposed horizontal vibrations will rock the drop more when the drop is tall, and thus more compliant, compared to when the drop is flattened and less compliant.
Various models with differing assumptions and approximations have been proposed to explain the cause of climbing drops (Benilov Reference Benilov2010; John & Thiele Reference John and Thiele2010; Benilov Reference Benilov2011; Benilov & Billingham Reference Benilov and Billingham2011; Benilov & Cummins Reference Benilov and Cummins2013; Borcia, Borcia & Bestehorn Reference Borcia, Borcia and Bestehorn2014; Sartori et al.
Reference Sartori, Quagliati, Varagnolo, Pierno, Mistura, Magaletti and Casciola2015; Ding et al.
Reference Ding, Zhu, Gao and Lu2018). A recent overview of these is given in Bradshaw & Billingham (Reference Bradshaw and Billingham2018). Recurring questions in these theoretical models are the role of and need for contact line hysteresis and the appropriate model for the contact line. All models are able to produce climbing drops, and all either explicitly show that contact line pinning is unnecessary or leave it out entirely.
Figure 2. Phase diagram for a water drop (a) on a PMMA surface from (Sartori et al.
Reference Sartori, Quagliati, Varagnolo, Pierno, Mistura, Magaletti and Casciola2015) and (b) on a LIS from Sartori et al. (Reference Sartori, Guglielmin, Ferraro, Filippi, Zaltron, Pierno and Mistura2019). Note that the climbing region is reduced to a small patch on the LIS, whereas it is unbounded on the solid plate.
Sartori et al. (Reference Sartori, Guglielmin, Ferraro, Filippi, Zaltron, Pierno and Mistura2019) have performed the first experiments to directly address the issue of contact line pinning. They use a liquid impregnated surface (LIS) that consists of a silicone surface with photoresist pillars, silanized, and coated with a fluorinated oil. These surfaces can be made with vanishingly low hysteresis (Keiser et al.
Reference Keiser, Keiser, Clanet and Quere2017), though Sartori et al. (Reference Sartori, Guglielmin, Ferraro, Filippi, Zaltron, Pierno and Mistura2019) report that their LIS have a hysteresis of the order of
$5^{\circ }$
. As shown by the comparison of a solid surface with an LIS in figure 2, the experiments reveal that the climbing regime is almost extinguished on the LIS. This surprising result appears to be incompatible with all current models, though there may be some wiggle room because the substrate is actually a liquid, albeit highly viscous, and gummed up with pillars, rather than a solid. In addition, Sartori et al. (Reference Sartori, Guglielmin, Ferraro, Filippi, Zaltron, Pierno and Mistura2019) find two distinct modes by which the drop can slide down the plate: distinguished primarily by the speed of descent, but also by the shape of the drop and phase of the contact area relative to the drive. The latter in particular is suggestive of the role of inertia.
3 Future
There are few model systems in which inertially dominated spreading can be studied easily with experiments. The work of Sartori et al. (Reference Sartori, Guglielmin, Ferraro, Filippi, Zaltron, Pierno and Mistura2019) raises the possibility that the community now has a model system in which the effects of inertia on contact line dynamics can be disentangled from those of pinning. A number of interesting issues remain to be resolved. Are liquid impregnated surfaces a perfect substitute for the ideal non-pinning solid surface? Is contact line hysteresis necessary for the asymmetry force to be significant? Does the climbing regime vanish in the zero-hysteresis limit? How would the experiments turn out in the nullified gravity configuration (figure 1
b)? What causes the two distinct descending regimes of sliding?
1 Introduction
The flow of a film or drop over a solid surface is ubiquitous in industry and science, with applications in microfluidics, ink-jet printing, coatings and crop spraying, to name a few (Bonn et al. Reference Bonn, Eggers, Indekeu, Meunier and Rolley2009). A prerequisite for understanding such phenomena is an accurate model of the contact line – the curve defined by the edge of the drop where the free surface meets the solid surface. For the drop to move, the contact line must also move. This seemingly obvious and innocuous statement hides a conundrum: moving the contact line while respecting the no-slip boundary condition leads to a divergence of the shear stress, or equivalently the dissipation rate. Research on this problem, though far from over, has proved to be a rich source of insights, as well as new physics and mathematics.
For a drop on a smooth homogeneous surface spreading due to capillarity, the motion of the contact line is largely understood (see, for example, Snoeijer & Andreotti Reference Snoeijer, Andreotti, Davis and Moin2013). The same cannot be said about inertia-dominated spreading, as occurs when a drop is subjected to vibrations or impacts a solid surface at speed. Moreover, most spreading applications must contend with contact line pinning – an effect epitomized by a drop tenaciously clinging to a windshield even when the car is in motion. Pinning is caused by microscopic irregularities that act as energy barriers hindering the motion of a drop, and are present on even the smoothest looking surfaces, such as glass (Good Reference Good1992; Mistura & Pierno Reference Mistura and Pierno2017). In the quasistatic limit, pinning manifests as hysteresis in the relationship between contact line speed and the contact angle. Inertia-dominated spreading on a regular surface is currently poorly understood – partly because of the difficulty in disentangling pinning and inertia. In this issue, Sartori et al. (Reference Sartori, Guglielmin, Ferraro, Filippi, Zaltron, Pierno and Mistura2019) investigate the motion of a drop induced by vibrations on a surface with very low hysteresis, shedding needed light on this regime.
Figure 1. (a) Experimental configuration in climbing-drop experiments. A drop rests on an inclined substrate undergoing harmonic oscillations along the vertical axis. The drop moves rightwards on the substrate. (b) Alternative experimental configuration where gravity plays no role but the drop still moves rightwards. (c) Schematic indicating that the drop is more susceptible to sideways oscillations during the down stroke of the oscillation.
2 Overview
Since the work of Daniel, Chaudhury & de Gennes (Reference Daniel, Chaudhury and de Gennes2005), it is known that drops can be moved across a surface with vibrations. (We omit from this discussion the surface acoustic wave technique, which also employs vibrations but with much higher frequencies.) They showed how a drop on a horizontal substrate vibrated in the horizontal direction with an anharmonic waveform will cause the drop to translate. Daniel et al. (Reference Daniel, Chaudhury and de Gennes2005) ascribed the movement to a ratchet-like response of the contact line in the presence of pinning. Brunet, Eggers & Deegan (Reference Brunet, Eggers and Deegan2007) discovered that a drop will climb up an inclined substrate oscillated vertically with a sufficiently large harmonic amplitude. In their experiment, a drop of silicone oil was placed on an inclined plate of polymethylmethacrylate (PMMA) and vibrated in the vertical direction, as illustrated in figure 1(a). Initially the drop was pinned by the surface. Several thresholds for qualitatively different responses were observed as the amplitude of vibration was increased. Above the first threshold the drop moves down the plate. Above the next threshold the drop stops moving. Above yet a higher threshold the drop moves up the plate. This last regime was found to persist up to the highest accelerations obtainable with their apparatus. A typical phase diagram of this behaviour is shown in figure 2(a). Additional experiments by Brunet, Eggers & Deegan (Reference Brunet, Eggers and Deegan2009) and Sartori et al. (Reference Sartori, Quagliati, Varagnolo, Pierno, Mistura, Magaletti and Casciola2015) confirmed these results and extended them to other liquids.
While the ability of drops to climb may appear paradoxical at first glance, the experiments of Brunet et al. (Reference Brunet, Eggers and Deegan2007) show that gravity is a confounding factor and the problem is better understood by configuring experiments as shown in figure 1(b), where the effect of gravity is nullified. In this configuration, drops are pinned at the lower accelerations, while above a threshold they de-pin and move to the right. Noblin, Kofman & Celestini (Reference Noblin, Kofman and Celestini2009) showed that the problem is better conceptualized by decomposing the angled vibrations into vertical and horizontal components, with a phase difference that can be tuned to vary the mean speed of the drop from positive to negative. As shown in figure 1(c), the vertical oscillations alternately make the drop tall or flat, depending on the direction of the acceleration; superimposed horizontal vibrations will rock the drop more when the drop is tall, and thus more compliant, compared to when the drop is flattened and less compliant.
Various models with differing assumptions and approximations have been proposed to explain the cause of climbing drops (Benilov Reference Benilov2010; John & Thiele Reference John and Thiele2010; Benilov Reference Benilov2011; Benilov & Billingham Reference Benilov and Billingham2011; Benilov & Cummins Reference Benilov and Cummins2013; Borcia, Borcia & Bestehorn Reference Borcia, Borcia and Bestehorn2014; Sartori et al. Reference Sartori, Quagliati, Varagnolo, Pierno, Mistura, Magaletti and Casciola2015; Ding et al. Reference Ding, Zhu, Gao and Lu2018). A recent overview of these is given in Bradshaw & Billingham (Reference Bradshaw and Billingham2018). Recurring questions in these theoretical models are the role of and need for contact line hysteresis and the appropriate model for the contact line. All models are able to produce climbing drops, and all either explicitly show that contact line pinning is unnecessary or leave it out entirely.
Figure 2. Phase diagram for a water drop (a) on a PMMA surface from (Sartori et al. Reference Sartori, Quagliati, Varagnolo, Pierno, Mistura, Magaletti and Casciola2015) and (b) on a LIS from Sartori et al. (Reference Sartori, Guglielmin, Ferraro, Filippi, Zaltron, Pierno and Mistura2019). Note that the climbing region is reduced to a small patch on the LIS, whereas it is unbounded on the solid plate.
Sartori et al. (Reference Sartori, Guglielmin, Ferraro, Filippi, Zaltron, Pierno and Mistura2019) have performed the first experiments to directly address the issue of contact line pinning. They use a liquid impregnated surface (LIS) that consists of a silicone surface with photoresist pillars, silanized, and coated with a fluorinated oil. These surfaces can be made with vanishingly low hysteresis (Keiser et al. Reference Keiser, Keiser, Clanet and Quere2017), though Sartori et al. (Reference Sartori, Guglielmin, Ferraro, Filippi, Zaltron, Pierno and Mistura2019) report that their LIS have a hysteresis of the order of
$5^{\circ }$
. As shown by the comparison of a solid surface with an LIS in figure 2, the experiments reveal that the climbing regime is almost extinguished on the LIS. This surprising result appears to be incompatible with all current models, though there may be some wiggle room because the substrate is actually a liquid, albeit highly viscous, and gummed up with pillars, rather than a solid. In addition, Sartori et al. (Reference Sartori, Guglielmin, Ferraro, Filippi, Zaltron, Pierno and Mistura2019) find two distinct modes by which the drop can slide down the plate: distinguished primarily by the speed of descent, but also by the shape of the drop and phase of the contact area relative to the drive. The latter in particular is suggestive of the role of inertia.
3 Future
There are few model systems in which inertially dominated spreading can be studied easily with experiments. The work of Sartori et al. (Reference Sartori, Guglielmin, Ferraro, Filippi, Zaltron, Pierno and Mistura2019) raises the possibility that the community now has a model system in which the effects of inertia on contact line dynamics can be disentangled from those of pinning. A number of interesting issues remain to be resolved. Are liquid impregnated surfaces a perfect substitute for the ideal non-pinning solid surface? Is contact line hysteresis necessary for the asymmetry force to be significant? Does the climbing regime vanish in the zero-hysteresis limit? How would the experiments turn out in the nullified gravity configuration (figure 1 b)? What causes the two distinct descending regimes of sliding?