1. Introduction
East Ellsworth Land (EEL), an area of the West Antarctic ice sheet (WAIS) south of the Antarctica Peninsula, flows into the Ronne Ice Shelf. There are a number of ice streams in this area, Evans Ice Stream and Rutford Ice Stream (RIS) being the largest, and in between them the smaller Carlson and Talutis Inlets. While flow of these ice streams and of the Ronne Ice Shelf itself is strongly affected by tides (Reference GudmundssonGud-mundsson, 2011;Reference Makinson, King, Nicholls and GudmundssonMakinson and others, 2012), repeated GPS measurements over 25 years have failed to show any decadal changes in flow velocity on RIS (Reference Gudmundsson and JenkinsGudmundsson and Jenkins, 2009). Vaughan and others (2008) suggested there had been a flow reorganization in RIS and Carlson Inlet >240 years BP, but internal radar data contradict this claim, showing that Carlson Inlet has been stagnant for at least 6 ka (Reference Hindmarsh, King, Mulvaney, Corr, Hiess and ChauletKing, 2011). Here we adduce further evidence from an ice- divide analysis suggesting near-stationary flow conditions in this area over timescales of a few thousand years.
The central idea in this work is that if the stratigraphy of an ice divide is in steady state, there is a strong indication that the flow in surrounding areas has been stationary for, at least, a time comparable to the stratigraphy evolution timescale of the ice divide. Martin and others (2009) and Martin and Gudmundsson (2012) showed that an ice divide evolving towards a steady state develops an internal stratigraphy dominated by a prominent combination of synclines and anticlines known as double-peaked Raymond bumps, while at the same time linear dips running parallel to the ridge form at the surface. Furthermore, Martin and others (2009) showed that these features are reproduced assuming, and only assuming, anisotropic nonlinear flow.
Ice is known to be a highly anisotropic material (e.g. Reference Pimienta and LipenkovPimienta and others, 1987). The crystals that constitute meteoric ice are randomly oriented, and macroscopic ice behaves as an isotropic material;but under certain conditions, ice flow and recrystallization processes create preferred orientations for the crystals and ice behaves as an anisotropic material. The evolution of crystal orientation fabric (COF) has been analysed from ice-core samples (e.g. Siple Dome (Di Reference DiPrinzio, Wilen, Alley, Fitzpatrick, Spencer and GowPrinzio and others, 2005), Byrd (Reference Alley, Gow and MeeseAlley and others, 1995) and GRIP (Greenland Ice Core Project; Reference Thorsteinsson, Kipfstuhl and MillerThorsteinsson and others, 1997)), but there is no direct measurement of the horizontal variation of COF in ice divides, and our knowledge of its horizontal variation is based on the interpretation of radar reflections (e.g. Reference MatsuokaMatsuoka and others, 2003;Reference Eisen, Hamann, Kipfstuhl, Steinhage and WilhelmsEisen and others, 2007) or inverse modelling of radar layers (e.g. Reference Pettit, Thorsteinsson, Jacobson and WaddingtonPettit and others, 2007;Reference Drews, Martin, Steinhage and EisenDrews and others, 2013).
In general, ice flow in a divide area is dominated by horizontal stretching and vertical compression. This flow regime induces a fabric that varies from isotropic at the surface, to a vertical girdle in the top half of the thickness, to a vertical single-maximum fabric (Reference Alley, Gow and MeeseAlley and others, 1995). Recrystallization processes, mainly polygonization and migration, also affect the COF (e.g. Reference ThorsteinssonThorsteinsson, 2002; Reference Gagliardini, Gillet-Chaulet Fand Montagnat and HondohGagliardini and others, 2009).
In addition to the effects of ice fabric on flow, it is particularly important in divides to consider the nonlinearity of ice rheology. One of the consequences of nonlinear flow is the formation of a relatively stiff zone of ice close to the bed (Reference RaymondRaymond, 1983). This effect produces, after a time comparable to the characteristic time of the divide (ice thickness divided by accumulation rate), the formation of synclines in the radar stratigraphy known as Raymond bumps (e.g. Reference Conway, Hall, Denton, Gades and WaddingtonConway and others, 1999;Martin and others, 2009), and Martin and Gudmundsson (2012) showed that if the divide stays under stationary ice-flow conditions for a time comparable to several characteristic times, subtle evolution of flow-induced fabric produces the development of anti- clines that are superimposed on the Raymond synclines. As a conseqence, the Raymond bump splits into two, leading to the formation of ‘double-peaked Raymond bumps’.

Fig. 1. MODIS Mosaic of Antarctica (MOA) image map (Reference Haran, Bohlander, Scambos and FahnestockHaran and others, 2005), showing the Ellsworth Land area around Kealey Ice Rise (delineated in yellow). The fast-flowing areas are highlighted from Rignot and others’ (2011) velocity map. The locations of ground-penetrating radar (GPR) profiles M, K and L are shown in blue, red and green, respectively.
Different models of anisotropic rheology have been proposed in the past (e.g. Reference LliboutryLliboutry, 1993;Reference Castelnau, Duval, Lebensohn and CanovaCastelnau and others, 1996;Reference Mangeney, Califano and HutterMangeney and others, 1997;Reference ThorsteinssonThorsteinsson, 2001;Gödert, 2003;Reference Gillet-ChauletGillet-Chaulet, 2007;Reference Pettit, Thorsteinsson, Jacobson and WaddingtonPettit and others, 2007;Reference Castelnau, Duval, Montagnat and BrennerCastelnau and others, 2008). All these models differ in various details with regard to the crystal model used (Schmid law;a basal slip system model;transversely isotropic), the description of the fabric (discrete or continuous through an orientation distribution function or an orientation tensor) and in the homogenization procedure used (uniform strain- rate, uniform stress or intermediate self-consistent proce- dures). A detailed review of all these models is provided by Gagliardini and others (2009).
The model we use is described in Martfn and others (2009) and Martfn and Gudmundsson (2012), but we summarize its main aspects in Appendices A-E for convenience. It incorporates a nonlinear extension to the flow-induced anisotropic rheology described by Godert (2003) and Gillet-Chaulet (2007).
The objective of this paper is twofold. Firstly, we provide new evidence of stationary flow conditions on the EEL area on the century to millennium timescale from the surface and internal stratigraphy of the area. To that end, we model flow and internal stratigraphy of Kealey Ice Rise and we look for signs of transient flow behaviour. Secondly, we use these data to validate our modelling approach and analyse the uncertainty in our model free parameters.
2. Data
Kealey Ice Rise is located north of the junction of Talutis Inlet and Carlson Inlet, at the southwest side of the Ronne Ice Shelf. AGPS and radio-echo sounding survey was carried out during the 1996/97 austral summer with a pulseEKKO 100 ground-based radar system. The radar surveys were con- ducted using a central frequency of 25 MHz, and the data processed using the processing software Reflexw (http://www.sandmeier-geo.de/GPR.html). The GPS data were collected using a number of Trimble 4000 and Leica 1200 units and processed using kinematic Precise Point Positioning technique with the Bernese GPS processing software (Reference Dach and HugentoblerDach and others, 2007).
The main profile locations are shown in Figure 1, and the radargrams M, K and L are shown in Figure 2. In the deepest areas of the ridge (profile M), the radar was unable to acquire the bedrock topography and we used BEDMAP bed topography (Reference Lythe and VaughanLythe and others, 2001).

Fig. 2. GPR profiles M, K and L at Kealey Ice Rise (see Fig. 1 for location). Some internal horizons are highlighted in red and the bedrock topography in blue. The bedrock topography in profile M was extracted from BEDMAP bed topography (Reference Lythe and VaughanLythe and others, 2001).
In addition to the geometry of the divides, we use the mean snow accumulation from Arthern and others (2006), and the mean surface temperature from Comiso (2000) (see Table 1).
Table 1. Numerical values of the parameters used in the simulations

3. Numerical Modelling
The lack of both laboratory and in situ measurements makes detailed validation of the rheology more difficult (Appendix C). Martin and others (2009) and Martin and Gudmundsson (2012) determined values for rheological parameters of the model for which the qualitative observed features (e.g. the number of synclines or anticlines in the ice stratigraphy) are reproduced. In this section, we use the radargrams from Kealey Ice Rise to further validate and tune the model.
We use a transient full-Stokes thermomechanical solver and a nonlinear flow-induced anisotropic rheology that is described in Martin and Gudmundsson (2012) as an extension of Martin and others (2009). We reproduce the main details of the numerical model in Appendix E for convenience.
3.1. Model parameters
The key parameters entering our rheology model are the two relative viscosities ß and γ, and the rheological index n (Appendix C). γ is the ratio of the viscosity in compression or tension along the c-axis to that in the basal plane, and is assumed to be close to unity (Reference Gillet-Chaulet, Gagliardini, Meyssonnier, Zwinger and RuokolainenGillet-Chaulet and others, 2006). In this study we therefore only vary the two parameters β, the ratio of viscosity of the grain for shear parallel to the basal plane to that in the basal plane, and n, the rheological index.
The laboratory experiments by Pimienta and others (1987) show that ice exhibiting a single-maximum fabric is ten times softer to deform perpendicularly to the c-axis than isotropic ice, and ten times harder to deform in the c-axis direction than isotropic ice. With the rheology described in Appendix C, the enhancements for shear Es and compression Ec for a single-maximum fabric with respect to an isotropic fabric are

Figure 3 shows the values of n and ß that, using the rheology described in Appendix C, follow the experimental results of Pimienta and others (1987), i.e. Es = (1 /10)1/n and Ec = 101/n.
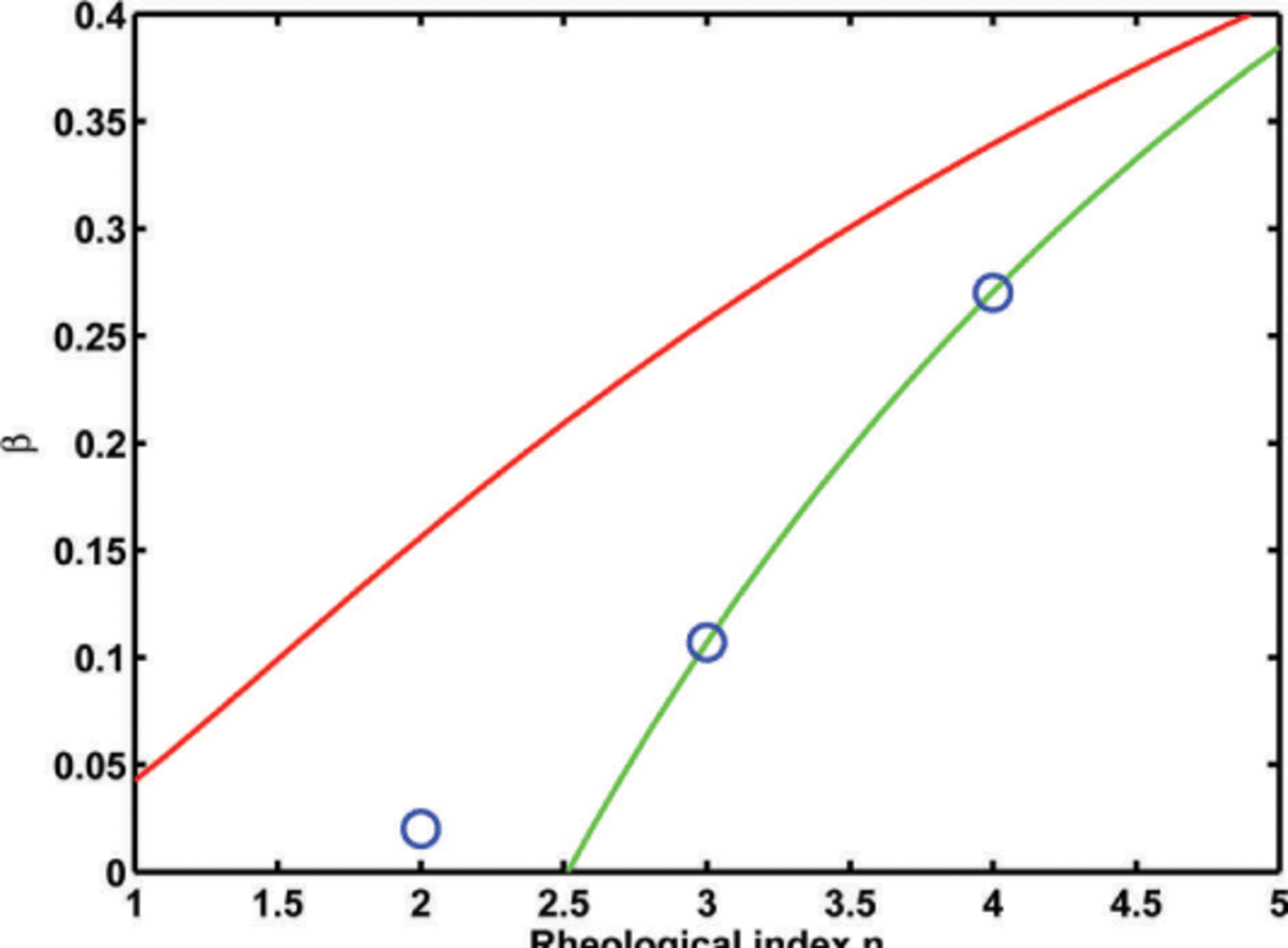
Fig. 3. Representation of the laboratory experiments by Pimienta and others (1987) in the model parameter space. The parameters are the rheological index n and the relative viscosity β. The red line represents the result that ice with single-maximum fabric is ten times softer to deform perpendicularly to the c –axis than isotropic ice, and the green line that ice exhibiting a single-maximum fabric is ten times harder to deform in the c-axis direction than the isotropic ice. The blue circles represent the values used in this study.
In order to understand the effect of n and ß on the ice stratigraphy, we show in Figure 4 the isochrone layering for different parameter values. We chose the values n = 2,3,4 and the corresponding values of ß so that the resulting pair is consistent with the shearing experiments of Pimienta and others (1987). The values of n and ß chosen are shown in Figure 3.

Fig. 4. Steady-state ice stratigraphy (isochrones) for an ice divide over a flat bedrock for different values of the rheological index n and relative viscosity. The parameters chosen are shown in Figure 3. They are n = 2 and β =0.02 in the left panel, n = 3 and β =0.10 in the central panel and n = 4 and β =0.27 in the right panel.
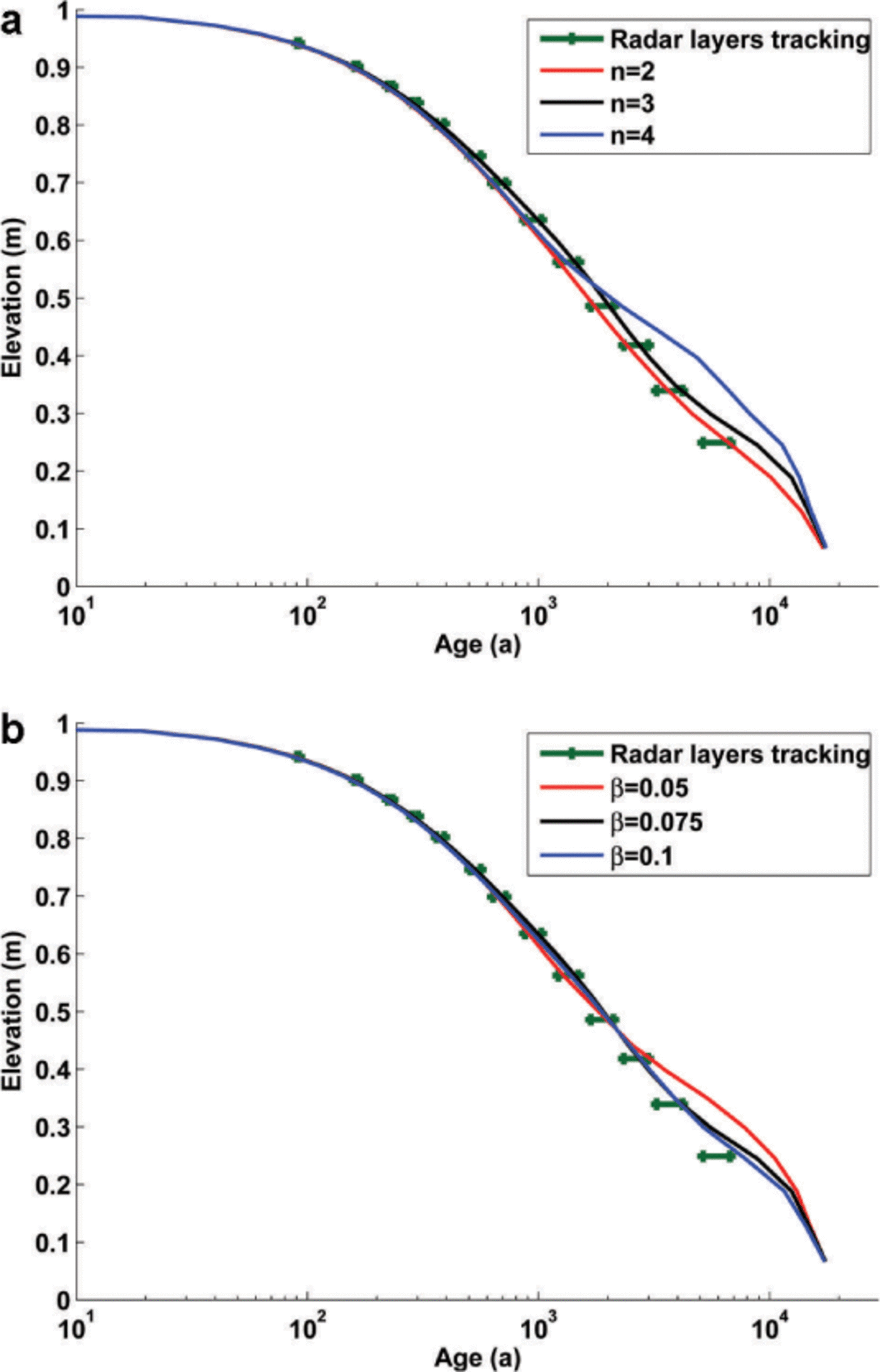
Fig. 5. Sensitivity of age versus depth distribution to (a) rheological index n and (b) relative viscosity β. Solid lines represent the age– depth distribution predicted by the model using β = 0.1 for the sensitivity analysis of n, and n = 3 for the sensitivity analysis of β. We compare the modelled age vs depth distribution at the divide with the estimated age of the picked radar reflecting horizons. We estimate the age of radar horizons at the margins where the effect of flow and fabric evolution is minimal (Martin and Gudmundsson, 2012), and represent the horizontal variation of the one-dimensional age estimates along the radar layers as an interval.
3.2. Modelling profiles M, K and L of Kealey Ice Rise
We show here that the present stratigraphy of Kealey Ice Rise can be reproduced assuming that Kealey Ice Rise has been stationary for a period of, at least, several times the characteristic time of the divide (tD), ice thickness divided by accumulation. We model the transversal profiles M, K and L (Figs 1 and 2).
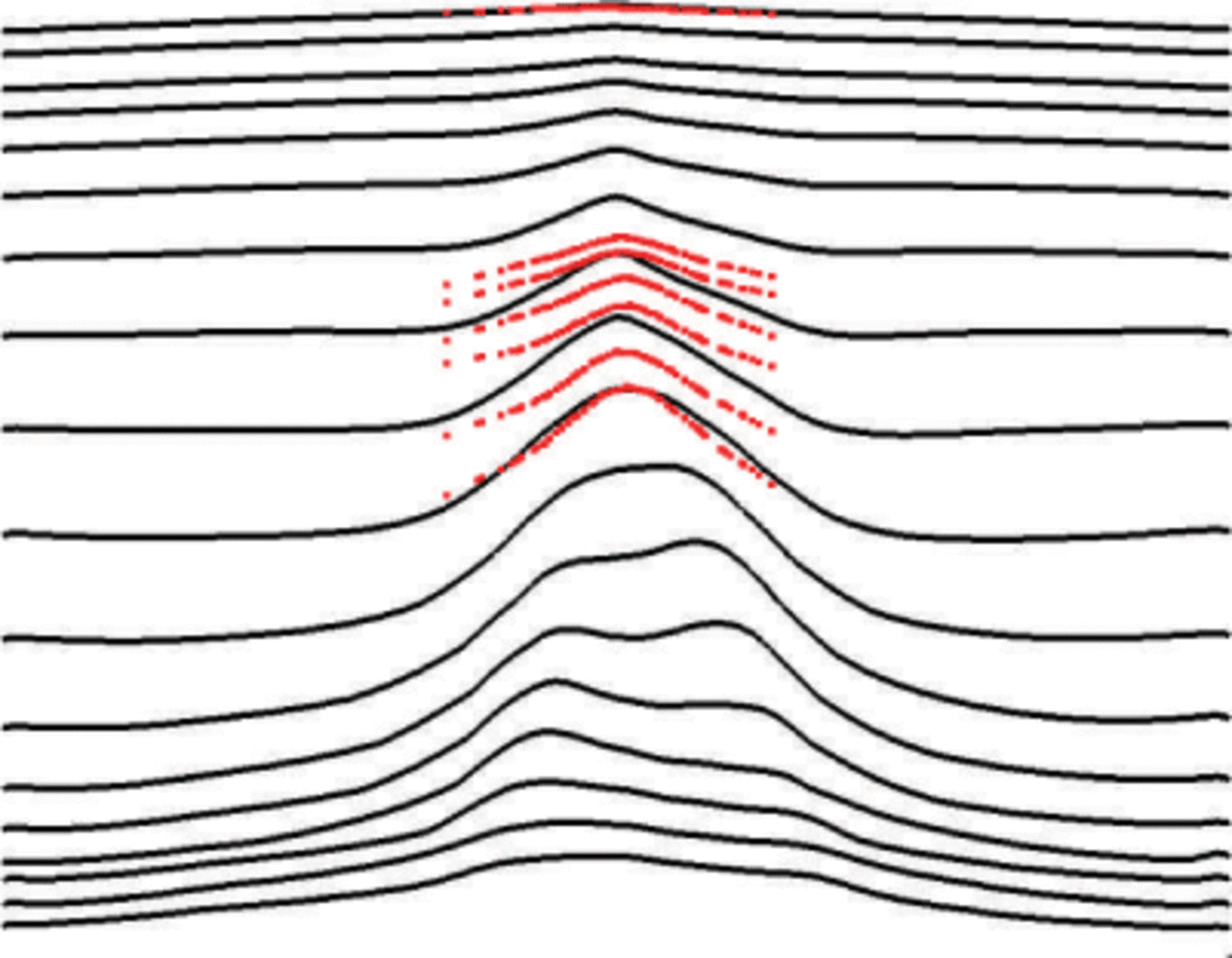
Fig. 6. Modelled isochrones (black) and radar layers (red) at profile M (see Fig. 1). n = 3 and β = 0. 1.
We initialize the models with the present geometry, fabric linearly varying from isotropic at the surface to vertically aligned single-maximum at the base, temperature following Robin's (1955) analytical approximation, and age distributed as the steady-state solution assuming anisotropic shallow-ice approximation flow (Appendix D). As discussed in Martin and others (2009), the initial conditions affect the solution in the first stages of the divide development but not the steady state. The model parameters are provided in Table 1.
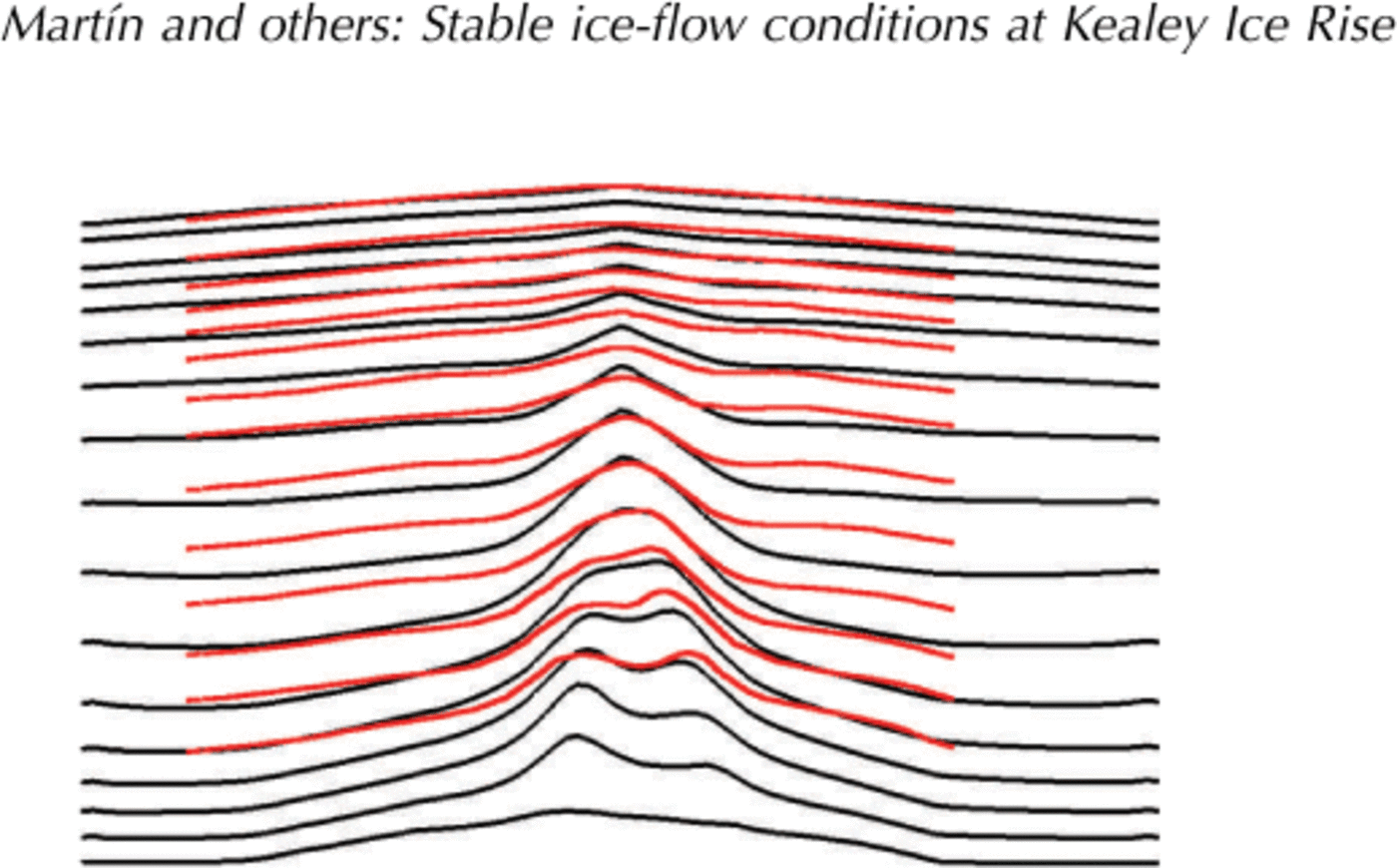
Fig. 7. Modelled isochrones (black) and radar layers (red) at profile K (see Fig. 1). n = 3 and β = 0. 1.
In order to study the impact of the free parameters n and ß on modelled internal stratigraphy, we consider profile K, for which the best data on bedrock geometry are available. This is also the profile most closely corresponding to a plane-flow situation (Section 2). For given values of n and β we simulate the evolution of flow, fabric, temperature and surface topography towards steady state. We stop the simulation at t = 10 fD because, after that, changes in ice age only occur in a small layer, of ~2.5% of the ice thickness, close to the bedrock.
Parameters n and ß are not fully independent, and the modelled isochrones and radar horizons are difficult to compare due to the complex flow regime in the area and the bedrock topography. Our approach is to compare the modelled age vs depth distribution at the divide with the estimated age of the picked radar reflecting horizons. We estimate the age of radar horizons at the margins where the effect of flow and fabric evolution is minimal (Reference Makinson, King, Nicholls and GudmundssonMartin and Gudmundsson, 2012). The sensitivity of the results with different values of n and ß is shown in Figure 5.
The results in Figure 5 show that the parameters n and ß that best fit the data are in the range 2 < n < 4 and 0.05 < ß < 0.1. We choose n = 3 and ß = 0.1 as represen- tative of these values.
Finally, Figures 6–8 compare the modelled stratigraphy for profiles M, K and L with their respective radargrams for these values. The modelled steady-state stratigraphy for the three profiles shows double-peaked Raymond bumps, in agreement with the general case presented in Martin and Gudmundsson (2012). The model of profile K (Fig. 7) reproduces the qualitative observed features. In profile M (Fig. 6) the radar was unable to acquire the deeper section of the profile. In profile L (Fig. 8) the radargram shows a single Raymond bump. Similar to the sensitivity analysis presented in Figure 5, there are small variations in the modelled stratigraphy within the range 2 ≤ n < 4 and 0.05 ß ≤ 0.1.We choose n = 3 and β = 0.1 as representative of these values.

Fig. 8. Modelled isochrones (black) and radar layers (red) at profile L (see Fig. 1). n = 3 and β = 0. 1.
Finally, Figures 6–8 compare the modelled stratigraphy for profiles M, K and L with their respective radargrams for these values. The modelled steady-state stratigraphy for the three profiles shows double-peaked Raymond bumps, in agreement with the general case presented in Martin and Gudmundsson (2012). The model of profile K (Fig. 7) reproduces the qualitative observed features. In profile M (Fig. 6) the radar was unable to acquire the deeper section of the profile. In profile L (Fig. 8) the radargram shows a single Raymond bump. Similar to the sensitivity analysis presented in Figure 5, there are small variations in the modeled stratigraphy within the range 2 ≤ n < 4 and 0: 05 < β ≤ 0. 1.
4. Discussion
The results above (Section 3.2) show that our modelling approach reproduces the general features observed in the stratigraphy of profiles M and K of Kealey Ice Rise.
Kealey Ice Rise profiles M and K are relatively flat across the ridge: the across-ridge slope at a distance of one ice thickness from the divide (0.01) is larger than the along-ridge slope at the divide (0.005). As discussed in Martin and others (2009), we expect negligible influence of along-ridge flow in profiles M and K but not in L, where the across-ridge slope at a distance of one ice thickness from the divide (0.01) is about the same as the along-ridge slope at the divide (0.01). Kealey Ice Rise profile L does not show a two-dimensional steady-state stratigraphy, and this suggests either along-ridge flow or a recent or ongoing migration of that shallow section of the divide.
The values for the rheological parameters n and ß that fit the data best are in the range 2 < n < 4 and 0.05 < ß < 0.1. These n values are smaller than previous estimates by Martin and others (2006) and Hindmarsh and others (2011) who both found that n = 4 gives the best fit to measurements of internal stratigraphy at Roosevelt Island and Fletcher Prom- ontory, respectively. They are also smaller than the estimate of n = 4.5 obtained by Gillet-Chaulet and others (2011) from in situ measurement of rheology at Summit, Greenland.
We stress, however, that Martin and others (2006), Gillet- Chaulet and others (2011) and Hindmarsh and others (2011) employed isotropic flow models, and the numerical values obtained for n can therefore not be compared directly with values from anisotropic flow models such as used here. Our model optimized values for ß are, as discussed in Section 3.1, compatible with the laboratory measurements by Pimienta and others (1987). The sensitivity analysis presented in Figure 5 shows that our results are not particularly sensitive to the values of n and ß within those ranges, but we stress that we are only able to reproduce observations by using an anisotropic nonlinear rheology.
It could be argued that the stationary flow conditions on Kealey Ice Rise and its surrounding ice masses are unique to this particular area, but the presence of double-peaked Raymond bumps in the stratigraphy of Fletcher Promontory (Reference Gillet-Chaulet, Hindmarsh, Corr, King and JenkinsGillet-Chaulet and others, 2011) and Raymond bumps in airborne radar data of Fowler Ice Rise (personal communication from J. Kingslake, 2013) suggest stationary ice-flow conditions on the millennia timescale for the area (Fig. 1).
5. Summary
We have shown that Kealey Ice Rise, a divide situated between Rutford and Evans Ice Streams, has not been subjected to large-scale flow reorganization over a period of at least twice the characteristic time of the divide (~2.8 ka at profile K). We find that we can successfully reproduce internal flow features (e.g. single and double Raymond bumps), as well as surface topographic features (e.g. the lineations running on both sides parallel to the ridge of the ice divide), without the need to resort to changes in external forcing with time. Hence, all these observed features of Kealey Ice Rise can be explained assuming stationary flow conditions over the past ~3 ka.
We furthermore argue that near-stationary flow conditions are required for the formation of the internal and surface structures seen in the data from Kealey Ice Rise. The double- peaked Raymond bumps can only develop given sufficient time (comparable to or longer than the characteristic time), and their existence therefore implies stationary flow conditions over these timescales. The small tilt visible in the data can, as discussed above, be explained as a consequence of the bed topography. Had the ice divide migrated horizontally by a distance more than a few times the ice thickness over the past few thousand years, this would have left a clear signature in the alignment ofthe Raymond bumps. Such a signature is not seen in the data. Hence, we can conclusively exclude the possibility of any significant ice-divide migration over the past few thousand years.
Finally we point out that the double-peaked Raymond bumps on the stratigraphy of Kealey Ice Rise are seen widely on other ice divides in the area. This suggests that not just Kealey Ice Rise but the whole of EEL has been near- stationary over recent millennia.
Our modelling approach uses a nonlinear flow-induced anisotropic rheology. In agreement with Martin and others (2009) and Martin and Gudmundsson (2012), we find that the qualitative behaviour of divide development and the timescales involved are not affected by the particular details ofthe rheology as long as we consider a nonlinear rheology (n > 1) and flow-induced anisotropy. The best model fit to observed internal stratigraphy ofthe Kealey Ice Rise is obtained using a rheological index in the range 2–4 and for a relative anisotropic viscosity ratio ß in the range 0.05 < ß < 0.1.
Acknowledgements
We thank the scientific editor, Ralf Greve, and two anony- mous reviewers for comments that helped to improve the quality of this paper.
Appendix A. Field Equations And Boundary Conditions
We solve flow in an x-z plane orthogonal to the axis of an ice divide. The z-axis is aligned vertically, the x-axis represents the horizontal direction of flow and in the y direction we assume plane strain. The ice surface and bed are given by z = s(x, t) and z = b(x) respectively.
The Stokes system and its boundary conditions are (Greve and Blatter, 2009)
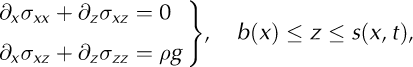
Equation (A1a) expresses the conservation of mass, and Eqn (A1b) the conservation of momentum. Here σ is the Cauchy stress tensor, ρ is the density of ice, g is the vertical component of the gravitational acceleration, and ![]() is the velocity vector. Equations (A1c) and (A1d) are the boundary conditions at the surface and bed respectively. At the lateral boundaries we assume for the velocity field the anisotropic shallow-ice approximation. This approximation is discussed in Appendix D.
is the velocity vector. Equations (A1c) and (A1d) are the boundary conditions at the surface and bed respectively. At the lateral boundaries we assume for the velocity field the anisotropic shallow-ice approximation. This approximation is discussed in Appendix D.
The kinematic boundary condition at the surface is
where a is accumulation rate of ice, expressed as a volume rate per unit area.
The heat equation and boundary conditions are
where ᶱ s is the prescribed surface temperature, K is the thermal diffusivity of ice, c is the specific heat capacity, Q D = trace (S • D) is the dissipation power, D and S are the strain-rate and deviatoric-stress tensors, K is the thermal conductivity and Q G is the geothermal heat flux. We assume that the horizontal gradient of temperature is zero at the lateral margins.
Isochrones are lines connecting ice particles of equal age ψ where age is calculated from
Appendix B. Ice Fabric: Description And Evolution
To describe the ice fabric we use the second- and fourth- order orientation tensors, a (2) and a(4) respectively (e.g. Godert, 2003;Gillet-Chaulet and others, 2006). We assume that the ice fabric is primarily induced by deformation rather than recrystallization. In that case, following Godert (2003) and Gillet-Chaulet and others (2006) the evolution of the second-order orientation tensor a (2) and boundary conditions can be written as
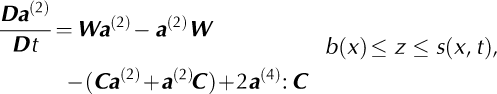
where W is the spin tensor (the skew-symmetric part of the gradient tensor),
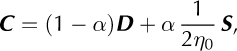
and α is the interaction parameter. α controls the relative weighting of the strain-rate tensor (D) and the deviatoric- stress tensor (S) in the fabric-evolution equation (Eqn (B1)).
The evolution of the second-order orientation tensor a (2) given by Eqn (B1) depends on a (4), and for that reason the system of equations listed above is not closed. A common approach for obtaining a closed system is to express the components of the fourth-order orientation tensor as functions of those of the second-order orientation tensor (e.g. Advani and Tucker, 1990). We follow this approach and use the invariant-based closure approximation (IBOF). As shown by Chung and Kwon (2002), the general form of the IBOF closure approximation is
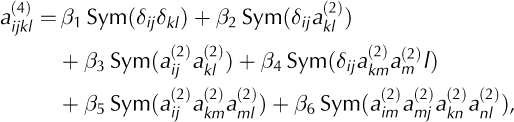
where ‘Sym’ denotes the symmetrical part of its argument and ßi are six functions of the second and third invariants of a (2). Following Chung and Kwon (2002), we assume that ßi are polynomials of degree 5 in the second and third invariant of a (2), and we use the coefficients computed by Gillet-Chaulet and others (2006) so that a (4) given by Eqn (B3) fits the fourth-order orientation tensor given by the orientation distribution function proposed by Gagliardini and Meyssonnier (1999).
Appendix C. Rheology
We assume that the monocrystal grain behaves as a viscous transversely isotropic medium and that there is a uniform stress distribution within the polycrystal (uniform-stress or static model (e.g. Gagliardini and Meyssonnier, 1999; Thorsteinsson, 2001;Gödert, 2003). Following Gcidert (2003) and Gillet-Chaulet and others (2005), we write the orthotropic rheology of the polycrystal as
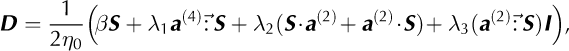
where I is the identity matrix, the symbols • and ![]() denote the contracted product and the double contracted product, respectively, and the three λ symbols are defined as
denote the contracted product and the double contracted product, respectively, and the three λ symbols are defined as

The mechanical properties of the monocrystal can then be described by the basal shear viscosity ŋ 0, and the two relative viscosity ratios ß and γ, i.e. ß, the ratio of viscosity of the grain for shear parallel to the basal plane to that in the basal plane, and 7, the ratio of the viscosity in compression or tension along the c-axis to that in the basal plane (e.g. Lliboutry, 1987;Meyssonnier and Philip, 1996). The viscosity ratio parameter ß is known to be smaller than unity, and the parameter 7 to be close to unity (Gillet-Chaulet and others, 2006).
In accordance with Glen's flow law, we propose a nonlinear extension of the rheology described in Eqn (C1):
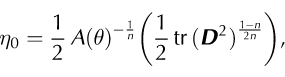
where A(θ)is the rate factor and is temperature-dependent,n is the rheological index and ‘tr’ denotes trace. We use the Dahl-Jensen (1989) relationship for the rate factor,
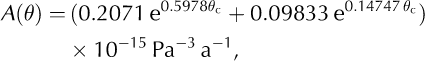
with n= 3 and θ c is the temperature (°C).
Pettit and others (2007) and Ma and others (2010) propose a similar nonlinear extension to Glen’s flow law (Eqn (C2)) that depends only on the stress tensor instead of on the strain-rate tensor. As observed by Ma and others (2010), no theoretical or experimental results are available that allow us to discard either of these solutions. We adopt the nonlinear extension described in Eqn (C9) because it reproduces qualitative aspects of the layering in the stratigraphy of a divide evolving towards steady state. Further numerical experiments (not reported here) showed that those observations cannot be reproduced using the model described above when using a nonlinear extension depending on the stress tensor only.
Appendix D. Anisotropic Shallow-Ice Approximation And Outflow Boundary Conditions
Mangeney and Califano (1998) proposed the extension of the shallow-ice approximation (Hutter, 1983) for anisotropic ice. Its use as lateral boundary conditions in full-Stokes models is described by Gagliardini and Meyssonnier (2002). The zeroth-order shallow ice expansion approximates Eqns (A1a) and (A1b) as (Mangeney and Califano, 1998; Gagliardini and Meyssonnier, 2002)

where, η xzxz is, from Eqn (C1), the reduced component of the viscosity tensor linking strain-rate and stress shear com- ponents.
Appendix E. Numerical Details
The model presented in Appendices A–D is similar to that described in Martin and others (2009) aside from the coupling between heat equation and ice flow through the viscosity (Eqn (C2)) and the dissipation power (Eqn (A3a)). The numerical algorithms are, however, different.
The system represented by Eqns (A1–A4), with their respective boundary conditions, is solved with the open- source software Elmer/Ice (http://elmerice.elmerfem.org/) (Gagliardini and others, 2013). The Stokes system, heat equation and free surface evolution are solved with the Elmer build-in finite-element solvers, using linear elements and stabilized with residual-free bubbles (see Elmer docu- mentation for details). In contrast, fabric evolution and age equations are solved using a semi-Lagrangian method using a two-time-level scheme and linear interpolation (details in Martin and others, 2009). The reason for not using a finite- element solver in the equations for fabric and age is that we find the semi-Lagrangian approach more stable close to the base of the divide where the ice is stagnant.











