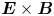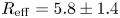1. Introduction
The feasibility of achieving fusion-grade plasma in open magnetic systems has been re-evaluated in the last decade (Bagryansky, Beklemishev & Postupaev Reference Bagryansky, Beklemishev and Postupaev2019). It became possible due to the advances in the investigation of plasma stability and suppression of the axial energy and particle losses (Burdakov et al. Reference Burdakov, Azhannikov, Astrelin, Beklemishev, Burmasov, Derevyankin, Ivanenko, Ivanov, Ivantsivskiy and Kandaurov2007; Bagryansky et al. Reference Bagryansky, Anikeev, Denisov, Gospodchikov, Ivanov, Lizunov, Kovalenko, Malygin, Maximov and Korobeinikova2015; Gota et al. Reference Gota, Binderbauer, Tajima, Putvinski, Tuszewski, Deng, Dettrick, Gupta, Korepanov and Magee2019). New concepts of the next-generation linear machines include a central gas-dynamic cell and separate modules for improved axial confinement (Beklemishev et al. Reference Beklemishev, Anikeev, Astrelin, Bagryansky, Burdakov, Davydenko, Gavrilenko, Ivanov, Ivanov and Ivantsivsky2013). The most tried and tested methods of the axial losses suppression are either a tandem mirror or a multiple-mirror system (see the review papers Dimov Reference Dimov1997; Burdakov & Postupaev Reference Burdakov and Postupaev2018). At the same time, new ideas for the confinement improvement can provide better losses suppression and should be comprehensively verified in experiment.
In the paper, we present new experimental results on plasma flows in the helical mirror system. Helical mirror confinement was proposed by Beklemishev (Reference Beklemishev2013). This proposal extends an idea of the multiple-mirror confinement. Periodic variations of the magnetic field required for the multiple mirrors are arranged in the helically symmetric form. Such a system resembles a straightened stellarator with one important difference. In the closed magnetic surfaces of a stellarator, the radial electric field is maintained by plasma self-organization processes. In a helical mirror system, a required spatial profile of the radial electric field can be set by proper biasing of endplates and limiters. This allows the direct control of the $\boldsymbol{E} \times \boldsymbol{B}$![]() plasma rotation. In the reference frame of the rotating plasma, the periodical variations of the magnetic field move in the direction defined by the directions of the rotation and the helicity. The locally trapped particles gain additional momentum in the same direction. If this direction is opposite to the direction of the plasma outflow, the helical mirror improves the confinement (Budker, Mirnov & Ryutov Reference Budker, Mirnov and Ryutov1982; Be'ery, Gertsman & Seeman Reference Be'ery, Gertsman and Seeman2018). Motion of the rotating plasma in a helical magnetic field was described theoretically by Beklemishev (Reference Beklemishev2016) and Chernoshtanov & Ayupov (Reference Chernoshtanov and Ayupov2021). In terms of macroscopic parameters, the axial component of pressure gradient becomes steeper in the presence of the axial Ampere's force. This force is created by the radial ion current and azimuthal component of the magnetic field. The potential energy of the ions in the external or ambipolar electric field is the energy source which drives the plasma motion. Therefore, Beklemishev (Reference Beklemishev2016) predicts radial plasma expansion if the plasma axis is charged positively (including the case of the rotation in ambipolar electric field) and radial plasma contraction if the plasma axis is charged negatively.
plasma rotation. In the reference frame of the rotating plasma, the periodical variations of the magnetic field move in the direction defined by the directions of the rotation and the helicity. The locally trapped particles gain additional momentum in the same direction. If this direction is opposite to the direction of the plasma outflow, the helical mirror improves the confinement (Budker, Mirnov & Ryutov Reference Budker, Mirnov and Ryutov1982; Be'ery, Gertsman & Seeman Reference Be'ery, Gertsman and Seeman2018). Motion of the rotating plasma in a helical magnetic field was described theoretically by Beklemishev (Reference Beklemishev2016) and Chernoshtanov & Ayupov (Reference Chernoshtanov and Ayupov2021). In terms of macroscopic parameters, the axial component of pressure gradient becomes steeper in the presence of the axial Ampere's force. This force is created by the radial ion current and azimuthal component of the magnetic field. The potential energy of the ions in the external or ambipolar electric field is the energy source which drives the plasma motion. Therefore, Beklemishev (Reference Beklemishev2016) predicts radial plasma expansion if the plasma axis is charged positively (including the case of the rotation in ambipolar electric field) and radial plasma contraction if the plasma axis is charged negatively.
An important feature of the multiple-mirror confinement is the necessity of the equal scales of ion free path length and the corrugation period (Mirnov & Ryutov Reference Mirnov and Ryutov1972) to provide momentum exchange between trapped and passing particles. At low density or high temperature, this process requires an additional turbulent scattering of ions to be effective.
Plasma flows in the helical magnetic field are investigated on the small-scale helical mirror SMOLA (Postupaev et al. Reference Postupaev, Sudnikov, Beklemishev and Ivanov2016; Sudnikov et al. Reference Sudnikov, Beklemishev, Postupaev, Burdakov, Ivanov, Vasilyeva, Kuklin and Sidorov2017). Axial plasma flow suppression by the helical section was demonstrated earlier, where an integral suppression ratio of 2–2.5 was achieved (Sudnikov et al. Reference Sudnikov, Beklemishev, Postupaev, Ivanov, Inzhevatkina, Sklyarov, Burdakov, Kuklin, Rovenskikh and Melnikov2019). An improvement of the suppression ratio with the increase of the magnetic field, corrugation ratio and plasma rotation velocity was observed (Sudnikov et al. Reference Sudnikov, Beklemishev, Inzhevatkina, Ivanov, Postupaev, Burdakov, Glinsky, Kuklin, Rovenskikh and Ustyuzhanin2020). The increase in plasma density in the entrance trap by a factor of 1.6 in the helical configuration was demonstrated (Sudnikov et al. Reference Sudnikov, Ivanov, Inzhevatkina, Larichkin, Lomov, Postupaev, Tolkachev and Ustyuzhanin2022). This paper presents the latest experimental results on the axial plasma flows in the helical mirror system at different directions of the plasma rotation and therefore different directions of the axial force that the trapped particles experience. The pinching to the axis is the same in both configurations.
2. Experimental set-up and parameters
The layout of the SMOLA helical mirror is presented in figure 1. The device was built for studies of a low-temperature hydrogen plasma flow through a 2.5-m-long transport section with the helically symmetric magnetic field. Plasma was generated in a source with a magnetically insulated heated ${\rm LaB}_6$![]() cathode (Ivanov et al. Reference Ivanov, Ustyuzhanin, Sudnikov and Inzhevatkina2021). Then the plasma was injected into a compact mirror trap in the entrance tank. Later in the text, we will call it the confinement region. In the discussed experiments, the mirrors of this trap were asymmetric with mirror ratios $R \approx 8$
cathode (Ivanov et al. Reference Ivanov, Ustyuzhanin, Sudnikov and Inzhevatkina2021). Then the plasma was injected into a compact mirror trap in the entrance tank. Later in the text, we will call it the confinement region. In the discussed experiments, the mirrors of this trap were asymmetric with mirror ratios $R \approx 8$![]() on the plasma source side and $R \approx 3$
on the plasma source side and $R \approx 3$![]() on the helical mirror side. Plasma flows in the axial direction from the confinement region to the transport section. This section has two independent magnetic systems, a solenoid for a straight field and a bispiral helical winding that forms helical magnetic mirrors. The spiral has $N = 12$
on the helical mirror side. Plasma flows in the axial direction from the confinement region to the transport section. This section has two independent magnetic systems, a solenoid for a straight field and a bispiral helical winding that forms helical magnetic mirrors. The spiral has $N = 12$![]() corrugation periods. We denote the field line without the periodic variation of the magnetic field module as the magnetic axis of the transport section. This axis has a spiral shape, and its radius depends on the helical to axial components of the magnetic field ratio. The last part of the device is the exit expander that contains an exit limiter and a radially segmented plasma receiver endplate. The axially symmetric confinement region, helically symmetric transport section and axially symmetric exit expander are matched together by the special correction units. The centre of the cathode is projected by the magnetic field line to the magnetic axis of the transport section and to the centre of the endplates. Vacuum tanks of the confinement region and the exit expander have the same volume and are pumped by the identical turbomolecular pumps. Vacuum conductivity of the transport section is an order of magnitude lower than the pumping speed of each TMP unit. The detailed description of the device can be found in Sudnikov et al. (Reference Sudnikov, Beklemishev, Postupaev, Burdakov, Ivanov, Vasilyeva, Kuklin and Sidorov2017).
corrugation periods. We denote the field line without the periodic variation of the magnetic field module as the magnetic axis of the transport section. This axis has a spiral shape, and its radius depends on the helical to axial components of the magnetic field ratio. The last part of the device is the exit expander that contains an exit limiter and a radially segmented plasma receiver endplate. The axially symmetric confinement region, helically symmetric transport section and axially symmetric exit expander are matched together by the special correction units. The centre of the cathode is projected by the magnetic field line to the magnetic axis of the transport section and to the centre of the endplates. Vacuum tanks of the confinement region and the exit expander have the same volume and are pumped by the identical turbomolecular pumps. Vacuum conductivity of the transport section is an order of magnitude lower than the pumping speed of each TMP unit. The detailed description of the device can be found in Sudnikov et al. (Reference Sudnikov, Beklemishev, Postupaev, Burdakov, Ivanov, Vasilyeva, Kuklin and Sidorov2017).

Figure 1. Layout of the SMOLA helical mirror. Positions of the main diagnostics are indicated. Probe, set of electrostatic probes including a double probe and one or two emissive probes; D.Sp, Doppler spectroscopy; Mirnov, 12-channel array of Mirnov coils; 38 GHz,microwave interferometer.
The experiments described in this paper were focused on the differences in plasma flows at different directions of the magnetic mirrors movement in the plasma reference frame. One can estimate that a helical mirror system should improve the confinement only if this direction is opposite to the plasma flow direction. In the other case, trapped ions are being moved away from the entrance region of the transport section. Minor improvement of the confinement is nevertheless possible in this configuration due to static multiple-mirror effect, but its effectiveness presumably should be significantly lower. The second process is pumping out the trapped ions that could result in degradation of the confinement and higher particle loss rate through the transport section. Later in this paper, we will denote the case of opposite directions of the magnetic mirror movement and plasma outflow as ‘confinement’ and another case as ‘pumping out’.
The direction of the force that the trapped particles experience is determined by the direction of the radial electric field, the direction of the axial magnetic field and the sign of the helicity. The direction of the radial electric field is determined by the design of the plasma gun which has negatively biased cathode on the axis and grounded anode on the periphery. Right-hand helicity of the magnetic field in the transport section is also fixed by the design of the transport section winding. At the same time, the direction of the magnetic field can be easily altered by simultaneous switching of the polarity of the current in every magnetic coil. The effect of any error magnetic field was compensated by the appropriate feeding of the correction coils at the ends of the transport section.
The distribution of the guiding magnetic field is shown in figure 2. Later in this paper, the magnetic configuration will be referred to by the guiding magnetic field in the transport section, all other magnetic fields vary proportionally. Another parameter of the magnetic system is the mean corrugation ratio $R_{{\rm mean}}$![]() , which is the ratio of the maximal and the minimal magnetic field along the field line within the transport section averaged over the plasma cross-section. This parameter defines the fraction of locally trapped particles in the plasma. In the discussed experiments, the magnetic field was in the range $B_z = 70\unicode{x2013}100\ {\rm mT}$
, which is the ratio of the maximal and the minimal magnetic field along the field line within the transport section averaged over the plasma cross-section. This parameter defines the fraction of locally trapped particles in the plasma. In the discussed experiments, the magnetic field was in the range $B_z = 70\unicode{x2013}100\ {\rm mT}$![]() , and the mean corrugation ratio was in the range $R_{{\rm mean}} = 1\unicode{x2013}1.7$
, and the mean corrugation ratio was in the range $R_{{\rm mean}} = 1\unicode{x2013}1.7$![]() , where $R_{{\rm mean}} = 1$
, where $R_{{\rm mean}} = 1$![]() stands for the straight field without the helical component. High corrugation ratios were achievable only at $B_z \leqslant 70\ {\rm mT}$
stands for the straight field without the helical component. High corrugation ratios were achievable only at $B_z \leqslant 70\ {\rm mT}$![]() due to restrictions of the power system.
due to restrictions of the power system.

Figure 2. Guiding magnetic field profiles for different radii.

Figure 3. Average plasma density in the confinement region and at the entrance of the transport section in different regimes.
The plasma density between the mirrors in the confinement region was determined by the hydrogen flow rate from the gas feeding system into the plasma source. The density was in the range $n = (0.6\unicode{x2013}5.5)\times 10^{18}\ {\rm m}^{-3}$![]() , average ion temperature was $T_i = 3.5\unicode{x2013}4.5\ {\rm eV}$
, average ion temperature was $T_i = 3.5\unicode{x2013}4.5\ {\rm eV}$![]() and electron temperature on the axis was $T_e = 20\unicode{x2013}30\ {\rm eV}$
and electron temperature on the axis was $T_e = 20\unicode{x2013}30\ {\rm eV}$![]() (Ivanov et al. Reference Ivanov, Ustyuzhanin, Sudnikov and Inzhevatkina2021). The density in the entrance region of the transport section was roughly 2-times lower in all regimes, giving $n = (0.3\unicode{x2013}2.5)\times 10^{18}\ {\rm m}^{-3}$
(Ivanov et al. Reference Ivanov, Ustyuzhanin, Sudnikov and Inzhevatkina2021). The density in the entrance region of the transport section was roughly 2-times lower in all regimes, giving $n = (0.3\unicode{x2013}2.5)\times 10^{18}\ {\rm m}^{-3}$![]() . These values correspond to the mean free path of an ion in the helical field with respect to the binary collisions $\lambda = 0.3\unicode{x2013}2.5\ {\rm m}$
. These values correspond to the mean free path of an ion in the helical field with respect to the binary collisions $\lambda = 0.3\unicode{x2013}2.5\ {\rm m}$![]() . Therefore, the ratio of the mean free path to the period of the helical corrugation was $\lambda /h \sim 1$
. Therefore, the ratio of the mean free path to the period of the helical corrugation was $\lambda /h \sim 1$![]() on the high density bound (in most high density cases, $\lambda \approx 2h$
on the high density bound (in most high density cases, $\lambda \approx 2h$![]() ) and $\lambda /h \sim N$
) and $\lambda /h \sim N$![]() on the low density bound. The first case meets the criterion of an efficient multiple-mirror confinement with binary collisions only, the second one requires anomalous scattering for the flow suppression. The ion temperature measured in the exit expander was the same as in the entrance tank. The helical mirror concept requires fast rotation of plasma due to $\boldsymbol{E}\times \boldsymbol{B}$
on the low density bound. The first case meets the criterion of an efficient multiple-mirror confinement with binary collisions only, the second one requires anomalous scattering for the flow suppression. The ion temperature measured in the exit expander was the same as in the entrance tank. The helical mirror concept requires fast rotation of plasma due to $\boldsymbol{E}\times \boldsymbol{B}$![]() drift. The detailed description of the particle drift in the helical magnetic field with the rotational velocity of the order of the thermal velocity is presented by Chernoshtanov & Ayupov (Reference Chernoshtanov and Ayupov2021). Plasma rotation velocity in the discussed experiments was $\omega = (1\unicode{x2013}1.1)\times 10^6\ {\rm s}^{-1}$
drift. The detailed description of the particle drift in the helical magnetic field with the rotational velocity of the order of the thermal velocity is presented by Chernoshtanov & Ayupov (Reference Chernoshtanov and Ayupov2021). Plasma rotation velocity in the discussed experiments was $\omega = (1\unicode{x2013}1.1)\times 10^6\ {\rm s}^{-1}$![]() in the entrance tank ($z = 1.15$
in the entrance tank ($z = 1.15$![]() m) and $\omega = (0.4\unicode{x2013}0.65)\times 10^6\ {\rm s}^{-1}$
m) and $\omega = (0.4\unicode{x2013}0.65)\times 10^6\ {\rm s}^{-1}$![]() in the exit expander ($z = 4.34$
in the exit expander ($z = 4.34$![]() m).
m).
The following diagnostics were actively used in the described experiments. Radially movable sets of electrostatic probes were installed in the confinement region ($z = 0.4$![]() m), in the entrance of the transport section ($z = 2.04$
m), in the entrance of the transport section ($z = 2.04$![]() m), in the exit from the transport section ($z = 3.48$
m), in the exit from the transport section ($z = 3.48$![]() m) and in the exit expander ($z = 4.34$
m) and in the exit expander ($z = 4.34$![]() m). Sets in the confinement region and in the transport section include a double probe and two radially shifted emissive probes. Double probes were used alternately in the ion saturation or in the $I$
m). Sets in the confinement region and in the transport section include a double probe and two radially shifted emissive probes. Double probes were used alternately in the ion saturation or in the $I$![]() –$V$
–$V$![]() characteristic regime. The emissive probes with thoriated tungsten wires were heated by the plasma during the initial part of the discharge, and then provided simultaneous measurements of plasma potential and radial electric field. Reaching the working temperature of the probe was verified by the thermal radiation of the wire. Set in the exit expander is a double probe in the ion saturation regime and one emissive probe heated by an external current prior to the experiment. Two imaging Doppler spectrometers ($z = 1.15$
characteristic regime. The emissive probes with thoriated tungsten wires were heated by the plasma during the initial part of the discharge, and then provided simultaneous measurements of plasma potential and radial electric field. Reaching the working temperature of the probe was verified by the thermal radiation of the wire. Set in the exit expander is a double probe in the ion saturation regime and one emissive probe heated by an external current prior to the experiment. Two imaging Doppler spectrometers ($z = 1.15$![]() m and $z = 4.34$
m and $z = 4.34$![]() m) and the array of Mirnov coils ($z = 2.76$
m) and the array of Mirnov coils ($z = 2.76$![]() m) were used to measure plasma rotation (Inzhevatkina et al. Reference Inzhevatkina, Burdakov, Ivanov, Lomov, Postupaev, Sudnikov and Ustyuzhanin2021). The spectrometers are also capable of measuring the Doppler broadening of the emission line of the charge-exchanged hydrogen, which depends on the ion temperature. Microwave interferometer (frequency $f = 38$
m) were used to measure plasma rotation (Inzhevatkina et al. Reference Inzhevatkina, Burdakov, Ivanov, Lomov, Postupaev, Sudnikov and Ustyuzhanin2021). The spectrometers are also capable of measuring the Doppler broadening of the emission line of the charge-exchanged hydrogen, which depends on the ion temperature. Microwave interferometer (frequency $f = 38$![]() GHz) in the distant half of the transport section ($z = 3.12$
GHz) in the distant half of the transport section ($z = 3.12$![]() m) provided an additional information about the plasma density.
m) provided an additional information about the plasma density.
The typical experimental waveforms are shown in figure 4. Time $t=0$![]() corresponds to the discharge initiation. The stationary plasma discharge builds up during the first 40 ms. Stationary neutral gas distribution, which depends on the hydrogen flow rate in the plasma source, discharge current and configuration, is achieved in ${\sim }80$
corresponds to the discharge initiation. The stationary plasma discharge builds up during the first 40 ms. Stationary neutral gas distribution, which depends on the hydrogen flow rate in the plasma source, discharge current and configuration, is achieved in ${\sim }80$![]() ms. Hydrogen flows through the transport section mostly in ionized form during the discharge (figure 4i). Average values on the flattop of the discharge ($t=90\unicode{x2013}150\ {\rm ms}$
ms. Hydrogen flows through the transport section mostly in ionized form during the discharge (figure 4i). Average values on the flattop of the discharge ($t=90\unicode{x2013}150\ {\rm ms}$![]() ) are used to plot radial profiles of the plasma parameters. The emissive probe reaches working temperature in $t\leqslant 40\ {\rm ms}$
) are used to plot radial profiles of the plasma parameters. The emissive probe reaches working temperature in $t\leqslant 40\ {\rm ms}$![]() at radial coordinates $r\leqslant 6\ {\rm cm}$
at radial coordinates $r\leqslant 6\ {\rm cm}$![]() . At the outer region ($r=6\unicode{x2013}8\ {\rm cm}$
. At the outer region ($r=6\unicode{x2013}8\ {\rm cm}$![]() ), the heating takes up to $t=90\ {\rm ms}$
), the heating takes up to $t=90\ {\rm ms}$![]() . The temperature rise time is consistent with the estimations similar to Hershkowitz et al. (Reference Hershkowitz, Nelson, Pew and Gates1983). At $t=165\ {\rm ms}$
. The temperature rise time is consistent with the estimations similar to Hershkowitz et al. (Reference Hershkowitz, Nelson, Pew and Gates1983). At $t=165\ {\rm ms}$![]() , the plasma source switches off to avoid damaging of the probes. Radial distributions of the plasma parameters were measured and integrated assuming axial symmetry of the plasma cross-section. Plasma axis was found for every magnetic configuration as the point of zero radial electric field.
, the plasma source switches off to avoid damaging of the probes. Radial distributions of the plasma parameters were measured and integrated assuming axial symmetry of the plasma cross-section. Plasma axis was found for every magnetic configuration as the point of zero radial electric field.

Figure 4. Typical waveforms of plasma parameters in discharges with straight ($R_{{\rm mean}} = 1$![]() , red curves) and helically corrugated ($R_{{\rm mean}} = 1.52$
, red curves) and helically corrugated ($R_{{\rm mean}} = 1.52$![]() ) magnetic configurations at the ‘confinement’ (blue curves) regime and ‘pumping-out’ (green curves) regime. Waveforms of the gas pressure without the discharge (orange curves) are shown for comparison. From top to bottom: (a) the discharge current; (b) the voltage between the anode and the cathode of the plasma source; (c) the potential of the emissive probe at $z=0.4\ {\rm m}$
) magnetic configurations at the ‘confinement’ (blue curves) regime and ‘pumping-out’ (green curves) regime. Waveforms of the gas pressure without the discharge (orange curves) are shown for comparison. From top to bottom: (a) the discharge current; (b) the voltage between the anode and the cathode of the plasma source; (c) the potential of the emissive probe at $z=0.4\ {\rm m}$![]() ; (d) the potential of the emissive probe at $z=2.04\ {\rm m}$
; (d) the potential of the emissive probe at $z=2.04\ {\rm m}$![]() ; (e) the current of the double probe at $z=0.4$
; (e) the current of the double probe at $z=0.4$![]() m ($I$
m ($I$![]() –$V$
–$V$![]() curve measurement); ( f) the current of the double probe at $z = 2.04 {\rm m}$
curve measurement); ( f) the current of the double probe at $z = 2.04 {\rm m}$![]() (the ion saturation current measurement); (g) linear plasma density from the interferometry data; (h) the neutral hydrogen pressure at $z=0.4$
(the ion saturation current measurement); (g) linear plasma density from the interferometry data; (h) the neutral hydrogen pressure at $z=0.4$![]() m; (i) the neutral hydrogen pressure at $z=4.34$
m; (i) the neutral hydrogen pressure at $z=4.34$![]() m.
m.
3. Radial distribution of plasma parameters
We assumed that the radial distributions of plasma parameters are axially symmetric and that the vertical displacement of the plasma axis is negligible compared to the plasma radius for all operation regimes. The first assumption relies on the axially symmetric configuration of the plasma source and confinement region, and on the bispiral configuration of the helical magnetic system which does not deform the plasma shape at small displacements of the plasma axis. The second one is based on the second-order rotational symmetry of the helical magnetic system with respect to the axis of the diagnostic port.
We integrated the plasma parameters over the cross-section of the plasma column to find the global effects of the helical magnetic field. Integration of the local plasma density returns the number of particles per unit length in the axial direction. This value multiplied by the distance between the simple and helical mirrors returns the number of particles in the confinement region. Integration of the ion saturation current of the probes in the transport section returns the value proportional to the particle flux in the axial direction in assumption of the constant electron temperature along the field line. Fitting of the experimental radial profiles by the analytical functions was used to find the integral values described above. The following function was used:

In this equation, $r$![]() is the radial coordinate relative to the geometric axis of the vacuum chamber, $r_0$
is the radial coordinate relative to the geometric axis of the vacuum chamber, $r_0$![]() is the position of the centre of the plasma stream where the radial electric field changes sign, fitting parameters $r_1$
is the position of the centre of the plasma stream where the radial electric field changes sign, fitting parameters $r_1$![]() and $r_2$
and $r_2$![]() are characteristic radii of the plasma stream and the density flat-top, and $a_1$
are characteristic radii of the plasma stream and the density flat-top, and $a_1$![]() and $a_2$
and $a_2$![]() are the corresponding amplitudes.
are the corresponding amplitudes.
Radial profiles of the plasma density and radial electric field for the cases of the simple and helical mirrors are shown in figure 5. The vertical error bars in these graphs correspond to the shot-to-shot reproducibility (${\sim }6\,\%$![]() of the corresponding value), the horizontal error bars correspond to the probe dimensions (probe length is 6 mm for the units installed in $z=0.40$
of the corresponding value), the horizontal error bars correspond to the probe dimensions (probe length is 6 mm for the units installed in $z=0.40$![]() m and $z=4.34$
m and $z=4.34$![]() m, 4 mm for all other units). The main reason of the systematic error in the experimental campaign was the drift of the gas feed rate at constant settings of the feeding system which depended on the number of discharges since the last operation at atmospheric pressure. This drift resulted in ${\sim }5\,\%$
m, 4 mm for all other units). The main reason of the systematic error in the experimental campaign was the drift of the gas feed rate at constant settings of the feeding system which depended on the number of discharges since the last operation at atmospheric pressure. This drift resulted in ${\sim }5\,\%$![]() difference of the plasma density between ‘pumping-out’ and ‘confinement’ sub-campaigns. The described systematic error does not play a role in comparison with the data inside one sub-campaign because the difference in the number of discharges is sufficiently lower. Other error sources for these measurements are negligible. These profiles show remarkable differences between the confinement and pumping out. In the confinement regime, the plasma density grows with the activation of the helical mirror (figure 5a). This growth is consistent with the previous experimental observations (Sudnikov et al. Reference Sudnikov, Ivanov, Inzhevatkina, Larichkin, Lomov, Postupaev, Tolkachev and Ustyuzhanin2022). In contrast, the density does not depend on the mirror ratio in the transport section at pumping out (figure 5b). Also, the radial electric field decreases in the pumping-out configuration if the helical field is activated (figure 5d). A reduced electric field can be the sign of the higher transversal conductivity. The definite reason of this effect requires further investigation.
difference of the plasma density between ‘pumping-out’ and ‘confinement’ sub-campaigns. The described systematic error does not play a role in comparison with the data inside one sub-campaign because the difference in the number of discharges is sufficiently lower. Other error sources for these measurements are negligible. These profiles show remarkable differences between the confinement and pumping out. In the confinement regime, the plasma density grows with the activation of the helical mirror (figure 5a). This growth is consistent with the previous experimental observations (Sudnikov et al. Reference Sudnikov, Ivanov, Inzhevatkina, Larichkin, Lomov, Postupaev, Tolkachev and Ustyuzhanin2022). In contrast, the density does not depend on the mirror ratio in the transport section at pumping out (figure 5b). Also, the radial electric field decreases in the pumping-out configuration if the helical field is activated (figure 5d). A reduced electric field can be the sign of the higher transversal conductivity. The definite reason of this effect requires further investigation.

Figure 5. Sample radial profiles in the confinement region: (a) plasma density in the confinement regime; (b) plasma density in the pumping-out regime; (c) radial electric field in the confinement regime; (d) radial electric field in the pumping-out regime. Dots show experimental data, lines are fitting functions.
The fluxes in the transport section also show different dependencies on the magnetic configuration at different directions of the rotation (figure 6). In the confinement regime, the plasma density at the entrance of the transport section grows proportionally to the density in the trap, and the plasma column width does not change significantly (figure 6a). At the exit from the transport section, both peak density and width of the plasma column decrease (figure 6c). Both these effects stand in agreement with the theory (Beklemishev Reference Beklemishev2013) and previous experiments (Sudnikov et al. Reference Sudnikov, Ivanov, Inzhevatkina, Larichkin, Lomov, Postupaev, Tolkachev and Ustyuzhanin2022). The suppression factor is higher at the plasma periphery, where the mirror ratio is larger, and close to unity at the magnetic axis where the field modulation from the helical winding vanishes. Radial transport towards the negatively biased axis also causes radial contraction of the plasma, as described by Beklemishev (Reference Beklemishev2016).

Figure 6. Sample radial profiles of the ion saturation current density in the transport section: (a) entrance of the transport section, confinement; (b) entrance of the transport section, pumping out; (c) exit from the transport section, confinement; (d) exit from the transport section, pumping out. Dots show experimental data, lines are fitting functions.
In the pumping-out configuration, the plasma density at the entrance of the transport section also grows, but the width of the plasma column in most profiles becomes slightly narrower. The radial density distribution at the exit from the transport section changes differently compared to the confinement region. The plasma column becomes significantly narrower, while the maximal density grows and becomes higher than in the straight field configuration. It stands in agreement with the assumption that the plasma loss is not suppressed in this configuration, only the radial transport of the trapped ions affects the observed density distribution.
The plasma potential in the pumping-out regime reaches $\phi \approx (2\unicode{x2013}3)T_e$![]() (figure 7), which is enough to transfer momentum to the trapped particles (Sudnikov et al. Reference Sudnikov, Beklemishev, Postupaev, Burdakov, Ivanov, Vasilyeva, Kuklin and Sidorov2017). In the confinement regime, the potential was lower, $\phi \approx (1.5\unicode{x2013}2)T_e$
(figure 7), which is enough to transfer momentum to the trapped particles (Sudnikov et al. Reference Sudnikov, Beklemishev, Postupaev, Burdakov, Ivanov, Vasilyeva, Kuklin and Sidorov2017). In the confinement regime, the potential was lower, $\phi \approx (1.5\unicode{x2013}2)T_e$![]() , which limits the effectiveness of the helical mirror. The shape of radial profiles in this regime was roughly the same as at the pumping out.
, which limits the effectiveness of the helical mirror. The shape of radial profiles in this regime was roughly the same as at the pumping out.

Figure 7. Sample radial profiles near the entrance of the transport section in the pumping-out regime: (a) electron temperature; (b) electrostatic potential. Dots show experimental data, lines are fitting functions.
Average ion temperature at both directions of the magnetic field was $\langle T_i \rangle \sim 4.5\ {\rm eV}$![]() in the straight configuration and $\langle T_i \rangle \sim 3.5\ {\rm eV}$
in the straight configuration and $\langle T_i \rangle \sim 3.5\ {\rm eV}$![]() in the helical configuration which is consistent with the data presented by Ivanov et al. (Reference Ivanov, Ustyuzhanin, Sudnikov and Inzhevatkina2021). Ion temperature at the axis reaches $T_i=7.5\pm 1\ {\rm eV}$
in the helical configuration which is consistent with the data presented by Ivanov et al. (Reference Ivanov, Ustyuzhanin, Sudnikov and Inzhevatkina2021). Ion temperature at the axis reaches $T_i=7.5\pm 1\ {\rm eV}$![]() in the straight configuration (figure 8). The temperature in the helical configuration is lower, giving $T_i=6\pm 1\ {\rm eV}$
in the straight configuration (figure 8). The temperature in the helical configuration is lower, giving $T_i=6\pm 1\ {\rm eV}$![]() at the axis. The temperature drops to $T_i=2\pm 0.5\ {\rm eV}$
at the axis. The temperature drops to $T_i=2\pm 0.5\ {\rm eV}$![]() on the plasma periphery in both regimes.
on the plasma periphery in both regimes.

Figure 8. Sample radial profiles of the ion temperature in the confinement region: (a) pumping-out regime; (b) confinement regime.
4. Dependencies of the integral parameters
The difference between the confinement and pumping out can be described by the plasma parameters integrated over the plasma cross-section. The dependencies of the integrated densities $n$![]() and fluxes $F$
and fluxes $F$![]() on the relative amplitude of the helical component of the magnetic field are shown in figure 9. Caps of the error bars correspond to uncertainties of the integral values calculated from the fitted profiles and play a role for comparison inside one regime (confinement or pumping out). The ends of lines of the error bars include a systematic error due to the density drift between different sub-campaigns. Average plasma density in the confinement region was $n \approx 4\times 10^{18}\ {\rm m}^{-3}$
on the relative amplitude of the helical component of the magnetic field are shown in figure 9. Caps of the error bars correspond to uncertainties of the integral values calculated from the fitted profiles and play a role for comparison inside one regime (confinement or pumping out). The ends of lines of the error bars include a systematic error due to the density drift between different sub-campaigns. Average plasma density in the confinement region was $n \approx 4\times 10^{18}\ {\rm m}^{-3}$![]() . In the confinement regime, the number of the particles between the mirrors increases by a factor of 1.3 (figure 9a), the average density at the entrance of the transport section also increases (figure 9b). The fluxes through the distant part of the transport section and in the exit expander decrease two-fold (figure 9c,d). Here we should note that the decrease of the particle flux through the exit from the transport section is balanced by the generation of the return flux in the middle part of the transport section close to the plasma axis (Sudnikov et al. Reference Sudnikov, Ivanov, Inzhevatkina, Larichkin, Lomov, Postupaev, Tolkachev and Ustyuzhanin2022). This return flux reduces or even reverses the average velocity in the entrance part of the transport section. In the distant part of the transport section, the density of this return flux is negligible and the reversed flow does not occur. The fluxes in the pumping-out regime do not show clear dependence on the mean corrugation. Variation of the flux in all cross-sections are below the statistically significant level.
. In the confinement regime, the number of the particles between the mirrors increases by a factor of 1.3 (figure 9a), the average density at the entrance of the transport section also increases (figure 9b). The fluxes through the distant part of the transport section and in the exit expander decrease two-fold (figure 9c,d). Here we should note that the decrease of the particle flux through the exit from the transport section is balanced by the generation of the return flux in the middle part of the transport section close to the plasma axis (Sudnikov et al. Reference Sudnikov, Ivanov, Inzhevatkina, Larichkin, Lomov, Postupaev, Tolkachev and Ustyuzhanin2022). This return flux reduces or even reverses the average velocity in the entrance part of the transport section. In the distant part of the transport section, the density of this return flux is negligible and the reversed flow does not occur. The fluxes in the pumping-out regime do not show clear dependence on the mean corrugation. Variation of the flux in all cross-sections are below the statistically significant level.

Figure 9. Dependencies of the particle number and integral flux on the mean corrugation ratio, $B_z=70\ {\rm mT}$![]() . (a) Number of particles in the confinement region; (b) average density at the entrance of the transport section. Plasma fluxes: (c) at the exit from the transport section; (d) in the exit expander.
. (a) Number of particles in the confinement region; (b) average density at the entrance of the transport section. Plasma fluxes: (c) at the exit from the transport section; (d) in the exit expander.
The dependence of the particle flux through the transport section on the plasma collisionality plays an important role in the multiple-mirror confinement. Classical theory of the multiple-mirror confinement (Mirnov & Ryutov Reference Mirnov and Ryutov1972; Kotelnikov Reference Kotelnikov2007) suggests that a multiple-mirror section is effective only if the period of the magnetic field variation is comparable with the ion mean free path. Ion scattering may occur either due to the binary collisions or due to microinstabilities in non-equilibrium plasma. Variation of the Coulomb collisionality in SMOLA is obtained by the variation of the gas feeding of the plasma source. In previous experiments in the confinement regime at a plasma density between the mirrors of $n = (0.8\unicode{x2013}4)\times 10^{18}\ {\rm m}^{-3}$![]() (Sudnikov et al. Reference Sudnikov, Ivanov, Inzhevatkina, Larichkin, Lomov, Postupaev, Tolkachev and Ustyuzhanin2022), no statistically significant difference was found between low- and high-density cases. In the described experiments, the density range was broader, and the level of the data uncertainty was reduced. The obtained integral values in the helical configuration were normalized by the corresponding values in the straight field regime, i.e. the normalized flux in the straight field was set to unity. The dependencies of the normalized integral values on the average density in the confinement region are shown in figure 10.
(Sudnikov et al. Reference Sudnikov, Ivanov, Inzhevatkina, Larichkin, Lomov, Postupaev, Tolkachev and Ustyuzhanin2022), no statistically significant difference was found between low- and high-density cases. In the described experiments, the density range was broader, and the level of the data uncertainty was reduced. The obtained integral values in the helical configuration were normalized by the corresponding values in the straight field regime, i.e. the normalized flux in the straight field was set to unity. The dependencies of the normalized integral values on the average density in the confinement region are shown in figure 10.

Figure 10. Dependencies of the normalized integral values at different coordinates on the average density in the confinement region. (a,c,g) Pumping-out regime, (b,d,h) confinement regime. From top to bottom: (a,b) at the entrance of the transport section; (c,d) in the distant part of the transport section; (e, f) at the exit from the transport section; (g,h) particle fluxes at the exit expander.
The normalized integral values do not show clear dependence on the plasma density in the confinement regime (figure 10b,d, f,h). In this regime, the integral flux at the end of the transport section decreases by a factor of approximately $F_{{\rm norm}}=0.66\pm 0.13$![]() at a corrugation ratio $R_{{\rm mean}} = 1.35$
at a corrugation ratio $R_{{\rm mean}} = 1.35$![]() and by a factor of approximately $F_{{\rm norm}}=0.43\pm 0.10$
and by a factor of approximately $F_{{\rm norm}}=0.43\pm 0.10$![]() at a corrugation ratio $R_{{\rm mean}} = 1.52$
at a corrugation ratio $R_{{\rm mean}} = 1.52$![]() . No statistically significant deviation from the average values was found at any cross-section ($p$
. No statistically significant deviation from the average values was found at any cross-section ($p$![]() -value for different cross-sections $p=0.35\unicode{x2013}0.65$
-value for different cross-sections $p=0.35\unicode{x2013}0.65$![]() ).
).
In contrast, in the pumping-out regime, the normalized integral values depend on plasma density significantly. The normalized flux stays constant only at the entrance of the transport section (figure 10a). At the distant part of the transport section, the normalized flux statistically significantly deviates from the constant ($p<0.003$![]() ). At high densities, the flux in the helical regime is slightly lower than in the straight field ($F_{{\rm norm}}=0.79\pm 0.17$
). At high densities, the flux in the helical regime is slightly lower than in the straight field ($F_{{\rm norm}}=0.79\pm 0.17$![]() ). This flux also reduces significantly at the lowest densities achieved in experiment ($F_{{\rm norm}}=0.63\pm 0.21$
). This flux also reduces significantly at the lowest densities achieved in experiment ($F_{{\rm norm}}=0.63\pm 0.21$![]() ). In contrast, at an average plasma density $n = 3\times 10^{18}\ {\rm m}^{-3}$
). In contrast, at an average plasma density $n = 3\times 10^{18}\ {\rm m}^{-3}$![]() , the flux through the transport section rises in the case of the helical magnetic field by a factor of approximately $F_{{\rm norm}}=1.40\pm 0.16$
, the flux through the transport section rises in the case of the helical magnetic field by a factor of approximately $F_{{\rm norm}}=1.40\pm 0.16$![]() . The increasing particle flux is consistent with the decrease of the effective mirror ratio of the helical mirror (estimation is given later, see (4.6)). The same dependence is observed at any magnetic field used in the experiment $B_z=50\unicode{x2013}100\ {\rm mT}$
. The increasing particle flux is consistent with the decrease of the effective mirror ratio of the helical mirror (estimation is given later, see (4.6)). The same dependence is observed at any magnetic field used in the experiment $B_z=50\unicode{x2013}100\ {\rm mT}$![]() and at any corrugation ratio $R_{{\rm mean}}=1.35\unicode{x2013}1.7$
and at any corrugation ratio $R_{{\rm mean}}=1.35\unicode{x2013}1.7$![]() .
.
The observed dependencies can be explained in the following way. In both cases, a fraction of ions becomes trapped between the maxima of the periodical magnetic field. In the confinement regime, the flux of the trapped ions moves in the direction opposite to the plasma outflow. In the previous experiments (Sudnikov et al. Reference Sudnikov, Ivanov, Inzhevatkina, Larichkin, Lomov, Postupaev, Tolkachev and Ustyuzhanin2022), the local density of the trapped ions flux near the plasma axis exceeded the density of the outflow. The velocity of the trapped ions was comparable to the axial velocity of the magnetic mirrors in the plasma reference frame. Such flux by itself can be an energy source for microinstabilities that can lead to an anomalous scattering. In this case, an improved confinement can take place in the broad range of the plasma density.
In the pumping-out regime, the flux of the trapped ions moves in the same direction as the plasma outflow; therefore, the relative velocity of the trapped and passing ions is lower than in the previous case. At the density $n = 4\times 10^{18}\ {\rm m}^{-3}$![]() , the trapped ions travel approximately one period of the magnetic corrugation before they scatter, giving a low rate of the pumping out. In this case, the helical magnetic field works similarly with the stationary multiple mirrors, which has the particle lifetime in the transport section (Burdakov & Postupaev Reference Burdakov and Postupaev2018):
, the trapped ions travel approximately one period of the magnetic corrugation before they scatter, giving a low rate of the pumping out. In this case, the helical magnetic field works similarly with the stationary multiple mirrors, which has the particle lifetime in the transport section (Burdakov & Postupaev Reference Burdakov and Postupaev2018):
where $\tau _0=L/v_{{\rm Ti}}$![]() is the time of flight with thermal velocity, $v_{{\rm Ti}}$
is the time of flight with thermal velocity, $v_{{\rm Ti}}$![]() is the ion thermal velocity, $L$
is the ion thermal velocity, $L$![]() is the length of the multiple-mirror section and $R$
is the length of the multiple-mirror section and $R$![]() is the mirror ratio. We should note that in classical multiple-mirror theory, this mirror ratio does not depend on the radius. In a helical mirror, a weighted average of the local corrugation ratio should be used to take into account varying fraction of the trapped particles. Local ion density can be taken as a weighting coefficient:
is the mirror ratio. We should note that in classical multiple-mirror theory, this mirror ratio does not depend on the radius. In a helical mirror, a weighted average of the local corrugation ratio should be used to take into account varying fraction of the trapped particles. Local ion density can be taken as a weighting coefficient:
In the case of a constant density across the plasma, this average gives $\langle (R(r)-1)^2 \rangle =\frac {4}{3}(R_{{\rm mean}}-1)^2$![]() taking into account that the ratio of the maximal and the minimal magnetic field along the field line depends on the radius as $(R-1)\sim r^2$
taking into account that the ratio of the maximal and the minimal magnetic field along the field line depends on the radius as $(R-1)\sim r^2$![]() . This calculation overestimates the last factor in (4.2) due to the low density on the plasma periphery where $(R-1)^2$
. This calculation overestimates the last factor in (4.2) due to the low density on the plasma periphery where $(R-1)^2$![]() rises. Numerical calculation of the particle lifetime with experimentally measured density and corrugation distribution gives $\tau \approx (1.1\unicode{x2013}1.3)\tau _0$
rises. Numerical calculation of the particle lifetime with experimentally measured density and corrugation distribution gives $\tau \approx (1.1\unicode{x2013}1.3)\tau _0$![]() .
.
At low density, the fraction of the trapped particles decreases because the mean free path becomes comparable to the length of the transport section if no anomalous scattering exist. In this case, the particle lifetime corresponds to the simple time of flight:
In the middle range of densities, the collisionality is high enough to maintain a fraction of the trapped particles $\kappa$![]() , which move a few periods of corrugation before being scattered again. This fraction is sufficient to contribute to the average flow velocity, but still too low to form an ion distribution function appropriate for a middle-scale corrugation regime in the multiple mirror magnetic system. In this case, in every individual cell of the multiple-mirror system, the loss cone corresponding to the particles returning back to the confinement region is depleted. Therefore, we have three ion populations: trapped particles which move with the axial velocity of the moving mirrors $V_z$
, which move a few periods of corrugation before being scattered again. This fraction is sufficient to contribute to the average flow velocity, but still too low to form an ion distribution function appropriate for a middle-scale corrugation regime in the multiple mirror magnetic system. In this case, in every individual cell of the multiple-mirror system, the loss cone corresponding to the particles returning back to the confinement region is depleted. Therefore, we have three ion populations: trapped particles which move with the axial velocity of the moving mirrors $V_z$![]() (fraction of this population is $\kappa$
(fraction of this population is $\kappa$![]() ); passing particles moving upstream with thermal velocity $v_{Ti}$
); passing particles moving upstream with thermal velocity $v_{Ti}$![]() (fraction of this population is $\kappa _u \leqslant \kappa /2$
(fraction of this population is $\kappa _u \leqslant \kappa /2$![]() ) and passing particles moving downstream with thermal velocity $v_{{\rm Ti}}$
) and passing particles moving downstream with thermal velocity $v_{{\rm Ti}}$![]() (fraction of this population is $1 - \kappa - \kappa _u$
(fraction of this population is $1 - \kappa - \kappa _u$![]() ). The particle lifetime can be estimated as
). The particle lifetime can be estimated as

This lifetime is lower than the corresponding value both in the classical multiple-mirror case and in the collisionless case if the axial velocity of the magnetic mirror movement exceeds the thermal velocity twofold. In experiment, the axial velocity of the magnetic mirror movement can be evaluated as $V_z=\omega h\sim (7.2\unicode{x2013}20)\times 10^4\ {\rm m}\ {\rm s}^{-1}$![]() , where $\omega \sim (0.4\unicode{x2013}1.1)\times 10^5\ {\rm s}^{-1}$
, where $\omega \sim (0.4\unicode{x2013}1.1)\times 10^5\ {\rm s}^{-1}$![]() is the rotational velocity and $h=18\ {\rm cm}$
is the rotational velocity and $h=18\ {\rm cm}$![]() is the period of corrugation. The thermal velocity for the ion temperature $T_i<7\ {\rm eV}$
is the period of corrugation. The thermal velocity for the ion temperature $T_i<7\ {\rm eV}$![]() is $v_{{\rm Ti}}<3.6\times 10^4\ {\rm m}\ {\rm s}^{-1}$
is $v_{{\rm Ti}}<3.6\times 10^4\ {\rm m}\ {\rm s}^{-1}$![]() . Therefore, the trapped particles are effectively transported to the exit from the transport section.
. Therefore, the trapped particles are effectively transported to the exit from the transport section.
The particle balance in the trap can be estimated in the same way as done by Sudnikov et al. (Reference Sudnikov, Ivanov, Inzhevatkina, Larichkin, Lomov, Postupaev, Tolkachev and Ustyuzhanin2022). If the density in the entrance trap exceeds $n\sim 10^{18}\ {\rm m}^{-3}$![]() , the losses are gasdynamic. In other words, if the ion mean free path becomes shorter than the confinement region, each mirror disturbs the ion distribution function only in its own vicinity. The losses through each mirror can be estimated as $F = n v_T S_m$
, the losses are gasdynamic. In other words, if the ion mean free path becomes shorter than the confinement region, each mirror disturbs the ion distribution function only in its own vicinity. The losses through each mirror can be estimated as $F = n v_T S_m$![]() (Ryutov Reference Ryutov1988), where $n$
(Ryutov Reference Ryutov1988), where $n$![]() and $v_T$
and $v_T$![]() are the density and the thermal velocity of ions in the entrance trap, and $S_m$
are the density and the thermal velocity of ions in the entrance trap, and $S_m$![]() is the cross-section of the plasma in the mirror. The losses are usually re-determined using the plasma cross-section in the minimal magnetic field $S_0 = S_m R$
is the cross-section of the plasma in the mirror. The losses are usually re-determined using the plasma cross-section in the minimal magnetic field $S_0 = S_m R$![]() , where $R$
, where $R$![]() is the corresponding mirror ratio.
is the corresponding mirror ratio.
The losses are balanced with new ions from the plasma source and the return flux, which is generated by the transport section. The rate of plasma neutralization and neutral gas pumping matches the rate of plasma source feeding in the steady state. The radial losses in the confinement region are assumed to be independent of the chosen magnetic configuration of the transport section. The particle balance inside the confinement region can be described in the following form:
where $R_1 = 8$![]() and $R_2 = 3$
and $R_2 = 3$![]() are the simple mirror ratios of the minimal magnetic field to the plasma source field and to the guide magnetic field of the transport section, $F_{{\rm feed}}$
are the simple mirror ratios of the minimal magnetic field to the plasma source field and to the guide magnetic field of the transport section, $F_{{\rm feed}}$![]() is the flux from the plasma source and $F_{{\rm return}}$
is the flux from the plasma source and $F_{{\rm return}}$![]() is the return flux from the transport section. The difference of the outflow $nvS_0$
is the return flux from the transport section. The difference of the outflow $nvS_0$![]() and return $F_{{\rm return}}$
and return $F_{{\rm return}}$![]() fluxes at the inlet of the transport section can be used to define the effective mirror ratio of the helical confinement system $R_{{\rm eff}}$
fluxes at the inlet of the transport section can be used to define the effective mirror ratio of the helical confinement system $R_{{\rm eff}}$![]() :
:
An important point of this definition is that the effective mirror ratio cannot be less than the simple mirror ratio, $R_{{\rm eff}}>R_2$![]() . In a simple mirror, any ion which reaches the point of highest magnetic field is immediately lost, $F_{{\rm return}}=0$
. In a simple mirror, any ion which reaches the point of highest magnetic field is immediately lost, $F_{{\rm return}}=0$![]() . Negative values of the return flux correspond to the situation where the particles come to the entrance of the transport section faster than with a simple mirror. Therefore, any modification which does not affect the confinement region either does not modify the effective mirror ratio or increases it.
. Negative values of the return flux correspond to the situation where the particles come to the entrance of the transport section faster than with a simple mirror. Therefore, any modification which does not affect the confinement region either does not modify the effective mirror ratio or increases it.
Estimation of the effective mirror ratio in the pumping-out regime gives $R_{{\rm eff}} = 4.0\pm 1.0$![]() at $R_{{\rm mean}} = 1.52$
at $R_{{\rm mean}} = 1.52$![]() , $\langle n_{z=0.4\ {\rm m}}\rangle =5\times 10^{18}\ {\rm m}^{-3}$
, $\langle n_{z=0.4\ {\rm m}}\rangle =5\times 10^{18}\ {\rm m}^{-3}$![]() and $R_{{\rm eff}} = 3.3\pm 0.8$
and $R_{{\rm eff}} = 3.3\pm 0.8$![]() at $R_{{\rm mean}} = 1.52$
at $R_{{\rm mean}} = 1.52$![]() , $\langle n_{z=0.4\ {\rm m}}\rangle =3\times 10^{18}\ {\rm m}^{-3}$
, $\langle n_{z=0.4\ {\rm m}}\rangle =3\times 10^{18}\ {\rm m}^{-3}$![]() . The same value can be estimated as $R_{{\rm eff}} = 5.8\pm 1.4$
. The same value can be estimated as $R_{{\rm eff}} = 5.8\pm 1.4$![]() at $R_{{\rm mean}} = 1.52$
at $R_{{\rm mean}} = 1.52$![]() for the confinement regime at all densities. A formally calculated effective mirror ratio in the straight magnetic field at $\langle n_{z=0.4\ {\rm m}}\rangle =5\times 10^{18}\ {\rm m}^{-3}$
for the confinement regime at all densities. A formally calculated effective mirror ratio in the straight magnetic field at $\langle n_{z=0.4\ {\rm m}}\rangle =5\times 10^{18}\ {\rm m}^{-3}$![]() gives $R_{{\rm eff}} = 3.5\pm 0.9$
gives $R_{{\rm eff}} = 3.5\pm 0.9$![]() . The main sources of errors of this value are uncertainty of the integral density $n$
. The main sources of errors of this value are uncertainty of the integral density $n$![]() (see figure 9a), uncertainty of the ion temperature $T_i$
(see figure 9a), uncertainty of the ion temperature $T_i$![]() (see figure 8) and plasma source flux $F_{{\rm feed}}$
(see figure 8) and plasma source flux $F_{{\rm feed}}$![]() measurement error (20 % of the readout value). These values are consistent with the variation of the particle flux at the exit from the transport section. The difference between the confinement and pumping-out regime shows that the improvement of the particle lifetime is not the result of the static multiple mirror effect. We should note here that in the confinement regime, the plasma potential and rotation velocity were limited compared to the previous experiments (Sudnikov et al. Reference Sudnikov, Ivanov, Inzhevatkina, Larichkin, Lomov, Postupaev, Tolkachev and Ustyuzhanin2022), thus limiting the confinement effectiveness.
measurement error (20 % of the readout value). These values are consistent with the variation of the particle flux at the exit from the transport section. The difference between the confinement and pumping-out regime shows that the improvement of the particle lifetime is not the result of the static multiple mirror effect. We should note here that in the confinement regime, the plasma potential and rotation velocity were limited compared to the previous experiments (Sudnikov et al. Reference Sudnikov, Ivanov, Inzhevatkina, Larichkin, Lomov, Postupaev, Tolkachev and Ustyuzhanin2022), thus limiting the confinement effectiveness.
5. Summary
Direct comparison of the different directions of the magnetic mirrors movement in the helically symmetric multiple-mirror confinement system demonstrated a significant difference in the plasma behaviour. In the confinement regime, i.e. if the force that trapped particles experience from the helical mirror system is opposite to the direction of the axial losses, the confinement improves with the increase of the fraction of the trapped particles. The plasma stream contracts in the radial direction and its maximal density decreases. Integral flux through the section with the helical magnetic field decreases. These results are consistent with the previous experimental results (Sudnikov et al. Reference Sudnikov, Beklemishev, Inzhevatkina, Ivanov, Postupaev, Burdakov, Glinsky, Kuklin, Rovenskikh and Ustyuzhanin2020, Reference Sudnikov, Ivanov, Inzhevatkina, Larichkin, Lomov, Postupaev, Tolkachev and Ustyuzhanin2022) and the theoretical estimations (Beklemishev Reference Beklemishev2016). No degradation of the confinement was observed with the rise of the mean free path of an ion with respect to the binary collisional scattering up to the length of the transport section.
In contrast, if the direction of the axial force is the same as the direction of the axial losses, i.e. in the pumping-out regime, the confinement does not depend on the magnetic configuration significantly. The plasma stream also contracts in the radial direction but its maximal density rises. The integral flux changes insignificantly with the variation of the magnetic field corrugation. At the intermediate densities corresponding to the mean free path of an ion with respect to the binary collisional scattering approximately 3–6 periods of the corrugation, the integral flux through the transport section increases compared to the case of the straight magnetic field. This effect presumably corresponds to the high axial velocity of the trapped particles, long distance of their travel before scattering and depleted loss cone corresponding to the particles returning back to the confinement region (4.4).
The difference in plasma flows at different directions of the plasma rotation allows to conclude that the axial losses are suppressed in the confinement regime due to the helical mirror effect rather than due to the classical multiple-mirror confinement. The presence of the confinement at low densities and higher pumping out at moderate densities outline the significance of the self-sustained processes of anomalous ion scattering for helical mirror concept and draws attention to the significance of their further investigation.
Acknowledgements
The authors thank Professor A. Burdakov, Dr D. Skovorodin, Dr A. Beklemishev, Professor P. Bagryansky, Professor I. Kotelnikov, Dr V. Burmasov, Professor V. Davydenko, Dr V. Astrelin and M. Khristo for valuable discussions.
Editor Cary Forest thanks the referees for their advice in evaluating this article.
Funding
This work was supported by the grant of the Russian Science Foundation 22-12-00133 (https://rscf.ru/project/22-12-00133/). Maintenance of the SMOLA device was supported by the Ministry of Science and Higher Education of the Russian Federation. Parts of the study related to the particle balance were supported by the grant of the President of the Russian Federation SP-1242.2021.2.
Declaration of interests
The authors report no conflict of interest.