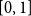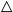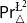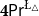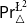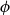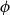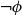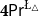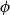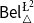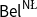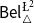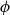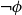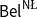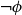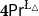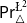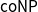1. Introduction
Classical probability and Dempster–Shafer theories study probability measures and belief functions. These are maps from the set of events of a sample space
![]() $W$
(i.e., from
$W$
(i.e., from
![]() $2^W$
) to
$2^W$
) to
![]() $[0,1]$
that are monotone w.r.t.
$[0,1]$
that are monotone w.r.t.
![]() $\subseteq$
with additional conditions. Probability measures satisfy the (finite or countable) additivity condition
$\subseteq$
with additional conditions. Probability measures satisfy the (finite or countable) additivity condition
 \begin{align*} \mu \left (\bigcup \limits _{i\in I}E_i\right )&=\sum \limits _{i\in I}\mu (E_i)\qquad \qquad \qquad (I\subseteq 2^W,\forall i,j\in I:i\neq j\Rightarrow E_i\cap E_j=\varnothing ) \end{align*}
\begin{align*} \mu \left (\bigcup \limits _{i\in I}E_i\right )&=\sum \limits _{i\in I}\mu (E_i)\qquad \qquad \qquad (I\subseteq 2^W,\forall i,j\in I:i\neq j\Rightarrow E_i\cap E_j=\varnothing ) \end{align*}
and belief functions its weaker version (total monotonicity in the terminology of Zhou Reference Zhou2013)
 \begin{align*} {\texttt {bel}}(W)&=1&{\texttt {bel}}\left (\bigcup \limits _{1\leq i\leq k}E_i\right )&\geq \sum \limits _{\scriptsize {\begin{matrix}J\subseteq \{1,\ldots, k\}\\J\neq \varnothing \end{matrix}}}\!\!\!(-1)^{|J|+1}\cdot {\texttt {bel}}\left (\bigcap \limits _{j\in J}E_j\right )& {\texttt {bel}}(\varnothing )&=0 \end{align*}
\begin{align*} {\texttt {bel}}(W)&=1&{\texttt {bel}}\left (\bigcup \limits _{1\leq i\leq k}E_i\right )&\geq \sum \limits _{\scriptsize {\begin{matrix}J\subseteq \{1,\ldots, k\}\\J\neq \varnothing \end{matrix}}}\!\!\!(-1)^{|J|+1}\cdot {\texttt {bel}}\left (\bigcap \limits _{j\in J}E_j\right )& {\texttt {bel}}(\varnothing )&=0 \end{align*}
Above, the disjointness of
![]() $E_i$
and
$E_i$
and
![]() $E_j$
can be understood as their incompatibility. Most importantly, if a propositional formula
$E_j$
can be understood as their incompatibility. Most importantly, if a propositional formula
![]() $\phi$
is associated with an event
$\phi$
is associated with an event
![]() $\|\phi \|$
(and interpreted as a statement about it), then
$\|\phi \|$
(and interpreted as a statement about it), then
(since
![]() $\|\phi \|$
and
$\|\phi \|$
and
![]() $\|\neg \phi \|$
are incompatible) and
$\|\neg \phi \|$
are incompatible) and
![]() $\|\phi \vee \neg \phi \|$
exhausts the entire sample space, whence
$\|\phi \vee \neg \phi \|$
exhausts the entire sample space, whence
Paraconsistent uncertainty theory, on the other hand, assumes that the measure of an event represents not the likelihood of it happening but an agent’s certainty therein which they infer from the information given by the sources. In this respect, it is close to the classical Dempster–Shafer theory that can also be considered as a generalisation of the subjective probability theory.
The main difference between the classical and paraconsistent approaches is the treatment of negation. Dempster–Shafer theory usually deals with contradictions between different sources. However, it is reasonable to assume that even a single source can give contradictory information (or give no information at all): for instance, a witness in court can provide a contradictory testimony; likewise, a newspaper article can fail to mention some event at all, without explicitly denying or confirming it. Thus, a ‘contradictory’ event
![]() $\|\phi \wedge \neg \phi \|$
can have a positive probability or belief assignment and
$\|\phi \wedge \neg \phi \|$
can have a positive probability or belief assignment and
![]() $\|\phi \vee \neg \phi \|$
does not necessarily exhaust the sample space. Thus, a logic describing events should allow them to be both true and false (if the source gives contradictory information) or neither true nor false (when the source does not give information). Formally, this means that
$\|\phi \vee \neg \phi \|$
does not necessarily exhaust the sample space. Thus, a logic describing events should allow them to be both true and false (if the source gives contradictory information) or neither true nor false (when the source does not give information). Formally, this means that
![]() $\neg$
does not correspond to the complement in the sample space.
$\neg$
does not correspond to the complement in the sample space.
1.1 Belnap–Dunn logic
As one can see from the previous paragraph, we need a very special kind of negation: the one that allows for true contradictions (and thus, rejects the principle of explosion), and, additionally, invalidates the law of excluded middle. Thus, the following principles are no longer valid
The logics that lack
![]() $\mathsf {EFQ}$
are called paraconsistent, those that do not have
$\mathsf {EFQ}$
are called paraconsistent, those that do not have
![]() $\mathsf {LEM}$
are paracomplete, and those that fail both principles are paradefinite or paranormal (cf., e.g., Arieli and Avron Reference Arieli and Avron2017 for the terminology).
$\mathsf {LEM}$
are paracomplete, and those that fail both principles are paradefinite or paranormal (cf., e.g., Arieli and Avron Reference Arieli and Avron2017 for the terminology).
The simplest paradefinite logic to represent reasoning about information provided by sources is the Belnap–Dunn logic (
![]() $\mathsf {BD}$
) from Belnap (Reference Belnap, Dunn and Epstein1977, Reference Belnap, Omori and Wansing2019) and Belnap (Reference Belnap, Dunn and Epstein1977, Reference Belnap, Omori and Wansing2019). Originally,
$\mathsf {BD}$
) from Belnap (Reference Belnap, Dunn and Epstein1977, Reference Belnap, Omori and Wansing2019) and Belnap (Reference Belnap, Dunn and Epstein1977, Reference Belnap, Omori and Wansing2019). Originally,
![]() $\mathsf {BD}$
was presented as a four-valued propositional logic in the
$\mathsf {BD}$
was presented as a four-valued propositional logic in the
![]() $\{\neg, \wedge, \vee \}$
language. The values (which we will henceforth call Belnapian values) represent different accounts a source can give regarding a statement
$\{\neg, \wedge, \vee \}$
language. The values (which we will henceforth call Belnapian values) represent different accounts a source can give regarding a statement
![]() $\phi$
:
$\phi$
:
-
•
 $\mathbf {T}$
stands for ‘the source only says that
$\mathbf {T}$
stands for ‘the source only says that
 $\phi$
is true’
$\phi$
is true’ -
•
 $\mathbf {F}$
stands for ‘the source only says that
$\mathbf {F}$
stands for ‘the source only says that
 $\phi$
is false’
$\phi$
is false’ -
•
 $\mathbf {B}$
stands for ‘the source says both that
$\mathbf {B}$
stands for ‘the source says both that
 $\phi$
is false and that
$\phi$
is false and that
 $\phi$
is true’
$\phi$
is true’ -
•
 $\mathbf {N}$
stands for ‘the source does not say that
$\mathbf {N}$
stands for ‘the source does not say that
 $\phi$
is false nor that it is true’.
$\phi$
is false nor that it is true’.
The interpretation of the truth values allows for reformulating
![]() $\mathsf {BD}$
semantics in terms of two classical but independent valuations. Namely,
$\mathsf {BD}$
semantics in terms of two classical but independent valuations. Namely,

It is easy to see that there are no universally true nor universally false formulas in
![]() $\mathsf {BD}$
. Thus,
$\mathsf {BD}$
. Thus,
![]() $\mathsf {BD}$
satisfies the desiderata outlined above. Moreover, even if we define
$\mathsf {BD}$
satisfies the desiderata outlined above. Moreover, even if we define
![]() $\phi \supset \chi$
as
$\phi \supset \chi$
as
![]() $\neg \phi \vee \chi$
, it is clear that neither Modus Ponens, nor the Deduction theorem will hold for
$\neg \phi \vee \chi$
, it is clear that neither Modus Ponens, nor the Deduction theorem will hold for
![]() $\supset$
. That is,
$\supset$
. That is,
![]() $\mathsf {BD}$
lacks the (definable) implication (cf. Omori and Wansing Reference Omori and Wansing2017, Section 5.1) for a detailed discussion of the implication in
$\mathsf {BD}$
lacks the (definable) implication (cf. Omori and Wansing Reference Omori and Wansing2017, Section 5.1) for a detailed discussion of the implication in
![]() $\mathsf {BD}$
). This, however, is not problematic since we are going to use
$\mathsf {BD}$
). This, however, is not problematic since we are going to use
![]() $\mathsf {BD}$
only to represent events and conditional statements which are usually formalised with an implication do not correspond to descriptions of events.
$\mathsf {BD}$
only to represent events and conditional statements which are usually formalised with an implication do not correspond to descriptions of events.
1.2 Probabilities and belief functions in
 $\mathsf {BD}$
$\mathsf {BD}$
The original interpretation of the Belnapian truth values that we gave above is presented in terms of the information one has. In this approach, however, the information is assumed to be crisp. Theories of uncertainty over
![]() $\mathsf {BD}$
were introduced to formalise situations where one has access to graded information. For instance, the first source could tell that
$\mathsf {BD}$
were introduced to formalise situations where one has access to graded information. For instance, the first source could tell that
![]() $p$
is true with the likelihood
$p$
is true with the likelihood
![]() $0.4$
and the second that
$0.4$
and the second that
![]() $p$
is false with probability
$p$
is false with probability
![]() $0.7$
. If one follows
$0.7$
. If one follows
![]() $\mathsf {BD}$
and treats positive and negative evidence independently, one needs a non-classical notion of uncertainty measures to represent this information.
$\mathsf {BD}$
and treats positive and negative evidence independently, one needs a non-classical notion of uncertainty measures to represent this information.
To the best of our knowledge, the earliest formalisation of probability theory in terms of
![]() $\mathsf {BD}$
was provided by Mares (Reference Mares1997). The formalisation is very similar to the one that we are going to use in this paper but bears one significant distinction. Namely, normalised measures (i.e., those where
$\mathsf {BD}$
was provided by Mares (Reference Mares1997). The formalisation is very similar to the one that we are going to use in this paper but bears one significant distinction. Namely, normalised measures (i.e., those where
![]() $\mu (W)=1$
and
$\mu (W)=1$
and
![]() $\mu (\varnothing )=0$
) are used by Mares (Reference Mares1997). This requirement, however, is superfluous since
$\mu (\varnothing )=0$
) are used by Mares (Reference Mares1997). This requirement, however, is superfluous since
![]() $\mathsf {BD}$
lacks universally (in)valid formulas.
$\mathsf {BD}$
lacks universally (in)valid formulas.
Another formalisation is given by Dunn (Reference Dunn2010). Dunn proposes to divide the sample space into four exhaustive and mutually exclusive parts depending on the Belnapian value of
![]() $\phi$
. An alternative approach was proposed by Klein et al. (Reference Klein, Majer and Rafiee Rad2021). There, the authors propose two equivalent interpretations based on the two formulations of semantics. The first option (which we call here
$\phi$
. An alternative approach was proposed by Klein et al. (Reference Klein, Majer and Rafiee Rad2021). There, the authors propose two equivalent interpretations based on the two formulations of semantics. The first option (which we call here
![]() $\pm$
-probability) is to give
$\pm$
-probability) is to give
![]() $\phi$
two independent probability measures: the one determining the likelihood of
$\phi$
two independent probability measures: the one determining the likelihood of
![]() $\phi$
to be true and the other the likelihood of
$\phi$
to be true and the other the likelihood of
![]() $\phi$
to be false. The second option (
$\phi$
to be false. The second option (
![]() $\mathbf {4}$
-probabilities) follows Dunn and divides the sample space according to whether
$\mathbf {4}$
-probabilities) follows Dunn and divides the sample space according to whether
![]() $\phi$
has value
$\phi$
has value
![]() $\mathbf {T}$
,
$\mathbf {T}$
,
![]() $\mathbf {B}$
,
$\mathbf {B}$
,
![]() $\mathbf {N}$
, or
$\mathbf {N}$
, or
![]() $\mathbf {F}$
in a given state. Note that in both cases, the probabilities are interpreted subjectively.
$\mathbf {F}$
in a given state. Note that in both cases, the probabilities are interpreted subjectively.
The main difference between the approaches of Dunn (Reference Dunn2010) and Klein et al. (Reference Klein, Majer and Rafiee Rad2021) is that in the former, the probability of
![]() $\phi \wedge \phi '$
is entirely determined by those of
$\phi \wedge \phi '$
is entirely determined by those of
![]() $\phi$
and
$\phi$
and
![]() $\phi '$
which makes it compositional. On the other hand, the paraconsistent probabilities proposed by Klein et al. (Reference Klein, Majer and Rafiee Rad2021) are not compositional w.r.t. conjunction. In this paper, we choose the latter approach since it can be argued (cf. Dubois Reference Dubois2008 for the details) that belief is not compositional when it comes to contradictory information.
$\phi '$
which makes it compositional. On the other hand, the paraconsistent probabilities proposed by Klein et al. (Reference Klein, Majer and Rafiee Rad2021) are not compositional w.r.t. conjunction. In this paper, we choose the latter approach since it can be argued (cf. Dubois Reference Dubois2008 for the details) that belief is not compositional when it comes to contradictory information.
A similar approach to paraconsistent probabilities was proposed by, for example, Bueno-Soler and Carnielli (Reference Bueno-Soler and Carnielli2016) and Rodrigues et al. (Reference Rodrigues, Bueno-Soler and Carnielli2021). There, probabilities are defined over an extension of
![]() $\mathsf {BD}$
with classicality and non-classicality operators. It is worth mentioning that the proposed axioms of probability are very close to those from Klein et al. (Reference Klein, Majer and Rafiee Rad2021): for example, both allow measures
$\mathsf {BD}$
with classicality and non-classicality operators. It is worth mentioning that the proposed axioms of probability are very close to those from Klein et al. (Reference Klein, Majer and Rafiee Rad2021): for example, both allow measures
![]() $\pi$
s.t.
$\pi$
s.t.
![]() $\pi (\phi )+\pi (\neg \phi )\lt 1$
(if the information regarding
$\pi (\phi )+\pi (\neg \phi )\lt 1$
(if the information regarding
![]() $\phi$
is incomplete) or
$\phi$
is incomplete) or
![]() $\pi (\phi )+\pi (\neg \phi )\gt 1$
(when the information is contradictory).
$\pi (\phi )+\pi (\neg \phi )\gt 1$
(when the information is contradictory).
Belief functions over
![]() $\mathsf {BD}$
were first defined by Zhou (Reference Zhou2013). There, they were presented on the ordered sets of states. Each formula
$\mathsf {BD}$
were first defined by Zhou (Reference Zhou2013). There, they were presented on the ordered sets of states. Each formula
![]() $\phi$
in this approach corresponds to two sets of states:
$\phi$
in this approach corresponds to two sets of states:
![]() $|\phi |^+$
(states where
$|\phi |^+$
(states where
![]() $\phi$
has value
$\phi$
has value
![]() $\mathbf {T}$
or
$\mathbf {T}$
or
![]() $\mathbf {B}$
) and
$\mathbf {B}$
) and
![]() $|\phi |^-$
(states where it is evaluated at
$|\phi |^-$
(states where it is evaluated at
![]() $\mathbf {B}$
or
$\mathbf {B}$
or
![]() $\mathbf {F}$
). Moreover, a logic formalising reasoning with belief functions was presented. A similar treatment of (non-normalised or general in the terminology of the paper) belief functions in
$\mathbf {F}$
). Moreover, a logic formalising reasoning with belief functions was presented. A similar treatment of (non-normalised or general in the terminology of the paper) belief functions in
![]() $\mathsf {BD}$
was given by Bílková et al. (Reference Bílková, Frittella, Kozhemiachenko, Majer and Nazari2023d). The main difference between the two treatments of belief functions was that Bílková et al. (Reference Bílková, Frittella, Kozhemiachenko, Majer and Nazari2023d) considered two options for interpreting
$\mathsf {BD}$
was given by Bílková et al. (Reference Bílková, Frittella, Kozhemiachenko, Majer and Nazari2023d). The main difference between the two treatments of belief functions was that Bílková et al. (Reference Bílková, Frittella, Kozhemiachenko, Majer and Nazari2023d) considered two options for interpreting
![]() ${\texttt {bel}}(|\phi |^-)$
: the first one was to treat it as the belief of
${\texttt {bel}}(|\phi |^-)$
: the first one was to treat it as the belief of
![]() $\neg \phi$
, and the second one – as the plausibility of
$\neg \phi$
, and the second one – as the plausibility of
![]() $\neg \phi$
. Another distinction was in the formalisation: Zhou (Reference Zhou2013) constructs a logic for reasoning about belief functions following Fagin et al. (Reference Fagin, Halpern and Megiddo1990): That is, incorporating the arithmetical operations and inequalities containing them into the language. Bílková et al. (Reference Bílková, Frittella, Kozhemiachenko, Majer and Nazari2023d) utilised a different approach: instead of using arithmetic inequalities, the reasoning about belief functions is conducted in a paraconsistent expansion of the Łukasiewicz logic
$\neg \phi$
. Another distinction was in the formalisation: Zhou (Reference Zhou2013) constructs a logic for reasoning about belief functions following Fagin et al. (Reference Fagin, Halpern and Megiddo1990): That is, incorporating the arithmetical operations and inequalities containing them into the language. Bílková et al. (Reference Bílková, Frittella, Kozhemiachenko, Majer and Nazari2023d) utilised a different approach: instead of using arithmetic inequalities, the reasoning about belief functions is conducted in a paraconsistent expansion of the Łukasiewicz logic
![]() $\mathsf {\unicode {x0141}}$
capable of expressing arithmetic operations on
$\mathsf {\unicode {x0141}}$
capable of expressing arithmetic operations on
![]() $[0,1]$
.
$[0,1]$
.
1.3 Two-layered logics for uncertainty
Reasoning about uncertainty can be formalised via modal logics where the modality is understood as a measure of an event. The concrete semantics of the modality can be defined in two ways. First, using a modal language with Kripke semantics where the measure is defined on the set of states as done by, for example, Gärdenfors (Reference Gärdenfors1975),Delgrande and Renne (Reference Delgrande and Renne2015), Delgrande et al. (Reference Delgrande, Renne and Sack2019) for qualitative probabilities, by Dautović et al. (Reference Dautović, Doder and Ognjanović2021) for the quantitative ones, and by Rodriguez et al. (Reference Rodriguez, Tuyt, Esteva and Godo2022) for the possibility and necessity measures. Second, employing a two-layered formalism (cf. Baldi et al. Reference Baldi, Cintula and Noguera2020; Fagin et al. Reference Fagin, Halpern and Megiddo1990; Fagin and Halpern Reference Fagin and Halpern1991; Hájek et al. Reference Hájek, Godo, Esteva, Besnard and Hanks1995, and Bílková et al. Reference Bílková, Frittella, Kozhemiachenko and Majer2023a,b,d) for examples). There, the logic is split into two levels: the inner layer describes events, and the outer layer describes the reasoning with the measure defined on events. The measure is a non-nesting modality
![]() $\texttt {M}$
, and the outer-layer formulas are built from ‘modal atoms’ – formulas of the form
$\texttt {M}$
, and the outer-layer formulas are built from ‘modal atoms’ – formulas of the form
![]() $\texttt {M}\phi$
with
$\texttt {M}\phi$
with
![]() $\phi$
being an inner-layer formula. The outer-layer formulas are then equipped with the semantics of a fuzzy logic that permits necessary operations (e.g., Łukasiewicz for the quantitative reasoning and Gödel for the qualitative).
$\phi$
being an inner-layer formula. The outer-layer formulas are then equipped with the semantics of a fuzzy logic that permits necessary operations (e.g., Łukasiewicz for the quantitative reasoning and Gödel for the qualitative).
An alternative to the two-layered logics is to use the language of linear inequalities to reason about measures of events. This is done by Fagin et al. (Reference Fagin, Halpern and Megiddo1990) for the classical reasoning about probabilities and by Zhou (Reference Zhou2013) for the reasoning with the belief functions over
![]() $\mathsf {BD}$
. In both cases, it is established that the logics with inequalities and the two-layered logics are equivalent – cf. Baldi et al. (Reference Baldi, Cintula and Noguera2020) for the case of classical probabilities and Bílková et al. (Reference Bílková, Frittella, Kozhemiachenko, Majer and Nazari2023d) for the reasoning with belief functions and probabilities over
$\mathsf {BD}$
. In both cases, it is established that the logics with inequalities and the two-layered logics are equivalent – cf. Baldi et al. (Reference Baldi, Cintula and Noguera2020) for the case of classical probabilities and Bílková et al. (Reference Bílková, Frittella, Kozhemiachenko, Majer and Nazari2023d) for the reasoning with belief functions and probabilities over
![]() $\mathsf {BD}$
.
$\mathsf {BD}$
.
In this paper, we study reasoning about uncertainty in a paraconsistent framework. For this, we choose two-layered logics. First, they are more modular than the usual Kripke semantics: as long as the logic of the event description is chosen, we can define different measures on top of it using different outer-layer logics. Second, two-layered logics provide a uniform way to prove completeness. This is done by translating the axioms of a given measure into formulas of the outer-layer logic (cf. Cintula and Noguera Reference Cintula and Noguera2014 for more details). Third, the techniques that are used to establish the decidability of the outer-layer logic can be applied to the decidability proof of the two-layered logic. Finally, even though the traditional Kripke semantics is more expressive than two-layered logics, this expressivity is not necessary in many contexts. Indeed, people rarely say something like ‘it is probable that it is probable that
![]() $\phi$
’. Moreover, it is considerably more difficult to motivate the assignment of truth values in the nesting case, in particular, when the same measure is applied both to a propositional and modalised formula as in, for example,
$\phi$
’. Moreover, it is considerably more difficult to motivate the assignment of truth values in the nesting case, in particular, when the same measure is applied both to a propositional and modalised formula as in, for example,
![]() $\texttt {M}(p\wedge \texttt {M}q)$
.
$\texttt {M}(p\wedge \texttt {M}q)$
.
We will also be formalising the quantitative reasoning. That is, we assume that the agents can assign numerical values to their certainty in a given proposition or say something like ‘I think that rain is twice more likely than snow’. Thus, we need a logic that can express the paraconsistent counterparts of the additivity condition as well as basic arithmetic operations. We choose the Łukasiewicz logic (
![]() $\mathsf {\unicode {x0141}}$
) for the outer layer since it can define (truncated) addition and subtraction on
$\mathsf {\unicode {x0141}}$
) for the outer layer since it can define (truncated) addition and subtraction on
![]() $[0,1]$
.
$[0,1]$
.
We will focus on four logics. Two probabilistic ones:
![]() $\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
(the logic of
$\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
(the logic of
![]() $\pm$
-probabilities),
$\pm$
-probabilities),
![]() $\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
(the logic of
$\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
(the logic of
![]() $\mathbf {4}$
-probabilities); and two logics for belief and plausibility functions over
$\mathbf {4}$
-probabilities); and two logics for belief and plausibility functions over
![]() $\mathsf {BD}$
introduced by Bílková et al. (Reference Bílková, Frittella, Kozhemiachenko, Majer and Nazari2023d) –
$\mathsf {BD}$
introduced by Bílková et al. (Reference Bílková, Frittella, Kozhemiachenko, Majer and Nazari2023d) –
![]() $\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
where belief and plausibility are defined via one another, and
$\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
where belief and plausibility are defined via one another, and
![]() $\mathsf {Bel}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}$
where belief and plausibility are assumed to be independent.
$\mathsf {Bel}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}$
where belief and plausibility are assumed to be independent.
1.4 Contributions and plan of the paper
This paper extends an earlier conference submission by Bílková et al. (Reference Bílková, Frittella, Kozhemiachenko, Majer, Hansen, Scedrov and de Queiroz2023b). We provide omitted details for the proofs of
![]() $\mathsf {coNP}$
-completeness of
$\mathsf {coNP}$
-completeness of
![]() $\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
and
$\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
and
![]() $\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
and of the finite strong completeness proof of
$\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
and of the finite strong completeness proof of
![]() $\mathscr {H}\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
– the Hilbert-style axiomatisation of
$\mathscr {H}\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
– the Hilbert-style axiomatisation of
![]() $\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
. The novel contribution of this manuscript is the proof of the
$\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
. The novel contribution of this manuscript is the proof of the
![]() $\mathsf {coNP}$
-completeness of
$\mathsf {coNP}$
-completeness of
![]() $\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
and
$\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
and
![]() $\mathsf {Bel}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}$
. We obtain this result by establishing a correspondence between these logics and
$\mathsf {Bel}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}$
. We obtain this result by establishing a correspondence between these logics and
![]() $\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}$
and
$\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}$
and
![]() $\mathsf {Pr}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}_{\mathbf {S5}}$
– two logics for reasoning about probabilities of modal
$\mathsf {Pr}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}_{\mathbf {S5}}$
– two logics for reasoning about probabilities of modal
![]() $\mathsf {BD}$
formulas that we introduce in the present paper. To apply the technique from Hájek and Tulipani (Reference Hájek and Tulipani2001), we establish a version of the small model property for the canonical models of
$\mathsf {BD}$
formulas that we introduce in the present paper. To apply the technique from Hájek and Tulipani (Reference Hájek and Tulipani2001), we establish a version of the small model property for the canonical models of
![]() $\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}$
and
$\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}$
and
![]() $\mathsf {Pr}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}_{\mathbf {S5}}$
. Thus, we continue the study of uncertainty via paraconsistent logics proposed by Bílková et al. (Reference Bílková, Frittella, Majer and Nazari2020) and carried on by Bílková et al. (Reference Bílková, Frittella, Kozhemiachenko and Majer2023a,c,d). The overarching goal of the project is to study logics that can express the following properties of beliefs.
$\mathsf {Pr}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}_{\mathbf {S5}}$
. Thus, we continue the study of uncertainty via paraconsistent logics proposed by Bílková et al. (Reference Bílková, Frittella, Majer and Nazari2020) and carried on by Bílková et al. (Reference Bílková, Frittella, Kozhemiachenko and Majer2023a,c,d). The overarching goal of the project is to study logics that can express the following properties of beliefs.
-
1. Given two statements
 $\phi$
and
$\phi$
and
 $\chi$
, one can be more certain in
$\chi$
, one can be more certain in
 $\phi$
than in
$\phi$
than in
 $\chi$
but still, neither believe in
$\chi$
but still, neither believe in
 $\phi$
completely nor consider
$\phi$
completely nor consider
 $\chi$
completely impossible.
$\chi$
completely impossible. -
2. Given two trusted sources, one can still prefer one source to the other.
-
3. One can believe in a contradiction but still not believe in something else.
-
4. Given two statements, it is possible that one cannot always compare their degrees of certainty in them (if, e.g., these statements have no common content).
The remainder of the text is structured as follows. In Section 2, we recall two approaches to probabilities over
![]() $\mathsf {BD}$
from Klein et al. (Reference Klein, Majer and Rafiee Rad2021) –
$\mathsf {BD}$
from Klein et al. (Reference Klein, Majer and Rafiee Rad2021) –
![]() $\pm$
-probabilities and
$\pm$
-probabilities and
![]() $\mathbf {4}$
-probabilities. In Section 3, we provide the semantics and axiomatisations of
$\mathbf {4}$
-probabilities. In Section 3, we provide the semantics and axiomatisations of
![]() $\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
and
$\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
and
![]() $\mathbf {4}\mathsf {Pr}^{\mathsf {\unicode {x0141}}_\triangle }$
– two-layered logics for probabilities and establish their
$\mathbf {4}\mathsf {Pr}^{\mathsf {\unicode {x0141}}_\triangle }$
– two-layered logics for probabilities and establish their
![]() $\mathsf {NP}$
-completeness. In Section 4, we recall two treatments of belief functions over
$\mathsf {NP}$
-completeness. In Section 4, we recall two treatments of belief functions over
![]() $\mathsf {BD}$
that were presented by Bílková et al. (Reference Bílková, Frittella, Kozhemiachenko, Majer and Nazari2023d). In Section 5, we discuss the two-layered logics for belief functions (
$\mathsf {BD}$
that were presented by Bílková et al. (Reference Bílková, Frittella, Kozhemiachenko, Majer and Nazari2023d). In Section 5, we discuss the two-layered logics for belief functions (
![]() $\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
and
$\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
and
![]() $\mathsf {Bel}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}$
), establish their connections with modal probabilistic logics
$\mathsf {Bel}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}$
), establish their connections with modal probabilistic logics
![]() $\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}$
and
$\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}$
and
![]() $\mathsf {Pr}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}_{\mathbf {S5}}$
, and provide a complexity evaluation of their validity problems. Finally, we summarise our results and set goals for future research in Section 6.
$\mathsf {Pr}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}_{\mathbf {S5}}$
, and provide a complexity evaluation of their validity problems. Finally, we summarise our results and set goals for future research in Section 6.
2. Probabilities over
 $\mathbf {BD}$
$\mathbf {BD}$
In the previous section, we gave an informal presentation of
![]() $\mathsf {BD}$
as a four-valued logic. Since we are going to use it to describe events, we will formulate its semantics in terms of sets of states. The language of
$\mathsf {BD}$
as a four-valued logic. Since we are going to use it to describe events, we will formulate its semantics in terms of sets of states. The language of
![]() $\mathsf {BD}$
is given by the following grammar (with
$\mathsf {BD}$
is given by the following grammar (with
![]() $\texttt {Prop}$
being a countable set of propositional variables).
$\texttt {Prop}$
being a countable set of propositional variables).
Convention 1 (Notation). In what follows,
![]() $\texttt {Prop}(\phi )$
denotes the set of variables occurring in
$\texttt {Prop}(\phi )$
denotes the set of variables occurring in
![]() $\phi$
and
$\phi$
and
![]() $\mathsf {Lit}(\phi )$
stands for the set of literals (i.e., variables or their negations) occurring in
$\mathsf {Lit}(\phi )$
stands for the set of literals (i.e., variables or their negations) occurring in
![]() $\phi$
. Moreover,
$\phi$
. Moreover,
![]() $\texttt {Sf}(\phi )$
is the set of all subformulas of
$\texttt {Sf}(\phi )$
is the set of all subformulas of
![]() $\phi$
. The length (i.e., the number of symbols) of
$\phi$
. The length (i.e., the number of symbols) of
![]() $\phi$
is denoted with
$\phi$
is denoted with
![]() $\unicode{x1D4C1}(\phi )$
.
$\unicode{x1D4C1}(\phi )$
.
We are also going to use two kinds of formulas: the single- and the two-layered ones. To make the differentiation between them simpler, we use Greek letters from the end of the alphabet (
![]() $\phi$
,
$\phi$
,
![]() $\chi$
,
$\chi$
,
![]() $\psi$
, etc.) to designate the first kind and the letters from the beginning of the alphabet (
$\psi$
, etc.) to designate the first kind and the letters from the beginning of the alphabet (
![]() $\alpha$
,
$\alpha$
,
![]() $\beta$
,
$\beta$
,
![]() $\gamma$
, …) for the second kind. We use
$\gamma$
, …) for the second kind. We use
![]() $v$
(with indices) to stand for the valuations of single-layered formulas and
$v$
(with indices) to stand for the valuations of single-layered formulas and
![]() $e$
(with indices) for the two-layered formulas.
$e$
(with indices) for the two-layered formulas.
Finally, we will use angular brackets
![]() $\langle \ldots \rangle$
for tuples that designate models of logics and pairs of valuations and round brackets
$\langle \ldots \rangle$
for tuples that designate models of logics and pairs of valuations and round brackets
![]() $(\ldots )$
for pairs of numbers that are values of formulas.
$(\ldots )$
for pairs of numbers that are values of formulas.
Definition 2 (Set semantics of
![]() $\mathsf {BD}$
). Let
$\mathsf {BD}$
). Let
![]() $\phi, \phi '\in \mathscr {L}_{\mathsf {BD}}$
,
$\phi, \phi '\in \mathscr {L}_{\mathsf {BD}}$
,
![]() $W\neq \varnothing$
, and
$W\neq \varnothing$
, and
![]() $v^+,v^-:\texttt {Prop}\to 2^W$
. For a model
$v^+,v^-:\texttt {Prop}\to 2^W$
. For a model
![]() $\mathfrak {M}=\langle W,v^+,v^-\rangle$
, we define notions of
$\mathfrak {M}=\langle W,v^+,v^-\rangle$
, we define notions of
![]() $w\vDash ^+\phi$
and
$w\vDash ^+\phi$
and
![]() $w\vDash ^-\phi$
for
$w\vDash ^-\phi$
for
![]() $w\in W$
as follows.
$w\in W$
as follows.
 \begin{align*} w\vDash ^+p&\text { iff }w\in v^+(p)&w\vDash ^-p&\text { iff }w\in v^-(p)\\ w\vDash ^+\neg \phi &\text { iff }w\vDash ^-\phi &w\vDash ^-\neg \phi &\text { iff }w\vDash ^+\phi \\ w\vDash ^+\phi \wedge \phi '&\text { iff }w\vDash ^+\phi \text { and }w\vDash ^+\phi '&w\vDash ^-\phi \wedge \phi '&\text { iff }w\vDash ^-\phi \text { or }w\vDash ^-\phi '\\ w\vDash ^+\phi \vee \phi '&\text { iff }w\vDash ^+\phi \text { or }w\vDash ^+\phi '&w\vDash ^-\phi \vee \phi '&\text { iff }w\vDash ^-\phi \text { and }w\vDash ^-\phi ' \end{align*}
\begin{align*} w\vDash ^+p&\text { iff }w\in v^+(p)&w\vDash ^-p&\text { iff }w\in v^-(p)\\ w\vDash ^+\neg \phi &\text { iff }w\vDash ^-\phi &w\vDash ^-\neg \phi &\text { iff }w\vDash ^+\phi \\ w\vDash ^+\phi \wedge \phi '&\text { iff }w\vDash ^+\phi \text { and }w\vDash ^+\phi '&w\vDash ^-\phi \wedge \phi '&\text { iff }w\vDash ^-\phi \text { or }w\vDash ^-\phi '\\ w\vDash ^+\phi \vee \phi '&\text { iff }w\vDash ^+\phi \text { or }w\vDash ^+\phi '&w\vDash ^-\phi \vee \phi '&\text { iff }w\vDash ^-\phi \text { and }w\vDash ^-\phi ' \end{align*}
Given a model
![]() $\mathfrak {M}$
, we denote the positive and negative extensions of a formula as follows:
$\mathfrak {M}$
, we denote the positive and negative extensions of a formula as follows:
A sequent
![]() $\phi \vdash \chi$
is satisfied on
$\phi \vdash \chi$
is satisfied on
![]() $\mathfrak {M}=\langle W,v^+,v^-\rangle$
(denoted,
$\mathfrak {M}=\langle W,v^+,v^-\rangle$
(denoted,
![]() $\mathfrak {M}\models [\phi \vdash \chi ]$
) iff
$\mathfrak {M}\models [\phi \vdash \chi ]$
) iff
![]() $|\phi |^+\subseteq |\chi |^+$
. A sequent
$|\phi |^+\subseteq |\chi |^+$
. A sequent
![]() $\phi \vdash \chi$
is
$\phi \vdash \chi$
is
![]() $\mathsf {BD}$
-valid (
$\mathsf {BD}$
-valid (
![]() $\phi \models _{\mathsf {BD}}\chi$
) iff it is satisfied on every model. In this case, we will say that
$\phi \models _{\mathsf {BD}}\chi$
) iff it is satisfied on every model. In this case, we will say that
![]() $\phi$
entails
$\phi$
entails
![]() $\chi$
in
$\chi$
in
![]() $\mathsf {BD}$
.
$\mathsf {BD}$
.
Remark 3.
One can see that every
![]() $\phi \in \mathscr {L}_{\mathsf {BD}}$
can be turned into its negation normal form
$\phi \in \mathscr {L}_{\mathsf {BD}}$
can be turned into its negation normal form
![]() $\mathsf {NNF}(\phi )$
where
$\mathsf {NNF}(\phi )$
where
![]() $\neg$
is applied to variables only. This can be done via the following transformations:
$\neg$
is applied to variables only. This can be done via the following transformations:
Moreover, it is clear that
![]() $|\phi |^+_{\mathfrak {M}}=|\mathsf {NNF}(\phi )|^+_{\mathfrak {M}}$
and
$|\phi |^+_{\mathfrak {M}}=|\mathsf {NNF}(\phi )|^+_{\mathfrak {M}}$
and
![]() $|\phi |^-_{\mathfrak {M}}=|\mathsf {NNF}(\phi )|^-_{\mathfrak {M}}$
in every model
$|\phi |^-_{\mathfrak {M}}=|\mathsf {NNF}(\phi )|^-_{\mathfrak {M}}$
in every model
![]() $\mathfrak {M}$
and that
$\mathfrak {M}$
and that
![]() $ \unicode{x1D4C1} (\mathsf {NNF}(\phi ))={\mathscr {O}}(\unicode{x1D4C1}(\phi ))$
.
$ \unicode{x1D4C1} (\mathsf {NNF}(\phi ))={\mathscr {O}}(\unicode{x1D4C1}(\phi ))$
.
Note that the semantics in Definition 2 is a formalisation of the truth and falsity conditions of
![]() $\{\neg, \wedge, \vee \}$
-formulas we saw in the table in Section 1.1. We can now use it to define probabilities on the models. We adapt the definitions from Klein et al. (Reference Klein, Majer and Rafiee Rad2021).
$\{\neg, \wedge, \vee \}$
-formulas we saw in the table in Section 1.1. We can now use it to define probabilities on the models. We adapt the definitions from Klein et al. (Reference Klein, Majer and Rafiee Rad2021).
Definition 4 (
![]() $\mathsf {BD}$
-models with
$\mathsf {BD}$
-models with
![]() $\pm$
-probabilities). A
$\pm$
-probabilities). A
![]() $\mathsf {BD}$
-model with a
$\mathsf {BD}$
-model with a
![]() $\pm$
-probability is a tuple
$\pm$
-probability is a tuple
![]() $\mathfrak {M}_\pm =\langle \mathfrak {M},\mu \rangle$
with
$\mathfrak {M}_\pm =\langle \mathfrak {M},\mu \rangle$
with
![]() $\mathfrak {M}$
being a
$\mathfrak {M}$
being a
![]() $\mathsf {BD}$
-model and
$\mathsf {BD}$
-model and
![]() $\mu :2^W\rightarrow [0,1]$
satisfying:
$\mu :2^W\rightarrow [0,1]$
satisfying:
-
 $\mathbf {mon}$
: if
$\mathbf {mon}$
: if
 $X\subseteq Y$
, then
$X\subseteq Y$
, then
 $\mu (X)\leq \mu (Y)$
;
$\mu (X)\leq \mu (Y)$
; -
 $\mathbf {neg}$
:
$\mathbf {neg}$
:
 $\mu (|\phi |^-_{\mathfrak {M}})=\mu (|\neg \phi |^+_{\mathfrak {M}})$
;
$\mu (|\phi |^-_{\mathfrak {M}})=\mu (|\neg \phi |^+_{\mathfrak {M}})$
; -
 $\mathbf {ex}$
:
$\mathbf {ex}$
:
 $\mu (|\phi \vee \chi |^+_{\mathfrak {M}})=\mu (|\phi |^+_{\mathfrak {M}})+\mu (|\chi |^+_{\mathfrak {M}})-\mu (|\phi \wedge \chi |^+_{\mathfrak {M}})$
.
$\mu (|\phi \vee \chi |^+_{\mathfrak {M}})=\mu (|\phi |^+_{\mathfrak {M}})+\mu (|\chi |^+_{\mathfrak {M}})-\mu (|\phi \wedge \chi |^+_{\mathfrak {M}})$
.
To facilitate the presentation of the four-valued probabilities defined over
![]() $\mathsf {BD}$
-models, we introduce additional extensions of
$\mathsf {BD}$
-models, we introduce additional extensions of
![]() $\phi$
defined via
$\phi$
defined via
![]() $|\phi |^+$
and
$|\phi |^+$
and
![]() $|\phi |^-$
.
$|\phi |^-$
.
Convention 5.
Let
![]() $\mathfrak {M}=\langle W,v^+,v^-\rangle$
be a
$\mathfrak {M}=\langle W,v^+,v^-\rangle$
be a
![]() $\mathsf {BD}$
-model,
$\mathsf {BD}$
-model,
![]() $\phi \in \mathscr {L}_{\mathsf {BD}}$
. We set
$\phi \in \mathscr {L}_{\mathsf {BD}}$
. We set
We call these extensions, respectively, pure belief, pure disbelief, conflict, and uncertainty in
![]() $\phi$
, following Klein et al. (Reference Klein, Majer and Rafiee Rad2021).
$\phi$
, following Klein et al. (Reference Klein, Majer and Rafiee Rad2021).
One can observe that these extensions correspond to the Belnapian values of
![]() $\phi$
(recall Section 1.1):
$\phi$
(recall Section 1.1):
-
• pure belief extension of
 $\phi$
is the set of states where
$\phi$
is the set of states where
 $\phi$
has value
$\phi$
has value
 $\mathbf {T}$
(i.e., exactly true, in other words, true and not false);
$\mathbf {T}$
(i.e., exactly true, in other words, true and not false); -
• pure disbelief extension of
 $\phi$
is the set of states where
$\phi$
is the set of states where
 $\phi$
has value
$\phi$
has value
 $\mathbf {F}$
(i.e., exactly false, in other words, false and not true);
$\mathbf {F}$
(i.e., exactly false, in other words, false and not true); -
• conflict extension of
 $\phi$
is the set of states where
$\phi$
is the set of states where
 $\phi$
has value
$\phi$
has value
 $\mathbf {B}$
(i.e., both true and false);
$\mathbf {B}$
(i.e., both true and false); -
• uncertainty extension of
 $\phi$
is the set of states where
$\phi$
is the set of states where
 $\phi$
has value
$\phi$
has value
 $\mathbf {N}$
(i.e., neither true nor false).
$\mathbf {N}$
(i.e., neither true nor false).
Definition 6 (
![]() $\mathsf {BD}$
-models with
$\mathsf {BD}$
-models with
![]() $\mathbf {4}$
-probabilities). A
$\mathbf {4}$
-probabilities). A
![]() $\mathsf {BD}$
-model with a
$\mathsf {BD}$
-model with a
![]() $\mathbf {4}$
-probability is a tuple
$\mathbf {4}$
-probability is a tuple
![]() $\mathfrak {M}_{\mathbf {4}} =\langle \mathfrak {M},\mu _v\rangle$
with
$\mathfrak {M}_{\mathbf {4}} =\langle \mathfrak {M},\mu _v\rangle$
with
![]() $\mathfrak {M}$
being a
$\mathfrak {M}$
being a
![]() $\mathsf {BD}$
-model and
$\mathsf {BD}$
-model and
![]() $\mu _{\mathbf {4}}:2^W\rightarrow [0,1]$
satisfying:
$\mu _{\mathbf {4}}:2^W\rightarrow [0,1]$
satisfying:
-
 $\mathbf {part}$
:
$\mathbf {part}$
:
 $\mu _{\mathbf {4}}(|\phi |^{\mathsf {b}}_{\mathfrak {M}})+\mu _{\mathbf {4}}(|\phi |^{\mathsf {d}}_{\mathfrak {M}})+\mu _{\mathbf {4}}(|\phi |^{\mathsf {u}}_{\mathfrak {M}})+\mu _{\mathbf {4}}(|\phi |^{\mathsf {c}}_{\mathfrak {M}})=1$
;
$\mu _{\mathbf {4}}(|\phi |^{\mathsf {b}}_{\mathfrak {M}})+\mu _{\mathbf {4}}(|\phi |^{\mathsf {d}}_{\mathfrak {M}})+\mu _{\mathbf {4}}(|\phi |^{\mathsf {u}}_{\mathfrak {M}})+\mu _{\mathbf {4}}(|\phi |^{\mathsf {c}}_{\mathfrak {M}})=1$
; -
 $\mathbf {neg}$
:
$\mathbf {neg}$
:
 $\mu _{\mathbf {4}}(|\neg \phi |^{\mathsf {b}}_{\mathfrak {M}})=\mu _{\mathbf {4}}(|\phi |^{\mathsf {d}}_{\mathfrak {M}})$
,
$\mu _{\mathbf {4}}(|\neg \phi |^{\mathsf {b}}_{\mathfrak {M}})=\mu _{\mathbf {4}}(|\phi |^{\mathsf {d}}_{\mathfrak {M}})$
,
 $\mu _{\mathbf {4}}(|\neg \phi |^{\mathsf {c}}_{\mathfrak {M}})=\mu _{\mathbf {4}}(|\phi |^{\mathsf {c}}_{\mathfrak {M}})$
;
$\mu _{\mathbf {4}}(|\neg \phi |^{\mathsf {c}}_{\mathfrak {M}})=\mu _{\mathbf {4}}(|\phi |^{\mathsf {c}}_{\mathfrak {M}})$
; -
 $\mathbf {contr}$
:
$\mathbf {contr}$
:
 $\mu _{\mathbf {4}}(|\phi \wedge \neg \phi |^{\mathsf {b}}_{\mathfrak {M}})=0$
,
$\mu _{\mathbf {4}}(|\phi \wedge \neg \phi |^{\mathsf {b}}_{\mathfrak {M}})=0$
,
 $\mu _{\mathbf {4}}(|\phi \wedge \neg \phi |^{\mathsf {c}}_{\mathfrak {M}})=\mu _{\mathbf {4}}(|\phi |^{\mathsf {c}}_{\mathfrak {M}})$
;
$\mu _{\mathbf {4}}(|\phi \wedge \neg \phi |^{\mathsf {c}}_{\mathfrak {M}})=\mu _{\mathbf {4}}(|\phi |^{\mathsf {c}}_{\mathfrak {M}})$
; -
 $\mathbf {BCmon}$
: if
$\mathbf {BCmon}$
: if
 $\mathfrak {M}\models [\phi \vdash \chi ]$
, then
$\mathfrak {M}\models [\phi \vdash \chi ]$
, then
 $\mu _{\mathbf {4}}(|\phi |^{\mathsf {b}}_{\mathfrak {M}})+\mu _{\mathbf {4}}(|\phi |^{\mathsf {c}}_{\mathfrak {M}})\leq \mu _{\mathbf {4}}(|\chi |^{\mathsf {b}}_{\mathfrak {M}})+\mu _{\mathbf {4}}(|\chi |^{\mathsf {c}}_{\mathfrak {M}})$
;
$\mu _{\mathbf {4}}(|\phi |^{\mathsf {b}}_{\mathfrak {M}})+\mu _{\mathbf {4}}(|\phi |^{\mathsf {c}}_{\mathfrak {M}})\leq \mu _{\mathbf {4}}(|\chi |^{\mathsf {b}}_{\mathfrak {M}})+\mu _{\mathbf {4}}(|\chi |^{\mathsf {c}}_{\mathfrak {M}})$
; -
 $\mathbf {BCex}$
:
$\mathbf {BCex}$
:
 $\mu _{\mathbf {4}}(|\phi |^{\mathsf {b}})+\mu _{\mathbf {4}}(|\phi |^{\mathsf {c}})+\mu _{\mathbf {4}}(|\psi |^{\mathsf {b}})+\mu _{\mathbf {4}}(|\psi |^{\mathsf {c}})=\mu _{\mathbf {4}}(|\phi \wedge \psi |^{\mathsf {b}})+\mu _{\mathbf {4}}(|\phi \wedge \psi |^{\mathsf {c}})+\\\mu _{\mathbf {4}}(|\phi \vee \psi |^{\mathsf {b}})+ \mu _{\mathbf {4}}(|\phi \vee \psi |^{\mathsf {c}})$
.
$\mu _{\mathbf {4}}(|\phi |^{\mathsf {b}})+\mu _{\mathbf {4}}(|\phi |^{\mathsf {c}})+\mu _{\mathbf {4}}(|\psi |^{\mathsf {b}})+\mu _{\mathbf {4}}(|\psi |^{\mathsf {c}})=\mu _{\mathbf {4}}(|\phi \wedge \psi |^{\mathsf {b}})+\mu _{\mathbf {4}}(|\phi \wedge \psi |^{\mathsf {c}})+\\\mu _{\mathbf {4}}(|\phi \vee \psi |^{\mathsf {b}})+ \mu _{\mathbf {4}}(|\phi \vee \psi |^{\mathsf {c}})$
.
Convention 7.
We will further omit lower indices in
![]() $|\phi |^+_{\mathfrak {M}}$
,
$|\phi |^+_{\mathfrak {M}}$
,
![]() $|\phi |^-_{\mathfrak {M}}$
,
$|\phi |^-_{\mathfrak {M}}$
,
![]() $|\phi |^{\mathsf {b}}_{\mathfrak {M}}$
, etc. and write
$|\phi |^{\mathsf {b}}_{\mathfrak {M}}$
, etc. and write
![]() $|\phi |^+$
,
$|\phi |^+$
,
![]() $|\phi |^-$
,
$|\phi |^-$
,
![]() $|\phi |^{\mathsf {b}}$
, etc. when the model is clear from the context.
$|\phi |^{\mathsf {b}}$
, etc. when the model is clear from the context.
We will utilise the following naming convention:
-
• we use the term ‘
 $\pm$
-probability’ to stand for
$\pm$
-probability’ to stand for
 $\mu$
from Definition 4
;
$\mu$
from Definition 4
; -
• we call
 $\mu _{\mathbf {4}}$
from Definition 6 a ‘
$\mu _{\mathbf {4}}$
from Definition 6 a ‘
 $\mathbf {4}$
-probability’ or a ‘four-valued probability’.
$\mathbf {4}$
-probability’ or a ‘four-valued probability’.
Recall that
![]() $\pm$
-probabilities are referred to as ‘non-standard’ by Klein et al. (Reference Klein, Majer and Rafiee Rad2021) and Bílková et al. (Reference Bílková, Frittella, Kozhemiachenko, Majer and Nazari2023). As this term is too broad (four-valued probabilities are not ‘standard’ either), we use a different designation.
$\pm$
-probabilities are referred to as ‘non-standard’ by Klein et al. (Reference Klein, Majer and Rafiee Rad2021) and Bílková et al. (Reference Bílková, Frittella, Kozhemiachenko, Majer and Nazari2023). As this term is too broad (four-valued probabilities are not ‘standard’ either), we use a different designation.
Let us quickly discuss the measures defined above. First, observe that
![]() $\mu (|\phi |^+)$
and
$\mu (|\phi |^+)$
and
![]() $\mu (|\phi |^-)$
are independent from one another. Thus,
$\mu (|\phi |^-)$
are independent from one another. Thus,
![]() $\mu$
gives two measures to each
$\mu$
gives two measures to each
![]() $\phi$
, as desired. Second, recall (Klein et al. Reference Klein, Majer and Rafiee Rad2021, Theorems 2–3) that every
$\phi$
, as desired. Second, recall (Klein et al. Reference Klein, Majer and Rafiee Rad2021, Theorems 2–3) that every
![]() $\mathbf {4}$
-probability on a
$\mathbf {4}$
-probability on a
![]() $\mathsf {BD}$
-model induces a
$\mathsf {BD}$
-model induces a
![]() $\pm$
-probability and vice versa. In the following sections, we will define two-layered logics for
$\pm$
-probability and vice versa. In the following sections, we will define two-layered logics for
![]() $\mathsf {BD}$
-models with
$\mathsf {BD}$
-models with
![]() $\pm$
- and
$\pm$
- and
![]() $\mathbf {4}$
-probabilities and show that they can be faithfully embedded into each other. It is instructive to note, moreover, that while
$\mathbf {4}$
-probabilities and show that they can be faithfully embedded into each other. It is instructive to note, moreover, that while
![]() $\pm$
- and
$\pm$
- and
![]() $\mathbf {4}$
-probabilities can be simulated by the classical ones, they do behave in a very different way.
$\mathbf {4}$
-probabilities can be simulated by the classical ones, they do behave in a very different way.
Convention 8 (Notation in models). Throughout the paper, we are going to give examples of various models. We use the following notation for values of variables in the states of a given model.

Example 9 (Paraconsistent vs. classical probabilities). First of all, observe that a
![]() $\pm$
-probability can be uniform. Indeed, for every
$\pm$
-probability can be uniform. Indeed, for every
![]() $c\in [0,1]$
and every
$c\in [0,1]$
and every
![]() $\mathsf {BD}$
-model
$\mathsf {BD}$
-model
![]() $\langle W,v^+,v^-\rangle$
, it is easy to check that the assignment
$\langle W,v^+,v^-\rangle$
, it is easy to check that the assignment
![]() $\forall X\subseteq W:\mu (X)=c$
is a
$\forall X\subseteq W:\mu (X)=c$
is a
![]() $\pm$
-probability.
$\pm$
-probability.
Second, the general import-export condition
that is true for the classical probabilities does not hold if
![]() $\mu$
is a
$\mu$
is a
![]() $\pm$
-probability. For consider Fig.
1
. One can see that
$\pm$
-probability. For consider Fig.
1
. One can see that
![]() $\mu$
is monotone and that
$\mu$
is monotone and that
![]() $\mu (|\phi |^+)=\mu (|\phi |^-)=0$
for every
$\mu (|\phi |^+)=\mu (|\phi |^-)=0$
for every
![]() $\phi \in \mathscr {L}_{\mathsf {BD}}$
(whence,
$\phi \in \mathscr {L}_{\mathsf {BD}}$
(whence,
![]() $\mu$
is a
$\mu$
is a
![]() $\pm$
-probability). On the other hand, it is clear that
$\pm$
-probability). On the other hand, it is clear that
![]() $\mu (W)\neq \mu (\{u_1\})+\mu (\{u_2\})-\mu (\varnothing )$
.
$\mu (W)\neq \mu (\{u_1\})+\mu (\{u_2\})-\mu (\varnothing )$
.
This, however, is not a problem since for every
![]() $\mathsf {BD}$
-model with a
$\mathsf {BD}$
-model with a
![]() $\pm$
-probability
$\pm$
-probability
![]() $\langle W,v^{+},v^{-},\mu \rangle$
, there exists a
$\langle W,v^{+},v^{-},\mu \rangle$
, there exists a
![]() $\mathsf {BD}$
-model
$\mathsf {BD}$
-model
![]() $\langle W',v^{'+},v^{'-},\pi \rangle$
with a classical probability measure
$\langle W',v^{'+},v^{'-},\pi \rangle$
with a classical probability measure
![]() $\pi$
s.t.
$\pi$
s.t.
![]() $\pi (|\phi |^+)=\mu (|\phi |^+)$
(Klein et al. Reference Klein, Majer and Rafiee Rad2021, Theorem 4).
$\pi (|\phi |^+)=\mu (|\phi |^+)$
(Klein et al. Reference Klein, Majer and Rafiee Rad2021, Theorem 4).
First of all, for the case of the model shown in Fig.
1
, one can either define
![]() $\pi (\{u_1\})=\pi (\{u_2\})=\frac {1}{2}$
or add a new state
$\pi (\{u_1\})=\pi (\{u_2\})=\frac {1}{2}$
or add a new state
![]() $u_3$
where all variables are neither true nor false. For a bit more refined example, consider Fig.
2
and set
$u_3$
where all variables are neither true nor false. For a bit more refined example, consider Fig.
2
and set
![]() $W=\{w_1,w_2\}$
and
$W=\{w_1,w_2\}$
and
![]() $W'=\{w'_1,w'_2,w'_3\}$
. It is clear that for every
$W'=\{w'_1,w'_2,w'_3\}$
. It is clear that for every
![]() $\phi \in \mathscr {L}_{\mathsf {BD}}$
,
$\phi \in \mathscr {L}_{\mathsf {BD}}$
,
![]() $\mu (|\phi |^+)=\pi (|\phi |^+)=\frac {1}{2}$
.
$\mu (|\phi |^+)=\pi (|\phi |^+)=\frac {1}{2}$
.
Likewise,
![]() $\mu _{\mathbf {4}}$
is not necessarily monotone w.r.t.
$\mu _{\mathbf {4}}$
is not necessarily monotone w.r.t.
![]() $\subseteq$
(which is required of the classical probabilities) since not every subset of a model is represented by an extension of an
$\subseteq$
(which is required of the classical probabilities) since not every subset of a model is represented by an extension of an
![]() $\mathscr {L}_{\mathsf {BD}}$
formula. Again, it is not a problem since for every
$\mathscr {L}_{\mathsf {BD}}$
formula. Again, it is not a problem since for every
![]() $\mathsf {BD}$
-model with
$\mathsf {BD}$
-model with
![]() $\mathbf {4}$
-probability
$\mathbf {4}$
-probability
![]() $\langle W,v^+,v^-,\mu _{\mathbf {4}}\rangle$
, there exist a
$\langle W,v^+,v^-,\mu _{\mathbf {4}}\rangle$
, there exist a
![]() $\mathsf {BD}$
-model
$\mathsf {BD}$
-model
![]() $\langle W',v^{'+},v^{'-},\pi \rangle$
with a classical probability measure
$\langle W',v^{'+},v^{'-},\pi \rangle$
with a classical probability measure
![]() $\pi$
s.t.
$\pi$
s.t.
![]() $\pi (|\phi |^{\mathsf {x}})=\mu _{\mathbf {4}}(|\phi |^{\mathsf {x}})$
for
$\pi (|\phi |^{\mathsf {x}})=\mu _{\mathbf {4}}(|\phi |^{\mathsf {x}})$
for
![]() $\mathsf {x}\in \{\mathsf {b},\mathsf {d},\mathsf {c},\mathsf {u}\}$
(Klein et al. Reference Klein, Majer and Rafiee Rad2021, Theorem 5).
$\mathsf {x}\in \{\mathsf {b},\mathsf {d},\mathsf {c},\mathsf {u}\}$
(Klein et al. Reference Klein, Majer and Rafiee Rad2021, Theorem 5).
Thus, we will further assume w.l.o.g. that
![]() $\mu$
and
$\mu$
and
![]() $\mu _{\mathbf {4}}$
are classical probability measures on
$\mu _{\mathbf {4}}$
are classical probability measures on
![]() $W$
.
$W$
.
Figure 1. A counterexample to (
![]() $\mathsf {IE}$
):
$\mathsf {IE}$
):
![]() $\mu (\{u_1\})=\mu (\{u_2\})=\frac {1}{3}$
,
$\mu (\{u_1\})=\mu (\{u_2\})=\frac {1}{3}$
,
![]() $\mu (W)=1$
, and
$\mu (W)=1$
, and
![]() $\mu (\varnothing )=0$
. All variables have the same values exemplified by
$\mu (\varnothing )=0$
. All variables have the same values exemplified by
![]() $p$
.
$p$
.
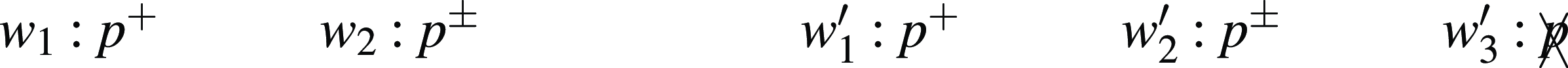
Figure 2. The values of all variables coincide with the values of
![]() $p$
state-wise.
$p$
state-wise.
![]() $\mu (X)=\frac {1}{2}$
for every
$\mu (X)=\frac {1}{2}$
for every
![]() $X\subseteq W$
;
$X\subseteq W$
;
![]() $\pi (\varnothing )=\pi (\{w'_1\})=0$
,
$\pi (\varnothing )=\pi (\{w'_1\})=0$
,
![]() $\pi (W')=1$
,
$\pi (W')=1$
,
![]() $\pi (X')=\frac {1}{2}$
otherwise.
$\pi (X')=\frac {1}{2}$
otherwise.
3. Logics for paraconsistent probabilities
In the Introduction, we saw that there could be two views on formalising paraconsistent probabilities (or uncertainty measures in general). The first option is to define probabilities in a paraconsistent logic. This is done, for example, by Dunn (Reference Dunn2010), Bueno-Soler and Carnielli (Reference Bueno-Soler and Carnielli2016), and Klein et al. (Reference Klein, Majer and Rafiee Rad2021). Another option is to employ a two-layered framework where the outer layer is not explosive as Flaminio et al. (Reference Flaminio, Godo, Ugolini, Dupin de Saint-Cyr, Öztürk Escoffier and Potyka2022) do. Our approach can be thought of as a combination of these two. Not only are our probabilities defined over a paraconsistent logic, but the logic with which we reason about them is also non-explosive.
In this section, we provide two-layered logics that are (weakly) complete w.r.t.
![]() $\mathsf {BD}$
-models with
$\mathsf {BD}$
-models with
![]() $\pm$
- and
$\pm$
- and
![]() $\mathbf {4}$
-probabilities. Since conditions on measures contain arithmetic operations on
$\mathbf {4}$
-probabilities. Since conditions on measures contain arithmetic operations on
![]() $[0,1]$
, we choose an expansion of Łukasiewicz logic, namely, Łukasiewicz logic with
$[0,1]$
, we choose an expansion of Łukasiewicz logic, namely, Łukasiewicz logic with
![]() $\triangle$
(
$\triangle$
(
![]() ${\mathsf {\unicode {x0141}}}_\triangle$
), for the outer layer. Furthermore,
${\mathsf {\unicode {x0141}}}_\triangle$
), for the outer layer. Furthermore,
![]() $\pm$
-probabilities work with both positive and negative extensions of formulas, whence it is reasonable to use
$\pm$
-probabilities work with both positive and negative extensions of formulas, whence it is reasonable to use
![]() $\mathsf {\unicode {x0141}}^2_{(\triangle, \rightarrow )}$
– a paraconsistent expansion of
$\mathsf {\unicode {x0141}}^2_{(\triangle, \rightarrow )}$
– a paraconsistent expansion of
![]() $\mathsf {\unicode {x0141}}$
(cf. Bílková et al. Reference Bílková, Frittella, Majer and Nazari2020 and Reference Bílková, Frittella, Kozhemiachenko, Das and Negri2021 for details) with two valuations –
$\mathsf {\unicode {x0141}}$
(cf. Bílková et al. Reference Bílková, Frittella, Majer and Nazari2020 and Reference Bílková, Frittella, Kozhemiachenko, Das and Negri2021 for details) with two valuations –
![]() $v_1$
(support of truth) and
$v_1$
(support of truth) and
![]() $v_2$
(support of falsity) – on
$v_2$
(support of falsity) – on
![]() $[0,1]$
.
$[0,1]$
.
3.1 Languages, semantics, and equivalence
Let us first recall the semantics of
![]() ${\mathsf {\unicode {x0141}}}_\triangle$
and
${\mathsf {\unicode {x0141}}}_\triangle$
and
![]() ${\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}$
. To facilitate the presentation, we begin with the definition of the standard
${\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}$
. To facilitate the presentation, we begin with the definition of the standard
![]() $\mathsf {\unicode {x0141}}_\triangle$
algebra on
$\mathsf {\unicode {x0141}}_\triangle$
algebra on
![]() $[0,1]$
that we will then use to define the semantics of both
$[0,1]$
that we will then use to define the semantics of both
![]() ${\mathsf {\unicode {x0141}}}_\triangle$
and
${\mathsf {\unicode {x0141}}}_\triangle$
and
![]() ${\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}$
.
${\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}$
.
Definition 10.
The standard
![]() ${\mathsf {\unicode {x0141}}}_\triangle$
algebra is a tuple
${\mathsf {\unicode {x0141}}}_\triangle$
algebra is a tuple
![]() $\langle [0,1],{\sim _{\mathsf {\unicode {x0141}}}},\triangle _{\mathsf {\unicode {x0141}}},\wedge _{\mathsf {\unicode {x0141}}},\vee _{\mathsf {\unicode {x0141}}},\rightarrow _{\mathsf {\unicode {x0141}}},\odot _{\mathsf {\unicode {x0141}}},\oplus _{\mathsf {\unicode {x0141}}},\ominus _{\mathsf {\unicode {x0141}}}\rangle$
with the operations are defined as follows.
$\langle [0,1],{\sim _{\mathsf {\unicode {x0141}}}},\triangle _{\mathsf {\unicode {x0141}}},\wedge _{\mathsf {\unicode {x0141}}},\vee _{\mathsf {\unicode {x0141}}},\rightarrow _{\mathsf {\unicode {x0141}}},\odot _{\mathsf {\unicode {x0141}}},\oplus _{\mathsf {\unicode {x0141}}},\ominus _{\mathsf {\unicode {x0141}}}\rangle$
with the operations are defined as follows.
 \begin{align*} {\sim _{\mathsf {\unicode {x0141}}}}a:=1-a \qquad\qquad\qquad\qquad \triangle _{\mathsf {\unicode {x0141}}}a:=\begin{cases}1\,\,\text {if }a=1\\0\,\,\text {otherwise}\end{cases} \end{align*}
\begin{align*} {\sim _{\mathsf {\unicode {x0141}}}}a:=1-a \qquad\qquad\qquad\qquad \triangle _{\mathsf {\unicode {x0141}}}a:=\begin{cases}1\,\,\text {if }a=1\\0\,\,\text {otherwise}\end{cases} \end{align*}
Definition 11 (
![]() ${\mathsf {\unicode {x0141}}}_\triangle$
) The language of
${\mathsf {\unicode {x0141}}}_\triangle$
) The language of
![]() ${\mathsf {\unicode {x0141}}}_\triangle$
is given via the following grammar
${\mathsf {\unicode {x0141}}}_\triangle$
is given via the following grammar
We will also write
![]() $\phi \leftrightarrow \chi$
as a shorthand for
$\phi \leftrightarrow \chi$
as a shorthand for
![]() $(\phi \rightarrow \chi )\odot (\chi \rightarrow \phi )$
.
$(\phi \rightarrow \chi )\odot (\chi \rightarrow \phi )$
.
A valuation is a map
![]() $v:\texttt {Prop}\rightarrow [0,1]$
that is extended to the complex formulas as expected:
$v:\texttt {Prop}\rightarrow [0,1]$
that is extended to the complex formulas as expected:
![]() $v(\phi \circ \chi )=v(\phi )\circ _{\mathsf {\unicode {x0141}}} v(\chi )$
.
$v(\phi \circ \chi )=v(\phi )\circ _{\mathsf {\unicode {x0141}}} v(\chi )$
.
![]() $\phi$
is
$\phi$
is
![]() ${\mathsf {\unicode {x0141}}}_\triangle$
-valid iff
${\mathsf {\unicode {x0141}}}_\triangle$
-valid iff
![]() $v(\phi )=1$
for every v.
$v(\phi )=1$
for every v.
![]() $\Gamma$
entails
$\Gamma$
entails
![]() $\chi$
(denoted
$\chi$
(denoted
![]() $\Gamma \models _{{\mathsf {\unicode {x0141}}}_\triangle }\chi$
) iff for every
$\Gamma \models _{{\mathsf {\unicode {x0141}}}_\triangle }\chi$
) iff for every
![]() $v$
s.t.
$v$
s.t.
![]() $v(\phi )=1$
for all
$v(\phi )=1$
for all
![]() $\phi \in \Gamma$
, it holds that
$\phi \in \Gamma$
, it holds that
![]() $v(\chi )=1$
as well.
$v(\chi )=1$
as well.
Definition 12 (
![]() ${\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}$
). The language is constructed using the following grammar.
${\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}$
). The language is constructed using the following grammar.
The semantics is given by two valuations
![]() $v_1$
(support of truth) and
$v_1$
(support of truth) and
![]() $v_2$
(support of falsity)
$v_2$
(support of falsity)
![]() $v_1,v_2:\texttt {Prop}\rightarrow [0,1]$
that are extended as follows.
$v_1,v_2:\texttt {Prop}\rightarrow [0,1]$
that are extended as follows.
 \begin{align*} v_1(\neg \phi )&=v_2(\phi )&v_2(\neg \phi )&=v_1(\phi )\\ v_1({\sim }\phi )&={\sim _{\mathsf {\unicode {x0141}}}}v_1(\phi )&v_2({\sim }\phi )&={\sim _{\mathsf {\unicode {x0141}}}}v_2(\phi )\\ v_1(\triangle \phi )&=\triangle _{\mathsf {\unicode {x0141}}} v_1(\phi )&v_2(\triangle \phi )&={\sim _{\mathsf {\unicode {x0141}}}}\triangle _{\mathsf {\unicode {x0141}}}{\sim }_{\mathsf {\unicode {x0141}}} v_2(\phi )\\ v_1(\phi \rightarrow \chi )&=v_1(\phi )\rightarrow _{\mathsf {\unicode {x0141}}} v_1(\chi )&v_2(\phi \rightarrow \chi )&=v_2(\chi )\ominus _{\mathsf {\unicode {x0141}}} v_2(\phi ) \end{align*}
\begin{align*} v_1(\neg \phi )&=v_2(\phi )&v_2(\neg \phi )&=v_1(\phi )\\ v_1({\sim }\phi )&={\sim _{\mathsf {\unicode {x0141}}}}v_1(\phi )&v_2({\sim }\phi )&={\sim _{\mathsf {\unicode {x0141}}}}v_2(\phi )\\ v_1(\triangle \phi )&=\triangle _{\mathsf {\unicode {x0141}}} v_1(\phi )&v_2(\triangle \phi )&={\sim _{\mathsf {\unicode {x0141}}}}\triangle _{\mathsf {\unicode {x0141}}}{\sim }_{\mathsf {\unicode {x0141}}} v_2(\phi )\\ v_1(\phi \rightarrow \chi )&=v_1(\phi )\rightarrow _{\mathsf {\unicode {x0141}}} v_1(\chi )&v_2(\phi \rightarrow \chi )&=v_2(\chi )\ominus _{\mathsf {\unicode {x0141}}} v_2(\phi ) \end{align*}
We say that
![]() $\phi$
is
$\phi$
is
![]() ${\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}$
-valid iff for every
${\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}$
-valid iff for every
![]() $v_1$
and
$v_1$
and
![]() $v_2$
, it holds that
$v_2$
, it holds that
![]() $v_1(\phi )=1$
and
$v_1(\phi )=1$
and
![]() $v_2(\phi )=0$
.
$v_2(\phi )=0$
.
Convention 13.
When there is no risk of confusion, we will use
![]() $v(\phi )=(x,y)$
to stand for
$v(\phi )=(x,y)$
to stand for
![]() $v_1(\phi )=x$
and
$v_1(\phi )=x$
and
![]() $v_2(\phi )=y$
.
$v_2(\phi )=y$
.
Remark 14.
Note that
![]() $\sim$
and
$\sim$
and
![]() $\rightarrow$
can define all other binary connectives in
$\rightarrow$
can define all other binary connectives in
![]() ${\mathsf {\unicode {x0141}}}_\triangle$
and
${\mathsf {\unicode {x0141}}}_\triangle$
and
![]() ${\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}$
.
${\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}$
.
We are now ready to present our two-layered logics for paraconsistent probabilities:
![]() $\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
– the logic of
$\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
– the logic of
![]() $\pm$
-probabilities and
$\pm$
-probabilities and
![]() $\mathbf {4}\mathsf {Pr}^{\mathsf {\unicode {x0141}}_\triangle }$
– the logic of
$\mathbf {4}\mathsf {Pr}^{\mathsf {\unicode {x0141}}_\triangle }$
– the logic of
![]() $\mathbf {4}$
-probabilities.
$\mathbf {4}$
-probabilities.
Definition 15 (
![]() $\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
: language and semantics). The language of
$\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
: language and semantics). The language of
![]() $\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
is constructed via the following grammar:
$\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
is constructed via the following grammar:
A
![]() $\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
-model is a tuple
$\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
-model is a tuple
![]() $\mathbb {M}=\langle \mathfrak {M},\mu _{\mathbf {4}},e\rangle$
s.t.
$\mathbb {M}=\langle \mathfrak {M},\mu _{\mathbf {4}},e\rangle$
s.t.
-
•
 $\langle \mathfrak {M},\mu _{\mathbf {4}}\rangle$
is a
$\langle \mathfrak {M},\mu _{\mathbf {4}}\rangle$
is a
 $\mathsf {BD}$
-model with
$\mathsf {BD}$
-model with
 $\mathbf {4}$
-probability;
$\mathbf {4}$
-probability;
-
•
 $e$
is a
$e$
is a
 ${\mathsf {\unicode {x0141}}}_\triangle$
valuation induced by
${\mathsf {\unicode {x0141}}}_\triangle$
valuation induced by
 $\mu _{\mathbf {4}}$
, that is:
$\mu _{\mathbf {4}}$
, that is:
-
–
 $e(\mathsf {Bl}\phi )=\mu _{\mathbf {4}}(|\phi |^{\mathsf {b}})$
,
$e(\mathsf {Bl}\phi )=\mu _{\mathbf {4}}(|\phi |^{\mathsf {b}})$
,
 $e(\mathsf {Db}\phi )=\mu _{\mathbf {4}}(|\phi |^{\mathsf {d}})$
,
$e(\mathsf {Db}\phi )=\mu _{\mathbf {4}}(|\phi |^{\mathsf {d}})$
,
 $e(\mathsf {Cf}\phi )=\mu _{\mathbf {4}}(|\phi |^{\mathsf {c}})$
,
$e(\mathsf {Cf}\phi )=\mu _{\mathbf {4}}(|\phi |^{\mathsf {c}})$
,
 $e(\mathsf {Uc}\phi )=\mu _{\mathbf {4}}(|\phi |^{\mathsf {u}})$
;
$e(\mathsf {Uc}\phi )=\mu _{\mathbf {4}}(|\phi |^{\mathsf {u}})$
; -
– values of complex
 $\mathscr {L}_{\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }}$
-formulas are computed via Definition 11
.
$\mathscr {L}_{\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }}$
-formulas are computed via Definition 11
.
-
We say that
![]() $\alpha$
is
$\alpha$
is
![]() ${\mathbf{4}\mathsf{Pr}^{\unicode{x0141}\triangle}}$
-valid iff
${\mathbf{4}\mathsf{Pr}^{\unicode{x0141}\triangle}}$
-valid iff
![]() $e(\alpha)=1$
in every
$e(\alpha)=1$
in every
![]() ${\mathbf{4}\mathsf{Pr}^{\unicode{x0141}\triangle}}$
-model. A set of formulas
${\mathbf{4}\mathsf{Pr}^{\unicode{x0141}\triangle}}$
-model. A set of formulas
![]() $\Gamma$
entails
$\Gamma$
entails
![]() $\alpha$
(
$\alpha$
(
![]() $\Gamma\models_{\mathbf{4}\mathsf{Pr}^{\unicode{x0141}\triangle}}\alpha$
) iff there is no
$\Gamma\models_{\mathbf{4}\mathsf{Pr}^{\unicode{x0141}\triangle}}\alpha$
) iff there is no
![]() $\mathbb{M}$
s.t.
$\mathbb{M}$
s.t.
![]() $e(\gamma)=1$
for every
$e(\gamma)=1$
for every
![]() $\gamma\in\Gamma$
but
$\gamma\in\Gamma$
but
![]() $e(\alpha)\neq1$
.
$e(\alpha)\neq1$
.
Definition 16 (
![]() $\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
: language and semantics). The language of
$\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
: language and semantics). The language of
![]() $\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
is given by the following grammar
$\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
is given by the following grammar
A
![]() $\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
-model is a tuple
$\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
-model is a tuple
![]() $\mathbb {M}=\langle \mathfrak {M},\mu, e_1,e_2\rangle$
s.t.
$\mathbb {M}=\langle \mathfrak {M},\mu, e_1,e_2\rangle$
s.t.
-
•
 $\langle \mathfrak {M},\mu \rangle$
is a
$\langle \mathfrak {M},\mu \rangle$
is a
 $\mathsf {BD}$
-model with
$\mathsf {BD}$
-model with
 $\pm$
-probability;
$\pm$
-probability;
-
•
 $e_1$
and
$e_1$
and
 $e_2$
are
$e_2$
are
 ${\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}$
valuations induced by
${\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}$
valuations induced by
 $\mu$
, that is:
$\mu$
, that is:
-
–
 $e_1(\mathsf {Pr}\phi )=\mu (|\phi |^+)$
,
$e_1(\mathsf {Pr}\phi )=\mu (|\phi |^+)$
,
 $e_2(\mathsf {Pr}\phi )=\mu (|\phi |^-)$
;
$e_2(\mathsf {Pr}\phi )=\mu (|\phi |^-)$
; -
– the values of complex
 $\mathscr {L}_{\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle }$
formulas are computed following Definition 12
.
$\mathscr {L}_{\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle }$
formulas are computed following Definition 12
.
-
We say that
![]() $\alpha$
is
$\alpha$
is
![]() ${\mathbf{4}\mathsf{Pr}^{\unicode{x0141}\triangle}}$
-valid iff
${\mathbf{4}\mathsf{Pr}^{\unicode{x0141}\triangle}}$
-valid iff
![]() $e(\alpha)=1$
in every
$e(\alpha)=1$
in every
![]() ${\mathbf{4}\mathsf{Pr}^{\unicode{x0141}\triangle}}$
-model. A set of formulas
${\mathbf{4}\mathsf{Pr}^{\unicode{x0141}\triangle}}$
-model. A set of formulas
![]() $\Gamma$
entails
$\Gamma$
entails
![]() $\alpha$
(
$\alpha$
(
![]() $\Gamma\models_{\mathbf{4}\mathsf{Pr}^{\unicode{x0141}\triangle}}\alpha$
) iff there is no
$\Gamma\models_{\mathbf{4}\mathsf{Pr}^{\unicode{x0141}\triangle}}\alpha$
) iff there is no
![]() $\mathbb{M}$
s.t.
$\mathbb{M}$
s.t.
![]() $e(\gamma)=1$
for every
$e(\gamma)=1$
for every
![]() $\gamma\in\Gamma$
but
$\gamma\in\Gamma$
but
![]() $e(\alpha)\neq1$
.
$e(\alpha)\neq1$
.
We note quickly that in Definitions 15 and 16,
![]() $e$
(as well as
$e$
(as well as
![]() $e_1$
and
$e_1$
and
![]() $e_2$
) are valuations of outer-layer formulas. Thus, they are defined only on modal atoms, not propositional variables. Propositional variables, in turn, have their values assigned by
$e_2$
) are valuations of outer-layer formulas. Thus, they are defined only on modal atoms, not propositional variables. Propositional variables, in turn, have their values assigned by
![]() $v^+$
and
$v^+$
and
![]() $v^-$
valuations of the
$v^-$
valuations of the
![]() $\mathsf {BD}$
-model over which the
$\mathsf {BD}$
-model over which the
![]() $\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
- or
$\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
- or
![]() $\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
-model is built.
$\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
-model is built.
The following property of
![]() $\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
will be useful further in the section.
$\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
will be useful further in the section.
Lemma 17.
Let
![]() $\alpha \in \mathscr {L}_{\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle }$
. Then,
$\alpha \in \mathscr {L}_{\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle }$
. Then,
![]() $\alpha$
is
$\alpha$
is
![]() $\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
-valid iff
$\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
-valid iff
![]() $e_1(\alpha )=1$
in every
$e_1(\alpha )=1$
in every
![]() $\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
-model.
$\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
-model.
Proof.
Let
![]() $\mathbb {M}=\langle W,v^+,v^-,\mu, e_1,e_2\rangle$
be a
$\mathbb {M}=\langle W,v^+,v^-,\mu, e_1,e_2\rangle$
be a
![]() $\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
-model s.t.
$\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
-model s.t.
![]() $e_2(\alpha )\neq 0$
. We construct a model
$e_2(\alpha )\neq 0$
. We construct a model
![]() $\mathbb {M}^*=\langle W,(v^*)^+,(v^*)^-,\mu, e^*_1,e^*_2\rangle$
where
$\mathbb {M}^*=\langle W,(v^*)^+,(v^*)^-,\mu, e^*_1,e^*_2\rangle$
where
![]() $e^*_1(\alpha )\neq 1$
. To do this, we define new
$e^*_1(\alpha )\neq 1$
. To do this, we define new
![]() $\mathsf {BD}$
valuations
$\mathsf {BD}$
valuations
![]() $(v^*)^+$
and
$(v^*)^+$
and
![]() $(v^*)^-$
on
$(v^*)^-$
on
![]() $W$
as follows.
$W$
as follows.
It can be easily checked by induction on
![]() $\phi \in \mathscr {L}_{\mathsf {BD}}$
that
$\phi \in \mathscr {L}_{\mathsf {BD}}$
that
Now, since we can w.l.o.g. assume that
![]() $\mu$
is a (classical) probability measure on
$\mu$
is a (classical) probability measure on
![]() $W$
(recall Example 9), we have that
$W$
(recall Example 9), we have that
It remains to show that
![]() $e^*(\alpha )=(1-e_2(\alpha ),1-e_1(\alpha ))$
for every
$e^*(\alpha )=(1-e_2(\alpha ),1-e_1(\alpha ))$
for every
![]() $\alpha \in \mathscr {L}_{\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle }$
. We proceed by induction on formulas. The basis case of
$\alpha \in \mathscr {L}_{\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle }$
. We proceed by induction on formulas. The basis case of
![]() $\alpha =\mathsf {Pr}\phi$
holds by (2).
$\alpha =\mathsf {Pr}\phi$
holds by (2).
Consider
![]() $\alpha =\beta \rightarrow \beta '$
.
$\alpha =\beta \rightarrow \beta '$
.
 \begin{align*} e^*_1(\beta \rightarrow \beta ')&=\min (1,1-e^*_1(\beta )+e^*_1(\beta '))\\ &=\min (1,1-(1-e_2(\beta ))+(1-e_2(\beta ')))\,\,{(\text{ by } IH)}\\ &=\min (1,1-e_2(\beta ')+e_2(\beta ))\\ &=1-\max (0,e_2(\beta ')-e_2(\beta ))\\ &=1-e_2(\beta \rightarrow \beta ') \end{align*}
\begin{align*} e^*_1(\beta \rightarrow \beta ')&=\min (1,1-e^*_1(\beta )+e^*_1(\beta '))\\ &=\min (1,1-(1-e_2(\beta ))+(1-e_2(\beta ')))\,\,{(\text{ by } IH)}\\ &=\min (1,1-e_2(\beta ')+e_2(\beta ))\\ &=1-\max (0,e_2(\beta ')-e_2(\beta ))\\ &=1-e_2(\beta \rightarrow \beta ') \end{align*}
 \begin{align*} e^*_2(\beta \rightarrow \beta ')&=\max (0,e^*_2(\beta ')-e^*_2(\beta ))\\ &=\max (0,1-e_1(\beta ')-(1-e_1(\beta )))\qquad \qquad {(\text{ by } IH)}\\ &=\max (0,e_1(\beta )-e_1(\beta '))\\ &=1-\min (1,1-e_1(\beta )+e_1(\beta ')) \end{align*}
\begin{align*} e^*_2(\beta \rightarrow \beta ')&=\max (0,e^*_2(\beta ')-e^*_2(\beta ))\\ &=\max (0,1-e_1(\beta ')-(1-e_1(\beta )))\qquad \qquad {(\text{ by } IH)}\\ &=\max (0,e_1(\beta )-e_1(\beta '))\\ &=1-\min (1,1-e_1(\beta )+e_1(\beta ')) \end{align*}
The remaining cases of
![]() $\alpha =\neg \beta$
,
$\alpha =\neg \beta$
,
![]() $\alpha ={\sim }\beta$
, and
$\alpha ={\sim }\beta$
, and
![]() $\alpha =\triangle \beta$
can be tackled similarly.
$\alpha =\triangle \beta$
can be tackled similarly.
It is now clear that if
![]() $e(\alpha )=(1,y)$
for some
$e(\alpha )=(1,y)$
for some
![]() $y\gt 0$
, we have
$y\gt 0$
, we have
![]() $e^*(\alpha )=(1-y,0)$
, that is,
$e^*(\alpha )=(1-y,0)$
, that is,
![]() $e^*_1(\alpha )\lt 1$
, as required. The result follows.
$e^*_1(\alpha )\lt 1$
, as required. The result follows.
Example 18 (Values of formulas in models). Consider Fig.
3
with a classical probability
![]() $\mu$
. Let us compute the values of the following (atomic) formulas:
$\mu$
. Let us compute the values of the following (atomic) formulas:
![]() $\mathsf {Pr}(p\wedge \neg q)$
,
$\mathsf {Pr}(p\wedge \neg q)$
,
![]() $\mathsf {Db}(p\wedge \neg q)$
, and
$\mathsf {Db}(p\wedge \neg q)$
, and
![]() $\mathsf {Bl}(q\vee \neg q)$
.
$\mathsf {Bl}(q\vee \neg q)$
.
We have
![]() $|p\wedge \neg q|^+=\{w_1\}$
and
$|p\wedge \neg q|^+=\{w_1\}$
and
![]() $|p\wedge \neg p|^-=\{w_1,w_3\}$
. Thus,
$|p\wedge \neg p|^-=\{w_1,w_3\}$
. Thus,
![]() $\mu (|p\wedge \neg q|^+)=\frac {1}{3}$
and
$\mu (|p\wedge \neg q|^+)=\frac {1}{3}$
and
![]() $\mu (|p\wedge \neg q|^-)=\frac {1}{2}$
which gives us
$\mu (|p\wedge \neg q|^-)=\frac {1}{2}$
which gives us
![]() $e(\mathsf {Pr}(p\wedge \neg q))=\left (\frac {1}{3},\frac {1}{2}\right )$
. Moreover,
$e(\mathsf {Pr}(p\wedge \neg q))=\left (\frac {1}{3},\frac {1}{2}\right )$
. Moreover,
![]() $|p\wedge \neg q|^{\mathsf {d}}=\{w_3\}$
, whence
$|p\wedge \neg q|^{\mathsf {d}}=\{w_3\}$
, whence
![]() $\mathsf {Db}(p\wedge \neg q)=\frac {1}{6}$
. For
$\mathsf {Db}(p\wedge \neg q)=\frac {1}{6}$
. For
![]() $q\vee \neg q$
, we have
$q\vee \neg q$
, we have
![]() $|q\vee \neg q|^{\mathsf {b}}=\{w_2\}$
, and thus,
$|q\vee \neg q|^{\mathsf {b}}=\{w_2\}$
, and thus,
![]() $e(\mathsf {Bl}(q\vee \neg q))=\frac {1}{2}$
.
$e(\mathsf {Bl}(q\vee \neg q))=\frac {1}{2}$
.

Figure 3.
![]() $\mu (\{w_1\})=\frac {1}{3}$
,
$\mu (\{w_1\})=\frac {1}{3}$
,
![]() $\mu (\{w_2\})=\frac {1}{2}$
,
$\mu (\{w_2\})=\frac {1}{2}$
,
![]() $\mu (\{w_3\})=\frac {1}{6}$
.
$\mu (\{w_3\})=\frac {1}{6}$
.
Before establishing faithful translations between
![]() $\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
and
$\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
and
![]() $\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
, let us recall that in the Introduction, we mentioned that quantitative statements about uncertainty expressed in the natural language may sound like ‘I think that rain is twice more likely than snow’. We show how to formalise this statement.
$\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
, let us recall that in the Introduction, we mentioned that quantitative statements about uncertainty expressed in the natural language may sound like ‘I think that rain is twice more likely than snow’. We show how to formalise this statement.
Example 19 (Formalisation).
-
 $\texttt {twice}$
: I think that rain is twice more likely than snow.
$\texttt {twice}$
: I think that rain is twice more likely than snow.
We are going to translate this statement into
![]() $\mathscr {L}_{\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }}$
and treat ‘I think that’ as pure belief modality. We denote ‘it is going to rain’ with
$\mathscr {L}_{\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }}$
and treat ‘I think that’ as pure belief modality. We denote ‘it is going to rain’ with
![]() $r$
and ‘it is going to snow’ with
$r$
and ‘it is going to snow’ with
![]() $s$
. It remains to write down a formula
$s$
. It remains to write down a formula
![]() $\phi _{\texttt {twice}}$
that has value
$\phi _{\texttt {twice}}$
that has value
![]() $1$
iff
$1$
iff
![]() $e(\mathsf {Bl} r)=2\cdot e(\mathsf {Bl} s)$
. Consider the following formula
$e(\mathsf {Bl} r)=2\cdot e(\mathsf {Bl} s)$
. Consider the following formula
Note that a more intuitive formalisation –
![]() $\triangle (\mathsf {Bl} r\leftrightarrow (\mathsf {Bl} s\oplus \mathsf {Bl} s))$
– would not work:
$\triangle (\mathsf {Bl} r\leftrightarrow (\mathsf {Bl} s\oplus \mathsf {Bl} s))$
– would not work:
![]() $\oplus$
is a truncated sum, whence it, e.g., does not exclude the situation with both
$\oplus$
is a truncated sum, whence it, e.g., does not exclude the situation with both
![]() $\mathsf {Bl} r$
and
$\mathsf {Bl} r$
and
![]() $\mathsf {Bl} s$
having value
$\mathsf {Bl} s$
having value
![]() $1$
. It can, however, be altered as follows:
$1$
. It can, however, be altered as follows:
![]() $\triangle (\mathsf {Bl} r\leftrightarrow (\mathsf {Bl} s\oplus \mathsf {Bl} s))\wedge {\sim }(\mathsf {Bl} s\odot \mathsf {Bl} s)$
which will give the desired outcome.
$\triangle (\mathsf {Bl} r\leftrightarrow (\mathsf {Bl} s\oplus \mathsf {Bl} s))\wedge {\sim }(\mathsf {Bl} s\odot \mathsf {Bl} s)$
which will give the desired outcome.
It is also clear that desiderata (1), (3), and (4) listed in Section 1.4 are satisfied by both
![]() $\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
and
$\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
and
![]() $\mathsf {Pr}^{\mathsf {\unicode {x0141}}^2}_\triangle$
. It is less straightforward, however, to see how we can formalise preferring one source to another (desideratum (2)). We explain this in the following remark.
$\mathsf {Pr}^{\mathsf {\unicode {x0141}}^2}_\triangle$
. It is less straightforward, however, to see how we can formalise preferring one source to another (desideratum (2)). We explain this in the following remark.
Remark 20.
To represent different sources, one can consider
![]() $\mathsf {BD}$
-models with several measures, each representing a source, and, accordingly, expand the language with other modalities corresponding to these new measures. We can state, for example, that one source (
$\mathsf {BD}$
-models with several measures, each representing a source, and, accordingly, expand the language with other modalities corresponding to these new measures. We can state, for example, that one source (
![]() $s_1$
) considers
$s_1$
) considers
![]() $\phi$
to be more likely than the other source (
$\phi$
to be more likely than the other source (
![]() $s_2$
) does. In
$s_2$
) does. In
![]() $\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
we can interpret this as the value of
$\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
we can interpret this as the value of
![]() $\mathsf {Bl}_{s_1}\phi$
being smaller than the value of
$\mathsf {Bl}_{s_1}\phi$
being smaller than the value of
![]() $\mathsf {Bl}_{s_2}\phi$
. This is formalised as follows:
$\mathsf {Bl}_{s_2}\phi$
. This is formalised as follows:
Unfortunately, there seems to be no direct way of representing the degrees of trust the agent assigns to
![]() $s_1$
and
$s_1$
and
![]() $s_2$
using only modalities treated as measures in the Łukasiewicz setting. A traditional way (cf., e.g., Shafer Reference Shafer1976, p. 252) of accounting for the degree of trust in a given source is to multiply the value a mass function gives to
$s_2$
using only modalities treated as measures in the Łukasiewicz setting. A traditional way (cf., e.g., Shafer Reference Shafer1976, p. 252) of accounting for the degree of trust in a given source is to multiply the value a mass function gives to
![]() $X\subseteq W$
by some
$X\subseteq W$
by some
![]() $x\in [0,1]$
. Thus, to model this approach, one would need a combination of Rational Pavelka and Product logics. Another option would be to redefine
$x\in [0,1]$
. Thus, to model this approach, one would need a combination of Rational Pavelka and Product logics. Another option would be to redefine
![]() $e(\mathsf {Bl}_s\phi )=(\mathsf {tr}_s\odot _{\mathsf {\unicode {x0141}}}\mu (|\phi |^{\mathsf {b}}))$
and similarly for other modalities (with
$e(\mathsf {Bl}_s\phi )=(\mathsf {tr}_s\odot _{\mathsf {\unicode {x0141}}}\mu (|\phi |^{\mathsf {b}}))$
and similarly for other modalities (with
![]() $\mathsf {tr}_s\in [0,1]$
standing for the trust in source
$\mathsf {tr}_s\in [0,1]$
standing for the trust in source
![]() $s$
). It is unclear, however, how to axiomatise this logic.
$s$
). It is unclear, however, how to axiomatise this logic.
It is possible, though, to make different modalities stand for different types of measures (e.g.,
![]() $\mathsf {Bl}_{s_1}$
can be generated by a
$\mathsf {Bl}_{s_1}$
can be generated by a
![]() $\mathbf {4}$
-probability while
$\mathbf {4}$
-probability while
![]() $\mathsf {Bl}_{s_2}$
by a belief function). This represents the different ways of aggregating the data the agent can have.
$\mathsf {Bl}_{s_2}$
by a belief function). This represents the different ways of aggregating the data the agent can have.
We finish the section by establishing faithful embeddings of
![]() $\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
and
$\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
and
![]() $\mathsf {Pr}^{\mathsf {\unicode {x0141}}^2}_\triangle$
into one another. First, we introduce some technical notions that will simplify the proof.
$\mathsf {Pr}^{\mathsf {\unicode {x0141}}^2}_\triangle$
into one another. First, we introduce some technical notions that will simplify the proof.
Convention 21.
We say that
![]() $\alpha \in \mathscr {L}_{\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle }$
is outer-
$\alpha \in \mathscr {L}_{\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle }$
is outer-
![]() $\neg$
-free when
$\neg$
-free when
![]() $\neg$
’s appear only inside modal atoms.
$\neg$
’s appear only inside modal atoms.
Definition 22.
Let
![]() $\phi \in \mathscr {L}_{\mathsf {BD}}$
and
$\phi \in \mathscr {L}_{\mathsf {BD}}$
and
![]() $\alpha \in \mathscr {L}_{\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle }$
.
$\alpha \in \mathscr {L}_{\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle }$
.
![]() $\alpha ^\neg$
is produced from
$\alpha ^\neg$
is produced from
![]() $\alpha$
by successively applying the following transformations.
$\alpha$
by successively applying the following transformations.
It is easy to see that
![]() $\alpha ^\neg$
is outer-
$\alpha ^\neg$
is outer-
![]() $\neg$
-free. Using Definitions 12 and 16, one can also check that
$\neg$
-free. Using Definitions 12 and 16, one can also check that
![]() $e(\alpha )=e(\alpha ^\neg )$
in every
$e(\alpha )=e(\alpha ^\neg )$
in every
![]() $\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
-model.
$\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
-model.
Definition 23.
Let
![]() $\phi \in \mathscr {L}_{\mathsf {BD}}$
and
$\phi \in \mathscr {L}_{\mathsf {BD}}$
and
![]() $\alpha \in \mathscr {L}_{\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle }$
be outer-
$\alpha \in \mathscr {L}_{\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle }$
be outer-
![]() $\neg$
-free. We define
$\neg$
-free. We define
![]() $\alpha ^{\mathbf {4}}\in \mathscr {L}_{\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }}$
as follows.
$\alpha ^{\mathbf {4}}\in \mathscr {L}_{\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }}$
as follows.
 \begin{align*} (\mathsf {Pr}\phi )^{\mathbf {4}}&=\mathsf {Bl}\phi \oplus \mathsf {Cf}\phi \\ (\heartsuit \alpha )^{\mathbf {4}}&=\heartsuit \alpha ^{\mathbf {4}}\qquad\qquad {(\heartsuit \in \{\triangle, {\sim }\})}\\ (\alpha \rightarrow \alpha ')^{\mathbf {4}}&=\alpha ^{\mathbf {4}}\rightarrow \alpha ^{'\mathbf {4}} \end{align*}
\begin{align*} (\mathsf {Pr}\phi )^{\mathbf {4}}&=\mathsf {Bl}\phi \oplus \mathsf {Cf}\phi \\ (\heartsuit \alpha )^{\mathbf {4}}&=\heartsuit \alpha ^{\mathbf {4}}\qquad\qquad {(\heartsuit \in \{\triangle, {\sim }\})}\\ (\alpha \rightarrow \alpha ')^{\mathbf {4}}&=\alpha ^{\mathbf {4}}\rightarrow \alpha ^{'\mathbf {4}} \end{align*}
Let
![]() $\beta \in \mathscr {L}_{\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }}$
. We define
$\beta \in \mathscr {L}_{\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }}$
. We define
![]() $\beta ^\pm$
as follows.
$\beta ^\pm$
as follows.
 \begin{align*} (\mathsf {Bl}\phi )^\pm &=\mathsf {Pr}\phi \ominus \mathsf {Pr}(\phi \wedge \neg \phi )\\ (\mathsf {Cf}\phi )^\pm &=\mathsf {Pr}(\phi \wedge \neg \phi )\\ (\mathsf {Uc}\phi )^\pm &={\sim }\mathsf {Pr}(\phi \vee \neg \phi )\\ (\mathsf {Db}\phi )^\pm &=\mathsf {Pr}\neg \phi \ominus \mathsf {Pr}(\phi \wedge \neg \phi )\\ (\heartsuit \beta )^\pm &=\heartsuit \beta ^\pm \qquad \qquad {(\heartsuit \in \{\triangle, {\sim }\})}\\ (\beta \rightarrow \beta ')^\pm &=\beta ^\pm \rightarrow \beta ^{'\pm } \end{align*}
\begin{align*} (\mathsf {Bl}\phi )^\pm &=\mathsf {Pr}\phi \ominus \mathsf {Pr}(\phi \wedge \neg \phi )\\ (\mathsf {Cf}\phi )^\pm &=\mathsf {Pr}(\phi \wedge \neg \phi )\\ (\mathsf {Uc}\phi )^\pm &={\sim }\mathsf {Pr}(\phi \vee \neg \phi )\\ (\mathsf {Db}\phi )^\pm &=\mathsf {Pr}\neg \phi \ominus \mathsf {Pr}(\phi \wedge \neg \phi )\\ (\heartsuit \beta )^\pm &=\heartsuit \beta ^\pm \qquad \qquad {(\heartsuit \in \{\triangle, {\sim }\})}\\ (\beta \rightarrow \beta ')^\pm &=\beta ^\pm \rightarrow \beta ^{'\pm } \end{align*}
Theorem 24.
![]() $\alpha \in \mathscr {L}_{\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle }$
is
$\alpha \in \mathscr {L}_{\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle }$
is
![]() $\mathsf {Pr}^{\mathsf {\unicode {x0141}}^2}_\triangle$
-valid iff
$\mathsf {Pr}^{\mathsf {\unicode {x0141}}^2}_\triangle$
-valid iff
![]() $(\alpha ^\neg )^{\mathbf {4}}$
is
$(\alpha ^\neg )^{\mathbf {4}}$
is
![]() $\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
-valid.
$\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
-valid.
Proof.
Let w.l.o.g.
![]() $\mathbb {M}=\langle W,v^+,v^-,\mu, e_1,e_2\rangle$
be a
$\mathbb {M}=\langle W,v^+,v^-,\mu, e_1,e_2\rangle$
be a
![]() $\mathsf {BD}$
-model with
$\mathsf {BD}$
-model with
![]() $\pm$
-probability where
$\pm$
-probability where
![]() $\mu$
is a classical probability measure and let
$\mu$
is a classical probability measure and let
![]() $e(\alpha )=(x,y)$
. We show that in the
$e(\alpha )=(x,y)$
. We show that in the
![]() $\mathsf {BD}$
-model
$\mathsf {BD}$
-model
![]() $\mathbb {M}_{\mathbf {4}}=\langle W,v^+,v^-,\mu, e_1\rangle$
with four-probability
$\mathbb {M}_{\mathbf {4}}=\langle W,v^+,v^-,\mu, e_1\rangle$
with four-probability
![]() $\mu$
and
$\mu$
and
![]() $e^{\mathbf {4}}$
induced by
$e^{\mathbf {4}}$
induced by
![]() $\mu$
,
$\mu$
,
![]() $e^{\mathbf {4}}((\alpha ^\neg )^{\mathbf {4}})=x$
. This is sufficient to prove the result because if
$e^{\mathbf {4}}((\alpha ^\neg )^{\mathbf {4}})=x$
. This is sufficient to prove the result because if
![]() $\alpha ^\neg$
is not
$\alpha ^\neg$
is not
![]() $\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
-valid,
$\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
-valid,
![]() $\mathsf {Pr}^{\mathsf {\unicode {x0141}}^2}_\triangle$
-valid
$\mathsf {Pr}^{\mathsf {\unicode {x0141}}^2}_\triangle$
-valid
![]() $\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
-valid either.
$\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
-valid either.
We proceed by induction on
![]() $\alpha ^\neg$
. For the basis case, we have that
$\alpha ^\neg$
. For the basis case, we have that
 \begin{align*} e_1(\mathsf {Pr}\phi )&=\mu (|\phi |^+)\\&=\mu (|\phi |^{\mathsf {b}}\cup |\phi |^{\mathsf {c}})\\& \begin{array}{l@{\qquad\qquad\qquad\qquad}c} =\mu (|\phi |^{\mathsf {b}})\cup \mu (|\phi |^{\mathsf {c}})\qquad & {(|\phi |^{\mathsf {b}} \text{ and } |\phi |^{\mathsf {c}} \text{ are disjoint })}\\ =e^{\mathbf {4}}(\mathsf {Bl}\phi )+e_{\mathbf {4}}(\mathsf {Cf}\phi ) & {(e^{\mathbf {4}} \text{ is induced by } \mu )}\\ =e^{\mathbf {4}}(\mathsf {Bl}\phi \oplus \mathsf {Cf}\phi )& {(e^{\mathbf {4}}(\mathsf {Bl}\phi )+e_{\mathbf {4}}(\mathsf {Cf}\phi )\leq 1)}\end{array} \end{align*}
\begin{align*} e_1(\mathsf {Pr}\phi )&=\mu (|\phi |^+)\\&=\mu (|\phi |^{\mathsf {b}}\cup |\phi |^{\mathsf {c}})\\& \begin{array}{l@{\qquad\qquad\qquad\qquad}c} =\mu (|\phi |^{\mathsf {b}})\cup \mu (|\phi |^{\mathsf {c}})\qquad & {(|\phi |^{\mathsf {b}} \text{ and } |\phi |^{\mathsf {c}} \text{ are disjoint })}\\ =e^{\mathbf {4}}(\mathsf {Bl}\phi )+e_{\mathbf {4}}(\mathsf {Cf}\phi ) & {(e^{\mathbf {4}} \text{ is induced by } \mu )}\\ =e^{\mathbf {4}}(\mathsf {Bl}\phi \oplus \mathsf {Cf}\phi )& {(e^{\mathbf {4}}(\mathsf {Bl}\phi )+e_{\mathbf {4}}(\mathsf {Cf}\phi )\leq 1)}\end{array} \end{align*}
The cases of connectives can be obtained by an application of the induction hypothesis.
Conversely, since the support of truth conditions in
![]() ${\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}$
coincide with the semantics of
${\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}$
coincide with the semantics of
![]() ${\mathsf {\unicode {x0141}}}_\triangle$
(cf. Definitions 11 and 12) and since
${\mathsf {\unicode {x0141}}}_\triangle$
(cf. Definitions 11 and 12) and since
![]() $\alpha ^\neg$
is outer-
$\alpha ^\neg$
is outer-
![]() $\neg$
-free, if
$\neg$
-free, if
![]() $e(\alpha ^\neg )\lt 1$
for some
$e(\alpha ^\neg )\lt 1$
for some
![]() $\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
-model
$\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
-model
![]() $\mathbb {M}_{\mathbf {4}}=\langle W,v^+,v^-,\mu, e\rangle$
, then
$\mathbb {M}_{\mathbf {4}}=\langle W,v^+,v^-,\mu, e\rangle$
, then
![]() $e_1(\alpha ^\neg )\lt 1$
for
$e_1(\alpha ^\neg )\lt 1$
for
![]() $\mathbb {M}=\langle W,v^+,v^-,\mu, e_1,e_2\rangle$
with
$\mathbb {M}=\langle W,v^+,v^-,\mu, e_1,e_2\rangle$
with
![]() $e=e_1$
.
$e=e_1$
.
We proceed by induction on
![]() $\alpha ^\neg$
(recall that
$\alpha ^\neg$
(recall that
![]() $e(\alpha )=e(\alpha ^\neg )$
in all
$e(\alpha )=e(\alpha ^\neg )$
in all
![]() $\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
-models). If
$\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
-models). If
![]() $\alpha =\mathsf {Pr}\phi$
, then
$\alpha =\mathsf {Pr}\phi$
, then
![]() $e_1(\mathsf {Pr}\phi )=\mu (|\phi |^+)=\mu (|\phi |^{\mathsf {b}}\cup |\phi |^{\mathsf {c}})$
. But
$e_1(\mathsf {Pr}\phi )=\mu (|\phi |^+)=\mu (|\phi |^{\mathsf {b}}\cup |\phi |^{\mathsf {c}})$
. But
![]() $|\phi |^{\mathsf {b}}$
and
$|\phi |^{\mathsf {b}}$
and
![]() $|\phi |^{\mathsf {c}}$
are disjoint, whence
$|\phi |^{\mathsf {c}}$
are disjoint, whence
![]() $\mu (|\phi |^{\mathsf {b}}\cup |\phi |^{\mathsf {c}})=\mu (|\phi |^{\mathsf {b}})+\mu (|\phi |^{\mathsf {c}})$
, and since
$\mu (|\phi |^{\mathsf {b}}\cup |\phi |^{\mathsf {c}})=\mu (|\phi |^{\mathsf {b}})+\mu (|\phi |^{\mathsf {c}})$
, and since
![]() $\mu (|\phi |^{\mathsf {b}})+\mu (|\phi |^{\mathsf {c}})\leq 1$
, we have that
$\mu (|\phi |^{\mathsf {b}})+\mu (|\phi |^{\mathsf {c}})\leq 1$
, we have that
![]() $e_1(\mathsf {Bl}\phi \oplus \mathsf {Cf}\phi )=\mu (|\phi |^{\mathsf {b}})+\mu (|\phi |^{\mathsf {c}})=e_1(\mathsf {Pr}\phi )$
, as required.
$e_1(\mathsf {Bl}\phi \oplus \mathsf {Cf}\phi )=\mu (|\phi |^{\mathsf {b}})+\mu (|\phi |^{\mathsf {c}})=e_1(\mathsf {Pr}\phi )$
, as required.
The induction steps are straightforward since the semantic conditions of support of truth in
![]() ${\mathsf {\unicode {x0141}}}^2_\triangle$
coincide with the semantics of
${\mathsf {\unicode {x0141}}}^2_\triangle$
coincide with the semantics of
![]() ${\mathsf {\unicode {x0141}}}_\triangle$
(cf. Definitions 12 and 11).
${\mathsf {\unicode {x0141}}}_\triangle$
(cf. Definitions 12 and 11).
Theorem 25.
![]() $\beta \in \mathscr {L}_{\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }}$
is
$\beta \in \mathscr {L}_{\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }}$
is
![]() $\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
-valid iff
$\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
-valid iff
![]() $\beta ^\pm$
is
$\beta ^\pm$
is
![]() $\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
-valid.
$\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
-valid.
Proof.
Assume w.l.o.g. that
![]() $\mathbb {M}=\langle W,v^+,v^-,\mu _{\mathbf {4}},e\rangle$
is a
$\mathbb {M}=\langle W,v^+,v^-,\mu _{\mathbf {4}},e\rangle$
is a
![]() $\mathsf {BD}$
-model with a
$\mathsf {BD}$
-model with a
![]() $\mathbf {4}$
-probability where
$\mathbf {4}$
-probability where
![]() $\mu _{\mathbf {4}}$
is a classical probability measure and
$\mu _{\mathbf {4}}$
is a classical probability measure and
![]() $e(\beta )=x$
. It suffices to define a
$e(\beta )=x$
. It suffices to define a
![]() $\mathsf {BD}$
-model with
$\mathsf {BD}$
-model with
![]() $\pm$
-probability
$\pm$
-probability
![]() $\mathbb {M}^\pm =\langle W,v^+,v^-,\mu _{\mathbf {4}},e_1,e_2\rangle$
and show that
$\mathbb {M}^\pm =\langle W,v^+,v^-,\mu _{\mathbf {4}},e_1,e_2\rangle$
and show that
![]() $e_1(\beta ^\pm )=x$
. If
$e_1(\beta ^\pm )=x$
. If
![]() $e(\beta )\lt 1$
, then
$e(\beta )\lt 1$
, then
![]() $e(\beta ^\pm )\lt 1$
(and thus, is not valid). If
$e(\beta ^\pm )\lt 1$
(and thus, is not valid). If
![]() $\beta ^\pm$
is not valid, we have that
$\beta ^\pm$
is not valid, we have that
![]() $e_1(\beta ^\pm )\lt 1$
by Lemma 17, whence
$e_1(\beta ^\pm )\lt 1$
by Lemma 17, whence
![]() $e(\beta )\lt 1$
, as well.
$e(\beta )\lt 1$
, as well.
We proceed by induction on
![]() $\beta$
. If
$\beta$
. If
![]() $\beta =\mathsf {Bl}\phi$
, then
$\beta =\mathsf {Bl}\phi$
, then
![]() $e(\mathsf {Bl}\phi )=\mu _{\mathbf {4}}(|\phi |^{\mathsf {b}})$
. Now observe that
$e(\mathsf {Bl}\phi )=\mu _{\mathbf {4}}(|\phi |^{\mathsf {b}})$
. Now observe that
![]() $\mu _{\mathbf {4}}(|\phi |^+)=\mu (|\phi |^{\mathsf {b}}\cup |\phi |^{\mathsf {c}})=\mu _{\mathbf {4}}(|\phi |^{\mathsf {b}})+\mu _{\mathbf {4}}(|\phi |^{\mathsf {c}})$
since
$\mu _{\mathbf {4}}(|\phi |^+)=\mu (|\phi |^{\mathsf {b}}\cup |\phi |^{\mathsf {c}})=\mu _{\mathbf {4}}(|\phi |^{\mathsf {b}})+\mu _{\mathbf {4}}(|\phi |^{\mathsf {c}})$
since
![]() $|\phi |^{\mathsf {b}}$
and
$|\phi |^{\mathsf {b}}$
and
![]() $|\phi |^{\mathsf {c}}$
are disjoint. But
$|\phi |^{\mathsf {c}}$
are disjoint. But
![]() $\mu _{\mathbf {4}}(|\phi |^+)\!=\!e_1(\mathsf {Pr}\phi )$
and
$\mu _{\mathbf {4}}(|\phi |^+)\!=\!e_1(\mathsf {Pr}\phi )$
and
![]() $\mu _{\mathbf {4}}(|\phi |^{\mathsf {c}})\!=\!\mu _{\mathbf {4}}(|\phi \!\wedge \!\neg \phi |^+)$
since
$\mu _{\mathbf {4}}(|\phi |^{\mathsf {c}})\!=\!\mu _{\mathbf {4}}(|\phi \!\wedge \!\neg \phi |^+)$
since
![]() $|\phi \!\wedge \!\neg \phi |^+\!=\!|\phi |^{\mathsf {c}}$
. Thus,
$|\phi \!\wedge \!\neg \phi |^+\!=\!|\phi |^{\mathsf {c}}$
. Thus,
![]() $\mu _{\mathbf {4}}(|\phi |^{\mathsf {b}})=e_1(\mathsf {Pr}\phi \ominus \mathsf {Pr}(\phi \wedge \neg \phi ))$
as required.
$\mu _{\mathbf {4}}(|\phi |^{\mathsf {b}})=e_1(\mathsf {Pr}\phi \ominus \mathsf {Pr}(\phi \wedge \neg \phi ))$
as required.
Other basis cases of
![]() $\mathsf {Cf}\phi$
,
$\mathsf {Cf}\phi$
,
![]() $\mathsf {Uc}\phi$
, and
$\mathsf {Uc}\phi$
, and
![]() $\mathsf {Db}\phi$
can be tackled similarly. The induction steps are straightforward since the support of truth in
$\mathsf {Db}\phi$
can be tackled similarly. The induction steps are straightforward since the support of truth in
![]() ${\mathsf {\unicode {x0141}}}^2_\triangle$
coincides with semantical conditions in
${\mathsf {\unicode {x0141}}}^2_\triangle$
coincides with semantical conditions in
![]() ${\mathsf {\unicode {x0141}}}_\triangle$
.
${\mathsf {\unicode {x0141}}}_\triangle$
.
We finish the section with a straightforward observation.
Lemma 26.
Let
![]() $\alpha \in \mathscr {L}_{\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle }$
and
$\alpha \in \mathscr {L}_{\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle }$
and
![]() $\beta \in \mathscr {L}_{\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }}$
. Then
$\beta \in \mathscr {L}_{\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }}$
. Then
![]() $\unicode{x1D4C1}((\alpha ^\neg )^{\mathbf {4}})={\mathscr {O}}(\unicode{x1D4C1}(\alpha ))$
and
$\unicode{x1D4C1}((\alpha ^\neg )^{\mathbf {4}})={\mathscr {O}}(\unicode{x1D4C1}(\alpha ))$
and
![]() $\unicode{x1D4C1}(\beta )={\mathscr {O}}(\unicode{x1D4C1}(\beta ^\pm ))$
.
$\unicode{x1D4C1}(\beta )={\mathscr {O}}(\unicode{x1D4C1}(\beta ^\pm ))$
.
Proof.
To simplify the presentation of the proof, we will further assume that
![]() $\unicode{x1D4C1}(\mathsf {Y}\phi )=\unicode{x1D4C1}(\phi )+2$
for every
$\unicode{x1D4C1}(\mathsf {Y}\phi )=\unicode{x1D4C1}(\phi )+2$
for every
![]() $\mathsf {Y}\in \{\mathsf {Pr},\mathsf {Bl},\mathsf {Cf},\mathsf {Uc},\mathsf {Db}\}$
. We begin with
$\mathsf {Y}\in \{\mathsf {Pr},\mathsf {Bl},\mathsf {Cf},\mathsf {Uc},\mathsf {Db}\}$
. We begin with
![]() $\alpha$
. From Definition 22, it is clear that
$\alpha$
. From Definition 22, it is clear that
![]() $\unicode{x1D4C1}(\alpha ^\neg )={\mathscr {O}}(\unicode{x1D4C1}(\alpha ))$
. It remains to show by induction on
$\unicode{x1D4C1}(\alpha ^\neg )={\mathscr {O}}(\unicode{x1D4C1}(\alpha ))$
. It remains to show by induction on
![]() $\alpha ^\neg$
that
$\alpha ^\neg$
that
![]() $\unicode{x1D4C1}((\alpha ^\neg )^{\mathbf {4}})={\mathscr {O}}(\unicode{x1D4C1}(\alpha ^\neg ))$
.
$\unicode{x1D4C1}((\alpha ^\neg )^{\mathbf {4}})={\mathscr {O}}(\unicode{x1D4C1}(\alpha ^\neg ))$
.
The basis case of
![]() $\alpha ^\neg =\mathsf {Pr}\phi$
is simple:
$\alpha ^\neg =\mathsf {Pr}\phi$
is simple:
![]() $\unicode{x1D4C1}(\mathsf {Pr}\phi )=\unicode{x1D4C1}(\phi )+2$
, whence
$\unicode{x1D4C1}(\mathsf {Pr}\phi )=\unicode{x1D4C1}(\phi )+2$
, whence
Here,
![]() $7$
is the sum of lengths of modalities,
$7$
is the sum of lengths of modalities,
![]() $\oplus$
, and outer brackets in
$\oplus$
, and outer brackets in
![]() $(\mathsf {Pr}\phi )^{\mathbf {4}}$
.
$(\mathsf {Pr}\phi )^{\mathbf {4}}$
.
Now let
![]() $\alpha ^\neg =(\alpha _1\rightarrow \alpha _2)$
. Then
$\alpha ^\neg =(\alpha _1\rightarrow \alpha _2)$
. Then
![]() $\unicode{x1D4C1}(\alpha ^\neg )=\unicode{x1D4C1}(\alpha _1)+\unicode{x1D4C1}(\alpha _2)+3$
(we count outer brackets here). Since
$\unicode{x1D4C1}(\alpha ^\neg )=\unicode{x1D4C1}(\alpha _1)+\unicode{x1D4C1}(\alpha _2)+3$
(we count outer brackets here). Since
![]() $(\alpha _1\rightarrow \alpha _2)^{\mathbf {4}}=\alpha ^{\mathbf {4}}_1\rightarrow \alpha ^{\mathbf {4}}_2$
, we have
$(\alpha _1\rightarrow \alpha _2)^{\mathbf {4}}=\alpha ^{\mathbf {4}}_1\rightarrow \alpha ^{\mathbf {4}}_2$
, we have
![]() $\unicode{x1D4C1}(\alpha ^{\mathbf {4}}_1\rightarrow \alpha ^{\mathbf {4}}_2)=\unicode{x1D4C1}(\alpha ^{\mathbf {4}}_1)+\unicode{x1D4C1}(\alpha ^{\mathbf {4}}_2)+3$
. We apply the induction hypothesis and obtain that
$\unicode{x1D4C1}(\alpha ^{\mathbf {4}}_1\rightarrow \alpha ^{\mathbf {4}}_2)=\unicode{x1D4C1}(\alpha ^{\mathbf {4}}_1)+\unicode{x1D4C1}(\alpha ^{\mathbf {4}}_2)+3$
. We apply the induction hypothesis and obtain that
![]() $\unicode{x1D4C1}(\alpha ^{\mathbf {4}}_1\rightarrow \alpha ^{\mathbf {4}}_2)={\mathscr {O}}(\unicode{x1D4C1}(\alpha _1))+{\mathscr {O}}(\unicode{x1D4C1}(\alpha _2))+3={\mathscr {O}}(\unicode{x1D4C1}(\alpha _1\rightarrow \alpha _2))$
.
$\unicode{x1D4C1}(\alpha ^{\mathbf {4}}_1\rightarrow \alpha ^{\mathbf {4}}_2)={\mathscr {O}}(\unicode{x1D4C1}(\alpha _1))+{\mathscr {O}}(\unicode{x1D4C1}(\alpha _2))+3={\mathscr {O}}(\unicode{x1D4C1}(\alpha _1\rightarrow \alpha _2))$
.
The cases of
![]() $\alpha =\triangle \alpha '$
and
$\alpha =\triangle \alpha '$
and
![]() $\alpha ={\sim }\alpha '$
can be dealt with in the same manner.
$\alpha ={\sim }\alpha '$
can be dealt with in the same manner.
Consider now
![]() $\beta \in \mathscr {L}_{\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }}$
. We show by induction on
$\beta \in \mathscr {L}_{\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }}$
. We show by induction on
![]() $\beta$
that
$\beta$
that
![]() $\unicode{x1D4C1}(\beta ^\pm )={\mathscr {O}}(\unicode{x1D4C1}(\beta ))$
. Assume that
$\unicode{x1D4C1}(\beta ^\pm )={\mathscr {O}}(\unicode{x1D4C1}(\beta ))$
. Assume that
![]() $\beta =\mathsf {Bl}\phi$
. Then
$\beta =\mathsf {Bl}\phi$
. Then
![]() $(\mathsf {Bl}\phi )^\pm =\mathsf {Pr}\phi \ominus \mathsf {Pr}(\phi \wedge \neg \phi )$
. Observe that
$(\mathsf {Bl}\phi )^\pm =\mathsf {Pr}\phi \ominus \mathsf {Pr}(\phi \wedge \neg \phi )$
. Observe that
![]() $\mathsf {Pr}\phi \ominus \mathsf {Pr}(\phi \wedge \neg \phi )$
is a shorthand for
$\mathsf {Pr}\phi \ominus \mathsf {Pr}(\phi \wedge \neg \phi )$
is a shorthand for
![]() ${\sim }(\mathsf {Pr}\phi \rightarrow \mathsf {Pr}(\phi \wedge \neg \phi ))$
. Thus, we have
${\sim }(\mathsf {Pr}\phi \rightarrow \mathsf {Pr}(\phi \wedge \neg \phi ))$
. Thus, we have
Note again that
![]() $12$
is the sum of the lengths of modalities,
$12$
is the sum of the lengths of modalities,
![]() $\wedge$
,
$\wedge$
,
![]() $\neg$
,
$\neg$
,
![]() $\rightarrow$
,
$\rightarrow$
,
![]() $\sim$
, and brackets in
$\sim$
, and brackets in
![]() ${\sim }(\mathsf {Pr}\phi \rightarrow \mathsf {Pr}(\phi \wedge \neg \phi ))$
. The cases of other modal atoms are similar. The cases of
${\sim }(\mathsf {Pr}\phi \rightarrow \mathsf {Pr}(\phi \wedge \neg \phi ))$
. The cases of other modal atoms are similar. The cases of
![]() $\beta =\beta _1\rightarrow \beta _2$
,
$\beta =\beta _1\rightarrow \beta _2$
,
![]() $\beta =\triangle \beta '$
, and
$\beta =\triangle \beta '$
, and
![]() $\beta ={\sim }\beta '$
can be considered in the same way as we did
$\beta ={\sim }\beta '$
can be considered in the same way as we did
![]() $(\alpha ^\neg )^{\mathbf {4}}$
. The result now follows since modalities do not nest.
$(\alpha ^\neg )^{\mathbf {4}}$
. The result now follows since modalities do not nest.
3.2 Axiomatisations
In this section, we present Hilbert-style calculi
![]() $\mathscr {H}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
and
$\mathscr {H}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
and
![]() $\mathscr {H}\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
that axiomatise
$\mathscr {H}\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
that axiomatise
![]() $\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
and
$\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
and
![]() $\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
. The completeness of
$\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
. The completeness of
![]() $\mathscr {H}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
w.r.t. finite theories (
$\mathscr {H}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
w.r.t. finite theories (
![]() $\mathsf {\unicode {x0141}}$
is not compact, whence there are no finite calculi for expansions of
$\mathsf {\unicode {x0141}}$
is not compact, whence there are no finite calculi for expansions of
![]() $\mathsf {\unicode {x0141}}$
complete w.r.t. countable theories) was established by Bílková et al. (Reference Bílková, Frittella, Kozhemiachenko, Majer and Nazari2023d). Here, we prove the completeness of
$\mathsf {\unicode {x0141}}$
complete w.r.t. countable theories) was established by Bílková et al. (Reference Bílková, Frittella, Kozhemiachenko, Majer and Nazari2023d). Here, we prove the completeness of
![]() $\mathscr {H}\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
.
$\mathscr {H}\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
.
To construct the calculi, we translate the conditions on measures from Definitions 4 and 6 into
![]() $\mathscr {L}_{\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle }$
and
$\mathscr {L}_{\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle }$
and
![]() $\mathscr {L}_{\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}_\triangle }}}$
formulas. We then use these translated conditions as additional axioms that extend Hilbert-style calculi for
$\mathscr {L}_{\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}_\triangle }}}$
formulas. We then use these translated conditions as additional axioms that extend Hilbert-style calculi for
![]() $\mathsf {\unicode {x0141}}_\triangle$
and
$\mathsf {\unicode {x0141}}_\triangle$
and
![]() ${\mathsf {\unicode {x0141}}}_\triangle$
and
${\mathsf {\unicode {x0141}}}_\triangle$
and
![]() ${\mathsf {\unicode {x0141}}}^2_ {(\triangle, \rightarrow )}$
.
${\mathsf {\unicode {x0141}}}^2_ {(\triangle, \rightarrow )}$
.
To facilitate the presentation, we recall these Hilbert calculi for
![]() ${\mathsf {\unicode {x0141}}}_\triangle$
. The axiomatisation of
${\mathsf {\unicode {x0141}}}_\triangle$
. The axiomatisation of
![]() $\unicode{x0141}\triangle$
can be obtained by adding
$\unicode{x0141}\triangle$
can be obtained by adding
![]() $\triangle$
-axioms and rules from Baaz (Reference Baaz1996), Hájek (Reference Hájek1998, Definition 2.4.5), or Běhounek et al. (Reference Běhounek, Cintula, Hájek, Cintula, Hájek and Noguera2011, Chapter I, 2.2.1) to the Hilbert-style calculus for
$\triangle$
-axioms and rules from Baaz (Reference Baaz1996), Hájek (Reference Hájek1998, Definition 2.4.5), or Běhounek et al. (Reference Běhounek, Cintula, Hájek, Cintula, Hájek and Noguera2011, Chapter I, 2.2.1) to the Hilbert-style calculus for
![]() $\unicode {x0141}$
from Metcalfe et al. (Reference Metcalfe, Olivetti and Gabbay2008, Section 6.2).
$\unicode {x0141}$
from Metcalfe et al. (Reference Metcalfe, Olivetti and Gabbay2008, Section 6.2).
Definition 27 (
![]() $\mathscr {H}{\mathsf {\unicode {x0141}}}_\triangle$
– the Hilbert-style calculus for
$\mathscr {H}{\mathsf {\unicode {x0141}}}_\triangle$
– the Hilbert-style calculus for
![]() ${\mathsf {\unicode {x0141}}}_\triangle$
). The calculus contains the following axioms and rules.
${\mathsf {\unicode {x0141}}}_\triangle$
). The calculus contains the following axioms and rules.
-
 $\mathbf {w}$
:
$\mathbf {w}$
:
 $\phi \rightarrow (\chi \rightarrow \phi )$
.
$\phi \rightarrow (\chi \rightarrow \phi )$
. -
 $\mathbf {sf}$
:
$\mathbf {sf}$
:
 $(\phi \rightarrow \chi )\rightarrow ((\chi \rightarrow \psi )\rightarrow (\phi \rightarrow \psi ))$
.
$(\phi \rightarrow \chi )\rightarrow ((\chi \rightarrow \psi )\rightarrow (\phi \rightarrow \psi ))$
. -
 $\mathbf {waj}$
:
$\mathbf {waj}$
:
 $((\phi \rightarrow \chi )\rightarrow \chi )\rightarrow ((\chi \rightarrow \phi )\rightarrow \phi )$
.
$((\phi \rightarrow \chi )\rightarrow \chi )\rightarrow ((\chi \rightarrow \phi )\rightarrow \phi )$
. -
 $\mathbf {co}$
:
$\mathbf {co}$
:
 $({\sim }\chi \rightarrow {\sim }\phi )\rightarrow (\phi \rightarrow \chi )$
.
$({\sim }\chi \rightarrow {\sim }\phi )\rightarrow (\phi \rightarrow \chi )$
. -
 $\mathbf {MP}$
:
$\mathbf {MP}$
:
 $\dfrac {\phi \quad \phi \rightarrow \chi }{\chi }$
.
$\dfrac {\phi \quad \phi \rightarrow \chi }{\chi }$
. -
 $\triangle 1$
:
$\triangle 1$
:
 $\triangle \phi \vee {\sim }\triangle \phi$
.
$\triangle \phi \vee {\sim }\triangle \phi$
. -
 $\triangle 2$
:
$\triangle 2$
:
 $\triangle \phi \rightarrow \phi$
.
$\triangle \phi \rightarrow \phi$
. -
 $\triangle 3$
:
$\triangle 3$
:
 $\triangle \phi \rightarrow \triangle \triangle \phi$
.
$\triangle \phi \rightarrow \triangle \triangle \phi$
. -
 $\triangle 4$
:
$\triangle 4$
:
 $\triangle (\phi \vee \chi )\rightarrow \triangle \phi \vee \triangle \chi$
.
$\triangle (\phi \vee \chi )\rightarrow \triangle \phi \vee \triangle \chi$
. -
 $\triangle 5$
:
$\triangle 5$
:
 $\triangle (\phi \rightarrow \chi )\rightarrow \triangle \phi \rightarrow \triangle \chi$
.
$\triangle (\phi \rightarrow \chi )\rightarrow \triangle \phi \rightarrow \triangle \chi$
. -
 $\triangle \mathbf {nec}$
:
$\triangle \mathbf {nec}$
:
 $\dfrac {\phi }{\triangle \phi }$
.
$\dfrac {\phi }{\triangle \phi }$
.
Proposition 28 (Finite strong completeness of
![]() $\mathscr {H}{\mathsf {\unicode {x0141}}}_\triangle$
). Let
$\mathscr {H}{\mathsf {\unicode {x0141}}}_\triangle$
). Let
![]() $\Gamma$
be finite. Then
$\Gamma$
be finite. Then
![]() $\Gamma \models _{{\mathsf {\unicode {x0141}}}_\triangle }\phi$
iff
$\Gamma \models _{{\mathsf {\unicode {x0141}}}_\triangle }\phi$
iff
![]() $\Gamma \vdash _{\mathscr {H}{\mathsf {\unicode {x0141}}}_\triangle }\phi$
.
$\Gamma \vdash _{\mathscr {H}{\mathsf {\unicode {x0141}}}_\triangle }\phi$
.
The calculus for
![]() ${\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}$
is acquired by adding the axioms for
${\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}$
is acquired by adding the axioms for
![]() $\neg$
(cf. Bílková et al. Reference Bílková, Frittella, Kozhemiachenko, Majer and Nazari2023 for details).
$\neg$
(cf. Bílková et al. Reference Bílková, Frittella, Kozhemiachenko, Majer and Nazari2023 for details).
Definition 29 (
![]() $\mathscr {H}{\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}$
– Hilbert-style calculus for
$\mathscr {H}{\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}$
– Hilbert-style calculus for
![]() ${\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}$
). The calculus expands
${\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}$
). The calculus expands
![]() $\mathscr {H}{\mathsf {\unicode {x0141}}}_\triangle$
with the following axioms and rules.
$\mathscr {H}{\mathsf {\unicode {x0141}}}_\triangle$
with the following axioms and rules.
-
 $\neg \neg$
:
$\neg \neg$
:
 $\neg \neg \phi \leftrightarrow \phi$
.
$\neg \neg \phi \leftrightarrow \phi$
. -
 $\neg {\sim }$
:
$\neg {\sim }$
:
 $\neg {\sim }\phi \leftrightarrow {\sim }\neg \phi$
.
$\neg {\sim }\phi \leftrightarrow {\sim }\neg \phi$
. -
 ${\sim }\neg \!\rightarrow$
:
${\sim }\neg \!\rightarrow$
:
 $({\sim }\neg \phi \rightarrow {\sim }\neg \chi ) \leftrightarrow {\sim }\neg (\phi \rightarrow \chi )$
.
$({\sim }\neg \phi \rightarrow {\sim }\neg \chi ) \leftrightarrow {\sim }\neg (\phi \rightarrow \chi )$
. -
 $\neg \triangle$
:
$\neg \triangle$
:
 $\neg \triangle \phi \leftrightarrow {\sim }\triangle {\sim }\neg \phi$
.
$\neg \triangle \phi \leftrightarrow {\sim }\triangle {\sim }\neg \phi$
. -
 $\mathbf {conf}$
:
$\mathbf {conf}$
:
 $\dfrac {\phi }{{\sim }\neg \phi }$
.
$\dfrac {\phi }{{\sim }\neg \phi }$
.
The completeness of
![]() $\mathscr {H}{\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}$
was shown in Bílková et al. (Reference Bílková, Frittella, Kozhemiachenko, Majer and Nazari2023, Lemma 4.16) (there, the logic is called
$\mathscr {H}{\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}$
was shown in Bílková et al. (Reference Bílková, Frittella, Kozhemiachenko, Majer and Nazari2023, Lemma 4.16) (there, the logic is called
![]() ${\mathsf {\unicode {x0141}}}^2$
).
${\mathsf {\unicode {x0141}}}^2$
).
The calculi for
![]() $\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
and
$\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
and
![]() $\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
are as follows.
$\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
are as follows.
Definition 30 (
![]() $\mathscr {H}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
– a Hilbert-style calculus for
$\mathscr {H}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
– a Hilbert-style calculus for
![]() $\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
). The calculus has the following axioms and rules.
$\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
). The calculus has the following axioms and rules.
-
 ${\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}$
:
${\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}$
:
 ${\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}$
-valid formulas and
${\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}$
-valid formulas and
 $\mathscr {H}{\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}$
rules instantiated in
$\mathscr {H}{\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}$
rules instantiated in
 $\mathscr {L}_{\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle }$
;
$\mathscr {L}_{\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle }$
; -
 $\pm \mathsf {mon}$
:
$\pm \mathsf {mon}$
:
 $\mathsf {Pr}\phi \rightarrow \mathsf {Pr}\chi$
if
$\mathsf {Pr}\phi \rightarrow \mathsf {Pr}\chi$
if
 $\phi \models _{\mathsf {BD}}\chi$
;
$\phi \models _{\mathsf {BD}}\chi$
; -
 $\pm \mathsf {neg}$
:
$\pm \mathsf {neg}$
:
 $\mathsf {Pr}\neg \phi \leftrightarrow \neg \mathsf {Pr}\phi$
;
$\mathsf {Pr}\neg \phi \leftrightarrow \neg \mathsf {Pr}\phi$
; -
 $\pm \mathsf {ex}$
:
$\pm \mathsf {ex}$
:
 $\mathsf {Pr}(\phi \vee \chi )\leftrightarrow ((\mathsf {Pr}\phi \ominus \mathsf {Pr}(\phi \wedge \chi ))\oplus \mathsf {Pr}\chi )$
.
$\mathsf {Pr}(\phi \vee \chi )\leftrightarrow ((\mathsf {Pr}\phi \ominus \mathsf {Pr}(\phi \wedge \chi ))\oplus \mathsf {Pr}\chi )$
.
It is important to note that
![]() $\pm \mathsf {neg}$
is not connected to the
$\pm \mathsf {neg}$
is not connected to the
![]() $\pm$
-probability of the complement of an event. Indeed, it contains only
$\pm$
-probability of the complement of an event. Indeed, it contains only
![]() $\mathsf {BD}$
negations and is, thus, a translation of the
$\mathsf {BD}$
negations and is, thus, a translation of the
![]() $\mathbf {neg}$
property from Definition 4.
$\mathbf {neg}$
property from Definition 4.
Proposition 31 (Finite strong completeness of
![]() $\mathscr {H}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
Bílková et al. Reference Bílková, Frittella, Kozhemiachenko, Majer and Nazari2023d, Theorem 4.24). Let
$\mathscr {H}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
Bílková et al. Reference Bílková, Frittella, Kozhemiachenko, Majer and Nazari2023d, Theorem 4.24). Let
![]() $\Xi \subseteq \mathscr {L}_{\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle }$
be finite. Then
$\Xi \subseteq \mathscr {L}_{\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle }$
be finite. Then
![]() $\Xi \models _{\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle }\alpha$
iff
$\Xi \models _{\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle }\alpha$
iff
![]() $\Xi \vdash _{\mathscr {H}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle }\alpha$
.
$\Xi \vdash _{\mathscr {H}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle }\alpha$
.
Definition 32 (
![]() $\mathscr {H}\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
– Hilbert-style calculus for
$\mathscr {H}\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
– Hilbert-style calculus for
![]() $\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
). The calculus
$\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
). The calculus
![]() $\mathscr {H}\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
consists of the following axioms and rules.
$\mathscr {H}\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
consists of the following axioms and rules.
-
 ${\mathsf {\unicode {x0141}}}_\triangle$
:
${\mathsf {\unicode {x0141}}}_\triangle$
:
 ${\mathsf {\unicode {x0141}}}_\triangle$
-valid formulas and sound rules instantiated in
${\mathsf {\unicode {x0141}}}_\triangle$
-valid formulas and sound rules instantiated in
 $\mathscr {L}_{\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }}$
.
$\mathscr {L}_{\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }}$
. -
 ${\mathbf {4}}\mathsf {equiv}$
:
${\mathbf {4}}\mathsf {equiv}$
:
 $\mathsf {X}\phi \leftrightarrow \mathsf {X}\chi$
for every
$\mathsf {X}\phi \leftrightarrow \mathsf {X}\chi$
for every
 $\phi, \chi \in \mathscr {L}_{\mathsf {BD}}$
s.t.
$\phi, \chi \in \mathscr {L}_{\mathsf {BD}}$
s.t.
 $\phi \dashv \vdash \chi$
is
$\phi \dashv \vdash \chi$
is
 $\mathsf {BD}$
-valid and
$\mathsf {BD}$
-valid and
 $\mathsf {X}\in \{\mathsf {Bl},\mathsf {Db},\mathsf {Cf},\mathsf {Uc}\}$
.
$\mathsf {X}\in \{\mathsf {Bl},\mathsf {Db},\mathsf {Cf},\mathsf {Uc}\}$
. -
 ${\mathbf {4}}\mathsf {contr}$
:
${\mathbf {4}}\mathsf {contr}$
:
 ${\sim }\mathsf {Bl}(\phi \wedge \neg \phi )$
;
${\sim }\mathsf {Bl}(\phi \wedge \neg \phi )$
;
 $\mathsf {Cf}\phi \leftrightarrow \mathsf {Cf}(\phi \wedge \neg \phi )$
.
$\mathsf {Cf}\phi \leftrightarrow \mathsf {Cf}(\phi \wedge \neg \phi )$
. -
 ${\mathbf {4}}\mathsf {neg}$
:
${\mathbf {4}}\mathsf {neg}$
:
 $\mathsf {Bl}\neg \phi \leftrightarrow \mathsf {Db}\phi$
;
$\mathsf {Bl}\neg \phi \leftrightarrow \mathsf {Db}\phi$
;
 $\mathsf {Cf}\neg \phi \leftrightarrow \mathsf {Cf}\phi$
.
$\mathsf {Cf}\neg \phi \leftrightarrow \mathsf {Cf}\phi$
. -
 ${\mathbf {4}}\mathsf {mon}$
:
${\mathbf {4}}\mathsf {mon}$
:
 $(\mathsf {Bl}\phi \oplus \mathsf {Cf}\phi )\rightarrow (\mathsf {Bl}\chi \oplus \mathsf {Cf}\chi )$
for every
$(\mathsf {Bl}\phi \oplus \mathsf {Cf}\phi )\rightarrow (\mathsf {Bl}\chi \oplus \mathsf {Cf}\chi )$
for every
 $\phi, \chi \in \mathscr {L}_{\mathsf {BD}}$
s.t.
$\phi, \chi \in \mathscr {L}_{\mathsf {BD}}$
s.t.
 $\phi \vdash \chi$
is
$\phi \vdash \chi$
is
 $\mathsf {BD}$
-valid.
$\mathsf {BD}$
-valid.
-
 ${\mathbf {4}}\mathsf {part1}$
:
${\mathbf {4}}\mathsf {part1}$
:
 $\mathsf {Bl}\phi \oplus \mathsf {Db}\phi \oplus \mathsf {Cf}\phi \oplus \mathsf {Uc}\phi$
.
$\mathsf {Bl}\phi \oplus \mathsf {Db}\phi \oplus \mathsf {Cf}\phi \oplus \mathsf {Uc}\phi$
. -
 ${\mathbf {4}}\mathsf {part2}$
:
${\mathbf {4}}\mathsf {part2}$
:
 $((\mathsf {X}_1\phi \oplus \mathsf {X}_2\phi \oplus \mathsf {X}_3\phi \oplus \mathsf {X}_4\phi )\ominus \mathsf {X}_4\phi )\leftrightarrow (\mathsf {X}_1\phi \oplus \mathsf {X}_2\phi \oplus \mathsf {X}_3\phi )$
with
$((\mathsf {X}_1\phi \oplus \mathsf {X}_2\phi \oplus \mathsf {X}_3\phi \oplus \mathsf {X}_4\phi )\ominus \mathsf {X}_4\phi )\leftrightarrow (\mathsf {X}_1\phi \oplus \mathsf {X}_2\phi \oplus \mathsf {X}_3\phi )$
with
 $\mathsf {X}_i\neq \mathsf {X}_j$
,
$\mathsf {X}_i\neq \mathsf {X}_j$
,
 $\mathsf {X}_i\in \{\mathsf {Bl},\mathsf {Db},\mathsf {Cf},\mathsf {Uc}\}$
.
$\mathsf {X}_i\in \{\mathsf {Bl},\mathsf {Db},\mathsf {Cf},\mathsf {Uc}\}$
. -
 ${\mathbf {4}}\mathsf {ex}$
:
${\mathbf {4}}\mathsf {ex}$
:
 $(\mathsf {Bl}(\phi \vee \chi )\oplus \mathsf {Cf}(\phi \vee \chi ))\leftrightarrow ((\mathsf {Bl}\phi \oplus \mathsf {Cf}\phi )\ominus (\mathsf {Bl}(\phi \wedge \chi )\oplus \mathsf {Cf}(\phi \wedge \chi ))\oplus (\mathsf {Bl}\chi \oplus$
$(\mathsf {Bl}(\phi \vee \chi )\oplus \mathsf {Cf}(\phi \vee \chi ))\leftrightarrow ((\mathsf {Bl}\phi \oplus \mathsf {Cf}\phi )\ominus (\mathsf {Bl}(\phi \wedge \chi )\oplus \mathsf {Cf}(\phi \wedge \chi ))\oplus (\mathsf {Bl}\chi \oplus$
 $ \mathsf {Cf}\chi ))$
.
$ \mathsf {Cf}\chi ))$
.
As one can see, the axioms in the calculi above are translations of properties from Definitions 4 and 6. In
![]() $\mathscr {H}\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
, we split
$\mathscr {H}\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
, we split
![]() ${\mathbf {4}}\mathbf {part}$
in two axioms to ensure that the values of
${\mathbf {4}}\mathbf {part}$
in two axioms to ensure that the values of
![]() $\mathsf {Bl}\phi$
,
$\mathsf {Bl}\phi$
,
![]() $\mathsf {Db}\phi$
,
$\mathsf {Db}\phi$
,
![]() $\mathsf {Cf}\phi$
, and
$\mathsf {Cf}\phi$
, and
![]() $\mathsf {Uc}\phi$
sum up exactly to
$\mathsf {Uc}\phi$
sum up exactly to
![]() $1$
. Note, moreover, that
$1$
. Note, moreover, that
![]() ${\mathbf {4}}\mathsf {mon}$
and
${\mathbf {4}}\mathsf {mon}$
and
![]() ${\mathbf {4}}\mathsf {ex}$
are translations of
${\mathbf {4}}\mathsf {ex}$
are translations of
![]() $\pm \mathsf {mon}$
and
$\pm \mathsf {mon}$
and
![]() $\pm \mathsf {ex}$
(cf. Definition 23). However, since other
$\pm \mathsf {ex}$
(cf. Definition 23). However, since other
![]() $\mathscr {H}\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
-axioms cannot be obtained as translations of
$\mathscr {H}\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
-axioms cannot be obtained as translations of
![]() $\mathscr {H}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
-axioms (nor, in fact, any
$\mathscr {H}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
-axioms (nor, in fact, any
![]() $\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
-valid formulas), soundness and completeness of
$\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
-valid formulas), soundness and completeness of
![]() $\mathscr {H}\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
cannot be established as a consequence of Theorem24 and completeness of
$\mathscr {H}\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
cannot be established as a consequence of Theorem24 and completeness of
![]() $\mathscr {H}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
(Proposition 31).
$\mathscr {H}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
(Proposition 31).
In the remainder of this section, we prove the completeness of
![]() $\mathscr {H}\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
w.r.t. finite theories.
$\mathscr {H}\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
w.r.t. finite theories.
Theorem 33.
Let
![]() $\Xi \subseteq \mathscr {L}_{\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }}$
be finite. Then
$\Xi \subseteq \mathscr {L}_{\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }}$
be finite. Then
![]() $\Xi \models _{\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }}\alpha$
iff
$\Xi \models _{\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }}\alpha$
iff
![]() $\Xi \vdash _{\mathscr {H}\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }}\alpha$
.
$\Xi \vdash _{\mathscr {H}\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }}\alpha$
.
Proof.
Soundness can be established by the routine check of the validity of the axioms. For example for
![]() ${\mathbf {4}}\mathsf {equiv}$
, observe that if
${\mathbf {4}}\mathsf {equiv}$
, observe that if
![]() $\phi$
and
$\phi$
and
![]() $\chi$
are equivalent in
$\chi$
are equivalent in
![]() $\mathsf {BD}$
, then
$\mathsf {BD}$
, then
![]() $|\phi |^+=|\chi |^+$
and
$|\phi |^+=|\chi |^+$
and
![]() $|\phi |^-=|\chi |^-$
, whence
$|\phi |^-=|\chi |^-$
, whence
![]() $|\phi |^{\mathsf {x}}=|\chi |^{\mathsf {x}}$
for every
$|\phi |^{\mathsf {x}}=|\chi |^{\mathsf {x}}$
for every
![]() $\mathsf {x}\in \{\mathsf {b},\mathsf {d},\mathsf {c},\mathsf {u}\}$
. Thus,
$\mathsf {x}\in \{\mathsf {b},\mathsf {d},\mathsf {c},\mathsf {u}\}$
. Thus,
![]() $e(\mathsf {X}\phi )=e(\mathsf {X}\chi )$
for each
$e(\mathsf {X}\phi )=e(\mathsf {X}\chi )$
for each
![]() $\mathsf {X}\in \{\mathsf {Bl},\mathsf {Db},\mathsf {Cf},\mathsf {Uc}\}$
, from where
$\mathsf {X}\in \{\mathsf {Bl},\mathsf {Db},\mathsf {Cf},\mathsf {Uc}\}$
, from where
![]() $\mathsf {X}\phi \leftrightarrow \mathsf {X}\chi$
is valid.
$\mathsf {X}\phi \leftrightarrow \mathsf {X}\chi$
is valid.
![]() ${\mathbf {4}}\mathsf {contr}$
,
${\mathbf {4}}\mathsf {contr}$
,
![]() ${\mathbf {4}}\mathsf {neg}$
, and
${\mathbf {4}}\mathsf {neg}$
, and
![]() ${\mathbf {4}}\mathsf {mon}$
are straightforward translations of
${\mathbf {4}}\mathsf {mon}$
are straightforward translations of
![]() $\mathbf {contr}$
,
$\mathbf {contr}$
,
![]() $\mathbf {neg}$
, and
$\mathbf {neg}$
, and
![]() $\mathbf {BCmon}$
.
$\mathbf {BCmon}$
.
![]() ${\mathbf {4}}\mathsf {ex}$
is the translation of
${\mathbf {4}}\mathsf {ex}$
is the translation of
![]() $\pm \mathsf {ex}$
, whence are valid by Theorem24.
$\pm \mathsf {ex}$
, whence are valid by Theorem24.
Last, consider
![]() ${\mathbf {4}}\mathsf {part1}$
and
${\mathbf {4}}\mathsf {part1}$
and
![]() ${\mathbf {4}}\mathsf {part2}$
. We have
${\mathbf {4}}\mathsf {part2}$
. We have
![]() $\sum \limits _{\mathsf {x}\in \{\mathsf {b},\mathsf {d},\mathsf {c},\mathsf {u}\}}\!\!\!\!|\phi |^{\mathsf {x}}=1$
. Hence,
$\sum \limits _{\mathsf {x}\in \{\mathsf {b},\mathsf {d},\mathsf {c},\mathsf {u}\}}\!\!\!\!|\phi |^{\mathsf {x}}=1$
. Hence,
![]() $\sum \limits _{\mathsf {X}\in \{\mathsf {Bl},\mathsf {Db},\mathsf {Cf},\mathsf {Uc}\}}\!\!\!\!e(\mathsf {X}\phi )=1$
. Thus, we have that
$\sum \limits _{\mathsf {X}\in \{\mathsf {Bl},\mathsf {Db},\mathsf {Cf},\mathsf {Uc}\}}\!\!\!\!e(\mathsf {X}\phi )=1$
. Thus, we have that
![]() ${\mathbf {4}}\mathsf {part1}$
and
${\mathbf {4}}\mathsf {part1}$
and
![]() ${\mathbf {4}}\mathsf {part2}$
are valid.
${\mathbf {4}}\mathsf {part2}$
are valid.
Let us now prove the completeness. We reason by contraposition. Assume that
![]() $\Xi \nvdash _{\mathscr {H}\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }}\alpha$
. Now, observe that
$\Xi \nvdash _{\mathscr {H}\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }}\alpha$
. Now, observe that
![]() $\mathscr {H}\mathbf {4}\mathsf {Pr}^{\mathsf {\unicode {x0141}}_\triangle }$
proofs are, actually,
$\mathscr {H}\mathbf {4}\mathsf {Pr}^{\mathsf {\unicode {x0141}}_\triangle }$
proofs are, actually,
![]() ${\mathsf {\unicode {x0141}}}_\triangle$
proofs with additional probabilistic axioms. Let
${\mathsf {\unicode {x0141}}}_\triangle$
proofs with additional probabilistic axioms. Let
![]() $\Xi ^*$
stand for
$\Xi ^*$
stand for
![]() $\Xi$
extended with probabilistic axioms built over all pairwise non-equivalent
$\Xi$
extended with probabilistic axioms built over all pairwise non-equivalent
![]() $\mathscr {L}_{\mathsf {BD}}$
formulas constructed from
$\mathscr {L}_{\mathsf {BD}}$
formulas constructed from
![]() $\texttt {Prop}[\Xi \cup \{\alpha \}]$
. Clearly,
$\texttt {Prop}[\Xi \cup \{\alpha \}]$
. Clearly,
![]() $\Xi ^*\nvdash _{\mathscr {H}\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }}\alpha$
either. Moreover,
$\Xi ^*\nvdash _{\mathscr {H}\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }}\alpha$
either. Moreover,
![]() $\Xi ^*$
is finite as well since
$\Xi ^*$
is finite as well since
![]() $\mathsf {BD}$
is tabular (and whence, there exist only finitely many pairwise non-equivalent
$\mathsf {BD}$
is tabular (and whence, there exist only finitely many pairwise non-equivalent
![]() $\mathscr {L}_{\mathsf {BD}}$
formulas over a finite set of variables). Now, by the weak completeness of
$\mathscr {L}_{\mathsf {BD}}$
formulas over a finite set of variables). Now, by the weak completeness of
![]() ${\mathsf {\unicode {x0141}}}_\triangle$
(Proposition 28), there exists an
${\mathsf {\unicode {x0141}}}_\triangle$
(Proposition 28), there exists an
![]() ${\mathsf {\unicode {x0141}}}_\triangle$
valuation
${\mathsf {\unicode {x0141}}}_\triangle$
valuation
![]() $e$
s.t.
$e$
s.t.
![]() $e[\Xi ^*]=1$
and
$e[\Xi ^*]=1$
and
![]() $e(\alpha )\neq 1$
.
$e(\alpha )\neq 1$
.
It remains to construct a
![]() $\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
-model
$\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
-model
![]() $\Xi ^*\models _{\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}_\triangle }}}\alpha$
using
$\Xi ^*\models _{\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}_\triangle }}}\alpha$
using
![]() $e$
. We proceed as follows. First, we set
$e$
. We proceed as follows. First, we set
![]() $W=2^{\mathsf {Lit}[\Xi ^*\cup \{\alpha \}]}$
, and for every
$W=2^{\mathsf {Lit}[\Xi ^*\cup \{\alpha \}]}$
, and for every
![]() $w\in W$
define
$w\in W$
define
![]() $w\in v^+(p)$
iff
$w\in v^+(p)$
iff
![]() $p\in w$
and
$p\in w$
and
![]() $w\in v^-(p)$
iff
$w\in v^-(p)$
iff
![]() $\neg p\in w$
. We extend the valuations to
$\neg p\in w$
. We extend the valuations to
![]() $\phi \in \mathscr {L}_{\mathsf {BD}}$
in the usual manner. Then, for
$\phi \in \mathscr {L}_{\mathsf {BD}}$
in the usual manner. Then, for
![]() $\mathsf {X}\phi \in \texttt {Sf}[\Xi ^*\cup \{\alpha \}]$
, we set
$\mathsf {X}\phi \in \texttt {Sf}[\Xi ^*\cup \{\alpha \}]$
, we set
![]() $\mu _{\mathbf {4}}(|\phi |^{\mathsf {x}})=e(\mathsf {X}\phi )$
according to modality
$\mu _{\mathbf {4}}(|\phi |^{\mathsf {x}})=e(\mathsf {X}\phi )$
according to modality
![]() $\mathsf {X}$
.
$\mathsf {X}$
.
It remains to extend
![]() $\mu _{\mathbf {4}}$
to the whole
$\mu _{\mathbf {4}}$
to the whole
![]() $2^W$
. Observe, however, that any map from
$2^W$
. Observe, however, that any map from
![]() $2^W$
to
$2^W$
to
![]() $[0,1]$
that extends
$[0,1]$
that extends
![]() $\mu _{\mathbf {4}}$
is, in fact, a
$\mu _{\mathbf {4}}$
is, in fact, a
![]() $\mathbf {4}$
-probability. Indeed, all requirements from Definition 6 concern only the extensions of formulas. But the model is finite,
$\mathbf {4}$
-probability. Indeed, all requirements from Definition 6 concern only the extensions of formulas. But the model is finite,
![]() $\mathsf {BD}$
is tabular, and
$\mathsf {BD}$
is tabular, and
![]() $\Xi ^*$
contains all the necessary instances of probabilistic axioms and
$\Xi ^*$
contains all the necessary instances of probabilistic axioms and
![]() $e[\Xi ^*]=1$
, whence all constraints on the formulas are satisfied.
$e[\Xi ^*]=1$
, whence all constraints on the formulas are satisfied.
3.3 Complexity
Let us now establish the complexity of
![]() $\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
and
$\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
and
![]() $\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
. Namely, we prove their NP-completeness. Since the mutual embeddings given in Definition 23 result in an at most linear increase in the size of the
$\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
. Namely, we prove their NP-completeness. Since the mutual embeddings given in Definition 23 result in an at most linear increase in the size of the
![]() $\mathsf {Pr}^{\mathsf {\unicode {x0141}}^2}_\triangle$
polynomial algorithm for
$\mathsf {Pr}^{\mathsf {\unicode {x0141}}^2}_\triangle$
polynomial algorithm for
![]() $\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
since it contains only one modality which will simplify the presentation. Note, furthermore, that
$\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
since it contains only one modality which will simplify the presentation. Note, furthermore, that
![]() ${\mathsf {\unicode {x0141}}}_\triangle$
(and thus,
${\mathsf {\unicode {x0141}}}_\triangle$
(and thus,
![]() ${\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}$
) are
${\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}$
) are
![]() $\mathsf {NP}$
-hard, thus,
$\mathsf {NP}$
-hard, thus,
![]() $\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
and
$\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
and
![]() $\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
are
$\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
are
![]() $\mathsf {NP}$
-hard as well. Thus, we only need to establish the upper bound.
$\mathsf {NP}$
-hard as well. Thus, we only need to establish the upper bound.
For the proof, we adapt constraint tableaux for
![]() ${\mathsf {\unicode {x0141}}}^2$
defined by Bílková et al. (Reference Bílková, Frittella, Kozhemiachenko, Das and Negri2021) and expand them with
${\mathsf {\unicode {x0141}}}^2$
defined by Bílková et al. (Reference Bílková, Frittella, Kozhemiachenko, Das and Negri2021) and expand them with
![]() $\mathsf {FP}(\mathsf {\unicode {x0141}})$
of Hájek and Tulipani (Reference Hájek and Tulipani2001) to establish our result. of Hájek and Tulipani (Reference Hájek and Tulipani2001) to establish our result.
$\mathsf {FP}(\mathsf {\unicode {x0141}})$
of Hájek and Tulipani (Reference Hájek and Tulipani2001) to establish our result. of Hájek and Tulipani (Reference Hájek and Tulipani2001) to establish our result.
Definition 34 (Constraint tableaux for
![]() ${\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}$
–
${\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}$
–
![]() $\mathscr {T}\big ({\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}\big )$
). Branches contain labelled formulas of the form
$\mathscr {T}\big ({\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}\big )$
). Branches contain labelled formulas of the form
![]() $\phi \leqslant _1i$
,
$\phi \leqslant _1i$
,
![]() $\phi \leqslant _2 i$
,
$\phi \leqslant _2 i$
,
![]() $\phi \geqslant _1i$
, or
$\phi \geqslant _1i$
, or
![]() $\phi \geqslant _2i$
, and numerical constraints of the form
$\phi \geqslant _2i$
, and numerical constraints of the form
![]() $i\leq j$
with
$i\leq j$
with
![]() $i$
and
$i$
and
![]() $j$
(labels) being linear polynomials over
$j$
(labels) being linear polynomials over
![]() $[0,1]$
. Each branch can be extended by an application of a rule below.
$[0,1]$
. Each branch can be extended by an application of a rule below.
 \begin{align*} &\quad\qquad \neg \!\leqslant _1\!\dfrac {\neg \phi \leqslant _1i}{\phi \leqslant _2i} \quad\qquad\neg \!\leqslant _2\!\dfrac {\neg \phi \leqslant _2i}{\phi \leqslant _1i}\quad\qquad \neg \!\geqslant _1\!\dfrac {\neg \phi \geqslant _1i}{\phi \geqslant _2i} \quad\qquad\neg \!\geqslant _2\!\dfrac {\neg \phi \geqslant _2i}{\phi \geqslant _1i}\\[10pt] &\quad\qquad {\sim }\leqslant _1\!\dfrac {{\sim }\phi \leqslant _1i}{\phi \geqslant _11-i}\quad\qquad {\sim }\!\leqslant _2\!\dfrac {{\sim }\phi \leqslant _2i}{\phi \geqslant _21-i} \quad\qquad {\sim }\!\geqslant _1\!\dfrac {{\sim }\phi \geqslant _1i}{\phi \leqslant _11-i} \quad\qquad{\sim }\!\geqslant _2\!\dfrac {{\sim }\phi \geqslant _2i}{\phi \leqslant _21-i}\\[10pt] &\triangle \!\geqslant _1\!\dfrac {\triangle \phi \geqslant _1i}{i\leq 0\left |\begin{matrix}\phi \geqslant _1j\\j\geq 1\end{matrix}\right .}\quad\qquad \triangle \!\leqslant _1\!\dfrac {\triangle \phi \leqslant _1i}{i\geq 1\left |\begin{matrix}\phi \leqslant _1j\\j\lt 1\end{matrix}\right .}\quad\qquad\triangle \!\leqslant _2\!\dfrac {\triangle \phi \leqslant _2i}{i\geq 1\left |\begin{matrix}\phi \leqslant j\\j\leq 0\end{matrix}\right .} \quad\qquad\triangle \!\geqslant _2\!\dfrac {\triangle \phi \geqslant _2i}{i\leq 0\left |\begin{matrix}\phi \geqslant j\\j\gt 0\end{matrix}\right .}\\[10pt] &\rightarrow \leqslant _1\dfrac {\phi _1\rightarrow \phi _2\leqslant _1i}{i\!\geq \!1\left |\begin{matrix}\phi _1\!\geqslant _1\!1\!-\!i\!+\!j\\\phi _2\leqslant _1j\\j\leq i\end{matrix}\right .} \quad\rightarrow \leqslant _2\dfrac {\phi _1\!\rightarrow \!\phi _2\!\leqslant _2\!i}{\begin{matrix}\phi _1\geqslant _2j\\\phi _2\!\leqslant _2\!i\!+\!j\end{matrix}}\quad \rightarrow \geqslant _1\dfrac {\phi _1\!\rightarrow \!\phi _2\geqslant _1 i}{\begin{matrix}\phi _1\!\leqslant _1\!1\!-\!i\!+\!j\\\phi _2\geqslant _1j\end{matrix}}\quad\rightarrow \geqslant _2\dfrac {\phi _1\rightarrow \phi _2\geqslant _2i}{i\!\leq \!0\left |\begin{matrix}\phi _1\!\leqslant _2\!j\\\phi _2\!\geqslant _2\!i\!+\!j\\j\leq 1-i\end{matrix}\right .} \end{align*}
\begin{align*} &\quad\qquad \neg \!\leqslant _1\!\dfrac {\neg \phi \leqslant _1i}{\phi \leqslant _2i} \quad\qquad\neg \!\leqslant _2\!\dfrac {\neg \phi \leqslant _2i}{\phi \leqslant _1i}\quad\qquad \neg \!\geqslant _1\!\dfrac {\neg \phi \geqslant _1i}{\phi \geqslant _2i} \quad\qquad\neg \!\geqslant _2\!\dfrac {\neg \phi \geqslant _2i}{\phi \geqslant _1i}\\[10pt] &\quad\qquad {\sim }\leqslant _1\!\dfrac {{\sim }\phi \leqslant _1i}{\phi \geqslant _11-i}\quad\qquad {\sim }\!\leqslant _2\!\dfrac {{\sim }\phi \leqslant _2i}{\phi \geqslant _21-i} \quad\qquad {\sim }\!\geqslant _1\!\dfrac {{\sim }\phi \geqslant _1i}{\phi \leqslant _11-i} \quad\qquad{\sim }\!\geqslant _2\!\dfrac {{\sim }\phi \geqslant _2i}{\phi \leqslant _21-i}\\[10pt] &\triangle \!\geqslant _1\!\dfrac {\triangle \phi \geqslant _1i}{i\leq 0\left |\begin{matrix}\phi \geqslant _1j\\j\geq 1\end{matrix}\right .}\quad\qquad \triangle \!\leqslant _1\!\dfrac {\triangle \phi \leqslant _1i}{i\geq 1\left |\begin{matrix}\phi \leqslant _1j\\j\lt 1\end{matrix}\right .}\quad\qquad\triangle \!\leqslant _2\!\dfrac {\triangle \phi \leqslant _2i}{i\geq 1\left |\begin{matrix}\phi \leqslant j\\j\leq 0\end{matrix}\right .} \quad\qquad\triangle \!\geqslant _2\!\dfrac {\triangle \phi \geqslant _2i}{i\leq 0\left |\begin{matrix}\phi \geqslant j\\j\gt 0\end{matrix}\right .}\\[10pt] &\rightarrow \leqslant _1\dfrac {\phi _1\rightarrow \phi _2\leqslant _1i}{i\!\geq \!1\left |\begin{matrix}\phi _1\!\geqslant _1\!1\!-\!i\!+\!j\\\phi _2\leqslant _1j\\j\leq i\end{matrix}\right .} \quad\rightarrow \leqslant _2\dfrac {\phi _1\!\rightarrow \!\phi _2\!\leqslant _2\!i}{\begin{matrix}\phi _1\geqslant _2j\\\phi _2\!\leqslant _2\!i\!+\!j\end{matrix}}\quad \rightarrow \geqslant _1\dfrac {\phi _1\!\rightarrow \!\phi _2\geqslant _1 i}{\begin{matrix}\phi _1\!\leqslant _1\!1\!-\!i\!+\!j\\\phi _2\geqslant _1j\end{matrix}}\quad\rightarrow \geqslant _2\dfrac {\phi _1\rightarrow \phi _2\geqslant _2i}{i\!\leq \!0\left |\begin{matrix}\phi _1\!\leqslant _2\!j\\\phi _2\!\geqslant _2\!i\!+\!j\\j\leq 1-i\end{matrix}\right .} \end{align*}
Let
![]() $i$
’s be linear polynomials that label the formulas in the branch and
$i$
’s be linear polynomials that label the formulas in the branch and
![]() $x$
’s be variables ranging over
$x$
’s be variables ranging over
![]() $[0,1]$
. We define the translation
$[0,1]$
. We define the translation
![]() $\unicode{x1D4C9}$
from labelled formulas to linear inequalities as follows:
$\unicode{x1D4C9}$
from labelled formulas to linear inequalities as follows:
Let
![]() $\triangledown \in \{\leqslant _1,\geqslant _1,\leqslant _2,\geqslant _2\}$
. A tableau branch
$\triangledown \in \{\leqslant _1,\geqslant _1,\leqslant _2,\geqslant _2\}$
. A tableau branch
is closed if the system of inequalities
does not have solutions. Otherwise,
![]() $\mathscr {B}$
is open. If no rule application adds new entries to
$\mathscr {B}$
is open. If no rule application adds new entries to
![]() $\mathscr {B}$
, it is called complete. A tableau is closed if all its branches are closed.
$\mathscr {B}$
, it is called complete. A tableau is closed if all its branches are closed.
![]() $\phi$
has a
$\phi$
has a
![]() $\mathscr {T}\left ({\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}\right )$
proof if the tableau beginning with
$\mathscr {T}\left ({\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}\right )$
proof if the tableau beginning with
![]() $\{\phi \leqslant _1c, c\lt 1\}$
is closed.
$\{\phi \leqslant _1c, c\lt 1\}$
is closed.
Remark 35.
Let us briefly remark on how to interpret rules and entries in the tableau. Consider, for instance, the rule
![]() $\rightarrow \leqslant _2$
. It’s meaning is:
$\rightarrow \leqslant _2$
. It’s meaning is:
![]() $v_2(\phi _1\rightarrow \phi _2)\leq i$
iff there is
$v_2(\phi _1\rightarrow \phi _2)\leq i$
iff there is
![]() $j \in [0,1]$
s.t.
$j \in [0,1]$
s.t.
![]() $v_2(\phi _1)\geq j$
and
$v_2(\phi _1)\geq j$
and
![]() $v_2(\phi _2)\leq i+j$
. Thus,
$v_2(\phi _2)\leq i+j$
. Thus,
![]() $\psi \leqslant _1i$
means that
$\psi \leqslant _1i$
means that
![]() $v_1(\phi )\leq i$
,
$v_1(\phi )\leq i$
,
![]() $\psi \geqslant _2i$
that
$\psi \geqslant _2i$
that
![]() $v_2(\psi )\geq i$
, etc.
$v_2(\psi )\geq i$
, etc.
Furthermore, our tableaux rules for
![]() $\triangle$
are necessarily branching in contrast to the rules for standard
$\triangle$
are necessarily branching in contrast to the rules for standard
![]() $\mathsf {\unicode {x0141}}$
connectives proposed by Hähnle (Reference Hähnle1992Reference Hähnle1994). This is because all connectives
$\mathsf {\unicode {x0141}}$
connectives proposed by Hähnle (Reference Hähnle1992Reference Hähnle1994). This is because all connectives
![]() $\mathsf {\unicode {x0141}}$
are continuous. On the other hand,
$\mathsf {\unicode {x0141}}$
are continuous. On the other hand,
![]() $\triangle$
is not continuous, hence, there cannot be a non-branching rule for it.
$\triangle$
is not continuous, hence, there cannot be a non-branching rule for it.
Definition 36 (Satisfying valuation of a branch). Let
![]() $v_1$
and
$v_1$
and
![]() $v_2$
be
$v_2$
be
![]() ${\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}$
valuations.
${\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}$
valuations.
![]() $v_1$
satisfies a labelled formula
$v_1$
satisfies a labelled formula
![]() $\phi \leqslant _1i$
(
$\phi \leqslant _1i$
(
![]() $v_2$
satisfies
$v_2$
satisfies
![]() $\phi \geqslant _2i$
) iff
$\phi \geqslant _2i$
) iff
![]() $v_{\mathrm {1}}(\phi )\leq i$
(resp.,
$v_{\mathrm {1}}(\phi )\leq i$
(resp.,
![]() $v_2(\phi )\geq i$
).
$v_2(\phi )\geq i$
).
![]() $v_1$
satisfies a branch
$v_1$
satisfies a branch
![]() $\mathscr {B}$
iff
$\mathscr {B}$
iff
![]() $v_1$
satisfies every labelled formula in
$v_1$
satisfies every labelled formula in
![]() $\mathscr {B}$
(and similarly for
$\mathscr {B}$
(and similarly for
![]() $v_2$
). A branch
$v_2$
). A branch
![]() $\mathscr {B}$
is satisfiable iff there is a pair of valuations
$\mathscr {B}$
is satisfiable iff there is a pair of valuations
![]() $\langle v_1,v_2\rangle$
that satisfies it.
$\langle v_1,v_2\rangle$
that satisfies it.
Theorem 37 (Completeness of tableaux).
-
1.
 $\phi$
is
$\phi$
is
 ${\mathsf {\unicode {x0141}}}_\triangle$
-valid iff it has a
${\mathsf {\unicode {x0141}}}_\triangle$
-valid iff it has a
 $\mathscr {T}\left ({\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}\right )$
proof.
$\mathscr {T}\left ({\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}\right )$
proof.
-
2.
 $\phi$
is
$\phi$
is
 ${\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}$
-valid iff it has a
${\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}$
-valid iff it has a
 $\mathscr {T}\left ({\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}\right )$
proof.
$\mathscr {T}\left ({\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}\right )$
proof.
Proof.
The proof follows Bílková et al. (Reference Bílková, Frittella, Kozhemiachenko, Das and Negri2021, Theorem 1). For soundness, we show that if
![]() $\langle v_1,v_2\rangle$
satisfies the premise of a rule, then it also satisfies one of its conclusions. We consider the case of
$\langle v_1,v_2\rangle$
satisfies the premise of a rule, then it also satisfies one of its conclusions. We consider the case of
![]() $\triangle \!\geqslant _1$
(the rules for other connectives are tackled by Bílková et al. (Reference Bílková, Frittella, Kozhemiachenko, Das and Negri2021); the remaining rules for
$\triangle \!\geqslant _1$
(the rules for other connectives are tackled by Bílková et al. (Reference Bílková, Frittella, Kozhemiachenko, Das and Negri2021); the remaining rules for
![]() $\triangle$
can be dealt with analogously).
$\triangle$
can be dealt with analogously).
Let
![]() $\triangle \phi \geqslant _1i$
be satisfied by
$\triangle \phi \geqslant _1i$
be satisfied by
![]() $\langle v_1,v_2\rangle$
. Then,
$\langle v_1,v_2\rangle$
. Then,
![]() $v_1(\triangle \phi )\geqslant i$
. We have two cases: (i)
$v_1(\triangle \phi )\geqslant i$
. We have two cases: (i)
![]() $i=0$
and (ii)
$i=0$
and (ii)
![]() $i\gt 0$
. In the first case, the left conclusion is satisfied. In the second case,
$i\gt 0$
. In the first case, the left conclusion is satisfied. In the second case,
![]() $v_1(\triangle \phi )=1$
. Hence,
$v_1(\triangle \phi )=1$
. Hence,
![]() $v_1(\phi )=1$
, that is, the right conclusion is satisfied.
$v_1(\phi )=1$
, that is, the right conclusion is satisfied.
For completeness, note from Bílková et al. (Reference Bílková, Frittella, Kozhemiachenko, Das and Negri2021, Proposition 1) that
![]() $\phi$
is
$\phi$
is
![]() ${\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}$
-valid iff
${\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}$
-valid iff
![]() $v_1(\phi )=1$
for every
$v_1(\phi )=1$
for every
![]() $v$
. Let us now show that every complete open branch can be satisfied. Assume that
$v$
. Let us now show that every complete open branch can be satisfied. Assume that
![]() $\mathscr {B}$
is a complete open branch. We construct the satisfying valuation as follows. Let
$\mathscr {B}$
is a complete open branch. We construct the satisfying valuation as follows. Let
![]() $\triangledown \!\in \!\{\leqslant _1,\geqslant _1,\leqslant _2,\geqslant _2\}$
and
$\triangledown \!\in \!\{\leqslant _1,\geqslant _1,\leqslant _2,\geqslant _2\}$
and
![]() $p_1,\ldots, p_m$
be the propositional variables appearing in the atomic labelled formulas in
$p_1,\ldots, p_m$
be the propositional variables appearing in the atomic labelled formulas in
![]() $\mathscr {B}$
.
$\mathscr {B}$
.
Let
![]() $\{p_1\triangledown j_1,\ldots, p_m\triangledown j_n\}$
and
$\{p_1\triangledown j_1,\ldots, p_m\triangledown j_n\}$
and
![]() $\{k_1\leq l_1,\ldots, k_q\leq l_q\}$
be the sets of all atomic labelled formulas and all numerical constraints in
$\{k_1\leq l_1,\ldots, k_q\leq l_q\}$
be the sets of all atomic labelled formulas and all numerical constraints in
![]() $\mathscr {B}$
. Notice that one variable might appear in many atomic labelled formulas, hence we might have
$\mathscr {B}$
. Notice that one variable might appear in many atomic labelled formulas, hence we might have
![]() $m \neq n$
. Since
$m \neq n$
. Since
![]() $\mathscr {B}$
is complete and open, the following system of linear inequalities over the set of variables
$\mathscr {B}$
is complete and open, the following system of linear inequalities over the set of variables
![]() $\{x_{p_1}^L,x_{p_1}^R,\ldots, x_{p_m}^L,x_{p_m}^R\}$
must have at least one solution under the constraints listed:
$\{x_{p_1}^L,x_{p_1}^R,\ldots, x_{p_m}^L,x_{p_m}^R\}$
must have at least one solution under the constraints listed:
Let
![]() $c=(c^L_1,c^R_1,\ldots, c^L_m,c^R_m)$
be a solution to the above system of inequalities such that
$c=(c^L_1,c^R_1,\ldots, c^L_m,c^R_m)$
be a solution to the above system of inequalities such that
![]() $c^L_j$
(
$c^L_j$
(
![]() $c^R_j$
) is the value of
$c^R_j$
) is the value of
![]() $x_{p_j}^L$
(
$x_{p_j}^L$
(
![]() $x_{p_j}^R$
). Define valuations as follows:
$x_{p_j}^R$
). Define valuations as follows:
![]() $v_1(p_j)=c^L_j$
and
$v_1(p_j)=c^L_j$
and
![]() $v_2(p_j)=c^R_j$
.
$v_2(p_j)=c^R_j$
.
It remains to show by induction on
![]() $\phi$
that all formulas present at
$\phi$
that all formulas present at
![]() $\mathscr {B}$
are satisfied by
$\mathscr {B}$
are satisfied by
![]() $v_1$
and
$v_1$
and
![]() $v_2$
. The basis case of variables holds by the construction of
$v_2$
. The basis case of variables holds by the construction of
![]() $v_1$
and
$v_1$
and
![]() $v_2$
. We consider the case of
$v_2$
. We consider the case of
![]() $\triangle \phi \geqslant _1i$
(the cases of other variables can be dealt with similarly).
$\triangle \phi \geqslant _1i$
(the cases of other variables can be dealt with similarly).
Assume that
![]() $\triangle \phi \geqslant _1i\in \mathscr {B}$
. Since
$\triangle \phi \geqslant _1i\in \mathscr {B}$
. Since
![]() $\mathscr {B}$
is complete and open, we have that either (i)
$\mathscr {B}$
is complete and open, we have that either (i)
![]() $i\leq 0\in \mathscr {B}$
or (ii)
$i\leq 0\in \mathscr {B}$
or (ii)
![]() $\{\phi \geqslant _1j,j\geq 1\}\subseteq \mathscr {B}$
. In the first case, since there is a solution for
$\{\phi \geqslant _1j,j\geq 1\}\subseteq \mathscr {B}$
. In the first case, since there is a solution for
![]() $\mathscr {B}^{\unicode{x1D4C9}}$
, we have that
$\mathscr {B}^{\unicode{x1D4C9}}$
, we have that
![]() $i=0$
, and thus
$i=0$
, and thus
![]() $\triangle \phi \geqslant _1i$
is satisfied by any
$\triangle \phi \geqslant _1i$
is satisfied by any
![]() $v_1$
. In the second case, we have that
$v_1$
. In the second case, we have that
![]() $\{\phi \geqslant _1j,j\geq 1\}$
is satisfied by the induction hypothesis, whence
$\{\phi \geqslant _1j,j\geq 1\}$
is satisfied by the induction hypothesis, whence
![]() $v_1(\phi )=1$
, and thus,
$v_1(\phi )=1$
, and thus,
![]() $v_1(\triangle \phi )=1$
, as required.
$v_1(\triangle \phi )=1$
, as required.
Definition 38 (Mixed-integer problem). Let
![]() $\mathbf {x}=(x_1,\ldots, x_k)\in \mathbb {R}^k$
and
$\mathbf {x}=(x_1,\ldots, x_k)\in \mathbb {R}^k$
and
![]() $\mathbf {y}=(y_1,\ldots, y_m)\in \mathbb {Z}^m$
be variables,
$\mathbf {y}=(y_1,\ldots, y_m)\in \mathbb {Z}^m$
be variables,
![]() $A$
and
$A$
and
![]() $B$
be integer matrices,
$B$
be integer matrices,
![]() $h$
an integer vector, and
$h$
an integer vector, and
![]() $f(\mathbf {x},\mathbf {y})$
be a
$f(\mathbf {x},\mathbf {y})$
be a
![]() $k+m$
-place linear function.
$k+m$
-place linear function.
-
1. A general MIP is to find
 $\mathbf {x}$
and
$\mathbf {x}$
and
 $\mathbf {y}$
s.t.
$\mathbf {y}$
s.t.
 $f(\mathbf {x},\mathbf {y})=\min \{f(\mathbf {x},\mathbf {y}):A\mathbf {x}+B\mathbf {y}\geq h\}$
.
$f(\mathbf {x},\mathbf {y})=\min \{f(\mathbf {x},\mathbf {y}):A\mathbf {x}+B\mathbf {y}\geq h\}$
. -
2. A bounded MIP (bMIP) is to find all solutions that belong to
 $[0,1]$
.
$[0,1]$
.
Proposition 39.
Bounded MIP is
![]() $\mathsf {NP}$
-complete.
$\mathsf {NP}$
-complete.
Remark 40.
The proof of
![]() $\mathsf {\unicode {x0141}}$
’s
$\mathsf {\unicode {x0141}}$
’s
![]() $\mathsf {NP}$
-completeness by Hähnle (Reference Hähnle1992, Reference Hähnle1994) uses the reduction of a Łukasiewicz formula
$\mathsf {NP}$
-completeness by Hähnle (Reference Hähnle1992, Reference Hähnle1994) uses the reduction of a Łukasiewicz formula
![]() $\phi$
to one instance of a bMIP of the size
$\phi$
to one instance of a bMIP of the size
![]() ${\mathscr {O}}(\unicode{x1D4C1}(\phi ))$
. This is because the rules are linear. In our case (cf. Remark 35), we cannot avoid branching. This, however, does not affect the complexity of
${\mathscr {O}}(\unicode{x1D4C1}(\phi ))$
. This is because the rules are linear. In our case (cf. Remark 35), we cannot avoid branching. This, however, does not affect the complexity of
![]() ${\mathsf {\unicode {x0141}}}_\triangle$
and tableau and then solve the system of inequalities corresponding to it. Note that in our setting all variables can be evaluated over
${\mathsf {\unicode {x0141}}}_\triangle$
and tableau and then solve the system of inequalities corresponding to it. Note that in our setting all variables can be evaluated over
![]() $\mathbb {R}\cap [0,1]$
; in addition, lengths of branches are polynomial in
$\mathbb {R}\cap [0,1]$
; in addition, lengths of branches are polynomial in
![]() $\unicode{x1D4C1}(\phi )$
. Hence, we can solve the system of inequalities obtained from the branch in the time polynomial w.r.t.
$\unicode{x1D4C1}(\phi )$
. Hence, we can solve the system of inequalities obtained from the branch in the time polynomial w.r.t.
![]() $\unicode{x1D4C1}(\phi )$
(and if there is no solution, then the branch is closed and we need to guess again). Thus,
$\unicode{x1D4C1}(\phi )$
(and if there is no solution, then the branch is closed and we need to guess again). Thus,
![]() $\mathsf {\unicode {x0141}}_\triangle$
and
$\mathsf {\unicode {x0141}}_\triangle$
and
![]() ${\mathsf {\unicode {x0141}}}_\triangle$
and
${\mathsf {\unicode {x0141}}}_\triangle$
and
![]() ${\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}$
are also
${\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}$
are also
![]() $\mathsf {NP}$
-complete.
$\mathsf {NP}$
-complete.
Let us now proceed to the proof of
![]() $\mathsf {NP}$
-completeness of
$\mathsf {NP}$
-completeness of
![]() $\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
. First, we show that we can completely remove
$\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
. First, we show that we can completely remove
![]() $\neg$
’s from
$\neg$
’s from
![]() $\mathscr {L}_{\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle }$
formulas while preserving their satisfiability.
$\mathscr {L}_{\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle }$
formulas while preserving their satisfiability.
Lemma 41.
For any outer-
![]() $\neg$
-free
$\neg$
-free
![]() $\alpha \in \mathscr {L}_{\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle }$
,
$\alpha \in \mathscr {L}_{\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle }$
,
![]() $\mathsf {Pr}^{\mathsf {\unicode {x0141}}^2}_\triangle$
-valid
$\mathsf {Pr}^{\mathsf {\unicode {x0141}}^2}_\triangle$
-valid
![]() $\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
-valid iff
$\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
-valid iff
![]() $\alpha ^*$
is
$\alpha ^*$
is
![]() $\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
-valid.
$\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
-valid.
Proof.
We construct
![]() $\alpha ^*$
as follows. First, we take every modal atom
$\alpha ^*$
as follows. First, we take every modal atom
![]() $\mathsf {Pr}\phi$
(recall that
$\mathsf {Pr}\phi$
(recall that
![]() $\phi \in \mathscr {L}_{\mathsf {BD}}$
) and replace
$\phi \in \mathscr {L}_{\mathsf {BD}}$
) and replace
![]() $\phi$
with its
$\phi$
with its
![]() $\mathsf {NNF}$
. Second, we replace every literal
$\mathsf {NNF}$
. Second, we replace every literal
![]() $\neg p$
occurring in
$\neg p$
occurring in
![]() $\mathsf {Pr}(\mathsf {NNF}(\phi ))$
with a corresponding fresh variable
$\mathsf {Pr}(\mathsf {NNF}(\phi ))$
with a corresponding fresh variable
![]() $p'$
. That is,
$p'$
. That is,
![]() $\neg p$
is replaced with
$\neg p$
is replaced with
![]() $p'$
,
$p'$
,
![]() $\neg q$
with
$\neg q$
with
![]() $q'$
, etc. Outer-layer connectives remain the same. Observe, that this increases the number of symbols in
$q'$
, etc. Outer-layer connectives remain the same. Observe, that this increases the number of symbols in
![]() $\alpha$
at most linearly: indeed, the transformation of
$\alpha$
at most linearly: indeed, the transformation of
![]() $\phi$
into
$\phi$
into
![]() $\mathsf {NNF}(\phi )$
is linear (recall Remark 3) and then we replace every occurrence of
$\mathsf {NNF}(\phi )$
is linear (recall Remark 3) and then we replace every occurrence of
![]() $\neg p$
with a fresh variable
$\neg p$
with a fresh variable
![]() $p^*$
. It remains to check that validity is preserved.
$p^*$
. It remains to check that validity is preserved.
Let
![]() $\alpha$
be not
$\alpha$
be not
![]() $\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
-valid,
$\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
-valid,
![]() $\mathsf {Pr}^{\mathsf {\unicode {x0141}}^2}_\triangle$
-model.
$\mathsf {Pr}^{\mathsf {\unicode {x0141}}^2}_\triangle$
-model.
![]() $\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
-model. By Lemma 17, this is equivalent to
$\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
-model. By Lemma 17, this is equivalent to
![]() $e_1(\alpha )\neq 1$
in some
$e_1(\alpha )\neq 1$
in some
![]() $\mathbb {M}=\langle W,v^+,v^-,\mu, e_1,e_2\rangle$
. Now, let
$\mathbb {M}=\langle W,v^+,v^-,\mu, e_1,e_2\rangle$
. Now, let
![]() $\mathbb {M}^*=\langle W,{v^*}^+,{v^*}^-,\mu, e^*_1,e^*_2\rangle$
s.t.
$\mathbb {M}^*=\langle W,{v^*}^+,{v^*}^-,\mu, e^*_1,e^*_2\rangle$
s.t.
![]() ${v^*}^+(p)=v^+(p)$
and
${v^*}^+(p)=v^+(p)$
and
![]() ${v^*}^+(p')=v^-(p)$
. It suffices to show that
${v^*}^+(p')=v^-(p)$
. It suffices to show that
![]() $e_1(\alpha )=e^*_1(\alpha ^*)$
.
$e_1(\alpha )=e^*_1(\alpha ^*)$
.
We proceed by induction on
![]() $\alpha$
. Let
$\alpha$
. Let
![]() $\alpha =\mathsf {Pr}\phi$
for some
$\alpha =\mathsf {Pr}\phi$
for some
![]() $\phi \in \mathscr {L}_{\mathsf {BD}}$
. We have that
$\phi \in \mathscr {L}_{\mathsf {BD}}$
. We have that
![]() $e_1(\alpha )=\mu (|\phi |^+)=\mu (|\mathsf {NNF}(\phi )|^+)$
. We check that
$e_1(\alpha )=\mu (|\phi |^+)=\mu (|\mathsf {NNF}(\phi )|^+)$
. We check that
![]() $|\mathsf {NNF}(\phi )|^+_{\mathbb {M}}=|\mathsf {NNF}(\phi )^*|^+_{\mathbb {M}^*}$
by induction on
$|\mathsf {NNF}(\phi )|^+_{\mathbb {M}}=|\mathsf {NNF}(\phi )^*|^+_{\mathbb {M}^*}$
by induction on
![]() $\mathsf {NNF}(\phi )$
.
$\mathsf {NNF}(\phi )$
.
If
![]() $\mathsf {NNF}(\phi )=p$
, then
$\mathsf {NNF}(\phi )=p$
, then
![]() $p^*=p$
and
$p^*=p$
and
![]() $v^+(p)={v^*}^+(p)$
by construction. If
$v^+(p)={v^*}^+(p)$
by construction. If
![]() $\mathsf {NNF}(\phi )=\neg p$
, then
$\mathsf {NNF}(\phi )=\neg p$
, then
![]() $(\neg p)^*=p'$
and
$(\neg p)^*=p'$
and
![]() $|\neg p|^+=v^-(p)={v^*}^+(p')$
by construction. If
$|\neg p|^+=v^-(p)={v^*}^+(p')$
by construction. If
![]() $\mathsf {NNF}(\phi )=\chi \wedge \psi$
, then
$\mathsf {NNF}(\phi )=\chi \wedge \psi$
, then
![]() $\mathsf {NNF}(\phi )=(\chi \wedge \psi )^*=\chi ^*\wedge \psi ^*$
. By the induction hypothesis,
$\mathsf {NNF}(\phi )=(\chi \wedge \psi )^*=\chi ^*\wedge \psi ^*$
. By the induction hypothesis,
![]() $|\chi |^+=|\chi ^*|^+$
and
$|\chi |^+=|\chi ^*|^+$
and
![]() $|\psi |^+=|\psi ^*|^+$
. Hence,
$|\psi |^+=|\psi ^*|^+$
. Hence,
![]() $|\chi \wedge \psi |^+_{\mathbb {M}}=|(\chi \wedge \psi )^*|^+_{\mathbb {M}^*}$
. The case of
$|\chi \wedge \psi |^+_{\mathbb {M}}=|(\chi \wedge \psi )^*|^+_{\mathbb {M}^*}$
. The case of
![]() $\mathsf {NNF}(\phi )=\chi \vee \psi$
can be considered in the same way.
$\mathsf {NNF}(\phi )=\chi \vee \psi$
can be considered in the same way.
It follows that
![]() $e_1(\mathsf {Pr}\phi )=e^*_1(\mathsf {Pr}(\mathsf {NNF}(\phi )^*))$
. The cases of
$e_1(\mathsf {Pr}\phi )=e^*_1(\mathsf {Pr}(\mathsf {NNF}(\phi )^*))$
. The cases of
![]() ${\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}$
connectives can be proven by a straightforward application of the induction hypothesis.
${\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}$
connectives can be proven by a straightforward application of the induction hypothesis.
For the converse, assume that
![]() $\alpha ^*$
is not
$\alpha ^*$
is not
![]() $\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
-valid. Hence,
$\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
-valid. Hence,
![]() $e_1(\alpha ^*)\neq 1$
in some model
$e_1(\alpha ^*)\neq 1$
in some model
![]() $\mathbb {M}=\langle W,v^+,v^-,\mu, e_1,e_2\rangle$
by Lemma 17. We define
$\mathbb {M}=\langle W,v^+,v^-,\mu, e_1,e_2\rangle$
by Lemma 17. We define
![]() $\mathbb {M}^\bullet =\langle W,{v^\bullet }^+,{v^\bullet }^-,\mu, e^\bullet _1,e^\bullet _2\rangle$
with
$\mathbb {M}^\bullet =\langle W,{v^\bullet }^+,{v^\bullet }^-,\mu, e^\bullet _1,e^\bullet _2\rangle$
with
![]() ${v^\bullet }^-(p)=v^+(p')$
and
${v^\bullet }^-(p)=v^+(p')$
and
![]() ${v^\bullet }^+(p)=v^+(p)$
. We can now show that
${v^\bullet }^+(p)=v^+(p)$
. We can now show that
![]() $e_1(\alpha ^*)=e^\bullet _1(\alpha )$
(i.e.,
$e_1(\alpha ^*)=e^\bullet _1(\alpha )$
(i.e.,
![]() $e^\bullet _1(\alpha )\neq 1$
) as in the previous case. The result is as follows.
$e^\bullet _1(\alpha )\neq 1$
) as in the previous case. The result is as follows.
We can now apply this lemma to adapt the proof of the
![]() $\mathsf {NP}$
-completeness of
$\mathsf {NP}$
-completeness of
![]() $\mathsf {FP}({\mathsf {\unicode {x0141}}})$
.
$\mathsf {FP}({\mathsf {\unicode {x0141}}})$
.
Theorem 42.
Validity of
![]() $\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
and
$\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
and
![]() $\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
is
$\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
is
![]() $\mathsf {coNP}$
-complete.
$\mathsf {coNP}$
-complete.
Proof.
Recall that
![]() $\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
and
$\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
and
![]() $\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
can be linearly embedded into one another (Theorems24 and 25 and Lemma 26). Thus, it remains to provide a non-deterministic polynomial algorithm that decides whether a formula is falsifiable (i.e., non-valid) for one of these logics. We choose
$\mathbf {4}\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}_\triangle }$
can be linearly embedded into one another (Theorems24 and 25 and Lemma 26). Thus, it remains to provide a non-deterministic polynomial algorithm that decides whether a formula is falsifiable (i.e., non-valid) for one of these logics. We choose
![]() $\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
since it has only one modality.
$\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
since it has only one modality.
Let
![]() $\alpha \in \mathscr {L}_{\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle }$
be over modal atoms
$\alpha \in \mathscr {L}_{\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle }$
be over modal atoms
![]() $\mathsf {Pr}\phi _1$
, …,
$\mathsf {Pr}\phi _1$
, …,
![]() $\mathsf {Pr}\phi _n$
. By Lemma 41, we can w.l.o.g. assume that
$\mathsf {Pr}\phi _n$
. By Lemma 41, we can w.l.o.g. assume that
![]() $\alpha$
does
$\alpha$
does
![]() $\mathsf {Pr}^{\mathsf {\unicode {x0141}}^2}_\triangle$
-valuation
$\mathsf {Pr}^{\mathsf {\unicode {x0141}}^2}_\triangle$
-valuation
![]() $\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
-valuation for
$\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
-valuation for
![]() $\alpha$
.
$\alpha$
.
First, we replace every modal atom
![]() $\mathsf {Pr}\phi _i$
with a fresh variable
$\mathsf {Pr}\phi _i$
with a fresh variable
![]() $q_{\phi _i}$
. Denote the new formula
$q_{\phi _i}$
. Denote the new formula
![]() $\alpha ^-$
. It is clear that
$\alpha ^-$
. It is clear that
![]() $\unicode{x1D4C1}(\alpha ^-)={\mathscr {O}}(\unicode{x1D4C1}(\alpha ))$
. We construct a
$\unicode{x1D4C1}(\alpha ^-)={\mathscr {O}}(\unicode{x1D4C1}(\alpha ))$
. We construct a
![]() $\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
tableau beginning with
$\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
tableau beginning with
![]() $\{\alpha ^-\leqslant _1c,c\lt 1\}$
. As
$\{\alpha ^-\leqslant _1c,c\lt 1\}$
. As
![]() $\alpha ^-$
does not contain
$\alpha ^-$
does not contain
![]() $\neg$
, every branch gives us an a system of linear inequalities that has a solution iff
$\neg$
, every branch gives us an a system of linear inequalities that has a solution iff
![]() $\alpha ^-$
is
$\alpha ^-$
is
![]() ${\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}$
-falsifiable:
${\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}$
-falsifiable:
![]() $\alpha ^-$
is
$\alpha ^-$
is
![]() ${\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}$
-falsifiable iff at least one system of inequalities corresponding to a tableau branch has a solution. Clearly, if
${\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}$
-falsifiable iff at least one system of inequalities corresponding to a tableau branch has a solution. Clearly, if
![]() $\alpha ^-$
is not
$\alpha ^-$
is not
![]() ${\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}$
-falsifiable, it is not
${\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}$
-falsifiable, it is not
![]() $\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
-falsifiable either.
$\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
-falsifiable either.
Now let
![]() $\mathfrak {Br}=\{\mathscr {B}_1,\ldots, \mathscr {B}_w\}$
be the set of all open branches in the
$\mathfrak {Br}=\{\mathscr {B}_1,\ldots, \mathscr {B}_w\}$
be the set of all open branches in the
![]() $\mathscr {T}\left ({\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}\right )$
tableau for
$\mathscr {T}\left ({\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}\right )$
tableau for
![]() $\alpha ^-$
. We guess a
$\alpha ^-$
. We guess a
![]() $\mathscr {B}\in \mathfrak {Br}$
and consider the following system of (in)equalities:
$\mathscr {B}\in \mathfrak {Br}$
and consider the following system of (in)equalities:
Here,
![]() $z_i$
’s correspond to the values of
$z_i$
’s correspond to the values of
![]() $q_{\phi _i}$
’s in
$q_{\phi _i}$
’s in
![]() $\alpha ^-$
and
$\alpha ^-$
and
![]() $t_i$
’s are linear polynomials that label
$t_i$
’s are linear polynomials that label
![]() $q_{\phi _i}$
’s. Numerical constraints give us
$q_{\phi _i}$
’s. Numerical constraints give us
![]() $k$
’s,
$k$
’s,
![]() $k'$
’s,
$k'$
’s,
![]() $m$
’s, and
$m$
’s, and
![]() $m'$
’s. Denote the number of inequalities and the number of variables in (
$m'$
’s. Denote the number of inequalities and the number of variables in (
![]() $\mathrm {LI}(1)^{\mathscr {B}}$
) with
$\mathrm {LI}(1)^{\mathscr {B}}$
) with
![]() $l_1$
and
$l_1$
and
![]() $l_2$
, respectively. It is clear that
$l_2$
, respectively. It is clear that
![]() $l_1={\mathscr {O}}(\unicode{x1D4C1}(\alpha ^-))$
and
$l_1={\mathscr {O}}(\unicode{x1D4C1}(\alpha ^-))$
and
![]() $l_2={\mathscr {O}}(\unicode{x1D4C1}(\alpha ^-))$
.
$l_2={\mathscr {O}}(\unicode{x1D4C1}(\alpha ^-))$
.
We need to check whether
![]() $z_i$
’s are coherent as probabilities of
$z_i$
’s are coherent as probabilities of
![]() $\phi _i$
’s. that is that there is a probability measure
$\phi _i$
’s. that is that there is a probability measure
![]() $\mu$
on
$\mu$
on
![]() $2^{\texttt {Prop}(\alpha )}$
s.t.
$2^{\texttt {Prop}(\alpha )}$
s.t.
![]() $\mu (|\phi _i|^+)=z_i$
. Recall again that because of Klein et al. (Reference Klein, Majer and Rafiee Rad2021, Theorem 4), we can assume that the probabilities are classical. Moreover, we can assume that there are
$\mu (|\phi _i|^+)=z_i$
. Recall again that because of Klein et al. (Reference Klein, Majer and Rafiee Rad2021, Theorem 4), we can assume that the probabilities are classical. Moreover, we can assume that there are
![]() $n$
propositional variables in
$n$
propositional variables in
![]() $\alpha$
(we can always add new superfluous variables or modal atoms to
$\alpha$
(we can always add new superfluous variables or modal atoms to
![]() $\alpha$
to make their numbers equal).
$\alpha$
to make their numbers equal).
Now, introduce
![]() $2^n$
variables
$2^n$
variables
![]() $u_v$
indexed by
$u_v$
indexed by
![]() $n$
-letter words over
$n$
-letter words over
![]() $\{0,1\}$
. These denote whether the variables of
$\{0,1\}$
. These denote whether the variables of
![]() $\phi _i$
’s are true under
$\phi _i$
’s are true under
![]() $v^+$
and thus correspond to subsets of
$v^+$
and thus correspond to subsets of
![]() $\texttt {Prop}(\alpha )$
. For example, if
$\texttt {Prop}(\alpha )$
. For example, if
![]() $\texttt {Prop}(\alpha )=\{p_1,p_2,p_3,p_4\}$
, then
$\texttt {Prop}(\alpha )=\{p_1,p_2,p_3,p_4\}$
, then
![]() $u_{1001}$
encodes
$u_{1001}$
encodes
![]() $\{p_1,p_4\}$
. Note that
$\{p_1,p_4\}$
. Note that
![]() $\neg$
does not occur in
$\neg$
does not occur in
![]() $\alpha ^-$
and thus we care only about
$\alpha ^-$
and thus we care only about
![]() $e_1$
and
$e_1$
and
![]() $v^+$
. Furthermore, while
$v^+$
. Furthermore, while
![]() $n$
is the number of
$n$
is the number of
![]() $\phi _i$
’s, we can add extra modal atoms or variables to make it also the number of variables. We let
$\phi _i$
’s, we can add extra modal atoms or variables to make it also the number of variables. We let
![]() $a_{i,v}=1$
when
$a_{i,v}=1$
when
![]() $\phi _i$
is true under
$\phi _i$
is true under
![]() $v^+$
and
$v^+$
and
![]() $a_{i,v}=0$
otherwise. Now add new equations to
$a_{i,v}=0$
otherwise. Now add new equations to
![]() $\mathrm{LI}(1)^{\mathscr {B}}$
, namely
$\mathrm{LI}(1)^{\mathscr {B}}$
, namely
The new problem – (
![]() $\mathrm {LI}(1)^{\mathscr {B}}$
)
$\mathrm {LI}(1)^{\mathscr {B}}$
)
![]() $\cup$
(
$\cup$
(
![]() $\mathrm {LI}(2\exp )^{\mathscr {B}}$
) – has a solution over
$\mathrm {LI}(2\exp )^{\mathscr {B}}$
) – has a solution over
![]() $[0,1]$
iff
$[0,1]$
iff
![]() $\alpha$
is
$\alpha$
is
![]() $\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
-satisfiable since (
$\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
-satisfiable since (
![]() $\mathrm {LI}(2\exp )^{\mathscr {B}}$
) encodes a measure on
$\mathrm {LI}(2\exp )^{\mathscr {B}}$
) encodes a measure on
![]() $\texttt {Prop}(\alpha )$
while the existence of a solution for (
$\texttt {Prop}(\alpha )$
while the existence of a solution for (
![]() $\mathrm {LI}(1)^{\mathscr {B}}$
) ensures that
$\mathrm {LI}(1)^{\mathscr {B}}$
) ensures that
![]() $\alpha$
is
$\alpha$
is
![]() ${\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}$
-satisfiable. Furthermore, although there are
${\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}$
-satisfiable. Furthermore, although there are
![]() $l_2+2^n+n$
variables in (
$l_2+2^n+n$
variables in (
![]() $\mathrm {LI}(1)^{\mathscr {B}}$
)
$\mathrm {LI}(1)^{\mathscr {B}}$
)
![]() $\cup$
(
$\cup$
(
![]() $\mathrm {LI}(2\exp )^{\mathscr {B}}$
), it has no more than
$\mathrm {LI}(2\exp )^{\mathscr {B}}$
), it has no more than
![]() $l_1+n+1$
(in)equalities. Thus by Fagin et al. (Reference Fagin, Halpern and Megiddo1990, Lemma 2.5), it has a solution with at most
$l_1+n+1$
(in)equalities. Thus by Fagin et al. (Reference Fagin, Halpern and Megiddo1990, Lemma 2.5), it has a solution with at most
![]() $l_1+n+1$
non-zero entries. We guess a list
$l_1+n+1$
non-zero entries. We guess a list
![]() $L$
of at most
$L$
of at most
![]() $l_1+n+1$
words
$l_1+n+1$
words
![]() $v$
(its size is
$v$
(its size is
![]() $n\cdot (l_1+n+1)$
). We can now compute the values of
$n\cdot (l_1+n+1)$
). We can now compute the values of
![]() $a_{i,v}$
’s for
$a_{i,v}$
’s for
![]() $i\leq n$
and
$i\leq n$
and
![]() $v\in L$
and obtain a new system of inequalities:
$v\in L$
and obtain a new system of inequalities:
It is clear that (
![]() $\mathrm {LI}(1)^{\mathscr {B}}$
)
$\mathrm {LI}(1)^{\mathscr {B}}$
)
![]() $\cup$
(
$\cup$
(
![]() $\mathrm {LI}(2\mathrm {poly})^{\mathscr {B}}$
) is of polynomial size w.r.t.
$\mathrm {LI}(2\mathrm {poly})^{\mathscr {B}}$
) is of polynomial size w.r.t.
![]() $\unicode{x1D4C1}(\alpha ^-)$
and thus can be solved in polynomial time. Moreover, (
$\unicode{x1D4C1}(\alpha ^-)$
and thus can be solved in polynomial time. Moreover, (
![]() $\mathrm {LI}(1)^{\mathscr {B}}$
)
$\mathrm {LI}(1)^{\mathscr {B}}$
)
![]() $\cup$
(
$\cup$
(
![]() $\mathrm {LI}(2\mathrm {poly})^{\mathscr {B}}$
) has a solution iff the values of
$\mathrm {LI}(2\mathrm {poly})^{\mathscr {B}}$
) has a solution iff the values of
![]() $\mathsf {Pr}\phi _i$
’s occurring on
$\mathsf {Pr}\phi _i$
’s occurring on
![]() $\mathscr {B}$
are coherent as probabilities. If there is no solution for (
$\mathscr {B}$
are coherent as probabilities. If there is no solution for (
![]() $\mathrm {LI}(1)^{\mathscr {B}}$
)
$\mathrm {LI}(1)^{\mathscr {B}}$
)
![]() $\cup$
(
$\cup$
(
![]() $\mathrm {LI}(2\mathrm {poly})^{\mathscr {B}}$
), we guess another open branch from the tableau and repeat the procedure. If there is no open branch
$\mathrm {LI}(2\mathrm {poly})^{\mathscr {B}}$
), we guess another open branch from the tableau and repeat the procedure. If there is no open branch
![]() $\mathscr {B}'\in \mathfrak {Br}$
s.t. its corresponding system of inequalities
$\mathscr {B}'\in \mathfrak {Br}$
s.t. its corresponding system of inequalities
![]() $\mathrm {LI}(1)^{\mathscr {B}'}\cup \mathrm {LI}(2\mathrm {poly})^{\mathscr {B}'}$
has a solution, then
$\mathrm {LI}(1)^{\mathscr {B}'}\cup \mathrm {LI}(2\mathrm {poly})^{\mathscr {B}'}$
has a solution, then
![]() $\alpha$
is
$\alpha$
is
![]() $\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
-valid as well by Lemma 41.
$\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
-valid as well by Lemma 41.
4. Belief and plausibility functions over
 $\mathsf {BD}$
$\mathsf {BD}$
In this section, we introduce
![]() $\mathsf {BD}$
-models with belief and plausibility functions. We adapt the definitions from Zhou (Reference Zhou2013) and Bílková et al. (Reference Bílková, Frittella, Kozhemiachenko, Majer and Nazari2023d).
$\mathsf {BD}$
-models with belief and plausibility functions. We adapt the definitions from Zhou (Reference Zhou2013) and Bílková et al. (Reference Bílková, Frittella, Kozhemiachenko, Majer and Nazari2023d).
Definition 43 (Belief function). A belief function on
![]() $W\neq \varnothing$
is a map
$W\neq \varnothing$
is a map
![]() ${\texttt {bel}}:2^W\rightarrow [0,1]$
s.t.
${\texttt {bel}}:2^W\rightarrow [0,1]$
s.t.
-
•
 $\texttt {bel}$
is monotone w.r.t.
$\texttt {bel}$
is monotone w.r.t.
 $\subseteq$
: if
$\subseteq$
: if
 $X\subseteq Y$
, then
$X\subseteq Y$
, then
 ${\texttt {bel}}(X)\leq {\texttt {bel}}(Y)$
;
${\texttt {bel}}(X)\leq {\texttt {bel}}(Y)$
; -
• for every
 $X_1,\ldots, X_k\subseteq W$
, it holds that
$X_1,\ldots, X_k\subseteq W$
, it holds that
 \begin{align*} {\texttt {bel}}\left (\bigcup \limits _{1\leq i\leq k}X_i\right )&\geq \sum \limits _{\scriptsize {\begin{matrix}J\subseteq \{1,\ldots, k\}\\J\neq \varnothing \end{matrix}}}(-1)^{|J|+1}\cdot {\texttt {bel}}\left (\bigcap \limits _{j\in J}X_j\right ) \end{align*}
\begin{align*} {\texttt {bel}}\left (\bigcup \limits _{1\leq i\leq k}X_i\right )&\geq \sum \limits _{\scriptsize {\begin{matrix}J\subseteq \{1,\ldots, k\}\\J\neq \varnothing \end{matrix}}}(-1)^{|J|+1}\cdot {\texttt {bel}}\left (\bigcap \limits _{j\in J}X_j\right ) \end{align*}
-
•
 ${\texttt {bel}}(\varnothing )=0$
and
${\texttt {bel}}(\varnothing )=0$
and
 ${\texttt {bel}}(W)=1$
.
${\texttt {bel}}(W)=1$
.
Definition 44 (Plausibility function). A plausibility function on
![]() $W\!\neq \!\varnothing$
is a map
$W\!\neq \!\varnothing$
is a map
![]() $\texttt {pl}\!:\!2^W\!\rightarrow \![0,1]$
s.t.
$\texttt {pl}\!:\!2^W\!\rightarrow \![0,1]$
s.t.
-
•
 $\texttt {pl}$
is monotone w.r.t.
$\texttt {pl}$
is monotone w.r.t.
 $\subseteq$
;
$\subseteq$
; -
• for every
 $X_1,\ldots, X_k\subseteq W$
, it holds that
$X_1,\ldots, X_k\subseteq W$
, it holds that
 \begin{align*} \texttt {pl}\left (\bigcap \limits _{1\leq i\leq k}X_i\right )\leq \sum \limits _{\scriptsize {\begin{matrix}J\subseteq \{1,\ldots, k\}\\J\neq \varnothing \end{matrix}}}(-1)^{|J|+1}\cdot \texttt {pl}\left (\bigcup \limits _{j\in J}X_j\right ) \end{align*}
\begin{align*} \texttt {pl}\left (\bigcap \limits _{1\leq i\leq k}X_i\right )\leq \sum \limits _{\scriptsize {\begin{matrix}J\subseteq \{1,\ldots, k\}\\J\neq \varnothing \end{matrix}}}(-1)^{|J|+1}\cdot \texttt {pl}\left (\bigcup \limits _{j\in J}X_j\right ) \end{align*}
-
•
 $\texttt {pl}(\varnothing )=0$
and
$\texttt {pl}(\varnothing )=0$
and
 $\texttt {pl}(W)=1$
.
$\texttt {pl}(W)=1$
.
Recall that every plausibility function
![]() $\texttt {pl}$
on
$\texttt {pl}$
on
![]() $W$
gives rise to a belief function
$W$
gives rise to a belief function
![]() ${\texttt {bel}}_{\texttt {pl}}$
and vice versa: given a belief function
${\texttt {bel}}_{\texttt {pl}}$
and vice versa: given a belief function
![]() $\texttt {bel}$
on
$\texttt {bel}$
on
![]() $W$
, one can construct a plausibility function
$W$
, one can construct a plausibility function
![]() $\texttt {pl}_{\texttt {bel}}$
.
$\texttt {pl}_{\texttt {bel}}$
.
Moreover, it was shown in Bílková et al. (Reference Bílková, Frittella, Kozhemiachenko, Majer and Nazari2023d, Lemmas 2.10 and 2.11) that a similar statement holds for
![]() $\mathsf {BD}$
-models. That is, belief and plausibility functions can be defined via one another even without set-theoretic complements.
$\mathsf {BD}$
-models. That is, belief and plausibility functions can be defined via one another even without set-theoretic complements.
In what follows, we will be using two kinds of
![]() $\mathsf {BD}$
-models with belief functions introduced by Bílková et al. (Reference Bílková, Frittella, Kozhemiachenko, Majer and Nazari2023): in the first one, belief and plausibility will be interdefinable via (4); in the second one, we will assume them to be independent.
$\mathsf {BD}$
-models with belief functions introduced by Bílková et al. (Reference Bílková, Frittella, Kozhemiachenko, Majer and Nazari2023): in the first one, belief and plausibility will be interdefinable via (4); in the second one, we will assume them to be independent.
Definition 45 (
![]() $\mathsf {BD}$
$\mathsf {BD}$
![]() $\texttt {bel}$
-models). A
$\texttt {bel}$
-models). A
![]() $\mathsf {BD}$
$\mathsf {BD}$
![]() $\texttt {bel}$
-model is a tuple
$\texttt {bel}$
-model is a tuple
![]() $\mathfrak {M}_{\texttt {bel}}=\langle \mathfrak {M},{\texttt {bel}}\rangle$
with
$\mathfrak {M}_{\texttt {bel}}=\langle \mathfrak {M},{\texttt {bel}}\rangle$
with
![]() $\mathfrak {M}$
being a
$\mathfrak {M}$
being a
![]() $\mathsf {BD}$
-model (recall Definition 2) and
$\mathsf {BD}$
-model (recall Definition 2) and
![]() $\texttt {bel}$
a belief function on
$\texttt {bel}$
a belief function on
![]() $W$
.
$W$
.
Definition 46 (
![]() $\mathsf {BD}$
$\mathsf {BD}$
![]() ${\texttt {bel}}/\texttt {pl}$
-models). A
${\texttt {bel}}/\texttt {pl}$
-models). A
![]() $\mathsf {BD}$
$\mathsf {BD}$
![]() ${\texttt {bel}}/\texttt {pl}$
-model is a tuple
${\texttt {bel}}/\texttt {pl}$
-model is a tuple
![]() $\mathfrak {M}_{{\texttt {bel}}/\texttt {pl}}=\langle \mathfrak {M},{\texttt {bel}},\texttt {pl}\rangle$
with
$\mathfrak {M}_{{\texttt {bel}}/\texttt {pl}}=\langle \mathfrak {M},{\texttt {bel}},\texttt {pl}\rangle$
with
![]() $\mathfrak {M}$
being a
$\mathfrak {M}$
being a
![]() $\mathsf {BD}$
-model (recall Definition 2),
$\mathsf {BD}$
-model (recall Definition 2),
![]() $\texttt {bel}$
a belief function on
$\texttt {bel}$
a belief function on
![]() $W$
, and
$W$
, and
![]() $\texttt {pl}$
a plausibility function on
$\texttt {pl}$
a plausibility function on
![]() $W$
.
$W$
.
Observe from Definitions 43 and 44 that the traditional axiomatisation of belief and plausibility functions is infinite. In the classical case, this can be circumvented following Godo et al. (Reference Godo, Hájek, Esteva and Nebel2001Reference Godo, Hájek and Esteva2003) if we define belief in
![]() $\phi$
as the probability of
$\phi$
as the probability of
![]() $\Box \phi$
(with
$\Box \phi$
(with
![]() $\Box$
being the non-nesting
$\Box$
being the non-nesting
![]() $\mathbf {S5}$
modality). Then, we can use (3) to define the plausibility of
$\mathbf {S5}$
modality). Then, we can use (3) to define the plausibility of
![]() $\phi$
as the probability of
$\phi$
as the probability of
![]() $\lozenge \phi$
since
$\lozenge \phi$
since
![]() $\lozenge \phi \equiv {\sim }\Box {\sim }\phi$
(here,
$\lozenge \phi \equiv {\sim }\Box {\sim }\phi$
(here,
![]() $\equiv$
is the classical equivalence and
$\equiv$
is the classical equivalence and
![]() $\sim$
is the classical negation). In the remainder of the section, we show that the same can be done in
$\sim$
is the classical negation). In the remainder of the section, we show that the same can be done in
![]() $\mathsf {BD}$
.
$\mathsf {BD}$
.
Let us first recall the classical result.
Definition 47.
A classical uncertainty model is a tuple
![]() $\mathfrak {M}=\langle W,v,\mu \rangle$
with
$\mathfrak {M}=\langle W,v,\mu \rangle$
with
![]() $W\neq \varnothing$
,
$W\neq \varnothing$
,
![]() $\mu :2^W\rightarrow [0,1]$
, and
$\mu :2^W\rightarrow [0,1]$
, and
![]() $v:\texttt {Prop}\rightarrow 2^W$
extended to the satisfaction relation
$v:\texttt {Prop}\rightarrow 2^W$
extended to the satisfaction relation
![]() $\mathfrak {M},w\vDash \phi$
as follows.
$\mathfrak {M},w\vDash \phi$
as follows.
If
![]() $\mu$
is a belief function, plausibility, probability, etc., we call
$\mu$
is a belief function, plausibility, probability, etc., we call
![]() $\mathfrak {M}$
belief, plausibility, probabilistic, etc. model.
$\mathfrak {M}$
belief, plausibility, probabilistic, etc. model.
The extension of a formula
![]() $\phi$
is defined as
$\phi$
is defined as
![]() $\|\phi \|=\{w:\mathfrak {M},w\vDash \phi \}$
.
$\|\phi \|=\{w:\mathfrak {M},w\vDash \phi \}$
.
Definition 48 (Classical probabilistic Kripke model). A classical probabilistic Kripke model is a tuple
![]() $\mathfrak {M}=\langle W,R,v,\pi \rangle$
with
$\mathfrak {M}=\langle W,R,v,\pi \rangle$
with
![]() $W\neq \varnothing$
,
$W\neq \varnothing$
,
![]() $R$
being an equivalence relation on
$R$
being an equivalence relation on
![]() $W$
,
$W$
,
![]() $\pi$
being a classical probability measure on
$\pi$
being a classical probability measure on
![]() $W$
and
$W$
and
![]() $v:\texttt {Prop}\rightarrow 2^W$
extended to the satisfaction relation
$v:\texttt {Prop}\rightarrow 2^W$
extended to the satisfaction relation
![]() $\mathfrak {M},w\vDash \phi$
as follows.
$\mathfrak {M},w\vDash \phi$
as follows.
 \begin{align*} \mathfrak {M},w\vDash p&\text { iff }w\in v(p)\\ \mathfrak {M},w\vDash {\sim }\phi &\text { iff }\mathfrak {M},w\nvDash \phi &\mathfrak {M},w\vDash \phi \wedge \chi &\text { iff }\mathfrak {M},w\vDash \phi \text { and }\mathfrak {M},w\vDash \chi \\ \mathfrak {M},w\vDash \Box \phi &\text { iff }\forall w':wRw'\Rightarrow \mathfrak {M},w'\vDash \phi &\mathfrak {M},w\vDash \lozenge \phi &\text { iff }\exists w':wRw'\,\&\,\mathfrak {M},w'\vDash \phi \end{align*}
\begin{align*} \mathfrak {M},w\vDash p&\text { iff }w\in v(p)\\ \mathfrak {M},w\vDash {\sim }\phi &\text { iff }\mathfrak {M},w\nvDash \phi &\mathfrak {M},w\vDash \phi \wedge \chi &\text { iff }\mathfrak {M},w\vDash \phi \text { and }\mathfrak {M},w\vDash \chi \\ \mathfrak {M},w\vDash \Box \phi &\text { iff }\forall w':wRw'\Rightarrow \mathfrak {M},w'\vDash \phi &\mathfrak {M},w\vDash \lozenge \phi &\text { iff }\exists w':wRw'\,\&\,\mathfrak {M},w'\vDash \phi \end{align*}
Theorem 49 (Godo et al. Reference Godo, Hájek, Esteva and Nebel2001, Theorem 1). Let
![]() $\phi$
be a propositional classical formula and let
$\phi$
be a propositional classical formula and let
![]() $\mathfrak {M}_{\texttt {bel}}=\langle W,v,{\texttt {bel}}\rangle$
and
$\mathfrak {M}_{\texttt {bel}}=\langle W,v,{\texttt {bel}}\rangle$
and
![]() $\mathfrak {M}=\langle W,v,\texttt {pl}\rangle$
be, respectively, a belief and plausibility models, then:
$\mathfrak {M}=\langle W,v,\texttt {pl}\rangle$
be, respectively, a belief and plausibility models, then:
-
(i) there is a classical probabilistic model
 $\mathfrak {M}_\Box \!=\!\langle W_\Box, \!R_\Box, \!v_\Box, \!\pi _\Box \rangle$
s.t.
$\mathfrak {M}_\Box \!=\!\langle W_\Box, \!R_\Box, \!v_\Box, \!\pi _\Box \rangle$
s.t.
 $\pi _\Box (\|\Box \phi \|)\!=\!{\texttt {bel}}(\|\phi \|)$
;
$\pi _\Box (\|\Box \phi \|)\!=\!{\texttt {bel}}(\|\phi \|)$
; -
(ii) there is a classical probabilistic model
 $\mathfrak {M}_\lozenge =\langle W_\lozenge, R_\lozenge, v_\lozenge, \pi _\lozenge \rangle$
s.t.
$\mathfrak {M}_\lozenge =\langle W_\lozenge, R_\lozenge, v_\lozenge, \pi _\lozenge \rangle$
s.t.
 $\pi _\lozenge (\|\lozenge \phi \|)=\texttt {pl}(\|\phi \|)$
.
$\pi _\lozenge (\|\lozenge \phi \|)=\texttt {pl}(\|\phi \|)$
.
We draw the attention of our readers to the fact that
![]() $\Box$
and
$\Box$
and
![]() $\lozenge$
do not have to be
$\lozenge$
do not have to be
![]() $\mathbf {S5}$
: it suffices that the underlying modal logic be normal. The original motivation for choosing
$\mathbf {S5}$
: it suffices that the underlying modal logic be normal. The original motivation for choosing
![]() $\mathbf {S5}$
was that it is locally finite. Note, however, that local finiteness can be achieved in other modal logics as well because
$\mathbf {S5}$
was that it is locally finite. Note, however, that local finiteness can be achieved in other modal logics as well because
![]() $\Box$
and
$\Box$
and
![]() $\lozenge$
do not nest (cf. Flaminio et al. Reference Flaminio, Godo and Marchioni2013, Section 6) for a detailed discussion).
$\lozenge$
do not nest (cf. Flaminio et al. Reference Flaminio, Godo and Marchioni2013, Section 6) for a detailed discussion).
Moreover, originally only (i) is proven by Godo et al. (Reference Godo, Hájek, Esteva and Nebel2001Reference Godo, Hájek and Esteva2003). Observe, however, that (ii) can be obtained from (i) using (3) since
 \begin{align*} \pi (\|\lozenge \phi \|)&=\pi (\|{\sim }\Box {\sim }\phi \|)\\ &=1-\pi (\|\Box {\sim }\phi \|)\\ &=1-{\texttt {bel}}(\|{\sim }\phi \|)\\ &=1-{\texttt {bel}}(W\setminus \|\phi \|)\\ &=\texttt {pl}_{\texttt {bel}}(\|\phi \|) \end{align*}
\begin{align*} \pi (\|\lozenge \phi \|)&=\pi (\|{\sim }\Box {\sim }\phi \|)\\ &=1-\pi (\|\Box {\sim }\phi \|)\\ &=1-{\texttt {bel}}(\|{\sim }\phi \|)\\ &=1-{\texttt {bel}}(W\setminus \|\phi \|)\\ &=\texttt {pl}_{\texttt {bel}}(\|\phi \|) \end{align*}
Let us now introduce probabilistic models for modal
![]() $\mathsf {BD}$
formulas. We borrow the definition of modalities in
$\mathsf {BD}$
formulas. We borrow the definition of modalities in
![]() $\mathsf {BD}$
from Odintsov and Wansing (Reference Odintsov and Wansing2017).
$\mathsf {BD}$
from Odintsov and Wansing (Reference Odintsov and Wansing2017).
Definition 50 (
![]() $\mathsf {BD}$
probabilistic Kripke models). A
$\mathsf {BD}$
probabilistic Kripke models). A
![]() $\mathsf {BD}$
probabilistic Kripke model is a tuple
$\mathsf {BD}$
probabilistic Kripke model is a tuple
![]() $\mathfrak {M}=\langle W,R,v^+,v^-,\pi \rangle$
with
$\mathfrak {M}=\langle W,R,v^+,v^-,\pi \rangle$
with
![]() $W\neq \varnothing$
,
$W\neq \varnothing$
,
![]() $R$
being an equivalence relation on
$R$
being an equivalence relation on
![]() $W$
,
$W$
,
![]() $\pi$
being a classical probability measure on
$\pi$
being a classical probability measure on
![]() $W$
and
$W$
and
![]() $v^+,v^-:\texttt {Prop}\rightarrow 2^W$
extended to
$v^+,v^-:\texttt {Prop}\rightarrow 2^W$
extended to
![]() $\mathfrak {M},w\vDash ^+\phi$
and
$\mathfrak {M},w\vDash ^+\phi$
and
![]() $\mathfrak {M},w\vDash ^-\phi$
as in Definition 2 for propositional connectives and as below for modalities.
$\mathfrak {M},w\vDash ^-\phi$
as in Definition 2 for propositional connectives and as below for modalities.
Positive and negative extensions of
![]() $\phi$
are as in Definition 2
.
$\phi$
are as in Definition 2
.
We also call the
![]() $\langle W,R,v^+,v^-\rangle$
reduct a
$\langle W,R,v^+,v^-\rangle$
reduct a
![]() $\mathsf {BD}$
Kripke model.
$\mathsf {BD}$
Kripke model.
Remark 51.
Since
![]() $\vDash ^+$
conditions for
$\vDash ^+$
conditions for
![]() $\Box$
and
$\Box$
and
![]() $\lozenge$
in the classical logic and in
$\lozenge$
in the classical logic and in
![]() $\mathsf {BD}$
coincide, it is clear (cf. Hájek Reference Hájek1996 for a detailed discussion of the classical case) that given a probability
$\mathsf {BD}$
coincide, it is clear (cf. Hájek Reference Hájek1996 for a detailed discussion of the classical case) that given a probability
![]() $\pi$
on a Kripke model
$\pi$
on a Kripke model
![]() $\mathfrak {M}$
, there are a belief and plausibility functions
$\mathfrak {M}$
, there are a belief and plausibility functions
![]() $\texttt {bel}$
and
$\texttt {bel}$
and
![]() $\texttt {pl}$
on
$\texttt {pl}$
on
![]() $\mathfrak {M}$
s.t.
$\mathfrak {M}$
s.t.
![]() ${\texttt {bel}}(|\phi |^+)=\pi (|\Box \phi |^+)$
and
${\texttt {bel}}(|\phi |^+)=\pi (|\Box \phi |^+)$
and
![]() $\texttt {pl}(|\phi |^+)=\pi (|\lozenge \phi |^+)$
for every
$\texttt {pl}(|\phi |^+)=\pi (|\lozenge \phi |^+)$
for every
![]() $\phi \in \mathscr {L}_{\mathsf {BD}}$
.
$\phi \in \mathscr {L}_{\mathsf {BD}}$
.
Theorem 52.
Let
![]() $\phi _1,\ldots, \phi _n\in \mathscr {L}_{\mathsf {BD}}$
and consider a
$\phi _1,\ldots, \phi _n\in \mathscr {L}_{\mathsf {BD}}$
and consider a
![]() $\mathsf {BD}$
$\mathsf {BD}$
![]() $\texttt {bel}$
-model
$\texttt {bel}$
-model
![]() $\mathfrak {M}_{\texttt {bel}}=\langle \mathfrak {M},{\texttt {bel}}\rangle$
and a
$\mathfrak {M}_{\texttt {bel}}=\langle \mathfrak {M},{\texttt {bel}}\rangle$
and a
![]() $\mathsf {BD}$
$\mathsf {BD}$
![]() ${\texttt {bel}}/\texttt {pl}$
-model
${\texttt {bel}}/\texttt {pl}$
-model
![]() $\mathfrak {M}'_{{\texttt {bel}}/\texttt {pl}}=\langle \mathfrak {M}',{\texttt {bel}}',\texttt {pl}'\rangle$
. Then, there exist
$\mathfrak {M}'_{{\texttt {bel}}/\texttt {pl}}=\langle \mathfrak {M}',{\texttt {bel}}',\texttt {pl}'\rangle$
. Then, there exist
-
1. a
 $\mathsf {BD}$
probabilistic Kripke model
$\mathsf {BD}$
probabilistic Kripke model
 $\mathfrak {M}_\Box =\langle W_\Box, R_\Box, v^+_\Box, v^-_\Box, \pi _\Box \rangle$
with
$\mathfrak {M}_\Box =\langle W_\Box, R_\Box, v^+_\Box, v^-_\Box, \pi _\Box \rangle$
with
 ${\texttt {bel}}(|\phi _i|^+)=\pi _\Box (|\Box \phi _i|^+)$
for each
${\texttt {bel}}(|\phi _i|^+)=\pi _\Box (|\Box \phi _i|^+)$
for each
 $i\in \{1,\ldots, n\}$
;
$i\in \{1,\ldots, n\}$
; -
2. a
 $\mathsf {BD}$
probabilistic Kripke model
$\mathsf {BD}$
probabilistic Kripke model
 $\mathfrak {M}_{\Box, \lozenge }=\langle W_{\Box, \lozenge },R_1,R_2,v^+_{\Box, \lozenge },v^-_{\Box, \lozenge },\pi _{\Box, \lozenge }\rangle$
with
$\mathfrak {M}_{\Box, \lozenge }=\langle W_{\Box, \lozenge },R_1,R_2,v^+_{\Box, \lozenge },v^-_{\Box, \lozenge },\pi _{\Box, \lozenge }\rangle$
with
 ${\texttt {bel}}'(|\phi _i|^+)=\pi _{\Box, \lozenge }(|\Box _1\phi _i|^+)$
and
${\texttt {bel}}'(|\phi _i|^+)=\pi _{\Box, \lozenge }(|\Box _1\phi _i|^+)$
and
 $\texttt {pl}'(|\phi _i|^+)=\pi _{\Box, \lozenge }(|\lozenge _2\phi _i|^+)$
for each
$\texttt {pl}'(|\phi _i|^+)=\pi _{\Box, \lozenge }(|\lozenge _2\phi _i|^+)$
for each
 $i\in \{1,\ldots, n\}$
(here,
$i\in \{1,\ldots, n\}$
(here,
 $\Box _1$
and
$\Box _1$
and
 $\lozenge _2$
are associated to
$\lozenge _2$
are associated to
 $R_1$
and
$R_1$
and
 $R_2$
, respectively).
$R_2$
, respectively).
Proof.
We prove (1) as (2) can be dealt with similarly. Let w.l.o.g.
![]() $\phi$
be in
$\phi$
be in
![]() $\mathsf {NNF}$
and denote
$\mathsf {NNF}$
and denote
![]() $\phi ^*$
the result of replacing every negated variable
$\phi ^*$
the result of replacing every negated variable
![]() $\neg p$
occurring in
$\neg p$
occurring in
![]() $\phi$
with a fresh variable
$\phi$
with a fresh variable
![]() $p^*$
. Consider
$p^*$
. Consider
![]() $\mathfrak {M}_{\texttt {bel}}=\langle W,v^+,v^-,{\texttt {bel}}\rangle$
and
$\mathfrak {M}_{\texttt {bel}}=\langle W,v^+,v^-,{\texttt {bel}}\rangle$
and
![]() $\mathfrak {M}^*_{\texttt {bel}}$
(cf. the proof of Lemma 41). It is easy to see that
$\mathfrak {M}^*_{\texttt {bel}}$
(cf. the proof of Lemma 41). It is easy to see that
![]() ${\texttt {bel}}(|\phi _i|^+)={\texttt {bel}}(|\phi ^*_i|^+)$
for every
${\texttt {bel}}(|\phi _i|^+)={\texttt {bel}}(|\phi ^*_i|^+)$
for every
![]() $i$
.
$i$
.
Now define a classical belief model
![]() $\mathfrak {M}^{\mathsf {cl}}_{\texttt {bel}}=\langle W,v^{\mathsf {cl}},{\texttt {bel}}\rangle$
with
$\mathfrak {M}^{\mathsf {cl}}_{\texttt {bel}}=\langle W,v^{\mathsf {cl}},{\texttt {bel}}\rangle$
with
![]() $v^{\mathsf {cl}}(q)=v^+(q)$
for every
$v^{\mathsf {cl}}(q)=v^+(q)$
for every
![]() $q\in \texttt {Prop}$
. Clearly,
$q\in \texttt {Prop}$
. Clearly,
![]() ${\texttt {bel}}(|\phi ^*_i|^+)={\texttt {bel}}(\|\phi ^*_i\|)$
for all
${\texttt {bel}}(|\phi ^*_i|^+)={\texttt {bel}}(\|\phi ^*_i\|)$
for all
![]() $\phi ^*_i$
’s. Thus, by Theorem49, we have that there is a classical Kripke probabilistic model
$\phi ^*_i$
’s. Thus, by Theorem49, we have that there is a classical Kripke probabilistic model
![]() $\mathfrak {M}_\Box \!=\!\langle W_\Box, \!R_\Box, \!v_\Box, \!\pi _\Box \rangle$
s.t.
$\mathfrak {M}_\Box \!=\!\langle W_\Box, \!R_\Box, \!v_\Box, \!\pi _\Box \rangle$
s.t.
![]() $\pi _\Box (\|\Box \phi ^*_i\|)\!=\!{\texttt {bel}}(\|\phi ^*_i\|)$
for every
$\pi _\Box (\|\Box \phi ^*_i\|)\!=\!{\texttt {bel}}(\|\phi ^*_i\|)$
for every
![]() $i$
. It remains to construct a suitable
$i$
. It remains to construct a suitable
![]() $\mathsf {BD}$
probabilistic Kripke model.
$\mathsf {BD}$
probabilistic Kripke model.
We define
![]() $\mathfrak {M}^{\mathsf {BD}}_\Box =\langle W_\Box, R_\Box, v^+_\Box, v^-_\Box, \pi _\Box \rangle$
with
$\mathfrak {M}^{\mathsf {BD}}_\Box =\langle W_\Box, R_\Box, v^+_\Box, v^-_\Box, \pi _\Box \rangle$
with
![]() $v^+_\Box (p)=v_\Box (p)$
and
$v^+_\Box (p)=v_\Box (p)$
and
![]() $v^-_\Box (p)=v_\Box (p^*)$
. One can show by induction on
$v^-_\Box (p)=v_\Box (p^*)$
. One can show by induction on
![]() $\phi ^*_i$
’s that
$\phi ^*_i$
’s that
![]() $\|\phi ^*_i\|=|\phi _i|^+$
, and thus
$\|\phi ^*_i\|=|\phi _i|^+$
, and thus
![]() $\|\Box \phi ^*_i\|=|\Box \phi _i|^+$
for every
$\|\Box \phi ^*_i\|=|\Box \phi _i|^+$
for every
![]() $i$
: indeed, cf. semantical conditions for
$i$
: indeed, cf. semantical conditions for
![]() $\Box$
in Definitions 48 and 50. Hence,
$\Box$
in Definitions 48 and 50. Hence,
![]() $\pi _\Box (\|\Box \phi ^*_i\|)=\pi _\Box (|\Box \phi _i|^+)$
, as required.
$\pi _\Box (\|\Box \phi ^*_i\|)=\pi _\Box (|\Box \phi _i|^+)$
, as required.
We finish the section with a brief observation.
Remark 53.
Just as in the classical case,
![]() $\Box$
and
$\Box$
and
![]() $\lozenge$
do not need to be
$\lozenge$
do not need to be
![]() $\mathbf {S5}$
. We choose
$\mathbf {S5}$
. We choose
![]() $\mathsf {BD}$
version of
$\mathsf {BD}$
version of
![]() $\mathbf {S5}$
because of the following property: if
$\mathbf {S5}$
because of the following property: if
![]() $\mathfrak {M}=\langle W,R,v^+,v^-,\pi \rangle$
is a
$\mathfrak {M}=\langle W,R,v^+,v^-,\pi \rangle$
is a
![]() $\mathsf {BD}$
probabilistic Kripke model and
$\mathsf {BD}$
probabilistic Kripke model and
![]() $\psi$
is a modal formula where all propositional variables are in the scope of a modality, and
$\psi$
is a modal formula where all propositional variables are in the scope of a modality, and
![]() $wRw'$
, then
$wRw'$
, then
![]() $\mathfrak {M},w\vDash ^+\psi$
iff
$\mathfrak {M},w\vDash ^+\psi$
iff
![]() $\mathfrak {M},w'\vDash ^+\psi$
and
$\mathfrak {M},w'\vDash ^+\psi$
and
![]() $\mathfrak {M},w\vDash ^-\psi$
iff
$\mathfrak {M},w\vDash ^-\psi$
iff
![]() $\mathfrak {M},w'\vDash ^-\psi$
.
$\mathfrak {M},w'\vDash ^-\psi$
.
5. Logics for belief and plausibility functions over
 $\mathsf {BD}$
$\mathsf {BD}$
In this section, we recall two-layered logics
![]() $\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
and
$\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
and
![]() $\mathsf {Bel}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}$
for reasoning with belief and plausibility functions over
$\mathsf {Bel}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}$
for reasoning with belief and plausibility functions over
![]() $\mathsf {BD}$
that were presented by Bílková et al., (2023). We then combine the technique of Hájek and Tulipani (Reference Hájek and Tulipani2001) with the results of Godo et al. (Reference Godo, Hájek, Esteva and Nebel2001Reference Godo, Hájek and Esteva2003) and Theorem52 to obtain the
$\mathsf {BD}$
that were presented by Bílková et al., (2023). We then combine the technique of Hájek and Tulipani (Reference Hájek and Tulipani2001) with the results of Godo et al. (Reference Godo, Hájek, Esteva and Nebel2001Reference Godo, Hájek and Esteva2003) and Theorem52 to obtain the
![]() $\mathsf {coNP}$
-completeness of
$\mathsf {coNP}$
-completeness of
![]() $\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
and
$\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
and
![]() $\mathsf {Bel}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}$
.
$\mathsf {Bel}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}$
.
5.1 Languages and semantics
Definition 54 (
![]() $\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
: language and semantics). The language of
$\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
: language and semantics). The language of
![]() $\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
is constructed using the grammar below.
$\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
is constructed using the grammar below.
A
![]() $\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
-model is a tuple
$\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
-model is a tuple
![]() $\mathbb {M}_{\texttt {bel}}=\langle \mathfrak {M},{\texttt {bel}},e_1,e_2\rangle$
with
$\mathbb {M}_{\texttt {bel}}=\langle \mathfrak {M},{\texttt {bel}},e_1,e_2\rangle$
with
-
•
 $\langle \mathfrak {M},{\texttt {bel}}\rangle$
being a
$\langle \mathfrak {M},{\texttt {bel}}\rangle$
being a
 $\mathsf {BD}$
$\mathsf {BD}$
 $\texttt {bel}$
-model (cf. Definition 45);
$\texttt {bel}$
-model (cf. Definition 45);
-
•
 $e_1$
and
$e_1$
and
 $e_2$
being
$e_2$
being
 ${\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}$
valuations induced by
${\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}$
valuations induced by
 $\texttt {bel}$
:
$\texttt {bel}$
:-
–
 $e_1({\mathsf {B}}\phi )={\texttt {bel}}(|\phi |^+)$
,
$e_1({\mathsf {B}}\phi )={\texttt {bel}}(|\phi |^+)$
,
 $e_2({\mathsf {B}}\phi )={\texttt {bel}}(|\phi |^-)$
;
$e_2({\mathsf {B}}\phi )={\texttt {bel}}(|\phi |^-)$
; -
– values of complex
 $\mathscr {L}_{\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle }$
-formulas are computed via Definition 12
.
$\mathscr {L}_{\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle }$
-formulas are computed via Definition 12
.
-
We say that
![]() $\alpha$
is
$\alpha$
is
![]() ${\mathsf{Bel}^{{\unicode {x0141}}^2}_\triangle}$
-valid iff
${\mathsf{Bel}^{{\unicode {x0141}}^2}_\triangle}$
-valid iff
![]() $e_1(\alpha)=1$
and
$e_1(\alpha)=1$
and
![]() $e_2(\alpha)=0$
in all models. A set of formulas
$e_2(\alpha)=0$
in all models. A set of formulas
![]() $\Gamma$
entails
$\Gamma$
entails
![]() $\alpha$
(
$\alpha$
(
![]() $\Gamma\models_{{\mathsf{Bel}^{{\unicode {x0141}}^2}_\triangle}}\alpha$
) iff there is no
$\Gamma\models_{{\mathsf{Bel}^{{\unicode {x0141}}^2}_\triangle}}\alpha$
) iff there is no
![]() ${\mathsf{Bel}^{{\unicode {x0141}}^2}_\triangle}$
-model s.t.
${\mathsf{Bel}^{{\unicode {x0141}}^2}_\triangle}$
-model s.t.
![]() $e(\gamma)=(1,0)$
for all
$e(\gamma)=(1,0)$
for all
![]() $\gamma\in\Gamma$
but
$\gamma\in\Gamma$
but
![]() $e(\alpha)\neq(1,0)$
.
$e(\alpha)\neq(1,0)$
.
Remark 55.
Note that we cannot utilise the technique from Lemma 17 to reduce
![]() $\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
-validity to checking whether
$\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
-validity to checking whether
![]() $e_1(\alpha )=1$
in every model. This is because belief functions are not additive. Thus, even though we can construct
$e_1(\alpha )=1$
in every model. This is because belief functions are not additive. Thus, even though we can construct
![]() $(v^*)^+$
and
$(v^*)^+$
and
![]() $(v^*)^-$
s.t.
(1)
holds, we cannot use it to infer the following counterpart of
(2)
:
$(v^*)^-$
s.t.
(1)
holds, we cannot use it to infer the following counterpart of
(2)
:
Indeed,
(5)
does not hold in general since it is not necessarily the case that
![]() ${\texttt {bel}}(W\setminus X)=1-{\texttt {bel}}(X)$
for
${\texttt {bel}}(W\setminus X)=1-{\texttt {bel}}(X)$
for
![]() $X\subseteq W$
.
$X\subseteq W$
.
![]() $\mathsf {Bel}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}$
logic (
$\mathsf {Bel}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}$
logic (
![]() $\mathsf {N}{\mathsf {\unicode {x0141}}}$
) that is (
$\mathsf {N}{\mathsf {\unicode {x0141}}}$
) that is (
![]() $\mathsf {N}{\mathsf {\unicode {x0141}}}$
) that is inspired by Nelson’s paraconsistent logic from Nelson (Reference Nelson1949). The logic was introduced by Bílková et al. (Reference Bílková, Frittella, Kozhemiachenko, Das and Negri2021) and further investigated by Bílková et al. (Reference Bílková, Frittella, Kozhemiachenko, Majer and Nazari2023d). We recall its language and semantics below.
$\mathsf {N}{\mathsf {\unicode {x0141}}}$
) that is inspired by Nelson’s paraconsistent logic from Nelson (Reference Nelson1949). The logic was introduced by Bílková et al. (Reference Bílková, Frittella, Kozhemiachenko, Das and Negri2021) and further investigated by Bílková et al. (Reference Bílková, Frittella, Kozhemiachenko, Majer and Nazari2023d). We recall its language and semantics below.
Definition 56 (
![]() $\mathsf {N}{\mathsf {\unicode {x0141}}}$
: language and semantics). The language is constructed via the following grammar.
$\mathsf {N}{\mathsf {\unicode {x0141}}}$
: language and semantics). The language is constructed via the following grammar.
The support of truth and support of falsity conditions are given by the following extensions of
![]() $v_1,v_2:\texttt {Prop}\rightarrow [0,1]$
(
$v_1,v_2:\texttt {Prop}\rightarrow [0,1]$
(
![]() $\mathsf {N}{\mathsf {\unicode {x0141}}}$
valuations) to the complex formulas.
$\mathsf {N}{\mathsf {\unicode {x0141}}}$
valuations) to the complex formulas.

We say that
![]() $\alpha$
is
$\alpha$
is
![]() ${\mathsf{Bel}^{\mathsf{N}{\unicode {x0141}}}}$
-valid iff
${\mathsf{Bel}^{\mathsf{N}{\unicode {x0141}}}}$
-valid iff
![]() $e_1(\alpha)=1$
for every
$e_1(\alpha)=1$
for every
![]() ${\mathsf{Bel}^{\mathsf{N}{\unicode {x0141}}}}$
-model.
${\mathsf{Bel}^{\mathsf{N}{\unicode {x0141}}}}$
-model.
![]() $\Gamma$
entails
$\Gamma$
entails
![]() $\alpha$
(
$\alpha$
(
![]() $\Gamma\models_{\mathsf{Bel}^{\mathsf{N}{\unicode {x0141}}}}\alpha$
) iff there is no
$\Gamma\models_{\mathsf{Bel}^{\mathsf{N}{\unicode {x0141}}}}\alpha$
) iff there is no
![]() ${\mathsf{Bel}^{\mathsf{N}{\unicode {x0141}}}}$
-model s.t.
${\mathsf{Bel}^{\mathsf{N}{\unicode {x0141}}}}$
-model s.t.
![]() $e_1(\gamma)=1$
for every
$e_1(\gamma)=1$
for every
![]() $\gamma\in\Gamma$
and
$\gamma\in\Gamma$
and
![]() $e_1(\alpha)\neq1$
.
$e_1(\alpha)\neq1$
.
Definition 57 (
![]() $\mathsf {Bel}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}$
: language and semantics). The language is given by the grammar below.
$\mathsf {Bel}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}$
: language and semantics). The language is given by the grammar below.
A
![]() $\mathsf {Bel}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}$
-model is a tuple
$\mathsf {Bel}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}$
-model is a tuple
![]() $\mathbb {M}_{{\texttt {bel}}/\texttt {pl}}=\langle \mathfrak {M},{\texttt {bel}},\texttt {pl},e_1,e_2\rangle$
with
$\mathbb {M}_{{\texttt {bel}}/\texttt {pl}}=\langle \mathfrak {M},{\texttt {bel}},\texttt {pl},e_1,e_2\rangle$
with
-
•
 $\langle \mathfrak {M},{\texttt {bel}},\texttt {pl}\rangle$
being a
$\langle \mathfrak {M},{\texttt {bel}},\texttt {pl}\rangle$
being a
 $\mathsf {BD}$
$\mathsf {BD}$
 ${\texttt {bel}}/\texttt {pl}$
-model (cf. Definition 46);
${\texttt {bel}}/\texttt {pl}$
-model (cf. Definition 46);
-
•
 $e_1$
and
$e_1$
and
 $e_2$
being
$e_2$
being
 $\mathsf {N}{\mathsf {\unicode {x0141}}}$
valuations induced by
$\mathsf {N}{\mathsf {\unicode {x0141}}}$
valuations induced by
 $\texttt {bel}$
and
$\texttt {bel}$
and
 $\texttt {pl}$
:
$\texttt {pl}$
:-
–
 $e_1({\mathsf {B}}\phi )={\texttt {bel}}(|\phi |^+)$
,
$e_1({\mathsf {B}}\phi )={\texttt {bel}}(|\phi |^+)$
,
 $e_2({\mathsf {B}}\phi )=\texttt {pl}(|\phi |^-)$
,
$e_2({\mathsf {B}}\phi )=\texttt {pl}(|\phi |^-)$
,
 $e_1(\mathsf {Pl}\phi )=\texttt {pl}(|\phi |^+)$
,
$e_1(\mathsf {Pl}\phi )=\texttt {pl}(|\phi |^+)$
,
 $e_2(\mathsf {Pl}\phi )={\texttt {bel}}(|\phi |^-)$
;
$e_2(\mathsf {Pl}\phi )={\texttt {bel}}(|\phi |^-)$
; -
– values of complex
 $\mathscr {L}_{\mathsf {Bel}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}}$
-formulas are computed via Definition 56
.
$\mathscr {L}_{\mathsf {Bel}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}}$
-formulas are computed via Definition 56
.
-
We say that
![]() $\alpha$
is
$\alpha$
is
![]() ${\mathsf{Bel}^{\mathsf{N}{\unicode {x0141}}}}$
-valid iff
${\mathsf{Bel}^{\mathsf{N}{\unicode {x0141}}}}$
-valid iff
![]() $e_1(\alpha)=1$
for every
$e_1(\alpha)=1$
for every
![]() ${\mathsf{Bel}^{\mathsf{N}{\unicode {x0141}}}}$
-model.
${\mathsf{Bel}^{\mathsf{N}{\unicode {x0141}}}}$
-model.
![]() $\Gamma$
entails
$\Gamma$
entails
![]() $\alpha$
(
$\alpha$
(
![]() $\Gamma\models_{\mathsf{Bel}^{\mathsf{N}{\unicode {x0141}}}}\alpha$
) iff there is no
$\Gamma\models_{\mathsf{Bel}^{\mathsf{N}{\unicode {x0141}}}}\alpha$
) iff there is no
![]() ${\mathsf{Bel}^{\mathsf{N}{\unicode {x0141}}}}$
-model s.t.
${\mathsf{Bel}^{\mathsf{N}{\unicode {x0141}}}}$
-model s.t.
![]() $e_1(\gamma)=1$
for every
$e_1(\gamma)=1$
for every
![]() $\gamma\in\Gamma$
and
$\gamma\in\Gamma$
and
![]() $e_1(\alpha)\neq1$
.
$e_1(\alpha)\neq1$
.
Note that using (4), we can define a plausibility operator
![]() $\mathsf {Pl}_{\mathsf {B}}$
in
$\mathsf {Pl}_{\mathsf {B}}$
in
![]() $\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
as
$\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
as
![]() $\mathsf {Pl_B}\phi := \sim \mathsf {B}\neg \phi$
. The main difference between it and
$\mathsf {Pl_B}\phi := \sim \mathsf {B}\neg \phi$
. The main difference between it and
![]() $\mathsf {PI}$
in
$\mathsf {PI}$
in
![]() $\mathsf {Bel}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}$
is that the latter is independent of belief. We refer readers to Bílková et al. (Reference Bílková, Frittella, Kozhemiachenko, Majer and Nazari2023d) for a more detailed discussion of differences between
$\mathsf {Bel}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}$
is that the latter is independent of belief. We refer readers to Bílková et al. (Reference Bílková, Frittella, Kozhemiachenko, Majer and Nazari2023d) for a more detailed discussion of differences between
![]() $\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
and
$\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
and
![]() $\mathsf {Bel}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}$
.
$\mathsf {Bel}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}$
.
Moreover,
![]() $\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
is complete w.r.t. models with classical probability measures (recall Klein et al. Reference Klein, Majer and Rafiee Rad2021, Theorems 3–4 and Bílková et al. Reference Bílková, Frittella, Kozhemiachenko, Majer and Nazari2023, Theorem 4.24). Thus, as belief and plausibility functions are generalisations of probabilities, it means that if a statement about belief functions is valid, then it is valid about probabilities as well. Formally, let
$\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
is complete w.r.t. models with classical probability measures (recall Klein et al. Reference Klein, Majer and Rafiee Rad2021, Theorems 3–4 and Bílková et al. Reference Bílková, Frittella, Kozhemiachenko, Majer and Nazari2023, Theorem 4.24). Thus, as belief and plausibility functions are generalisations of probabilities, it means that if a statement about belief functions is valid, then it is valid about probabilities as well. Formally, let
![]() $\alpha \in \mathscr {L}_{\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle }$
and let further
$\alpha \in \mathscr {L}_{\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle }$
and let further
![]() $\alpha ^{\mathsf {Pr}}$
be the result of the replacement of
$\alpha ^{\mathsf {Pr}}$
be the result of the replacement of
![]() ${\mathsf {B}}\phi$
’s with
${\mathsf {B}}\phi$
’s with
![]() $\mathsf {Pr}\phi$
’s. Then if
$\mathsf {Pr}\phi$
’s. Then if
![]() $\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle \models \alpha$
, it follows that
$\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle \models \alpha$
, it follows that
![]() $\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle \models \alpha ^{\mathsf {Pr}}$
. This means that
$\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle \models \alpha ^{\mathsf {Pr}}$
. This means that
![]() $\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
can be thought of as an extension or a semantical restriction of
$\mathsf {Pr}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
can be thought of as an extension or a semantical restriction of
![]() $\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
.
$\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
.
In the previous section, we showed (Theorem52) that belief and plausibility in
![]() $\mathsf {BD}$
can be represented as probabilities of modal formulas. We are going to introduce two logics –
$\mathsf {BD}$
can be represented as probabilities of modal formulas. We are going to introduce two logics –
![]() $\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}$
and
$\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}$
and
![]() $\mathsf {Pr}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}_{\mathbf {S5}}$
–
$\mathsf {Pr}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}_{\mathbf {S5}}$
–
![]() $\mathsf {Bel}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}$
– that deal with those and show that
$\mathsf {Bel}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}$
– that deal with those and show that
![]() $\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
and
$\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
and
![]() $\mathsf {Bel}^{{\mathsf {N\unicode {x0141}}}}$
$\mathsf {Bel}^{{\mathsf {N\unicode {x0141}}}}$
Definition 58 (
![]() $\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}$
: language and semantics). The language is constructed as follows.
$\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}$
: language and semantics). The language is constructed as follows.
A
![]() $\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}$
-model is a tuple
$\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}$
-model is a tuple
![]() $\mathbb {M}_\pi =\langle \mathfrak {M},\pi, e_1,e_2\rangle$
s.t.
$\mathbb {M}_\pi =\langle \mathfrak {M},\pi, e_1,e_2\rangle$
s.t.
-
•
 $\langle \mathfrak {M},\pi \rangle$
is a
$\langle \mathfrak {M},\pi \rangle$
is a
 $\mathsf {BD}$
probabilistic Kripke model;
$\mathsf {BD}$
probabilistic Kripke model;
-
•
 $e_1$
and
$e_1$
and
 $e_2$
are
$e_2$
are
 ${\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}$
valuations induced by
${\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}$
valuations induced by
 $\pi$
:
$\pi$
:-
–
 $e_1(\mathsf {Pr}\heartsuit \phi )=\pi (|\heartsuit \phi |^+)$
,
$e_1(\mathsf {Pr}\heartsuit \phi )=\pi (|\heartsuit \phi |^+)$
,
 $e_2(\mathsf {Pr}\heartsuit \phi )=\pi (|\heartsuit \phi |^-)$
with
$e_2(\mathsf {Pr}\heartsuit \phi )=\pi (|\heartsuit \phi |^-)$
with
 $\heartsuit \in \{\Box, \lozenge \}$
;
$\heartsuit \in \{\Box, \lozenge \}$
; -
– values of complex
 $\mathscr {L}_{\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}}$
-formulas are computed via Definition 12
.
$\mathscr {L}_{\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}}$
-formulas are computed via Definition 12
.
-
We say that
![]() $\alpha$
is
$\alpha$
is
![]() $\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}$
-valid iff
$\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}$
-valid iff
![]() $e_1(\alpha )=1$
and
$e_1(\alpha )=1$
and
![]() $e_2(\alpha )=0$
in all
$e_2(\alpha )=0$
in all
![]() $\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}$
-models. A set of formulas
$\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}$
-models. A set of formulas
![]() $\Gamma$
entails
$\Gamma$
entails
![]() $\alpha$
(
$\alpha$
(
![]() $\Gamma \models _{\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}}\alpha$
) iff there is no
$\Gamma \models _{\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}}\alpha$
) iff there is no
![]() $\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}$
-model s.t.
$\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}$
-model s.t.
![]() $e(\gamma )=(1,0)$
for all
$e(\gamma )=(1,0)$
for all
![]() $\gamma \in \Gamma$
but
$\gamma \in \Gamma$
but
![]() $e(\alpha )\neq (1,0)$
.
$e(\alpha )\neq (1,0)$
.
The next statements can be proven in the same manner as Lemmas 17 and 41, respectively.
Lemma 59.
Let
![]() $\alpha \in \mathscr {L}_{\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}}$
. Then
$\alpha \in \mathscr {L}_{\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}}$
. Then
![]() $\alpha$
is
$\alpha$
is
![]() $\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}$
-valid iff
$\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}$
-valid iff
![]() $e_1(\alpha )=1$
in all
$e_1(\alpha )=1$
in all
![]() $\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}$
-models.
$\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}$
-models.
Lemma 60.
Let
![]() $\alpha \in \mathscr {L}_{\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}}$
. Then there is
$\alpha \in \mathscr {L}_{\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}}$
. Then there is
![]() $\alpha ^*$
where
$\alpha ^*$
where
![]() $\neg$
does not occur at all s.t.
$\neg$
does not occur at all s.t.
![]() $\alpha ^*$
is
$\alpha ^*$
is
![]() $\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}$
-valid iff
$\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}$
-valid iff
![]() $\alpha$
is
$\alpha$
is
![]() $\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}$
-valid.
$\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}$
-valid.
Definition 61 (
![]() $\mathsf {Pr}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}_{\mathbf {S5}}$
: language and semantics). The language is generated by the following grammar.
$\mathsf {Pr}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}_{\mathbf {S5}}$
: language and semantics). The language is generated by the following grammar.
A
![]() $\mathsf {Pr}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}_{\mathbf {S5}}$
-model is a tuple
$\mathsf {Pr}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}_{\mathbf {S5}}$
-model is a tuple
![]() $\mathbb {M}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}_{\pi _1,\pi _2}=\langle W,R_1,R_2,v^+,v^-,\pi _1,\pi _2,e_1,e_2\rangle$
s.t.
$\mathbb {M}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}_{\pi _1,\pi _2}=\langle W,R_1,R_2,v^+,v^-,\pi _1,\pi _2,e_1,e_2\rangle$
s.t.
-
•
 $\langle W,R_1,R_2,v^+,v^-,\pi _1,\pi _2\rangle$
is a
$\langle W,R_1,R_2,v^+,v^-,\pi _1,\pi _2\rangle$
is a
 $\mathsf {BD}$
probabilistic Kripke model with two relations and two measures;
$\mathsf {BD}$
probabilistic Kripke model with two relations and two measures;
-
•
 $e_1$
and
$e_1$
and
 $e_2$
are
$e_2$
are
 $\mathsf {N}{\mathsf {\unicode {x0141}}}$
valuations induced by
$\mathsf {N}{\mathsf {\unicode {x0141}}}$
valuations induced by
 $\pi _1$
and
$\pi _1$
and
 $\pi _2$
:
$\pi _2$
:-
–
 $e_1(\mathsf {Pr}_1\heartsuit _1\phi )=\pi _1(|\heartsuit _1\phi |^+)$
,
$e_1(\mathsf {Pr}_1\heartsuit _1\phi )=\pi _1(|\heartsuit _1\phi |^+)$
,
 $e_2(\mathsf {Pr}_1\heartsuit _1\phi )=\pi _1(|\heartsuit _1\phi |^-)$
with
$e_2(\mathsf {Pr}_1\heartsuit _1\phi )=\pi _1(|\heartsuit _1\phi |^-)$
with
 $\heartsuit \in \{\Box, \lozenge \}$
;
$\heartsuit \in \{\Box, \lozenge \}$
; -
–
 $e_1(\mathsf {Pr}_2\heartsuit _2\phi )=\pi _2(|\heartsuit _2\phi |^+)$
,
$e_1(\mathsf {Pr}_2\heartsuit _2\phi )=\pi _2(|\heartsuit _2\phi |^+)$
,
 $e_2(\mathsf {Pr}_2\heartsuit _2\phi )=\pi _2(|\heartsuit _2\phi |^-)$
with
$e_2(\mathsf {Pr}_2\heartsuit _2\phi )=\pi _2(|\heartsuit _2\phi |^-)$
with
 $\heartsuit \in \{\lozenge, \Box \}$
;
$\heartsuit \in \{\lozenge, \Box \}$
; -
– values of complex
 $\mathscr {L}_{\mathsf {Pr}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}_{\mathbf {S5}}}$
-formulas are computed via Definition 56
.
$\mathscr {L}_{\mathsf {Pr}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}_{\mathbf {S5}}}$
-formulas are computed via Definition 56
.
-
We say that
![]() $\alpha$
is
$\alpha$
is
![]() ${{\mathsf{Pr}}^{\mathsf{N}{\unicode {x0141}}}_{\mathbf{S5}}}$
-valid iff
${{\mathsf{Pr}}^{\mathsf{N}{\unicode {x0141}}}_{\mathbf{S5}}}$
-valid iff
![]() $e_1(\alpha)=1$
in all
$e_1(\alpha)=1$
in all
![]() ${{\mathsf{Pr}}^{\mathsf{N}{\unicode {x0141}}}_{\mathbf{S5}}}$
-models. A set of formulas
${{\mathsf{Pr}}^{\mathsf{N}{\unicode {x0141}}}_{\mathbf{S5}}}$
-models. A set of formulas
![]() $\Gamma$
entails
$\Gamma$
entails
![]() $\alpha$
(
$\alpha$
(
![]() $\Gamma\models_{\mathsf{Pr}^{(\triangle,\rightarrow)}_{\mathbf{S5}}}\alpha$
) iff there is no
$\Gamma\models_{\mathsf{Pr}^{(\triangle,\rightarrow)}_{\mathbf{S5}}}\alpha$
) iff there is no
![]() ${{\mathsf{Pr}}^{\mathsf{N}{\unicode {x0141}}}_{\mathbf{S5}}}$
-model s.t.
${{\mathsf{Pr}}^{\mathsf{N}{\unicode {x0141}}}_{\mathbf{S5}}}$
-model s.t.
![]() $e(\gamma)=1$
for all
$e(\gamma)=1$
for all
![]() $\gamma\in\Gamma$
but
$\gamma\in\Gamma$
but
![]() $e(\alpha)\neq 1$
.
$e(\alpha)\neq 1$
.
5.2 Embedding of belief logics into probabilistic logics
Theorem52 shows that beliefs can be represented as probabilities of modal formulas. In this section, we use this result to prove that we can faithfully embed
![]() $\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
and
$\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
and
![]() $\mathsf {Bel}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}$
into
$\mathsf {Bel}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}$
into
![]() $\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}$
and
$\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}$
and
![]() $\mathsf {Pr}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}_{\mathbf {S5}}$
. To simplify the presentation, observe that all
$\mathsf {Pr}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}_{\mathbf {S5}}$
. To simplify the presentation, observe that all
![]() $\mathscr {L}_{\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle }$
- and
$\mathscr {L}_{\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle }$
- and
![]() $\mathscr {L}_{\mathsf {Bel}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}}$
-formulas can be transformed into an outer-
$\mathscr {L}_{\mathsf {Bel}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}}$
-formulas can be transformed into an outer-
![]() $\neg$
-free form since
$\neg$
-free form since
![]() ${\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}$
and
${\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}$
and
![]() $\mathsf {N}{\mathsf {\unicode {x0141}}}$
permit
$\mathsf {N}{\mathsf {\unicode {x0141}}}$
permit
![]() $\mathsf {NNF}$
’s and since the following holds.
$\mathsf {NNF}$
’s and since the following holds.
 \begin{align*} \begin{array}{l@{\quad\quad}l@{\qquad\qquad\qquad \qquad}l}e(\neg {\mathsf {B}}\phi )=e({\mathsf {B}}\neg \phi )& & {(\text{ in } \mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle)}\\ e(\neg {\mathsf {B}}\phi )=e(\mathsf {Pl}\neg \phi )& e(\neg \mathsf {Pl}\phi )=e({\mathsf {B}}\neg \phi ) & {(\text{ in } \mathsf {Bel}^{\mathsf {N}{\mathsf {\unicode {x0141}}}})} \end{array} \end{align*}
\begin{align*} \begin{array}{l@{\quad\quad}l@{\qquad\qquad\qquad \qquad}l}e(\neg {\mathsf {B}}\phi )=e({\mathsf {B}}\neg \phi )& & {(\text{ in } \mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle)}\\ e(\neg {\mathsf {B}}\phi )=e(\mathsf {Pl}\neg \phi )& e(\neg \mathsf {Pl}\phi )=e({\mathsf {B}}\neg \phi ) & {(\text{ in } \mathsf {Bel}^{\mathsf {N}{\mathsf {\unicode {x0141}}}})} \end{array} \end{align*}
Definition 62 (Embedding of
![]() $\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
into
$\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
into
![]() $\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}$
). Let
$\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}$
). Let
![]() $\alpha \in \mathscr {L}_{\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle }$
be outer-
$\alpha \in \mathscr {L}_{\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle }$
be outer-
![]() $\neg$
-free, we define
$\neg$
-free, we define
![]() $\alpha ^\boxplus$
and
$\alpha ^\boxplus$
and
![]() $\alpha ^\boxminus$
as follows.
$\alpha ^\boxminus$
as follows.
 \begin{align*} ({\mathsf {B}}\phi )^\boxplus &=\mathsf {Pr}(\Box \phi )&({\mathsf {B}}\phi )^\boxminus &=\mathsf {Pr}(\Box \neg \phi )\\ (\triangle \beta )^\boxplus &=\triangle (\beta ^\boxplus )&(\triangle \beta )^\boxminus &={\sim }\triangle {\sim }(\beta ^\boxminus )\\ ({\sim }\beta )^\boxplus &={\sim }(\beta ^\boxplus )&({\sim }\beta )^\boxminus &={\sim }(\beta ^\boxminus )\\ (\beta \rightarrow \gamma )^\boxplus &=\beta ^\boxplus \rightarrow \gamma ^\boxplus &(\beta \rightarrow \gamma )^\boxminus &=\gamma ^\boxminus \ominus \beta ^\boxminus \end{align*}
\begin{align*} ({\mathsf {B}}\phi )^\boxplus &=\mathsf {Pr}(\Box \phi )&({\mathsf {B}}\phi )^\boxminus &=\mathsf {Pr}(\Box \neg \phi )\\ (\triangle \beta )^\boxplus &=\triangle (\beta ^\boxplus )&(\triangle \beta )^\boxminus &={\sim }\triangle {\sim }(\beta ^\boxminus )\\ ({\sim }\beta )^\boxplus &={\sim }(\beta ^\boxplus )&({\sim }\beta )^\boxminus &={\sim }(\beta ^\boxminus )\\ (\beta \rightarrow \gamma )^\boxplus &=\beta ^\boxplus \rightarrow \gamma ^\boxplus &(\beta \rightarrow \gamma )^\boxminus &=\gamma ^\boxminus \ominus \beta ^\boxminus \end{align*}
Definition 63 (Embedding of
![]() $\mathsf {Bel}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}$
into
$\mathsf {Bel}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}$
into
![]() $\mathsf {Pr}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}_{\mathbf {S5}}$
). Let
$\mathsf {Pr}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}_{\mathbf {S5}}$
). Let
![]() $\alpha \in \mathscr {L}_{\mathsf {Bel}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}}$
be outer-
$\alpha \in \mathscr {L}_{\mathsf {Bel}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}}$
be outer-
![]() $\neg$
-free, we define
$\neg$
-free, we define
![]() $\alpha ^{\Box, \lozenge }$
as follows.
$\alpha ^{\Box, \lozenge }$
as follows.
We can now prove the following statement.
Theorem 64.
-
1.
 $\alpha \in \mathscr {L}_{\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle }$
is
$\alpha \in \mathscr {L}_{\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle }$
is
 $\mathsf {Bel}^{\mathsf {\unicode {x0141}}}_\triangle$
-valid iff (a)
$\mathsf {Bel}^{\mathsf {\unicode {x0141}}}_\triangle$
-valid iff (a)
 $e_1(\alpha ^\boxplus )=1$
in every
$e_1(\alpha ^\boxplus )=1$
in every
 $\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}$
-model and (b)
$\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}$
-model and (b)
 $e_1(\alpha ^\boxminus )=0$
in every
$e_1(\alpha ^\boxminus )=0$
in every
 $\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}$
-model.
$\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}$
-model.
-
2.
 $\alpha \in \mathscr {L}_{\mathsf {Bel}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}}$
is
$\alpha \in \mathscr {L}_{\mathsf {Bel}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}}$
is
 $\mathsf {Bel}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}$
-valid iff
$\mathsf {Bel}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}$
-valid iff
 $\alpha ^{\Box, \lozenge }$
is
$\alpha ^{\Box, \lozenge }$
is
 $\mathsf {Pr}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}_{\mathbf {S5}}$
-valid.
$\mathsf {Pr}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}_{\mathbf {S5}}$
-valid.
Proof.
We begin with (1). Consider the ‘only if’ direction: we assume that either (i)
![]() $e_1(\alpha ^\boxplus )=x\lt 1$
in some
$e_1(\alpha ^\boxplus )=x\lt 1$
in some
![]() $\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}$
-model or (ii)
$\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}$
-model or (ii)
![]() $e_1(\alpha ^\boxminus )=y\gt 0$
in some
$e_1(\alpha ^\boxminus )=y\gt 0$
in some
![]() $\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}$
-model. We prove by induction that in this case, there are some
$\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}$
-model. We prove by induction that in this case, there are some
![]() $\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
-models where
$\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
-models where
![]() $e'_1(\alpha )=x$
or
$e'_1(\alpha )=x$
or
![]() $e'_2(\alpha )=y$
, respectively.
$e'_2(\alpha )=y$
, respectively.
Let
![]() $\alpha ^\boxplus =\mathsf {Pr}(\Box \phi )$
and
$\alpha ^\boxplus =\mathsf {Pr}(\Box \phi )$
and
![]() $e_1(\mathsf {Pr}(\Box \phi ))=x\lt 1$
. This means that
$e_1(\mathsf {Pr}(\Box \phi ))=x\lt 1$
. This means that
![]() $\pi (|\mathsf {Pr}(\Box \phi )|^+)=x$
. Using Remark 51, we obtain that there is a belief function
$\pi (|\mathsf {Pr}(\Box \phi )|^+)=x$
. Using Remark 51, we obtain that there is a belief function
![]() $\texttt {bel}$
s.t.
$\texttt {bel}$
s.t.
![]() ${\texttt {bel}}(|\phi |^+)=x\lt 1$
. Thus,
${\texttt {bel}}(|\phi |^+)=x\lt 1$
. Thus,
![]() $e^{\texttt {bel}}_1({\mathsf {B}}\phi )=x\lt 1$
for the evaluation
$e^{\texttt {bel}}_1({\mathsf {B}}\phi )=x\lt 1$
for the evaluation
![]() $e^{\texttt {bel}}_1$
induced by
$e^{\texttt {bel}}_1$
induced by
![]() $\texttt {bel}$
, as required. The induction steps can be obtained by a simple application of the induction hypothesis since
$\texttt {bel}$
, as required. The induction steps can be obtained by a simple application of the induction hypothesis since
![]() $\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}$
and
$\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}$
and
![]() $\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
use
$\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
use
![]() ${\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}$
as their outer-layer logic. Thus, (i) is tackled.
${\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}$
as their outer-layer logic. Thus, (i) is tackled.
For (ii), we proceed similarly. Let
![]() $\alpha ^{\boxminus }=\mathsf {Pr}(\Box \neg \phi )=y\gt 0$
. Again, we obtain that there is a belief function
$\alpha ^{\boxminus }=\mathsf {Pr}(\Box \neg \phi )=y\gt 0$
. Again, we obtain that there is a belief function
![]() $\texttt {bel}$
s.t.
$\texttt {bel}$
s.t.
![]() ${\texttt {bel}}(|\neg \phi |^+)=x\gt 0$
(i.e.,
${\texttt {bel}}(|\neg \phi |^+)=x\gt 0$
(i.e.,
![]() ${\texttt {bel}}(|\phi |^-)=y\gt 0$
). Hence,
${\texttt {bel}}(|\phi |^-)=y\gt 0$
). Hence,
![]() $e^{\texttt {bel}}_2({\mathsf {B}}\phi )=x\gt 0$
for the evaluation induced by
$e^{\texttt {bel}}_2({\mathsf {B}}\phi )=x\gt 0$
for the evaluation induced by
![]() $\texttt {bel}$
. The cases of propositional connectives can be tackled similarly, so, we only consider
$\texttt {bel}$
. The cases of propositional connectives can be tackled similarly, so, we only consider
![]() $\alpha ^\boxminus =\gamma ^\boxminus \ominus \beta ^\boxminus$
. Let
$\alpha ^\boxminus =\gamma ^\boxminus \ominus \beta ^\boxminus$
. Let
![]() $e_1(\gamma ^\boxminus \ominus \beta ^\boxminus )=y\gt 0$
. Thus,
$e_1(\gamma ^\boxminus \ominus \beta ^\boxminus )=y\gt 0$
. Thus,
![]() $z\!=\!e_1(\gamma ^\boxminus )\!\gt \!e_1(\beta ^\boxminus )\!=\!z'$
with
$z\!=\!e_1(\gamma ^\boxminus )\!\gt \!e_1(\beta ^\boxminus )\!=\!z'$
with
![]() $z\!-\!z'\!=\!y$
. Applying the induction hypothesis, we have that
$z\!-\!z'\!=\!y$
. Applying the induction hypothesis, we have that
![]() $e'_2(\gamma )\!=\!z$
,
$e'_2(\gamma )\!=\!z$
,
![]() $e'_2(\beta )\!=\!z'$
, and
$e'_2(\beta )\!=\!z'$
, and
![]() $z\!-\!z'\!=\!y$
. Hence,
$z\!-\!z'\!=\!y$
. Hence,
![]() $e'_2(\beta \rightarrow \gamma )=y\gt 0$
.
$e'_2(\beta \rightarrow \gamma )=y\gt 0$
.
Let us now deal with the ‘if’ direction. Assume that
![]() $\alpha$
is not
$\alpha$
is not
![]() $\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
-valid,
$\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
-valid,
![]() $\mathsf {Bel}^{\mathsf {\unicode {x0141}}^2}_\triangle$
-model where
$\mathsf {Bel}^{\mathsf {\unicode {x0141}}^2}_\triangle$
-model where
![]() $e_1(\alpha )=x\lt 1$
or (ii) there is a model where
$e_1(\alpha )=x\lt 1$
or (ii) there is a model where
![]() $e_2(\alpha )=y\gt 0$
. We prove by induction that there is where
$e_2(\alpha )=y\gt 0$
. We prove by induction that there is where
![]() $e_1(\alpha )=x\lt 1$
or (ii) there is a model where
$e_1(\alpha )=x\lt 1$
or (ii) there is a model where
![]() $e_2(\alpha )=y\gt 0$
. We prove by induction that there is a
$e_2(\alpha )=y\gt 0$
. We prove by induction that there is a
![]() $\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}$
-model s.t.
$\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}$
-model s.t.
![]() $e'_1(\alpha ^\boxplus )=x\lt 1$
or
$e'_1(\alpha ^\boxplus )=x\lt 1$
or
![]() $e'_1(\alpha ^\boxminus )=y\gt 0$
.
$e'_1(\alpha ^\boxminus )=y\gt 0$
.
First, if
![]() $\alpha ={\mathsf {B}}\phi$
and
$\alpha ={\mathsf {B}}\phi$
and
![]() $e_1({\mathsf {B}}\phi )=x\lt 1$
in some
$e_1({\mathsf {B}}\phi )=x\lt 1$
in some
![]() $\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
-model, then we have that there is a
$\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
-model, then we have that there is a
![]() $\mathsf {BD}$
$\mathsf {BD}$
![]() $\texttt {bel}$
-model s.t.
$\texttt {bel}$
-model s.t.
![]() ${\texttt {bel}}(|\phi |^+)=x$
. Hence, by Theorem52, there is a
${\texttt {bel}}(|\phi |^+)=x$
. Hence, by Theorem52, there is a
![]() $\mathsf {BD}$
probabilistic Kripke model s.t.
$\mathsf {BD}$
probabilistic Kripke model s.t.
![]() $\pi (|\Box \phi |^+)=x$
, and thus,
$\pi (|\Box \phi |^+)=x$
, and thus,
![]() $e^\pi _1(\mathsf {Pr}(\Box \phi ))=x\lt 1$
for the induced valuation
$e^\pi _1(\mathsf {Pr}(\Box \phi ))=x\lt 1$
for the induced valuation
![]() $e^\pi _1$
. In the second case, we have
$e^\pi _1$
. In the second case, we have
![]() $\mathsf {Bel}^{\mathsf {\unicode {x0141}}^2}_\triangle$
-model. Thus,
$\mathsf {Bel}^{\mathsf {\unicode {x0141}}^2}_\triangle$
-model. Thus,
![]() ${\texttt {bel}}(|\phi |^-)=y$
which is equivalent to
${\texttt {bel}}(|\phi |^-)=y$
which is equivalent to
![]() ${\texttt {bel}}(|\neg \phi |^+)=x$
. Again, applying Theorem52, we obtain that there is a probabilistic Kripke model with
${\texttt {bel}}(|\neg \phi |^+)=x$
. Again, applying Theorem52, we obtain that there is a probabilistic Kripke model with
![]() $\pi (|\Box \neg \phi |^+)=y\gt 0$
. Hence,
$\pi (|\Box \neg \phi |^+)=y\gt 0$
. Hence,
![]() $e^\pi _1(\mathsf {Pr}(\Box \neg \phi ))=y\gt 0$
, as required. The cases of propositional connectives can be obtained by simple applications of the induction hypothesis as in the ‘only if’ direction. hypothesis as in the ‘only if’ direction.
$e^\pi _1(\mathsf {Pr}(\Box \neg \phi ))=y\gt 0$
, as required. The cases of propositional connectives can be obtained by simple applications of the induction hypothesis as in the ‘only if’ direction. hypothesis as in the ‘only if’ direction.
(2) can be shown similarly. Assume that
![]() $e_1(\alpha ^{\Box, \lozenge })=x\lt 1$
in some
$e_1(\alpha ^{\Box, \lozenge })=x\lt 1$
in some
![]() $\mathsf {Pr}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}_{\mathbf {S5}}$
-model. Applying Remark 51, one can show by induction that there is a
$\mathsf {Pr}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}_{\mathbf {S5}}$
-model. Applying Remark 51, one can show by induction that there is a
![]() $\mathsf {Bel}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}$
-model with
$\mathsf {Bel}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}$
-model with
![]() $e'_1(\alpha )=x$
. Conversely, using Theorem52 one obtains that if
$e'_1(\alpha )=x$
. Conversely, using Theorem52 one obtains that if
![]() $\alpha$
is not
$\alpha$
is not
![]() $\mathsf {Bel}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}$
-valid, then
$\mathsf {Bel}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}$
-valid, then
![]() $\alpha$
is not
$\alpha$
is not
![]() $\mathsf {Pr}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}_{\mathbf {S5}}$
-valid either.
$\mathsf {Pr}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}_{\mathbf {S5}}$
-valid either.
One can show that both translations are linear.
Lemma 65.
-
1. Let
 $\alpha \in \mathscr {L}_{\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle }$
. Then
$\alpha \in \mathscr {L}_{\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle }$
. Then
 $\unicode{x1D4C1}(\alpha ^\boxplus )={\mathscr {O}}(\unicode{x1D4C1}(\alpha ))$
and
$\unicode{x1D4C1}(\alpha ^\boxplus )={\mathscr {O}}(\unicode{x1D4C1}(\alpha ))$
and
 $\unicode{x1D4C1}(\alpha ^\boxminus )={\mathscr {O}}(\unicode{x1D4C1}(\alpha ))$
.
$\unicode{x1D4C1}(\alpha ^\boxminus )={\mathscr {O}}(\unicode{x1D4C1}(\alpha ))$
. -
2. Let
 $\beta \in \mathscr {L}_{\mathsf {Bel}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}}$
. Then
$\beta \in \mathscr {L}_{\mathsf {Bel}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}}$
. Then
 $\unicode{x1D4C1}(\beta ^{\Box, \lozenge })={\mathscr {O}}(\unicode{x1D4C1}(\alpha ))$
.
$\unicode{x1D4C1}(\beta ^{\Box, \lozenge })={\mathscr {O}}(\unicode{x1D4C1}(\alpha ))$
.
Proof. Analogously to Lemma 26
5.3 Complexity
Theorem64 and Lemma 65 give us a polynomial reduction from validity in
![]() $\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
and
$\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
and
![]() $\mathsf {Bel}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}$
to
$\mathsf {Bel}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}$
to
![]() $\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}$
and
$\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}$
and
![]() $\mathsf {Pr}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}_{\mathbf {S5}}$
. It is, thus, sufficient to prove that
$\mathsf {Pr}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}_{\mathbf {S5}}$
. It is, thus, sufficient to prove that
![]() $\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}$
-validity and
$\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}$
-validity and
![]() $\mathsf {Pr}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}_{\mathbf {S5}}$
-validity are
$\mathsf {Pr}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}_{\mathbf {S5}}$
-validity are
![]() $\mathsf {coNP}$
-complete. Recall that in the proof of Theorem42, we used canonical models of
$\mathsf {coNP}$
-complete. Recall that in the proof of Theorem42, we used canonical models of
![]() $\mathsf {BD}$
built over the powerset of all literals occurring in a formula which we encoded via
$\mathsf {BD}$
built over the powerset of all literals occurring in a formula which we encoded via
![]() $u_v$
variables. We define canonical models for
$u_v$
variables. We define canonical models for
![]() $\mathsf {BD}$
with
$\mathsf {BD}$
with
![]() $\mathbf {S5}$
modalities.
$\mathbf {S5}$
modalities.
Definition 66 (Clusters). Let
![]() $\mathfrak {M}=\langle W,R,v^+,v^-\rangle$
be a
$\mathfrak {M}=\langle W,R,v^+,v^-\rangle$
be a
![]() $\mathsf {BD}$
Kripke model. A cluster is any subset
$\mathsf {BD}$
Kripke model. A cluster is any subset
![]() $X\subseteq W$
closed under
$X\subseteq W$
closed under
![]() $R$
. That is, if
$R$
. That is, if
![]() $w\in X$
and
$w\in X$
and
![]() $wRw'$
, then
$wRw'$
, then
![]() $w'\in X$
.
$w'\in X$
.
Definition 67 (Bisimilarity). Two
![]() $\mathsf {BD}$
Kripke models
$\mathsf {BD}$
Kripke models
![]() $\mathfrak {M}=\langle W,R,v^+,v^-\rangle$
and
$\mathfrak {M}=\langle W,R,v^+,v^-\rangle$
and
![]() $\mathfrak {M}'=\langle W',R',v^{'+},v^{'-}\rangle$
are called bisimilar (denoted
$\mathfrak {M}'=\langle W',R',v^{'+},v^{'-}\rangle$
are called bisimilar (denoted
![]() $\mathfrak {M}\simeq \mathfrak {M}'$
) if there is a relation
$\mathfrak {M}\simeq \mathfrak {M}'$
) if there is a relation
![]() ${\mathscr {Z}}\subseteq W\times W'$
s.t. for every
${\mathscr {Z}}\subseteq W\times W'$
s.t. for every
![]() $p\in \texttt {Prop}$
,
$p\in \texttt {Prop}$
,
![]() $x\in W$
, and
$x\in W$
, and
![]() $x'\in W$
, the following conditions hold:
$x'\in W$
, the following conditions hold:
-
1.
 $\mathfrak {M},x\vDash ^+p$
iff
$\mathfrak {M},x\vDash ^+p$
iff
 $\mathfrak {M}',x'\vDash ^+p$
and
$\mathfrak {M}',x'\vDash ^+p$
and
 $\mathfrak {M},x\vDash ^-p$
iff
$\mathfrak {M},x\vDash ^-p$
iff
 $\mathfrak {M}',x'\vDash ^-p$
for every
$\mathfrak {M}',x'\vDash ^-p$
for every
 $x\in W$
and
$x\in W$
and
 $x'\in W'$
s.t.
$x'\in W'$
s.t.
 $x{\mathscr {Z}} x'$
;
$x{\mathscr {Z}} x'$
; -
2. if
 $wRx$
and
$wRx$
and
 $w{\mathscr {Z}} w'$
, then there is
$w{\mathscr {Z}} w'$
, then there is
 $x'\in W'$
s.t.
$x'\in W'$
s.t.
 $w'R'x'$
and
$w'R'x'$
and
 $x{\mathscr {Z}} x'$
;
$x{\mathscr {Z}} x'$
; -
3. if
 $w'R'x'$
and
$w'R'x'$
and
 $w{\mathscr {Z}} w'$
, then there is
$w{\mathscr {Z}} w'$
, then there is
 $x\in X$
s.t.
$x\in X$
s.t.
 $wRx$
and
$wRx$
and
 $x{\mathscr {Z}} x'$
.
$x{\mathscr {Z}} x'$
.
Bisimilarity of Kripke models with two relations are defined similarly but conditions (2) and (3) have to hold for both relations.
The following statement is straightforward to establish.
Proposition 68.
Let
![]() $\mathfrak {M}\simeq \mathfrak {M}'$
,
$\mathfrak {M}\simeq \mathfrak {M}'$
,
![]() $\mathscr {Z}$
be the bisimilarity relation, and
$\mathscr {Z}$
be the bisimilarity relation, and
![]() $w{\mathscr {Z}} w'$
. Then for every
$w{\mathscr {Z}} w'$
. Then for every
![]() $\sigma$
over
$\sigma$
over
![]() $\{\neg, \wedge, \vee, \Box, \lozenge \}$
, it follows that
$\{\neg, \wedge, \vee, \Box, \lozenge \}$
, it follows that
Definition 69 (Canonical model for
![]() $\mathsf {BD}$
with
$\mathsf {BD}$
with
![]() $\mathbf {S5}$
$\mathbf {S5}$
![]() $\Box$
). Let
$\Box$
). Let
![]() $\Gamma =\{\Box \phi _1,\ldots \Box \phi _m\}$
and
$\Gamma =\{\Box \phi _1,\ldots \Box \phi _m\}$
and
![]() $\mathsf {Lit}[\Gamma ]=\{l_1,\ldots, l_n\}$
. The canonical model of
$\mathsf {Lit}[\Gamma ]=\{l_1,\ldots, l_n\}$
. The canonical model of
![]() $\Gamma$
is the disjoint union of all pairwise non-bisimilar clusters on
$\Gamma$
is the disjoint union of all pairwise non-bisimilar clusters on
![]() $2^{\mathsf {Lit}[\Gamma ]}$
, that is the following structure:
$2^{\mathsf {Lit}[\Gamma ]}$
, that is the following structure:
with valuations
![]() $v^+$
and
$v^+$
and
![]() $v^-$
defined as below:
$v^-$
defined as below:
Importantly, as the next statements show, we can prove a version of the small model property for probabilities of
![]() $\Box \phi$
and
$\Box \phi$
and
![]() $\lozenge \phi$
formulas where
$\lozenge \phi$
formulas where
![]() $\phi \in \mathscr {L}_{\mathsf {BD}}$
. Namely, we show that in arbitrary models, we only need clusters whose size is linearly bounded by the number of formulas and that we can assume the measure to be positive only on clusters with linearly bounded size in
$\phi \in \mathscr {L}_{\mathsf {BD}}$
. Namely, we show that in arbitrary models, we only need clusters whose size is linearly bounded by the number of formulas and that we can assume the measure to be positive only on clusters with linearly bounded size in
![]() $\mathfrak {M}^{\mathsf {\mathsf {BD}\mathbf {{S5}}}}$
.
$\mathfrak {M}^{\mathsf {\mathsf {BD}\mathbf {{S5}}}}$
.
Lemma 70 (Small model property). Let
![]() $\mathfrak {M}=\langle W,R,v^+,v^-,\pi \rangle$
be a
$\mathfrak {M}=\langle W,R,v^+,v^-,\pi \rangle$
be a
![]() $\mathsf {BD}$
probabilistic Kripke model,
$\mathsf {BD}$
probabilistic Kripke model,
![]() $\phi _1,\ldots, \phi _m\subseteq \mathscr {L}_{\mathsf {BD}}$
,
$\phi _1,\ldots, \phi _m\subseteq \mathscr {L}_{\mathsf {BD}}$
,
![]() $1\leq k\leq m$
and
$1\leq k\leq m$
and
![]() $\Gamma =\{\Box \phi _i\mid i\leq k\}\cup \{\lozenge \phi _i\mid k\lt i\leq m\}$
. Then there is a model
$\Gamma =\{\Box \phi _i\mid i\leq k\}\cup \{\lozenge \phi _i\mid k\lt i\leq m\}$
. Then there is a model
![]() $\mathfrak {M}_{\mathsf {s}}=\langle W_{\mathsf {s}},R_{\mathsf {s}},v^+_{\mathsf {s}},v^-_{\mathsf {s}},\pi _{\mathsf {s}}\rangle$
s.t.
$\mathfrak {M}_{\mathsf {s}}=\langle W_{\mathsf {s}},R_{\mathsf {s}},v^+_{\mathsf {s}},v^-_{\mathsf {s}},\pi _{\mathsf {s}}\rangle$
s.t.
![]() $W_{\mathsf {s}}\subseteq W$
,
$W_{\mathsf {s}}\subseteq W$
,
![]() $R_{\mathsf {s}}=R_{|W_{\mathsf {s}}}$
,
$R_{\mathsf {s}}=R_{|W_{\mathsf {s}}}$
,
![]() $v^+_{\mathsf {s}}$
and
$v^+_{\mathsf {s}}$
and
![]() $v^-_{\mathsf {s}}$
are restrictions of
$v^-_{\mathsf {s}}$
are restrictions of
![]() $v^+$
and
$v^+$
and
![]() $v^-$
on
$v^-$
on
![]() $W_{\mathsf {s}}$
, every cluster of
$W_{\mathsf {s}}$
, every cluster of
![]() $\mathfrak {M}_{\mathsf {s}}$
contains at most
$\mathfrak {M}_{\mathsf {s}}$
contains at most
![]() $2m+1$
states, and for every
$2m+1$
states, and for every
![]() $\sigma \in \Gamma$
, it holds that
$\sigma \in \Gamma$
, it holds that
Proof.
Observe that
![]() $\mathfrak {M}$
is a disjoint union of all its clusters and that for every
$\mathfrak {M}$
is a disjoint union of all its clusters and that for every
![]() $\sigma \in \Gamma$
and every cluster
$\sigma \in \Gamma$
and every cluster
![]() $X\subseteq W$
the following two statements hold:
$X\subseteq W$
the following two statements hold:
We show how to remove ‘redundant’ states from clusters containing more than
![]() $2m+1$
states and redefine the measure accordingly.
$2m+1$
states and redefine the measure accordingly.
Now let
![]() $X$
be a cluster in
$X$
be a cluster in
![]() $W$
with more than
$W$
with more than
![]() $2m+1$
states. Let further,
$2m+1$
states. Let further,
![]() $\Phi ^\forall _X,\Phi ^\exists _X\subseteq \Gamma$
be such that
$\Phi ^\forall _X,\Phi ^\exists _X\subseteq \Gamma$
be such that
It is clear from the semantics of
![]() $\mathsf {BD}$
with
$\mathsf {BD}$
with
![]() $\mathbf {S5}$
modalities (recall Definition 50) that no matter which and how many states we remove from
$\mathbf {S5}$
modalities (recall Definition 50) that no matter which and how many states we remove from
![]() $X$
$X$
-
1. all
 $\Box$
-formulas from
$\Box$
-formulas from
 $\Phi ^\forall _X$
will remain true in every state non-removed of
$\Phi ^\forall _X$
will remain true in every state non-removed of
 $X$
while all
$X$
while all
 $\Box$
-formulas from
$\Box$
-formulas from
 $\Gamma \setminus \Phi ^\exists _X$
will remain non-false in every non-removed state of
$\Gamma \setminus \Phi ^\exists _X$
will remain non-false in every non-removed state of
 $X$
;
$X$
; -
2. dually, all
 $\lozenge$
-formulas from
$\lozenge$
-formulas from
 $\Phi ^\forall _X$
will remain false in every state non-removed of
$\Phi ^\forall _X$
will remain false in every state non-removed of
 $X$
while all
$X$
while all
 $\lozenge$
-formulas from
$\lozenge$
-formulas from
 $\Gamma \setminus \Phi ^\exists _X$
will remain non-true in every non-removed state of
$\Gamma \setminus \Phi ^\exists _X$
will remain non-true in every non-removed state of
 $X$
.
$X$
.
Let us now show how to construct a cluster
![]() $X_{\mathsf {s}}$
containing at most
$X_{\mathsf {s}}$
containing at most
![]() $2m+1$
states s.t.
$2m+1$
states s.t.
![]() $\Phi ^\forall _X=\Phi ^\forall _{X_{\mathsf {s}}}$
and
$\Phi ^\forall _X=\Phi ^\forall _{X_{\mathsf {s}}}$
and
![]() $\Phi ^\exists _X=\Phi ^\exists _{X_{\mathsf {s}}}$
.
$\Phi ^\exists _X=\Phi ^\exists _{X_{\mathsf {s}}}$
.
First, we take any state
![]() $x\in X$
. Clearly, all
$x\in X$
. Clearly, all
![]() $\Box$
- and
$\Box$
- and
![]() $\lozenge$
-formulas from
$\lozenge$
-formulas from
![]() $\Phi ^\forall _X$
will remain true (or, respectively, false) in
$\Phi ^\forall _X$
will remain true (or, respectively, false) in
![]() $x$
. Likewise,
$x$
. Likewise,
![]() $\Box$
-formulas from
$\Box$
-formulas from
![]() $\Gamma \setminus \Phi ^\exists _X$
will remain non-false in
$\Gamma \setminus \Phi ^\exists _X$
will remain non-false in
![]() $x$
and
$x$
and
![]() $\lozenge$
-formulas from
$\lozenge$
-formulas from
![]() $\Gamma \setminus \Phi ^\exists _X$
will remain non-true.
$\Gamma \setminus \Phi ^\exists _X$
will remain non-true.
Now let
![]() $\Box \phi \in \Phi ^\exists _X$
be a formula s.t. it was false in
$\Box \phi \in \Phi ^\exists _X$
be a formula s.t. it was false in
![]() $X$
but became non-false in
$X$
but became non-false in
![]() $x$
. This means that there was some
$x$
. This means that there was some
![]() $x_{\Box \phi }\in X$
s.t.
$x_{\Box \phi }\in X$
s.t.
![]() $\mathfrak {M},x_{\Box \phi }\vDash ^-\phi$
but
$\mathfrak {M},x_{\Box \phi }\vDash ^-\phi$
but
![]() $x_{\Box \phi }\neq x$
. We set
$x_{\Box \phi }\neq x$
. We set
![]() $X_{\Box \phi }=\{x,x_{\Box \phi }\}$
. It is clear that
$X_{\Box \phi }=\{x,x_{\Box \phi }\}$
. It is clear that
![]() $\Box \phi$
is false in
$\Box \phi$
is false in
![]() $X_{\Box \phi }$
but all other formulas remained true or non-false because they were true or non-false in
$X_{\Box \phi }$
but all other formulas remained true or non-false because they were true or non-false in
![]() $X$
and
$X$
and
![]() $X_{\Box \phi }\subseteq X$
. Now we take the next formula, say,
$X_{\Box \phi }\subseteq X$
. Now we take the next formula, say,
![]() $\Box \phi '\in \Phi ^\exists _X$
that was false in
$\Box \phi '\in \Phi ^\exists _X$
that was false in
![]() $X$
but became non-false in
$X$
but became non-false in
![]() $x$
. If it is still non-false in
$x$
. If it is still non-false in
![]() $X_{\Box \phi }$
, it means that there is some
$X_{\Box \phi }$
, it means that there is some
![]() $x_{\Box \phi '}\in X\setminus X_{\Box \phi }$
s.t.
$x_{\Box \phi '}\in X\setminus X_{\Box \phi }$
s.t.
![]() $\mathfrak {M},x_{\Box \phi '}\vDash ^-\phi '$
. Thus, we set
$\mathfrak {M},x_{\Box \phi '}\vDash ^-\phi '$
. Thus, we set
![]() $X_{\Box \phi '}=X_{\Box \phi }\cup \{x_{\Box \phi '}\}$
. We repeat this procedure until we tackle all
$X_{\Box \phi '}=X_{\Box \phi }\cup \{x_{\Box \phi '}\}$
. We repeat this procedure until we tackle all
![]() $\Box$
-formulas from
$\Box$
-formulas from
![]() $\Phi ^\exists _X$
that became non-false in
$\Phi ^\exists _X$
that became non-false in
![]() $x$
. Then we do the same with
$x$
. Then we do the same with
![]() $\lozenge$
-formulas from
$\lozenge$
-formulas from
![]() $\Phi ^\exists _X$
that became non-true in
$\Phi ^\exists _X$
that became non-true in
![]() $x$
. Since there are at most
$x$
. Since there are at most
![]() $m$
formulas in
$m$
formulas in
![]() $\Phi ^\exists _X$
, we will have added at most
$\Phi ^\exists _X$
, we will have added at most
![]() $m$
states to
$m$
states to
![]() $\{x\}$
. Denote the resulting cluster
$\{x\}$
. Denote the resulting cluster
![]() $X_-$
.
$X_-$
.
After that, we do the same with
![]() $\Box$
-formulas from
$\Box$
-formulas from
![]() $\Gamma \setminus \Phi ^\forall _X$
that became true in
$\Gamma \setminus \Phi ^\forall _X$
that became true in
![]() $x$
and
$x$
and
![]() $\lozenge$
-formulas from
$\lozenge$
-formulas from
![]() $\Gamma \setminus \Phi ^\forall _X$
that became false in
$\Gamma \setminus \Phi ^\forall _X$
that became false in
![]() $x$
. This will also add at most
$x$
. This will also add at most
![]() $m$
states to
$m$
states to
![]() $X_-$
. The resulting cluster which we call
$X_-$
. The resulting cluster which we call
![]() $X_{\mathsf {s}}$
will, thus, contain at most
$X_{\mathsf {s}}$
will, thus, contain at most
![]() $2m+1$
states. Moreover, we have that
$2m+1$
states. Moreover, we have that
![]() $\Phi ^\forall _X=\Phi ^\forall _{X_{\mathsf {s}}}$
and
$\Phi ^\forall _X=\Phi ^\forall _{X_{\mathsf {s}}}$
and
![]() $\Phi ^\exists _X=\Phi ^\exists _{X_{\mathsf {s}}}$
, as required.
$\Phi ^\exists _X=\Phi ^\exists _{X_{\mathsf {s}}}$
, as required.
It remains to define
![]() $\pi _{\mathsf {s}}$
on
$\pi _{\mathsf {s}}$
on
![]() $X_{\mathsf {s}}$
. As
$X_{\mathsf {s}}$
. As
![]() $X_{\mathsf {s}}\subseteq X$
, let
$X_{\mathsf {s}}\subseteq X$
, let
![]() $X_{\mathsf {s}}=X'\cup \{x''\}$
and define
$X_{\mathsf {s}}=X'\cup \{x''\}$
and define
 \begin{align*} \pi _{\mathsf {s}}(\{x'\})&= \begin{cases} \pi (\{x'\})&\text { if }x'\in X'\\ \displaystyle \sum \limits _{y\in X\setminus X_{\mathsf {s}}}\!\!\pi (\{y\})&\text { if }x'=x'' \end{cases} \end{align*}
\begin{align*} \pi _{\mathsf {s}}(\{x'\})&= \begin{cases} \pi (\{x'\})&\text { if }x'\in X'\\ \displaystyle \sum \limits _{y\in X\setminus X_{\mathsf {s}}}\!\!\pi (\{y\})&\text { if }x'=x'' \end{cases} \end{align*}
We repeat this procedure with every cluster. It is clear that the obtained model will consist of clusters containing at most
![]() $2m+1$
states and that
$2m+1$
states and that
![]() $\pi (|\sigma |^+)=\pi _{\mathsf {s}}(|\sigma |^+)$
and
$\pi (|\sigma |^+)=\pi _{\mathsf {s}}(|\sigma |^+)$
and
![]() $\pi (|\sigma |^-)=\pi _{\mathsf {s}}(|\sigma |^-)$
for every
$\pi (|\sigma |^-)=\pi _{\mathsf {s}}(|\sigma |^-)$
for every
![]() $\sigma \in \Gamma$
, it holds that
$\sigma \in \Gamma$
, it holds that
The next statement shows that any measure assignment to formulas of the form
![]() $\Box \phi$
and
$\Box \phi$
and
![]() $\lozenge \phi$
on a given
$\lozenge \phi$
on a given
![]() $\mathsf {BD}$
probabilistic Kripke model can be transferred to a measure assignment on
$\mathsf {BD}$
probabilistic Kripke model can be transferred to a measure assignment on
![]() $\mathfrak {M}^{\mathsf {\mathsf {BD}\mathbf {{S5}}}}$
.
$\mathfrak {M}^{\mathsf {\mathsf {BD}\mathbf {{S5}}}}$
.
Theorem 71.
-
1. Let
 $\phi _1,\ldots, \phi _m\in \mathscr {L}_{\mathsf {BD}}$
,
$\phi _1,\ldots, \phi _m\in \mathscr {L}_{\mathsf {BD}}$
,
 $\Gamma =\{\Box \phi _1,\ldots \Box \phi _{l},\lozenge \phi _{l+1},\ldots, \lozenge \phi _m\}$
, and
$\Gamma =\{\Box \phi _1,\ldots \Box \phi _{l},\lozenge \phi _{l+1},\ldots, \lozenge \phi _m\}$
, and
 $\mathfrak {M}=\langle W,R,v^+,v^-,\pi \rangle$
be a probabilistic Kripke model. Then there is a probability measure
$\mathfrak {M}=\langle W,R,v^+,v^-,\pi \rangle$
be a probabilistic Kripke model. Then there is a probability measure
 $\pi ^{\mathsf {C}}$
on
$\pi ^{\mathsf {C}}$
on
 $\mathfrak {M}^{\mathsf {\mathsf {BD}\mathbf {{S5}}}}_{\Gamma }$
s.t.
$\mathfrak {M}^{\mathsf {\mathsf {BD}\mathbf {{S5}}}}_{\Gamma }$
s.t.
-
(a)
 $\pi ^{\mathsf {C}}(|\sigma |^+)=\pi (|\sigma |^+)$
and
$\pi ^{\mathsf {C}}(|\sigma |^+)=\pi (|\sigma |^+)$
and
 $\pi ^{\mathsf {C}}(|\sigma |^-)=\pi (|\sigma |^-)$
for every
$\pi ^{\mathsf {C}}(|\sigma |^-)=\pi (|\sigma |^-)$
for every
 $\sigma \in \Gamma$
;
$\sigma \in \Gamma$
; -
(b) if
 $X$
is a cluster in
$X$
is a cluster in
 $\mathfrak {M}^{\mathsf {\mathsf {BD}\mathbf {{S5}}}}_\Gamma$
s.t.
$\mathfrak {M}^{\mathsf {\mathsf {BD}\mathbf {{S5}}}}_\Gamma$
s.t.
 $|X|\gt 2m+1$
, then
$|X|\gt 2m+1$
, then
 $\pi ^{\mathsf {C}}(X)=0$
.
$\pi ^{\mathsf {C}}(X)=0$
.
-
-
2. Let
 $\{\phi _i\mid i\leq k\}\cup \{\chi _j\mid j\leq l\}\subseteq \mathscr {L}_{\mathsf {BD}}$
,
$\{\phi _i\mid i\leq k\}\cup \{\chi _j\mid j\leq l\}\subseteq \mathscr {L}_{\mathsf {BD}}$
,
 $k+l=m$
,
$k+l=m$
,
 $k'\leq k$
,
$k'\leq k$
,
 $l'\leq l$
,
$l'\leq l$
,
 $\Gamma _1=\{\Box _1\phi _i\mid i\leq k'\}\cup \{\lozenge _1\phi _i\mid k'\lt i\leq k\}$
,
$\Gamma _1=\{\Box _1\phi _i\mid i\leq k'\}\cup \{\lozenge _1\phi _i\mid k'\lt i\leq k\}$
,
 $\Gamma _2=\{\Box _2\chi _j\mid j\leq l'\}\cup \{\lozenge _2\chi _j\mid l'\lt j\leq l\}$
,
$\Gamma _2=\{\Box _2\chi _j\mid j\leq l'\}\cup \{\lozenge _2\chi _j\mid l'\lt j\leq l\}$
,
 $\Gamma =\Gamma _1\cup \Gamma _2$
, and
$\Gamma =\Gamma _1\cup \Gamma _2$
, and
 $\mathfrak {M}=\langle W,R_1,R_2,v^+,v^-,\pi _1,\pi _2\rangle$
be a probabilistic Kripke model. Then there are probability measures
$\mathfrak {M}=\langle W,R_1,R_2,v^+,v^-,\pi _1,\pi _2\rangle$
be a probabilistic Kripke model. Then there are probability measures
 $\pi ^{\mathsf {C}}_1$
and
$\pi ^{\mathsf {C}}_1$
and
 $\pi ^{\mathsf {C}}_2$
on
$\pi ^{\mathsf {C}}_2$
on
 $\mathfrak {M}^{\mathsf {\mathsf {BD}\mathbf {{S5}}}}_{\Gamma }$
s.t.
$\mathfrak {M}^{\mathsf {\mathsf {BD}\mathbf {{S5}}}}_{\Gamma }$
s.t.
-
(a)
 $\pi ^{\mathsf {C}}_1(|\sigma |^+)=\pi _1(|\sigma |^+)$
,
$\pi ^{\mathsf {C}}_1(|\sigma |^+)=\pi _1(|\sigma |^+)$
,
 $\pi ^{\mathsf {C}}_1(|\sigma |^-)=\pi _1(|\sigma |^-)$
,
$\pi ^{\mathsf {C}}_1(|\sigma |^-)=\pi _1(|\sigma |^-)$
,
 $\pi ^{\mathsf {C}}_2(|\tau |^+)=\pi _2(|\tau |^+)$
, and
$\pi ^{\mathsf {C}}_2(|\tau |^+)=\pi _2(|\tau |^+)$
, and
 $\pi ^{\mathsf {C}}_2(|\tau |^-)=\pi _2(|\tau |^-)$
for every
$\pi ^{\mathsf {C}}_2(|\tau |^-)=\pi _2(|\tau |^-)$
for every
 $\sigma \in \Gamma _1$
and
$\sigma \in \Gamma _1$
and
 $\tau \in \Gamma _2$
;
$\tau \in \Gamma _2$
; -
(b) if
 $X$
is a cluster in
$X$
is a cluster in
 $\mathfrak {M}^{\mathsf {\mathsf {BD}\mathbf {{S5}}}}_\Gamma$
s.t.
$\mathfrak {M}^{\mathsf {\mathsf {BD}\mathbf {{S5}}}}_\Gamma$
s.t.
 $|X|\gt 2m+1$
, then
$|X|\gt 2m+1$
, then
 $\pi ^{\mathsf {C}}_1(X)=\pi ^{\mathsf {C}}_2(X)=0$
.
$\pi ^{\mathsf {C}}_1(X)=\pi ^{\mathsf {C}}_2(X)=0$
.
-
Proof.
We begin with (1). As there are only
![]() $m$
formulas, it is clear that
$m$
formulas, it is clear that
![]() $\mathsf {Lit}[\Gamma ]$
is finite. We let
$\mathsf {Lit}[\Gamma ]$
is finite. We let
![]() $|\mathsf {Lit}[\Gamma ]|=k$
. Thus,
$|\mathsf {Lit}[\Gamma ]|=k$
. Thus,
![]() $\mathfrak {M}$
contains at most
$\mathfrak {M}$
contains at most
 $\displaystyle \sum \limits _{j=1}^{2^k}\binom {2^k}{j}=2^{2^k}-1$
pairwise non-bisimilar clusters (recall Definition 66 for the notion of cluster). In addition to that, using Lemma 70, we can w.l.o.g. assume that these clusters contain at most
$\displaystyle \sum \limits _{j=1}^{2^k}\binom {2^k}{j}=2^{2^k}-1$
pairwise non-bisimilar clusters (recall Definition 66 for the notion of cluster). In addition to that, using Lemma 70, we can w.l.o.g. assume that these clusters contain at most
![]() $2m+1$
states. Moreover,
$2m+1$
states. Moreover,
![]() $W$
is the disjoint union of all clusters, whence,
$W$
is the disjoint union of all clusters, whence,
![]() $\displaystyle \sum \limits _{X\text { is a\,cluster}}\!\!\!\!\!\!\!\!\pi (X)\!=\!1$
, and furthermore, for every cluster
$\displaystyle \sum \limits _{X\text { is a\,cluster}}\!\!\!\!\!\!\!\!\pi (X)\!=\!1$
, and furthermore, for every cluster
![]() $X\subseteq \mathfrak {M}$
, there is a cluster
$X\subseteq \mathfrak {M}$
, there is a cluster
![]() $X^{\mathsf {C}}\subseteq \mathfrak {M}^{\mathsf {\mathsf {BD}\mathbf {{S5}}}}_\Gamma$
s.t.
$X^{\mathsf {C}}\subseteq \mathfrak {M}^{\mathsf {\mathsf {BD}\mathbf {{S5}}}}_\Gamma$
s.t.
![]() $X\simeq X^{\mathsf {C}}$
. From here, it is clear that
$X\simeq X^{\mathsf {C}}$
. From here, it is clear that
holds for every
![]() $\sigma$
when
$\sigma$
when
![]() $w{\mathscr {Z}} w^{\mathsf {C}}$
.
$w{\mathscr {Z}} w^{\mathsf {C}}$
.
Now, recall from Definition 69 that
![]() $\mathfrak {M}^{\mathsf {\mathsf {BD}\mathbf {{S5}}}}_{\Gamma }$
is the disjoint union of all pairwise non-bisimilar clusters. Thus, we can define
$\mathfrak {M}^{\mathsf {\mathsf {BD}\mathbf {{S5}}}}_{\Gamma }$
is the disjoint union of all pairwise non-bisimilar clusters. Thus, we can define
![]() $\pi ^{\mathsf {C}}$
as follows:
$\pi ^{\mathsf {C}}$
as follows:
 \begin{align*} \pi ^{\mathsf {C}}(\{w^{\mathsf {C}}\})&=\sum \limits _{\scriptsize {\begin{matrix}w{\mathscr {Z}} w^{\mathsf {C}}\\w\!\in \!W\end{matrix}}}\pi (\{w\}) \end{align*}
\begin{align*} \pi ^{\mathsf {C}}(\{w^{\mathsf {C}}\})&=\sum \limits _{\scriptsize {\begin{matrix}w{\mathscr {Z}} w^{\mathsf {C}}\\w\!\in \!W\end{matrix}}}\pi (\{w\}) \end{align*}
It is now easy to see that
![]() $\pi ^{\mathsf {C}}(|\sigma |^+)=\pi (|\sigma |^+)$
and
$\pi ^{\mathsf {C}}(|\sigma |^+)=\pi (|\sigma |^+)$
and
![]() $\pi ^{\mathsf {C}}(|\sigma |^-)=\pi (|\sigma |^-)$
for every
$\pi ^{\mathsf {C}}(|\sigma |^-)=\pi (|\sigma |^-)$
for every
![]() $\sigma \in \Gamma$
, as required. Moreover, since
$\sigma \in \Gamma$
, as required. Moreover, since
![]() $\mathfrak {M}$
w.l.o.g. contains only clusters with at most
$\mathfrak {M}$
w.l.o.g. contains only clusters with at most
![]() $2m+1$
states, no cluster in
$2m+1$
states, no cluster in
![]() $\mathfrak {M}^{\mathsf {\mathsf {BD}\mathbf {{S5}}}}_\Gamma$
with a greater number of states has a positive measure assignment under
$\mathfrak {M}^{\mathsf {\mathsf {BD}\mathbf {{S5}}}}_\Gamma$
with a greater number of states has a positive measure assignment under
![]() $\pi ^{\mathsf {C}}$
.
$\pi ^{\mathsf {C}}$
.
The proof of (2) is similar. First, we take the mono-relational reducts of
![]() $\mathfrak {M}$
, that is, the following two models:
$\mathfrak {M}$
, that is, the following two models:
![]() $\mathfrak {M}_{R_1}=\langle W,R_1,v^+,v^-,\pi \rangle$
and
$\mathfrak {M}_{R_1}=\langle W,R_1,v^+,v^-,\pi \rangle$
and
![]() $\mathfrak {M}_{R_2}=\langle W,R_2,v^+,v^-,\pi \rangle$
. Since every formula in
$\mathfrak {M}_{R_2}=\langle W,R_2,v^+,v^-,\pi \rangle$
. Since every formula in
![]() $\Gamma$
contains only one modality and thus depends only on
$\Gamma$
contains only one modality and thus depends only on
![]() $R_1$
or only on
$R_1$
or only on
![]() $R_2$
, it is clear that the following equivalences hold for every
$R_2$
, it is clear that the following equivalences hold for every
![]() $w\in W$
,
$w\in W$
,
![]() $\sigma \in \Gamma _1$
, and
$\sigma \in \Gamma _1$
, and
![]() $\tau \in \Gamma _2$
:
$\tau \in \Gamma _2$
:
Now, it is clear that
![]() $\mathfrak {M}_{R_1}$
and
$\mathfrak {M}_{R_1}$
and
![]() $\mathfrak {M}_{R_2}$
are disjoint unions of clusters (w.r.t.
$\mathfrak {M}_{R_2}$
are disjoint unions of clusters (w.r.t.
![]() $R_1$
and
$R_1$
and
![]() $R_2$
, respectively). We can again use Lemma 70 and assume w.l.o.g. that clusters w.r.t.
$R_2$
, respectively). We can again use Lemma 70 and assume w.l.o.g. that clusters w.r.t.
![]() $R_1$
and
$R_1$
and
![]() $R_2$
contain at most
$R_2$
contain at most
![]() $2m+1$
states. Hence:
$2m+1$
states. Hence:
-
(a) for every cluster
 $X\subseteq \mathfrak {M}_{R_1}$
, there is a cluster
$X\subseteq \mathfrak {M}_{R_1}$
, there is a cluster
 $X^{\mathsf {C}}\subseteq \mathfrak {M}^{\mathsf {\mathsf {BD}\mathbf {{S5}}}}_\Gamma$
s.t.
$X^{\mathsf {C}}\subseteq \mathfrak {M}^{\mathsf {\mathsf {BD}\mathbf {{S5}}}}_\Gamma$
s.t.
 $X\simeq X^{\mathsf {C}}$
;
$X\simeq X^{\mathsf {C}}$
; -
(b) for every cluster
 $Y\subseteq \mathfrak {M}_{R_2}$
, there is a cluster
$Y\subseteq \mathfrak {M}_{R_2}$
, there is a cluster
 $Y^{\mathsf {C}}\subseteq \mathfrak {M}^{\mathsf {\mathsf {BD}\mathbf {{S5}}}}_\Gamma$
s.t.
$Y^{\mathsf {C}}\subseteq \mathfrak {M}^{\mathsf {\mathsf {BD}\mathbf {{S5}}}}_\Gamma$
s.t.
 $Y\simeq Y^{\mathsf {C}}$
.
$Y\simeq Y^{\mathsf {C}}$
.
We use
![]() ${\mathscr {Z}}_1$
and
${\mathscr {Z}}_1$
and
![]() ${\mathscr {Z}}_2$
to denote bisimilarity relations that witness (a) and (b), respectively. Now, we define
${\mathscr {Z}}_2$
to denote bisimilarity relations that witness (a) and (b), respectively. Now, we define
![]() $\pi ^{\mathsf {C}}_1$
and
$\pi ^{\mathsf {C}}_1$
and
![]() $\pi ^{\mathsf {C}}_2$
as below.
$\pi ^{\mathsf {C}}_2$
as below.
 \begin{align*} \pi ^{\mathsf {C}}_1(\{w^{\mathsf {C}}\})&=\sum \limits _{\scriptsize {\begin{matrix}w{\mathscr {Z}}_1 w^{\mathsf {C}}\\w\!\in \!W\end{matrix}}}\pi _1(\{w\})&\pi ^{\mathsf {C}}_2(\{w^{\mathsf {C}}\})&=\sum \limits _{\scriptsize {\begin{matrix}w{\mathscr {Z}}_2 w^{\mathsf {C}}\\w\!\in \!W\end{matrix}}}\pi _2(\{w\}) \end{align*}
\begin{align*} \pi ^{\mathsf {C}}_1(\{w^{\mathsf {C}}\})&=\sum \limits _{\scriptsize {\begin{matrix}w{\mathscr {Z}}_1 w^{\mathsf {C}}\\w\!\in \!W\end{matrix}}}\pi _1(\{w\})&\pi ^{\mathsf {C}}_2(\{w^{\mathsf {C}}\})&=\sum \limits _{\scriptsize {\begin{matrix}w{\mathscr {Z}}_2 w^{\mathsf {C}}\\w\!\in \!W\end{matrix}}}\pi _2(\{w\}) \end{align*}
Again, it is straightforward to check that
![]() $\pi ^{\mathsf {C}}_1(|\sigma |^+)=\pi _1(|\sigma |^+)$
,
$\pi ^{\mathsf {C}}_1(|\sigma |^+)=\pi _1(|\sigma |^+)$
,
![]() $\pi ^{\mathsf {C}}_1(|\sigma |^-)=\pi _1(|\sigma |^-)$
,
$\pi ^{\mathsf {C}}_1(|\sigma |^-)=\pi _1(|\sigma |^-)$
,
![]() $\pi ^{\mathsf {C}}_2(|\tau |^+)=\pi _2(|\tau |^+)$
, and
$\pi ^{\mathsf {C}}_2(|\tau |^+)=\pi _2(|\tau |^+)$
, and
![]() $\pi ^{\mathsf {C}}_2(|\tau |^-)=\pi _2(|\tau |^-)$
for every
$\pi ^{\mathsf {C}}_2(|\tau |^-)=\pi _2(|\tau |^-)$
for every
![]() $\sigma \in \Gamma _1$
and
$\sigma \in \Gamma _1$
and
![]() $\tau \in \Gamma _2$
.
$\tau \in \Gamma _2$
.
The decision algorithms for
![]() $\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}$
and
$\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}$
and
![]() $\mathsf {Pr}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}_{\mathbf {S5}}$
are based upon the one presented in Theorem42. Thus, we need a tableaux calculus for
$\mathsf {Pr}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}_{\mathbf {S5}}$
are based upon the one presented in Theorem42. Thus, we need a tableaux calculus for
![]() $\mathsf {N}{\mathsf {\unicode {x0141}}}$
. It was given by Bílková et al. (Reference Bílková, Frittella, Kozhemiachenko, Das and Negri2021), and we recall it here. All notions – open and closed branches, interpretations of entries, and satisfying valuations of branches – are the same as in
$\mathsf {N}{\mathsf {\unicode {x0141}}}$
. It was given by Bílková et al. (Reference Bílková, Frittella, Kozhemiachenko, Das and Negri2021), and we recall it here. All notions – open and closed branches, interpretations of entries, and satisfying valuations of branches – are the same as in
![]() $\mathscr {T}\left ({\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}\right )$
(cf. Definitions 34 and 36), so we only list the rules in the next definition.
$\mathscr {T}\left ({\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}\right )$
(cf. Definitions 34 and 36), so we only list the rules in the next definition.
Definition 72 (
![]() $\mathscr {T}\!\!\left (\mathsf {N}{\mathsf {\unicode {x0141}}}\right )$
– the tableau calculus for
$\mathscr {T}\!\!\left (\mathsf {N}{\mathsf {\unicode {x0141}}}\right )$
– the tableau calculus for
![]() $\mathsf {N}{\mathsf {\unicode {x0141}}}$
). The rules are as follows.
$\mathsf {N}{\mathsf {\unicode {x0141}}}$
). The rules are as follows.

Remark 73.
Note that all connectives in
![]() $\mathsf {N}{\mathsf {\unicode {x0141}}}$
are continuous and thus all rules of
$\mathsf {N}{\mathsf {\unicode {x0141}}}$
are continuous and thus all rules of
![]() $\mathscr {T}\left (\mathsf {N}{\mathsf {\unicode {x0141}}}\right )$
can be linearised. This will require the introduction of another sort of variables that range over
$\mathscr {T}\left (\mathsf {N}{\mathsf {\unicode {x0141}}}\right )$
can be linearised. This will require the introduction of another sort of variables that range over
![]() $\{0,1\}$
. To make the presentation of both tableaux calculi uniform, however, we decided against the linear version of the tableau rules.
$\{0,1\}$
. To make the presentation of both tableaux calculi uniform, however, we decided against the linear version of the tableau rules.
Theorem 74.
Validity in
![]() $\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}$
and
$\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}$
and
![]() $\mathsf {Pr}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}_{\mathbf {S5}}$
is
$\mathsf {Pr}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}_{\mathbf {S5}}$
is
![]() $\mathsf {coNP}$
-complete.
$\mathsf {coNP}$
-complete.
Proof.
As
![]() ${\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}$
and
${\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}$
and
![]() $\mathsf {N}{\mathsf {\unicode {x0141}}}$
are
$\mathsf {N}{\mathsf {\unicode {x0141}}}$
are
![]() $\mathsf {coNP}$
-complete (cf. Bílková et al. Reference Bílková, Frittella, Kozhemiachenko, Das and Negri2021), we only show the upper bound. The proof is similar to that of Theorem42, so we address the main differences.
$\mathsf {coNP}$
-complete (cf. Bílková et al. Reference Bílková, Frittella, Kozhemiachenko, Das and Negri2021), we only show the upper bound. The proof is similar to that of Theorem42, so we address the main differences.
We begin with
![]() $\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}$
. We show how to check the falsifiability of
$\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}$
. We show how to check the falsifiability of
![]() $\alpha \in \mathscr {L}_{\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}}$
in nondeterministic polynomial time. Assume that
$\alpha \in \mathscr {L}_{\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}}$
in nondeterministic polynomial time. Assume that
![]() $\alpha$
is built over
$\alpha$
is built over
![]() $\mathsf {Pr}\sigma _1$
, …,
$\mathsf {Pr}\sigma _1$
, …,
![]() $\mathsf {Pr}\sigma _n$
and that
$\mathsf {Pr}\sigma _n$
and that
![]() $|\mathsf {Lit}(\alpha )|=n$
(just as in Theorem42, we can add superfluous modal atoms) and that
$|\mathsf {Lit}(\alpha )|=n$
(just as in Theorem42, we can add superfluous modal atoms) and that
![]() $\alpha$
is outer-
$\alpha$
is outer-
![]() $\neg$
-free (this holds because
$\neg$
-free (this holds because
![]() $e(\neg \mathsf {Pr}\Box \phi )=e(\mathsf {Pr}\lozenge \neg \phi )$
and
$e(\neg \mathsf {Pr}\Box \phi )=e(\mathsf {Pr}\lozenge \neg \phi )$
and
![]() $e(\neg \mathsf {Pr}\lozenge \phi )=e(\mathsf {Pr}\Box \neg \phi )$
in every model).
$e(\neg \mathsf {Pr}\lozenge \phi )=e(\mathsf {Pr}\Box \neg \phi )$
in every model).
We construct a
![]() $\mathscr {T}\left ({\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}\right )$
constraint tableau beginning with
$\mathscr {T}\left ({\mathsf {\unicode {x0141}}}^2_{(\triangle, \rightarrow )}\right )$
constraint tableau beginning with
![]() $\{\alpha ^-\leqslant _1c,c\lt 1\}$
where
$\{\alpha ^-\leqslant _1c,c\lt 1\}$
where
![]() $\alpha ^-$
is the result of replacement of every modal atom
$\alpha ^-$
is the result of replacement of every modal atom
![]() $\mathsf {Pr}\sigma _i$
with a fresh variable
$\mathsf {Pr}\sigma _i$
with a fresh variable
![]() $q_{\sigma _i}$
and check in nondeterministic polynomial time whether it is closed. If it has open branches, we guess one (say,
$q_{\sigma _i}$
and check in nondeterministic polynomial time whether it is closed. If it has open branches, we guess one (say,
![]() $\mathscr {B}$
) and consider its corresponding system of linear inequalities.
$\mathscr {B}$
) and consider its corresponding system of linear inequalities.
Here,
![]() $z_i$
’s correspond to the values of
$z_i$
’s correspond to the values of
![]() $q_{\sigma _i}$
’s in
$q_{\sigma _i}$
’s in
![]() $\alpha ^-$
and
$\alpha ^-$
and
![]() $t_i$
’s are linear polynomials that label
$t_i$
’s are linear polynomials that label
![]() $q_{\sigma _i}$
’s. Numerical constraints give us
$q_{\sigma _i}$
’s. Numerical constraints give us
![]() $k$
’s,
$k$
’s,
![]() $k'$
’s,
$k'$
’s,
![]() $m$
’s and
$m$
’s and
![]() $m'$
’s. Denote the number of inequalities and the number of variables in (
$m'$
’s. Denote the number of inequalities and the number of variables in (
![]() $\mathrm {LI}(1)_\Box ^{\mathscr {B}}$
) with
$\mathrm {LI}(1)_\Box ^{\mathscr {B}}$
) with
![]() $l_1$
and
$l_1$
and
![]() $l_2$
, respectively. It is clear that
$l_2$
, respectively. It is clear that
![]() $l_1={\mathscr {O}}(\unicode{x1D4C1}(\alpha ^-))$
and
$l_1={\mathscr {O}}(\unicode{x1D4C1}(\alpha ^-))$
and
![]() $l_2={\mathscr {O}}(\unicode{x1D4C1}(\alpha ^-))$
.
$l_2={\mathscr {O}}(\unicode{x1D4C1}(\alpha ^-))$
.
To check that
![]() $z_i$
’s are coherent as probabilities of
$z_i$
’s are coherent as probabilities of
![]() $\sigma _i$
’s, we introduce
$\sigma _i$
’s, we introduce
![]() $2^{2^n}-1$
new variables of the form
$2^{2^n}-1$
new variables of the form
![]() $u_v$
with
$u_v$
with
![]() $v\in \{0,1,;\}^*$
. Here,
$v\in \{0,1,;\}^*$
. Here,
![]() $v$
encodes the valuation of literals of
$v$
encodes the valuation of literals of
![]() $\alpha$
in the corresponding cluster of
$\alpha$
in the corresponding cluster of
![]() $\mathfrak {M}^{\mathsf {\mathsf {BD}\mathbf {{S5}}}}_{\alpha }$
(cf. Definitions 66 and 69). For example, if
$\mathfrak {M}^{\mathsf {\mathsf {BD}\mathbf {{S5}}}}_{\alpha }$
(cf. Definitions 66 and 69). For example, if
![]() $\mathsf {Lit}(\alpha )=\{p_1,\neg p_1,p_2,\neg p_2\}$
,
$\mathsf {Lit}(\alpha )=\{p_1,\neg p_1,p_2,\neg p_2\}$
,
![]() $u_{1000;1100;0101}$
encodes
$u_{1000;1100;0101}$
encodes
![]() $\{\{p_1\},\{p_1,\neg p_1\},\{\neg p_1,\neg p_2\}\}$
. Additionally, we put
$\{\{p_1\},\{p_1,\neg p_1\},\{\neg p_1,\neg p_2\}\}$
. Additionally, we put
![]() $a_{i,v}=1$
if
$a_{i,v}=1$
if
![]() $\mathfrak {M}^{\mathsf {\mathsf {BD}\mathbf {{S5}}}}_{\alpha },w\vDash ^+\sigma _i$
for every state
$\mathfrak {M}^{\mathsf {\mathsf {BD}\mathbf {{S5}}}}_{\alpha },w\vDash ^+\sigma _i$
for every state
![]() $w$
in the cluster corresponding to
$w$
in the cluster corresponding to
![]() $v$
and
$v$
and
![]() $a_{i,v}=0$
, otherwise. We then add the following equalities for every
$a_{i,v}=0$
, otherwise. We then add the following equalities for every
![]() $i$
.
$i$
.
As in Theorem42, we guess a list
![]() $L$
of at most
$L$
of at most
![]() $l_1+n+1$
words
$l_1+n+1$
words
![]() $v$
. By Theorem71, we w.l.o.g. assume that only clusters with at most
$v$
. By Theorem71, we w.l.o.g. assume that only clusters with at most
![]() $2n+1$
states have a positive measure assignment. Thus,
$2n+1$
states have a positive measure assignment. Thus,
![]() $L$
contains only
$L$
contains only
![]() $u_v$
’s whose length is not greater than
$u_v$
’s whose length is not greater than
![]() $n\cdot (2n+1)$
, whence, the size of
$n\cdot (2n+1)$
, whence, the size of
![]() $L$
is not greater than
$L$
is not greater than
![]() $n\cdot (2n+1)\cdot (l_1+n+1)$
. We compute the values of
$n\cdot (2n+1)\cdot (l_1+n+1)$
. We compute the values of
![]() $a_{i,v}$
’s for
$a_{i,v}$
’s for
![]() $i\leq n$
and
$i\leq n$
and
![]() $v\in L$
which takes deterministic polynomial time w.r.t.
$v\in L$
which takes deterministic polynomial time w.r.t.
![]() $\unicode{x1D4C1}(\alpha ^-)$
because clusters contain at most
$\unicode{x1D4C1}(\alpha ^-)$
because clusters contain at most
![]() $2n+1$
states. This gives us the following system of inequalities.
$2n+1$
states. This gives us the following system of inequalities.
One can see that the size of (
![]() $\mathrm {LI}(1)_\Box ^{\mathscr {B}}$
)
$\mathrm {LI}(1)_\Box ^{\mathscr {B}}$
)
![]() $\cup$
(
$\cup$
(
![]() $\mathrm {LI}(2\mathrm {poly})_\Box ^{\mathscr {B}}$
) is polynomial in
$\mathrm {LI}(2\mathrm {poly})_\Box ^{\mathscr {B}}$
) is polynomial in
![]() $\unicode{x1D4C1}(\alpha ^-)$
as there are polynomially many (in)equalities containing polynomially many variables with linearly bounded labels. Hence, it can be solved in nondeterministic polynomial time. The rest of the proof follows that of Theorem42.
$\unicode{x1D4C1}(\alpha ^-)$
as there are polynomially many (in)equalities containing polynomially many variables with linearly bounded labels. Hence, it can be solved in nondeterministic polynomial time. The rest of the proof follows that of Theorem42.
The
![]() $\mathsf {coNP}$
-membership proof for
$\mathsf {coNP}$
-membership proof for
![]() $\mathsf {Pr}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}_{\mathbf {S5}}$
is similar, so, we provide only a sketch. The main differences are as follows. First, there are two modalities –
$\mathsf {Pr}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}_{\mathbf {S5}}$
is similar, so, we provide only a sketch. The main differences are as follows. First, there are two modalities –
![]() $\mathsf {Pr}_1$
and
$\mathsf {Pr}_1$
and
![]() $\mathsf {Pr}_2$
; this is why, when transforming
$\mathsf {Pr}_2$
; this is why, when transforming
![]() $\alpha$
into
$\alpha$
into
![]() $\alpha ^-$
, we replace
$\alpha ^-$
, we replace
![]() $\mathsf {Pr}_1\sigma _i$
’s with
$\mathsf {Pr}_1\sigma _i$
’s with
![]() $q_{\sigma _{1_i}}$
’s and
$q_{\sigma _{1_i}}$
’s and
![]() $\mathsf {Pr}_2\sigma _i$
’s with
$\mathsf {Pr}_2\sigma _i$
’s with
![]() $q_{\sigma _{2_i}}$
’s. Thus, we introduce two sorts of
$q_{\sigma _{2_i}}$
’s. Thus, we introduce two sorts of
![]() $z$
’s (
$z$
’s (
![]() $z_{1_i}$
’s and
$z_{1_i}$
’s and
![]() $z_{2_i}$
’s) in the system of inequalities corresponding to an open branch in the
$z_{2_i}$
’s) in the system of inequalities corresponding to an open branch in the
![]() $\mathscr {T}\!\!\left (\mathsf {N}{\mathsf {\unicode {x0141}}}\right )$
tableau for
$\mathscr {T}\!\!\left (\mathsf {N}{\mathsf {\unicode {x0141}}}\right )$
tableau for
![]() $\alpha ^-$
. Note, however, that since
$\alpha ^-$
. Note, however, that since
![]() $\Box _1$
and
$\Box _1$
and
![]() $\lozenge _1$
do not occur in the same modal atom as
$\lozenge _1$
do not occur in the same modal atom as
![]() $\Box _2$
or
$\Box _2$
or
![]() $\lozenge _2$
, we can utilise
$\lozenge _2$
, we can utilise
![]() $\mathfrak {M}^{\mathsf {\mathsf {BD}\mathbf {{S5}}}}_{\alpha ^-}$
for both sets of modalities. However (recall Theorem71), we will need two independent measures.
$\mathfrak {M}^{\mathsf {\mathsf {BD}\mathbf {{S5}}}}_{\alpha ^-}$
for both sets of modalities. However (recall Theorem71), we will need two independent measures.
Second, we need two sorts of
![]() $u_v$
’s –
$u_v$
’s –
![]() $u^1_v$
and
$u^1_v$
and
![]() $u^2_v$
(
$u^2_v$
(
![]() $v$
’s are defined as in the case of
$v$
’s are defined as in the case of
![]() $\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}$
) – to differentiate between two measures on
$\mathsf {Pr}^{(\triangle, \rightarrow )}_{\mathbf {S5}}$
) – to differentiate between two measures on
![]() $\mathfrak {M}^{\mathsf {\mathsf {BD}\mathbf {{S5}}}}_{\alpha }$
. This means that (
$\mathfrak {M}^{\mathsf {\mathsf {BD}\mathbf {{S5}}}}_{\alpha }$
. This means that (
![]() $\mathrm {LI}(2\exp )_\Box ^{\mathscr {B}}$
) will have the following form:
$\mathrm {LI}(2\exp )_\Box ^{\mathscr {B}}$
) will have the following form:
Thus, we have
![]() $l_1+2n+2$
inequalities in total. Hence, we can guess the list
$l_1+2n+2$
inequalities in total. Hence, we can guess the list
![]() $L$
containing
$L$
containing
![]() $l_1+2n+2$
variables. By Theorem71, we need only
$l_1+2n+2$
variables. By Theorem71, we need only
![]() $v$
’s of length at most
$v$
’s of length at most
![]() $n\cdot (2n+1)$
. Therefore, the size of
$n\cdot (2n+1)$
. Therefore, the size of
![]() $L$
is at most
$L$
is at most
![]() $n\cdot (2n+1)\cdot (l_1+2n+2)$
, which means that it takes nondeterministic polynomial time to solve the system of inequalities obtained after guessing
$n\cdot (2n+1)\cdot (l_1+2n+2)$
, which means that it takes nondeterministic polynomial time to solve the system of inequalities obtained after guessing
![]() $L$
. The result is as follows.
$L$
. The result is as follows.
Corollary 75.
Validity in
![]() $\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
and
$\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
and
![]() $\mathsf {Bel}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}$
is
$\mathsf {Bel}^{\mathsf {N}{\mathsf {\unicode {x0141}}}}$
is
![]() $\mathsf {coNP}$
-complete.
$\mathsf {coNP}$
-complete.
6. Conclusion
In this paper, we considered several two-layered logics for reasoning with probability measures and belief functions defined in the
![]() $\mathsf {BD}$
-framework. In particular, we established that the logics of
$\mathsf {BD}$
-framework. In particular, we established that the logics of
![]() $\mathbf {4}$
- and
$\mathbf {4}$
- and
![]() $\pm$
-probabilities can be faithfully embedded into one another (Theorems24 and 25) and constructed a complete Hilbert axiomatisation for the logic of
$\pm$
-probabilities can be faithfully embedded into one another (Theorems24 and 25) and constructed a complete Hilbert axiomatisation for the logic of
![]() $\mathbf {4}$
-probabilities (Theorem33). We also established
$\mathbf {4}$
-probabilities (Theorem33). We also established
![]() $\mathsf {coNP}$
-completeness for logics of
$\mathsf {coNP}$
-completeness for logics of
![]() $\pm$
- and
$\pm$
- and
![]() $\mathbf {4}$
-probabilities and
$\mathbf {4}$
-probabilities and
![]() $\mathsf {coNP}$
-completeness for logics of belief and plausibility functions in
$\mathsf {coNP}$
-completeness for logics of belief and plausibility functions in
![]() $\mathsf {BD}$
(Theorem42 and Corollary 75) utilising the connection between belief assignments of propositional and modal formulas (Theorem52) and a version of the small model property for the canonical model (Theorem71). Still, several important questions remain open.
$\mathsf {BD}$
(Theorem42 and Corollary 75) utilising the connection between belief assignments of propositional and modal formulas (Theorem52) and a version of the small model property for the canonical model (Theorem71). Still, several important questions remain open.
First, our belief and plausibility functions are close to
![]() $\pm$
-probabilities because they assign each statement
$\pm$
-probabilities because they assign each statement
![]() $\phi$
two measures: the measure of its positive extension and the measure of its negative extension. It is thus instructive to define
$\phi$
two measures: the measure of its positive extension and the measure of its negative extension. It is thus instructive to define
![]() $\mathbf {4}$
-valued belief and plausibility functions that will assign measures to
$\mathbf {4}$
-valued belief and plausibility functions that will assign measures to
![]() $\phi$
according to the pure belief, pure disbelief, conflict and uncertainty extensions (cf. Convention 5). This is not a trivial task since belief and plausibility functions are not additive, whence, the measures of these extensions cannot be directly obtained from
$\phi$
according to the pure belief, pure disbelief, conflict and uncertainty extensions (cf. Convention 5). This is not a trivial task since belief and plausibility functions are not additive, whence, the measures of these extensions cannot be directly obtained from
![]() ${\texttt {bel}}(|\phi |^+)$
and
${\texttt {bel}}(|\phi |^+)$
and
![]() ${\texttt {bel}}(|\phi |^-)$
.
${\texttt {bel}}(|\phi |^-)$
.
Third, observe that axiomatisations of
![]() $\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
proposed by Bílková et al. (Reference Bílková, Frittella, Kozhemiachenko, Majer and Nazari2023d) are infinite. In the case of belief functions over the classical logic, it is shown by Godo et al. (Reference Godo, Hájek, Esteva and Nebel2001, Reference Godo, Hájek and Esteva2003) how to produce a finite axiomatisation for the two-layered logics of belief functions in the classical case using the representation of
$\mathsf {Bel}^{{\mathsf {\unicode {x0141}}}^2}_\triangle$
proposed by Bílková et al. (Reference Bílková, Frittella, Kozhemiachenko, Majer and Nazari2023d) are infinite. In the case of belief functions over the classical logic, it is shown by Godo et al. (Reference Godo, Hájek, Esteva and Nebel2001, Reference Godo, Hájek and Esteva2003) how to produce a finite axiomatisation for the two-layered logics of belief functions in the classical case using the representation of
![]() ${\texttt {bel}}(\|\phi \|)$
as
${\texttt {bel}}(\|\phi \|)$
as
![]() $\pi (\|\Box \phi \|)$
. Recall that a similar property (Theorem52) holds for the
$\pi (\|\Box \phi \|)$
. Recall that a similar property (Theorem52) holds for the
![]() $\mathsf {BD}$
as well. It makes sense to use it to obtain a finite axiomatisation of belief and plausibility functions over
$\mathsf {BD}$
as well. It makes sense to use it to obtain a finite axiomatisation of belief and plausibility functions over
![]() $\mathsf {BD}$
.
$\mathsf {BD}$
.
Finally, Bílková et al. (Reference Bílková, Frittella, Kozhemiachenko and Majer2023a) proposed two-layered logics for qualitative reasoning about different uncertainty measures. In particular, we constructed logics for qualitative reasoning with belief functions and probabilities. These logics utilised the bi-Gödel logic (
![]() $\mathsf {biG}$
) in the outer layer. Since
$\mathsf {biG}$
) in the outer layer. Since
![]() $\mathsf {biG}$
is also
$\mathsf {biG}$
is also
![]() $\mathsf {NP}$
-complete, the question arises whether we can apply the technique of Hájek and Tulipani (Reference Hájek and Tulipani2001) to prove the
$\mathsf {NP}$
-complete, the question arises whether we can apply the technique of Hájek and Tulipani (Reference Hájek and Tulipani2001) to prove the
![]() $\mathsf {NP}$
-completeness of two-layered logics for qualitative reasoning about uncertainty.
$\mathsf {NP}$
-completeness of two-layered logics for qualitative reasoning about uncertainty.
Acknowledgements
The first and the last author were supported by the grant numero 22-23022L CELIA of Grantová Agentura České Republiky. The second and third authors were supported by the grant ANR-19-CE48-0006 of Agence Nationale de la Recherche. The third author was, in addition, supported by the grant ANR-19-CHIA-0014 of Agence Nationale de la Recherche. The paper is a part of the MOSAIC project financed by the European Union’s Marie Skłodowska-Curie grant numero 101007627.
The authors also wish to thank the editors and the reviewers for their comments that greatly enhanced the paper.
Competing interests
No conflict of interest to declare.