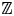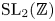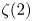1. Introduction
We begin by motivating the results of this paper from two apparently different, but in fact equivalent, perspectives.
1.1 Depth filtration on multiple zeta values
Multiple zeta values are defined for integers ![]() $n_1,\ldots , n_{r-1}\geq 1$ and
$n_1,\ldots , n_{r-1}\geq 1$ and ![]() $n_r\geq 2$ by
$n_r\geq 2$ by
 \[ \zeta(n_1,\ldots, n_r) = \sum_{1\leq k_1< \cdots < k_r} \frac{1}{k_1^{n_1} \ldots k_r^{n_r} } . \]
\[ \zeta(n_1,\ldots, n_r) = \sum_{1\leq k_1< \cdots < k_r} \frac{1}{k_1^{n_1} \ldots k_r^{n_r} } . \]
Their weight is the quantity ![]() $n_1+\dots +n_r$, and their depth is the number of indices
$n_1+\dots +n_r$, and their depth is the number of indices ![]() $r$. Relations between multiple zeta values of depth 2 were first studied by Euler. Let
$r$. Relations between multiple zeta values of depth 2 were first studied by Euler. Let ![]() $\mathcal {Z}_N$ denote the
$\mathcal {Z}_N$ denote the ![]() $\mathbb {Q}$-vector space spanned by multiple zeta values in weight
$\mathbb {Q}$-vector space spanned by multiple zeta values in weight ![]() $N$. Zagier conjectured, firstly, that the space
$N$. Zagier conjectured, firstly, that the space ![]() $\mathcal {Z}$ of multiple zeta values is isomorphic to the direct sum of the
$\mathcal {Z}$ of multiple zeta values is isomorphic to the direct sum of the ![]() $\mathcal {Z}_N$ (in other words, the weight is a grading), and secondly, that the dimension of
$\mathcal {Z}_N$ (in other words, the weight is a grading), and secondly, that the dimension of ![]() $\mathcal {Z}_N$ can be expressed using the generating series
$\mathcal {Z}_N$ can be expressed using the generating series
 \begin{equation} \sum_{N\geq 0} \dim_{\mathbb{Q}} \, (\mathcal{Z}_N) s^N = \frac{1}{1-s^2-s^3}. \end{equation}
\begin{equation} \sum_{N\geq 0} \dim_{\mathbb{Q}} \, (\mathcal{Z}_N) s^N = \frac{1}{1-s^2-s^3}. \end{equation}
Using the theory [Reference LevineLev93, Reference Deligne and GoncharovDG05] of mixed Tate motives over ![]() $\mathbb {Z}$, Goncharov [Reference GoncharovGon01a] and Terasoma [Reference TerasomaTer02] independently showed that
$\mathbb {Z}$, Goncharov [Reference GoncharovGon01a] and Terasoma [Reference TerasomaTer02] independently showed that ![]() $\dim _{\mathbb {Q}} \mathcal {Z}_N$ is bounded above by the coefficient of
$\dim _{\mathbb {Q}} \mathcal {Z}_N$ is bounded above by the coefficient of ![]() $s^N$ in the right-hand side of (1.1). Furthermore, if one replaces
$s^N$ in the right-hand side of (1.1). Furthermore, if one replaces ![]() $\mathcal {Z}_N$ with the
$\mathcal {Z}_N$ with the ![]() $\mathbb {Q}$-vector space of motivic multiple zeta values
$\mathbb {Q}$-vector space of motivic multiple zeta values ![]() $\zeta ^{{\mathfrak {m}}}(n_1,\ldots , n_r)$ of weight
$\zeta ^{{\mathfrak {m}}}(n_1,\ldots , n_r)$ of weight ![]() $N$, then (1.1) is a theorem [Reference BrownBro12, Reference DeligneDel13]. The rational function on the right-hand side of (1.1) can be interpreted as follows: it is the Poincaré series of the free graded module, generated by
$N$, then (1.1) is a theorem [Reference BrownBro12, Reference DeligneDel13]. The rational function on the right-hand side of (1.1) can be interpreted as follows: it is the Poincaré series of the free graded module, generated by ![]() $\zeta ^{{\mathfrak {m}}}(2n)$ for
$\zeta ^{{\mathfrak {m}}}(2n)$ for ![]() $n\geq 1$, over the graded dual of the universal enveloping algebra of the Lie algebra of the category of mixed Tate motives over
$n\geq 1$, over the graded dual of the universal enveloping algebra of the Lie algebra of the category of mixed Tate motives over ![]() $\mathbb {Z}$, which is free with one generator in every odd degree
$\mathbb {Z}$, which is free with one generator in every odd degree ![]() $\leq -3$ (see [Reference Deligne and GoncharovDG05, Reference DeligneDel13] for further details).
$\leq -3$ (see [Reference Deligne and GoncharovDG05, Reference DeligneDel13] for further details).
Based on numerical experiments, Broadhurst and Kreimer [Reference Broadhurst and KreimerBK97] formulated a fascinating and more refined conjecture which takes into account the depth. The depth, by contrast with the conjectural properties of the weight, is only a filtration, and not a grading. Let ![]() $\mathcal {Z}_{N,d}$ denote the
$\mathcal {Z}_{N,d}$ denote the ![]() $\mathbb {Q}$-vector space spanned by multiple zeta values in weight
$\mathbb {Q}$-vector space spanned by multiple zeta values in weight ![]() $N$ and depth
$N$ and depth ![]() $d$, modulo multiple zeta values of weight
$d$, modulo multiple zeta values of weight ![]() $N$ and strictly lower depth. They propose that
$N$ and strictly lower depth. They propose that
 \begin{equation} \sum_{N, d\geq 0} \dim_{\mathbb{Q}}\, (\mathcal{Z}_{N,d}) s^N t^d = \frac{ 1 + \mathbb{E}(s) t}{1- \mathbb{O}(s) t + \mathbb{S}(s) t^2 - \mathbb{S}(s) t^4} , \end{equation}
\begin{equation} \sum_{N, d\geq 0} \dim_{\mathbb{Q}}\, (\mathcal{Z}_{N,d}) s^N t^d = \frac{ 1 + \mathbb{E}(s) t}{1- \mathbb{O}(s) t + \mathbb{S}(s) t^2 - \mathbb{S}(s) t^4} , \end{equation}where, using the notation from [Reference Ihara, Kaneko and ZagierIKZ06, Appendix],
Formula (1.2) specializes to the statement (1.1) upon setting ![]() $t=1$.
$t=1$.
The meaning of this conjecture is still mysterious, but one goal of this paper is to offer a homological interpretation of (1.2). The series ![]() $\mathbb {E}(s)$ and
$\mathbb {E}(s)$ and ![]() $\mathbb {O}(s)$ are the generating series for the dimensions of the spaces of even and odd single zeta values respectively, and
$\mathbb {O}(s)$ are the generating series for the dimensions of the spaces of even and odd single zeta values respectively, and ![]() $\mathbb {S}(s)$ is the generating series for the dimensions of the space of cusp forms for the full modular group
$\mathbb {S}(s)$ is the generating series for the dimensions of the space of cusp forms for the full modular group ![]() $\mathrm {SL}_2(\mathbb {Z})$. The first prediction of (1.2), due to the presence of a non-trivial coefficient of
$\mathrm {SL}_2(\mathbb {Z})$. The first prediction of (1.2), due to the presence of a non-trivial coefficient of ![]() $t^2$ in the denominator of the right-hand side, is the existence of an extra relation between double zeta values of even weight for every cusp form, modulo multiple zeta values of lower depth (single zeta values). These relations have indeed been shown to exist and are well understood by the work of Gangl et al. [Reference Gangl, Kaneko and ZagierGKZ06], who exhibited an infinite family of such relations. The smallest one corresponds to the Ramanujan cusp form of weight 12:
$t^2$ in the denominator of the right-hand side, is the existence of an extra relation between double zeta values of even weight for every cusp form, modulo multiple zeta values of lower depth (single zeta values). These relations have indeed been shown to exist and are well understood by the work of Gangl et al. [Reference Gangl, Kaneko and ZagierGKZ06], who exhibited an infinite family of such relations. The smallest one corresponds to the Ramanujan cusp form of weight 12:
The coefficients in this and all such equations can be related to period polynomials for cusp forms, or equivalently, to group cocycles for ![]() $\mathrm {SL}_2(\mathbb {Z})$. Furthermore, a geometric mechanism for these relations is by now fairly well understood [Reference BrownBro14b].
$\mathrm {SL}_2(\mathbb {Z})$. Furthermore, a geometric mechanism for these relations is by now fairly well understood [Reference BrownBro14b].
The situation in higher depths remains very unclear. It is known by work of Zagier [Reference ZagierZag93] and Goncharov [Reference GoncharovGon01b] that (1.2) is true (in a suitable setting, i.e. for solutions to the double shuffle equations as discussed below) in depths 2 and 3, respectively. Nevertheless, the presence of the term in ![]() $t^4$ in the right-hand side of (1.2) suggests a new phenomenon in depth 4. If we interpret the right-hand side of (1.2) in terms of the Poincaré series of a depth-graded version of the Lie algebra of the category of mixed Tate motives over
$t^4$ in the right-hand side of (1.2) suggests a new phenomenon in depth 4. If we interpret the right-hand side of (1.2) in terms of the Poincaré series of a depth-graded version of the Lie algebra of the category of mixed Tate motives over ![]() $\mathbb {Z}$, the term in
$\mathbb {Z}$, the term in ![]() $t^4$ suggests the existence of new generators in this Lie algebra in depth 4, corresponding to cusp forms for the full modular group.
$t^4$ suggests the existence of new generators in this Lie algebra in depth 4, corresponding to cusp forms for the full modular group.
In this paper we supply candidates for these ‘exceptional’ generators by constructing them explicitly out of period polynomials of cusp forms. As a result, we can formulate a much more precise conjecture than (1.2) which predicts not only the dimensions of the spaces of multiple zeta values in all weights and depths, but also their relations and modulo lower depths. In order to get some sense of these exceptional generators, consider the first one, which occurs in depth 4 and weight 12. It turns out that all multiple zeta values in weight 12 and depth 4 are proportional to a single element ![]() $\zeta (1,1,2,8)$ modulo terms of lower depth and products, for example,
$\zeta (1,1,2,8)$ modulo terms of lower depth and products, for example,
The exceptional generator corresponding to the Ramanujan cusp form ![]() $\Delta$ annihilates every such relation, and therefore gives an interpretation of the coefficients (in this case, the number 116) in terms of ratios of critical values of the
$\Delta$ annihilates every such relation, and therefore gives an interpretation of the coefficients (in this case, the number 116) in terms of ratios of critical values of the ![]() $L$-function of
$L$-function of ![]() $\Delta$.
$\Delta$.
1.2 The projective line minus three points
Let ![]() $\mathcal {G}^{\mathrm {dR}}_{\mathcal {MT}(\mathbb {Z})}=\mathrm {Aut}^{\otimes }_{\mathcal {MT}(\mathbb {Z})}(\omega _{\mathrm {dR}})$ denote the motivic Galois group of the Tannakian category
$\mathcal {G}^{\mathrm {dR}}_{\mathcal {MT}(\mathbb {Z})}=\mathrm {Aut}^{\otimes }_{\mathcal {MT}(\mathbb {Z})}(\omega _{\mathrm {dR}})$ denote the motivic Galois group of the Tannakian category ![]() $\mathcal {MT}(\mathbb {Z})$ of mixed Tate motives over the integers [Reference Deligne and GoncharovDG05], and let
$\mathcal {MT}(\mathbb {Z})$ of mixed Tate motives over the integers [Reference Deligne and GoncharovDG05], and let ![]() $\mathcal {U}^{\mathrm {dR}}_{\mathcal {MT}(\mathbb {Z})}\leq \mathcal {G}^{\mathrm {dR}}_{\mathcal {MT}(\mathbb {Z})}$ denote its unipotent radical. One has a canonical isomorphism
$\mathcal {U}^{\mathrm {dR}}_{\mathcal {MT}(\mathbb {Z})}\leq \mathcal {G}^{\mathrm {dR}}_{\mathcal {MT}(\mathbb {Z})}$ denote its unipotent radical. One has a canonical isomorphism ![]() $\mathcal {G}^{\mathrm {dR}}_{\mathcal {MT}(\mathbb {Z})}= \mathcal {U}^{\mathrm {dR}}_{\mathcal {MT}(\mathbb {Z})} \rtimes \mathbb {G}_m$. Let
$\mathcal {G}^{\mathrm {dR}}_{\mathcal {MT}(\mathbb {Z})}= \mathcal {U}^{\mathrm {dR}}_{\mathcal {MT}(\mathbb {Z})} \rtimes \mathbb {G}_m$. Let
denote the de Rham fundamental group (respectively, torsor of paths) at a tangential base point at ![]() $0$ (respectively, between tangential basepoints at
$0$ (respectively, between tangential basepoints at ![]() $0$ and
$0$ and ![]() $1$) [Reference DeligneDel89]. The latter is a torsor over the former, via compositionFootnote 1 of paths
$1$) [Reference DeligneDel89]. The latter is a torsor over the former, via compositionFootnote 1 of paths ![]() ${}_0 \Pi _{0} \times {}_0 \Pi _{1} \rightarrow {}_0 \Pi _{1}$. Since
${}_0 \Pi _{0} \times {}_0 \Pi _{1} \rightarrow {}_0 \Pi _{1}$. Since ![]() ${}_0 \Pi _{0}, {}_0 \Pi _{1}$ are the de Rham realizations of (pro)-objects in the category of mixed Tate motives over
${}_0 \Pi _{0}, {}_0 \Pi _{1}$ are the de Rham realizations of (pro)-objects in the category of mixed Tate motives over ![]() $\mathbb {Z}$, the group
$\mathbb {Z}$, the group ![]() $\mathcal {G}^{\mathrm {dR}}_{\mathcal {MT}(\mathbb {Z})}$ acts upon them, and there is a canonical representation
$\mathcal {G}^{\mathrm {dR}}_{\mathcal {MT}(\mathbb {Z})}$ acts upon them, and there is a canonical representation
where the group of automorphisms on the right denotes those automorphisms which respect the structure ![]() ${}_0 \Pi _{0} \times {}_0\Pi _x \rightarrow {}_0\Pi _x$ for
${}_0 \Pi _{0} \times {}_0\Pi _x \rightarrow {}_0\Pi _x$ for ![]() $x \in \{0,1\}$. This action is the motivic version of the outer action of the absolute Galois group
$x \in \{0,1\}$. This action is the motivic version of the outer action of the absolute Galois group ![]() $\mathrm {Gal}(\bar {\mathbb {Q}}/\mathbb {Q})$ on the pro-
$\mathrm {Gal}(\bar {\mathbb {Q}}/\mathbb {Q})$ on the pro-![]() $\ell$ completion of the fundamental group of
$\ell$ completion of the fundamental group of ![]() $X$ which was first studied extensively by Deligne, Drinfeld, and Ihara [Reference DeligneDel13, Reference DrinfeldDri90, Reference IharaIha02]. Deligne conjectured that this action is faithful, or equivalently, that the motivic torsor of paths on
$X$ which was first studied extensively by Deligne, Drinfeld, and Ihara [Reference DeligneDel13, Reference DrinfeldDri90, Reference IharaIha02]. Deligne conjectured that this action is faithful, or equivalently, that the motivic torsor of paths on ![]() $X$ generates the category
$X$ generates the category ![]() $\mathcal {MT}(\mathbb {Z})$, which was shown in [Reference BrownBro12, Reference DeligneDel13]. The graded Lie algebraFootnote 2 of
$\mathcal {MT}(\mathbb {Z})$, which was shown in [Reference BrownBro12, Reference DeligneDel13]. The graded Lie algebraFootnote 2 of ![]() ${}_0 \Pi _{0}$ is the free graded Lie algebra
${}_0 \Pi _{0}$ is the free graded Lie algebra ![]() $\mathbb {L}( e_0,e_1)$ on two generators
$\mathbb {L}( e_0,e_1)$ on two generators ![]() $e_0,e_1$. Therefore, the infinitesimal version of the action of
$e_0,e_1$. Therefore, the infinitesimal version of the action of ![]() $\mathcal {U}^{\mathrm {dR}}_{\mathcal {MT}(\mathbb {Z})}$ on
$\mathcal {U}^{\mathrm {dR}}_{\mathcal {MT}(\mathbb {Z})}$ on ![]() ${}_0 \Pi _{0}$ gives a very concrete way to study the motivic Galois group, or equivalently, its graded Lie algebra
${}_0 \Pi _{0}$ gives a very concrete way to study the motivic Galois group, or equivalently, its graded Lie algebra ![]() $\mathfrak {g}^{\mathfrak {m}}$ together with its representation:
$\mathfrak {g}^{\mathfrak {m}}$ together with its representation:
One shows that the image of ![]() $\mathfrak {g}^{\mathfrak {m}}$ lies in the Lie subalgebra of derivations which are in the image of the linear map
$\mathfrak {g}^{\mathfrak {m}}$ lies in the Lie subalgebra of derivations which are in the image of the linear map
 \begin{align*} \mathbb{L}(e_0,e_1) & \mapsto \mathrm{Der}\, \mathbb{L}(e_0,e_1) \\ f & \mapsto D_f, \end{align*}
\begin{align*} \mathbb{L}(e_0,e_1) & \mapsto \mathrm{Der}\, \mathbb{L}(e_0,e_1) \\ f & \mapsto D_f, \end{align*}
where ![]() $D_f(e_0)=0$ and
$D_f(e_0)=0$ and ![]() $D_f(e_1) = [f,e_1]$. One can equip
$D_f(e_1) = [f,e_1]$. One can equip ![]() $\mathbb {L}(e_0,e_1)$ with a new Lie algebra structure
$\mathbb {L}(e_0,e_1)$ with a new Lie algebra structure ![]() $\{\,{,}\,\}$, called the Ihara bracket, such that the previous map becomes a morphism of Lie algebras (i.e.
$\{\,{,}\,\}$, called the Ihara bracket, such that the previous map becomes a morphism of Lie algebras (i.e. ![]() $D_{\{f,g\}} = [D_f, D_g]$), where the bracket on the right is the usual Lie bracket on derivations. Let us denote the graded vector space
$D_{\{f,g\}} = [D_f, D_g]$), where the bracket on the right is the usual Lie bracket on derivations. Let us denote the graded vector space ![]() $\mathbb {L}(e_0,e_1)$ together with this new Lie algebra structure by
$\mathbb {L}(e_0,e_1)$ together with this new Lie algebra structure by ![]() $\mathfrak {g} := (\mathbb {L}(e_0,e_1) , \{\,{,}\,\} )$.
$\mathfrak {g} := (\mathbb {L}(e_0,e_1) , \{\,{,}\,\} )$.
One obtains from all this a canonical embedding of the motivic Lie algebra
By abuse of notation, we shall identify ![]() $\mathfrak {g}^{\mathfrak {m}}$ with its image in
$\mathfrak {g}^{\mathfrak {m}}$ with its image in ![]() $\mathfrak {g}$. The injectivity of
$\mathfrak {g}$. The injectivity of ![]() $\mathfrak {g}^{\mathfrak {m}} \rightarrow \mathfrak {g}$ follows from [Reference BrownBro12].
$\mathfrak {g}^{\mathfrak {m}} \rightarrow \mathfrak {g}$ follows from [Reference BrownBro12].
A major problem is to describe this Lie algebra as precisely as possible. We know that it has generators called ‘zeta elements’ for every ![]() $n\geq 1$:
$n\geq 1$:
but they are not canonicalFootnote 3 (e.g. ![]() $\sigma _{11}$ is only well defined up to addition of rational multiples of
$\sigma _{11}$ is only well defined up to addition of rational multiples of ![]() $\{\sigma _3, \{\sigma _5, \sigma _3\}\}$). Deligne's conjecture in its originally stated form was that the
$\{\sigma _3, \{\sigma _5, \sigma _3\}\}$). Deligne's conjecture in its originally stated form was that the ![]() $\ell$-adic versions of the
$\ell$-adic versions of the ![]() $\sigma _{2n+1}$, which are elements in a certain Lie algebra constructed out of
$\sigma _{2n+1}$, which are elements in a certain Lie algebra constructed out of ![]() $\mathrm {Gal}(\bar {\mathbb {Q}}/\mathbb {Q})$, form a free Lie algebra for the Ihara bracket.
$\mathrm {Gal}(\bar {\mathbb {Q}}/\mathbb {Q})$, form a free Lie algebra for the Ihara bracket.
Theorem 1.1 [Reference BrownBro12]
The graded Lie algebra ![]() $\mathfrak {g}^{\mathfrak {m}}$ is a free Lie algebra on (some choice of) generators
$\mathfrak {g}^{\mathfrak {m}}$ is a free Lie algebra on (some choice of) generators ![]() $\sigma _{2n+1}$ in each degree
$\sigma _{2n+1}$ in each degree ![]() $-(2n+1)$ for
$-(2n+1)$ for ![]() $n \geq 1$.
$n \geq 1$.
Only the classes ![]() $[\sigma _{2n+1}]$ in the abelianization
$[\sigma _{2n+1}]$ in the abelianization ![]() $(\mathfrak {g}^{\mathfrak {m}} )^{\mathrm {ab}}= \mathfrak {g}^{\mathfrak {m}} /\{\mathfrak {g}^{\mathfrak {m}} ,\mathfrak {g}^{\mathfrak {m}} \}$ are canonical. Since
$(\mathfrak {g}^{\mathfrak {m}} )^{\mathrm {ab}}= \mathfrak {g}^{\mathfrak {m}} /\{\mathfrak {g}^{\mathfrak {m}} ,\mathfrak {g}^{\mathfrak {m}} \}$ are canonical. Since ![]() $H_1(\mathfrak {g}^{\mathfrak {m}} ;\mathbb {Q})= (\mathfrak {g}^{\mathfrak {m}} )^{\mathrm {ab}}$, one can rephrase the previous theorem by saying that
$H_1(\mathfrak {g}^{\mathfrak {m}} ;\mathbb {Q})= (\mathfrak {g}^{\mathfrak {m}} )^{\mathrm {ab}}$, one can rephrase the previous theorem by saying that
 \begin{equation} \begin{gathered} H_1(\mathfrak{g}^{\mathfrak{m}} ; \mathbb{Q} ) \cong \bigoplus_{n\geq 1} [\sigma_{2n+1}] \mathbb{Q} ,\\ H_i(\mathfrak{g}^{\mathfrak{m}} ; \mathbb{Q}) = 0, \quad \hbox{for} \ i \geq 2. \end{gathered} \end{equation}
\begin{equation} \begin{gathered} H_1(\mathfrak{g}^{\mathfrak{m}} ; \mathbb{Q} ) \cong \bigoplus_{n\geq 1} [\sigma_{2n+1}] \mathbb{Q} ,\\ H_i(\mathfrak{g}^{\mathfrak{m}} ; \mathbb{Q}) = 0, \quad \hbox{for} \ i \geq 2. \end{gathered} \end{equation}
The abstract structure of the Lie algebra ![]() $\mathfrak {g}^{\mathfrak {m}}$ is therefore very simple, but the information about linear relations between multiple zeta values is encoded in the coefficients of the generators
$\mathfrak {g}^{\mathfrak {m}}$ is therefore very simple, but the information about linear relations between multiple zeta values is encoded in the coefficients of the generators ![]() $\sigma _{2n+1}$, which are not known explicitly. In this paper we study the associated graded version
$\sigma _{2n+1}$, which are not known explicitly. In this paper we study the associated graded version ![]() $\mathfrak {dg}^{\mathfrak {m}}$ of this Lie algebra for a filtration called the depth, which is related to the depth filtration on multiple zeta values. By contrast with the case of
$\mathfrak {dg}^{\mathfrak {m}}$ of this Lie algebra for a filtration called the depth, which is related to the depth filtration on multiple zeta values. By contrast with the case of ![]() $\mathfrak {g}^{\mathfrak {m}}$, we will provide an explicit conjectural description of all the generators of
$\mathfrak {g}^{\mathfrak {m}}$, we will provide an explicit conjectural description of all the generators of ![]() $\mathfrak {dg}^{\mathfrak {m}}$. It is not a free Lie algebra, but a little more complicated.
$\mathfrak {dg}^{\mathfrak {m}}$. It is not a free Lie algebra, but a little more complicated.
1.3 Depth filtration on the motivic Lie algebra
As defined in [Reference Deligne and GoncharovDG05], the depth filtration is induced geometrically by the inclusion ![]() $\mathbb {P}^1\backslash \{0,1,\infty \} \subset \mathbb {G}_m$ and is the decreasing filtration
$\mathbb {P}^1\backslash \{0,1,\infty \} \subset \mathbb {G}_m$ and is the decreasing filtration ![]() $\mathfrak {D}$ on
$\mathfrak {D}$ on ![]() $\mathbb {L}(e_0,e_1)$, where
$\mathbb {L}(e_0,e_1)$, where ![]() $\mathfrak {D}^r$ consists of Lie brackets containing at least
$\mathfrak {D}^r$ consists of Lie brackets containing at least ![]() $r$ occurrences of the letter
$r$ occurrences of the letter ![]() $e_1$. It is preserved by the Ihara bracket
$e_1$. It is preserved by the Ihara bracket ![]() $\{\,{,}\,\}$, and therefore defines a filtration on
$\{\,{,}\,\}$, and therefore defines a filtration on ![]() $\mathfrak {g}$. One defines the depth filtration
$\mathfrak {g}$. One defines the depth filtration ![]() $\mathfrak {D}^r \mathfrak {g}^{\mathfrak {m}}$ to be the induced filtration. An element in
$\mathfrak {D}^r \mathfrak {g}^{\mathfrak {m}}$ to be the induced filtration. An element in ![]() $\mathfrak {g}^{\mathfrak {m}}$ lies in
$\mathfrak {g}^{\mathfrak {m}}$ lies in ![]() $\mathfrak {D}^r \mathfrak {g}^{\mathfrak {m}}$ if and only if the corresponding derivation of
$\mathfrak {D}^r \mathfrak {g}^{\mathfrak {m}}$ if and only if the corresponding derivation of ![]() $\mathrm {Lie}\, {}_0 \Pi _{0}= \mathbb {L}(e_0,e_1)$ sends
$\mathrm {Lie}\, {}_0 \Pi _{0}= \mathbb {L}(e_0,e_1)$ sends ![]() $\mathfrak {D}^s$ to
$\mathfrak {D}^s$ to ![]() $\mathfrak {D}^{s+r}$ for all
$\mathfrak {D}^{s+r}$ for all ![]() $s$. This makes the motivic nature of
$s$. This makes the motivic nature of ![]() $\mathfrak {D}$ clear since the
$\mathfrak {D}$ clear since the ![]() $\sigma _{2n+1}$ increase the depth by at least 1.
$\sigma _{2n+1}$ increase the depth by at least 1.
We consider the associated graded Lie algebra:
It is bigraded by weight and depth: the depth will be indicated by a subscript, thus ![]() $\mathfrak {dg}^{\mathfrak {m}}_r = \mathrm {gr}^r_{\mathfrak {D}} \mathfrak {g}^{\mathfrak {m}}$. We identify
$\mathfrak {dg}^{\mathfrak {m}}_r = \mathrm {gr}^r_{\mathfrak {D}} \mathfrak {g}^{\mathfrak {m}}$. We identify ![]() $\mathfrak {dg}^{\mathfrak {m}}$ with a Lie subalgebra of
$\mathfrak {dg}^{\mathfrak {m}}$ with a Lie subalgebra of ![]() $\mathrm {gr}_{\mathfrak {D}} \mathfrak {g}$ which as a bigraded vector space is identified with
$\mathrm {gr}_{\mathfrak {D}} \mathfrak {g}$ which as a bigraded vector space is identified with ![]() $\mathbb {L}(e_0,e_1)$. Note that, in fact, the Ihara bracket
$\mathbb {L}(e_0,e_1)$. Note that, in fact, the Ihara bracket ![]() $\{\,{,}\,\}$ respects the depth grading on the free Lie algebra
$\{\,{,}\,\}$ respects the depth grading on the free Lie algebra ![]() $\mathbb {L}(e_0,e_1)$, so the Lie bracket on
$\mathbb {L}(e_0,e_1)$, so the Lie bracket on ![]() $\mathrm {gr}_{\mathfrak {D}} \mathfrak {g}$ is given by the identical formula to that for
$\mathrm {gr}_{\mathfrak {D}} \mathfrak {g}$ is given by the identical formula to that for ![]() $\{\,{,}\,\}$.
$\{\,{,}\,\}$.
In depth 1, ![]() $\mathfrak {dg}^{\mathfrak {m}}$ inherits canonical ‘zeta’ generators which are the images of
$\mathfrak {dg}^{\mathfrak {m}}$ inherits canonical ‘zeta’ generators which are the images of ![]() $\sigma _{2n+1}$:
$\sigma _{2n+1}$:
Ihara discovered, astonishingly, that in the depth-graded Lie algebra the generators ![]() $\bar {\sigma }_{2n+1}$ are not free. The first relation occurs in weight 12:
$\bar {\sigma }_{2n+1}$ are not free. The first relation occurs in weight 12:
In order to reconcile this relation with the freeness theorem (Theorem 1.1), there must exist an extra generator in ![]() $\mathfrak {dg}^{\mathfrak {m}}$ in weight 12 to compensate for it: the new generator is given by the lowest depth part of
$\mathfrak {dg}^{\mathfrak {m}}$ in weight 12 to compensate for it: the new generator is given by the lowest depth part of ![]() $\{\sigma _3, \sigma _9\} - 3 \{\sigma _5, \sigma _7\}$, which is in depth
$\{\sigma _3, \sigma _9\} - 3 \{\sigma _5, \sigma _7\}$, which is in depth ![]() $\geq 4$. Exceptional generators such as these (but defined in a direct and somewhat different manner) are one of the main objects of study of this paper.
$\geq 4$. Exceptional generators such as these (but defined in a direct and somewhat different manner) are one of the main objects of study of this paper.
The general quadratic relations between the ![]() $\bar {\sigma }_{2n+1}$ have been known explicitly for some time [Reference Ihara and TakaoIT93, Reference SchnepsSch06, Reference GoncharovGon05, Reference Gangl, Kaneko and ZagierGKZ06] and will be re-derived as an immediate consequence of the formalism we introduce below. To describe them, let
$\bar {\sigma }_{2n+1}$ have been known explicitly for some time [Reference Ihara and TakaoIT93, Reference SchnepsSch06, Reference GoncharovGon05, Reference Gangl, Kaneko and ZagierGKZ06] and will be re-derived as an immediate consequence of the formalism we introduce below. To describe them, let ![]() $V_{n} = \bigoplus _{i+j=n} \mathbb {Q} X^i Y^j$ denote the vector space of homogeneous polynomials of degree
$V_{n} = \bigoplus _{i+j=n} \mathbb {Q} X^i Y^j$ denote the vector space of homogeneous polynomials of degree ![]() $n$ in two variables, with its right action of
$n$ in two variables, with its right action of ![]() $\mathrm {SL}_2(\mathbb {Z})$. Evaluating cocycles on the matrix
$\mathrm {SL}_2(\mathbb {Z})$. Evaluating cocycles on the matrix ![]() $\big (\begin {smallmatrix} 0 & -1 \\ 1 & 0 \end {smallmatrix}\big )$ induces an isomorphism
$\big (\begin {smallmatrix} 0 & -1 \\ 1 & 0 \end {smallmatrix}\big )$ induces an isomorphism
where ![]() $+$ denotes invariants under the involution which sends a cocycle
$+$ denotes invariants under the involution which sends a cocycle ![]() $\gamma \mapsto C_{\gamma }$ to the cocycle
$\gamma \mapsto C_{\gamma }$ to the cocycle ![]() $\gamma \mapsto C_{\epsilon \gamma \epsilon ^{-1}}\big |_{\epsilon }$, where
$\gamma \mapsto C_{\epsilon \gamma \epsilon ^{-1}}\big |_{\epsilon }$, where ![]() $\epsilon = \big (\begin {smallmatrix} 1 & 0 \\ 0 & -1 \end {smallmatrix}\big )$. One can show that this involution is induced by the action of complex conjugation on
$\epsilon = \big (\begin {smallmatrix} 1 & 0 \\ 0 & -1 \end {smallmatrix}\big )$. One can show that this involution is induced by the action of complex conjugation on ![]() $(\mathbb {C} \backslash \mathbb {R}) / \mathrm {GL}_2(\mathbb {Z})$. The space
$(\mathbb {C} \backslash \mathbb {R}) / \mathrm {GL}_2(\mathbb {Z})$. The space ![]() $\mathsf {S} _{2n} \subset \mathbb {Q}[X,Y]$ is the space of even-period polynomials: it is the space of antisymmetric homogeneous polynomials
$\mathsf {S} _{2n} \subset \mathbb {Q}[X,Y]$ is the space of even-period polynomials: it is the space of antisymmetric homogeneous polynomials ![]() $P(X,Y)$ of degree
$P(X,Y)$ of degree ![]() $2n-2$, divisible by
$2n-2$, divisible by ![]() $Y$, satisfying
$Y$, satisfying ![]() $P(\pm X, \pm Y)=P(X,Y)$ and
$P(\pm X, \pm Y)=P(X,Y)$ and
One shows that the quadratic relations between ![]() $\bar {\sigma }_{2i+1}$ in weight
$\bar {\sigma }_{2i+1}$ in weight ![]() $2n+2$ are completely described by period polynomials in
$2n+2$ are completely described by period polynomials in ![]() $\mathsf {S} _{2n}$:
$\mathsf {S} _{2n}$:
where ![]() $i+j=n$ in both equations. The first goal of this paper is to provide a complete conjectural description of
$i+j=n$ in both equations. The first goal of this paper is to provide a complete conjectural description of ![]() $\mathfrak {dg}^{\mathfrak {m}}$.
$\mathfrak {dg}^{\mathfrak {m}}$.
1.4 Results
1.4.1 Missing generators
Firstly, we construct the candidate exceptional generators in depth 4 using period polynomials for cusp forms. We define an explicit map
which, to every even-period polynomial associates a Lie word in two generators ![]() $e_0,e_1$, of degree
$e_0,e_1$, of degree ![]() $4$ in
$4$ in ![]() $e_1$. A different source of extra generators in depth 4 are the lowest- depth part of expressions of the form
$e_1$. A different source of extra generators in depth 4 are the lowest- depth part of expressions of the form ![]() $\sum _{i < j} \lambda _{i,j} \{ \sigma _{2i+1}, \sigma _{2j+1}\}$ where the
$\sum _{i < j} \lambda _{i,j} \{ \sigma _{2i+1}, \sigma _{2j+1}\}$ where the ![]() $\lambda _{i,j}$ are as in (1.8) (these expressions have depth
$\lambda _{i,j}$ are as in (1.8) (these expressions have depth ![]() $\geq 4$) but such generators depend on a choice of generators
$\geq 4$) but such generators depend on a choice of generators ![]() $\sigma _{2n+1}$. A canonical choice of such generators was given in [Reference BrownBro17a], but the relationship with the elements
$\sigma _{2n+1}$. A canonical choice of such generators was given in [Reference BrownBro17a], but the relationship with the elements ![]() $\mathsf {e}$, which are introduced in the present paper and defined very differently, is not completely understood. For instance, even if one works modulo commutators, these two possible definitions of generators in depth 4 are related by a non-trivial isomorphism on the space of period polynomials (see §§ 1.4.3, 8.4).
$\mathsf {e}$, which are introduced in the present paper and defined very differently, is not completely understood. For instance, even if one works modulo commutators, these two possible definitions of generators in depth 4 are related by a non-trivial isomorphism on the space of period polynomials (see §§ 1.4.3, 8.4).
The simplest possible conjecture that one can make is that the depth-graded motivic Lie algebra is generated by the canonical generators ![]() $\bar {\sigma }_{2n+1}$ in depth 1, the image of the exceptional map
$\bar {\sigma }_{2n+1}$ in depth 1, the image of the exceptional map ![]() $\mathsf {e}$ in depth 4 and subject only to the known quadratic relations between the
$\mathsf {e}$ in depth 4 and subject only to the known quadratic relations between the ![]() $\bar {\sigma }_{2n+1}$ in depth 2. This is equivalent to a statement about
$\bar {\sigma }_{2n+1}$ in depth 2. This is equivalent to a statement about ![]() $H_i(\mathfrak {dg}^{\mathfrak {m}};\mathbb {Q})$ for
$H_i(\mathfrak {dg}^{\mathfrak {m}};\mathbb {Q})$ for ![]() $i=1,2$, and suggests the following reformulation of the Broadhurst–Kreimer conjecture.
$i=1,2$, and suggests the following reformulation of the Broadhurst–Kreimer conjecture.
Conjecture 1 The image of ![]() $\mathsf {e}$ lies in
$\mathsf {e}$ lies in ![]() $\mathfrak {dg}^{\mathfrak {m}}$, and
$\mathfrak {dg}^{\mathfrak {m}}$, and
 \begin{equation} \begin{aligned}H_1(\mathfrak{dg}^{\mathfrak{m}};\mathbb{Q}) &\cong \bigoplus_{n\geq 1} \bar{\sigma}_{2n+1} \mathbb{Q} \oplus \bigoplus_{n} \mathsf{e}(\mathsf{S} _{2n}), \\ H_2(\mathfrak{dg}^{\mathfrak{m}};\mathbb{Q}) &\cong {\bigoplus_n} \mathsf{S} _{2n}, \\ H_i(\mathfrak{dg}^{\mathfrak{m}};\mathbb{Q}) &= 0, \quad \hbox{for} \ i\geq 3 . \end{aligned} \end{equation}
\begin{equation} \begin{aligned}H_1(\mathfrak{dg}^{\mathfrak{m}};\mathbb{Q}) &\cong \bigoplus_{n\geq 1} \bar{\sigma}_{2n+1} \mathbb{Q} \oplus \bigoplus_{n} \mathsf{e}(\mathsf{S} _{2n}), \\ H_2(\mathfrak{dg}^{\mathfrak{m}};\mathbb{Q}) &\cong {\bigoplus_n} \mathsf{S} _{2n}, \\ H_i(\mathfrak{dg}^{\mathfrak{m}};\mathbb{Q}) &= 0, \quad \hbox{for} \ i\geq 3 . \end{aligned} \end{equation} We show in § 10.2 that Conjecture 1 implies the version of (1.2) in which multiple zeta values are replaced by motivic multiple zeta values. This is in turn equivalent to (1.2) if one assumes the period conjecture for mixed Tate motives over ![]() $\mathbb {Z}$.
$\mathbb {Z}$.
Conjecture 1 describes all relations between depth-graded motivic multiple zeta values (modulo products and ![]() $\zeta ^{{\mathfrak {m}}}(2)$). More precisely, consider the ring
$\zeta ^{{\mathfrak {m}}}(2)$). More precisely, consider the ring ![]() $\mathcal {H}$ of shuffle-regularized motivic multiple zeta values
$\mathcal {H}$ of shuffle-regularized motivic multiple zeta values ![]() $\zeta ^{{\mathfrak {m}}}(w)$ where
$\zeta ^{{\mathfrak {m}}}(w)$ where ![]() $w$ is a word in
$w$ is a word in ![]() $\{e_0,e_1\}$. It is weight-graded, and also has a depth filtration
$\{e_0,e_1\}$. It is weight-graded, and also has a depth filtration ![]() $\mathfrak {D}$, which counts the number of
$\mathfrak {D}$, which counts the number of ![]() $e_1$'s. Let
$e_1$'s. Let ![]() $\mathrm {gr}^{\mathfrak {D}} \mathcal {H}$ denote the associated graded ring and let
$\mathrm {gr}^{\mathfrak {D}} \mathcal {H}$ denote the associated graded ring and let ![]() $\mathrm {gr}^{\mathfrak {D}} I$ denote its augmentation ideal. Then a linear relation of weight
$\mathrm {gr}^{\mathfrak {D}} I$ denote its augmentation ideal. Then a linear relation of weight ![]() $N$ and depth
$N$ and depth ![]() $d$ of the form
$d$ of the form
where ![]() $\lambda _w \in \mathbb {Q}$ and
$\lambda _w \in \mathbb {Q}$ and ![]() $w$ ranges over words in
$w$ ranges over words in ![]() $e_0,e_1$ of length
$e_0,e_1$ of length ![]() $N$ with
$N$ with ![]() $d$ letters
$d$ letters ![]() $e_1$, holds in the quotientFootnote 4
$e_1$, holds in the quotientFootnote 4 ![]() $(\mathrm {gr}^{\mathfrak {D}} \mathcal {H}) / ((\mathrm {gr}^{\mathfrak {D}} I)^2 + (\zeta ^{{\mathfrak {m}}}(2)))$ if and only if, for all
$(\mathrm {gr}^{\mathfrak {D}} \mathcal {H}) / ((\mathrm {gr}^{\mathfrak {D}} I)^2 + (\zeta ^{{\mathfrak {m}}}(2)))$ if and only if, for all ![]() $x \in \mathfrak {dg}^{\mathfrak {m}}_d$ of weight
$x \in \mathfrak {dg}^{\mathfrak {m}}_d$ of weight ![]() $N$ and depth
$N$ and depth ![]() $d$ of the form
$d$ of the form ![]() $x= \sum _{w} c_w w$, one has
$x= \sum _{w} c_w w$, one has ![]() $\sum _{w} c_w \lambda _w =0.$ Since Conjecture 1 provides an explicit presentation for
$\sum _{w} c_w \lambda _w =0.$ Since Conjecture 1 provides an explicit presentation for ![]() $\mathfrak {dg}^{\mathfrak {m}}$, it conjecturally describes all such relations between (motivic) depth-graded multiple zeta values (see Example 8.4).
$\mathfrak {dg}^{\mathfrak {m}}$, it conjecturally describes all such relations between (motivic) depth-graded multiple zeta values (see Example 8.4).
In fact, the formalism developed here enables one to describe all relations between depth-graded motivic multiple zeta values (and not necessarily modulo products or modulo ![]() $\zeta ^{{\mathfrak {m}}}(2)$). These are described by the linear forms which vanish not on
$\zeta ^{{\mathfrak {m}}}(2)$). These are described by the linear forms which vanish not on ![]() $\mathfrak {dg}^{\mathfrak {m}}$ but rather on the bigraded right-module over the universal enveloping algebra
$\mathfrak {dg}^{\mathfrak {m}}$ but rather on the bigraded right-module over the universal enveloping algebra ![]() $\mathcal {U} \mathfrak {dg}^{\mathfrak {m}}$ generated by the depth 1 components of a rational associator
$\mathcal {U} \mathfrak {dg}^{\mathfrak {m}}$ generated by the depth 1 components of a rational associator ![]() $\tau ^{(1)}$ (defined in [Reference BrownBro17a]). This can be made completely explicit: see § 6.7.
$\tau ^{(1)}$ (defined in [Reference BrownBro17a]). This can be made completely explicit: see § 6.7.
1.4.2 Linearized double shuffle equations
The main evidence for the previous conjecture comes from the double shuffle equations. It is known that
where ![]() $\mathfrak {grt}$ is Drinfeld's Grothendieck–Teichmüller Lie algebra, and
$\mathfrak {grt}$ is Drinfeld's Grothendieck–Teichmüller Lie algebra, and ![]() $\mathfrak {dm}_0$ is Racinet's regularized double shuffle Lie algebra, both of which are defined by explicit equations. The inclusion of
$\mathfrak {dm}_0$ is Racinet's regularized double shuffle Lie algebra, both of which are defined by explicit equations. The inclusion of ![]() $\mathfrak {g}^{\mathfrak {m}}$ in
$\mathfrak {g}^{\mathfrak {m}}$ in ![]() $\mathfrak {grt}$ and
$\mathfrak {grt}$ and ![]() $\mathfrak {dm}_0$ follow from Theorem 1.1 and results of Drinfeld [Reference DrinfeldDri90] and Racinet [Reference RacinetRac02], respectively. The inclusion
$\mathfrak {dm}_0$ follow from Theorem 1.1 and results of Drinfeld [Reference DrinfeldDri90] and Racinet [Reference RacinetRac02], respectively. The inclusion ![]() $\mathfrak {grt} \subset \mathfrak {dm}_0$ is due to Furusho [Reference FurushoFur11].
$\mathfrak {grt} \subset \mathfrak {dm}_0$ is due to Furusho [Reference FurushoFur11].
If we pass to the depth-graded Lie algebras, we have
where ![]() $\mathfrak {ls}$ are the linearized double shuffle equations defined in [Reference Ihara, Kaneko and ZagierIKZ06]. The advantage of these equations are that they are extremely simple to define:
$\mathfrak {ls}$ are the linearized double shuffle equations defined in [Reference Ihara, Kaneko and ZagierIKZ06]. The advantage of these equations are that they are extremely simple to define: ![]() $\mathfrak {ls}$ is essentially the intersection of two shuffle algebras. Hitherto,
$\mathfrak {ls}$ is essentially the intersection of two shuffle algebras. Hitherto, ![]() $\mathfrak {ls}$ was studied merely as a vector space, but it turns out, as a consequence of the work of Racinet, that it also inherits a Lie algebra structure for the linearized Ihara bracket. We offer a complete conjectural description of
$\mathfrak {ls}$ was studied merely as a vector space, but it turns out, as a consequence of the work of Racinet, that it also inherits a Lie algebra structure for the linearized Ihara bracket. We offer a complete conjectural description of ![]() $\mathfrak {ls}$ below.
$\mathfrak {ls}$ below.
The first theorem states that the exceptional elements are solutions to the linearized double shuffle equations in depth 4.
Theorem 1.2 There is an explicit injective linear map
The formula for the map ![]() $\mathsf {e}$ is given in § 8, and associates to every even-period polynomial
$\mathsf {e}$ is given in § 8, and associates to every even-period polynomial ![]() $f$ a solution
$f$ a solution ![]() $\mathsf {e}_f$ of the linearized double shuffle equations. The question of whether the elements
$\mathsf {e}_f$ of the linearized double shuffle equations. The question of whether the elements ![]() $\mathsf {e}_f$ are motivic (i.e. whether they lie in the subspace
$\mathsf {e}_f$ are motivic (i.e. whether they lie in the subspace ![]() $\mathfrak {dg}^{\mathfrak {m}}$) is open.
$\mathfrak {dg}^{\mathfrak {m}}$) is open.
Conjecture 2 One has
 \begin{equation} \begin{aligned}H_1(\mathfrak{ls} ;\mathbb{Q}) &\cong \bigoplus_{n\geq 1} \bar{\sigma}_{2n+1} \mathbb{Q} \oplus \bigoplus_{n} \mathsf{e}(\mathsf{S} _{2n}), \\ H_2(\mathfrak{ls} ;\mathbb{Q}) &\cong {\bigoplus_n} \mathsf{S} _{2n}, \\ H_i(\mathfrak{ls} ;\mathbb{Q}) &= 0, \quad \hbox{for}\ i\geq 3.\end{aligned} \end{equation}
\begin{equation} \begin{aligned}H_1(\mathfrak{ls} ;\mathbb{Q}) &\cong \bigoplus_{n\geq 1} \bar{\sigma}_{2n+1} \mathbb{Q} \oplus \bigoplus_{n} \mathsf{e}(\mathsf{S} _{2n}), \\ H_2(\mathfrak{ls} ;\mathbb{Q}) &\cong {\bigoplus_n} \mathsf{S} _{2n}, \\ H_i(\mathfrak{ls} ;\mathbb{Q}) &= 0, \quad \hbox{for}\ i\geq 3.\end{aligned} \end{equation} This conjecture states, in particular, that ![]() $\mathfrak {ls}$ is generated by zeta elements and the exceptional generators in depth 4 subject only to the known quadratic relations between zeta elements. It is at the same time, the simplest and the strongest conjecture that one can formulate. It implies several open conjectures about relations between multiple zeta values. For example, it implies: Conjecture 1, and hence the motivic version of the Broadhurst–Kreimer conjecture; the conjecture
$\mathfrak {ls}$ is generated by zeta elements and the exceptional generators in depth 4 subject only to the known quadratic relations between zeta elements. It is at the same time, the simplest and the strongest conjecture that one can formulate. It implies several open conjectures about relations between multiple zeta values. For example, it implies: Conjecture 1, and hence the motivic version of the Broadhurst–Kreimer conjecture; the conjecture ![]() $\mathfrak {dg}^{\mathfrak {m}}=\mathfrak {ls}$ (which in turn implies a conjecture in [Reference Ihara, Kaneko and ZagierIKZ06]); and the conjectures
$\mathfrak {dg}^{\mathfrak {m}}=\mathfrak {ls}$ (which in turn implies a conjecture in [Reference Ihara, Kaneko and ZagierIKZ06]); and the conjectures ![]() $\mathfrak {g}^{\mathfrak {m}} = \mathfrak {grt}$ (Drinfeld) and
$\mathfrak {g}^{\mathfrak {m}} = \mathfrak {grt}$ (Drinfeld) and ![]() $\mathfrak {g}^{\mathfrak {m}} = \mathfrak {dm}_0$ (Zagier, Racinet). The proofs of these implications use Theorem 1.1 and Furusho's theorem [Reference FurushoFur11] in an essential way. Since the Lie algebra
$\mathfrak {g}^{\mathfrak {m}} = \mathfrak {dm}_0$ (Zagier, Racinet). The proofs of these implications use Theorem 1.1 and Furusho's theorem [Reference FurushoFur11] in an essential way. Since the Lie algebra ![]() $\mathfrak {ls}$ is defined in a very simple and completely elementary way, the previous conjecture suggest a possibility of seeking a proof of all of the above conjectures intrinsically within the theory of modular forms.
$\mathfrak {ls}$ is defined in a very simple and completely elementary way, the previous conjecture suggest a possibility of seeking a proof of all of the above conjectures intrinsically within the theory of modular forms.
1.4.3 Discussion
Note that the vanishing of ![]() $H_i(\mathfrak {ls} )$ for
$H_i(\mathfrak {ls} )$ for ![]() $i\geq 3$ is equivalent to the vanishing for
$i\geq 3$ is equivalent to the vanishing for ![]() $i=3$. This follows from the well-known fact that the vanishing of a Yoneda Ext group causes all higher Ext groups to vanish ([Reference Enriques and LochakEL16], [Reference BrownBro17a, Remark 8.6]).
$i=3$. This follows from the well-known fact that the vanishing of a Yoneda Ext group causes all higher Ext groups to vanish ([Reference Enriques and LochakEL16], [Reference BrownBro17a, Remark 8.6]).
The exceptional elements ![]() $\mathsf {e}$ satisfy a range of special properties which are studied in §§ 8 and 9. Using these, we can prove that they satisfy no quadratic relations, which provides some meagre evidence in favour of the previous conjectures. We do not know, however, that the
$\mathsf {e}$ satisfy a range of special properties which are studied in §§ 8 and 9. Using these, we can prove that they satisfy no quadratic relations, which provides some meagre evidence in favour of the previous conjectures. We do not know, however, that the ![]() $\mathsf {e}_f$ are non-trivial in the abelianization of
$\mathsf {e}_f$ are non-trivial in the abelianization of ![]() $\mathfrak {ls}$, nor can we presently rule out the existence of relations among the elements of the form
$\mathfrak {ls}$, nor can we presently rule out the existence of relations among the elements of the form
which are in depth ![]() $5$ and in weights
$5$ and in weights ![]() $\geq 15$ (respectively, 17). Relations which are quadratic in the
$\geq 15$ (respectively, 17). Relations which are quadratic in the ![]() $\mathsf {e}_f$ could first occur in weight 28 and depth 8. Viewed from this perspective, the current numerical data in favour of the standard conjectures on multiple zeta values is lacking, since new phenomena could potentially occur in weights and depths beyond the range of current experimentation. Any such phenomena would point to new and fascinating connections between mixed Tate motives over
$\mathsf {e}_f$ could first occur in weight 28 and depth 8. Viewed from this perspective, the current numerical data in favour of the standard conjectures on multiple zeta values is lacking, since new phenomena could potentially occur in weights and depths beyond the range of current experimentation. Any such phenomena would point to new and fascinating connections between mixed Tate motives over ![]() $\mathbb {Z}$ with geometry and arithmetic. Indeed, the methods introduced in this paper should enable one to test the validity of Conjecture 2 to far higher weights than presently known.
$\mathbb {Z}$ with geometry and arithmetic. Indeed, the methods introduced in this paper should enable one to test the validity of Conjecture 2 to far higher weights than presently known.
The motivic Lie algebra ![]() $\mathfrak {g}^{\mathfrak {m}}$ together with its depth filtration
$\mathfrak {g}^{\mathfrak {m}}$ together with its depth filtration ![]() $\mathfrak {D}$ naturally gives rise to a spectral sequence (§ 4.5), and the Broadhurst–Kreimer conjecture is equivalent to the statement that this spectral sequence should behave as simply as possible (given the existence of the quadratic relations between
$\mathfrak {D}$ naturally gives rise to a spectral sequence (§ 4.5), and the Broadhurst–Kreimer conjecture is equivalent to the statement that this spectral sequence should behave as simply as possible (given the existence of the quadratic relations between ![]() $\bar {\sigma }_{2n+1}$); there is only one non-trivial differential,
$\bar {\sigma }_{2n+1}$); there is only one non-trivial differential,
This is possibly also an argument in favour of Conjecture 1. In [Reference BrownBro17a] we computed this differential by finding canonical lifts of the zeta elements to depth 3. The relation with the map ![]() $\mathsf {e}$ is mysterious, although Yasuda has subsequently found a conjectural relation between
$\mathsf {e}$ is mysterious, although Yasuda has subsequently found a conjectural relation between ![]() $\mathsf {e}$ and the image of
$\mathsf {e}$ and the image of ![]() $d$ in the abelianization of
$d$ in the abelianization of ![]() $\mathfrak {ls}$ (private correspondence) involving critical values of
$\mathfrak {ls}$ (private correspondence) involving critical values of ![]() $L$-functions of cusp forms. See Example 8.5.
$L$-functions of cusp forms. See Example 8.5.
Finally, we investigate the Lie subalgebra of ![]() $\mathfrak {dg}^{\mathfrak {m}}$ which is generated only by the elements
$\mathfrak {dg}^{\mathfrak {m}}$ which is generated only by the elements ![]() $\bar {\sigma }_{2n+1}$ (without exceptional elements), and conjecture that it describes the structure of totally odd depth-graded motivic multiple zeta values.
$\bar {\sigma }_{2n+1}$ (without exceptional elements), and conjecture that it describes the structure of totally odd depth-graded motivic multiple zeta values.
1.5 Contents of the paper
In §§ 2–4 we recall some background on the motivic fundamental group of ![]() $\mathbb {P}^1\backslash \{ 0, 1, \infty \}$, the Ihara action and the depth filtration. In § 5 we discuss the linearized double shuffle relations from the Hopf algebra point of view. In § 6, and throughout the rest of the paper, we use polynomial representations to replace words of fixed
$\mathbb {P}^1\backslash \{ 0, 1, \infty \}$, the Ihara action and the depth filtration. In § 5 we discuss the linearized double shuffle relations from the Hopf algebra point of view. In § 6, and throughout the rest of the paper, we use polynomial representations to replace words of fixed ![]() $\mathfrak {D}$-degree
$\mathfrak {D}$-degree ![]() $r$ in
$r$ in ![]() $e_0,e_1$ with polynomials in
$e_0,e_1$ with polynomials in ![]() $r$ variables:
$r$ variables:
which sends words beginning in ![]() $e_0$ to zero, and
$e_0$ to zero, and ![]() $\bar {\rho } (e_1 e_0^{n_1} \ldots e_1 e_0^{n_r})=x_1^{n_1}\ldots x_r^{n_r}$. This replaces identities between non-commutative formal power series with functional equations in commutative polynomials, strongly reminiscent of those considered in [Reference EcalleEca03, Reference Ihara, Kaneko and ZagierIKZ06]. We show that in the polynomial representation, the Ihara bracket has an extremely simple form (§ 6.5). A simple way to view the duality between depth-graded motivic multiple zeta values and polynomials is via the generating series
$\bar {\rho } (e_1 e_0^{n_1} \ldots e_1 e_0^{n_r})=x_1^{n_1}\ldots x_r^{n_r}$. This replaces identities between non-commutative formal power series with functional equations in commutative polynomials, strongly reminiscent of those considered in [Reference EcalleEca03, Reference Ihara, Kaneko and ZagierIKZ06]. We show that in the polynomial representation, the Ihara bracket has an extremely simple form (§ 6.5). A simple way to view the duality between depth-graded motivic multiple zeta values and polynomials is via the generating series
The generators (1.6) are simply the coefficients of ![]() $\zeta ^{{\mathfrak {m}}}_{\mathfrak {D}}(2n+1)$:
$\zeta ^{{\mathfrak {m}}}_{\mathfrak {D}}(2n+1)$:
In § 7 we review the relation between period polynomials and depth 2 multiple zeta values, and in § 8 we define, for each period polynomial ![]() $P$, an element
$P$, an element
which defines the exceptional elements in ![]() $\mathfrak {ls} _4$. These elements satisfy some remarkable properties (§ 9) which are stable under the Ihara bracket. In § 10 we discuss Conjecture 1 and its consequences, and in § 11 we discuss some applications for the enumeration of the totally odd multiple zeta values
$\mathfrak {ls} _4$. These elements satisfy some remarkable properties (§ 9) which are stable under the Ihara bracket. In § 10 we discuss Conjecture 1 and its consequences, and in § 11 we discuss some applications for the enumeration of the totally odd multiple zeta values ![]() $\zeta (2n_1+1, \ldots , 2n_r+1)$ where
$\zeta (2n_1+1, \ldots , 2n_r+1)$ where ![]() $n_i\geq 1$.
$n_i\geq 1$.
1.5.1 Related work
Since the first draft of this paper appeared, there have been a number of related developments, which cannot all be mentioned here for reasons of space. I apologize to the many people who have subsequently extended some of the ideas in this paper in various directions [Reference MatthesMat16, Reference TasakaTas16, Reference MaMa16, Reference LiLi19], not only for the delay in publishing this work, but also for being unable to give a complete survey of subsequent developments of the subject here.
First of all, an alternative description of depth 4 exceptional generators was given in [Reference BrownBro17a], by constructing canonical zeta elements in ![]() $\mathfrak {g}^{\mathfrak {m}} /\mathfrak {D}^4 \mathfrak {g}^{\mathfrak {m}}$ and applying the differential in the depth spectral sequence. These elements are motivic (i.e. lie in
$\mathfrak {g}^{\mathfrak {m}} /\mathfrak {D}^4 \mathfrak {g}^{\mathfrak {m}}$ and applying the differential in the depth spectral sequence. These elements are motivic (i.e. lie in ![]() $\mathfrak {dg}^{\mathfrak {m}}_4$), but their relationship to the exceptional elements
$\mathfrak {dg}^{\mathfrak {m}}_4$), but their relationship to the exceptional elements ![]() $\mathsf {e}$ defined here is far from clear. The entire construction relies on the relationship between
$\mathsf {e}$ defined here is far from clear. The entire construction relies on the relationship between ![]() $\mathbb {P}^1 \backslash \{0,1,\infty \}$ (genus 0) and the unipotent completion of the fundamental group Tate elliptic curve (genus 1), and the fact that the depth filtration is induced by natural filtrations in the elliptic setting. Similarly, the precise relationship between the work of Pollack [Reference PollackPol09] and the present paper is now partially understood but warrants further investigation.
$\mathbb {P}^1 \backslash \{0,1,\infty \}$ (genus 0) and the unipotent completion of the fundamental group Tate elliptic curve (genus 1), and the fact that the depth filtration is induced by natural filtrations in the elliptic setting. Similarly, the precise relationship between the work of Pollack [Reference PollackPol09] and the present paper is now partially understood but warrants further investigation.
Subsequently, the work [Reference BrownBro14b] explains the origin of the quadratic relations between ![]() $\bar {\sigma }_{2n+1}$ by proving that they come from ‘modular elements’ corresponding to non-critical values of L-functions of cusp forms, which act on the relative completion of the fundamental group on the moduli stack
$\bar {\sigma }_{2n+1}$ by proving that they come from ‘modular elements’ corresponding to non-critical values of L-functions of cusp forms, which act on the relative completion of the fundamental group on the moduli stack ![]() $\mathcal {M}_{1,1}$ of elliptic curves. From this perspective, the canonical generators
$\mathcal {M}_{1,1}$ of elliptic curves. From this perspective, the canonical generators ![]() $\bar {\sigma }_{2n+1}$ can be understood as coming from Eisenstein series, which supports the philosophy that Conjecture 2 relates entirely to modular forms. Nevertheless, the connection between modular elements and the phenomena in depth 4 studied in the present paper remain unexplored.
$\bar {\sigma }_{2n+1}$ can be understood as coming from Eisenstein series, which supports the philosophy that Conjecture 2 relates entirely to modular forms. Nevertheless, the connection between modular elements and the phenomena in depth 4 studied in the present paper remain unexplored.
In a very different direction, Goncharov [Reference GoncharovGon05] has studied the depth filtration from the perspective of the homology of the general linear group ![]() $\mathrm {GL}_d(\mathbb {Z})$, which he relates to the structure of multiple zeta values in depth
$\mathrm {GL}_d(\mathbb {Z})$, which he relates to the structure of multiple zeta values in depth ![]() $d$. We have no understanding of the relationship between this point of view and conjecture (1.11).
$d$. We have no understanding of the relationship between this point of view and conjecture (1.11).
After the first draft of this paper appeared, Conjecture 4 was related to questions of Koszulity in the paper [Reference Enriques and LochakEL16].
Finally, the interested reader may wish to consult the notesFootnote 5 where, in answer to a question due to Zagier, we reformulated the Broadhurst–Kreimer conjecture as a short exact sequence, which suggests another line of attack on Conjecture 2.
2. Reminders on  $\pi _1^{\mathfrak {m}}(\mathbb {P}^1\backslash \{0,1,\infty \})$
$\pi _1^{\mathfrak {m}}(\mathbb {P}^1\backslash \{0,1,\infty \})$
2.1 The motivic  $\pi _1$ of
$\pi _1$ of  $\mathbb {P}^1\backslash \{0,1,\infty \}$
$\mathbb {P}^1\backslash \{0,1,\infty \}$
Let ![]() $X=\mathbb {P}^1\backslash \{0,1,\infty \}$, and let
$X=\mathbb {P}^1\backslash \{0,1,\infty \}$, and let ![]() $\overset {\rightarrow }{1}\!_0, -\overset {\rightarrow }{1}\!_1$ denote the tangential base points on
$\overset {\rightarrow }{1}\!_0, -\overset {\rightarrow }{1}\!_1$ denote the tangential base points on ![]() $X$ given by the tangent vector
$X$ given by the tangent vector ![]() $1$ at
$1$ at ![]() $0$, and the tangent vector
$0$, and the tangent vector ![]() $-1$ at
$-1$ at ![]() $1$. Denote the de Rham realization of the motivic fundamental torsor of paths on
$1$. Denote the de Rham realization of the motivic fundamental torsor of paths on ![]() $X$ with respect to these basepoints by
$X$ with respect to these basepoints by
It is the affine scheme over ![]() $\mathbb {Q}$ which to any commutative unitary
$\mathbb {Q}$ which to any commutative unitary ![]() $\mathbb {Q}$-algebra
$\mathbb {Q}$-algebra ![]() $R$ associates the set of group-like formal power series in two non-commuting variables
$R$ associates the set of group-like formal power series in two non-commuting variables ![]() $e_0$ and
$e_0$ and ![]() $e_1$,
$e_1$,
where ![]() $\Delta$ is the completed coproduct for which the elements
$\Delta$ is the completed coproduct for which the elements ![]() $e_0$ and
$e_0$ and ![]() $e_1$ are primitive:
$e_1$ are primitive: ![]() $\Delta e_i = 1\otimes e_i + e_i \otimes 1$ for
$\Delta e_i = 1\otimes e_i + e_i \otimes 1$ for ![]() $i=0,1$. The ring of regular functions on
$i=0,1$. The ring of regular functions on ![]() ${}_0 \Pi _{1}$ is the
${}_0 \Pi _{1}$ is the ![]() $\mathbb {Q}$-algebra
$\mathbb {Q}$-algebra
whose underlying vector space is spanned by the set of words ![]() $w$ in the letters
$w$ in the letters ![]() $e^0, e^1$, together with the empty word, and whose multiplication is given by the shuffle product
$e^0, e^1$, together with the empty word, and whose multiplication is given by the shuffle product ![]() $\, \unicode{x0448} \,: \mathbb {Q} \langle e^0, e^1 \rangle \otimes _{\mathbb {Q}} \mathbb {Q} \langle e^0, e^1 \rangle \rightarrow \mathbb {Q} \langle e^0, e^1 \rangle$. The deconcatenation of words defines a coproduct, making
$\, \unicode{x0448} \,: \mathbb {Q} \langle e^0, e^1 \rangle \otimes _{\mathbb {Q}} \mathbb {Q} \langle e^0, e^1 \rangle \rightarrow \mathbb {Q} \langle e^0, e^1 \rangle$. The deconcatenation of words defines a coproduct, making ![]() $\mathcal {O}({}_0 \Pi _{1})$ into a Hopf algebra. This gives rise to a group structure on
$\mathcal {O}({}_0 \Pi _{1})$ into a Hopf algebra. This gives rise to a group structure on ![]() ${}_0 \Pi _{1}(\mathbb {Q})$ (corresponding to the fact that in the de Rham realization there is a canonical path between any two points on
${}_0 \Pi _{1}(\mathbb {Q})$ (corresponding to the fact that in the de Rham realization there is a canonical path between any two points on ![]() $X$). Any word
$X$). Any word ![]() $w$ in
$w$ in ![]() $e^0,e^1$ defines a function
$e^0,e^1$ defines a function
which extracts the coefficient ![]() $S_w$ of the word
$S_w$ of the word ![]() $w$ (viewed in
$w$ (viewed in ![]() $e_0,e_1$) in a group-like series
$e_0,e_1$) in a group-like series ![]() $S \in R\langle \!\langle e_0, e_1 \rangle \! \rangle ^{\times }$. The Lie algebra of
$S \in R\langle \!\langle e_0, e_1 \rangle \! \rangle ^{\times }$. The Lie algebra of ![]() ${}_0 \Pi _{1}(\mathbb {Q})$ is the completed Lie algebra
${}_0 \Pi _{1}(\mathbb {Q})$ is the completed Lie algebra ![]() $\mathbb {L}(e_0,e_1)^\wedge$ of the graded Lie algebra
$\mathbb {L}(e_0,e_1)^\wedge$ of the graded Lie algebra ![]() $\mathbb {L}(e_0,e_1)$ which is freely generated by the two elements
$\mathbb {L}(e_0,e_1)$ which is freely generated by the two elements ![]() $e_0,e_1$ in degree
$e_0,e_1$ in degree ![]() $-1$. The universal enveloping algebra
$-1$. The universal enveloping algebra ![]() $\mathcal {U} \, \mathbb {L}(e_0,e_1)$ of
$\mathcal {U} \, \mathbb {L}(e_0,e_1)$ of ![]() $\mathbb {L}(e_0,e_1)$ is the tensor (co)algebra on
$\mathbb {L}(e_0,e_1)$ is the tensor (co)algebra on ![]() $e_0,e_1$:
$e_0,e_1$:
It is the graded cocommutative Hopf algebra which is the graded dual of ![]() $\mathcal {O}({}_0 \Pi _{1})$. Its multiplication is given by the concatenation product, and its coproduct is the unique coproduct for which
$\mathcal {O}({}_0 \Pi _{1})$. Its multiplication is given by the concatenation product, and its coproduct is the unique coproduct for which ![]() $e_0$ and
$e_0$ and ![]() $e_1$ are primitive.
$e_1$ are primitive.
2.2 Action of the motivic Galois group
Now let ![]() $\mathcal {MT}(\mathbb {Z})$ denote the Tannakian category of mixed Tate motives over
$\mathcal {MT}(\mathbb {Z})$ denote the Tannakian category of mixed Tate motives over ![]() $\mathbb {Z}$, with canonical fiber functor given by the de Rham realization. Let
$\mathbb {Z}$, with canonical fiber functor given by the de Rham realization. Let ![]() $\mathcal {G}_{\mathcal {MT}(\mathbb {Z})}$ denote the group of automorphisms of this fiber functor. It is an affine group scheme over
$\mathcal {G}_{\mathcal {MT}(\mathbb {Z})}$ denote the group of automorphisms of this fiber functor. It is an affine group scheme over ![]() $\mathbb {Q}$. It has a decomposition as a semi-direct product
$\mathbb {Q}$. It has a decomposition as a semi-direct product
where ![]() $\mathcal {U}_{\mathcal {MT}(\mathbb {Z})}$ is pro-unipotent. Furthermore, one knows from the relationship between the Ext groups in
$\mathcal {U}_{\mathcal {MT}(\mathbb {Z})}$ is pro-unipotent. Furthermore, one knows from the relationship between the Ext groups in ![]() $\mathcal {MT}(\mathbb {Z})$ and Borel's results on the rational algebraic
$\mathcal {MT}(\mathbb {Z})$ and Borel's results on the rational algebraic ![]() $K$-theory of
$K$-theory of ![]() $\mathbb {Q}$ that the graded Lie algebra of
$\mathbb {Q}$ that the graded Lie algebra of ![]() $\mathcal {U}_{\mathcal {MT}(\mathbb {Z})}$ is non-canonically isomorphic to the Lie algebra freely generated by one generator
$\mathcal {U}_{\mathcal {MT}(\mathbb {Z})}$ is non-canonically isomorphic to the Lie algebra freely generated by one generator ![]() $\sigma _{2i+1}$ in degree
$\sigma _{2i+1}$ in degree ![]() $-(2i+1)$ for every
$-(2i+1)$ for every ![]() $i\geq 1$. It is important to note that only the classes of the elements
$i\geq 1$. It is important to note that only the classes of the elements ![]() $\sigma _{2i+1}$ in the abelianization
$\sigma _{2i+1}$ in the abelianization ![]() $\mathcal {U}_{\mathcal {MT}(\mathbb {Z})}^{\mathrm {ab}}$ are canonical, the elements
$\mathcal {U}_{\mathcal {MT}(\mathbb {Z})}^{\mathrm {ab}}$ are canonical, the elements ![]() $\sigma _{2i+1}$ themselves are not.
$\sigma _{2i+1}$ themselves are not.
Since ![]() $\mathcal {O}({}_0 \Pi _{1})$ is the de Rham realization of an Ind-object in the category
$\mathcal {O}({}_0 \Pi _{1})$ is the de Rham realization of an Ind-object in the category ![]() $\mathcal {MT}(\mathbb {Z})$, there is an action of the motivic Galois group
$\mathcal {MT}(\mathbb {Z})$, there is an action of the motivic Galois group ![]() $\mathcal {G}_{\mathcal {MT}(\mathbb {Z})}$ on
$\mathcal {G}_{\mathcal {MT}(\mathbb {Z})}$ on ![]() ${}_0 \Pi _{1}$ and hence
${}_0 \Pi _{1}$ and hence
The action of ![]() $\mathcal {U}_{\mathcal {MT}(\mathbb {Z})}$ on the unit element
$\mathcal {U}_{\mathcal {MT}(\mathbb {Z})}$ on the unit element ![]() $1\in {}_0 \Pi _{1}$ defines a map
$1\in {}_0 \Pi _{1}$ defines a map
and the action (2.2) factors through a map
first computed by Ihara. It is obtained from [Reference Deligne and GoncharovDG05, §§ 5.9, 5.13], by reversing all words in order to be consistent with our convention for composition of paths. An element ![]() $a\in {}_0 \Pi _{1}$ defines an action denoted by
$a\in {}_0 \Pi _{1}$ defines an action denoted by ![]() $\langle a \rangle _0$ on
$\langle a \rangle _0$ on ![]() ${}_0 \Pi _{0}$ which is compatible with (2.4) via the composition of paths
${}_0 \Pi _{0}$ which is compatible with (2.4) via the composition of paths ![]() ${}_0 \Pi _{0} \times {}_0 \Pi _{1} \rightarrow {}_0 \Pi _{1}$. Therefore, writing
${}_0 \Pi _{0} \times {}_0 \Pi _{1} \rightarrow {}_0 \Pi _{1}$. Therefore, writing ![]() $x_{00}$ (respectively,
$x_{00}$ (respectively, ![]() $x_{01}$) for the element
$x_{01}$) for the element ![]() $x$ in
$x$ in ![]() ${}_0 \Pi _{0}$ (respectively,
${}_0 \Pi _{0}$ (respectively, ![]() ${}_0 \Pi _{1})$, one finds that for
${}_0 \Pi _{1})$, one finds that for ![]() $g\in {}_0 \Pi _{1}$,
$g\in {}_0 \Pi _{1}$,
where ![]() $\langle a \rangle _0$ acts on the generators
$\langle a \rangle _0$ acts on the generators ![]() $\exp (e_i)$ in
$\exp (e_i)$ in ![]() ${}_0 \Pi _{0}$, for
${}_0 \Pi _{0}$, for ![]() $i=0,1$, by
$i=0,1$, by
We now give a concrete way to compute ![]() $\circ$ by expressing it as the restriction of a combinatorially defined map
$\circ$ by expressing it as the restriction of a combinatorially defined map ![]() $\, \underline {\circ }\,$ on a larger space.
$\, \underline {\circ }\,$ on a larger space.
Definition 2.1 Inductively define a ![]() $\mathbb {Q}$-bilinear map
$\mathbb {Q}$-bilinear map
as follows. For any two words ![]() $a, w$ in
$a, w$ in ![]() $e_0,e_1$, and any integer
$e_0,e_1$, and any integer ![]() $n\geq 0$, let
$n\geq 0$, let
where ![]() $a \, \underline {\circ }\, e_0^n = e_0^n a$, and for any
$a \, \underline {\circ }\, e_0^n = e_0^n a$, and for any ![]() $a_i \in \{e_0,e_1\}$,
$a_i \in \{e_0,e_1\}$, ![]() $(a_1\ldots a_n)^* = (-1)^n a_n \ldots a_1$.
$(a_1\ldots a_n)^* = (-1)^n a_n \ldots a_1$.
We now show that the map ![]() $\, \underline {\circ }\,$ restricts to the full action
$\, \underline {\circ }\,$ restricts to the full action
induced by (2.4). To see this, identify the universal enveloping of the graded Lie algebra ![]() $\mathcal {U} \,\mathrm {Lie} \, {}_0 \Pi _{1} = \mathcal {U} \mathbb {L}(e_0,e_1)$ with
$\mathcal {U} \,\mathrm {Lie} \, {}_0 \Pi _{1} = \mathcal {U} \mathbb {L}(e_0,e_1)$ with ![]() $T(e_0, e_1)$. Since
$T(e_0, e_1)$. Since ![]() $\mathfrak {g}$ is isomorphic (as a vector space) to
$\mathfrak {g}$ is isomorphic (as a vector space) to ![]() $\mathbb {L}(e_0,e_1)$, there is also a natural embedding
$\mathbb {L}(e_0,e_1)$, there is also a natural embedding ![]() $i: \mathfrak {g}\rightarrow T(e_0,e_1)$.
$i: \mathfrak {g}\rightarrow T(e_0,e_1)$.
Proposition 2.2 The action (2.8) is obtained by restriction of ![]() $\, \underline {\circ }\,$, that is,
$\, \underline {\circ }\,$, that is,
Proof. For any ![]() $S \in {}_0 \Pi _{1}$, the coefficient of
$S \in {}_0 \Pi _{1}$, the coefficient of ![]() $w$ in
$w$ in ![]() $S^{-1}$ is equal to the coefficient of
$S^{-1}$ is equal to the coefficient of ![]() $w^*$ in
$w^*$ in ![]() $S$, since the map
$S$, since the map ![]() $*$ is the antipode in
$*$ is the antipode in ![]() $\mathcal {O}({}_0 \Pi _{1})$. Identifying the (vector space)
$\mathcal {O}({}_0 \Pi _{1})$. Identifying the (vector space) ![]() $\mathfrak {g}\cong \mathbb {L}(e_0,e_1)$ with its image in
$\mathfrak {g}\cong \mathbb {L}(e_0,e_1)$ with its image in ![]() $T(e_0,e_1)$, it follows that the infinitesimal, weight-graded, version of the map (2.6) is the derivation
$T(e_0,e_1)$, it follows that the infinitesimal, weight-graded, version of the map (2.6) is the derivation ![]() $\langle f\rangle _0:\mathbb {L}(e_0,e_1) \rightarrow \mathbb {L}(e_0,e_1)$ which for any
$\langle f\rangle _0:\mathbb {L}(e_0,e_1) \rightarrow \mathbb {L}(e_0,e_1)$ which for any ![]() $f\in \mathbb {L}(e_0,e_1)$ is given by
$f\in \mathbb {L}(e_0,e_1)$ is given by
Thus ![]() $\langle f\rangle _0 : T(e_0,e_1) \rightarrow T(e_0,e_1)$ is the map
$\langle f\rangle _0 : T(e_0,e_1) \rightarrow T(e_0,e_1)$ is the map
Adding the term ![]() $e_0^{m_0} e_1 \ldots e_1 e_0^{m_r} f$ corresponding to concatenation on the right by
$e_0^{m_0} e_1 \ldots e_1 e_0^{m_r} f$ corresponding to concatenation on the right by ![]() $f$ gives precisely the map defined by (2.7).
$f$ gives precisely the map defined by (2.7).
2.3 The motivic Lie algebra
By (2.3), we obtain a map of Lie algebras
where the Ihara bracket satisfies ![]() $\{f,g\}= f\circ g- g \circ f$. It follows from Theorem 1.1 that this map is injective [Reference BrownBro12]. In this paper, we shall identify
$\{f,g\}= f\circ g- g \circ f$. It follows from Theorem 1.1 that this map is injective [Reference BrownBro12]. In this paper, we shall identify ![]() $\mathrm {Lie} (\mathcal {U}_{\mathcal {MT}(\mathbb {Z})})$ with its image, and abusively call it the motivic Lie algebra.
$\mathrm {Lie} (\mathcal {U}_{\mathcal {MT}(\mathbb {Z})})$ with its image, and abusively call it the motivic Lie algebra.
Definition 2.3 The motivic Lie algebra ![]() $\mathfrak {g}^{\mathfrak {m}} \subseteq \mathfrak {g}$ is the image of the map (2.9).
$\mathfrak {g}^{\mathfrak {m}} \subseteq \mathfrak {g}$ is the image of the map (2.9).
The Lie algebra ![]() $\mathfrak {g}^{\mathfrak {m}}$ is non-canonically isomorphic to the free Lie algebra with one generator
$\mathfrak {g}^{\mathfrak {m}}$ is non-canonically isomorphic to the free Lie algebra with one generator ![]() $\sigma _{2i+1}$ in each degree
$\sigma _{2i+1}$ in each degree ![]() $-(2i+1)$ for
$-(2i+1)$ for ![]() $i \geq 1$.
$i \geq 1$.
3. Motivic multiple zeta values
Let ![]() $\mathcal {A}^{\mathcal {MT}}$ denote the graded Hopf algebra of functions on
$\mathcal {A}^{\mathcal {MT}}$ denote the graded Hopf algebra of functions on ![]() $\mathcal {U}_{\mathcal {MT}(\mathbb {Z})}$. Dualizing (2.2) gives the motivic coaction (written in this paper as a left coaction)
$\mathcal {U}_{\mathcal {MT}(\mathbb {Z})}$. Dualizing (2.2) gives the motivic coaction (written in this paper as a left coaction)
Furthermore, the image in ![]() ${}_0 \Pi _{1}(\mathbb {C})$ of the straight path
${}_0 \Pi _{1}(\mathbb {C})$ of the straight path ![]() $dch$ from
$dch$ from ![]() $0$ to
$0$ to ![]() $1$ in
$1$ in ![]() $X$ under the comparison isomorphism is the Drinfeld associator element
$X$ under the comparison isomorphism is the Drinfeld associator element ![]() $\Phi \in {}_0 \Pi _{1}(\mathbb {R})$ which begins
$\Phi \in {}_0 \Pi _{1}(\mathbb {R})$ which begins
The map which takes the coefficient of a word ![]() $w$ in
$w$ in ![]() $\Phi$ defines the period homomorphism
$\Phi$ defines the period homomorphism
Here, we use the convention from [Reference BrownBro12]: the coefficient of the word ![]() $e_{a_1}\ldots e_{a_n}$ in
$e_{a_1}\ldots e_{a_n}$ in ![]() $\Phi$, for
$\Phi$, for ![]() $a_i \in \{0,1\}$, is the iterated integral
$a_i \in \{0,1\}$, is the iterated integral
regularized with respect to the tangent vector ![]() $1$ at
$1$ at ![]() $0$, and
$0$, and ![]() $-1$ at
$-1$ at ![]() $1$, where the integration begins on the left, and
$1$, where the integration begins on the left, and ![]() $\omega _0 = {dt }/{t}$ and
$\omega _0 = {dt }/{t}$ and ![]() $\omega _1 = {dt }/({1-t})$.
$\omega _1 = {dt }/({1-t})$.
Definition 3.1 The algebra of motivic multiple zeta values is defined as follows. The ideal of motivic relations between multiple zeta values is defined to be ![]() $J^{\mathcal {MT}} \leq \mathcal {O}({}_0 \Pi _{1})$, the largest graded ideal contained in the kernel of
$J^{\mathcal {MT}} \leq \mathcal {O}({}_0 \Pi _{1})$, the largest graded ideal contained in the kernel of ![]() $per$ which is stable under
$per$ which is stable under ![]() $\Delta ^{\mathcal {M}}$. We set
$\Delta ^{\mathcal {M}}$. We set
and let ![]() $\zeta ^{{\mathfrak {m}}}(n_1,\ldots , n_r)$ denote the image of the word
$\zeta ^{{\mathfrak {m}}}(n_1,\ldots , n_r)$ denote the image of the word ![]() $e^1(e^0)^{n_1-1} \ldots e^1 (e^0)^{n_r-1}$ in
$e^1(e^0)^{n_1-1} \ldots e^1 (e^0)^{n_r-1}$ in ![]() $\mathcal {H}$. Likewise, for any
$\mathcal {H}$. Likewise, for any ![]() $a_1,\ldots , a_n \in \{0,1\}$, we let
$a_1,\ldots , a_n \in \{0,1\}$, we let ![]() $I^{\mathfrak {m}}(0;a_1,\ldots , a_n;1)$ denote the image of the word
$I^{\mathfrak {m}}(0;a_1,\ldots , a_n;1)$ denote the image of the word ![]() $e^{a_1}\ldots e^{a_n}$ in
$e^{a_1}\ldots e^{a_n}$ in ![]() $\mathcal {H}$. Equivalently, one can define
$\mathcal {H}$. Equivalently, one can define
where the right-hand side is a motivic period [Reference BrownBro14a] of the category ![]() $\mathcal {MT}(\mathbb {Z})$, and define the motivic multiple zeta values by specializing to the case when
$\mathcal {MT}(\mathbb {Z})$, and define the motivic multiple zeta values by specializing to the case when ![]() $a_1=1$ and
$a_1=1$ and ![]() $a_n=0$.
$a_n=0$.
Remark 3.2 The algebra of motivic multiple zeta values has the following geometric interpretation: ![]() $J^{\mathcal {MT}}$ is the ideal of functions which vanishes on the orbit of the de Rham image of
$J^{\mathcal {MT}}$ is the ideal of functions which vanishes on the orbit of the de Rham image of ![]() $dch$ in
$dch$ in ![]() ${}_0 \Pi _{1}(\mathbb {C})$. The latter is defined over
${}_0 \Pi _{1}(\mathbb {C})$. The latter is defined over ![]() $\mathbb {Q}$ because it is the image under the comparison isomorphism of the orbit under the Betti Galois group
$\mathbb {Q}$ because it is the image under the comparison isomorphism of the orbit under the Betti Galois group ![]() $\mathrm {Aut}^{\otimes }_{\mathcal {MT}(\mathbb {Z})}(\omega _B)$ of the Betti image of the straight-line path, which is rational.
$\mathrm {Aut}^{\otimes }_{\mathcal {MT}(\mathbb {Z})}(\omega _B)$ of the Betti image of the straight-line path, which is rational.
The space ![]() $\mathcal {H}$ is naturally graded by the weight, and has a graded coaction
$\mathcal {H}$ is naturally graded by the weight, and has a graded coaction
and a period map ![]() $per: \mathcal {H} \rightarrow \mathbb {R}$. The period of
$per: \mathcal {H} \rightarrow \mathbb {R}$. The period of ![]() $\zeta ^{{\mathfrak {m}}}(n_1,\ldots , n_r)$ is
$\zeta ^{{\mathfrak {m}}}(n_1,\ldots , n_r)$ is ![]() $\zeta (n_1,\ldots , n_r)$. One obtains partial information about the motivic coaction (3.1) using the fact that it factors through the coaction which is dual to the Ihara action (2.4).
$\zeta (n_1,\ldots , n_r)$. One obtains partial information about the motivic coaction (3.1) using the fact that it factors through the coaction which is dual to the Ihara action (2.4).
3.1 The Ihara coaction
For any graded Hopf algebra ![]() $H$, let
$H$, let ![]() $IH= H_{>0}/H^2_{>0}$ denote the Lie coalgebra of indecomposable elements of
$IH= H_{>0}/H^2_{>0}$ denote the Lie coalgebra of indecomposable elements of ![]() $H$, and let
$H$, and let ![]() $\pi : H_{>0} \rightarrow IH$ denote the natural map. Dualizing (2.8) (and making it into a left coaction) gives an infinitesimal coaction
$\pi : H_{>0} \rightarrow IH$ denote the natural map. Dualizing (2.8) (and making it into a left coaction) gives an infinitesimal coaction
Let ![]() $D_{r}: \mathcal {O}({}_0 \Pi _{1}) \rightarrow I \mathcal {O}({}_0 \Pi _{1})_r \otimes _{\mathbb {Q}} \mathcal {O}({}_0 \Pi _{1})$ denote its component of degree
$D_{r}: \mathcal {O}({}_0 \Pi _{1}) \rightarrow I \mathcal {O}({}_0 \Pi _{1})_r \otimes _{\mathbb {Q}} \mathcal {O}({}_0 \Pi _{1})$ denote its component of degree ![]() $(r,\cdot )$, and let us denote the element
$(r,\cdot )$, and let us denote the element ![]() $e^{a_1}\ldots e^{a_n}$ in
$e^{a_1}\ldots e^{a_n}$ in ![]() $\mathcal {O}({}_0 \Pi _{1})$ by
$\mathcal {O}({}_0 \Pi _{1})$ by ![]() $\mathbb {I}(0;a_1,\ldots , a_n;1)$, where
$\mathbb {I}(0;a_1,\ldots , a_n;1)$, where ![]() $a_i \in \{0,1\}$.
$a_i \in \{0,1\}$.
Proposition 3.3 Set ![]() $a_0=0, a_{n+1}=1$. For all
$a_0=0, a_{n+1}=1$. For all ![]() $r\geq 1$, and
$r\geq 1$, and ![]() $a_1,\ldots , a_n \in \{0,1\}$,
$a_1,\ldots , a_n \in \{0,1\}$,
 \begin{align} D_r \, \mathbb{I}( 0; a_1, \ldots, a_n; 1 ) =\sum_{p=0}^{n-r} \pi( \mathbb{I}(a_{p} ;a_{p+1},.\, .\,, a_{p+r}; a_{p+r+1})) \otimes \mathbb{I}(0; a_1, .\, .\,, a_{p}, a_{p+r+1}, .\, .\, , a_n ; 1) , \end{align}
\begin{align} D_r \, \mathbb{I}( 0; a_1, \ldots, a_n; 1 ) =\sum_{p=0}^{n-r} \pi( \mathbb{I}(a_{p} ;a_{p+1},.\, .\,, a_{p+r}; a_{p+r+1})) \otimes \mathbb{I}(0; a_1, .\, .\,, a_{p}, a_{p+r+1}, .\, .\, , a_n ; 1) , \end{align}
where ![]() $\mathbb {I}(a_{p} ;a_{p+1},.\, .\,, a_{p+r}; a_{p+r+1}) \in \mathcal {O}({}_0 \Pi _{1})$ is defined to be zero if
$\mathbb {I}(a_{p} ;a_{p+1},.\, .\,, a_{p+r}; a_{p+r+1}) \in \mathcal {O}({}_0 \Pi _{1})$ is defined to be zero if ![]() $a_p=a_{p+r+1}$, and equal to
$a_p=a_{p+r+1}$, and equal to ![]() $(-1)^r \mathbb {I}( a_{p+r+1} ;a_{p+r},.\, .\,, a_{p+1}; a_{p})$ if
$(-1)^r \mathbb {I}( a_{p+r+1} ;a_{p+r},.\, .\,, a_{p+1}; a_{p})$ if ![]() $a_p=1$ and
$a_p=1$ and ![]() $a_{p+r+1}=0$.
$a_{p+r+1}=0$.
Proof. One checks that this formula is dual to ![]() $\, \underline {\circ }\,$ (see also [Reference BrownBro14a, § 2.5]).
$\, \underline {\circ }\,$ (see also [Reference BrownBro14a, § 2.5]).
Since the motivic coaction on ![]() $\mathcal {H}$ factors through the Ihara coaction, it follows that the degree
$\mathcal {H}$ factors through the Ihara coaction, it follows that the degree ![]() $(r,\cdot )$ component factors through operators
$(r,\cdot )$ component factors through operators
given by the same formula as (3.3) in which each term ![]() $\mathbb {I}$ is replaced by its image
$\mathbb {I}$ is replaced by its image ![]() $I^{\mathfrak {m}}$ in
$I^{\mathfrak {m}}$ in ![]() $\mathcal {H}$ (respectively,
$\mathcal {H}$ (respectively, ![]() $\mathcal {A}$). Since
$\mathcal {A}$). Since ![]() $\mathcal {A}^{\mathcal {MT}}$ is cogenerated in odd degrees only, the motivic coaction on
$\mathcal {A}^{\mathcal {MT}}$ is cogenerated in odd degrees only, the motivic coaction on ![]() $\mathcal {H}$ is completely determined by the set of operators
$\mathcal {H}$ is completely determined by the set of operators ![]() $D_{2r+1}$ for all
$D_{2r+1}$ for all ![]() $r\geq 1$ (see [Reference BrownBro12]).
$r\geq 1$ (see [Reference BrownBro12]).
4. The depth filtration
4.1 Definition
The depth filtration was defined in [Reference Deligne and GoncharovDG05, § 6.1]. We recall the definition in a slightly different language. The inclusion ![]() $\mathbb {P}^1\backslash \{0,1,\infty \} \hookrightarrow \mathbb {P}^1\backslash \{0,\infty \}$ induces a map on the motivic fundamental groupoids
$\mathbb {P}^1\backslash \{0,1,\infty \} \hookrightarrow \mathbb {P}^1\backslash \{0,\infty \}$ induces a map on the motivic fundamental groupoids
and hence on the de Rham realizations
and similarly for ![]() $\mathcal {O}(\pi ^{\mathrm {dR}}_1(\mathbb {G}_m, \overset {\rightarrow }{1}\!_0))\rightarrow \mathcal {O}({}_0 \Pi _{0})$. They are given by the inclusion of
$\mathcal {O}(\pi ^{\mathrm {dR}}_1(\mathbb {G}_m, \overset {\rightarrow }{1}\!_0))\rightarrow \mathcal {O}({}_0 \Pi _{0})$. They are given by the inclusion of ![]() $\mathbb {Q}\langle e^0 \rangle$ into
$\mathbb {Q}\langle e^0 \rangle$ into ![]() $\mathbb {Q} \langle e^0, e^1 \rangle$. Define their images to be
$\mathbb {Q} \langle e^0, e^1 \rangle$. Define their images to be ![]() $\mathfrak {D}_0 \mathcal {O}({}_0 \Pi _{1})$ and
$\mathfrak {D}_0 \mathcal {O}({}_0 \Pi _{1})$ and ![]() $\mathfrak {D}_0 \mathcal {O}({}_0 \Pi _{0})$, respectively. Now define increasing filtrations
$\mathfrak {D}_0 \mathcal {O}({}_0 \Pi _{0})$, respectively. Now define increasing filtrations ![]() $\mathfrak {D}_d$ on
$\mathfrak {D}_d$ on ![]() $\mathcal {O}({}_0 \Pi _{0})$ and
$\mathcal {O}({}_0 \Pi _{0})$ and ![]() $\mathcal {O}({}_0 \Pi _{1})$ by induction on
$\mathcal {O}({}_0 \Pi _{1})$ by induction on ![]() $d \geq 0$ as follows:
$d \geq 0$ as follows: ![]() $\mathfrak {D}_d$ is the largest subspace such that
$\mathfrak {D}_d$ is the largest subspace such that ![]() $\Delta \mathfrak {D}_d \subset \sum _{i+j=d} \mathfrak {D}_i\otimes \mathfrak {D}_j$, where
$\Delta \mathfrak {D}_d \subset \sum _{i+j=d} \mathfrak {D}_i\otimes \mathfrak {D}_j$, where ![]() $\Delta ^{\mathrm {dec}}: \mathcal {O}({}_0 \Pi _{x}) \rightarrow \mathcal {O}({}_0\Pi _{x}) \otimes \mathcal {O}({}_0 \Pi _{0})$ is dual to composition of paths, for
$\Delta ^{\mathrm {dec}}: \mathcal {O}({}_0 \Pi _{x}) \rightarrow \mathcal {O}({}_0\Pi _{x}) \otimes \mathcal {O}({}_0 \Pi _{0})$ is dual to composition of paths, for ![]() $x=0,1$. Since
$x=0,1$. Since ![]() $\Delta ^{\mathrm {dec}}$, on identifying
$\Delta ^{\mathrm {dec}}$, on identifying ![]() $\mathcal {O}({}_0 \Pi _{0}) \cong \mathcal {O}({}_0 \Pi _{1}) \cong \mathbb {Q}\langle e_0,e_1\rangle$, is nothing other than the deconcatenation coproduct, the filtration
$\mathcal {O}({}_0 \Pi _{0}) \cong \mathcal {O}({}_0 \Pi _{1}) \cong \mathbb {Q}\langle e_0,e_1\rangle$, is nothing other than the deconcatenation coproduct, the filtration ![]() $\mathfrak {D}_d \mathcal {O}({}_0 \Pi _{1})$ is given by
$\mathfrak {D}_d \mathcal {O}({}_0 \Pi _{1})$ is given by
with respect to which ![]() $\mathcal {O}({}_0 \Pi _{1})$ is a filtered comodule over the filtered Hopf algebra
$\mathcal {O}({}_0 \Pi _{1})$ is a filtered comodule over the filtered Hopf algebra ![]() $\mathcal {O}({}_0 \Pi _{0})$, with respect to
$\mathcal {O}({}_0 \Pi _{0})$, with respect to ![]() $\Delta ^{\mathrm {dec}}$. Furthermore, since the map (4.1) is motivic, it follows that
$\Delta ^{\mathrm {dec}}$. Furthermore, since the map (4.1) is motivic, it follows that ![]() $\mathfrak {D}_0$ is preserved by the action of the motivic Galois group. The same is true for all
$\mathfrak {D}_0$ is preserved by the action of the motivic Galois group. The same is true for all ![]() $d$ by induction: if
$d$ by induction: if ![]() $g \in G^{\mathrm {dR}}_{\mathcal {MT}(\mathbb {Z})}$ and
$g \in G^{\mathrm {dR}}_{\mathcal {MT}(\mathbb {Z})}$ and ![]() $g\, \mathfrak {D}_i \subset \mathfrak {D}_i$ for all
$g\, \mathfrak {D}_i \subset \mathfrak {D}_i$ for all ![]() $i < d$, then we also have
$i < d$, then we also have ![]() $g \mathfrak {D}_d \subset \mathfrak {D}_d$ by definition of
$g \mathfrak {D}_d \subset \mathfrak {D}_d$ by definition of ![]() $\mathfrak {D}_d$, since
$\mathfrak {D}_d$, since ![]() $g$ commutes with
$g$ commutes with ![]() $\Delta ^{\mathrm {dec}}$, which is motivic. Therefore the depth is also motivic and descends to the algebra
$\Delta ^{\mathrm {dec}}$, which is motivic. Therefore the depth is also motivic and descends to the algebra ![]() $\mathcal {H}$. By Definition 3.1 the depth filtration
$\mathcal {H}$. By Definition 3.1 the depth filtration ![]() $\mathfrak {D}_d \mathcal {H}$ is the increasing filtration defined by
$\mathfrak {D}_d \mathcal {H}$ is the increasing filtration defined by
Following [Reference DeligneDel10], it is convenient to define the ![]() $\mathfrak {D}$-degree on
$\mathfrak {D}$-degree on ![]() $\mathcal {O} ({}_0 \Pi _{1})$ to be the degree in
$\mathcal {O} ({}_0 \Pi _{1})$ to be the degree in ![]() $e^1$. It defines a grading on
$e^1$. It defines a grading on ![]() ${}_0 \Pi _{1}$ which is not motivic. By (4.2), the depth filtration (which is motivic) is simply the increasing filtration associated to the
${}_0 \Pi _{1}$ which is not motivic. By (4.2), the depth filtration (which is motivic) is simply the increasing filtration associated to the ![]() $\mathfrak {D}$-degree.
$\mathfrak {D}$-degree.
4.2 Depth-graded motivic multiple zeta values
Definition 4.1 Let ![]() $\mathfrak {D}_d \mathcal {A}$ be the induced filtration on the quotient
$\mathfrak {D}_d \mathcal {A}$ be the induced filtration on the quotient ![]() $\mathcal {A} = \mathcal {H}/\zeta ^{{\mathfrak {m}}}(2) \mathcal {H}$. We define the depth-graded motivic multiple zeta value
$\mathcal {A} = \mathcal {H}/\zeta ^{{\mathfrak {m}}}(2) \mathcal {H}$. We define the depth-graded motivic multiple zeta value
to be the image of ![]() $\zeta ^{{\mathfrak {m}}}(n_1,\ldots , n_r)$ in
$\zeta ^{{\mathfrak {m}}}(n_1,\ldots , n_r)$ in ![]() $\mathrm {gr}_r^{\mathfrak {D}} \mathcal {H}$.
$\mathrm {gr}_r^{\mathfrak {D}} \mathcal {H}$.
Proposition 4.2 There is a non-canonical isomorphism of bigraded vector spaces:
where ![]() $\zeta ^{{\mathfrak {m}}}_{\mathfrak {D}}(2)^n$ are in depth
$\zeta ^{{\mathfrak {m}}}_{\mathfrak {D}}(2)^n$ are in depth ![]() $1$ for all
$1$ for all ![]() $n\geq 1$.
$n\geq 1$.
Proof. Choose a homomorphism ![]() $\pi _2: \mathcal {H} \rightarrow \mathbb {Q}[\zeta ^{{\mathfrak {m}}}(2)]$ which respects the weight-grading and such that
$\pi _2: \mathcal {H} \rightarrow \mathbb {Q}[\zeta ^{{\mathfrak {m}}}(2)]$ which respects the weight-grading and such that ![]() $\pi _2(\zeta ^{{\mathfrak {m}}}(2))=\zeta ^{{\mathfrak {m}}}(2)$. Such a homomorphism exists by [Reference Deligne and GoncharovDG05, § 5.20] (see [Reference BrownBro12, § 2.3]). Composing with the coaction (3.1), we obtain a map
$\pi _2(\zeta ^{{\mathfrak {m}}}(2))=\zeta ^{{\mathfrak {m}}}(2)$. Such a homomorphism exists by [Reference Deligne and GoncharovDG05, § 5.20] (see [Reference BrownBro12, § 2.3]). Composing with the coaction (3.1), we obtain a map
By a motivic version [Reference BrownBro12] of Euler's theorem, ![]() $\zeta ^{{\mathfrak {m}}}(2)^n$ is a rational multiple of
$\zeta ^{{\mathfrak {m}}}(2)^n$ is a rational multiple of ![]() $\zeta ^{{\mathfrak {m}}}(2n)$, and so all powers of
$\zeta ^{{\mathfrak {m}}}(2n)$, and so all powers of ![]() $\zeta ^{{\mathfrak {m}}}(2)$ have depth 1. The depth filtration thus satisfies
$\zeta ^{{\mathfrak {m}}}(2)$ have depth 1. The depth filtration thus satisfies
Since ![]() $\mathfrak {D}_0 \mathcal {H}=\mathbb {Q}$, it follows trivially that
$\mathfrak {D}_0 \mathcal {H}=\mathbb {Q}$, it follows trivially that ![]() $\pi _2$ respects the depth filtration because it is
$\pi _2$ respects the depth filtration because it is ![]() $\mathbb {Q}$-linear. Since the depth filtration is motivic, it is also respected by
$\mathbb {Q}$-linear. Since the depth filtration is motivic, it is also respected by ![]() $\Delta ^{\mathcal {M}}$, and therefore the map
$\Delta ^{\mathcal {M}}$, and therefore the map ![]() $(id \otimes \pi _2) \,\Delta ^{\mathcal {M}}: \mathcal {H}\rightarrow \mathcal {A} \otimes _{\mathbb {Q}}\mathbb {Q}[\zeta ^{{\mathfrak {m}}}(2)]$ defined above also respects the depth filtration. The statement (4.3) follows since we know that this map is an isomorphism (by [Reference BrownBro12, (2.13)] or [Reference DeligneDel10, Proposition 5.8]).
$(id \otimes \pi _2) \,\Delta ^{\mathcal {M}}: \mathcal {H}\rightarrow \mathcal {A} \otimes _{\mathbb {Q}}\mathbb {Q}[\zeta ^{{\mathfrak {m}}}(2)]$ defined above also respects the depth filtration. The statement (4.3) follows since we know that this map is an isomorphism (by [Reference BrownBro12, (2.13)] or [Reference DeligneDel10, Proposition 5.8]).
Since ![]() $\mathrm {gr}^\mathfrak {D} \mathcal {A}$ is a commutative graded Hopf algebra (for the coproduct induced by
$\mathrm {gr}^\mathfrak {D} \mathcal {A}$ is a commutative graded Hopf algebra (for the coproduct induced by ![]() $\Delta ^{\mathcal {M}}$), it is a polynomial algebra. The same is then true for
$\Delta ^{\mathcal {M}}$), it is a polynomial algebra. The same is then true for ![]() $\mathrm {gr}^{\mathfrak {D}} \mathcal {H}$, by (4.3). If
$\mathrm {gr}^{\mathfrak {D}} \mathcal {H}$, by (4.3). If ![]() $I$ denotes indecomposable elements, then it follows that
$I$ denotes indecomposable elements, then it follows that ![]() $I (\mathrm {gr}^{\mathfrak {D}} \mathcal {A})\cong \mathrm {gr}^{\mathfrak {D}} \, I \mathcal {A}$.
$I (\mathrm {gr}^{\mathfrak {D}} \mathcal {A})\cong \mathrm {gr}^{\mathfrak {D}} \, I \mathcal {A}$.
4.3 Depth-graded motivic Lie algebra
The depth filtration defines a decreasing filtration ![]() $\mathfrak {D}^r$ on
$\mathfrak {D}^r$ on ![]() $\mathfrak {g}^{\mathfrak {m}}$ where
$\mathfrak {g}^{\mathfrak {m}}$ where ![]() $\mathfrak {D}^r$ consists of words with at least
$\mathfrak {D}^r$ consists of words with at least ![]() $r$ occurrences of
$r$ occurrences of ![]() $e_1$:
$e_1$:
We denote the associated graded Lie algebra by ![]() $\mathfrak {dg}^{\mathfrak {m}}$. There is correspondingly a decreasing depth filtration on
$\mathfrak {dg}^{\mathfrak {m}}$. There is correspondingly a decreasing depth filtration on ![]() $\mathcal {U} \mathfrak {g}^{\mathfrak {m}}$, also denoted by
$\mathcal {U} \mathfrak {g}^{\mathfrak {m}}$, also denoted by ![]() $\mathfrak {D}$.
$\mathfrak {D}$.
It follows from the definitions above that ![]() $\mathfrak {dg}^{\mathfrak {m}}$ is the bigraded Lie algebra dual to the bigraded coalgebra
$\mathfrak {dg}^{\mathfrak {m}}$ is the bigraded Lie algebra dual to the bigraded coalgebra ![]() $I (\mathrm {gr}^{\mathfrak {D}} \mathcal {A})\cong \mathrm {gr}^{\mathfrak {D}} \, I \mathcal {A}$ of depth-graded motivic multiple zeta values modulo products. Thus the problem of studying relations between (motivic) multiple zeta values modulo lower depth (and modulo
$I (\mathrm {gr}^{\mathfrak {D}} \mathcal {A})\cong \mathrm {gr}^{\mathfrak {D}} \, I \mathcal {A}$ of depth-graded motivic multiple zeta values modulo products. Thus the problem of studying relations between (motivic) multiple zeta values modulo lower depth (and modulo ![]() $\zeta ^{{\mathfrak {m}}}(2)$) and the algebra
$\zeta ^{{\mathfrak {m}}}(2)$) and the algebra ![]() $\mathfrak {dg}^{\mathfrak {m}}$ are equivalent.
$\mathfrak {dg}^{\mathfrak {m}}$ are equivalent.
4.4 Depth-parity
The following proposition is a consequence of Tsumura's result on double shuffle equations (Proposition 6.4).
Proposition 4.3 The depth-graded motivic Lie algebra ![]() $\mathfrak {dg}^{\mathfrak {m}}$ vanishes in bidegrees with different parity. More precisely, it vanishes in weight
$\mathfrak {dg}^{\mathfrak {m}}$ vanishes in bidegrees with different parity. More precisely, it vanishes in weight ![]() $N$ and depth
$N$ and depth ![]() $r$ if
$r$ if ![]() $N\not \equiv r \pmod 2$.
$N\not \equiv r \pmod 2$.
Equivalently, if ![]() $n_1+\cdots + n_r \not \equiv r \pmod 2$, and
$n_1+\cdots + n_r \not \equiv r \pmod 2$, and ![]() $n_1+\cdots + n_r >2$ then
$n_1+\cdots + n_r >2$ then
We do not need to work modulo ![]() $\zeta ^{{\mathfrak {m}}}_{\mathfrak {D}}(2)$ in the previous equation since the weight is larger than
$\zeta ^{{\mathfrak {m}}}_{\mathfrak {D}}(2)$ in the previous equation since the weight is larger than ![]() $2$ by assumption and all other even zeta values
$2$ by assumption and all other even zeta values ![]() $\zeta ^{{\mathfrak {m}}}(2n)$,
$\zeta ^{{\mathfrak {m}}}(2n)$, ![]() $n\geq 2$, are products.
$n\geq 2$, are products.
4.5 Depth spectral sequence
The depth filtration on the motivic Lie algebra ![]() $\mathfrak {g}^{\mathfrak {m}}$ induces a homology spectral sequence which converges to the associated graded for the depth of the homology of
$\mathfrak {g}^{\mathfrak {m}}$ induces a homology spectral sequence which converges to the associated graded for the depth of the homology of ![]() $\mathfrak {g}^{\mathfrak {m}}$. By Theorem 1.1, the latter satisfies
$\mathfrak {g}^{\mathfrak {m}}$. By Theorem 1.1, the latter satisfies
 \[ H_i(\mathfrak{g}^{\mathfrak{m}} ) = \begin{cases} \bigoplus\limits_{n\geq 1} \mathbb{Q} [\sigma_{2n+1}] & \hbox{if } i =1 \\ 0 & \hbox{if } i \geq 1 \end{cases} \]
\[ H_i(\mathfrak{g}^{\mathfrak{m}} ) = \begin{cases} \bigoplus\limits_{n\geq 1} \mathbb{Q} [\sigma_{2n+1}] & \hbox{if } i =1 \\ 0 & \hbox{if } i \geq 1 \end{cases} \]
and is entirely concentrated in depth ![]() $1$.
$1$.
The depth spectral sequence satisfies
where ![]() $E^1_{-p,q}$ vanishes unless
$E^1_{-p,q}$ vanishes unless ![]() $p\geq 1$ and
$p\geq 1$ and ![]() $p< q \leq 2p$, as can easily be seen from the Chevalley–Eilenberg chain complex which computes the homology of a Lie algebra (see § 10.2 and (10.3)). The differentials satisfy
$p< q \leq 2p$, as can easily be seen from the Chevalley–Eilenberg chain complex which computes the homology of a Lie algebra (see § 10.2 and (10.3)). The differentials satisfy
Proposition 4.4 The differentials ![]() $d^r$ vanish if
$d^r$ vanish if ![]() $r$ is odd.
$r$ is odd.
Proof. The weight grading on ![]() $\mathfrak {dg}^{\mathfrak {m}}$ induces a weight grading on the depth spectral sequence, with respect to which the differentials are of degree
$\mathfrak {dg}^{\mathfrak {m}}$ induces a weight grading on the depth spectral sequence, with respect to which the differentials are of degree ![]() $0$. It follows from Proposition 4.3 and
$0$. It follows from Proposition 4.3 and ![]() $E^1_{-p,q} = \mathrm {gr}_{\mathfrak {D}}^p H_{q-p} (\mathfrak {dg}^{\mathfrak {m}})$ that
$E^1_{-p,q} = \mathrm {gr}_{\mathfrak {D}}^p H_{q-p} (\mathfrak {dg}^{\mathfrak {m}})$ that ![]() $E^1_{p,q}$, and hence all
$E^1_{p,q}$, and hence all ![]() $E^r_{p,q}$, vanish unless the depth and weight have the same parity. The result follows since
$E^r_{p,q}$, vanish unless the depth and weight have the same parity. The result follows since ![]() $d^r$ has (weight, depth)-bidegree
$d^r$ has (weight, depth)-bidegree ![]() $(0,r)$.
$(0,r)$.
Here is a picture of the potentially non-vanishing ![]() $E^1=E^2$ terms:
$E^1=E^2$ terms:

In fact, we know by Theorem 1.1 that
and therefore everything to the left of the column indexed ![]() $-1$ converges to zero. Furthermore, one knows that
$-1$ converges to zero. Furthermore, one knows that ![]() $\mathrm {gr}^2_{\mathfrak {D}} H_1 (\mathfrak {dg}^{\mathfrak {m}})=0$, and
$\mathrm {gr}^2_{\mathfrak {D}} H_1 (\mathfrak {dg}^{\mathfrak {m}})=0$, and ![]() $\mathrm {gr}^3_{\mathfrak {D}} H_i (\mathfrak {dg}^{\mathfrak {m}})$ vanish for all
$\mathrm {gr}^3_{\mathfrak {D}} H_i (\mathfrak {dg}^{\mathfrak {m}})$ vanish for all ![]() $i$. One also has a complete description of
$i$. One also has a complete description of ![]() $\mathrm {gr}^2_{\mathfrak {D}} H_2(\mathfrak {dg}^{\mathfrak {m}})$ in terms of period polynomials of cusp forms, as discussed below. Therefore, the first interesting part of the differential is
$\mathrm {gr}^2_{\mathfrak {D}} H_2(\mathfrak {dg}^{\mathfrak {m}})$ in terms of period polynomials of cusp forms, as discussed below. Therefore, the first interesting part of the differential is
and the main Conjecture 1 can be reformulated as saying that the components of all other differentials in the depth spectral sequence vanish.
5. Linearized double shuffle relations
5.1 Reminders on the standard relations
We briefly review the double shuffle relations and their depth-linearized versions. See [Reference CartierCar02, Reference RacinetRac02, Reference BrownBro17b] for further background.
5.1.1 Shuffle product
Consider the algebra ![]() $\mathbb {Q}\langle e_0, e_1 \rangle$ of words in the two letters
$\mathbb {Q}\langle e_0, e_1 \rangle$ of words in the two letters ![]() $e_0, e_1$, equipped with the shuffle product
$e_0, e_1$, equipped with the shuffle product ![]() $\, \unicode{x0448} \,$ (§ 2.1). It is defined recursively by
$\, \unicode{x0448} \,$ (§ 2.1). It is defined recursively by
for all ![]() $w,w'\in \{e_0,e_1\}^\times$ and
$w,w'\in \{e_0,e_1\}^\times$ and ![]() $i,j\in \{0,1\}$, and the property that the empty word
$i,j\in \{0,1\}$, and the property that the empty word ![]() $1$ satisfies
$1$ satisfies ![]() $1\, \unicode{x0448} \, w=w\, \unicode{x0448} \, 1=w$. It is a Hopf algebra for the deconcatenation coproduct. A linear map
$1\, \unicode{x0448} \, w=w\, \unicode{x0448} \, 1=w$. It is a Hopf algebra for the deconcatenation coproduct. A linear map ![]() $\Phi : \mathbb {Q}\langle e_0, e_1 \rangle \rightarrow \mathbb {Q}$ is a homomorphism for the shuffle multiplication, or
$\Phi : \mathbb {Q}\langle e_0, e_1 \rangle \rightarrow \mathbb {Q}$ is a homomorphism for the shuffle multiplication, or ![]() $\Phi _{w} \Phi _{w'} = \Phi _{w \, \unicode{x0448} \, w'}$ for all
$\Phi _{w} \Phi _{w'} = \Phi _{w \, \unicode{x0448} \, w'}$ for all ![]() $w,w'\in \{e_0,e_1\}^\times$ and
$w,w'\in \{e_0,e_1\}^\times$ and ![]() $\Phi _1=1$, if and only if the series
$\Phi _1=1$, if and only if the series
is invertible and group-like for the (completed) coproduct ![]() $\Delta _{\!\, \unicode{x0448} \,}$ with respect to which
$\Delta _{\!\, \unicode{x0448} \,}$ with respect to which ![]() $e_0$ and
$e_0$ and ![]() $e_1$ are primitive (compare § 2.1). In other words, there is an equivalence:
$e_1$ are primitive (compare § 2.1). In other words, there is an equivalence:
One says that ![]() $\Phi$ satisfies the shuffle relations if either of the equivalent conditions (5.2) holds. Passing to the corresponding Lie algebra, we have an equivalence
$\Phi$ satisfies the shuffle relations if either of the equivalent conditions (5.2) holds. Passing to the corresponding Lie algebra, we have an equivalence
One says that ![]() $\Phi$ satisfies the shuffle relations modulo products if either of the equivalent conditions (5.3) holds.
$\Phi$ satisfies the shuffle relations modulo products if either of the equivalent conditions (5.3) holds.
The algebra ![]() $\mathbb {Q}\langle e_0, e_1\rangle$ is bigraded for the degree, or weight (for which
$\mathbb {Q}\langle e_0, e_1\rangle$ is bigraded for the degree, or weight (for which ![]() $e_0,e_1$ both have degree
$e_0,e_1$ both have degree ![]() $-1$), and the
$-1$), and the ![]() $\mathfrak {D}$-degree for which
$\mathfrak {D}$-degree for which ![]() $e_1$ has degree
$e_1$ has degree ![]() $1$, and
$1$, and ![]() $e_0$ degree
$e_0$ degree ![]() $0$. The relations (5.1)–(5.3) evidently respect both gradings. In this case, then, passing to the depth grading does not change the relations in any way, and the linearized shuffle relations are identical to the shuffle relations modulo products.
$0$. The relations (5.1)–(5.3) evidently respect both gradings. In this case, then, passing to the depth grading does not change the relations in any way, and the linearized shuffle relations are identical to the shuffle relations modulo products.
Definition 5.1 Let ![]() $\Phi \in \mathrm {gr}_{\mathfrak {D}}^r T(e_0,e_1)$ be of weight
$\Phi \in \mathrm {gr}_{\mathfrak {D}}^r T(e_0,e_1)$ be of weight ![]() $N$. It defines a linear form
$N$. It defines a linear form ![]() $w\mapsto \Phi _w$ on words of weight
$w\mapsto \Phi _w$ on words of weight ![]() $N\geq 2$ and
$N\geq 2$ and ![]() $\mathfrak {D}$-degree
$\mathfrak {D}$-degree ![]() $r$. It satisfies the linearized shuffle relations if
$r$. It satisfies the linearized shuffle relations if
where ![]() $\Delta '_{\!\, \unicode{x0448} \,}$ is the reduced coproduct
$\Delta '_{\!\, \unicode{x0448} \,}$ is the reduced coproduct ![]() $\Delta '_{\!\, \unicode{x0448} \,}(\Phi )= \Delta _{\!\, \unicode{x0448} \,}(\Phi ) - 1 \otimes \Phi - \Phi \otimes 1$. Equivalently,
$\Delta '_{\!\, \unicode{x0448} \,}(\Phi )= \Delta _{\!\, \unicode{x0448} \,}(\Phi ) - 1 \otimes \Phi - \Phi \otimes 1$. Equivalently, ![]() $\Phi _{w\, \unicode{x0448} \, w'} = 0$ for all words
$\Phi _{w\, \unicode{x0448} \, w'} = 0$ for all words ![]() $w,w'\in \{e_0,e_1\}^{\times }$ of total weight
$w,w'\in \{e_0,e_1\}^{\times }$ of total weight ![]() $N$ and total
$N$ and total ![]() $\mathfrak {D}$-degree
$\mathfrak {D}$-degree ![]() $r$.
$r$.
5.1.2 Stuffle product
Let ![]() $Y=\{ \mathsf {y} _n, n\geq 1\}$ denote an alphabet with one letter
$Y=\{ \mathsf {y} _n, n\geq 1\}$ denote an alphabet with one letter ![]() $\mathsf {y} _i$ in every degree
$\mathsf {y} _i$ in every degree ![]() $\geq 1$, and consider the graded algebra
$\geq 1$, and consider the graded algebra ![]() $\mathbb {Q}\langle Y\rangle$ equipped with the stuffle product [Reference RacinetRac02]. It is defined recursively by
$\mathbb {Q}\langle Y\rangle$ equipped with the stuffle product [Reference RacinetRac02]. It is defined recursively by
for all ![]() $w,w'\in Y^\times$ and
$w,w'\in Y^\times$ and ![]() $i,j \geq 1$, and the property that the empty word
$i,j \geq 1$, and the property that the empty word ![]() $1$ satisfies
$1$ satisfies ![]() $1* w= w* 1=w$. A linear map
$1* w= w* 1=w$. A linear map ![]() $\Phi : \mathbb {Q}\langle Y \rangle \rightarrow \mathbb {Q}$ is a homomorphism for the stuffle multiplication, or
$\Phi : \mathbb {Q}\langle Y \rangle \rightarrow \mathbb {Q}$ is a homomorphism for the stuffle multiplication, or ![]() $\Phi _{w} \Phi _{w'} = \Phi _{w * w'}$ for all
$\Phi _{w} \Phi _{w'} = \Phi _{w * w'}$ for all ![]() $w,w'\in Y^{\times }$ and
$w,w'\in Y^{\times }$ and ![]() $\Phi _1=1$, if and only if
$\Phi _1=1$, if and only if
is group-like for the (completed) coproduct ![]() $\Delta _{*} : \mathbb {Q} \langle \langle Y \rangle \rangle \rightarrow \mathbb {Q} \langle \langle Y \rangle \rangle \hat {\otimes }_{\mathbb {Q}} \mathbb {Q} \langle \langle Y \rangle \rangle$ which is a homomorphism for the concatenation product and defined on generators by
$\Delta _{*} : \mathbb {Q} \langle \langle Y \rangle \rangle \rightarrow \mathbb {Q} \langle \langle Y \rangle \rangle \hat {\otimes }_{\mathbb {Q}} \mathbb {Q} \langle \langle Y \rangle \rangle$ which is a homomorphism for the concatenation product and defined on generators by
 \begin{equation} \Delta_{*} \mathsf{y} _n = \sum_{i=0}^n \mathsf{y} _i \otimes \mathsf{y} _{n-i} . \end{equation}
\begin{equation} \Delta_{*} \mathsf{y} _n = \sum_{i=0}^n \mathsf{y} _i \otimes \mathsf{y} _{n-i} . \end{equation}
Thus the stuffle relations are equivalent to being group-like for ![]() $\Delta _{*}$:
$\Delta _{*}$:
One says that ![]() $\Phi$ satisfies the stuffle relations if either of the equivalent conditions (5.6) holds. Passing to the corresponding Lie algebra, we have an equivalence
$\Phi$ satisfies the stuffle relations if either of the equivalent conditions (5.6) holds. Passing to the corresponding Lie algebra, we have an equivalence
One says that ![]() $\Phi$ satisfies the stuffle relations modulo products if either of the equivalent conditions (5.7) holds.
$\Phi$ satisfies the stuffle relations modulo products if either of the equivalent conditions (5.7) holds.
The algebra ![]() $\mathbb {Q}\langle Y\rangle$ is graded for the degree (where
$\mathbb {Q}\langle Y\rangle$ is graded for the degree (where ![]() $\mathsf {y} _n$ has degree
$\mathsf {y} _n$ has degree ![]() $n$), and filtered for the depth (where
$n$), and filtered for the depth (where ![]() $\mathsf {y} _n$ has depth
$\mathsf {y} _n$ has depth ![]() $1$). By inspection of (5.4), we notice that the rightmost term is of lower depth than the other terms and therefore drops out in the associated graded. The associated graded of
$1$). By inspection of (5.4), we notice that the rightmost term is of lower depth than the other terms and therefore drops out in the associated graded. The associated graded of ![]() $*$ therefore satisfies the same recursive definition as for
$*$ therefore satisfies the same recursive definition as for ![]() $\, \unicode{x0448} \,$ and it follows that the associated depth-graded
$\, \unicode{x0448} \,$ and it follows that the associated depth-graded
is simply the shuffle algebra on ![]() $Y$. The depth induces a decreasing filtration on the (dual) completed Hopf algebra
$Y$. The depth induces a decreasing filtration on the (dual) completed Hopf algebra ![]() $\mathbb {Q}\langle \langle Y \rangle \rangle$, and it follows from (5.5) that the images of the elements
$\mathbb {Q}\langle \langle Y \rangle \rangle$, and it follows from (5.5) that the images of the elements ![]() $\mathsf {y} _n$ are primitive in the associated graded. Thus
$\mathsf {y} _n$ are primitive in the associated graded. Thus
where ![]() $\Delta _{\, \unicode{x0448} \,,Y}: \mathbb {Q}\langle \langle Y \rangle \rangle \rightarrow \mathbb {Q}\langle \langle Y \rangle \rangle \hat {\otimes }_{\mathbb {Q}} \mathbb {Q}\langle \langle Y \rangle \rangle$ is the (completed) coproduct for which the elements
$\Delta _{\, \unicode{x0448} \,,Y}: \mathbb {Q}\langle \langle Y \rangle \rangle \rightarrow \mathbb {Q}\langle \langle Y \rangle \rangle \hat {\otimes }_{\mathbb {Q}} \mathbb {Q}\langle \langle Y \rangle \rangle$ is the (completed) coproduct for which the elements ![]() $\mathsf {y} _n$ are primitive, and which is a homomorphism for concatenation.
$\mathsf {y} _n$ are primitive, and which is a homomorphism for concatenation.
Definition 5.2 Let ![]() $\Phi \in T(Y)$, the tensor (co)algebra on
$\Phi \in T(Y)$, the tensor (co)algebra on ![]() $Y$, of degree
$Y$, of degree ![]() $N\geq 2$ and
$N\geq 2$ and ![]() $\mathfrak {D}$-degree
$\mathfrak {D}$-degree ![]() $r$. It defines a linear map
$r$. It defines a linear map ![]() $w\mapsto \Phi _w$ on words in
$w\mapsto \Phi _w$ on words in ![]() $Y$ of weight
$Y$ of weight ![]() $N$ and
$N$ and ![]() $\mathfrak {D}$-degree
$\mathfrak {D}$-degree ![]() $r$. We say that it satisfies the linearized stuffle relations if
$r$. We say that it satisfies the linearized stuffle relations if
where ![]() $\Delta '_{\, \unicode{x0448} \,, Y}= \Delta _{\, \unicode{x0448} \,,Y} - 1 \otimes \mathrm {id} - \mathrm {id} \otimes 1$ is the reduced coproduct of
$\Delta '_{\, \unicode{x0448} \,, Y}= \Delta _{\, \unicode{x0448} \,,Y} - 1 \otimes \mathrm {id} - \mathrm {id} \otimes 1$ is the reduced coproduct of ![]() $\Delta _{\, \unicode{x0448} \,, Y}$ for which the
$\Delta _{\, \unicode{x0448} \,, Y}$ for which the ![]() $\mathsf {y} _n$ are primitive. Equivalently,
$\mathsf {y} _n$ are primitive. Equivalently, ![]() $\Phi _{w\, \unicode{x0448} \, w'} = 0$ for all words
$\Phi _{w\, \unicode{x0448} \, w'} = 0$ for all words ![]() $w,w'\in Y$ of total weight
$w,w'\in Y$ of total weight ![]() $N$ and total
$N$ and total ![]() $\mathfrak {D}$-degree
$\mathfrak {D}$-degree ![]() $r$.
$r$.
5.1.3 Linearized double shuffle relations
In order to consider both relations simultaneously, define a linear map
which maps every word beginning in ![]() $e_0$ to
$e_0$ to ![]() $0$, and such that
$0$, and such that
In [Reference RacinetRac02], Racinet considered a certain graded vector space, denoted ![]() $\mathfrak {dm}_0(\mathbb {Q})$ [Reference RacinetRac02, Définition 2.4], of series satisfying the shuffle and stuffle relations and a regularization condition, and showed that it is a Lie algebra for the Ihara bracket. Since we consider the depth-graded version of this algebra, the regularization plays no role here.
$\mathfrak {dm}_0(\mathbb {Q})$ [Reference RacinetRac02, Définition 2.4], of series satisfying the shuffle and stuffle relations and a regularization condition, and showed that it is a Lie algebra for the Ihara bracket. Since we consider the depth-graded version of this algebra, the regularization plays no role here.
Definition 5.3 Let ![]() $\Phi \in \mathrm {gr}^{\mathfrak {D}}_r T(e_0,e_1)$ of weight
$\Phi \in \mathrm {gr}^{\mathfrak {D}}_r T(e_0,e_1)$ of weight ![]() $N$. The linear form
$N$. The linear form ![]() $w\mapsto \Phi _w$ on words of weight
$w\mapsto \Phi _w$ on words of weight ![]() $N$ and
$N$ and ![]() $\mathfrak {D}$-degree
$\mathfrak {D}$-degree ![]() $r$ satisfies the linearized double shuffle relations if
$r$ satisfies the linearized double shuffle relations if
When ![]() $r=1$, we add the extra condition that
$r=1$, we add the extra condition that ![]() $\Phi =0$ when
$\Phi =0$ when ![]() $N$ is even, and
$N$ is even, and ![]() $\Phi (e_0)=\Phi (e_1)=0$. Let
$\Phi (e_0)=\Phi (e_1)=0$. Let ![]() $\mathfrak {ls} \subset \mathcal {U} \mathfrak {g}$ denote the vector space of elements satisfying the linearized double shuffle relations. It is bigraded by weight and depth.
$\mathfrak {ls} \subset \mathcal {U} \mathfrak {g}$ denote the vector space of elements satisfying the linearized double shuffle relations. It is bigraded by weight and depth.
Remark 5.4 There is a natural inclusion
The graded subspace of ![]() $\mathfrak {ls}$ of weight
$\mathfrak {ls}$ of weight ![]() $N$ and depth
$N$ and depth ![]() $d$ is isomorphic to the vector space denoted
$d$ is isomorphic to the vector space denoted ![]() $D_{N+d,d}$ in [Reference Ihara, Kaneko and ZagierIKZ06]. In [Reference Ihara, Kaneko and ZagierIKZ06] it is conjectured that (5.10) is an isomorphism.
$D_{N+d,d}$ in [Reference Ihara, Kaneko and ZagierIKZ06]. In [Reference Ihara, Kaneko and ZagierIKZ06] it is conjectured that (5.10) is an isomorphism.
Racinet proved that ![]() $\mathfrak {dm}_0(\mathbb {Q})$ is preserved by the Ihara bracket. Since the latter is homogeneous for the
$\mathfrak {dm}_0(\mathbb {Q})$ is preserved by the Ihara bracket. Since the latter is homogeneous for the ![]() $\mathfrak {D}$-degree, it follows that
$\mathfrak {D}$-degree, it follows that ![]() $\mathrm {gr}_{\mathfrak {D}} \mathfrak {dm}_0(\mathbb {Q})$ is also preserved by the bracket, but this is not quite enough to prove that
$\mathrm {gr}_{\mathfrak {D}} \mathfrak {dm}_0(\mathbb {Q})$ is also preserved by the bracket, but this is not quite enough to prove that ![]() $\mathfrak {ls}$ is too.
$\mathfrak {ls}$ is too.
Theorem 5.5 The bigraded vector space ![]() $\mathfrak {ls}$ is preserved by the Ihara bracket.
$\mathfrak {ls}$ is preserved by the Ihara bracket.
Proof. The compatibility of the shuffle product with the Ihara bracket follows by definition. It therefore suffices to check that the linearized stuffle relation is preserved by the bracket. The proof of [Reference RacinetRac02] goes through identically, and uses in an essential way the fact that the images of the elements ![]() $\mathsf {y} _{2n}$ in
$\mathsf {y} _{2n}$ in ![]() $\mathrm {gr}^1_{\mathfrak {D}} \mathfrak {dm}_0(\mathbb {Q})$ are zero (which in
$\mathrm {gr}^1_{\mathfrak {D}} \mathfrak {dm}_0(\mathbb {Q})$ are zero (which in ![]() $\mathfrak {dm}_0(\mathbb {Q})$ follows from [Reference RacinetRac02, Proposition 2.2], but holds in
$\mathfrak {dm}_0(\mathbb {Q})$ follows from [Reference RacinetRac02, Proposition 2.2], but holds in ![]() $\mathfrak {ls}$ by Definition 5.3).
$\mathfrak {ls}$ by Definition 5.3).
Many thanks to a referee for pointing out at least two places in the literature which have subsequently provided a more detailed proof of this statement: [Reference MaassaraniMaa19] and also [Reference SchnepsSch15, Theorem 3.4.3]. It would be interesting to know if a suitable linearized version of the associator relations is equivalent to the linearized double shuffle relations.
5.2 Summary of definitions
We have the following Lie subalgebras of the Lie algebra ![]() $\mathfrak {g}\cong (\mathbb {L}(e_0,e_1), \{\,{,}\,\})$, equipped with the Ihara bracket:
$\mathfrak {g}\cong (\mathbb {L}(e_0,e_1), \{\,{,}\,\})$, equipped with the Ihara bracket:
where ![]() $\mathfrak {g}^{\mathfrak {m}}$ is the image of the (weight-graded) Lie algebra of
$\mathfrak {g}^{\mathfrak {m}}$ is the image of the (weight-graded) Lie algebra of ![]() $\mathcal {U}_{\mathcal {MT}(\mathbb {Z})}$ and is isomorphic to the free graded Lie algebra on (non-canonical) generators
$\mathcal {U}_{\mathcal {MT}(\mathbb {Z})}$ and is isomorphic to the free graded Lie algebra on (non-canonical) generators ![]() $\sigma _{2i+1}$ for
$\sigma _{2i+1}$ for ![]() $i\geq 1$. A standard conjecture states that
$i\geq 1$. A standard conjecture states that ![]() $\mathfrak {g}^{\mathfrak {m}} \subseteq \mathfrak {dm}_0(\mathbb {Q})$ is an isomorphism. Passing to the depth-graded versions, and writing
$\mathfrak {g}^{\mathfrak {m}} \subseteq \mathfrak {dm}_0(\mathbb {Q})$ is an isomorphism. Passing to the depth-graded versions, and writing ![]() $\mathfrak {dg}^{\mathfrak {m}}= \mathrm {gr}_{\mathfrak {D}}\mathfrak {g}^{\mathfrak {m}}$, we have inclusions of bigraded Lie algebras
$\mathfrak {dg}^{\mathfrak {m}}= \mathrm {gr}_{\mathfrak {D}}\mathfrak {g}^{\mathfrak {m}}$, we have inclusions of bigraded Lie algebras
where ![]() $\mathfrak {ls}$ stands for the linearized double shuffle algebra. Once again, all Lie algebras in (5.11) are conjectured to be equal. The bigraded dual space
$\mathfrak {ls}$ stands for the linearized double shuffle algebra. Once again, all Lie algebras in (5.11) are conjectured to be equal. The bigraded dual space ![]() $(\mathfrak {dg}^{\mathfrak {m}})^{\vee }$ is isomorphic to the Lie coalgebra of depth-graded motivic multiple zeta values, modulo
$(\mathfrak {dg}^{\mathfrak {m}})^{\vee }$ is isomorphic to the Lie coalgebra of depth-graded motivic multiple zeta values, modulo ![]() $\zeta ^{{\mathfrak {m}}}(2)$ and modulo products. The Lie algebras (5.11) are Lie subalgebras of
$\zeta ^{{\mathfrak {m}}}(2)$ and modulo products. The Lie algebras (5.11) are Lie subalgebras of ![]() $\mathrm {gr}_{\mathfrak {D}} \mathfrak {g} \cong \mathfrak {g}$, since the Ihara bracket is homogeneous with respect to
$\mathrm {gr}_{\mathfrak {D}} \mathfrak {g} \cong \mathfrak {g}$, since the Ihara bracket is homogeneous with respect to ![]() $\mathfrak {D}$-degree.
$\mathfrak {D}$-degree.
All the above Lie algebras can, in particular, be viewed inside the vector space ![]() $\mathcal {U} \mathbb {L}(e_0,e_1)= T(\mathbb {Q} e_0 \oplus \mathbb {Q} e_1)$, which is graded for the
$\mathcal {U} \mathbb {L}(e_0,e_1)= T(\mathbb {Q} e_0 \oplus \mathbb {Q} e_1)$, which is graded for the ![]() $\mathfrak {D}$-degree. Next, we show that complicated expressions in the non-commutative algebra
$\mathfrak {D}$-degree. Next, we show that complicated expressions in the non-commutative algebra ![]() $T(\mathbb {Q} e_0 \oplus \mathbb {Q} e_1)$ can be greatly simplified by encoding words of fixed
$T(\mathbb {Q} e_0 \oplus \mathbb {Q} e_1)$ can be greatly simplified by encoding words of fixed ![]() $\mathfrak {D}$-degree in terms of polynomials.
$\mathfrak {D}$-degree in terms of polynomials.
6. Polynomial representations
6.1 Composition of polynomials
Recall from (2.1) that ![]() $\mathcal {U} \,\mathbb {L}(e_0,e_1)$ is isomorphic to the bigraded tensor algebra
$\mathcal {U} \,\mathbb {L}(e_0,e_1)$ is isomorphic to the bigraded tensor algebra ![]() $T(e_0,e_1)$, and the space
$T(e_0,e_1)$, and the space ![]() $\mathrm {gr}_{\mathfrak {D}}^r \, \mathcal {U}\, \mathbb {L}(e_0,e_1)=\mathrm {gr}_{\mathfrak {D}}^r \, T(e_0,e_1)$ of
$\mathrm {gr}_{\mathfrak {D}}^r \, \mathcal {U}\, \mathbb {L}(e_0,e_1)=\mathrm {gr}_{\mathfrak {D}}^r \, T(e_0,e_1)$ of ![]() $\mathfrak {D}$-degree
$\mathfrak {D}$-degree ![]() $r$ is the spanned by words in
$r$ is the spanned by words in ![]() $e_0,e_1$ with exactly
$e_0,e_1$ with exactly ![]() $r$ occurrences of
$r$ occurrences of ![]() $e_1$.
$e_1$.
Definition 6.1 Consider the isomorphism of vector spaces
It maps elements of degree ![]() $n$ to elements of degree
$n$ to elements of degree ![]() $n-r$.
$n-r$.
The operator ![]() $\, \underline {\circ }\, : T(e_0,e_1) \otimes _{\mathbb {Q}} T(e_0,e_1) \rightarrow T(e_0,e_1)$ respects the
$\, \underline {\circ }\, : T(e_0,e_1) \otimes _{\mathbb {Q}} T(e_0,e_1) \rightarrow T(e_0,e_1)$ respects the ![]() $\mathfrak {D}$-grading, so defines a map
$\mathfrak {D}$-grading, so defines a map
which can be read off from (2.7). Explicitly, it is
 \begin{align} f \, \underline{\circ}\, g (y_0,\ldots, y_{r+s}) &= \sum_{i=0}^s f(y_i,y_{i+1}, \ldots, y_{i+r}) g(y_0,\ldots, y_i, y_{i+r+1}, \ldots, y_{r+s}) \nonumber\\ &\quad + ({-}1)^{\deg f + r} \sum_{i=1}^s f(y_{i+r},\ldots, y_{i+1},y_i) g(y_0,\ldots, y_{i-1}, y_{i+r}, \ldots, y_{r+s}). \end{align}
\begin{align} f \, \underline{\circ}\, g (y_0,\ldots, y_{r+s}) &= \sum_{i=0}^s f(y_i,y_{i+1}, \ldots, y_{i+r}) g(y_0,\ldots, y_i, y_{i+r+1}, \ldots, y_{r+s}) \nonumber\\ &\quad + ({-}1)^{\deg f + r} \sum_{i=1}^s f(y_{i+r},\ldots, y_{i+1},y_i) g(y_0,\ldots, y_{i-1}, y_{i+r}, \ldots, y_{r+s}). \end{align}Antisymmetrizing, and using Proposition 2.2, we obtain a formula for the Ihara bracket
The linearized double shuffle relations on words translate into functional equations for polynomials after applying the map ![]() $\rho$. We describe some of these below.
$\rho$. We describe some of these below.
6.2 Translation invariance
The additive group ![]() $\mathbb {G}_a$ acts on
$\mathbb {G}_a$ acts on ![]() $\mathbb {A}^{r+1}$ by translation, and hence
$\mathbb {A}^{r+1}$ by translation, and hence ![]() $\mathbb {G}_a(\mathbb {Q})$ acts on its ring of functions via
$\mathbb {G}_a(\mathbb {Q})$ acts on its ring of functions via ![]() $\lambda : (y_0,\ldots , y_r) \mapsto (y_0+\lambda ,\ldots , y_r+\lambda )$.
$\lambda : (y_0,\ldots , y_r) \mapsto (y_0+\lambda ,\ldots , y_r+\lambda )$.
Lemma 6.2 The image of ![]() $\mathfrak {g}^{\mathfrak {m}}$ under
$\mathfrak {g}^{\mathfrak {m}}$ under ![]() $\rho$ is contained in the subspace of polynomials in
$\rho$ is contained in the subspace of polynomials in ![]() $\mathbb {Q}[y_0,\ldots , y_r]$ which are invariant under translation.
$\mathbb {Q}[y_0,\ldots , y_r]$ which are invariant under translation.
Proof. The subspace ![]() $\mathfrak {g}^{\mathfrak {m}} \subset \mathfrak {g} \cong \mathbb {L}(e_0,e_1) \subset T(e_0,e_1)$ is contained in the subspace of elements which are primitive with respect to the shuffle coproduct
$\mathfrak {g}^{\mathfrak {m}} \subset \mathfrak {g} \cong \mathbb {L}(e_0,e_1) \subset T(e_0,e_1)$ is contained in the subspace of elements which are primitive with respect to the shuffle coproduct ![]() $\Delta _{\, \unicode{x0448} \,}$. Let
$\Delta _{\, \unicode{x0448} \,}$. Let ![]() $\pi _0: T(e_0,e_1) \rightarrow \mathbb {Q}$ denote the linear map which sends the word
$\pi _0: T(e_0,e_1) \rightarrow \mathbb {Q}$ denote the linear map which sends the word ![]() $e_0$ to
$e_0$ to ![]() $1$ and all other words to
$1$ and all other words to ![]() $0$, and consider the map
$0$, and consider the map ![]() $\partial _0 = (\pi _0 \otimes id) \circ \Delta _{\, \unicode{x0448} \,}$. It defines a derivation
$\partial _0 = (\pi _0 \otimes id) \circ \Delta _{\, \unicode{x0448} \,}$. It defines a derivation ![]() $\partial _0: T(e_0,e_1) \longrightarrow T(e_0,e_1)$ which satisfies
$\partial _0: T(e_0,e_1) \longrightarrow T(e_0,e_1)$ which satisfies
 \[ \partial_0 (e_0^{a_0} e_1 \ldots e_1 e_0^{a_r} )= \sum_{i=0}^r a_i \, e_0^{a_0} e_1 \ldots e_1 e_0^{a_i-1}e_1 \ldots e_1 e_0^{a_r} \]
\[ \partial_0 (e_0^{a_0} e_1 \ldots e_1 e_0^{a_r} )= \sum_{i=0}^r a_i \, e_0^{a_0} e_1 \ldots e_1 e_0^{a_i-1}e_1 \ldots e_1 e_0^{a_r} \]
for all non-negative integers ![]() $a_0,\ldots , a_r$. Let
$a_0,\ldots , a_r$. Let ![]() $r\geq 1$,
$r\geq 1$, ![]() $\xi \in \mathrm {gr}_{\mathfrak {D}}^r T(e_0,e_1)$, and
$\xi \in \mathrm {gr}_{\mathfrak {D}}^r T(e_0,e_1)$, and ![]() $f=\rho (\xi )$. If
$f=\rho (\xi )$. If ![]() $\xi$ is primitive for
$\xi$ is primitive for ![]() $\Delta _{\, \unicode{x0448} \,}$, it satisfies
$\Delta _{\, \unicode{x0448} \,}$, it satisfies ![]() $\partial _0 \xi =0$ and the previous equation is
$\partial _0 \xi =0$ and the previous equation is
 \begin{equation} \sum_{i=0}^r \frac{ \partial f }{\partial y_i }=0 . \end{equation}
\begin{equation} \sum_{i=0}^r \frac{ \partial f }{\partial y_i }=0 . \end{equation}
This is equivalent to ![]() $({\partial }/{\partial \lambda }) g=0$, where
$({\partial }/{\partial \lambda }) g=0$, where ![]() $g= f(y_0,\ldots , y_r) - f(y_0+\lambda ,\ldots , y_r+\lambda )$. Therefore
$g= f(y_0,\ldots , y_r) - f(y_0+\lambda ,\ldots , y_r+\lambda )$. Therefore ![]() $g$ is constant in
$g$ is constant in ![]() $\lambda$. It vanishes at
$\lambda$. It vanishes at ![]() $\lambda =0$, so
$\lambda =0$, so ![]() $g\equiv 0$ and
$g\equiv 0$ and ![]() $f$ is translation invariant.
$f$ is translation invariant.
Let us denote the map which sends ![]() $y_0$ to zero and
$y_0$ to zero and ![]() $y_i$ to
$y_i$ to ![]() $x_i$ for
$x_i$ for ![]() $i=1,\ldots , r$ by
$i=1,\ldots , r$ by
where ![]() $\bar {f}$ is the ‘reduced’ polynomial
$\bar {f}$ is the ‘reduced’ polynomial ![]() $\bar {f}(x_1,\ldots , x_r)= f(0,x_1,\ldots , x_r)$. In the case when
$\bar {f}(x_1,\ldots , x_r)= f(0,x_1,\ldots , x_r)$. In the case when ![]() $f$ is translation invariant, we can retrieve
$f$ is translation invariant, we can retrieve ![]() $f$ from
$f$ from ![]() $\bar {f}$ via
$\bar {f}$ via
Taking the coefficients of (6.7) gives equation I2 of [Reference BrownBro12], which gives a formula for the shuffle-regularization of iterated integrals which begin with any sequence of ![]() $0$'s.
$0$'s.
Definition 6.3 For any element ![]() $\xi \in \mathfrak {dg}^{\mathfrak {m}}$ of depth
$\xi \in \mathfrak {dg}^{\mathfrak {m}}$ of depth ![]() $r$ we denote its reduced polynomial representation by
$r$ we denote its reduced polynomial representation by ![]() $\bar {\rho }(\xi )\in \mathbb {Q}[x_1,\ldots , x_r]$.
$\bar {\rho }(\xi )\in \mathbb {Q}[x_1,\ldots , x_r]$.
To avoid confusion, we reserve the variables ![]() $x_1,\ldots , x_r$ for the reduced polynomial
$x_1,\ldots , x_r$ for the reduced polynomial ![]() $\bar {\rho }(\xi )$ and use the variables
$\bar {\rho }(\xi )$ and use the variables ![]() $y_0, \ldots , y_r$ as above to denote the full polynomial
$y_0, \ldots , y_r$ as above to denote the full polynomial ![]() $\rho (\xi )$.
$\rho (\xi )$.
6.3 Antipodal symmetries
The set of primitive elements in a Hopf algebra is stable under the antipode. For the shuffle Hopf algebra this is the map ![]() $* : T(e_0,e_1) \rightarrow T(e_0,e_1)$ which sends
$* : T(e_0,e_1) \rightarrow T(e_0,e_1)$ which sends ![]() $w \mapsto (-1)^{|w|} \tilde {w}$, where
$w \mapsto (-1)^{|w|} \tilde {w}$, where ![]() $\tilde {w}$ is the reversed word and
$\tilde {w}$ is the reversed word and ![]() $|w|$ the length of
$|w|$ the length of ![]() $w$. Restricting to
$w$. Restricting to ![]() $\mathfrak {D}$-degree
$\mathfrak {D}$-degree ![]() $r$ and transporting via
$r$ and transporting via ![]() $\rho$, we obtain a map
$\rho$, we obtain a map
 \begin{equation} \begin{gathered} \sigma: \mathbb{Q}[y_0,\ldots, y_r] \longrightarrow \mathbb{Q}[y_0,\ldots, y_r] \\ \sigma( f) (y_0,\ldots, y_r) = ({-}1)^{\deg(f) +r} f(y_r,\ldots, y_0). \end{gathered} \end{equation}
\begin{equation} \begin{gathered} \sigma: \mathbb{Q}[y_0,\ldots, y_r] \longrightarrow \mathbb{Q}[y_0,\ldots, y_r] \\ \sigma( f) (y_0,\ldots, y_r) = ({-}1)^{\deg(f) +r} f(y_r,\ldots, y_0). \end{gathered} \end{equation}
Therefore, if ![]() $f\in \mathbb {Q}[y_0,\ldots , y_r]$ satisfies the shuffle relations (5.3), then
$f\in \mathbb {Q}[y_0,\ldots , y_r]$ satisfies the shuffle relations (5.3), then
Since the stuffle algebra, graded for the depth filtration, is isomorphic to the shuffle algebra on ![]() $Y$ (5.9), it follows that its antipode is the map
$Y$ (5.9), it follows that its antipode is the map ![]() $\mathsf {y} _{i_1}\ldots \mathsf {y} _{i_r} \mapsto (-1)^r\mathsf {y} _{i_r}\ldots \mathsf {y} _{i_1}$. This defines an involution
$\mathsf {y} _{i_1}\ldots \mathsf {y} _{i_r} \mapsto (-1)^r\mathsf {y} _{i_r}\ldots \mathsf {y} _{i_1}$. This defines an involution
Therefore if ![]() $\bar {f}\in \mathbb {Q}[x_1,\ldots , x_r]$ satisfies the linearized stuffle relations, then
$\bar {f}\in \mathbb {Q}[x_1,\ldots , x_r]$ satisfies the linearized stuffle relations, then ![]() $\bar {f} + \bar {\tau }(\bar {f})=0$. Note that the involution
$\bar {f} + \bar {\tau }(\bar {f})=0$. Note that the involution ![]() $\bar {\tau }$ lifts to an involution
$\bar {\tau }$ lifts to an involution
and therefore if ![]() $f\in \mathbb {Q}[y_0,\ldots , y_r]$ satisfies both translational invariance and the linearized stuffle relations, we have
$f\in \mathbb {Q}[y_0,\ldots , y_r]$ satisfies both translational invariance and the linearized stuffle relations, we have
The composition ![]() $\tau \sigma$ is the signed cyclic rotation of order
$\tau \sigma$ is the signed cyclic rotation of order ![]() $r+1$,
$r+1$,
and plays an important role in the rest of this paper.
6.4 Parity relations
The following result is well known, and was first proved by Tsumura [Reference TsumuraTsu04], and subsequently in ([Reference Ihara, Kaneko and ZagierIKZ06, Theorem 7]). We repeat the proof for convenience.
Proposition 6.4 The components of ![]() $\mathfrak {ls}$ in weight
$\mathfrak {ls}$ in weight ![]() $N$ and depth
$N$ and depth ![]() $r$ vanish unless
$r$ vanish unless ![]() $N\equiv r\ \mathrm {mod} 2$. Equivalently,
$N\equiv r\ \mathrm {mod} 2$. Equivalently, ![]() $\rho (\mathfrak {ls} )$ consists of polynomials of even degree only.
$\rho (\mathfrak {ls} )$ consists of polynomials of even degree only.
Proof. Let ![]() $f\in \mathbb {Q}[y_0,\ldots , y_r]$ be in the image of
$f\in \mathbb {Q}[y_0,\ldots , y_r]$ be in the image of ![]() $\rho (\mathfrak {dg}^{\mathfrak {m}}_r)$. In particular, it satisfies the linearized stuffle relations (6.9) and (6.12). Following [Reference Ihara, Kaneko and ZagierIKZ06], consider the relation
$\rho (\mathfrak {dg}^{\mathfrak {m}}_r)$. In particular, it satisfies the linearized stuffle relations (6.9) and (6.12). Following [Reference Ihara, Kaneko and ZagierIKZ06], consider the relation
 \[ \mathsf{y} _1 \, \unicode{x0448} \, \mathsf{y} _2 \ldots \mathsf{y} _r = \mathsf{y} _1\ldots \mathsf{y} _r + \sum_{i=2}^{r} \mathsf{y} _2 \ldots \mathsf{y} _i \mathsf{y} _1 \mathsf{y} _{i+1} \ldots \mathsf{y} _r , \]
\[ \mathsf{y} _1 \, \unicode{x0448} \, \mathsf{y} _2 \ldots \mathsf{y} _r = \mathsf{y} _1\ldots \mathsf{y} _r + \sum_{i=2}^{r} \mathsf{y} _2 \ldots \mathsf{y} _i \mathsf{y} _1 \mathsf{y} _{i+1} \ldots \mathsf{y} _r , \]
where ![]() $r\geq 2$ (the case
$r\geq 2$ (the case ![]() $r=1$ follows from Definition 5.3). Then we have
$r=1$ follows from Definition 5.3). Then we have
 \[ f(y_0,y_1,\ldots, y_r) + \sum_{i=2}^{r} f(y_0,y_2,\ldots, y_i, y_1, y_{i+1}, \ldots, y_r) =0 . \]
\[ f(y_0,y_1,\ldots, y_r) + \sum_{i=2}^{r} f(y_0,y_2,\ldots, y_i, y_1, y_{i+1}, \ldots, y_r) =0 . \]
Now apply the automorphism of ![]() $\mathbb {Q}[y_0,\ldots , y_r]$ defined on generators by
$\mathbb {Q}[y_0,\ldots , y_r]$ defined on generators by ![]() $y_i \mapsto y_{i+1}$, where
$y_i \mapsto y_{i+1}$, where ![]() $i$ is taken modulo
$i$ is taken modulo ![]() $r+1$. This leads to the equation
$r+1$. This leads to the equation
 \[ f(y_1,y_2,\ldots, y_r, y_0) + \sum_{i=3}^{r+1} f(y_1,y_3,\ldots, y_i, y_2, y_{i+1}, \ldots,y_r, y_0) =0 . \]
\[ f(y_1,y_2,\ldots, y_r, y_0) + \sum_{i=3}^{r+1} f(y_1,y_3,\ldots, y_i, y_2, y_{i+1}, \ldots,y_r, y_0) =0 . \]
By applying a cyclic rotation ![]() $\tau \sigma$ to each term, we get
$\tau \sigma$ to each term, we get
 \[ f(y_0, y_1,y_2,\ldots, y_r) + \sum_{i=3}^{r} f(y_0, y_1,y_3,\ldots, y_i, y_2, y_{i+1}, \ldots, y_r) + f(y_2, y_1, y_3,\ldots, y_r,y_0) =0 . \]
\[ f(y_0, y_1,y_2,\ldots, y_r) + \sum_{i=3}^{r} f(y_0, y_1,y_3,\ldots, y_i, y_2, y_{i+1}, \ldots, y_r) + f(y_2, y_1, y_3,\ldots, y_r,y_0) =0 . \]
The first two terms can be interpreted as the terms occurring in the linearized stuffle product (![]() $\mathsf {y} _2 \, \unicode{x0448} \, \mathsf {y} _1\mathsf {y} _3 \ldots \mathsf {y} _r$) minus the first term. As a result, one obtains the equation
$\mathsf {y} _2 \, \unicode{x0448} \, \mathsf {y} _1\mathsf {y} _3 \ldots \mathsf {y} _r$) minus the first term. As a result, one obtains the equation
which, by a final application of ![]() $\tau \sigma$ to the right-hand term, yields
$\tau \sigma$ to the right-hand term, yields
Therefore, in the case when ![]() $\deg f$ is odd, the polynomial
$\deg f$ is odd, the polynomial ![]() $f$ must vanish.
$f$ must vanish.
6.5 Dihedral symmetry and the Ihara bracket
For all ![]() $r\geq 1$, consider the graded vector space
$r\geq 1$, consider the graded vector space ![]() $\mathfrak {p} _r$ of polynomials
$\mathfrak {p} _r$ of polynomials ![]() $f\in \mathbb {Q}[y_0,\ldots , y_r]$ which satisfy
$f\in \mathbb {Q}[y_0,\ldots , y_r]$ which satisfy
The maps ![]() $\sigma ,\tau$ generate a dihedral group
$\sigma ,\tau$ generate a dihedral group ![]() $D_{r+1}=\langle \sigma , \tau \rangle$ of symmetries acting on
$D_{r+1}=\langle \sigma , \tau \rangle$ of symmetries acting on ![]() $\mathfrak {p} _r$ of order
$\mathfrak {p} _r$ of order ![]() $2r+2$, and any element
$2r+2$, and any element ![]() $f$ satisfying (6.13) is invariant under cyclic rotation:
$f$ satisfying (6.13) is invariant under cyclic rotation:
and anti-invariant under the reflections ![]() $\sigma$ and
$\sigma$ and ![]() $\tau$. Thus
$\tau$. Thus ![]() $\mathbb {Q} f \subset \mathfrak {p} _r$ is isomorphic to the one-dimensional sign (orientation) representation
$\mathbb {Q} f \subset \mathfrak {p} _r$ is isomorphic to the one-dimensional sign (orientation) representation ![]() $\varepsilon$ of the dihedral group
$\varepsilon$ of the dihedral group ![]() $D_{r+1}$.
$D_{r+1}$.
Proposition 6.5 Suppose that ![]() $f\in \mathfrak {p} _r$ and
$f\in \mathfrak {p} _r$ and ![]() $g\in \mathfrak {p} _s$ are polynomials satisfying (6.13). Then the Ihara bracket is the signed average over the dihedral symmetry group:
$g\in \mathfrak {p} _s$ are polynomials satisfying (6.13). Then the Ihara bracket is the signed average over the dihedral symmetry group:
In particular, ![]() $\{.\,{,}\,.\}: \mathfrak {p} _r \times \mathfrak {p} _s \rightarrow \mathfrak {p} _{r+s}$, and
$\{.\,{,}\,.\}: \mathfrak {p} _r \times \mathfrak {p} _s \rightarrow \mathfrak {p} _{r+s}$, and ![]() $\mathfrak {p} =\bigoplus _{r\geq 1} \mathfrak {p} _r$ is a bigraded Lie algebra.
$\mathfrak {p} =\bigoplus _{r\geq 1} \mathfrak {p} _r$ is a bigraded Lie algebra.
Proof. A straightforward calculation from (6.3) and definition (6.4) gives
where the summation indices are taken modulo ![]() $r+s+1$. Invoking dihedral symmetry of
$r+s+1$. Invoking dihedral symmetry of ![]() $f, g$ leads to formula (6.14). The Jacobi identity for
$f, g$ leads to formula (6.14). The Jacobi identity for ![]() $\{.\,{,}\,.\}$ is automatic since the Ihara action is an action, but can also be proved very easily by identifying its terms with the set of double cuts in a polygon (see [Reference BrownBro17b]). The fact that parity (first equation of (6.13)) is preserved by
$\{.\,{,}\,.\}$ is automatic since the Ihara action is an action, but can also be proved very easily by identifying its terms with the set of double cuts in a polygon (see [Reference BrownBro17b]). The fact that parity (first equation of (6.13)) is preserved by ![]() $\{\,{,}\,\}$ is clear. The anti-invariance under
$\{\,{,}\,\}$ is clear. The anti-invariance under ![]() $\sigma , \tau$ is also clear from the dihedral symmetry of (6.14).
$\sigma , \tau$ is also clear from the dihedral symmetry of (6.14).
A similar dihedral symmetry was also found by Goncharov [Reference GoncharovGon01b]; the interpretation of the dihedral reflections as antipodes may or may not be new. Since the Ihara action is, by definition, compatible with the shuffle product, it follows from Lemma 6.2 that translation invariance is preserved by the Ihara bracket. One can also easily verify this by direct computation:
 \[ \sum_{i=0}^r \frac{\partial f }{\partial y_i }=\sum_{i=0}^s \frac{\partial g }{\partial y_i }= 0 \quad \Longrightarrow \quad \sum_{i=0}^{r+s} \frac{\partial \{f,g\} }{\partial y_i } =0 . \]
\[ \sum_{i=0}^r \frac{\partial f }{\partial y_i }=\sum_{i=0}^s \frac{\partial g }{\partial y_i }= 0 \quad \Longrightarrow \quad \sum_{i=0}^{r+s} \frac{\partial \{f,g\} }{\partial y_i } =0 . \]Definition 6.6 Let ![]() $\bar {\mathfrak {p} }_r \subset \mathfrak {p} _r$ denote the subspace of polynomials which satisfy (6.13) and are invariant under translation, and write
$\bar {\mathfrak {p} }_r \subset \mathfrak {p} _r$ denote the subspace of polynomials which satisfy (6.13) and are invariant under translation, and write ![]() $\bar {\mathfrak {p} }= \bigoplus _{r \geq 1} \bar {\mathfrak {p} }_r$.
$\bar {\mathfrak {p} }= \bigoplus _{r \geq 1} \bar {\mathfrak {p} }_r$.
By abuse of notation, we can equivalently view ![]() $\bar {\mathfrak {p} }_r$ as the subspace of polynomials
$\bar {\mathfrak {p} }_r$ as the subspace of polynomials ![]() $\bar {f}\in \mathbb {Q}[x_1,\ldots , x_r]$ whose lift
$\bar {f}\in \mathbb {Q}[x_1,\ldots , x_r]$ whose lift ![]() $\bar {f}(y_1 -y_0,\ldots , y_r-y_0)$ lies in
$\bar {f}(y_1 -y_0,\ldots , y_r-y_0)$ lies in ![]() $\mathfrak {p} _r$. Explicitly,
$\mathfrak {p} _r$. Explicitly, ![]() $\bar {\mathfrak {p} }_r$ is the vector space of polynomials satisfying
$\bar {\mathfrak {p} }_r$ is the vector space of polynomials satisfying
(1)
 $\bar {f}(x_1,\ldots , x_r )= \bar {f}(-x_1,\ldots , -x_r )$,
$\bar {f}(x_1,\ldots , x_r )= \bar {f}(-x_1,\ldots , -x_r )$,(2)
 $\bar {f}(x_1,\ldots , x_r ) + (-1)^r \bar {f}(x_r,\ldots , x_1 ) =0$,
$\bar {f}(x_1,\ldots , x_r ) + (-1)^r \bar {f}(x_r,\ldots , x_1 ) =0$,(3)
 $\bar {f}(x_1,\ldots , x_r ) + (-1)^r \bar {f}(x_{r-1}-x_r,\ldots , x_1-x_r, -x_r ) =0$,
$\bar {f}(x_1,\ldots , x_r ) + (-1)^r \bar {f}(x_{r-1}-x_r,\ldots , x_1-x_r, -x_r ) =0$,
with Lie bracket induced by (6.14). To conclude the previous discussion, the map
is an injective map of bigraded Lie algebras.
Definition 6.7 We use the notation ![]() $\mathbb {D}_r\subset \mathbb {Q} [x_1,\ldots , x_r]$ to denote the space
$\mathbb {D}_r\subset \mathbb {Q} [x_1,\ldots , x_r]$ to denote the space ![]() $\bar {\rho }(\mathfrak {ls} _r)$ in depth
$\bar {\rho }(\mathfrak {ls} _r)$ in depth ![]() $r$. It is the space of polynomial solutions to the linearized double shuffle equations in depth
$r$. It is the space of polynomial solutions to the linearized double shuffle equations in depth ![]() $r$ and is the direct sum for all
$r$ and is the direct sum for all ![]() $n$, of spaces denoted
$n$, of spaces denoted ![]() $D_{n, r}$ in [Reference Ihara, Kaneko and ZagierIKZ06].
$D_{n, r}$ in [Reference Ihara, Kaneko and ZagierIKZ06].
6.6 Generators in depth  $1$ and examples
$1$ and examples
It follows from Theorem 1.1 that in depth ![]() $1$, the Lie algebra
$1$, the Lie algebra ![]() $\mathfrak {dg}^{\mathfrak {m}}$ has exactly one generator in every odd weight
$\mathfrak {dg}^{\mathfrak {m}}$ has exactly one generator in every odd weight ![]() $\geq 3$:
$\geq 3$:
In particular, the algebras ![]() $\mathfrak {dg}^{\mathfrak {m}} \subset \mathrm {gr}_{\mathfrak {D}} \mathfrak {dm}_0 (\mathbb {Q}) \subset \mathfrak {ls}$ are all isomorphic in depth
$\mathfrak {dg}^{\mathfrak {m}} \subset \mathrm {gr}_{\mathfrak {D}} \mathfrak {dm}_0 (\mathbb {Q}) \subset \mathfrak {ls}$ are all isomorphic in depth ![]() $1$.
$1$.
Definition 6.8 Denote the Lie subalgebra generated by ![]() $x_1^{2n}$, for
$x_1^{2n}$, for ![]() $n\geq 1$, by
$n\geq 1$, by
Example 6.9 The formula for the Ihara bracket in depth 2 can be written
6.7 Relations between depth-graded motivic multiple zeta values
We briefly explain how we may describe all relations between ![]() $\zeta ^{{\mathfrak {m}}}_{\mathfrak {D}}$ using this formalism.
$\zeta ^{{\mathfrak {m}}}_{\mathfrak {D}}$ using this formalism.
Proposition 4.2 states that ![]() $\mathrm {gr}^{\mathfrak {D}} \mathcal {H}$ is the free bigraded right
$\mathrm {gr}^{\mathfrak {D}} \mathcal {H}$ is the free bigraded right ![]() $\mathcal {U} \mathfrak {dg}^{\mathfrak {m}}$-module generated by the
$\mathcal {U} \mathfrak {dg}^{\mathfrak {m}}$-module generated by the ![]() $\zeta ^{{\mathfrak {m}}}_{\mathfrak {D}}(2n)$, and can be represented by polynomials as follows. The role of the even zeta value
$\zeta ^{{\mathfrak {m}}}_{\mathfrak {D}}(2n)$, and can be represented by polynomials as follows. The role of the even zeta value ![]() $\zeta ^{{\mathfrak {m}}}(2n)$, for
$\zeta ^{{\mathfrak {m}}}(2n)$, for ![]() $n\geq 1$, is played by the depth-graded associator element
$n\geq 1$, is played by the depth-graded associator element ![]() $\tau ^{(1)}$ in weight
$\tau ^{(1)}$ in weight ![]() $2n$ constructed in [Reference BrownBro17a, §§ 7.3 and 7.4], and is encoded by the monomial in one variable:
$2n$ constructed in [Reference BrownBro17a, §§ 7.3 and 7.4], and is encoded by the monomial in one variable:
Therefore, a relation
holds between (shuffle-regularized) depth-graded motivic multiple zeta values in depth ![]() $d$ and weight
$d$ and weight ![]() $N$ if and only if
$N$ if and only if ![]() $\sum _{\underline {n} = (n_1,\ldots , n_d)} \lambda _{\underline {n}} c_{\underline {n}} =0$ for all
$\sum _{\underline {n} = (n_1,\ldots , n_d)} \lambda _{\underline {n}} c_{\underline {n}} =0$ for all
where ![]() $\xi$ is of depth
$\xi$ is of depth ![]() $d$ and weight
$d$ and weight ![]() $N$ of the form
$N$ of the form
 \begin{align*} x&= g_1 \, \underline{\circ}\, \big( g_2 \, \underline{\circ}\, \big( \ldots \ldots \big( g_{d-1} \, \underline{\circ}\, g_d \big)\! \cdots \!\big)\big) \quad \hbox{ if } N\equiv d \pmod{2},\\ x&= g_1 \, \underline{\circ}\, \big( g_2 \, \underline{\circ}\, \big( \ldots \ldots \big( g_{d-1} \, \underline{\circ}\, \bar{\tau}_{2k} \big)\! \cdots \!\big)\big)\quad \hbox{ if } N\not\equiv d \pmod{2} , \end{align*}
\begin{align*} x&= g_1 \, \underline{\circ}\, \big( g_2 \, \underline{\circ}\, \big( \ldots \ldots \big( g_{d-1} \, \underline{\circ}\, g_d \big)\! \cdots \!\big)\big) \quad \hbox{ if } N\equiv d \pmod{2},\\ x&= g_1 \, \underline{\circ}\, \big( g_2 \, \underline{\circ}\, \big( \ldots \ldots \big( g_{d-1} \, \underline{\circ}\, \bar{\tau}_{2k} \big)\! \cdots \!\big)\big)\quad \hbox{ if } N\not\equiv d \pmod{2} , \end{align*}
in which the ![]() $g_i$ are the polynomial representatives of generators of
$g_i$ are the polynomial representatives of generators of ![]() $\mathfrak {dg}^{\mathfrak {m}}$ and
$\mathfrak {dg}^{\mathfrak {m}}$ and ![]() $k\geq 1$.
$k\geq 1$.
Examples 6.10 We give some simple examples in depth 2. For this, our formula for ![]() $\, \underline {\circ }\,$ gives, for any
$\, \underline {\circ }\,$ gives, for any ![]() $m,n\geq 1$,
$m,n\geq 1$,
(1) In weight 5, depth 2, ![]() $\mathrm {gr}_2^{\mathfrak {D}} \mathcal {H}_5$ is one-dimensional generated by the element
$\mathrm {gr}_2^{\mathfrak {D}} \mathcal {H}_5$ is one-dimensional generated by the element ![]() $\bar {\sigma }_3 \circ \bar {\tau }_2$, which we can compute using (6.16) to be
$\bar {\sigma }_3 \circ \bar {\tau }_2$, which we can compute using (6.16) to be
It encodes the coefficients of ![]() $\zeta ^{{\mathfrak {m}}}(3) \zeta ^{{\mathfrak {m}}}(2)$ in the following (shuffle-regularized) depth-graded multiple zeta values in depth 2 and weight 4, as one can see from the relations
$\zeta ^{{\mathfrak {m}}}(3) \zeta ^{{\mathfrak {m}}}(2)$ in the following (shuffle-regularized) depth-graded multiple zeta values in depth 2 and weight 4, as one can see from the relations
 \begin{align*} \zeta^{{\mathfrak{m}}}(3,2) &= \tfrac{9}{2}\, \zeta^{{\mathfrak{m}}}(5) - 2\, \zeta^{{\mathfrak{m}}}(3) \zeta^{{\mathfrak{m}}}(2), \\ \zeta^{{\mathfrak{m}}}(2,3) &={-}\tfrac{11}{2}\, \zeta^{{\mathfrak{m}}}(5) +3\, \zeta^{{\mathfrak{m}}}(3) \zeta^{{\mathfrak{m}}}(2), \\ \zeta^{{\mathfrak{m}}}(1,4) &= 2 \, \zeta(5) - \zeta^{{\mathfrak{m}}}(3) \zeta^{{\mathfrak{m}}}2). \end{align*}
\begin{align*} \zeta^{{\mathfrak{m}}}(3,2) &= \tfrac{9}{2}\, \zeta^{{\mathfrak{m}}}(5) - 2\, \zeta^{{\mathfrak{m}}}(3) \zeta^{{\mathfrak{m}}}(2), \\ \zeta^{{\mathfrak{m}}}(2,3) &={-}\tfrac{11}{2}\, \zeta^{{\mathfrak{m}}}(5) +3\, \zeta^{{\mathfrak{m}}}(3) \zeta^{{\mathfrak{m}}}(2), \\ \zeta^{{\mathfrak{m}}}(1,4) &= 2 \, \zeta(5) - \zeta^{{\mathfrak{m}}}(3) \zeta^{{\mathfrak{m}}}2). \end{align*}
For instance, we may read off the relation ![]() $3\, \zeta ^{{\mathfrak {m}}}_{\mathfrak {D}}(3,2)+2\, \zeta ^{{\mathfrak {m}}}_{\mathfrak {D}}(2,3)=0$ from
$3\, \zeta ^{{\mathfrak {m}}}_{\mathfrak {D}}(3,2)+2\, \zeta ^{{\mathfrak {m}}}_{\mathfrak {D}}(2,3)=0$ from ![]() $x_1^2 \, \underline {\circ }\, x_1$.
$x_1^2 \, \underline {\circ }\, x_1$.
(2) In weight 7, depth 2, ![]() $\mathrm {gr}_2^{\mathfrak {D}} \mathcal {H}_7$ is two-dimensional generated by the two elements
$\mathrm {gr}_2^{\mathfrak {D}} \mathcal {H}_7$ is two-dimensional generated by the two elements ![]() $\bar {\sigma }_5 \circ \bar {\tau }_2$ and
$\bar {\sigma }_5 \circ \bar {\tau }_2$ and ![]() $\bar {\sigma }_3 \circ \bar {\tau }_4$, which we compute via
$\bar {\sigma }_3 \circ \bar {\tau }_4$, which we compute via
 \begin{align*} x_1^4 \, \underline{\circ}\, x_1 &= x_1^5 - 4\,x_1^4 x_2 + 10 \, x_1^3 x_2^2 - 10 \, x_1^2 x_2^3 +5 \, x_1x_2^4 - x_2^5 \\ x_1^2 \, \underline{\circ}\, x^3_1 &= x_1^5 - 2 \, x_1^4 x_2 + x_1^3 x_2^2 +2 \, x_1 x_2^4 - x_2^5 . \end{align*}
\begin{align*} x_1^4 \, \underline{\circ}\, x_1 &= x_1^5 - 4\,x_1^4 x_2 + 10 \, x_1^3 x_2^2 - 10 \, x_1^2 x_2^3 +5 \, x_1x_2^4 - x_2^5 \\ x_1^2 \, \underline{\circ}\, x^3_1 &= x_1^5 - 2 \, x_1^4 x_2 + x_1^3 x_2^2 +2 \, x_1 x_2^4 - x_2^5 . \end{align*}
The coefficients in these expressions encode the coefficients of ![]() $\zeta ^{{\mathfrak {m}}}(5) \zeta ^{{\mathfrak {m}}}(2)$ and
$\zeta ^{{\mathfrak {m}}}(5) \zeta ^{{\mathfrak {m}}}(2)$ and ![]() $\zeta ^{{\mathfrak {m}}}(3) \zeta ^{{\mathfrak {m}}}(4)$ in depth 2 multiple zeta values of weight 7. For example,
$\zeta ^{{\mathfrak {m}}}(3) \zeta ^{{\mathfrak {m}}}(4)$ in depth 2 multiple zeta values of weight 7. For example,
 \begin{align*} \zeta^{{\mathfrak{m}}}(5,2) &= 10\, \zeta^{{\mathfrak{m}}}(7) - 4\, \zeta^{{\mathfrak{m}}}(5) \zeta^{{\mathfrak{m}}}(2) - 2 \, \zeta^{{\mathfrak{m}}}(3) \zeta^{{\mathfrak{m}}}(4), \\ \zeta^{{\mathfrak{m}}}(4,3) &={-}18\, \zeta^{{\mathfrak{m}}}(7) +10 \, \zeta^{{\mathfrak{m}}}(5) \zeta^{{\mathfrak{m}}}(2) + \zeta^{{\mathfrak{m}}}(3) \zeta^{{\mathfrak{m}}}(4), \\ \zeta^{{\mathfrak{m}}}(3,4) &= 17 \, \zeta^{{\mathfrak{m}}}(7) - 10 \, \zeta^{{\mathfrak{m}}}(5) \zeta^{{\mathfrak{m}}}(2), \\ \zeta^{{\mathfrak{m}}}(2,5) &={-}11 \, \zeta^{{\mathfrak{m}}}(7) +5 \, \zeta^{{\mathfrak{m}}}(5) \zeta^{{\mathfrak{m}}}(2) +2 \,\zeta^{{\mathfrak{m}}}(3) \zeta^{{\mathfrak{m}}}(4) . \end{align*}
\begin{align*} \zeta^{{\mathfrak{m}}}(5,2) &= 10\, \zeta^{{\mathfrak{m}}}(7) - 4\, \zeta^{{\mathfrak{m}}}(5) \zeta^{{\mathfrak{m}}}(2) - 2 \, \zeta^{{\mathfrak{m}}}(3) \zeta^{{\mathfrak{m}}}(4), \\ \zeta^{{\mathfrak{m}}}(4,3) &={-}18\, \zeta^{{\mathfrak{m}}}(7) +10 \, \zeta^{{\mathfrak{m}}}(5) \zeta^{{\mathfrak{m}}}(2) + \zeta^{{\mathfrak{m}}}(3) \zeta^{{\mathfrak{m}}}(4), \\ \zeta^{{\mathfrak{m}}}(3,4) &= 17 \, \zeta^{{\mathfrak{m}}}(7) - 10 \, \zeta^{{\mathfrak{m}}}(5) \zeta^{{\mathfrak{m}}}(2), \\ \zeta^{{\mathfrak{m}}}(2,5) &={-}11 \, \zeta^{{\mathfrak{m}}}(7) +5 \, \zeta^{{\mathfrak{m}}}(5) \zeta^{{\mathfrak{m}}}(2) +2 \,\zeta^{{\mathfrak{m}}}(3) \zeta^{{\mathfrak{m}}}(4) . \end{align*}
Choosing any linear functional on the coefficients of ![]() $x_1^4 x_2$,
$x_1^4 x_2$, ![]() $x_1^3 x_2^2$ and
$x_1^3 x_2^2$ and ![]() $x_1^2 x_2^3$ which vanishes on
$x_1^2 x_2^3$ which vanishes on ![]() $x_1^4 \, \underline {\circ }\, x_1$ and
$x_1^4 \, \underline {\circ }\, x_1$ and ![]() $x_1^2 \, \underline {\circ }\, x^3_1$ leads to a relation between depth-graded motivic multiple zeta values, for instance:
$x_1^2 \, \underline {\circ }\, x^3_1$ leads to a relation between depth-graded motivic multiple zeta values, for instance:
(3) In weight 8, depth 2, ![]() $\mathrm {gr}_2^{\mathfrak {D}} \mathcal {H}_8$ is two-dimensional generated by the pair of elements
$\mathrm {gr}_2^{\mathfrak {D}} \mathcal {H}_8$ is two-dimensional generated by the pair of elements ![]() $\bar {\sigma }_3 \circ \bar {\sigma }_5$ and
$\bar {\sigma }_3 \circ \bar {\sigma }_5$ and ![]() $\bar {\sigma }_5 \circ \bar {\sigma }_3$, which we compute using (6.16) by
$\bar {\sigma }_5 \circ \bar {\sigma }_3$, which we compute using (6.16) by
 \begin{align*} x_1^4 \, \underline{\circ}\, x^2_1 &= x_1^6 - 2 \, x_1^5 x_2 + x_1^4 x_2^2 +2 \, x_1 x_2^5 - x_2^6 \\ x_1^2 \, \underline{\circ}\, x^4_1 &= x_1^6 - 4 \, x_1^5 x_2 + 6 \, x_1^4 x_2^2 - 5\, x_1^2 x_2^4 + 4\, x_1 x_2^5 - x_2^6. \end{align*}
\begin{align*} x_1^4 \, \underline{\circ}\, x^2_1 &= x_1^6 - 2 \, x_1^5 x_2 + x_1^4 x_2^2 +2 \, x_1 x_2^5 - x_2^6 \\ x_1^2 \, \underline{\circ}\, x^4_1 &= x_1^6 - 4 \, x_1^5 x_2 + 6 \, x_1^4 x_2^2 - 5\, x_1^2 x_2^4 + 4\, x_1 x_2^5 - x_2^6. \end{align*}From these, we deduce all relations between depth-graded motivic multiple zeta values of weight 8 and depth 2, such as
since ![]() $2.( 0) + 5.(2) + 10. (-1) =0$ and
$2.( 0) + 5.(2) + 10. (-1) =0$ and ![]() $2.(-5) + 5.(4) + 10.(-1)=0$ where the numbers in brackets are the coefficients of
$2.(-5) + 5.(4) + 10.(-1)=0$ where the numbers in brackets are the coefficients of ![]() $x_1^2x_2^4$,
$x_1^2x_2^4$, ![]() $x_1 x_2^5$,
$x_1 x_2^5$, ![]() $x_2^6$ in
$x_2^6$ in ![]() $x_1^4 \, \underline {\circ }\, x^2_1$ and
$x_1^4 \, \underline {\circ }\, x^2_1$ and ![]() $x_1^2 \, \underline {\circ }\, x^2_3$. Indeed, one may check that
$x_1^2 \, \underline {\circ }\, x^2_3$. Indeed, one may check that ![]() $5 \, \zeta ^{{\mathfrak {m}}}(2,6) + 2\, \zeta ^{{\mathfrak {m}}}(3,5) + 10\, \zeta ^{{\mathfrak {m}}}(1,7) = \frac {6}{175} \zeta ^{{\mathfrak {m}}}(2)^4$.
$5 \, \zeta ^{{\mathfrak {m}}}(2,6) + 2\, \zeta ^{{\mathfrak {m}}}(3,5) + 10\, \zeta ^{{\mathfrak {m}}}(1,7) = \frac {6}{175} \zeta ^{{\mathfrak {m}}}(2)^4$.
7. Modular relations in depth 2
7.1 Reminders on period polynomials
We recall some definitions from [Reference Kohnen and ZagierKZ84, § 1.1]. Let ![]() $S_{2k}(\mathrm {SL}_2(\mathbb {Z}))$ denote the space of cusp forms of weight
$S_{2k}(\mathrm {SL}_2(\mathbb {Z}))$ denote the space of cusp forms of weight ![]() $2k$ for the full modular group
$2k$ for the full modular group ![]() $\mathrm {SL}_2(\mathbb {Z})$.
$\mathrm {SL}_2(\mathbb {Z})$.
Definition 7.1 Let ![]() $n\geq 1$ and let
$n\geq 1$ and let ![]() $W_{2n}^e\subset \mathbb {Q}[X,Y]$ denote the vector space of homogeneous polynomials
$W_{2n}^e\subset \mathbb {Q}[X,Y]$ denote the vector space of homogeneous polynomials ![]() $P(X,Y)$ of degree
$P(X,Y)$ of degree ![]() $2n-2$ satisfying
$2n-2$ satisfying
The space ![]() $W_{2n}^e$ contains the polynomial
$W_{2n}^e$ contains the polynomial ![]() $p_{2n}= X^{2n-2}-Y^{2n-2}$, and is a direct sum
$p_{2n}= X^{2n-2}-Y^{2n-2}$, and is a direct sum
where ![]() $\mathsf {S} _{2n}$ is the subspace of polynomials which vanish at
$\mathsf {S} _{2n}$ is the subspace of polynomials which vanish at ![]() $(X,Y)=(1,0)$. We write
$(X,Y)=(1,0)$. We write ![]() $\mathsf {S} = \bigoplus _{n} \mathsf {S} _{2n}$. The Eichler–Shimura–Manin theorem gives a map which associates, in particular, an even-period polynomial to every cusp form:
$\mathsf {S} = \bigoplus _{n} \mathsf {S} _{2n}$. The Eichler–Shimura–Manin theorem gives a map which associates, in particular, an even-period polynomial to every cusp form:
Explicitly, if ![]() $f$ is a cusp form of weight
$f$ is a cusp form of weight ![]() $2k$, the map is given by
$2k$, the map is given by
where ![]() $+$ denotes the projection onto invariants under the involution
$+$ denotes the projection onto invariants under the involution ![]() $(X,Y)\mapsto (X,-Y)$, that is,
$(X,Y)\mapsto (X,-Y)$, that is, ![]() $a^+(X,Y)= \frac {1}{2} (a (X,Y) + a(X,-Y))$. The three-term equation (7.2) follows from integrating around the geodesic triangle with vertices
$a^+(X,Y)= \frac {1}{2} (a (X,Y) + a(X,-Y))$. The three-term equation (7.2) follows from integrating around the geodesic triangle with vertices ![]() $0,1,i \infty$ and is reminiscent of the hexagon equation for associators. The map (7.3) is an isomorphism onto a subspace of
$0,1,i \infty$ and is reminiscent of the hexagon equation for associators. The map (7.3) is an isomorphism onto a subspace of ![]() $W^e_{2k} \otimes \mathbb {C}$ of codimension
$W^e_{2k} \otimes \mathbb {C}$ of codimension ![]() $1$. Thus
$1$. Thus ![]() $\dim S_{2k}(\mathrm {SL} _2(\mathbb {Z})) = \dim \mathsf {S} _{2k}$ and it follows from classical results on the space of modular forms of level 1 that
$\dim S_{2k}(\mathrm {SL} _2(\mathbb {Z})) = \dim \mathsf {S} _{2k}$ and it follows from classical results on the space of modular forms of level 1 that
 \begin{equation} \sum_{n\geq 0} \dim \mathsf{S} _{2n} s^{2n} = \frac{s^{12} }{(1-s^4)(1-s^6)} = \mathbb{S}(s) . \end{equation}
\begin{equation} \sum_{n\geq 0} \dim \mathsf{S} _{2n} s^{2n} = \frac{s^{12} }{(1-s^4)(1-s^6)} = \mathbb{S}(s) . \end{equation}7.2 Linearized double shuffle in depths 2 and 3
We first recall from [Reference Ihara, Kaneko and ZagierIKZ06] that ![]() $\mathbb {D}_2$ is the graded space of homogeneous polynomials
$\mathbb {D}_2$ is the graded space of homogeneous polynomials ![]() $f\in \mathbb {Q}[x_1,x_2]$ in two variables satisfying the linearized double shuffle equations in depth 2:
$f\in \mathbb {Q}[x_1,x_2]$ in two variables satisfying the linearized double shuffle equations in depth 2:
The space ![]() $\mathbb {D}_3$ consists of homogeneous polynomials
$\mathbb {D}_3$ consists of homogeneous polynomials ![]() $f \in \mathbb {Q}[x_1,x_2,x_3]$ such that
$f \in \mathbb {Q}[x_1,x_2,x_3]$ such that
 \begin{align*} f(x_1,x_2,x_3) + f(x_2,x_1,x_3) +f(x_2,x_3,x_1) & = 0, \\ f^{\sharp}(x_1,x_2,x_3) + f^{\sharp}(x_2,x_1,x_3) +f^{\sharp}(x_2,x_3,x_1) & = 0 , \end{align*}
\begin{align*} f(x_1,x_2,x_3) + f(x_2,x_1,x_3) +f(x_2,x_3,x_1) & = 0, \\ f^{\sharp}(x_1,x_2,x_3) + f^{\sharp}(x_2,x_1,x_3) +f^{\sharp}(x_2,x_3,x_1) & = 0 , \end{align*}
where ![]() $f^{\sharp }(x,y,z) = f(x,x+y, x+y+z)$. The general double shuffle equations and their linearized versions are derived in [Reference BrownBro17b, §§ 4–7] using Hopf-algebra-theoretic techniques.
$f^{\sharp }(x,y,z) = f(x,x+y, x+y+z)$. The general double shuffle equations and their linearized versions are derived in [Reference BrownBro17b, §§ 4–7] using Hopf-algebra-theoretic techniques.
7.3 A short exact sequence in depth 2
The Ihara bracket gives a map
Applying the isomorphism ![]() $\bar {\rho }$ leads to a map
$\bar {\rho }$ leads to a map
given by the formula in Example 6.9. Since ![]() $\mathbb {D}_1$ is isomorphic to the graded vector space
$\mathbb {D}_1$ is isomorphic to the graded vector space ![]() $\mathbb {Q}[x_1^{2n},{n\geq 1}]$, it follows that
$\mathbb {Q}[x_1^{2n},{n\geq 1}]$, it follows that ![]() $\mathbb {D}_1 \wedge \mathbb {D}_1$ is isomorphic to the space of antisymmetric even polynomials
$\mathbb {D}_1 \wedge \mathbb {D}_1$ is isomorphic to the space of antisymmetric even polynomials ![]() $p(x_1,x_2)$ with positive bidegrees, with basis
$p(x_1,x_2)$ with positive bidegrees, with basis ![]() $x_1^{2m} x_2^{2n} - x_1^{2n} x_2^{2m}$ for
$x_1^{2m} x_2^{2n} - x_1^{2n} x_2^{2m}$ for ![]() $m>n>0$. It follows from Example 6.9 that the image of
$m>n>0$. It follows from Example 6.9 that the image of ![]() $p(x_1,x_2)$ under (7.6) is
$p(x_1,x_2)$ under (7.6) is
Comparing with (7.2) and (7.1), we immediately deduce (cf. [Reference Ihara and TakaoIT93, Reference GoncharovGon05, Reference Gangl, Kaneko and ZagierGKZ06, Reference SchnepsSch06]) that
In fact, the dimensions of the space ![]() $\mathbb {D}_2$ have been computed several times in the literature (e.g. by some simple representation-theoretic arguments), and it is relatively easy to show [Reference Gangl, Kaneko and ZagierGKZ06] that the following sequence is exact:
$\mathbb {D}_2$ have been computed several times in the literature (e.g. by some simple representation-theoretic arguments), and it is relatively easy to show [Reference Gangl, Kaneko and ZagierGKZ06] that the following sequence is exact:
Example 7.2 The smallest non-trivial period polynomial occurs in degree 10 and is given by ![]() $s_{12} = X^2Y^2(X-Y)^3(X+Y)^3 = X^8 Y^2 -3 X^6 Y^4+3 X^4 Y^6-X^2Y^8.$ By the exact sequence (7.8) it immediately gives rise to the equation
$s_{12} = X^2Y^2(X-Y)^3(X+Y)^3 = X^8 Y^2 -3 X^6 Y^4+3 X^4 Y^6-X^2Y^8.$ By the exact sequence (7.8) it immediately gives rise to the equation
which, by the faithfulness of the map ![]() $\bar {\rho }$, is equivalent to Ihara's formula (1.7).
$\bar {\rho }$, is equivalent to Ihara's formula (1.7).
7.4 A short exact sequence in depth 3
If ![]() $V$ is a vector space let
$V$ is a vector space let ![]() $\mathrm {Lie}_n(V) \subset V^{\otimes n}$ denote the component of degree
$\mathrm {Lie}_n(V) \subset V^{\otimes n}$ denote the component of degree ![]() $n$ in the free graded Lie algebra
$n$ in the free graded Lie algebra ![]() $\mathrm {Lie}(V)$ generated by
$\mathrm {Lie}(V)$ generated by ![]() $V$, viewed inside the tensor algebra
$V$, viewed inside the tensor algebra ![]() $T(V)= \bigoplus _{n\geq 0} V^{\otimes n}$. It is the subspace spanned by Lie brackets of the form
$T(V)= \bigoplus _{n\geq 0} V^{\otimes n}$. It is the subspace spanned by Lie brackets of the form ![]() $[v_1,[v_2,\ldots , [v_{n-1},v_n]\ldots ]$ where the Lie bracket on
$[v_1,[v_2,\ldots , [v_{n-1},v_n]\ldots ]$ where the Lie bracket on ![]() $T(V)$ is the antisymmetrization of the tensor multiplication (i.e.
$T(V)$ is the antisymmetrization of the tensor multiplication (i.e.![]() $[v_1,v_2]=v_1v_2-v_2v_1$). Thus, as a graded vector space,
$[v_1,v_2]=v_1v_2-v_2v_1$). Thus, as a graded vector space, ![]() $\mathrm {Lie}(V) \cong \bigoplus _{n \geq 1} \mathrm {Lie}_n(V)$, and each
$\mathrm {Lie}(V) \cong \bigoplus _{n \geq 1} \mathrm {Lie}_n(V)$, and each ![]() $\mathrm {Lie}_n$ is a direct sum of Schur functors (e.g.
$\mathrm {Lie}_n$ is a direct sum of Schur functors (e.g. ![]() $\mathrm {Lie}_1(V) = V$ and
$\mathrm {Lie}_1(V) = V$ and ![]() $\mathrm {Lie}_2(V) = {\bigwedge} ^2 V$).
$\mathrm {Lie}_2(V) = {\bigwedge} ^2 V$).
The triple Ihara bracket gives a trilinear map
and hence a map ![]() $\mathrm {Lie}_3(\mathbb {D}_1) \rightarrow \mathbb {D}_3$ whose image is spanned by
$\mathrm {Lie}_3(\mathbb {D}_1) \rightarrow \mathbb {D}_3$ whose image is spanned by ![]() $\{x_1^{2a} , \{ x_1^{2b}, x_1^{2c}\} \!\}$, for
$\{x_1^{2a} , \{ x_1^{2b}, x_1^{2c}\} \!\}$, for ![]() $a,b,c\geq 1$. Goncharov has studied the space
$a,b,c\geq 1$. Goncharov has studied the space ![]() $\mathbb {D}_3$, and computed its dimensions in each weight [Reference GoncharovGon05]. It follows from his work that the sequence
$\mathbb {D}_3$, and computed its dimensions in each weight [Reference GoncharovGon05]. It follows from his work that the sequence
is exact, where the first map (identifying ![]() $\mathsf {S}$ with
$\mathsf {S}$ with ![]() $\ker (\Lambda ^2 \mathbb {D}_1 \rightarrow \mathbb {D}_2)$) is given by
$\ker (\Lambda ^2 \mathbb {D}_1 \rightarrow \mathbb {D}_2)$) is given by
and the second map in the sequence immediately above is ![]() $[a,b]\otimes c \mapsto [c, [a,b]]$. Starting from depth
$[a,b]\otimes c \mapsto [c, [a,b]]$. Starting from depth ![]() $4$, the structure of
$4$, the structure of ![]() $\mathfrak {ls} _d\cong \mathbb {D}_d$ is not known.Footnote 6 In particular, it is easy to show that the map given by the quadruple Ihara bracket
$\mathfrak {ls} _d\cong \mathbb {D}_d$ is not known.Footnote 6 In particular, it is easy to show that the map given by the quadruple Ihara bracket
is not surjective, since in weight ![]() $12$,
$12$, ![]() $\dim \mathbb {D}_4= 1$, but
$\dim \mathbb {D}_4= 1$, but ![]() $\mathrm {Lie}_4 (\mathbb {D}_1) = 0$. Our next purpose is to construct the missing elements in depth 4.
$\mathrm {Lie}_4 (\mathbb {D}_1) = 0$. Our next purpose is to construct the missing elements in depth 4.
Remark 7.3 A different way to think about the sequence (7.10) is via the curious equality ![]() $\dim \mathsf {S} \otimes _{\mathbb {Q}} \mathbb {D}_1 = \dim \Lambda ^3(\mathbb {D}_1)$ which follows from (7.4). I do not know if there is an appropriate combinatorial or modular interpretation of this identity which could be relevant to the previous exact sequence.
$\dim \mathsf {S} \otimes _{\mathbb {Q}} \mathbb {D}_1 = \dim \Lambda ^3(\mathbb {D}_1)$ which follows from (7.4). I do not know if there is an appropriate combinatorial or modular interpretation of this identity which could be relevant to the previous exact sequence.
8. Exceptional modular elements in depth 4
8.1 Linearized equations in depth 4
For the convenience of the reader, we write out the linearized double shuffle relations in full in depth 4. There are four equations. In order to write them down we shall use the following notation, where ![]() $f \in \mathbb {Q}[x_1,\ldots , x_4]$, and we are given any set of indices
$f \in \mathbb {Q}[x_1,\ldots , x_4]$, and we are given any set of indices ![]() $\{i,j,k,l\} = \{1,2,3,4\}$:
$\{i,j,k,l\} = \{1,2,3,4\}$:
 \begin{align} \begin{gathered} f(ijkl) = f(x_i,x_j,x_k,x_l), \\ f^{\sharp}(ijkl) = f(x_i,x_i+x_j,x_i+x_j+x_k,x_i+x_j+x_k+x_l) . \end{gathered} \end{align}
\begin{align} \begin{gathered} f(ijkl) = f(x_i,x_j,x_k,x_l), \\ f^{\sharp}(ijkl) = f(x_i,x_i+x_j,x_i+x_j+x_k,x_i+x_j+x_k+x_l) . \end{gathered} \end{align}
Then ![]() $\mathbb {D}_4$ (see [Reference Ihara, Kaneko and ZagierIKZ06, § 8]) is the subspace of polynomials
$\mathbb {D}_4$ (see [Reference Ihara, Kaneko and ZagierIKZ06, § 8]) is the subspace of polynomials ![]() $f\in \mathbb {Q}[x_1,\ldots , x_4]$ satisfying
$f\in \mathbb {Q}[x_1,\ldots , x_4]$ satisfying
where ![]() $f$ and
$f$ and ![]() $f^{\sharp }$ are extended by linearity in the obvious way, and
$f^{\sharp }$ are extended by linearity in the obvious way, and
For example, the first equation of (8.2) is simply
We construct some exceptional solutions to these equations from period polynomials.
8.2 Definition of the exceptional elements
Let ![]() $f(x,y) \in \mathsf {S} _{2n+2}$ be an even-period polynomial of degree
$f(x,y) \in \mathsf {S} _{2n+2}$ be an even-period polynomial of degree ![]() $2n$ which vanishes at
$2n$ which vanishes at ![]() $y=0$. It follows from (7.1) and (7.2) that it vanishes along
$y=0$. It follows from (7.1) and (7.2) that it vanishes along ![]() $x=0$ and
$x=0$ and ![]() $x-y=0$. Therefore we can write
$x-y=0$. Therefore we can write
where ![]() $f_0(x,y)\in \mathbb {Q}[x,y]$ is symmetric and homogeneous of degree
$f_0(x,y)\in \mathbb {Q}[x,y]$ is symmetric and homogeneous of degree ![]() $2n-3$, and satisfies
$2n-3$, and satisfies
Let us also write ![]() $f_1(x,y)= (x-y) f_0(x,y)$. We have
$f_1(x,y)= (x-y) f_0(x,y)$. We have ![]() $f_1(-x,y)=f_1(x,-y)=-f_1(x,y)$.
$f_1(-x,y)=f_1(x,-y)=-f_1(x,y)$.
Definition 8.1 Let ![]() $f\in \mathbb {Q}[x,y]$ be an even-period polynomial as above. Define
$f\in \mathbb {Q}[x,y]$ be an even-period polynomial as above. Define
 \begin{align} \begin{gathered} \mathsf{e}_f \in \mathbb{Q}[y_0,y_1,y_2,y_3,y_4], \\ \mathsf{e}_f = \sum_{\mathbb{Z}/ 5 \mathbb{Z} } \big( f_1(y_4-y_3,y_2-y_1) + (y_0-y_1) f_0 (y_2-y_3,y_4-y_3) \big) , \end{gathered} \end{align}
\begin{align} \begin{gathered} \mathsf{e}_f \in \mathbb{Q}[y_0,y_1,y_2,y_3,y_4], \\ \mathsf{e}_f = \sum_{\mathbb{Z}/ 5 \mathbb{Z} } \big( f_1(y_4-y_3,y_2-y_1) + (y_0-y_1) f_0 (y_2-y_3,y_4-y_3) \big) , \end{gathered} \end{align}
where the sum is over cyclic permutations ![]() $(y_0,y_1,y_2,y_3, y_4 ) \mapsto (y_1,y_2,y_3, y_4, y_0)$. Its reduction
$(y_0,y_1,y_2,y_3, y_4 ) \mapsto (y_1,y_2,y_3, y_4, y_0)$. Its reduction ![]() $\bar {\mathsf {e}}_f\in \mathbb {Q}[x_1,\ldots , x_4]$ is obtained by setting
$\bar {\mathsf {e}}_f\in \mathbb {Q}[x_1,\ldots , x_4]$ is obtained by setting ![]() $y_0=0, y_i =x_i$, for
$y_0=0, y_i =x_i$, for ![]() $i=1,\ldots , 4$.
$i=1,\ldots , 4$.
Remark 8.2 The full expression for ![]() $\bar {e}_f$ is explicitly
$\bar {e}_f$ is explicitly
 \begin{align} \bar{e}_f(x_1,x_2,x_3,x_4) &= f_1(x_4-x_3,x_2-x_1) + f_1({-}x_4,x_3-x_2) + f_1(x_1,x_4-x_3) \nonumber\\ &\quad + f_1(x_2-x_1,-x_4) +f_1(x_3-x_2,x_1) -x_1 f_0 (x_2-x_3,x_4-x_3) \nonumber\\ &\quad+ (x_1-x_2) f_0 (x_3-x_4,-x_4) + (x_2-x_3) f_0 (x_4, x_1) \nonumber\\ &\quad + (x_3-x_4) f_0 ({-}x_1, x_2-x_1)+ x_4 f_0 (x_1-x_2, x_3-x_2) . \end{align}
\begin{align} \bar{e}_f(x_1,x_2,x_3,x_4) &= f_1(x_4-x_3,x_2-x_1) + f_1({-}x_4,x_3-x_2) + f_1(x_1,x_4-x_3) \nonumber\\ &\quad + f_1(x_2-x_1,-x_4) +f_1(x_3-x_2,x_1) -x_1 f_0 (x_2-x_3,x_4-x_3) \nonumber\\ &\quad+ (x_1-x_2) f_0 (x_3-x_4,-x_4) + (x_2-x_3) f_0 (x_4, x_1) \nonumber\\ &\quad + (x_3-x_4) f_0 ({-}x_1, x_2-x_1)+ x_4 f_0 (x_1-x_2, x_3-x_2) . \end{align}
Since ![]() $f$ is even it vanishes to order
$f$ is even it vanishes to order ![]() $2$ along
$2$ along ![]() $x=0,y=0,x=y$. Therefore
$x=0,y=0,x=y$. Therefore
and the same holds a fortiori for ![]() $f_1$. If we set
$f_1$. If we set ![]() $x_3=x_4=0$ in equation (8.6) then all terms except for the fifth vanish and we are left with
$x_3=x_4=0$ in equation (8.6) then all terms except for the fifth vanish and we are left with
In this way, the period polynomial ![]() $f$ can be retrieved from
$f$ can be retrieved from ![]() $\bar {\mathsf {e}}_f$: it is
$\bar {\mathsf {e}}_f$: it is ![]() $xy\bar {\mathsf {e}}_f(x,y,0,0)$. This computation is related to the discussion in [Reference Blümlein, Broadhurst and VermaserenBBV10, § 9.2], regarding multiple zeta values of depth 4 of the form
$xy\bar {\mathsf {e}}_f(x,y,0,0)$. This computation is related to the discussion in [Reference Blümlein, Broadhurst and VermaserenBBV10, § 9.2], regarding multiple zeta values of depth 4 of the form ![]() $\zeta (1,1,m, n)$.
$\zeta (1,1,m, n)$.
8.3 Exceptional elements and linearized double shuffle equations
Theorem 8.3 The reduced polynomial ![]() $\bar {\mathsf {e}}_f$ obtained from (8.5) satisfies the linearized double shuffle relations. In particular, we have an injective linear map
$\bar {\mathsf {e}}_f$ obtained from (8.5) satisfies the linearized double shuffle relations. In particular, we have an injective linear map
Proof. The injectivity follows immediately from (8.7). The proof that the linearized double shuffle relations hold is a finite computation. In the absence of a purely conceptual proof, we shall break the calculation into more easily verifiable pieces.
We first consider the stuffle equations. It follows from general properties of the Dynkin operator on shuffle algebras that a homogeneous polynomial in four variables satisfies the two linearized stuffle equations (8.2) if and only if it is in the image of the map ![]() $\lambda :\mathbb {Q}[x_1,\ldots , x_4] \rightarrow \mathbb {Q}[x_1,\ldots , x_4]$, with eight terms defined by
$\lambda :\mathbb {Q}[x_1,\ldots , x_4] \rightarrow \mathbb {Q}[x_1,\ldots , x_4]$, with eight terms defined by
where ![]() $\alpha ( f)(x_1,\ldots , x_4)$ is the linear combination
$\alpha ( f)(x_1,\ldots , x_4)$ is the linear combination
For a detailed discussion and proofs, we refer to [Reference BrownBro17b, § 16.4 and Corollary 16.6]. The linearized stuffle relations (8.2) hold for the sum of the first five terms in ![]() $f_1$, and for the sum of the second five terms in
$f_1$, and for the sum of the second five terms in ![]() $f_0$ in (8.6) separately. Consider first the terms in
$f_0$ in (8.6) separately. Consider first the terms in ![]() $f_1$. They consist of two parts:
$f_1$. They consist of two parts:
and
One easily checks that ![]() $\lambda (T_1) = 4 \, T_1$, and that
$\lambda (T_1) = 4 \, T_1$, and that ![]() $\lambda (f_1(x_1,x_2-x_3))$ equals
$\lambda (f_1(x_1,x_2-x_3))$ equals
using only the fact that ![]() $f_1$ is antisymmetric and odd in
$f_1$ is antisymmetric and odd in ![]() $x$ and
$x$ and ![]() $y$. Thus
$y$. Thus ![]() $T_1, T_2$ lie in the image of
$T_1, T_2$ lie in the image of ![]() $\lambda$ and are solutions to the linearized stuffle equations.
$\lambda$ and are solutions to the linearized stuffle equations.
Now consider the terms in ![]() $f_0$ in (8.6). Once again, they break into two parts:
$f_0$ in (8.6). Once again, they break into two parts:
and
One checks that ![]() $\lambda (T_k ) = 4 \, T_k$ for
$\lambda (T_k ) = 4 \, T_k$ for ![]() $k=3,4$ using the three-term relation (8.4), and hence
$k=3,4$ using the three-term relation (8.4), and hence ![]() $T_3,T_4$ are solutions to the linearized stuffle equations. This is the only point in the proof where the three-term relation is needed.
$T_3,T_4$ are solutions to the linearized stuffle equations. This is the only point in the proof where the three-term relation is needed.
For the linearized shuffle relations, note that there exists ![]() $g \in \mathbb {Q}[x,y]$ such that
$g \in \mathbb {Q}[x,y]$ such that ![]() $f_0(x,y) = (x+y) g(x,y)$ and
$f_0(x,y) = (x+y) g(x,y)$ and ![]() $f_1 = (x^2-y^2) g(x,y)$ since an even-period polynomial
$f_1 = (x^2-y^2) g(x,y)$ since an even-period polynomial ![]() $f(x,y)$ vanishes along
$f(x,y)$ vanishes along ![]() $x=y$ and is even in both
$x=y$ and is even in both ![]() $x$ and
$x$ and ![]() $y$. The polynomial
$y$. The polynomial ![]() $g(x,y)$ is symmetric and odd in
$g(x,y)$ is symmetric and odd in ![]() $x$ and in
$x$ and in ![]() $y$ (i.e.
$y$ (i.e. ![]() $g(x,y)=g(y,x)$ and
$g(x,y)=g(y,x)$ and ![]() $g(-x,y)=g(x,-y)=-g(x,y)$). These properties suffice to prove that (8.6) satisfies the shuffle equations. The full expression again splits into two pieces with four and six terms, respectively:
$g(-x,y)=g(x,-y)=-g(x,y)$). These properties suffice to prove that (8.6) satisfies the shuffle equations. The full expression again splits into two pieces with four and six terms, respectively:
 \begin{align*} T_5&= (x_4^2-x_{23}^2) g(x_4, x_{23})+x_{23}(x_1+x_4)g(x_1, x_4) + x_{12}(x_{34}-x_4)g(x_{34}, -x_4)\\ &\quad +(x_{12}^2-x_4^2)g(x_{12}, x_4), \end{align*}
\begin{align*} T_5&= (x_4^2-x_{23}^2) g(x_4, x_{23})+x_{23}(x_1+x_4)g(x_1, x_4) + x_{12}(x_{34}-x_4)g(x_{34}, -x_4)\\ &\quad +(x_{12}^2-x_4^2)g(x_{12}, x_4), \end{align*}
where we use the notation ![]() $x_{ij} = x_i-x_j$, and
$x_{ij} = x_i-x_j$, and
 \begin{align*} T_6&= x_{34}(x_{21}-x_1)g(x_1, x_{12})+x_4(x_{32}+x_{12})g(x_{12}, x_{32})+(x_{32}^2-x_1^2)g(x_{32}, x_1) \\ &\quad +(x_1^2-x_{43}^2)g(x_1, x_{43}) + x_1(x_{34}+x_{32})g(x_{32}, x_{34})+(x_{43}^2-x_{21}^2)g(x_{43}, x_{21}). \end{align*}
\begin{align*} T_6&= x_{34}(x_{21}-x_1)g(x_1, x_{12})+x_4(x_{32}+x_{12})g(x_{12}, x_{32})+(x_{32}^2-x_1^2)g(x_{32}, x_1) \\ &\quad +(x_1^2-x_{43}^2)g(x_1, x_{43}) + x_1(x_{34}+x_{32})g(x_{32}, x_{34})+(x_{43}^2-x_{21}^2)g(x_{43}, x_{21}). \end{align*}
Both ![]() $T_5$ and
$T_5$ and ![]() $T_6$ can laboriously be verified to satisfy the two shuffle equations in depth 4. The statement follows since
$T_6$ can laboriously be verified to satisfy the two shuffle equations in depth 4. The statement follows since ![]() $\mathsf {e}_f$ equals
$\mathsf {e}_f$ equals ![]() $T_1+T_2+T_3+T_4 = T_5+T_6$.
$T_1+T_2+T_3+T_4 = T_5+T_6$.
Identifying ![]() $\mathfrak {ls} _4$ with
$\mathfrak {ls} _4$ with ![]() $\mathbb {D}_4$ via the map
$\mathbb {D}_4$ via the map ![]() $\bar {\rho }$, we can view
$\bar {\rho }$, we can view ![]() $\mathsf {e}$ as a map from
$\mathsf {e}$ as a map from ![]() $\mathsf {S}$ to
$\mathsf {S}$ to ![]() $\mathfrak {ls} _4$. Note that relation (7.2) is proved for the periods of modular forms by integrating round contours very similar to those which prove the symmetry and hexagonal relations for associators. It would be very interesting to see if there is any connection between the five-fold symmetry of the element
$\mathfrak {ls} _4$. Note that relation (7.2) is proved for the periods of modular forms by integrating round contours very similar to those which prove the symmetry and hexagonal relations for associators. It would be very interesting to see if there is any connection between the five-fold symmetry of the element ![]() $\mathsf {e}_f$ and the pentagon equation.
$\mathsf {e}_f$ and the pentagon equation.
Example 8.4 It follows from (7.4) that the space of period polynomials in degrees ![]() $12, 16, 18$ and
$12, 16, 18$ and ![]() $20$ is of dimension
$20$ is of dimension ![]() $1$. Choose integral generators:
$1$. Choose integral generators:
 \begin{align*} f_{12} &= [x_{{1}}^{8} , x_{{2}}^{2}]-3\,[x_{{1}}^{6},x_{{2}}^{4}], \\ f_{16} &= 2\,[x_{{1}}^{12},x_{{2}}^{2}]-7\,[x_{{1}}^{10},x_{{2}}^{4}]+11\,[x_{ {1}}^{8},x_{{2}}^{6}], \\ f_{18} &= 8\, [x_{{1}}^{14},x_{{2}}^{2}]-25\,[x_{{1}}^{12},x_{{2}}^{4}]+26\,[x_ {{1}}^{10},x_{{2}}^{6}], \\ f_{20} &= 3\,[x_{{1}}^{16},x_{{2}}^{2}]-10\,[x_{{1}}^{14},x_{{2}}^{4}]+14\,[x_ {{1}}^{12},x_{{2}}^{6}]-13\,[x_{{1}}^{10},x_{{2}}^{8}], \end{align*}
\begin{align*} f_{12} &= [x_{{1}}^{8} , x_{{2}}^{2}]-3\,[x_{{1}}^{6},x_{{2}}^{4}], \\ f_{16} &= 2\,[x_{{1}}^{12},x_{{2}}^{2}]-7\,[x_{{1}}^{10},x_{{2}}^{4}]+11\,[x_{ {1}}^{8},x_{{2}}^{6}], \\ f_{18} &= 8\, [x_{{1}}^{14},x_{{2}}^{2}]-25\,[x_{{1}}^{12},x_{{2}}^{4}]+26\,[x_ {{1}}^{10},x_{{2}}^{6}], \\ f_{20} &= 3\,[x_{{1}}^{16},x_{{2}}^{2}]-10\,[x_{{1}}^{14},x_{{2}}^{4}]+14\,[x_ {{1}}^{12},x_{{2}}^{6}]-13\,[x_{{1}}^{10},x_{{2}}^{8}], \end{align*}
where ![]() $[x_1^a,x_2^b]$ denotes
$[x_1^a,x_2^b]$ denotes ![]() $x_1^ax_2^b-x_1^bx_2^a$. Let
$x_1^ax_2^b-x_1^bx_2^a$. Let ![]() $\mathsf {e}_{12},\ldots , \mathsf {e}_{20}$ denote the corresponding exceptional elements. We know by Theorem 1.1 that
$\mathsf {e}_{12},\ldots , \mathsf {e}_{20}$ denote the corresponding exceptional elements. We know by Theorem 1.1 that ![]() $\mathfrak {g}^{\mathfrak {m}}$ is of dimension
$\mathfrak {g}^{\mathfrak {m}}$ is of dimension ![]() $2$ in weight
$2$ in weight ![]() $12$, spanned by
$12$, spanned by ![]() $\{ \sigma _3, \sigma _9\}$ and
$\{ \sigma _3, \sigma _9\}$ and ![]() $\{\sigma _5, \sigma _7\}$. We know by (7.9) that in weight 12,
$\{\sigma _5, \sigma _7\}$. We know by (7.9) that in weight 12, ![]() $\mathfrak {dg}^{\mathfrak {m}}_2$ is of dimension 1,
$\mathfrak {dg}^{\mathfrak {m}}_2$ is of dimension 1, ![]() $\mathfrak {dg}^{\mathfrak {m}}_3$ vanishes by parity, so it follows that
$\mathfrak {dg}^{\mathfrak {m}}_3$ vanishes by parity, so it follows that ![]() $\mathfrak {dg}^{\mathfrak {m}}_4$ is of dimension 1 and hence spanned by
$\mathfrak {dg}^{\mathfrak {m}}_4$ is of dimension 1 and hence spanned by ![]() $\bar {\mathsf {e}}_{12}$ (since we know that
$\bar {\mathsf {e}}_{12}$ (since we know that ![]() $\mathfrak {ls} _4$ in weight 12 is one-dimensional). Writing out just a few of its coefficients as an example, we have:
$\mathfrak {ls} _4$ in weight 12 is one-dimensional). Writing out just a few of its coefficients as an example, we have:
Using ![]() $\bar {\mathsf {e}}_{12}$, one can write all depth-graded motivic multiple zeta values of depth 4 and weight 12 as multiples of
$\bar {\mathsf {e}}_{12}$, one can write all depth-graded motivic multiple zeta values of depth 4 and weight 12 as multiples of ![]() $\zeta _{\mathfrak {D}}(1,1,8,2)$. For example, one has
$\zeta _{\mathfrak {D}}(1,1,8,2)$. For example, one has
modulo products and modulo multiple zeta values of depth ![]() $\leq 2$.
$\leq 2$.
8.4 Are the exceptional elements motivic?
We say that an exceptional element ![]() $\mathsf {e}_f$ is motivic if it lies in the depth-graded motivic Lie algebra:
$\mathsf {e}_f$ is motivic if it lies in the depth-graded motivic Lie algebra:
Conjecture 3 The exceptional elements ![]() $\mathsf {e}_f$ are all motivic.
$\mathsf {e}_f$ are all motivic.
Since ![]() $\mathfrak {dg}^{\mathfrak {m}}_k= \mathfrak {ls} _k$ for
$\mathfrak {dg}^{\mathfrak {m}}_k= \mathfrak {ls} _k$ for ![]() $k =1,2,3$, to prove that an exceptional element
$k =1,2,3$, to prove that an exceptional element ![]() $\mathsf {e}_f$ is motivic it is enough to show that, modulo commutators, it lies in the image of the map
$\mathsf {e}_f$ is motivic it is enough to show that, modulo commutators, it lies in the image of the map
where ![]() $\mathsf {S} \subset \Lambda ^2 \mathfrak {dg}^{\mathfrak {m}}_1$ is the space of relations in depth
$\mathsf {S} \subset \Lambda ^2 \mathfrak {dg}^{\mathfrak {m}}_1$ is the space of relations in depth ![]() $2$, and
$2$, and ![]() $d$ is the first non-trivial differential in the spectral sequence on
$d$ is the first non-trivial differential in the spectral sequence on ![]() $\mathfrak {g}^{\mathfrak {m}}$ associated to the depth filtration (§ 4.5).
$\mathfrak {g}^{\mathfrak {m}}$ associated to the depth filtration (§ 4.5).
The map ![]() $d$ can be computed explicitly as follows. Choose a lift
$d$ can be computed explicitly as follows. Choose a lift ![]() $\sigma _{2n+1} \in \mathfrak {g}^{\mathfrak {m}}$ of every generator
$\sigma _{2n+1} \in \mathfrak {g}^{\mathfrak {m}}$ of every generator ![]() $\bar {\sigma }_{2n+1} \in \mathfrak {dg}^{\mathfrak {m}}_1$, and decompose it according to the
$\bar {\sigma }_{2n+1} \in \mathfrak {dg}^{\mathfrak {m}}_1$, and decompose it according to the ![]() $\mathfrak {D}$-degree:
$\mathfrak {D}$-degree:
where ![]() $\sigma ^{(i)}_{2n+1}$ is of
$\sigma ^{(i)}_{2n+1}$ is of ![]() $\mathfrak {D}$-degree
$\mathfrak {D}$-degree ![]() $i$, and
$i$, and ![]() $\sigma ^{(1)}_{2n+1} =\bar {\sigma }_{2n+1}$. Then, for any element
$\sigma ^{(1)}_{2n+1} =\bar {\sigma }_{2n+1}$. Then, for any element
with ![]() $\lambda _{i,j} \in \mathbb {Q}$, we have
$\lambda _{i,j} \in \mathbb {Q}$, we have
where ![]() $\{.\,{,}\,. \}: {\bigwedge} ^2 \mathfrak {g}^{\mathfrak {m}} \rightarrow \mathfrak {g}^{\mathfrak {m}}$ can be computed on the level of polynomial representations by exactly the same formula as the one given in § 6.
$\{.\,{,}\,. \}: {\bigwedge} ^2 \mathfrak {g}^{\mathfrak {m}} \rightarrow \mathfrak {g}^{\mathfrak {m}}$ can be computed on the level of polynomial representations by exactly the same formula as the one given in § 6.
Examples 8.5 The elements ![]() $\sigma _3, \sigma _5, \sigma _7, \sigma _9$ defined by the coefficients of
$\sigma _3, \sigma _5, \sigma _7, \sigma _9$ defined by the coefficients of ![]() $\zeta (3),\zeta (5),\zeta (7)$, and
$\zeta (3),\zeta (5),\zeta (7)$, and ![]() $\zeta (9)$ in weights
$\zeta (9)$ in weights ![]() $3$,
$3$, ![]() $5$,
$5$, ![]() $7$,
$7$, ![]() $9$ in Drinfeld's associator are canonical, and we have
$9$ in Drinfeld's associator are canonical, and we have
which proves that the element ![]() $\mathsf {e}_{12}$ is motivic. Using the depth-parity proposition (Proposition 6.4), one can show that the corresponding congruence
$\mathsf {e}_{12}$ is motivic. Using the depth-parity proposition (Proposition 6.4), one can show that the corresponding congruence
propagates to depth 5 also. Compare with the ‘key example’ of [Reference IharaIha02, p. 258] and the ensuing discussion. Thereafter, one checks that
 \begin{align*} d \big(2 \, \sigma_3\wedge \sigma_{13} -7 \, \sigma_5 \wedge \sigma_{11} + 11 \, \sigma_7\wedge \sigma_{9} \big) &\equiv \tfrac{3617 } {720} \mathsf{e}_{16} \pmod{ \mathfrak{a}}, \\ d \big(8 \, \sigma_3 \wedge \sigma_{15} -25 \, \sigma_5 \wedge \sigma_{13} + 26 \, \sigma_7 \wedge \sigma_{11} \big) &\equiv \tfrac{43867 }{9000} \mathsf{e}_{18} \pmod{ \mathfrak{a}}, \\ d \big(3 \, \sigma_3 \wedge \sigma_{17} -10 \, \sigma_5 \wedge \sigma_{13} + 14 \, \sigma_7 \wedge \sigma_{13} -13 \, f_9 \wedge f_{11} \big) &\equiv \tfrac{174611 }{35280} \mathsf{e}_{20} \pmod{ \mathfrak{a}}, \end{align*}
\begin{align*} d \big(2 \, \sigma_3\wedge \sigma_{13} -7 \, \sigma_5 \wedge \sigma_{11} + 11 \, \sigma_7\wedge \sigma_{9} \big) &\equiv \tfrac{3617 } {720} \mathsf{e}_{16} \pmod{ \mathfrak{a}}, \\ d \big(8 \, \sigma_3 \wedge \sigma_{15} -25 \, \sigma_5 \wedge \sigma_{13} + 26 \, \sigma_7 \wedge \sigma_{11} \big) &\equiv \tfrac{43867 }{9000} \mathsf{e}_{18} \pmod{ \mathfrak{a}}, \\ d \big(3 \, \sigma_3 \wedge \sigma_{17} -10 \, \sigma_5 \wedge \sigma_{13} + 14 \, \sigma_7 \wedge \sigma_{13} -13 \, f_9 \wedge f_{11} \big) &\equiv \tfrac{174611 }{35280} \mathsf{e}_{20} \pmod{ \mathfrak{a}}, \end{align*}
where ![]() $\mathfrak {a} = \{\mathfrak {g}^{\mathfrak {m}} ,\mathfrak {g}^{\mathfrak {m}} \} + \mathfrak {D}^5 \mathfrak {g}^{\mathfrak {m}}$, that is, the previous identities hold modulo commutators and modulo terms of depth 5 or more. In this manner, I have checked that the elements
$\mathfrak {a} = \{\mathfrak {g}^{\mathfrak {m}} ,\mathfrak {g}^{\mathfrak {m}} \} + \mathfrak {D}^5 \mathfrak {g}^{\mathfrak {m}}$, that is, the previous identities hold modulo commutators and modulo terms of depth 5 or more. In this manner, I have checked that the elements ![]() $\mathsf {e}_f$ are motivic for all
$\mathsf {e}_f$ are motivic for all ![]() $f$ up to weight
$f$ up to weight ![]() $30$. In particular, it seems that the differential
$30$. In particular, it seems that the differential ![]() $d$ is related to our map
$d$ is related to our map ![]() $\mathsf {e}$ (which is defined over
$\mathsf {e}$ (which is defined over ![]() $\mathbb {Z}$) up to a non-trivial isomorphism of the space of period polynomials. The numerators on the right-hand side are the numerators of
$\mathbb {Z}$) up to a non-trivial isomorphism of the space of period polynomials. The numerators on the right-hand side are the numerators of ![]() $\zeta (16)\pi ^{-16}, \zeta (18)\pi ^{-18}$, and
$\zeta (16)\pi ^{-16}, \zeta (18)\pi ^{-18}$, and ![]() $\zeta (20)\pi ^{-20}$. Unfortunately, it does not seem possible to construct canonical zeta elements
$\zeta (20)\pi ^{-20}$. Unfortunately, it does not seem possible to construct canonical zeta elements ![]() $\sigma _{2n+1}$ for
$\sigma _{2n+1}$ for ![]() $n\geq 5$ in a consistent way such that the above relations hold exactly in
$n\geq 5$ in a consistent way such that the above relations hold exactly in ![]() $\mathfrak {g}^{\mathfrak {m}} _4$ (and not modulo
$\mathfrak {g}^{\mathfrak {m}} _4$ (and not modulo ![]() $\mathfrak {a}$).
$\mathfrak {a}$).
Using the theory of the unipotent fundamental group of the Tate elliptic curve, we showed in [Reference BrownBro17a] how to construct canonical elements ![]() $\sigma ^{(3)}_{2i+1}$ modulo depths
$\sigma ^{(3)}_{2i+1}$ modulo depths ![]() $\geq 5$, which enables one to write down the differential
$\geq 5$, which enables one to write down the differential ![]() $d$ explicitly. The only remaining difficulty in proving that the elements
$d$ explicitly. The only remaining difficulty in proving that the elements ![]() $\mathsf {e}_f$ are motivic is therefore to understand better the quotient
$\mathsf {e}_f$ are motivic is therefore to understand better the quotient ![]() $\mathfrak {ls} / \{ \mathfrak {ls} , \mathfrak {ls} \}$ in depth
$\mathfrak {ls} / \{ \mathfrak {ls} , \mathfrak {ls} \}$ in depth ![]() $4$. Yasuda has since shown, assuming that the
$4$. Yasuda has since shown, assuming that the ![]() $\mathsf {e}_f$ are motivic, how to relate the exceptional elements to the differential
$\mathsf {e}_f$ are motivic, how to relate the exceptional elements to the differential ![]() $d$ using the action of Hecke operators on the space of period polynomials.
$d$ using the action of Hecke operators on the space of period polynomials.
If the elements ![]() $\mathsf {e}_f$ can be shown to be motivic, then they provide in particular an answer to the question raised by Ihara [Reference IharaIha02, end of § 4, p. 259]. The appearance of the numerators of Bernoulli numbers is related to [Reference IharaIha02, Conjecture 2], and the Ihara–Takao relations [Reference Ihara and TakaoIT93], and has been studied from the Galois-theoretic perspective by Sharifi [Reference SharifiSha02] and McCallum and Sharifi [Reference McCallum and SharifiMS03].
$\mathsf {e}_f$ can be shown to be motivic, then they provide in particular an answer to the question raised by Ihara [Reference IharaIha02, end of § 4, p. 259]. The appearance of the numerators of Bernoulli numbers is related to [Reference IharaIha02, Conjecture 2], and the Ihara–Takao relations [Reference Ihara and TakaoIT93], and has been studied from the Galois-theoretic perspective by Sharifi [Reference SharifiSha02] and McCallum and Sharifi [Reference McCallum and SharifiMS03].
9. Some properties of the elements  $\mathsf {e}_f$
$\mathsf {e}_f$
The exceptional elements ![]() $\mathsf {e}_f$ satisfy many remarkable properties, only some of which will be outlined here. Of particular relevance are those properties which are motivic, that is, stable under the Ihara bracket.
$\mathsf {e}_f$ satisfy many remarkable properties, only some of which will be outlined here. Of particular relevance are those properties which are motivic, that is, stable under the Ihara bracket.
9.1 Unevenness
For any polynomial ![]() $f\in \mathbb {Q}[x_1,\ldots , x_r]$, let
$f\in \mathbb {Q}[x_1,\ldots , x_r]$, let
and denote the projection onto the even part in ![]() $x_i$ by
$x_i$ by
We can also write ![]() $\pi ^{\mathrm {ev}}_{x_i} f = \frac {1}{2} \big ( f(x_1,\ldots , x_i, \ldots , x_r) + f(x_1,\ldots , -x_i, \ldots , x_r) \big )$.
$\pi ^{\mathrm {ev}}_{x_i} f = \frac {1}{2} \big ( f(x_1,\ldots , x_i, \ldots , x_r) + f(x_1,\ldots , -x_i, \ldots , x_r) \big )$.
Lemma 9.1 The elements ![]() $\mathsf {e}_f(y_0, y_1, y_2, y_3, y_4)$ are uneven:
$\mathsf {e}_f(y_0, y_1, y_2, y_3, y_4)$ are uneven:
Proof. The term of the form ![]() $(y_0-y_1) f_0 (y_2-y_3,y_4-y_3)$ in definition (8.1) is obviously uneven since it is linear in
$(y_0-y_1) f_0 (y_2-y_3,y_4-y_3)$ in definition (8.1) is obviously uneven since it is linear in ![]() $y_0,y_1$. The term
$y_0,y_1$. The term ![]() $f_1(y_4-y_3, y_2-y_1)$ is likewise uneven because
$f_1(y_4-y_3, y_2-y_1)$ is likewise uneven because ![]() $f_1(x,y)$ is odd in
$f_1(x,y)$ is odd in ![]() $x$ and
$x$ and ![]() $y$. The fact that
$y$. The fact that ![]() $\mathsf {e}_f$ is uneven follows by cyclic symmetry.
$\mathsf {e}_f$ is uneven follows by cyclic symmetry.
We shall see later in § 11.1 that the property of being uneven is motivic, that is, stable under the Ihara bracket, and is related to the totally odd zeta values. We conjecture that a solution to the linearized double shuffle equations is uneven if and only if it is in the Lie ideal of ![]() $\mathfrak {ls}$ generated by exceptional elements.
$\mathfrak {ls}$ generated by exceptional elements.
9.2 Sparsity
Lemma 9.2 The elements ![]() $\mathsf {e}_f(y_0,y_1,y_2,y_3,y_4)$ are sparse:
$\mathsf {e}_f(y_0,y_1,y_2,y_3,y_4)$ are sparse:
In other words, ![]() $\mathsf {e}_f$ is a linear combination of monomials which only depend on four out of five of the variables
$\mathsf {e}_f$ is a linear combination of monomials which only depend on four out of five of the variables ![]() $y_0,\ldots , y_4$.
$y_0,\ldots , y_4$.
Proof. Immediate from the definition.
One can show that this property is also motivic, that is, forms an ideal under the Ihara bracket. Call an element ![]() $f\in \mathfrak {p}_r$ sparse if it is annihilated by
$f\in \mathfrak {p}_r$ sparse if it is annihilated by
Proposition 9.3 The sparse elements in ![]() $\bigoplus _{r} \mathfrak {p}_r$ form a Lie ideal.
$\bigoplus _{r} \mathfrak {p}_r$ form a Lie ideal.
Proof. Let ![]() $f \in \mathfrak {p}_r$ and
$f \in \mathfrak {p}_r$ and ![]() $g\in \mathfrak {p}_s$ where
$g\in \mathfrak {p}_s$ where ![]() $f$ is sparse. The Ihara bracket
$f$ is sparse. The Ihara bracket ![]() $\{f,g\}$ is given by (6.14) and consists of a cyclic sum over terms of the form
$\{f,g\}$ is given by (6.14) and consists of a cyclic sum over terms of the form
to which we apply the product of ![]() ${\partial }/{\partial y_i}$ for
${\partial }/{\partial y_i}$ for ![]() $0\leq i \leq r+s$. Using the chain rule with respect to
$0\leq i \leq r+s$. Using the chain rule with respect to ![]() ${\partial }/{\partial y_r}$ and
${\partial }/{\partial y_r}$ and ![]() ${\partial }/{\partial y_{r+s}}$ and invoking the sparsity of
${\partial }/{\partial y_{r+s}}$ and invoking the sparsity of ![]() $f$, we obtain
$f$, we obtain
 \begin{equation} \bigg(\prod_{i=0}^{r-1} \frac{\partial}{\partial y_i}\bigg) \big( f(y_0,\ldots, y_r) - f(y_{r+s}, y_0, \ldots, y_{r-1})\big) \times \bigg( \prod_{i=r}^{r+s} \frac{\partial}{\partial y_i} \bigg) g(y_r,\ldots, y_{r+s}) . \end{equation}
\begin{equation} \bigg(\prod_{i=0}^{r-1} \frac{\partial}{\partial y_i}\bigg) \big( f(y_0,\ldots, y_r) - f(y_{r+s}, y_0, \ldots, y_{r-1})\big) \times \bigg( \prod_{i=r}^{r+s} \frac{\partial}{\partial y_i} \bigg) g(y_r,\ldots, y_{r+s}) . \end{equation}
By cyclic symmetry of ![]() $f$, we have
$f$, we have
Using the sparsity of ![]() $f$ once more, we find that
$f$ once more, we find that
 \[ \bigg( \prod_{i=0}^{r-1} \frac{\partial}{\partial y_i}\bigg) f(y_0,\ldots, y_r) = \bigg( \prod_{i=0}^{r-1} \frac{\partial}{\partial y_i}\bigg) f( y_0, \ldots, y_{r-1},y_{r+s}) \]
\[ \bigg( \prod_{i=0}^{r-1} \frac{\partial}{\partial y_i}\bigg) f(y_0,\ldots, y_r) = \bigg( \prod_{i=0}^{r-1} \frac{\partial}{\partial y_i}\bigg) f( y_0, \ldots, y_{r-1},y_{r+s}) \]
since the left-hand side is a polynomial which is annihilated by ![]() ${\partial }/{\partial y_r}$, and hence does not depend on
${\partial }/{\partial y_r}$, and hence does not depend on ![]() $y_r$. In particular, it equals the right-hand side. It follows that the left-hand factor of (9.3) vanishes, which completes the proof.
$y_r$. In particular, it equals the right-hand side. It follows that the left-hand factor of (9.3) vanishes, which completes the proof.
In fact, there are other differential equations satisfied by the ![]() $\mathsf {e}_f$ and one can use these equations to define various filtrations on the Lie algebras
$\mathsf {e}_f$ and one can use these equations to define various filtrations on the Lie algebras ![]() $\mathfrak {p}$ and
$\mathfrak {p}$ and ![]() $\mathfrak {ls}$. It would be interesting to try to prove that the degree in the exceptional elements defines a grading on the Lie subalgebra of
$\mathfrak {ls}$. It would be interesting to try to prove that the degree in the exceptional elements defines a grading on the Lie subalgebra of ![]() $\bar {\mathfrak {p}}$ spanned by the
$\bar {\mathfrak {p}}$ spanned by the ![]() $x_1^{2n}$ and the
$x_1^{2n}$ and the ![]() $\bar {\mathsf {e}}_f$, as predicted by the conjectures below.
$\bar {\mathsf {e}}_f$, as predicted by the conjectures below.
Remark 9.4 The properties of unevenness and sparsity imply that almost all the coefficients of ![]() $\mathsf {e}_f$ are zero. This implies that the freeness of the motivic Lie algebra (Theorem 1.1) hangs by a thread (see, for example, (8.8)).
$\mathsf {e}_f$ are zero. This implies that the freeness of the motivic Lie algebra (Theorem 1.1) hangs by a thread (see, for example, (8.8)).
If we define the interior of a polynomial ![]() $p\in \mathbb {Q}[x_1,\ldots , x_r]$ to be
$p\in \mathbb {Q}[x_1,\ldots , x_r]$ to be ![]() $p^{o} = \pi ^{\geq 2}_1 \ldots \pi ^{\geq 2}_r p$, where
$p^{o} = \pi ^{\geq 2}_1 \ldots \pi ^{\geq 2}_r p$, where ![]() $\pi _i^{\geq 2}(f) = \sum _{k\geq 2} \pi ^k_{x_i}(f) \,x_i^k$, then in fact the majority of the non-trivial monomials in
$\pi _i^{\geq 2}(f) = \sum _{k\geq 2} \pi ^k_{x_i}(f) \,x_i^k$, then in fact the majority of the non-trivial monomials in ![]() $\bar {\mathsf {e}}_f$ are determined by a single term,
$\bar {\mathsf {e}}_f$ are determined by a single term,
which follows easily from the definition (8.6).
9.3 Other properties
We mention briefly some directions for further investigation. The proofs of the following facts are trivial yet sometimes lengthy applications of the definitions, basic properties of period polynomials, and the definition of ![]() $\{.\,{,}\,.\}$.
$\{.\,{,}\,.\}$.
Suppose that ![]() $f^{(1)}, \ldots , f^{(n)}$ are period polynomials, and let
$f^{(1)}, \ldots , f^{(n)}$ are period polynomials, and let ![]() $f^{(i)}_1$ be as defined in § 8.2. Then, generalizing (8.7), we have
$f^{(i)}_1$ be as defined in § 8.2. Then, generalizing (8.7), we have
 \begin{equation} \pi^0_{n+2}\pi^0_{n+3} \ldots\pi^0_{4n-1} \pi^0_{4n} \big(\bar{\mathsf{e}}_{f^{(1)}} \circ (\bar{\mathsf{e}}_{f^{(2)}} \circ \cdots (\bar{\mathsf{e}}_{f^{(n-1)}} \circ \bar{\mathsf{e}}_{f^{(n)}}) \cdots )\big) = \prod_{i=1}^n f_1^{(i)}(x_i,x_{i+1}). \end{equation}
\begin{equation} \pi^0_{n+2}\pi^0_{n+3} \ldots\pi^0_{4n-1} \pi^0_{4n} \big(\bar{\mathsf{e}}_{f^{(1)}} \circ (\bar{\mathsf{e}}_{f^{(2)}} \circ \cdots (\bar{\mathsf{e}}_{f^{(n-1)}} \circ \bar{\mathsf{e}}_{f^{(n)}}) \cdots )\big) = \prod_{i=1}^n f_1^{(i)}(x_i,x_{i+1}). \end{equation} Unfortunately, some information about the polynomials ![]() $f_i$ is lost in this equation, but one can do better by using the operators
$f_i$ is lost in this equation, but one can do better by using the operators ![]() $\pi _i^{\mathrm {ev}} = \pi _{x_i}^{\mathrm {ev}}$. For example, one checks that
$\pi _i^{\mathrm {ev}} = \pi _{x_i}^{\mathrm {ev}}$. For example, one checks that
factorizes. Applying the operator ![]() $\pi ^2_3$ to this equation gives
$\pi ^2_3$ to this equation gives
and causes the variables to separate. Next, one checks that
for some ![]() $\alpha \in \mathbb {Q}$, and it is easy to show that the right-hand side of the previous equation is non-zero and uniquely determines the period polynomial
$\alpha \in \mathbb {Q}$, and it is easy to show that the right-hand side of the previous equation is non-zero and uniquely determines the period polynomial ![]() $f$ (using the fact that the involutions
$f$ (using the fact that the involutions ![]() $(x_1,x_2)\mapsto (x_1,x_2-2x_1)$ and
$(x_1,x_2)\mapsto (x_1,x_2-2x_1)$ and ![]() $(x_1,x_2)\mapsto (-x_1,x_2)$ generate an infinite group). Putting these facts together shows the following result.
$(x_1,x_2)\mapsto (-x_1,x_2)$ generate an infinite group). Putting these facts together shows the following result.
Corollary 9.5 There are no non-trivial relations between commutators ![]() $\{\bar {\mathsf {e}}_f, \bar {\mathsf {e}}_g\}$.
$\{\bar {\mathsf {e}}_f, \bar {\mathsf {e}}_g\}$.
Since similar factorization properties to (9.6) hold in higher depths, one might hope to prove, in a similar manner, the conjecture that the Lie subalgebra of ![]() $\mathfrak {ls}$ generated by the exceptional elements
$\mathfrak {ls}$ generated by the exceptional elements ![]() $\mathsf {e}_f$ is free.
$\mathsf {e}_f$ is free.
10. Lie algebra structure and Broadhurst–Kreimer conjecture
10.1 Interpretation of the Broadhurst–Kreimer conjecture
In the light of the Broadhurst–Kreimer conjecture on the dimensions of the space of multiple zeta values graded by depth (1.2), and Zagier's conjecture which states that the regularized double shuffle relations generate all relations between multiple zeta values, it is natural to rephrase their conjectures, tentatively, in the Lie algebra setting as follows.
Conjecture 4 (Strong Broadhurst–Kreimer and Zagier conjecture)
 \begin{align} \begin{aligned} H_1(\mathfrak{ls} , \mathbb{Q}) &\cong \mathfrak{ls} _1 \oplus \mathsf{e}(\mathsf{S} ), \\ H_2(\mathfrak{ls} , \mathbb{Q}) &\cong \mathsf{S} , \\ H_i(\mathfrak{ls} , \mathbb{Q}) &= 0, \quad \hbox{for all } i \geq 3 . \end{aligned}\end{align}
\begin{align} \begin{aligned} H_1(\mathfrak{ls} , \mathbb{Q}) &\cong \mathfrak{ls} _1 \oplus \mathsf{e}(\mathsf{S} ), \\ H_2(\mathfrak{ls} , \mathbb{Q}) &\cong \mathsf{S} , \\ H_i(\mathfrak{ls} , \mathbb{Q}) &= 0, \quad \hbox{for all } i \geq 3 . \end{aligned}\end{align}This conjecture is the strongest possible conjecture that one could make: as we shall see below, it implies nearly all the remaining open problems concerning relations between (motivic) multiple zeta values. The numerical evidence for this conjecture is substantial [Reference Blümlein, Broadhurst and VermaserenBBV10], but not sufficient to remove all reasonable doubt. More conservatively, and without reference to the double shuffle relations, one could make a weaker reformulation of the Broadhurst–Kreimer conjecture.
Conjecture 5 (Motivic version of the Broadhurst–Kreimer conjecture)
The exceptional elements ![]() $\mathsf {e}_f$ are motivic (i.e.
$\mathsf {e}_f$ are motivic (i.e. ![]() $\mathsf {e}(\mathsf {S} ) \subset \mathfrak {dg}^{\mathfrak {m}}$), and
$\mathsf {e}(\mathsf {S} ) \subset \mathfrak {dg}^{\mathfrak {m}}$), and
 \begin{align} \begin{aligned} H_1(\mathfrak{dg}^{\mathfrak{m}}, \mathbb{Q}) &\cong \mathfrak{dg}^{\mathfrak{m}}_1 \oplus \mathsf{e}(\mathsf{S} ), \\ H_2(\mathfrak{dg}^{\mathfrak{m}}, \mathbb{Q}) &\cong \mathsf{S} ,\\ H_i(\mathfrak{dg}^{\mathfrak{m}}, \mathbb{Q}) &= 0, \quad \hbox{for all} \ i \geq 3 . \end{aligned} \end{align}
\begin{align} \begin{aligned} H_1(\mathfrak{dg}^{\mathfrak{m}}, \mathbb{Q}) &\cong \mathfrak{dg}^{\mathfrak{m}}_1 \oplus \mathsf{e}(\mathsf{S} ), \\ H_2(\mathfrak{dg}^{\mathfrak{m}}, \mathbb{Q}) &\cong \mathsf{S} ,\\ H_i(\mathfrak{dg}^{\mathfrak{m}}, \mathbb{Q}) &= 0, \quad \hbox{for all} \ i \geq 3 . \end{aligned} \end{align} Since the conjectural generators are totally explicit, it is possible to verify the independence of Lie brackets in the reduced polynomial representation ![]() $\bar {\rho }(\mathfrak {g}^{\mathfrak {m}} )$ simply by computing the coefficients of a small number of monomials. In this way, it should be possible to verify (10.2) to much higher weights and depths than is presently known. Note that the Broadhurst–Kreimer conjecture could fail if there existed non-trivial relations between commutators involving several exceptional elements
$\bar {\rho }(\mathfrak {g}^{\mathfrak {m}} )$ simply by computing the coefficients of a small number of monomials. In this way, it should be possible to verify (10.2) to much higher weights and depths than is presently known. Note that the Broadhurst–Kreimer conjecture could fail if there existed non-trivial relations between commutators involving several exceptional elements ![]() $\mathsf {e}_f$. These would necessarily have weight and depth far beyond the range of present computations.
$\mathsf {e}_f$. These would necessarily have weight and depth far beyond the range of present computations.
10.2 Enumeration of dimensions
Let ![]() $\mathfrak {h}$ be a Lie algebra over a field
$\mathfrak {h}$ be a Lie algebra over a field ![]() $k$, and let
$k$, and let ![]() $\mathcal {U} \mathfrak {h}$ be its universal enveloping algebra. The homology groups
$\mathcal {U} \mathfrak {h}$ be its universal enveloping algebra. The homology groups ![]() $H_i(\mathfrak {h};k)$ of
$H_i(\mathfrak {h};k)$ of ![]() $\mathfrak {h}$ are defined to be the homology of the following complex:
$\mathfrak {h}$ are defined to be the homology of the following complex:
Suppose that ![]() $\mathfrak {h}$ is bigraded, and finite-dimensional in each bigraded piece. Then
$\mathfrak {h}$ is bigraded, and finite-dimensional in each bigraded piece. Then ![]() $\Lambda ^i \mathfrak {h}, \mathcal {U} \mathfrak {h}, H_i(\mathfrak {h})$ inherit a bigrading. For any bigraded
$\Lambda ^i \mathfrak {h}, \mathcal {U} \mathfrak {h}, H_i(\mathfrak {h})$ inherit a bigrading. For any bigraded ![]() $k$-module
$k$-module ![]() $M_{\bullet ,\bullet }$, which is finite-dimensional in every bidegree, define its Poincaré–Hilbert series by
$M_{\bullet ,\bullet }$, which is finite-dimensional in every bidegree, define its Poincaré–Hilbert series by
Similarly, for a family of such bigraded ![]() $k$-modules
$k$-modules ![]() $M^l$, with
$M^l$, with ![]() $l\geq 0$, let us write
$l\geq 0$, let us write
The following proposition follows from standard homological algebra.
Proposition 10.1 With the above assumptions, the Poincaré series of ![]() $\mathcal {U} \mathfrak {h}$ and the homology of
$\mathcal {U} \mathfrak {h}$ and the homology of ![]() $\mathfrak {h}$ are related by the equation
$\mathfrak {h}$ are related by the equation
Proof. Let ![]() $\varepsilon : \mathcal {U}\mathfrak {h} \rightarrow k$ be the augmentation map. Recall that the Chevalley–Eilenberg complex [Reference WeibelWei94, § 7.7] is exact in all degrees:
$\varepsilon : \mathcal {U}\mathfrak {h} \rightarrow k$ be the augmentation map. Recall that the Chevalley–Eilenberg complex [Reference WeibelWei94, § 7.7] is exact in all degrees:
It therefore defines a resolution of ![]() $k$. Viewing
$k$. Viewing ![]() $k$ as a
$k$ as a ![]() $\mathcal {U} \mathfrak {h}$-module via
$\mathcal {U} \mathfrak {h}$-module via ![]() $\varepsilon$ and applying the functor
$\varepsilon$ and applying the functor ![]() $M\mapsto k\otimes _{\mathcal {U} \mathfrak {h}} M$ to (10.5) gives a complex whose truncation is exactly (10.3).
$M\mapsto k\otimes _{\mathcal {U} \mathfrak {h}} M$ to (10.5) gives a complex whose truncation is exactly (10.3).
Writing ![]() $\Lambda ^1 \mathfrak {h} = \mathfrak {h}$, and
$\Lambda ^1 \mathfrak {h} = \mathfrak {h}$, and ![]() $\Lambda ^0 \mathfrak {h} =k$, the exactness of (10.5) yields
$\Lambda ^0 \mathfrak {h} =k$, the exactness of (10.5) yields
since this is nothing other than the bigraded Euler characteristic. Since (10.3) computes the homology of ![]() $\mathfrak {h}$, we deduce similarly that
$\mathfrak {h}$, we deduce similarly that
which implies formula (10.4).
10.3 Corollaries of Conjectures 4 and 5
Let us first apply Proposition 10.1 to the algebra ![]() $\mathfrak {ls}$, bigraded by weight and depth.
$\mathfrak {ls}$, bigraded by weight and depth.
Lemma 10.2 Conjecture 4 implies that
If we identify ![]() $\mathfrak {ls} _d$ via the isomorphism
$\mathfrak {ls} _d$ via the isomorphism ![]() $\bar {\rho }$ with the space of polynomials
$\bar {\rho }$ with the space of polynomials ![]() $\mathbb {D}_d$ satisfying the linearized double shuffle relations, we obtain the conjecture stated in [Reference Ihara, Kaneko and ZagierIKZ06, Appendix].
$\mathbb {D}_d$ satisfying the linearized double shuffle relations, we obtain the conjecture stated in [Reference Ihara, Kaneko and ZagierIKZ06, Appendix].
Proof. Assuming Conjecture 4, we have
 \begin{align*} \mathcal{X}_{H_1(\mathfrak{ls} )}(s,t) &= \mathbb{O}(s)\, t + \mathbb{S}(s) \, t^4, \\ \mathcal{X}_{H_2(\mathfrak{ls} )} (s,t) &= \mathbb{S}(s) \, t^2 , \end{align*}
\begin{align*} \mathcal{X}_{H_1(\mathfrak{ls} )}(s,t) &= \mathbb{O}(s)\, t + \mathbb{S}(s) \, t^4, \\ \mathcal{X}_{H_2(\mathfrak{ls} )} (s,t) &= \mathbb{S}(s) \, t^2 , \end{align*}
where ![]() $\mathbb {O}$ and
$\mathbb {O}$ and ![]() $\mathbb {S}$ were defined in (1.3). Apply (10.4) to conclude.
$\mathbb {S}$ were defined in (1.3). Apply (10.4) to conclude.
Proposition 10.3 Conjecture 4 is equivalent to Conjecture 5, together with ![]() $\mathfrak {dg}^{\mathfrak {m}} = \mathfrak {ls}$.
$\mathfrak {dg}^{\mathfrak {m}} = \mathfrak {ls}$.
Proof. The inclusion ![]() $\mathfrak {dg}^{\mathfrak {m}} \subset \mathfrak {ls}$ implies that, for all weights
$\mathfrak {dg}^{\mathfrak {m}} \subset \mathfrak {ls}$ implies that, for all weights ![]() $N$ and depths
$N$ and depths ![]() $d$,
$d$,
This uses the fact that ![]() $\mathrm {gr}_{\mathfrak {D}} \mathcal {U} \mathfrak {g}^{\mathfrak {m}} \cong \mathcal {U} \mathfrak {dg}^{\mathfrak {m}}$, which follows from the Poincaré–Birkoff–Witt theorem. Now we know from Theorem 1.1 that
$\mathrm {gr}_{\mathfrak {D}} \mathcal {U} \mathfrak {g}^{\mathfrak {m}} \cong \mathcal {U} \mathfrak {dg}^{\mathfrak {m}}$, which follows from the Poincaré–Birkoff–Witt theorem. Now we know from Theorem 1.1 that
 \[ \frac{1 }{1- \mathbb{O}(s)} = \sum_{N\geq 0} \bigg(\sum_{d\geq 0} \dim_{\mathbb{Q}} (\mathcal{U} \mathfrak{g}^{\mathfrak{m}} )_{N,d} \bigg) s^N . \]
\[ \frac{1 }{1- \mathbb{O}(s)} = \sum_{N\geq 0} \bigg(\sum_{d\geq 0} \dim_{\mathbb{Q}} (\mathcal{U} \mathfrak{g}^{\mathfrak{m}} )_{N,d} \bigg) s^N . \]
If conjecture 4 holds then, specializing (10.6) to ![]() $t=1$, we obtain
$t=1$, we obtain
 \[ \frac{1 }{1- \mathbb{O}(s)} = \sum_{N\geq 0} \bigg( \sum_{d\geq 0} \dim_{\mathbb{Q}} (\mathcal{U} \mathfrak{ls} )_{N,d} \bigg) s^N , \]
\[ \frac{1 }{1- \mathbb{O}(s)} = \sum_{N\geq 0} \bigg( \sum_{d\geq 0} \dim_{\mathbb{Q}} (\mathcal{U} \mathfrak{ls} )_{N,d} \bigg) s^N , \]
and therefore, for all ![]() $N$,
$N$,
Since the dimensions in (10.7) are non-negative, this implies equality in (10.7), and so ![]() $\mathrm {gr}_{\mathfrak {D}} \mathcal {U} \mathfrak {g}^{\mathfrak {m}} \cong \mathcal {U} \mathfrak {dg}^{\mathfrak {m}} = \mathcal {U} \mathfrak {ls}$ and hence
$\mathrm {gr}_{\mathfrak {D}} \mathcal {U} \mathfrak {g}^{\mathfrak {m}} \cong \mathcal {U} \mathfrak {dg}^{\mathfrak {m}} = \mathcal {U} \mathfrak {ls}$ and hence ![]() $\mathfrak {dg}^{\mathfrak {m}} = \mathfrak {ls}$. Replacing
$\mathfrak {dg}^{\mathfrak {m}} = \mathfrak {ls}$. Replacing ![]() $\mathfrak {dg}^{\mathfrak {m}}$ with
$\mathfrak {dg}^{\mathfrak {m}}$ with ![]() $\mathfrak {ls}$ in Conjecture 4 gives the statement of Conjecture 5, and proves the first direction of the implication. The converse is obvious.
$\mathfrak {ls}$ in Conjecture 4 gives the statement of Conjecture 5, and proves the first direction of the implication. The converse is obvious.
The conjecture ![]() $\mathfrak {dg}^{\mathfrak {m}}=\mathfrak {ls}$ implies that
$\mathfrak {dg}^{\mathfrak {m}}=\mathfrak {ls}$ implies that ![]() $\mathfrak {g}^{\mathfrak {m}} = \mathfrak {dm}_0(\mathbb {Q})$, which is the statement that all relations between motivic multiple zeta values are generated by the regularized double shuffle relations (which is equivalent to a conjecture of Zagier's). By Furusho's theorem [Reference FurushoFur11], it would in turn imply Drinfeld's conjecture that
$\mathfrak {g}^{\mathfrak {m}} = \mathfrak {dm}_0(\mathbb {Q})$, which is the statement that all relations between motivic multiple zeta values are generated by the regularized double shuffle relations (which is equivalent to a conjecture of Zagier's). By Furusho's theorem [Reference FurushoFur11], it would in turn imply Drinfeld's conjecture that ![]() $\mathfrak {grt}$ is free with one generator in every odd degree
$\mathfrak {grt}$ is free with one generator in every odd degree ![]() $\leq -3$ (which is in turn equivalent, in the light of Theorem 1.1, to the statement that all relations between (motivic) multiple zeta values are generated by the associator relations.)
$\leq -3$ (which is in turn equivalent, in the light of Theorem 1.1, to the statement that all relations between (motivic) multiple zeta values are generated by the associator relations.)
Corollary 10.4 Conjecture 5 implies a Broadhurst–Kreimer conjecture for motivic multiple zeta values. More precisely, Conjecture 5 implies that
 \begin{equation} \sum_{N, d\geq 0} (\dim_{\mathbb{Q}} \mathrm{gr}^{\mathfrak{D}}_d \mathcal{H}_{N}) \, s^N t^d = \frac{ 1 + \mathbb{E}(s) t }{1- \mathbb{O}(s) t + \mathbb{S}(s) t^2 - \mathbb{S}(s) t^4} , \end{equation}
\begin{equation} \sum_{N, d\geq 0} (\dim_{\mathbb{Q}} \mathrm{gr}^{\mathfrak{D}}_d \mathcal{H}_{N}) \, s^N t^d = \frac{ 1 + \mathbb{E}(s) t }{1- \mathbb{O}(s) t + \mathbb{S}(s) t^2 - \mathbb{S}(s) t^4} , \end{equation}
where ![]() $\mathcal {H}_{N}$ is the
$\mathcal {H}_{N}$ is the ![]() $\mathbb {Q}$-vector space generated by motivic multiple zeta values of weight
$\mathbb {Q}$-vector space generated by motivic multiple zeta values of weight ![]() $N$.
$N$.
Proof. Apply Proposition 10.1 to ![]() $\mathfrak {dg}^{\mathfrak {m}}$. Then Conjecture 5 implies via (10.4) that
$\mathfrak {dg}^{\mathfrak {m}}$. Then Conjecture 5 implies via (10.4) that
 \begin{equation} \sum_{N,d\geq 0} (\dim_{\mathbb{Q}} \mathrm{gr}_{\mathfrak{D}}^d \mathcal{U} \mathfrak{g}^{\mathfrak{m}} _{N}) s^N t^d=\frac{ 1 }{1- \mathbb{O}(s)\, t + \mathbb{S}(s) \, t^2 - \mathbb{S}(s) \, t^4 } . \end{equation}
\begin{equation} \sum_{N,d\geq 0} (\dim_{\mathbb{Q}} \mathrm{gr}_{\mathfrak{D}}^d \mathcal{U} \mathfrak{g}^{\mathfrak{m}} _{N}) s^N t^d=\frac{ 1 }{1- \mathbb{O}(s)\, t + \mathbb{S}(s) \, t^2 - \mathbb{S}(s) \, t^4 } . \end{equation}Equation (10.8) follows from (4.3), which states that
The statement follows from ![]() $\mathrm {gr}^{\mathfrak {D}} \mathcal {A} \cong (\mathrm {gr}_{\mathfrak {D}}\mathcal {U} \mathfrak {g}^{\mathfrak {m}} )^{\vee }$ (see § 4.2) and the fact that
$\mathrm {gr}^{\mathfrak {D}} \mathcal {A} \cong (\mathrm {gr}_{\mathfrak {D}}\mathcal {U} \mathfrak {g}^{\mathfrak {m}} )^{\vee }$ (see § 4.2) and the fact that ![]() $1 + \mathbb {E}(s) t$ is the Poincaré series for the bigraded algebra
$1 + \mathbb {E}(s) t$ is the Poincaré series for the bigraded algebra
using a corollary [Reference BrownBro12] of the motivic version of Euler's theorem: ![]() $\mathbb {Q} \zeta ^{{\mathfrak {m}}}(2n) = \mathbb {Q} \zeta ^{{\mathfrak {m}}}(2)^n$.
$\mathbb {Q} \zeta ^{{\mathfrak {m}}}(2n) = \mathbb {Q} \zeta ^{{\mathfrak {m}}}(2)^n$.
11. Totally odd multiple zeta values
Let ![]() $\mathcal {H}^{\mathrm {odd}}\subset \mathcal {H}$ denote the vector subspace generated by the elements
$\mathcal {H}^{\mathrm {odd}}\subset \mathcal {H}$ denote the vector subspace generated by the elements
where ![]() $n_1,\ldots , n_r$ are integers
$n_1,\ldots , n_r$ are integers ![]() $\geq 1$. Then
$\geq 1$. Then ![]() $\mathrm {gr}^{\mathfrak {D}}\mathcal {H}^{\mathrm {odd}} \subset \mathrm {gr}^{\mathfrak {D}} \mathcal {H}$ is the vector subspace spanned by the depth-graded versions
$\mathrm {gr}^{\mathfrak {D}}\mathcal {H}^{\mathrm {odd}} \subset \mathrm {gr}^{\mathfrak {D}} \mathcal {H}$ is the vector subspace spanned by the depth-graded versions ![]() $\zeta ^{{\mathfrak {m}}}_{\mathfrak {D}}(2n_1+1,\ldots , 2n_r+1)$ of (11.1). It is clear from the linearized stuffle product formula that
$\zeta ^{{\mathfrak {m}}}_{\mathfrak {D}}(2n_1+1,\ldots , 2n_r+1)$ of (11.1). It is clear from the linearized stuffle product formula that ![]() $\mathrm {gr}^{\mathfrak {D}} \mathcal {H}^{\mathrm {odd}}$ is an algebra, indeed, it is a quotient of the shuffle algebra
$\mathrm {gr}^{\mathfrak {D}} \mathcal {H}^{\mathrm {odd}}$ is an algebra, indeed, it is a quotient of the shuffle algebra
with exactly one generator ![]() $\mathsf {2n+1}$ in each degree
$\mathsf {2n+1}$ in each degree ![]() $2n+1$, for
$2n+1$, for ![]() $n\geq 1$. Let
$n\geq 1$. Let ![]() $\mathcal {A} ^{\mathrm {odd}}$ denote
$\mathcal {A} ^{\mathrm {odd}}$ denote ![]() $\mathcal {H}^{\mathrm {odd}}$ modulo the ideal generated by
$\mathcal {H}^{\mathrm {odd}}$ modulo the ideal generated by ![]() $\zeta ^{{\mathfrak {m}}}(2)$, and let
$\zeta ^{{\mathfrak {m}}}(2)$, and let ![]() $\mathrm {gr}^{\mathfrak {D}} \mathcal {A} ^{\mathrm {odd}}$ denote
$\mathrm {gr}^{\mathfrak {D}} \mathcal {A} ^{\mathrm {odd}}$ denote ![]() $\mathrm {gr}^{\mathfrak {D}} \mathcal {H}^{\mathrm {odd}}$ modulo the ideal generated by
$\mathrm {gr}^{\mathfrak {D}} \mathcal {H}^{\mathrm {odd}}$ modulo the ideal generated by ![]() $\zeta ^{{\mathfrak {m}}}_{\mathfrak {D}}(2)$.
$\zeta ^{{\mathfrak {m}}}_{\mathfrak {D}}(2)$.
Proposition 11.1 The space ![]() $\mathcal {H}^{\mathrm {odd}}$ is almost stable under the motivic coaction:
$\mathcal {H}^{\mathrm {odd}}$ is almost stable under the motivic coaction:
Furthermore, the group ![]() $\mathcal {U}_{\mathcal {MT}(\mathbb {Z})}$ acts trivially on the associated graded
$\mathcal {U}_{\mathcal {MT}(\mathbb {Z})}$ acts trivially on the associated graded ![]() $\mathrm {gr}^{\mathfrak {D}} \mathcal {H}^{\mathrm {odd}}$.
$\mathrm {gr}^{\mathfrak {D}} \mathcal {H}^{\mathrm {odd}}$.
Proof. By the remarks at the end of § 3.1, it suffices to compute the infinitesimal coaction (3.3) in odd degrees only. Therefore apply the operator ![]() $D_{2s+1}$ to the element
$D_{2s+1}$ to the element
We use the terminology ‘subsequence’ to denote a term which occurs on the left-hand side of (3.3), and ‘quotient sequence’ to denote a term which occurs on the right. Every subsequence with two or more ![]() $1$'s gives rise to a quotient sequence of depth
$1$'s gives rise to a quotient sequence of depth ![]() $\leq r-2$. Every subsequence of depth exactly 1 and of odd length is either of the form
$\leq r-2$. Every subsequence of depth exactly 1 and of odd length is either of the form
(which cannot occur since every pair of successive ![]() $1$'s in the original sequence are separated by an even number of
$1$'s in the original sequence are separated by an even number of ![]() $0$'s), or of the form
$0$'s), or of the form
In this case, the quotient sequence has the property that every pair of successive ![]() $1$'s are separated by an even number of
$1$'s are separated by an even number of ![]() $0$'s, which defines an element of
$0$'s, which defines an element of ![]() $\mathcal {H}^{\mathrm {odd}}$. In the case when the subsequence has no
$\mathcal {H}^{\mathrm {odd}}$. In the case when the subsequence has no ![]() $1$'s, the left-hand side of (3.3) is zero and the action is trivial, which proves the last statement.
$1$'s, the left-hand side of (3.3) is zero and the action is trivial, which proves the last statement.
It follows immediately from the proposition that the action of the graded Lie algebra ![]() $\mathrm {Lie}\, \mathcal {U}_{\mathcal {MT}(\mathbb {Z})}$ on the two-step quotients
$\mathrm {Lie}\, \mathcal {U}_{\mathcal {MT}(\mathbb {Z})}$ on the two-step quotients ![]() ${\mathfrak {D}}_r \mathcal {H}^{\mathrm {odd}}/ {\mathfrak {D}}_{r-2} \mathcal {H}^{\mathrm {odd}}$ factors through its abelianization
${\mathfrak {D}}_r \mathcal {H}^{\mathrm {odd}}/ {\mathfrak {D}}_{r-2} \mathcal {H}^{\mathrm {odd}}$ factors through its abelianization ![]() $(\mathrm {Lie}\, \mathcal {U}_{\mathcal {MT}(\mathbb {Z})})^{\mathrm {ab}}$, which has canonical generators in every odd degree
$(\mathrm {Lie}\, \mathcal {U}_{\mathcal {MT}(\mathbb {Z})})^{\mathrm {ab}}$, which has canonical generators in every odd degree ![]() $2r+1$, for
$2r+1$, for ![]() $r\geq 1$. Thus for every integer
$r\geq 1$. Thus for every integer ![]() $n\geq 1$, there is a well-defined derivation
$n\geq 1$, there is a well-defined derivation
which corresponds to the action of the canonical generator ![]() $\sigma _{2n+1} \in (\mathrm {Lie}\, \mathcal {U}_{\mathcal {MT}(\mathbb {Z})})^{\mathrm {ab}}$. If
$\sigma _{2n+1} \in (\mathrm {Lie}\, \mathcal {U}_{\mathcal {MT}(\mathbb {Z})})^{\mathrm {ab}}$. If ![]() $m_1+\cdots +m_r = n_1+\cdots +n_r$ are integers
$m_1+\cdots +m_r = n_1+\cdots +n_r$ are integers ![]() $\geq 1$, then we obtain numbers
$\geq 1$, then we obtain numbers
where, by duality,
Recall that the action ![]() $\, \underline {\circ }\,$ is given by the formula
$\, \underline {\circ }\,$ is given by the formula
 \begin{gather*} \mathbb{Q}[x^2_1] \otimes_{\mathbb{Q}} \mathbb{Q}[x_1,\ldots, x_{r-1}] \longrightarrow \mathbb{Q}[x_1,\ldots, x_r] \\ x_1^{2n} \, \underline{\circ}\, g(x_1,\ldots, x_{r-1} ) = \sum_{i=1}^r \big( (x_i - x_{i-1})^{2n} - (x_i - x_{i+1})^{2n}\big) g(x_1,\ldots, \widehat{x_i}, \ldots, x_r), \end{gather*}
\begin{gather*} \mathbb{Q}[x^2_1] \otimes_{\mathbb{Q}} \mathbb{Q}[x_1,\ldots, x_{r-1}] \longrightarrow \mathbb{Q}[x_1,\ldots, x_r] \\ x_1^{2n} \, \underline{\circ}\, g(x_1,\ldots, x_{r-1} ) = \sum_{i=1}^r \big( (x_i - x_{i-1})^{2n} - (x_i - x_{i+1})^{2n}\big) g(x_1,\ldots, \widehat{x_i}, \ldots, x_r), \end{gather*}
where ![]() $x_0=0$ and
$x_0=0$ and ![]() $x_{r+1}=x_r$ (i.e. the term
$x_{r+1}=x_r$ (i.e. the term ![]() $(x_r-x_{r+1})^{2n}$ is discarded). Note that
$(x_r-x_{r+1})^{2n}$ is discarded). Note that ![]() $\, \underline {\circ }\,$ coincides with
$\, \underline {\circ }\,$ coincides with ![]() $\circ$ here by Proposition 2.2 since
$\circ$ here by Proposition 2.2 since ![]() $x_1^{2n}$ lies in the image of
$x_1^{2n}$ lies in the image of ![]() $\mathfrak {g}^{\mathfrak {m}}$.
$\mathfrak {g}^{\mathfrak {m}}$.
If ![]() $S_{N,r}$ denotes the set of compositions of an integer
$S_{N,r}$ denotes the set of compositions of an integer ![]() $N$ as a sum of
$N$ as a sum of ![]() $r$ positive integers, let
$r$ positive integers, let ![]() $C_{N,r}$ denote the
$C_{N,r}$ denote the ![]() $|S_{N,r}| \times |S_{N,r}|$ square matrix whose entries are the integers
$|S_{N,r}| \times |S_{N,r}|$ square matrix whose entries are the integers
11.1 Enumeration of totally odd depth-graded multiple zeta values
Definition 11.2 We say that a polynomial ![]() $f \in \mathbb {Q}[y_0, y_1,\ldots , y_r]$ is uneven if the coefficient of
$f \in \mathbb {Q}[y_0, y_1,\ldots , y_r]$ is uneven if the coefficient of ![]() $y_0^{2n_0} \ldots y_r^{2n_r}$ in
$y_0^{2n_0} \ldots y_r^{2n_r}$ in ![]() $f$ vanishes for all
$f$ vanishes for all ![]() $n_0,\ldots , n_r \geq 0$.
$n_0,\ldots , n_r \geq 0$.
Recall from (9.1) that the exceptional elements ![]() $e_f \in \mathfrak {ls}$ are uneven. The following proposition is a kind of dual to the previous one.
$e_f \in \mathfrak {ls}$ are uneven. The following proposition is a kind of dual to the previous one.
Proposition 11.3 The set of uneven elements in ![]() $\mathfrak {ls}$ is an ideal for the Ihara bracket.
$\mathfrak {ls}$ is an ideal for the Ihara bracket.
Proof. Let ![]() $f, g\in \rho (\mathfrak {ls} )$ such that
$f, g\in \rho (\mathfrak {ls} )$ such that ![]() $f$ is uneven. It suffices to show that
$f$ is uneven. It suffices to show that ![]() $\{f,g\}$ is uneven. By the parity result (Proposition 6.4), we know that
$\{f,g\}$ is uneven. By the parity result (Proposition 6.4), we know that ![]() $f$ and
$f$ and ![]() $g$ are of even degree. It follows from (6.3) that
$g$ are of even degree. It follows from (6.3) that ![]() $\{f,g\}$ is a linear combination of terms of the form
$\{f,g\}$ is a linear combination of terms of the form
where ![]() $\alpha , \beta$ are sets of indices with
$\alpha , \beta$ are sets of indices with ![]() $|\alpha \cap \beta | = 1$. Since the polynomial
$|\alpha \cap \beta | = 1$. Since the polynomial ![]() $f$ is homogeneous of even degree, it follows that the coefficient of
$f$ is homogeneous of even degree, it follows that the coefficient of ![]() $y_0^{2n_0} \ldots y_N^{2n_N}$ in
$y_0^{2n_0} \ldots y_N^{2n_N}$ in ![]() $\{f,g\}$ is a linear combination of the coefficients of totally even monomials in
$\{f,g\}$ is a linear combination of the coefficients of totally even monomials in ![]() $f$, which all vanish. In more detail, let us consider two sets of indices with
$f$, which all vanish. In more detail, let us consider two sets of indices with ![]() $\alpha \cap \beta = \{\gamma \}$, and the corresponding monomials which occur in
$\alpha \cap \beta = \{\gamma \}$, and the corresponding monomials which occur in ![]() $f,g$ respectively:
$f,g$ respectively:
where ![]() $c^f_{\alpha }, c^g_{\beta } \in \mathbb {Q}$. A monomial in
$c^f_{\alpha }, c^g_{\beta } \in \mathbb {Q}$. A monomial in ![]() $\{f,g\}$ is of the form
$\{f,g\}$ is of the form
Suppose that ![]() $m_{\gamma }+n_{\gamma }$ and all
$m_{\gamma }+n_{\gamma }$ and all ![]() $m_a, n_b$ are even for
$m_a, n_b$ are even for ![]() $a \in \alpha \backslash \{\gamma \}$ and
$a \in \alpha \backslash \{\gamma \}$ and ![]() $b \in \beta \backslash \{\gamma \}$. If
$b \in \beta \backslash \{\gamma \}$. If ![]() $m_{\gamma }$ is odd, then
$m_{\gamma }$ is odd, then ![]() $c^f_{\alpha }=0$ since
$c^f_{\alpha }=0$ since ![]() $f$ is of even degree by Proposition 6.4. In the case when
$f$ is of even degree by Proposition 6.4. In the case when ![]() $m_{\gamma }$ is even,
$m_{\gamma }$ is even, ![]() $c^f_{\alpha }= 0$ since
$c^f_{\alpha }= 0$ since ![]() $f$ is uneven. Therefore
$f$ is uneven. Therefore ![]() $\{f,g\}$ is uneven.
$\{f,g\}$ is uneven.
Corollary 11.4 The Lie ideal in ![]() $\mathfrak {ls}$ generated by the exceptional elements is orthogonal to (i.e. annihilated by)
$\mathfrak {ls}$ generated by the exceptional elements is orthogonal to (i.e. annihilated by) ![]() $\mathrm {gr}^{\mathfrak {D}}\mathcal {A} ^{\mathrm {odd}}$.
$\mathrm {gr}^{\mathfrak {D}}\mathcal {A} ^{\mathrm {odd}}$.
Proof. The elements ![]() $\mathsf {e}_f$ are uneven.
$\mathsf {e}_f$ are uneven.
In the light of Conjecture 5 it is therefore natural to expect that ![]() $\mathrm {gr}^{\mathfrak {D}} \mathcal {A} ^{\mathrm {odd}}$ is dual to
$\mathrm {gr}^{\mathfrak {D}} \mathcal {A} ^{\mathrm {odd}}$ is dual to ![]() $\mathfrak {g}^{\mathrm {odd}}$, which suggests the following conjecture.
$\mathfrak {g}^{\mathrm {odd}}$, which suggests the following conjecture.
Conjecture 6 (‘Uneven’ part of motivic Broadhurst–Kreimer conjecture)
 \begin{equation} \sum_{N\geq 0, d\geq 0} ( \dim_{\mathbb{Q}} \mathrm{gr}^{\mathfrak{D}}_d \mathcal{A} ^{\mathrm{odd}}_{N}) s^N t^d = \frac{1 } {1- \mathbb{O}(s) t + \mathbb{S}(s) t^2} . \end{equation}
\begin{equation} \sum_{N\geq 0, d\geq 0} ( \dim_{\mathbb{Q}} \mathrm{gr}^{\mathfrak{D}}_d \mathcal{A} ^{\mathrm{odd}}_{N}) s^N t^d = \frac{1 } {1- \mathbb{O}(s) t + \mathbb{S}(s) t^2} . \end{equation} Since the action of the operators ![]() $\partial _{2n+1}$ on the totally odd depth-graded motivic multiple zeta values can be computed explicitly in terms of binomial coefficients, one can hope to prove a version of this conjecture by elementary methods. Indeed, assuming Conjecture 5, the left-hand side of (11.3) is the generating series
$\partial _{2n+1}$ on the totally odd depth-graded motivic multiple zeta values can be computed explicitly in terms of binomial coefficients, one can hope to prove a version of this conjecture by elementary methods. Indeed, assuming Conjecture 5, the left-hand side of (11.3) is the generating series
where ![]() $C_{N,r}$ are the matrices of binomial coefficients defined in (11.2). Therefore, one is led to conjecture that this generating series also coincides with the right-hand side of (11.3). I have verified this up to weight 30.
$C_{N,r}$ are the matrices of binomial coefficients defined in (11.2). Therefore, one is led to conjecture that this generating series also coincides with the right-hand side of (11.3). I have verified this up to weight 30.
Standard transcendence conjectures for multiple zeta values would then have it that if ![]() $\mathcal {Z}^{\mathrm {odd}}_{N,d}$ denotes the space of totally odd depth-graded multiple zeta values modulo
$\mathcal {Z}^{\mathrm {odd}}_{N,d}$ denotes the space of totally odd depth-graded multiple zeta values modulo ![]() $\zeta (2)$, of weight
$\zeta (2)$, of weight ![]() $N$ and depth
$N$ and depth ![]() $d$, then we obtain the new conjecture
$d$, then we obtain the new conjecture
 \begin{equation} \sum_{N\geq 0, d\geq 0} \big( \dim_{\mathbb{Q}} \mathcal{Z}^{\mathrm{odd}}_{N,d} \big) s^N t^d = \frac{1 }{1- \mathbb{O}(s) t + \mathbb{S}(s) t^2} . \end{equation}
\begin{equation} \sum_{N\geq 0, d\geq 0} \big( \dim_{\mathbb{Q}} \mathcal{Z}^{\mathrm{odd}}_{N,d} \big) s^N t^d = \frac{1 }{1- \mathbb{O}(s) t + \mathbb{S}(s) t^2} . \end{equation}Remark 11.5 These conjectures measure the relations between totally odd (motivic) multiple zeta values modulo all (motivic) multiple zeta values of lower depth, not just modulo totally odd (motivic) multiple zeta values of lower depth (in other words, ![]() $\mathcal {Z}^{\mathrm {odd}}_{N,d}$ denotes the span of the totally odd zetas in the space of depth- graded multiple zeta values, and not the depth-graded of the space of totally odd multiple zeta values).
$\mathcal {Z}^{\mathrm {odd}}_{N,d}$ denotes the span of the totally odd zetas in the space of depth- graded multiple zeta values, and not the depth-graded of the space of totally odd multiple zeta values).
Acknowledgements
This project has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (grant agreement nos. 257638 and 724638). I would like to thank the Institute for Advanced Study and the Humboldt Foundation. This work was partly inspired by Zagier's lectures at the Collège de France in October 2011, in which he explained parts of [Reference Ihara, Kaneko and ZagierIKZ06, § 8], and partly based on a talk at a conference in June 2012 at the IHES in honour of P. Cartier's eightieth birthday. It is a pleasure to dedicate this work to him, with my deepest gratitude.