Published online by Cambridge University Press: 29 November 2024
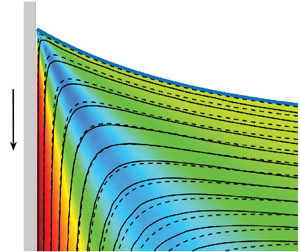
The flow near a moving contact line depends on the dynamic contact angle, viscosity ratio and capillary number. We report experiments involving immersing a plate into a liquid bath, concurrently measuring the interface shape, interfacial velocity and fluid flow using digital image processing and particle image velocimetry. All experiments were performed at low plate speeds to maintain small Reynolds and capillary numbers for comparison with viscous theories. The dynamic contact angle, measured in the viscous phase, was kept below  $90^{\circ }$ and the viscosity ratio,
$90^{\circ }$ and the viscosity ratio,  $\lambda < 1$. This region of parameter space is largely unexplored for advancing contact lines. An important aim of the present study is to provide new experimental data against which new contact line models can be developed. The flow field is directly compared against the prediction from the viscous theory of Huh & Scriven (J. Colloid Interface Sci., vol. 35, issue 1, 1971, pp. 85–101) but with a slight modification involving the curved interface. Remarkable agreement is found between experiments and theory across a wide parameter range. The prediction for interfacial speed from Huh & Scriven is also in excellent agreement with experiments except in the vicinity of the contact line. Material points along the interface were found to rapidly slow down near the contact line, thus alleviating the singularity at the moving contact line. To the best of our knowledge, such a detailed test of theoretical models has not been performed before and we hope the present study will spur new modelling efforts in the field.
$\lambda < 1$. This region of parameter space is largely unexplored for advancing contact lines. An important aim of the present study is to provide new experimental data against which new contact line models can be developed. The flow field is directly compared against the prediction from the viscous theory of Huh & Scriven (J. Colloid Interface Sci., vol. 35, issue 1, 1971, pp. 85–101) but with a slight modification involving the curved interface. Remarkable agreement is found between experiments and theory across a wide parameter range. The prediction for interfacial speed from Huh & Scriven is also in excellent agreement with experiments except in the vicinity of the contact line. Material points along the interface were found to rapidly slow down near the contact line, thus alleviating the singularity at the moving contact line. To the best of our knowledge, such a detailed test of theoretical models has not been performed before and we hope the present study will spur new modelling efforts in the field.