INTRODUCTION
Rapid transmission of influenza in the form of institutional outbreaks has been associated with closed communities [Reference Mook1–Reference Besselaar4], a pattern which has also been observed for the 2009 pandemic strain [Reference Smith5, Reference Marchand-Austin6]. High levels of transmission are also associated with extensive and sometimes rapid spread in school-age children [Reference Smith5, Reference Sasaki7–Reference Lyytikainen9] and are facilitated by social as well as classroom interaction [Reference Kar-Purkayastha10]. Close contact allowing droplet spread may be more important than aerosol transmission in such close social groupings [Reference Han11]. The introduction of a novel strain of influenza A to residential communities has also been reported to produce high attack rates [Reference Besselaar4]. Spread to new susceptible cohorts can extend and prolong institutional outbreaks [Reference Young2]. Here we describe an outbreak in a residential summer school with substantial social contact and a high turnover of cohorts during the first wave of the influenza A(H1N1) 2009 pandemic. Factors associated with transmission were identified. The observed outbreak was fitted to models of transmission dynamics in order to estimate the impact of interventions.
METHODS
Setting and population
An international summer school opened in the UK on 5 July 2009 with 276 teenage students coming from 18 countries. Of these, 247 were housed in university accommodation (five buildings on one college site) and 29 (26 students from Belgium plus three others) with host families. The age range was 12–16 years (median 14·2) and 59% were female. Students from different countries and age groups were mixed across the five accommodation buildings. All students participated in morning classes and an extensive social programme. Allocation to classes was based on ability and not on age or nationality. The summer school was scheduled to run for 8 weeks, with overlapping cohorts arriving and departing weekly.
Epidemiological methods
Case definition
Two cases were laboratory-confirmed by PCR testing throat swab samples. Otherwise cases were defined by the combination of both clinical and epidemiological criteria, i.e. pyrexia ⩾38°C and two or more symptoms of cough, sore throat, rhinorrhoea, limb/joint pain or headache as clinical criteria and the epidemiological criterion of close contact with a confirmed case. Sharing a school setting with cases in the context of an outbreak was considered as close contact so that all students meeting the clinical case definition were counted as cases. This was in line with the national operational case definition at the time [12].
Data gathering and analysis
Symptoms and onset dates were recorded by the summer school nursing staff. Exposure information was obtained from summer school administrative data including age, gender, nationality, teaching groups, classrooms and accommodation. Data were summarized by an epidemic curve and tabulation. Relative risk associated with exposures was calculated and 95% confidence intervals (CIs) estimated using standard errors calculated from the square root of the variance of the score statistic. Independence of identified risks was assessed using likelihood ratio tests from multivariate logistic regression models.
Public health interventions
An outbreak control team was established following the confirmation of pandemic (H1N1) 2009 infection, including public health, clinical and summer school representatives. Advice on hygiene and increased hand washing was given from the outset in accordance with the UK's ‘Catch it, Bin it, Kill it’ campaign [13]. The provision of alcohol gels and enhanced cleaning of communal areas was implemented as was rapid assessment of symptomatic students and access to prescriptions to enable antiviral medication to be commenced within 24 h of symptom onset. Strict isolation of all symptomatic individuals was maintained until 24 h after their symptoms had resolved. Increased staffing was put in place to support these activities. These measures were generally fully established by 11 July and maintained apart from temporary difficulties in environmental cleaning due to staffing difficulties. Social events were risk assessed and a disco cancelled, but school outings including coach trips and classes continued as usual for those who were not ill. The next incoming cohort was reduced to 76 of the planned 138, with 62 of the expected students deferred until later in the summer.
Modelling
The ‘basic reproduction number’ R 0 is the mean number of secondary cases arising from a single infected case, in an otherwise susceptible population [Reference Giesecke14]. It is a compact measure of transmissibility: self-sustaining spread of a virus requires R 0>1, and thus successful non-vaccination interventions (as in this study) must reduce R 0 below this threshold. The effective reproduction number R eff removes the requirement for the whole population to be susceptible.
Two separate modelling approaches were used to estimate the effect of interventions on transmission. First, the Wallinga–Teunis method [Reference Wallinga and Teunis15] was used to estimate R eff from the incidence data. This method requires the input of a distribution for the generation interval, the time between infection of an index case and infection of a secondary case. Following previous studies the generation interval was assumed to follow a gamma distribution, with mean 3 days and variance 2 days [Reference Fraser16]. Sensitivity analysis was performed and results compared for different assumed values of the mean and variance for the generation time.
Second, incidence data was used to fit simple deterministic models of transmission dynamics, to estimate basic transmission parameters (constituents of R 0) before and after interventions. Specifically, to allow for clustering of individuals, the student population was partitioned into n distinct ‘groups’ of infection risk (to be motivated by the epidemiological data – see Results section). Writing S i, I i, N i as the numbers of susceptible, infectious and total individuals in group i respectively, governing equations for group i read, in the absence of interventions:
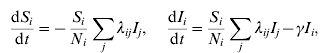
where 1/γ is the mean infectious period. The coefficients λij constitute the ‘transmission matrix’, and denote the rate of infection in group i, due to an infected case in group j. Three different forms for the transmission matrix were considered, as described below. Writing ρ(λ) for the largest eigenvalue of the matrix λij, R 0 in the pre-intervention period is thus
Interventions were assumed to be in effect from 11 July onwards (see ‘Public health interventions’ subsection described above), or day 6 of the outbreak. It was further assumed that interventions would affect transmission parameters in all groups equally. Hence interventions would multiply λij by a constant scalar ![]() , and effect a new infectious period 1/
, and effect a new infectious period 1/![]() , yielding post-intervention equations:
, yielding post-intervention equations:
with basic reproduction number:
The parenthetical terms on the right-hand side of equation (3) therefore allow estimation of the effect of interventions on basic transmission parameters, unconfounded by the influence of immunity at the time of intervention.
The transmission matrix λij is a composite of the contact structure, or ‘mixing’ between groups, and the probability of transmission per contact between a susceptible and infected case (the latter taken to be constant across groups). Three different forms of mixing were considered, described briefly here with further details given in the Supplementary material (available online): (i) Homogeneous mixing, i.e. λij=b for all i, j, for a single parameter b to be estimated. (ii) Uniform within- and between-group mixing, ‘uniform’ in the sense that all groups have the same within-group mixing coefficient b W. Together with the between-group coefficient b B, this provided two parameters to be estimated. (iii) Non-uniform within- and between-group mixing. Here separate within-group mixing coefficients are taken for each group. Together with the between-group coefficient, these provided n+1 parameters to be estimated.
For a given initial infectious period 1/γ, therefore, total parameters to be estimated were: λij (subject to model choice), ![]() These parameters were fitted by the least-squares method. Specifically, for a given initial parameter set, epidemic time-courses were simulated using equations (1) and (2). The residuals were calculated as the squared difference between simulated and observed daily incidence in each group, and the objective function was computed as the sum of all of these residuals. The downhill simplex algorithm [Reference Nelder and Mead17] was used to minimize this objective function. The process was repeated for 1000 initial parameter sets generated by Latin hypercube sampling, from which was selected the parameter set yielding the least sum of squares.
These parameters were fitted by the least-squares method. Specifically, for a given initial parameter set, epidemic time-courses were simulated using equations (1) and (2). The residuals were calculated as the squared difference between simulated and observed daily incidence in each group, and the objective function was computed as the sum of all of these residuals. The downhill simplex algorithm [Reference Nelder and Mead17] was used to minimize this objective function. The process was repeated for 1000 initial parameter sets generated by Latin hypercube sampling, from which was selected the parameter set yielding the least sum of squares.
RESULTS
The summer school sought advice on 8 July 2009 from a local general practice physician regarding six students with influenza-like illness. On 9 July, nasopharyngeal swabs were taken from two students which confirmed pandemic influenza A(H1N1) 2009. The number of affected students increased rapidly (Fig. 1). Between 7 and 16 July, 115 clinically presumed cases and two laboratory-confirmed cases produced a clinical attack rate of 42·4%. The clinical attack rate was 49% for males and 38% for females (P=0·06). The attack rate did not vary significantly with age group (range 38–57% in 1-year age bands, P=0·48). No significant association was found between illness and classes in specific teaching groups (P=0·21) or classrooms (P=0·59).

Fig. 1. Epidemic curve for influenza-like illness in summer school participants, 7–16 July 2009, by block of residence with block F representing those living externally with families (n=117).
Six of the 18 nationalities participating in the summer school were represented by ⩾15 students. Clinical attack rates ranged from 40·6% to 57·9%, with no significant evidence for variation by nationality (Fisher's exact test P=0·47) in the five national groups of size ⩾15 that were accommodated on-site in university accommodation. Of the 26 Belgian students, who were accommodated with host families, only two (7·7%) met the case definition. Overall, students staying on-site in university accommodation experienced a clinical attack rate of 46·6%, which was 6·8 times greater than the risk of symptomatic infection for students staying with host families (95% CI 1·8–25·8). Within the university accommodation, clinical attack rates varied significantly between buildings, from 22·8% to 73·1% (P=0·002, Table 1). Students staying in single rooms in university accommodation had 1·35 times lower risk of symptomatic infection than those in twin rooms (95% CI 1·01–1·79), with clinical attack rates of 39·8% and 53·7%, respectively. Multivariate logistic regression analysis including room type (single or double) and building among the 236 students resident within the college and for whom full data were available showed no evidence for interaction between these exposures (likelihood ratio test P=0·66 for interaction terms). The effect of building was maintained in the multivariate analysis remaining significant, with minor alterations of the coefficients associated with each building (compared to building A as baseline) and similar explanatory value for the building exposure when considered with and without room type in the model (pseudo-R 2 value of 0·053 and 0·051, respectively). The effect size of room type decreased in the multivariate model lost statistical significance (Table 2).
Table 1. Attack rate of influenza-like illness by accommodation building in those accommodated on site (Fisher's exact P=0·002)
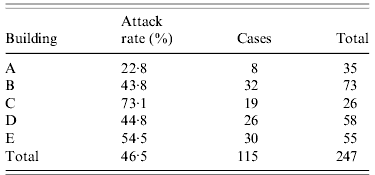
Table 2. Association of building of residence and sharing a double room with illness in students with complete data for accommodation type (n=236)
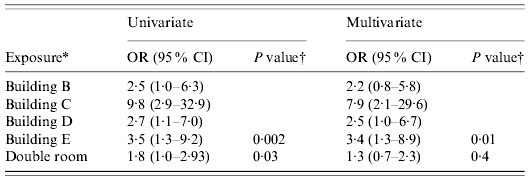
OR, Odds ratio; CI, confidence interval.
* Buildings compared to building A and sharing a double room compared to single room accommodation.
† P values from likelihood ratio test for evidence of an effect of building of residence and Wald test from double room compared to single room.
The estimated R eff by the Wallinga–Teunis method was 5 (95% CI 2·8–7·2) at the start of the outbreak and dropped daily until it was <1 on 12 July (Fig. 2), when the epidemic curve showed the greatest number of new cases (Fig. 1). Sensitivity analysis, which varied the generation time distribution, altered the estimates of R eff. However, these estimates remained substantially >1 initially and dropped rapidly between 10 and 12 July in each of these analyses (Supplementary Fig. S1, online).

Fig. 2. Estimated effective reproductive numbers each day during the outbreak with error bars representing 1·96 standard deviations.
Given the apparent significance of university accommodation buildings in risk of symptomatic infection, the ‘groups’ described in equations (1) and (2) were identified with buildings A–E, thus taking n=5. Table 3 shows resulting parameter estimates under the three different model scenarios described above, while Figure 3 shows the simulated daily incidence aggregated across all five buildings: epidemic curves for individual buildings are provided in the Supplementary online material. Here it is assumed that the mean infectious period in the absence of interventions is 3 days, consistent with Figure 2: corresponding results for other plausible infectious periods are also provided in the Supplementary material.

Fig. 3. Comparison of observed and simulated daily incidence, under the model scenarios described in the text. Incidence aggregated over all buildings is shown (see Supplementary online material for incidence curves for individual buildings). Simulation results of model (i) are omitted for clarity, as they are indistinguishable here from those of model (ii).
Table 3. Parameters estimated from transmission models under three different scenarios, assuming an infectious period before intervention of 3 days. Bracketed values in the final row are obtained by constraining pre- and post-intervention transmission parameters to be the same, and re-evaluating best fits

Table 3 illustrates a qualitatively consistent result across all three scenarios, that intervention substantially reduced the infectious period ![]() , to approximately 1 day. There is less agreement between models about the impact on infectiousness, with models (i) and (ii) counterintuitively suggesting a mild increase (
, to approximately 1 day. There is less agreement between models about the impact on infectiousness, with models (i) and (ii) counterintuitively suggesting a mild increase (![]() ~1·1) and only model (iii) suggesting a reduction, of around 33% (
~1·1) and only model (iii) suggesting a reduction, of around 33% (![]() ~0·64). However, it is also model (iii) that appears to reproduce the incidence data best, in particular the sharpness of the peak in incidence on day 6, both on an aggregate level (Fig. 3) as well as in individual buildings (Supplementary Fig. S2). Overall, parameter estimates suggest consistently that interventions may have succeeded in bringing the basic reproductive number R 0 just below 1. Moreover, in all models the inclusion of interventions substantially improves the goodness-of-fit (bottom row, Table 3). Several important caveats for these simple models are discussed below.
~0·64). However, it is also model (iii) that appears to reproduce the incidence data best, in particular the sharpness of the peak in incidence on day 6, both on an aggregate level (Fig. 3) as well as in individual buildings (Supplementary Fig. S2). Overall, parameter estimates suggest consistently that interventions may have succeeded in bringing the basic reproductive number R 0 just below 1. Moreover, in all models the inclusion of interventions substantially improves the goodness-of-fit (bottom row, Table 3). Several important caveats for these simple models are discussed below.
DISCUSSION
This outbreak illustrates the rapidity of spread and high attack rates typical of influenza in residential communities. The high attack rates of respiratory infections in residential settings, including influenza [Reference Young2–Reference Besselaar4] and other respiratory viruses [Reference Marchand-Austin6], have been well described. New strains of influenza A introduced to naive populations have generated especially high attack rates, with 60% of pupils and 25% of staff in the first French school identified as affected by pandemic influenza A(H1N1) 2009 [Reference Guinard18], and 34% of those resident in a South African police residential college when influenza A/Fujian/411/2002-like virus was first introduced to the country in 2003 [Reference Besselaar4]. In the present context, the opening of the language school similarly represents a population with minimal immunity to a novel virus: students arrived from outside the UK and, within Europe at this time, only the UK reported widespread geographical spread of pandemic (H1N1) 2009 influenza, with sporadic spread in a small minority of other countries [19].
The association of illness with residence in on-site accommodation buildings compared to accommodation with host families, variation in attack rate in these on-site buildings, and possibly increased rates of illness in those sharing a twin room, all support residential social contact as having an important role in transmission. The variation in risk by building of residence is consistent with reports in residential college [Reference Besselaar4] and boarding school [Reference Smith5] outbreaks.
The increased risk of symptomatic infection associated with twin bedrooms in univariate analysis of this outbreak echoes findings of previous studies, although the effect was substantially lost in multivariate analysis. In an Italian residential drug-rehabilitation community, the clinical attack rate was 15·9% overall but ranged from 8·05% in detached houses in the main community to 21·67% in dormitories, with attack rates of only 2·65% in residents of a smaller satellite community on another site [Reference Boschini3]. In an Australian prison outbreak illness was associated with sharing a cell, and the outbreak began in a crowded remand prison with between 1 and 6 occupants per cell [Reference Young2]. In contrast age, classroom setting and nationality (apart from a low attack rate in Belgian students living off-site) did not appear to be associated with risk of illness. Spread between school classmates has been described [Reference Kar-Purkayastha10, Reference Guinard18, Reference Cauchemez20] in other pandemic (H1N1) 2009 outbreaks. In the current outbreak population classes were formed based on ability in the week of the outbreak. Thus a lack of social identity within classes may explain the difference between the current outbreak and others where class was more important as a risk factor.
Modelling-based estimates of transmission in this outbreak showed high initial levels that then decreased markedly. This suggests that basic interventions may have been effective in controlling the outbreak, even in this high-risk setting. Indeed, it is possible to interpret the parameter estimates in terms of specific interventions: case isolation and treatment, through essentially curtailing the infectious period, reduce 1/![]() in equation (3); conversely, increased hygiene measures, by reducing infectiousness per contact, reduces
in equation (3); conversely, increased hygiene measures, by reducing infectiousness per contact, reduces ![]() . On the basis of model (iii) – which appears to best fit the incidence data – there are indications that both of these effects occurred, suggesting that hygiene and case isolation and treatment may have had concomitant effects on overall transmission. A third intervention was the cancellation of social activities, such as a disco, while maintaining normal educational activities as far as possible. From a modelling perspective such measures may be considered to ‘stabilize’ contact rates, essentially avoiding the transient increases in contact associated with social gatherings.
. On the basis of model (iii) – which appears to best fit the incidence data – there are indications that both of these effects occurred, suggesting that hygiene and case isolation and treatment may have had concomitant effects on overall transmission. A third intervention was the cancellation of social activities, such as a disco, while maintaining normal educational activities as far as possible. From a modelling perspective such measures may be considered to ‘stabilize’ contact rates, essentially avoiding the transient increases in contact associated with social gatherings.
We note that the simplicity of these models, while affording a transparent framework, must be interpreted with caution. Here we have put forward three simple mixing scenarios, as a tentative exploration of how heterogeneity in the student population may affect the overall results, but these are by no means exhaustive. For example we have neglected the possibility of asymptomatic infection, potential ‘superspreader’ events, and stochasticity. The latter, although perhaps not significant when aggregating across buildings, may nevertheless play a role in specific settings such as building A, where case numbers were particularly low. Moreover the presence of superspreaders, or relatively few individuals accounting for a disproportionate amount of transmission, may offer an alternative explanation for the distinctive, sharp peak in incidence. Further work may seek to explore these factors.
Such caveats notwithstanding, we note also that the two independent modelling approaches used here – the Wallinga–Teunis method and the deterministic transmission model (iii) – give consistent estimates for R 0 of ~5–6 in the absence of interventions. These levels exceed population-scale estimates of R 0 for this pandemic (the latter being typically 1–3 [Reference Yang21]) and, if accurate, would seem to reflect the elevated transmission potential in this residential school setting, typical of residential institutions [Reference Young2–Reference Besselaar4], compared to that in the wider community.
In this outbreak other evidence supports the model indication that interventions decreased transmission and, in particular, that it was not due to the development of immunity. First, the relatively low attack rate in some accommodation buildings indicates that the outbreak finished early when many susceptibles were still present. Second, the timescale of decrease is early in comparison to the effects that would be seen if acquired immunity were the cause. Third, control was maintained without new cases until the fifth week of the summer school, when a second outbreak occurred in building A, the building which showed a low initial attack rate in the outbreak described here. This second outbreak was again controlled without spread into succeeding cohorts. Finally, the structure of the summer school with new but overlapping cohorts joining weekly was ideal to provide fresh susceptible populations to allow sustained, high-level transmission in the absence of interventions.
The only interventions employed were rapid treatment and isolation of cases, basic hygiene measures and avoidance of particularly high-risk social events. Chemoprophylaxis was not employed and vaccination was not available. Previous studies have found these implemented measures to be effective. Several systematic reviews identify hand hygiene as protective against transmission of respiratory illnesses [Reference Rabie and Curtis22, Reference Jefferson23] including in institutional settings [Reference Rabie and Curtis22]. Moreover, published reviews suggest that multiple interventions may be more effective than single intervention approaches [Reference Jefferson23], a notion echoed here by the multiplicative effects of intervention in equation (3).
The effectiveness of infection control measures in different settings is an important public health question since all such interventions have some cost and some, such as school closures, can have substantial social and economic impact. Evaluation of effectiveness is difficult with randomized, trial-based evidence rarely available, and most evidence coming from opportunistic studies such as this one, studies inherently limited by the context and nature of the outbreak and population. This outbreak provided the useful opportunity of a susceptible residential population, founded on the opening date of the summer school, followed by rapid transmission of a novel virus. The multi-stranded evidence from available data, epidemiological and modelling techniques suggests that basic public health measures alone, without chemoprophylaxis or vaccination, appeared to control spread during the outbreak described. Notably, such control was achieved despite the very high rate of initial transmission and the ongoing renewal of a susceptible population by new but overlapping weekly student cohorts. This would have implications beyond residential schools to other institutional settings, especially those sharing the challenge of frequent turnover of susceptible cohorts. It also indicates that simple measures within schools may provide an alternative means to control spread without school closure, a costly intervention that was widely debated and extensively used [Reference Smith5, Reference Sasaki7, Reference Kar-Purkayastha10, Reference Sypsa and Hatzakis24, Reference Cauchemez25] during the early stages of the 2009 pandemic.
NOTE
Supplementary material accompanies this paper on the Journal's website (http://journals.cambridge.org/hyg).
ACKNOWLEDGEMENTS
The authors thank the South East Regional Microbiology Laboratory for exceptional provision of laboratory services and collaboration during this incident and the first wave of the pandemic generally and for helpful comments to this paper. N. A. also thanks Dr Sebastien Ballesteros for helpful discussion.
DECLARATION OF INTEREST
None.








