Hostname: page-component-669899f699-ggqkh Total loading time: 0 Render date: 2025-04-25T04:59:18.186Z Has data issue: false hasContentIssue false
  • English
  • Français

Uniqueness of ground states to fractional nonlinear elliptic equations with harmonic potential

Part of: Miscellaneous topics - Partial differential equations Partial differential equations

Published online by Cambridge University Press:  11 April 2024

Tianxiang Gou
Tianxiang Gou*
Affiliation:
School of Mathematics and Statistics, Xi'an Jiaotong University, 710049 Xi'an, Shaanxi, China ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we prove the uniqueness of ground states to the following fractional nonlinear elliptic equation with harmonic potential,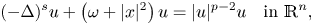

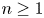\[ (-\Delta)^s u+ \left(\omega+|x|^2\right) u=|u|^{p-2}u \quad \mbox{in}\ \mathbb{R}^n, \]
where $n \geq 1$, $0< s<1$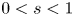, $\omega >-\lambda _{1,s}$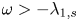, $2< p< {2n}/{(n-2s)^+}$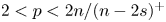, $\lambda _{1,s}>0$ 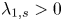is the lowest eigenvalue of $(-\Delta )^s + |x|^2$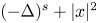. The fractional Laplacian $(-\Delta )^s$ 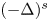is characterized as $\mathcal {F}((-\Delta )^{s}u)(\xi )=|\xi |^{2s} \mathcal {F}(u)(\xi )$ 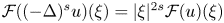for $\xi \in \mathbb {R}^n$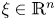, where $\mathcal {F}$ 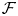denotes the Fourier transform. This solves an open question in [M. Stanislavova and A. G. Stefanov. J. Evol. Equ. 21 (2021), 671–697.] concerning the uniqueness of ground states.

Keywords

Uniquenessground statesharmonic potentialfractional elliptic equations

MSC classification

Primary: 35A02: Uniqueness problems
Secondary: 35R11: Fractional partial differential equations
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 14
Check for updates
Copyright
Copyright © The Author(s), 2024. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Ding, Z. and Hajaiej, H.. On a fractional Schrödinger equation in the presence of harmonic potential. Electron. Res. Arch. 29 (2021), 3449–3469.CrossRefGoogle Scholar
Felmer, P., Quaas, A. and Tan, J.. Positive solutions of nonlinear Schrödinger equation with the fractional Laplacian. Proc. Roy. Soc. Edinburgh Sect. A 142 (2012), 1237–1262.CrossRefGoogle Scholar
Frank, R. L. and Lenzmann, E.. Uniqueness of non-linear ground states for fractional Laplacians in $\mathbb {R}$. Acta Math. 210 (2013), 261–318.CrossRefGoogle Scholar
Frank, R. L., Lenzmann, E. and Silvestre, L.. Uniqueness of radial solutions for the fractional Laplacian. Comm. Pure Appl. Math. 69 (2016), 167–1726.CrossRefGoogle Scholar
Hirose, M. and Ohta, M.. Structure of positive radial solutions to scalar field equations with harmonic potential. J. Differ. Equ. 178 (2002), 519–540.CrossRefGoogle Scholar
Hirose, M. and Ohta, M.. Uniqueness of positive solutions to scalar field equations with harmonic potential. Funkcial. Ekvac. 50 (2007), 67–100.CrossRefGoogle Scholar
Kabeya, Y. and Tanaka, K.. Uniqueness of positive radial solutions of semilinear elliptic equations in $\mathbb {R}^n$ and Séré's non-degeneracy condition. Comm. Partial Differ. Equ. 24 (1999), 563–598.CrossRefGoogle Scholar
Laskin, N.. Fractional quantum mechanics and Lévy path integrals. Phys. Lett. A 268 (2000), 298–305.CrossRefGoogle Scholar
Laskin, N.. Fractional Schrödinger equation. Phys. Rev. E (3) 66 (2002), 056108. 7 pp.CrossRefGoogle ScholarPubMed
Stanislavova, M. and Stefanov, A. G.. Ground states for the nonlinear Schrödinger equation under a general trapping potential. J. Evol. Equ. 21 (2021), 671–697.CrossRefGoogle Scholar
Willem, M.. Minimax Theorems (Birkhauser Verlag, Boston, Basel, Berlin, 1996).CrossRefGoogle Scholar