Published online by Cambridge University Press: 06 June 2022
In a ball $\Omega \subset \mathbb {R}^{n}$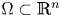 with $n\ge 2$
with $n\ge 2$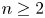 , the chemotaxis system
, the chemotaxis system
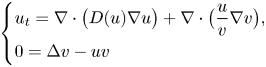
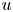 and with prescribed constant positive Dirichlet boundary data for $v$
and with prescribed constant positive Dirichlet boundary data for $v$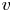 . It is shown that if $D\in C^{3}([0,\infty ))$
. It is shown that if $D\in C^{3}([0,\infty ))$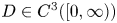 is such that $0< D(\xi ) \le {K_D} (\xi +1)^{-\alpha }$
is such that $0< D(\xi ) \le {K_D} (\xi +1)^{-\alpha }$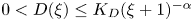 for all $\xi >0$
for all $\xi >0$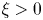 with some ${K_D}>0$
with some ${K_D}>0$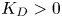 and $\alpha >0$
and $\alpha >0$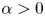 , then for all initial data from a considerably large set of radial functions on $\Omega$
, then for all initial data from a considerably large set of radial functions on $\Omega$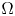 , the corresponding initial-boundary value problem admits a solution blowing up in finite time.
, the corresponding initial-boundary value problem admits a solution blowing up in finite time.