Introduction
The size and orientation of crystals in a sea-ice cover growing upon a supercooled ocean (Fig. 1) is not the same as that seen in sea ice growing away from the influence of ice shelves (Reference WeeksWeeks, 2010). We investigate the processes which affect the mass balance and crystal structure of sea ice near an ice shelf.

Fig. 1. Typical sea-ice cover and resulting crystal fabrics late in the winter close to an ice shelf. A granular ice (1) cover forms from frazil ice and grows to form columnar ice (2) which is then aligned by currents, resulting in aligned columnar ice (3). Later, platelet ice (4) is formed as the ice bottom advances into a porous matrix of large, disordered platelet crystals which form the sub-ice platelet layer. Small ice crystals float freely in the ocean beneath the ice.
In most circumstances, sea ice forms first by the consolidation of frazil crystals at the ocean surface formed by rapid loss of heat to the cold air, then by conduction of heat from the ice/water interface to the atmosphere. Heat is transferred from the ocean upwards through the sea ice. Individual grains within the ice compete and geometric selection favours grains with horizontal c-axes, forming columnar ice. Further selection occurs and the mean grain diameter increases with depth (Reference Weeks and AckleyWeeks and Ackley, 1982). Currents below the ice also provide a growth advantage to grains whose c-axis is parallel to the current direction, forming an aligned crystal fabric (e.g. Reference Langhorne and RobinsonLanghorne and Robinson, 1986).
In the vicinity of ice shelves, which fringe 44% of the continent of Antarctica (Reference Le Brocq, Payne and VieliLe Brocq and others, 2010), supercooled water can emerge from the ice-shelf cavity. This is generated because of the pressure dependence of the freezing point of sea water. The pressure at the base of an ice shelf allows melting if High Salinity Shelf Water (HSSW) is able to enter the ice-shelf cavity. This produces less saline water which rises, reducing its pressure and causing its freezing point to increase (e.g. Reference Foldvik and KvingeFoldvik and Kvinge, 1974). This water may become supercooled as it rises. Supercooling of this Ice Shelf Water (ISW) is relieved through the formation of frazil crystals (Reference Williams, Jenkins, Determann, Jacobs and WeissWilliams and others, 1998; Reference Holland and FelthamHolland and Feltham, 2005). By the end of winter the ocean below regions of sea ice adjacent to ice shelves can be supercooled by as much as 45 mK (Reference Lewis, Perkin and JacobsLewis and Perkin, 1985). The observations of Reference LeonardLeonard and others (2011), for instance, show in situ supercooling from the surface to 40 m depth in early September 2003, with a maximum supercooling of ~20 mK. Consequently a layer of large plate-like ice crystals fused together in a porous matrix is seen below the sea ice (e.g. Reference Crocker and WadhamsCrocker and Wadhams, 1989), forming the subice platelet layer (Fig. 1). This porous layer of crystals is similar to the layers of marine ice sometimes seen below ice shelves (e.g. Reference Craven, Allison, Fricker and WarnerCraven and others, 2009), although the physical conditions below a sea-ice cover and a deep ice shelf can differ, resulting in different consolidation mechanisms and different ice fabrics (e.g. Reference Tison, Lorrain, Bouzette, Dini, Bondesan and StievenardTison and others, 1997). Sub-ice platelet layers and associated platelet ice (Fig. 1) in cores have been observed in many locations around Antarctica: in McMurdo Sound and close to the Drygalski Ice Tongue (Reference PaigePaige, 1966; Reference Jeffries, Weeks, Shaw and MorrisJeffries and others, 1993; Reference Gow, Ackley, Govoni, Weeks and JeffriesGow and others, 1998; Reference Jones and HillJones and Hill, 2001; Reference Smith, Langhorne, Haskell, Trodahl, Frew and VennellSmith and others, 2001); in fast ice attached to ice shelves along the length of the coast of the Weddell Sea (Reference Eicken and LangeEicken and Lange, 1989; Reference KipfstuhlKipfstuhl, 1991); and in East Antarctica close to the Lazarev Ice Shelf (Reference SerikovSerikov, 1963). The lower parts of sea-ice cores taken in these areas display a characteristic platelet ice texture, with bladed crystals of a range of sizes and random orientations of their c-axes. A typical ice cover with a sub-ice platelet layer is shown schematically in Figure 1.
Other observations of ice production are associated with supercooled oceans. Growth of ice crystals on suspended ropes and instruments is common (Reference Leonard, Purdie, Langhorne, Haskell, Williams and FrewLeonard and others, 2006; Reference MahoneyMahoney and others, 2011) and must occur by relief of supercooling in the water column as no other heat sink exists. Ice crystals with diameters between 10 and 25 mm have been captured by trawl nets at depths of 125 and 250 m in front of both the Amery and Filchner Ice Shelves (Reference Dieckmann, Rohardt, Hellmer and KipfstuhlDieckmann and others, 1986; Reference Penrose, Conde and PaulyPenrose and others, 1994). Short-term observations by Reference Smith, Langhorne, Haskell, Trodahl, Frew and VennellSmith and others (2001) have measured in situ supercooling of the sea water directly below a sub-ice platelet layer (such as sketched in Fig. 1) and they presented evidence that the crystals that make up the sub-ice platelet layer in McMurdo Sound achieve much of theirgrowth while attached to the base of the sea ice.
Few combined observations of the ocean, sub-ice platelet layer and sea ice are available during the winter growth season for sea ice near an ice shelf. Reference Leonard, Purdie, Langhorne, Haskell, Williams and FrewLeonard and others (2006) demonstrated that the arrival of supercooled water in McMurdo Sound is associated with an increase in the level of acoustic backscatter from the water column. They attribute this to the presence of frazil crystals. In turn they showed that these crystals are associated with the presence of a platelet ice texture in sea-ice cores. Further, Reference Purdie, Langhorne, Leonard and HaskellPurdie and others (2006) showed that supercooled water in the ocean led to a negative heat flux to the sea ice that enhanced the growth of the sea ice by contributing 10% of the total ice thickness.
Away from ice shelves, disruptions to a columnar fabric can also occur. Several authors (e.g. Reference Jeffries, Weeks, Shaw and MorrisJeffries and others, 1993; Reference Wei, Johnston and DempseyWei and others, 1995; Reference Gow, Ackley, Govoni, Weeks and JeffriesGow and others, 1998) suggest new grains are introduced to the growing sea ice from a range of sources. Reference Wei, Johnston and DempseyWei and others (1995) explain transitions between columnar and isotropic fabrics in Arctic sea ice by suggesting that small seed crystals are created through a multiplication process after collisions at the ice/water interface. Frazil formed in leads may be swept under a growing ice sheet by currents, where it becomes frozen into the ice cover (Reference Weeks, Ackley and UntersteinerWeeks and Ackley, 1986), or doublediffusion from descending plumes of cold brine around ice- stalactites may produce small ice crystals close to the plumes (Reference MartinMartin, 1974). Alternatively, seed crystals can be produced by processes remote from the sea ice and supplied to the ice/water interface directly from the ocean (Reference Dieckmann, Rohardt, Hellmer and KipfstuhlDieckmann and others, 1986; Reference Jenkins and BomboschJenkins and Bombosch, 1995; Reference Leonard, Purdie, Langhorne, Haskell, Williams and FrewLeonard and others, 2006). Whatever the source, an input of new grains will tend to depress the mean size of grains, opposing the tendency for geometric selection to increase the mean grain size (Reference KolmogorovKolmogorov, 1940; Reference Weeks, Ackley and UntersteinerWeeks and Ackley, 1986).
If small crystals are supplied from the water column we expect that the rate at which crystals leave suspension may change if levels of turbulence in the ocean change, or if there are changes in the ocean circulation (Reference Holland, Jacobs and JenkinsHolland and others, 2003; Reference Leonard, Purdie, Langhorne, Haskell, Williams and FrewLeonard and others, 2006; Reference MahoneyMahoney and others, 2011). Reference McGuinness, Williams, Langhorne, Purdie and CrookMcGuinness and others (2009) suggest that as sea ice thickens, its growth rate willslow, reducing the net amount of brine rejected to the ocean which, in turn, reduces stirring of the ocean and results in more crystals settling as turbulence is reduced. Reference Dempsey, Langhorne, Robinson, Williams, Haskell and FrewDempsey and others (2010) modelled the transition in cores from columnar ice to platelet ice by considering a flux of ice platelets from the ocean. This model, driven only by geometric factors, concludes that the formation of a subice platelet layer is determined by the relative magnitudes of the rate of advance of the ice bottom and the flux of ice crystals from the ocean.
There is considerable interest in determining Antarctic sea-ice thickness from freeboard measurement by satellites (e.g. Reference Giles, Laxon and WorbyGiles and others, 2008), yet little is known about the properties of the sub-ice platelet layer. It contributes to the buoyancy of the sea ice and so appears as a mass contribution that will be correctly determined from freeboard measurements. However, it will not be possible to determine the thickness of the sea ice or sub-ice platelet layer. Thus the mechanical strength or effective thermal conductivity of the sea ice cannot be found without knowing the thickness and solid volume fraction of the sub-ice platelet layer. The sub-ice platelet layer will also exhibit different electrical properties from those of sea water or sea ice and so will require special treatment if measured using electromagnetic sounding (Reference Haas, Lobach, Hendricks, Rabenstein and PfafflingHaas and others, 2009). The open structure of the sub-ice platelet layer facilitates melting of the layer as the ocean warms in the spring, enhances biological productivity by providing increased surface area for microorganisms to inhabit and acts as shelter from prey organisms (Reference SmetacekSmetacek and others, 1992; Reference Arrigo, Robinson and SulliVanArrigo and others, 1993).
In this paper, which completes a preliminary study presented by Reference GoughGough and others (2010), we report measurements of sea-ice thickness, salinity, sea-ice temperatures and crystallography, along with contemporaneous measurements of the underlying ocean temperature and salinity during the transition from aligned columnar growth to randomly oriented platelet ice (Fig. 1). We show that the ocean affects the heat budget, grain size and crystal fabric of the ice before a sub-ice platelet layer forms at the ice/water interface and before platelet ice can be identified in a core. We demonstrate that platelet ice is recorded in ice cores simultaneously with the establishment of a sub-ice platelet layer. For the first time, we measure the volume fraction of a sub-ice platelet layer and, by comparing the establishment of a platelet ice fabric at two sites with different growth rates, we show that slowly growing sea ice forms a sub-ice platelet layer earlier than faster-growing sea ice, in keeping with the model predictions of Reference Dempsey, Langhorne, Robinson, Williams, Haskell and FrewDempsey and others (2010). A detailed description of the oceanographic conditions and the appearance of ISW during this study is given by Reference MahoneyMahoney and others (2011).
Field Site
McMurdo Sound (Fig. 2) connects the Ross Sea to the north with the cavity below the Ross Ice Shelf to the south through Haskell Strait, a 500-600m deep channel which passes under the McMurdo Ice Shelf. In 2009, multi-year sea ice covered the southern part of the Sound and ranged from 2 to 8 m in thickness. First-year ice in the north of the Sound broke out during January 2009 and an open channel was cleared by icebreakers to reach McMurdo Station in early February. Sea ice usually forms on the surface in early March, but is often cleared away by autumn storms. In 2009, ice formed in the sheltered tanker channel Fig. 2) between 7 and 20 March. However, the fast-ice cover in the open embayment at the end of the tanker channel did not persist until 28 April. Two ice study sites were established, one situated in the mouth of the tanker channel (TC, 77°46.90’S, 166° 18.92’ E) and one in the open embayment at its end, which we refer to as Erebus Bay (EB, 77°46.55’S, 166°18.77’E). TC was 800 m south of EB. The water depth at EB was measured as 515 m and both sites were at least 12 km from the coast.

Fig. 2. Top: Our study site is located in McMurdo Sound, in the Ross Sea region of Antarctica. Floating ice shelves are grey, grounded ice or land is blue. Bottom: Synthetic aperture radar image from June 2009 showing our study sites and the sea ice in McMurdo Sound, with the area at the end of the tanker channel shown in an inset.
Two designs of temperature strings were installed during this experiment. The first design, which was used for three of the four strings, used prongs to hold the 2 mm diameter sensors away from a polycarbonate support, with wires running horizontally for a distance of 70 mm to minimize vertical heat transport in the vicinity of the thermistors. Thermistor spacing for these probes was 30 mm, with larger spacing near the top of the ice. In the second design, an oil- filled, 8 mm diameter, aluminium tube mimics the thermal properties of the expected ice cover (Reference TrodahlTrodahl and others, 2000). Sensors have vertical spacing of 100 mm. The dates of operation and configuration for each string are shown in Table 1.
Table 1. Temperature strings installed during the experiment in 2009

Thermistors were logged every 10 min using Campbell Scientific CR10X or CR3000 loggers. At the start and end of each scan, standard resistors were measured to guard against drift in the loggers. Thermistors were calibrated at the University of Otago in their housings but before mounting on their supports. An Industrial Research Ltd RT200 platinum resistance thermometer (±0.03°C) was used in ice/water or ice/brine baths maintained in the range 0 to -13°C. Some thermistors drifted from their calibration before becoming frozen into the sea ice. We use a procedure outlined in Appendix A to apply an offset to these temperature measurements. Our estimated accuracy for each string is shown in Table 1 for temperatures between 0°C and -10°C.
Sea-Ice Thickness
Ice thickness was measured approximately weekly at EB using a set of four hot-wire gauges. These comprise a 4m wire weighted with a horizontal bar, which is inserted into an auger hole and allowed to freeze in place (Reference UntersteinerUntersteiner, 1961; Reference Mahoney, Gearheard, Oshima and QillaqMahoney and others, 2009). At each measurement the wire is heated to allow it to be pulled upwards, with both the position of first resistance and the position of the ice bottom (defined in Fig. 1) being noted. We also performed thickness measurements at both sites through 50mm auger and 120mm core holes using tapes weighted with horizontal bars. Following Reference CrockerCrocker (1988), we located the lower edge of the sub-ice platelet layer by noting the first resistance encountered by the tape. We then forced the bar upwards through the sub-ice platelet layer to locate the solid ice bottom (the traditional ice thickness). We confirmed that this method locates the bottom of the subice platelet layer by drilling and coring in the field of view of an underwater video camera suspended on an L-shaped arm. Ice thickness (defined by the position of the ice bottom; see Fig. 1) measured by hot wires matched the drilled measurements well (Fig. 3). The position of first resistance did not always correspond with the sub-ice platelet layer measured through recently drilled holes with thickness tapes, suggesting that ice platelets grew on the suspended hot-wire cables. Snow accumulation at TC was measured by taking spot measurements and at EB with a grid of nine snow stakes.

Fig. 3. Ice thickness, sub-ice platelet layer thickness and snow cover at (a) the tanker channel and (b) Erebus Bay. ‘ThA’, ‘ThB’, ‘ThC’ and ‘ThV’ show the bottom determined from temperature profiles. ‘Drill’, ‘Hot wire’ and ‘Core length’ show mechanically determined thickness. ‘Snow +’ and ‘Snow −’ show the range of snow cover at a stake array. ‘Formation’ is the time the ice cover formed and remained fast. ‘Sub-ice platelet layer’ shows the thickness of the sub-ice platelet layer at the coring site. ‘Hot-wire platelets’ shows the position of first resistance felt on the hot wires at EB.
The ice thickness at the thermistor arrays was determined from hourly mean temperature profiles using the algorithm outlined in Appendix B. This ice bottom was then smoothed with a 7 day moving average. We estimate an error of ±0.01 m for this ice thickness measurement.
Temperature measurements (before correction) from thermistors within the sub-ice platelet layer were indistinguishable from ocean temperature measurements taken with a conductivity-temperature-depth (CTD) profiler within a few metres of the ice bottom (see Reference MahoneyMahoney and others, 2011). As a result, it was not possible to determine the thickness of the sub-ice platelet layer using temperature measurements alone.
Ice-thickness and snow-cover measurements are shown in Figure 3. Once deployment holes were frozen (i.e. within 7-10 days of deployment), thickness determined from temperature measurements corresponded well with drilled measurements.
Several ice cores were collected on two occasions (12 May and 29 June) at TC and fortnightly (from 12 May to 29 September) at EB. Each time, three to six full-thickness, 90mm diameter cores were taken from a previously undrilled area. As well as full-thickness cores, some bottom cores were taken to measure the salinity of the sea ice in the lowest 0.3 m. In situ temperatures were measured using an Omega 866C thermometer inserted into a 2 mm hole drilled to the middle of the core. The thickness of the sea ice and sub-ice platelet layer was measured through core holes as described above. As sections were brought to the surface they were quickly cut into 100 mm (full-thickness cores) or 30 mm (bottom cores) pieces on a wooden bench and sealed in plastic pots. On return to Scott Base these pieces were melted at room temperature and theirsalinity measured using a YSI-30 salinometer with an accuracy of ±0.1.
The mean salinities of melted core segments from 63 fullthickness cores from EB and 6 cores from TC are shown in Figure 4. The mean is calculated from all cores collected at each site through the winter, so there are more samples contributing to values at the top of the ice than at the bottom. Samples are included in the average only if the entire sample was at least 0.05 m above the bottom of the sea ice. The salinity is higher near the top of the sea ice as the ice there grew rapidly. Later the ice thickness, air temperatures and contributions from the ocean conspired to produce an almost constant growth rate (Fig. 3), and thus an approximately constant salinity profile (Reference WeeksWeeks, 2010).

Fig. 4. Average salinity profiles from (a) the tanker channel (6 cores) and (b) Erebus Bay (63 cores). Average salinity is shown in blue with one standard deviation in red. The green line shows the ±0.1m smoothed profile used when calculating heat fluxes.
Ice growth on suspended hot wires at EB was first recorded on 12 July and increased until 23 July (Figs 3 and 5a). None was recorded on 28 July. From the next visit (5 August) onwards additional ice was always present. Ice growth on longer weighted ropes hung from our oceanographic huts (Reference MahoneyMahoney and others, 2011) was first observed on 8 July, when we saw a small accretion of thumbnail-sized platelets. No further growth was observed on these weighted ropes until 4 August, when the rope had not been visited since 29 July.

Fig. 5. (a)Observations of platelet ice growth on hot wires suspended below the ice cover at EB. (b) Residual (oceanic) heat flux, Fw, from TC (ThA: red) and EB (ThB: green, ThV: light blue and ThC: blue). Errors are indicated by width of the coloured swath. (c) Isotropy parameter from c-axis measurements at TC (red) and EB (blue). I = 0 for clustered or aligned fabrics, and approaches 1 for isotropic fabrics. (d) Rate of change of grain size, dD n /dz, from 10 cm depth bins of Dn . Values from thick sections are shown as squares, and from thin sections as circles. TC in purple/red and EB in light blue/blue. A dashed grey line shows the expected value of Reference Weeks, Ackley and UntersteinerWeeks and Ackley (1986) for thin Arctic sea ice. (e) Potential supercooling in the ocean from measured temperature and salinity at 50m. (f) Thickness at TC (red) and EB (blue).
No sub-ice platelet layer was detected at EB through drill or core holes until 4 August, when a 0.02 m layer was detected. Small thumbnail-sized platelets were also seen protruding from the otherwise cellular ice bottom on 4 August. From 1 September the interface became distinctly rough and platelets a few centimetres in diameter, probably broken away from the sub-ice platelet layer by coring, were seen in most core holes.
While fewer measurements were made at TC, drill measurements until 16 July found no sub-ice platelet layer. A down-hole camera, deployed on 28 July at a site 3 km south of TC through sea ice with a similar snow cover and formation history, showed a 0.10 m layer of sharply bladed platelets attached to the bottom of the sea ice, while none were seen on the same day at EB, suggesting that a sub-ice platelet layer formed earlier at TC than EB.
Heat Flux
By considering the energy balance for a small layer of ice near the bottom of the growing sea-ice cover, we calculate a residual flux, Fw, which is not accounted for by conductive heat transfer through the sea ice to the air, internal cooling of the sea ice or phase changes at the ice bottom or within the sea ice. This can be identified as an oceanic heat flux, and can be determined using ice temperatures and growth- rate measurements by employing a residual method (Reference McPhee and UntersteinerMcPhee and Untersteiner, 1982; Reference Purdie, Langhorne, Leonard and HaskellPurdie and others, 2006). We select a reference layer close to the ice bottom, but above the likely influence of convective heat transport in the ‘mushy’ skeletal layer (Reference Wettlaufer, Worster and HuppertWettlaufer and others, 1997). We assume that sea ice is created at the temperature of that layer until we move our reference layer downwards to compensate for further ice growth. The energy balance of our reference layer can be split into four components:

where

is the conductive heat flux, with thermal conductivity, K si(ρ, S, T), given by Reference Pringle, Eicken, Trodahl and BackstromPringle and others (2007), T the sea- ice temperature and z a vertical coordinate;

is the latent heat flux, where L si(S, T) is the latent heat, given by Reference YenYen (1981) with a typographical error in one term corrected as described by Reference Pringle, Eicken, Trodahl and BackstromPringle and others (2007), H is the position of the ice bottom and t is time; and

is the specific heat required to cool the reference layer. The specific heat capacity, C si(S, T), is given by Reference YenYen (1981). This small correction is necessary before we move our reference level downwards at the next time-step because the advance of isotherms through this reference layer cools this layer slightly below its formation temperature.
F w, the oceanic heat flux, is the residual. Upward heat fluxes, warming and melting have positive sign, and z and H decrease from zero at the snow/ice interface.
At an ice/water interface heat is transferred by both conduction within the solid ice and by convection of brine through the permeable skeletal layer. As we do not account for convection in our energy balance, we must solve the balance at a point in the sea ice where convection is unlikely to be important. This should occur where the bulk salinity of the sea ice has reached a stable value (Reference Petrich, Langhorne and SimPetrich and others, 2006). Comparing the salinity of our bottom cores with that measured in later full-thickness cores we located this horizon, which occurred 0.15m above the ice bottom, and we use this as the level at which we solve the energy balance.
We find H, the position of the ice bottom, and dH/dt from the ice thickness determined from temperature profiles (Appendix B), and thus set our reference level z r = H +0.15. We find the temperature, T, and dT/dz for our reference layer using a linear fit to all thermistors within ±0.1 m of z r. dT/dt is determined from T at the same level in the previous and following time-steps. We find the salinity, S, from a smoothed mean about z r, as shown in Figure 4. Stepping in discrete time-steps of Δt we grow a portion of ice at our reference level of thickness |Δt dH/dt| with temperature T and salinity S. We take ρ as 934 kgm-3 throughout. This is near the top of the range reviewed by Reference Timco and FrederkingTimco and Frederking (1996), and was calculated using isostatic balance from a number of widely separated drillholes in snow-free ice a few kilometres north of EB in November.
In Figure 6 we show F c, F 1 and F s for all temperature strings. The thicker snow and ice cover at TC is evident in smaller F 1 and F c than at EB in June and July. Variation between temperature strings at EB is consistent with variations in snow cover. The residual, F w, is displayed i n Figure 5b. Mean values of the residual heat flux vary between (5 ± 6) and (-15± 10) Wm-2 in May, and settle to between (-6.0±2.0) and (-10.6 ± 2.0)Wm-2 by September, with less variation after mid-August. We calculate the fraction of ice growth not accounted for by heat conducted to the atmosphere These, averaged over month-long periods, are shown in Table 2.

Fig. 6. Daily heat fluxes calculated 0.15m above the ice bottom from temperature strings at TC (red) and EB (others). F c is the heat conducted upwards through the ice. F l is the latent heat required to form the thickness of sea ice added. Fs accounts for internal cooling at our reference level. Errors are indicated by the width of the coloured swatch, which is smaller than the line thickness for F s, which is also always close to zero.
Table 2. Ice growth at EB in 2009

It is important to note that F w is not always a true heat flux. When F w is negative, it may be a consequence of a flow of heat from the sea ice to the ocean locally. Alternatively, it may appear in the form of latent heat through the accumulation of ice crystals from the ocean and these may have formed elsewhere. The most likely scenario is a mixture of both processes.
Sea-Ice Structure
Near the end of the field experiment a series of full-depth cores was taken from both sites and these were used to analyse ice structure. An azimuth was marked on the cores, and care was taken to record the alignment between breaks in the core. Cores were processed in a cold laboratory at Scott Base at -22°C. Thick (8-9 mm) sections were cut horizontally and vertically, and thin (<0.5 mm) sections prepared from these using a microtome. Crystal c-axis orientation measurements were made from the thin sections at a range of depths using a universal stage, as described by Reference LangwayLangway (1958). Crystals were selected for measurement using a 10 mm grid, with ~60 measurements made for each thin section. All thick and thin sections were photographed shortly after preparation under four distinct orientations between the sample and the direction of crossed polarizing filters. Examples from EB and TC are shown in Figure 7.

Fig. 7. Left: Horizontal thin and vertical thick sections from TC. Vertical sections from 102 to 172 cm depth. Middle: c-axis Schmidt-net plots and shape triangles for three levels formed at the same time, G: girdle, C: cluster, I: isotropic (Fig. 8). N: number of c-axis measurements, I: isotropy parameter, Dn: mean grain diameter (cm) (see text for details). TC 140 and EB 140 from 12 July, TC 150 and EB 147 from 28 July, and TC 160 and EB 157 from 9 August. Right: Vertical and horizontal thin sections from EB. Vertical sections from 122 to 175 cm. All thin sections are 90mm in diameter. Grain boundaries detected using the method in Appendix C are shown in white on the right halves of horizontal thin sections.
A number of measurements of F w in regions with and without nearby ice shelves are shown in Table 3. Away from ice shelves, small and positive fluxes contrast with our larger negative values of F w, confirming that the ocean in McMurdo Sound enhances sea-ice growth by acting as a sink for latent heat through relief of supercooling, or through the introduction of platelet ice crystals ahead of the ice bottom. Our calculation of the residual flux, F w, does not account for ice deposited in a sub-ice platelet layer until it has been incorporated into the sea ice by the advance of the ice bottom, because we cannot detect the sub-ice platelet layer with temperature measurements. This suggests that our values will underestimate both the magnitude and levels of variation in the heat flux from the ocean after early August.
Table 3. Selected measurements of wintertime oceanic heat flux under sea ice

The c-axis measurements of crystal orientations at a given level in the sea ice can be summarized using orientation tensors. Following Reference WoodcockWoodcock (1977) we consider each c-axis measurement from a given thin section as a point of unit ‘mass’ distributed on the surface of a unit sphere. We calculate normalized eigenvalues, S 1, S 2 and S 3, which are the three moments of inertia about the principal axes of the distribution of ‘mass’. Frazil, snow ice and platelet ice display a uniform c-axis distribution (S 1 ≈ S 2 ≈ S 3), columnar ice forms a horizontal girdle of c-axis directions Tanker channel (S1 ≈ S2 > S3) and current-aligned columnar ice has c-axes clustered along the current direction (S1 > S2 ≈ S3) (Reference Weeks, Ackley and UntersteinerWeeks and Ackley, 1986).
We can study the degree to which the grains in an ice cover are clustered using the isotropy, I = S 3/S 1, and elongation, E =1 - (S 2/S 1), parameters as defined by Reference BennBenn (1994). I varies from 0 for girdle (columnar) and clustered (aligned) fabrics to 1 for uniform (platelet) fabrics. E varies from 0 for girdle and uniform fabrics to 1 for clustered fabrics. Plots of these parameters as shape triangles are shown for selected thin sections in Figure 7 and are summarized for both sites in Figure 8. As deeper sea ice was sampled, c-axis orientations at TC followed a simple trajectory from an aligned columnar fabric to an isotropic fabric. However, in the faster-growing ice at EB, c-axis orientations followed a complicated path. Close to the snow/ice interface fabrics were those of well- aligned columnar ice, but at a depth of 1.40 m these tended towards isotropic fabrics. Following this, the fabric became columnar and partially aligned by 1.50m, before returning towards isotropic once again.

Fig. 8. Shape triangles for TC (left) and EB (right). Depth of each thin section is indicated by its colour. Elongation, E, is high for aligned fabrics, but low otherwise. Isotropy, I, is high for isotropic fabrics, but low otherwise. TC evolves in a simple way with depth, while EB follows a complicated path on the diagram.
In Figure 5c the isotropy parameter, I, is shown for 11 sections from one core at TC and 30 sections from three cores at EB. Depth into the sea ice is converted to time of formation by interpolating drilled thickness measurements from Figure 3, giving an error of ±2 days.
Inspection of horizontal thin sections suggests that the ice cover was composed of strongly aligned columnar growth by May, the start time for Figure 5c. Both sites then exhibit columnar or aligned columnar fabrics during June and early July as thicknesses approach 1.40 m. In mid-July, crystal orientations at both sites become more isotropic (Fig. 7). At TC this situation persisted into August (1.50 and 1.60 m) with a random distribution of c-axes, as shown in Schmidt- net plots in Figures 7b and c and 8. Conversely, at EB the ice returned to an aligned columnar fabric with high E values by 28 July (1.47 m; Figs 7e and 8), with alignment matching the current direction in late June of ~110° (west or northwest). By early August (1.57 m), order in the crystal structure had been disrupted, and an isotropic fabric restored.
Grain boundaries in photographs of horizontal thick and thin sections were detected using an algorithm described in Appendix C. This procedure does not detect grains smaller than 5 mm2 but serves to adequately trace depth-dependent changes in the size of grains larger than this. Examples of detected grain boundaries are displayed in Figure 7.
From these grain boundaries we calculate a mean linear grain size, Dn , using a method outlined in Appendix C. We then group sections in 0.1 m depth intervals and average Dn values for thin and thick sections separately. Figure 9 shows these averaged values with the central depth of each bin converted to time by interpolating thickness measurements from Figure 3. In all, 11 thin and 83 thick sections from one core at TC were analysed, and 32 thin and 108 thick sections from four cores at EB. Thin sections yield different mean grain sizes from thick sections, as the thick sections include more grains and produce weaker contrast between grains for the grain-detection algorithm. Thus grain-size comparisons should be made within one type of section only.

Fig. 9. Mean grain sizes, Dn, for both sites. Values calculated from thin or thick horizontal sections and averaged in 10 cm depth bins, before converting depth into time of formation.
Reference Weeks, Ackley and UntersteinerWeeks and Ackley (1986) examined the grain-size measurements of Reference WeeksWeeks (1958), Reference Tabata and OnoTabata and Ono (1962) and Reference Weeks and HamiltonWeeks and Hamilton (1962), and determined a relationship for the mean diameter, ![]() of grains with horizontal dimensions l and w, as a function of depth in a growing ice cover. For the first 0.6 m of growth in the columnar zone, they found that
of grains with horizontal dimensions l and w, as a function of depth in a growing ice cover. For the first 0.6 m of growth in the columnar zone, they found that ![]() increases with depth, z, as
increases with depth, z, as ![]() If the sea ice in our study grew in the same conditions as thin Arctic fast ice, we would expect a similar relationship to hold for our Dn
values and so plot dD
n
/dz = (D
n
(z) - Dn
(z - 0.1))/0.1 for both sites in Figure 5d. We expect a dD
n
/dz value of 0.035. For the EB site this indeed occurred in early May, when the sea ice was <0.5 m thick, but we then observed a period when episodes of increasing grain size (dD
n
/dz > 0) were followed by an influx of small crystals (dD
n
/dz < 0), so that our grains never grew to the sizes reported by Reference Weeks, Ackley and UntersteinerWeeks and Ackley (1986). Eventually the grain size reached an approximately constant value and the dD
n
/dz values clustered around zero. For the slower- growing TC site, at depths greater than 1.2 m, the behaviour was less complex, with no periods when the rate of increase of grain size approached 0.035, and a reduced spread of values in June and July. Reference Weeks, Ackley and UntersteinerWeeks and Ackley (1986) caution that one should not expect a linear increase in grain size through the whole thickness of the sea ice, especially where frazil from leads might be swept under the ice cover and seed new grains. We believe that a dD
n
/dz value close to 0 provides evidence that new grains are incorporated into the ice cover.
If the sea ice in our study grew in the same conditions as thin Arctic fast ice, we would expect a similar relationship to hold for our Dn
values and so plot dD
n
/dz = (D
n
(z) - Dn
(z - 0.1))/0.1 for both sites in Figure 5d. We expect a dD
n
/dz value of 0.035. For the EB site this indeed occurred in early May, when the sea ice was <0.5 m thick, but we then observed a period when episodes of increasing grain size (dD
n
/dz > 0) were followed by an influx of small crystals (dD
n
/dz < 0), so that our grains never grew to the sizes reported by Reference Weeks, Ackley and UntersteinerWeeks and Ackley (1986). Eventually the grain size reached an approximately constant value and the dD
n
/dz values clustered around zero. For the slower- growing TC site, at depths greater than 1.2 m, the behaviour was less complex, with no periods when the rate of increase of grain size approached 0.035, and a reduced spread of values in June and July. Reference Weeks, Ackley and UntersteinerWeeks and Ackley (1986) caution that one should not expect a linear increase in grain size through the whole thickness of the sea ice, especially where frazil from leads might be swept under the ice cover and seed new grains. We believe that a dD
n
/dz value close to 0 provides evidence that new grains are incorporated into the ice cover.
Observations In The Ocean
Heated huts were placed on the ice 300 m north of EB, where holes were melted and kept open to allow access to the ocean. Using a back-lit camera system developed during the experiment (Fig. 10), we observed small suspended ice crystals in the ocean down to 25 m from our first observation on 6 June until the end of the experiment (20 October). Most crystals observed in the water column at EB had a diameter less than 5 mm, but a few larger crystals were sometimes observed. The camera configuration is shown in Figure 10 along with frames from 23 July. Full videos are available from http://youtu.be/4BT6ehbtEKo and http://youtu.be/PRe0zwlm_ME

Fig. 10. (a) Camera configuration to image scatterers in the water column. The camera sees crystals and other scatterers in the volume where the light cone intersects the camera’s field of view (FOV). A laser beam is set up a known distance from the camera and aligned perpendicular to the camera’s field of view to allow the size of objects illuminated by the laser to be determined. Resulting images are 58 cm wide in the plane of the laser beam. The system can be suspended horizontally from floats under the sea ice, or vertically on a weighted rope deeper in the ocean. (b) Camera suspended horizontally 0.5m below the sea ice looking towards one of our holes. A small crystal (circled) has drifted into the path of the laser beam and has a diameter of 5mm. (c) Camera hanging vertically, looking upwards, at a depth of 23m. The larger crystal (circled) is at least 25mm × 16mm. Both images were captured on 23 July.
An oceanographic mooring was installed 500 m south of TC from July to September (see Reference MahoneyMahoney and others, 2011, for details). In this paper we include data from one of the instruments. At 50 m an unpumped Sea-Bird Electronics SBE-37 (MicroCAT) recorded conductivity, temperature and pressure at 10 min intervals, with an accuracy of ±0.002°C in temperature and ±0.004 in salinity.
From measurements of ocean temperature and pressure we calculate the potential temperature, θ. From recorded salinity and pressure, we calculate T fs the freezing point at the surface, using the standard algorithms adopted by UNESCO (Reference Fofonoff and MillardFofonoff and Millard, 1983). Our error in θ is ±0.005°C, and in T fs is ±0.003°C. In Figure 5e we plot a 1 day running mean of θ - T fs the potential supercooling. In June and early July, θ varies about its surface freezing point. After late July the ocean at 50 m is persistently below its surface freezing point, implying contact with an ice shelf and suggesting the presence of in situ supercooled water near the ocean surface below the sea-ice cover. In this time period, 280 full-depth CTD casts were taken in McMurdo Sound and confirm this interpretation of the mooring data. These oceanographic measurements are explored in more detail by Reference MahoneyMahoney and others (2011).
Transition From Columnar Ice
In early July we observe a transition from an ordered columnar fabric to a disordered fabric at 1.40m in the EB cores (Fig. 7d). If there was not a strong source of seed crystals from the ocean to cause this change in the sea ice then we would expect the columnar fabric to persist at 1.40 m. Following this disruption at 1.40 m a columnar fabric was reestablished by 1.50 m (Fig. 7e), without a significant change in the growth rate of the sea ice (Fig. 3). It is therefore unlikely that the rate of brine rejection from the sea ice changed, so levels of stirring through brine rejection would be constant as the ice grew from 1.40 to 1.50 m. This suggests that changes in the oceanic conditions are responsible for changes in the ice cover, and not forcing from the ice cover as postulated by Reference McGuinness, Williams, Langhorne, Purdie and CrookMcGuinness and others (2009).
At TC the mean grain size changed little after June, the first time for which we have grain-size measurements from TC, and dD n /dz ≈ 0 for the entire period for which we have measurements. This suggests that the rate at which new seeds are supplied to the ice is high enough, relative to the rate of growth of the ice bottom, that individual grains are not able to expand in area before being interrupted by new grains.
At EB, where the ice was growing faster, the behaviour is more complicated (Fig. 8). During May and June, when the ocean below the sea ice was only occasionally cooled below its surface freezing point (Reference MahoneyMahoney and others, 2011) and no growth was detected on suspended hot wires (Fig. 5e and a), the mean grain size, D n , sometimes decreased and sometimes increased (Fig. 9). This suggests that there are both periods when new grains are introduced to the growing ice sheet at a rate which partially resets the effects of geometric selection, and periods when the rate at which new grains are introduced is low enough for geometric selection to occur (Reference Dempsey, Langhorne, Robinson, Williams, Haskell and FrewDempsey and others, 2010). We believe this was not observed at TC because the ice there was always growing at a slower rate (Fig. 3), and so this episodic signal was not resolved. This episodic signature in the sea ice may reflect a variable presence of small ice crystals in the water column. Reference Leonard, Purdie, Langhorne, Haskell, Williams and FrewLeonard and others (2006), in a winter-long study in McMurdo Sound, described episodic changes in the strength of backscatter from an acoustic Doppler current profiler, which they deduced were due to variations in the number and/or size of crystals in the water column.
Platelet Ice
We also observe disruption to the crystal fabric when a subice platelet layer forms below the sea ice. During periods of greater or sustained supercooling, some grains, either newly seeded or already present, gain a growth advantage putting them slightly further from the ice/ocean interface than their neighbours. This allows them to grow beyond the base of the ice by relieving some of the supercooling (Reference Smith, Langhorne, Haskell, Trodahl, Frew and VennellSmith and others, 2001), while their peers are shrouded by the boundary layer which is held at the ice/sea-water freezing point. These crystals, the vanguard of a sub-ice platelet layer, will also shield the remaining grains from the effects of current alignment by increasing drag and increasing the depth of the boundary layer, effectively decoupling the ocean from the grains at the ice bottom (Fig. 1). This process is seen in our cores in early July (1.45 m) at TC and in early August (1.57 m) at EB, where I → 1 implies we no longer see aligned columnar fabrics (Fig. 5c). However, the transition from columnar to platelet ice is not the same at both sites.
At TC the crystal fabric was initially typical of columnar ice but became isotropic (I → 1) in mid-July, at about the same time as the ocean at 50 m depth dropped to a temperature persistently below its surface freezing point (Fig. 5e). This indicates that a sub-ice platelet layer may have formed at TC in mid-July and remained for the rest of the winter.
Similarly at EB, in mid-July, the crystal fabric became isotropic (I → 1) and the mean grain size was constant (dD n /dz → 0). This was also when ice growth was first detected on suspended hot wires (Fig. 5a). However, after this disruption, a columnar fabric returned (I → 0) and even became aligned (E → 0) towards the end of July (Fig. 5c). We can speculate that a temporary sub-ice platelet layer had formed at EB but was overtaken by conductively driven growth of the ice bottom in late July. After early August, an isotropic fabric dominates (I → 1) again, and the texture finally became characteristic of platelet ice in late August (Fig. 7). This was when we first detected a sub-ice platelet layer below the ice at EB using thickness tapes (Fig. 3), a layer that persisted until the end of winter.
Thus we need to explain why a sustained sub-ice platelet layer, and hence incorporated platelet ice, was established earlier in the ice at TC than at EB, when both were subject to the same oceanic conditions. As suggested by Reference Dempsey, Langhorne, Robinson, Williams, Haskell and FrewDempsey and others (2010), there is clearly a competition between the growth rate forced by conduction of heat away from the base of the sea ice and the rate at which a few crystals at the base of the ice can outpace others in response to supercooling in the ocean. It seems likely that the thicker snow cover at TC (Fig. 3) sufficiently reduced the conductive growth rate of the sea ice there, that by mid-July it had established a sub-ice platelet layer. Consequently, platelet ice formed in late July. Over the same time period at EB the thinner snow cover meant that conductive growth caused the ice bottom to advance beyond the thin sub-ice platelet layer that may have grown, so all grains could again participate in geometric selection and be exposed to current-driven alignment, forming columnar and aligned columnar ice.
The Sub-Ice Platelet Layer
Let us postulate that two modes of sea-ice growth are possible when Fw is negative. In the first mode, columnar or aligned columnar sea ice grows and simply gains extra thickness from the oceanic heat flux, which could be provided in the form of crystals floating up from the ocean, or through relief of supercooling at the ice bottom (Fig. 1). In the second mode, a sub-ice platelet layer forms ahead of the ice bottom either through accumulation of platelet crystals from the water column or as supercooling is relieved to increase the size of smaller seed grains. The sub-ice platelet layer is incorporated into the ice cover by growth in its interstices to form platelet ice. We believe that the following analysis holds if Fw is a true heat flux, or if it is provided in the form of a flux of ice crystals, or a combination of both. The measurements in this study and those of Reference Leonard, Purdie, Langhorne, Haskell, Williams and FrewLeonard and others (2006) suggest that a flux of small crystals exists, but that most growth due to Fw occurs at the ice bottom or, later in the growth season, at the lower edge of the sub-ice platelet layer (Reference Smith, Langhorne, Haskell, Trodahl, Frew and VennellSmith and others, 2001).
If we assume that a sub-ice platelet layer has a solid volume fraction of (β, that Fw is used to generate the leading edge of the sub-ice platelet layer (the growth of individual platelet crystals), that Fc is used to fill the interstices in the sub-ice platelet layer (consolidation), that both the sub-ice platelet layer and bulk sea ice are composed of sea ice with the same energy of formation, E = ρL, and that Fs can be neglected, then in the first (columnar) mode, the ice bottom grows at a rate of

For the second mode in which a sub-ice platelet layer can grow, the sub-ice platelet layer advances at a rate of

while the ice bottom advances at a rate of

A sub-ice platelet layer will exist if the sub-ice platelet layer growth rate is faster than the sea-ice growth rate (Reference Dempsey, Langhorne, Robinson, Williams, Haskell and FrewDempsey and others, 2010). So, noting that R is a negative quantity, a sub-ice platelet layer will exist if

leading to

Thus, as long as sub-ice platelet layers everywhere are the same, platelet ice, seen in ice cores, is evidence of -F w/F c exceeding this ratio.
In reality, the porous sub-ice platelet layer is connected to the ocean, so if growth is due to relief of supercooling we might expect some supercooled water to penetrate the layer and perhaps increase the rate at which the congelation growth interface can advance, especially if the sub-ice platelet layer is thin. This will reduce the effective value of F w and increase the effective value of F c, making a sub-ice platelet layer form for larger values of F w than would be predicted here. We also assume that none of the growth of the sub-ice platelet layer is due to heat conducted upwards from the sub-ice platelet layer, which may occur once the sub-ice platelet layer has become established. Within the accuracy of our temperature measurements we were not able to detect a temperature gradient within the sub-ice platelet layer, so we believe that neither of these processes was very important in our case, once the sub-ice platelet layer became established.
For slowly growing multi-year ice with a thick snow cover, F c will be small, so a sub-ice platelet layer will establish itself as soon as F w becomes negative. For more rapidly growing first-year ice, such as the just-formed pack at the edge of a polynya, F c will be large, so although there might be a significant flux of heat to the ocean, a sub-ice platelet layer will not form and evidence of this will not be recorded in the sea-ice crystal structure as platelet ice.
During winter 2009 a sub-ice platelet layer formed below the sea ice at EB in early August when the ice cover was ~ 1.65 m thick (Fig. 3), and caused the ice to form an isotropic platelet fabric as it grew into this matrix of pre-existing crystals. During September, when a sub-ice platelet layer was always present, our measurement of the residual flux did not represent the value of Fw experienced by the leading edge of the sub-ice platelet layer, but instead measured the volume fraction of the sub-ice platelet layer being captured by the advancing ice bottom. In effect, we only accounted for the latent heat of the ice in the sub-ice platelet layer once the conductive flux had caused it to become consolidated by the advancing ice bottom.
After the establishment of a sub-ice platelet layer, the residual heat flux was consistently negative (downwards) with F w = -10 ± 2 W m-2, F 1 = -40 ± 1 W m -2, |F s| < 0.1W m-2 and F c = 30 ± 1W m-2 (Fig. 6). If we assume that our measured Fw accounts for the ice present in the subice platelet layer with an ice volume fraction of β and if F c accounts for all sea ice that forms in the interstices of the sub-ice platelet layer then, from above,

giving β =0.25 ± 0.06. We assume that none of the latent heat released by the advancing sub-ice platelet layer is conducted to the atmosphere through the sea ice and this may underestimate the solid volume fraction of the sub-ice platelet layer. If the sub-ice platelet layer is hydraulically connected to the ocean and so forms ice by relieving supercooling internally as well as at its leading edge, then this value will only be representative of the volume fraction of ice in established sub-ice platelet layers. The volume fraction in the sub-ice platelet layer close to the ocean may be lower. If voids within the sub-ice platelet layer were filled by freezing due to the relief of supercooling, then our value of β will be an overestimate. Few estimates of the sub-ice platelet layer’s physical properties exist, as it is difficult to sample. We summarize previous estimates of the sub-ice platelet layer ice volume fraction in Table 4, our result being the most precise to date.
Table 4. Selected estimates for the ice volume fraction of a sub-ice platelet layer

Conclusion
Simultaneous measurements of the ocean and the sea ice have been made over the winter sea-ice growth season, including frequent observations of the state of the ice/water interface and detailed measurements of the sea-ice crystal structure. We have documented the various stages of sea- ice growth in regions where supercooled water, formed by the outflow of ISW from the Ross and McMurdo Ice Shelf cavities, is present below the sea ice. These processes probably extend for 200 km beyond the ice shelves that form much of the coastline of Antarctica (Reference Stevens, Robinson, Williams and HaskellStevens and others, 2009), and models of sea ice or the ocean should strive to include them.
Using multiple thermistor strings we measured a residual heat flux which varied between (5 ± 6) and (-15 ± 10) Wm-2 in May. By September this flux had settled to between (-6.0 ± 2.0) and (-10.6 ± 2.0) W m-2. In total, 12% of the ice grown from June to September was not accounted for by heat conducted to the atmosphere. Using heat flux measurements combined with observations of the state of the ice/water interface we measured an ice volume fraction, β, of 0.25 ± 0.06 in the sub-ice platelet layer.
By comparing the establishment of a sub-ice platelet layer at two sites, we have demonstrated that a sub-ice platelet layer forms below the sea ice once the ratio of the oceanic heat flux to the conductive heat flux exceeds a critical value that depends on the solid volume fraction of the sub-ice platelet layer (Eqn (9)). This led to the incorporation of platelet ice fabrics into the sea-ice cover with an isotropy parameter I → 1.
Nonetheless, we supply evidence that the sea ice was affected by the ocean beneath it before the formation of a sub-ice platelet layer and before a platelet ice fabric emerged. For example, at EB in June and July a columnar fabric was recorded with I → 0, in spite of the fact that 5% of the ice growth was not due to heat conducted to the atmosphere. However, at this time small ice crystals were observed in the water column and these interfered with geometric selection, causing the grain size in the columnar ice to be held at a constant value.
In Antarctic first-year landfast sea ice, platelet ice is the signature of sustained supercooling and sustained negative oceanic heat fluxes. However, we have demonstrated that a columnar fabric results when as much as 5% of the ice growth was caused by heat transferred to the ocean. The effects of ice-shelf-conditioned water may therefore spread further than has been previously suspected based on observations of platelet ice in ice cores. In areas where sea ice grows slowly, such as multi-year sea ice or where there is a thick snow cover, much of the ice volume gained in the winter may be in the form of a sub-ice platelet layer.
Since the sea-ice cover contains a signature of the past states of the near-surface ocean, our study highlights the need to understand the freezing process of sea ice in very cold, ice-shelf affected waters.
Acknowledgements
This work, a part of New Zealand’s contribution to the International Polar Year, was funded by the Foundation for Research Science and Technology, the University of Otago, Industrial Research Ltd and the National Institute of Water and Atmospheric Research Ltd. A.J.G. was supported by a University of Otago Postgraduate Scholarship. We are grateful to Antarctica New Zealand for logistical support and Myles Thayer, Richard Sparrow and Peter Stroud for help constructing instruments. We thank Brian Staite and the Scott Base 2009 winter team for field support, Wolfgang Rack for supplying RADARSAT imagery for Figure 2, Joe Trodahl for some temperature data, and Craig Stevens and Craig Stewart for help with the mooring. The comments of two anonymous reviewers significantly improved the paper.
Appendix A: Thermistor Drift Correction
We use a two-pass method to correct drift in our thermistor calibrations. In the first pass we determine a tentative position for the freezing front (Appendix B) using uncorrected temperatures, T*. At each time-step thermistors are marked as being in the ocean (those >7 cm below the ice bottom) or not in the ocean (all other thermistors). We then calculate the mean ocean temperature, T ocean, from those thermistors marked as being in the ocean and calculate an offset, δth, for each thermistor so that the corrected temperature T th = T ocean = Tth* + δth Once a thermistor is no longer marked as being in the ocean, we continue to apply the offset we calculated for that thermistor when it was last labelled as being in the ocean. In the calculations of heat fluxes that we have described, we only use thermistors which are close to the freezing front of the sea ice, so we have not corrected the drift of thermistors after they are frozen into the sea ice.
Appendix B: Ice Thickness From Temperature Profiles
The location of the freezing front is found by applying the following procedure to a temperature profile. For each profile the thermistors are divided into trial ocean and trial ice groups. The process starts with all thermistors in a trial ice group. An attempt is made to fit a temperature profile. At each attempt, a linear profile is fitted to the four ice thermistors nearest the ocean and T ocean is determined from the average of all thermistors in the ocean group. If no thermistor is in the ocean group the last measured T ocean or -1.9°C is used. If the linear fit to the ice thermistors intersects T ocean between the lowest ice and highest ocean thermistor, within ±0.01 m, then this intersect is used as the ice thickness. If unsuccessful, the lowest thermistor in the ice group is moved to the ocean group and the test repeated.
Appendix C: Grain Boundaries
Grain boundaries in digital images of thin and thick sections were detected using an algorithm developed for terrestrial ice cores by Gay and Weiss (1999), modified by Durand and others (2006) and adapted here for images of sea-ice sections. A series of colour images, taken under different orientations between the sample and cross-polarizing filters, were first co-registered then downscaled to a resolution of 0.09 mm pixel-1. Edges are then detected in each colour channel of each image. As sea ice contains brine inclusions, refrozen brine channels and sloping grain boundaries, we first apply an eight-pixel wide opening, closing and median filtering operator. The MatlabTM implementation of the Canny method (Canny, 1986) is used to detect edges using a threshold of 0.20 for all thin sections and a threshold between 0.16 and 0.24 for thick sections. These values were chosen manually to best select the largest grains. A larger threshold reduces the number of boundaries found. Finally the channel is skeletonized, and edges summed from each channel and each image. Open edges are then pruned. As the algorithm is difficult to tune for small grains, we have chosen these parameters to find the larger grains well.
To determine a mean linear grain size for each horizontal section, we select the largest grains from the grain-size distribution and take an average. Some sections have a smaller area, as they were taken from a core which was also used to make vertical sections, so we must select an area-weighted number of grains from which to find the mean linear grain size. We select α = 0.8grainscm-2 from each section, so that the total number, Nn , selected for each section varies from 35 to 50. The mean linear grain size for section n, Dn , is then calculated by sorting the grains by area, and finding
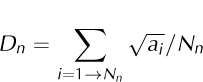
with a i the area of grain i.
















