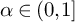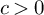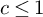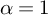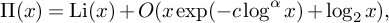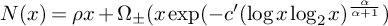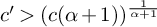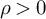1 Introduction
In this paper, we study the optimality of Malliavin-type remainders in the asymptotic density approximation formula for Beurling generalized integers, a problem that has its roots in a long-standing open question of Bateman and Diamond [Reference Bateman and Diamond2, Reference Landau13B, p. 199]. Let
![]() $\mathcal {P}:\:p_{1}\leq p_{2}\leq \dots $
be a Beurling generalized prime system, namely, an unbounded and nondecreasing sequence of positive real numbers satisfying
$\mathcal {P}:\:p_{1}\leq p_{2}\leq \dots $
be a Beurling generalized prime system, namely, an unbounded and nondecreasing sequence of positive real numbers satisfying
![]() $p_{1}>1$
, and let
$p_{1}>1$
, and let
![]() $\mathcal {N}$
be its associated system of generalized integers, that is, the multiplicative semigroup generated by 1 and
$\mathcal {N}$
be its associated system of generalized integers, that is, the multiplicative semigroup generated by 1 and
![]() $\mathcal {P}$
[Reference Bateman and Diamond2, Reference Beurling3, Reference Diamond and Zhang10]. We consider the functions
$\mathcal {P}$
[Reference Bateman and Diamond2, Reference Beurling3, Reference Diamond and Zhang10]. We consider the functions
![]() $\pi (x)$
and
$\pi (x)$
and
![]() $N(x)$
counting the number of generalized primes and integers, respectively, not exceeding x.
$N(x)$
counting the number of generalized primes and integers, respectively, not exceeding x.
Malliavin discovered [Reference Malliavin14] that the two asymptotic relations
and
for some
![]() $c>0$
and
$c>0$
and
![]() $c'>0$
, are closely related to each other in the sense that if (Nβ
) holds for a given
$c'>0$
, are closely related to each other in the sense that if (Nβ
) holds for a given
![]() $0<\beta \leq 1$
, then (P
$0<\beta \leq 1$
, then (P
![]() $_{\alpha ^{\ast }}$
) is satisfied for some
$_{\alpha ^{\ast }}$
) is satisfied for some
![]() $\alpha ^\ast $
, and vice versa the relation (Pα
) for a given
$\alpha ^\ast $
, and vice versa the relation (Pα
) for a given
![]() $0<\alpha \leq 1$
ensures that (N
$0<\alpha \leq 1$
ensures that (N
![]() $_{\beta ^{\ast }}$
) holds for a certain
$_{\beta ^{\ast }}$
) holds for a certain
![]() $\beta ^{\ast }$
. A natural question is then what the optimal error terms of Malliavin-type are. Writing
$\beta ^{\ast }$
. A natural question is then what the optimal error terms of Malliavin-type are. Writing
![]() $\alpha ^{\ast }(\beta )$
and
$\alpha ^{\ast }(\beta )$
and
![]() $\beta ^{\ast }(\alpha )$
for the best possibleFootnote
1
exponents in these implications, we have:
$\beta ^{\ast }(\alpha )$
for the best possibleFootnote
1
exponents in these implications, we have:
Problem 1.1. Given any
![]() $\alpha ,\beta \in (0,1]$
, find the best exponents
$\alpha ,\beta \in (0,1]$
, find the best exponents
![]() $\alpha ^{\ast }(\beta )$
and
$\alpha ^{\ast }(\beta )$
and
![]() $\beta ^{\ast }(\alpha )$
.
$\beta ^{\ast }(\alpha )$
.
So far, there are only two instances where a solution to Problem 1.1 is known. In 2006, Diamond, Montgomery and Vorhauer [Reference Diamond, Montgomery and Vorhauer9] (cf. [Reference Zhang16]) demonstrated that
![]() $\alpha ^{\ast }(1) = 1/2$
, while in our recent work [7] we have shown that
$\alpha ^{\ast }(1) = 1/2$
, while in our recent work [7] we have shown that
![]() $\beta ^{\ast }(1)=1/2$
. The former result proves that the de la Vallée Poussin remainder is best possible in Landau’s classical prime number theorem (PNT) [Reference Landau13], whereas the latter one yields the optimality of a theorem of Hilberdink and Lapidus [Reference Hilberdink and Lapidus12].
$\beta ^{\ast }(1)=1/2$
. The former result proves that the de la Vallée Poussin remainder is best possible in Landau’s classical prime number theorem (PNT) [Reference Landau13], whereas the latter one yields the optimality of a theorem of Hilberdink and Lapidus [Reference Hilberdink and Lapidus12].
We shall solve here Problem 1.1 for any value
![]() $\alpha \in (0,1]$
. Improving upon Malliavin’s results, Diamond [Reference Diamond8] (cf. [Reference Hilberdink and Lapidus12]) established the lower bound
$\alpha \in (0,1]$
. Improving upon Malliavin’s results, Diamond [Reference Diamond8] (cf. [Reference Hilberdink and Lapidus12]) established the lower bound
![]() $\beta ^{\ast }(\alpha )\geq \alpha /(1+\alpha )$
. We will prove the reverse inequality:
$\beta ^{\ast }(\alpha )\geq \alpha /(1+\alpha )$
. We will prove the reverse inequality:
Theorem 1.2. We have
![]() $\beta ^{\ast }(\alpha )=\alpha /(1+\alpha )$
for any
$\beta ^{\ast }(\alpha )=\alpha /(1+\alpha )$
for any
![]() $\alpha \in (0,1]$
.
$\alpha \in (0,1]$
.
Our main result actually supplies more accurate information, and, in particular, it exhibits the best possible value of the constant
![]() $c'$
in (Nβ
). In order to explain it, let us first state Diamond’s result in a refined form, showing the explicit dependency of the constant
$c'$
in (Nβ
). In order to explain it, let us first state Diamond’s result in a refined form, showing the explicit dependency of the constant
![]() $c'$
on c and
$c'$
on c and
![]() $\alpha $
. We write
$\alpha $
. We write
![]() $\log _{k} x$
for the k times iterated logarithm. The Riemann prime counting function of the generalized number system naturally occurs in our considerations;Footnote
2
as in classical number theory, it is defined as
$\log _{k} x$
for the k times iterated logarithm. The Riemann prime counting function of the generalized number system naturally occurs in our considerations;Footnote
2
as in classical number theory, it is defined as
![]() $\Pi (x)=\sum _{n=1}^{\infty }\pi (x^{1/n})/n$
. We also mention that, for the sake of convenience, we choose to define the logarithmic integral as
$\Pi (x)=\sum _{n=1}^{\infty }\pi (x^{1/n})/n$
. We also mention that, for the sake of convenience, we choose to define the logarithmic integral as
 $$ \begin{align} \operatorname{\mathrm{Li}} (x):= \int_{1}^{x} \frac{1-u^{-1}}{\log u} \mathrm{d} u. \end{align} $$
$$ \begin{align} \operatorname{\mathrm{Li}} (x):= \int_{1}^{x} \frac{1-u^{-1}}{\log u} \mathrm{d} u. \end{align} $$
Theorem 1.3. Suppose there exist constants
![]() $\alpha \in (0,1]$
and
$\alpha \in (0,1]$
and
![]() $c>0$
, with the additional requirement
$c>0$
, with the additional requirement
![]() $c\leq 1$
when
$c\leq 1$
when
![]() $\alpha =1$
, such that
$\alpha =1$
, such that
Then, there is a constant
![]() $\rho>0$
such that
$\rho>0$
such that
 $$ \begin{align} N(x) = \rho x + O\biggl\{x\exp\biggl(-(c(\alpha+1))^{\frac{1}{\alpha+1}}(\log x\log_{2} x)^{\frac{\alpha}{\alpha+1}}\biggl(1+O\biggl(\frac{\log_{3}x}{\log_{2} x}\biggr)\biggr)\biggr)\biggr\}. \end{align} $$
$$ \begin{align} N(x) = \rho x + O\biggl\{x\exp\biggl(-(c(\alpha+1))^{\frac{1}{\alpha+1}}(\log x\log_{2} x)^{\frac{\alpha}{\alpha+1}}\biggl(1+O\biggl(\frac{\log_{3}x}{\log_{2} x}\biggr)\biggr)\biggr)\biggr\}. \end{align} $$
A proof of Theorem 1.3 can be given as in [Reference Broucke, Debruyne and Vindas5, Theorem A.1] (cf. [Reference Balazard1]), starting from the identity [Reference Diamond and Zhang10]
 $$ \begin{align} \mathrm{d} N = \exp^{\ast}(\mathrm{d} \Pi) = \sum_{n=0}^{\infty}\frac{1}{n!}(\mathrm{d}\Pi)^{\ast n} \end{align} $$
$$ \begin{align} \mathrm{d} N = \exp^{\ast}(\mathrm{d} \Pi) = \sum_{n=0}^{\infty}\frac{1}{n!}(\mathrm{d}\Pi)^{\ast n} \end{align} $$
and using a version of the Dirichlet hyperbola method to estimate the convolution powers
![]() $(\mathrm{d} \Pi )^{\ast n}$
. The current article is devoted to showing the optimality of Theorem 1.3, including the optimality of the constant
$(\mathrm{d} \Pi )^{\ast n}$
. The current article is devoted to showing the optimality of Theorem 1.3, including the optimality of the constant
![]() $c' = (c(\alpha +1))^{1/(\alpha +1)}$
in the asymptotic estimate (1.3), as established by the next theorem. Note that Theorem 1.2 follows at once upon combining Theorem 1.3 and Theorem 1.4.
$c' = (c(\alpha +1))^{1/(\alpha +1)}$
in the asymptotic estimate (1.3), as established by the next theorem. Note that Theorem 1.2 follows at once upon combining Theorem 1.3 and Theorem 1.4.
Theorem 1.4. Let
![]() $\alpha $
and c be constants such that
$\alpha $
and c be constants such that
![]() $\alpha \in (0,1]$
and
$\alpha \in (0,1]$
and
![]() $c>0$
, where we additionally require
$c>0$
, where we additionally require
![]() $c\le 1$
if
$c\le 1$
if
![]() $\alpha =1$
. Then there exists a Beurling generalized number system such that
$\alpha =1$
. Then there exists a Beurling generalized number system such that
 $$ \begin{align} \Pi(x) - \operatorname{\mathrm{Li}}(x) \ll \begin{cases} x\exp(-c(\log x)^{\alpha}) &\mbox{if}\ \alpha<1\ \mbox{or}\ \alpha=1\ \mbox{and}\ c<1, \\ \log_{2}x &\mbox{if}\ \alpha=c=1, \end{cases} \end{align} $$
$$ \begin{align} \Pi(x) - \operatorname{\mathrm{Li}}(x) \ll \begin{cases} x\exp(-c(\log x)^{\alpha}) &\mbox{if}\ \alpha<1\ \mbox{or}\ \alpha=1\ \mbox{and}\ c<1, \\ \log_{2}x &\mbox{if}\ \alpha=c=1, \end{cases} \end{align} $$
and
 $$ \begin{align} N(x) = \rho x + \Omega_{\pm}\biggl\{x\exp\biggl(-(c(\alpha+1))^{\frac{1}{\alpha+1}}(\log x\log_{2} x)^{\frac{\alpha}{\alpha+1}}\biggl(1 + b\frac{\log_{3} x}{\log_{2} x}\biggr)\biggr)\biggr\}, \end{align} $$
$$ \begin{align} N(x) = \rho x + \Omega_{\pm}\biggl\{x\exp\biggl(-(c(\alpha+1))^{\frac{1}{\alpha+1}}(\log x\log_{2} x)^{\frac{\alpha}{\alpha+1}}\biggl(1 + b\frac{\log_{3} x}{\log_{2} x}\biggr)\biggr)\biggr\}, \end{align} $$
where
![]() $\rho>0$
is the asymptotic density of N and b is some positive constant.Footnote
3
$\rho>0$
is the asymptotic density of N and b is some positive constant.Footnote
3
The proof of Theorem 1.4 consists of two main steps. We shall first construct an explicit example of a continuous analog [Reference Beurling3, Reference Diamond and Zhang10] of a number system fulfilling all requirements from Theorem 1.4, and then we will discretize it by means of a probabilistic procedure. The second step will be accomplished in Section 6 with the aid of a recently improved version [Reference Broucke and Vindas6] of the Diamond–Montgomery–Vorhauer–Zhang random prime approximation method [Reference Diamond, Montgomery and Vorhauer9, Reference Zhang16]. The construction and analysis of the continuous example will be carried out in Sections 2–5.
Our method is in the same spirit as in [Reference Broucke, Debruyne and Vindas5], particularly making extensive use of saddle point analysis. Nevertheless, it is worthwhile to point out that showing Theorem 1.4 requires devising a new example. Even in the case
![]() $\alpha =1$
, our treatment here delivers novel important information that cannot be reached with the earlier construction. Direct generalizations of the example from [Reference Broucke, Debruyne and Vindas5] are unable to reveal the optimal constant
$\alpha =1$
, our treatment here delivers novel important information that cannot be reached with the earlier construction. Direct generalizations of the example from [Reference Broucke, Debruyne and Vindas5] are unable to reveal the optimal constant
![]() $c'$
in the remainder
$c'$
in the remainder
![]() $O(x\exp (-c' (\log x \log _2 x)^{\alpha /(\alpha +1)}(1+o(1))))$
of equation (1.3). In fact, upon sharpening the technique from [Reference Broucke, Debruyne and Vindas5] when
$O(x\exp (-c' (\log x \log _2 x)^{\alpha /(\alpha +1)}(1+o(1))))$
of equation (1.3). In fact, upon sharpening the technique from [Reference Broucke, Debruyne and Vindas5] when
![]() $\alpha =1$
, one would only be able to obtain the
$\alpha =1$
, one would only be able to obtain the
![]() $\Omega _{\pm }$
-estimate with
$\Omega _{\pm }$
-estimate with
![]() $c'>2\sqrt {c}$
, which falls short of the actual optimal value
$c'>2\sqrt {c}$
, which falls short of the actual optimal value
![]() $c'=\sqrt {2c}$
that we establish with our new construction. Furthermore, we deal here with the general case
$c'=\sqrt {2c}$
that we establish with our new construction. Furthermore, we deal here with the general case
![]() $0<\alpha \leq 1$
. There is a notable difference between generalized number systems satisfying equation (1.5) with
$0<\alpha \leq 1$
. There is a notable difference between generalized number systems satisfying equation (1.5) with
![]() $\alpha =1$
and those satisfying it with
$\alpha =1$
and those satisfying it with
![]() $0<\alpha <1$
. In the latter case, the zeta function admits, in general, no meromorphic continuationFootnote
4
beyond the line
$0<\alpha <1$
. In the latter case, the zeta function admits, in general, no meromorphic continuationFootnote
4
beyond the line
![]() $\sigma =1$
, which a priori renders direct use of complex analysis arguments impossible. We will overcome this difficulty with a truncation idea, where the analyzed continuous number system is approximated by a sequence of continuous number systems having very regular zeta functions in the sense that they are actually analytic on
$\sigma =1$
, which a priori renders direct use of complex analysis arguments impossible. We will overcome this difficulty with a truncation idea, where the analyzed continuous number system is approximated by a sequence of continuous number systems having very regular zeta functions in the sense that they are actually analytic on
![]() $\mathbb {C}\setminus \{1\}$
.
$\mathbb {C}\setminus \{1\}$
.
We conclude this introduction by mentioning that determining the best exponent
![]() $\alpha ^{\ast }(\beta )$
from Problem 1.1 remains wide open for
$\alpha ^{\ast }(\beta )$
from Problem 1.1 remains wide open for
![]() $0<\beta <1$
. Bateman and Diamond have conjectured that
$0<\beta <1$
. Bateman and Diamond have conjectured that
![]() $\alpha ^{\ast }(\beta )=\beta /(\beta +1)$
. The validity of this conjecture has only been verified [Reference Diamond, Montgomery and Vorhauer9] for
$\alpha ^{\ast }(\beta )=\beta /(\beta +1)$
. The validity of this conjecture has only been verified [Reference Diamond, Montgomery and Vorhauer9] for
![]() $\beta =1$
. It has recently been shown [Reference Broucke4] that
$\beta =1$
. It has recently been shown [Reference Broucke4] that
![]() $\alpha ^{\ast }(\beta )\leq \beta /(\beta +1)$
. However, the best-known admissible value [Reference Diamond and Zhang10, Theorem 16.8, p. 187] when
$\alpha ^{\ast }(\beta )\leq \beta /(\beta +1)$
. However, the best-known admissible value [Reference Diamond and Zhang10, Theorem 16.8, p. 187] when
![]() $0<\beta <1$
is
$0<\beta <1$
is
![]() $\alpha ^{*}\approx \beta /(\beta + 6.91)$
, which is still far from the conjectural exponent.
$\alpha ^{*}\approx \beta /(\beta + 6.91)$
, which is still far from the conjectural exponent.
2 Construction of the continuous example
We explain here the setup for the construction of our continuous example, whose analysis shall be the subject of Sections 3–5. Let us first clarify what is meant by a not necessarily discrete generalized number system. In a broader sense [Reference Beurling3, Reference Diamond and Zhang10], a Beurling generalized number system is merely a pair of nondecreasing right continuous functions
![]() $(\Pi ,N)$
with
$(\Pi ,N)$
with
![]() $\Pi (1)=0$
and
$\Pi (1)=0$
and
![]() $N(1)=1$
, both having support in
$N(1)=1$
, both having support in
![]() $[1,\infty )$
, and subject to the relation (1.4), where the exponential is taken with respect to the (multiplicative) convolution of measures [Reference Diamond and Zhang10]. Since our hypotheses always guarantee convergence of the Mellin transforms, the latter becomes equivalent to the zeta function identity
$[1,\infty )$
, and subject to the relation (1.4), where the exponential is taken with respect to the (multiplicative) convolution of measures [Reference Diamond and Zhang10]. Since our hypotheses always guarantee convergence of the Mellin transforms, the latter becomes equivalent to the zeta function identity
 $$\begin{align*}\zeta(s) :=\int^{\infty}_{1^{-}} x^{-s}\mathrm{d}N(x)= \exp\left(\int^{\infty}_{1}x^{-s}\mathrm{d}\Pi(x)\right). \end{align*}$$
$$\begin{align*}\zeta(s) :=\int^{\infty}_{1^{-}} x^{-s}\mathrm{d}N(x)= \exp\left(\int^{\infty}_{1}x^{-s}\mathrm{d}\Pi(x)\right). \end{align*}$$
We define our continuous Beurling system via its Chebyshev function
![]() $\psi _{C}$
. This uniquely defines
$\psi _{C}$
. This uniquely defines
![]() $\Pi _{C}$
and
$\Pi _{C}$
and
![]() $N_{C}$
by means of the relations
$N_{C}$
by means of the relations
![]() $\mathrm{d} \Pi _{C}(u) = (1/\log u)\mathrm{d} \psi _{C}(u)$
and
$\mathrm{d} \Pi _{C}(u) = (1/\log u)\mathrm{d} \psi _{C}(u)$
and
![]() $\mathrm{d} N_{C} = \exp ^{\ast }(\mathrm{d} \Pi _{C})$
. For
$\mathrm{d} N_{C} = \exp ^{\ast }(\mathrm{d} \Pi _{C})$
. For
![]() $x\ge 1$
, set
$x\ge 1$
, set
 $$ \begin{align} \psi_{C}(x) = x - 1 - \log x + \sum_{k=0}^{\infty}(R_{k}(x) + S_{k}(x)). \end{align} $$
$$ \begin{align} \psi_{C}(x) = x - 1 - \log x + \sum_{k=0}^{\infty}(R_{k}(x) + S_{k}(x)). \end{align} $$
Here,
![]() $x-1-\log x = \int _{1}^{x}\log u \mathrm{d} \operatorname {\mathrm {Li}}(u)$
is the main term (cf. equation (1.1)), the terms
$x-1-\log x = \int _{1}^{x}\log u \mathrm{d} \operatorname {\mathrm {Li}}(u)$
is the main term (cf. equation (1.1)), the terms
![]() $R_{k}$
are the deviations which will create a large oscillation in the integers, while the
$R_{k}$
are the deviations which will create a large oscillation in the integers, while the
![]() $S_{k}$
are introduced to mitigate the jump discontinuity of
$S_{k}$
are introduced to mitigate the jump discontinuity of
![]() $R_{k}$
and make
$R_{k}$
and make
![]() $\psi _{C}$
absolutely continuous. The effect of the terms
$\psi _{C}$
absolutely continuous. The effect of the terms
![]() $S_{k}$
on the asymptotics of
$S_{k}$
on the asymptotics of
![]() $N_{C}$
will be harmless. Concretely, we consider fast growing sequences
$N_{C}$
will be harmless. Concretely, we consider fast growing sequences
![]() $(A_{k})_{k}$
,
$(A_{k})_{k}$
,
![]() $(B_{k})_{k}$
,
$(B_{k})_{k}$
,
![]() $(C_{k})_{k}$
and
$(C_{k})_{k}$
and
![]() $(\tau _{k})_{k}$
with
$(\tau _{k})_{k}$
with
![]() $A_{k}<B_{k}<C_{k}<A_{k+1}$
, and defineFootnote
5
$A_{k}<B_{k}<C_{k}<A_{k+1}$
, and defineFootnote
5

We require that
![]() $\tau _{k}\log A_{k}, \tau _{k}\log B_{k} \in 2\pi \mathbb {Z}$
and define
$\tau _{k}\log A_{k}, \tau _{k}\log B_{k} \in 2\pi \mathbb {Z}$
and define
![]() $C_{k}$
as the unique solution of
$C_{k}$
as the unique solution of
![]() $R_{k}(B_{k}) + (1/2)\bigl (B_{k}-1-\log B_{k} - (C_{k}-1-\log C_{k})\bigr )= 0$
. Notice that for
$R_{k}(B_{k}) + (1/2)\bigl (B_{k}-1-\log B_{k} - (C_{k}-1-\log C_{k})\bigr )= 0$
. Notice that for
![]() $A_{k}\le x \le B_{k}$
,
$A_{k}\le x \le B_{k}$
,
 $$ \begin{align*} R_{k}(x) &= \frac{\tau_{k}^{2}}{2(\tau_{k}^{2}+1)}\biggl(\frac{x}{\tau_{k}}\sin(\tau_{k}\log x) + \frac{x}{\tau_{k}^{2}}\cos(\tau_{k} \log x) - \frac{A_{k}}{\tau_{k}^{2}}\biggr) - \frac{\sin(\tau_{k}\log x)}{2\tau_{k}}, \\ R_{k}(B_{k}) &= \frac{B_{k}-A_{k}}{2(\tau_{k}^{2}+1)}> 0, \end{align*} $$
$$ \begin{align*} R_{k}(x) &= \frac{\tau_{k}^{2}}{2(\tau_{k}^{2}+1)}\biggl(\frac{x}{\tau_{k}}\sin(\tau_{k}\log x) + \frac{x}{\tau_{k}^{2}}\cos(\tau_{k} \log x) - \frac{A_{k}}{\tau_{k}^{2}}\biggr) - \frac{\sin(\tau_{k}\log x)}{2\tau_{k}}, \\ R_{k}(B_{k}) &= \frac{B_{k}-A_{k}}{2(\tau_{k}^{2}+1)}> 0, \end{align*} $$
so the definition of
![]() $C_{k}$
makes sense (i.e.,
$C_{k}$
makes sense (i.e.,
![]() $C_{k}>B_{k}$
). We will also set
$C_{k}>B_{k}$
). We will also set
![]() $A_{k}=\sqrt {B_{k}}$
and
$A_{k}=\sqrt {B_{k}}$
and
then
With these definitions in place, we have that
![]() $\psi _{C}$
is absolutely continuous, nondecreasing, and satisfies
$\psi _{C}$
is absolutely continuous, nondecreasing, and satisfies
![]() $\psi _{C}(x) = x + O\bigl (x\exp (-c(\log x)^{\alpha })\bigr )$
, which implies thatFootnote
6
equation (1.5) holds for
$\psi _{C}(x) = x + O\bigl (x\exp (-c(\log x)^{\alpha })\bigr )$
, which implies thatFootnote
6
equation (1.5) holds for
![]() $\Pi _{C}(x) = \int _{1}^{x}(1/\log u)\mathrm{d} \psi _{C}(u)$
. Finally we define a sequence
$\Pi _{C}(x) = \int _{1}^{x}(1/\log u)\mathrm{d} \psi _{C}(u)$
. Finally we define a sequence
![]() $(x_{k})_{k}$
via the relation
$(x_{k})_{k}$
via the relation
Here,
![]() $(\varepsilon _{k})_{k}$
is a bounded sequence which is introduced to control the value of
$(\varepsilon _{k})_{k}$
is a bounded sequence which is introduced to control the value of
![]() $\tau _{k}\log x_{k}$
mod
$\tau _{k}\log x_{k}$
mod
![]() $2\pi $
(this will be needed later on). It is on the sequence
$2\pi $
(this will be needed later on). It is on the sequence
![]() $(x_{k})_{k}$
that we will show the oscillation estimate (1.6).
$(x_{k})_{k}$
that we will show the oscillation estimate (1.6).
We collect all technical requirements of the considered sequences in the following lemma. The rapid growth of the sequence
![]() $(B_{k})_{k}$
will be formulated as a general inequality
$(B_{k})_{k}$
will be formulated as a general inequality
![]() $B_{k+1}>\max \{F(B_{k}), G(k)\}$
, for some functions F and G. We will not specify here what F and G we require. At each point later on where the rapid growth is used, it will be clear what kind of growth (and what F, G) is needed.
$B_{k+1}>\max \{F(B_{k}), G(k)\}$
, for some functions F and G. We will not specify here what F and G we require. At each point later on where the rapid growth is used, it will be clear what kind of growth (and what F, G) is needed.
Lemma 2.1. Let F, G be increasing functions. There exist sequences
![]() $(B_{k})_{k}$
and
$(B_{k})_{k}$
and
![]() $(\varepsilon _{k})_{k}$
such that, with the definitions of
$(\varepsilon _{k})_{k}$
such that, with the definitions of
![]() $(A_{k})_{k}$
,
$(A_{k})_{k}$
,
![]() $(C_{k})_{k}$
,
$(C_{k})_{k}$
,
![]() $(\tau _{k})_{k}$
and
$(\tau _{k})_{k}$
and
![]() $(x_{k})_{k}$
as above, the following properties hold:
$(x_{k})_{k}$
as above, the following properties hold:
-
(a)
 $B_{k+1}> \max \{F(B_{k}), G(k)\}$
;
$B_{k+1}> \max \{F(B_{k}), G(k)\}$
; -
(b)
 $\tau _{k}\log A_{k}\in 2\pi \mathbb {Z}$
and
$\tau _{k}\log A_{k}\in 2\pi \mathbb {Z}$
and
 $\tau _{k}\log B_{k} \in 2\pi \mathbb {Z}$
;
$\tau _{k}\log B_{k} \in 2\pi \mathbb {Z}$
; -
(c)
 $\tau _{k}\log x_{k} \in \pi /2 + 2\pi \mathbb {Z}$
when k is even, and
$\tau _{k}\log x_{k} \in \pi /2 + 2\pi \mathbb {Z}$
when k is even, and
 $\tau _{k}\log x_{k} \in 3\pi /2 + 2\pi \mathbb {Z}$
when k is odd;
$\tau _{k}\log x_{k} \in 3\pi /2 + 2\pi \mathbb {Z}$
when k is odd; -
(d)
 $(\varepsilon _{k})_{k}$
is a bounded sequence.
$(\varepsilon _{k})_{k}$
is a bounded sequence.
Proof. We define the sequences inductively. Consider the function
![]() $f(u) = u\mathrm {e}^{cu^{\alpha }}$
. Let
$f(u) = u\mathrm {e}^{cu^{\alpha }}$
. Let
![]() $B_{0}$
be some (large) number with
$B_{0}$
be some (large) number with
![]() $f(\log B_{0})\in 4\pi \mathbb {Z}$
so that (b) is satisfied with
$f(\log B_{0})\in 4\pi \mathbb {Z}$
so that (b) is satisfied with
![]() $k=0$
. Define
$k=0$
. Define
![]() $y_{0}$
via
$y_{0}$
via
![]() $\log B_{0} = (c(\alpha +1))^{\frac {-1}{\alpha +1}}(\log y_{0}\log _{2} y_{0})^{\frac {1}{\alpha +1}}$
. We have that
$\log B_{0} = (c(\alpha +1))^{\frac {-1}{\alpha +1}}(\log y_{0}\log _{2} y_{0})^{\frac {1}{\alpha +1}}$
. We have that
![]() $\tau _{0}\log x_{0} - \tau _{0}\log y_{0} \asymp -\varepsilon _{0}\tau _{0}(\log B_{0})^{\alpha }/\log _{2}B_{0}$
, if
$\tau _{0}\log x_{0} - \tau _{0}\log y_{0} \asymp -\varepsilon _{0}\tau _{0}(\log B_{0})^{\alpha }/\log _{2}B_{0}$
, if
![]() $\varepsilon _{0}$
is bounded, say, so we may pick an
$\varepsilon _{0}$
is bounded, say, so we may pick an
![]() $\varepsilon _{0}$
satisfying even
$\varepsilon _{0}$
satisfying even
![]() $0 \le \varepsilon _{0} \ll \tau _{0}^{-1}(\log B_{0})^{-\alpha }\log _{2}B_{0}$
so that
$0 \le \varepsilon _{0} \ll \tau _{0}^{-1}(\log B_{0})^{-\alpha }\log _{2}B_{0}$
so that
![]() $\tau _{0}\log x_{0} \in \pi /2+2\pi \mathbb {Z}$
.
$\tau _{0}\log x_{0} \in \pi /2+2\pi \mathbb {Z}$
.
Now suppose that
![]() $B_{k}$
and
$B_{k}$
and
![]() $\varepsilon _{k}$
,
$\varepsilon _{k}$
,
![]() $0\le k \le K$
are defined. Choose a number
$0\le k \le K$
are defined. Choose a number
![]() $B_{K+1}>\max \{4(C_{K})^{2}, F(B_{K}), G(k)\}$
with
$B_{K+1}>\max \{4(C_{K})^{2}, F(B_{K}), G(k)\}$
with
![]() $f(\log B_{K+1}) \in 4\pi \mathbb {Z}$
, taking care of (a) and (b). As before, one might choose
$f(\log B_{K+1}) \in 4\pi \mathbb {Z}$
, taking care of (a) and (b). As before, one might choose
![]() $\varepsilon _{K+1}$
,
$\varepsilon _{K+1}$
,
![]() $0\le \varepsilon _{K+1}\ll \tau _{K+1}^{-1}(\log B_{K+1})^{-\alpha }\log _{2}B_{K+1}$
such that (c) holds. Property (d) is obvious.
$0\le \varepsilon _{K+1}\ll \tau _{K+1}^{-1}(\log B_{K+1})^{-\alpha }\log _{2}B_{K+1}$
such that (c) holds. Property (d) is obvious.
In order to deduce the asymptotics of
![]() $N_{C}$
, we shall analyze its zeta function
$N_{C}$
, we shall analyze its zeta function
![]() $\zeta _{C}$
and use an effective Perron formula:
$\zeta _{C}$
and use an effective Perron formula:
 $$ \begin{align} N_{C}(x) = \frac{1}{2\pi\mathrm{i}}\int_{\kappa-\mathrm{i} T}^{\kappa+\mathrm{i} T}x^{s}\zeta_{C}(s)\frac{\mathrm{d} s}{s} + \mbox{ error term}. \end{align} $$
$$ \begin{align} N_{C}(x) = \frac{1}{2\pi\mathrm{i}}\int_{\kappa-\mathrm{i} T}^{\kappa+\mathrm{i} T}x^{s}\zeta_{C}(s)\frac{\mathrm{d} s}{s} + \mbox{ error term}. \end{align} $$
Here,
![]() $\kappa>1$
, the parameter
$\kappa>1$
, the parameter
![]() $T>0$
is some large number, and the error term depends on these numbers. The usual strategy is then to push the contour of integration to the left of
$T>0$
is some large number, and the error term depends on these numbers. The usual strategy is then to push the contour of integration to the left of
![]() $\sigma = \operatorname {Re} s =1$
; the pole of
$\sigma = \operatorname {Re} s =1$
; the pole of
![]() $\zeta _{C}$
at
$\zeta _{C}$
at
![]() $s=1$
will give the main term, while lower order terms will arise from the integral over the new contour (whose shape will be dictated by the growth of
$s=1$
will give the main term, while lower order terms will arise from the integral over the new contour (whose shape will be dictated by the growth of
![]() $\zeta _{C}$
). In its current form, this approach is not suited for our problem since it is not clear if our zeta function admits a meromorphic continuation to the left of
$\zeta _{C}$
). In its current form, this approach is not suited for our problem since it is not clear if our zeta function admits a meromorphic continuation to the left of
![]() $\sigma =1$
. However, we can remedy this with the following truncation idea.
$\sigma =1$
. However, we can remedy this with the following truncation idea.
Consider
![]() $x\ge 1$
, and let K be such that
$x\ge 1$
, and let K be such that
![]() $x < A_{K+1}$
. We denote by
$x < A_{K+1}$
. We denote by
![]() $\psi _{C,K}$
the Chebyshev function defined by equation (2.1) but where the summation range in the series is altered to the restricted range
$\psi _{C,K}$
the Chebyshev function defined by equation (2.1) but where the summation range in the series is altered to the restricted range
![]() $ 0\le k\le K$
. For
$ 0\le k\le K$
. For
![]() $x<A_{K+1}$
, we have
$x<A_{K+1}$
, we have
![]() $\psi _{C,K}(x) = \psi _{C}(x)$
, and, setting
$\psi _{C,K}(x) = \psi _{C}(x)$
, and, setting
![]() $\mathrm{d} \Pi _{C,K}(u) = (1/\log u) \mathrm{d} \psi _{C,K}(u)$
and
$\mathrm{d} \Pi _{C,K}(u) = (1/\log u) \mathrm{d} \psi _{C,K}(u)$
and
![]() $\mathrm{d} N_{C,K}(u) = \exp ^{\ast }(\mathrm{d} \Pi _{C,K}(u))$
, we also have that
$\mathrm{d} N_{C,K}(u) = \exp ^{\ast }(\mathrm{d} \Pi _{C,K}(u))$
, we also have that
![]() $N_{C,K}(x) = N_{C}(x)$
holds in this range. Hence, for these x, the above Perron formula (2.5) remains valid if we replace
$N_{C,K}(x) = N_{C}(x)$
holds in this range. Hence, for these x, the above Perron formula (2.5) remains valid if we replace
![]() $\zeta _{C}$
by
$\zeta _{C}$
by
![]() $\zeta _{C,K}$
, the zeta function of
$\zeta _{C,K}$
, the zeta function of
![]() $N_{C,K}$
, which does admit meromorphic continuation beyond
$N_{C,K}$
, which does admit meromorphic continuation beyond
![]() $\sigma =1$
.
$\sigma =1$
.
In the following two sections, we will study the Perron integral in equation (2.5) for
![]() $x = x_{K}$
and with
$x = x_{K}$
and with
![]() $\zeta _{C}$
replaced by
$\zeta _{C}$
replaced by
![]() $\zeta _{C,K}$
. Note that by (a), we may assume that
$\zeta _{C,K}$
. Note that by (a), we may assume that
![]() $x_{K} < A_{K+1}$
. To asymptotically evaluate this integral, we will use the saddle point method, also known as the method of steepest descent. For an introduction to the saddle point method, we refer to [Reference de Bruijn7, Chapters 5 and 6] or [Reference Estrada and Kanwal11, Section 3.6].
$x_{K} < A_{K+1}$
. To asymptotically evaluate this integral, we will use the saddle point method, also known as the method of steepest descent. For an introduction to the saddle point method, we refer to [Reference de Bruijn7, Chapters 5 and 6] or [Reference Estrada and Kanwal11, Section 3.6].
In Section 3, we will estimate the contribution from the integral over the steepest paths through the saddle points. This contribution will match the oscillation term in equation (1.6). In Section 4, we will connect these steepest paths to each other and to the vertical line
![]() $[\kappa -\mathrm {i} T, \kappa +\mathrm {i} T]$
and determine that the contribution of these connecting pieces to equation (2.5) is of lower order than the contribution from the saddle points. We also estimate the error term in the effective Perron formula in Section 5 and conclude the analysis of the continuous example. Finally, in Section 6 we use probabilistic methods to show the existence of a discrete Beurling system
$[\kappa -\mathrm {i} T, \kappa +\mathrm {i} T]$
and determine that the contribution of these connecting pieces to equation (2.5) is of lower order than the contribution from the saddle points. We also estimate the error term in the effective Perron formula in Section 5 and conclude the analysis of the continuous example. Finally, in Section 6 we use probabilistic methods to show the existence of a discrete Beurling system
![]() $(\Pi , N)$
that inherits the asymptotics of the continuous system
$(\Pi , N)$
that inherits the asymptotics of the continuous system
![]() $(\Pi _{C}, N_{C})$
.
$(\Pi _{C}, N_{C})$
.
3 Analysis of the saddle points
First we compute the zeta function
![]() $\zeta _{C,K}$
. Computing the Mellin transform of
$\zeta _{C,K}$
. Computing the Mellin transform of
![]() $\psi _{C,K}$
gives that
$\psi _{C,K}$
gives that
 $$\begin{align*}-\frac{\zeta_{C,K}'}{\zeta_{C,K}}(s) = \frac{1}{s-1} - \frac{1}{s} + \sum_{k=0}^{K}\bigl( \eta_{k}(s) + \tilde{\eta}_{k}(s) + \xi_{k}(s) - \eta_{k}(s+1) - \tilde{\eta}_{k}(s+1) - \xi_{k}(s+1)\bigr), \end{align*}$$
$$\begin{align*}-\frac{\zeta_{C,K}'}{\zeta_{C,K}}(s) = \frac{1}{s-1} - \frac{1}{s} + \sum_{k=0}^{K}\bigl( \eta_{k}(s) + \tilde{\eta}_{k}(s) + \xi_{k}(s) - \eta_{k}(s+1) - \tilde{\eta}_{k}(s+1) - \xi_{k}(s+1)\bigr), \end{align*}$$
where
 $$ \begin{align} \eta_{k}(s) = \frac{B_{k}^{1-s} - A_{k}^{1-s}}{4(1+\mathrm{i}\tau_{k} -s)}, \quad \tilde{\eta}_{k}(s) = \frac{B_{k}^{1-s} - A_{k}^{1-s}}{4(1-\mathrm{i}\tau_{k} -s)}, \quad \xi_{k}(s) = \frac{B_{k}^{1-s}-C_{k}^{1-s}}{2(1-s)}, \end{align} $$
$$ \begin{align} \eta_{k}(s) = \frac{B_{k}^{1-s} - A_{k}^{1-s}}{4(1+\mathrm{i}\tau_{k} -s)}, \quad \tilde{\eta}_{k}(s) = \frac{B_{k}^{1-s} - A_{k}^{1-s}}{4(1-\mathrm{i}\tau_{k} -s)}, \quad \xi_{k}(s) = \frac{B_{k}^{1-s}-C_{k}^{1-s}}{2(1-s)}, \end{align} $$
and where we used property (b) of the sequences
![]() $(A_{k})_{k}$
,
$(A_{k})_{k}$
,
![]() $(B_{k})_{k}$
. Integrating gives
$(B_{k})_{k}$
. Integrating gives
 $$\begin{align*}\log \zeta_{C,K}(s) = \log\frac{s}{s-1} + \sum_{k=0}^{K}\int_{s}^{s+1}\bigl(\eta_{k}(z) + \tilde{\eta}_{k}(z) + \xi_{k}(z)\bigr)\mathrm{d} z, \end{align*}$$
$$\begin{align*}\log \zeta_{C,K}(s) = \log\frac{s}{s-1} + \sum_{k=0}^{K}\int_{s}^{s+1}\bigl(\eta_{k}(z) + \tilde{\eta}_{k}(z) + \xi_{k}(z)\bigr)\mathrm{d} z, \end{align*}$$
the integration constant being
![]() $0$
because
$0$
because
![]() $\log \zeta _{C,K}(\sigma ) \rightarrow 0$
as
$\log \zeta _{C,K}(\sigma ) \rightarrow 0$
as
![]() $\sigma \rightarrow \infty $
. The main term of the Perron integral formula for
$\sigma \rightarrow \infty $
. The main term of the Perron integral formula for
![]() $N_{C,K}(x_{K})$
becomes
$N_{C,K}(x_{K})$
becomes
 $$\begin{align*}\frac{1}{2\pi\mathrm{i}}\int_{\kappa-\mathrm{i} T}^{\kappa+\mathrm{i} T}\frac{x_{K}^{s}}{s-1}\exp\biggl(\sum_{k=0}^{K}\int_{s}^{s+1}\bigl(\eta_{k}(z) + \tilde{\eta}_{k}(z) + \xi_{k}(z)\bigr)\mathrm{d} z\biggr)\mathrm{d} s. \end{align*}$$
$$\begin{align*}\frac{1}{2\pi\mathrm{i}}\int_{\kappa-\mathrm{i} T}^{\kappa+\mathrm{i} T}\frac{x_{K}^{s}}{s-1}\exp\biggl(\sum_{k=0}^{K}\int_{s}^{s+1}\bigl(\eta_{k}(z) + \tilde{\eta}_{k}(z) + \xi_{k}(z)\bigr)\mathrm{d} z\biggr)\mathrm{d} s. \end{align*}$$
The idea of the saddle point method is to estimate an integral of the form
![]() $\int _{\Gamma }\mathrm {e}^{f(s)}g(s)\mathrm{d} s$
, with f and g analytic, by shifting the contour
$\int _{\Gamma }\mathrm {e}^{f(s)}g(s)\mathrm{d} s$
, with f and g analytic, by shifting the contour
![]() $\Gamma $
to a contour which passes through the saddle points of f via the paths of steepest descent. Since the main contribution in the Perron integral will come from
$\Gamma $
to a contour which passes through the saddle points of f via the paths of steepest descent. Since the main contribution in the Perron integral will come from
![]() $x_{K}^{s}\exp (\int _{s}^{\infty }\eta _{K}(z)\mathrm{d} z)$
, we will apply the method with
$x_{K}^{s}\exp (\int _{s}^{\infty }\eta _{K}(z)\mathrm{d} z)$
, we will apply the method with
 $$ \begin{align} f(s) &= f_{K}(s) = s\log x_{K} + \int_{s}^{\infty}\eta_{K}(z)\mathrm{d} z,\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad \end{align} $$
$$ \begin{align} f(s) &= f_{K}(s) = s\log x_{K} + \int_{s}^{\infty}\eta_{K}(z)\mathrm{d} z,\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad \end{align} $$
 $$ \begin{align} g(s) &= g_{K}(s) = \frac{1}{s-1}\exp\biggl(\sum_{k=0}^{K}\int_{s}^{s+1}\bigl(\eta_{k}(z) + \tilde{\eta}_{k}(z) + \xi_{k}(z)\bigr)\mathrm{d} z - \int_{s}^{\infty}\eta_{K}(z)\mathrm{d} z\biggr). \end{align} $$
$$ \begin{align} g(s) &= g_{K}(s) = \frac{1}{s-1}\exp\biggl(\sum_{k=0}^{K}\int_{s}^{s+1}\bigl(\eta_{k}(z) + \tilde{\eta}_{k}(z) + \xi_{k}(z)\bigr)\mathrm{d} z - \int_{s}^{\infty}\eta_{K}(z)\mathrm{d} z\biggr). \end{align} $$
Note also that by writing
![]() $\int _{s}^{\infty }\eta _{K}(z)\mathrm{d} z $
as a Mellin transform, we obtain the alternative representation
$\int _{s}^{\infty }\eta _{K}(z)\mathrm{d} z $
as a Mellin transform, we obtain the alternative representation
 $$ \begin{align} \int_{s}^{\infty}\eta_{K}(z)\mathrm{d} z = \frac{1}{4}\int_{A_{K}}^{B_{K}}x^{-s}\mathrm{e}^{\mathrm{i}\tau\log x}\frac{1}{\log x}\mathrm{d} x = \frac{1}{4}\int_{1/2}^{1}\frac{B_{K}^{(1+\mathrm{i}\tau_{K} - s)u}}{u}\mathrm{d} u, \end{align} $$
$$ \begin{align} \int_{s}^{\infty}\eta_{K}(z)\mathrm{d} z = \frac{1}{4}\int_{A_{K}}^{B_{K}}x^{-s}\mathrm{e}^{\mathrm{i}\tau\log x}\frac{1}{\log x}\mathrm{d} x = \frac{1}{4}\int_{1/2}^{1}\frac{B_{K}^{(1+\mathrm{i}\tau_{K} - s)u}}{u}\mathrm{d} u, \end{align} $$
as we have set
![]() $A_{K} = \sqrt {B_{K}}$
. In the rest of this section, we will mostly work with
$A_{K} = \sqrt {B_{K}}$
. In the rest of this section, we will mostly work with
![]() $f_{K}$
, and we will drop the subscripts K where there is no risk of confusion.
$f_{K}$
, and we will drop the subscripts K where there is no risk of confusion.
3.1 The saddle points
We will now compute the saddle points of f, which are solutions of the equation
For integers m, set numbers
![]() $t^{\pm }_{m}$
as
$t^{\pm }_{m}$
as
![]() $t^{\pm }_{m} = \tau + (2\pi m \pm \pi /2)/\log B$
, and let
$t^{\pm }_{m} = \tau + (2\pi m \pm \pi /2)/\log B$
, and let
![]() $V_{m}$
be the rectangle with vertices
$V_{m}$
be the rectangle with vertices
 $$\begin{align*}1-\frac{\frac{\alpha}{2}\log_{2} B}{\log B} + \mathrm{i} t^{\pm}_{m}, \quad \frac{1}{2} + \mathrm{i} t^{\pm}_{m}. \end{align*}$$
$$\begin{align*}1-\frac{\frac{\alpha}{2}\log_{2} B}{\log B} + \mathrm{i} t^{\pm}_{m}, \quad \frac{1}{2} + \mathrm{i} t^{\pm}_{m}. \end{align*}$$
Lemma 3.1. Suppose that
![]() $\left \lvert m \right \rvert < \log _{2} B$
. Then
$\left \lvert m \right \rvert < \log _{2} B$
. Then
![]() $f'$
has a unique simple zero
$f'$
has a unique simple zero
![]() $s_{m}$
in the interior of
$s_{m}$
in the interior of
![]() $V_{m}$
.
$V_{m}$
.
Proof. We apply the argument principle. Note that from equation (2.4) it follows that
 $$ \begin{align*} f'\biggl(\frac{1}{2} + \mathrm{i} t^{-}_{m}\biggr) \!&= -\frac{\mathrm{i}}{2}B^{1/2}\bigl(1+o(1)\bigr), & f'\biggl(\kern-1.2pt 1-\frac{\frac{\alpha}{2}\log_{2} B}{\log B} + \mathrm{i} t^{-}_{m}\biggr) \!&=\log x\bigl(1+o(1)\bigr), \\ f'\biggl(1-\frac{\frac{\alpha}{2}\log_{2} B}{\log B} + \mathrm{i} t^{+}_{m}\biggr) \!&=\log x\bigl(1+o(1)\bigr), & f'\biggl(\frac{1}{2} + \mathrm{i} t^{+}_{m}\biggr)\! &= \frac{\mathrm{i}}{2}B^{1/2}\bigl(1+o(1)\bigr)\kern-1.2pt. \end{align*} $$
$$ \begin{align*} f'\biggl(\frac{1}{2} + \mathrm{i} t^{-}_{m}\biggr) \!&= -\frac{\mathrm{i}}{2}B^{1/2}\bigl(1+o(1)\bigr), & f'\biggl(\kern-1.2pt 1-\frac{\frac{\alpha}{2}\log_{2} B}{\log B} + \mathrm{i} t^{-}_{m}\biggr) \!&=\log x\bigl(1+o(1)\bigr), \\ f'\biggl(1-\frac{\frac{\alpha}{2}\log_{2} B}{\log B} + \mathrm{i} t^{+}_{m}\biggr) \!&=\log x\bigl(1+o(1)\bigr), & f'\biggl(\frac{1}{2} + \mathrm{i} t^{+}_{m}\biggr)\! &= \frac{\mathrm{i}}{2}B^{1/2}\bigl(1+o(1)\bigr)\kern-1.2pt. \end{align*} $$
On the lower horizontal side of
![]() $V_{m}$
, we have
$V_{m}$
, we have
 $$\begin{align*}\operatorname{Im} f'(\sigma+\mathrm{i} t^{-}_{m}) = -\frac{B^{1-\sigma}/4}{(1-\sigma)^{2}+(\tau-t_{m}^{-})^{2}}\biggl\{ \biggl(1-\frac{\sqrt{2}}{2}B^{\frac{\sigma-1}{2}}\biggr)(1-\sigma) + \frac{\sqrt{2}}{2}B^{\frac{\sigma-1}{2}}(\tau-t_{m}^{-})\biggr\} < 0, \end{align*}$$
$$\begin{align*}\operatorname{Im} f'(\sigma+\mathrm{i} t^{-}_{m}) = -\frac{B^{1-\sigma}/4}{(1-\sigma)^{2}+(\tau-t_{m}^{-})^{2}}\biggl\{ \biggl(1-\frac{\sqrt{2}}{2}B^{\frac{\sigma-1}{2}}\biggr)(1-\sigma) + \frac{\sqrt{2}}{2}B^{\frac{\sigma-1}{2}}(\tau-t_{m}^{-})\biggr\} < 0, \end{align*}$$
as the factor inside the curly brackets is positive in the considered ranges for
![]() $\sigma $
and m. Similarly, we have
$\sigma $
and m. Similarly, we have
![]() $\operatorname {Im} f'(\sigma +\mathrm {i} t^{+}_{m})>0$
on the upper horizontal edge of
$\operatorname {Im} f'(\sigma +\mathrm {i} t^{+}_{m})>0$
on the upper horizontal edge of
![]() $V_{m}$
. On the right vertical edge,
$V_{m}$
. On the right vertical edge,
 $$\begin{align*}\operatorname{Re} f'\biggl(1-\frac{\frac{\alpha}{2}\log_{2}B}{\log B} +\mathrm{i} t\biggr)>0, \end{align*}$$
$$\begin{align*}\operatorname{Re} f'\biggl(1-\frac{\frac{\alpha}{2}\log_{2}B}{\log B} +\mathrm{i} t\biggr)>0, \end{align*}$$
and on the left vertical edge,
 $$\begin{align*}f'\biggl(\frac{1}{2}+\mathrm{i} t\biggr) = \frac{B^{1/2}}{2}\mathrm{e}^{\mathrm{i}\pi-\mathrm{i}(t-\tau)\log B}\bigl(1+o(1)\bigr). \end{align*}$$
$$\begin{align*}f'\biggl(\frac{1}{2}+\mathrm{i} t\biggr) = \frac{B^{1/2}}{2}\mathrm{e}^{\mathrm{i}\pi-\mathrm{i}(t-\tau)\log B}\bigl(1+o(1)\bigr). \end{align*}$$
Starting from the lower left vertex of
![]() $V_{m}$
and moving in the counterclockwise direction, we see that the argument of
$V_{m}$
and moving in the counterclockwise direction, we see that the argument of
![]() $f'$
starts off close to
$f'$
starts off close to
![]() $-\pi /2$
, increases to about
$-\pi /2$
, increases to about
![]() $0$
on the lower horizontal edge, remains close to
$0$
on the lower horizontal edge, remains close to
![]() $0$
on the right vertical edge, increases to about
$0$
on the right vertical edge, increases to about
![]() $\pi /2$
on the upper horizontal edge and finally increases to approximately
$\pi /2$
on the upper horizontal edge and finally increases to approximately
![]() $3\pi /2$
on the left vertical edge. This proves the lemma.
$3\pi /2$
on the left vertical edge. This proves the lemma.
From now on, we assume that
![]() $\left \lvert m \right \rvert < \varepsilon \log _{2} B$
for some small
$\left \lvert m \right \rvert < \varepsilon \log _{2} B$
for some small
![]() $\varepsilon>0$
. (In fact, later on we will further reduce the range to
$\varepsilon>0$
. (In fact, later on we will further reduce the range to
![]() $\left \lvert m \right \rvert \le (\log _{2} B)^{3/4}$
.) We denote the unique saddle point in the rectangle
$\left \lvert m \right \rvert \le (\log _{2} B)^{3/4}$
.) We denote the unique saddle point in the rectangle
![]() $V_{m}$
by
$V_{m}$
by
![]() $s_{m} = \sigma _{m} + \mathrm {i} t_{m}$
. The saddle point equation (3.5) implies that
$s_{m} = \sigma _{m} + \mathrm {i} t_{m}$
. The saddle point equation (3.5) implies that
 $$ \begin{align*} \sigma_{m} &= 1-\frac{1}{\log B}\biggl(\log_{2} x + \log 4 - \log\left\lvert 1-B^{(s_{m}-1)/2} \right\rvert - \log\left\lvert \frac{1}{1+\mathrm{i}\tau-s_{m}} \right\rvert \,\biggr), \\ t_{m} &= \tau + \frac{1}{\log B}\biggl(2\pi m + \arg\bigl(1-B^{(s_{m}-1)/2}\bigr) - \arg\bigl(1+\mathrm{i}\tau - s_{m}\bigr)\biggr), \end{align*} $$
$$ \begin{align*} \sigma_{m} &= 1-\frac{1}{\log B}\biggl(\log_{2} x + \log 4 - \log\left\lvert 1-B^{(s_{m}-1)/2} \right\rvert - \log\left\lvert \frac{1}{1+\mathrm{i}\tau-s_{m}} \right\rvert \,\biggr), \\ t_{m} &= \tau + \frac{1}{\log B}\biggl(2\pi m + \arg\bigl(1-B^{(s_{m}-1)/2}\bigr) - \arg\bigl(1+\mathrm{i}\tau - s_{m}\bigr)\biggr), \end{align*} $$
with the understanding that the difference of the arguments in the formula for
![]() $t_{m}$
lies in
$t_{m}$
lies in
![]() $[-\pi /2,\pi /2]$
. We set
$[-\pi /2,\pi /2]$
. We set
 $$\begin{align*}E_{m} = \log\left\lvert \frac{1}{1+\mathrm{i}\tau - s_{m}} \right\rvert. \end{align*}$$
$$\begin{align*}E_{m} = \log\left\lvert \frac{1}{1+\mathrm{i}\tau - s_{m}} \right\rvert. \end{align*}$$
Since
![]() $s_{m}\in V_{m}$
, we have
$s_{m}\in V_{m}$
, we have
![]() $0\le E_{m}\le \log _{2} B$
. Also
$0\le E_{m}\le \log _{2} B$
. Also
![]() $\log \left \lvert 1-B^{(s_{m}-1)/2} \right \rvert = O(1)$
. This implies that
$\log \left \lvert 1-B^{(s_{m}-1)/2} \right \rvert = O(1)$
. This implies that
so that
![]() $E_{m} = \log _{2} B - \log _{3}x + O(1)$
. Here, we have also used that
$E_{m} = \log _{2} B - \log _{3}x + O(1)$
. Here, we have also used that
the last formula following from equation (2.4). This in turn implies that
where we again used equation (2.4). Combining this with equation (3.5), we get in particular that
 $$ \begin{align} \log x = \frac{B^{1-s_{m}}}{4(1+\mathrm{i}\tau-s_{m})}\bigl(1+O\bigl((\log B)^{-\alpha/2}\bigr)\bigr). \end{align} $$
$$ \begin{align} \log x = \frac{B^{1-s_{m}}}{4(1+\mathrm{i}\tau-s_{m})}\bigl(1+O\bigl((\log B)^{-\alpha/2}\bigr)\bigr). \end{align} $$
For
![]() $t_{m}$
, we have that
$t_{m}$
, we have that
 $$ \begin{align*} \arg(1-B^{(s_{m}-1)/2}) &\ll (\log B)^{-\alpha/2}, \\ \arg(1+\mathrm{i}\tau - s_{m}) &= -\frac{2\pi m}{\alpha\log_{2} B} + O\biggl(\frac{1}{\log_{2} B} + \frac{\left\lvert m \right\rvert }{(\log_{2} B)^{2}} + \frac{\left\lvert m \right\rvert ^{3}}{(\log_{2} B)^{3}}\biggr). \end{align*} $$
$$ \begin{align*} \arg(1-B^{(s_{m}-1)/2}) &\ll (\log B)^{-\alpha/2}, \\ \arg(1+\mathrm{i}\tau - s_{m}) &= -\frac{2\pi m}{\alpha\log_{2} B} + O\biggl(\frac{1}{\log_{2} B} + \frac{\left\lvert m \right\rvert }{(\log_{2} B)^{2}} + \frac{\left\lvert m \right\rvert ^{3}}{(\log_{2} B)^{3}}\biggr). \end{align*} $$
We get that
 $$ \begin{align} t_{m} = \tau + \frac{1}{\log B}\biggl\{2\pi m\biggl(1+\frac{1}{\alpha\log_{2} B}\biggr) + O\biggl(\frac{1}{\log_{2} B} + \frac{\left\lvert m \right\rvert }{(\log_{2} B)^{2}} + \frac{\left\lvert m \right\rvert ^{3}}{(\log_{2} B)^{3}}\biggr) \biggr\}. \end{align} $$
$$ \begin{align} t_{m} = \tau + \frac{1}{\log B}\biggl\{2\pi m\biggl(1+\frac{1}{\alpha\log_{2} B}\biggr) + O\biggl(\frac{1}{\log_{2} B} + \frac{\left\lvert m \right\rvert }{(\log_{2} B)^{2}} + \frac{\left\lvert m \right\rvert ^{3}}{(\log_{2} B)^{3}}\biggr) \biggr\}. \end{align} $$
Also, it is important to notice that
![]() $t_{0} = \tau $
.
$t_{0} = \tau $
.
The main contribution to the Perron integral (2.5) will come from the saddle point
![]() $s_{0}$
; see Subsection 3.3. We will show in Subsection 3.5 that the contribution from the other saddle points
$s_{0}$
; see Subsection 3.3. We will show in Subsection 3.5 that the contribution from the other saddle points
![]() $s_{m}$
,
$s_{m}$
,
![]() $m\neq 0$
, is of lower order. This will require a finer estimate for
$m\neq 0$
, is of lower order. This will require a finer estimate for
![]() $\sigma _{m}$
, which is the subject of the following lemma.
$\sigma _{m}$
, which is the subject of the following lemma.
Lemma 3.2. There exists a fixed constant
![]() $d>0$
, independent of K and m such that for
$d>0$
, independent of K and m such that for
![]() $\left \lvert m \right \rvert \le (\log _{2}B)^{3/4}$
,
$\left \lvert m \right \rvert \le (\log _{2}B)^{3/4}$
,
![]() $m\neq 0$
,
$m\neq 0$
,
 $$\begin{align*}\sigma_{m} \le \sigma_{0} - \frac{d}{\log B(\log_{2} B)^{2}}. \end{align*}$$
$$\begin{align*}\sigma_{m} \le \sigma_{0} - \frac{d}{\log B(\log_{2} B)^{2}}. \end{align*}$$
Proof. We use equations (3.6) and (3.8) to get a better estimate for
![]() $E_{m}$
, which will in turn yield a better estimate for
$E_{m}$
, which will in turn yield a better estimate for
![]() $\sigma _{m}$
. We iterate this procedure three times.
$\sigma _{m}$
. We iterate this procedure three times.
The first iteration yields
 $$\begin{align*}\sigma_{m} = 1 - \frac{1}{\log B}\biggl\{\log_{2} x - \log_{2} B + \log_{3} B + \log 4 + \log\alpha + O\biggl(\frac{1+\left\lvert m \right\rvert }{\log_{2} B}\biggr)\biggr\}. \end{align*}$$
$$\begin{align*}\sigma_{m} = 1 - \frac{1}{\log B}\biggl\{\log_{2} x - \log_{2} B + \log_{3} B + \log 4 + \log\alpha + O\biggl(\frac{1+\left\lvert m \right\rvert }{\log_{2} B}\biggr)\biggr\}. \end{align*}$$
Write
![]() $Y = \log _{2}x - \log _{2}B + \log _{3}B$
, and note that
$Y = \log _{2}x - \log _{2}B + \log _{3}B$
, and note that
![]() $Y \asymp \log _{2}B$
. Iterating a second time, we get
$Y \asymp \log _{2}B$
. Iterating a second time, we get
 $$\begin{align*}\sigma_{m} = 1-\frac{1}{\log B}\biggl\{\log_{2}x - \log_{2}B + \log Y +\log 4 + \frac{\log4+\log\alpha}{Y} + O\biggl(\frac{1+m^{2}}{(\log_{2}B)^{2}}\biggr)\biggr\}. \end{align*}$$
$$\begin{align*}\sigma_{m} = 1-\frac{1}{\log B}\biggl\{\log_{2}x - \log_{2}B + \log Y +\log 4 + \frac{\log4+\log\alpha}{Y} + O\biggl(\frac{1+m^{2}}{(\log_{2}B)^{2}}\biggr)\biggr\}. \end{align*}$$
We now set
![]() $Y' = \log _{2}x-\log _{2}B + \log Y$
and note again that
$Y' = \log _{2}x-\log _{2}B + \log Y$
and note again that
![]() $Y'\asymp \log _{2}B$
. A final iteration gives
$Y'\asymp \log _{2}B$
. A final iteration gives
 $$ \begin{align*} \sigma_{m} = 1 - \frac{1}{\log B}\biggl\{\log_{2}x - \log_{2}B &+ \log Y' + \log4 + \frac{\log 4}{Y'} + \frac{\log4+\log\alpha}{YY'} \\ & -\frac{(\log4)^{2}}{2Y^{\prime2}} +\frac{2\pi^{2}m^{2}}{Y^{\prime2}} - \frac{4\pi^{4}m^{4}}{Y^{\prime4}} + O\biggl(\frac{1+m^{2}}{(\log_{2}B)^{3}}\biggr)\biggr\}. \end{align*} $$
$$ \begin{align*} \sigma_{m} = 1 - \frac{1}{\log B}\biggl\{\log_{2}x - \log_{2}B &+ \log Y' + \log4 + \frac{\log 4}{Y'} + \frac{\log4+\log\alpha}{YY'} \\ & -\frac{(\log4)^{2}}{2Y^{\prime2}} +\frac{2\pi^{2}m^{2}}{Y^{\prime2}} - \frac{4\pi^{4}m^{4}}{Y^{\prime4}} + O\biggl(\frac{1+m^{2}}{(\log_{2}B)^{3}}\biggr)\biggr\}. \end{align*} $$
The lemma now follows from comparing the above formula in the case
![]() $m=0$
with the case
$m=0$
with the case
![]() $m\neq 0$
.
$m\neq 0$
.
Near the saddle points, we will approximate f and
![]() $f'$
by their Taylor polynomials.
$f'$
by their Taylor polynomials.
Lemma 3.3. There are holomorphic functions
![]() $\lambda _{m}$
and
$\lambda _{m}$
and
![]() $\tilde {\lambda }_{m}$
such that
$\tilde {\lambda }_{m}$
such that
 $$ \begin{align*} f(s) &= f(s_{m}) + \frac{f"(s_{m})}{2}(s-s_{m})^{2}(1+\lambda_{m}(s)), \\ f'(s) &= f"(s_{m})(s-s_{m})(1+\tilde{\lambda}_{m}(s)), \end{align*} $$
$$ \begin{align*} f(s) &= f(s_{m}) + \frac{f"(s_{m})}{2}(s-s_{m})^{2}(1+\lambda_{m}(s)), \\ f'(s) &= f"(s_{m})(s-s_{m})(1+\tilde{\lambda}_{m}(s)), \end{align*} $$
and with the property that for each
![]() $\varepsilon>0$
, there exists a
$\varepsilon>0$
, there exists a
![]() $\delta>0$
, independent of K and m such that
$\delta>0$
, independent of K and m such that
Proof. We have
 $$\begin{align*}f"(s) = (\log B)\frac{B^{1-s} - \frac{1}{2} B^{(1-s)/2}}{4(1+\mathrm{i}\tau - s)} - \frac{B^{1-s} - B^{(1-s)/2}}{4(1+\mathrm{i}\tau-s)^{2}}, \quad \left\lvert f"(s_{m}) \right\rvert \asymp \frac{(\log B)^{\alpha}(\log B)^{2}}{\log_{2}B}, \end{align*}$$
$$\begin{align*}f"(s) = (\log B)\frac{B^{1-s} - \frac{1}{2} B^{(1-s)/2}}{4(1+\mathrm{i}\tau - s)} - \frac{B^{1-s} - B^{(1-s)/2}}{4(1+\mathrm{i}\tau-s)^{2}}, \quad \left\lvert f"(s_{m}) \right\rvert \asymp \frac{(\log B)^{\alpha}(\log B)^{2}}{\log_{2}B}, \end{align*}$$
where we have used equation (3.6), and
 $$\begin{align*}f"'(s) = -(\log B)^{2}\frac{B^{1-s} - \frac{1}{4}B^{(1-s)/2}}{4(1+\mathrm{i}\tau-s)} + (\log B)\frac{B^{1-s}-\frac{1}{2}B^{(1-s)/2}}{2(1+\mathrm{i}\tau-s)^{2}} - \frac{B^{1-s}-B^{(1-s)/2}}{2(1+\mathrm{i}\tau-s)^{3}}. \end{align*}$$
$$\begin{align*}f"'(s) = -(\log B)^{2}\frac{B^{1-s} - \frac{1}{4}B^{(1-s)/2}}{4(1+\mathrm{i}\tau-s)} + (\log B)\frac{B^{1-s}-\frac{1}{2}B^{(1-s)/2}}{2(1+\mathrm{i}\tau-s)^{2}} - \frac{B^{1-s}-B^{(1-s)/2}}{2(1+\mathrm{i}\tau-s)^{3}}. \end{align*}$$
If
![]() $\left \lvert s-s_{m} \right \rvert \ll 1/\log B$
, then
$\left \lvert s-s_{m} \right \rvert \ll 1/\log B$
, then
 $$\begin{align*}\left\lvert f"'(s) \right\rvert \ll \frac{(\log B)^{\alpha}(\log B)^{3}}{\log_{2}B}. \end{align*}$$
$$\begin{align*}\left\lvert f"'(s) \right\rvert \ll \frac{(\log B)^{\alpha}(\log B)^{3}}{\log_{2}B}. \end{align*}$$
It follows that
 $$\begin{align*}\left\lvert \frac{f"'(s)}{f"(s_{m})}(s-s_{m}) \right\rvert < \varepsilon, \end{align*}$$
$$\begin{align*}\left\lvert \frac{f"'(s)}{f"(s_{m})}(s-s_{m}) \right\rvert < \varepsilon, \end{align*}$$
if
![]() $\left \lvert s-s_{m} \right \rvert < \delta /\log B$
, for sufficiently small
$\left \lvert s-s_{m} \right \rvert < \delta /\log B$
, for sufficiently small
![]() $\delta $
. The lemma now follows from Taylor’s formula.
$\delta $
. The lemma now follows from Taylor’s formula.
3.2 The steepest path through
 $s_{0}$
$s_{0}$
The equation for the path of steepest descent through
![]() $s_{0}$
is
$s_{0}$
is
Using the formula (3.4) for
![]() $\int _{s}^{\infty }\eta (z)\mathrm{d} z$
, we get the equation
$\int _{s}^{\infty }\eta (z)\mathrm{d} z$
, we get the equation
 $$\begin{align*}t\log x - \frac{1}{4}\int_{1/2}^{1}B^{(1-\sigma)u}\sin\bigl((t-\tau)(\log B) u\bigr)\frac{\mathrm{d} u}{u} = \tau\log x. \end{align*}$$
$$\begin{align*}t\log x - \frac{1}{4}\int_{1/2}^{1}B^{(1-\sigma)u}\sin\bigl((t-\tau)(\log B) u\bigr)\frac{\mathrm{d} u}{u} = \tau\log x. \end{align*}$$
Setting
![]() $\theta =(t-\tau )\log B$
, this is equivalent to
$\theta =(t-\tau )\log B$
, this is equivalent to
 $$ \begin{align} \theta\frac{\log x}{\log B} = \frac{1}{4}\int_{1/2}^{1}B^{(1-\sigma)u}\sin(\theta u)\frac{\mathrm{d} u}{u}. \end{align} $$
$$ \begin{align} \theta\frac{\log x}{\log B} = \frac{1}{4}\int_{1/2}^{1}B^{(1-\sigma)u}\sin(\theta u)\frac{\mathrm{d} u}{u}. \end{align} $$
Note that, as t varies between
![]() $t_{0}^{-}$
and
$t_{0}^{-}$
and
![]() $t_{0}^{+}$
,
$t_{0}^{+}$
,
![]() $\theta $
varies between
$\theta $
varies between
![]() $-\pi /2$
and
$-\pi /2$
and
![]() $\pi /2$
. This equation has every point of the line
$\pi /2$
. This equation has every point of the line
![]() $\theta =0$
as a solution. However, one sees that the line
$\theta =0$
as a solution. However, one sees that the line
![]() $\theta =0$
is the path of steepest ascent since
$\theta =0$
is the path of steepest ascent since
![]() $\operatorname {Re} f(s) \ge \operatorname {Re} f(s_{0})$
there. We now show the existence of a different curve through
$\operatorname {Re} f(s) \ge \operatorname {Re} f(s_{0})$
there. We now show the existence of a different curve through
![]() $s_{0}$
of which each point is a solution of equation (3.9). This is then necessarily the path of steepest descent. For each fixed
$s_{0}$
of which each point is a solution of equation (3.9). This is then necessarily the path of steepest descent. For each fixed
![]() $\theta \in [-\pi /2, \pi /2] \setminus \{0\}$
, equation (3.9) has a unique solution
$\theta \in [-\pi /2, \pi /2] \setminus \{0\}$
, equation (3.9) has a unique solution
![]() $\sigma =\sigma _{\theta }$
since the right-hand side is a continuous and monotone function of
$\sigma =\sigma _{\theta }$
since the right-hand side is a continuous and monotone function of
![]() $\sigma $
, with range
$\sigma $
, with range
![]() $\mathbb {R}_{\gtrless 0}$
, if
$\mathbb {R}_{\gtrless 0}$
, if
![]() $\theta \gtrless 0$
. This shows the existence of the path of steepest descent
$\theta \gtrless 0$
. This shows the existence of the path of steepest descent
![]() $\Gamma _{0}$
through
$\Gamma _{0}$
through
![]() $s_{0}$
. This path connects the lines
$s_{0}$
. This path connects the lines
![]() $\theta =-\pi /2$
and
$\theta =-\pi /2$
and
![]() $\theta =\pi /2$
.
$\theta =\pi /2$
.
One can readily see that
Integrating by parts, we see that
 $$ \begin{align*} \frac{1}{4}\int_{1/2}^{1}B^{(1-\sigma_{\theta})u}\sin(\theta u)\frac{\mathrm{d} u}{u} &= \frac{1}{4}\sin\theta \frac{B^{1-\sigma_{\theta}}}{(1-\sigma_{\theta})\log B}\bigl(1+O\bigl((\log B)^{-\alpha/2}\bigr) + O\bigl((\log_{2} B)^{-1}\bigr)\bigr) \\ &=\frac{\sin\theta}{4\log B}\frac{B^{1-\sigma_{0}}}{1-\sigma_{0}}\mathrm{e}^{a_{\theta}}\bigl(1+O\bigl((\log_{2} B)^{-1}\bigr)\bigr) \\ &=\sin\theta\frac{\log x}{\log B}\mathrm{e}^{a_{\theta}}\bigl(1+O\bigl((\log_{2} B)^{-1}\bigr)\bigr), \end{align*} $$
$$ \begin{align*} \frac{1}{4}\int_{1/2}^{1}B^{(1-\sigma_{\theta})u}\sin(\theta u)\frac{\mathrm{d} u}{u} &= \frac{1}{4}\sin\theta \frac{B^{1-\sigma_{\theta}}}{(1-\sigma_{\theta})\log B}\bigl(1+O\bigl((\log B)^{-\alpha/2}\bigr) + O\bigl((\log_{2} B)^{-1}\bigr)\bigr) \\ &=\frac{\sin\theta}{4\log B}\frac{B^{1-\sigma_{0}}}{1-\sigma_{0}}\mathrm{e}^{a_{\theta}}\bigl(1+O\bigl((\log_{2} B)^{-1}\bigr)\bigr) \\ &=\sin\theta\frac{\log x}{\log B}\mathrm{e}^{a_{\theta}}\bigl(1+O\bigl((\log_{2} B)^{-1}\bigr)\bigr), \end{align*} $$
where we used equation (3.7) in the last line. Equation (3.9) then implies that
Let
![]() $\gamma $
now be a unit speed parametrization of this path of steepest descent:
$\gamma $
now be a unit speed parametrization of this path of steepest descent:
The fact that
![]() $\Gamma _{0}$
is the path of steepest descent implies that for
$\Gamma _{0}$
is the path of steepest descent implies that for
![]() $y<0$
,
$y<0$
,
![]() $\gamma '(y)$
is a positive multiple of
$\gamma '(y)$
is a positive multiple of
![]() $\overline {f'}(\gamma (y))$
, while for
$\overline {f'}(\gamma (y))$
, while for
![]() $y>0$
,
$y>0$
,
![]() $\gamma '(y)$
is a negative multiple of
$\gamma '(y)$
is a negative multiple of
![]() $\overline {f'}(\gamma (y))$
. We now show that the argument of the tangent vector
$\overline {f'}(\gamma (y))$
. We now show that the argument of the tangent vector
![]() $\gamma '(y)$
is sufficiently close to
$\gamma '(y)$
is sufficiently close to
![]() $\pi /2$
.
$\pi /2$
.
Lemma 3.4. For
![]() $y\in [y^{-}, y^{+}]$
,
$y\in [y^{-}, y^{+}]$
,
![]() $\left \lvert \arg \bigl (\gamma '(y)\mathrm {e}^{-\mathrm {i}\pi /2}\bigr ) \right \rvert < \pi /5$
.
$\left \lvert \arg \bigl (\gamma '(y)\mathrm {e}^{-\mathrm {i}\pi /2}\bigr ) \right \rvert < \pi /5$
.
Proof. We consider two cases: the case where s is sufficiently close to
![]() $s_{0}$
so that we can apply Lemma 3.3 to estimate the argument of
$s_{0}$
so that we can apply Lemma 3.3 to estimate the argument of
![]() $\overline {f'}$
and the remaining case, where we will estimate this argument via the definition of f.
$\overline {f'}$
and the remaining case, where we will estimate this argument via the definition of f.
We apply Lemma 3.3 with
![]() $\varepsilon = 1/5$
to find a
$\varepsilon = 1/5$
to find a
![]() $\delta>0$
such that for
$\delta>0$
such that for
![]() $\left \lvert s-s_{0} \right \rvert < \delta /\log B$
,
$\left \lvert s-s_{0} \right \rvert < \delta /\log B$
,
Set
![]() $s-s_{0} = r\mathrm {e}^{\mathrm {i}\phi }$
with
$s-s_{0} = r\mathrm {e}^{\mathrm {i}\phi }$
with
![]() $r<\delta /\log B$
and
$r<\delta /\log B$
and
![]() $-\pi < \phi \le \pi $
. Using that
$-\pi < \phi \le \pi $
. Using that
![]() $f"(s_{0})$
is real and positive, we have
$f"(s_{0})$
is real and positive, we have
 $$ \begin{align*} \operatorname{Re} h(s) &= \frac{f"(s_{0})}{2}r^{2}\bigl((1+\operatorname{Re}\lambda_{0}(s))\cos2\phi - (\operatorname{Im}\lambda_{0}(s))\sin2\phi\bigr)\\ \operatorname{Im} h(s) &= \frac{f"(s_{0})}{2}r^{2}\bigl((1+\operatorname{Re}\lambda_{0}(s))\sin2\phi + (\operatorname{Im}\lambda_{0}(s))\cos2\phi\bigr). \end{align*} $$
$$ \begin{align*} \operatorname{Re} h(s) &= \frac{f"(s_{0})}{2}r^{2}\bigl((1+\operatorname{Re}\lambda_{0}(s))\cos2\phi - (\operatorname{Im}\lambda_{0}(s))\sin2\phi\bigr)\\ \operatorname{Im} h(s) &= \frac{f"(s_{0})}{2}r^{2}\bigl((1+\operatorname{Re}\lambda_{0}(s))\sin2\phi + (\operatorname{Im}\lambda_{0}(s))\cos2\phi\bigr). \end{align*} $$
Suppose
![]() $s\in \Gamma _{0}\setminus \{s_{0}\}$
with
$s\in \Gamma _{0}\setminus \{s_{0}\}$
with
![]() $\left \lvert s-s_{0} \right \rvert < \delta /\log B$
. Then
$\left \lvert s-s_{0} \right \rvert < \delta /\log B$
. Then
![]() $\operatorname {Re} h(s)<0$
and
$\operatorname {Re} h(s)<0$
and
![]() $\operatorname {Im} h(s)=0$
. The condition
$\operatorname {Im} h(s)=0$
. The condition
![]() $\operatorname {Re} h(s) < 0$
implies that
$\operatorname {Re} h(s) < 0$
implies that
![]() $\phi \in (-4\pi /5, -\pi /5) \cup (\pi /5, 4\pi /5)$
say, as
$\phi \in (-4\pi /5, -\pi /5) \cup (\pi /5, 4\pi /5)$
say, as
![]() $\left \lvert \lambda _{0}(s) \right \rvert < 1/5$
. In combination with
$\left \lvert \lambda _{0}(s) \right \rvert < 1/5$
. In combination with
![]() $\operatorname {Im} h(s) = 0$
, this implies that
$\operatorname {Im} h(s) = 0$
, this implies that
![]() $\phi \in (-3\pi /5,-2\pi /5) \cup (2\pi /5, 3\pi /5)$
whenever
$\phi \in (-3\pi /5,-2\pi /5) \cup (2\pi /5, 3\pi /5)$
whenever
![]() $s\in \Gamma _{0}\setminus \{s_{0}\}$
,
$s\in \Gamma _{0}\setminus \{s_{0}\}$
,
![]() $\left \lvert s-s_{0} \right \rvert < \delta /\log B$
. Again by Lemma 3.3,
$\left \lvert s-s_{0} \right \rvert < \delta /\log B$
. Again by Lemma 3.3,
It follows that
![]() $\left \lvert \arg \bigl (\gamma '(y)\mathrm {e}^{-\mathrm {i}\pi /2}\bigr ) \right \rvert < \pi /5$
when
$\left \lvert \arg \bigl (\gamma '(y)\mathrm {e}^{-\mathrm {i}\pi /2}\bigr ) \right \rvert < \pi /5$
when
![]() $\left \lvert \gamma (y)-s_{0} \right \rvert < \delta /\log B$
.
$\left \lvert \gamma (y)-s_{0} \right \rvert < \delta /\log B$
.
It remains to treat the case
![]() $\left \lvert \gamma (y)-s_{0} \right \rvert \ge \delta /\log B$
. For these points, we have that
$\left \lvert \gamma (y)-s_{0} \right \rvert \ge \delta /\log B$
. For these points, we have that
![]() $\delta /2 \le \left \lvert \theta \right \rvert \le \pi /2$
, where we used the notation
$\delta /2 \le \left \lvert \theta \right \rvert \le \pi /2$
, where we used the notation
![]() $\theta = (\operatorname {Im} \gamma (y) -\tau )\log B$
as before. Set
$\theta = (\operatorname {Im} \gamma (y) -\tau )\log B$
as before. Set
![]() $\gamma (y) = s = \sigma +\mathrm {i} t$
with
$\gamma (y) = s = \sigma +\mathrm {i} t$
with
![]() $\sigma =\sigma _{0} - a_{\theta }/\log B$
. Recalling that
$\sigma =\sigma _{0} - a_{\theta }/\log B$
. Recalling that
![]() $\tau \log B\in 4\pi \mathbb {Z}$
, we obtain the following explicit expression for
$\tau \log B\in 4\pi \mathbb {Z}$
, we obtain the following explicit expression for
![]() $\overline {f'}$
:
$\overline {f'}$
:
 $$ \begin{align*} \overline{f'}(s)& = \log x - \frac{1/4}{(1-\sigma)^{2}+(t-\tau)^{2}}\biggl\{ B^{1-\sigma}\biggl(\!\biggl((1-\sigma)\cos\theta + \frac{\theta\sin\theta}{\log B}\biggr) + \mathrm{i}\biggl((1-\sigma)\sin\theta - \frac{\theta\cos\theta}{\log B}\biggr)\!\biggr) \\[5pt] &\quad-B^{(1-\sigma)/2}\biggl(\biggl((1-\sigma)\cos(\theta/2) + \frac{\theta\sin(\theta/2)}{\log B}\biggr) + \mathrm{i}\biggl((1-\sigma)\sin(\theta/2) - \frac{\theta\cos(\theta/2)}{\log B}\biggr)\biggr)\biggr\}. \end{align*} $$
$$ \begin{align*} \overline{f'}(s)& = \log x - \frac{1/4}{(1-\sigma)^{2}+(t-\tau)^{2}}\biggl\{ B^{1-\sigma}\biggl(\!\biggl((1-\sigma)\cos\theta + \frac{\theta\sin\theta}{\log B}\biggr) + \mathrm{i}\biggl((1-\sigma)\sin\theta - \frac{\theta\cos\theta}{\log B}\biggr)\!\biggr) \\[5pt] &\quad-B^{(1-\sigma)/2}\biggl(\biggl((1-\sigma)\cos(\theta/2) + \frac{\theta\sin(\theta/2)}{\log B}\biggr) + \mathrm{i}\biggl((1-\sigma)\sin(\theta/2) - \frac{\theta\cos(\theta/2)}{\log B}\biggr)\biggr)\biggr\}. \end{align*} $$
Using equations (3.7) and (3.10), we see that

This implies
The last inequality follows from the fact that
![]() $\left \lvert 1/\theta -\cot \theta \right \rvert < 2/\pi $
for
$\left \lvert 1/\theta -\cot \theta \right \rvert < 2/\pi $
for
![]() $\theta \in [-\pi /2, \pi /2]$
and that
$\theta \in [-\pi /2, \pi /2]$
and that
![]() $\arctan (2/\pi ) \approx 0.18\pi < \pi /5$
.
$\arctan (2/\pi ) \approx 0.18\pi < \pi /5$
.
3.3 The contribution from
 $s_{0}$
$s_{0}$
We will now estimate the contribution from
![]() $s_{0}$
, by which we mean
$s_{0}$
, by which we mean
 $$\begin{align*}\frac{1}{\pi}\operatorname{Im}\int_{\Gamma_{0}}\mathrm{e}^{f(s)}g(s)\mathrm{d} s, \end{align*}$$
$$\begin{align*}\frac{1}{\pi}\operatorname{Im}\int_{\Gamma_{0}}\mathrm{e}^{f(s)}g(s)\mathrm{d} s, \end{align*}$$
and where f and g are given by equations (3.2) and (3.3), respectively. We have combined the two pieces in the upper and lower half plane
![]() $\int _{\Gamma _{0}}$
and
$\int _{\Gamma _{0}}$
and
![]() $-\int _{\overline {\Gamma _{0}}}$
into one integral using
$-\int _{\overline {\Gamma _{0}}}$
into one integral using
![]() $\zeta _{C}(\overline {s}) = \overline {\zeta _{C}(s)}$
. To estimate this integral, we will use the following simple lemma (see, e.g., [Reference Broucke, Debruyne and Vindas5, Lemma 3.3]).
$\zeta _{C}(\overline {s}) = \overline {\zeta _{C}(s)}$
. To estimate this integral, we will use the following simple lemma (see, e.g., [Reference Broucke, Debruyne and Vindas5, Lemma 3.3]).
Lemma 3.5. Let
![]() $a<b$
, and suppose that
$a<b$
, and suppose that
![]() $F: [a,b] \to \mathbb {C}$
is integrable. If there exist
$F: [a,b] \to \mathbb {C}$
is integrable. If there exist
![]() $\theta _{0}$
and
$\theta _{0}$
and
![]() $\omega $
with
$\omega $
with
![]() $0\le \omega < \pi /2$
such that
$0\le \omega < \pi /2$
such that
![]() $\left \lvert \arg (F\mathrm {e}^{-\mathrm {i}\theta _{0}}) \right \rvert \le \omega $
, then
$\left \lvert \arg (F\mathrm {e}^{-\mathrm {i}\theta _{0}}) \right \rvert \le \omega $
, then
 $$\begin{align*}\int_{a}^{b}F(u)\mathrm{d} u = \rho\mathrm{e}^{\mathrm{i}(\theta_{0}+\varphi)} \end{align*}$$
$$\begin{align*}\int_{a}^{b}F(u)\mathrm{d} u = \rho\mathrm{e}^{\mathrm{i}(\theta_{0}+\varphi)} \end{align*}$$
for some real numbers
![]() $\rho $
and
$\rho $
and
![]() $\varphi $
satisfying
$\varphi $
satisfying
 $$\begin{align*}\rho \ge (\cos \omega)\int_{a}^{b}\left\lvert F(u) \right\rvert \mathrm{d} u \quad \mbox{and} \quad \left\lvert \varphi \right\rvert \le \omega. \end{align*}$$
$$\begin{align*}\rho \ge (\cos \omega)\int_{a}^{b}\left\lvert F(u) \right\rvert \mathrm{d} u \quad \mbox{and} \quad \left\lvert \varphi \right\rvert \le \omega. \end{align*}$$
We will estimate g with the following lemma.
Lemma 3.6. Let
![]() $\varepsilon>0$
, and suppose that
$\varepsilon>0$
, and suppose that
![]() $s=\sigma +\mathrm {i} t$
satisfies
$s=\sigma +\mathrm {i} t$
satisfies
 $$\begin{align*}\sigma \ge 1 - O\left(\frac{\log_{2}B_{K}}{\log B_{K}} \right), \quad t \gg \tau_{K}. \end{align*}$$
$$\begin{align*}\sigma \ge 1 - O\left(\frac{\log_{2}B_{K}}{\log B_{K}} \right), \quad t \gg \tau_{K}. \end{align*}$$
Then for
![]() $K (> K(\varepsilon ))$
sufficiently large,
$K (> K(\varepsilon ))$
sufficiently large,
 $$\begin{align*}\left\lvert \sum_{k=0}^{K-1}\int_{s}^{s+1}\bigl(\eta_{k}(z) + \tilde{\eta}_{k}(z) + \xi_{k}(z)\bigr)\mathrm{d} z + \int_{s}^{s+1}\bigl(\tilde{\eta}_{K}(z)+\xi_{K}(z)\bigr)\mathrm{d} z - \int_{s+1}^{\infty}\eta_{K}(z)\mathrm{d} z \right\rvert < \varepsilon. \end{align*}$$
$$\begin{align*}\left\lvert \sum_{k=0}^{K-1}\int_{s}^{s+1}\bigl(\eta_{k}(z) + \tilde{\eta}_{k}(z) + \xi_{k}(z)\bigr)\mathrm{d} z + \int_{s}^{s+1}\bigl(\tilde{\eta}_{K}(z)+\xi_{K}(z)\bigr)\mathrm{d} z - \int_{s+1}^{\infty}\eta_{K}(z)\mathrm{d} z \right\rvert < \varepsilon. \end{align*}$$
Proof. By the definition (3.1) of the functions
![]() $\eta _{k}$
,
$\eta _{k}$
,
![]() $\tilde {\eta }_{k}$
, and
$\tilde {\eta }_{k}$
, and
![]() $\xi _{k}$
, we have
$\xi _{k}$
, we have
 $$\begin{align*}\sum_{k=0}^{K}\int_{s}^{s+1}\xi_{k}(z)\mathrm{d} z \ll \sum_{k=0}^{K}\frac{C_{k}^{1-\sigma}}{\left\lvert s \right\rvert \log C_{k}} \ll K\frac{(\log B_{K})^{O(1)}}{\tau_{K}}, \end{align*}$$
$$\begin{align*}\sum_{k=0}^{K}\int_{s}^{s+1}\xi_{k}(z)\mathrm{d} z \ll \sum_{k=0}^{K}\frac{C_{k}^{1-\sigma}}{\left\lvert s \right\rvert \log C_{k}} \ll K\frac{(\log B_{K})^{O(1)}}{\tau_{K}}, \end{align*}$$
where in the last step we used that
![]() $C_{K} \asymp B_{K}$
by equation (2.3). This quantity is bounded by
$C_{K} \asymp B_{K}$
by equation (2.3). This quantity is bounded by
![]() $\exp \bigl (\log K - c(\log B_{K})^{\alpha } + O(\log _{2}B_{K})\bigr )$
, which can be made arbitrarily small by taking K sufficiently large, due to the rapid growth of
$\exp \bigl (\log K - c(\log B_{K})^{\alpha } + O(\log _{2}B_{K})\bigr )$
, which can be made arbitrarily small by taking K sufficiently large, due to the rapid growth of
![]() $(B_{k})_{k}$
(property (a)). The condition
$(B_{k})_{k}$
(property (a)). The condition
![]() $t \gg \tau _{K}$
together with the rapid growth of
$t \gg \tau _{K}$
together with the rapid growth of
![]() $(\tau _{k})_{k}$
implies that
$(\tau _{k})_{k}$
implies that
![]() $\left \lvert 1 \pm \mathrm {i}\tau _{k} - s \right \rvert \gg \tau _{K}$
, for
$\left \lvert 1 \pm \mathrm {i}\tau _{k} - s \right \rvert \gg \tau _{K}$
, for
![]() $0\le k \le K-1$
(at least when K is sufficiently large). Hence,
$0\le k \le K-1$
(at least when K is sufficiently large). Hence,
 $$\begin{align*}\sum_{k=0}^{K-1}\int_{s}^{s+1}(\eta_{k}(z)+\tilde{\eta}_{k}(z))\mathrm{d} z \ll \sum_{k=0}^{K-1}\frac{B_{k}^{1-\sigma}}{\tau_{K}\log B_{k}} \ll \exp\bigl(\log K - c(\log B_{K})^{\alpha} + O(\log_{2}B_{K})\bigr). \end{align*}$$
$$\begin{align*}\sum_{k=0}^{K-1}\int_{s}^{s+1}(\eta_{k}(z)+\tilde{\eta}_{k}(z))\mathrm{d} z \ll \sum_{k=0}^{K-1}\frac{B_{k}^{1-\sigma}}{\tau_{K}\log B_{k}} \ll \exp\bigl(\log K - c(\log B_{K})^{\alpha} + O(\log_{2}B_{K})\bigr). \end{align*}$$
Finally, we have
 $$ \begin{align*} \int_{s}^{s+1}\tilde{\eta}_{K}(z)\mathrm{d} z &\ll \frac{B_{K}^{1-\sigma}}{\tau_{K}\log B_{K}} = \exp\bigl(-c(\log B_{K})^{\alpha} + O(\log_{2}B_{K})\bigr), \\ \int_{s+1}^{\infty}\eta_{K}(z)\mathrm{d} z &\ll \frac{B_{K}^{-\sigma}}{\log B_{K}}.\\[-36pt] \end{align*} $$
$$ \begin{align*} \int_{s}^{s+1}\tilde{\eta}_{K}(z)\mathrm{d} z &\ll \frac{B_{K}^{1-\sigma}}{\tau_{K}\log B_{K}} = \exp\bigl(-c(\log B_{K})^{\alpha} + O(\log_{2}B_{K})\bigr), \\ \int_{s+1}^{\infty}\eta_{K}(z)\mathrm{d} z &\ll \frac{B_{K}^{-\sigma}}{\log B_{K}}.\\[-36pt] \end{align*} $$
In particular, we may assume that on the contour
![]() $\Gamma _{0}$
, these terms are in absolute value smaller than
$\Gamma _{0}$
, these terms are in absolute value smaller than
![]() $\pi /40$
, say. Also,
$\pi /40$
, say. Also,
![]() $1/\left \lvert s-1 \right \rvert \sim 1/\tau _{K}$
and
$1/\left \lvert s-1 \right \rvert \sim 1/\tau _{K}$
and
![]() $\left \lvert \arg \bigl (\mathrm {e}^{\mathrm {i}\pi /2}/(s-1)\bigr ) \right \rvert < \pi /40$
on
$\left \lvert \arg \bigl (\mathrm {e}^{\mathrm {i}\pi /2}/(s-1)\bigr ) \right \rvert < \pi /40$
on
![]() $\Gamma _{0}$
. We have
$\Gamma _{0}$
. We have
 $$\begin{align*}\int_{\Gamma_{0}}\mathrm{e}^{f(s)}g(s)\mathrm{d} s = \mathrm{e}^{f(s_{0})}\int_{\Gamma_{0}}\mathrm{e}^{f(s)-f(s_{0})}g(s)\mathrm{d} s. \end{align*}$$
$$\begin{align*}\int_{\Gamma_{0}}\mathrm{e}^{f(s)}g(s)\mathrm{d} s = \mathrm{e}^{f(s_{0})}\int_{\Gamma_{0}}\mathrm{e}^{f(s)-f(s_{0})}g(s)\mathrm{d} s. \end{align*}$$
We now apply Lemma 3.5 to estimate the size and argument of this integral. By Property (c) and Lemma 3.4 we get that
 $$ \begin{gather*} \int_{\Gamma_{0}}\mathrm{e}^{f(s)}g(s)\mathrm{d} s = (-1)^{K}R\mathrm{e}^{\mathrm{i}(\pi/2 + \varphi)}, \\ R \gg \frac{\mathrm{e}^{\operatorname{Re} f(s_{0})}}{\tau_{K}}\int_{y^{-}}^{y^{+}}\exp\bigl( f(\gamma(y))-f(s_{0})\bigr)\mathrm{d} y, \quad \left\lvert \varphi \right\rvert < \frac{\pi}{5} + \frac{\pi}{40} + \frac{\pi}{40} = \frac{\pi}{4}. \end{gather*} $$
$$ \begin{gather*} \int_{\Gamma_{0}}\mathrm{e}^{f(s)}g(s)\mathrm{d} s = (-1)^{K}R\mathrm{e}^{\mathrm{i}(\pi/2 + \varphi)}, \\ R \gg \frac{\mathrm{e}^{\operatorname{Re} f(s_{0})}}{\tau_{K}}\int_{y^{-}}^{y^{+}}\exp\bigl( f(\gamma(y))-f(s_{0})\bigr)\mathrm{d} y, \quad \left\lvert \varphi \right\rvert < \frac{\pi}{5} + \frac{\pi}{40} + \frac{\pi}{40} = \frac{\pi}{4}. \end{gather*} $$
Note that
![]() $f(\gamma (y))-f(s_{0})$
is real. In order to bound the remaining integral from below, we restrict the range of integration to the points
$f(\gamma (y))-f(s_{0})$
is real. In order to bound the remaining integral from below, we restrict the range of integration to the points
![]() $s=\gamma (y)$
in the disk
$s=\gamma (y)$
in the disk
![]() $B(s_{0}, \delta /\log B)$
so that we may approximate f by means of Lemma 3.3. We have
$B(s_{0}, \delta /\log B)$
so that we may approximate f by means of Lemma 3.3. We have
Now
![]() $f"(s_{0})$
is real, and
$f"(s_{0})$
is real, and
![]() $f"(s_{0}) = \log B\log x\bigl (1+O((\log _{2}B)^{-1})\bigr )$
and
$f"(s_{0}) = \log B\log x\bigl (1+O((\log _{2}B)^{-1})\bigr )$
and
if we take a value for
![]() $\delta $
provided by Lemma 3.3 corresponding to the choice
$\delta $
provided by Lemma 3.3 corresponding to the choice
![]() $\varepsilon =1$
say. Hence, the integral
$\varepsilon =1$
say. Hence, the integral
![]() $\int _{y^{-}}^{y^{+}}\exp \bigl ( f(\gamma (y))-f(s_{0})\bigr )\mathrm{d} y$
is bounded from below by
$\int _{y^{-}}^{y^{+}}\exp \bigl ( f(\gamma (y))-f(s_{0})\bigr )\mathrm{d} y$
is bounded from below by
 $$\begin{align*}\int_{-\delta/\log B}^{\delta/\log B}\exp\bigl(-2(\log B\log x) y^{2}\bigr)\mathrm{d} y \gg_{\delta} \min\biggl(\frac{1}{\log B}, \frac{1}{\sqrt{\log B\log x}}\biggr) = \frac{1}{\sqrt{\log B\log x}}. \end{align*}$$
$$\begin{align*}\int_{-\delta/\log B}^{\delta/\log B}\exp\bigl(-2(\log B\log x) y^{2}\bigr)\mathrm{d} y \gg_{\delta} \min\biggl(\frac{1}{\log B}, \frac{1}{\sqrt{\log B\log x}}\biggr) = \frac{1}{\sqrt{\log B\log x}}. \end{align*}$$
We conclude that the contribution from
![]() $s_{0}$
has sign
$s_{0}$
has sign
![]() $(-1)^{K}$
and has absolute value bounded from below by
$(-1)^{K}$
and has absolute value bounded from below by
 $$ \begin{align} \frac{x}{\tau}\exp\biggl(-(1-\sigma_{0})\log x + \int_{s_{0}}^{\infty}\eta(z)\mathrm{d} z + O(\log_{2}x)\biggr). \end{align} $$
$$ \begin{align} \frac{x}{\tau}\exp\biggl(-(1-\sigma_{0})\log x + \int_{s_{0}}^{\infty}\eta(z)\mathrm{d} z + O(\log_{2}x)\biggr). \end{align} $$
Let us now estimate
![]() $\int _{s}^{\infty }\eta (z)\mathrm{d} z$
. We use the representation (3.4) and integrate by parts three times,
$\int _{s}^{\infty }\eta (z)\mathrm{d} z$
. We use the representation (3.4) and integrate by parts three times,
 $$ \begin{align} \int_{s}^{\infty}\eta(z)\mathrm{d} z &= \frac{B^{1+\mathrm{i}\tau-s}-2B^{(1+\mathrm{i}\tau-s)/2}}{4(1+\mathrm{i}\tau -s)\log B} + \frac{B^{1+\mathrm{i}\tau-s}-4B^{(1+\mathrm{i}\tau-s)/2}}{4((1+\mathrm{i}\tau -s)\log B)^{2}} \nonumber \\ &\quad+ \frac{B^{1+\mathrm{i}\tau-s}-8B^{(1+\mathrm{i}\tau-s)/2}}{2((1+\mathrm{i}\tau -s)\log B)^{3}} + \frac{3}{2((1+\mathrm{i}\tau -s )\log B)^{3}}\int_{1/2}^{1}\frac{B^{(1+\mathrm{i}\tau-s)u}}{u^{4}}\mathrm{d} u. \end{align} $$
$$ \begin{align} \int_{s}^{\infty}\eta(z)\mathrm{d} z &= \frac{B^{1+\mathrm{i}\tau-s}-2B^{(1+\mathrm{i}\tau-s)/2}}{4(1+\mathrm{i}\tau -s)\log B} + \frac{B^{1+\mathrm{i}\tau-s}-4B^{(1+\mathrm{i}\tau-s)/2}}{4((1+\mathrm{i}\tau -s)\log B)^{2}} \nonumber \\ &\quad+ \frac{B^{1+\mathrm{i}\tau-s}-8B^{(1+\mathrm{i}\tau-s)/2}}{2((1+\mathrm{i}\tau -s)\log B)^{3}} + \frac{3}{2((1+\mathrm{i}\tau -s )\log B)^{3}}\int_{1/2}^{1}\frac{B^{(1+\mathrm{i}\tau-s)u}}{u^{4}}\mathrm{d} u. \end{align} $$
Although we did not have to perform partial integration to obtain the contribution (3.14) from
![]() $s_{0}$
below, we shall require these finer estimates for
$s_{0}$
below, we shall require these finer estimates for
![]() $\int ^{\infty }_{s} \eta (z) \mathrm{d} z$
later on. For
$\int ^{\infty }_{s} \eta (z) \mathrm{d} z$
later on. For
![]() $s=s_{0}$
we get
$s=s_{0}$
we get
 $$ \begin{align} \int_{s_{0}}^{\infty}\eta(z)\mathrm{d} z &= \frac{B^{1-\sigma_{0}}}{4(1-\sigma_{0})}\frac{1}{\log B} + \frac{B^{1-\sigma_{0}}}{4(1-\sigma_{0})}\frac{1}{(1-\sigma_{0})(\log B)^{2}} \nonumber \\ &\quad+ \frac{B^{1-\sigma_{0}}}{4(1-\sigma_{0})}\frac{2}{(1-\sigma_{0})^{2}(\log B)^{3}} + O\biggl(\frac{B^{1-\sigma_{0}}}{1-\sigma_{0}}\frac{1}{(1-\sigma_{0})^{3}(\log B)^{4}}\biggr) \nonumber \\ &= \frac{\log x}{\log B}\biggl(1+\frac{1}{(1-\sigma_{0})\log B}+\frac{2}{((1-\sigma_{0})\log B)^{2}} + O\biggl(\frac{1}{((1-\sigma_{0})\log B)^{3}}\biggr)\biggr), \end{align} $$
$$ \begin{align} \int_{s_{0}}^{\infty}\eta(z)\mathrm{d} z &= \frac{B^{1-\sigma_{0}}}{4(1-\sigma_{0})}\frac{1}{\log B} + \frac{B^{1-\sigma_{0}}}{4(1-\sigma_{0})}\frac{1}{(1-\sigma_{0})(\log B)^{2}} \nonumber \\ &\quad+ \frac{B^{1-\sigma_{0}}}{4(1-\sigma_{0})}\frac{2}{(1-\sigma_{0})^{2}(\log B)^{3}} + O\biggl(\frac{B^{1-\sigma_{0}}}{1-\sigma_{0}}\frac{1}{(1-\sigma_{0})^{3}(\log B)^{4}}\biggr) \nonumber \\ &= \frac{\log x}{\log B}\biggl(1+\frac{1}{(1-\sigma_{0})\log B}+\frac{2}{((1-\sigma_{0})\log B)^{2}} + O\biggl(\frac{1}{((1-\sigma_{0})\log B)^{3}}\biggr)\biggr), \end{align} $$
where we have used equation (3.7). Combining the above with the estimate (3.6) for
![]() $\sigma _{0}$
and the relations (2.2) and (2.4) between
$\sigma _{0}$
and the relations (2.2) and (2.4) between
![]() $\tau $
and B, and x and B, respectively, we get that the contribution from
$\tau $
and B, and x and B, respectively, we get that the contribution from
![]() $s_{0}$
has absolute value which is bounded from below by
$s_{0}$
has absolute value which is bounded from below by
 $$ \begin{align} x\exp\biggl\{-(c(\alpha+1))^{\frac{1}{\alpha+1}}(\log x\log_{2}x)^{\frac{\alpha}{\alpha+1}}\biggl(1+\frac{\alpha}{\alpha+1}\frac{\log_{3}x}{\log_{2}x}+ O\biggl(\frac{1}{\log_{2}x}\biggr)\biggr)\biggr\}. \end{align} $$
$$ \begin{align} x\exp\biggl\{-(c(\alpha+1))^{\frac{1}{\alpha+1}}(\log x\log_{2}x)^{\frac{\alpha}{\alpha+1}}\biggl(1+\frac{\alpha}{\alpha+1}\frac{\log_{3}x}{\log_{2}x}+ O\biggl(\frac{1}{\log_{2}x}\biggr)\biggr)\biggr\}. \end{align} $$
3.4 The steepest paths through
 $s_{m}$
,
$s_{m}$
,
 $m\neq 0$
$m\neq 0$
We now consider the contributions from the other saddle points. In this case by such contributions we mean
where
![]() $\Gamma _{m}$
is some contour which connects the two horizontal lines
$\Gamma _{m}$
is some contour which connects the two horizontal lines
![]() $t=t_{m}^{-}$
and
$t=t_{m}^{-}$
and
![]() $t=t_{m}^{+}$
. This contribution will be of lower order than that of
$t=t_{m}^{+}$
. This contribution will be of lower order than that of
![]() $s_{0}$
. We shall again use the method of steepest descent; just taking some simple choice for
$s_{0}$
. We shall again use the method of steepest descent; just taking some simple choice for
![]() $\Gamma _{m}$
(e.g. a vertical line segment) and estimating the integral via the triangle inequality appears to be insufficient for small m. We consider
$\Gamma _{m}$
(e.g. a vertical line segment) and estimating the integral via the triangle inequality appears to be insufficient for small m. We consider
![]() $\left \lvert m \right \rvert \le M := \lfloor (\log _{2}B)^{3/4}\rfloor $
. The part of the Perron integral where
$\left \lvert m \right \rvert \le M := \lfloor (\log _{2}B)^{3/4}\rfloor $
. The part of the Perron integral where
![]() $t<t_{-M}^{-}$
or
$t<t_{-M}^{-}$
or
![]() $t>t_{M}^{+}$
can be estimated without appealing to the saddle point method, and this will be done in the next section.
$t>t_{M}^{+}$
can be estimated without appealing to the saddle point method, and this will be done in the next section.
We want to show that we can connect the two lines
![]() $t=t_{m}^{-}$
and
$t=t_{m}^{-}$
and
![]() $t=t_{m}^{+}$
with the path of steepest decent through
$t=t_{m}^{+}$
with the path of steepest decent through
![]() $s_{m}$
. We first consider the steepest path in a small neighborhood of
$s_{m}$
. We first consider the steepest path in a small neighborhood of
![]() $s_{m}$
. By applying Lemma 3.3 with
$s_{m}$
. By applying Lemma 3.3 with
![]() $\varepsilon =1/5$
, we find some
$\varepsilon =1/5$
, we find some
![]() $\delta '> 0$
(independent of K and m) such that
$\delta '> 0$
(independent of K and m) such that
where
![]() $\left \lvert \lambda _{m}(s) \right \rvert < 1/5$
for
$\left \lvert \lambda _{m}(s) \right \rvert < 1/5$
for
![]() $s\in B(s_{m}, \delta '/\log B)$
, and where
$s\in B(s_{m}, \delta '/\log B)$
, and where
![]() $\psi _{m}$
is a holomorphic bijection of
$\psi _{m}$
is a holomorphic bijection of
![]() $B(s_{m}, \delta '/\log B)$
onto some neighborhood U of
$B(s_{m}, \delta '/\log B)$
onto some neighborhood U of
![]() $0$
. The path of steepest descent
$0$
. The path of steepest descent
![]() $\Gamma _{m}$
in
$\Gamma _{m}$
in
![]() $B(s_{m}, \delta '/\log B)$
is the inverse image under
$B(s_{m}, \delta '/\log B)$
is the inverse image under
![]() $\psi _{m}$
of the curve
$\psi _{m}$
of the curve
![]() $\{ z\in U: \operatorname {Re} z=0\}$
. Since
$\{ z\in U: \operatorname {Re} z=0\}$
. Since
![]() $f"(s_{m}) = \log B\log x\bigl (1+O((\log _{2}B)^{-1})\bigr )$
(which follows from equation (3.7)), we have that
$f"(s_{m}) = \log B\log x\bigl (1+O((\log _{2}B)^{-1})\bigr )$
(which follows from equation (3.7)), we have that
where we have set
![]() $s-s_{m}=r\mathrm {e}^{\mathrm {i}\phi }$
. Points
$s-s_{m}=r\mathrm {e}^{\mathrm {i}\phi }$
. Points
![]() $s \in \Gamma _{m}\setminus \{s_{m}\}$
satisfy
$s \in \Gamma _{m}\setminus \{s_{m}\}$
satisfy
![]() $\operatorname {Re}\bigl ( f(s) - f(s_{m}) \bigr ) < 0$
, and since
$\operatorname {Re}\bigl ( f(s) - f(s_{m}) \bigr ) < 0$
, and since
![]() $\left \lvert \lambda _{m}(s) \right \rvert < 1/5$
, it follows from the above equation that such points lie in the union of the sectors
$\left \lvert \lambda _{m}(s) \right \rvert < 1/5$
, it follows from the above equation that such points lie in the union of the sectors
![]() $\phi \in (\pi /5, 4\pi /5) \cup (-\pi /5, -4\pi /5)$
, say. We have that
$\phi \in (\pi /5, 4\pi /5) \cup (-\pi /5, -4\pi /5)$
, say. We have that
![]() $\Gamma _{m}\setminus \{s_{m}\}$
is the union of two curves
$\Gamma _{m}\setminus \{s_{m}\}$
is the union of two curves
![]() $\Gamma _{m}^{+}$
and
$\Gamma _{m}^{+}$
and
![]() $\Gamma _{m}^{-}$
, where
$\Gamma _{m}^{-}$
, where
![]() $\Gamma _{m}^{+}$
lies in the sector
$\Gamma _{m}^{+}$
lies in the sector
![]() $\phi \in (\pi /5, 4\pi /5)$
, and
$\phi \in (\pi /5, 4\pi /5)$
, and
![]() $\Gamma _{m}^{-}$
lies in the sector
$\Gamma _{m}^{-}$
lies in the sector
![]() $\phi \in (-\pi /5, -4\pi /5)$
. (It is impossible that both pieces lie in the same sector since the angle between
$\phi \in (-\pi /5, -4\pi /5)$
. (It is impossible that both pieces lie in the same sector since the angle between
![]() $\Gamma _{m}^{+}$
and
$\Gamma _{m}^{+}$
and
![]() $\Gamma _{m}^{-}$
at
$\Gamma _{m}^{-}$
at
![]() $s_{m}$
equals
$s_{m}$
equals
![]() $\pi $
, as
$\pi $
, as
![]() $\psi _{m}^{-1}$
is conformal.) Both
$\psi _{m}^{-1}$
is conformal.) Both
![]() $\Gamma _{m}^{+}$
and
$\Gamma _{m}^{+}$
and
![]() $\Gamma _{m}^{-}$
intersect the circle
$\Gamma _{m}^{-}$
intersect the circle
![]() $\partial B(s_{m}, \delta '/(2\log B))$
, which can be seen from the fact that
$\partial B(s_{m}, \delta '/(2\log B))$
, which can be seen from the fact that
![]() $\psi _{m}(\Gamma _{m}^{+})$
and
$\psi _{m}(\Gamma _{m}^{+})$
and
![]() $\psi _{m}(\Gamma _{m}^{-})$
both intersect the closed curve
$\psi _{m}(\Gamma _{m}^{-})$
both intersect the closed curve
![]() $\psi _{m}(\partial B(s_{m}, \delta '/(2\log B)))$
. From this it follows that the path of steepest descent
$\psi _{m}(\partial B(s_{m}, \delta '/(2\log B)))$
. From this it follows that the path of steepest descent
![]() $\Gamma _{m}$
connects the lines
$\Gamma _{m}$
connects the lines
![]() $t=t_{m}-\delta /\log B$
and
$t=t_{m}-\delta /\log B$
and
![]() $t=t_{m}+\delta /\log B$
, where
$t=t_{m}+\delta /\log B$
, where
![]() $\delta =(\delta '/2)\sin (\pi /5)$
. Since
$\delta =(\delta '/2)\sin (\pi /5)$
. Since
![]() $f'(s) = f"(s_{m})(s-s_{m})(1+\tilde {\lambda }_{m}(s))$
, with also
$f'(s) = f"(s_{m})(s-s_{m})(1+\tilde {\lambda }_{m}(s))$
, with also
![]() $\left \lvert \tilde {\lambda }_{m}(s) \right \rvert < 1/5$
, it follows that
$\left \lvert \tilde {\lambda }_{m}(s) \right \rvert < 1/5$
, it follows that
![]() $\arg f'(s) \in (\pi /10, 9\pi /10)$
if
$\arg f'(s) \in (\pi /10, 9\pi /10)$
if
![]() $\phi \in (\pi /5, 4\pi /5)$
, and
$\phi \in (\pi /5, 4\pi /5)$
, and
![]() $\arg f'(s) \in (-9\pi /10, -\pi /10)$
if
$\arg f'(s) \in (-9\pi /10, -\pi /10)$
if
![]() $\phi \in (-4\pi /5, -\pi /5)$
. This implies that the tangent vector of
$\phi \in (-4\pi /5, -\pi /5)$
. This implies that the tangent vector of
![]() $\Gamma _{m}$
has argument contained in
$\Gamma _{m}$
has argument contained in
![]() $(\pi /10, 9\pi /10)$
(when
$(\pi /10, 9\pi /10)$
(when
![]() $\Gamma _{m}$
is parametrized in such a way that we move in the upward direction). From this it follows that the length of
$\Gamma _{m}$
is parametrized in such a way that we move in the upward direction). From this it follows that the length of
![]() $\Gamma _{m}$
in the neighborhood
$\Gamma _{m}$
in the neighborhood
![]() $B(s_{m}, \delta '/(2\log B))$
is bounded by
$B(s_{m}, \delta '/(2\log B))$
is bounded by
![]() $O(\delta /\log B)$
.
$O(\delta /\log B)$
.
For the continuation of
![]() $\Gamma _{m}$
outside this neighborhood of
$\Gamma _{m}$
outside this neighborhood of
![]() $s_{m}$
, we argue as follows. We again set
$s_{m}$
, we argue as follows. We again set
![]() $\theta =(t-\tau )\log B$
, and we consider the range
$\theta =(t-\tau )\log B$
, and we consider the range
The equation for the steepest paths through
![]() $s_{m}$
,
$s_{m}$
,
![]() $\operatorname {Im} f(s) = \operatorname {Im} f(s_{m})$
, gives
$\operatorname {Im} f(s) = \operatorname {Im} f(s_{m})$
, gives
 $$\begin{align*}t_{m}\log x - \frac{1}{4}\int_{1/2}^{1}B^{(1-\sigma_{m})u}\sin\bigl((t_{m}-\tau)(\log B)u\bigr)\frac{\mathrm{d} u}{u} = t\log x - \frac{1}{4}\int_{1/2}^{1}B^{(1-\sigma)u}\sin(\theta u)\frac{\mathrm{d} u}{u}, \end{align*}$$
$$\begin{align*}t_{m}\log x - \frac{1}{4}\int_{1/2}^{1}B^{(1-\sigma_{m})u}\sin\bigl((t_{m}-\tau)(\log B)u\bigr)\frac{\mathrm{d} u}{u} = t\log x - \frac{1}{4}\int_{1/2}^{1}B^{(1-\sigma)u}\sin(\theta u)\frac{\mathrm{d} u}{u}, \end{align*}$$
which is equivalent to
 $$ \begin{align} (t-t_{m})\log x + \frac{1}{4}\int_{1/2}^{1}B^{(1-\sigma_{m})u}\sin\bigl((t_{m}-\tau)(\log B)u\bigr)\frac{\mathrm{d} u}{u} = \frac{1}{4}\int_{1/2}^{1}B^{(1-\sigma)u}\sin(\theta u)\frac{\mathrm{d} u}{u}. \end{align} $$
$$ \begin{align} (t-t_{m})\log x + \frac{1}{4}\int_{1/2}^{1}B^{(1-\sigma_{m})u}\sin\bigl((t_{m}-\tau)(\log B)u\bigr)\frac{\mathrm{d} u}{u} = \frac{1}{4}\int_{1/2}^{1}B^{(1-\sigma)u}\sin(\theta u)\frac{\mathrm{d} u}{u}. \end{align} $$
Also, the points on the path of steepest ascent satisfy this equation, but we will show that for fixed
![]() $\theta $
in the range (3.15), the above equation has a unique solution for
$\theta $
in the range (3.15), the above equation has a unique solution for
![]() $\sigma $
(in a sufficiently large range for
$\sigma $
(in a sufficiently large range for
![]() $\sigma $
that contains
$\sigma $
that contains
![]() $\sigma _{m}$
). These solutions necessarily form the continuation of the path of steepest descent in the neighborhood
$\sigma _{m}$
). These solutions necessarily form the continuation of the path of steepest descent in the neighborhood
![]() $B(s_{m}, \delta '/ (2\log B))$
.
$B(s_{m}, \delta '/ (2\log B))$
.
We consider
![]() $\theta $
in the range (3.15) fixed (so also t is fixed). We have
$\theta $
in the range (3.15) fixed (so also t is fixed). We have
![]() $\sin \theta \gg _{\delta } 1$
. The right-hand side of equation (3.16) is a monotone function of
$\sin \theta \gg _{\delta } 1$
. The right-hand side of equation (3.16) is a monotone function of
![]() $\sigma $
for
$\sigma $
for
![]() $\sigma $
in the range
$\sigma $
in the range
![]() $\sigma = 1-\alpha \bigl (\log _{2}B + O(1)\bigr )/\log B$
:
$\sigma = 1-\alpha \bigl (\log _{2}B + O(1)\bigr )/\log B$
:
 $$ \begin{align*} \frac{\partial\text{RHS}}{\partial\sigma} &= -\frac{1}{4}\int_{1/2}^{1}B^{(1-\sigma)u}\log B\sin(\theta u)\mathrm{d} u \\[4pt] &=-\frac{1}{4}\frac{B^{1-\sigma}}{(1-\sigma)^{2}+(\theta/\log B)^{2}}\biggl((1-\sigma)\sin\theta - \frac{\theta\cos\theta}{\log B}\biggr)\bigl(1+O_{\delta}(B^{(\sigma-1)/2})\bigr). \end{align*} $$
$$ \begin{align*} \frac{\partial\text{RHS}}{\partial\sigma} &= -\frac{1}{4}\int_{1/2}^{1}B^{(1-\sigma)u}\log B\sin(\theta u)\mathrm{d} u \\[4pt] &=-\frac{1}{4}\frac{B^{1-\sigma}}{(1-\sigma)^{2}+(\theta/\log B)^{2}}\biggl((1-\sigma)\sin\theta - \frac{\theta\cos\theta}{\log B}\biggr)\bigl(1+O_{\delta}(B^{(\sigma-1)/2})\bigr). \end{align*} $$
Since
![]() $\left \lvert \theta \right \rvert \ll (\log _{2}B)^{3/4}$
, this indeed has a fixed sign in the aforementioned range. By setting
$\left \lvert \theta \right \rvert \ll (\log _{2}B)^{3/4}$
, this indeed has a fixed sign in the aforementioned range. By setting
![]() $\sigma =\sigma _{m}-a/\log B$
for some large positive and negative values of a, one can conclude that equation (3.16) has a unique solution. Indeed, integrating by parts gives
$\sigma =\sigma _{m}-a/\log B$
for some large positive and negative values of a, one can conclude that equation (3.16) has a unique solution. Indeed, integrating by parts gives
 $$ \begin{align*} \text{LHS} &= (t-t_{m})\log x + O\biggl(\frac{\log x}{\log B}\frac{\left\lvert m \right\rvert }{\log_{2}B}\biggr), \\[4pt] \text{RHS} &= \mathrm{e}^{a}\frac{\log x}{\log B}\sin\theta\biggl(1+O_{\delta}\biggl(\frac{\left\lvert m \right\rvert }{\log_{2}B}\biggr)\biggr). \end{align*} $$
$$ \begin{align*} \text{LHS} &= (t-t_{m})\log x + O\biggl(\frac{\log x}{\log B}\frac{\left\lvert m \right\rvert }{\log_{2}B}\biggr), \\[4pt] \text{RHS} &= \mathrm{e}^{a}\frac{\log x}{\log B}\sin\theta\biggl(1+O_{\delta}\biggl(\frac{\left\lvert m \right\rvert }{\log_{2}B}\biggr)\biggr). \end{align*} $$
Here, we used that
 $$\begin{align*}\sin((t_{m}-\tau)\log B) \ll \frac{\left\lvert m \right\rvert }{\log_{2}B}, \quad \frac{B^{1-\sigma}}{4(1-\sigma)} = \mathrm{e}^{a}\log x\biggl(1+O\biggl(\frac{\left\lvert m \right\rvert }{\log_{2}B}\biggr)\biggr), \end{align*}$$
$$\begin{align*}\sin((t_{m}-\tau)\log B) \ll \frac{\left\lvert m \right\rvert }{\log_{2}B}, \quad \frac{B^{1-\sigma}}{4(1-\sigma)} = \mathrm{e}^{a}\log x\biggl(1+O\biggl(\frac{\left\lvert m \right\rvert }{\log_{2}B}\biggr)\biggr), \end{align*}$$
by equations (3.8) and (3.7), (3.6), (3.8), respectively. Since
![]() $t-t_{m} = (\theta -2\pi m)/\log B + O(\,\left \lvert m \right \rvert /(\log B\log _{2}B))$
by equation (3.8), it follows that
$t-t_{m} = (\theta -2\pi m)/\log B + O(\,\left \lvert m \right \rvert /(\log B\log _{2}B))$
by equation (3.8), it follows that
![]() $\text {LHS} \lessgtr \text {RHS}$
if a is sufficiently large, resp. small. This shows that we can connect the lines
$\text {LHS} \lessgtr \text {RHS}$
if a is sufficiently large, resp. small. This shows that we can connect the lines
![]() $t=t_{m}^{-}$
and
$t=t_{m}^{-}$
and
![]() $t=t_{m}^{+}$
with the path of steepest descent
$t=t_{m}^{+}$
with the path of steepest descent
![]() $\Gamma _{m}$
.
$\Gamma _{m}$
.
Denoting the solutions of equation (3.16) for
![]() $\sigma $
at
$\sigma $
at
![]() $\theta = 2\pi m \pm \pi /2$
by
$\theta = 2\pi m \pm \pi /2$
by
![]() $\sigma _{m}^{\pm }$
and setting
$\sigma _{m}^{\pm }$
and setting
![]() $\sigma _{m}^{\pm } = \sigma _{m} - a_{m}^{\pm }/\log B$
, the above calculations also show that
$\sigma _{m}^{\pm } = \sigma _{m} - a_{m}^{\pm }/\log B$
, the above calculations also show that
 $$ \begin{align} a_{m}^{\pm} = \log\frac{\pi}{2} + O\biggl(\frac{\left\lvert m \right\rvert }{\log_{2}B}\biggr), \quad \mbox{so} \quad \sigma_{m}^{\pm} = \sigma_{m} - \frac{\log(\pi/2)}{\log B} + O\bigl((\log B)^{-1}(\log_{2}B)^{-1/4}\bigr). \end{align} $$
$$ \begin{align} a_{m}^{\pm} = \log\frac{\pi}{2} + O\biggl(\frac{\left\lvert m \right\rvert }{\log_{2}B}\biggr), \quad \mbox{so} \quad \sigma_{m}^{\pm} = \sigma_{m} - \frac{\log(\pi/2)}{\log B} + O\bigl((\log B)^{-1}(\log_{2}B)^{-1/4}\bigr). \end{align} $$
Finally, we need that the length of
![]() $\Gamma _{m}$
is not too large. For the part inside the neighborhood
$\Gamma _{m}$
is not too large. For the part inside the neighborhood
![]() $B(s_{m}, \delta '/(2\log B))$
, this was already remarked at the beginning of this subsection. Outside this neighborhood, we use that
$B(s_{m}, \delta '/(2\log B))$
, this was already remarked at the beginning of this subsection. Outside this neighborhood, we use that
![]() $\frac{\partial}{\partial\sigma }\text {RHS} \gg _{\delta } \log x$
,
$\frac{\partial}{\partial\sigma }\text {RHS} \gg _{\delta } \log x$
,
![]() $\frac{\partial}{\partial\theta }\text {RHS} \ll \log x/\log B$
and
$\frac{\partial}{\partial\theta }\text {RHS} \ll \log x/\log B$
and
![]() $\frac{\partial}{\partial\theta }\text {LHS} = \log x/\log B$
so that
$\frac{\partial}{\partial\theta }\text {LHS} = \log x/\log B$
so that
![]() $\frac{\mathrm{d}}{\mathrm{d}\theta }\sigma (\theta ) \ll _{\delta } 1/\log B$
. This implies that
$\frac{\mathrm{d}}{\mathrm{d}\theta }\sigma (\theta ) \ll _{\delta } 1/\log B$
. This implies that
![]() $\operatorname {\mathrm {length}}(\Gamma _{m}) \ll 1/\log B$
.
$\operatorname {\mathrm {length}}(\Gamma _{m}) \ll 1/\log B$
.
3.5 The contributions from
 $s_{m}$
,
$s_{m}$
,
 $m\neq 0$
$m\neq 0$
On the path of steepest descent
![]() $\Gamma _{m}$
,
$\Gamma _{m}$
,
![]() $\operatorname {Re} f$
reaches its maximum at
$\operatorname {Re} f$
reaches its maximum at
![]() $s_{m}$
. This together with Lemma 3.6 implies the following bound for the contribution of
$s_{m}$
. This together with Lemma 3.6 implies the following bound for the contribution of
![]() $s_{m}$
,
$s_{m}$
,
![]() $m\neq 0$
:
$m\neq 0$
:
 $$\begin{align*}\operatorname{Im} \frac{1}{\pi}\int_{\Gamma_{m}}\mathrm{e}^{f(s)}g(s)\mathrm{d} s \ll \frac{x}{\tau}\exp\biggl(-(1-\sigma_{m})\log x + \operatorname{Re} \int_{s_{m}}^{\infty}\eta(z)\mathrm{d} z\biggr) \operatorname{\mathrm{length}}(\Gamma_{m}). \end{align*}$$
$$\begin{align*}\operatorname{Im} \frac{1}{\pi}\int_{\Gamma_{m}}\mathrm{e}^{f(s)}g(s)\mathrm{d} s \ll \frac{x}{\tau}\exp\biggl(-(1-\sigma_{m})\log x + \operatorname{Re} \int_{s_{m}}^{\infty}\eta(z)\mathrm{d} z\biggr) \operatorname{\mathrm{length}}(\Gamma_{m}). \end{align*}$$
Using equations (3.12), (3.7), the inequality
![]() $\left \lvert 1+\mathrm {i}\tau -s_{m} \right \rvert> 1-\sigma _{0}$
and equation (3.13), we get
$\left \lvert 1+\mathrm {i}\tau -s_{m} \right \rvert> 1-\sigma _{0}$
and equation (3.13), we get
 $$ \begin{align*} \operatorname{Re}\int_{s_{m}}^{\infty}\eta(z)\mathrm{d} z &\le \frac{\log x}{\log B}\biggl(1+\frac{1}{\left\lvert 1+\mathrm{i}\tau -s_{m} \right\rvert \log B} + \frac{2}{(\,\left\lvert 1+\mathrm{i}\tau -s_{m} \right\rvert \log B)^{2}} + O\biggl(\frac{1}{(\,\left\lvert 1+\mathrm{i}\tau -s_{m} \right\rvert \log B)^{3}}\biggr)\!\!\biggr) \\ &\le \int_{s_{0}}^{\infty}\eta(z)\mathrm{d} z + O\biggl(\frac{\log x}{(\log B)(\log_{2}B)^{3}}\biggr). \end{align*} $$
$$ \begin{align*} \operatorname{Re}\int_{s_{m}}^{\infty}\eta(z)\mathrm{d} z &\le \frac{\log x}{\log B}\biggl(1+\frac{1}{\left\lvert 1+\mathrm{i}\tau -s_{m} \right\rvert \log B} + \frac{2}{(\,\left\lvert 1+\mathrm{i}\tau -s_{m} \right\rvert \log B)^{2}} + O\biggl(\frac{1}{(\,\left\lvert 1+\mathrm{i}\tau -s_{m} \right\rvert \log B)^{3}}\biggr)\!\!\biggr) \\ &\le \int_{s_{0}}^{\infty}\eta(z)\mathrm{d} z + O\biggl(\frac{\log x}{(\log B)(\log_{2}B)^{3}}\biggr). \end{align*} $$
Combining this with Lemma 3.2, we see that the contribution of
![]() $s_{m}$
is bounded by
$s_{m}$
is bounded by
 $$\begin{align*}\frac{x}{\tau}\exp\biggl(-(1-\sigma_{0})\log x + \int_{s_{0}}^{\infty}\eta(z)\mathrm{d} z - d\frac{\log x}{\log B(\log_{2}B)^{2}} + O\biggl(\frac{\log x}{\log B(\log_{2}B)^{3}}\biggr)\biggr). \end{align*}$$
$$\begin{align*}\frac{x}{\tau}\exp\biggl(-(1-\sigma_{0})\log x + \int_{s_{0}}^{\infty}\eta(z)\mathrm{d} z - d\frac{\log x}{\log B(\log_{2}B)^{2}} + O\biggl(\frac{\log x}{\log B(\log_{2}B)^{3}}\biggr)\biggr). \end{align*}$$
Since
 $$\begin{align*}\frac{\log x}{\log B(\log_{2}B)^{2}} \asymp \frac{(\log x)^{\frac{\alpha}{\alpha+1}}}{(\log_{2}x)^{\frac{2\alpha+3}{\alpha+1}}} \end{align*}$$
$$\begin{align*}\frac{\log x}{\log B(\log_{2}B)^{2}} \asymp \frac{(\log x)^{\frac{\alpha}{\alpha+1}}}{(\log_{2}x)^{\frac{2\alpha+3}{\alpha+1}}} \end{align*}$$
tends to infinity, this is of strictly lower order than the contribution of
![]() $s_{0}$
, equation (3.11). The same holds for
$s_{0}$
, equation (3.11). The same holds for
![]() $\sum _{0<\,\left \lvert m \right \rvert \le M}\int _{\Gamma _{m}}\mathrm {e}^{f(z)}g(z)\mathrm{d} z$
since summing all these contributions enlarges the bound only by a factor
$\sum _{0<\,\left \lvert m \right \rvert \le M}\int _{\Gamma _{m}}\mathrm {e}^{f(z)}g(z)\mathrm{d} z$
since summing all these contributions enlarges the bound only by a factor
![]() $M=\exp (O(\log _{3}x))$
.
$M=\exp (O(\log _{3}x))$
.
4 The remainder in the contour integral
Let us recall that the main goal is to estimate the Perron integral
where the integral is along some suitable contour connecting the points
![]() $\kappa \pm \mathrm {i} T$
for some
$\kappa \pm \mathrm {i} T$
for some
![]() $\kappa>1$
,
$\kappa>1$
,
![]() $T>0$
, which will be specified later. We refer again to the definitions of f and g: equations (3.2) and (3.3). In the previous section, we have used the fact that
$T>0$
, which will be specified later. We refer again to the definitions of f and g: equations (3.2) and (3.3). In the previous section, we have used the fact that
![]() $\zeta _{C,K}$
is very large near the saddle point
$\zeta _{C,K}$
is very large near the saddle point
![]() $s_{0}$
to show that the integral along a small contour
$s_{0}$
to show that the integral along a small contour
![]() $\Gamma _{0}$
passing through
$\Gamma _{0}$
passing through
![]() $s_{0}$
is also very large. This should be considered the ‘main term’ in our estimate for the Perron integral. The zeta function is also large around the other saddle points
$s_{0}$
is also very large. This should be considered the ‘main term’ in our estimate for the Perron integral. The zeta function is also large around the other saddle points
![]() $s_{m}$
,
$s_{m}$
,
![]() $m\neq 0$
, but since these are slightly to the left of
$m\neq 0$
, but since these are slightly to the left of
![]() $s_{0}$
,
$s_{0}$
,
![]() $x^{s}$
is smaller there. This turned out to be enough to show that the integrals along similar contours
$x^{s}$
is smaller there. This turned out to be enough to show that the integrals along similar contours
![]() $\Gamma _{m}$
through
$\Gamma _{m}$
through
![]() $s_{m}$
,
$s_{m}$
,
![]() $m\neq 0$
combined are of lower order than the main term.
$m\neq 0$
combined are of lower order than the main term.
In this section, we estimate ‘the remainder’, which consists of three parts. First, we have to connect the steepest paths
![]() $\Gamma _{m}$
to each other. This forms one contour near the saddle points, which we have to connect to the ‘standard’ Perron contour
$\Gamma _{m}$
to each other. This forms one contour near the saddle points, which we have to connect to the ‘standard’ Perron contour
![]() $[\kappa -\mathrm {i} T, \kappa +\mathrm {i} T]$
. Finally, we also have to estimate the remainder in the effective Perron formula (2.5).
$[\kappa -\mathrm {i} T, \kappa +\mathrm {i} T]$
. Finally, we also have to estimate the remainder in the effective Perron formula (2.5).
4.1 Connecting the steepest paths
Let
![]() $\Upsilon _{m}$
be the line segment connecting
$\Upsilon _{m}$
be the line segment connecting
![]() $\sigma _{m-1}^{+}+\mathrm {i} t_{m-1}^{+}$
to
$\sigma _{m-1}^{+}+\mathrm {i} t_{m-1}^{+}$
to
![]() $\sigma _{m}^{-}+\mathrm {i} t_{m}^{-}$
if
$\sigma _{m}^{-}+\mathrm {i} t_{m}^{-}$
if
![]() $m>0$
and connecting
$m>0$
and connecting
![]() $\sigma _{m}^{+}+\mathrm {i} t_{m}^{+}$
to
$\sigma _{m}^{+}+\mathrm {i} t_{m}^{+}$
to
![]() $\sigma _{m+1}^{-}+\mathrm {i} t_{m+1}^{-}$
if
$\sigma _{m+1}^{-}+\mathrm {i} t_{m+1}^{-}$
if
![]() $m<0$
. By previous calculations (equations (3.10) and (3.17)), we know that the real part on these lines is bounded by
$m<0$
. By previous calculations (equations (3.10) and (3.17)), we know that the real part on these lines is bounded by
![]() $\sigma _{0} - \frac {\log (\pi /2)}{2\log B}$
, say. Furthermore,
$\sigma _{0} - \frac {\log (\pi /2)}{2\log B}$
, say. Furthermore,
![]() $\operatorname {Re} \int _{s}^{\infty }\eta (z)\mathrm{d} z$
is significantly smaller on these lines than at the saddle points. Indeed, using equation (3.12) and the fact that
$\operatorname {Re} \int _{s}^{\infty }\eta (z)\mathrm{d} z$
is significantly smaller on these lines than at the saddle points. Indeed, using equation (3.12) and the fact that
 $$\begin{align*}\operatorname{Re} \frac{B^{1+\mathrm{i}\tau-s}}{1+\mathrm{i}\tau-s} = \frac{B^{1-\sigma}}{(1-\sigma)^{2}+(t-\tau)^{2}}\biggl(\cos\bigl((t-\tau)\log B\bigr)(1-\sigma) + (t-\tau)\sin\bigl((t-\tau)\log B\bigr)\biggr), \end{align*}$$
$$\begin{align*}\operatorname{Re} \frac{B^{1+\mathrm{i}\tau-s}}{1+\mathrm{i}\tau-s} = \frac{B^{1-\sigma}}{(1-\sigma)^{2}+(t-\tau)^{2}}\biggl(\cos\bigl((t-\tau)\log B\bigr)(1-\sigma) + (t-\tau)\sin\bigl((t-\tau)\log B\bigr)\biggr), \end{align*}$$
we have
 $$ \begin{align} \operatorname{Re}\int_{s}^{\infty}\eta(z)\mathrm{d} z &= \operatorname{Re} \frac{B^{1+\mathrm{i}\tau-s} - 2B^{(1+\mathrm{i}\tau-s)/2}}{4(1+\mathrm{i}\tau-s)\log B} + O\biggl(\frac{B^{1-\sigma}}{(\log_{2}B)^{2}}\biggr) \nonumber \\[4pt] &\le \frac{(t-\tau)B^{1-\sigma}}{4(1-\sigma)^{2}\log B} + O\biggl(\frac{B^{1-\sigma}}{(\log_{2}B)^{2}}\biggr) \nonumber \\[4pt] &\ll \frac{\log x}{(\log B)(\log_{2}B)^{1/4}} , \end{align} $$
$$ \begin{align} \operatorname{Re}\int_{s}^{\infty}\eta(z)\mathrm{d} z &= \operatorname{Re} \frac{B^{1+\mathrm{i}\tau-s} - 2B^{(1+\mathrm{i}\tau-s)/2}}{4(1+\mathrm{i}\tau-s)\log B} + O\biggl(\frac{B^{1-\sigma}}{(\log_{2}B)^{2}}\biggr) \nonumber \\[4pt] &\le \frac{(t-\tau)B^{1-\sigma}}{4(1-\sigma)^{2}\log B} + O\biggl(\frac{B^{1-\sigma}}{(\log_{2}B)^{2}}\biggr) \nonumber \\[4pt] &\ll \frac{\log x}{(\log B)(\log_{2}B)^{1/4}} , \end{align} $$
for
![]() $s\in \Upsilon _{m}$
. In the first inequality, we used that
$s\in \Upsilon _{m}$
. In the first inequality, we used that
![]() $\cos \bigl ((t-\tau )\log B\bigr ) \le 0$
, and for the second estimate we used equation (3.7) and that
$\cos \bigl ((t-\tau )\log B\bigr ) \le 0$
, and for the second estimate we used equation (3.7) and that
![]() $\sigma -\sigma _{0}\ll 1/\log B$
(which follows from equations (3.17) and equation (3.6)), together with
$\sigma -\sigma _{0}\ll 1/\log B$
(which follows from equations (3.17) and equation (3.6)), together with
![]() $(t-\tau )/(1-\sigma ) \ll (\log _{2}B)^{-1/4}$
. Using Lemma 3.6 to bound g, we see that
$(t-\tau )/(1-\sigma ) \ll (\log _{2}B)^{-1/4}$
. Using Lemma 3.6 to bound g, we see that
 $$\begin{align*}\sum_{0 < \, \left\lvert m \right\rvert \leq M} \int_{\Upsilon_{m} }\!\mathrm{e}^{f(s)}g(s)\mathrm{d} s \ll \frac{x}{\tau}\exp\biggl(\kern-1pt\!-(1-\sigma_{0})\log x -\frac{\log(\pi/2)}{2}\frac{\log x}{\log B} + O\biggl(\frac{\log x}{(\log B)(\log_{2}B)^{1/4}}\biggr)\!\!\kern-1pt\biggr), \end{align*}$$
$$\begin{align*}\sum_{0 < \, \left\lvert m \right\rvert \leq M} \int_{\Upsilon_{m} }\!\mathrm{e}^{f(s)}g(s)\mathrm{d} s \ll \frac{x}{\tau}\exp\biggl(\kern-1pt\!-(1-\sigma_{0})\log x -\frac{\log(\pi/2)}{2}\frac{\log x}{\log B} + O\biggl(\frac{\log x}{(\log B)(\log_{2}B)^{1/4}}\biggr)\!\!\kern-1pt\biggr), \end{align*}$$
which is negligible with respect to the contribution from
![]() $s_{0}$
, in view of equations (3.11) and (3.13).
$s_{0}$
, in view of equations (3.11) and (3.13).
4.2 Returning to the line
 $[\kappa -\mathrm {i} T, \kappa +\mathrm {i} T]$
$[\kappa -\mathrm {i} T, \kappa +\mathrm {i} T]$
We will now connect the contour near the saddle points to the line
![]() $[\kappa -\mathrm {i} T, \kappa +\mathrm {i} T]$
. First, we need another lemma to bound g.
$[\kappa -\mathrm {i} T, \kappa +\mathrm {i} T]$
. First, we need another lemma to bound g.
Lemma 4.1. Suppose
![]() $s=\sigma +\mathrm {i} t$
satisfies
$s=\sigma +\mathrm {i} t$
satisfies
 $$\begin{align*}\sigma \ge 1 - O\left(\frac{\log_{2}B_{K}}{\log B_{K}}\right), \quad t\ge0. \end{align*}$$
$$\begin{align*}\sigma \ge 1 - O\left(\frac{\log_{2}B_{K}}{\log B_{K}}\right), \quad t\ge0. \end{align*}$$
Then,
 $$\begin{align*}\sum_{k=0}^{K-1}\int_{s}^{s+1}\bigl(\eta_{k}(z) + \tilde{\eta}_{k}(z) + \xi_{k}(z)\bigr)\mathrm{d} z + \int_{s}^{s+1}\bigl(\tilde{\eta}_{K}(z)+\xi_{K}(z)\bigr)\mathrm{d} z - \int_{s+1}^{\infty}\eta_{K}(z)\mathrm{d} z \ll 1. \end{align*}$$
$$\begin{align*}\sum_{k=0}^{K-1}\int_{s}^{s+1}\bigl(\eta_{k}(z) + \tilde{\eta}_{k}(z) + \xi_{k}(z)\bigr)\mathrm{d} z + \int_{s}^{s+1}\bigl(\tilde{\eta}_{K}(z)+\xi_{K}(z)\bigr)\mathrm{d} z - \int_{s+1}^{\infty}\eta_{K}(z)\mathrm{d} z \ll 1. \end{align*}$$
Proof. The sum of the integrals
![]() $\int _{s+1}^{\infty }$
is trivially bounded. Recall that
$\int _{s+1}^{\infty }$
is trivially bounded. Recall that
 $$\begin{align*}\int_{s}^{\infty}\eta_{k}(z)\mathrm{d} z = \frac{1}{4}\int_{s}^{\infty}\frac{B_{k}^{1-z}-B_{k}^{(1-z)/2}}{1+\mathrm{i}\tau_{k}-z}\mathrm{d} z = \frac{1}{4}\int_{1/2}^{1}\frac{B_{k}^{(1+\mathrm{i}\tau_{k}-s)u}}{u}\mathrm{d} u. \end{align*}$$
$$\begin{align*}\int_{s}^{\infty}\eta_{k}(z)\mathrm{d} z = \frac{1}{4}\int_{s}^{\infty}\frac{B_{k}^{1-z}-B_{k}^{(1-z)/2}}{1+\mathrm{i}\tau_{k}-z}\mathrm{d} z = \frac{1}{4}\int_{1/2}^{1}\frac{B_{k}^{(1+\mathrm{i}\tau_{k}-s)u}}{u}\mathrm{d} u. \end{align*}$$
Let
![]() $k<K$
.
$k<K$
.
Case 1:
![]() $t\le \tau _{k}/2$
or
$t\le \tau _{k}/2$
or
![]() $t\ge 2\tau _{k}$
. Then the above integral is bounded by
$t\ge 2\tau _{k}$
. Then the above integral is bounded by
 $$\begin{align*}\frac{B_{k}^{1-\sigma}}{\tau_{k}\log B_{k}} \le \frac{1}{\tau_{k}}\exp\biggl\{O\biggl(\frac{\log_{2}B_{K}}{\log B_{K}}\log B_{k}\biggr)\biggr\} \ll \frac{1}{\tau_{k}}, \end{align*}$$
$$\begin{align*}\frac{B_{k}^{1-\sigma}}{\tau_{k}\log B_{k}} \le \frac{1}{\tau_{k}}\exp\biggl\{O\biggl(\frac{\log_{2}B_{K}}{\log B_{K}}\log B_{k}\biggr)\biggr\} \ll \frac{1}{\tau_{k}}, \end{align*}$$
where the fast growth of
![]() $(B_{k})_{k}$
was used (property (a)).
$(B_{k})_{k}$
was used (property (a)).
Case 2:
![]() $\tau _{k}/2 < t < 2\tau _{k}$
. Then we use the second integral representation for
$\tau _{k}/2 < t < 2\tau _{k}$
. Then we use the second integral representation for
![]() $\int ^{\infty }_{s} \eta _{k}(z) \mathrm{d} z$
and get the bound
$\int ^{\infty }_{s} \eta _{k}(z) \mathrm{d} z$
and get the bound
![]() $B_{k}^{1-\sigma } \ll 1$
. This case occurs at most once.
$B_{k}^{1-\sigma } \ll 1$
. This case occurs at most once.
Since
![]() $\sum _{k}(1/\tau _{k})$
converges, this deals with the terms involving
$\sum _{k}(1/\tau _{k})$
converges, this deals with the terms involving
![]() $\eta _{k}$
; bounding the terms with
$\eta _{k}$
; bounding the terms with
![]() $\tilde {\eta }_{k}$
,
$\tilde {\eta }_{k}$
,
![]() $k<K$
is completely analogous, except that in this case we can always use the bound from Case 1 since
$k<K$
is completely analogous, except that in this case we can always use the bound from Case 1 since
![]() $\left \lvert 1-\mathrm {i}\tau _{k}-s \right \rvert \gg \tau _{k}$
(since
$\left \lvert 1-\mathrm {i}\tau _{k}-s \right \rvert \gg \tau _{k}$
(since
![]() $t\ge 0$
). Also
$t\ge 0$
). Also
 $$\begin{align*}\int_{s}^{\infty}\tilde{\eta}_{K}(z)\mathrm{d} z \ll \frac{1}{\tau_{K}}\exp(O(\log_{2}B_{K})) = \exp\bigl(O(\log_{2}B_{K}) - c(\log B_{K})^{\alpha}\bigr) \ll 1. \end{align*}$$
$$\begin{align*}\int_{s}^{\infty}\tilde{\eta}_{K}(z)\mathrm{d} z \ll \frac{1}{\tau_{K}}\exp(O(\log_{2}B_{K})) = \exp\bigl(O(\log_{2}B_{K}) - c(\log B_{K})^{\alpha}\bigr) \ll 1. \end{align*}$$
Finally, for
![]() $k\le K$
,
$k\le K$
,
 $$ \begin{align*} \int_{s}^{\infty}\xi_{k}(z)\mathrm{d} z &= -\frac{1}{2}\int_{1}^{\log C_{k}/\log B_{k}}\frac{B_{k}^{(1-s)u}}{u}\mathrm{d} u \ll \biggl(\frac{\log C_{k}}{\log B_{k}}-1\biggr)C_{k}^{1-\sigma} \\ &\ll \exp\biggl\{-2c(\log B_{k})^{\alpha} + O\biggl(\frac{\log_{2}B_{K}}{\log B_{K}}\log C_{k}\biggr)\biggr\} \ll \exp\bigl(-c(\log B_{k})^{\alpha}\bigr) = \frac{1}{\tau_{k}}, \end{align*} $$
$$ \begin{align*} \int_{s}^{\infty}\xi_{k}(z)\mathrm{d} z &= -\frac{1}{2}\int_{1}^{\log C_{k}/\log B_{k}}\frac{B_{k}^{(1-s)u}}{u}\mathrm{d} u \ll \biggl(\frac{\log C_{k}}{\log B_{k}}-1\biggr)C_{k}^{1-\sigma} \\ &\ll \exp\biggl\{-2c(\log B_{k})^{\alpha} + O\biggl(\frac{\log_{2}B_{K}}{\log B_{K}}\log C_{k}\biggr)\biggr\} \ll \exp\bigl(-c(\log B_{k})^{\alpha}\bigr) = \frac{1}{\tau_{k}}, \end{align*} $$
where we used equation (2.3).
Recall that we have set
![]() $M = \lfloor (\log _{2}B)^{3/4}\rfloor $
. Set
$M = \lfloor (\log _{2}B)^{3/4}\rfloor $
. Set
![]() $T_{1}^{\pm } = t_{\pm M}^{\pm }$
. We now connect the point
$T_{1}^{\pm } = t_{\pm M}^{\pm }$
. We now connect the point
![]() $\sigma _{-M}^{-}+ \mathrm {i} T_{1}^{-}$
to some point on the real axisFootnote
7
, and
$\sigma _{-M}^{-}+ \mathrm {i} T_{1}^{-}$
to some point on the real axisFootnote
7
, and
![]() $\sigma _{M}^{+}+\mathrm {i} T_{1}^{+}$
to the point
$\sigma _{M}^{+}+\mathrm {i} T_{1}^{+}$
to the point
![]() $\kappa +\mathrm {i} T$
by a number of line segments (
$\kappa +\mathrm {i} T$
by a number of line segments (
![]() $\kappa $
and T will be specified later). In what follows, we will use expressions in the style ‘The segment
$\kappa $
and T will be specified later). In what follows, we will use expressions in the style ‘The segment
![]() $\Delta $
contributes
$\Delta $
contributes
![]() $\ll F$
, which is negligible’, by which we mean that
$\ll F$
, which is negligible’, by which we mean that
![]() $\int _{\Delta }\mathrm {e}^{f(s)}g(s)\mathrm{d} s \ll F$
and that F is of lower order than the contribution of
$\int _{\Delta }\mathrm {e}^{f(s)}g(s)\mathrm{d} s \ll F$
and that F is of lower order than the contribution of
![]() $s_{0}$
(3.11). We will also apply Lemma 4.1 repeatedly, without referring to it each time.
$s_{0}$
(3.11). We will also apply Lemma 4.1 repeatedly, without referring to it each time.
First, we connect
![]() $\sigma _{M}^{+}+\mathrm {i} T_{1}^{+}$
to
$\sigma _{M}^{+}+\mathrm {i} T_{1}^{+}$
to
![]() $\sigma _{0}+\mathrm {i} T_{1}^{+}$
, and similarly
$\sigma _{0}+\mathrm {i} T_{1}^{+}$
, and similarly
![]() $\sigma _{-M}^{-}+\mathrm {i} T_{1}^{-}$
to
$\sigma _{-M}^{-}+\mathrm {i} T_{1}^{-}$
to
![]() $\sigma _{0}+\mathrm {i} T_{1}^{-}$
. By equation (4.1), this contributes
$\sigma _{0}+\mathrm {i} T_{1}^{-}$
. By equation (4.1), this contributes
 $$\begin{align*}\ll \frac{x^{\sigma_{0}}}{\tau}\exp\biggl(O\biggl(\frac{\log x}{(\log B)(\log_{2}B)^{1/4}}\biggr)\biggr), \end{align*}$$
$$\begin{align*}\ll \frac{x^{\sigma_{0}}}{\tau}\exp\biggl(O\biggl(\frac{\log x}{(\log B)(\log_{2}B)^{1/4}}\biggr)\biggr), \end{align*}$$
which is negligible. Next, set
![]() $T_{2}^{\pm } = \tau \pm \exp \bigl ((\log B)^{\alpha /2}\bigr )$
,
$T_{2}^{\pm } = \tau \pm \exp \bigl ((\log B)^{\alpha /2}\bigr )$
,
![]() $\Delta _{1}^{+}=[\sigma _{0}+\mathrm {i} T_{1}^{+}, \sigma _{0}+\mathrm {i} T_{2}^{+}]$
,
$\Delta _{1}^{+}=[\sigma _{0}+\mathrm {i} T_{1}^{+}, \sigma _{0}+\mathrm {i} T_{2}^{+}]$
,
![]() $\Delta _{1}^{-}=[\sigma _{0}+\mathrm {i} T_{2}^{-}, \sigma _{0}+ \mathrm {i} T_{1}^{-}]$
. We require a better bound for
$\Delta _{1}^{-}=[\sigma _{0}+\mathrm {i} T_{2}^{-}, \sigma _{0}+ \mathrm {i} T_{1}^{-}]$
. We require a better bound for
![]() $\int _{s}^{\infty }\eta (z)\mathrm{d} z$
on these lines. Integrating by parts, one sees that
$\int _{s}^{\infty }\eta (z)\mathrm{d} z$
on these lines. Integrating by parts, one sees that
 $$\begin{align*}\int_{s}^{\infty}\eta(z)\mathrm{d} z = \frac{1}{4}\int_{s}^{\infty}\frac{B^{1-z}-B^{(1-z)/2}}{1+\mathrm{i}\tau-z}\mathrm{d} z = \frac{B^{1-s} - 2B^{(1-s)/2}}{4(1+\mathrm{i}\tau-s)(\log B)} + O\biggl(\frac{(\log B)^{\alpha}}{(\log_{2}B)^{2}}\biggr), \end{align*}$$
$$\begin{align*}\int_{s}^{\infty}\eta(z)\mathrm{d} z = \frac{1}{4}\int_{s}^{\infty}\frac{B^{1-z}-B^{(1-z)/2}}{1+\mathrm{i}\tau-z}\mathrm{d} z = \frac{B^{1-s} - 2B^{(1-s)/2}}{4(1+\mathrm{i}\tau-s)(\log B)} + O\biggl(\frac{(\log B)^{\alpha}}{(\log_{2}B)^{2}}\biggr), \end{align*}$$
if
![]() $\operatorname {Re} s=\sigma _{0}$
. If
$\operatorname {Re} s=\sigma _{0}$
. If
![]() $\left \lvert t-\tau _{K} \right \rvert \ge (\log _{2}B)^{3/4}/(2\log B)$
say, then for some
$\left \lvert t-\tau _{K} \right \rvert \ge (\log _{2}B)^{3/4}/(2\log B)$
say, then for some
![]() $r>0$
,
$r>0$
,
 $$\begin{align*}\frac{1}{\left\lvert 1+\mathrm{i}\tau-s \right\rvert } \le \frac{1}{1-\sigma_{0}}\biggl(1-r\biggl(\frac{t-\tau}{1-\sigma_{0}}\biggr)^{2}\biggr) \le \frac{1}{1-\sigma_{0}}\biggl(1-\frac{r/4}{(\log_{2}B)^{1/2}}\biggr). \end{align*}$$
$$\begin{align*}\frac{1}{\left\lvert 1+\mathrm{i}\tau-s \right\rvert } \le \frac{1}{1-\sigma_{0}}\biggl(1-r\biggl(\frac{t-\tau}{1-\sigma_{0}}\biggr)^{2}\biggr) \le \frac{1}{1-\sigma_{0}}\biggl(1-\frac{r/4}{(\log_{2}B)^{1/2}}\biggr). \end{align*}$$
Hence,
 $$\begin{align*}\operatorname{Re} \int_{s}^{\infty}\eta(z)\mathrm{d} z \le \frac{\log x}{\log B}\biggl(1-\frac{r/4}{(\log_{2}B)^{1/2}}\biggr) + O\biggl(\frac{\log x}{(\log B)(\log_{2}B)}\biggr). \end{align*}$$
$$\begin{align*}\operatorname{Re} \int_{s}^{\infty}\eta(z)\mathrm{d} z \le \frac{\log x}{\log B}\biggl(1-\frac{r/4}{(\log_{2}B)^{1/2}}\biggr) + O\biggl(\frac{\log x}{(\log B)(\log_{2}B)}\biggr). \end{align*}$$
If furthermore
![]() $\left \lvert t-\tau \right \rvert \ge 1$
, then
$\left \lvert t-\tau \right \rvert \ge 1$
, then
 $$\begin{align*}\operatorname{Re} \int_{s}^{\infty}\eta(z)\mathrm{d} z \ll \frac{B^{1-\sigma_{0}}}{\log B} \asymp (\log B)^{\alpha-1} \ll 1. \end{align*}$$
$$\begin{align*}\operatorname{Re} \int_{s}^{\infty}\eta(z)\mathrm{d} z \ll \frac{B^{1-\sigma_{0}}}{\log B} \asymp (\log B)^{\alpha-1} \ll 1. \end{align*}$$
These bounds imply that the contribution from
![]() $\Delta _{1}^{\pm }$
is
$\Delta _{1}^{\pm }$
is
 $$\begin{align*}\ll \frac{x^{\sigma_{0}}}{\tau}\biggl\{\exp\biggl(\frac{\log x}{\log B}\biggl(1-\frac{r/4}{(\log_{2}B)^{1/2}}\biggr) + O\biggl(\frac{\log x}{(\log B)(\log_{2}B)}\biggr)\biggr) + \exp\bigl((\log B)^{\alpha/2}\bigr) \biggr\}, \end{align*}$$
$$\begin{align*}\ll \frac{x^{\sigma_{0}}}{\tau}\biggl\{\exp\biggl(\frac{\log x}{\log B}\biggl(1-\frac{r/4}{(\log_{2}B)^{1/2}}\biggr) + O\biggl(\frac{\log x}{(\log B)(\log_{2}B)}\biggr)\biggr) + \exp\bigl((\log B)^{\alpha/2}\bigr) \biggr\}, \end{align*}$$
which is admissible. Next, we set
 $$\begin{align*}\sigma' = \sigma_{0} -2\frac{c(\log B)^{\alpha}}{\log x} = \sigma_{0} - O\biggl(\frac{\log_{2}B}{\log B}\biggr) \end{align*}$$
$$\begin{align*}\sigma' = \sigma_{0} -2\frac{c(\log B)^{\alpha}}{\log x} = \sigma_{0} - O\biggl(\frac{\log_{2}B}{\log B}\biggr) \end{align*}$$
so that
![]() $x^{\sigma '} = x^{\sigma _{0}}/\tau ^{2}$
. Set
$x^{\sigma '} = x^{\sigma _{0}}/\tau ^{2}$
. Set
![]() $\Delta _{2}^{\pm } = [\sigma '+\mathrm {i} T_{2}^{\pm }, \sigma _{0}+\mathrm {i} T_{2}^{\pm }]$
. For
$\Delta _{2}^{\pm } = [\sigma '+\mathrm {i} T_{2}^{\pm }, \sigma _{0}+\mathrm {i} T_{2}^{\pm }]$
. For
![]() $\sigma \ge 1 - O\bigl (\log _{2}B/\log B\bigr )$
and
$\sigma \ge 1 - O\bigl (\log _{2}B/\log B\bigr )$
and
![]() $\left \lvert t-\tau \right \rvert \ge \exp \bigl ((\log B)^{\alpha /2}\bigr )$
,
$\left \lvert t-\tau \right \rvert \ge \exp \bigl ((\log B)^{\alpha /2}\bigr )$
,
 $$\begin{align*}\operatorname{Re} \int_{s}^{\infty}\eta(z)\mathrm{d} z \ll \exp\bigl(-(\log B)^{\alpha/2} + O(\log_{2}B)\bigr) \ll 1, \end{align*}$$
$$\begin{align*}\operatorname{Re} \int_{s}^{\infty}\eta(z)\mathrm{d} z \ll \exp\bigl(-(\log B)^{\alpha/2} + O(\log_{2}B)\bigr) \ll 1, \end{align*}$$
so the contribution from
![]() $\Delta _{2}^{\pm }$
is
$\Delta _{2}^{\pm }$
is
![]() $\ll x^{\sigma _{0}}/\tau $
, which is negligible. Let now
$\ll x^{\sigma _{0}}/\tau $
, which is negligible. Let now
![]() $T_{3}^{+} = x^{2}$
,
$T_{3}^{+} = x^{2}$
,
![]() $\Delta _{3}^{+} = [\sigma ' + \mathrm {i} T_{2}^{+}, \sigma '+\mathrm {i} T_{3}^{+}]$
, and
$\Delta _{3}^{+} = [\sigma ' + \mathrm {i} T_{2}^{+}, \sigma '+\mathrm {i} T_{3}^{+}]$
, and
![]() $\Delta _{3}^{-} = [\sigma ', \sigma '+ \mathrm {i} T_{2}^{-}]$
. We have that
$\Delta _{3}^{-} = [\sigma ', \sigma '+ \mathrm {i} T_{2}^{-}]$
. We have that
 $$ \begin{align*} \int_{\Delta_{3}^{+}} &\ll x^{\sigma'}\int_{T_{2}^{+}}^{T_{3}^{+}}\frac{\mathrm{d} t}{t} \ll \frac{x^{\sigma_{0}}}{\tau^{2}}\log x, \\ \int_{\Delta_{3}^{-}} &\ll x^{\sigma'}\biggl(\int_{1}^{T_{2}^{-}}\frac{\mathrm{d} t}{t} + \frac{1}{\left\lvert \sigma'-1 \right\rvert }\biggr) \ll \frac{x^{\sigma_{0}}}{\tau^{2}}\biggl( (\log B)^{\alpha} + \frac{\log B}{\log_{2}B}\biggr). \end{align*} $$
$$ \begin{align*} \int_{\Delta_{3}^{+}} &\ll x^{\sigma'}\int_{T_{2}^{+}}^{T_{3}^{+}}\frac{\mathrm{d} t}{t} \ll \frac{x^{\sigma_{0}}}{\tau^{2}}\log x, \\ \int_{\Delta_{3}^{-}} &\ll x^{\sigma'}\biggl(\int_{1}^{T_{2}^{-}}\frac{\mathrm{d} t}{t} + \frac{1}{\left\lvert \sigma'-1 \right\rvert }\biggr) \ll \frac{x^{\sigma_{0}}}{\tau^{2}}\biggl( (\log B)^{\alpha} + \frac{\log B}{\log_{2}B}\biggr). \end{align*} $$
Both of these are admissible. Finally, we set
![]() $\Delta _{4}^{+} = [\sigma '+\mathrm {i} T_{3}^{+}, 3/2 + \mathrm {i} T_{3}^{+}]$
. This segment only contributes
$\Delta _{4}^{+} = [\sigma '+\mathrm {i} T_{3}^{+}, 3/2 + \mathrm {i} T_{3}^{+}]$
. This segment only contributes
![]() $\ll x^{3/2}/T_{3}^{+} = 1/\sqrt {x}$
.
$\ll x^{3/2}/T_{3}^{+} = 1/\sqrt {x}$
.
We have now connected our contour to the line
![]() $[\kappa -\mathrm {i} T, \kappa +\mathrm {i} T]$
, with
$[\kappa -\mathrm {i} T, \kappa +\mathrm {i} T]$
, with
![]() $\kappa =3/2$
and
$\kappa =3/2$
and
![]() $T=T_{3}^{+}=x^{2}$
.
$T=T_{3}^{+}=x^{2}$
.
5 Conclusion of the analysis of the continuous example
By an effective Perron formula, e.g., [Reference Tenenbaum15, Theorem II.2.3], we have thatFootnote 8
 $$ \begin{align*} N_{C,K}(x) &= \frac{1}{2}\bigl(N_{C,K}(x^{+})+N_{C,K}(x^{-})\bigr) \\[6pt] &= \frac{1}{2\pi\mathrm{i}}\int_{\kappa-\mathrm{i} T}^{\kappa+\mathrm{i} T}\zeta_{C,K}(s)\frac{x^{s}}{s}\mathrm{d} s + O\biggl(x^{\kappa}\int_{1^{-}}^{\infty}\frac{1}{u^{\kappa}\bigl(1+T\left\lvert \log(x/u) \right\rvert \bigr)}\mathrm{d} N_{C,K}(u)\biggr). \end{align*} $$
$$ \begin{align*} N_{C,K}(x) &= \frac{1}{2}\bigl(N_{C,K}(x^{+})+N_{C,K}(x^{-})\bigr) \\[6pt] &= \frac{1}{2\pi\mathrm{i}}\int_{\kappa-\mathrm{i} T}^{\kappa+\mathrm{i} T}\zeta_{C,K}(s)\frac{x^{s}}{s}\mathrm{d} s + O\biggl(x^{\kappa}\int_{1^{-}}^{\infty}\frac{1}{u^{\kappa}\bigl(1+T\left\lvert \log(x/u) \right\rvert \bigr)}\mathrm{d} N_{C,K}(u)\biggr). \end{align*} $$
We apply it with
![]() $x=x_{K}$
,
$x=x_{K}$
,
![]() $\kappa =3/2$
, and
$\kappa =3/2$
, and
![]() $T=(x_{K})^{2}$
. Let us first deal with the error term in the effective Perron formula. We have for every K:
$T=(x_{K})^{2}$
. Let us first deal with the error term in the effective Perron formula. We have for every K:
 $$\begin{align*}\mathrm{d} N_{C,K}(u) &= \exp^{\ast}(\mathrm{d}\Pi_{C,K}(u)) \\[6pt]&\quad\le \exp^{\ast}(2\mathrm{d}\operatorname{\mathrm{Li}}(u)) = (\delta_{1}(u)+\mathrm{d} u)\ast(\delta_{1}(u)+\mathrm{d} u) = \delta_{1}(u) + 2\mathrm{d} u + \log u\mathrm{d} u. \end{align*}$$
$$\begin{align*}\mathrm{d} N_{C,K}(u) &= \exp^{\ast}(\mathrm{d}\Pi_{C,K}(u)) \\[6pt]&\quad\le \exp^{\ast}(2\mathrm{d}\operatorname{\mathrm{Li}}(u)) = (\delta_{1}(u)+\mathrm{d} u)\ast(\delta_{1}(u)+\mathrm{d} u) = \delta_{1}(u) + 2\mathrm{d} u + \log u\mathrm{d} u. \end{align*}$$
Hence, this error term is bounded by
 $$ \begin{align*} &\frac{x^{3/2}}{T\log x} + x^{3/2}\biggl(\int_{1}^{x/2} + \int_{x/2}^{x-1} + \int_{x-1}^{x+1} + \int_{x+1}^{\infty}\biggr)\frac{2 + \log u}{u^{3/2}\bigl(1+T\left\lvert \log(x/u) \right\rvert \bigr)}\mathrm{d} u \\[6pt] &\quad\ll \frac{1}{\sqrt{x}\log x} + x^{3/2}\biggl(\frac{1}{x^{2}} + \frac{\log x}{x^{3/2}}\biggr) \ll \log x. \end{align*} $$
$$ \begin{align*} &\frac{x^{3/2}}{T\log x} + x^{3/2}\biggl(\int_{1}^{x/2} + \int_{x/2}^{x-1} + \int_{x-1}^{x+1} + \int_{x+1}^{\infty}\biggr)\frac{2 + \log u}{u^{3/2}\bigl(1+T\left\lvert \log(x/u) \right\rvert \bigr)}\mathrm{d} u \\[6pt] &\quad\ll \frac{1}{\sqrt{x}\log x} + x^{3/2}\biggl(\frac{1}{x^{2}} + \frac{\log x}{x^{3/2}}\biggr) \ll \log x. \end{align*} $$
We shift the contour in the integral to the contour described in the previous (sub)sections. We showed that the integral along the shifted contour has sign
![]() $(-1)^{K}$
and has absolute value bounded from below by
$(-1)^{K}$
and has absolute value bounded from below by
 $$\begin{align*}x_{K}\exp\biggl\{-(c(\alpha+1))^{\frac{1}{\alpha+1}}(\log x_{K}\log_{2}x_{K})^{\frac{\alpha}{\alpha+1}}\biggl(1+\frac{\alpha}{\alpha+1}\frac{\log_{3}x_{K}}{\log_{2}x_{K}}+ O\biggl(\frac{1}{\log_{2}x_{K}}\biggr)\biggr)\biggr\}; \end{align*}$$
$$\begin{align*}x_{K}\exp\biggl\{-(c(\alpha+1))^{\frac{1}{\alpha+1}}(\log x_{K}\log_{2}x_{K})^{\frac{\alpha}{\alpha+1}}\biggl(1+\frac{\alpha}{\alpha+1}\frac{\log_{3}x_{K}}{\log_{2}x_{K}}+ O\biggl(\frac{1}{\log_{2}x_{K}}\biggr)\biggr)\biggr\}; \end{align*}$$
see equation (3.14). Shifting the contour also gives a contribution from the pole at
![]() $s=1$
, which is
$s=1$
, which is
![]() $\rho _{C,K}x_{K}$
, where
$\rho _{C,K}x_{K}$
, where
 $$\begin{align*}\rho_{C,K} = \operatorname*{\mathrm{Res}}_{s=1}\zeta_{C,K}(s) = \exp\biggl(\sum_{k=0}^{K}\int_{1}^{2}\bigl(\eta_{k}(z)+\tilde{\eta}_{k}(z)+\xi_{k}(z)\bigr)\mathrm{d} z\biggr). \end{align*}$$
$$\begin{align*}\rho_{C,K} = \operatorname*{\mathrm{Res}}_{s=1}\zeta_{C,K}(s) = \exp\biggl(\sum_{k=0}^{K}\int_{1}^{2}\bigl(\eta_{k}(z)+\tilde{\eta}_{k}(z)+\xi_{k}(z)\bigr)\mathrm{d} z\biggr). \end{align*}$$
To conclude the analysis of the continuous example
![]() $(\Pi _{C}, N_{C})$
, we need to show that the oscillation result holds for
$(\Pi _{C}, N_{C})$
, we need to show that the oscillation result holds for
![]() $N_{C}$
, i.e., that
$N_{C}$
, i.e., that
![]() $N_{C}(x) - \rho _{C}x$
displays the desired oscillation. The density
$N_{C}(x) - \rho _{C}x$
displays the desired oscillation. The density
![]() $\rho _{C}$
of
$\rho _{C}$
of
![]() $N_{C}$
equals the right-hand residue of
$N_{C}$
equals the right-hand residue of
![]() $\zeta _{C}$
at
$\zeta _{C}$
at
![]() $s=1$
, that is
$s=1$
, that is
![]() $\lim _{s\to 1^{+}}(s-1)\zeta _{C}(s)$
(see, e.g., [Reference Diamond and Zhang10, Theorem 7.3]):
$\lim _{s\to 1^{+}}(s-1)\zeta _{C}(s)$
(see, e.g., [Reference Diamond and Zhang10, Theorem 7.3]):
 $$\begin{align*}\rho_{C} = \exp\biggl(\sum_{k=0}^{\infty}\int_{1}^{2}\bigl(\eta_{k}(z)+\tilde{\eta}_{k}(z)+\xi_{k}(z)\bigr)\mathrm{d} z\biggr). \end{align*}$$
$$\begin{align*}\rho_{C} = \exp\biggl(\sum_{k=0}^{\infty}\int_{1}^{2}\bigl(\eta_{k}(z)+\tilde{\eta}_{k}(z)+\xi_{k}(z)\bigr)\mathrm{d} z\biggr). \end{align*}$$
Now
 $$ \begin{gather*} \int_{1}^{2}\bigl(\eta_{k}(s) + \tilde{\eta}_{k}(z)\bigr)\mathrm{d} z \ll \int_{1}^{2}\frac{B_{k}^{1-z}-B_{k}^{(1-z)/2}}{1 \pm\mathrm{i}\tau_{k}-z}\mathrm{d} z \ll \frac{1}{\tau_{k}\log B_{k}}, \\[5pt] \int_{1}^{2}\xi_{k}(z)\mathrm{d} z = \frac{1}{2}\int_{\log B_{k}}^{\log C_{k}}\frac{\mathrm{e}^{-u}-1}{u}\mathrm{d} u \ll \frac{\log C_{k}-\log B_{k}}{\log B_{k}} \ll \frac{1}{\tau_{k}^{2}}, \end{gather*} $$
$$ \begin{gather*} \int_{1}^{2}\bigl(\eta_{k}(s) + \tilde{\eta}_{k}(z)\bigr)\mathrm{d} z \ll \int_{1}^{2}\frac{B_{k}^{1-z}-B_{k}^{(1-z)/2}}{1 \pm\mathrm{i}\tau_{k}-z}\mathrm{d} z \ll \frac{1}{\tau_{k}\log B_{k}}, \\[5pt] \int_{1}^{2}\xi_{k}(z)\mathrm{d} z = \frac{1}{2}\int_{\log B_{k}}^{\log C_{k}}\frac{\mathrm{e}^{-u}-1}{u}\mathrm{d} u \ll \frac{\log C_{k}-\log B_{k}}{\log B_{k}} \ll \frac{1}{\tau_{k}^{2}}, \end{gather*} $$
where we used equation (2.3) in the last step. By property (a), we may assume that
 $$\begin{align*}\sum_{k=K+1}^{\infty}\frac{1}{\tau_{k}\log B_{k}} \le \frac{2}{\tau_{K+1}\log B_{K+1}} \le \frac{1}{x_{K}}. \end{align*}$$
$$\begin{align*}\sum_{k=K+1}^{\infty}\frac{1}{\tau_{k}\log B_{k}} \le \frac{2}{\tau_{K+1}\log B_{K+1}} \le \frac{1}{x_{K}}. \end{align*}$$
Hence, we have
 $$\begin{align*}\rho_{C,K} - \rho_{C} = \rho_{C}\biggl\{\exp\biggl(-\sum_{k=K+1}^{\infty}\int_{1}^{2}\bigl(\eta_{k}(z)+\tilde{\eta}_{k}(z)+\xi_{k}(z)\bigr) \mathrm{d} z\biggr)-1\biggr\} \ll \frac{1}{x_{K}} \end{align*}$$
$$\begin{align*}\rho_{C,K} - \rho_{C} = \rho_{C}\biggl\{\exp\biggl(-\sum_{k=K+1}^{\infty}\int_{1}^{2}\bigl(\eta_{k}(z)+\tilde{\eta}_{k}(z)+\xi_{k}(z)\bigr) \mathrm{d} z\biggr)-1\biggr\} \ll \frac{1}{x_{K}} \end{align*}$$
so that
 $$ \begin{align*} N_{C}(x_{K}) -\rho_{C}x_{K} &= N_{C,K}(x_{K}) -\rho_{C,K}x_{K} + (\rho_{C,K}-\rho_{C})x_{K} \\ &= \Omega_{\pm}\Bigl(x_{K}\exp\bigl(-(c(\alpha+1))^{\frac{1}{\alpha+1}}(\log x_{K}\log_{2}x_{K})^{\frac{\alpha}{\alpha+1}}(1+\dotso)\bigr)\Bigr) +O(1). \end{align*} $$
$$ \begin{align*} N_{C}(x_{K}) -\rho_{C}x_{K} &= N_{C,K}(x_{K}) -\rho_{C,K}x_{K} + (\rho_{C,K}-\rho_{C})x_{K} \\ &= \Omega_{\pm}\Bigl(x_{K}\exp\bigl(-(c(\alpha+1))^{\frac{1}{\alpha+1}}(\log x_{K}\log_{2}x_{K})^{\frac{\alpha}{\alpha+1}}(1+\dotso)\bigr)\Bigr) +O(1). \end{align*} $$
This concludes the proof of the existence of a continuous Beurling prime system satisfying equations (1.5) and (1.6).
6 The discrete example
We will now show the existence of a discrete Beurling prime system
![]() $(\Pi ,N)$
arising from a sequence of Beurling primes
$(\Pi ,N)$
arising from a sequence of Beurling primes
![]() $1<p_{1}\le p_{2}\le \dotso $
and satisfying equations (1.5) and (1.6). This will be done by approximating the continuous system
$1<p_{1}\le p_{2}\le \dotso $
and satisfying equations (1.5) and (1.6). This will be done by approximating the continuous system
![]() $(\Pi _{C}, N_{C})$
with a discrete one via a probabilistic procedure devised by the first and third named authors in [Reference Broucke and Vindas6]. This random approximation method is an improvement of that of Diamond, Montgomery and Vorhauer [Reference Diamond, Montgomery and Vorhauer9, Section 7] (see also Zhang [Reference Zhang16, Section 2]). We also use a trick introduced by the authors in [Reference Broucke, Debruyne and Vindas5, Section 6] in order to control the argument of the zeta function at some specific points; this is done by adding a well-chosen prime finitely many times to the system.
$(\Pi _{C}, N_{C})$
with a discrete one via a probabilistic procedure devised by the first and third named authors in [Reference Broucke and Vindas6]. This random approximation method is an improvement of that of Diamond, Montgomery and Vorhauer [Reference Diamond, Montgomery and Vorhauer9, Section 7] (see also Zhang [Reference Zhang16, Section 2]). We also use a trick introduced by the authors in [Reference Broucke, Debruyne and Vindas5, Section 6] in order to control the argument of the zeta function at some specific points; this is done by adding a well-chosen prime finitely many times to the system.
Given a nondecreasing right-continuous function F, which tends to
![]() $\infty $
and satisfies
$\infty $
and satisfies
![]() $F(1)=0$
and
$F(1)=0$
and
![]() $F(x) \ll x/\log x$
, the approximation procedure from [Reference Broucke and Vindas6] guarantees the existence of a sequence of Beurling primes
$F(x) \ll x/\log x$
, the approximation procedure from [Reference Broucke and Vindas6] guarantees the existence of a sequence of Beurling primes
![]() $\mathcal {P}_{D} = (p_{j})_{j}$
with counting function
$\mathcal {P}_{D} = (p_{j})_{j}$
with counting function
![]() $\pi _{D}$
satisfying
$\pi _{D}$
satisfying
 $$ \begin{align} \forall y\ge1, \forall t\ge0: \left\lvert \sum_{p_{j}\le y}p_{j}^{-\mathrm{i} t} - \int_{1}^{y}u^{-\mathrm{i} t}\mathrm{d} F(u) \right\rvert \ll \sqrt{y} + \sqrt{\frac{y\log(\,\left\lvert t \right\rvert +1)}{\log(y+1)}}. \end{align} $$
$$ \begin{align} \forall y\ge1, \forall t\ge0: \left\lvert \sum_{p_{j}\le y}p_{j}^{-\mathrm{i} t} - \int_{1}^{y}u^{-\mathrm{i} t}\mathrm{d} F(u) \right\rvert \ll \sqrt{y} + \sqrt{\frac{y\log(\,\left\lvert t \right\rvert +1)}{\log(y+1)}}. \end{align} $$
We will apply this withFootnote
9
![]() $F=\pi _{C}$
, where
$F=\pi _{C}$
, where
![]() $\pi _{C}$
is defined as
$\pi _{C}$
is defined as
 $$\begin{align*}\pi_{C}(x) = \sum_{\nu=1}^{\infty}\frac{\mu(\nu)}{\nu} \Pi_{C}(x^{1/\nu}), \quad \mbox{ so that } \quad \Pi_{C}(x) = \sum_{\nu=1}^{\infty}\frac{\pi_{C}(x^{1/\nu})}{\nu}. \end{align*}$$
$$\begin{align*}\pi_{C}(x) = \sum_{\nu=1}^{\infty}\frac{\mu(\nu)}{\nu} \Pi_{C}(x^{1/\nu}), \quad \mbox{ so that } \quad \Pi_{C}(x) = \sum_{\nu=1}^{\infty}\frac{\pi_{C}(x^{1/\nu})}{\nu}. \end{align*}$$
Here,
![]() $\mu $
stands for the classical Möbius function.
$\mu $
stands for the classical Möbius function.
Lemma 6.1. The function
![]() $\pi _{C}$
is nondecreasing, right-continuous, tends to
$\pi _{C}$
is nondecreasing, right-continuous, tends to
![]() $\infty $
and satisfies
$\infty $
and satisfies
![]() $\pi _{C}(1)=0$
and
$\pi _{C}(1)=0$
and
![]() $\pi _{C}(x) \ll x/\log x$
.
$\pi _{C}(x) \ll x/\log x$
.
Proof. We only need to show that
![]() $\pi _{C}$
is nondecreasing; the other assertions are obvious. Using the series expansion
$\pi _{C}$
is nondecreasing; the other assertions are obvious. Using the series expansion
![]() $\operatorname {\mathrm {Li}}(x) = \sum _{n=1}^{\infty }\frac {(\log x)^{n}}{n!n}$
, we have
$\operatorname {\mathrm {Li}}(x) = \sum _{n=1}^{\infty }\frac {(\log x)^{n}}{n!n}$
, we have
 $$\begin{align*}\pi_{C}(x) = \operatorname{\mathrm{li}}(x) + \sum_{k=0}^{\infty}\sum_{\nu=1}^{\infty}\bigl(r_{k,\nu}(x) + s_{k,\nu}(x)\bigr), \end{align*}$$
$$\begin{align*}\pi_{C}(x) = \operatorname{\mathrm{li}}(x) + \sum_{k=0}^{\infty}\sum_{\nu=1}^{\infty}\bigl(r_{k,\nu}(x) + s_{k,\nu}(x)\bigr), \end{align*}$$
where

Note that the notation
![]() $\operatorname {\mathrm {li}}(x)$
is not standard: Here it does not refer to (a variant of) the logarithmic integral, but rather
$\operatorname {\mathrm {li}}(x)$
is not standard: Here it does not refer to (a variant of) the logarithmic integral, but rather
![]() $\operatorname {\mathrm {li}}(x)$
relates to
$\operatorname {\mathrm {li}}(x)$
relates to
![]() $\operatorname {\mathrm {Li}}(x)$
in the same way as
$\operatorname {\mathrm {Li}}(x)$
in the same way as
![]() $\pi (x)$
relates to
$\pi (x)$
relates to
![]() $\Pi (x)$
.
$\Pi (x)$
.
We have
![]() $\operatorname {\mathrm {supp}}(r_{k,\nu }+s_{k,\nu }) = [A_{k}^{\nu }, C_{k}^{\nu }] =: I_{k, \nu }$
. The function
$\operatorname {\mathrm {supp}}(r_{k,\nu }+s_{k,\nu }) = [A_{k}^{\nu }, C_{k}^{\nu }] =: I_{k, \nu }$
. The function
![]() $\pi _{C}$
is absolutely continuous, so it will follow that it is nondecreasing if we show that
$\pi _{C}$
is absolutely continuous, so it will follow that it is nondecreasing if we show that
![]() $\pi _{C}'$
is nonnegative. If x is contained in no
$\pi _{C}'$
is nonnegative. If x is contained in no
![]() $I_{k,\nu }$
, then
$I_{k,\nu }$
, then
![]() $\pi _{C}'(x) = \operatorname {\mathrm {li}}'(x)>0$
. Suppose now the contrary, and let m be the largest integer such that
$\pi _{C}'(x) = \operatorname {\mathrm {li}}'(x)>0$
. Suppose now the contrary, and let m be the largest integer such that
![]() $x\in I_{k, m}$
for some
$x\in I_{k, m}$
for some
![]() $k\ge 0$
. Note that
$k\ge 0$
. Note that
![]() $m\le \log x/\log A_{0}$
. Since, for each
$m\le \log x/\log A_{0}$
. Since, for each
![]() $\nu \le m$
, there is at most one value of k for which
$\nu \le m$
, there is at most one value of k for which
![]() $x\in I_{k,\nu }$
, we have
$x\in I_{k,\nu }$
, we have
 $$ \begin{align*} \left\lvert \biggl(\sum_{k=0}^{\infty}\sum_{\nu=1}^{\infty}\bigl(r_{k,\nu}(x) + s_{k,\nu}(x)\bigr)\biggr)' \right\rvert &\le \frac{1}{2}\sum_{\substack{k,\nu \\[6pt] x\in I_{k,\nu}}}\frac{1-x^{-1/\nu}}{\nu\log x}x^{1/\nu-1} \\ &\le \frac{1}{2\log x}\sum_{\nu=1}^{m}\frac{x^{1/\nu-1}}{\nu} \le \frac{1}{2\log x}\biggl(1 + \frac{\log_{2}x}{\sqrt{x}}\biggr). \end{align*} $$
$$ \begin{align*} \left\lvert \biggl(\sum_{k=0}^{\infty}\sum_{\nu=1}^{\infty}\bigl(r_{k,\nu}(x) + s_{k,\nu}(x)\bigr)\biggr)' \right\rvert &\le \frac{1}{2}\sum_{\substack{k,\nu \\[6pt] x\in I_{k,\nu}}}\frac{1-x^{-1/\nu}}{\nu\log x}x^{1/\nu-1} \\ &\le \frac{1}{2\log x}\sum_{\nu=1}^{m}\frac{x^{1/\nu-1}}{\nu} \le \frac{1}{2\log x}\biggl(1 + \frac{\log_{2}x}{\sqrt{x}}\biggr). \end{align*} $$
On the other hand,
 $$\begin{align*}\operatorname{\mathrm{li}}'(x) \ge \frac{1}{\zeta(2)}\frac{1-x^{-1}}{\log x} \ge 0.6\frac{1-x^{-1}}{\log x},\\[-12pt] \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{li}}'(x) \ge \frac{1}{\zeta(2)}\frac{1-x^{-1}}{\log x} \ge 0.6\frac{1-x^{-1}}{\log x},\\[-12pt] \end{align*}$$
and together with
![]() $x\ge A_{0}$
, this implies that
$x\ge A_{0}$
, this implies that
![]() $\pi _{C}'(x)> 0$
(we may assume that
$\pi _{C}'(x)> 0$
(we may assume that
![]() $A_{0}$
is sufficiently large).
$A_{0}$
is sufficiently large).
Applying the discretization procedure to
![]() $F=\pi _{C}$
shows the existence of a sequence of Beurling primes
$F=\pi _{C}$
shows the existence of a sequence of Beurling primes
![]() $\mathcal {P}_{D} = (p_{j})_{j}$
with counting function
$\mathcal {P}_{D} = (p_{j})_{j}$
with counting function
![]() $\pi _{D}$
satisfying equations (6.1) and (6.2). Denote the Riemann prime counting function of
$\pi _{D}$
satisfying equations (6.1) and (6.2). Denote the Riemann prime counting function of
![]() $\mathcal {P}_{D}$
by
$\mathcal {P}_{D}$
by
![]() $\Pi _{D}$
, and set
$\Pi _{D}$
, and set
 $$\begin{align*}\mathrm{d}\Pi_{D,K}(u) = \sum_{p_{j}^{\nu}<A_{K+1}}\frac{1}{\nu}\delta_{p_{j}^{\nu}}(u) + \chi_{[A_{K+1},\infty)}(u)\mathrm{d}\operatorname{\mathrm{Li}}(u),\\[-12pt] \end{align*}$$
$$\begin{align*}\mathrm{d}\Pi_{D,K}(u) = \sum_{p_{j}^{\nu}<A_{K+1}}\frac{1}{\nu}\delta_{p_{j}^{\nu}}(u) + \chi_{[A_{K+1},\infty)}(u)\mathrm{d}\operatorname{\mathrm{Li}}(u),\\[-12pt] \end{align*}$$
where
![]() $\chi _{E}$
denotes the characteristic function of the set E. Let
$\chi _{E}$
denotes the characteristic function of the set E. Let
![]() $\log \zeta _{D,K}(s)$
be the Mellin–Stieltjes transform of
$\log \zeta _{D,K}(s)$
be the Mellin–Stieltjes transform of
![]() $\mathrm{d} \Pi _{D,K}$
. Set
$\mathrm{d} \Pi _{D,K}$
. Set
 $$\begin{align*}S_{l} = \biggl[l\frac{\pi}{80}-\frac{\pi}{160}, l\frac{\pi}{80}+\frac{\pi}{160}\biggr) + 2\pi\mathbb{Z} \quad \mbox{for } l=0,1,\dotso,159.\\[-12pt] \end{align*}$$
$$\begin{align*}S_{l} = \biggl[l\frac{\pi}{80}-\frac{\pi}{160}, l\frac{\pi}{80}+\frac{\pi}{160}\biggr) + 2\pi\mathbb{Z} \quad \mbox{for } l=0,1,\dotso,159.\\[-12pt] \end{align*}$$
Then for some l (resp. r), we have that for infinitely many even (resp. odd) values of K
Assume without loss of generality that
![]() $l\ge r$
. Then there exists a number q, close to
$l\ge r$
. Then there exists a number q, close to
![]() $80/\pi $
such that
$80/\pi $
such that
 $$ \begin{align} \left\lvert \operatorname{Im}\bigl(-l\log(1-q^{-(1+\mathrm{i}\tau_{K})})\bigr) + l\frac{\pi}{80} \right\rvert &< \frac{\pi}{40} \quad \mbox{if}\ K\ \mbox{is even},\\[-12pt]\nonumber \end{align} $$
$$ \begin{align} \left\lvert \operatorname{Im}\bigl(-l\log(1-q^{-(1+\mathrm{i}\tau_{K})})\bigr) + l\frac{\pi}{80} \right\rvert &< \frac{\pi}{40} \quad \mbox{if}\ K\ \mbox{is even},\\[-12pt]\nonumber \end{align} $$
 $$ \begin{align} \left\lvert \operatorname{Im}\bigl(-l\log(1-q^{-(1+\mathrm{i}\tau_{K})})\bigr) + r\frac{\pi}{80} \right\rvert &< \frac{\pi}{40} \quad \mbox{if}\ K\ \mbox{is odd}.\\[-12pt]\nonumber \end{align} $$
$$ \begin{align} \left\lvert \operatorname{Im}\bigl(-l\log(1-q^{-(1+\mathrm{i}\tau_{K})})\bigr) + r\frac{\pi}{80} \right\rvert &< \frac{\pi}{40} \quad \mbox{if}\ K\ \mbox{is odd}.\\[-12pt]\nonumber \end{align} $$
We refer to [Reference Broucke, Debruyne and Vindas5, Section 6] for a proof of this statement. That proof only requires some fast growth of the sequence
![]() $(\tau _{k})_{k}$
, which we may assume.
$(\tau _{k})_{k}$
, which we may assume.
We define our final prime system
![]() $\mathcal {P}$
as the prime system obtained by adding the prime q with multiplicity l to the system
$\mathcal {P}$
as the prime system obtained by adding the prime q with multiplicity l to the system
![]() $\mathcal {P}_{D}$
. Denote its Riemann prime counting function by
$\mathcal {P}_{D}$
. Denote its Riemann prime counting function by
![]() $\Pi $
and its integer counting function by N. We have
$\Pi $
and its integer counting function by N. We have
where in the last step we used equation (6.1). Since
![]() $\Pi _{C}$
satisfies equation (1.5), it is clear that
$\Pi _{C}$
satisfies equation (1.5), it is clear that
![]() $\Pi $
also satisfiesFootnote
10
(1.5).
$\Pi $
also satisfiesFootnote
10
(1.5).
SetFootnote 11
 $$ \begin{align*} \mathrm{d}\Pi_{K}(u) &= \mathrm{d}\Pi_{D,K}(u) + l \sum_{q^{\nu}<A_{K+1}}\frac{1}{\nu}\delta_{q^{\nu}}(u); \\[6pt] \mathrm{d} \pi_{K}(u) &= \sum_{p_{j}<A_{K+1}}\delta_{p_{j}}(u) + l\delta_{q}(u).\\[-12pt] \end{align*} $$
$$ \begin{align*} \mathrm{d}\Pi_{K}(u) &= \mathrm{d}\Pi_{D,K}(u) + l \sum_{q^{\nu}<A_{K+1}}\frac{1}{\nu}\delta_{q^{\nu}}(u); \\[6pt] \mathrm{d} \pi_{K}(u) &= \sum_{p_{j}<A_{K+1}}\delta_{p_{j}}(u) + l\delta_{q}(u).\\[-12pt] \end{align*} $$
If
![]() $x<A_{K+1}$
,
$x<A_{K+1}$
,
![]() $N(x)=N_{K}(x)$
and applying the effective Perron formula gives that for
$N(x)=N_{K}(x)$
and applying the effective Perron formula gives that for
![]() $\kappa>1$
and
$\kappa>1$
and
![]() $T\ge 0$
$T\ge 0$
 $$ \begin{align} \frac{1}{2}(N(x^{+})+N(x^{-})) &= \frac{1}{2\pi\mathrm{i}}\int_{\kappa-\mathrm{i} T}^{\kappa+\mathrm{i} T}\zeta_{C,K}(s)\frac{x^{s}}{s}\exp\bigl(\log\zeta_{K}(s)-\log\zeta_{C,K}(s)\bigr)\mathrm{d} s \nonumber\\[6pt] &\quad+ O\biggl(x^{\kappa}\int_{1^{-}}^{\infty}\frac{1}{u^{\kappa}\bigl(1+T\left\lvert \log(x/u) \right\rvert \bigr)}\mathrm{d} N_{K}(u)\biggr).\\[-12pt]\nonumber \end{align} $$
$$ \begin{align} \frac{1}{2}(N(x^{+})+N(x^{-})) &= \frac{1}{2\pi\mathrm{i}}\int_{\kappa-\mathrm{i} T}^{\kappa+\mathrm{i} T}\zeta_{C,K}(s)\frac{x^{s}}{s}\exp\bigl(\log\zeta_{K}(s)-\log\zeta_{C,K}(s)\bigr)\mathrm{d} s \nonumber\\[6pt] &\quad+ O\biggl(x^{\kappa}\int_{1^{-}}^{\infty}\frac{1}{u^{\kappa}\bigl(1+T\left\lvert \log(x/u) \right\rvert \bigr)}\mathrm{d} N_{K}(u)\biggr).\\[-12pt]\nonumber \end{align} $$
We will shift the contour of the first integral to one which is (up to some of the line segments
![]() $\Delta _{i}^{+}$
) identical to the contour considered in the analysis of the continuous example
$\Delta _{i}^{+}$
) identical to the contour considered in the analysis of the continuous example
![]() $\Pi _{C}$
. One can then repeat the whole analysis in Sections 3 and 4 to estimate this integral, provided that we have a good bound on
$\Pi _{C}$
. One can then repeat the whole analysis in Sections 3 and 4 to estimate this integral, provided that we have a good bound on
![]() $\left \lvert \exp (\log \zeta _{K}(s)-\log \zeta _{C,K}(s)) \right \rvert $
and that
$\left \lvert \exp (\log \zeta _{K}(s)-\log \zeta _{C,K}(s)) \right \rvert $
and that
![]() $\arg \bigl (\exp (\log \zeta _{K}(s)-\log \zeta _{C,K}(s))\bigr )$
is sufficiently small for s on the steepest path
$\arg \bigl (\exp (\log \zeta _{K}(s)-\log \zeta _{C,K}(s))\bigr )$
is sufficiently small for s on the steepest path
![]() $\Gamma _{0}$
. We now show that this is the case.
$\Gamma _{0}$
. We now show that this is the case.
Integrating by parts and using that
![]() $\mathrm{d} \Pi _{K} = \mathrm{d} \Pi _{C,K}$
on
$\mathrm{d} \Pi _{K} = \mathrm{d} \Pi _{C,K}$
on
![]() $[A_{K+1},\infty )$
and
$[A_{K+1},\infty )$
and
![]() $\mathrm{d} \Pi _{C,K}=\mathrm{d} \Pi _{C}$
on
$\mathrm{d} \Pi _{C,K}=\mathrm{d} \Pi _{C}$
on
![]() $[1,A_{K+1}]$
, we see that, for
$[1,A_{K+1}]$
, we see that, for
![]() $\sigma> 1/2$
,
$\sigma> 1/2$
,
 $$ \begin{align*} \log\zeta_{K}(s)-\log\zeta_{C,K}(s) &= \int_{1}^{A_{K+1}}y^{-s}\mathrm{d}\,\bigl(\Pi_{K}(y)-\Pi_{C,K}(y)\bigr) \nonumber\\[6pt] &= O(1) + \int_{1}^{A_{K+1}}\kern-0.2pt y^{-s}\mathrm{d}\,\bigl(\Pi_{K}(y) - \pi_{K}(y)\bigr) - \int_{1}^{A_{K+1}}\kern-0.2pt y^{-s}\mathrm{d}\,\bigl(\Pi_{C}(y)-\pi_{C}(y)\bigr) \\[6pt] &\quad + \int_{1}^{A_{K+1}}y^{-\sigma}\mathrm{d}\,\biggl(\sum_{p_{j}\le y}p_{j}^{-\mathrm{i} t} - \int_{1}^{y}u^{-\mathrm{i} t}\mathrm{d}\pi_{C}(u)\biggr).\\[-20pt] \end{align*} $$
$$ \begin{align*} \log\zeta_{K}(s)-\log\zeta_{C,K}(s) &= \int_{1}^{A_{K+1}}y^{-s}\mathrm{d}\,\bigl(\Pi_{K}(y)-\Pi_{C,K}(y)\bigr) \nonumber\\[6pt] &= O(1) + \int_{1}^{A_{K+1}}\kern-0.2pt y^{-s}\mathrm{d}\,\bigl(\Pi_{K}(y) - \pi_{K}(y)\bigr) - \int_{1}^{A_{K+1}}\kern-0.2pt y^{-s}\mathrm{d}\,\bigl(\Pi_{C}(y)-\pi_{C}(y)\bigr) \\[6pt] &\quad + \int_{1}^{A_{K+1}}y^{-\sigma}\mathrm{d}\,\biggl(\sum_{p_{j}\le y}p_{j}^{-\mathrm{i} t} - \int_{1}^{y}u^{-\mathrm{i} t}\mathrm{d}\pi_{C}(u)\biggr).\\[-20pt] \end{align*} $$
The bound (6.2) and the fact that
![]() $\mathrm{d} \,(\Pi _{K} - \pi _{K})$
,
$\mathrm{d} \,(\Pi _{K} - \pi _{K})$
,
![]() $\mathrm{d} \,\bigl (\Pi _{C}-\pi _{C}\bigr )$
are positive measures now imply that uniformly for
$\mathrm{d} \,\bigl (\Pi _{C}-\pi _{C}\bigr )$
are positive measures now imply that uniformly for
![]() $\sigma \ge 3/4$
, say,
$\sigma \ge 3/4$
, say,
where
![]() $D>0$
is a constant which depends on the implicit constant in equation (6.2) but which is independent of K. Similarly,
$D>0$
is a constant which depends on the implicit constant in equation (6.2) but which is independent of K. Similarly,
Also, for infinitely many even and odd K,
 $$ \begin{align*} &\operatorname{Im}\bigl(\log\zeta_{K}(1+\mathrm{i}\tau_{K}) - \log\zeta_{C,K}(1+\mathrm{i}\tau_{K})\bigr) \\ &= \operatorname{Im}\biggl\{\log\zeta_{D,K}(1+\mathrm{i}\tau_{K})-\log\zeta_{C,K}(1+\mathrm{i}\tau_{K}) - l\log(1-q^{-(1+\mathrm{i}\tau_{K})}) \\ &\qquad\qquad + l\biggl(\log(1-q^{-(1+\mathrm{i}\tau_{K})})+\sum_{q^{\nu}<A_{K+1}}\frac{q^{-\nu(1+\mathrm{i}\tau_{K})}}{\nu}\biggr)\biggr\} \in \biggl[-\frac{6\pi}{160},\frac{6\pi}{160}\biggr]+2\pi\mathbb{Z}, \end{align*} $$
$$ \begin{align*} &\operatorname{Im}\bigl(\log\zeta_{K}(1+\mathrm{i}\tau_{K}) - \log\zeta_{C,K}(1+\mathrm{i}\tau_{K})\bigr) \\ &= \operatorname{Im}\biggl\{\log\zeta_{D,K}(1+\mathrm{i}\tau_{K})-\log\zeta_{C,K}(1+\mathrm{i}\tau_{K}) - l\log(1-q^{-(1+\mathrm{i}\tau_{K})}) \\ &\qquad\qquad + l\biggl(\log(1-q^{-(1+\mathrm{i}\tau_{K})})+\sum_{q^{\nu}<A_{K+1}}\frac{q^{-\nu(1+\mathrm{i}\tau_{K})}}{\nu}\biggr)\biggr\} \in \biggl[-\frac{6\pi}{160},\frac{6\pi}{160}\biggr]+2\pi\mathbb{Z}, \end{align*} $$
by equations (6.3) and (6.4) and since
 $$\begin{align*}l\left\lvert \log(1-q^{-(1+\mathrm{i}\tau_{K})})+\sum_{q^{\nu}<A_{K+1}}\frac{q^{-\nu(1+\mathrm{i}\tau_{K})}}{\nu} \right\rvert \ll (1/q)^{\frac{\log A_{K+1}}{\log q}} < \frac{\pi}{160}, \end{align*}$$
$$\begin{align*}l\left\lvert \log(1-q^{-(1+\mathrm{i}\tau_{K})})+\sum_{q^{\nu}<A_{K+1}}\frac{q^{-\nu(1+\mathrm{i}\tau_{K})}}{\nu} \right\rvert \ll (1/q)^{\frac{\log A_{K+1}}{\log q}} < \frac{\pi}{160}, \end{align*}$$
say. Let now
![]() $s\in \Gamma _{0}$
, the steepest path through
$s\in \Gamma _{0}$
, the steepest path through
![]() $s_{0}$
. Then
$s_{0}$
. Then
![]() $\left \lvert s-(1+\mathrm {i}\tau _{K}) \right \rvert \ll \log _{2}B_{K}/\log B_{K}$
, and
$\left \lvert s-(1+\mathrm {i}\tau _{K}) \right \rvert \ll \log _{2}B_{K}/\log B_{K}$
, and
 $$ \begin{align*} &\log\zeta_{K}(s) - \log\zeta_{C,K}(s) \\&\quad= \log\zeta_{K}(1+\mathrm{i}\tau_{k})-\log\zeta_{C,K}(1+\mathrm{i}\tau_{K}) + \int_{1+\mathrm{i}\tau_{K}}^{s}\bigl(\log\zeta_{K}(z)-\log\zeta_{C,K}(z)\bigr)'\mathrm{d} z \\ &\quad= \log\zeta_{K}(1+\mathrm{i}\tau_{k})-\log\zeta_{C,K}(1+\mathrm{i}\tau_{K}) + O\biggl(\sqrt{\log\tau_{K}}\frac{\log_{2}B_{K}}{\log B_{K}}\biggr), \end{align*} $$
$$ \begin{align*} &\log\zeta_{K}(s) - \log\zeta_{C,K}(s) \\&\quad= \log\zeta_{K}(1+\mathrm{i}\tau_{k})-\log\zeta_{C,K}(1+\mathrm{i}\tau_{K}) + \int_{1+\mathrm{i}\tau_{K}}^{s}\bigl(\log\zeta_{K}(z)-\log\zeta_{C,K}(z)\bigr)'\mathrm{d} z \\ &\quad= \log\zeta_{K}(1+\mathrm{i}\tau_{k})-\log\zeta_{C,K}(1+\mathrm{i}\tau_{K}) + O\biggl(\sqrt{\log\tau_{K}}\frac{\log_{2}B_{K}}{\log B_{K}}\biggr), \end{align*} $$
so for such s,
 $$\begin{align*}\operatorname{Im}\bigl(\log\zeta_{K}(s)-\log\zeta_{C,K}(s)\bigr) \in \biggl[-\frac{7\pi}{160},\frac{7\pi}{160}\biggr] + 2\pi\mathbb{Z}. \end{align*}$$
$$\begin{align*}\operatorname{Im}\bigl(\log\zeta_{K}(s)-\log\zeta_{C,K}(s)\bigr) \in \biggl[-\frac{7\pi}{160},\frac{7\pi}{160}\biggr] + 2\pi\mathbb{Z}. \end{align*}$$
Since
![]() $N(x) \ll x$
(which follows for instance from Theorem 1.3), there exists some
$N(x) \ll x$
(which follows for instance from Theorem 1.3), there exists some
![]() $\tilde {x}_{K}\in (x_{K}-1,x_{K})$
such that
$\tilde {x}_{K}\in (x_{K}-1,x_{K})$
such that
 $$\begin{align*}\biggl(\tilde{x}_{K} - \frac{1}{\tilde{x}_{K}^{2}}, \tilde{x}_{K} + \frac{1}{\tilde{x}_{K}^{2}}\biggr)\cap\mathcal{N} = \varnothing, \end{align*}$$
$$\begin{align*}\biggl(\tilde{x}_{K} - \frac{1}{\tilde{x}_{K}^{2}}, \tilde{x}_{K} + \frac{1}{\tilde{x}_{K}^{2}}\biggr)\cap\mathcal{N} = \varnothing, \end{align*}$$
where
![]() $\mathcal {N}$
is the set of integers generated by
$\mathcal {N}$
is the set of integers generated by
![]() $\mathcal {P}$
. We will apply the effective Perron formula (6.5) with
$\mathcal {P}$
. We will apply the effective Perron formula (6.5) with
![]() $x=\tilde {x}_{K}$
instead of
$x=\tilde {x}_{K}$
instead of
![]() $x_{K}$
in order to avoid a technical difficulty in bounding the error term in this formula. Changing
$x_{K}$
in order to avoid a technical difficulty in bounding the error term in this formula. Changing
![]() $x_{K}$
to
$x_{K}$
to
![]() $\tilde {x}_{K}$
is not problematic, since
$\tilde {x}_{K}$
is not problematic, since
![]() ${\sigma \log (x_{K}/\tilde {x}_{K}) \ll 1}$
, and on the steepest path
${\sigma \log (x_{K}/\tilde {x}_{K}) \ll 1}$
, and on the steepest path
![]() $\Gamma _{0}$
,
$\Gamma _{0}$
,
![]() $\operatorname {Im}(s\log (x_{K}/\tilde {x}_{K})) \ll \tau _{K}/x_{K} < \pi /160$
say. This implies that on the steepest path
$\operatorname {Im}(s\log (x_{K}/\tilde {x}_{K})) \ll \tau _{K}/x_{K} < \pi /160$
say. This implies that on the steepest path
![]() $\Gamma _{0}$
through
$\Gamma _{0}$
through
![]() $s_{0}$
the argument of the integrand in equation (6.5) when
$s_{0}$
the argument of the integrand in equation (6.5) when
![]() $x=\tilde {x}_{K}$
belongs to
$x=\tilde {x}_{K}$
belongs to
![]() $\pi /2 + [-3\pi /10, 3\pi /10] + 2\pi \mathbb {Z}$
(resp.
$\pi /2 + [-3\pi /10, 3\pi /10] + 2\pi \mathbb {Z}$
(resp.
![]() $\in 3\pi /2 + [-3\pi /10, 3\pi /10] + 2\pi \mathbb {Z}$
) for infinitely many even (resp. odd) K. Together with the bound (6.6) this yields that for infinitely many even and odd K the contribution from
$\in 3\pi /2 + [-3\pi /10, 3\pi /10] + 2\pi \mathbb {Z}$
) for infinitely many even (resp. odd) K. Together with the bound (6.6) this yields that for infinitely many even and odd K the contribution from
![]() $s_{0}$
is the same as in equation (3.14) (but possibly with a different value for the implicit constant). One might check that the bound (6.6) is also sufficient to treat all the other pieces of the contour, except for the line segment
$s_{0}$
is the same as in equation (3.14) (but possibly with a different value for the implicit constant). One might check that the bound (6.6) is also sufficient to treat all the other pieces of the contour, except for the line segment
![]() $\Delta _{3}^{+}$
. We will replace this segment together with
$\Delta _{3}^{+}$
. We will replace this segment together with
![]() $\Delta _{4}^{+}$
by a different contour, a little more to the left, so that
$\Delta _{4}^{+}$
by a different contour, a little more to the left, so that
![]() $x^{s}$
can counter the additional factor
$x^{s}$
can counter the additional factor
![]() $\exp (D\sqrt {\log t})$
. We will also need a larger value of T to bound the error term in the effective Perron formula, so we now take
$\exp (D\sqrt {\log t})$
. We will also need a larger value of T to bound the error term in the effective Perron formula, so we now take
![]() $T=(x_{K})^{4}$
instead of
$T=(x_{K})^{4}$
instead of
![]() $T=(x_{K})^{2}$
.
$T=(x_{K})^{2}$
.
Recall that
![]() $\Delta _{2}^{+}$
brought us to the point
$\Delta _{2}^{+}$
brought us to the point
![]() $\sigma '+\mathrm {i} T_{2}^{+}$
. First, set
$\sigma '+\mathrm {i} T_{2}^{+}$
. First, set
![]() $\tilde {\Delta }_{3}^{+}=[\sigma '+\mathrm {i} T_{2}^{+}, \sigma '+2\mathrm {i}\tau ]$
. This segment contributes
$\tilde {\Delta }_{3}^{+}=[\sigma '+\mathrm {i} T_{2}^{+}, \sigma '+2\mathrm {i}\tau ]$
. This segment contributes
![]() $\ll x^{\sigma '}\exp (D\sqrt {\log (2\tau )})$
, which is admissible. Next, we want to move to the left in such a way that
$\ll x^{\sigma '}\exp (D\sqrt {\log (2\tau )})$
, which is admissible. Next, we want to move to the left in such a way that
![]() $\int _{s}^{\infty }\eta _{K}$
remains under control. Set
$\int _{s}^{\infty }\eta _{K}$
remains under control. Set
![]() $\sigma (t)=1-\log t/\log B_{K}$
. If
$\sigma (t)=1-\log t/\log B_{K}$
. If
![]() $\sigma \ge \sigma (t)$
and
$\sigma \ge \sigma (t)$
and
![]() $t\ge 2\tau _{K}$
, then
$t\ge 2\tau _{K}$
, then
 $$\begin{align*}\sum_{k=0}^{K}\int_{s}^{s+1}\bigl(\eta_{k}(z) + \tilde{\eta}_{k}(z) + \xi_{k}(z)\bigr)\mathrm{d} z \ll \sum_{k=0}^{K}\frac{B_{k}^{1-\sigma(t)}}{t\log B_{k}} \ll \sum_{k=0}^{K}\frac{1}{\log B_{k}} \ll 1, \end{align*}$$
$$\begin{align*}\sum_{k=0}^{K}\int_{s}^{s+1}\bigl(\eta_{k}(z) + \tilde{\eta}_{k}(z) + \xi_{k}(z)\bigr)\mathrm{d} z \ll \sum_{k=0}^{K}\frac{B_{k}^{1-\sigma(t)}}{t\log B_{k}} \ll \sum_{k=0}^{K}\frac{1}{\log B_{k}} \ll 1, \end{align*}$$
by the rapid growth of
![]() $(B_{k})_{k}$
(see (a)). Set
$(B_{k})_{k}$
(see (a)). Set
![]() $\tilde {\Delta }_{4}^{+}=[\sigma (2\tau )+2\mathrm {i}\tau , \sigma '+2\mathrm {i}\tau ]$
(note that
$\tilde {\Delta }_{4}^{+}=[\sigma (2\tau )+2\mathrm {i}\tau , \sigma '+2\mathrm {i}\tau ]$
(note that
![]() ${\sigma (2\tau )<\sigma '}$
). The contribution of
${\sigma (2\tau )<\sigma '}$
). The contribution of
![]() $\tilde {\Delta }_{4}^{+}$
is bounded by
$\tilde {\Delta }_{4}^{+}$
is bounded by
![]() $(x^{\sigma '}/\tau )\exp (D\sqrt {\log (2\tau )})$
, which is negligible. Now set
$(x^{\sigma '}/\tau )\exp (D\sqrt {\log (2\tau )})$
, which is negligible. Now set
![]() $\sigma "=\sigma '-2D/\sqrt {\log x}$
. We consider two cases.
$\sigma "=\sigma '-2D/\sqrt {\log x}$
. We consider two cases.
Case 1:
![]() $\sigma (2\tau ) \le \sigma "$
, that is,
$\sigma (2\tau ) \le \sigma "$
, that is,
![]() $\alpha> 1/3$
. Then we set
$\alpha> 1/3$
. Then we set
![]() $\tilde {\Delta }_{5}^{+} = [\sigma (2\tau )+2\mathrm {i}\tau , \sigma (2\tau )+\mathrm {i} x^{4}]$
, its contribution is
$\tilde {\Delta }_{5}^{+} = [\sigma (2\tau )+2\mathrm {i}\tau , \sigma (2\tau )+\mathrm {i} x^{4}]$
, its contribution is
![]() $\ll x^{\sigma "}(\log x)\exp \bigl (D\sqrt {\log x^{4}}\bigr ) = x^{\sigma '}\log x$
, which is admissible.
$\ll x^{\sigma "}(\log x)\exp \bigl (D\sqrt {\log x^{4}}\bigr ) = x^{\sigma '}\log x$
, which is admissible.
Case 2:
![]() $\sigma (2\tau )>\sigma "$
, that is,
$\sigma (2\tau )>\sigma "$
, that is,
![]() $\alpha \leq 1/3$
. Let
$\alpha \leq 1/3$
. Let
![]() $T_{3}^{+}$
be the solution of
$T_{3}^{+}$
be the solution of
![]() $\sigma (T_{3}^{+}) = \sigma "$
, and set
$\sigma (T_{3}^{+}) = \sigma "$
, and set
![]() $\tilde {\Delta }_{5}^{+}=\{\sigma (t)+\mathrm {i} t: 2\tau \le t\le T_{3}^{+}\} \cup [\sigma "+\mathrm {i} T_{3}^{+}, \sigma "+\mathrm {i} x^{4}]$
. This contributes
$\tilde {\Delta }_{5}^{+}=\{\sigma (t)+\mathrm {i} t: 2\tau \le t\le T_{3}^{+}\} \cup [\sigma "+\mathrm {i} T_{3}^{+}, \sigma "+\mathrm {i} x^{4}]$
. This contributes
 $$\begin{align*}\ll x\int_{2\tau}^{T_{3}^{+}}\exp\biggl(-\frac{\log x}{\log B}\log t + D\sqrt{\log t}\biggr)\frac{\mathrm{d} t}{t} + x^{\sigma"}(\log x)\exp\bigl(D\sqrt{\log x^{4}}\bigr). \end{align*}$$
$$\begin{align*}\ll x\int_{2\tau}^{T_{3}^{+}}\exp\biggl(-\frac{\log x}{\log B}\log t + D\sqrt{\log t}\biggr)\frac{\mathrm{d} t}{t} + x^{\sigma"}(\log x)\exp\bigl(D\sqrt{\log x^{4}}\bigr). \end{align*}$$
The first integral is bounded by
 $$\begin{align*}x\int_{2\tau}^{T_{3}^{+}}\exp\biggl(-\frac{\log x}{2\log B}\log t\biggr)\frac{\mathrm{d} t}{t} \ll x\exp\biggl(-\frac{\log x}{2\log B}\log(2\tau)\biggr) \ll x \exp\biggl(-\frac{c\log x}{2(\log B)^{1-\alpha}}\biggr), \end{align*}$$
$$\begin{align*}x\int_{2\tau}^{T_{3}^{+}}\exp\biggl(-\frac{\log x}{2\log B}\log t\biggr)\frac{\mathrm{d} t}{t} \ll x\exp\biggl(-\frac{\log x}{2\log B}\log(2\tau)\biggr) \ll x \exp\biggl(-\frac{c\log x}{2(\log B)^{1-\alpha}}\biggr), \end{align*}$$
which is again admissible.
Finally, we set
![]() $\tilde {\Delta }_{6}^{+} = [\sigma (2\tau )+\mathrm {i} x^{4}, 3/2 + \mathrm {i} x^{4}]$
or
$\tilde {\Delta }_{6}^{+} = [\sigma (2\tau )+\mathrm {i} x^{4}, 3/2 + \mathrm {i} x^{4}]$
or
![]() $[\sigma " + \mathrm {i} x^{4}, 3/2 + \mathrm {i} x^{4}]$
, this contributes
$[\sigma " + \mathrm {i} x^{4}, 3/2 + \mathrm {i} x^{4}]$
, this contributes
![]() $x^{3/2 - 4}\exp \bigl (D\sqrt {\log x^{4}}\bigr )$
, which is negligible.
$x^{3/2 - 4}\exp \bigl (D\sqrt {\log x^{4}}\bigr )$
, which is negligible.
Next, we need to estimate the error term in the effective Perron formula
 $$ \begin{align} x^{3/2}\int_{1^{-}}^{\infty}\frac{1}{u^{3/2}\bigl(1+x^{4}\left\lvert \log(x/u) \right\rvert \bigr)}\mathrm{d} N_{K}(u), \quad x=\tilde{x}_{K}. \end{align} $$
$$ \begin{align} x^{3/2}\int_{1^{-}}^{\infty}\frac{1}{u^{3/2}\bigl(1+x^{4}\left\lvert \log(x/u) \right\rvert \bigr)}\mathrm{d} N_{K}(u), \quad x=\tilde{x}_{K}. \end{align} $$
We have that
 $$ \begin{align*} & \mathrm{d} N_{K} = \exp^{\ast}(\mathrm{d}\Pi_{K}) = \exp^{\ast}\biggl(\sum_{p_{j}^{\nu}<A_{K+1}}\frac{1}{\nu}\delta_{p_{j}^{\nu}} + l \sum_{q^{\nu}<A_{K+1}}\frac{1}{\nu}\delta_{q^{\nu}}\biggr) \\ & + \exp^{\ast}\biggl(\sum_{p_{j}^{\nu}<A_{K+1}}\!\frac{1}{\nu}\delta_{p_{j}^{\nu}} + l \!\sum_{q^{\nu}<A_{K+1}}\!\frac{1}{\nu}\delta_{q^{\nu}}\!\biggr) {\ast} \biggl(\chi_{[A_{K+1},\infty)}\mathrm{d}\operatorname{\mathrm{Li}} + \frac{1}{2}\bigl(\chi_{[A_{K+1},\infty)}\mathrm{d}\operatorname{\mathrm{Li}}\bigr)^{\ast 2} + \dotso\!\biggr) =: \mathrm{d} m_{1} + \mathrm{d} m_{2}. \end{align*} $$
$$ \begin{align*} & \mathrm{d} N_{K} = \exp^{\ast}(\mathrm{d}\Pi_{K}) = \exp^{\ast}\biggl(\sum_{p_{j}^{\nu}<A_{K+1}}\frac{1}{\nu}\delta_{p_{j}^{\nu}} + l \sum_{q^{\nu}<A_{K+1}}\frac{1}{\nu}\delta_{q^{\nu}}\biggr) \\ & + \exp^{\ast}\biggl(\sum_{p_{j}^{\nu}<A_{K+1}}\!\frac{1}{\nu}\delta_{p_{j}^{\nu}} + l \!\sum_{q^{\nu}<A_{K+1}}\!\frac{1}{\nu}\delta_{q^{\nu}}\!\biggr) {\ast} \biggl(\chi_{[A_{K+1},\infty)}\mathrm{d}\operatorname{\mathrm{Li}} + \frac{1}{2}\bigl(\chi_{[A_{K+1},\infty)}\mathrm{d}\operatorname{\mathrm{Li}}\bigr)^{\ast 2} + \dotso\!\biggr) =: \mathrm{d} m_{1} + \mathrm{d} m_{2}. \end{align*} $$
Since
![]() $\mathrm{d} m_{1} \le \mathrm{d} N$
, the contribution of
$\mathrm{d} m_{1} \le \mathrm{d} N$
, the contribution of
![]() $\mathrm{d} m_{1}$
to equation (6.7) is bounded by
$\mathrm{d} m_{1}$
to equation (6.7) is bounded by
 $$\begin{align*}x^{3/2}\sum_{n\in \mathcal{N}}\frac{1}{n^{3/2}\bigl(1+x^{4}\left\lvert \log (x/n) \right\rvert \bigr)} \ll x^{3/2-4} + \sum_{\substack{n\in\mathcal{N} \\ x/2\le n\le 2x}}\frac{x}{x^{4}\left\lvert n-x \right\rvert }, \end{align*}$$
$$\begin{align*}x^{3/2}\sum_{n\in \mathcal{N}}\frac{1}{n^{3/2}\bigl(1+x^{4}\left\lvert \log (x/n) \right\rvert \bigr)} \ll x^{3/2-4} + \sum_{\substack{n\in\mathcal{N} \\ x/2\le n\le 2x}}\frac{x}{x^{4}\left\lvert n-x \right\rvert }, \end{align*}$$
where we used
![]() $\left \lvert \log (x/n) \right \rvert \gg \left \lvert n-x \right \rvert /x$
when
$\left \lvert \log (x/n) \right \rvert \gg \left \lvert n-x \right \rvert /x$
when
![]() $x/2\le n\le 2x$
. By the choice of
$x/2\le n\le 2x$
. By the choice of
![]() $x=\tilde {x}_{K}$
,
$x=\tilde {x}_{K}$
,
![]() $\left \lvert n-x \right \rvert \ge 1/x^{2}$
, so the last sum is bounded by
$\left \lvert n-x \right \rvert \ge 1/x^{2}$
, so the last sum is bounded by
![]() $(1/x)N_{K}(2x)$
, which is bounded. The second measure
$(1/x)N_{K}(2x)$
, which is bounded. The second measure
![]() $\mathrm{d} m_{2}$
has support in
$\mathrm{d} m_{2}$
has support in
![]() $[A_{K+1},\infty )$
. Since we may assume that
$[A_{K+1},\infty )$
. Since we may assume that
![]() $A_{K+1}>2x_{K}$
by (a) and since
$A_{K+1}>2x_{K}$
by (a) and since
![]() $\mathrm{d} m_{2} \le \mathrm{d} N_{K}$
, the contribution of
$\mathrm{d} m_{2} \le \mathrm{d} N_{K}$
, the contribution of
![]() $\mathrm{d} m_{2}$
to equation (6.7) is bounded by
$\mathrm{d} m_{2}$
to equation (6.7) is bounded by
 $$\begin{align*}\frac{1}{x^{4}}\int_{A_{K+1}}^{\infty}\frac{\mathrm{d} N_{K}(u)}{u^{3/2}} \ll \frac{1}{x^{4}}. \end{align*}$$
$$\begin{align*}\frac{1}{x^{4}}\int_{A_{K+1}}^{\infty}\frac{\mathrm{d} N_{K}(u)}{u^{3/2}} \ll \frac{1}{x^{4}}. \end{align*}$$
(The integral is bounded by
![]() $\zeta _{K}(3/2)$
, which is bounded independent of K.)
$\zeta _{K}(3/2)$
, which is bounded independent of K.)
To complete the proof, it remains to bound
![]() $\rho -\rho _{K}$
, where
$\rho -\rho _{K}$
, where
![]() $\rho $
and
$\rho $
and
![]() $\rho _{K}$
are the asymptotic densities of N and
$\rho _{K}$
are the asymptotic densities of N and
![]() $N_{K}$
, respectively. We have
$N_{K}$
, respectively. We have
 $$ \begin{align*} \log \rho - \log \rho_{K} &= \int_{1^{-}}^{\infty}\frac{1}{u}\biggl(\sum_{p_{j}^{\nu}\ge A_{K+1}}\frac{1}{\nu}\delta_{p_{j}^{\nu}}(u) + l\sum_{q^{\nu}\ge A_{K+1}}\frac{1}{\nu}\delta_{q^{\nu}}(u) - \chi_{[A_{K+1},\infty)}\mathrm{d}\operatorname{\mathrm{Li}}(u)\biggr)\\ &\ll \int_{A_{K+1}}^{\infty}\frac{1}{u^{2}}\left\lvert \Pi(u)-\Pi(A_{K+1}^{-})-\operatorname{\mathrm{Li}}(u)+\operatorname{\mathrm{Li}}(A_{K+1}) \right\rvert \mathrm{d} u\\ &\ll \int_{A_{K+1}}^{\infty}\frac{\exp\bigl(-c(\log u)^{\alpha}\bigr)}{u}\mathrm{d} u \ll \exp\bigl(-(c/2)(\log A_{K+1})^{\alpha}\bigr)\le \frac{1}{x_{K}}, \end{align*} $$
$$ \begin{align*} \log \rho - \log \rho_{K} &= \int_{1^{-}}^{\infty}\frac{1}{u}\biggl(\sum_{p_{j}^{\nu}\ge A_{K+1}}\frac{1}{\nu}\delta_{p_{j}^{\nu}}(u) + l\sum_{q^{\nu}\ge A_{K+1}}\frac{1}{\nu}\delta_{q^{\nu}}(u) - \chi_{[A_{K+1},\infty)}\mathrm{d}\operatorname{\mathrm{Li}}(u)\biggr)\\ &\ll \int_{A_{K+1}}^{\infty}\frac{1}{u^{2}}\left\lvert \Pi(u)-\Pi(A_{K+1}^{-})-\operatorname{\mathrm{Li}}(u)+\operatorname{\mathrm{Li}}(A_{K+1}) \right\rvert \mathrm{d} u\\ &\ll \int_{A_{K+1}}^{\infty}\frac{\exp\bigl(-c(\log u)^{\alpha}\bigr)}{u}\mathrm{d} u \ll \exp\bigl(-(c/2)(\log A_{K+1})^{\alpha}\bigr)\le \frac{1}{x_{K}}, \end{align*} $$
where we may assume the last bound in view of (a). In conclusion, we have that (on some subsequence containing infinitely many even and odd K):
 $$ \begin{align*} N(\tilde{x}_{K}) - \rho\tilde{x}_{K} &= N_{K}(\tilde{x}_{K})-\rho_{K}\tilde{x}_{K} + (\rho-\rho_{K})\tilde{x}_{K} \\ &= \Omega_{\pm}\Bigl(\tilde{x}_{K}\exp\bigl(-(c(\alpha+1))^{\frac{1}{\alpha+1}}(\log \tilde{x}_{K}\log_{2}\tilde{x}_{K})^{\frac{\alpha}{\alpha+1}}(1+\dotso)\bigr)\Bigr) + O(1). \end{align*} $$
$$ \begin{align*} N(\tilde{x}_{K}) - \rho\tilde{x}_{K} &= N_{K}(\tilde{x}_{K})-\rho_{K}\tilde{x}_{K} + (\rho-\rho_{K})\tilde{x}_{K} \\ &= \Omega_{\pm}\Bigl(\tilde{x}_{K}\exp\bigl(-(c(\alpha+1))^{\frac{1}{\alpha+1}}(\log \tilde{x}_{K}\log_{2}\tilde{x}_{K})^{\frac{\alpha}{\alpha+1}}(1+\dotso)\bigr)\Bigr) + O(1). \end{align*} $$
Competing Interests
None.