1. Introduction and motivation
The energy spectrum associated with water waves encompasses a vast range of frequencies. On one end of the spectrum are low-frequency tidal waves generated by the mutual attraction of the Sun, Moon and Earth while on the other end are high-frequency ripples, the periods of which are fractions of a second (see figure 1 in Conroy et al. (Reference Conroy, Kubatko, Nappi, Sebian, West and Mandli2018)). A significant portion of energy contained within this spectrum resides in a high-frequency band of water waves generated by air–water interactions known as the wind sea. When a wind sea is created by a large storm – such as a hurricane – it can wreak havoc among coastal communities. In total, 210 billion US dollars was spent on the recoveries of Hurricane Katrina and Superstorm Sandy (e.g. Blake Reference Blake2013; GSO 2015).
As time progresses into the twenty-first century, the probability of an increase in the intensity of global tropical cyclones along with their destruction potential is likely (probability ![]() $>$66 %) (GFDL 2020). A recent report by the World Meteorological Organization task team (Knutson et al. Reference Knutson2020) also concludes that it is likely that rainfall rates associated with these cyclones will increase and sea level rise caused by anthropogenic warming should cause higher inundation levels when tropical cyclones do occur, which can lead to an increase in coastal community damages (GFDL 2020). In an effort to adapt to this situation and create coastal communities that are resilient to hurricane storm surge, researchers and coastal managers are attempting to use ensemble storm surge studies and real time forecast guidance to gauge how coastal flood dynamics responds to variations in storm strength, track and duration. Both approaches can employ hundreds to thousands of storm surge computer simulations to quantify the risk of a particular storm event. The computer simulations rely on two distinct mathematical models that share information in terms of stress to quantify the total storm surge inundation. These models consist of a long wave model that quantifies storm surge dynamics due to (i) the tides (waves with a period of 12 h or 24 h) and (ii) waves created by the large pressure gradient at the sea surface associated with the storm (waves with a period greater than 2.5 min). The long wave model is coupled to a short wave model (high-frequency gravity water waves with a period between 1 and 30 s), which quantifies the wind sea that forms in conjunction with the long waves. Advanced short wave models (see WAMDI 1988; Booij, Ris & Holthuijsen Reference Booij, Ris and Holthuijsen1999; Tolman Reference Tolman2009; Smit, Janssen & Herbers Reference Smit, Janssen and Herbers2015) can capture a multitude of surface water-wave phenomena on a wide variety of scales. This complexity, however, comes at a steep computational cost. ‘Operational’ short wave ocean models typically increase the computational load by a factor of three for coupled models using an unstructured mesh (Dietrich et al. Reference Dietrich2012), and can run up to
$>$66 %) (GFDL 2020). A recent report by the World Meteorological Organization task team (Knutson et al. Reference Knutson2020) also concludes that it is likely that rainfall rates associated with these cyclones will increase and sea level rise caused by anthropogenic warming should cause higher inundation levels when tropical cyclones do occur, which can lead to an increase in coastal community damages (GFDL 2020). In an effort to adapt to this situation and create coastal communities that are resilient to hurricane storm surge, researchers and coastal managers are attempting to use ensemble storm surge studies and real time forecast guidance to gauge how coastal flood dynamics responds to variations in storm strength, track and duration. Both approaches can employ hundreds to thousands of storm surge computer simulations to quantify the risk of a particular storm event. The computer simulations rely on two distinct mathematical models that share information in terms of stress to quantify the total storm surge inundation. These models consist of a long wave model that quantifies storm surge dynamics due to (i) the tides (waves with a period of 12 h or 24 h) and (ii) waves created by the large pressure gradient at the sea surface associated with the storm (waves with a period greater than 2.5 min). The long wave model is coupled to a short wave model (high-frequency gravity water waves with a period between 1 and 30 s), which quantifies the wind sea that forms in conjunction with the long waves. Advanced short wave models (see WAMDI 1988; Booij, Ris & Holthuijsen Reference Booij, Ris and Holthuijsen1999; Tolman Reference Tolman2009; Smit, Janssen & Herbers Reference Smit, Janssen and Herbers2015) can capture a multitude of surface water-wave phenomena on a wide variety of scales. This complexity, however, comes at a steep computational cost. ‘Operational’ short wave ocean models typically increase the computational load by a factor of three for coupled models using an unstructured mesh (Dietrich et al. Reference Dietrich2012), and can run up to ![]() $86$ times as slow as a structured grid long wave model (Mellor, Donelan & Oey Reference Mellor, Donelan and Oey2008). Due to the expense of the short wave component, ensemble storm surge studies routinely disregard (Liberto et al. Reference Liberto, Colle, Georgas, Blumberg and Taylor2011) or relax the convergence criteria of the short wave numerical solution (Ning, Emanuel & Vanmarcke Reference Ning, Emanuel and Vanmarcke2014), which can have a negative impact in terms of the reliability of model results. Beyond danger of inaccuracy during disaster scenarios, these ‘quick’ fixes can ultimately perpetuate a public distrust in the validity of such computational tools.
$86$ times as slow as a structured grid long wave model (Mellor, Donelan & Oey Reference Mellor, Donelan and Oey2008). Due to the expense of the short wave component, ensemble storm surge studies routinely disregard (Liberto et al. Reference Liberto, Colle, Georgas, Blumberg and Taylor2011) or relax the convergence criteria of the short wave numerical solution (Ning, Emanuel & Vanmarcke Reference Ning, Emanuel and Vanmarcke2014), which can have a negative impact in terms of the reliability of model results. Beyond danger of inaccuracy during disaster scenarios, these ‘quick’ fixes can ultimately perpetuate a public distrust in the validity of such computational tools.
The primary goal of this investigation is to leverage the 60-plus years of wind, water-wave and turbulence research to develop a rigorous framework to quantify the wind sea in a fashion that is computationally efficient and extendable (in terms of future work) to incorporate swell and coastal effects. To achieve this goal we focus our efforts on two main parts: (i) the development of a mathematical model to quantify the generation and propagation of various conservative quantities (momentum, energy, etc.) of the wind sea and (ii) the development of a statistical method to quantify the input in terms of the cause and effect of air–water interactions that transfer energy and grow the wind sea.
The secondary goal is to introduce a recursive integration method that extracts a measure of nonlinearity of the air–water interaction from observational wind speed data measured at 10 m above the sea surface, denoted by ![]() $U_{10}$, and uses this measure to interpolate
$U_{10}$, and uses this measure to interpolate ![]() $U_{10}$ to shorter time scales. The measure is known as the Hurst exponent (Hurst Reference Hurst1951, Reference Hurst1955; Mandelbrot Reference Mandelbrot1977) and it is an important measure in terms of quantifying dependence driven variability of the wind data (see the details provided in § 3, as well as our companion paper Conroy, Kubatko & Mandli (Reference Conroy, Kubatko and Mandli2021) and Mandelbrot (Reference Mandelbrot1977)). When the Hurst exponent is set to
$U_{10}$ to shorter time scales. The measure is known as the Hurst exponent (Hurst Reference Hurst1951, Reference Hurst1955; Mandelbrot Reference Mandelbrot1977) and it is an important measure in terms of quantifying dependence driven variability of the wind data (see the details provided in § 3, as well as our companion paper Conroy, Kubatko & Mandli (Reference Conroy, Kubatko and Mandli2021) and Mandelbrot (Reference Mandelbrot1977)). When the Hurst exponent is set to ![]() $H = 1/2$, the water surface is composed of linear waves. However, numerical findings indicate that for a wind sea created by air–water interactions the Hurst exponent falls within the bounds
$H = 1/2$, the water surface is composed of linear waves. However, numerical findings indicate that for a wind sea created by air–water interactions the Hurst exponent falls within the bounds ![]() $0.33 < H < 0.45$ and varies at a given spatial coordinate in time. The fact that
$0.33 < H < 0.45$ and varies at a given spatial coordinate in time. The fact that ![]() $H < 1/2$ for the wind sea is significant because it corresponds to anti-persistent behaviour. Physically, this can be attributed to vortices that form in the turbulent air–water interaction which store information and give the flow field a ‘memory’ of the generator of the turbulence. The cyclonic nature of the vortices leads to the anti-correlated motion and vortex stretching leads to singular regions of energy dissipation at small scales that have a multifractal (statistical) distribution (Frisch Reference Frisch1996; Yakhot Reference Yakhot2006). Balanced source terms for wave generation in spectral resolving phase-averaged wave models are a function of
$H < 1/2$ for the wind sea is significant because it corresponds to anti-persistent behaviour. Physically, this can be attributed to vortices that form in the turbulent air–water interaction which store information and give the flow field a ‘memory’ of the generator of the turbulence. The cyclonic nature of the vortices leads to the anti-correlated motion and vortex stretching leads to singular regions of energy dissipation at small scales that have a multifractal (statistical) distribution (Frisch Reference Frisch1996; Yakhot Reference Yakhot2006). Balanced source terms for wave generation in spectral resolving phase-averaged wave models are a function of ![]() $U_{10}$. It is rare to have access to observational data for
$U_{10}$. It is rare to have access to observational data for ![]() $U_{10}$ that are observed at the time scales necessary to integrate the action balance equation in time. Therefore,
$U_{10}$ that are observed at the time scales necessary to integrate the action balance equation in time. Therefore, ![]() $U_{10}$ must be interpolated to smaller time scales. This is predominantly accomplished via linear interpolation, which does not capture non-Gaussian behaviour. The recursive integration methods presented in § 3 can be used in spectral resolving phase-averaged models to capture the non-Gaussian behaviour of
$U_{10}$ must be interpolated to smaller time scales. This is predominantly accomplished via linear interpolation, which does not capture non-Gaussian behaviour. The recursive integration methods presented in § 3 can be used in spectral resolving phase-averaged models to capture the non-Gaussian behaviour of ![]() $U_{10}$. In fact, Cavaleri (Reference Cavaleri2009) draws attention to the fact that phase-averaged water-wave models typically under-predict peak wave heights and peak wave periods in strong storms unless ‘strong, but effective tuning’ is used. In our companion paper (Conroy et al. Reference Conroy, Kubatko and Mandli2021) we show that this effect can be alleviated with our recursive integration methods and we conjecture that using our recursive integration methods to generate
$U_{10}$. In fact, Cavaleri (Reference Cavaleri2009) draws attention to the fact that phase-averaged water-wave models typically under-predict peak wave heights and peak wave periods in strong storms unless ‘strong, but effective tuning’ is used. In our companion paper (Conroy et al. Reference Conroy, Kubatko and Mandli2021) we show that this effect can be alleviated with our recursive integration methods and we conjecture that using our recursive integration methods to generate ![]() $U_{10}$ coupled with a source term such as, for example, the Zakharov–Resio–Pushkarev wind input source term (Zakharov, Resio & Pushkarev Reference Zakharov, Resio and Pushkarev2017), will help remedy this effect in spectral resolving wave models. Details for obtaining the numerical code for the recursive integration method can be found in Appendix A.
$U_{10}$ coupled with a source term such as, for example, the Zakharov–Resio–Pushkarev wind input source term (Zakharov, Resio & Pushkarev Reference Zakharov, Resio and Pushkarev2017), will help remedy this effect in spectral resolving wave models. Details for obtaining the numerical code for the recursive integration method can be found in Appendix A.
1.1. Background
Before we delve into the specifics of the mathematical treatment of our investigation it seems prudent that we provide the reader with some background information in regard to how our investigation leverages water-wave research and fits in with existing water-wave models and theories.
More specifically, our model fits into the phase-averaging classification of water-wave models that seeks to quantify the bulk movement of the short waves of the sea surface. Due to the large range of scales (both spatial and temporal) that span water-wave dynamics (see Salmon Reference Salmon1998) it is impossible to resolve all of the individual wave trains that comprise the water surface. Phase-averaging models circumvent this issue by characterizing the water-wave environment in a statistical sense, and make use of a probability density function to determine the water-wave dynamics that is most likely to occur at a specific geographic coordinate of interest under a given physical condition. Many short wave models quantify the water-wave heights and frequencies generated by air–water interactions by solving an energy balance equation (or action balance equation if the wind sea forms in the presence of currents). The energy balance equation involves operators in both geographic space and spectral space, and results in a five-dimensional equation whose solution is exacerbated by its spectral resolving source term, which is a function of atmospheric input, nonlinear wave–wave interactions and dissipation (see Hasselmann et al. Reference Hasselmann1973; Janssen Reference Janssen2004).
Rather than solve the action balance equation, we solve a system of balance equations derived from the Navier–Stokes equations (see Appendix B). These equations preserve statistical moments of quantities of interest (e.g. momentum, energy, energy flux) of the short water waves and can be described as moment field equations. The main advantage of our approach is twofold: (i) the final form of the system of equations we solve to quantify air–water turbulence consists of conservative hyperbolic partial differential equations (PDEs) with source terms, which are amenable to advanced discretization methods and are relatively easy to solve numerically, and (ii) the air–water energy transfer terms allow for non-Gaussian energy transfer (non-Gaussian loosely means that events in the tails of the distribution play an important role in the process). In other words, we do not assume a priori that the stochastic random variables that quantify the turbulent energy of the atmosphere are Gaussian. Indeed, there are some near-Gaussian features of turbulence but energy transfer is not one of them. Further, it should be emphasized that near Gaussian is not synonymous with Gaussian; if the turbulent velocity were truly Gaussian then the energy flux through the wavenumber ![]() $k$ would identically vanish (Frisch Reference Frisch1996).
$k$ would identically vanish (Frisch Reference Frisch1996).
Due to the fact that the moment field equations consist of moments of the Navier–Stokes equation we have to deal with the issue of moment closure (each equation for the ![]() $n$th-order moment involves terms of the
$n$th-order moment involves terms of the ![]() $(n+1)$th-order moment which means the equations cannot be solved without some kind of closure scheme, see Friedrich & Peinke (Reference Friedrich and Peinke2020), for example). Previous water-wave investigations make use of the Reynolds-averaged Navier–Stokes (RANS) equation to quantify air–water turbulence (Janssen Reference Janssen2004). Many of these investigations used variations of an eddy viscosity mixing length approach to close the RANS equation. However, these efforts were more focused on investigating critical layer dynamics and largely did not attempt to track the water waves after they were created (Janssen Reference Janssen2004).
$(n+1)$th-order moment which means the equations cannot be solved without some kind of closure scheme, see Friedrich & Peinke (Reference Friedrich and Peinke2020), for example). Previous water-wave investigations make use of the Reynolds-averaged Navier–Stokes (RANS) equation to quantify air–water turbulence (Janssen Reference Janssen2004). Many of these investigations used variations of an eddy viscosity mixing length approach to close the RANS equation. However, these efforts were more focused on investigating critical layer dynamics and largely did not attempt to track the water waves after they were created (Janssen Reference Janssen2004).
Because we are concerned with generating and tracking the water waves, we close the moment field equations with a novel approach that transforms the turbulent diffusion operator to a wave propagation term. The wave propagation term quantifies energy transfer between the wind and water in terms of a pulsation – a pulsation in the energy of the atmosphere creates a corresponding pulsation of energy in the water surface – whether or not the energy pulsation transferred from the wind to the water surface grows into a longer wave depends on the strength of the pulsation and the speed of the water wave and the duration (or fetch) of the wind. More specifically, because we model air and water as inviscid fluids, if the physical conditions are such that an inflection point exists between the speed of the wind and water wave then at least one instability exists and the water wave will grow if the wind continues to blow at the same speed (see Moreland, Saffman & Yuen Reference Moreland, Saffman and Yuen1991). Rather than explicitly calculate these instabilities we quantify the probability of an instability occurring via a parameter that we denote by ![]() $q$, and use this information in a statistical operator that generates the expected energy pulse in the water surface.
$q$, and use this information in a statistical operator that generates the expected energy pulse in the water surface.
We define the exact quantitative relation connecting the wind velocity to the corresponding energy pulse (created in the water surface) via the original energy transfer parameterization of Hasselmann et al. (Reference Hasselmann, Ross, Muller and Sell1975), which takes into account atmospheric input, nonlinear wave interactions and dissipation, and has been verified by the direct numerical simulations of Tanaka (Reference Tanaka2001). It can be noted that Hasselmann's original nonlinear energy parameterization is only valid for growing wind seas and is not applicable to swell waves, and therefore, we limit the current investigation to water waves with a non-dimensional frequency ![]() $\nu = f_m U_{10}/g > 14$, where
$\nu = f_m U_{10}/g > 14$, where ![]() $f_m$ is the peak frequency of the water waves,
$f_m$ is the peak frequency of the water waves, ![]() $U_{10}$ is the wind speed measured at
$U_{10}$ is the wind speed measured at ![]() $10$ m from the water surface and
$10$ m from the water surface and ![]() $g$ is acceleration due to gravity.
$g$ is acceleration due to gravity.
The resonance mechanism described above is originally due to Phillips (Reference Phillips1957) and Miles (Reference Miles1957), who both independently conjectured that resonance between the wind and the water surface generates water waves. Phillips considers a resonance mechanism involving turbulent pressure fluctuations while the Miles theory takes into account the resonance between wave induced pressure fluctuations and the free surface of the water (Janssen Reference Janssen2004). The Phillips mechanism leads to a linear growth rate while the Miles mechanism leads to an exponential growth rate caused by shear flow instability. Recent laboratory experiments by Liberzon & Shemer (Reference Liberzon and Shemer2011) show that wave growth is exponential, however, these same experiments invalidate some of the consequences of Miles’ theory, although it has received support from experiments examining longer waves (Janssen Reference Janssen2004).
In this investigation, we assume that the wave growth is exponential, however, we do not explicitly resolve the shear flow instability mechanism posited by Miles. Instead, we consider the probability of the likeliness of an instability occurring based on the current physical state of the atmosphere and body of water and quantify the temporal distribution of these instabilities. Because we neglect viscosity effects in our model, these instabilities take the form of singularities.
As in the work of Phillips, we also develop the resonance mechanism in terms of a reference frame that moves in tandem with the water surface and transfers energy via pressure and shear stress. Rather than characterize the frame of reference of this energy transfer (between air and water) with the speed of the stress distribution, however, we characterize the frame of reference using a speed, ![]() $\|\boldsymbol {u}_0\|$, linked to the flow of energy in the wind-sea spectrum. Further, unlike Phillips, who assumes that the stress fluctuations are random, we utilize a formulation such that the characteristic speed of each stress pulsation depends on the previous stress pulsation, so that all of the turbulent pulsations are connected to a generating event. In other words, the stress pulsations have a memory of the event that generated the turbulence.
$\|\boldsymbol {u}_0\|$, linked to the flow of energy in the wind-sea spectrum. Further, unlike Phillips, who assumes that the stress fluctuations are random, we utilize a formulation such that the characteristic speed of each stress pulsation depends on the previous stress pulsation, so that all of the turbulent pulsations are connected to a generating event. In other words, the stress pulsations have a memory of the event that generated the turbulence.
To illustrate this point, consider the simple example of a laminar fluid flowing past a dense screen mesh. As the fluid flows past the screen mesh turbulence will be created and energy dissipation will occur nearly everywhere within the fluid. The turbulence in this case is nearly space filling (to the extent that the screen mesh is space filling) and the energy transfer can be quantified (in terms of low-order moments) using the famous theory of Kolmogorov (Reference Kolmogorov1941).
For wind flowing over a body of water the generating event of the turbulence, for example, could be due to the wind initially flowing over rough topography before flowing over a rough coastline and then over the body of water. The energy dissipation caused by these generating events result in a distribution of eddies that is not space filling but is fractal (Frisch Reference Frisch1996; Mandelbrot Reference Mandelbrot1974); the dimension of the statistical signature of energy transfer lies between a dimension of 2 and 3. In this case, the turbulence is said to be intermittent, and Kolmogorov's 1941 theory is no longer applicable (Yakhot Reference Yakhot2006). In fact, turbulence observed in nature is multifractal (Frisch Reference Frisch1996; Mandelbrot Reference Mandelbrot1998), there is a spectrum of fractal dimensions associated with a given flow field which it acquires through interactions with its environment. In the example of the wind flowing over a body of water, the spectrum of fractal dimensions (in terms of the eddy distribution) results from the wind's interaction with the topography, coastline and body of water where each event injects a different statistical pattern into the flow field. The recursive integration method we introduce in § 3 is general enough to extract the statistical distribution of energy transfer from the flow field regardless of the generating event.
More specifically, we generate multifractal measures of the eddy distribution in the wind by decomposing observational wind data into a series of duration limited pulses where the temporal distribution of the wind speed and direction are modelled using a power law. The characteristic speed/direction of each pulse can change with each duration. The power law exponent also changes with each pulsation, and measures the extent of the turbulence associated with each pulse. In particular, a large absolute value of the exponent indicates a greater probability that an instability will occur and is associated with either injection or dissipation of energy/momentum at the air–water interface.
It can be noted that when we refer to air–water turbulence we refer to small scale, high-frequency turbulence where the period of the turbulence is less than the period of the water waves. In this case the small scale turbulence is so fast that it is always in equilibrium with the shear flow which generates an instability and transfers energy between the air and water (Janssen Reference Janssen2004). Large scale turbulence (classified as having a period greater than the water waves) is excluded from the current investigation.
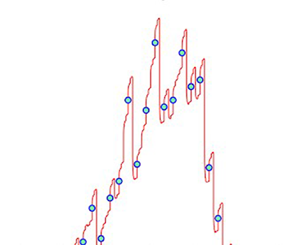
Due to the fact that wind data are typically presented in hourly averages, and because we are concerned with small scale turbulence, we introduce a recursive integration procedure that generates a refined distribution of the wind turbulence for shorter time scales. The method leverages the fact that the Navier–Stokes equations are invariant under scaling transformations in the form of self-affine power laws that hold for small viscosity values (Frisch Reference Frisch1996). Typically, such scaling properties only hold over a range of scales delineated by an inner cutoff and outer cutoff. The outer cutoff is usually specified in terms of the integral length scale while the inner cutoff is typically associated with molecular diffusion. Because of this fact, scaling laws can typically can only be employed over 3–5 decades of refinement.
The recursive integration method we develop herein proceeds in a similar iterative fashion as cascade models such as the ![]() $p$ model (Meneveau & Sreenivasan Reference Meneveau and Sreenivasan1987) and
$p$ model (Meneveau & Sreenivasan Reference Meneveau and Sreenivasan1987) and ![]() $\beta$ model (Frisch Reference Frisch1996), and was originally inspired by the curdling models of Mandelbrot (Reference Mandelbrot1974), however, there are some important distinctions. In the
$\beta$ model (Frisch Reference Frisch1996), and was originally inspired by the curdling models of Mandelbrot (Reference Mandelbrot1974), however, there are some important distinctions. In the ![]() $p$ model, the probabilities of a binomial distribution were chosen so as to reproduce the generalized dimensions of the multifractal spectrum of the dissipation field of several fully developed turbulent flows. The
$p$ model, the probabilities of a binomial distribution were chosen so as to reproduce the generalized dimensions of the multifractal spectrum of the dissipation field of several fully developed turbulent flows. The ![]() $\beta$ model (which was introduced by Mandelbrot (Reference Mandelbrot1974) and popularized by Frisch (Reference Frisch1996)) also uses a pre-determined value for
$\beta$ model (which was introduced by Mandelbrot (Reference Mandelbrot1974) and popularized by Frisch (Reference Frisch1996)) also uses a pre-determined value for ![]() $\beta$ that determines the fractal dimension of the energy dissipation, and the weighted curdling model of Mandelbrot is typically used by prescribing the distribution of the weights using a priori considerations.
$\beta$ that determines the fractal dimension of the energy dissipation, and the weighted curdling model of Mandelbrot is typically used by prescribing the distribution of the weights using a priori considerations.
In our approach, rather than use a priori considerations, we use a conditional probability and determine the weights based on the current state and previous state of the dynamics of the wind field. We achieve this by preserving the area and endpoint values of the data over each time interval that the average wind data are reported, and calculate the characteristic velocity, ![]() $\|\boldsymbol {u}_0\|$, and power law exponent,
$\|\boldsymbol {u}_0\|$, and power law exponent, ![]() $q$, that defines the velocity distribution. Each successive iteration is initialized by integrating over a sub-region of the distribution to determine a new set of averages that are used to determine the velocity distribution over a shorter duration of time. An important component of our recursive integration concerns the fact that we are able to cut out temporal regions during the integration process to produce a fractal support of the measure which falls within the range of observations with each recursion. This is markedly different than most cascade models that begin from a uniform measure and require a number of recursions before the fractal measure of the dissipation falls within the range of observations. In this respect, our recursive integration procedure can generate what Mandelbrot (Reference Mandelbrot1974) refers to as conservative and non-conservative cascades. The recursive integration method coupled with the source terms developed in § 2.1 are the key to capturing the non-Gaussian behaviour of the energy transfer. Further, we would like to emphasize that the recursive integration method presented herein is by no means meant to represent a physical mechanism of energy transfer in a turbulent fluid; it is purely a mathematical construct to interpolate the data in a non-Gaussian fashion.
$q$, that defines the velocity distribution. Each successive iteration is initialized by integrating over a sub-region of the distribution to determine a new set of averages that are used to determine the velocity distribution over a shorter duration of time. An important component of our recursive integration concerns the fact that we are able to cut out temporal regions during the integration process to produce a fractal support of the measure which falls within the range of observations with each recursion. This is markedly different than most cascade models that begin from a uniform measure and require a number of recursions before the fractal measure of the dissipation falls within the range of observations. In this respect, our recursive integration procedure can generate what Mandelbrot (Reference Mandelbrot1974) refers to as conservative and non-conservative cascades. The recursive integration method coupled with the source terms developed in § 2.1 are the key to capturing the non-Gaussian behaviour of the energy transfer. Further, we would like to emphasize that the recursive integration method presented herein is by no means meant to represent a physical mechanism of energy transfer in a turbulent fluid; it is purely a mathematical construct to interpolate the data in a non-Gaussian fashion.
The remainder of this paper is organized as follows; in § 2 we introduce the moment field equations and derive source terms that quantify air–water energy transfer. We close these source terms in § 3 and introduce our recursive integration method and the corresponding energy measures. Finally, in § 4 we apply our methods to air–water turbulence over Lake Erie and measure the fractal dimension of the turbulent energy as well as the generating and propagating of short water waves over Lake Erie. We compare numerical results to observations and close the paper with a discussion of conclusions and future work.
2. Moment field equations
Let ![]() $\varOmega$ be a bounded domain in
$\varOmega$ be a bounded domain in ![]() $\mathbb {R}^3$. We track energy associated with the short water waves generated by air–water interactions within
$\mathbb {R}^3$. We track energy associated with the short water waves generated by air–water interactions within ![]() $\varOmega$ by solving a set of moment field equations,
$\varOmega$ by solving a set of moment field equations,
 \begin{equation} \frac{\partial m_n}{\partial t} + \nabla_{xy} \cdot \left(m_n \boldsymbol{c}_0+ \sum_{i=0}^n m_{n-i}\boldsymbol{c}_{i+1}\right) = \mu_n \varDelta_{xy} m_n,\quad n = 0,1,\ldots ,N, \end{equation}
\begin{equation} \frac{\partial m_n}{\partial t} + \nabla_{xy} \cdot \left(m_n \boldsymbol{c}_0+ \sum_{i=0}^n m_{n-i}\boldsymbol{c}_{i+1}\right) = \mu_n \varDelta_{xy} m_n,\quad n = 0,1,\ldots ,N, \end{equation}
where c 0 is the group speed of the long wave that the short gravity waves are travelling with, c 1 is the speed associated with the short wave group, c 2 is the acceleration of the short wave group, etc., ![]() $\mu$ is a diffusion coefficient,
$\mu$ is a diffusion coefficient, ![]() $\nabla _{xy} = \partial / \partial x \hat {i} + \partial / \partial y\hat {j}$,
$\nabla _{xy} = \partial / \partial x \hat {i} + \partial / \partial y\hat {j}$, ![]() $\varDelta _{xy} = \partial ^2 / \partial x^2 + \partial ^2 / \partial y^2$ and
$\varDelta _{xy} = \partial ^2 / \partial x^2 + \partial ^2 / \partial y^2$ and ![]() $n$ corresponds to the order of the moment,
$n$ corresponds to the order of the moment, ![]() $m_n$, of the one-dimensional density (
$m_n$, of the one-dimensional density (![]() $F(\boldsymbol {x}_0,k,t)$) of the short water waves at the geographic point
$F(\boldsymbol {x}_0,k,t)$) of the short water waves at the geographic point ![]() $\boldsymbol {x}_0$,
$\boldsymbol {x}_0$,
Here, ![]() $k = \| \boldsymbol {k} \|$ is the magnitude of the water wavenumber vector with mean direction
$k = \| \boldsymbol {k} \|$ is the magnitude of the water wavenumber vector with mean direction ![]() $\bar {\theta }$ and
$\bar {\theta }$ and ![]() $k_i$ and
$k_i$ and ![]() $k_f$ are the low and high wavenumber cutoffs of the wind sea. The mean direction satisfies the differential equation,
$k_f$ are the low and high wavenumber cutoffs of the wind sea. The mean direction satisfies the differential equation,
where ![]() $D(\boldsymbol {x},t)$ parameterizes the inhomogeneities of the medium of propagation, see Salmon (Reference Salmon1998), for example. It can be noted that
$D(\boldsymbol {x},t)$ parameterizes the inhomogeneities of the medium of propagation, see Salmon (Reference Salmon1998), for example. It can be noted that ![]() $D$ incorporates atmospheric input, fluid depths, etc.; the
$D$ incorporates atmospheric input, fluid depths, etc.; the ![]() $\boldsymbol {c}_{i}$ are coefficients that represent the velocity, acceleration, etc. of the water-wave group (see Appendix B), and are functions of a dispersion relation,
$\boldsymbol {c}_{i}$ are coefficients that represent the velocity, acceleration, etc. of the water-wave group (see Appendix B), and are functions of a dispersion relation,
which relates the angular frequencies (![]() $\bar {\omega }_{n+1} = 2{\rm \pi} \bar {f}_{n+1}$) to the characteristic wavenumbers,
$\bar {\omega }_{n+1} = 2{\rm \pi} \bar {f}_{n+1}$) to the characteristic wavenumbers, ![]() $\bar {k}_{n+1}$, defined as
$\bar {k}_{n+1}$, defined as
 \begin{equation} \bar{k}_{n+1}=\frac{\displaystyle\int{k^{n+1} F(\boldsymbol{x}_0,k,t)\,\textrm{d}k}}{ \displaystyle\int{k^n F(\boldsymbol{x}_0,k,t)\,\textrm{d}k}}=\frac{m_{n+1}}{m_n}, \end{equation}
\begin{equation} \bar{k}_{n+1}=\frac{\displaystyle\int{k^{n+1} F(\boldsymbol{x}_0,k,t)\,\textrm{d}k}}{ \displaystyle\int{k^n F(\boldsymbol{x}_0,k,t)\,\textrm{d}k}}=\frac{m_{n+1}}{m_n}, \end{equation}
where the bounds of integration in (2.5) are from ![]() $k_i$ to
$k_i$ to ![]() $k_f$. The number of moments preserved in (2.1) is a function of the water-wave dynamics under consideration. In this initial investigation, we set
$k_f$. The number of moments preserved in (2.1) is a function of the water-wave dynamics under consideration. In this initial investigation, we set ![]() $N = 1$ and solve the system of equations,
$N = 1$ and solve the system of equations,
where ![]() $\mathcal {E}$ is energy supplied to the water waves from the atmosphere,
$\mathcal {E}$ is energy supplied to the water waves from the atmosphere, ![]() $\bar {\theta }_w$ is the mean direction of the atmospheric velocity in the boundary layer,
$\bar {\theta }_w$ is the mean direction of the atmospheric velocity in the boundary layer, ![]() $m_0$ is a characteristic quantity (momentum, energy or energy flux) of the short water-wave group,
$m_0$ is a characteristic quantity (momentum, energy or energy flux) of the short water-wave group, ![]() $m_1$ is a measure of the representative water wavenumber and
$m_1$ is a measure of the representative water wavenumber and ![]() $\tilde {\mu }_0$ and
$\tilde {\mu }_0$ and ![]() $\tilde {\mu }_1$ are diffusion coefficients to be defined in the next subsection. It can be noted that in this work we neglect the high-order wave group acceleration term (c 2)m 0 in (2.7) and assume that
$\tilde {\mu }_1$ are diffusion coefficients to be defined in the next subsection. It can be noted that in this work we neglect the high-order wave group acceleration term (c 2)m 0 in (2.7) and assume that ![]() $\boldsymbol {c}_0 = 0$ (the air–water interactions create a wind sea in the absence of any ambient current).
$\boldsymbol {c}_0 = 0$ (the air–water interactions create a wind sea in the absence of any ambient current).
2.1. Air–water energy transfer
The physical model described by (2.1) can be enunciated in the following fashion; we have a set of moment ‘masses’ that characterize the energy of a group of water waves propagating through a medium at a velocity that depends on the specific properties of the medium as well as the water-wave group itself. In the case of air–water turbulence, pressure pulsations in the local atmosphere tend to transfer energy to the moment masses causing them to deviate from their reference energy level – this is the energy transfer that we wish to quantify – the scales of the problem, however, render the inner workings of this process opaque, giving it the appearance of a random process. Classically, this process is modelled with a diffusive operator that attempts to quantify the potential for a space–time region to deviate from its current energy configuration due to subscale energy transfer. Let us leverage this diffusive operator to derive an air–water energy transfer term.
Choosing a reference frame that moves with the velocity of the water-wave group, the propensity for the moment field to fluctuate from its spectral configuration is
where ![]() $\bar {\mu }_n$ is a function of the variance supplied by the atmospheric turbulence. Equation (2.9) gives the probability that a certain measure of moment mass lies within the interval
$\bar {\mu }_n$ is a function of the variance supplied by the atmospheric turbulence. Equation (2.9) gives the probability that a certain measure of moment mass lies within the interval ![]() $[\boldsymbol {x}_0-\delta \boldsymbol {x}/2,\boldsymbol {x}_0+\delta \boldsymbol {x}/2]$ at a given instant in time
$[\boldsymbol {x}_0-\delta \boldsymbol {x}/2,\boldsymbol {x}_0+\delta \boldsymbol {x}/2]$ at a given instant in time ![]() $t$. However, we are interested in the energy transfer along a path that is fixed in space and interval in time, so what we really require is an expression that gives the probability that a certain measure of moment mass lies in the interval
$t$. However, we are interested in the energy transfer along a path that is fixed in space and interval in time, so what we really require is an expression that gives the probability that a certain measure of moment mass lies in the interval ![]() $[t_i,t_f]$ (where
$[t_i,t_f]$ (where ![]() $t_f - t_i \equiv l \equiv \varDelta t$) at the spatial point
$t_f - t_i \equiv l \equiv \varDelta t$) at the spatial point ![]() $\boldsymbol {x}_0$. In other words, we need an expression for diffusion in time. We can achieve this through the use of the wave equation along with a relation due to Kolmogorov. In particular, the wave equation is
$\boldsymbol {x}_0$. In other words, we need an expression for diffusion in time. We can achieve this through the use of the wave equation along with a relation due to Kolmogorov. In particular, the wave equation is
where ![]() $\|\boldsymbol {c}_{g_f}\|$ is the speed of a group of fluctuations in the moment field that results from pressure pulsations in the atmosphere. It can be noted that in the previous equation and the remainder of this subsection,
$\|\boldsymbol {c}_{g_f}\|$ is the speed of a group of fluctuations in the moment field that results from pressure pulsations in the atmosphere. It can be noted that in the previous equation and the remainder of this subsection, ![]() $n = 0,1$. We assume a relation exists between
$n = 0,1$. We assume a relation exists between ![]() $\bar {\mu }_n$ and
$\bar {\mu }_n$ and ![]() $\|\boldsymbol {c}_{g_f}\|^2$ so that we can make use of (2.9) and (2.10) to write,
$\|\boldsymbol {c}_{g_f}\|^2$ so that we can make use of (2.9) and (2.10) to write,
where we have rewritten ![]() $m_n$ on the right-hand side of (2.9) and (2.10) as
$m_n$ on the right-hand side of (2.9) and (2.10) as ![]() $\mathcal {E}_n$ to emphasize that this corresponds to moments of the water-wave energy pulsation generated by pulsations in the wind. We then utilize the idea of probability space–time paths from No. 9 in Kolmogorov (Reference Kolmogorov1992) to rewrite this expression solely as a function of the separation in time. Specifically, we have
$\mathcal {E}_n$ to emphasize that this corresponds to moments of the water-wave energy pulsation generated by pulsations in the wind. We then utilize the idea of probability space–time paths from No. 9 in Kolmogorov (Reference Kolmogorov1992) to rewrite this expression solely as a function of the separation in time. Specifically, we have
 \begin{equation} \frac{\partial m_n}{\partial t}=\tilde{\mu}_n\varDelta_{xy} \mathcal{E}_n = \mathcal{A}\frac{\partial ^2\mathcal{E}_n}{\partial t^2} = \sum_{i} A_{in} \frac{{\rm d} \mathcal{E}_n}{{\rm d}t}, \end{equation}
\begin{equation} \frac{\partial m_n}{\partial t}=\tilde{\mu}_n\varDelta_{xy} \mathcal{E}_n = \mathcal{A}\frac{\partial ^2\mathcal{E}_n}{\partial t^2} = \sum_{i} A_{in} \frac{{\rm d} \mathcal{E}_n}{{\rm d}t}, \end{equation}
where the last term follows from the general result presented in § 10 in No. 9 of Kolmogorov (Reference Kolmogorov1992). It can be emphasized that ![]() ${\rm d} \mathcal {E}_n/{\rm d}t$ is the change in the local energy field due to changes in the atmospheric velocity in the boundary layer (or energy transfer) over a duration limited interval
${\rm d} \mathcal {E}_n/{\rm d}t$ is the change in the local energy field due to changes in the atmospheric velocity in the boundary layer (or energy transfer) over a duration limited interval ![]() $\varDelta t$. In other words,
$\varDelta t$. In other words, ![]() ${{\rm d} \mathcal {E}_n}/{\rm d}t$ represents the energy pulsation generated in the water by a stress pulsation in the wind. What remains is to determine the
${{\rm d} \mathcal {E}_n}/{\rm d}t$ represents the energy pulsation generated in the water by a stress pulsation in the wind. What remains is to determine the ![]() $A_{nk}$ that measure the probability for the water-wave field to pass from state
$A_{nk}$ that measure the probability for the water-wave field to pass from state ![]() $\varrho _j$ to state
$\varrho _j$ to state ![]() $\varrho _k$ in the local (temporal) neighbourhood under consideration (Kolmogorov Reference Kolmogorov1992). Assuming that the energy transfer travels with the group velocity of the fluctuation in the moment field,
$\varrho _k$ in the local (temporal) neighbourhood under consideration (Kolmogorov Reference Kolmogorov1992). Assuming that the energy transfer travels with the group velocity of the fluctuation in the moment field, ![]() $\|\boldsymbol {c}_{g_f}\|$, we can write
$\|\boldsymbol {c}_{g_f}\|$, we can write
 \begin{gather} \frac{\partial m_n}{\partial t}=\tilde{\mu}_n\left(\frac{\partial ^2\mathcal{E}_n}{\partial x^2}+\frac{\partial ^2\mathcal{E}_n}{\partial y^2}\right) =\tilde{\mu}_n\left(\frac{{\rm d}^2\mathcal{E}_n}{(c_{g_{f_x}}\,{\rm d}t)^2} +\frac{{\rm d}^2\mathcal{E}_n}{(c_{g_{f_y}}\,{\rm d}t)^2}\right), \end{gather}
\begin{gather} \frac{\partial m_n}{\partial t}=\tilde{\mu}_n\left(\frac{\partial ^2\mathcal{E}_n}{\partial x^2}+\frac{\partial ^2\mathcal{E}_n}{\partial y^2}\right) =\tilde{\mu}_n\left(\frac{{\rm d}^2\mathcal{E}_n}{(c_{g_{f_x}}\,{\rm d}t)^2} +\frac{{\rm d}^2\mathcal{E}_n}{(c_{g_{f_y}}\,{\rm d}t)^2}\right), \end{gather} \begin{gather}\frac{\partial m_n}{\partial t}=\frac{\tilde{\mu}_n}{\|\boldsymbol{c}_{g_f}\|^2\cos^2\theta} \frac{{\rm d}^2\mathcal{E}_n}{{\rm d}t^2}+\frac{\tilde{\mu}_n}{\|\boldsymbol{c}_{g_f}\|^2\sin^2\theta} \frac{{\rm d}^2\mathcal{E}_n}{{\rm d}t^2}. \end{gather}
\begin{gather}\frac{\partial m_n}{\partial t}=\frac{\tilde{\mu}_n}{\|\boldsymbol{c}_{g_f}\|^2\cos^2\theta} \frac{{\rm d}^2\mathcal{E}_n}{{\rm d}t^2}+\frac{\tilde{\mu}_n}{\|\boldsymbol{c}_{g_f}\|^2\sin^2\theta} \frac{{\rm d}^2\mathcal{E}_n}{{\rm d}t^2}. \end{gather}Substitution of the general relation (74) in No. 9 of Kolmogorov (Reference Kolmogorov1992) gives,
For expression (2.15) to hold true, we must set
where the ![]() $\mathcal {C}_n$ terms relate
$\mathcal {C}_n$ terms relate ![]() $\partial m_n / \partial t$ to
$\partial m_n / \partial t$ to ![]() ${\rm d}\mathcal {E} / {\rm d}t$. The final air–sea transfer source terms (
${\rm d}\mathcal {E} / {\rm d}t$. The final air–sea transfer source terms (![]() $S_n$) are,
$S_n$) are,
The ![]() $\tilde {\mu }_n$ term in (2.20) scales the spectral transfer of the local neighbourhood under consideration and is simply equal to
$\tilde {\mu }_n$ term in (2.20) scales the spectral transfer of the local neighbourhood under consideration and is simply equal to ![]() $1/2\|\boldsymbol {c}_{g_f}\|^2$. The exact value of
$1/2\|\boldsymbol {c}_{g_f}\|^2$. The exact value of ![]() $\mathcal {C}_0$ will depend on the specific density function being conserved by the moment field equations. For instance, if the density function quantifies momentum (
$\mathcal {C}_0$ will depend on the specific density function being conserved by the moment field equations. For instance, if the density function quantifies momentum (![]() $P = \mathcal {E}/c_p$ where
$P = \mathcal {E}/c_p$ where ![]() $c_p= \omega / k$ is the phase speed of the water waves), then, for
$c_p= \omega / k$ is the phase speed of the water waves), then, for ![]() $n = 0$, we have,
$n = 0$, we have,
where ![]() $\|\boldsymbol {c}_{p_f}\|$ is the phase speed of the water-wave pulsation. If the density function quantifies water-wave energy, then for
$\|\boldsymbol {c}_{p_f}\|$ is the phase speed of the water-wave pulsation. If the density function quantifies water-wave energy, then for ![]() $n=0$,
$n=0$, ![]() $\mathcal {C}_0$ is set to,
$\mathcal {C}_0$ is set to,
Finally, in the case of energy flux we have,
Regardless of the probability density quantified by the moment field equations, the ![]() $\mathcal {C}_1$ term takes the form,
$\mathcal {C}_1$ term takes the form,
which qualitatively is similar to the inverse of the wave age ![]() $\chi _{10} = c_p / U_{10}$. The key difference between expression (2.24) and the inverse wave age involves the fact that expression (2.24) is written in terms of the speed of the water-wave pulsation generated in the water surface by the wind rather than being written in terms of the wind speed
$\chi _{10} = c_p / U_{10}$. The key difference between expression (2.24) and the inverse wave age involves the fact that expression (2.24) is written in terms of the speed of the water-wave pulsation generated in the water surface by the wind rather than being written in terms of the wind speed ![]() $U_{10}$. Substitution of (2.23) and (2.24) into (2.20), for example, yields the source terms for the moment field equations that quantify the energy flux transferred from the wind to the water waves,
$U_{10}$. Substitution of (2.23) and (2.24) into (2.20), for example, yields the source terms for the moment field equations that quantify the energy flux transferred from the wind to the water waves,
and
Here, we emphasize the fact that the ![]() ${{\rm d}\mathcal {E}_n}/{{\rm d}t}$ terms are explicit functions of the wind speed. More specifically, the
${{\rm d}\mathcal {E}_n}/{{\rm d}t}$ terms are explicit functions of the wind speed. More specifically, the ![]() ${{\rm d}\mathcal {E}_n}/{{\rm d}t}$ terms are duration limited pulsations in the local energy field of the water-wave group that result from air–water interactions in the atmospheric boundary layer and satisfy the energy balance equation of nonlinear energy transfer that accounts for atmospheric input, nonlinear wave interactions and dissipation as quantified by Hasselmann et al. (Reference Hasselmann, Ross, Muller and Sell1975). We define these terms as well as the explicit form of the duration limited wind velocity in the next section.
${{\rm d}\mathcal {E}_n}/{{\rm d}t}$ terms are duration limited pulsations in the local energy field of the water-wave group that result from air–water interactions in the atmospheric boundary layer and satisfy the energy balance equation of nonlinear energy transfer that accounts for atmospheric input, nonlinear wave interactions and dissipation as quantified by Hasselmann et al. (Reference Hasselmann, Ross, Muller and Sell1975). We define these terms as well as the explicit form of the duration limited wind velocity in the next section.
3. The wind-sea generator: air–water interactions
We define the atmospheric turbulence that generates the wind sea by considering the incompressible Navier–Stokes equations,
where ![]() $p$ is the pressure,
$p$ is the pressure, ![]() $\rho _a$ is the density of air and
$\rho _a$ is the density of air and ![]() $\mu$ is the fluid viscosity. Rather than attempt to explicitly solve these equations we leverage scaling properties of (3.1) to measure the energy transfer associated with the air–sea turbulence. That is, in the limit
$\mu$ is the fluid viscosity. Rather than attempt to explicitly solve these equations we leverage scaling properties of (3.1) to measure the energy transfer associated with the air–sea turbulence. That is, in the limit ![]() $\mu \rightarrow 0$ the Navier–Stokes equations are invariant under scaling transformations (Frisch Reference Frisch1996),
$\mu \rightarrow 0$ the Navier–Stokes equations are invariant under scaling transformations (Frisch Reference Frisch1996),
The scaling also holds at small viscosity (see Frisch Reference Frisch1996) if,
which implies that the dissipation, defined as ![]() $\epsilon = \mu \langle (\boldsymbol {\nabla } \boldsymbol {u})^2\rangle$ (
$\epsilon = \mu \langle (\boldsymbol {\nabla } \boldsymbol {u})^2\rangle$ (![]() $\langle \cdot \rangle$ denotes ensemble averages), scales as,
$\langle \cdot \rangle$ denotes ensemble averages), scales as,
From this, it follows that the absolute probability of encountering an active region of turbulence is,
for ![]() $\ell _{\eta } < r \ll L$, where
$\ell _{\eta } < r \ll L$, where ![]() $\ell _{\eta }$ is a dissipation cutoff,
$\ell _{\eta }$ is a dissipation cutoff, ![]() $L$ is the integral length scale and
$L$ is the integral length scale and ![]() $r$ is a spatial distance, see Frisch (Reference Frisch1996) for more details. It can be noted that scaling exponent (
$r$ is a spatial distance, see Frisch (Reference Frisch1996) for more details. It can be noted that scaling exponent (![]() $h$) of the Navier–Stokes equation is related to the Hurst exponent (
$h$) of the Navier–Stokes equation is related to the Hurst exponent (![]() $H$) via
$H$) via
In the case ![]() $h \geq 1/3$ energy is conserved, however, if
$h \geq 1/3$ energy is conserved, however, if ![]() $h < 1/3$ then the scaling relations are non-conservative and energy is lost to due to a loss of regularity (Frisch Reference Frisch1996).
$h < 1/3$ then the scaling relations are non-conservative and energy is lost to due to a loss of regularity (Frisch Reference Frisch1996).
The Hurst exponent is important in a statistical context because it measures the extent of the memory of the process (Mandelbrot Reference Mandelbrot1977). If a process is random and Gaussian then the variance of the process is connected to the square root of the period and the process is ‘memoryless’; past events have no influence on future events and ![]() $H = 1/2$ (the variance is tied to the square root operator). To illustrate this point further, imagine we are studying the time series of a variable with temporal movements that are generated by a process that is unknown to the observer. Let us denote these movements by
$H = 1/2$ (the variance is tied to the square root operator). To illustrate this point further, imagine we are studying the time series of a variable with temporal movements that are generated by a process that is unknown to the observer. Let us denote these movements by ![]() $B_{H}(t)$. If the expectation of the motion is zero for all time
$B_{H}(t)$. If the expectation of the motion is zero for all time ![]() $t$, then the expected variance of the motion over a period
$t$, then the expected variance of the motion over a period ![]() $T$ can be expressed in terms of the Hurst exponent (Mandelbrot Reference Mandelbrot1977),
$T$ can be expressed in terms of the Hurst exponent (Mandelbrot Reference Mandelbrot1977),
where ![]() $\mathbb {V}[\cdot ]$ is the expected variance and
$\mathbb {V}[\cdot ]$ is the expected variance and ![]() $0 < H < 1$ (Mandelbrot Reference Mandelbrot1977). When
$0 < H < 1$ (Mandelbrot Reference Mandelbrot1977). When ![]() $H < 1/2$ the motion is antipersistent; it has a tendency to return to some past condition, whereas if
$H < 1/2$ the motion is antipersistent; it has a tendency to return to some past condition, whereas if ![]() $H > 1/2$ the motion is persistent and a given condition tends to persist for long intervals of time (Mandelbrot Reference Mandelbrot1977). It can be noted that the graph dimension of the corresponding time series is
$H > 1/2$ the motion is persistent and a given condition tends to persist for long intervals of time (Mandelbrot Reference Mandelbrot1977). It can be noted that the graph dimension of the corresponding time series is ![]() $D_G = 2 - H$ and is always greater than the topological dimension. There is a self-similar trail (
$D_G = 2 - H$ and is always greater than the topological dimension. There is a self-similar trail (![]() $(X(t),Y(t))=f(B_H(t))$) connected to the graph dimension that corresponds to the spatial path of the motion and the dimension of this trail is given by
$(X(t),Y(t))=f(B_H(t))$) connected to the graph dimension that corresponds to the spatial path of the motion and the dimension of this trail is given by ![]() $D_E = 1/H > D_G$, and corresponds to the dimension that the trail is embedded in. If the trail occurs in Cartesian space and ‘fills’ all three dimensions, for instance, then the trail is said to be space filling. However,
$D_E = 1/H > D_G$, and corresponds to the dimension that the trail is embedded in. If the trail occurs in Cartesian space and ‘fills’ all three dimensions, for instance, then the trail is said to be space filling. However, ![]() $D_E$ does not have to be an integer. In the case it is a non-integer,
$D_E$ does not have to be an integer. In the case it is a non-integer, ![]() $D_E$, is known as the fractal dimension. When a process is multifractal there is a spectrum of fractal dimensions associated with the flow and
$D_E$, is known as the fractal dimension. When a process is multifractal there is a spectrum of fractal dimensions associated with the flow and ![]() $D_E > D_G$, however, the relation
$D_E > D_G$, however, the relation ![]() $D_E = 1/H$ no longer holds, see Mandelbrot (Reference Mandelbrot1997, Reference Mandelbrot1998) for more details. In this case the dimension of the self-similar support of the multifractal measure is determined via other considerations, see § 3.5.3.
$D_E = 1/H$ no longer holds, see Mandelbrot (Reference Mandelbrot1997, Reference Mandelbrot1998) for more details. In this case the dimension of the self-similar support of the multifractal measure is determined via other considerations, see § 3.5.3.
It is interesting to note that Kolmogorov (Reference Kolmogorov1941) assumes energy interactions are local in wavenumber space; energy transfer concentrates on a singular set of points with ![]() $H = 1/3$. Clearly, the motion has a memory of the generating event because
$H = 1/3$. Clearly, the motion has a memory of the generating event because ![]() $H < 1/2$ and the set is also space filling because we have
$H < 1/2$ and the set is also space filling because we have ![]() $D_E = 1/(1/3) = 3$. Experiments and observations, however, tend to point to the fact that energy transfer in a turbulent fluid is not space filling but is intermittent at small scales (Frisch Reference Frisch1996).
$D_E = 1/(1/3) = 3$. Experiments and observations, however, tend to point to the fact that energy transfer in a turbulent fluid is not space filling but is intermittent at small scales (Frisch Reference Frisch1996).
3.1. Distribution of the wind velocity
Rather than utilize the absolute probability given by (3.5) (which is highly dependent on ![]() $L$) we utilize a conditional probability to generate measures of the velocity and energy transfer connected to air–water interactions. That is, given the condition that an active region of turbulence occurs within the period
$L$) we utilize a conditional probability to generate measures of the velocity and energy transfer connected to air–water interactions. That is, given the condition that an active region of turbulence occurs within the period ![]() $l_{d_{\eta }} \ll l_{d_{\epsilon }} < t_l < l_0 \ll L_T$ (
$l_{d_{\eta }} \ll l_{d_{\epsilon }} < t_l < l_0 \ll L_T$ (![]() $l_{d_{\eta }}$ is the molecule length scale,
$l_{d_{\eta }}$ is the molecule length scale, ![]() $l_{d_{\epsilon }} \approx 1 \times 10^{-6}$ and
$l_{d_{\epsilon }} \approx 1 \times 10^{-6}$ and ![]() $L_T$ is the temporal integral length scale), then we assume that the local distribution of the atmospheric velocity at the spatial point
$L_T$ is the temporal integral length scale), then we assume that the local distribution of the atmospheric velocity at the spatial point ![]() $\boldsymbol {x}_0$ is temporally hyperbolic, with magnitude,
$\boldsymbol {x}_0$ is temporally hyperbolic, with magnitude,
and direction,
where ![]() $t_{l}$ is the local time,
$t_{l}$ is the local time, ![]() $g$ is acceleration due to gravity,
$g$ is acceleration due to gravity, ![]() $(\|\boldsymbol {u}_0\|,\theta _0)$ are local constants and
$(\|\boldsymbol {u}_0\|,\theta _0)$ are local constants and ![]() $\omega _{\theta }$ is the minimum turning frequency of the characteristic reference velocity (
$\omega _{\theta }$ is the minimum turning frequency of the characteristic reference velocity (![]() $\boldsymbol {u}_0$),
$\boldsymbol {u}_0$),
i.e. the representative velocity of the large scale flow field of the space–time region under consideration. It can be noted that the exponents ![]() $(q,\varUpsilon )$ quantify the amount of change (from the reference velocity field
$(q,\varUpsilon )$ quantify the amount of change (from the reference velocity field ![]() $\boldsymbol {u}_0$) that
$\boldsymbol {u}_0$) that ![]() $\boldsymbol {u}$ undergoes over the time interval
$\boldsymbol {u}$ undergoes over the time interval ![]() $l_0 - l_{d_{\epsilon }}$ (if
$l_0 - l_{d_{\epsilon }}$ (if ![]() $q = 0$ and
$q = 0$ and ![]() $\varUpsilon = 0$ then
$\varUpsilon = 0$ then ![]() $\boldsymbol {u} = \boldsymbol {u}_0$). For a given time series the global distribution of the atmospheric turbulent velocity consists of the union of all the local regions used to pave the temporal velocity curve, i.e.
$\boldsymbol {u} = \boldsymbol {u}_0$). For a given time series the global distribution of the atmospheric turbulent velocity consists of the union of all the local regions used to pave the temporal velocity curve, i.e.
 \begin{equation} \boldsymbol{u}_{l}=\mathop{\bigcup}\limits_{j=1}^{\mathcal{N}}\boldsymbol{u}^{(\,j)} =\mathop{\bigcup}\limits_{j=1}^{\mathcal{N}}\{\|\boldsymbol{u}^{(\,j)}\|\, \textrm{e}^{{\rm i}\theta_w^{(\,j)}}\}, \end{equation}
\begin{equation} \boldsymbol{u}_{l}=\mathop{\bigcup}\limits_{j=1}^{\mathcal{N}}\boldsymbol{u}^{(\,j)} =\mathop{\bigcup}\limits_{j=1}^{\mathcal{N}}\{\|\boldsymbol{u}^{(\,j)}\|\, \textrm{e}^{{\rm i}\theta_w^{(\,j)}}\}, \end{equation}
where the magnitude ![]() $\|\boldsymbol {u}^{(\,j)}\|$ and direction
$\|\boldsymbol {u}^{(\,j)}\|$ and direction ![]() $\theta ^{(\,j)}_w$ are functions of the spatial coordinate
$\theta ^{(\,j)}_w$ are functions of the spatial coordinate ![]() $\boldsymbol {x}_0$ and global time
$\boldsymbol {x}_0$ and global time ![]() $t$, and
$t$, and ![]() $\mathcal {N}$ is the total number of local regions used to pave the temporal velocity curve. It can be noted that the
$\mathcal {N}$ is the total number of local regions used to pave the temporal velocity curve. It can be noted that the ![]() $l$ attached to
$l$ attached to ![]() $\boldsymbol {u}_{l}$ indicates that the temporal continuity of the representation of the distribution of the atmospheric velocity depends on the inner cutoff of the kernel. More specifically, we define a temporal region
$\boldsymbol {u}_{l}$ indicates that the temporal continuity of the representation of the distribution of the atmospheric velocity depends on the inner cutoff of the kernel. More specifically, we define a temporal region ![]() $\mathcal {R}^{(\,j)}$ located at the geographical coordinate
$\mathcal {R}^{(\,j)}$ located at the geographical coordinate ![]() $\boldsymbol {x}_0$ of height,
$\boldsymbol {x}_0$ of height,
and length,
Each ![]() $\mathcal {R}^{(\,j)}$ is a local reference frame that wholly contains the dynamic perturbations of the flow field in the time interval
$\mathcal {R}^{(\,j)}$ is a local reference frame that wholly contains the dynamic perturbations of the flow field in the time interval ![]() $l_0$ (at the point
$l_0$ (at the point ![]() $\boldsymbol {x}_0$). Embedded within each
$\boldsymbol {x}_0$). Embedded within each ![]() $\mathcal {R}^{(\,j)}$ is a cut out region
$\mathcal {R}^{(\,j)}$ is a cut out region ![]() $]l_{d_{\epsilon }}, l_{d}[$ where functions (3.8) and (3.9) are no longer valid. This region corresponds to a measure of uncertainty in terms of the measure of the turbulent velocity on the length scale,
$]l_{d_{\epsilon }}, l_{d}[$ where functions (3.8) and (3.9) are no longer valid. This region corresponds to a measure of uncertainty in terms of the measure of the turbulent velocity on the length scale, ![]() $l_0$, and therefore, we would like to make
$l_0$, and therefore, we would like to make ![]() $l_d$ as small as possible. We address this issue in § 3.5.
$l_d$ as small as possible. We address this issue in § 3.5.
3.1.1. Determination of characteristic pressure
To complete the description of the atmospheric flow field we need to determine the pressure field associated with the velocity distribution given by (3.11). In the limit ![]() $\mu \rightarrow 0$ local accelerations along a space–time path in the atmosphere are solely due to pressure gradients,
$\mu \rightarrow 0$ local accelerations along a space–time path in the atmosphere are solely due to pressure gradients,
where ![]() ${\mathrm {D}\cdot }/{(\mathrm {D}t)}$ is the total derivative. In general, the total pressure will vary in both the
${\mathrm {D}\cdot }/{(\mathrm {D}t)}$ is the total derivative. In general, the total pressure will vary in both the ![]() $x$ and
$x$ and ![]() $y$ directions of the domain,
$y$ directions of the domain,
Substituting (3.14) into (3.15) and rearranging gives
Integrating yields the total pressure,
where ![]() $p_0$ is the characteristic reference pressure associated with the large scale flow field. In general,
$p_0$ is the characteristic reference pressure associated with the large scale flow field. In general, ![]() $p_0$ is a function of the large scale thermodynamic properties of the atmosphere as well as the topography and boundary of the domain. If we make use of the fact that
$p_0$ is a function of the large scale thermodynamic properties of the atmosphere as well as the topography and boundary of the domain. If we make use of the fact that ![]() $u = \| \boldsymbol {u}^{(\,j)}\| \cos (\theta )$ and
$u = \| \boldsymbol {u}^{(\,j)}\| \cos (\theta )$ and ![]() $v = \| \boldsymbol {u}^{(\,j)} \| \sin (\theta )$ over a given
$v = \| \boldsymbol {u}^{(\,j)} \| \sin (\theta )$ over a given ![]() $\mathcal {R}^{(\,j)}$, then (3.17) simplifies to,
$\mathcal {R}^{(\,j)}$, then (3.17) simplifies to,
and it becomes apparent that the pressure fluctuations in the local atmosphere with respect to ![]() $p_0$ are equivalent to the kinetic energy of the atmosphere.
$p_0$ are equivalent to the kinetic energy of the atmosphere.
We close the description of the turbulent flow field by relating ![]() $p_0^{(\,j)}$ to the average pressure (or expected pressure)
$p_0^{(\,j)}$ to the average pressure (or expected pressure) ![]() $\bar {p}^{(\,j)}$ over a given
$\bar {p}^{(\,j)}$ over a given ![]() $\mathcal {R}^{(\,j)}$. In particular, the average pressure (
$\mathcal {R}^{(\,j)}$. In particular, the average pressure (![]() $\bar {p}^{(\,j)}$) can be expressed in terms of the total pressure (
$\bar {p}^{(\,j)}$) can be expressed in terms of the total pressure (![]() $p_T^{(\,j)}$) as,
$p_T^{(\,j)}$) as,
 \begin{equation} \bar{p}^{(\,j)}=\frac{1}{(l_0-l_{d_{\epsilon}})}\int_{l_{d_{\epsilon}}}^{l_0}{p_T^{(\,j)}\,\mathrm{d}t_l} =\frac{1}{(l_0-l_{d_{\epsilon}})}\int_{l_{d_{\epsilon}}}^{l_0}\left(p_0^{(\,j)}-\underbrace{\frac{\rho_a}{2}\|\boldsymbol{u}^{(\,j)}\|^2}_{{\equiv} p'^{(\,j)}}\right)\mathrm{d}t_l. \end{equation}
\begin{equation} \bar{p}^{(\,j)}=\frac{1}{(l_0-l_{d_{\epsilon}})}\int_{l_{d_{\epsilon}}}^{l_0}{p_T^{(\,j)}\,\mathrm{d}t_l} =\frac{1}{(l_0-l_{d_{\epsilon}})}\int_{l_{d_{\epsilon}}}^{l_0}\left(p_0^{(\,j)}-\underbrace{\frac{\rho_a}{2}\|\boldsymbol{u}^{(\,j)}\|^2}_{{\equiv} p'^{(\,j)}}\right)\mathrm{d}t_l. \end{equation}Inserting (3.8) into (3.19) while evaluating the integral yields,
 \begin{align} \bar{p}^{(\,j)}&=p_0^{(\,j)}-\frac{1}{(l_0-l_{d_{\epsilon}})} \int_{l_{d_{\epsilon}}}^{l_0}{\frac{\rho_a}{2}\|\boldsymbol{u}^{(\,j)}\|^2\,\mathrm{d}t_l}\nonumber\\ &=p_0^{(\,j)}-\left(\frac{\rho_a \|\boldsymbol{u}_0^{(\,j)}\|^2}{2(2q^{(\,j)}+1)}\left(\frac{g(l_0)}{\|\boldsymbol{u}_0^{(\,j)}\|}\right)^{2q^{(\,j)}+1} -\frac{\rho_a\|\boldsymbol{u}_0^{(\,j)}\|^2}{2(2q^{(\,j)}+1)}\left(\frac{g(l_{d_{\epsilon}})}{\|\boldsymbol{u}_0^{(\,j)}\|}\right)^{2q^{(\,j)}+1}\right). \end{align}
\begin{align} \bar{p}^{(\,j)}&=p_0^{(\,j)}-\frac{1}{(l_0-l_{d_{\epsilon}})} \int_{l_{d_{\epsilon}}}^{l_0}{\frac{\rho_a}{2}\|\boldsymbol{u}^{(\,j)}\|^2\,\mathrm{d}t_l}\nonumber\\ &=p_0^{(\,j)}-\left(\frac{\rho_a \|\boldsymbol{u}_0^{(\,j)}\|^2}{2(2q^{(\,j)}+1)}\left(\frac{g(l_0)}{\|\boldsymbol{u}_0^{(\,j)}\|}\right)^{2q^{(\,j)}+1} -\frac{\rho_a\|\boldsymbol{u}_0^{(\,j)}\|^2}{2(2q^{(\,j)}+1)}\left(\frac{g(l_{d_{\epsilon}})}{\|\boldsymbol{u}_0^{(\,j)}\|}\right)^{2q^{(\,j)}+1}\right). \end{align}
Re-arranging the latter expression gives the relation for ![]() $p_0^{(\,j)}$ in terms of
$p_0^{(\,j)}$ in terms of ![]() $\bar {p}^{(\,j)}$,
$\bar {p}^{(\,j)}$,
 \begin{equation} p_0^{(\,j)} = \bar{p}^{(\,j)}+\left(\frac{\rho_a \|\boldsymbol{u}_0^{(\,j)}\|^2}{2(2q^{(\,j)}+1)}\left(\frac{g(l_0)}{\|\boldsymbol{u}_0^{(\,j)}\|}\right)^{2q^{(\,j)}+1} -\frac{\rho_a\|\boldsymbol{u}_0^{(\,j)}\|^2}{2(2q^{(\,j)}+1)} \left(\frac{g(l_{d_{\epsilon}})}{\|\boldsymbol{u}_0^{(\,j)}\|}\right)^{2q^{(\,j)}+1}\right). \end{equation}
\begin{equation} p_0^{(\,j)} = \bar{p}^{(\,j)}+\left(\frac{\rho_a \|\boldsymbol{u}_0^{(\,j)}\|^2}{2(2q^{(\,j)}+1)}\left(\frac{g(l_0)}{\|\boldsymbol{u}_0^{(\,j)}\|}\right)^{2q^{(\,j)}+1} -\frac{\rho_a\|\boldsymbol{u}_0^{(\,j)}\|^2}{2(2q^{(\,j)}+1)} \left(\frac{g(l_{d_{\epsilon}})}{\|\boldsymbol{u}_0^{(\,j)}\|}\right)^{2q^{(\,j)}+1}\right). \end{equation}
The local distribution of the total pressure, ![]() $p_T^{(\,j)} = p_0^{(\,j)} - p^{'(\,j)}$, over a given
$p_T^{(\,j)} = p_0^{(\,j)} - p^{'(\,j)}$, over a given ![]() $\mathcal {R}^{(\,j)}$ is then
$\mathcal {R}^{(\,j)}$ is then
 \begin{align} p_T^{(\,j)}&=\bar{p}^{(\,j)}+\frac{\rho_a}{2}\left[\frac{\|\boldsymbol{u}_0^{(\,j)}\|^2}{(2q^{(\,j)}+1)} \left(\frac{g(l_0)}{\|\boldsymbol{u}_0^{(\,j)}\|}\right)^{2q^{(\,j)}+1}-\frac{\rho_a \|\boldsymbol{u}_0^{(\,j)}\|^2}{2(2q^{(\,j)}+1)}\left(\frac{g(l_{d_{\epsilon}})}{\|\boldsymbol{u}_0^{(\,j)}\|}\right)^{2q^{(\,j)}+1}\right. \nonumber\\ &\quad \left. -\|\boldsymbol{u}_0^{(\,j)}\|^2\left(\frac{g(t_{l})}{\|\boldsymbol{u}_0^{(\,j)}\|}\right)^{2q^{(\,j)}}\right], \end{align}
\begin{align} p_T^{(\,j)}&=\bar{p}^{(\,j)}+\frac{\rho_a}{2}\left[\frac{\|\boldsymbol{u}_0^{(\,j)}\|^2}{(2q^{(\,j)}+1)} \left(\frac{g(l_0)}{\|\boldsymbol{u}_0^{(\,j)}\|}\right)^{2q^{(\,j)}+1}-\frac{\rho_a \|\boldsymbol{u}_0^{(\,j)}\|^2}{2(2q^{(\,j)}+1)}\left(\frac{g(l_{d_{\epsilon}})}{\|\boldsymbol{u}_0^{(\,j)}\|}\right)^{2q^{(\,j)}+1}\right. \nonumber\\ &\quad \left. -\|\boldsymbol{u}_0^{(\,j)}\|^2\left(\frac{g(t_{l})}{\|\boldsymbol{u}_0^{(\,j)}\|}\right)^{2q^{(\,j)}}\right], \end{align}
and the global distribution of the total pressure is the union of the pressure kernels associated with each ![]() $\mathcal {R}^{(\,j)}$,
$\mathcal {R}^{(\,j)}$,
 \begin{equation} p_{l} =\mathop{\bigcup}\limits_{j=1}^{\mathcal{N}} p_T^{(\,j)}. \end{equation}
\begin{equation} p_{l} =\mathop{\bigcup}\limits_{j=1}^{\mathcal{N}} p_T^{(\,j)}. \end{equation}3.2. Group velocity of water-wave pulsations
To close the energy transfer source terms, we assume that the water-wave pulsations generated by the turbulent pressure pulsations of the wind are small amplitude waves. This allows us to use linear wave theory (see figure 1) to define the group velocity of the water-wave pulsations created by the wind. We acknowledge that the process through which momentum and energy is fluxed into the water column is significantly more complicated than the linear model depicted in figure 1, see Fedorov & Melville (Reference Fedorov and Melville1998) for a more rigorous theoretical description. However, the goal of this section is not to accurately quantify the complicated momentum and energy flux between the air and water surface, but rather, to show in simple terms how the singularity (or instability) that is associated with energy transfer arises within our statistical formulation. More specifically, the mathematical model described in figure 1 can be solved over the local duration, ![]() $t_l\in (l_{d_{\epsilon }},l_0)$, using a velocity potential of the form,
$t_l\in (l_{d_{\epsilon }},l_0)$, using a velocity potential of the form,
with amplitude,
and surface elevation,
where ![]() $\rho _w$ is the density of water,
$\rho _w$ is the density of water, ![]() $k = \|\boldsymbol {k}\|$ is the magnitude of the wavenumber, and
$k = \|\boldsymbol {k}\|$ is the magnitude of the wavenumber, and ![]() $a = f(z,t)$ is a coefficient that ensures the solution,
$a = f(z,t)$ is a coefficient that ensures the solution, ![]() $\phi (x,z,t)$, satisfies the top and bottom boundary conditions. The dispersion relation for the advection of the energy pulsation created in the water waves by the turbulent pressure of the wind over the duration,
$\phi (x,z,t)$, satisfies the top and bottom boundary conditions. The dispersion relation for the advection of the energy pulsation created in the water waves by the turbulent pressure of the wind over the duration, ![]() $t_l\in (l_{d_{\epsilon }},l_0)$, is determined using the dynamic boundary condition. At time
$t_l\in (l_{d_{\epsilon }},l_0)$, is determined using the dynamic boundary condition. At time ![]() $t=0$, before the fluctuation in the atmospheric pressure begins, the pressure of the water and atmosphere at the free surface is in balance and is equal to
$t=0$, before the fluctuation in the atmospheric pressure begins, the pressure of the water and atmosphere at the free surface is in balance and is equal to ![]() $p_0$. When
$p_0$. When ![]() $t>0$, the pressure fluctuation in the atmosphere begins to transfer energy to the water waves and the pressure at the free surface dynamically adjusts. Therefore, at
$t>0$, the pressure fluctuation in the atmosphere begins to transfer energy to the water waves and the pressure at the free surface dynamically adjusts. Therefore, at ![]() $z = \eta$ the dynamic boundary condition becomes,
$z = \eta$ the dynamic boundary condition becomes,
where ![]() $\mathcal {T}\eta _{xx}$ is the net normal force per unit area that represents the surface tension of the water. Substitution of
$\mathcal {T}\eta _{xx}$ is the net normal force per unit area that represents the surface tension of the water. Substitution of ![]() $\phi$ along with the dynamic pressure (3.18) into (3.27) while rearranging and simplifying gives the dispersion relation,
$\phi$ along with the dynamic pressure (3.18) into (3.27) while rearranging and simplifying gives the dispersion relation,
Equation (3.28) is singular when ![]() $\eta = 0$. The singularity arises in our mathematical formulation from the pressure pulsation in the wind due to its kinetic energy and corresponds to a potential instability in the water surface; it is a relic of our simple mathematical approach. It can be noted that the pressure adjustment at the free surface is of the order
$\eta = 0$. The singularity arises in our mathematical formulation from the pressure pulsation in the wind due to its kinetic energy and corresponds to a potential instability in the water surface; it is a relic of our simple mathematical approach. It can be noted that the pressure adjustment at the free surface is of the order ![]() $10^{-3}$ and is only relevant when the surface elevation of the water is a relatively ‘small’ value but larger than an inner cutoff (say,
$10^{-3}$ and is only relevant when the surface elevation of the water is a relatively ‘small’ value but larger than an inner cutoff (say, ![]() $10^{-6}$). Making use of (3.28) the phase speed of the water wave pulsation is,
$10^{-6}$). Making use of (3.28) the phase speed of the water wave pulsation is,
 \begin{equation} \|\boldsymbol{c}_{p_f}\|=c_{p_f} = \frac{\omega}{k}= \sqrt{\frac{g}{k}\tanh(kd)\left(1-\frac{\rho_a/2 \|\boldsymbol{u}\|^2 }{\rho_w g\eta}-\frac{\mathcal{T}}{\rho_w}k^2\right)}, \end{equation}
\begin{equation} \|\boldsymbol{c}_{p_f}\|=c_{p_f} = \frac{\omega}{k}= \sqrt{\frac{g}{k}\tanh(kd)\left(1-\frac{\rho_a/2 \|\boldsymbol{u}\|^2 }{\rho_w g\eta}-\frac{\mathcal{T}}{\rho_w}k^2\right)}, \end{equation}while an expression for the group velocity can be derived via,
which ends up being a function of ![]() $\partial \eta / \partial k$. Clearly, the phase speed of the water-wave pulsation as defined by (3.29) depends on the ratio of kinetic energy of the wind to the potential energy of the sea surface. Another important consequence that immediately can be seen is that at the moment
$\partial \eta / \partial k$. Clearly, the phase speed of the water-wave pulsation as defined by (3.29) depends on the ratio of kinetic energy of the wind to the potential energy of the sea surface. Another important consequence that immediately can be seen is that at the moment ![]() $t_l > 0$, just as the energy transfer begins and before an appreciable change in the velocity of the water pulsation forms (where the singularity exists in our representation of the wind velocity), the surface elevation of the water waves is the solution to a partial differential equation involving the pressure and the surface tension of the free surface,
$t_l > 0$, just as the energy transfer begins and before an appreciable change in the velocity of the water pulsation forms (where the singularity exists in our representation of the wind velocity), the surface elevation of the water waves is the solution to a partial differential equation involving the pressure and the surface tension of the free surface,
which demonstrates the role that the pressure pulsation plays in the initial generation of the water waves. For instance, substitution of the expression ![]() $\eta$ into the PDE above would give the dependence of the amplitude of
$\eta$ into the PDE above would give the dependence of the amplitude of ![]() $\eta$ on the pressure pulsation, which is a function of time. The initial excitation of the surface elevation will be controlled by the absolute value of the exponent
$\eta$ on the pressure pulsation, which is a function of time. The initial excitation of the surface elevation will be controlled by the absolute value of the exponent ![]() $q$ in expression (3.8). The larger the absolute value of the exponent, the larger the jump that will occur in the surface elevation at time
$q$ in expression (3.8). The larger the absolute value of the exponent, the larger the jump that will occur in the surface elevation at time ![]() $t_l > 0$, see figure
$t_l > 0$, see figure ![]() $3$ in our companion paper (Conroy et al. Reference Conroy, Kubatko and Mandli2021) for an illustration of the jumps in
$3$ in our companion paper (Conroy et al. Reference Conroy, Kubatko and Mandli2021) for an illustration of the jumps in ![]() $\|\boldsymbol {u}\|$. Because we are not explicitly concerned with resolving the initial water waves of the air–water transfer (and because the local pressure term is
$\|\boldsymbol {u}\|$. Because we are not explicitly concerned with resolving the initial water waves of the air–water transfer (and because the local pressure term is ![]() ${\approx }10^{-3}$), we ignore the pressure term and the surface tension term in the calculations of
${\approx }10^{-3}$), we ignore the pressure term and the surface tension term in the calculations of ![]() $c_{p_f}$ and
$c_{p_f}$ and ![]() $c_{g_f}$ in our numerical simulations. It can be noted that the above analysis does not examine the effect of the water surface on the atmosphere, however, in this investigation we only make use of observational wind data which already have this effect built in. Finally, there is ample evidence that the water-wave generation mechanism should make use of the friction wind speed
$c_{g_f}$ in our numerical simulations. It can be noted that the above analysis does not examine the effect of the water surface on the atmosphere, however, in this investigation we only make use of observational wind data which already have this effect built in. Finally, there is ample evidence that the water-wave generation mechanism should make use of the friction wind speed ![]() $u_{*}$ as opposed to the wind speed
$u_{*}$ as opposed to the wind speed ![]() $U_{10}$ (see Janssen (Reference Janssen2004), for example). We utilize
$U_{10}$ (see Janssen (Reference Janssen2004), for example). We utilize ![]() $U_{10}$ in this work simply because the closure scheme developed by Hasselmann et al. (Reference Hasselmann, Ross, Muller and Sell1975) uses
$U_{10}$ in this work simply because the closure scheme developed by Hasselmann et al. (Reference Hasselmann, Ross, Muller and Sell1975) uses ![]() $U_{10}$.
$U_{10}$.

Figure 1. Model problem of linear wave theory.
3.3. Duration limited solutions to the energy balance equation
When the speed of the wind can be represented locally by the power law given by (3.8) then closed form solutions exist to a parameterized form of the energy balance equation. More specifically, Hasselmann et al. (Reference Hasselmann, Ross, Muller and Sell1975) derived a rigorous parameterization of the spectral energy balance that takes into account nonlinear wave–wave interactions, dissipation and atmospheric input, and has been verified by the direct numerical simulations of Tanaka (Reference Tanaka2001). For duration limited wind waves, the non-dimensional representative frequency and energy of the corresponding water-wave pulsations can be expressed solely in terms of the characteristic constants (see Hasselmann et al. (Reference Hasselmann, Ross, Muller and Sell1975) for details),
 \begin{equation} \left.\begin{array}{c} \nu^{(\,j)} =a^{(\,j)}\left[\dfrac{g}{\|\boldsymbol{u}_0^{(\,j)}\|}(t_{l})\right]^{\varphi^{(\,j)}},\quad \varphi^{(\,j)}=3/7(q^{(\,j)}-1),\\ \epsilon^{(\,j)} = d^{(\,j)}(\nu^{(\,j)})^{{-}10/3}, \end{array}\right\} \end{equation}
\begin{equation} \left.\begin{array}{c} \nu^{(\,j)} =a^{(\,j)}\left[\dfrac{g}{\|\boldsymbol{u}_0^{(\,j)}\|}(t_{l})\right]^{\varphi^{(\,j)}},\quad \varphi^{(\,j)}=3/7(q^{(\,j)}-1),\\ \epsilon^{(\,j)} = d^{(\,j)}(\nu^{(\,j)})^{{-}10/3}, \end{array}\right\} \end{equation}where
 \begin{equation} \left.\begin{array}{c} a^{(\,j)} = 16.8(1+1.51q^{(\,j)})^{3/7}, \\ b^{(\,j)} = 0.031\left(\dfrac{1+1.33q^{(\,j)}}{1+1.51q^{(\,j)}}\right)^{1/2}, \end{array}\right\} \end{equation}
\begin{equation} \left.\begin{array}{c} a^{(\,j)} = 16.8(1+1.51q^{(\,j)})^{3/7}, \\ b^{(\,j)} = 0.031\left(\dfrac{1+1.33q^{(\,j)}}{1+1.51q^{(\,j)}}\right)^{1/2}, \end{array}\right\} \end{equation}and
The shape parameter, ![]() $\varLambda$, relates the representative frequency, energy and dissipation parameter,
$\varLambda$, relates the representative frequency, energy and dissipation parameter, ![]() $\alpha ^{(\,j)}$, via
$\alpha ^{(\,j)}$, via
where ![]() $\varLambda = 1.60 (\pm 0.02) (10^{-4})$ arises from wind-wave observations (Hasselmann et al. Reference Hasselmann1973) and is directly proportional to the graph dimension of the atmospheric turbulent velocity in the air–sea boundary layer. The measure of the high-frequency spectral cutoff,
$\varLambda = 1.60 (\pm 0.02) (10^{-4})$ arises from wind-wave observations (Hasselmann et al. Reference Hasselmann1973) and is directly proportional to the graph dimension of the atmospheric turbulent velocity in the air–sea boundary layer. The measure of the high-frequency spectral cutoff, ![]() $\alpha ^{(\,j)}$, which parameterizes dissipation, is proportional to the fourth-order moment but can be expressed in terms of
$\alpha ^{(\,j)}$, which parameterizes dissipation, is proportional to the fourth-order moment but can be expressed in terms of ![]() $\|\boldsymbol {u}_0^{(\,j)}\|$ and
$\|\boldsymbol {u}_0^{(\,j)}\|$ and ![]() $q^{(\,j)}$ as,
$q^{(\,j)}$ as,
where ![]() $b^{(\,j)}$ is given by (3.33), and
$b^{(\,j)}$ is given by (3.33), and ![]() $\nu ^{(\,j)}$ by (3.32). The global distributions of the representative non-dimensional frequency and energy of the wind sea are,
$\nu ^{(\,j)}$ by (3.32). The global distributions of the representative non-dimensional frequency and energy of the wind sea are,
 \begin{equation} \nu_{l} =\mathop{\bigcup}\limits_{j=1}^{\mathcal{N}} \nu^{(\,j)}, \end{equation}
\begin{equation} \nu_{l} =\mathop{\bigcup}\limits_{j=1}^{\mathcal{N}} \nu^{(\,j)}, \end{equation}and
 \begin{equation} \mathcal{\epsilon}_{l} =\mathop{\bigcup}\limits_{j=1}^{\mathcal{N}} \mathcal{\epsilon}^{(\,j)}, \end{equation}
\begin{equation} \mathcal{\epsilon}_{l} =\mathop{\bigcup}\limits_{j=1}^{\mathcal{N}} \mathcal{\epsilon}^{(\,j)}, \end{equation}
where ![]() $\nu = f_m U_{10}/g$ and
$\nu = f_m U_{10}/g$ and ![]() $\epsilon = \mathcal {E} g^2/ U_{10}^4$. It can be noted that other closure schemes besides Hasselmann et al. (Reference Hasselmann, Ross, Muller and Sell1975) can be used to define the duration limited pulsations in the water surface. For instance, the Zakharov–Resio–Pushkarev wind input source term (Zakharov et al. Reference Zakharov, Resio and Pushkarev2017) can be used as well. When the short water waves are not duration limited then we can use (3.32) to determine the
$\epsilon = \mathcal {E} g^2/ U_{10}^4$. It can be noted that other closure schemes besides Hasselmann et al. (Reference Hasselmann, Ross, Muller and Sell1975) can be used to define the duration limited pulsations in the water surface. For instance, the Zakharov–Resio–Pushkarev wind input source term (Zakharov et al. Reference Zakharov, Resio and Pushkarev2017) can be used as well. When the short water waves are not duration limited then we can use (3.32) to determine the ![]() ${\rm d} \mathcal {E}_0 / {\rm d}t$ and
${\rm d} \mathcal {E}_0 / {\rm d}t$ and ![]() ${\rm d} \mathcal {E}_1 / {\rm d}t$ terms needed for the air–water energy transfer source terms (2.25) and (2.26). Making use of (3.32) and differentiating with respect to time yields,
${\rm d} \mathcal {E}_1 / {\rm d}t$ terms needed for the air–water energy transfer source terms (2.25) and (2.26). Making use of (3.32) and differentiating with respect to time yields,
 \begin{equation} \frac{{\rm d} \mathcal{E}_0^{(\,j)}}{ {\rm d}t} = \frac{C_0 \varLambda \|\boldsymbol{u}_0^{(\,j)}\|^4\mathcal{Q}^{(\,j)}(9q^{(\,j)}+5)(151q^{(\,j)}+100)^{3/7} \left(\dfrac{g}{\|\boldsymbol{u}_0^{(\,j)}\|}(t_{l})\right)^{(31/7)q^{(\,j)}-3/7}} {g^2(t_{l})\left[(151q^{(\,j)}+100)^{3/7}\left(\dfrac{g}{\|\boldsymbol{u}_0^{(\,j)}\|}(t_{l})\right)^{(3/7)q^{(\,j)}-3/7}\right]^{13/3}}, \end{equation}
\begin{equation} \frac{{\rm d} \mathcal{E}_0^{(\,j)}}{ {\rm d}t} = \frac{C_0 \varLambda \|\boldsymbol{u}_0^{(\,j)}\|^4\mathcal{Q}^{(\,j)}(9q^{(\,j)}+5)(151q^{(\,j)}+100)^{3/7} \left(\dfrac{g}{\|\boldsymbol{u}_0^{(\,j)}\|}(t_{l})\right)^{(31/7)q^{(\,j)}-3/7}} {g^2(t_{l})\left[(151q^{(\,j)}+100)^{3/7}\left(\dfrac{g}{\|\boldsymbol{u}_0^{(\,j)}\|}(t_{l})\right)^{(3/7)q^{(\,j)}-3/7}\right]^{13/3}}, \end{equation}and
 \begin{equation} \frac{{\rm d} \mathcal{E}_1^{(\,j)}}{ {\rm d}t} = \frac{C_1\varLambda \|\boldsymbol{u}_0^{(\,j)}\|^3\mathcal{Q}^{(\,j)}(2q^{(\,j)}+1)(151q^{(\,j)}+100)^{6/7} \left(\dfrac{g}{\|\boldsymbol{u}_0^{(\,j)}\|}(t_{l})\right)^{(27/7)q^{(\,j)}-6/7}} {g(t_{l})\left[(151q^{(\,j)}+100)^{3/7}\left(\dfrac{g}{\|\boldsymbol{u}_0^{(\,j)}\|}(t_{l})\right)^{(3/7)q^{(\,j)}-3/7}\right]^{13/3}}, \end{equation}
\begin{equation} \frac{{\rm d} \mathcal{E}_1^{(\,j)}}{ {\rm d}t} = \frac{C_1\varLambda \|\boldsymbol{u}_0^{(\,j)}\|^3\mathcal{Q}^{(\,j)}(2q^{(\,j)}+1)(151q^{(\,j)}+100)^{6/7} \left(\dfrac{g}{\|\boldsymbol{u}_0^{(\,j)}\|}(t_{l})\right)^{(27/7)q^{(\,j)}-6/7}} {g(t_{l})\left[(151q^{(\,j)}+100)^{3/7}\left(\dfrac{g}{\|\boldsymbol{u}_0^{(\,j)}\|}(t_{l})\right)^{(3/7)q^{(\,j)}-3/7}\right]^{13/3}}, \end{equation}where
 \begin{equation} \mathcal{Q}^{(\,j)} =\left(\frac{133q^{(\,j)}+100}{151q^{(\,j)}+100}\right)^{1/2}, \end{equation}
\begin{equation} \mathcal{Q}^{(\,j)} =\left(\frac{133q^{(\,j)}+100}{151q^{(\,j)}+100}\right)^{1/2}, \end{equation}
and ![]() $C_0 = 5.25(10^{-4})$ and
$C_0 = 5.25(10^{-4})$ and ![]() $C_1 = 4.20(10^{-3})$. Due to the fact that the pulsations
$C_1 = 4.20(10^{-3})$. Due to the fact that the pulsations ![]() ${\rm d} \mathcal {E}_0 / {\rm d}t$ and
${\rm d} \mathcal {E}_0 / {\rm d}t$ and ![]() ${\rm d} \mathcal {E}_1 / {\rm d}t$ correspond to high frequency pulsations that are typically of a much shorter wavelength than the water depth, the fluctuations travel with a deep water-wave phase speed,
${\rm d} \mathcal {E}_1 / {\rm d}t$ correspond to high frequency pulsations that are typically of a much shorter wavelength than the water depth, the fluctuations travel with a deep water-wave phase speed,
 \begin{equation} \|\boldsymbol{c}_{p_f}\|_{l} =\mathop{\bigcup}\limits_{j=1}^{\mathcal{N}} \frac{g}{2 {\rm \pi}f_m^{(\,j)}}, \end{equation}
\begin{equation} \|\boldsymbol{c}_{p_f}\|_{l} =\mathop{\bigcup}\limits_{j=1}^{\mathcal{N}} \frac{g}{2 {\rm \pi}f_m^{(\,j)}}, \end{equation}and group speed,
 \begin{equation} \|\boldsymbol{c}_{g_f}\|_{l} =\mathop{\bigcup}\limits_{j=1}^{\mathcal{N}} \frac{g}{4 {\rm \pi}f_m^{(\,j)}}, \end{equation}
\begin{equation} \|\boldsymbol{c}_{g_f}\|_{l} =\mathop{\bigcup}\limits_{j=1}^{\mathcal{N}} \frac{g}{4 {\rm \pi}f_m^{(\,j)}}, \end{equation}where we have neglected the high-order term of (3.29). Substitution of (3.40) and (3.43) into (2.20) reduces the closure of the moment field equations to the calculation of the characteristic constants that define the distribution of the wind velocity.
3.4. Calculation of characteristic constants
We calculate the set of characteristic constants ![]() $\{ \|\boldsymbol {u}_0^{(\,j)}\|, \theta _0^{(\,j)}, q^{(\,j)}, \varUpsilon ^{(\,j)} \}_{j=1}^{\mathcal {N}}$ that define the velocity kernels and the corresponding duration limited water-wave pulsations through preservation of large scale averages of observational atmospheric velocity data combined with some reconstruction of the endpoint values of each
$\{ \|\boldsymbol {u}_0^{(\,j)}\|, \theta _0^{(\,j)}, q^{(\,j)}, \varUpsilon ^{(\,j)} \}_{j=1}^{\mathcal {N}}$ that define the velocity kernels and the corresponding duration limited water-wave pulsations through preservation of large scale averages of observational atmospheric velocity data combined with some reconstruction of the endpoint values of each ![]() $\mathcal {R}^{(\,j)}$. We denote these reconstructed endpoint values as
$\mathcal {R}^{(\,j)}$. We denote these reconstructed endpoint values as ![]() $u^{(\,j)}_i$ and
$u^{(\,j)}_i$ and ![]() $u^{(\,j)}_f$. For a given
$u^{(\,j)}_f$. For a given ![]() $\mathcal {R}^{(\,j)}$ located at
$\mathcal {R}^{(\,j)}$ located at ![]() $\boldsymbol {x}_0$ of length
$\boldsymbol {x}_0$ of length ![]() $l_0$ the initial and final speed values are,
$l_0$ the initial and final speed values are,
 \begin{equation} \left.\begin{array}{c}
\|\boldsymbol{u}^{(\,j)}(t_{l}=l_{d_{\epsilon}})\| =
\|\boldsymbol{u}_0^{(\,j)}\|\left(\dfrac{g(l_{d_{\epsilon}})}{\|\boldsymbol{u}_0^{(\,j)}\|}\right)^{q^{(\,j)}}=u_i^{(\,j)},\\
\|\boldsymbol{u}^{(\,j)}(t_{l}=l_0)\| =
\|\boldsymbol{u}_0^{(\,j)}\| \left(\dfrac{g
(l_0)}{\|\boldsymbol{u}_0^{(\,j)}\|}\right)^{q^{(\,j)}}=u_f^{(\,j)}.
\end{array}\right\} \end{equation}
\begin{equation} \left.\begin{array}{c}
\|\boldsymbol{u}^{(\,j)}(t_{l}=l_{d_{\epsilon}})\| =
\|\boldsymbol{u}_0^{(\,j)}\|\left(\dfrac{g(l_{d_{\epsilon}})}{\|\boldsymbol{u}_0^{(\,j)}\|}\right)^{q^{(\,j)}}=u_i^{(\,j)},\\
\|\boldsymbol{u}^{(\,j)}(t_{l}=l_0)\| =
\|\boldsymbol{u}_0^{(\,j)}\| \left(\dfrac{g
(l_0)}{\|\boldsymbol{u}_0^{(\,j)}\|}\right)^{q^{(\,j)}}=u_f^{(\,j)}.
\end{array}\right\} \end{equation}
Solving for ![]() $q^{(\,j)}$ we have,
$q^{(\,j)}$ we have,
 \begin{equation} q^{(\,j)} =\log\left(\frac{u_i^{(\,j)}}{\|\boldsymbol{u}_0^{(\,j)}\|}\right)\left/\,\log \left(\frac{g(l_{d_{\epsilon}})}{\|\boldsymbol{u}_0^{(\,j)}\|}\right), \right. \end{equation}
\begin{equation} q^{(\,j)} =\log\left(\frac{u_i^{(\,j)}}{\|\boldsymbol{u}_0^{(\,j)}\|}\right)\left/\,\log \left(\frac{g(l_{d_{\epsilon}})}{\|\boldsymbol{u}_0^{(\,j)}\|}\right), \right. \end{equation} \begin{equation}q^{(\,j)}=\log\left(\frac{u_f^{(\,j)}}{\|\boldsymbol{u}_0^{(\,j)}\|}\right)\left/\,\log \left(\frac{g(l_0)}{\|\boldsymbol{u}_0^{(\,j)}\|}\right)\right. . \end{equation}
\begin{equation}q^{(\,j)}=\log\left(\frac{u_f^{(\,j)}}{\|\boldsymbol{u}_0^{(\,j)}\|}\right)\left/\,\log \left(\frac{g(l_0)}{\|\boldsymbol{u}_0^{(\,j)}\|}\right)\right. . \end{equation}
Setting these equations equal to one another and simplifying leads to an expression that can be solved for ![]() $\|\boldsymbol {u}_0^{(\,j)}\|$,
$\|\boldsymbol {u}_0^{(\,j)}\|$,
 \begin{equation} \log\left(\frac{u_i^{(\,j)}}{\|\boldsymbol{u}_0^{(\,j)}\|}\right) \log\left(\frac{g(l_0)}{\|\boldsymbol{u}_0^{(\,j)}\|}\right) - \log\left(\frac{u_f^{(\,j)}}{\|\boldsymbol{u}_0^{(\,j)}\|}\right) \log\left(\frac{g(l_{d_{\epsilon}})}{\|\boldsymbol{u}_0^{(\,j)}\|}\right) = 0. \end{equation}
\begin{equation} \log\left(\frac{u_i^{(\,j)}}{\|\boldsymbol{u}_0^{(\,j)}\|}\right) \log\left(\frac{g(l_0)}{\|\boldsymbol{u}_0^{(\,j)}\|}\right) - \log\left(\frac{u_f^{(\,j)}}{\|\boldsymbol{u}_0^{(\,j)}\|}\right) \log\left(\frac{g(l_{d_{\epsilon}})}{\|\boldsymbol{u}_0^{(\,j)}\|}\right) = 0. \end{equation}
The exponent ![]() $q^{(\,j)}$ can be determined by preserving large scale averages of observational wind data, i.e. the area. In particular, the integral of (3.8) is
$q^{(\,j)}$ can be determined by preserving large scale averages of observational wind data, i.e. the area. In particular, the integral of (3.8) is
 \begin{equation} \left.\begin{aligned} \underbrace{\int_{l_{d_{\epsilon}}}^{l_0}{\|\boldsymbol{u}_0^{(\,j)}\| \left(\frac{g(t_{l})}{\|\boldsymbol{u}_0^{(\,j)}\|}\right)^{q^{(\,j)}}\,{\rm d}t_{l}}} & =\left.\frac{(\|\boldsymbol{u}_0^{(\,j)}\|)^2}{g(q^{(\,j)}+1)}\left(\frac{g(t_{\ell})}{\|\boldsymbol{u}_0^{(\,j)}\|}\right)^{q^{(\,j)}+1} \right|_{l_{d_{\epsilon}}}^{l_0},\\ \bar{u}^{(\,j)}(l_0-l_{d_{\epsilon}}) & =\left[ \frac{(\|\boldsymbol{u}_0^{(\,j)}\|)^2}{g(q^{(\,j)}+1)}\left(\frac{g(l_0)}{\|\boldsymbol{u}_0^{(\,j)}\|}\right)^{q^{(\,j)}+1}\right.\\ & \quad \left.-\, \frac{(\|\boldsymbol{u}_0^{(\,j)}\|)^2}{g(q^{(\,j)}+1)} \left(\frac{g(l_{d_{\epsilon}})}{\|\boldsymbol{u}_0^{(\,j)}\|}\right)^{q^{(\,j)}+1}\right], \end{aligned}\right\} \end{equation}
\begin{equation} \left.\begin{aligned} \underbrace{\int_{l_{d_{\epsilon}}}^{l_0}{\|\boldsymbol{u}_0^{(\,j)}\| \left(\frac{g(t_{l})}{\|\boldsymbol{u}_0^{(\,j)}\|}\right)^{q^{(\,j)}}\,{\rm d}t_{l}}} & =\left.\frac{(\|\boldsymbol{u}_0^{(\,j)}\|)^2}{g(q^{(\,j)}+1)}\left(\frac{g(t_{\ell})}{\|\boldsymbol{u}_0^{(\,j)}\|}\right)^{q^{(\,j)}+1} \right|_{l_{d_{\epsilon}}}^{l_0},\\ \bar{u}^{(\,j)}(l_0-l_{d_{\epsilon}}) & =\left[ \frac{(\|\boldsymbol{u}_0^{(\,j)}\|)^2}{g(q^{(\,j)}+1)}\left(\frac{g(l_0)}{\|\boldsymbol{u}_0^{(\,j)}\|}\right)^{q^{(\,j)}+1}\right.\\ & \quad \left.-\, \frac{(\|\boldsymbol{u}_0^{(\,j)}\|)^2}{g(q^{(\,j)}+1)} \left(\frac{g(l_{d_{\epsilon}})}{\|\boldsymbol{u}_0^{(\,j)}\|}\right)^{q^{(\,j)}+1}\right], \end{aligned}\right\} \end{equation}
where ![]() $t_{l}$ is the local time,
$t_{l}$ is the local time, ![]() $\bar {u}^{(\,j)}$ is the average wind speed over the region
$\bar {u}^{(\,j)}$ is the average wind speed over the region ![]() $\mathcal {R}^{(\,j)}$. We solve (3.47) and (3.48) simultaneously with the help of a Newton solver, see our companion paper (Conroy et al. Reference Conroy, Kubatko and Mandli2021) for details.
$\mathcal {R}^{(\,j)}$. We solve (3.47) and (3.48) simultaneously with the help of a Newton solver, see our companion paper (Conroy et al. Reference Conroy, Kubatko and Mandli2021) for details.
Here, we emphasize that our solution method for the characteristic constants introduces a dependency between distributions, where the explicit dependence is a function of the chosen reconstruction scheme. For instance, if an upwind reconstruction scheme is used then the distribution ![]() $\boldsymbol {u}^{(\,j)}$ over a given
$\boldsymbol {u}^{(\,j)}$ over a given ![]() $\mathcal {R}^{(\,j)}$ will be conditioned by past expectations (
$\mathcal {R}^{(\,j)}$ will be conditioned by past expectations (![]() $\bar {u}^{(j-1)}$), however, if any other reconstruction scheme is utilized then the distribution will depend on past and future expectations (
$\bar {u}^{(j-1)}$), however, if any other reconstruction scheme is utilized then the distribution will depend on past and future expectations (![]() $\bar {u}^{(j+1)}$) in a ratio defined by the reconstruction.
$\bar {u}^{(j+1)}$) in a ratio defined by the reconstruction.
Because we are concerned with small scale turbulence a major question concerns the optimal length of the local ![]() $\mathcal {R}^{(\,j)}$ over which the velocity kernels are well defined in terms of transferring momentum to the water and in terms of numerical consistency. That is, the calculation of the characteristic constants depends on time averaged values of velocity and pressure which in some instances could be defined on a scale whose region of uncertainty,
$\mathcal {R}^{(\,j)}$ over which the velocity kernels are well defined in terms of transferring momentum to the water and in terms of numerical consistency. That is, the calculation of the characteristic constants depends on time averaged values of velocity and pressure which in some instances could be defined on a scale whose region of uncertainty, ![]() $] l_{d_{\epsilon }}, l_{d} [$, is too large to correspond to small scale turbulence and too large to consistently integrate the moment field equations (this corresponds to the case where the numerical time step necessary to integrate (2.1) is less than the length of the region of uncertainty, see Conroy et al. (Reference Conroy, Kubatko and Mandli2021) for details). We address this issue and shrink the region of uncertainty through a recursive integration process to construct a refined distribution of the velocity of the turbulent medium so that
$] l_{d_{\epsilon }}, l_{d} [$, is too large to correspond to small scale turbulence and too large to consistently integrate the moment field equations (this corresponds to the case where the numerical time step necessary to integrate (2.1) is less than the length of the region of uncertainty, see Conroy et al. (Reference Conroy, Kubatko and Mandli2021) for details). We address this issue and shrink the region of uncertainty through a recursive integration process to construct a refined distribution of the velocity of the turbulent medium so that ![]() $] l_{d_{\epsilon }}, l_{d} [ < {\rm d}t$ where
$] l_{d_{\epsilon }}, l_{d} [ < {\rm d}t$ where ![]() ${\rm d}t$ is the time step of the numerical integrator of (2.1).
${\rm d}t$ is the time step of the numerical integrator of (2.1).
3.5. Recursive integration and energy measures
The goal of the recursive integration process is to shrink the region of uncertainty associated with each velocity distribution ![]() $\boldsymbol {u}^{(\,j)}$ in a manner such that
$\boldsymbol {u}^{(\,j)}$ in a manner such that ![]() $] l_{d_{\epsilon }}, l_{d} [ < {\rm d}t$. We proceed by first subdividing each
$] l_{d_{\epsilon }}, l_{d} [ < {\rm d}t$. We proceed by first subdividing each ![]() $\mathcal {R}^{(\,j)}$ into two subregions
$\mathcal {R}^{(\,j)}$ into two subregions ![]() $\mathcal {R}^{(\,j)}_{1}$ and
$\mathcal {R}^{(\,j)}_{1}$ and ![]() $\mathcal {R}^{(\,j)}_{2}$ ; we then calculate the expected velocity of each subregion and pair these values with the nonlinear solution method described in Conroy et al. (Reference Conroy, Kubatko and Mandli2021) to create a new set of velocity kernels. This new set is composed of twice as many
$\mathcal {R}^{(\,j)}_{2}$ ; we then calculate the expected velocity of each subregion and pair these values with the nonlinear solution method described in Conroy et al. (Reference Conroy, Kubatko and Mandli2021) to create a new set of velocity kernels. This new set is composed of twice as many ![]() $\mathcal {R}^{(\,j)}$ as the original set and adds cut outs along the space–time path while shrinking the region of uncertainty
$\mathcal {R}^{(\,j)}$ as the original set and adds cut outs along the space–time path while shrinking the region of uncertainty ![]() $] l_{d_{\epsilon }}, l_{d_{i}} [$ associated with these cut outs toward zero, see Conroy et al. (Reference Conroy, Kubatko and Mandli2021) for the full algorithm.
$] l_{d_{\epsilon }}, l_{d_{i}} [$ associated with these cut outs toward zero, see Conroy et al. (Reference Conroy, Kubatko and Mandli2021) for the full algorithm.
3.5.1. Velocity measure
Consider the discrete sequence of lengths associated with a given ![]() $\mathcal {R}^{(\,j)}$,
$\mathcal {R}^{(\,j)}$,
The average, or expected speed of each subregion of level ![]() $i+1$ is connected to the expectation of level
$i+1$ is connected to the expectation of level ![]() $i$ via
$i$ via
 \begin{equation} \bar{u}^{(\,j)}_{i} = \frac{1}{C_{i+1}}\sum_{s = 1}^{C_{i+1}} w^{(\,j)}_{s} \bar{u}^{(\,j)}_{s}, \end{equation}
\begin{equation} \bar{u}^{(\,j)}_{i} = \frac{1}{C_{i+1}}\sum_{s = 1}^{C_{i+1}} w^{(\,j)}_{s} \bar{u}^{(\,j)}_{s}, \end{equation}
where ![]() $C_{i+1}$ is the number of sub-regions of level
$C_{i+1}$ is the number of sub-regions of level ![]() $i+1$ and the
$i+1$ and the ![]() $w^{(\,j)}_{s}$ correspond to the measure (or weights) of each subregion
$w^{(\,j)}_{s}$ correspond to the measure (or weights) of each subregion ![]() $s$, which are defined as,
$s$, which are defined as,
 \begin{equation} w^{(\,j)}_{s} = \frac{\bar{u}^{(\,j)}_{i}}{\bar{u}^{(\,j)}_{s}}. \end{equation}
\begin{equation} w^{(\,j)}_{s} = \frac{\bar{u}^{(\,j)}_{i}}{\bar{u}^{(\,j)}_{s}}. \end{equation}
The expectation of the parent kernel ![]() $\bar {u}^{(\,j)}_{i}$ is
$\bar {u}^{(\,j)}_{i}$ is
 \begin{equation} \bar{u}^{(\,j)}_{i}=\frac{1}{(l_{i}-l_{d_{\epsilon}})} \int^{l_{i}}_{l_{d_{\epsilon}}}{\| \boldsymbol{u}_0^{(\,j)} \| \left(\frac{g}{\| \boldsymbol{u}_0^{(\,j)} \|}t_{l}\right)^{q^{(\,j)}}\,{\rm d}t_{l}}, \end{equation}
\begin{equation} \bar{u}^{(\,j)}_{i}=\frac{1}{(l_{i}-l_{d_{\epsilon}})} \int^{l_{i}}_{l_{d_{\epsilon}}}{\| \boldsymbol{u}_0^{(\,j)} \| \left(\frac{g}{\| \boldsymbol{u}_0^{(\,j)} \|}t_{l}\right)^{q^{(\,j)}}\,{\rm d}t_{l}}, \end{equation}
and the offspring, ![]() $\bar {u}^{(\,j)}_{s}$, corresponds to the expected speed of the turbulent velocity over an interior time interval,
$\bar {u}^{(\,j)}_{s}$, corresponds to the expected speed of the turbulent velocity over an interior time interval, ![]() $l_{d_{\epsilon }} < (l_{s+1} - l_{s}) < l_{i}$,
$l_{d_{\epsilon }} < (l_{s+1} - l_{s}) < l_{i}$,
 \begin{align} \bar{u}^{(\,j)}_{s} &=\frac{1}{(l_{s+1} - l_{s})} \int_{l_{s}}^{l_{s+1}} {\| \boldsymbol{u}_0^{(\,j)} \| \left(\frac{g}{\| \boldsymbol{u}_0^{(\,j)} \|}t_{l}\right)^{q^{(\,j)}}\,{\rm d}t_{l}},\nonumber\\ & = \left[\frac{\| \boldsymbol{u}_0^{(\,j)} \|^2}{g(l_{s+1} - l_{s})(q^{(\,j)}+1)}\left(\frac{g}{\| \boldsymbol{u}_0^{(\,j)} \|}l_{s+1}\right)^{q^{(\,j)}+1}\right.\nonumber\\ &\quad - \left. \frac{\| \boldsymbol{u}_0 \|^2}{g(l_{s+1} - l_{s})(q^{(\,j)}+1)}\left(\frac{g}{\| \boldsymbol{u}_0^{(\,j)} \|}l_{s}\right)^{q^{(\,j)}+1}\right]. \end{align}
\begin{align} \bar{u}^{(\,j)}_{s} &=\frac{1}{(l_{s+1} - l_{s})} \int_{l_{s}}^{l_{s+1}} {\| \boldsymbol{u}_0^{(\,j)} \| \left(\frac{g}{\| \boldsymbol{u}_0^{(\,j)} \|}t_{l}\right)^{q^{(\,j)}}\,{\rm d}t_{l}},\nonumber\\ & = \left[\frac{\| \boldsymbol{u}_0^{(\,j)} \|^2}{g(l_{s+1} - l_{s})(q^{(\,j)}+1)}\left(\frac{g}{\| \boldsymbol{u}_0^{(\,j)} \|}l_{s+1}\right)^{q^{(\,j)}+1}\right.\nonumber\\ &\quad - \left. \frac{\| \boldsymbol{u}_0 \|^2}{g(l_{s+1} - l_{s})(q^{(\,j)}+1)}\left(\frac{g}{\| \boldsymbol{u}_0^{(\,j)} \|}l_{s}\right)^{q^{(\,j)}+1}\right]. \end{align}When dyadic intervals serve as the refinement mechanism, the averages used to initiate the next level of integration are,
 \begin{equation} \bar{u}_1^{(\,j)}= \frac{1}{(l_{i}/2 - l_{d_i})} \int_{l_{d_i}}^{l_{i}/2} {\| \boldsymbol{u}_0^{(\,j)} \| \left(\frac{g}{\| \boldsymbol{u}_0^{(\,j)} \|}t_{l}\right)^{q^{(\,j)}}\,\textrm{d}t_{l}}, \end{equation}
\begin{equation} \bar{u}_1^{(\,j)}= \frac{1}{(l_{i}/2 - l_{d_i})} \int_{l_{d_i}}^{l_{i}/2} {\| \boldsymbol{u}_0^{(\,j)} \| \left(\frac{g}{\| \boldsymbol{u}_0^{(\,j)} \|}t_{l}\right)^{q^{(\,j)}}\,\textrm{d}t_{l}}, \end{equation}and
 \begin{equation} \bar{u}_2^{(\,j)}= \frac{1}{(l_{i} - l_{i}/2)} \int_{l_{i}/2}^{l_{i}} {\| \boldsymbol{u}_0^{(\,j)} \| \left(\frac{g}{\| \boldsymbol{u}_0^{(\,j)} \|}t_{l}\right)^{q^{(\,j)}}\,\textrm{d}t_{l}}. \end{equation}
\begin{equation} \bar{u}_2^{(\,j)}= \frac{1}{(l_{i} - l_{i}/2)} \int_{l_{i}/2}^{l_{i}} {\| \boldsymbol{u}_0^{(\,j)} \| \left(\frac{g}{\| \boldsymbol{u}_0^{(\,j)} \|}t_{l}\right)^{q^{(\,j)}}\,\textrm{d}t_{l}}. \end{equation}
It can be noted that the interval ![]() $] l_{d_{\epsilon }},l_{d_i} [$ is cut out of the integration. The manner in which this interval is handled during the recursion process leads to markedly different measures and dimensions of the support. More specifically, when the length of the cut out is set to a relatively small number, such as
$] l_{d_{\epsilon }},l_{d_i} [$ is cut out of the integration. The manner in which this interval is handled during the recursion process leads to markedly different measures and dimensions of the support. More specifically, when the length of the cut out is set to a relatively small number, such as ![]() $1 \times 10^{-7}$ and kept constant with each level of integration, the sum of the weights equals
$1 \times 10^{-7}$ and kept constant with each level of integration, the sum of the weights equals ![]() $C_{i+1}$ and the refinement cascade is said to be conservative, or microcanonical (Mandelbrot Reference Mandelbrot1974). In this case
$C_{i+1}$ and the refinement cascade is said to be conservative, or microcanonical (Mandelbrot Reference Mandelbrot1974). In this case ![]() $] l_{d_{\epsilon }},l_{d_i} [$ is always less than
$] l_{d_{\epsilon }},l_{d_i} [$ is always less than ![]() ${\rm d}t$, however, the graph dimension of the resulting velocity distribution will not be in a range that matches theory and observation until after five levels of recursive integration. The dimension of the support in this case is approximately equal to the embedding dimension
${\rm d}t$, however, the graph dimension of the resulting velocity distribution will not be in a range that matches theory and observation until after five levels of recursive integration. The dimension of the support in this case is approximately equal to the embedding dimension ![]() $E$ (the resulting measure of the turbulence is
$E$ (the resulting measure of the turbulence is ![]() $E$-filling). Conversely, if we allow the cut out
$E$-filling). Conversely, if we allow the cut out ![]() $] l_{d_{\epsilon }},l_{d_i} [$ to vary in length (more specifically to shrink or become thinner) with each integration, then the sum of the weights only equals
$] l_{d_{\epsilon }},l_{d_i} [$ to vary in length (more specifically to shrink or become thinner) with each integration, then the sum of the weights only equals ![]() $C_{i+1}$ on average, local conservation is not maintained and the recursion is said to be canonical (Mandelbrot Reference Mandelbrot1974). In this scenario, the graph dimension of the velocity distribution is in the range of observations and theory with each recursion and we can re-write (3.50) as
$C_{i+1}$ on average, local conservation is not maintained and the recursion is said to be canonical (Mandelbrot Reference Mandelbrot1974). In this scenario, the graph dimension of the velocity distribution is in the range of observations and theory with each recursion and we can re-write (3.50) as
 \begin{equation} \bar{u}^{(\,j)}_i = \frac{1}{C_{i+1}}\sum_{s=1}^{C_{i+1}}\bar{u}^{(\,j)}_s + \bar{u}^{(\,j)}_{\bar{\epsilon}}, \end{equation}
\begin{equation} \bar{u}^{(\,j)}_i = \frac{1}{C_{i+1}}\sum_{s=1}^{C_{i+1}}\bar{u}^{(\,j)}_s + \bar{u}^{(\,j)}_{\bar{\epsilon}}, \end{equation}
where ![]() $\bar {u}^{(\,j)}_{\bar {\epsilon }}$ is the value of velocity cut out from the refinement of level
$\bar {u}^{(\,j)}_{\bar {\epsilon }}$ is the value of velocity cut out from the refinement of level ![]() $i$. This cut out represents a loss of regularity in the velocity field in the spirit of Onsager (Reference Onsager1949).
$i$. This cut out represents a loss of regularity in the velocity field in the spirit of Onsager (Reference Onsager1949).
3.5.2. Energy measures
We measure the distribution of turbulent energy in the wind by defining the following measure (or weight),
 \begin{equation} w^{(\,j)}_{\mathcal{E}s}=\frac{(\bar{u}^{(\,j)}_i)^2}{(\bar{u}_s^{(\,j)})^2}, \end{equation}
\begin{equation} w^{(\,j)}_{\mathcal{E}s}=\frac{(\bar{u}^{(\,j)}_i)^2}{(\bar{u}_s^{(\,j)})^2}, \end{equation}
where ![]() $\bar {u}^{(\,j)}_i$ and
$\bar {u}^{(\,j)}_i$ and ![]() $\bar {u}_s^{(\,j)}$ correspond to the measures of the parent and offspring kernels presented in the previous subsection. The weights,
$\bar {u}_s^{(\,j)}$ correspond to the measures of the parent and offspring kernels presented in the previous subsection. The weights, ![]() $w_{\mathcal {E}s}$, measure the redistribution of energy across temporal scales,
$w_{\mathcal {E}s}$, measure the redistribution of energy across temporal scales,
 \begin{equation} \langle \mathcal{E} \rangle^{(\,j)}_i = \frac{1}{C_{i+1}}\sum_{s = 1}^{C_{i+1}} w^{(\,j)}_{\mathcal{E}s} \mathcal{E}_s^{(\,j)}, \end{equation}
\begin{equation} \langle \mathcal{E} \rangle^{(\,j)}_i = \frac{1}{C_{i+1}}\sum_{s = 1}^{C_{i+1}} w^{(\,j)}_{\mathcal{E}s} \mathcal{E}_s^{(\,j)}, \end{equation}and the total ensemble averages of the energy measure are,
 \begin{equation} \langle \mathcal{E} \rangle_l= \frac{1}{\mathcal{N}}\sum_{j = 1}^{\mathcal{N}} \langle \mathcal{E} \rangle^{(\,j)}_M. \end{equation}
\begin{equation} \langle \mathcal{E} \rangle_l= \frac{1}{\mathcal{N}}\sum_{j = 1}^{\mathcal{N}} \langle \mathcal{E} \rangle^{(\,j)}_M. \end{equation}It can be noted that when definitions (3.52) and (3.53) are substituted into (3.57), then (3.57) is qualitatively similar to the expressions used in She & Leveque (Reference She and Leveque1994) to measure the hierarchy of dissipation structures within a turbulent fluid. The energy transfer moments take the form,
where the exponent function of the moments, ![]() $\tau (n)$, are defined as in Mandelbrot (Reference Mandelbrot1998),
$\tau (n)$, are defined as in Mandelbrot (Reference Mandelbrot1998),
Here, ![]() $E$ is the dimension of the embedding space and the determining function is,
$E$ is the dimension of the embedding space and the determining function is,
where the ensemble average is over the indices ![]() $s$ and
$s$ and ![]() $j$ (see Mandelbrot (Reference Mandelbrot1998) for more details). It can be noted that the
$j$ (see Mandelbrot (Reference Mandelbrot1998) for more details). It can be noted that the ![]() $\tau$-functions (and therefore the moments) remain bounded below some critical value
$\tau$-functions (and therefore the moments) remain bounded below some critical value ![]() $n_{crit}$. For values greater than
$n_{crit}$. For values greater than ![]() $n_{crit}$, however, values for the
$n_{crit}$, however, values for the ![]() $\tau$-functions become large and tend toward infinity as
$\tau$-functions become large and tend toward infinity as ![]() $n \rightarrow \infty$. This critical
$n \rightarrow \infty$. This critical ![]() $n$-value serves as a scale factor for the velocity structure functions (Mandelbrot Reference Mandelbrot1974, Reference Mandelbrot1997),
$n$-value serves as a scale factor for the velocity structure functions (Mandelbrot Reference Mandelbrot1974, Reference Mandelbrot1997),
and determines the length of the virtual cut out of the velocity in the canonical case at each scale length ![]() $l_i$. That is, the slope of the graph of
$l_i$. That is, the slope of the graph of ![]() $\log {(l_{d_i})}$ vs
$\log {(l_{d_i})}$ vs ![]() $\log {(l_i)}$ has a slope equal to
$\log {(l_i)}$ has a slope equal to ![]() $n_{crit}$, and we have,
$n_{crit}$, and we have,
This relationship was revealed in our numerical studies of the recursive integration, where we find that ![]() $n_{{\rm crit}} \approx 5$. This is significant because
$n_{{\rm crit}} \approx 5$. This is significant because ![]() $n_{{\rm crit}}$ corresponds to the asymptotically scaling tail of the distribution of the energy weights of our multifractal measures, the value of which (
$n_{{\rm crit}}$ corresponds to the asymptotically scaling tail of the distribution of the energy weights of our multifractal measures, the value of which (![]() $n_{{\rm crit}} \approx 5$) happens to be equal to the high-frequency tail representing dissipation of the water-wave spectrum; see Zakharov et al. (Reference Zakharov, Resio and Pushkarev2017), for instance. It can be noted that we choose the initial inner cutoff,
$n_{{\rm crit}} \approx 5$) happens to be equal to the high-frequency tail representing dissipation of the water-wave spectrum; see Zakharov et al. (Reference Zakharov, Resio and Pushkarev2017), for instance. It can be noted that we choose the initial inner cutoff, ![]() $l_{d_0}$, of the recursive integration process in a manner such that the structure function of the velocity distribution lies in the range of theory and observation, see figures 2 and 3 and our companion paper (Conroy et al. Reference Conroy, Kubatko and Mandli2021) for details.
$l_{d_0}$, of the recursive integration process in a manner such that the structure function of the velocity distribution lies in the range of theory and observation, see figures 2 and 3 and our companion paper (Conroy et al. Reference Conroy, Kubatko and Mandli2021) for details.

Figure 2. Velocity structure function exponents at Lake Erie Buoy 45005 vs experimental data of Anselmet et al. (Reference Anselmet, Gagne, Hopfinger and Antonia1984) and Benzi et al. (Reference Benzi, Ciliberto, Tripiccione, Baudet, Massaioli and Succi1993) and theoretical relation of She & Leveque (Reference She and Leveque1994) (black dashed line). Diamonds correspond to average structure functions (May–October) of the recursive integration methods, black crosses (![]() $+$) correspond to the data of Benzi et al. (Reference Benzi, Ciliberto, Tripiccione, Baudet, Massaioli and Succi1993) and all other markers correspond to data of Anselmet et al. (Reference Anselmet, Gagne, Hopfinger and Antonia1984).
$+$) correspond to the data of Benzi et al. (Reference Benzi, Ciliberto, Tripiccione, Baudet, Massaioli and Succi1993) and all other markers correspond to data of Anselmet et al. (Reference Anselmet, Gagne, Hopfinger and Antonia1984).

Figure 3. Velocity structure function exponents at Lake Erie Buoy 45005 vs experimental data of Anselmet et al. (Reference Anselmet, Gagne, Hopfinger and Antonia1984) and Benzi et al. (Reference Benzi, Ciliberto, Tripiccione, Baudet, Massaioli and Succi1993) and theoretical relation of She & Leveque (Reference She and Leveque1994) (black dashed line). Diamonds correspond to average structure functions (May–October) of the recursive integration methods, black crosses (![]() $+$) correspond to the data of Benzi et al. (Reference Benzi, Ciliberto, Tripiccione, Baudet, Massaioli and Succi1993) and all other markers correspond to data of Anselmet et al. (Reference Anselmet, Gagne, Hopfinger and Antonia1984).
$+$) correspond to the data of Benzi et al. (Reference Benzi, Ciliberto, Tripiccione, Baudet, Massaioli and Succi1993) and all other markers correspond to data of Anselmet et al. (Reference Anselmet, Gagne, Hopfinger and Antonia1984).
3.5.3. Dimension of the support of the measure
The slopes of the ![]() $\tau$-functions for
$\tau$-functions for ![]() $n = 1$ are (Mandelbrot Reference Mandelbrot1974),
$n = 1$ are (Mandelbrot Reference Mandelbrot1974),
When ![]() $D_E > 0$,
$D_E > 0$, ![]() $D_E$ is the intrinsic dimension of the support of the measure
$D_E$ is the intrinsic dimension of the support of the measure ![]() $w_s$ in the
$w_s$ in the ![]() $E-$dimension embedding space. In the case
$E-$dimension embedding space. In the case ![]() $E = 3$,
$E = 3$, ![]() $D_E$ corresponds to the fractal dimension of the spatial trail of the self-affine measure of the turbulent energy transfer (Mandelbrot Reference Mandelbrot1974). It is a measure of how the local variation of a function grows as the characteristic length scale over which the function is defined shrinks towards a relative zero (inner cutoff) (Mandelbrot Reference Mandelbrot1977, Reference Mandelbrot1985; Dubuc et al. Reference Dubuc, Quiniou, Roques-Carmes, Tricot and Zucker1989). It can be noted that, in the turbulence literature,
$D_E$ corresponds to the fractal dimension of the spatial trail of the self-affine measure of the turbulent energy transfer (Mandelbrot Reference Mandelbrot1974). It is a measure of how the local variation of a function grows as the characteristic length scale over which the function is defined shrinks towards a relative zero (inner cutoff) (Mandelbrot Reference Mandelbrot1977, Reference Mandelbrot1985; Dubuc et al. Reference Dubuc, Quiniou, Roques-Carmes, Tricot and Zucker1989). It can be noted that, in the turbulence literature, ![]() $D_E$ typically lies in the range
$D_E$ typically lies in the range ![]() $2.95 \geq D_E \geq 2.27$ (Mandelbrot Reference Mandelbrot1974; Schertzer & Lovejoy Reference Schertzer and Lovejoy1985; Frisch Reference Frisch1996).
$2.95 \geq D_E \geq 2.27$ (Mandelbrot Reference Mandelbrot1974; Schertzer & Lovejoy Reference Schertzer and Lovejoy1985; Frisch Reference Frisch1996).
4. Quantifying air–water turbulence over Lake Erie
We apply our quantitative methods to air–water turbulence over Lake Erie, the tenth largest lake in the world and the fourth largest lake (by surface area) of the Great Lakes. Lake Erie commerce generates approximately ![]() $10.7$ billion US dollars in annual revenue (OEC 2015), and due to its orientation, large surface area and (relatively) shallow water depth, is extremely susceptible to wind water-wave generation, with seiches known to form on the lake of up to
$10.7$ billion US dollars in annual revenue (OEC 2015), and due to its orientation, large surface area and (relatively) shallow water depth, is extremely susceptible to wind water-wave generation, with seiches known to form on the lake of up to ![]() $5$ m (NOAA 2016). Tidal ranges on the lake are less than
$5$ m (NOAA 2016). Tidal ranges on the lake are less than ![]() $5$ cm, and thus, the main driver of the circulation of the system is due to gravity water waves generated by air–water interactions.
$5$ cm, and thus, the main driver of the circulation of the system is due to gravity water waves generated by air–water interactions.
4.1. Air–water interactions
To quantify air–water interactions over Lake Erie and generate input data for the moment field equations, we apply the nonlinear solution method outlined in § 3.4 to observational atmospheric data obtained from 27 meteorological stations owned and operated by the National Oceanic and Atmospheric Association (NOAA); the positions of the 27 stations are illustrated in figure 7 in Conroy et al. (Reference Conroy, Kubatko, Nappi, Sebian, West and Mandli2018). The exponents of the structure functions of the velocity measure (3.51) are shown in figures 2 and 3 while the dimension of the support of the energy measures are shown in table 1. In general, our methods produce structure functions and a fractal embedding dimension, ![]() $D_E$, that match theory and analysis of experimental data. The value of
$D_E$, that match theory and analysis of experimental data. The value of ![]() $D_E$ lies in the range
$D_E$ lies in the range ![]() $2.82 \geq D_E \geq 2.27$ with an average value
$2.82 \geq D_E \geq 2.27$ with an average value ![]() $D_E = 2.58$. Analysis of atmospheric boundary layer data puts a lower bound on the graph dimension of the velocity of
$D_E = 2.58$. Analysis of atmospheric boundary layer data puts a lower bound on the graph dimension of the velocity of ![]() $D_G = 1.56$ (Syu & Kirchoff Reference Syu and Kirchoff1993), which in the uniscaling case gives an embedding dimension
$D_G = 1.56$ (Syu & Kirchoff Reference Syu and Kirchoff1993), which in the uniscaling case gives an embedding dimension ![]() $D_E = 2.27$. This is a reflection of the fact that atmospheric turbulence can be very intermittent. It can be noted that, after four recursive integrations, the length of each
$D_E = 2.27$. This is a reflection of the fact that atmospheric turbulence can be very intermittent. It can be noted that, after four recursive integrations, the length of each ![]() $\mathcal {R}^{(\,j)}$ is
$\mathcal {R}^{(\,j)}$ is ![]() $\varDelta t_l = l_3= 3.75$ min, and the average exponent in the velocity distribution (3.8) is
$\varDelta t_l = l_3= 3.75$ min, and the average exponent in the velocity distribution (3.8) is ![]() $\bar {q} \approx 5.0 \times 10^{-4}$. In other words, on average, at relatively small scales the energy transfer as measured by
$\bar {q} \approx 5.0 \times 10^{-4}$. In other words, on average, at relatively small scales the energy transfer as measured by ![]() $q^{(\,j)}$ is rather negligible and the bulk of the energy transfer (at these scales) is due to a few ‘rare’ events (typical minimum and maximum values of
$q^{(\,j)}$ is rather negligible and the bulk of the energy transfer (at these scales) is due to a few ‘rare’ events (typical minimum and maximum values of ![]() $q^{(\,j)}$ are
$q^{(\,j)}$ are ![]() $\approx \pm 0.03$ which is
$\approx \pm 0.03$ which is ![]() $\approx 13$ times the standard deviation). This highlights the intermittency of the turbulence at relatively small scales which is a phenomenon that is well documented in the literature (Frisch Reference Frisch1996; Hentschel & Procaccia Reference Hentschel and Procaccia1982, Reference Hentschel and Procaccia1983; Schertzer & Lovejoy Reference Schertzer and Lovejoy1985). See Conroy et al. (Reference Conroy, Kubatko and Mandli2021) for a complete numerical investigation of the recursive integration process.
$\approx 13$ times the standard deviation). This highlights the intermittency of the turbulence at relatively small scales which is a phenomenon that is well documented in the literature (Frisch Reference Frisch1996; Hentschel & Procaccia Reference Hentschel and Procaccia1982, Reference Hentschel and Procaccia1983; Schertzer & Lovejoy Reference Schertzer and Lovejoy1985). See Conroy et al. (Reference Conroy, Kubatko and Mandli2021) for a complete numerical investigation of the recursive integration process.
4.2. Short water waves on Lake Erie
We perform hindcast simulations of the short water-wave energy over Lake Erie for the month of August 2011 using the input data detailed in the previous subsection. We begin by simply using the duration limited relation given by (3.33) coupled with our recursive integration method and calculate significant wave height over the lake associated with the velocity distributions (3.8). It can be noted that significant wave height is the average wave height of the third highest waves of the wind sea, which we define as,
where ![]() $H = 0.43$ is the Hurst exponent calculated via the methods presented in our companion paper (Conroy et al. Reference Conroy, Kubatko and Mandli2021) and
$H = 0.43$ is the Hurst exponent calculated via the methods presented in our companion paper (Conroy et al. Reference Conroy, Kubatko and Mandli2021) and ![]() $\mathcal {E}_l$ is given by (3.32). Results are shown in figures 4 and 5, where numerical results match the observational significant water-wave height quantitatively well. In fact, the root-mean-square (r.m.s.) error in this case is
$\mathcal {E}_l$ is given by (3.32). Results are shown in figures 4 and 5, where numerical results match the observational significant water-wave height quantitatively well. In fact, the root-mean-square (r.m.s.) error in this case is ![]() $0.132$ m and the correlation coefficient is
$0.132$ m and the correlation coefficient is ![]() $R = 0.91$. The agreement between observed and calculated significant water-wave height using the duration limited kernel (3.32) coupled with the recursive integration method of § 3.5 is satisfactory, however, it can be noted that there are certain events in figure 4 that indicate the wave field cannot be fully approximated by a duration limited kernel. In other words, there is some advection effect that needs to be included in the model, for instance, see the events from 4 August to 7 August and the event just before 15 August.
$R = 0.91$. The agreement between observed and calculated significant water-wave height using the duration limited kernel (3.32) coupled with the recursive integration method of § 3.5 is satisfactory, however, it can be noted that there are certain events in figure 4 that indicate the wave field cannot be fully approximated by a duration limited kernel. In other words, there is some advection effect that needs to be included in the model, for instance, see the events from 4 August to 7 August and the event just before 15 August.
To account for advection of water-wave energy through Lake Erie we solve the moment field equations and perform hindcast simulations for the months of August 2011 and July 2011. We use a deep water-wave dispersion relation for (2.4),
and set the moment field to quantify the energy flux so that the variance of the sea surface is calculated via,
where ![]() $\| \boldsymbol {c}_1\|$ corresponds to the peak phase speed of the water waves and calculate significant wave height via the approximation
$\| \boldsymbol {c}_1\|$ corresponds to the peak phase speed of the water waves and calculate significant wave height via the approximation ![]() $H_s \approx 4\sqrt {\sigma ^2}$ (Holthuijsen Reference Holthuijsen2007). The moment field equations are discretized with an unstructured discontinuous Galerkin (DG) finite element method (see Conroy et al. (Reference Conroy, Kubatko and Mandli2021) for details). Model simulations were performed with
$H_s \approx 4\sqrt {\sigma ^2}$ (Holthuijsen Reference Holthuijsen2007). The moment field equations are discretized with an unstructured discontinuous Galerkin (DG) finite element method (see Conroy et al. (Reference Conroy, Kubatko and Mandli2021) for details). Model simulations were performed with ![]() $\mathbb {P}^0$ polynomials using a time step
$\mathbb {P}^0$ polynomials using a time step ![]() ${\rm d}t = 2$ min, which on average took
${\rm d}t = 2$ min, which on average took ![]() $5$ min (of CPU time) to execute on an Apple laptop. With
$5$ min (of CPU time) to execute on an Apple laptop. With ![]() ${\rm d}t = 2$ min the numerical results generated by the model are ‘noisy’, just as any physical wave record observed at such a frequency would be. Therefore, to compare model output to buoy observations we correspondingly average the model output over hourly time windows. Results are shown in figures 6–9 and tables 2 and 3.
${\rm d}t = 2$ min the numerical results generated by the model are ‘noisy’, just as any physical wave record observed at such a frequency would be. Therefore, to compare model output to buoy observations we correspondingly average the model output over hourly time windows. Results are shown in figures 6–9 and tables 2 and 3.

Figure 6. Hourly averaged significant water-wave height (a) and average water-wave period (b) at NDBC Buoy 45005 (NDBC 2016) in Lake Erie for August 2011. Note how, qualitatively, both SWAN (blue line) and the moment field model (red line) are well correlated to the buoy data (black line) in panel (a).

Figure 7. August 2011 linear regression of the moment field model results at Buoy 45005 (NDBC 2016) in Lake Erie. Panel (a) shows the regression for significant water-wave height while (b) is average water-wave period, (![]() $T_{avg}=1/\bar {f}_0$) of the moment field model.
$T_{avg}=1/\bar {f}_0$) of the moment field model.

Figure 8. Hourly averaged significant water-wave height (a) and average water-wave period (b) at NDBC Buoy 45005 (NDBC 2016) in Lake Erie for July 2011. Note how qualitatively, both SWAN (blue line) and the moment field model (red line) are well correlated to the buoy data (black line) in panel (a)

Figure 9. July 2011 linear regression of the moment field model results at Buoy 45005 (NDBC 2016) in Lake Erie. Panel (a) shows the regression for significant water-wave height while (b) is average water-wave period, (![]() $T_{avg}=1/\bar {f}_0$) of the moment field model.
$T_{avg}=1/\bar {f}_0$) of the moment field model.
Table 2. Statistical comparison of moment field model (MFM) and SWAN with Lake Erie Buoy 45005 (NDBC 2016) for significant water-wave height.

Table 3. Statistical comparison of moment field model with Lake Erie Buoy 45005 (NDBC 2016) for average water-wave period.

In general, model output is well correlated to the buoy observations and to the water wave model known as Simulating WAves Nearshore (SWAN) (SWAN 2015). SWAN solves the action balance equation and on average took ![]() $3$ h to execute a monthly simulation. In fact, the moment field model executes almost
$3$ h to execute a monthly simulation. In fact, the moment field model executes almost ![]() $40$ times as fast as SWAN while producing similar error measures in terms of significant wave height – the r.m.s. error for the moment field model was
$40$ times as fast as SWAN while producing similar error measures in terms of significant wave height – the r.m.s. error for the moment field model was ![]() $0.100$ m in August 2011 and
$0.100$ m in August 2011 and ![]() $0.095$ m for July 2011, while SWAN produced r.m.s. errors of
$0.095$ m for July 2011, while SWAN produced r.m.s. errors of ![]() $0.097$ and
$0.097$ and ![]() $0.092$ m, respectively. It can be noted that the moment field equations produce lower error measures in terms of matching the mean and standard deviation of the buoy data as compared to SWAN. However, there are durations in the water-wave record where both SWAN and the moment field equations over or under-predict buoy observations (there does not seem to be any discernible bias in either case). One observation to make note of is the fact that the moment field model slightly misses the timing in the local minimum that occurs in significant wave height on 17 August 2011 and 30 August 2011, an issue that we will explore in future work.
$0.092$ m, respectively. It can be noted that the moment field equations produce lower error measures in terms of matching the mean and standard deviation of the buoy data as compared to SWAN. However, there are durations in the water-wave record where both SWAN and the moment field equations over or under-predict buoy observations (there does not seem to be any discernible bias in either case). One observation to make note of is the fact that the moment field model slightly misses the timing in the local minimum that occurs in significant wave height on 17 August 2011 and 30 August 2011, an issue that we will explore in future work.
To emphasize the fact that our model captures nonlinear energy transfer we calculate the graph dimension ![]() $D_G$ of the pulsation group velocity of the water waves used in the model source terms at NDBC Buoy 45005. We calculate
$D_G$ of the pulsation group velocity of the water waves used in the model source terms at NDBC Buoy 45005. We calculate ![]() $D_G$ using the method described in our companion paper (Conroy et al. Reference Conroy, Kubatko and Mandli2021) where the slope of the best fit line in figure 10 corresponds to the graph dimension of the pulsation velocity, which has a value of
$D_G$ using the method described in our companion paper (Conroy et al. Reference Conroy, Kubatko and Mandli2021) where the slope of the best fit line in figure 10 corresponds to the graph dimension of the pulsation velocity, which has a value of ![]() $1.57$ (
$1.57$ (![]() $H = 0.43$) and mirrors the graph dimension of the wind, see Conroy et al. (Reference Conroy, Kubatko and Mandli2021) for more details.
$H = 0.43$) and mirrors the graph dimension of the wind, see Conroy et al. (Reference Conroy, Kubatko and Mandli2021) for more details.

Figure 10. Least squares approximation of the graph dimension, ![]() $D_G$, of the pulsation group velocity of the water waves,
$D_G$, of the pulsation group velocity of the water waves, ![]() $\boldsymbol {c}_{g_f}$, for August 2011.
$\boldsymbol {c}_{g_f}$, for August 2011.
The correlation between the model output of water-wave period and observed water-wave period is not as high of a value as the correlation of significant wave height, and the r.m.s. error is also a higher value for the water-wave period as compared to significant wave height. This is a common theme among short wave models (Holthuijsen Reference Holthuijsen2007), and ultimately, high numerical resolution via ![]() $p$-refinement and
$p$-refinement and ![]() $h$-refinement (or adaptation) needs to be used in spatial areas where the peak frequency is rapidly changing to accurately resolve the water-wave period (Conroy et al. Reference Conroy, Kubatko and Mandli2021).
$h$-refinement (or adaptation) needs to be used in spatial areas where the peak frequency is rapidly changing to accurately resolve the water-wave period (Conroy et al. Reference Conroy, Kubatko and Mandli2021).
5. Conclusions
Energy transfer in turbulent fluids is non-Gaussian. We quantify this non-Gaussian transfer between wind and water using self-affine velocity distributions and a recursive integration method that redistributes and concentrates this transfer in time. The resulting energy measures are multifractal and the dimension of the support of the energy distribution is consistent with theory and observation. The self-affine velocity distributions satisfy a parametrized form of the energy balance equation for water waves as well as invariant properties of the Navier–Stokes equation and are used to construct source terms for a system of moment field equations that track and propagate the short water waves created by air–water interactions.
Our methods are accurate and efficient; application to Lake Erie produces embedding dimensions that lie in the range ![]() $2.82 \geq D_E \geq 2.27$, and correspondingly, water-wave periods and significant water-wave heights are well correlated with observational buoy data and the water-wave model known as SWAN. Further, our methods execute almost 40 times as quickly as SWAN.
$2.82 \geq D_E \geq 2.27$, and correspondingly, water-wave periods and significant water-wave heights are well correlated with observational buoy data and the water-wave model known as SWAN. Further, our methods execute almost 40 times as quickly as SWAN.
The recursive integration method presented herein can be used by a full spectral model to interpolate the wind data (![]() $U_{10}$) in a non-Gaussian fashion. Typical short water-wave models interpolate the wind input to smaller time scales using linear interpolation, which does not extend the variability dependence of the observational data to small scales (hourly averaged data down to minutes or seconds), and can distort the timing of how energy flows within the water-wave spectrum. In fact, this could be part of the reason why phase-averaged water-wave models have had trouble capturing peak water-wave heights and periods in strong storms, as described by Cavaleri (Reference Cavaleri2009).
$U_{10}$) in a non-Gaussian fashion. Typical short water-wave models interpolate the wind input to smaller time scales using linear interpolation, which does not extend the variability dependence of the observational data to small scales (hourly averaged data down to minutes or seconds), and can distort the timing of how energy flows within the water-wave spectrum. In fact, this could be part of the reason why phase-averaged water-wave models have had trouble capturing peak water-wave heights and periods in strong storms, as described by Cavaleri (Reference Cavaleri2009).
Future work could follow a number of different paths (for instance, in regards to the recursive integration), but our ultimate goal is to utilize the model in ensemble storm surge studies. To fully depict the short water-wave field in this case an additional swell phase needs to be included in the moment field equations as well as the appropriate transfer and dissipation terms. One can argue that swell dissipation is the largest source of error in phase-averaging water-wave models (Stopa et al. Reference Stopa, Ardhuin, Husson, Jiang, Chapron and Collard2016) and we plan to collaborate with scientists (see Zappa et al. (Reference Zappa, Banner, Schultz, Corrada-Emmanuel, Wolff and Yalcin2008) for instance) to obtain more accurate estimates of swell decay. In addition to modelling swell and its dissipation, we will need to develop source terms that account for coastal effects as the short water waves propagate into coastal regions, which we could base on the work of Holthuijsen, Booij & Herbers (Reference Holthuijsen, Booij and Herbers1989). This work is well under way and future investigations will examine how to consistently transfer energy between the wind-sea and swell phases, as well as the longer circulation waves that the short water waves form on.
Declaration of interests
The authors report no conflict of interest.
Appendix A. Recursive integration computer code
The recursive integration computer code can be obtained at https://doi.org/10.5281/zenodo.4570654.
Appendix B. Derivation of energy based moment field equations
Consider a constant density flow field described by the Navier–Stokes equations (Salmon Reference Salmon1998),
where repeated subscripts imply the summation convention. The moment field equations can be derived in terms of the energy of the water waves by contracting the momentum (B1) with ![]() $v_i$, namely
$v_i$, namely
 \begin{align} \frac{\partial }{\partial t}\left(\frac{1}{2}v_i v_i\right)+\frac{\partial }{\partial x_j}\left(\frac{1}{2}v_i v_i v_j\right)&={-}\frac{\partial }{\partial x_i}(v_i p)-\tilde{\nu}\frac{\partial }{\partial x_j}\left(v_i\frac{\partial v_i}{\partial x_j}\right)\nonumber\\ &\quad +\tilde{\mu}\frac{\partial }{\partial x_j}\left(\frac{\partial }{\partial x_j}\left(\frac{1}{2}v_i v_i\right)\right), \end{align}
\begin{align} \frac{\partial }{\partial t}\left(\frac{1}{2}v_i v_i\right)+\frac{\partial }{\partial x_j}\left(\frac{1}{2}v_i v_i v_j\right)&={-}\frac{\partial }{\partial x_i}(v_i p)-\tilde{\nu}\frac{\partial }{\partial x_j}\left(v_i\frac{\partial v_i}{\partial x_j}\right)\nonumber\\ &\quad +\tilde{\mu}\frac{\partial }{\partial x_j}\left(\frac{\partial }{\partial x_j}\left(\frac{1}{2}v_i v_i\right)\right), \end{align}which is the energy equation for a constant density fluid (Salmon Reference Salmon1998). Re-arranging the above expression,
while defining,
and setting,
we arrive at a balance equation for ![]() $\varPhi$,
$\varPhi$,
It can be noted that ![]() $\varPhi$ is the energy of the flow field over its entire range of scales (or wavelengths), and can be represented by the characteristic function,
$\varPhi$ is the energy of the flow field over its entire range of scales (or wavelengths), and can be represented by the characteristic function,
where ![]() $\ell$ is length and
$\ell$ is length and ![]() $k=\|\boldsymbol {k}\|$ is the magnitude of the wave vector with mean direction
$k=\|\boldsymbol {k}\|$ is the magnitude of the wave vector with mean direction ![]() $\bar {\theta }$ at the geographic point
$\bar {\theta }$ at the geographic point ![]() $\boldsymbol {x}_0$ and
$\boldsymbol {x}_0$ and ![]() ${\rm i} = \sqrt {-1}$. We quantify spectral fluctuations clustered about a characteristic energy level,
${\rm i} = \sqrt {-1}$. We quantify spectral fluctuations clustered about a characteristic energy level, ![]() $m_0$,
$m_0$,
by expanding ![]() $\varPhi _N$ into a series of moments about the variance of the high-frequency gravity water waves,
$\varPhi _N$ into a series of moments about the variance of the high-frequency gravity water waves,
 \begin{align} \varPhi_N(\ell) &= \int_{k_i}^{k_f}{ F(k)\exp{({\rm i}k\ell)}\,{\rm d}k} \approx \sum_{n=0}^{N} \left(\frac{m_n}{n!}\right)\ell^n \nonumber\\ &\approx m_0+(m_0\bar{k}_1)\ell+(m_1\bar{k}_2)\frac{\ell^2}{2!}+\cdots +(m_{N-1}\bar{k}_{N})\frac{\ell^N}{N!}, \end{align}
\begin{align} \varPhi_N(\ell) &= \int_{k_i}^{k_f}{ F(k)\exp{({\rm i}k\ell)}\,{\rm d}k} \approx \sum_{n=0}^{N} \left(\frac{m_n}{n!}\right)\ell^n \nonumber\\ &\approx m_0+(m_0\bar{k}_1)\ell+(m_1\bar{k}_2)\frac{\ell^2}{2!}+\cdots +(m_{N-1}\bar{k}_{N})\frac{\ell^N}{N!}, \end{align}
where ![]() $N$ represents the spectral cutoff associated with the wind sea and
$N$ represents the spectral cutoff associated with the wind sea and ![]() $\bar {k}_{n+1} = {m_{n+1}}/{m_n}$ is the representative wavenumber of level
$\bar {k}_{n+1} = {m_{n+1}}/{m_n}$ is the representative wavenumber of level ![]() $n+1$. The corresponding expansion of the magnitude of the energy transport velocity
$n+1$. The corresponding expansion of the magnitude of the energy transport velocity ![]() $V_N$ is,
$V_N$ is,
 \begin{align} V_{N}(\ell) &=c_0+\sum_{n=1}^{N} \left(\int_{k_0}^{k_N} k^{n-1} G(k)\,{\rm d}k\right)\frac{\ell^{(n-1)}}{(n-1)!} \nonumber\\ & = c_{0}+c_1+c_2 ( \ell )+\cdots+c_{N}\left(\frac{\ell^{(N-1)}}{(N-1)!}\right), \end{align}
\begin{align} V_{N}(\ell) &=c_0+\sum_{n=1}^{N} \left(\int_{k_0}^{k_N} k^{n-1} G(k)\,{\rm d}k\right)\frac{\ell^{(n-1)}}{(n-1)!} \nonumber\\ & = c_{0}+c_1+c_2 ( \ell )+\cdots+c_{N}\left(\frac{\ell^{(N-1)}}{(N-1)!}\right), \end{align}
where ![]() $G(k)$ is the probability density of
$G(k)$ is the probability density of ![]() $V$,
$V$, ![]() $c_0$ is the speed of the reference frame that the high-frequency gravity water waves are travelling with (say, a baroclinic current),
$c_0$ is the speed of the reference frame that the high-frequency gravity water waves are travelling with (say, a baroclinic current), ![]() $c_1$ is the speed associated with the water-wave group,
$c_1$ is the speed associated with the water-wave group, ![]() $c_2$ is the acceleration of the water-wave group, etc. Substituting (B11) and (B12) into (B8), we have,
$c_2$ is the acceleration of the water-wave group, etc. Substituting (B11) and (B12) into (B8), we have,
 \begin{align} \frac{\partial }{\partial t}\left(\sum_{n=0}^{N} \left(\frac{m_n}{n!}\right)\ell^n\right)&= \tilde{\mu}\frac{\partial }{\partial x_j}\left(\frac{\partial }{\partial x_j}\sum_{n=0}^{N} \left(\frac{m_n}{n!}\right)\ell^n\right) \nonumber\\ &\quad -\frac{\partial }{\partial x_j}\left[\left(\sum_{n=0}^{N} \left(\frac{m_n}{n!}\right)\ell^n\right)\left(c_0 + \sum_{n=1}^{N} c_n \frac{\ell^{(n-1)}}{(n-1)!} \right)_j\right]. \end{align}
\begin{align} \frac{\partial }{\partial t}\left(\sum_{n=0}^{N} \left(\frac{m_n}{n!}\right)\ell^n\right)&= \tilde{\mu}\frac{\partial }{\partial x_j}\left(\frac{\partial }{\partial x_j}\sum_{n=0}^{N} \left(\frac{m_n}{n!}\right)\ell^n\right) \nonumber\\ &\quad -\frac{\partial }{\partial x_j}\left[\left(\sum_{n=0}^{N} \left(\frac{m_n}{n!}\right)\ell^n\right)\left(c_0 + \sum_{n=1}^{N} c_n \frac{\ell^{(n-1)}}{(n-1)!} \right)_j\right]. \end{align}
Evaluating (B13) at ![]() $\ell = 0$ gives,
$\ell = 0$ gives,
 \begin{equation} \frac{\partial m_{0}}{\partial t}+\frac{\partial }{\partial x_j}\left(m_{0}\sum_{i=0}^1 c_{ji}\right)=\tilde{\mu}\frac{\partial }{\partial x_j}\left( \frac{\partial m_{0}}{\partial x_j}\right). \end{equation}
\begin{equation} \frac{\partial m_{0}}{\partial t}+\frac{\partial }{\partial x_j}\left(m_{0}\sum_{i=0}^1 c_{ji}\right)=\tilde{\mu}\frac{\partial }{\partial x_j}\left( \frac{\partial m_{0}}{\partial x_j}\right). \end{equation}
Taking the derivative of (B13) with respect to ![]() $\ell$ and setting
$\ell$ and setting ![]() $\ell = 0$ yields
$\ell = 0$ yields ![]() $m_1$,
$m_1$,
 \begin{equation} \frac{\partial m_{1}}{\partial t}+\frac{\partial }{\partial x_j}\left(m_{1}\sum_{i=0}^1 c_{ji}+m_0c_{j2}\right)=\tilde{\mu}\frac{\partial }{\partial x_j}\left( \frac{\partial m_{1}}{\partial x_j}\right). \end{equation}
\begin{equation} \frac{\partial m_{1}}{\partial t}+\frac{\partial }{\partial x_j}\left(m_{1}\sum_{i=0}^1 c_{ji}+m_0c_{j2}\right)=\tilde{\mu}\frac{\partial }{\partial x_j}\left( \frac{\partial m_{1}}{\partial x_j}\right). \end{equation}
Repeating this process of taking the ![]() $n$th derivative of (B13) and setting
$n$th derivative of (B13) and setting ![]() $\ell = 0$ we arrive at the moment field equations,
$\ell = 0$ we arrive at the moment field equations,
 \begin{equation} \frac{\partial m_{n}}{\partial t}+\frac{\partial }{\partial x_j}\left(m_{n}c_{j,0}+\sum_{i=0}^n m_{n-i} c_{j,i+1}\right)=\tilde{\mu}\frac{\partial }{\partial x_j}\left( \frac{\partial m_{n}}{\partial x_j}\right),\quad n = 0, 1, \ldots, N, \end{equation}
\begin{equation} \frac{\partial m_{n}}{\partial t}+\frac{\partial }{\partial x_j}\left(m_{n}c_{j,0}+\sum_{i=0}^n m_{n-i} c_{j,i+1}\right)=\tilde{\mu}\frac{\partial }{\partial x_j}\left( \frac{\partial m_{n}}{\partial x_j}\right),\quad n = 0, 1, \ldots, N, \end{equation}
a system of ![]() $N$ balance equations that are coupled together through the representative wavenumbers
$N$ balance equations that are coupled together through the representative wavenumbers ![]() $\bar {k}_{n+1}$ (the
$\bar {k}_{n+1}$ (the ![]() $c_{ji}$ coefficients are functions of these wavenumbers), where
$c_{ji}$ coefficients are functions of these wavenumbers), where ![]() $c_{1i} = c_i(\bar {k}_{n+1}) \cos \bar {\theta }_i$ and
$c_{1i} = c_i(\bar {k}_{n+1}) \cos \bar {\theta }_i$ and ![]() $c_{2i} = c_i(\bar {k}_{n+1}) \sin \bar {\theta }_i$ and
$c_{2i} = c_i(\bar {k}_{n+1}) \sin \bar {\theta }_i$ and ![]() $\bar {\theta }_0$ is the mean direction of the ambient current and
$\bar {\theta }_0$ is the mean direction of the ambient current and ![]() $\bar {\theta }_i$ (
$\bar {\theta }_i$ (![]() $i > 0$) is given by,
$i > 0$) is given by,
where ![]() $D(\boldsymbol {x},t)$ parameterizes the inhomogeneities of the medium of propagation, see Salmon (Reference Salmon1998) for example. It can be noted that a similar procedure can be performed to derive a system of moment field equations for the momentum (in which case the moment field would be similar to the RANS equation) and for the energy flux (in which case one would just contract the energy equation with
$D(\boldsymbol {x},t)$ parameterizes the inhomogeneities of the medium of propagation, see Salmon (Reference Salmon1998) for example. It can be noted that a similar procedure can be performed to derive a system of moment field equations for the momentum (in which case the moment field would be similar to the RANS equation) and for the energy flux (in which case one would just contract the energy equation with ![]() $v_i$).
$v_i$).