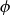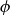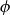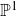1. Introduction
A celebrated theorem of Silverman [ Reference Silverman24 ] states that there are only finitely many integral points in an orbit under a rational function defined over a number field, as long as the second iterate of the function is not a polynomial. Hsia–Silverman [ Reference Hsia and Silverman9 ] then made this theorem explicit and uniform: the upper bound for the number of integral points is given by an explicit formula in terms of the height of the initial point, and the largest iterate which can be integral is given uniformly independent of the initial point. The results of Hsia–Silverman have already been generalised in many directions. Just to name a few, Mello [ Reference Mello21 ] has considered integral points in orbits under several (not necessarily commuting) rational functions and obtained similar upper bounds, and Hindes [ Reference Hindes7 ] has proved that the number of integral points in an orbit is uniformly bounded in a suitable one-parameter family of initial points and rational functions and that the average over such a family is in fact zero.
In this paper, we consider another generalisation of Hsia–Silverman, namely to morphisms on higher-dimensional projective spaces. The author [ Reference Yasufuku29 ] has considered some cases of higher-dimensional analogs of Silverman’s result [ Reference Silverman24 ], so in some sense this paper is the combination of the two generalisations of [ Reference Silverman24 ]: namely, Hsia–Silverman [ Reference Hsia and Silverman9 ] and the author [ Reference Yasufuku29 ]. Higher-dimensional Diophantine geometry is in general quite difficult; the Bombieri–Lang conjecture, which states the sparsity of rational points on varieties of general type, is already open in dimension 2. There has been plethora of recent research surrounding uniformity of rational points on abelian varieties (e.g. [ Reference Dimitrov, Gao and Habegger3, Reference Gao, Ge and Kühne5 ]), but still, working with higher-dimensional varieties often forces us to either restrict to certain cases or assume various deep conjectures.
We prove two results in this paper on uniformity of quasi-integral points in higher-dimensional orbits. The results are uniform in two senses: independent of the initial point of the orbit, and independent of a specific number field as long as the degree is bounded. The first result applies when the pullback of a divisor by some iterate of
![]() $\phi$
breaks up into enough irreducible components which are numerical multiples of each other. For this result, we use Le’s algebraic-point version [
Reference Le13
] of the recent result of Ji–Yan–Yu [
Reference Ji, Yan and Yu10
] which is a type of Schmidt subspace theorem for divisors in subgeneral position. The second result applies more generally, but it assumes the algebraic-point version of Vojta’s conjecture. This conjecture, in the special form of the abc conjecture and the abcd conjecture, was used by Looper [
Reference Looper15, Reference Looper16
] to show uniform boundedness of preperiodic points for polynomials. The second result is more dynamical in nature, as it uses arithmetic degrees introduced by Kawaguchi–Silverman as well as the theory of asymptotic multiplicities of forward orbits, which were used in a recent result of Matsuzawa [
Reference Matsuzawa20
].
$\phi$
breaks up into enough irreducible components which are numerical multiples of each other. For this result, we use Le’s algebraic-point version [
Reference Le13
] of the recent result of Ji–Yan–Yu [
Reference Ji, Yan and Yu10
] which is a type of Schmidt subspace theorem for divisors in subgeneral position. The second result applies more generally, but it assumes the algebraic-point version of Vojta’s conjecture. This conjecture, in the special form of the abc conjecture and the abcd conjecture, was used by Looper [
Reference Looper15, Reference Looper16
] to show uniform boundedness of preperiodic points for polynomials. The second result is more dynamical in nature, as it uses arithmetic degrees introduced by Kawaguchi–Silverman as well as the theory of asymptotic multiplicities of forward orbits, which were used in a recent result of Matsuzawa [
Reference Matsuzawa20
].
We now state our main results precisely. For the first result, we follow [
Reference Le13
] to define
![]() $C(m, M, \delta)$
as
$C(m, M, \delta)$
as
 \begin{equation}C(m, M, \delta) = \begin{cases}(\delta m - \delta M + 1)(\delta M +1) &M\le \frac m2\\[5pt] (\frac {\delta m}2 + 1)^2 &M \gt \frac m2 \text{ and } \delta m \text{ is even}\\[5pt] (\lfloor\frac {\delta m}2\rfloor + 1)(\lfloor\frac {\delta m}2\rfloor + 2) &M \gt \frac m2 \text{ and } \delta m \text{ is odd}\end{cases}\end{equation}
\begin{equation}C(m, M, \delta) = \begin{cases}(\delta m - \delta M + 1)(\delta M +1) &M\le \frac m2\\[5pt] (\frac {\delta m}2 + 1)^2 &M \gt \frac m2 \text{ and } \delta m \text{ is even}\\[5pt] (\lfloor\frac {\delta m}2\rfloor + 1)(\lfloor\frac {\delta m}2\rfloor + 2) &M \gt \frac m2 \text{ and } \delta m \text{ is odd}\end{cases}\end{equation}
for natural numbers
![]() $m, M, \delta$
, where
$m, M, \delta$
, where
![]() $\lfloor \,\,\rfloor$
is the floor function. Throughout the paper, we use the notation of
$\lfloor \,\,\rfloor$
is the floor function. Throughout the paper, we use the notation of
![]() $ \phi^{{\circ}t}$
for the tth iterate of
$ \phi^{{\circ}t}$
for the tth iterate of
![]() $\phi$
, and the degree of
$\phi$
, and the degree of
![]() $\phi$
is the polarisation degree (not the topological degree which counts the number of preimages). The first result is as follows.
$\phi$
is the polarisation degree (not the topological degree which counts the number of preimages). The first result is as follows.
Theorem 1. Let
![]() $m, M, \delta$
be natural numbers,
$m, M, \delta$
be natural numbers,
![]() $d$
be a natural number at least 2, and let
$d$
be a natural number at least 2, and let
![]() $\epsilon$
be a positive real number at most 1. Let
$\epsilon$
be a positive real number at most 1. Let
![]() $k$
be a number field, and suppose that:
$k$
be a number field, and suppose that:
-
(i)
 $\phi\;:\; {\mathbb{P}}^M {\longrightarrow} {\mathbb{P}}^M$
is a morphism of degree
$\phi\;:\; {\mathbb{P}}^M {\longrightarrow} {\mathbb{P}}^M$
is a morphism of degree
 $d$
defined over k;
$d$
defined over k; -
(ii)
 $D$
is a (possibly reducible) hypersurface in
$D$
is a (possibly reducible) hypersurface in
 ${\mathbb{P}}^M$
;
${\mathbb{P}}^M$
; -
(iii) there exists a natural number
 $t$
such that where
$t$
such that where \[\left( \phi^{{\circ}t} \right)^*D = D_1 + \cdots + D_q + D',\]
\[\left( \phi^{{\circ}t} \right)^*D = D_1 + \cdots + D_q + D',\]
 $D_1, \ldots, D_q$
are in
$D_1, \ldots, D_q$
are in
 $m$
-subgeneral position,
$m$
-subgeneral position,
 $D'$
is an effective divisor, and
$D'$
is an effective divisor, and  \[\frac {\epsilon d^t {(\deg D)}- (\deg D')}{\displaystyle \max_i \deg D_i} \gt C(m, M, \delta);\]
\[\frac {\epsilon d^t {(\deg D)}- (\deg D')}{\displaystyle \max_i \deg D_i} \gt C(m, M, \delta);\]
-
(iv)
 $S$
is a finite set of places of
$S$
is a finite set of places of
 $k$
including all archimedean ones, and
$k$
including all archimedean ones, and
 $\mathcal R_\epsilon$
is a set of
$\mathcal R_\epsilon$
is a set of
 $(D,S,\epsilon)$
-quasi-integral points.
$(D,S,\epsilon)$
-quasi-integral points.
Then
and
are both finite sets, and moreover, there exists
![]() $N = N(\phi, S, \epsilon, \delta, m)$
such that whenever
$N = N(\phi, S, \epsilon, \delta, m)$
such that whenever
![]() $\phi^{{\circ} n} (P)\in \mathcal R_\epsilon\backslash {|D|}$
for
$\phi^{{\circ} n} (P)\in \mathcal R_\epsilon\backslash {|D|}$
for
![]() $P\in {\mathbb{P}}^M(K)$
with
$P\in {\mathbb{P}}^M(K)$
with
![]() $[K\;:\;k]\le \delta$
and
$[K\;:\;k]\le \delta$
and
![]() $n\in {\mathbb{N}}$
, n is at most N.
$n\in {\mathbb{N}}$
, n is at most N.
The definitions of m-subgeneral positions and quasi-integral points will be given in the next section. We only note here that the
![]() $\epsilon=1$
case of
$\epsilon=1$
case of
![]() $(D,S,\epsilon)$
-quasi-integral points corresponds to the usual notion of (
$(D,S,\epsilon)$
-quasi-integral points corresponds to the usual notion of (
![]() $D$
,
$D$
,
![]() $S$
)-integral points.
$S$
)-integral points.
By conjugating with a linear polynomial with a highly divisible leading coefficient, one can force the first N iterates to be integral (cf. [
Reference Silverman25
, proposition 3·46]). Therefore, N has to depend on
![]() $\phi$
(and thus also on d). N also has to depend on S, since enlarging S makes more iterates integral.
$\phi$
(and thus also on d). N also has to depend on S, since enlarging S makes more iterates integral.
Theorem 1 for the case of
![]() ${\mathbb{P}}^1$
does not quite recover the result of Hsia–Silverman [
Reference Hsia and Silverman9
], as there are non-polynomial maps not satisfying hypothesis (iii). On the other hand, we can modify the proof in the case of
${\mathbb{P}}^1$
does not quite recover the result of Hsia–Silverman [
Reference Hsia and Silverman9
], as there are non-polynomial maps not satisfying hypothesis (iii). On the other hand, we can modify the proof in the case of
![]() ${\mathbb{P}}^1$
to obtain a stronger statement, from which the results of Hsia–Silverman easily follow. With this modification, Theorem 1 for the case of
${\mathbb{P}}^1$
to obtain a stronger statement, from which the results of Hsia–Silverman easily follow. With this modification, Theorem 1 for the case of
![]() ${\mathbb{P}}^1$
easily implies that the ‘average’ number of integral points in orbits is zero as first proved by Gunther–Hindes [
Reference Gunther and Hindes6
], because finiteness of (1·3) implies that orbits of points with sufficiently large height contain no integral points. See Remark 6 for more details. Also, we discuss in Remark 7 the inter-relationship among the three conclusions of the theorem, and we discuss some generalisations to projective varieties in Remark 8.
${\mathbb{P}}^1$
easily implies that the ‘average’ number of integral points in orbits is zero as first proved by Gunther–Hindes [
Reference Gunther and Hindes6
], because finiteness of (1·3) implies that orbits of points with sufficiently large height contain no integral points. See Remark 6 for more details. Also, we discuss in Remark 7 the inter-relationship among the three conclusions of the theorem, and we discuss some generalisations to projective varieties in Remark 8.
Example 2. Let
![]() $\mathfrak R_S$
be the subset of
$\mathfrak R_S$
be the subset of
![]() $\overline {\mathbb{Q}}$
consisting of elements which are integral over the the ring of
$\overline {\mathbb{Q}}$
consisting of elements which are integral over the the ring of
![]() $S$
-integers of
$S$
-integers of
![]() $k$
. Let
$k$
. Let
![]() $L_1,\ldots, L_q\in k[X_0,\ldots, X_M]$
be linear forms in general position,
$L_1,\ldots, L_q\in k[X_0,\ldots, X_M]$
be linear forms in general position,
![]() $F_1,\ldots, F_M\in k[X_0,\ldots, X_M]$
be homogeneous of degree
$F_1,\ldots, F_M\in k[X_0,\ldots, X_M]$
be homogeneous of degree
![]() $d$
, and let
$d$
, and let
![]() $F_0\in k[X_0,\ldots, X_M]$
be homogeneous of degree
$F_0\in k[X_0,\ldots, X_M]$
be homogeneous of degree
![]() $d-q$
. Let
$d-q$
. Let
![]() $\phi = [L_1\cdots L_q \cdot F_0\;:\; F_1 \;:\; \cdots \;:\; F_M]$
, and for any
$\phi = [L_1\cdots L_q \cdot F_0\;:\; F_1 \;:\; \cdots \;:\; F_M]$
, and for any
![]() $P\in {\mathbb{P}}^M(\overline {\mathbb{Q}})$
, we write
$P\in {\mathbb{P}}^M(\overline {\mathbb{Q}})$
, we write
![]() $\phi^{{\circ} n} (P) = [ {a_0}^{{\circ} n} \;:\; \cdots \;:\; {a_M}^{{\circ} n}]$
. Then Theorem 1 shows that as long as
$\phi^{{\circ} n} (P) = [ {a_0}^{{\circ} n} \;:\; \cdots \;:\; {a_M}^{{\circ} n}]$
. Then Theorem 1 shows that as long as
![]() $q \gt C(M, M, \delta)$
,
$q \gt C(M, M, \delta)$
,
and
are both finite sets, and there exists a uniform bound for
![]() $n$
(independently of
$n$
(independently of
![]() $P$
) for which
$P$
) for which
![]() ${{a_1}^{{\circ} n}}/{ {a_0}^{{\circ} n}},\ldots, {{a_M}^{{\circ} n}}/{{a_0}^{{\circ} n}}\in \mathfrak R_S$
. In particular, for quadratic points (the case of
${{a_1}^{{\circ} n}}/{ {a_0}^{{\circ} n}},\ldots, {{a_M}^{{\circ} n}}/{{a_0}^{{\circ} n}}\in \mathfrak R_S$
. In particular, for quadratic points (the case of
![]() $\delta = 2$
), we get these conclusions if
$\delta = 2$
), we get these conclusions if
![]() $q \gt (M+1)^2$
.
$q \gt (M+1)^2$
.
Next, we state our second result, this time with a less restrictive hypothesis but under assuming a deep conjecture from Diophantine geometry.
Theorem 3. Let
![]() $\phi\;:\; {\mathbb{P}}^M \longrightarrow {\mathbb{P}}^M$
be a surjective morphism of degree
$\phi\;:\; {\mathbb{P}}^M \longrightarrow {\mathbb{P}}^M$
be a surjective morphism of degree
![]() $d\ge 2$
defined over a number field
$d\ge 2$
defined over a number field
![]() $k$
, and let S be a finite subset of
$k$
, and let S be a finite subset of
![]() $M_k$
. Let
$M_k$
. Let
![]() $D$
be a nontrivial effective divisor on
$D$
be a nontrivial effective divisor on
![]() ${\mathbb{P}}^M$
defined over
${\mathbb{P}}^M$
defined over
![]() $k$
,
$k$
,
![]() $\epsilon$
be a positive real number at most 1, and let
$\epsilon$
be a positive real number at most 1, and let
![]() $\mathcal R_\epsilon$
be a set of
$\mathcal R_\epsilon$
be a set of
![]() $(D,S,\epsilon)$
-quasi-integral points. Assume that Vojta’s General Conjecture (Conjecture 9) holds for a certain blowup of projective spaces determined by
$(D,S,\epsilon)$
-quasi-integral points. Assume that Vojta’s General Conjecture (Conjecture 9) holds for a certain blowup of projective spaces determined by
![]() $\phi$
and
$\phi$
and
![]() $D$
. Then there exist a Zariski-closed
$D$
. Then there exist a Zariski-closed
![]() $Z=Z(D,S,\epsilon) \subsetneq {\mathbb{P}}^M$
and a constant N such that if
$Z=Z(D,S,\epsilon) \subsetneq {\mathbb{P}}^M$
and a constant N such that if
![]() $P$
satisfies:
$P$
satisfies:
-
(i)
 $P\in {\mathbb{P}}^M(K)$
with
$P\in {\mathbb{P}}^M(K)$
with
 $[K\;:\;k] \le \delta$
;
$[K\;:\;k] \le \delta$
; -
(ii) P is not a preperiodic point under
 $\phi$
;
$\phi$
; -
(iii) for every
 $\phi$
-periodic irreducible subvariety Y with
$\phi$
-periodic irreducible subvariety Y with
 $Y\cap D \neq \emptyset$
,
$Y\cap D \neq \emptyset$
,
 $e_{\phi, +}(Y) \lt \alpha_\phi(P)$
;
$e_{\phi, +}(Y) \lt \alpha_\phi(P)$
; -
(iv)
 $\phi^{{\circ} n} (P) \in \mathcal R_\epsilon$
,
$\phi^{{\circ} n} (P) \in \mathcal R_\epsilon$
,
then either
![]() $\phi^{{\circ} n} (P) \in Z$
or n is bounded above by N.
$\phi^{{\circ} n} (P) \in Z$
or n is bounded above by N.
Here,
![]() $\alpha_\phi(P)$
is the arithmetic degree and
$\alpha_\phi(P)$
is the arithmetic degree and
![]() $e_{\phi,+}(Y)$
is the asymptotic multiplicity of the forward orbit of the scheme point Y: the precise definitions will be given in Section 3. For the case of
$e_{\phi,+}(Y)$
is the asymptotic multiplicity of the forward orbit of the scheme point Y: the precise definitions will be given in Section 3. For the case of
![]() ${\mathbb{P}}^1$
, there exist no nontrivial blowups, and Vojta’s General conjecture is known to be equivalent to the abc conjecture ([
Reference Vojta27
]). Moreover, since Z is a finite set in this case, the proof in Section 3 will show the existence of a uniform bound N without the exceptional set Z. This way, we obtain the algebraic-point version of Hsia–Silverman [
Reference Hsia and Silverman9
, theorem 11]. Also, in Remark 11, we show an example which demonstrates that the hypothesis
${\mathbb{P}}^1$
, there exist no nontrivial blowups, and Vojta’s General conjecture is known to be equivalent to the abc conjecture ([
Reference Vojta27
]). Moreover, since Z is a finite set in this case, the proof in Section 3 will show the existence of a uniform bound N without the exceptional set Z. This way, we obtain the algebraic-point version of Hsia–Silverman [
Reference Hsia and Silverman9
, theorem 11]. Also, in Remark 11, we show an example which demonstrates that the hypothesis
![]() $e_{\phi, +}(Y) \lt \alpha_\phi(P)$
is necessary, and in Remark 12, we discuss a generalisation of this theorem to polarised morphisms on projective varieties. In the final remark, we consider whether the exceptional set Z is really necessary in Theorem 3.
$e_{\phi, +}(Y) \lt \alpha_\phi(P)$
is necessary, and in Remark 12, we discuss a generalisation of this theorem to polarised morphisms on projective varieties. In the final remark, we consider whether the exceptional set Z is really necessary in Theorem 3.
2. Notations, and the Proof of Theorem 1
Let k be a number field, and let
![]() $M_k$
be the set of places of k. For each
$M_k$
be the set of places of k. For each
![]() $v\in M_k$
, we define the normalised absolute value
$v\in M_k$
, we define the normalised absolute value
![]() $|\cdot |_v$
as follows: for
$|\cdot |_v$
as follows: for
![]() $k = {\mathbb{Q}}$
,
$k = {\mathbb{Q}}$
,
![]() $|\cdot |_\infty$
is the usual absolute value on
$|\cdot |_\infty$
is the usual absolute value on
![]() ${\mathbb{R}}$
, and for each prime p, we define the normalised p-adic absolute value
${\mathbb{R}}$
, and for each prime p, we define the normalised p-adic absolute value
![]() $|\cdot |_p$
by setting
$|\cdot |_p$
by setting
![]() $|p|_p = 1/p$
. For a general number field k, we define
$|p|_p = 1/p$
. For a general number field k, we define
![]() $|\cdot |_v$
to be the
$|\cdot |_v$
to be the
![]() ${[k_v\;:\; {\mathbb{Q}}_v]}/{[k\;:\;{\mathbb{Q}}]}$
-th power of the v-adic absolute value which restricts to one of the normalised absolute values on
${[k_v\;:\; {\mathbb{Q}}_v]}/{[k\;:\;{\mathbb{Q}}]}$
-th power of the v-adic absolute value which restricts to one of the normalised absolute values on
![]() ${\mathbb{Q}}$
. With this normalisation, the product formula
${\mathbb{Q}}$
. With this normalisation, the product formula
holds for all
![]() $x\in k^*$
.
$x\in k^*$
.
The height of a point
![]() $P = [a_0:\cdots \;:\; a_M]\in {\mathbb{P}}^M(k)$
is defined by
$P = [a_0:\cdots \;:\; a_M]\in {\mathbb{P}}^M(k)$
is defined by
For an effective divisor D on
![]() ${\mathbb{P}}^M$
defined by a homogeneous polynomial
${\mathbb{P}}^M$
defined by a homogeneous polynomial
![]() $F\in k[x_0, \ldots, x_M]$
, the Weil height is defined simply by
$F\in k[x_0, \ldots, x_M]$
, the Weil height is defined simply by
and the local height is defined by
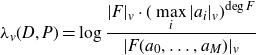 \[\lambda_v(D, P) = \log \frac{|F|_v \cdot \displaystyle (\max_i |a_i|_v)^{\deg F}}{|F(a_0,\ldots, a_M)|_v}\]
\[\lambda_v(D, P) = \log \frac{|F|_v \cdot \displaystyle (\max_i |a_i|_v)^{\deg F}}{|F(a_0,\ldots, a_M)|_v}\]
for
![]() $v\in M_k$
and
$v\in M_k$
and
![]() $P\in ({\mathbb{P}}^M \backslash D)(k)$
, where
$P\in ({\mathbb{P}}^M \backslash D)(k)$
, where
![]() $|F|_v$
is the maximum of the
$|F|_v$
is the maximum of the
![]() $v$
-adic absolute values of the coefficients of
$v$
-adic absolute values of the coefficients of
![]() $F$
. The notions of Weil heights and local heights can be generalised to any projective variety X, and
$F$
. The notions of Weil heights and local heights can be generalised to any projective variety X, and
is a bounded function on
![]() $(X \backslash D)(\overline {\mathbb{Q}})$
. For more details, see for example [
Reference Bombieri and Gubler2, Reference Hindry and Silverman8
].
$(X \backslash D)(\overline {\mathbb{Q}})$
. For more details, see for example [
Reference Bombieri and Gubler2, Reference Hindry and Silverman8
].
We can now define the notion of quasi-integral points.
Definition 4. Let
![]() $X$
be a projective variety defined over a number field
$X$
be a projective variety defined over a number field
![]() $k$
, and
$k$
, and
![]() $D$
be an effective divisor defined over
$D$
be an effective divisor defined over
![]() $k$
. Let
$k$
. Let
![]() $S$
be a finite set of places of
$S$
be a finite set of places of
![]() $k$
, and let
$k$
, and let
![]() $\epsilon$
be a positive real number at most 1. A set of
$\epsilon$
be a positive real number at most 1. A set of
![]() $(D,S,\epsilon)$
-quasi-integral points is a set of the form
$(D,S,\epsilon)$
-quasi-integral points is a set of the form
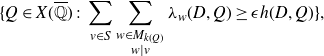 \[\{Q\in X(\overline {\mathbb{Q}})\;:\; \sum_{v\in S} \sum_{\substack{w\in M_{k(Q)}\\ w \mid v}} \lambda_w (D, Q) \ge \epsilon h(D, Q)\},\]
\[\{Q\in X(\overline {\mathbb{Q}})\;:\; \sum_{v\in S} \sum_{\substack{w\in M_{k(Q)}\\ w \mid v}} \lambda_w (D, Q) \ge \epsilon h(D, Q)\},\]
where
![]() $k(Q)$
is the field of definition of
$k(Q)$
is the field of definition of
![]() $Q$
.
$Q$
.
A set of (D, S,1)-quasi-integral points corresponds to the notion of (D, S)-integral points. In particular, when
![]() $D = (X_0 = 0)$
is the hyperplane in
$D = (X_0 = 0)$
is the hyperplane in
![]() ${\mathbb{P}}^M$
,
${\mathbb{P}}^M$
,
is a set of (D, S)-integral points, where
![]() $\mathfrak R_{S}$
is the subset of
$\mathfrak R_{S}$
is the subset of
![]() $\overline {\mathbb{Q}}$
consisting of elements which are integral over the the ring of S-integers of k.
$\overline {\mathbb{Q}}$
consisting of elements which are integral over the the ring of S-integers of k.
To prove Theorem 1, we use the following theorem of [
Reference Le13
], which is an algebraic-point version of [
Reference Ji, Yan and Yu10
]. We recall that effective divisors
![]() $D_1, \ldots, D_q$
are in m-subgeneral position if for any subset
$D_1, \ldots, D_q$
are in m-subgeneral position if for any subset
![]() $I\subseteq \{1,\ldots, q\}$
with
$I\subseteq \{1,\ldots, q\}$
with
![]() $|I| \le m+1$
, we have
$|I| \le m+1$
, we have
Theorem 5 ([
Reference Le13
, theorem 2]). Let
![]() $m, M, \delta$
be natural numbers, and let
$m, M, \delta$
be natural numbers, and let
![]() $C(m,M,\delta)$
as in (1·1). Let
$C(m,M,\delta)$
as in (1·1). Let
![]() $D_1,\ldots, D_q$
be effective nontrivial Cartier divisors on
$D_1,\ldots, D_q$
be effective nontrivial Cartier divisors on
![]() ${\mathbb{P}}^M$
which are defined over a number field k and are in m-subgeneral position. Then given
${\mathbb{P}}^M$
which are defined over a number field k and are in m-subgeneral position. Then given
![]() $\epsilon' \gt 0$
and a finite set S of places of k including all archimedean ones,
$\epsilon' \gt 0$
and a finite set S of places of k including all archimedean ones,
 \[\sum_{v\in S} \sum_{\substack{w\in M_{k(P)}\\ w \mid v}} \sum_{i=1}^q \frac {\lambda_w(D_i, P)}{\deg D_i} \lt (C(m, M,\delta) + \epsilon') h(P)\]
\[\sum_{v\in S} \sum_{\substack{w\in M_{k(P)}\\ w \mid v}} \sum_{i=1}^q \frac {\lambda_w(D_i, P)}{\deg D_i} \lt (C(m, M,\delta) + \epsilon') h(P)\]
holds for all but finitely many points
![]() $P\in {\mathbb{P}}^M(\overline k)\setminus \bigcup_{i=1}^q |D_i|$
satisfying
$P\in {\mathbb{P}}^M(\overline k)\setminus \bigcup_{i=1}^q |D_i|$
satisfying
![]() $[k(P)\;:\; k] \le \delta$
.
$[k(P)\;:\; k] \le \delta$
.
Proof of Theorem
1. By a standard Weil height property, there exists a constant
![]() ${C_{1}}$
such that
${C_{1}}$
such that
for all
![]() $Q\in {\mathbb{P}}^M(\overline {\mathbb{Q}})$
. As
$Q\in {\mathbb{P}}^M(\overline {\mathbb{Q}})$
. As
![]() $d \gt 1$
, we can rearrange terms to obtain
$d \gt 1$
, we can rearrange terms to obtain
so by letting
![]() ${C_{2}} = \displaystyle \frac {(d^t - 1) {C_{1}}}{d-1}$
, we have
${C_{2}} = \displaystyle \frac {(d^t - 1) {C_{1}}}{d-1}$
, we have
for all
![]() $Q\in {\mathbb{P}}^M(\overline {\mathbb{Q}})$
. By a standard property of local heights and by the fact that the Néron–Severi rank of
$Q\in {\mathbb{P}}^M(\overline {\mathbb{Q}})$
. By a standard property of local heights and by the fact that the Néron–Severi rank of
![]() ${\mathbb{P}}^M$
is one, it also follows that there exist constants
${\mathbb{P}}^M$
is one, it also follows that there exist constants
![]() ${C_{3}}$
and
${C_{3}}$
and
![]() ${C_{3}}'$
such that
${C_{3}}'$
such that
 \begin{equation}\sum_{v\in S} \sum_{\substack{w\in M_{k(Q)}\\ w\mid v}} \lambda_w(D', Q) \le h(D', Q) + {C_{3}}'\le (\deg D') h(Q) + {C_{3}}\end{equation}
\begin{equation}\sum_{v\in S} \sum_{\substack{w\in M_{k(Q)}\\ w\mid v}} \lambda_w(D', Q) \le h(D', Q) + {C_{3}}'\le (\deg D') h(Q) + {C_{3}}\end{equation}
for all
![]() $Q\in ({\mathbb{P}}^M\backslash D')(\overline {\mathbb{Q}})$
. There also exists a constant
$Q\in ({\mathbb{P}}^M\backslash D')(\overline {\mathbb{Q}})$
. There also exists a constant
![]() ${C_{4}}$
such that
${C_{4}}$
such that
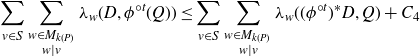 \begin{equation}\sum_{v\in S} \sum_{\substack{w\in M_{k(P)}\\ w\mid v}} \lambda_w(D, \phi^{{\circ} t} (Q))\le \sum_{v\in S} \sum_{\substack{w\in M_{k(P)}\\ w\mid v}} \lambda_w((\phi^{{\circ} t})^* D, Q) + {C_{4}}\end{equation}
\begin{equation}\sum_{v\in S} \sum_{\substack{w\in M_{k(P)}\\ w\mid v}} \lambda_w(D, \phi^{{\circ} t} (Q))\le \sum_{v\in S} \sum_{\substack{w\in M_{k(P)}\\ w\mid v}} \lambda_w((\phi^{{\circ} t})^* D, Q) + {C_{4}}\end{equation}
for all
![]() $Q\in {\mathbb{P}}^M(\overline {\mathbb{Q}})\setminus |(\phi^{{\circ} t})^{-1} D|$
.
$Q\in {\mathbb{P}}^M(\overline {\mathbb{Q}})\setminus |(\phi^{{\circ} t})^{-1} D|$
.
Now, suppose that
![]() $[K\;:\;k] \le \delta$
,
$[K\;:\;k] \le \delta$
,
![]() $P\in {\mathbb{P}}^M(K)$
, and
$P\in {\mathbb{P}}^M(K)$
, and
![]() $\phi ^{{\circ} n}(P) \in \mathcal R_\epsilon \backslash \phi^{{\circ} t}(|D'|\cup \bigcup_{i=1}^q |D_i|)$
with
$\phi ^{{\circ} n}(P) \in \mathcal R_\epsilon \backslash \phi^{{\circ} t}(|D'|\cup \bigcup_{i=1}^q |D_i|)$
with
![]() $n\ge t$
. By definition and by equations (2·3) and (2·4),
$n\ge t$
. By definition and by equations (2·3) and (2·4),
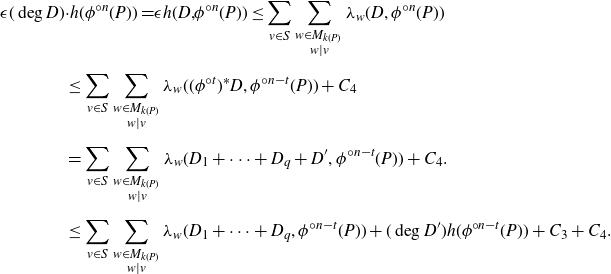 \begin{align*}{\epsilon (\deg D) }&{\cdot h(\phi^{{\circ} n} (P)) = } \epsilon h({D, }\phi^{{\circ} n} (P)) \le \sum_{v\in S} \sum_{\substack{w\in M_{k(P)}\\ w\mid v}} \lambda_w(D, \phi^{{\circ} n} (P))\\[5pt] &\le \sum_{v\in S} \sum_{\substack{w\in M_{k(P)}\\ w\mid v}} \lambda_w((\phi^{{\circ} t})^* D, \phi^{{\circ} n-t} (P)) + {C_{4}}\\[5pt] &= \sum_{v\in S} \sum_{\substack{w\in M_{k(P)}\\ w\mid v}} \lambda_w(D_1+\cdots + D_q + D', \phi^{{\circ} n-t} (P)) + {C_{4}}. \\[5pt] &\le \sum_{v\in S} \sum_{\substack{w\in M_{k(P)}\\ w\mid v}} \lambda_w(D_1+\cdots + D_q, \phi^{{\circ} n-t} (P)) + (\deg D') h(\phi^{{\circ} n-t}(P)) +{C_{3}} + {C_{4}}.\end{align*}
\begin{align*}{\epsilon (\deg D) }&{\cdot h(\phi^{{\circ} n} (P)) = } \epsilon h({D, }\phi^{{\circ} n} (P)) \le \sum_{v\in S} \sum_{\substack{w\in M_{k(P)}\\ w\mid v}} \lambda_w(D, \phi^{{\circ} n} (P))\\[5pt] &\le \sum_{v\in S} \sum_{\substack{w\in M_{k(P)}\\ w\mid v}} \lambda_w((\phi^{{\circ} t})^* D, \phi^{{\circ} n-t} (P)) + {C_{4}}\\[5pt] &= \sum_{v\in S} \sum_{\substack{w\in M_{k(P)}\\ w\mid v}} \lambda_w(D_1+\cdots + D_q + D', \phi^{{\circ} n-t} (P)) + {C_{4}}. \\[5pt] &\le \sum_{v\in S} \sum_{\substack{w\in M_{k(P)}\\ w\mid v}} \lambda_w(D_1+\cdots + D_q, \phi^{{\circ} n-t} (P)) + (\deg D') h(\phi^{{\circ} n-t}(P)) +{C_{3}} + {C_{4}}.\end{align*}
Therefore, combining with (2·2), we have
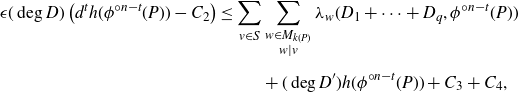 \begin{align}\epsilon {(\deg D)}\left(d^t h(\phi^{{\circ} n-t}(P)) - {C_{2}}\right) \le \sum_{v\in S} &\sum_{\substack{w\in M_{k(P)}\\ w\mid v}} \lambda_w(D_1+\cdots + D_q, \phi^{{\circ} n-t} (P)) \notag \\[5pt] & + (\deg D') h(\phi^{{\circ} n-t}(P)) + {C_{3}} + {C_{4}}, \end{align}
\begin{align}\epsilon {(\deg D)}\left(d^t h(\phi^{{\circ} n-t}(P)) - {C_{2}}\right) \le \sum_{v\in S} &\sum_{\substack{w\in M_{k(P)}\\ w\mid v}} \lambda_w(D_1+\cdots + D_q, \phi^{{\circ} n-t} (P)) \notag \\[5pt] & + (\deg D') h(\phi^{{\circ} n-t}(P)) + {C_{3}} + {C_{4}}, \end{align}
hence by letting
![]() ${C_{5}} = \epsilon {(\deg D)}{C_{2}} + {C_{3}} + {C_{4}}$
, we have
${C_{5}} = \epsilon {(\deg D)}{C_{2}} + {C_{3}} + {C_{4}}$
, we have
 \begin{equation}(\epsilon {(\deg D)} d^t - (\deg D')) h(\phi^{{\circ} n-t}(P)) \le \sum_{v\in S} \sum_{\substack{w\in M_{k(P)}\\ w\mid v}} \lambda_w(D_1+\cdots + D_q, \phi^{{\circ} n-t} (P)) + {C_{5}}.\end{equation}
\begin{equation}(\epsilon {(\deg D)} d^t - (\deg D')) h(\phi^{{\circ} n-t}(P)) \le \sum_{v\in S} \sum_{\substack{w\in M_{k(P)}\\ w\mid v}} \lambda_w(D_1+\cdots + D_q, \phi^{{\circ} n-t} (P)) + {C_{5}}.\end{equation}
By assumption,
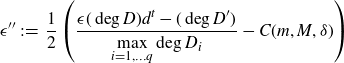 \[\epsilon'' \;:\!=\; \frac 12 \left(\frac{\epsilon {(\deg D)} d^t - (\deg D')}{\displaystyle \max_{i=1,\ldots q} \deg D_i} - C(m, M, \delta)\right)\]
\[\epsilon'' \;:\!=\; \frac 12 \left(\frac{\epsilon {(\deg D)} d^t - (\deg D')}{\displaystyle \max_{i=1,\ldots q} \deg D_i} - C(m, M, \delta)\right)\]
is positive, and we have
 \begin{align*}\sum_{v\in S} \sum_{\substack{w\in M_{k(P)}\\ w\mid v}} &\sum_{i=1}^q \frac{\lambda_w(D_i, \phi^{{\circ} n-t} (P))}{\deg D_i}\\[5pt] &\ge \sum_{v\in S} \sum_{\substack{w\in M_{k(P)}\\ w\mid v}} \frac{\lambda_w(D_1+\cdots + D_q, \phi^{{\circ} n-t} (P))}{\displaystyle \max_{i=1,\ldots q} \deg D_i}\\[5pt] &\ge \frac{\epsilon {(\deg D)} d^t - (\deg D')}{\displaystyle \max_{i=1,\ldots q} \deg D_i} h(\phi^{{\circ} n-t}(P)) - \frac {{C_{5}}}{\displaystyle \max_{i=1,\ldots q} \deg D_i} \qquad (\because (2.6))\\[5pt] & \gt \left(C(m, M, \delta) + \epsilon''\right) h(\phi^{{\circ} n-t}(P)) - \frac {{C_{5}}}{\displaystyle \max_{i=1,\ldots q} \deg D_i}.\end{align*}
\begin{align*}\sum_{v\in S} \sum_{\substack{w\in M_{k(P)}\\ w\mid v}} &\sum_{i=1}^q \frac{\lambda_w(D_i, \phi^{{\circ} n-t} (P))}{\deg D_i}\\[5pt] &\ge \sum_{v\in S} \sum_{\substack{w\in M_{k(P)}\\ w\mid v}} \frac{\lambda_w(D_1+\cdots + D_q, \phi^{{\circ} n-t} (P))}{\displaystyle \max_{i=1,\ldots q} \deg D_i}\\[5pt] &\ge \frac{\epsilon {(\deg D)} d^t - (\deg D')}{\displaystyle \max_{i=1,\ldots q} \deg D_i} h(\phi^{{\circ} n-t}(P)) - \frac {{C_{5}}}{\displaystyle \max_{i=1,\ldots q} \deg D_i} \qquad (\because (2.6))\\[5pt] & \gt \left(C(m, M, \delta) + \epsilon''\right) h(\phi^{{\circ} n-t}(P)) - \frac {{C_{5}}}{\displaystyle \max_{i=1,\ldots q} \deg D_i}.\end{align*}
Therefore, applying Theorem 5 with
![]() $\epsilon' = {\epsilon''}/2$
,
$\epsilon' = {\epsilon''}/2$
,
![]() $\phi^{{\circ} n-t}(P)$
lies either in the finite set of exceptions coming from Le’s theorem or in the finite set of height bounded above by
$\phi^{{\circ} n-t}(P)$
lies either in the finite set of exceptions coming from Le’s theorem or in the finite set of height bounded above by
![]() $\displaystyle {2 {C_{5}}}/{\Big(\epsilon'' \displaystyle \max_{i=1,\ldots q} \deg D_i}\Big)$
. By taking the image under
$\displaystyle {2 {C_{5}}}/{\Big(\epsilon'' \displaystyle \max_{i=1,\ldots q} \deg D_i}\Big)$
. By taking the image under
![]() $\phi^{{\circ} t}$
, it follows that
$\phi^{{\circ} t}$
, it follows that
![]() $\phi^{{\circ} n}(P)$
lies in a finite set
$\phi^{{\circ} n}(P)$
lies in a finite set
![]() $\mathcal F = \mathcal F(\phi, S, \epsilon, \delta, m)$
. In particular, for a non-preperiodic P, the number of n’s for which
$\mathcal F = \mathcal F(\phi, S, \epsilon, \delta, m)$
. In particular, for a non-preperiodic P, the number of n’s for which
![]() $\phi^{{\circ} n}(P)\in \mathcal R_\epsilon \backslash \phi^{{\circ} t}(|D'|\cup \bigcup_{i=1}^q |D_i|)$
is uniformly bounded above by
$\phi^{{\circ} n}(P)\in \mathcal R_\epsilon \backslash \phi^{{\circ} t}(|D'|\cup \bigcup_{i=1}^q |D_i|)$
is uniformly bounded above by
![]() ${t+ }\# \mathcal F$
.
${t+ }\# \mathcal F$
.
By the Northcott property, there exists
![]() $\alpha$
such that any
$\alpha$
such that any
![]() $Q\in {\mathbb{P}}^M(K)$
with
$Q\in {\mathbb{P}}^M(K)$
with
![]() $[K\;:\;k]\le \delta$
and
$[K\;:\;k]\le \delta$
and
![]() $h(Q) \gt {{C_{1}}}/({d-1})$
satisfies
$h(Q) \gt {{C_{1}}}/({d-1})$
satisfies
![]() $h(Q) \ge \alpha$
. Therefore, by letting
$h(Q) \ge \alpha$
. Therefore, by letting
![]() $\beta$
be the maximum height of the finite set
$\beta$
be the maximum height of the finite set
![]() $\mathcal F$
, it follows from (2·1) that any time
$\mathcal F$
, it follows from (2·1) that any time
![]() $\phi^{{\circ} n}(P)$
is in
$\phi^{{\circ} n}(P)$
is in
![]() $\mathcal R_\epsilon \backslash \phi^{{\circ} t}(|D'|\cup \bigcup_{i=1}^q |D_i|)$
with
$\mathcal R_\epsilon \backslash \phi^{{\circ} t}(|D'|\cup \bigcup_{i=1}^q |D_i|)$
with
![]() $h(P) \gt {{C_{1}}}/({d-1})$
,
$h(P) \gt {{C_{1}}}/({d-1})$
,
is satisfied, so we obtain
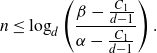 \[n \le \log_d \left(\frac {\beta - \frac{{C_{1}}}{d-1}}{\alpha - \frac{{C_{1}}}{d-1}}\right).\]
\[n \le \log_d \left(\frac {\beta - \frac{{C_{1}}}{d-1}}{\alpha - \frac{{C_{1}}}{d-1}}\right).\]
On the other hand, if P is not preperiodic, then after at most
iterations, the point will have height at least
![]() ${{C_{1}}}/({d-1})$
. So it follows that after at most
${{C_{1}}}/({d-1})$
. So it follows that after at most
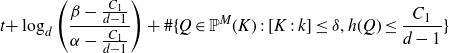 \[{t+ }\log_d \left(\frac {\beta - \frac{{C_{1}}}{d-1}}{\alpha - \frac{{C_{1}}}{d-1}}\right) + \#\{Q\in {\mathbb{P}}^M(K)\;:\; [K\;:\;k] \le \delta, h(Q) \le \frac{{C_{1}}}{d-1} \}\]
\[{t+ }\log_d \left(\frac {\beta - \frac{{C_{1}}}{d-1}}{\alpha - \frac{{C_{1}}}{d-1}}\right) + \#\{Q\in {\mathbb{P}}^M(K)\;:\; [K\;:\;k] \le \delta, h(Q) \le \frac{{C_{1}}}{d-1} \}\]
iterations, no orbit point will be in
![]() $\mathcal R_\epsilon$
. It is also immediate that whenever
$\mathcal R_\epsilon$
. It is also immediate that whenever
![]() $\phi^{{\circ} n}(P)$
is in
$\phi^{{\circ} n}(P)$
is in
![]() $\mathcal R_\epsilon \backslash \phi^{{\circ} t}(|D'|\cup \bigcup_{i=1}^q |D_i|)$
for some n, (2·7) implies that the height of P is bounded above by
$\mathcal R_\epsilon \backslash \phi^{{\circ} t}(|D'|\cup \bigcup_{i=1}^q |D_i|)$
for some n, (2·7) implies that the height of P is bounded above by
![]() $\max(\beta, {{C_{1}}}/({d-1}))$
, so such a P comes from a finite set when
$\max(\beta, {{C_{1}}}/({d-1}))$
, so such a P comes from a finite set when
![]() $P\in {\mathbb{P}}^M(K)$
with
$P\in {\mathbb{P}}^M(K)$
with
![]() $[K\;:\;k]\le \delta$
. This finishes all parts of the proof.
$[K\;:\;k]\le \delta$
. This finishes all parts of the proof.
Remark 6. As noted in the introduction, Theorem 1 for the case of
![]() ${\mathbb{P}}^1$
does not recover Hsia–Silverman [
Reference Hsia and Silverman9
]. Indeed, for example for
${\mathbb{P}}^1$
does not recover Hsia–Silverman [
Reference Hsia and Silverman9
]. Indeed, for example for
![]() $\phi(x) = x/{(x-1)^d}$
,
$\phi(x) = x/{(x-1)^d}$
,
![]() $\phi^{-1}(\infty) = \{1\}$
,
$\phi^{-1}(\infty) = \{1\}$
,
![]() $\phi^{-1}(0) = \{\infty, 0 \}$
, and the ramification points are
$\phi^{-1}(0) = \{\infty, 0 \}$
, and the ramification points are
![]() $1, \infty, 1/({1-d})$
. Since
$1, \infty, 1/({1-d})$
. Since
![]() $(x-1)^d - x$
does not have a root in
$(x-1)^d - x$
does not have a root in
![]() ${\mathbb{Q}}$
, the preimages of 1 are not in
${\mathbb{Q}}$
, the preimages of 1 are not in
![]() ${\mathbb{Q}}$
, so from here on the points in the preimage tree are not in
${\mathbb{Q}}$
, so from here on the points in the preimage tree are not in
![]() ${\mathbb{Q}}$
. So in particular, they are not ramified. Therefore, the number of preimage points of
${\mathbb{Q}}$
. So in particular, they are not ramified. Therefore, the number of preimage points of
![]() $\infty$
by
$\infty$
by
![]() $\phi^{{\circ} t}$
is
$\phi^{{\circ} t}$
is
![]() $d^{t-1}$
, so
$d^{t-1}$
, so
![]() $\deg D'$
is
$\deg D'$
is
![]() $d^t - d^{t-1} = (({d-1})/d) \cdot d^t$
. Hence, when
$d^t - d^{t-1} = (({d-1})/d) \cdot d^t$
. Hence, when
![]() $\epsilon \le ({d-1})/d$
, one can never satisfy hypothesis (iii).
$\epsilon \le ({d-1})/d$
, one can never satisfy hypothesis (iii).
On the other hand, by modifying the proof argument slightly, we recover the result of Hsia–Silverman. By [
Reference Silverman25
, lemma 3·52], for any small
![]() $\epsilon'' \gt 0$
, there exists t such that the maximal multiplicity of points in
$\epsilon'' \gt 0$
, there exists t such that the maximal multiplicity of points in
![]() $(\phi^{{\circ} t})^*(\infty)$
is at most
$(\phi^{{\circ} t})^*(\infty)$
is at most
![]() $\epsilon'' d^t$
. Then instead of using divisor
$\epsilon'' d^t$
. Then instead of using divisor
![]() $D'$
and obtaining (2·5), letting
$D'$
and obtaining (2·5), letting
![]() $D_1 + \cdots + D_q$
be the reduced induced closed subscheme of
$D_1 + \cdots + D_q$
be the reduced induced closed subscheme of
![]() $(\phi^{{\circ} t})^*(\infty)$
(i.e. just making the multiplicity of each preimage point to 1), we have
$(\phi^{{\circ} t})^*(\infty)$
(i.e. just making the multiplicity of each preimage point to 1), we have
 \[\epsilon \left(d^t h(\phi^{{\circ} n-t}(P)) - {C_{2}}\right) \le \epsilon'' d^t \sum_{v\in S} \sum_{\substack{w\in M_{k(P)}\\ w\mid v}} \lambda_w(D_1+\cdots + D_q, \phi^{{\circ} n-t} (P)) + {C_{3}} + {C_{4}}.\]
\[\epsilon \left(d^t h(\phi^{{\circ} n-t}(P)) - {C_{2}}\right) \le \epsilon'' d^t \sum_{v\in S} \sum_{\substack{w\in M_{k(P)}\\ w\mid v}} \lambda_w(D_1+\cdots + D_q, \phi^{{\circ} n-t} (P)) + {C_{3}} + {C_{4}}.\]
Therefore,
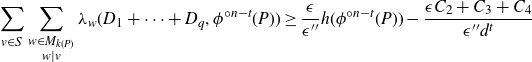 \[\sum_{v\in S} \sum_{\substack{w\in M_{k(P)}\\ w\mid v}} \lambda_w(D_1+\cdots + D_q, \phi^{{\circ} n-t} (P)) \ge \frac {\epsilon}{\epsilon''} h(\phi^{{\circ} n-t}(P)) - \frac{\epsilon {C_{2}} + {C_{3}} + {C_{4}}}{\epsilon'' d^t}\]
\[\sum_{v\in S} \sum_{\substack{w\in M_{k(P)}\\ w\mid v}} \lambda_w(D_1+\cdots + D_q, \phi^{{\circ} n-t} (P)) \ge \frac {\epsilon}{\epsilon''} h(\phi^{{\circ} n-t}(P)) - \frac{\epsilon {C_{2}} + {C_{3}} + {C_{4}}}{\epsilon'' d^t}\]
and thus by choosing
![]() $\epsilon''$
so that
$\epsilon''$
so that
![]() ${\epsilon}/{\epsilon''} \gt C(1,1,\delta)$
, the rest of the argument goes through and we obtain the result of Hsia–Silverman [
Reference Hsia and Silverman9
, theorem 11].
${\epsilon}/{\epsilon''} \gt C(1,1,\delta)$
, the rest of the argument goes through and we obtain the result of Hsia–Silverman [
Reference Hsia and Silverman9
, theorem 11].
Remark 7. We observe that the three conclusions of the theorem are related, but none implies another directly. Indeed, the set of initial points (1·3) can be finite while larger and larger iterate could be in
![]() $\mathcal R_\epsilon$
to make (1·2) infinite and force nonexistence of a uniform bound
$\mathcal R_\epsilon$
to make (1·2) infinite and force nonexistence of a uniform bound
![]() $N$
. Similarly, even if the set (1·2) of integral points in orbits is finite, this may occur with larger and larger iterate with (infinitely many) different initial points. Of course, as is evident from the proof, finiteness of either (1·2) or (1·3) will imply the finiteness of the other as well as the existence of the uniform bound
$N$
. Similarly, even if the set (1·2) of integral points in orbits is finite, this may occur with larger and larger iterate with (infinitely many) different initial points. Of course, as is evident from the proof, finiteness of either (1·2) or (1·3) will imply the finiteness of the other as well as the existence of the uniform bound
![]() $N$
, by the Northcott property and by the fact that every morphism on projective space is polarised.
$N$
, by the Northcott property and by the fact that every morphism on projective space is polarised.
Remark 8. Since Le’s theorem holds for projective varieties as long as there exists an ample divisor
![]() $A$
such that each
$A$
such that each
![]() $D_i$
is numerically equivalent to a multiple of
$D_i$
is numerically equivalent to a multiple of
![]() $A$
, Theorem 1 also holds under this setting as long as the divisor
$A$
, Theorem 1 also holds under this setting as long as the divisor
![]() $D'$
is also numerically equivalent to a multiple of
$D'$
is also numerically equivalent to a multiple of
![]() $A$
(we define the ‘degree’ by the multiple of
$A$
(we define the ‘degree’ by the multiple of
![]() $A$
to which each
$A$
to which each
![]() $D_i$
is numerically equivalent). In particular, the theorem holds for projective varieties with Néron–Severi rank one.
$D_i$
is numerically equivalent). In particular, the theorem holds for projective varieties with Néron–Severi rank one.
3. Proof of Theorem 3
In this section, we apply results of Matsuzawa [ Reference Matsuzawa20 ] to obtain a similar result as Theorem 1, but with different hypotheses. Since Matsuzawa’s result assumes Vojta’s conjecture, the result of this section will also be conditional on this conjecture. Matsuzawa used the so-called “Main Conjecture” of Vojta [ Reference Vojta27 , conjecture 3·4·3], which works over a fixed number field. In contrast, since we would like to obtain an algebraic-point version, here we assume the so-called “General Conjecture” of Vojta [ Reference Vojta27 , conjecture 5·2·6], which applies for algebraic points but with a discriminant term on the right-hand side. In the following, we define the absolute logarithmic discriminant by
where
![]() $D_{L/{\mathbb{Q}}}$
is the (usual) discriminant of the number field L.
$D_{L/{\mathbb{Q}}}$
is the (usual) discriminant of the number field L.
Conjecture 9 (Vojta’s General Conjecture). Let X be a smooth projective variety defined over a number field k, with
![]() $K_X$
as a canonical divisor. Let D be a normal-crossings divisor on X and A be an ample divisor both defined over k, and let S be a finite subset of
$K_X$
as a canonical divisor. Let D be a normal-crossings divisor on X and A be an ample divisor both defined over k, and let S be a finite subset of
![]() $M_k$
. Let
$M_k$
. Let
![]() $\delta $
be a natural number. Then given
$\delta $
be a natural number. Then given
![]() $\epsilon \gt 0$
, there exist a Zariski-closed
$\epsilon \gt 0$
, there exist a Zariski-closed
![]() $Z = Z(\epsilon) \subsetneq X$
and a constant
$Z = Z(\epsilon) \subsetneq X$
and a constant
![]() $c_{X,k}$
such that
$c_{X,k}$
such that
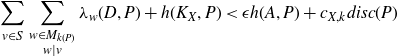 $$\sum_{v\in S} \sum_{\substack{w\in M_{k(P)}\\ w\mid v}} \lambda_{{w}}(D, P) + h(K_X, P) \lt \epsilon h(A, P) + {c_{X,k}} \, {disc}(P)$$
$$\sum_{v\in S} \sum_{\substack{w\in M_{k(P)}\\ w\mid v}} \lambda_{{w}}(D, P) + h(K_X, P) \lt \epsilon h(A, P) + {c_{X,k}} \, {disc}(P)$$
for
![]() $P\in X(K)\setminus Z$
with
$P\in X(K)\setminus Z$
with
![]() $[K\;:\;k] \le \delta$
.
$[K\;:\;k] \le \delta$
.
In [
Reference Vojta27
, conjecture 5·2·6], Vojta originally set
![]() $c_{X,k}$
to be
$c_{X,k}$
to be
![]() $\dim X$
. Later in [
Reference Vojta28
, conjecture 2·1], Vojta set
$\dim X$
. Later in [
Reference Vojta28
, conjecture 2·1], Vojta set
![]() $c_{X,k}$
to be simply 1. On the other hand, Masser [
Reference Masser18
] has shown a counterexample for
$c_{X,k}$
to be simply 1. On the other hand, Masser [
Reference Masser18
] has shown a counterexample for
![]() $c_{X,k} = 1$
, and Levin [
Reference Levin14
] has constructed a surface for which
$c_{X,k} = 1$
, and Levin [
Reference Levin14
] has constructed a surface for which
![]() $c_{X,k}$
needs to be at least
$c_{X,k}$
needs to be at least
![]() $3/2$
. In [
Reference Levin14
], Levin also discusses why the same statement for all algebraic points at once does not hold, i.e. why cannot let
$3/2$
. In [
Reference Levin14
], Levin also discusses why the same statement for all algebraic points at once does not hold, i.e. why cannot let
![]() $\delta = \infty$
. Perhaps,
$\delta = \infty$
. Perhaps,
![]() $c_{X,k} = \dim X$
is suitable, but the exact constant seems not quite settled, and it will be sufficient for our purposes as long as
$c_{X,k} = \dim X$
is suitable, but the exact constant seems not quite settled, and it will be sufficient for our purposes as long as
![]() $c_{X,k}$
does not depend on P (it could even depend on
$c_{X,k}$
does not depend on P (it could even depend on
![]() $\epsilon$
, S and D), thus we state this conjecture in this fashion with
$\epsilon$
, S and D), thus we state this conjecture in this fashion with
![]() $c_{X,k}$
in this paper. We note that this conjecture is extremely deep: for example the conjecture for Fermat curves easily implies the abc conjecture.
$c_{X,k}$
in this paper. We note that this conjecture is extremely deep: for example the conjecture for Fermat curves easily implies the abc conjecture.
The arithmetic degree
![]() $\alpha_\phi(P)$
, introduced by Kawaguchi–Silverman [
Reference Kawaguchi and Silverman12
], is
$\alpha_\phi(P)$
, introduced by Kawaguchi–Silverman [
Reference Kawaguchi and Silverman12
], is
when the limit exists.
Finally, we also need the notion of ‘asymptotic’ multiplicity of the forward orbit of a scheme point.
Definition 10. Let
![]() $\phi\;:\; X{\longrightarrow} X$
be a finite flat self-morphism of a separated scheme of finite type over a number field. For a scheme point
$\phi\;:\; X{\longrightarrow} X$
be a finite flat self-morphism of a separated scheme of finite type over a number field. For a scheme point
![]() $x$
, we define the multiplicity of
$x$
, we define the multiplicity of
![]() $\phi$
at
$\phi$
at
![]() $x$
as
$x$
as
where
![]() $\mathfrak m_{\phi(x)}$
is the maximal ideal of
$\mathfrak m_{\phi(x)}$
is the maximal ideal of
![]() $\mathcal O_{X,\phi(x)}$
and
$\mathcal O_{X,\phi(x)}$
and
![]() $l_{\mathcal O_{X,x}}$
stands for the length as an
$l_{\mathcal O_{X,x}}$
stands for the length as an
![]() $\mathcal O_{X,x}$
-module. We then define the asymptotic multiplicity as
$\mathcal O_{X,x}$
-module. We then define the asymptotic multiplicity as
Favre [
Reference Favre4
, theorem 2·5·8] has shown that this limit exists. When
![]() $Y$
is an irreducible subvariety with the generic point
$Y$
is an irreducible subvariety with the generic point
![]() $\eta$
, we also write
$\eta$
, we also write
![]() $e_{\phi,+}(Y)$
for
$e_{\phi,+}(Y)$
for
![]() $e_{\phi, +}(\eta)$
.
$e_{\phi, +}(\eta)$
.
By Matsuzawa [ Reference Matsuzawa20 , theorem 4·8], the function
is well-defined and upper-semicontinuous. In particular,
exists, and hypothesis (iii) of Theorem 3 is satisfied if and only if
![]() $\alpha_\phi(P)$
is bigger than (3·1).
$\alpha_\phi(P)$
is bigger than (3·1).
We are now ready to prove Theorem 3.
Proof of Theorem
3. The proof is based on the proofs of Lemma 7.17 and Theorem 1.16 of Matsuzawa [
Reference Matsuzawa20
], but one needs to take care to make N independent of P and its field of definition. First, letting H be an ample divisor on
![]() ${\mathbb{P}}^M$
(e.g. a hyperplane), there exists a constant
${\mathbb{P}}^M$
(e.g. a hyperplane), there exists a constant
![]() ${C_{6}}$
such that
${C_{6}}$
such that
This is an immediate consequence of the ampleness of H, but in this setting of
![]() ${\mathbb{P}}^M$
, we can let
${\mathbb{P}}^M$
, we can let
![]() ${C_{6}}$
be
${C_{6}}$
be
![]() $M+2$
.
$M+2$
.
Next, let e be the quantity defined by (3·1). For morphisms on normal projective varieties, the set of all arithmetic degrees is finite by Kawaguchi–Silverman [
Reference Kawaguchi and Silverman11
] (in fact, for polarised morphisms as in this case, it is clear from their proof that the arithmetic degree can only be 1 or
![]() $\deg \phi$
). In particular,
$\deg \phi$
). In particular,
is a finite set, and we let the minimum of this set be r (if this set is empty, then the statement of Theorem 3 will also be vacuous). Letting
![]() $\epsilon_1 = ({r - e})/2 \gt 0$
, we have
$\epsilon_1 = ({r - e})/2 \gt 0$
, we have
so for sufficiently large t,
Moreover, from [
Reference Matsuzawa20
, corollary 7·13], for all sufficiently large t, the log canonical threshold of
![]() $(\phi^{{\circ} t})^{-1}(D)$
is at least
$(\phi^{{\circ} t})^{-1}(D)$
is at least
![]() $\left( 1/({e+\epsilon_1})\right)^t$
. So from here on, we fix a large enough t satisfying this as well as (3·3). Applying Conjecture 9 (instead of the conjecture for
$\left( 1/({e+\epsilon_1})\right)^t$
. So from here on, we fix a large enough t satisfying this as well as (3·3). Applying Conjecture 9 (instead of the conjecture for
![]() $\delta =1$
without the discriminant term) to the log resolution X of
$\delta =1$
without the discriminant term) to the log resolution X of
![]() $({\mathbb{P}}^M, (\phi^{{\circ} t})^{-1}(D))$
, the proof of [
Reference Matsuzawa20
, proposition 7·15] shows that there exist a Zariski-closed
$({\mathbb{P}}^M, (\phi^{{\circ} t})^{-1}(D))$
, the proof of [
Reference Matsuzawa20
, proposition 7·15] shows that there exist a Zariski-closed
![]() $Z_0\subsetneq {\mathbb{P}}^M$
and a constant
$Z_0\subsetneq {\mathbb{P}}^M$
and a constant
![]() ${C_{7}}$
(depending on t, but recall that we have already fixed a large enough t) such that
${C_{7}}$
(depending on t, but recall that we have already fixed a large enough t) such that
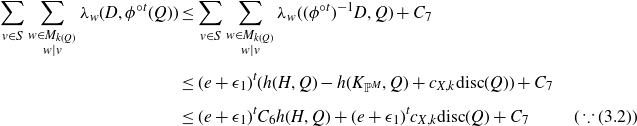 \begin{align}\sum_{v\in S} \sum_{\substack{w\in M_{k(Q)}\\ w\mid v}} \lambda_{{w}}(D, \phi^{{\circ} t} (Q)) &\le \sum_{v\in S} \sum_{\substack{w\in M_{k(Q)}\\ w\mid v}} \lambda_{{w}}((\phi^{{\circ} t})^{-1}D, Q) + {C_{7}} \notag \\[5pt] &\le (e+\epsilon_1)^t (h(H, Q) - h(K_{{\mathbb{P}}^M}, Q) + {c_{X,k}} \textrm{disc}(Q)) + {C_{7}} \notag\\[5pt] &\le (e+\epsilon_1)^t {C_{6}} h(H, Q) + (e+\epsilon_1)^t {c_{X,k}} \textrm{disc}(Q) + {C_{7}} \quad\quad\;\;\, (\because (3.2)) \end{align}
\begin{align}\sum_{v\in S} \sum_{\substack{w\in M_{k(Q)}\\ w\mid v}} \lambda_{{w}}(D, \phi^{{\circ} t} (Q)) &\le \sum_{v\in S} \sum_{\substack{w\in M_{k(Q)}\\ w\mid v}} \lambda_{{w}}((\phi^{{\circ} t})^{-1}D, Q) + {C_{7}} \notag \\[5pt] &\le (e+\epsilon_1)^t (h(H, Q) - h(K_{{\mathbb{P}}^M}, Q) + {c_{X,k}} \textrm{disc}(Q)) + {C_{7}} \notag\\[5pt] &\le (e+\epsilon_1)^t {C_{6}} h(H, Q) + (e+\epsilon_1)^t {c_{X,k}} \textrm{disc}(Q) + {C_{7}} \quad\quad\;\;\, (\because (3.2)) \end{align}
for all Q of degree bounded by
![]() $\delta$
lying outside of
$\delta$
lying outside of
![]() $Z_0$
.
$Z_0$
.
From Mahler [
Reference Mahler17
], there exists a constant
![]() ${C_{8}}$
so that
${C_{8}}$
so that
More explicitly Silverman [
Reference Silverman23
, theorem 2] has shown that we can take
![]() ${C_{8}} = \log \delta$
. Since
${C_{8}} = \log \delta$
. Since
![]() $\phi$
is a morphism of degree d, we also have
$\phi$
is a morphism of degree d, we also have
for some constant
![]() ${C_{9}} \ge 0$
. By setting
${C_{9}} \ge 0$
. By setting
![]() ${C_{10}} = {{C_{9}}}/({d-1})$
, we have
${C_{10}} = {{C_{9}}}/({d-1})$
, we have
so
for any m.
Now, let P and n satisfy the hypotheses of the theorem. By hypothesis (iii) and the fact that e is equal to (3·1), we have
![]() $e \lt \alpha_\phi(P)$
. By our definition of r and (3·3),
$e \lt \alpha_\phi(P)$
. By our definition of r and (3·3),
holds. Moreover,
This is proved by Silverman [ Reference Silverman26 , proposition 12] for rational maps on projective spaces, and proved for general projective varieties by Matsuzawa [ Reference Matsuzawa19 , theorem 1·4]. In all, we have
Therefore, we have
 \begin{align}(e+\epsilon_1)^t h(H, \phi^{{\circ} n-t} (P)) &\le \frac {\epsilon {\cdot (\deg D)}}{2{C_{6}}} \alpha_\phi(P)^t h(H, \phi^{{\circ} n-t} (P)) \qquad (\because (3.8))\notag\\[5pt] &\le \frac {\epsilon {\cdot (\deg D)}}{2{C_{6}}} d^t h(H, \phi^{{\circ} n-t} (P))\notag \\[5pt] &\le \frac {\epsilon {\cdot (\deg D)}}{2{C_{6}}} \big(h(H, \phi^{{\circ} {n}} (P)) + d^t {C_{10}} \big) \qquad (\because (3.7))\end{align}
\begin{align}(e+\epsilon_1)^t h(H, \phi^{{\circ} n-t} (P)) &\le \frac {\epsilon {\cdot (\deg D)}}{2{C_{6}}} \alpha_\phi(P)^t h(H, \phi^{{\circ} n-t} (P)) \qquad (\because (3.8))\notag\\[5pt] &\le \frac {\epsilon {\cdot (\deg D)}}{2{C_{6}}} d^t h(H, \phi^{{\circ} n-t} (P))\notag \\[5pt] &\le \frac {\epsilon {\cdot (\deg D)}}{2{C_{6}}} \big(h(H, \phi^{{\circ} {n}} (P)) + d^t {C_{10}} \big) \qquad (\because (3.7))\end{align}
We now combine all of these together. We divide the argument into two cases, depending on whether
![]() $\textrm{disc}(P)$
is bigger than the following quantity or not:
$\textrm{disc}(P)$
is bigger than the following quantity or not:
Case I:
![]() $\textrm{disc}(P) \gt $
(3·11)
$\textrm{disc}(P) \gt $
(3·11)
In this case,
![]() $k(P) \neq k$
, so in particular,
$k(P) \neq k$
, so in particular,
![]() $\delta \gt 1$
. The assumption implies
$\delta \gt 1$
. The assumption implies
thus by Mahler’s inequality (3·5),
Hence, by (3·7), we have
We now compute from (3·4):
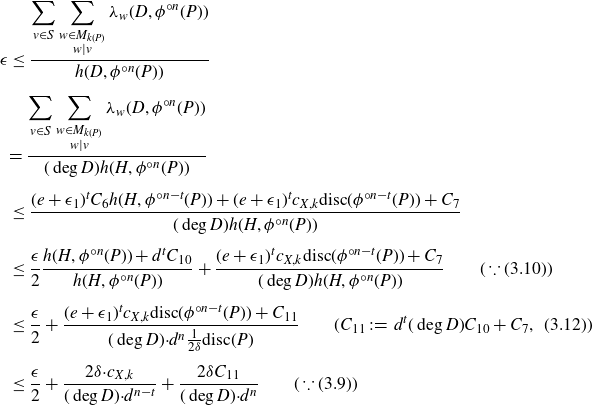 \begin{align}\epsilon &\le \frac{\displaystyle \sum_{v\in S} \sum_{\substack{w\in M_{k(P)}\\ w\mid v}} \lambda_{{w}}(D, \phi^{{\circ} n} (P))}{h({D}, \phi^{{\circ} n} (P))} \notag \\[5pt] &{= \frac{\displaystyle \sum_{v\in S} \sum_{\substack{w\in M_{k(P)}\\ w\mid v}} \lambda_{w}(D, \phi^{{\circ} n} (P))}{(\deg D) h(H, \phi^{{\circ} n} (P))}} \\[5pt] &\le \frac{(e+\epsilon_1)^t {C_{6}} h(H, \phi^{{\circ} n-t}(P)) + (e+\epsilon_1)^t {c_{X,k}} \textrm{disc}(\phi^{{\circ} n-t}(P)) + {C_{7}}}{{(\deg D)} h(H, \phi^{{\circ} n} (P))}\notag \\[5pt] &\le \frac {\epsilon} 2 \frac{h(H, \phi^{{\circ} {n}}(P)) + d^t {C_{10}}}{h(H, \phi^{{\circ} {n}}(P))} + \frac {(e+\epsilon_1)^t {c_{X,k}} \textrm{disc}(\phi^{{\circ} n-t}(P)) + {C_{7}}}{{(\deg D)} h(H, \phi^{{\circ} {n}}(P))} \qquad (\because (3.10))\notag \\[5pt] &\le \frac {\epsilon} 2 + \frac {(e+\epsilon_1)^t {c_{X,k}} \textrm{disc}(\phi^{{\circ} n-t}(P)) + {C_{11}}}{{(\deg D) \cdot } d^n \frac 1{2\delta} \textrm{disc}(P)} \qquad ({C_{11}}\;:\!=\; d^t {(\deg D)} {C_{10}}+{C_{7}}, \,\, (3.12))\notag \\[5pt] &\le \frac {\epsilon} 2 + \frac {2\delta {\cdot c_{X,k}}}{{(\deg D) \cdot } d^{n-t}} + \frac {2\delta {C_{11}}}{{(\deg D) \cdot } d^n} \qquad (\because (3.9))\notag\end{align}
\begin{align}\epsilon &\le \frac{\displaystyle \sum_{v\in S} \sum_{\substack{w\in M_{k(P)}\\ w\mid v}} \lambda_{{w}}(D, \phi^{{\circ} n} (P))}{h({D}, \phi^{{\circ} n} (P))} \notag \\[5pt] &{= \frac{\displaystyle \sum_{v\in S} \sum_{\substack{w\in M_{k(P)}\\ w\mid v}} \lambda_{w}(D, \phi^{{\circ} n} (P))}{(\deg D) h(H, \phi^{{\circ} n} (P))}} \\[5pt] &\le \frac{(e+\epsilon_1)^t {C_{6}} h(H, \phi^{{\circ} n-t}(P)) + (e+\epsilon_1)^t {c_{X,k}} \textrm{disc}(\phi^{{\circ} n-t}(P)) + {C_{7}}}{{(\deg D)} h(H, \phi^{{\circ} n} (P))}\notag \\[5pt] &\le \frac {\epsilon} 2 \frac{h(H, \phi^{{\circ} {n}}(P)) + d^t {C_{10}}}{h(H, \phi^{{\circ} {n}}(P))} + \frac {(e+\epsilon_1)^t {c_{X,k}} \textrm{disc}(\phi^{{\circ} n-t}(P)) + {C_{7}}}{{(\deg D)} h(H, \phi^{{\circ} {n}}(P))} \qquad (\because (3.10))\notag \\[5pt] &\le \frac {\epsilon} 2 + \frac {(e+\epsilon_1)^t {c_{X,k}} \textrm{disc}(\phi^{{\circ} n-t}(P)) + {C_{11}}}{{(\deg D) \cdot } d^n \frac 1{2\delta} \textrm{disc}(P)} \qquad ({C_{11}}\;:\!=\; d^t {(\deg D)} {C_{10}}+{C_{7}}, \,\, (3.12))\notag \\[5pt] &\le \frac {\epsilon} 2 + \frac {2\delta {\cdot c_{X,k}}}{{(\deg D) \cdot } d^{n-t}} + \frac {2\delta {C_{11}}}{{(\deg D) \cdot } d^n} \qquad (\because (3.9))\notag\end{align}
as long as
![]() $\phi^{{\circ} n-t}(P)\notin Z_0$
, i.e. as long as
$\phi^{{\circ} n-t}(P)\notin Z_0$
, i.e. as long as
![]() $\phi^{{\circ} n}(P) \notin \phi^{{\circ} t}(Z_0)$
. Note that here we use the fact that the discriminant remains the same in an orbit, as
$\phi^{{\circ} n}(P) \notin \phi^{{\circ} t}(Z_0)$
. Note that here we use the fact that the discriminant remains the same in an orbit, as
![]() $\phi$
itself is defined over k. For sufficiently large n, which can be evidently chosen independently of P, the sum of the last two terms is less than
$\phi$
itself is defined over k. For sufficiently large n, which can be evidently chosen independently of P, the sum of the last two terms is less than
![]() ${\epsilon}/2$
. This contradicts the fact that
${\epsilon}/2$
. This contradicts the fact that
![]() $\phi^{{\circ} n}(P)$
was
$\phi^{{\circ} n}(P)$
was
![]() $(D,S,\epsilon)$
-quasi-integral. Therefore, quasi-integral points must appear in earlier iterations.
$(D,S,\epsilon)$
-quasi-integral. Therefore, quasi-integral points must appear in earlier iterations.
Case II:
![]() $\textrm{disc}(P) \le $
(3·11)
$\textrm{disc}(P) \le $
(3·11)
We compute in a similar fashion as above:
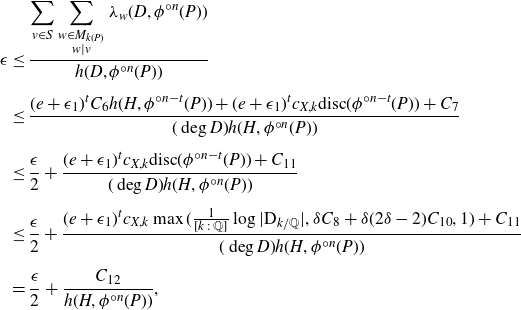 \begin{align*}\epsilon &\le \frac{\displaystyle \sum_{v\in S} \sum_{\substack{w\in M_{k(P)}\\ w\mid v}} \lambda_{{w}}(D, \phi^{{\circ} n} (P))}{h({D}, \phi^{{\circ} n} (P))} \\[5pt] &\le \frac{(e+\epsilon_1)^t {C_{6}} h(H, \phi^{{\circ} n-t}(P)) + (e+\epsilon_1)^t {c_{X,k}} \textrm{disc}(\phi^{{\circ} n-t}(P)) + {C_{7}}}{{(\deg D)} h(H, \phi^{{\circ} n} (P))}\\[5pt] &\le \frac {\epsilon} 2 + \frac {(e+\epsilon_1)^t {c_{X,k}} \textrm{disc}(\phi^{{\circ} n-t}(P)) + {C_{11}}}{{(\deg D)} h(H, \phi^{{\circ} n} (P))}\\[5pt] &\le \frac {\epsilon} 2 + \frac{(e+\epsilon_1)^t {c_{X,k}} \max(\frac 1{[k\;:\;{\mathbb{Q}}]} \log |\textrm D_{k/{\mathbb{Q}}}|, \delta {C_{8}} + \delta(2\delta -2) {C_{10}}, 1) + {C_{11}}}{{(\deg D)} h(H, \phi^{{\circ} n} (P))}\\[5pt] &= \frac {\epsilon} 2 + \frac{{C_{12}}}{h(H, \phi^{{\circ} n} (P))},\end{align*}
\begin{align*}\epsilon &\le \frac{\displaystyle \sum_{v\in S} \sum_{\substack{w\in M_{k(P)}\\ w\mid v}} \lambda_{{w}}(D, \phi^{{\circ} n} (P))}{h({D}, \phi^{{\circ} n} (P))} \\[5pt] &\le \frac{(e+\epsilon_1)^t {C_{6}} h(H, \phi^{{\circ} n-t}(P)) + (e+\epsilon_1)^t {c_{X,k}} \textrm{disc}(\phi^{{\circ} n-t}(P)) + {C_{7}}}{{(\deg D)} h(H, \phi^{{\circ} n} (P))}\\[5pt] &\le \frac {\epsilon} 2 + \frac {(e+\epsilon_1)^t {c_{X,k}} \textrm{disc}(\phi^{{\circ} n-t}(P)) + {C_{11}}}{{(\deg D)} h(H, \phi^{{\circ} n} (P))}\\[5pt] &\le \frac {\epsilon} 2 + \frac{(e+\epsilon_1)^t {c_{X,k}} \max(\frac 1{[k\;:\;{\mathbb{Q}}]} \log |\textrm D_{k/{\mathbb{Q}}}|, \delta {C_{8}} + \delta(2\delta -2) {C_{10}}, 1) + {C_{11}}}{{(\deg D)} h(H, \phi^{{\circ} n} (P))}\\[5pt] &= \frac {\epsilon} 2 + \frac{{C_{12}}}{h(H, \phi^{{\circ} n} (P))},\end{align*}
as long as
![]() $\phi^{{\circ} n}(P) \notin \phi^{{\circ} t}(Z_0)$
, where
$\phi^{{\circ} n}(P) \notin \phi^{{\circ} t}(Z_0)$
, where
![]() ${C_{12}}$
is defined to be
${C_{12}}$
is defined to be
![]() $1/{\deg D}$
times the numerator of the previous equation (which is a constant since t is fixed). In particular,
$1/{\deg D}$
times the numerator of the previous equation (which is a constant since t is fixed). In particular,
By the Northcott property, there exists
![]() ${C_{13}} \gt {C_{10}}$
such that any point
${C_{13}} \gt {C_{10}}$
such that any point
![]() $Q\in {\mathbb{P}}^M(K)$
with
$Q\in {\mathbb{P}}^M(K)$
with
![]() $[K\;:\;k]\le \delta$
and
$[K\;:\;k]\le \delta$
and
![]() $h(Q) \gt {C_{10}}$
satisfies
$h(Q) \gt {C_{10}}$
satisfies
![]() $h(Q) \ge {C_{13}}$
. Therefore, if
$h(Q) \ge {C_{13}}$
. Therefore, if
![]() $h(P) \gt {C_{10}}$
, (3·7) implies
$h(P) \gt {C_{10}}$
, (3·7) implies
![]() $h(\phi^{{\circ} n}(P)) \gt d^n (h(P) - {C_{10}}) \ge d^n ({C_{13}} - {C_{10}})$
. This together with (3·14) implies
$h(\phi^{{\circ} n}(P)) \gt d^n (h(P) - {C_{10}}) \ge d^n ({C_{13}} - {C_{10}})$
. This together with (3·14) implies
On the other hand, if P is not preperiodic and
![]() $h(P) \le {C_{10}}$
, after at most
$h(P) \le {C_{10}}$
, after at most
iterations, all the remaining iterations have height above
![]() ${C_{10}}$
, so we now obtain a uniform bound for n.
${C_{10}}$
, so we now obtain a uniform bound for n.
We end this paper with several remarks.
Remark 11. The condition that
![]() $e_{\phi, +}(Y) \lt \alpha_\phi(P)$
is necessary. For example, if
$e_{\phi, +}(Y) \lt \alpha_\phi(P)$
is necessary. For example, if
![]() $\phi = [Z_0^d\;:\; F_1 \;:\; \cdots \;:\; F_M]$
is a morphism with
$\phi = [Z_0^d\;:\; F_1 \;:\; \cdots \;:\; F_M]$
is a morphism with
![]() $F_i$
having coefficients in the ring of integers, then the entire orbit of
$F_i$
having coefficients in the ring of integers, then the entire orbit of
![]() $P = [1\;:\;a_1 \;:\; \cdots \;:\; a_M]$
lies in the set of integral points (i.e. in
$P = [1\;:\;a_1 \;:\; \cdots \;:\; a_M]$
lies in the set of integral points (i.e. in
![]() $\mathcal R_1$
) with respect to the hyperplane
$\mathcal R_1$
) with respect to the hyperplane
![]() $D = (Z_0 = 0)$
if each
$D = (Z_0 = 0)$
if each
![]() $a_i$
is integral. In this case,
$a_i$
is integral. In this case,
![]() $D$
is
$D$
is
![]() $\phi$
-fixed and
$\phi$
-fixed and
![]() $e_{\phi, +}(D) = d = \alpha_\phi(P)$
. For general choices of
$e_{\phi, +}(D) = d = \alpha_\phi(P)$
. For general choices of
![]() $F_i$
and
$F_i$
and
![]() $P$
, the orbit is conjectured to be also Zariski-dense; for example, [
Reference Amerik, Bogomolov and Rovinsky1
, corollary 2·7] shows the existence of such a
$P$
, the orbit is conjectured to be also Zariski-dense; for example, [
Reference Amerik, Bogomolov and Rovinsky1
, corollary 2·7] shows the existence of such a
![]() $P$
whenever there is a fixed point of
$P$
whenever there is a fixed point of
![]() $\phi$
such that the eigenvalues of the tangent map at that point are multiplicatively independent.
$\phi$
such that the eigenvalues of the tangent map at that point are multiplicatively independent.
Remark 12. We can generalise
![]() $\phi$
to any polarised morphism on a projective variety, as long as
$\phi$
to any polarised morphism on a projective variety, as long as
![]() $D$
is numerically equivalent to a multiple of
$D$
is numerically equivalent to a multiple of
![]() $H$
(for example, if the Néron–Severi rank is one). Indeed, (3·6) holds for polarised endomorphisms, the results of Matsuzawa hold for morphisms on projective varieties, and Mahler’s inequality (3·5) holds by embedding the variety as a closed subvariety of a projective space. Moreover, if
$H$
(for example, if the Néron–Severi rank is one). Indeed, (3·6) holds for polarised endomorphisms, the results of Matsuzawa hold for morphisms on projective varieties, and Mahler’s inequality (3·5) holds by embedding the variety as a closed subvariety of a projective space. Moreover, if
![]() $D$
is numerically equivalent to a positive multiple of
$D$
is numerically equivalent to a positive multiple of
![]() $H$
, there exists
$H$
, there exists
![]() $d' \gt 0$
such that
$d' \gt 0$
such that
![]() $h(D, Q) \ge d' h(H, Q)$
for all
$h(D, Q) \ge d' h(H, Q)$
for all
![]() $Q$
with sufficiently large height, so by replacing
$Q$
with sufficiently large height, so by replacing
![]() $\deg D$
by
$\deg D$
by
![]() $d'$
in (3·3) and (3·13) and in equations thereafter, the argument goes through.
$d'$
in (3·3) and (3·13) and in equations thereafter, the argument goes through.
Remark 13. From Sano [ Reference Sano22 , theorem 1·1], we know
for some
![]() $l$
, but as
$l$
, but as
![]() ${C_{14}}$
and
${C_{14}}$
and
![]() ${C_{15}}$
depend on the canonical height of
${C_{15}}$
depend on the canonical height of
![]() $P$
with respect to a basis of Néron–Severi group, it seems difficult to use these bounds for our purposes of showing uniformity. Here, we use a more elementary height inequality involving
$P$
with respect to a basis of Néron–Severi group, it seems difficult to use these bounds for our purposes of showing uniformity. Here, we use a more elementary height inequality involving
![]() $h(\phi^{{\circ} t} (P))$
instead.
$h(\phi^{{\circ} t} (P))$
instead.
Remark 14. It is natural to ask whether the exceptional set
![]() $Z$
can be removed from the statement of the theorem. That is, does there exist a subvariety
$Z$
can be removed from the statement of the theorem. That is, does there exist a subvariety
![]() $Z\subsetneq {\mathbb{P}}^M$
such that
$Z\subsetneq {\mathbb{P}}^M$
such that
![]() $Z\cap \mathcal R_\epsilon$
contains
$Z\cap \mathcal R_\epsilon$
contains
![]() $\phi^{{\circ} n}(P)$
for arbitrarily large
$\phi^{{\circ} n}(P)$
for arbitrarily large
![]() $n$
with
$n$
with
![]() $P\in {\mathbb{P}}^M(K)$
,
$P\in {\mathbb{P}}^M(K)$
,
![]() $[K\;:\;k] \le \delta$
,
$[K\;:\;k] \le \delta$
,
![]() $P$
non-
$P$
non-
![]() $\phi$
-preperiodic, and every
$\phi$
-preperiodic, and every
![]() $\phi$
-periodic subvariety
$\phi$
-periodic subvariety
![]() $Y$
with
$Y$
with
![]() $Y\cap D \neq \emptyset$
satisfying
$Y\cap D \neq \emptyset$
satisfying
![]() $e_{\phi, +}(Y) \lt \alpha_\phi(P)$
?
$e_{\phi, +}(Y) \lt \alpha_\phi(P)$
?
If we ask
![]() $Z$
to satisfy the stronger condition that it contains infinitely many points of the orbit of a single point, then the dynamical Mordell–Lang conjecture would imply that there is a periodic subvariety containing infinitely many integral points. Replacing by an iterate, we may assume that we have a fixed subvariety. If
$Z$
to satisfy the stronger condition that it contains infinitely many points of the orbit of a single point, then the dynamical Mordell–Lang conjecture would imply that there is a periodic subvariety containing infinitely many integral points. Replacing by an iterate, we may assume that we have a fixed subvariety. If
![]() $\phi$
is a map on
$\phi$
is a map on
![]() ${\mathbb{P}}^2$
, then such a fixed curve must be rational as it contains infinitely many integral points, and by Silverman’s theorem, the second iterate of the map restricted to this rational curve must be a polynomial. Then the intersection point of this curve with
${\mathbb{P}}^2$
, then such a fixed curve must be rational as it contains infinitely many integral points, and by Silverman’s theorem, the second iterate of the map restricted to this rational curve must be a polynomial. Then the intersection point of this curve with
![]() $|D|$
must be a fixed point whose multiplicity is equal to (so not strictly less than) the degree. Since the arithmetic degree is equal to the degree, this is a contradiction to the assumption. This heuristic argument seems to indicate that if such a
$|D|$
must be a fixed point whose multiplicity is equal to (so not strictly less than) the degree. Since the arithmetic degree is equal to the degree, this is a contradiction to the assumption. This heuristic argument seems to indicate that if such a
![]() $Z$
exists for a morphism on
$Z$
exists for a morphism on
![]() ${\mathbb{P}}^2$
, it must contain integral points which are arbitrarily high iterates coming from different initial points.
${\mathbb{P}}^2$
, it must contain integral points which are arbitrarily high iterates coming from different initial points.