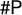1 Introduction
The Kronecker coefficients
![]() ${\texttt {k}}(\lambda ,\mu ,\nu )$
of the symmetric group
${\texttt {k}}(\lambda ,\mu ,\nu )$
of the symmetric group
![]() $S_n$
are some of the most classical, yet largely mysterious, quantities in algebraic combinatorics and representation theory. The Kronecker coefficient is the multiplicity of the irreducible
$S_n$
are some of the most classical, yet largely mysterious, quantities in algebraic combinatorics and representation theory. The Kronecker coefficient is the multiplicity of the irreducible
![]() $S_n$
representation
$S_n$
representation
![]() $\mathbb {S}_{\nu }$
in the tensor product
$\mathbb {S}_{\nu }$
in the tensor product
![]() $\mathbb {S}_\lambda \otimes \mathbb {S}_\mu $
of two other irreducible
$\mathbb {S}_\lambda \otimes \mathbb {S}_\mu $
of two other irreducible
![]() $S_n$
representations. Murnaghan defined them in 1938 as an analogue of the Littlewood-Richardson coefficients
$S_n$
representations. Murnaghan defined them in 1938 as an analogue of the Littlewood-Richardson coefficients
![]() $c^{\lambda }_{\mu \nu }$
of the general linear group
$c^{\lambda }_{\mu \nu }$
of the general linear group
![]() ${GL}_N$
, which are the multiplicity of the irreducible Weyl modules
${GL}_N$
, which are the multiplicity of the irreducible Weyl modules
![]() $V_\lambda $
in the tensor products
$V_\lambda $
in the tensor products
![]() $V_{\mu } \otimes V_{\nu }$
. Yet, the analogy has not translated far into their properties. The Littlewood-Richardson coefficients have a beautiful positive combinatorial interpretation, and their positivity is “easy” to decide, formally, it is in
$V_{\mu } \otimes V_{\nu }$
. Yet, the analogy has not translated far into their properties. The Littlewood-Richardson coefficients have a beautiful positive combinatorial interpretation, and their positivity is “easy” to decide, formally, it is in
![]() ${{{\textsf {P}} }}$
. However, positive combinatorial formulas for the Kronecker coefficients have eluded us so far, see Section 1.2, and their positivity is hard to decide. The reduced Kronecker coefficients
${{{\textsf {P}} }}$
. However, positive combinatorial formulas for the Kronecker coefficients have eluded us so far, see Section 1.2, and their positivity is hard to decide. The reduced Kronecker coefficients
![]() $\overline {\texttt {k}}(\alpha ,\beta ,\gamma )$
are defined as the stable limit of the ordinary Kronecker coefficients
$\overline {\texttt {k}}(\alpha ,\beta ,\gamma )$
are defined as the stable limit of the ordinary Kronecker coefficients
These coefficients are called extended Littlewood-Richardson numbers in [Reference KirillovKir04], since in the special case when
![]() $|\alpha |=|\beta |+|\gamma |$
, we have
$|\alpha |=|\beta |+|\gamma |$
, we have
the Littlewood-Richardson coefficient. As such, they have been considered as an intermediate, an interpolation, between the Littlewood-Richardson and Kronecker coefficients. Problem 2.32 in [Reference KirillovKir04] asks for a combinatorial interpretation of
![]() $\overline {{\texttt {k}}}(\alpha ,\beta ,\gamma )$
. They have been an object of independent interest, see [Reference MurnaghanMur38, Reference MurnaghanMur56, Reference BrionBri93, Reference VallejoVal99, Reference KirillovKir04, Reference Briand, Orellana and RosasBOR11, Reference Bowman, De Visscher and OrellanaBDVO15, Reference Colmenarejo and RosasCR15, Reference ManivelMan15, Reference Sam and SnowdenSS16, Reference Ikenmeyer and PanovaIP17, Reference Pak and PanovaPP20b, Reference Orellana and ZabrockiOZ19, Reference Orellana and ZabrockiOZ21], and considered better behaved than the ordinary Kronecker coefficients.
$\overline {{\texttt {k}}}(\alpha ,\beta ,\gamma )$
. They have been an object of independent interest, see [Reference MurnaghanMur38, Reference MurnaghanMur56, Reference BrionBri93, Reference VallejoVal99, Reference KirillovKir04, Reference Briand, Orellana and RosasBOR11, Reference Bowman, De Visscher and OrellanaBDVO15, Reference Colmenarejo and RosasCR15, Reference ManivelMan15, Reference Sam and SnowdenSS16, Reference Ikenmeyer and PanovaIP17, Reference Pak and PanovaPP20b, Reference Orellana and ZabrockiOZ19, Reference Orellana and ZabrockiOZ21], and considered better behaved than the ordinary Kronecker coefficients.
This is, however, not the case. As we show, every Kronecker coefficient is equal to an explicit reduced Kronecker coefficient of not much larger partitions, in particular:
Theorem 1. For all partitions
![]() $\lambda $
,
$\lambda $
,
![]() $\mu $
,
$\mu $
,
![]() $\nu $
of equal sizes, we have
$\nu $
of equal sizes, we have
Here,
 $a^b := (\underbrace {a,\ldots ,a}_{b \text { many}})$
and
$a^b := (\underbrace {a,\ldots ,a}_{b \text { many}})$
and
 $(\nu _1^b,\nu ) := (\underbrace {\nu _1,\ldots ,\nu _1}_{b \text { many}},\nu _1,\nu _2,\nu _3,\ldots )$
.
$(\nu _1^b,\nu ) := (\underbrace {\nu _1,\ldots ,\nu _1}_{b \text { many}},\nu _1,\nu _2,\nu _3,\ldots )$
.
Theorem 1 implies that in a very strong sense, on the spectrum between Littlewood-Richardson and Kronecker coefficients, the reduced Kronecker coefficients are at the same point as the ordinary Kronecker coefficients. In particular, Theorem 1 implies that Problem 2.32 in [Reference KirillovKir04] is equivalent to Problem 10 in [Reference StanleySta00]: Finding a combinatorial interpretation for the Kronecker coefficient or for the reduced Kronecker coefficient are the same problem. Formally, Conjectures 9.1 and 9.4 in [Reference PakPak22] are the same. Our result can be interpreted in a positive or in a negative way. On the one hand, the reduced Kronecker coefficients cannot be easier to understand than the ordinary Kronecker coefficients. On the other hand, understanding the reduced Kronecker coefficients is sufficient to understand all ordinary Kronecker coefficients. As a corollary, we settle the conjecture from [Reference Pak and PanovaPP20b, Section 4.4] on the hardness of deciding the positivity of
![]() $\overline {{\texttt {k}}}(\alpha ,\beta ,\gamma )$
.
$\overline {{\texttt {k}}}(\alpha ,\beta ,\gamma )$
.
Corollary 1 (settles conjecture in [Reference Pak and PanovaPP20b, Section 4.4]).
Given
![]() $\alpha ,\beta ,\gamma $
in unary, deciding if
$\alpha ,\beta ,\gamma $
in unary, deciding if
![]() ${\overline {{\texttt {k}}}(\alpha ,\beta ,\gamma )>0}$
is
${\overline {{\texttt {k}}}(\alpha ,\beta ,\gamma )>0}$
is
![]() ${{{{\textsf {NP}}}}}$
-hard.
${{{{\textsf {NP}}}}}$
-hard.
Proof. This follows directly from Theorem 1 and the fact that deciding
![]() ${\texttt {k}}(\lambda ,\mu ,\nu )>0$
is
${\texttt {k}}(\lambda ,\mu ,\nu )>0$
is
![]() ${{{{\textsf {NP}}}}}$
-hard [Reference Ikenmeyer, Mulmuley and WalterIMW17].
${{{{\textsf {NP}}}}}$
-hard [Reference Ikenmeyer, Mulmuley and WalterIMW17].
Moreover, by the same immediate argument, it is now clear that computing the reduced Kronecker coefficient is strongly #P-hard under parsimonious many-one reductions (the argument in [Reference Pak and PanovaPP20b] gives only the #P-hardness under Turing reductions).
We discovered the partition triple construction in Theorem 1 by analyzing the natural interpretation of
![]() ${\texttt {k}}(\lambda ,\mu ,\nu )$
via the general linear group, see Section 3, and the relationship with 3-dimensional binary contingency arrays. Once the precise statement of Theorem 1 is found, one can give short and self-contained proofs (see Section 2). In particular, in Section 3, we prove Theorem 1 by giving an explicit isomorphism between the corresponding highest weight vector spaces. In Section 4, we give elementary purely combinatorial proofs via symmetric functions, which also bridge the two methodologies. Theorem 1 (but not the explicit isomorphism) can also be deduced from a formula from 2011 by E. Briand, R. Orellana and M. Rosas, [Reference Briand, Orellana and RosasBOR11] (see the discussion at the end of Section 4.2).
${\texttt {k}}(\lambda ,\mu ,\nu )$
via the general linear group, see Section 3, and the relationship with 3-dimensional binary contingency arrays. Once the precise statement of Theorem 1 is found, one can give short and self-contained proofs (see Section 2). In particular, in Section 3, we prove Theorem 1 by giving an explicit isomorphism between the corresponding highest weight vector spaces. In Section 4, we give elementary purely combinatorial proofs via symmetric functions, which also bridge the two methodologies. Theorem 1 (but not the explicit isomorphism) can also be deduced from a formula from 2011 by E. Briand, R. Orellana and M. Rosas, [Reference Briand, Orellana and RosasBOR11] (see the discussion at the end of Section 4.2).
1.1 Background and definitions
We refer to [Reference James and KerberJK84, Reference StanleySta99, Reference SaganSag13] for basic definitions and properties from algebraic combinatorics and representation theory, and employ the following notation. We write
![]() $[a,b]:=\{a,a+1,\ldots ,b\}$
, and
$[a,b]:=\{a,a+1,\ldots ,b\}$
, and
![]() $[n]:=[1,n]$
. A composition of n is a sequence of nonnegative integers that sum up to n. A partition
$[n]:=[1,n]$
. A composition of n is a sequence of nonnegative integers that sum up to n. A partition
![]() $\lambda =(\lambda _1,\lambda _2,\ldots )$
of n, denoted
$\lambda =(\lambda _1,\lambda _2,\ldots )$
of n, denoted
![]() $\lambda \vdash n$
, is a weakly decreasing composition. Its size is
$\lambda \vdash n$
, is a weakly decreasing composition. Its size is
![]() $|\lambda | := \sum _i \lambda _i$
. Denote by
$|\lambda | := \sum _i \lambda _i$
. Denote by
![]() $\ell (\lambda )=\max \{i \mid \lambda _i> 0\}$
the length of
$\ell (\lambda )=\max \{i \mid \lambda _i> 0\}$
the length of
![]() $\lambda $
. We interpret
$\lambda $
. We interpret
![]() $\lambda $
as a vector of arbitrary length
$\lambda $
as a vector of arbitrary length
![]() $\geq \ell (\lambda )$
by appending zeros. We denote by
$\geq \ell (\lambda )$
by appending zeros. We denote by
![]() $(n)$
the partition of n of length 1. To every partition, we associate its Young diagram, which is a list of left-justified rows of boxes,
$(n)$
the partition of n of length 1. To every partition, we associate its Young diagram, which is a list of left-justified rows of boxes,
![]() $\lambda _i$
many boxes in row i. We write
$\lambda _i$
many boxes in row i. We write
![]() $\lambda '$
do denote the transpose partition, that is, the partition that arises from reflecting the Young diagram at the main diagonal. Formally,
$\lambda '$
do denote the transpose partition, that is, the partition that arises from reflecting the Young diagram at the main diagonal. Formally,
![]() $\lambda ^{\prime }_j := \max \{i \mid \lambda _i\geq j\}$
. We add partitions row-wise:
$\lambda ^{\prime }_j := \max \{i \mid \lambda _i\geq j\}$
. We add partitions row-wise:
![]() $(\lambda +\mu )_i=\lambda _i+\mu _i$
. We define
$(\lambda +\mu )_i=\lambda _i+\mu _i$
. We define
![]() $\lambda \mathbin {\diamond }\mu := (\lambda '+\mu ')'$
, adding partitions column-wise as Young diagrams. Note that
$\lambda \mathbin {\diamond }\mu := (\lambda '+\mu ')'$
, adding partitions column-wise as Young diagrams. Note that
![]() $\mathbin {\diamond }$
is commutative and associative, and that if
$\mathbin {\diamond }$
is commutative and associative, and that if
![]() $\lambda _{\ell (\lambda )}\geq \mu _1$
, then
$\lambda _{\ell (\lambda )}\geq \mu _1$
, then
![]() $\lambda \mathbin {\diamond }\mu =(\lambda _1,\ldots ,\mu _1,\ldots )$
is just the concatenation of rows. The Specht modules
$\lambda \mathbin {\diamond }\mu =(\lambda _1,\ldots ,\mu _1,\ldots )$
is just the concatenation of rows. The Specht modules
![]() $\mathbb {S}_{\lambda }$
for
$\mathbb {S}_{\lambda }$
for
![]() $\lambda \vdash n$
are the irreducible representation of the symmetric group
$\lambda \vdash n$
are the irreducible representation of the symmetric group
![]() $S_{n}$
(see [Reference James and KerberJK84, Reference StanleySta99, Reference SaganSag13]).
$S_{n}$
(see [Reference James and KerberJK84, Reference StanleySta99, Reference SaganSag13]).
The Kronecker coefficient
![]() ${\texttt {k}}(\lambda ,\mu ,\nu )$
is the structure constantFootnote
1
defined via
${\texttt {k}}(\lambda ,\mu ,\nu )$
is the structure constantFootnote
1
defined via
or, equivalently, via Specht modules as
From this description, it is immediately clear that
![]() ${\texttt {k}}(\lambda ,\mu ,\nu )$
is a nonnegative integer. Yet, the problem of finding a combinatorial interpretation of
${\texttt {k}}(\lambda ,\mu ,\nu )$
is a nonnegative integer. Yet, the problem of finding a combinatorial interpretation of
![]() ${\texttt {k}}(\lambda ,\mu ,\nu )$
is wide open [Reference StanleySta00, Reference Ikenmeyer and PakIP22, Reference PanovaPan23].
${\texttt {k}}(\lambda ,\mu ,\nu )$
is wide open [Reference StanleySta00, Reference Ikenmeyer and PakIP22, Reference PanovaPan23].
The Kronecker coefficients were defined by Murnaghan [Reference MurnaghanMur38] in 1938 as the analogues of the Littlewood-Richardson coefficients
![]() $c^{\lambda }_{\mu \nu }$
, which are the structure constants in the ring of irreducible
$c^{\lambda }_{\mu \nu }$
, which are the structure constants in the ring of irreducible
![]() ${GL}_N$
representations, the Weyl modules
${GL}_N$
representations, the Weyl modules
![]() $V_{\lambda }$
, given as
$V_{\lambda }$
, given as
![]() $V_\mu \otimes V_\nu = \bigoplus _\lambda V_{\lambda }^{\oplus c^{\lambda }_{\mu \nu }}.$
Some simple properties, see [Reference James and KerberJK84, Reference SaganSag13], include the transposition invariance
$V_\mu \otimes V_\nu = \bigoplus _\lambda V_{\lambda }^{\oplus c^{\lambda }_{\mu \nu }}.$
Some simple properties, see [Reference James and KerberJK84, Reference SaganSag13], include the transposition invariance
![]() ${\texttt {k}}(\lambda ,\mu ,\nu ) = {\texttt {k}}(\lambda ',\mu ',\nu )$
, since
${\texttt {k}}(\lambda ,\mu ,\nu ) = {\texttt {k}}(\lambda ',\mu ',\nu )$
, since
![]() $\mathbb {S}_{1^n}\otimes \mathbb {S}_{\lambda }=\mathbb {S}_{\lambda '}$
[Reference James and KerberJK84]. From their definition, and the fact that
$\mathbb {S}_{1^n}\otimes \mathbb {S}_{\lambda }=\mathbb {S}_{\lambda '}$
[Reference James and KerberJK84]. From their definition, and the fact that
![]() $\chi ^\lambda (\pi ) \in \mathbb {Z}$
, see [Reference James and KerberJK84, Reference SaganSag13], we have
$\chi ^\lambda (\pi ) \in \mathbb {Z}$
, see [Reference James and KerberJK84, Reference SaganSag13], we have
and thus we have the
![]() $S_3$
invariance
$S_3$
invariance
![]() ${\texttt {k}}(\lambda ,\mu ,\nu )={\texttt {k}}(\lambda ,\nu ,\mu )={\texttt {k}}(\mu ,\nu ,\lambda )=\cdots $
. Note that the Kronecker coefficient is not invariant under transposing an odd number of partitions, and we define
${\texttt {k}}(\lambda ,\mu ,\nu )={\texttt {k}}(\lambda ,\nu ,\mu )={\texttt {k}}(\mu ,\nu ,\lambda )=\cdots $
. Note that the Kronecker coefficient is not invariant under transposing an odd number of partitions, and we define
It is known that
![]() ${\texttt {k}}(\lambda ,\mu ,\nu )=0$
if
${\texttt {k}}(\lambda ,\mu ,\nu )=0$
if
![]() $\ell (\lambda )>\ell (\mu )\cdot \ell (\nu )$
[Reference DvirDvi93], which also follows by combining
$\ell (\lambda )>\ell (\mu )\cdot \ell (\nu )$
[Reference DvirDvi93], which also follows by combining
![]() ${\texttt {k}}(\lambda ,\mu ,\nu )={\texttt {k}}(\lambda ,\mu ',\nu ')$
with Lemma 3. We define the stable range as the set of triples
${\texttt {k}}(\lambda ,\mu ,\nu )={\texttt {k}}(\lambda ,\mu ',\nu ')$
with Lemma 3. We define the stable range as the set of triples
![]() $(\lambda ,\mu ,\nu )$
that satisfy
$(\lambda ,\mu ,\nu )$
that satisfy
There are several proofs for the fact that for arbitrary
![]() $(\alpha ,\beta ,\gamma )$
with
$(\alpha ,\beta ,\gamma )$
with
![]() $|\alpha |=|\beta |=|\gamma |$
, the triple
$|\alpha |=|\beta |=|\gamma |$
, the triple
![]() $(\alpha +(i), \ \beta +(i) ,\gamma +(i))$
is in the stable range for i large enough (and hence for all i from then on), and upper bounds on the necessary i are known (see, e.g. [Reference BrionBri93], [Reference DvirDvi93], [Reference VallejoVal99], [Reference Briand, Orellana and RosasBOR11], [Reference IkenmeyerIke12, Section 7.4], [Reference Pak and PanovaPP14]). The reduced Kronecker coefficient is defined as the limit value in (1.1), namely,
$(\alpha +(i), \ \beta +(i) ,\gamma +(i))$
is in the stable range for i large enough (and hence for all i from then on), and upper bounds on the necessary i are known (see, e.g. [Reference BrionBri93], [Reference DvirDvi93], [Reference VallejoVal99], [Reference Briand, Orellana and RosasBOR11], [Reference IkenmeyerIke12, Section 7.4], [Reference Pak and PanovaPP14]). The reduced Kronecker coefficient is defined as the limit value in (1.1), namely,
![]() $\overline {{\texttt {k}}}(\alpha ,\beta ,\gamma ) := \lim _{n \to \infty } {\texttt {k}}(\, (n-|\alpha |,\alpha ), \ (n-|\beta |,\beta ), \ (n-|\gamma |,\gamma ) \,)$
for arbitrary partitions
$\overline {{\texttt {k}}}(\alpha ,\beta ,\gamma ) := \lim _{n \to \infty } {\texttt {k}}(\, (n-|\alpha |,\alpha ), \ (n-|\beta |,\beta ), \ (n-|\gamma |,\gamma ) \,)$
for arbitrary partitions
![]() $\alpha $
,
$\alpha $
,
![]() $\beta $
,
$\beta $
,
![]() $\gamma $
(in particular, we do not require
$\gamma $
(in particular, we do not require
![]() $|\alpha |=|\beta |=|\gamma |$
). When
$|\alpha |=|\beta |=|\gamma |$
). When
![]() $|\alpha |=|\beta |+|\gamma |$
, then it coincides with the Littlewood-Richardson coefficient
$|\alpha |=|\beta |+|\gamma |$
, then it coincides with the Littlewood-Richardson coefficient
![]() $c^{\alpha }_{\beta \gamma }$
from (1.2) (see, e.g. [Reference MurnaghanMur56, Reference LittlewoodLit58, Reference DvirDvi93], and [Reference Christandl, Şahinoğlu and WalterCŞW18, Section 6]).
$c^{\alpha }_{\beta \gamma }$
from (1.2) (see, e.g. [Reference MurnaghanMur56, Reference LittlewoodLit58, Reference DvirDvi93], and [Reference Christandl, Şahinoğlu and WalterCŞW18, Section 6]).
1.2 Related work
The Littlewood-Richardson (LR) coefficients can be computed by the Littlewood-Richardson rule, stated in 1934 and proven formally about 40 years later. It says that
![]() $c^{\lambda }_{\mu \nu }$
is equal to the number of LR tableaux of shape
$c^{\lambda }_{\mu \nu }$
is equal to the number of LR tableaux of shape
![]() $\lambda /\mu $
and content
$\lambda /\mu $
and content
![]() $\nu $
(see Section 4.1 and [Reference StanleySta99, Reference SaganSag13]). The apparent analogy in definitions motivates the community to search for such interpretations for the Kronecker coefficients. Interest in efficient ways to compute
$\nu $
(see Section 4.1 and [Reference StanleySta99, Reference SaganSag13]). The apparent analogy in definitions motivates the community to search for such interpretations for the Kronecker coefficients. Interest in efficient ways to compute
![]() ${\texttt {k}}(\lambda ,\mu ,\nu )$
and
${\texttt {k}}(\lambda ,\mu ,\nu )$
and
![]() $\overline {{\texttt {k}}}(\alpha ,\beta \gamma )$
dates back at least to Murnaghan [Reference MurnaghanMur38]. Specific interest in nonnegative combinatorial interpretations of
$\overline {{\texttt {k}}}(\alpha ,\beta \gamma )$
dates back at least to Murnaghan [Reference MurnaghanMur38]. Specific interest in nonnegative combinatorial interpretations of
![]() ${\texttt {k}}(\lambda ,\mu ,\nu )$
can be found in [Reference LascouxLas79, Reference Garsia and RemmelGR85], and was formulated clearly again by Stanley as Problem 10 in his list “Open Problems in Algebraic Combinatorics” [Reference StanleySta00]: “Find a combinatorial interpretation of the Kronecker product coefficients
${\texttt {k}}(\lambda ,\mu ,\nu )$
can be found in [Reference LascouxLas79, Reference Garsia and RemmelGR85], and was formulated clearly again by Stanley as Problem 10 in his list “Open Problems in Algebraic Combinatorics” [Reference StanleySta00]: “Find a combinatorial interpretation of the Kronecker product coefficients
![]() ${\texttt {k}}(\lambda ,\mu ,\nu )$
, thereby combinatorially reproving that they are nonnegative” (see also [Reference PanovaPan23] for a detailed discussion on this topic). Despite its natural and fundamental nature and the variety of efforts, this question has seen relatively little progress. In 1989, Remmel found a combinatorial rule for
${\texttt {k}}(\lambda ,\mu ,\nu )$
, thereby combinatorially reproving that they are nonnegative” (see also [Reference PanovaPan23] for a detailed discussion on this topic). Despite its natural and fundamental nature and the variety of efforts, this question has seen relatively little progress. In 1989, Remmel found a combinatorial rule for
![]() ${\texttt {k}}(\lambda ,\mu ,\nu )$
when two of the partitions are hooks [Reference RemmelRem89]. In 1994, Remmel and Whitehead [Reference Remmel and WhiteheadRW94] found
${\texttt {k}}(\lambda ,\mu ,\nu )$
when two of the partitions are hooks [Reference RemmelRem89]. In 1994, Remmel and Whitehead [Reference Remmel and WhiteheadRW94] found
![]() ${\texttt {k}}(\lambda ,\mu ,\nu )$
for
${\texttt {k}}(\lambda ,\mu ,\nu )$
for
![]() $\ell (\lambda ), \ell (\mu )\leq 2$
, which was subsequently studied also in [Reference Blasiak, Mulmuley and SohoniBMS15]. In 2006, Ballantine and Orellana [Reference Ballantine and OrellanaBO06] established a rule for
$\ell (\lambda ), \ell (\mu )\leq 2$
, which was subsequently studied also in [Reference Blasiak, Mulmuley and SohoniBMS15]. In 2006, Ballantine and Orellana [Reference Ballantine and OrellanaBO06] established a rule for
![]() ${\texttt {k}}(\lambda ,\mu ,\nu )$
when
${\texttt {k}}(\lambda ,\mu ,\nu )$
when
![]() $\mu =(n-k,k)$
and
$\mu =(n-k,k)$
and
![]() $\lambda _1 \geq 2k-1$
. In general, when the number of rows is fixed,
$\lambda _1 \geq 2k-1$
. In general, when the number of rows is fixed,
![]() ${\texttt {k}}(\lambda ,\mu ,\nu )$
can be computed in polynomial time [Reference Christandl, Doran and WalterCDW12] (see also [Reference Pak and PanovaPP17b] for a different approach and related results). The most general rule for
${\texttt {k}}(\lambda ,\mu ,\nu )$
can be computed in polynomial time [Reference Christandl, Doran and WalterCDW12] (see also [Reference Pak and PanovaPP17b] for a different approach and related results). The most general rule for
![]() $\nu =(n-k,1^k)$
, a hook, and any other two partitions, was established by Blasiak in 2012 [Reference BlasiakBla17], and later simplified in [Reference LiuLiu17, Reference Blasiak and LiuBL18]. Other special cases include multiplicity-free Kronecker products by Bessenrodt-Bowman [Reference Bessenrodt and BowmanBB17], triples of partitions which are marginals of pyramids by Ikenmeyer-Mulmuley-Walter [Reference Ikenmeyer, Mulmuley and WalterIMW17],
$\nu =(n-k,1^k)$
, a hook, and any other two partitions, was established by Blasiak in 2012 [Reference BlasiakBla17], and later simplified in [Reference LiuLiu17, Reference Blasiak and LiuBL18]. Other special cases include multiplicity-free Kronecker products by Bessenrodt-Bowman [Reference Bessenrodt and BowmanBB17], triples of partitions which are marginals of pyramids by Ikenmeyer-Mulmuley-Walter [Reference Ikenmeyer, Mulmuley and WalterIMW17],
![]() ${\texttt {k}}(m^k,m^k,(mk-n,n))$
as counting labeled trees by Pak-Panova [Reference PanovaPan15, slide 9], near-rectangular partitions by Tewari in [Reference TewariTew15], etc. As shown in [Reference Ikenmeyer, Mulmuley and WalterIMW17], computing the Kronecker coefficients is
${\texttt {k}}(m^k,m^k,(mk-n,n))$
as counting labeled trees by Pak-Panova [Reference PanovaPan15, slide 9], near-rectangular partitions by Tewari in [Reference TewariTew15], etc. As shown in [Reference Ikenmeyer, Mulmuley and WalterIMW17], computing the Kronecker coefficients is
![]() ${{{\textsf {\#P}}}}$
-hard, and deciding positivity is
${{{\textsf {\#P}}}}$
-hard, and deciding positivity is
![]() ${{{{\textsf {NP}}}}}$
-hard, while in [Reference Bravyi, Chowdhury, Gosset, Havlícĕk and ZhuBCG+23] it is shown that deciding positivity is in QMA.
${{{{\textsf {NP}}}}}$
-hard, while in [Reference Bravyi, Chowdhury, Gosset, Havlícĕk and ZhuBCG+23] it is shown that deciding positivity is in QMA.
It was shown by Murnaghan [Reference MurnaghanMur56] that the reduced Kronecker coefficients generalize the Littlewood-Richardson coefficients (see equation (1.2)). This motivated Kirillov to name
![]() $\overline {{\texttt {k}}}$
as “extended Littlewood-Richardson numbers”. This relationship and other properties have motivated an independent interest in the reduced Kronecker coefficients as intermediates between Littlewood-Richardson and ordinary Kronecker coefficients. Some special cases of combinatorial interpretations can be derived from the existing ones for the ordinary Kronecker coefficients. A combinatorial interpretation of
$\overline {{\texttt {k}}}$
as “extended Littlewood-Richardson numbers”. This relationship and other properties have motivated an independent interest in the reduced Kronecker coefficients as intermediates between Littlewood-Richardson and ordinary Kronecker coefficients. Some special cases of combinatorial interpretations can be derived from the existing ones for the ordinary Kronecker coefficients. A combinatorial interpretation of
![]() $\overline {{\texttt {k}}}(\alpha ,\beta ,\gamma )$
in the subcase where
$\overline {{\texttt {k}}}(\alpha ,\beta ,\gamma )$
in the subcase where
![]() $\ell (\alpha )=1$
was obtained in [Reference Ballantine and OrellanaBO05, Reference Ballantine and OrellanaBO06] (see also [Reference Colmenarejo and RosasCR15]). Methods to compute them have been discussed in [Reference MurnaghanMur38, Reference MurnaghanMur56] and have been developed in a series of papers (see [Reference Briand, Orellana and RosasBOR11, Reference Bowman, De Visscher and OrellanaBDVO15, Reference Orellana and ZabrockiOZ19, Reference Orellana and ZabrockiOZ21]). As observed in [Reference Bowman, De Visscher and OrellanaBDVO15], the reduced Kronecker coefficients are also the structure constants for the ring of so-called character polynomials [Reference MacdonaldMac98]. The reduced Kronecker coefficients are a special case of a more general stability phenomenon that, if
$\ell (\alpha )=1$
was obtained in [Reference Ballantine and OrellanaBO05, Reference Ballantine and OrellanaBO06] (see also [Reference Colmenarejo and RosasCR15]). Methods to compute them have been discussed in [Reference MurnaghanMur38, Reference MurnaghanMur56] and have been developed in a series of papers (see [Reference Briand, Orellana and RosasBOR11, Reference Bowman, De Visscher and OrellanaBDVO15, Reference Orellana and ZabrockiOZ19, Reference Orellana and ZabrockiOZ21]). As observed in [Reference Bowman, De Visscher and OrellanaBDVO15], the reduced Kronecker coefficients are also the structure constants for the ring of so-called character polynomials [Reference MacdonaldMac98]. The reduced Kronecker coefficients are a special case of a more general stability phenomenon that, if
![]() ${\texttt {k}}(i\alpha ,i\beta ,i\gamma )=1$
for all i, then
${\texttt {k}}(i\alpha ,i\beta ,i\gamma )=1$
for all i, then
![]() ${\texttt {k}}(\lambda +N\alpha ,\mu +N\beta ,\nu +N\gamma )$
stabilizes as
${\texttt {k}}(\lambda +N\alpha ,\mu +N\beta ,\nu +N\gamma )$
stabilizes as
![]() $N\to \infty $
(see [Reference StembridgeSte, Reference Sam and SnowdenSS16, Reference VallejoVal20]).
$N\to \infty $
(see [Reference StembridgeSte, Reference Sam and SnowdenSS16, Reference VallejoVal20]).
The Kronecker coefficients can be expressed as a small alternating sum of reduced Kronecker coefficients, and reduced Kronecker coefficients are certain sums of ordinary Kronecker coefficients for smaller partitions (see [Reference Briand, Orellana and RosasBOR11]). These relationships showed that reduced Kronecker coefficients are also #P-hard to compute (see [Reference Pak and PanovaPP20b]). However, these relations did not imply that deciding positivity of reduced Kronecker coefficients is NP-hard.
It is important to note that deciding if
![]() $c^{\lambda }_{\mu \nu }>0$
is in
$c^{\lambda }_{\mu \nu }>0$
is in
![]() ${{{\textsf {P}} }}$
, since they count integer points in a polytope that has an integral vertex whenever it is nonempty. This was shown in [Reference Mulmuley, Narayanan and SohoniMNS12, Reference De Loera and McAllisterDLM06] and follows from Knutson-Tao’s proof of the saturation theorem for Littlewood-Richardson coefficients [Reference Knutson and TaoKT99], namely, that
${{{\textsf {P}} }}$
, since they count integer points in a polytope that has an integral vertex whenever it is nonempty. This was shown in [Reference Mulmuley, Narayanan and SohoniMNS12, Reference De Loera and McAllisterDLM06] and follows from Knutson-Tao’s proof of the saturation theorem for Littlewood-Richardson coefficients [Reference Knutson and TaoKT99], namely, that
![]() $c^{N\lambda }_{N\mu , N\nu }>0 \Longleftrightarrow c^{\lambda }_{\mu \nu }>0$
. The Kronecker coefficients do not satisfy the saturation property, because
$c^{N\lambda }_{N\mu , N\nu }>0 \Longleftrightarrow c^{\lambda }_{\mu \nu }>0$
. The Kronecker coefficients do not satisfy the saturation property, because
![]() ${\texttt {k}}(2^2,2^2,2^2)=1$
, but
${\texttt {k}}(2^2,2^2,2^2)=1$
, but
![]() ${\texttt {k}}(1^2,1^2,1^2)=0$
. Until recently, it was believed that the reduced Kronecker coefficients have the saturation property: It was conjectured in [Reference KirillovKir04, Reference KlyachkoKly04] that if
${\texttt {k}}(1^2,1^2,1^2)=0$
. Until recently, it was believed that the reduced Kronecker coefficients have the saturation property: It was conjectured in [Reference KirillovKir04, Reference KlyachkoKly04] that if
![]() $\overline {{\texttt {k}}}(N\alpha ,N\beta , N\gamma )> 0$
for some
$\overline {{\texttt {k}}}(N\alpha ,N\beta , N\gamma )> 0$
for some
![]() $N>0$
, then
$N>0$
, then
![]() $\overline {{\texttt {k}}}(\alpha ,\beta ,\gamma )> 0 .$
This was disproved in [Reference Pak and PanovaPP20b] in 2020 and moved the reduced Kroneckers away from the Littlewood-Richardson coefficients on that spectrum.
$\overline {{\texttt {k}}}(\alpha ,\beta ,\gamma )> 0 .$
This was disproved in [Reference Pak and PanovaPP20b] in 2020 and moved the reduced Kroneckers away from the Littlewood-Richardson coefficients on that spectrum.
It is known that the Kronecker coefficients (and hence also the reduced Kronecker coefficients) satisfy the so-called semigroup property [Reference ChristandlChr06, Theorem 2.7], which implies that if
![]() ${\texttt {k}}(\lambda ,\mu ,\nu )>0$
, then
${\texttt {k}}(\lambda ,\mu ,\nu )>0$
, then
![]() $\forall N>0: {\texttt {k}}(N\lambda ,N\mu ,N\nu )>0$
, and if
$\forall N>0: {\texttt {k}}(N\lambda ,N\mu ,N\nu )>0$
, and if
![]() $\overline {{\texttt {k}}}(\alpha ,\beta ,\gamma )>0$
, then
$\overline {{\texttt {k}}}(\alpha ,\beta ,\gamma )>0$
, then
![]() $\forall N>0: \overline {{\texttt {k}}}(N\alpha ,N\beta ,N\gamma )>0$
. Deciding whether or not
$\forall N>0: \overline {{\texttt {k}}}(N\alpha ,N\beta ,N\gamma )>0$
. Deciding whether or not
![]() $\exists N :{\texttt {k}}(N\lambda ,N\mu ,N\nu )> 0$
is in
$\exists N :{\texttt {k}}(N\lambda ,N\mu ,N\nu )> 0$
is in
![]() ${{{{\textsf {NP}}}}}\cap {{{\textsf {coNP}} }}$
, and analogously for
${{{{\textsf {NP}}}}}\cap {{{\textsf {coNP}} }}$
, and analogously for
![]() $\overline {{\texttt {k}}}(N\alpha ,N\beta ,N\gamma )$
[Reference Bürgisser, Christandl, Mulmuley and WalterBCMW17].
$\overline {{\texttt {k}}}(N\alpha ,N\beta ,N\gamma )$
[Reference Bürgisser, Christandl, Mulmuley and WalterBCMW17].
2 Setting up the proof of Theorem 1
We set up the proof in this section, reducing to a more general Theorem 2, which has a short proof via
![]() $GL_N$
in Section 3. We also give two short, self-contained proofs using basic symmetric function techniques in Section 4.
$GL_N$
in Section 3. We also give two short, self-contained proofs using basic symmetric function techniques in Section 4.
We prove a slightly stronger statement than Theorem 1: For
![]() $l\geq \ell (\lambda )$
,
$l\geq \ell (\lambda )$
,
![]() $m\geq \ell (\mu )$
,
$m\geq \ell (\mu )$
,
![]() $c\geq \nu _1$
, we have
$c\geq \nu _1$
, we have
We start with Lemma 1, a classical identity that can be proved in several ways (see, e.g. [Reference DvirDvi93, Theorem 2.4’], [Reference Briand, Orellana and RosasBOR09, Proof of Lemma 2.1], [Reference VallejoVal09, Theorem 3.1], [Reference IkenmeyerIke12, Corollary 4.4.14]).
Lemma 1. Let
![]() $\lambda ,\mu ,\nu $
be partitions with
$\lambda ,\mu ,\nu $
be partitions with
![]() $\ell (\lambda )\leq l$
,
$\ell (\lambda )\leq l$
,
![]() $\ell (\mu )\leq m$
. Then
$\ell (\mu )\leq m$
. Then
The situation is depicted in Figure 1.

Figure 1 An example of the situation in Lemma 1 with
![]() $\lambda =(4,2,1)$
,
$\lambda =(4,2,1)$
,
![]() $\mu =(3,2,1,1)$
,
$\mu =(3,2,1,1)$
,
![]() $\nu =(3,3,1)$
,
$\nu =(3,3,1)$
,
![]() $l=3$
and
$l=3$
and
![]() $m=4$
.
$m=4$
.
In terms of
![]() ${\texttt {k}}'$
, instead of
${\texttt {k}}'$
, instead of
![]() ${\texttt {k}}$
, we can alternatively phrase Lemma 1 as
${\texttt {k}}$
, we can alternatively phrase Lemma 1 as
which has a direct proof via an isomorphism of highest weight vector spaces (see (3.3)).
Note that if
![]() $\ell (\nu )>lm$
, then
$\ell (\nu )>lm$
, then
![]() $\ell (\nu )>lm\geq \ell (\lambda )\cdot \ell (\mu )$
, and hence
$\ell (\nu )>lm\geq \ell (\lambda )\cdot \ell (\mu )$
, and hence
![]() ${\texttt {k}}(\lambda ,\mu ,\nu )=0$
. Moreover,
${\texttt {k}}(\lambda ,\mu ,\nu )=0$
. Moreover,
![]() $\ell (1^{lm}+\nu )=\ell (\nu )>lm\geq \ell (\lambda )\cdot \ell (\mu ) = \ell (m^l+\lambda )\cdot \ell (l^m+\mu )$
, and hence
$\ell (1^{lm}+\nu )=\ell (\nu )>lm\geq \ell (\lambda )\cdot \ell (\mu ) = \ell (m^l+\lambda )\cdot \ell (l^m+\mu )$
, and hence
![]() ${\texttt {k}}( \, m^l+\lambda , \ l^m+\mu , \ 1^{lm}+\nu \, )=0$
. So we can assume that
${\texttt {k}}( \, m^l+\lambda , \ l^m+\mu , \ 1^{lm}+\nu \, )=0$
. So we can assume that
![]() $\ell (\nu )\leq lm$
. We give two proofs in this case, one in Section 3 and one in Section 4.
$\ell (\nu )\leq lm$
. We give two proofs in this case, one in Section 3 and one in Section 4.
The following Lemma 2 is proved by applying Lemma 1 twice, in different directions. An illustration of the situation is given in Figure 2.
Lemma 2. Let
![]() $\lambda $
,
$\lambda $
,
![]() $\mu $
,
$\mu $
,
![]() $\nu $
be partitions of the same size, and let
$\nu $
be partitions of the same size, and let
![]() $l \geq \ell (\lambda )$
,
$l \geq \ell (\lambda )$
,
![]() $m \geq \ell (\mu )$
and
$m \geq \ell (\mu )$
and
![]() $c \geq \nu _1$
. Let
$c \geq \nu _1$
. Let
![]() $d=(m+1)c$
,
$d=(m+1)c$
,
![]() $e=(l+1)c$
. Then
$e=(l+1)c$
. Then
Proof. We apply Lemma 1 twice as follows.
 $$ \begin{align*} {\texttt{k}}'(\lambda,\mu,\nu') &\stackrel{{({2.2})}}{=} {\texttt{k}}'( \, (mc)\mathbin{\diamond}\lambda , \ c^m + \mu, \ m^c+\nu' \, )\\ &\stackrel{{({2.2})}}{=} {\texttt{k}}'( \, c^{l+1} + ((mc) \mathbin{\diamond} \lambda) , \ (e)\mathbin{\diamond}(m^c +\mu), \ (l+m+1)^c+\nu' \, ).\\[-38pt] \end{align*} $$
$$ \begin{align*} {\texttt{k}}'(\lambda,\mu,\nu') &\stackrel{{({2.2})}}{=} {\texttt{k}}'( \, (mc)\mathbin{\diamond}\lambda , \ c^m + \mu, \ m^c+\nu' \, )\\ &\stackrel{{({2.2})}}{=} {\texttt{k}}'( \, c^{l+1} + ((mc) \mathbin{\diamond} \lambda) , \ (e)\mathbin{\diamond}(m^c +\mu), \ (l+m+1)^c+\nu' \, ).\\[-38pt] \end{align*} $$
Theorem 2. Let
![]() $\lambda $
,
$\lambda $
,
![]() $\mu $
,
$\mu $
,
![]() $\nu $
be partitions of the same size, such that
$\nu $
be partitions of the same size, such that
![]() $\lambda _1 \geq \ell (\mu ) \cdot \nu _1$
and
$\lambda _1 \geq \ell (\mu ) \cdot \nu _1$
and
![]() $\mu _1 \geq \ell (\lambda ) \cdot \nu _1$
. Then, for every
$\mu _1 \geq \ell (\lambda ) \cdot \nu _1$
. Then, for every
![]() $h \geq 0$
, we have
$h \geq 0$
, we have
We provide three proofs of this fact, one in Section 3, and two in Section 4. Those sections can be read independently of each other. The proofs make use of an observation on 3-dimensional contingency arrays with zeros and ones as entries (Lemma 4), but they use it in different ways.
We identify subsets
![]() $Q \subseteq \mathbb {N}^3$
with their characteristic functions
$Q \subseteq \mathbb {N}^3$
with their characteristic functions
![]() $Q : \mathbb {N}^3\to \{0,1\}$
, and we call Q a binary or
$Q : \mathbb {N}^3\to \{0,1\}$
, and we call Q a binary or
![]() $\{0,1\}$
-contingency array. This means, we interpret Q as a function to
$\{0,1\}$
-contingency array. This means, we interpret Q as a function to
![]() $\{0,1\}$
, and as the point set of its support. The interpretation will always be clear from the context. The 2-dimensional marginals of Q are defined as
$\{0,1\}$
, and as the point set of its support. The interpretation will always be clear from the context. The 2-dimensional marginals of Q are defined as
![]() $Q_{i\ast \ast } := \sum _{j,k}Q_{i,j,k} = |Q\cap (\{i\}\times \mathbb {N}\times \mathbb {N})|$
,
$Q_{i\ast \ast } := \sum _{j,k}Q_{i,j,k} = |Q\cap (\{i\}\times \mathbb {N}\times \mathbb {N})|$
,
![]() $Q_{\ast i \ast } := \sum _{j,k}Q_{j,i,k} = |Q\cap (\mathbb {N}\times \{i\}\times \mathbb {N})|$
,
$Q_{\ast i \ast } := \sum _{j,k}Q_{j,i,k} = |Q\cap (\mathbb {N}\times \{i\}\times \mathbb {N})|$
,
![]() $Q_{\ast \ast i} := \sum _{j,k}Q_{j,k,i} = |Q\cap (\mathbb {N}\times \mathbb {N}\times \{i\})|$
. For
$Q_{\ast \ast i} := \sum _{j,k}Q_{j,k,i} = |Q\cap (\mathbb {N}\times \mathbb {N}\times \{i\})|$
. For
![]() $\alpha \in {\mathbb {N}}^{\mathbb {N}}$
,
$\alpha \in {\mathbb {N}}^{\mathbb {N}}$
,
![]() $\beta \in {\mathbb {N}}^{\mathbb {N}}$
,
$\beta \in {\mathbb {N}}^{\mathbb {N}}$
,
![]() $\gamma \in {\mathbb {N}}^{\mathbb {N}}$
,
$\gamma \in {\mathbb {N}}^{\mathbb {N}}$
,
![]() $|\alpha |=|\beta |=|\gamma |<\infty $
, we denote by
$|\alpha |=|\beta |=|\gamma |<\infty $
, we denote by
There is a close connection to the Kronecker coefficients via the following lemma.
Lemma 3. For partitions
![]() $\alpha $
,
$\alpha $
,
![]() $\beta $
,
$\beta $
,
![]() $\gamma $
of equal size, we have
$\gamma $
of equal size, we have
![]() ${\texttt {k}}'(\alpha ,\beta ,\gamma )\leq |\mathcal C(\alpha ,\beta ,\gamma )|$
.
${\texttt {k}}'(\alpha ,\beta ,\gamma )\leq |\mathcal C(\alpha ,\beta ,\gamma )|$
.
Proof. There are different proofs of this fact, for example [Reference Ikenmeyer, Mulmuley and WalterIMW17, Lemma 2.6] and [Reference Pak and PanovaPP20a, Theorem 5.3] (see also Sections 3.1 and 4.1).
The following lemma shows how restrictions on the marginals can result in strong restrictions on the sets Q, a technique that was also applied in [Reference Ikenmeyer, Mulmuley and WalterIMW17].
Lemma 4. Let
![]() $\alpha ,\beta ,\gamma $
be compositions with
$\alpha ,\beta ,\gamma $
be compositions with
![]() $|\alpha |=|\beta |=|\gamma |$
. Let
$|\alpha |=|\beta |=|\gamma |$
. Let
![]() $a\geq \ell (\alpha )$
,
$a\geq \ell (\alpha )$
,
![]() $b\geq \ell (\beta )$
, and let the integers
$b\geq \ell (\beta )$
, and let the integers
![]() $c,h$
be such that
$c,h$
be such that
![]() $c+h \geq \ell (\gamma )$
and
$c+h \geq \ell (\gamma )$
and
![]() $\sum _{i>c} \gamma _i \leq h$
. Furthermore, let
$\sum _{i>c} \gamma _i \leq h$
. Furthermore, let
![]() $\alpha _1\geq bc+h$
,
$\alpha _1\geq bc+h$
,
![]() $\beta _1\geq ac+h$
.
$\beta _1\geq ac+h$
.
Then, for every
![]() $Q\in \mathcal {C}(\alpha ,\beta ,\gamma )$
, we have
$Q\in \mathcal {C}(\alpha ,\beta ,\gamma )$
, we have
 $$ \begin{align*} & \{1\}\times[b]\times[c] \subseteq Q, \quad [a]\times\{1\}\times[c] \subseteq Q, \quad \{1\}\times\{1\}\times[c+h] \subseteq Q, \text{ and}\\ & Q \cap (\mathbb{N} \times \mathbb{N} \times [c+1,c+h]) = \{1\} \times \{1\} \times [c+1,c+h]. \end{align*} $$
$$ \begin{align*} & \{1\}\times[b]\times[c] \subseteq Q, \quad [a]\times\{1\}\times[c] \subseteq Q, \quad \{1\}\times\{1\}\times[c+h] \subseteq Q, \text{ and}\\ & Q \cap (\mathbb{N} \times \mathbb{N} \times [c+1,c+h]) = \{1\} \times \{1\} \times [c+1,c+h]. \end{align*} $$
In particular, if
![]() $\mathcal {C}(\alpha ,\beta ,\gamma )$
is nonempty, then
$\mathcal {C}(\alpha ,\beta ,\gamma )$
is nonempty, then
![]() $a=\ell (\alpha )$
,
$a=\ell (\alpha )$
,
![]() $b=\ell (\beta )$
,
$b=\ell (\beta )$
,
![]() $\gamma _i=1$
for all
$\gamma _i=1$
for all
![]() $c+1\leq i\leq c+h$
, and
$c+1\leq i\leq c+h$
, and
![]() $\alpha _1=bc+h$
,
$\alpha _1=bc+h$
,
![]() $\beta _1=ac+h$
,
$\beta _1=ac+h$
,
![]() $\alpha _2\leq bc$
and
$\alpha _2\leq bc$
and
![]() $\beta _2\leq ac$
.
$\beta _2\leq ac$
.

Figure 3 Lemma 4 for
![]() $a=5$
,
$a=5$
,
![]() $b=4$
,
$b=4$
,
![]() $c=2$
,
$c=2$
,
![]() $h=4$
. A gray cube represents a forced 1 in the contingency array. Absence of color represents a forced 0 in the contingency array. The blue box shows the area where both zeros and ones are possible.
$h=4$
. A gray cube represents a forced 1 in the contingency array. Absence of color represents a forced 0 in the contingency array. The blue box shows the area where both zeros and ones are possible.
In other words, if we have 3-dimensional point configurations with such marginals, then the walls consist of two rectangles and a long column as depicted in Figure 3.
Proof. Assume that there exists a binary contingency array
![]() $Q\in \mathcal C(\alpha ,\beta ,\gamma )$
. Let
$Q\in \mathcal C(\alpha ,\beta ,\gamma )$
. Let
![]() $B_\cup := \{1\}\times [b]\times [c+h] \ \cup \ [a]\times \{1\}\times [c+h]$
be the set of points in the planes
$B_\cup := \{1\}\times [b]\times [c+h] \ \cup \ [a]\times \{1\}\times [c+h]$
be the set of points in the planes
![]() $x=1$
and
$x=1$
and
![]() $y=1$
, and let
$y=1$
, and let
![]() $B_\cap := \{1\}\times \{1\}\times [c+h]$
be the set of points on the line
$B_\cap := \{1\}\times \{1\}\times [c+h]$
be the set of points on the line
![]() $x=y=1$
. Let
$x=y=1$
. Let
![]() $H_i := Q \cap (\mathbb {N}\times \mathbb {N}\times \{i\}) \cap B_\cup $
be the entries of Q in
$H_i := Q \cap (\mathbb {N}\times \mathbb {N}\times \{i\}) \cap B_\cup $
be the entries of Q in
![]() $B_\cup $
at the section with the plane
$B_\cup $
at the section with the plane
![]() $z=i$
. In particular,
$z=i$
. In particular,
 $$ \begin{align*}\sum_{i=1}^{c+h}|H_i|=|Q\cap B_\cup|.\end{align*} $$
$$ \begin{align*}\sum_{i=1}^{c+h}|H_i|=|Q\cap B_\cup|.\end{align*} $$
We have
![]() $\sum _{i=c+1}^{c+h} |H_i|\leq \sum _{i=c+1}^{c+h} \gamma _i \leq h$
,
$\sum _{i=c+1}^{c+h} |H_i|\leq \sum _{i=c+1}^{c+h} \gamma _i \leq h$
,
![]() $|H_i|\leq a+b-1$
for all
$|H_i|\leq a+b-1$
for all
![]() $0<i\leq c$
and
$0<i\leq c$
and
![]() $|Q\cap B_\cap | \leq c+h$
. All these inequalities must be met with equality, because
$|Q\cap B_\cap | \leq c+h$
. All these inequalities must be met with equality, because
 $$ \begin{align*} \alpha_1+\beta_1 &= |Q\cap B_\cap| + |Q\cap B_\cup| \\ &= \textstyle|Q\cap B_\cap| + \sum_{i=1}^{c+h}|H_i| \\ &= \textstyle|Q\cap B_\cap| + \sum_{i=1}^{c}|H_i| + \sum_{i=c+1}^{c+h}|H_i| \\ &\leq (c+h)+(a+b-1)c + h \\ &= (a+b)c+2h \\ &\leq \alpha_1+\beta_1. \end{align*} $$
$$ \begin{align*} \alpha_1+\beta_1 &= |Q\cap B_\cap| + |Q\cap B_\cup| \\ &= \textstyle|Q\cap B_\cap| + \sum_{i=1}^{c+h}|H_i| \\ &= \textstyle|Q\cap B_\cap| + \sum_{i=1}^{c}|H_i| + \sum_{i=c+1}^{c+h}|H_i| \\ &\leq (c+h)+(a+b-1)c + h \\ &= (a+b)c+2h \\ &\leq \alpha_1+\beta_1. \end{align*} $$
We thus have the following equalities:
![]() $|Q\cap B_\cap |=c+h=|B_\cap |$
and
$|Q\cap B_\cap |=c+h=|B_\cap |$
and
![]() $\forall i\in [c]$
, we have
$\forall i\in [c]$
, we have
![]() $|H_i|=a+b-1 = |(\mathbb {N}\times \mathbb {N}\times \{i\}) \cap B_\cup |$
. Thus, we have
$|H_i|=a+b-1 = |(\mathbb {N}\times \mathbb {N}\times \{i\}) \cap B_\cup |$
. Thus, we have
![]() $B_\cap \subseteq Q$
and
$B_\cap \subseteq Q$
and
![]() $\{1\}\times [b]\times [c]\subseteq Q$
and
$\{1\}\times [b]\times [c]\subseteq Q$
and
![]() $[a]\times \{1\}\times [c]\subseteq Q$
and
$[a]\times \{1\}\times [c]\subseteq Q$
and
![]() $Q \cap (\mathbb {N}\times \mathbb {N}\times [c+1,c+h])=\{1\}\times \{1\}\times [c+1,c+h]$
. This gives the desired marginals, and the claim follows.
$Q \cap (\mathbb {N}\times \mathbb {N}\times [c+1,c+h])=\{1\}\times \{1\}\times [c+1,c+h]$
. This gives the desired marginals, and the claim follows.
We now prove (2.1), which implies Theorem 1.
Proof. Proof of (2.1).
Let
![]() $d=mc+c$
and
$d=mc+c$
and
![]() $e=lc+c$
. Suppose first that
$e=lc+c$
. Suppose first that
![]() $\lambda _1 \leq mc$
and
$\lambda _1 \leq mc$
and
![]() $\mu _1 \leq lc$
. We apply Lemma 2, and obtain
$\mu _1 \leq lc$
. We apply Lemma 2, and obtain
 $$ \begin{align*}{\texttt{k}}(\lambda,\mu,\nu) = {\texttt{k}}\big( \underbrace{ (d) \mathbin{\diamond} (c^l+\lambda) }_{=:\,\hat{\lambda}}, \, \underbrace{(e) \mathbin{\diamond} (c^m + \mu)}_{=:\,\hat{\mu}}, \, \underbrace{c^{l+m+1} \mathbin{\diamond} \nu}_{=:\,\hat{\nu}} \big).\end{align*} $$
$$ \begin{align*}{\texttt{k}}(\lambda,\mu,\nu) = {\texttt{k}}\big( \underbrace{ (d) \mathbin{\diamond} (c^l+\lambda) }_{=:\,\hat{\lambda}}, \, \underbrace{(e) \mathbin{\diamond} (c^m + \mu)}_{=:\,\hat{\mu}}, \, \underbrace{c^{l+m+1} \mathbin{\diamond} \nu}_{=:\,\hat{\nu}} \big).\end{align*} $$
The top rows of
![]() $\hat {\lambda },\hat {\mu },\hat {\nu }$
are
$\hat {\lambda },\hat {\mu },\hat {\nu }$
are
![]() $d, e, c$
, respectively, and thus Theorem 2 gives that for all
$d, e, c$
, respectively, and thus Theorem 2 gives that for all
![]() $h \in \mathbb {N}$
we have
$h \in \mathbb {N}$
we have
 $$ \begin{align*} {\texttt{k}}(\hat{\lambda},\,\hat{\mu},\,\hat{\nu} ) &= {\texttt{k}}( \hat{\lambda}+h,\, \hat{\mu}+h,\, \hat{\nu}+h) \\ &= {\texttt{k}}( \, (d+h) \mathbin{\diamond} (c^l+\lambda) , \, (e+h) \mathbin{\diamond} (c^m + \mu), \, (c+h)\mathbin{\diamond} c^{l+m} \mathbin{\diamond} \nu \, ) \\ &= \overline{{\texttt{k}}}( c^l+\lambda,\, c^m + \mu,\, c^{l+m} \mathbin{\diamond} \nu ), \end{align*} $$
$$ \begin{align*} {\texttt{k}}(\hat{\lambda},\,\hat{\mu},\,\hat{\nu} ) &= {\texttt{k}}( \hat{\lambda}+h,\, \hat{\mu}+h,\, \hat{\nu}+h) \\ &= {\texttt{k}}( \, (d+h) \mathbin{\diamond} (c^l+\lambda) , \, (e+h) \mathbin{\diamond} (c^m + \mu), \, (c+h)\mathbin{\diamond} c^{l+m} \mathbin{\diamond} \nu \, ) \\ &= \overline{{\texttt{k}}}( c^l+\lambda,\, c^m + \mu,\, c^{l+m} \mathbin{\diamond} \nu ), \end{align*} $$
where the last identity follows by letting
![]() $h \to \infty $
. This proves (2.1) in the first case.
$h \to \infty $
. This proves (2.1) in the first case.
Suppose now that
![]() $\lambda _1> mc$
, the case
$\lambda _1> mc$
, the case
![]() $\mu _1>lc$
is completely analogous. Set
$\mu _1>lc$
is completely analogous. Set
![]() $b:=m+1$
. Then we have
$b:=m+1$
. Then we have
![]() ${\texttt {k}}(\lambda ,\mu ,\nu ) = {\texttt {k}}(\lambda ',\mu ,\nu ') =0$
since
${\texttt {k}}(\lambda ,\mu ,\nu ) = {\texttt {k}}(\lambda ',\mu ,\nu ') =0$
since
![]() $\ell (\lambda ') =\lambda _1>mc \geq \ell (\mu )\ell (\nu ')$
. On the other hand, the reduced Kronecker coefficient is obtained by adding long first rows,
$\ell (\lambda ') =\lambda _1>mc \geq \ell (\mu )\ell (\nu ')$
. On the other hand, the reduced Kronecker coefficient is obtained by adding long first rows,
![]() $cm+c+ h$
,
$cm+c+ h$
,
![]() $cl+c+h$
,
$cl+c+h$
,
![]() $c+h$
, respectively, so
$c+h$
, respectively, so
 $$ \begin{align*} & \hspace{0.52cm}\overline{{\texttt{k}}}( c^l+\lambda, \, c^m + \mu, \, c^{l+m} \mathbin{\diamond} \nu) \\ &= {\texttt{k}}\big( (cm +c+ h) \mathbin{\diamond} (c^l+\lambda),\, (lc+c+h) \mathbin{\diamond} (c^m+\mu),\, (c+h)\mathbin{\diamond} c^{l+m} \mathbin{\diamond} \nu)\big) \\ &= {\texttt{k}}'\big( \underbrace{(cm +c+ h) \mathbin{\diamond} (c^l+\lambda)}_{=:\,\alpha},\, \underbrace{(lc+c+h) \mathbin{\diamond} (c^m+\mu)}_{=:\,\beta},\, \underbrace{( (l+b)^{c} + \nu')\mathbin{\diamond}(1^h)}_{=:\,\gamma}\big) \end{align*} $$
$$ \begin{align*} & \hspace{0.52cm}\overline{{\texttt{k}}}( c^l+\lambda, \, c^m + \mu, \, c^{l+m} \mathbin{\diamond} \nu) \\ &= {\texttt{k}}\big( (cm +c+ h) \mathbin{\diamond} (c^l+\lambda),\, (lc+c+h) \mathbin{\diamond} (c^m+\mu),\, (c+h)\mathbin{\diamond} c^{l+m} \mathbin{\diamond} \nu)\big) \\ &= {\texttt{k}}'\big( \underbrace{(cm +c+ h) \mathbin{\diamond} (c^l+\lambda)}_{=:\,\alpha},\, \underbrace{(lc+c+h) \mathbin{\diamond} (c^m+\mu)}_{=:\,\beta},\, \underbrace{( (l+b)^{c} + \nu')\mathbin{\diamond}(1^h)}_{=:\,\gamma}\big) \end{align*} $$
for sufficiently large h. Let
![]() $\hat \gamma = (l+b)^c+\nu '$
be
$\hat \gamma = (l+b)^c+\nu '$
be
![]() $\gamma $
without the h many trailing 1s. We observe that
$\gamma $
without the h many trailing 1s. We observe that
![]() $\alpha _2 = \lambda _1+c$
,
$\alpha _2 = \lambda _1+c$
,
![]() $\ell (\beta )=b$
and
$\ell (\beta )=b$
and
![]() $\ell (\hat \gamma )=c$
. From
$\ell (\hat \gamma )=c$
. From
![]() $\lambda _1> mc$
, we conclude
$\lambda _1> mc$
, we conclude
![]() $\alpha _2>bc$
. Lemma 4 shows that
$\alpha _2>bc$
. Lemma 4 shows that
![]() $\mathcal C(\alpha ,\beta ,\gamma )=\emptyset $
. Hence,
$\mathcal C(\alpha ,\beta ,\gamma )=\emptyset $
. Hence,
![]() ${\texttt {k}}'(\alpha ,\beta ,\gamma )=0$
by Lemma 3.
${\texttt {k}}'(\alpha ,\beta ,\gamma )=0$
by Lemma 3.
3 Proofs via the general linear group
3.1 Tools from the general linear group viewpoint
We refer to [Reference FultonFul97, Section 8] for the basic properties of the irreducible representations of the general linear group. The irreducible representations
![]() $V_{a^b}(\mathbb {C}^b)$
of the general linear group
$V_{a^b}(\mathbb {C}^b)$
of the general linear group
![]() $\text {GL}_b$
are 1-dimensional: For
$\text {GL}_b$
are 1-dimensional: For
![]() $g\in \text {GL}_b$
,
$g\in \text {GL}_b$
,
![]() $v\in V_{a^b}(\mathbb {C}^b)$
, we have
$v\in V_{a^b}(\mathbb {C}^b)$
, we have
![]() $gv := \det (g)^a v$
. Hence, if we decompose
$gv := \det (g)^a v$
. Hence, if we decompose
![]() $V_{1^{ab}}(\mathbb {C}^{ab})$
as a
$V_{1^{ab}}(\mathbb {C}^{ab})$
as a
![]() $\text {GL}_a\times \text {GL}_b$
representation via the group homomorphism
$\text {GL}_a\times \text {GL}_b$
representation via the group homomorphism
![]() $\text {GL}_a\times \text {GL}_b\to \text {GL}_{ab}$
,
$\text {GL}_a\times \text {GL}_b\to \text {GL}_{ab}$
,
![]() $(g_1,g_2)\mapsto g_1\otimes g_2$
, then we obtain
$(g_1,g_2)\mapsto g_1\otimes g_2$
, then we obtain
![]() $V_{1^{ab}}(\mathbb {C}^{ab})\simeq V_{b^a}(\mathbb {C}^a)\otimes V_{a^b}(\mathbb {C}^b)$
. Tensoring with such a 1-dimensional representation preserves irreducibility:
$V_{1^{ab}}(\mathbb {C}^{ab})\simeq V_{b^a}(\mathbb {C}^a)\otimes V_{a^b}(\mathbb {C}^b)$
. Tensoring with such a 1-dimensional representation preserves irreducibility:
![]() $V_\lambda (\mathbb {C}^a)\otimes V_{b^a}(\mathbb {C}^a) \simeq V_{b^a+\lambda }(\mathbb {C}^a)$
.
$V_\lambda (\mathbb {C}^a)\otimes V_{b^a}(\mathbb {C}^a) \simeq V_{b^a+\lambda }(\mathbb {C}^a)$
.
The Kronecker coefficients have an interpretation as the structure coefficients arising when decomposing irreducible
![]() $\text {GL}_{ab}$
representations as
$\text {GL}_{ab}$
representations as
![]() $\text {GL}_a\times \text {GL}_b$
representations:
$\text {GL}_a\times \text {GL}_b$
representations:
 $$\begin{align*}V_\nu(\mathbb{C}^{ab}) \simeq \bigoplus_{\substack{\lambda \vdash_a |\nu| \\ \mu \vdash_b |\nu|}} \left( V_\lambda(\mathbb{C}^{a}) \otimes V_\mu(\mathbb{C}^{b}) \right)^{\oplus{\texttt{k}}(\lambda,\mu,\nu)}. \end{align*}$$
$$\begin{align*}V_\nu(\mathbb{C}^{ab}) \simeq \bigoplus_{\substack{\lambda \vdash_a |\nu| \\ \mu \vdash_b |\nu|}} \left( V_\lambda(\mathbb{C}^{a}) \otimes V_\mu(\mathbb{C}^{b}) \right)^{\oplus{\texttt{k}}(\lambda,\mu,\nu)}. \end{align*}$$
This can be seen directly from Schur-Weyl duality (see, e.g. [Reference ChristandlChr06, (2.2)] or [Reference IkenmeyerIke12, Proposition 4.4.11]). Another formulation is via the multiplicity of the irreducible
![]() $G := \text {GL}_a\times \text {GL}_b\times \text {GL}_c$
representation
$G := \text {GL}_a\times \text {GL}_b\times \text {GL}_c$
representation
![]() $V_\alpha (\mathbb {C}^a)\otimes V_\beta (\mathbb {C}^b)\otimes V_\gamma (\mathbb {C}^c)$
in the D-th wedge power of
$V_\alpha (\mathbb {C}^a)\otimes V_\beta (\mathbb {C}^b)\otimes V_\gamma (\mathbb {C}^c)$
in the D-th wedge power of
![]() $\mathbb {C}^{a}\otimes \mathbb {C}^{b}\otimes \mathbb {C}^{c}$
(see [Reference Ikenmeyer, Mulmuley and WalterIMW17]). Formally for partitions
$\mathbb {C}^{a}\otimes \mathbb {C}^{b}\otimes \mathbb {C}^{c}$
(see [Reference Ikenmeyer, Mulmuley and WalterIMW17]). Formally for partitions
![]() $\alpha ,\beta ,\gamma \vdash D$
, we have
$\alpha ,\beta ,\gamma \vdash D$
, we have
A vector v for which
![]() $\big (\text {diag}(r_1,\ldots ,r_a),\text {diag}(s_1,\ldots ,s_b),\text {diag}(t_1,\ldots ,t_c)\big )v = r_1^{\lambda _1}\cdots r_a^{\lambda _a}\cdot s_1^{\mu _1}\cdots s_b^{\mu _b}\cdot t_1^{\nu _1}\cdots t_c^{\nu _c} v$
is called a weight vector of weight
$\big (\text {diag}(r_1,\ldots ,r_a),\text {diag}(s_1,\ldots ,s_b),\text {diag}(t_1,\ldots ,t_c)\big )v = r_1^{\lambda _1}\cdots r_a^{\lambda _a}\cdot s_1^{\mu _1}\cdots s_b^{\mu _b}\cdot t_1^{\nu _1}\cdots t_c^{\nu _c} v$
is called a weight vector of weight
![]() $(\lambda ,\mu ,\nu )$
.
$(\lambda ,\mu ,\nu )$
.
For
![]() $(A,B,C)\in \mathbb {C}^{a\times a} \times \mathbb {C}^{b\times b} \times \mathbb {C}^{c\times c}$
, the Lie algebra action on
$(A,B,C)\in \mathbb {C}^{a\times a} \times \mathbb {C}^{b\times b} \times \mathbb {C}^{c\times c}$
, the Lie algebra action on
![]() ${\bigwedge }^D(\mathbb {C}^a\otimes \mathbb {C}^b\otimes \mathbb {C}^c)$
is defined as
${\bigwedge }^D(\mathbb {C}^a\otimes \mathbb {C}^b\otimes \mathbb {C}^c)$
is defined as
![]() $(A,B,C).v := \lim _{\varepsilon \to 0}\varepsilon ^{-1}((\varepsilon (A,B,C) + (\text {id}_a,\text {id}_b,\text {id}_c))v-v)$
. A raising operator is the Lie algebra action of
$(A,B,C).v := \lim _{\varepsilon \to 0}\varepsilon ^{-1}((\varepsilon (A,B,C) + (\text {id}_a,\text {id}_b,\text {id}_c))v-v)$
. A raising operator is the Lie algebra action of
![]() $(E_{i-1,i},0,0)$
, where
$(E_{i-1,i},0,0)$
, where
![]() $E_{i,j}$
is the matrix with a 1 at position
$E_{i,j}$
is the matrix with a 1 at position
![]() $(i,j)$
and zeros everywhere else. The other raising operators are
$(i,j)$
and zeros everywhere else. The other raising operators are
![]() $(0,E_{i-1,i},0)$
and
$(0,E_{i-1,i},0)$
and
![]() $(0,0,E_{i-1,i})$
. Let
$(0,0,E_{i-1,i})$
. Let
![]() $e_i := (0,\ldots ,0,1,0,\ldots ,0)^T$
, and let
$e_i := (0,\ldots ,0,1,0,\ldots ,0)^T$
, and let
![]() $e_{i,j,k} := e_i \otimes e_j \otimes e_k$
. Then, for example,
$e_{i,j,k} := e_i \otimes e_j \otimes e_k$
. Then, for example,
![]() $(E_{i,j},0,0) e_{r,1,1} = e_{i,1,1}$
iff
$(E_{i,j},0,0) e_{r,1,1} = e_{i,1,1}$
iff
![]() $r=j$
and 0 otherwise. A highest weight vector (HWV) of weight
$r=j$
and 0 otherwise. A highest weight vector (HWV) of weight
![]() $(\alpha ,\beta ,\gamma )$
is a nonzero weight vector of weight
$(\alpha ,\beta ,\gamma )$
is a nonzero weight vector of weight
![]() $(\alpha ,\beta ,\gamma )$
that is mapped to zero by all raising operators. The irreducible
$(\alpha ,\beta ,\gamma )$
that is mapped to zero by all raising operators. The irreducible
![]() $\text {GL}_a\times \text {GL}_b\times \text {GL}_c$
representation
$\text {GL}_a\times \text {GL}_b\times \text {GL}_c$
representation
![]() $V_{\alpha }\otimes V_{\beta }\otimes V_{\gamma }$
contains exactly one HWV (up to scale), and that is of weight
$V_{\alpha }\otimes V_{\beta }\otimes V_{\gamma }$
contains exactly one HWV (up to scale), and that is of weight
![]() $(\alpha ,\beta ,\gamma )$
. Hence, ([Reference Ikenmeyer, Mulmuley and WalterIMW17, Lemma 2.1]),
$(\alpha ,\beta ,\gamma )$
. Hence, ([Reference Ikenmeyer, Mulmuley and WalterIMW17, Lemma 2.1]),
where
![]() $\text {HWV}_{\alpha ,\beta ,\gamma }$
denotes the space of HWVs of weight
$\text {HWV}_{\alpha ,\beta ,\gamma }$
denotes the space of HWVs of weight
![]() $(\alpha ,\beta ,\gamma )$
. Note that each standard basis vector in
$(\alpha ,\beta ,\gamma )$
. Note that each standard basis vector in
![]() ${\bigwedge }^D(\mathbb {C}^{a}\otimes \mathbb {C}^{b}\otimes \mathbb {C}^c)$
is a weight vector, and hence for each weight vector space of weight w, we have a basis given by the set of standard basis vectors of weight w. Let
${\bigwedge }^D(\mathbb {C}^{a}\otimes \mathbb {C}^{b}\otimes \mathbb {C}^c)$
is a weight vector, and hence for each weight vector space of weight w, we have a basis given by the set of standard basis vectors of weight w. Let
![]() $e_{i,j,k} := e_i \otimes e_j \otimes e_k$
, and for a list of points
$e_{i,j,k} := e_i \otimes e_j \otimes e_k$
, and for a list of points
![]() $Q \in (\mathbb {N}^3)^D$
, we define
$Q \in (\mathbb {N}^3)^D$
, we define
![]() $\psi _Q := e_{Q_1} \wedge e_{Q_2} \wedge \cdots \wedge e_{Q_D}$
. If Q has marginals
$\psi _Q := e_{Q_1} \wedge e_{Q_2} \wedge \cdots \wedge e_{Q_D}$
. If Q has marginals
![]() $(\alpha ,\beta ,\gamma )$
, then
$(\alpha ,\beta ,\gamma )$
, then
![]() $\psi _Q$
has weight
$\psi _Q$
has weight
![]() $(\alpha ,\beta ,\gamma )$
. This immediately implies the result of Lemma 3.
$(\alpha ,\beta ,\gamma )$
. This immediately implies the result of Lemma 3.
We illustrate the concept with some examples. The HWVs in
![]() $\bigwedge ^2(\mathbb {C}^2\otimes \mathbb {C}^2\otimes \mathbb {C}^1)$
are
$\bigwedge ^2(\mathbb {C}^2\otimes \mathbb {C}^2\otimes \mathbb {C}^1)$
are
![]() $e_{1,1,1}\wedge e_{2,1,1}$
and
$e_{1,1,1}\wedge e_{2,1,1}$
and
![]() $e_{1,1,1}\wedge e_{1,2,1}$
. A nontrivial example is the HWV
$e_{1,1,1}\wedge e_{1,2,1}$
. A nontrivial example is the HWV
of weight
![]() $((2,1),(2,1),(2,1))$
in
$((2,1),(2,1),(2,1))$
in
![]() $\bigwedge ^3(\mathbb {C}^2\otimes \mathbb {C}^2\otimes \mathbb {C}^2)$
, which can be seen as follows:
$\bigwedge ^3(\mathbb {C}^2\otimes \mathbb {C}^2\otimes \mathbb {C}^2)$
, which can be seen as follows:
 $$ \begin{align*} (E_{1,2},0,0)t &= e_{1,1,1}\wedge e_{1,2,1} \wedge e_{1,1,2} + e_{1,1,1}\wedge e_{1,1,2} \wedge e_{1,2,1} =0, \\ (0,E_{1,2},0)t &= e_{1,1,1}\wedge e_{2,1,1} \wedge e_{1,1,2} + e_{1,1,1}\wedge e_{1,1,2} \wedge e_{2,1,1} =0 , \\ (0,0,E_{1,2})t &= e_{1,1,1}\wedge e_{2,1,1} \wedge e_{1,2,1} + e_{1,1,1}\wedge e_{1,2,1} \wedge e_{2,1,1} =0. \end{align*} $$
$$ \begin{align*} (E_{1,2},0,0)t &= e_{1,1,1}\wedge e_{1,2,1} \wedge e_{1,1,2} + e_{1,1,1}\wedge e_{1,1,2} \wedge e_{1,2,1} =0, \\ (0,E_{1,2},0)t &= e_{1,1,1}\wedge e_{2,1,1} \wedge e_{1,1,2} + e_{1,1,1}\wedge e_{1,1,2} \wedge e_{2,1,1} =0 , \\ (0,0,E_{1,2})t &= e_{1,1,1}\wedge e_{2,1,1} \wedge e_{1,2,1} + e_{1,1,1}\wedge e_{1,2,1} \wedge e_{2,1,1} =0. \end{align*} $$
3.2 Proofs from the general linear group viewpoint
For the sake of completeness, we present the short proof of Lemma 1 from [Reference Briand, Orellana and RosasBOR09, Proof of Lemma 2.1] and [Reference IkenmeyerIke12, Corollary 4.4.14].
Proof of Lemma 1 via the general linear group.
We have that
![]() $V_{m^l+\lambda }(\mathbb {C}^l)\otimes V_{l^m+\mu }(\mathbb {C}^m)$
occurs in
$V_{m^l+\lambda }(\mathbb {C}^l)\otimes V_{l^m+\mu }(\mathbb {C}^m)$
occurs in
![]() $V_{1^{lm}+\nu }(\mathbb {C}^{lm})$
with multiplicity
$V_{1^{lm}+\nu }(\mathbb {C}^{lm})$
with multiplicity
![]() ${\texttt {k}}(m^l+\lambda ,\ l^m+\mu ,\ 1^{lm}+\nu )$
. But we also have
${\texttt {k}}(m^l+\lambda ,\ l^m+\mu ,\ 1^{lm}+\nu )$
. But we also have
 $$ \begin{align*} V_{1^{lm}+\nu}(\mathbb{C}^{lm}) &\!\!\simeq\!\! V_{1^{lm}}(\mathbb{C}^{lm}) \otimes V_{\nu}(\mathbb{C}^{lm}) \\ &\!\!\simeq\!\! (V_{m^l}(\mathbb{C}^l)\otimes V_{l^m}(\mathbb{C}^m)) \ \otimes \ \bigoplus_{\substack{\lambda \vdash_l |\nu| \\ \mu \vdash_m |\nu|}} \left( V_\lambda(\mathbb{C}^{l}) \otimes V_\mu(\mathbb{C}^{m}) \right)^{\oplus{\texttt{k}}(\lambda,\mu,\nu)} \\ &\!\!\simeq\!\! \bigoplus_{\substack{\lambda \vdash_a |\nu| \\ \mu \vdash_b |\nu|}} \left( V_{m^l+\lambda}(\mathbb{C}^{l}) \otimes V_{l^m+\mu}(\mathbb{C}^{m}) \right)^{\oplus{\texttt{k}}(\lambda,\mu,\nu)}.\\[-57pt] \end{align*} $$
$$ \begin{align*} V_{1^{lm}+\nu}(\mathbb{C}^{lm}) &\!\!\simeq\!\! V_{1^{lm}}(\mathbb{C}^{lm}) \otimes V_{\nu}(\mathbb{C}^{lm}) \\ &\!\!\simeq\!\! (V_{m^l}(\mathbb{C}^l)\otimes V_{l^m}(\mathbb{C}^m)) \ \otimes \ \bigoplus_{\substack{\lambda \vdash_l |\nu| \\ \mu \vdash_m |\nu|}} \left( V_\lambda(\mathbb{C}^{l}) \otimes V_\mu(\mathbb{C}^{m}) \right)^{\oplus{\texttt{k}}(\lambda,\mu,\nu)} \\ &\!\!\simeq\!\! \bigoplus_{\substack{\lambda \vdash_a |\nu| \\ \mu \vdash_b |\nu|}} \left( V_{m^l+\lambda}(\mathbb{C}^{l}) \otimes V_{l^m+\mu}(\mathbb{C}^{m}) \right)^{\oplus{\texttt{k}}(\lambda,\mu,\nu)}.\\[-57pt] \end{align*} $$
Proof of Theorem 2 via contingency arrays and highest weight vectors.
Let
![]() $a:=\ell (\lambda )$
,
$a:=\ell (\lambda )$
,
![]() $b:=\ell (\mu )$
,
$b:=\ell (\mu )$
,
![]() $c:=\nu _1$
. Let
$c:=\nu _1$
. Let
![]() $\gamma := \nu '$
, so
$\gamma := \nu '$
, so
![]() $\ell (\gamma )=c$
. We have
$\ell (\gamma )=c$
. We have
![]() $\lambda _1 \geq bc$
and
$\lambda _1 \geq bc$
and
![]() $\mu _1 \geq ac$
. Observe that
$\mu _1 \geq ac$
. Observe that
![]() ${\texttt {k}}(\lambda ,\mu ,\nu ) = {\texttt {k}}'(\lambda ,\mu ,\gamma )$
. Let
${\texttt {k}}(\lambda ,\mu ,\nu ) = {\texttt {k}}'(\lambda ,\mu ,\gamma )$
. Let
![]() $\widetilde \lambda = \lambda + (h)$
,
$\widetilde \lambda = \lambda + (h)$
,
![]() $\widetilde \mu = \mu + (h)$
,
$\widetilde \mu = \mu + (h)$
,
![]() $\widetilde \gamma = \gamma \mathbin {\diamond } (1^h)$
. We define an injective linear map
$\widetilde \gamma = \gamma \mathbin {\diamond } (1^h)$
. We define an injective linear map
![]() $\varphi $
as follows
$\varphi $
as follows
 $$ \begin{align} \varphi : \ {\bigwedge}^D(\mathbb{C}^{a}\otimes\mathbb{C}^{b}\otimes\mathbb{C}^{c}) &\to {\bigwedge}^{D+h}(\mathbb{C}^{a}\otimes\mathbb{C}^{b}\otimes\mathbb{C}^{c+h}) \nonumber \\ v &\mapsto v \wedge e_{1,1,c+1} \wedge e_{1,1,c+2} \wedge \cdots \wedge e_{1,1,c+h}. \end{align} $$
$$ \begin{align} \varphi : \ {\bigwedge}^D(\mathbb{C}^{a}\otimes\mathbb{C}^{b}\otimes\mathbb{C}^{c}) &\to {\bigwedge}^{D+h}(\mathbb{C}^{a}\otimes\mathbb{C}^{b}\otimes\mathbb{C}^{c+h}) \nonumber \\ v &\mapsto v \wedge e_{1,1,c+1} \wedge e_{1,1,c+2} \wedge \cdots \wedge e_{1,1,c+h}. \end{align} $$
Note that
![]() $\varphi $
maps vectors of weight
$\varphi $
maps vectors of weight
![]() $(\lambda ,\mu ,\gamma )$
to vectors of weight
$(\lambda ,\mu ,\gamma )$
to vectors of weight
![]() $(\widetilde \lambda ,\widetilde \mu ,\widetilde \gamma )$
. It remains to show that
$(\widetilde \lambda ,\widetilde \mu ,\widetilde \gamma )$
. It remains to show that
![]() $\varphi $
maps HWVs to HWVs, and that every HWV of weight
$\varphi $
maps HWVs to HWVs, and that every HWV of weight
![]() $(\widetilde \lambda ,\widetilde \mu ,\widetilde \gamma )$
has a preimage under
$(\widetilde \lambda ,\widetilde \mu ,\widetilde \gamma )$
has a preimage under
![]() $\varphi $
.
$\varphi $
.
We first prove that
![]() $\varphi $
sends HWVs to HWVs. By construction of
$\varphi $
sends HWVs to HWVs. By construction of
![]() $\varphi $
, we observe that for
$\varphi $
, we observe that for
![]() $1 \leq i < i' \leq a$
, we have
$1 \leq i < i' \leq a$
, we have
Analogously,
![]() $(0,E_{j,j'},0) \varphi (u) = 0$
for
$(0,E_{j,j'},0) \varphi (u) = 0$
for
![]() $1 \leq j < j' \leq b$
, and
$1 \leq j < j' \leq b$
, and
![]() $(0,0,E_{k,k'}) \varphi (u) = 0$
for
$(0,0,E_{k,k'}) \varphi (u) = 0$
for
![]() $1 \leq k < k' \leq c$
. The remaining raising operators also vanish by construction of
$1 \leq k < k' \leq c$
. The remaining raising operators also vanish by construction of
![]() $\varphi $
, because
$\varphi $
, because
 $$ \begin{align*} &(0,0,E_{c+k,c+k'}) (v \wedge e_{1,1,c+1} \wedge \cdots \wedge e_{1,1,c+h}) \\ &\quad= v \wedge e_{1,1,c+1} \wedge \cdots \wedge {e_{1,1,c+k}} \wedge e_{1,1,c+k} \wedge \widehat{e_{1,1,c+k'}} \wedge \cdots \wedge e_{1,1,c+h} \\&\quad= 0, \end{align*} $$
$$ \begin{align*} &(0,0,E_{c+k,c+k'}) (v \wedge e_{1,1,c+1} \wedge \cdots \wedge e_{1,1,c+h}) \\ &\quad= v \wedge e_{1,1,c+1} \wedge \cdots \wedge {e_{1,1,c+k}} \wedge e_{1,1,c+k} \wedge \widehat{e_{1,1,c+k'}} \wedge \cdots \wedge e_{1,1,c+h} \\&\quad= 0, \end{align*} $$
because of the repeated factor
![]() $e_{1,1,c+k}$
. Here, the
$e_{1,1,c+k}$
. Here, the
![]() $\widehat {e_{1,1,c+k'}}$
means omission of that factor. For every basis vector
$\widehat {e_{1,1,c+k'}}$
means omission of that factor. For every basis vector
![]() $\psi _Q$
of weight
$\psi _Q$
of weight
![]() $(\widetilde \lambda ,\widetilde \mu ,\widetilde \gamma )$
, by Lemma 4, we have
$(\widetilde \lambda ,\widetilde \mu ,\widetilde \gamma )$
, by Lemma 4, we have
![]() $(1,1,c)\in Q$
and
$(1,1,c)\in Q$
and
![]() $Q\cap (\mathbb {N}\times \mathbb {N}\times \{c+1\})=\{(1,1,c+1)\}$
, hence,
$Q\cap (\mathbb {N}\times \mathbb {N}\times \{c+1\})=\{(1,1,c+1)\}$
, hence,
![]() $(0,0,E_{c,c+1})\psi _Q = 0$
as well.
$(0,0,E_{c,c+1})\psi _Q = 0$
as well.
We now show that every weight vector of weight
![]() $(\widetilde \lambda ,\widetilde \mu ,\widetilde \gamma )$
has a preimage under
$(\widetilde \lambda ,\widetilde \mu ,\widetilde \gamma )$
has a preimage under
![]() $\varphi $
, which finishes the proof. It is sufficient to show this for basis vectors. Let
$\varphi $
, which finishes the proof. It is sufficient to show this for basis vectors. Let
![]() $\psi _Q$
be a basis weight vector of weight
$\psi _Q$
be a basis weight vector of weight
![]() $(\widetilde \lambda ,\widetilde \mu ,\widetilde \gamma )$
, that is,
$(\widetilde \lambda ,\widetilde \mu ,\widetilde \gamma )$
, that is,
![]() $Q\subseteq \mathbb {N}^3$
with marginals
$Q\subseteq \mathbb {N}^3$
with marginals
![]() $(\widetilde \lambda ,\widetilde \mu ,\widetilde \gamma )$
. We apply Lemma 4 to see that
$(\widetilde \lambda ,\widetilde \mu ,\widetilde \gamma )$
. We apply Lemma 4 to see that
![]() $\{1\}\times \{1\}\times [c+1,c+h]\subset Q$
and
$\{1\}\times \{1\}\times [c+1,c+h]\subset Q$
and
![]() $Q\cap (\mathbb {N}\times \mathbb {N}\times \{i\})=\{(1,1,i)\}$
for all
$Q\cap (\mathbb {N}\times \mathbb {N}\times \{i\})=\{(1,1,i)\}$
for all
![]() $c+1\leq i\leq c+h$
. Therefore,
$c+1\leq i\leq c+h$
. Therefore,
![]() $\psi _Q$
has a preimage under
$\psi _Q$
has a preimage under
![]() $\varphi $
, namely,
$\varphi $
, namely,
![]() $\psi _{P}$
, where P arises from Q by deleting all points with 3
$\psi _{P}$
, where P arises from Q by deleting all points with 3
![]() $^{\text {rd}}$
coordinate
$^{\text {rd}}$
coordinate
![]() $>c$
.
$>c$
.
Note that (2.2) (and hence also Lemma 2) can alternatively be proved by a simple explicit linear map between highest weight vector spaces
 $$ \begin{align} \text{HWV}_{\lambda,\mu,\nu^t}\big({\bigwedge}^D(\mathbb{C}^{l}\otimes\mathbb{C}^{m}\otimes\mathbb{C}^{c})\big) & \to \text{HWV}_{m^l + \lambda,\ l^m + \mu, \ (lm)\mathbin{\diamond}\nu^t}\big({\bigwedge}^{D+lm}(\mathbb{C}^{l}\otimes\mathbb{C}^{m}\otimes\mathbb{C}^{c+1})\big) \nonumber \\ e_{i_1,j_1,k_1}\wedge\cdots\wedge e_{i_D,j_D,k_D} & \mapsto e_{i_1,j_1,k_1+1}\wedge\cdots\wedge e_{i_D,j_D,k_D+1} \wedge e_{1,1,1} \wedge \cdots \wedge e_{l,m,1} \end{align} $$
$$ \begin{align} \text{HWV}_{\lambda,\mu,\nu^t}\big({\bigwedge}^D(\mathbb{C}^{l}\otimes\mathbb{C}^{m}\otimes\mathbb{C}^{c})\big) & \to \text{HWV}_{m^l + \lambda,\ l^m + \mu, \ (lm)\mathbin{\diamond}\nu^t}\big({\bigwedge}^{D+lm}(\mathbb{C}^{l}\otimes\mathbb{C}^{m}\otimes\mathbb{C}^{c+1})\big) \nonumber \\ e_{i_1,j_1,k_1}\wedge\cdots\wedge e_{i_D,j_D,k_D} & \mapsto e_{i_1,j_1,k_1+1}\wedge\cdots\wedge e_{i_D,j_D,k_D+1} \wedge e_{1,1,1} \wedge \cdots \wedge e_{l,m,1} \end{align} $$
for
![]() $D=|\lambda |$
. Combining this with the construction in Theorem 2, Theorem 1 is now fully proved by an explicit isomorphism of highest weight vector spaces.
$D=|\lambda |$
. Combining this with the construction in Theorem 2, Theorem 1 is now fully proved by an explicit isomorphism of highest weight vector spaces.
4 Proofs via symmetric functions
4.1 Tools from symmetric functions
Here, we recall basic definitions and facts from symmetric function theory (see [Reference StanleySta99, Reference SaganSag13, Reference MacdonaldMac98]).
The standard Young tableaux (SYT) of shape
![]() $\lambda \vdash n$
are assignments of
$\lambda \vdash n$
are assignments of
![]() $1,2,\ldots ,n$
to the Young diagram of
$1,2,\ldots ,n$
to the Young diagram of
![]() $\lambda $
, so that the numbers are decreasing along rows and down columns, and each number appears exactly once. A semi-standard Young tableaux (SSYT) of skew shape
$\lambda $
, so that the numbers are decreasing along rows and down columns, and each number appears exactly once. A semi-standard Young tableaux (SSYT) of skew shape
![]() $\lambda /\mu $
is an assignment of integers
$\lambda /\mu $
is an assignment of integers
![]() $1,2,\ldots ,N$
to the boxes of the skew Young diagram
$1,2,\ldots ,N$
to the boxes of the skew Young diagram
![]() $\lambda /\mu $
, such that the values weakly increase along rows and strictly down columns. We say that an SSYT T has type (weight)
$\lambda /\mu $
, such that the values weakly increase along rows and strictly down columns. We say that an SSYT T has type (weight)
![]() $type(T)=\alpha $
if there are
$type(T)=\alpha $
if there are
![]() $\alpha _i$
entries equal to i for each i.
$\alpha _i$
entries equal to i for each i.
As an example,  is an SSYT of shape
is an SSYT of shape
![]() $(5,4,4)/(2,1)$
and type
$(5,4,4)/(2,1)$
and type
![]() $(3,1,4,2)$
.
$(3,1,4,2)$
.
The ring of symmetric functions
![]() $\Lambda $
has several fundamental bases. Here, we will use the monomial basis
$\Lambda $
has several fundamental bases. Here, we will use the monomial basis
![]() $\{ m_\lambda \}$
given by
$\{ m_\lambda \}$
given by
![]() $m_\lambda =x_1^{\lambda _1}x_2^{\lambda _2}\ldots +\cdots $
, summing over all distinct monomials with exponents
$m_\lambda =x_1^{\lambda _1}x_2^{\lambda _2}\ldots +\cdots $
, summing over all distinct monomials with exponents
![]() $\lambda _1,\lambda _2,\ldots $
. We will also use the homogeneous symmetric functions
$\lambda _1,\lambda _2,\ldots $
. We will also use the homogeneous symmetric functions
![]() $\{h_\lambda \}$
given by
$\{h_\lambda \}$
given by
![]() $h_0=1; \ h_{m}=0 \text { for }m<0 \text { and } h_\lambda := h_{\lambda _1} h_{\lambda _2}\cdots $
. The Schur functions
$h_0=1; \ h_{m}=0 \text { for }m<0 \text { and } h_\lambda := h_{\lambda _1} h_{\lambda _2}\cdots $
. The Schur functions
![]() $s_\lambda $
are one of the fundamental bases of the ring
$s_\lambda $
are one of the fundamental bases of the ring
![]() $\Lambda $
of symmetric functions. Moreover,
$\Lambda $
of symmetric functions. Moreover,
![]() $s_\lambda (x_1,\ldots ,x_N)$
is the value of the character of
$s_\lambda (x_1,\ldots ,x_N)$
is the value of the character of
![]() $V_\lambda $
at a matrix with eigenvalues
$V_\lambda $
at a matrix with eigenvalues
![]() $x_1,\ldots ,x_N$
. We have the following formulas for them, where
$x_1,\ldots ,x_N$
. We have the following formulas for them, where
![]() $\ell =\ell (\lambda )$
,
$\ell =\ell (\lambda )$
,
 $$ \begin{align} \text{Weyl determinantal formula:} \quad & s_\lambda(x_1,\ldots,x_N) = \frac{ \det[ x_i^{\lambda_j+N-j}]_{i,j=1}^N }{\det[x_i^{N-j}] }\ \qquad \end{align} $$
$$ \begin{align} \text{Weyl determinantal formula:} \quad & s_\lambda(x_1,\ldots,x_N) = \frac{ \det[ x_i^{\lambda_j+N-j}]_{i,j=1}^N }{\det[x_i^{N-j}] }\ \qquad \end{align} $$
The Littlewood-Richardson coefficients are the structure constants in the ring of symmetric functions as
They can be computed combinatorially via the Littlewood-Richardson rule:
![]() $c^{\lambda }_{\mu \nu }$
is equal to the number of SSYTs T of shape
$c^{\lambda }_{\mu \nu }$
is equal to the number of SSYTs T of shape
![]() $\lambda /\mu $
, type
$\lambda /\mu $
, type
![]() $\nu $
and whose reading words are a ballot sequence. The reading word is obtained by reading the tableaux right to left along rows, top to bottom, and a word is a ballot sequence if, in every prefix, the number of i’s is not less than the number of
$\nu $
and whose reading words are a ballot sequence. The reading word is obtained by reading the tableaux right to left along rows, top to bottom, and a word is a ballot sequence if, in every prefix, the number of i’s is not less than the number of
![]() $i+1$
’s for every i. The multi-LR coefficients
$i+1$
’s for every i. The multi-LR coefficients
![]() $c^{\lambda }_{\alpha ^1 \cdots \alpha ^k}$
are defined as
$c^{\lambda }_{\alpha ^1 \cdots \alpha ^k}$
are defined as
 $$ \begin{align} c^{\lambda}_{\alpha^1\cdots \alpha^k} := \langle s_\lambda, s_{\alpha_1} s_{\alpha^2}\cdots s_{\alpha^k} \rangle = \sum_{\beta^1,\beta^2,\ldots} c^{\lambda}_{\alpha^1 \beta^1} c^{\beta^1}_{\alpha^2 \beta^2} \cdots c^{\beta^{k-1}}_{\alpha^{k-1}\alpha^k}, \end{align} $$
$$ \begin{align} c^{\lambda}_{\alpha^1\cdots \alpha^k} := \langle s_\lambda, s_{\alpha_1} s_{\alpha^2}\cdots s_{\alpha^k} \rangle = \sum_{\beta^1,\beta^2,\ldots} c^{\lambda}_{\alpha^1 \beta^1} c^{\beta^1}_{\alpha^2 \beta^2} \cdots c^{\beta^{k-1}}_{\alpha^{k-1}\alpha^k}, \end{align} $$
where the sum is over partitions
![]() $\beta ^i \vdash |\beta ^{i-1}|- |\alpha ^i|$
with
$\beta ^i \vdash |\beta ^{i-1}|- |\alpha ^i|$
with
![]() $\beta ^0:=\lambda $
. It is then easy to see that they count SSYTs T of shape
$\beta ^0:=\lambda $
. It is then easy to see that they count SSYTs T of shape
![]() $\lambda $
and type
$\lambda $
and type
![]() $(\alpha ^1 \mathbin {\diamond } \alpha ^2 \mathbin {\diamond } \cdots )$
, such that the reading word of each skew subtableau corresponding to the entries with values between
$(\alpha ^1 \mathbin {\diamond } \alpha ^2 \mathbin {\diamond } \cdots )$
, such that the reading word of each skew subtableau corresponding to the entries with values between
![]() $1+\sum _{i=1}^r \ell (\alpha ^i)$
and
$1+\sum _{i=1}^r \ell (\alpha ^i)$
and
![]() $\sum _{i=1}^{r+1} \ell (\alpha ^i)$
is a lattice permutation for every
$\sum _{i=1}^{r+1} \ell (\alpha ^i)$
is a lattice permutation for every
![]() $r=1,\ldots ,k-1$
. For example,
$r=1,\ldots ,k-1$
. For example,

are two multi-LR tableaux of shape
![]() $\lambda =(7,6,5)$
and types
$\lambda =(7,6,5)$
and types
![]() $\alpha ^1=(4,3,1)$
,
$\alpha ^1=(4,3,1)$
,
![]() $\alpha ^2 =(3,3)$
,
$\alpha ^2 =(3,3)$
,
![]() $\alpha ^3=(3,1)$
.
$\alpha ^3=(3,1)$
.
The Kronecker coefficient can be studied via the following expansions
where
![]() $x \cdot y = (x_1y_1,x_1y_2,\ldots ,x_2y_1,\ldots )$
consists of the pairwise products of the two sets of variables. In particular, this gives that
$x \cdot y = (x_1y_1,x_1y_2,\ldots ,x_2y_1,\ldots )$
consists of the pairwise products of the two sets of variables. In particular, this gives that
From the Jacobi-Trudy identity, we thus obtain
 $$ \begin{align*} s_\lambda[x\cdot y]&= \det[ h_{\lambda_i-i+j}[x\cdot y]] \\&= \sum_{\sigma \in S_{\ell}} {\mathrm{sgn}}(\sigma) \sum_{\, \alpha^i \vdash \lambda_i-i+\sigma_i} s_{\alpha^1}(x)\cdots s_{\alpha^\ell}(x)s_{\alpha^1}(y)\cdots s_{\alpha^\ell}(y), \end{align*} $$
$$ \begin{align*} s_\lambda[x\cdot y]&= \det[ h_{\lambda_i-i+j}[x\cdot y]] \\&= \sum_{\sigma \in S_{\ell}} {\mathrm{sgn}}(\sigma) \sum_{\, \alpha^i \vdash \lambda_i-i+\sigma_i} s_{\alpha^1}(x)\cdots s_{\alpha^\ell}(x)s_{\alpha^1}(y)\cdots s_{\alpha^\ell}(y), \end{align*} $$
so
 $$ \begin{align} {\texttt{k}}(\lambda,\mu,\nu) = \sum_{\sigma \in S_{\ell}} {\mathrm{sgn}}(\sigma) \sum_{\, \alpha^i \vdash \lambda_i-i+\sigma_i} c^{\mu}_{\alpha^1\cdots \alpha^k}c^{\nu}_{\alpha^1\cdots \alpha^k}. \end{align} $$
$$ \begin{align} {\texttt{k}}(\lambda,\mu,\nu) = \sum_{\sigma \in S_{\ell}} {\mathrm{sgn}}(\sigma) \sum_{\, \alpha^i \vdash \lambda_i-i+\sigma_i} c^{\mu}_{\alpha^1\cdots \alpha^k}c^{\nu}_{\alpha^1\cdots \alpha^k}. \end{align} $$
Note that this identity appears many times in the literature, including [Reference VallejoVal09, Reference Pak and PanovaPP17b, Reference Pak and PanovaPP17a].
The following are referred to as the “triple Cauchy identities” (see, e.g. [Reference StanleySta99, Exercise 7.78]):
 $$ \begin{align*}\sum_{\lambda,\mu,\nu} {\texttt{k}}(\lambda,\mu,\nu) s_\lambda(x) s_\mu(y) s_\nu(z) = \prod_{i,j,k} \frac{1}{1-x_iy_jz_k},\end{align*} $$
$$ \begin{align*}\sum_{\lambda,\mu,\nu} {\texttt{k}}(\lambda,\mu,\nu) s_\lambda(x) s_\mu(y) s_\nu(z) = \prod_{i,j,k} \frac{1}{1-x_iy_jz_k},\end{align*} $$
 $$ \begin{align*}\sum_{\lambda,\mu,\nu} {\texttt{k}}(\lambda,\mu,\nu) s_\lambda(x) s_\mu(y) s_{\nu'}(z) = \prod_{i,j,k} (1+x_iy_jz_k),\end{align*} $$
$$ \begin{align*}\sum_{\lambda,\mu,\nu} {\texttt{k}}(\lambda,\mu,\nu) s_\lambda(x) s_\mu(y) s_{\nu'}(z) = \prod_{i,j,k} (1+x_iy_jz_k),\end{align*} $$
where the second identity follows from the first via the involution
![]() $\omega $
on the symmetric functions in the variables z. Denote by
$\omega $
on the symmetric functions in the variables z. Denote by
![]() $C(\alpha ,\beta ,\gamma ):=|\mathcal {C}(\alpha ,\beta ,\gamma )|$
. Then the second identity becomes
$C(\alpha ,\beta ,\gamma ):=|\mathcal {C}(\alpha ,\beta ,\gamma )|$
. Then the second identity becomes
 $$ \begin{align} \sum_{\lambda,\mu,\nu} {\texttt{k}}(\lambda,\mu,\nu) s_\lambda(x) s_\mu(y) s_{\nu'}(z) = \sum_{\alpha,\beta,\gamma} C(\alpha,\beta,\gamma) x^\alpha y^\beta z^\gamma. \end{align} $$
$$ \begin{align} \sum_{\lambda,\mu,\nu} {\texttt{k}}(\lambda,\mu,\nu) s_\lambda(x) s_\mu(y) s_{\nu'}(z) = \sum_{\alpha,\beta,\gamma} C(\alpha,\beta,\gamma) x^\alpha y^\beta z^\gamma. \end{align} $$
Note that this identity immediately gives the upper bound in Lemma 3 by comparing coefficients at
![]() $x^\lambda y^\mu z^{\nu '}$
on both sides.
$x^\lambda y^\mu z^{\nu '}$
on both sides.
We now express
![]() ${\texttt {k}}(\lambda ,\mu ,\nu )$
as an alternating sum over contingency arrays. Denote by
${\texttt {k}}(\lambda ,\mu ,\nu )$
as an alternating sum over contingency arrays. Denote by
and multiply by
![]() $\Delta (x) \Delta (y) \Delta (z)$
both sides of equation (4.7). Expressing the Schur functions via the ratio of determinants in 4.2, we obtain
$\Delta (x) \Delta (y) \Delta (z)$
both sides of equation (4.7). Expressing the Schur functions via the ratio of determinants in 4.2, we obtain
 $$ \begin{align*} \sum_{\lambda,\mu,\nu} {\texttt{k}}(\lambda,\mu,\nu) \det[x_i^{\lambda_j+a-j}]\det[y_i^{\mu_j+b-j}] \det[z_i^{\nu^{\prime}_j +c-j}] \\ \quad = \Delta(x)\Delta(y)\Delta(z) \sum_{\alpha,\beta,\gamma} C(\alpha,\beta,\gamma) x^\alpha y^\beta z^\gamma. \end{align*} $$
$$ \begin{align*} \sum_{\lambda,\mu,\nu} {\texttt{k}}(\lambda,\mu,\nu) \det[x_i^{\lambda_j+a-j}]\det[y_i^{\mu_j+b-j}] \det[z_i^{\nu^{\prime}_j +c-j}] \\ \quad = \Delta(x)\Delta(y)\Delta(z) \sum_{\alpha,\beta,\gamma} C(\alpha,\beta,\gamma) x^\alpha y^\beta z^\gamma. \end{align*} $$
Comparing coefficients at
![]() $x_1^{\lambda _1+a-1}\ldots y_1^{\mu _1+b-1}\ldots z_1^{\nu ^{\prime }_1 + c-1} \ldots $
on both sides, we obtain
$x_1^{\lambda _1+a-1}\ldots y_1^{\mu _1+b-1}\ldots z_1^{\nu ^{\prime }_1 + c-1} \ldots $
on both sides, we obtain
![]() ${\texttt {k}}(\lambda ,\mu ,\nu ) = $
${\texttt {k}}(\lambda ,\mu ,\nu ) = $
 $$ \begin{align*}[x_1^{\lambda_1+a-1}\ldots y_1^{\mu_1+b-1}\ldots z_1^{\nu^{\prime}_1 + c-1} \ldots]\Delta(x)\Delta(y)\Delta(z) \sum_{\alpha,\beta,\gamma} C(\alpha,\beta,\gamma) x^\alpha y^\beta z^\gamma,\end{align*} $$
$$ \begin{align*}[x_1^{\lambda_1+a-1}\ldots y_1^{\mu_1+b-1}\ldots z_1^{\nu^{\prime}_1 + c-1} \ldots]\Delta(x)\Delta(y)\Delta(z) \sum_{\alpha,\beta,\gamma} C(\alpha,\beta,\gamma) x^\alpha y^\beta z^\gamma,\end{align*} $$
where the
![]() $[\cdots ]$
denotes the coefficient extraction. Expanding the
$[\cdots ]$
denotes the coefficient extraction. Expanding the
![]() $\Delta $
s into monomials, whose marginals we incorporate, we get that we must have
$\Delta $
s into monomials, whose marginals we incorporate, we get that we must have
![]() $\lambda _i + a - i = \alpha _i + a-\sigma _i$
etc., so
$\lambda _i + a - i = \alpha _i + a-\sigma _i$
etc., so
![]() $\alpha _i = \lambda _i+\sigma _i-i$
, and we obtain, see also [Reference Pak and PanovaPP20a],
$\alpha _i = \lambda _i+\sigma _i-i$
, and we obtain, see also [Reference Pak and PanovaPP20a],
![]() ${\texttt {k}}(\lambda ,\mu ,\nu ) = $
${\texttt {k}}(\lambda ,\mu ,\nu ) = $

where a permutation
![]() $\sigma $
is interpreted as the vector
$\sigma $
is interpreted as the vector
![]() $(\sigma (1),\ldots ,\sigma (a))$
and
$(\sigma (1),\ldots ,\sigma (a))$
and
![]() $\text {id}=(1,2,\ldots )$
is the identity permutation of the corresponding size.
$\text {id}=(1,2,\ldots )$
is the identity permutation of the corresponding size.
4.2 Proofs via symmetric functions
Proof of Lemma 1 via symmetric functions.
Let
![]() $\hat {\nu }=1^{l m}+ \nu $
. We use Schur functions as follows. We apply equation (4.5) with variables
$\hat {\nu }=1^{l m}+ \nu $
. We use Schur functions as follows. We apply equation (4.5) with variables
![]() $x_1,\ldots ,x_\ell $
and
$x_1,\ldots ,x_\ell $
and
![]() $y_1,\ldots ,y_m$
, so
$y_1,\ldots ,y_m$
, so
![]() $x_i=0$
for
$x_i=0$
for
![]() $i>l$
and
$i>l$
and
![]() $y_j=0$
for
$y_j=0$
for
![]() $j>m$
, and we obtain
$j>m$
, and we obtain
If
![]() ${\texttt {k}}(\hat {\nu },\theta ,\tau )>0$
, we must have
${\texttt {k}}(\hat {\nu },\theta ,\tau )>0$
, we must have
![]() $\ell (\theta ) \ell (\tau ) \geq \ell (\hat {\nu }) = l m$
. Since
$\ell (\theta ) \ell (\tau ) \geq \ell (\hat {\nu }) = l m$
. Since
![]() $s_\theta (x_1,\ldots ,x_l)=0$
if
$s_\theta (x_1,\ldots ,x_l)=0$
if
![]() $\ell (\theta )>l$
and
$\ell (\theta )>l$
and
![]() $s_\tau (y_1,\ldots ,y_m)=0$
if
$s_\tau (y_1,\ldots ,y_m)=0$
if
![]() $\ell (\tau )>m$
, we then must have only the partitions with
$\ell (\tau )>m$
, we then must have only the partitions with
![]() $\ell (\theta )=l$
,
$\ell (\theta )=l$
,
![]() $\ell (\tau )=m$
appearing.
$\ell (\tau )=m$
appearing.
Since
![]() $s_{\hat {\nu }}$
is the generating function over SSYTs with entries
$s_{\hat {\nu }}$
is the generating function over SSYTs with entries
![]() $x_1y_1,\ldots ,x_ly_m$
, and its first column has length exactly
$x_1y_1,\ldots ,x_ly_m$
, and its first column has length exactly
![]() $lc$
, we must have all the entries
$lc$
, we must have all the entries
![]() $x_iy_j$
appearing exactly once in that column. As this is the minimal possible column, the rest of the SSYT can be any of the SSYTs of the remaining shape and entries
$x_iy_j$
appearing exactly once in that column. As this is the minimal possible column, the rest of the SSYT can be any of the SSYTs of the remaining shape and entries
![]() $x_1y_1,\ldots ,x_ly_m$
. Thus
$x_1y_1,\ldots ,x_ly_m$
. Thus
We also note that
![]() $s_{l^m + \mu }(y_1,\ldots ,y_m) = (y_1\ldots y_m)^l s_\mu (y)$
, since the first l columns of length m are forced to be filled with
$s_{l^m + \mu }(y_1,\ldots ,y_m) = (y_1\ldots y_m)^l s_\mu (y)$
, since the first l columns of length m are forced to be filled with
![]() $1,\ldots ,m$
, and for the remaining tableaux, there are no restrictions other than being an SSYT. Similarly,
$1,\ldots ,m$
, and for the remaining tableaux, there are no restrictions other than being an SSYT. Similarly,
![]() $s_{m^l + \lambda }(x_1,\ldots ,x_l) = (x_1\ldots x_l)^m s_\lambda (x)$
. Comparing coefficients of
$s_{m^l + \lambda }(x_1,\ldots ,x_l) = (x_1\ldots x_l)^m s_\lambda (x)$
. Comparing coefficients of
![]() $s_\lambda (x)s_\mu (y)$
at equations (4.9) and (4.10), we thus see that
$s_\lambda (x)s_\mu (y)$
at equations (4.9) and (4.10), we thus see that
Proof of Theorem 2 via contingency arrays and symmetric functions.
From now on, we will use formula (4.8) and Lemma 4 to show that the only possible contingency arrays are the ones in Figure 2.
Consider now
![]() ${\texttt {k}}(\lambda + h, \mu +h, \nu +h)$
as in the problem, and let
${\texttt {k}}(\lambda + h, \mu +h, \nu +h)$
as in the problem, and let
![]() $\alpha = (\lambda +h), \beta = (\mu +h)$
,
$\alpha = (\lambda +h), \beta = (\mu +h)$
,
![]() $\gamma =(\nu +h)'$
, so that
$\gamma =(\nu +h)'$
, so that
![]() ${\texttt {k}}(\alpha ,\beta ,\gamma ') = {\texttt {k}}(\lambda + h, \mu +h, \nu +h)$
. Let
${\texttt {k}}(\alpha ,\beta ,\gamma ') = {\texttt {k}}(\lambda + h, \mu +h, \nu +h)$
. Let
![]() $\nu _1=c$
,
$\nu _1=c$
,
![]() $\ell (\lambda )=a$
and
$\ell (\lambda )=a$
and
![]() $\ell (\mu )=b$
, so we have
$\ell (\mu )=b$
, so we have
![]() $\alpha _1 \geq bc+h, \beta _1 \geq ac+h$
,
$\alpha _1 \geq bc+h, \beta _1 \geq ac+h$
,
![]() $\gamma _i =1$
for
$\gamma _i =1$
for
![]() $i=c+1,\ldots ,c+h$
and
$i=c+1,\ldots ,c+h$
and
![]() ${\texttt {k}}(\alpha ,\beta ,\gamma ')=$
${\texttt {k}}(\alpha ,\beta ,\gamma ')=$

In formula (4.11), we then consider
![]() $\{0,1\}$
-contingency arrays Q with marginals
$\{0,1\}$
-contingency arrays Q with marginals
 $$ \begin{align*} Q_{1\ast\ast}:= & \sum_{j,k} Q_{1,j,k} = \lambda_1 +\sigma_1-1 \geq bc+h, \\Q_{\ast 1 \ast}:= & \sum_{i,k} Q_{i,1,k} = \mu_1+ \pi_1-1 \geq ac+h, \\Q_{\ast \ast k}:= & \sum_{i,j} Q_{i,j,k} = 1+ \rho_k - k, \text{ for } k=c+1,\ldots,c+h. \end{align*} $$
$$ \begin{align*} Q_{1\ast\ast}:= & \sum_{j,k} Q_{1,j,k} = \lambda_1 +\sigma_1-1 \geq bc+h, \\Q_{\ast 1 \ast}:= & \sum_{i,k} Q_{i,1,k} = \mu_1+ \pi_1-1 \geq ac+h, \\Q_{\ast \ast k}:= & \sum_{i,j} Q_{i,j,k} = 1+ \rho_k - k, \text{ for } k=c+1,\ldots,c+h. \end{align*} $$
Note that then we have
 $$ \begin{align} \sum_{k>c} Q_{\ast\ast k} = h + \sum_{k=c+1}^{c+h} \rho_k - \sum_{k=c+1}^{c+h} k \leq h, \end{align} $$
$$ \begin{align} \sum_{k>c} Q_{\ast\ast k} = h + \sum_{k=c+1}^{c+h} \rho_k - \sum_{k=c+1}^{c+h} k \leq h, \end{align} $$
and the support of the array is in
![]() $[1,a]\times [1,b] \times [1,c+h]$
, so we can apply Lemma 4 and conclude that
$[1,a]\times [1,b] \times [1,c+h]$
, so we can apply Lemma 4 and conclude that
![]() $Q_{1,j,k}=0 \text { iff } (j,k) \in [2,b]\times [c+1,c+h]$
and
$Q_{1,j,k}=0 \text { iff } (j,k) \in [2,b]\times [c+1,c+h]$
and
![]() $Q_{i,1,k}=0 \text { iff } (i,k) \in [2,a] \times [c+1,c+h].$
$Q_{i,1,k}=0 \text { iff } (i,k) \in [2,a] \times [c+1,c+h].$
Thus, we must have
![]() $Q_{1\ast \ast }=bc+h$
,
$Q_{1\ast \ast }=bc+h$
,
![]() $Q_{\ast 1 \ast } =ac+h$
, and so
$Q_{\ast 1 \ast } =ac+h$
, and so
![]() $\sigma _1=\pi _1=1$
,
$\sigma _1=\pi _1=1$
,
![]() $\{\rho _{c+1},\ldots ,\rho _{c+h}\}=\{c+1,\ldots ,c+h\}$
, and for
$\{\rho _{c+1},\ldots ,\rho _{c+h}\}=\{c+1,\ldots ,c+h\}$
, and for
![]() $k \in [c+1,c+h]$
, we must have
$k \in [c+1,c+h]$
, we must have
![]() $Q_{i,j,k}=0$
unless
$Q_{i,j,k}=0$
unless
![]() $i=j=1$
. This also forces us to have
$i=j=1$
. This also forces us to have
![]() $Q_{1,1,k}=1$
for all these k, and so
$Q_{1,1,k}=1$
for all these k, and so
![]() $\rho _k =k$
for
$\rho _k =k$
for
![]() $k=c+1,\ldots ,c+h$
.
$k=c+1,\ldots ,c+h$
.
This completely determines
![]() $Q_{i,j,k}$
for
$Q_{i,j,k}$
for
![]() $k>c$
, as well as
$k>c$
, as well as
![]() $\rho _k$
for
$\rho _k$
for
![]() $k>c$
, and
$k>c$
, and
![]() $\rho = \bar {\rho },(c+1),\ldots ,(c+h)$
for
$\rho = \bar {\rho },(c+1),\ldots ,(c+h)$
for
![]() $\bar {\rho }\in S_c$
. We can thus write formula (4.11) as
$\bar {\rho }\in S_c$
. We can thus write formula (4.11) as

where
![]() $\bar {\alpha } = \alpha - (h) = \lambda $
,
$\bar {\alpha } = \alpha - (h) = \lambda $
,
![]() $\bar {\beta } = \beta - (h) = \mu $
and
$\bar {\beta } = \beta - (h) = \mu $
and
![]() $\bar {\gamma } = (\gamma _1\ldots ,\gamma _c) = \nu '$
. As the last part coincides with the expression for
$\bar {\gamma } = (\gamma _1\ldots ,\gamma _c) = \nu '$
. As the last part coincides with the expression for
![]() ${\texttt {k}}(\lambda ,\mu ,\nu )$
in (4.8), we get the desired identity.
${\texttt {k}}(\lambda ,\mu ,\nu )$
in (4.8), we get the desired identity.
Proof of Theorem 2 via Littlewood-Richardson coefficients.
Let again
![]() $\ell (\lambda )=a$
,
$\ell (\lambda )=a$
,
![]() $\ell (\mu )=b$
and
$\ell (\mu )=b$
and
![]() $\nu _1=c$
.
$\nu _1=c$
.
We have that
![]() ${\texttt {k}}(\lambda +h,\mu +h,\nu +h) = {\texttt {k}}( \nu '\mathbin {\diamond } (1^h), \lambda ' \mathbin {\diamond } (1^h), \mu +h)$
, and we are going to apply formula (4.6) with that triple of partitions. Set
${\texttt {k}}(\lambda +h,\mu +h,\nu +h) = {\texttt {k}}( \nu '\mathbin {\diamond } (1^h), \lambda ' \mathbin {\diamond } (1^h), \mu +h)$
, and we are going to apply formula (4.6) with that triple of partitions. Set
![]() $\hat {\mu }=\mu +h$
,
$\hat {\mu }=\mu +h$
,
![]() $\hat {\lambda } = \lambda ' \mathbin {\diamond } (1^h) = (\lambda +h)'$
and
$\hat {\lambda } = \lambda ' \mathbin {\diamond } (1^h) = (\lambda +h)'$
and
![]() $\hat {\nu }=\nu '\mathbin {\diamond }(1^h)(\nu +h)'$
. Here,
$\hat {\nu }=\nu '\mathbin {\diamond }(1^h)(\nu +h)'$
. Here,
![]() $\ell (\nu '\mathbin {\diamond }(1^h)) = c+h$
, so
$\ell (\nu '\mathbin {\diamond }(1^h)) = c+h$
, so
 $$ \begin{align*}{\texttt{k}}(\lambda+h, \mu+h,\nu+h) = \sum_{\sigma \in S_{c+h} } {\mathrm{sgn}}(\sigma) \sum_{\alpha^i \vdash \hat{\nu}_i-i+\sigma_i} c^{\hat{\lambda}}_{\alpha^1 \alpha^2 \cdots} c^{\hat{\mu}}_{\alpha^1 \alpha^2 \cdots}.\end{align*} $$
$$ \begin{align*}{\texttt{k}}(\lambda+h, \mu+h,\nu+h) = \sum_{\sigma \in S_{c+h} } {\mathrm{sgn}}(\sigma) \sum_{\alpha^i \vdash \hat{\nu}_i-i+\sigma_i} c^{\hat{\lambda}}_{\alpha^1 \alpha^2 \cdots} c^{\hat{\mu}}_{\alpha^1 \alpha^2 \cdots}.\end{align*} $$
We will now characterize the possible partitions
![]() $\alpha ^i$
involved in this sum. From the iterated definition of the multi-LR coefficients (4.4), we see that in order for the coefficients to be nonzero, we must have
$\alpha ^i$
involved in this sum. From the iterated definition of the multi-LR coefficients (4.4), we see that in order for the coefficients to be nonzero, we must have
![]() $\alpha ^i \subset \hat {\mu }$
and
$\alpha ^i \subset \hat {\mu }$
and
![]() $\alpha ^i \subset \hat {\lambda }$
. In particular, then
$\alpha ^i \subset \hat {\lambda }$
. In particular, then
![]() $\ell (\alpha ^i) \leq \ell (\mu ) =b$
and
$\ell (\alpha ^i) \leq \ell (\mu ) =b$
and
![]() $\alpha ^i_1 \leq \hat {\lambda }_1 = a$
. Note that multi-LR coefficients count certain SSYTs of type
$\alpha ^i_1 \leq \hat {\lambda }_1 = a$
. Note that multi-LR coefficients count certain SSYTs of type
![]() $(\alpha ^1\mathbin {\diamond } \alpha ^2 \mathbin {\diamond }\ldots \mathbin {\diamond } \alpha ^c \mathbin {\diamond } \ldots )$
, and thus in the shape
$(\alpha ^1\mathbin {\diamond } \alpha ^2 \mathbin {\diamond }\ldots \mathbin {\diamond } \alpha ^c \mathbin {\diamond } \ldots )$
, and thus in the shape
![]() $\hat {\lambda }$
, the first column will have at most
$\hat {\lambda }$
, the first column will have at most
![]() $\ell (\alpha ^1) + \cdots +\ell (\alpha ^c) \leq bc$
many entries from the first c partitions. So there are at least h boxes in the first column which need to be covered by the partitions
$\ell (\alpha ^1) + \cdots +\ell (\alpha ^c) \leq bc$
many entries from the first c partitions. So there are at least h boxes in the first column which need to be covered by the partitions
![]() $\alpha ^{c+1},\ldots , \alpha ^{c+h}$
. We then have
$\alpha ^{c+1},\ldots , \alpha ^{c+h}$
. We then have
 $$ \begin{align*}h \leq \ell(\alpha^{c+1})+\cdots+\ell(\alpha^{c+h}) \leq |\alpha^{c+1}| + \cdots + |\alpha^{c+h}| = \sum_{i=c+1}^{c+h} 1 -i +\sigma_i \leq h,\end{align*} $$
$$ \begin{align*}h \leq \ell(\alpha^{c+1})+\cdots+\ell(\alpha^{c+h}) \leq |\alpha^{c+1}| + \cdots + |\alpha^{c+h}| = \sum_{i=c+1}^{c+h} 1 -i +\sigma_i \leq h,\end{align*} $$
as
![]() $\sigma _{c+1}+\cdots +\sigma _{c+h} \leq c+1+\cdots c+h$
. Thus, we need to have equalities, and so
$\sigma _{c+1}+\cdots +\sigma _{c+h} \leq c+1+\cdots c+h$
. Thus, we need to have equalities, and so
so
![]() $\alpha ^i$
are single column partitions, possibly empty.
$\alpha ^i$
are single column partitions, possibly empty.
Further, we have
![]() $\alpha ^i \leq a$
,
$\alpha ^i \leq a$
,
![]() $\alpha ^i \subset \hat {\mu }$
. As there is a multi-LR of type
$\alpha ^i \subset \hat {\mu }$
. As there is a multi-LR of type
![]() $(\alpha ^1 \mathbin {\diamond } \alpha ^2 \cdots )$
, the first row of that tableaux can only be occupied by the smallest entries of each type. So we must have
$(\alpha ^1 \mathbin {\diamond } \alpha ^2 \cdots )$
, the first row of that tableaux can only be occupied by the smallest entries of each type. So we must have
 $$ \begin{align*}ac+h =\hat{\mu}_1 \leq \sum_i \alpha^i_1 \leq \sum_{i=1}^c a + \sum_{i=c+1}^{c+h} \alpha^i_1.\end{align*} $$
$$ \begin{align*}ac+h =\hat{\mu}_1 \leq \sum_i \alpha^i_1 \leq \sum_{i=1}^c a + \sum_{i=c+1}^{c+h} \alpha^i_1.\end{align*} $$
Thus,
![]() $\alpha _1^{c+1}+\cdots + \alpha ^{c+h}_1 \geq h$
. Since
$\alpha _1^{c+1}+\cdots + \alpha ^{c+h}_1 \geq h$
. Since
![]() $\alpha ^i_1\leq 1$
by the above consideration, we must have
$\alpha ^i_1\leq 1$
by the above consideration, we must have
![]() $\alpha ^i=(1)$
for all
$\alpha ^i=(1)$
for all
![]() $i>c$
. So
$i>c$
. So
![]() $\sigma _i=i$
for
$\sigma _i=i$
for
![]() $i=c+1,\ldots ,c+h$
.
$i=c+1,\ldots ,c+h$
.
Then
We thus get that
 $$ \begin{align*} {\texttt{k}}(\lambda+h, \mu+h,\nu+h) = \sum_{\sigma \in S_{c+h} } {\mathrm{sgn}}(\sigma) \sum_{\alpha^i \vdash \hat{\nu}_i-i+\sigma_i} c^{\hat{\lambda}}_{\alpha^1 \alpha^2 \cdots} c^{\hat{\mu}}_{\alpha^1 \alpha^2 \cdots}\\ =\sum_{\sigma \in S_{c} } {\mathrm{sgn}}(\sigma) \sum_{\alpha^i \vdash \nu^{\prime}_i-i+\sigma_i} c^{\lambda'}_{\alpha^1 \alpha^2 \cdots} c^{\mu}_{\alpha^1 \alpha^2 \cdots} ={\texttt{k}}(\nu',\lambda',\mu)={\texttt{k}}(\lambda,\mu,\nu), \end{align*} $$
$$ \begin{align*} {\texttt{k}}(\lambda+h, \mu+h,\nu+h) = \sum_{\sigma \in S_{c+h} } {\mathrm{sgn}}(\sigma) \sum_{\alpha^i \vdash \hat{\nu}_i-i+\sigma_i} c^{\hat{\lambda}}_{\alpha^1 \alpha^2 \cdots} c^{\hat{\mu}}_{\alpha^1 \alpha^2 \cdots}\\ =\sum_{\sigma \in S_{c} } {\mathrm{sgn}}(\sigma) \sum_{\alpha^i \vdash \nu^{\prime}_i-i+\sigma_i} c^{\lambda'}_{\alpha^1 \alpha^2 \cdots} c^{\mu}_{\alpha^1 \alpha^2 \cdots} ={\texttt{k}}(\nu',\lambda',\mu)={\texttt{k}}(\lambda,\mu,\nu), \end{align*} $$
which completes the proof.
We now discuss how Theorem 1 can be seen from the following identity, which first appeared in [Reference Briand, Orellana and RosasBOR11], where it was proven using symmetric function operators. It was then reformulated in [Reference Bowman, De Visscher and OrellanaBDVO15, Theorem 4.3], which studies the partition algebra, as follows.
Set
![]() $m = r + s$
, and let
$m = r + s$
, and let
![]() $\nu \vdash m-l$
,
$\nu \vdash m-l$
,
![]() $\lambda \vdash r$
,
$\lambda \vdash r$
,
![]() $\mu \vdash s$
for some nonnegative integer l. Then
$\mu \vdash s$
for some nonnegative integer l. Then
 $$\begin{align*}\overline{{\texttt{k}}}(\lambda,\mu,\nu) = \sum_{\substack{l_1, l_2\\unicode{x0142}=l_1+2l_2}} \sum_{\substack{\alpha\vdash r-l_1-l_2\\\beta\vdash s-l_1-l_2}} \sum_{\substack{\pi,\rho,\sigma\vdash l_1\\\gamma\vdash l_2}} c_{\alpha,\beta,\pi}^\nu c_{\alpha,\rho,\gamma}^\lambda c_{\gamma,\sigma,\beta}^\mu {\texttt{k}}(\pi,\rho,\sigma) .\end{align*}$$
$$\begin{align*}\overline{{\texttt{k}}}(\lambda,\mu,\nu) = \sum_{\substack{l_1, l_2\\unicode{x0142}=l_1+2l_2}} \sum_{\substack{\alpha\vdash r-l_1-l_2\\\beta\vdash s-l_1-l_2}} \sum_{\substack{\pi,\rho,\sigma\vdash l_1\\\gamma\vdash l_2}} c_{\alpha,\beta,\pi}^\nu c_{\alpha,\rho,\gamma}^\lambda c_{\gamma,\sigma,\beta}^\mu {\texttt{k}}(\pi,\rho,\sigma) .\end{align*}$$
We now apply it to compute the reduced Kronecker coefficient in Theorem 1. Let
![]() $\hat {\lambda } = \nu _1^{\ell (\lambda )}+\lambda $
,
$\hat {\lambda } = \nu _1^{\ell (\lambda )}+\lambda $
,
![]() $\hat {\mu } = \nu _1^{\ell (\mu )}+\mu $
and
$\hat {\mu } = \nu _1^{\ell (\mu )}+\mu $
and
![]() $\hat {\nu } = (\nu _1^{\ell (\lambda )+\ell (\mu )},\nu )$
. Then
$\hat {\nu } = (\nu _1^{\ell (\lambda )+\ell (\mu )},\nu )$
. Then
![]() $m -l = (\ell (\lambda )+\ell (\mu ))\nu _1 + n$
,
$m -l = (\ell (\lambda )+\ell (\mu ))\nu _1 + n$
,
![]() $r= \ell (\lambda )\nu _1+n$
,
$r= \ell (\lambda )\nu _1+n$
,
![]() $s =\ell (\mu )\nu _1+n$
, so
$s =\ell (\mu )\nu _1+n$
, so
![]() $l=n$
and the above identity translates to
$l=n$
and the above identity translates to
 $$ \begin{align*}\overline{{\texttt{k}}}(\hat{\lambda},\hat{\mu},\hat{\nu}) = \sum_{\substack{l_1, l_2\\n=l_1+2l_2}} \sum_{\substack{\alpha\vdash r-l_1-l_2\\\beta\vdash s-l_1-l_2}} \sum_{\substack{\pi,\rho,\sigma\vdash l_1\\\gamma\vdash l_2}} c_{\alpha,\beta,\pi}^{\hat{\nu}} c_{\alpha,\rho,\gamma}^{\hat{\lambda}} c_{\gamma,\sigma,\beta}^{\hat{\mu}} {\texttt{k}}(\pi,\rho,\sigma) .\end{align*} $$
$$ \begin{align*}\overline{{\texttt{k}}}(\hat{\lambda},\hat{\mu},\hat{\nu}) = \sum_{\substack{l_1, l_2\\n=l_1+2l_2}} \sum_{\substack{\alpha\vdash r-l_1-l_2\\\beta\vdash s-l_1-l_2}} \sum_{\substack{\pi,\rho,\sigma\vdash l_1\\\gamma\vdash l_2}} c_{\alpha,\beta,\pi}^{\hat{\nu}} c_{\alpha,\rho,\gamma}^{\hat{\lambda}} c_{\gamma,\sigma,\beta}^{\hat{\mu}} {\texttt{k}}(\pi,\rho,\sigma) .\end{align*} $$
We now observe that
![]() $|\alpha | \geq \ell (\lambda )\nu _1$
, and if
$|\alpha | \geq \ell (\lambda )\nu _1$
, and if
![]() $c^{\hat {\lambda }}_{\alpha ,\rho ,\gamma }>0$
,
$c^{\hat {\lambda }}_{\alpha ,\rho ,\gamma }>0$
,
![]() $c^{\hat {\nu }}_{\alpha ,\beta ,\pi }>0$
, then
$c^{\hat {\nu }}_{\alpha ,\beta ,\pi }>0$
, then
![]() $\alpha \subset \hat {\nu } \cap \hat {\lambda } = (\nu _1^{\ell (\lambda )})$
. Then we must have
$\alpha \subset \hat {\nu } \cap \hat {\lambda } = (\nu _1^{\ell (\lambda )})$
. Then we must have
![]() $\alpha = \nu _1^{\ell (\lambda )}$
, and so
$\alpha = \nu _1^{\ell (\lambda )}$
, and so
![]() $l_1+l_2=n$
. Since
$l_1+l_2=n$
. Since
![]() $l_1 +2l_2=n$
, we must have
$l_1 +2l_2=n$
, we must have
![]() $l_2=0$
and
$l_2=0$
and
![]() $l_1=n$
, so
$l_1=n$
, so
![]() $\gamma =\emptyset $
. Similarly, we obtain
$\gamma =\emptyset $
. Similarly, we obtain
![]() $\beta =(\nu _1^{\ell (\mu )})$
, leaving us with
$\beta =(\nu _1^{\ell (\mu )})$
, leaving us with
 $$ \begin{align*} \overline{\mathtt{k}}(\hat{\lambda},\hat{\mu},\hat{\nu}) =\sum_{\pi,\rho,\sigma\vdash n} c_{\alpha,\beta,\pi}^{\hat{\nu}}c_{\alpha,\rho}^{\hat{\lambda}}c_{\sigma,\beta}^{\hat{\mu}}{\mathtt{k}}(\pi,\rho,\sigma). \end{align*} $$
$$ \begin{align*} \overline{\mathtt{k}}(\hat{\lambda},\hat{\mu},\hat{\nu}) =\sum_{\pi,\rho,\sigma\vdash n} c_{\alpha,\beta,\pi}^{\hat{\nu}}c_{\alpha,\rho}^{\hat{\lambda}}c_{\sigma,\beta}^{\hat{\mu}}{\mathtt{k}}(\pi,\rho,\sigma). \end{align*} $$
Observe that the Littlewood-Richardson rule gives, since
![]() $\alpha $
is the rectangle in the beginning of
$\alpha $
is the rectangle in the beginning of
![]() $\hat {\lambda }$
, that
$\hat {\lambda }$
, that
![]() $c^{\hat {\lambda }}_{\alpha ,\rho } = 0$
if
$c^{\hat {\lambda }}_{\alpha ,\rho } = 0$
if
![]() $\rho \neq \hat {\lambda } /\alpha = \lambda $
, and is
$\rho \neq \hat {\lambda } /\alpha = \lambda $
, and is
![]() $1$
otherwise. Similarly, the other Littlewood-Richardson coefficients are zero unless
$1$
otherwise. Similarly, the other Littlewood-Richardson coefficients are zero unless
![]() $\sigma =\mu $
and
$\sigma =\mu $
and
![]() $\pi =\nu $
, we are left with only one partition triple
$\pi =\nu $
, we are left with only one partition triple
![]() $(\pi ,\rho ,\sigma ) = (\nu ,\lambda ,\mu )$
, whose coefficient is 1 and the identity in Theorem 1 follows.
$(\pi ,\rho ,\sigma ) = (\nu ,\lambda ,\mu )$
, whose coefficient is 1 and the identity in Theorem 1 follows.
Competing interests
The authors have no competing interest to declare.
Ethical standards
The research meets all ethical guidelines, including adherence to the legal requirements of the study country.
Funding statement
This research was supported by grants from Engineering and Physics Sciences Research Council grant EP/W014882/1 and National Science Foundation CCF:AF grant 2007652.