1. Introduction
Dual-arm robots, specifically humanoid robots, represent the most adaptable kinds of robots suited for human-designed environments. Over the last decade’s developments in autonomous robotics systems, humanoid robots are an example of potentially dual-arm robots, and their applications have gained significance. Humanoid robots and dual-arm robots advances can enable us to undertake varied, complex applications, such as rescue missions (Saeedvand, Reference Saeedvand2019), service robots (Saeedvand, Reference Saeedvand2019), etc. Consequently, dual-arm architecture, and this study specifically a humanoid robot, can serve as autonomous entities, executing intricate tasks (Lioutikov, Reference Lioutikov2016; Yan, Reference Yan2016; Qu, Reference Qu2019; Weng et al., Reference Weng, Tan and Chen2019). Interacting with different objects is a challenging problem for a mobile robot with robotics arms, encompassing factors like perception, trajectory planning, and control to grasping (Lenz et al., Reference Lenz, Lee and Saxena2015; Khansari, Reference Khansari2020), as well as manipulation (Fang, Reference Fang2020). In certain situations, robots may need to use a computer as a standard user might. For instance, in rescue scenarios, network connection issues might necessitate a humanoid robot to operate a computer or server when remote access is not possible (Saeedvand et al., Reference Saeedvand, Aghdasi and Baltes2019, Reference Saeedvand, Aghdasi and Baltes2020), or another example can be the service robot applications that a robot might need to use a computer to perform some tasks as a service in a home or even in an industry environment.
The ability to type with an arbitrary computer keyboard requires highly dexterous skills that a dual-arm robot needs to have. Using different keyboards with variable locations and random orientations makes the type problem challenging for a humanoid robot. In this regard, in order to complete the typing task successfully, both arms of a humanoid robot with independent sequences of movement primitives demand very accurate control strategies.
Typing on a conventional computer keyboard necessitates a level of dexterity that challenges even the most advanced dual-arm robots. As keyboards can vary in design, location, and orientation, enabling a humanoid robot to type with these variables requires sophisticated control and learning strategies. Previous studies have largely centered on manipulating objects with dual-arm robots (Lioutikov, Reference Lioutikov2016; Weng et al., Reference Weng, Tan and Chen2019; Li, Reference Li2017; Mandala et al., Reference Mandala, Saeedvand and Baltes2020) or single manipulators (Lenz et al., Reference Lenz, Lee and Saxena2015; Fang, Reference Fang2020; Zhu, Reference Zhu2019; Seker et al., Reference Seker, Tekden and Ugur2019). Notably absent from this body of work are learning-based approaches tailored to keyboard operation. A humanoid robot, when faced with a mispositioned or improperly angled keyboard, may initially employ algorithms to adjust it. Yet, even after such adjustments, achieving precise alignment relative to the robot’s trunk for predefined motion control can be elusive. This challenge is further compounded when the robot confronts different keyboard types. In essence, the primary challenges confronting robotic typing include: (i) the keyboard location and orientation are not precisely related to the robot’s trunk to use predefined motion control, (ii) the typing process requires two arms to use, and (iii) there can be different types of keyboards to be used by the robot. Figure 1 depicts our humanoid robot that types with a keyboard.

Figure 1. Modified THORMANG3 dual-arm humanoid robot to type with the keyboard
Deep learning techniques have consistently showcased remarkable results across diverse domains, from object detection (Liu, Reference Liu2020) and face recognition (Guo and Zhang, Reference Guo and Zhang2019; Wu et al., Reference Wu, Shen and Van Den Hengel2019) to control systems (Chen and Guhl, Reference Chen and Guhl2018). In the realm of robotics, both supervised and unsupervised learning approaches have been employed depending on the specific application. Within the traditional reinforcement learning (RL) paradigm, Q-learning emerges as a prevalent method, enjoying wide application in robotics (Kober et al., Reference Kober, Bagnell and Peters2013). However, a significant limitation of Q-learning lies in its suitability, mostly for problems characterized by a small state space. To address this limitation, deep neural networks (DNNs) have been integrated with Q-learning, essentially using the DNN as a function approximator to map states to Q-values for all potential actions within the state space. This hybrid approach gave rise to deep Q-Learning (DQL) (Mnih, Reference Mnih2015), adept at handling large-scale problems.
However, the DQL, despite its advancements, still faces challenges in managing high-dimensional action spaces or continuous environments effectively. This shortcoming paved the way for the development of the Deep Deterministic Policy Gradient (DDPG) algorithm (Lillicrap, Reference Lillicrap2015). The DDPG, an evolution of the Deterministic Policy Gradient (DPG) (Silver, Reference Silver2014) within the Actor-Critic framework, not only learns efficient policies but also supports off-policy exploration in continuous spaces.
In order to achieve a low number of trial and error to learn with a low-dimension state presentation for DRL algorithms, there are recent advanced approaches that are encoding sequences of images using the Convolutional Neural Network (CNN) (Hafner, Reference Hafner2020). In deep learning research, the Convolutional Auto-Encoder (CAE) is one of the most useful architectures. One auto-encoder includes a paradigm similar to the encoder-decoder in which the inputs transform into a lower-dimensional space as the encoder part, and then they expand to reproduce the initial inputs as the decoder part (Masci, Reference Masci2011). The CAE is suited well to image processing tasks in comparison to the classic stacked auto-encoder (Hinton & Salakhutdinov, Reference Hinton and Salakhutdinov2006). The reason is that CAE in image processing utilizes the properties of convolutional neural networks completely, which have been proven to deliver superior results on different conditions of input data, such as on corrupted, noisy, or sifted image data (LeCun, Reference LeCun1998). Different research techniques used CAE in combination with deep reinforcement learning algorithms to reduce environment state-space complexity and improve the performance of their algorithms (Kim & Park, Reference Kim and Park2019; Han, Reference Han2020; Liu, Reference Liu2017; Finn, Reference Finn2016). Based on this fact, in this paper, to reduce the state-space complexity that comes directly from camera images and to increase the real-time response of the proposed algorithm, we propose a convolutional auto-encoder-decoder as a preprocessing step on the proposed DDPG algorithm in our hierarchical platform named HDDPG.
Due to the described problem for typing with different keyboards, the main contributions of this paper are summarized as follows. (i) Proposing a hierarchical DRL algorithm to address the typing on various keyboards using a dual-arm humanoid robot, (ii) merging CAE with DRL in a hierarchical platform to decrease the environment’s state-space dimension, (iii) Implementing the proposed algorithm in both a simulation and on a real robot to demonstrate the algorithm’s efficiency.
The remainder of this paper is organized as follows. In Section 2, a literature review of related research studies is presented. The proposed hierarchical algorithm is presented in Section 3. In Section 4, the experimental evaluations are proposed in two phases, including simulation results and empirical implementation of the dual-armed humanoid robot. Finally, section 5 is a conclusion to the paper.
2. Literature review
Computer keyboards were designed to be used by humans, and the process of developing a humanoid typist robot offers the potential of revealing new insights into the control of manipulation in a human behavior manner. The applications for robots with the ability to type can be rescue operations, service robots, research and development, entertainment, customer Service, etc. As one example of rescue operations, disasters or dangerous areas often are dangerous for teams of rescue workers. Therefore, using a rescue robot has greatly benefited from overcoming this problem (Magid, Reference Magid2020). Conversely, unlike other robot rescue platforms (Moosavian et al., Reference Moosavian, Semsarilar and Kalantari2006; Bogue, Reference Bogue2015; Apvrille et al., Reference Apvrille, Tanzi and Dugelay2014; Murphy, Reference Murphy2012), the humanoid robot is built to structurally imitate the human body from every aspect as much as possible, and DARPA Robot Competition (DRC) (Kohlbrecher et al., Reference Kohlbrecher2015; Johnson et al., Reference Johnson2015) is an example of rescue task by robots. Therefore, in a rescue scenario, in certain cases, the robot might need to be able to use the computer keyboard to take control of different operations, which indicates the importance of the problem stated in this paper.
Correspondingly, there are prior studies that developed typist robots (Kurnia et al., Reference Kurnia2017; Kurniawan et al., Reference Kurniawan2017a, Reference Kurniawanb). Their aims relied on helping people with physical disabilities on their hands (quadriplegic persons) by giving them the ability to type with a computer keyboard. These research studies used two-arm robots (each arm with four degrees of freedom (DOFs)) attached to fixed distances with a standard keyboard. Other related works similar to typing computer keyboards are playing piano (Zhang et al. Reference Zhang2009, Reference Zhang, Malhotra and Matsuoka2011; Lin et al., Reference Lin2010 Li & Chuang, Reference Li and Chuang2013). These studies used a manipulation hand designed to mimic the biomechanics of the human finger that achieved the robotics systems able to play human-level piano skills. The shortcoming with these approaches is the robot’s hand coordinates that can move in the single axis attached to the horizontal rail track. For this reason, such solutions are not quite suitable for a rescue mission. In contrast, a humanoid robot can manipulate different tasks to support the high-dimensional space of computer keyboard design.
As mentioned above, therefore, the solution for flexible typing with a computer keyboard needs to employ a dual-arm robot. To the best of our knowledge, there is no autonomous typist humanoid robot up to date. However, typing with a computer keyboard by a humanoid robot has its similarities to playing musical keyboard instruments. The first instrument robotic player was developed by Sugano and Kato (Reference Sugano and Kato1987) in early 1980. They use WABOT-2 humanoid robot to play the piano. The WABOT -2’s arm has 21 DOFs with wired flexible fingers with high dexterity. In Batula and Kim (Reference Batula and Kim2010), the authors used both hands of a mini-humanoid robot to play the piano. This robot’s hands’ shape is not like human hand anatomy, and they have used a simple solid object to represent the end effector for pressing the piano. A simple song (kid-level) was successfully played by the ROBONOVA robot. However, agility and workspace limitations were using a mini-sized humanoid robot. Moreover, the design of the hands was not suitable for typing buttons on the computer keyboard. On the other hand, the authors solved the problem of a workspace (Maier et al., Reference Maier, Zohouri and Bennewitz2014) and showed an NAO humanoid robot playing metallophone.
In Ren et al. (Reference Ren, Han and Wang2022), the authors study the challenge of controlling the dual-arm lunar-assisted robot, particularly when assisting astronauts in an unstructured lunar environment. Given the complexities of the lunar surface and the need to automate trajectories, a hierarchical reinforcement learning model is proposed for dual-arm control. The model views trajectory planning as a two-layer Markov decision process. Key limitations addressed include efficiently exploring and deciding in high-dimensional action spaces and setting up an appropriate reward function to optimize strategies quickly. The methodology simplifies the vast data from astronaut postures into 20 key models, streamlining the robot’s decision-making process. Simulation results using a dual-arm robot manipulator validate the proposed methods, emphasizing their potential in advancing lunar exploration and astronaut-robot collaboration. In Wang et al. (Reference Wang2020), the authors introduce a novel framework for mobile robotic manipulation, combining deep reinforcement learning with visual perception from an onboard RGB camera. It’s designed for the transition from simulation to real-world applications. Despite the advancements, challenges arise from the intricate coordination of mobile and manipulative functions, potential inconsistencies between simulated and real-world environments, and dependencies on visual perception, which may face real-world limitations or obscurations.
Generally, the reinforcement algorithm (RL) has shown remarkable results in the robotic area (Kober et al., Reference Kober, Bagnell and Peters2013). Problems in robotics are often best represented with high-dimensional, continuous states and actions (Laschi et al., Reference Laschi2000), especially in a robotic manipulation task. This is why RL can be used to train policies to perform complex robotic manipulation skills (Levine et al., Reference Levine2016). In RL, an agent learns an optimal policy for solving a task. This policy tells the robot which action to perform in a particular state. The robot acquires the policy incrementally by performing experiments. The following review of the literature (respectively) confirms that the manipulation problem in the robotics system has been extensively studied, and the RL algorithm has made significant progress in dealing with this. The RL-based approaches on humanoid robots have been used in different vision-based manipulation problems. In our previous study (Saeedvand et al., Reference Saeedvand, Mandala and Baltes2021), we proposed a DRL algorithm to balance control for dragging heavy objects by an adult-sized humanoid robot. In another study (Baltes et al., Reference Baltes, Christmann and Saeedvand2023), we proposed a successful DRL based on the Proximal Policy Optimization (PPO) approach for balance control and driving a two-wheeled scooter using the same adult-sized humanoid robot.
In Zhang et al. (Reference Zhang2015), the authors used solely gray images to feed into the DQL on a simulated 3-DOF arm robot. The result shows feasibility performance from exploration in simulation without prior knowledge. Also, several works in manipulation dexterous problems have been studied. In Rajeswara et al. (Reference Rajeswaran2017), the authors showed the first empirical result on a model-free deep reinforcement learning algorithm (DRL) to train high-dimensional human-like five-finger hands on several dexterous manipulation tasks, such as object relocation, in-hand manipulation, tool use, and opening doors. Then, in Gu et al. (Reference Gu2017), the authors improved a DRL on deep Q-function off-policy training time that uses a single asynchronous policy to train across dual-arm robots on opening complex doors from scratch. On the contrary, in the compliant manipulation problem (Kalakrishna et al., Reference Kalakrishnan2011), the authors presented Policy Improvement with Path Integrals (PI2) algorithm to learn the force/torque profile on the Barrett WAM robot arm performing manipulation tasks: opening a door with a lever door handle and picking up a pen off the table. Similarly, in Huang et al. (Reference Huang2019), the authors have used DRL to train policies for gentle object manipulation, where the force sensor is attached in Shadow Dexterous Hand to give reward value based on the ‘pain’ signal given on the grasping level.
In the human-robot collaborative manipulation problem (Ye et al., Reference Ye, Thobbi and Sheng2011), the authors developed a framework based on a Q-learning algorithm with a guided exploration strategy to learn the optimal state-action policy on the human-robot collaborative manipulation task on the table lifting task. Conversely, in the manipulation imitation learning problem (Pasto et al., Reference Pastor2011), the authors employed the Dynamic Movement Primitive (DMP) algorithm to allow the PR2 robot on the pool stroke task to refine manipulation skills based on a demonstration shown by a human expert. On the one hand, in the manipulation trajectory problem (Stulp et al., Reference Stulp, Theodorou and Schaal2012), the authors improved robust trajectory manipulation by a utilized set of sequence motion primitives (PI2 Seq), where shape parameter trajectory between the start and endpoint of movement has extended to take goal parameters into account. Whereas, in the manipulation grasping problem (Hoof et al., Reference Hoof2015), the authors validated unknown object grasping in-hand robots using the RL algorithm to train robot hand manipulation with tactile features (angular velocity sensor) (Ozawa et al., Reference Ozawa2005), where the analytic dynamic or kinematic of the object model is unknown. Next (Boularias et al., Reference Boularias, Bagnell and Stentz2015), the authors solved manipulation planning on unknown and arbitrary objects grasping in a cluttered environment by using RL with the UCB algorithm.
By looking at the existing literature, the limitations of studies can be stated as follows.
-
• Typing Robots: Previous studies have developed robots that can type, primarily aimed at assisting those with physical disabilities. The major limitation was the restricted mobility of the robot’s hand coordinates and their limitation in using different kinds of keyboards.
-
• Instrumental Robotics: Playing instruments, especially the piano, is somewhat similar to typing on a keyboard. Certain limitations in the instrument models can efficient keyboard typing.
-
• Progress in RL-based Robotic Manipulation: Several studies have showcased the capabilities of RL in diverse manipulation tasks, from simple object relocation to more intricate tasks like opening doors and gentle object handling, but they have not focused on typing tasks.
-
• Collaborative and Imitative Learning: RL techniques have been applied in collaborative tasks, where robots and humans work together, as well as in imitative learning, where robots refine their skills based on human demonstrations. However, typing with the keyboard hasn’t been studied well.
In general, dual-arm robots can be used in different kinds of scenarios. However, research on typing with a computer keyboard by autonomous robots has not been focused so far. Several traditional approaches have been addressed for typing by keyboard problems, but their solution is far from being applied to dynamic environmental situations. Motivated by this, in this paper, we propose a novel hierarchical RL algorithm for an adult-sized humanoid robot as a robust algorithm to achieve typing on a computer keyboard in a real environment.
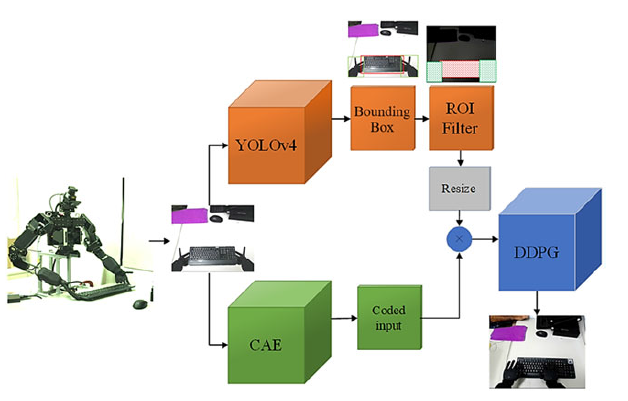
Figure 2. Proposed architecture for typing with the keyboard, including convolutional auto-encoder and deep reinforcement learning
3. Proposed algorithm
In this section, we describe the proposed hierarchical deep reinforcement learning algorithm in detail, which is based on the DRL. The goal of the proposed algorithm is to type with an arbitrary keyboard by a dual-arm adult-sized humanoid robot. So, the proposed algorithm generates the best actions based on the detected keyboard that is already placed in a proper position with the error at position and orientation. In this regard, many related works (Lenz et al., Reference Lenz, Lee and Saxena2015; Khansari, Reference Khansari2020), Saxen et al. (Reference Saxena, Driemeyer and Ng2008) and Jiang et al. (Reference Jiang, Moseson and Saxena2011) address the perception aspect of the grasping and placement problems. Thus, in general, the rule of typing with a keyboard is to propose a hierarchical DDPG algorithm that learns how to generate a series of actions based on a real and empirical strategy for typing. In Figure 2, the high-level architecture for typing with the keyboard is shown.
As demonstrated in Figure 2, the proposed hierarchical algorithm unfolds in several distinct steps:
-
1. Object Detection and Localization: Once frames are captured from the robot’s camera, our first step involves the use of the YOLOv4-tiny algorithm. This step precisely detects and localizes both the keyboard and the robot arms within the scene, producing the resulting bounding boxes (Bochkovskiy et al., Reference Bochkovskiy, Wang and Liao2020).
-
2. Region of Interest (ROI) Creation: Based on the bounding boxes of the detected objects (in this case, the keyboard and robot arms), we formulate our ROI filter. This filter is a binary matrix, matching the size of the original input image frame, populated with ones and zeros. In this matrix, ones correspond to areas where objects are detected by YOLO, while zeros represent the remainder of the image.
-
3. Convolutional Autoencoder (CAE) Application: Simultaneously, the input frames are subjected to an unsupervised pre-trained CAE. This CAE, which has been trained on our comprehensive dataset of target objects, acts as a pivotal dimensionality reduction component within our deep reinforcement learning model.
-
4. Integration of ROI and CAE Outputs: To seamlessly integrate outputs from both the ROI filter and CAE, we resize the binary ROI matrix to align with the dimensions of the CAE output, ensuring the matrix’s properties remain intact. Following this, an element-wise multiplication is performed between the CAE-encoded frame and the resized binary matrix. The outcome of this process is a condensed input, emphasizing key environmental features and accentuating encoded areas of the frame.
-
5. Implementation of Deep Deterministic DDPG: With the processed low-dimensional frames in hand, our next step involves the deep deterministic DDPG algorithm. As the core of our methodology, the DDPG algorithm utilizes these frames as input states. Its mission? To discern and master the optimal policy guiding the robot arms’ movements.
The following sections delve deeper into each component of the hierarchical algorithm, offering a more granular view of the processes at play.
3.1. Object detection
In robotic applications, a vision-based object detection system plays an important role in building robots that can perceive the world and their movements for accomplishing different tasks. Therefore, the most notable object detection method utilizing a deep learning algorithm is called You Only Look Once (YOLO). It can achieve high accuracy by being able to run on a real-time video stream. In other words, it uses one-stage anchor-based detectors to feed forward propagation over the neural network to combine the classification and localization problem (Bochkovskiy et al., Reference Bochkovskiy, Wang and Liao2020). The one-stage object detector, YOLOv4, is also capable of achieving reasonable accuracy on both the classifier and detector (Bochkovskiy et al., Reference Bochkovskiy, Wang and Liao2020). So, we used Yolov4 to localize the keyboard position in the environment. Therefore, the projected keyboard position from vision coordinates are transformed into a global coordinate system of the robot’s inverse kinematic for typing purpose and will be described in the next section.
3.2. Inverse Kinematic (IK) and Trajectory Planning (TP)
Independent dual-arm manipulations with respect to the orientation target of the object are still a challenging task for a humanoid robot. Inverse Kinematics (IK) in arm positioning methods formulate many solutions of motion processes in the robot with links structure (Colomé & Torras, Reference Colomé and Torras2020). Therefore, a humanoid robot with arms structurally designed like a human obviously could be controlled by using IK. The intuition behind IK is to derive the positions of each joint to comply with the end effector in Cartesian coordinates concerning a given position and orientation (Kajita et al., Reference Kajita2014). We illustrate the right arm kinematic link of the THORMANG3 upper body robot in Figure 3.
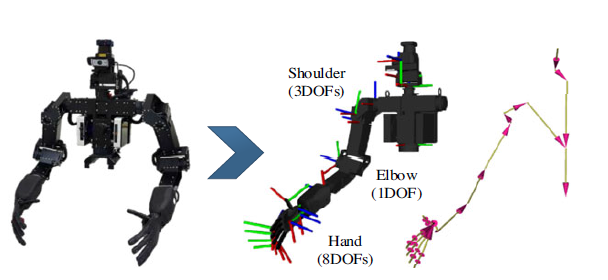
Figure 3. THORMANG3 right arm kinematic chain (real and modeled robot)
In linear algebra, to determine the relationship between the position and orientation of a link structure, we used affine matrix transformation in rotations and translations. To denote a matrix rotation, we used
![]() ${R_z}(\varphi ){R_y}(\theta ){R_x}(\phi )$
to describe roll, pitch, and yaw rotations, respectively. Therefore, a given rotation angle will be transformed to the current point
${R_z}(\varphi ){R_y}(\theta ){R_x}(\phi )$
to describe roll, pitch, and yaw rotations, respectively. Therefore, a given rotation angle will be transformed to the current point
![]() $p$
in the Equation (1).
$p$
in the Equation (1).
On the other hand, we can obtain the new transformation matrix with translation
![]() $x,y,z$
axes according to the current point
$x,y,z$
axes according to the current point
![]() $p$
in the Equation (2).
$p$
in the Equation (2).
 \begin{align}Tran{s_{(x,y,z)}} = \left[ {\begin{array}{c@{\quad}c@{\quad}c@{\quad}c}1 {}&0 {}&0 {}&x\\0 {}&1& {}0& {}y\\0& {}0& {}1& {}z\\0& {}0& {}0& {}1\end{array}} \right]p\end{align}
\begin{align}Tran{s_{(x,y,z)}} = \left[ {\begin{array}{c@{\quad}c@{\quad}c@{\quad}c}1 {}&0 {}&0 {}&x\\0 {}&1& {}0& {}y\\0& {}0& {}1& {}z\\0& {}0& {}0& {}1\end{array}} \right]p\end{align}
Generally, solving the IK solution is still a challenging problem since the relation of link orientation and position with the joint angle is defined by nonlinear equations. However, if we take the relationship of derivatives between the link position and orientation with the joint angles, it can be expressed by linear equations. Therefore, the IK solution problem can be solved by calculating linear equations over the numerical method. Moreover, the Inverse Jacobian methods are well-known for providing simple solutions of numerical methods towards linear equations. As shown in Figure 3, our THORMANG3 robot’s kinematic and dynamic models are interpreted using the Unified Robot Description Format (URDF). As a result, it formed a kinematic chain structure. Therefore, to enhance the simplicity of solving our robot’s IK problem, we used the most notable Orocos Kinematic Dynamic Library (KDL) that utilizes Jacobian Pseudo Inverse (JPI) (Beeson & Ames, Reference Beeson and Ames2015). Inputs of this KDL IK solver are given by the robot kinematic chains based on the mechanical structure of the robot.
Trajectory planning (TP) manipulations for the humanoid robot’s arm are widely proposed in various types of approaches. In this paper, we adopted a robust dynamic torque compliance control from Piazzi and Visioli (Reference Piazzi and Visioli2000) to perform all required trajectories. This is significant due to collision trajectories between each arm’s independence can be avoided. In this regard, during typing, each letter is typed by the minimum trajectory of each arm concerning the predefined workspace of each arm. We defined the workspace of each arm by taking the middle position of the keyboard as a reference and dividing by two for the left and right arm, respectively. Therefore, using an adopted trajectory planner after the robot knows the keyboard location can increase the efficiency of typing speed for future work. This generated trajectory only to prevent collision during typing letters that are near the cross border of each arm workspace.
3.3. Convolutional Auto-Encoder (CAE)
In general, an auto-encoder is a type of artificial neural network that learns data coding, whereas, in deep learning areas, the convolutional auto-encoder (CAE) is the most successful method for coding an image data type (Masci, Reference Masci2011). The CAE method consists of an encoder-decoder paradigm that learns how to code image inputs to image outputs in an unsupervised learning manner. It has an internal hidden layer and is composed of two main parts: an encoder transforms the input image into a lower-dimensional space, and then the decoder maps the reconstructed images back into the original input. The advantage of CAE is that it can extract important features from unlabeled data by removing redundant information. As a result, the data are more robust and efficient (Masci, Reference Masci2011). Recently, CAE methods have been widely used in many pre-training tasks for many scientific research applications (Hinton & Salakhutdinov, Reference Hinton and Salakhutdinov2006). The reasons are referred to as the advantages of a convolutional neural network (CNN) in image processing applications that are robust or insensitive processing types of image data (i.e. blurry, noisy, corrupted images) (LeCun, Reference LeCun1998). Therefore, in this paper, we adopted the CAE algorithm as a part of our deep reinforcement learning method. The encoder-decoder algorithm is applied as input environment states to reduce the input complexity and to solve the diversity between simulation and real environments. Since the theoretical literature of CAE is well mentioned in Masci (Reference Masci2011), Ranzat et al. (Reference Ranzato2007), Vincent et al. (Reference Vincent2008), Hinton et al. (Reference Hinton, Krizhevsky and Wang2011), we proposed an adopted CAE as part of the proposed algorithm. In this regard, the CAE is trained with real-environment data and then feeds into lower-dimensional input for the proposed DDPG algorithm. In Figure 4, we depicted the proposed CAE architecture (the encoder part).
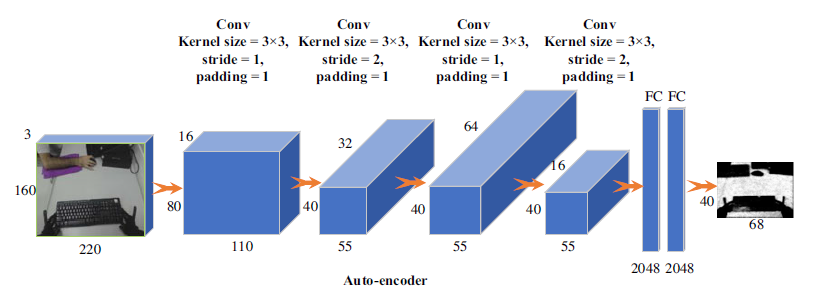
Figure 4. The structure of the proposed CAE algorithm
3.4. The deep reinforcement learning algorithms
In this section, we delve into the intricacies of various deep reinforcement learning methodologies, emphasizing their foundational concepts and their distinct applications.
3.4.1 Deep reinforcement learning
Arguably the most prominent traditional Reinforcement Learning (RL) method, the Q-learning algorithm finds widespread use (Mnih, Reference Mnih2015). Deep Q-learning, its deep learning counterpart, incorporates a value-based function approximator, employing neural networks to compute Q-values using state-action pairs (Mnih, Reference Mnih2015). Designed for discrete control in environments characterized by high-dimensional state and action spaces, Deep Q-learning generally applies the Bellman equation (Equation (3)) to compute Q-values for each state-action pair, typically employing an epsilon-greedy strategy.
Where,
![]() $t$
indicates the time step,
$t$
indicates the time step,
![]() $s$
indicates the state,
$s$
indicates the state,
![]() $a$
specifies the action,
$a$
specifies the action,
![]() $\alpha $
is the learning rate, and
$\alpha $
is the learning rate, and
![]() $\gamma $
is the discount factor.
$\gamma $
is the discount factor.
3.4.2 Policy Gradient (PG) and Deterministic Policy Gradient (DPG)
For continuous control challenges in RL, the PG algorithm directly models and optimizes policy (Sutton et al., Reference Sutton2000). By directly selecting actions based on the current state and skipping intermediary steps, PG algorithms aim to optimize long-term cumulative rewards using gradient descent. However, achieving action value sampling with PG demands exhaustive integration across the action space, which is computationally intensive. As a response, the DPG algorithm emerged, notable for directly determining action values at each stage and enabling policy learning without any dynamic model (Silver, Reference Silver2014).
3.4.3 Actor-critic framework
Leveraging the strengths of both value-based RL and policy-based RL, the Actor-Critic framework comprises two discrete entities: an actor and a critic network. The actor network, responsible for exploring the state space, calculates the strategy function value, while the critic network determines this value. Both networks operate on distinct policies, ensuring comprehensive exploration through a mix of random and deterministic policies. By employing gradient descent, the critic policy identifies maximum cumulative rewards, and the overall system can be updated per action step, enabling faster value judgment compared to traditional PG.
3.4.4 Deep Deterministic Policy Gradient (DDPG)
The Actor-Critic framework stands as a prominent method that capitalizes on the strengths of both value-based RL and policy-based RL algorithms. Within this structure, there are two distinct networks: the actor and the critic. The actor network takes on the role of a policy network, exploring the state space, while the strategy function value network is determined by the critic network. Both networks operate with different policies, ensuring comprehensive exploration by merging a random policy with a deterministic one sourced from the critic network. This critic policy harnesses gradient descent to pinpoint the maximum cumulative rewards. Moreover, the flexibility of the actor-critic algorithm allows for updates during single-step actions, which fosters a faster value judgment compared to the traditional PG approach.
Nevertheless, despite its many advantages, the Actor-Critic framework grapples with convergence issues. Stepping in to address this drawback is the DDPG (Lillicrap, Reference Lillicrap2015), which, while rooted in the DPG, employs an actor-critic model akin to its predecessors (Mnih, Reference Mnih2015). Similar to its antecedents, DDPG leverages the Bellman equation for Q-value computation. It then projects expected rewards based on actor-network parameters, invoking the chain rule (Lillicrap, Reference Lillicrap2015).
The DPG’s inherent strengths lie in its ability to decide on action values directly at every stage and to master control policies without a dependency on dynamic models. By navigating the state space, it becomes feasible to apply an off-policy and model-free algorithm using distinct control policies. However, as noted earlier, the convergence challenges faced by the Actor-Critic system prompted the advent of DDPG. Predominantly derived from DPG, the DDPG adopts an actor-critic approach similar to the one mentioned previously (Mnih, Reference Mnih2015). It continues to use the Bellman equation to determine the Q-value, further approximating the expected rewards via actor-network parameters and employing the chain rule (Lillicrap, Reference Lillicrap2015).
The same Bellman Equation (3) is also being used to calculate the Q-value
![]() ${\rm{Q(}}{{\rm{s}}_{\rm{t}}}{\rm{,}}{{\rm{a}}_{\rm{t}}}{\rm{)}}$
in the DDPG algorithm. Hence, it approximates the expected rewards in the actor-network parameters, and the chain rule in the Equation (4) is utilized (Lillicrap, Reference Lillicrap2015).
${\rm{Q(}}{{\rm{s}}_{\rm{t}}}{\rm{,}}{{\rm{a}}_{\rm{t}}}{\rm{)}}$
in the DDPG algorithm. Hence, it approximates the expected rewards in the actor-network parameters, and the chain rule in the Equation (4) is utilized (Lillicrap, Reference Lillicrap2015).
Where
![]() $\mu \left( {s|{\beta ^\mu }} \right)$
specifies the defined parameters of the actor function with
$\mu \left( {s|{\beta ^\mu }} \right)$
specifies the defined parameters of the actor function with
![]() ${\beta ^\mu }$
the policy network parameter. In DDPG, the action
${\beta ^\mu }$
the policy network parameter. In DDPG, the action
![]() $a$
is straightly calculated from the continuous search action space using the deep neural network. Moreover, to boost training stability, the actor-critic networks are updating progressively (Lillicrap, Reference Lillicrap2015). Then, to increase the robustness of the algorithm, during the exploration process, the exploration policy
$a$
is straightly calculated from the continuous search action space using the deep neural network. Moreover, to boost training stability, the actor-critic networks are updating progressively (Lillicrap, Reference Lillicrap2015). Then, to increase the robustness of the algorithm, during the exploration process, the exploration policy
![]() $\mu '$
is acquired by randomly decaying noise
$\mu '$
is acquired by randomly decaying noise
![]() $\varepsilon $
in the Equation (5).
$\varepsilon $
in the Equation (5).
where the equivalent of
![]() ${\varepsilon _i} + 1$
is
${\varepsilon _i} + 1$
is
![]() ${r_d}*{\varepsilon _i}$
,
${r_d}*{\varepsilon _i}$
,
![]() ${r_d}$
specifies the decay rate. Therefore, to summarize the DRL algorithms, the DDPG algorithm solves the shortcomings of the DQL in terms of a continuous environment. As a result, the DDPG algorithm has an advantage in learning with multi-policies and off-policy exploration in continuous environment spaces. So, the proposed hierarchical algorithm in this paper is based on the DDPG algorithm.
${r_d}$
specifies the decay rate. Therefore, to summarize the DRL algorithms, the DDPG algorithm solves the shortcomings of the DQL in terms of a continuous environment. As a result, the DDPG algorithm has an advantage in learning with multi-policies and off-policy exploration in continuous environment spaces. So, the proposed hierarchical algorithm in this paper is based on the DDPG algorithm.
3.5. Proposed DDPG algorithm
The core objective of our proposed DDPG algorithm is to guide each arm of the dual-armed robot to accurately press designated buttons. In each action step, the algorithm generates commands for both arms, leading to rotations that help align the robot’s end effectors with the desired buttons. It is essential to note that by this stage, the robot has already adjusted the keyboard’s position. However, the exact location and orientation of the keyboard remain arbitrary.
The overarching goal is to train a DRL model that can deduce the final pressing positions for both of the robot’s independent arms using inverse kinematics (IK) control, all within the framework of the DDPG algorithm. In a given episode, based on the robot arms’ initial positions and the object’s location (which form the current state), the DDPG algorithm produces control actions per arm.
As outlined in Figure 2, both the CAE and the ROI filters process the image directly captured from the robot’s camera. These components work together to simplify the input states received from the environment. Therefore, the combination of the CAE and the object detection and ROI filters serves as a dimensionality reduction step for the DDPG algorithm. The resulting processed state comprises encoded frames that encapsulate the vital information from each input frame. With these refined input states, the DDPG algorithm is trained to produce optimal actions for the robot’s arm movements.
Figure 4 delves deeper into the structure of the deep networks used for the CAE algorithm. Meanwhile, Figure 5 provides a control block diagram illustrating how the DDPG algorithm interfaces with the THORMANG3 humanoid robot platform model.
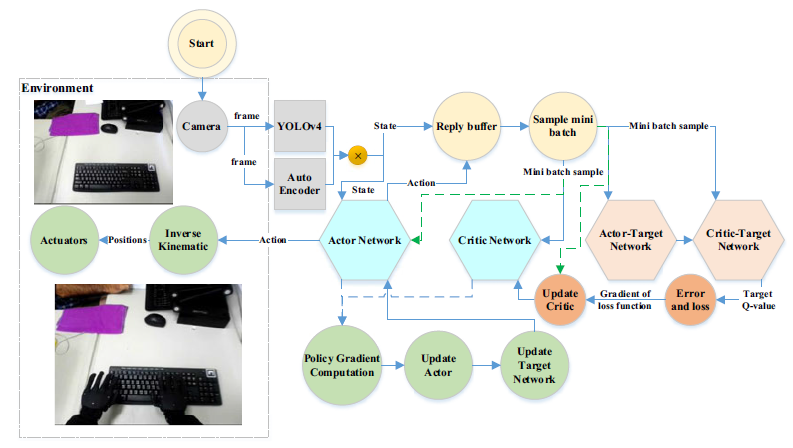
Figure 5. Block diagram of the DDPG algorithm and its interface with the environment
As mentioned earlier, using IK, the robot’s arms move from their current position on a 3D coordinate system to the target position to press the buttons of a keyboard. We define the robot pointing figure as an end effector and per arm. Based on this, actions in the proposed algorithm are based on the control of each independent arm on (x and y coordinate) with IK parallel to the table. For our dual-armed robot, the action space is defined in a continuous domain for each arm. The three primary actions for each arm are:
-
1. Horizontal Movement (x): Dictates the left or right movement of the arm. Its value ranges in a continuous form, typically between [–1, 1], where –1 represents the maximum leftward movement, and 1 represents the maximum rightward movement.
-
2. Vertical Movement (y): Defines the upward or downward motion of the arm. Its value also lies in the continuous range [–1, 1], with –1 indicating the maximum downward movement and 1 indicating the maximum upward movement.
-
3. Press Action: This action determines the pressing mechanism of the arm. In a continuous form, it can range between [0, 1], where 0 denotes no pressing force and 1 denotes the maximum pressing force.
Hence, for our dual-armed robot, the combined action space becomes a 6-dimensional continuous vector, with each dimension corresponding to one of the actions for each arm, as shown in Equation (6) as follows.
where,
![]() ${l_x},{L_y}$
, and
${l_x},{L_y}$
, and
![]() ${L_{press}}$
are the actions for the left arm.
${L_{press}}$
are the actions for the left arm.
![]() ${R_x},{R_y}$
, and
${R_x},{R_y}$
, and
![]() ${R_{press}}$
indicating the actions for the second arm. This 6-dimensional action space allows our DDPG algorithm to generate precise control for each arm, enabling the robot to interact successfully with its environment. Besides, the environmental constraints of the robot’s arms, such as the distance to the table to prevent collisions, are assessed using a LiDAR scanner and mapped into the workspace of the robot’s arms.
${R_{press}}$
indicating the actions for the second arm. This 6-dimensional action space allows our DDPG algorithm to generate precise control for each arm, enabling the robot to interact successfully with its environment. Besides, the environmental constraints of the robot’s arms, such as the distance to the table to prevent collisions, are assessed using a LiDAR scanner and mapped into the workspace of the robot’s arms.
At the onset of each episode, we strategically position the robot’s arms over the ‘A’ and ‘L’ keys, which serve as pivotal reference points. This choice is influenced by the spatial distribution of these keys: they’re situated nearly at opposite ends of the home row on a standard keyboard, thereby providing a broad frame of reference. Starting from these keys not only ensures a consistent beginning across episodes but also simplifies the subsequent movements the robot needs to make (this idea is similar to how a human tries to initialize the hands on the keyboard).
Our preprocessing mechanism, powered by YOLO, detects the keyboard’s layout and determines the initial positioning over the ‘A’ and ‘L’ keys, although not quite precise. To provide clarity on the spatial computations, consider the Equation (7).
 \begin{align}\left\{ {\begin{array}{l}{{L_x} = {x_1} + \dfrac{{{x_2}}}{{12}}}\\[8pt]{{L_y} = {R_y} = {y_1} + \dfrac{{{y_2}}}{2}}\\[8pt]{{R_x} = {x_1} + \dfrac{{{x_2}}}{2}}\end{array}} \right.\end{align}
\begin{align}\left\{ {\begin{array}{l}{{L_x} = {x_1} + \dfrac{{{x_2}}}{{12}}}\\[8pt]{{L_y} = {R_y} = {y_1} + \dfrac{{{y_2}}}{2}}\\[8pt]{{R_x} = {x_1} + \dfrac{{{x_2}}}{2}}\end{array}} \right.\end{align}
Here,
![]() ${L_x}$
and
${L_x}$
and
![]() ${R_x}$
represent the approximate x-coordinates for the ‘A’ and ‘L’ keys, respectively, while
${R_x}$
represent the approximate x-coordinates for the ‘A’ and ‘L’ keys, respectively, while
![]() ${L_y}$
and
${L_y}$
and
![]() ${R_y}$
capture their approximate y-coordinates on the keyboard. The variables
${R_y}$
capture their approximate y-coordinates on the keyboard. The variables
![]() ${x_1},{x_2},{y_1}$
, and
${x_1},{x_2},{y_1}$
, and
![]() ${y_2}$
are parameters derived from the YOLO’s frame detection, giving us the relative positions of the keys on the detected keyboard. This formulation aids in deriving a consistent and reliable starting point for the robot’s actions across episodes, facilitating efficient and meaningful learning.
${y_2}$
are parameters derived from the YOLO’s frame detection, giving us the relative positions of the keys on the detected keyboard. This formulation aids in deriving a consistent and reliable starting point for the robot’s actions across episodes, facilitating efficient and meaningful learning.
The primary objective of the HDDPG algorithm is to train the robot to accurately press two reference keys on the keyboard, starting from these initial positions. By learning to precisely press these two keys, the algorithm can compute the distances between them and determine their relative angle with respect to the robot’s trunk. This understanding enables us to extend a coordinate system centered on these two reference keys, facilitating the identification of positions for all other keys within the robot’s environment.
By narrowing down our action space to focus on one key per arm, we drastically reduce the enormity of potential control actions, condensing it into a manageable 3D continuous action space. Consequently, once the algorithm learns to press the reference keys accurately, it can deduce the positions of all other keys on any keyboard by mapping the coordinates of these reference points. It’s noteworthy that the pressing action, executed by the robot’s arms, utilizes force control, thereby sidestepping the complexities involved in managing pressing depth. To identify individual keys across various keyboard types, we employ a vision-based keyboard classification approach facilitated by YOLOv4.
The reward function is a signal to evaluate the performance of taking an action at a state. Assuming accrete implementation of trajectory planner for the robot’s arms with
![]() $\varepsilon $
execution error, which
$\varepsilon $
execution error, which
![]() $\varepsilon $
is ignorable, in type problem, we can define the objectives as follows. (i) Evaluating if the robot presses the defined buttons properly or not. (ii) how far the pressed buttons are from initialized reference keys, ‘A’ and ‘L’ keys for left and right arms, respectively. Therefore, we can define and calculate the reward
$\varepsilon $
is ignorable, in type problem, we can define the objectives as follows. (i) Evaluating if the robot presses the defined buttons properly or not. (ii) how far the pressed buttons are from initialized reference keys, ‘A’ and ‘L’ keys for left and right arms, respectively. Therefore, we can define and calculate the reward
![]() ${R_i}$
for the
${R_i}$
for the
![]() $i$
th iteration as shown in the Equation (8).
$i$
th iteration as shown in the Equation (8).
 \begin{align}{R_i} = \left\{ {\begin{array}{l@{\quad}l}{\left( {\dfrac{1}{{{{\left| {\left| {{P_L} - {R_A}} \right|} \right|}^2} + {{\left| {\left| {{P_R} - {R_L}} \right|} \right|}^2}}}} \right) + 1}& {}{if\;press\left( L \right)\;and\;press\left( R \right)}\\[12pt]{\dfrac{1}{{{{\left| {\left| {{P_L} - {R_A}} \right|} \right|}^2}}}} {}&{\;else\;if\;press\left( L \right)}\\[12pt]{\dfrac{1}{{{{\left| {\left| {{P_R} - {R_L}} \right|} \right|}^2}}}}&{else\;if\;press\left( R \right)}\\[10pt]0 {}&{else}\end{array}} \right.\end{align}
\begin{align}{R_i} = \left\{ {\begin{array}{l@{\quad}l}{\left( {\dfrac{1}{{{{\left| {\left| {{P_L} - {R_A}} \right|} \right|}^2} + {{\left| {\left| {{P_R} - {R_L}} \right|} \right|}^2}}}} \right) + 1}& {}{if\;press\left( L \right)\;and\;press\left( R \right)}\\[12pt]{\dfrac{1}{{{{\left| {\left| {{P_L} - {R_A}} \right|} \right|}^2}}}} {}&{\;else\;if\;press\left( L \right)}\\[12pt]{\dfrac{1}{{{{\left| {\left| {{P_R} - {R_L}} \right|} \right|}^2}}}}&{else\;if\;press\left( R \right)}\\[10pt]0 {}&{else}\end{array}} \right.\end{align}
where
![]() ${P_L}$
and
${P_L}$
and
![]() ${P_R}$
indicate the left and right arm pressing position, respectively.
${P_R}$
indicate the left and right arm pressing position, respectively.
![]() ${R_A}$
and
${R_A}$
and
![]() ${R_L}$
indicate the correct position of the ‘A’ and ‘L’ keys. The calculation of Euclidean distance between the pressing position and the correct position indicates the error of correct pressing.
${R_L}$
indicate the correct position of the ‘A’ and ‘L’ keys. The calculation of Euclidean distance between the pressing position and the correct position indicates the error of correct pressing.
![]() $press(L)$
and
$press(L)$
and
![]() $press(R)$
return qualitative logical values for success and unsuccessful pressing procedures. Note that in our reward function
$press(R)$
return qualitative logical values for success and unsuccessful pressing procedures. Note that in our reward function
![]() ${R_i}$
, there are divisions that involve terms such as
${R_i}$
, there are divisions that involve terms such as
![]() ${\left| {\left| {{P_L} - {R_A}} \right|} \right|^2} + {\left| {\left| {{P_R} - {R_L}} \right|} \right|^2}$
,
${\left| {\left| {{P_L} - {R_A}} \right|} \right|^2} + {\left| {\left| {{P_R} - {R_L}} \right|} \right|^2}$
,
![]() ${\left| {\left| {{P_L} - {R_A}} \right|} \right|^2}$
, and
${\left| {\left| {{P_L} - {R_A}} \right|} \right|^2}$
, and
![]() ${\left| {\left| {{P_R} - {R_L}} \right|} \right|^2}$
. We recognize that in certain scenarios, the values of these terms can be zero. If any of these terms result in zero, their maximum predefined reward value in each term will be used.
${\left| {\left| {{P_R} - {R_L}} \right|} \right|^2}$
. We recognize that in certain scenarios, the values of these terms can be zero. If any of these terms result in zero, their maximum predefined reward value in each term will be used.
As shown in Figure 5, the HDDPG algorithm, in general, learns the policy to map current states to best actions. It saves the previous experiences in a reply buffer, and based on the received rewards, it computes the gradients to update the network parameters. In this regard, it obtains the optimal policy without establishing the dynamic model of object placement for the robot. In Table 1, we demonstrated the HDDPG algorithm’s pseudocode for object placement on the gym toolkit. In this regard, the simulation part of training is performed on the gym toolkit.
Table 1. HDDPG algorithm’s pseudocode for object placement on gym toolkit

4. Experimental results
Our experiments consist of two distinct phases. In the first phase, we utilize the Gym toolkit, an open-source interface popularly used for reinforcement learning tasks (Brockman et al., Reference Brockman, Sutskever and Altman2020). Specifically, within the Gym framework, we developed our custom environment to closely simulate our target scenario. This custom environment provided us with a controlled setting to evaluate our algorithm’s preliminary performance. Following this, in the second phase, we transition to implementing the algorithm on a real robot in an actual environment. For a holistic evaluation of our proposed algorithm, our experiments are organized into two sections: the simulation implementations using our custom Gym environment and empirical real-world trials.
4.1. Experiments setup
To have a realistic simulation and to be able to use training output in the real environment, we use the robot’s camera frames from different perspectives, including the robot’s arms and keyboards. In the proposed DDPG algorithm, some hyper-parameters play important roles in the final performance. The hyper-parameters numerical definition and settings in our proposed DDPG algorithm structure are as follows. The number of episodes (
![]() $i$
) is considered as 14 000, the number of steps (
$i$
) is considered as 14 000, the number of steps (
![]() $t$
) is 30, and the step size is considered 2mm movement of the end effector. In each episode, the robot moves both arms to press two keys (one per each). Note that the initial orientations of arms are defined as constant values, and both arms initialize parallel to the robot’s trunk. In the experiments, keyboards are initialized by random position and angle at each episode.
$t$
) is 30, and the step size is considered 2mm movement of the end effector. In each episode, the robot moves both arms to press two keys (one per each). Note that the initial orientations of arms are defined as constant values, and both arms initialize parallel to the robot’s trunk. In the experiments, keyboards are initialized by random position and angle at each episode.
In each episode’s training procedure, the target network’s parameters are also replicating from the original network. Each episode terminates in two conditions: (i) two keys were pressed, and (ii) the robot’s pressure sensors triggered the termination signal for both arms. Reply memory size is defined as 10 000, which indicates the number of past experiences. The mini-batch size is defined as 64, which controls the number of utilized experiences during each gradient update. The actor learning rate is defined as 0.0004, and the critic learning rate is chosen as 0.002 by trying different values. These learning rates determine the gradient update step size for performing the optimization of the networks. The discount factor as the weight of future rewards is chosen as 0.98. The maximum value of the angle of keyboards is chosen
![]() $ \pm 5^\circ $
. In the actor network, there are two convolutional layers with 5×5 kernel sizes, stride two, and padding 0, along with a fully connected layer. The details of the actor-network are summarized in Table 2.
$ \pm 5^\circ $
. In the actor network, there are two convolutional layers with 5×5 kernel sizes, stride two, and padding 0, along with a fully connected layer. The details of the actor-network are summarized in Table 2.
Table 2. The actor-network structure and layers’ details
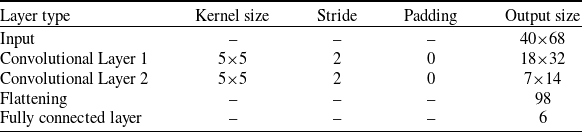
In addition to the described specifications, it is worth noting that the activation functions of the DDPG network structure in hidden layers are rectified linear units (Relu) activation functions. Also, in the output layer in the actor network, the tangent hyperbolic activation function is applied. In the experiments, we used a modified THORMANG3 humanoid robot with 12 DOFs. We performed each experiment 60 times per keyboard with a slight initial random location and orientation (within the robot workspace). We track the robot’s pressed keys by reading the wireless keyboard’s pressed keys. Also, we calculated the correct position of the ‘A’ and ‘L’ keys from the real environment by using a Charuco marker mounted on the keyboard, which we calibrated with the robot’s camera. We consider the distance of the robot from the table in the z-axis adjusted by the robot standing z, and we initialized the robot’s arms distance from the table once. In Table 3, we illustrated the specifications of the object.
Table 3. Dimensions and weights of the used objects in the experiments

4.2. Simulation implementation
As mentioned earlier, in simulation experiments, we used our developed simulator using the gym toolkit. The input for the proposed algorithm is the direct frames captured from the robot’s camera that indicate the environment states. Thus, in order to have as realistic and close to real-environment simulations as possible, we used robot vision camera frames in our simulation process. In our simulation, we juxtapose DDPG, a method inherently designed for continuous action spaces, with the traditionally discrete-action-based DQL. To facilitate this, we employed a discretization technique, segmenting the continuous action spectrum into intervals for DQL’s use. This comparison serves a dual purpose: it allows DQL, with its foundational significance in DRL, to benchmark against DDPG, and it highlights the nuanced advantages of genuine continuous action approaches. Readers are encouraged to consider the results with the underlying differences between these algorithms and the accommodations made for DQL in mind.
In Figure 6, we illustrated two examples of the dragging simulation process from initial random positions and orientations.

Figure 6. Examples of simulations in the gym toolkit that the robot is typing with a keyboard
As shown in Figure 6, we illustrated typing simulations with the proposed hierarchical DDPG algorithm. In our simulations, the keyboards are located in different random initial positions and angles on each episode within the robot’s arms’ workspace. The simulation result for the accumulated reward at each episode for training the proposed HDDPG algorithm in comparison to the DDPG algorithm and a conventional DQL algorithm is illustrated in Figure 7(a), and the average keys pressing error in Figure 7(b). Note that the DDPG and DQL algorithms in these experiments are not using our proposed CAE.
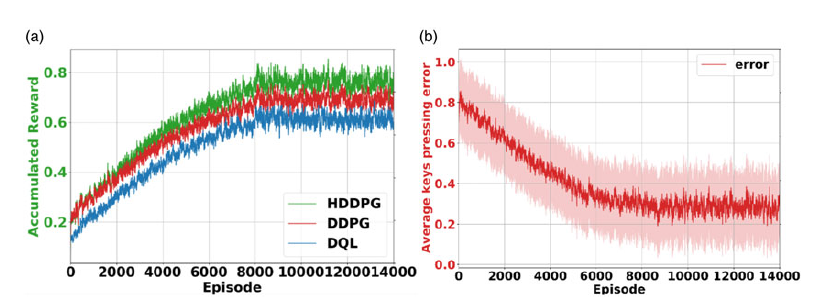
Figure 7. (a) Accumulated reward during training episodes; comparing proposed HDDPG, DDPG, and DQL algorithms; (b) average keys pressing error for HDDPG algorithm in simulation
As shown in Figure 7, the proposed HDDPG achieved higher accumulated rewards due to state-space complexity reduction by the proposed CAE in comparison to DDPG and DQL algorithms. In Figure 8, the success rate of the 50 pressing attempts per keyboard at the simulation phase has been shown.
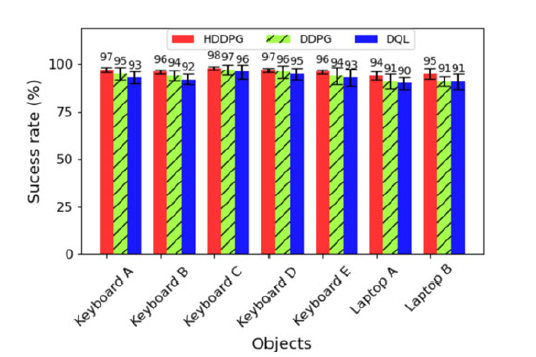
Figure 8. Success rate comparison of HDDPG, DDPG, and DQL algorithms for different keyboards on simulations
In Figure 8, the average success rate for all keyboards in 60 tries has been shown. The total average success rate of HDDPG for all objects is 96.14%, while the results are 94% and 92.85% for DDPG and DQL algorithms, respectively. Therefore, in these results, it is clear that the HDDPG algorithm achieved a higher success rate.
4.3. Empirical experiment implementation
In this section, we discuss the results of experiments in the real environment. As explained earlier, we implemented the proposed algorithm on the modified THORMANG3 humanoid robot, which has 12 DoFs per arm and a total of 27 DoFs in the upper body part.
In our approach, the heart of bridging the gap between the simulated environment and the real world lies in the way we’ve gathered data. By sourcing data directly from the robot’s perspective, we ensure that the simulation encompasses real-world intricacies. The environment in our study is predominantly constrained to the robot arms and keyboards. Given this limited scope and also using CAE, which helps to generalize state space, we’ve been able to create a simulation that is highly representative of the real world. The physics, dynamics, and interaction of the robot arms with the keyboards in the simulation are finely tuned to mimic real-world conditions. Yet, even with a closely mirrored simulation, transitioning from the digital realm to the tangible world isn’t seamless. Minor discrepancies inevitably arise due to factors like hardware limitations, sensor noise, or unexpected physical interactions. To manage this, we’ve introduced a post-simulation mapping phase. Once the training in the simulated environment concludes, we introduce the learned behavior to the real robot. During this phase, we make slight adjustments to the policy, ensuring it caters to any slight differences between the simulation and reality. This method of adaptation ensures that the robot’s actions in the real world are both accurate and efficient, leveraging the deep learning it underwent in the simulation.
You can see a short video example of the type experiment with all keys on the keyboard at https://youtu.be/rEvVCUgX17U. In Figure 9, we illustrated the object’s type procedure example in the real world.
Table 4. Success rate comparison for different objects in the real environment
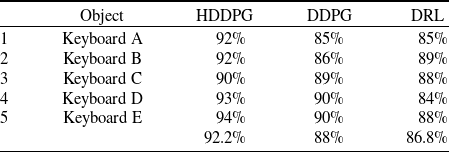

Figure 9. The type procedure snapshots on the real environment
As shown in Figure 9, the robot types with keyboards with both arms using the proposed HDDPG algorithm. In this regard, we implemented experiments on different keyboards and illustrated the results. The detailed success rate for individual objects in real-environment experiments is shown in Table 4.
Although The results for real experiments, with 92.2%, are lower than the simulation results (96.14%), the proposed algorithm presents the highest success rate in comparison to DDPG and DQL algorithms, with 88% and 86.8%, respectively. So, considering the uncertainty factors of the real environment, the results of the proposed algorithm are outstanding.
5. Conclusion
Dual-arm robot configurations are uniquely poised to interact within human-designed environments, from undertaking rescue missions to acting as service robots. A particularly nuanced aspect of this interaction lies in enabling these robots to type on keyboards, which come in a myriad of designs and orientations. This paper undertook the ambitious challenge of not only equipping humanoid robots with the capability to type across variable keyboard setups but also ensuring high levels of accuracy in their performance. The key to our approach was the introduction of the HDDPG algorithm, a hierarchical extension of the DDPG. By integrating the Convolutional Auto-Encoder, our approach managed the complexities presented by continuous state and action spaces, showcasing that deep learning techniques, when appropriately applied, can markedly elevate the efficiency and precision of robotic applications. Our empirical evaluations, conducted in both simulated and real-world scenarios, bore testament to the prowess of the HDDPG. Achieving success rates of 96.14% in simulations and 92.2% in real-world settings, the results stand as a significant leap forward in the journey to achieve seamless human-robot interaction. Not only did our approach demonstrate a robust performance, but it also outshined established algorithms such as DDPG and Deep Q-Learning, establishing its promise as a potent tool in the robotics domain.
In our current research, the focus has been on enabling robots to type on keyboards within controlled settings. However, our vision expands well beyond this. We envisage a world where dual-arm robots can seamlessly interact with a vast array of devices, from computers to life-saving equipment like automatic electric defibrillators. By increasing typing speeds, utilizing multiple robot fingers, and generalizing our approach to other objects, we aim to redefine the capabilities of humanoid robots. To further enhance robustness, future work will explore adaptive visual techniques for varied conditions, such as smoky environments or worn-out keyboards, integrate infrared imaging, and delve into multi-modal sensing. Moreover, the exploration of alternative reinforcement learning methodologies, such as Proximal Policy Optimization (PPO), is on our horizon to ensure resilience and efficiency in diverse scenarios.
Acknowledgments
This work was financially supported by the ‘Chinese Language and Technology Center’ of the National Taiwan Normal University (NTNU) from The Featured Areas Research Center Program within the framework of the Higher Education Sprout Project by the Ministry of Education (MOE) in Taiwan and the Ministry of Science and Technology, Taiwan, under Grant Nos. MOST 108-2634-F-003-002, MOST 108-2634-F-003-003, and MOST 108-2634-F-003-004 (administered through Pervasive Artificial Intelligence Research (PAIR) Labs) as well as MOST 107-2811-E-003-503. We are grateful to the National Center for High-performance Computing for computer time and facilities to conduct this research.
Funding
This work was financially supported by the ‘Chinese Language and Technology Center’ of the National Taiwan Normal University (NTNU) from The Featured Areas Research Center Program within the framework of the Higher Education Sprout Project by the Ministry of Education (MOE) in Taiwan and Ministry of Science and Technology, Taiwan, under Grants No. MOST 108-2634-F-003-002, MOST 108-2634-F-003-003, MOST 113-2221-E-003-009, and MOST 108-2634-F-003-004 (administered through Pervasive Artificial Intelligence Research (PAIR) Labs), as well as MOST 107-2811-E-003-503. We are grateful to the National Center for High-performance Computing for computer time and facilities to conduct this research.
Competing interests
Jacky Baltes, Hanjaya Mandala, and Saeed Saeedvand are employed at the National Taiwan Normal University. Jacky Baltes and Saeed Saeedvand have received grants from the National Taiwan Normal University. ‘Competing interests: All the authors declare none’.
Ethical approval
This article does not contain any studies with human participants or animals performed by any of the authors.
















