1 Introduction
People often need to make rapid decisions on the relative allocation of behaviour between competing alternatives in daily life. The choice for each alternative may lead to a conflict with immediate and long-term consequences. For instance, after a day in class, a student may face a choice between exercising versus playing computer games. Students might harm their long-term health by choosing to play a computer game for long periods rather than to exercise because playing a game gives an immediate reward and is therefore more attractive. There is a famous experiment known as the Harvard Game that examines how humans navigate decisions with conflict in the immediate and long-term consequences (Reference Rachlin and LaibsonRachlin and Laibson, 2000).
In the Harvard Game, participants were asked to make an uninterrupted sequence of choices between two alternatives (matching and maximising options) with the goal of maximising the rewards they receive over the entire session. On a given trial, the matching (suboptimal) option always returns more reward than the maximising option. However, the more the matching option is chosen, the less the future utility of both alternatives becomes. Therefore, to receive maximal total rewards in the game, participants on every trial need to choose the maximising option that appears, at the time, to be the inferior option of the two.
Over the past several decades, numerous behavioural results in the Harvard game or variations of the game (Gray, 1999, Herrnstein, 1991, Otto et al., 2012, Reference Tunney and ShanksTunney and Shanks, 2002) have shown that humans and other animals often fail to inhibit the tendency to select the matching option with higher local rates of reward, a phenomena referred to as melioration (Reference Herrnstein and PrelecHerrnstein and Prelec, 1991, Vaughan, 1981). Melioration deviates from rational choice in the consideration of local rates of reward (suboptimal or melioration strategy) rather than the global maximisation of utility (optimal or maximising strategy). According to the melioration theory (Reference Herrnstein and PrelecHerrnstein and Prelec, 1991), human (or other animal) choice is governed by a myopic tendency towards alternatives with higher local rates of reward. However, the melioration strategy does not explain how the optimal behavioural result might emerge from tasks that have a reward structure similar to the Harvard game.
The present study was to examine how people could discover the optimal strategy in such Harvard-type games through the use of additional cues to indicate the increment of reward over rounds for each option. The experimental paradigm that we used are rising optimum tasks (Reference Montague and BernsMontague and Berns, 2002, Li et al., 2006, Bogacz et al., 2007), which are an extension of the Harvard Game. In experimental condition 1, we largely established that behaviour in the task replicates previous work. In experimental condition 2, we presented an extension of the task by providing participants with past actions and rewards indicative of the underlying reward contingencies. We find that a snapshot of recent experiences by itself (Bogacz et al., 2007, Sims et al., 2013, Reference SakaiSakai and Fukai, 2008, Cheng et al., 2011, Reference Iigaya and FusiIigaya and Fusi, 2013, Reference Loewenstein and SeungLoewenstein and Seung, 2006, Reference SoltaniSoltani and Wang, 2006) is insufficient to facilitate participants acquiring optimal strategy. In experimental condition 3, we rearranged past choices and rewards, showing the sequence for each alternative separately, to help participants to understand the change of reward over rounds for each option. This display was effective in helping participants learn to make the optimal choice.
2 Method
A total of 141 undergraduate students from Zhejiang University of Technology participated in three conditions (69 males, 72 females; ages ranging from 18 to 22, with a mean age of 19.8). All of them had normal or corrected-to-normal vision and normal colour vision. They were randomly divided into three groups, with 47 participants in each of the three conditions. They were told that they would earn money according to the total score they obtained in a sequential two-choice task.
The experimental equipment was a Lenovo Shaoyang desktop computer, the display equipment was a 17-inch flat CRT monitor, the screen resolution was set to 1024 × 768 pixels, and the mouse resolution was 1000 dpi.
The three different conditions are shown in the Figure 1A–C. In each condition, participants choose sequentially between two actions by pressing one of the two buttons: A or B. Clicking on the button A or B cause the colour bar (red or cyan, respectively) in a square window to update, and the height of the bar indicated the score from that choice. The cumulative score of the choices is displayed numerically in the upper part of the rectangle window. In the second condition, the recent choices (at most 20 trials) before the current trial are displayed on the top of the screen (Figure 1B). In the third condition, the recent choice is displayed beside the two buttons, respectively. After each choice, the little bar is separately displayed beside the two buttons according to the choice. As shown in Figure 1C, the button A is chosen in the first trial, and then the B, A, A, A and B buttons are selected in turn in next five trials. After the sixth trials, the four (two) red (cyan) little bars are displayed beside the button A (B).

Figure 1: The task and reward structure. A-C) the three conditions in the task. A) Sample two trials during the first condition. The participant selects the button A and obtain score of 55 in the first trial. Then the button B is chosen in the second trial and obtain score of 38. After each choice, a scale bar is updated to reflect the reward earned for that choice, and the bar height following a choice depends on the obtained score for that choice. B) The previous choices and scores are shown on the top of the screen in the second condition. C) The previous choices and scores are separated on both sides of the screen according to the choices in the third condition. D) Reward functions (blue and green curve) for two choices as the function of choice allocation to A. The dashed red curve shows the utility rate for different proportions of responses to A.
On each trial, the reward is a function of past choices. Such history dependence is modelled through the reward equation used for the same purpose by Reference Montague and BernsMontague and Berns (2002), as follows:
where g, c 1, c 2, c 3 and c 4 determine the shape of the function R. q A(t) is the ratio of chosen button A over the last W (= 20) trials. The q(t) is defined as
where a i(t) is participant’s choice at trial t. If the button A is chosen, a A(t) = 1 and a B(t) = 0; if button B is chosen, a A(t) = 0 and a B(t) = 1. We refer to the proportion of A choices in the last W trials as allocation to A.
As shown in Figure 1D, the blue curve shows the score after pressing button A for different allocations to A during the last 20 trials, and the green curve shows the score after pressing button B (g = 240, c 1 = 1.05, c 2 = 0.215, c 3 = 1.2 and c 4 = 0.4). For example, if the participant had pressed equal number of A and B within the last 20 trials and the last choice was A, then the resulting score is 92 — it can be read from Figure 1D by looking at blue line.
The matching behaviour is at the intersection of the blue and green lines in a way that the returns of the two alternative targets are equal (Herrnstein, 1961, Herrnstein, 1979). Thus, the strategy for matching behaviour is to choose button A (matching target) with probability 0.75. The crossing point of the blue and green lines is called the matching point. The dashed red line in Figure 1D is the utility rate for different proportions of responses to A. The utility rate is defined as the global average rate of return from the two alternatives. To gain the maximal reward, participants need to press button B (maximizing target) on every choice. Thus, the far left end point of the red dashed curve is called the optimizing point. For simplicity, we call the matching target button A, and the maximizing target button B. In fact, button A and button B were randomly assigned to the matching target and the maximising target for each participant.
Participants were instructed to maximise the reward (score) over the course of the task. Each participant had 10 trials to familiarise themselves and performed 100 trials during each condition. The cash they gained is equal to the total score (× 0.001 CNY) after conducted a condition.
3 Results
Figure 2 shows the average proportion of matching alternative and average reward rate for each participant in the three conditions, where each black point represents a participant. In conditions 1 and 2, except for a few outliers, all participants chose on average to stay near the matching point rather than the optimising point. In condition 3, however, a majority of participants chose on average to stay near the optimising point.

Figure 2: Average proportion choice A and average reward rate for each participant (black points), overlaid over the reward structure for button A (blue) and B (green).
Figure 3 shows the distribution of choice A and reward. Most participants chose to stay with the point in which the allocation to A was near 0.7 in conditions 1 and 2. At this point, the total score (reward) roughly equals to 5000. In condition 3, some participants chose to stay at the point where the allocation to A was near 0. At this point, the total score was approximately 12,000. The difference in total score between conditions 2 and 3 was significant at p<.001 by a t test.
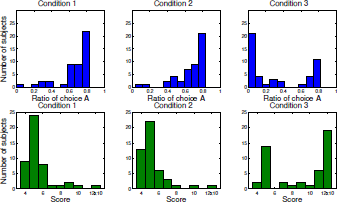
Figure 3: Distributions of allocation to A (top panels) and total rewards (bottom panels) in the three conditions.
To more precisely quantify participants’ behaviour with regard to type of strategy, we calculated the fraction of trials that followed the optimal and the melioration strategies for each participant. Because the optimal strategy is always to choose option B, we define the optimising fraction simply as the fraction of choices B. In addition, the meliorating fraction is defined as the proportion of choices that satisfy this strategy among the trials where the allocation to A was between 0.72 and 0.82. For each subject, we determined the strategy that was followed on the greatest number of trials. The fraction of all participants with a preference of each strategy in two conditions is shown in Figure 4. In conditions 1 and 2, nearly 60% of participants adopted the melioration strategy, whereas, in condition 3, only about 25% of participants adopted the melioration strategy, and about 55% of participants adopted the optimal strategy. Interestingly, not all of behavioural results of participants reached the matching or maximising points.
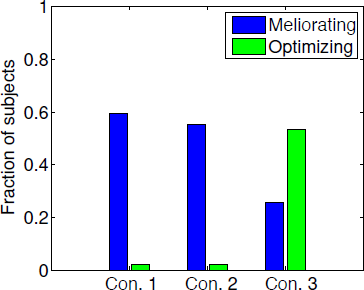
Figure 4: Proportion of participants with melioration and optimal strategy in the three conditions.
4 Discussion
We used rising optimum tasks, which have been used previously to investigate simple reinforcement learning behaviour and short-term memory traces for action bias in human sequential decision-making (Bogacz et al., 2007). We examined the effects of recent experiences on choice in the rising optimum task that placed short- and long-term rewards in conflict. The results of our first condition showed that most participants become stuck in a local cycle around the matching point of the reward curves where the fractional allocation to target A is approximately 0.75, which are consistent with several previous studies (Bogacz et al., 2007, Reference Gureckis and LoveGureckis and Love, 2009). Furthermore, the results of the second condition demonstrated the snapshot of recent experiences is insufficient to facilitate participants acquiring optimal performance in the task, where the fractional allocation to target B is nearly 1. In the third condition, we found that participants more easily reach optimal performance by adding cues to indicate the increment of reward for each option, separately, so that the change over rounds was more salient.
Participants in the first condition appear to have favoured the matching option, although they can obtain the maximal total income by selecting the maximal option on every choice. However, the optimal strategy is not obvious to the participants because choosing A results in greater immediate reward than choosing B for allocations A lesser than 0.7. Continuing to select A will produce gradually lesser reward (diminishing return), but these will remain greater than selecting B until the allocation to A higher than 0.7. At that point, choosing B will obtain greater immediate reward than choosing A. Thus, most of participants in the first condition reach matching behaviour since they are driven primarily by concerns about immediate reward.
Participants could adopt the optimal strategy while they learn to take account of the recent history of actions. However, most of the participants kept adopting the melioration strategy even though the snapshot of recent experiences is given in the second condition. The existing theory often uses the eligibility trace model of reinforcement learning to explain the decision-making results converging to the optimisation point in the rising optimum task (Bogacz et al., 2007, Neth et al., 2006), but the eligibility trace model requires the participants to take advantage of all of the past experience. The behavioural results in condition 2 demonstrated that even given the necessary information (i.e., the snapshot of recent experiences) for the optimal strategy, the participants still find it hard to find the strategy (Brunsson, 1982, Reference Hastie and DawesHastie and Dawes, 2010, Simon, 1982).
In the third condition, we rearranged past choices and rewards for each alternative to help participants to easily find payoffs from consecutively choosing the target A decrease, whereas the payoff from consecutively choosing the target B increase. Thus, participants in the third condition could directly perceive the increment of payoff on each option. The behavioural results in condition 3 indicated that providing cues indicating the immediate feedback about the increment of payoff to participants could make it easier for participants to adopt the optimal strategy. Our finding in the third condition is largely consistent with previous works demonstrating how cues indicative of underlying dynamics for decision-making task may help decision makers develop optimal strategies (Reference Gureckis and LoveGureckis and Love, 2009, Herrnstein et al., 1993, Reference Stillwell and TunneyStillwell and Tunney, 2009). For example, perceptual cues that readily align with the underlying state of the Farming on Mars task environment help participants overcome the impulsive appeal of short-term rewards (Reference Gureckis and LoveGureckis and Love, 2009). The participants were more likely to maximise profit when provided with an arrow that indicated the number of responses the participant made to the maximising choice option over the relevant choice history (Herrnstein et al., 1993). Our results indicate that preferring the option for local payoff can, in some circumstances, be overcome by providing informative cues that indicate a clear immediate outcome for another option.






