Hostname: page-component-745bb68f8f-b95js Total loading time: 0 Render date: 2025-01-11T23:21:14.574Z Has data issue: false hasContentIssue false
  • English
  • Français

On the homotopy and strong homotopy type of complexes of discrete Morse functions

Part of: Applied homological algebra and category theory Algebraic structures PL-topology

Published online by Cambridge University Press:  02 February 2022

Connor Donovan ,
Maxwell Lin  and
Nicholas A. Scoville Open the ORCID record for Nicholas A. Scoville [Opens in a new window]
Connor Donovan
Affiliation:
Department of Mathematics and Computer Science, Ursinus College, Collegeville, PA 19426, USA e-mail: [email protected]
Maxwell Lin
Affiliation:
Department of Mathematics, University of California, Berkeley, Berkeley, CA 94720, USA e-mail: [email protected]
Nicholas A. Scoville*
Affiliation:
Department of Mathematics and Computer Science, Ursinus College, Collegeville, PA 19426, USA e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we determine the homotopy types of the Morse complexes of certain collections of simplicial complexes by studying dominating vertices or strong collapses. We show that if K contains two leaves that share a common vertex, then its Morse complex is strongly collapsible and hence has the homotopy type of a point. We also show that the pure Morse complex of a tree is strongly collapsible, thereby recovering as a corollary a result of Ayala et al. (2008, Topology and Its Applications 155, 2084–2089). In addition, we prove that the Morse complex of a disjoint union 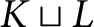$K\sqcup L$ is the Morse complex of the join $K*L$ . This result is used to compute the homotopy type of the Morse complex of some families of graphs, including Caterpillar graphs, as well as the automorphism group of a disjoint union for a large collection of disjoint complexes.

Keywords

Discrete Morse theoryMorse complexdominated vertexstrong collapsibilityhomotopy

MSC classification

Primary: 55U05: Abstract complexes
Secondary: 57Q05: General topology of complexes 08A35: Automorphisms, endomorphisms
Type
Article
Information
Canadian Mathematical Bulletin , Volume 66 , Issue 1 , March 2023 , pp. 19 - 37
Check for updates
Copyright
© Canadian Mathematical Society, 2022

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ayala, R., Fernández, L. M., Quintero, A., and Vilches, J. A., A note on the pure Morse complex of a graph . Topology Appl. 155(2008), nos. 17–18, 2084–2089.CrossRefGoogle Scholar
Barmak, J. A., Algebraic topology of finite topological spaces and applications, Lecture Notes in Mathematics, 2032, Springer, Heidelberg, 2011.CrossRefGoogle Scholar
Barmak, J. A. and Minian, E. G., Strong homotopy types, nerves and collapses . Discrete Comput. Geom. 47(2012), no. 2, 301–328.CrossRefGoogle Scholar
Bickle, A., Fundamentals of graph theory, Pure and Applied Undergraduate Texts, 43, American Mathematical Society, Providence, RI, 2020.Google Scholar
Capitelli, N. A. and Minian, E. G., A simplicial complex is uniquely determined by its set of discrete Morse functions . Discrete Comput. Geom. 58(2017), no. 1, 144–157.CrossRefGoogle Scholar
Chari, M. K. and Joswig, M., Complexes of discrete Morse functions . Discrete Math. 302(2005), nos. 1–3, 39–51.CrossRefGoogle Scholar
Ferrario, D. L. and Piccinini, R. A., Simplicial structures in topology, CMS Books in Mathematics, 1613–5237, Springer, New York, 2011, Translated from the 2009 Italian original by Maria Nair Piccinini.CrossRefGoogle Scholar
Forman, R., Morse theory for cell complexes . Adv. Math. 134(1998), no. 1, 90–145.CrossRefGoogle Scholar
Forman, R., A user’s guide to discrete Morse theory , Sém. Lothar. Combin. 48(2002), Article no. B48c, 35 pp.Google Scholar
Jonsson, J., Introduction to simplicial homology, 2011, Available at https://people.kth.se/~jakobj/homology.html.Google Scholar
Knudson, K., Morse theory: smooth and discrete, World Scientific, Hackensack, NJ, 2015.CrossRefGoogle Scholar
Kozlov, D. N., Complexes of directed trees . J. Combin. Theory Ser. A. 88(1999), no. 1, 112–122.CrossRefGoogle Scholar
Lin, M. and Scoville, N. A., On the automorphism group of the Morse complex . Adv. Appl. Math. 131(2021), 102250.CrossRefGoogle Scholar
Scoville, N. A., Discrete Morse theory, Student Mathematical Library, 90, American Mathematical Society, Providence, RI, 2019.CrossRefGoogle Scholar
Scoville, N. A. and Zaremsky, M. C. B., Higher connectivity of the morse complex. Proc. Amer. Math. Soc., to appear.Google Scholar