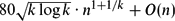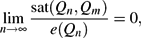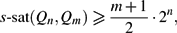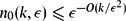Paper
A Bound on the Number of Edges in Graphs Without an Even Cycle
- Part of:
-
- Published online by Cambridge University Press:
- 07 April 2016, pp. 1-15
-
- Article
- Export citation
Monotonicity of Avoidance Coupling on KN
- Part of:
-
- Published online by Cambridge University Press:
- 03 June 2016, pp. 16-23
-
- Article
- Export citation
Patterns in Random Permutations Avoiding the Pattern 132
-
- Published online by Cambridge University Press:
- 18 May 2016, pp. 24-51
-
- Article
- Export citation
Saturated Subgraphs of the Hypercube
- Part of:
-
- Published online by Cambridge University Press:
- 19 September 2016, pp. 52-67
-
- Article
- Export citation
Large Unavoidable Subtournaments
- Part of:
-
- Published online by Cambridge University Press:
- 21 June 2016, pp. 68-77
-
- Article
- Export citation
Saturation in the Hypercube and Bootstrap Percolation
- Part of:
-
- Published online by Cambridge University Press:
- 31 March 2016, pp. 78-98
-
- Article
- Export citation
Distinct Distances on Algebraic Curves in the Plane
-
- Published online by Cambridge University Press:
- 15 July 2016, pp. 99-117
-
- Article
- Export citation
Pfaffian Formulas for Spanning Tree Probabilities
- Part of:
-
- Published online by Cambridge University Press:
- 30 May 2016, pp. 118-137
-
- Article
- Export citation
Asymptotic Structure of Graphs with the Minimum Number of Triangles
- Part of:
-
- Published online by Cambridge University Press:
- 04 May 2016, pp. 138-160
-
- Article
-
- You have access
- Open access
- Export citation