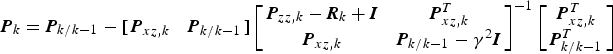1. INTRODUCTION
The integration of a Strap-down Inertial Navigation System (SINS) and the Global Positioning System (GPS) has been widely utilised for real-time navigation, mobile mapping, Location-based Services, transport and many other applications. Kalman Filtering (KF) is the most common technique for data fusion of GPS and SINS (Grejner-Brzezinska et al., Reference Grejner-Brzezinska, Da and Toth1998). However, the operations of the KF rely on the proper definition of the dynamic stochastic models and the standard KF can only be used to deal with linear systems (Yi and Grejner-Brzezinska, Reference Yi and Grejner-Brzezinska2006). Furthermore, due to the nonlinear characteristics of the low-cost SINS error model and the uncertainty of the stochastic model, the KF estimation is not optimal and may produce an unreliable result, or even lead to filtering divergence (Geng and Wang, Reference Geng and Wang2008).
Over the past few decades, nonlinear KF algorithms have been intensively investigated to deal with the nonlinear issues of low-cost SINS (Gustafsson, Reference Gustafsson2010; Wendel et al., Reference Wendel, Metzger, Moenikes, Maier and Trommer2006). The recently proposed Cubature Kalman Filtering (CKF) is a Gaussian approximation to the Bayesian filtering. It has more accurate filtering performance than traditional methods, and less computational cost (Arasaratnam and Haykin, Reference Arasaratnam and Haykin2009). The CKF was introduced to deal with the data fusion of the integrated GPS/INS system (Sun and Tang, Reference Sun and Tang2012). However, the standard CKF may still face difficulty in providing stable results and cannot deal with the outliers in the measurements effectively. Robust Cubature Kalman Filtering (RCKF) based on an H∞ filter was proposed for integrated GPS/INS navigation applications (Liu et al., Reference Liu, Cai, Tang and Wang2010).
The RCKF algorithm makes use of the H∞ robust filter to overcome the interference of outliers. For the H∞ robust filter, the given restrict parameter γ is used to show the bound level and assess the robustness of the H∞ filter to this uncertain interference (Simon, Reference Simon2006). The parameter γ can be chosen appropriately according to the detailed performance index and there is a balance between system average accuracy and its robustness performance (Einicke and White, Reference Einicke and White1999). Certainly, γ must be larger than a positive number to output a normal filtering result. It is found that the smaller the value of γ the stronger the robustness of the filter (Liu et al., Reference Liu, Cai, Tang and Wang2010). However, a disproportionately small value can easily lead to a non-positive definite state covariance and cause filter divergence. Based on the error variance constraints or minimum variance principle, the modified robust filters were proposed (Hung and Yang, Reference Hung and Yang2003; Shaked and Souza, Reference Shaked and Souza1995). An a priori robust filter for linear uncertain systems was presented by (Yahali and Shake, Reference Yahali and Shake1996) which guarantees a certain bound on the error covariance of the estimate. Furthermore, the nonlinear robust Kalman filtering problem with norm-bound parameter uncertainties was also studied by Xiong et al. (Reference Xiong, Wei and Liu2012). However, how to improve the performance of a robust filter under a small given parameter γ has rarely been investigated.
In this paper, the authors compare the performance of a robust cubature Kalman filter for integrated GPS/SINS navigation applications under different given parameters γ. In order to maintain a high level of numerical stability, a Singular Value Decomposition (SVD) algorithm is introduced to replace the Cholesky decomposition in the RCKF. Land vehicle tests have been carried out to compare the performance of this algorithm with other cubature Kalman filter algorithms. The results show that the SVD-based Robust Cubature Kalman Filter (SVD-RCKF) algorithm can significantly improve the filtering stability and has better robustness to the impact of outliers.
The structure of this paper is as follows. Section 2 includes the nonlinear description of the H∞ filter and the calculation steps of the RCKF based on SVD is presented in Section 3. Section 4 lists the formulae of the system and observation equations of the GPS/SINS system. Two test results and data analysis are given in Section 5. The final part of the paper is the preliminary conclusions attained through this study.
2. H∞ FILTER AND ITS NONLINEAR DESCRIPTION
2.1. The Principle of an H∞ filter
An H∞ filter is a typical implementation of the robust filtering theory (Simon, Reference Simon2006). It defines a cost function as follows:
$$J = \displaystyle{\sum\limits_{k = 1}^N \left\vert {\bi x}_k - \hat{\bi x}_k \right\vert^2 \over \left\vert {\bi x}_0 - \hat{\bi x}_0 \right\vert_{{\bi P}_0^{ - 1}}^2 + \sum\limits_{k = 1}^N (\left\vert {\bi w}_k \right\vert_{{\bi Q}_k^{-1}}^2 + \left\vert {\bi v}_k \right\vert_{{\bi R}_k^{-1}}^2}$$
where N is the total number of filtering time limit and k = 1,2,··· N. w k and v k are the unrelated system noise and measurement noise, and Q k and R k are their covariance matrices respectively. x 0 is the initial value of the system state vector x k with covariance P 0, whilst 
$\hat{\bi x}_0 $ and 
$\hat{\bi x}_k $ are the estimated values of x 0 and x k. In this equation, 
$\left\vert {{\bi x}_0} - {\hat {\bi x}}_0 \right\vert_{P_0^{ - 1}} ^2 = ({\bi x}_0 - {\hat {\bi x}}_0 )^T {{\bi P}_0^{ - 1}} ({\bi x}_0 - {\hat {\bi x}}_0 )$. Other similar terms can be obtained recursively.
The goal of an optimal H∞ filter is to find an estimate of x k that minimizes J, under the condition 
${\hat{\bi x}}_k = \arg \min \left\vert {\bi J} \right\vert_\infty $. Normally, it is difficult to get the analytical solution of an optimal H∞ filter problem. Therefore, we need find a suboptimal iterative algorithm. We can set a threshold value γ, which meets 
$\left\vert {\bi J} \right\vert_\infty = {\rm sup}\ {\bi J} \le {\gamma}^2 (\left\vert {\bi J} \right\vert_\infty $ refers to the infinity-norm of J and supis the supremum of a set). The threshold value γ is equivalent to the following Riccati inequality (Chen and Yuan, Reference Chen and Yuan2009):
$${\bi P}_k^{ - 1} + {\bi H}_k^T {\bi H}_k - \gamma ^{ - 2} {\bi L}_k^T {\bi L}_k \gt 0$$where, L k is a user-defined matrix (assumed to be full rank). If we want to directly estimate x k (as in the Kalman filtering), then we set L k = I. H k is the matrix of measurement function after linearization, and P k is the covariance matrix of x k.
For an H∞ filter, the estimation error in the most unfavourable conditions is controlled by the threshold value γ that is called the designed restrict parameter. When the designed restrict parameter γ is smaller, the robustness of a filter is stronger. When γ approaches infinity, the H∞ filter is approaching the standard Kalman filter.
2.2. The nonlinear description of an H∞ filter
In order to apply the H∞ filter in the nonlinear models, the recursive Riccati equation for a linear model is transformed to implement the nonlinear filter. Due to P k/k−1H kT = P xz,k, H kP k/k−1H kT = P zz,k−R k (Yan et al., Reference Yan, Yan and Xu2008), the formula for computing the state vector covariance matrix of the nonlinear H∞ filter can be modified as follows:
$${\bi P}_k = {\bi P}_{k/k - 1} - \left[\matrix{{\bi P}_{xz,k} & {\bi P}_{k/k - 1}} \right]\left[\matrix{{\bi P}_{zz,k} - {\bi R}_k + {\bi I} &{\bi P}_{xz,k}^T \cr {\bi P}_{xz,k} &{\bi P}_{k/k - 1} - \gamma^2 {\bi I}} \right]^{ - 1} \left[\matrix{{\bi P}_{xz,k}^T \cr {\bi P}_{k/k - 1}^T} \right]$$where, innovation covariance matrices P zz,k and cross-covariance matrix P xz,k can be gained by nonlinear filtering methods such as the cubature Kalman filter and the unscented Kalman filter.
For nonlinear models, we can calculate the mean and covariance of the state vectors by cubature point transformation instead of a Taylor expansion as discussed by Arasaratnam and Haykin (Reference Arasaratnam and Haykin2009) and then we can obtain the nonlinear H∞ robust filter based on the cubature Kalman filter.
3. ROBUST CUBATURE KALMAN FILTER BASED ON SVD
Based on a cubature Kalman filter frame, we developed a new filter algorithm by introducing an H∞ robust filter. It is called a Robust Cubature Kalman Filter (RCKF). However, after many iterations of the RCKF, P k/k−1 and P k can easily lose their positive definiteness and this will lead to the instability of the numerical value. Meanwhile a much smaller restrict parameter γ may lead to non-positive definiteness of P k/k−1 and P k. Therefore singular value decomposition (Gao et al., Reference Gao, Wang and Jiao2010) is applied in the calculation of the covariance matrix for the RCKF instead of the Cholesky decomposition in this paper.
Consider the following discrete nonlinear system:
$${\bi x}_k = f\,({\bi x}_{k - 1} ) + {\bi w}_{k - 1} $$
$${\bi z}_k = h({\bi x}_k ) + {\bi v}_k $$where x k and z k are the state and measurements of the dynamic system; f(·) and h(·) are known nonlinear functions; w k−1 and v k are the independent process and measurement Gaussian noise sequences with zero means and co-variances, Q k−1 and R k, respectively. Then the procedure of the Robust Cubature Kalman Filter based on Singular Value Decomposition (SVD-RCKF) can be expressed as follows:
1) Calculate the basic cubature sampling points ξ i and weights ω i based on the cubature rule.
(6)where m is the number of cubature points, and n x is the dimension of state vector. [1] represents a set that is similar to the following set of points:
$${\bi \xi} _i = \sqrt {\displaystyle{m \over 2}} [1]_i, \,\omega _i = \displaystyle{1 \over m},\,i = 1,2, \cdots m,\,m = 2n_x $$$\left\{ {\left( {\matrix{1 \cr 0 \cr}} \right),\left( {\matrix{ 0 \cr 1 \cr}} \right),\left( {\matrix{ { - 1} \cr 0 \cr}} \right),\left( {\matrix{ 0 \cr { - 1} \cr}} \right)} \right\}$. Here, the generator is $\left( {\matrix{ 1 \cr 0 \cr}} \right)$.2) Time update:
Factorise P k−1 based on SVD, and we get:
where S = diags{1 ,s 2,···s n} is a diagonal matrix. Normally, the co-variance matrix P k−1 is a symmetric one, so its eigenvalues are s i2(i = 1,2,···n) and U = V. Then the factorisation formula can be described as follows:$${\bi P}_{k - 1}^{} = {\bi U}\left[ {\matrix{ {\bi S} & 0 \cr 0 & 0 \cr}} \right]{\bi V}^T $$(7)$${\bi P}_{k - 1} = {\bi U}_{k - 1} {\bi S}_{k - 1} {\bi V}_{k - 1}^T $$Evaluate the cubature points X i,k−1
(8)$${\bi X}_{i,k - 1} = {\bi U}_{i,k - 1} \sqrt {s_i} {\xi} _i + {\hat {\bi x}}_{k - 1} $$Evaluate the propagated cubature points X i,k*
(9)$${\bi X}_{i,k}^{\ast} = f\,({\bi X}_{i,k - 1} )$$Estimate the predicted state
$\bar{\bi x}_k $ and error covariance P k/k−1(10)$$\left\{\matrix{\bar{\bi x}_k = \sum\limits_{i = 1}^m {\omega_i} {\bi X}_{i,k}^{\ast} \hfill \cr {\bi P}_{k/k - 1} = \sum\limits_{i = 1}^m {\omega _i} {\bi X}_{i,k}^{\ast} {\bi X}_{i,k}^{{\ast} T} - \bar{\bi x}_k \bar{\bi x}_k^T + {\bi Q}_{k - 1} \hfill} \right.$$3) Measurement update
SVD factorisation
(11)$${{\bi P}_{k/k - 1}} = {{\bi U}_{k/k - 1}}{{\bi S}_{k/k - 1}}{\bi V}_{k/k - 1}^T $$Calculate the cubature points
(12)$${{\bi X}_{i,k/k - 1}} = {{\bi U}_{i,k/k - 1}}\sqrt {{s_i}} {{\xi }_i} + {\bar{\bi x}_k}$$Calculate the propagated cubature points of measurement vector Z i,k
(13)$${\bi Z}_{i,k} = h({\bi X}_{i,k/k - 1} )$$Calculate the predicted measurement vector
$\bar{\bi z}_k $, the innovation covariance matrices P zz,k and the cross-covariance matrix P xz,k(14)$$\left\{ \matrix{\bar{\bi z}_k = \sum\limits_{i = 1}^m {\omega _i} {\bi Z}_{i,k} \hfill \cr {\bi P}_{zz,k} = \sum\limits_{i = 1}^m {\omega _i} {\bi Z}_{i,k} {\bi Z}_{i,k} ^T - \bar{\bi z}_k \bar{\bi z}_k^T + {\bi R}_k \hfill \cr {\bi P}_{xz,k} = \sum\limits_{i = 1}^m {\omega _i} {\bi X}_{i,k} {\bi Z}_{i,k} ^T - \bar{\bi x}_k \bar{\bi z}_k^T \hfill} \right.$$Calculate the gain matrix K k, the updated state
$\hat{\bi x}_k $ and the corresponding covariance P k(15)$${\bi K}_k = {\bi P}_{xz,k} /{\bi P}_{zz,k} $$(16)$$\hat{\bi x}_k = \bar{\bi x}_k + {\bi K}_k ({\bi z}_k - \bar{\bi z}_k )$$(17)$${\bi P}_k = {\bi P}_{k/k - 1} - {\bi K}_k {\bi P}_{zz,k} {\bi K}_k^T $$Considering the state covariance update formula of the H∞ robust filter:
(18)$${\bi P}_k = {\bi P}_{k/k - 1} - \left[\matrix{{\bi P}_{xz,k} &{\bi P}_{k/k - 1}} \right] \left[\matrix{{\bi P}_{zz,k} - {\bi R}_k + {\bi I} &{\bi P}_{xz,k}^T \cr {\bi P}_{xz,k} &{\bi P}_{k/k - 1} - \gamma^2 {\bi I}} \right]^{- 1} \left[\matrix{{\bi P}_{xz,k}^T \cr {\bi P}_{k/k - 1}^T} \right]$$
Equations (4) to (16) and (18) constitute the calculation procedure of the Robust Cubature Kalman Filter based on SVD (SVD-RCKF).
4. THE DYNAMIC AND OBSERVATION EQUATIONS OF A GPS/SINS SYSTEM
The loosely coupled GPS/SINS system is adopted. The state vectors are composed of the position and velocity error in an Earth-Centred and Earth-Fixed frame (ECEF frame, e frame), the attitude error between computer e frame and platform e′ frame, and the gyro and accelerometer drift errors in the body frame (b frame), which can be expressed as (Petovello, Reference Petovello2003):
$${\bi x}_k = \left[\matrix{\Delta {\bi R}^e &\Delta {\bi V}^e &{\bi \varphi}^e &\nabla^b & {\bi \varepsilon}^b} \right]^T $The nonlinear differential error model for low-cost SINS is as follows:
$$\left\{\matrix{\Delta \dot{\bi R}^e = \Delta {\bi V}^e \hfill \cr \Delta \dot{\bi V}^e = ({\bi I}_{3 \times 3} - {\bi C}_{e^{\prime}}^e) {\bi f}^{e^{\prime}} + {\bi C}_b^{e^{\prime}} \nabla^b - 2{\bi \Omega} _{ie}^e \Delta {\bi V}^e \hfill \cr \dot{\bi \varphi} ^e = ({\bi I}_{3 \times 3} - {\bi C}_e^{e^{\prime}}) {\bi \omega}_{ie}^e - {\bi C}_b^{e^{\prime}} {\bi \varepsilon}^b \hfill \cr \dot{\nabla}^b = 0 \hfill \cr \dot{\bi \varepsilon} ^b = 0 \hfill} \right.$$
where ΔR e and ΔV e are the position and velocity error in the e frame, 
${\dot {\bi \varphi}} ^e $ is the attitude error between computer e frame and platform e′ frame, I 3×3 is the 3 × 3 unit matrix, C e′e is the rotation matrix between the computer e frame and the platform e′ frame; C be′ is the rotation matrix between the body frame and the platform e′ frame; Ωiee is the skew symmetric matrix of earth rotation rate ω iee; ε b and ▿b are the gyro and accelerometer drift errors in the body frame.
The dynamical model of a loosely coupled GPS/SINS system can be expressed as follows
$${\dot {\bi x}}_k = f\,({\bi x}_{k - 1} ) + {\bi w}_k $$Generally, the measurement model can be expressed as:
$${\bi z}_k = \left[ {\matrix{ {\hat{\bi R}_{INS}^e - \hat{\bi R}_{GPS}^e} \cr {\hat{\bi V}_{INS}^e - \hat{\bi V}_{GPS}^e} \cr}} \right] = {\bi Hx}_{\bi k} + {\bi v}_k = \left[ {\matrix{ {{\bi I}_{3 \times 3}} & {{\bi 0}_{3 \times 3}} & {{\bi 0}_{3 \times 3}} & {{\bi 0}_{3 \times 3}} & {{\bi 0}_{3 \times 3}} \cr {{\bi 0}_{3 \times 3}} & {{\bi I}_{3 \times 3}} & {{\bi 0}_{3 \times 3}} & {{\bi 0}_{3 \times 3}} & {{\bi 0}_{3 \times 3}} \cr}} \right]{\bi x}_k + {\bi v}_k $$
where 
$\hat{\bi R}_{INS}^e $ and
$\hat{\bi V}_{INS}^e $ are the computed position and velocity vectors by the SINS in the e frame, 
$\hat{\bi R}_{GPS}^e $ and
$\hat{\bi V}_{GPS}^e $ are those output by GPS, and v k is the noise vector.
5. TEST CASES AND DATA ANALYSIS
To demonstrate the performance of the SVD-RCKF algorithm, data was collected under real world conditions with a probe vehicle. The tests were performed in Xuzhou (China) and Nottingham (UK) respectively.
5.1. Case study 1
The first dataset was collected at the China University of Mining and Technology (CUMT), Xuzhou, China in January 2011. The test employed two GPS receivers and one low-cost Inertial Measurement Unit (IMU) (SPAN-CPT). One of the GPS receivers was set on the rooftop as the reference station, and the second was placed on the top of the test vehicle together with the IMU. The data was logged for post processing. The SPAN-CPT IMU consists of a three-axis open-loop fibre optic gyroscope and three-axis MEMS accelerometers. The technical data is shown in Table 1. The specified parameters were used in setting up the Q estimation in the filtering process. Figure 1 shows the ground track of the test vehicle. The update rates of the INS and GPS were 100 Hz and 1 Hz, respectively. The high accuracy double difference carrier-phase GPS position results are used as reference values.
Figure 1. The vehicle trajectory of Case 1.
Table 1. IMU technical specifications.
The test results plotted in Figure 2 are based on the cubature Kalman filter. It is worth noting here that the results contain some outlier values due to the vehicle driving over speed bumps. These indicate that the robustness of the CKF needs to be improved.
Figure 2. The position error of CKF in Case 1.
Figure 3 shows the positioning error when using the robust cubature Kalman filter and the parameter γ is set to 2. Comparing Figures 2 and 3, it is apparent how effective the robust filter is. The error amplitude in Figure 3 is reduced by improving the robustness of the filter. Figure 4 is the position error result for the SVD-based robust cubature Kalman filter (SVD-RCKF) with γ set to 2. Figures 3 and 4 show that the results are almost the same when the parameter γ is set to 2. The reason is that the Cholesky decomposition and the SVD method can achieve a similar effect when the RCKF is relatively stable. Table 2 shows the statistical information for the different filter algorithms.
Figure 3. The position error of RCKF (γ = 2) in Case 1.
Figure 4. The position error of SVD-RCKF (γ = 2) in Case 1.
Table 2. Position errors of different filters in Case 1(γ = 2).
The performance of the robust cubature Kalman filter with different values of the parameter γ was further analysed. Table 3 presents the statistical information. For the RCKF, the larger value for the parameter γ, the less the robustness of the filter. Compared with the result of the RCKF on the value of 2500, the results when using the value of 1·5 improved the performance by 6·5%, 7·1% and 3·7% in three directions. This indicates that the RCKF can achieve jarless robustness performance if the different design parameters are within limits.
Table 3. The position errors of different restrict parameter in Case 1.
From the fundamental of the H∞ robust filter, we know that the smaller the restrict parameter γ, the stronger the robustness of the filter. To get more robust performance, case studies with smaller γ values were compared. The result is shown in Table 3. We find that the RCKF sometimes does not work well. The reason is that after many iterations of the RCKF with a much smaller restrict parameter γ, P k/k−1 and P k lose their positive definiteness and this consequently leads to the instability of the numerical value. In order to further improve the numerical stability of the RCKF, the SVD-RCKF method is proposed. Figure 5 gives the position errors when using the new filter algorithm with γ set to 1. Compared with the result from the RCKF with γ set to 2, the result of SVD-RCKF with the value of 1 improved the performance by 56·0%, 60·8% and 50·9% in three directions. As expected, the results are better than the other algorithms previously mentioned. However, it was found that the relationship between γ and the robustness of a filter does not exist anymore if γ is much smaller. That is because there is no solution to the Riccati inequality if the γ is too small. For instance, the estimation error increases when γ is set smaller than 0·7, as shown in Table 3.
Figure 5. The position error of SVD-RCKF (γ = 1) in Case 1.
5.2. Case study 2
The second test was carried out in Nottingham, UK in November 2013. The test setup was similar to Case study 1. A Global Navigation Satellite System (GNSS) antenna, a GNSS receiver and a SPAN-LCI IMU were mounted in a van and data was logged from the receiver's serial ports to a laptop for storage and processing. The vector between the IMU centre and GPS antenna was accurately surveyed using a total station and is considered to be known to within 1 cm. A base station was set up on the roof of the NGB building to provide Differential GPS (DGPS) and Real-Time Kinematic (RTK) corrections. The update rates of the INS and GPS are 200 Hz and 1 Hz, respectively. The average baseline length was less than 3 km for the test. Figure 6 is the test trajectory and Figure 7 is a photograph taken of the test van. The high accuracy real-time output results of a SPAN-CIMU system are used as the reference value and the double difference code GPS position and velocity results are used as the input measurements.
Figure 6. The vehicle trajectory of Case 2.
Figure 7. The testing van in Case 2.
The position error of the CKF is shown in Figure 8. It indicates that there are many epochs of outlier data and the amplitude is a little big. The robustness of the CKF should be enhanced to tackle the problem of gross errors or an inaccurate system.
Figure 8. The position error of CKF in Case 2.
Figure 9 shows the position error when using the SVD based Robust Cubature Kalman Filter (SVD-RCKF) and the parameter γ is set as 3. As we can see by comparing Figure 8 and Figure 9, the error amplitude in Figure 9 is reduced through improving the robustness of the filter. As is the situation in Case 1, the position error of the RCKF is almost the same as the SVD-RCKF, so the corresponding plot of the RCKF is omitted in Case 2 to keep the description concise. Table 4 shows the statistical information of the plots.
Figure 9. The position error of SVD-RCKF (γ = 3) in Case 2.
Table 4. Position errors of different filters in Case 2 (γ = 3).
As in Case 1, the performance of the robust cubature Kalman filter with different values for parameter γ were also compared. The result is very similar to Case 1. Table 5 shows the corresponding statistical result. From Table 5, we know that the larger the value of the parameter γ, the worse the robustness of the filter. Compared with the result of the RCKF with the value of 5000, the results for the value of 3 only improved the performance by 7·0%, 0·0% and 6·2%, in three directions. Similar to Case 1, this result demonstrates that the RCKF can achieve jarless robustness performance if the different design parameter is within limits.
Table 5. The position errors of different strict parameter in case 2.
To achieve more robust performance, case studies with smaller γ were compared. The results from Case 2 are shown in Table 5. We find that the RCKF cannot work when the parameter γ is smaller than 2. The reason is that after many iterations in the RCKF with a much smaller restrict parameter γ, P k/k−1 and P k lose their positive definiteness and this consequently leads to the instability of the numerical value. As is the situation in Case 1, the SVD-RCKF is introduced to further improve the numerical stability of the RCKF. Figure 10 gives the position errors when using the new filter algorithm with γ set to 1·44. Compared with the result from the RCKF with γ set to 3, the result from the SVD-RCKF with the value of 1·44 improved the performance by 30·3%, 31·3% and 26·2% in three directions. As expected, the results are better than the other algorithms previously mentioned. However, the same problem remains as in Case 1, where the robust filter will diverge when the parameter γ is set too small. That is because there is no solution to the Riccati inequality if the γ is too small. In this case study, the estimation error shown in Table 5 increases when γ is set smaller than 1·44.
Figure 10. The position error of SVD-RCKF(γ = 1·414) in Case 2.
Case 2 displays a difference from Case 1, as the outlier may still exist in the position error series. The reason could be that the test van was driven around corners sharply, and at fairly high speed.
Combining the analysis of Case 1 and Case 2, we know that the nonlinear robust filtering could gain a stable performance if the restrict parameter were assigned properly. If a more robust performance was expected, the restrict parameter should be assigned adventurously. However, due to the existence criteria of the Riccati inequality, the restrict parameter cannot be assigned without bounding. From the analysis of the two cases, the restrict parameter should be equal to, or bigger than 1, and the optimal value should vary in different cases. Therefore, how to assign the parameter properly is the future work for the nonlinear robust filter.
6. CONCLUSIONS
The robust cubature Kalman filter based on the H∞ filter is very effective at detecting outlier data in GPS/SINS integration systems. It has been found that a smaller restrict parameter γ can improve the overall performance of the RCKF. However, it is also apparent that the RCKF easily diverges if the parameter is too small. The robust cubature Kalman filter based on SVD is proposed to maintain stronger robustness on the wider conditions for the design parameters. Two case studies indicate that the new filtering method is effective. It is also anticipated that more work needs to be carried out regarding how to set the optimal parameter and quantify the stability of the SVD-RCKF.
ACKNOWLEDGEMENTS
The authors would like to thank Yang Gao and Scott Stephenson from the University of Nottingham for their help in collecting the testing data in Nottingham. The paper was partially funded by the National Natural Science Foundation of China (No.41371423, No.41204011), the National High Technology Research and Development Program of China (No.2013AA12A201) and the Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD, NO.SZBF 2011-6-B35). The University of Nottingham provided a scholarship to support the first author's visit to Nottingham.
