1. Introduction
In a wide variety of fluid dynamical systems sound waves play no significant role on the time and length scales of interest. Yet their presence generally requires them to be resolved in numerical calculations in order to maintain numerical stability. For explicit numerical schemes, the time step ![]() $\Delta t$ cannot exceed
$\Delta t$ cannot exceed ![]() $\Delta x / \max \{c,u\}$, where
$\Delta x / \max \{c,u\}$, where ![]() $\Delta x$ is the smallest scale resolved in the simulation,
$\Delta x$ is the smallest scale resolved in the simulation, ![]() $c$ is the sound speed and
$c$ is the sound speed and ![]() $u$ is the magnitude of the fluid velocity. For flows of very low Mach number, i.e. flows with
$u$ is the magnitude of the fluid velocity. For flows of very low Mach number, i.e. flows with ![]() $u \ll c$, this imposes an impracticable limit on the numerical time step. So-called ‘sound-proof’ models explicitly remove sound waves from the equations that are solved, so that the time step is no longer constrained by the sound speed. In practical applications this may result in a reduction in computational time by several orders of magnitude. Various sound-proof models have been derived for different applications, each of which requires particular physical assumptions and has its own domain of validity.
$u \ll c$, this imposes an impracticable limit on the numerical time step. So-called ‘sound-proof’ models explicitly remove sound waves from the equations that are solved, so that the time step is no longer constrained by the sound speed. In practical applications this may result in a reduction in computational time by several orders of magnitude. Various sound-proof models have been derived for different applications, each of which requires particular physical assumptions and has its own domain of validity.
A completely different approach is to solve the fully compressible equations using an implicit (or semi-implicit) numerical scheme, which avoids the need for very small computational time steps (e.g. Viallet et al. Reference Viallet, Goffrey, Baraffe, Folini, Geroux, Popov, Pratt and Walder2016). However, such methods do not remove sound waves from the dynamics; rather they introduce numerical dissipation that prevents sound waves from growing to significant amplitudes. To minimise the effect of this numerical dissipation on the results, such models use preconditioning techniques that are tailored to the particular problem of interest (Goffrey et al. Reference Goffrey, Pratt, Viallet, Baraffe, Popov, Walder, Folini, Geroux and Constantino2017).
Of the various sound-proof approximations, the pseudo-incompressible approximation has the advantage that it can be derived under a single assumption: that the (Eulerian) pressure perturbations are small (Durran Reference Durran1989, Reference Durran2008; Vasil et al. Reference Vasil, Lecoanet, Brown, Wood and Zweibel2013). In particular, Vasil et al. (Reference Vasil, Lecoanet, Brown, Wood and Zweibel2013) have shown that the pseudo-incompressible equations can be obtained by applying Hamilton's principle to a suitable action, which is obtained simply by linearising the pressure variable about a given ‘background’ field, ![]() $P_0$. Although the resulting equations describe only ideal (i.e. adiabatic) dynamics, they can be extended to include non-ideal processes by invoking ‘thermodynamic consistency’ (Klein & Pauluis Reference Klein and Pauluis2012), or by using an extended variational principle (Gay-Balmaz Reference Gay-Balmaz2019). The main advantage of using a variational formalism is that it guarantees (via Noether's theorem) that the equations obey conservation laws that are directly analogous to those of the unapproximated system.
$P_0$. Although the resulting equations describe only ideal (i.e. adiabatic) dynamics, they can be extended to include non-ideal processes by invoking ‘thermodynamic consistency’ (Klein & Pauluis Reference Klein and Pauluis2012), or by using an extended variational principle (Gay-Balmaz Reference Gay-Balmaz2019). The main advantage of using a variational formalism is that it guarantees (via Noether's theorem) that the equations obey conservation laws that are directly analogous to those of the unapproximated system.
In the simplest implementation of the pseudo-incompressible approximation, the background pressure, ![]() $P_0$, is a fixed function of altitude. However, the resulting equations have two shortcomings:
$P_0$, is a fixed function of altitude. However, the resulting equations have two shortcomings:
(i) they become inaccurate on large horizontal scales (for which pressure perturbations are significant e.g. Davies et al. Reference Davies, Staniforth, Wood and Thuburn2003); and
(ii) they imply a constraint on the velocity field that cannot generally be maintained in the presence of heat sources, at least for certain choices of the boundary conditions (e.g. Rehm & Baum Reference Rehm and Baum1978; Lecoanet et al. Reference Lecoanet, Brown, Zweibel, Burns, Oishi and Vasil2014).
For these reasons, and for the sake of greater generality, it is desirable to allow the background pressure field to evolve in time, whilst maintaining hydrostatic balance (Almgren Reference Almgren2000; Almgren et al. Reference Almgren, Bell, Nonaka and Zingale2008; O'Neill & Klein Reference O'Neill and Klein2014). We refer to this as the hybrid pseudo-incompressible–hydrostatic model. However, by allowing the background pressure to evolve we violate one of the assumptions under which the variational derivations were performed, and as a result the hybrid model generally does not maintain exact energy conservation.
The purpose of this paper is to resolve this problem by generalising the method of Vasil et al. (Reference Vasil, Lecoanet, Brown, Wood and Zweibel2013) to allow the background pressure ![]() $P_0$ to vary in time, subject to the constraint that the horizontally averaged dynamics is hydrostatic. To enforce this additional constraint, we introduce an additional Lagrange multiplier into the fluid action, which results in an additional force in the momentum equation. (Such a force is expected whenever an additional constraint is imposed, though this point does not always seem to have been recognised in the literature.) As a proof of concept we present an implementation of our hybrid equations using the MAESTROeX code (Fan et al. Reference Fan, Nonaka, Almgren, Harpole and Zingale2019a).
$P_0$ to vary in time, subject to the constraint that the horizontally averaged dynamics is hydrostatic. To enforce this additional constraint, we introduce an additional Lagrange multiplier into the fluid action, which results in an additional force in the momentum equation. (Such a force is expected whenever an additional constraint is imposed, though this point does not always seem to have been recognised in the literature.) As a proof of concept we present an implementation of our hybrid equations using the MAESTROeX code (Fan et al. Reference Fan, Nonaka, Almgren, Harpole and Zingale2019a).
We note that an alternative hybrid model can be obtained by generalising the hydrostatic approximation (Miller & Pearce Reference Miller and Pearce1974; White Reference White1989; Arakawa & Konor Reference Arakawa and Konor2009), and a variational formalism has already been used to obtain ‘quasi-hydrostatic’ and ‘semi-hydrostatic’ approximations (Salmon & Smith Reference Salmon and Smith1994; Dubos & Voitus Reference Dubos and Voitus2014). Such approximations are well suited to many meteorological applications, in which the dynamics occurs on large horizontal scales (measured relative to a typical vertical scale height). However, the pseudo-incompressible approximation is generally more accurate for modelling dynamics on small horizontal length scales, such as atmospheric convection and other buoyancy processes, which form the motivation for the present work.
2. The constrained fluid action
2.1. The fully compressible fluid
To obtain the equations of motion using Hamilton's principle, we first need to identify the appropriate action for the dynamical system in question. For a fluid, the most natural representation of the action is in terms of Lagrangian coordinates (Salmon Reference Salmon1988). However, in applications it is far more convenient to express the equations in Eulerian form, and so in what follows we take the standard ‘hybrid Lagrangian–Eulerian’ approach (Bretherton Reference Bretherton1970). The action is expressed in Eulerian form as the space–time integral
where ![]() $\mathcal {L}$ is the Lagrangian density, the most concise form of which for a fully compressible fluid is
$\mathcal {L}$ is the Lagrangian density, the most concise form of which for a fully compressible fluid is
Here, ![]() $\rho$ is the fluid density,
$\rho$ is the fluid density, ![]() $\boldsymbol {u}$ is the velocity,
$\boldsymbol {u}$ is the velocity, ![]() $\varPhi$ is the gravitational potential and
$\varPhi$ is the gravitational potential and ![]() $U$ is the specific internal energy, which is naturally a function of the density and specific entropy,
$U$ is the specific internal energy, which is naturally a function of the density and specific entropy, ![]() $s$. We make the Cowling approximation by assuming that
$s$. We make the Cowling approximation by assuming that ![]() $\varPhi$ is a given function of space only, although the method can be generalised to include self-gravity if required. We now calculate the first variation of the action with respect to the fields
$\varPhi$ is a given function of space only, although the method can be generalised to include self-gravity if required. We now calculate the first variation of the action with respect to the fields ![]() $\rho$,
$\rho$, ![]() $s$ and
$s$ and ![]() $\boldsymbol {u}$:
$\boldsymbol {u}$:
The variations ![]() $\delta S$,
$\delta S$, ![]() $\delta \rho$ and
$\delta \rho$ and ![]() $\delta \boldsymbol {u}$ are not independent, since they all result from the same variation in the fluid element trajectories. We can express each of them in terms of the Lagrangian displacement,
$\delta \boldsymbol {u}$ are not independent, since they all result from the same variation in the fluid element trajectories. We can express each of them in terms of the Lagrangian displacement, ![]() $\boldsymbol {\xi }$, as follows (Newcomb Reference Newcomb1962):
$\boldsymbol {\xi }$, as follows (Newcomb Reference Newcomb1962):
From these expressions, and integrating by parts, we can write the first variation of the action as
where
represents the usual Lagrangian derivative and ![]() $P$ is the fluid pressure:
$P$ is the fluid pressure:
We use the subscript ‘EoS’ to indicate a quantity that can be expressed explicitly as a function of ![]() $\rho$ and
$\rho$ and ![]() $s$ via an equation of state.
$s$ via an equation of state.
Hamilton's principle states that ![]() $\delta \mathcal {S}$ must vanish for all possible choices of
$\delta \mathcal {S}$ must vanish for all possible choices of ![]() $\boldsymbol {\xi }$, and hence we obtain the usual Euler equation:
$\boldsymbol {\xi }$, and hence we obtain the usual Euler equation:
Moreover, the forms assumed for ![]() $\delta \rho$ and
$\delta \rho$ and ![]() $\delta s$ in (2.4a–c) guarantee the conservation of mass and entropy, so we also have
$\delta s$ in (2.4a–c) guarantee the conservation of mass and entropy, so we also have
Since the action contains no explicit time dependence, it follows from Noether's theorem that the system conserves a total energy, whose density, ![]() $E$ say, we can deduce easily from the action:
$E$ say, we can deduce easily from the action:
We note that the correct definition of the fluid pressure, given by (2.7), follows directly from the derivation. By contrast, since the dynamics arising from Hamilton's principle is necessarily adiabatic, we have not needed to define the fluid temperature. However, the correct definition can be deduced by requiring that the laws of thermodynamics are obeyed. Specifically, in the presence of a volumetric heat source, ![]() $Q$, we expect the fluid entropy to obey a prognostic equation of the form
$Q$, we expect the fluid entropy to obey a prognostic equation of the form
and the temperature, ![]() $T$, must be defined such that the energy,
$T$, must be defined such that the energy, ![]() $E$, remains a conserved quantity; Klein & Pauluis (Reference Klein and Pauluis2012) refer to this as the principle of ‘thermodynamic consistency’. In the case of a fully compressible fluid this leads, of course, to the usual definition:
$E$, remains a conserved quantity; Klein & Pauluis (Reference Klein and Pauluis2012) refer to this as the principle of ‘thermodynamic consistency’. In the case of a fully compressible fluid this leads, of course, to the usual definition:
2.2. The pseudo-incompressible fluid
As shown by Vasil et al. (Reference Vasil, Lecoanet, Brown, Wood and Zweibel2013), the pseudo-incompressible approximation can be obtained in a general form simply by supplementing the Lagrangian density ![]() $\mathcal {L}$ with an additional term
$\mathcal {L}$ with an additional term
Here, ![]() $P_{EoS}(\rho,s)$ is defined as previously,
$P_{EoS}(\rho,s)$ is defined as previously, ![]() $P_0(\boldsymbol {x})$ is a prescribed background pressure and
$P_0(\boldsymbol {x})$ is a prescribed background pressure and ![]() $\lambda (\boldsymbol {x},t)$ is a Lagrange multiplier. When Hamilton's principle is applied,
$\lambda (\boldsymbol {x},t)$ is a Lagrange multiplier. When Hamilton's principle is applied, ![]() $\lambda$ is regarded as an additional, independent variable, and therefore serves to enforce the constraint
$\lambda$ is regarded as an additional, independent variable, and therefore serves to enforce the constraint ![]() $P_{EoS} = P_0$. This constraint implies that the density, and hence the volume, of each fluid element depends entirely on its entropy and its Eulerian position, without any reference to pressure perturbations. In this way, acoustic waves are removed from the system (Durran Reference Durran2008).
$P_{EoS} = P_0$. This constraint implies that the density, and hence the volume, of each fluid element depends entirely on its entropy and its Eulerian position, without any reference to pressure perturbations. In this way, acoustic waves are removed from the system (Durran Reference Durran2008).
As discussed in the Introduction, the ‘generalised pseudo-incompressible’ equations obtained by Vasil et al. (Reference Vasil, Lecoanet, Brown, Wood and Zweibel2013) can be extended to include diabatic processes by invoking thermodynamic consistency. However, if the background pressure ![]() $P_0$ is still regarded as a fixed function of space only, then the resulting equations become ill-posed for certain boundary conditions. To see why, we take the Lagrangian derivative of the constraint equation
$P_0$ is still regarded as a fixed function of space only, then the resulting equations become ill-posed for certain boundary conditions. To see why, we take the Lagrangian derivative of the constraint equation ![]() $P_{EoS}(\rho,s) = P_0(\boldsymbol {x})$, which tells us that
$P_{EoS}(\rho,s) = P_0(\boldsymbol {x})$, which tells us that
Using mass conservation and the diabatic heating equation (2.11), this becomes
where ![]() $c^2(\rho,s) \equiv {\partial P_{EoS}}/{\partial \rho }$ is the square of the sound speed. If, for example,
$c^2(\rho,s) \equiv {\partial P_{EoS}}/{\partial \rho }$ is the square of the sound speed. If, for example, ![]() $Q$ represents an external injection of heat into the fluid, then we expect the right-hand side of this equation to be positive. This implies that the left-hand side must also be positive, and hence the fluid must expand. But if we impose impenetrable boundary conditions over the entire surface of the fluid, then expansion in any region of the fluid must be balanced by contraction elsewhere, which is not compatible with (2.15). The obvious solution to this problem is to allow the pressure
$Q$ represents an external injection of heat into the fluid, then we expect the right-hand side of this equation to be positive. This implies that the left-hand side must also be positive, and hence the fluid must expand. But if we impose impenetrable boundary conditions over the entire surface of the fluid, then expansion in any region of the fluid must be balanced by contraction elsewhere, which is not compatible with (2.15). The obvious solution to this problem is to allow the pressure ![]() $P_0$ to change in response to heating, and as described in the Introduction this has long been recognised in numerical implementations of the pseudo-incompressible approximation. A further advantage of allowing the background state to evolve is that it is more self-consistent, and leads to a more ‘universal’ model that is free from any imposed background profiles. But if
$P_0$ to change in response to heating, and as described in the Introduction this has long been recognised in numerical implementations of the pseudo-incompressible approximation. A further advantage of allowing the background state to evolve is that it is more self-consistent, and leads to a more ‘universal’ model that is free from any imposed background profiles. But if ![]() $P_0$ is allowed to vary in time then there is no longer any reason to expect the model to conserve energy.
$P_0$ is allowed to vary in time then there is no longer any reason to expect the model to conserve energy.
2.3. The hybrid pseudo-incompressible–hydrostatic model
Our goal is to generalise the derivation of Vasil et al. (Reference Vasil, Lecoanet, Brown, Wood and Zweibel2013) to allow the background pressure to evolve, but subject to the condition that it remains horizontally invariant, and hydrostatic. At the level of the action, we can enforce this as a constraint by supplementing the Lagrangian density with a term
where for simplicity we have assumed a plane-parallel atmosphere, with uniform gravitational acceleration ![]() $\boldsymbol {g} = - \boldsymbol {\nabla }\varPhi = g\boldsymbol {e}_{z}$. (We use the convention that
$\boldsymbol {g} = - \boldsymbol {\nabla }\varPhi = g\boldsymbol {e}_{z}$. (We use the convention that ![]() $g$ is negative.) A similar constraint has previously been used to derive a ‘semi-hydrostatic’ model (Dubos & Voitus Reference Dubos and Voitus2014), but the difference here is that we only wish to impose this constraint on the horizontally averaged fields. We therefore take the Lagrange multiplier
$g$ is negative.) A similar constraint has previously been used to derive a ‘semi-hydrostatic’ model (Dubos & Voitus Reference Dubos and Voitus2014), but the difference here is that we only wish to impose this constraint on the horizontally averaged fields. We therefore take the Lagrange multiplier ![]() $\mu$ to be horizontally invariant, i.e.
$\mu$ to be horizontally invariant, i.e. ![]() $\mu (z,t)$, so that the constraint it enforces is
$\mu (z,t)$, so that the constraint it enforces is
where an overbar represents a horizontal average. Since we still want to make the pseudo-incompressible approximation, we simultaneously enforce the constraint ![]() $P_{EoS} = \overline {P_{EoS}}$. Thus, our pseudo-incompressible–hydrostatic action has the form
$P_{EoS} = \overline {P_{EoS}}$. Thus, our pseudo-incompressible–hydrostatic action has the form
where we have used the fact that
to remove any explicit reference to ![]() $\overline {P_{EoS}}$ from the action. We note that the action (2.18) only depends on the non-horizontally averaged part of
$\overline {P_{EoS}}$ from the action. We note that the action (2.18) only depends on the non-horizontally averaged part of ![]() $\lambda$, that is
$\lambda$, that is ![]() $(\lambda -\bar {\lambda })$, and so
$(\lambda -\bar {\lambda })$, and so ![]() $\bar {\lambda }$ is essentially arbitrary; we will take advantage of this fact shortly.
$\bar {\lambda }$ is essentially arbitrary; we will take advantage of this fact shortly.
It is now straightforward to obtain the equations of motion via Hamilton's principle, which leads to the following momentum equation:
Given that the horizontal average of ![]() $\lambda$ is essentially arbitrary, we can simplify this result by declaring that
$\lambda$ is essentially arbitrary, we can simplify this result by declaring that ![]() $\bar {\lambda } = {\partial \mu }/{\partial z}$. Our complete set of equations is then
$\bar {\lambda } = {\partial \mu }/{\partial z}$. Our complete set of equations is then
where, for brevity, we use the symbol ![]() $P$ to refer to both
$P$ to refer to both ![]() $P_{EoS}$ and its horizontal average, which are equal by construction. From this point onwards, it is more convenient to regard
$P_{EoS}$ and its horizontal average, which are equal by construction. From this point onwards, it is more convenient to regard ![]() $P(z,t)$ as an independent variable, alongside
$P(z,t)$ as an independent variable, alongside ![]() $\rho (\boldsymbol {x},t)$, rather than as a function of
$\rho (\boldsymbol {x},t)$, rather than as a function of ![]() $\rho$ and
$\rho$ and ![]() $s$. We will therefore henceforth regard the quantities
$s$. We will therefore henceforth regard the quantities ![]() $s$ and
$s$ and ![]() $c$ as functions of
$c$ as functions of ![]() $P$ and
$P$ and ![]() $\rho$, and for later convenience we introduce the quantity
$\rho$, and for later convenience we introduce the quantity
We note that our momentum equation (2.21) differs from that of Vasil et al. (Reference Vasil, Lecoanet, Brown, Wood and Zweibel2013) and Klein & Pauluis (Reference Klein and Pauluis2012) only in the presence of ![]() $\bar {\lambda }$, which serves to modify the effective gravitational field. As in the model of Dubos & Voitus (Reference Dubos and Voitus2014), it is possible to interpret
$\bar {\lambda }$, which serves to modify the effective gravitational field. As in the model of Dubos & Voitus (Reference Dubos and Voitus2014), it is possible to interpret ![]() $\mu$ (and hence
$\mu$ (and hence ![]() $\bar {\lambda }$) as a correction to the geopotential height.
$\bar {\lambda }$) as a correction to the geopotential height.
As mentioned earlier, a major advantage of having made all of our approximations at the level of the action is that the model is guaranteed to admit conservation laws similar to those of the exact system, provided that our approximations do not violate the relevant mathematical symmetries. In particular, the additional constraint terms in (2.18) do not explicitly depend on either position or time, and so our hybrid model is guaranteed to conserve momentum and energy in some form. Another conserved quantity, which is of central importance in meteorology, is the potential vorticity, which owes its existence to the indistinguishability of fluid particles lying within surfaces of constant entropy (Salmon Reference Salmon1982). In terms of our Lagrangian–Eulerian description, it can be shown that potential vorticity is a materially conserved quantity provided that the first variation of the action depends on ![]() $\boldsymbol {\xi }$ only through
$\boldsymbol {\xi }$ only through ![]() $\delta \rho$,
$\delta \rho$, ![]() $\delta s$ and
$\delta s$ and ![]() $\delta \boldsymbol {u}$ (Vasil et al. Reference Vasil, Lecoanet, Brown, Wood and Zweibel2013). This result can also be derived directly from our momentum equation (2.21), whose curl yields the vorticity equation
$\delta \boldsymbol {u}$ (Vasil et al. Reference Vasil, Lecoanet, Brown, Wood and Zweibel2013). This result can also be derived directly from our momentum equation (2.21), whose curl yields the vorticity equation
where ![]() $\boldsymbol {\omega } \equiv \boldsymbol {\nabla }\times \boldsymbol {u}$ is the vorticity. Because the right-hand side here is perpendicular to
$\boldsymbol {\omega } \equiv \boldsymbol {\nabla }\times \boldsymbol {u}$ is the vorticity. Because the right-hand side here is perpendicular to ![]() $\boldsymbol {\nabla } s$, it follows that the circulation around any isentropic material curve remains constant in time, and hence that the quantity
$\boldsymbol {\nabla } s$, it follows that the circulation around any isentropic material curve remains constant in time, and hence that the quantity
is materially conserved.
2.4. Thermodynamic consistency
As just mentioned, (2.21)–(2.24) are guaranteed to conserve energy in some form. In fact, since the action (2.18) only differs from the fully compressible action by constraint terms, the conserved energy must have exactly the form given by (2.10). Indeed, using (2.21)–(2.24) it can be shown that
This result demonstrates that ![]() $E$ is no longer a locally conserved quantity in our hybrid approximation, i.e. it does not satisfy a local conservation law, unless the right-hand side happens to be zero. However, the right-hand side has zero horizontal average, and so the horizontally averaged energy,
$E$ is no longer a locally conserved quantity in our hybrid approximation, i.e. it does not satisfy a local conservation law, unless the right-hand side happens to be zero. However, the right-hand side has zero horizontal average, and so the horizontally averaged energy, ![]() $\bar {E}$, is still a conserved quantity, i.e. it does satisfy a local conservation law. In other words, imposing hydrostatic balance causes energy to be instantaneously redistributed within each horizontal surface, but energy is still conserved locally in the vertical direction, and hence also globally.
$\bar {E}$, is still a conserved quantity, i.e. it does satisfy a local conservation law. In other words, imposing hydrostatic balance causes energy to be instantaneously redistributed within each horizontal surface, but energy is still conserved locally in the vertical direction, and hence also globally.
We emphasise that in order to obtain this result, we needed to use the momentum equation (2.21), which includes an additional force not present in previous pseudo-incompressible models (e.g. Durran Reference Durran1989; Almgren et al. Reference Almgren, Bell, Nonaka and Zingale2008; Klein & Pauluis Reference Klein and Pauluis2012; Vasil et al. Reference Vasil, Lecoanet, Brown, Wood and Zweibel2013; O'Neill & Klein Reference O'Neill and Klein2014; Fan et al. Reference Fan, Nonaka, Almgren, Harpole and Zingale2019a). The presence of this force follows directly from Hamilton's principle.
Another important feature of (2.28) is that it contains additional energy flux terms compared with the fully compressible energy equation. The first of these, ![]() $\lambda \rho c^2$, was already present in previous pseudo-incompressible models, where it was identified as a pressure perturbation and often denoted as
$\lambda \rho c^2$, was already present in previous pseudo-incompressible models, where it was identified as a pressure perturbation and often denoted as ![]() $p'$ or
$p'$ or ![]() ${\rm \pi}$. The other terms involve our new Lagrange multiplier
${\rm \pi}$. The other terms involve our new Lagrange multiplier ![]() $\mu$ and therefore have not previously arisen. Their contribution to the total energy budget can be made to vanish by imposing either that
$\mu$ and therefore have not previously arisen. Their contribution to the total energy budget can be made to vanish by imposing either that ![]() $\mu =0$ or that
$\mu =0$ or that ![]() ${\partial P}/{\partial t} = - g\overline {\rho u_z}$ on the upper and lower boundaries. As we show in § 3, the latter is appropriate if the domain has open boundaries, whereas the former is required for a closed domain.
${\partial P}/{\partial t} = - g\overline {\rho u_z}$ on the upper and lower boundaries. As we show in § 3, the latter is appropriate if the domain has open boundaries, whereas the former is required for a closed domain.
We now invoke thermodynamic consistency to identify the appropriate definition of the temperature in our hybrid model. If we replace the adiabatic heat equation (2.23) with its diabatic counterpart (2.11), we find that the energy equation (2.28) now acquires an additional source term on its right-hand side,
but is otherwise unchanged. To preserve the first law of thermodynamics, we must therefore define the temperature to be
The same result was obtained by Klein & Pauluis (Reference Klein and Pauluis2012) and Gay-Balmaz (Reference Gay-Balmaz2019). We emphasise that, since this formula for ![]() $T$ depends on the quantity
$T$ depends on the quantity ![]() $\lambda$, the ‘correct’ temperature cannot generally be obtained from the usual equation of state.
$\lambda$, the ‘correct’ temperature cannot generally be obtained from the usual equation of state.
2.5. The velocity constraint and solvability
In summary, our diabatic equations are
Although the set of (2.31)–(2.35) is complete, for the sake of obtaining solutions it is convenient to rearrange them a little. First, the heat equation (2.33) can be expressed as an evolution equation for ![]() $P$:
$P$:
However, only the horizontally averaged part of this equation is required to evolve ![]() $P$, and the rest serves as a constraint on the velocity. An alternative equation for
$P$, and the rest serves as a constraint on the velocity. An alternative equation for ![]() ${\partial P}/{\partial t}$ can be obtained by taking the Eulerian time derivative of the hydrostatic constraint (2.34). Using the continuity equation (2.32), and assuming periodic or impenetrable side boundaries and an impenetrable lower boundary, we find that
${\partial P}/{\partial t}$ can be obtained by taking the Eulerian time derivative of the hydrostatic constraint (2.34). Using the continuity equation (2.32), and assuming periodic or impenetrable side boundaries and an impenetrable lower boundary, we find that
 \begin{align} \frac{\partial}{\partial z}\frac{\partial P}{\partial t} &={-} g\frac{\partial}{\partial z}\overline{\rho u_z} \nonumber\\ \Rightarrow\quad \frac{\partial P}{\partial t} &={-} g\overline{\rho u_z} + \dot{P}_b, \end{align}
\begin{align} \frac{\partial}{\partial z}\frac{\partial P}{\partial t} &={-} g\frac{\partial}{\partial z}\overline{\rho u_z} \nonumber\\ \Rightarrow\quad \frac{\partial P}{\partial t} &={-} g\overline{\rho u_z} + \dot{P}_b, \end{align}
where ![]() $\dot {P}_b(t)$ is the rate of change of the pressure on the lower boundary. This function will depend on the choice of boundary condition at the upper boundary. For example, in the case where the upper boundary is impenetrable it is convenient to eliminate
$\dot {P}_b(t)$ is the rate of change of the pressure on the lower boundary. This function will depend on the choice of boundary condition at the upper boundary. For example, in the case where the upper boundary is impenetrable it is convenient to eliminate ![]() ${\partial P}/{\partial t}$ between (2.36) and (2.37), leading to a constraint equation for the velocity field:
${\partial P}/{\partial t}$ between (2.36) and (2.37), leading to a constraint equation for the velocity field:
where we have defined
to match the notation used in the low-Mach-number literature (Fan et al. Reference Fan, Nonaka, Almgren, Harpole and Zingale2019a). If we neglect the ![]() $\dot {P}_b$ term here then in general this equation has no solutions that meet the impenetrable boundary conditions; this is just an example of the problem mentioned in § 2.2, and indicates that the velocity constraint is degenerate for this choice of boundary conditions. The correct value for
$\dot {P}_b$ term here then in general this equation has no solutions that meet the impenetrable boundary conditions; this is just an example of the problem mentioned in § 2.2, and indicates that the velocity constraint is degenerate for this choice of boundary conditions. The correct value for ![]() $\dot {P}_b$ must therefore be obtained as a solvability condition for (2.38). For example, if the horizontal average of the first term in (2.38) can be neglected, then taking the volume average of this equation we deduce that
$\dot {P}_b$ must therefore be obtained as a solvability condition for (2.38). For example, if the horizontal average of the first term in (2.38) can be neglected, then taking the volume average of this equation we deduce that
(O'Neill & Klein Reference O'Neill and Klein2014). An alternative scenario, more relevant to atmospheric applications, is that of a semi-infinite atmosphere with an impenetrable lower boundary. Since the total mass of the semi-infinite atmosphere remains constant, and is assumed to remain in hydrostatic balance, it is arguable that the pressure on the lower boundary should remain approximately constant, i.e. that ![]() $\dot {P}_b\simeq 0$ (Almgren Reference Almgren2000). This assumption is implicit in the MAESTROeX model, which neglects the function
$\dot {P}_b\simeq 0$ (Almgren Reference Almgren2000). This assumption is implicit in the MAESTROeX model, which neglects the function ![]() $\dot {P}_b$ (Almgren et al. Reference Almgren, Bell, Nonaka and Zingale2008), although in practice the equations are solved in a finite computational domain, and the upper boundary is taken either to be impenetrable or to have a fixed pressure. Furthermore (2.40) shows that, even in the limit of a semi-infinite atmosphere, we obtain
$\dot {P}_b$ (Almgren et al. Reference Almgren, Bell, Nonaka and Zingale2008), although in practice the equations are solved in a finite computational domain, and the upper boundary is taken either to be impenetrable or to have a fixed pressure. Furthermore (2.40) shows that, even in the limit of a semi-infinite atmosphere, we obtain ![]() $\dot {P}_b=0$ only if the injected heat,
$\dot {P}_b=0$ only if the injected heat, ![]() $Q$, vanishes sufficiently rapidly with height.
$Q$, vanishes sufficiently rapidly with height.
In both of the cases just described, we arrive at an approximate expression for the function ![]() $\dot {P}_b$. Because the result is only approximate, if we use it we must necessarily abandon (at least) one of the ‘exact’ (2.31)–(2.34). For example, O'Neill & Klein (Reference O'Neill and Klein2014) chose to abandon hydrostatic balance and/or mass conservation in their model. (More precisely, they allowed the ‘pseudo-density’, which satisfies the continuity equation, to depart from the ‘background density’, which satisfies hydrostatic balance). In the MAESTROeX model, which assumes that
$\dot {P}_b$. Because the result is only approximate, if we use it we must necessarily abandon (at least) one of the ‘exact’ (2.31)–(2.34). For example, O'Neill & Klein (Reference O'Neill and Klein2014) chose to abandon hydrostatic balance and/or mass conservation in their model. (More precisely, they allowed the ‘pseudo-density’, which satisfies the continuity equation, to depart from the ‘background density’, which satisfies hydrostatic balance). In the MAESTROeX model, which assumes that ![]() $\dot {P}_b=0$, the heat equation (2.33) is not used.
$\dot {P}_b=0$, the heat equation (2.33) is not used.
In the next section we describe a more consistent procedure for determining the value of ![]() $\dot {P}_b$, and how this can be implemented within the existing framework of the MAESTROeX code. For definiteness we focus on the case of a closed domain, in which the upper and lower boundaries are both impenetrable, so that the total energy ought to be conserved.
$\dot {P}_b$, and how this can be implemented within the existing framework of the MAESTROeX code. For definiteness we focus on the case of a closed domain, in which the upper and lower boundaries are both impenetrable, so that the total energy ought to be conserved.
3. The solution procedure
To avoid inessential complications, in what follows we consider an ideal gas, so that the relations between the thermodynamic variables can be stated explicitly. Our complete set of equations is then
 \begin{gather}S = \frac{Q/(\gamma P)}{\dfrac{1}{\gamma-1} + \lambda}. \end{gather}
\begin{gather}S = \frac{Q/(\gamma P)}{\dfrac{1}{\gamma-1} + \lambda}. \end{gather}
The MAESTROeX code (Fan et al. Reference Fan, Nonaka, Almgren, Harpole and Zingale2019a,Reference Fan, Nonaka, Almgren, Willcox, Harpole and Zingaleb) is a massively parallel, finite-volume solver for low-Mach-number astrophysical flows. It allows us to solve the above equations after having modified the code to include the terms involving ![]() $\bar {\lambda }$ and
$\bar {\lambda }$ and ![]() $\dot {P}_b$ for planar geometry (avoiding the additional complexity of the spherical implementation for now). It also allows for adaptive mesh refinement and reactions between multiple species, but we do not consider those features here. Although we only consider an ideal gas here, our changes to the code have been implemented for an arbitrary equation of state.
$\dot {P}_b$ for planar geometry (avoiding the additional complexity of the spherical implementation for now). It also allows for adaptive mesh refinement and reactions between multiple species, but we do not consider those features here. Although we only consider an ideal gas here, our changes to the code have been implemented for an arbitrary equation of state.
The code uses a predictor–corrector scheme, in which most quantities are updated several times over the course of a single time step. However, for our purposes the essential steps of the algorithm are:
(i) Timestep the momentum equation (3.1) using an ‘old’ value of
 $\lambda$.
$\lambda$.(ii) Calculate the necessary correction to
 $\lambda$ and
$\lambda$ and  $\boldsymbol {u}$ in order to meet the velocity constraint (3.4).
$\boldsymbol {u}$ in order to meet the velocity constraint (3.4).(iii) Timestep the continuity equation (3.2).
(iv) Update the pressure by integrating the hydrostatic balance equation (3.3).
The critical step here is determining the correction to ![]() $\lambda$ (which in practice is only updated at the end of each time step). Suppose that the ‘true’ value of
$\lambda$ (which in practice is only updated at the end of each time step). Suppose that the ‘true’ value of ![]() $\lambda$ is larger than the old value by
$\lambda$ is larger than the old value by ![]() $\Delta \lambda$. Then the velocity we initially obtain after taking a time step of size
$\Delta \lambda$. Then the velocity we initially obtain after taking a time step of size ![]() $\Delta t$ will be
$\Delta t$ will be
where ![]() $\boldsymbol {u}$ represents the ‘true’ velocity, and where we have defined
$\boldsymbol {u}$ represents the ‘true’ velocity, and where we have defined ![]() $\phi \equiv \gamma P^{1-1/\gamma }\,\Delta \lambda \,\Delta t$. Substituting this into the velocity constraint (3.4), we obtain the following equation for
$\phi \equiv \gamma P^{1-1/\gamma }\,\Delta \lambda \,\Delta t$. Substituting this into the velocity constraint (3.4), we obtain the following equation for ![]() $\phi$:
$\phi$:
In Appendix A we describe how this equation can be solved, by formulating its adjoint problem, and the associated solvability condition for ![]() $\dot {P}_b$. However, since implementing this would require significant changes to the existing MAESTROeX algorithm, we here present an approximate solution procedure that is more in keeping with the existing code. We also note that MAESTROeX uses a slightly different definition for the quantity
$\dot {P}_b$. However, since implementing this would require significant changes to the existing MAESTROeX algorithm, we here present an approximate solution procedure that is more in keeping with the existing code. We also note that MAESTROeX uses a slightly different definition for the quantity ![]() $\phi$, which has been found to improve numerical stability (Almgren, Bell & Crutchfield Reference Almgren, Bell and Crutchfield2000; Almgren et al. Reference Almgren, Bell, Nonaka and Zingale2008) but is mathematically equivalent to what we present here.
$\phi$, which has been found to improve numerical stability (Almgren, Bell & Crutchfield Reference Almgren, Bell and Crutchfield2000; Almgren et al. Reference Almgren, Bell, Nonaka and Zingale2008) but is mathematically equivalent to what we present here.
Currently, MAESTROeX actually implements the velocity constraint in two parts, by writing the density and velocity fields as the sums of horizontally averaged and remainder contributions: ![]() $\rho = \bar {\rho } + \tilde {\rho }$ and
$\rho = \bar {\rho } + \tilde {\rho }$ and ![]() $\boldsymbol {u} = \overline {u_z}\boldsymbol {e}_{z} + \tilde {\boldsymbol {u}}$. The velocity constraint (3.4) can then be separated into two equations:
$\boldsymbol {u} = \overline {u_z}\boldsymbol {e}_{z} + \tilde {\boldsymbol {u}}$. The velocity constraint (3.4) can then be separated into two equations:
Equation (3.8) is solved for ![]() $\overline {u_z}$ by integrating upward from the lower boundary, and using an ‘old’ value of
$\overline {u_z}$ by integrating upward from the lower boundary, and using an ‘old’ value of ![]() $\overline {\tilde {\rho } \tilde {u}_z}$. The quantity
$\overline {\tilde {\rho } \tilde {u}_z}$. The quantity ![]() $\dot {P}_b$ is currently neglected in this calculation, which means that the solution cannot generally be made to satisfy an impenetrable upper boundary condition. In order to allow for impenetrable boundaries above and below, we must take
$\dot {P}_b$ is currently neglected in this calculation, which means that the solution cannot generally be made to satisfy an impenetrable upper boundary condition. In order to allow for impenetrable boundaries above and below, we must take
which is a straightforward generalisation of the result (2.40) used by O'Neill & Klein (Reference O'Neill and Klein2014). The value of ![]() $\dot {P}_b$ obtained here can then be used later for the lower boundary condition in step (iv) of the algorithm described above. After
$\dot {P}_b$ obtained here can then be used later for the lower boundary condition in step (iv) of the algorithm described above. After ![]() $\overline {u_z}$ is calculated from (3.8), we can substitute (3.6) into (3.9), which leads to the following equation for
$\overline {u_z}$ is calculated from (3.8), we can substitute (3.6) into (3.9), which leads to the following equation for ![]() $\phi$:
$\phi$:
This differs from the equation currently solved in MAESTROeX because of the ![]() $\bar {\phi }$ term, which arises because of the additional
$\bar {\phi }$ term, which arises because of the additional ![]() $\bar {\lambda }$ term in the momentum (3.1). To solve this equation using the existing MAESTROeX algorithm, we can use an ‘old’ value for
$\bar {\lambda }$ term in the momentum (3.1). To solve this equation using the existing MAESTROeX algorithm, we can use an ‘old’ value for ![]() $\bar {\phi }$ and, if desired, iterate to convergence. We then update
$\bar {\phi }$ and, if desired, iterate to convergence. We then update ![]() $\lambda$ and use (3.6) to obtain the corrected velocity,
$\lambda$ and use (3.6) to obtain the corrected velocity, ![]() $\boldsymbol {u}$. The boundary conditions for (3.11) are chosen such that the corrected velocity satisfies the impenetrable boundary conditions. However, the solution for
$\boldsymbol {u}$. The boundary conditions for (3.11) are chosen such that the corrected velocity satisfies the impenetrable boundary conditions. However, the solution for ![]() $\phi$ is then determined only up to a constant, which is a consequence of the degeneracy of the velocity constraint for impenetrable boundary conditions. The value of this constant is not arbitrary, because it affects the updated value of
$\phi$ is then determined only up to a constant, which is a consequence of the degeneracy of the velocity constraint for impenetrable boundary conditions. The value of this constant is not arbitrary, because it affects the updated value of ![]() $\lambda$, and hence the temperature. To determine this constant, we return to the point mentioned in § 2.4, that
$\lambda$, and hence the temperature. To determine this constant, we return to the point mentioned in § 2.4, that ![]() $\mu$ should vanish on both of the impenetrable horizontal boundaries. Since
$\mu$ should vanish on both of the impenetrable horizontal boundaries. Since ![]() ${\partial \mu }/{\partial z} = \bar {\lambda }$, this condition requires that the domain integral (or domain average) of
${\partial \mu }/{\partial z} = \bar {\lambda }$, this condition requires that the domain integral (or domain average) of ![]() $\lambda$ must be zero, and so the domain average of
$\lambda$ must be zero, and so the domain average of ![]() $\Delta \lambda \propto \phi /P^{1-1/\gamma }$ must be zero also. In this way, the appropriate solution of (3.11) can be determined uniquely.
$\Delta \lambda \propto \phi /P^{1-1/\gamma }$ must be zero also. In this way, the appropriate solution of (3.11) can be determined uniquely.
4. Numerical tests
We have implemented the above solution procedure into a fork of the MAESTROeX code at version 21.06. (The fork of the code can be found at https://github.com/asnodin/MAESTROeX-hybrid.) Here we compare results obtained using this implementation, in a number of test problems, with results obtained using the existing pseudo-incompressible implementation in MAESTROeX (Fan et al. Reference Fan, Nonaka, Almgren, Harpole and Zingale2019a) and the fully compressible CASTRO code (Almgren et al. Reference Almgren, Beckner, Bell, Day, Howell, Joggerst, Lijewski, Nonaka, Singer and Zingale2010). To demonstrate the effect of each of our separate changes to the model, we consider four levels of refinement: ![]() $M_0$ denotes the original implementation;
$M_0$ denotes the original implementation; ![]() $M_1$, as
$M_1$, as ![]() $M_0$, but including the
$M_0$, but including the ![]() $\dot {P}_b$ term;
$\dot {P}_b$ term; ![]() $M_2$, as
$M_2$, as ![]() $M_1$, but including the
$M_1$, but including the ![]() $\bar {\lambda }$ term in the momentum equation; and
$\bar {\lambda }$ term in the momentum equation; and ![]() $M_3$, as
$M_3$, as ![]() $M_2$, but also using the thermodynamically consistent
$M_2$, but also using the thermodynamically consistent ![]() $T$, rather than
$T$, rather than ![]() $T_{EoS}$. Results from CASTRO are denoted with a
$T_{EoS}$. Results from CASTRO are denoted with a ![]() $C$. Unless otherwise specified, all tests here are for an ideal gas with
$C$. Unless otherwise specified, all tests here are for an ideal gas with ![]() $\gamma =5/3$ in a two-dimensional Cartesian box of size
$\gamma =5/3$ in a two-dimensional Cartesian box of size ![]() $L_x \times L_z$, with periodic boundary conditions in the horizontal (
$L_x \times L_z$, with periodic boundary conditions in the horizontal (![]() $x$) direction and impenetrable upper and lower boundaries in the vertical (
$x$) direction and impenetrable upper and lower boundaries in the vertical (![]() $z$) direction. The comparison with model
$z$) direction. The comparison with model ![]() $M_0$ is complicated by the fact that, with the
$M_0$ is complicated by the fact that, with the ![]() $\dot {P}_b$ term omitted, it is not possible to satisfy the velocity constraint (3.4) exactly for impenetrable boundary conditions. Moreover, because the value of
$\dot {P}_b$ term omitted, it is not possible to satisfy the velocity constraint (3.4) exactly for impenetrable boundary conditions. Moreover, because the value of ![]() $\dot {P}_b$ in this model is not calculated, the pressure on the lower boundary is simply held fixed. We note that MAESTROeX provides several methods for calculating the temperature, for example by solving an auxiliary equation for the specific enthalpy,
$\dot {P}_b$ in this model is not calculated, the pressure on the lower boundary is simply held fixed. We note that MAESTROeX provides several methods for calculating the temperature, for example by solving an auxiliary equation for the specific enthalpy, ![]() $H$, or specific internal energy,
$H$, or specific internal energy, ![]() $U$. To avoid potential inconsistencies, in all of our results using MAESTROeX the quantity
$U$. To avoid potential inconsistencies, in all of our results using MAESTROeX the quantity ![]() $T_{EoS}$ is derived from
$T_{EoS}$ is derived from ![]() $P$ and
$P$ and ![]() $\rho$. In Appendix B we present evolution equations for
$\rho$. In Appendix B we present evolution equations for ![]() $H$ and
$H$ and ![]() $U$ that are consistent with our model
$U$ that are consistent with our model ![]() $M_3$. Unless otherwise specified, our results are presented in c.g.s. units, which are the default in MAESTROeX.
$M_3$. Unless otherwise specified, our results are presented in c.g.s. units, which are the default in MAESTROeX.
4.1. Internal gravity waves
We consider perturbations to an atmosphere that is initially isothermal and in hydrostatic equilibrium. The domain has size ![]() $L_x = L_z = L = 10^9\,{\rm cm}$, and a numerical resolution of
$L_x = L_z = L = 10^9\,{\rm cm}$, and a numerical resolution of ![]() $64\times 64$ cells. The initial density field is
$64\times 64$ cells. The initial density field is
where ![]() $\rho _0=1/3\,{\rm g}\,{\rm cm}^{-3}$,
$\rho _0=1/3\,{\rm g}\,{\rm cm}^{-3}$, ![]() $m=4$ and
$m=4$ and ![]() $n=2$. The initial pressure is calculated assuming hydrostatic balance, with uniform gravity
$n=2$. The initial pressure is calculated assuming hydrostatic balance, with uniform gravity ![]() $g=-3\times 10^{4}\,{\rm cm}\,{\rm s}^{-2}$, and bottom pressure
$g=-3\times 10^{4}\,{\rm cm}\,{\rm s}^{-2}$, and bottom pressure ![]() $P_b =10^{13}\,{\rm dyn}\,{\rm cm}^{-2}$. The form of the perturbation has been chosen to match a single eigenmode of the linearised equations. For a small-amplitude perturbation, we would therefore expect to see an oscillation with frequency
$P_b =10^{13}\,{\rm dyn}\,{\rm cm}^{-2}$. The form of the perturbation has been chosen to match a single eigenmode of the linearised equations. For a small-amplitude perturbation, we would therefore expect to see an oscillation with frequency ![]() $\omega$ given by the dispersion relation
$\omega$ given by the dispersion relation
where ![]() $N^2 = (\gamma -1) (-g)/(\gamma L)$ is the Brunt–Väisälä frequency. We have chosen a relatively large amplitude for the perturbation in order to test the conservation of energy, which means that the waves break after only a few oscillation periods,
$N^2 = (\gamma -1) (-g)/(\gamma L)$ is the Brunt–Väisälä frequency. We have chosen a relatively large amplitude for the perturbation in order to test the conservation of energy, which means that the waves break after only a few oscillation periods, ![]() $t_0=2{\rm \pi} /\omega$. We integrate the adiabatic equations up to
$t_0=2{\rm \pi} /\omega$. We integrate the adiabatic equations up to ![]() $t = 7t_0$ for models
$t = 7t_0$ for models ![]() $M_0$,
$M_0$, ![]() $M_1$ and
$M_1$ and ![]() $M_2$. (Since this test is adiabatic, model
$M_2$. (Since this test is adiabatic, model ![]() $M_3$ is identical to
$M_3$ is identical to ![]() $M_2$.) Time series of the energy in each simulation are plotted in figure 1. In model
$M_2$.) Time series of the energy in each simulation are plotted in figure 1. In model ![]() $M_0$, the total energy oscillates significantly, by an amount comparable to the oscillation in the individual contributions from internal, kinetic and gravitational potential energy. By contrast, in models
$M_0$, the total energy oscillates significantly, by an amount comparable to the oscillation in the individual contributions from internal, kinetic and gravitational potential energy. By contrast, in models ![]() $M_1$ and
$M_1$ and ![]() $M_2$ the total energy is fairly well conserved, to within approximately
$M_2$ the total energy is fairly well conserved, to within approximately ![]() $0.01\,\%$ while the waves remain essentially linear, and approximately
$0.01\,\%$ while the waves remain essentially linear, and approximately ![]() $0.1\,\%$ once wave breaking occurs, at which point numerical dissipation becomes significant. The flow in all three cases is very similar, and the main difference is in the internal energy, as shown in figure 1(a,b). In this test, models
$0.1\,\%$ once wave breaking occurs, at which point numerical dissipation becomes significant. The flow in all three cases is very similar, and the main difference is in the internal energy, as shown in figure 1(a,b). In this test, models ![]() $M_1$ and
$M_1$ and ![]() $M_2$ produce very similar results, indicating that the
$M_2$ produce very similar results, indicating that the ![]() $\bar {\lambda }$ term in the momentum equation has a negligible effect. This is perhaps unsurprising given that the horizontally averaged flow is very weak in this case. The spurious oscillations in the internal energy in model
$\bar {\lambda }$ term in the momentum equation has a negligible effect. This is perhaps unsurprising given that the horizontally averaged flow is very weak in this case. The spurious oscillations in the internal energy in model ![]() $M_0$ result from the imposition of constant boundary pressure, which is relaxed in model
$M_0$ result from the imposition of constant boundary pressure, which is relaxed in model ![]() $M_1$.
$M_1$.

Figure 1. Time series of internal energy (![]() $E_{int}$), kinetic energy (
$E_{int}$), kinetic energy (![]() $E_{kin}$) and gravitational potential energy (
$E_{kin}$) and gravitational potential energy (![]() $E_{grav}$) in the internal gravity wave test, for models
$E_{grav}$) in the internal gravity wave test, for models ![]() ${M_0}$ (a) and
${M_0}$ (a) and ![]() $M_2$ (b). Each plot shows the change relative to the initial value as a fraction of the total initial energy. Plots for model
$M_2$ (b). Each plot shows the change relative to the initial value as a fraction of the total initial energy. Plots for model ![]() $M_1$ (not shown) are very similar to those in (b). (c) The evolution of the total energy in models
$M_1$ (not shown) are very similar to those in (b). (c) The evolution of the total energy in models ![]() $M_0, M_1$ and
$M_0, M_1$ and ![]() $M_2$.
$M_2$.
4.2. Rayleigh–Taylor instability
For this test, we begin with a layer of fluid with density ![]() $\rho _1$ overlaid by a layer with density
$\rho _1$ overlaid by a layer with density ![]() $\rho _2 > \rho _1$. The entire domain is initially hydrostatic, with a piecewise linear pressure profile. Following the procedure described in Almgren et al. (Reference Almgren, Beckner, Bell, Day, Howell, Joggerst, Lijewski, Nonaka, Singer and Zingale2010), the density interface is then slightly smoothed and perturbed, with
$\rho _2 > \rho _1$. The entire domain is initially hydrostatic, with a piecewise linear pressure profile. Following the procedure described in Almgren et al. (Reference Almgren, Beckner, Bell, Day, Howell, Joggerst, Lijewski, Nonaka, Singer and Zingale2010), the density interface is then slightly smoothed and perturbed, with
where ![]() $w$ is the smoothing width and
$w$ is the smoothing width and ![]() $Z(x)$ is the interface height:
$Z(x)$ is the interface height:
We take the domain size to be ![]() $L_x \times L_z = 0.5\,{\rm cm}\times 1\,{\rm cm}$, with a resolution of
$L_x \times L_z = 0.5\,{\rm cm}\times 1\,{\rm cm}$, with a resolution of ![]() $256\times 512$ grid cells. We choose
$256\times 512$ grid cells. We choose ![]() $\rho _1 = 1\,{\rm g}\,{\rm cm}^{-3}$,
$\rho _1 = 1\,{\rm g}\,{\rm cm}^{-3}$, ![]() $\rho _2 = 2\,{\rm g}\,{\rm cm}^{-3}$,
$\rho _2 = 2\,{\rm g}\,{\rm cm}^{-3}$, ![]() $w = 0.005\,{\rm cm}$,
$w = 0.005\,{\rm cm}$, ![]() $A = 0.01\,{\rm cm}$,
$A = 0.01\,{\rm cm}$, ![]() $g=-1\,{\rm cm}\,{\rm s}^{-2}$ and a bottom pressure of
$g=-1\,{\rm cm}\,{\rm s}^{-2}$ and a bottom pressure of ![]() $P_b =5\,{\rm dyn}\,{\rm cm}^{-2}$. This initial set-up was evolved for models
$P_b =5\,{\rm dyn}\,{\rm cm}^{-2}$. This initial set-up was evolved for models ![]() $C$,
$C$, ![]() $M_0$,
$M_0$, ![]() $M_1$ and
$M_1$ and ![]() $M_2$ up to a time of
$M_2$ up to a time of ![]() $t=10\,{\rm s}$. In figure 2(a) we show contours of the density in models
$t=10\,{\rm s}$. In figure 2(a) we show contours of the density in models ![]() $C$ and
$C$ and ![]() $M_2$ at times
$M_2$ at times ![]() $t=2$ and
$t=2$ and ![]() $3\,{\rm s}$. (Model
$3\,{\rm s}$. (Model ![]() $M_1$ is very similar to
$M_1$ is very similar to ![]() $M_2$ at both of these times.) Up to time
$M_2$ at both of these times.) Up to time ![]() $t=2\,{\rm s}$ models
$t=2\,{\rm s}$ models ![]() $C$ and
$C$ and ![]() $M_2$ show close agreement, but by
$M_2$ show close agreement, but by ![]() $t=3\,{\rm s}$ the simulations diverge as secondary instabilities develop. These differences are likely explained by the different advection schemes used in the two codes (Almgren et al. Reference Almgren, Beckner, Bell, Day, Howell, Joggerst, Lijewski, Nonaka, Singer and Zingale2010), rather than by differences in the models themselves. In fact, the qualitative agreement between models
$t=3\,{\rm s}$ the simulations diverge as secondary instabilities develop. These differences are likely explained by the different advection schemes used in the two codes (Almgren et al. Reference Almgren, Beckner, Bell, Day, Howell, Joggerst, Lijewski, Nonaka, Singer and Zingale2010), rather than by differences in the models themselves. In fact, the qualitative agreement between models ![]() $C$ and
$C$ and ![]() $M_2$ is surprising good, given that the Mach number reaches a maximum of around
$M_2$ is surprising good, given that the Mach number reaches a maximum of around ![]() $0.7$ during the simulation, because the pseudo-incompressible approximation is generally only expected to hold for low Mach number. Moreover, our hybrid model assumes that the (horizontally averaged) pressure remains in hydrostatic balance at all times, whereas in the CASTRO simulation there are inversions in the horizontally averaged pressure profile, as shown in figure 2(b). The pressure profiles in models
$0.7$ during the simulation, because the pseudo-incompressible approximation is generally only expected to hold for low Mach number. Moreover, our hybrid model assumes that the (horizontally averaged) pressure remains in hydrostatic balance at all times, whereas in the CASTRO simulation there are inversions in the horizontally averaged pressure profile, as shown in figure 2(b). The pressure profiles in models ![]() $M_1$ and
$M_1$ and ![]() $M_2$ are essentially identical, whereas model
$M_2$ are essentially identical, whereas model ![]() $M_0$ has a significantly lower pressure, as a result of its pressure being fixed at the lower boundary. Models
$M_0$ has a significantly lower pressure, as a result of its pressure being fixed at the lower boundary. Models ![]() $M_1$ and
$M_1$ and ![]() $M_2$ conserve the total energy to within approximately 0.1 %, as shown in figure 2(c), whereas in model
$M_2$ conserve the total energy to within approximately 0.1 %, as shown in figure 2(c), whereas in model ![]() $M_0$ the energy change is about an order of magnitude larger, and is therefore not shown.
$M_0$ the energy change is about an order of magnitude larger, and is therefore not shown.

Figure 2. Contour plots of density (in ![]() ${\rm g}\,{\rm cm}^{-3}$) in the Rayleigh–Taylor test for models
${\rm g}\,{\rm cm}^{-3}$) in the Rayleigh–Taylor test for models ![]() $C$ and
$C$ and ![]() $M_2$ at two times (a). The two simulations remain in close agreement until
$M_2$ at two times (a). The two simulations remain in close agreement until ![]() $t=2\,{\rm s}$, but then diverge as secondary instabilities develop. At the same time, pressure inversions appear in the horizontally averaged pressure in model
$t=2\,{\rm s}$, but then diverge as secondary instabilities develop. At the same time, pressure inversions appear in the horizontally averaged pressure in model ![]() $C$ (b), whereas the pressure in model
$C$ (b), whereas the pressure in model ![]() $M_2$ is hydrostatic and therefore monotonic. In model
$M_2$ is hydrostatic and therefore monotonic. In model ![]() $M_0$, which omits the
$M_0$, which omits the ![]() $\dot {P}_b$ term, the pressure remains fixed at the upper and lower boundaries. (c) The evolution of the total energy in models
$\dot {P}_b$ term, the pressure remains fixed at the upper and lower boundaries. (c) The evolution of the total energy in models ![]() $C$,
$C$, ![]() $M_1$ and
$M_1$ and ![]() $M_2$.
$M_2$.
Despite the eventual divergence of solutions between models ![]() $C$,
$C$, ![]() $M_1$ and
$M_1$ and ![]() $M_2$, we observe quite similar energy evolution, as shown in figure 3. Model
$M_2$, we observe quite similar energy evolution, as shown in figure 3. Model ![]() $M_2$ exhibits slightly better agreement with model
$M_2$ exhibits slightly better agreement with model ![]() $C$, although there are more significant oscillations in the gravitational and kinetic energy in model
$C$, although there are more significant oscillations in the gravitational and kinetic energy in model ![]() $C$. As shown in figure 2(c), model
$C$. As shown in figure 2(c), model ![]() $M_2$ maintains better energy conservation than model
$M_2$ maintains better energy conservation than model ![]() $M_1$ up to approximately
$M_1$ up to approximately ![]() $t = 3.5\,{\rm s}$, at which point the Mach number reaches
$t = 3.5\,{\rm s}$, at which point the Mach number reaches ![]() ${Ma} \simeq 0.4$. This suggests slightly better energy conservation when we include the
${Ma} \simeq 0.4$. This suggests slightly better energy conservation when we include the ![]() $\bar {\lambda }$ term in our equations.
$\bar {\lambda }$ term in our equations.

Figure 3. Evolution of energy contributions (as described in figure 1) in the Rayleigh–Taylor test for (a) model ![]() $C$, (b) model
$C$, (b) model ![]() $M_1$ and (c) model
$M_1$ and (c) model ![]() $M_2$.
$M_2$.
4.3. Rising and falling bubbles in an atmosphere
The test cases considered so far were adiabatic, and so the ‘thermodynamically consistent’ expression for the temperature, used in model ![]() $M_3$, had no effect on the results. We now present a test case involving both prescribed heat sources and thermal diffusion, in order to elucidate the effect of this change on the model. For this case the total heating,
$M_3$, had no effect on the results. We now present a test case involving both prescribed heat sources and thermal diffusion, in order to elucidate the effect of this change on the model. For this case the total heating, ![]() $Q$, has the form
$Q$, has the form
where ![]() $K$ is the thermal conductivity, which we take to be constant, and
$K$ is the thermal conductivity, which we take to be constant, and ![]() $\varPi _{t_0,t_1}$ is the boxcar function, meaning that external heating is applied only for
$\varPi _{t_0,t_1}$ is the boxcar function, meaning that external heating is applied only for ![]() $t_0\leqslant t\leqslant t_1$. By default, thermal diffusion is implemented in MAESTROeX in terms of the specific enthalpy (Malone et al. Reference Malone, Nonaka, Almgren, Bell and Zingale2011), but for this test case we use the alternative implementation in terms of temperature, so that we can work with the corrected temperature,
$t_0\leqslant t\leqslant t_1$. By default, thermal diffusion is implemented in MAESTROeX in terms of the specific enthalpy (Malone et al. Reference Malone, Nonaka, Almgren, Bell and Zingale2011), but for this test case we use the alternative implementation in terms of temperature, so that we can work with the corrected temperature, ![]() $T$, rather than
$T$, rather than ![]() $T_{EoS}$. This is important because, when the heating (4.5) is introduced into the heat equation (2.33), we find that
$T_{EoS}$. This is important because, when the heating (4.5) is introduced into the heat equation (2.33), we find that
So thermal diffusion introduces a positive-definite source of entropy, consistent with the second law of thermodynamics.
The initial pressure and density are chosen to be
which implies that the initial temperature, ![]() $T\propto P/\rho$, is linear in
$T\propto P/\rho$, is linear in ![]() $z$ and the initial specific entropy,
$z$ and the initial specific entropy, ![]() $s \propto \ln (P/\rho ^\gamma )$, is constant. This background state is chosen because it is steady and marginally stable to convection. The temperature gradient is fixed to its initial value at the top and bottom boundaries, so that there is no net heat flux into the domain. We use a domain of size
$s \propto \ln (P/\rho ^\gamma )$, is constant. This background state is chosen because it is steady and marginally stable to convection. The temperature gradient is fixed to its initial value at the top and bottom boundaries, so that there is no net heat flux into the domain. We use a domain of size ![]() $L_x = L_z = 2\,{\rm cm}$, with
$L_x = L_z = 2\,{\rm cm}$, with ![]() $1024 \times 1024$ grid cells. The parameter values are set as
$1024 \times 1024$ grid cells. The parameter values are set as ![]() $L = 2.5\,{\rm cm}$,
$L = 2.5\,{\rm cm}$, ![]() $P_0 = 1.65\times 10^6\,{\rm dyn}\,{\rm cm}^{-2}$,
$P_0 = 1.65\times 10^6\,{\rm dyn}\,{\rm cm}^{-2}$, ![]() $g = -1\times 10^9\,{\rm cm}\,{\rm s}^{-2}$ and
$g = -1\times 10^9\,{\rm cm}\,{\rm s}^{-2}$ and ![]() $K = 4\times 10^{4}\,{\rm erg}\,{\rm K}^{-1}\,{\rm cm}^{-1}\,{\rm s}^{-1}$.
$K = 4\times 10^{4}\,{\rm erg}\,{\rm K}^{-1}\,{\rm cm}^{-1}\,{\rm s}^{-1}$.
The form of the heating function, ![]() $f(x,z)$, is chosen to produce a number of positively or negatively buoyant ‘bubbles’, via localised heat sources:
$f(x,z)$, is chosen to produce a number of positively or negatively buoyant ‘bubbles’, via localised heat sources:
with the ![]() $i$th source centred at
$i$th source centred at ![]() $\boldsymbol {x}_i$, with a width
$\boldsymbol {x}_i$, with a width ![]() $w_i$ and an amplitude
$w_i$ and an amplitude ![]() $A_i$.
$A_i$.
We first consider the case of a single rising bubble, by taking ![]() $\boldsymbol {x}_1 = (1,0.7)\,{\rm cm}$,
$\boldsymbol {x}_1 = (1,0.7)\,{\rm cm}$, ![]() $A_1 = 1\times 10^{13}\,{\rm erg}\,{\rm cm}^{-3}\,{\rm s}^{-1}$ and
$A_1 = 1\times 10^{13}\,{\rm erg}\,{\rm cm}^{-3}\,{\rm s}^{-1}$ and ![]() $w_1 = 0.025\,{\rm cm}$. This heating is applied between
$w_1 = 0.025\,{\rm cm}$. This heating is applied between ![]() $t_0 = 1\times 10^{-5}\,{\rm s}$ and
$t_0 = 1\times 10^{-5}\,{\rm s}$ and ![]() $t_1 = 2\times 10^{-5}\,{\rm s}$. Figure 4 shows close-ups of the bubble at
$t_1 = 2\times 10^{-5}\,{\rm s}$. Figure 4 shows close-ups of the bubble at ![]() $t = 2\times 10^{-4}\,{\rm s}$, for models
$t = 2\times 10^{-4}\,{\rm s}$, for models ![]() $M_2$,
$M_2$, ![]() $M_3$ and
$M_3$ and ![]() $C$; this is the time at which differences between the simulations became measurable. We do not present results from model
$C$; this is the time at which differences between the simulations became measurable. We do not present results from model ![]() $M_1$ because in that simulation the velocity projection failed to converge, which suggests that the
$M_1$ because in that simulation the velocity projection failed to converge, which suggests that the ![]() $\bar {\lambda }$ term in the momentum equation is essential to this test case. Figure 4(a–c) shows temperature contours for each model; the contours for model
$\bar {\lambda }$ term in the momentum equation is essential to this test case. Figure 4(a–c) shows temperature contours for each model; the contours for model ![]() $C$ are slightly sharper, which we attribute to the different advection scheme used in CASTRO because all of the models have the same thermal conductivity. The differences between the models are made clearer by plotting the relative temperature differences, as is done in figure 4(d–f). We see that the temperature correction introduced in model
$C$ are slightly sharper, which we attribute to the different advection scheme used in CASTRO because all of the models have the same thermal conductivity. The differences between the models are made clearer by plotting the relative temperature differences, as is done in figure 4(d–f). We see that the temperature correction introduced in model ![]() $M_3$ is positive in the vicinity of the bubble, making that bubble slightly more buoyant compared to model
$M_3$ is positive in the vicinity of the bubble, making that bubble slightly more buoyant compared to model ![]() $M_2$. This correction to the temperature also produces a better agreement between models
$M_2$. This correction to the temperature also produces a better agreement between models ![]() $M_3$ and
$M_3$ and ![]() $C$. Figure 4(g–i) shows the local Mach number in the three models, which all agree to within 1 %.
$C$. Figure 4(g–i) shows the local Mach number in the three models, which all agree to within 1 %.

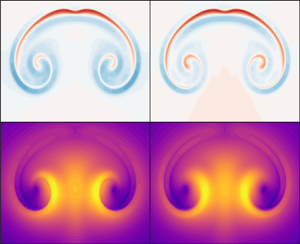
Figure 4. Contour plots of temperature for a single rising bubble at ![]() $t = 2\times 10^{-4}\,{\rm s}$ for cases
$t = 2\times 10^{-4}\,{\rm s}$ for cases ![]() $M_2, M_3$ and
$M_2, M_3$ and ![]() $C$ (a–c). (d–f) Relative temperature differences between plots in (a–c) as indicated in each panel. (g–i) Contours of Mach number corresponding to the cases as in (a–c).
$C$ (a–c). (d–f) Relative temperature differences between plots in (a–c) as indicated in each panel. (g–i) Contours of Mach number corresponding to the cases as in (a–c).
Figure 5 shows time series of energy in the same simulations. After the initial injection of heat, the total energy is conserved almost perfectly in model ![]() $C$ and to within
$C$ and to within ![]() $0.001\,\%$ in models
$0.001\,\%$ in models ![]() $M_2$ and
$M_2$ and ![]() $M_3$. Cases
$M_3$. Cases ![]() $M_2$ and
$M_2$ and ![]() $M_3$ are essentially indistinguishable; in both cases the gravitational potential energy steadily decreases as the bubble rises, leading to an increase in kinetic energy and internal energy (through dissipative heating). The kinetic energy in model
$M_3$ are essentially indistinguishable; in both cases the gravitational potential energy steadily decreases as the bubble rises, leading to an increase in kinetic energy and internal energy (through dissipative heating). The kinetic energy in model ![]() $C$ follows a very similar trajectory, as expected given the similarities in the flow seen in figure 4. However, the internal and gravitational energy terms in model
$C$ follows a very similar trajectory, as expected given the similarities in the flow seen in figure 4. However, the internal and gravitational energy terms in model ![]() $C$ exhibit a more dramatic, quasi-periodic oscillation, which we attribute to lack of hydrostatic balance in the horizontally averaged dynamics. The injection of heat in this fully compressible model establishes a gentle vertical ‘sloshing’ that is associated with very small velocities yet large changes in the internal and gravitational energy terms. In an attempt to reduce this effect, and allow a more meaningful comparison with model
$C$ exhibit a more dramatic, quasi-periodic oscillation, which we attribute to lack of hydrostatic balance in the horizontally averaged dynamics. The injection of heat in this fully compressible model establishes a gentle vertical ‘sloshing’ that is associated with very small velocities yet large changes in the internal and gravitational energy terms. In an attempt to reduce this effect, and allow a more meaningful comparison with model ![]() $C$, we have considered a second configuration with one rising bubble and one sinking bubble, as illustrated in figure 6. For this case, we place heat sources at
$C$, we have considered a second configuration with one rising bubble and one sinking bubble, as illustrated in figure 6. For this case, we place heat sources at ![]() $\boldsymbol {x}_+=(2/3,1)\,{\rm cm}$ and
$\boldsymbol {x}_+=(2/3,1)\,{\rm cm}$ and ![]() $\boldsymbol {x}_-=(4/3,1)\,{\rm cm}$, with amplitudes
$\boldsymbol {x}_-=(4/3,1)\,{\rm cm}$, with amplitudes ![]() $A = \pm 2\times 10^{13}\,{\rm erg}\,{\rm cm}^{-3}\,{\rm s}^{-1}$ and the same width
$A = \pm 2\times 10^{13}\,{\rm erg}\,{\rm cm}^{-3}\,{\rm s}^{-1}$ and the same width ![]() $w = 0.025\,{\rm cm}$. These heat sources are both applied between
$w = 0.025\,{\rm cm}$. These heat sources are both applied between ![]() $t_0 = 1\times 10^{-5}\,{\rm s}$ and
$t_0 = 1\times 10^{-5}\,{\rm s}$ and ![]() $t_1 = 7\times 10^{-5}\,{\rm s}$. For these simulations we use a numerical resolution of
$t_1 = 7\times 10^{-5}\,{\rm s}$. For these simulations we use a numerical resolution of ![]() $512\times 512$ grid cells. The energy evolution for this configuration is shown in figure 7 for models
$512\times 512$ grid cells. The energy evolution for this configuration is shown in figure 7 for models ![]() $C$,
$C$, ![]() $M_2$ and
$M_2$ and ![]() $M_3$. We note that the heat source and sink are not implemented exactly symmetrically, and so there is a slight drop in the total energy between times
$M_3$. We note that the heat source and sink are not implemented exactly symmetrically, and so there is a slight drop in the total energy between times ![]() $t_0$ and
$t_0$ and ![]() $t_1$. However, after this time the total energy is conserved just as well as in the single bubble case. There are still significant fluctuations in the gravitational and internal energy in model
$t_1$. However, after this time the total energy is conserved just as well as in the single bubble case. There are still significant fluctuations in the gravitational and internal energy in model ![]() $C$, but these are of much lower amplitude than in the single bubble case. Models
$C$, but these are of much lower amplitude than in the single bubble case. Models ![]() $M_2$ and
$M_2$ and ![]() $M_3$ again produce very similar results, although both have a slightly lower kinetic energy than model
$M_3$ again produce very similar results, although both have a slightly lower kinetic energy than model ![]() $C$. In model
$C$. In model ![]() $C$, as shown in figure 7(a), the gravitational potential energy remains nearly constant until
$C$, as shown in figure 7(a), the gravitational potential energy remains nearly constant until ![]() $t \simeq 3\times 10^{-5}\,{\rm s}$, which is roughly equal to the sound-crossing time in the domain. Up to this time, the imposed heating produces an increase in the local fluid pressure without much change in density. In models
$t \simeq 3\times 10^{-5}\,{\rm s}$, which is roughly equal to the sound-crossing time in the domain. Up to this time, the imposed heating produces an increase in the local fluid pressure without much change in density. In models ![]() $M_2$ and
$M_2$ and ![]() $M_3$, by contrast, the imposed heating produces an instantaneous expansion or contraction of the fluid, as dictated by the velocity constraint (3.4).
$M_3$, by contrast, the imposed heating produces an instantaneous expansion or contraction of the fluid, as dictated by the velocity constraint (3.4).

Figure 5. Evolution of the energy for the single rising bubble test for case ![]() $C$ (a), case
$C$ (a), case ![]() $M_2$ (b) and case
$M_2$ (b) and case ![]() $M_3$ (c). The plotted components are as described in figure 1. The time axis starts at
$M_3$ (c). The plotted components are as described in figure 1. The time axis starts at ![]() $t = 1\times 10^{-5}\,{\rm s}$, when the heating is turned on.
$t = 1\times 10^{-5}\,{\rm s}$, when the heating is turned on.

Figure 6. The temperature at ![]() $t=1.9\times 10^{-4}\,{\rm s}$, minus the initial temperature, in the two-bubble test with model
$t=1.9\times 10^{-4}\,{\rm s}$, minus the initial temperature, in the two-bubble test with model ![]() $C$. (The results of models
$C$. (The results of models ![]() $M_2$ and
$M_2$ and ![]() $M_3$ are very similar.)
$M_3$ are very similar.)

Figure 7. Evolution of the energy as in figure 5, but for the rising and falling bubble test.
5. Summary and discussion
By formulating an appropriate action, we have derived a hybrid pseudo-incompressible– hydrostatic model that conserves energy. In the case of closed boundaries, the velocity must satisfy a degenerate constraint equation, and this degeneracy is broken by requiring that the energy flux through the boundaries vanishes. We have implemented this model within the existing MAESTROeX framework and validated it in a number of test cases, including comparison with results from the fully compressible code CASTRO. Our changes to the MAESTROeX algorithm generally have a small effect on the numerical results, but in at least some cases they produce better energy conservation and better agreement with the fully compressible code. The main benefit of using a sound-proof model is that larger time steps can be used. For example, in the case shown in figure 4, we used a time step of ![]() $3.28\times 10^{-7}\,{\rm s}$, whereas CASTRO required a time step of
$3.28\times 10^{-7}\,{\rm s}$, whereas CASTRO required a time step of ![]() $3.34\times 10^{-8}\,{\rm s}$, a factor of 10 smaller. In our test cases the Mach number was typically
$3.34\times 10^{-8}\,{\rm s}$, a factor of 10 smaller. In our test cases the Mach number was typically ![]() ${Ma} \simeq 0.5$, whereas in many practical applications one would have
${Ma} \simeq 0.5$, whereas in many practical applications one would have ![]() ${Ma} \ll 1$, in which case a sound-proof model becomes much more efficient, as well as more accurate. Of course, the time step may still be limited by other factors, such as the presence of high-frequency internal gravity waves (Higl, Müller & Weiss Reference Higl, Müller and Weiss2021). In such cases, other numerical techniques such as Runge–Kutta time integration may lead to greater numerical stability.
${Ma} \ll 1$, in which case a sound-proof model becomes much more efficient, as well as more accurate. Of course, the time step may still be limited by other factors, such as the presence of high-frequency internal gravity waves (Higl, Müller & Weiss Reference Higl, Müller and Weiss2021). In such cases, other numerical techniques such as Runge–Kutta time integration may lead to greater numerical stability.
Although we have chosen to focus on the case of closed boundary conditions, the approach we have outlined can also be applied to the case of ‘open’ boundary conditions. If either the lower or upper boundary is open then the background pressure should be evolved according to (2.37) but with the ![]() $\dot {P}_b$ term set to zero, as is already implemented in MAESTROeX. As mentioned in § 2.4, this ensures that there are no unphysical boundary fluxes associated with the Lagrange multiplier
$\dot {P}_b$ term set to zero, as is already implemented in MAESTROeX. As mentioned in § 2.4, this ensures that there are no unphysical boundary fluxes associated with the Lagrange multiplier ![]() $\mu$. For similar reasons, the other Lagrange multiplier,
$\mu$. For similar reasons, the other Lagrange multiplier, ![]() $\lambda$, should be set to zero on any open boundaries; this also removes any degeneracy when calculating the velocity correction.
$\lambda$, should be set to zero on any open boundaries; this also removes any degeneracy when calculating the velocity correction.
All of the numerical test cases we have presented here involve a single (ideal) gas, but MAESTROeX is designed for multi-fluid applications with complex reaction networks. In such applications the reaction rates are often very temperature-sensitive, and we plan to test whether using the corrected temperature, rather than ![]() $T_{EoS}$, produces more accurate results.
$T_{EoS}$, produces more accurate results.
Acknowledgements
We thank J. Thurgood for his work on the early stages of this project. We also thank M. Zingale, A. Harpole, D. Fan, A. Nonaka and M. Katz for helpful discussions about this work and about the MAESTROeX code.
Funding
This work was supported by EPSRC grant EP/R024952/1.
Declaration of interests
The authors report no conflict of interest.
Data availability statement
Data used to produce figures can be found at https://doi.org/10.25405/data.ncl.c.5752439.
Appendix A. Unsplit velocity projection
We would like to solve the equation
subject to the boundary condition
on the upper and lower boundaries, which is obtained via (3.6), taking ![]() $\boldsymbol {u}$ to satisfy the impenetrable boundary condition.
$\boldsymbol {u}$ to satisfy the impenetrable boundary condition.
We consider the adjoint of (A1), using ![]() $\phi ^{\dagger}$ to denote the adjoint variable. Since the operator on the left-hand side of this equation is self-adjoint with respect to the usual
$\phi ^{\dagger}$ to denote the adjoint variable. Since the operator on the left-hand side of this equation is self-adjoint with respect to the usual ![]() $L^2$-norm, the adjoint problem is simply the homogeneous version of (A1)–(A2):
$L^2$-norm, the adjoint problem is simply the homogeneous version of (A1)–(A2):
with boundary condition
The solution of this adjoint problem is unique, up to a constant multiplicative factor. Multiplying (A1) by this solution, integrating by parts and applying the boundary conditions for ![]() $\phi$ and
$\phi$ and ![]() $\phi ^{\dagger}$, we eventually obtain the solvability condition
$\phi ^{\dagger}$, we eventually obtain the solvability condition
Therefore, assuming that the adjoint solution ![]() $\phi ^{\dagger}$ can be computed, the necessary value for
$\phi ^{\dagger}$ can be computed, the necessary value for ![]() $\dot {P}_b$ can be expressed as the ratio of two domain integrals. We recover our result (3.10) if we approximate
$\dot {P}_b$ can be expressed as the ratio of two domain integrals. We recover our result (3.10) if we approximate ![]() $\phi ^{\dagger} \simeq P^{-1/\gamma }$ and
$\phi ^{\dagger} \simeq P^{-1/\gamma }$ and ![]() $\tilde {u}_z^{\dagger} = \tilde {u}_z$; these approximations become exact if
$\tilde {u}_z^{\dagger} = \tilde {u}_z$; these approximations become exact if ![]() $\rho$ happens to be a function of
$\rho$ happens to be a function of ![]() $z$ only, in which case we recover the formula (2.40) of O'Neill & Klein (Reference O'Neill and Klein2014).
$z$ only, in which case we recover the formula (2.40) of O'Neill & Klein (Reference O'Neill and Klein2014).
For this value of ![]() $\dot {P}_b$, (A1) can be solved for
$\dot {P}_b$, (A1) can be solved for ![]() $\phi$, up to an arbitrary multiple of
$\phi$, up to an arbitrary multiple of ![]() $\phi ^{\dagger}$. As in § 3, this remaining degeneracy is removed by the requirement that the domain average of
$\phi ^{\dagger}$. As in § 3, this remaining degeneracy is removed by the requirement that the domain average of ![]() $\phi /P^{1-1/\gamma }$ must be zero.
$\phi /P^{1-1/\gamma }$ must be zero.
Appendix B. Auxiliary evolution equations
The general hybrid equations (2.31)–(2.34) can be used to obtain evolution equations for other thermodynamic quantities, e.g. the specific internal energy, ![]() $U(\rho,s)$, or the specific enthalpy,
$U(\rho,s)$, or the specific enthalpy, ![]() $H = U + P/\rho$:
$H = U + P/\rho$:
We note that, in both cases, the applied heating, ![]() $Q$, must be multiplied by the correction factor
$Q$, must be multiplied by the correction factor ![]() $T_{EoS}/T$.
$T_{EoS}/T$.