Hostname: page-component-669899f699-chc8l Total loading time: 0 Render date: 2025-05-04T01:53:01.207Z Has data issue: false hasContentIssue false
  • English
  • Français

The Schwarzian norm estimates for Janowski convex functions

Part of: Geometric function theory

Published online by Cambridge University Press:  12 February 2024

Md Firoz Ali Open the ORCID record for Md Firoz Ali [Opens in a new window]  and
Sanjit Pal Open the ORCID record for Sanjit Pal [Opens in a new window]
Md Firoz Ali
Affiliation:
Department of Mathematics, National Institute of Technology Durgapur, Durgapur 713209, West Bengal, India ([email protected]; [email protected]; [email protected])
Sanjit Pal
Affiliation:
Department of Mathematics, National Institute of Technology Durgapur, Durgapur 713209, West Bengal, India ([email protected]; [email protected]; [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

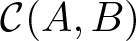For $-1\leq B \lt A\leq 1$, let $\mathcal{C}(A,B)$ denote the class of normalized Janowski convex functions defined in the unit disk $\mathbb{D}:=\{z\in\mathbb{C}:|z| \lt 1\}$ that satisfy the subordination relation $1+zf''(z)/f'(z)\prec (1+Az)/(1+Bz)$. In the present article, we determine the sharp estimate of the Schwarzian norm for functions in the class $\mathcal{C}(A,B)$. The Dieudonné’s lemma which gives the exact region of variability for derivatives at a point of bounded functions, plays the key role in this study, and we also use this lemma to construct the extremal functions for the sharpness by a new method.

Keywords

analytic functionsunivalent functionsJanowski convex functionsSchwarzian norm

MSC classification

Primary: 30C45: Special classes of univalent and multivalent functions (starlike, convex, bounded rotation, etc.) 30C55: General theory of univalent and multivalent functions
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 67 , Issue 2 , May 2024 , pp. 299 - 315
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Ahlfors, L. V. and Weill, G., A uniqueness theorem for Beltrami equations, Proc. Amer. Math. Soc. 13 (1962), 975–978.CrossRefGoogle Scholar
Ali, M. F. and Pal, S., Schwarzian norm estimates for some classes of analytic functions, Mediterr. J. Math. 20 (2023), .CrossRefGoogle Scholar
Bhowmik, B. and Wirths, K. J., A sharp bound for the Schwarzian derivative of concave functions, Colloq. Math. 128(2) (2012), 245–251.CrossRefGoogle Scholar
Chiang, Y. M., Schwarzian derivative and second order differential equations, Ph.D. thesis, (Univ. of London, 1991).Google Scholar
Dieudonné, J. A., Recherches sur quelques problèmes relatifs aux polynômes et aux fonctions bornées d’une variable complexe, Ann. Sci. Éc. Norm. Supér. 48 (1931), 247–358.CrossRefGoogle Scholar
Duren, P. L., Univalent functions, (Grundlehren der mathematischen Wissenschaften 259), (New York, Berlin, Heidelberg, Tokyo, 1983).Google Scholar
Fait, M., Krzyż, J. G. and Zygmunt, J., Explicit quasiconformal extensions for some classes of univalent functions, Comment. Math. Helv. 51 (1976), 279–285.CrossRefGoogle Scholar
Goodman, A. W.. Univalent functions, Vols. I and II (Mariner Publishing Co., Tampa, Florida, 1983).Google Scholar
Goodman, A. W., On uniformly convex functions, Ann. Polon. Math. 56(1) (1991), 87–92.CrossRefGoogle Scholar
Janowski, W., Some extremal problems for certain families of analytic functions I, Ann. Polon. Math. 28 (1973), 297–326.CrossRefGoogle Scholar
Janowski, W., Some extremal problems for certain families of analytic functions II, Bull. Acad. Polon. Sci. Ser. Sci. Math. Astron. Phys. 21 (1973) 17–25.Google Scholar
Sugawa, T., A self-duality of strong starlikeness, Kodai Math. J. 28 (2005), 382–389.CrossRefGoogle Scholar
Kanas, S. and Sugawa, T., Strong starlikeness for a class of convex functions, J. Math. Anal. Appl. 336 (2007), 1005–1017.CrossRefGoogle Scholar
Kanas, S. and Sugawa, T., Sharp norm estimate of Schwarzian derivative for a class of convex functions, Ann. Polon. Math. 101(1) (2011), 75–86.CrossRefGoogle Scholar
Kim, Y.C. and Sugawa, T., Norm estimates of the pre-Schwarzian derivatives for certain classes of univalent functions, Proc. Edinb. Math. Soc. 49(1) (2006), 131–143.CrossRefGoogle Scholar
Kraus, W., Über den Zusamenhang einiger Charakteristiken eines einfach zusammenhängenden Bereiches mit der Kreisabbildung, Mitt. Math. Sem., Giessen 21 (1932), 1–28.Google Scholar
Kühnau, R., Verzerrungssätze und Koeffizientenbedingungen vom Grunskyschen Typ für quasikonforme Abbildungen, Math. Nachr. 48 (1971), 77–105.CrossRefGoogle Scholar
Lehto, O., Domain constants associated with Schwarzian derivative, Comment. Math. Helv. 52 (1977), 603–610.CrossRefGoogle Scholar
Lehto, O., Univalent functions and Teichmüller spaces, (New York: Springer-Verlag, 1987).CrossRefGoogle Scholar
Ma, W. and Minda, D., Uniformly convex functions, Ann. Polon. Math. 57 (1992), 165–175.CrossRefGoogle Scholar
Nehari, Z., The Schwarzian derivative and schlicht functions, Bull. Amer. Math. Soc. 55(6) (1949), 545–551.CrossRefGoogle Scholar
Nehari, Z., A property of convex conformal maps, J. Anal. Math. 30 (1976), 390–393.CrossRefGoogle Scholar
Ponnusamy, S. and Sahoo, S. K., Norm estimates for convolution transforms of certain classes of analytic functions, J. Math. Anal. Appl. 342 (2008), 171–180.CrossRefGoogle Scholar
Robertson, M. S., The theory of univalent functions, Ann. Math. 2) 37 (1936), 374–408.CrossRefGoogle Scholar
Robertson, M. S., Univalent functions f(z) for which zf’(z) is spirallike, Michigan Math. J. 16 (1969), 97–101.CrossRefGoogle Scholar
Rønning, F., Uniformly convex functions and a corresponding class of starlike functions, Proc. Amer. Math. Soc. 118 (1993), 189–196.CrossRefGoogle Scholar
Silverman, H. and Silvia, E. M., Subclasses of starlike functions subordinate to convex functions, Canad. J. Math. 37(1) (1985), 48–61.CrossRefGoogle Scholar
Suita, N., Schwarzian derivatives of convex functions, J. Hokkaido Univ. Ed. Sect. II A 46 (1996), 113–117.Google Scholar