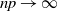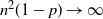Average Jaccard index of random graphs

Abstract

The asymptotic behavior of the Jaccard index in G(n, p), the classical Erdös–Rényi random graph model, is studied as n goes to infinity. We first derive the asymptotic distribution of the Jaccard index of any pair of distinct vertices, as well as the first two moments of this index. Then the average of the Jaccard indices over all vertex pairs in G(n, p) is shown to be asymptotically normal under an additional mild condition that $np\to\infty$ and $n^2(1-p)\to\infty$.

1. Introduction

The Jaccard index, also known as the Jaccard similarity coefficient, was originally introduced by Paul Jaccard to measure the similarity between two sets [13]. For any two finite sets $\mathcal{A}$ and $\mathcal{B}$ , the Jaccard index $J(\mathcal{A},\mathcal{B})$ is the ratio of the size of their intersection to the size of their union. That is,

\begin{equation*} J(\mathcal{A},\mathcal{B}) = \frac{|\mathcal{A}\cap \mathcal{B}|}{|\mathcal{A}\cup \mathcal{B}|} = \frac{|\mathcal{A}\cap \mathcal{B}|}{|\mathcal{A}|+|\mathcal{B}|-|\mathcal{A}\cap \mathcal{B}|},\end{equation*}

where the symbol $|\cdot|$ denotes the cardinality of a set. It is clear that this index ranges from 0 to 1. The associated Jaccard distance for quantifying the dissimilarity between two sets is defined as one minus the Jaccard index (see, e.g., [11, 17]). In statistics and data science, the Jaccard index is employed as a statistic to measure the similarity between sample sets, especially for binary and categorical data (see, e.g., [6, 15]). For extensive generalizations of the Jaccard index in many other mathematical structures, such as scalars, vectors, matrices, and multisets, we refer the reader to [7]. Due to its simplicity and popularity, many applications of the Jaccard index and its variants have been developed in various fields, such as cell formation [29], pattern recognition [12], data mining [24], natural language processing [27], recommendation systems [3], medical image segmentation [8], and machine learning [1].

Following the original definition on sets, the Jaccard index of two vertices in a graph can naturally be extended to equal the number of common neighbors divided by the number of vertices that are neighbors of at least one of them (see, e.g., [9]). As a graph benchmark suitable for real-world applications, the Jaccard index has also been proposed to determine the similarity in graphs or networks [16], because of its clear interpretability and computational scalability. This index, as well as its variants, is employed to find core nodes for community detection in complex networks [4, 20], to estimate the coupling strength between temporal graphs [19], and to do link prediction [18, 21, 30], among others.

Erdös–Rényi random graphs are widely used as a benchmark model in statistical network analysis (see, e.g., [2, 26]). In the simulation study of [22], it is shown that the empirical cumulative distribution functions of Jaccard indices over all vertex pairs in two network models, the Erdös–Rényi random graph and the stochastic block model, are quite different. Despite the widespread applications of the Jaccard index in network analysis, to the best of our knowledge there is a lack of comprehensive study of theoretical results on this simple index defined on statistical graph models. As the first step toward filling this gap, our main concern in this paper is derive the asymptotic behavior of the basic Jaccard index in Erdös–Rényi random graphs. For numerous probabilistic results on this classical random graph model we refer the reader to [5, 14, 25].

Throughout this paper we use the following notation. For any integer $n\ge2$ , we denote by [n] the vertex set $\{1,2,\ldots,n\}$ . For an event ${\mathcal E}$ , let $|{\mathcal E}|$ be the cardinality, $\overline{\mathcal E}$ the complement, and $\mathbf{1}({\mathcal E})$ the indicator of ${\mathcal E}$ . For real numbers a, b, we write $a\vee b$ to denote the maximum of a and b. For probabilistic convergence, we use $\buildrel \textrm{D} \over \longrightarrow $ and $\buildrel \textrm{P} \over \longrightarrow$ to denote convergence in distribution and in probability, respectively.

The rest of this paper is organized as follows. The Jaccard index of any pair of distinct vertices in the Erdös–Rényi random graph G(n, p) is considered in Section 2. We first compute the mean and variance of this index, and then obtain the phase changes of its asymptotic distribution for $p\in [0,1]$ in all regimes as $n\to \infty$ . In Section 3, we prove the asymptotic normality of the average of the Jaccard indices over all vertex pairs in G(n, p) as $np\to \infty$ and $n^2(1-p)\to \infty$ .

2. Jaccard index of a vertex pair

Let us denote by G(n, p) an Erdös–Rényi random graph on the vertex set [n], where each edge is present independently with probability p. In this paper we consider $p = p(n)$ as a function of the graph size n. For any two vertices $i, j \in [n]$ , let $\mathbf{1}_{ij}$ be the indicator that takes the value 1 if an edge between i and j is present in G(n, p), and takes the value 0 otherwise. It follows that $\mathbf{1}_{ii} = 0$ , $\mathbf{1}_{ij} = \mathbf{1}_{ji}$ , and $\{\mathbf{1}_{ij} \,:\, 1 \leq i < j \leq n\}$ is a sequence of independent Bernoulli variables with success rate p. The $n\times n$ matrix $\boldsymbol{A}=(\mathbf{1}_{ij})$ is usually called the adjacent matrix of G(n, p), and is a symmetric matrix with all diagonal entries equal to zero.

For any vertex $i\in[n]$ , let the set ${\mathcal N}_i$ be its neighborhood, i.e., ${\mathcal N}_{i}=\{k\,:\,\mathbf{1}_{ik}=1, k\in [n]\}$ . For any pair of vertices $i,j\in[n]$ , we also define their union neighborhood as

\begin{equation*} {\mathcal N}_{ij} = \{k\,:\,\mathbf{1}_{ik}\vee \mathbf{1}_{jk}=1,\,k\in[n]\,\mbox{and}\,k\neq i,j\}, \quad i\neq j.\end{equation*}

Notice that here the neighborhood set ${\mathcal N}_{ij}$ does not contain vertices i and j themselves, even if $\mathbf{1}_{ij}=1$ . Then the Jaccard index of vertices i and j in G(n, p) is formally defined as

(1) \begin{equation} J_{ij}^{(n)} = \frac{|{\mathcal N}_{i}\cap {\mathcal N}_{j}|}{|{\mathcal N}_{ij}|} \,=\!:\, \frac{S_{ij}^{(n)}}{T_{ij}^{(n)}}, \quad i\neq j.\end{equation}

We can see that the index $J_{ij}^{(n)}$ given in (1) is not well defined when ${\mathcal N}_{ij}$ is an empty set or $T_{ij}^{(n)}=0$ . For convenience, following the idea in [6], we define $J_{ij}^{(n)}=p/(2-p)$ in this special case. Indeed, it is shown later that the conditional expectation of $J_{ij}^{(n)}$ is exactly $p/(2-p)$ given that $T_{ij}^{(n)}>0$ . In terms of the adjacent matrix $\boldsymbol{A}$ , the numerator and denominator in (1) can be rewritten as

(2) \begin{equation} S_{ij}^{(n)} = \sum\limits_{k\neq i,j}\mathbf{1}_{ik}\mathbf{1}_{jk}, \qquad T_{ij}^{(n)} = \sum\limits_{k\neq i,j}\mathbf{1}_{ik} \vee \mathbf{1}_{jk}.\end{equation}

Due to the independence of the elements in $\boldsymbol{A}$ , it is clear that the random variables $S_{ij}^{(n)}$ and $T_{ij}^{(n)}$ follow the binomial distributions $\textrm{Bin}(n-2,p^2)$ and $\textrm{Bin}(n-2,p(2-p))$ , respectively. Hence, the Jaccard index of a vertex pair in G(n, p) is a quotient of two dependent binomial random variables.

2.1. Mean and variance

We first calculate the mean and variance of the Jaccard index of any pair of vertices in G. By (1) and (2), we can see that $\big\{J_{ij}^{(n)},\, 1\le i<j\le n\big\}$ is a sequence of random variables that are pairwise dependent but identically distributed. Without loss of generality, we only consider $J_{12}^{(n)}$ .

For any vertex $3\le k\le n$ , the conditional probability

\begin{equation*} \mathbb{P}(\mathbf{1}_{1k}\mathbf{1}_{2k}=1 \mid \mathbf{1}_{1k} \vee \mathbf{1}_{2k} = 1) = \frac{\mathbb{P}(\mathbf{1}_{1k}\mathbf{1}_{2k} = 1)}{\mathbb{P}(\mathbf{1}_{1k} \vee \mathbf{1}_{2k} = 1)} = \frac{p}{2-p},\end{equation*}

which is independent of k. Then, for any positive integer $1\le m\le n-2$ , given the event $T_{12}^{(n)}=m$ , the conditional distribution of $S_{12}^{(n)}$ is $\textrm{Bin}(m,p/(2-p))$ , due to independence of the indicators $\{\mathbf{1}_{1k},\mathbf{1}_{2k},\,3\le k\le n\}$ . Consequently, we have

(3) \begin{align} {\mathbb E}\Big[S_{12}^{(n)} \mid T_{12}^{(n)} = m\Big] & = \frac{mp}{2-p}, \end{align}

(4) \begin{align} \textrm{Var}\Big[S_{12}^{(n)} \mid T_{12}^{(n)} = m\Big] & = \frac{2mp(1-p)}{(2-p)^{2}}. \end{align}

Noting that $J_{12}^{(n)}=p/(2-p)$ in the special case $T_{12}^{(n)}=0$ , by (1) and (3) we thus have ${\mathbb E}\Big[J_{12}^{(n)} \mid T_{12}^{(n)}\Big] = {p}/({2-p})$ , which implies that ${\mathbb E}\Big[J_{12}^{(n)}\Big]=p/(2-p)$ and $\textrm{Var}\Big[{\mathbb E}\Big(J_{12}^{(n)} \mid T_{12}^{(n)}\Big)\Big] = 0$ . Using the law of total variance, it follows from this and (4) that

(5) \begin{align} \textrm{Var}\Big[J_{12}^{(n)}\Big] = {\mathbb E}\Big[\textrm{Var}\Big(J_{12}^{(n)} \mid T_{12}^{(n)}\Big)\Big] & = \sum_{m=1}^{n-2}{\mathbb P}\Big(T_{12}^{(n)} = m\Big) \textrm{Var}\bigg[\frac{S_{12}^{(n)}}{m} \mid T_{12}^{(n)} = m\bigg] \notag \\ & = \frac{2p(1-p)}{(2-p)^{2}}\sum_{m=1}^{n-2}\frac{1}{m}{\mathbb P}\Big(T_{12}^{(n)}=m\Big),\end{align}

which involves the first inverse moment of the binomial distribution. Recalling that $T_{12}^{(n)}$ has the distribution $\textrm{Bin}(n-2,p(2-p))$ , it follows by [28, Corollary 1] that

(6) \begin{equation} \sum_{m=1}^{n-2}\frac{1}{m}{\mathbb P}\Big(T_{12}^{(n)} = m\Big) = \frac{1}{np(2-p)}\bigg(1 + O\bigg(\frac{1}{np}\bigg)\bigg)\end{equation}

as $np\to\infty$ . By (5) and (6), we thus have

\begin{equation*} \textrm{Var}\Big[J_{12}^{(n)}\Big] = \frac{2(1-p)}{n(2-p)^{3}}\bigg(1 + O\bigg(\frac{1}{np}\bigg)\bigg).\end{equation*}

Collecting the above findings, by Chebyshev’s inequality we thus prove the following result.

Proposition 1. Let $J_{ij}^{(n)}$ be the Jaccard index of any distinct vertices $i,j\in[n]$ in G(n,p). Then ${\mathbb E}\Big[J_{ij}^{(n)}\Big]=p/(2-p)$ for all $n\ge 2$ . In particular, as $np\to\infty$ , it further follows that

\begin{equation*} \textrm{Var}\Big[J_{ij}^{(n)}\Big] = \frac{2(1-p)}{n(2-p)^{3}}\bigg(1 + O\bigg(\frac{1}{np}\bigg)\bigg), \end{equation*}

and $J_{ij}^{(n)}-p/(2-p)$ converges to 0 in probability.

2.2. Asymptotic distribution

We now establish the asymptotic distribution of the Jaccard index of any vertex pair in G(n, p).

Theorem 1. Let $J_{ij}^{(n)}$ be the Jaccard index of any distinct vertices $i,j\in[n]$ in G(n,p).

1. (i) If $np^{2}(1-p)\to\infty$ , then

   \begin{equation*} \sqrt{\frac{n(2-p)^{3}}{2(1-p)}}\bigg(J_{ij}^{(n)}-\frac{p}{2-p}\bigg) \buildrel \textrm{D} \over \longrightarrow Z, \end{equation*}
   where Z denotes a standard normal random variable.

2. (ii) If $np^2\to \lambda$ for some constant $\lambda>0$ , then $2npJ_{ij}^{(n)}\buildrel \textrm{D} \over \longrightarrow \textrm{Poi}(\lambda)$ , where $\textrm{Poi}(\lambda)$ denotes the Poisson distribution with parameter $\lambda$ .

3. (iii) If $np^2\to0$ , then $npJ_{ij}^{(n)}\buildrel \textrm{P} \over \longrightarrow 0$ .

4. (iv) If $n(1-p)\to c$ for some constant $c>0$ , then $n\Big(1-J_{ij}^{(n)}\Big)\buildrel \textrm{D} \over \longrightarrow \textrm{Poi}(2c)$ .

5. (v) If $n(1-p)\to 0$ , then $n\big(1-J_{ij}^{(n)}\big)\buildrel \textrm{P} \over \longrightarrow 0$ .

Proof. As presented in the previous subsection, it is sufficient to consider a single index $J_{12}^{(n)}$ . To prove (i), we first rewrite

(7) \begin{align} \sqrt{\frac{(n-2)(2-p)^{3}}{2(1-p)}}\bigg(J_{12}^{(n)}-\frac{p}{2-p}\bigg) & = \sqrt{\frac{(n-2)(2-p)}{2(1-p)}}\cdot\frac{(2-p)S_{12}^{(n)}-pT_{12}^{(n)}}{T_{12}^{(n)}} \notag \\ & = \frac{(2-p)S_{12}^{(n)}-pT_{12}^{(n)}}{\sqrt{2(n-2)p^{2}(1-p)(2-p)}\,}\cdot\frac{(n-2)p(2-p)}{T_{12}^{(n)}}. \end{align}

For any distinct vertices $i,j,k\in[n]$ , we write

(8) \begin{equation} V_{ij,k} = (2-p)\mathbf{1}_{ik}\mathbf{1}_{jk}-p(\mathbf{1}_{ik}\vee \mathbf{1}_{jk}). \end{equation}

Then, for any fixed two vertices $i,j\in[n]$ , the random variables $\{V_{ij,k},\,k\in[n],k\neq i,j\}$ are independent and identically distributed with common mean 0 and common variance $2p^{2}(1-p)$ $(2-p)$ . Since it follows by (2) that

(9) \begin{equation} (2-p)S_{12}^{(n)} - pT_{12}^{(n)} = \sum_{k=3}^{n} V_{12,k}, \end{equation}

a direct application of the Lindeberg–Feller central limit theorem yields

(10) \begin{equation} \frac{(2-p)S_{12}^{(n)}-pT_{12}^{(n)}}{\sqrt{2(n-2)p^{2}(1-p)(2-p)}\,} \buildrel \textrm{D} \over \longrightarrow Z \end{equation}

whenever $np^2(1-p)\to\infty$ . By Chebyshev’s inequality, the fact that $T_{12}^{(n)}\sim \textrm{Bin}((n-2),$ $p(2-p))$ gives us that, as $np\to\infty$ ,

(11) \begin{equation} \frac{T_{12}^{(n)}}{(n-2)p(2-p)}\buildrel \textrm{P} \over \longrightarrow 1, \end{equation}

which, together with (7) and (10), proves (i) by Slutsky’s lemma.

If $np^{2}\to \lambda$ for some constant $\lambda>0$ , we must have that $p\to 0$ and $np\to\infty$ . Since $S_{12}^{(n)}\sim \textrm{Bin}(n-2,p^2)$ , the Poisson limit theorem yields that $S_{12}^{(n)}\buildrel \textrm{D} \over \longrightarrow \textrm{Poi}(\lambda)$ . By (11), again using Slutsky’s lemma, we obtain

\begin{equation*} 2npJ_{12}^{(n)} = \frac{2np}{T_{12}^{(n)}}\cdot S_{12}^{(n)}\buildrel \textrm{D} \over \longrightarrow \textrm{Poi}(\lambda), \end{equation*}

which proves (ii).

If $np^2\to0$ , to prove (iii) we only need to prove that the probability ${\mathbb P}\Big(npJ_{ij}^{(n)}>np^2/$ $(2-p)\Big)$ tends to 0. Note that if the event $\Big\{S_{12}^{(n)}=0\Big\}$ occurs, the Jaccard index $J_{ij}^{(n)}$ must be 0 or $p/(2-p)$ . Therefore,

\begin{equation*} {\mathbb P}\bigg(npJ_{ij}^{(n)}>\frac{np^2}{2-p}\bigg) = {\mathbb P}\bigg(J_{ij}^{(n)}>\frac{p}{2-p}\bigg) \le {\mathbb P}\Big(S_{12}^{(n)}\neq0\Big) = 1 - {\mathbb P}\Big(S_{12}^{(n)}=0\Big). \end{equation*}

Again by the fact that $S_{12}^{(n)}\sim \textrm{Bin}(n-2,p^2)$ , we have $1-{\mathbb P}\big(S_{12}^{(n)}=0\big)\to 0$ if $np^2\to0$ . This implies (iii).

Analogously to (7), we have

(12) \begin{equation} \frac{p}{2-p}-J_{12}^{(n)} = \frac{-(2-p)S_{12}^{(n)}+pT_{12}^{(n)}}{(n-2)p(2-p)^2} \cdot \frac{(n-2)p(2-p)}{T_{12}^{(n)}}. \end{equation}

Note that (11) still holds, and $n[1-p/(2-p)]$ has the limit 2c if $n(1-p)\to c$ for some constant $c>0$ . To prove (iv), by (12) it is now sufficient to show that

(13) \begin{equation} -(2-p)S_{12}^{(n)}+pT_{12}^{(n)}\buildrel \textrm{D} \over \longrightarrow \textrm{Poi}(2c)-2c. \end{equation}

For any distinct vertices $i,j,k\in[n]$ , we can directly obtain from (8) that the characteristic function of $-V_{ij,k}$ is

\begin{equation*} f_n(t) = {\mathbb E}\big[\textrm{e}^{-\textrm{i}tV_{ij,k}}\big] = p^2\textrm{e}^{-2\textrm{i}t(1-p)} + 2p(1-p)\textrm{e}^{\textrm{i}tp}+(1-p)^2, \end{equation*}

where $\textrm{i}=\sqrt{-1}$ denotes the imaginary unit. Then, by (9) and independence, we have that the characteristic function of $-(2-p)S_{12}^{(n)}+pT_{12}^{(n)}$ is equal to

\begin{equation*} f_n^{n-2}(t) = \big[p^2\textrm{e}^{-2\textrm{i}t(1-p)}+2p(1-p)\textrm{e}^{\textrm{i}tp}+(1-p)^2\big]^{n-2}, \quad t\in\mathbb{R}. \end{equation*}

Note that

\begin{align*} \lim_{n\to\infty}n\big[p^2\textrm{e}^{-2\textrm{i}t(1-p)}+2p(1-p)\textrm{e}^{\textrm{i}tp}+(1-p)^2-1\big] & = 2c\textrm{e}^{\textrm{i}t}+\lim_{n\to\infty}n\big[p^2\textrm{e}^{-2\textrm{i}t(1-p)}-1\big] \\ & = 2c\textrm{e}^{\textrm{i}t}+\lim_{n\to\infty}n\big[p^2\big(\textrm{e}^{-2\textrm{i}t(1-p)}-1\big)\\ & \quad +\big(p^2-1\big)\big] \\ & = 2c\big(\textrm{e}^{\textrm{i}t}-\textrm{i}t-1\big) \end{align*}

if $n(1-p)\to c$ . Therefore, the limit of the characteristic function of $-(2-p)S_{12}^{(n)}+pT_{12}^{(n)}$ satisfies

\begin{equation*} \lim_{n\to\infty}f_n^{n-2}(t)=\exp\big\{2c\big(\textrm{e}^{\textrm{i}t}-\textrm{i}t-1\big)\big\}, \end{equation*}

which implies (13) and completes the proof of (iv).

We only sketch the proof of (v), since it is very similar to (iv). By (11) and (12), it is sufficient to show that $-(2-p)S_{12}^{(n)}+pT_{12}^{(n)}$ converges in probability to 0 under the condition $n(1-p)\to 0$ . In fact, following the proof of (13), in this case we can deduce that its characteristic function $f_n^{n-2}(t)\to 1$ .

3. Average Jaccard index

In this section we derive asymptotic properties of the average Jaccard index of G(n, p), which is given by

(14) \begin{equation} J_n = \frac{2}{n(n-1)}\sum_{i=1}^{n-1} \sum_{j=i+1}^n J_{ij}^{(n)}.\end{equation}

That is, the average Jaccard index $J_n$ is the average of the Jaccard indices over all vertex pairs in the Erdös–Rényi random graph G(n, p). An immediate consequence of Proposition 1 is that the expectation of $J_n$ is equal to $p/(2-p)$ .

We now state the main results of this paper.

Theorem 2. Let $J_n$ be the average Jaccard index of G(n,p). If $np\to\infty$ and $n^2(1-p)\to\infty$ , then

\begin{equation*} \frac{n(2-p)^2}{\sqrt{8p(1-p)}\,}\bigg(J_n-\frac{p}{2-p}\bigg)\buildrel \textrm{D} \over \longrightarrow Z, \end{equation*}

where Z denotes a standard normal random variable.

It is remarkable that the quantity $n^2(1-p)/2$ is the asymptotic expected number of unoccupied edges in G(n, p). Theorem 2 suggests that if G(n, p) is neither too sparse (see, e.g., [25, Section 1.8]) nor close to a complete graph, then its average Jaccard index $J_n$ has asymptotic normality. In order to prove Theorem 2, we first introduce two auxiliary lemmas, both of which involve the inverse moments of the binomial distribution.

Lemma 1. If the random variable $X_n$ has a binomial distribution with parameters n and p, then, for any fixed constants $a\ge0$ and $b>0$ , as $np\to\infty$ ,

\begin{equation*} {\mathbb E}\bigg[\bigg(\frac{(n+a)p}{b+X_n}-1\bigg)^2\bigg] = O\bigg(\frac{1}{np}\bigg). \end{equation*}

Proof. For any $\varepsilon\in (0,1)$ , we define ${\mathcal A}_n \,:\!=\,\{(1-\varepsilon)(n+a)p \le b + X_n \le (1+\varepsilon)(n+a)p\}$ . Applying Chernoff’s bound for the binomial distribution (see, e.g., [14, Corollary 2.3]) gives, for sufficiently large n,

\begin{equation*} {\mathbb P}\big(\overline{{\mathcal A}}_n\big) \le {\mathbb P}\bigg(\bigg|\frac{X_n}{np}-1\bigg| > \frac{\varepsilon}{2}\bigg) \le 2\exp\bigg\{{-}\frac{\varepsilon^2}{12}np\bigg\} = O\bigg(\frac{1}{n^3p^3}\bigg). \end{equation*}

Then, for sufficiently large n, by noting that

\begin{equation*} \bigg(\frac{(n+a)p}{b+X_n}-1\bigg)^2 \le \bigg(\frac{(n+a)p}{b}\bigg)^2 + 1 \le 2n^2p^2, \end{equation*}

we have

\begin{align*} {\mathbb E}\bigg[\bigg(\frac{(n+a)p}{b+X_n}-1\bigg)^2\bigg] & = {\mathbb E}\bigg[\bigg(\frac{(n+a)p}{b+X_n}-1\bigg)^2\mathbf{1}({\mathcal A}_n)\bigg] + {\mathbb E}\bigg[\bigg(\frac{(n+a)p}{b+X_n}-1\bigg)^2\mathbf{1}\big(\overline{{\mathcal A}}_n\big)\bigg] \\ & \le {\mathbb E}\bigg[\frac{(n+a)^2p^2}{(b+X_n)^2}\bigg(\frac{b+X_n}{(n+a)p}-1\bigg)^2 \mathbf{1}({\mathcal A}_n)\bigg] + 2n^2p^2\mathbb{P}\big(\overline{{\mathcal A}}_n\big) \\ & \le (1-\varepsilon)^{-2}{\mathbb E}\bigg[\bigg(\frac{b+X_n}{(n+a)p}-1\bigg)^2\bigg] + 2n^2p^2\mathbb{P}\big(\overline{{\mathcal A}}_n\big) \\ & = O\bigg(\frac{1}{np}\bigg), \end{align*}

where we used the inequality

\begin{equation*} {\mathbb E}\bigg[\bigg(\frac{b+X_n}{(n+a)p}-1\bigg)^2\bigg] \le \frac{2}{(n+a)^2p^2}\big(\mathbb{E}\big[(X_n-np)^2\big] + (b-ap)^2\big) = O\bigg(\frac{1}{np}\bigg). \end{equation*}

Lemma 2. If the random variable $X_n$ has a binomial distribution with parameters n and p, then, for any fixed positive constants b and $\alpha$ , as $np\to\infty$ ,

\begin{equation*} {\mathbb E}\bigg[\frac{1}{(b+X_n)^{\alpha}}\bigg] = \frac{1}{(np)^{\alpha}}(1+o(1)). \end{equation*}

Proof. This is an immediate consequence of [23, Theorem 2].

We now give a formal proof of Theorem 2.

Proof of Theorem 2. By (12), the index $J_{ij}^{(n)}$ can be expressed as

(15) \begin{equation} J_{ij}^{(n)} = \frac{p}{2-p} + \frac{(2-p)S_{ij}^{(n)}-pT_{ij}^{(n)}}{(n-2)p(2-p)^2} + R_{ij}^{(n)}, \quad 1 \le i \neq j \le n, \end{equation}

where the remainder term is

(16) \begin{equation} R_{ij}^{(n)} = \frac{(2-p)S_{ij}^{(n)}-pT_{ij}^{(n)}}{(n-2)p(2-p)^2}\bigg(\frac{(n-2)p(2-p)}{T_{ij}^{(n)}}-1\bigg). \end{equation}

Note the special case in (15) that the remainder term $R_{ij}^{(n)}$ vanishes if $T_{ij}^{(n)}=0$ . Taking expectation on both sides of (15) gives, for any distinct vertices $i,j\in[n]$ ,

(17) \begin{equation} {\mathbb E}\Big[R_{ij}^{(n)}\Big]=0. \end{equation}

Denote by $R_n$ the sum of all the remainder terms, i.e.,

(18) \begin{equation} R_{n} = \sum_{i=1}^{n-1}\sum_{j=i+1}^nR_{ij}^{(n)}. \end{equation}

Then it follows by (17) that ${\mathbb E}[R_n]=0$ . By (2) and the simple fact that $\mathbf{1}_{ik}\vee \mathbf{1}_{jk}=\mathbf{1}_{ik}+\mathbf{1}_{jk}-\mathbf{1}_{ik}\mathbf{1}_{jk}$ , we have, for any $1\le i\neq j\le n$ ,

\begin{equation*} (2-p)S_{ij}^{(n)} - pT_{ij}^{(n)} = \sum_{k\neq i,j}\big[(2-p)\mathbf{1}_{ik}\mathbf{1}_{jk}-p\mathbf{1}_{ik}\vee \mathbf{1}_{jk}\big] = \sum_{k\neq i,j}\big[2\mathbf{1}_{ik}\mathbf{1}_{jk}-p\big(\mathbf{1}_{ik}+\mathbf{1}_{jk}\big)\big], \end{equation*}

which, together with (14) and (15), implies that

(19) \begin{align} J_{n} & = \frac{p}{2-p} + \frac{2}{n(n-1)} \sum_{i=1}^{n-1}\sum_{j=i+1}^n\bigg(\frac{(2-p)S_{ij}^{(n)}-pT_{ij}^{(n)}}{(n-2)p(2-p)^2} + R_{ij}^{(n)}\bigg) \notag \\ & = \frac{p}{2-p} + \frac{2}{n(n-1)(n-2)(2-p)^{2}}\sum_{i=1}^{n-1} \sum_{j=i+1}^n\sum_{k\neq i,j}\bigg(\frac{2\mathbf{1}_{ik}\mathbf{1}_{jk}}{p} - (\mathbf{1}_{ik}+\mathbf{1}_{jk})\bigg) + \frac{2}{n(n-1)}R_{n} \notag \\ & = \frac{p}{2-p} - \frac{4P_{1,n}}{n(n-1)(2-p)^{2}} + \frac{4P_{2,n}}{n(n-1)(n-2)p(2-p)^{2}} + \frac{2}{n(n-1)}R_{n}, \end{align}

where

\begin{equation*} P_{1,n} = \sum_{i=1}^{n-1}\sum_{j=i+1}^n\mathbf{1}_{ij}, \qquad P_{2,n} = \sum_{i=1}^{n-1}\sum_{j=i+1}^n\sum_{k\neq i,j}\mathbf{1}_{ij}\mathbf{1}_{ik} \end{equation*}

denote the number of edges and the number of paths of length two in G(n, p), respectively. Further, we can rewrite (19) as

(20) \begin{equation} \frac{(n-1)(2-p)^2}{\sqrt{8p(1-p)}}\bigg(J_n-\frac{p}{2-p}\bigg) = \sqrt{\frac{2p}{1-p}}\bigg({-}\frac{P_{1,n}}{np} + \frac{P_{2,n}}{n(n-2)p^2}\bigg) + \frac{(2-p)^2}{n\sqrt{2p(1-p)}\,}R_n. \end{equation}

For $P_{1,n}$ and $P_{2,n}$ , it is not hard to obtain that their expectations are given by ${\mathbb E}[P_{1,n}] = \frac12n(n-1)p$ and ${\mathbb E}[P_{2,n}] = \frac12n(n-1)(n-2)p^2$ . Applying [10, Theorem 3(iii)] yields that if $np\to\infty$ and $n^2(1-p)\to \infty$ ,

\begin{equation*} \sqrt{\frac{2p}{1-p}}\bigg(\frac{P_{1,n}-\frac12n(n-1)p}{np}, \frac{P_{2,n}-\frac12n(n-1)(n-2)p^2}{2n(n-2)p^2}\bigg)\buildrel \textrm{D} \over \longrightarrow (Z,Z), \end{equation*}

which implies that

(21) \begin{equation} \sqrt{\frac{2p}{1-p}}\bigg({-}\frac{P_{1,n}}{np}+\frac{P_{2,n}}{n(n-2)p^2}\bigg) \buildrel \textrm{D} \over \longrightarrow Z. \end{equation}

To prove Theorem 2, by (20) and (21) it is sufficient to show that

\begin{equation*} \frac{R_n}{n\sqrt{p(1-p)}\,}\buildrel \textrm{P} \over \longrightarrow 0. \end{equation*}

That is, by Chebyshev’s inequality and the fact that ${\mathbb E}[R_n]=0$ , we only need to prove that

(22) \begin{equation} \textrm{Var}[R_n] = o\big(n^2p(1-p)\big). \end{equation}

On the other hand, by symmetry, it follows by (18) that

(23) \begin{align} \textrm{Var}[R_{n}] & = \textrm{cov}\Bigg(\sum_{i=1}^{n-1}\sum_{j=i+1}^n R_{ij}^{(n)},\sum_{i=1}^{n-1}\sum_{j=i+1}^n R_{ij}^{(n)}\Bigg) \notag \\ & = \frac{n(n-1)}{2}\textrm{cov}\Bigg(R_{12}^{(n)},\sum_{i=1}^{n-1}\sum_{j=i+1}^n R_{ij}^{(n)}\Bigg) \notag \\ & = \frac12n(n-1)\textrm{Var}\Big[R_{12}^{(n)}\Big] + n(n-1)(n-2)\textrm{cov}\Big(R_{12}^{(n)},R_{13}^{(n)}\Big) \notag \\ & \quad + \frac14n(n-1)(n-2)(n-3)\textrm{cov}\Big(R_{12}^{(n)},R_{34}^{(n)}\Big). \end{align}

To prove (22), we next estimate the variance and covariances in (23) separately. By the law of total expectation and (17), for the variance of $R_{12}^{(n)}$ we have

(24) \begin{equation} \textrm{Var}\Big[R_{12}^{(n)}\Big] = {\mathbb E}\Big[\Big(R_{12}^{(n)}\Big)^{2}\Big] = {\mathbb E}\Big[{\mathbb E}\Big[\Big(R_{12}^{(n)}\Big)^{2} \mid T_{12}^{(n)}\Big]\Big] = \sum_{m=0}^{n-2}{\mathbb E}\Big[\Big(R_{12}^{(n)}\Big)^{2} \mid T_{12}^{(n)}=m\Big]{\mathbb P}\Big(T_{12}^{(n)}=m\Big). \end{equation}

Recalling that $T_{12}^{(n)}\sim \textrm{Bin}(n-2,p(2-p))$ , and $R_{12}^{(n)}=0$ if $T_{12}^{(n)}=0$ , By (3), (4), and (16), it follows that

\begin{align*} {\mathbb E}\Big[\Big(R_{12}^{(n)}\Big)^{2} \mid T_{12}^{(n)}=m\Big] & = \frac1{(n-2)^2p^2(2-p)^2}\bigg(\frac{(n-2)p(2-p)}{m}-1\bigg)^2 \textrm{Var}\Big(S_{12}^{(n)} \mid T_{12}^{(n)}=m\Big) \\ & = \frac{2(1-p)}{(n-2)^2p(2-p)^4}\bigg(\frac{(n-2)^2p^2(2-p)^2}{m}-2(n-2)p(2-p)+m\bigg), \end{align*}

which, together with (6) and (24), implies that

(25) \begin{align} \textrm{Var}\Big[R_{12}^{(n)}\Big] & = \frac{2(1-p)}{(n-2)^2p(2-p)^4}\sum_{m=1}^{n-2}\!\bigg(\frac{(n-2)^2p^2(2-p)^2}{m}-2(n-2)p(2-p)+m\bigg) {\mathbb P}\Big(T_{12}^{(n)}=m\Big) \notag \\ & = \frac{2(1-p)}{(n-2)(2-p)^3}\bigg((n-2)p(2-p)\sum_{m=1}^{n-2}\frac1m{\mathbb P}\Big(T_{12}^{(n)}=m\Big) - 1 + 2{\mathbb P}\Big(T_{12}^{(n)}=0\Big)\bigg) \notag \\ & = O\bigg(\frac{1-p}{n^2p}\bigg), \end{align}

where in the last equality we used the simple fact that

\begin{equation*} 0<{\mathbb P}\Big(T_{12}^{(n)}=0\Big)=(1-p)^{2(n-2)}\leq \textrm{e}^{-2(n-2)p}=o\bigg(\frac{1}{np}\bigg). \end{equation*}

To calculate the covariance of $R_{12}^{(n)}$ and $R_{13}^{(n)}$ , by convention we introduce the shorthand notation

\begin{equation*} \widetilde{T}_{ij}^{(n)}\,:\!=\,\frac{(n-2)p(2-p)}{T_{ij}^{(n)}}-1 \end{equation*}

for distinct vertices $i,j\in [n]$ . Recalling (8), we have

\begin{equation*} (2-p)S_{ij}^{(n)}-pT_{ij}^{(n)}=\sum_{k\neq i,j} V_{ij,k}, \quad i,j\in [n]. \end{equation*}

By symmetry and (16), it thus follows that

(26) \begin{align} \textrm{cov}\Big(R_{12}^{(n)},R_{13}^{(n)}\Big) & = \frac{1}{(n-2)^{2}p^{2}(2-p)^{4}}\sum_{k=3}^n\sum_{l\neq1,3} {\mathbb E}\Big[V_{12,k}V_{13,l}\widetilde{T}_{12}^{(n)}\widetilde{T}_{13}^{(n)} \mathbf{1}\Big(T_{12}^{(n)}T_{13}^{(n)}>0\Big)\Big] \notag \\ & = \frac{1}{(n-2)p^{2}(2-p)^{4}} {\mathbb E}\Big[V_{12,3}V_{13,2}\widetilde{T}_{12}^{(n)}\widetilde{T}_{13}^{(n)} \mathbf{1}\Big(T_{12}^{(n)}T_{13}^{(n)}>0\Big)\Big] \notag \\ & \quad + \frac{(n-3)}{(n-2)p^{2}(2-p)^{4}} {\mathbb E}\Big[V_{12,3}V_{13,4}\widetilde{T}_{12}^{(n)}\widetilde{T}_{13}^{(n)} \mathbf{1}\Big(T_{12}^{(n)}T_{13}^{(n)}>0\Big)\Big], \end{align}

which splits the covariance into two parts. Notice that, by (8), the discrete random variable $V_{ij,k}\neq 0$ if and only if $\mathbf{1}_{ik}\vee \mathbf{1}_{jk}=1$ . This implies that if $V_{12,3}V_{13,2}\neq 0$ , we have $T_{12}^{(n)}=1+\sum_{k=4}^{n} \mathbf{1}_{1k}\vee \mathbf{1}_{2k}$ and $T_{13}^{(n)}=1+\sum_{k=4}^{n} \mathbf{1}_{1k}\vee \mathbf{1}_{3k}$ , and they have the same distribution. Since it follows that, by conditioning on $\mathbf{1}_{23}$ ,

\begin{align*} {\mathbb E}[V_{12,3}V_{13,2}] & = {\mathbb E}\big[\big((2-p)\mathbf{1}_{13}\mathbf{1}_{23}-p(\mathbf{1}_{13}\vee \mathbf{1}_{23})\big) \big((2-p)\mathbf{1}_{12}\mathbf{1}_{23}-p(\mathbf{1}_{12}\vee \mathbf{1}_{23})\big)\big] \\ & = p{\mathbb E}\big[\big((2-p)\mathbf{1}_{13}-p\big)\big((2-p)\mathbf{1}_{12}-p\big)\big] + (1-p){\mathbb E}\big[p^2\mathbf{1}_{13}\mathbf{1}_{12}\big] \\ & = p^3(1-p)^2+p^4(1-p) = p^3(1-p), \end{align*}

and that, by Lemma 1 and the Cauchy–Schwarz inequality,

\begin{multline*} \bigg|\mathbb{E}\bigg[\bigg(\frac{(n-2)p(2-p)}{1+\sum_{k=4}^{n}\mathbf{1}_{1k}\vee\mathbf{1}_{2k}}-1\bigg) \bigg(\frac{(n-2)p(2-p)}{1+\sum_{k=4}^{n}\mathbf{1}_{1k}\vee\mathbf{1}_{3k}}-1\bigg)\bigg]\bigg| \\ \leq \mathbb{E}\bigg[\bigg(\frac{(n-2)p(2-p)}{1+\sum_{k=4}^{n}\mathbf{1}_{1k}\vee\mathbf{1}_{2k}}-1\bigg)^2\bigg] = O \bigg(\frac{1}{np}\bigg), \end{multline*}

we have

(27) \begin{align} & {\mathbb E}\Big[V_{12,3}V_{13,2}\widetilde{T}_{12}^{(n)}\widetilde{T}_{13}^{(n)} \mathbf{1}\Big(T_{12}^{(n)}T_{13}^{(n)}>0\Big)\Big] \notag \\ & \qquad = {\mathbb E}\bigg[V_{12,3}V_{13,2} \bigg(\frac{(n-2)p(2-p)}{1+\sum_{k=4}^{n}\mathbf{1}_{1k}\vee\mathbf{1}_{2k}}-1\bigg) \bigg(\frac{(n-2)p(2-p)}{1+\sum_{k=4}^{n}\mathbf{1}_{1k}\vee\mathbf{1}_{3k}}-1\bigg)\bigg] \notag \\ & \qquad = p^{3}(1-p)\mathbb{E}\bigg[ \bigg(\frac{(n-2)p(2-p)}{1+\sum_{k=4}^{n}\mathbf{1}_{1k}\vee\mathbf{1}_{2k}}-1\bigg) \bigg(\frac{(n-2)p(2-p)}{1+\sum_{k=4}^{n}\mathbf{1}_{1k}\vee\mathbf{1}_{3k}}-1\bigg)\bigg] \notag \\ & \qquad = O\bigg(\frac{p^{2}(1-p)}{n}\bigg). \end{align}

Let us define ${\mathcal B}_{ab}\,:\!=\,\{\mathbf{1}_{12}\vee \mathbf{1}_{23}=a,\, \mathbf{1}_{14}\vee \mathbf{1}_{24}=b\}$ , $a,b \in\{0,1\}$ . Noting that $\mathbb{E}[V_{12,3}]=0$ , we have

\begin{equation*} \mathbb{E}\big[V_{12,3}\mathbf{1}(\mathbf{1}_{12}\vee \mathbf{1}_{23}=1)\big] = -\mathbb{E}\big[V_{12,3}\mathbf{1}(\mathbf{1}_{12}\vee \mathbf{1}_{23}=0)\big] = p\mathbb{E}\big[\mathbf{1}_{13}\mathbf{1}(\mathbf{1}_{12}=\mathbf{1}_{23}=0)\big] = p^2(1-p)^2, \end{equation*}

which implies that, for any $a,b=0$ or 1,

\begin{align*} \mathbb{E}[V_{12,3}V_{13,4}\mathbf{1}({\mathcal B}_{ab})] & = \mathbb{E}[V_{12,3}\mathbf{1}(\mathbf{1}_{12}\vee \mathbf{1}_{23}=a)] \mathbb{E}[V_{13,4}\mathbf{1}(\mathbf{1}_{14}\vee \mathbf{1}_{24}=b)] \\ & = \mathbb{E}[V_{12,3}\mathbf{1}(\mathbf{1}_{12}\vee \mathbf{1}_{23}=a)] \mathbb{E}[V_{12,3}\mathbf{1}(\mathbf{1}_{12}\vee \mathbf{1}_{23}=b)] \\ & = ({-}1)^{a+b}p^4(1-p)^4. \end{align*}

Analogously to (27), we have

(28) \begin{align} & \mathbb{E}\Big[V_{12,3}V_{13,4}\widetilde{T}_{12}^{(n)}\widetilde{T}_{13}^{(n)} \mathbf{1}\Big(T_{12}^{(n)}T_{13}^{(n)}>0\Big)\Big] \notag \\ & \qquad = \sum_{a=0}^1\sum_{b=0}^1\mathbb{E} \Big[V_{12,3}V_{13,4}\widetilde{T}_{12}^{(n)}\widetilde{T}_{13}^{(n)}\mathbf{1}({\mathcal B}_{ab})\Big] \notag \\ & \qquad = \sum_{a=0}^1\sum_{b=0}^1 \mathbb{E}\big[V_{12,3}V_{13,4}W_{12}(b)W_{13}(a)\mathbf{1}({\mathcal B}_{ab})\big] \notag \\ & \qquad = \sum_{a=0}^1\sum_{b=0}^1\mathbb{E}\big[V_{12,3}V_{13,4}\mathbf{1}({\mathcal B}_{ab})\big] \mathbb{E}\big[W_{12}(b)W_{13}(a)\big] \notag \\ & \qquad = p^{4}(1-p)^{4}\mathbb{E}\big[(W_{12}(0)-W_{12}(1))(W_{13}(0)-W_{13}(1))\big], \end{align}

where

\begin{equation*} W_{ij}(a) \,:\!=\, \frac{(n-2)p(2-p)}{1+a+\sum_{k=5}^{n}\mathbf{1}_{ik}\vee \mathbf{1}_{jk}}-1, \quad i,j\in [n], \,a=0,1. \end{equation*}

Noting that $W_{12}(0)-W_{12}(1)$ and $W_{13}(0)-W_{13}(1)$ have the same distribution, by Lemma 2 and the Cauchy–Schwarz inequality we have

\begin{align*} {\mathbb E}\big|\big(W_{12}(0)-W_{12}(1)\big)\big(W_{13}(0)-W_{13}(1)\big)\big| & \le {\mathbb E}\big[(W_{12}(0)-W_{12}(1))^2\big] \\ & \le (n-2)^{2}p^{2}(2-p)^{2} {\mathbb E}\left[\frac{1}{\Big(1+\sum_{k=5}^{n}\mathbf{1}_{1k}\vee \mathbf{1}_{2k}\Big)^{4}}\right] \\ & = O\bigg(\frac{1}{n^{2}p^{2}}\bigg), \end{align*}

which, together with (26), (27), and (28), implies that

(29) \begin{equation} \textrm{cov}\Big(R_{12}^{(n)},R_{13}^{(n)}\Big) = O\bigg(\frac{1-p}{n^2}\bigg). \end{equation}

It remains to calculate the second covariance $\mathbf{Cov}\Big(R_{12}^{(n)},R_{34}^{(n)}\Big)$ on the right-hand side of (23), and the procedure is similar to the previous one. We sketch the calculations below, omitting a few specific interpretations. Analogously to (26), we have

(30) \begin{align} \textrm{cov}\Big(R_{12}^{(n)},R_{34}^{(n)}\Big) & = \frac{1}{(n-2)^{2}p^{2}(2-p)^4}\sum_{k=3}^n\sum_{l\neq 3,4} {\mathbb E}\Big[V_{12,k}V_{34,l}\widetilde{T}_{12}^{(n)}\widetilde{T}_{34}^{(n)} \mathbf{1}\Big(T_{12}^{(n)}T_{34}^{(n)}>0\Big)\Big] \notag \\ & = \frac{4}{(n-2)^{2}p^{2}(2-p)^4}{\mathbb E}\Big[V_{12,3}V_{34,1}\widetilde{T}_{12}^{(n)}\widetilde{T}_{34}^{(n)} \mathbf{1}\Big(T_{12}^{(n)}T_{34}^{(n)}>0\Big)\Big] \notag \\ & \quad + \frac{2}{(n-2)p^{2}(2-p)^4}{\mathbb E}\Big[V_{12,3}V_{34,5}\widetilde{T}_{12}^{(n)}\widetilde{T}_{34}^{(n)} \mathbf{1}\Big(T_{12}^{(n)}T_{34}^{(n)}>0\Big)\Big] \notag \\ & \quad + \frac{(n-4)^2}{(n-2)^{2}p^{2}(2-p)^4} {\mathbb E}\Big[V_{12,5}V_{34,5}\widetilde{T}_{12}^{(n)}\widetilde{T}_{34}^{(n)} \mathbf{1}\Big(T_{12}^{(n)}T_{34}^{(n)}>0\Big)\Big]. \end{align}

Define ${\mathcal C}_{ab} \,:\!=\, \{\mathbf{1}_{14}\vee \mathbf{1}_{24}=a,\,\mathbf{1}_{23}\vee \mathbf{1}_{24}=b\}$ , $a,b \in\{0,1\}$ . After straightforward calculations, we have

\begin{align*} {\mathbb E}\big[V_{12,3}V_{34,1}\mathbf{1}({\mathcal C}_{00})\big] & = p^3(1-p)^3, \\ {\mathbb E}\big[V_{12,3}V_{34,1}\mathbf{1}({\mathcal C}_{11})\big] & = p^{3}(1-p)\big(1+3(1-p)^{2}\big), \\ {\mathbb E}\big[V_{12,3}V_{34,1}\mathbf{1}({\mathcal C}_{01})\big] & = {\mathbb E}\big[V_{12,3}V_{34,1}\mathbf{1}({\mathcal C}_{10})\big] = -2p^3(1-p)^3. \end{align*}

Then we can conclude that ${\mathbb E}[V_{12,3}V_{34,1}\mathbf{1}({\mathcal C}_{ab})] = O(p^3(1-p))$ . Hence, by the Cauchy–Schwarz inequality and Lemma 1,

(31) \begin{align} {\mathbb E}\Big[V_{12,3}V_{34,1}\widetilde{T}_{12}^{(n)}\widetilde{T}_{34}^{(n)} \mathbf{1}\Big(T_{12}^{(n)}T_{34}^{(n)}>0\Big)\Big] & = \sum_{a=0}^1\sum_{b=0}^1{\mathbb E}\big[V_{12,3}V_{34,1}W_{12}(a)W_{34}(b)\mathbf{1}({\mathcal C}_{ab})\big] \notag \\ & = \sum_{a=0}^1\sum_{b=0}^1{\mathbb E}[V_{12,3}V_{34,1}\mathbf{1}({\mathcal C}_{ab})] {\mathbb E}[W_{12}(a)]{\mathbb E}[W_{34}(b)] \notag \\ & = O\bigg(\frac{p^2(1-p)}{n}\bigg). \end{align}

Since $V_{12,3}$ and $V_{34,5}$ are independent and have the common mean 0, it follows that

(32) \begin{align} & {\mathbb E}\Big[V_{12,3}V_{34,5}\widetilde{T}_{12}^{(n)}\widetilde{T}_{34}^{(n)} \mathbf{1}\Big(T_{12}^{(n)}T_{34}^{(n)}>0\Big)\Big] \notag \\ & = {\mathbb E}\Big[V_{12,3}V_{34,5}\widetilde{T}_{12}^{(n)}\widetilde{T}_{34}^{(n)} \mathbf{1}(\mathbf{1}_{13}\vee\mathbf{1}_{23}=1)\mathbf{1}(\mathbf{1}_{35}\vee\mathbf{1}_{45}=1)\Big] \notag \\ & = {\mathbb E}[V_{34,5}\mathbf{1}(\mathbf{1}_{35}\vee\mathbf{1}_{45}=1)] {\mathbb E}\bigg[V_{12,3}\widetilde{T}_{12}^{(n)}\mathbf{1}(\mathbf{1}_{13}\vee \mathbf{1}_{23}=1) \bigg(\frac{(n-2)p(2-p)}{1+\sum_{k\neq 3,4,5}(\mathbf{1}_{3k}\vee\mathbf{1}_{4k})}-1\bigg)\bigg] \notag \\ & = {\mathbb E}[V_{34,5}]{\mathbb E}\bigg[V_{12,3}\widetilde{T}_{12}^{(n)} \mathbf{1}(\mathbf{1}_{13}\vee\mathbf{1}_{23}=1) \bigg(\frac{(n-2)p(2-p)}{1+\sum_{k\neq 3,4,5}(\mathbf{1}_{3k}\vee\mathbf{1}_{4k})}-1\bigg)\bigg] = 0. \end{align}

Similarly, we also have ${\mathbb E}\big[V_{12,5}V_{34,5}\widetilde{T}_{12}^{(n)}\widetilde{T}_{34}^{(n)} \mathbf{1}\big(T_{12}^{(n)}T_{34}^{(n)}>0\big)\big] = 0$ . Plugging this, (31), and (32) into (30) yields

\begin{equation*} \textrm{cov}\Big(R_{12}^{(n)},R_{34}^{(n)}\Big) = O\bigg(\frac{1-p}{n^3}\bigg), \end{equation*}

which, together with (23), (25), and (29), implies that

\begin{equation*} \textrm{Var}[R_n] = O\bigg(\frac{1-p}{p}\bigg) + O(n(1-p)) + O(n(1-p)) = O(n(1-p)) \end{equation*}

as $np\to\infty$ . This proves (22), and thus completes the proof of Theorem 2.