1 INTRODUCTION
Magnetars are neutron stars (NSs) whose energy budget is dominated by dissipation of electric currents supporting magnetic fields. Known objects of this type have strong fields: poloidal (in particular, dipolar) or/and toroidal. The origin of these strong fields is still not clear.
In their foundational paper, Duncan & Thompson (Reference Duncan and Thompson1992) proposed that strong fields are enhanced via a dynamo mechanism. This scenario requires rapid initial rotation of an NS. Field of the order of 1015 G can be reached if the initial spin is ~1 msecFootnote 1 . This is a strong prediction that potentially can be tested.
Vink & Kuiper (Reference Vink and Kuiper2006) studied supernova remnants (SNRs) with magnetars to check if traces of additional energy release due to a rapidly spinning down magnetar can be found. Indeed, a young magnetar is a very powerful source with a luminosity L ~ 9.6 × 1048 B 2 15 P −4 msec erg s−1. Such objects were even considered as central engines of gamma-ray bursts (Usov Reference Usov1992). Though no additional energy input in magnetars’ SNRs has been found (Vink & Kuiper Reference Vink and Kuiper2006), still this result does not exclude the original scenario by Duncan & Thompson (Reference Duncan and Thompson1992). Note also, that alternatives related to fossil fields (Ferrario & Wickramasinghe Reference Ferrario and Wickramasinghe2006) have been seriously criticised (Spruit Reference Spruit, Bassa, Wang, Cumming and Kaspi2008), as just a small fraction of the total stellar magnetic flux can end in an NS.
Unfortunately, due to a rapid spin-down and field decay, initial periods of magnetars are quickly ‘forgotten’. However, there is a situation, when the initial period can be ‘frozen’. This is related to strong fall-back which results in burying of the magnetic field (Muslimov & Page Reference Muslimov and Page1995; Ho Reference Ho2011; Viganò & Pons Reference Viganò and Pons2012; Bernal, Page, & Lee Reference Bernal, Page and Lee2013). Such an NS—magnetar inside, anti-magnetar outside—can be a Rosetta stone for understanding the origin of strong magnetic fields. Potentially, an NS in the SNR Kes 79 could be such an object.
The NS in Kes 79 (PSR J1852+0040) belongs to the class of so-called ‘anti-magnetars’(Halpern & Gotthelf Reference Halpern and Gotthelf2010). It has a spin period p = 0.105 s,
![]() $\dot{p}=8.7 \times 10^{-18}$
, and so the polar magnetic field for an orthogonal rotator is about 6.2 × 1010 G. The SNR age is estimated as ~6 × 103 years. The source has one peculiar feature: large (64%) pulse fraction. Shabaltas & Lai (Reference Shabaltas and Lai2012) show that large pulse fraction of the NS in Kes 79 can be explained if its magnetic field in the crust is very strong: few ×1014 G. In their study, the authors assumed that the strong component of the field is the toroidal one. Potentially, this opens two possibilities. First, despite its young age, the NS in Kes 79 is an analogue of so-called low-field magnetars (see a review in Turolla & Esposito Reference Turolla and Esposito2013). Second, both components are strong, and they have been significantly submerged due to a strong fall-back episode (Geppert, Page, & Zannias Reference Geppert, Page and Zannias1999 called such sources ‘hidden magnetars’). Below, we analyse how this can be used to put constraints on the origin of magnetars’ magnetic field.
$\dot{p}=8.7 \times 10^{-18}$
, and so the polar magnetic field for an orthogonal rotator is about 6.2 × 1010 G. The SNR age is estimated as ~6 × 103 years. The source has one peculiar feature: large (64%) pulse fraction. Shabaltas & Lai (Reference Shabaltas and Lai2012) show that large pulse fraction of the NS in Kes 79 can be explained if its magnetic field in the crust is very strong: few ×1014 G. In their study, the authors assumed that the strong component of the field is the toroidal one. Potentially, this opens two possibilities. First, despite its young age, the NS in Kes 79 is an analogue of so-called low-field magnetars (see a review in Turolla & Esposito Reference Turolla and Esposito2013). Second, both components are strong, and they have been significantly submerged due to a strong fall-back episode (Geppert, Page, & Zannias Reference Geppert, Page and Zannias1999 called such sources ‘hidden magnetars’). Below, we analyse how this can be used to put constraints on the origin of magnetars’ magnetic field.
2 ANALYSIS AND ESTIMATES
The process of fall-back on a newborn magnetar can be a very complicated one. However, in this section, we apply simple formulae to perform a qualitative analysis of the consequences of such a process.
At first, we recall that accretion on the surface of an NS can be prohibited either by a relativistic wind (so-called ejector stage), or by a rapidly rotating magnetosphere (propeller stage), see a detailed description of stages, for example, in Lipunov (Reference Lipunov1992). Transition between stages can be formalised in terms of critical spin periods (back transitions can not be symmetric, and so corresponding critical periods can be different, also additional conditions can be important, but we do not discuss here situations not applicable to the fall-back case).
The first one, p E, corresponds to the transition ejector→propeller. The second, p A, corresponds to the transition propeller→accretor. We are interested mainly in the latter one, as the fall-back we are interested in, is strong enough to switch off the pulsar.
 \begin{equation}
p_\mathrm{A}\approx 20 \mu _{32}^{6/7} \left(\frac{M}{\text{M}_\odot }\right)^{-5/7} \left(\frac{\dot{M}}{\text{M}_\odot \mathrm{yr}^{-1}}\right)^{-3/7} \, \mathrm{msec}.
\end{equation}
\begin{equation}
p_\mathrm{A}\approx 20 \mu _{32}^{6/7} \left(\frac{M}{\text{M}_\odot }\right)^{-5/7} \left(\frac{\dot{M}}{\text{M}_\odot \mathrm{yr}^{-1}}\right)^{-3/7} \, \mathrm{msec}.
\end{equation}
If the initial dipole magnetic field is strong and the spin period is short, then accretion is possible only for a very large accretion rate
![]() $\sim 100 \text{M}_\odot$
yr −1. Such rates are not unexpected. For example, Chevalier (Reference Chevalier1989) estimated the accretion rate for SN1987A as
$\sim 100 \text{M}_\odot$
yr −1. Such rates are not unexpected. For example, Chevalier (Reference Chevalier1989) estimated the accretion rate for SN1987A as
![]() $350 \text{M}_\odot$
yr−1 (lower values about tens of solar masses per year also have been reported by other authors).
$350 \text{M}_\odot$
yr−1 (lower values about tens of solar masses per year also have been reported by other authors).
Bernal et al. (Reference Bernal, Page and Lee2013) demonstrated that for such strong fall-back the field is rapidly (~100 msec) submerged. Then it can diffuse out on a time scale of thousands or tens of thousand years (Ho Reference Ho2011; Viganò & Pons Reference Viganò and Pons2012). While the field is submerged, the NS appears as an anti-magnetar. Rotation braking is very slow in this case. The spin period is nearly constant, frozen. A similar situation appears if the initial dipolar field was small, but the toroidal is large. In this case, the accretion gates are opened even for lower
![]() $\dot{M}$
. Discovery of an anti-magnetar with a large crustal field and a millisecond-scale spin period would be a proof for a dynamo-mechanism field origin. Oppositely, PSR J1852+0040 (with its large spin period) most probably represents a counter example.
$\dot{M}$
. Discovery of an anti-magnetar with a large crustal field and a millisecond-scale spin period would be a proof for a dynamo-mechanism field origin. Oppositely, PSR J1852+0040 (with its large spin period) most probably represents a counter example.
In PSR J1852+0040, the present day spin period is nearly the same as the initial one because
![]() $\dot{p}$
is low due to the low field and the relatively long spin period. And it is easy to estimate that no spin-down mechanism (magneto-rotational or similar ones, propeller, interaction with a disc, etc.) can slow the rotation from few milliseconds down to 100 msec in a very short time before the field is buried.
$\dot{p}$
is low due to the low field and the relatively long spin period. And it is easy to estimate that no spin-down mechanism (magneto-rotational or similar ones, propeller, interaction with a disc, etc.) can slow the rotation from few milliseconds down to 100 msec in a very short time before the field is buried.
One of the most effective spin-down mechanisms ever discussed was proposed by Shakura (Reference Shakura1975) (see a list of other spin-down formulae for the propeller stage in Lipunov & Popov Reference Lipunov and Popov1995):
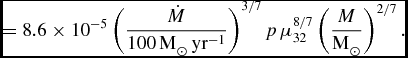 $$
=8.6\times 10^{-5} \left(\frac{\dot{M}}{100 \, \text{M}_\odot \,{\mathrm{yr}}^{-1}}\right)^{3/7} p \, \mu _{32}^{8/7} \left(\frac{M}{\text{M}_\odot }\right)^{2/7}.
$$
$$
=8.6\times 10^{-5} \left(\frac{\dot{M}}{100 \, \text{M}_\odot \,{\mathrm{yr}}^{-1}}\right)^{3/7} p \, \mu _{32}^{8/7} \left(\frac{M}{\text{M}_\odot }\right)^{2/7}.
$$
We conclude that a strong crustal toroidal magnetic field in Kes 79 could not be generated with a dynamo mechanism.
3 DISCUSSION
Shabaltas & Lai (Reference Shabaltas and Lai2012) comment that the field configuration they obtained can not be a unique one which explains the large pulse fraction of PSR J1852+0040. This means that we cannot be sure if the dipolar component of the field was strong before the fall-back episode, or not.
Bernal et al. (Reference Bernal, Page and Lee2013) mention that the accretion of magnetised matter can modify the magnetic field of a NS, reducing the dipolar component while making the general shape of the field configuration more complicated. If this is the case for PSR J1852+0040, then it can be much different from normal magnetars. Even if the strength of toroidal field in the crust is high, the total energy of the field can be orders of magnitude smaller than in magnetars (Viganò, Pons, & Miralles Reference Viganò, Pons and Miralles2012). Probably, an effective dynamo mechanism is not necessary in this case. Then accretion could start for 100 msec period even for relatively low accretion rates.
High accretion rates normally result in a large total accreted mass, comparable with the mass of the crust. Roughly, the mass of the crust is accreted in one hour for the rate
![]() $\dot{M}=100\, \text{M}_\odot \,$
yr−1:
$\dot{M}=100\, \text{M}_\odot \,$
yr−1:
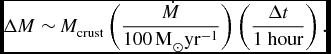 $$
\Delta M \sim M_\mathrm{crust} \left(\frac{\dot{M}}{100\, \text{M}_\odot {\mathrm{ yr}}^{-1}}\right) \left( \frac{\Delta t}{1\; {\mathrm{hour}}}\right).
$$
$$
\Delta M \sim M_\mathrm{crust} \left(\frac{\dot{M}}{100\, \text{M}_\odot {\mathrm{ yr}}^{-1}}\right) \left( \frac{\Delta t}{1\; {\mathrm{hour}}}\right).
$$
It would be important to estimate for PSR J1852+0040 the total amount of accreted matter. This can allow the calculation of the maximum accretion rate during the fall-back. Then all estimates above can be made in a more robust way.
As a determination of initial spin periods for known magnetarsFootnote 2 is impossible, a promising way to get solid arguments in favour of the dynamo mechanism hypothesis is to find a real ‘frozen magnetar’. In the modern picture of unified NS population (see, for example, Pons, Viganò, & Geppert Reference Pons, Viganò and Geppert2012 for description of different possibilities and evolutionary histories, especially their Figure 2 for evolutionary tracks), such sources are quite natural. However, they must be relatively rare.
Magnetars form up to 10% of all NSs as both observations and population synthesis studies indicate (see Gill & Heyl Reference Gill and Heyl2007, and also Popov et al. Reference Popov, Pons, Miralles, Boldin and Posselt2010 for a unified description of magnetars, pulsars and cooling NSs, and references therein). If we assume that the submergence of the magnetic field happens in magnetars as often, as in other NSs, and that central compact objects (CCOs) are NSs with submerged fields, then the number of ‘frozen’ magnetars is ≲10% of the number of CCOs. However, it is natural to assume that the larger the fields, the more difficult it is to bury them. Then, the fraction of ‘frozen magnetars’ is even lower. In addition, if magnetars are born in binary systems where spin of the progenitor was increased due to interaction with the companion (Popov & Prokhorov Reference Popov and Prokhorov2006; Bogomazov & Popov Reference Bogomazov and Popov2009), then the amount of fall-back can be smaller as a significant parts of the outer layers of the star are already removed (this was mentioned, for example, by Chevalier Reference Chevalier1989). The problem of identification (the detectability of millisecond periods for complicated field topology in the crust, pulse profiles, etc.) can also prevent easy discovery of ‘frozen magnetars’ (but see a recent discussion in Perna et al. Reference Perna, Viganó, Pons and Rea2013). On the other hand, an additional energy source—field decay —can help such sources to stay bright for a longer time, which favours their discovery (Heyl & Kulkarni Reference Heyl and Kulkarni1998).
4 CONCLUSIONS
The CCO in Kes 79 has a relatively long spin period (0.1 s) and might have a strong crustal field (Shabaltas & Lai Reference Shabaltas and Lai2012). We argue that this field could not be generated by a dynamo mechanism as, on one hand, known mechanisms of NS spin-down applicable in the case of this source cannot slow down rotation form ~ msec to the present day period before the field is buried, on the other—the present day low field also excludes a significant spin-down during the lifetime of the source. Discovery of a ‘frozen magnetar’—a CCO-like source with a millisecond period and indications of a strong crustal field—would be a strong argument in favour of the dynamo mechanism scenario by Duncan & Thompson (Reference Duncan and Thompson1992).
ACKNOWLEDGEMENTS
I thank participants of the Madrid-2013 conference ‘Fast and furious’, in particular Dr. Daniele Viganó, for discussions. Special thanks to prof. D. Page, who made useful comments on the draft of the paper. Comments by an unknown referee helped to improve the paper. This work was supported by the RFBR grant 12-02-00186.



