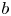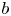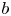1. Introduction
Black holes and neutron stars are among the most remarkable objects in the universe. In addition to warping space–time, they generate powerful plasma outflows, which, in the case of supermassive black holes, can manifest as radio sources that extend up to a million light years through intergalactic space. Because the plasma around these compact objects and their outflows are often relativistic, with flow velocities comparable to the speed of light and magnetic energy density comparable to (or much greater than) the rest-mass energy density of the plasma, the plasma physics of these environments has been the subject of a great deal of recent study (Thompson & Blaes Reference Thompson and Blaes1998; Blandford Reference Blandford2002; Chandran, Foucart & Tchekhovskoy Reference Chandran, Foucart and Tchekhovskoy2018; Li, Zrake & Beloborodov Reference Li, Zrake and Beloborodov2019; Nathanail et al. Reference Nathanail, Gill, Porth, Fromm and Rezzolla2020; Ripperda, Bacchini & Philippov Reference Ripperda, Bacchini and Philippov2020; Yuan et al. Reference Yuan, Beloborodov, Chen and Levin2020; Chashkina, Bromberg & Levinson Reference Chashkina, Bromberg and Levinson2021; Li, Beloborodov & Sironi Reference Li, Beloborodov and Sironi2021; Ripperda et al. Reference Ripperda, Mahlmann, Chernoglazov, TenBarge, Most, Juno, Yuan, Philippov and Bhattacharjee2021; TenBarge et al. Reference TenBarge, Ripperda, Chernoglazov, Bhattacharjee, Mahlmann, Most, Juno, Yuan and Philippov2021; Yuan et al. Reference Yuan, Levin, Bransgrove and Philippov2021). It is therefore of interest to study how the basic building blocks of plasma physics, for example the plasma waves, behave in a relativistic system.
One of the most important waves in non-relativistic plasma physics is the Alfvén wave (AW) (Alfvén Reference Alfvén1942; Barnes & Suffolk Reference Barnes and Suffolk1971; Barnes & Hollweg Reference Barnes and Hollweg1974; Goldstein, Klimas & Barish Reference Goldstein, Klimas and Barish1974). This wave has prompted a great deal of study, in part because of its ubiquitous presence in spacecraft observations of the solar wind (Belcher & Davis Reference Belcher and Davis1971). The prevalence of this wave in the solar wind may be due to the fact that long-wavelength propagating fluctuations that are not AWs quickly dissipate, either through steepening into shocks, turbulent mixing or damping due to wave–particle interactions (Barnes & Hollweg Reference Barnes and Hollweg1974; Cohen & Kulsrud Reference Cohen and Kulsrud1974; Vasquez & Hollweg Reference Vasquez and Hollweg1996; Schekochihin et al. Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009). In contrast, AWs are undamped in a collisionless plasma in the long-wavelength limit (Barnes & Suffolk Reference Barnes and Suffolk1971), and they undergo only weak turbulent mixing when most of the AWs propagate in a single direction along the background magnetic field lines (as happens in the solar wind, in which most of the AWs propagate away from the Sun in the plasma rest frame). AWs in non-relativistic plasmas also possess a polarization state in which the waves do not steepen into shocks, irrespective of their amplitude. This is the ‘spherical polarization state’, in which the total magnetic-field strength B is a constant. Indeed, in a homogeneous, non-relativistic plasma, a nonlinear, three-dimensional AW packet in which the total magnetic-field strength, density and pressure are constant is an exact solution to the compressible magnetohydrodynamic (MHD) equations (Goldstein et al. Reference Goldstein, Klimas and Barish1974). In the solar wind, the observed AWs are often nearly perfectly spherically polarized.
AWs play an important role in space and astrophysical plasmas. For example, they contribute substantially to the heating of the solar corona and the energization of the solar wind. Convective motions at the solar photosphere shake the magnetic field lines that connect the solar surface to the distant interplanetary medium, thereby launching AWs that transport energy outward from the solar surface. In many models, the dissipation of this AW energy flux is the dominant heating mechanism in the solar corona and solar wind (Cranmer, Van Ballegooijen & Edgar Reference Cranmer, Van Ballegooijen and Edgar2007; Verdini et al. Reference Verdini, Velli, Matthaeus, Oughton and Dmitruk2009; van der Holst et al. Reference van der Holst, Sokolov, Meng, Jin, Manchester IV, Toth and Gombosi2014; Chandran Reference Chandran2021). A similar energization mechanism could arise in relativistic astrophysical plasmas, in which a dense central object (e.g. a black-hole accretion disk, or the surface of a proto-neutron star) has a turbulent surface and is threaded by a magnetic field (e.g. Metzger, Thompson & Quataert Reference Metzger, Thompson and Quataert2007). Relativistic AW turbulence has been the subject of several recent studies (e.g. Thompson & Blaes Reference Thompson and Blaes1998; Cho Reference Cho2005; Chandran et al. Reference Chandran, Foucart and Tchekhovskoy2018; Ripperda et al. Reference Ripperda, Mahlmann, Chernoglazov, TenBarge, Most, Juno, Yuan, Philippov and Bhattacharjee2021; TenBarge et al. Reference TenBarge, Ripperda, Chernoglazov, Bhattacharjee, Mahlmann, Most, Juno, Yuan and Philippov2021) and relativistic AW in the magnetically dominated regime have been implicated in the energization of pulsar and magnetar magnetospheres (Bransgrove, Beloborodov & Levin Reference Bransgrove, Beloborodov and Levin2020; Yuan et al. Reference Yuan, Beloborodov, Chen and Levin2020, Reference Yuan, Levin, Bransgrove and Philippov2021; Beloborodov Reference Beloborodov2021).
AWs also play a crucial role in the transport and confinement of cosmic rays. When the average cosmic-ray drift velocity through a plasma exceeds the Alfvén speed, the AW becomes unstable and grows, leading to wave pitch-angle scattering of the cosmic rays (Lerche Reference Lerche1966; Wentzel Reference Wentzel1968; Kulsrud & Pearce Reference Kulsrud and Pearce1969). This same process plays a critical role in diffusive shock acceleration. The streaming of cosmic rays away from a shock in the upstream direction amplifies AWs, which scatter the cosmic rays, causing them to return to the shock, thereby enabling the repeated shock crossings required to accelerate particles to high energies (Bell Reference Bell1978).
The tendency for AWs to develop spherical polarization in non-relativistic plasmas has important implications for the way that AWs affect the transport of energetic particles and energize plasma outflows. For example, in contrast to large-amplitude, linearly polarized AWs, large-amplitude spherically polarized AWs do not cause magnetic mirroring of cosmic rays. In addition, numerical simulations suggest that when the amplitudes of the fluctuating and background magnetic fields are comparable, spherically polarized AWs necessarily develop discontinuous magnetic-field rotations (Valentini et al. Reference Valentini, Malara, Sorriso-Valvo, Bruno and Primavera2019; Squire, Chandran & Meyrand Reference Squire, Chandran and Meyrand2020; Shoda, Chandran & Cranmer Reference Shoda, Chandran and Cranmer2021). Copious abrupt magnetic-field rotations are indeed observed in the solar wind close to the Sun (Bale et al. Reference Bale, Badman, Bonnell, Bowen, Burgess, Case, Cattell, Chandran, Chaston and Chen2019; Kasper et al. Reference Kasper, Bale, Belcher, Berthomier, Case, Chandran, Curtis, Gallagher, Gary and Golub2019; Horbury et al. Reference Horbury, Woolley, Laker, Matteini, Eastwood, Bale, Velli, Chandran, Phan and Raouafi2020), but fewer are observed farther away, implying that these discontinuities erode over time, possibly via plasma instabilities (Tenerani et al. Reference Tenerani, Velli, Matteini, Réville, Shi, Bale, Kasper, Bonnell, Case and de Wit2020). The development and decay of these discontinuities provide a dissipation channel for AWs that can alter the rate at which wave energy is thermalized and, in principle, the way that the dissipated wave energy is apportioned among different particle species (cf. Howes Reference Howes2010; Kawazura et al. Reference Kawazura, Schekochihin, Barnes, TenBarge, Tong, Klein and Dorland2020). If a relativistic analogue of the spherically polarized state exists for the relativistic AW, this could have important implications for energetic particle propagation and turbulent heating in relativistic plasmas. This possibility is the focus of this Letter.
Previous work on large-amplitude relativistic AWs has been limited to two simplified cases. First, in the magnetically dominated limit, where the magnetic energy density is much larger than the energy density of the plasma, the inertia of the plasma may be neglected and arbitrary AW are exact nonlinear solutions, travelling at the speed of light $c$![]() (Thompson & Blaes Reference Thompson and Blaes1998). Second, when the magnetic field is not so dominant and the plasma inertia may not be neglected, exact nonlinear AW solutions have been found for the so-called ‘simple wave’, in which the magnetic-field strength in the local fluid frame is a constant and the fluctuations depend only on a single scalar variable $\phi (x^{\mu })$
(Thompson & Blaes Reference Thompson and Blaes1998). Second, when the magnetic field is not so dominant and the plasma inertia may not be neglected, exact nonlinear AW solutions have been found for the so-called ‘simple wave’, in which the magnetic-field strength in the local fluid frame is a constant and the fluctuations depend only on a single scalar variable $\phi (x^{\mu })$![]() (Barnes & Suffolk Reference Barnes and Suffolk1971; Greco Reference Greco1972; Anile Reference Anile1989). It was shown that the simple AW propagates without steepening. This was apparently rediscovered by Heyvaerts, Lehner & Mottez (Reference Heyvaerts, Lehner and Mottez2012), who also showed that the simple AWs are necessarily planar ($1+1$
(Barnes & Suffolk Reference Barnes and Suffolk1971; Greco Reference Greco1972; Anile Reference Anile1989). It was shown that the simple AW propagates without steepening. This was apparently rediscovered by Heyvaerts, Lehner & Mottez (Reference Heyvaerts, Lehner and Mottez2012), who also showed that the simple AWs are necessarily planar ($1+1$![]() -dimensional).
-dimensional).
In this Letter, we extend this work to more general $3+1$![]() -dimensional structures, without assuming plane polarization or that the system is magnetically dominated. We show that any fluctuations in the magnetic-field 4-vector and velocity 4-vector that are proportional to each other in the same way as linear AWs are exact nonlinear solutions to the relativistic MHD equations in flat space–time, provided that the mass density, internal energy, pressure and background magnetic field are constants. In these solutions, the magnetic-field strength in the local fluid rest frame is a constant. The resulting wave packets propagate through the plasma at the relativistic Alfvén velocity without steepening into shocks.
-dimensional structures, without assuming plane polarization or that the system is magnetically dominated. We show that any fluctuations in the magnetic-field 4-vector and velocity 4-vector that are proportional to each other in the same way as linear AWs are exact nonlinear solutions to the relativistic MHD equations in flat space–time, provided that the mass density, internal energy, pressure and background magnetic field are constants. In these solutions, the magnetic-field strength in the local fluid rest frame is a constant. The resulting wave packets propagate through the plasma at the relativistic Alfvén velocity without steepening into shocks.
2. Elsasser formulation of general relativistic magnetohydrodynamics
The equations of general relativistic magnetohydrodynamics (GRMHD) (Anile Reference Anile1989) describe the motion of a perfectly conducting fluid under the influence of the electromagnetic fields and gravity,Footnote 1 and may be derived assuming that the electric field vanishes in the local fluid rest frame. These equations are, first, the conservation of mass
the stress–energy equation
and the induction equation
In these equations, $\nabla _\nu$![]() denotes the covariant derivative, $\rho$
denotes the covariant derivative, $\rho$![]() is the mass density, $u^{\mu }$
is the mass density, $u^{\mu }$![]() is the fluid 4-velocity, the GRMHD stress–energy tensor is
is the fluid 4-velocity, the GRMHD stress–energy tensor is
where $g^{\mu \nu }$![]() is the metric tensor, the magnetic-field 4-vector is
is the metric tensor, the magnetic-field 4-vector is
with $b^{2} = b^{\mu } b_\mu >0$![]() , $F_{\lambda \kappa }$
, $F_{\lambda \kappa }$![]() the Faraday tensor divided by $\sqrt {4{\rm \pi} }$
the Faraday tensor divided by $\sqrt {4{\rm \pi} }$![]() , $\epsilon ^{\mu \nu \kappa \lambda }$
, $\epsilon ^{\mu \nu \kappa \lambda }$![]() the Levi-Civita tensor, and
the Levi-Civita tensor, and
where $U$![]() is the internal energy and $p$
is the internal energy and $p$![]() is the thermal pressure. We use units such that the speed of light $c=1$
is the thermal pressure. We use units such that the speed of light $c=1$![]() . We use the notation
. We use the notation
to denote the magnitude squared of any 4-vector $A^{\mu }$![]() ; for spacelike 4-vectors, we also write $A=\sqrt {A^{2}}$
; for spacelike 4-vectors, we also write $A=\sqrt {A^{2}}$![]() .
.
The 4-velocity satisfies
and (2.5) implies that
Chandran et al. (Reference Chandran, Foucart and Tchekhovskoy2018) noticed that, just as in non-relativistic MHD, (2.2) and (2.3) may be cast in a useful pseudo-symmetric Elsasser (Reference Elsasser1950) form by multiplying (2.3) by $\pm \mathcal {E}^{1/2}$![]() , adding to (2.2) and dividing the two resulting equations by $\mathcal {E}$
, adding to (2.2) and dividing the two resulting equations by $\mathcal {E}$![]() . This results in
. This results in
where
and $\partial _\nu$![]() refers to differentiation with respect to the coordinate $\nu$
refers to differentiation with respect to the coordinate $\nu$![]() . Equation (2.10), along with (2.1) and an equation of state, comprise the Elsasser formulation of GRMHD. These equations have been used recently by TenBarge et al. (Reference TenBarge, Ripperda, Chernoglazov, Bhattacharjee, Mahlmann, Most, Juno, Yuan and Philippov2021) to study weak AW turbulence in the small-amplitude, magnetically dominated, anisotropic limit.
. Equation (2.10), along with (2.1) and an equation of state, comprise the Elsasser formulation of GRMHD. These equations have been used recently by TenBarge et al. (Reference TenBarge, Ripperda, Chernoglazov, Bhattacharjee, Mahlmann, Most, Juno, Yuan and Philippov2021) to study weak AW turbulence in the small-amplitude, magnetically dominated, anisotropic limit.
In the following, we restrict ourselves to the case of special relativity, for which the Minkowski metric may be written in Cartesian coordinates $g^{\mu \nu }=\mathrm {diag}(-1,1,1,1)$![]() , and the covariant derivative reduces to the simpler 4-gradient operator $\nabla _\nu = \partial _\nu$
, and the covariant derivative reduces to the simpler 4-gradient operator $\nabla _\nu = \partial _\nu$![]() . Thus, our results only apply when the length and time scales of the fluctuations are small compared with the scales over which the metric changes significantly.
. Thus, our results only apply when the length and time scales of the fluctuations are small compared with the scales over which the metric changes significantly.
3. Fluctuations on a uniform background
We take each quantity to be the sum of a background value plus a fluctuation

We take the background quantities to be uniform in space and time,
and consider fluctuations satisfying
The final equation of (3.3a,b) implies that $\tilde {z}_-^{\mu } = 0$![]() . We assume that the fluctuations are localized in space–time around a sequence of events $X^{\mu }$
. We assume that the fluctuations are localized in space–time around a sequence of events $X^{\mu }$![]() ; at another sequence of events ${X'}^{\mu }$
; at another sequence of events ${X'}^{\mu }$![]() , $b^{\nu }(X'^{\mu }) \to \overline {b}^{\mu }$
, $b^{\nu }(X'^{\mu }) \to \overline {b}^{\mu }$![]() and $u^{\mu }(X'^{\mu }) \to \overline {u}^{\mu }$
and $u^{\mu }(X'^{\mu }) \to \overline {u}^{\mu }$![]() as $|(X-X')^{2}|\to \infty$
as $|(X-X')^{2}|\to \infty$![]() .
.
It follows from (2.8) that
The space–time localization of the fluctuations combined with the constancy of $\bar {u}^{\mu }$![]() implies that $\overline {u}^{2}=-1$
implies that $\overline {u}^{2}=-1$![]() , and hence
, and hence
Equation (2.9) further restricts the solution by requiring that
The localization of the fluctuations and the constancy of $\bar {u}^{\mu }$![]() and $\bar {b}^{\mu }$
and $\bar {b}^{\mu }$![]() imply that $\overline {u}^{\mu }\overline {b}_\mu =0$
imply that $\overline {u}^{\mu }\overline {b}_\mu =0$![]() , so (3.6) becomes
, so (3.6) becomes
Subtracting (3.5) from twice (3.7), we find that
Finally, we calculate the scalar $b^{2}$![]() . This is
. This is
a constant, where we have used (3.8) in the last equality. Thus, the wave packet has constant 4-magnetic-field magnitude, analogous to the constant-$B^{2}$![]() constraint for a large-amplitude AW in non-relativistic MHD (Barnes & Hollweg Reference Barnes and Hollweg1974; Goldstein et al. Reference Goldstein, Klimas and Barish1974).
constraint for a large-amplitude AW in non-relativistic MHD (Barnes & Hollweg Reference Barnes and Hollweg1974; Goldstein et al. Reference Goldstein, Klimas and Barish1974).
At each point in space–time, we may boost into an accelerating frame moving with the instantaneous local fluid velocity $u^{\mu }$![]() , the local fluid rest frame. In this frame, $b^{t}=0$
, the local fluid rest frame. In this frame, $b^{t}=0$![]() and, therefore, the magnetic-field 3-vector has magnitude squared $B^{2}=b^{2}$
and, therefore, the magnetic-field 3-vector has magnitude squared $B^{2}=b^{2}$![]() , which is a constant and therefore the same at each point; $B^{2}$
, which is a constant and therefore the same at each point; $B^{2}$![]() is not spatially constant in an arbitrary fixed inertial frame.
is not spatially constant in an arbitrary fixed inertial frame.
Equation (2.1) with $\rho$![]() constant and flat space–time gives
constant and flat space–time gives
and the $+$![]() Elsasser equation (2.10) then gives
Elsasser equation (2.10) then gives
with the $-$![]() Elsasser equation vanishing by virtue of (3.10) and (3.3a,b). (3.11) is a linear wave equation for the evolution of $\tilde {z}_+^{\mu }$
Elsasser equation vanishing by virtue of (3.10) and (3.3a,b). (3.11) is a linear wave equation for the evolution of $\tilde {z}_+^{\mu }$![]() ; thus, a three-dimensional Alfvénic wavepacket of (apparently; see (5.1)) arbitrary amplitude and arbitrary shape propagates without distortion on a homogeneous background.
; thus, a three-dimensional Alfvénic wavepacket of (apparently; see (5.1)) arbitrary amplitude and arbitrary shape propagates without distortion on a homogeneous background.
4. Components in the background rest frame
We define a background rest frame (BRF)Footnote 2 in which the homogeneous background (3.2) is at rest. In this frame $\overline {u}^{\mu } = (1,0,0,0)$![]() , and $\overline {b}^{\mu } = (0, 0,0,b)$
, and $\overline {b}^{\mu } = (0, 0,0,b)$![]() , where we have chosen to align the $z$
, where we have chosen to align the $z$![]() direction with the background magnetic field. Since $u^{\mu }$
direction with the background magnetic field. Since $u^{\mu }$![]() is a future-directed 4-velocity, it is straightforward to show, working in the BRF and using (3.4), that $\tilde {u}^{2} \geq 0$
is a future-directed 4-velocity, it is straightforward to show, working in the BRF and using (3.4), that $\tilde {u}^{2} \geq 0$![]() , a relation that holds in all frames since $\tilde {u}^{2}$
, a relation that holds in all frames since $\tilde {u}^{2}$![]() is a scalar. (The equality $\tilde {u}^{2} = 0$
is a scalar. (The equality $\tilde {u}^{2} = 0$![]() is obtained only when $\tilde {u}^{\mu } = 0$
is obtained only when $\tilde {u}^{\mu } = 0$![]() .) Calculating (3.5) and (3.8) in the BRF, the $t$
.) Calculating (3.5) and (3.8) in the BRF, the $t$![]() and $z$
and $z$![]() components of the fluctuation are given by
components of the fluctuation are given by
and the magnitude of the remaining (perpendicular) fluctuation components $\tilde {u}_\perp =\sqrt {(\tilde {u}^{x})^{2} + (\tilde {u}^{y})^{2}}$![]() is
is
where $\sigma = b^{2}/(\rho +U+p)$![]() . Providing $\tilde {u}^{2}$
. Providing $\tilde {u}^{2}$![]() thus gives us nearly all the information in the fluctuation 4-vector, apart from the direction in the $y$
thus gives us nearly all the information in the fluctuation 4-vector, apart from the direction in the $y$![]() -$z$
-$z$![]() plane that the perpendicular fluctuation points. To determine this, we must use (3.10) and a particular functional form for $\tilde {u}^{2}$
plane that the perpendicular fluctuation points. To determine this, we must use (3.10) and a particular functional form for $\tilde {u}^{2}$![]() . This amounts to solving a two-dimensional first-order quasilinear partial differential equation with analytic coefficients for one of the components (say, $\tilde {u}^{x}$
. This amounts to solving a two-dimensional first-order quasilinear partial differential equation with analytic coefficients for one of the components (say, $\tilde {u}^{x}$![]() ).
).
Evaluating the fluid 3-velocity $v^{i}=u^{i}/u^{t}$![]() and magnetic-field 3-vector $B^{i}=b^{i} u^{t} - b^{t} u^{i}$
and magnetic-field 3-vector $B^{i}=b^{i} u^{t} - b^{t} u^{i}$![]() , it is clear that, in the BRF, $B^{2}$
, it is clear that, in the BRF, $B^{2}$![]() is not constant, the 3-vector magnetic and velocity fluctuations are not related to each other by a constant of proportionality, and do not in general even point in the same direction.
is not constant, the 3-vector magnetic and velocity fluctuations are not related to each other by a constant of proportionality, and do not in general even point in the same direction.
5. Maximum amplitude
Equation (4.2) implies an upper limit on the magnitude of the fluctuations,
In the non-relativistic case, this has been recently noticed in solar wind AWs by (Matteini et al. Reference Matteini, Stansby, Horbury and Chen2018). The observed magnitude of the fluid 3-velocity in the BRF is
an increasing function of $\tilde {u}$![]() ; $v<1$
; $v<1$![]() and $v\to 1$
and $v\to 1$![]() as $\tilde {u}\to \infty$
as $\tilde {u}\to \infty$![]() .
.
6. Alfvén velocity and wave frame
The propagation of the wave is controlled by the constant time-like 4-vector $\overline {z}_-^{\mu }$![]() , with
, with
(In the limit $b^{2}\to \infty$![]() while keeping $\rho$
while keeping $\rho$![]() , $U$
, $U$![]() and $p$
and $p$![]() constant, $\overline {z}_-^{2} \to 0$
constant, $\overline {z}_-^{2} \to 0$![]() .) An observer moving with 4-velocity $\overline {z}_-^{\mu } / \sqrt {-\overline {z}_-^{2}}$
.) An observer moving with 4-velocity $\overline {z}_-^{\mu } / \sqrt {-\overline {z}_-^{2}}$![]() sees a time-independent structure; such an observer is in the wave frame (WF). The WF 3-velocity relative to another frame is $v_w^{i} = \overline {z}_-^{i}/\overline {z}_-^{t}$
sees a time-independent structure; such an observer is in the wave frame (WF). The WF 3-velocity relative to another frame is $v_w^{i} = \overline {z}_-^{i}/\overline {z}_-^{t}$![]() , and specifically, relative to the BRF is
, and specifically, relative to the BRF is
Thus, the three-dimensional relativistic AW propagates along the background field lines at this relativistic Alfvén velocity, just like the planar AW (Barnes & Suffolk Reference Barnes and Suffolk1971; Heyvaerts et al. Reference Heyvaerts, Lehner and Mottez2012). Note that this does not depend on $\tilde {u}^{\mu }$![]() , so the wave does not steepen into a shock. If all of $b^{2}/\rho,U/\rho,p/\rho \ll 1$
, so the wave does not steepen into a shock. If all of $b^{2}/\rho,U/\rho,p/\rho \ll 1$![]() , we recover the usual non-relativistic Alfvén velocity. As $b^{2}\to \infty$
, we recover the usual non-relativistic Alfvén velocity. As $b^{2}\to \infty$![]() , $v_A^{2}\to 1$
, $v_A^{2}\to 1$![]() , the ultra-relativistic limit of the AW previously studied by (for example) Thompson & Blaes (Reference Thompson and Blaes1998) and Heyl & Hernquist (Reference Heyl and Hernquist1999).
, the ultra-relativistic limit of the AW previously studied by (for example) Thompson & Blaes (Reference Thompson and Blaes1998) and Heyl & Hernquist (Reference Heyl and Hernquist1999).
7. Structure in the WF
In the WF, the spatial components of $z_-^{\mu } = \overline {z}_-^{\mu }$![]() are zero and so
are zero and so
Using (2.9), we may obtain
where $v^{2}$![]() is the square of the 3-velocity $v^{i}=u^{i}/\gamma$
is the square of the 3-velocity $v^{i}=u^{i}/\gamma$![]() and $\gamma =u^{t}$
and $\gamma =u^{t}$![]() . Then, we may calculate the magnetic-field 3-vector,
. Then, we may calculate the magnetic-field 3-vector,
so in the WF the 3-velocity is parallel and proportional to the magnetic-field 3-vector, just like in the non-relativistic case. This also implies $\partial _i v^{i}=0$![]() in the WF. We may also calculate
in the WF. We may also calculate
and so, since $b^{2}$![]() is constant, in the WF $v^{2}$
is constant, in the WF $v^{2}$![]() and $B^{2}$
and $B^{2}$![]() are both constant, just like in the non-relativistic case (Matteini et al. Reference Matteini, Horbury, Pantellini, Velli and Schwartz2015).
are both constant, just like in the non-relativistic case (Matteini et al. Reference Matteini, Horbury, Pantellini, Velli and Schwartz2015).
Let us consider the components of the stress–energy tensor (2.4) in the WF. First, using (7.2) and (7.4),
a space–time constant for our solution. Applying (7.2) again,
which from (7.3) has no spatial divergence, maintaining the constancy of $T^{tt}$![]() in the equation $\partial _\nu T^{t\nu } = 0$
in the equation $\partial _\nu T^{t\nu } = 0$![]() . Finally,
. Finally,
a space–time constant, thus enforcing the constancy in time of $T^{it}$![]() in the equations $\partial _\nu T^{i\nu } = 0$
in the equations $\partial _\nu T^{i\nu } = 0$![]() . The cancellation of the first two terms in the space–space components of (2.4) in the WF generalizes the result for the non-relativistic AW that the centrifugal force exactly balances the tension force in the magnetic field, keeping the fluid flowing exactly along the field lines in the WF.
. The cancellation of the first two terms in the space–space components of (2.4) in the WF generalizes the result for the non-relativistic AW that the centrifugal force exactly balances the tension force in the magnetic field, keeping the fluid flowing exactly along the field lines in the WF.
8. Discussion
Our analysis has shown that some of the unique properties of the AW survive, even with relativistic fluctuation velocities and arbitrarily strong magnetic-field strength. Specifically, just as in the non-relativistic case (Goldstein et al. Reference Goldstein, Klimas and Barish1974), a three-dimensional Alfvénic structure propagates in time without steepening into a shock,Footnote 3 no matter its fluctuation amplitude; equivalently, the propagation velocity in the rest frame of the background is always the relativistic Alfvén velocity (6.2), which is independent of the fluctuation amplitude. Also analogous to the non-relativistic case, the magnitude $b^{2}$![]() of the magnetic-field 4-vector $b^{\mu }$
of the magnetic-field 4-vector $b^{\mu }$![]() is a space–time constant. This implies correlations between different components of the fluctuation to enforce this constraint. Unlike in the non-relativistic case, in a general inertial frame the magnetic-field 3-vector does not have constant magnitude; however, in the WF moving at the Alfvén velocity, both the velocity and magnetic field 3-vectors have constant magnitude, as in the non-relativistic case. Also in the WF, the plasma 3-velocity is parallel and proportional to the magnetic-field 3-vector.
is a space–time constant. This implies correlations between different components of the fluctuation to enforce this constraint. Unlike in the non-relativistic case, in a general inertial frame the magnetic-field 3-vector does not have constant magnitude; however, in the WF moving at the Alfvén velocity, both the velocity and magnetic field 3-vectors have constant magnitude, as in the non-relativistic case. Also in the WF, the plasma 3-velocity is parallel and proportional to the magnetic-field 3-vector.
In what situations might one see large-amplitude relativistic AWs? In a statistically homogeneous medium, one might expect equal fluxes of $\tilde {z}_\pm ^{\mu }$![]() AWs, a nonlinear, turbulent situation. However, if the waves are excited by some particular event or set of events, they will mainly travel away from that event. We might postulate (inspired by non-relativistic plasma physics) that sufficiently far from the source, the other, non-Alfvénic modes largely dissipate, and then we are left with just the AWs. This situation would be relevant, for example, in outflows around a compact object like a black hole (Chandran et al. Reference Chandran, Foucart and Tchekhovskoy2018). One caveat is that in this case the background is likely to be highly inhomogeneous, and these inhomogeneities will reflect the waves and thus drive turbulence. However, as previously mentioned, in the non-relativistic case it can be shown that even including this turbulence (Cranmer & Van Ballegooijen Reference Cranmer and Van Ballegooijen2005; Verdini & Velli Reference Verdini and Velli2007; Perez & Chandran Reference Perez and Chandran2013; Van Ballegooijen & Asgari-Targhi Reference Van Ballegooijen and Asgari-Targhi2016; van Ballegooijen & Asgari-Targhi Reference van Ballegooijen and Asgari-Targhi2017; Chandran & Perez Reference Chandran and Perez2019), in fact the normalized amplitude $\tilde {B}/\overline {B}$
AWs, a nonlinear, turbulent situation. However, if the waves are excited by some particular event or set of events, they will mainly travel away from that event. We might postulate (inspired by non-relativistic plasma physics) that sufficiently far from the source, the other, non-Alfvénic modes largely dissipate, and then we are left with just the AWs. This situation would be relevant, for example, in outflows around a compact object like a black hole (Chandran et al. Reference Chandran, Foucart and Tchekhovskoy2018). One caveat is that in this case the background is likely to be highly inhomogeneous, and these inhomogeneities will reflect the waves and thus drive turbulence. However, as previously mentioned, in the non-relativistic case it can be shown that even including this turbulence (Cranmer & Van Ballegooijen Reference Cranmer and Van Ballegooijen2005; Verdini & Velli Reference Verdini and Velli2007; Perez & Chandran Reference Perez and Chandran2013; Van Ballegooijen & Asgari-Targhi Reference Van Ballegooijen and Asgari-Targhi2016; van Ballegooijen & Asgari-Targhi Reference van Ballegooijen and Asgari-Targhi2017; Chandran & Perez Reference Chandran and Perez2019), in fact the normalized amplitude $\tilde {B}/\overline {B}$![]() of the primary outward-travelling AWs tends to grow with distance from the central object (in the solar wind case, the Sun Parker Reference Parker1965; Hollweg Reference Hollweg1974), with the other, reflected, components remaining relatively small: i.e. the fluctuations are approximately large-amplitude AWs. This is thought to be a possible origin for the ‘switchbacks’; abrupt magnetic-field reversals recently observed by NASA's Parker Solar Probe in the near-Sun solar wind (Squire et al. Reference Squire, Chandran and Meyrand2020). If this result carries over to the relativistic case (as it appears to, cf. Chandran et al. Reference Chandran, Foucart and Tchekhovskoy2018), large-amplitude AWs of the type discussed in this Letter may also exist in relativistic environments. Energization by large-amplitude AW have already been studied in the magnetically dominated limit (Thompson & Blaes Reference Thompson and Blaes1998; Cho Reference Cho2005; Yuan et al. Reference Yuan, Beloborodov, Chen and Levin2020; Li et al. Reference Li, Beloborodov and Sironi2021; Ripperda et al. Reference Ripperda, Mahlmann, Chernoglazov, TenBarge, Most, Juno, Yuan, Philippov and Bhattacharjee2021): our results apply both in this limit and when the magnetization is less extreme, and thus may be important for the study of the heating and observed dynamics of plasma around compact objects (Akiyama et al. Reference Akiyama, Algaba, Alberdi, Alef, Anantua, Asada, Azulay, Baczko, Ball and Baloković2021a,Reference Akiyama, Algaba, Alberdi, Alef, Anantua, Asada, Azulay, Baczko, Ball and Balokovićb).
of the primary outward-travelling AWs tends to grow with distance from the central object (in the solar wind case, the Sun Parker Reference Parker1965; Hollweg Reference Hollweg1974), with the other, reflected, components remaining relatively small: i.e. the fluctuations are approximately large-amplitude AWs. This is thought to be a possible origin for the ‘switchbacks’; abrupt magnetic-field reversals recently observed by NASA's Parker Solar Probe in the near-Sun solar wind (Squire et al. Reference Squire, Chandran and Meyrand2020). If this result carries over to the relativistic case (as it appears to, cf. Chandran et al. Reference Chandran, Foucart and Tchekhovskoy2018), large-amplitude AWs of the type discussed in this Letter may also exist in relativistic environments. Energization by large-amplitude AW have already been studied in the magnetically dominated limit (Thompson & Blaes Reference Thompson and Blaes1998; Cho Reference Cho2005; Yuan et al. Reference Yuan, Beloborodov, Chen and Levin2020; Li et al. Reference Li, Beloborodov and Sironi2021; Ripperda et al. Reference Ripperda, Mahlmann, Chernoglazov, TenBarge, Most, Juno, Yuan, Philippov and Bhattacharjee2021): our results apply both in this limit and when the magnetization is less extreme, and thus may be important for the study of the heating and observed dynamics of plasma around compact objects (Akiyama et al. Reference Akiyama, Algaba, Alberdi, Alef, Anantua, Asada, Azulay, Baczko, Ball and Baloković2021a,Reference Akiyama, Algaba, Alberdi, Alef, Anantua, Asada, Azulay, Baczko, Ball and Balokovićb).
Acknowledgements
We are grateful to the two referees for their erudite comments and suggestions.
Editor Roger Blandford thanks the referees for their advice in evaluating this article.
Funding
A.M. was supported by NASA grant 80NSSC21K0462 and NASA contract NNN06AA01C. B.D.G.C. was supported in part by NASA grants NNX17AI18G and 80NSSC19K0829.
Declaration of interest
The authors report no conflict of interest.