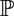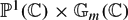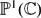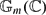Research Article
Automorphisms of the 3-sphere that preserve spatial graphs and handlebody-knots
-
- Published online by Cambridge University Press:
- 03 February 2015, pp. 1-22
-
- Article
- Export citation
Stability of L1 contractions†
-
- Published online by Cambridge University Press:
- 01 April 2015, pp. 23-46
-
- Article
- Export citation
A Jarník type theorem for planar curves: everything about the parabola
-
- Published online by Cambridge University Press:
- 01 April 2015, pp. 47-60
-
- Article
- Export citation
Gottlieb groups of function spaces
-
- Published online by Cambridge University Press:
- 10 April 2015, pp. 61-77
-
- Article
- Export citation
Uniqueness of higher genus bridge surfaces for torus knots
-
- Published online by Cambridge University Press:
- 11 May 2015, pp. 79-88
-
- Article
- Export citation
Centralisers of Dehn twist automorphisms of free groups
-
- Published online by Cambridge University Press:
- 08 May 2015, pp. 89-114
-
- Article
- Export citation
On the Hilbert functions of sets of points in
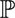 $\mathbb{P}$1 ×
$\mathbb{P}$1 × 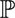 $\mathbb{P}$1 ×
$\mathbb{P}$1 × 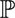 $\mathbb{P}$1
$\mathbb{P}$1
-
- Published online by Cambridge University Press:
- 04 May 2015, pp. 115-123
-
- Article
- Export citation
The stretch-length tradeoff in geometric networks: average case and worst case study
-
- Published online by Cambridge University Press:
- 05 May 2015, pp. 125-151
-
- Article
- Export citation
An explicit André–Oort type result for
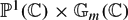 $\mathbb{P}^1(\mathbb{C}) \times \mathbb{G}_m(\mathbb{C})$
$\mathbb{P}^1(\mathbb{C}) \times \mathbb{G}_m(\mathbb{C})$
-
- Published online by Cambridge University Press:
- 30 April 2015, pp. 153-163
-
- Article
- Export citation
Portraits of preperiodic points for rational maps
-
- Published online by Cambridge University Press:
- 08 May 2015, pp. 165-186
-
- Article
- Export citation
Erratum
Erratum to “On surface links whose link groups are abelian”
-
- Published online by Cambridge University Press:
- 10 April 2015, p. 187
-
- Article
-
- You have access
- Export citation
Front Cover (OFC, IFC) and matter
PSP volume 159 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 22 May 2015, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
PSP volume 159 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 22 May 2015, pp. b1-b2
-
- Article
-
- You have access
- Export citation