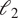Impact Statement
This work demonstrates that the tenet of representation learning also applies to atmospheric dynamics and that the intermediate activations of trained neural networks can provide an informative embedding for atmospheric data. We show this with a novel, self-supervised learning task derived from the underlying physics that makes large amounts of unlabeled observational and simulation data accessible for machine learning. We exemplify the utility of our learned representations by deriving from these a distance metric for atmospheric dynamics that leads to improved performance in applications such as downscaling and missing data interpolation.
1. Introduction
Representation learning is an important methodology in machine learning where the focus is on the data transformations that are provided by a neural network. The motivation for it is to obtain an embedding of the input data that will facilitate a range of applications, for example, by revealing intrinsic aspects of the data or by being invariant to perturbations that are irrelevant to tasks. Representation learning is today central to application areas such as machine translation (e.g., Devlin et al., Reference Devlin, Chang, Lee and Toutanova2019; Brown et al., Reference Brown, Mann, Ryder, Subbiah, Kaplan, Dhariwal, Neelakantan, Shyam, Sastry, Askell, Agarwal, Herbert-Voss, Krueger, Henighan, Child, Ramesh, Ziegler, Wu, Winter, Hesse, Chen, Sigler, Litwin, Gray, Chess, Clark, Berner, McCandlish, Radford, Sutskever, Amodei, Larochelle, Ranzato, Hadsell, Balcan and Lin2020), and image understanding (e.g., Caron et al., Reference Caron, Touvron, Misra, Jegou, Mairal, Bojanowski and Joulin2021; Bao et al., Reference Bao, Dong, Piao and Wei2022; He et al., Reference He, Chen, Xie, Li, Dollár and Girshick2022), and has led there to significantly improved performance on a variety of tasks.
In the geosciences, representation learning has so far received only limited attention. One reason is the lack of large-scale, labeled datasets that are classically used for training. As has been shown for other domains (e.g., Devlin et al., Reference Devlin, Chang, Lee and Toutanova2019; He et al., Reference He, Fan, Wu, Xie and Girshick2020; Caron et al., Reference Caron, Touvron, Misra, Jegou, Mairal, Bojanowski and Joulin2021), representation learning can, however, benefit from working with unlabeled data and performing self-supervised learning with loss functions derived from the data itself. One reason for this is that a self-supervised task can be more challenging than, for example, choosing from a small set of possible answers or labels. Hence, with a self-supervised task the neural network is forced to learn more expressive and explanatory internal representations. A second reason for the efficiency of self-supervised training is that it makes much larger amounts of data available since no labels are required (e.g., Devlin et al., Reference Devlin, Chang, Lee and Toutanova2019; Brown et al., Reference Brown, Mann, Ryder, Subbiah, Kaplan, Dhariwal, Neelakantan, Shyam, Sastry, Askell, Agarwal, Herbert-Voss, Krueger, Henighan, Child, Ramesh, Ziegler, Wu, Winter, Hesse, Chen, Sigler, Litwin, Gray, Chess, Clark, Berner, McCandlish, Radford, Sutskever, Amodei, Larochelle, Ranzato, Hadsell, Balcan and Lin2020; Zhai et al., Reference Zhai, Kolesnikov, Houlsby and Beyer2021).
In this work, we introduce self-supervised representation learning for atmospheric dynamics and demonstrate its utility by defining a novel, data-driven distance metric for atmospheric states based on it. For the self-supervised training, we propose a novel learning task that is applicable to a wide range of datasets in atmospheric science. Specifically, given a temporal sequence of datum, for example, spatial fields in a reanalysis or from a simulation, the task of the neural network is to predict the temporal distance between two randomly selected, close-by sequence elements. Performing well on the task requires the network to develop an internal representation of the underlying dynamics, which will typically be useful for a range of tasks.
We demonstrate the effectiveness and practicality of our self-supervised training task by learning a representation network for vorticity and divergence (which are equivalent to the wind velocity field) from ERA5 reanalysis (Hersbach et al., Reference Hersbach, Bell, Berrisford, Hirahara, Horányi, Muñoz-Sabater, Nicolas, Peubey, Radu, Schepers, Simmons, Soci, Abdalla, Abellan, Balsamo, Bechtold, Biavati, Bidlot, Bonavita, De Chiara, Dahlgren, Dee, Diamantakis, Dragani, Flemming, Forbes, Fuentes, Geer, Haimberger, Healy, Hogan, Hólm, Janisková, Keeley, Laloyaux, Lopez, Lupu, Radnoti, de Rosnay, Rozum, Vamborg, Villaume and Thépaut2020), see Figure 1 for an overview. From the learned representation, we subsequently derive a data-driven distance metric for atmospheric states, which we call the AtmoDist distance. To demonstrate its potential, we use it as a loss function in the generative adversarial network (GAN)-based downscaling as well as to interpolate missing data. Building on the state-of-the-art GAN by Stengel et al. (Reference Stengel, Glaws, Hettinger and King2020) we show that the AtmoDist loss significantly improves downscaling results compared to the
![]() $ {\mathrm{\ell}}_2 $
-loss used in the original work. For missing data interpolation, AtmoDist leads to more realistic fine-scale details and better local statistics. As a baseline, we use in the experiments an auto-encoder, which provides an alternative means to obtain a feature space representation with self-supervised training. We also report results on experiments with AtmoDist on the predictability of atmospheric states where the data-driven loss reproduces known dependencies on season and spatial location.
$ {\mathrm{\ell}}_2 $
-loss used in the original work. For missing data interpolation, AtmoDist leads to more realistic fine-scale details and better local statistics. As a baseline, we use in the experiments an auto-encoder, which provides an alternative means to obtain a feature space representation with self-supervised training. We also report results on experiments with AtmoDist on the predictability of atmospheric states where the data-driven loss reproduces known dependencies on season and spatial location.

Figure 1. Overview of the methodology for AtmoDist. From a temporal sequence of atmospheric fields (bottom), two nearby ones are selected at random (red) and stored together with their temporal separation
![]() $ \Delta t $
as a training sample. Both fields are then passed through the same representation network (blue), which embeds them into a high-dimensional feature space (left). These embeddings are subsequently used by the tail network to predict the temporal separation
$ \Delta t $
as a training sample. Both fields are then passed through the same representation network (blue), which embeds them into a high-dimensional feature space (left). These embeddings are subsequently used by the tail network to predict the temporal separation
![]() $ \Delta t $
(top, orange). The whole architecture is trained end-to-end. Once training is completed, the embeddings can be used in downstream tasks, for example, through a distance measure
$ \Delta t $
(top, orange). The whole architecture is trained end-to-end. Once training is completed, the embeddings can be used in downstream tasks, for example, through a distance measure
![]() $ d\left({X}_{t_1},{X}_{t_2}\right) $
in embedding space.
$ d\left({X}_{t_1},{X}_{t_2}\right) $
in embedding space.
The tasks evaluated in our work, that is, downscaling and missing data interpolation, are only two possible applications that we selected to demonstrate the usefulness of the learned representations of AtmoDist. Forecasting (Rasp et al., Reference Rasp, Dueben, Scher, Weyn, Mouatadid and Thuerey2020; Bi et al., Reference Bi, Xie, Zhang, Chen, Gu and Tian2022; Lam et al., Reference Lam, Sanchez-Gonzalez, Willson, Wirnsberger, Fortunato, Pritzel, Ravuri, Ewalds, Alet, Eaton-Rosen, Hu, Merose, Hoyer, Holland, Stott, Vinyals, Mohamed and Battaglia2022; Pathak et al., Reference Pathak, Subramanian, Harrington, Raja, Chattopadhyay, Mardani, Kurth, Hall, Li, Azizzadenesheli, Hassanzadeh, Kashinath and Anandkumar2022), climate response modeling (Watson-Parris et al., Reference Watson-Parris, Rao, Olivié, Seland, Nowack, Camps-Valls, Stier, Bouabid, Dewey, Fons, Gonzalez, Harder, Jeggle, Lenhardt, Manshausen, Novitasari, Ricard and Roesch2022), or the detection and modeling of extreme weather events (Racah et al., Reference Racah, Beckham, Maharaj, Kahou, Prabhat, Pal, Guyon, Luxburg, Bengio, Wallach, Fergus, Vishwanathan and Garnett2017; Blanchard et al., Reference Blanchard, Parashar, Dodov, Lessig and Sapsis2022), are other potential tasks that could benefit from improved representation learning.
We believe that self-supervised representation learning for atmospheric data has significant potential and we hence consider the present work as a first step in this direction. Self-supervised learning only requires unlabeled data, which is available in significant quantities, for example, in the form of satellite observations, reanalyses, and simulation outputs. Given the difficulty of obtaining large, labeled datasets, this removes an obstacle to the use of large-scale machine learning in the atmospheric sciences. At the same time, representation learning can “distill” effective representations from very large amounts of data (Devlin et al., Reference Devlin, Chang, Lee and Toutanova2019; Zhai et al., Reference Zhai, Kolesnikov, Houlsby and Beyer2021), which might, for example, provide a new avenue to process the outputs produced by large simulation runs (Eyring et al., Reference Eyring, Bony, Meehl, Senior, Stevens, Stouffer and Taylor2016). We believe that learned representation can also be useful to gain novel scientific insights into the physics, similar to how proper orthogonal decompositions have been used in the past. This is, in our opinion, a particularly inspiring direction for future work (Toms et al., Reference Toms, Barnes and Ebert-Uphoff2020).
2. Related Work
In the following, we will discuss pertinent related work from the geosciences and machine learning.
2.1. Geosciences
Distance measures for atmospheric states play an important role in classical weather and climate predictions. For example, ensemble methods require a well-defined notion of nearby atmospheric states for their initialization. Various distance measures have therefore been proposed in the literature, typically grounded in mathematical and physical considerations, for example, conservation laws. The importance of an appropriate distance measure for atmospheric states already appears in the classical work by Lorenz (Reference Lorenz1969) where atmospheric predictability depends on the closeness of initial states and is also affected by the characteristics of their spectrum that is, a Sobolev-type measure. Talagrand (Reference Talagrand1981) considered an energy metric around a reference state obtained from the primitive equations in work on 4D data assimilation. Palmer et al. (Reference Palmer, Gelaro, Barkmeijer and Buizza1998) argue that within the framework of linearized equations and with singular vectors as coordinates, a metric for targeting observations should not only be informed by geophysical fluid dynamics considerations but also consider the operational observing network. Recently, Koh and Wan (Reference Koh and Wan2015) introduce an energy metric that does not require an atmospheric reference state but is intrinsically defined. For the case of an ideal barotropic fluid, the metric of Koh and Wan (Reference Koh and Wan2015) also coincides with the geodesic metric that was introduced by Arnold (Reference Arnold1966) and studied by Ebin and Marsden (Reference Ebin and Marsden1970) to describe the fluid motion as a geodesic on the infinite-dimensional group of volume preserving diffeomorphisms. Although of utility in classical applications, the aforementioned distance measures lack the sensitivity desirable for machine-learning techniques, for example, with respect to small-scale features, and are agnostic to applications. In the context of downscaling, this deficiency has recently been noted by Stengel et al. (Reference Stengel, Glaws, Hettinger and King2020).
2.2. Representation learning and learned distance measures
Representation learning (Bengio et al., Reference Bengio, Courville and Vincent2013) focuses on the nonlinear transformations that are realized by a neural network and understands these as a mapping of the input data to a feature space adapted to the data domain. The feature space is informative and explanatory, for example, when different classes are well separated and interdependencies are transparently encoded. This then allows to solve so-called downstream applications in a simple and efficient manner, for example, by appending a linear transformation or a small neural network to the pre-trained one. Good representations will also be useful for a wide range of applications.
A pertinent example of the importance of representations in neural networks is classification. There, the bulk of the overall network architecture is usually devoted to transforming the data into a feature space where the different classes correspond to linear and well-separated subspaces. A linear mapping in the classification head then suffices to accurately solve the task and the entire preceding network can thus be considered as a representation one. With deep neural networks, one obtains a hierarchy of representations where deeper once typically correspond to more abstract features, see, for example, Zeiler and Fergus (Reference Zeiler, Fergus, Fleet, Pajdla, Schiele and Tuytelaars2014) for visualizations. The hierarchical structure is of importance, for example, for generative machine-learning models (e.g., Ronneberger et al., Reference Ronneberger, Fischer, Brox, Navab, Hornegger, Wells and Frangi2015; Karras et al., Reference Karras, Laine and Aila2019, Reference Karras, Laine, Aittala, Hellsten, Lehtinen and Aila2020; Ranftl et al., Reference Ranftl, Bochkovskiy and Koltun2021) where features at all scales have to match the target distribution.
An important applications of representation learning is the design of domain-specific loss functions, sometimes also denoted as content losses (Zhang et al., Reference Zhang, Isola, Efros, Shechtman and Wang2018). The rationale for these is that feature spaces are designed to capture the essential aspects of an input data domain and computing a distance there is hence more discriminative than on the raw inputs (Achille and Soatto, Reference Achille and Soatto2018). Furthermore, deeper layers typically have invariance against “irrelevant” perturbations, for example, translation, rotation, and noise in images. A domain where content losses play an important role is computer vision where
![]() $ {\mathrm{\ell}}_p $
-norms in the pixel domain of images are usually not well suited for machine learning, for example, because a small shift in the image content can lead to a large distance in an
$ {\mathrm{\ell}}_p $
-norms in the pixel domain of images are usually not well suited for machine learning, for example, because a small shift in the image content can lead to a large distance in an
![]() $ {\mathrm{\ell}}_p $
-norm despite the image being semantically unchanged. Loss functions computed in the feature spaces of networks such as VGG (Simonyan and Zisserman, Reference Simonyan and Zisserman2015), in contrast, can lead to substantially improved performance in task such as in-painting (Yang et al., Reference Yang, Lu, Lin, Shechtman, Wang and Li2017), style transfer (Gatys et al., Reference Gatys, Ecker and Bethge2016), and image synthesis (Ledig et al., Reference Ledig, Theis, Huszar, Caballero, Cunningham, Acosta, Aitken, Tejani, Totz, Wang and Shi2017; Karras et al., Reference Karras, Laine and Aila2019).
$ {\mathrm{\ell}}_p $
-norm despite the image being semantically unchanged. Loss functions computed in the feature spaces of networks such as VGG (Simonyan and Zisserman, Reference Simonyan and Zisserman2015), in contrast, can lead to substantially improved performance in task such as in-painting (Yang et al., Reference Yang, Lu, Lin, Shechtman, Wang and Li2017), style transfer (Gatys et al., Reference Gatys, Ecker and Bethge2016), and image synthesis (Ledig et al., Reference Ledig, Theis, Huszar, Caballero, Cunningham, Acosta, Aitken, Tejani, Totz, Wang and Shi2017; Karras et al., Reference Karras, Laine and Aila2019).
2.3. Self-supervised learning
Closely related to representation learning is self-supervised learning that is today the state-of-the-art methodology for obtaining informative and explanatory representations. The appeal of self-supervised learning is that it does not require labeled data but uses for training a loss function that solely depends on the data itself. In computer vision, for example, a common self-supervised learning task is to in-paint (or predict) a region that was cropped out from a given image (Pathak et al., Reference Pathak, Krahenbuhl, Donahue, Darrell and Efros2016). Since training is typically informed by the data and not a specific application, self-supervised learning fits naturally with representation learning where one seeks domain- or data-specific but task-independent representations. The ability to use very large amounts of training data, which is usually much easier than in supervised training since no labels are required, also helps in most instances to significantly improve representations (Radford et al., Reference Radford, Narasimhan, Salimans and Sutskever2018; Devlin et al., Reference Devlin, Chang, Lee and Toutanova2019; Brown et al., Reference Brown, Mann, Ryder, Subbiah, Kaplan, Dhariwal, Neelakantan, Shyam, Sastry, Askell, Agarwal, Herbert-Voss, Krueger, Henighan, Child, Ramesh, Ziegler, Wu, Winter, Hesse, Chen, Sigler, Litwin, Gray, Chess, Clark, Berner, McCandlish, Radford, Sutskever, Amodei, Larochelle, Ranzato, Hadsell, Balcan and Lin2020; Zhai et al., Reference Zhai, Kolesnikov, Houlsby and Beyer2021).
Prominent examples of pretext tasks for computer vision include solving jigsaw puzzles (Noroozi and Favaro, Reference Noroozi, Favaro, Leibe, Matas, Sebe and Welling2016), learning image rotations (Gidaris et al., Reference Gidaris, Singh and Komodakis2018), predicting color channels from grayscale images and vice versa (Zhang et al., Reference Zhang, Isola and Efros2017), or inpainting cropped out regions of an image (Pathak et al., Reference Pathak, Krahenbuhl, Donahue, Darrell and Efros2016). An early approach that has been used for representation learning is the denoising autoencoder (Vincent et al., Reference Vincent, Larochelle, Lajoie, Bengio and Manzagol2010). The work of Misra et al. (Reference Misra, Zitnick, Hebert, Leibe, Matas, Sebe and Welling2016) is directly related to ours in the sense that they train a network to predict the temporal order of a video sequence using a triplet loss. In contrast, our approach relies on predicting the exact (categorical) temporal distance between two patches and not the order, which we believe forces the network to learn more informative representations.
Recently, consistency-based methods have received considerable attention in the literature on self-supervised learning, for example, in the form of contrastive loss functions or student-teacher methods. Since our work employs a pretext task, we will not discuss these methods but refer to Le-Khac et al. (Reference Le-Khac, Healy and Smeaton2020) for an overview.
2.4. Machine learning for the geoscience
Deep neural networks have become an important tool in the geosciences in the last years and will likely be relevant for a wide range of problems in the future (e.g., Dueben and Bauer, Reference Dueben and Bauer2018; Toms et al., Reference Toms, Barnes and Ebert-Uphoff2020; Schultz et al., Reference Schultz, Betancourt, Gong, Kleinert, Langguth, Leufen, Mozaffari and Stadtler2021; Balaji et al., Reference Balaji, Couvreux, Deshayes, Gautrais, Hourdin and Rio2022). Reichstein et al. (Reference Reichstein, Camps-Valls, Stevens, Jung, Denzler, Carvalhais and Prabhat2019) pointed out the importance of spatiotemporal approaches to machine learning in the field. This implies the need for network architectures adapted to spatiotemporal data as well as suitable learning protocols and loss functions. AtmoDist addresses the last aspect.
An early example of spatial representation learning in the geosciences is Tile2Vec (Jean et al., Reference Jean, Wang, Samar, Azzari, Lobell and Ermon2019) for remote sensing. The work demonstrates that local tiles, or patches, can serve as analogues to words in geospatial data and that this allows for the adoption of ideas from natural language processing to geoscience. Related is Space2Vec which can be considered as a multi-scale representation learning approach of geolocations. A spatiotemporal machine-learning approach is used by Barnes et al. (Reference Barnes, Anderson and Ebert-Uphoff2018) where a neural network is trained to predict the global year of a temperature field. This is similar to AtmoDist where the training task is also the prediction of temporal information given a spatial field. Barnes et al. (Reference Barnes, Anderson and Ebert-Uphoff2018), however, use their trained network for questions related to global warming whereas we are interested in representation learning. Semi-supervised learning, that is, the combination of a supervised and self-supervised loss function, is employed by Racah et al. (Reference Racah, Beckham, Maharaj, Kahou, Prabhat, Pal, Guyon, Luxburg, Bengio, Wallach, Fergus, Vishwanathan and Garnett2017) to improve the detection accuracy of extra-tropical and tropical cyclones. As a self-supervised loss, the
![]() $ {\mathrm{\ell}}_2 $
reconstruction error of atmospheric fields using an autoencoder is chosen. We also employ an autoencoder as a baseline in this work and find that it leads to significantly worse results on the two downstream tasks we consider.
$ {\mathrm{\ell}}_2 $
reconstruction error of atmospheric fields using an autoencoder is chosen. We also employ an autoencoder as a baseline in this work and find that it leads to significantly worse results on the two downstream tasks we consider.
Apart from the above examples, spatiotemporal representation learning has, to our knowledge, not received widespread attention in atmospheric science. This is in contrast to, for instance, natural language processing (Vaswani et al., Reference Vaswani, Shazeer, Parmar, Uszkoreit, Jones, Gomez, Kaiser, Polosukhin, Guyon, Luxburg, Bengio, Wallach, Fergus, Vishwanathan and Garnett2017; Devlin et al., Reference Devlin, Chang, Lee and Toutanova2019) or computer vision (Dosovitskiy et al., Reference Dosovitskiy, Beyer, Kolesnikov, Weissenborn, Zhai, Unterthiner, Dehghani, Minderer, Heigold, Gelly, Uszkoreit and Houlsby2020; Caron et al., Reference Caron, Touvron, Misra, Jegou, Mairal, Bojanowski and Joulin2021; He et al., Reference He, Chen, Xie, Li, Dollár and Girshick2022). In the past, dimensionality reduction techniques such as Principal Component Analysis (PCA), kernel-PCA, or Maximum Variance Unfolding, have been used extensively to analyze atmospheric dynamics (e.g., Lima et al., Reference Lima, Lall, Jebara and Barnston2009; Mercer and Richman, Reference Mercer and Richman2012; Hannachi and Iqbal, Reference Hannachi and Iqbal2019). These can be seen as simple forms of representation learning since they also provide a data transformation to a coordinate system adapted to the input. The need for more expressive representations than those obtained by these methods has been one of the main motivations behind deep neural networks (cf. Bengio et al., Reference Bengio, Courville and Vincent2013).
Several GANs dedicated to geoscience applications have been proposed in the literature (e.g., Stengel et al., Reference Stengel, Glaws, Hettinger and King2020; Zhu et al., Reference Zhu, Cheng, Zhang, Yao, Gao and Liu2020; Klemmer and Neill, Reference Klemmer and Neill2021; Klemmer et al., Reference Klemmer, Xu, Acciaio and Neill2022). Noteworthy is SPATE-GAN (Klemmer et al., Reference Klemmer, Xu, Acciaio and Neill2022) that uses a custom metric for spatiotemporal autocorrelation and determines an embedding loss based on it. The authors demonstrate that this improves GAN performance across different datasets without changes to the neural network architecture of the generative model. It hence provides an alternative to AtmoDist proposed in our work. We compare with Stengel et al. (Reference Stengel, Glaws, Hettinger and King2020) which uses SRGAN (Ledig et al., Reference Ledig, Theis, Huszar, Caballero, Cunningham, Acosta, Aitken, Tejani, Totz, Wang and Shi2017) to address applications such as wind farm placement. SRGAN was the first work that advocated the use of perceptual loss functions for single-image super-resolution in computer vision. While numerous extensions to the original SRGAN model exist (Lim et al., Reference Lim, Son, Kim, Nah and Lee2017; Wang et al., Reference Wang, Yu, Wu, Gu, Liu, Dong, Qiao and Change2018), they achieve increased performance by introducing additional complexities to the neural network architecture and training procedure compared to the vanilla SRGAN. In our opinion, this makes them less suited to explore the quality of learned representations and derived loss-functions due to an increased amount of possibly confounding factors. Furthermore, Kurinchi-Vendhan et al. (Reference Kurinchi-Vendhan, Lütjens, Gupta, Werner and Newman2021) find that neither of these methods, when applied to atmospheric data, gives a definite advantage over the others and they instead vary in performance depending on what kind of evaluation criterion is used. CEDGAN by Zhu et al. (Reference Zhu, Cheng, Zhang, Yao, Gao and Liu2020) is an encoder-decoder conditional GAN that is used by the authors for spatial interpolation of orography, a task closely related to super-resolution. The authors solely rely on the adversarial loss term conditioned on the known parts of the field to ensure that the interpolated field is consistent. Such an approach could be easily extended to and possibly benefit from the use of a content-loss that compares the output directly with the ground truth image. GAN-based super-resolution methods could potentially also benefit from additionally conditioning the discriminator on the low-resolution input image. Indeed, the potential to directly use features learned by a discriminator (or generator) has been recognized before (Radford et al., Reference Radford, Metz and Chintala2015).
3. Method
We perform self-supervised representation learning for atmospheric dynamics and derive a data-driven distance function for atmospheric states from it. For this, we employ a siamese neural network (Chicco, Reference Chicco2021) and combine it with a novel, domain-specific spatiotemporal pretext task that derives from the theory of geophysical fluid dynamics. Specifically, for a given temporal sequence of unlabeled atmospheric states, a neural network is trained to predict the temporal separation between two nearby ones. For the predictions to be accurate, the network has to learn an internal representation that captured the intrinsic properties of atmospheric flows and hence provides feature spaces adapted to atmospheric dynamics. For training, we employ ERA5 reanalysis (Hersbach et al., Reference Hersbach, Bell, Berrisford, Hirahara, Horányi, Muñoz-Sabater, Nicolas, Peubey, Radu, Schepers, Simmons, Soci, Abdalla, Abellan, Balsamo, Bechtold, Biavati, Bidlot, Bonavita, De Chiara, Dahlgren, Dee, Diamantakis, Dragani, Flemming, Forbes, Fuentes, Geer, Haimberger, Healy, Hogan, Hólm, Janisková, Keeley, Laloyaux, Lopez, Lupu, Radnoti, de Rosnay, Rozum, Vamborg, Villaume and Thépaut2020), which we consider a good approximation to observations. An overview of the AtmoDist methodology is provided in Figure 1.
3.1. Dataset and preprocessing
We employ relative vorticity and divergence to represent an atmospheric state. The two scalar fields are equivalent to the wind velocity vector field, which is the most important dynamic variable and hence a good proxy for the overall state. Our data is from model level 120 of ERA5, which corresponds approximately to the pressure level
![]() $ 883\mathrm{hPa}\pm 85 $
, and a temporal resolution of 3 hr is used. Vorticity and divergence fields are obtained from the native spectral coefficients of ERA5 by mapping them onto a Gaussian grid with resolution
$ 883\mathrm{hPa}\pm 85 $
, and a temporal resolution of 3 hr is used. Vorticity and divergence fields are obtained from the native spectral coefficients of ERA5 by mapping them onto a Gaussian grid with resolution
![]() $ 1280\times 2560 $
(we use pyshtools for this [Wieczorek and Meschede, Reference Wieczorek and Meschede2018]). The grids are subsequently sampled into patches of size
$ 1280\times 2560 $
(we use pyshtools for this [Wieczorek and Meschede, Reference Wieczorek and Meschede2018]). The grids are subsequently sampled into patches of size
![]() $ 160\times 160 $
, which corresponds approximately to
$ 160\times 160 $
, which corresponds approximately to
![]() $ 2500\hskip0.1em \mathrm{km}\times 2500\hskip0.1em \mathrm{km} $
, with randomly selected centers. Following Stengel et al. (Reference Stengel, Glaws, Hettinger and King2020), we restrict the centers to
$ 2500\hskip0.1em \mathrm{km}\times 2500\hskip0.1em \mathrm{km} $
, with randomly selected centers. Following Stengel et al. (Reference Stengel, Glaws, Hettinger and King2020), we restrict the centers to
![]() $ \pm 60{}^{\circ} $
latitude to avoid the severe distortions close to the poles.
$ \pm 60{}^{\circ} $
latitude to avoid the severe distortions close to the poles.
We found that both vorticity and divergence roughly follow a zero-centered Laplace distribution. This led to instabilities, in particular in the training of the downstream task. While clipping values larger than 70 standard deviations was sufficient to stabilize training, this discards information about extreme events that are of particular relevance in many applications. We therefore apply an invertible log-transform to the input data in a preprocessing step and train and evaluate in the log-transformed space, see Appendix A.1 for details.
Training is performed on
![]() $ 3 $
-hourly data from 1979 to 1998 (20 years) while the period from 2000 to 2005 is reserved for evaluation (6 years). This results in
$ 3 $
-hourly data from 1979 to 1998 (20 years) while the period from 2000 to 2005 is reserved for evaluation (6 years). This results in
![]() $ 58440\times {N}_p $
spatial fields for the training and
$ 58440\times {N}_p $
spatial fields for the training and
![]() $ 17536\times {N}_p $
fields for the evaluation set, where
$ 17536\times {N}_p $
fields for the evaluation set, where
![]() $ {N}_p $
is the number of patches per global field of size
$ {N}_p $
is the number of patches per global field of size
![]() $ 1280\times 2560 $
. We used
$ 1280\times 2560 $
. We used
![]() $ {N}_p=31 $
in our experiments. The maximum time lag, that is, the maximum temporal separation between spatial fields, was
$ {N}_p=31 $
in our experiments. The maximum time lag, that is, the maximum temporal separation between spatial fields, was
![]() $ \Delta {t}_{\mathrm{max}}=69\hskip0.22em \mathrm{hr} $
. This is equivalent to 23 categories for the training of the representation network. An overview of the dataset is given in Table 1.
$ \Delta {t}_{\mathrm{max}}=69\hskip0.22em \mathrm{hr} $
. This is equivalent to 23 categories for the training of the representation network. An overview of the dataset is given in Table 1.
Table 1. Overview of the data used in this work.

3.2. Pretext task
Our pretext task is defined for a temporal sequence of spatial fields, for example, atmospheric states from reanalysis or a simulation, and it defines a categorial loss function for self-supervised training. The task is derived from the theory of geophysical fluid dynamics and motivated by the fact that the time evolution of an ideal barotropic fluid is described by a geodesic flow (Arnold, Reference Arnold1966; Ebin and Marsden, Reference Ebin and Marsden1970). Since a geodesic flow is one of shortest distance, the temporal separation between two nearby states corresponds to an intrinsic distance between them. As a spatiotemporal pretext task for learning a distance measure for atmospheric dynamics, we thus use the prediction of the temporal separation between close-by states. More specifically, given two local patches of atmospheric states
![]() $ {X}_{t_1},{X}_{t_2} $
centered at the same spatial location but at different, nearby times
$ {X}_{t_1},{X}_{t_2} $
centered at the same spatial location but at different, nearby times
![]() $ {t}_1 $
and
$ {t}_1 $
and
![]() $ {t}_2 $
, the task for the neural network is to predict their temporal separation
$ {t}_2 $
, the task for the neural network is to predict their temporal separation
![]() $ \Delta t={t}_2-{t}_1=n\cdot {h}_t $
given by a multiple of the time step
$ \Delta t={t}_2-{t}_1=n\cdot {h}_t $
given by a multiple of the time step
![]() $ {h}_t $
(3 hr in our case). The categorical label of a tuple
$ {h}_t $
(3 hr in our case). The categorical label of a tuple
![]() $ \left({X}_{t_1},{X}_{t_2}\right) $
of input patches, each consisting of the vorticity and divergence field at the respective time
$ \left({X}_{t_1},{X}_{t_2}\right) $
of input patches, each consisting of the vorticity and divergence field at the respective time
![]() $ {t}_k=k\cdot {h}_t $
for the patch region, is thus defined as the number of time steps
$ {t}_k=k\cdot {h}_t $
for the patch region, is thus defined as the number of time steps
![]() $ n $
in between them. Following standard methodology for classification problems, for each training item
$ n $
in between them. Following standard methodology for classification problems, for each training item
![]() $ \left({X}_{t_1},{X}_{t_2}\right) $
, our representation network predicts a probability distribution over the finite set of allowed values for
$ \left({X}_{t_1},{X}_{t_2}\right) $
, our representation network predicts a probability distribution over the finite set of allowed values for
![]() $ n $
. Training can thus be performed with cross-entropy loss, which is known to be highly effective.
$ n $
. Training can thus be performed with cross-entropy loss, which is known to be highly effective.
For a distance metric one expects
![]() $ F\left({X}_{t_1},{X}_{t_2}\right)=F\left({X}_{t_2},{X}_{t_1}\right) $
. However, we found that reversing the order of inputs results in prediction errors being reversed as well and training the network on randomly ordered pairs did not prevent this behavior. As a consequence, we train the network using a fixed order, that is, we only evaluate
$ F\left({X}_{t_1},{X}_{t_2}\right)=F\left({X}_{t_2},{X}_{t_1}\right) $
. However, we found that reversing the order of inputs results in prediction errors being reversed as well and training the network on randomly ordered pairs did not prevent this behavior. As a consequence, we train the network using a fixed order, that is, we only evaluate
![]() $ F\left({X}_{t_1},{X}_{t_2}\right) $
with
$ F\left({X}_{t_1},{X}_{t_2}\right) $
with
![]() $ {t}_1<{t}_2 $
.
$ {t}_1<{t}_2 $
.
3.3. Neural network architecture
The architecture of the neural network we use for representation learning consists of two parts and is schematically depicted in Figure 2. The first part is the representation network. It provides an encoder that maps an atmospheric field
![]() $ X $
to its feature space representation
$ X $
to its feature space representation
![]() $ \mathrm{\mathcal{F}}(X)\hskip0.2em \subseteq \hskip0.2em {\mathrm{\mathbb{R}}}^N $
. Since both states
$ \mathrm{\mathcal{F}}(X)\hskip0.2em \subseteq \hskip0.2em {\mathrm{\mathbb{R}}}^N $
. Since both states
![]() $ {X}_{t_k} $
of the tuple
$ {X}_{t_k} $
of the tuple
![]() $ \left({X}_{t_1},{X}_{t_2}\right) $
that form a training item are used separately as input to the encoder, it is a siamese network (Chicco, Reference Chicco2021). The second part of our overall architecture is a tail or comparison network
$ \left({X}_{t_1},{X}_{t_2}\right) $
that form a training item are used separately as input to the encoder, it is a siamese network (Chicco, Reference Chicco2021). The second part of our overall architecture is a tail or comparison network
![]() $ T\left(\mathrm{\mathcal{F}}\left({X}_{t_1}\right),\mathrm{\mathcal{F}}\left({X}_{t_2}\right)\right) $
that maps the tuple
$ T\left(\mathrm{\mathcal{F}}\left({X}_{t_1}\right),\mathrm{\mathcal{F}}\left({X}_{t_2}\right)\right) $
that maps the tuple
![]() $ \left(\mathrm{\mathcal{F}}\left({X}_{t_1}\right),\mathrm{\mathcal{F}}\left({X}_{t_2}\right)\right) $
of representations to a probability density
$ \left(\mathrm{\mathcal{F}}\left({X}_{t_1}\right),\mathrm{\mathcal{F}}\left({X}_{t_2}\right)\right) $
of representations to a probability density
![]() $ p\left(\Delta t|{X}_{t_1},{X}_{t_2}\right) $
for their temporal separation
$ p\left(\Delta t|{X}_{t_1},{X}_{t_2}\right) $
for their temporal separation
![]() $ \Delta t=n\cdot {h}_t $
. The representation and tail networks are trained simultaneously in an end-to-end manner. After training, only the representation network is of relevance since its activations at the final layer provide the feature space
$ \Delta t=n\cdot {h}_t $
. The representation and tail networks are trained simultaneously in an end-to-end manner. After training, only the representation network is of relevance since its activations at the final layer provide the feature space
![]() $ \mathrm{\mathcal{F}}(X) $
for the input
$ \mathrm{\mathcal{F}}(X) $
for the input
![]() $ {X}_t $
that defines the learned representation. The use of activations at intermediate layers is also possible but was not considered in the present work. Note that the tail network should be much smaller than the representation network to facilitate discriminative and explanatory representations.
$ {X}_t $
that defines the learned representation. The use of activations at intermediate layers is also possible but was not considered in the present work. Note that the tail network should be much smaller than the representation network to facilitate discriminative and explanatory representations.

Figure 2. The AtmoDist network used for learning the pretext task. Numbers after layer names indicate the number of filters/feature maps of an operation. The comparison network is only required during training and can be discarded afterward.
The representation network follows a residual architecture (He et al., Reference He, Zhang, Ren and Sun2015) although with a slightly reduced number of feature maps compared to the standard configurations used in computer vision. It maps an input
![]() $ X $
of size
$ X $
of size
![]() $ 2\times 160\times 160 $
to a representation vector
$ 2\times 160\times 160 $
to a representation vector
![]() $ \mathrm{\mathcal{F}}(X) $
of size
$ \mathrm{\mathcal{F}}(X) $
of size
![]() $ 128\times 5\times 5 $
. This corresponds to a compression rate of 16. The tail network is a simple convolutional network with a softmax layer at the end to obtain a discrete probability distribution. Both networks together consist of 2,747,856 parameters with 2,271,920 in the encoder and 470,144 in the tail network.
$ 128\times 5\times 5 $
. This corresponds to a compression rate of 16. The tail network is a simple convolutional network with a softmax layer at the end to obtain a discrete probability distribution. Both networks together consist of 2,747,856 parameters with 2,271,920 in the encoder and 470,144 in the tail network.
3.4. Training
We train AtmoDist on the dataset described in Section 3.1 using stochastic gradient descent. Since training failed to converge in early experiments, we introduced a pre-training scheme where we initially use only about 10% of the data before switching to the full dataset. For further details on the training procedure, we refer to Appendix A.2.
As can be seen in Figure 3, with pre-training the training loss converges well although overfitting sets in from epoch 27 onwards. Our experiments indicate that the overfitting results from using a fixed, pre-computed set of randomly sampled patches and it could likely be alleviated by sampling these dynamically during training. The noise seen in the evaluation loss is a consequence of the different training and evaluation behavior of the batch normalization layers. While there exist methods to address this issue (Ioffe, Reference Ioffe2017), we found them insufficient in our case. Instance normalization (Ulyanov et al., Reference Ulyanov, Vedaldi and Lempitsky2017) or layer normalization (Ba et al., Reference Ba, Kiros and Hinton2016) are viable alternatives that should be explored in the future.

Figure 3. Loss (left) and Top-1 accuracy (right) during training calculated on the training (1979–1998) and the evaluation dataset (2000–2005). Drops in loss correspond to learning rate reductions. The best loss and accuracy are achieved in epoch 27; afterward the network begins to overfit.
3.5. Construction of AtmoDist metric
The final layer of the representation network provides an embedding
![]() $ \mathrm{\mathcal{F}}\left({X}_t\right) $
of the vorticity and divergence fields, which together form
$ \mathrm{\mathcal{F}}\left({X}_t\right) $
of the vorticity and divergence fields, which together form
![]() $ {X}_t $
, into a feature space (cf. Figure 2). Although this representation can potentially be useful for many different applications, we employ it to define a domain-specific distance functions for atmospheric states.
$ {X}_t $
, into a feature space (cf. Figure 2). Although this representation can potentially be useful for many different applications, we employ it to define a domain-specific distance functions for atmospheric states.
The feature space representation
![]() $ \mathrm{\mathcal{F}}\left({X}_t\right) $
is a tensor of size
$ \mathrm{\mathcal{F}}\left({X}_t\right) $
is a tensor of size
![]() $ 128\times 5\times 5 $
that we interpret as a vector, that is, we consider
$ 128\times 5\times 5 $
that we interpret as a vector, that is, we consider
![]() $ \mathrm{\mathcal{F}}\left({X}_t\right)\in {\mathrm{\mathbb{R}}}^N $
with
$ \mathrm{\mathcal{F}}\left({X}_t\right)\in {\mathrm{\mathbb{R}}}^N $
with
![]() $ N=3200 $
. We then define the AtmoDist metric
$ N=3200 $
. We then define the AtmoDist metric
![]() $ d\left({X}_1,{X}_2\right) $
for two atmospheric states
$ d\left({X}_1,{X}_2\right) $
for two atmospheric states
![]() $ {X}_1,{X}_2 $
as
$ {X}_1,{X}_2 $
as
where
![]() $ \parallel \cdot \parallel $
denotes the standard
$ \parallel \cdot \parallel $
denotes the standard
![]() $ {\mathrm{\ell}}_2 $
-norm. The
$ {\mathrm{\ell}}_2 $
-norm. The
![]() $ {\mathrm{\ell}}_2 $
-norm is commonly used for the construction of metrics based on neural network activations (Gatys et al., Reference Gatys, Ecker and Bethge2016; Ledig et al., Reference Ledig, Theis, Huszar, Caballero, Cunningham, Acosta, Aitken, Tejani, Totz, Wang and Shi2017). Other
$ {\mathrm{\ell}}_2 $
-norm is commonly used for the construction of metrics based on neural network activations (Gatys et al., Reference Gatys, Ecker and Bethge2016; Ledig et al., Reference Ledig, Theis, Huszar, Caballero, Cunningham, Acosta, Aitken, Tejani, Totz, Wang and Shi2017). Other
![]() $ {\mathrm{\ell}}_p $
-norms or weighted norms could potentially also be useful although preliminary experiments indicated that these provide results comparable to Equation (1).
$ {\mathrm{\ell}}_p $
-norms or weighted norms could potentially also be useful although preliminary experiments indicated that these provide results comparable to Equation (1).
4. Evaluation
The evaluation of representation learning techniques usually employs a collection of downstream applications, since the embedding into the abstract and high-dimensional feature space is in itself rarely insightful. To facilitate interpretation, one thereby typically relies on well-known classification problems. Simple techniques are also employed for the mapping from the representation to the prediction, for example, a small neural network similar to our tail network, to indeed evaluate the representations and not any subsequent computations.
Unfortunately, standardized labeled benchmark datasets akin to MNIST (LeCun et al., Reference LeCun, Bottou, Bengio and Haffner1998) or ImageNet (Russakovsky et al., Reference Russakovsky, Deng, Su, Krause, Satheesh, Ma, Huang, Karpathy, Khosla, Bernstein, Berg and Fei-Fei2015) currently do not exist for atmospheric dynamics and it is their lack that inspired our self-supervised pretext task. We thus demonstrate the effectiveness of our representations using downscaling, that is, super-resolution, and the interpolation of a partially missing field. Both can be considered as standard problems and have been considered in a variety of previous works (e.g., Requena-Mesa et al., Reference Requena-Mesa, Reichstein, Mahecha, Kraft and Denzler2019; Groenke et al., Reference Groenke, Madaus and Monteleoni2020; Meraner et al., Reference Meraner, Ebel, Zhu and Schmitt2020; Stengel et al., Reference Stengel, Glaws, Hettinger and King2020). For downscaling we build on the recent work by Stengel et al. (Reference Stengel, Glaws, Hettinger and King2020) that provides a state-of-the-art GAN-based downscaling technique and, to facilitate a direct comparison, employ their implementation and replace only the
![]() $ {\mathrm{\ell}}_2 $
-norm in their code with the AtmoDist distance metric introduced in Section 3.5. For missing data interpolation, we interpret it as a variant of inpainting and use a network inspired by those successful with the problem in computer vision.
$ {\mathrm{\ell}}_2 $
-norm in their code with the AtmoDist distance metric introduced in Section 3.5. For missing data interpolation, we interpret it as a variant of inpainting and use a network inspired by those successful with the problem in computer vision.
As a baseline, we compare our learned representations against those of an autoencoder (Bengio et al., Reference Bengio, Courville and Vincent2013), one of the earliest representation learning methods. To facilitate a fair comparison, the encoder of the autoencoder is identical to representation network described in Section 3.3. The decoder is a mirrored version of the encoder, replacing downscaling convolutions with upscaling ones. For details, refer to Appendix A.4. After training, the autoencoder is able to produce decent, yet overly -smooth, reconstructions as can be seen in Figure 5.

Figure 4. Mean
![]() $ {\mathrm{\ell}}_1 $
-norm (left) and mean
$ {\mathrm{\ell}}_1 $
-norm (left) and mean
![]() $ {\mathrm{\ell}}_2 $
-norm (right) between samples that are a fixed time-interval apart calculated on the training set. Shaded areas indicate standard deviation. For comparability, the AtmoDist distance has been normalized in each case with the method described in Appendix A.3. To give equal weight to divergence and vorticity, they have been normalized to zero mean and unit variance before calculating grid point-wise metrics.
$ {\mathrm{\ell}}_2 $
-norm (right) between samples that are a fixed time-interval apart calculated on the training set. Shaded areas indicate standard deviation. For comparability, the AtmoDist distance has been normalized in each case with the method described in Appendix A.3. To give equal weight to divergence and vorticity, they have been normalized to zero mean and unit variance before calculating grid point-wise metrics.

Figure 5. Divergence field (left) and its reconstruction produced by the autoencoder (right). While the reconstructed field lacks finer details, large-scale structures are properly captured by the autoencoder.
Before we turn to the downstream applications, we begin with an intrinsic evaluation of the AtmoDist metric using the average distance between atmospheric states with a fixed temporal separation
![]() $ \Delta t $
. Since this is close to the training task for AtmoDist, it provides a favorable setting for it. Nonetheless, we believe that the comparison still provides useful insights into our work.
$ \Delta t $
. Since this is close to the training task for AtmoDist, it provides a favorable setting for it. Nonetheless, we believe that the comparison still provides useful insights into our work.
4.1. Intrinsic evaluation of the AtmoDist distance
In order to obtain an intrinsic, application-independent evaluation of the AtmoDist distance in Equation (1), we determine it as a function of temporal separation
![]() $ \Delta t $
between two atmospheric states
$ \Delta t $
between two atmospheric states
![]() $ {X}_{t_1} $
and
$ {X}_{t_1} $
and
![]() $ {X}_{t_2} $
. Note that although the training also employed
$ {X}_{t_2} $
. Note that although the training also employed
![]() $ \Delta t $
, the AtmoDist distance metric does no longer use the tail network and the computations are thus different than those during training. Because of the quasi-chaotic nature of the atmosphere (Lorenz, Reference Lorenz1969), one expects that any distance measure for it will saturate when the decorrelation time has been reached. To be effective, for example, for machine-learning applications, the distance between states should, however, dependent approximately linear on their temporal separation before the decorrelation time, at least in a statistical sense when a large number of pairs
$ \Delta t $
, the AtmoDist distance metric does no longer use the tail network and the computations are thus different than those during training. Because of the quasi-chaotic nature of the atmosphere (Lorenz, Reference Lorenz1969), one expects that any distance measure for it will saturate when the decorrelation time has been reached. To be effective, for example, for machine-learning applications, the distance between states should, however, dependent approximately linear on their temporal separation before the decorrelation time, at least in a statistical sense when a large number of pairs
![]() $ {X}_{t_1} $
and
$ {X}_{t_1} $
and
![]() $ {X}_{t_2} $
for fixed
$ {X}_{t_2} $
for fixed
![]() $ \Delta t $
is considered.
$ \Delta t $
is considered.
4.1.1. Comparison to
 $ {\mathrm{\ell}}_p $
-norm
$ {\mathrm{\ell}}_p $
-norm
We compute
![]() $ {\mathrm{\ell}}_1 $
-norm,
$ {\mathrm{\ell}}_1 $
-norm,
![]() $ {\mathrm{\ell}}_2 $
-norm, and AtmoDist distance as a function of
$ {\mathrm{\ell}}_2 $
-norm, and AtmoDist distance as a function of
![]() $ \Delta t $
for all atmospheric states that form the training set for AtmoDist and report averaged distances for the different
$ \Delta t $
for all atmospheric states that form the training set for AtmoDist and report averaged distances for the different
![]() $ \Delta t $
. As shown in Figure 4, the AtmoDist distance takes longer to saturate than mean
$ \Delta t $
. As shown in Figure 4, the AtmoDist distance takes longer to saturate than mean
![]() $ {\mathrm{\ell}}_1 $
-norm and
$ {\mathrm{\ell}}_1 $
-norm and
![]() $ {\mathrm{\ell}}_2 $
-norm and increases more linearly. Also, its standard deviation is significantly smaller and AtmoDist hence provides more consistent distances. Qualitatively similar results are obtained for SSIM (Wang et al., Reference Wang, Bovik, Sheikh and Simoncelli2004) and PSNR, two popular metric in computer vision, and we report the results for these in Figure 15 in the Appendix.
$ {\mathrm{\ell}}_2 $
-norm and increases more linearly. Also, its standard deviation is significantly smaller and AtmoDist hence provides more consistent distances. Qualitatively similar results are obtained for SSIM (Wang et al., Reference Wang, Bovik, Sheikh and Simoncelli2004) and PSNR, two popular metric in computer vision, and we report the results for these in Figure 15 in the Appendix.
4.1.2. Temporal behavior
To obtain further insight into the temporal behavior of AtmoDist, we consider the confusion matrix as a function of temporal separation
![]() $ \Delta t $
when AtmoDist is used in the training of the network, that is, with the tail network. Figure 6 confirms the expected behavior that predictions get less certain as
$ \Delta t $
when AtmoDist is used in the training of the network, that is, with the tail network. Figure 6 confirms the expected behavior that predictions get less certain as
![]() $ \Delta t $
increases and the states become less correlated. Interestingly, the emergence of sub-diagonals indicates that the network is able to infer the time of the day, that is, the phase of Earth’s rotation, with high precision, but it can for large
$ \Delta t $
increases and the states become less correlated. Interestingly, the emergence of sub-diagonals indicates that the network is able to infer the time of the day, that is, the phase of Earth’s rotation, with high precision, but it can for large
![]() $ \Delta t $
no longer separate different days.
$ \Delta t $
no longer separate different days.

Figure 6. The confusion matrix shows the accuracy for the evaluation set as a function of predicted time lag and actual time lag. The side-diagonals indicate that AtmoDist is able to infer the time of the day for an atmospheric state with high precision solely based on a local patch of divergence and vorticity fields but might err on the day. A logarithmic color scale has been used to better highlight the side-diagonals.
4.1.3. Spatial behavior
The predictability of atmospheric dynamics is not spatially and temporally homogeneous but has a strong dependence on the location as well as the season. One hence would expect that also the error of AtmoDist reflects these intrinsic atmospheric properties. In Figure 7 we show the spatial distribution of the error of AtmoDist, again in the setup used during training with the tail network. As can been seen there, AtmoDist yields good predictions when evaluated near land but performance degrades drastically over the oceans. Apparent in Figure 7 is also a strong difference in predictability between the cold and warm season. This indicates that the model primarily focusses on detecting mesoscale convective activities and not on tracing Lagrangian coherent structures.

Figure 7. Accuracy of AtmoDist to correctly predict that two patches are 48 hr apart as a function of space with an error margin of 3 hr (i.e., 45 and 51 hr are also counted as correct prediction). The red rectangle in the lower left corner indicates the patch size used as input for the network.
4.2. Downscaling
Downscaling, or super-resolution, is a classical problem in both climate science and computer vision. The objective is to obtain a high-resolution field
![]() $ {X}^{\mathrm{hr}} $
given only a low-resolution version
$ {X}^{\mathrm{hr}} $
given only a low-resolution version
![]() $ {X}^{\mathrm{lr}} $
of it. This problem is inherently ill-posed since a given
$ {X}^{\mathrm{lr}} $
of it. This problem is inherently ill-posed since a given
![]() $ {X}^{\mathrm{lr}} $
is compatible with a large number of valid high-resolution
$ {X}^{\mathrm{lr}} $
is compatible with a large number of valid high-resolution
![]() $ {X}^{\mathrm{hr}} $
. Despite this, state-of-the-art methods can often provide valid
$ {X}^{\mathrm{hr}} $
. Despite this, state-of-the-art methods can often provide valid
![]() $ {X}^{\mathrm{hr}} $
whose statistics match those of the true fields. In the last years, in particular approaches based on GANs (Goodfellow et al., Reference Goodfellow, Pouget-Abadie, Mirza, Xu, Warde-Farley, Ozair, Courville and Bengio2014) have become the de facto standard (e.g., Jiang et al., Reference Jiang, Esmaeilzadeh, Azizzadenesheli, Kashinath, Mustafa, Tchelepi, Marcus, Prabhat and Anandkumar2020; Stengel et al., Reference Stengel, Glaws, Hettinger and King2020; Klemmer et al., Reference Klemmer, Xu, Acciaio and Neill2022).
$ {X}^{\mathrm{hr}} $
whose statistics match those of the true fields. In the last years, in particular approaches based on GANs (Goodfellow et al., Reference Goodfellow, Pouget-Abadie, Mirza, Xu, Warde-Farley, Ozair, Courville and Bengio2014) have become the de facto standard (e.g., Jiang et al., Reference Jiang, Esmaeilzadeh, Azizzadenesheli, Kashinath, Mustafa, Tchelepi, Marcus, Prabhat and Anandkumar2020; Stengel et al., Reference Stengel, Glaws, Hettinger and King2020; Klemmer et al., Reference Klemmer, Xu, Acciaio and Neill2022).
Stengel et al. (Reference Stengel, Glaws, Hettinger and King2020) recently applied GAN-based super-resolution to wind and solar data in North America, demonstrating physically consistent results that outperform competing methods. The authors build on the SRGAN from Ledig et al. (Reference Ledig, Theis, Huszar, Caballero, Cunningham, Acosta, Aitken, Tejani, Totz, Wang and Shi2017) but instead of the VGG network (Simonyan and Zisserman, Reference Simonyan and Zisserman2015) that was used as a representation-based content loss in the original work, Stengel et al. (Reference Stengel, Glaws, Hettinger and King2020) had to resort to an
![]() $ {\mathrm{\ell}}_2 $
-loss since no analogue for the atmosphere was available. Our work fills this gap and we demonstrate that the learned AtmoDist metric in Equation (1) leads to significantly improved results for atmospheric downscaling. The only modifications to the implementation from Stengel et al. (Reference Stengel, Glaws, Hettinger and King2020) are a restriction to 4X super-resolution in our work (mainly due to the high computational costs for GAN training), incorporation of an improved initialization scheme for upscaling sub-pixel convolutions (Aitken et al., Reference Aitken, Ledig, Theis, Caballero, Wang and Shi2017), as well as replacing transposed convolutions in the generator with regular ones as in the original SRGAN. We also do not use batch normalization in the generator, as suggested by Stengel et al. (Reference Stengel, Glaws, Hettinger and King2020). For both the
$ {\mathrm{\ell}}_2 $
-loss since no analogue for the atmosphere was available. Our work fills this gap and we demonstrate that the learned AtmoDist metric in Equation (1) leads to significantly improved results for atmospheric downscaling. The only modifications to the implementation from Stengel et al. (Reference Stengel, Glaws, Hettinger and King2020) are a restriction to 4X super-resolution in our work (mainly due to the high computational costs for GAN training), incorporation of an improved initialization scheme for upscaling sub-pixel convolutions (Aitken et al., Reference Aitken, Ledig, Theis, Caballero, Wang and Shi2017), as well as replacing transposed convolutions in the generator with regular ones as in the original SRGAN. We also do not use batch normalization in the generator, as suggested by Stengel et al. (Reference Stengel, Glaws, Hettinger and King2020). For both the
![]() $ {\mathrm{\ell}}_2 $
-based downscaling as well as the AtmoDist-based downscaling, the model is trained for 18 epochs.
$ {\mathrm{\ell}}_2 $
-based downscaling as well as the AtmoDist-based downscaling, the model is trained for 18 epochs.
Downscaled divergence fields are shown in Figure 8. Examples for vorticity can be found in Figure 16 in the appendix. Qualitatively, the fields obtained with the AtmoDist metric look sharper than those with an
![]() $ {\mathrm{\ell}}_2 $
-loss. This overly smooth appearance with
$ {\mathrm{\ell}}_2 $
-loss. This overly smooth appearance with
![]() $ {\mathrm{\ell}}_2 $
-loss is a well-known problem and one of the original motivations for learned content loss functions (Ledig et al., Reference Ledig, Theis, Huszar, Caballero, Cunningham, Acosta, Aitken, Tejani, Totz, Wang and Shi2017). In Figure 9 (left) we show the average energy spectrum of the downscaled fields. Also with respect to this measure, the AtmoDist metric provides significantly improved results and yields a spectrum very close to the ERA5 ground truth. Following Stengel et al. (Reference Stengel, Glaws, Hettinger and King2020), we also compare the semivariogram of the downscaled fields that measures the spatial variance of a field
$ {\mathrm{\ell}}_2 $
-loss is a well-known problem and one of the original motivations for learned content loss functions (Ledig et al., Reference Ledig, Theis, Huszar, Caballero, Cunningham, Acosta, Aitken, Tejani, Totz, Wang and Shi2017). In Figure 9 (left) we show the average energy spectrum of the downscaled fields. Also with respect to this measure, the AtmoDist metric provides significantly improved results and yields a spectrum very close to the ERA5 ground truth. Following Stengel et al. (Reference Stengel, Glaws, Hettinger and King2020), we also compare the semivariogram of the downscaled fields that measures the spatial variance of a field
![]() $ f(x) $
as a function of the lag distance
$ f(x) $
as a function of the lag distance
![]() $ r $
(Matheron, Reference Matheron1963) (see Appendix A.6 for details on the calculation of the semivariogram). As can be seen in Figure 9 (right) we find that our approach again captures the real geostatistics much better than an
$ r $
(Matheron, Reference Matheron1963) (see Appendix A.6 for details on the calculation of the semivariogram). As can be seen in Figure 9 (right) we find that our approach again captures the real geostatistics much better than an
![]() $ {\mathrm{\ell}}_2 $
-based downscaling. The fields obtained from the autoencoder-based loss are visually of lower quality than with the other two loss functions and the same holds true for the quantitative evaluation metrics (Figure 10).
$ {\mathrm{\ell}}_2 $
-based downscaling. The fields obtained from the autoencoder-based loss are visually of lower quality than with the other two loss functions and the same holds true for the quantitative evaluation metrics (Figure 10).

Figure 8. Uncurated set of downscaled divergence fields over the Gulf of Thailand at different time steps. Coastlines are shown in the first ground truth field and then omitted for better comparability.

Figure 9. Left: The energy spectrum starting from wavenumber 200 and averaged over the whole evaluation period. The spectra below wavenumber 200 are almost identical. The spectrum has been calculated by first converting divergence and vorticity to eastwardly and northwardly wind fields, and then evaluating the kinetic energy. Right: Semivariogram of divergence.

Figure 10. Histogram of reconstruction errors measured in
![]() $ {\mathrm{\ell}}_2 $
norm (left) and difference of total variation (right) for relative vorticity. We define the difference of total variation between the original field
$ {\mathrm{\ell}}_2 $
norm (left) and difference of total variation (right) for relative vorticity. We define the difference of total variation between the original field
![]() $ f $
and its super-resolved approximation
$ f $
and its super-resolved approximation
![]() $ g $
as
$ g $
as
![]() $ {d}_{\mathrm{tv}}\left(f,g\right)={\int}_{\mathcal{D}}\left|\nabla f(x)\right|-\left|\nabla g(x)\right| dx $
. Values closer to zero are better. Despite performing better with regards to the
$ {d}_{\mathrm{tv}}\left(f,g\right)={\int}_{\mathcal{D}}\left|\nabla f(x)\right|-\left|\nabla g(x)\right| dx $
. Values closer to zero are better. Despite performing better with regards to the
![]() $ {\mathrm{\ell}}_2 $
reconstruction error, the
$ {\mathrm{\ell}}_2 $
reconstruction error, the
![]() $ {\mathrm{\ell}}_2 $
-based super-resolution performs worse with regards to the difference of total variation. Notice that the approach by Stengel et al. (Reference Stengel, Glaws, Hettinger and King2020) minimizes the
$ {\mathrm{\ell}}_2 $
-based super-resolution performs worse with regards to the difference of total variation. Notice that the approach by Stengel et al. (Reference Stengel, Glaws, Hettinger and King2020) minimizes the
![]() $ {\mathrm{\ell}}_2 $
reconstruction error during training. Interestingly, all three approaches have solely negative total variation differences, implying that the super-resolved fields are overly smooth compared to the ground truth fields. Similar results are obtained for divergence.
$ {\mathrm{\ell}}_2 $
reconstruction error during training. Interestingly, all three approaches have solely negative total variation differences, implying that the super-resolved fields are overly smooth compared to the ground truth fields. Similar results are obtained for divergence.
Finally, we investigate local statistics for the GAN-based downscaling. In Figure 13 (left) we show these for vorticity. The AtmoDist metric again improves the obtained results although a discrepancy to the ERA5 ground truth is still apparent. In Table 2 we report better/worse scores for AtmoDist-based downscaling and those using the
![]() $ {\mathrm{\ell}}_2 $
-loss for the Wasserstein-1 distance calculated on the empirical distributions (akin to those in Figure 13) for 150 randomly selected, quasi-uniformly distributed cities. A location is thereby scored as better if the Wasserstein-1 distance of the
$ {\mathrm{\ell}}_2 $
-loss for the Wasserstein-1 distance calculated on the empirical distributions (akin to those in Figure 13) for 150 randomly selected, quasi-uniformly distributed cities. A location is thereby scored as better if the Wasserstein-1 distance of the
![]() $ {\mathrm{\ell}}_2 $
-based super-resolution exceeds 10% of the Wasserstein-1 distance of our approach, and as worse in the opposite case. If neither is the case, that is, both approaches have a comparable error, the location is scored as equal. We find that for divergence we achieve better Wasserstein-1 distances in 102 out of 150 locations while only being worse in 36 out of 150. Similar results are obtained for vorticity.
$ {\mathrm{\ell}}_2 $
-based super-resolution exceeds 10% of the Wasserstein-1 distance of our approach, and as worse in the opposite case. If neither is the case, that is, both approaches have a comparable error, the location is scored as equal. We find that for divergence we achieve better Wasserstein-1 distances in 102 out of 150 locations while only being worse in 36 out of 150. Similar results are obtained for vorticity.
Table 2. Better/worse scores for local statistics of GAN-based super-resolution.


Figure 11. Interpolated vorticity fields (center, in the yellow square) for deleted regions for, from left to right, ground truth, AtmoDist,
![]() $ {\mathrm{\ell}}_2 $
-norm, and autoencoder. Both
$ {\mathrm{\ell}}_2 $
-norm, and autoencoder. Both
![]() $ {\mathrm{\ell}}_2 $
-loss and autoencoder-loss produce overly smooth results. The AtmoDist-based reconstruction captures more of the higher-frequency features present in the data although it suffers from some blocking artifacts. The horizontal artifacts for the autoencoder occurred frequently in our results.
$ {\mathrm{\ell}}_2 $
-loss and autoencoder-loss produce overly smooth results. The AtmoDist-based reconstruction captures more of the higher-frequency features present in the data although it suffers from some blocking artifacts. The horizontal artifacts for the autoencoder occurred frequently in our results.

Figure 12. Semivariograms for the reconstruction of partially occluded fields for divergence (left) and vorticity (right). The autoencoder performs better on divergence than the
![]() $ {\mathrm{\ell}}_2 $
-loss while the roles are interchanged for vorticity. We hypothesize that this is due to the larger high-frequency content of divergence.
$ {\mathrm{\ell}}_2 $
-loss while the roles are interchanged for vorticity. We hypothesize that this is due to the larger high-frequency content of divergence.

Figure 13. Left: Kernel density estimate of vorticity distribution at Milan (Italy). The
![]() $ {\mathrm{\ell}}_2 $
-based GAN achieves a Wasserstein distance of
$ {\mathrm{\ell}}_2 $
-based GAN achieves a Wasserstein distance of
![]() $ 5.3\cdot {10}^{-6} $
while our approach achieves a Wasserstein distance of
$ 5.3\cdot {10}^{-6} $
while our approach achieves a Wasserstein distance of
![]() $ 2.0\cdot {10}^{-6} $
. The autoencoder-based GAN yields significant worse statistics. Right: Reconstruction error measured as difference of total variation of divergence for the
$ 2.0\cdot {10}^{-6} $
. The autoencoder-based GAN yields significant worse statistics. Right: Reconstruction error measured as difference of total variation of divergence for the
![]() $ {\mathrm{\ell}}_2 $
-based super-resolution as a function of time. To highlight the oscillations, the errors have been smoothed by a 30 day moving average. The oscillations are also present in the AtmoDist-based super-resolution, when comparing vorticity, or when the reconstruction error is measured using the
$ {\mathrm{\ell}}_2 $
-based super-resolution as a function of time. To highlight the oscillations, the errors have been smoothed by a 30 day moving average. The oscillations are also present in the AtmoDist-based super-resolution, when comparing vorticity, or when the reconstruction error is measured using the
![]() $ {\mathrm{\ell}}_2 $
norm.
$ {\mathrm{\ell}}_2 $
norm.
4.2.1. Biennial oscillations
In Figure 13 (right) we show the downscaling error for divergence over the six year evaluation period. Clearly visible is an oscillation in the error with a period of approximately two years, which exist also for vorticity and when
![]() $ {\mathrm{\ell}}_2 $
-loss is used. It is likely that these oscillations are related to the quasi-biennial oscillation (QBO) (Baldwin et al., Reference Baldwin, Gray, Dunkerton, Hamilton, Haynes, Randel, Holton, Alexander, Hirota, Horinouchi, Jones, Kinnersley, Marquardt, Sato and Takahashi2001) and thus reflect intrinsic changes in the predicability in the atmosphere. We leave a further investigation of the effect of the QBO on AtmoDist to future work.
$ {\mathrm{\ell}}_2 $
-loss is used. It is likely that these oscillations are related to the quasi-biennial oscillation (QBO) (Baldwin et al., Reference Baldwin, Gray, Dunkerton, Hamilton, Haynes, Randel, Holton, Alexander, Hirota, Horinouchi, Jones, Kinnersley, Marquardt, Sato and Takahashi2001) and thus reflect intrinsic changes in the predicability in the atmosphere. We leave a further investigation of the effect of the QBO on AtmoDist to future work.
4.3. Reconstruction of partially occluded fields
In the atmospheric sciences, the complete reconstruction of partially occluded or missing fields, for example, because of clouds, is an important problem (e.g., Meraner et al., Reference Meraner, Ebel, Zhu and Schmitt2020). It appears in a similar form in computer vision as inpainting.
To further evaluate the performance of AtmoDist, we also use it as a loss for this problem and compare it again against the
![]() $ {\mathrm{\ell}}_2 $
-loss. For simplicity, we use again ERA5 divergence and vorticity fields as dataset and artificially add occlusion by cropping out a
$ {\mathrm{\ell}}_2 $
-loss. For simplicity, we use again ERA5 divergence and vorticity fields as dataset and artificially add occlusion by cropping out a
![]() $ 40\times 40 $
region centrally from the
$ 40\times 40 $
region centrally from the
![]() $ 160\times 160 $
patches used in the training of the representation network.
$ 160\times 160 $
patches used in the training of the representation network.
As the network for the inpaiting, we choose the identical architecture as for the autoencoder (see Appendix A.4). The
![]() $ 160\times 160 $
image with a cropped-out center is passed as input and the network outputs an equally sized image. From that output, only the central region is considered when calculating the loss during training. Details are presented in Appendix A.5.
$ 160\times 160 $
image with a cropped-out center is passed as input and the network outputs an equally sized image. From that output, only the central region is considered when calculating the loss during training. Details are presented in Appendix A.5.
Figure 11 shows reconstructed fields for all three loss functions. The AtmoDist-based reconstruction produces the most detailed field although it suffers from some blocking artifacts. The
![]() $ {\mathrm{\ell}}_2 $
-based reconstruction is overly smooth and has homogenous structures instead of fine details. The autoencoder-based field is even smoother than the reconstruction based on the
$ {\mathrm{\ell}}_2 $
-based reconstruction is overly smooth and has homogenous structures instead of fine details. The autoencoder-based field is even smoother than the reconstruction based on the
![]() $ {\mathrm{\ell}}_2 $
loss. In fact, we had to tune our training procedure by switching to Adam and lowering the learning rate to prevent this model from generating constant fields. This was not necessary for either the
$ {\mathrm{\ell}}_2 $
loss. In fact, we had to tune our training procedure by switching to Adam and lowering the learning rate to prevent this model from generating constant fields. This was not necessary for either the
![]() $ {\mathrm{\ell}}_2 $
-based or AtmoDist-based reconstructions. Semiovariograms for the reconstructions are shown in Figure 12. These also verify that AtmoDist provides reconstructions with more realistic fine-scale details. The average
$ {\mathrm{\ell}}_2 $
-based or AtmoDist-based reconstructions. Semiovariograms for the reconstructions are shown in Figure 12. These also verify that AtmoDist provides reconstructions with more realistic fine-scale details. The average
![]() $ {\mathrm{\ell}}_2 $
norms for AtmoDist,
$ {\mathrm{\ell}}_2 $
norms for AtmoDist,
![]() $ {\mathrm{\ell}}_2 $
-loss, and autoencoder loss are 0.62, 0.50, and 0.88. Again a clearly better performance of AtmoDist compared to the autoencoder can be observed.
$ {\mathrm{\ell}}_2 $
-loss, and autoencoder loss are 0.62, 0.50, and 0.88. Again a clearly better performance of AtmoDist compared to the autoencoder can be observed.
4.4. Ablation study
We performed an ablation study to better understand the effect of the maximum temporal separation
![]() $ \Delta {t}_{\mathrm{max}} $
on the performance of AtmoDist. If
$ \Delta {t}_{\mathrm{max}} $
on the performance of AtmoDist. If
![]() $ \Delta {t}_{\mathrm{max}} $
is chosen too small, the pretext task might become too easy and a low training error might be achieved with sub-optimal representations. If
$ \Delta {t}_{\mathrm{max}} $
is chosen too small, the pretext task might become too easy and a low training error might be achieved with sub-optimal representations. If
![]() $ \Delta {t}_{\mathrm{max}} $
is chosen too large, the task might, however, become too difficult and also lead to representations that do not capture the desired effects. We thus trained AtmoDist with
$ \Delta {t}_{\mathrm{max}} $
is chosen too large, the task might, however, become too difficult and also lead to representations that do not capture the desired effects. We thus trained AtmoDist with
![]() $ \Delta {t}_{\mathrm{max}}=\left\{45\hskip0.22em \mathrm{hr},69\hskip0.22em \mathrm{hr},93\hskip0.22em \mathrm{hr}\right\} $
on a reduced dataset with only 66% of the original size. Afterwards, we train three SRGAN models, one for each maximum temporal separation, for 9 epochs using the same hyper-parameters and dataset as in the original downscaling experiment.
$ \Delta {t}_{\mathrm{max}}=\left\{45\hskip0.22em \mathrm{hr},69\hskip0.22em \mathrm{hr},93\hskip0.22em \mathrm{hr}\right\} $
on a reduced dataset with only 66% of the original size. Afterwards, we train three SRGAN models, one for each maximum temporal separation, for 9 epochs using the same hyper-parameters and dataset as in the original downscaling experiment.
Results for the energy spectrum, semivariogram, and downscaling errors are shown in Figure 14. We find that with
![]() $ \Delta {t}_{\mathrm{max}}=69\hskip0.22em \mathrm{hr} $
the downscaling performs slightly better than with
$ \Delta {t}_{\mathrm{max}}=69\hskip0.22em \mathrm{hr} $
the downscaling performs slightly better than with
![]() $ \Delta {t}_{\mathrm{max}}=45\hskip0.22em \mathrm{hr} $
with respect to all three metrics. For
$ \Delta {t}_{\mathrm{max}}=45\hskip0.22em \mathrm{hr} $
with respect to all three metrics. For
![]() $ \Delta {t}_{\mathrm{max}}=93\hskip0.22em \mathrm{hr} $
, the model performs significantly worse than the other two, implying that past a certain threshold, performance begins to degrade. Notably, all three models outperform the
$ \Delta {t}_{\mathrm{max}}=93\hskip0.22em \mathrm{hr} $
, the model performs significantly worse than the other two, implying that past a certain threshold, performance begins to degrade. Notably, all three models outperform the
![]() $ {\mathrm{\ell}}_2 $
-based downscaling model even though the representations networks have been trained with less data as in the main experiment.
$ {\mathrm{\ell}}_2 $
-based downscaling model even though the representations networks have been trained with less data as in the main experiment.

Figure 14. The energy spectrum (left), semivariogram (center), and distribution of total variation difference errors (right) for models trained with different maximum
![]() $ \Delta {t}_{\mathrm{max}} $
for our ablation study. The semivariogram and error distributions are calculated on divergence, but qualitatively similar results are obtained for vorticity.
$ \Delta {t}_{\mathrm{max}} $
for our ablation study. The semivariogram and error distributions are calculated on divergence, but qualitatively similar results are obtained for vorticity.
5. Conclusion and Future Work
We have presented AtmoDist, a representation learning approach for atmospheric dynamics. It is based on a novel spatiotemporal pretext task designed for atmospheric data that is applicable to a wide range of different fields. We used the representations learned by AtmoDist to introduce a data-driven metric for atmospheric states and showed that it improves the state-of-the-art for downscaling when used as a loss function there. For the reconstruction of missing field data, it also led to more detailed and more realistic results. Surprisingly, AtmoDist improved the performance even for local statistics, although locality played no role in the pretext task. These results validate the quality of our learned representations.
5.1. Possible extensions of AtmoDist
We believe that different extensions of AtmoDist should be explored in the future. One possible direction is the use of a contrastive loss instead of our current pretext task. For this, samples within a certain temporal distance from each other can be used as positive pairs and samples above that threshold as negative ones, akin to word2vec (Mikolov et al., Reference Mikolov, Chen, Corrado, Dean, Bengio and LeCun2013). However, we believe that predicting the exact time lag between two atmospheric states provides a much more challenging task and hence a better training signal than solely predicting if two states are within a certain distance of each other. Exploring a triplet loss (Hoffer and Ailon, Reference Hoffer and Ailon2015) is another interesting direction.
We also want to explore other downstream tasks, for example, the classification and prediction of hurricanes (Prabhat et al., Reference Prabhat, Kashinath, Mudigonda, Kim, Kapp-Schwoerer, Graubner, Karaismailoglu, von Kleist, Kurth, Greiner, Mahesh, Yang, Lewis, Chen, Lou, Chandran, Toms, Chapman, Dagon, Shields, O’Brien, Wehner and Collins2021) or extreme events (Racah et al., Reference Racah, Beckham, Maharaj, Kahou, Prabhat, Pal, Guyon, Luxburg, Bengio, Wallach, Fergus, Vishwanathan and Garnett2017). Interesting would also be to explore transfer learning for AtmoDist, for example, to train on historical data and then adapt to a regime with significant
![]() $ {\mathrm{CO}}_2 $
forcing, similar to Barnes et al. (Reference Barnes, Anderson and Ebert-Uphoff2018). This could be explored with simulation data, which can be used to train AtmoDist without modifications.
$ {\mathrm{CO}}_2 $
forcing, similar to Barnes et al. (Reference Barnes, Anderson and Ebert-Uphoff2018). This could be explored with simulation data, which can be used to train AtmoDist without modifications.
We employed only divergence and vorticity and a single vertical layer in AtmoDist. In the future, we want to validate our approach using additional variables, for example, those appearing in the primitive equations, and with more vertical layers. It is also likely that better representations can be obtained when not only a single time step but a temporal window of nearby states is provided to the network.
5.2. Outlook
We consider AtmoDist as a first proof-of-concept for the utility of representation learning for analyzing, understanding, and improving applications in the context of weather and climate dynamics.
Representation learning in computer vision relies heavily on data augmentation (e.g., Chen et al., Reference Chen, Kornblith, Norouzi, Hinton, HD and Singh2020; Caron et al., Reference Caron, Touvron, Misra, Jegou, Mairal, Bojanowski and Joulin2021). While this is a well-understood subject for natural images, the same does not hold true for atmospheric and more general climate dynamics data. Compared to computer vision, many more physical constraints have to be considered. We hence believe that the design and validation of novel data augmentations is an important direction for future work.
Another currently unexplored research direction is representation learning using (unlabeled) simulation data. For example, one could perform pre-training on the very large amounts of simulation data that are available from Climate Model Intercomparison Project (CMIP) runs (Eyring et al., Reference Eyring, Bony, Meehl, Senior, Stevens, Stouffer and Taylor2016) and use fine-tuning (Devlin et al., Reference Devlin, Chang, Lee and Toutanova2019), transfer learning, or domain adaptation to derive a network that is well suited for observational data. Another interesting direction is to compare representations obtained for reanalysis and simulation data, which has the potential to provide insights into subtle biases that persist in simulations.
Our current work focused on improving downstream applications using representation learning. However, we believe that it also has the potential to provide new insights into the physical processes in the atmosphere, analogous to how tools such as proper orthogonal decompositions helped to analyze the physics in the past. In our opinion, in particular attention-based network architectures, such as transformers (Vaswani et al., Reference Vaswani, Shazeer, Parmar, Uszkoreit, Jones, Gomez, Kaiser, Polosukhin, Guyon, Luxburg, Bengio, Wallach, Fergus, Vishwanathan and Garnett2017), provide a promising approach to this.
Acknowledgments
We gratefully acknowledge discussions with the participants of the workshop Machine Learning and the Physics of Climate at the Kavli Institute of Theoretical Physics in Santa Barbara that helped to shaped our overall understanding of the potential of representation learning for weather and climate dynamics. Special thanks to Yi Deng for many helpful discussions and explanations.
Author Contributions
Conceptualization: S.H. and C.L. Data curation: S.H. Data visualization: S.H. Methodology: S.H. and C.L. Writing original draft: S.H. and C.L. All authors approved the final submitted draft.
Competing Interests
The authors declare no competing interests exist.
Data Availability Statement
Our code is made available at https://github.com/sehoffmann/AtmoDist. Instructions on how to download ERA5 can be found at https://confluence.ecmwf.int/display/CKB/How+to+download+ERA5.
Ethics Statement
The research meets all ethical guidelines, including adherence to the legal requirements of the study country.
Funding Statement
This work was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)—Project-ID 422037413–TRR 287.
A. Appendix.
A.1. Preprocessing
Divergence and vorticity are transformed in a preprocessing step by
![]() $ y=f\left(g\left(h(x)\right)\right) $
where
$ y=f\left(g\left(h(x)\right)\right) $
where
and which is applied element-wise and independently for vorticity and divergence. Here
![]() $ {\mu}_1 $
and
$ {\mu}_1 $
and
![]() $ {\sigma}_1 $
denote the mean and standard deviation of the corresponding fields, respectively, while
$ {\sigma}_1 $
denote the mean and standard deviation of the corresponding fields, respectively, while
![]() $ {\mu}_2 $
and
$ {\mu}_2 $
and
![]() $ {\sigma}_2 $
denote the mean and standard deviation of the log-transformed field
$ {\sigma}_2 $
denote the mean and standard deviation of the log-transformed field
![]() $ w $
. All moments are calculated across the training dataset and are shown in Table 3. The parameter
$ w $
. All moments are calculated across the training dataset and are shown in Table 3. The parameter
![]() $ \alpha $
controls the strength by which the dynamic range at the tails of the distribution is compressed. We found that
$ \alpha $
controls the strength by which the dynamic range at the tails of the distribution is compressed. We found that
![]() $ \alpha \hskip0.35em =\hskip0.35em 0.2 $
is sufficient to stabilize training while it avoids an aggressive compression of the original data. Notice that the log function behaves approximately linear around 1, thus leaving small values almost unaffected.
$ \alpha \hskip0.35em =\hskip0.35em 0.2 $
is sufficient to stabilize training while it avoids an aggressive compression of the original data. Notice that the log function behaves approximately linear around 1, thus leaving small values almost unaffected.
Table 3. Mean and standard deviations calculated on the training dataset (1979–1998) on model level 120 for divergence and relative vorticity.

A.2. AtmoDist Training
The AtmoDist network is trained using standard stochastic gradient descent with momentum
![]() $ \beta \hskip0.35em =\hskip0.35em 0.9 $
and an initial learning rate of
$ \beta \hskip0.35em =\hskip0.35em 0.9 $
and an initial learning rate of
![]() $ \eta \hskip0.35em =\hskip0.35em {10}^{-1} $
. If training encounters a plateau, the learning rate is reduced by an order of magnitude to a minimum of
$ \eta \hskip0.35em =\hskip0.35em {10}^{-1} $
. If training encounters a plateau, the learning rate is reduced by an order of magnitude to a minimum of
![]() $ {\eta}_{\mathrm{min}}\hskip0.35em =\hskip0.35em {10}^{-5} $
. Additionally, gradient clipping is employed, ensuring that the
$ {\eta}_{\mathrm{min}}\hskip0.35em =\hskip0.35em {10}^{-5} $
. Additionally, gradient clipping is employed, ensuring that the
![]() $ {l}_2 $
-norm of the gradient does not exceed
$ {l}_2 $
-norm of the gradient does not exceed
![]() $ {G}_{\mathrm{max}}\hskip0.35em =\hskip0.35em 5.0 $
. Finally, to counteract overfitting, weight decay of
$ {G}_{\mathrm{max}}\hskip0.35em =\hskip0.35em 5.0 $
. Finally, to counteract overfitting, weight decay of
![]() $ {10}^{-4} $
is used.
$ {10}^{-4} $
is used.

Figure 15. Mean SSIM and PSNR as a function of the temporal separation
![]() $ \Delta t $
. Since in both cases higher quantities indicate more similarity between samples, we apply the following transformations to make the plots comparable to Figure 4: SSIM:
$ \Delta t $
. Since in both cases higher quantities indicate more similarity between samples, we apply the following transformations to make the plots comparable to Figure 4: SSIM:
![]() $ y=1-\left(1+ SSIM\left({X}_{t_1},{X}_{t_2}\right)\right)/2 $
; PSNR:
$ y=1-\left(1+ SSIM\left({X}_{t_1},{X}_{t_2}\right)\right)/2 $
; PSNR:
![]() $ y=50\hskip0.1em dB- PSNR\left({X}_{t_1},{X}_{t_2}\right) $
.
$ y=50\hskip0.1em dB- PSNR\left({X}_{t_1},{X}_{t_2}\right) $
.
Despite the network converging on lower resolutions in preliminary experiments, once we trained on 160x160 patches at native resolution (1280x2560) the network failed to converge. We hypothesize that the issue is the difficulty of the pretext task combined with an initial lack of discerning features. We thus employ a pre-training scheme inspired by curriculum learning (Bengio et al., Reference Bengio, Louradour, Collobert and Weston2009). More specifically, we initially train the network only on about 10% of the data so that it can first focus on solving the task there. After 20 epochs, we then reset the learning rate to
![]() $ \eta \hskip0.35em =\hskip0.35em {10}^{-1} $
and start training on the whole dataset.
$ \eta \hskip0.35em =\hskip0.35em {10}^{-1} $
and start training on the whole dataset.
A.3. Scaling the Loss Function
To ensure that downscaling with
![]() $ {\mathrm{\ell}}_2 $
-loss and the AtmoDist metric exhibit the same training dynamics, we normalize our loss function. This is particularly important with respect to the
$ {\mathrm{\ell}}_2 $
-loss and the AtmoDist metric exhibit the same training dynamics, we normalize our loss function. This is particularly important with respect to the
![]() $ {\alpha}_{\mathrm{adv}} $
parameter which controls the trade-off between content-loss and adversarial-loss in SRGAN (Ledig et al., Reference Ledig, Theis, Huszar, Caballero, Cunningham, Acosta, Aitken, Tejani, Totz, Wang and Shi2017). The same procedure is also applied to the loss function derived from the autoencoder.
$ {\alpha}_{\mathrm{adv}} $
parameter which controls the trade-off between content-loss and adversarial-loss in SRGAN (Ledig et al., Reference Ledig, Theis, Huszar, Caballero, Cunningham, Acosta, Aitken, Tejani, Totz, Wang and Shi2017). The same procedure is also applied to the loss function derived from the autoencoder.
We hypothesize that due to the chaotic dynamics of the atmosphere, any loss function should on average converge to a specific level after a certain time period (ignoring daily and annual oscillations). Thus, we normalize our content-loss by ensuring that the equilibrium levels are roughly the same in terms of least squares by solving the following optimization problem for the scaling factor
![]() $ \alpha $
$ \alpha $
 $$ \hat{\alpha}\hskip0.35em =\hskip0.35em \underset{\alpha \in \mathrm{\mathbb{R}}}{\mathrm{argmin}}\sum \limits_{t\hskip0.35em =\hskip0.35em \frac{N}{2}}^N{\left(\alpha {c}_t-{m}_t\right)}^2 $$
$$ \hat{\alpha}\hskip0.35em =\hskip0.35em \underset{\alpha \in \mathrm{\mathbb{R}}}{\mathrm{argmin}}\sum \limits_{t\hskip0.35em =\hskip0.35em \frac{N}{2}}^N{\left(\alpha {c}_t-{m}_t\right)}^2 $$
where
![]() $ {c}_t $
denote the average AtmoDist distance of samples that are
$ {c}_t $
denote the average AtmoDist distance of samples that are
![]() $ \Delta t $
apart and
$ \Delta t $
apart and
![]() $ {m}_t $
their average
$ {m}_t $
their average
![]() $ {\mathrm{\ell}}_2 $
distance. It is easy to verify that the above optimization problem has the unique solution
$ {\mathrm{\ell}}_2 $
distance. It is easy to verify that the above optimization problem has the unique solution
 $$ \hat{\alpha}\hskip0.35em =\hskip0.35em \frac{\sum_{t\hskip0.35em =\hskip0.35em \frac{N}{2}}^N{c}_t{m}_t}{\sum_{t\hskip0.35em =\hskip0.35em \frac{N}{2}}^N{c}_t^2}. $$
$$ \hat{\alpha}\hskip0.35em =\hskip0.35em \frac{\sum_{t\hskip0.35em =\hskip0.35em \frac{N}{2}}^N{c}_t{m}_t}{\sum_{t\hskip0.35em =\hskip0.35em \frac{N}{2}}^N{c}_t^2}. $$
A.4. Autoencoder Architecture
The autoencoder takes as input a divergence and vorticity field of size
![]() $ 160\times 160 $
. It consists of an encoder part that compresses the input field to a suitable representation, and a decoder that takes the representation and reconstructs the original field from it.
$ 160\times 160 $
. It consists of an encoder part that compresses the input field to a suitable representation, and a decoder that takes the representation and reconstructs the original field from it.
The encoder is identical to the representation network used for the AtmoDist task. The decoder is a mirrored version of the encoder where downscaling convolutions were replaced by upscaling ones. Upscaling is done by bilinear interpolation followed by a standard residual block.
In the middle, that is in-between encoder and decoder, no feed-forward layer is used. It would have contained the majority of parameters of the overall network and thus potentially also of its capacity. Instead, we use an approach inspired by Tolstikhin et al. (Reference Tolstikhin, Houlsby, Kolesnikov, Beyer, Zhai, Unterthiner, Yung, Steiner, Keysers, Uszkoreit, Lucic and Dosovitskiy2021) to ensure that information can propagate between each spatial position.
First, the
![]() $ H\times \mathrm{W}\times C $
feature map of the last encoder layer, where
$ H\times \mathrm{W}\times C $
feature map of the last encoder layer, where
![]() $ H,W,C $
denote height, width, and number of channels, respectively, is interpreted as
$ H,W,C $
denote height, width, and number of channels, respectively, is interpreted as
![]() $ C $
vectors of dimensionality
$ C $
vectors of dimensionality
![]() $ H\cdot W $
. Each vector is then transformed by a feed-forward layer, mixing information spatially for each channel. Afterwards, the same procedure is repeated for the
$ H\cdot W $
. Each vector is then transformed by a feed-forward layer, mixing information spatially for each channel. Afterwards, the same procedure is repeated for the
![]() $ H\cdot W $
vectors of dimensionality
$ H\cdot W $
vectors of dimensionality
![]() $ C $
to mix information channel-wise as well. This approach allows us to propagate information globally without bloating the size of the network in a significant way.
$ C $
to mix information channel-wise as well. This approach allows us to propagate information globally without bloating the size of the network in a significant way.
The autoencoder is trained in the same way as the AtmoDist representation network, compare Appendix A.2, except that no pre-training is used.
A.5. Inpainting Training
Our network used for inpainting follows the same architecture as the autoencoder described above.
When training with either the AtmoDist- or autoencoder-based loss function, we initialize the network with a pre-trained version in the same way as we did for the super-resolution already. Furthermore, a small
![]() $ l2 $
-loss term is added as a regularization. Specifically, the total loss is given by
$ l2 $
-loss term is added as a regularization. Specifically, the total loss is given by
where
![]() $ \gamma \hskip0.35em =\hskip0.35em 0.1 $
and
$ \gamma \hskip0.35em =\hskip0.35em 0.1 $
and
![]() $ {L}_{\mathrm{content}} $
is either the already scaled AtmoDist or autoencoder loss. This is done to prevent local minima and artifacts during training.
$ {L}_{\mathrm{content}} $
is either the already scaled AtmoDist or autoencoder loss. This is done to prevent local minima and artifacts during training.
A.6. Semivariogram Calculation
The semivariogram, given by
can be calculated in different ways. We approximate the integral that defines it using Monte-Carlo sampling. In particular, for each time-step and each lag-distance
![]() $ r $
, 300 random locations and 300 random directions are sampled and the field is evaluated at these points. This procedure is done for the complete evaluation period and in the end the semivariogram is obtained by averaging.
$ r $
, 300 random locations and 300 random directions are sampled and the field is evaluated at these points. This procedure is done for the complete evaluation period and in the end the semivariogram is obtained by averaging.

Figure 16. Uncurated set of downscaled vorticity fields over the Mediterranean Sea and Eastern Europe at different time steps. Coastlines are shown in the first ground truth field and then omitted for better comparability.