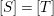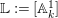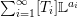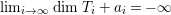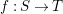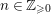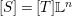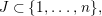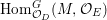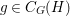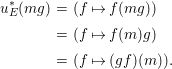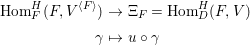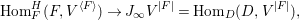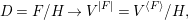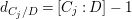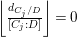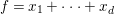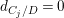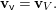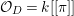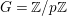1 Introduction
The McKay correspondence in terms of stringy invariants was first studied by Batyrev and Dais [Reference Batyrev and DaisBD96] and Batyrev [Reference BatyrevBat99]. Denef and Loeser [Reference Denef and LoeserDL02] later took a more conceptual approach, where the McKay correspondence directly follows from the theory of motivic integration suitably generalized to a situation involving finite group actions.
These works were confined to characteristic zero. Except for some works for the tame case (the finite group has order coprime to the characteristic), attempts to generalize to arbitrary characteristics, including the wild (nontame) case, were only recently started in [Reference YasudaYas14, Reference YasudaYasa]. There, a conjectural generalization of results in characteristic zero was formulated. Subsequently, it turned out in [Reference Wood and YasudaWY15] that the conjecture is closely related to the number theory, in particular, the problem of counting local Galois representations. In these papers, however, only linear actions on affine spaces were discussed. In characteristic zero, since every finite group action on a smooth variety is locally linearizable, many studies can be reduced to the linear case. This is no longer true in positive or mixed characteristics. The conjecture has been verified in very special cases, by computing stringy invariants explicitly. The aims of this paper are first to generalize the conjecture to nonlinear actions on a (possibly singular) affine variety, and second to make it possible to compute stringy invariants in more complicated examples.
We now recall the conjecture from [Reference YasudaYasa]. Set the base scheme to be 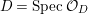 $D=\text{Spec}\,{\mathcal{O}}_{D}$, with
$D=\text{Spec}\,{\mathcal{O}}_{D}$, with ![]() ${\mathcal{O}}_{D}$ a complete discrete valuation ring, and suppose that its residue field, denoted by
${\mathcal{O}}_{D}$ a complete discrete valuation ring, and suppose that its residue field, denoted by ![]() $k$, is algebraically closed.
$k$, is algebraically closed.
Remark 1.1. Working over a discrete valuation ring rather than a field is natural in our arguments. We can easily switch from a field to a discrete valuation ring by the base change 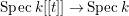 $\text{Spec}\,k[[t]]\rightarrow \text{Spec}\,k$.
$\text{Spec}\,k[[t]]\rightarrow \text{Spec}\,k$.
We consider a linear action of a finite group ![]() $G$ on the affine
$G$ on the affine ![]() $d$-space
$d$-space 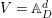 $V=\mathbb{A}_{D}^{d}$ over
$V=\mathbb{A}_{D}^{d}$ over ![]() $D$ and the associated quotient scheme
$D$ and the associated quotient scheme 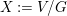 $X:=V/G$.
$X:=V/G$.
Conjecture 1.2. (The wild McKay correspondence conjecture [Reference YasudaYasa])
Let 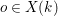 $o\in X(k)$ denote the image of the origin, and let
$o\in X(k)$ denote the image of the origin, and let 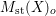 $M_{\text{st}}(X)_{o}$ denote the stringy motif of
$M_{\text{st}}(X)_{o}$ denote the stringy motif of ![]() $X$ at
$X$ at ![]() $o$. Suppose that the quotient morphism
$o$. Suppose that the quotient morphism ![]() $V\rightarrow X$ is étale in codimension one. Then
$V\rightarrow X$ is étale in codimension one. Then
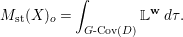 $$\begin{eqnarray}M_{\text{st}}(X)_{o}=\int _{G\text{-}\text{Cov}(D)}\mathbb{L}^{\mathbf{w}}\,d{\it\tau}.\end{eqnarray}$$
$$\begin{eqnarray}M_{\text{st}}(X)_{o}=\int _{G\text{-}\text{Cov}(D)}\mathbb{L}^{\mathbf{w}}\,d{\it\tau}.\end{eqnarray}$$ Here, 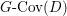 $G\text{-}\text{Cov}(D)$ is the (conjectural) moduli space of
$G\text{-}\text{Cov}(D)$ is the (conjectural) moduli space of ![]() $G$-covers of
$G$-covers of ![]() $D$,
$D$, ![]() $\mathbf{w}$ is the weight function on
$\mathbf{w}$ is the weight function on 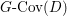 $G\text{-}\text{Cov}(D)$ associated to the
$G\text{-}\text{Cov}(D)$ associated to the ![]() $G$-representation
$G$-representation ![]() $V$, and
$V$, and ![]() ${\it\tau}$ is the tautological motivic measure on
${\it\tau}$ is the tautological motivic measure on 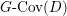 $G\text{-}\text{Cov}(D)$.
$G\text{-}\text{Cov}(D)$.
In [Reference YasudaYas14], Conjecture 1.2 was verified, when 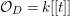 ${\mathcal{O}}_{D}=k[[t]]$ with
${\mathcal{O}}_{D}=k[[t]]$ with ![]() $k$ of characteristic
$k$ of characteristic ![]() $p>0$,
$p>0$, ![]() $G$ is the cyclic group of order
$G$ is the cyclic group of order ![]() $p$ and the
$p$ and the ![]() $G$-action on
$G$-action on ![]() $\mathbb{A}_{D}^{d}$ is defined over
$\mathbb{A}_{D}^{d}$ is defined over ![]() $k$. In [Reference Wood and YasudaWY15], a variant conjecture was verified when the symmetric group
$k$. In [Reference Wood and YasudaWY15], a variant conjecture was verified when the symmetric group ![]() $S_{n}$ acts on
$S_{n}$ acts on ![]() $\mathbb{A}_{D}^{2n}$ by two copies of the standard representation. In the same paper, a generalization to the case where
$\mathbb{A}_{D}^{2n}$ by two copies of the standard representation. In the same paper, a generalization to the case where ![]() $k$ is only perfect was formulated by modifying the function
$k$ is only perfect was formulated by modifying the function ![]() $\mathbf{w}$.
$\mathbf{w}$.
Roughly, the conjecture was derived as follows. We first express 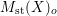 $M_{\text{st}}(X)_{o}$ as a motivic integral over the space of arcs of
$M_{\text{st}}(X)_{o}$ as a motivic integral over the space of arcs of ![]() $X$, that is,
$X$, that is, ![]() $D$-morphisms
$D$-morphisms ![]() $D\rightarrow X$. We then transform the motivic integral to a motivic integral over the space of
$D\rightarrow X$. We then transform the motivic integral to a motivic integral over the space of ![]() $G$-arcs of
$G$-arcs of ![]() $V$, that is,
$V$, that is, ![]() $G$-equivariant
$G$-equivariant ![]() $D$-morphisms
$D$-morphisms ![]() $E\rightarrow V$ for
$E\rightarrow V$ for ![]() $G$-covers
$G$-covers ![]() $E\rightarrow D$. Using the technique of untwisting, we reduce the study of
$E\rightarrow D$. Using the technique of untwisting, we reduce the study of ![]() $G$-arcs to that of ordinary arcs, and can see that the contribution of each
$G$-arcs to that of ordinary arcs, and can see that the contribution of each ![]() $G$-cover
$G$-cover ![]() $E\rightarrow D$ to
$E\rightarrow D$ to 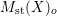 $M_{\text{st}}(X)_{o}$ is
$M_{\text{st}}(X)_{o}$ is ![]() $\mathbb{L}^{\mathbf{w}(E)}$, and hence the conjecture. A prototype of untwisting was introduced by Denef and Loeser [Reference Denef and LoeserDL02]. In [Reference YasudaYasa], the author developed it so that we can use it even in the wild case. In this paper, we refine the technique slightly more. For each
$\mathbb{L}^{\mathbf{w}(E)}$, and hence the conjecture. A prototype of untwisting was introduced by Denef and Loeser [Reference Denef and LoeserDL02]. In [Reference YasudaYasa], the author developed it so that we can use it even in the wild case. In this paper, we refine the technique slightly more. For each ![]() $G$-cover
$G$-cover ![]() $E$ of
$E$ of ![]() $D$ with a connected component
$D$ with a connected component ![]() $F$, we can construct another affine space
$F$, we can construct another affine space 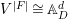 $V^{|F|}\cong \mathbb{A}_{D}^{d}$ and a morphism
$V^{|F|}\cong \mathbb{A}_{D}^{d}$ and a morphism 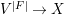 $V^{|F|}\rightarrow X$ such that there is a correspondence between
$V^{|F|}\rightarrow X$ such that there is a correspondence between ![]() $G$-arcs of
$G$-arcs of ![]() $V$ and ordinary arcs of
$V$ and ordinary arcs of ![]() $V^{|F|}$. Through the correspondence, we can represent the contribution of
$V^{|F|}$. Through the correspondence, we can represent the contribution of ![]() $E$ to
$E$ to 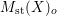 $M_{\text{st}}(X)_{o}$ as a motivic integral over the ordinary arcs
$M_{\text{st}}(X)_{o}$ as a motivic integral over the ordinary arcs 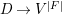 $D\rightarrow V^{|F|}$.
$D\rightarrow V^{|F|}$.
Our strategy of generalization to the nonlinear case is quite simple. Given an affine variety ![]() $\mathsf{v}$ with a
$\mathsf{v}$ with a ![]() $G$-action, we equivariantly embed
$G$-action, we equivariantly embed ![]() $\mathsf{v}$ into an affine space
$\mathsf{v}$ into an affine space ![]() $V$ with a linear
$V$ with a linear ![]() $G$-action. For each
$G$-action. For each ![]() $G$-cover
$G$-cover ![]() $E\rightarrow D$ with a connected component
$E\rightarrow D$ with a connected component ![]() $F$, we take the subvariety
$F$, we take the subvariety 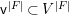 $\mathsf{v}^{|F|}\subset V^{|F|}$ corresponding to
$\mathsf{v}^{|F|}\subset V^{|F|}$ corresponding to ![]() $\mathsf{v}\subset V$, which plays the same role as
$\mathsf{v}\subset V$, which plays the same role as ![]() $V^{|F|}$ in the linear case.
$V^{|F|}$ in the linear case.
We also need an idea from the minimal model program, that is, working with varieties endowed with divisors rather than varieties themselves. Encapsulating one more piece of information, we introduce the notion of centered log structures or centered log ![]() $D$-varieties, which are just triples
$D$-varieties, which are just triples 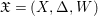 $\mathfrak{X}=(X,{\rm\Delta},W)$ of a normal
$\mathfrak{X}=(X,{\rm\Delta},W)$ of a normal ![]() $D$-variety
$D$-variety ![]() $X$, a
$X$, a ![]() $\mathbb{Q}$-divisor
$\mathbb{Q}$-divisor ![]() ${\rm\Delta}$ and a closed subset
${\rm\Delta}$ and a closed subset ![]() $W$ of
$W$ of 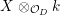 $X\otimes _{{\mathcal{O}}_{D}}k$ with
$X\otimes _{{\mathcal{O}}_{D}}k$ with 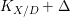 $K_{X/D}+{\rm\Delta}$
$K_{X/D}+{\rm\Delta}$![]() $\mathbb{Q}$-Cartier. It is straightforward to generalize the stringy motif to centered log
$\mathbb{Q}$-Cartier. It is straightforward to generalize the stringy motif to centered log ![]() $D$-varieties. We write it as
$D$-varieties. We write it as ![]() $M_{\text{st}}(\mathfrak{X})$. For instance, the stringy motif
$M_{\text{st}}(\mathfrak{X})$. For instance, the stringy motif 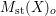 $M_{\text{st}}(X)_{o}$ mentioned above is the same as
$M_{\text{st}}(X)_{o}$ mentioned above is the same as 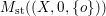 $M_{\text{st}}((X,0,\{o\}))$.
$M_{\text{st}}((X,0,\{o\}))$.
Returning to the equivariant immersion ![]() $\mathsf{v}{\hookrightarrow}V$, if
$\mathsf{v}{\hookrightarrow}V$, if ![]() $\mathsf{v}$ is given a centered log structure
$\mathsf{v}$ is given a centered log structure 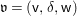 $\mathfrak{v}=(\mathsf{v},{\it\delta},\mathsf{w})$, then there exist unique centered log structures
$\mathfrak{v}=(\mathsf{v},{\it\delta},\mathsf{w})$, then there exist unique centered log structures ![]() $\mathfrak{x}$ on
$\mathfrak{x}$ on 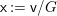 $\mathsf{x}:=\mathsf{v}/G$ and
$\mathsf{x}:=\mathsf{v}/G$ and ![]() $\mathfrak{v}^{|F|,{\it\nu}}$ on the normalization
$\mathfrak{v}^{|F|,{\it\nu}}$ on the normalization ![]() $\mathsf{v}^{|F|,{\it\nu}}$ of
$\mathsf{v}^{|F|,{\it\nu}}$ of ![]() $\mathsf{v}^{|F|}$ so that all the morphisms connecting them are crepant (see Section 2.2 for details). If
$\mathsf{v}^{|F|}$ so that all the morphisms connecting them are crepant (see Section 2.2 for details). If ![]() $H\subset G$ is the stabilizer of the component
$H\subset G$ is the stabilizer of the component ![]() $F\subset E$, then the centralizer
$F\subset E$, then the centralizer ![]() $C_{G}(H)$ of
$C_{G}(H)$ of ![]() $H$ acts on
$H$ acts on ![]() $\mathsf{v}^{|F|,{\it\nu}}$ and on its arc space
$\mathsf{v}^{|F|,{\it\nu}}$ and on its arc space 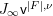 $J_{\infty }\mathsf{v}^{|F|,{\it\nu}}$. We define
$J_{\infty }\mathsf{v}^{|F|,{\it\nu}}$. We define 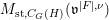 $M_{\text{st},C_{G}(H)}(\mathfrak{v}^{|F|,{\it\nu}})$ in the same way as defining the ordinary stringy motif except that we use the quotient space
$M_{\text{st},C_{G}(H)}(\mathfrak{v}^{|F|,{\it\nu}})$ in the same way as defining the ordinary stringy motif except that we use the quotient space 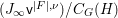 $(J_{\infty }\mathsf{v}^{|F|,{\it\nu}})/C_{G}(H)$ rather than the arc space
$(J_{\infty }\mathsf{v}^{|F|,{\it\nu}})/C_{G}(H)$ rather than the arc space 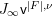 $J_{\infty }\mathsf{v}^{|F|,{\it\nu}}$ itself. We formulate the following conjecture which generalizes Conjecture 1.2.
$J_{\infty }\mathsf{v}^{|F|,{\it\nu}}$ itself. We formulate the following conjecture which generalizes Conjecture 1.2.
Conjecture 1.3. (Conjecture 7.3)
We have
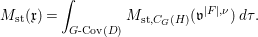 $$\begin{eqnarray}M_{\text{st}}(\mathfrak{x})=\int _{G\text{-}\text{Cov}(D)}M_{\text{st},C_{G}(H)}(\mathfrak{v}^{|F|,{\it\nu}})\,d{\it\tau}.\end{eqnarray}$$
$$\begin{eqnarray}M_{\text{st}}(\mathfrak{x})=\int _{G\text{-}\text{Cov}(D)}M_{\text{st},C_{G}(H)}(\mathfrak{v}^{|F|,{\it\nu}})\,d{\it\tau}.\end{eqnarray}$$We verify Conjecture 1.3 in two examples from the simplest ones, computing both sides of the equality independently. One example is a tame action on a singular variety and the other is a wild nonlinear action on a smooth variety.
Keeping the above arguments in mind, let us return to the linear case. One difficulty in computing the right-hand side of the equality in Conjecture 1.2 is in computing the weights ![]() $\mathbf{w}(E)$ explicitly, and another is in computing the moduli space
$\mathbf{w}(E)$ explicitly, and another is in computing the moduli space 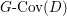 $G\text{-}\text{Cov}(D)$. Taking an equivariant immersion
$G\text{-}\text{Cov}(D)$. Taking an equivariant immersion ![]() $\mathsf{v}{\hookrightarrow}V$ is useful also in solving the former difficulty for some linear actions. With
$\mathsf{v}{\hookrightarrow}V$ is useful also in solving the former difficulty for some linear actions. With ![]() $E$,
$E$, ![]() $F$ and
$F$ and ![]() $H$ as before, if
$H$ as before, if 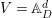 $V=\mathbb{A}_{D}^{d}$ has a linear
$V=\mathbb{A}_{D}^{d}$ has a linear ![]() $G$-action, and if
$G$-action, and if 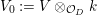 $V_{0}:=V\otimes _{{\mathcal{O}}_{D}}k$, then the weight of
$V_{0}:=V\otimes _{{\mathcal{O}}_{D}}k$, then the weight of ![]() $E$ with respect to
$E$ with respect to ![]() $V$ is, by definition,
$V$ is, by definition,
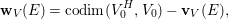 $$\begin{eqnarray}\mathbf{w}_{V}(E)=\text{codim}(V_{0}^{H},V_{0})-\boldsymbol{v}_{V}(E),\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{w}_{V}(E)=\text{codim}(V_{0}^{H},V_{0})-\boldsymbol{v}_{V}(E),\end{eqnarray}$$ with another function ![]() $\boldsymbol{v}_{V}$ on
$\boldsymbol{v}_{V}$ on 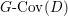 $G\text{-}\text{Cov}(D)$, and
$G\text{-}\text{Cov}(D)$, and ![]() $V_{0}^{H}$ the
$V_{0}^{H}$ the ![]() $H$-fixed-point locus in
$H$-fixed-point locus in ![]() $V_{0}$. The first term,
$V_{0}$. The first term, 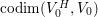 $\text{codim}(V_{0}^{H},V_{0})$, is easy to compute, while the second is generally not. However, if
$\text{codim}(V_{0}^{H},V_{0})$, is easy to compute, while the second is generally not. However, if ![]() $G$ acts on
$G$ acts on ![]() $V$ by permutations of coordinates, then
$V$ by permutations of coordinates, then ![]() $\boldsymbol{v}_{V}(E)$ is represented in terms of the discriminant [Reference Wood and YasudaWY15]. In this situation, we can associate a degree
$\boldsymbol{v}_{V}(E)$ is represented in terms of the discriminant [Reference Wood and YasudaWY15]. In this situation, we can associate a degree ![]() $d$ cover
$d$ cover ![]() $C\rightarrow D$ to a
$C\rightarrow D$ to a ![]() $G$-cover
$G$-cover ![]() $E\rightarrow D$, and
$E\rightarrow D$, and
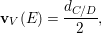 $$\begin{eqnarray}\boldsymbol{v}_{V}(E)=\frac{d_{C/D}}{2},\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{v}_{V}(E)=\frac{d_{C/D}}{2},\end{eqnarray}$$ with ![]() $d_{C/D}$ the discriminant exponent of the cover
$d_{C/D}$ the discriminant exponent of the cover ![]() $C\rightarrow D$. We generalize this equality to hyperplanes in
$C\rightarrow D$. We generalize this equality to hyperplanes in ![]() $V$ defined by a
$V$ defined by a ![]() $G$-invariant linear form. For simplicity, we consider the case where
$G$-invariant linear form. For simplicity, we consider the case where ![]() $\mathsf{v}\subset V$ is defined by
$\mathsf{v}\subset V$ is defined by
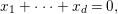 $$\begin{eqnarray}x_{1}+\cdots +x_{d}=0,\end{eqnarray}$$
$$\begin{eqnarray}x_{1}+\cdots +x_{d}=0,\end{eqnarray}$$ with 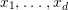 $x_{1},\ldots ,x_{d}$ coordinates of
$x_{1},\ldots ,x_{d}$ coordinates of ![]() $V$.
$V$.
Proposition 1.4. (See Corollary 11.4 for a slightly more general result)
Let 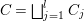 $C=\sqcup _{j=1}^{l}C_{j}$ be the decomposition of
$C=\sqcup _{j=1}^{l}C_{j}$ be the decomposition of ![]() $C$ into the connected components. Then
$C$ into the connected components. Then
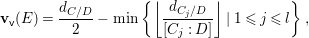 $$\begin{eqnarray}\boldsymbol{v}_{\mathsf{v}}(E)=\frac{d_{C/D}}{2}-\min \left\{\left\lfloor \frac{d_{C_{j}/D}}{[C_{j}:D]}\right\rfloor \mid 1\leqslant j\leqslant l\right\},\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{v}_{\mathsf{v}}(E)=\frac{d_{C/D}}{2}-\min \left\{\left\lfloor \frac{d_{C_{j}/D}}{[C_{j}:D]}\right\rfloor \mid 1\leqslant j\leqslant l\right\},\end{eqnarray}$$ with ![]() $[C_{j}:D]$ the degree of
$[C_{j}:D]$ the degree of 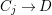 $C_{j}\rightarrow D$.
$C_{j}\rightarrow D$.
Using this and assuming a motivic version of Krasner’s formula [Reference KrasnerKra66] for counting local field extensions, we explicitly compute
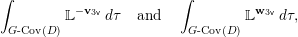 $$\begin{eqnarray}\int _{G\text{-}\text{Cov}(D)}\mathbb{L}^{-\boldsymbol{v}_{3\mathsf{v}}}\,d{\it\tau}\quad \text{and}\quad \int _{G\text{-}\text{Cov}(D)}\mathbb{L}^{\mathbf{w}_{3\mathsf{v}}}\,d{\it\tau},\end{eqnarray}$$
$$\begin{eqnarray}\int _{G\text{-}\text{Cov}(D)}\mathbb{L}^{-\boldsymbol{v}_{3\mathsf{v}}}\,d{\it\tau}\quad \text{and}\quad \int _{G\text{-}\text{Cov}(D)}\mathbb{L}^{\mathbf{w}_{3\mathsf{v}}}\,d{\it\tau},\end{eqnarray}$$ when ![]() $G=S_{4}$ acts on
$G=S_{4}$ acts on 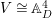 $V\cong \mathbb{A}_{D}^{4}$ by the standard representation,
$V\cong \mathbb{A}_{D}^{4}$ by the standard representation, ![]() $\mathsf{v}\subset V$ is given by
$\mathsf{v}\subset V$ is given by 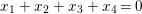 $x_{1}+x_{2}+x_{3}+x_{4}=0$ and
$x_{1}+x_{2}+x_{3}+x_{4}=0$ and ![]() $3\mathsf{v}$ is the direct sum of three copies of
$3\mathsf{v}$ is the direct sum of three copies of ![]() $\mathsf{v}$. We find that the two integrals are dual to each other. The same kind of duality was observed in [Reference Wood and YasudaWY15] and will be discussed in [Reference Wood and YasudaWY] in more detail. The formulas obtained for these integrals are motivic versions of mass formulas for local Galois representations [Reference BhargavaBha07, Reference KedlayaKed07, Reference WoodWoo08] with respect to weights coming from a nonpermutation representation.
$\mathsf{v}$. We find that the two integrals are dual to each other. The same kind of duality was observed in [Reference Wood and YasudaWY15] and will be discussed in [Reference Wood and YasudaWY] in more detail. The formulas obtained for these integrals are motivic versions of mass formulas for local Galois representations [Reference BhargavaBha07, Reference KedlayaKed07, Reference WoodWoo08] with respect to weights coming from a nonpermutation representation.
From Section 2 to 6, we review the theory in the linear case and finally formulate the McKay correspondence for linear actions. Most material here is not new and is found, for instance, in [Reference YasudaYasa], although arguments are refined and adjusted to our purpose. In Section 7, we formulate the McKay correspondence for nonlinear actions. In Section 8, we study how to determine the centered log structure ![]() $\mathfrak{v}^{|F|,{\it\nu}}$ under some assumptions. In Sections 9 and 10, we compute nonlinear examples. In Sections 11 and 12, we treat hyperplanes in permutation representations. We end the paper with concluding remarks in Section 13.
$\mathfrak{v}^{|F|,{\it\nu}}$ under some assumptions. In Sections 9 and 10, we compute nonlinear examples. In Sections 11 and 12, we treat hyperplanes in permutation representations. We end the paper with concluding remarks in Section 13.
1.1 Note added on October 16, 2015
It seems to be better to replace 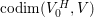 $\text{codim}(V_{0}^{H},V)$ with the dimension of
$\text{codim}(V_{0}^{H},V)$ with the dimension of ![]() $u^{-1}(o)$ in various places, notably in the definition of
$u^{-1}(o)$ in various places, notably in the definition of ![]() $\mathbf{w}$. Here,
$\mathbf{w}$. Here, ![]() $u$ is the morphism
$u$ is the morphism 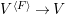 $V^{\left\langle F\right\rangle }\rightarrow V$ given in Definition 4.8 and
$V^{\left\langle F\right\rangle }\rightarrow V$ given in Definition 4.8 and ![]() $o\in V_{0}$ is the origin. This was realized in the later work [Reference YasudaYasb]. The problem is that there seems to be no reason for the map
$o\in V_{0}$ is the origin. This was realized in the later work [Reference YasudaYasb]. The problem is that there seems to be no reason for the map ![]() ${\it\beta}$ in diagrams (4.3) and (4.4) to be surjective, though I do not know of any counterexample. When it is surjective, the mentioned replacement does not change anything. For several important cases it is indeed surjective; see [Reference YasudaYasb, Lemma 8.3].
${\it\beta}$ in diagrams (4.3) and (4.4) to be surjective, though I do not know of any counterexample. When it is surjective, the mentioned replacement does not change anything. For several important cases it is indeed surjective; see [Reference YasudaYasb, Lemma 8.3].
1.2 Convention and notation
If ![]() $X$ is an affine scheme,
$X$ is an affine scheme, ![]() ${\mathcal{O}}_{X}$ denotes its coordinate ring. By the same symbol
${\mathcal{O}}_{X}$ denotes its coordinate ring. By the same symbol ![]() ${\mathcal{O}}_{X}$, we sometimes denote also the structure sheaf on a scheme
${\mathcal{O}}_{X}$, we sometimes denote also the structure sheaf on a scheme ![]() $X$. This abuse of notation does not cause any problems. When a group
$X$. This abuse of notation does not cause any problems. When a group ![]() $G$ acts on
$G$ acts on ![]() $X$ from the left, then we suppose that
$X$ from the left, then we suppose that ![]() $G$ acts on
$G$ acts on ![]() ${\mathcal{O}}_{X}$ from the right: for
${\mathcal{O}}_{X}$ from the right: for ![]() $g\in G$, if
$g\in G$, if 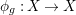 ${\it\phi}_{g}:X\rightarrow X$ is the
${\it\phi}_{g}:X\rightarrow X$ is the ![]() $g$-action on
$g$-action on ![]() $X$, then
$X$, then ![]() $g$ acts on
$g$ acts on ![]() ${\mathcal{O}}_{X}$ by the pullback of functions by
${\mathcal{O}}_{X}$ by the pullback of functions by ![]() ${\it\phi}_{g}$. Throughout the paper, we fix an affine scheme
${\it\phi}_{g}$. Throughout the paper, we fix an affine scheme ![]() $D$, with
$D$, with ![]() ${\mathcal{O}}_{D}$ a complete discrete valuation ring. We denote the residue field of
${\mathcal{O}}_{D}$ a complete discrete valuation ring. We denote the residue field of ![]() ${\mathcal{O}}_{D}$ by
${\mathcal{O}}_{D}$ by ![]() $k$ and suppose that
$k$ and suppose that ![]() $k$ is algebraically closed. For an integral scheme
$k$ is algebraically closed. For an integral scheme ![]() $X$, we denote by
$X$, we denote by ![]() $K(X)$ its function field. If
$K(X)$ its function field. If ![]() $X$ is affine, then
$X$ is affine, then ![]() $K(X)$ is the fraction (quotient) field of the ring
$K(X)$ is the fraction (quotient) field of the ring ![]() ${\mathcal{O}}_{X}$. Again, by abuse of notation,
${\mathcal{O}}_{X}$. Again, by abuse of notation, ![]() $K(X)$ also denotes the constant sheaf on
$K(X)$ also denotes the constant sheaf on ![]() $X$ associated to the function field. For a
$X$ associated to the function field. For a ![]() $D$-scheme
$D$-scheme ![]() $X$, we denote by
$X$, we denote by ![]() $X_{0}$ the special fiber with the reduced structure:
$X_{0}$ the special fiber with the reduced structure: 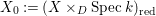 $X_{0}:=(X\times _{D}\text{Spec}\,k)_{\text{red}}$.
$X_{0}:=(X\times _{D}\text{Spec}\,k)_{\text{red}}$.
2 Motivic integration and stringy motifs
In this section, we review the theories of motivic integration over ordinary (untwisted) arcs and stringy invariants, mainly developed in [Reference KontsevichKon95, Reference Denef and LoeserDL99, Reference BatyrevBat98, Reference BatyrevBat99, Reference Denef and LoeserDL02, Reference SebagSeb04].
2.1 Centered log varieties
We call an integral ![]() $D$-scheme
$D$-scheme ![]() $X$ a
$X$ a ![]() $D$-variety if
$D$-variety if ![]() $X$ is flat, separated and of finite type over
$X$ is flat, separated and of finite type over ![]() $D$, and
$D$, and ![]() $X$ is smooth over
$X$ is smooth over ![]() $D$ at the generic point of
$D$ at the generic point of ![]() $X$. For a
$X$. For a ![]() $D$-variety
$D$-variety ![]() $X$, we denote the smooth locus of
$X$, we denote the smooth locus of ![]() $X$ by
$X$ by ![]() $X_{\text{sm}}$ and the regular locus by
$X_{\text{sm}}$ and the regular locus by ![]() $X_{\text{reg}}$.
$X_{\text{reg}}$.
Let ![]() $X$ be a normal
$X$ be a normal ![]() $D$-variety. We can define the canonical sheaf
$D$-variety. We can define the canonical sheaf 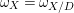 ${\it\omega}_{X}={\it\omega}_{X/D}$ of
${\it\omega}_{X}={\it\omega}_{X/D}$ of ![]() $X$ over
$X$ over ![]() $D$ as in [Reference KollárKol13, page 8]. On
$D$ as in [Reference KollárKol13, page 8]. On ![]() $X_{\text{sm}}$, the canonical sheaf is isomorphic to
$X_{\text{sm}}$, the canonical sheaf is isomorphic to 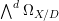 $\wedge ^{d}{\rm\Omega}_{X/D}$, with
$\wedge ^{d}{\rm\Omega}_{X/D}$, with ![]() $d$ the relative dimension of
$d$ the relative dimension of ![]() $X$ over
$X$ over ![]() $D$. Therefore, we can think of
$D$. Therefore, we can think of ![]() ${\it\omega}_{X}$ as a subsheaf of
${\it\omega}_{X}$ as a subsheaf of 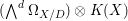 $(\wedge ^{d}{\rm\Omega}_{X/D})\otimes K(X)$. We define the canonical divisor of
$(\wedge ^{d}{\rm\Omega}_{X/D})\otimes K(X)$. We define the canonical divisor of ![]() $X$, denoted by
$X$, denoted by 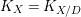 $K_{X}=K_{X/D}$, to be the linear equivalence class of Weil divisors corresponding to
$K_{X}=K_{X/D}$, to be the linear equivalence class of Weil divisors corresponding to ![]() ${\it\omega}_{X}$.
${\it\omega}_{X}$.
A log ![]() $D$-variety is a pair
$D$-variety is a pair ![]() $(X,{\rm\Delta})$ of a normal
$(X,{\rm\Delta})$ of a normal ![]() $D$-variety
$D$-variety ![]() $X$ and a Weil
$X$ and a Weil ![]() $\mathbb{Q}$-divisor
$\mathbb{Q}$-divisor ![]() ${\rm\Delta}$ such that
${\rm\Delta}$ such that 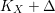 $K_{X}+{\rm\Delta}$ is
$K_{X}+{\rm\Delta}$ is ![]() $\mathbb{Q}$-Cartier. We call
$\mathbb{Q}$-Cartier. We call ![]() ${\rm\Delta}$ the boundary of the log variety. The canonical divisor of a log
${\rm\Delta}$ the boundary of the log variety. The canonical divisor of a log ![]() $D$-variety
$D$-variety ![]() $(X,{\rm\Delta})$ is
$(X,{\rm\Delta})$ is 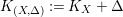 $K_{(X,{\rm\Delta})}:=K_{X}+{\rm\Delta}$.
$K_{(X,{\rm\Delta})}:=K_{X}+{\rm\Delta}$.
A centered log ![]() $D$-variety is a triple
$D$-variety is a triple 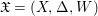 $\mathfrak{X}=(X,{\rm\Delta},W)$ such that
$\mathfrak{X}=(X,{\rm\Delta},W)$ such that ![]() $(X,{\rm\Delta})$ is a log
$(X,{\rm\Delta})$ is a log ![]() $D$-variety and
$D$-variety and ![]() $W$ is a closed subset of
$W$ is a closed subset of ![]() $X_{0}$, where
$X_{0}$, where ![]() $X_{0}$ denotes the special fiber of the structure morphism
$X_{0}$ denotes the special fiber of the structure morphism ![]() $X\rightarrow D$ with the reduced structure. We call
$X\rightarrow D$ with the reduced structure. We call ![]() $W$ the center of
$W$ the center of ![]() $\mathfrak{X}$. We also say that
$\mathfrak{X}$. We also say that ![]() $\mathfrak{X}$ is a centered log structure on
$\mathfrak{X}$ is a centered log structure on ![]() $X$. For a centered log variety
$X$. For a centered log variety 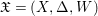 $\mathfrak{X}=(X,{\rm\Delta},W)$, we define a canonical divisor of
$\mathfrak{X}=(X,{\rm\Delta},W)$, we define a canonical divisor of ![]() $\mathfrak{X}$ as the one of
$\mathfrak{X}$ as the one of ![]() $(X,{\rm\Delta})$:
$(X,{\rm\Delta})$:
 $$\begin{eqnarray}K_{\mathfrak{X}}:=K_{(X,{\rm\Delta})}=K_{X}+{\rm\Delta}.\end{eqnarray}$$
$$\begin{eqnarray}K_{\mathfrak{X}}:=K_{(X,{\rm\Delta})}=K_{X}+{\rm\Delta}.\end{eqnarray}$$ Sometimes, we identify a normal ![]() $\mathbb{Q}$-Gorenstein (
$\mathbb{Q}$-Gorenstein (![]() $K_{X}$ is
$K_{X}$ is ![]() $\mathbb{Q}$-Cartier)
$\mathbb{Q}$-Cartier) ![]() $D$-variety
$D$-variety ![]() $X$ with the log
$X$ with the log ![]() $D$-variety
$D$-variety ![]() $(X,0)$, and identify a log
$(X,0)$, and identify a log ![]() $D$-variety
$D$-variety ![]() $(X,{\rm\Delta})$ with the centered log
$(X,{\rm\Delta})$ with the centered log ![]() $D$-variety
$D$-variety  $(X,{\rm\Delta},X_{0})$:
$(X,{\rm\Delta},X_{0})$:
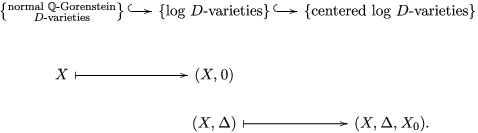 $$\begin{eqnarray}\begin{array}{@{}c@{}}\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}c@{}}\end{array}\end{eqnarray}$$2.2 Crepant morphisms
For centered log ![]() $D$-varieties
$D$-varieties  $\mathfrak{X}=(X,{\rm\Delta},W)$ and
$\mathfrak{X}=(X,{\rm\Delta},W)$ and 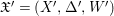 $\mathfrak{X}^{\prime }=(X^{\prime },{\rm\Delta}^{\prime },W^{\prime })$, a morphism
$\mathfrak{X}^{\prime }=(X^{\prime },{\rm\Delta}^{\prime },W^{\prime })$, a morphism 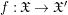 $f:\mathfrak{X}\rightarrow \mathfrak{X}^{\prime }$ is just a morphism
$f:\mathfrak{X}\rightarrow \mathfrak{X}^{\prime }$ is just a morphism 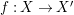 $f:X\rightarrow X^{\prime }$ of the underlying varieties with
$f:X\rightarrow X^{\prime }$ of the underlying varieties with 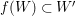 $f(W)\subset W^{\prime }$. We say that a morphism
$f(W)\subset W^{\prime }$. We say that a morphism ![]() $\mathfrak{X}\rightarrow \mathfrak{X}^{\prime }$ is proper or birational if it is so as the morphism
$\mathfrak{X}\rightarrow \mathfrak{X}^{\prime }$ is proper or birational if it is so as the morphism 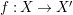 $f:X\rightarrow X^{\prime }$ of the underlying varieties. We say that a morphism
$f:X\rightarrow X^{\prime }$ of the underlying varieties. We say that a morphism  $f:\mathfrak{X}\rightarrow \mathfrak{X}^{\prime }$ is crepant if
$f:\mathfrak{X}\rightarrow \mathfrak{X}^{\prime }$ is crepant if
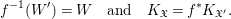 $$\begin{eqnarray}f^{-1}(W^{\prime })=W\quad \text{and}\quad K_{\mathfrak{ X}}=f^{\ast }K_{\mathfrak{ X}^{\prime }}.\end{eqnarray}$$
$$\begin{eqnarray}f^{-1}(W^{\prime })=W\quad \text{and}\quad K_{\mathfrak{ X}}=f^{\ast }K_{\mathfrak{ X}^{\prime }}.\end{eqnarray}$$ The right equality should be understood as that for ![]() $r\in \mathbb{Z}_{{>}0}$ such that
$r\in \mathbb{Z}_{{>}0}$ such that 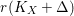 $r(K_{X}+{\rm\Delta})$ and
$r(K_{X}+{\rm\Delta})$ and  $r(K_{X^{\prime }}+{\rm\Delta}^{\prime })$ are Cartier, we have a natural isomorphism
$r(K_{X^{\prime }}+{\rm\Delta}^{\prime })$ are Cartier, we have a natural isomorphism
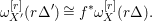 $$\begin{eqnarray}{\it\omega}_{X^{\prime }}^{[r]}(r{\rm\Delta}^{\prime })\cong f^{\ast }{\it\omega}_{X}^{[r]}(r{\rm\Delta}).\end{eqnarray}$$
$$\begin{eqnarray}{\it\omega}_{X^{\prime }}^{[r]}(r{\rm\Delta}^{\prime })\cong f^{\ast }{\it\omega}_{X}^{[r]}(r{\rm\Delta}).\end{eqnarray}$$ Here, 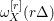 ${\it\omega}_{X}^{[r]}(r{\rm\Delta})$ is the invertible sheaf, which is identical to
${\it\omega}_{X}^{[r]}(r{\rm\Delta})$ is the invertible sheaf, which is identical to 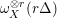 ${\it\omega}_{X}^{\otimes r}(r{\rm\Delta})$ on
${\it\omega}_{X}^{\otimes r}(r{\rm\Delta})$ on ![]() $X_{\text{reg}}$. We adopt this convention throughout the paper.
$X_{\text{reg}}$. We adopt this convention throughout the paper.
Given a generically étale morphism 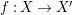 $f:X\rightarrow X^{\prime }$ of normal
$f:X\rightarrow X^{\prime }$ of normal ![]() $D$-varieties, a centered log structure
$D$-varieties, a centered log structure ![]() $\mathfrak{X}^{\prime }$ on
$\mathfrak{X}^{\prime }$ on ![]() $X^{\prime }$ induces a unique centered log structure
$X^{\prime }$ induces a unique centered log structure ![]() $\mathfrak{X}$ on
$\mathfrak{X}$ on ![]() $X$ such that the morphism
$X$ such that the morphism 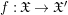 $f:\mathfrak{X}\rightarrow \mathfrak{X}^{\prime }$ is crepant. Conversely, if
$f:\mathfrak{X}\rightarrow \mathfrak{X}^{\prime }$ is crepant. Conversely, if 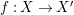 $f:X\rightarrow X^{\prime }$ is additionally proper, then for each centered log structure
$f:X\rightarrow X^{\prime }$ is additionally proper, then for each centered log structure ![]() $\mathfrak{X}$ on
$\mathfrak{X}$ on ![]() $X$, there exists at most one centered log structure on
$X$, there exists at most one centered log structure on ![]() $\mathfrak{X}^{\prime }$ such that
$\mathfrak{X}^{\prime }$ such that 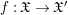 $f:\mathfrak{X}\rightarrow \mathfrak{X}^{\prime }$ is crepant.
$f:\mathfrak{X}\rightarrow \mathfrak{X}^{\prime }$ is crepant.
Remark 2.1. For our purposes, we may slightly weaken the assumptions in the definition of crepant morphisms. For instance, concerning the equality 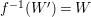 $f^{-1}(W^{\prime })=W$, we only need this equality outside
$f^{-1}(W^{\prime })=W$, we only need this equality outside 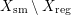 $X_{\text{sm}}\setminus X_{\text{reg}}$. This is because the locus
$X_{\text{sm}}\setminus X_{\text{reg}}$. This is because the locus 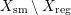 $X_{\text{sm}}\setminus X_{\text{reg}}$ does not contribute to stringy motifs at all, which are defined below. However, for simplicity, we will cling to our definition as above.
$X_{\text{sm}}\setminus X_{\text{reg}}$ does not contribute to stringy motifs at all, which are defined below. However, for simplicity, we will cling to our definition as above.
2.3 Motivic integration
Let 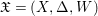 $\mathfrak{X}=(X,{\rm\Delta},W)$ be a centered log
$\mathfrak{X}=(X,{\rm\Delta},W)$ be a centered log ![]() $D$-variety. An arc of
$D$-variety. An arc of ![]() $\mathfrak{X}$ is a
$\mathfrak{X}$ is a ![]() $D$-morphism
$D$-morphism ![]() $D\rightarrow X$ sending the closed point of
$D\rightarrow X$ sending the closed point of ![]() $D$ into
$D$ into ![]() $W$. The arc space of
$W$. The arc space of ![]() $\mathfrak{X}$, denoted
$\mathfrak{X}$, denoted ![]() $J_{\infty }\mathfrak{X}$, is a
$J_{\infty }\mathfrak{X}$, is a ![]() $k$-scheme parameterizing the arcs of
$k$-scheme parameterizing the arcs of ![]() $\mathfrak{X}$. We put
$\mathfrak{X}$. We put 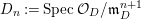 $D_{n}:=\text{Spec}\,{\mathcal{O}}_{D}/\mathfrak{m}_{D}^{n+1}$, with
$D_{n}:=\text{Spec}\,{\mathcal{O}}_{D}/\mathfrak{m}_{D}^{n+1}$, with ![]() $\mathfrak{m}_{D}$ the maximal ideal of
$\mathfrak{m}_{D}$ the maximal ideal of ![]() ${\mathcal{O}}_{D}$. An
${\mathcal{O}}_{D}$. An ![]() $n$-jet of
$n$-jet of ![]() $\mathfrak{X}$ is a
$\mathfrak{X}$ is a ![]() $D$-morphism
$D$-morphism  $D_{n}\rightarrow X$ sending the unique point of
$D_{n}\rightarrow X$ sending the unique point of ![]() $D_{n}$ into
$D_{n}$ into ![]() $W$. For each
$W$. For each ![]() $n$, there exists a
$n$, there exists a ![]() $k$-scheme
$k$-scheme ![]() $J_{n}\mathfrak{X}$ parametrizing
$J_{n}\mathfrak{X}$ parametrizing ![]() $n$-jets of
$n$-jets of ![]() $\mathfrak{X}$. For
$\mathfrak{X}$. For ![]() $n\geqslant m$, we have natural morphisms
$n\geqslant m$, we have natural morphisms  $J_{n}\mathfrak{X}\rightarrow J_{m}\mathfrak{X}$, and the arc space
$J_{n}\mathfrak{X}\rightarrow J_{m}\mathfrak{X}$, and the arc space ![]() $J_{\infty }\mathfrak{X}$ is identified with the projective limit of
$J_{\infty }\mathfrak{X}$ is identified with the projective limit of ![]() $J_{n}\mathfrak{X}$,
$J_{n}\mathfrak{X}$, ![]() $n\geqslant 0$ with respect to these maps. We have the induced maps
$n\geqslant 0$ with respect to these maps. We have the induced maps
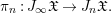 $$\begin{eqnarray}{\it\pi}_{n}:J_{\infty }\mathfrak{X}\rightarrow J_{n}\mathfrak{X}.\end{eqnarray}$$
$$\begin{eqnarray}{\it\pi}_{n}:J_{\infty }\mathfrak{X}\rightarrow J_{n}\mathfrak{X}.\end{eqnarray}$$ For ![]() $n<\infty$,
$n<\infty$, ![]() $J_{n}\mathfrak{X}$ are of finite type over
$J_{n}\mathfrak{X}$ are of finite type over ![]() $k$. For a morphism
$k$. For a morphism 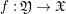 $f:\mathfrak{Y}\rightarrow \mathfrak{X}$ and each
$f:\mathfrak{Y}\rightarrow \mathfrak{X}$ and each 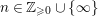 $n\in \mathbb{Z}_{{\geqslant}0}\cup \{\infty \}$, there exists a natural map
$n\in \mathbb{Z}_{{\geqslant}0}\cup \{\infty \}$, there exists a natural map
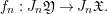 $$\begin{eqnarray}f_{n}:J_{n}\mathfrak{Y}\rightarrow J_{n}\mathfrak{X}.\end{eqnarray}$$
$$\begin{eqnarray}f_{n}:J_{n}\mathfrak{Y}\rightarrow J_{n}\mathfrak{X}.\end{eqnarray}$$ The arc space ![]() $J_{\infty }\mathfrak{X}$ has the so-called motivic measure, denoted by
$J_{\infty }\mathfrak{X}$ has the so-called motivic measure, denoted by ![]() ${\it\mu}_{J_{\infty }\mathfrak{X}}$. The measure takes values in some (semi-)ring, say
${\it\mu}_{J_{\infty }\mathfrak{X}}$. The measure takes values in some (semi-)ring, say ![]() ${\mathcal{R}}$, which is often a suitable modification of the Grothendieck (semi-)ring of
${\mathcal{R}}$, which is often a suitable modification of the Grothendieck (semi-)ring of ![]() $k$-varieties. In this paper, we fix
$k$-varieties. In this paper, we fix ![]() ${\mathcal{R}}$ satisfying the following properties. Denoting by
${\mathcal{R}}$ satisfying the following properties. Denoting by ![]() $[T]$ the class of a
$[T]$ the class of a ![]() $k$-variety
$k$-variety ![]() $T$ in
$T$ in ![]() ${\mathcal{R}}$,
${\mathcal{R}}$,
∙ for a bijective morphism
 $S\rightarrow T$, we have
$S\rightarrow T$, we have  $[S]=[T]$ in
$[S]=[T]$ in  ${\mathcal{R}}$;
${\mathcal{R}}$;∙ putting
 $\mathbb{L}:=[\mathbb{A}_{k}^{1}]$, we have all fractional powers
$\mathbb{L}:=[\mathbb{A}_{k}^{1}]$, we have all fractional powers  $\mathbb{L}^{a}$,
$\mathbb{L}^{a}$,  $a\in \mathbb{Q}$ in
$a\in \mathbb{Q}$ in  ${\mathcal{R}}$;
${\mathcal{R}}$;∙ an infinite series
 $\sum _{i=1}^{\infty }[T_{i}]\mathbb{L}^{a_{i}}$ with
$\sum _{i=1}^{\infty }[T_{i}]\mathbb{L}^{a_{i}}$ with  $\lim _{i\rightarrow \infty }\dim T_{i}+a_{i}=-\infty$ converges;
$\lim _{i\rightarrow \infty }\dim T_{i}+a_{i}=-\infty$ converges;∙ for a morphism
 $f:S\rightarrow T$, and for
$f:S\rightarrow T$, and for  $n\in \mathbb{Z}_{{\geqslant}0}$, if every fiber of
$n\in \mathbb{Z}_{{\geqslant}0}$, if every fiber of  $f$ admits a homeomorphism from or to the quotient
$f$ admits a homeomorphism from or to the quotient  $\mathbb{A}_{k}^{n}/G$ for some linear action of a finite group
$\mathbb{A}_{k}^{n}/G$ for some linear action of a finite group  $G$ on
$G$ on  $\mathbb{A}_{k}^{n}$, then
$\mathbb{A}_{k}^{n}$, then  $[S]=[T]\mathbb{L}^{n}$.
$[S]=[T]\mathbb{L}^{n}$.
One possible choice is the field of Puiseux series in ![]() $t^{-1}$,
$t^{-1}$,
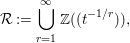 $$\begin{eqnarray}{\mathcal{R}}:=\mathop{\bigcup }_{r=1}^{\infty }\mathbb{Z}((t^{-1/r})),\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{R}}:=\mathop{\bigcup }_{r=1}^{\infty }\mathbb{Z}((t^{-1/r})),\end{eqnarray}$$ where we put ![]() $[T]$ to be the Poincaré polynomial as in [Reference NicaiseNic11].
$[T]$ to be the Poincaré polynomial as in [Reference NicaiseNic11].
A subset 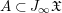 $A\subset J_{\infty }\mathfrak{X}$ is called stable if there exists
$A\subset J_{\infty }\mathfrak{X}$ is called stable if there exists 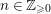 $n\in \mathbb{Z}_{{\geqslant}0}$ such that
$n\in \mathbb{Z}_{{\geqslant}0}$ such that  ${\it\pi}_{n}(A)\subset J_{n}\mathfrak{X}$ is a constructible subset and
${\it\pi}_{n}(A)\subset J_{n}\mathfrak{X}$ is a constructible subset and 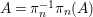 $A={\it\pi}_{n}^{-1}{\it\pi}_{n}(A)$, and for every
$A={\it\pi}_{n}^{-1}{\it\pi}_{n}(A)$, and for every ![]() $m\geqslant n$, every fiber of the map
$m\geqslant n$, every fiber of the map 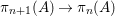 ${\it\pi}_{n+1}(A)\rightarrow {\it\pi}_{n}(A)$ is homeomorphic to
${\it\pi}_{n+1}(A)\rightarrow {\it\pi}_{n}(A)$ is homeomorphic to ![]() $\mathbb{A}_{k}^{n}$. The measure of a stable subset
$\mathbb{A}_{k}^{n}$. The measure of a stable subset ![]() $A$ is given by
$A$ is given by
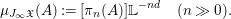 $$\begin{eqnarray}{\it\mu}_{J_{\infty }\mathfrak{X}}(A):=[{\it\pi}_{n}(A)]\mathbb{L}^{-nd}\quad (n\gg 0).\end{eqnarray}$$
$$\begin{eqnarray}{\it\mu}_{J_{\infty }\mathfrak{X}}(A):=[{\it\pi}_{n}(A)]\mathbb{L}^{-nd}\quad (n\gg 0).\end{eqnarray}$$More generally, we can define the measure for measurable subsets, which are roughly the limits of stable subsets.
Let 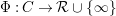 ${\rm\Phi}:C\rightarrow {\mathcal{R}}\cup \{\infty \}$ be a measurable function on a subset
${\rm\Phi}:C\rightarrow {\mathcal{R}}\cup \{\infty \}$ be a measurable function on a subset  $C\subset J_{\infty }\mathfrak{X}$. That is, the image of
$C\subset J_{\infty }\mathfrak{X}$. That is, the image of ![]() ${\rm\Phi}$ is countable, all fibers
${\rm\Phi}$ is countable, all fibers ![]() ${\rm\Phi}^{-1}(a)$ are measurable and
${\rm\Phi}^{-1}(a)$ are measurable and 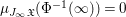 ${\it\mu}_{J_{\infty }\mathfrak{X}}({\rm\Phi}^{-1}(\infty ))=0$. We define
${\it\mu}_{J_{\infty }\mathfrak{X}}({\rm\Phi}^{-1}(\infty ))=0$. We define
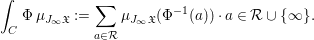 $$\begin{eqnarray}\int _{C}{\rm\Phi}\,{\it\mu}_{J_{\infty }\mathfrak{X}}:=\mathop{\sum }_{a\in {\mathcal{R}}}{\it\mu}_{J_{\infty }\mathfrak{X}}({\rm\Phi}^{-1}(a))\cdot a\in {\mathcal{R}}\cup \{\infty \}.\end{eqnarray}$$
$$\begin{eqnarray}\int _{C}{\rm\Phi}\,{\it\mu}_{J_{\infty }\mathfrak{X}}:=\mathop{\sum }_{a\in {\mathcal{R}}}{\it\mu}_{J_{\infty }\mathfrak{X}}({\rm\Phi}^{-1}(a))\cdot a\in {\mathcal{R}}\cup \{\infty \}.\end{eqnarray}$$2.4 Stringy invariants
We still suppose that 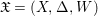 $\mathfrak{X}=(X,{\rm\Delta},W)$ is a centered log
$\mathfrak{X}=(X,{\rm\Delta},W)$ is a centered log ![]() $D$-variety.
$D$-variety.
Definition 2.2. To a coherent ideal sheaf ![]() $I\neq 0$ on
$I\neq 0$ on ![]() $X$ defining a closed subscheme
$X$ defining a closed subscheme ![]() $Z\subsetneq X$, we associate the order function,
$Z\subsetneq X$, we associate the order function,
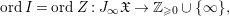 $$\begin{eqnarray}\text{ord}\,I=\text{ord}\,Z:J_{\infty }\mathfrak{X}\rightarrow \mathbb{Z}_{{\geqslant}0}\cup \{\infty \},\end{eqnarray}$$
$$\begin{eqnarray}\text{ord}\,I=\text{ord}\,Z:J_{\infty }\mathfrak{X}\rightarrow \mathbb{Z}_{{\geqslant}0}\cup \{\infty \},\end{eqnarray}$$ as follows. For an arc  ${\it\gamma}:D\rightarrow X$, the pullback
${\it\gamma}:D\rightarrow X$, the pullback ![]() ${\it\gamma}^{-1}I$ of
${\it\gamma}^{-1}I$ of ![]() $I$ is an ideal of
$I$ is an ideal of ![]() ${\mathcal{O}}_{D}$ and of the form
${\mathcal{O}}_{D}$ and of the form ![]() $\mathfrak{m}_{D}^{l}$ for some
$\mathfrak{m}_{D}^{l}$ for some 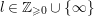 $l\in \mathbb{Z}_{{\geqslant}0}\cup \{\infty \}$, where we put
$l\in \mathbb{Z}_{{\geqslant}0}\cup \{\infty \}$, where we put 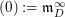 $(0):=\mathfrak{m}_{D}^{\infty }$ by convention. For a fractional ideal
$(0):=\mathfrak{m}_{D}^{\infty }$ by convention. For a fractional ideal ![]() $I$ (that is, a coherent
$I$ (that is, a coherent ![]() ${\mathcal{O}}_{X}$-submodule of
${\mathcal{O}}_{X}$-submodule of ![]() $K(X)$), if we write
$K(X)$), if we write 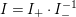 $I=I_{+}\cdot I_{-}^{-1}$ for ideal sheaves
$I=I_{+}\cdot I_{-}^{-1}$ for ideal sheaves ![]() $I_{+}$ and
$I_{+}$ and ![]() $I_{-}$ with
$I_{-}$ with ![]() $I_{-}$ locally principal, then we put
$I_{-}$ locally principal, then we put
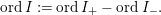 $$\begin{eqnarray}\text{ord}\,I:=\text{ord}\,I_{+}-\text{ord}\,I_{-}.\end{eqnarray}$$
$$\begin{eqnarray}\text{ord}\,I:=\text{ord}\,I_{+}-\text{ord}\,I_{-}.\end{eqnarray}$$ Here, we put 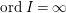 $\text{ord}\,I=\infty$ if either
$\text{ord}\,I=\infty$ if either  $\text{ord}\,I_{+}=\infty$ or
$\text{ord}\,I_{+}=\infty$ or 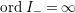 $\text{ord}\,I_{-}=\infty$. Similarly, for a
$\text{ord}\,I_{-}=\infty$. Similarly, for a ![]() $\mathbb{Q}$-linear combination
$\mathbb{Q}$-linear combination  $Z=\sum _{i=1}^{n}a_{i}Z_{i}$ of closed subschemes
$Z=\sum _{i=1}^{n}a_{i}Z_{i}$ of closed subschemes ![]() $Z_{i}\subsetneq X$, we define
$Z_{i}\subsetneq X$, we define
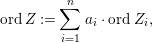 $$\begin{eqnarray}\text{ord}\,Z:=\mathop{\sum }_{i=1}^{n}a_{i}\cdot \text{ord}\,Z_{i},\end{eqnarray}$$
$$\begin{eqnarray}\text{ord}\,Z:=\mathop{\sum }_{i=1}^{n}a_{i}\cdot \text{ord}\,Z_{i},\end{eqnarray}$$ taking values in 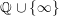 $\mathbb{Q}\cup \{\infty \}$.
$\mathbb{Q}\cup \{\infty \}$.
Remark 2.3. For a closed subscheme ![]() $Z\subsetneq X$, we expect that
$Z\subsetneq X$, we expect that 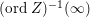 $(\text{ord}\,Z)^{-1}(\infty )$ has measure zero. The author does not know whether this has been proved, but this follows from the change of variables formula, if there exists a resolution of singularities
$(\text{ord}\,Z)^{-1}(\infty )$ has measure zero. The author does not know whether this has been proved, but this follows from the change of variables formula, if there exists a resolution of singularities 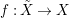 $f:\tilde{X}\rightarrow X$ so that
$f:\tilde{X}\rightarrow X$ so that ![]() $\tilde{X}$ is regular and
$\tilde{X}$ is regular and 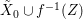 $\tilde{X}_{0}\cup f^{-1}(Z)$ is a simple normal crossing divisor. If the expectation is actually true, then order functions for fractional ideals and
$\tilde{X}_{0}\cup f^{-1}(Z)$ is a simple normal crossing divisor. If the expectation is actually true, then order functions for fractional ideals and ![]() $\mathbb{Q}$-linear combination of closed subschemes are well-defined modulo measure zero subsets.
$\mathbb{Q}$-linear combination of closed subschemes are well-defined modulo measure zero subsets.
Let ![]() $r\in \mathbb{Z}_{{>}0}$ be such that
$r\in \mathbb{Z}_{{>}0}$ be such that ![]() $rK_{\mathfrak{X}}$ is Cartier. Since the sheaf
$rK_{\mathfrak{X}}$ is Cartier. Since the sheaf 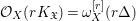 ${\mathcal{O}}_{X}(rK_{\mathfrak{X}})={\it\omega}_{X}^{[r]}(r{\rm\Delta})$ is invertible and thought of as a subsheaf of the constant sheaf
${\mathcal{O}}_{X}(rK_{\mathfrak{X}})={\it\omega}_{X}^{[r]}(r{\rm\Delta})$ is invertible and thought of as a subsheaf of the constant sheaf 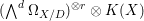 $(\wedge ^{d}{\rm\Omega}_{X/D})^{\otimes r}\otimes K(X)$, we can define a fractional ideal sheaf
$(\wedge ^{d}{\rm\Omega}_{X/D})^{\otimes r}\otimes K(X)$, we can define a fractional ideal sheaf ![]() $I_{\mathfrak{X}}^{r}$ by the equality of subsheaves of
$I_{\mathfrak{X}}^{r}$ by the equality of subsheaves of 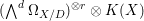 $(\wedge ^{d}{\rm\Omega}_{X/D})^{\otimes r}\otimes K(X)$,
$(\wedge ^{d}{\rm\Omega}_{X/D})^{\otimes r}\otimes K(X)$,
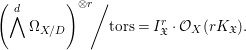 $$\begin{eqnarray}\left.\left(\mathop{d}^{\wedge }{\rm\Omega}_{X/D}\right)^{\otimes r}\!\right/\!\text{tors}=I_{\mathfrak{ X}}^{r}\cdot {\mathcal{O}}_{X}(rK_{\mathfrak{X}}).\end{eqnarray}$$
$$\begin{eqnarray}\left.\left(\mathop{d}^{\wedge }{\rm\Omega}_{X/D}\right)^{\otimes r}\!\right/\!\text{tors}=I_{\mathfrak{ X}}^{r}\cdot {\mathcal{O}}_{X}(rK_{\mathfrak{X}}).\end{eqnarray}$$ We then put a function ![]() $\mathbf{f}_{\mathfrak{X}}$ on
$\mathbf{f}_{\mathfrak{X}}$ on ![]() $J_{\infty }\mathfrak{X}$ by
$J_{\infty }\mathfrak{X}$ by
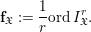 $$\begin{eqnarray}\mathbf{f}_{\mathfrak{X}}:=\frac{1}{r}\text{ord}\,I_{\mathfrak{X}}^{r}.\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{f}_{\mathfrak{X}}:=\frac{1}{r}\text{ord}\,I_{\mathfrak{X}}^{r}.\end{eqnarray}$$ Since 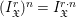 $(I_{\mathfrak{X}}^{r})^{n}=I_{\mathfrak{X}}^{r\cdot n}$, the function
$(I_{\mathfrak{X}}^{r})^{n}=I_{\mathfrak{X}}^{r\cdot n}$, the function ![]() $\mathbf{f}_{\mathfrak{X}}$ is independent of the choice of
$\mathbf{f}_{\mathfrak{X}}$ is independent of the choice of ![]() $r$.
$r$. ![]() $$If
$$If ![]() $X$ is smooth, then we simply have
$X$ is smooth, then we simply have 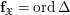 $\mathbf{f}_{\mathfrak{X}}=\text{ord}\,{\rm\Delta}$.
$\mathbf{f}_{\mathfrak{X}}=\text{ord}\,{\rm\Delta}$.
Definition 2.4. The stringy motif of ![]() $\mathfrak{X}$ is defined to be
$\mathfrak{X}$ is defined to be
 $$\begin{eqnarray}M_{\text{st}}(\mathfrak{X}):=\int _{J_{\infty }\mathfrak{X}}\mathbb{L}^{\mathbf{f}_{\mathfrak{X}}}\,d{\it\mu}_{J_{\infty }\mathfrak{X}}.\end{eqnarray}$$
$$\begin{eqnarray}M_{\text{st}}(\mathfrak{X}):=\int _{J_{\infty }\mathfrak{X}}\mathbb{L}^{\mathbf{f}_{\mathfrak{X}}}\,d{\it\mu}_{J_{\infty }\mathfrak{X}}.\end{eqnarray}$$ We also write 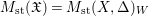 $M_{\text{st}}(\mathfrak{X})=M_{\text{st}}(X,{\rm\Delta})_{W}$, and sometimes omit
$M_{\text{st}}(\mathfrak{X})=M_{\text{st}}(X,{\rm\Delta})_{W}$, and sometimes omit ![]() ${\rm\Delta}$ if
${\rm\Delta}$ if ![]() ${\rm\Delta}=0$, and
${\rm\Delta}=0$, and ![]() $W$ if
$W$ if 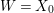 $W=X_{0}$. When the integral above converges, we call
$W=X_{0}$. When the integral above converges, we call ![]() $\mathfrak{X}$stringily log terminal. When it diverges, we put
$\mathfrak{X}$stringily log terminal. When it diverges, we put 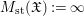 $M_{\text{st}}(\mathfrak{X}):=\infty$.
$M_{\text{st}}(\mathfrak{X}):=\infty$.
Conjecture 2.5. If a morphism 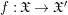 $f:\mathfrak{X}\rightarrow \mathfrak{X}^{\prime }$ of centered log
$f:\mathfrak{X}\rightarrow \mathfrak{X}^{\prime }$ of centered log ![]() $D$-varieties is proper, birational and crepant, then
$D$-varieties is proper, birational and crepant, then
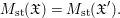 $$\begin{eqnarray}M_{\text{st}}(\mathfrak{X})=M_{\text{st}}(\mathfrak{X}^{\prime }).\end{eqnarray}$$
$$\begin{eqnarray}M_{\text{st}}(\mathfrak{X})=M_{\text{st}}(\mathfrak{X}^{\prime }).\end{eqnarray}$$Proposition 2.6. Conjecture 2.5 holds if there exists a proper birational morphism ![]() $Y\rightarrow X$ of
$Y\rightarrow X$ of ![]() $D$-varieties such that
$D$-varieties such that 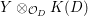 $Y\otimes _{{\mathcal{O}}_{D}}K(D)$ is smooth over
$Y\otimes _{{\mathcal{O}}_{D}}K(D)$ is smooth over ![]() $K(D)$. In particular, Conjecture 2.5 holds if
$K(D)$. In particular, Conjecture 2.5 holds if ![]() $K(D)$ has characteristic zero.
$K(D)$ has characteristic zero.
Proof. Let ![]() $X_{{\it\eta}}$ be the generic fiber of
$X_{{\it\eta}}$ be the generic fiber of ![]() $X\rightarrow D$. From the Hironaka theorem, there exists a coherent ideal sheaf
$X\rightarrow D$. From the Hironaka theorem, there exists a coherent ideal sheaf 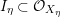 $I_{{\it\eta}}\subset {\mathcal{O}}_{X_{{\it\eta}}}$ such that the blowup of
$I_{{\it\eta}}\subset {\mathcal{O}}_{X_{{\it\eta}}}$ such that the blowup of ![]() $X_{{\it\eta}}$ along
$X_{{\it\eta}}$ along ![]() $I_{{\it\eta}}$ is smooth over
$I_{{\it\eta}}$ is smooth over ![]() $K(D)$. Let
$K(D)$. Let ![]() $I\subset {\mathcal{O}}_{X}$ be a coherent ideal sheaf such that
$I\subset {\mathcal{O}}_{X}$ be a coherent ideal sheaf such that 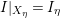 $I|_{X_{{\it\eta}}}=I_{{\it\eta}}$. The blowup of
$I|_{X_{{\it\eta}}}=I_{{\it\eta}}$. The blowup of ![]() $X$ along
$X$ along ![]() $I$ has a smooth generic fiber. Hence, the second assertion of the lemma follows from the first one.
$I$ has a smooth generic fiber. Hence, the second assertion of the lemma follows from the first one.
To prove the first one, we can apply the version of the change of variables formula proved by Sebag [Reference SebagSeb04, Theorem 8.0.5] (see also [Reference Nicaise and SebagNS11]). If ![]() $\mathfrak{Y}$ is the centered log structure on
$\mathfrak{Y}$ is the centered log structure on ![]() $Y$ such that the induced morphism
$Y$ such that the induced morphism  $f:\mathfrak{Y}\rightarrow \mathfrak{X}$ is crepant, then the change of variables formula shows that
$f:\mathfrak{Y}\rightarrow \mathfrak{X}$ is crepant, then the change of variables formula shows that
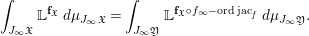 $$\begin{eqnarray}\int _{J_{\infty }\mathfrak{X}}\mathbb{L}^{\mathbf{f}_{\mathfrak{X}}}\,d{\it\mu}_{J_{\infty }\mathfrak{X}}=\int _{J_{\infty }\mathfrak{Y}}\mathbb{L}^{\mathbf{f}_{\mathfrak{X}}\circ f_{\infty }-\text{ord}\,\text{jac}_{f}}\,d{\it\mu}_{J_{\infty }\mathfrak{Y}}.\end{eqnarray}$$
$$\begin{eqnarray}\int _{J_{\infty }\mathfrak{X}}\mathbb{L}^{\mathbf{f}_{\mathfrak{X}}}\,d{\it\mu}_{J_{\infty }\mathfrak{X}}=\int _{J_{\infty }\mathfrak{Y}}\mathbb{L}^{\mathbf{f}_{\mathfrak{X}}\circ f_{\infty }-\text{ord}\,\text{jac}_{f}}\,d{\it\mu}_{J_{\infty }\mathfrak{Y}}.\end{eqnarray}$$ Here, 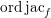 $\text{ord}\,\text{jac}_{f}$ is the function of Jacobian orders as defined in [Reference SebagSeb04, page 29]. For
$\text{ord}\,\text{jac}_{f}$ is the function of Jacobian orders as defined in [Reference SebagSeb04, page 29]. For  $r\in \mathbb{Z}_{{>}0}$ such that
$r\in \mathbb{Z}_{{>}0}$ such that ![]() $rK_{\mathfrak{X}}$ and
$rK_{\mathfrak{X}}$ and ![]() $rK_{\mathfrak{Y}}$ are Cartier, we have
$rK_{\mathfrak{Y}}$ are Cartier, we have
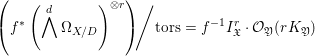 $$\begin{eqnarray}\displaystyle \left.\left(f^{\ast }\left(\mathop{d}^{\wedge }{\rm\Omega}_{X/D}\right)^{\otimes r}\right)\!\right/\!\text{tors} & = & \displaystyle f^{-1}I_{\mathfrak{X}}^{r}\cdot {\mathcal{O}}_{\mathfrak{Y}}(rK_{\mathfrak{Y}})\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\left(f^{\ast }\left(\mathop{d}^{\wedge }{\rm\Omega}_{X/D}\right)^{\otimes r}\right)\!\right/\!\text{tors} & = & \displaystyle f^{-1}I_{\mathfrak{X}}^{r}\cdot {\mathcal{O}}_{\mathfrak{Y}}(rK_{\mathfrak{Y}})\nonumber\end{eqnarray}$$and
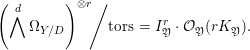 $$\begin{eqnarray}\displaystyle \left.\left(\mathop{d}^{\wedge }{\rm\Omega}_{Y/D}\right)^{\otimes r}\!\right/\!\text{tors} & = & \displaystyle I_{\mathfrak{Y}}^{r}\cdot {\mathcal{O}}_{\mathfrak{Y}}(rK_{\mathfrak{Y}}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\left(\mathop{d}^{\wedge }{\rm\Omega}_{Y/D}\right)^{\otimes r}\!\right/\!\text{tors} & = & \displaystyle I_{\mathfrak{Y}}^{r}\cdot {\mathcal{O}}_{\mathfrak{Y}}(rK_{\mathfrak{Y}}).\nonumber\end{eqnarray}$$This shows that
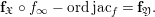 $$\begin{eqnarray}\mathbf{f}_{\mathfrak{X}}\circ f_{\infty }-\text{ord}\,\text{jac}_{f}=\mathbf{f}_{\mathfrak{Y}}.\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{f}_{\mathfrak{X}}\circ f_{\infty }-\text{ord}\,\text{jac}_{f}=\mathbf{f}_{\mathfrak{Y}}.\end{eqnarray}$$ We obtain 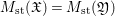 $M_{\text{st}}(\mathfrak{X})=M_{\text{st}}(\mathfrak{Y})$, and similarly
$M_{\text{st}}(\mathfrak{X})=M_{\text{st}}(\mathfrak{Y})$, and similarly  $M_{\text{st}}(\mathfrak{X}^{\prime })=M_{\text{st}}(\mathfrak{Y})$. We have proved the proposition.◻
$M_{\text{st}}(\mathfrak{X}^{\prime })=M_{\text{st}}(\mathfrak{Y})$. We have proved the proposition.◻
Proposition 2.7. Let 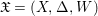 $\mathfrak{X}=(X,{\rm\Delta},W)$ be a centered log
$\mathfrak{X}=(X,{\rm\Delta},W)$ be a centered log ![]() $D$-variety and write
$D$-variety and write
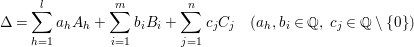 $$\begin{eqnarray}{\rm\Delta}=\mathop{\sum }_{h=1}^{l}a_{h}A_{h}+\mathop{\sum }_{i=1}^{m}b_{i}B_{i}+\mathop{\sum }_{j=1}^{n}c_{j}C_{j}\quad (a_{h},b_{i}\in \mathbb{Q},\,c_{j}\in \mathbb{Q}\setminus \{0\})\end{eqnarray}$$
$$\begin{eqnarray}{\rm\Delta}=\mathop{\sum }_{h=1}^{l}a_{h}A_{h}+\mathop{\sum }_{i=1}^{m}b_{i}B_{i}+\mathop{\sum }_{j=1}^{n}c_{j}C_{j}\quad (a_{h},b_{i}\in \mathbb{Q},\,c_{j}\in \mathbb{Q}\setminus \{0\})\end{eqnarray}$$ such that ![]() $A_{h}$ are the irreducible components of the closure of
$A_{h}$ are the irreducible components of the closure of 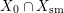 $X_{0}\cap X_{\text{sm}}$,
$X_{0}\cap X_{\text{sm}}$, ![]() $B_{i}$ are the irreducible components of
$B_{i}$ are the irreducible components of 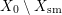 $X_{0}\setminus X_{\text{sm}}$ and
$X_{0}\setminus X_{\text{sm}}$ and ![]() $C_{j}$ are prime divisors not contained in
$C_{j}$ are prime divisors not contained in ![]() $X_{0}$. Let
$X_{0}$. Let
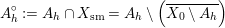 $$\begin{eqnarray}\displaystyle A_{h}^{\circ }:=A_{h}\cap X_{\text{sm}}=A_{h}\setminus \left(\overline{X_{0}\setminus A_{h}}\right) & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle A_{h}^{\circ }:=A_{h}\cap X_{\text{sm}}=A_{h}\setminus \left(\overline{X_{0}\setminus A_{h}}\right) & & \displaystyle \nonumber\end{eqnarray}$$and
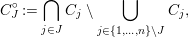 $$\begin{eqnarray}\displaystyle C_{J}^{\circ }:=\mathop{\bigcap }_{j\in J}C_{j}\setminus \mathop{\bigcup }_{j\in \{1,\ldots ,n\}\setminus J}C_{j}, & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle C_{J}^{\circ }:=\mathop{\bigcap }_{j\in J}C_{j}\setminus \mathop{\bigcup }_{j\in \{1,\ldots ,n\}\setminus J}C_{j}, & & \displaystyle \nonumber\end{eqnarray}$$ with 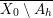 $\overline{X_{0}\setminus A_{h}}$ the closure of
$\overline{X_{0}\setminus A_{h}}$ the closure of 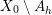 $X_{0}\setminus A_{h}$. We suppose that
$X_{0}\setminus A_{h}$. We suppose that ![]() $X$ is regular and that
$X$ is regular and that 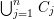 $\bigcup _{j=1}^{n}C_{j}$ is simple normal crossing, that is, for any
$\bigcup _{j=1}^{n}C_{j}$ is simple normal crossing, that is, for any 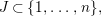 $J\subset \{1,\ldots ,n\},$ the scheme-theoretic intersection
$J\subset \{1,\ldots ,n\},$ the scheme-theoretic intersection 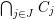 $\bigcap _{j\in J}C_{j}$ is smooth over
$\bigcap _{j\in J}C_{j}$ is smooth over ![]() $D$. Then
$D$. Then ![]() $\mathfrak{X}$ is stringily log terminal if and only if
$\mathfrak{X}$ is stringily log terminal if and only if ![]() $c_{j}<1$ for every
$c_{j}<1$ for every ![]() $j$, with
$j$, with 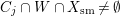 $C_{j}\cap W\cap X_{\text{sm}}\neq \emptyset$. Moreover, if this is the case,
$C_{j}\cap W\cap X_{\text{sm}}\neq \emptyset$. Moreover, if this is the case,
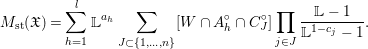 $$\begin{eqnarray}M_{\text{st}}(\mathfrak{X})=\mathop{\sum }_{h=1}^{l}\mathbb{L}^{a_{h}}\mathop{\sum }_{J\subset \{1,\ldots ,n\}}[W\cap A_{h}^{\circ }\cap C_{J}^{\circ }]\mathop{\prod }_{j\in J}\frac{\mathbb{L}-1}{\mathbb{L}^{1-c_{j}}-1}.\end{eqnarray}$$
$$\begin{eqnarray}M_{\text{st}}(\mathfrak{X})=\mathop{\sum }_{h=1}^{l}\mathbb{L}^{a_{h}}\mathop{\sum }_{J\subset \{1,\ldots ,n\}}[W\cap A_{h}^{\circ }\cap C_{J}^{\circ }]\mathop{\prod }_{j\in J}\frac{\mathbb{L}-1}{\mathbb{L}^{1-c_{j}}-1}.\end{eqnarray}$$Proof. We first note that the locus 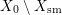 $X_{0}\setminus X_{\text{sm}}$ does not have any arc, and hence does not contribute to
$X_{0}\setminus X_{\text{sm}}$ does not have any arc, and hence does not contribute to ![]() $M_{\text{st}}(\mathfrak{X})$. Since
$M_{\text{st}}(\mathfrak{X})$. Since
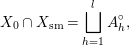 $$\begin{eqnarray}X_{0}\cap X_{\text{sm}}=\mathop{\sqcup }_{h=1}^{l}A_{h}^{\circ },\end{eqnarray}$$
$$\begin{eqnarray}X_{0}\cap X_{\text{sm}}=\mathop{\sqcup }_{h=1}^{l}A_{h}^{\circ },\end{eqnarray}$$ we can decompose ![]() $M_{\text{st}}(\mathfrak{X})$ into the sum of components corresponding to
$M_{\text{st}}(\mathfrak{X})$ into the sum of components corresponding to ![]() $A_{h}^{\circ }$,
$A_{h}^{\circ }$,  $h=1,\ldots ,l$. The divisor
$h=1,\ldots ,l$. The divisor ![]() $a_{h}A_{h}$ contributes to the component corresponding to
$a_{h}A_{h}$ contributes to the component corresponding to ![]() $A_{h}^{\circ }$ by the multiplication with
$A_{h}^{\circ }$ by the multiplication with ![]() $\mathbb{L}^{a_{h}}$. From all of these arguments, the proposition has been reduced to the formula
$\mathbb{L}^{a_{h}}$. From all of these arguments, the proposition has been reduced to the formula
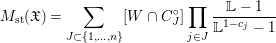 $$\begin{eqnarray}M_{\text{st}}(\mathfrak{X})=\mathop{\sum }_{J\subset \{1,\ldots ,n\}}[W\cap C_{J}^{\circ }]\mathop{\prod }_{j\in J}\frac{\mathbb{L}-1}{\mathbb{L}^{1-c_{j}}-1}\end{eqnarray}$$
$$\begin{eqnarray}M_{\text{st}}(\mathfrak{X})=\mathop{\sum }_{J\subset \{1,\ldots ,n\}}[W\cap C_{J}^{\circ }]\mathop{\prod }_{j\in J}\frac{\mathbb{L}-1}{\mathbb{L}^{1-c_{j}}-1}\end{eqnarray}$$ in the case where ![]() $X$ is smooth and
$X$ is smooth and 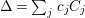 ${\rm\Delta}=\sum _{j}c_{j}C_{j}$. This is the standard explicit formula (see for instance [Reference BatyrevBat98]).◻
${\rm\Delta}=\sum _{j}c_{j}C_{j}$. This is the standard explicit formula (see for instance [Reference BatyrevBat98]).◻
2.5 Group actions
Definition 2.8. A centered log ![]() $G$-
$G$-![]() $D$-variety is a centered log
$D$-variety is a centered log ![]() $D$-variety
$D$-variety 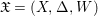 $\mathfrak{X}=(X,{\rm\Delta},W)$ endowed with a faithful
$\mathfrak{X}=(X,{\rm\Delta},W)$ endowed with a faithful ![]() $G$-action on
$G$-action on ![]() $X$ such that
$X$ such that ![]() ${\rm\Delta}$ and
${\rm\Delta}$ and ![]() $W$ are stable under the
$W$ are stable under the ![]() $G$-action. Given a variety
$G$-action. Given a variety ![]() $X$ with a faithful
$X$ with a faithful ![]() $G$-action, we say that a centered log structure
$G$-action, we say that a centered log structure ![]() $\mathfrak{X}$ on
$\mathfrak{X}$ on ![]() $X$ is
$X$ is ![]() $G$-equivariant if it is a centered log
$G$-equivariant if it is a centered log ![]() $G$-
$G$-![]() $D$-variety.
$D$-variety.
For a centered log ![]() $G$-
$G$-![]() $D$-variety
$D$-variety ![]() $\mathfrak{X}$, the arc space
$\mathfrak{X}$, the arc space ![]() $J_{\infty }\mathfrak{X}$ has a natural
$J_{\infty }\mathfrak{X}$ has a natural ![]() $G$-action. We define a motivic measure on
$G$-action. We define a motivic measure on 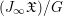 $(J_{\infty }\mathfrak{X})/G$, denoted by
$(J_{\infty }\mathfrak{X})/G$, denoted by 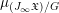 ${\it\mu}_{(J_{\infty }\mathfrak{X})/G}$, in the same way as defining the motivic measure on
${\it\mu}_{(J_{\infty }\mathfrak{X})/G}$, in the same way as defining the motivic measure on ![]() $J_{\infty }\mathfrak{X}$, except that in the definition of stable subsets, say
$J_{\infty }\mathfrak{X}$, except that in the definition of stable subsets, say ![]() $A$, fibers of
$A$, fibers of 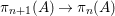 ${\it\pi}_{n+1}(A)\rightarrow {\it\pi}_{n}(A)$ are only assumed to be homeomorphic to the quotient
${\it\pi}_{n+1}(A)\rightarrow {\it\pi}_{n}(A)$ are only assumed to be homeomorphic to the quotient ![]() $\mathbb{A}_{k}^{d}/H$ for some linear action of a finite group
$\mathbb{A}_{k}^{d}/H$ for some linear action of a finite group ![]() $H$ on
$H$ on ![]() $\mathbb{A}_{k}^{d}$.
$\mathbb{A}_{k}^{d}$.
The function ![]() $\mathbf{f}_{\mathfrak{X}}$ on
$\mathbf{f}_{\mathfrak{X}}$ on ![]() $J_{\infty }\mathfrak{X}$ is
$J_{\infty }\mathfrak{X}$ is ![]() $G$-invariant and gives a function on
$G$-invariant and gives a function on 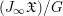 $(J_{\infty }\mathfrak{X})/G$, which we again denote by
$(J_{\infty }\mathfrak{X})/G$, which we again denote by ![]() $\mathbf{f}_{\mathfrak{X}}$. We define
$\mathbf{f}_{\mathfrak{X}}$. We define
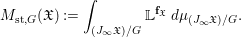 $$\begin{eqnarray}M_{\text{st},G}(\mathfrak{X}):=\int _{(J_{\infty }\mathfrak{X})/G}\mathbb{L}^{\mathbf{f}_{\mathfrak{X}}}\,d{\it\mu}_{(J_{\infty }\mathfrak{X})/G}.\end{eqnarray}$$
$$\begin{eqnarray}M_{\text{st},G}(\mathfrak{X}):=\int _{(J_{\infty }\mathfrak{X})/G}\mathbb{L}^{\mathbf{f}_{\mathfrak{X}}}\,d{\it\mu}_{(J_{\infty }\mathfrak{X})/G}.\end{eqnarray}$$ The reader should not confuse 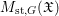 $M_{\text{st},G}(\mathfrak{X})$ with the orbifold stringy motif
$M_{\text{st},G}(\mathfrak{X})$ with the orbifold stringy motif ![]() $M_{\text{st}}^{G}(\mathfrak{X})$, defined later.
$M_{\text{st}}^{G}(\mathfrak{X})$, defined later.
Let us define a ![]() $G$-prime divisor as a divisor of the form
$G$-prime divisor as a divisor of the form 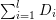 $\sum _{i=1}^{l}D_{i}$, where
$\sum _{i=1}^{l}D_{i}$, where ![]() $D_{i}$ are prime divisors permuted transitively by the
$D_{i}$ are prime divisors permuted transitively by the ![]() $G$-actions.
$G$-actions.
Proposition 2.9. Let 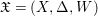 $\mathfrak{X}=(X,{\rm\Delta},W)$ be a centered log
$\mathfrak{X}=(X,{\rm\Delta},W)$ be a centered log ![]() $G$-
$G$-![]() $D$-variety and write
$D$-variety and write
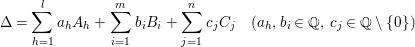 $$\begin{eqnarray}{\rm\Delta}=\mathop{\sum }_{h=1}^{l}a_{h}A_{h}+\mathop{\sum }_{i=1}^{m}b_{i}B_{i}+\mathop{\sum }_{j=1}^{n}c_{j}C_{j}\quad (a_{h},b_{i}\in \mathbb{Q},\,c_{j}\in \mathbb{Q}\setminus \{0\})\end{eqnarray}$$
$$\begin{eqnarray}{\rm\Delta}=\mathop{\sum }_{h=1}^{l}a_{h}A_{h}+\mathop{\sum }_{i=1}^{m}b_{i}B_{i}+\mathop{\sum }_{j=1}^{n}c_{j}C_{j}\quad (a_{h},b_{i}\in \mathbb{Q},\,c_{j}\in \mathbb{Q}\setminus \{0\})\end{eqnarray}$$ such that ![]() $A_{h}$ are the distinct
$A_{h}$ are the distinct ![]() $G$-prime divisors such that
$G$-prime divisors such that ![]() $\bigcup A_{h}$ is equal to the closure of
$\bigcup A_{h}$ is equal to the closure of 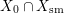 $X_{0}\cap X_{\text{sm}}$,
$X_{0}\cap X_{\text{sm}}$, ![]() $B_{i}$ are the distinct
$B_{i}$ are the distinct ![]() $G$-prime divisors with
$G$-prime divisors with 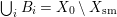 $\bigcup _{i}B_{i}=X_{0}\setminus X_{\text{sm}}$ and
$\bigcup _{i}B_{i}=X_{0}\setminus X_{\text{sm}}$ and ![]() $C_{j}$ are
$C_{j}$ are ![]() $G$-prime divisors not contained in
$G$-prime divisors not contained in ![]() $X_{0}$. We suppose that
$X_{0}$. We suppose that
∙
 $X$ is regular,
$X$ is regular,∙ for any
 $J\subset \{1,\ldots ,n\},$ the scheme-theoretic intersection
$J\subset \{1,\ldots ,n\},$ the scheme-theoretic intersection  $\bigcap _{j\in J}C_{j}$ is smooth over
$\bigcap _{j\in J}C_{j}$ is smooth over  $D$, and
$D$, and∙ for every
 $j$ with
$j$ with  $C_{j}\cap W\cap X_{\text{sm}}\neq \emptyset$,
$C_{j}\cap W\cap X_{\text{sm}}\neq \emptyset$,  $c_{j}<1$.
$c_{j}<1$.
With the same notation as in Proposition 2.7, we have
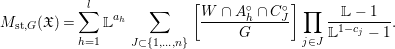 $$\begin{eqnarray}M_{\text{st},G}(\mathfrak{X})=\mathop{\sum }_{h=1}^{l}\mathbb{L}^{a_{h}}\mathop{\sum }_{J\subset \{1,\ldots ,n\}}\left[\frac{W\cap A_{h}^{\circ }\cap C_{J}^{\circ }}{G}\right]\mathop{\prod }_{j\in J}\frac{\mathbb{L}-1}{\mathbb{L}^{1-c_{j}}-1}.\end{eqnarray}$$
$$\begin{eqnarray}M_{\text{st},G}(\mathfrak{X})=\mathop{\sum }_{h=1}^{l}\mathbb{L}^{a_{h}}\mathop{\sum }_{J\subset \{1,\ldots ,n\}}\left[\frac{W\cap A_{h}^{\circ }\cap C_{J}^{\circ }}{G}\right]\mathop{\prod }_{j\in J}\frac{\mathbb{L}-1}{\mathbb{L}^{1-c_{j}}-1}.\end{eqnarray}$$3  $G$-arcs
$G$-arcs
In the last subsection, we considered motivic integration over varieties endowed with finite group actions. However, we considered only ordinary (untwisted) arcs, which are not general enough to apply to the McKay correspondence. Suitably generalized arcs were introduced by Denef and Loeser [Reference Denef and LoeserDL02] in characteristic zero. The author [Reference YasudaYasa] further generalized them to arbitrary characteristics. We may use generalized arcs of orbifolds or Deligne–Mumford stacks as in [Reference Lupercio and PoddarLP04, Reference YasudaYas04, Reference YasudaYas06, Reference YasudaYasa], so that we can treat general orbifolds, having group actions only locally. We do not pursue generalization in this direction, however.
From now on, we fix a finite group ![]() $G$.
$G$.
Definition 3.1. By a ![]() $G$-cover of
$G$-cover of ![]() $D$, we mean a
$D$, we mean a ![]() $D$-scheme
$D$-scheme ![]() $E$ endowed with a left
$E$ endowed with a left ![]() $G$-action such that
$G$-action such that 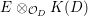 $E\otimes _{{\mathcal{O}}_{D}}K(D)$ is an étale
$E\otimes _{{\mathcal{O}}_{D}}K(D)$ is an étale ![]() $G$-torsor over
$G$-torsor over 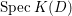 $\text{Spec}\,K(D)$ and
$\text{Spec}\,K(D)$ and ![]() $E$ is the normalization of
$E$ is the normalization of ![]() $D$ in
$D$ in 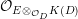 ${\mathcal{O}}_{E\otimes _{{\mathcal{O}}_{D}}K(D)}$. We denote by
${\mathcal{O}}_{E\otimes _{{\mathcal{O}}_{D}}K(D)}$. We denote by 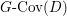 $G\text{-}\text{Cov}(D)$ the set of
$G\text{-}\text{Cov}(D)$ the set of ![]() $G$-covers of
$G$-covers of ![]() $D$ up to isomorphism.
$D$ up to isomorphism.
Remark 3.2. In the tame case, there is a one-to-one correspondence between the points of 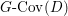 $G\text{-}\text{Cov}(D)$ and the conjugacy classes in
$G\text{-}\text{Cov}(D)$ and the conjugacy classes in ![]() $G$. In the wild case, however,
$G$. In the wild case, however, 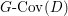 $G\text{-}\text{Cov}(D)$ is expected to be an infinite-dimensional space having a countable stratification with finite-dimensional strata.
$G\text{-}\text{Cov}(D)$ is expected to be an infinite-dimensional space having a countable stratification with finite-dimensional strata.
We now fix the following notation: ![]() $E$ is a
$E$ is a ![]() $G$-cover of
$G$-cover of ![]() $D$,
$D$, ![]() $F$ is a connected component of
$F$ is a connected component of ![]() $E$ with a stabilizer
$E$ with a stabilizer ![]() $H$ so that
$H$ so that ![]() $F$ is an
$F$ is an ![]() $H$-cover of
$H$-cover of ![]() $D$.
$D$.

Lemma 3.3. Let ![]() $\text{Aut}(E)$ be the automorphism group of
$\text{Aut}(E)$ be the automorphism group of ![]() $E$ as a
$E$ as a ![]() $G$-cover of
$G$-cover of ![]() $D$. That is, it consists of
$D$. That is, it consists of ![]() $G$-equivariant
$G$-equivariant ![]() $D$-automorphisms of
$D$-automorphisms of ![]() $E$. We have a natural isomorphism
$E$. We have a natural isomorphism
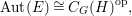 $$\begin{eqnarray}\text{Aut}(E)\cong C_{G}(H)^{\text{op}},\end{eqnarray}$$
$$\begin{eqnarray}\text{Aut}(E)\cong C_{G}(H)^{\text{op}},\end{eqnarray}$$ where the right-hand side is the opposite group of the centralizer of ![]() $H$ in
$H$ in ![]() $G$.
$G$.
Proof. If ![]() $E$ is the trivial
$E$ is the trivial ![]() $G$-cover
$G$-cover ![]() $D\times G$ of
$D\times G$ of ![]() $D$, then its automorphisms are nothing but the right
$D$, then its automorphisms are nothing but the right ![]() $G$-action on
$G$-action on ![]() $G$. Therefore,
$G$. Therefore, 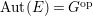 $\text{Aut}(E)=G^{\text{op}}$.
$\text{Aut}(E)=G^{\text{op}}$.
For the general case, let ![]() $E_{F}$ be the normalization of the fiber product
$E_{F}$ be the normalization of the fiber product 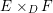 $E\times _{D}F$. This is a trivial
$E\times _{D}F$. This is a trivial ![]() $G$-cover of
$G$-cover of ![]() $F$, and we have a natural injection
$F$, and we have a natural injection
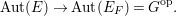 $$\begin{eqnarray}\text{Aut}(E)\rightarrow \text{Aut}(E_{F})=G^{\text{op}}.\end{eqnarray}$$
$$\begin{eqnarray}\text{Aut}(E)\rightarrow \text{Aut}(E_{F})=G^{\text{op}}.\end{eqnarray}$$ Its image is the automorphisms of ![]() $E_{F}$ compatible with the action of
$E_{F}$ compatible with the action of 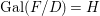 $\text{Gal}(F/D)=H$. This shows the lemma.◻
$\text{Gal}(F/D)=H$. This shows the lemma.◻
Let ![]() $V$ be a
$V$ be a ![]() $D$-variety endowed with a faithful left
$D$-variety endowed with a faithful left ![]() $G$-action.
$G$-action.
Definition 3.4. We define an ![]() $E$-twisted
$E$-twisted ![]() $G$-arc of
$G$-arc of ![]() $V$ as a
$V$ as a ![]() $G$-equivariant
$G$-equivariant ![]() $D$-morphism
$D$-morphism ![]() $E\rightarrow V$, and a
$E\rightarrow V$, and a ![]() $G$-arc of
$G$-arc of ![]() $V$ as an
$V$ as an ![]() $E$-twisted
$E$-twisted ![]() $G$-arc for some
$G$-arc for some ![]() $E$. Two
$E$. Two ![]() $G$-arcs
$G$-arcs ![]() $E\rightarrow V$ and
$E\rightarrow V$ and  $E^{\prime }\rightarrow V$ are said to be isomorphic if there exists a
$E^{\prime }\rightarrow V$ are said to be isomorphic if there exists a ![]() $G$-equivariant
$G$-equivariant ![]() $D$-isomorphism
$D$-isomorphism 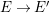 $E\rightarrow E^{\prime }$ compatible with the morphisms to
$E\rightarrow E^{\prime }$ compatible with the morphisms to ![]() $V$. We denote by
$V$. We denote by ![]() $J_{\infty }^{G,E}V$ the set of isomorphism classes of
$J_{\infty }^{G,E}V$ the set of isomorphism classes of ![]() $E$-twisted
$E$-twisted ![]() $G$-arcs of
$G$-arcs of ![]() $V$ and by
$V$ and by ![]() $J_{\infty }^{G}V$ the set of isomorphism classes of
$J_{\infty }^{G}V$ the set of isomorphism classes of ![]() $G$-arcs of
$G$-arcs of ![]() $V$.
$V$.
Obviously,
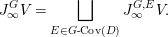 $$\begin{eqnarray}J_{\infty }^{G}V=\mathop{\sqcup }_{E\in G\text{-}\text{Cov}(D)}J_{\infty }^{G,E}V.\end{eqnarray}$$
$$\begin{eqnarray}J_{\infty }^{G}V=\mathop{\sqcup }_{E\in G\text{-}\text{Cov}(D)}J_{\infty }^{G,E}V.\end{eqnarray}$$ Let 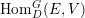 $\text{Hom}_{D}^{G}(E,V)$ be the space of
$\text{Hom}_{D}^{G}(E,V)$ be the space of ![]() $G$-equivariant
$G$-equivariant ![]() $D$-morphisms
$D$-morphisms ![]() $E\rightarrow V$. We define a left action of
$E\rightarrow V$. We define a left action of 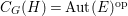 $C_{G}(H)=\text{Aut}(E)^{\text{op}}$ on
$C_{G}(H)=\text{Aut}(E)^{\text{op}}$ on 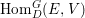 $\text{Hom}_{D}^{G}(E,V)$ as follows. For
$\text{Hom}_{D}^{G}(E,V)$ as follows. For 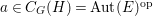 $a\in C_{G}(H)=\text{Aut}(E)^{\text{op}}$ and
$a\in C_{G}(H)=\text{Aut}(E)^{\text{op}}$ and 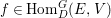 $f\in \text{Hom}_{D}^{G}(E,V)$,
$f\in \text{Hom}_{D}^{G}(E,V)$,
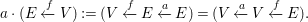 $$\begin{eqnarray}\displaystyle a\cdot (E\xleftarrow[]{f}V):=(V\xleftarrow[]{f}E\xleftarrow[]{a}E)=(V\xleftarrow[]{a}V\xleftarrow[]{f}E). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle a\cdot (E\xleftarrow[]{f}V):=(V\xleftarrow[]{f}E\xleftarrow[]{a}E)=(V\xleftarrow[]{a}V\xleftarrow[]{f}E). & & \displaystyle\end{eqnarray}$$By definition, we have
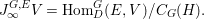 $$\begin{eqnarray}J_{\infty }^{G,E}V=\text{Hom}_{D}^{G}(E,V)/C_{G}(H).\end{eqnarray}$$
$$\begin{eqnarray}J_{\infty }^{G,E}V=\text{Hom}_{D}^{G}(E,V)/C_{G}(H).\end{eqnarray}$$ For 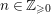 $n\in \mathbb{Z}_{{\geqslant}0}$, we put
$n\in \mathbb{Z}_{{\geqslant}0}$, we put 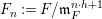 $F_{n}:=F/\mathfrak{m}_{F}^{n\cdot h+1}$, with
$F_{n}:=F/\mathfrak{m}_{F}^{n\cdot h+1}$, with 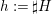 $h:=\sharp H$, and define
$h:=\sharp H$, and define 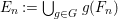 $E_{n}:=\bigcup _{g\in G}g(F_{n})$. In particular,
$E_{n}:=\bigcup _{g\in G}g(F_{n})$. In particular, 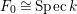 $F_{0}\cong \text{Spec}\,k$, and
$F_{0}\cong \text{Spec}\,k$, and ![]() $E_{0}$ consists of the closed points of
$E_{0}$ consists of the closed points of ![]() $E$ with the reduced scheme structure.
$E$ with the reduced scheme structure.
Definition 3.5. We define an ![]() $E$-twisted
$E$-twisted ![]() $G$-n-jet of
$G$-n-jet of ![]() $V$ as a
$V$ as a ![]() $G$-equivariant
$G$-equivariant ![]() $D$-morphism
$D$-morphism 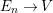 $E_{n}\rightarrow V$, and put
$E_{n}\rightarrow V$, and put
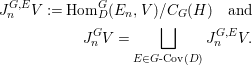 $$\begin{eqnarray}\displaystyle J_{n}^{G,E}V:=\text{Hom}_{D}^{G}(E_{n},V)/C_{G}(H)\quad \text{and} & & \displaystyle \nonumber\\ \displaystyle J_{n}^{G}V=\mathop{\sqcup }_{E\in G\text{-}\text{Cov}(D)}J_{n}^{G,E}V. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle J_{n}^{G,E}V:=\text{Hom}_{D}^{G}(E_{n},V)/C_{G}(H)\quad \text{and} & & \displaystyle \nonumber\\ \displaystyle J_{n}^{G}V=\mathop{\sqcup }_{E\in G\text{-}\text{Cov}(D)}J_{n}^{G,E}V. & & \displaystyle \nonumber\end{eqnarray}$$ Here, the ![]() $C_{G}(H)$-action on
$C_{G}(H)$-action on 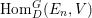 $\text{Hom}_{D}^{G}(E_{n},V)$ is similarly defined to (3.1).
$\text{Hom}_{D}^{G}(E_{n},V)$ is similarly defined to (3.1).
Note that if ![]() $E\not \cong E^{\prime }$, then
$E\not \cong E^{\prime }$, then ![]() $E$-twisted and
$E$-twisted and ![]() $E^{\prime }$-twisted
$E^{\prime }$-twisted ![]() $G$-
$G$-![]() $n$-jets never give the same point of
$n$-jets never give the same point of ![]() $J_{n}^{G}V$. For each
$J_{n}^{G}V$. For each  $n\in \mathbb{Z}_{{\geqslant}0}$ and
$n\in \mathbb{Z}_{{\geqslant}0}$ and 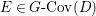 $E\in G\text{-}\text{Cov}(D)$, we have natural maps
$E\in G\text{-}\text{Cov}(D)$, we have natural maps
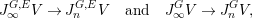 $$\begin{eqnarray}J_{\infty }^{G,E}V\rightarrow J_{n}^{G,E}V\quad \text{and}\quad J_{\infty }^{G}V\rightarrow J_{n}^{G}V,\end{eqnarray}$$
$$\begin{eqnarray}J_{\infty }^{G,E}V\rightarrow J_{n}^{G,E}V\quad \text{and}\quad J_{\infty }^{G}V\rightarrow J_{n}^{G}V,\end{eqnarray}$$ both of which we will denote by ![]() ${\it\pi}_{n}$. We have obtained the following commutative diagram:
${\it\pi}_{n}$. We have obtained the following commutative diagram:
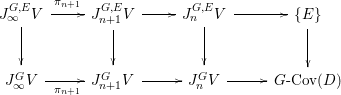
Remark 3.6. In [Reference YasudaYasa], the author conjectured that the sets 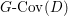 $G\text{-}\text{Cov}(D)$,
$G\text{-}\text{Cov}(D)$, ![]() $J_{n}^{G,E}V$,
$J_{n}^{G,E}V$, ![]() $J_{n}^{G}V$
$J_{n}^{G}V$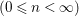 $(0\leqslant n<\infty )$ are realized as
$(0\leqslant n<\infty )$ are realized as ![]() $k$-schemes admitting stratifications with at most countably many finite-dimensional strata, which will be necessary below to define the motivic measure.
$k$-schemes admitting stratifications with at most countably many finite-dimensional strata, which will be necessary below to define the motivic measure.
Let ![]() $X$ be the quotient scheme
$X$ be the quotient scheme ![]() $V/G$, writing the quotient morphism as
$V/G$, writing the quotient morphism as
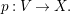 $$\begin{eqnarray}p:V\rightarrow X.\end{eqnarray}$$
$$\begin{eqnarray}p:V\rightarrow X.\end{eqnarray}$$ Given a ![]() $G$-arc
$G$-arc ![]() $E\rightarrow V$, we get an arc
$E\rightarrow V$, we get an arc ![]() $D\rightarrow X$ by taking the
$D\rightarrow X$ by taking the ![]() $G$-quotients of the source and the target. This gives a natural map
$G$-quotients of the source and the target. This gives a natural map
 $$\begin{eqnarray}p_{\infty }:J_{\infty }^{G}V\rightarrow J_{\infty }X.\end{eqnarray}$$
$$\begin{eqnarray}p_{\infty }:J_{\infty }^{G}V\rightarrow J_{\infty }X.\end{eqnarray}$$ Let ![]() $T\subset V$ be the ramification locus of
$T\subset V$ be the ramification locus of ![]() ${\it\pi}$, say, with the reduced scheme structure and
${\it\pi}$, say, with the reduced scheme structure and ![]() $\bar{T}\subset X$ its image. The map
$\bar{T}\subset X$ its image. The map ![]() $p_{\infty }$ restricts to the bijection
$p_{\infty }$ restricts to the bijection
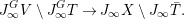 $$\begin{eqnarray}J_{\infty }^{G}V\setminus J_{\infty }^{G}T\rightarrow J_{\infty }X\setminus J_{\infty }\bar{T}.\end{eqnarray}$$
$$\begin{eqnarray}J_{\infty }^{G}V\setminus J_{\infty }^{G}T\rightarrow J_{\infty }X\setminus J_{\infty }\bar{T}.\end{eqnarray}$$ For ![]() $n<\infty$, we have a natural map
$n<\infty$, we have a natural map
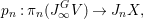 $$\begin{eqnarray}p_{n}:{\it\pi}_{n}(J_{\infty }^{G}V)\rightarrow J_{n}X,\end{eqnarray}$$
$$\begin{eqnarray}p_{n}:{\it\pi}_{n}(J_{\infty }^{G}V)\rightarrow J_{n}X,\end{eqnarray}$$ where ![]() ${\it\pi}_{n}$ denotes the natural map
${\it\pi}_{n}$ denotes the natural map 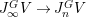 $J_{\infty }^{G}V\rightarrow J_{n}^{G}V$.
$J_{\infty }^{G}V\rightarrow J_{n}^{G}V$.
For a centered log ![]() $G$-
$G$-![]() $D$-variety
$D$-variety ![]() $\mathfrak{V}$ and
$\mathfrak{V}$ and  $n\in \mathbb{Z}_{{\geqslant}0}\cup \{\infty \}$, we define
$n\in \mathbb{Z}_{{\geqslant}0}\cup \{\infty \}$, we define ![]() $J_{n}^{G}\mathfrak{V}$ and
$J_{n}^{G}\mathfrak{V}$ and ![]() $J_{n}^{G,E}\mathfrak{V}$ as the subsets of
$J_{n}^{G,E}\mathfrak{V}$ as the subsets of ![]() $J_{n}^{G}V$ and
$J_{n}^{G}V$ and ![]() $J_{n}^{G,E}V$ consisting of the morphisms
$J_{n}^{G,E}V$ consisting of the morphisms  $E_{n}\rightarrow V$ sending the closed points of
$E_{n}\rightarrow V$ sending the closed points of ![]() $E_{n}$ into the center of
$E_{n}$ into the center of ![]() $\mathfrak{V}$.
$\mathfrak{V}$.
4 The untwisting technique revisited
In this section, we revisit the technique of untwisting, which was first used by Denef and Loeser [Reference Denef and LoeserDL02] in characteristic zero, and generalized to arbitrary characteristics by the author [Reference YasudaYasa]. Our constructions below are slightly different and refined from the ones in [Reference YasudaYasa].
Let us now turn to the case where ![]() $V$ is an affine space over
$V$ is an affine space over ![]() $D$ and the given
$D$ and the given ![]() $G$-action is linear. We keep fixed a
$G$-action is linear. We keep fixed a ![]() $G$-cover
$G$-cover ![]() $E$ of
$E$ of ![]() $D$ and a connected component
$D$ and a connected component ![]() $F$ of
$F$ of ![]() $E$ with stabilizer
$E$ with stabilizer ![]() $H$.
$H$.
For a free ![]() ${\mathcal{O}}_{D}$-module
${\mathcal{O}}_{D}$-module ![]() $M$ of rank
$M$ of rank ![]() $d$, let
$d$, let  ${\mathcal{O}}_{V}:=S_{{\mathcal{O}}_{D}}^{\bullet }M$ be its symmetric algebra, and put
${\mathcal{O}}_{V}:=S_{{\mathcal{O}}_{D}}^{\bullet }M$ be its symmetric algebra, and put
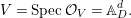 $$\begin{eqnarray}V=\text{Spec}\,{\mathcal{O}}_{V}=\mathbb{A}_{D}^{d}.\end{eqnarray}$$
$$\begin{eqnarray}V=\text{Spec}\,{\mathcal{O}}_{V}=\mathbb{A}_{D}^{d}.\end{eqnarray}$$ We suppose that the module ![]() $M$ and hence the
$M$ and hence the ![]() ${\mathcal{O}}_{D}$-algebra
${\mathcal{O}}_{D}$-algebra ![]() ${\mathcal{O}}_{V}$ have faithful right
${\mathcal{O}}_{V}$ have faithful right ![]() $G$-actions. Then
$G$-actions. Then ![]() $V$ has the induced left
$V$ has the induced left ![]() $G$-action. The set
$G$-action. The set 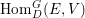 $\text{Hom}_{D}^{G}(E,V)$ can be identified with the
$\text{Hom}_{D}^{G}(E,V)$ can be identified with the ![]() ${\mathcal{O}}_{D}$-module
${\mathcal{O}}_{D}$-module
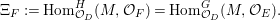 $$\begin{eqnarray}\displaystyle {\rm\Xi}_{F}:=\text{Hom}_{{\mathcal{O}}_{D}}^{H}(M,{\mathcal{O}}_{F})=\text{Hom}_{{\mathcal{O}}_{D}}^{G}(M,{\mathcal{O}}_{E}). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\rm\Xi}_{F}:=\text{Hom}_{{\mathcal{O}}_{D}}^{H}(M,{\mathcal{O}}_{F})=\text{Hom}_{{\mathcal{O}}_{D}}^{G}(M,{\mathcal{O}}_{E}). & & \displaystyle \nonumber\end{eqnarray}$$ We call ![]() ${\rm\Xi}_{F}$ the tuning module.
${\rm\Xi}_{F}$ the tuning module.
Remark 4.1. If we fix a basis of ![]() $M$, then the module
$M$, then the module 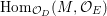 $\text{Hom}_{{\mathcal{O}}_{D}}(M,{\mathcal{O}}_{E})$ is identified with
$\text{Hom}_{{\mathcal{O}}_{D}}(M,{\mathcal{O}}_{E})$ is identified with ![]() ${\mathcal{O}}_{E}^{\oplus d}$. This module
${\mathcal{O}}_{E}^{\oplus d}$. This module ![]() ${\mathcal{O}}_{E}^{\oplus d}$ has two
${\mathcal{O}}_{E}^{\oplus d}$ has two ![]() $G$-actions: one is the diagonal
$G$-actions: one is the diagonal ![]() $G$-action induced from the given
$G$-action induced from the given ![]() $G$-action on
$G$-action on ![]() ${\mathcal{O}}_{E}$ and the other is the one induced from the
${\mathcal{O}}_{E}$ and the other is the one induced from the ![]() $G$-action on
$G$-action on ![]() $M$. For an element of
$M$. For an element of ![]() ${\mathcal{O}}_{E}^{\oplus d}$ corresponding to a
${\mathcal{O}}_{E}^{\oplus d}$ corresponding to a ![]() $G$-equivariant map
$G$-equivariant map 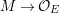 $M\rightarrow {\mathcal{O}}_{E}$, the two actions must coincide. We thus can identify
$M\rightarrow {\mathcal{O}}_{E}$, the two actions must coincide. We thus can identify ![]() ${\rm\Xi}_{F}$ with the locus in
${\rm\Xi}_{F}$ with the locus in ![]() ${\mathcal{O}}_{E}^{\oplus d}$ where the two actions coincide. This was how the module
${\mathcal{O}}_{E}^{\oplus d}$ where the two actions coincide. This was how the module ![]() ${\rm\Xi}_{F}$ was presented in previous papers [Reference YasudaYasa, Reference Wood and YasudaWY15].
${\rm\Xi}_{F}$ was presented in previous papers [Reference YasudaYasa, Reference Wood and YasudaWY15].
Lemma 4.2. [Reference YasudaYasa, Reference Wood and YasudaWY15]
The module ![]() ${\rm\Xi}_{F}$ is a free
${\rm\Xi}_{F}$ is a free ![]() ${\mathcal{O}}_{D}$-module of rank
${\mathcal{O}}_{D}$-module of rank ![]() $d$. Moreover, it is a saturated
$d$. Moreover, it is a saturated ![]() ${\mathcal{O}}_{D}$-submodule of
${\mathcal{O}}_{D}$-submodule of 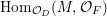 $\text{Hom}_{{\mathcal{O}}_{D}}(M,{\mathcal{O}}_{F})$ and of
$\text{Hom}_{{\mathcal{O}}_{D}}(M,{\mathcal{O}}_{F})$ and of 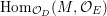 $\text{Hom}_{{\mathcal{O}}_{D}}(M,{\mathcal{O}}_{E})$: for
$\text{Hom}_{{\mathcal{O}}_{D}}(M,{\mathcal{O}}_{E})$: for ![]() $a\in {\mathcal{O}}_{D}$ and
$a\in {\mathcal{O}}_{D}$ and 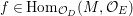 $f\in \text{Hom}_{{\mathcal{O}}_{D}}(M,{\mathcal{O}}_{E})$, if
$f\in \text{Hom}_{{\mathcal{O}}_{D}}(M,{\mathcal{O}}_{E})$, if 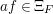 $af\in {\rm\Xi}_{F}$, then
$af\in {\rm\Xi}_{F}$, then ![]() $f\in {\rm\Xi}_{F}$.
$f\in {\rm\Xi}_{F}$.
From (3.2),
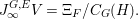 $$\begin{eqnarray}J_{\infty }^{G,E}V={\rm\Xi}_{F}/C_{G}(H).\end{eqnarray}$$
$$\begin{eqnarray}J_{\infty }^{G,E}V={\rm\Xi}_{F}/C_{G}(H).\end{eqnarray}$$ Note that the ![]() $C_{G}(H)$-action on
$C_{G}(H)$-action on ![]() ${\rm\Xi}_{F}$ is
${\rm\Xi}_{F}$ is ![]() ${\mathcal{O}}_{D}$-linear.
${\mathcal{O}}_{D}$-linear.
Lemma 4.3. The maps
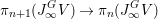 $$\begin{eqnarray}{\it\pi}_{n+1}(J_{\infty }^{G}V)\rightarrow {\it\pi}_{n}(J_{\infty }^{G}V)\end{eqnarray}$$
$$\begin{eqnarray}{\it\pi}_{n+1}(J_{\infty }^{G}V)\rightarrow {\it\pi}_{n}(J_{\infty }^{G}V)\end{eqnarray}$$ have fibers homeomorphic to the quotient of ![]() $\mathbb{A}_{k}^{d}$ by a linear action of a finite group.
$\mathbb{A}_{k}^{d}$ by a linear action of a finite group.
Proof. If we denote the map 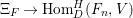 ${\rm\Xi}_{F}\rightarrow \text{Hom}_{D}^{H}(F_{n},V)$ again by
${\rm\Xi}_{F}\rightarrow \text{Hom}_{D}^{H}(F_{n},V)$ again by ![]() ${\it\pi}_{n}$, the image
${\it\pi}_{n}$, the image ![]() ${\it\pi}_{n}({\rm\Xi}_{F})$ is isomorphic to
${\it\pi}_{n}({\rm\Xi}_{F})$ is isomorphic to 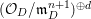 $({\mathcal{O}}_{D}/\mathfrak{m}_{D}^{n+1})^{\oplus d}$. This shows that the fibers of
$({\mathcal{O}}_{D}/\mathfrak{m}_{D}^{n+1})^{\oplus d}$. This shows that the fibers of
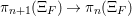 $$\begin{eqnarray}{\it\pi}_{n+1}({\rm\Xi}_{F})\rightarrow {\it\pi}_{n}({\rm\Xi}_{F})\end{eqnarray}$$
$$\begin{eqnarray}{\it\pi}_{n+1}({\rm\Xi}_{F})\rightarrow {\it\pi}_{n}({\rm\Xi}_{F})\end{eqnarray}$$ are isomorphic to ![]() $\mathbb{A}_{k}^{d}$, proving the lemma.◻
$\mathbb{A}_{k}^{d}$, proving the lemma.◻
Definition 4.4. We define a motivic measure ![]() ${\it\mu}_{J_{\infty }^{G}V}$ on
${\it\mu}_{J_{\infty }^{G}V}$ on ![]() $J_{\infty }^{G}V$ in the same way as the ones on
$J_{\infty }^{G}V$ in the same way as the ones on ![]() $J_{\infty }V$ and
$J_{\infty }V$ and 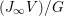 $(J_{\infty }V)/G$. If
$(J_{\infty }V)/G$. If ![]() $\mathfrak{V}$ is a
$\mathfrak{V}$ is a ![]() $G$-equivariant centered log structure on
$G$-equivariant centered log structure on ![]() $V$, we define the measure
$V$, we define the measure ![]() ${\it\mu}_{J_{\infty }^{G}\mathfrak{V}}$ on
${\it\mu}_{J_{\infty }^{G}\mathfrak{V}}$ on ![]() $J_{\infty }^{G}\mathfrak{V}$ as the restriction of
$J_{\infty }^{G}\mathfrak{V}$ as the restriction of ![]() ${\it\mu}_{J_{\infty }^{G}V}$.
${\it\mu}_{J_{\infty }^{G}V}$.
Remark 4.5. For the definition above to make sense, we need the conjecture that moduli spaces 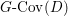 $G\text{-}\text{Cov}(D)$ and
$G\text{-}\text{Cov}(D)$ and ![]() $J_{n}^{G}V$ exist and have some finiteness (see Remark 3.6).
$J_{n}^{G}V$ exist and have some finiteness (see Remark 3.6).
Definition 4.6. We define modules,
 $$\begin{eqnarray}\displaystyle & M^{|F|}:=\text{Hom}_{{\mathcal{O}}_{D}}({\rm\Xi}_{F},{\mathcal{O}}_{D})\quad \text{and} & \displaystyle \nonumber\\ \displaystyle & M^{\left\langle F\right\rangle }:=M^{|F|}\otimes _{{\mathcal{O}}_{D}}{\mathcal{O}}_{F}=\text{Hom}_{{\mathcal{O}}_{D}}({\rm\Xi}_{F},{\mathcal{O}}_{F}), & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & M^{|F|}:=\text{Hom}_{{\mathcal{O}}_{D}}({\rm\Xi}_{F},{\mathcal{O}}_{D})\quad \text{and} & \displaystyle \nonumber\\ \displaystyle & M^{\left\langle F\right\rangle }:=M^{|F|}\otimes _{{\mathcal{O}}_{D}}{\mathcal{O}}_{F}=\text{Hom}_{{\mathcal{O}}_{D}}({\rm\Xi}_{F},{\mathcal{O}}_{F}), & \displaystyle \nonumber\end{eqnarray}$$ which are free modules of rank ![]() $d$ over
$d$ over ![]() ${\mathcal{O}}_{D}$ and
${\mathcal{O}}_{D}$ and ![]() ${\mathcal{O}}_{F}$ respectively. We define an
${\mathcal{O}}_{F}$ respectively. We define an ![]() ${\mathcal{O}}_{D}$-linear map
${\mathcal{O}}_{D}$-linear map
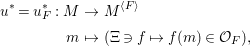 $$\begin{eqnarray}\displaystyle u^{\ast }=u_{F}^{\ast }:M & \rightarrow & \displaystyle M^{\left\langle F\right\rangle }\nonumber\\ \displaystyle m & \mapsto & \displaystyle ({\rm\Xi}\ni f\mapsto f(m)\in {\mathcal{O}}_{F}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle u^{\ast }=u_{F}^{\ast }:M & \rightarrow & \displaystyle M^{\left\langle F\right\rangle }\nonumber\\ \displaystyle m & \mapsto & \displaystyle ({\rm\Xi}\ni f\mapsto f(m)\in {\mathcal{O}}_{F}),\nonumber\end{eqnarray}$$ identifying ![]() ${\rm\Xi}_{F}$ with
${\rm\Xi}_{F}$ with  $\text{Hom}_{{\mathcal{O}}_{D}}^{H}(M,{\mathcal{O}}_{F})$ rather than
$\text{Hom}_{{\mathcal{O}}_{D}}^{H}(M,{\mathcal{O}}_{F})$ rather than 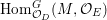 $\text{Hom}_{{\mathcal{O}}_{D}}^{G}(M,{\mathcal{O}}_{E})$.
$\text{Hom}_{{\mathcal{O}}_{D}}^{G}(M,{\mathcal{O}}_{E})$.
Lemma 4.7. We suppose that ![]() $H$ and
$H$ and ![]() $C_{G}(H)$ act on
$C_{G}(H)$ act on ![]() $M$ by restricting the given
$M$ by restricting the given ![]() $G$-action.
$G$-action.
(1) With respect to the
 $H$-action on
$H$-action on  $M^{\left\langle F\right\rangle }$ induced from the
$M^{\left\langle F\right\rangle }$ induced from the  $H$-action on
$H$-action on  ${\mathcal{O}}_{F}$, the map
${\mathcal{O}}_{F}$, the map  $u^{\ast }$ is
$u^{\ast }$ is  $H$-equivariant.
$H$-equivariant.(2) With respect to the
 $C_{G}(H)$-action on
$C_{G}(H)$-action on  $M^{\left\langle F\right\rangle }$ induced from the (left)
$M^{\left\langle F\right\rangle }$ induced from the (left)  $C_{G}(H)$-action on
$C_{G}(H)$-action on  ${\rm\Xi}_{F}$, the map
${\rm\Xi}_{F}$, the map  $u^{\ast }$ is
$u^{\ast }$ is  $C_{G}(H)$-equivariant.
$C_{G}(H)$-equivariant.
(1) For
 $h\in H$ and
$h\in H$ and  $m\in M$, we have since
$m\in M$, we have since $$\begin{eqnarray}\displaystyle u^{\ast }(mh) & = & \displaystyle (f\mapsto f(mh))\nonumber\\ \displaystyle & = & \displaystyle (f\mapsto f(m)h)\nonumber\\ \displaystyle & = & \displaystyle (f\mapsto f(m))h,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle u^{\ast }(mh) & = & \displaystyle (f\mapsto f(mh))\nonumber\\ \displaystyle & = & \displaystyle (f\mapsto f(m)h)\nonumber\\ \displaystyle & = & \displaystyle (f\mapsto f(m))h,\nonumber\end{eqnarray}$$ $f\in {\rm\Xi}$ are
$f\in {\rm\Xi}$ are  $H$-equivariant. This shows the assertion.
$H$-equivariant. This shows the assertion.(2) Let
 $M^{\left\langle E\right\rangle }:=\text{Hom}_{{\mathcal{O}}_{D}}({\rm\Xi}_{F},{\mathcal{O}}_{E})$ and consider the natural map now identifying
$M^{\left\langle E\right\rangle }:=\text{Hom}_{{\mathcal{O}}_{D}}({\rm\Xi}_{F},{\mathcal{O}}_{E})$ and consider the natural map now identifying $$\begin{eqnarray}u_{E}^{\ast }:M\rightarrow M^{\left\langle E\right\rangle },\,m\mapsto (f\mapsto f(m)),\end{eqnarray}$$
$$\begin{eqnarray}u_{E}^{\ast }:M\rightarrow M^{\left\langle E\right\rangle },\,m\mapsto (f\mapsto f(m)),\end{eqnarray}$$ ${\rm\Xi}_{F}$ with
${\rm\Xi}_{F}$ with  $\text{Hom}_{{\mathcal{O}}_{D}}^{G}(M,{\mathcal{O}}_{E})$. This map is
$\text{Hom}_{{\mathcal{O}}_{D}}^{G}(M,{\mathcal{O}}_{E})$. This map is  $C_{G}(H)$-equivariant. Indeed, for
$C_{G}(H)$-equivariant. Indeed, for  $g\in C_{G}(H)$ and
$g\in C_{G}(H)$ and  $m\in M$, from (3.1), we have The map
$m\in M$, from (3.1), we have The map $$\begin{eqnarray}\displaystyle u_{E}^{\ast }(mg) & = & \displaystyle (f\mapsto f(mg))\nonumber\\ \displaystyle & = & \displaystyle (f\mapsto f(m)g)\nonumber\\ \displaystyle & = & \displaystyle (f\mapsto (gf)(m)).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle u_{E}^{\ast }(mg) & = & \displaystyle (f\mapsto f(mg))\nonumber\\ \displaystyle & = & \displaystyle (f\mapsto f(m)g)\nonumber\\ \displaystyle & = & \displaystyle (f\mapsto (gf)(m)).\nonumber\end{eqnarray}$$ $u_{E}^{\ast }$ factors as Since the inclusion
$u_{E}^{\ast }$ factors as Since the inclusion $$\begin{eqnarray}M\xrightarrow[]{u_{F}^{\ast }}M^{\left\langle F\right\rangle }{\hookrightarrow}M^{\left\langle E\right\rangle }.\end{eqnarray}$$
$$\begin{eqnarray}M\xrightarrow[]{u_{F}^{\ast }}M^{\left\langle F\right\rangle }{\hookrightarrow}M^{\left\langle E\right\rangle }.\end{eqnarray}$$ $M^{\left\langle F\right\rangle }{\hookrightarrow}M^{\left\langle E\right\rangle }$ is also
$M^{\left\langle F\right\rangle }{\hookrightarrow}M^{\left\langle E\right\rangle }$ is also  $C_{G}(H)$-equivariant, so does
$C_{G}(H)$-equivariant, so does  $u_{F}^{\ast }$. ◻
$u_{F}^{\ast }$. ◻
Note that the ![]() $H$- and
$H$- and ![]() $C_{G}(H)$-actions above on
$C_{G}(H)$-actions above on ![]() $M^{\left\langle F\right\rangle }$ commute.
$M^{\left\langle F\right\rangle }$ commute.
Definition 4.8. We define the untwisting variety (resp. pre-untwisting variety) of ![]() $V$ with respect to
$V$ with respect to ![]() $F$ as
$F$ as
 $$\begin{eqnarray}V^{|F|}:=\text{Spec}\,S_{{\mathcal{O}}_{D}}^{\bullet }M^{|F|}=\mathbb{A}_{D}^{d}~(\text{resp. }V^{\left\langle F\right\rangle }:=\text{Spec}\,S_{{\mathcal{O}}_{F}}^{\bullet }M^{\left\langle F\right\rangle }=\mathbb{A}_{F}^{d}).\end{eqnarray}$$
$$\begin{eqnarray}V^{|F|}:=\text{Spec}\,S_{{\mathcal{O}}_{D}}^{\bullet }M^{|F|}=\mathbb{A}_{D}^{d}~(\text{resp. }V^{\left\langle F\right\rangle }:=\text{Spec}\,S_{{\mathcal{O}}_{F}}^{\bullet }M^{\left\langle F\right\rangle }=\mathbb{A}_{F}^{d}).\end{eqnarray}$$ We denote the projection 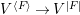 $V^{\langle F\rangle }\rightarrow V^{|F|}$ by
$V^{\langle F\rangle }\rightarrow V^{|F|}$ by ![]() $r=r_{F}$, where
$r=r_{F}$, where ![]() $r$ stands for the restriction of scalars (see diagram (4.1) below). The map
$r$ stands for the restriction of scalars (see diagram (4.1) below). The map ![]() $u^{\ast }$ defines a
$u^{\ast }$ defines a ![]() $D$-morphism
$D$-morphism
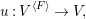 $$\begin{eqnarray}u:V^{\left\langle F\right\rangle }\rightarrow V,\end{eqnarray}$$
$$\begin{eqnarray}u:V^{\left\langle F\right\rangle }\rightarrow V,\end{eqnarray}$$ which is both ![]() $H$- and
$H$- and ![]() $C_{G}(H)$-equivariant. We call the pair of
$C_{G}(H)$-equivariant. We call the pair of ![]() $r$ and
$r$ and ![]() $u$ the untwisting correspondence of
$u$ the untwisting correspondence of ![]() $V$ with respect to
$V$ with respect to ![]() $F$.
$F$.
Let 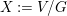 $X:=V/G$, and identify
$X:=V/G$, and identify ![]() ${\mathcal{O}}_{X}$ with
${\mathcal{O}}_{X}$ with ![]() $({\mathcal{O}}_{V})^{G}$. Since the
$({\mathcal{O}}_{V})^{G}$. Since the ![]() $H$-invariant subring of
$H$-invariant subring of ![]() ${\mathcal{O}}_{V^{\left\langle F\right\rangle }}$ is
${\mathcal{O}}_{V^{\left\langle F\right\rangle }}$ is
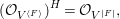 $$\begin{eqnarray}({\mathcal{O}}_{V^{\left\langle F\right\rangle }})^{H}={\mathcal{O}}_{V^{|F|}},\end{eqnarray}$$
$$\begin{eqnarray}({\mathcal{O}}_{V^{\left\langle F\right\rangle }})^{H}={\mathcal{O}}_{V^{|F|}},\end{eqnarray}$$we have
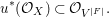 $$\begin{eqnarray}u^{\ast }({\mathcal{O}}_{X})\subset {\mathcal{O}}_{V^{|F|}}.\end{eqnarray}$$
$$\begin{eqnarray}u^{\ast }({\mathcal{O}}_{X})\subset {\mathcal{O}}_{V^{|F|}}.\end{eqnarray}$$ We denote the induced morphism  $V^{|F|}\rightarrow X$ by
$V^{|F|}\rightarrow X$ by ![]() $p^{|F|}$. We have the following commutative diagram:
$p^{|F|}$. We have the following commutative diagram:
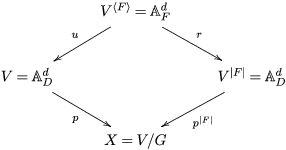 $$\begin{eqnarray}\begin{array}{@{}c@{}}\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}c@{}}\end{array}\end{eqnarray}$$(1) The map
is bijective. $$\begin{eqnarray}\displaystyle \text{Hom}_{F}^{H}(F,V^{\left\langle F\right\rangle }) & \rightarrow & \displaystyle {\rm\Xi}_{F}=\text{Hom}_{D}^{H}(F,V)\nonumber\\ \displaystyle {\it\gamma} & \mapsto & \displaystyle u\circ {\it\gamma}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{Hom}_{F}^{H}(F,V^{\left\langle F\right\rangle }) & \rightarrow & \displaystyle {\rm\Xi}_{F}=\text{Hom}_{D}^{H}(F,V)\nonumber\\ \displaystyle {\it\gamma} & \mapsto & \displaystyle u\circ {\it\gamma}\nonumber\end{eqnarray}$$(2) The map
sending a morphism $$\begin{eqnarray}\text{Hom}_{F}^{H}(F,V^{\left\langle F\right\rangle })\rightarrow J_{\infty }V^{|F|}=\text{Hom}_{D}(D,V^{|F|}),\end{eqnarray}$$
$$\begin{eqnarray}\text{Hom}_{F}^{H}(F,V^{\left\langle F\right\rangle })\rightarrow J_{\infty }V^{|F|}=\text{Hom}_{D}(D,V^{|F|}),\end{eqnarray}$$ $F\rightarrow V^{\left\langle F\right\rangle }$ to the induced one of quotients, is bijective.
$F\rightarrow V^{\left\langle F\right\rangle }$ to the induced one of quotients, is bijective. $$\begin{eqnarray}D=F/H\rightarrow V^{|F|}=V^{\left\langle F\right\rangle }/H,\end{eqnarray}$$
$$\begin{eqnarray}D=F/H\rightarrow V^{|F|}=V^{\left\langle F\right\rangle }/H,\end{eqnarray}$$
(1) With the identification
the map of the assertion is identified with the map $$\begin{eqnarray}\text{Hom}_{F}^{H}(F,V^{\left\langle F\right\rangle })=\text{Hom}_{{\mathcal{O}}_{F}}^{H}(\text{Hom}_{{\mathcal{O}}_{D}}({\rm\Xi}_{F},{\mathcal{O}}_{F}),{\mathcal{O}}_{F}),\end{eqnarray}$$where
$$\begin{eqnarray}\text{Hom}_{F}^{H}(F,V^{\left\langle F\right\rangle })=\text{Hom}_{{\mathcal{O}}_{F}}^{H}(\text{Hom}_{{\mathcal{O}}_{D}}({\rm\Xi}_{F},{\mathcal{O}}_{F}),{\mathcal{O}}_{F}),\end{eqnarray}$$where $$\begin{eqnarray}\displaystyle a:\text{Hom}_{{\mathcal{O}}_{F}}^{H}(\text{Hom}_{{\mathcal{O}}_{D}}({\rm\Xi}_{F},{\mathcal{O}}_{F}),{\mathcal{O}}_{F}) & \rightarrow & \displaystyle {\rm\Xi}_{F}\nonumber\\ \displaystyle {\it\phi} & \mapsto & \displaystyle (m\mapsto {\it\phi}((f\mapsto f(m)))),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle a:\text{Hom}_{{\mathcal{O}}_{F}}^{H}(\text{Hom}_{{\mathcal{O}}_{D}}({\rm\Xi}_{F},{\mathcal{O}}_{F}),{\mathcal{O}}_{F}) & \rightarrow & \displaystyle {\rm\Xi}_{F}\nonumber\\ \displaystyle {\it\phi} & \mapsto & \displaystyle (m\mapsto {\it\phi}((f\mapsto f(m)))),\nonumber\end{eqnarray}$$ $m\in M$ and
$m\in M$ and  $f\in {\rm\Xi}_{F}$. Let us consider the map where
$f\in {\rm\Xi}_{F}$. Let us consider the map where $$\begin{eqnarray}\displaystyle b:{\rm\Xi}_{F} & \rightarrow & \displaystyle \text{Hom}_{{\mathcal{O}}_{F}}^{H}(\text{Hom}_{{\mathcal{O}}_{D}}({\rm\Xi}_{F},{\mathcal{O}}_{F}),{\mathcal{O}}_{F})\nonumber\\ \displaystyle f & \mapsto & \displaystyle (z\mapsto z(f)),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle b:{\rm\Xi}_{F} & \rightarrow & \displaystyle \text{Hom}_{{\mathcal{O}}_{F}}^{H}(\text{Hom}_{{\mathcal{O}}_{D}}({\rm\Xi}_{F},{\mathcal{O}}_{F}),{\mathcal{O}}_{F})\nonumber\\ \displaystyle f & \mapsto & \displaystyle (z\mapsto z(f)),\nonumber\end{eqnarray}$$ $z\in \text{Hom}_{{\mathcal{O}}_{D}}({\rm\Xi}_{F},{\mathcal{O}}_{F})$. The composition
$z\in \text{Hom}_{{\mathcal{O}}_{D}}({\rm\Xi}_{F},{\mathcal{O}}_{F})$. The composition  $a\circ b$ sends
$a\circ b$ sends  $f\in {\rm\Xi}_{F}$ to and hence is the identity map. It follows that
$f\in {\rm\Xi}_{F}$ to and hence is the identity map. It follows that $$\begin{eqnarray}\displaystyle \left(m\mapsto \left(z\mapsto z(f)\right)\left(h\mapsto h(m)\right)\right) & = & \displaystyle \left(m\mapsto f(m)\right)\nonumber\\ \displaystyle & = & \displaystyle f,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left(m\mapsto \left(z\mapsto z(f)\right)\left(h\mapsto h(m)\right)\right) & = & \displaystyle \left(m\mapsto f(m)\right)\nonumber\\ \displaystyle & = & \displaystyle f,\nonumber\end{eqnarray}$$ $a$ is surjective. Now the assertion follows from the fact that the source and target of
$a$ is surjective. Now the assertion follows from the fact that the source and target of  $a$ are free
$a$ are free  ${\mathcal{O}}_{D}$-modules of the same rank and
${\mathcal{O}}_{D}$-modules of the same rank and  $a$ is a homomorphism of
$a$ is a homomorphism of  ${\mathcal{O}}_{D}$-modules.
${\mathcal{O}}_{D}$-modules.(2) We can give the converse by the base change associated to
 $F\rightarrow D$. ◻
$F\rightarrow D$. ◻
In summary, we have a one-to-one correspondence between ![]() ${\rm\Xi}_{F}$ and
${\rm\Xi}_{F}$ and ![]() $J_{\infty }V^{|F|}$, induced from the untwisting correspondence. From Lemma 4.7, the correspondence is compatible with the
$J_{\infty }V^{|F|}$, induced from the untwisting correspondence. From Lemma 4.7, the correspondence is compatible with the ![]() $C_{G}(H)$-actions on both sides. Therefore, it descends to a one-to-one correspondence between
$C_{G}(H)$-actions on both sides. Therefore, it descends to a one-to-one correspondence between ![]() $J_{\infty }^{G,E}V$ and
$J_{\infty }^{G,E}V$ and  $(J_{\infty }V^{|F|})/C_{G}(H)$. We obtain the following commutative diagram:
$(J_{\infty }V^{|F|})/C_{G}(H)$. We obtain the following commutative diagram:
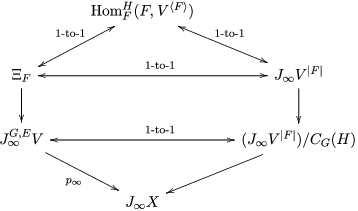 $$\begin{eqnarray}\begin{array}{@{}c@{}}\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}c@{}}\end{array}\end{eqnarray}$$ For ![]() $n<\infty$, we have a similar diagram:
$n<\infty$, we have a similar diagram:
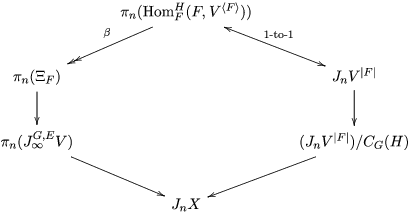 $$\begin{eqnarray}\begin{array}{@{}c@{}}\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}c@{}}\end{array}\end{eqnarray}$$ Note that the arrow ![]() ${\it\beta}$ is no longer bijective. When
${\it\beta}$ is no longer bijective. When ![]() $n=0$, the diagram is represented as
$n=0$, the diagram is represented as
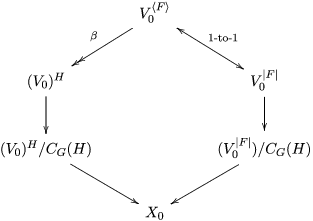 $$\begin{eqnarray}\begin{array}{@{}c@{}}\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}c@{}}\end{array}\end{eqnarray}$$ Here, ![]() $(V_{0})^{H}$ is the fixed-point locus of the
$(V_{0})^{H}$ is the fixed-point locus of the ![]() $H$-action on
$H$-action on ![]() $V_{0}$.
$V_{0}$.
5 The change of variables formula
The untwisting technique, discussed in the last section, enables us to deduce a conjectural change of variables formula for the map  $p_{\infty }:J_{\infty }^{G}V\rightarrow J_{\infty }X$. In turn, it derives the McKay correspondence for linear actions in the next section.
$p_{\infty }:J_{\infty }^{G}V\rightarrow J_{\infty }X$. In turn, it derives the McKay correspondence for linear actions in the next section.
We keep the notation from the last section.
Definition 5.1. Let 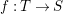 $f:T\rightarrow S$ be a morphism of
$f:T\rightarrow S$ be a morphism of ![]() $D$-varieties which is generically étale. The Jacobian ideal (sheaf)
$D$-varieties which is generically étale. The Jacobian ideal (sheaf)
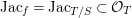 $$\begin{eqnarray}\text{Jac}_{f}=\text{Jac}_{T/S}\subset {\mathcal{O}}_{T}\end{eqnarray}$$
$$\begin{eqnarray}\text{Jac}_{f}=\text{Jac}_{T/S}\subset {\mathcal{O}}_{T}\end{eqnarray}$$ is defined as the zeroth Fitting ideal (sheaf) of ![]() ${\rm\Omega}_{T/S}$, the sheaf of Kähler differentials. We denote by
${\rm\Omega}_{T/S}$, the sheaf of Kähler differentials. We denote by ![]() $\mathbf{j}_{f}$ the order function of
$\mathbf{j}_{f}$ the order function of ![]() $\text{Jac}_{f}$ on
$\text{Jac}_{f}$ on ![]() $J_{\infty }T$,
$J_{\infty }T$, 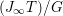 $(J_{\infty }T)/G$ or
$(J_{\infty }T)/G$ or ![]() $J_{\infty }^{G}T$ if
$J_{\infty }^{G}T$ if ![]() $T$ has a faithful action of a finite group
$T$ has a faithful action of a finite group ![]() $G$. The ambiguity of the domain will not cause confusion.
$G$. The ambiguity of the domain will not cause confusion.
Remark 5.2. When ![]() $T$ is smooth, the function
$T$ is smooth, the function ![]() $\mathbf{j}_{f}$ on
$\mathbf{j}_{f}$ on ![]() $J_{\infty }T$ coincides with the Jacobian order function, denoted by
$J_{\infty }T$ coincides with the Jacobian order function, denoted by 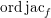 $\text{ord}\,\text{jac}_{f}$, in [Reference SebagSeb04] and mentioned in the proof of Proposition 2.6.
$\text{ord}\,\text{jac}_{f}$, in [Reference SebagSeb04] and mentioned in the proof of Proposition 2.6.
Conjecture 5.3. Let the assumption be as in Section 4. Let 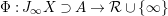 ${\rm\Phi}:J_{\infty }X\supset A\rightarrow {\mathcal{R}}\cup \{\infty \}$ be a measurable function, with
${\rm\Phi}:J_{\infty }X\supset A\rightarrow {\mathcal{R}}\cup \{\infty \}$ be a measurable function, with 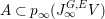 $A\subset p_{\infty }(J_{\infty }^{G,E}V)$, and let
$A\subset p_{\infty }(J_{\infty }^{G,E}V)$, and let ![]() $p_{(\infty )}^{|F|}$ be the natural map
$p_{(\infty )}^{|F|}$ be the natural map 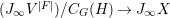 $(J_{\infty }V^{|F|})/C_{G}(H)\rightarrow J_{\infty }X$. We have
$(J_{\infty }V^{|F|})/C_{G}(H)\rightarrow J_{\infty }X$. We have
 $$\begin{eqnarray}\displaystyle \int _{A}{\rm\Phi}\,d{\it\mu}_{J_{\infty }X}=\int _{(p_{(\infty )}^{|F|})^{-1}(A)}({\rm\Phi}\circ p_{(\infty )}^{|F|})\mathbb{L}^{-\mathbf{j}_{p^{|F|}}}\,d{\it\mu}_{(J_{\infty }V^{|F|})/C_{G}(H)}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{A}{\rm\Phi}\,d{\it\mu}_{J_{\infty }X}=\int _{(p_{(\infty )}^{|F|})^{-1}(A)}({\rm\Phi}\circ p_{(\infty )}^{|F|})\mathbb{L}^{-\mathbf{j}_{p^{|F|}}}\,d{\it\mu}_{(J_{\infty }V^{|F|})/C_{G}(H)}. & & \displaystyle \nonumber\end{eqnarray}$$Although there is no written proof of the conjecture in this general form in the literature as far as the author knows, the conjecture is likely to be proved by using existing techniques and arguments from [Reference Denef and LoeserDL02] and [Reference SebagSeb04].
Definition 5.4. [Reference YasudaYasa]
For 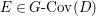 $E\in G\text{-}\text{Cov}(D)$ with a connected component
$E\in G\text{-}\text{Cov}(D)$ with a connected component ![]() $F$, we define the weights of
$F$, we define the weights of ![]() $E$ and
$E$ and ![]() $F$ with respect to
$F$ with respect to ![]() $V$ as
$V$ as
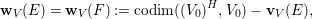 $$\begin{eqnarray}\displaystyle \mathbf{w}_{V}(E)=\mathbf{w}_{V}(F):=\text{codim}((V_{0})^{H},V_{0})-\boldsymbol{v}_{V}(E), & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathbf{w}_{V}(E)=\mathbf{w}_{V}(F):=\text{codim}((V_{0})^{H},V_{0})-\boldsymbol{v}_{V}(E), & & \displaystyle \nonumber\end{eqnarray}$$with
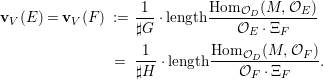 $$\begin{eqnarray}\displaystyle \boldsymbol{v}_{V}(E)=\boldsymbol{v}_{V}(F) & := & \displaystyle \frac{1}{\sharp G}\cdot \text{length}\frac{\text{Hom}_{{\mathcal{O}}_{D}}(M,{\mathcal{O}}_{E})}{{\mathcal{O}}_{E}\cdot {\rm\Xi}_{F}}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{\sharp H}\cdot \text{length}\frac{\text{Hom}_{{\mathcal{O}}_{D}}(M,{\mathcal{O}}_{F})}{{\mathcal{O}}_{F}\cdot {\rm\Xi}_{F}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{v}_{V}(E)=\boldsymbol{v}_{V}(F) & := & \displaystyle \frac{1}{\sharp G}\cdot \text{length}\frac{\text{Hom}_{{\mathcal{O}}_{D}}(M,{\mathcal{O}}_{E})}{{\mathcal{O}}_{E}\cdot {\rm\Xi}_{F}}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{\sharp H}\cdot \text{length}\frac{\text{Hom}_{{\mathcal{O}}_{D}}(M,{\mathcal{O}}_{F})}{{\mathcal{O}}_{F}\cdot {\rm\Xi}_{F}}.\nonumber\end{eqnarray}$$ For the generalization to the case where ![]() $k$ is only perfect, see [Reference Wood and YasudaWY15].
$k$ is only perfect, see [Reference Wood and YasudaWY15].
The definition above gives the weight function,
 $$\begin{eqnarray}\mathbf{w}_{V}:G\text{-}\text{Cov}(D)\rightarrow \frac{1}{\sharp G}\mathbb{Z}.\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{w}_{V}:G\text{-}\text{Cov}(D)\rightarrow \frac{1}{\sharp G}\mathbb{Z}.\end{eqnarray}$$We will denote the composition
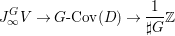 $$\begin{eqnarray}J_{\infty }^{G}V\rightarrow G\text{-}\text{Cov}(D)\rightarrow \frac{1}{\sharp G}\mathbb{Z}\end{eqnarray}$$
$$\begin{eqnarray}J_{\infty }^{G}V\rightarrow G\text{-}\text{Cov}(D)\rightarrow \frac{1}{\sharp G}\mathbb{Z}\end{eqnarray}$$ again by ![]() $\mathbf{w}_{V}$.
$\mathbf{w}_{V}$.
Definition 5.5. For an ideal ![]() $I\subset {\mathcal{O}}_{V}$ stable under the
$I\subset {\mathcal{O}}_{V}$ stable under the ![]() $G$-action and a
$G$-action and a ![]() $G$-arc
$G$-arc 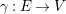 ${\it\gamma}:E\rightarrow V$, we define a function
${\it\gamma}:E\rightarrow V$, we define a function
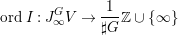 $$\begin{eqnarray}\text{ord}\,I:J_{\infty }^{G}V\rightarrow \frac{1}{\sharp G}\mathbb{Z}\cup \{\infty \}\end{eqnarray}$$
$$\begin{eqnarray}\text{ord}\,I:J_{\infty }^{G}V\rightarrow \frac{1}{\sharp G}\mathbb{Z}\cup \{\infty \}\end{eqnarray}$$by
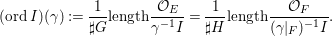 $$\begin{eqnarray}(\text{ord}\,I)({\it\gamma}):=\frac{1}{\sharp G}\text{length}\frac{{\mathcal{O}}_{E}}{{\it\gamma}^{-1}I}=\frac{1}{\sharp H}\text{length}\frac{{\mathcal{O}}_{F}}{({\it\gamma}|_{F})^{-1}I}.\end{eqnarray}$$
$$\begin{eqnarray}(\text{ord}\,I)({\it\gamma}):=\frac{1}{\sharp G}\text{length}\frac{{\mathcal{O}}_{E}}{{\it\gamma}^{-1}I}=\frac{1}{\sharp H}\text{length}\frac{{\mathcal{O}}_{F}}{({\it\gamma}|_{F})^{-1}I}.\end{eqnarray}$$ We then extend this to ![]() $G$-stable fractional ideals and
$G$-stable fractional ideals and ![]() $G$-stable
$G$-stable ![]() $\mathbb{Q}$-linear combinations of closed subschemes as in Definition 2.2.
$\mathbb{Q}$-linear combinations of closed subschemes as in Definition 2.2.
The conjectural change of variables formula is stated as follows.
Conjecture 5.6. [Reference YasudaYasa]
For a measurable function 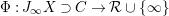 ${\rm\Phi}:J_{\infty }X\supset C\rightarrow {\mathcal{R}}\cup \{\infty \}$, we have
${\rm\Phi}:J_{\infty }X\supset C\rightarrow {\mathcal{R}}\cup \{\infty \}$, we have
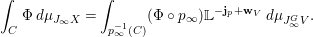 $$\begin{eqnarray}\int _{C}{\rm\Phi}\,d{\it\mu}_{J_{\infty }X}=\int _{p_{\infty }^{-1}(C)}({\rm\Phi}\circ p_{\infty })\mathbb{L}^{-\mathbf{j}_{p}+\mathbf{w}_{V}}\,d{\it\mu}_{J_{\infty }^{G}V}.\end{eqnarray}$$
$$\begin{eqnarray}\int _{C}{\rm\Phi}\,d{\it\mu}_{J_{\infty }X}=\int _{p_{\infty }^{-1}(C)}({\rm\Phi}\circ p_{\infty })\mathbb{L}^{-\mathbf{j}_{p}+\mathbf{w}_{V}}\,d{\it\mu}_{J_{\infty }^{G}V}.\end{eqnarray}$$To explain where the formula comes from, we first show a lemma.
Lemma 5.7. We have
 $$\begin{eqnarray}\text{Jac}_{V^{\left\langle F\right\rangle }/V\times _{D}F}=\mathfrak{m}_{F}^{\sharp H\cdot \boldsymbol{v}_{V}(F)}{\mathcal{O}}_{V^{\left\langle F\right\rangle }}.\end{eqnarray}$$
$$\begin{eqnarray}\text{Jac}_{V^{\left\langle F\right\rangle }/V\times _{D}F}=\mathfrak{m}_{F}^{\sharp H\cdot \boldsymbol{v}_{V}(F)}{\mathcal{O}}_{V^{\left\langle F\right\rangle }}.\end{eqnarray}$$Proof. Let  $u^{\prime }:V^{\left\langle F\right\rangle }\rightarrow V\times _{D}F$ be the natural map. We have the standard exact sequence
$u^{\prime }:V^{\left\langle F\right\rangle }\rightarrow V\times _{D}F$ be the natural map. We have the standard exact sequence
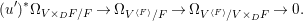 $$\begin{eqnarray}(u^{\prime })^{\ast }{\rm\Omega}_{V\times _{D}F/F}\rightarrow {\rm\Omega}_{V^{\left\langle F\right\rangle }/F}\rightarrow {\rm\Omega}_{V^{\left\langle F\right\rangle }/V\times _{D}F}\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}(u^{\prime })^{\ast }{\rm\Omega}_{V\times _{D}F/F}\rightarrow {\rm\Omega}_{V^{\left\langle F\right\rangle }/F}\rightarrow {\rm\Omega}_{V^{\left\langle F\right\rangle }/V\times _{D}F}\rightarrow 0.\end{eqnarray}$$The left map is identical to the map
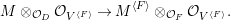 $$\begin{eqnarray}M\otimes _{{\mathcal{O}}_{D}}{\mathcal{O}}_{V^{\left\langle F\right\rangle }}\rightarrow M^{\left\langle F\right\rangle }\otimes _{{\mathcal{O}}_{F}}{\mathcal{O}}_{V^{\left\langle F\right\rangle }}.\end{eqnarray}$$
$$\begin{eqnarray}M\otimes _{{\mathcal{O}}_{D}}{\mathcal{O}}_{V^{\left\langle F\right\rangle }}\rightarrow M^{\left\langle F\right\rangle }\otimes _{{\mathcal{O}}_{F}}{\mathcal{O}}_{V^{\left\langle F\right\rangle }}.\end{eqnarray}$$ Since the Fitting ideal is compatible with base changes (for instance, see [Reference EisenbudEis95, Corollary 20.5]), if ![]() $I$ denotes the zeroth Fitting ideal of
$I$ denotes the zeroth Fitting ideal of
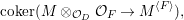 $$\begin{eqnarray}\text{coker}(M\otimes _{{\mathcal{O}}_{D}}{\mathcal{O}}_{F}\rightarrow M^{\left\langle F\right\rangle }),\end{eqnarray}$$
$$\begin{eqnarray}\text{coker}(M\otimes _{{\mathcal{O}}_{D}}{\mathcal{O}}_{F}\rightarrow M^{\left\langle F\right\rangle }),\end{eqnarray}$$ we have 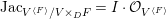 $\text{Jac}_{V^{\left\langle F\right\rangle }/V\times _{D}F}=I\cdot {\mathcal{O}}_{V^{\left\langle F\right\rangle }}$. It is now easy to see that
$\text{Jac}_{V^{\left\langle F\right\rangle }/V\times _{D}F}=I\cdot {\mathcal{O}}_{V^{\left\langle F\right\rangle }}$. It is now easy to see that 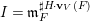 $I=\mathfrak{m}_{F}^{\sharp H\cdot \boldsymbol{v}_{V}(F)}$, for instance, by considering a triangular matrix representing the map
$I=\mathfrak{m}_{F}^{\sharp H\cdot \boldsymbol{v}_{V}(F)}$, for instance, by considering a triangular matrix representing the map 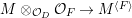 $M\otimes _{{\mathcal{O}}_{D}}{\mathcal{O}}_{F}\rightarrow M^{\left\langle F\right\rangle }$ for suitable bases.◻
$M\otimes _{{\mathcal{O}}_{D}}{\mathcal{O}}_{F}\rightarrow M^{\left\langle F\right\rangle }$ for suitable bases.◻
Conjecture 5.6 can be guessed from the following conjecture.
Conjecture 5.8. For 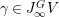 ${\it\gamma}\in J_{\infty }^{G}V$ and
${\it\gamma}\in J_{\infty }^{G}V$ and ![]() $n\gg 0$, the fiber of the map
$n\gg 0$, the fiber of the map
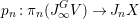 $$\begin{eqnarray}p_{n}:{\it\pi}_{n}(J_{\infty }^{G}V)\rightarrow J_{n}X\end{eqnarray}$$
$$\begin{eqnarray}p_{n}:{\it\pi}_{n}(J_{\infty }^{G}V)\rightarrow J_{n}X\end{eqnarray}$$ over the image of ![]() ${\it\gamma}$ is homeomorphic to a quotient of the affine space
${\it\gamma}$ is homeomorphic to a quotient of the affine space
 $$\begin{eqnarray}\mathbb{A}_{k}^{(\mathbf{j}_{p}-\mathbf{w}_{V})({\it\gamma})}\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{A}_{k}^{(\mathbf{j}_{p}-\mathbf{w}_{V})({\it\gamma})}\end{eqnarray}$$by a linear finite group action.
To see this, we first note that since two ![]() $G$-arcs
$G$-arcs ![]() $E\rightarrow V$ and
$E\rightarrow V$ and 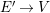 $E^{\prime }\rightarrow V$ with
$E^{\prime }\rightarrow V$ with ![]() $E\not \cong E^{\prime }$ have distinct images in
$E\not \cong E^{\prime }$ have distinct images in ![]() $J_{n}X$ for
$J_{n}X$ for ![]() $n\gg 0$, we can focus on
$n\gg 0$, we can focus on ![]() $J_{\infty }^{G,E}V$ for fixed
$J_{\infty }^{G,E}V$ for fixed ![]() $E$. Fixing a
$E$. Fixing a ![]() $G$-arc
$G$-arc 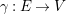 ${\it\gamma}:E\rightarrow V$, we consider the map
${\it\gamma}:E\rightarrow V$, we consider the map
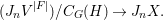 $$\begin{eqnarray}(J_{n}V^{|F|})/C_{G}(H)\rightarrow J_{n}X.\end{eqnarray}$$
$$\begin{eqnarray}(J_{n}V^{|F|})/C_{G}(H)\rightarrow J_{n}X.\end{eqnarray}$$ The fiber of this map over the image of ![]() ${\it\gamma}$ should be homeomorphic to
${\it\gamma}$ should be homeomorphic to
 $$\begin{eqnarray}\mathbb{A}_{k}^{\boldsymbol{ j}_{p^{|F|}}({\it\gamma}^{\prime })}/A,\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{A}_{k}^{\boldsymbol{ j}_{p^{|F|}}({\it\gamma}^{\prime })}/A,\end{eqnarray}$$ where ![]() ${\it\gamma}^{\prime }$ is an arc of
${\it\gamma}^{\prime }$ is an arc of ![]() $V^{|F|}$ corresponding to
$V^{|F|}$ corresponding to ![]() ${\it\gamma}$, and
${\it\gamma}$, and ![]() $A$ is a certain subgroup of
$A$ is a certain subgroup of ![]() $C_{G}(H)$ acting linearly on the affine space. This fact would be proved in the course of proving Conjecture 5.3. On the other hand, the map
$C_{G}(H)$ acting linearly on the affine space. This fact would be proved in the course of proving Conjecture 5.3. On the other hand, the map
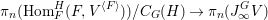 $$\begin{eqnarray}{\it\pi}_{n}(\text{Hom}_{F}^{H}(F,V^{\left\langle F\right\rangle }))/C_{G}(H)\rightarrow {\it\pi}_{n}(J_{\infty }^{G}V)\end{eqnarray}$$
$$\begin{eqnarray}{\it\pi}_{n}(\text{Hom}_{F}^{H}(F,V^{\left\langle F\right\rangle }))/C_{G}(H)\rightarrow {\it\pi}_{n}(J_{\infty }^{G}V)\end{eqnarray}$$ induced by ![]() $u$ has fibers homeomorphic to
$u$ has fibers homeomorphic to
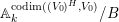 $$\begin{eqnarray}\mathbb{A}_{k}^{\text{codim}((V_{0})^{H},V_{0})}/B\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{A}_{k}^{\text{codim}((V_{0})^{H},V_{0})}/B\end{eqnarray}$$ for some finite group ![]() $B$, which can be seen by looking at diagrams (4.2)–(4.4). From Lemma 5.7,
$B$, which can be seen by looking at diagrams (4.2)–(4.4). From Lemma 5.7,
 $$\begin{eqnarray}\displaystyle \mathbf{j}_{p^{|F|}}\hspace{-1.0pt}-\hspace{-1.0pt}\text{codim}((V_{0})^{H},V_{0}) & = & \displaystyle \mathbf{j}_{V^{\left\langle F\right\rangle }/X\times _{D}F}-\text{codim}((V_{0})^{H},V_{0})\nonumber\\ \displaystyle & = & \displaystyle (\mathbf{j}_{V\times _{D}F/X\times _{D}F}+\mathbf{j}_{V^{\left\langle F\right\rangle }/V\times _{D}F})\hspace{-2.0pt}-\hspace{-2.0pt}\text{codim}((V_{0})^{H},V_{0})\nonumber\\ \displaystyle & = & \displaystyle \mathbf{j}_{p}-\mathbf{w}_{V},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathbf{j}_{p^{|F|}}\hspace{-1.0pt}-\hspace{-1.0pt}\text{codim}((V_{0})^{H},V_{0}) & = & \displaystyle \mathbf{j}_{V^{\left\langle F\right\rangle }/X\times _{D}F}-\text{codim}((V_{0})^{H},V_{0})\nonumber\\ \displaystyle & = & \displaystyle (\mathbf{j}_{V\times _{D}F/X\times _{D}F}+\mathbf{j}_{V^{\left\langle F\right\rangle }/V\times _{D}F})\hspace{-2.0pt}-\hspace{-2.0pt}\text{codim}((V_{0})^{H},V_{0})\nonumber\\ \displaystyle & = & \displaystyle \mathbf{j}_{p}-\mathbf{w}_{V},\nonumber\end{eqnarray}$$concluding Conjecture 5.8.
6 The McKay correspondence for linear actions
To state the McKay correspondence conjecture for linear actions, we first define the notion of orbifold stringy motifs. Keeping the notation from the last section, let ![]() $\mathfrak{X}$,
$\mathfrak{X}$, ![]() $\mathfrak{V}$,
$\mathfrak{V}$, ![]() $\mathfrak{V}^{\left\langle F\right\rangle }$ and
$\mathfrak{V}^{\left\langle F\right\rangle }$ and ![]() $\mathfrak{V}^{|F|}$ be centered log structures on
$\mathfrak{V}^{|F|}$ be centered log structures on ![]() $X$,
$X$, ![]() $V$,
$V$, ![]() $V^{\left\langle F\right\rangle }$ and
$V^{\left\langle F\right\rangle }$ and ![]() $V^{|F|}$ respectively, so that the following morphisms are all crepant:
$V^{|F|}$ respectively, so that the following morphisms are all crepant:

Since ![]() $X$ is
$X$ is ![]() $\mathbb{Q}$-factorial, either
$\mathbb{Q}$-factorial, either ![]() $\mathfrak{X}$ or
$\mathfrak{X}$ or ![]() $\mathfrak{V}$ determines the other centered log structures. The centered log structure
$\mathfrak{V}$ determines the other centered log structures. The centered log structure ![]() $\mathfrak{V}$ is
$\mathfrak{V}$ is ![]() $G$-equivariant and
$G$-equivariant and ![]() $\mathfrak{V}^{|F|}$
$\mathfrak{V}^{|F|}$![]() $C_{G}(H)$-equivariant.
$C_{G}(H)$-equivariant.
Definition 6.1. We define the orbifold stringy motif of the centered log ![]() $G$-
$G$-![]() $D$-variety
$D$-variety ![]() $\mathfrak{V}$ to be
$\mathfrak{V}$ to be
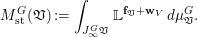 $$\begin{eqnarray}M_{\text{st}}^{G}(\mathfrak{V}):=\int _{J_{\infty }^{G}\mathfrak{V}}\mathbb{L}^{\mathbf{f}_{\mathfrak{V}}+\mathbf{w}_{V}}\,d{\it\mu}_{\mathfrak{V}}^{G}.\end{eqnarray}$$
$$\begin{eqnarray}M_{\text{st}}^{G}(\mathfrak{V}):=\int _{J_{\infty }^{G}\mathfrak{V}}\mathbb{L}^{\mathbf{f}_{\mathfrak{V}}+\mathbf{w}_{V}}\,d{\it\mu}_{\mathfrak{V}}^{G}.\end{eqnarray}$$ Note that since ![]() $\mathfrak{V}$ is smooth over
$\mathfrak{V}$ is smooth over ![]() $D$, we have
$D$, we have 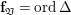 $\mathbf{f}_{\mathfrak{V}}=\text{ord}\,{\rm\Delta}$ for the boundary
$\mathbf{f}_{\mathfrak{V}}=\text{ord}\,{\rm\Delta}$ for the boundary ![]() ${\rm\Delta}$ of
${\rm\Delta}$ of ![]() $\mathfrak{V}$.
$\mathfrak{V}$.
Arguments as in the proof of Proposition 2.6 deduce the following conjecture from Conjecture 5.6.
Conjecture 6.2. (The motivic McKay correspondence for linear actions I)
We have
 $$\begin{eqnarray}M_{\text{st}}(\mathfrak{X})=M_{\text{st}}^{G}(\mathfrak{V}).\end{eqnarray}$$
$$\begin{eqnarray}M_{\text{st}}(\mathfrak{X})=M_{\text{st}}^{G}(\mathfrak{V}).\end{eqnarray}$$We next formulate a conjecture presented in a slightly different way so that we are able to generalize it to the nonlinear case easily.
Definition 6.3. For 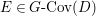 $E\in G\text{-}\text{Cov}(D)$, we define the
$E\in G\text{-}\text{Cov}(D)$, we define the ![]() $E$-parts of
$E$-parts of 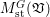 $M_{\text{st}}^{G}(\mathfrak{V})$ and
$M_{\text{st}}^{G}(\mathfrak{V})$ and ![]() $M_{\text{st}}(\mathfrak{X})$ respectively by
$M_{\text{st}}(\mathfrak{X})$ respectively by
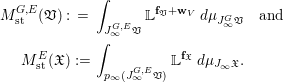 $$\begin{eqnarray}\displaystyle M_{\text{st}}^{G,E}(\mathfrak{V}): & = & \displaystyle \int _{J_{\infty }^{G,E}\mathfrak{V}}\mathbb{L}^{\mathbf{f}_{\mathfrak{V}}+\mathbf{w}_{V}}\,d{\it\mu}_{J_{\infty }^{G}\mathfrak{V}}\quad \text{and}\nonumber\\ \displaystyle M_{\text{st}}^{E}(\mathfrak{X}) & := & \displaystyle \int _{p_{\infty }(J_{\infty }^{G,E}\mathfrak{V})}\mathbb{L}^{\mathbf{f}_{\mathfrak{X}}}\,d{\it\mu}_{J_{\infty }\mathfrak{X}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle M_{\text{st}}^{G,E}(\mathfrak{V}): & = & \displaystyle \int _{J_{\infty }^{G,E}\mathfrak{V}}\mathbb{L}^{\mathbf{f}_{\mathfrak{V}}+\mathbf{w}_{V}}\,d{\it\mu}_{J_{\infty }^{G}\mathfrak{V}}\quad \text{and}\nonumber\\ \displaystyle M_{\text{st}}^{E}(\mathfrak{X}) & := & \displaystyle \int _{p_{\infty }(J_{\infty }^{G,E}\mathfrak{V})}\mathbb{L}^{\mathbf{f}_{\mathfrak{X}}}\,d{\it\mu}_{J_{\infty }\mathfrak{X}}.\nonumber\end{eqnarray}$$By the same reasoning as that for the last conjecture, we would have
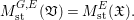 $$\begin{eqnarray}M_{\text{st}}^{G,E}(\mathfrak{V})=M_{\text{st}}^{E}(\mathfrak{X}).\end{eqnarray}$$
$$\begin{eqnarray}M_{\text{st}}^{G,E}(\mathfrak{V})=M_{\text{st}}^{E}(\mathfrak{X}).\end{eqnarray}$$On the other hand, from Conjecture 5.3, we would have
 $$\begin{eqnarray}M_{\text{st}}^{E}(\mathfrak{X})=M_{\text{st},C_{G}(H)}(\mathfrak{V}^{|F|}).\end{eqnarray}$$
$$\begin{eqnarray}M_{\text{st}}^{E}(\mathfrak{X})=M_{\text{st},C_{G}(H)}(\mathfrak{V}^{|F|}).\end{eqnarray}$$ Let 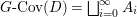 $G\text{-}\text{Cov}(D)=\sqcup _{i=0}^{\infty }A_{i}$ be a conjectural stratification with finite-dimensional strata
$G\text{-}\text{Cov}(D)=\sqcup _{i=0}^{\infty }A_{i}$ be a conjectural stratification with finite-dimensional strata ![]() $A_{i}$ (see Remark 3.6). The author [Reference YasudaYasa] conjectures also that each stratum
$A_{i}$ (see Remark 3.6). The author [Reference YasudaYasa] conjectures also that each stratum ![]() $A_{i}$ may not be of finite type over
$A_{i}$ may not be of finite type over ![]() $k$, but the limit of a family
$k$, but the limit of a family
 $$\begin{eqnarray}X_{1}\xrightarrow[]{f_{1}}X_{2}\xrightarrow[]{f_{2}}\cdots\end{eqnarray}$$
$$\begin{eqnarray}X_{1}\xrightarrow[]{f_{1}}X_{2}\xrightarrow[]{f_{2}}\cdots\end{eqnarray}$$ such that ![]() $X_{j}$ are of finite type and
$X_{j}$ are of finite type and ![]() $f_{i}$ are homeomorphisms. We then define a constructible subset of
$f_{i}$ are homeomorphisms. We then define a constructible subset of 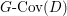 $G\text{-}\text{Cov}(D)$ as a constructible subset of
$G\text{-}\text{Cov}(D)$ as a constructible subset of 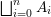 $\sqcup _{i=0}^{n}A_{i}$ for some
$\sqcup _{i=0}^{n}A_{i}$ for some ![]() $n<\infty$, which would be well defined thanks to this conjecture. For a constructible subset
$n<\infty$, which would be well defined thanks to this conjecture. For a constructible subset ![]() $C$ of
$C$ of 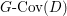 $G\text{-}\text{Cov}(D)$, its class
$G\text{-}\text{Cov}(D)$, its class ![]() $[C]$ in
$[C]$ in ![]() ${\mathcal{R}}$ is well defined. Let
${\mathcal{R}}$ is well defined. Let ![]() ${\it\tau}$ denote the tautological motivic measure on
${\it\tau}$ denote the tautological motivic measure on 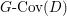 $G\text{-}\text{Cov}(D)$ given by
$G\text{-}\text{Cov}(D)$ given by 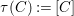 ${\it\tau}(C):=[C]$ for a constructible subset
${\it\tau}(C):=[C]$ for a constructible subset ![]() $C$. If a function
$C$. If a function 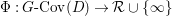 ${\rm\Phi}:G\text{-}\text{Cov}(D)\rightarrow {\mathcal{R}}\cup \{\infty \}$ is constructible, that is, its image is countable and all fibers
${\rm\Phi}:G\text{-}\text{Cov}(D)\rightarrow {\mathcal{R}}\cup \{\infty \}$ is constructible, that is, its image is countable and all fibers ![]() ${\rm\Phi}^{-1}(a)$,
${\rm\Phi}^{-1}(a)$, ![]() $a\in {\mathcal{R}}$ are constructible, then the integral
$a\in {\mathcal{R}}$ are constructible, then the integral 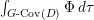 $\int _{G\text{-}\text{Cov}(D)}{\rm\Phi}\,d{\it\tau}$ is defined by
$\int _{G\text{-}\text{Cov}(D)}{\rm\Phi}\,d{\it\tau}$ is defined by
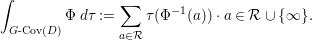 $$\begin{eqnarray}\int _{G\text{-}\text{Cov}(D)}{\rm\Phi}\,d{\it\tau}:=\mathop{\sum }_{a\in {\mathcal{R}}}{\it\tau}({\rm\Phi}^{-1}(a))\cdot a\in {\mathcal{R}}\cup \{\infty \}.\end{eqnarray}$$
$$\begin{eqnarray}\int _{G\text{-}\text{Cov}(D)}{\rm\Phi}\,d{\it\tau}:=\mathop{\sum }_{a\in {\mathcal{R}}}{\it\tau}({\rm\Phi}^{-1}(a))\cdot a\in {\mathcal{R}}\cup \{\infty \}.\end{eqnarray}$$From Conjecture 6.2 and conjectural equations (6.1) and (6.2), it seems natural to expect
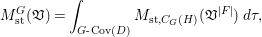 $$\begin{eqnarray}M_{\text{st}}^{G}(\mathfrak{V})=\int _{G\text{-}\text{Cov}(D)}M_{\text{st},C_{G}(H)}(\mathfrak{V}^{|F|})\,d{\it\tau},\end{eqnarray}$$
$$\begin{eqnarray}M_{\text{st}}^{G}(\mathfrak{V})=\int _{G\text{-}\text{Cov}(D)}M_{\text{st},C_{G}(H)}(\mathfrak{V}^{|F|})\,d{\it\tau},\end{eqnarray}$$and hence we have the following conjecture.
Conjecture 6.4. (The motivic McKay correspondence for linear actions II)
We have
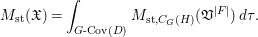 $$\begin{eqnarray}M_{\text{st}}(\mathfrak{X})=\int _{G\text{-}\text{Cov}(D)}M_{\text{st},C_{G}(H)}(\mathfrak{V}^{|F|})\,d{\it\tau}.\end{eqnarray}$$
$$\begin{eqnarray}M_{\text{st}}(\mathfrak{X})=\int _{G\text{-}\text{Cov}(D)}M_{\text{st},C_{G}(H)}(\mathfrak{V}^{|F|})\,d{\it\tau}.\end{eqnarray}$$This formulation of the McKay correspondence is what we generalize to the nonlinear case.
To make this conjecture more meaningful, it would be nice if we could compute  $M_{\text{st},C_{G}(H)}(\mathfrak{V}^{|F|})$ explicitly. For this purpose, next we see how to determine the centered log structures
$M_{\text{st},C_{G}(H)}(\mathfrak{V}^{|F|})$ explicitly. For this purpose, next we see how to determine the centered log structures ![]() $\mathfrak{V}^{\left\langle F\right\rangle }$ and
$\mathfrak{V}^{\left\langle F\right\rangle }$ and ![]() $\mathfrak{V}^{|F|}$ from
$\mathfrak{V}^{|F|}$ from ![]() $\mathfrak{V}$. Let us write
$\mathfrak{V}$. Let us write  $\mathfrak{V}=(V,{\rm\Delta},W)$,
$\mathfrak{V}=(V,{\rm\Delta},W)$, 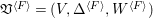 $\mathfrak{V}^{\left\langle F\right\rangle }=(V,{\rm\Delta}^{\left\langle F\right\rangle },W^{\left\langle F\right\rangle })$ and
$\mathfrak{V}^{\left\langle F\right\rangle }=(V,{\rm\Delta}^{\left\langle F\right\rangle },W^{\left\langle F\right\rangle })$ and 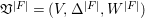 $\mathfrak{V}^{|F|}=(V,{\rm\Delta}^{|F|},W^{|F|})$. The centers
$\mathfrak{V}^{|F|}=(V,{\rm\Delta}^{|F|},W^{|F|})$. The centers ![]() $W^{\left\langle F\right\rangle }$ and
$W^{\left\langle F\right\rangle }$ and ![]() $W^{|F|}$ are simply determined by
$W^{|F|}$ are simply determined by
 $$\begin{eqnarray}W^{\left\langle F\right\rangle }=u^{-1}(W)\quad \text{and}\quad W^{|F|}=r(W^{\left\langle F\right\rangle }).\end{eqnarray}$$
$$\begin{eqnarray}W^{\left\langle F\right\rangle }=u^{-1}(W)\quad \text{and}\quad W^{|F|}=r(W^{\left\langle F\right\rangle }).\end{eqnarray}$$ The boundaries ![]() ${\rm\Delta}^{\left\langle F\right\rangle }$ and
${\rm\Delta}^{\left\langle F\right\rangle }$ and ![]() ${\rm\Delta}^{|F|}$ are determined as follows.
${\rm\Delta}^{|F|}$ are determined as follows.
Lemma 6.5. Regarding ![]() $V_{0}^{\left\langle F\right\rangle }$ and
$V_{0}^{\left\langle F\right\rangle }$ and ![]() $V_{0}^{|F|}$ prime divisors on
$V_{0}^{|F|}$ prime divisors on ![]() $V^{\left\langle F\right\rangle }$ and
$V^{\left\langle F\right\rangle }$ and ![]() $V^{|F|}$, we have
$V^{|F|}$, we have
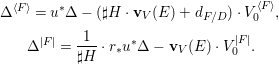 $$\begin{eqnarray}\displaystyle & {\rm\Delta}^{\left\langle F\right\rangle }=u^{\ast }{\rm\Delta}-(\sharp H\cdot \boldsymbol{v}_{V}(E)+d_{F/D})\cdot V_{0}^{\left\langle F\right\rangle }, & \displaystyle \nonumber\\ \displaystyle & {\rm\Delta}^{|F|}=\displaystyle \frac{1}{\sharp H}\cdot r_{\ast }u^{\ast }{\rm\Delta}-\boldsymbol{v}_{V}(E)\cdot V_{0}^{|F|}. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & {\rm\Delta}^{\left\langle F\right\rangle }=u^{\ast }{\rm\Delta}-(\sharp H\cdot \boldsymbol{v}_{V}(E)+d_{F/D})\cdot V_{0}^{\left\langle F\right\rangle }, & \displaystyle \nonumber\\ \displaystyle & {\rm\Delta}^{|F|}=\displaystyle \frac{1}{\sharp H}\cdot r_{\ast }u^{\ast }{\rm\Delta}-\boldsymbol{v}_{V}(E)\cdot V_{0}^{|F|}. & \displaystyle \nonumber\end{eqnarray}$$ Here, ![]() $d_{F/D}$ is the different exponent of
$d_{F/D}$ is the different exponent of ![]() $F/D$, characterized by
$F/D$, characterized by  ${\rm\Omega}_{F/D}\cong {\mathcal{O}}_{F}/\mathfrak{m}_{F}^{d_{F/D}}$.
${\rm\Omega}_{F/D}\cong {\mathcal{O}}_{F}/\mathfrak{m}_{F}^{d_{F/D}}$.
Proof. For the first equality, we have
 $$\begin{eqnarray}\displaystyle u^{\ast }(K_{V}+{\rm\Delta}) & = & \displaystyle K_{V^{\left\langle F\right\rangle }}-K_{V^{\left\langle F\right\rangle }/V}+u^{\ast }{\rm\Delta}\nonumber\\ \displaystyle & = & \displaystyle K_{V^{\left\langle F\right\rangle }}-K_{V^{\left\langle F\right\rangle }/V\times _{D}F}-(u^{\prime })^{\ast }K_{V\times _{D}F/V}+u^{\ast }{\rm\Delta}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle u^{\ast }(K_{V}+{\rm\Delta}) & = & \displaystyle K_{V^{\left\langle F\right\rangle }}-K_{V^{\left\langle F\right\rangle }/V}+u^{\ast }{\rm\Delta}\nonumber\\ \displaystyle & = & \displaystyle K_{V^{\left\langle F\right\rangle }}-K_{V^{\left\langle F\right\rangle }/V\times _{D}F}-(u^{\prime })^{\ast }K_{V\times _{D}F/V}+u^{\ast }{\rm\Delta}.\nonumber\end{eqnarray}$$ Here, ![]() $K_{V^{\left\langle F\right\rangle }}$ is the canonical divisor of
$K_{V^{\left\langle F\right\rangle }}$ is the canonical divisor of ![]() $V^{\left\langle F\right\rangle }$ as a
$V^{\left\langle F\right\rangle }$ as a ![]() $D$-variety rather than an
$D$-variety rather than an ![]() $F$-variety, and
$F$-variety, and ![]() $u^{\prime }$ denotes the natural morphism
$u^{\prime }$ denotes the natural morphism 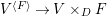 $V^{\left\langle F\right\rangle }\rightarrow V\times _{D}F$. From Lemma 5.7,
$V^{\left\langle F\right\rangle }\rightarrow V\times _{D}F$. From Lemma 5.7,
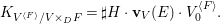 $$\begin{eqnarray}K_{V^{\left\langle F\right\rangle }/V\times _{D}F}=\sharp H\cdot \boldsymbol{v}_{V}(E)\cdot V_{0}^{\left\langle F\right\rangle }.\end{eqnarray}$$
$$\begin{eqnarray}K_{V^{\left\langle F\right\rangle }/V\times _{D}F}=\sharp H\cdot \boldsymbol{v}_{V}(E)\cdot V_{0}^{\left\langle F\right\rangle }.\end{eqnarray}$$ Since 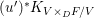 $(u^{\prime })^{\ast }K_{V\times _{D}F/V}$ is the pullback of
$(u^{\prime })^{\ast }K_{V\times _{D}F/V}$ is the pullback of ![]() $K_{F/D}$, we have
$K_{F/D}$, we have
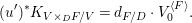 $$\begin{eqnarray}(u^{\prime })^{\ast }K_{V\times _{D}F/V}=d_{F/D}\cdot V_{0}^{\left\langle F\right\rangle }.\end{eqnarray}$$
$$\begin{eqnarray}(u^{\prime })^{\ast }K_{V\times _{D}F/V}=d_{F/D}\cdot V_{0}^{\left\langle F\right\rangle }.\end{eqnarray}$$These equalities show the first equality of the lemma.
The second one follows from
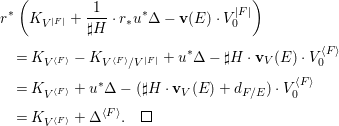 $$\begin{eqnarray}\displaystyle & & \displaystyle r^{\ast }\left(K_{V^{|F|}}+\frac{1}{\sharp H}\cdot r_{\ast }u^{\ast }{\rm\Delta}-\boldsymbol{v}(E)\cdot V_{0}^{|F|}\right)\nonumber\\ \displaystyle & & \displaystyle \quad =K_{V^{\left\langle F\right\rangle }}-K_{V^{\left\langle F\right\rangle }/V^{|F|}}+u^{\ast }{\rm\Delta}-\sharp H\cdot \boldsymbol{v}_{V}(E)\cdot V_{0}^{\left\langle F\right\rangle }\nonumber\\ \displaystyle & & \displaystyle \quad =K_{V^{\left\langle F\right\rangle }}+u^{\ast }{\rm\Delta}-(\sharp H\cdot \boldsymbol{v}_{V}(E)+d_{F/E})\cdot V_{0}^{\left\langle F\right\rangle }\nonumber\\ \displaystyle & & \displaystyle \quad =K_{V^{\left\langle F\right\rangle }}+{\rm\Delta}^{\left\langle F\right\rangle }.\square\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle r^{\ast }\left(K_{V^{|F|}}+\frac{1}{\sharp H}\cdot r_{\ast }u^{\ast }{\rm\Delta}-\boldsymbol{v}(E)\cdot V_{0}^{|F|}\right)\nonumber\\ \displaystyle & & \displaystyle \quad =K_{V^{\left\langle F\right\rangle }}-K_{V^{\left\langle F\right\rangle }/V^{|F|}}+u^{\ast }{\rm\Delta}-\sharp H\cdot \boldsymbol{v}_{V}(E)\cdot V_{0}^{\left\langle F\right\rangle }\nonumber\\ \displaystyle & & \displaystyle \quad =K_{V^{\left\langle F\right\rangle }}+u^{\ast }{\rm\Delta}-(\sharp H\cdot \boldsymbol{v}_{V}(E)+d_{F/E})\cdot V_{0}^{\left\langle F\right\rangle }\nonumber\\ \displaystyle & & \displaystyle \quad =K_{V^{\left\langle F\right\rangle }}+{\rm\Delta}^{\left\langle F\right\rangle }.\square\nonumber\end{eqnarray}$$Example 6.6. Suppose that ![]() ${\rm\Delta}=0$ and
${\rm\Delta}=0$ and  $W=\{o\}$, with
$W=\{o\}$, with ![]() $o\in V_{0}$ the origin. Then
$o\in V_{0}$ the origin. Then 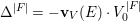 ${\rm\Delta}^{|F|}=-\boldsymbol{v}_{V}(E)\cdot V_{0}^{|F|}$ and
${\rm\Delta}^{|F|}=-\boldsymbol{v}_{V}(E)\cdot V_{0}^{|F|}$ and 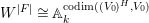 $W^{|F|}\cong \mathbb{A}_{k}^{\text{codim}((V_{0})^{H},V_{0})}$. Hence,
$W^{|F|}\cong \mathbb{A}_{k}^{\text{codim}((V_{0})^{H},V_{0})}$. Hence,
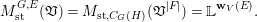 $$\begin{eqnarray}M_{\text{st}}^{G,E}(\mathfrak{V})=M_{\text{st},C_{G}(H)}(\mathfrak{V}^{|F|})=\mathbb{L}^{\mathbf{w}_{V}(E)}.\end{eqnarray}$$
$$\begin{eqnarray}M_{\text{st}}^{G,E}(\mathfrak{V})=M_{\text{st},C_{G}(H)}(\mathfrak{V}^{|F|})=\mathbb{L}^{\mathbf{w}_{V}(E)}.\end{eqnarray}$$Conjecture 6.4 is reduced to the form
 $$\begin{eqnarray}M_{\text{st}}(\mathfrak{X})=\int _{G\text{-}\text{Cov}(D)}\mathbb{L}^{\mathbf{w}_{V}}\,d{\it\tau}.\end{eqnarray}$$
$$\begin{eqnarray}M_{\text{st}}(\mathfrak{X})=\int _{G\text{-}\text{Cov}(D)}\mathbb{L}^{\mathbf{w}_{V}}\,d{\it\tau}.\end{eqnarray}$$ If 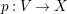 $p:V\rightarrow X$ is étale in codimension one, and if we denote
$p:V\rightarrow X$ is étale in codimension one, and if we denote ![]() $p(o)$ again by
$p(o)$ again by ![]() $o$, then
$o$, then 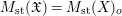 $M_{\text{st}}(\mathfrak{X})=M_{\text{st}}(X)_{o}$, and the last equality is exactly what was conjectured in [Reference YasudaYasa].
$M_{\text{st}}(\mathfrak{X})=M_{\text{st}}(X)_{o}$, and the last equality is exactly what was conjectured in [Reference YasudaYasa].
Remark 6.7. If ![]() $\sharp G$ is prime to the characteristic of
$\sharp G$ is prime to the characteristic of ![]() $k$, then
$k$, then 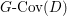 $G\text{-}\text{Cov}(D)$ is identified with the set of conjugacy classes of
$G\text{-}\text{Cov}(D)$ is identified with the set of conjugacy classes of ![]() $G$, denoted by
$G$, denoted by  $\text{Conj}(G)$. Equality (6.3) in the last example is then written as
$\text{Conj}(G)$. Equality (6.3) in the last example is then written as
 $$\begin{eqnarray}M_{\text{st}}(\mathfrak{X})=\mathop{\sum }_{[g]\in \text{Conj}(G)}\mathbb{L}^{\mathbf{w}_{V}(g)}.\end{eqnarray}$$
$$\begin{eqnarray}M_{\text{st}}(\mathfrak{X})=\mathop{\sum }_{[g]\in \text{Conj}(G)}\mathbb{L}^{\mathbf{w}_{V}(g)}.\end{eqnarray}$$ Expressing the weights ![]() $\mathbf{w}_{V}(g)$ in terms of eigenvalues, we recover results by Batyrev [Reference BatyrevBat99] and Denef and Loeser [Reference Denef and LoeserDL02].
$\mathbf{w}_{V}(g)$ in terms of eigenvalues, we recover results by Batyrev [Reference BatyrevBat99] and Denef and Loeser [Reference Denef and LoeserDL02].
7 The McKay correspondence for nonlinear actions
In this section, we generalize Conjecture 6.4 to the nonlinear case. This is rather easy, once we have formulated the conjecture as it is.
Let us consider an affine ![]() $D$-variety
$D$-variety 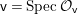 $\mathsf{v}=\text{Spec}\,{\mathcal{O}}_{\mathsf{v}}$ endowed with a faithful
$\mathsf{v}=\text{Spec}\,{\mathcal{O}}_{\mathsf{v}}$ endowed with a faithful ![]() $G$-action. We fix a
$G$-action. We fix a ![]() $G$-equivariant (locally closed) immersion
$G$-equivariant (locally closed) immersion
into an affine space 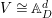 $V\cong \mathbb{A}_{D}^{d}$ endowed with a linear
$V\cong \mathbb{A}_{D}^{d}$ endowed with a linear ![]() $G$-action. Identifying
$G$-action. Identifying ![]() $G$-arcs of
$G$-arcs of ![]() $\mathsf{v}$ with those of
$\mathsf{v}$ with those of ![]() $V$ factoring through
$V$ factoring through ![]() $\mathsf{v}$, we regard
$\mathsf{v}$, we regard ![]() $J_{\infty }^{G}\mathsf{v}$ as a subset of
$J_{\infty }^{G}\mathsf{v}$ as a subset of ![]() $J_{\infty }^{G}V$.
$J_{\infty }^{G}V$.
Remark 7.1. Such an immersion always exists. Indeed, let 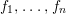 $f_{1},\ldots ,f_{n}$ be generators of
$f_{1},\ldots ,f_{n}$ be generators of ![]() ${\mathcal{O}}_{\mathsf{v}}$ as an
${\mathcal{O}}_{\mathsf{v}}$ as an ![]() ${\mathcal{O}}_{D}$-algebra, let
${\mathcal{O}}_{D}$-algebra, let 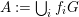 $A:=\bigcup _{i}f_{i}G$, the union of their orbits, and let
$A:=\bigcup _{i}f_{i}G$, the union of their orbits, and let 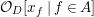 ${\mathcal{O}}_{D}[x_{f}\mid f\in A]$ be the polynomial ring with variables
${\mathcal{O}}_{D}[x_{f}\mid f\in A]$ be the polynomial ring with variables ![]() $x_{f}$,
$x_{f}$, ![]() $f\in A$ over
$f\in A$ over ![]() ${\mathcal{O}}_{D}$. The ring has a natural
${\mathcal{O}}_{D}$. The ring has a natural ![]() $G$-action by permutations of variables. The
$G$-action by permutations of variables. The ![]() ${\mathcal{O}}_{D}$-algebra homomorphism
${\mathcal{O}}_{D}$-algebra homomorphism
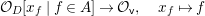 $$\begin{eqnarray}{\mathcal{O}}_{D}[x_{f}\mid f\in A]\rightarrow {\mathcal{O}}_{\mathsf{v}},\quad x_{f}\mapsto f\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{O}}_{D}[x_{f}\mid f\in A]\rightarrow {\mathcal{O}}_{\mathsf{v}},\quad x_{f}\mapsto f\end{eqnarray}$$ defines a desired immersion. Moreover, this construction gives a closed immersion into ![]() $V$ on which
$V$ on which ![]() $G$ acts by permutations. In this case, our weight function
$G$ acts by permutations. In this case, our weight function ![]() $\mathbf{w}_{V}$ is closely related to the Artin and Swan conductors [Reference Wood and YasudaWY15], although we do not use this fact in this paper.
$\mathbf{w}_{V}$ is closely related to the Artin and Swan conductors [Reference Wood and YasudaWY15], although we do not use this fact in this paper.
Definition 7.2. For 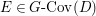 $E\in G\text{-}\text{Cov}(D)$ with a connected component
$E\in G\text{-}\text{Cov}(D)$ with a connected component ![]() $F$, we define the pre-untwisting variety of
$F$, we define the pre-untwisting variety of ![]() $\mathsf{v}$, denoted by
$\mathsf{v}$, denoted by ![]() $\mathsf{v}^{\left\langle F\right\rangle }$, as the irreducible component of
$\mathsf{v}^{\left\langle F\right\rangle }$, as the irreducible component of 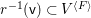 $r^{-1}(\mathsf{v})\subset V^{\left\langle F\right\rangle }$ which dominates
$r^{-1}(\mathsf{v})\subset V^{\left\langle F\right\rangle }$ which dominates ![]() $\mathsf{v}$. We then define the untwisting variety, denoted by
$\mathsf{v}$. We then define the untwisting variety, denoted by ![]() $\mathsf{v}^{|F|}$, as the image of
$\mathsf{v}^{|F|}$, as the image of ![]() $\mathsf{v}^{\left\langle F\right\rangle }$ in
$\mathsf{v}^{\left\langle F\right\rangle }$ in ![]() $V^{|F|}$. We also define the normalized pre-untwisting
$V^{|F|}$. We also define the normalized pre-untwisting ![]() $\mathsf{v}^{\left\langle F\right\rangle ,{\it\nu}}$and untwisting varieties
$\mathsf{v}^{\left\langle F\right\rangle ,{\it\nu}}$and untwisting varieties ![]() $\mathsf{v}^{|F|,{\it\nu}}$ to be the normalizations of
$\mathsf{v}^{|F|,{\it\nu}}$ to be the normalizations of ![]() $\mathsf{v}^{\left\langle F\right\rangle }$ and
$\mathsf{v}^{\left\langle F\right\rangle }$ and ![]() $\mathsf{v}^{|F|}$ respectively.
$\mathsf{v}^{|F|}$ respectively.
Let 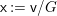 $\mathsf{x}:=\mathsf{v}/G$. The following diagram shows natural morphisms of relevant varieties, and the symbols
$\mathsf{x}:=\mathsf{v}/G$. The following diagram shows natural morphisms of relevant varieties, and the symbols ![]() $t$,
$t$, ![]() $s$ and
$s$ and ![]() $q$ denote morphisms as indicated:
$q$ denote morphisms as indicated:
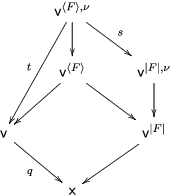 $$\begin{eqnarray}\begin{array}{@{}c@{}}\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}c@{}}\end{array}\end{eqnarray}$$The one-to-one correspondence obtained in the last section,
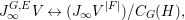 $$\begin{eqnarray}J_{\infty }^{G,E}V\leftrightarrow (J_{\infty }V^{|F|})/C_{G}(H),\end{eqnarray}$$
$$\begin{eqnarray}J_{\infty }^{G,E}V\leftrightarrow (J_{\infty }V^{|F|})/C_{G}(H),\end{eqnarray}$$induces a one-to-one correspondence
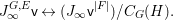 $$\begin{eqnarray}J_{\infty }^{G,E}\mathsf{v}\leftrightarrow (J_{\infty }\mathsf{v}^{|F|})/C_{G}(H).\end{eqnarray}$$
$$\begin{eqnarray}J_{\infty }^{G,E}\mathsf{v}\leftrightarrow (J_{\infty }\mathsf{v}^{|F|})/C_{G}(H).\end{eqnarray}$$We obtain the following diagram:
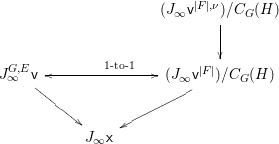
If we put ![]() $J_{\infty }^{E}\mathsf{x}$ to be the image of
$J_{\infty }^{E}\mathsf{x}$ to be the image of ![]() $J_{\infty }^{G,E}\mathsf{v}$ in
$J_{\infty }^{G,E}\mathsf{v}$ in ![]() $J_{\infty }\mathsf{x}$, then we can naturally expect that
$J_{\infty }\mathsf{x}$, then we can naturally expect that ![]() $J_{\infty }^{E}\mathsf{x}$ coincides with the images of
$J_{\infty }^{E}\mathsf{x}$ coincides with the images of ![]() $J_{\infty }\mathsf{v}^{|F|}$ and
$J_{\infty }\mathsf{v}^{|F|}$ and 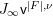 $J_{\infty }\mathsf{v}^{|F|,{\it\nu}}$ modulo measure zero subsets.
$J_{\infty }\mathsf{v}^{|F|,{\it\nu}}$ modulo measure zero subsets.
From now on, we suppose that ![]() $\mathsf{v}$ is normal. Let
$\mathsf{v}$ is normal. Let ![]() $\mathfrak{v}$,
$\mathfrak{v}$, ![]() $\mathfrak{v}^{\left\langle F\right\rangle ,{\it\nu}}$,
$\mathfrak{v}^{\left\langle F\right\rangle ,{\it\nu}}$, ![]() $\mathfrak{v}^{|F|,{\it\nu}}$ and
$\mathfrak{v}^{|F|,{\it\nu}}$ and ![]() $\mathfrak{x}$ be centered log structures on
$\mathfrak{x}$ be centered log structures on ![]() $\mathsf{v}$,
$\mathsf{v}$, ![]() $\mathsf{v}^{\left\langle F\right\rangle ,{\it\nu}}$ and
$\mathsf{v}^{\left\langle F\right\rangle ,{\it\nu}}$ and ![]() $\mathsf{v}^{|F|,{\it\nu}}$ respectively such that the morphisms
$\mathsf{v}^{|F|,{\it\nu}}$ respectively such that the morphisms
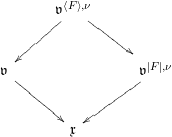
are all crepant. The centered log ![]() $D$-varieties
$D$-varieties ![]() $\mathfrak{v}$ and
$\mathfrak{v}$ and ![]() $\mathfrak{v}^{|F|,{\it\nu}}$ are
$\mathfrak{v}^{|F|,{\it\nu}}$ are ![]() $G$- and
$G$- and ![]() $C_{G}(H)$-equivariant respectively. If we define the
$C_{G}(H)$-equivariant respectively. If we define the ![]() $E$-part
$E$-part ![]() $M_{\text{st}}^{E}(\mathfrak{x})$ of
$M_{\text{st}}^{E}(\mathfrak{x})$ of ![]() $M_{\text{st}}(\mathfrak{x})$, we can expect
$M_{\text{st}}(\mathfrak{x})$, we can expect
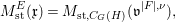 $$\begin{eqnarray}M_{\text{st}}^{E}(\mathfrak{x})=M_{\text{st},C_{G}(H)}(\mathfrak{v}^{|F|,{\it\nu}}),\end{eqnarray}$$
$$\begin{eqnarray}M_{\text{st}}^{E}(\mathfrak{x})=M_{\text{st},C_{G}(H)}(\mathfrak{v}^{|F|,{\it\nu}}),\end{eqnarray}$$similarly to the linear case. The equality is a slight generalization of Conjecture 2.5 and would follow from the change of variables formula generalized along the line of [Reference Denef and LoeserDL02], applied to the almost bijection
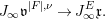 $$\begin{eqnarray}J_{\infty }\mathfrak{v}^{|F|,{\it\nu}}\rightarrow J_{\infty }^{E}\mathfrak{x}.\end{eqnarray}$$
$$\begin{eqnarray}J_{\infty }\mathfrak{v}^{|F|,{\it\nu}}\rightarrow J_{\infty }^{E}\mathfrak{x}.\end{eqnarray}$$It is then natural to expect the following conjecture.
Conjecture 7.3. (The McKay correspondence for nonlinear actions)
We have
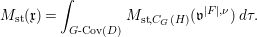 $$\begin{eqnarray}M_{\text{st}}(\mathfrak{x})=\int _{G\text{-}\text{Cov}(D)}M_{\text{st},C_{G}(H)}(\mathfrak{v}^{|F|,{\it\nu}})\,d{\it\tau}.\end{eqnarray}$$
$$\begin{eqnarray}M_{\text{st}}(\mathfrak{x})=\int _{G\text{-}\text{Cov}(D)}M_{\text{st},C_{G}(H)}(\mathfrak{v}^{|F|,{\it\nu}})\,d{\it\tau}.\end{eqnarray}$$Definition 7.4. We define the ![]() $E$-part of the orbifold stringy motif of
$E$-part of the orbifold stringy motif of ![]() $\mathfrak{v}$ as
$\mathfrak{v}$ as
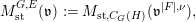 $$\begin{eqnarray}\displaystyle M_{\text{st}}^{G,E}(\mathfrak{v}) & :=M_{\text{st},C_{G}(H)}(\mathfrak{v}^{|F|,{\it\nu}}), & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle M_{\text{st}}^{G,E}(\mathfrak{v}) & :=M_{\text{st},C_{G}(H)}(\mathfrak{v}^{|F|,{\it\nu}}), & \displaystyle \nonumber\end{eqnarray}$$ and the orbifold stringy motif of ![]() $\mathfrak{v}$ as
$\mathfrak{v}$ as
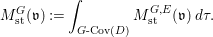 $$\begin{eqnarray}M_{\text{st}}^{G}(\mathfrak{v}):=\int _{G\text{-}\text{Cov}(D)}M_{\text{st}}^{G,E}(\mathfrak{v})\,d{\it\tau}.\end{eqnarray}$$
$$\begin{eqnarray}M_{\text{st}}^{G}(\mathfrak{v}):=\int _{G\text{-}\text{Cov}(D)}M_{\text{st}}^{G,E}(\mathfrak{v})\,d{\it\tau}.\end{eqnarray}$$With this definition, the last conjecture simply says
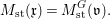 $$\begin{eqnarray}M_{\text{st}}(\mathfrak{x})=M_{\text{st}}^{G}(\mathfrak{v}).\end{eqnarray}$$
$$\begin{eqnarray}M_{\text{st}}(\mathfrak{x})=M_{\text{st}}^{G}(\mathfrak{v}).\end{eqnarray}$$Remark 7.5. The reader may wonder why we do not define ![]() $M_{\text{st}}^{G}(\mathfrak{v})$ as a motivic integral on
$M_{\text{st}}^{G}(\mathfrak{v})$ as a motivic integral on ![]() $J_{\infty }^{G}\mathfrak{v}$, which appears to be more natural. It is because the author does not know whether one can define a motivic measure on
$J_{\infty }^{G}\mathfrak{v}$, which appears to be more natural. It is because the author does not know whether one can define a motivic measure on ![]() $J_{\infty }^{G}\mathfrak{v}$, as he does not know how to compute dimensions of fibers of
$J_{\infty }^{G}\mathfrak{v}$, as he does not know how to compute dimensions of fibers of
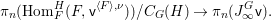 $$\begin{eqnarray}{\it\pi}_{n}(\text{Hom}_{F}^{H}(F,\mathsf{v}^{\left\langle F\right\rangle ,{\it\nu}}))/C_{G}(H)\rightarrow {\it\pi}_{n}(J_{\infty }^{G}\mathsf{v}).\end{eqnarray}$$
$$\begin{eqnarray}{\it\pi}_{n}(\text{Hom}_{F}^{H}(F,\mathsf{v}^{\left\langle F\right\rangle ,{\it\nu}}))/C_{G}(H)\rightarrow {\it\pi}_{n}(J_{\infty }^{G}\mathsf{v}).\end{eqnarray}$$ Knowing it was, in the linear case, a key in formulating the change of variables formula (Conjecture 5.6) and determining the integrand 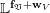 $\mathbb{L}^{\mathbf{f}_{\mathfrak{V}}+\mathbf{w}_{V}}$ in the definition of
$\mathbb{L}^{\mathbf{f}_{\mathfrak{V}}+\mathbf{w}_{V}}$ in the definition of 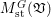 $M_{\text{st}}^{G}(\mathfrak{V})$.
$M_{\text{st}}^{G}(\mathfrak{V})$.
8 Computing boundaries of untwisting varieties
To compute examples of the wild McKay correspondence, we need to determine centered log varieties ![]() $\mathfrak{v}^{|F|,{\it\nu}}$. It is easy to determine the center. In this section, supposing that
$\mathfrak{v}^{|F|,{\it\nu}}$. It is easy to determine the center. In this section, supposing that ![]() $\mathsf{v}$ and
$\mathsf{v}$ and ![]() $\mathsf{v}^{|F|}$ are both normal and complete intersections in
$\mathsf{v}^{|F|}$ are both normal and complete intersections in ![]() $V$ and
$V$ and ![]() $V^{|F|}$ respectively, we compute the boundary of
$V^{|F|}$ respectively, we compute the boundary of ![]() $\mathfrak{v}^{|F|}$.
$\mathfrak{v}^{|F|}$.
Let
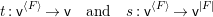 $$\begin{eqnarray}t:\mathsf{v}^{\left\langle F\right\rangle }\rightarrow \mathsf{v}\quad \text{and}\quad s:\mathsf{v}^{\left\langle F\right\rangle }\rightarrow \mathsf{v}^{|F|}\end{eqnarray}$$
$$\begin{eqnarray}t:\mathsf{v}^{\left\langle F\right\rangle }\rightarrow \mathsf{v}\quad \text{and}\quad s:\mathsf{v}^{\left\langle F\right\rangle }\rightarrow \mathsf{v}^{|F|}\end{eqnarray}$$ be the natural morphisms, although they are different from the morphisms denoted by the same symbols in diagram (7.1) unless ![]() $\mathsf{v}^{\left\langle F\right\rangle }$ is also normal. The subvariety
$\mathsf{v}^{\left\langle F\right\rangle }$ is also normal. The subvariety 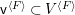 $\mathsf{v}^{\left\langle F\right\rangle }\subset V^{\left\langle F\right\rangle }$ is a complete intersection. To see this, first note that if
$\mathsf{v}^{\left\langle F\right\rangle }\subset V^{\left\langle F\right\rangle }$ is a complete intersection. To see this, first note that if 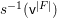 $s^{-1}(\mathsf{v}^{|F|})$ denotes the scheme-theoretic preimage, then
$s^{-1}(\mathsf{v}^{|F|})$ denotes the scheme-theoretic preimage, then 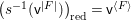 $\left(s^{-1}(\mathsf{v}^{|F|})\right)_{\text{red}}=\mathsf{v}^{\left\langle F\right\rangle }$. The subscheme
$\left(s^{-1}(\mathsf{v}^{|F|})\right)_{\text{red}}=\mathsf{v}^{\left\langle F\right\rangle }$. The subscheme  $s^{-1}(\mathsf{v}^{|F|})\subset V^{\left\langle F\right\rangle }$ is a complete intersection, hence Cohen–Macaulay, and generically reduced. From [Reference EisenbudEis95, Theorem 18.15],
$s^{-1}(\mathsf{v}^{|F|})\subset V^{\left\langle F\right\rangle }$ is a complete intersection, hence Cohen–Macaulay, and generically reduced. From [Reference EisenbudEis95, Theorem 18.15], 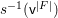 $s^{-1}(\mathsf{v}^{|F|})$ is actually reduced and
$s^{-1}(\mathsf{v}^{|F|})$ is actually reduced and
 $$\begin{eqnarray}s^{-1}(\mathsf{v}^{|F|})=\mathsf{v}^{\left\langle F\right\rangle }.\end{eqnarray}$$
$$\begin{eqnarray}s^{-1}(\mathsf{v}^{|F|})=\mathsf{v}^{\left\langle F\right\rangle }.\end{eqnarray}$$ In general, for a complete intersection subvariety ![]() $Y\subset X$, its conormal sheaf
$Y\subset X$, its conormal sheaf ![]() ${\mathcal{C}}_{Y/X}$ is defined as
${\mathcal{C}}_{Y/X}$ is defined as ![]() $I_{Y}/I_{Y}^{2}$, with
$I_{Y}/I_{Y}^{2}$, with 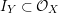 $I_{Y}\subset {\mathcal{O}}_{X}$ the defining ideal sheaf of
$I_{Y}\subset {\mathcal{O}}_{X}$ the defining ideal sheaf of ![]() $Y$. We put
$Y$. We put
 $$\begin{eqnarray}\det {\mathcal{C}}_{Y/X}:=\mathop{\text{codim}(Y,X)}^{\wedge }{\mathcal{C}}_{Y/X}.\end{eqnarray}$$
$$\begin{eqnarray}\det {\mathcal{C}}_{Y/X}:=\mathop{\text{codim}(Y,X)}^{\wedge }{\mathcal{C}}_{Y/X}.\end{eqnarray}$$ There exists a unique effective ![]() $H$-stable Cartier divisor
$H$-stable Cartier divisor ![]() $A_{F}$ on
$A_{F}$ on ![]() $\mathsf{v}^{\left\langle F\right\rangle }$ such that
$\mathsf{v}^{\left\langle F\right\rangle }$ such that
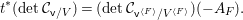 $$\begin{eqnarray}t^{\ast }(\det {\mathcal{C}}_{\mathsf{v}/V})=(\det {\mathcal{C}}_{\mathsf{v}^{\left\langle F\right\rangle }/V^{\left\langle F\right\rangle }})(-A_{F}).\end{eqnarray}$$
$$\begin{eqnarray}t^{\ast }(\det {\mathcal{C}}_{\mathsf{v}/V})=(\det {\mathcal{C}}_{\mathsf{v}^{\left\langle F\right\rangle }/V^{\left\langle F\right\rangle }})(-A_{F}).\end{eqnarray}$$Proposition 8.1. Let ![]() ${\it\delta}$ and
${\it\delta}$ and ![]() ${\it\delta}^{|F|}$ be the boundaries of
${\it\delta}^{|F|}$ be the boundaries of ![]() $\mathfrak{v}$ and
$\mathfrak{v}$ and ![]() $\mathfrak{v}^{|F|}$ respectively, and
$\mathfrak{v}^{|F|}$ respectively, and 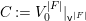 $C:=V_{0}^{|F|}|_{\mathsf{v}^{|F|}}$, the restriction of the prime divisor
$C:=V_{0}^{|F|}|_{\mathsf{v}^{|F|}}$, the restriction of the prime divisor ![]() $V_{0}^{|F|}$ on
$V_{0}^{|F|}$ on ![]() $V^{|F|}$ to
$V^{|F|}$ to ![]() $\mathsf{v}^{|F|}$. Then
$\mathsf{v}^{|F|}$. Then
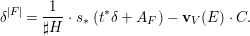 $$\begin{eqnarray}{\it\delta}^{|F|}=\frac{1}{\sharp H}\cdot s_{\ast }\left(t^{\ast }{\it\delta}+A_{F}\right)-\boldsymbol{v}_{V}(E)\cdot C.\end{eqnarray}$$
$$\begin{eqnarray}{\it\delta}^{|F|}=\frac{1}{\sharp H}\cdot s_{\ast }\left(t^{\ast }{\it\delta}+A_{F}\right)-\boldsymbol{v}_{V}(E)\cdot C.\end{eqnarray}$$Proof. Let ![]() ${\it\epsilon}^{|F|}$ be the right-hand side of the equality. As in the proof of Lemma 6.5, it suffices to show that the pullbacks of divisors
${\it\epsilon}^{|F|}$ be the right-hand side of the equality. As in the proof of Lemma 6.5, it suffices to show that the pullbacks of divisors ![]() $K_{\mathsf{v}}+{\it\delta}$ and
$K_{\mathsf{v}}+{\it\delta}$ and 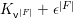 $K_{\mathsf{v}^{|F|}}+{\it\epsilon}^{|F|}$ to
$K_{\mathsf{v}^{|F|}}+{\it\epsilon}^{|F|}$ to ![]() $\mathsf{v}^{\left\langle F\right\rangle }$ coincide. Since
$\mathsf{v}^{\left\langle F\right\rangle }$ coincide. Since
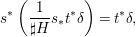 $$\begin{eqnarray}s^{\ast }\left(\frac{1}{\sharp H}s_{\ast }t^{\ast }{\it\delta}\right)=t^{\ast }{\it\delta},\end{eqnarray}$$
$$\begin{eqnarray}s^{\ast }\left(\frac{1}{\sharp H}s_{\ast }t^{\ast }{\it\delta}\right)=t^{\ast }{\it\delta},\end{eqnarray}$$ we may suppose ![]() ${\it\delta}=0$ and hence
${\it\delta}=0$ and hence
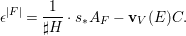 $$\begin{eqnarray}{\it\epsilon}^{|F|}=\frac{1}{\sharp H}\cdot s_{\ast }A_{F}-\boldsymbol{v}_{V}(E)C.\end{eqnarray}$$
$$\begin{eqnarray}{\it\epsilon}^{|F|}=\frac{1}{\sharp H}\cdot s_{\ast }A_{F}-\boldsymbol{v}_{V}(E)C.\end{eqnarray}$$By abuse of notation, identifying a divisor corresponding to an invertible sheaf, from the adjunction formula, we have
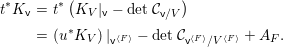 $$\begin{eqnarray}\displaystyle t^{\ast }K_{\mathsf{v}} & = & \displaystyle t^{\ast }\left(K_{V}|_{\mathsf{v}}-\det {\mathcal{C}}_{\mathsf{v}/V}\right)\nonumber\\ \displaystyle & = & \displaystyle \left(u^{\ast }K_{V}\right)|_{\mathsf{v}^{\left\langle F\right\rangle }}-\det {\mathcal{C}}_{\mathsf{v}^{\left\langle F\right\rangle }/V^{\left\langle F\right\rangle }}+A_{F}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle t^{\ast }K_{\mathsf{v}} & = & \displaystyle t^{\ast }\left(K_{V}|_{\mathsf{v}}-\det {\mathcal{C}}_{\mathsf{v}/V}\right)\nonumber\\ \displaystyle & = & \displaystyle \left(u^{\ast }K_{V}\right)|_{\mathsf{v}^{\left\langle F\right\rangle }}-\det {\mathcal{C}}_{\mathsf{v}^{\left\langle F\right\rangle }/V^{\left\langle F\right\rangle }}+A_{F}.\nonumber\end{eqnarray}$$ On the other hand, since  $s^{\ast }(\det {\mathcal{C}}_{\mathsf{v}^{|F|}/V^{|F|}})=\det {\mathcal{C}}_{\mathsf{v}^{\left\langle F\right\rangle }/V^{\left\langle F\right\rangle }}$,
$s^{\ast }(\det {\mathcal{C}}_{\mathsf{v}^{|F|}/V^{|F|}})=\det {\mathcal{C}}_{\mathsf{v}^{\left\langle F\right\rangle }/V^{\left\langle F\right\rangle }}$,
 $$\begin{eqnarray}\displaystyle s^{\ast }(K_{\mathsf{v}^{|F|}}+{\it\epsilon}^{|F|}) & = & \displaystyle s^{\ast }(K_{V^{|F|}}|_{\mathsf{v}^{|F|}}\hspace{-2.0pt}-\hspace{-2.0pt}\det {\mathcal{C}}_{\mathsf{v}^{|F|}/V^{|F|}})\hspace{-2.0pt}-\hspace{-2.0pt}\sharp H\cdot \boldsymbol{v}_{V}(E)V_{0}^{\left\langle F\right\rangle }|_{\mathsf{v}^{\left\langle F\right\rangle }}\hspace{-1.0pt}+\hspace{-1.0pt}A_{F}\nonumber\\ \displaystyle & = & \displaystyle (r^{\ast }K_{V^{|F|}}-\sharp H\cdot \boldsymbol{v}_{V}(E)V_{0}^{\left\langle F\right\rangle })|_{\mathsf{v}^{\left\langle F\right\rangle }}-\det {\mathcal{C}}_{\mathsf{v}^{\left\langle F\right\rangle }/V^{\left\langle F\right\rangle }}+A_{F}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle s^{\ast }(K_{\mathsf{v}^{|F|}}+{\it\epsilon}^{|F|}) & = & \displaystyle s^{\ast }(K_{V^{|F|}}|_{\mathsf{v}^{|F|}}\hspace{-2.0pt}-\hspace{-2.0pt}\det {\mathcal{C}}_{\mathsf{v}^{|F|}/V^{|F|}})\hspace{-2.0pt}-\hspace{-2.0pt}\sharp H\cdot \boldsymbol{v}_{V}(E)V_{0}^{\left\langle F\right\rangle }|_{\mathsf{v}^{\left\langle F\right\rangle }}\hspace{-1.0pt}+\hspace{-1.0pt}A_{F}\nonumber\\ \displaystyle & = & \displaystyle (r^{\ast }K_{V^{|F|}}-\sharp H\cdot \boldsymbol{v}_{V}(E)V_{0}^{\left\langle F\right\rangle })|_{\mathsf{v}^{\left\langle F\right\rangle }}-\det {\mathcal{C}}_{\mathsf{v}^{\left\langle F\right\rangle }/V^{\left\langle F\right\rangle }}+A_{F}.\nonumber\end{eqnarray}$$From Lemma 6.5,
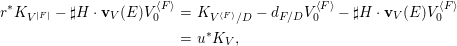 $$\begin{eqnarray}\displaystyle r^{\ast }K_{V^{|F|}}-\sharp H\cdot \boldsymbol{v}_{V}(E)V_{0}^{\left\langle F\right\rangle } & = & \displaystyle K_{V^{\left\langle F\right\rangle }/D}-d_{F/D}V_{0}^{\left\langle F\right\rangle }-\sharp H\cdot \boldsymbol{v}_{V}(E)V_{0}^{\left\langle F\right\rangle }\nonumber\\ \displaystyle & = & \displaystyle u^{\ast }K_{V},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle r^{\ast }K_{V^{|F|}}-\sharp H\cdot \boldsymbol{v}_{V}(E)V_{0}^{\left\langle F\right\rangle } & = & \displaystyle K_{V^{\left\langle F\right\rangle }/D}-d_{F/D}V_{0}^{\left\langle F\right\rangle }-\sharp H\cdot \boldsymbol{v}_{V}(E)V_{0}^{\left\langle F\right\rangle }\nonumber\\ \displaystyle & = & \displaystyle u^{\ast }K_{V},\nonumber\end{eqnarray}$$which shows the proposition. ◻
It is handy to rewrite the proposition in the case of hypersurfaces as follows.
Corollary 8.2. Suppose that ![]() $\mathsf{v}\subset V$ is a hypersurface defined by a polynomial
$\mathsf{v}\subset V$ is a hypersurface defined by a polynomial ![]() $f\in {\mathcal{O}}_{V}$, and write
$f\in {\mathcal{O}}_{V}$, and write
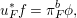 $$\begin{eqnarray}u_{F}^{\ast }f={\it\pi}_{F}^{b}{\it\phi},\end{eqnarray}$$
$$\begin{eqnarray}u_{F}^{\ast }f={\it\pi}_{F}^{b}{\it\phi},\end{eqnarray}$$ where ![]() ${\it\pi}_{F}$ is a uniformizer of
${\it\pi}_{F}$ is a uniformizer of ![]() ${\mathcal{O}}_{F}$,
${\mathcal{O}}_{F}$, ![]() $b$ is an integer
$b$ is an integer ![]() $b\geqslant 0$, and
$b\geqslant 0$, and  ${\it\phi}\in {\mathcal{O}}_{V^{\left\langle F\right\rangle }}$, with
${\it\phi}\in {\mathcal{O}}_{V^{\left\langle F\right\rangle }}$, with ![]() ${\it\pi}_{F}\nmid {\it\phi}$. Then, with the notation as above, we have
${\it\pi}_{F}\nmid {\it\phi}$. Then, with the notation as above, we have
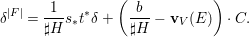 $$\begin{eqnarray}{\it\delta}^{|F|}=\frac{1}{\sharp H}s_{\ast }t^{\ast }{\it\delta}+\left(\frac{b}{\sharp H}-\boldsymbol{v}_{V}(E)\right)\cdot C.\end{eqnarray}$$
$$\begin{eqnarray}{\it\delta}^{|F|}=\frac{1}{\sharp H}s_{\ast }t^{\ast }{\it\delta}+\left(\frac{b}{\sharp H}-\boldsymbol{v}_{V}(E)\right)\cdot C.\end{eqnarray}$$Proof. The corollary follows from
 $$\begin{eqnarray}A_{F}=b\cdot (V_{0}^{\left\langle F\right\rangle }|_{\mathsf{v}_{0}^{\left\langle F\right\rangle }})\quad \text{and}\quad s_{\ast }A_{F}=b\cdot C.\square\end{eqnarray}$$
$$\begin{eqnarray}A_{F}=b\cdot (V_{0}^{\left\langle F\right\rangle }|_{\mathsf{v}_{0}^{\left\langle F\right\rangle }})\quad \text{and}\quad s_{\ast }A_{F}=b\cdot C.\square\end{eqnarray}$$Remark 8.3. In the corollary above, if ![]() $f$ is
$f$ is ![]() $G$-invariant, then
$G$-invariant, then ![]() $b$ is a multiple of
$b$ is a multiple of ![]() $\sharp H$ and hence
$\sharp H$ and hence ![]() $b/\sharp H$ is an integer.
$b/\sharp H$ is an integer.
9 A tame singular example
In this section, we verify Conjecture 7.3 for an example of the tame case where ![]() $\mathsf{v}$ is not regular.
$\mathsf{v}$ is not regular.
Suppose that ![]() $k$ has characteristic
$k$ has characteristic ![]() $\neq 2$. Let
$\neq 2$. Let 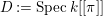 $D:=\text{Spec}\,k[[{\it\pi}]]$,
$D:=\text{Spec}\,k[[{\it\pi}]]$, 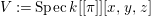 $V:=\text{Spec}\,k[[{\it\pi}]][x,y,z]$ and
$V:=\text{Spec}\,k[[{\it\pi}]][x,y,z]$ and 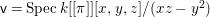 $\mathsf{v}=\text{Spec}\,k[[{\it\pi}]][x,y,z]/(xz-y^{2})$, the trivial family of the
$\mathsf{v}=\text{Spec}\,k[[{\it\pi}]][x,y,z]/(xz-y^{2})$, the trivial family of the ![]() $A_{1}$-singularity over
$A_{1}$-singularity over 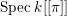 $\text{Spec}\,k[[{\it\pi}]]$. We suppose that
$\text{Spec}\,k[[{\it\pi}]]$. We suppose that  $G=\mathbb{Z}/2\mathbb{Z}=\{1,g\}$ acts on
$G=\mathbb{Z}/2\mathbb{Z}=\{1,g\}$ acts on ![]() $V$ by
$V$ by
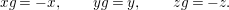 $$\begin{eqnarray}xg=-x,\qquad yg=y,\qquad zg=-z.\end{eqnarray}$$
$$\begin{eqnarray}xg=-x,\qquad yg=y,\qquad zg=-z.\end{eqnarray}$$ The subvariety ![]() $\mathsf{v}$ is stable under the
$\mathsf{v}$ is stable under the ![]() $G$-action, and the quotient variety
$G$-action, and the quotient variety 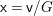 $\mathsf{x}=\mathsf{v}/G$ can be embedded into
$\mathsf{x}=\mathsf{v}/G$ can be embedded into 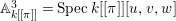 $\mathbb{A}_{k[[{\it\pi}]]}^{3}=\text{Spec}\,k[[{\it\pi}]][u,v,w]$ and gives the hypersurface defined by the equation
$\mathbb{A}_{k[[{\it\pi}]]}^{3}=\text{Spec}\,k[[{\it\pi}]][u,v,w]$ and gives the hypersurface defined by the equation 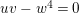 $uv-w^{4}=0$. Thus,
$uv-w^{4}=0$. Thus, ![]() $\mathsf{x}$ is the trivial family of the
$\mathsf{x}$ is the trivial family of the ![]() $A_{3}$-singularity over
$A_{3}$-singularity over 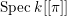 $\text{Spec}\,k[[{\it\pi}]]$.
$\text{Spec}\,k[[{\it\pi}]]$.
Since the morphism ![]() $\mathsf{v}\rightarrow \mathsf{x}$ is étale in codimension one, it is crepant (with the identification (2.1)). Let
$\mathsf{v}\rightarrow \mathsf{x}$ is étale in codimension one, it is crepant (with the identification (2.1)). Let ![]() $\tilde{\mathsf{x}}_{0}\rightarrow \mathsf{x}_{0}$ be the minimal resolution, and let
$\tilde{\mathsf{x}}_{0}\rightarrow \mathsf{x}_{0}$ be the minimal resolution, and let 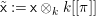 $\tilde{\mathsf{x}}:=\mathsf{x}\otimes _{k}k[[{\it\pi}]]$. The natural morphism
$\tilde{\mathsf{x}}:=\mathsf{x}\otimes _{k}k[[{\it\pi}]]$. The natural morphism ![]() $\tilde{\mathsf{x}}\rightarrow \mathsf{x}$ is crepant. From Proposition 2.7,
$\tilde{\mathsf{x}}\rightarrow \mathsf{x}$ is crepant. From Proposition 2.7,
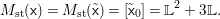 $$\begin{eqnarray}M_{\text{st}}(\mathsf{x})=M_{\text{st}}(\tilde{\mathsf{x}})=[\tilde{\mathsf{x}}_{0}]=\mathbb{L}^{2}+3\mathbb{L}.\end{eqnarray}$$
$$\begin{eqnarray}M_{\text{st}}(\mathsf{x})=M_{\text{st}}(\tilde{\mathsf{x}})=[\tilde{\mathsf{x}}_{0}]=\mathbb{L}^{2}+3\mathbb{L}.\end{eqnarray}$$ Next, we will compute ![]() $M_{\text{st}}^{G}(\mathsf{v})$ and verify that it coincides with
$M_{\text{st}}^{G}(\mathsf{v})$ and verify that it coincides with ![]() $M_{\text{st}}(\mathsf{x})$. There are exactly two
$M_{\text{st}}(\mathsf{x})$. There are exactly two ![]() $G$-covers of
$G$-covers of ![]() $D$ up to isomorphism: the trivial one
$D$ up to isomorphism: the trivial one 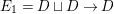 $E_{1}=D\sqcup D\rightarrow D$ and the nontrivial one
$E_{1}=D\sqcup D\rightarrow D$ and the nontrivial one
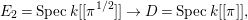 $$\begin{eqnarray}E_{2}=\text{Spec}\,k[[{\it\pi}^{1/2}]]\rightarrow D=\text{Spec}\,k[[{\it\pi}]],\end{eqnarray}$$
$$\begin{eqnarray}E_{2}=\text{Spec}\,k[[{\it\pi}^{1/2}]]\rightarrow D=\text{Spec}\,k[[{\it\pi}]],\end{eqnarray}$$and hence
 $$\begin{eqnarray}M_{\text{st}}^{G}(\mathsf{v})=M_{\text{st}}^{G,E_{1}}(\mathsf{v})+M_{\text{st}}^{G,E_{2}}(\mathsf{v}).\end{eqnarray}$$
$$\begin{eqnarray}M_{\text{st}}^{G}(\mathsf{v})=M_{\text{st}}^{G,E_{1}}(\mathsf{v})+M_{\text{st}}^{G,E_{2}}(\mathsf{v}).\end{eqnarray}$$ As for the first term 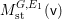 $M_{\text{st}}^{G,E_{1}}(\mathsf{v})$, we have
$M_{\text{st}}^{G,E_{1}}(\mathsf{v})$, we have 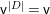 $\mathsf{v}^{|D|}=\mathsf{v}$. Consider the minimal resolution
$\mathsf{v}^{|D|}=\mathsf{v}$. Consider the minimal resolution ![]() $\tilde{\mathsf{v}}_{0}\rightarrow \mathsf{v}_{0}$ and put
$\tilde{\mathsf{v}}_{0}\rightarrow \mathsf{v}_{0}$ and put 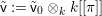 $\tilde{\mathsf{v}}:=\tilde{\mathsf{v}}_{0}\otimes _{k}k[[{\it\pi}]]$. Then the morphism
$\tilde{\mathsf{v}}:=\tilde{\mathsf{v}}_{0}\otimes _{k}k[[{\it\pi}]]$. Then the morphism ![]() $\tilde{\mathsf{v}}\rightarrow \mathsf{v}$ is crepant. Since the
$\tilde{\mathsf{v}}\rightarrow \mathsf{v}$ is crepant. Since the ![]() $G$-action on the exceptional locus is trivial, from Proposition 2.9,
$G$-action on the exceptional locus is trivial, from Proposition 2.9,
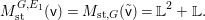 $$\begin{eqnarray}M_{\text{st}}^{G,E_{1}}(\mathsf{v})=M_{\text{st},G}(\tilde{\mathsf{v}})=\mathbb{L}^{2}+\mathbb{L}.\end{eqnarray}$$
$$\begin{eqnarray}M_{\text{st}}^{G,E_{1}}(\mathsf{v})=M_{\text{st},G}(\tilde{\mathsf{v}})=\mathbb{L}^{2}+\mathbb{L}.\end{eqnarray}$$ Next, we compute 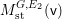 $M_{\text{st}}^{G,E_{2}}(\mathsf{v})$. For
$M_{\text{st}}^{G,E_{2}}(\mathsf{v})$. For ![]() $F=E_{2}$, the tuning module
$F=E_{2}$, the tuning module ![]() ${\rm\Xi}_{F}$ has a basis
${\rm\Xi}_{F}$ has a basis
 $$\begin{eqnarray}{\it\pi}^{1/2}x^{\ast },y^{\ast },{\it\pi}^{1/2}z^{\ast },\end{eqnarray}$$
$$\begin{eqnarray}{\it\pi}^{1/2}x^{\ast },y^{\ast },{\it\pi}^{1/2}z^{\ast },\end{eqnarray}$$ with 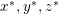 $x^{\ast },y^{\ast },z^{\ast }$ the dual basis of
$x^{\ast },y^{\ast },z^{\ast }$ the dual basis of ![]() $x$,
$x$, ![]() $y$,
$y$, ![]() $z$. If we denote the dual basis of (9.1) by
$z$. If we denote the dual basis of (9.1) by ![]() $\text{x}$,
$\text{x}$, ![]() $\text{y}$,
$\text{y}$, ![]() $\text{z}$, then we can write
$\text{z}$, then we can write ![]() $u^{\ast }$ as
$u^{\ast }$ as
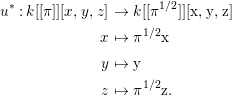 $$\begin{eqnarray}\displaystyle u^{\ast }:k[[{\it\pi}]][x,y,z] & \rightarrow & \displaystyle k[[{\it\pi}^{1/2}]][\text{x},\text{y},\text{z}]\nonumber\\ \displaystyle x & \mapsto & \displaystyle {\it\pi}^{1/2}\text{x}\nonumber\\ \displaystyle y & \mapsto & \displaystyle \text{y}\nonumber\\ \displaystyle z & \mapsto & \displaystyle {\it\pi}^{1/2}\text{z}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle u^{\ast }:k[[{\it\pi}]][x,y,z] & \rightarrow & \displaystyle k[[{\it\pi}^{1/2}]][\text{x},\text{y},\text{z}]\nonumber\\ \displaystyle x & \mapsto & \displaystyle {\it\pi}^{1/2}\text{x}\nonumber\\ \displaystyle y & \mapsto & \displaystyle \text{y}\nonumber\\ \displaystyle z & \mapsto & \displaystyle {\it\pi}^{1/2}\text{z}.\nonumber\end{eqnarray}$$ We see that ![]() $\mathsf{v}^{|F|}$ is given by
$\mathsf{v}^{|F|}$ is given by
 $$\begin{eqnarray}{\it\pi}\text{x}\text{z}-\text{y}^{2}=0.\end{eqnarray}$$
$$\begin{eqnarray}{\it\pi}\text{x}\text{z}-\text{y}^{2}=0.\end{eqnarray}$$ Since the nonregular locus of ![]() $\mathsf{v}^{|F|}$ has dimension one, the variety
$\mathsf{v}^{|F|}$ has dimension one, the variety ![]() $\mathsf{v}^{|F|}$ is normal. From Corollary 8.2, the boundary
$\mathsf{v}^{|F|}$ is normal. From Corollary 8.2, the boundary ![]() ${\it\delta}^{|F|}$ of
${\it\delta}^{|F|}$ of ![]() $\mathfrak{v}^{|F|}$ is given by
$\mathfrak{v}^{|F|}$ is given by
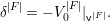 $$\begin{eqnarray}{\it\delta}^{|F|}=-V_{0}^{|F|}|_{\mathsf{v}^{|F|}}.\end{eqnarray}$$
$$\begin{eqnarray}{\it\delta}^{|F|}=-V_{0}^{|F|}|_{\mathsf{v}^{|F|}}.\end{eqnarray}$$Hence,
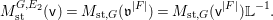 $$\begin{eqnarray}M_{\text{st}}^{G,E_{2}}(\mathsf{v})=M_{\text{st},G}(\mathfrak{v}^{|F|})=M_{\text{st},G}(\mathsf{v}^{|F|})\mathbb{L}^{-1}.\end{eqnarray}$$
$$\begin{eqnarray}M_{\text{st}}^{G,E_{2}}(\mathsf{v})=M_{\text{st},G}(\mathfrak{v}^{|F|})=M_{\text{st},G}(\mathsf{v}^{|F|})\mathbb{L}^{-1}.\end{eqnarray}$$ The ![]() $G$-action on
$G$-action on ![]() $\mathsf{v}^{|F|}$ is given by
$\mathsf{v}^{|F|}$ is given by
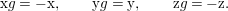 $$\begin{eqnarray}\text{x}g=-\text{x},\qquad \text{y}g=\text{y},\qquad \text{z}g=-\text{z}.\end{eqnarray}$$
$$\begin{eqnarray}\text{x}g=-\text{x},\qquad \text{y}g=\text{y},\qquad \text{z}g=-\text{z}.\end{eqnarray}$$ The nonregular locus of ![]() $\mathsf{v}^{|F|}$ consists of three irreducible components
$\mathsf{v}^{|F|}$ consists of three irreducible components
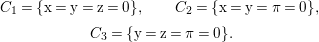 $$\begin{eqnarray}\displaystyle & C_{1}=\{\text{x}=\text{y}=\text{z}=0\},\qquad C_{2}=\{\text{x}=\text{y}={\it\pi}=0\}, & \displaystyle \nonumber\\ \displaystyle & C_{3}=\{\text{y}=\text{z}={\it\pi}=0\}. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & C_{1}=\{\text{x}=\text{y}=\text{z}=0\},\qquad C_{2}=\{\text{x}=\text{y}={\it\pi}=0\}, & \displaystyle \nonumber\\ \displaystyle & C_{3}=\{\text{y}=\text{z}={\it\pi}=0\}. & \displaystyle \nonumber\end{eqnarray}$$ Let  $\mathsf{v}_{1}\rightarrow \mathsf{v}^{|F|}$ be the blowup along
$\mathsf{v}_{1}\rightarrow \mathsf{v}^{|F|}$ be the blowup along ![]() $C_{1}$. Then the nonregular locus of
$C_{1}$. Then the nonregular locus of ![]() $\mathsf{v}_{1}$ is exactly the union of the strict transforms
$\mathsf{v}_{1}$ is exactly the union of the strict transforms ![]() $C_{2}^{\prime }$ and
$C_{2}^{\prime }$ and ![]() $C_{3}^{\prime }$ of
$C_{3}^{\prime }$ of ![]() $C_{2}$ and
$C_{2}$ and ![]() $C_{3}$. Moreover, the singularities of
$C_{3}$. Moreover, the singularities of ![]() $\mathsf{v}_{1}$ are two trivial families of the
$\mathsf{v}_{1}$ are two trivial families of the ![]() $A_{1}$-singularity over
$A_{1}$-singularity over ![]() $\mathbb{A}_{k}^{1}$. Let
$\mathbb{A}_{k}^{1}$. Let ![]() $\mathsf{v}_{2}\rightarrow \mathsf{v}_{1}$ be the blowup along
$\mathsf{v}_{2}\rightarrow \mathsf{v}_{1}$ be the blowup along ![]() $C_{2}^{\prime }$ and
$C_{2}^{\prime }$ and ![]() $C_{3}^{\prime }$. Then
$C_{3}^{\prime }$. Then ![]() $\mathsf{v}_{2}$ is regular. If
$\mathsf{v}_{2}$ is regular. If ![]() $A_{2}$ and
$A_{2}$ and ![]() $A_{3}$ are the exceptional prime divisors over
$A_{3}$ are the exceptional prime divisors over ![]() $C_{2}^{\prime }$ and
$C_{2}^{\prime }$ and ![]() $C_{3}^{\prime }$ respectively, then the smooth locus of
$C_{3}^{\prime }$ respectively, then the smooth locus of ![]() $\mathsf{v}_{2}\rightarrow D$ in the special fiber is the disjoint union of open subsets
$\mathsf{v}_{2}\rightarrow D$ in the special fiber is the disjoint union of open subsets  $A_{2}^{\prime }\subset E_{2}$ and
$A_{2}^{\prime }\subset E_{2}$ and  $A_{3}^{\prime }\subset E_{3}$ with
$A_{3}^{\prime }\subset E_{3}$ with  $A_{2}^{\prime }\cong A_{3}^{\prime }\cong \mathbb{A}_{k}^{2}$. Since the morphism
$A_{2}^{\prime }\cong A_{3}^{\prime }\cong \mathbb{A}_{k}^{2}$. Since the morphism 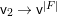 $\mathsf{v}_{2}\rightarrow \mathsf{v}^{|F|}$ is crepant and the
$\mathsf{v}_{2}\rightarrow \mathsf{v}^{|F|}$ is crepant and the ![]() $G$-action on its exceptional locus is trivial,
$G$-action on its exceptional locus is trivial,
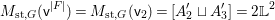 $$\begin{eqnarray}M_{\text{st},G}(\mathsf{v}^{|F|})=M_{\text{st},G}(\mathsf{v}_{2})=[A_{2}^{\prime }\sqcup A_{3}^{\prime }]=2\mathbb{L}^{2}\end{eqnarray}$$
$$\begin{eqnarray}M_{\text{st},G}(\mathsf{v}^{|F|})=M_{\text{st},G}(\mathsf{v}_{2})=[A_{2}^{\prime }\sqcup A_{3}^{\prime }]=2\mathbb{L}^{2}\end{eqnarray}$$and
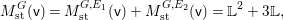 $$\begin{eqnarray}M_{\text{st}}^{G}(\mathsf{v})=M_{\text{st}}^{G,E_{1}}(\mathsf{v})+M_{\text{st}}^{G,E_{2}}(\mathsf{v})=\mathbb{L}^{2}+3\mathbb{L},\end{eqnarray}$$
$$\begin{eqnarray}M_{\text{st}}^{G}(\mathsf{v})=M_{\text{st}}^{G,E_{1}}(\mathsf{v})+M_{\text{st}}^{G,E_{2}}(\mathsf{v})=\mathbb{L}^{2}+3\mathbb{L},\end{eqnarray}$$as desired.
10 A wild nonlinear example
In this section, we verify Conjecture 7.3 for an example of wild nonlinear actions.
Suppose that ![]() $k$ has characteristic two. Let
$k$ has characteristic two. Let 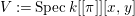 $V:=\text{Spec}\,k[[{\it\pi}]][x,y]$, on which the group
$V:=\text{Spec}\,k[[{\it\pi}]][x,y]$, on which the group 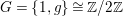 $G=\{1,g\}\cong \mathbb{Z}/2\mathbb{Z}$ acts by the transposition of
$G=\{1,g\}\cong \mathbb{Z}/2\mathbb{Z}$ acts by the transposition of ![]() $x$ and
$x$ and ![]() $y$, and
$y$, and 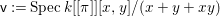 $\mathsf{v}:=\text{Spec}\,k[[{\it\pi}]][x,y]/(x+y+xy)$. The completion of
$\mathsf{v}:=\text{Spec}\,k[[{\it\pi}]][x,y]/(x+y+xy)$. The completion of ![]() $\mathsf{v}$ at the origin
$\mathsf{v}$ at the origin 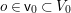 $o\in \mathsf{v}_{0}\subset V_{0}$ gives
$o\in \mathsf{v}_{0}\subset V_{0}$ gives
 $$\begin{eqnarray}\text{Spec}\,k[[{\it\pi},x]],\end{eqnarray}$$
$$\begin{eqnarray}\text{Spec}\,k[[{\it\pi},x]],\end{eqnarray}$$ with the ![]() $G$-action by
$G$-action by
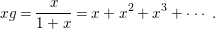 $$\begin{eqnarray}xg=\frac{x}{1+x}=x+x^{2}+x^{3}+\cdots \,.\end{eqnarray}$$
$$\begin{eqnarray}xg=\frac{x}{1+x}=x+x^{2}+x^{3}+\cdots \,.\end{eqnarray}$$ The invariant subring of 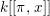 $k[[{\it\pi},x]]$ is
$k[[{\it\pi},x]]$ is
 $$\begin{eqnarray}k[[{\it\pi},x]]^{g}=k\left[\!\left[{\it\pi},\frac{x^{2}}{1+x}\right]\!\right].\end{eqnarray}$$
$$\begin{eqnarray}k[[{\it\pi},x]]^{g}=k\left[\!\left[{\it\pi},\frac{x^{2}}{1+x}\right]\!\right].\end{eqnarray}$$Since
 $$\begin{eqnarray}k[[x]]=\frac{k[[\frac{x^{2}}{1+x}]][X]}{\left\langle F(X)\right\rangle },\qquad F(X):=X^{2}+\frac{x^{2}}{1+x}X+\frac{x^{2}}{1+x},\end{eqnarray}$$
$$\begin{eqnarray}k[[x]]=\frac{k[[\frac{x^{2}}{1+x}]][X]}{\left\langle F(X)\right\rangle },\qquad F(X):=X^{2}+\frac{x^{2}}{1+x}X+\frac{x^{2}}{1+x},\end{eqnarray}$$ the different of 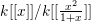 $k[[x]]/k[[\frac{x^{2}}{1+x}]]$ is
$k[[x]]/k[[\frac{x^{2}}{1+x}]]$ is
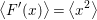 $$\begin{eqnarray}\left\langle F^{\prime }(x)\right\rangle =\left\langle x^{2}\right\rangle\end{eqnarray}$$
$$\begin{eqnarray}\left\langle F^{\prime }(x)\right\rangle =\left\langle x^{2}\right\rangle\end{eqnarray}$$ (see [Reference SerreSer79, page 56, Corollary 2]). Let ![]() $Z\subset V$ be the zero section of
$Z\subset V$ be the zero section of ![]() $V\rightarrow D$, defined by the ideal
$V\rightarrow D$, defined by the ideal 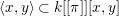 $\left\langle x,y\right\rangle \subset k[[{\it\pi}]][x,y]$. We regard
$\left\langle x,y\right\rangle \subset k[[{\it\pi}]][x,y]$. We regard ![]() $Z$ as a prime divisor on
$Z$ as a prime divisor on ![]() $\mathsf{v}$. Note that
$\mathsf{v}$. Note that ![]() $2Z$ is defined by
$2Z$ is defined by  $x+y=0$.
$x+y=0$.
If we put 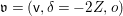 $\mathfrak{v}=(\mathsf{v},{\it\delta}=-2Z,o)$ and
$\mathfrak{v}=(\mathsf{v},{\it\delta}=-2Z,o)$ and 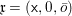 $\mathfrak{x}=(\mathsf{x},0,\bar{o})$, with
$\mathfrak{x}=(\mathsf{x},0,\bar{o})$, with ![]() $\bar{o}$ the image of
$\bar{o}$ the image of ![]() $o$, then the quotient morphism
$o$, then the quotient morphism  $q:\mathfrak{v}\rightarrow \mathfrak{x}$ is crepant. We obviously have
$q:\mathfrak{v}\rightarrow \mathfrak{x}$ is crepant. We obviously have
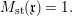 $$\begin{eqnarray}M_{\text{st}}(\mathfrak{x})=1.\end{eqnarray}$$
$$\begin{eqnarray}M_{\text{st}}(\mathfrak{x})=1.\end{eqnarray}$$ Next, we will verify that 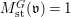 $M_{\text{st}}^{G}(\mathfrak{v})=1$. For the trivial
$M_{\text{st}}^{G}(\mathfrak{v})=1$. For the trivial ![]() $G$-cover
$G$-cover 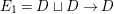 $E_{1}=D\sqcup D\rightarrow D$, since
$E_{1}=D\sqcup D\rightarrow D$, since 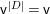 $\mathsf{v}^{|D|}=\mathsf{v}$, from Proposition 2.9, we have
$\mathsf{v}^{|D|}=\mathsf{v}$, from Proposition 2.9, we have
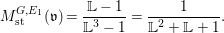 $$\begin{eqnarray}M_{\text{st}}^{G,E_{1}}(\mathfrak{v})=\frac{\mathbb{L}-1}{\mathbb{L}^{3}-1}=\frac{1}{\mathbb{L}^{2}+\mathbb{L}+1}.\end{eqnarray}$$
$$\begin{eqnarray}M_{\text{st}}^{G,E_{1}}(\mathfrak{v})=\frac{\mathbb{L}-1}{\mathbb{L}^{3}-1}=\frac{1}{\mathbb{L}^{2}+\mathbb{L}+1}.\end{eqnarray}$$ Let  $E=F=\text{Spec}\,k[[{\it\rho}]]$ be any nontrivial
$E=F=\text{Spec}\,k[[{\it\rho}]]$ be any nontrivial ![]() $G$-cover of
$G$-cover of 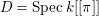 $D=\text{Spec}\,k[[{\it\pi}]]$. The associated tuning module
$D=\text{Spec}\,k[[{\it\pi}]]$. The associated tuning module ![]() ${\rm\Xi}_{F}$ is generated by two elements
${\rm\Xi}_{F}$ is generated by two elements ![]() ${\it\alpha}_{1}$ and
${\it\alpha}_{1}$ and ![]() ${\it\alpha}_{2}$ given by
${\it\alpha}_{2}$ given by
 $$\begin{eqnarray}{\it\alpha}_{1}:x\mapsto 1,\,y\mapsto 1\end{eqnarray}$$
$$\begin{eqnarray}{\it\alpha}_{1}:x\mapsto 1,\,y\mapsto 1\end{eqnarray}$$and
 $$\begin{eqnarray}{\it\alpha}_{2}:x\mapsto {\it\rho},\,y\mapsto {\it\rho}g.\end{eqnarray}$$
$$\begin{eqnarray}{\it\alpha}_{2}:x\mapsto {\it\rho},\,y\mapsto {\it\rho}g.\end{eqnarray}$$ Let ![]() $\text{x}$ and
$\text{x}$ and ![]() $\text{y}$ be the dual basis of
$\text{y}$ be the dual basis of ![]() ${\it\alpha}_{1}$ and
${\it\alpha}_{1}$ and ![]() ${\it\alpha}_{2}$. Then
${\it\alpha}_{2}$. Then ![]() $u^{\ast }$ is given by
$u^{\ast }$ is given by
 $$\begin{eqnarray}\displaystyle k[[{\it\pi}]][x,y] & \rightarrow & \displaystyle k[[{\it\rho}]][\text{x},\text{y}]\nonumber\\ \displaystyle x & \mapsto & \displaystyle \text{x}+{\it\rho}\text{y}\nonumber\\ \displaystyle y & \mapsto & \displaystyle \text{x}+({\it\rho}g)\text{y}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle k[[{\it\pi}]][x,y] & \rightarrow & \displaystyle k[[{\it\rho}]][\text{x},\text{y}]\nonumber\\ \displaystyle x & \mapsto & \displaystyle \text{x}+{\it\rho}\text{y}\nonumber\\ \displaystyle y & \mapsto & \displaystyle \text{x}+({\it\rho}g)\text{y}.\nonumber\end{eqnarray}$$ Therefore, ![]() $\mathsf{v}^{\left\langle F\right\rangle }$ and
$\mathsf{v}^{\left\langle F\right\rangle }$ and ![]() $\mathsf{v}^{|F|}$ are defined by
$\mathsf{v}^{|F|}$ are defined by
 $$\begin{eqnarray}\displaystyle & & \displaystyle (\text{x}+{\it\rho}\text{y})(\text{x}+({\it\rho}g)\text{y})+(\text{x}+{\it\rho}\text{y})+(\text{x}+({\it\rho}g)\text{y})\nonumber\\ \displaystyle & & \displaystyle \quad =\text{x}^{2}+\text{Nr}({\it\rho})\text{y}^{2}+\text{Tr}({\it\rho})\text{y}(1+\text{x})\nonumber\\ \displaystyle & & \displaystyle \quad =0.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle (\text{x}+{\it\rho}\text{y})(\text{x}+({\it\rho}g)\text{y})+(\text{x}+{\it\rho}\text{y})+(\text{x}+({\it\rho}g)\text{y})\nonumber\\ \displaystyle & & \displaystyle \quad =\text{x}^{2}+\text{Nr}({\it\rho})\text{y}^{2}+\text{Tr}({\it\rho})\text{y}(1+\text{x})\nonumber\\ \displaystyle & & \displaystyle \quad =0.\nonumber\end{eqnarray}$$ The ![]() $G$-action on
$G$-action on 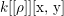 $k[[{\it\rho}]][\text{x},\text{y}]$ is given by
$k[[{\it\rho}]][\text{x},\text{y}]$ is given by
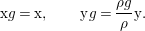 $$\begin{eqnarray}\text{x}g=\text{x},\qquad \text{y}g=\frac{{\it\rho}g}{{\it\rho}}\text{y}.\end{eqnarray}$$
$$\begin{eqnarray}\text{x}g=\text{x},\qquad \text{y}g=\frac{{\it\rho}g}{{\it\rho}}\text{y}.\end{eqnarray}$$ The pullback of ![]() $2Z$ to
$2Z$ to ![]() $\mathsf{v}^{\left\langle F\right\rangle }$ is defined by
$\mathsf{v}^{\left\langle F\right\rangle }$ is defined by ![]() $\text{Tr}({\it\rho})\text{y}$. Let
$\text{Tr}({\it\rho})\text{y}$. Let  $S:=\mathsf{v}_{0}^{|F|}$, regarded as a prime divisor on
$S:=\mathsf{v}_{0}^{|F|}$, regarded as a prime divisor on ![]() $\mathsf{v}^{|F|}$, and let
$\mathsf{v}^{|F|}$, and let ![]() $B$ be the prime divisor on
$B$ be the prime divisor on ![]() $\mathsf{v}^{|F|}$ such that
$\mathsf{v}^{|F|}$ such that ![]() $2B$ is defined by
$2B$ is defined by ![]() $\text{y}=0$. From Corollary 8.2, the boundary
$\text{y}=0$. From Corollary 8.2, the boundary ![]() ${\it\delta}^{|F|}$ of
${\it\delta}^{|F|}$ of ![]() $\mathfrak{v}^{|F|}$ is
$\mathfrak{v}^{|F|}$ is
 $$\begin{eqnarray}-4nS-2B,\end{eqnarray}$$
$$\begin{eqnarray}-4nS-2B,\end{eqnarray}$$ with 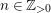 $n\in \mathbb{Z}_{{>}0}$ given by
$n\in \mathbb{Z}_{{>}0}$ given by 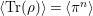 $\left\langle \text{Tr}({\it\rho})\right\rangle =\left\langle {\it\pi}^{n}\right\rangle$. The center of
$\left\langle \text{Tr}({\it\rho})\right\rangle =\left\langle {\it\pi}^{n}\right\rangle$. The center of ![]() $\mathfrak{v}^{|F|}$ is
$\mathfrak{v}^{|F|}$ is ![]() $\mathsf{v}_{0}^{|F|}$. Hence,
$\mathsf{v}_{0}^{|F|}$. Hence,
 $$\begin{eqnarray}M_{\text{st},G}(\mathfrak{v}^{|F|})=M_{\text{st},G}(\mathsf{v}^{|F|},-2B)\mathbb{L}^{-2n}.\end{eqnarray}$$
$$\begin{eqnarray}M_{\text{st},G}(\mathfrak{v}^{|F|})=M_{\text{st},G}(\mathsf{v}^{|F|},-2B)\mathbb{L}^{-2n}.\end{eqnarray}$$ Let us now consider the case ![]() $n=1$. The variety
$n=1$. The variety ![]() $\mathsf{v}^{|F|}$ has two
$\mathsf{v}^{|F|}$ has two ![]() $A_{1}$-singularities at
$A_{1}$-singularities at
 $$\begin{eqnarray}(\text{x},\text{y},{\it\pi})=(0,0,0),\,(0,1,0).\end{eqnarray}$$
$$\begin{eqnarray}(\text{x},\text{y},{\it\pi})=(0,0,0),\,(0,1,0).\end{eqnarray}$$ Blowing them up, we get a crepant morphism 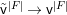 $\tilde{\mathsf{v}}^{|F|}\rightarrow \mathsf{v}^{|F|}$. Let
$\tilde{\mathsf{v}}^{|F|}\rightarrow \mathsf{v}^{|F|}$. Let ![]() $N_{0}$ and
$N_{0}$ and ![]() $N_{1}$ be the exceptional prime divisors over
$N_{1}$ be the exceptional prime divisors over ![]() $(0,0,0)$ and
$(0,0,0)$ and ![]() $(0,1,0)$ respectively. The
$(0,1,0)$ respectively. The ![]() $G$-action on
$G$-action on ![]() $N_{0}$ is trivial, and the one on
$N_{0}$ is trivial, and the one on ![]() $N_{1}$ is linear. Let
$N_{1}$ is linear. Let 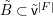 $\tilde{B}\subset \tilde{\mathsf{v}}^{|F|}$ be the strict transform of
$\tilde{B}\subset \tilde{\mathsf{v}}^{|F|}$ be the strict transform of ![]() $B$. The morphism
$B$. The morphism 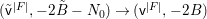 $(\tilde{\mathsf{v}}^{|F|},-2\tilde{B}-N_{0})\rightarrow (\mathsf{v}^{|F|},-2B)$ is crepant. Since
$(\tilde{\mathsf{v}}^{|F|},-2\tilde{B}-N_{0})\rightarrow (\mathsf{v}^{|F|},-2B)$ is crepant. Since ![]() $\tilde{\mathsf{v}}^{|F|}$ is regular, the smooth locus of
$\tilde{\mathsf{v}}^{|F|}$ is regular, the smooth locus of  $\tilde{\mathsf{v}}^{|F|}\rightarrow D$ in the special fiber is
$\tilde{\mathsf{v}}^{|F|}\rightarrow D$ in the special fiber is
 $$\begin{eqnarray}N_{0}\setminus \{1\text{ point}\}\sqcup N_{1}\setminus \{1\text{ point}\},\end{eqnarray}$$
$$\begin{eqnarray}N_{0}\setminus \{1\text{ point}\}\sqcup N_{1}\setminus \{1\text{ point}\},\end{eqnarray}$$ where the removed point of ![]() $N_{0}$ is different from the intersection
$N_{0}$ is different from the intersection ![]() $N_{0}\cap \tilde{B}$. Therefore,
$N_{0}\cap \tilde{B}$. Therefore,
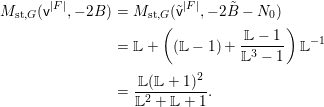 $$\begin{eqnarray}\displaystyle M_{\text{st},G}(\mathsf{v}^{|F|},-2B) & = & \displaystyle M_{\text{st},G}(\tilde{\mathsf{v}}^{|F|},-2\tilde{B}-N_{0})\nonumber\\ \displaystyle & = & \displaystyle \mathbb{L}+\left((\mathbb{L}-1)+\frac{\mathbb{L}-1}{\mathbb{L}^{3}-1}\right)\mathbb{L}^{-1}\nonumber\\ \displaystyle & = & \displaystyle \frac{\mathbb{L}(\mathbb{L}+1)^{2}}{\mathbb{L}^{2}+\mathbb{L}+1}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle M_{\text{st},G}(\mathsf{v}^{|F|},-2B) & = & \displaystyle M_{\text{st},G}(\tilde{\mathsf{v}}^{|F|},-2\tilde{B}-N_{0})\nonumber\\ \displaystyle & = & \displaystyle \mathbb{L}+\left((\mathbb{L}-1)+\frac{\mathbb{L}-1}{\mathbb{L}^{3}-1}\right)\mathbb{L}^{-1}\nonumber\\ \displaystyle & = & \displaystyle \frac{\mathbb{L}(\mathbb{L}+1)^{2}}{\mathbb{L}^{2}+\mathbb{L}+1}.\nonumber\end{eqnarray}$$ Next, consider the case ![]() $n\geqslant 2$. Then
$n\geqslant 2$. Then ![]() $\mathsf{v}^{|F|}$ is nonregular only at the origin
$\mathsf{v}^{|F|}$ is nonregular only at the origin 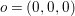 $o=(0,0,0)$. The completion of
$o=(0,0,0)$. The completion of ![]() $\mathsf{v}^{|F|}$ at the origin is
$\mathsf{v}^{|F|}$ at the origin is
 $$\begin{eqnarray}\text{Spec}\,\frac{k[[{\it\pi},\text{x},\text{y}]]}{\left\langle \text{x}^{2}+{\it\pi}\text{y}^{2}+{\it\pi}^{n}\text{y}\right\rangle }\end{eqnarray}$$
$$\begin{eqnarray}\text{Spec}\,\frac{k[[{\it\pi},\text{x},\text{y}]]}{\left\langle \text{x}^{2}+{\it\pi}\text{y}^{2}+{\it\pi}^{n}\text{y}\right\rangle }\end{eqnarray}$$ after a suitable change of coordinates, which is the ![]() $D_{2n}^{0}$-singularity in Artin’s classification [Reference ArtinArt77]. Let
$D_{2n}^{0}$-singularity in Artin’s classification [Reference ArtinArt77]. Let 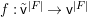 $f:\tilde{\mathsf{v}}^{|F|}\rightarrow \mathsf{v}^{|F|}$ be the minimal resolution. The exceptional prime divisors
$f:\tilde{\mathsf{v}}^{|F|}\rightarrow \mathsf{v}^{|F|}$ be the minimal resolution. The exceptional prime divisors  $N_{1},\ldots ,N_{2n}$, the strict transform
$N_{1},\ldots ,N_{2n}$, the strict transform ![]() $\tilde{B}$ of
$\tilde{B}$ of ![]() $B$ and the one
$B$ and the one ![]() $\tilde{S}$ of
$\tilde{S}$ of ![]() $S$ are arranged as indicated in the following dual graph:
$S$ are arranged as indicated in the following dual graph:
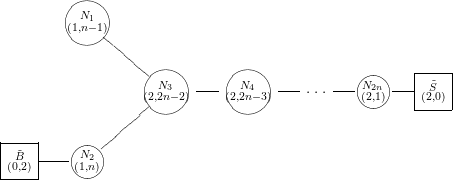
Here, the pairs of numbers, say ![]() $(a,b)$, mean that
$(a,b)$, mean that ![]() $a$ is the multiplicity of the relevant prime divisor in
$a$ is the multiplicity of the relevant prime divisor in ![]() $f^{\ast }(2S)$, and
$f^{\ast }(2S)$, and ![]() $b$ is the one in
$b$ is the one in ![]() $f^{\ast }(2B)$. If we put
$f^{\ast }(2B)$. If we put
 $$\begin{eqnarray}\tilde{{\it\delta}}^{|F|}:=-2\tilde{B}-(n-1)N_{1}-nN_{2}-\mathop{\sum }_{i=2}^{2n-1}(2n-i)N_{i+1},\end{eqnarray}$$
$$\begin{eqnarray}\tilde{{\it\delta}}^{|F|}:=-2\tilde{B}-(n-1)N_{1}-nN_{2}-\mathop{\sum }_{i=2}^{2n-1}(2n-i)N_{i+1},\end{eqnarray}$$then the morphism
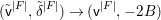 $$\begin{eqnarray}(\tilde{\mathsf{v}}^{|F|},\tilde{{\it\delta}}^{|F|})\rightarrow (\mathsf{v}^{|F|},-2B)\end{eqnarray}$$
$$\begin{eqnarray}(\tilde{\mathsf{v}}^{|F|},\tilde{{\it\delta}}^{|F|})\rightarrow (\mathsf{v}^{|F|},-2B)\end{eqnarray}$$ is crepant. Since ![]() $N_{1}$ and
$N_{1}$ and ![]() $N_{2}$ are the only prime divisors having multiplicity one in
$N_{2}$ are the only prime divisors having multiplicity one in ![]() $f^{\ast }(2S)$, the smooth locus of the morphism
$f^{\ast }(2S)$, the smooth locus of the morphism 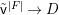 $\tilde{\mathsf{v}}^{|F|}\rightarrow D$ in the special fiber is
$\tilde{\mathsf{v}}^{|F|}\rightarrow D$ in the special fiber is
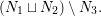 $$\begin{eqnarray}(N_{1}\sqcup N_{2})\setminus N_{3}.\end{eqnarray}$$
$$\begin{eqnarray}(N_{1}\sqcup N_{2})\setminus N_{3}.\end{eqnarray}$$ Since the ![]() $G$-action on the exceptional locus of
$G$-action on the exceptional locus of ![]() $f$ is trivial, we have
$f$ is trivial, we have
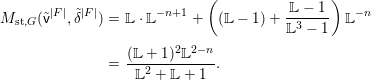 $$\begin{eqnarray}\displaystyle M_{\text{st},G}(\tilde{\mathsf{v}}^{|F|},\tilde{{\it\delta}}^{|F|}) & = & \displaystyle \mathbb{L}\cdot \mathbb{L}^{-n+1}+\left((\mathbb{L}-1)+\frac{\mathbb{L}-1}{\mathbb{L}^{3}-1}\right)\mathbb{L}^{-n}\nonumber\\ \displaystyle & = & \displaystyle \frac{(\mathbb{L}+1)^{2}\mathbb{L}^{2-n}}{\mathbb{L}^{2}+\mathbb{L}+1}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle M_{\text{st},G}(\tilde{\mathsf{v}}^{|F|},\tilde{{\it\delta}}^{|F|}) & = & \displaystyle \mathbb{L}\cdot \mathbb{L}^{-n+1}+\left((\mathbb{L}-1)+\frac{\mathbb{L}-1}{\mathbb{L}^{3}-1}\right)\mathbb{L}^{-n}\nonumber\\ \displaystyle & = & \displaystyle \frac{(\mathbb{L}+1)^{2}\mathbb{L}^{2-n}}{\mathbb{L}^{2}+\mathbb{L}+1}.\nonumber\end{eqnarray}$$ In summary, for ![]() $n>0$, we have
$n>0$, we have
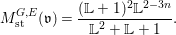 $$\begin{eqnarray}M_{\text{st}}^{G,E}(\mathfrak{v})=\frac{(\mathbb{L}+1)^{2}\mathbb{L}^{2-3n}}{\mathbb{L}^{2}+\mathbb{L}+1}.\end{eqnarray}$$
$$\begin{eqnarray}M_{\text{st}}^{G,E}(\mathfrak{v})=\frac{(\mathbb{L}+1)^{2}\mathbb{L}^{2-3n}}{\mathbb{L}^{2}+\mathbb{L}+1}.\end{eqnarray}$$ Since the locus of 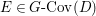 $E\in G\text{-}\text{Cov}(D)$ with
$E\in G\text{-}\text{Cov}(D)$ with 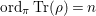 $\text{ord}_{{\it\pi}}\,\text{Tr}({\it\rho})=n$ is homeomorphic to
$\text{ord}_{{\it\pi}}\,\text{Tr}({\it\rho})=n$ is homeomorphic to  $\mathbb{G}_{m,k}\times \mathbb{A}_{k}^{n-1}$ (see [Reference YasudaYas14]),
$\mathbb{G}_{m,k}\times \mathbb{A}_{k}^{n-1}$ (see [Reference YasudaYas14]),
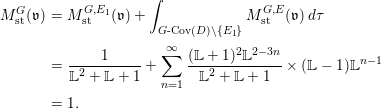 $$\begin{eqnarray}\displaystyle M_{\text{st}}^{G}(\mathfrak{v}) & = & \displaystyle M_{\text{st}}^{G,E_{1}}(\mathfrak{v})+\int _{G\text{-}\text{Cov}(D)\setminus \{E_{1}\}}M_{\text{st}}^{G,E}(\mathfrak{v})\,d{\it\tau}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{\mathbb{L}^{2}+\mathbb{L}+1}+\mathop{\sum }_{n=1}^{\infty }\frac{(\mathbb{L}+1)^{2}\mathbb{L}^{2-3n}}{\mathbb{L}^{2}+\mathbb{L}+1}\times (\mathbb{L}-1)\mathbb{L}^{n-1}\nonumber\\ \displaystyle & = & \displaystyle 1.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle M_{\text{st}}^{G}(\mathfrak{v}) & = & \displaystyle M_{\text{st}}^{G,E_{1}}(\mathfrak{v})+\int _{G\text{-}\text{Cov}(D)\setminus \{E_{1}\}}M_{\text{st}}^{G,E}(\mathfrak{v})\,d{\it\tau}\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{\mathbb{L}^{2}+\mathbb{L}+1}+\mathop{\sum }_{n=1}^{\infty }\frac{(\mathbb{L}+1)^{2}\mathbb{L}^{2-3n}}{\mathbb{L}^{2}+\mathbb{L}+1}\times (\mathbb{L}-1)\mathbb{L}^{n-1}\nonumber\\ \displaystyle & = & \displaystyle 1.\nonumber\end{eqnarray}$$11 Stable hyperplanes in permutation representations
When ![]() $G$ acts on
$G$ acts on ![]() $V$ by permutations of coordinates, then the functions
$V$ by permutations of coordinates, then the functions ![]() $\boldsymbol{v}_{V}$ and
$\boldsymbol{v}_{V}$ and ![]() $\mathbf{w}_{V}$ can be computed by using Artin or Swan conductors, or discriminants or differents [Reference Wood and YasudaWY15]. In this section, we generalize to the case of a hyperplane in a permutation representation defined by an invariant linear form.
$\mathbf{w}_{V}$ can be computed by using Artin or Swan conductors, or discriminants or differents [Reference Wood and YasudaWY15]. In this section, we generalize to the case of a hyperplane in a permutation representation defined by an invariant linear form.
Suppose that ![]() $G$ acts on
$G$ acts on
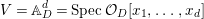 $$\begin{eqnarray}V=\mathbb{A}_{D}^{d}=\text{Spec}\,{\mathcal{O}}_{D}[x_{1},\ldots ,x_{d}]\end{eqnarray}$$
$$\begin{eqnarray}V=\mathbb{A}_{D}^{d}=\text{Spec}\,{\mathcal{O}}_{D}[x_{1},\ldots ,x_{d}]\end{eqnarray}$$by permutations of coordinates, and
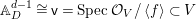 $$\begin{eqnarray}\mathbb{A}_{D}^{d-1}\cong \mathsf{v}=\text{Spec}\,{\mathcal{O}}_{V}/\left\langle f\right\rangle \subset V\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{A}_{D}^{d-1}\cong \mathsf{v}=\text{Spec}\,{\mathcal{O}}_{V}/\left\langle f\right\rangle \subset V\end{eqnarray}$$ is a hyperplane defined by a ![]() $G$-invariant linear form
$G$-invariant linear form
 $$\begin{eqnarray}f=\mathop{\sum }_{i=1}^{d}f_{i}x_{i}\in M^{G}\qquad \left(M:=\bigoplus _{i=1}^{d}{\mathcal{O}}_{D}x_{i}\right).\end{eqnarray}$$
$$\begin{eqnarray}f=\mathop{\sum }_{i=1}^{d}f_{i}x_{i}\in M^{G}\qquad \left(M:=\bigoplus _{i=1}^{d}{\mathcal{O}}_{D}x_{i}\right).\end{eqnarray}$$ The assumption that 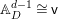 $\mathbb{A}_{D}^{d-1}\cong \mathsf{v}$ means that at least one coefficient
$\mathbb{A}_{D}^{d-1}\cong \mathsf{v}$ means that at least one coefficient ![]() $f_{i}$ is a unit in
$f_{i}$ is a unit in ![]() ${\mathcal{O}}_{D}$.
${\mathcal{O}}_{D}$.
Fix  $E\in G\text{-}\text{Cov}(D)$ and a connected component
$E\in G\text{-}\text{Cov}(D)$ and a connected component ![]() $F$ of
$F$ of ![]() $E$ with stabilizer
$E$ with stabilizer ![]() $H$. Let
$H$. Let
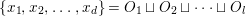 $$\begin{eqnarray}\{x_{1},x_{2},\ldots ,x_{d}\}=O_{1}\sqcup O_{2}\sqcup \cdots \sqcup O_{l}\end{eqnarray}$$
$$\begin{eqnarray}\{x_{1},x_{2},\ldots ,x_{d}\}=O_{1}\sqcup O_{2}\sqcup \cdots \sqcup O_{l}\end{eqnarray}$$ be the decomposition into the ![]() $H$-orbits. Reordering
$H$-orbits. Reordering 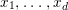 $x_{1},\ldots ,x_{d}$ if necessary, we suppose that
$x_{1},\ldots ,x_{d}$ if necessary, we suppose that
 $$\begin{eqnarray}O_{j}=x_{j}H,\quad 1\leqslant j\leqslant l.\end{eqnarray}$$
$$\begin{eqnarray}O_{j}=x_{j}H,\quad 1\leqslant j\leqslant l.\end{eqnarray}$$ The assumption  $f\in M^{G}$ now means that if
$f\in M^{G}$ now means that if ![]() $i\in O_{j}$, and if
$i\in O_{j}$, and if ![]() $h_{i}\in H$ is any element sending
$h_{i}\in H$ is any element sending ![]() $x_{j}$ to
$x_{j}$ to ![]() $x_{i}$, then
$x_{i}$, then
 $$\begin{eqnarray}f_{i}=f_{j}h_{i}.\end{eqnarray}$$
$$\begin{eqnarray}f_{i}=f_{j}h_{i}.\end{eqnarray}$$ For 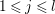 $1\leqslant j\leqslant l$, we put
$1\leqslant j\leqslant l$, we put 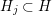 $H_{j}\subset H$ to be the stabilizer of
$H_{j}\subset H$ to be the stabilizer of ![]() $j$, which has order
$j$, which has order  $\sharp H/\sharp O_{j}$, and put
$\sharp H/\sharp O_{j}$, and put 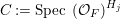 $C:=\text{Spec}\,\left({\mathcal{O}}_{F}\right)^{H_{j}}$, which is a cover of
$C:=\text{Spec}\,\left({\mathcal{O}}_{F}\right)^{H_{j}}$, which is a cover of ![]() $D$ of degree
$D$ of degree ![]() $\sharp O_{j}$. Accordingly,
$\sharp O_{j}$. Accordingly,
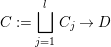 $$\begin{eqnarray}C:=\displaystyle \mathop{\sqcup }_{j=1}^{l}C_{j}\rightarrow D\end{eqnarray}$$
$$\begin{eqnarray}C:=\displaystyle \mathop{\sqcup }_{j=1}^{l}C_{j}\rightarrow D\end{eqnarray}$$ is a cover of degree ![]() $d$. Here, we say that a morphism
$d$. Here, we say that a morphism ![]() $C\rightarrow D$ is a cover if
$C\rightarrow D$ is a cover if ![]() $C$ is the normalization of
$C$ is the normalization of ![]() $D$ in some finite étale (not necessarily Galois)
$D$ in some finite étale (not necessarily Galois) ![]() $K(D)$-algebra. We obtain
$K(D)$-algebra. We obtain ![]() $C$ from
$C$ from ![]() $E$ also in the following way. If
$E$ also in the following way. If ![]() $G_{D}$ is the absolute Galois group of
$G_{D}$ is the absolute Galois group of ![]() $K(D)$, then the
$K(D)$, then the ![]() $G$-cover
$G$-cover ![]() $E$ corresponds to a continuous homomorphism
$E$ corresponds to a continuous homomorphism 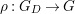 ${\it\rho}:G_{D}\rightarrow G$ (up to conjugation). Since
${\it\rho}:G_{D}\rightarrow G$ (up to conjugation). Since ![]() $G$ acts on
$G$ acts on 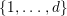 $\{1,\ldots ,d\}$ by conjugation, we get a continuous action of
$\{1,\ldots ,d\}$ by conjugation, we get a continuous action of ![]() $G_{D}$ on
$G_{D}$ on 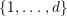 $\{1,\ldots ,d\}$, giving a finite étale cover
$\{1,\ldots ,d\}$, giving a finite étale cover 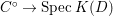 $C^{\circ }\rightarrow \text{Spec}\,K(D)$. Taking the normalization of
$C^{\circ }\rightarrow \text{Spec}\,K(D)$. Taking the normalization of ![]() $D$ in
$D$ in ![]() $C^{\circ }$, we get
$C^{\circ }$, we get ![]() $C$ (up to isomorphism).
$C$ (up to isomorphism).
For a cover ![]() $C\rightarrow D$, we denote by
$C\rightarrow D$, we denote by ![]() $d_{C/D}$ its discriminant exponent: the discriminant of the extension
$d_{C/D}$ its discriminant exponent: the discriminant of the extension 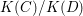 $K(C)/K(D)$ is
$K(C)/K(D)$ is ![]() $\mathfrak{m}_{D}^{d_{C/D}}$. If
$\mathfrak{m}_{D}^{d_{C/D}}$. If ![]() $C$ is connected, then
$C$ is connected, then ![]() $d_{C/D}$ is the same as the different exponent appearing in Lemma 6.5. (Note that since
$d_{C/D}$ is the same as the different exponent appearing in Lemma 6.5. (Note that since ![]() $C$ and
$C$ and ![]() $D$ have the same algebraically closed residue field, the ramification index of a cover
$D$ have the same algebraically closed residue field, the ramification index of a cover ![]() $C\rightarrow D$ is equal to its degree.)
$C\rightarrow D$ is equal to its degree.)
Lemma 11.1. We have
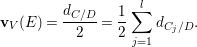 $$\begin{eqnarray}\boldsymbol{v}_{V}(E)=\frac{d_{C/D}}{2}=\frac{1}{2}\mathop{\sum }_{j=1}^{l}d_{C_{j}/D}.\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{v}_{V}(E)=\frac{d_{C/D}}{2}=\frac{1}{2}\mathop{\sum }_{j=1}^{l}d_{C_{j}/D}.\end{eqnarray}$$Proof. This follows from [Reference KedlayaKed07, Lemma 3.4] and [Reference Wood and YasudaWY15, Theorem 4.7].◻
We have an isomorphism
 $$\begin{eqnarray}\displaystyle \begin{array}{@{}rcl@{}}{\it\alpha}:{\rm\Xi}_{F}=\text{Hom}_{{\mathcal{O}}_{D}}^{H}(M,{\mathcal{O}}_{F})\hspace{3.0pt} & \rightarrow \hspace{3.0pt} & \displaystyle \mathop{\bigoplus }_{j=1}^{l}{\mathcal{O}}_{C_{j}}\\ {\it\phi}\hspace{3.0pt} & \mapsto \hspace{3.0pt} & ({\it\phi}(x_{1}),\ldots ,{\it\phi}(x_{l})).\end{array} & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \begin{array}{@{}rcl@{}}{\it\alpha}:{\rm\Xi}_{F}=\text{Hom}_{{\mathcal{O}}_{D}}^{H}(M,{\mathcal{O}}_{F})\hspace{3.0pt} & \rightarrow \hspace{3.0pt} & \displaystyle \mathop{\bigoplus }_{j=1}^{l}{\mathcal{O}}_{C_{j}}\\ {\it\phi}\hspace{3.0pt} & \mapsto \hspace{3.0pt} & ({\it\phi}(x_{1}),\ldots ,{\it\phi}(x_{l})).\end{array} & & \displaystyle \nonumber\end{eqnarray}$$ For each ![]() $e\geqslant 0$, we choose an element
$e\geqslant 0$, we choose an element 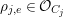 ${\it\rho}_{j,e}\in {\mathcal{O}}_{C_{j}}$, with
${\it\rho}_{j,e}\in {\mathcal{O}}_{C_{j}}$, with 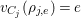 $v_{C_{j}}({\it\rho}_{j,e})=e$, where
$v_{C_{j}}({\it\rho}_{j,e})=e$, where ![]() $v_{C_{j}}$ is the normalized valuation of
$v_{C_{j}}$ is the normalized valuation of ![]() $K(C_{j})$. The elements
$K(C_{j})$. The elements
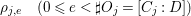 $$\begin{eqnarray}{\it\rho}_{j,e}\quad (0\leqslant e<\sharp O_{j}=[C_{j}:D])\end{eqnarray}$$
$$\begin{eqnarray}{\it\rho}_{j,e}\quad (0\leqslant e<\sharp O_{j}=[C_{j}:D])\end{eqnarray}$$ form a basis of ![]() ${\mathcal{O}}_{C_{j}}$ as an
${\mathcal{O}}_{C_{j}}$ as an ![]() ${\mathcal{O}}_{D}$-module, and
${\mathcal{O}}_{D}$-module, and
 $$\begin{eqnarray}{\it\sigma}_{j,e}:=(0,\ldots ,0,\overset{\underset{\smallsmile }{j}}{{\it\rho}_{j,e}},0,\ldots ,0)\quad (1\leqslant j\leqslant l,\,0\leqslant e<\sharp O_{j})\end{eqnarray}$$
$$\begin{eqnarray}{\it\sigma}_{j,e}:=(0,\ldots ,0,\overset{\underset{\smallsmile }{j}}{{\it\rho}_{j,e}},0,\ldots ,0)\quad (1\leqslant j\leqslant l,\,0\leqslant e<\sharp O_{j})\end{eqnarray}$$ form a basis of 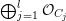 $\bigoplus _{j=1}^{l}{\mathcal{O}}_{C_{j}}$. Let
$\bigoplus _{j=1}^{l}{\mathcal{O}}_{C_{j}}$. Let 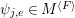 ${\it\psi}_{j,e}\in M^{\left\langle F\right\rangle }$,
${\it\psi}_{j,e}\in M^{\left\langle F\right\rangle }$, 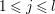 $1\leqslant j\leqslant l$,
$1\leqslant j\leqslant l$, 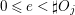 $0\leqslant e<\sharp O_{j}$, be the dual basis of
$0\leqslant e<\sharp O_{j}$, be the dual basis of ![]() ${\it\sigma}_{j,e}$ through the isomorphism
${\it\sigma}_{j,e}$ through the isomorphism ![]() ${\it\alpha}$. The map
${\it\alpha}$. The map 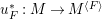 $u_{F}^{\ast }:M\rightarrow M^{\left\langle F\right\rangle }$ sends
$u_{F}^{\ast }:M\rightarrow M^{\left\langle F\right\rangle }$ sends ![]() $x_{i}$ with
$x_{i}$ with ![]() $i\in O_{j}$ to
$i\in O_{j}$ to
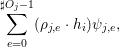 $$\begin{eqnarray}\mathop{\sum }_{e=0}^{\sharp O_{j}-1}({\it\rho}_{j,e}\cdot h_{i}){\it\psi}_{j,e},\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{e=0}^{\sharp O_{j}-1}({\it\rho}_{j,e}\cdot h_{i}){\it\psi}_{j,e},\end{eqnarray}$$ where ![]() $h_{i}$ is any element of
$h_{i}$ is any element of ![]() $H$ sending
$H$ sending ![]() $x_{j}$ to
$x_{j}$ to ![]() $x_{i}$ as above, and
$x_{i}$ as above, and ![]() $f$ to
$f$ to
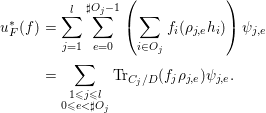 $$\begin{eqnarray}\displaystyle u_{F}^{\ast }(f) & = & \displaystyle \mathop{\sum }_{j=1}^{l}\mathop{\sum }_{e=0}^{\sharp O_{j}-1}\left(\mathop{\sum }_{i\in O_{j}}f_{i}({\it\rho}_{j,e}h_{i})\right){\it\psi}_{j,e}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\substack{ 1\leqslant j\leqslant l \\ 0\leqslant e<\sharp O_{j}}}\text{Tr}_{C_{j}/D}(f_{j}{\it\rho}_{j,e}){\it\psi}_{j,e}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle u_{F}^{\ast }(f) & = & \displaystyle \mathop{\sum }_{j=1}^{l}\mathop{\sum }_{e=0}^{\sharp O_{j}-1}\left(\mathop{\sum }_{i\in O_{j}}f_{i}({\it\rho}_{j,e}h_{i})\right){\it\psi}_{j,e}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\substack{ 1\leqslant j\leqslant l \\ 0\leqslant e<\sharp O_{j}}}\text{Tr}_{C_{j}/D}(f_{j}{\it\rho}_{j,e}){\it\psi}_{j,e}.\nonumber\end{eqnarray}$$ Here, ![]() $\text{Tr}_{C_{j}/D}$ is the trace map
$\text{Tr}_{C_{j}/D}$ is the trace map 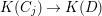 $K(C_{j})\rightarrow K(D)$.
$K(C_{j})\rightarrow K(D)$.
Lemma 11.2. Let ![]() $B\rightarrow D$ be a connected cover of degree
$B\rightarrow D$ be a connected cover of degree ![]() $n$. For
$n$. For ![]() $e\in \mathbb{Z}_{{\geqslant}0}$, we have
$e\in \mathbb{Z}_{{\geqslant}0}$, we have
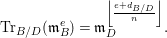 $$\begin{eqnarray}\text{Tr}_{B/D}(\mathfrak{m}_{B}^{e})=\mathfrak{m}_{D}^{\left\lfloor \frac{e+d_{B/D}}{n}\right\rfloor }.\end{eqnarray}$$
$$\begin{eqnarray}\text{Tr}_{B/D}(\mathfrak{m}_{B}^{e})=\mathfrak{m}_{D}^{\left\lfloor \frac{e+d_{B/D}}{n}\right\rfloor }.\end{eqnarray}$$ Here, ![]() $\left\lfloor r\right\rfloor$ is the largest integer
$\left\lfloor r\right\rfloor$ is the largest integer ![]() ${\leqslant}r$. In particular, there exists a generator
${\leqslant}r$. In particular, there exists a generator ![]() ${\it\rho}_{e}$ of
${\it\rho}_{e}$ of ![]() $\mathfrak{m}_{B}^{e}$ such that
$\mathfrak{m}_{B}^{e}$ such that
 $$\begin{eqnarray}v_{D}(\text{Tr}_{B/D}({\it\rho}_{e}))=\left\lfloor \frac{e+d_{B/D}}{n}\right\rfloor ,\end{eqnarray}$$
$$\begin{eqnarray}v_{D}(\text{Tr}_{B/D}({\it\rho}_{e}))=\left\lfloor \frac{e+d_{B/D}}{n}\right\rfloor ,\end{eqnarray}$$ where ![]() $v_{D}$ is the normalized valuation of
$v_{D}$ is the normalized valuation of ![]() $K(D)$.
$K(D)$.
Proof. From [Reference SerreSer79, Proposition 7, page 50], for ![]() $a\in \mathbb{Z}$,
$a\in \mathbb{Z}$,
 $$\begin{eqnarray}\displaystyle \text{Tr}_{B/D}(\mathfrak{m}_{B}^{e})\subset \mathfrak{m}_{D}^{a} & \Leftrightarrow & \displaystyle \mathfrak{m}_{B}^{e}\subset \mathfrak{m}_{B}^{an-d_{B/D}}\nonumber\\ \displaystyle & \Leftrightarrow & \displaystyle a\leqslant \frac{e+d_{B/D}}{n}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{Tr}_{B/D}(\mathfrak{m}_{B}^{e})\subset \mathfrak{m}_{D}^{a} & \Leftrightarrow & \displaystyle \mathfrak{m}_{B}^{e}\subset \mathfrak{m}_{B}^{an-d_{B/D}}\nonumber\\ \displaystyle & \Leftrightarrow & \displaystyle a\leqslant \frac{e+d_{B/D}}{n}.\nonumber\end{eqnarray}$$ This shows the first assertion. To show the second assertion, suppose, on the contrary, that there does not exist such a generator of ![]() $\mathfrak{m}_{B}^{e}$. From the first assertion, there exists an element
$\mathfrak{m}_{B}^{e}$. From the first assertion, there exists an element  ${\it\tau}\in \mathfrak{m}_{B}^{e+1}$ with
${\it\tau}\in \mathfrak{m}_{B}^{e+1}$ with
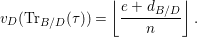 $$\begin{eqnarray}v_{D}(\text{Tr}_{B/D}({\it\tau}))=\left\lfloor \frac{e+d_{B/D}}{n}\right\rfloor .\end{eqnarray}$$
$$\begin{eqnarray}v_{D}(\text{Tr}_{B/D}({\it\tau}))=\left\lfloor \frac{e+d_{B/D}}{n}\right\rfloor .\end{eqnarray}$$ For any generator ![]() ${\it\rho}$ of
${\it\rho}$ of ![]() $\mathfrak{m}_{B}^{e}$,
$\mathfrak{m}_{B}^{e}$, ![]() ${\it\rho}+{\it\tau}$ is a generator with the desired property, a contradiction.◻
${\it\rho}+{\it\tau}$ is a generator with the desired property, a contradiction.◻
Proposition 11.3. Let us write 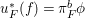 $u_{F}^{\ast }(f)={\it\pi}_{F}^{b}{\it\phi}$, with
$u_{F}^{\ast }(f)={\it\pi}_{F}^{b}{\it\phi}$, with ![]() ${\it\phi}$ irreducible (a linear form over
${\it\phi}$ irreducible (a linear form over ![]() ${\mathcal{O}}_{D}$ with at least one coefficient a unit). Namely,
${\mathcal{O}}_{D}$ with at least one coefficient a unit). Namely, ![]() $b$ is the order of
$b$ is the order of ![]() $u_{F}^{\ast }(f)$ along
$u_{F}^{\ast }(f)$ along ![]() $V_{0}^{\left\langle F\right\rangle }$. Then
$V_{0}^{\left\langle F\right\rangle }$. Then
 $$\begin{eqnarray}\displaystyle b=\sharp H\cdot \min \left\{v_{D}(f_{j})+\left\lfloor \frac{d_{C_{j}/D}}{[C_{j}:D]}\right\rfloor \mid 1\leqslant j\leqslant l\right\}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle b=\sharp H\cdot \min \left\{v_{D}(f_{j})+\left\lfloor \frac{d_{C_{j}/D}}{[C_{j}:D]}\right\rfloor \mid 1\leqslant j\leqslant l\right\}. & & \displaystyle \nonumber\end{eqnarray}$$ Here, we put  $v_{D}(0):=+\infty$ by convention.
$v_{D}(0):=+\infty$ by convention.
Proof. From the lemma above, for a suitable choice of ![]() ${\it\rho}_{j,e}$, we have
${\it\rho}_{j,e}$, we have
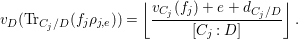 $$\begin{eqnarray}v_{D}(\text{Tr}_{C_{j}/D}(f_{j}{\it\rho}_{j,e}))=\left\lfloor \frac{v_{C_{j}}(f_{j})+e+d_{C_{j}/D}}{[C_{j}:D]}\right\rfloor .\end{eqnarray}$$
$$\begin{eqnarray}v_{D}(\text{Tr}_{C_{j}/D}(f_{j}{\it\rho}_{j,e}))=\left\lfloor \frac{v_{C_{j}}(f_{j})+e+d_{C_{j}/D}}{[C_{j}:D]}\right\rfloor .\end{eqnarray}$$Then
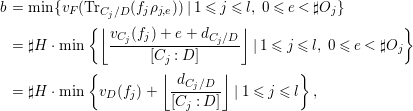 $$\begin{eqnarray}\displaystyle b & = & \displaystyle \min \{v_{F}(\text{Tr}_{C_{j}/D}(f_{j}{\it\rho}_{j,e}))\mid 1\leqslant j\leqslant l,\,0\leqslant e<\sharp O_{j}\}\nonumber\\ \displaystyle & = & \displaystyle \sharp H\cdot \min \left\{\left\lfloor \frac{v_{C_{j}}(f_{j})+e+d_{C_{j}/D}}{[C_{j}:D]}\right\rfloor \mid 1\leqslant j\leqslant l,\,0\leqslant e<\sharp O_{j}\right\}\nonumber\\ \displaystyle & = & \displaystyle \sharp H\cdot \min \left\{v_{D}(f_{j})+\left\lfloor \frac{d_{C_{j}/D}}{[C_{j}:D]}\right\rfloor \mid 1\leqslant j\leqslant l\right\},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle b & = & \displaystyle \min \{v_{F}(\text{Tr}_{C_{j}/D}(f_{j}{\it\rho}_{j,e}))\mid 1\leqslant j\leqslant l,\,0\leqslant e<\sharp O_{j}\}\nonumber\\ \displaystyle & = & \displaystyle \sharp H\cdot \min \left\{\left\lfloor \frac{v_{C_{j}}(f_{j})+e+d_{C_{j}/D}}{[C_{j}:D]}\right\rfloor \mid 1\leqslant j\leqslant l,\,0\leqslant e<\sharp O_{j}\right\}\nonumber\\ \displaystyle & = & \displaystyle \sharp H\cdot \min \left\{v_{D}(f_{j})+\left\lfloor \frac{d_{C_{j}/D}}{[C_{j}:D]}\right\rfloor \mid 1\leqslant j\leqslant l\right\},\nonumber\end{eqnarray}$$which shows the proposition.◻
Corollary 11.4. For 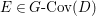 $E\in G\text{-}\text{Cov}(D)$, we have
$E\in G\text{-}\text{Cov}(D)$, we have
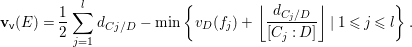 $$\begin{eqnarray}\displaystyle \boldsymbol{v}_{\mathsf{v}}(E)=\frac{1}{2}\mathop{\sum }_{j=1}^{l}d_{Cj/D}-\min \left\{v_{D}(f_{j})+\left\lfloor \frac{d_{C_{j}/D}}{[C_{j}:D]}\right\rfloor \mid 1\leqslant j\leqslant l\right\}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{v}_{\mathsf{v}}(E)=\frac{1}{2}\mathop{\sum }_{j=1}^{l}d_{Cj/D}-\min \left\{v_{D}(f_{j})+\left\lfloor \frac{d_{C_{j}/D}}{[C_{j}:D]}\right\rfloor \mid 1\leqslant j\leqslant l\right\}. & & \displaystyle \nonumber\end{eqnarray}$$ In particular, if 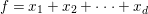 $f=x_{1}+x_{2}+\cdots +x_{d}$, then
$f=x_{1}+x_{2}+\cdots +x_{d}$, then
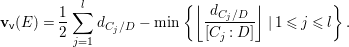 $$\begin{eqnarray}\displaystyle \boldsymbol{v}_{\mathsf{v}}(E)=\frac{1}{2}\mathop{\sum }_{j=1}^{l}d_{C_{j}/D}-\min \left\{\left\lfloor \frac{d_{C_{j}/D}}{[C_{j}:D]}\right\rfloor \mid 1\leqslant j\leqslant l\right\}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{v}_{\mathsf{v}}(E)=\frac{1}{2}\mathop{\sum }_{j=1}^{l}d_{C_{j}/D}-\min \left\{\left\lfloor \frac{d_{C_{j}/D}}{[C_{j}:D]}\right\rfloor \mid 1\leqslant j\leqslant l\right\}. & & \displaystyle \nonumber\end{eqnarray}$$Proof. In our situation, the symbol ![]() $\mathsf{v}^{|F|}$ has, a priori, two meanings: one is obtained by applying the untwisting technique directly to
$\mathsf{v}^{|F|}$ has, a priori, two meanings: one is obtained by applying the untwisting technique directly to ![]() $\mathsf{v}$ and the other by first applying it to
$\mathsf{v}$ and the other by first applying it to ![]() $V$ and taking the induced subvariety in
$V$ and taking the induced subvariety in ![]() $V^{|F|}$. However, the two constructions actually coincide. Indeed, if
$V^{|F|}$. However, the two constructions actually coincide. Indeed, if ![]() $\mathsf{m}$ is the linear part of
$\mathsf{m}$ is the linear part of ![]() ${\mathcal{O}}_{\mathsf{v}}$, then we have a surjection
${\mathcal{O}}_{\mathsf{v}}$, then we have a surjection ![]() $M{\twoheadrightarrow}\mathsf{m}$. It induces a surjection
$M{\twoheadrightarrow}\mathsf{m}$. It induces a surjection 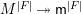 $M^{|F|}{\twoheadrightarrow}\mathsf{m}^{|F|}$ and a closed immersion
$M^{|F|}{\twoheadrightarrow}\mathsf{m}^{|F|}$ and a closed immersion 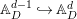 $\mathbb{A}_{D}^{d-1}{\hookrightarrow}\mathbb{A}_{D}^{d}$. This shows the claim. Therefore, there is no confusion in the use of the symbol as well as
$\mathbb{A}_{D}^{d-1}{\hookrightarrow}\mathbb{A}_{D}^{d}$. This shows the claim. Therefore, there is no confusion in the use of the symbol as well as ![]() $\mathfrak{v}^{|F|}$.
$\mathfrak{v}^{|F|}$.
The boundary of ![]() $\mathfrak{v}^{|F|}$ is
$\mathfrak{v}^{|F|}$ is 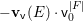 $-\boldsymbol{v}_{\mathsf{v}}(E)\cdot \mathsf{v}_{0}^{|F|}$ from Lemma 6.5, while
$-\boldsymbol{v}_{\mathsf{v}}(E)\cdot \mathsf{v}_{0}^{|F|}$ from Lemma 6.5, while
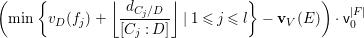 $$\begin{eqnarray}\left(\min \left\{v_{D}(f_{j})+\left\lfloor \frac{d_{C_{j}/D}}{[C_{j}:D]}\right\rfloor \mid 1\leqslant j\leqslant l\right\}-\boldsymbol{v}_{V}(E)\right)\cdot \mathsf{v}_{0}^{|F|}\end{eqnarray}$$
$$\begin{eqnarray}\left(\min \left\{v_{D}(f_{j})+\left\lfloor \frac{d_{C_{j}/D}}{[C_{j}:D]}\right\rfloor \mid 1\leqslant j\leqslant l\right\}-\boldsymbol{v}_{V}(E)\right)\cdot \mathsf{v}_{0}^{|F|}\end{eqnarray}$$from Propositions 8.1 and 11.3. Comparing the coefficients shows the corollary.◻
(1) Let
 $p$ denote the characteristic of
$p$ denote the characteristic of  $k$. If
$k$. If  $p\nmid [C_{j}:D]$, then
$p\nmid [C_{j}:D]$, then  $d_{C_{j}/D}=[C_{j}:D]-1$ and
$d_{C_{j}/D}=[C_{j}:D]-1$ and  $\left\lfloor \frac{d_{C_{j}/D}}{[C_{j}:D]}\right\rfloor =0$. Therefore, if
$\left\lfloor \frac{d_{C_{j}/D}}{[C_{j}:D]}\right\rfloor =0$. Therefore, if  $p\nmid d$ and if
$p\nmid d$ and if  $f=x_{1}+\cdots +x_{d}$, then since at least one
$f=x_{1}+\cdots +x_{d}$, then since at least one  $C_{j}$ satisfies
$C_{j}$ satisfies  $p\nmid [C_{j}:D]$, we have
$p\nmid [C_{j}:D]$, we have  $\boldsymbol{v}_{\mathsf{v}}=\boldsymbol{v}_{V}$. This equality is also explained as follows. We have the exact sequence whether we have
$\boldsymbol{v}_{\mathsf{v}}=\boldsymbol{v}_{V}$. This equality is also explained as follows. We have the exact sequence whether we have $$\begin{eqnarray}0\rightarrow \mathsf{v}\rightarrow V\xrightarrow[]{(x_{1},\ldots ,x_{d})\mapsto \sum x_{i}}\mathbb{A}_{D}^{1}\rightarrow 0,\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow \mathsf{v}\rightarrow V\xrightarrow[]{(x_{1},\ldots ,x_{d})\mapsto \sum x_{i}}\mathbb{A}_{D}^{1}\rightarrow 0,\end{eqnarray}$$ $p\mid d$ or not. If
$p\mid d$ or not. If  $p\nmid d$, this sequence splits. The equality follows from the additivity of
$p\nmid d$, this sequence splits. The equality follows from the additivity of  $\boldsymbol{v}_{\bullet }$ (see [Reference Wood and YasudaWY15]).
$\boldsymbol{v}_{\bullet }$ (see [Reference Wood and YasudaWY15]).(2) If, for some
 $j$,
$j$,  $f_{j}$ is a unit and
$f_{j}$ is a unit and  $\sharp O_{j}=1$ (hence
$\sharp O_{j}=1$ (hence  $C_{j}=D$ and
$C_{j}=D$ and  $d_{C_{j}/D}=0$), then the corollary above deduces that
$d_{C_{j}/D}=0$), then the corollary above deduces that  $\boldsymbol{v}_{\mathsf{v}}=\boldsymbol{v}_{V}.$ Again,
$\boldsymbol{v}_{\mathsf{v}}=\boldsymbol{v}_{V}.$ Again,  $V$ is isomorphic to the direct sum of
$V$ is isomorphic to the direct sum of  $\mathsf{v}$ and a one-dimensional trivial representation, this time as an
$\mathsf{v}$ and a one-dimensional trivial representation, this time as an  $H$-representation.
$H$-representation.
Example 11.6. Let ![]() $p$ be a prime number, and let
$p$ be a prime number, and let 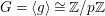 $G=\left\langle g\right\rangle \cong \mathbb{Z}/p\mathbb{Z}$. Suppose that
$G=\left\langle g\right\rangle \cong \mathbb{Z}/p\mathbb{Z}$. Suppose that 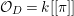 ${\mathcal{O}}_{D}=k[[{\it\pi}]]$, with
${\mathcal{O}}_{D}=k[[{\it\pi}]]$, with ![]() $k$ of characteristic
$k$ of characteristic ![]() $p$, and that
$p$, and that ![]() $G$ acts on
$G$ acts on 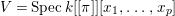 $V=\text{Spec}\,k[[{\it\pi}]][x_{1},\ldots ,x_{p}]$ by
$V=\text{Spec}\,k[[{\it\pi}]][x_{1},\ldots ,x_{p}]$ by
 $$\begin{eqnarray}g(x_{i})=\left\{\begin{array}{@{}ll@{}}x_{i+1}\quad & (1\leqslant i<p),\\ x_{1}\quad & (i=p),\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}g(x_{i})=\left\{\begin{array}{@{}ll@{}}x_{i+1}\quad & (1\leqslant i<p),\\ x_{1}\quad & (i=p),\end{array}\right.\end{eqnarray}$$ and that ![]() $\mathsf{v}\subset V$ is the hyperplane defined by
$\mathsf{v}\subset V$ is the hyperplane defined by 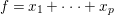 $f=x_{1}+\cdots +x_{p}$. Let
$f=x_{1}+\cdots +x_{p}$. Let 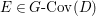 $E\in G\text{-}\text{Cov}(D)$ be a connected
$E\in G\text{-}\text{Cov}(D)$ be a connected ![]() $G$-cover. The ramification jump
$G$-cover. The ramification jump  $j\in \mathbb{Z}_{{>}0}$ of
$j\in \mathbb{Z}_{{>}0}$ of ![]() $E$ is given by
$E$ is given by
 $$\begin{eqnarray}j:=v_{D}({\it\pi}_{E}g-{\it\pi}_{E})-1,\end{eqnarray}$$
$$\begin{eqnarray}j:=v_{D}({\it\pi}_{E}g-{\it\pi}_{E})-1,\end{eqnarray}$$ which is not divisible by ![]() $p$. From [Reference SerreSer79, page 83, Lemma 3],
$p$. From [Reference SerreSer79, page 83, Lemma 3],
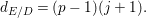 $$\begin{eqnarray}d_{E/D}=(p-1)(j+1).\end{eqnarray}$$
$$\begin{eqnarray}d_{E/D}=(p-1)(j+1).\end{eqnarray}$$Accordingly,
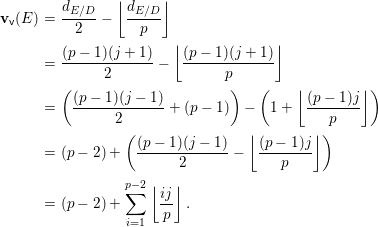 $$\begin{eqnarray}\displaystyle \boldsymbol{v}_{\mathsf{v}}(E) & = & \displaystyle \frac{d_{E/D}}{2}-\left\lfloor \frac{d_{E/D}}{p}\right\rfloor \nonumber\\ \displaystyle & = & \displaystyle \frac{(p-1)(j+1)}{2}-\left\lfloor \frac{(p-1)(j+1)}{p}\right\rfloor \nonumber\\ \displaystyle & = & \displaystyle \left(\frac{(p-1)(j-1)}{2}+(p-1)\right)-\left(1+\left\lfloor \frac{(p-1)j}{p}\right\rfloor \right)\nonumber\\ \displaystyle & = & \displaystyle (p-2)+\left(\frac{(p-1)(j-1)}{2}-\left\lfloor \frac{(p-1)j}{p}\right\rfloor \right)\nonumber\\ \displaystyle & = & \displaystyle (p-2)+\mathop{\sum }_{i=1}^{p-2}\left\lfloor \frac{ij}{p}\right\rfloor .\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{v}_{\mathsf{v}}(E) & = & \displaystyle \frac{d_{E/D}}{2}-\left\lfloor \frac{d_{E/D}}{p}\right\rfloor \nonumber\\ \displaystyle & = & \displaystyle \frac{(p-1)(j+1)}{2}-\left\lfloor \frac{(p-1)(j+1)}{p}\right\rfloor \nonumber\\ \displaystyle & = & \displaystyle \left(\frac{(p-1)(j-1)}{2}+(p-1)\right)-\left(1+\left\lfloor \frac{(p-1)j}{p}\right\rfloor \right)\nonumber\\ \displaystyle & = & \displaystyle (p-2)+\left(\frac{(p-1)(j-1)}{2}-\left\lfloor \frac{(p-1)j}{p}\right\rfloor \right)\nonumber\\ \displaystyle & = & \displaystyle (p-2)+\mathop{\sum }_{i=1}^{p-2}\left\lfloor \frac{ij}{p}\right\rfloor .\nonumber\end{eqnarray}$$The last equality follows from
 $$\begin{eqnarray}\frac{(p-1)(j-1)}{2}=\mathop{\sum }_{i=1}^{p-1}\left\lfloor \frac{ij}{p}\right\rfloor\end{eqnarray}$$
$$\begin{eqnarray}\frac{(p-1)(j-1)}{2}=\mathop{\sum }_{i=1}^{p-1}\left\lfloor \frac{ij}{p}\right\rfloor\end{eqnarray}$$ (for instance, see [Reference Graham, Knuth and PatashnikGKP89, page 94]). Since 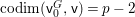 $\text{codim}(\mathsf{v}_{0}^{G},\mathsf{v})=p-2$,
$\text{codim}(\mathsf{v}_{0}^{G},\mathsf{v})=p-2$,
 $$\begin{eqnarray}\mathbf{w}_{\mathsf{v}}(E)=(p-2)-\boldsymbol{v}_{\mathsf{v}}(E)=-\mathop{\sum }_{i=1}^{p-2}\left\lfloor \frac{ij}{p}\right\rfloor ,\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{w}_{\mathsf{v}}(E)=(p-2)-\boldsymbol{v}_{\mathsf{v}}(E)=-\mathop{\sum }_{i=1}^{p-2}\left\lfloor \frac{ij}{p}\right\rfloor ,\end{eqnarray}$$which coincides with computation in [Reference YasudaYas14] (see also [Reference YasudaYasa]).
12 Some  $S_{4}$-masses in characteristic two
$S_{4}$-masses in characteristic two
In this section, we consider the case where ![]() ${\mathcal{O}}_{D}$ has characteristic two,
${\mathcal{O}}_{D}$ has characteristic two, ![]() $G$ is the symmetric group
$G$ is the symmetric group ![]() $S_{4}$,
$S_{4}$, 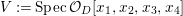 $V:=\text{Spec}\,{\mathcal{O}}_{D}[x_{1},x_{2},x_{3},x_{4}]$, with the standard
$V:=\text{Spec}\,{\mathcal{O}}_{D}[x_{1},x_{2},x_{3},x_{4}]$, with the standard ![]() $G$-action, and
$G$-action, and ![]() $\mathsf{v}\subset V$ is the hyperplane defined by
$\mathsf{v}\subset V$ is the hyperplane defined by 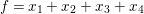 $f=x_{1}+x_{2}+x_{3}+x_{4}$. The induced
$f=x_{1}+x_{2}+x_{3}+x_{4}$. The induced ![]() $G$-action on
$G$-action on ![]() $\mathsf{v}$ is still faithful, since
$\mathsf{v}$ is still faithful, since ![]() $\mathsf{v}$ contains a point whose coordinates are distinct one another, for instance,
$\mathsf{v}$ contains a point whose coordinates are distinct one another, for instance,  $(0,1,a,a+1)$ with
$(0,1,a,a+1)$ with 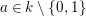 $a\in k\setminus \{0,1\}$. As an application of the computation of
$a\in k\setminus \{0,1\}$. As an application of the computation of ![]() $\boldsymbol{v}_{\mathsf{v}}$ in the last section, we compute motivic integrals
$\boldsymbol{v}_{\mathsf{v}}$ in the last section, we compute motivic integrals
 $$\begin{eqnarray}\mathbb{M}=\int _{G\text{-}\text{Cov}(D)}\mathbb{L}^{-3\boldsymbol{v}_{\mathsf{v}}}\,d{\it\tau}\quad \text{and}\quad \mathbb{M}^{\prime }:=\int _{G\text{-}\text{Cov}(D)}\mathbb{L}^{3\mathbf{w}_{\mathsf{v}}}\,d{\it\tau}\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{M}=\int _{G\text{-}\text{Cov}(D)}\mathbb{L}^{-3\boldsymbol{v}_{\mathsf{v}}}\,d{\it\tau}\quad \text{and}\quad \mathbb{M}^{\prime }:=\int _{G\text{-}\text{Cov}(D)}\mathbb{L}^{3\mathbf{w}_{\mathsf{v}}}\,d{\it\tau}\end{eqnarray}$$ under some assumptions, and observe that ![]() $\mathbb{M}$ and
$\mathbb{M}$ and ![]() $\mathbb{M}^{\prime }$ are dual to each other. Such a duality was first observed in [Reference Wood and YasudaWY15] and is discussed in more detail in [Reference Wood and YasudaWY]. It is also related to the Poincaré duality of stringy motifs. The number 3 in the integrals is chosen because for
$\mathbb{M}^{\prime }$ are dual to each other. Such a duality was first observed in [Reference Wood and YasudaWY15] and is discussed in more detail in [Reference Wood and YasudaWY]. It is also related to the Poincaré duality of stringy motifs. The number 3 in the integrals is chosen because for  $n=1,2$, the integrals
$n=1,2$, the integrals 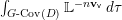 $\int _{G\text{-}\text{Cov}(D)}\mathbb{L}^{-n\boldsymbol{v}_{\mathsf{v}}}\,d{\it\tau}$ and
$\int _{G\text{-}\text{Cov}(D)}\mathbb{L}^{-n\boldsymbol{v}_{\mathsf{v}}}\,d{\it\tau}$ and 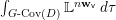 $\int _{G\text{-}\text{Cov}(D)}\mathbb{L}^{n\mathbf{w}_{\mathsf{v}}}\,d{\it\tau}$ diverge.
$\int _{G\text{-}\text{Cov}(D)}\mathbb{L}^{n\mathbf{w}_{\mathsf{v}}}\,d{\it\tau}$ diverge.
To compute ![]() $\mathbb{M}$ and
$\mathbb{M}$ and ![]() $\mathbb{M}^{\prime }$, we decompose them into the sums of 5 terms respectively. For
$\mathbb{M}^{\prime }$, we decompose them into the sums of 5 terms respectively. For ![]() $n\geqslant 0$, let
$n\geqslant 0$, let ![]() $\text{Fie}_{n}$ and
$\text{Fie}_{n}$ and ![]() $\text{Eta}_{n}$ be the (conjectural) moduli spaces of degree
$\text{Eta}_{n}$ be the (conjectural) moduli spaces of degree ![]() $n$ field extensions and étale extensions of
$n$ field extensions and étale extensions of ![]() $K(D)$ respectively. Since
$K(D)$ respectively. Since ![]() $G=S_{4}$, giving a continuous homomorphism
$G=S_{4}$, giving a continuous homomorphism 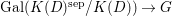 $\text{Gal}(K(D)^{\text{sep}}/K(D))\rightarrow G$ is equivalent to giving a continuous
$\text{Gal}(K(D)^{\text{sep}}/K(D))\rightarrow G$ is equivalent to giving a continuous 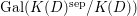 $\text{Gal}(K(D)^{\text{sep}}/K(D))$-action on
$\text{Gal}(K(D)^{\text{sep}}/K(D))$-action on  $\{1,\ldots ,n\}$. Therefore, the map
$\{1,\ldots ,n\}$. Therefore, the map
 $$\begin{eqnarray}\displaystyle G\text{-}\text{Cov}(D) & \rightarrow & \displaystyle \text{Eta}_{4}\nonumber\\ \displaystyle E & \mapsto & \displaystyle {\mathcal{O}}_{D}\otimes _{{\mathcal{O}}_{D}}K(D)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle G\text{-}\text{Cov}(D) & \rightarrow & \displaystyle \text{Eta}_{4}\nonumber\\ \displaystyle E & \mapsto & \displaystyle {\mathcal{O}}_{D}\otimes _{{\mathcal{O}}_{D}}K(D)\nonumber\end{eqnarray}$$is bijective. Since there are exactly 5 partitions of 4,
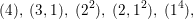 $$\begin{eqnarray}(4),\,(3,1),\,(2^{2}),\,(2,1^{2}),\,(1^{4}),\end{eqnarray}$$
$$\begin{eqnarray}(4),\,(3,1),\,(2^{2}),\,(2,1^{2}),\,(1^{4}),\end{eqnarray}$$ and ![]() $\text{Fie}_{1}$ is a singleton, we have the following decomposition of
$\text{Fie}_{1}$ is a singleton, we have the following decomposition of ![]() $\text{Eta}_{4}$:
$\text{Eta}_{4}$:
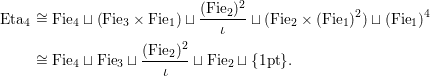 $$\begin{eqnarray}\displaystyle \text{Eta}_{4} & \cong & \displaystyle \text{Fie}_{4}\sqcup \left(\text{Fie}_{3}\times \text{Fie}_{1}\right)\sqcup \frac{(\text{Fie}_{2})^{2}}{{\it\iota}}\sqcup (\text{Fie}_{2}\times \left(\text{Fie}_{1}\right)^{2})\sqcup \left(\text{Fie}_{1}\right)^{4}\nonumber\\ \displaystyle & \cong & \displaystyle \text{Fie}_{4}\sqcup \text{Fie}_{3}\sqcup \frac{(\text{Fie}_{2})^{2}}{{\it\iota}}\sqcup \text{Fie}_{2}\sqcup \{1\text{pt}\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{Eta}_{4} & \cong & \displaystyle \text{Fie}_{4}\sqcup \left(\text{Fie}_{3}\times \text{Fie}_{1}\right)\sqcup \frac{(\text{Fie}_{2})^{2}}{{\it\iota}}\sqcup (\text{Fie}_{2}\times \left(\text{Fie}_{1}\right)^{2})\sqcup \left(\text{Fie}_{1}\right)^{4}\nonumber\\ \displaystyle & \cong & \displaystyle \text{Fie}_{4}\sqcup \text{Fie}_{3}\sqcup \frac{(\text{Fie}_{2})^{2}}{{\it\iota}}\sqcup \text{Fie}_{2}\sqcup \{1\text{pt}\}.\nonumber\end{eqnarray}$$ Here, ![]() ${\it\iota}$ is the involution of
${\it\iota}$ is the involution of ![]() $(\text{Fie}_{2})^{2}$ given by the transposition of components. We have the corresponding stratification
$(\text{Fie}_{2})^{2}$ given by the transposition of components. We have the corresponding stratification
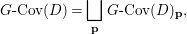 $$\begin{eqnarray}G\text{-}\text{Cov}(D)=\mathop{\sqcup }_{\mathbf{p}}G\text{-}\text{Cov}(D)_{\mathbf{p}},\end{eqnarray}$$
$$\begin{eqnarray}G\text{-}\text{Cov}(D)=\mathop{\sqcup }_{\mathbf{p}}G\text{-}\text{Cov}(D)_{\mathbf{p}},\end{eqnarray}$$ where ![]() $\mathbf{p}$ runs over the partitions of
$\mathbf{p}$ runs over the partitions of ![]() $4$ and the corresponding decompositions of
$4$ and the corresponding decompositions of ![]() $\mathbb{M}$ and
$\mathbb{M}$ and ![]() $\mathbb{M}^{\prime }$,
$\mathbb{M}^{\prime }$,
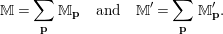 $$\begin{eqnarray}\displaystyle \mathbb{M}=\mathop{\sum }_{\mathbf{p}}\mathbb{M}_{\mathbf{p}}\quad \text{and}\quad \mathbb{M}^{\prime }=\mathop{\sum }_{\mathbf{p}}\mathbb{M}_{\mathbf{p}}^{\prime }. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathbb{M}=\mathop{\sum }_{\mathbf{p}}\mathbb{M}_{\mathbf{p}}\quad \text{and}\quad \mathbb{M}^{\prime }=\mathop{\sum }_{\mathbf{p}}\mathbb{M}_{\mathbf{p}}^{\prime }. & & \displaystyle \nonumber\end{eqnarray}$$To further computations, we need to assume the following conjecture.
Conjecture 12.1. (The motivic version of Krasner’s formula)
Suppose that ![]() $k$ has characteristic
$k$ has characteristic ![]() $p>0$. Let
$p>0$. Let ![]() $m\geqslant 2$ be an integer, and let
$m\geqslant 2$ be an integer, and let 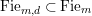 $\text{Fie}_{m,d}\subset \text{Fie}_{m}$ be the locus of degree
$\text{Fie}_{m,d}\subset \text{Fie}_{m}$ be the locus of degree ![]() $m$ field extensions of
$m$ field extensions of ![]() $k(({\it\pi}))$ with discriminant exponent
$k(({\it\pi}))$ with discriminant exponent ![]() $d$. Then we have the equality in
$d$. Then we have the equality in ![]() ${\mathcal{R}}$,
${\mathcal{R}}$,
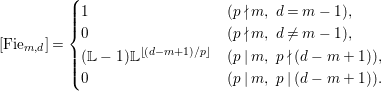 $$\begin{eqnarray}[\text{Fie}_{m,d}]=\left\{\begin{array}{@{}ll@{}}1\quad & (p\nmid m,\,d=m-1),\\ 0\quad & (p\nmid m,\,d\neq m-1),\\ (\mathbb{L}-1)\mathbb{L}^{\left\lfloor (d-m+1)/p\right\rfloor }\quad & (p\mid m,\,p\nmid (d-m+1)),\\ 0\quad & (p\mid m,\,p\mid (d-m+1)).\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}[\text{Fie}_{m,d}]=\left\{\begin{array}{@{}ll@{}}1\quad & (p\nmid m,\,d=m-1),\\ 0\quad & (p\nmid m,\,d\neq m-1),\\ (\mathbb{L}-1)\mathbb{L}^{\left\lfloor (d-m+1)/p\right\rfloor }\quad & (p\mid m,\,p\nmid (d-m+1)),\\ 0\quad & (p\mid m,\,p\mid (d-m+1)).\end{array}\right.\end{eqnarray}$$ Krasner [Reference KrasnerKra66] showed that if ![]() $q=p^{e}$ is a power of a prime number
$q=p^{e}$ is a power of a prime number ![]() $p$, then the number of totally ramified degree
$p$, then the number of totally ramified degree ![]() $m$ extensions of the power series field
$m$ extensions of the power series field ![]() $\mathbb{F}_{q}(({\it\pi}))$ in its algebraic closure
$\mathbb{F}_{q}(({\it\pi}))$ in its algebraic closure ![]() $\overline{\mathbb{F}_{q}(({\it\pi}))}$ is exactly
$\overline{\mathbb{F}_{q}(({\it\pi}))}$ is exactly
 $$\begin{eqnarray}\left\{\begin{array}{@{}ll@{}}m\quad & (p\nmid m,\,d=m-1),\\ 0\quad & (p\nmid m,\,d\neq m-1),\\ m(q-1)q^{\left\lfloor (d-m+1)/p\right\rfloor }\quad & (p\mid m,\,p\nmid (d-m+1)),\\ 0\quad & (p\mid m,\,p\mid (d-m+1)).\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\left\{\begin{array}{@{}ll@{}}m\quad & (p\nmid m,\,d=m-1),\\ 0\quad & (p\nmid m,\,d\neq m-1),\\ m(q-1)q^{\left\lfloor (d-m+1)/p\right\rfloor }\quad & (p\mid m,\,p\nmid (d-m+1)),\\ 0\quad & (p\mid m,\,p\mid (d-m+1)).\end{array}\right.\end{eqnarray}$$ Counting isomorphism classes (with weights coming from automorphisms) rather than subfields of ![]() $\overline{\mathbb{F}_{q}(({\it\pi}))}$ as done in [Reference SerreSer78], we can kill the factor
$\overline{\mathbb{F}_{q}(({\it\pi}))}$ as done in [Reference SerreSer78], we can kill the factor ![]() $m$. The conjecture above seems to be the only reasonable possibility.
$m$. The conjecture above seems to be the only reasonable possibility.
In what follows, we exhibit how to compute ![]() $\mathbb{M}_{(2^{2})}$ and
$\mathbb{M}_{(2^{2})}$ and ![]() $\mathbb{M}_{(2^{2})}^{\prime }$. Computation of the other terms is similar and easier. We go back to the assumption that
$\mathbb{M}_{(2^{2})}^{\prime }$. Computation of the other terms is similar and easier. We go back to the assumption that ![]() $k$ has characteristic two. If
$k$ has characteristic two. If 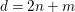 $d=2n+m$, then the conjecture reads
$d=2n+m$, then the conjecture reads
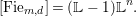 $$\begin{eqnarray}[\text{Fie}_{m,d}]=(\mathbb{L}-1)\mathbb{L}^{n}.\end{eqnarray}$$
$$\begin{eqnarray}[\text{Fie}_{m,d}]=(\mathbb{L}-1)\mathbb{L}^{n}.\end{eqnarray}$$ Let 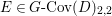 $E\in G\text{-}\text{Cov}(D)_{2,2}$, and let
$E\in G\text{-}\text{Cov}(D)_{2,2}$, and let  $C=C_{1}\sqcup C_{2}$ be the associated quartic cover of
$C=C_{1}\sqcup C_{2}$ be the associated quartic cover of ![]() $D$, where
$D$, where ![]() $C_{1}$ and
$C_{1}$ and ![]() $C_{2}$ are double covers of
$C_{2}$ are double covers of ![]() $D$ with
$D$ with 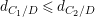 $d_{C_{1}/D}\leqslant d_{C_{2}/D}$. Then
$d_{C_{1}/D}\leqslant d_{C_{2}/D}$. Then
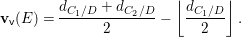 $$\begin{eqnarray}\boldsymbol{v}_{\mathsf{v}}(E)=\frac{d_{C_{1}/D}+d_{C_{2}/D}}{2}-\left\lfloor \frac{d_{C_{1}/D}}{2}\right\rfloor .\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{v}_{\mathsf{v}}(E)=\frac{d_{C_{1}/D}+d_{C_{2}/D}}{2}-\left\lfloor \frac{d_{C_{1}/D}}{2}\right\rfloor .\end{eqnarray}$$ If we write 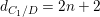 $d_{C_{1}/D}=2n+2$ and
$d_{C_{1}/D}=2n+2$ and 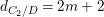 $d_{C_{2}/D}=2m+2$ for some
$d_{C_{2}/D}=2m+2$ for some 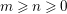 $m\geqslant n\geqslant 0$,
$m\geqslant n\geqslant 0$,
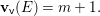 $$\begin{eqnarray}\boldsymbol{v}_{\mathsf{v}}(E)=m+1.\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{v}_{\mathsf{v}}(E)=m+1.\end{eqnarray}$$ From the last property of ![]() ${\mathcal{R}}$ in the list in Section 2.3, we have
${\mathcal{R}}$ in the list in Section 2.3, we have
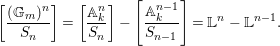 $$\begin{eqnarray}\left[\frac{(\mathbb{G}_{m})^{n}}{S_{n}}\right]=\left[\frac{\mathbb{A}_{k}^{n}}{S_{n}}\right]-\left[\frac{\mathbb{A}_{k}^{n-1}}{S_{n-1}}\right]=\mathbb{L}^{n}-\mathbb{L}^{n-1}.\end{eqnarray}$$
$$\begin{eqnarray}\left[\frac{(\mathbb{G}_{m})^{n}}{S_{n}}\right]=\left[\frac{\mathbb{A}_{k}^{n}}{S_{n}}\right]-\left[\frac{\mathbb{A}_{k}^{n-1}}{S_{n-1}}\right]=\mathbb{L}^{n}-\mathbb{L}^{n-1}.\end{eqnarray}$$Accordingly,
 $$\begin{eqnarray}\left[\frac{\left(\text{Fie}_{2,2n+2}\right)^{2}}{{\it\iota}}\right]=(\mathbb{L}-1)\mathbb{L}^{2n+1}.\end{eqnarray}$$
$$\begin{eqnarray}\left[\frac{\left(\text{Fie}_{2,2n+2}\right)^{2}}{{\it\iota}}\right]=(\mathbb{L}-1)\mathbb{L}^{2n+1}.\end{eqnarray}$$We have
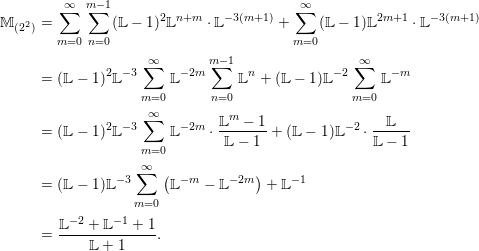 $$\begin{eqnarray}\displaystyle \mathbb{M}_{(2^{2})} & = & \displaystyle \mathop{\sum }_{m=0}^{\infty }\mathop{\sum }_{n=0}^{m-1}(\mathbb{L}-1)^{2}\mathbb{L}^{n+m}\cdot \mathbb{L}^{-3(m+1)}+\mathop{\sum }_{m=0}^{\infty }(\mathbb{L}-1)\mathbb{L}^{2m+1}\cdot \mathbb{L}^{-3(m+1)}\nonumber\\ \displaystyle & = & \displaystyle (\mathbb{L}-1)^{2}\mathbb{L}^{-3}\mathop{\sum }_{m=0}^{\infty }\mathbb{L}^{-2m}\mathop{\sum }_{n=0}^{m-1}\mathbb{L}^{n}+(\mathbb{L}-1)\mathbb{L}^{-2}\mathop{\sum }_{m=0}^{\infty }\mathbb{L}^{-m}\nonumber\\ \displaystyle & = & \displaystyle (\mathbb{L}-1)^{2}\mathbb{L}^{-3}\mathop{\sum }_{m=0}^{\infty }\mathbb{L}^{-2m}\cdot \frac{\mathbb{L}^{m}-1}{\mathbb{L}-1}+(\mathbb{L}-1)\mathbb{L}^{-2}\cdot \frac{\mathbb{L}}{\mathbb{L}-1}\nonumber\\ \displaystyle & = & \displaystyle (\mathbb{L}-1)\mathbb{L}^{-3}\mathop{\sum }_{m=0}^{\infty }\left(\mathbb{L}^{-m}-\mathbb{L}^{-2m}\right)+\mathbb{L}^{-1}\nonumber\\ \displaystyle & = & \displaystyle \frac{\mathbb{L}^{-2}+\mathbb{L}^{-1}+1}{\mathbb{L}+1}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathbb{M}_{(2^{2})} & = & \displaystyle \mathop{\sum }_{m=0}^{\infty }\mathop{\sum }_{n=0}^{m-1}(\mathbb{L}-1)^{2}\mathbb{L}^{n+m}\cdot \mathbb{L}^{-3(m+1)}+\mathop{\sum }_{m=0}^{\infty }(\mathbb{L}-1)\mathbb{L}^{2m+1}\cdot \mathbb{L}^{-3(m+1)}\nonumber\\ \displaystyle & = & \displaystyle (\mathbb{L}-1)^{2}\mathbb{L}^{-3}\mathop{\sum }_{m=0}^{\infty }\mathbb{L}^{-2m}\mathop{\sum }_{n=0}^{m-1}\mathbb{L}^{n}+(\mathbb{L}-1)\mathbb{L}^{-2}\mathop{\sum }_{m=0}^{\infty }\mathbb{L}^{-m}\nonumber\\ \displaystyle & = & \displaystyle (\mathbb{L}-1)^{2}\mathbb{L}^{-3}\mathop{\sum }_{m=0}^{\infty }\mathbb{L}^{-2m}\cdot \frac{\mathbb{L}^{m}-1}{\mathbb{L}-1}+(\mathbb{L}-1)\mathbb{L}^{-2}\cdot \frac{\mathbb{L}}{\mathbb{L}-1}\nonumber\\ \displaystyle & = & \displaystyle (\mathbb{L}-1)\mathbb{L}^{-3}\mathop{\sum }_{m=0}^{\infty }\left(\mathbb{L}^{-m}-\mathbb{L}^{-2m}\right)+\mathbb{L}^{-1}\nonumber\\ \displaystyle & = & \displaystyle \frac{\mathbb{L}^{-2}+\mathbb{L}^{-1}+1}{\mathbb{L}+1}.\nonumber\end{eqnarray}$$ If we suppose that the ![]() $H$-orbits in
$H$-orbits in 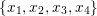 $\{x_{1},x_{2},x_{3},x_{4}\}$ are
$\{x_{1},x_{2},x_{3},x_{4}\}$ are 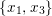 $\{x_{1},x_{3}\}$ and
$\{x_{1},x_{3}\}$ and  $\{x_{2},x_{4}\}$, then
$\{x_{2},x_{4}\}$, then
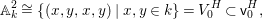 $$\begin{eqnarray}\mathbb{A}_{k}^{2}\cong \{(x,y,x,y)\mid x,y\in k\}=V_{0}^{H}\subset \mathsf{v}_{0}^{H},\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{A}_{k}^{2}\cong \{(x,y,x,y)\mid x,y\in k\}=V_{0}^{H}\subset \mathsf{v}_{0}^{H},\end{eqnarray}$$ we have  $\text{codim}(\mathsf{v}_{0}^{H},\mathsf{v}_{0})=1$ and
$\text{codim}(\mathsf{v}_{0}^{H},\mathsf{v}_{0})=1$ and
 $$\begin{eqnarray}\mathbb{M}_{(2^{2})}^{\prime }=\mathbb{L}^{3}\cdot \mathbb{M}_{(2^{2})}=\frac{\mathbb{L}+\mathbb{L}^{2}+\mathbb{L}^{3}}{\mathbb{L}+1}.\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{M}_{(2^{2})}^{\prime }=\mathbb{L}^{3}\cdot \mathbb{M}_{(2^{2})}=\frac{\mathbb{L}+\mathbb{L}^{2}+\mathbb{L}^{3}}{\mathbb{L}+1}.\end{eqnarray}$$ Thus, ![]() $\mathbb{M}_{(2^{2})}$ and
$\mathbb{M}_{(2^{2})}$ and ![]() $\mathbb{M}_{(2^{2})}^{\prime }$ are dual to each other in the sense that they interchange by substituting
$\mathbb{M}_{(2^{2})}^{\prime }$ are dual to each other in the sense that they interchange by substituting ![]() $\mathbb{L}^{-1}$ for
$\mathbb{L}^{-1}$ for ![]() $\mathbb{L}$.
$\mathbb{L}$.
For the other terms ![]() $\mathbb{M}_{\mathbf{p}}$ and
$\mathbb{M}_{\mathbf{p}}$ and ![]() $\mathbb{M}_{\mathbf{p}}^{\prime }$, we see that
$\mathbb{M}_{\mathbf{p}}^{\prime }$, we see that
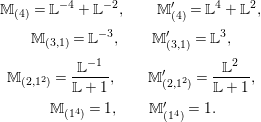 $$\begin{eqnarray}\displaystyle & \mathbb{M}_{(4)}=\mathbb{L}^{-4}+\mathbb{L}^{-2},\qquad \mathbb{M}_{(4)}^{\prime }=\mathbb{L}^{4}+\mathbb{L}^{2}, & \displaystyle \nonumber\\ \displaystyle & \mathbb{M}_{(3,1)}=\mathbb{L}^{-3},\qquad \mathbb{M}_{(3,1)}^{\prime }=\mathbb{L}^{3}, & \displaystyle \nonumber\\ \displaystyle & \mathbb{M}_{(2,1^{2})}=\displaystyle \frac{\mathbb{L}^{-1}}{\mathbb{L}+1},\qquad \mathbb{M}_{(2,1^{2})}^{\prime }=\frac{\mathbb{L}^{2}}{\mathbb{L}+1}, & \displaystyle \nonumber\\ \displaystyle & \mathbb{M}_{(1^{4})}=1,\qquad \mathbb{M}_{(1^{4})}^{\prime }=1. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \mathbb{M}_{(4)}=\mathbb{L}^{-4}+\mathbb{L}^{-2},\qquad \mathbb{M}_{(4)}^{\prime }=\mathbb{L}^{4}+\mathbb{L}^{2}, & \displaystyle \nonumber\\ \displaystyle & \mathbb{M}_{(3,1)}=\mathbb{L}^{-3},\qquad \mathbb{M}_{(3,1)}^{\prime }=\mathbb{L}^{3}, & \displaystyle \nonumber\\ \displaystyle & \mathbb{M}_{(2,1^{2})}=\displaystyle \frac{\mathbb{L}^{-1}}{\mathbb{L}+1},\qquad \mathbb{M}_{(2,1^{2})}^{\prime }=\frac{\mathbb{L}^{2}}{\mathbb{L}+1}, & \displaystyle \nonumber\\ \displaystyle & \mathbb{M}_{(1^{4})}=1,\qquad \mathbb{M}_{(1^{4})}^{\prime }=1. & \displaystyle \nonumber\end{eqnarray}$$ For each partition ![]() $\mathbf{p}$, we would have the duality. Summing these up, we get
$\mathbf{p}$, we would have the duality. Summing these up, we get
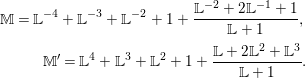 $$\begin{eqnarray}\displaystyle \mathbb{M}=\mathbb{L}^{-4}+\mathbb{L}^{-3}+\mathbb{L}^{-2}+1+\frac{\mathbb{L}^{-2}+2\mathbb{L}^{-1}+1}{\mathbb{L}+1}, & & \displaystyle \nonumber\\ \displaystyle \mathbb{M}^{\prime }=\mathbb{L}^{4}+\mathbb{L}^{3}+\mathbb{L}^{2}+1+\frac{\mathbb{L}+2\mathbb{L}^{2}+\mathbb{L}^{3}}{\mathbb{L}+1}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathbb{M}=\mathbb{L}^{-4}+\mathbb{L}^{-3}+\mathbb{L}^{-2}+1+\frac{\mathbb{L}^{-2}+2\mathbb{L}^{-1}+1}{\mathbb{L}+1}, & & \displaystyle \nonumber\\ \displaystyle \mathbb{M}^{\prime }=\mathbb{L}^{4}+\mathbb{L}^{3}+\mathbb{L}^{2}+1+\frac{\mathbb{L}+2\mathbb{L}^{2}+\mathbb{L}^{3}}{\mathbb{L}+1}. & & \displaystyle \nonumber\end{eqnarray}$$Remark 12.2. By similar computations, we can easily deduce the motivic counterpart of Serre’s mass formula [Reference SerreSer78] from Conjecture 12.1. In any characteristic and for any ![]() $m$,
$m$,
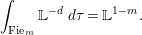 $$\begin{eqnarray}\int _{\text{Fie}_{m}}\mathbb{L}^{-d}\,d{\it\tau}=\mathbb{L}^{1-m}.\end{eqnarray}$$
$$\begin{eqnarray}\int _{\text{Fie}_{m}}\mathbb{L}^{-d}\,d{\it\tau}=\mathbb{L}^{1-m}.\end{eqnarray}$$ Here,  $d:\text{Fie}_{m}\rightarrow \mathbb{Z}$ is the function associating the discriminant exponent to a field extension and
$d:\text{Fie}_{m}\rightarrow \mathbb{Z}$ is the function associating the discriminant exponent to a field extension and ![]() ${\it\tau}$ is the tautological motivic measure on
${\it\tau}$ is the tautological motivic measure on ![]() $\text{Fie}_{n}$. This too justifies the conjecture. With some more computation, it would be possible to also get the motivic version of Bhargava’s formula [Reference BhargavaBha07].
$\text{Fie}_{n}$. This too justifies the conjecture. With some more computation, it would be possible to also get the motivic version of Bhargava’s formula [Reference BhargavaBha07].
13 Concluding remarks
We end the paper by making some remarks and raising several problems for the future.
13.1 Singularities of  $\mathsf{v}$,
$\mathsf{v}$,  $\mathsf{v}^{|F|}$ and
$\mathsf{v}^{|F|}$ and  $\mathsf{v}^{|F|,{\it\nu}}$
$\mathsf{v}^{|F|,{\it\nu}}$
In the definition of log varieties, we assumed that the ambient variety is always normal. It forced us to take the normalization ![]() $\mathsf{v}^{|F|,{\it\nu}}$ of the untwisting variety
$\mathsf{v}^{|F|,{\it\nu}}$ of the untwisting variety ![]() $\mathsf{v}^{|F|}$. The normality assumption enabled us to work in a standard setting of the minimal model program and to use familiar computations of divisors. However, this restriction seems not to be really necessary. For instance, we can define the stringy motif if we specify an invertible subsheaf of
$\mathsf{v}^{|F|}$. The normality assumption enabled us to work in a standard setting of the minimal model program and to use familiar computations of divisors. However, this restriction seems not to be really necessary. For instance, we can define the stringy motif if we specify an invertible subsheaf of
 $$\begin{eqnarray}\left(\mathop{d}^{\wedge }{\rm\Omega}_{X/D}\right)^{\otimes r}\otimes K(X)\end{eqnarray}$$
$$\begin{eqnarray}\left(\mathop{d}^{\wedge }{\rm\Omega}_{X/D}\right)^{\otimes r}\otimes K(X)\end{eqnarray}$$ rather than a boundary divisor ![]() ${\rm\Delta}$. We then would be able to replace most of the arguments in this paper with ones using subsheaves rather than divisors.
${\rm\Delta}$. We then would be able to replace most of the arguments in this paper with ones using subsheaves rather than divisors.
What kind of singularities can ![]() $\mathsf{v}^{|F|}$ and
$\mathsf{v}^{|F|}$ and ![]() $\mathsf{v}^{|F|,{\it\nu}}$ have? In the examples in Sections 9 and 10, rather mild singularities appeared. Indeed, in both examples, for every
$\mathsf{v}^{|F|,{\it\nu}}$ have? In the examples in Sections 9 and 10, rather mild singularities appeared. Indeed, in both examples, for every 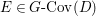 $E\in G\text{-}\text{Cov}(D)$, the untwisting variety
$E\in G\text{-}\text{Cov}(D)$, the untwisting variety ![]() $\mathsf{v}^{|F|}$ had only normal hypersurface singularities having a crepant resolution. In general, if
$\mathsf{v}^{|F|}$ had only normal hypersurface singularities having a crepant resolution. In general, if ![]() $\mathsf{v}\subset V$ is a hypersurface, then so is
$\mathsf{v}\subset V$ is a hypersurface, then so is 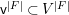 $\mathsf{v}^{|F|}\subset V^{|F|}$, although the author does not know if it is always normal. What about complete intersections? If the answer is positive, then we would be able to use Proposition 8.1 to compute the boundary of
$\mathsf{v}^{|F|}\subset V^{|F|}$, although the author does not know if it is always normal. What about complete intersections? If the answer is positive, then we would be able to use Proposition 8.1 to compute the boundary of ![]() $\mathfrak{v}^{|F|}$. Moreover, we might be able to generalize, for instance, the semicontinuity of the minimal log discrepancies to quotients of local complete intersections by combining arguments used for local complete intersections [Reference Ein, Mustaţă and YasudaEMY03, Reference Ein and MustaţǎEM04] and quotient singularities [Reference NakamuraNak].
$\mathfrak{v}^{|F|}$. Moreover, we might be able to generalize, for instance, the semicontinuity of the minimal log discrepancies to quotients of local complete intersections by combining arguments used for local complete intersections [Reference Ein, Mustaţă and YasudaEMY03, Reference Ein and MustaţǎEM04] and quotient singularities [Reference NakamuraNak].
In the tame case, if 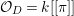 ${\mathcal{O}}_{D}=k[[{\it\pi}]]$, then, as we saw in Section 9, the map
${\mathcal{O}}_{D}=k[[{\it\pi}]]$, then, as we saw in Section 9, the map 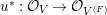 $u^{\ast }:{\mathcal{O}}_{V}\rightarrow {\mathcal{O}}_{V^{\left\langle F\right\rangle }}$ is simply given by
$u^{\ast }:{\mathcal{O}}_{V}\rightarrow {\mathcal{O}}_{V^{\left\langle F\right\rangle }}$ is simply given by 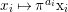 $x_{i}\mapsto {\it\pi}^{a_{i}}\text{x}_{i}$,
$x_{i}\mapsto {\it\pi}^{a_{i}}\text{x}_{i}$, ![]() $a_{i}\in \mathbb{Q}$ for a suitable choice of coordinates
$a_{i}\in \mathbb{Q}$ for a suitable choice of coordinates 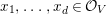 $x_{1},\ldots ,x_{d}\in {\mathcal{O}}_{V}$ and
$x_{1},\ldots ,x_{d}\in {\mathcal{O}}_{V}$ and 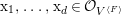 $\text{x}_{1},\ldots ,\text{x}_{d}\in {\mathcal{O}}_{V^{\left\langle F\right\rangle }}$. Therefore, if
$\text{x}_{1},\ldots ,\text{x}_{d}\in {\mathcal{O}}_{V^{\left\langle F\right\rangle }}$. Therefore, if ![]() $\mathsf{v}\subset V$ is defined by
$\mathsf{v}\subset V$ is defined by 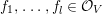 $f_{1},\ldots ,f_{l}\in {\mathcal{O}}_{V}$, then the scheme-theoretic preimage
$f_{1},\ldots ,f_{l}\in {\mathcal{O}}_{V}$, then the scheme-theoretic preimage 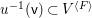 $u^{-1}(\mathsf{v})\subset V^{\left\langle F\right\rangle }$ is defined by
$u^{-1}(\mathsf{v})\subset V^{\left\langle F\right\rangle }$ is defined by 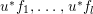 $u^{\ast }f_{1},\ldots ,u^{\ast }f_{l}$, which have the same number of terms as
$u^{\ast }f_{1},\ldots ,u^{\ast }f_{l}$, which have the same number of terms as 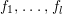 $f_{1},\ldots ,f_{l}$ respectively. In particular, if
$f_{1},\ldots ,f_{l}$ respectively. In particular, if ![]() $\mathsf{v}$ is an affine toric variety, then it is embedded into
$\mathsf{v}$ is an affine toric variety, then it is embedded into ![]() $V$ as a closed subvariety defined by binomials
$V$ as a closed subvariety defined by binomials  $f_{1},\ldots ,f_{l}$, and then
$f_{1},\ldots ,f_{l}$, and then ![]() $u^{-1}(\mathsf{v})$ is also defined by binomials. Thanks to this fact, we might be able to study
$u^{-1}(\mathsf{v})$ is also defined by binomials. Thanks to this fact, we might be able to study ![]() $\mathsf{v}^{|F|}$ from the combinatorial viewpoint.
$\mathsf{v}^{|F|}$ from the combinatorial viewpoint.
In the example in Section 10, ![]() $\mathsf{v}^{|F|}$ had
$\mathsf{v}^{|F|}$ had ![]() $A_{1}$-singularities and
$A_{1}$-singularities and ![]() $D_{2n}^{0}$-singularities, from Artin’s classification of rational double points in positive characteristics [Reference ArtinArt77]. In general, when
$D_{2n}^{0}$-singularities, from Artin’s classification of rational double points in positive characteristics [Reference ArtinArt77]. In general, when ![]() $\mathsf{v}$ and hence
$\mathsf{v}$ and hence ![]() $\mathsf{v}^{|F|}$ are surfaces (relative dimension one over
$\mathsf{v}^{|F|}$ are surfaces (relative dimension one over ![]() $D$), then what kind of singularities can
$D$), then what kind of singularities can ![]() $\mathsf{v}^{|F|}$ have? Does every rational double point appear on some
$\mathsf{v}^{|F|}$ have? Does every rational double point appear on some ![]() $\mathsf{v}^{|F|}$? If we can compute singularities of
$\mathsf{v}^{|F|}$? If we can compute singularities of ![]() $\mathsf{v}^{|F|}$ systematically, we would be able to compute the right-hand side of the equality in Conjecture 7.3 explicitly and to derive many mass formulas, explained below.
$\mathsf{v}^{|F|}$ systematically, we would be able to compute the right-hand side of the equality in Conjecture 7.3 explicitly and to derive many mass formulas, explained below.
13.2 Mass formulas for extensions of a local field and local Galois representations
For a constructible function 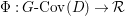 ${\rm\Phi}:G\text{-}\text{Cov}(D)\rightarrow {\mathcal{R}}$, the integral
${\rm\Phi}:G\text{-}\text{Cov}(D)\rightarrow {\mathcal{R}}$, the integral
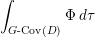 $$\begin{eqnarray}\int _{G\text{-}\text{Cov}(D)}{\rm\Phi}\,d{\it\tau}\end{eqnarray}$$
$$\begin{eqnarray}\int _{G\text{-}\text{Cov}(D)}{\rm\Phi}\,d{\it\tau}\end{eqnarray}$$ can be regarded as the motivic count of ![]() $G$-covers of
$G$-covers of ![]() $D$ with
$D$ with  $E\in G\text{-}\text{Cov}(D)$ weighted by
$E\in G\text{-}\text{Cov}(D)$ weighted by ![]() ${\rm\Phi}(E)$. If
${\rm\Phi}(E)$. If ![]() ${\mathcal{O}}_{D}$ has a finite residue field
${\mathcal{O}}_{D}$ has a finite residue field ![]() $k=\mathbb{F}_{q}$ rather than an algebraically closed one, then the motif
$k=\mathbb{F}_{q}$ rather than an algebraically closed one, then the motif 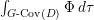 $\int _{G\text{-}\text{Cov}(D)}{\rm\Phi}\,d{\it\tau}$ should give an actual weighted count of
$\int _{G\text{-}\text{Cov}(D)}{\rm\Phi}\,d{\it\tau}$ should give an actual weighted count of ![]() $G$-covers of
$G$-covers of ![]() $D$ as its point-counting realization. This observation was made in [Reference YasudaYas14, Reference Wood and YasudaWY15] in the context of the wild McKay correspondence for linear actions. Such counts are number-theoretic problems by nature. Indeed, as clarified in [Reference Wood and YasudaWY15], counts appearing in the McKay correspondence are closely related to counts of extensions of a local field and to counts of local Galois representations, for instance, studied in [Reference KrasnerKra66, Reference SerreSer78, Reference BhargavaBha07, Reference KedlayaKed07, Reference WoodWoo08]: formulas for such counts are called mass formulas. The weights previously considered have the form
$D$ as its point-counting realization. This observation was made in [Reference YasudaYas14, Reference Wood and YasudaWY15] in the context of the wild McKay correspondence for linear actions. Such counts are number-theoretic problems by nature. Indeed, as clarified in [Reference Wood and YasudaWY15], counts appearing in the McKay correspondence are closely related to counts of extensions of a local field and to counts of local Galois representations, for instance, studied in [Reference KrasnerKra66, Reference SerreSer78, Reference BhargavaBha07, Reference KedlayaKed07, Reference WoodWoo08]: formulas for such counts are called mass formulas. The weights previously considered have the form ![]() $\mathbb{L}^{{\it\alpha}}$ for some function
$\mathbb{L}^{{\it\alpha}}$ for some function 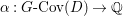 ${\it\alpha}:G\text{-}\text{Cov}(D)\rightarrow \mathbb{Q}$, corresponding to weights of the form
${\it\alpha}:G\text{-}\text{Cov}(D)\rightarrow \mathbb{Q}$, corresponding to weights of the form ![]() $\frac{1}{\sharp H}q^{{\it\alpha}}$ in actual counts if
$\frac{1}{\sharp H}q^{{\it\alpha}}$ in actual counts if ![]() $k=\mathbb{F}_{q}$. However, in Conjecture 7.3, we have fancier weights
$k=\mathbb{F}_{q}$. However, in Conjecture 7.3, we have fancier weights 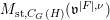 $M_{\text{st},C_{G}(H)}(\mathfrak{v}^{|F|,{\it\nu}})$, which are expected to often be rational functions in
$M_{\text{st},C_{G}(H)}(\mathfrak{v}^{|F|,{\it\nu}})$, which are expected to often be rational functions in ![]() $\mathbb{L}$ or
$\mathbb{L}$ or ![]() $\mathbb{L}^{1/n}$,
$\mathbb{L}^{1/n}$, 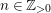 $n\in \mathbb{Z}_{{>}0}$ (this is actually the case in examples in Sections 9 and 10). The new weights clearly have geometric meaning and might provide some insight into the number theory.
$n\in \mathbb{Z}_{{>}0}$ (this is actually the case in examples in Sections 9 and 10). The new weights clearly have geometric meaning and might provide some insight into the number theory.
13.3 Weight functions for general representations
How do we compute functions ![]() $\mathbf{w}_{V}$ and
$\mathbf{w}_{V}$ and ![]() $\boldsymbol{v}_{V}$ for general linear actions
$\boldsymbol{v}_{V}$ for general linear actions 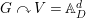 $G\curvearrowright V=\mathbb{A}_{D}^{d}$? By now, we have satisfactory answers in the following cases:
$G\curvearrowright V=\mathbb{A}_{D}^{d}$? By now, we have satisfactory answers in the following cases:
∙ the tame case [Reference YasudaYasa, Reference Wood and YasudaWY15],
∙ the case where
 ${\mathcal{O}}_{D}=k[[{\it\pi}]]$, with
${\mathcal{O}}_{D}=k[[{\it\pi}]]$, with  $k$ of characteristic
$k$ of characteristic  $p>0$, and
$p>0$, and  $G=\mathbb{Z}/p\mathbb{Z}$ [Reference YasudaYas14],
$G=\mathbb{Z}/p\mathbb{Z}$ [Reference YasudaYas14],∙ permutation representations [Reference Wood and YasudaWY15],
∙ a hyperplane in a permutation representation defined by an invariant linear form (Corollary 11.4).
For the general case, we can always embed a given representation into a permutation representation and apply Corollary 8.1. The problem is to compute the divisor ![]() $A_{F}$, which appears to be almost equivalent to computing functions
$A_{F}$, which appears to be almost equivalent to computing functions ![]() $\mathbf{w}_{V}$ and
$\mathbf{w}_{V}$ and ![]() $\boldsymbol{v}_{V}$.
$\boldsymbol{v}_{V}$.
13.4 The convergence or divergence of motivic integrals
The motivic integrals discussed in this paper do not generally converge, and stringy motifs and motivic masses can be infinite. In such a case, the wild McKay correspondence conjecture does not mean much. In characteristic zero, the convergence of a stringy motif is equivalent to the given singularities being (Kawamata) log terminal. The author then called stringily log terminal singularities whose stringy motif converges, which is equivalent to the usual notion of log terminal if singularities admit a log resolution. Since quotient singularities in characteristic zero are always log terminal, this divergence problem did not occur in the study of the McKay correspondence in characteristic zero. However, wild quotient singularities are sometimes stringily log terminal and sometimes not. It is an interesting problem to know when they are and when they are not. If 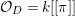 ${\mathcal{O}}_{D}=k[[{\it\pi}]]$ has characteristic
${\mathcal{O}}_{D}=k[[{\it\pi}]]$ has characteristic ![]() $p>0$, and
$p>0$, and 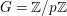 $G=\mathbb{Z}/p\mathbb{Z}$, then the convergence is determined by the value of a simple representation-theoretic invariant denoted by
$G=\mathbb{Z}/p\mathbb{Z}$, then the convergence is determined by the value of a simple representation-theoretic invariant denoted by ![]() $D_{V}$ in [Reference YasudaYas14]. Is it possible to generalize this invariant to other groups?
$D_{V}$ in [Reference YasudaYas14]. Is it possible to generalize this invariant to other groups?
Another problem is that of attaching finite values to divergent motivic integrals by “renormalizing” them somehow, for instance, as tried by Veys [Reference VeysVey04, Reference VeysVey03] for stringy invariants in characteristic zero.
Acknowledgments
I wish to thank Yusuke Nakamura and Shuji Saito for useful discussions directing my interests to nonlinear actions, Johannes Nicaise and Julien Sebag for their kind answers to my questions on motivic integration over formal schemes, and Melanie Matchett Wood for stimulating discussions on our joint work.