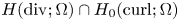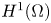1. Introduction
The relaxed micromorphic model is a novel generalized continuum model allowing to describe size effects and band-gap behaviour of microstructured solids with effective equations ignoring the detailed microstructure [Reference Alberdi, Robbins, Walsh and Dingreville2, Reference Demore, Rizzi, Collet, Neff and Madeo6, Reference Ghiba, Neff, Madeo, Placidi and Rosi8, Reference Madeo, Neff, Ghiba and Rosi21, Reference Neff, Ghiba, Madeo, Placidi and Rosi25, Reference Owczarek, Ghiba and Neff28]. As a micromorphic model it couples the classical displacement $u:\Omega \subset \mathbb{R} ^3\to \mathbb{R} ^3$![]() with a non-symmetric tensor field $P:\Omega \subset \mathbb{R} ^3\to \mathbb{R} ^{3\times 3}$
with a non-symmetric tensor field $P:\Omega \subset \mathbb{R} ^3\to \mathbb{R} ^{3\times 3}$![]() called the microdistortion through the variational problem
called the microdistortion through the variational problem

subject to suitable boundary conditions. The tensor ${\mathbb {L}}_{{\rm c}}$![]() introduces a size-dependence into the model in the sense that smaller samples respond relatively stiffer. The existence and uniqueness in the static case follows from the incompatible Korn's inequality [Reference Gmeineder, Lewintan and Neff13, Reference Lewintan, Müller and Neff18–Reference Lewintan and Neff20, Reference Neff, Pauly and Witsch27]. The constitutive tensors ${\mathbb {C}_{{\rm e}}}$
introduces a size-dependence into the model in the sense that smaller samples respond relatively stiffer. The existence and uniqueness in the static case follows from the incompatible Korn's inequality [Reference Gmeineder, Lewintan and Neff13, Reference Lewintan, Müller and Neff18–Reference Lewintan and Neff20, Reference Neff, Pauly and Witsch27]. The constitutive tensors ${\mathbb {C}_{{\rm e}}}$![]() , ${\mathbb {C}_{{\rm micro}}}$
, ${\mathbb {C}_{{\rm micro}}}$![]() and ${\mathbb {L}}_{{\rm c}}$
and ${\mathbb {L}}_{{\rm c}}$![]() are to be found by novel homogenization strategies [Reference Neff, Eidel, d'Agostino and Madeo23, Reference Sarhil, Scheunemann, J. Schröder and Neff35–Reference Schröder, Sarhil, Scheunemann and Neff37]. Letting ${\mathbb {C}_{{\rm micro}}}\rightarrow +\infty$
are to be found by novel homogenization strategies [Reference Neff, Eidel, d'Agostino and Madeo23, Reference Sarhil, Scheunemann, J. Schröder and Neff35–Reference Schröder, Sarhil, Scheunemann and Neff37]. Letting ${\mathbb {C}_{{\rm micro}}}\rightarrow +\infty$![]() the models response tends to the linear Cosserat model [Reference Ghiba, Rizzi, Madeo and Neff9]. A range of engineering relevant analytical solutions are already available for the relaxed micromorphic model [Reference Rizzi, Hütter, Khan, Ghiba, Madeo and Neff34]. The solution is naturally found as $u\in H^1(\Omega )$
the models response tends to the linear Cosserat model [Reference Ghiba, Rizzi, Madeo and Neff9]. A range of engineering relevant analytical solutions are already available for the relaxed micromorphic model [Reference Rizzi, Hütter, Khan, Ghiba, Madeo and Neff34]. The solution is naturally found as $u\in H^1(\Omega )$![]() and $P\in H(\operatorname {Curl};\Omega )$
and $P\in H(\operatorname {Curl};\Omega )$![]() , thus the microdistortion $P$
, thus the microdistortion $P$![]() may have jumps in normal direction. The implementation in the finite element context needs standard element formulations for the displacement $u$
may have jumps in normal direction. The implementation in the finite element context needs standard element formulations for the displacement $u$![]() , but e.g. Nédélec - spaces for $P$
, but e.g. Nédélec - spaces for $P$![]() in order to achieve optimal convergence rates [Reference Rizzi, d'Agostino, Neff and Madeo33, Reference Schröder, Sarhil, Scheunemann and Neff37–Reference Sky, Neunteufel, Münch, Schöberl and Neff40].
in order to achieve optimal convergence rates [Reference Rizzi, d'Agostino, Neff and Madeo33, Reference Schröder, Sarhil, Scheunemann and Neff37–Reference Sky, Neunteufel, Münch, Schöberl and Neff40].
However, it is sometimes preferred to circumvent the Nédélec - framework and to work with $H^1(\Omega )$![]() for the microdistortion tensor $P$
for the microdistortion tensor $P$![]() . For these cases it is mandatory to clarify in advance whether the regularity of $P$
. For these cases it is mandatory to clarify in advance whether the regularity of $P$![]() allows for a faithful result. In this spirit, we continue here the investigation of regularity in the static case and we will be able to derive a global higher regularity result for weak solutions of the relaxed micromorphic model (global as opposed to only interior regularity). It extends the local result from [Reference Knees, Owczarek and Neff15] to smooth domains. The latter is formulated on a bounded domain $\Omega \subset \mathbb{R} ^3$
allows for a faithful result. In this spirit, we continue here the investigation of regularity in the static case and we will be able to derive a global higher regularity result for weak solutions of the relaxed micromorphic model (global as opposed to only interior regularity). It extends the local result from [Reference Knees, Owczarek and Neff15] to smooth domains. The latter is formulated on a bounded domain $\Omega \subset \mathbb{R} ^3$![]() and the Euler-Lagrange equations to (1.1) read as follows ([Reference Alberdi, Robbins, Walsh and Dingreville2, Reference Ghiba, Neff, Madeo, Placidi and Rosi8, Reference Neff, Ghiba, Madeo, Placidi and Rosi25, Reference Owczarek, Ghiba and Neff28, Reference Owczarek, Ghiba and Neff29]): given positive definite and symmetric material dependent coefficient tensors $\mathbb{C} _e:\Omega \rightarrow \operatorname{Lin} (\operatorname {Sym}(3),\,\operatorname {Sym}(3))$
and the Euler-Lagrange equations to (1.1) read as follows ([Reference Alberdi, Robbins, Walsh and Dingreville2, Reference Ghiba, Neff, Madeo, Placidi and Rosi8, Reference Neff, Ghiba, Madeo, Placidi and Rosi25, Reference Owczarek, Ghiba and Neff28, Reference Owczarek, Ghiba and Neff29]): given positive definite and symmetric material dependent coefficient tensors $\mathbb{C} _e:\Omega \rightarrow \operatorname{Lin} (\operatorname {Sym}(3),\,\operatorname {Sym}(3))$![]() , $\mathbb{C} _\text {micro}:\Omega \rightarrow \operatorname{Lin} (\operatorname {Sym}(3),\,\operatorname {Sym}(3))$
, $\mathbb{C} _\text {micro}:\Omega \rightarrow \operatorname{Lin} (\operatorname {Sym}(3),\,\operatorname {Sym}(3))$![]() and $\mathbb{L} _c:\Omega \rightarrow \operatorname{Lin} (\mathbb{R} ^{3\times 3},\,\mathbb{R} ^{3\times 3})$
and $\mathbb{L} _c:\Omega \rightarrow \operatorname{Lin} (\mathbb{R} ^{3\times 3},\,\mathbb{R} ^{3\times 3})$![]() determine a displacement field $u:\Omega \to \mathbb{R} ^3$
determine a displacement field $u:\Omega \to \mathbb{R} ^3$![]() and a non-symmetric microdistortion tensor $P:\Omega \to \mathbb{R} ^{3\times 3}$
and a non-symmetric microdistortion tensor $P:\Omega \to \mathbb{R} ^{3\times 3}$![]() satisfying
satisfying

together with suitable boundary conditions. Here, $f:\Omega \to \mathbb{R} ^3$![]() is a given volume force density, $M:\Omega \to \mathbb{R} ^{3\times 3}$
is a given volume force density, $M:\Omega \to \mathbb{R} ^{3\times 3}$![]() a body moment tensor and $\sigma =\mathbb{C} _e\operatorname {sym}(\mathrm {D} u - P)$
a body moment tensor and $\sigma =\mathbb{C} _e\operatorname {sym}(\mathrm {D} u - P)$![]() is the symmetric force stress tensor while $m={\mathbb {L}}_{{\rm c}}\operatorname {Curl} P$
is the symmetric force stress tensor while $m={\mathbb {L}}_{{\rm c}}\operatorname {Curl} P$![]() is the non-symmetric moment tensor.
is the non-symmetric moment tensor.
The main result of the present contribution is theorem 4.1 which states that on smooth domains and with smooth coefficients weak solutions of (1.2) are more regular and satisfy
where the last regularity in (1.3) follows from equation (1.2). Moreover, if $\mathbb{L} _c$![]() has a special block diagonal structure (see corollary 4.2), then we in addition have
has a special block diagonal structure (see corollary 4.2), then we in addition have
The results (1.3) are obtained by a combination of the Helmholtz decomposition for the matrix field $P$![]() , regularity results for linear elliptic systems of elasticity-type and the classical Maxwell embedding recalled in theorem 2.4. The additional regularity formulated in (1.4) relies on a weighted version of the Maxwell embedding theorem, [Reference Weber42].
, regularity results for linear elliptic systems of elasticity-type and the classical Maxwell embedding recalled in theorem 2.4. The additional regularity formulated in (1.4) relies on a weighted version of the Maxwell embedding theorem, [Reference Weber42].
2. Background from function space theory
2.1 Notation, assumptions
For vectors $a,\,b\in \mathbb{R} ^3$![]() , we define the scalar product $\langle a,\,b\rangle :=\sum _{i=1}^3 a_ib_i$
, we define the scalar product $\langle a,\,b\rangle :=\sum _{i=1}^3 a_ib_i$![]() , the Euclidean norm $|a|^2:=\langle a,\,a\rangle$
, the Euclidean norm $|a|^2:=\langle a,\,a\rangle$![]() and the dyadic product $a\otimes b=(a_ib_j)_{i,j=1}^3\in \mathbb{R} ^{3\times 3}$
and the dyadic product $a\otimes b=(a_ib_j)_{i,j=1}^3\in \mathbb{R} ^{3\times 3}$![]() , where $\mathbb{R} ^{3\times 3}$
, where $\mathbb{R} ^{3\times 3}$![]() will denote the set of real $3\times 3$
will denote the set of real $3\times 3$![]() matrices. For matrices $P,\,Q\in \mathbb{R} ^{3\times 3}$
matrices. For matrices $P,\,Q\in \mathbb{R} ^{3\times 3}$![]() , we define the standard Euclidean scalar product $\langle P,\,Q\rangle :=\sum _{i=1}^3\sum _{j=1}^3 P_{ij}Q_{ij}$
, we define the standard Euclidean scalar product $\langle P,\,Q\rangle :=\sum _{i=1}^3\sum _{j=1}^3 P_{ij}Q_{ij}$![]() and the Frobenius-norm $\|P\|^2:=\langle P,\,P\rangle$
and the Frobenius-norm $\|P\|^2:=\langle P,\,P\rangle$![]() . $P^T\in \mathbb{R} ^{3\times 3}$
. $P^T\in \mathbb{R} ^{3\times 3}$![]() denotes the transposition of the matrix $P\in \mathbb{R} ^{3\times 3}$
denotes the transposition of the matrix $P\in \mathbb{R} ^{3\times 3}$![]() and for $P\in \mathbb{R} ^{3\times 3}$
and for $P\in \mathbb{R} ^{3\times 3}$![]() , the symmetric part of $P$
, the symmetric part of $P$![]() will be denoted by $\operatorname {sym} P={1}/{2}(P+P^T)\in \operatorname {Sym}(3)$
will be denoted by $\operatorname {sym} P={1}/{2}(P+P^T)\in \operatorname {Sym}(3)$![]() .
.
Let $\Omega \subset \mathbb{R} ^3$![]() be a bounded domain. As a minimal requirement, we assume in this paper that the boundary $\partial \Omega$
be a bounded domain. As a minimal requirement, we assume in this paper that the boundary $\partial \Omega$![]() is Lipschitz continuous, meaning that it can locally be described as the graph of a Lipschitz continuous function, see [Reference Grisvard14] for a precise definition. In a similar spirit we speak of $C^1$
is Lipschitz continuous, meaning that it can locally be described as the graph of a Lipschitz continuous function, see [Reference Grisvard14] for a precise definition. In a similar spirit we speak of $C^1$![]() or $C^{1,1}$
or $C^{1,1}$![]() -regular boundaries. For a function $u=(u^1,\,u^2,\,u^3)^T:\Omega \to \mathbb{R} ^3$
-regular boundaries. For a function $u=(u^1,\,u^2,\,u^3)^T:\Omega \to \mathbb{R} ^3$![]() , the differential $\mathrm {D} u$
, the differential $\mathrm {D} u$![]() is given by
is given by

with $(\mathrm {D} u^k)_{l}= \partial _{x_l} u^k$![]() for $1\leq k\leq 3$
for $1\leq k\leq 3$![]() and $1\leq \ell \leq 3$
and $1\leq \ell \leq 3$![]() and with $\mathrm {D} u^k\in \mathbb{R} ^{1\times 3}$
and with $\mathrm {D} u^k\in \mathbb{R} ^{1\times 3}$![]() . For a vector field $w:\Omega \to \mathbb{R} ^3$
. For a vector field $w:\Omega \to \mathbb{R} ^3$![]() , the divergence and the curl are given as
, the divergence and the curl are given as

For tensor fields $Q:\Omega \to \mathbb{R} ^{3\times 3}$![]() , $\operatorname {Curl} Q$
, $\operatorname {Curl} Q$![]() and $\operatorname {Div} Q$
and $\operatorname {Div} Q$![]() are defined row-wise:
are defined row-wise:

where $Q^i$![]() denotes the $i$
denotes the $i$![]() -th row of $Q$
-th row of $Q$![]() . With these definitions, for $u:\Omega \to \mathbb{R} ^3$
. With these definitions, for $u:\Omega \to \mathbb{R} ^3$![]() we have consistently $\operatorname {Curl}\mathrm {D} u=0\in \mathbb{R} ^{3 \times 3}$
we have consistently $\operatorname {Curl}\mathrm {D} u=0\in \mathbb{R} ^{3 \times 3}$![]() .
.
The Sobolev spaces [Reference Adams and Fournier1, Reference Girault and Raviart11] used in this paper are

spaces for tensor valued functions are denoted by $H(\operatorname {Curl};\Omega )$![]() and $H(\operatorname {Div};\Omega )$
and $H(\operatorname {Div};\Omega )$![]() . Moreover, $H_0^1(\Omega )$
. Moreover, $H_0^1(\Omega )$![]() is the completion of $C_0^{\infty }(\Omega )$
is the completion of $C_0^{\infty }(\Omega )$![]() with respect to the $H^1$
with respect to the $H^1$![]() -norm and $H_0({\rm curl};\Omega )$
-norm and $H_0({\rm curl};\Omega )$![]() and $H_0(\operatorname {div};\Omega )$
and $H_0(\operatorname {div};\Omega )$![]() are the completions of $C_0^{\infty }(\Omega )$
are the completions of $C_0^{\infty }(\Omega )$![]() with respect to the $H(\operatorname {curl})$
with respect to the $H(\operatorname {curl})$![]() -norm and the $H(\operatorname {div})$
-norm and the $H(\operatorname {div})$![]() -norm, respectively. By $H^{-1}(\Omega )$
-norm, respectively. By $H^{-1}(\Omega )$![]() we denote the dual of $H_0^1(\Omega )$
we denote the dual of $H_0^1(\Omega )$![]() . Finally we define
. Finally we define
and set
Assumption A: We assume that the coefficient functions ${\mathbb {C}_{{\rm e}}},\,{\mathbb {C}_{{\rm micro}}}$![]() and ${\mathbb {L}}_{{\rm c}}$
and ${\mathbb {L}}_{{\rm c}}$![]() in (1.2) are fourth order elasticity tensors from $C^{0,1}(\overline \Omega ;\operatorname{Lin} (\mathbb{R} ^{3\times 3};\mathbb{R} ^{3\times 3}))$
in (1.2) are fourth order elasticity tensors from $C^{0,1}(\overline \Omega ;\operatorname{Lin} (\mathbb{R} ^{3\times 3};\mathbb{R} ^{3\times 3}))$![]() and are symmetric and positive definite in the following sense
and are symmetric and positive definite in the following sense
(i) For every $\sigma,\,\tau \in \operatorname {Sym}(3)$
 , $\eta _1,\,\eta _2\in \mathbb{R} ^{3\times 3}$
, $\eta _1,\,\eta _2\in \mathbb{R} ^{3\times 3}$ and all $x\in \overline \Omega$
and all $x\in \overline \Omega$ :
(2.3)\begin{align} \langle \mathbb{C}_e(x)\sigma,\tau\rangle = \langle \sigma,\mathbb{C}_e(x)\tau\rangle, \quad \langle \mathbb{C}_\text{micro}(x)\sigma,\tau\rangle & = \langle \sigma,\mathbb{C}_\text{micro}(x)\tau\rangle, \nonumber\\ \langle \mathbb{L}_c(x)\eta_1,\eta_2\rangle & = \langle\eta_1, \mathbb{L}_c(x)\eta_2\rangle. \end{align}
:
(2.3)\begin{align} \langle \mathbb{C}_e(x)\sigma,\tau\rangle = \langle \sigma,\mathbb{C}_e(x)\tau\rangle, \quad \langle \mathbb{C}_\text{micro}(x)\sigma,\tau\rangle & = \langle \sigma,\mathbb{C}_\text{micro}(x)\tau\rangle, \nonumber\\ \langle \mathbb{L}_c(x)\eta_1,\eta_2\rangle & = \langle\eta_1, \mathbb{L}_c(x)\eta_2\rangle. \end{align}
(ii) There exists positive constants $C_{\mathrm {e}}$
 , $C_{\mathrm {micro}}$
, $C_{\mathrm {micro}}$ and $L_{\mathrm {c}}$
and $L_{\mathrm {c}}$ such that for all $x\in \overline \Omega$
such that for all $x\in \overline \Omega$ , $\sigma \in \operatorname {Sym}(3)$
, $\sigma \in \operatorname {Sym}(3)$ and $\eta \in \mathbb{R} ^{3\times 3}$
and $\eta \in \mathbb{R} ^{3\times 3}$ :
(2.4)\begin{equation} \langle{\mathbb{C}_{{\rm e}}}(x)\sigma,\sigma\rangle\geq C_{\mathrm{e}}|\sigma|^2 ,\quad \langle{\mathbb{C}_{{\rm micro}}}(x)\sigma,\sigma\rangle\geq C_{\mathrm{micro}}|\sigma|^2\,,\quad\,\, \langle{\mathbb{L}}_{{\rm c}}(x)\eta,\eta\rangle\geq L_{\mathrm{c}}|\eta|^2. \end{equation}
:
(2.4)\begin{equation} \langle{\mathbb{C}_{{\rm e}}}(x)\sigma,\sigma\rangle\geq C_{\mathrm{e}}|\sigma|^2 ,\quad \langle{\mathbb{C}_{{\rm micro}}}(x)\sigma,\sigma\rangle\geq C_{\mathrm{micro}}|\sigma|^2\,,\quad\,\, \langle{\mathbb{L}}_{{\rm c}}(x)\eta,\eta\rangle\geq L_{\mathrm{c}}|\eta|^2. \end{equation}
2.2 Helmholtz decomposition, embeddings, elliptic regularity
Based on the results from Section 3.3 of the book [Reference Girault and Raviart11] (Corollary $3.4$![]() ), see also [Reference Bauer, Pauly and Schomburg4, Theorem 5.3], the following version of the Helmholtz decomposition will be used:
), see also [Reference Bauer, Pauly and Schomburg4, Theorem 5.3], the following version of the Helmholtz decomposition will be used:
Theorem 2.1 Helmholtz decomposition
Let $\Omega \subset \mathbb{R} ^3$![]() be a bounded domain with a Lipschitz boundary. Then
be a bounded domain with a Lipschitz boundary. Then
and hence, for every $p\in L^2(\Omega ;\mathbb{R} ^3)$![]() there exist unique $v\in H_0^1(\Omega )$
there exist unique $v\in H_0^1(\Omega )$![]() and $q\in H (\operatorname {div},\,0;\Omega )$
and $q\in H (\operatorname {div},\,0;\Omega )$![]() such that $p=\mathrm {D} v + q$
such that $p=\mathrm {D} v + q$![]() .
.
It is worth mentioning that in the case of the $L^2$![]() -theory, theorem 2.1 holds for any bounded domain $\Omega \subset \mathbb{R} ^3$
-theory, theorem 2.1 holds for any bounded domain $\Omega \subset \mathbb{R} ^3$![]() without having a Lipschitz boundary, see e.g. [Reference Farwig, Kozono and Sohr7]. An immediate consequence of the Helmholtz decomposition theorem is
without having a Lipschitz boundary, see e.g. [Reference Farwig, Kozono and Sohr7]. An immediate consequence of the Helmholtz decomposition theorem is
Proposition 2.2 Let $\Omega \subset \mathbb{R} ^3$![]() be a bounded domain and let $p\in L^2(\Omega )$
be a bounded domain and let $p\in L^2(\Omega )$![]() with $p=\mathrm {D} v + q$
with $p=\mathrm {D} v + q$![]() , where $v\in H_0^1(\Omega )$
, where $v\in H_0^1(\Omega )$![]() and $q\in H(\operatorname {div},\,0;\Omega )$
and $q\in H(\operatorname {div},\,0;\Omega )$![]() are given according to the Helmholtz decomposition. Then $\mathrm {D} v\in H_0(\operatorname {curl},\,0;\Omega )$
are given according to the Helmholtz decomposition. Then $\mathrm {D} v\in H_0(\operatorname {curl},\,0;\Omega )$![]() .
.
Proof. Notice that it is sufficient to prove that
For this, let us assume that $v\in H_0^1(\Omega )$![]() and let $\{v_n\}\subset C_0^\infty (\Omega )$
and let $\{v_n\}\subset C_0^\infty (\Omega )$![]() such that $v_n\rightarrow v$
such that $v_n\rightarrow v$![]() in $H^1(\Omega )$
in $H^1(\Omega )$![]() . Then, for all $\phi \in C^\infty _0(\Omega )$
. Then, for all $\phi \in C^\infty _0(\Omega )$![]() we obtain
we obtain
and $\mathrm {D} v\in H(\operatorname {curl},\,0;\Omega )$![]() . Moreover, $\{\mathrm {D} v_n\}\subset C_0^\infty (\Omega )\cap H_0(\operatorname {curl},\,0;\Omega )$
. Moreover, $\{\mathrm {D} v_n\}\subset C_0^\infty (\Omega )\cap H_0(\operatorname {curl},\,0;\Omega )$![]() and $\mathrm {D} v_n\rightarrow \mathrm {D} v$
and $\mathrm {D} v_n\rightarrow \mathrm {D} v$![]() in $H(\operatorname {curl};\Omega )$
in $H(\operatorname {curl};\Omega )$![]() . As $H_0(\operatorname {curl},\,0;\Omega )$
. As $H_0(\operatorname {curl},\,0;\Omega )$![]() is a closed subspace of $H(\operatorname {curl};\Omega )$
is a closed subspace of $H(\operatorname {curl};\Omega )$![]() we conclude that $\mathrm {D} v\in H_0(\operatorname {curl},\,0;\Omega )$
we conclude that $\mathrm {D} v\in H_0(\operatorname {curl},\,0;\Omega )$![]() .
.
In an analogous way to proposition 2.2, we can prove the following lemma, from which additional regularities will be derived for the solution of system (1.2) (see corollary 4.2).
Lemma 2.3 For any bounded domain $\Omega \subset \mathbb{R} ^3$![]() it holds
it holds
Proof. Let us assume that $\{E_n\}\subset C_0^\infty (\Omega )$![]() such that $E_n\rightarrow E$
such that $E_n\rightarrow E$![]() in $H(\operatorname {curl};\Omega )$
in $H(\operatorname {curl};\Omega )$![]() . Then, for all $\phi \in C^\infty _0(\Omega )$
. Then, for all $\phi \in C^\infty _0(\Omega )$![]() we obtain
we obtain
and $\operatorname {curl} E\in H(\operatorname {div},\,0;\Omega )$![]() . Moreover, $\{\operatorname {curl} E_n\}\subset C_0^\infty (\Omega )\cap H_0(\operatorname {div},\,0;\Omega )$
. Moreover, $\{\operatorname {curl} E_n\}\subset C_0^\infty (\Omega )\cap H_0(\operatorname {div},\,0;\Omega )$![]() and $\operatorname {curl} E _n\rightarrow \operatorname {curl} E$
and $\operatorname {curl} E _n\rightarrow \operatorname {curl} E$![]() in $H(\operatorname {div};\Omega )$
in $H(\operatorname {div};\Omega )$![]() . As $H_0(\operatorname {div},\,0;\Omega )$
. As $H_0(\operatorname {div},\,0;\Omega )$![]() is a closed subspace of $H(\operatorname {div};\Omega )$
is a closed subspace of $H(\operatorname {div};\Omega )$![]() we conclude that $\operatorname {curl} E\in H_0(\operatorname {div},\,0;\Omega )$
we conclude that $\operatorname {curl} E\in H_0(\operatorname {div},\,0;\Omega )$![]() .
.
The next embedding theorem is for instance proved in [Reference Girault and Raviart11, Sections 3.4, 3.5] and [Reference Kuhn and Pauly16] (see [Reference Grisvard14] for properties of convex sets):
Theorem 2.4 Embedding theorem
Let $\Omega \subset \mathbb{R} ^3$![]() be a convex domain or a domain with a $C^{1,1}$
be a convex domain or a domain with a $C^{1,1}$![]() -smooth boundary $\partial \Omega$
-smooth boundary $\partial \Omega$![]() . Then
. Then
and there exists a constant $C>0$![]() such that for every $p\in H(\operatorname {curl};\Omega )\cap H_0(\operatorname {div};\Omega )$
such that for every $p\in H(\operatorname {curl};\Omega )\cap H_0(\operatorname {div};\Omega )$![]() or $p\in H_0(\operatorname {curl};\Omega )\cap H(\operatorname {div};\Omega )$
or $p\in H_0(\operatorname {curl};\Omega )\cap H(\operatorname {div};\Omega )$![]() we have
we have
A version of this result for Lipschitz domains showing $H^{{1}/{2}}(\Omega )$![]() - regularity is given in [Reference Costabel5] (similar results for bounded strong Lipschitz domains with strong Lipschitz boundary interface parts may be found in [Reference Pauly and Schomburg31, Reference Pauly and Schomburg32]). In addition, it can be noted that convex domains are strongly Lipschitz, cf. [Reference Grisvard14]. A proof for convex domains including a family of relevant boundary conditions can be found in [Reference Pauly30]. For the previous embedding theorem there are also some versions with weights, and we cite here Theorem 2.2 from [Reference Weber42] with $k=1$
- regularity is given in [Reference Costabel5] (similar results for bounded strong Lipschitz domains with strong Lipschitz boundary interface parts may be found in [Reference Pauly and Schomburg31, Reference Pauly and Schomburg32]). In addition, it can be noted that convex domains are strongly Lipschitz, cf. [Reference Grisvard14]. A proof for convex domains including a family of relevant boundary conditions can be found in [Reference Pauly30]. For the previous embedding theorem there are also some versions with weights, and we cite here Theorem 2.2 from [Reference Weber42] with $k=1$![]() and $\ell =0$
and $\ell =0$![]() . We assume that the weight function $\varepsilon :\overline \Omega \to \mathbb{R} ^{3\times 3}$
. We assume that the weight function $\varepsilon :\overline \Omega \to \mathbb{R} ^{3\times 3}$![]() for every $x\in \overline \Omega$
for every $x\in \overline \Omega$![]() is symmetric and positive definite, uniformly in $x$
is symmetric and positive definite, uniformly in $x$![]() .
.
Theorem 2.5 Let $\Omega \subset \mathbb{R} ^3$![]() be a bounded domain with a $C^2$
be a bounded domain with a $C^2$![]() -smooth boundary and let $\varepsilon \in C^1(\overline \Omega,\,\mathbb{R} ^{3\times 3})$
-smooth boundary and let $\varepsilon \in C^1(\overline \Omega,\,\mathbb{R} ^{3\times 3})$![]() be a symmetric and positive definite weight function. Assume that $p:\Omega \to \mathbb{R} ^3$
be a symmetric and positive definite weight function. Assume that $p:\Omega \to \mathbb{R} ^3$![]() belongs to one of the following spaces:
belongs to one of the following spaces:
or
Then $p\in H^1(\Omega )$![]() and there exists a constant $C>0$
and there exists a constant $C>0$![]() (independent of $p$
(independent of $p$![]() ) such that
) such that
Remark 2.6 Assuming higher regularity on the weight function $\varepsilon$![]() and the smoothness of $\partial \Omega$
and the smoothness of $\partial \Omega$![]() (i.e. $\varepsilon \in C^k(\overline {\Omega },\,\mathbb{R} ^{3\times 3})$
(i.e. $\varepsilon \in C^k(\overline {\Omega },\,\mathbb{R} ^{3\times 3})$![]() and $\partial \Omega \in C^{k+1})$
and $\partial \Omega \in C^{k+1})$![]() , Theorem 2.2 from [Reference Weber42] guarantees a corresponding higher regularity of $p$
, Theorem 2.2 from [Reference Weber42] guarantees a corresponding higher regularity of $p$![]() .
.
In the proof of theorem 4.1 we will decompose the microdistortion tensor $P$![]() as $P=\mathrm {D} q + Q$
as $P=\mathrm {D} q + Q$![]() and apply theorem 2.4 to $Q$
and apply theorem 2.4 to $Q$![]() . The regularity for the displacement field $u$
. The regularity for the displacement field $u$![]() and the vector $q$
and the vector $q$![]() then is a consequence of an elliptic regularity result that we discuss next.
then is a consequence of an elliptic regularity result that we discuss next.
Let us consider the following auxiliary bilinear form: for $(u,\,q)\in H^1_0(\Omega ;\mathbb{R} ^{3+3})$![]() and $(u,\,v)\in H^1_0(\Omega ;\mathbb{R} ^{3+3})$
and $(u,\,v)\in H^1_0(\Omega ;\mathbb{R} ^{3+3})$![]() we define
we define
where $\mathbb{A} :\Omega \rightarrow (\operatorname{Lin} (\operatorname {Sym}(3),\,\operatorname {Sym}(3)))^4$![]() is defined by the following formula
is defined by the following formula
Corollary 2.7 Let Assumption $\bf {A}_{(ii)}$![]() be satisfied. Then, there exists a positive constant $C_{\mathbb{A} }$
be satisfied. Then, there exists a positive constant $C_{\mathbb{A} }$![]() such that for all $x\in \overline \Omega$
such that for all $x\in \overline \Omega$![]() and $\sigma =(\sigma _1,\,\sigma _2)\in \operatorname {Sym}(3)\times \operatorname {Sym}(3)$
and $\sigma =(\sigma _1,\,\sigma _2)\in \operatorname {Sym}(3)\times \operatorname {Sym}(3)$![]() we have:
we have:
Proof. Fix $x\in \overline \Omega$![]() and $\sigma =(\sigma _1,\,\sigma _2)\in \operatorname {Sym}(3)\times \operatorname {Sym}(3)$
and $\sigma =(\sigma _1,\,\sigma _2)\in \operatorname {Sym}(3)\times \operatorname {Sym}(3)$![]() , then
, then
Assumption $\bf {A}_{(ii)}$![]() implies
implies

and the proof is completed.
Now, for all $(u,\,q)\in H^1_0(\Omega ;\mathbb{R} ^{3+3})$![]() we have
we have

where the constant $C_{K}$![]() is a constant resulting from the standard Korn's inequality [Reference Neff22]. This shows that the bilinear form (2.7) is coercive on the space $H^1_0(\Omega ;\mathbb{R} ^{3+3})$
is a constant resulting from the standard Korn's inequality [Reference Neff22]. This shows that the bilinear form (2.7) is coercive on the space $H^1_0(\Omega ;\mathbb{R} ^{3+3})$![]() . The form (2.7) defines the following auxiliary problem: for $(F_1,\,F_2)\in L^2(\Omega ;\mathbb{R} ^{3+3})$
. The form (2.7) defines the following auxiliary problem: for $(F_1,\,F_2)\in L^2(\Omega ;\mathbb{R} ^{3+3})$![]() find $(u,\,q)\in H^1_0(\Omega ;\mathbb{R} ^{3+3})$
find $(u,\,q)\in H^1_0(\Omega ;\mathbb{R} ^{3+3})$![]() with
with
for all $(v,\,w)\in H^1_0(\Omega ;\mathbb{R} ^{3+3})$![]() . Modifying the results concerning the regularity of elliptic partial differential equations, it would be possible to obtain the existence of a solution for system (2.11) with the regularity $(u,\,q)\in H^1_0(\Omega ;\mathbb{R} ^{3+3})\cap H^2(\Omega ;\mathbb{R} ^{3+3})$
. Modifying the results concerning the regularity of elliptic partial differential equations, it would be possible to obtain the existence of a solution for system (2.11) with the regularity $(u,\,q)\in H^1_0(\Omega ;\mathbb{R} ^{3+3})\cap H^2(\Omega ;\mathbb{R} ^{3+3})$![]() (see for example [Reference Gilbarg and Trudinger10, Theorem 9.15, Section 9.6]). However, system (2.11) fits perfectly into the class considered in [Reference Neff and Knees26]. There, the global regularity of weak solutions to a quasilinear elliptic system with a rank-one-monotone nonlinearity was investigated. As an application of the result from [Reference Neff and Knees26] we obtain
(see for example [Reference Gilbarg and Trudinger10, Theorem 9.15, Section 9.6]). However, system (2.11) fits perfectly into the class considered in [Reference Neff and Knees26]. There, the global regularity of weak solutions to a quasilinear elliptic system with a rank-one-monotone nonlinearity was investigated. As an application of the result from [Reference Neff and Knees26] we obtain
Lemma 2.8 Let $\Omega \subset \mathbb{R} ^3$![]() be a bounded domain with a $C^{1,1}$
be a bounded domain with a $C^{1,1}$![]() -smooth boundary $\partial \Omega$
-smooth boundary $\partial \Omega$![]() . Let furthermore $(F_1,\,F_2)\in L^2(\Omega ;\mathbb{R} ^{3+3})$
. Let furthermore $(F_1,\,F_2)\in L^2(\Omega ;\mathbb{R} ^{3+3})$![]() and ${\mathbb {C}_{{\rm e}}},\,{\mathbb {C}_{{\rm micro}}}\in C^{0,1}(\overline \Omega ; \operatorname{Lin} (\mathbb{R} ^{3\times 3};\mathbb{R} ^{3\times 3}))$
and ${\mathbb {C}_{{\rm e}}},\,{\mathbb {C}_{{\rm micro}}}\in C^{0,1}(\overline \Omega ; \operatorname{Lin} (\mathbb{R} ^{3\times 3};\mathbb{R} ^{3\times 3}))$![]() . Then the problem (2.11) has a unique solution $(u,\,q)\in H^1_0(\Omega ;\mathbb{R} ^{3+3})\cap H^2(\Omega ;\mathbb{R} ^{3+3})$
. Then the problem (2.11) has a unique solution $(u,\,q)\in H^1_0(\Omega ;\mathbb{R} ^{3+3})\cap H^2(\Omega ;\mathbb{R} ^{3+3})$![]() .
.
Proof. Coercivity (2.10) of the bilinear form (3.1) and the Lax-Milgram theorem imply the existence of exactly one weak solution $(u,\,q)\in H^1_0(\Omega ;\mathbb{R} ^{3+3})$![]() . In order to prove higher regularity of this solution we will use Theorem $5.2$
. In order to prove higher regularity of this solution we will use Theorem $5.2$![]() of [Reference Neff and Knees26].
of [Reference Neff and Knees26].
Let us introduce $\mathbb {B}:\overline \Omega \times \mathbb{R} ^{(3+3)\times 3}\rightarrow \mathbb{R} ^{(3+3)\times 3}$![]() as the unique $x$
as the unique $x$![]() -dependent linear mapping satisfying
-dependent linear mapping satisfying
for all $A_1,\,A_2,\,B_1,\,B_2\in \mathbb{R} ^{3\times 3}$![]() and $x\in \overline \Omega$
and $x\in \overline \Omega$![]() . Then for every $x\in \overline {\Omega }$
. Then for every $x\in \overline {\Omega }$![]() , $A=(A_1,\,A_2)\in \mathbb{R} ^{(3+3)\times 3}$
, $A=(A_1,\,A_2)\in \mathbb{R} ^{(3+3)\times 3}$![]() , $\xi =(\xi _1,\,\xi _2)\in \mathbb{R} ^{3+3}$
, $\xi =(\xi _1,\,\xi _2)\in \mathbb{R} ^{3+3}$![]() and $\eta \in \mathbb{R} ^3$
and $\eta \in \mathbb{R} ^3$![]() we have thanks to the positive definiteness of $\mathbb{A}$
we have thanks to the positive definiteness of $\mathbb{A}$![]()

Since $\|\operatorname {sym}(\xi _i\otimes \eta )\|^2=1/2(\|\xi _i\|^2\|\eta\|^2 + \|\langle \xi _i,\,\eta \rangle\|^2)$![]() , this ultimately implies that $\mathbb {B}$
, this ultimately implies that $\mathbb {B}$![]() is strongly rank-one monotone/satisfies the Legendre-Hadamard condition. Due to the Lipschitz continuity of ${\mathbb {C}_{{\rm e}}}$
is strongly rank-one monotone/satisfies the Legendre-Hadamard condition. Due to the Lipschitz continuity of ${\mathbb {C}_{{\rm e}}}$![]() and ${\mathbb {C}_{{\rm micro}}}$
and ${\mathbb {C}_{{\rm micro}}}$![]() the remaining assumptions of Theorem $5.2$
the remaining assumptions of Theorem $5.2$![]() of [Reference Neff and Knees26] can easily be verified. Hence, [Reference Neff and Knees26, Theorem 5.2] implies $(u,\,q)\in H^2(\Omega ;\mathbb{R} ^{3+3})$
of [Reference Neff and Knees26] can easily be verified. Hence, [Reference Neff and Knees26, Theorem 5.2] implies $(u,\,q)\in H^2(\Omega ;\mathbb{R} ^{3+3})$![]() .
.
3. Weak formulation of the relaxed micromorphic model
For $u,\,v\in H^1_0(\Omega,\,\mathbb{R} ^3)$![]() and $P,\,W\in H_0(\operatorname {Curl};\Omega )$
and $P,\,W\in H_0(\operatorname {Curl};\Omega )$![]() the following bilinear form is associated with the system (1.2)
the following bilinear form is associated with the system (1.2)

where the tensor $\mathbb{A}$![]() is defined in (2.8). Here, homogeneous boundary conditions $u\big |_{\partial \Omega }=0$
is defined in (2.8). Here, homogeneous boundary conditions $u\big |_{\partial \Omega }=0$![]() and $(P\times n)\big |_{\partial \Omega }=0$
and $(P\times n)\big |_{\partial \Omega }=0$![]() are considered.
are considered.
Theorem 3.1 Existence of weak solutions
Let $\Omega \subset \mathbb{R} ^3$![]() be a bounded domain with a Lipschitz boundary and assume that ${\mathbb {C}_{{\rm e}}},\,{\mathbb {C}_{{\rm micro}}},\,{\mathbb {L}}_{{\rm c}}\in L^\infty (\Omega ;\operatorname{Lin} (\mathbb{R} ^{3\times 3};\mathbb{R} ^{3\times 3}))$
be a bounded domain with a Lipschitz boundary and assume that ${\mathbb {C}_{{\rm e}}},\,{\mathbb {C}_{{\rm micro}}},\,{\mathbb {L}}_{{\rm c}}\in L^\infty (\Omega ;\operatorname{Lin} (\mathbb{R} ^{3\times 3};\mathbb{R} ^{3\times 3}))$![]() comply with the symmetry and positivity properties formulated in (2.3)–(2.4). Then for every $f\in H^{-1}(\Omega )$
comply with the symmetry and positivity properties formulated in (2.3)–(2.4). Then for every $f\in H^{-1}(\Omega )$![]() and $M\in (H_0(\operatorname {Curl};\Omega ))^{\ast }$
and $M\in (H_0(\operatorname {Curl};\Omega ))^{\ast }$![]() there exists a unique pair $(u,\,P)\in H_0^1(\Omega )\times H_0(\operatorname {Curl};\Omega )$
there exists a unique pair $(u,\,P)\in H_0^1(\Omega )\times H_0(\operatorname {Curl};\Omega )$![]() such that
such that
Proof. For a bounded domain $\Omega \subset \mathbb{R} ^3$![]() with Lipschitz boundary $\partial \Omega$
with Lipschitz boundary $\partial \Omega$![]() the incompatible Korn's inequality [Reference Gmeineder, Lewintan and Neff12, Reference Lewintan and Neff19, Reference Lewintan and Neff20, Reference Neff, Pauly and Witsch27] implies that there is a constant $\tilde {c}>0$
the incompatible Korn's inequality [Reference Gmeineder, Lewintan and Neff12, Reference Lewintan and Neff19, Reference Lewintan and Neff20, Reference Neff, Pauly and Witsch27] implies that there is a constant $\tilde {c}>0$![]() such that
such that
for all $P\in {\rm H}_0(\operatorname {Curl};\Omega )$![]() . Positive definiteness of the tensors $\mathbb{A}$
. Positive definiteness of the tensors $\mathbb{A}$![]() and ${\mathbb {L}}_{{\rm c}}$
and ${\mathbb {L}}_{{\rm c}}$![]() entail
entail
Hence, by (3.3) and Korn's inequality the bilinear form (3.1) is coercive on $H_0^1(\Omega )\times H_0(\operatorname {Curl};\Omega )$![]() and the Lax-Milgram theorem finishes the proof.
and the Lax-Milgram theorem finishes the proof.
Thanks to the Helmholtz decomposition, weak solutions can equivalently be characterized as follows:
Lemma 3.2 Let the assumptions of theorem 3.1 be satisfied, $f\in H^{-1}(\Omega )$![]() and $M\in (H_0(\operatorname {Curl};\Omega ))^{\ast }$
and $M\in (H_0(\operatorname {Curl};\Omega ))^{\ast }$![]() . Let furthermore $(u,\,P)\in H_0^1(\Omega )\times H_0(\operatorname {Curl};\Omega )$
. Let furthermore $(u,\,P)\in H_0^1(\Omega )\times H_0(\operatorname {Curl};\Omega )$![]() and let $(q,\,Q)\in H_0^1(\Omega ;\mathbb{R} ^3)\times H(\operatorname {Div},\,0;\Omega )$
and let $(q,\,Q)\in H_0^1(\Omega ;\mathbb{R} ^3)\times H(\operatorname {Div},\,0;\Omega )$![]() such that $P=\mathrm {D} q + Q$
such that $P=\mathrm {D} q + Q$![]() . Then the following (a) and (b) are equivalent:
. Then the following (a) and (b) are equivalent:
(a) $(u,\,P)$
 is a weak solution of (1.2) in the sense of (3.2).
is a weak solution of (1.2) in the sense of (3.2).(b) For all $(v,\,W)\in H_0^1(\Omega )\times H_0(\operatorname {Curl};\Omega )$
 the triple $(u,\,q,\,Q)$
the triple $(u,\,q,\,Q)$ satisfies
(3.5)\begin{align} \int_\Omega \langle \mathbb{A} & \begin{pmatrix} \operatorname{sym}\mathrm{D} u\\ \operatorname{sym}\mathrm{D} q + \operatorname{sym} Q \end{pmatrix},\quad \begin{pmatrix} \operatorname{sym}\mathrm{D} v\\ \operatorname{sym} W \end{pmatrix} \rangle\, {\mathrm d} x\nonumber\\ & \quad+ \int_\Omega \langle{\mathbb{L}}_{{\rm c}} \operatorname{Curl} Q,\operatorname{Curl} W\rangle\,{\mathrm d} x= \int_{\Omega}\langle f,v\rangle + \langle M,W\rangle\,{\mathrm d} x. \end{align}
satisfies
(3.5)\begin{align} \int_\Omega \langle \mathbb{A} & \begin{pmatrix} \operatorname{sym}\mathrm{D} u\\ \operatorname{sym}\mathrm{D} q + \operatorname{sym} Q \end{pmatrix},\quad \begin{pmatrix} \operatorname{sym}\mathrm{D} v\\ \operatorname{sym} W \end{pmatrix} \rangle\, {\mathrm d} x\nonumber\\ & \quad+ \int_\Omega \langle{\mathbb{L}}_{{\rm c}} \operatorname{Curl} Q,\operatorname{Curl} W\rangle\,{\mathrm d} x= \int_{\Omega}\langle f,v\rangle + \langle M,W\rangle\,{\mathrm d} x. \end{align}
Proof. $(a)\implies (b):$![]() Assume that $(u,\,P)\in H_0^1(\Omega )\times H_0(\operatorname {Curl};\Omega )$
Assume that $(u,\,P)\in H_0^1(\Omega )\times H_0(\operatorname {Curl};\Omega )$![]() is a weak solution of (1.2) in the sense of (3.2). Then theorem 2.1 implies that for $i=1,\,2,\,3$
is a weak solution of (1.2) in the sense of (3.2). Then theorem 2.1 implies that for $i=1,\,2,\,3$![]() there exists unique $q_i\in H_0^1(\Omega )$
there exists unique $q_i\in H_0^1(\Omega )$![]() and $Q_i\in H_0(\operatorname {Div},\,0;\Omega )$
and $Q_i\in H_0(\operatorname {Div},\,0;\Omega )$![]() such that $P_i=\mathrm {D} q_i + Q_i$
such that $P_i=\mathrm {D} q_i + Q_i$![]() , where $P_i$
, where $P_i$![]() denotes the rows of the matrix $P$
denotes the rows of the matrix $P$![]() . Inserting $P=(\nabla q_1 + Q_1,\, \nabla q_2 + Q_2,\, \nabla q_3 + Q_3)^T$
. Inserting $P=(\nabla q_1 + Q_1,\, \nabla q_2 + Q_2,\, \nabla q_3 + Q_3)^T$![]() into (3.2) we obtain (3.5), where $Q=(Q_1,\, Q_2,\, Q_3)^T$
into (3.2) we obtain (3.5), where $Q=(Q_1,\, Q_2,\, Q_3)^T$![]() .
.
$(b)\implies (a):$![]() Let for all $(v,\,W)\in H_0^1(\Omega )\times H_0(\operatorname {Curl};\Omega )$
Let for all $(v,\,W)\in H_0^1(\Omega )\times H_0(\operatorname {Curl};\Omega )$![]() the triple $(u,\,q,\,Q)\in H_0^1(\Omega ;\mathbb{R} ^3)\times H_0^1(\Omega ;\mathbb{R} ^3)\times H(\operatorname {Div},\,0;\Omega )$
the triple $(u,\,q,\,Q)\in H_0^1(\Omega ;\mathbb{R} ^3)\times H_0^1(\Omega ;\mathbb{R} ^3)\times H(\operatorname {Div},\,0;\Omega )$![]() satisfy (3.5). Then (3.5) can be written in the form
satisfy (3.5). Then (3.5) can be written in the form

and the function $(u,\,\mathrm {D} q+Q)$![]() satisfies (3.2) for all $(v,\,W)\in H_0^1(\Omega )\times H_0(\operatorname {Curl};\Omega )$
satisfies (3.2) for all $(v,\,W)\in H_0^1(\Omega )\times H_0(\operatorname {Curl};\Omega )$![]() . Uniqueness of a weak solution of the problem (1.2) implies that $P=\mathrm {D} q+Q$
. Uniqueness of a weak solution of the problem (1.2) implies that $P=\mathrm {D} q+Q$![]() .
.
4. Global regularity on smooth domains
The aim of this section is to prove the following regularity theorem
Theorem 4.1 Let $\Omega \subset \mathbb{R} ^3$![]() be a bounded domain with a $C^{1,1}$
be a bounded domain with a $C^{1,1}$![]() -smooth boundary. Moreover, in addition to the assumptions of theorem 3.1 let ${\mathbb {C}_{{\rm e}}},\,{\mathbb {C}_{{\rm micro}}},\,{\mathbb {L}}_{{\rm c}}\in C^{0,1}(\overline \Omega ; \operatorname{Lin} (\mathbb{R} ^{3\times 3};\mathbb{R} ^{3\times 3}))$
-smooth boundary. Moreover, in addition to the assumptions of theorem 3.1 let ${\mathbb {C}_{{\rm e}}},\,{\mathbb {C}_{{\rm micro}}},\,{\mathbb {L}}_{{\rm c}}\in C^{0,1}(\overline \Omega ; \operatorname{Lin} (\mathbb{R} ^{3\times 3};\mathbb{R} ^{3\times 3}))$![]() . Finally, we assume that $f\in L^2(\Omega )$
. Finally, we assume that $f\in L^2(\Omega )$![]() and $M\in H(\operatorname {Div};\Omega )$
and $M\in H(\operatorname {Div};\Omega )$![]() . Then for every weak solution $(u,\,P)\in H_0^1(\Omega )\times H_0(\operatorname {Curl};\Omega )$
. Then for every weak solution $(u,\,P)\in H_0^1(\Omega )\times H_0(\operatorname {Curl};\Omega )$![]() we have
we have
and there exists a constant $C>0$![]() (independent of $f$
(independent of $f$![]() and $M$
and $M$![]() ) such that
) such that
The proof relies on the Helmholtz decomposition of $P$![]() , the embedding theorem 2.4 and theorem 2.8 about the global regularity for the auxiliary problem (2.11).
, the embedding theorem 2.4 and theorem 2.8 about the global regularity for the auxiliary problem (2.11).
Proof. Let $(u,\,P)\in H_0^1(\Omega )\times H_0(\operatorname {Curl};\Omega )$![]() satisfy (3.2) with $f\in L^2(\Omega )$
satisfy (3.2) with $f\in L^2(\Omega )$![]() and $M\in H(\operatorname {Div};\Omega )$
and $M\in H(\operatorname {Div};\Omega )$![]() .
.
We first show that $(u,\,P)\in H^2(\Omega )\times H^1(\Omega )$![]() . Let $P=\mathrm {D} q + Q$
. Let $P=\mathrm {D} q + Q$![]() , where $q\in H_0^1(\Omega ;\mathbb{R} ^3)$
, where $q\in H_0^1(\Omega ;\mathbb{R} ^3)$![]() and $Q\in H(\operatorname {Div},\,0;\Omega )$
and $Q\in H(\operatorname {Div},\,0;\Omega )$![]() are given according to the Helmholtz decomposition. By proposition 2.2 it follows that $Q\in H(\operatorname {Div},\,0;\Omega )\cap H_0(\operatorname {Curl};\Omega )$
are given according to the Helmholtz decomposition. By proposition 2.2 it follows that $Q\in H(\operatorname {Div},\,0;\Omega )\cap H_0(\operatorname {Curl};\Omega )$![]() and thanks to the assumed regularity of $\partial \Omega$
and thanks to the assumed regularity of $\partial \Omega$![]() , theorem 2.4 implies that $Q\in H^1(\Omega )$
, theorem 2.4 implies that $Q\in H^1(\Omega )$![]() . Next, choosing $W=\mathrm {D} w$
. Next, choosing $W=\mathrm {D} w$![]() for $w\in C_0^\infty (\Omega ;\mathbb{R} ^d)$
for $w\in C_0^\infty (\Omega ;\mathbb{R} ^d)$![]() , the weak form (3.5) in combination with a density argument implies that for all $v,\,w\in H_0^1(\Omega )$
, the weak form (3.5) in combination with a density argument implies that for all $v,\,w\in H_0^1(\Omega )$![]() we have
we have

Since $Q\in H^1(\Omega )$![]() and $M\in H(\operatorname {Div};\Omega )$
and $M\in H(\operatorname {Div};\Omega )$![]() , by partial integration the right hand side of (4.3) can be rewritten as $\int _\Omega \langle F_1,\, v\rangle + \langle F_2,\, w\rangle \textrm{d}x$
, by partial integration the right hand side of (4.3) can be rewritten as $\int _\Omega \langle F_1,\, v\rangle + \langle F_2,\, w\rangle \textrm{d}x$![]() with functions $F_1,\,F_2\in L^2(\Omega )$
with functions $F_1,\,F_2\in L^2(\Omega )$![]() . theorem 2.8 implies that $u,\,q\in H^2(\Omega )$
. theorem 2.8 implies that $u,\,q\in H^2(\Omega )$![]() and hence $P=\mathrm {D} q +Q\in H^1(\Omega )$
and hence $P=\mathrm {D} q +Q\in H^1(\Omega )$![]() .
.
Let us next choose $v=0$![]() and $W\in C_0^\infty (\Omega )$
and $W\in C_0^\infty (\Omega )$![]() in (3.1). Rearranging the terms we find that
in (3.1). Rearranging the terms we find that

which implies that $\operatorname {Curl}({\mathbb {L}}_{{\rm c}}\operatorname {Curl} P)\in L^2(\Omega )$![]() and ${\mathbb {L}}_{{\rm c}}\operatorname {Curl} P\in H(\operatorname {Curl};\Omega )$
and ${\mathbb {L}}_{{\rm c}}\operatorname {Curl} P\in H(\operatorname {Curl};\Omega )$![]() .
.
If we additionally assume that $\mathbb {L}_c$![]() has a block-diagonal structure, we may also achieve $\operatorname {Curl} P\in H^1(\Omega )$
has a block-diagonal structure, we may also achieve $\operatorname {Curl} P\in H^1(\Omega )$![]() by applying the weighted embedding theorem 2.5.
by applying the weighted embedding theorem 2.5.
Corollary 4.2 In addition to the assumptions of theorem 4.1 let $\mathbb {L}_c\in C^1(\overline \Omega ;\operatorname{Lin} (\mathbb{R} ^{3\times 3},\,\mathbb{R} ^{3\times 3}))$![]() be of block diagonal structure, meaning that there exist $\mathbb {L}_i\in C^1(\overline \Omega ;\mathbb{R} ^{3\times 3})$
be of block diagonal structure, meaning that there exist $\mathbb {L}_i\in C^1(\overline \Omega ;\mathbb{R} ^{3\times 3})$![]() , $1\leq i\leq 3$
, $1\leq i\leq 3$![]() , such that for every $W\in \mathbb{R} ^{3\times 3}$
, such that for every $W\in \mathbb{R} ^{3\times 3}$![]() we have $(\mathbb {L}_c W)_{i\text {-th row}}= \mathbb {L}_i (W_{i\text {-th row}})$
we have $(\mathbb {L}_c W)_{i\text {-th row}}= \mathbb {L}_i (W_{i\text {-th row}})$![]() . Then $\mathbb {L}_c\operatorname {Curl} P\in H^1(\Omega )$
. Then $\mathbb {L}_c\operatorname {Curl} P\in H^1(\Omega )$![]() and $\operatorname {Curl} P\in H^1(\Omega )$
and $\operatorname {Curl} P\in H^1(\Omega )$![]() .
.
Proof. We focus on the $i$![]() -th row $P^i$
-th row $P^i$![]() of $P$
of $P$![]() . Let $\varepsilon =(\mathbb {L}_i)^{-1}$
. Let $\varepsilon =(\mathbb {L}_i)^{-1}$![]() . Then $\varepsilon \in C^1(\overline \Omega ;\mathbb{R} ^{3\times 3})$
. Then $\varepsilon \in C^1(\overline \Omega ;\mathbb{R} ^{3\times 3})$![]() and $\varepsilon (x)$
and $\varepsilon (x)$![]() is symmetric and uniformly positive definite with respect to $x\in \overline \Omega$
is symmetric and uniformly positive definite with respect to $x\in \overline \Omega$![]() .
.
We know that $P^i\in H_0(\operatorname {curl};\Omega )$![]() , hence lemma 2.3 implies immediately that
, hence lemma 2.3 implies immediately that
The weighted embedding theorem 2.5 implies $\mathbb {L}_i \operatorname {curl} P^i\in H^1(\Omega )$![]() , and since $\varepsilon =\mathbb {L}_i^{-1}$
, and since $\varepsilon =\mathbb {L}_i^{-1}$![]() is a multiplyer on $H^1(\Omega )$
is a multiplyer on $H^1(\Omega )$![]() , we finally obtain $\operatorname {curl} P^i\in H^1(\Omega )$
, we finally obtain $\operatorname {curl} P^i\in H^1(\Omega )$![]() .
.
Remark 4.3 The previous result may be applied to the simple uni-constant isotropic curvature case $L^2_{\mathrm {c}}\,\|\operatorname {Curl} P\|^2$![]() .
.
Remark 4.4 It is clear that the same higher regularity result can be established for the linear Cosserat model [Reference Ghiba, Rizzi, Madeo and Neff9].
5. Global regularity for a gauge-invariant incompatible elasticity model
The method presented above for obtaining regularity of solution for the static relaxed micromorphic model can be directly applied to the following gauge-invariant incompatible elasticity model [Reference Lazar and Anastassiadis17, Reference Neff, Ghiba, Lazar and Madeo24]
where the unknown function is the non-symmetric incompatible elastic distortion $e:\Omega \rightarrow \mathbb{R} ^{3\times 3}$![]() while $M:\Omega \rightarrow \mathbb{R} ^{3\times 3}$
while $M:\Omega \rightarrow \mathbb{R} ^{3\times 3}$![]() is a given body moment tensor. The constitutive tensors ${\mathbb {C}_{{\rm e}}}$
is a given body moment tensor. The constitutive tensors ${\mathbb {C}_{{\rm e}}}$![]() , ${\mathbb {L}}_{{\rm c}}$
, ${\mathbb {L}}_{{\rm c}}$![]() are positive definite fourth order tensors (fulfilling the Assumption A) while ${\mathbb {C}_{{\rm c}}}:\operatorname {\mathfrak {so}}(3)\rightarrow \operatorname {\mathfrak {so}}(3)$
are positive definite fourth order tensors (fulfilling the Assumption A) while ${\mathbb {C}_{{\rm c}}}:\operatorname {\mathfrak {so}}(3)\rightarrow \operatorname {\mathfrak {so}}(3)$![]() is positive semi-definite. The system (5.1) is considered with homogeneous tangential boundary conditions, i.e.
is positive semi-definite. The system (5.1) is considered with homogeneous tangential boundary conditions, i.e.
where $\times$![]() denotes the vector product, $n$
denotes the vector product, $n$![]() is the unit outward normal vector at the surface $\partial \Omega$
is the unit outward normal vector at the surface $\partial \Omega$![]() , $e_i$
, $e_i$![]() ($i=1,\,2,\,3$
($i=1,\,2,\,3$![]() ) are the rows of the tensor $e$
) are the rows of the tensor $e$![]() . Problem (5.1) generalizes the time-harmonic Maxwell-type eigenvalue problem [Reference Alberti and Capdeboscq3, Reference Yin43] from the vectorial to the tensorial setting. On the other hand, equation (5.1) corresponds to the second equation of (1.2) upon setting ${\mathbb {C}_{{\rm micro}}}\equiv 0$
. Problem (5.1) generalizes the time-harmonic Maxwell-type eigenvalue problem [Reference Alberti and Capdeboscq3, Reference Yin43] from the vectorial to the tensorial setting. On the other hand, equation (5.1) corresponds to the second equation of (1.2) upon setting ${\mathbb {C}_{{\rm micro}}}\equiv 0$![]() , assuming ${\mathbb {C}_{{\rm c}}}\equiv 0$
, assuming ${\mathbb {C}_{{\rm c}}}\equiv 0$![]() , identifying the elastic distortion $e$
, identifying the elastic distortion $e$![]() with $e=\mathrm {D} u-P$
with $e=\mathrm {D} u-P$![]() and observing that
and observing that
Smooth solutions of (5.1) satisfy the balance of linear momentum equation
Gauge-invariance means here that the solution $e$![]() is invariant under
is invariant under
which invariance is only possible since ${\mathbb {C}_{{\rm micro}}}\equiv 0$![]() (${\mathbb {C}_{{\rm micro}}}> 0$
(${\mathbb {C}_{{\rm micro}}}> 0$![]() breaks the gauge-invariance). Here $\tau$
breaks the gauge-invariance). Here $\tau$![]() is a space-dependent (or local) translation vector. The elastic energy can then be expressed as
is a space-dependent (or local) translation vector. The elastic energy can then be expressed as
in which the first term accounts for the energy due to elastic distortion, the second term takes into account the energy due to incompatibility in the presence of dislocations and the last term is representing the forcing.
For $e,\,v\in H_0(\operatorname {Curl};\Omega )$![]() the following bilinear form is associated with the system (5.1)
the following bilinear form is associated with the system (5.1)
Let us assume that $M\in H(\operatorname {Div};\Omega )$![]() . Coercivity of the bilinear form (5.7) (the generalized incompatible Korn's inequality (3.3)) and the Lax-Milgram theorem imply the existence of exactly one weak solution $e\in H_0(\operatorname {Curl};\Omega )$
. Coercivity of the bilinear form (5.7) (the generalized incompatible Korn's inequality (3.3)) and the Lax-Milgram theorem imply the existence of exactly one weak solution $e\in H_0(\operatorname {Curl};\Omega )$![]() of the system (5.1). The Helmholtz decomposition yields that $e=\mathrm {D} q + Q$
of the system (5.1). The Helmholtz decomposition yields that $e=\mathrm {D} q + Q$![]() , where $q\in H_0^1(\Omega ;\mathbb{R} ^3)$
, where $q\in H_0^1(\Omega ;\mathbb{R} ^3)$![]() and $Q\in H(\operatorname {Div},\,0;\Omega )$
and $Q\in H(\operatorname {Div},\,0;\Omega )$![]() . By proposition 2.2 it follows that $Q\in H(\operatorname {Div},\,0;\Omega )\cap H_0(\operatorname {Curl};\Omega )$
. By proposition 2.2 it follows that $Q\in H(\operatorname {Div},\,0;\Omega )\cap H_0(\operatorname {Curl};\Omega )$![]() and theorem 2.4 implies that $Q\in H^1(\Omega )$
and theorem 2.4 implies that $Q\in H^1(\Omega )$![]() . Inserting the decomposed form of the tensor $e$
. Inserting the decomposed form of the tensor $e$![]() into the weak form of system (5.1), we obtain
into the weak form of system (5.1), we obtain

for all $W\in H_0(\operatorname {Curl};\Omega )$![]() . Again, choosing $W=\mathrm {D} w$
. Again, choosing $W=\mathrm {D} w$![]() for $w\in C_0^\infty (\Omega ;\mathbb{R} ^3)$
for $w\in C_0^\infty (\Omega ;\mathbb{R} ^3)$![]() , the weak form (5.8) in combination with a density argument implies that for all $w\in H_0^1(\Omega )$
, the weak form (5.8) in combination with a density argument implies that for all $w\in H_0^1(\Omega )$![]() we have
we have

Since $Q\in H^1(\Omega )$![]() and $M\in H(\operatorname {Div};\Omega )$
and $M\in H(\operatorname {Div};\Omega )$![]() , by partial integration the right hand side of (4.3) can be rewritten as $\int _\Omega \langle F_2,\, w\rangle \textrm{d}x$
, by partial integration the right hand side of (4.3) can be rewritten as $\int _\Omega \langle F_2,\, w\rangle \textrm{d}x$![]() with functions $F_2\in L^2(\Omega )$
with functions $F_2\in L^2(\Omega )$![]() . Note that the auxiliary problem (??) obtained this time is a problem from standard linear elasticity. Thus, in this case we do not need to go through lemma 2.8: just from the standard theory of regularity in the linear elasticity we obtain that $q\in H^2(\Omega )$
. Note that the auxiliary problem (??) obtained this time is a problem from standard linear elasticity. Thus, in this case we do not need to go through lemma 2.8: just from the standard theory of regularity in the linear elasticity we obtain that $q\in H^2(\Omega )$![]() ([Reference Valent41]). The result is that on smooth domains and with smooth coefficients the weak solution of (5.1) is more regular and satisfies
([Reference Valent41]). The result is that on smooth domains and with smooth coefficients the weak solution of (5.1) is more regular and satisfies
where the last regularity in (5.10) follows from equation (5.1). Moreover, if ${\mathbb {L}}_{{\rm c}}$![]() has a special block diagonal structure, then we have
has a special block diagonal structure, then we have
Acknowledgements
The authors wish to thank Dirk Pauly (TU Dresden) for inspiring discussions on this subject dating to 2013. Patrizio Neff and Dorothee Knees acknowledge support in the framework of the Priority Programme SPP 2256 ‘Variational Methods for Predicting Complex Phenomena in Engineering Structures and Materials’ funded by the Deutsche Forschungsgemeinschaft (DFG, German research foundation): P. Neff within the project ‘A variational scale-dependent transition scheme - from Cauchy elasticity to the relaxed micromorphic continuum’ (Project-ID 440935806), D. Knees within the project ‘Rate-independent systems in solid mechanics: physical properties, mathematical analysis, efficient numerical algorithms’ (Project-ID 441222077). D.K. and P.N. enjoyed the welcoming atmosphere at the Hausdorff Research Institute for Mathematics, Bonn, funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany's Excellence Strategy – EXC-2047/1 – 390685813.