Lidar measurement of surface melt for a temperate Alpine glacier at the seasonal and hourly scales

Abstract

This study shows how a new generation of terrestrial laser scanners can be used to investigate glacier surface ablation and other elements of glacial hydrodynamics at exceptionally high spatial and temporal resolution. The study area is an Alpine valley glacier, Haut Glacier d’Arolla, Switzerland. Here we use an ultra-long-range lidar RIEGL VZ-6000 scanner, having a laser specifically designed for measurement of snow- and ice-cover surfaces. We focus on two timescales: seasonal and daily. Our results show that a near-infrared scanning laser system can provide high-precision elevation change and ablation data from long ranges, and over relatively large sections of the glacier surface. We use it to quantify spatial variations in the patterns of surface melt at the seasonal scale, as controlled by both aspect and differential debris cover. At the daily scale, we quantify the effects of ogive-related differences in ice surface debris content on spatial patterns of ablation. Daily scale measurements point to possible hydraulic jacking of the glacier associated with short-term water pressure rises. This latter demonstration shows that this type of lidar may be used to address subglacial hydrologic questions, in addition to motion and ablation measurements.

Introduction

Methods for detecting changes in glacier volume and their spatial distribution have made increasing use of remote sensing, following from the work of Sebastian Finsterwalder who, at the end of the 19th century, showed that oblique images could be used to quantify glacier morphology using photogrammetry. It is not surprising that, since this early progress, the number of techniques available to measure glaciers using remote sensing has burgeoned, to include radar altimetry and interferometry (e.g. Iken and others, 1983; Reinhardt and Rentsch, 1986; Andreassen and others, 2002; Rippin and others, 2003; Mair and others, 2008; Herman and others, 2011), digital aerial photogrammetry (e.g. Brecher, 1986; Baltsavias and others, 2001; Keutterling and Thomas, 2006; Barrand and others, 2009; Heid and Kääb, 2012) and airborne laser scanning (ALS; e.g. Rees and Arnold, 2007; Notebaert and others, 2009; Deems and others, 2013; Helfricht and others, 2013).

One emerging technique is terrestrial laser scanning (TLS). This has been used extensively in the geosciences (e.g. Heritage and Hetherington, 2007; Alho and others, 2009; Hodge and others, 2009; Smith and others, 2012; Williams and others, 2013) but less so in cryosphere studies (e.g. Bauer and others, 2003; Avian and Bauer, 2006; Schwalbe and others, 2008; Deems and others, 2013).

Unlike ALS systems, which typically have wavelengths of 1064 nm, most existing TLS operate at wavelengths of ∼1500 nm, a wavelength with high rates of absorption and low ice reflectance (Deems and others, 2013). This limits the possible scanning distance to a maximum of ∼150 m (Deems and others, 2013). New TLS systems are now available with wavelengths in the near-infrared, which allow long-range scanning of glacier surfaces as developed here. Producing reliable measurements of ice and snow surface changes will require careful consideration of experimental design, including handling the sources of error associated with the method. Thus, the main objective of this study is to show how the new generation of long-range TLS systems can be used to quantify: (1) glacier surface change and hence ablation, and (2) other elements of glacial hydrodynamics, over two scales, seasonal and sub-daily. As the time between measurements reduces, so the magnitude of expected changes should reduce, and the limits of detection (determined by instrument- and deployment-related uncertainties) are approached. At the same time, to aid with the development and validation of high-resolution cryosphere models (e.g. surface ablation models), high-frequency, potentially sub-daily measurements may be of very high value. To achieve this requires careful emphasis on experimental protocols and errors. Here we seek to outline such a protocol and in so doing to determine the timescales over which meaningful results may be obtained. We use a new type of laser scanner, which has a laser 3B (wavelength 1064 nm) specifically designed for measurement of snow- and ice-cover surfaces, and hence is suitable for application over much larger ranges than hitherto. Unlike drone-based techniques that rely on photogrammetric methods and sunlit surfaces, TLS methods do not require surface structures or contrast, and can operate during both day and night.

Study Area

The catchment of Haut Glacier d’Arolla is located in the Val d’Hérens, Valais, in the Swiss Alps. The glacier had a surface area of 3.5 km² in 2010 (Fischer and others, 2015), a mean elevation of 2987 m and a snout elevation of 2579 m. Its average slope is 16.9°. It rests on a bed of unconsolidated sediments with some bedrock outcrops (Hubbard and Nienow, 1997). The area has been the subject of extensive scientific research, including subglacial hydrology (e.g. Nienow and others, 1998; Kulessa and others, 2003; Willis and others, 2003), surface ice-flow acceleration during spring events (e.g. Mair and others, 2002a, 2003, 2008; Fischer and others, 2011), ice-flow velocity (e.g. Harbor and others, 1997) and studies of the controls on surface melt (e.g. Brock and Arnold 2000; Hubbard and others, 2000; Pellicciotti and others, 2005; Brock and others, 2006).

The climate of Haut Glacier d’Arolla is temperate, with warm summers (mean temperature for 2013 was 9.8°C), and cold and fairly wet winters (mean temperature for 2013 was −6.2°C and cumulative precipitations were 170 mm) (according to data provided by HYDRO Exploitation SA for the Arolla meteorological station situated ∼2100 m a.s.l.), although this general pattern is strongly affected by local relief (Arnold, 2005). The glacier has been in continual recession since at least the 1960s, even during cooler and snowier periods when adjacent glaciers (e.g. Tsijiore Nouve, Bas Glacier d’Arolla) advanced (e.g. Zryd, 2001; Fischer and others, 2015).

The focus of this study is application of a laser scanner at the melt season and sub-daily timescales in the ablation zone of the glacier. To do this, two regions were considered (Fig. 1).

Fig. 1. Study site and scans extension. (a) Haut Glacier d’Arolla shown on orthoimage 2009 provided by the Swiss Federal Office of Topography (Swisstopo). (b) Picture taken at the exact location of the lidar instrument on 5 August 2013 during the 12 hour scan, representing the field of vision of the scanner. In yellow, lidar location; in blue, visual approximation of the area selected for the seasonal survey; in red, visual approximation of the area selected for the sub-daily survey.

Methodology

Terrestrial laser scanner: RIEGL VZ-6000

Terrestrial laser scanners emit near-infrared laser signals and measure the time required for a return of that signal after reflection from a target of interest, based on echo digitization and waveform processing (RIEGL Laser Measurement Systems, 2013a). Here a RIEGL VZ-6000 scanner was used, an instrument that can provide ultra-long-range measurements (up to 6000 m) at two rates, ∼220 000 or 23 000 measurements s⁻¹ (RIEGL Laser Measurement Systems, 2013a; Fig. 2). Its laser beam footprint is 240 mm at 2000 m.

Fig. 2. Terrestrial laser scanner RIEGL VZ-6000 used for the surveys, in front of Haut Glacier d’Arolla.

Both distance and surface properties influence the intensity of the signal. This study focuses on snow- and ice-covered surfaces whose reflectivity is high at visible wavelengths but lower in the near-infrared because of their high liquid water content. The reflectivity varies according to the level of purity of the snow surface. Traditionally, terrestrial scanners have used Class 1 laser beams, with relatively shorter wavelengths. The lidar RIEGL VZ-6000 uses a longer near-infrared wavelength (1064 nm through a Class 3B laser) such that high rates of reflection (>80%) from snow- and ice-covered terrains are theoretically possible even at distances of >1 km (RIEGL Laser Measurement Systems, 2013b), although this is something that has to be validated. To achieve returns at long distances, the instrument needs to be operated at the low measurement frequency (23 000 measurements s⁻¹). At this frequency, a measurement step of 0.005° is possible, implying an average point spacing of ∼0.090 m at 1 km and ∼0.180 m at 2 km. Since the system uses a wavelength classified as a 3B laser (hazardous), important precautions have to be taken by the instrument operators, and also to manage the optical risk of people in the landscape (according to the standards of RIEGL Laser Measurement Systems, 2012).

Application to Haut Glacier d’Arolla

A series of scans were performed during the 2013 melt season, using the same approximate instrument site (±0.100 m) in all cases. The upper part of the glacier was not detectable because of the geometry of the valley, but the central (∼3 km from the instrument) and bottom (∼1 km from the instrument) portions were clearly visible and were scanned on the following dates: 6 July, 30 July, 5 August, 11 August and 15 September 2013, at ∼12:00 in all cases. To test the capacity of the scanner to collect a longer daily cycle of datasets, a scan was performed every hour between 09:00 and 17:00 on 5 August in a zone of predominantly glacier ice, away from the moraines. On 5 August, two consecutive scans were undertaken at ∼12:00, one for the smaller study area immediately followed by a larger area scan that was acquired once per day. There were two options to orient and to tie each scan into the same coordinate system: absolute orientation using specially positioned ground control points (GCPs) measured by the scanner; and relative orientation, in which each scan is tied to one reference scan, using natural features known to be stable during the measurement period. The latter has the advantage that it is not necessary to distribute and to measure points across potentially inaccessible terrain, and so was the option chosen here.

For all scans, stable bedrock outcrops were identified during post-processing, and the 6 July 2013 scan was used as the reference scan. For this reason, the point clouds covered a larger area than that which was of interest. Tables 1 and 2 show the parameters used in the scans. Data were collected with a measurement step of 0.005°. In theory, at a scan distance of 2 km, this should produce a point spacing of 0.180 m, or a point density of ∼30 points m⁻². Tables 1 and 2 show that the actual point density obtained is reduced, and this is due to poor reflection, notably where there is a thin film of water at the surface (i.e. surface melt). This emphasizes that for daily scans, measurements are more likely to be optimal earlier in the morning.

Table 1. Seasonal survey parameters

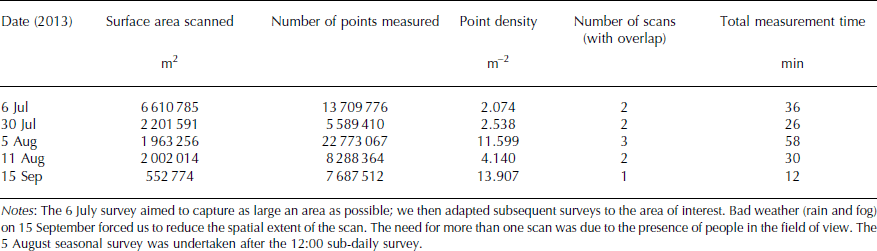
Table 2. Sub-daily survey parameters

Point cloud processing

Point cloud processing required: (1) combining the overlapped scans to one layer and removing clear visual outliers due to, for example, atmospheric reflections such as dust or moisture, which were still present despite scanning on cloud-free days; (2) co-registering the data, initially by manually identifying a small number of points to orient and to displace the data approximately into the same local coordinate system; (3) improving the precision of the coregistration using automated comparison of points (e.g. bedrock outcrops) that could be taken as stable over the study period; (4) determining the quality of each final registration; (5) trimming the data to the area of interest (only the glacier); and (6) transforming the remaining point cloud into a surface (mesh) and manipulating the surfaces to estimate surface change.

The software used for processing point clouds from the RIEGL VZ-6000 is RiSCAN PRO^® (RIEGL Laser Measurement Systems, 2005). The processing was undertaken for two separate projects: (1) the seasonal scale and (2) the sub-daily scale, reflecting the fact that the precision of the latter should be better than the former because the instrument was not moved between scans.

For both steps of the registration, the coordinate systems for the first seasonal survey (6 July 2013) and the first sub-daily survey (09:00, 5 August 2013) were used as the datum onto which the other seasonal and sub-daily surveys respectively were registered. For the approximate coregistration (step 2 above), a small number (minimum 4) of manually identified common points were used to provide an initial estimate. The density of the point clouds was then reduced to facilitate and to shorten the time of computation for the precise orientation (step 3), and patches of data associated with bedrock outcrops were identified. The precise orientation was then undertaken through an iterative closest point (ICP) process (Zhang, 1992) in which the orientation and the position of each scan is iteratively modified in order to calculate the best fit between the point patches based upon least-squares minimization of residuals. The output includes an indication of the quality of the fit as a root-mean-square error, but it is also possible to obtain a full set of fitted point residuals, such that more useful error statistics can be determined. We explain below that the latter were critical in order to distinguish signals of change from noise associated with the registration process.

After trimming to the zone of interest, each co-registered point cloud was triangulated using nearest-neighbour interpolation with a two-dimensional (2-D) Delaunay triangulation algorithm. The lowest point density measured was 1.89 points m⁻², or a mean point spacing of ∼0.730 m. We aimed to produce digital elevation models (DEMs) with a point spacing of 0.30 m (see below) and, given the limited level of interpolation that this implies, we judged the Delaunay method to be sufficient. We did adopt criteria that limited the maximum length of triangle edges and triangle angles. The maximum edge length was defined as 5 m with the aim of avoiding large data gaps while removing triangles that would otherwise become too elongated, mainly at the margins of the DEMs. The maximum angle between the triangle normal and the line of sight was 90° given the relatively flat glacier surface.

Finally, the points were exported to the SURFER^® software (Golden Software, 2014). A regular grid with a 0.30 m spacing (reflecting the approximate point density) was interpolated using kriging because we could assume the spatial variation in the phenomenon represented by the z-values to be statistically homogeneous throughout the surface (Golden Software, 2014). SURFER^® uses a variogram model that measures the deviations from the average within the dataset as a function of distance scale. A linear component for trend removal was employed, with the slope and the anisotropy equal to 1.

The resulting DEMs could be compared by differencing, in order to visualize surface changes and also to perform volume calculations.

Data quality

Following Cooper (1998), the derived data could have two types of error: systematic error associated with point errors that are highly intercorrelated (e.g. a clear mean error); and random error associated with individual data points that are pairwise locally uncorrelated with one another. It is necessary to consider both these error sources in lidar DEM data, especially because random error associated with sensor position and orientation can translate into systematic error in a DEM surface (e.g. surface tilt) (Lane and others, 2004).

Ideally, the mean error should be zero. If it is not, it should be spatially uniform, with no spatial non-stationarity (i.e. areas with more mean error than others). To assess the mean error associated with the scale of our study, and in particular to assess whether it was spatially stationary, we focus on the sub-daily scale of measurement. At the sub-daily scale, we can be more certain that the hillslopes surrounding the glacier are stable and this allows us to identify a number of stable bedrock zones where there should be no change between surveys. In all cases there were at least 20 such zones. For these stable bedrock zones, we quantify the mean error.

Under the assumption that the mean error is negligible within the study area and that the random errors are Gaussian and pairwise uncorrelated, the standard deviation of error can be used to identify limits of detection for surface change. To have 95% confidence in a measured change (Lane and others, 2003),

(1)

where z_i is the elevation of a point at times 1 and 2 and σ_i is the standard deviation of error taken as characteristic of the entire dataset. This calculation was used to identify a range for which estimated changes were too small to be statistically significant and so could be considered as noise. In all cases, we took the standard deviation of error determined from the set of residuals obtained from registering the datasets to the 6 July 2013 data (seasonal scale) and the 5 August 2013 09:00 data (daily scale).

Results

Data quality

Figure 3 shows the mean error calculated by comparing bedrock zones thought to be stable at the sub-daily scale. While there remains some mean error, even at distances >3.5 km, this is less than ∼0.040 m. At the distance typical of the study area (∼1.8 km), the mean error is likely to be ∼0.020 m, so the results are encouraging.

Fig. 3. Mean errors for bedrock zones thought to be stable at the sub-daily timescale, also showing the outline of the DEMs of difference for the sub-daily survey. D is the distance from the scanner to each area; the mean error is shown with reference to 09:00 for 11:00, 13:00, 15:00 and 17:00.

Tables 3 and 4 show the standard deviations of error of each compared dataset and the associated limits of detection (LoD) using Eqn (1) for each pairwise surface comparison. As follows from the methodology, there is no registration error associated with the 6 July and 5 August 09:00 data. As the lidar was not moved on 5 August between scans, the standard deviations were significantly smaller (approximately six times) than those of the seasonal survey and this lower error propagates into better limits of detection (Tables 3 and 4).

Table 3. Standard deviation diagonal and limits of detection for the seasonal scale. Units are meters

Table 4. Standard deviation diagonal and limits of detection for the hourly scale. Units are meters

Surface changes at the seasonal scale

Tables 5 and 6 show the average melt volume per day for each period (m³ d⁻¹) and the same melt volumes divided by the surface to provide an average surface lowering (effectively a spatially averaged melt rate) (m d⁻¹). The same calculations were performed for the sub-daily survey (m³ m⁻² h⁻¹). These calculations allow spatial mapping of the rates of melting and elevation change across the two temporal scales. To compare these two timescales, the melt rate results were also normalized by hour. This calculation assumes that at the scale of the study, there is negligible flux from upstream. This assumption is discussed below.

Table 5. Melt volumes and melt rates for the seasonal survey with uncertainty. Note that care should be shown in relation to the sub-daily melt rates and mean hourly temperatures as the weather station and the high-frequency study areas have very different sub-daily patterns of shading and hence insolation

Table 6. Melt volumes and melt rates for the sub-daily survey with uncertainty. Note that care should be shown in relating the sub-daily melt rates and mean hourly temperatures as the weather station and the high-frequency study areas have very different sub-daily patterns of shading and hence insolation

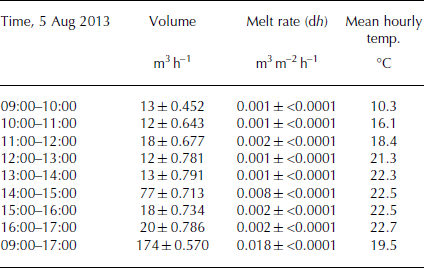
The results reflect the seasonal evolution of meteorological conditions (Fig. 4). The melt rates during July and early August are similar; they then decline gradually during the transition from midsummer to early autumn. The progressive reduction in solar insolation due to increased valley shading is the main factor in reducing melt rate. Averaged over the entire period, for the area studied, the glacier lost ∼0.05 ± 0.002 m³ m⁻² of ice per day, equivalent to 5 ± 0.20 cm of spatially averaged daily surface melt. Figure 5 illustrates the total melt for each time interval (Fig. 5a) and melt rate (Fig. 5b). In practice, the melt rates are spatially variable: while showing the generally decreasing melt rates through time, there are clear areas of lower melt that trend north–south and which are related to medial moraines (Fig. 6). There are some diagonal lines, which are related to slight imprecisions in the orientation of individual laser lines. As they are smaller than ∼0.010 m, substantially smaller than typical daily melt rates during the study period, they will therefore have little impact on results.

Fig. 4. Temperatures and precipitations during the study period (6 July to 15 September 2013) for Arolla. Date format is dd/mm.

Fig. 5. DEMs of difference for the seasonal survey. Top: raw periodic melt rate (effective changes); bottom: changes normalized by day. The axes are in the lidar coordinate system; the proportionality between the scale and the LoD is conserved. Date format is dd/mm (2013).

Fig. 6. Outline of the seasonal survey shown on orthoimage 2009 provided by Swisstopo. Note that the orthoimage is older than the scan data (2009 vs 2013) and the glacier has retreated; however, the patterns of the moraines are visible and some are highlighted in the figure.

It should be noted that these observations may underestimate melt because there is no correction for the effects of ice mass flux. Given velocity measurements made at Haut Glacier d’Arolla of up to ∼4 m a⁻¹ (inferred from Mair and others, 2001, 2003) and that much of this velocity comes from short-duration ‘spring’ events, the amount of lateral displacement depends upon the number and scale of the springtime advance events during the period. However, even this flux effect may be relatively unimportant if the glacier surface slope is low. In the study area it was ∼0.083, such that every time a glacier point moves through a gridcell in terms of distance, there should be an additional 0.025 m of melt. Data from Mair and others (2001) suggest maximum 5 day average velocities of 0.120 m d⁻¹ (associated with a spring event) but more typical values of 0.020–0.040 cm d⁻¹. Given the latter, ∼10 days are needed to achieve a lateral displacement sufficient for 0.025 m vertical change. This suggests when compared with Table 5 that the lidar-derived surface elevation changes need to be corrected for flux effects for the seasonal-scale comparisons, and this could be done either through tracking specially inserted markers (e.g. a differential GPS (dGPS) receiver) or by analysis of repeat images of the zone of interest to identify surface displacements. As the frequency of survey goes up, so the lidar data will approximate more correctly true surface elevation change.

Surface changes at the sub-daily scale

Figure 7 illustrates the difference in DEMs (DEMs of difference) for 09:00 (reference) relative to 11:00, 13:00, 15:00 and 17:00 on 5 August 2013. This was one of the warmest days of the summer (Fig. 3; Tables 5 and 6) and the melt rate recorded between 09:00 and 17:00 was typical of the period (Table 6). It was comparable with but slightly higher than that expected given the melt rates observed between late July and mid-August for the larger area survey (Table 5), especially given that the high-frequency area is on the lowest part of the glacier. There was no precipitation and a high insolation rate, which increased the temperature rapidly (Fig. 8). The maximum reached 22.9°C in Arolla at 17:00. At this scale, it is possible to note two important elements of the surface change. The first is clear spatially coherent measurements of differential melt on the glacier surface. At the sub-daily scale, as compared with the seasonal scale, the typical ice surface velocities mean that changes cannot be attributed to flux effects, even with a ‘spring’ event, leading to a down-glacier velocity of 0.120 m d⁻¹. The vertical elevation changes are present in a 0.30 m DEM over 2 hours, and the length scale of the features is many metres. Rather we conclude that they reflect differential melt rates associated with the effects of ogive-related differences in surface debris content and hence albedo. We justify this interpretation below.

Fig. 7. DEMs of difference for the sub-daily survey: (a) 09:00–11:00; (b) 09:00–13:00; (c) 09:00–15:00; (d) 09:00–17:00. The axes are in the lidar coordinate system.

Fig. 8. Temperatures and insolation conditions on 5 August 2013. These values are issued from Evolène station (insolation – Météosuisse) and Arolla usine station (temperature – HYDRO Exploitation SA).

The second pattern is associated with a positive surface change in the upper (southerly) portion of the study area, early in the morning, which decays progressively during the day. We discuss reasons for this pattern below.

Discussion

Methodological issues and data quality

In methodological terms, this paper shows that long-range terrestrial laser scanners that use wavelengths suitable for reflection by snow and ice are able to provide exceptional levels of detail on surface ice melt: the data we have obtained have revealed spatial variability in melt related to moraine cover at the seasonal scale and the presence of ogives in the ice surface at the sub-daily scale.

The typical survey distance for these measures was ∼1.8 km, and data with a mean spatial resolution of 0.170 m were obtained. The acquisition time for the larger seasonal-scale area was less than ∼20 min and for the smaller sub-daily-scale area <8 min. Acquisition of these data comes with the following caveats: (1) atmospheric absorption (clouds and rain) both reduces the possible survey distances and introduces substantial noise; (2) the actual scan areas had to be enlarged to allow measurement of stable bedrock zones during the study periods; (3) better precision was possible where the scanner did not need to be moved between surveys (i.e. at the sub-daily timescale); (4) use of the scanner required attention to be given to safety-related issues; and (5) a complex glacier surface requires more than a single scan position. In this case, only a single position was needed because a suitable vantage point of the glacier could be identified. These issues notwithstanding, the data obtained appeared to be highly realistic, with only minimal artefacts present (Fig. 5). In theory, the scan can be used to provide highly reliable and spatially rich data on surface melt patterns, without further correction, provided that the time between scans is short relative to the lateral glacier surface velocity. If the scanner is not moved between scans, and despite the 2–3 km distance from the area scanned, changes in surface elevation of ≥0.020 m can be detected.

Seasonal surface changes

There is a broad association between overall melt rate and the evolution of temperature from early July until mid- September (Table 5). The spatial variability in melt was clearly associated with the effects of debris cover related to medial moraines (Fig. 6). Haut Glacier d’Arolla possesses three medial moraines: (1) an ablation-dominated moraine east of the glacier centre line, (2) an ice-stream interaction moraine west of the glacier centre line, and (3) a medial–lateral supraglacial moraine complex along the western margin of the glacier (Gomez and Small, 1985). The first corresponds to the linear-curved feature in the eastern part of the study area and the second is found in the centre of the figure (Fig. 5). These melting differences result from debris-cover thickness effects, with thicker debris cover on the ablation-dominated eastern moraine. A thin debris cover (<∼0.050 m) enhances ablation due to a reduced albedo and an increased absorption of shortwave radiation, whereas thicker debris insulates the underlying ice and reduces ablation, because of its low thermal conductivity (e.g. Khodakov, 1972; Nakawo and Young, 1981; Mattson and others, 1992; Hagg and others, 2008; Pratap and others, 2015). As the scanner also provides data on the net surface reflectance, it is possible that in addition to obtaining surface elevation change data, it may also be able to infer debris-cover characteristics, something that will be explored in future projects. It was also possible to identify aspect controls on the patterns of surface change. Figure 9 shows the distribution by aspect of the surface change (6 July to 15 September 2013) compared with the distribution of points. It shows that the majority of data points had aspects west through north but the surface changes were dominant for aspects from east through southwest. Although, at the seasonal scale, these surface changes are not an exact measurement of melt due to uncorrected flux effects, they nonetheless confirm the expected aspect control on melt rates, and the potential for detailed investigation of controls on the spatial patterns of melt using long-range TLS.

Fig. 9. Distribution by aspect of the surface elevation change (6 July 2013 to 15 September 2013) compared with the distribution of points on the glacier surface.

Sub-daily surface changes

We hypothesize that the spatially coherent measurements of differential melt on the glacier surface are ogives (see above). It is well established that a low density of debris cover enhances melt. As debris cover increases, melt rate further increases until a critical thickness is reached, the underlying ice becomes isolated from the insolation and the melt rates are reduced. The form of the patterns observed in Figure 7 suggests that the melt pattern may be related to ogives (Fig. 1b). Following Posamentier (1978) and Goodsell and others (2002), surface ogives (or Forbes bands) are the expression of shearing (small- or large-scale) and faulting, thought to bring basally derived ice to the surface adjacent to more recently formed and whiter surface ice. The bed-originating bands develop many small ridges that can trap dust and dirt, causing them to appear to be debris-rich, and so to have a lower albedo, even if there is not necessarily an increase in debris content below the surface layer (Goodsell and others, 2002). Thus, the darkness of the bed-originating band starts to develop once the ogive has started to move downstream, while dust accumulates. As it does so, shear on either side of the glacier and greater velocity along the centre line causes the ogive form to develop (Hambrey and others, 1980). Here the ogives occupy one-half of the glacier width, on the west side (Fig. 1b) associated with ice that originates from the Col Collon and the base of Mont Brûlé. Their visual presence in both imagery (Fig. 1b) and associated melt patterns (Fig. 7) suggests that we have been able to measure at a very high temporal resolution the differential melt associated with these features. Note that it is not possible to see ogives at the seasonal scale because of ice mass flux effects that obliterate the ogive signal.

The more intriguing part of these data is the measurement of surface uplift occurring early in the day and gradually diminishing, allowing the ogive pattern to become more dominant across the glacier. Such a change could have several origins: (1) a registration error, with one or more surfaces having an incorrect spatial trend; (2) the effects of differential ice flux which would lead to thickening in the upstream part of the area of interest; (3) the effects of aspect on differential surface melt; or (4) the effects of sub-daily hydraulic jacking (e.g. Kulessa and others, 2008).

Figure 3 suggests mean registration errors substantially less than the magnitude of the surface uplift, with a maximum error <0.05 m at 3.7 km. Our study area is at 1.8 km, with a measured surface uplift of at least >0.05 m, thus eliminating the first hypothesis. The second hypothesis can be evaluated by considering the magnitude of the observed changes. These are typically ∼0.10 m in 2 hours (09:00–11:00; Fig. 7). That is, ice that is 0.10 m higher than any one gridcell will need to move downstream by 0.30 m, the gridcell resolution, in order for the magnitude of change to be due to an ice flux effect. We noted above that a lateral displacement of 0.30 m should create a vertical change of 0.0249 m. Thus, a vertical change of 0.10 m should require a lateral displacement of ∼1.20 m in 2 hours. This is an order of magnitude greater than the maximum daily velocities measured on Haut Glacier d’Arolla, associated with relatively infrequent spring-melt-related speed-up events (e.g. Mair and others, 2001). This is highly unlikely. Additionally, feature tracking using point clouds (e.g. of structual weaknesses evident in the surface) showed no lateral displacement at the 2 hour timescale.

The possibility that aspect and debris cover could explain this difference, even if correct, does not explain surface uplift. At the sub-daily scale, it may be added that the slope down-glacier was the same throughout the area. Indeed, the zone that experienced the uplift had an aspect that probably made it more subject to higher insolation, which also counters this explanation.

The remaining hypothesis is that sub-daily hydraulic jacking was measured. Kulessa and others (2008) suggest that this may happen at a sub-daily scale associated with the onset of melting and the associated local build-up of subglacial water pressure. The transition from a distributed to a canalized system has been observed and explained at the seasonal scale (e.g. Nienow and others, 1998; Mair and others, 2002b, 2008; Kulessa and others, 2008). The hydraulic jacking may occur because after partial closure of the channels overnight, there was a rapid input of meltwater linked to high insolation and rapid temperature rise (Fig. 8), at a rate greater than the capacity of the channels to melt (Hock and Hooke, 1993), such that the pressure builds up locally (Mair and others, 2003). Local ice-bed decoupling occurs, resulting from an uplift of the ice and a strengthening of the subglacial lubrication (Mair and others, 2003). The fact that this is restricted to the upper part of the study area may reflect the steep gradient in ice thickness up-glacier, which will drive overnight closure rates. To further evaluate this assumption, repeat surveys of this area, coupled with measurements of subglacial channels using ground-penetrating radar, are required.

Conclusions

This study has shown that elements of the melting and dynamic processes of an Alpine temperate valley glacier can be measured using long-range terrestrial laser scanning. This was demonstrated using data obtained at two temporal scales: seasonal and sub-daily. At the seasonal scale, mean surface changes of 0.050 ± 0.002 m³ m⁻² d⁻¹, uncorrected for flux effects, were measured between July and mid- September. The data show how surface changes declined with the transition from midsummer to early autumn (Table 5), and how they were spatially variable in relation to glacier debris cover. At the sub-daily scale, spatially variable surface change was measured associated with ogive-related variability in debris cover as well as a possible hydraulic jacking early in the day.

At the spatial scale of study (a scan distance centred on 1.8 km but extending to 3 km), use of a laser wavelength optimal for snow and ice cover allowed data to be obtained with a mean point spacing of <0.200 m. The surface changes that could be detected depended on: (1) whether or not the scanner was moved between surveys, leading to better precision at the sub-daily scale when the scanner was fixed; and (2) the quality of the co-registration process.