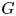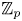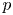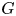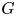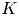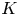1. Introduction
The homological theory of group actions began with the results of P.A. Smith [Reference Smith22] that, if ![]() $G$ is a
$G$ is a ![]() $p$-group acting on a contractible space, then the fixed set is
$p$-group acting on a contractible space, then the fixed set is ![]() ${\mathbb {Z}}_p$-acyclic. While originally the connection between the order of the group and the nature of acyclicity seemed like an artefact of the proof, it was soon realised that this was not the case.
${\mathbb {Z}}_p$-acyclic. While originally the connection between the order of the group and the nature of acyclicity seemed like an artefact of the proof, it was soon realised that this was not the case.
A definitive refutation of this was the result of L. Jones that any ![]() ${\mathbb {Z}}_n$-acyclic, finite CW-complex is the fixed set of semi-free
${\mathbb {Z}}_n$-acyclic, finite CW-complex is the fixed set of semi-free ![]() ${\mathbb {Z}}_n$-action on a finite, contractible CW-complex [Reference Jones12]. Here we recall that a group action is semi-free if all isotropy subgroups are either trivial or the whole group. If one removes the semi-free condition, then R. Oliver's work [Reference Oliver16] shows that, when
${\mathbb {Z}}_n$-action on a finite, contractible CW-complex [Reference Jones12]. Here we recall that a group action is semi-free if all isotropy subgroups are either trivial or the whole group. If one removes the semi-free condition, then R. Oliver's work [Reference Oliver16] shows that, when ![]() $n$ is not a prime power, the necessary and sufficient condition for a finite CW-complex
$n$ is not a prime power, the necessary and sufficient condition for a finite CW-complex ![]() $F$ to be a fixed set is that the Euler characteristic
$F$ to be a fixed set is that the Euler characteristic ![]() $\chi (F)=1$. Incidentally, this is not necessary for general topological actions, but it is for the so called ANR-actions. By an ANR action, we mean a
$\chi (F)=1$. Incidentally, this is not necessary for general topological actions, but it is for the so called ANR-actions. By an ANR action, we mean a ![]() $G$-action on a space
$G$-action on a space ![]() $X$, which makes
$X$, which makes ![]() $X$ into a finite dimensional
$X$ into a finite dimensional ![]() $G$-ANR (equivariant absolute neighbourhood retract)Footnote 1.
$G$-ANR (equivariant absolute neighbourhood retract)Footnote 1.
This paper and a companion one [Reference Cappell, Weinberger and Yan8] study the extensions of the work of Jones and of Oliver, respectively, to non-simply connected spaces. The simply connected theory was interestingly explored by Assadi [Reference Assadi1] and Oliver-Petrie [Reference Oliver and Petrie17], and is largely understood. Both theories depend on a kind of ‘equivariant surgery’ and involve ![]() $K_0$. Assadi-Vogel [Reference Assadi and Vogel2] developed a non-simply connected, semi-free theory for actions on manifolds (therefore only for certain restricted families of groups). Our work extends theirs, in the situation of finite CW-complexes which allows for many more possible finite groups.
$K_0$. Assadi-Vogel [Reference Assadi and Vogel2] developed a non-simply connected, semi-free theory for actions on manifolds (therefore only for certain restricted families of groups). Our work extends theirs, in the situation of finite CW-complexes which allows for many more possible finite groups.
The main results of our companion paper [Reference Cappell, Weinberger and Yan8] show that the analogue of Oliver's theorem does not become substantially more subtle in the presence of the fundamental group. The following is a special case:
Theorem Suppose ![]() $X$ and
$X$ and ![]() $F$ are finite CW-complexes, and
$F$ are finite CW-complexes, and ![]() $G={\mathbb {Z}}_n$ is a cyclic group with
$G={\mathbb {Z}}_n$ is a cyclic group with ![]() $n$ not prime power. Then there is a finite
$n$ not prime power. Then there is a finite ![]() $G$-CW-complex
$G$-CW-complex ![]() $Y$ with
$Y$ with ![]() $Y^G=F$ and a
$Y^G=F$ and a ![]() $G$-map
$G$-map ![]() $Y\to X$ (giving
$Y\to X$ (giving ![]() $X$ the trivial
$X$ the trivial ![]() $G$-action) which is a homotopy equivalence, if and only if
$G$-action) which is a homotopy equivalence, if and only if ![]() $\chi (F)=\chi (X)$.
$\chi (F)=\chi (X)$.
Here and below we see, by generalising Oliver's work, including to non-simply connected settings, that the complete analysis of fixed point sets is governed by the Euler characteristics of combinations of the components of putative fixed sets.
The necessity in the theorem is a consequence of the Lefschetz fixed point theorem, and therefore also holds for the ![]() $G$-ANR case. The proof of sufficiency in [Reference Cappell, Weinberger and Yan8] builds on Oliver's work by a series of purely geometric constructions; for our purposes, we remark that the fundamental group of
$G$-ANR case. The proof of sufficiency in [Reference Cappell, Weinberger and Yan8] builds on Oliver's work by a series of purely geometric constructions; for our purposes, we remark that the fundamental group of ![]() $X$ does not enter.
$X$ does not enter.
In this paper, we will see that, even for ![]() $G={\mathbb {Z}}_p$ there is a rich set of phenomena visible in trying to understand the homotopy types of fixed sets, in contrast to the situation for non-
$G={\mathbb {Z}}_p$ there is a rich set of phenomena visible in trying to understand the homotopy types of fixed sets, in contrast to the situation for non-![]() $p$-groups. In contrast to the generalisation of Oliver's theorem, an analysis of semi-free actions shows a number of interesting phenomena. We will mention some examples before describing our main theorems: theorems 1 and 2.
$p$-groups. In contrast to the generalisation of Oliver's theorem, an analysis of semi-free actions shows a number of interesting phenomena. We will mention some examples before describing our main theorems: theorems 1 and 2.
Example 1.1 Let ![]() $T(r)$ be the mapping torus of a degree
$T(r)$ be the mapping torus of a degree ![]() $r$ map from a sphere
$r$ map from a sphere ![]() $S^d$ to itself. Notice that the map
$S^d$ to itself. Notice that the map ![]() $T(r)\to S^1$ is a
$T(r)\to S^1$ is a ![]() ${\mathbb {Z}}_n[{\mathbb {Z}}]$-homology equivalence if and only if
${\mathbb {Z}}_n[{\mathbb {Z}}]$-homology equivalence if and only if ![]() $n$ divides a power of
$n$ divides a power of ![]() $r$ (i.e., all the primes in
$r$ (i.e., all the primes in ![]() $n$ occur in
$n$ occur in ![]() $r$). The infinite cyclic cover has nontrivial
$r$). The infinite cyclic cover has nontrivial ![]() ${\mathbb {Q}}$-homology, but is also
${\mathbb {Q}}$-homology, but is also ![]() ${\mathbb {Z}}_n$-acyclic under this divisibility condition.
${\mathbb {Z}}_n$-acyclic under this divisibility condition.
We will see that there is a semi-free ![]() ${\mathbb {Z}}_n$-action on a finite CW-complex homotopy equivalent to
${\mathbb {Z}}_n$-action on a finite CW-complex homotopy equivalent to ![]() $S^1$ with fixed set
$S^1$ with fixed set ![]() $T(r)$ if and only if
$T(r)$ if and only if ![]() $n$ divides
$n$ divides ![]() $r$. When
$r$. When ![]() $n$ is not square-free, this condition goes beyond Smith theory. It is related to
$n$ is not square-free, this condition goes beyond Smith theory. It is related to ![]() $\widetilde {K}_0({\mathbb {Z}}[{\mathbb {Z}}\times {\mathbb {Z}}_n])$, and the role of the non-square-free condition is well known to be the condition for the Nil factor to be nontrivial in the Bass–Heller–Swan formula of algebraic
$\widetilde {K}_0({\mathbb {Z}}[{\mathbb {Z}}\times {\mathbb {Z}}_n])$, and the role of the non-square-free condition is well known to be the condition for the Nil factor to be nontrivial in the Bass–Heller–Swan formula of algebraic ![]() $K$-theory (see Bass–Murthy [Reference Bass and Murthy6]). Concretely,
$K$-theory (see Bass–Murthy [Reference Bass and Murthy6]). Concretely, ![]() $T(p)$ is fixed under a
$T(p)$ is fixed under a ![]() ${\mathbb {Z}}_p$-action, but not a semi-free
${\mathbb {Z}}_p$-action, but not a semi-free ![]() ${\mathbb {Z}}_{p^2}$-action on some homotopy circle. Its two fold cover
${\mathbb {Z}}_{p^2}$-action on some homotopy circle. Its two fold cover ![]() $T(p^2)$ is fixed under a semi-free
$T(p^2)$ is fixed under a semi-free ![]() ${\mathbb {Z}}_{p^2}$-action, but not a semi-free
${\mathbb {Z}}_{p^2}$-action, but not a semi-free ![]() ${\mathbb {Z}}_{p^3}$-action, etc.
${\mathbb {Z}}_{p^3}$-action, etc.
If one studies topological actions on manifolds that are locally smooth, one does not necessarily obtain a finite ![]() $G$-CW-complex [Reference Quinn19, Reference Quinn20, Reference Steinberger23, Reference Weinberger29]. The non-uniqueness of such structures, even when they exist, is implicated in the phenomenon of nonlinear similarity of linear actions on the sphere [Reference Cappell and Shaneson7]. In the above examples one can obtain a locally smooth action (or equivalently a
$G$-CW-complex [Reference Quinn19, Reference Quinn20, Reference Steinberger23, Reference Weinberger29]. The non-uniqueness of such structures, even when they exist, is implicated in the phenomenon of nonlinear similarity of linear actions on the sphere [Reference Cappell and Shaneson7]. In the above examples one can obtain a locally smooth action (or equivalently a ![]() $G$-ANR action) with
$G$-ANR action) with ![]() $T(r)$ as fixed set if and only if one can construct such a
$T(r)$ as fixed set if and only if one can construct such a ![]() $G$-action on finite CW-complex. The following example shows a difference between these categories.
$G$-action on finite CW-complex. The following example shows a difference between these categories.
Example 1.2 Let ![]() $T(r_1,\,r_2)$ be the double mapping torus, obtained by glueing two ends of
$T(r_1,\,r_2)$ be the double mapping torus, obtained by glueing two ends of ![]() $S^d\times [0,\,1]$ to a copy of
$S^d\times [0,\,1]$ to a copy of ![]() $S^d$ by maps of degrees
$S^d$ by maps of degrees ![]() $r_1,\,r_2$. Then
$r_1,\,r_2$. Then ![]() $T(2,\,3)$ is
$T(2,\,3)$ is ![]() ${\mathbb {Z}}_6[{\mathbb {Z}}]$-acyclic. It is the fixed set of a semi-free
${\mathbb {Z}}_6[{\mathbb {Z}}]$-acyclic. It is the fixed set of a semi-free ![]() ${\mathbb {Z}}_6$-ANR action. On the other hand, it is not the fixed set (up to homotopy) of any finite
${\mathbb {Z}}_6$-ANR action. On the other hand, it is not the fixed set (up to homotopy) of any finite ![]() $G$-CW-complex homotopy equivalent to the circle
$G$-CW-complex homotopy equivalent to the circle ![]() $S^1$.
$S^1$.
In this case, the obstructions are nontrivial elements of ![]() $K_{-1}({\mathbb {Z}}[{\mathbb {Z}}_6])$ that enter via the Bass–Heller–Swan formula into the obstruction group
$K_{-1}({\mathbb {Z}}[{\mathbb {Z}}_6])$ that enter via the Bass–Heller–Swan formula into the obstruction group ![]() $\widetilde {K}_0({\mathbb {Z}}[{\mathbb {Z}}\times {\mathbb {Z}}_6])$; there are similar examples arising for all groups of not prime power order.
$\widetilde {K}_0({\mathbb {Z}}[{\mathbb {Z}}\times {\mathbb {Z}}_6])$; there are similar examples arising for all groups of not prime power order.
One of the reasons to focus so strongly on the case of the circle is the special role that it plays in the Farrell–Jones conjecture in algebraic ![]() $K$-theory [Reference Farrell and Jones11]. The circle is central to this problem because, as we shall soon explain more systematically, the examples on the circle can be promoted to examples on any finite CW-complex whose fundamental group is a torsion free hyperbolic group, or a lattice.
$K$-theory [Reference Farrell and Jones11]. The circle is central to this problem because, as we shall soon explain more systematically, the examples on the circle can be promoted to examples on any finite CW-complex whose fundamental group is a torsion free hyperbolic group, or a lattice.
Assuming the Farrell–Jones conjecture, if the fundamental group is torsion free, there are no examples of fixed sets obstructed for ![]() ${\mathbb {Z}}_p$-actions when the Smith condition holds. To give an example where there is an obstruction, we turn to finite fundamental group.
${\mathbb {Z}}_p$-actions when the Smith condition holds. To give an example where there is an obstruction, we turn to finite fundamental group.
Example 1.3 Let ![]() $f\colon L(kp;1) \to L(p;1)$ be a degree
$f\colon L(kp;1) \to L(p;1)$ be a degree ![]() $r$ map of three dimensional lens spaces, with
$r$ map of three dimensional lens spaces, with ![]() $k,\,p$ coprime. There is a
$k,\,p$ coprime. There is a ![]() ${\mathbb {Z}}_p$-action on a space of the homotopy type of
${\mathbb {Z}}_p$-action on a space of the homotopy type of ![]() $L(p;1)$, such that the inclusion map from the fixed set is homotopic to
$L(p;1)$, such that the inclusion map from the fixed set is homotopic to ![]() $f$, if and only if
$f$, if and only if ![]() $r^{p-1}=k^{p-1}$ mod
$r^{p-1}=k^{p-1}$ mod ![]() $p^2$. The details are in proposition 4.6.
$p^2$. The details are in proposition 4.6.
We now state the results from which the above examples follow.
Let ![]() $G$ be a group. A
$G$ be a group. A ![]() $G$-map between finite
$G$-map between finite ![]() $G$-CW-complexes (or compact
$G$-CW-complexes (or compact ![]() $G$-ANRs) is a pseudo-equivalence if it is a homotopy equivalence after ignoring the group action. Given a
$G$-ANRs) is a pseudo-equivalence if it is a homotopy equivalence after ignoring the group action. Given a ![]() $G$-map
$G$-map ![]() $f\colon F\to Y$, we ask whether it is possible to extend
$f\colon F\to Y$, we ask whether it is possible to extend ![]() $F$ to a bigger finite
$F$ to a bigger finite ![]() $G$-CW-complex (or compact
$G$-CW-complex (or compact ![]() $G$-ANR)
$G$-ANR) ![]() $X$, and extend
$X$, and extend ![]() $f$ to a pseudo-equivalent
$f$ to a pseudo-equivalent ![]() $G$-map
$G$-map ![]() $g\colon X\to Y$. We call
$g\colon X\to Y$. We call ![]() $g$ a pseudo-equivalence extension of
$g$ a pseudo-equivalence extension of ![]() $f$.
$f$.
In this paper, we concentrate on the following setting. The group ![]() $G$ is finite, and all spaces are finite, semi-free
$G$ is finite, and all spaces are finite, semi-free ![]() $G$-CW-complexes. Moreover, we only consider
$G$-CW-complexes. Moreover, we only consider ![]() $F=X^G$ in the pseudo-equivalence extension. In other words, the extension from
$F=X^G$ in the pseudo-equivalence extension. In other words, the extension from ![]() $F$ to
$F$ to ![]() $X$ is obtained by attaching free
$X$ is obtained by attaching free ![]() $G$-cells.
$G$-cells.
The concept of pseudo-equivalence was introduced by Oliver and Petrie [Reference Oliver and Petrie17, Reference Petrie18]. A pseudo-equivalence becomes a homotopy equivalence upon applying the Borel construction. However, a characterisation in terms of Borel equivalence would be inadequate for our present purpose because we require our ![]() $G$-spaces to be finite
$G$-spaces to be finite ![]() $G$-CW-complexes.
$G$-CW-complexes.
For the special case ![]() $Y$ is a point, the question of the existence of a pseudo-equivalence extension becomes whether a given space
$Y$ is a point, the question of the existence of a pseudo-equivalence extension becomes whether a given space ![]() $F$ can be the fixed point set of a semi-free
$F$ can be the fixed point set of a semi-free ![]() $G$-action on a contractible, finite CW-complex
$G$-action on a contractible, finite CW-complex ![]() $X$. The classical results of Smith [Reference Smith22] and of Jones [Reference Jones12] give necessary and sufficient condition for semi-free actions by cyclic groups.
$X$. The classical results of Smith [Reference Smith22] and of Jones [Reference Jones12] give necessary and sufficient condition for semi-free actions by cyclic groups.
Theorem Smith and Jones
A finite CW-complex ![]() $F$ is the fixed set of a finite, contractible, semi-free
$F$ is the fixed set of a finite, contractible, semi-free ![]() ${\mathbb {Z}}_n$-CW-complex if and only if
${\mathbb {Z}}_n$-CW-complex if and only if ![]() $\widetilde {H}_*(F;{\mathbb {Z}}_n)=0$.
$\widetilde {H}_*(F;{\mathbb {Z}}_n)=0$.
For a general semi-free action of ![]() $G$ on contractible
$G$ on contractible ![]() $X$, and any prime factor
$X$, and any prime factor ![]() $p$ of
$p$ of ![]() $|G|$, the fixed set
$|G|$, the fixed set ![]() $F=X^G$ is the same as the fixed set
$F=X^G$ is the same as the fixed set ![]() $X^C$ of a cyclic subgroup
$X^C$ of a cyclic subgroup ![]() $C$ of order
$C$ of order ![]() $p$. Then the homological condition in the theorem becomes
$p$. Then the homological condition in the theorem becomes ![]() $\widetilde {H}_*(F;{\mathbb {F}}_p)=0$ for all prime factors
$\widetilde {H}_*(F;{\mathbb {F}}_p)=0$ for all prime factors ![]() $p$ of
$p$ of ![]() $G$ (
$G$ (![]() ${\mathbb {F}}_p={\mathbb {Z}}_p$ is a field for prime
${\mathbb {F}}_p={\mathbb {Z}}_p$ is a field for prime ![]() $p$). This is equivalent to
$p$). This is equivalent to ![]() $\widetilde {H}_*(F;{\mathbb {Z}}_{|G|})=0$. We call this the Smith condition.
$\widetilde {H}_*(F;{\mathbb {Z}}_{|G|})=0$. We call this the Smith condition.
In general, we let ![]() $Y$ be a connected
$Y$ be a connected ![]() $G$-CW-complex. Let
$G$-CW-complex. Let ![]() $\widetilde {Y}$ be the universal cover of
$\widetilde {Y}$ be the universal cover of ![]() $Y$, with action by the fundamental group
$Y$, with action by the fundamental group ![]() $\pi =\pi _1(Y)$. Then all actions on
$\pi =\pi _1(Y)$. Then all actions on ![]() $\widetilde {Y}$ covering
$\widetilde {Y}$ covering ![]() $G$-actions on
$G$-actions on ![]() $Y$ form a group
$Y$ form a group ![]() $\Gamma$ that fits into an exact sequence
$\Gamma$ that fits into an exact sequence
The definition of ![]() $\Gamma$ here is not always exactly correct, because it ignores the effectiveness of the
$\Gamma$ here is not always exactly correct, because it ignores the effectiveness of the ![]() $G$-action. See § 2 for the precise definition. In particular, we have
$G$-action. See § 2 for the precise definition. In particular, we have ![]() $\Gamma =\pi \times G$ if
$\Gamma =\pi \times G$ if ![]() $G$ acts trivially on
$G$ acts trivially on ![]() $Y$.
$Y$.
Suppose a ![]() $G$-map
$G$-map ![]() $g\colon X\to Y$ is a pseudo-equivalence between semi-free
$g\colon X\to Y$ is a pseudo-equivalence between semi-free ![]() $G$-CW-complexes. Then the mapping cone of
$G$-CW-complexes. Then the mapping cone of ![]() $g$ is a contractible semi-free
$g$ is a contractible semi-free ![]() $G$-CW-complex, and the Smith condition can be applied to the mapping cone to give isomorphisms
$G$-CW-complex, and the Smith condition can be applied to the mapping cone to give isomorphisms ![]() $H_*(X^G;{\mathbb {F}}_p)\cong H_*(Y^G;{\mathbb {F}}_p)$ for all prime factors
$H_*(X^G;{\mathbb {F}}_p)\cong H_*(Y^G;{\mathbb {F}}_p)$ for all prime factors ![]() $p$ of
$p$ of ![]() $|G|$. In fact, in § 2, we apply the Smith condition to the universal cover and get isomorphisms
$|G|$. In fact, in § 2, we apply the Smith condition to the universal cover and get isomorphisms ![]() $H_*(X^G;{\mathbb {F}}_p\pi )\cong H_*(Y^G;{\mathbb {F}}_p\pi )$. This is the necessary Smith condition for constructing pseudo-equivalence extension.
$H_*(X^G;{\mathbb {F}}_p\pi )\cong H_*(Y^G;{\mathbb {F}}_p\pi )$. This is the necessary Smith condition for constructing pseudo-equivalence extension.
However, it turns out that there is additionally an algebraic ![]() $K$-theoretic obstruction. The following is our first main result, for the case the
$K$-theoretic obstruction. The following is our first main result, for the case the ![]() $G$-action on
$G$-action on ![]() $Y$ is trivial.
$Y$ is trivial.
Theorem 1.4 Suppose ![]() $f\colon F\to Y$ is a map of finite CW-complexes, with
$f\colon F\to Y$ is a map of finite CW-complexes, with ![]() $Y$ connected and
$Y$ connected and ![]() $\pi =\pi _1(Y)$. Then
$\pi =\pi _1(Y)$. Then ![]() $F$ can be the fixed set of a finite, semi-free
$F$ can be the fixed set of a finite, semi-free ![]() $G$-CW-complex
$G$-CW-complex ![]() $X$, and
$X$, and ![]() $f$ has pseudo-equivalence extension
$f$ has pseudo-equivalence extension ![]() $g\colon X\to Y$, if and only if the following are satisfied:
$g\colon X\to Y$, if and only if the following are satisfied:
1. The map
 $f$ induces isomorphisms
$f$ induces isomorphisms  $H_*(F;{\mathbb {F}}_p\pi )\cong H_*(Y;{\mathbb {F}}_p\pi )$ for all prime factors
$H_*(F;{\mathbb {F}}_p\pi )\cong H_*(Y;{\mathbb {F}}_p\pi )$ for all prime factors  $p$ of
$p$ of  $|G|$.
$|G|$.2. An obstruction
 $[C_*(\widetilde {f})]\in \widetilde {K}_0({\mathbb {Z}}[\pi \times G])$ vanishes.
$[C_*(\widetilde {f})]\in \widetilde {K}_0({\mathbb {Z}}[\pi \times G])$ vanishes.
The first is what we have called the Smith condition. In the second condition, the chain complex ![]() $C_*(\widetilde {f})$ of the
$C_*(\widetilde {f})$ of the ![]() $\pi$-cover
$\pi$-cover ![]() $\widetilde {f}\colon \widetilde {F}\to \widetilde {Y}$ of
$\widetilde {f}\colon \widetilde {F}\to \widetilde {Y}$ of ![]() $f$ is a
$f$ is a ![]() ${\mathbb {Z}}\pi$-chain complex. Then we regard
${\mathbb {Z}}\pi$-chain complex. Then we regard ![]() $C_*(\widetilde {f})$ as a
$C_*(\widetilde {f})$ as a ![]() ${\mathbb {Z}}[\pi \times G]$-chain complex with trivial
${\mathbb {Z}}[\pi \times G]$-chain complex with trivial ![]() $G$-action. We will argue that the Smith condition implies that
$G$-action. We will argue that the Smith condition implies that ![]() $C_*(\widetilde {f})$ is chain homotopy equivalent to a finite chain complex of finitely generated projective
$C_*(\widetilde {f})$ is chain homotopy equivalent to a finite chain complex of finitely generated projective ![]() ${\mathbb {Z}}[\pi \times G]$-modules, and therefore gives a well-defined element
${\mathbb {Z}}[\pi \times G]$-modules, and therefore gives a well-defined element ![]() $[C_*(\widetilde {f})]\in \widetilde {K}_0({\mathbb {Z}}[\pi \times G])$. Moreover, since the terms in
$[C_*(\widetilde {f})]\in \widetilde {K}_0({\mathbb {Z}}[\pi \times G])$. Moreover, since the terms in ![]() $C_*(\widetilde {f})$ are finitely generated free
$C_*(\widetilde {f})$ are finitely generated free ![]() ${\mathbb {Z}}[\pi ]$-modules, the obstruction lies in the kernel of the homomorphism that forgets the
${\mathbb {Z}}[\pi ]$-modules, the obstruction lies in the kernel of the homomorphism that forgets the ![]() $G$-action:
$G$-action:
Theorem 1.5 Suppose ![]() $Y$ is a finite, semi-free, connected
$Y$ is a finite, semi-free, connected ![]() $G$-CW-complex, with
$G$-CW-complex, with ![]() $\pi =\pi _1(Y)$. Suppose
$\pi =\pi _1(Y)$. Suppose ![]() $F$ is a finite CW-complex and
$F$ is a finite CW-complex and ![]() $f\colon F\to Y^G$ is a map. Then
$f\colon F\to Y^G$ is a map. Then ![]() $F$ can be the fixed set of a finite, semi-free
$F$ can be the fixed set of a finite, semi-free ![]() $G$-CW-complex
$G$-CW-complex ![]() $X,$ and
$X,$ and ![]() $f$ has pseudo-equivalence extension
$f$ has pseudo-equivalence extension ![]() $g\colon X\to Y,$ if and only if the following are satisfied:
$g\colon X\to Y,$ if and only if the following are satisfied:
1. The map
 $f$ induces isomorphisms
$f$ induces isomorphisms  $H_*(F;{\mathbb {F}}_p\pi )\cong H_*(Y^G;{\mathbb {F}}_p\pi )$ for all prime factors
$H_*(F;{\mathbb {F}}_p\pi )\cong H_*(Y^G;{\mathbb {F}}_p\pi )$ for all prime factors  $p$ of
$p$ of  $|G|$.
$|G|$.2. A well-defined obstruction
 $[C_*(\widetilde {f})]\in \widetilde {K}_0({\mathbb {Z}}[\Gamma ])$ vanishes.
$[C_*(\widetilde {f})]\in \widetilde {K}_0({\mathbb {Z}}[\Gamma ])$ vanishes.
The meaning of the two conditions is explained in § 2 and 3. The Smith condition is equivalent to the condition being satisfied on each connected component of ![]() $Y^G$. Then we get a
$Y^G$. Then we get a ![]() $K$-theory element on each connected component similar to the first main theorem, and the obstruction
$K$-theory element on each connected component similar to the first main theorem, and the obstruction ![]() $[C_*(\widetilde {f})]$ is the sum of these. Moreover, similar to the remark for theorem 1.4, we know the obstruction lies in the kernel of the forgetful homomorphism
$[C_*(\widetilde {f})]$ is the sum of these. Moreover, similar to the remark for theorem 1.4, we know the obstruction lies in the kernel of the forgetful homomorphism ![]() $\widetilde {K}_0({\mathbb {Z}}[\Gamma ])\to \widetilde {K}_0({\mathbb {Z}}[\pi ])$.
$\widetilde {K}_0({\mathbb {Z}}[\Gamma ])\to \widetilde {K}_0({\mathbb {Z}}[\pi ])$.
We also describe how ![]() $\widetilde {K}^{top}$ enters to modify the above results in the simple homotopy setting (theorem 3.1) and the
$\widetilde {K}^{top}$ enters to modify the above results in the simple homotopy setting (theorem 3.1) and the ![]() $G$-ANR setting (theorem 3.2).
$G$-ANR setting (theorem 3.2).
We remark that Oliver and Petrie [Reference Oliver and Petrie17] studied the extension problem in a generally different setting (see also Assadi [Reference Assadi1], and Morimoto and Iizuka [Reference Morimoto and Iizuka15]). When restricted to our problem, they gave the obstruction such that the extension ![]() $g$ induces isomorphism on the integral homology. Therefore they solved our problem for the case
$g$ induces isomorphism on the integral homology. Therefore they solved our problem for the case ![]() $Y$ is simply connected. What is new in our theorem is the non-simply connected case for homotopy equivalences.
$Y$ is simply connected. What is new in our theorem is the non-simply connected case for homotopy equivalences.
Another important paper in this direction was Assadi-Vogel [Reference Assadi and Vogel2], that works in a manifold setting. It is quite close to what we do, although their techniques are different (based on ideas of homology propagation rather than ![]() $G$-surgery), formally have less generality (since
$G$-surgery), formally have less generality (since ![]() ${\mathbb {Z}}_p\times {\mathbb {Z}}_p$ cannot act semi-freely on a manifold, for example), and their calculations focus on finite fundamental groups. Our focus here is mainly on the phenomena that arise when fundamental groups are torsion free, as this paper is intended to provide foundations for later studies of group actions on aspherical manifolds.
${\mathbb {Z}}_p\times {\mathbb {Z}}_p$ cannot act semi-freely on a manifold, for example), and their calculations focus on finite fundamental groups. Our focus here is mainly on the phenomena that arise when fundamental groups are torsion free, as this paper is intended to provide foundations for later studies of group actions on aspherical manifolds.
Finally, we would like to thank the referee for a careful reading and a number of useful suggestions.
2. Smith condition
We explain the Smith condition in more detail.
Let ![]() $G$ be a finite group. Let
$G$ be a finite group. Let ![]() $X$ and
$X$ and ![]() $Y$ be semi-free
$Y$ be semi-free ![]() $G$-CW-complexes. Let
$G$-CW-complexes. Let ![]() $g\colon X\to Y$ be a
$g\colon X\to Y$ be a ![]() $G$-map and a (non-equivariant) homotopy equivalence, i.e.,
$G$-map and a (non-equivariant) homotopy equivalence, i.e., ![]() $g$ is a pseudo-equivalent
$g$ is a pseudo-equivalent ![]() $G$-map. Let
$G$-map. Let ![]() $f\colon F=X^G\to Y$ be the restriction of
$f\colon F=X^G\to Y$ be the restriction of ![]() $g$ to the fixed set. Let
$g$ to the fixed set. Let ![]() $Y$ be connected, and let
$Y$ be connected, and let ![]() $p\colon \widetilde {Y}\to Y$ be the universal cover, equipped with the free action by the fundamental group
$p\colon \widetilde {Y}\to Y$ be the universal cover, equipped with the free action by the fundamental group ![]() $\pi =\pi _1(Y)$.
$\pi =\pi _1(Y)$.
An element ![]() $u\in G$ gives an action
$u\in G$ gives an action ![]() $u\colon Y\to Y$. The action lifts to self homeomorphisms
$u\colon Y\to Y$. The action lifts to self homeomorphisms ![]() $\widetilde {u}\colon \widetilde {Y}\to \widetilde {Y}$ of the universal cover, in the sense that
$\widetilde {u}\colon \widetilde {Y}\to \widetilde {Y}$ of the universal cover, in the sense that ![]() $p\widetilde {u}=up$. If we fix one lifting
$p\widetilde {u}=up$. If we fix one lifting ![]() $\widetilde {u}$ of
$\widetilde {u}$ of ![]() $u$, then the other liftings of
$u$, then the other liftings of ![]() $u$ are
$u$ are ![]() $a\widetilde {u}$, for
$a\widetilde {u}$, for ![]() $a\in \pi$. Let
$a\in \pi$. Let ![]() $\Gamma '$ be the collections of all such liftings. Then
$\Gamma '$ be the collections of all such liftings. Then ![]() $\Gamma '$ is a group fitting into an exact sequence
$\Gamma '$ is a group fitting into an exact sequence
We remark that ![]() $G_0$ consists of those
$G_0$ consists of those ![]() $u\in G$ that act trivially on
$u\in G$ that act trivially on ![]() $Y$, because the liftings
$Y$, because the liftings ![]() $\widetilde {u}$ can only distinguish
$\widetilde {u}$ can only distinguish ![]() $u\in G$ through their actions on
$u\in G$ through their actions on ![]() $Y$. To further distinguish distinct elements of
$Y$. To further distinguish distinct elements of ![]() $G$ that may act the same way on
$G$ that may act the same way on ![]() $Y$, we introduce the group
$Y$, we introduce the group ![]() $\Gamma$ as the pullback of
$\Gamma$ as the pullback of ![]() $\Gamma '\to G/G_0\leftarrow G$:
$\Gamma '\to G/G_0\leftarrow G$:
Then we get an exact sequence
As an extreme case, if ![]() $G$ acts trivially on
$G$ acts trivially on ![]() $Y$, then
$Y$, then ![]() $\Gamma =\pi \times G$.
$\Gamma =\pi \times G$.
As an example, consider ![]() $G={\mathbb {Z}}_2=\langle u\rangle$ acting on the real projective space
$G={\mathbb {Z}}_2=\langle u\rangle$ acting on the real projective space ![]() ${\mathbb {R}P}^2$ by
${\mathbb {R}P}^2$ by ![]() $u([x_0,\,x_1,\,x_2])=[x_0,\,x_1,\,-x_2]=[-x_0,\,-x_1,\,x_2]$. The universal cover of
$u([x_0,\,x_1,\,x_2])=[x_0,\,x_1,\,-x_2]=[-x_0,\,-x_1,\,x_2]$. The universal cover of ![]() ${\mathbb {R}P}^2$ is the sphere
${\mathbb {R}P}^2$ is the sphere ![]() $S^2$, with the covering group
$S^2$, with the covering group ![]() $\pi$ generated by the antipode
$\pi$ generated by the antipode ![]() $a(x_1,\,x_2,\,x_3)=(-x_1,\,-x_2,\,-x_3)$. The action
$a(x_1,\,x_2,\,x_3)=(-x_1,\,-x_2,\,-x_3)$. The action ![]() $u$ lifts to
$u$ lifts to ![]() $\widetilde {u}_1(x_0,\,x_1,\,x_2)=(x_0,\,x_1,\,-x_2)$ and
$\widetilde {u}_1(x_0,\,x_1,\,x_2)=(x_0,\,x_1,\,-x_2)$ and ![]() $\widetilde {u}_2(x_0,\,x_1,\,x_2)=(-x_0,\,-x_1,\,x_2)$. The group
$\widetilde {u}_2(x_0,\,x_1,\,x_2)=(-x_0,\,-x_1,\,x_2)$. The group ![]() $\Gamma ={\mathbb {Z}}_2\times {\mathbb {Z}}_2=\langle \widetilde {u}_1\rangle \times \langle \widetilde {u}_2\rangle$, and
$\Gamma ={\mathbb {Z}}_2\times {\mathbb {Z}}_2=\langle \widetilde {u}_1\rangle \times \langle \widetilde {u}_2\rangle$, and ![]() $\pi$ is a subgroup of
$\pi$ is a subgroup of ![]() $\Gamma$ by
$\Gamma$ by ![]() $a=\widetilde {u}_1\widetilde {u}_2$.
$a=\widetilde {u}_1\widetilde {u}_2$.
We use ![]() $\;\widetilde {}\;$ to denote the lifting/pullback along the universal cover of
$\;\widetilde {}\;$ to denote the lifting/pullback along the universal cover of ![]() $Y$. For example, we have the pullbacks (note that
$Y$. For example, we have the pullbacks (note that ![]() $\widetilde {X}$ is generally not the universal cover of
$\widetilde {X}$ is generally not the universal cover of ![]() $X$):
$X$):

For a connected component ![]() $C$ of
$C$ of ![]() $Y^G$, we have the pullback
$Y^G$, we have the pullback

In our example, we have ![]() $({\mathbb {R}P}^2)^G=\{[x_0,\,x_1,\,0]\}\sqcup \{[0,\,0,\,1]\}={\mathbb {R}P}^1\sqcup \{[0,\,0,\,1]\}$, and
$({\mathbb {R}P}^2)^G=\{[x_0,\,x_1,\,0]\}\sqcup \{[0,\,0,\,1]\}={\mathbb {R}P}^1\sqcup \{[0,\,0,\,1]\}$, and ![]() $\widetilde {({\mathbb {R}P}^2)^G}=\{(x_0,\,x_1,\,0)\}\sqcup \{(0,\,0,\,1)\}\sqcup \{(0,\,0,\,-1)\}=S^1\sqcup N\sqcup S$ (
$\widetilde {({\mathbb {R}P}^2)^G}=\{(x_0,\,x_1,\,0)\}\sqcup \{(0,\,0,\,1)\}\sqcup \{(0,\,0,\,-1)\}=S^1\sqcup N\sqcup S$ (![]() $N$ and
$N$ and ![]() $S$ are the north and south poles).
$S$ are the north and south poles).
Let ![]() $\widetilde {y}\in \widetilde {Y^G}$ and
$\widetilde {y}\in \widetilde {Y^G}$ and ![]() $y=p(\widetilde {y})\in Y^G$. Let
$y=p(\widetilde {y})\in Y^G$. Let ![]() $C$ and
$C$ and ![]() $\widehat {C}$ be the connected components of
$\widehat {C}$ be the connected components of ![]() $Y^G$ and
$Y^G$ and ![]() $\widetilde {Y^G}$ containing
$\widetilde {Y^G}$ containing ![]() $y$ and
$y$ and ![]() $\widetilde {y}$. Then
$\widetilde {y}$. Then ![]() $\widehat {C}$ covers
$\widehat {C}$ covers ![]() $C$. We may use
$C$. We may use ![]() $\widetilde {y}$ to get an isomorphism
$\widetilde {y}$ to get an isomorphism ![]() $\pi _1(Y,\,y)\cong \pi$. Then the deck transformations
$\pi _1(Y,\,y)\cong \pi$. Then the deck transformations ![]() $\pi _{\widehat {C}}\subset \pi$ of the covering
$\pi _{\widehat {C}}\subset \pi$ of the covering ![]() $\widehat {C}\to C$ is the image of the homomorphism
$\widehat {C}\to C$ is the image of the homomorphism ![]() $\pi _1(C,\,y)\to \pi _1(Y,\,y)$, and we get
$\pi _1(C,\,y)\to \pi _1(Y,\,y)$, and we get ![]() $\widetilde {C}=\pi \times _{\pi _{\widehat {C}}} \widehat {C}$.
$\widetilde {C}=\pi \times _{\pi _{\widehat {C}}} \widehat {C}$.
In general, for ![]() $\widetilde {y}\in \widetilde {Y}$ and
$\widetilde {y}\in \widetilde {Y}$ and ![]() $y=p(\widetilde {y})\in Y$, the induced homomorphism
$y=p(\widetilde {y})\in Y$, the induced homomorphism ![]() $\Gamma _{\widetilde {y}}\to G_y$ of isotropy groups is an isomorphism. In particular, for
$\Gamma _{\widetilde {y}}\to G_y$ of isotropy groups is an isomorphism. In particular, for ![]() $y\in Y^G$, the isomorphism gives a splitting
$y\in Y^G$, the isomorphism gives a splitting ![]() $G=G_y\cong \Gamma _{\widetilde {y}}\subset \Gamma$ of (2.1). The splitting depends only upon the connected component
$G=G_y\cong \Gamma _{\widetilde {y}}\subset \Gamma$ of (2.1). The splitting depends only upon the connected component ![]() $\widehat {C}$ containing
$\widehat {C}$ containing ![]() $\widetilde {y}$. Therefore we may denote
$\widetilde {y}$. Therefore we may denote ![]() $\Gamma _{\widehat {C}}=\Gamma _{\widetilde {y}}$, and get
$\Gamma _{\widehat {C}}=\Gamma _{\widetilde {y}}$, and get ![]() $\Gamma =\pi \rtimes \Gamma _{\widehat {C}}$.
$\Gamma =\pi \rtimes \Gamma _{\widehat {C}}$.
The other connected components of ![]() $\widetilde {C}$ are
$\widetilde {C}$ are ![]() $a\widehat {C}$,
$a\widehat {C}$, ![]() $a\in \pi$. Therefore the connected component
$a\in \pi$. Therefore the connected component ![]() $C$ gives a
$C$ gives a ![]() $\pi$-conjugation class of isotropy groups (equivalently, a
$\pi$-conjugation class of isotropy groups (equivalently, a ![]() $\pi$-conjugation class of splittings of (2.1))
$\pi$-conjugation class of splittings of (2.1))
In our example, ![]() $({\mathbb {R}P}^2)^G$ has two connected components
$({\mathbb {R}P}^2)^G$ has two connected components ![]() $C_1={\mathbb {R}P}^1$ and
$C_1={\mathbb {R}P}^1$ and ![]() $C_2=[0,\,0,\,1]$. Their preimages in
$C_2=[0,\,0,\,1]$. Their preimages in ![]() $\widetilde {({\mathbb {R}P}^2)^G}$ are respectively
$\widetilde {({\mathbb {R}P}^2)^G}$ are respectively ![]() $\widetilde {C}_1=S^1$ and
$\widetilde {C}_1=S^1$ and ![]() $\widetilde {C}_2=\{N,\,S\}$. We may take
$\widetilde {C}_2=\{N,\,S\}$. We may take ![]() $\widehat {C}_1=S^1$,
$\widehat {C}_1=S^1$, ![]() $\widehat {C}_2=N$, with
$\widehat {C}_2=N$, with ![]() $a\widehat {C}_1=\widehat {C}_1$,
$a\widehat {C}_1=\widehat {C}_1$, ![]() $a\widehat {C}_2=S$. Then
$a\widehat {C}_2=S$. Then ![]() $\Gamma _{S^1}=\langle \widetilde {u}_1\rangle$, and
$\Gamma _{S^1}=\langle \widetilde {u}_1\rangle$, and ![]() $\Gamma _N=\Gamma _S=\langle \widetilde {u}_2\rangle$. The semi-direct products
$\Gamma _N=\Gamma _S=\langle \widetilde {u}_2\rangle$. The semi-direct products ![]() $\Gamma =\pi \rtimes \Gamma _{S^1}=\langle a\rangle \times \langle \widetilde {u}_1\rangle$ and
$\Gamma =\pi \rtimes \Gamma _{S^1}=\langle a\rangle \times \langle \widetilde {u}_1\rangle$ and ![]() $\Gamma =\pi \rtimes \Gamma _N=\pi \rtimes \Gamma _S=\langle a\rangle \times \langle \widetilde {u}_2\rangle$ are the usual products. Moreover, we have the two-fold cover
$\Gamma =\pi \rtimes \Gamma _N=\pi \rtimes \Gamma _S=\langle a\rangle \times \langle \widetilde {u}_2\rangle$ are the usual products. Moreover, we have the two-fold cover ![]() $\widehat {C}_1=S^1\to C_1={\mathbb {R}P}^1$ with the covering group
$\widehat {C}_1=S^1\to C_1={\mathbb {R}P}^1$ with the covering group ![]() $\pi _{\widehat {C}_1}=\pi$, and
$\pi _{\widehat {C}_1}=\pi$, and ![]() $\widetilde {C}_1=\widehat {C}_1=\pi \times _{\pi }\widehat {C}_1$. We also have the one-fold cover
$\widetilde {C}_1=\widehat {C}_1=\pi \times _{\pi }\widehat {C}_1$. We also have the one-fold cover ![]() $\widehat {C}_2\to C_2$ with the covering group
$\widehat {C}_2\to C_2$ with the covering group ![]() $\pi _{\widehat {C}_2}=1$, and
$\pi _{\widehat {C}_2}=1$, and ![]() $\widetilde {C}_2=\widehat {C}_2\sqcup a\widehat {C}_2=\pi \times _1 \widehat {C}_2$.
$\widetilde {C}_2=\widehat {C}_2\sqcup a\widehat {C}_2=\pi \times _1 \widehat {C}_2$.
Denote the homomorphism ![]() $G\cong \Gamma _{\widehat {C}}\subset \Gamma$ by
$G\cong \Gamma _{\widehat {C}}\subset \Gamma$ by ![]() $u\to \widetilde {u}$. Then the elements of
$u\to \widetilde {u}$. Then the elements of ![]() $\Gamma =\pi \rtimes \Gamma _{\widehat {C}}\cong \pi \rtimes G$ are
$\Gamma =\pi \rtimes \Gamma _{\widehat {C}}\cong \pi \rtimes G$ are ![]() $a\widetilde {u}$, with
$a\widetilde {u}$, with ![]() $a\in \pi$ and
$a\in \pi$ and ![]() $u\in G$. The multiplication in
$u\in G$. The multiplication in ![]() $\Gamma$ is given by
$\Gamma$ is given by ![]() $a_1\widetilde {u}_1a_2\widetilde {u}_2=a_1u_1(a_2)\widetilde {u_1u_2}$. Here
$a_1\widetilde {u}_1a_2\widetilde {u}_2=a_1u_1(a_2)\widetilde {u_1u_2}$. Here ![]() $u(a)$ is obtained by regarding
$u(a)$ is obtained by regarding ![]() $a\in \pi _1(Y,\,y)$ as a loop at
$a\in \pi _1(Y,\,y)$ as a loop at ![]() $y$ and applying the action of
$y$ and applying the action of ![]() $u\in G$ to the loop. In particular, if
$u\in G$ to the loop. In particular, if ![]() $a\in \pi _1(C,\,y)$ lies in the deck transformation group
$a\in \pi _1(C,\,y)$ lies in the deck transformation group ![]() $\pi _{{\widehat {C}}}$, then
$\pi _{{\widehat {C}}}$, then ![]() $u(a)=a$. This means
$u(a)=a$. This means ![]() $\Gamma _{\widehat {C}}$ acts trivially on
$\Gamma _{\widehat {C}}$ acts trivially on ![]() $\pi _{{\widehat {C}}}$, and
$\pi _{{\widehat {C}}}$, and ![]() $\pi _{\widehat {C}}\times \Gamma _{\widehat {C}}\cong \pi _{\widehat {C}}\times G$ is a subgroup of
$\pi _{\widehat {C}}\times \Gamma _{\widehat {C}}\cong \pi _{\widehat {C}}\times G$ is a subgroup of ![]() $\Gamma$.
$\Gamma$.
We have the ![]() ${\mathbb {Z}}[\Gamma ]$-chain complexes
${\mathbb {Z}}[\Gamma ]$-chain complexes
Since the isotropy group ![]() $\Gamma _{\widehat {C}}$ acts trivially on
$\Gamma _{\widehat {C}}$ acts trivially on ![]() ${\widehat {C}}$, we may regard
${\widehat {C}}$, we may regard ![]() $C_*({\widehat {C}})$ as a
$C_*({\widehat {C}})$ as a ![]() ${\mathbb {Z}}[\pi _{\widehat {C}}\times \Gamma _{\widehat {C}}]$-chain complex (with trivial action by
${\mathbb {Z}}[\pi _{\widehat {C}}\times \Gamma _{\widehat {C}}]$-chain complex (with trivial action by ![]() $\Gamma _{\widehat {C}}$). By
$\Gamma _{\widehat {C}}$). By ![]() $\Gamma =\pi \rtimes \Gamma _{\widehat {C}}$, we get the following interpretation of the
$\Gamma =\pi \rtimes \Gamma _{\widehat {C}}$, we get the following interpretation of the ![]() ${\mathbb {Z}}[\Gamma ]$-chain complex
${\mathbb {Z}}[\Gamma ]$-chain complex ![]() $C_*(\widetilde {C})$
$C_*(\widetilde {C})$
Similarly, let ![]() $\widehat {F}_C\subset \widetilde {F}_C$ correspond to
$\widehat {F}_C\subset \widetilde {F}_C$ correspond to ![]() $\widehat {C}\subset \widetilde {C}$. Then we have
$\widehat {C}\subset \widetilde {C}$. Then we have
The pseudo-equivalent ![]() $G$-map
$G$-map ![]() $g\colon X\to Y$ between semi-free
$g\colon X\to Y$ between semi-free ![]() $G$-CW-complexes lifts to a pseudo-equivalent
$G$-CW-complexes lifts to a pseudo-equivalent ![]() $\Gamma$-map
$\Gamma$-map ![]() $\widetilde {g}\colon \widetilde {X}\to \widetilde {Y}$, and
$\widetilde {g}\colon \widetilde {X}\to \widetilde {Y}$, and ![]() $\widetilde {g}$ has the ‘fixed part”
$\widetilde {g}$ has the ‘fixed part” ![]() $\widetilde {f}\colon \widetilde {F}\to \widetilde {Y^G}$. Here the fixed part is not fixed by the whole
$\widetilde {f}\colon \widetilde {F}\to \widetilde {Y^G}$. Here the fixed part is not fixed by the whole ![]() $\Gamma$, but by various isotropy subgroups
$\Gamma$, but by various isotropy subgroups ![]() $\Gamma _{\widehat {C}}\subset \Gamma$. We regard the pseudo-equivalent
$\Gamma _{\widehat {C}}\subset \Gamma$. We regard the pseudo-equivalent ![]() $\Gamma$-map
$\Gamma$-map ![]() $\widetilde {g}$ as a pseudo-equivalent
$\widetilde {g}$ as a pseudo-equivalent ![]() $\Gamma _{\widehat {C}}$-map. This implies that the mapping cone
$\Gamma _{\widehat {C}}$-map. This implies that the mapping cone ![]() $C(\widetilde {g})$ is a contractible, semi-free
$C(\widetilde {g})$ is a contractible, semi-free ![]() $\Gamma _{\widehat {C}}$-space. The fixed set
$\Gamma _{\widehat {C}}$-space. The fixed set ![]() $C(\widetilde {g})^{\Gamma _{\widehat {C}}}$ is the mapping cone of the map
$C(\widetilde {g})^{\Gamma _{\widehat {C}}}$ is the mapping cone of the map ![]() $\widetilde {X}^{\Gamma _{\widehat {C}}}\to \widetilde {Y}^{\Gamma _{\widehat {C}}}$. By the classical Smith theory [Reference Smith22],
$\widetilde {X}^{\Gamma _{\widehat {C}}}\to \widetilde {Y}^{\Gamma _{\widehat {C}}}$. By the classical Smith theory [Reference Smith22], ![]() $C(\widetilde {g})^{\Gamma _{\widehat {C}}}$ has trivial
$C(\widetilde {g})^{\Gamma _{\widehat {C}}}$ has trivial ![]() ${\mathbb {F}}_p$-homology for all prime factors
${\mathbb {F}}_p$-homology for all prime factors ![]() $p$ of
$p$ of ![]() $|\Gamma _{\widehat {C}}|=|G|$. This implies an isomorphism
$|\Gamma _{\widehat {C}}|=|G|$. This implies an isomorphism ![]() $H_*(\widetilde {X}^{\Gamma _{\widehat {C}}};{\mathbb {F}}_p)\cong H_*(\widetilde {Y}^{\Gamma _{\widehat {C}}};{\mathbb {F}}_p)$.
$H_*(\widetilde {X}^{\Gamma _{\widehat {C}}};{\mathbb {F}}_p)\cong H_*(\widetilde {Y}^{\Gamma _{\widehat {C}}};{\mathbb {F}}_p)$.
We note that ![]() $\Gamma _{\widehat {C}}$ may fix several connected components
$\Gamma _{\widehat {C}}$ may fix several connected components ![]() $\widehat {C}_0,\,\widehat {C}_1,\,\dots,\,\widehat {C}_k$ of
$\widehat {C}_0,\,\widehat {C}_1,\,\dots,\,\widehat {C}_k$ of ![]() $\widetilde {Y^G}$, in addition to
$\widetilde {Y^G}$, in addition to ![]() $\widehat {C}_0=\widehat {C}$. Then the isomorphism
$\widehat {C}_0=\widehat {C}$. Then the isomorphism ![]() $H_*(\widetilde {X}^{\Gamma _{\widehat {C}}};{\mathbb {F}}_p)\cong H_*(\widetilde {Y}^{\Gamma _{\widehat {C}}};{\mathbb {F}}_p)$ is a direct sum of isomorphisms
$H_*(\widetilde {X}^{\Gamma _{\widehat {C}}};{\mathbb {F}}_p)\cong H_*(\widetilde {Y}^{\Gamma _{\widehat {C}}};{\mathbb {F}}_p)$ is a direct sum of isomorphisms ![]() $H_*(\widehat {F}_{C_i};{\mathbb {F}}_p) \cong H_*(\widehat {C}_i;{\mathbb {F}}_p)$. For
$H_*(\widehat {F}_{C_i};{\mathbb {F}}_p) \cong H_*(\widehat {C}_i;{\mathbb {F}}_p)$. For ![]() $i=0$, this gives the local Smith condition
$i=0$, this gives the local Smith condition
For our example, we have the Smith condition on ![]() $\widehat {C}_1=S^1$ with the antipode action by
$\widehat {C}_1=S^1$ with the antipode action by ![]() $\pi =\langle a\rangle$, and the Smith condition on
$\pi =\langle a\rangle$, and the Smith condition on ![]() $\widehat {C}_2=N$ with the trivial group action. The first condition is obtained by applying the usual Smith condition to the action of
$\widehat {C}_2=N$ with the trivial group action. The first condition is obtained by applying the usual Smith condition to the action of ![]() $\Gamma _{S^1}=\langle \widetilde {u}_1\rangle$ on
$\Gamma _{S^1}=\langle \widetilde {u}_1\rangle$ on ![]() $S^2$. The second condition is obtained by applying the usual Smith condition to the action of
$S^2$. The second condition is obtained by applying the usual Smith condition to the action of ![]() $\Gamma _N=\Gamma _S=\langle \widetilde {u}_2\rangle$ on
$\Gamma _N=\Gamma _S=\langle \widetilde {u}_2\rangle$ on ![]() $S^2$. Although the second condition consists of conditions on
$S^2$. Although the second condition consists of conditions on ![]() $N$ and
$N$ and ![]() $S$, the two conditions are equivalent by the action of
$S$, the two conditions are equivalent by the action of ![]() $\pi =\langle a\rangle$.
$\pi =\langle a\rangle$.
Finally, we combine the local Smith conditions into the global Smith condition in theorems 1.4 and 1.5. We pick one connected component ![]() $\widehat {C}$ of
$\widehat {C}$ of ![]() $\widetilde {C}$ for each connected component
$\widetilde {C}$ for each connected component ![]() $C$ of
$C$ of ![]() $Y^G$. Then
$Y^G$. Then
and
 \begin{align*} H_*(Y^G;{\mathbb{F}}_p\pi) &=H_*(\widetilde{Y^G};{\mathbb{F}}_p) \\ &=\oplus_{C\in \pi_0Y^G}H_*(\pi\times_{\pi_{\widehat{C}}}\widehat{C};{\mathbb{F}}_p) \\ &=\oplus_{C\in \pi_0Y^G}{\mathbb{F}}_p\pi\otimes_{{\mathbb{F}}_p\pi_{\widehat{C}}}H_*(\widehat{C};{\mathbb{F}}_p), \end{align*}
\begin{align*} H_*(Y^G;{\mathbb{F}}_p\pi) &=H_*(\widetilde{Y^G};{\mathbb{F}}_p) \\ &=\oplus_{C\in \pi_0Y^G}H_*(\pi\times_{\pi_{\widehat{C}}}\widehat{C};{\mathbb{F}}_p) \\ &=\oplus_{C\in \pi_0Y^G}{\mathbb{F}}_p\pi\otimes_{{\mathbb{F}}_p\pi_{\widehat{C}}}H_*(\widehat{C};{\mathbb{F}}_p), \end{align*}
Similarly, we have
Then the direct sum of the local Smith condition (2.2) is the global Smith condition
For our example, the global Smith condition is the direct sum of the Smith conditions on ![]() $S^1$,
$S^1$, ![]() $N$, and
$N$, and ![]() $S$.
$S$.
3. Proof of main theorems
The proof of the main theorems in the introduction involves an equivariant version of Wall's finiteness obstruction [Reference Wall28].
Proof of theorem 1.4. Proof of theorem 1.4
We assume that the first (Smith) condition is satisfied and try to construct a pseudo-equivalence extension ![]() $g$. In the process, we will encounter the obstruction in the second condition, and will see that it is well-defined.
$g$. In the process, we will encounter the obstruction in the second condition, and will see that it is well-defined.
By ![]() $H_0(F;{\mathbb {F}}_p\pi )\cong H_0(Y;{\mathbb {F}}_p\pi )={\mathbb {F}}_p$, we know
$H_0(F;{\mathbb {F}}_p\pi )\cong H_0(Y;{\mathbb {F}}_p\pi )={\mathbb {F}}_p$, we know ![]() $F$ is connected. We choose a base point in
$F$ is connected. We choose a base point in ![]() $F$ and use its image in
$F$ and use its image in ![]() $Y$ as the base point of
$Y$ as the base point of ![]() $Y$. For any loop
$Y$. For any loop ![]() $\epsilon$ in
$\epsilon$ in ![]() $Y$ at the base point, we may attach
$Y$ at the base point, we may attach ![]() $G$ copies of loops to
$G$ copies of loops to ![]() $F$, and equivariantly map these loops to the loop
$F$, and equivariantly map these loops to the loop ![]() $\epsilon$. Since
$\epsilon$. Since ![]() $Y$ is a finite CW-complex, we may attach finitely many such loops to get a finite, semi-free
$Y$ is a finite CW-complex, we may attach finitely many such loops to get a finite, semi-free ![]() $G$-CW-complex
$G$-CW-complex ![]() $X^1$ with fixed point set
$X^1$ with fixed point set ![]() $F$, and get a
$F$, and get a ![]() $G$-map
$G$-map ![]() $f^1\colon X^1\to Y$ that is surjective on
$f^1\colon X^1\to Y$ that is surjective on ![]() $\pi _1$.
$\pi _1$.
Since ![]() $X^1$ is a finite
$X^1$ is a finite ![]() $G$-CW-complex, there are finitely many loops
$G$-CW-complex, there are finitely many loops ![]() $\epsilon _i$ generating
$\epsilon _i$ generating ![]() $\pi _1(X^1)$. Since
$\pi _1(X^1)$. Since ![]() $f^1$ is surjective on
$f^1$ is surjective on ![]() $\pi _1$, the images
$\pi _1$, the images ![]() $f^1(\epsilon _i)$ generate
$f^1(\epsilon _i)$ generate ![]() $\pi$, which is finitely presented because
$\pi$, which is finitely presented because ![]() $Y$ is a finite CW-complex. Therefore
$Y$ is a finite CW-complex. Therefore ![]() $\pi$ can be presented by
$\pi$ can be presented by ![]() $f^1(\epsilon _i)$ as generators, with finitely many words
$f^1(\epsilon _i)$ as generators, with finitely many words ![]() $f^1(w_j)$ of these loops as relations. For each such word
$f^1(w_j)$ of these loops as relations. For each such word ![]() $f^1(w_j)$, we glue
$f^1(w_j)$, we glue ![]() $G$-copies of
$G$-copies of ![]() $D^2$ to
$D^2$ to ![]() $X^1$ along
$X^1$ along ![]() $Gw_j$ and equivariantly map these
$Gw_j$ and equivariantly map these ![]() $2$-cells to
$2$-cells to ![]() $Y$. We thus get a finite, semi-free
$Y$. We thus get a finite, semi-free ![]() $G$-CW-complex
$G$-CW-complex ![]() $X^{1.5}$ with fixed point set
$X^{1.5}$ with fixed point set ![]() $F$, and extend
$F$, and extend ![]() $f^1$ to a
$f^1$ to a ![]() $G$-map
$G$-map ![]() $f^{1.5}\colon X^{1.5}\to Y$ that induces an isomorphism on
$f^{1.5}\colon X^{1.5}\to Y$ that induces an isomorphism on ![]() $\pi _1$.
$\pi _1$.
Since ![]() $f^{1.5}$ induces an isomorphism on
$f^{1.5}$ induces an isomorphism on ![]() $\pi _1$, by the Hurewicz theorem, we have
$\pi _1$, by the Hurewicz theorem, we have ![]() $\pi _2(f^{1.5})=H_2(f^{1.5};{\mathbb {Z}}\pi )$. This implies that
$\pi _2(f^{1.5})=H_2(f^{1.5};{\mathbb {Z}}\pi )$. This implies that ![]() $\pi _2(f^{1.5})$ is finitely generated as a
$\pi _2(f^{1.5})$ is finitely generated as a ![]() ${\mathbb {Z}}\pi$-module. In fact, as
${\mathbb {Z}}\pi$-module. In fact, as ![]() $G$ is a finite group, the
$G$ is a finite group, the ![]() $G$-action also makes
$G$-action also makes ![]() $\pi _2(f^{1.5})$ into a finitely generated
$\pi _2(f^{1.5})$ into a finitely generated ![]() ${\mathbb {Z}}[\pi \times G]$-module. We represent a finite set of
${\mathbb {Z}}[\pi \times G]$-module. We represent a finite set of ![]() ${\mathbb {Z}}[\pi \times G]$-generators by maps
${\mathbb {Z}}[\pi \times G]$-generators by maps ![]() $S^1\to X^{1.5}$ and
$S^1\to X^{1.5}$ and ![]() $D^2\to Y$ compatible with
$D^2\to Y$ compatible with ![]() $f^2$. Then we glue
$f^2$. Then we glue ![]() $G$-copies of
$G$-copies of ![]() $D^2$ along
$D^2$ along ![]() $G(S^1\to X^{1.5})$ to
$G(S^1\to X^{1.5})$ to ![]() $X^{1.5}$ and equivariantly map these
$X^{1.5}$ and equivariantly map these ![]() $2$-cells to
$2$-cells to ![]() $Y$ by
$Y$ by ![]() $G(D^2\to Y)$ (for the current case that the
$G(D^2\to Y)$ (for the current case that the ![]() $G$-action on
$G$-action on ![]() $Y$ is trivial, this is
$Y$ is trivial, this is ![]() $D^2\to Y$). We get a finite, semi-free
$D^2\to Y$). We get a finite, semi-free ![]() $G$-CW-complex
$G$-CW-complex ![]() $X^2$ with fixed point set
$X^2$ with fixed point set ![]() $F$, and extend
$F$, and extend ![]() $f^{1.5}$ to a
$f^{1.5}$ to a ![]() $G$-map
$G$-map ![]() $f^2\colon X^2\to Y$, such that
$f^2\colon X^2\to Y$, such that ![]() $f^2$ satisfies
$f^2$ satisfies ![]() $\pi _1(f^2)=\pi _2(f^2)=0$.
$\pi _1(f^2)=\pi _2(f^2)=0$.
The construction from ![]() $f^{1.5}$ to
$f^{1.5}$ to ![]() $f^2$ can be inductively extended to higher dimensions. If we have a
$f^2$ can be inductively extended to higher dimensions. If we have a ![]() $G$-map
$G$-map ![]() $f^i\colon X^i\to Y$ satisfying
$f^i\colon X^i\to Y$ satisfying ![]() $\pi _j(f^i)=0$ for
$\pi _j(f^i)=0$ for ![]() $j\le i$, then we can use a finite set of
$j\le i$, then we can use a finite set of ![]() ${\mathbb {Z}}[\pi \times G]$-generators of
${\mathbb {Z}}[\pi \times G]$-generators of ![]() $\pi _{i+1}(f^i)=H_{i+1}(f^i;{\mathbb {Z}}\pi )$ to equivariantly attach
$\pi _{i+1}(f^i)=H_{i+1}(f^i;{\mathbb {Z}}\pi )$ to equivariantly attach ![]() $(i+1)$-dimensional free
$(i+1)$-dimensional free ![]() $G$-cells to
$G$-cells to ![]() $X^i$, and extend
$X^i$, and extend ![]() $f^i$ to a
$f^i$ to a ![]() $G$-map
$G$-map ![]() $f^{i+1}\colon X^{i+1}\to Y$ satisfying
$f^{i+1}\colon X^{i+1}\to Y$ satisfying ![]() $\pi _j(f^{i+1})=0$ for
$\pi _j(f^{i+1})=0$ for ![]() $j\le i+1$. Inductively, we get
$j\le i+1$. Inductively, we get ![]() $f^n\colon X^n\to Y$ for some
$f^n\colon X^n\to Y$ for some ![]() $n>\max \{\dim F,\,\dim Y\}$, such that
$n>\max \{\dim F,\,\dim Y\}$, such that ![]() $\pi _j(f^n)=0$ for
$\pi _j(f^n)=0$ for ![]() $j\le n$.
$j\le n$.
Let us consider the effect of one more construction to get ![]() $f^{n+1}\colon X^{n+1}\to Y$. The generators used for the construction can be interpreted as a basis of a finitely generated free
$f^{n+1}\colon X^{n+1}\to Y$. The generators used for the construction can be interpreted as a basis of a finitely generated free ![]() ${\mathbb {Z}}[\pi \times G]$-module
${\mathbb {Z}}[\pi \times G]$-module ![]() $A$ in a surjective
$A$ in a surjective ![]() ${\mathbb {Z}}[\pi \times G]$-homomorphism
${\mathbb {Z}}[\pi \times G]$-homomorphism ![]() $A\to H_{n+1}(f^n;{\mathbb {Z}}\pi )$. By
$A\to H_{n+1}(f^n;{\mathbb {Z}}\pi )$. By ![]() $n+1>\max \{\dim X^n,\,\dim Y\}$, we have
$n+1>\max \{\dim X^n,\,\dim Y\}$, we have ![]() $H_{n+2}(f^n;{\mathbb {Z}}\pi )=0$ and an exact sequence
$H_{n+2}(f^n;{\mathbb {Z}}\pi )=0$ and an exact sequence
 \begin{align*} & H_{n+2}(f^n;{\mathbb{Z}}\pi)=0 \to H_{n+2}(f^{n+1};{\mathbb{Z}}\pi) \to H_{n+1}(X^{n+1},X^n;{\mathbb{Z}}\pi)=A \\ & \to H_{n+1}(f^n;{\mathbb{Z}}\pi)\to H_{n+1}(f^{n+1};{\mathbb{Z}}\pi) \to H_n(X^{n+1},X^n;{\mathbb{Z}}\pi)=0 \to\cdots \end{align*}
\begin{align*} & H_{n+2}(f^n;{\mathbb{Z}}\pi)=0 \to H_{n+2}(f^{n+1};{\mathbb{Z}}\pi) \to H_{n+1}(X^{n+1},X^n;{\mathbb{Z}}\pi)=A \\ & \to H_{n+1}(f^n;{\mathbb{Z}}\pi)\to H_{n+1}(f^{n+1};{\mathbb{Z}}\pi) \to H_n(X^{n+1},X^n;{\mathbb{Z}}\pi)=0 \to\cdots \end{align*}
By the Hurewicz theorem, the exact sequence gives ![]() $\pi _j(f^{n+1})=H_j(f^{n+1};{\mathbb {Z}}\pi )=0$ for
$\pi _j(f^{n+1})=H_j(f^{n+1};{\mathbb {Z}}\pi )=0$ for ![]() $j\le n+1$, and a short exact sequence
$j\le n+1$, and a short exact sequence
Note that ![]() $\pi _{n+2}(f^{n+1})$ is to be used for the further construction based on
$\pi _{n+2}(f^{n+1})$ is to be used for the further construction based on ![]() $f^{n+1}$. Therefore, the short exact sequence shows that, if
$f^{n+1}$. Therefore, the short exact sequence shows that, if ![]() $H_{n+1}(f^n;{\mathbb {Z}}\pi )$ has a finite resolution of finitely generated free
$H_{n+1}(f^n;{\mathbb {Z}}\pi )$ has a finite resolution of finitely generated free ![]() ${\mathbb {Z}}[\pi \times G]$-modules
${\mathbb {Z}}[\pi \times G]$-modules
then the resolution can be used as a recipe for constructing a ![]() $G$-map
$G$-map ![]() $f^{n+k}\colon X^{n+k}\to Y$, such that
$f^{n+k}\colon X^{n+k}\to Y$, such that ![]() $X^{n+k}$ is a finite, semi-free
$X^{n+k}$ is a finite, semi-free ![]() $G$-CW-complex with fixed point set
$G$-CW-complex with fixed point set ![]() $F$, and
$F$, and ![]() $f^{n+k}$ extends
$f^{n+k}$ extends ![]() $f$ and is a (non-equivariant) homotopy equivalence. This
$f$ and is a (non-equivariant) homotopy equivalence. This ![]() $f^{n+k}$ is the pseudo-equivalence extension in the theorem.
$f^{n+k}$ is the pseudo-equivalence extension in the theorem.
Next we argue that the Smith condition implies that the ![]() ${\mathbb {Z}}[\pi \times G]$-module
${\mathbb {Z}}[\pi \times G]$-module ![]() $H_{n+1}(f^n;{\mathbb {Z}}\pi )$ has a finite resolution by finitely generated projective
$H_{n+1}(f^n;{\mathbb {Z}}\pi )$ has a finite resolution by finitely generated projective ![]() ${\mathbb {Z}}[\pi \times G]$-modules. This induces (by § 3 of [Reference Mislin14], for example) an element
${\mathbb {Z}}[\pi \times G]$-modules. This induces (by § 3 of [Reference Mislin14], for example) an element ![]() $[H_{n+1}(f^n;{\mathbb {Z}}\pi )]\in \widetilde {K}_0({\mathbb {Z}}[\pi \times G])$, such that the element vanishes if and only if all the projective modules in the resolution can be chosen to be free. Therefore the element is the obstruction for completing our construction.
$[H_{n+1}(f^n;{\mathbb {Z}}\pi )]\in \widetilde {K}_0({\mathbb {Z}}[\pi \times G])$, such that the element vanishes if and only if all the projective modules in the resolution can be chosen to be free. Therefore the element is the obstruction for completing our construction.
We identify this obstruction with the ![]() $K$-theory element represented by the
$K$-theory element represented by the ![]() ${\mathbb {Z}}\pi$-chain complex
${\mathbb {Z}}\pi$-chain complex ![]() $C_*(\widetilde {f})$, regarded as a
$C_*(\widetilde {f})$, regarded as a ![]() ${\mathbb {Z}}[\pi \times G]$-chain complex with the trivial
${\mathbb {Z}}[\pi \times G]$-chain complex with the trivial ![]() $G$-action. This is crucial for detailed calculations. This fact is essentially Lemma 1.7 of [Reference Assadi and Vogel2]; but we give a detailed explanation anyway.
$G$-action. This is crucial for detailed calculations. This fact is essentially Lemma 1.7 of [Reference Assadi and Vogel2]; but we give a detailed explanation anyway.
There is a (possibly infinite) free ![]() ${\mathbb {Z}}G$-resolution
${\mathbb {Z}}G$-resolution ![]() $P$ of the trivial
$P$ of the trivial ![]() ${\mathbb {Z}}G$-module
${\mathbb {Z}}G$-module ![]() ${\mathbb {Z}}$, such that
${\mathbb {Z}}$, such that ![]() $P$ is finitely generated in each dimension. Then we have
$P$ is finitely generated in each dimension. Then we have
where each term in the ![]() ${\mathbb {Z}}[\pi \times G]$-chain complex
${\mathbb {Z}}[\pi \times G]$-chain complex ![]() $C_*(\widetilde {f})\otimes P$ is finitely generated and free.
$C_*(\widetilde {f})\otimes P$ is finitely generated and free.
There is also a (infinitely generated) projective ![]() ${\mathbb {Z}}[{1}/{|G|}][G]$-resolution
${\mathbb {Z}}[{1}/{|G|}][G]$-resolution ![]() $P'$ of the trivial
$P'$ of the trivial ![]() ${\mathbb {Z}}[{1}/{|G|}][G]$-module
${\mathbb {Z}}[{1}/{|G|}][G]$-module ![]() ${\mathbb {Z}}[{1}/{|G|}]$, such that
${\mathbb {Z}}[{1}/{|G|}]$, such that ![]() $P'$ is nonzero only in dimensions
$P'$ is nonzero only in dimensions ![]() $0$ and
$0$ and ![]() $1$. This implies the second chain homotopy equivalence below
$1$. This implies the second chain homotopy equivalence below
The first chain homotopy equivalence is due to the Smith condition, ![]() $H_*(C_*(\widetilde {f});{\mathbb {F}}_p)=H_*(f;{\mathbb {F}}_p\pi )=0$, for all prime factors
$H_*(C_*(\widetilde {f});{\mathbb {F}}_p)=H_*(f;{\mathbb {F}}_p\pi )=0$, for all prime factors ![]() $p$ of
$p$ of ![]() $|G|$. Since
$|G|$. Since ![]() $C_*(\widetilde {f})$ vanishes above dimension
$C_*(\widetilde {f})$ vanishes above dimension ![]() $n$, and
$n$, and ![]() $P'$ vanishes away from dimensions
$P'$ vanishes away from dimensions ![]() $0$ and
$0$ and ![]() $1$, the chain complex
$1$, the chain complex ![]() $C_*(\widetilde {f})\otimes P'$ has cohomological dimension
$C_*(\widetilde {f})\otimes P'$ has cohomological dimension ![]() $\le n+1$.
$\le n+1$.
By Theorem 3.5 of [Reference Mislin14], and the special properties of the two ![]() ${\mathbb {Z}}[\pi \times G]$-chain complexes that are chain homotopy equivalent to
${\mathbb {Z}}[\pi \times G]$-chain complexes that are chain homotopy equivalent to ![]() $C_*(\widetilde {f})$, we know
$C_*(\widetilde {f})$, we know ![]() $C_*(\widetilde {f})$ is chain homotopy equivalent to a finite chain complex of finitely generated projective
$C_*(\widetilde {f})$ is chain homotopy equivalent to a finite chain complex of finitely generated projective ![]() ${\mathbb {Z}}[\pi \times G]$-modules. This gives a well-defined element
${\mathbb {Z}}[\pi \times G]$-modules. This gives a well-defined element ![]() $[C_*(\widetilde {f})]\in \widetilde {K}_0({\mathbb {Z}}[\pi \times G])$.
$[C_*(\widetilde {f})]\in \widetilde {K}_0({\mathbb {Z}}[\pi \times G])$.
The chain complex ![]() $C_*(\widetilde {f})$ fits into an exact sequence of
$C_*(\widetilde {f})$ fits into an exact sequence of ![]() ${\mathbb {Z}}[\pi \times G]$-chain complexes
${\mathbb {Z}}[\pi \times G]$-chain complexes
Since ![]() $C_{*-1}(\widetilde {X}^n,\,\widetilde {F})$ is a finite chain complex of finitely generated free
$C_{*-1}(\widetilde {X}^n,\,\widetilde {F})$ is a finite chain complex of finitely generated free ![]() ${\mathbb {Z}}[\pi \times G]$-modules,
${\mathbb {Z}}[\pi \times G]$-modules, ![]() $C_*(\widetilde {f}^n)$ is also chain homotopy equivalent to a finite chain complex of finitely generated projective
$C_*(\widetilde {f}^n)$ is also chain homotopy equivalent to a finite chain complex of finitely generated projective ![]() ${\mathbb {Z}}[\pi \times G]$-modules, and
${\mathbb {Z}}[\pi \times G]$-modules, and ![]() $[C_*(\widetilde {f}^n)]=[C_*(\widetilde {f})]\in \widetilde {K}_0(\pi \times G)$. On the other hand, we know the homology of
$[C_*(\widetilde {f}^n)]=[C_*(\widetilde {f})]\in \widetilde {K}_0(\pi \times G)$. On the other hand, we know the homology of ![]() $C_*(\widetilde {f}^n)$ vanishes in all dimensions except for
$C_*(\widetilde {f}^n)$ vanishes in all dimensions except for ![]() $H_{n+1}(f^n;{\mathbb {Z}}\pi )$. Therefore the
$H_{n+1}(f^n;{\mathbb {Z}}\pi )$. Therefore the ![]() ${\mathbb {Z}}[\pi \times G]$-chain complex
${\mathbb {Z}}[\pi \times G]$-chain complex ![]() $\cdots \to 0\to H_{n+1}(f^n;{\mathbb {Z}}\pi )\to 0\to \cdots$ is chain homotopy equivalent to
$\cdots \to 0\to H_{n+1}(f^n;{\mathbb {Z}}\pi )\to 0\to \cdots$ is chain homotopy equivalent to ![]() $C_*(\widetilde {f}^n)$. This implies that
$C_*(\widetilde {f}^n)$. This implies that ![]() $H_{n+1}(f^n;{\mathbb {Z}}\pi )$ has a finite resolution by finitely generated projective
$H_{n+1}(f^n;{\mathbb {Z}}\pi )$ has a finite resolution by finitely generated projective ![]() ${\mathbb {Z}}[\pi \times G]$-modules, and
${\mathbb {Z}}[\pi \times G]$-modules, and
The equality to ![]() $[C_*(\widetilde {f})]$ shows that the obstruction
$[C_*(\widetilde {f})]$ shows that the obstruction ![]() $(-1)^{n+1}[H_{n+1}(f^n;{\mathbb {Z}}\pi )]$ is independent of our choice of construction.
$(-1)^{n+1}[H_{n+1}(f^n;{\mathbb {Z}}\pi )]$ is independent of our choice of construction.
Proof of Theorem 1.5. Proof of theorem 1.5
The proof is similar to theorem 1.4. The inductive construction of ![]() $f^n\colon X^n\to Y$ is the same, except that the new cells can be mapped to
$f^n\colon X^n\to Y$ is the same, except that the new cells can be mapped to ![]() $Y$ instead of just the fixed set, and all the homotopy groups and homology groups (at the universal cover level) are
$Y$ instead of just the fixed set, and all the homotopy groups and homology groups (at the universal cover level) are ![]() ${\mathbb {Z}}[\Gamma ]$-modules. For sufficiently large
${\mathbb {Z}}[\Gamma ]$-modules. For sufficiently large ![]() $n$, the obstruction for constructing the pseudo-equivalence is
$n$, the obstruction for constructing the pseudo-equivalence is ![]() $[H_{n+1}(f^n;{\mathbb {Z}}\pi )]\in \widetilde {K}_0({\mathbb {Z}}[\Gamma ])$. We need to argue that
$[H_{n+1}(f^n;{\mathbb {Z}}\pi )]\in \widetilde {K}_0({\mathbb {Z}}[\Gamma ])$. We need to argue that ![]() $C_*(\widetilde {f})$ represents an element in
$C_*(\widetilde {f})$ represents an element in ![]() $\widetilde {K}_0({\mathbb {Z}}[\Gamma ])$ that is the same as
$\widetilde {K}_0({\mathbb {Z}}[\Gamma ])$ that is the same as ![]() $(-1)^{n+1}[H_{n+1}(f^n;{\mathbb {Z}}\pi )]$.
$(-1)^{n+1}[H_{n+1}(f^n;{\mathbb {Z}}\pi )]$.
In § 2, we saw that the global Smith condition (2.3) in theorem 1.5 is equivalent to the local Smith condition (2.2) for each connected component ![]() $C$ of
$C$ of ![]() $Y^G$. Following the same argument for theorem 1.4, we know the
$Y^G$. Following the same argument for theorem 1.4, we know the ![]() ${\mathbb {Z}}[\pi _{\widehat {C}}\times \Gamma _{\widehat {C}}]$-chain complex
${\mathbb {Z}}[\pi _{\widehat {C}}\times \Gamma _{\widehat {C}}]$-chain complex ![]() $C_*(\widehat {F}_C\to \widehat {C})$ is chain homotopy equivalent to a finite chain complex of finitely generated projective
$C_*(\widehat {F}_C\to \widehat {C})$ is chain homotopy equivalent to a finite chain complex of finitely generated projective ![]() ${\mathbb {Z}}[\pi _{\widehat {C}}\times \Gamma _{\widehat {C}}]$-modules. This gives a well-defined
${\mathbb {Z}}[\pi _{\widehat {C}}\times \Gamma _{\widehat {C}}]$-modules. This gives a well-defined ![]() $K$-theory element
$K$-theory element
By ![]() $\pi _{\widehat {C}}\times \Gamma _{\widehat {C}}\subset \pi \rtimes \Gamma _{\widehat {C}}=\Gamma$, this inducts to
$\pi _{\widehat {C}}\times \Gamma _{\widehat {C}}\subset \pi \rtimes \Gamma _{\widehat {C}}=\Gamma$, this inducts to
 \begin{align*} [C_*(\widetilde{F}_C\to \widetilde{C})] &=[{\mathbb{Z}}[\Gamma]\otimes_{{\mathbb{Z}}[\pi_{\widehat{C}}\times \Gamma_{\widehat{C}}]}C_*(\widehat{F}_C\to \widehat{C})] \\ &=\text{Ind}_{{\mathbb{Z}}[\pi_{\widehat{C}}\times \Gamma_{\widehat{C}}]}^{{\mathbb{Z}}[\Gamma]}[C_*(\widehat{F}_C\to \widehat{C})] \in \widetilde{K}_0({\mathbb{Z}}[\Gamma]), \end{align*}
\begin{align*} [C_*(\widetilde{F}_C\to \widetilde{C})] &=[{\mathbb{Z}}[\Gamma]\otimes_{{\mathbb{Z}}[\pi_{\widehat{C}}\times \Gamma_{\widehat{C}}]}C_*(\widehat{F}_C\to \widehat{C})] \\ &=\text{Ind}_{{\mathbb{Z}}[\pi_{\widehat{C}}\times \Gamma_{\widehat{C}}]}^{{\mathbb{Z}}[\Gamma]}[C_*(\widehat{F}_C\to \widehat{C})] \in \widetilde{K}_0({\mathbb{Z}}[\Gamma]), \end{align*}
which further adds up to
Now we know the ![]() ${\mathbb {Z}}[\Gamma ]$–chain complex
${\mathbb {Z}}[\Gamma ]$–chain complex ![]() $C_*(\widetilde {f})$ is chain homotopy equivalent to a finite chain complex of finitely generated projective
$C_*(\widetilde {f})$ is chain homotopy equivalent to a finite chain complex of finitely generated projective ![]() ${\mathbb {Z}}[\Gamma ]$-modules and gives a
${\mathbb {Z}}[\Gamma ]$-modules and gives a ![]() $K$-theory element. Then we have short exact sequences of
$K$-theory element. Then we have short exact sequences of ![]() ${\mathbb {Z}}[\Gamma ]$-chain complexes
${\mathbb {Z}}[\Gamma ]$-chain complexes
 \begin{align*} 0&\to C_*(\widetilde{f}\colon \widetilde{F}\to \widetilde{Y^G}) \to C_*(\widetilde{F}\to \widetilde{Y}) \to C_{*-1}(\widetilde{Y},\widetilde{Y^G})\to 0, \\ 0&\to C_*(\widetilde{F}\to \widetilde{Y}) \to C_*(\widetilde{f}^n\colon \widetilde{X}^n\to \widetilde{Y}) \to C_{*-1}(\widetilde{X}^n,\widetilde{F}) \to 0. \end{align*}
\begin{align*} 0&\to C_*(\widetilde{f}\colon \widetilde{F}\to \widetilde{Y^G}) \to C_*(\widetilde{F}\to \widetilde{Y}) \to C_{*-1}(\widetilde{Y},\widetilde{Y^G})\to 0, \\ 0&\to C_*(\widetilde{F}\to \widetilde{Y}) \to C_*(\widetilde{f}^n\colon \widetilde{X}^n\to \widetilde{Y}) \to C_{*-1}(\widetilde{X}^n,\widetilde{F}) \to 0. \end{align*}
Since ![]() $Y$ is a semi-free
$Y$ is a semi-free ![]() $G$-CW-complex, and
$G$-CW-complex, and ![]() $X^n$ is obtained by glueing free
$X^n$ is obtained by glueing free ![]() $G$-cells to
$G$-cells to ![]() $F$, both
$F$, both ![]() $C_{*-1}(\widetilde {Y},\,\widetilde {Y^G})$ and
$C_{*-1}(\widetilde {Y},\,\widetilde {Y^G})$ and ![]() $C_{*-1}(\widetilde {X}^n,\,\widetilde {F})$ are finite chain complexes of finitely generated free
$C_{*-1}(\widetilde {X}^n,\,\widetilde {F})$ are finite chain complexes of finitely generated free ![]() ${\mathbb {Z}}[\Gamma ]$-modules. Therefore
${\mathbb {Z}}[\Gamma ]$-modules. Therefore
 \begin{align*} [C_*(\widetilde{f})] &=[C_*(\widetilde{F}\to \widetilde{Y})] \\ &=[C_*(\widetilde{f}^n\colon \widetilde{X}^n\to \widetilde{Y})] \\ &=({-}1)^{n+1}[H_{n+1}(f^n;{\mathbb{Z}}\pi)] \in \widetilde{K}_0({\mathbb{Z}}[\Gamma]). \end{align*}
\begin{align*} [C_*(\widetilde{f})] &=[C_*(\widetilde{F}\to \widetilde{Y})] \\ &=[C_*(\widetilde{f}^n\colon \widetilde{X}^n\to \widetilde{Y})] \\ &=({-}1)^{n+1}[H_{n+1}(f^n;{\mathbb{Z}}\pi)] \in \widetilde{K}_0({\mathbb{Z}}[\Gamma]). \end{align*}
This completes the identification of the ![]() $K$-theory obstruction.
$K$-theory obstruction.
The main theorems can be modified to get the pseudo-equivalence extension to be a simple homotopy equivalence. The only change is the ![]() $K$-theory in which the obstruction lives. The following is the analogue of theorem 1.4 making use of an algebraic
$K$-theory in which the obstruction lives. The following is the analogue of theorem 1.4 making use of an algebraic ![]() $K$-theory introduced in [Reference Assadi and Vogel2].
$K$-theory introduced in [Reference Assadi and Vogel2].
Theorem 3.1 Suppose ![]() $f\colon F\to Y$ is a map of finite CW-complexes, with
$f\colon F\to Y$ is a map of finite CW-complexes, with ![]() $Y$ connected and
$Y$ connected and ![]() $\pi =\pi _1(Y)$. Then
$\pi =\pi _1(Y)$. Then ![]() $F$ can be the fixed set of a finite, semi-free
$F$ can be the fixed set of a finite, semi-free ![]() $G$-CW-complex
$G$-CW-complex ![]() $X$, and
$X$, and ![]() $f$ has simple pseudo-equivalence extension
$f$ has simple pseudo-equivalence extension ![]() $g\colon X\to Y$, if and only if the following are satisfied:
$g\colon X\to Y$, if and only if the following are satisfied:
1. The map
 $f$ induces isomorphisms
$f$ induces isomorphisms  $H_*(F;{\mathbb {F}}_p\pi )\cong H_*(Y;{\mathbb {F}}_p\pi )$ for all prime factors
$H_*(F;{\mathbb {F}}_p\pi )\cong H_*(Y;{\mathbb {F}}_p\pi )$ for all prime factors  $p$ of
$p$ of  $|G|$.
$|G|$.2. A well-defined obstruction
 $[C_*(\widetilde {f})]\in Wh_1^T(\pi \subset \pi \times G)$ vanishes.
$[C_*(\widetilde {f})]\in Wh_1^T(\pi \subset \pi \times G)$ vanishes.
Assadi and Vogel [Reference Assadi and Vogel2] introduced the Grothendick group ![]() $Wh_1^T(\pi \subset \pi \times G)$ of the additive category of finitely generated
$Wh_1^T(\pi \subset \pi \times G)$ of the additive category of finitely generated ![]() ${\mathbb {Z}}\pi$-based projective
${\mathbb {Z}}\pi$-based projective ![]() ${\mathbb {Z}}[\pi \times G]$-modules, such that the
${\mathbb {Z}}[\pi \times G]$-modules, such that the ![]() ${\mathbb {Z}}[\pi \times G]$-module
${\mathbb {Z}}[\pi \times G]$-module ![]() ${\mathbb {Z}}[\pi \times G]$ with the choice of
${\mathbb {Z}}[\pi \times G]$ with the choice of ![]() $G$ as
$G$ as ![]() ${\mathbb {Z}}\pi$-basis is trivial in
${\mathbb {Z}}\pi$-basis is trivial in ![]() $Wh_1^T$. They showed that there is an exact sequence (
$Wh_1^T$. They showed that there is an exact sequence (![]() $\widetilde {K}_0(\pi )$ is denoted
$\widetilde {K}_0(\pi )$ is denoted ![]() $Wh_0(\pi )$ in [Reference Assadi and Vogel2])
$Wh_0(\pi )$ in [Reference Assadi and Vogel2])
The cells of ![]() $F$ and
$F$ and ![]() $Y$ give natural
$Y$ give natural ![]() ${\mathbb {Z}}\pi$-bases for the modules in
${\mathbb {Z}}\pi$-bases for the modules in ![]() $C_*(\widetilde {f})$. By Lemmas 1.6 and 1.7 of [Reference Assadi and Vogel2], under the Smith condition, the chain complex
$C_*(\widetilde {f})$. By Lemmas 1.6 and 1.7 of [Reference Assadi and Vogel2], under the Smith condition, the chain complex ![]() $C_*(\widetilde {f})$ with the natural
$C_*(\widetilde {f})$ with the natural ![]() ${\mathbb {Z}}\pi$-bases gives a well-defined element
${\mathbb {Z}}\pi$-bases gives a well-defined element ![]() $[C_*(\widetilde {f})]\in Wh_1^T(\pi \subset \pi \times G)$. The image of this element in
$[C_*(\widetilde {f})]\in Wh_1^T(\pi \subset \pi \times G)$. The image of this element in ![]() $\widetilde {K}_0({\mathbb {Z}}[\pi \times G])$ is the obstruction in the main theorem.
$\widetilde {K}_0({\mathbb {Z}}[\pi \times G])$ is the obstruction in the main theorem.
The proof of theorem 3.1 is the same as the proof of theorem 1.4, with additional tracking of the basis in the construction. The key point is that the free ![]() $G$-cells used in the construction give the chain complex
$G$-cells used in the construction give the chain complex ![]() $C_{*-1}(\widetilde {X}^n,\,\widetilde {F})$, where each term is the direct sum of finitely many copies of
$C_{*-1}(\widetilde {X}^n,\,\widetilde {F})$, where each term is the direct sum of finitely many copies of ![]() ${\mathbb {Z}}[\pi \times G]$ with the
${\mathbb {Z}}[\pi \times G]$ with the ![]() ${\mathbb {Z}}\pi$-basis
${\mathbb {Z}}\pi$-basis ![]() $G$. Therefore
$G$. Therefore ![]() $[C_{*-1}(\widetilde {X}^n,\,\widetilde {F})]=0\in Wh_1^T(\pi \subset \pi \times G)$.
$[C_{*-1}(\widetilde {X}^n,\,\widetilde {F})]=0\in Wh_1^T(\pi \subset \pi \times G)$.
In the context of theorem 1.5, we may also extend the ![]() $K$-theory to
$K$-theory to ![]() $Wh_1^T(\pi \subset \Gamma )$, by considering the additive category of finitely generated
$Wh_1^T(\pi \subset \Gamma )$, by considering the additive category of finitely generated ![]() ${\mathbb {Z}}\pi$-based projective
${\mathbb {Z}}\pi$-based projective ![]() ${\mathbb {Z}}[\Gamma ]$-modules. For the
${\mathbb {Z}}[\Gamma ]$-modules. For the ![]() ${\mathbb {Z}}[\Gamma ]$-module
${\mathbb {Z}}[\Gamma ]$-module ![]() ${\mathbb {Z}}[\Gamma ]$, we find a subset
${\mathbb {Z}}[\Gamma ]$, we find a subset ![]() $\Gamma _0\subset \Gamma$, such that the multiplication map
$\Gamma _0\subset \Gamma$, such that the multiplication map ![]() $\pi \times \Gamma _0\to \Gamma$ is a one-to-one correspondence. Then
$\pi \times \Gamma _0\to \Gamma$ is a one-to-one correspondence. Then ![]() $\Gamma _0$ is a
$\Gamma _0$ is a ![]() ${\mathbb {Z}}\pi$-basis of
${\mathbb {Z}}\pi$-basis of ![]() ${\mathbb {Z}}[\Gamma ]$, and this represents the trivial element in
${\mathbb {Z}}[\Gamma ]$, and this represents the trivial element in ![]() $Wh_1^T(\pi \subset \Gamma )$. Using this
$Wh_1^T(\pi \subset \Gamma )$. Using this ![]() $K$-theory, we also have the simple homotopy version of theorem 1.5.
$K$-theory, we also have the simple homotopy version of theorem 1.5.
The main theorems can also be modified to treat compact ANR-spaces in place of finite CW-complexes. We only present the analogue of theorem 1.4.
Theorem 3.2 Suppose ![]() $f\colon F\to Y$ is a map of compact ANR-spaces, with
$f\colon F\to Y$ is a map of compact ANR-spaces, with ![]() $Y$ connected and
$Y$ connected and ![]() $\pi =\pi _1(Y)$. Then
$\pi =\pi _1(Y)$. Then ![]() $F$ can be the fixed set of a semi-free compact
$F$ can be the fixed set of a semi-free compact ![]() $G$-ANR-space
$G$-ANR-space ![]() $X,$ and
$X,$ and ![]() $f$ has pseudo-equivalence extension
$f$ has pseudo-equivalence extension ![]() $g\colon X\to Y,$ if and only if the following are satisfied:
$g\colon X\to Y,$ if and only if the following are satisfied:
1. The map
 $f$ induces isomorphisms
$f$ induces isomorphisms  $H_*(F;{\mathbb {F}}_p\pi )\cong H_*(Y;{\mathbb {F}}_p\pi )$ for all prime factors
$H_*(F;{\mathbb {F}}_p\pi )\cong H_*(Y;{\mathbb {F}}_p\pi )$ for all prime factors  $p$ of
$p$ of  $|G|$.
$|G|$.2. A well-defined obstruction
 $[C_*(\widetilde {f})]\in \widetilde {K}_0^{top}({\mathbb {Z}}\pi \subset {\mathbb {Z}}[\pi \times G])$ vanishes.
$[C_*(\widetilde {f})]\in \widetilde {K}_0^{top}({\mathbb {Z}}\pi \subset {\mathbb {Z}}[\pi \times G])$ vanishes.
The topological ![]() $K$-theory
$K$-theory ![]() $\widetilde {K}_0^{top}$ was introduced by M. Steinberger and J. West [Reference Steinberger23, Reference Steinberger and West24], and by F. Quinn [Reference Quinn19, Reference Quinn20] as the
$\widetilde {K}_0^{top}$ was introduced by M. Steinberger and J. West [Reference Steinberger23, Reference Steinberger and West24], and by F. Quinn [Reference Quinn19, Reference Quinn20] as the ![]() $K$-theoretical obstruction for the topological version of the finiteness theorems for
$K$-theoretical obstruction for the topological version of the finiteness theorems for ![]() $G$-ANR-spaces. It fits into an exact sequence
$G$-ANR-spaces. It fits into an exact sequence
 \begin{align} & H_1(\pi;\widetilde{\bf K}({\mathbb{Z}}[G]))\to Wh(\pi\times G)\to Wh^{top}(\pi\subset\pi\times G) \nonumber\\ &\to H_0(\pi;\widetilde{\bf K}({\mathbb{Z}}[G]))\to \widetilde{K}_0({\mathbb{Z}}[\pi\times G])\to \widetilde{K}_0^{top}({\mathbb{Z}}\pi\subset {\mathbb{Z}}[\pi\times G]) \to\cdots \end{align}
\begin{align} & H_1(\pi;\widetilde{\bf K}({\mathbb{Z}}[G]))\to Wh(\pi\times G)\to Wh^{top}(\pi\subset\pi\times G) \nonumber\\ &\to H_0(\pi;\widetilde{\bf K}({\mathbb{Z}}[G]))\to \widetilde{K}_0({\mathbb{Z}}[\pi\times G])\to \widetilde{K}_0^{top}({\mathbb{Z}}\pi\subset {\mathbb{Z}}[\pi\times G]) \to\cdots \end{align} By a theorem of West [Reference West30], compact ANRs are homotopy equivalent to finite CW-complexes. Therefore we have an obstruction ![]() $[C_*(\widetilde {f})]\in \widetilde {K}_0({\mathbb {Z}}[\pi \times G])$ in our main pseudo-equivalence extension theorem. Quinn [Reference Quinn19] showed that controlled finitely dominated CW-complexes over
$[C_*(\widetilde {f})]\in \widetilde {K}_0({\mathbb {Z}}[\pi \times G])$ in our main pseudo-equivalence extension theorem. Quinn [Reference Quinn19] showed that controlled finitely dominated CW-complexes over ![]() $F$ with free
$F$ with free ![]() $G$-actions have controlled Wall finiteness obstructions in
$G$-actions have controlled Wall finiteness obstructions in ![]() $H_0(F;\widetilde {\bf K}({\mathbb {Z}}[G]))$, and all elements of this group can be realised. By glueing on such an element, we can change the obstruction
$H_0(F;\widetilde {\bf K}({\mathbb {Z}}[G]))$, and all elements of this group can be realised. By glueing on such an element, we can change the obstruction ![]() $[C_*(\widetilde {f})]\in \widetilde {K}_0({\mathbb {Z}}[\pi \times G])$ by any element in the image of
$[C_*(\widetilde {f})]\in \widetilde {K}_0({\mathbb {Z}}[\pi \times G])$ by any element in the image of ![]() $H_0(F;\widetilde {\bf K}({\mathbb {Z}}[G]))$. We will explain in the next paragraph that the natural map
$H_0(F;\widetilde {\bf K}({\mathbb {Z}}[G]))$. We will explain in the next paragraph that the natural map ![]() $H_0(F;\widetilde {\bf K}({\mathbb {Z}}[G]))\to H_0(Y;\widetilde {\bf K}({\mathbb {Z}}[G]))\to H_0(\pi; \widetilde {\bf K}({\mathbb {Z}}[G]))$ is surjective. Therefore
$H_0(F;\widetilde {\bf K}({\mathbb {Z}}[G]))\to H_0(Y;\widetilde {\bf K}({\mathbb {Z}}[G]))\to H_0(\pi; \widetilde {\bf K}({\mathbb {Z}}[G]))$ is surjective. Therefore ![]() $H_0(F;\widetilde {\bf K}({\mathbb {Z}}[G]))$ and
$H_0(F;\widetilde {\bf K}({\mathbb {Z}}[G]))$ and ![]() $H_0(\pi; \widetilde {\bf K}({\mathbb {Z}}[G]))$ have the same image in
$H_0(\pi; \widetilde {\bf K}({\mathbb {Z}}[G]))$ have the same image in ![]() $\widetilde {K}_0({\mathbb {Z}}[\pi \times G])$. Thus we conclude that the obstruction for
$\widetilde {K}_0({\mathbb {Z}}[\pi \times G])$. Thus we conclude that the obstruction for ![]() $G$-ANR pseudo-equivalence extension problem actually lies in the image of
$G$-ANR pseudo-equivalence extension problem actually lies in the image of ![]() $\widetilde {K}_0({\mathbb {Z}}[\pi \times G])$ in
$\widetilde {K}_0({\mathbb {Z}}[\pi \times G])$ in ![]() $\widetilde {K}_0^{top}({\mathbb {Z}}\pi \subset {\mathbb {Z}}[\pi \times G])$.
$\widetilde {K}_0^{top}({\mathbb {Z}}\pi \subset {\mathbb {Z}}[\pi \times G])$.
Carter's vanishing theorem [Reference Carter9] says that ![]() $K_{-i}({\mathbb {Z}}[G])=0$ for all finite groups
$K_{-i}({\mathbb {Z}}[G])=0$ for all finite groups ![]() $G$ and
$G$ and ![]() $i>1$. Therefore the spectral sequence that computes
$i>1$. Therefore the spectral sequence that computes ![]() $H_0(F;\widetilde {\bf K}({\mathbb {Z}}[G]))$ consists of only
$H_0(F;\widetilde {\bf K}({\mathbb {Z}}[G]))$ consists of only ![]() $H_0(F;\widetilde {K}_0({\mathbb {Z}}[G]))$ and
$H_0(F;\widetilde {K}_0({\mathbb {Z}}[G]))$ and ![]() $H_1(F;\widetilde {K}_{-1}({\mathbb {Z}}[G]))$. The same is true for
$H_1(F;\widetilde {K}_{-1}({\mathbb {Z}}[G]))$. The same is true for ![]() $H_0(Y;\widetilde {\bf K}({\mathbb {Z}}[G]))$ and
$H_0(Y;\widetilde {\bf K}({\mathbb {Z}}[G]))$ and ![]() $H_0(\pi; \widetilde {\bf K}({\mathbb {Z}}[G]))$. To show the surjection, therefore, we only need to show that
$H_0(\pi; \widetilde {\bf K}({\mathbb {Z}}[G]))$. To show the surjection, therefore, we only need to show that ![]() $H_i(F;\widetilde {K}_{-i}({\mathbb {Z}}[G]))\to H_i(Y;\widetilde {K}_{-i}({\mathbb {Z}}[G]))\to H_i(\pi; \widetilde {K}_{-i}({\mathbb {Z}}[G]))$ is surjective for
$H_i(F;\widetilde {K}_{-i}({\mathbb {Z}}[G]))\to H_i(Y;\widetilde {K}_{-i}({\mathbb {Z}}[G]))\to H_i(\pi; \widetilde {K}_{-i}({\mathbb {Z}}[G]))$ is surjective for ![]() $i=0,\,1$. The Smith condition implies that
$i=0,\,1$. The Smith condition implies that ![]() $\pi _iF\to \pi _iY$ is surjective for
$\pi _iF\to \pi _iY$ is surjective for ![]() $i=0,\,1$. This implies the surjections on
$i=0,\,1$. This implies the surjections on ![]() $H_i(*;\widetilde {K}_{-i}({\mathbb {Z}}[G]))$ for
$H_i(*;\widetilde {K}_{-i}({\mathbb {Z}}[G]))$ for ![]() $i=0,\,1$.
$i=0,\,1$.
4. Calculations and examples
Let ![]() $T(r)$ be the mapping torus of a map
$T(r)$ be the mapping torus of a map ![]() $S^d\to S^d$ of degree
$S^d\to S^d$ of degree ![]() $r$. Let
$r$. Let
be the projection map. For a finite group ![]() $G$ of order
$G$ of order ![]() $n$, we try to extend
$n$, we try to extend ![]() $F$ to be the fixed set of a finite, semi-free
$F$ to be the fixed set of a finite, semi-free ![]() $G$-CW-complex
$G$-CW-complex ![]() $X$, and extend
$X$, and extend ![]() $f$ to a pseudo-equivalence
$f$ to a pseudo-equivalence ![]() $g\colon X\to S^1$.
$g\colon X\to S^1$.
We have ![]() $\pi _1(Y)=\langle t\rangle =\{t^i\colon i\in {\mathbb {Z}}\}\cong {\mathbb {Z}}$, and the only non-trivial
$\pi _1(Y)=\langle t\rangle =\{t^i\colon i\in {\mathbb {Z}}\}\cong {\mathbb {Z}}$, and the only non-trivial ![]() ${\mathbb {Z}}\langle t\rangle$-homologyFootnote 2 of
${\mathbb {Z}}\langle t\rangle$-homologyFootnote 2 of ![]() $f$ is
$f$ is
For a prime ![]() $p$, we have
$p$, we have ![]() $H_d(f;{\mathbb {Z}}_p\langle t\rangle )=0$ if and only if
$H_d(f;{\mathbb {Z}}_p\langle t\rangle )=0$ if and only if ![]() $p|r$. Therefore, the Smith condition is satisfied for
$p|r$. Therefore, the Smith condition is satisfied for ![]() $G$ if and only if
$G$ if and only if
This is equivalent to ![]() $n$ dividing some power of
$n$ dividing some power of ![]() $r$. Under this assumption, the condition for the semi-free pseudo-equivalence extension is the vanishing of
$r$. Under this assumption, the condition for the semi-free pseudo-equivalence extension is the vanishing of
Proposition 4.1 Suppose ![]() $G$ is a finite group of order
$G$ is a finite group of order ![]() $n$. If
$n$. If ![]() $r$ is a multiple of
$r$ is a multiple of ![]() $n$, then
$n$, then ![]() $T(r)\to S^1$ has semi-free pseudo-equivalence extension. Moreover, if
$T(r)\to S^1$ has semi-free pseudo-equivalence extension. Moreover, if ![]() $G$ is abelian, then the converse is also true.
$G$ is abelian, then the converse is also true.
Example 1.1 in the introduction is a direct consequence of proposition 4.1. In fact, ![]() $T(p)$ is not only not the fixed set of a semi-free
$T(p)$ is not only not the fixed set of a semi-free ![]() ${\mathbb {Z}}_{p^2}$-action on homotopy circle, it is also not the fixed set of a semi-free
${\mathbb {Z}}_{p^2}$-action on homotopy circle, it is also not the fixed set of a semi-free ![]() ${\mathbb {Z}}_p\times {\mathbb {Z}}_p$-action. The proof given below also shows that
${\mathbb {Z}}_p\times {\mathbb {Z}}_p$-action. The proof given below also shows that ![]() $T(p^2)$ is not fixed under a semi-free
$T(p^2)$ is not fixed under a semi-free ![]() ${\mathbb {Z}}_p\times {\mathbb {Z}}_{p^2}$-action or
${\mathbb {Z}}_p\times {\mathbb {Z}}_{p^2}$-action or ![]() ${\mathbb {Z}}_p\times {\mathbb {Z}}_p\times {\mathbb {Z}}_p$-action, etc.
${\mathbb {Z}}_p\times {\mathbb {Z}}_p\times {\mathbb {Z}}_p$-action, etc.
Proof. We have the Bass–Heller–Swan decompositions [Reference Bass, Heller and Swan5]
We also have the pullbacks of rings [Reference Milnor13] (![]() $\Sigma _G=\sum _{g\in G}g$)
$\Sigma _G=\sum _{g\in G}g$)

that induce the Swan homomorphismsFootnote 3 that are compatible with the Bass–Heller–Swan decompositions
 \begin{align*} \partial &\colon K_1({\mathbb{Z}}_n\langle t\rangle)\to \widetilde{K}_0({\mathbb{Z}}[G]\langle t\rangle), \\ \partial &\colon K_1({\mathbb{Z}}_n)\to \widetilde{K}_0({\mathbb{Z}}[G]), \\ \partial &\colon K_0({\mathbb{Z}}_n)\to K_{{-}1}({\mathbb{Z}}[G]), \\ \partial &\colon NK_1({\mathbb{Z}}_n)\to NK_0({\mathbb{Z}}[G]). \end{align*}
\begin{align*} \partial &\colon K_1({\mathbb{Z}}_n\langle t\rangle)\to \widetilde{K}_0({\mathbb{Z}}[G]\langle t\rangle), \\ \partial &\colon K_1({\mathbb{Z}}_n)\to \widetilde{K}_0({\mathbb{Z}}[G]), \\ \partial &\colon K_0({\mathbb{Z}}_n)\to K_{{-}1}({\mathbb{Z}}[G]), \\ \partial &\colon NK_1({\mathbb{Z}}_n)\to NK_0({\mathbb{Z}}[G]). \end{align*}
We note that our obstruction is an image of the Swan homomorphism
Since ![]() $n$ divides
$n$ divides ![]() $r$, we get
$r$, we get ![]() $[rt-1]=[-1]$, which comes from
$[rt-1]=[-1]$, which comes from ![]() $K_1({\mathbb {Z}}\langle t\rangle )$. Therefore,
$K_1({\mathbb {Z}}\langle t\rangle )$. Therefore, ![]() $\partial [rt-1]=0$, and the sufficient part of the proposition.
$\partial [rt-1]=0$, and the sufficient part of the proposition.
For the necessary part, we note that the Smith condition requires ![]() $n$ dividing some power of
$n$ dividing some power of ![]() $r$. Now we identify the obstruction in the Bass–Heller–Swan decomposition. By the proof of the decomposition in [Reference Rosenberg21, Theorem 3.2.22], we write the automorphism of
$r$. Now we identify the obstruction in the Bass–Heller–Swan decomposition. By the proof of the decomposition in [Reference Rosenberg21, Theorem 3.2.22], we write the automorphism of ![]() $R\langle t\rangle$ as an automorphism of
$R\langle t\rangle$ as an automorphism of ![]() $R$ with a nilpotent correction
$R$ with a nilpotent correction
where ![]() $r-1$ is invertible and
$r-1$ is invertible and ![]() $(r-1)^{-1}r$ is nilpotent by the Smith condition. This shows that the element
$(r-1)^{-1}r$ is nilpotent by the Smith condition. This shows that the element ![]() $[rt-1]$ becomes
$[rt-1]$ becomes ![]() $([r-1],\,0,\,0,\,[(r-1)^{-1}r])$ in the decomposition, and our obstruction is
$([r-1],\,0,\,0,\,[(r-1)^{-1}r])$ in the decomposition, and our obstruction is ![]() $\partial [r-1]\in \widetilde {K}_0({\mathbb {Z}}[G])$ and
$\partial [r-1]\in \widetilde {K}_0({\mathbb {Z}}[G])$ and ![]() $\partial [(r-1)^{-1}r]\in NK_0({\mathbb {Z}}[G])$. We will concentrate on the vanishing of
$\partial [(r-1)^{-1}r]\in NK_0({\mathbb {Z}}[G])$. We will concentrate on the vanishing of ![]() $\partial [(r-1)^{-1}r]$, which is the image of
$\partial [(r-1)^{-1}r]$, which is the image of ![]() $(r-1)^{-1}(rt-1)\in K_1({\mathbb {Z}}_n\langle t\rangle )$ under the Swan homomorphism.
$(r-1)^{-1}(rt-1)\in K_1({\mathbb {Z}}_n\langle t\rangle )$ under the Swan homomorphism.
Now we assume ![]() $G$ is abelian. Then we have the determinant maps from
$G$ is abelian. Then we have the determinant maps from ![]() $K_1$ to the groups of invertible elements. The Swan homomorphism is part of an exact sequence compatible with the determinants
$K_1$ to the groups of invertible elements. The Swan homomorphism is part of an exact sequence compatible with the determinants

The vanishing of ![]() $\partial [(r-1)^{-1}r]$ implies that
$\partial [(r-1)^{-1}r]$ implies that ![]() $[(r-1)^{-1}(rt-1)]$ is in the image of
$[(r-1)^{-1}(rt-1)]$ is in the image of ![]() $\alpha$. This further implies that
$\alpha$. This further implies that ![]() $\det [(r-1)^{-1}(rt-1)]=(r-1)^{-1}(rt-1)$ is in the image of
$\det [(r-1)^{-1}(rt-1)]=(r-1)^{-1}(rt-1)$ is in the image of ![]() $\beta$. In the appendix of this paper, we prove that
$\beta$. In the appendix of this paper, we prove that ![]() $({\mathbb {Z}}[G]/\Sigma _G)\langle t\rangle ^*=({\mathbb {Z}}[G]/\Sigma _G)^*\langle t\rangle$. In other words, the units (i.e., multiplicatively invertible elements) in
$({\mathbb {Z}}[G]/\Sigma _G)\langle t\rangle ^*=({\mathbb {Z}}[G]/\Sigma _G)^*\langle t\rangle$. In other words, the units (i.e., multiplicatively invertible elements) in ![]() $({\mathbb {Z}}[G]/\Sigma _G)\langle t\rangle$ are monomials. If
$({\mathbb {Z}}[G]/\Sigma _G)\langle t\rangle$ are monomials. If ![]() $n$ does not divide
$n$ does not divide ![]() $r$, then
$r$, then ![]() $(r-1)^{-1}(rt-1)$ is not a monomial, and we get a contradiction. This proves the necessary part.
$(r-1)^{-1}(rt-1)$ is not a monomial, and we get a contradiction. This proves the necessary part.
The necessary part of the proof shows that, if ![]() $G$ is abelian and
$G$ is abelian and ![]() $r$ is not a multiple of
$r$ is not a multiple of ![]() $n$ (and
$n$ (and ![]() $n$ divides a power of
$n$ divides a power of ![]() $r$), then the
$r$), then the ![]() $K$-theory obstruction
$K$-theory obstruction ![]() $\partial [rt-1]\in \widetilde {K}_0({\mathbb {Z}}[G]\langle t\rangle )$ for
$\partial [rt-1]\in \widetilde {K}_0({\mathbb {Z}}[G]\langle t\rangle )$ for ![]() $T(r)\to S^1$ has nonzero component
$T(r)\to S^1$ has nonzero component ![]() $\partial [(r-1)^{-1}r]$ in the Bass Nil group
$\partial [(r-1)^{-1}r]$ in the Bass Nil group ![]() $NK_0({\mathbb {Z}}[G])$. The Nil group is the
$NK_0({\mathbb {Z}}[G])$. The Nil group is the ![]() $K$-theory of the additive category of finitely generated
$K$-theory of the additive category of finitely generated ![]() $R$-modules equipped with nilpotent endomorphisms. It is introduced in [Reference Bass4] to account for the difference between the
$R$-modules equipped with nilpotent endomorphisms. It is introduced in [Reference Bass4] to account for the difference between the ![]() $K$-theory of a ring
$K$-theory of a ring ![]() $R$ and its polynomial extension
$R$ and its polynomial extension ![]() $R[t]$ or the Laurent extension
$R[t]$ or the Laurent extension ![]() $R\langle t\rangle$. In case
$R\langle t\rangle$. In case ![]() $\pi ={\mathbb {Z}}=\langle t\rangle$ in the exact sequence (3.1), the map
$\pi ={\mathbb {Z}}=\langle t\rangle$ in the exact sequence (3.1), the map ![]() $H_0({\mathbb {Z}};\widetilde {\bf K}({\mathbb {Z}}[G]))\to \widetilde {K}_0({\mathbb {Z}}[{\mathbb {Z}}\times G])$ is exactly the comparison (i.e., the inclusion in (4.1)) between
$H_0({\mathbb {Z}};\widetilde {\bf K}({\mathbb {Z}}[G]))\to \widetilde {K}_0({\mathbb {Z}}[{\mathbb {Z}}\times G])$ is exactly the comparison (i.e., the inclusion in (4.1)) between ![]() $\widetilde {K}_0({\mathbb {Z}}[G])\oplus K_{-1}({\mathbb {Z}}[G])$ and
$\widetilde {K}_0({\mathbb {Z}}[G])\oplus K_{-1}({\mathbb {Z}}[G])$ and ![]() $\widetilde {K}_0({\mathbb {Z}}[G]\langle t\rangle )$. Therefore, the component
$\widetilde {K}_0({\mathbb {Z}}[G]\langle t\rangle )$. Therefore, the component ![]() $\partial [(r-1)^{-1}r]$ in the
$\partial [(r-1)^{-1}r]$ in the ![]() $NK_0({\mathbb {Z}}[G])$ part of
$NK_0({\mathbb {Z}}[G])$ part of ![]() $\widetilde {K}_0({\mathbb {Z}}[G]\langle t\rangle )$, being nonzero, implies that the image of the obstruction
$\widetilde {K}_0({\mathbb {Z}}[G]\langle t\rangle )$, being nonzero, implies that the image of the obstruction ![]() $\partial [rt-1]\in \widetilde {K}_0({\mathbb {Z}}[G]\langle t\rangle )$ in
$\partial [rt-1]\in \widetilde {K}_0({\mathbb {Z}}[G]\langle t\rangle )$ in ![]() $\widetilde {K}_0^{top}({\mathbb {Z}}[{\mathbb {Z}}]\subset {\mathbb {Z}}[{\mathbb {Z}}\times G])$ is nonzero. This image is the
$\widetilde {K}_0^{top}({\mathbb {Z}}[{\mathbb {Z}}]\subset {\mathbb {Z}}[{\mathbb {Z}}\times G])$ is nonzero. This image is the ![]() $K$-theory obstruction in theorem 3.2. Therefore, the map
$K$-theory obstruction in theorem 3.2. Therefore, the map ![]() $T(r)\to S^1$ does not even have semi-free pseudo-equivalence extension in the
$T(r)\to S^1$ does not even have semi-free pseudo-equivalence extension in the ![]() $G$-ANR category.
$G$-ANR category.
In short, there are examples of non-existence of semi-free extension in the ![]() $G$-ANR category if and only if the order of
$G$-ANR category if and only if the order of ![]() $G$ has a square factor.
$G$ has a square factor.
For the sufficiency part of proposition 4.1, we also give an explicit construction for the special case that ![]() $G$ acts freely on a sphere. There is, for example, the case
$G$ acts freely on a sphere. There is, for example, the case ![]() $G$ is a cyclic group acting on the circle
$G$ is a cyclic group acting on the circle ![]() $S^1$ by the standard rotations.
$S^1$ by the standard rotations.
Example 4.2 Suppose ![]() $r$ is a multiple of
$r$ is a multiple of ![]() $n=|G|$, and
$n=|G|$, and ![]() $G$ acts freely on a sphere
$G$ acts freely on a sphere ![]() $S^e$. By replacing
$S^e$. By replacing ![]() $S^e$ with
$S^e$ with ![]() $S^e*S^e=S^{2e+1}$ and taking the join of
$S^e*S^e=S^{2e+1}$ and taking the join of ![]() $G$-actions, we may further assume that the action preserves the orientation of
$G$-actions, we may further assume that the action preserves the orientation of ![]() $S^e$. Consider the join
$S^e$. Consider the join ![]() $S^{d+e+1}=S^d*S^e$, with the trivial
$S^{d+e+1}=S^d*S^e$, with the trivial ![]() $G$-action on
$G$-action on ![]() $S^d$ and the given
$S^d$ and the given ![]() $G$-action on
$G$-action on ![]() $S^e$. The action is semi-free with fixed set
$S^e$. The action is semi-free with fixed set ![]() $(S^{d+e+1})^G=S^d$. Let
$(S^{d+e+1})^G=S^d$. Let ![]() $h$ be a self map of
$h$ be a self map of ![]() $S^{d+e+1}$ that is the join of the degree
$S^{d+e+1}$ that is the join of the degree ![]() $r$ map on
$r$ map on ![]() $S^d$ and the identity map on
$S^d$ and the identity map on ![]() $S^e$. Then
$S^e$. Then ![]() $h$ is a
$h$ is a ![]() $G$-map of degree
$G$-map of degree ![]() $r$. For any free point
$r$. For any free point ![]() $x\in S^{d+e+1}-S^d$, let
$x\in S^{d+e+1}-S^d$, let ![]() $D$ be a small disk around
$D$ be a small disk around ![]() $x$, such that the action of
$x$, such that the action of ![]() $G$ on
$G$ on ![]() $D$ gives disjoint copies. By shrinking the boundary
$D$ gives disjoint copies. By shrinking the boundary ![]() $\partial D$ of
$\partial D$ of ![]() $D$ to the point
$D$ to the point ![]() $x$, we get a map
$x$, we get a map ![]() $S^{d+e+1}\to S^{d+e+1}\vee _x(D/\partial D)$. Combining the identity on
$S^{d+e+1}\to S^{d+e+1}\vee _x(D/\partial D)$. Combining the identity on ![]() $S^{d+e+1}$ and a homeomorphism
$S^{d+e+1}$ and a homeomorphism ![]() $D/\partial D\to S^{d+e+1}$, we get a map
$D/\partial D\to S^{d+e+1}$, we get a map ![]() $S^{d+e+1}\to S^{d+e+1}\vee _xS^{d+e+1}\to S^{d+e+1}$. If we do this for all
$S^{d+e+1}\to S^{d+e+1}\vee _xS^{d+e+1}\to S^{d+e+1}$. If we do this for all ![]() $G$ copies of
$G$ copies of ![]() $D$, then we get a
$D$, then we get a ![]() $G$-map
$G$-map ![]() $h'\colon S^{d+e+1}\to S^{d+e+1}\vee _{Gx}G(D/\partial D)\to S^{d+e+1}$. By choosing a suitable homeomorphism
$h'\colon S^{d+e+1}\to S^{d+e+1}\vee _{Gx}G(D/\partial D)\to S^{d+e+1}$. By choosing a suitable homeomorphism ![]() $D/\partial D\to S^{d+e+1}$, the degree of
$D/\partial D\to S^{d+e+1}$, the degree of ![]() $h'$ is
$h'$ is ![]() $r+n$ or
$r+n$ or ![]() $r-n$. By repeating the construction for several points in
$r-n$. By repeating the construction for several points in ![]() $S^{d+e+1}-S^d$, we get a
$S^{d+e+1}-S^d$, we get a ![]() $G$-map
$G$-map ![]() $h''\colon S^{d+e+1}\to S^{d+e+1}$ of degree
$h''\colon S^{d+e+1}\to S^{d+e+1}$ of degree ![]() $r+an$ for any integer
$r+an$ for any integer ![]() $a$. Since
$a$. Since ![]() $r$ is a multiple of
$r$ is a multiple of ![]() $n$, we take
$n$, we take ![]() $a=-{r}/{n}$ and get a
$a=-{r}/{n}$ and get a ![]() $G$-map
$G$-map ![]() $h''\colon S^{d+e+1}\to S^{d+e+1}$ of degree
$h''\colon S^{d+e+1}\to S^{d+e+1}$ of degree ![]() $0$. On the other hand, since the modification happens only on the free part of
$0$. On the other hand, since the modification happens only on the free part of ![]() $S^{d+e+1}$, the restriction of
$S^{d+e+1}$, the restriction of ![]() $h''$ on the fixed part is still the original degree
$h''$ on the fixed part is still the original degree ![]() $r$ map
$r$ map ![]() $S^d\to S^d$. The mapping torus
$S^d\to S^d$. The mapping torus ![]() $T(h'')$ has semi-free
$T(h'')$ has semi-free ![]() $G$-action with fixed set
$G$-action with fixed set ![]() $T(r)$, and
$T(r)$, and ![]() $T(h'')\to S^1$ extends
$T(h'')\to S^1$ extends ![]() $T(r)\to S^1$. Moreover, since the degree of
$T(r)\to S^1$. Moreover, since the degree of ![]() $h''$ is
$h''$ is ![]() $0$, the map
$0$, the map ![]() $T(h'')\to S^1$ is a homotopy equivalence.
$T(h'')\to S^1$ is a homotopy equivalence.
Now we turn to another application showing other phenomena. Suppose ![]() $n$ is not a prime power. Then
$n$ is not a prime power. Then ![]() $n=n_1n_2$, with
$n=n_1n_2$, with ![]() $n_1,\,n_2>1$ and coprime. Let
$n_1,\,n_2>1$ and coprime. Let ![]() $a$ satisfy
$a$ satisfy ![]() $a=1$ mod
$a=1$ mod ![]() $n_1$ and
$n_1$ and ![]() $a=0$ mod
$a=0$ mod ![]() $n_2$. Then
$n_2$. Then ![]() $b=1-a$ satisfies
$b=1-a$ satisfies ![]() $b=0$ mod
$b=0$ mod ![]() $n_1$ and
$n_1$ and ![]() $b=1$ mod
$b=1$ mod ![]() $n_2$. Let
$n_2$. Let ![]() $T(a,\,b)$ be the double torus of two maps of
$T(a,\,b)$ be the double torus of two maps of ![]() $S^d$ to itself of respective degrees
$S^d$ to itself of respective degrees ![]() $a,\,b$. Let
$a,\,b$. Let ![]() $f\colon T(a,\,b)\to S^1$ be the projection map. We consider the pseudo-equivalence extension of
$f\colon T(a,\,b)\to S^1$ be the projection map. We consider the pseudo-equivalence extension of ![]() $f$ for the action by the cyclic group
$f$ for the action by the cyclic group ![]() $G={\mathbb {Z}}_n$.
$G={\mathbb {Z}}_n$.
Similar to the mapping torus in the earlier example, the only non-trivial ![]() ${\mathbb {Z}}\langle t\rangle$-homology of
${\mathbb {Z}}\langle t\rangle$-homology of ![]() $f$ is
$f$ is
By ![]() $(at-b)(at^{-1}-b)=a^2=1$ mod
$(at-b)(at^{-1}-b)=a^2=1$ mod ![]() $n_1$, and
$n_1$, and ![]() $(at-b)(at^{-1}-b)=b^2=1$ mod
$(at-b)(at^{-1}-b)=b^2=1$ mod ![]() $n_2$, and
$n_2$, and ![]() $n_1,\,n_2$ coprime, we know
$n_1,\,n_2$ coprime, we know ![]() $at-b$ is invertible in
$at-b$ is invertible in ![]() ${\mathbb {Z}}_n\langle t\rangle$. This verifies the Smith condition for
${\mathbb {Z}}_n\langle t\rangle$. This verifies the Smith condition for ![]() $f$.
$f$.
Proposition 4.3 Suppose ![]() $G={\mathbb {Z}}_n$ is the cyclic group of not prime power order
$G={\mathbb {Z}}_n$ is the cyclic group of not prime power order ![]() $n$. Then for suitable
$n$. Then for suitable ![]() $a,\,b,$ the map
$a,\,b,$ the map ![]() $T(a,\,b)\to S^1$ satisfies the Smith condition for
$T(a,\,b)\to S^1$ satisfies the Smith condition for ![]() $G,$ but has no semi-free pseudo-equivalence extension.
$G,$ but has no semi-free pseudo-equivalence extension.
Example 1.2 in the introduction is a direct consequence of proposition 4.3. The proof shows that the obstruction effectively lies in the direct summand ![]() $K_{-1}({\mathbb {Z}}[{\mathbb {Z}}_n])\subset \widetilde {K}_0({\mathbb {Z}}[{\mathbb {Z}}_n]\langle t\rangle )$ according to (4.1). By theorem 3.2 and the explanation after the proof of proposition 4.1, this implies that, although
$K_{-1}({\mathbb {Z}}[{\mathbb {Z}}_n])\subset \widetilde {K}_0({\mathbb {Z}}[{\mathbb {Z}}_n]\langle t\rangle )$ according to (4.1). By theorem 3.2 and the explanation after the proof of proposition 4.1, this implies that, although ![]() $T(a,\,b)\to S^1$ has no semi-free pseudo-equivalence extension in the
$T(a,\,b)\to S^1$ has no semi-free pseudo-equivalence extension in the ![]() $G$-CW-complex category, the map does have semi-free pseudo-equivalence extension in the
$G$-CW-complex category, the map does have semi-free pseudo-equivalence extension in the ![]() $G$-ANR category.
$G$-ANR category.
Proof. The obstruction for pseudo-equivalence extension is
This is the image of
under the Swan homomorphism. We carry out the argument similarly to proposition 4.1.
We have ![]() $a(1-a)=ab=0$ mod
$a(1-a)=ab=0$ mod ![]() $n$. This means
$n$. This means ![]() $a^2=a$ mod
$a^2=a$ mod ![]() $n$, or
$n$, or ![]() $a$ is an idempotent mod
$a$ is an idempotent mod ![]() $n$. In particular,
$n$. In particular, ![]() $a{\mathbb {Z}}_n$ is a projective
$a{\mathbb {Z}}_n$ is a projective ![]() ${\mathbb {Z}}_n$-module. By the proof of [Reference Rosenberg21, Theorem 3.2.22], the obstruction
${\mathbb {Z}}_n$-module. By the proof of [Reference Rosenberg21, Theorem 3.2.22], the obstruction ![]() $[at-b]$ on the left of (4.2) corresponds to
$[at-b]$ on the left of (4.2) corresponds to ![]() $(0,\,[a{\mathbb {Z}}_n],\,0,\,0)$ on the right, with
$(0,\,[a{\mathbb {Z}}_n],\,0,\,0)$ on the right, with ![]() $[a{\mathbb {Z}}_n]\in K_0({\mathbb {Z}}_n)$. Therefore our obstruction is the image
$[a{\mathbb {Z}}_n]\in K_0({\mathbb {Z}}_n)$. Therefore our obstruction is the image ![]() $\partial [a{\mathbb {Z}}_n]\in K_{-1}({\mathbb {Z}}[{\mathbb {Z}}_n])$ under the Swan homomorphism. By the calculation of [Reference Bass and Murthy6], this element is a non-divisible element of
$\partial [a{\mathbb {Z}}_n]\in K_{-1}({\mathbb {Z}}[{\mathbb {Z}}_n])$ under the Swan homomorphism. By the calculation of [Reference Bass and Murthy6], this element is a non-divisible element of ![]() $K_{-1}({\mathbb {Z}}[{\mathbb {Z}}_n])$.
$K_{-1}({\mathbb {Z}}[{\mathbb {Z}}_n])$.
The Swan homomorphism fits into an exact sequence
 \begin{align*} &\widetilde{K}_0({\mathbb{Z}})\oplus \widetilde{K}_0({\mathbb{Z}}[{\mathbb{Z}}_n]/\Sigma_{{\mathbb{Z}}_n}) \to \widetilde{K}_0({\mathbb{Z}}_n) \xrightarrow{\partial} K_{{-}1}({\mathbb{Z}}[{\mathbb{Z}}_n]) \\ &\quad\to K_{{-}1}({\mathbb{Z}})\oplus K_{{-}1}({\mathbb{Z}}[{\mathbb{Z}}_n]/\Sigma_{{\mathbb{Z}}_n}) \to K_{{-}1}({\mathbb{Z}}_n). \end{align*}
\begin{align*} &\widetilde{K}_0({\mathbb{Z}})\oplus \widetilde{K}_0({\mathbb{Z}}[{\mathbb{Z}}_n]/\Sigma_{{\mathbb{Z}}_n}) \to \widetilde{K}_0({\mathbb{Z}}_n) \xrightarrow{\partial} K_{{-}1}({\mathbb{Z}}[{\mathbb{Z}}_n]) \\ &\quad\to K_{{-}1}({\mathbb{Z}})\oplus K_{{-}1}({\mathbb{Z}}[{\mathbb{Z}}_n]/\Sigma_{{\mathbb{Z}}_n}) \to K_{{-}1}({\mathbb{Z}}_n). \end{align*}
Here the image of ![]() $\widetilde {K}_0({\mathbb {Z}}_n)$ is the same as the image of
$\widetilde {K}_0({\mathbb {Z}}_n)$ is the same as the image of ![]() $K_0({\mathbb {Z}}_n)$. By [Reference Bass and Murthy6, Reference Swan and Evans26], we have
$K_0({\mathbb {Z}}_n)$. By [Reference Bass and Murthy6, Reference Swan and Evans26], we have ![]() $\widetilde {K}_0({\mathbb {Z}})=K_{-1}({\mathbb {Z}})=0$,
$\widetilde {K}_0({\mathbb {Z}})=K_{-1}({\mathbb {Z}})=0$, ![]() $\widetilde {K}_0({\mathbb {Z}}[{\mathbb {Z}}_n]/\Sigma _{{\mathbb {Z}}_n})$ is finite, and
$\widetilde {K}_0({\mathbb {Z}}[{\mathbb {Z}}_n]/\Sigma _{{\mathbb {Z}}_n})$ is finite, and ![]() $\widetilde {K}_0({\mathbb {Z}}_n)$ and
$\widetilde {K}_0({\mathbb {Z}}_n)$ and ![]() $K_{-1}({\mathbb {Z}}[{\mathbb {Z}}_n]/\Sigma _{{\mathbb {Z}}_n})$ are free abelian. Therefore
$K_{-1}({\mathbb {Z}}[{\mathbb {Z}}_n]/\Sigma _{{\mathbb {Z}}_n})$ are free abelian. Therefore ![]() $\widetilde {K}_0({\mathbb {Z}}_n)$ embeds as a direct summand of
$\widetilde {K}_0({\mathbb {Z}}_n)$ embeds as a direct summand of ![]() $K_{-1}({\mathbb {Z}}[{\mathbb {Z}}_n])$.
$K_{-1}({\mathbb {Z}}[{\mathbb {Z}}_n])$.
If ![]() $n=p_1^{m_1}\dots p_l^{m_l}$ is the decomposition into distinct primes, then
$n=p_1^{m_1}\dots p_l^{m_l}$ is the decomposition into distinct primes, then
We note that the projective ![]() ${\mathbb {Z}}_n$-module
${\mathbb {Z}}_n$-module ![]() $a{\mathbb {Z}}_n$ is isomorphic to
$a{\mathbb {Z}}_n$ is isomorphic to ![]() ${\mathbb {Z}}_{n_1}$. Under the isomorphism
${\mathbb {Z}}_{n_1}$. Under the isomorphism ![]() $K_0({\mathbb {Z}}_n)=K_0({\mathbb {Z}}_{n_1})\oplus K_0({\mathbb {Z}}_{n_2})$,
$K_0({\mathbb {Z}}_n)=K_0({\mathbb {Z}}_{n_1})\oplus K_0({\mathbb {Z}}_{n_2})$, ![]() $[a{\mathbb {Z}}_n]\in K_0({\mathbb {Z}}_n)$ corresponds to
$[a{\mathbb {Z}}_n]\in K_0({\mathbb {Z}}_n)$ corresponds to ![]() $([{\mathbb {Z}}_{n_1}],\,0)\in K_0({\mathbb {Z}}_{n_1})\oplus K_0({\mathbb {Z}}_{n_2})$. If we start by choosing
$([{\mathbb {Z}}_{n_1}],\,0)\in K_0({\mathbb {Z}}_{n_1})\oplus K_0({\mathbb {Z}}_{n_2})$. If we start by choosing ![]() $n_1=p_1^{m_1}$ and
$n_1=p_1^{m_1}$ and ![]() $n_2={n}/{n_1}$, then the obstruction for
$n_2={n}/{n_1}$, then the obstruction for ![]() $f\colon T(a,\,b)\to S^1$ is the image of
$f\colon T(a,\,b)\to S^1$ is the image of ![]() $(1,\,0,\,\dots,\,0)\in K_0({\mathbb {Z}}_n)$ under the injective Swan homomorphism. Similarly, we can make other choices of
$(1,\,0,\,\dots,\,0)\in K_0({\mathbb {Z}}_n)$ under the injective Swan homomorphism. Similarly, we can make other choices of ![]() $n_1,\,n_2$, such that the obstructions for the corresponding
$n_1,\,n_2$, such that the obstructions for the corresponding ![]() $f\colon T(a,\,b)\to S^1$ are the images of other unit vectors, in
$f\colon T(a,\,b)\to S^1$ are the images of other unit vectors, in ![]() $K_0({\mathbb {Z}}_n)$. The upshot is that, if
$K_0({\mathbb {Z}}_n)$. The upshot is that, if ![]() $n$ is not a prime power, then we can construct
$n$ is not a prime power, then we can construct ![]() $f\colon F\to S^1$ satisfying the Smith condition, and the obstruction is a nonzero element in
$f\colon F\to S^1$ satisfying the Smith condition, and the obstruction is a nonzero element in ![]() $K_{-1}({\mathbb {Z}}[{\mathbb {Z}}_n])$.
$K_{-1}({\mathbb {Z}}[{\mathbb {Z}}_n])$.
The examples in propositions 4.1 and 4.3 can fit into other spaces.
Theorem 4.4 Suppose ![]() $Y$ is a finite CW-complex with torsion free
$Y$ is a finite CW-complex with torsion free ![]() $\pi =\pi _1(Y)$. Suppose the Farrell–Jones conjecture holds for
$\pi =\pi _1(Y)$. Suppose the Farrell–Jones conjecture holds for ![]() $\pi$. Suppose
$\pi$. Suppose ![]() $G$ is finite cyclic, and
$G$ is finite cyclic, and ![]() $|G|$ is not a prime and has no square factor. Then there is a map
$|G|$ is not a prime and has no square factor. Then there is a map ![]() $F\to Y$ satisfying the Smith condition but has no semi-free pseudo-equivalence extension, if and only if
$F\to Y$ satisfying the Smith condition but has no semi-free pseudo-equivalence extension, if and only if ![]() $H_1\pi \ne 0$.
$H_1\pi \ne 0$.
The condition on the order of ![]() $G$ is that
$G$ is that ![]() $|G|$ is a product of more than one distinct primes.
$|G|$ is a product of more than one distinct primes.
Proof. The hypothesis that ![]() $|G|$ has no square factor implies that
$|G|$ has no square factor implies that ![]() $NK_0({\mathbb {Z}}[G])=0$. Then for torsion free
$NK_0({\mathbb {Z}}[G])=0$. Then for torsion free ![]() $\pi$, the Farrell–Jones conjecture asserts that
$\pi$, the Farrell–Jones conjecture asserts that
If ![]() $H_1\pi =0$, then
$H_1\pi =0$, then ![]() $H_1(\pi; K_{-1}({\mathbb {Z}}[G]))=0$, and the Swan homomorphism relevant to constructing the
$H_1(\pi; K_{-1}({\mathbb {Z}}[G]))=0$, and the Swan homomorphism relevant to constructing the ![]() $G$-action lies in the
$G$-action lies in the ![]() $K_0({\mathbb {Z}}[G])$ part. Thus we are reduced to the classical Swan homomorphism. By [Reference Swan25, Corollary 6.1], the Swan homomorphism vanishes for cyclic
$K_0({\mathbb {Z}}[G])$ part. Thus we are reduced to the classical Swan homomorphism. By [Reference Swan25, Corollary 6.1], the Swan homomorphism vanishes for cyclic ![]() $G$.
$G$.
If ![]() $H_1\pi \ne 0$, then a generator of
$H_1\pi \ne 0$, then a generator of ![]() $H_1\pi =H_1Y$ can be represented by a loop
$H_1\pi =H_1Y$ can be represented by a loop ![]() $S^1\to Y$. By proposition 4.3, there is a map
$S^1\to Y$. By proposition 4.3, there is a map ![]() $f\colon F\to S^1$ satisfying the Smith condition but has non-vanishing pseudo-equivalence extension obstruction
$f\colon F\to S^1$ satisfying the Smith condition but has non-vanishing pseudo-equivalence extension obstruction ![]() $[C(\widetilde {f})]\in \widetilde {K}_{-1}({\mathbb {Z}}[G])=H_1(S^1,\,\widetilde {K}_{-1}({\mathbb {Z}}[G]))\subset \widetilde {K}_0({\mathbb {Z}}[G]\langle t\rangle )$, where
$[C(\widetilde {f})]\in \widetilde {K}_{-1}({\mathbb {Z}}[G])=H_1(S^1,\,\widetilde {K}_{-1}({\mathbb {Z}}[G]))\subset \widetilde {K}_0({\mathbb {Z}}[G]\langle t\rangle )$, where ![]() $t$ is the generator of
$t$ is the generator of ![]() $\pi _1(S^1)$. We use the loop
$\pi _1(S^1)$. We use the loop ![]() $S^1\to Y$ to extend
$S^1\to Y$ to extend ![]() $f$ to
$f$ to ![]() $f'\colon F\cup _{S_1}Y\to Y$. Then
$f'\colon F\cup _{S_1}Y\to Y$. Then ![]() $f'$ also satisfies the Smith condition, and the pseudo-equivalence extension obstruction
$f'$ also satisfies the Smith condition, and the pseudo-equivalence extension obstruction ![]() $[C(\widetilde {f'})]$ for
$[C(\widetilde {f'})]$ for ![]() $f'$ is the image of
$f'$ is the image of ![]() $[C(\widetilde {f})]$ under the homomorphism
$[C(\widetilde {f})]$ under the homomorphism
Since the circle represents a generator of ![]() $H_1\pi$, the image obstruction is still nonzero.
$H_1\pi$, the image obstruction is still nonzero.
Theorem 4.5 Suppose ![]() $Y$ is a finite CW-complex with torsion free
$Y$ is a finite CW-complex with torsion free ![]() $\pi =\pi _1(Y)$, the Farrell–Jones conjecture holds for
$\pi =\pi _1(Y)$, the Farrell–Jones conjecture holds for ![]() $\pi$, and
$\pi$, and ![]() $\pi$ has maximal infinite cyclic subgroup
$\pi$ has maximal infinite cyclic subgroup ![]() $C,$ such that the normaliser of
$C,$ such that the normaliser of ![]() $C$ is
$C$ is ![]() $C$ itself. Suppose
$C$ itself. Suppose ![]() $G$ is a finite abelian group, such that
$G$ is a finite abelian group, such that ![]() $|G|$ has square factor. Then there is a map
$|G|$ has square factor. Then there is a map ![]() $F\to Y$ satisfying the Smith condition, but has no semi-free pseudo-equivalence extension.
$F\to Y$ satisfying the Smith condition, but has no semi-free pseudo-equivalence extension.
The theorem implies that, if every map ![]() $F\to Y$ satisfying the Smith condition has semi-free pseudo-equivalence extension for
$F\to Y$ satisfying the Smith condition has semi-free pseudo-equivalence extension for ![]() ${\mathbb {Z}}_n$-action, then
${\mathbb {Z}}_n$-action, then ![]() $n$ is a product of at least two distinct primes.
$n$ is a product of at least two distinct primes.
Proof. The proof is similar to theorem 4.4, except that the Farrell–Jones conjecture is more complicated because ![]() $NK_0({\mathbb {Z}}[G])\ne 0$. In this case, by [Reference Bartels3], the formula for
$NK_0({\mathbb {Z}}[G])\ne 0$. In this case, by [Reference Bartels3], the formula for ![]() $K_0({\mathbb {Z}}[\pi \times G])$ has another factor (i.e., a direct summand), namely
$K_0({\mathbb {Z}}[\pi \times G])$ has another factor (i.e., a direct summand), namely ![]() $H_*^{\pi \times G}(E_{{\mathcal {V}}{\mathcal {C}}}(\pi \times G),\, E_{{\mathcal {F}}{\mathcal {I}}{\mathcal {N}}}(\pi \times G); {\bf K})$. Here
$H_*^{\pi \times G}(E_{{\mathcal {V}}{\mathcal {C}}}(\pi \times G),\, E_{{\mathcal {F}}{\mathcal {I}}{\mathcal {N}}}(\pi \times G); {\bf K})$. Here ![]() $H_*^{\pi \times G}$ is the homology over the category of
$H_*^{\pi \times G}$ is the homology over the category of ![]() $\pi \times G$-orbits (by Davis and Lück [Reference Davis and Lück10]),
$\pi \times G$-orbits (by Davis and Lück [Reference Davis and Lück10]), ![]() $E_{{\mathcal {V}}{\mathcal {C}}}$ is the classifying space for the family of virtually cyclic subgroups,
$E_{{\mathcal {V}}{\mathcal {C}}}$ is the classifying space for the family of virtually cyclic subgroups, ![]() $E_{{\mathcal {F}}{\mathcal {I}}{\mathcal {N}}}$ is the classifying space for finite subgroups, and
$E_{{\mathcal {F}}{\mathcal {I}}{\mathcal {N}}}$ is the classifying space for finite subgroups, and ![]() ${\bf K}$ is the non-connective
${\bf K}$ is the non-connective ![]() $K$-theory spectrum of the isotropy groups of points. Note that this relative homology is concentrated on points with infinite isotropy. Under the condition of
$K$-theory spectrum of the isotropy groups of points. Note that this relative homology is concentrated on points with infinite isotropy. Under the condition of ![]() $C$ being normalised only by itself, by [Reference Farrell and Jones11], the set of points with isotropy
$C$ being normalised only by itself, by [Reference Farrell and Jones11], the set of points with isotropy ![]() $C$ contributes two copies of
$C$ contributes two copies of ![]() $NK_0({\mathbb {Z}}[G])$, and the glueing trick using our example from proposition 4.1 constructs an obstructed example.
$NK_0({\mathbb {Z}}[G])$, and the glueing trick using our example from proposition 4.1 constructs an obstructed example.
Since this element is nonzero in ![]() $\widetilde {K}_0^{G,top}$ in the sense of [Reference Quinn20, Reference Steinberger23], it even obstructs the existence of an ANR-action.
$\widetilde {K}_0^{G,top}$ in the sense of [Reference Quinn20, Reference Steinberger23], it even obstructs the existence of an ANR-action.
Finally, we study the pseudo-equivalence extension of a map between ![]() $3$-dimensional lens spaces.
$3$-dimensional lens spaces.
Proposition 4.6 Suppose ![]() $f\colon L(kp;1) \to L(p;1)$ is a degree
$f\colon L(kp;1) \to L(p;1)$ is a degree ![]() $d$ map, where
$d$ map, where ![]() $p$ is a prime not dividing
$p$ is a prime not dividing ![]() $d$ and
$d$ and ![]() $k$. Then
$k$. Then ![]() $f$ has a pseudo-equivalence extension for
$f$ has a pseudo-equivalence extension for ![]() ${\mathbb {Z}}_p$-action if and only if
${\mathbb {Z}}_p$-action if and only if ![]() $d^{p-1}=k^{p-1}$ mod
$d^{p-1}=k^{p-1}$ mod ![]() $p^2$.
$p^2$.
Proof. The obstruction lies in ![]() $\widetilde {K}_0({\mathbb {Z}}[{\mathbb {Z}}_p\times {\mathbb {Z}}_p])$, where the first
$\widetilde {K}_0({\mathbb {Z}}[{\mathbb {Z}}_p\times {\mathbb {Z}}_p])$, where the first ![]() ${\mathbb {Z}}_p=\pi _1(L(p;1))$, and the second
${\mathbb {Z}}_p=\pi _1(L(p;1))$, and the second ![]() ${\mathbb {Z}}_p$ is the action group. The obstruction is given by the chain complex of the map
${\mathbb {Z}}_p$ is the action group. The obstruction is given by the chain complex of the map ![]() $\widetilde {f}\colon \widetilde {L}(kp;1)\to \widetilde {L}(p;1)$ obtained by pulling back along the universal cover
$\widetilde {f}\colon \widetilde {L}(kp;1)\to \widetilde {L}(p;1)$ obtained by pulling back along the universal cover ![]() $\widetilde {L}(p;1)=S^3\to L(p;1)$. We have the long exact sequence
$\widetilde {L}(p;1)=S^3\to L(p;1)$. We have the long exact sequence
 \begin{align*} & H_3(L(kp;1);{\mathbb{Z}}[{\mathbb{Z}}_p])={\mathbb{Z}}\to H_3(L(p;1);{\mathbb{Z}}[{\mathbb{Z}}_p])={\mathbb{Z}}\to H_3(f;{\mathbb{Z}}[{\mathbb{Z}}_p])={\mathbb{Z}}_d \\ &\quad\to H_2(L(kp;1);{\mathbb{Z}}[{\mathbb{Z}}_p])=0\to H_2(L(p;1);{\mathbb{Z}}[{\mathbb{Z}}_p])=0\to H_2(f;{\mathbb{Z}}[{\mathbb{Z}}_p])={\mathbb{Z}}_k \\ &\quad\to H_1(L(kp;1);{\mathbb{Z}}[{\mathbb{Z}}_p])={\mathbb{Z}}_{kp}\to H_1(L(p;1);{\mathbb{Z}}[{\mathbb{Z}}_p])={\mathbb{Z}}_p\to H_1(f;{\mathbb{Z}}[{\mathbb{Z}}_p])=0. \end{align*}
\begin{align*} & H_3(L(kp;1);{\mathbb{Z}}[{\mathbb{Z}}_p])={\mathbb{Z}}\to H_3(L(p;1);{\mathbb{Z}}[{\mathbb{Z}}_p])={\mathbb{Z}}\to H_3(f;{\mathbb{Z}}[{\mathbb{Z}}_p])={\mathbb{Z}}_d \\ &\quad\to H_2(L(kp;1);{\mathbb{Z}}[{\mathbb{Z}}_p])=0\to H_2(L(p;1);{\mathbb{Z}}[{\mathbb{Z}}_p])=0\to H_2(f;{\mathbb{Z}}[{\mathbb{Z}}_p])={\mathbb{Z}}_k \\ &\quad\to H_1(L(kp;1);{\mathbb{Z}}[{\mathbb{Z}}_p])={\mathbb{Z}}_{kp}\to H_1(L(p;1);{\mathbb{Z}}[{\mathbb{Z}}_p])={\mathbb{Z}}_p\to H_1(f;{\mathbb{Z}}[{\mathbb{Z}}_p])=0. \end{align*}
We note that ![]() $H_*(f;{\mathbb {Z}}[{\mathbb {Z}}_p])=0,\,0,\,{\mathbb {Z}}_k,\,{\mathbb {Z}}_d,\,0,\,\dots$ are trivial
$H_*(f;{\mathbb {Z}}[{\mathbb {Z}}_p])=0,\,0,\,{\mathbb {Z}}_k,\,{\mathbb {Z}}_d,\,0,\,\dots$ are trivial ![]() ${\mathbb {Z}}[{\mathbb {Z}}_p\times {\mathbb {Z}}_p]$-modules, and have
${\mathbb {Z}}[{\mathbb {Z}}_p\times {\mathbb {Z}}_p]$-modules, and have ![]() ${\mathbb {Z}}[{\mathbb {Z}}_p\times {\mathbb {Z}}_p]$-projective resolutions. Therefore, the Euler characteristic of
${\mathbb {Z}}[{\mathbb {Z}}_p\times {\mathbb {Z}}_p]$-projective resolutions. Therefore, the Euler characteristic of ![]() $H_*(f;{\mathbb {Z}}[{\mathbb {Z}}_p])$ gives an element of
$H_*(f;{\mathbb {Z}}[{\mathbb {Z}}_p])$ gives an element of ![]() $K_1({\mathbb {Z}}_{p^2})$ (
$K_1({\mathbb {Z}}_{p^2})$ (![]() $p^2$ is the order of the group
$p^2$ is the order of the group ![]() ${\mathbb {Z}}_p\times {\mathbb {Z}}_p$), and the obstruction is the image of this element under the Swan homomorphism for the group
${\mathbb {Z}}_p\times {\mathbb {Z}}_p$), and the obstruction is the image of this element under the Swan homomorphism for the group ![]() ${\mathbb {Z}}_p\times {\mathbb {Z}}_p$
${\mathbb {Z}}_p\times {\mathbb {Z}}_p$
In the multiplicative group ![]() $({\mathbb {Z}}_{p^2})^*$, the Euler characteristic of
$({\mathbb {Z}}_{p^2})^*$, the Euler characteristic of ![]() $H_*(f;{\mathbb {Z}}[{\mathbb {Z}}_p])$ is
$H_*(f;{\mathbb {Z}}[{\mathbb {Z}}_p])$ is ![]() ${k}/{d}$. The group
${k}/{d}$. The group ![]() $({\mathbb {Z}}_{p^2})^*$ is additively isomorphic to
$({\mathbb {Z}}_{p^2})^*$ is additively isomorphic to ![]() ${\mathbb {Z}}_p\oplus {\mathbb {Z}}_{p-1}$. By [Reference Ullom27, Proposition 3], the image of the Swan homomorphism is an additive group
${\mathbb {Z}}_p\oplus {\mathbb {Z}}_{p-1}$. By [Reference Ullom27, Proposition 3], the image of the Swan homomorphism is an additive group ![]() ${\mathbb {Z}}_p\subset \widetilde {K}_0({\mathbb {Z}}[{\mathbb {Z}}_p\times {\mathbb {Z}}_p])$. Therefore an element
${\mathbb {Z}}_p\subset \widetilde {K}_0({\mathbb {Z}}[{\mathbb {Z}}_p\times {\mathbb {Z}}_p])$. Therefore an element ![]() $r$ is in the kernel of the Swan homomorphism
$r$ is in the kernel of the Swan homomorphism ![]() $({\mathbb {Z}}_{p^2})^*\cong {\mathbb {Z}}_p\oplus {\mathbb {Z}}_{p-1}\to {\mathbb {Z}}_p$ if and only if
$({\mathbb {Z}}_{p^2})^*\cong {\mathbb {Z}}_p\oplus {\mathbb {Z}}_{p-1}\to {\mathbb {Z}}_p$ if and only if ![]() $r^{p-1}=1$. In particular, the pseudo-equivalence extension obstruction
$r^{p-1}=1$. In particular, the pseudo-equivalence extension obstruction ![]() $\frac {k}{d}\in ({\mathbb {Z}}_{p^2})^*$ for
$\frac {k}{d}\in ({\mathbb {Z}}_{p^2})^*$ for ![]() $f$ vanishes if and only if
$f$ vanishes if and only if ![]() $({k}/{d})^{p-1}=1$ in
$({k}/{d})^{p-1}=1$ in ![]() $({\mathbb {Z}}_{p^2})^*$. This gives the condition
$({\mathbb {Z}}_{p^2})^*$. This gives the condition ![]() $d^{p-1}=k^{p-1}$ mod
$d^{p-1}=k^{p-1}$ mod ![]() $p^2$ in the proposition.
$p^2$ in the proposition.
Acknowledgements
Research was partially supported by NSF grant DMS-2105451. Research was partially supported by NYU Silver Professorship. Research was supported by Hong Kong RGC General Research Fund 16308018.
Appendix A Units of  $({\mathbb {Z}}[G]/\Sigma _G)\langle t\rangle$
$({\mathbb {Z}}[G]/\Sigma _G)\langle t\rangle$
Lemma A.1 If ![]() $G$ is a finite abelian group, then the units of
$G$ is a finite abelian group, then the units of ![]() $({\mathbb {Z}}[G]/\Sigma _G)\langle t\rangle$ are monomials.
$({\mathbb {Z}}[G]/\Sigma _G)\langle t\rangle$ are monomials.
Proof. The proof is based on the fact that ![]() $R\langle t\rangle ^*=R^*\langle t\rangle$ for an integral domain
$R\langle t\rangle ^*=R^*\langle t\rangle$ for an integral domain ![]() $R$. In other words, the units in the polynomial ring
$R$. In other words, the units in the polynomial ring ![]() $R\langle t\rangle$ are monomials. In general,
$R\langle t\rangle$ are monomials. In general, ![]() ${\mathbb {Z}}[G]/\Sigma _G$ is not an integral domain, but can be detected by sufficiently many homomorphisms to integral domains. Specifically, a character
${\mathbb {Z}}[G]/\Sigma _G$ is not an integral domain, but can be detected by sufficiently many homomorphisms to integral domains. Specifically, a character ![]() $\lambda \colon G\to \langle \xi _n\rangle \subset {\mathbb {C}}$ (
$\lambda \colon G\to \langle \xi _n\rangle \subset {\mathbb {C}}$ (![]() $\xi _n=e^{{2\pi i}/{n}}$ is the
$\xi _n=e^{{2\pi i}/{n}}$ is the ![]() $n$-th root of unity and
$n$-th root of unity and ![]() $\langle \xi \rangle$ is all powers of
$\langle \xi \rangle$ is all powers of ![]() $\xi$) induces a ring homomorphism
$\xi$) induces a ring homomorphism ![]() $\lambda \colon {\mathbb {Z}}[G]\to {\mathbb {Z}}[\xi _n]={\mathbb {Z}}[s]/\varphi _n(s)$, where
$\lambda \colon {\mathbb {Z}}[G]\to {\mathbb {Z}}[\xi _n]={\mathbb {Z}}[s]/\varphi _n(s)$, where ![]() $\varphi _n$ is the minimal polynomial of
$\varphi _n$ is the minimal polynomial of ![]() $\xi _n$. This further induces a homomorphism
$\xi _n$. This further induces a homomorphism ![]() $\lambda \colon {\mathbb {Z}}[G]/\Sigma _G\to {\mathbb {Z}}[\xi _n]$ unless
$\lambda \colon {\mathbb {Z}}[G]/\Sigma _G\to {\mathbb {Z}}[\xi _n]$ unless ![]() $\lambda$ is trivial. Then we get a homomorphism of units
$\lambda$ is trivial. Then we get a homomorphism of units
The equality is due to the fact that ![]() ${\mathbb {Z}}[\xi _n]$ is an integral domain. Then for a unit
${\mathbb {Z}}[\xi _n]$ is an integral domain. Then for a unit ![]() $x=\sum x_it^i$,
$x=\sum x_it^i$, ![]() $x_i\in {\mathbb {Z}}[G]$, on the left, we know
$x_i\in {\mathbb {Z}}[G]$, on the left, we know ![]() $\lambda (x)=\sum \lambda (x_i)t^i\in {\mathbb {Z}}[\xi _n]^*\langle t\rangle$ means that there is
$\lambda (x)=\sum \lambda (x_i)t^i\in {\mathbb {Z}}[\xi _n]^*\langle t\rangle$ means that there is ![]() $i(\lambda )$, such that
$i(\lambda )$, such that ![]() $\lambda (x)=\lambda (x_{i(\lambda )})t^{i(\lambda )}$ (i.e.,
$\lambda (x)=\lambda (x_{i(\lambda )})t^{i(\lambda )}$ (i.e., ![]() $\lambda (x_i)=0$ for all
$\lambda (x_i)=0$ for all ![]() $i\ne i(\lambda )$).
$i\ne i(\lambda )$).
If we take ![]() $\lambda$ to be all non-trivial characters, with the corresponding
$\lambda$ to be all non-trivial characters, with the corresponding ![]() $n=p^k$ being prime powers, then we get an embedding
$n=p^k$ being prime powers, then we get an embedding
This induces an embedding of the units (for the specific selections of ![]() $\lambda$)
$\lambda$)
The embedding of the units shows that, if we prove that ![]() $i(\lambda )$ is independent of the choice of
$i(\lambda )$ is independent of the choice of ![]() $\lambda$, then the original unit
$\lambda$, then the original unit ![]() $x=\sum x_it^i$ on the left is also a monomial. This proves the lemma.
$x=\sum x_it^i$ on the left is also a monomial. This proves the lemma.
First, by ![]() $\varphi _{p^k}(s)=(1-s^{p^k})/(1-s^{p^{k-1}})=1+s^{p^{k-1}}+s^{2p^{k-1}}+\dots +s^{(p-1)p^{k-1}}$, we have a homomorphism by sending
$\varphi _{p^k}(s)=(1-s^{p^k})/(1-s^{p^{k-1}})=1+s^{p^{k-1}}+s^{2p^{k-1}}+\dots +s^{(p-1)p^{k-1}}$, we have a homomorphism by sending ![]() $s$ to
$s$ to ![]() $1$
$1$
Then we have the composition ![]() $\mu \circ \lambda \colon {\mathbb {Z}}[G]/\Sigma _G\to {\mathbb {F}}_p$ that sends every group element to
$\mu \circ \lambda \colon {\mathbb {Z}}[G]/\Sigma _G\to {\mathbb {F}}_p$ that sends every group element to ![]() $1$. In particular, the induced map
$1$. In particular, the induced map ![]() $\mu \circ \lambda \colon ({\mathbb {Z}}[G]/\Sigma _G)\langle t\rangle \to {\mathbb {F}}_p\langle t\rangle$ depends only on
$\mu \circ \lambda \colon ({\mathbb {Z}}[G]/\Sigma _G)\langle t\rangle \to {\mathbb {F}}_p\langle t\rangle$ depends only on ![]() $p$. Then
$p$. Then ![]() $\mu \circ \lambda (x)=\mu (x_{i(\lambda )})t^{i(\lambda )}$ depends only on
$\mu \circ \lambda (x)=\mu (x_{i(\lambda )})t^{i(\lambda )}$ depends only on ![]() $p$. This implies that, if two characters
$p$. This implies that, if two characters ![]() $\lambda$ and
$\lambda$ and ![]() $\lambda '$ correspond to the same prime, then
$\lambda '$ correspond to the same prime, then ![]() $i(\lambda )=i(\lambda ')$.
$i(\lambda )=i(\lambda ')$.
It remains to show that, if ![]() $\lambda$ and
$\lambda$ and ![]() $\lambda '$ correspond to
$\lambda '$ correspond to ![]() $\xi _p$ and
$\xi _p$ and ![]() $\xi _q$, where
$\xi _q$, where ![]() $p,\,q$ are distinct primes, then
$p,\,q$ are distinct primes, then ![]() $i(\lambda )=i(\lambda ')$. By what we proved above, we only need to verify this for any one pair
$i(\lambda )=i(\lambda ')$. By what we proved above, we only need to verify this for any one pair ![]() $\lambda$ and
$\lambda$ and ![]() $\lambda '$ corresponding to
$\lambda '$ corresponding to ![]() $\xi _p$ and
$\xi _p$ and ![]() $\xi _q$. Consider a character
$\xi _q$. Consider a character ![]() $\Lambda \colon G\to C=\langle \xi _{pq}\rangle \subset {\mathbb {C}}$. Then we have
$\Lambda \colon G\to C=\langle \xi _{pq}\rangle \subset {\mathbb {C}}$. Then we have

The compositions to ![]() ${\mathbb {Z}}[\xi _p]$ and
${\mathbb {Z}}[\xi _p]$ and ![]() ${\mathbb {Z}}[\xi _{pq}]$ are respectively
${\mathbb {Z}}[\xi _{pq}]$ are respectively ![]() $\lambda$ and
$\lambda$ and ![]() $\Lambda$. Therefore, the images of a unit
$\Lambda$. Therefore, the images of a unit ![]() $x=\sum x_it^i \in ({\mathbb {Z}}[G]/\Sigma _G)\langle t\rangle ^*$ are respectively
$x=\sum x_it^i \in ({\mathbb {Z}}[G]/\Sigma _G)\langle t\rangle ^*$ are respectively ![]() $\lambda (x_{i(\lambda )})t^{i(\lambda )}\in {\mathbb {Z}}[\xi _p]^*\langle t\rangle$ and
$\lambda (x_{i(\lambda )})t^{i(\lambda )}\in {\mathbb {Z}}[\xi _p]^*\langle t\rangle$ and ![]() $\lambda (x_{i(\Lambda )})t^{i(\Lambda )}\in {\mathbb {Z}}[\xi _{pq}]^*\langle t\rangle$. Both are further mapped to
$\lambda (x_{i(\Lambda )})t^{i(\Lambda )}\in {\mathbb {Z}}[\xi _{pq}]^*\langle t\rangle$. Both are further mapped to ![]() $({\mathbb {Z}}[\xi _{pq}]/\varphi _p(\xi _{pq}))^*\langle t\rangle$. To show
$({\mathbb {Z}}[\xi _{pq}]/\varphi _p(\xi _{pq}))^*\langle t\rangle$. To show ![]() $i(\Lambda )=i(\lambda )$, therefore, we only need to show that
$i(\Lambda )=i(\lambda )$, therefore, we only need to show that ![]() ${\mathbb {Z}}[\xi _{pq}]/\varphi _p(\xi _{pq})\ne 0$.
${\mathbb {Z}}[\xi _{pq}]/\varphi _p(\xi _{pq})\ne 0$.
By ![]() ${\mathbb {Z}}[\xi _{pq}]/\varphi _p(\xi _{pq})={\mathbb {Z}}[s]/(\varphi _{pq}(s),\, \varphi _p(s))$, the ring is
${\mathbb {Z}}[\xi _{pq}]/\varphi _p(\xi _{pq})={\mathbb {Z}}[s]/(\varphi _{pq}(s),\, \varphi _p(s))$, the ring is ![]() $0$ if and only if
$0$ if and only if ![]() $1=\varphi _{pq}(s)u(s)+\varphi _p(s)v(s)$ for some polynomials
$1=\varphi _{pq}(s)u(s)+\varphi _p(s)v(s)$ for some polynomials ![]() $u(s),\,v(s)\in {\mathbb {Z}}[s]$. Taking
$u(s),\,v(s)\in {\mathbb {Z}}[s]$. Taking ![]() $s=\xi _p$, we get
$s=\xi _p$, we get ![]() $1=\varphi _{pq}(\xi _p)v(\xi _p)$. By
$1=\varphi _{pq}(\xi _p)v(\xi _p)$. By
we have
Then ![]() $1=\varphi _{pq}(\xi _p)v(\xi _p)$ means
$1=\varphi _{pq}(\xi _p)v(\xi _p)$ means ![]() $1+\xi _p+\xi _p^2+\dots +\xi _p^{q-1}=qv(\xi _p)$ is a multiple of
$1+\xi _p+\xi _p^2+\dots +\xi _p^{q-1}=qv(\xi _p)$ is a multiple of ![]() $q$ in
$q$ in ![]() ${\mathbb {Z}}[\xi _p]$. Since
${\mathbb {Z}}[\xi _p]$. Since ![]() $p,\,q$ are coprime, this is not true.
$p,\,q$ are coprime, this is not true.
We conclude that the ring is non-zero. This implies ![]() $i(\Lambda )=i(\lambda )$. Switching
$i(\Lambda )=i(\lambda )$. Switching ![]() $p$ and
$p$ and ![]() $q$, we also get
$q$, we also get ![]() $i(\Lambda )=i(\lambda ')$. This completes the proof of
$i(\Lambda )=i(\lambda ')$. This completes the proof of ![]() $i(\lambda )=i(\lambda ')$.
$i(\lambda )=i(\lambda ')$.