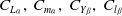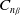Nomenclature
 $\boldsymbol{{A}}$
$\boldsymbol{{A}}$steady-state state matrix
 $b$
$b$Wingspan in m
 $\overline{c}$
$\overline{c}$mean aerodynamic chord in m
 $\boldsymbol{{C}}$
$\boldsymbol{{C}}$steady-state observation matrix
 ${C_{{D_0}}}$
${C_{{D_0}}}$drag force coefficient at zero lift
 ${C_{{L_{{\delta _e}}}}}$
${C_{{L_{{\delta _e}}}}}$derivative of lift force coefficient w.r.t. elevator deflection
 ${C_{{L_0}}}$
${C_{{L_0}}}$lift force coefficient at zero angle-of-attack
 ${C_{{L_\alpha }}}$
${C_{{L_\alpha }}}$derivative of lift force coefficient w.r.t. angle-of-attack
 ${C_{{Y_{{\delta _r}}}}}$
${C_{{Y_{{\delta _r}}}}}$derivative of side force coefficient w.r.t. rudder deflection
 ${C_{{Y_0}}}$
${C_{{Y_0}}}$side force coefficient at zero sideslip angle
 ${C_{{Y_p}}}$
${C_{{Y_p}}}$derivative of side force coefficient w.r.t. roll rate
 ${C_{{Y_r}}}$
${C_{{Y_r}}}$derivative of side force coefficient w.r.t. yaw rate
 ${C_{{Y_\beta }}}$
${C_{{Y_\beta }}}$derivative of side force coefficient w.r.t. sideslip angle
 ${C_{{l_{{\delta _a}}}}}$
${C_{{l_{{\delta _a}}}}}$derivative of rolling moment coefficient w.r.t. aileron deflection
 ${C_{{l_{{\delta _r}}}}}$
${C_{{l_{{\delta _r}}}}}$derivative of rolling moment coefficient w.r.t. rudder deflection
 ${C_{{l_0}}}$
${C_{{l_0}}}$rolling moment coefficient at zero sideslip angle
 ${C_{{l_p}}}$
${C_{{l_p}}}$derivative of rolling moment coefficient w.r.t. roll rate
 ${C_{{l_r}}}$
${C_{{l_r}}}$derivative of rolling moment coefficient w.r.t. yaw rate
 ${C_{{l_\beta }}}$
${C_{{l_\beta }}}$derivative of rolling moment coefficient w.r.t. sideslip angle
 ${C_{{m_{{\delta _e}}}}}$
${C_{{m_{{\delta _e}}}}}$derivative of pitching moment coefficient w.r.t. elevator deflection
 ${C_{{m_0}}}$
${C_{{m_0}}}$pitching moment coefficient at zero angle-of-attack
 ${C_{{m_q}}}$
${C_{{m_q}}}$derivative of pitching moment coefficient w.r.t. pitch rate
 ${C_{{m_\alpha }}}$
${C_{{m_\alpha }}}$derivative of pitching moment coefficient w.r.t. angle-of-attack
 ${C_{{n_{{\delta _r}}}}}$
${C_{{n_{{\delta _r}}}}}$derivative of yawing moment coefficient w.r.t. rudder deflection
 ${C_{{n_0}}}$
${C_{{n_0}}}$Yawing moment coefficient at zero sideslip angle
 ${C_{{n_p}}}$
${C_{{n_p}}}$derivative of yawing moment coefficient w.r.t. roll rate
 ${C_{{n_r}}}$
${C_{{n_r}}}$derivative of yawing moment coefficient w.r.t. yaw rate
 ${C_{{n_\beta }}}$
${C_{{n_\beta }}}$derivative of yawing moment coefficient w.r.t. sideslip angle
 ${C_D}$
${C_D}$nondimensional drag force coefficient
 ${C_L}$
${C_L}$nondimensional lift force coefficient
 ${C_Y}$
${C_Y}$nondimensional side force coefficient
 ${C_{\boldsymbol{{l}}}}$
${C_{\boldsymbol{{l}}}}$nondimensional rolling moment coefficient
 ${C_{\boldsymbol{{m}}}}$
${C_{\boldsymbol{{m}}}}$nondimensional pitching moment coefficient
 ${C_{\boldsymbol{{n}}}}$
${C_{\boldsymbol{{n}}}}$nondimensional yawing moment coefficient
 $\boldsymbol{\mathcal{F}}$
$\boldsymbol{\mathcal{F}}$Fisher information matrix
 $\boldsymbol{{F}}$
$\boldsymbol{{F}}$process noise distribution matrix
 ${F_t}$
${F_t}$thrust force in N
- g
acceleration due to gravity in
 ${\textrm{m}}/{{\textrm{s}}^2}$
${\textrm{m}}/{{\textrm{s}}^2}$ $\boldsymbol{\mathcal{G}}$
$\boldsymbol{\mathcal{G}}$gradient vector
 $G$
$G$measurement noise distribution matrix
 ${I_{xx}}$
${I_{xx}}$mass moment of inertia about body x-axis in
 ${\textrm{kg }}{{\textrm{m}}^2}$
${\textrm{kg }}{{\textrm{m}}^2}$ ${I_{xz}}$
${I_{xz}}$product moment of inertia in body xz-plane in
 ${\textrm{kg }}{{\textrm{m}}^2}$
${\textrm{kg }}{{\textrm{m}}^2}$ ${I_{yy}}$
${I_{yy}}$mass moment of inertia about body y-axis in
 ${\textrm{kg }}{{\textrm{m}}^2}$
${\textrm{kg }}{{\textrm{m}}^2}$ ${I_{zz}}$
${I_{zz}}$mass moment of inertia about body z-axis in
 ${\textrm{kg }}{{\textrm{m}}^2}$
${\textrm{kg }}{{\textrm{m}}^2}$ $\boldsymbol{{J}}$
$\boldsymbol{{J}}$cost function
 $k$
$k$induced drag force correction factor
 $\boldsymbol{{K}}$
$\boldsymbol{{K}}$steady-state Kalman gain matrix
 $\boldsymbol{{L}}$
$\boldsymbol{{L}}$likelihood function
- m
mass of UAV in kg
 ${n_p}$
${n_p}$number of parameters
 ${n_x}$
${n_x}$number of state variables
 ${n_y}$
${n_y}$number of observation variables
 $p$
$p$roll rate in rad/s
 $\boldsymbol{{P}}$
$\boldsymbol{{P}}$steady-state prediction error covariance matrix
- q
pitch rate in rad/s
 $r$
$r$Yaw rate in
 ${\textrm{rad}}/{\textrm{s}}$
${\textrm{rad}}/{\textrm{s}}$ $\boldsymbol{{R}}$
$\boldsymbol{{R}}$measurement noise covariance matrix
- S
Wing planform area in
 ${{\textrm{m}}^2}$
${{\textrm{m}}^2}$ ${t_k}$
${t_k}$discrete-time
 $\boldsymbol{{u}}$
$\boldsymbol{{u}}$control input vector
 $\overline{\boldsymbol{{u}}}$
$\overline{\boldsymbol{{u}}}$discrete-time control input vector
 $\boldsymbol{{v}}$
$\boldsymbol{{v}}$measurement noise vector
- V
freestream velocity in m/s
 $\boldsymbol{{V}}$
$\boldsymbol{{V}}$measurement noise matrix
 $\boldsymbol{{w}}$
$\boldsymbol{{w}}$process noise vector
 $\boldsymbol{{x}}$
$\boldsymbol{{x}}$state vector
 $\widehat{\boldsymbol{{x}}}$
$\widehat{\boldsymbol{{x}}}$corrected state vector
 $\widetilde{\boldsymbol{{x}}}$
$\widetilde{\boldsymbol{{x}}}$predicted state vector
 $\boldsymbol{{y}}$
$\boldsymbol{{y}}$output vector
 $\widetilde{\boldsymbol{{{y}}}}$
$\widetilde{\boldsymbol{{{y}}}}$predicted output vector
 ${\textbf{z}}$
${\textbf{z}}$measurement vector
Greek symbol
 $\alpha $
$\alpha $angle-of-attack in rad
 $\beta $
$\beta $sideslip angle in rad
 ${\delta _a}$
${\delta _a}$aileron deflection angle in rad
 ${\delta _e}$
${\delta _e}$elevator deflection angle in rad
 ${\delta _r}$
${\delta _r}$rudder deflection angle in rad
 $\theta $
$\theta $pitch angle in rad
 $\mu $
$\mu $mean of a scalar Gaussian random variable
- ρ
density of air in
 ${\textrm{kg}}/{{\textrm{m}}^3}$
${\textrm{kg}}/{{\textrm{m}}^3}$ $\sigma $
$\sigma $standard deviation of a scalar Gaussian random variable
 $\phi $
$\phi $roll angle in rad
- M
mean of a Gaussian random vector
 ${\boldsymbol{\Sigma }}$
${\boldsymbol{\Sigma }}$covariance of a Gaussian random vector
 ${\boldsymbol{\Theta }}$
${\boldsymbol{\Theta }}$parameter vector
1.0 Introduction
Following their tremendous success in the military arena, unmanned aerial vehicles (UAVs) are rapidly finding their way into civilian applications. The UAV was initially designed as a tool for aerial photography, surveillance and reconnaissance during the last century [Reference Fahlstrom and Gleason1]. Sooner they became a valuable military asset with a broader range of applications, including decoying, jamming, relaying radio signals, detecting land mines and so on [Reference Austin2]. UAVs have also been used for aerial photography, agriculture, search and rescue and crowd control by civilians and governments over the last two decades. Since most of these applications demand the UAV to be highly manoeuvrable, they are designed to have marginal stability or even instability [Reference Fahlstrom and Gleason1], demanding a dedicated fly-by-wire onboard autopilot. The robustness and effectiveness of an onboard autopilot are significantly influenced by the UAV dynamics, which is indeed described by its aerodynamic model [Reference Saderla, Kim and Ghosh3]. Besides the above purpose, the aerodynamic model also plays an integral part in developing a realistic flight simulator for the training of pilots.
Aerodynamic characterisation is already a well-established discipline with ever-growing scientific literature. There are a wide variety of techniques available such as analytical methods [Reference Pamadi4], wind tunnel testing [Reference Morelli and DeLoach5], computational fluid dynamics (CFD) methods [Reference Murphy, Klein, Frink and Vicroy6] and system identification methods. The analytical methods are based on sets of empirical and semi-empirical equations, which provide complete information about the aerodynamic derivatives in the preliminary design stages, albeit with low accuracy in most cases. One of the famous analytical procedures, called US DATCOM, has been used for evaluating the aerodynamic coefficients of a UAS-S4 aircraft, and these estimates are found to be as accurate as CFD-based estimates [Reference Kuitche and Botez7]. Wind tunnel testing and CFD methods can be used to estimate parameters with better accuracy than those estimated using analytical methods. However, both are expensive in terms of cost and time [Reference Khatri8]. Furthermore, the parameters estimated using static wind tunnel testing suffer errors due to wall effects, Reynold’s number and sting interferences. Its inability to provide damping derivatives is another severe limitation [Reference Saderla, Dhayalan and Ghosh9]. Even though damping derivatives of a scaled model can be obtained from dynamic wind tunnel testing, it requires sophisticated instruments and actuators [Reference Balakrishna, Niranjana, Rajamurthy, Srinathkumar, Rajan and Singh10]. System identification methods based on flight testing can overcome most of the limitations mentioned earlier and can help to formulate complex aerodynamic models by considering realistic flight scenarios.
System identification is defined as “a methodology for building mathematical models of dynamic systems using measurements of input and output signals of the system” [11]. In the case of UAVs, the structure of the dynamic model is well defined using rigid body Newtonian mechanics; the system identification problem reduces to a parameter estimation problem where the numerical value of the parameters governing the UAV dynamics are determined statistically using flight data [Reference Jategaonkar12]. These flight data that are to be used for the system identification process are obtained by carrying out specific manoeuvres that exogenously excite the dynamics of the aircraft [Reference Morelli13]. The advancement in sensor technology has made the fabrication of micro-electro-sensor systems possible, which helps in logging the flight data acquired while performing system identification manoeuvres, even in small UAVs. Equation error methods (EEM), output error methods (OEM) [Reference Özger14–Reference Licitra, Bürger, Williams, Ruiterkamp and Diehl16], filter error methods (FEM) [Reference Mohamed and Joy17–Reference Moszczynski, Leung and Grant19] and Artificial Intelligence- (AI) based methods [Reference Kumar and Ghosh20–Reference Dhayalan, Saderla and Ghosh24] are primary aerodynamic parameter estimation methods. The least square cost function-based EEM has been touted as a promising alternative for a rapid parameter estimation technique because of its computational simplicity. This method does not require any initial value for the estimation of parameters and does not possess numerical instability. Though it is the simplest method in terms of mathematical formulation, its estimates are discrepant when the flight data is corrupted with random noise, which is usually the case. In the presence of measurement noise, the OEM, based on the maximum-likelihood cost function, performs exceedingly better than EEM because it considers the statistical properties of random noise in its cost function. However, when there are uncertainties in the model dynamics, termed process noise, OEM is a less-reliable method [Reference Schetz, Klein and Morelli25]. It is well observed that OEM estimates are susceptible to a priori information, which may lead to significant inaccuracies if the initial value of the parameters is at a significant offset from the nominal value [Reference Lichota and Lasek26]. FEM is considered an exemplary method for estimating parameters in the presence of measurement and process noise. FEM is mainly classified into extended Kalman filter (EKF), unscented Kalman filter (UKF), and augmented unscented Kalman filter (UKFa). Though the UKF method performs better in some cases, the overall performance of all three variants remains similar [Reference Chowdhary and Jategaonkar27]. Over the past two decades, the widespread accessibility of extensive computational resources has significantly popularised the usage of AI techniques, primarily based on Machine Learning (ML) and Deep Learning (DL) algorithms, to solve existing problems in different disciplines. One of the popular AI-based estimation methods is Neural-Gauss-Newton (NGN), in which a feed-forward neural network, trained using flight data, replaces the system dynamics [Reference Peyada and Ghosh28]. Though the NGN method accurately estimates the parameters, the trained neural network does not necessarily represent a generalised flight dynamic model. Instead, it is a restricted model sensitive to flight data used to train the model. Apart from the time-domain parameter estimation methods, some procedures use frequency-domain formulation based on the finite Fourier transform [Reference Morelli and Grauer29–Reference Mohamed31].
Despite its versatility, the conventional FEM requires significant computational resources because it involves the computation of Jacobian matrices, Kalman gain obtained by solving the Ricatti equation, and parameter updation through the Gauss-Newton (GN) method. The heavy computational aspects of FEM can be minimised by considering steady-state EKF instead of its time-varying counterpart, which is regarded as a valid simplification if the system under investigation is time-invariant and the deviation from the nominal trajectory is minimal [Reference Jategaonkar12]. Furthermore, reduction in computational resources is possible by replacing the gradient-based parameter updation technique with a solution search-based approach such as particle swarm optimisation (PSO) and genetic algorithms (GA). The PSO algorithm [Reference Kennedy and Eberhart32], discovered in 1995, is an evolutionary computation technique like GA in many of the aspects wherein the potential solutions (particles) move through the solution search space following the current optimum particle [33]. The PSO method has already been used in many aerospace applications as a tool for optimisation [Reference Li and Zhang34]. The present work attempts to couple the advantages of steady-state EKF and PSO to develop an efficient FEM without compromising the accuracy of the estimated parameters, and the proposed method is termed FEM-PSO. The parameters estimated using the proposed FEM-PSO method are compared with those obtained using the conventional FEM method and wind tunnel. Further, a proof-of-match exercise has been carried out using the estimated parameters. The manuscript has been organised as follows: Mathematical modelling of the flight dynamics of the UAV for longitudinal and lateral-directional cases has been presented in Section 2. The parameter estimation methodology, including the formulations for conventional FEM and FEM-PSO, has been organised in Section 3. A description of data gathering has been provided in Section 4. Section 5 contains the analysis of the results obtained in the current research. The advantages and limitations of using FEM-PSO have been presented in Section 6.
2.0 Mathematical modelling
The flight data for this research was acquired using two indigenously designed propeller-driven wing-alone UAVs, namely CDFP and CDRW [Reference Saderla, Kim and Ghosh3]. CDFP, with a gross take-off mass of 3.5 kg, features a cropped delta wing with a flat-plate aerofoil, while CDRW, with a gross take-off mass of 3.6 kg, features a reflex aerofoil. The UAVs house their separate fuselages, and they have an all-moving vertical tail, which acts as both a vertical stabiliser and rudder. Both UAVs do not have a dedicated horizontal tail, but they feature elevons that act as the control surface to induce pitching and rolling moments independently [Reference Saderla, Dhayalan and Ghosh35]. Both CDFP and CDRW, whose prototypes are given in Fig. 1, were developed, instrumented and tested at the Flight Laboratory of IIT Kanpur. The standard geometrical parameters of CDFP and CDRW have been listed in Table 1.
Table 1. Standard geometric parameters of CDFP and CDRW


Figure 1. Cropped Delta wing UAVs [Reference Saderla, Dhayalan and Ghosh35].

Figure 2. A schematic representation of the cropped Delta UAV [Reference Kumar, Saderla and Kim36].
The UAVs can be treated as rigid bodies and their six DOF dynamics can be described using differential equations, which are nonlinear and coupled in nature. These governing equations of motion are decoupled, retaining their original non-linearity, under appropriate assumptions based on flight manoeuvres to represent longitudinal and lateral-directional motion independently. The simplifying assumptions include the thrust from the propulsion system being perfectly aligned with the body’s x-axis and the angle-of-attack ![]() $\alpha $ being small. A schematic representation of the UAV is given in Fig. 2. The description of the symbols used in the forthcoming sections is given in nomenclature. The governing equations for longitudinal motion used in the current research are given by Equation (1) as follows [Reference Schetz, Klein and Morelli25]:
$\alpha $ being small. A schematic representation of the UAV is given in Fig. 2. The description of the symbols used in the forthcoming sections is given in nomenclature. The governing equations for longitudinal motion used in the current research are given by Equation (1) as follows [Reference Schetz, Klein and Morelli25]:
 \begin{align}\dot V & = - \frac{{\rho S{V^2}}}{{2m}} C_D + g\sin\! ( {\alpha - \theta } ) + \frac{{{F_t}}}{m}\cos\! ( \alpha ) \nonumber\\
\dot \alpha & = - \frac{{\rho SV}}{{2m}}{C_L} + \frac{g}{V}\cos\! ( {\alpha - \theta } ) - \frac{{{F_t}}}{{mV}}\sin\! ( \alpha ) + q \nonumber\\
\dot q & = \frac{{\rho S\overline{c}{V^2}}}{{2{I_{yy}}}}{C_m} \nonumber\\
\dot \theta & = q \end{align}
\begin{align}\dot V & = - \frac{{\rho S{V^2}}}{{2m}} C_D + g\sin\! ( {\alpha - \theta } ) + \frac{{{F_t}}}{m}\cos\! ( \alpha ) \nonumber\\
\dot \alpha & = - \frac{{\rho SV}}{{2m}}{C_L} + \frac{g}{V}\cos\! ( {\alpha - \theta } ) - \frac{{{F_t}}}{{mV}}\sin\! ( \alpha ) + q \nonumber\\
\dot q & = \frac{{\rho S\overline{c}{V^2}}}{{2{I_{yy}}}}{C_m} \nonumber\\
\dot \theta & = q \end{align}The lateral-directional dynamic equations in current research are given by Equation (2) as follows [Reference Schetz, Klein and Morelli25]:
 \begin{align}\dot \beta & = - \frac{{\rho SV}}{{2m}}{C_Y} - \frac{{{F_t}}}{{mV}}\sin\! ( \beta ) + \frac{g}{V}\sin\! ( \phi ) - r \nonumber\\
\dot p & = \frac{1}{2}\left( {\frac{{\rho S{V^2}b\left( {{I_{zz}}{C_l} + {I_{xz}}{C_n}} \right)}}{{{I_{xx}}{I_{zz}} - I_{xz}^2}}} \right) \nonumber\\
\dot r & = \frac{1}{2}\left( {\frac{{\rho S{V^2}b\left( {{I_{xz}}{C_l} + {I_{xx}}{C_n}} \right)}}{{{I_{xx}}{I_{zz}} - I_{xz}^2}}} \right) \nonumber\\
\dot \phi & = p \end{align}
\begin{align}\dot \beta & = - \frac{{\rho SV}}{{2m}}{C_Y} - \frac{{{F_t}}}{{mV}}\sin\! ( \beta ) + \frac{g}{V}\sin\! ( \phi ) - r \nonumber\\
\dot p & = \frac{1}{2}\left( {\frac{{\rho S{V^2}b\left( {{I_{zz}}{C_l} + {I_{xz}}{C_n}} \right)}}{{{I_{xx}}{I_{zz}} - I_{xz}^2}}} \right) \nonumber\\
\dot r & = \frac{1}{2}\left( {\frac{{\rho S{V^2}b\left( {{I_{xz}}{C_l} + {I_{xx}}{C_n}} \right)}}{{{I_{xx}}{I_{zz}} - I_{xz}^2}}} \right) \nonumber\\
\dot \phi & = p \end{align}
The aerodynamic coefficients involved in the dynamic equations, if the UAV is operated at a low angle-of-attack, can be modelled using the linear equations as follows [Reference Saderla, Kim and Ghosh3, Reference Bryan37]:
 \begin{align}{C_L} & = {C_{{L_0}}} + {C_{{L_\alpha }}}\alpha + {C_{{L_q}}}\frac{{q\overline{c}}}{{2V}} + {C_{{L_{{\delta _e}}}}}{\delta _e} \nonumber\\
{C_D} & = {C_{{D_0}}} + kC_L^2 \nonumber\\
{C_m} & = {C_{{m_0}}} + {C_{{m_\alpha }}}\alpha + {C_{{m_q}}}\frac{{q\overline{c}}}{{2V}} + {C_{{m_{{\delta _e}}}}}{\delta _e} \nonumber
\\
{C_Y} & = {C_{{Y_0}}} + {C_{{Y_\beta }}}\beta + {C_{{Y_p}}}\frac{{pb}}{{2V}} + {C_{{Y_r}}}\frac{{rb}}{{2V}} + {C_{{Y_{{\delta _r}}}}}{\delta _r} \nonumber\\
{C_l} & = {C_{{l_0}}} + {C_{{l_\beta }}}\beta + {C_{{l_p}}}\frac{{pb}}{{2V}} + {C_{{l_r}}}\frac{{rb}}{{2V}} + {C_{{l_{{\delta _a}}}}}{\delta _a} + {C_{{l_{{\delta _r}}}}}{\delta _r} \nonumber\\
{C_n} & = {C_{{n_0}}} + {C_{{n_\beta }}}\beta + {C_{{n_p}}}\frac{{pb}}{{2V}} + {C_{{n_r}}}\frac{{rb}}{{2V}} + {C_{{n_{{\delta _r}}}}}{\delta _r} \end{align}
\begin{align}{C_L} & = {C_{{L_0}}} + {C_{{L_\alpha }}}\alpha + {C_{{L_q}}}\frac{{q\overline{c}}}{{2V}} + {C_{{L_{{\delta _e}}}}}{\delta _e} \nonumber\\
{C_D} & = {C_{{D_0}}} + kC_L^2 \nonumber\\
{C_m} & = {C_{{m_0}}} + {C_{{m_\alpha }}}\alpha + {C_{{m_q}}}\frac{{q\overline{c}}}{{2V}} + {C_{{m_{{\delta _e}}}}}{\delta _e} \nonumber
\\
{C_Y} & = {C_{{Y_0}}} + {C_{{Y_\beta }}}\beta + {C_{{Y_p}}}\frac{{pb}}{{2V}} + {C_{{Y_r}}}\frac{{rb}}{{2V}} + {C_{{Y_{{\delta _r}}}}}{\delta _r} \nonumber\\
{C_l} & = {C_{{l_0}}} + {C_{{l_\beta }}}\beta + {C_{{l_p}}}\frac{{pb}}{{2V}} + {C_{{l_r}}}\frac{{rb}}{{2V}} + {C_{{l_{{\delta _a}}}}}{\delta _a} + {C_{{l_{{\delta _r}}}}}{\delta _r} \nonumber\\
{C_n} & = {C_{{n_0}}} + {C_{{n_\beta }}}\beta + {C_{{n_p}}}\frac{{pb}}{{2V}} + {C_{{n_r}}}\frac{{rb}}{{2V}} + {C_{{n_{{\delta _r}}}}}{\delta _r} \end{align}
Equation (1) can be rewritten in the following vector form,
In Equation (4),
are the state variables, control variables, and parameters for the longitudinal dynamics, respectively.
Equation (2) can be rewritten in the following vector form,
In Equation (5),
are the state variables, control variables and parameters for the lateral-directional dynamics, respectively.
In general, the nonlinear equations of motion describing the longitudinal and lateral-directional dynamics of a UAV can be represented in state space [Reference Jategaonkar12] as follows in Equation (6),
Equation (6) does not necessarily capture the dynamics perfectly because of the inaccuracies in the model arising due to unmodelled dynamics and uncertainties in the parameters. These uncertainties in the model can be quantified by modelling the process noise. This research assumes that the process noise follows the Gaussian distribution with zero mean and identical covariance. During flight tests, the variables of interest are measured using sensors. However, all sensors are not perfect. The data captured by the sensors contain undesirable frequencies, which is termed measurement noise. In this research, it is assumed that the measurement noise is Gaussian with zero mean and identical covariance.
When measurement and process noise are added to Equation (6), it becomes [Reference Morelli and DeLoach5]
 \begin{align}\dot{\boldsymbol{{x}}}(t)& = \boldsymbol{{f}}( {\boldsymbol{{x}}(t),\boldsymbol{{u}}(t),{\boldsymbol{\Theta }}} ) + \boldsymbol{{Fw}}(t) \nonumber\\
\boldsymbol{{y}}(t)& = \boldsymbol{{g}}( {\boldsymbol{{x}}(t),\boldsymbol{{u}}(t),{\boldsymbol{\Theta }}} ) \nonumber\\
\boldsymbol{{z}}( {{t_k}} ) & = \boldsymbol{{y}}( {{t_k}} ) + \boldsymbol{{Gv}}( {{t_k}} ) \end{align}
\begin{align}\dot{\boldsymbol{{x}}}(t)& = \boldsymbol{{f}}( {\boldsymbol{{x}}(t),\boldsymbol{{u}}(t),{\boldsymbol{\Theta }}} ) + \boldsymbol{{Fw}}(t) \nonumber\\
\boldsymbol{{y}}(t)& = \boldsymbol{{g}}( {\boldsymbol{{x}}(t),\boldsymbol{{u}}(t),{\boldsymbol{\Theta }}} ) \nonumber\\
\boldsymbol{{z}}( {{t_k}} ) & = \boldsymbol{{y}}( {{t_k}} ) + \boldsymbol{{Gv}}( {{t_k}} ) \end{align}
F and G are process and measurement noise distribution matrices, respectively.
Since the noises are assumed to be random, w and v can be treated as random vectors, which means that the system states x is also a random vector, complicating the parameter estimation process because the state cannot be obtained by direct integration of state equations. It must be estimated using a suitable minimum variance estimator, as described in Section 3.
3.0 Parameter estimation methodology
3.1 Multivariate Gaussian distribution
From [Reference Bertsekas and Tsitsiklis38], if ![]() $X$ is a Gaussian random variable that takes on values from a discrete set
$X$ is a Gaussian random variable that takes on values from a discrete set ![]() $s\{ {{x_1},{x_2}, \ldots ,{x_m}} \}$ with mean
$s\{ {{x_1},{x_2}, \ldots ,{x_m}} \}$ with mean ![]() $\mu $ and variance
$\mu $ and variance ![]() ${\sigma ^2}$, then its probability distribution function
${\sigma ^2}$, then its probability distribution function ![]() ${p_X}( x )$ is given by,
${p_X}( x )$ is given by,
If ![]() $\boldsymbol{{X}}$ is a Gaussian random vector with mean
$\boldsymbol{{X}}$ is a Gaussian random vector with mean ![]() $\boldsymbol{{M}}$ and covariance
$\boldsymbol{{M}}$ and covariance ![]() ${\boldsymbol{\Sigma }}$, of dimension
${\boldsymbol{\Sigma }}$, of dimension ![]() $n \times 1$ where each of its elements
$n \times 1$ where each of its elements ![]() ${X_i}$ take on values from discrete sets
${X_i}$ take on values from discrete sets ![]() ${s_i}\{ {{x_{i1}},{x_{i2}}, \ldots ,{x_{im}}} \}$ and if all
${s_i}\{ {{x_{i1}},{x_{i2}}, \ldots ,{x_{im}}} \}$ and if all ![]() ${X_i}$ are independent of each other, the joint probability distribution function
${X_i}$ are independent of each other, the joint probability distribution function ![]() ${p_{\boldsymbol{{X}}}}(\boldsymbol{{x}})$ is given by,
${p_{\boldsymbol{{X}}}}(\boldsymbol{{x}})$ is given by,
If ![]() $\boldsymbol{{X}}$ is a Gaussian random matrix of dimension
$\boldsymbol{{X}}$ is a Gaussian random matrix of dimension ![]() $n \times N$ where each of its
$n \times N$ where each of its ![]() $N$ columns
$N$ columns ![]() ${X_i}$ are independent random vectors with identical variance
${X_i}$ are independent random vectors with identical variance ![]() $\boldsymbol{{M}}$, the joint probability distribution
$\boldsymbol{{M}}$, the joint probability distribution ![]() ${p_{\boldsymbol{{X}}}}( \boldsymbol{\mathcal{X}} )$ is given by,
${p_{\boldsymbol{{X}}}}( \boldsymbol{\mathcal{X}} )$ is given by,
3.2 Conventional filter error method (FEM)
The need for a state estimator is described briefly in this subsection. Since the dynamics of the UAV is nonlinear in both longitudinal and lateral cases, EKF has been preferred as the state estimator. In this research, the steady-state EKF algorithm has been used because it dramatically reduces the computation costs if the system is linear time-invariant (LTI) and the deviations from the nominal trajectory are minor. The steady-state EKF algorithm consists of prediction and correction steps given by [Reference Jategaonkar12].
Prediction step
 \begin{align}
\widetilde{\boldsymbol{{x}}} ( {{t_{k + 1}}} ) & = \widehat{\boldsymbol{{x}}} ( {{t_k}} ) + \mathop \int\limits_{{t_k}}^{{t_{k + 1}}} \boldsymbol{{f}}( {x(t),\overline{\boldsymbol{{u}}}({{t_k}}),{\boldsymbol{\Theta }}} ) {\textrm{d}}t,\quad \widehat{\boldsymbol{{x}}}( {{t_0}} ) = {\boldsymbol{{x}}_{\boldsymbol{0}}} \nonumber\\
\widetilde{\boldsymbol{{y}}} ({{t_k}} ) & = \boldsymbol{{g}}( {\widetilde{\boldsymbol{{x}}}( {{t_k}} ), \overline{\boldsymbol{{u}}}( {{t_k}} ), {\boldsymbol{\Theta }}} )
\end{align}
\begin{align}
\widetilde{\boldsymbol{{x}}} ( {{t_{k + 1}}} ) & = \widehat{\boldsymbol{{x}}} ( {{t_k}} ) + \mathop \int\limits_{{t_k}}^{{t_{k + 1}}} \boldsymbol{{f}}( {x(t),\overline{\boldsymbol{{u}}}({{t_k}}),{\boldsymbol{\Theta }}} ) {\textrm{d}}t,\quad \widehat{\boldsymbol{{x}}}( {{t_0}} ) = {\boldsymbol{{x}}_{\boldsymbol{0}}} \nonumber\\
\widetilde{\boldsymbol{{y}}} ({{t_k}} ) & = \boldsymbol{{g}}( {\widetilde{\boldsymbol{{x}}}( {{t_k}} ), \overline{\boldsymbol{{u}}}( {{t_k}} ), {\boldsymbol{\Theta }}} )
\end{align}
Correction step
The steady-state Kalman gain ![]() $\boldsymbol{{K}}$ in Equation (12) is obtained by solving the steady-state Ricatti equation given by Equation (13) for steady-state prediction error covariance matrix
$\boldsymbol{{K}}$ in Equation (12) is obtained by solving the steady-state Ricatti equation given by Equation (13) for steady-state prediction error covariance matrix ![]() $\boldsymbol{{P}}$ as follows,
$\boldsymbol{{P}}$ as follows,
 \begin{align} \boldsymbol{{AP}} + {\boldsymbol{{PA}}^{\boldsymbol{{T}}}} & \! - \frac{1}{{\Delta t}}\boldsymbol{{P}}{\boldsymbol{{C}}^{\boldsymbol{{T}}}}{\boldsymbol{{R}}^{ - \boldsymbol{1}}}\boldsymbol{{CP}} + \boldsymbol{{F}}{\boldsymbol{{F}}^{\boldsymbol{{T}}}} = \boldsymbol{0} \nonumber\\
& \qquad\boldsymbol{{K}} = \boldsymbol{{P}}{\boldsymbol{{C}}^{\boldsymbol{{T}}}}{R^{ - \boldsymbol{1}}} \end{align}
\begin{align} \boldsymbol{{AP}} + {\boldsymbol{{PA}}^{\boldsymbol{{T}}}} & \! - \frac{1}{{\Delta t}}\boldsymbol{{P}}{\boldsymbol{{C}}^{\boldsymbol{{T}}}}{\boldsymbol{{R}}^{ - \boldsymbol{1}}}\boldsymbol{{CP}} + \boldsymbol{{F}}{\boldsymbol{{F}}^{\boldsymbol{{T}}}} = \boldsymbol{0} \nonumber\\
& \qquad\boldsymbol{{K}} = \boldsymbol{{P}}{\boldsymbol{{C}}^{\boldsymbol{{T}}}}{R^{ - \boldsymbol{1}}} \end{align}
The State and Observation matrices in Equation (13) are obtained using Newton’s Central Difference scheme. Proper tuning of F and G matrices decides the success of EKF. This adaptive filtering problem is solved using the combined formulation technique proposed by Maine and Iliff in Ref. [Reference Maine and Iliff15]. The EKF by itself does not do parameter estimation. It gives the best estimate of the state based on current parameters. The goodness of this generated estimate is measured with a cost function. This cost function must be minimised for the parameters using an optimisation algorithm. In conventional EKF implementation, Gauss-Newton (GN) method is used for carrying out the optimisation.
Using Equations (7) and (10), the likelihood function ![]() $L( {\boldsymbol{{z}}{\textrm{|}}{\boldsymbol{\Theta }}} ),$ which captures the probability of observing the data
$L( {\boldsymbol{{z}}{\textrm{|}}{\boldsymbol{\Theta }}} ),$ which captures the probability of observing the data ![]() $\boldsymbol{{z}}$ given the parameters
$\boldsymbol{{z}}$ given the parameters ![]() ${\boldsymbol{\Theta }}$ for the case of
${\boldsymbol{\Theta }}$ for the case of ![]() $\boldsymbol{{z}}$ being drawn from Gaussian distribution is given by,
$\boldsymbol{{z}}$ being drawn from Gaussian distribution is given by,
It is possible to convert the parameter estimation problem into a nonlinear optimisation problem constrained by dynamic equations. If the measurement z and covariance R are fixed, when the optimal value of parameters ![]() ${{\boldsymbol{\Theta }}^*}$ is used in Equation (14),
${{\boldsymbol{\Theta }}^*}$ is used in Equation (14), ![]() $L$ will have its maximum value, which is the maximum likelihood estimate (MLE) for
$L$ will have its maximum value, which is the maximum likelihood estimate (MLE) for ![]() $\boldsymbol{{z}}$. In this research, the cost
$\boldsymbol{{z}}$. In this research, the cost ![]() $J$ is taken as the negative logarithm of Equation (14), as given below,
$J$ is taken as the negative logarithm of Equation (14), as given below,
If the value of ![]() $\boldsymbol{{R}}$ is unknown, it is taken to be the value that minimises Equation (15) when
$\boldsymbol{{R}}$ is unknown, it is taken to be the value that minimises Equation (15) when ![]() ${\boldsymbol{\Theta }}$ is a known value as proposed in the two-step relaxation strategy [Reference Jategaonkar12]. It is found by partially differentiating Equation (15) with respect to
${\boldsymbol{\Theta }}$ is a known value as proposed in the two-step relaxation strategy [Reference Jategaonkar12]. It is found by partially differentiating Equation (15) with respect to ![]() $\boldsymbol{{R}}$ and equating it to
$\boldsymbol{{R}}$ and equating it to ![]() $\boldsymbol{0}$ as follows,
$\boldsymbol{0}$ as follows,
From, [Reference Petersen and Pedersen39]
Substituting Equation (17) in Equation (15),
Since ![]() $J$ is to be optimised for
$J$ is to be optimised for ![]() ${\boldsymbol{\Theta }}$, for a given measurement z, Equation (18) can further be reduced into [Reference Jategaonkar12]
${\boldsymbol{\Theta }}$, for a given measurement z, Equation (18) can further be reduced into [Reference Jategaonkar12]
GN optimisation algorithm is used to optimise Equation (19) w.r.t. ![]() ${\boldsymbol{\Theta }}$. The parameter
${\boldsymbol{\Theta }}$. The parameter ![]() ${\boldsymbol{\Theta }}$ iteratively converges towards the optimal solution
${\boldsymbol{\Theta }}$ iteratively converges towards the optimal solution ![]() ${{\boldsymbol{\Theta }}^*}$ using the gradient information of the cost function. The cost function
${{\boldsymbol{\Theta }}^*}$ using the gradient information of the cost function. The cost function ![]() $J ( {\boldsymbol{\Theta }} )$ can be linearly approximated [Reference Peyada and Ghosh28], and parameter correction
$J ( {\boldsymbol{\Theta }} )$ can be linearly approximated [Reference Peyada and Ghosh28], and parameter correction ![]() ${\boldsymbol{\Delta }}{\boldsymbol{\Theta }}$ [Reference Jategaonkar12] is given as follows,
${\boldsymbol{\Delta }}{\boldsymbol{\Theta }}$ [Reference Jategaonkar12] is given as follows,
In Equation (20), the first derivative of ![]() $J$ w.r.t.
$J$ w.r.t. ![]() ${\boldsymbol{\Theta }}$ represents the gradient
${\boldsymbol{\Theta }}$ represents the gradient ![]() $\boldsymbol{\mathcal{G}}$ and an approximation of the second derivate represents the Fisher information matrix
$\boldsymbol{\mathcal{G}}$ and an approximation of the second derivate represents the Fisher information matrix ![]() $\boldsymbol{\mathcal{F}}$. They are evaluated as follows [Reference Jategaonkar12]:
$\boldsymbol{\mathcal{F}}$. They are evaluated as follows [Reference Jategaonkar12]:
 \begin{align} \boldsymbol{\mathcal{G}} & = - {\boldsymbol{{S}}}^{\boldsymbol{{T}}}{\boldsymbol{{R}}^{ - \boldsymbol{1}}}\mathop \sum \nolimits_{i = 1}^N [ {{\boldsymbol{{z}}_i} - {{\widetilde{\boldsymbol{{y}}}}_i}} ] \nonumber\\
\boldsymbol{\mathcal{F}} & = {\boldsymbol{{S}}^{\boldsymbol{{T}}}}{\boldsymbol{{R}}^{ - \boldsymbol{1}}}\boldsymbol{{S}} \end{align}
\begin{align} \boldsymbol{\mathcal{G}} & = - {\boldsymbol{{S}}}^{\boldsymbol{{T}}}{\boldsymbol{{R}}^{ - \boldsymbol{1}}}\mathop \sum \nolimits_{i = 1}^N [ {{\boldsymbol{{z}}_i} - {{\widetilde{\boldsymbol{{y}}}}_i}} ] \nonumber\\
\boldsymbol{\mathcal{F}} & = {\boldsymbol{{S}}^{\boldsymbol{{T}}}}{\boldsymbol{{R}}^{ - \boldsymbol{1}}}\boldsymbol{{S}} \end{align}
In Equation (21), ![]() $\boldsymbol{{S}}$ is a matrix of dimension (
$\boldsymbol{{S}}$ is a matrix of dimension (![]() ${n_y} \times {n_p}$) and it is known as the sensitivity matrix, which quantifies the effect of change in parameters on the estimated output vector
${n_y} \times {n_p}$) and it is known as the sensitivity matrix, which quantifies the effect of change in parameters on the estimated output vector ![]() $\widetilde{\boldsymbol{{y}}}$. Mathematically, it is given as,
$\widetilde{\boldsymbol{{y}}}$. Mathematically, it is given as,
The response gradience ![]() $\dfrac{{\partial \widetilde{\boldsymbol{{y}}}}}{{\partial {\boldsymbol{\Theta }}}}$ in Equation (22) is obtained numerically by giving a small perturbation
$\dfrac{{\partial \widetilde{\boldsymbol{{y}}}}}{{\partial {\boldsymbol{\Theta }}}}$ in Equation (22) is obtained numerically by giving a small perturbation ![]() $\delta {\boldsymbol{\Theta }}$ to each element of the parameter vector and computing the corresponding perturbed response
$\delta {\boldsymbol{\Theta }}$ to each element of the parameter vector and computing the corresponding perturbed response ![]() ${\widetilde{\boldsymbol{{y}}}}_{\boldsymbol{{p}}}$. The
${\widetilde{\boldsymbol{{y}}}}_{\boldsymbol{{p}}}$. The ![]() ${l^{th}}$ column of the response gradience is computed using the following linear approximation:
${l^{th}}$ column of the response gradience is computed using the following linear approximation:
Finally, the parameter update is given by,
3.3. FEM augmented with particle swarm optimisation (FEM-PSO)
The cost function in Equation (19) is optimised using the PSO algorithm. The PSO belongs to a class of computational techniques inspired by biological systems. This evolutionary computational technique performs stochastic optimisation based on the social behaviour of particles. The main advantage of using the PSO algorithm over the conventional Gauss-Newton (GN) algorithm is that the PSO does not require gradience computation at each iteration which significantly reduces the computation cost of the onboard computer. The working of the PSO algorithm for parameter estimation is briefly explained as follows:
Initialise The search space ![]() $S$ where the optimal solution
$S$ where the optimal solution ![]() ${{\boldsymbol{\Theta }}^*}$ is likely to be observed is chosen as
${{\boldsymbol{\Theta }}^*}$ is likely to be observed is chosen as ![]() $\left[ {{\boldsymbol{\Theta }}_{\boldsymbol{{min}}}^{\boldsymbol{{i}}}, {\boldsymbol{\Theta }}_{\boldsymbol{{max}}}^{\boldsymbol{{i}}}} \right]$ where
$\left[ {{\boldsymbol{\Theta }}_{\boldsymbol{{min}}}^{\boldsymbol{{i}}}, {\boldsymbol{\Theta }}_{\boldsymbol{{max}}}^{\boldsymbol{{i}}}} \right]$ where ![]() ${\boldsymbol{\Theta }}_{\boldsymbol{{min}}}^{\boldsymbol{{i}}}$ and
${\boldsymbol{\Theta }}_{\boldsymbol{{min}}}^{\boldsymbol{{i}}}$ and ![]() ${\boldsymbol{\Theta }}_{\boldsymbol{{max}}}^{\boldsymbol{{i}}}$ represent the maximum and minimum limits of the solution. The initial position of all the particles
${\boldsymbol{\Theta }}_{\boldsymbol{{max}}}^{\boldsymbol{{i}}}$ represent the maximum and minimum limits of the solution. The initial position of all the particles ![]() ${{\boldsymbol{\Theta }}^{\boldsymbol{{i}}}}( 0 )$ are chosen randomly within
${{\boldsymbol{\Theta }}^{\boldsymbol{{i}}}}( 0 )$ are chosen randomly within ![]() $S.$ The initial velocity of all the particles
$S.$ The initial velocity of all the particles ![]() ${\boldsymbol{\Delta }}{{\boldsymbol{\Theta }}^{\boldsymbol{{i}}}}(0)$ are chosen to be
${\boldsymbol{\Delta }}{{\boldsymbol{\Theta }}^{\boldsymbol{{i}}}}(0)$ are chosen to be ![]() $0$. Initial value of personal best position for each particle
$0$. Initial value of personal best position for each particle ![]() ${\boldsymbol{\Theta }}_{\boldsymbol{{pb}}}^{\boldsymbol{{i}}}(0)$ is chosen to be their respective initial positions since the particles have not started moving yet. The initial global best position
${\boldsymbol{\Theta }}_{\boldsymbol{{pb}}}^{\boldsymbol{{i}}}(0)$ is chosen to be their respective initial positions since the particles have not started moving yet. The initial global best position ![]() ${{\boldsymbol{\Theta }}_{\boldsymbol{{gb}}}}(0)$ is chosen to be the personal best position that minimises the cost function given in Equation (19).
${{\boldsymbol{\Theta }}_{\boldsymbol{{gb}}}}(0)$ is chosen to be the personal best position that minimises the cost function given in Equation (19).
 \begin{align} {{\boldsymbol{\Theta }}^{\boldsymbol{{i}}}}(0) &\, :\!=\, {\textrm{rand}}\left[ {{\boldsymbol{\Theta }}_{\boldsymbol{{min}}}^{\boldsymbol{{i}}},{\textrm{ }}{\boldsymbol{\Theta }}_{\boldsymbol{{max}}}^{\boldsymbol{{i}}}} \right],\forall {\textrm{ }}i \in [ {1,2, \ldots ,{N_p}} ] \nonumber\\
{\boldsymbol{\Delta }}{{\boldsymbol{\Theta }}^{\boldsymbol{{i}}}}(0)&\, :\!=\, \boldsymbol{0} \nonumber\\
{\boldsymbol{\Theta }}_{\boldsymbol{{pb}}}^i(0)&\, :\!=\, {{\boldsymbol{\Theta }}^{\boldsymbol{{i}}}}(0) \nonumber\\
{{\boldsymbol{\Theta }}_{\boldsymbol{{gb}}}}(0)&\, :\!=\, \mathop {{\textrm{argmin}}}\limits_{{{\boldsymbol{\Theta }}_{\boldsymbol{{pb}}}}} J\left( {{\boldsymbol{\Theta }}_{pb}^i} \right) \end{align}
\begin{align} {{\boldsymbol{\Theta }}^{\boldsymbol{{i}}}}(0) &\, :\!=\, {\textrm{rand}}\left[ {{\boldsymbol{\Theta }}_{\boldsymbol{{min}}}^{\boldsymbol{{i}}},{\textrm{ }}{\boldsymbol{\Theta }}_{\boldsymbol{{max}}}^{\boldsymbol{{i}}}} \right],\forall {\textrm{ }}i \in [ {1,2, \ldots ,{N_p}} ] \nonumber\\
{\boldsymbol{\Delta }}{{\boldsymbol{\Theta }}^{\boldsymbol{{i}}}}(0)&\, :\!=\, \boldsymbol{0} \nonumber\\
{\boldsymbol{\Theta }}_{\boldsymbol{{pb}}}^i(0)&\, :\!=\, {{\boldsymbol{\Theta }}^{\boldsymbol{{i}}}}(0) \nonumber\\
{{\boldsymbol{\Theta }}_{\boldsymbol{{gb}}}}(0)&\, :\!=\, \mathop {{\textrm{argmin}}}\limits_{{{\boldsymbol{\Theta }}_{\boldsymbol{{pb}}}}} J\left( {{\boldsymbol{\Theta }}_{pb}^i} \right) \end{align}
Update The position of the particles is updated iteratively, followed by its velocity update to give a new generation of particles. The velocity is updated based on the relative position of the particle from its personal best position and global best position in the current iteration. The following equations list the velocity and position updates of the particles, respectively, for a given generation ![]() $t$,
$t$,
In Equation (26), ![]() $w, c_1$, and
$w, c_1$, and ![]() ${c_2}$ are the hyperparameters of the PSO algorithm and are called the inertial coefficient, personal cognitive coefficient, and social cognitive coefficient, respectively. In this research, the values of
${c_2}$ are the hyperparameters of the PSO algorithm and are called the inertial coefficient, personal cognitive coefficient, and social cognitive coefficient, respectively. In this research, the values of ![]() ${c_1}$ and
${c_1}$ and ![]() ${c_2}$ are chosen to be 2 as given in [Reference Kennedy and Eberhart32]. The value of
${c_2}$ are chosen to be 2 as given in [Reference Kennedy and Eberhart32]. The value of ![]() $w$ is chosen to decrease with each iteration by the rule
$w$ is chosen to decrease with each iteration by the rule ![]() $w( {t + 1} ) = 0.99 w(t)$ to encourage the particles to follow the optimal direction as given in [Reference Kumar, Saderla and Kim36].
$w( {t + 1} ) = 0.99 w(t)$ to encourage the particles to follow the optimal direction as given in [Reference Kumar, Saderla and Kim36]. ![]() ${\boldsymbol{{a}}_{\boldsymbol{1}}}$ and
${\boldsymbol{{a}}_{\boldsymbol{1}}}$ and ![]() ${\boldsymbol{{a}}_{\boldsymbol{2}}}$ in Equation (26) are random vectors of appropriate dimensions.
${\boldsymbol{{a}}_{\boldsymbol{2}}}$ in Equation (26) are random vectors of appropriate dimensions.
It is to be asserted that ![]() ${{\boldsymbol{\Theta }}^{\textbf{i}}}( {t + 1} ) \in S, \forall \in [ {1, 2, \ldots ,{N_p}} ]$. If the
${{\boldsymbol{\Theta }}^{\textbf{i}}}( {t + 1} ) \in S, \forall \in [ {1, 2, \ldots ,{N_p}} ]$. If the ![]() ${i^{th}}$ particle is not in
${i^{th}}$ particle is not in ![]() $S$, it is to be re-initialised. The personal best position of the particles and the global best position are updated iteratively as follows:
$S$, it is to be re-initialised. The personal best position of the particles and the global best position are updated iteratively as follows:
 \begin{align} {\boldsymbol{\Theta }}_{\boldsymbol{{pb}}}^{\boldsymbol{{i}}}( {t + 1} )& =
\begin{cases}{{\boldsymbol{\Theta }}^{\boldsymbol{{i}}}}( {t + 1} ), & \ \ \text{if}\ J\left( {{{\boldsymbol{\Theta }}^{\boldsymbol{{i}}}}( {t + 1} )} \right) \le J\left( {{\boldsymbol{\Theta }}_{\boldsymbol{{pb}}}^{\boldsymbol{{i}}}(t)} \right)\\
{\boldsymbol{\Theta }}_{\boldsymbol{{pb}}}^{\boldsymbol{{i}}}(t), & \ \ \text{Otherwise}\end{cases} \nonumber\\
{{\boldsymbol{\Theta }}_{\boldsymbol{{gb}}}}( {t + 1} ) &= \begin{cases}{\boldsymbol{\Theta }}_{\boldsymbol{{pb}}}^{\boldsymbol{{i}}}( {t + 1} ), & \text{if}\ \ J\left( {{\boldsymbol{\Theta }}_{{{\boldsymbol{{pb}}}}}^{\boldsymbol{{i}}}( {t + 1} )} \right) \le J\left( {{{\boldsymbol{\Theta }}_{\boldsymbol{{gb}}}}(t)} \right)\\
{{\boldsymbol{\Theta }}_{\boldsymbol{{gb}}}}(t),& \text{Otherwise}\end{cases} \end{align}
\begin{align} {\boldsymbol{\Theta }}_{\boldsymbol{{pb}}}^{\boldsymbol{{i}}}( {t + 1} )& =
\begin{cases}{{\boldsymbol{\Theta }}^{\boldsymbol{{i}}}}( {t + 1} ), & \ \ \text{if}\ J\left( {{{\boldsymbol{\Theta }}^{\boldsymbol{{i}}}}( {t + 1} )} \right) \le J\left( {{\boldsymbol{\Theta }}_{\boldsymbol{{pb}}}^{\boldsymbol{{i}}}(t)} \right)\\
{\boldsymbol{\Theta }}_{\boldsymbol{{pb}}}^{\boldsymbol{{i}}}(t), & \ \ \text{Otherwise}\end{cases} \nonumber\\
{{\boldsymbol{\Theta }}_{\boldsymbol{{gb}}}}( {t + 1} ) &= \begin{cases}{\boldsymbol{\Theta }}_{\boldsymbol{{pb}}}^{\boldsymbol{{i}}}( {t + 1} ), & \text{if}\ \ J\left( {{\boldsymbol{\Theta }}_{{{\boldsymbol{{pb}}}}}^{\boldsymbol{{i}}}( {t + 1} )} \right) \le J\left( {{{\boldsymbol{\Theta }}_{\boldsymbol{{gb}}}}(t)} \right)\\
{{\boldsymbol{\Theta }}_{\boldsymbol{{gb}}}}(t),& \text{Otherwise}\end{cases} \end{align}
Convergence If ![]() $t \geqslant {t_{max}}$, the iteration is stopped and
$t \geqslant {t_{max}}$, the iteration is stopped and ![]() ${{\boldsymbol{\Theta }}_{\boldsymbol{{gb}}}}$ is taken as
${{\boldsymbol{\Theta }}_{\boldsymbol{{gb}}}}$ is taken as ![]() ${{\boldsymbol{\Theta }}^*}$.
${{\boldsymbol{\Theta }}^*}$.

Figure 3. PSO algorithm for parameter estimation.

Figure 4. Comparison between actual flight data and simulated data for CDFP in the longitudinal flight regime.

Figure 5. Comparison between flight data and simulated data for CDRW in the longitudinal flight regime.
The above description has been summarised in Fig. 3 as a flowchart.
4.0 Flight data gathering
Flight data gathering (FDG) can be defined as acquiring the time history of motion variables and the corresponding applied control inputs. FDG is such an essential step in the parameter estimation process that the accuracy and reliability of the estimated parameters directly depend on the quality of the gathered data. The amount of information content is a direct measure of the quality of flight data, and it can be held high only when the control input sufficiently excites the dynamics of the UAV independently. For this purpose, the UAV should house an industrial-grade data acquisition system with an inertial measurement unit (IMU) to capture motion variables, standard quality pressure sensors to indirectly measure velocity, and flow angle sensors to measure the angle-of-attack and sideslip angles. The technical details of the data acquisition system and the nature of the flight tests performed with CDFP and CDRW are presented briefly in Ref. [Reference Saderla, Dhayalan and Ghosh35]. The generated flight data are labelled with the UAV name followed by the nature of excitation – L for longitudinal and LD for lateral directional, followed by the serial number of the flight test. Therefore, CDFP_Li would mean that it is the ![]() ${i^{\textrm{th}}}$ CDFP dataset where its longitudinal mode is excited.
${i^{\textrm{th}}}$ CDFP dataset where its longitudinal mode is excited.
A total of 16 compatible flight data sets, 4 for longitudinal parameter estimation and 4 for lateral-directional parameter estimation for CDFP and CDRW each, are used in the current research. From Figs 4 and 5, it can be noticed that sinusoidal elevator inputs are applied to the UAVs for the excitation of longitudinal dynamics. Since the maximum angle-of-attack observed in the manoeuvres performed by the UAVs is close to ![]() ${10^ \circ }$ and from the wind tunnel experiments carried out using the above UAVs [Reference Saderla40], it was observed that the variation of the aerodynamic coefficients was linear when the angle-of-attack varied between
${10^ \circ }$ and from the wind tunnel experiments carried out using the above UAVs [Reference Saderla40], it was observed that the variation of the aerodynamic coefficients was linear when the angle-of-attack varied between ![]() $ - 5^\circ $ and
$ - 5^\circ $ and ![]() $10^\circ $. Hence the use of the linear aerodynamic model presented in Equation (3) is suitable for the aerodynamic characterisation of the above UAVs. From Figs 7 and 8, it can be referred that the aileron is subjected to sinusoidal inputs varied between
$10^\circ $. Hence the use of the linear aerodynamic model presented in Equation (3) is suitable for the aerodynamic characterisation of the above UAVs. From Figs 7 and 8, it can be referred that the aileron is subjected to sinusoidal inputs varied between ![]() $ \pm 10^\circ $ to excite the lateral-directional dynamics of the UAVs. It can be observed that the rudder inputs are negligible in most cases because the UAVs have a high aspect ratio all-movable vertical tail rudder, which indicates high control power, and the slightest deflection of the rudder can make the task of controlling the UAV difficult for a ground stationed pilot. Therefore, lateral-directional dynamics are excited through aileron deflection alone [Reference Saderla, Kim and Ghosh3].
$ \pm 10^\circ $ to excite the lateral-directional dynamics of the UAVs. It can be observed that the rudder inputs are negligible in most cases because the UAVs have a high aspect ratio all-movable vertical tail rudder, which indicates high control power, and the slightest deflection of the rudder can make the task of controlling the UAV difficult for a ground stationed pilot. Therefore, lateral-directional dynamics are excited through aileron deflection alone [Reference Saderla, Kim and Ghosh3].
Table 2. Estimated longitudinal parameters for CDFP_L1, CDFP_L2

Note: Values in the () denote Cramer-Rao lower bounds.
Table 3. Estimated longitudinal parameters for CDFP_L3, CDFP_L4

Table 4. Estimated longitudinal parameters for CDRW_L1, CDRW_L2

Table 5. Estimated longitudinal parameters for CDRW_L3, CDRW_L4


Figure 6. Scatter plot comparing the estimated longitudinal parameters with wind tunnel estimates.

Figure 7. Comparison between flight data and simulated data for CDFP in the lateral-directional flight regime.

Figure 8. Comparison between flight data and simulated data for CDRW in the lateral-directional flight regime.
Table 6. Estimated lateral-directional parameters for CDFP_LD1, CDFP_LD2

Table 7. Estimated lateral-directional parameters for CDFP_LD3, CDFP_LD4

Table 8. Estimated lateral-directional parameters for CDRW_LD1, CDRW_LD2

Table 9. Estimated lateral-directional parameters for CDRW_LD3, CDRW_LD4

5.0 Results and discussions
Some of the longitudinal and lateral-directional parameters of both CDFP and CDRW UAVs have already been estimated using wind tunnel testing in Refs [Reference Saderla40–Reference Saderla, Dhayalan, Singh, Kumar and Ghosh42]. The parameters estimated using FEM and FEM-PSO are compared against the corresponding wind tunnel estimates for both CDFP and CDRW. Further, longitudinal and lateral-directional flight simulations are constructed using the estimated FEM and FEM-PSO parameters subjected to the same control inputs as the flight data, and the reconstructed simulations are graphically compared against the flight data in this section.
5.1 Validation of longitudinal parameters
The longitudinal aerodynamic parameters corresponding to CDFP datasets, estimated using conventional FEM and FEM-PSO, are presented in Tables 2 and 3. From the tables, it can be observed that both the FEM and FEM-PSO estimates of the longitudinal static stability parameter ![]() ${C_{{m_\alpha }}}$ are fairly consistent across all the datasets. Their mean offsets from the wind tunnel estimate for CDFP_L1, CDFP_L2, CDFP_L3, and CDFP_L4 are found to be 0.18%, 0.15%, 0.18% and 0.18% for FEM, and 0.77%, 3.57%, 0.18% and 2.23% for FEM-PSO, respectively. In the case of lift curve slope
${C_{{m_\alpha }}}$ are fairly consistent across all the datasets. Their mean offsets from the wind tunnel estimate for CDFP_L1, CDFP_L2, CDFP_L3, and CDFP_L4 are found to be 0.18%, 0.15%, 0.18% and 0.18% for FEM, and 0.77%, 3.57%, 0.18% and 2.23% for FEM-PSO, respectively. In the case of lift curve slope ![]() ${C_{{L_\alpha }}}$, the FEM estimates are off from wind tunnel estimate by 2.58%, 2.86%, 2.86% and 2.85%, while the FEM-PSO estimates are off by 2.58%, 1.94%, 2.65% and 2.84%. The estimated parameters are then used to simulate the longitudinal motion variables given by Equation (1), where the thrust and elevator input correspond to the respective flight data set. They are compared against the originally recorded motion variables in the flight data, as shown in Fig. 4. It can be noted from the figure that although the elevator inputs are unique in each of the datasets, the responses simulated using both the FEM and FEM-PSO estimates match with the actual flight data reasonably well.
${C_{{L_\alpha }}}$, the FEM estimates are off from wind tunnel estimate by 2.58%, 2.86%, 2.86% and 2.85%, while the FEM-PSO estimates are off by 2.58%, 1.94%, 2.65% and 2.84%. The estimated parameters are then used to simulate the longitudinal motion variables given by Equation (1), where the thrust and elevator input correspond to the respective flight data set. They are compared against the originally recorded motion variables in the flight data, as shown in Fig. 4. It can be noted from the figure that although the elevator inputs are unique in each of the datasets, the responses simulated using both the FEM and FEM-PSO estimates match with the actual flight data reasonably well.
Tables 4 and 5 contain the longitudinal parameters estimated for CDRW datasets using FEM and FEM-PSO. The estimated parameters and recorded control inputs are then used to reconstruct the motion variables using the dynamic equations given in Equation (1). A comparison has been made between the reconstructed and actual responses in Fig. 5. It can be observed that all the simulated responses are consistent with measured flight data except ![]() ${V_\infty }$ in CDRW_L1. The FEM estimates of
${V_\infty }$ in CDRW_L1. The FEM estimates of ![]() ${C_{{L_\alpha }}}$ are off from the wind tunnel estimate by 0.02%, 0.01%, 0.02% and 0.02%, while the FEM-PSO estimates are off by 6.37%, 0.64%, 1.98% and 2.06%. The variation in
${C_{{L_\alpha }}}$ are off from the wind tunnel estimate by 0.02%, 0.01%, 0.02% and 0.02%, while the FEM-PSO estimates are off by 6.37%, 0.64%, 1.98% and 2.06%. The variation in ![]() ${C_{{m_\alpha }}}$ estimates are lower in FEM estimate than in the FEM-PSO. FEM estimates of
${C_{{m_\alpha }}}$ estimates are lower in FEM estimate than in the FEM-PSO. FEM estimates of ![]() ${C_{{m_\alpha }}}$ have a variation of
${C_{{m_\alpha }}}$ have a variation of ![]() $ \lt 1\% $ in all the cases, while the offsets in FEM-PSO estimates are 15.89%, 4.73%, 2.32% and 5.27%.
$ \lt 1\% $ in all the cases, while the offsets in FEM-PSO estimates are 15.89%, 4.73%, 2.32% and 5.27%.
From Fig. 6, in ![]() ${C_{{L_\alpha }}}$ estimation for CDFP, the FEM-PSO with a mean deviation of 2.5% w.r.t. the wind tunnel estimate performs slightly better than FEM with a mean deviation of 2.85%. The FEM estimates of longitudinal damping derivative
${C_{{L_\alpha }}}$ estimation for CDFP, the FEM-PSO with a mean deviation of 2.5% w.r.t. the wind tunnel estimate performs slightly better than FEM with a mean deviation of 2.85%. The FEM estimates of longitudinal damping derivative ![]() ${C_{{m_q}}}$ with a median deviation of 0.18% and 0.58% for CDFP and CDRW, respectively, perform better than FEM-PSO estimates with a median deviation of 1.5% and 5%. It can also be noticed that in the case of CDFP, the elevator control power
${C_{{m_q}}}$ with a median deviation of 0.18% and 0.58% for CDFP and CDRW, respectively, perform better than FEM-PSO estimates with a median deviation of 1.5% and 5%. It can also be noticed that in the case of CDFP, the elevator control power ![]() ${C_{{m_{\delta e}}}}$ estimates obtained by FEM have a lower standard deviation of
${C_{{m_{\delta e}}}}$ estimates obtained by FEM have a lower standard deviation of ![]() $5 \times {10^{ - 5}}$ when compared against FEM-PSO estimates with a standard deviation of
$5 \times {10^{ - 5}}$ when compared against FEM-PSO estimates with a standard deviation of ![]() $5.79 \times {10^{ - 3}}$.
$5.79 \times {10^{ - 3}}$.
5.2 Validation of lateral-directional parameters
The estimated aerodynamic parameters pertaining to the lateral-directional datasets of CDFP are listed in Tables 6 and 7. These are used to generate simulated responses using the dynamic equations given by Equation (2) for the same aileron and rudder control inputs corresponding to the respective flight data. A comparison between the simulated results and the flight data has been made in Fig. 7. It can be seen that both the FEM and FEM-PSO simulated motion variables agree with the flight data except for y-acceleration ![]() ${a_y}$. The FEM-PSO estimates of
${a_y}$. The FEM-PSO estimates of ![]() ${C_{{Y_\beta }}}$ have a significantly lower offset (<12%) from the wind tunnel estimate when compared against the FEM estimates with relative offsets of 39.42%, 45.58%, 50.58% and 37.88%. In the case of lateral static stability derivative
${C_{{Y_\beta }}}$ have a significantly lower offset (<12%) from the wind tunnel estimate when compared against the FEM estimates with relative offsets of 39.42%, 45.58%, 50.58% and 37.88%. In the case of lateral static stability derivative ![]() ${C_{{l_\beta }}}$, all the FEM estimates have a relative error of 0.11% w.r.t. wind tunnel value, while the FEM-PSO estimates have offsets of 1.89%, 2%, 10.56% and 0.89%. The relative error in directional static stability derivative
${C_{{l_\beta }}}$, all the FEM estimates have a relative error of 0.11% w.r.t. wind tunnel value, while the FEM-PSO estimates have offsets of 1.89%, 2%, 10.56% and 0.89%. The relative error in directional static stability derivative ![]() ${C_{{n_\beta }}}$ w.r.t. wind tunnel value is observed to be 7% in all FEM estimates, while it is 6.5%, 9.5%, 5% and 9.5% in FEM-PSO estimates.
${C_{{n_\beta }}}$ w.r.t. wind tunnel value is observed to be 7% in all FEM estimates, while it is 6.5%, 9.5%, 5% and 9.5% in FEM-PSO estimates.
The lateral-directional derivatives of CDRW datasets estimated using FEM and FEM-PSO are presented in Tables 8 and 9. In Fig. 8, a comparison is made for the motion variables simulated using FEM and FEM-PSO estimated derivatives against the actual flight data. Similar to CDFP, a slight deviation is observed in ![]() ${a_y}$ from the flight data. Significant difference in relative error is observed between estimates of
${a_y}$ from the flight data. Significant difference in relative error is observed between estimates of ![]() ${C_{{Y_\beta }}}$ by FEM and FEM-PSO; FEM-PSO estimates having a lower relative error than the FEM estimates. The relative errors in
${C_{{Y_\beta }}}$ by FEM and FEM-PSO; FEM-PSO estimates having a lower relative error than the FEM estimates. The relative errors in ![]() ${C_{{Y_\beta }}}$ w.r.t. wind tunnel value for FEM estimates are observed to be 38.85%, 48.85%, 20.61% and 18.17%, while for FEM-PSO estimates the relative errors are 10.92%, 12.82%, 6.49% and 4.96%. In the case of lateral static stability derivative
${C_{{Y_\beta }}}$ w.r.t. wind tunnel value for FEM estimates are observed to be 38.85%, 48.85%, 20.61% and 18.17%, while for FEM-PSO estimates the relative errors are 10.92%, 12.82%, 6.49% and 4.96%. In the case of lateral static stability derivative ![]() ${C_{{l_\beta }}}$, all the FEM estimates have a relative error of 10.99% w.r.t. wind tunnel value, while the FEM-PSO estimates have offsets of 10.59%, 8.02%, 13.47% and 6.34%. The relative error in directional static stability derivative
${C_{{l_\beta }}}$, all the FEM estimates have a relative error of 10.99% w.r.t. wind tunnel value, while the FEM-PSO estimates have offsets of 10.59%, 8.02%, 13.47% and 6.34%. The relative error in directional static stability derivative ![]() ${C_{{n_\beta }}}$ w.r.t. wind tunnel value is observed to be 7% in all FEM estimates, while it is 6.5%, 7%, 8% and 8.5% in FEM-PSO estimates.
${C_{{n_\beta }}}$ w.r.t. wind tunnel value is observed to be 7% in all FEM estimates, while it is 6.5%, 7%, 8% and 8.5% in FEM-PSO estimates.
Since the rudder is not used in most of the manoeuvres intentionally, it is natural to have inaccuracies in rudder deflection-dependent derivatives. From Fig. 9, the ![]() ${C_{{Y_{\delta r}}}}$ estimates of FEM-PSO are closer to wind tunnel estimates than the FEM estimates. However, both the FEM and FEM-PSO estimates of rudder control power
${C_{{Y_{\delta r}}}}$ estimates of FEM-PSO are closer to wind tunnel estimates than the FEM estimates. However, both the FEM and FEM-PSO estimates of rudder control power ![]() ${C_{{n_{\delta r}}}}$suffer noticeable offset with a maximum of 15.45% in FEM and 19.09% in FEM-PSO w.r.t. wind tunnel estimates.
${C_{{n_{\delta r}}}}$suffer noticeable offset with a maximum of 15.45% in FEM and 19.09% in FEM-PSO w.r.t. wind tunnel estimates.

Figure 9. Scatter plot comparing the estimated lateral directional parameters with wind tunnel estimates.
5.3 Convergence comparison between FEM and FEM-PSO
PSO is a metaheuristic optimisation algorithm, whereas GN is a second-order derivative-based algorithm. The nonlinear dependence of the output variables with the system parameters makes the MLE cost function non-convex and, along with the approximation of the Hessian matrix, introduces numerical instabilities in the GN algorithm when inappropriate initial values are given [Reference Schetz, Klein and Morelli25]. In this research, parameters estimated using the EEM are fed as initial values to the GN algorithm, and it is observed that it narrows down to the optimal parameter set in a finite number of iterations (at most 28 iterations when tolerance was set at ![]() ${10^{ - 4}}$). Figure 10 shows the result of a convergence comparison between GN-employed conventional FEM and FEM-PSO for CDFP_L1. It can be noticed that for the same initial parameters and number of maximum iterations, FEM is roughly three times faster than the FEM-PSO method. Even though the convergence is poor in PSO, it does not suffer the numerical difficulties encountered with GN. From Tables 2–9, it can be observed that the Cramer-Rao Lower Bounds (CRLB) of FEM estimates are lower in magnitude when compared with the FEM-PSO estimates, which shows that there is relatively little room for uncertainty in FEM estimates than FEM-PSO estimates. This might be possible because FEM offers the optimal parameters within the given number of iterations, which is not the case with FEM-PSO. Although FEM-PSO estimates come with more uncertainty, analysis of the simulation results with FEM-PSO estimates against the actual flight data shows that they are as good as FEM for practical purposes.
${10^{ - 4}}$). Figure 10 shows the result of a convergence comparison between GN-employed conventional FEM and FEM-PSO for CDFP_L1. It can be noticed that for the same initial parameters and number of maximum iterations, FEM is roughly three times faster than the FEM-PSO method. Even though the convergence is poor in PSO, it does not suffer the numerical difficulties encountered with GN. From Tables 2–9, it can be observed that the Cramer-Rao Lower Bounds (CRLB) of FEM estimates are lower in magnitude when compared with the FEM-PSO estimates, which shows that there is relatively little room for uncertainty in FEM estimates than FEM-PSO estimates. This might be possible because FEM offers the optimal parameters within the given number of iterations, which is not the case with FEM-PSO. Although FEM-PSO estimates come with more uncertainty, analysis of the simulation results with FEM-PSO estimates against the actual flight data shows that they are as good as FEM for practical purposes.

Figure 10. Convergence time comparison between FEM and FEM-PSO.
5.4 Proof-of-match exercise
The estimated aerodynamic parameters of the individual datasets are used to carry out the proof-of-match exercise for longitudinal and lateral-directional cases separately. The longitudinal parameters estimated using the eight datasets are averaged and are used to simulate the response for the elevator inputs of CDFP_L5 and CDRW_L5, respectively. The simulated response is compared with the recorded response of CDFP_L5 and CDRW_L5, as shown in Fig. 11a and b, where it can be observed that the simulated output variables are in close agreement with the flight data. Similarly, the lateral-directional proof-of-match is performed using CDFP_LD5 and CDRW_LD5, where the mean of the eight lateral-directional estimated parameters is used to generate the response corresponding to the aileron and rudder inputs of CDFP_LD5 and CDRW_LD5, respectively. The generated response is matched against the recorded response, as shown in Fig. 11c and d. It can be noticed that all the motion variables are consistent with the flight data.

Figure 11. Proof-of-match exercise.
6.0 Conclusion
In the current research work, a filter error method augmented with particle swarm optimisation, FEM-PSO, is proposed and successfully implemented for the aerodynamic characterisation of CDFP and CDRW UAVs. Various compatible data sets pertaining to linear longitudinal and lateral-directional flight regimes are used to demonstrate and compare the effectiveness of the proposed method with conventional computationally intensive FEM. It is clear from the results that estimated aerodynamic derivatives using FEM-PSO are consistent with full-scale wind tunnel and FEM estimates. With the considered initial parameters of the PSO algorithm and search space, the Cramer-Rao bounds of estimated aerodynamic parameters are slightly higher than the FEM method, indicating less confidence in estimates; however, simulated responses are in good agreement with measured flight data. With the proof-of-match exercise, it is observed that all simulated responses using FEM-PSO estimates are very close to measured flight data, which further strengthens the faith in the estimated parameters. The main advantages of the FEM-PSO method are ease of implementation and lower dependencies on initial values of aerodynamic parameters. Although the cost of gradience computation is saved, the seemingly random motion of the particles through the search space affects the rate of convergence in the FEM-PSO method, mainly when the number of particles is large, and the search space is higher dimensional. The convergence rate of the proposed method can be made faster by employing an advanced variant of the PSO algorithm and an optimised number of search particles, which may lead to another research problem.
Acknowledgments
This research work is supported by Core Research Grant funded by Science and Engineering Research Board (SERB), India (Grant no. CRG/2019/005676). The fourth author’s research is supported by the National Research Foundation of Korea (NRF), funded by the Ministry of Science and ICT, Republic of Korea (Grant no. NRF-2017R1A5A1015311). The authors sincerely thank IIT Kanpur for providing facilities to conduct flight tests.