1. Introduction
In high-speed flows, turbulent boundary layers are known to severely affect the surface drag and heat transfer, so accurate predictive models are strongly desired for reliable vehicle design and flow control (Bradshaw Reference Bradshaw1977). Among various simulation strategies, the Reynolds-averaged Navier–Stokes (RANS) models are long established yet still prevailing, especially for engineering problems, owing to their simplicity, efficiency and robustness (Wilcox Reference Wilcox2006). Compared with the incompressible counterpart, however, compressible RANS models have weaker theoretical foundations, and suffer from the complications brought about by intrinsic compressibility, heat transfer, shocks, high-enthalpy effects and other factors (Gatski & Bonnet Reference Gatski and Bonnet2013; Cheng et al. Reference Cheng, Chen, Zhu, Shyy and Fu2024).
The RANS models are usually divided into four categories by the number of additional equations introduced: the algebraic (zero-equation), one-equation, two-equation and stress-transport models. The algebraic models are the simplest ones, which directly model the eddy viscosity ![]() $\mu _t$ (and eddy diffusivity
$\mu _t$ (and eddy diffusivity ![]() $\kappa _t$) using theoretical/empirical algebraic relations. Two standout models are the Cebeci–Smith (CS) model (Cebeci & Smith Reference Cebeci and Smith1974) and the Baldwin–Lomax (BL) model (Baldwin & Lomax Reference Baldwin and Lomax1978), both of which formulate
$\kappa _t$) using theoretical/empirical algebraic relations. Two standout models are the Cebeci–Smith (CS) model (Cebeci & Smith Reference Cebeci and Smith1974) and the Baldwin–Lomax (BL) model (Baldwin & Lomax Reference Baldwin and Lomax1978), both of which formulate ![]() $\mu _t$ into a two-layer structure. The inner layer part is based on the mixing length model with a viscous damping correction devised by van Driest (Reference van Driest1956). The outer portion is built on the defect layer scaling by Clauser (Reference Clauser1956) and the intermittent function by Klebanoff (Reference Klebanoff1955). In incompressible applications, the algebraic models can faithfully reproduce mean velocity profiles and skin friction for attached boundary layers, though they become unreliable when subject to strong pressure gradient and separation (Wilcox Reference Wilcox2006). Furthermore, the CS and BL models can attain comparable accuracy levels. The latter is more commonly considered for complex flows since it avoids directly using the boundary layer thickness. When extended to compressible flows, no special compressibility correction was considered in early investigations, observing the insensitivity of classical mixing length to the Mach number
$\mu _t$ into a two-layer structure. The inner layer part is based on the mixing length model with a viscous damping correction devised by van Driest (Reference van Driest1956). The outer portion is built on the defect layer scaling by Clauser (Reference Clauser1956) and the intermittent function by Klebanoff (Reference Klebanoff1955). In incompressible applications, the algebraic models can faithfully reproduce mean velocity profiles and skin friction for attached boundary layers, though they become unreliable when subject to strong pressure gradient and separation (Wilcox Reference Wilcox2006). Furthermore, the CS and BL models can attain comparable accuracy levels. The latter is more commonly considered for complex flows since it avoids directly using the boundary layer thickness. When extended to compressible flows, no special compressibility correction was considered in early investigations, observing the insensitivity of classical mixing length to the Mach number ![]() ${\textit {Ma}}$ (Maise & McDonald Reference Maise and McDonald1968; Baldwin & Lomax Reference Baldwin and Lomax1978). To close the problem,
${\textit {Ma}}$ (Maise & McDonald Reference Maise and McDonald1968; Baldwin & Lomax Reference Baldwin and Lomax1978). To close the problem, ![]() $\kappa _t$ in the energy equation is related to
$\kappa _t$ in the energy equation is related to ![]() $\mu _t$ through a prescribed turbulent Prandtl number
$\mu _t$ through a prescribed turbulent Prandtl number ![]() ${\textit {Pr}}_t$. The resulting compressible models can reproduce well the mean flows in high-speed adiabatic flows with minor pressure gradients, but they deteriorate under diabatic walls (with surface heat transfer; (Maise & McDonald Reference Maise and McDonald1968; Shang, Hankey & Dwoyer Reference Shang, Hankey and Dwoyer1973; York & Knight Reference York and Knight1985)). As one improvement, the wall viscous unit for the inner layer scaling can be replaced by the semilocal one (though not in this terminology originally) based upon local density and viscosity (Gupta et al. Reference Gupta, Lee, Zoby, Moss and Thompson1990; Cheatwood & Thompson Reference Cheatwood and Thompson1993). Dilley & McClinton (Reference Dilley and McClinton2001) showed that this modification in BL largely improved the mean flows in hypersonic cold-wall cases, and the predicted surface friction and heat flux agreed well with experiments. Further improvements for complex three-dimensional boundary layers were contributed by, for example, Degani & Schiff (Reference Degani and Schiff1983) and Panaras (Reference Panaras1997), among others. Consequently, the BL models are extensively adopted in high-speed applications and numerous commercial solvers (Cheatwood & Thompson Reference Cheatwood and Thompson1993; Srinivasan, Bittner & Bobskill Reference Srinivasan, Bittner and Bobskill1993; Rumsey, Biedron & Thomas Reference Rumsey, Biedron and Thomas1997; Townend et al. Reference Townend, Muylaert, Walpot and Vennemann1999; Candler et al. Reference Candler, Johnson, Nompelis, Gidzak, Subbareddy and Barnhardt2015).
${\textit {Pr}}_t$. The resulting compressible models can reproduce well the mean flows in high-speed adiabatic flows with minor pressure gradients, but they deteriorate under diabatic walls (with surface heat transfer; (Maise & McDonald Reference Maise and McDonald1968; Shang, Hankey & Dwoyer Reference Shang, Hankey and Dwoyer1973; York & Knight Reference York and Knight1985)). As one improvement, the wall viscous unit for the inner layer scaling can be replaced by the semilocal one (though not in this terminology originally) based upon local density and viscosity (Gupta et al. Reference Gupta, Lee, Zoby, Moss and Thompson1990; Cheatwood & Thompson Reference Cheatwood and Thompson1993). Dilley & McClinton (Reference Dilley and McClinton2001) showed that this modification in BL largely improved the mean flows in hypersonic cold-wall cases, and the predicted surface friction and heat flux agreed well with experiments. Further improvements for complex three-dimensional boundary layers were contributed by, for example, Degani & Schiff (Reference Degani and Schiff1983) and Panaras (Reference Panaras1997), among others. Consequently, the BL models are extensively adopted in high-speed applications and numerous commercial solvers (Cheatwood & Thompson Reference Cheatwood and Thompson1993; Srinivasan, Bittner & Bobskill Reference Srinivasan, Bittner and Bobskill1993; Rumsey, Biedron & Thomas Reference Rumsey, Biedron and Thomas1997; Townend et al. Reference Townend, Muylaert, Walpot and Vennemann1999; Candler et al. Reference Candler, Johnson, Nompelis, Gidzak, Subbareddy and Barnhardt2015).
On the other hand, recently accumulated direct numerical simulation (DNS) data for high-speed canonical flows provides a chance to reassess the behaviour of the BL model. As analysed by Hendrickson et al. (Reference Hendrickson, Subbareddy, Candler and Macdonald2023), and as will be shown below, even for zero-pressure-gradient (ZPG) flat-plate boundary layers, there are clear disparities in mean profiles between BL and DNS under diabatic conditions, especially for the temperature. Also, there is room for improvement in adiabatic flows. Therefore, the objective of this work is to improve the velocity and temperature prediction by the BL model for canonical supersonic/hypersonic boundary layers, based on recently advanced knowledge of mean flow properties.
The established relations of mean velocity and temperature in compressible wall-bounded turbulence are briefly reviewed, to set the grounds for later discussions. First, the hypothesis of Morkovin (Reference Morkovin1962) earns wide support, which states that at moderate free stream Mach numbers (![]() ${\textit {Ma}}_\infty \lesssim 5$), the dilatation effect is small, so any differences from incompressible turbulence can be accounted for by variations of mean properties (Coleman, Kim & Moser Reference Coleman, Kim and Moser1995; Pirozzoli, Grasso & Gatski Reference Pirozzoli, Grasso and Gatski2004; Duan, Beekman & Martín Reference Duan, Beekman and Martín2010; Lagha et al. Reference Lagha, Kim, Eldredge and Zhong2011). As a result, velocity transformation can be built using only mean flow variables, expecting that the transformed streamwise velocity reproduces the incompressible law of the wall and outer-layer scalings. More attention has been paid to the former, i.e. the compressible law of the wall. Pioneering work is the transformation by van Driest (Reference van Driest1951) (denoted as VD hereinafter) built upon the mixing length assumption. This widely used transformation performs well for high-speed adiabatic flows, but deteriorates in diabatic conditions. Trettel & Larsson (Reference Trettel and Larsson2016) designed a transformation based on viscous stress and semilocal units (denoted as TL), which is particularly accurate for pipe and channel flows, but can also become less accurate in diabatic boundary layers (logarithmic region). Recently, Griffin, Fu & Moin (Reference Griffin, Fu and Moin2021) proposed a total-stress-based transformation (denoted as GFM), combining the advantages of the near-wall relation by TL and a modified version of the equilibrium arguments of Zhang et al. (Reference Zhang, Bi, Hussain, Li and She2012). The GFM transformation performs remarkably well in a wide range of air flows, particularly diabatic flows, hence successfully collapsing the channel, pipe and boundary layer cases within and below the logarithmic region. Very recently, Hasan et al. (Reference Hasan, Larsson, Pirozzoli and Pecnik2023b) proposed a transformation (termed HLPP) by introducing a correction to the TL transformation to interpret intrinsic compressibility effects (hence questioning the validity of Morkovin's hypothesis), so the logarithmic scaling in diabatic flows can be reasonably formulated. Besides, the non-air-like and supercritical flow cases can be accounted for, which can be a challenge for the GFM transformation (Bai, Griffin & Fu Reference Bai, Griffin and Fu2022). On the other hand, fewer transformations are available for the outer-layer velocity, presumably due to the greater reliance on flow configurations. Maise & McDonald (Reference Maise and McDonald1968) demonstrated that a compressible law of the wake was attainable for adiabatic boundary layers (
${\textit {Ma}}_\infty \lesssim 5$), the dilatation effect is small, so any differences from incompressible turbulence can be accounted for by variations of mean properties (Coleman, Kim & Moser Reference Coleman, Kim and Moser1995; Pirozzoli, Grasso & Gatski Reference Pirozzoli, Grasso and Gatski2004; Duan, Beekman & Martín Reference Duan, Beekman and Martín2010; Lagha et al. Reference Lagha, Kim, Eldredge and Zhong2011). As a result, velocity transformation can be built using only mean flow variables, expecting that the transformed streamwise velocity reproduces the incompressible law of the wall and outer-layer scalings. More attention has been paid to the former, i.e. the compressible law of the wall. Pioneering work is the transformation by van Driest (Reference van Driest1951) (denoted as VD hereinafter) built upon the mixing length assumption. This widely used transformation performs well for high-speed adiabatic flows, but deteriorates in diabatic conditions. Trettel & Larsson (Reference Trettel and Larsson2016) designed a transformation based on viscous stress and semilocal units (denoted as TL), which is particularly accurate for pipe and channel flows, but can also become less accurate in diabatic boundary layers (logarithmic region). Recently, Griffin, Fu & Moin (Reference Griffin, Fu and Moin2021) proposed a total-stress-based transformation (denoted as GFM), combining the advantages of the near-wall relation by TL and a modified version of the equilibrium arguments of Zhang et al. (Reference Zhang, Bi, Hussain, Li and She2012). The GFM transformation performs remarkably well in a wide range of air flows, particularly diabatic flows, hence successfully collapsing the channel, pipe and boundary layer cases within and below the logarithmic region. Very recently, Hasan et al. (Reference Hasan, Larsson, Pirozzoli and Pecnik2023b) proposed a transformation (termed HLPP) by introducing a correction to the TL transformation to interpret intrinsic compressibility effects (hence questioning the validity of Morkovin's hypothesis), so the logarithmic scaling in diabatic flows can be reasonably formulated. Besides, the non-air-like and supercritical flow cases can be accounted for, which can be a challenge for the GFM transformation (Bai, Griffin & Fu Reference Bai, Griffin and Fu2022). On the other hand, fewer transformations are available for the outer-layer velocity, presumably due to the greater reliance on flow configurations. Maise & McDonald (Reference Maise and McDonald1968) demonstrated that a compressible law of the wake was attainable for adiabatic boundary layers (![]() ${\textit {Ma}}_\infty$ from 1.5 to 5) using the VD transformation. Duan, Beekman & Martín (Reference Duan, Beekman and Martín2011) (and also Guarini et al. (Reference Guarini, Moser, Shariff and Wray2000), Pirozzoli et al. (Reference Pirozzoli, Grasso and Gatski2004) and Wenzel et al. (Reference Wenzel, Selent, Kloker and Rist2018)) suggest that the VD-transformed velocities collapse in the outer layer for adiabatic boundary layers with
${\textit {Ma}}_\infty$ from 1.5 to 5) using the VD transformation. Duan, Beekman & Martín (Reference Duan, Beekman and Martín2011) (and also Guarini et al. (Reference Guarini, Moser, Shariff and Wray2000), Pirozzoli et al. (Reference Pirozzoli, Grasso and Gatski2004) and Wenzel et al. (Reference Wenzel, Selent, Kloker and Rist2018)) suggest that the VD-transformed velocities collapse in the outer layer for adiabatic boundary layers with ![]() ${\textit {Ma}}_\infty$ from 0 to 12, provided comparable
${\textit {Ma}}_\infty$ from 0 to 12, provided comparable ![]() ${\textit {Re}}_{\delta _2}$ (defined later). Pirozzoli & Bernardini (Reference Pirozzoli and Bernardini2011) also noted that for supersonic adiabatic boundary layers, the VD-transformed defect velocity matched the incompressible counterpart well.
${\textit {Re}}_{\delta _2}$ (defined later). Pirozzoli & Bernardini (Reference Pirozzoli and Bernardini2011) also noted that for supersonic adiabatic boundary layers, the VD-transformed defect velocity matched the incompressible counterpart well.
In terms of temperature, the classical Crocco–Busemann relation (e.g. White Reference White2006) shows that, after assuming unity Prandtl numbers (![]() ${\textit {Pr}}$), the mean temperature is almost a quadratic function of the mean streamwise velocity. A less restrictive relation was proposed by Walz (Reference Walz1969) to incorporate non-unity
${\textit {Pr}}$), the mean temperature is almost a quadratic function of the mean streamwise velocity. A less restrictive relation was proposed by Walz (Reference Walz1969) to incorporate non-unity ![]() ${\textit {Pr}}$ effects by introducing the recovery temperature. Although this relation holds in high-speed adiabatic flows, the accuracy degrades severely in case of significant surface heat transfer. A crucial modification was contributed by Duan & Martín (Reference Duan and Martín2011), who introduced a semiempirical quadratic function of the velocity. The resulting quadratic temperature–velocity (TV) relation was shown to be highly accurate for a wide range of boundary layer, channel and pipe flows (Zhang, Duan & Choudhari Reference Zhang, Duan and Choudhari2018; Modesti & Pirozzoli Reference Modesti and Pirozzoli2019; Fu et al. Reference Fu, Karp, Bose, Moin and Urzay2021; Griffin, Fu & Moin Reference Griffin, Fu and Moin2023), even with high-enthalpy effects (using enthalpy instead; Passiatore et al. Reference Passiatore, Sciacovelli, Cinnella and Pascazio2022). Subsequently, Zhang et al. (Reference Zhang, Bi, Hussain and She2014) recast the above relation in terms of a generalized Reynolds analogy, where the Reynolds analogy factor is present for further physical interpretations of the closure constant.
${\textit {Pr}}$ effects by introducing the recovery temperature. Although this relation holds in high-speed adiabatic flows, the accuracy degrades severely in case of significant surface heat transfer. A crucial modification was contributed by Duan & Martín (Reference Duan and Martín2011), who introduced a semiempirical quadratic function of the velocity. The resulting quadratic temperature–velocity (TV) relation was shown to be highly accurate for a wide range of boundary layer, channel and pipe flows (Zhang, Duan & Choudhari Reference Zhang, Duan and Choudhari2018; Modesti & Pirozzoli Reference Modesti and Pirozzoli2019; Fu et al. Reference Fu, Karp, Bose, Moin and Urzay2021; Griffin, Fu & Moin Reference Griffin, Fu and Moin2023), even with high-enthalpy effects (using enthalpy instead; Passiatore et al. Reference Passiatore, Sciacovelli, Cinnella and Pascazio2022). Subsequently, Zhang et al. (Reference Zhang, Bi, Hussain and She2014) recast the above relation in terms of a generalized Reynolds analogy, where the Reynolds analogy factor is present for further physical interpretations of the closure constant.
The success of these mean flow relations makes it possible to recover the mean velocity and temperature by solving an inverse problem, which helps improve turbulence modelling. Pioneering work is the generalized velocity derived by van Driest (Reference van Driest1951) through combining the VD transformation and the quadratic TV relation throughout the boundary layer. This framework enables efficient computation of the mean profiles and skin friction (Huang, Bradshaw & Coakley Reference Huang, Bradshaw and Coakley1993; Kumar & Larsson Reference Kumar and Larsson2022). Owing to the continuously increased accuracy of these mean flow relations, more and more attention has been paid to the modelling aspect in recent years. For channel and pipe flows, the combination of the velocity transformation and TV relation leads to ordinary differential equations (ODEs) for the mean flow, which achieves a relatively high accuracy (Chen et al. Reference Chen, Cheng, Fu and Gan2023a; Song, Zhang & Xia Reference Song, Zhang and Xia2023). For ZPG boundary layers, Hasan et al. (Reference Hasan, Larsson, Pirozzoli and Pecnik2023a) supplemented a ![]() ${\textit {Re}}$-dependent function for Coles’ wake parameter (Coles Reference Coles1956). The ODE set for the inverse problem is thus formulated, and the results are in close agreement with DNS. In a more general set-up, Hendrickson, Subbareddy & Candler (Reference Hendrickson, Subbareddy and Candler2022) and Hendrickson et al. (Reference Hendrickson, Subbareddy, Candler and Macdonald2023) used velocity transformations to improve the inner-layer scaling of the BL model, also for ZPG boundary layers. Although the mean profile prediction is improved for the two cases displayed, there are still noticeable deviations in temperature from DNS for cold-wall cases. More encouragingly, the established relations can help improve the wall-modelled large-eddy simulations (WMLES). In a very recent work, Griffin et al. (Reference Griffin, Fu and Moin2023) proposed a near-wall model using the GFM transformation and the TV relation, with the outer boundary conditions provided by large-eddy simulations (LES). This model was shown to be significantly more accurate than the classical ODE wall model for a wide range of canonical cases examined. Hendrickson et al. (Reference Hendrickson, Subbareddy, Candler and Macdonald2023) made similar explorations, while the temperature prediction was less accurate for cold-wall boundary layers when velocity transformations alone were taken into account.
${\textit {Re}}$-dependent function for Coles’ wake parameter (Coles Reference Coles1956). The ODE set for the inverse problem is thus formulated, and the results are in close agreement with DNS. In a more general set-up, Hendrickson, Subbareddy & Candler (Reference Hendrickson, Subbareddy and Candler2022) and Hendrickson et al. (Reference Hendrickson, Subbareddy, Candler and Macdonald2023) used velocity transformations to improve the inner-layer scaling of the BL model, also for ZPG boundary layers. Although the mean profile prediction is improved for the two cases displayed, there are still noticeable deviations in temperature from DNS for cold-wall cases. More encouragingly, the established relations can help improve the wall-modelled large-eddy simulations (WMLES). In a very recent work, Griffin et al. (Reference Griffin, Fu and Moin2023) proposed a near-wall model using the GFM transformation and the TV relation, with the outer boundary conditions provided by large-eddy simulations (LES). This model was shown to be significantly more accurate than the classical ODE wall model for a wide range of canonical cases examined. Hendrickson et al. (Reference Hendrickson, Subbareddy, Candler and Macdonald2023) made similar explorations, while the temperature prediction was less accurate for cold-wall boundary layers when velocity transformations alone were taken into account.
As aforementioned, we aim to improve the compressible BL model for canonical boundary layers using the established relations for mean velocity and temperature. To make the improvement clean and solid, we strictly adhere to the following three principles.
(i) First, the BL model for incompressible flows is not altered. The compressible version is modified to achieve the same accuracy level as the incompressible one.
(ii) Second, only well-established relations are used, which have been widely verified. We avoid introducing any new functions or coefficients fitted by ourselves.
(iii) Last, the modification is made as simple as feasible.
For a priori inspiration and a posteriori examination, wide published DNS databases for ZPG boundary layers are employed containing 12 cases from different sources, with ![]() ${\textit {Ma}}_\infty$ ranging from 2 to 14 under adiabatic, cold and heated wall conditions. Of particular focus are the cold-wall cases, which are ubiquitous and even unavoidable in practical hypersonic applications. The remaining parts are organized as follows. Section 2 describes the governing equations, DNS database and the baseline BL model. Section 3 presents how established relations are implemented in the wall model, and provides a priori examination using the DNS data. The resulting modified BL model is examined in § 4 for all the cases, and the work is summarized in § 5. Although only ZPG boundary layers are considered, we believe that the present framework is promising. The applications, limitations and future steps are discussed in § 5.1.
${\textit {Ma}}_\infty$ ranging from 2 to 14 under adiabatic, cold and heated wall conditions. Of particular focus are the cold-wall cases, which are ubiquitous and even unavoidable in practical hypersonic applications. The remaining parts are organized as follows. Section 2 describes the governing equations, DNS database and the baseline BL model. Section 3 presents how established relations are implemented in the wall model, and provides a priori examination using the DNS data. The resulting modified BL model is examined in § 4 for all the cases, and the work is summarized in § 5. Although only ZPG boundary layers are considered, we believe that the present framework is promising. The applications, limitations and future steps are discussed in § 5.1.
2. Problem formulations and datasets
2.1. Governing equations and DNS datasets
The ZPG turbulent boundary layers are considered, as illustrated in figure 1. Assuming a calorically perfect gas, the zero-equation RANS equations are written as
 $$\begin{gather}
\bar{\rho} c_p
\bigg(\frac{\partial \tilde{T}}{\partial t} +
\tilde{\boldsymbol{u}}
\boldsymbol{\cdot}\boldsymbol{\nabla} \tilde{T} \bigg)
- \left(\frac{\partial \bar{p}}{\partial t} +
\tilde{\boldsymbol{u}}
\boldsymbol{\cdot}\boldsymbol{\nabla} \bar{p}
\right)\nonumber\\ =
\left(\tilde{\mu}+\mu_t\right) \Big[ \boldsymbol{\nabla}
\tilde{\boldsymbol{u}} \boldsymbol{:} \left(
{\boldsymbol{\nabla} \tilde{\boldsymbol{u}} +
\boldsymbol{\nabla} \tilde{\boldsymbol{u}}^{\text{T}}}
\right) - \frac{2}{3} \left( {\boldsymbol{\nabla}
\boldsymbol{\cdot} \tilde{\boldsymbol{u}}} \right)^2
\Big] + \boldsymbol{\nabla}
\boldsymbol{\cdot}[\left(\tilde{\kappa} +
\kappa_t\right) \boldsymbol{\nabla} \tilde{T}],
\end{gather}$$
$$\begin{gather}
\bar{\rho} c_p
\bigg(\frac{\partial \tilde{T}}{\partial t} +
\tilde{\boldsymbol{u}}
\boldsymbol{\cdot}\boldsymbol{\nabla} \tilde{T} \bigg)
- \left(\frac{\partial \bar{p}}{\partial t} +
\tilde{\boldsymbol{u}}
\boldsymbol{\cdot}\boldsymbol{\nabla} \bar{p}
\right)\nonumber\\ =
\left(\tilde{\mu}+\mu_t\right) \Big[ \boldsymbol{\nabla}
\tilde{\boldsymbol{u}} \boldsymbol{:} \left(
{\boldsymbol{\nabla} \tilde{\boldsymbol{u}} +
\boldsymbol{\nabla} \tilde{\boldsymbol{u}}^{\text{T}}}
\right) - \frac{2}{3} \left( {\boldsymbol{\nabla}
\boldsymbol{\cdot} \tilde{\boldsymbol{u}}} \right)^2
\Big] + \boldsymbol{\nabla}
\boldsymbol{\cdot}[\left(\tilde{\kappa} +
\kappa_t\right) \boldsymbol{\nabla} \tilde{T}],
\end{gather}$$
where ![]() $\rho$,
$\rho$, ![]() $\boldsymbol {u}$,
$\boldsymbol {u}$, ![]() $T$ and
$T$ and ![]() $p=\rho RT$ are the fluid's density, velocity, temperature and pressure;
$p=\rho RT$ are the fluid's density, velocity, temperature and pressure; ![]() $R$ and
$R$ and ![]() $c_p$ are the gas constant and isobaric specific heat;
$c_p$ are the gas constant and isobaric specific heat; ![]() $\mu$ and
$\mu$ and ![]() $\kappa$ are molecular viscosity and thermal conductivity. The Reynolds and Favre averages are denoted as
$\kappa$ are molecular viscosity and thermal conductivity. The Reynolds and Favre averages are denoted as ![]() $\bar {\phi }$ and
$\bar {\phi }$ and ![]() $\tilde{\phi }$ (fluctuations as
$\tilde{\phi }$ (fluctuations as ![]() $\phi ^{\prime }$ and
$\phi ^{\prime }$ and ![]() $\phi ^{{\prime \prime }}$), respectively. The quantities
$\phi ^{{\prime \prime }}$), respectively. The quantities ![]() $\mu _t$ and
$\mu _t$ and ![]() $\kappa _t$ model the Reynolds stress
$\kappa _t$ model the Reynolds stress ![]() $-\bar {\rho }\widetilde{\boldsymbol {u}^{{\prime \prime }}\boldsymbol {u}^{{\prime \prime }}}$ and turbulent heat flux
$-\bar {\rho }\widetilde{\boldsymbol {u}^{{\prime \prime }}\boldsymbol {u}^{{\prime \prime }}}$ and turbulent heat flux ![]() $-\bar {\rho }c_p \widetilde{\boldsymbol {u}^{{\prime \prime }} T^{{\prime \prime }}}$, whose formulations are described in § 2.3. The wall is set no-slip and isothermal or adiabatic. The variables in wall viscous units are expressed with a superscript
$-\bar {\rho }c_p \widetilde{\boldsymbol {u}^{{\prime \prime }} T^{{\prime \prime }}}$, whose formulations are described in § 2.3. The wall is set no-slip and isothermal or adiabatic. The variables in wall viscous units are expressed with a superscript ![]() $+$, as
$+$, as ![]() $\boldsymbol {x}^+={\boldsymbol {x}}/{\delta _\nu }$,
$\boldsymbol {x}^+={\boldsymbol {x}}/{\delta _\nu }$, ![]() $\bar {\rho }^+=\bar {\rho }/\rho _w$,
$\bar {\rho }^+=\bar {\rho }/\rho _w$, ![]() $\tilde{\boldsymbol u}^+=\tilde{\boldsymbol u}/{u_\tau }$ and
$\tilde{\boldsymbol u}^+=\tilde{\boldsymbol u}/{u_\tau }$ and ![]() $\tilde {\mu }^+=\tilde {\mu }/\mu _w$, where
$\tilde {\mu }^+=\tilde {\mu }/\mu _w$, where ![]() $w$ represents the wall variables,
$w$ represents the wall variables, ![]() $\delta _\nu =\mu _w/(\rho _w u_\tau )$ is the viscous length unit,
$\delta _\nu =\mu _w/(\rho _w u_\tau )$ is the viscous length unit, ![]() $u_\tau =(\tau _w/\rho _w)^{1/2}$ is the friction velocity,
$u_\tau =(\tau _w/\rho _w)^{1/2}$ is the friction velocity, ![]() $\tau _w$ is the wall shear. Correspondingly, the friction Reynolds number is
$\tau _w$ is the wall shear. Correspondingly, the friction Reynolds number is ![]() ${\textit {Re}}_\tau =\delta _{99}/\delta _v$ with
${\textit {Re}}_\tau =\delta _{99}/\delta _v$ with ![]() $\delta _{99}$ the nominal thickness based on streamwise velocity. Furthermore, semilocal units are adopted, with a superscript
$\delta _{99}$ the nominal thickness based on streamwise velocity. Furthermore, semilocal units are adopted, with a superscript ![]() $*$ as
$*$ as ![]() $u_\tau ^*=(\tau _w/\bar {\rho })^{1/2}$,
$u_\tau ^*=(\tau _w/\bar {\rho })^{1/2}$, ![]() $\delta _\nu ^*=\tilde {\mu }/(\bar {\rho } u_\tau ^*)$, so
$\delta _\nu ^*=\tilde {\mu }/(\bar {\rho } u_\tau ^*)$, so ![]() $y^*=y/\delta _v^*$. Most recent transformations are based on
$y^*=y/\delta _v^*$. Most recent transformations are based on ![]() $y^*$, so
$y^*$, so ![]() $y^*$ as the inner scaling can be used to classify different layers, in analogy to
$y^*$ as the inner scaling can be used to classify different layers, in analogy to ![]() $y^+$ in incompressible flows. Besides, two commonly used Reynolds numbers are
$y^+$ in incompressible flows. Besides, two commonly used Reynolds numbers are ![]() ${\textit {Re}}_\theta =\rho _\infty U_\infty \theta /\mu _\infty$ and
${\textit {Re}}_\theta =\rho _\infty U_\infty \theta /\mu _\infty$ and ![]() ${\textit {Re}}_{\delta _2}=\rho _\infty U_\infty \theta /\mu _w$ (Fernholz & Finley Reference Fernholz and Finley1980), where
${\textit {Re}}_{\delta _2}=\rho _\infty U_\infty \theta /\mu _w$ (Fernholz & Finley Reference Fernholz and Finley1980), where ![]() $\theta$ is the momentum thickness and
$\theta$ is the momentum thickness and ![]() $\infty$ denotes free stream variables.
$\infty$ denotes free stream variables.

Figure 1. Schematic of the compressible flat-plate ZPG boundary layers.
To comprehensively examine the modified BL model, wide elaborated DNS databases are employed for ZPG boundary layers from different sources, with ![]() ${\textit {Ma}}_\infty$ from 2 to 14 under adiabatic, cold and heated walls. The published data are from Pirozzoli & Bernardini (Reference Pirozzoli and Bernardini2011, Reference Pirozzoli and Bernardini2013), Zhang et al. (Reference Zhang, Duan and Choudhari2018) and Volpiani, Bernardini & Larsson (Reference Volpiani, Bernardini and Larsson2018, Reference Volpiani, Bernardini and Larsson2020), as summarized in table 1. Though
${\textit {Ma}}_\infty$ from 2 to 14 under adiabatic, cold and heated walls. The published data are from Pirozzoli & Bernardini (Reference Pirozzoli and Bernardini2011, Reference Pirozzoli and Bernardini2013), Zhang et al. (Reference Zhang, Duan and Choudhari2018) and Volpiani, Bernardini & Larsson (Reference Volpiani, Bernardini and Larsson2018, Reference Volpiani, Bernardini and Larsson2020), as summarized in table 1. Though ![]() ${\textit {Ma}}_\infty =14$ is reached, the high-enthalpy effects (e.g. Chen et al. Reference Chen, Xi, Ren and Fu2022b) are not considered following the reference set-up. Besides, the incompressible data from Schlatter & Örlü (Reference Schlatter and Örlü2010) are included, as a reference for the incompressible BL model. The viscous parameters in each case are computed according to the references. The viscosity is from Sutherland's law, the power law or the formula for
${\textit {Ma}}_\infty =14$ is reached, the high-enthalpy effects (e.g. Chen et al. Reference Chen, Xi, Ren and Fu2022b) are not considered following the reference set-up. Besides, the incompressible data from Schlatter & Örlü (Reference Schlatter and Örlü2010) are included, as a reference for the incompressible BL model. The viscous parameters in each case are computed according to the references. The viscosity is from Sutherland's law, the power law or the formula for ![]() $\rm {N}_2$ (the working fluid in case ZDC-M8Tw048R20). Constant
$\rm {N}_2$ (the working fluid in case ZDC-M8Tw048R20). Constant ![]() ${\textit {Pr}}=c_p\mu /\kappa$ are adopted for the thermal conductivity.
${\textit {Pr}}=c_p\mu /\kappa$ are adopted for the thermal conductivity.
Table 1. Parameters for the DNS datasets, where ![]() $T_r$ is the recovery temperature (
$T_r$ is the recovery temperature (![]() $T_w=T_r$ for adiabatic cases). The cases with multiple streamwise locations are labelled in the brackets of the case numbers. The abbreviations for data sources are used hereinafter, as SO for Schlatter & Örlü (Reference Schlatter and Örlü2010), PB for Pirozzoli & Bernardini (Reference Pirozzoli and Bernardini2011, Reference Pirozzoli and Bernardini2013), ZDC for Zhang et al. (Reference Zhang, Duan and Choudhari2018) and VBL for Volpiani et al. (Reference Volpiani, Bernardini and Larsson2018, Reference Volpiani, Bernardini and Larsson2020). The notation expresses
$T_w=T_r$ for adiabatic cases). The cases with multiple streamwise locations are labelled in the brackets of the case numbers. The abbreviations for data sources are used hereinafter, as SO for Schlatter & Örlü (Reference Schlatter and Örlü2010), PB for Pirozzoli & Bernardini (Reference Pirozzoli and Bernardini2011, Reference Pirozzoli and Bernardini2013), ZDC for Zhang et al. (Reference Zhang, Duan and Choudhari2018) and VBL for Volpiani et al. (Reference Volpiani, Bernardini and Larsson2018, Reference Volpiani, Bernardini and Larsson2020). The notation expresses ![]() ${\textit {Ma}}_\infty$,
${\textit {Ma}}_\infty$, ![]() $T_w/T_r$ and
$T_w/T_r$ and ![]() ${\textit {Re}}_{\delta _2}$ (divided by 100).
${\textit {Re}}_{\delta _2}$ (divided by 100).

Notably, (2.1) is expressed using the Favre-averaged variables (except for ![]() $\bar {\rho }$) to form a closed system (Gatski & Bonnet Reference Gatski and Bonnet2013). The difference between the Reynolds- and Favre-averaged results cannot be accounted for using the algebraic RANS models, so we simply use the Favre averages throughout for consistency of notation, though the DNS data mostly adopt the Reynolds averages. This simplification will not affect the main conclusions of this work because even for the M14Tw018R24 case of the highest
$\bar {\rho }$) to form a closed system (Gatski & Bonnet Reference Gatski and Bonnet2013). The difference between the Reynolds- and Favre-averaged results cannot be accounted for using the algebraic RANS models, so we simply use the Favre averages throughout for consistency of notation, though the DNS data mostly adopt the Reynolds averages. This simplification will not affect the main conclusions of this work because even for the M14Tw018R24 case of the highest ![]() ${\textit {Ma}}$, there are only slight differences between the DNS statistics from these two averages (Zhang et al. Reference Zhang, Duan and Choudhari2018).
${\textit {Ma}}$, there are only slight differences between the DNS statistics from these two averages (Zhang et al. Reference Zhang, Duan and Choudhari2018).
2.2. Solution of boundary layer equations
Based on the hypersonic interaction parameter (White Reference White2006), the effects of shock-boundary-layer interaction at the leading edge are evaluated to be minor on the downstream locations for the cases in table 1. Therefore, the boundary layer equations can be used for efficient computation of the mean flow, in the absence of impinging shock and separation. From (2.1), the boundary layer equations are written as (e.g. White Reference White2006)
 \begin{equation} \left. \begin{gathered}
\dfrac{\partial ( {\bar{\rho} \tilde{U}} )}{\partial x} +
\dfrac{\partial ( {\bar{\rho} \tilde{V}} )}{\partial y} =
0,\\ \bar{\rho} \bigg( {\tilde{U} \dfrac{\partial
\tilde{U}}{\partial x} + \tilde{V} \dfrac{\partial
\tilde{U}}{\partial y}} \bigg) ={-} \dfrac{{\mathrm{d}}
P_e}{{\mathrm{d}}\kern0.7pt x} + \dfrac{\partial }{\partial
y} \bigg[ \left({\tilde{\mu} + \mu_t}\right)
\dfrac{\partial \tilde{U}}{\partial y} \bigg],\\
\bar{\rho} c_p \bigg( {\tilde{U} \dfrac{\partial
\tilde{T}}{\partial x} + \tilde{V} \dfrac{\partial
\tilde{T}}{\partial y}} \bigg) = \tilde{U}
\dfrac{{\mathrm{d}} P_e}{{\mathrm{d}}\kern0.7pt x} +
\left({\tilde{\mu} + \mu_t}\right) \bigg( {\dfrac{\partial
\tilde{U}}{\partial y}} \bigg)^2 + \dfrac{\partial
}{\partial y} \bigg[ {\left( {\tilde{\kappa} + \kappa_t}
\right) \dfrac{\partial \tilde{T}}{\partial y}} \bigg],
\end{gathered} \right\}
\end{equation}
\begin{equation} \left. \begin{gathered}
\dfrac{\partial ( {\bar{\rho} \tilde{U}} )}{\partial x} +
\dfrac{\partial ( {\bar{\rho} \tilde{V}} )}{\partial y} =
0,\\ \bar{\rho} \bigg( {\tilde{U} \dfrac{\partial
\tilde{U}}{\partial x} + \tilde{V} \dfrac{\partial
\tilde{U}}{\partial y}} \bigg) ={-} \dfrac{{\mathrm{d}}
P_e}{{\mathrm{d}}\kern0.7pt x} + \dfrac{\partial }{\partial
y} \bigg[ \left({\tilde{\mu} + \mu_t}\right)
\dfrac{\partial \tilde{U}}{\partial y} \bigg],\\
\bar{\rho} c_p \bigg( {\tilde{U} \dfrac{\partial
\tilde{T}}{\partial x} + \tilde{V} \dfrac{\partial
\tilde{T}}{\partial y}} \bigg) = \tilde{U}
\dfrac{{\mathrm{d}} P_e}{{\mathrm{d}}\kern0.7pt x} +
\left({\tilde{\mu} + \mu_t}\right) \bigg( {\dfrac{\partial
\tilde{U}}{\partial y}} \bigg)^2 + \dfrac{\partial
}{\partial y} \bigg[ {\left( {\tilde{\kappa} + \kappa_t}
\right) \dfrac{\partial \tilde{T}}{\partial y}} \bigg],
\end{gathered} \right\}
\end{equation}
where ![]() $\tilde{U}$ and
$\tilde{U}$ and ![]() $\tilde{V}$ are the streamwise (
$\tilde{V}$ are the streamwise (![]() $x$) and wall-normal (
$x$) and wall-normal (![]() $y$) velocities. The pressure is assumed invariant along the
$y$) velocities. The pressure is assumed invariant along the ![]() $y$-direction (
$y$-direction (![]() $P_e$), so
$P_e$), so ![]() $\bar {\rho }=\rho _e T_e/\tilde{T}$ is satisfied, where
$\bar {\rho }=\rho _e T_e/\tilde{T}$ is satisfied, where ![]() $e$ denotes values at the boundary layer edge. More general formulations accounting for geometrical curvature, far-field shock and cross-flow can be found in Degani & Schiff (Reference Degani and Schiff1983) and Gupta et al. (Reference Gupta, Lee, Zoby, Moss and Thompson1990).
$e$ denotes values at the boundary layer edge. More general formulations accounting for geometrical curvature, far-field shock and cross-flow can be found in Degani & Schiff (Reference Degani and Schiff1983) and Gupta et al. (Reference Gupta, Lee, Zoby, Moss and Thompson1990).
Due to the complex formulation of ![]() $\mu _t$ and
$\mu _t$ and ![]() $\kappa _t$ (§ 2.3), the boundary layer profiles are not self-similar, even with ZPG. To solve the non-self-similar flow, the Mangler–Levy–Lees transformation can be used to remove the singularity at the leading edge
$\kappa _t$ (§ 2.3), the boundary layer profiles are not self-similar, even with ZPG. To solve the non-self-similar flow, the Mangler–Levy–Lees transformation can be used to remove the singularity at the leading edge ![]() $x=0$ (Probstein & Elliott Reference Probstein and Elliott1956). The transformed coordinate
$x=0$ (Probstein & Elliott Reference Probstein and Elliott1956). The transformed coordinate ![]() $(\xi,\eta )$ is defined as
$(\xi,\eta )$ is defined as
The continuity equation is then eliminated and the transformed momentum and energy equations are
where the normalized streamwise velocity and temperature are ![]() $F=\tilde{U}/U_e$ and
$F=\tilde{U}/U_e$ and ![]() $G=\tilde{T}/T_e$ and
$G=\tilde{T}/T_e$ and ![]() $\varPi =\int F\,{\mathrm {d}}\eta$. The other parameters are
$\varPi =\int F\,{\mathrm {d}}\eta$. The other parameters are ![]() $C_1=\bar {\rho }(\tilde {\mu }+\mu _t)/(\rho _e\mu _e)$,
$C_1=\bar {\rho }(\tilde {\mu }+\mu _t)/(\rho _e\mu _e)$, ![]() $C_2=\bar {\rho }(\tilde {\kappa }+\kappa _t)/(\rho _e c_p \mu _e)$ and the Eckert number
$C_2=\bar {\rho }(\tilde {\kappa }+\kappa _t)/(\rho _e c_p \mu _e)$ and the Eckert number ![]() ${\textit {Ec}}_e=U_e^2/(c_pT_e)$. The streamwise pressure gradient is reflected in
${\textit {Ec}}_e=U_e^2/(c_pT_e)$. The streamwise pressure gradient is reflected in ![]() ${\mathrm {d}} U_e/{\mathrm {d}} \xi$ through the Bernoulli equation, taken to be zero in the flows considered. The wall-normal boundary conditions at the wall and in the free stream are
${\mathrm {d}} U_e/{\mathrm {d}} \xi$ through the Bernoulli equation, taken to be zero in the flows considered. The wall-normal boundary conditions at the wall and in the free stream are
Equation (2.4) is solved using the streamwise marching procedure (Blottner Reference Blottner1963; Chen, Wang & Fu Reference Chen, Wang and Fu2021). At ![]() $\xi =0$, (2.4) degenerates into two ODEs in terms of
$\xi =0$, (2.4) degenerates into two ODEs in terms of ![]() $\eta$, which are solved using the shooting method and serve as the initial profile. Afterwards, the solution at
$\eta$, which are solved using the shooting method and serve as the initial profile. Afterwards, the solution at ![]() $\xi >0$ is feasible through streamwise marching. The streamwise (
$\xi >0$ is feasible through streamwise marching. The streamwise (![]() $\xi$) derivatives are discretized using the third-order finite-difference scheme. The Chebyshev collocation method is adopted for the wall-normal direction (
$\xi$) derivatives are discretized using the third-order finite-difference scheme. The Chebyshev collocation method is adopted for the wall-normal direction (![]() $\eta$), with more points clustering near the wall. A grid number
$\eta$), with more points clustering near the wall. A grid number ![]() $N_y=241$ is adequate to provide grid-independent results. A uniform
$N_y=241$ is adequate to provide grid-independent results. A uniform ![]() $\xi$ mesh is adopted, while the grid with increasing spacing can be used for better robustness. At each
$\xi$ mesh is adopted, while the grid with increasing spacing can be used for better robustness. At each ![]() $\xi _i$, Newtonian iteration is used for quick convergence of the nonlinear equations. Second-order convergence can be realized for laminar flows (e.g. Chen, Wang & Fu Reference Chen, Wang and Fu2022a), while for turbulent flows here, the derivatives of
$\xi _i$, Newtonian iteration is used for quick convergence of the nonlinear equations. Second-order convergence can be realized for laminar flows (e.g. Chen, Wang & Fu Reference Chen, Wang and Fu2022a), while for turbulent flows here, the derivatives of ![]() $\mu _t$ and
$\mu _t$ and ![]() $\kappa _t$ may not be smooth (due to the maximum and intersection functions, see § 2.3), so the convergence is only first order. The convergence criterion for
$\kappa _t$ may not be smooth (due to the maximum and intersection functions, see § 2.3), so the convergence is only first order. The convergence criterion for ![]() $[F,G]^{\textrm {T}}$ is set to
$[F,G]^{\textrm {T}}$ is set to ![]() $10^{-9}$ and at most 50 iterations are allowed at each streamwise location. The above procedure is substantially more efficient than solving (2.1). For the cases in table 1, the mean flow at the target
$10^{-9}$ and at most 50 iterations are allowed at each streamwise location. The above procedure is substantially more efficient than solving (2.1). For the cases in table 1, the mean flow at the target ![]() $x$ can be obtained within minutes on a desktop computer. The solver is verified (detailed in Appendix A) through comparing with Hendrickson et al. (Reference Hendrickson, Subbareddy, Candler and Macdonald2023), who solved the full Navier–Stokes (NS) equation with BL models using the US3D code.
$x$ can be obtained within minutes on a desktop computer. The solver is verified (detailed in Appendix A) through comparing with Hendrickson et al. (Reference Hendrickson, Subbareddy, Candler and Macdonald2023), who solved the full Navier–Stokes (NS) equation with BL models using the US3D code.
It is worth mentioning that ![]() $\mu _t$ and
$\mu _t$ and ![]() $\kappa _t$ from the BL model are zero at
$\kappa _t$ from the BL model are zero at ![]() $\xi =0$ (since
$\xi =0$ (since ![]() $y=0$), so the initial profile at
$y=0$), so the initial profile at ![]() $\xi =0$ is exactly the laminar counterpart. Thereby, there is a numerical (not physical) transition process downstream as
$\xi =0$ is exactly the laminar counterpart. Thereby, there is a numerical (not physical) transition process downstream as ![]() $\mu _t$ increases. If the transition is not desirable, the start point for marching
$\mu _t$ increases. If the transition is not desirable, the start point for marching ![]() $\xi _0$ can be placed somewhere downstream, where the maximum
$\xi _0$ can be placed somewhere downstream, where the maximum ![]() $\mu _t/\mu _\infty$ is already high and the flow is turbulent. The initial profile at
$\mu _t/\mu _\infty$ is already high and the flow is turbulent. The initial profile at ![]() $\xi _0>0$ can still be obtained by solving the ODEs with the streamwise derivatives (left-hand sides in (2.4)) artificially dropped. The regime of streamwise adjustment is short due to the parabolic nature of (2.2), so the results downstream are not sensitive to
$\xi _0>0$ can still be obtained by solving the ODEs with the streamwise derivatives (left-hand sides in (2.4)) artificially dropped. The regime of streamwise adjustment is short due to the parabolic nature of (2.2), so the results downstream are not sensitive to ![]() $\xi _0$.
$\xi _0$.
2.3. Baseline BL model
As mentioned in § 1, the BL model using semilocal units for the inner layer construction outperforms the one using wall-viscous units in high-speed applications (Dilley & McClinton Reference Dilley and McClinton2001). Therefore, the semilocal version is selected as the baseline BL model for modification. For future reference, it is termed the BL-local model in this work. The formulations are specified below, primarily following Cheatwood & Thompson (Reference Cheatwood and Thompson1993) for the LAURA code. The two-layer formulation of ![]() $\mu _t$ in BL (and also CS) is
$\mu _t$ in BL (and also CS) is
where ![]() $y_{m\mu }$ is the matching (intersection) point between the inner layer
$y_{m\mu }$ is the matching (intersection) point between the inner layer ![]() ${\mu _{t,i}}$ and outer layer
${\mu _{t,i}}$ and outer layer ![]() ${\mu _{t,o}}$. The former is based on the mixing length concept, as
${\mu _{t,o}}$. The former is based on the mixing length concept, as
where ![]() $\tilde{\omega }$ is the vorticity,
$\tilde{\omega }$ is the vorticity, ![]() $l_{mix}$ is the mixing length corrected by the exponential damping function of van Driest (Reference van Driest1956) and
$l_{mix}$ is the mixing length corrected by the exponential damping function of van Driest (Reference van Driest1956) and ![]() $\kappa _c$ is the von Kármán constant, taken as 0.40. There are two differences in (2.7a–c) from the original version of Baldwin & Lomax (Reference Baldwin and Lomax1978). First,
$\kappa _c$ is the von Kármán constant, taken as 0.40. There are two differences in (2.7a–c) from the original version of Baldwin & Lomax (Reference Baldwin and Lomax1978). First, ![]() $y^*$ is used in the exponent of
$y^*$ is used in the exponent of ![]() $l_{mix}$, instead of
$l_{mix}$, instead of ![]() $y^+$, which was also adopted in recent works on WMLES (Yang & Lv Reference Yang and Lv2018; Fu, Bose & Moin Reference Fu, Bose and Moin2022; Kamogawa, Tamaki & Kawai Reference Kamogawa, Tamaki and Kawai2023). Second,
$y^+$, which was also adopted in recent works on WMLES (Yang & Lv Reference Yang and Lv2018; Fu, Bose & Moin Reference Fu, Bose and Moin2022; Kamogawa, Tamaki & Kawai Reference Kamogawa, Tamaki and Kawai2023). Second, ![]() $A^+$ is not a constant, but dependent on the local total shear
$A^+$ is not a constant, but dependent on the local total shear ![]() $\bar {\tau }^+=\bar {\tau }/\tau _w$. For thin layer flows,
$\bar {\tau }^+=\bar {\tau }/\tau _w$. For thin layer flows, ![]() $|\tilde{\omega }|$ can be simplified to
$|\tilde{\omega }|$ can be simplified to ![]() $|{\partial \tilde{U}_{{\scriptscriptstyle /\!/}}}/{\partial n}|$, where
$|{\partial \tilde{U}_{{\scriptscriptstyle /\!/}}}/{\partial n}|$, where ![]() $\tilde{U}_{{\scriptscriptstyle /\!/}}$ is the velocity parallel to the wall, and
$\tilde{U}_{{\scriptscriptstyle /\!/}}$ is the velocity parallel to the wall, and ![]() $n$ is the wall-normal direction. For the configurations in figure 1, we simply have
$n$ is the wall-normal direction. For the configurations in figure 1, we simply have ![]() $|\tilde{\omega }|=|{\partial \tilde{U}}/{\partial y}|$.
$|\tilde{\omega }|=|{\partial \tilde{U}}/{\partial y}|$.
The outer-layer viscosity is evaluated by the Clauser–Klebanoff formulation (Klebanoff Reference Klebanoff1955; Clauser Reference Clauser1956). First, Clauser reasoned that for boundary layers, the eddies sufficiently away from the wall are no longer constrained by the wall, so their sizes should be proportional to the overall boundary layer thickness. The resulting maximum kinematic eddy viscosity in the outer layer is ![]() $\nu _{t,max}\sim U_e \delta _k^*$, or
$\nu _{t,max}\sim U_e \delta _k^*$, or ![]() $\nu _{t,max}=\alpha U_e \delta _k^*$, where
$\nu _{t,max}=\alpha U_e \delta _k^*$, where ![]() $\delta _k^*=\int (1-\tilde{U}/U_e)\,{\mathrm {d}} y$ is the kinematic displacement thickness (equals the displacement thickness in incompressible cases) and
$\delta _k^*=\int (1-\tilde{U}/U_e)\,{\mathrm {d}} y$ is the kinematic displacement thickness (equals the displacement thickness in incompressible cases) and ![]() $\alpha$ is a closure coefficient. Farther away from the wall, the flow becomes intermittent. An empirical intermittency factor
$\alpha$ is a closure coefficient. Farther away from the wall, the flow becomes intermittent. An empirical intermittency factor ![]() $F_{{Kleb}}$ (specified later) was introduced by Klebanoff, to model the diminishing of
$F_{{Kleb}}$ (specified later) was introduced by Klebanoff, to model the diminishing of ![]() $\nu _{t,o}$ with increasing height. Consequently,
$\nu _{t,o}$ with increasing height. Consequently, ![]() $\mu _{t,o}$ is computed as
$\mu _{t,o}$ is computed as ![]() $\bar {\rho }\nu _{t,max}F_{{Kleb}}$, which leads to the prevailing CS model. To avoid determining the boundary layer thicknesses, which is beneficial for complex flows,
$\bar {\rho }\nu _{t,max}F_{{Kleb}}$, which leads to the prevailing CS model. To avoid determining the boundary layer thicknesses, which is beneficial for complex flows, ![]() $U_e \delta _k^*$ in
$U_e \delta _k^*$ in ![]() $\nu _{t,max}$ is replaced by the wake function
$\nu _{t,max}$ is replaced by the wake function ![]() $C_{cp} y_{max} F_{max}$ in the BL model, which can be justified from the defect velocity scaling (detailed in § 3.2). Therefore, the outer-layer
$C_{cp} y_{max} F_{max}$ in the BL model, which can be justified from the defect velocity scaling (detailed in § 3.2). Therefore, the outer-layer ![]() $\mu _t$, adopted without explicit compressible corrections, is
$\mu _t$, adopted without explicit compressible corrections, is
where the vorticity function and the intermittency function are
Notably, ![]() $y_{max}$ is the peak position of the vorticity function following common usage, not the height of the computational domain. Compared with the CS model, the boundary layer thickness in
$y_{max}$ is the peak position of the vorticity function following common usage, not the height of the computational domain. Compared with the CS model, the boundary layer thickness in ![]() $F_{{Kleb}}$ is replaced by
$F_{{Kleb}}$ is replaced by ![]() $y_{max}/C_{{Kleb}}$. For more general flows,
$y_{max}/C_{{Kleb}}$. For more general flows, ![]() $\mu _{t,o}$ can be further restricted by a wake relation designed for free shear flows (see Wilcox Reference Wilcox2006). It is inactive in the present wall-bounded cases, thus not displayed for conciseness.
$\mu _{t,o}$ can be further restricted by a wake relation designed for free shear flows (see Wilcox Reference Wilcox2006). It is inactive in the present wall-bounded cases, thus not displayed for conciseness.
Besides ![]() $\kappa _c$ and
$\kappa _c$ and ![]() $A^+$, there are three closure coefficients
$A^+$, there are three closure coefficients ![]() $\alpha$,
$\alpha$, ![]() $C_{cp}$ and
$C_{cp}$ and ![]() $C_{{Kleb}}$ in the baseline model. Some works (e.g. Gupta et al. Reference Gupta, Lee, Zoby, Moss and Thompson1990) suggest their
$C_{{Kleb}}$ in the baseline model. Some works (e.g. Gupta et al. Reference Gupta, Lee, Zoby, Moss and Thompson1990) suggest their ![]() ${\textit {Ma}}$ dependence, but following the principles in § 1, we adopt the original constant values,
${\textit {Ma}}$ dependence, but following the principles in § 1, we adopt the original constant values, ![]() $\alpha =0.0168$,
$\alpha =0.0168$, ![]() $C_{cp}=1.6$ and
$C_{cp}=1.6$ and ![]() $C_{{Kleb}}=0.3$. After the numerical discretization, the intersection and maximum operations in (2.6) and (2.9a,b) are conducted after a third-order interpolation on adjacent grid points, to ensure smoothness and accuracy. After obtaining
$C_{{Kleb}}=0.3$. After the numerical discretization, the intersection and maximum operations in (2.6) and (2.9a,b) are conducted after a third-order interpolation on adjacent grid points, to ensure smoothness and accuracy. After obtaining ![]() $\mu _t$,
$\mu _t$, ![]() $\kappa _t=c_p\mu _t/{\textit {Pr}}_t$ is calculated through a prescribed
$\kappa _t=c_p\mu _t/{\textit {Pr}}_t$ is calculated through a prescribed ![]() ${\textit {Pr}}_t$. Although
${\textit {Pr}}_t$. Although ![]() ${\textit {Pr}}_t$ can be designed as a function of the wall-normal height (Subbareddy & Candler Reference Subbareddy and Candler2012), the simplest choice of a constant
${\textit {Pr}}_t$ can be designed as a function of the wall-normal height (Subbareddy & Candler Reference Subbareddy and Candler2012), the simplest choice of a constant ![]() ${\textit {Pr}}_t$ is adopted, equal to 0.9 as a common choice. The effects of
${\textit {Pr}}_t$ is adopted, equal to 0.9 as a common choice. The effects of ![]() ${\textit {Pr}}_t$ variations will be discussed in § 3.3.
${\textit {Pr}}_t$ variations will be discussed in § 3.3.
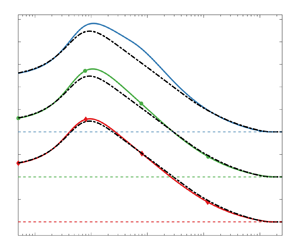
Two cases are employed to demonstrate the behaviour of the baseline BL-local model. First is an incompressible case from SO (![]() ${\textit {Ma}}_\infty$ set to 0.01 in our solver). The mean velocity and eddy viscosity are compared with the DNS data at
${\textit {Ma}}_\infty$ set to 0.01 in our solver). The mean velocity and eddy viscosity are compared with the DNS data at ![]() ${\textit {Re}}_\theta =2540$ in figure 2. Note that
${\textit {Re}}_\theta =2540$ in figure 2. Note that ![]() $\mu _t$ from DNS is evaluated by definition as
$\mu _t$ from DNS is evaluated by definition as ![]() $\mu _t=-\bar {\rho }\widetilde{u^{{\prime \prime }} v^{{\prime \prime }}}/(\partial \tilde{U}/\partial y)$;
$\mu _t=-\bar {\rho }\widetilde{u^{{\prime \prime }} v^{{\prime \prime }}}/(\partial \tilde{U}/\partial y)$; ![]() $\mu _t$ near the boundary layer edge is not displayed since both the numerator and denominator tend to zero. The predicted streamwise velocity is basically in line with DNS, showing the good capability of BL for incompressible flows. In the inner layer,
$\mu _t$ near the boundary layer edge is not displayed since both the numerator and denominator tend to zero. The predicted streamwise velocity is basically in line with DNS, showing the good capability of BL for incompressible flows. In the inner layer, ![]() $\mu _t^+$ faithfully follows the incompressible scaling by Johnson & King (Reference Johnson and King1985) as
$\mu _t^+$ faithfully follows the incompressible scaling by Johnson & King (Reference Johnson and King1985) as
where the last multiplier is termed the damping function. Note that (2.10) is more convenient than (2.7a–c) for comparisons between cases because ![]() $\tilde{\omega }$ does not explicitly appear. Away from the wall, the damping function is nearly unity, so the logarithmic scaling is formulated. In the outer layer, the peak value
$\tilde{\omega }$ does not explicitly appear. Away from the wall, the damping function is nearly unity, so the logarithmic scaling is formulated. In the outer layer, the peak value ![]() $\mu _{t,max}=\bar {\rho }\nu _{t,max}$ from the BL model is also close to the DNS (note that
$\mu _{t,max}=\bar {\rho }\nu _{t,max}$ from the BL model is also close to the DNS (note that ![]() $\bar {\rho }$ is invariant), so the matching point
$\bar {\rho }$ is invariant), so the matching point ![]() $y_{m\mu }^+=152$ (
$y_{m\mu }^+=152$ (![]() $\kern0.7pt y_{m\mu }=0.18\delta _{99}$) is near the upper bound of the logarithmic region, above which the outer-layer scaling is formulated. Although
$\kern0.7pt y_{m\mu }=0.18\delta _{99}$) is near the upper bound of the logarithmic region, above which the outer-layer scaling is formulated. Although ![]() $\mu _{t,o}$ damps (by
$\mu _{t,o}$ damps (by ![]() $F_{{Kleb}}$) more slowly than the DNS in the intermittent region, only a minor difference in
$F_{{Kleb}}$) more slowly than the DNS in the intermittent region, only a minor difference in ![]() $\tilde{U}$ appears due to the diminishing
$\tilde{U}$ appears due to the diminishing ![]() $\partial \tilde{U}/\partial y$.
$\partial \tilde{U}/\partial y$.

Figure 2. (a,c) Eddy viscosity and (b,d) mean streamwise velocity and temperature (only compressible case) from the baseline BL-local model and DNS for the (a,b) incompressible SO-M0R25 case and (c,d) hypersonic ZDC-M8Tw048R20 case.
For the hypersonic cold-wall case M8Tw048R20 from ZDC, however, ![]() $\tilde{U}$ and
$\tilde{U}$ and ![]() $\tilde{T}$ from the BL-local model have clear deviations from the DNS data, especially for
$\tilde{T}$ from the BL-local model have clear deviations from the DNS data, especially for ![]() $\tilde{T}$, as shown in figure 2(d). The discrepancy can be explained from figure 2(c). Compared with DNS,
$\tilde{T}$, as shown in figure 2(d). The discrepancy can be explained from figure 2(c). Compared with DNS, ![]() $\mu _{t,o}$ is severely underestimated, so the matching point
$\mu _{t,o}$ is severely underestimated, so the matching point ![]() $y_{m\mu }^*=67$ (
$y_{m\mu }^*=67$ (![]() $\kern0.7pt y_{m\mu }=0.09\delta _{99}$) is quite low. Consequently, the region
$\kern0.7pt y_{m\mu }=0.09\delta _{99}$) is quite low. Consequently, the region ![]() $67< y^*\lesssim 300$ (
$67< y^*\lesssim 300$ (![]() $0.09< y_{m\mu }/\delta _{99}\lesssim 0.27$) is not formulated by the logarithmic scaling in (2.7a), leading to the errors in
$0.09< y_{m\mu }/\delta _{99}\lesssim 0.27$) is not formulated by the logarithmic scaling in (2.7a), leading to the errors in ![]() $\tilde{U}$ and
$\tilde{U}$ and ![]() $\tilde{T}$ there. Meanwhile,
$\tilde{T}$ there. Meanwhile, ![]() $\tilde{T}$ around the temperature peak (
$\tilde{T}$ around the temperature peak (![]() $\kern0.7pt y^*\sim 7$) is over-predicted, possibly due to the inaccurate
$\kern0.7pt y^*\sim 7$) is over-predicted, possibly due to the inaccurate ![]() ${\textit {Pr}}_t$ there (specified in § 3.3).
${\textit {Pr}}_t$ there (specified in § 3.3).
In the following, the inner and outer-layer scalings of ![]() $\mu _t$ and
$\mu _t$ and ![]() $\kappa _t$ are investigated separately using the DNS data. Three targeted modifications are proposed based on established relations.
$\kappa _t$ are investigated separately using the DNS data. Three targeted modifications are proposed based on established relations.
3. Established relations and a priori examination
3.1. Inner-layer scaling
First, we demonstrate that the formulation of ![]() $\mu _{t,i}$ in the BL-local model is equivalent to applying the TL transformation. Analogous derivation was presented by Yang & Lv (Reference Yang and Lv2018) within the WMLES framework. Using the definition of
$\mu _{t,i}$ in the BL-local model is equivalent to applying the TL transformation. Analogous derivation was presented by Yang & Lv (Reference Yang and Lv2018) within the WMLES framework. Using the definition of ![]() $\mu _t$ and (2.7a–c), the mixing-length relation can be expressed, in wall-viscous units, as
$\mu _t$ and (2.7a–c), the mixing-length relation can be expressed, in wall-viscous units, as
The left-hand side, ![]() $-\bar {\rho }^+ \widetilde{u^{{{\prime \prime }}+}v^{{{\prime \prime }}+}}=-\bar {\rho } \widetilde{u^{{{\prime \prime }}}v^{{{\prime \prime }}}}/\tau _w=-\widetilde{u^{{{\prime \prime }}*}v^{{{\prime \prime }}*}}$, is the density-weighted or semilocal Reynolds shear stress (Morkovin's scaling), which is known to well match the incompressible counterpart in the inner layer in terms of
$-\bar {\rho }^+ \widetilde{u^{{{\prime \prime }}+}v^{{{\prime \prime }}+}}=-\bar {\rho } \widetilde{u^{{{\prime \prime }}}v^{{{\prime \prime }}}}/\tau _w=-\widetilde{u^{{{\prime \prime }}*}v^{{{\prime \prime }}*}}$, is the density-weighted or semilocal Reynolds shear stress (Morkovin's scaling), which is known to well match the incompressible counterpart in the inner layer in terms of ![]() $y^*$ (Coleman et al. Reference Coleman, Kim and Moser1995; Pirozzoli & Bernardini Reference Pirozzoli and Bernardini2011; Zhang et al. Reference Zhang, Duan and Choudhari2018; Hirai, Pecnik & Kawai Reference Hirai, Pecnik and Kawai2021; Cheng & Fu Reference Cheng and Fu2022; Cogo et al. Reference Cogo, Salvadore, Picano and Bernardini2022; Bai et al. Reference Bai, Cheng, Griffin, Li and Fu2023). Meanwhile, it is recognized that the right-hand side is related to the TL transformation,
$y^*$ (Coleman et al. Reference Coleman, Kim and Moser1995; Pirozzoli & Bernardini Reference Pirozzoli and Bernardini2011; Zhang et al. Reference Zhang, Duan and Choudhari2018; Hirai, Pecnik & Kawai Reference Hirai, Pecnik and Kawai2021; Cheng & Fu Reference Cheng and Fu2022; Cogo et al. Reference Cogo, Salvadore, Picano and Bernardini2022; Bai et al. Reference Bai, Cheng, Griffin, Li and Fu2023). Meanwhile, it is recognized that the right-hand side is related to the TL transformation, ![]() $U_{{TL}}^+(\kern0.7pt y^*)= \int \bar {\mu }^+(\partial y^*/\partial y^+) \,{\mathrm {d}} \bar {U}^+$. The resulting form, under the notation of Favre averages, is
$U_{{TL}}^+(\kern0.7pt y^*)= \int \bar {\mu }^+(\partial y^*/\partial y^+) \,{\mathrm {d}} \bar {U}^+$. The resulting form, under the notation of Favre averages, is
The left-hand side and right-hand side are both functions of ![]() $y^*$, so if the transformed inner layer shear well matches the incompressible counterpart, then (2.7a) will be a highly accurate modelling of
$y^*$, so if the transformed inner layer shear well matches the incompressible counterpart, then (2.7a) will be a highly accurate modelling of ![]() $\mu _{t,i}$. For diagnostic purposes, a semilocal eddy viscosity is defined as
$\mu _{t,i}$. For diagnostic purposes, a semilocal eddy viscosity is defined as
 \begin{equation} \mu_{t,{{TL}}}^*(\kern0.7pt y^*) = \frac{-\bar{\rho}^+ \widetilde{u^{{{\prime\prime}}+}v^{{{\prime\prime}}+}}}{{\partial {U}_{{TL}}^+}/{\partial y^*}} = \frac{\mu_t}{\tilde{\mu}}, \end{equation}
\begin{equation} \mu_{t,{{TL}}}^*(\kern0.7pt y^*) = \frac{-\bar{\rho}^+ \widetilde{u^{{{\prime\prime}}+}v^{{{\prime\prime}}+}}}{{\partial {U}_{{TL}}^+}/{\partial y^*}} = \frac{\mu_t}{\tilde{\mu}}, \end{equation}
which is expected to match the incompressible ![]() $\mu _{t,i}$ (or
$\mu _{t,i}$ (or ![]() $\nu _{t,i}$). Equation (3.3) is examined in figure 3(a) using all the DNS data in table 1. Since we are concerned with the inner layer part,
$\nu _{t,i}$). Equation (3.3) is examined in figure 3(a) using all the DNS data in table 1. Since we are concerned with the inner layer part, ![]() $\mu _{t,{{TL}}}^*$ is plotted in dotted lines after reaching its maximum. The reference line is the counterpart of (2.10) with
$\mu _{t,{{TL}}}^*$ is plotted in dotted lines after reaching its maximum. The reference line is the counterpart of (2.10) with ![]() $y^+$ replaced by
$y^+$ replaced by ![]() $y^*$ (Yang & Lv Reference Yang and Lv2018), as
$y^*$ (Yang & Lv Reference Yang and Lv2018), as
There is only a small scattering of ![]() $\mu _{t,{{TL}}}^*(\kern0.7pt y^*)$ within and below the buffer layer, showing the accuracy of the TL transformation for that region. This also explains the well-predicted surface quantities in the BL-local model for hypersonic cases (Dilley & McClinton Reference Dilley and McClinton2001). In the logarithmic region,
$\mu _{t,{{TL}}}^*(\kern0.7pt y^*)$ within and below the buffer layer, showing the accuracy of the TL transformation for that region. This also explains the well-predicted surface quantities in the BL-local model for hypersonic cases (Dilley & McClinton Reference Dilley and McClinton2001). In the logarithmic region, ![]() $\mu _{t,{{TL}}}^*$ tends to be lower than (3.4), especially for diabatic cases, suggesting an underestimated
$\mu _{t,{{TL}}}^*$ tends to be lower than (3.4), especially for diabatic cases, suggesting an underestimated ![]() $\mu _{t,i}$ in BL-local. This is consistent with the behaviour of
$\mu _{t,i}$ in BL-local. This is consistent with the behaviour of ![]() $U_{{TL}}^+$, which can lead to over-prediction in the logarithmic region in diabatic cases. Nevertheless, figure 2(c) indicates that
$U_{{TL}}^+$, which can lead to over-prediction in the logarithmic region in diabatic cases. Nevertheless, figure 2(c) indicates that ![]() $\mu _{t,i}$ in the BL-local model is somewhat higher than DNS, rather than lower. This inconsistency is due to the discrepancy in
$\mu _{t,i}$ in the BL-local model is somewhat higher than DNS, rather than lower. This inconsistency is due to the discrepancy in ![]() $\tilde{T}$, on which the variables for constructing the semilocal units (
$\tilde{T}$, on which the variables for constructing the semilocal units (![]() $\bar {\rho }$ and
$\bar {\rho }$ and ![]() $\tilde {\mu }$) are dependent.
$\tilde {\mu }$) are dependent.

Figure 3. Semilocal eddy viscosity using the (a) TL (as in the BL-local model) and (b) GFM transformations from the DNS datasets. The legends for panels (a,b) are the same, separately shown in the two boxes.
As an alternative, we employ the GFM transformation to construct ![]() $\mu _{t,i}$, a thought recently implemented by Griffin et al. (Reference Griffin, Fu and Moin2023) and Hendrickson et al. (Reference Hendrickson, Subbareddy, Candler and Macdonald2023) for model improvement. The results using the very recent HLPP transformation will be discussed in Appendix B. The GFM is shown to have better overall performances than TL for canonical air flows, particularly diabatic boundary layers in the logarithmic layer, though it can degrade for supercritical or non-air-like flows (Bai et al. Reference Bai, Griffin and Fu2022; Hasan et al. Reference Hasan, Larsson, Pirozzoli and Pecnik2023b). This transformation is defined as
$\mu _{t,i}$, a thought recently implemented by Griffin et al. (Reference Griffin, Fu and Moin2023) and Hendrickson et al. (Reference Hendrickson, Subbareddy, Candler and Macdonald2023) for model improvement. The results using the very recent HLPP transformation will be discussed in Appendix B. The GFM is shown to have better overall performances than TL for canonical air flows, particularly diabatic boundary layers in the logarithmic layer, though it can degrade for supercritical or non-air-like flows (Bai et al. Reference Bai, Griffin and Fu2022; Hasan et al. Reference Hasan, Larsson, Pirozzoli and Pecnik2023b). This transformation is defined as
 \begin{align} U_{{GFM}}^+ (\kern0.7pt y^*) = \int_0^{y^*} S_t^+ \,{\mathrm{d}} y^*, \quad S_t^+= \frac{S_{eq}^+}{1 + S_{eq}^+- S_{TL}^+} = \frac{\dfrac{1}{\tilde{\mu}^+} \dfrac{\partial \tilde{U}^+}{\partial y^*}}{1 + \dfrac{1}{\tilde{\mu}^+} \dfrac{\partial \tilde{U}^+}{\partial y^*} - \tilde{\mu}^+ \dfrac{\partial \tilde{U}^+}{\partial y^+}}, \end{align}
\begin{align} U_{{GFM}}^+ (\kern0.7pt y^*) = \int_0^{y^*} S_t^+ \,{\mathrm{d}} y^*, \quad S_t^+= \frac{S_{eq}^+}{1 + S_{eq}^+- S_{TL}^+} = \frac{\dfrac{1}{\tilde{\mu}^+} \dfrac{\partial \tilde{U}^+}{\partial y^*}}{1 + \dfrac{1}{\tilde{\mu}^+} \dfrac{\partial \tilde{U}^+}{\partial y^*} - \tilde{\mu}^+ \dfrac{\partial \tilde{U}^+}{\partial y^+}}, \end{align}
where ![]() $S_{TL}^+$ is the TL transformation kernel defined above, and
$S_{TL}^+$ is the TL transformation kernel defined above, and ![]() $S_{eq}^+$ results from the approximate balance of turbulence production and dissipation in the logarithmic region, as a modification to the arguments of Zhang et al. (Reference Zhang, Bi, Hussain, Li and She2012). Similar to (3.2), the GFM-based mixing length relation in the semilocal coordinate takes the form of
$S_{eq}^+$ results from the approximate balance of turbulence production and dissipation in the logarithmic region, as a modification to the arguments of Zhang et al. (Reference Zhang, Bi, Hussain, Li and She2012). Similar to (3.2), the GFM-based mixing length relation in the semilocal coordinate takes the form of
Accordingly, the semilocal eddy viscosity using GFM is
 \begin{equation} \mu_{t,{{GFM}}}^*(\kern0.7pt y^*) = \frac{-\bar{\rho}^+ \widetilde{u^{{{\prime\prime}}+}v^{{{\prime\prime}}+}}}{{\partial U_{{GFM}}^+}/{\partial y^*}} = \frac{\mu_t}{\tilde{\mu}} \frac{{\partial U_{{TL}}^+}/{\partial y}}{{\partial U_{{GFM}}^+}/{\partial y}}. \end{equation}
\begin{equation} \mu_{t,{{GFM}}}^*(\kern0.7pt y^*) = \frac{-\bar{\rho}^+ \widetilde{u^{{{\prime\prime}}+}v^{{{\prime\prime}}+}}}{{\partial U_{{GFM}}^+}/{\partial y^*}} = \frac{\mu_t}{\tilde{\mu}} \frac{{\partial U_{{TL}}^+}/{\partial y}}{{\partial U_{{GFM}}^+}/{\partial y}}. \end{equation}
As shown in figure 3(b), ![]() $\mu _{t,{{GFM}}}^*$ experiences smaller scattering than
$\mu _{t,{{GFM}}}^*$ experiences smaller scattering than ![]() $\mu _{t,{{TL}}}^*$ at
$\mu _{t,{{TL}}}^*$ at ![]() $y^*\lesssim 70$. Also,
$y^*\lesssim 70$. Also, ![]() $\mu _{t,{{GFM}}}^*$ in the logarithmic region follows (3.4) more closely, demonstrating better robustness for modelling
$\mu _{t,{{GFM}}}^*$ in the logarithmic region follows (3.4) more closely, demonstrating better robustness for modelling ![]() $\mu _{t,i}$ than (2.7a). For practical use, the incompressible analogy
$\mu _{t,i}$ than (2.7a). For practical use, the incompressible analogy ![]() $\mu _{t,{{GFM}}}^*$ is computed first using (3.6), based on
$\mu _{t,{{GFM}}}^*$ is computed first using (3.6), based on ![]() $y^*$ and
$y^*$ and ![]() ${\partial {U}_{{GFM}}^+}/{\partial y^*}$; afterward,
${\partial {U}_{{GFM}}^+}/{\partial y^*}$; afterward, ![]() $\mu _{t,i}$ is obtained from (3.7).
$\mu _{t,i}$ is obtained from (3.7).
Notably, the GFM and TL transformations are designed only for the region within and below the logarithmic layer, so their accuracy for the outer region is not guaranteed. Consequently, they may not be directly used to modify the outer-layer ![]() $\mu _t$. Our exploration to improve the
$\mu _t$. Our exploration to improve the ![]() $\mu _{t,o}$ modelling is presented below.
$\mu _{t,o}$ modelling is presented below.
3.2. Outer-layer scaling
The derivation of the outer-layer scaling in the baseline BL model is briefly reviewed first, to set the grounds for possible modifications.
The crucial part of modelling ![]() $\mu _{t,o}$ is the estimation of its peak value, as learned from figure 2. In (2.8), the peak value
$\mu _{t,o}$ is the estimation of its peak value, as learned from figure 2. In (2.8), the peak value ![]() $\nu _{t,max}$ is estimated first, then
$\nu _{t,max}$ is estimated first, then ![]() $\mu _{t,o}$ is formed as
$\mu _{t,o}$ is formed as ![]() $\bar {\rho }\nu _{t,max}$ before the diminishing by
$\bar {\rho }\nu _{t,max}$ before the diminishing by ![]() $F_{{Kleb}}$. Consequently,
$F_{{Kleb}}$. Consequently, ![]() $\mu _{t,o}$ can continue to increase at
$\mu _{t,o}$ can continue to increase at ![]() $y>y_{m\mu }$ due to the rising
$y>y_{m\mu }$ due to the rising ![]() $\bar {\rho }$ (see figure 2c), rather than monotonically decreasing as in incompressible cases. Therefore, it is first a question whether
$\bar {\rho }$ (see figure 2c), rather than monotonically decreasing as in incompressible cases. Therefore, it is first a question whether ![]() $\nu _{t,max}$ (then
$\nu _{t,max}$ (then ![]() $\mu _{t,o}=\bar {\rho }\nu _{t,max}F_{{Kleb}}$, as in BL-local) or
$\mu _{t,o}=\bar {\rho }\nu _{t,max}F_{{Kleb}}$, as in BL-local) or ![]() $\mu _{t,max}$ (the maximum
$\mu _{t,max}$ (the maximum ![]() $\mu _t$, then
$\mu _t$, then ![]() $\mu _{t,o}=\mu _{t,max}F_{{Kleb}}$ which monotonically decreases with
$\mu _{t,o}=\mu _{t,max}F_{{Kleb}}$ which monotonically decreases with ![]() $y$) should be modelled. In hypersonic cases,
$y$) should be modelled. In hypersonic cases, ![]() $\bar {\rho }$ can vary considerably in the outer region, so the two strategies can lead to significant differences. From existing works, the scaling for
$\bar {\rho }$ can vary considerably in the outer region, so the two strategies can lead to significant differences. From existing works, the scaling for ![]() $\mu _{t,max}$ is scarce while that for
$\mu _{t,max}$ is scarce while that for ![]() $\nu _{t,max}$ is prevailing, so the following investigation is mainly on
$\nu _{t,max}$ is prevailing, so the following investigation is mainly on ![]() $\nu _{t,max}$. As mentioned in § 2.3, Cebeci & Smith (Reference Cebeci and Smith1974) argued that
$\nu _{t,max}$. As mentioned in § 2.3, Cebeci & Smith (Reference Cebeci and Smith1974) argued that ![]() $\nu _{t,max}$ was proportional to the boundary layer thickness, and suggested two scalings,
$\nu _{t,max}$ was proportional to the boundary layer thickness, and suggested two scalings,
which also hold in compressible flows. The first closure constant ![]() $\alpha$ has been introduced in § 2.3, and the second one
$\alpha$ has been introduced in § 2.3, and the second one ![]() $\alpha _2$ is
$\alpha _2$ is ![]() $0.06\unicode{x2013} 0.075$. Although widely used, (3.8) is re-examined here using the DNS data for future reference. The ratios
$0.06\unicode{x2013} 0.075$. Although widely used, (3.8) is re-examined here using the DNS data for future reference. The ratios ![]() $\alpha _{2,DNS}=\nu _{t,max}/(u_\tau \delta _{99})$ and
$\alpha _{2,DNS}=\nu _{t,max}/(u_\tau \delta _{99})$ and ![]() $\alpha _{DNS}=\nu _{t,max}/(U_e \delta _k^*)$ for all cases are shown in figure 4(a,b), as functions of the corresponding Reynolds numbers. For incompressible cases,
$\alpha _{DNS}=\nu _{t,max}/(U_e \delta _k^*)$ for all cases are shown in figure 4(a,b), as functions of the corresponding Reynolds numbers. For incompressible cases, ![]() $\alpha _{2,DNS}$ varies more slightly than
$\alpha _{2,DNS}$ varies more slightly than ![]() $\alpha _{DNS}$ with increasing
$\alpha _{DNS}$ with increasing ![]() ${\textit {Re}}$. When compressible cases are included, however,
${\textit {Re}}$. When compressible cases are included, however, ![]() $\alpha _{2,DNS}$ is the less robust one. In particular,
$\alpha _{2,DNS}$ is the less robust one. In particular, ![]() $\alpha _{2,DNS}$ varies more than twice between the diabatic cases, which is not surprising due to its higher sensitivity to wall quantities by definition.
$\alpha _{2,DNS}$ varies more than twice between the diabatic cases, which is not surprising due to its higher sensitivity to wall quantities by definition.
For incompressible flows, the well-known velocity defect law provides another way to estimate ![]() $\nu _{t,max}$ without using the boundary layer thicknesses, as adopted in the BL model. Specifically, the Clauser defect law reads
$\nu _{t,max}$ without using the boundary layer thicknesses, as adopted in the BL model. Specifically, the Clauser defect law reads ![]() $U_e^+-\tilde{U}^+=U_{{df}}^+(\eta )$, where
$U_e^+-\tilde{U}^+=U_{{df}}^+(\eta )$, where ![]() $U_{{df}}^+$ is the defect velocity and the outer scale
$U_{{df}}^+$ is the defect velocity and the outer scale ![]() $\eta =y/\varDelta$ is based on the Rotta–Clauser boundary layer thickness
$\eta =y/\varDelta$ is based on the Rotta–Clauser boundary layer thickness ![]() $\varDelta =U_e^+\delta _k^*=\int (U_e^+-\tilde{U}^+)\,{\mathrm {d}} y$ (note that
$\varDelta =U_e^+\delta _k^*=\int (U_e^+-\tilde{U}^+)\,{\mathrm {d}} y$ (note that ![]() $\eta$ is no longer the transformed coordinate defined in § 2.2). Consequently, a collapse of the following function is suggested as
$\eta$ is no longer the transformed coordinate defined in § 2.2). Consequently, a collapse of the following function is suggested as
where the approximation holds in the outer layer where ![]() $y^*\gg A^+$ (see (2.7c)). The last term is the scaled vorticity function in (2.9a), and the first three terms are the diagnostic function commonly used to evaluate
$y^*\gg A^+$ (see (2.7c)). The last term is the scaled vorticity function in (2.9a), and the first three terms are the diagnostic function commonly used to evaluate ![]() $\kappa _c$, though the main focus here is on the outer layer. For a quantitative evaluation of (3.9) and then
$\kappa _c$, though the main focus here is on the outer layer. For a quantitative evaluation of (3.9) and then ![]() $y_{max} F_{max}$, the semiempirical relation by Monkewitz, Chauhan & Nagib (Reference Monkewitz, Chauhan and Nagib2007) for incompressible boundary layers in the large-
$y_{max} F_{max}$, the semiempirical relation by Monkewitz, Chauhan & Nagib (Reference Monkewitz, Chauhan and Nagib2007) for incompressible boundary layers in the large-![]() ${\textit {Re}}$ limit is employed, which gives one explicit expression of
${\textit {Re}}$ limit is employed, which gives one explicit expression of ![]() $U_{{df}}^+(\eta )$. As a result, the outer-layer maximum of
$U_{{df}}^+(\eta )$. As a result, the outer-layer maximum of ![]() $y\partial \tilde{U}^+/\partial y$ is equal to 5.55 at
$y\partial \tilde{U}^+/\partial y$ is equal to 5.55 at ![]() $\eta =0.155$. Therefore, the ratio of
$\eta =0.155$. Therefore, the ratio of ![]() $\nu _{t,max}$ to
$\nu _{t,max}$ to ![]() $y_{max} F_{max}$ using (3.8a), i.e.
$y_{max} F_{max}$ using (3.8a), i.e.
is a constant (namely ![]() $C_{cp}$, though not exactly the same value), which leads to (2.8) directly used in the compressible baseline BL model. Analogously, if
$C_{cp}$, though not exactly the same value), which leads to (2.8) directly used in the compressible baseline BL model. Analogously, if ![]() $\nu _{t,max}$ is from (3.8b), then the constant in (3.10) can be obtained from another form of incompressible defect law
$\nu _{t,max}$ is from (3.8b), then the constant in (3.10) can be obtained from another form of incompressible defect law ![]() $U_e^+-\tilde{U}^+=U_{{df}}^+(\kern0.7pt y/\delta _{99})$. Inspired by (3.9) and (3.10), the compressible defect velocity scalings and their derivatives are examined below, to explore possible compressible corrections to (2.8).
$U_e^+-\tilde{U}^+=U_{{df}}^+(\kern0.7pt y/\delta _{99})$. Inspired by (3.9) and (3.10), the compressible defect velocity scalings and their derivatives are examined below, to explore possible compressible corrections to (2.8).
As introduced in § 1, most of the existing compressible defect velocity scalings are based on the VD transformation. The VD is built upon the mixing length assumption for the region within and below the logarithmic layer, so the outer layer is not the targeted region for it to work, like other transformations (TL, GFM, etc.). Nevertheless, previous investigations actively support its usage for compressible defect velocity scalings (Maise & McDonald Reference Maise and McDonald1968; Fernholz & Finley Reference Fernholz and Finley1980; Guarini et al. Reference Guarini, Moser, Shariff and Wray2000; Pirozzoli et al. Reference Pirozzoli, Grasso and Gatski2004; Duan et al. Reference Duan, Beekman and Martín2011; Pirozzoli & Bernardini Reference Pirozzoli and Bernardini2011; Wenzel et al. Reference Wenzel, Selent, Kloker and Rist2018), suggesting its fundamentality in transforming compressible flows, though the diabatic cases are somewhat insufficiently examined. Therefore, the VD transformation is considered until future reports of more advanced ones. Following the incompressible procedures above, a VD-based displacement thickness can be defined, following Smits & Dussauge (Reference Smits and Dussauge2006), as
 \begin{equation} \delta_{{{VD}}}^* = \int_0^\infty \left( 1-\frac{U_{{VD}}}{U_{{{VD}},e}} \right)\,{\mathrm{d}} y, \quad \text{where} \ U_{{VD}}^+ (\kern0.7pt y^+) = \int_0^{\tilde{U}^+} {\sqrt{\bar{\rho}^+}\,{\mathrm{d}} \tilde{U}^+}. \end{equation}
\begin{equation} \delta_{{{VD}}}^* = \int_0^\infty \left( 1-\frac{U_{{VD}}}{U_{{{VD}},e}} \right)\,{\mathrm{d}} y, \quad \text{where} \ U_{{VD}}^+ (\kern0.7pt y^+) = \int_0^{\tilde{U}^+} {\sqrt{\bar{\rho}^+}\,{\mathrm{d}} \tilde{U}^+}. \end{equation}
The corresponding outer scale is ![]() $\eta _{{VD}}=y/\varDelta _{{VD}}$, where the transformed Rotta–Clauser thickness is
$\eta _{{VD}}=y/\varDelta _{{VD}}$, where the transformed Rotta–Clauser thickness is ![]() $\varDelta _{{VD}}=U_{{{VD}},e}^+\delta _{{{VD}}}^*=\int (U_{{{VD}},e}^+-U_{{VD}}^+)\,{\mathrm {d}} y$. Since VD may not be accurate enough in the inner layer, the transformed displacement thickness can be alternatively defined in a mixed manner,
$\varDelta _{{VD}}=U_{{{VD}},e}^+\delta _{{{VD}}}^*=\int (U_{{{VD}},e}^+-U_{{VD}}^+)\,{\mathrm {d}} y$. Since VD may not be accurate enough in the inner layer, the transformed displacement thickness can be alternatively defined in a mixed manner, ![]() $\delta _{mix}^*$, where the integrand in the inner region (say
$\delta _{mix}^*$, where the integrand in the inner region (say ![]() $y<0.15\delta _{99}$) is replaced by the TL- or GFM-based defect velocity. Taking GFM as an example, the difference between
$y<0.15\delta _{99}$) is replaced by the TL- or GFM-based defect velocity. Taking GFM as an example, the difference between ![]() $\delta _{mix}^*$ and
$\delta _{mix}^*$ and ![]() $\delta _{{{VD}}}^*$ turns out to be less than 2.5 % and 4.5 % for the supersonic and hypersonic cases, respectively. Since
$\delta _{{{VD}}}^*$ turns out to be less than 2.5 % and 4.5 % for the supersonic and hypersonic cases, respectively. Since ![]() $\delta _{\textit{VD} }^*$ is not finally used in the new model but to inform modification, we employ
$\delta _{\textit{VD} }^*$ is not finally used in the new model but to inform modification, we employ ![]() $\delta _{{{VD}}}^*$ instead of
$\delta _{{{VD}}}^*$ instead of ![]() $\delta _{mix}^*$ hereafter for simplicity and consistency. Similar to (3.8),
$\delta _{mix}^*$ hereafter for simplicity and consistency. Similar to (3.8), ![]() $\nu _{t,max}$ can be evaluated as
$\nu _{t,max}$ can be evaluated as ![]() $\nu _{t,max}=\alpha _{{{VD}}} U_e\delta _{{{VD}}}^*=\alpha _{{{VD}}} \nu _e {\textit {Re}}_{\delta _{{{VD}}}^*}$, which is examined in figure 4(c) by computing
$\nu _{t,max}=\alpha _{{{VD}}} U_e\delta _{{{VD}}}^*=\alpha _{{{VD}}} \nu _e {\textit {Re}}_{\delta _{{{VD}}}^*}$, which is examined in figure 4(c) by computing ![]() $\alpha _{VD,DNS}=\nu _{t,max}/(U_e\delta _{{{VD}}}^*)$ for all cases. The ratio
$\alpha _{VD,DNS}=\nu _{t,max}/(U_e\delta _{{{VD}}}^*)$ for all cases. The ratio ![]() $\alpha _{VD,DNS}$ experiences a comparably small variation with
$\alpha _{VD,DNS}$ experiences a comparably small variation with ![]() $\alpha _{DNS}$. Besides, there is generally a decreasing trend of
$\alpha _{DNS}$. Besides, there is generally a decreasing trend of ![]() $\alpha _{VD,DNS}$ with
$\alpha _{VD,DNS}$ with ![]() ${\textit {Re}}_{\delta _{{{VD}}}^*}$ rising, which awaits future examination using higher-
${\textit {Re}}_{\delta _{{{VD}}}^*}$ rising, which awaits future examination using higher-![]() ${\textit {Re}}$ data. Notably, the diabatic cases exhibit no larger departure than the incompressible and adiabatic cases, though the VD transformation tends to deteriorate. A possible reason is that (3.11) is defined in an integral manner, allowing error cancellation.
${\textit {Re}}$ data. Notably, the diabatic cases exhibit no larger departure than the incompressible and adiabatic cases, though the VD transformation tends to deteriorate. A possible reason is that (3.11) is defined in an integral manner, allowing error cancellation.
Afterwards, the compressible defect velocity scalings are studied, to establish connections with the vorticity function. The form examined by Pirozzoli & Bernardini (Reference Pirozzoli and Bernardini2011) for supersonic adiabatic boundary layers is ![]() $(U_{{{VD}},e}-U_{{VD}})/U_{{{VD}},e}=g_1(\kern0.7pt y/\delta _{99})$, where
$(U_{{{VD}},e}-U_{{VD}})/U_{{{VD}},e}=g_1(\kern0.7pt y/\delta _{99})$, where ![]() $g_1$ is a universal function. This function is computed in figure 5(c) for all the DNS cases, and the results before the VD transformation are plotted in figure 5(a) for comparison. As can be seen,
$g_1$ is a universal function. This function is computed in figure 5(c) for all the DNS cases, and the results before the VD transformation are plotted in figure 5(a) for comparison. As can be seen, ![]() $g_1$ for diabatic cases deviates more significantly from the incompressible counterpart. As an alternative to
$g_1$ for diabatic cases deviates more significantly from the incompressible counterpart. As an alternative to ![]() $g_1$, the VD-based analogy to the Clauser defect law takes the form of
$g_1$, the VD-based analogy to the Clauser defect law takes the form of ![]() $U_{{{VD}},e}^+-U_{{VD}}^+=g_2(\eta _{{VD}})$, which is examined in figure 5(b) between cases. For the present datasets,
$U_{{{VD}},e}^+-U_{{VD}}^+=g_2(\eta _{{VD}})$, which is examined in figure 5(b) between cases. For the present datasets, ![]() $g_2$ tends to achieve a somewhat better collapse than
$g_2$ tends to achieve a somewhat better collapse than ![]() $g_1$. We proceed to study the derivatives of these defect velocities, to connect with the diagnostic function and then the vorticity function. The diagnostic function used in (2.8) is displayed in figure 5(d), where a few strongly oscillating curves are not shown. Note that
$g_1$. We proceed to study the derivatives of these defect velocities, to connect with the diagnostic function and then the vorticity function. The diagnostic function used in (2.8) is displayed in figure 5(d), where a few strongly oscillating curves are not shown. Note that ![]() $y{\partial \tilde{U}^+}/{\partial y}$ is plotted instead of
$y{\partial \tilde{U}^+}/{\partial y}$ is plotted instead of ![]() $y{\partial \tilde{U}}/{\partial y}$ for direct connection with
$y{\partial \tilde{U}}/{\partial y}$ for direct connection with ![]() $\nu _{t,max}$ (see (3.10), there is a factor
$\nu _{t,max}$ (see (3.10), there is a factor ![]() $u_\tau$ in (3.8) or
$u_\tau$ in (3.8) or ![]() $\varDelta$). The main focus is on the outer layer, so the region
$\varDelta$). The main focus is on the outer layer, so the region ![]() $y<0.15\delta _{99}$ is plotted in dotted lines. If the outer-layer peaks of
$y<0.15\delta _{99}$ is plotted in dotted lines. If the outer-layer peaks of ![]() $y{\partial \tilde{U}^+}/{\partial y}$ are collapsed between cases, then the ratio
$y{\partial \tilde{U}^+}/{\partial y}$ are collapsed between cases, then the ratio ![]() $\nu _{t,max}/(\kern0.7pt y_{max}F_{max})$ would be nearly invariant, which would then provide a robust modelling for
$\nu _{t,max}/(\kern0.7pt y_{max}F_{max})$ would be nearly invariant, which would then provide a robust modelling for ![]() $\mu _{t,o}$, as derived in (3.10) for incompressible cases. First, the incompressible cases in figure 5(d) suggest a rough outer-layer similarity at this
$\mu _{t,o}$, as derived in (3.10) for incompressible cases. First, the incompressible cases in figure 5(d) suggest a rough outer-layer similarity at this ![]() ${\textit {Re}}$ range (
${\textit {Re}}$ range (![]() ${\textit {Re}}_\tau \gtrsim 400$,
${\textit {Re}}_\tau \gtrsim 400$, ![]() ${\textit {Re}}_{\delta _2}\gtrsim 1400$), though the collapse is not as close to perfect as in the large-
${\textit {Re}}_{\delta _2}\gtrsim 1400$), though the collapse is not as close to perfect as in the large-![]() ${\textit {Re}}$ limit (Nagib, Chauhan & Monkewitz Reference Nagib, Chauhan and Monkewitz2007). For the compressible cases, the peak locations in figure 5(d) all concentrate around
${\textit {Re}}$ limit (Nagib, Chauhan & Monkewitz Reference Nagib, Chauhan and Monkewitz2007). For the compressible cases, the peak locations in figure 5(d) all concentrate around ![]() $0.7\delta _{99}$, but the maximums vary considerably, especially for some cold-wall cases, even if the low-
$0.7\delta _{99}$, but the maximums vary considerably, especially for some cold-wall cases, even if the low-![]() ${\textit {Re}}$ cases are excluded. Consequently,
${\textit {Re}}$ cases are excluded. Consequently, ![]() $\mu _{t,o}$ can be severely under-predicted, as is observed in figure 2(c). For the VD-based defect velocity
$\mu _{t,o}$ can be severely under-predicted, as is observed in figure 2(c). For the VD-based defect velocity ![]() $g_2(\eta _{{VD}})$, the outer-layer relation analogous to (3.9) is derived as
$g_2(\eta _{{VD}})$, the outer-layer relation analogous to (3.9) is derived as
As noted by Smits & Dussauge (Reference Smits and Dussauge2006), (3.12) indicates a proper velocity scale in the outer layer to be ![]() $u_\tau /\sqrt {\bar {\rho }^+}$, which can be used to extend Coles’ law of the wake (Maise & McDonald Reference Maise and McDonald1968; Huang et al. Reference Huang, Bradshaw and Coakley1993; Hasan et al. Reference Hasan, Larsson, Pirozzoli and Pecnik2023a). Furthermore, the factor
$u_\tau /\sqrt {\bar {\rho }^+}$, which can be used to extend Coles’ law of the wake (Maise & McDonald Reference Maise and McDonald1968; Huang et al. Reference Huang, Bradshaw and Coakley1993; Hasan et al. Reference Hasan, Larsson, Pirozzoli and Pecnik2023a). Furthermore, the factor ![]() $\sqrt {\bar {\rho }^+}$ turns out to be fundamental to account for compressibility effects, and was suggested by Catris & Aupoix (Reference Catris and Aupoix2000) and Otero Rodriguez et al. (Reference Otero Rodriguez, Patel, Diez Sanhueza and Pecnik2018) to improve the eddy viscosity and diffusivity in sophisticated RANS models. The transformed function
$\sqrt {\bar {\rho }^+}$ turns out to be fundamental to account for compressibility effects, and was suggested by Catris & Aupoix (Reference Catris and Aupoix2000) and Otero Rodriguez et al. (Reference Otero Rodriguez, Patel, Diez Sanhueza and Pecnik2018) to improve the eddy viscosity and diffusivity in sophisticated RANS models. The transformed function ![]() $y{\partial U_{{VD}}^+}/{\partial y}$ is plotted in figure 5(e) in terms of
$y{\partial U_{{VD}}^+}/{\partial y}$ is plotted in figure 5(e) in terms of ![]() $\eta _{{VD}}$. Although obvious scattering in peak values and locations is still observable, better collapse is attained compared with figure 5(d), demonstrating the effectiveness of the VD density weighting.
$\eta _{{VD}}$. Although obvious scattering in peak values and locations is still observable, better collapse is attained compared with figure 5(d), demonstrating the effectiveness of the VD density weighting.

Figure 5. Different forms of (a–c) defect velocities and (d–f) diagnostic functions for all cases. The reference lines in panels (d–f) are from (3.10). The legends for all the panels are the same, separately shown in the three boxes.
Therefore, it is suggested that the VD-based vorticity function can be utilized in the outer layer scaling of the BL model, to replace the original one without compressible corrections. From (3.12), the vorticity function in (2.9a) is modified by simply adding a factor ![]() $\sqrt {\bar {\rho }^+}$ as
$\sqrt {\bar {\rho }^+}$ as
Here, the denominator ![]() $\sqrt {\rho _w}$ has been moved out of this function to combine with other factors in
$\sqrt {\rho _w}$ has been moved out of this function to combine with other factors in ![]() $\mu _{t,o}$, which does not affect the value of
$\mu _{t,o}$, which does not affect the value of ![]() $y_{{{VD}},max}$. Consequently, (2.8) is modified to be
$y_{{{VD}},max}$. Consequently, (2.8) is modified to be
Here, the denominator ![]() $\sqrt {\bar {\rho }}$ can be interpreted as a compensation to the amplified vorticity function (3.13). The final form also turns out to reach a compromise between the modelling of
$\sqrt {\bar {\rho }}$ can be interpreted as a compensation to the amplified vorticity function (3.13). The final form also turns out to reach a compromise between the modelling of ![]() $\nu _{t,max}$ and
$\nu _{t,max}$ and ![]() $\mu _{t,max}$, so
$\mu _{t,max}$, so ![]() $\mu _{t,o}\sim \bar {\rho }^{1/2}F_{{Kleb}}$ and
$\mu _{t,o}\sim \bar {\rho }^{1/2}F_{{Kleb}}$ and ![]() $\nu _{t,o}\sim \bar {\rho }^{-1/2}F_{{Kleb}}$. As a natural consequence, (3.14) produces the same results as (2.8) for incompressible flows with constant density.
$\nu _{t,o}\sim \bar {\rho }^{-1/2}F_{{Kleb}}$. As a natural consequence, (3.14) produces the same results as (2.8) for incompressible flows with constant density.
The empirical function ![]() $F_{{Kleb}}(\kern0.7pt y/y_{{{VD}},max})$ remains unmodified as in (2.9b) before acquiring more theoretical guidance. Also, the closure constants
$F_{{Kleb}}(\kern0.7pt y/y_{{{VD}},max})$ remains unmodified as in (2.9b) before acquiring more theoretical guidance. Also, the closure constants ![]() $\alpha$,
$\alpha$, ![]() $C_{cp}$ and
$C_{cp}$ and ![]() $C_{{Kleb}}$ remain unaltered, consistent with the incompressible version. Finally, since the quantity
$C_{{Kleb}}$ remain unaltered, consistent with the incompressible version. Finally, since the quantity ![]() $y_{{{VD}},max}/C_{{Kleb}}$ used in
$y_{{{VD}},max}/C_{{Kleb}}$ used in ![]() $F_{{Kleb}}$ represents an estimation of the boundary layer thickness, its relation to
$F_{{Kleb}}$ represents an estimation of the boundary layer thickness, its relation to ![]() $\delta _{99}$ is examined in figure 5(f) by plotting the transformed function in terms of
$\delta _{99}$ is examined in figure 5(f) by plotting the transformed function in terms of ![]() $y/\delta _{99}$. For most cases,
$y/\delta _{99}$. For most cases, ![]() $y_{{{VD}},max}/\delta _{99}$ is within 0.6–0.8, but it seems closer to the boundary layer edge than
$y_{{{VD}},max}/\delta _{99}$ is within 0.6–0.8, but it seems closer to the boundary layer edge than ![]() $y_{max}/\delta _{99}$, suggesting slower damping of
$y_{max}/\delta _{99}$, suggesting slower damping of ![]() $\mu _{t,o}$ in the intermittent region.
$\mu _{t,o}$ in the intermittent region.
3.3. The TV relation
As stated in § 2.3, the eddy diffusivity in RANS models for temperature prediction is obtained mostly through a specified ![]() ${\textit {Pr}}_t$, whose one common definition is
${\textit {Pr}}_t$, whose one common definition is
 \begin{equation} {\textit{Pr}}_t = \frac{\widetilde{u^{{\prime\prime}} v^{{\prime\prime}}} (\partial \tilde{T} / \partial y)}{\widetilde{v^{{\prime\prime}} T^{{\prime\prime}}} (\partial \tilde{U} / \partial y)}. \end{equation}
\begin{equation} {\textit{Pr}}_t = \frac{\widetilde{u^{{\prime\prime}} v^{{\prime\prime}}} (\partial \tilde{T} / \partial y)}{\widetilde{v^{{\prime\prime}} T^{{\prime\prime}}} (\partial \tilde{U} / \partial y)}. \end{equation}
It is widely shown that ![]() ${\textit {Pr}}_t$ is within 0.7–1.1 in most regions above the buffer layer and is typically equal to 0.85 in the logarithmic region, insensitive to
${\textit {Pr}}_t$ is within 0.7–1.1 in most regions above the buffer layer and is typically equal to 0.85 in the logarithmic region, insensitive to ![]() ${\textit {Ma}}$,
${\textit {Ma}}$, ![]() ${\textit {Re}}$ and wall cooling (Huang, Coleman & Bradshaw Reference Huang, Coleman and Bradshaw1995; Duan et al. Reference Duan, Beekman and Martín2010; Pirozzoli & Bernardini Reference Pirozzoli and Bernardini2011; Lusher & Coleman Reference Lusher and Coleman2022). However,
${\textit {Re}}$ and wall cooling (Huang, Coleman & Bradshaw Reference Huang, Coleman and Bradshaw1995; Duan et al. Reference Duan, Beekman and Martín2010; Pirozzoli & Bernardini Reference Pirozzoli and Bernardini2011; Lusher & Coleman Reference Lusher and Coleman2022). However, ![]() ${\textit {Pr}}_t$ can experience complicated variations within and below the buffer layer, especially in cold-wall boundary layers, which is illustrated in figure 6(a) using the DNS data from ZDC. At
${\textit {Pr}}_t$ can experience complicated variations within and below the buffer layer, especially in cold-wall boundary layers, which is illustrated in figure 6(a) using the DNS data from ZDC. At ![]() $y^*\gtrsim 25$, three
$y^*\gtrsim 25$, three ![]() ${\textit {Pr}}_t$ are quite close to each other, slowly decreasing towards the boundary layer edge. Near the temperature peak, however,
${\textit {Pr}}_t$ are quite close to each other, slowly decreasing towards the boundary layer edge. Near the temperature peak, however, ![]() $\partial \tilde{T}/\partial y$ and
$\partial \tilde{T}/\partial y$ and ![]() $\widetilde{v^{{\prime \prime }} T^{{\prime \prime }}}$ both change signs, so
$\widetilde{v^{{\prime \prime }} T^{{\prime \prime }}}$ both change signs, so ![]() ${\textit {Pr}}_t$ can be negative or even singular. This singularity is also observable in the adiabatic case M2p5Tw10R17, though very close to the wall (
${\textit {Pr}}_t$ can be negative or even singular. This singularity is also observable in the adiabatic case M2p5Tw10R17, though very close to the wall (![]() $\kern0.7pt y^*\approx 2$). Meanwhile,
$\kern0.7pt y^*\approx 2$). Meanwhile, ![]() ${\textit {Pr}}_t$ between the singular point and the wall is generally lower than 0.5 for the three cases. The rapid variation of
${\textit {Pr}}_t$ between the singular point and the wall is generally lower than 0.5 for the three cases. The rapid variation of ![]() ${\textit {Pr}}_t$ can lead to prediction errors for the temperature peak, as discussed for figure 2(d). For further demonstration, figure 6(b) compares between three cases with different
${\textit {Pr}}_t$ can lead to prediction errors for the temperature peak, as discussed for figure 2(d). For further demonstration, figure 6(b) compares between three cases with different ![]() ${\textit {Pr}}_t$ using the BL-local model (case M8Tw048R20). At
${\textit {Pr}}_t$ using the BL-local model (case M8Tw048R20). At ![]() $y^*\gtrsim 100$,
$y^*\gtrsim 100$, ![]() $\tilde{T}$ is quite insensitive to
$\tilde{T}$ is quite insensitive to ![]() ${\textit {Pr}}_t$ but at
${\textit {Pr}}_t$ but at ![]() $y^*\lesssim 100$, a continuous decrease of
$y^*\lesssim 100$, a continuous decrease of ![]() $\tilde{T}$ is observed with the drop of
$\tilde{T}$ is observed with the drop of ![]() ${\textit {Pr}}_t$ due to enhanced turbulent heat flux. The case
${\textit {Pr}}_t$ due to enhanced turbulent heat flux. The case ![]() ${\textit {Pr}}_t=0.8$ seems to best predict the temperature peak. For the colder-wall case M6Tw025R11, an even lower
${\textit {Pr}}_t=0.8$ seems to best predict the temperature peak. For the colder-wall case M6Tw025R11, an even lower ![]() ${\textit {Pr}}_t=0.6$ is required in a similar test (not shown) to capture reasonably the peak temperature. Therefore, accurate modelling of
${\textit {Pr}}_t=0.6$ is required in a similar test (not shown) to capture reasonably the peak temperature. Therefore, accurate modelling of ![]() ${\textit {Pr}}_t$ is significant for near-wall temperature prediction. A constant
${\textit {Pr}}_t$ is significant for near-wall temperature prediction. A constant ![]() ${\textit {Pr}}_t=0.9$ can lead to an over-predicted peak temperature for cold-wall cases.
${\textit {Pr}}_t=0.9$ can lead to an over-predicted peak temperature for cold-wall cases.

Figure 6. (a) Turbulent Prandtl numbers in different DNS cases from ZDC and (b) the mean temperature using the BL-local model with different ![]() ${\textit {Pr}}_t$ for case M8Tw048R20.
${\textit {Pr}}_t$ for case M8Tw048R20.
Besides constancy, ![]() ${\textit {Pr}}_t$ can be modelled as a function of the wall-normal height (Abe & Antonia Reference Abe and Antonia2017; Huang, Duan & Choudhari Reference Huang, Duan and Choudhari2022; Huang et al. Reference Huang, Coleman, Spalart and Yang2023); for example, the expression by Subbareddy & Candler (Reference Subbareddy and Candler2012) for boundary layers is
${\textit {Pr}}_t$ can be modelled as a function of the wall-normal height (Abe & Antonia Reference Abe and Antonia2017; Huang, Duan & Choudhari Reference Huang, Duan and Choudhari2022; Huang et al. Reference Huang, Coleman, Spalart and Yang2023); for example, the expression by Subbareddy & Candler (Reference Subbareddy and Candler2012) for boundary layers is ![]() ${\textit {Pr}}_t = 1-0.25y/\delta _{99}$. This formula is also examined in figure 6(b) within the BL model. The resulting temperature is close to the
${\textit {Pr}}_t = 1-0.25y/\delta _{99}$. This formula is also examined in figure 6(b) within the BL model. The resulting temperature is close to the ![]() ${\textit {Pr}}_t=1$ case and thus inaccurate for near-wall temperature prediction. Other available
${\textit {Pr}}_t=1$ case and thus inaccurate for near-wall temperature prediction. Other available ![]() ${\textit {Pr}}_t$ formulae are expected to have analogous behaviours because
${\textit {Pr}}_t$ formulae are expected to have analogous behaviours because ![]() ${\textit {Pr}}_t$ are all designed to monotonically decrease away from the wall, though most of the formulae are modelled based on channel flows. As discussed above, capturing the non-monotonic and singular behaviour of
${\textit {Pr}}_t$ are all designed to monotonically decrease away from the wall, though most of the formulae are modelled based on channel flows. As discussed above, capturing the non-monotonic and singular behaviour of ![]() ${\textit {Pr}}_t$ near the wall is crucial, but it seems difficult to summarize a universal expression of
${\textit {Pr}}_t$ near the wall is crucial, but it seems difficult to summarize a universal expression of ![]() ${\textit {Pr}}_t$ in the near-wall region. The location of the singular point may correlate with the temperature peak, but the
${\textit {Pr}}_t$ in the near-wall region. The location of the singular point may correlate with the temperature peak, but the ![]() ${\textit {Pr}}_t$ farther below towards the wall also differs considerably from case to case. Ad hoc fitting of
${\textit {Pr}}_t$ farther below towards the wall also differs considerably from case to case. Ad hoc fitting of ![]() ${\textit {Pr}}_t$ for each case is plausible, but no universality is guaranteed. Consequently, we seek alternatives to specifying
${\textit {Pr}}_t$ for each case is plausible, but no universality is guaranteed. Consequently, we seek alternatives to specifying ![]() ${\textit {Pr}}_t$. As mentioned in § 1, the algebraic TV relation by Duan & Martín (Reference Duan and Martín2011) and Zhang et al. (Reference Zhang, Bi, Hussain and She2014) is remarkably accurate for adiabatic and diabatic boundary layers, and channel and pipe flows. It is thus incorporated for efficient and accurate temperature prediction in several recent works within the frameworks of ODE solvers and WMLES (Chen et al. Reference Chen, Cheng, Fu and Gan2023a; Griffin et al. Reference Griffin, Fu and Moin2023; Hasan et al. Reference Hasan, Larsson, Pirozzoli and Pecnik2023a; Song et al. Reference Song, Zhang and Xia2023). Thereby, the TV relation is utilized to improve the temperature prediction in the BL model.
${\textit {Pr}}_t$. As mentioned in § 1, the algebraic TV relation by Duan & Martín (Reference Duan and Martín2011) and Zhang et al. (Reference Zhang, Bi, Hussain and She2014) is remarkably accurate for adiabatic and diabatic boundary layers, and channel and pipe flows. It is thus incorporated for efficient and accurate temperature prediction in several recent works within the frameworks of ODE solvers and WMLES (Chen et al. Reference Chen, Cheng, Fu and Gan2023a; Griffin et al. Reference Griffin, Fu and Moin2023; Hasan et al. Reference Hasan, Larsson, Pirozzoli and Pecnik2023a; Song et al. Reference Song, Zhang and Xia2023). Thereby, the TV relation is utilized to improve the temperature prediction in the BL model.
The quadratic algebraic relation is written as
where ![]() $\tilde{U}_\delta$ and
$\tilde{U}_\delta$ and ![]() $\tilde{T}_\delta$ are the values at the boundary-layer edge
$\tilde{T}_\delta$ are the values at the boundary-layer edge ![]() $\delta$ (specified later), and
$\delta$ (specified later), and ![]() $T_r=T_\infty (1+r{\textit {Ec}}_\infty /2)$ is the recovery temperature with
$T_r=T_\infty (1+r{\textit {Ec}}_\infty /2)$ is the recovery temperature with ![]() $r={\textit {Pr}}^{1/3}$ the recovery factor. The closure constant
$r={\textit {Pr}}^{1/3}$ the recovery factor. The closure constant ![]() $C_T$ is determined to be 0.8259 by Duan & Martín (Reference Duan and Martín2011) and is recast as
$C_T$ is determined to be 0.8259 by Duan & Martín (Reference Duan and Martín2011) and is recast as ![]() $s{\textit {Pr}}$ by Zhang et al. (Reference Zhang, Bi, Hussain and She2014), where the Reynolds analogy factor
$s{\textit {Pr}}$ by Zhang et al. (Reference Zhang, Bi, Hussain and She2014), where the Reynolds analogy factor ![]() $s$ is 1.14 following convention. The examination of (3.16) for the deployed DNS datasets is not presented since it has been extensively verified (e.g. Zhang et al. Reference Zhang, Duan and Choudhari2018; Modesti & Pirozzoli Reference Modesti and Pirozzoli2019; Fu et al. Reference Fu, Karp, Bose, Moin and Urzay2021; Zhang et al. Reference Zhang, Wan, Liu, Sun and Lu2022; Griffin et al. Reference Griffin, Fu and Moin2023). Its implementation into the model is discussed below. In the works of Song et al. (Reference Song, Zhang and Xia2023), Chen et al. (Reference Chen, Cheng, Fu and Gan2023a) and Hasan et al. (Reference Hasan, Larsson, Pirozzoli and Pecnik2023a), (3.16) is used throughout the boundary layer. In comparison, Griffin et al. (Reference Griffin, Fu and Moin2023) adopt it only in the near-wall region with the upper boundary condition matched by LES. The latter strategy is preferred for two reasons. First,
$s$ is 1.14 following convention. The examination of (3.16) for the deployed DNS datasets is not presented since it has been extensively verified (e.g. Zhang et al. Reference Zhang, Duan and Choudhari2018; Modesti & Pirozzoli Reference Modesti and Pirozzoli2019; Fu et al. Reference Fu, Karp, Bose, Moin and Urzay2021; Zhang et al. Reference Zhang, Wan, Liu, Sun and Lu2022; Griffin et al. Reference Griffin, Fu and Moin2023). Its implementation into the model is discussed below. In the works of Song et al. (Reference Song, Zhang and Xia2023), Chen et al. (Reference Chen, Cheng, Fu and Gan2023a) and Hasan et al. (Reference Hasan, Larsson, Pirozzoli and Pecnik2023a), (3.16) is used throughout the boundary layer. In comparison, Griffin et al. (Reference Griffin, Fu and Moin2023) adopt it only in the near-wall region with the upper boundary condition matched by LES. The latter strategy is preferred for two reasons. First, ![]() $\tilde{T}$ in the outer layer is already insensitive to
$\tilde{T}$ in the outer layer is already insensitive to ![]() ${\textit {Pr}}_t$ and
${\textit {Pr}}_t$ and ![]() ${\textit {Pr}}_t$ also varies mildly. Second, by solving the original energy (2.1c) in the outer layer, more flow information is retained, which is more applicable to general flows. To realize the multilayer formulation, a matching location
${\textit {Pr}}_t$ also varies mildly. Second, by solving the original energy (2.1c) in the outer layer, more flow information is retained, which is more applicable to general flows. To realize the multilayer formulation, a matching location ![]() $y_{mT}<\delta$ within the boundary layer is required, above which (2.1c) is solved and below which (3.16) is enforced. The resulting temperature formulation is also a two-layer structure, analogous to
$y_{mT}<\delta$ within the boundary layer is required, above which (2.1c) is solved and below which (3.16) is enforced. The resulting temperature formulation is also a two-layer structure, analogous to ![]() $\mu _t$ in (2.6). The outer boundary condition for (3.16) is now the temperature sample at
$\mu _t$ in (2.6). The outer boundary condition for (3.16) is now the temperature sample at ![]() $y_{mT}$. To enforce the matching temperature
$y_{mT}$. To enforce the matching temperature ![]() $\tilde{T}_m$ at
$\tilde{T}_m$ at ![]() $y_{mT}$, the original outer boundary condition
$y_{mT}$, the original outer boundary condition ![]() $\tilde{T}|_{y=\delta }=\tilde{T}_\delta$ is relaxed, and (3.16) is rewritten, following Griffin et al. (Reference Griffin, Fu and Moin2023), to be
$\tilde{T}|_{y=\delta }=\tilde{T}_\delta$ is relaxed, and (3.16) is rewritten, following Griffin et al. (Reference Griffin, Fu and Moin2023), to be
where ![]() $\tilde{U}_m$ is the velocity sample at
$\tilde{U}_m$ is the velocity sample at ![]() $y_{mT}$. Within the framework in § 2.2, the energy equation (2.4b) with constant
$y_{mT}$. Within the framework in § 2.2, the energy equation (2.4b) with constant ![]() ${\textit {Pr}}_t$ is solved first throughout the boundary layer. As a second step, (3.17) is used to update
${\textit {Pr}}_t$ is solved first throughout the boundary layer. As a second step, (3.17) is used to update ![]() $\tilde{T}$ at
$\tilde{T}$ at ![]() $y< y_{mT}$ once within each iteration, based on the quantities at
$y< y_{mT}$ once within each iteration, based on the quantities at ![]() $y_{mT}$ and
$y_{mT}$ and ![]() $\delta$. If solving the full RANS equation (2.1), then (3.17) can be directly imposed during the temporal stepping subject to an appropriate initial field.
$\delta$. If solving the full RANS equation (2.1), then (3.17) can be directly imposed during the temporal stepping subject to an appropriate initial field.
Note that only a zero-order continuity of ![]() $\tilde{T}$ at
$\tilde{T}$ at ![]() $y_{mT}$ is guaranteed by (3.17). Actually, such a high-order discontinuity also exists in
$y_{mT}$ is guaranteed by (3.17). Actually, such a high-order discontinuity also exists in ![]() $\mu _t$ at
$\mu _t$ at ![]() $y_{m\mu }$ (see figure 2). Numerical results prove negligible effects of the discontinuities on the mean profiles after the computation converges. Inspired by figure 6(b),
$y_{m\mu }$ (see figure 2). Numerical results prove negligible effects of the discontinuities on the mean profiles after the computation converges. Inspired by figure 6(b), ![]() $y_{mT}^*$ is fixed at 100 throughout. A sensitivity study of
$y_{mT}^*$ is fixed at 100 throughout. A sensitivity study of ![]() $y_{mT}^*$ is conducted in Appendix A, suggesting minor differences in the mean temperature with
$y_{mT}^*$ is conducted in Appendix A, suggesting minor differences in the mean temperature with ![]() $y_{mT}^*$ varied from 50 to 150. In the spirit of the BL model, the explicit determination of the boundary layer edge, required by
$y_{mT}^*$ varied from 50 to 150. In the spirit of the BL model, the explicit determination of the boundary layer edge, required by ![]() $\tilde{U}_\delta$ and
$\tilde{U}_\delta$ and ![]() $\tilde{T}_\delta$, should be avoided. Consistent with (2.9a),
$\tilde{T}_\delta$, should be avoided. Consistent with (2.9a), ![]() $\delta$ is set to
$\delta$ is set to ![]() $y_{max}/C_{{Kleb}}$ (
$y_{max}/C_{{Kleb}}$ (![]() $\kern0.7pt y_{{{VD}},max}/C_{{Kleb}}$ if using (3.14)), and the final results turn out to be quite insensitive to
$\kern0.7pt y_{{{VD}},max}/C_{{Kleb}}$ if using (3.14)), and the final results turn out to be quite insensitive to ![]() $\delta$. As a final remark, (3.17) is designed for fully developed turbulence and becomes invalid for laminar flows (however, see the recent results of Mo & Gao (Reference Mo and Gao2024)), so the numerical transition process mentioned in § 2.2 should be avoided; in other words, the initial profile should be placed downstream in the turbulent regime.
$\delta$. As a final remark, (3.17) is designed for fully developed turbulence and becomes invalid for laminar flows (however, see the recent results of Mo & Gao (Reference Mo and Gao2024)), so the numerical transition process mentioned in § 2.2 should be avoided; in other words, the initial profile should be placed downstream in the turbulent regime.
3.4. Modification summary
As described in §§ 3.1–3.3, three well-established mean flow relations are employed to modify the BL-local model. Two modifications are made to the two-layer ![]() $\mu _t$ in (2.6). To be specific, the GFM transformation is utilized for the inner layer
$\mu _t$ in (2.6). To be specific, the GFM transformation is utilized for the inner layer ![]() $\mu _{t,i}$ (3.7), and the VD transformation is adopted for the outer-layer
$\mu _{t,i}$ (3.7), and the VD transformation is adopted for the outer-layer ![]() $\mu _{t,o}$ (3.14). This version, without modifying the temperature relation, is termed the BL-GFM-VD model. Furthermore, one modification is made to the inner layer temperature. The algebraic TV relation (i.e. (3.17)) is enforced at
$\mu _{t,o}$ (3.14). This version, without modifying the temperature relation, is termed the BL-GFM-VD model. Furthermore, one modification is made to the inner layer temperature. The algebraic TV relation (i.e. (3.17)) is enforced at ![]() $y< y_{mT}$, instead of specifying
$y< y_{mT}$, instead of specifying ![]() ${\textit {Pr}}_t$ and solving the energy equation. This final version is called the BL-GFM-VD-TV model. For incompressible flows with constant thermodynamic properties, the two modified models (and also BL-local) degenerate to the original version by Baldwin & Lomax (Reference Baldwin and Lomax1978).
${\textit {Pr}}_t$ and solving the energy equation. This final version is called the BL-GFM-VD-TV model. For incompressible flows with constant thermodynamic properties, the two modified models (and also BL-local) degenerate to the original version by Baldwin & Lomax (Reference Baldwin and Lomax1978).
4. Results of the modified BL models
The two modified BL models are comprehensively evaluated using the 12 DNS cases. The primary quantities of interest are the mean profiles, and the wall and integral quantities. The fluctuation statistics are not expected to agree well with DNS considering the great simplicity in RANS.
The cold-wall Ma8Tw048R20 case from ZDC is focused on first, as examined in figure 2. The mean streamwise velocity and temperature predicted by the three BL models are shown in figure 7 in the inner scale. The distributions of ![]() $\mu _t$ and
$\mu _t$ and ![]() ${\textit {Pr}}_t$ are also displayed for diagnostic purposes. As mentioned above, the BL-local model underestimates the outer-layer
${\textit {Pr}}_t$ are also displayed for diagnostic purposes. As mentioned above, the BL-local model underestimates the outer-layer ![]() $\mu _t$ for this case, leading to a smaller
$\mu _t$ for this case, leading to a smaller ![]() $u_\tau$ and an upward tilting of
$u_\tau$ and an upward tilting of ![]() $\tilde{U}^+$ in the outer region, compared with the DNS data. This tilting of
$\tilde{U}^+$ in the outer region, compared with the DNS data. This tilting of ![]() $\tilde{U}^+$ suggests an under-predicted
$\tilde{U}^+$ suggests an under-predicted ![]() $\tilde{U}/U_\infty =\tilde{U}^+/U_\infty ^+$ in the logarithmic region, as displayed in figure 2(d). A notable improvement for the outer-layer
$\tilde{U}/U_\infty =\tilde{U}^+/U_\infty ^+$ in the logarithmic region, as displayed in figure 2(d). A notable improvement for the outer-layer ![]() $\tilde{U}^+$ is observed in the BL-GFM-VD model, and as a step forward,
$\tilde{U}^+$ is observed in the BL-GFM-VD model, and as a step forward, ![]() $\tilde{U}^+$ (and also
$\tilde{U}^+$ (and also ![]() $\tilde{U}/U_\infty$ in the outer scale) from BL-GFM-VD-TV is closely in line with DNS. From figure 7(c), the matching point
$\tilde{U}/U_\infty$ in the outer scale) from BL-GFM-VD-TV is closely in line with DNS. From figure 7(c), the matching point ![]() $y_{m\mu }^*=242$ (
$y_{m\mu }^*=242$ (![]() $\kern0.7pt y_{m\mu }=0.24\delta _{99}$) is much higher than that in BL-local (
$\kern0.7pt y_{m\mu }=0.24\delta _{99}$) is much higher than that in BL-local (![]() $\kern0.7pt y_{m\mu }^*=67$ in figure 2c), owing to the lifted
$\kern0.7pt y_{m\mu }^*=67$ in figure 2c), owing to the lifted ![]() $\mu _{t,o}$ after utilizing the VD transformation. Consequently, the region
$\mu _{t,o}$ after utilizing the VD transformation. Consequently, the region ![]() $y^*\lesssim 242$ obeys the logarithmic scaling formulated by the GFM transformation. In tandem with the more accurate
$y^*\lesssim 242$ obeys the logarithmic scaling formulated by the GFM transformation. In tandem with the more accurate ![]() $\tilde{U}$, clear improvement in predicting
$\tilde{U}$, clear improvement in predicting ![]() $\tilde{T}$ is observed in figure 7(b) from BL-local to BL-GFM-VD. Nevertheless, the predicted peak temperature and that in the logarithmic region are still higher than DNS. Further improvement coinciding with DNS is realized in the BL-GFM-VD-TV model, where the inner layer
$\tilde{T}$ is observed in figure 7(b) from BL-local to BL-GFM-VD. Nevertheless, the predicted peak temperature and that in the logarithmic region are still higher than DNS. Further improvement coinciding with DNS is realized in the BL-GFM-VD-TV model, where the inner layer ![]() $\tilde{T}$ is formulated by (3.17). The excellent agreement of
$\tilde{T}$ is formulated by (3.17). The excellent agreement of ![]() $\tilde{T}$ in the BL-GFM-VD-TV model can be explained from a posteriori diagnosis of
$\tilde{T}$ in the BL-GFM-VD-TV model can be explained from a posteriori diagnosis of ![]() ${\textit {Pr}}_t$, which is computed by substituting the BL results back to the energy equation (2.1c) or (2.4b). As shown in figure 7(d),
${\textit {Pr}}_t$, which is computed by substituting the BL results back to the energy equation (2.1c) or (2.4b). As shown in figure 7(d), ![]() ${\textit {Pr}}_t$ at
${\textit {Pr}}_t$ at ![]() $y^*>y_{mT}^*$ is 0.9 by construction. At
$y^*>y_{mT}^*$ is 0.9 by construction. At ![]() $y^*< y_{mT}^*$,
$y^*< y_{mT}^*$, ![]() ${\textit {Pr}}_t$ is not a constant but varies in a qualitatively consistent manner with DNS; a singular point also appears at
${\textit {Pr}}_t$ is not a constant but varies in a qualitatively consistent manner with DNS; a singular point also appears at ![]() $y^*\approx 8$. The slight discontinuity in
$y^*\approx 8$. The slight discontinuity in ![]() ${\textit {Pr}}_t$ around
${\textit {Pr}}_t$ around ![]() $y_{mT}^*$ is due to the matching procedure, as noted in § 3.3. In short, by employing the TV relation, the intricate variation of
$y_{mT}^*$ is due to the matching procedure, as noted in § 3.3. In short, by employing the TV relation, the intricate variation of ![]() ${\textit {Pr}}_t$ near the wall can be modelled, leading to an accurate temperature prediction combined with an appropriate
${\textit {Pr}}_t$ near the wall can be modelled, leading to an accurate temperature prediction combined with an appropriate ![]() $\mu _t$.
$\mu _t$.

Figure 7. (a) Mean streamwise velocity, (b) mean temperature, (c) eddy viscosity and (d) turbulent Prandtl number from different BL models and DNS for case ZDC-Ma8Tw048R20 (cold wall).
Similar intermodel comparisons are made for the remaining DNS cases. For conciseness, we demonstrate below the mean-flow profiles of three representative cases from different sources: one cold-wall case from ZDC (M6Tw025R11); one adiabatic-wall case from PB (M4Tw10R21); one heated-wall case from VBL (M2Tw19R3). Afterwards, more attention will be paid to diabatic cases, and the prediction errors of the remaining cases will be summarized collectively.
The results of the cold-wall M6Tw025R11 case are shown in figure 8 in both the inner and outer scales. The velocity prediction from the BL-GFM-VD model is close to BL-GFM-VD-TV, especially in the outer scale, so the former is not displayed. The model comparisons for velocity exhibit different features in the inner and outer scales. Both models tend to under-predict ![]() $u_\tau$, thus leading to higher
$u_\tau$, thus leading to higher ![]() $\tilde{U}^+$ in the outer region;
$\tilde{U}^+$ in the outer region; ![]() $\tilde{U}^+$ by BL-GFM-VD-TV tends to deviate more. If expressed in the outer scale, nevertheless,
$\tilde{U}^+$ by BL-GFM-VD-TV tends to deviate more. If expressed in the outer scale, nevertheless, ![]() $\tilde{U}$ by BL-GFM-VD-TV follows the DNS trend more closely, especially in the logarithmic region due to the elevated
$\tilde{U}$ by BL-GFM-VD-TV follows the DNS trend more closely, especially in the logarithmic region due to the elevated ![]() $\mu _{t,o}$ and hence a higher
$\mu _{t,o}$ and hence a higher ![]() $y_{m\mu }$ (
$y_{m\mu }$ (![]() $\kern0.7pt y_{m\mu }^*$ rises from 80 in BL-local to 224). The reversed trends in the inner and outer scales will be revisited later, along with more quantitative measurements of the prediction errors. The temperature predictions of the three BL models strongly resemble those in figure 7. The BL-local model severely over-predicts
$\kern0.7pt y_{m\mu }^*$ rises from 80 in BL-local to 224). The reversed trends in the inner and outer scales will be revisited later, along with more quantitative measurements of the prediction errors. The temperature predictions of the three BL models strongly resemble those in figure 7. The BL-local model severely over-predicts ![]() $\tilde{T}$ in most regions (
$\tilde{T}$ in most regions (![]() $\kern0.7pt y<0.7\delta _{99}$) within the boundary layer, especially when expressed in the outer scale (figure 8d). Though the error in the logarithmic region is reduced in the BL-GFM-VD model owing to the improved logarithmic scaling, clear over-prediction still exists due to the overrated
$\kern0.7pt y<0.7\delta _{99}$) within the boundary layer, especially when expressed in the outer scale (figure 8d). Though the error in the logarithmic region is reduced in the BL-GFM-VD model owing to the improved logarithmic scaling, clear over-prediction still exists due to the overrated ![]() ${\textit {Pr}}_t$ in the near-wall region. After employing the TV relation, excellent agreement with DNS is obtained in the BL-GFM-VD-TV model.
${\textit {Pr}}_t$ in the near-wall region. After employing the TV relation, excellent agreement with DNS is obtained in the BL-GFM-VD-TV model.

Figure 8. Mean (a,b) streamwise velocity and (c,d) temperature in the (a,c) inner and (b,d) outer scales from different BL models for case ZDC-M6Tw025R11 (cold wall).
The adiabatic case M4Tw10R21 is considered in figure 9. As extensively examined in previous works (see § 1), the BL-local model well reproduces the mean velocity, but ![]() $\tilde{T}$ in the logarithmic region is over-estimated. After using BL-GFM-VD and BL-GFM-VD-TV, the high accuracy for the velocity is retained with even a better prediction for
$\tilde{T}$ in the logarithmic region is over-estimated. After using BL-GFM-VD and BL-GFM-VD-TV, the high accuracy for the velocity is retained with even a better prediction for ![]() $\tilde{U}^+$, and the prediction for
$\tilde{U}^+$, and the prediction for ![]() $\tilde{T}$ is significantly improved. Again, this is attributed to the elevated
$\tilde{T}$ is significantly improved. Again, this is attributed to the elevated ![]() $\mu _{t,o}$ and
$\mu _{t,o}$ and ![]() $y_{m\mu }$, so the logarithmic scaling in (3.6) is more strictly followed up to
$y_{m\mu }$, so the logarithmic scaling in (3.6) is more strictly followed up to ![]() $y_{m\mu }^*=210$ for this case. The TV relation is of limited help for this adiabatic case because the singular point of
$y_{m\mu }^*=210$ for this case. The TV relation is of limited help for this adiabatic case because the singular point of ![]() ${\textit {Pr}}_t$, if it exists, is down to the viscous layer (see figure 6a), where
${\textit {Pr}}_t$, if it exists, is down to the viscous layer (see figure 6a), where ![]() $\kappa$ is dominant over
$\kappa$ is dominant over ![]() $\kappa _t$. Away from the singular point,
$\kappa _t$. Away from the singular point, ![]() ${\textit {Pr}}_t$ varies moderately and can be well approximated by a constant. For the heated-wall case in figure 10, the same conclusion as for figures 8 and 9 is drawn. Good agreement with DNS is realized for
${\textit {Pr}}_t$ varies moderately and can be well approximated by a constant. For the heated-wall case in figure 10, the same conclusion as for figures 8 and 9 is drawn. Good agreement with DNS is realized for ![]() $\tilde{U}$ and
$\tilde{U}$ and ![]() $\tilde{T}$ in the BL-GFM-VD-TV model. The improvement for velocity is more obvious when expressed in the outer scale. The mild under-prediction in
$\tilde{T}$ in the BL-GFM-VD-TV model. The improvement for velocity is more obvious when expressed in the outer scale. The mild under-prediction in ![]() $u_\tau$ is presumably related to the relatively low
$u_\tau$ is presumably related to the relatively low ![]() ${\textit {Re}}_{\delta _2}$ in the M2Tw19R3 and also M6Tw025R11 cases, so the outer-layer similarity of the defect velocity diminishes (see figure 5).
${\textit {Re}}_{\delta _2}$ in the M2Tw19R3 and also M6Tw025R11 cases, so the outer-layer similarity of the defect velocity diminishes (see figure 5).

Figure 9. Same as figure 8 except for case PB-M4Tw10R21 (adiabatic wall).

Figure 10. Same as figure 8 except for case VBL-M2Tw19R3 (heated wall).
More attention is paid to the diabatic cases considering their ubiquity in hypersonic applications and difficulty in prediction by the baseline model. The temperature predictions for four more diabatic cases (VBL-M2Tw05R13, VBL-M5Tw19R7, ZDC-M6Tw076R17 and ZDC-M14Tw018R24) are shown in figure 11, covering the lowest and highest ![]() ${\textit {Ma}}_\infty$ in the dataset. In addition to the same conclusions as for figures 8–10, two more points are concluded. For the heated and moderately cooled wall cases (figure 11b,c,
${\textit {Ma}}_\infty$ in the dataset. In addition to the same conclusions as for figures 8–10, two more points are concluded. For the heated and moderately cooled wall cases (figure 11b,c, ![]() $T_w/T_r>0.5$), abundant improvement in
$T_w/T_r>0.5$), abundant improvement in ![]() $\tilde{T}$ is achieved by BL-GFM-VD, over the BL-local model. For the highly cooled wall cases (figures 11a,d and 8c,
$\tilde{T}$ is achieved by BL-GFM-VD, over the BL-local model. For the highly cooled wall cases (figures 11a,d and 8c, ![]() $T_w/T_r\le 0.5$), however, modifying only
$T_w/T_r\le 0.5$), however, modifying only ![]() $\mu _t$ is insufficient due to the intricate variation of
$\mu _t$ is insufficient due to the intricate variation of ![]() ${\textit {Pr}}_t$ near the wall. The TV relation should be further incorporated for accurate temperature prediction. As demonstrated in figure 11(e,f), the
${\textit {Pr}}_t$ near the wall. The TV relation should be further incorporated for accurate temperature prediction. As demonstrated in figure 11(e,f), the ![]() ${\textit {Pr}}_t$ profiles from BL-GFM-VD-TV well match the DNS trends for these highly cooled wall cases, so the non-monotonic behaviour and the singularity of
${\textit {Pr}}_t$ profiles from BL-GFM-VD-TV well match the DNS trends for these highly cooled wall cases, so the non-monotonic behaviour and the singularity of ![]() ${\textit {Pr}}_t$ can be reasonably modelled. For reference, the velocity predictions for the four diabatic cases are also demonstrated in figure 12. In both the inner and outer scales, the velocities by the BL-GFM-VD-TV model are in good agreement with the DNS data.
${\textit {Pr}}_t$ can be reasonably modelled. For reference, the velocity predictions for the four diabatic cases are also demonstrated in figure 12. In both the inner and outer scales, the velocities by the BL-GFM-VD-TV model are in good agreement with the DNS data.

Figure 11. (a–d) Mean temperature and (e–f) turbulent Prandtl number profiles from different BL models for cases (a) VBL-M2Tw05R13 (cold wall), (b) VBL-M5Tw19R7 (heated wall), (c) ZDC-M6Tw076R17 (cold wall) and (d) ZDC-M14Tw018R24 (cold wall). Panels (e,f) are for the two highly cooled wall cases ZDC-M6Tw025R11 and M14Tw018R24.

Figure 12. Same as figure 11 except for the mean streamwise velocity (four diabatic cases). (a) M2Tw05R13, (b) M5Tw19R7, (c) M6Tw076R17, (d) M14Tw018R24.
Quantitative measurements of the prediction accuracy are presented using two types of relative errors to DNS, which are defined in terms of the inner-scale logarithmic coordinate and the outer-scale normal coordinate, respectively, as
 \begin{equation} \epsilon_{lg,U} =
\frac{\displaystyle\int_{0}^{\lg y_{{{up}}}^*} \big| {\tilde{U}_{BL}^+}
- { \tilde{U}_{DNS}^+} \big| \,{\mathrm{d}} \lg
y^*}{\displaystyle\int_{0}^{\lg y_{{{up}}}^*} { \tilde{U}_{DNS}^+}
\,{\mathrm{d}} \lg y^*}, \quad \epsilon_{n,U} =
\frac{\displaystyle\int_{0}^{y_{{{up}}}} \big| \tilde{U}_{BL} -
\tilde{U}_{DNS} \big| \,{\mathrm{d}} y
}{\displaystyle\int_{0}^{y_{{{up}}}} \tilde{U}_{DNS} \,{\mathrm{d}} y}.
\end{equation}
\begin{equation} \epsilon_{lg,U} =
\frac{\displaystyle\int_{0}^{\lg y_{{{up}}}^*} \big| {\tilde{U}_{BL}^+}
- { \tilde{U}_{DNS}^+} \big| \,{\mathrm{d}} \lg
y^*}{\displaystyle\int_{0}^{\lg y_{{{up}}}^*} { \tilde{U}_{DNS}^+}
\,{\mathrm{d}} \lg y^*}, \quad \epsilon_{n,U} =
\frac{\displaystyle\int_{0}^{y_{{{up}}}} \big| \tilde{U}_{BL} -
\tilde{U}_{DNS} \big| \,{\mathrm{d}} y
}{\displaystyle\int_{0}^{y_{{{up}}}} \tilde{U}_{DNS} \,{\mathrm{d}} y}.
\end{equation}
The two errors for temperature, ![]() $\epsilon _{lg,T}$ and
$\epsilon _{lg,T}$ and ![]() $\epsilon _{n,T}$, are defined likewise. The upper limits of the integral
$\epsilon _{n,T}$, are defined likewise. The upper limits of the integral ![]() $y_{{{up}}}$ for all four
$y_{{{up}}}$ for all four ![]() $\epsilon$ are fixed at
$\epsilon$ are fixed at ![]() $1.1\delta _{99}$. The four errors for all cases are displayed in figure 13 in the order of case numbers. Note that the algebraic averaged errors between locations are displayed for the cases with multiple streamwise locations. As mentioned above, the BL-local model satisfactorily reproduces
$1.1\delta _{99}$. The four errors for all cases are displayed in figure 13 in the order of case numbers. Note that the algebraic averaged errors between locations are displayed for the cases with multiple streamwise locations. As mentioned above, the BL-local model satisfactorily reproduces ![]() $\tilde{U}$ for the adiabatic cases (numbers 1–4), with
$\tilde{U}$ for the adiabatic cases (numbers 1–4), with ![]() $\epsilon _{lg,U}<1.0\,\%$ and
$\epsilon _{lg,U}<1.0\,\%$ and ![]() $\epsilon _{n,U}<1.6\,\%$ for all examined. These are also the accuracy levels of the incompressible BL model. In the presence of surface heat transfer, the two
$\epsilon _{n,U}<1.6\,\%$ for all examined. These are also the accuracy levels of the incompressible BL model. In the presence of surface heat transfer, the two ![]() $\epsilon _{U}$ rise a bit, and
$\epsilon _{U}$ rise a bit, and ![]() $\epsilon _{n,U}$ reaches over 3 % for the four hypersonic cases. Meanwhile, the temperature prediction has poor performance, where
$\epsilon _{n,U}$ reaches over 3 % for the four hypersonic cases. Meanwhile, the temperature prediction has poor performance, where ![]() $\epsilon _{n,T}$ exceeds 10 % for the five hypersonic diabatic cases and even surpasses 20 % for case 12 with a heated wall. In comparison, the velocity prediction is moderately improved using the BL-GFM-VD-TV model. The mean
$\epsilon _{n,T}$ exceeds 10 % for the five hypersonic diabatic cases and even surpasses 20 % for case 12 with a heated wall. In comparison, the velocity prediction is moderately improved using the BL-GFM-VD-TV model. The mean ![]() $\epsilon _{lg,U}$ for all cases is reduced from 1.2 % to 0.7 %, and the mean
$\epsilon _{lg,U}$ for all cases is reduced from 1.2 % to 0.7 %, and the mean ![]() $\epsilon _{n,U}$ is from 2.5 % to 1.3 %. More importantly, the two
$\epsilon _{n,U}$ is from 2.5 % to 1.3 %. More importantly, the two ![]() $\epsilon _{U}$ from BL-GFM-VD-TV do not exhibit an obviously increasing trend with
$\epsilon _{U}$ from BL-GFM-VD-TV do not exhibit an obviously increasing trend with ![]() ${\textit {Ma}}$ lifted or wall-cooling strengthened, indicating enhanced model robustness by employing established relations. It is worth mentioning that case 7 (M6Tw025R11) is the only one where
${\textit {Ma}}$ lifted or wall-cooling strengthened, indicating enhanced model robustness by employing established relations. It is worth mentioning that case 7 (M6Tw025R11) is the only one where ![]() $\epsilon _{lg,U}$ is not improved, as discussed for figure 8. This is acceptable considering the imperfect collapse of the outer-layer scaling in figure 5 due to compressibility and low-
$\epsilon _{lg,U}$ is not improved, as discussed for figure 8. This is acceptable considering the imperfect collapse of the outer-layer scaling in figure 5 due to compressibility and low-![]() ${\textit {Re}}$ effects. Compared with the velocity counterpart, a more significant improvement is realized in the temperature prediction. After deploying BL-GFM-VD-TV,
${\textit {Re}}$ effects. Compared with the velocity counterpart, a more significant improvement is realized in the temperature prediction. After deploying BL-GFM-VD-TV, ![]() $\epsilon _{lg,T}$ and
$\epsilon _{lg,T}$ and ![]() $\epsilon _{n,T}$ for all cases are notably decreased. As an overall measure, the mean
$\epsilon _{n,T}$ for all cases are notably decreased. As an overall measure, the mean ![]() $\epsilon _{lg,T}$ is reduced from 1.4 % to 0.4 %, and the mean
$\epsilon _{lg,T}$ is reduced from 1.4 % to 0.4 %, and the mean ![]() $\epsilon _{n,T}$ is reduced from 8.8 % to 3.4 %. Moreover, we plot in figure 13(b) the
$\epsilon _{n,T}$ is reduced from 8.8 % to 3.4 %. Moreover, we plot in figure 13(b) the ![]() $\epsilon _{lg,T}$ from BL-GFM-VD. It is between the errors of BL-local and BL-GFM-VD-TV for each case, demonstrating that the improved temperature prediction is jointly contributed by the velocity transformations and the TV relation.
$\epsilon _{lg,T}$ from BL-GFM-VD. It is between the errors of BL-local and BL-GFM-VD-TV for each case, demonstrating that the improved temperature prediction is jointly contributed by the velocity transformations and the TV relation.

Figure 13. Relative errors of different BL models to DNS for the mean (a,c) streamwise velocity and (b,d) temperature, measured in terms of (a,b) logarithmic and (c,d) normal coordinates, respectively, where (a) ![]() $\epsilon _{lg,U}$, (b)
$\epsilon _{lg,U}$, (b) ![]() $\epsilon _{lg,T}$, (c)
$\epsilon _{lg,T}$, (c) ![]() $\epsilon _{n,U}$, (d)
$\epsilon _{n,U}$, (d) ![]() $\epsilon _{n,T}$. The horizontal lines are their average errors. For reference, the
$\epsilon _{n,T}$. The horizontal lines are their average errors. For reference, the ![]() ${\textit {Ma}}_\infty$ and
${\textit {Ma}}_\infty$ and ![]() $T_w/T_r$ in each case are plotted in panels (e,f). Cases 1–4 are adiabatic walls, 5–10 are cold walls and 11–12 are heated walls, as categorized in shaded areas.
$T_w/T_r$ in each case are plotted in panels (e,f). Cases 1–4 are adiabatic walls, 5–10 are cold walls and 11–12 are heated walls, as categorized in shaded areas.
Besides the mean profiles, the wall and integral quantities are also of interest in RANS. The comparison between the BL models and DNS is listed in table 2 for the five ZDC cases at specific ![]() ${\textit {Re}}_\tau$, where
${\textit {Re}}_\tau$, where ![]() $H$ is the shape factor, and
$H$ is the shape factor, and ![]() $C_f$ and
$C_f$ and ![]() $B_q$ are the non-dimensional surface friction and heat flux. First, much better predictions for integral quantities, such as
$B_q$ are the non-dimensional surface friction and heat flux. First, much better predictions for integral quantities, such as ![]() $H$, are realized in the BL-GFM-VD-TV model, attributed to the overall improvement in mean profile shapes. Regarding the wall quantities, the BL-local model employs the TL transformation for the inner layer
$H$, are realized in the BL-GFM-VD-TV model, attributed to the overall improvement in mean profile shapes. Regarding the wall quantities, the BL-local model employs the TL transformation for the inner layer ![]() $\mu _t$ (see § 3.1). Since TL provides accurate scaling in the viscous layer, the wall quantities can be well predicted by the BL-local model including diabatic cases, as demonstrated by Dilley & McClinton (Reference Dilley and McClinton2001). After using BL-GFM-VD-TV, some improvements for the wall quantities can be observed, especially for
$\mu _t$ (see § 3.1). Since TL provides accurate scaling in the viscous layer, the wall quantities can be well predicted by the BL-local model including diabatic cases, as demonstrated by Dilley & McClinton (Reference Dilley and McClinton2001). After using BL-GFM-VD-TV, some improvements for the wall quantities can be observed, especially for ![]() $u_\tau$ and
$u_\tau$ and ![]() $C_f$. Nevertheless, not all the cases are improved at the specific limited streamwise locations, in particular the M6Tw025R11 case of relatively low
$C_f$. Nevertheless, not all the cases are improved at the specific limited streamwise locations, in particular the M6Tw025R11 case of relatively low ![]() ${\textit {Re}}_{\delta _2}$. A more comprehensive evaluation of the wall quantities is anticipated based on the data at a set of locations in each case.
${\textit {Re}}_{\delta _2}$. A more comprehensive evaluation of the wall quantities is anticipated based on the data at a set of locations in each case.
Table 2. Some wall and integral quantities from different BL models and DNS for the ZDC cases. The significant figures of the DNS data are the same as in the reference. Note that ![]() $C_f$ was not listed in the reference, so it is inferred here using
$C_f$ was not listed in the reference, so it is inferred here using ![]() $\rho _w$ and
$\rho _w$ and ![]() $u_\tau$.
$u_\tau$.

5. Discussions and summary
5.1. Discussions
The present work is designed for ZPG boundary layers, so its applications and limitations are further discussed. First, we demonstrate a promising framework of how to incorporate well-established mean flow relations to improve the BL wall model. The module-style modification allows direct substitutions of more accurate relations in the future. Second, a highly efficient and accurate mean-flow solver is feasible using the modified BL model, which can be further combined with, for example, the resolvent analysis to obtain the fluctuation characteristics over a wide parameter space (![]() ${\textit {Ma}}$,
${\textit {Ma}}$, ![]() ${\textit {Re}}$, wall cooling, etc.), as done by Cossu, Pujals & Depardon (Reference Cossu, Pujals and Depardon2009) for incompressible boundary layers and by Chen et al. (Reference Chen, Cheng, Fu and Gan2023a,Reference Chen, Cheng, Gan and Fub) for compressible channels. Third, the two modified models can be applied to high-speed channel and pipe flows, though we anticipate that the improvement over the BL-local model will not be as large as that for the boundary layer cases. Two possible reasons are that for channel and pipe flows, the TL transformation used for the inner layer is particularly accurate, and
${\textit {Re}}$, wall cooling, etc.), as done by Cossu, Pujals & Depardon (Reference Cossu, Pujals and Depardon2009) for incompressible boundary layers and by Chen et al. (Reference Chen, Cheng, Fu and Gan2023a,Reference Chen, Cheng, Gan and Fub) for compressible channels. Third, the two modified models can be applied to high-speed channel and pipe flows, though we anticipate that the improvement over the BL-local model will not be as large as that for the boundary layer cases. Two possible reasons are that for channel and pipe flows, the TL transformation used for the inner layer is particularly accurate, and ![]() ${\textit {Pr}}_t$ has no singularities in the near-wall region (e.g. Huang et al. Reference Huang, Coleman and Bradshaw1995; Cheng & Fu Reference Cheng and Fu2023).
${\textit {Pr}}_t$ has no singularities in the near-wall region (e.g. Huang et al. Reference Huang, Coleman and Bradshaw1995; Cheng & Fu Reference Cheng and Fu2023).
As discussed in § 3, the present modifications are limited to attached thin-layer flows (then ![]() $|\tilde{\omega }|=|{\partial \tilde{U}_{{\scriptscriptstyle /\!/}}}/{\partial n}|$ or
$|\tilde{\omega }|=|{\partial \tilde{U}_{{\scriptscriptstyle /\!/}}}/{\partial n}|$ or ![]() $|{\partial \tilde{U}}/{\partial y}|$), so it becomes inapplicable when other components of
$|{\partial \tilde{U}}/{\partial y}|$), so it becomes inapplicable when other components of ![]() $\tilde{\omega }$ are non-negligible. In this sense, the modified BL model is less general than the baseline one. On the one hand, it is known that computing the attached thin-layer flow is the strength of the BL model (and other algebraic ones) over other more sophisticated turbulence models, so the present modifications to the BL model can help maximize its strength. On the other hand, further extensions to more general flows with pressure gradients, separation, etc., are under investigation and will be reported separately. Taking the pressure gradient effects as an example, model improvement is anticipated owing to the following evidence. A valuable DNS database was elaborated by Wenzel et al. (Reference Wenzel, Gibis, Kloker and Rist2019) for supersonic boundary layers (Mach 2) under both favourable and adverse pressure gradients. Their results, and also those of Bai et al. (Reference Bai, Griffin and Fu2022), actively support the usage of various velocity transformations for the inner layer. With rising adverse pressure gradient strength, the VD transformation increasingly underestimates the velocity in the outer region, but it significantly reduces the compressibility effects. Moreover, Gibis et al. (Reference Gibis, Wenzel, Kloker and Rist2019) suggested appropriate compressible scalings for the outer-layer self-similarity under pressure gradients, which could, for example, improve the Rotta–Clauser parameter used in the CS model. Nevertheless, more non-ZPG DNS databases are highly desired in a range of
$\tilde{\omega }$ are non-negligible. In this sense, the modified BL model is less general than the baseline one. On the one hand, it is known that computing the attached thin-layer flow is the strength of the BL model (and other algebraic ones) over other more sophisticated turbulence models, so the present modifications to the BL model can help maximize its strength. On the other hand, further extensions to more general flows with pressure gradients, separation, etc., are under investigation and will be reported separately. Taking the pressure gradient effects as an example, model improvement is anticipated owing to the following evidence. A valuable DNS database was elaborated by Wenzel et al. (Reference Wenzel, Gibis, Kloker and Rist2019) for supersonic boundary layers (Mach 2) under both favourable and adverse pressure gradients. Their results, and also those of Bai et al. (Reference Bai, Griffin and Fu2022), actively support the usage of various velocity transformations for the inner layer. With rising adverse pressure gradient strength, the VD transformation increasingly underestimates the velocity in the outer region, but it significantly reduces the compressibility effects. Moreover, Gibis et al. (Reference Gibis, Wenzel, Kloker and Rist2019) suggested appropriate compressible scalings for the outer-layer self-similarity under pressure gradients, which could, for example, improve the Rotta–Clauser parameter used in the CS model. Nevertheless, more non-ZPG DNS databases are highly desired in a range of ![]() ${\textit {Ma}}$ and wall-cooling conditions.
${\textit {Ma}}$ and wall-cooling conditions.
5.2. Summary
Different forms of mean-flow relations for high-speed wall-bounded turbulence, including the velocity transformation and algebraic TV relation, have been established in previous works with increasing accuracy. The combination of these relations enables an efficient and accurate recovery of the mean flow as an inverse problem, which is a solid mean to accommodate compressibility effects. This thought is utilized in this work, and the core idea is to systematically improve the BL wall model for ZPG boundary layers using various established scalings. The objective is that BL can achieve comparable accuracy with the incompressible counterpart. Only well-established relations are adopted, and we avoid introducing any new functions or coefficients fitted by ourselves. Twelve published DNS datasets are employed for a priori inspiration and a posteriori examination. A large parameter space is covered, with ![]() ${\textit {Ma}}_\infty$ ranging from 2 to 14 under adiabatic, cold and heated wall conditions (
${\textit {Ma}}_\infty$ ranging from 2 to 14 under adiabatic, cold and heated wall conditions (![]() $T_w/T_r$ from 0.18 to 1.9).
$T_w/T_r$ from 0.18 to 1.9).
The baseline BL-local model is the classical one widely used in numerous commercial solvers, which uses semilocal units in the inner-layer damping function, and assumes a prescribed ![]() ${\textit {Pr}}_t$ distribution. The baseline model can well reproduce the velocity for adiabatic cases, but deteriorates subject to surface heat transfer. Meanwhile, the temperature prediction has obvious deviations from DNS in both adiabatic and diabatic cases.
${\textit {Pr}}_t$ distribution. The baseline model can well reproduce the velocity for adiabatic cases, but deteriorates subject to surface heat transfer. Meanwhile, the temperature prediction has obvious deviations from DNS in both adiabatic and diabatic cases.
Three modifications are made to the formulations of ![]() $\mu _t$ and
$\mu _t$ and ![]() $\tilde{T}$, corresponding to the three shortcomings of the BL-local model. First, we show that the inner-layer scaling of
$\tilde{T}$, corresponding to the three shortcomings of the BL-local model. First, we show that the inner-layer scaling of ![]() $\mu _t$ in BL-local is equivalent to applying the TL transformation, which degrades in the logarithmic region in diabatic boundary layers. Therefore, we adopt the GFM transformation instead, for improved logarithmic scaling of
$\mu _t$ in BL-local is equivalent to applying the TL transformation, which degrades in the logarithmic region in diabatic boundary layers. Therefore, we adopt the GFM transformation instead, for improved logarithmic scaling of ![]() $\mu _t$. Second, the outer-layer
$\mu _t$. Second, the outer-layer ![]() $\mu _t$ and thus the matching location can be severely underestimated (
$\mu _t$ and thus the matching location can be severely underestimated (![]() $\kern0.7pt y_{m\mu }^*$ down to 40–60) in BL-local, so the logarithmic scaling above this low
$\kern0.7pt y_{m\mu }^*$ down to 40–60) in BL-local, so the logarithmic scaling above this low ![]() $y_{m\mu }^*$ is not followed. For improvement, we adopt the VD transformation in the outer layer based on the compressible defect velocity scaling. Third, the inner layer temperature in cold-wall cases is quite sensitive to
$y_{m\mu }^*$ is not followed. For improvement, we adopt the VD transformation in the outer layer based on the compressible defect velocity scaling. Third, the inner layer temperature in cold-wall cases is quite sensitive to ![]() ${\textit {Pr}}_t$, and
${\textit {Pr}}_t$, and ![]() ${\textit {Pr}}_t$ varies considerably near the wall and exhibits a singularity around the temperature peak. Since there lacks a unified modelling of
${\textit {Pr}}_t$ varies considerably near the wall and exhibits a singularity around the temperature peak. Since there lacks a unified modelling of ![]() ${\textit {Pr}}_t$ near the wall, we design a novel two-layer formulation of
${\textit {Pr}}_t$ near the wall, we design a novel two-layer formulation of ![]() $\tilde{T}$. The energy equation with constant
$\tilde{T}$. The energy equation with constant ![]() ${\textit {Pr}}_t$ is only solved in the outer layer (
${\textit {Pr}}_t$ is only solved in the outer layer (![]() $\kern0.7pt y>y_{mT}$), and the inner layer (
$\kern0.7pt y>y_{mT}$), and the inner layer (![]() $\kern0.7pt y< y_{mT}$) temperature is formulated by the algebraic quadratic TV relation. The modified model is termed BL-GFM-VD-TV, where the latter three acronyms denote the three modifications, respectively; see § 3.4.
$\kern0.7pt y< y_{mT}$) temperature is formulated by the algebraic quadratic TV relation. The modified model is termed BL-GFM-VD-TV, where the latter three acronyms denote the three modifications, respectively; see § 3.4.
Numerical results between all the DNS cases demonstrate that the three modifications take effect as expected. For the mean streamwise velocity, the high accuracy of the BL-local model for adiabatic cases is retained, while that for diabatic cases is improved, especially in the logarithmic region. Meanwhile, significant improvement for the temperature is realized for both adiabatic and diabatic cases, that ![]() $\tilde{T}$ is in close agreement with DNS in most cases, which has not been realized before. The mean relative errors of
$\tilde{T}$ is in close agreement with DNS in most cases, which has not been realized before. The mean relative errors of ![]() $\tilde{T}$ to DNS for all cases are down to 0.4 % measured in the logarithmic wall-normal coordinate and 3.4 % in the outer coordinate, only around one-third of those in the baseline model. Furthermore, a posteriori diagnosis suggests that the non-monotonic and singular behaviours of
$\tilde{T}$ to DNS for all cases are down to 0.4 % measured in the logarithmic wall-normal coordinate and 3.4 % in the outer coordinate, only around one-third of those in the baseline model. Furthermore, a posteriori diagnosis suggests that the non-monotonic and singular behaviours of ![]() ${\textit {Pr}}_t$ in cold-wall cases can be modelled. We emphasize that modifying only
${\textit {Pr}}_t$ in cold-wall cases can be modelled. We emphasize that modifying only ![]() $\mu _t$ is insufficient for an accurate temperature prediction in highly cooled wall cases. The TV relation should be further incorporated in the near-wall region.
$\mu _t$ is insufficient for an accurate temperature prediction in highly cooled wall cases. The TV relation should be further incorporated in the near-wall region.
Future works will be on possible extensions of the modified models to more complex configurations, and their behaviours in the flows with moderate pressure gradients.
Acknowledgements
We are grateful to all the authors listed in table 1 for kindly sharing their elaborated DNS datasets.
Funding
This research was supported by CORE, a joint research centre between the Laoshan Laboratory and HKUST. L.F. acknowledges the fund from the Research Grant Council (RGC) of the Government of HKSAR with RGC/ECS Project (no. 26200222), RGC/GRF Project (no. 16201023) and RGC/STG Project (no. STG2/E-605/23-N), the fund from Guangdong Province Science and Technology Plan Project (no. 2023A0505030005) and the fund from the Project of Hetao Shenzhen–Hong Kong Science and Technology Innovation Cooperation Zone (no. HZQB-KCZYB-2020083).
Declaration of interests
The authors report no conflict of interest.
Data availability statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Appendix A. Solver verification and sensitivity study
To ensure the validity of the boundary layer equations and verify our solver, we first compare the mean flow results with Hendrickson et al. (Reference Hendrickson, Subbareddy, Candler and Macdonald2023), who solved the full NS equation with BL models using the US3D code. The ZDC-M6Tw025R11 case is computed using the standard BL model. The results are shown in figure 14(a), and close agreement with the reference is obtained. As discussed in § 2.2, the M14Tw018R24 case is most susceptible to shock-boundary-layer interaction at the leading edge. For further validation of the boundary layer equations at such a high ![]() ${\textit {Ma}}$, we additionally implement a second-order shock-capturing RANS simulation (Chen & Fu Reference Chen and Fu2020) on a
${\textit {Ma}}$, we additionally implement a second-order shock-capturing RANS simulation (Chen & Fu Reference Chen and Fu2020) on a ![]() $N_x\times N_y={300\times 163}$ mesh for this case. The comparisons of the velocity and temperature profiles are displayed in figure 14(b), where good agreement is demonstrated.
$N_x\times N_y={300\times 163}$ mesh for this case. The comparisons of the velocity and temperature profiles are displayed in figure 14(b), where good agreement is demonstrated.

Figure 14. Mean streamwise velocity and temperature from the standard BL model for cases (a) M6Tw025R11 and (b) M14Tw018R24. The reference data are from (a) Hendrickson et al. (Reference Hendrickson, Subbareddy, Candler and Macdonald2023) and (b) our RANS solver.
Next, a sensitivity study of ![]() $y_{mT}^*$ is conducted. Three
$y_{mT}^*$ is conducted. Three ![]() $y_{mT}^*=50$, 100, 150 are selected, and the BL-GFM-VD-TV results for two hypersonic cases are displayed in figure 15. Basically, there is a minor difference in
$y_{mT}^*=50$, 100, 150 are selected, and the BL-GFM-VD-TV results for two hypersonic cases are displayed in figure 15. Basically, there is a minor difference in ![]() $\tilde{T}$ with varying
$\tilde{T}$ with varying ![]() $y_{mT}^*$. A higher
$y_{mT}^*$. A higher ![]() $y_{mT}^*$ tends to provide closer results to DNS near the temperature peak. On the other hand, a lower
$y_{mT}^*$ tends to provide closer results to DNS near the temperature peak. On the other hand, a lower ![]() $y_{mT}^*$ can enhance the computational robustness, especially at the first few streamwise locations. Thereby, a moderate
$y_{mT}^*$ can enhance the computational robustness, especially at the first few streamwise locations. Thereby, a moderate ![]() $y_{mT}^*=100$ is used throughout.
$y_{mT}^*=100$ is used throughout.

Figure 15. Mean temperature from the BL-GFM-VD-TV model with different ![]() $y_{mT}^*$ for cases (a) M8Tw048R20 and (b) M6Tw025R11.
$y_{mT}^*$ for cases (a) M8Tw048R20 and (b) M6Tw025R11.
Appendix B. Results of the HLPP transformation
The very recent transformation of Hasan et al. (Reference Hasan, Larsson, Pirozzoli and Pecnik2023b) incorporates intrinsic compressibility effects by introducing a correction to the TL transformation, as
Here, ![]() $D^i$ is the classical damping function as in (3.4) representing the incompressible counterpart, and
$D^i$ is the classical damping function as in (3.4) representing the incompressible counterpart, and ![]() $D^c$ is the modified damping function to interpret intrinsic compressibility, where the correction function
$D^c$ is the modified damping function to interpret intrinsic compressibility, where the correction function ![]() $f({\textit {Ma}}_\tau )=19.3{\textit {Ma}}_\tau$ and
$f({\textit {Ma}}_\tau )=19.3{\textit {Ma}}_\tau$ and ![]() ${\textit {Ma}}_\tau$ is the friction Mach number. The transformed velocities
${\textit {Ma}}_\tau$ is the friction Mach number. The transformed velocities ![]() $U_{tsf}^+$ using TL, GFM and HLPP are shown in figure 16 for all the DNS cases (Reynolds-averaged values), and the relative errors to DNS are displayed as a function of
$U_{tsf}^+$ using TL, GFM and HLPP are shown in figure 16 for all the DNS cases (Reynolds-averaged values), and the relative errors to DNS are displayed as a function of ![]() ${\textit {Ma}}_\tau$, following Hasan et al. (Reference Hasan, Larsson, Pirozzoli and Pecnik2023b). The mean errors (also defined based on Reynolds averages) of GFM and HLPP between all cases are approximately the same, equal to 2.2 % and 2.4 %, respectively. Note that the errors in figure 16 are somewhat differently defined from Hasan et al. (Reference Hasan, Larsson, Pirozzoli and Pecnik2023b) (their figure 2) because the present errors are based on the absolute value of the velocity difference, hence non-negative by definition (see equation (8) in Griffin et al. (Reference Griffin, Fu and Moin2021) and (4.1a,b) above).
${\textit {Ma}}_\tau$, following Hasan et al. (Reference Hasan, Larsson, Pirozzoli and Pecnik2023b). The mean errors (also defined based on Reynolds averages) of GFM and HLPP between all cases are approximately the same, equal to 2.2 % and 2.4 %, respectively. Note that the errors in figure 16 are somewhat differently defined from Hasan et al. (Reference Hasan, Larsson, Pirozzoli and Pecnik2023b) (their figure 2) because the present errors are based on the absolute value of the velocity difference, hence non-negative by definition (see equation (8) in Griffin et al. (Reference Griffin, Fu and Moin2021) and (4.1a,b) above).

Figure 16. Transformed streamwise velocity using (a) TL, (b) GFM and (c) HLPP for all cases. The black dashed and dotted lines are the incompressible DNS data from Sillero, Jiménez & Moser (Reference Sillero, Jiménez and Moser2013) and Lee & Moser (Reference Lee and Moser2015), respectively. The subpanels display the relative errors to DNS as described in Griffin et al. (Reference Griffin, Fu and Moin2021) and Hasan et al. (Reference Hasan, Larsson, Pirozzoli and Pecnik2023b). The legends are the same as in figure 5 (pentacles represent the legends without symbols).
The HLPP transformation can also be employed, following the procedures in § 3.1, to improve the inner-layer scaling in the BL-local model. After incorporating VD for the outer layer and the TV relation, the final model can be termed BL-HLPP-VD-TV. We have also implemented this model and find that the mean relative errors in predicting velocity and temperature are comparable with BL-GFM-VD-TV, as expected from figure 16. Specifically, the four mean errors are ![]() $\epsilon _{lg,U}=0.6\,\%$,
$\epsilon _{lg,U}=0.6\,\%$, ![]() $\epsilon _{lg,T}=0.4\,\%$,
$\epsilon _{lg,T}=0.4\,\%$, ![]() $\epsilon _{n,U}=1.3\,\%$ and
$\epsilon _{n,U}=1.3\,\%$ and ![]() $\epsilon _{n,T}=3.5\,\%$.
$\epsilon _{n,T}=3.5\,\%$.