The Thermal Properties of Sea Ice

Abstract

Compared with freshwater ice, whose physical properties are well known, sea iceis a relatively complex substance whose transition to a completely solid mixtureof pure ice and solid salts is completed only at extremely low temperaturesrarely encountered in nature. The physical properties of sea ice are thusstrongly dependent on salinity, temperature and time. Many of these propertiesare still not fully understood or accurately known, particularly those importantfor the understanding of a natural ice cover. The specific heat for example isan important term in the calculation of the heat energy content of a cover.However, Malmgren (1927), whose calculatedvalues of the specific heat of sea ice are in general use, neglected the directcontribution of the brine present in inclusions. Re-examination of thequestion of specific and latent heats of sea ice has led to distinguishingbetween the freezing and melting points and enabled significant observations inthis range. Similarly, because the thermal conductivity is a necessary parameterin the description of the thermal behaviour of ice. the sea-ice modelsuggested by Anderson (1958) has beenmodified and extended in the present work to the case of saline ice containingair bubbles. This enabled the completion of calculations of density andconductivity. In order to illustrate the theoretically calculated values.measurements were made on sea-ice samples to determine the specific heat,density and thermal conductivity.

Résumé

Par comparaison avec la glace d’eau douce. dont lespropriétés physiques sont bien connues, la glace de mer est unesubstance relativement complexe dont le passage à un mélangeentièrement solide de glace pure et de sels n’estréalisé qu’à des températuresextrêmement basses que l’on rencontre rarement dans la nature.

Les propriétés physiques de la glace de mer dépendentfortement de la salinité, de la température et du temps. Denombreuses propriétés ne sont pas encore pleinement comprises ouconnues avec précision, en particulier celles qui sont importantes pourla compréhension d’une couverture de glace naturelle. Par exemplela chaleur spécifique est un terme important dans le calcul du contenu dechaleur d’une telle couverture. Cependant, Malmgren (1927), dont on utilise généralement lesvaleurs calculées pour la chaleur spécifique de la glace de mer, anégligé la contribution directe de la saumure présente dansles inclusions. Un nouvel examen du problème des chaleursspécifiques et latentes de la glace de mer a conduit à faire ladistinction entre les points de congelation et de fusion et permis desobservations significatives dans ce domaine. Parallèlement, puisque laconductivité thermique est un paramètre nécessaire àla description du comportement thermique dc la glace, le modèle de glacede mer suggéré par Anderson(1958) a été modifié et étendu dans leprésent travail au cas de la glace salée contenant des bullesd’air. Ceci a permis de completer les calculs de densité et deconductivité. De façon à illustrer les valeursthéoriques calculées, des mesures ont été faites surdes échantillons dc glace de mer pour déterminer la chaleurspécifique, la densité et la conductivité thermique.

Zusammenfassung

Verglichen mit Süsswassereis, dessert physikalische Eigenschaften gutbekannt sind, ist Meereis eine verhältnismässig komplizierteSubstanz, die erst bei schr tiefen, in der Natur selten verwirklichtenTemperaturen vollständig zu einer Eis-Salzmischung erstarrt. Diephysikalischen Eigenschaften des Meereises sind daher stark von Salzgehalt,Temperatur und Zeit abhängig. Viele dieser Eigenschaften. insbesonderedie für das Verständnis einer natürlichen Eisdeckewichtigen, sind noch nicht völlig geklärt oder bekannt. Z.B. diespezifische Wärme ist eine wichtige Grösse in der Berechnung desWärmeinhaltes einer Eisdecke. Malmgren’s (1927) allgemein verwandte Werte der spezifischenWärme vernachlässigen den Beitrag des vom Eise eingeschlossenenSalzwassers. Eine nähere Untersuchung der spezifischen und latentenWärme des Meereises hat zu einer Unterscheidung zwischen Gefrierpunkt undSchmelzpunkt geführt und bedeutsame Beobachtungen in demÜbergangsgebiet zwischen diesen Temperaturen ermöglicht.Ähnliches gilt für die Wärmeleitfähigkeit, diefür die Beschreibung des thermischen Verhaltens des Meereisesunerlässlichist. Das von Anderson(1958) vorgeschlagene Modell für Meereis ist modifiziert undauf den Fall des salzhaltigen Eises mit Luftbläschen erweitert worden.Dadurch wurden Berechnungen von Dichte und Wärmeleitung möglich.Die auf diese Weise erhaltenen theoretischen Werte wurden durch Messungen derspezifischen Wärme, der Dichte und der Wärmeleitfähigkeitan Meereis kontrolliert und bestätigt.

Introduction

The thermal diffusivity term in the diffusion equation is defined as the ratio of thermal conductivity to specific heat. It is thus convenient to consider these two terms, together with the latent heat and density, as thermal properties.

Because these quantities are strongly dependent on temperature and composition, in the case of sea ice their precise measurement has always posed considerable difficulty. In fact it still appears to be safer to rely on theoretical values for the thermal conductivity and specific heat. In the development of a suitable sea-ice model for the calculation of these quantities, an interesting progressive complexity appears. The specific heat can be obtained from knowledge of the composition alone. The density requires additional consideration of air bubble content. Finally, in order to calculate the thermal conductivity, information on the spatial distribution of all the components is required.

1. The Specific and Latent Heats of Sea Ice

1.1 The composition of sea ice

When sea-water is cooled to its freezing point, pure ice crystals form, separating from the brine which initially remains in contact with the sea. As freezing progresses, some pockets of brine are cut off so that the resulting ice as a whole is composed of pure ice, brine, solid salt crystals and air bubbles. The latter have negligible influence on the specific heat, but the continuous change in relative abundance of the other constituents with temperature leads to an abnormally large specific heat. At temperatures not far removed from the freezing point, further freezing of the interior brine is the major heat absorbing process.

The total mass of dissolved solid material in grams contained in one kilogram of solution is the usual oceanographic definition of salinity. This is also applied to sea ice and the mass of salt in grams per kilogram of sea ice is usually quoted in parts per thousand (‰). The salinity of sea ice may well be considered a convenient property to which other more complex properties, including thermal, electrical and mechanical, may be referred. However, because the salts in sea ice consist of many ions, chief amongst which are: Na⁺, K⁺, Ca⁺⁺, Mg⁺⁺, Cl⁻, SO₄⁻⁻ and CO₃⁻⁻, the specification is in general insufficient to fix the relative ionic content of the ice.

As shown in the phase diagram in Figure 1 of Assur (1960), based on the work of Nelson and Thompson (1954), above a temperature of −8.2° C. essentially all salts trapped within the body of sea ice are in solution. Down to this temperature limit, the relative concentration of the ions is as in sea-water and the specification of salinity alone is usually unambiguous. Below −8.2° C., Na₂SO₄.10H₂O is the first salt to precipitate, so that on migration of brine in the ice the relative local concentrations of ions in the ice will be altered. This has been shown by Addison (personal communication) in his ionic analysis of the upper 10 cm. of artificially grown sea ice. In this case, the specification of salinity alone is not always sufficient to account for all the properties of the ice. It should be noted however, that the dependence of the properties of sea ice on salinity is greatest above −8.2° C., in which region knowledge of the salinity alone is sufficient, unless the ice concerned has undergone a significant temperature excursion to colder temperatures and returned. Between −8.2° C. and −23° C., even the complete absence of Na₂SO₄.10H₂O crystals in a particular region of ice will affect the specific heat of 10‰ saline ice by less than 1% at −20° C. and 2% at −10° C. For ice of lower salinity this error will be even less. In geophysical investigations, this is not a serious discrepancy.

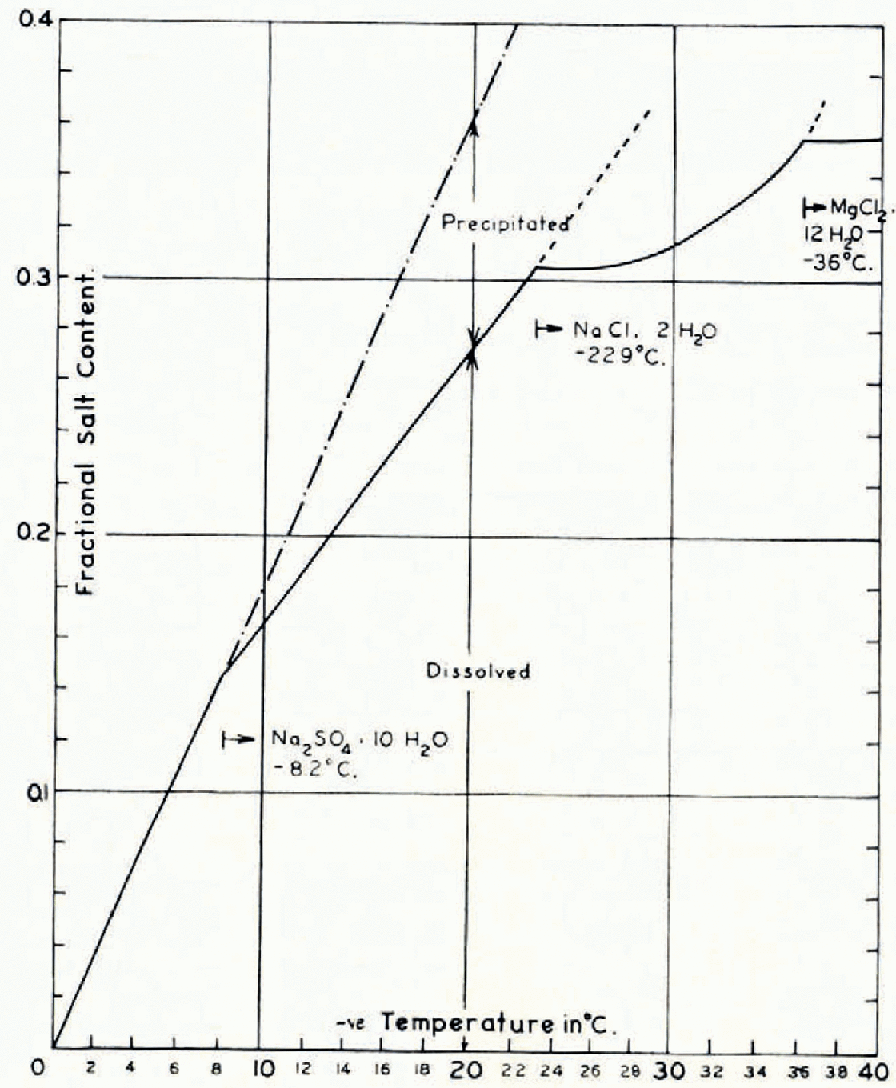
Fig. 1. Freezing point of brine as a function of the ratio of dissolved salts to pure water

Theories based on the salinity of ice expressed in terms of ions present would be time dependent and bound to the thermal history of the ice concerned. The complexity of the resulting mathematical expressions would preclude their use in any practical application.

A result of many measurements by Malmgren (1927) in the Arctic Ocean, was that the salinity calculated from chlorinity differed from that found by hydrometric determinations by less than 5 per cent for any given ice sample. This leads to the belief that the salinity is usually a sufficiently good parameter in analysis of the thermal behaviour of sea ice. It is important to note that in the results of Assur shown in Figure 1, the usual concept of salinity is not used. The composition is given by the fractional salt content, or ratio of the dissolved salts to pure water. For dilute solutions, the difference between salinity and fractional salt content may often be inappreciable, but it is most important when discussing solutions having the concentrations of the brines trapped in sea ice.

1.2 The specific heat of ice between the freezing point and −8.2° C.

There is no significant substitution of the ions listed earlier in the ice lattice, so that it is reasonable to assume that at the freezing point, the brine in the interior cells has the same salt content as the sea water from which the ice was formed.

If σ is the salinity of the sea ice as a whole, and s the fractional salt content of the brine, according to the usage of Assur, within the ice at a temperature θ, then the total mass of pure water in unit mass of sea ice at that temperature is given by

(1.2.1)

and the mass of pure ice by

(1.2.2)

A change in temperature of the ice causes a change in fractional salt content of the brine because of further freezing, and the difference in mass of unfrozen water per unit mass of sea ice may be expressed as

(1.2.3)

Figure 1 shows that the relation between s and θ is linear over the range being considered, so that

(1.2.4)

This linear relationship between s and θ is the sole reason for keeping the concept of fractional salt content for the brine. If the salinity of the brine is given by σ _b, then we have

so that the function connecting σ _b and θ is too complex for a simple interchange of variables.

Using equation (1.2.4) to eliminate s from (1.2.3), we obtain

(1.2.5)

Essentially the specific heat of sea ice depends on the amount of water substance changing state during temperature changes, and on the specific heats of pure ice and water. Since the direct contribution to the specific heat of sea ice of 4‰ salinity by the thermal capacity of its salts is of the order of 0.0008 cal.g.⁻¹ °C.⁻¹, this is considered negligible. The effects of heats of crystallization (or dilution) are also neglected, since for example, according to data quoted by Lange and Forker (1952), the infinite dilution of 0.004 g. of sodium chloride involves less than 0.008 cal. Considering the small change in dilution over a range of 1° C., the importance of this term vanishes completely, even though it may be of the order of ten times as large for an equal amount of sodium sulphate.

The heat dQ absorbed by unit mass of sea ice during a temperature increase of dθ can thus be written as:

(1.2.6)

where c _w is the specific heat of water, c _i that of pure ice and L _i its latent heat of formation. The specific heat of sea ice then follows from equations (1.2.5) and (1.2.6) as

or, substituting for s from equation (1.2.4),

(1.2.7)

The term σc _i may be considered negligible for natural sea ice.

Table I shows the results of calculation using the values L _i = 79·69 cal.g.⁻¹, c _i = 0·48 cal.g.⁻¹ °C.⁻¹, c _w = 1.01 cal.g.⁻¹ °C.⁻¹ and α = −0.0182° C⁻¹, for a number of ice salinities.

Table I The Specific Heat of Sea Ice Between −2° C. and −23° C.

1.3 The specific heat of ice between −8.2 and −23° C.

The results summarized in Figure 1 indicate that a continuous deposition, of Na₂SO₄.10H₂O only, takes place between −8.2° C. and 23° C. In this range it is convenient to consider s grams of dissolved salt and p grams of precipitate (not including its water of crystallization) to be associated with each gram of water. Assuming a linear rate of deposition of Na₂SO₄.10H₂O, the quantity of precipitate at any temperature can be calculated by extrapolating the initial section of the phase graph as shown. This extrapolated graph then indicates the salinity of the brine as it would have been had no crystallization taken place, so that the difference between the actual and projected values is equal to the corresponding relative mass of precipitate. In one gram of sea ice there are thus w grams of water, ws grams of dissolved salt, and wp grams of precipitated salt with which βwp grams of water are combined in crystals. For Na₂SO₄.10H₂O, β = 1·27. Thus in general, the mass of unfrozen pure water is given by

(1.3.1)

and the mass of pure ice by

(1.3.2)

The change in mass of unfrozen water substance per unit mass of sea ice for a change in salinity ds and associated precipitate dp is given by

(1.3.3)

Again, Figure 1 shows that

(1.3.4)

Hence

(1.3.5)

as before.

The heat dQ absorbed by unit mass of sea ice during a temperature increase of dθ is now

(1.3.6)

where c _h is the specific heat of the precipitated hydrate. The last term of equation (1.3.6) accounts for the direct contribution of the specific heat of sodium sulphate decahydrate crystals. Using equations (1.3.4), (1.3.5) and (1.3.6) the specific heat of sea ice becomes

Since

, and βc _i and (1+β)c _h are of the same order of magnitude, the last term may be neglected, so that we have again (cf. equation (1.2.7))

(1.3.7)

Calculations with this formula, with c _i varying monotonically from 0.48 to 0.46 cal.g.⁻¹ °C.⁻¹, and other constants as before in section 1.2 complete Table I. The information contained in this table is presented in Figure 2 in graphical form.

Fig. 2. Specific heat of sea ice as a function of temperature. Curves are for the salinities indicated

1.4 Latent heat of ice formation

The presence of salts in water depresses the freezing point by an amount which can be determined from the temperature-composition graph; at this temperature a definite amount of pure ice will form, enclosing brine having the salinity of the sea-water. The amount of pure ice present in unit mass of sea ice at the temperature of freezing is: (1−σ−σ/s). For ice frozen from water of salt content s, the latent heat of formation is thus

(1.4.1)

Table II shows the latent heat calculated as a function of ice salinity.

When the temperature of sea ice is increased, brine cells within the ice become more dilute by melting ice. This process continues until all the ice has melted. The resulting brine at this stage has a salinity equal to that of the original ice, so that for ice of salinity 4‰, the final melting point is about −0.2° C. The heat required in this process must be considered as specific heat, as it is associated with a continuous change in temperature. One is thus forced to conclude that a latent heat, which according to the usual concept implies a release or absorption of heat at constant temperature, does not exist during the melting of sea icc.

The apparent “latent heat anomaly” of sea ice is explained by the fact that on initial freezing, the ice is in contact with sea-water, from which, however, the ice on the surface of a cover, or ice removed for observation, is usually isolated. A true latent heat could be observed were ice to be melted while in contact with sea-water of constant concentration. This for example occurs during final stages of the break-up of an ice cover, when small floes are awash in the sea.

Since the bulk of the ice within a cover is usually not in contact with seawater, it is of interest to consider the specific heat of established ice between its final freezing point and the final melting point. The temperature records of Yakovlev (1958) for Arctic ice at about lat. 85° N. show that during July and August the upper ice surface is between 0° C. and −1° C., with all of the ice at a temperature above initial freezing point. It is thus clear that knowledge of the specific heat of sea ice is necessary for temperatures in this region.

The specific heat of ice at temperatures higher than −2° C., calculated from equation (1.2.7), is also tabulated in Table II. Figure 2 shows the specific heat of ice as a function of salinity over the entire temperature range considered in sections 1.3 and 1.4.

Table II Latent Heat of Sea Ice

Using equation (1.2.7) it is possible to calculate the heat Q _m required to melt unit mass of ice with a certain initial temperature θ ₀;

(1.4.2)

where θ _m = σ/α is the final melting point. Completing the integration of (1.4.2) we have

(1.4.3)

and inserting the values L _i = 79.67 cal.g.⁻¹, c _i = 0 48 cal.g.⁻¹,°C.⁻¹, θ ≥ −8.2°C., c _w = 1·0 cal.g.⁻¹ °C.⁻¹ and α = −1.8×10⁻² °C.⁻¹, enables the compilation of Table III.

Table III Heat Required for the Complete Melting of Isolated Sea Ice

1.5 The measurement of the specific heat of sea ice

The insufficiency of published data on the specific heat of saline ice has made it desirable to develop a method of checking the validity of the theoretically calculated values. There is a particular need for measurements which extend into the temperature interval between the freezing and final melting points for an extensive range of salinities.

Because the specific heat of sea ice is a continuous non-linear function of the temperature it would be extremely tedious and of questionable accuracy to measure the specific heat directly over the small temperature intervals necessary. Near to the melting point especially, the intervals would have to be so minute that normal laboratory thermometers capable of resolving to within 0.02° C. are inadequate. Both Malmgren (1927) and Nazintsev (1959) preferred to work over intervals of some 2° C., and thus obtain mean values for the specific heat over that temperature range. An alternative procedure has been chosen in the present instance. The total heat involved per unit mass of sea ice over arbitrary temperature intervals of up to several degrees centigrade was compared with the corresponding theoretical definite integral over the same range.

Electrical heating of samples in a vacuum flask calorimeter was chosen as the most convenient simple laboratory method for the determination of specific heats. In order to ensure a uniform temperature distribution, it is necessary to immerse ice samples in a liquid which is immiscible with water and which does not dissolve the inorganic salts found in sea ice. The liquid must have no components changing phase over a temperature range extending from about −40° C. to +30° C. Normal heptane is a suitable liquid, being a pure hydrocarbon freezing at −90.6° C. and boiling at 98.4° C.

The mixture in the vacuum flask was heated electrically through a central heating coil, the energy being uniformly distributed by a stirring rod surrounding the coil. A source of power at constant voltage was arranged by having a 12 V. accumulator on continual charge from a primary power source. A second heating coil duplicating that in the calorimeter was connected across the battery when the calorimeter’s heating coil was not in operation. As the charging current from the primary source was adjusted to match the discharge through one of the heating coils, there was no perceptible change in the accumulator’s condition during the calorimetry. This greatly simplified the accurate assessment of the energy absorbed by the mixture in the calorimeter.

Initially it was necessary to determine the thermal water equivalent of the calorimeter and the specific heat of normal heptane. This was accomplished using distilled water and pure ice respectively as standards. The specific heat of a sample of sea ice was then determined by using a mixture of approximately 300 g. of small pieces of ice and 300 g. normal heptane. After temperature equilibrium, this mixture was heated at the rate of about 50 W. for times of the order of ten minutes, the resulting change in temperature being observed.

The electrical method of calorimetry necessitates only one temperature difference being measured. An alternative method involving the method of mixtures required two temperature differences to be observed, and because the thermometry is crucial, this latter method proved less satisfactory.

The samples of laboratory-grown sea ice used in the calorimetry were crushed into small pieces which were then thoroughly mixed in a large cold container. Part of the crushed ice was removed and its melt brought to 15° C. for a salinity determination by calibrated hydrometer, the remainder being used in a number of trials in the calorimeter.

Table IV summarizes the results of the experimental determinations. When the ranges calculated for each result are taken into account, there is an overlap between experimental and theoretical values in each case. The error in the experimental determinations is due mainly to lack of accuracy in the measurement of the temperature interval, and to the uncertainties in the specific heat for normal heptane and the quantity of electrical power supplied. The accuracy of the theoretical values depends mainly on the validity of the phase diagram referred to earlier.

Table IV Experimental and Theoretical Values for the Heat Content of Sea Ice

2 The Density and Thermal Conductivity of Sea Ice

2.1 Introduction

The components of sea ice, namely pure ice, brine, air, and, below −8.2° C., solid salt crystals, have widely differing thermal conductivities. The thermal conductivity is thus strongly dependent on composition, which may be specified by the density, salinity and temperature.

In neglecting the presence of air bubbles in sea ice, Anderson (1958) has prevented his theory from demonstrating the two interesting and important asymptotic tendencies of the thermal conductivity. As will be shown, this quantity is mainly determined by the salinity at high temperatures and by the density at low temperatures. This is because the salinity determines the amount of brine, whose relative volume becomes more important near to the melting point. At the lower temperature range when the ice is largely solid, the most important factor in the density is the air bubble content.

As in the discussion of specific heat, it is simplest to consider ice in the temperature range between the freezing point and −8.2° C., below which the precipitation of Na₂SO₄.10H₂O commences and complicates the analysis. As the relative amount of liquid present in the ice becomes large towards the final melting point, the discussion of conductivity becomes meaningless as the increased mobility of the brine permits convective heat transfer.

2.2 The composition and air bubble content of sea ice above −8.2° C.

If the salinity of the ice is σ and the fractional salt content of the enclosed brine is s, then the mass of unfrozen brine in unit mass of sea ice is given by

(2.2.1)

and the mass of pure ice by

(2.2.2)

the mass of air being negligible.

By volume, however, unit mass of sea ice contains a volume (σ+σ/s)/ρ _w(1+s) of brine, and (1−σ−σ/s)/ρ _i of ice; ρ _w and ρ _i being the densities of pure water and ice respectively. Thus unit volume of sea ice contains a volume of brine given by

(2.2.3)

and of pure ice given by

(2.2.4)

where ρ _s is the density of sea ice. The simplifying assumption has been made that solutions’ volumes are independent of their concentration.

It is now seen that the volume of air contained in unit volume of sea ice is

(2.2.5)

In the range being considered, ρ _w = 9·999 g.cm.⁻³, ρ _i = 0·917 g.cm.⁻³, and s = αθ where θ is the temperature and 1/α = −55°C. (which value can be found from Figure 1). Inserting these values,

(2.2.6)

Using this equation it is possible to calculate the fractional volume of air bubbles in sea ice as a function of temperature, salinity and density, as is shown graphically in Figure 3.

Fig. 3. Air bubble content as a function of temperature for sea ice of different salinities and densities

2.3 The density of sea ice

From equation (2.2.5) it is seen that

Neglecting the term containing σs and replacing s by αθ, we have

(2.3.1)

Because the second term in the denominator above is small the following approximation often suffices:

(2.3.2)

The second of the above expressions shows that density increases with salinity provided that the air bubble content remains constant. Whilst the density is significantly temperature dependent near to the freezing point, this dependence diminishes considerably with lower temperatures. The change in density of a sample of normal sea ice between −10° C. and −20° C. is only of the order of 0.1 per cent.

Because faster growing sea ice tends to capture more air bubbles as well as more concentrated brine, it follows that an increase in salinity is accompanied by an increase in air bubble content. Since the effect of these two variables is for the former to increase and the latter to decrease the density, this quantity displays a constancy remarkable for a sea ice property.

Observations made on annual sea ice found in Hudson Bay near Churchill, Manitoba, illustrate this fact. The graphs in Figure 4 show that apart from the upper 10 to 15 cm. of ice, the time variation in density due to brine drainage is almost as large as the differences found throughout the ice at any time.

Fig. 4. Plots of density and of salinity as a function of depth. Curves from left to right are for density on 22 February, density on 3 April, salinity on 3 April, salinity on 22 February. The crystal structure of the core on 22 February is shown on the extreme right to the same scale. The horizontal bars indicate the range of the experimental values

The strip photograph in Figure 4 shows the crystal structure profile of the ice on 22 February. Rapidly grown ice is indicated by small crystal sizes and a relatively large retention of brine resulting in a higher salinity; this is seen from 0–15 cm. and 58–65 cm. on the composite figure. The latter band of small crystalline ice shows a definite effect on the density explicable only in terms of a greater air bubble content. Larger crystals resulting from ice growing more slowly are accompanied by a lower salinity as seen at about 40 cm.

Density was measured by weighing ice samples in both air and normal heptane. The density of the latter at any temperature was established by using an aluminium solid cylinder of known dimensions as a standard object for weighing. The salinities were found by hydrometer. Five samples were used for each ten centimetre section of ice, enabling the density to be established to within ±0.1 per cent and the salinity to ±10 per cent.

From equation (2.3.2), it can be seen that at −10° C., a 0.05 per cent change in the density of sea ice is to be expected when the salinity falls from 5‰ to 4‰ by compressive drainage alone.

2.4 Models for the calculation of the thermal conductivity of sea ice

Established sea ice has been shown by Langleben (1960) amongst others to consist of pure ice enclosing vertical cylinders of approximately elliptical cross-section of brine, whose lengths, especially at higher temperatures are long compared with their average diameters. Anderson has preferred to calculate the thermal conductivity on the basis of assuming spherical brine pockets. This assumption may have greater validity at lower temperatures. At these temperatures however, the small amount of brine plays a less significant role in determining the conductivity of the ice than at higher temperatures. It thus seems more reasonable to choose the shape of brine inclusions predominating at those higher temperatures where the brine is more important.

Since the flow of heat occurs along the direction of the cylindrical axes, a short vertical length of sea ice may be considered as a system of parallel connected conductors. It is immaterial for the purpose of calculation whether the conductors are specially grouped or not; the determining factor for the total conduction being the relative cross-sectional areas of pure ice and brine presented to the heat flux. It is, of course, assumed that no convective movement of brine takes place in the narrow cylinders. It is interesting to note that the thermal conductivity for horizontal heat flow, for which the brine and pure ice appear series connected, is much less than for vertical heat flow. It might thus be expected that non uniform heating or cooling of a sea ice surface, due to an irregular snow cover, tends to remain a local phenomenon.

Two methods of procedure are now available. One is to consider sea ice as consisting of uniformly bubbly pure ice enclosing vertical cylinders of brine. The other is to suppose that the brine pockets are more uniformly distributed within the ice than are the air bubbles. The majority of the air bubbles form during the initial freezing, and are found throughout the ice. Being more or less spherical in shape, the air bubbles are certainly more uniformly distributed within the bulk of the ice than the brine pockets. The method of calculation of the thermal conductivity will thus be to obtain an expression for the thermal conductivity of bubbly pure ice, and then to consider sea ice as a parallel connection of this material and brine.

2.5 The effect of air bubbles on the conductivity of ice

Maxwell (1892) obtained an expression for the resistivity r of a compound medium, consisting of a medium of resistivity r ₁, containing uniformly distributed small spheres of resistivity r _2. If there are n small spheres of radius a ₂ contained in a sphere of surrounding material of radius a ₁ and v = na ₂³/a ₁³, then

(2.5.1)

Since the air bubbles within a body of ice are approximately spherical, (2.5.1) may be used to obtain an expression for the thermal conductivity of bubbly ice. If k _a,k _i are the conductivities of air and ice respectively, and v:1 is the ratio of their volumes, then the conductivity of the compound medium is given by

(2.5.2)

The value of v under given conditions has been determined in section 2.2. Using the value 5×10⁻³ cal.cm.⁻¹sec.⁻¹ °C.⁻¹ for k _i it remains for us to assign a value for the conductivity of air.

In the range of interest, i.e. 0 to −20° C., the conductivity of air can be taken as 6×10⁻⁵ cal.cm.⁻¹ sec.⁻¹ °C.⁻¹, at atmospheric pressure. Increases in this value due to hydrostatic and contractive pressures are usually not sufficient to affect the conductivity of the compound medium by even 0.5 per cent.

Figure 5 shows the thermal conductivity and density of freshwater ice as functions of bubble content.

Fig. 5. Density (solid line) and thermal conductivity of bubbly freshwater ice

Table V The Thermal Conductivity of Bubbly Ice

2.6 A model for sea ice including air bubbles

The nature of brine cells in sea ice has already been discussed in section 2.4, so that we shall now proceed to consider sea ice as a compound bubbly pure ice medium enclosing a number of vertical brine cylinders, whose total cross-sectional area per unit area of sea ice can be specified.

From Figure 6, it may be seen that if A _bi and A _b are the cross-sectional areas of bubbly pure ice and brine whose normals are parallel to the heat flow respectively, and J _bi,J _b,J _s, represent the heat fluxes through the bubbly pure ice, brine and compound sea ice, then the following relations hold for a section of sea ice whose ends, at a vertical distance x apart, have temperatures θ ₁ and θ ₀:

where k _b is the conductivity of brine,

but

where k _s is the conductivity of sea ice, so

(2.6.1)

Fig. 6. A model for sea ice

The relative cross-sectional area of brine and bubbly pure ice are proportional to their relative volumes, which can be inferred from equation (2.2.3), so

and since A _w+A _bi = 1, we have for the conductivity of sea ice,

(2.6.2)

where k _bi is given by equation (2.5.2).

Replacing s by αθ as in section 2.2, we have

(2.6.3)

Although there are no systematic experimental data available on the conductivity of brine, a number of isolated determinations for solutions of several inorganic salts show that the thermal conductivity is strongly dependent on the concentration, and to a lesser extent on the temperature. Assuming that the relation between salt content and conductivity is linear for a fractional salt content less than 150‰ at constant temperature, then on the basis of a limited number of isolated conductivity determinations for NaCl and Na₂SO₄ solutions given by Lange and Forker (1952), the conductivity of brine at 0° C. may be approximated by

(2.6.4)

Assuming a temperature dependence similar to that for pure water suggested by the data of Lange and Forker, an additional factor generalizes equation (2.6.4) to

(2.6.5)

It is now possible to calculate the thermal conductivity of sea ice as a function of temperature, salinity and density, using equations (2.6.2) and (2.6.5) in conjunction with (2.6.3).

Fig. 7. Thermal conductivity of sea ice as a function of temperature. Curves drawn for various salinities and densities; salinity indicated by line thickness; density indicated by line pattern

The results of calculations based on a value of k _i at 0° C. of 5×10⁻³ cal. cm.⁻¹sec.⁻¹ ° C.⁻¹ given by Dorsey (1940) for pure ice, are shown graphically in Figure 7.

Fortunately, it can be noted that at lower temperatures, where equation (2.6.5) becomes less accurate, the actual value of k _b is of less importance since the relative volume of water present becomes negligible.

2.7 The thermal conductivity of sea ice below −8.2° C.

As has been hinted in section 2.1, the commencement of the precipitation of solid hydrates below −8.2° C. results in a rigorous theory becoming extremely involved. The lack of knowledge of the thermal conductivities of the inorganic hydrates found in sea ice and those of concentrated brines makes it unjustifiable to proceed theoretically from fundamental principles.

Inspection of the curves for the conductivities in Figure 7 suggests an alternative procedure. Since the salinity of sea ice is rarely greater than 10‰, it is unlikely that serious discontinuities will occur in the conductivity-temperature function at temperatures where salts begin to precipitate. Already at −8° C. all the curves shown in Figure 7 exhibit asymptotic behaviour. At lower temperatures, the conductivity of low salinity ice will tend to the value for freshwater ice. Using equation (2.5.2) for a uniform distribution of a large number of small centres of solid salt in a main body of pure ice, and assuming a low value, 10⁻³ cal.cm.⁻¹sec.^−1° C.⁻¹, for the conductivity of the solid salts, it is seen that a salinity of 8‰ lowers the conductivity by less than 1 per cent relative to non-saline ice. Almost all salts in the ice are precipitated by −40° C., it would thus be reasonable to suppose that at this point, the thermal conductivity of a sample of sea ice could be given by the corresponding value for freshwater ice of the same density.

2.8 Measurement of the thermal conductivity of sea ice

The thermal conductivity of Hudson Bay annual sea ice was measured in two ways. The first involved comparison of the temperature gradients in a layer of the sea ice cover and in a reference block of non-saline ice embedded in it. The reference ice was formed by freezing fresh water in a 1.5×1.5×0.3 m.³ pit prepared in the sea-ice surface. After freezing, a small core was extracted to check for the absence of salt and to measure its density. The thermal conductivity of the standard medium was then found by using equations (2.2.6) and (2.5.2). Over two months, the ice between the 10 and 30 cm. levels from the surface was observed to have a thermal conductivity of (4.7±0.7)×10⁻³ cal.cm.⁻¹ sec.^−1° C.⁻¹. The theoretical value for this type of ice whose mean temperature, salinity and density are −7° C., 6‰ and 0.91 g. cm.⁻³ respectively is 4.7×10⁻³ cal.cm.⁻¹ sec.^−1° C.⁻¹.

The second determination gave the mean thermal conductivity for the entire thickness of the ice cover over three months by observing the growth at the ice-water interface over an appropriate time interval. These values were used in a modified form of Stefan’s (1891) simple ice-growth equation which allowed for the change in heat content of the ice as well as for the time delay in the transfer of thermal energy from the ice-water interface to the surface. For the cover as a whole, whose mean temperature was −5.5° C., density 0.915 g.cm.⁻³ and salinity 5‰, the thermal conductivity of (4.9±0.5)×10⁻³ cal. cm.⁻¹ sec.^−1° C.⁻¹. calculated from the observations covered the value of 4.7×10⁻³ cal. cm.⁻¹ sec.⁻¹ ° C.⁻¹. predicted theoretically.

It is important to note that both the theoretical and experimental determinations of the thermal conductivity of sea ice are significantly greater than those given in many other works, e.g. Pounder and Little (1959). This is because these have used the simple ice growth formula of Stefan (1891) without corrections. For example, for a cover 1.5 m. thick, the time difference between surface cooling and consequent ice growth is of the order of 2 weeks. Thus when the surface temperature is integrated over three months commencing with the initial formation of the cover, an error of approximately 15 per cent is introduced if the integration is not terminated at a calculable time before the final ice thickness observation.

3.1 Conclusion on thermal diffusivity of sea ice

The thermal diffusivity is often the most directly observed thermal property as it is directly associated with the rate of temperature changes in a medium. Consequently it is interesting to examine the temperature dependence of this quantity. It has been seen that the specific heat c _s, density ρ _s and thermal conductivity k _s, of sea ice are all monotonic functions of the temperature. For increasing temperature, c _s increases, this will be denoted by c _s↑ ; ρ _s increases, i.e. ρ _s↑ and k _s decreases, k _s ↓. Hence the diffusivity, k _s, which is given by

is more temperature dependent than any of its constituent parameters. As a consequence, the precise analysis of temperature data is a complex undertaking for sea ice.

Table VI Specific Heat c _s Thermal Conductivity k _s and Thermal Diffusivity k _s of Sea Ice for Various Salinities, Temperatures and Densities

The thermal properties are summarized by Table VI. It is interesting to observe that in contrast to its dependence on salinity and temperature, the thermal diffusivity of ice is not greatly affected by density changes. In fact for fresh-water ice with the range of densities encountered in nature the thermal diffusivity can be regarded as independent of density.

Acknowledgements

The author completed much of this work whilst a member of the Ice Research Project in the Physics Department at McGill University, being supported in part by a National Research Council of Canada grant, A-820, and by the Canadian Defence Research Board through D.D.P. contracts GC-69–900109 and GC-69–000105.