Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-27T12:08:16.695Z Has data issue: false hasContentIssue false
  • English
  • Français

Metacyclic Invariants of Knots and Links

Published online by Cambridge University Press:  20 November 2018

R. H. Fox
R. H. Fox*
Affiliation:
Princeton University, Princeton, New Jersey
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

To each representation ρ on a transitive permutation group P of the group G = π(S – k) of an (ordered and oriented) link k = k1 ∪ k2 ∪ … ∪ kμ in the oriented 3-sphere S there is associated an oriented open 3-manifold M = Mρ(k), the covering space of S – k that belongs to ρ. 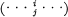The points 01, 02, … that lie over the base point o may be indexed in such a way that the elements g of G into which the paths from oi to oj project are represented by the permutations gρ of the form , and this property characterizes M. Of course M does not depend on the actual indices assigned to the points o1, o2, … but only on the equivalence class of ρ, where two representations ρ of G onto P and ρ′ of G onto P′ are equivalent when there is an inner automorphism θ of some symmetric group in which both P and P′ are contained which is such that ρ′ = θρ.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 22 , Issue 2 , 01 April 1970 , pp. 193 - 201
Copyright
Copyright © Canadian Mathematical Society 1970

References

1. Anger, A. L., Machine calculation of knot polynomials, Princeton senior thesis, Princeton University, Princeton, N. J., 1959.Google Scholar
2. Artin, M., On some invariants of some doubled knots, Princeton senior thesis, Princeton University, Princeton, N. J., 1955.Google Scholar
3. Bankwitz, C. and Schumann, H. G., Uber Viergeflechte, Abh. Math. Sem. Univ. Hamburg 10 (1934), 263–284.Google Scholar
4. Coxeter, H. S. M. and Moser, W. O. J., Generators and relations for discrete groups, 2nd éd., Ergebnisse der Math., Vol. 14 (Springer-Verlag, Berlin, 1965).Google Scholar
5. Crowell, R. H., On the van Kampen theorem, Pacific J. Math. 9 (1959), 43–50.Google Scholar
6. Fox, R. H., Free differential calculus. III : Subgroups, Ann. of Math. (2) 64 (1956), 407–419.Google Scholar
7. Fox, R. H., Covering spaces with singularities; Algebraic geometry and topology, A symposium in honor of S. Lefschetz, pp. 243–257 (Princeton Univ. Press, Princeton, N. J., 1957).Google Scholar
8. Fox, R. H., A quick trip through knot theory, Topology of 3-manifolds and related topics, Proc. The Univ. of Georgia Institute, 1961, pp. 120–167 (Prentice-Hall, Englewood Cliffs, N. J., 1962).Google Scholar
9. Fox, R. H., Construction of simply connected 3-manifolds, Topology of 3-manifolds and related topics, Proc. The Univ. of Georgia Institute, 1961, pp. 213–216 (Prentice-Hall, Englewood Cliffs, N. J., 1962).Google Scholar
10. Little, C. N., On knots with a census for order 10, Trans. Connecticut Acad. Sci. 7 (1885), 27–43.Google Scholar
11. Little, C. N., Alternate ± knots of order 11, Trans. Roy. Soc. Edinburgh 86 (1890), 253–255.Google Scholar
12. Little, C. N., Non alternate ± knots, Trans. Roy. Soc. Edinburgh 89 (1900), 771–778.Google Scholar
13. Perko, K. A. Jr., An invariant of certain knots, Princeton senior thesis, Princeton University, Princeton, N. J., 1964.Google Scholar
14. Reidemeister, K., Knotentheorie, Ergebnisse der Math, und ihrer Grenzgebiete, Vol. 1 (Julius Springer, Berlin, 1932).Google Scholar
15. Schubert, H., Knoten und Vollringe, Acta Math. 90 (1953), 131–286.Google Scholar
16. Seifert, H., Schlingknoten, Math. Z. 52 (1949), 62–80.Google Scholar
17. Tait, P. G., On knots. III; III; (Scientific Papers. I); (1877), 273-317; (1885), 318-334; (1885), 335–347.Google Scholar
18. Whitehead, J. H. C., On doubled knots, J. London Math. Soc. 12 (1937), 63–71.Google Scholar