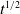1. Introduction
The drying of thin films that consist of a volatile solvent and a particulate phase is relevant to a wide range of industrial applications [Reference Kolegov and Barash24], such as the fabrication of electrodes for lithium-ion batteries [Reference Zhang, Courtier and Zhang41] and flexible conductive coatings [Reference Shimoni, Azoubel and Magdassi35]. As solvent is removed from the mixture by evaporation, the particulate phase aggregates to form a porous solid. The evaporation-driven flow of solvent through the pores will generate a pressure gradient that, in turn, can deform the solid. The removal of solvent from the pore space will also cause the solid to contract. If the film has been placed on a rigid substrate, then the adhesion of the solid to the substrate will restrict contractions in the horizontal plane. As a result, mechanical stresses will develop within the film [Reference Croll9]. The film stress can be relieved through a myriad of mechanical instabilities [Reference Giorgiutti-Dauphiné and Pauchard16], including fracture [Reference Bourrianne, Lilin, Sintès, Nîrca, McKinley and Bischofberger5, Reference Dufresne, Corwin and Greenblatt10], buckling [Reference Pauchard and Allain31] and delamination [Reference Giorgiutti-Dauphiné and Pauchard15, Reference Osman, Goehring, Stitt and Shokri30]. Although drying-induced instabilities have traditionally been viewed as detrimental, there is increasing interest in understanding how these can be harnessed in applications such as medical diagnostics [Reference Sefiane, Duursma and Arif34] and lithography [Reference Kim, Kim, Ha and Kim23].
Avoiding or triggering instabilities during film drying requires quantitative knowledge about the evolution of the film stress. However, directly measuring the mechanical stress during drying is difficult. A number of innovative experiments have therefore been designed around the aim of indirectly measuring the film stress [Reference Bouchaudy and Salmon4, Reference Xu, Engl and Jerison40]. The cantilever technique is one such experiment, whereby a thin film (or drop) is deposited onto the upper surface of a thin plate that is supported at one end by a wall [Reference Evans and Craig12]. Due to the adhesion between the film and the plate, the mechanical stresses that are generated in the film during drying are transmitted to the plate. In response, the plate will bend, causing a deflection that can be measured. The film stress can then be inferred from the deflection using mathematical modelling.
In the seminal work of Stoney [Reference Stoney36], a simple model is presented for the cantilever experiment. Using classical beam theory, Stoney was able to determine a relationship between the film stress and the beam deflection. Stoney’s derivation relies on a number of key assumptions, namely the film is thin compared to the beam, the film has a uniform and constant thickness, and bending is driven by a uniform longitudinal film stress. In the context of drying, the latter point implies that the film has a homogeneous composition. Moreover, Stoney’s derivation requires the explicit definition of a neutral axis, which is a longitudinal axis in the beam where no strain occurs. A number of authors have extended Stoney’s model by utilising more sophisticated beam theories [Reference Francis, McCormick, Vaessen and Payne14]. For example, Petersen et al. [Reference Petersen, Heldmann and Johannsmann32] accounted the finite thickness of the film. However, Chiu [Reference Chiu6] has criticised several of these models and argues that Stoney’s choice of neutral axis is only correct when the film and beam have the same Young’s modulus. As discussed by Francis et al. [Reference Francis, McCormick, Vaessen and Payne14], the Young’s modulus of the film is typically one or two orders of magnitude smaller than that of the plate. At the other end of the modelling spectrum, Lei et al. [Reference Lei, Francis, Gerberich and Scriven26] used the finite element method to simulate the drying of an elasto-viscoplastic film on a cantilever beam. To the best of our knowledge, no comparison has been made between simple models based on beam theory and finite element solutions of the full equations of continuum mechanics.
By analysing a cantilever experiment with a Stoney-like model, Croll [Reference Croll8] observed that the stress in the film is independent of the film height. Similar observations were recently made for drying polymer films by Tomar et al. [Reference Tomar, Shahin and Tirumkudulu39], who also noted that the kinetics of stress generation are sensitive to the Péclet number. The film stress was found to increase linearly with time for small Péclet numbers and nonlinearly for larger Péclet numbers. The nonlinear evolution of the stress was attributed to the formation of a polymer-rich skin at the film surface caused by a large rate of evaporation. When a skin forms, the longitudinal stress across the film will be highly non-uniform and the applicability of Stoney’s model to this scenario comes into question. Skin formation is particularly problematic when manufacturing electrodes for lithium-ion batteries, as stress and composition gradients can lead to mechanical failure and poor electrical conductivity [Reference Font, Protas, Richardson and Foster13, Reference Jaiser, Kumberg and Klaver20, Reference Jaiser, Müller, Baunach, Bauer, Scharfer and Schabel21]. Understanding the mechanics of skin formation is therefore crucial to improving battery performance.
The aim of this paper is to revisit the derivation of Stoney-like formulae using asymptotic methods. Starting from the time-dependent equations of three-dimensional continuum mechanics, a hierarchy of simplified models for the cantilever experiment will be derived. More specifically, the film will be modelled using nonlinear poroelasticity [Reference Biot3, Reference MacMinn, Dufresne and Wettlaufer29] and the plate using nonlinear elasticity [Reference Howell, Kozyreff and Ockendon19]. The asymptotic analysis is based on the small aspect ratios of the film and the plate. By using asymptotic methods to simplify the equations of elasticity rather than directly appealing to beam theory, the explicit definition of a neutral axis can be avoided. The reduced models that are presented here extend Stoney-like models by capturing the evolution of the film thickness, composition and stress, all of which can be highly non-uniform. Moreover, the analysis reveals parameter regimes where the plate deflection is driven by both the longitudinal and transverse stress in the film. The reduced models are validated by comparing them against finite element solutions of the full system of equations and found to be very accurate.
A key feature of the asymptotic reduction is that it leads to a one-way decoupling of the models, thus allowing the film and plate equations to be solved sequentially. Moreover, the dimensionality of the film and plate models are reduced. The combined result is a computationally efficient model that is able to resolve the spatio-temporal dynamics of drying and bending. In asymptotically reducing the equations for the film, we invoke a poroelastic version of lubrication theory [Reference Etzold, Fortune, Landel and Dalziel11, Reference Hewitt, Neufeld and Balmforth18, Reference Jensen, Glucksberg, Sachs and Grotberg22]. Furthermore, we extend our previous work on drying-induced stresses in poroelastic drops [Reference Hennessy, Craster and Matar17] by accounting for a wide range of drying regimes that are determined by the magnitude of the Péclet number. In all cases, the film model reduces to either a nonlinear ordinary differential equation or a nonlinear diffusion equation for the solvent concentration. The deformation of the plate can be described by an extended form of the Föppl-von Kármán (FvK) equations [Reference Landau and Lifshitz25] that accounts for gradients in the longitudinal traction exerted on the upper plate surface by the film. In order to derive a consistent set of boundary conditions at the free edges of the plate, a careful analysis of the Saint-Venant boundary layers is required [Reference Howell, Kozyreff and Ockendon19]. If considering a beam rather than a plate, we show that the FvK equations reduce to a linear second-order differential equation.
The governing equations for the film and the plate are presented in Section 2. A scaling analysis and preliminary reduction of the plate equations are carried out in Section 3. The equations are non-dimensionalised in Section 4. A detailed asymptotic reduction is then carried out in Section 5. In Section 6, the solutions of the asymptotically reduced models are compared against finite element solutions of the full model. A parametric study is also conducted. The paper concludes in Section 7.
2. Modelling
The formation of a coating is a complex process that involves the transformation of a liquid-like mixture into a solid. The generation of mechanical stress occurs after the gel point of the mixture has been crossed, and the mechanical response of the film becomes more solid-like than liquid-like. In cantilever experiments, the crossing of the gel point can be identified as the time at which the plate begins to bend. Before this time, film drying takes place but the deflection of the plate is negligible.
Given that we are interested in modelling the deflection of the plate, we will assume that the gel point has just been crossed so that a poroelastic matrix has formed throughout the film. One-dimensional models that couple solidification and poromechanics have been considered by Style and Peppin [Reference Style and Peppin37] and Punati and Tirumkudulu [Reference Punati and Tirumkudulu33]. We therefore consider a poroelastic film that is drying on a thin, flexible plate, as illustrated in Figure 1. The plate is assumed to be rectangular with length
![]() $L$
, width
$L$
, width
![]() $W$
and thickness
$W$
and thickness
![]() $H_p$
. The length and width are assumed to be comparable in size. However, the thickness of the plate is assumed to be much smaller than the length and width. The small aspect ratio of the plate is denoted by
$H_p$
. The length and width are assumed to be comparable in size. However, the thickness of the plate is assumed to be much smaller than the length and width. The small aspect ratio of the plate is denoted by
![]() $\delta = H_p/ L \ll 1$
.
$\delta = H_p/ L \ll 1$
.

Figure 1. Bending of a plate during film drying. The plate has length
![]() $L$
, width
$L$
, width
![]() $W$
and height
$W$
and height
![]() $H_p$
. The initial film thickness is given by
$H_p$
. The initial film thickness is given by
![]() $H_f(X_1, X_2)$
, where
$H_f(X_1, X_2)$
, where
![]() $X_1$
and
$X_1$
and
![]() $X_2$
are Lagrangian coordinates that lie in the plane spanned by the plate centreline (dashed line). The plate is clamped to a wall at
$X_2$
are Lagrangian coordinates that lie in the plane spanned by the plate centreline (dashed line). The plate is clamped to a wall at
![]() $X_1 = 0$
. The origin of the vertical Lagrangian coordinate
$X_1 = 0$
. The origin of the vertical Lagrangian coordinate
![]() $Z$
coincides with the plate centreline. Panels (a) and (b): Cross-sections of the Lagrangian (undeformed) configuration. Panel (c): Cross-section of the Eulerian (deformed) configuration.
$Z$
coincides with the plate centreline. Panels (a) and (b): Cross-sections of the Lagrangian (undeformed) configuration. Panel (c): Cross-section of the Eulerian (deformed) configuration.
We let
![]() $X_1$
,
$X_1$
,
![]() $X_2$
, and
$X_2$
, and
![]() $X_3 = Z$
denote Cartesian coordinates associated with the initial (Lagrangian) configuration of the system. The coordinates
$X_3 = Z$
denote Cartesian coordinates associated with the initial (Lagrangian) configuration of the system. The coordinates
![]() $X_1$
and
$X_1$
and
![]() $X_2$
are chosen to lie in the plane that is parallel to the upper and lower surfaces of the plate. The vertical (or transverse) Lagrangian coordinate,
$X_2$
are chosen to lie in the plane that is parallel to the upper and lower surfaces of the plate. The vertical (or transverse) Lagrangian coordinate,
![]() $Z$
, is chosen such that
$Z$
, is chosen such that
![]() $Z = 0$
corresponds to the centre surface of the plate. Consequently,
$Z = 0$
corresponds to the centre surface of the plate. Consequently,
![]() $Z = \pm H_p/2$
denotes the upper and lower surfaces. The plate is envisioned as being clamped to a wall at
$Z = \pm H_p/2$
denotes the upper and lower surfaces. The plate is envisioned as being clamped to a wall at
![]() $X_1 = 0$
and having free edges at
$X_1 = 0$
and having free edges at
![]() $X_1 = L$
and
$X_1 = L$
and
![]() $X_2 = \pm W/ 2$
.
$X_2 = \pm W/ 2$
.
The film has a non-uniform thickness that evolves in time. The initial film thickness is denoted by
![]() $H_f(X_1, X_2)$
and has a maximum value given by
$H_f(X_1, X_2)$
and has a maximum value given by
![]() $H_f^0 = \max (H_f)$
. The film is also assumed to be thin relative to the length of the plate so that
$H_f^0 = \max (H_f)$
. The film is also assumed to be thin relative to the length of the plate so that
![]() $\epsilon = H_f^0/ L \ll 1$
. We assume that the film thickness tends to zero as the edges of the plate are approached. That is, the contact line of the film is assumed to be static, in agreement with experiments [Reference Bourrianne, Lilin, Sintès, Nîrca, McKinley and Bischofberger5, Reference Osman, Goehring, Stitt and Shokri30], and pinned to the edges of the plate. Recession of the contact line during drying is typically prohibited by the strong adhesion of the solid constituents to the substrate [Reference Giorgiutti-Dauphiné and Pauchard16, Reference Tirumkudulu and Punati38]. Our modelling setup is similar to the experiments of Tomar et al. [Reference Tomar, Shahin and Tirumkudulu39], where a drop of polymer solution was deposited into the middle of a cantilever plate and allowed to dry.
$\epsilon = H_f^0/ L \ll 1$
. We assume that the film thickness tends to zero as the edges of the plate are approached. That is, the contact line of the film is assumed to be static, in agreement with experiments [Reference Bourrianne, Lilin, Sintès, Nîrca, McKinley and Bischofberger5, Reference Osman, Goehring, Stitt and Shokri30], and pinned to the edges of the plate. Recession of the contact line during drying is typically prohibited by the strong adhesion of the solid constituents to the substrate [Reference Giorgiutti-Dauphiné and Pauchard16, Reference Tirumkudulu and Punati38]. Our modelling setup is similar to the experiments of Tomar et al. [Reference Tomar, Shahin and Tirumkudulu39], where a drop of polymer solution was deposited into the middle of a cantilever plate and allowed to dry.
The film is assumed to remain bonded to the plate during drying. The upper surface of the plate, originally located at
![]() $Z = H_p/2$
, becomes vertically displaced to the Eulerian position
$Z = H_p/2$
, becomes vertically displaced to the Eulerian position
![]() $z = H_p/2 + w(x_1, x_2, t)$
, where
$z = H_p/2 + w(x_1, x_2, t)$
, where
![]() $x_1$
and
$x_1$
and
![]() $x_2$
are in-plane coordinates associated with the deformed (Eulerian) configuration and
$x_2$
are in-plane coordinates associated with the deformed (Eulerian) configuration and
![]() $t$
is time. The Eulerian thickness of the film is denoted by
$t$
is time. The Eulerian thickness of the film is denoted by
![]() $h_f(x_1, x_2,t)$
. Hence, the Eulerian position of the free surface of the film is given by
$h_f(x_1, x_2,t)$
. Hence, the Eulerian position of the free surface of the film is given by
![]() $z = H_p/ 2 + w(x_1, x_2,t) + h_f(x_1, x_2,t)$
.
$z = H_p/ 2 + w(x_1, x_2,t) + h_f(x_1, x_2,t)$
.
2.1. Notation
Occasionally, vector and tensor quantities will be decomposed into in-plane and vertical components that are parallel and perpendicular to the undeformed plate, respectively. We let
![]() $\boldsymbol{{e}}_1$
,
$\boldsymbol{{e}}_1$
,
![]() $\boldsymbol{{e}}_2$
, and
$\boldsymbol{{e}}_2$
, and
![]() $\boldsymbol{{e}}_3 = \boldsymbol{{e}}_z$
denote Cartesian basis vectors for the
$\boldsymbol{{e}}_3 = \boldsymbol{{e}}_z$
denote Cartesian basis vectors for the
![]() $X_1$
,
$X_1$
,
![]() $X_2$
, and
$X_2$
, and
![]() $X_3 = Z$
directions, as well as the
$X_3 = Z$
directions, as well as the
![]() $x_1$
,
$x_1$
,
![]() $x_2$
, and
$x_2$
, and
![]() $z = x_3$
directions. If
$z = x_3$
directions. If
![]() $\boldsymbol{{a}} = a_i \boldsymbol{{e}}_i$
denotes an arbitrary vector, then we can write
$\boldsymbol{{a}} = a_i \boldsymbol{{e}}_i$
denotes an arbitrary vector, then we can write
![]() $\boldsymbol{{a}} = \boldsymbol{{a}}_{\parallel } + a_z \boldsymbol{{e}}_z$
, where
$\boldsymbol{{a}} = \boldsymbol{{a}}_{\parallel } + a_z \boldsymbol{{e}}_z$
, where
![]() $\boldsymbol{{a}}_{\parallel } = a_\alpha \boldsymbol{{e}}_\alpha$
is defined as the vector of in-plane components and
$\boldsymbol{{a}}_{\parallel } = a_\alpha \boldsymbol{{e}}_\alpha$
is defined as the vector of in-plane components and
![]() $a_z = a_3$
is the vertical component. Einstein summation notation is used, and we adopt the convention that Greek indices are equal to 1 or 2. We let
$a_z = a_3$
is the vertical component. Einstein summation notation is used, and we adopt the convention that Greek indices are equal to 1 or 2. We let
![]() $\nabla$
denote the material gradient taken with respect to the Lagrangian coordinates
$\nabla$
denote the material gradient taken with respect to the Lagrangian coordinates
![]() $\boldsymbol{{X}} = X_i \boldsymbol{{e}}_i$
. The in-plane gradient operator is defined as
$\boldsymbol{{X}} = X_i \boldsymbol{{e}}_i$
. The in-plane gradient operator is defined as
![]() $\nabla _{\parallel } = \nabla - \boldsymbol{{e}}_z\,\partial/\partial Z$
. Tensors as written as
$\nabla _{\parallel } = \nabla - \boldsymbol{{e}}_z\,\partial/\partial Z$
. Tensors as written as
![]() ${\sf\boldsymbol T} = {\sf\boldsymbol T}_{\parallel } + {\sf\boldsymbol T}_{\perp } \otimes \boldsymbol{{e}}_z +{\textsf{T}}_{z\alpha } \boldsymbol{{e}}_z \otimes \boldsymbol{{e}}_\alpha +{\textsf{T}}_{zz} \boldsymbol{{e}}_z \otimes \boldsymbol{{e}}_z$
where
${\sf\boldsymbol T} = {\sf\boldsymbol T}_{\parallel } + {\sf\boldsymbol T}_{\perp } \otimes \boldsymbol{{e}}_z +{\textsf{T}}_{z\alpha } \boldsymbol{{e}}_z \otimes \boldsymbol{{e}}_\alpha +{\textsf{T}}_{zz} \boldsymbol{{e}}_z \otimes \boldsymbol{{e}}_z$
where
![]() ${\sf\boldsymbol T}_{\parallel } ={\textsf{T}}_{\alpha \beta } \boldsymbol{{e}}_\alpha \otimes \boldsymbol{{e}}_\beta$
and
${\sf\boldsymbol T}_{\parallel } ={\textsf{T}}_{\alpha \beta } \boldsymbol{{e}}_\alpha \otimes \boldsymbol{{e}}_\beta$
and
![]() ${\sf\boldsymbol T}_\perp ={\textsf{T}}_{\alpha z} \boldsymbol{{e}}_\alpha$
.
${\sf\boldsymbol T}_\perp ={\textsf{T}}_{\alpha z} \boldsymbol{{e}}_\alpha$
.
2.2. Kinematics
The governing equations are formulated in terms of Lagrangian coordinates
![]() $\boldsymbol{{X}} = X_i \boldsymbol{{e}}_i$
associated with the initial (undeformed) configuration of the film and plate. We let
$\boldsymbol{{X}} = X_i \boldsymbol{{e}}_i$
associated with the initial (undeformed) configuration of the film and plate. We let
![]() $\boldsymbol{{x}} = x_i(\boldsymbol{{X}},t) \boldsymbol{{e}}_i$
denote Eulerian coordinates associated with the current (deformed) configuration. During drying, the solid element originally located at
$\boldsymbol{{x}} = x_i(\boldsymbol{{X}},t) \boldsymbol{{e}}_i$
denote Eulerian coordinates associated with the current (deformed) configuration. During drying, the solid element originally located at
![]() $\boldsymbol{{X}}$
is displaced to
$\boldsymbol{{X}}$
is displaced to
![]() $\boldsymbol{{x}}$
, thereby generating a displacement
$\boldsymbol{{x}}$
, thereby generating a displacement
![]() $\boldsymbol{{u}} = \boldsymbol{{x}}(\boldsymbol{{X}},t) - \boldsymbol{{X}}$
. The deformation gradient tensor
$\boldsymbol{{u}} = \boldsymbol{{x}}(\boldsymbol{{X}},t) - \boldsymbol{{X}}$
. The deformation gradient tensor
![]() ${\sf\boldsymbol F}$
describes the distortion of material elements and is given by
${\sf\boldsymbol F}$
describes the distortion of material elements and is given by
where
![]() ${\sf\boldsymbol I}$
is the identity tensor. We adopt the convention that the gradient of a vector
${\sf\boldsymbol I}$
is the identity tensor. We adopt the convention that the gradient of a vector
![]() $\boldsymbol{{a}} = a_i \boldsymbol{{e}}_i$
is given by
$\boldsymbol{{a}} = a_i \boldsymbol{{e}}_i$
is given by
![]() $\nabla \boldsymbol{{a}} = (\partial a_{i}/\partial X_j)\,\boldsymbol{{e}}_i\otimes \boldsymbol{{e}}_j$
. The determinant of
$\nabla \boldsymbol{{a}} = (\partial a_{i}/\partial X_j)\,\boldsymbol{{e}}_i\otimes \boldsymbol{{e}}_j$
. The determinant of
![]() ${\sf\boldsymbol F}$
, denoted by
${\sf\boldsymbol F}$
, denoted by
![]() $J = \det {\sf\boldsymbol F}$
, accounts for volumetric changes of material elements.
$J = \det {\sf\boldsymbol F}$
, accounts for volumetric changes of material elements.
2.3. A model for a poroelastic film
Poroelastic materials consist of a porous and deformable solid matrix that is filled with fluid. The theory of poroelasticity was first developed by Biot [Reference Biot3] in the context of soil mechanics. Coussy [Reference Coussy7] provides a comprehensive overview of the theory. We treat the drying film as a poroelastic material and describe it using a Lagrangian version of the model proposed by MacMinn et al. [Reference MacMinn, Dufresne and Wettlaufer29]. In essence, the model couples the equations of nonlinear elasticity to those for flow in a porous medium.
Conservation of liquid in the porous film leads to
where
![]() $\Phi$
is the nominal volume fraction of fluid and
$\Phi$
is the nominal volume fraction of fluid and
![]() $\boldsymbol{{Q}}$
is the nominal fluid flux. The Eulerian volume fraction of fluid, which is equivalent to the film porosity, is given by
$\boldsymbol{{Q}}$
is the nominal fluid flux. The Eulerian volume fraction of fluid, which is equivalent to the film porosity, is given by
![]() $\phi = \Phi/ J$
. The transport of fluid within the pore space is governed by Darcy’s law, which can be written in terms of the reference configuration as
$\phi = \Phi/ J$
. The transport of fluid within the pore space is governed by Darcy’s law, which can be written in terms of the reference configuration as
where
![]() ${\sf\boldsymbol {K}}$
is a permeability tensor and
${\sf\boldsymbol {K}}$
is a permeability tensor and
![]() $p$
is the fluid pressure. The permeability tensor can be written in terms of the scalar permeability
$p$
is the fluid pressure. The permeability tensor can be written in terms of the scalar permeability
![]() $k(\phi )$
as
$k(\phi )$
as
![]() ${\sf\boldsymbol {K}} = (k(\phi )/ \mu _f) J {\sf\boldsymbol {C}}^{-1}$
, where
${\sf\boldsymbol {K}} = (k(\phi )/ \mu _f) J {\sf\boldsymbol {C}}^{-1}$
, where
![]() $\mu _f$
is the fluid viscosity and
$\mu _f$
is the fluid viscosity and
![]() ${\sf\boldsymbol {C}} = {\sf\boldsymbol F}^T {\sf\boldsymbol F}$
is the right Cauchy–Green tensor. The factor of
${\sf\boldsymbol {C}} = {\sf\boldsymbol F}^T {\sf\boldsymbol F}$
is the right Cauchy–Green tensor. The factor of
![]() $J {\sf\boldsymbol {C}}^{-1}$
in
$J {\sf\boldsymbol {C}}^{-1}$
in
![]() ${\sf\boldsymbol {K}}$
is the result of mapping Darcy’s law in the current configuration to the reference configuration. We let
${\sf\boldsymbol {K}}$
is the result of mapping Darcy’s law in the current configuration to the reference configuration. We let
![]() $k_0 = k(\phi _0)$
denote the initial permeability, where
$k_0 = k(\phi _0)$
denote the initial permeability, where
![]() $\phi _0$
is the initial volume fraction (or porosity) of the film. For simplicity, we assume that the initial fluid fraction is spatially uniform.
$\phi _0$
is the initial volume fraction (or porosity) of the film. For simplicity, we assume that the initial fluid fraction is spatially uniform.
At the microscopic level, the solid and fluid phases are assumed to be incompressible. However, at the macroscopic level, the film is compressible, with volumetric changes being accommodated by rearrangements of the pore geometry and the removal (or addition) of fluid from material elements. The connection between macroscopic volume changes and the amount of fluid in the pore space of a material element is captured through the incompressibility condition
Evaluating (2.4) at
![]() $t = 0$
gives
$t = 0$
gives
![]() $J = 1$
. Since drying leads to the removal of fluid from the pore space,
$J = 1$
. Since drying leads to the removal of fluid from the pore space,
![]() $\Phi$
decreases relative to
$\Phi$
decreases relative to
![]() $\phi _0$
, and we expect that
$\phi _0$
, and we expect that
![]() $J \leq 1$
. If the composition of the film remains uniform during drying, then
$J \leq 1$
. If the composition of the film remains uniform during drying, then
![]() $J$
can be written in terms of the total film volume
$J$
can be written in terms of the total film volume
![]() $V(t)$
as
$V(t)$
as
![]() $J = V(t)/ V(0)$
. In light of this, we will refer to
$J = V(t)/ V(0)$
. In light of this, we will refer to
![]() $J$
as the contraction ratio.
$J$
as the contraction ratio.
Conservation of linear and angular momentum in the film leads to
The first Piola–Kirchhoff (PK1) stress tensor
![]() ${\sf\boldsymbol S}$
is decomposed as
${\sf\boldsymbol S}$
is decomposed as
![]() ${\sf\boldsymbol S} = \boldsymbol{\mathsf{\Sigma }} - p J {\sf\boldsymbol F}^{-T}$
, where the first component,
${\sf\boldsymbol S} = \boldsymbol{\mathsf{\Sigma }} - p J {\sf\boldsymbol F}^{-T}$
, where the first component,
![]() $\boldsymbol{\mathsf{\Sigma }}$
, represents the effective (Terzaghi) elastic stress of the solid. The second contribution to
$\boldsymbol{\mathsf{\Sigma }}$
, represents the effective (Terzaghi) elastic stress of the solid. The second contribution to
![]() ${\sf\boldsymbol S}$
accounts for the stress exerted by the fluid. The solid matrix is assumed to be isotropic and obey a neo-Hookean equation of state. The elastic component of the stress tensor can be written as
${\sf\boldsymbol S}$
accounts for the stress exerted by the fluid. The solid matrix is assumed to be isotropic and obey a neo-Hookean equation of state. The elastic component of the stress tensor can be written as
where
![]() $E_f$
and
$E_f$
and
![]() $\nu _f$
are the Young’s modulus and Poisson’s ratio of the film, respectively. Both of these parameters are assumed to remain constant during the drying process. In the limit of small deformations,
$\nu _f$
are the Young’s modulus and Poisson’s ratio of the film, respectively. Both of these parameters are assumed to remain constant during the drying process. In the limit of small deformations,
![]() $\nabla \boldsymbol{{u}} \ll 1$
, we find that
$\nabla \boldsymbol{{u}} \ll 1$
, we find that
![]() ${\sf\boldsymbol F} \sim {\sf\boldsymbol I} + \nabla \boldsymbol{{u}}$
,
${\sf\boldsymbol F} \sim {\sf\boldsymbol I} + \nabla \boldsymbol{{u}}$
,
![]() ${\sf\boldsymbol F}^{-T} \sim {\sf\boldsymbol I} - (\nabla \boldsymbol{{u}})^T$
, and
${\sf\boldsymbol F}^{-T} \sim {\sf\boldsymbol I} - (\nabla \boldsymbol{{u}})^T$
, and
![]() $J = \det {\sf\boldsymbol F} \sim 1 + \nabla \cdot \boldsymbol{{u}}$
. Hence, the stress-strain relation (2.7) reduces to
$J = \det {\sf\boldsymbol F} \sim 1 + \nabla \cdot \boldsymbol{{u}}$
. Hence, the stress-strain relation (2.7) reduces to
thus recovering linear elasticity. When carrying out a scaling analysis in Section 3, it will be convenient to write the stress balance (2.5) in component form as
where the definitions of
![]() ${\sf\boldsymbol S}_{\parallel }$
and
${\sf\boldsymbol S}_{\parallel }$
and
![]() ${\sf\boldsymbol S}_{\perp }$
can be found in Section 2.1.
${\sf\boldsymbol S}_{\perp }$
can be found in Section 2.1.
2.4. A model for a deformable plate
Conservation of linear and angular momentum for the plate leads to
where
![]() ${\sf\boldsymbol S}$
is the PK1 stress tensor,
${\sf\boldsymbol S}$
is the PK1 stress tensor,
![]() ${\sf\boldsymbol F} = {\sf\boldsymbol I} + \nabla \boldsymbol{{u}}$
is the deformation gradient tensor, and
${\sf\boldsymbol F} = {\sf\boldsymbol I} + \nabla \boldsymbol{{u}}$
is the deformation gradient tensor, and
![]() $\boldsymbol{{u}}$
is the plate displacement. The mechanical response of the plate is described using the Saint-Venant–Kirchhoff constitutive relation given by
$\boldsymbol{{u}}$
is the plate displacement. The mechanical response of the plate is described using the Saint-Venant–Kirchhoff constitutive relation given by
where
![]() $\nu _p$
and
$\nu _p$
and
![]() $E_p$
are the Poisson’s ratio and Young’s modulus of the plate, respectively;
$E_p$
are the Poisson’s ratio and Young’s modulus of the plate, respectively;
![]() ${\sf\boldsymbol {P}}$
is the second Piola–Kirchhoff stress tensor, and
${\sf\boldsymbol {P}}$
is the second Piola–Kirchhoff stress tensor, and
![]() ${\sf\boldsymbol {E}} = (1/2) ({\sf\boldsymbol F}^T {\sf\boldsymbol F} - {\sf\boldsymbol I})$
is the strain tensor.
${\sf\boldsymbol {E}} = (1/2) ({\sf\boldsymbol F}^T {\sf\boldsymbol F} - {\sf\boldsymbol I})$
is the strain tensor.
2.5. Boundary and initial conditions
In the reference configuration, the film thickness is constant in time and given by
![]() $H_f(\boldsymbol{{X}}_{\parallel })$
. The position of the film surface is then
$H_f(\boldsymbol{{X}}_{\parallel })$
. The position of the film surface is then
![]() $Z =H_f + H_p/ 2$
. At the film surface, we assume that fluid evaporates with volumetric flux
$Z =H_f + H_p/ 2$
. At the film surface, we assume that fluid evaporates with volumetric flux
![]() $V_e$
that depends on the Eulerian fluid fraction. We therefore impose
$V_e$
that depends on the Eulerian fluid fraction. We therefore impose
where
![]() $\mathcal{S}({\sf\boldsymbol F}) = J |{\sf\boldsymbol F}^{-T} \cdot \boldsymbol{{N}}|$
is a dimensionless function that accounts for how the differential area element differs between the reference and deformed configurations. The unit normal vector can be written as
$\mathcal{S}({\sf\boldsymbol F}) = J |{\sf\boldsymbol F}^{-T} \cdot \boldsymbol{{N}}|$
is a dimensionless function that accounts for how the differential area element differs between the reference and deformed configurations. The unit normal vector can be written as
![]() $\boldsymbol{{N}} = \mathcal{N}^{-1}({-}\nabla _{\parallel } H_f + \boldsymbol{{e}}_z)$
where
$\boldsymbol{{N}} = \mathcal{N}^{-1}({-}\nabla _{\parallel } H_f + \boldsymbol{{e}}_z)$
where
![]() $\mathcal{N} = (1 + |\nabla _{\parallel } H_f|^2)^{1/2}$
. In addition, we assume that the film surface is stress-free:
$\mathcal{N} = (1 + |\nabla _{\parallel } H_f|^2)^{1/2}$
. In addition, we assume that the film surface is stress-free:
The adhesion between the film and the plate is assumed to be perfect; consequently, neither slip nor delamination can occur. The assumption of perfect adhesion manifests as continuity of displacement,
where
![]() $-$
means approaching
$-$
means approaching
![]() $Z = H_p/2$
from the plate and
$Z = H_p/2$
from the plate and
![]() $+$
means approaching
$+$
means approaching
![]() $Z = H_p/ 2$
from the film. The traction exerted by the film on the plate is denoted by
$Z = H_p/ 2$
from the film. The traction exerted by the film on the plate is denoted by
![]() $\boldsymbol{\tau }$
. Continuity of stress across the plate-film interface can therefore be expressed as
$\boldsymbol{\tau }$
. Continuity of stress across the plate-film interface can therefore be expressed as
The plate is assumed to be impermeable, and hence, the following no-flux condition is imposed:
The lower surface of the plate is assumed to be stress-free, resulting in
At the contact surface between the plate and the wall, zero-displacement conditions are imposed:
The free edges of the plate are stress-free; thus,
The initial condition for the nominal fluid fraction is given by
![]() $\Phi (\boldsymbol{{X}}_{\parallel },Z,0) = \phi _0$
.
$\Phi (\boldsymbol{{X}}_{\parallel },Z,0) = \phi _0$
.
3. Scaling analysis and reduction of the plate equations
The amplitude of the plate deflection can be estimated by carrying out a scaling analysis of the governing equations. This estimate will guide the asymptotic reduction of the plate model. To facilitate the scaling analysis, the film and plate are assumed to behave as linear elastic materials with stress-strain relations that are, respectively, identical or analogous to (2.8). In addition, it will be assumed that the deflection of the plate is driven by the in-plane traction, in line with Stoney-like models [Reference Evans and Craig12, Reference Stoney36]. We will show below that these two assumptions can be broken in the following ways. The vertical traction can play a comparable role to the in-plane traction. The shear stresses in the film,
![]() $\textsf{S}_{\alpha z}$
and
$\textsf{S}_{\alpha z}$
and
![]() $\textsf{S}_{z \alpha }$
, can have different orders of magnitude. These cases will be specifically addressed when constructing asymptotic solutions to the governing equations. The strategy behind the scaling analysis is to estimate the size of the in-plane traction from the film equations. Then, the magnitude of the plate displacements will be estimated by examining the plate equations.
$\textsf{S}_{z \alpha }$
, can have different orders of magnitude. These cases will be specifically addressed when constructing asymptotic solutions to the governing equations. The strategy behind the scaling analysis is to estimate the size of the in-plane traction from the film equations. Then, the magnitude of the plate displacements will be estimated by examining the plate equations.
To begin, we consider the stress balance in the film (2.9a). The size of the shear stress in the film can be found by noting that vertical gradients in the shear stress
![]() $\partial {\sf\boldsymbol S}_{\perp }/\partial Z \sim {\sf\boldsymbol S}_{\perp }/ H_f^0$
must balance in-plane gradients of the in-plane stress
$\partial {\sf\boldsymbol S}_{\perp }/\partial Z \sim {\sf\boldsymbol S}_{\perp }/ H_f^0$
must balance in-plane gradients of the in-plane stress
![]() $\nabla _{\parallel } \cdot {\sf\boldsymbol S}_{\parallel } \sim E_f/ L$
. Consequently, the shear stress and in-plane traction scale like
$\nabla _{\parallel } \cdot {\sf\boldsymbol S}_{\parallel } \sim E_f/ L$
. Consequently, the shear stress and in-plane traction scale like
![]() ${\sf\boldsymbol S}_{\perp } \sim \epsilon E_f$
and
${\sf\boldsymbol S}_{\perp } \sim \epsilon E_f$
and
![]() $\boldsymbol{\tau }_{\parallel } \sim \epsilon E_f$
. Applying similar arguments to the vertical component of the stress balance (2.9a) and assuming
$\boldsymbol{\tau }_{\parallel } \sim \epsilon E_f$
. Applying similar arguments to the vertical component of the stress balance (2.9a) and assuming
![]() $\textsf{S}_{z \alpha } \sim \textsf{S}_{\alpha z} \sim \epsilon E_f$
shows that
$\textsf{S}_{z \alpha } \sim \textsf{S}_{\alpha z} \sim \epsilon E_f$
shows that
![]() $\textsf{S}_{zz} \sim \epsilon ^2 E_f$
and hence
$\textsf{S}_{zz} \sim \epsilon ^2 E_f$
and hence
![]() $\tau _{z} \sim \epsilon ^2 E_f$
. Thus, under these assumptions, the vertical traction is much smaller than the in-plane traction.
$\tau _{z} \sim \epsilon ^2 E_f$
. Thus, under these assumptions, the vertical traction is much smaller than the in-plane traction.
The in-plane traction exerted on the surface of the plate generates an internal shear stress; thus,
![]() ${\sf\boldsymbol S}_{\perp } \sim \boldsymbol{\tau }_{\parallel } \sim \epsilon E_f$
. As in the film, the vertical gradients in the shear stress,
${\sf\boldsymbol S}_{\perp } \sim \boldsymbol{\tau }_{\parallel } \sim \epsilon E_f$
. As in the film, the vertical gradients in the shear stress,
![]() $\partial {\sf\boldsymbol S}_{\perp }/\partial Z \sim {\sf\boldsymbol S}_{\perp }/ H_p$
, are balanced by the in-plane gradients of the in-plane stresses,
$\partial {\sf\boldsymbol S}_{\perp }/\partial Z \sim {\sf\boldsymbol S}_{\perp }/ H_p$
, are balanced by the in-plane gradients of the in-plane stresses,
![]() $\nabla _{\parallel } \cdot {\sf\boldsymbol S}_{\parallel } \sim {\sf\boldsymbol S}_{\parallel }/ L$
, leading to
$\nabla _{\parallel } \cdot {\sf\boldsymbol S}_{\parallel } \sim {\sf\boldsymbol S}_{\parallel }/ L$
, leading to
![]() ${\sf\boldsymbol S}_{\parallel } \sim \delta ^{-1} \epsilon E_f$
. A linear stress-strain relation implies that
${\sf\boldsymbol S}_{\parallel } \sim \delta ^{-1} \epsilon E_f$
. A linear stress-strain relation implies that
![]() ${\sf\boldsymbol S}_{\parallel } \sim E_p \boldsymbol{{u}}_{\parallel }/ L$
. Thus, we find that the in-plane displacement in the plate scales as
${\sf\boldsymbol S}_{\parallel } \sim E_p \boldsymbol{{u}}_{\parallel }/ L$
. Thus, we find that the in-plane displacement in the plate scales as
![]() $\boldsymbol{{u}}_{\parallel } \sim \delta ^{-1} (E_f/ E_p) H_f^0$
. A scale for the vertical displacement of the plate is obtained by assuming that bending is the primary mode of deformation and balancing the components of the shear strains,
$\boldsymbol{{u}}_{\parallel } \sim \delta ^{-1} (E_f/ E_p) H_f^0$
. A scale for the vertical displacement of the plate is obtained by assuming that bending is the primary mode of deformation and balancing the components of the shear strains,
![]() $\boldsymbol{{u}}_{\parallel }/ H_p \sim u_z/ L$
, which leads to
$\boldsymbol{{u}}_{\parallel }/ H_p \sim u_z/ L$
, which leads to
![]() $u_z \sim \delta ^{-2} (E_f/ E_p) H_f^0$
. Since the displacements in the film and plate must match at the film-plate surface, these displacement scales also apply to the film.
$u_z \sim \delta ^{-2} (E_f/ E_p) H_f^0$
. Since the displacements in the film and plate must match at the film-plate surface, these displacement scales also apply to the film.
The scaling analysis motivates introducing the non-dimensional parameter
![]() $\mathcal{E} \equiv \delta ^{-2} E_f/ E_p$
, which compares the film modulus
$\mathcal{E} \equiv \delta ^{-2} E_f/ E_p$
, which compares the film modulus
![]() $E_f$
to a reduced modulus for the plate,
$E_f$
to a reduced modulus for the plate,
![]() $\delta ^2 E_p$
. Thus,
$\delta ^2 E_p$
. Thus,
![]() $\mathcal{E}$
characterises how stiff the film is relative to the plate. The displacements will therefore scale as
$\mathcal{E}$
characterises how stiff the film is relative to the plate. The displacements will therefore scale as
![]() $\boldsymbol{{u}}_{\parallel } \sim \delta \mathcal{E} H_f^0$
and
$\boldsymbol{{u}}_{\parallel } \sim \delta \mathcal{E} H_f^0$
and
![]() $u_z \sim \mathcal{E} H_f^0$
. The size of
$u_z \sim \mathcal{E} H_f^0$
. The size of
![]() $\mathcal{E}$
, therefore, plays a key role in determining the magnitudes of the displacements and controls the mechanics of the film and plate. For films that are thin relative to the plate,
$\mathcal{E}$
, therefore, plays a key role in determining the magnitudes of the displacements and controls the mechanics of the film and plate. For films that are thin relative to the plate,
![]() $\epsilon \ll \delta$
, three regimes of plate mechanics can be identified:
$\epsilon \ll \delta$
, three regimes of plate mechanics can be identified:
-
(i) Soft films:
 $\mathcal{E} = O(1)$
. The deflection of the plate scales like the film thickness, which is much smaller than the plate thickness. Linear plate theory can be applied.
$\mathcal{E} = O(1)$
. The deflection of the plate scales like the film thickness, which is much smaller than the plate thickness. Linear plate theory can be applied. -
(ii) Stiff films:
 $\mathcal{E} = O(\delta \epsilon ^{-1}) \gg 1$
. The plate deflection is proportional to its thickness. Föppl-von Kármán theory applies to the plate.
$\mathcal{E} = O(\delta \epsilon ^{-1}) \gg 1$
. The plate deflection is proportional to its thickness. Föppl-von Kármán theory applies to the plate. -
(iii) Very stiff films:
 $\mathcal{E} \gg O(\delta \epsilon ^{-1}) \gg 1$
. The deflection of the plate greatly exceeds its thickness. This regime is beyond the validity of Föppl-von Kármán theory.
$\mathcal{E} \gg O(\delta \epsilon ^{-1}) \gg 1$
. The deflection of the plate greatly exceeds its thickness. This regime is beyond the validity of Föppl-von Kármán theory.
The model reduction presented below will focus on the first two of these regimes. An analysis of Regime (iii), in which the film is very stiff, is left as an area of future work. The case when the film and the plate have similar thicknesses, i.e.
![]() $\delta = O(\epsilon )$
as
$\delta = O(\epsilon )$
as
![]() $\epsilon \to 0$
, is a distinguished limit. In this case, Regimes (i) and (ii) coincide and the plate can be modelled using a modified form of the Föppl-von Kármán (FvK) equations. The reduced equations for the plate are formulated by assuming that
$\epsilon \to 0$
, is a distinguished limit. In this case, Regimes (i) and (ii) coincide and the plate can be modelled using a modified form of the Föppl-von Kármán (FvK) equations. The reduced equations for the plate are formulated by assuming that
![]() $\delta = O(\epsilon )$
and are then specialised to the first two regimes when
$\delta = O(\epsilon )$
and are then specialised to the first two regimes when
![]() $\epsilon \ll \delta$
in Section 5.
$\epsilon \ll \delta$
in Section 5.
3.1. Reduced equations for the plate
The mechanics of the plate are described using a modified form of the Föppl-von Kármán (FvK) equations that accounts for non-uniform in-plane tractions. These equations are systematically derived from the equations of nonlinear elasticity in Appendix A.1. The leading-order contribution to the vertical displacement of the plate, which we denote by
![]() $w$
, is independent of
$w$
, is independent of
![]() $Z$
and satisfies
$Z$
and satisfies
where
![]() $B = \bar{E}_p H_p^3/ 12$
is the bending modulus and
$B = \bar{E}_p H_p^3/ 12$
is the bending modulus and
![]() $\bar{E}_p = E_p/ (1 - \nu _p^2)$
is the effective Young’s modulus. The first term on the right-hand side of (3.1a) is absent from traditional formulations of the FvK equations; see, e.g. Landau and Lifshitz [Reference Landau and Lifshitz25] or Howell et al. [Reference Howell, Kozyreff and Ockendon19]. The mean in-plane displacement
$\bar{E}_p = E_p/ (1 - \nu _p^2)$
is the effective Young’s modulus. The first term on the right-hand side of (3.1a) is absent from traditional formulations of the FvK equations; see, e.g. Landau and Lifshitz [Reference Landau and Lifshitz25] or Howell et al. [Reference Howell, Kozyreff and Ockendon19]. The mean in-plane displacement
![]() $\bar{\boldsymbol{{u}}}_{\parallel }$
can be obtained by solving the mean in-plane stress balance given by
$\bar{\boldsymbol{{u}}}_{\parallel }$
can be obtained by solving the mean in-plane stress balance given by
where the mean in-plane stress
![]() $\bar{{\sf\boldsymbol S}}_{\parallel }$
and strain
$\bar{{\sf\boldsymbol S}}_{\parallel }$
and strain
![]() $\bar{{\sf\boldsymbol {E}}}_{\parallel }$
are defined as
$\bar{{\sf\boldsymbol {E}}}_{\parallel }$
are defined as
The in-plane displacements are linked to the mean in-plane and vertical displacements via
3.2. Boundary conditions at the edges of the plate
At the clamped edge of the plate, located at
![]() $X_1 = 0$
, we impose
$X_1 = 0$
, we impose
The boundary conditions at a free edge can be derived by resolving the mechanics of the plate in a thin boundary layer where the stresses become large, details of which are provided in Appendix A.2. The boundary conditions at
![]() $X_1 = L$
are
$X_1 = L$
are
Similarly, the boundary conditions at
![]() $X_2 = \pm W/ 2$
are
$X_2 = \pm W/ 2$
are
4. Non-dimensionalisation
The governing equations for the film and plate are non-dimensionalised by scaling the in-plane coordinates as
![]() $\boldsymbol{{x}}_{\parallel } \sim L$
. Time is scaled as
$\boldsymbol{{x}}_{\parallel } \sim L$
. Time is scaled as
![]() $t \sim \tau _{\text{pe}}$
, where the poroelastic time scale
$t \sim \tau _{\text{pe}}$
, where the poroelastic time scale
![]() $\tau _{\text{pe}} = \mu _f L^2/ (k_0 E_f)$
describes the time required for a pressure gradient of magnitude
$\tau _{\text{pe}} = \mu _f L^2/ (k_0 E_f)$
describes the time required for a pressure gradient of magnitude
![]() $E_f/ L$
to transport fluid a distance
$E_f/ L$
to transport fluid a distance
![]() $L$
through a porous medium with permeability
$L$
through a porous medium with permeability
![]() $k_0$
.
$k_0$
.
4.1. Film model
In the film, the vertical coordinate is scaled according to
![]() $Z \sim H_f^0$
. The components of the fluxes are scaled as
$Z \sim H_f^0$
. The components of the fluxes are scaled as
![]() $\boldsymbol{{Q}}_\parallel \sim (k_0/ \mu _f) E_f/ L$
and
$\boldsymbol{{Q}}_\parallel \sim (k_0/ \mu _f) E_f/ L$
and
![]() $Q_z \sim \epsilon (k_0/ \mu _f) E_f/ L$
. The film displacements and stresses are scaled according to the estimates from Section 3; thus,
$Q_z \sim \epsilon (k_0/ \mu _f) E_f/ L$
. The film displacements and stresses are scaled according to the estimates from Section 3; thus,
![]() $\boldsymbol{{u}}_{\parallel } \sim \delta \mathcal{E} H_f^0$
,
$\boldsymbol{{u}}_{\parallel } \sim \delta \mathcal{E} H_f^0$
,
![]() $u_z \sim \mathcal{E} H_f^0$
,
$u_z \sim \mathcal{E} H_f^0$
,
![]() ${\sf\boldsymbol S}_{\parallel } \sim E_f$
,
${\sf\boldsymbol S}_{\parallel } \sim E_f$
,
![]() ${\sf\boldsymbol S}_{\perp } \sim \epsilon E_f$
,
${\sf\boldsymbol S}_{\perp } \sim \epsilon E_f$
,
![]() $\textsf{S}_{z \alpha } \sim \epsilon E_f$
, and
$\textsf{S}_{z \alpha } \sim \epsilon E_f$
, and
![]() $\textsf{S}_{zz} \sim \epsilon ^2 E_f$
. The pressure and the elastic stress tensor are scaled as
$\textsf{S}_{zz} \sim \epsilon ^2 E_f$
. The pressure and the elastic stress tensor are scaled as
![]() $p \sim E_f$
and
$p \sim E_f$
and
![]() $\boldsymbol{\mathsf{\Sigma }} \sim E_f$
.
$\boldsymbol{\mathsf{\Sigma }} \sim E_f$
.
Under this choice of scales, the conservation law for the nominal fluid fraction (2.2a) becomes
By writing the symmetric permeability tensor as
![]() ${\sf\boldsymbol {K}} = {\sf\boldsymbol {K}}_{\parallel } + {\sf\boldsymbol {K}}_{\perp } \otimes \boldsymbol{{e}}_z + \boldsymbol{{e}}_z \otimes {\sf\boldsymbol {K}}_{\perp } +{\textsf{K}}_{zz} \boldsymbol{{e}}_z \otimes \boldsymbol{{e}}_z$
, the non-dimensional components of the fluid flux (2.3) are
${\sf\boldsymbol {K}} = {\sf\boldsymbol {K}}_{\parallel } + {\sf\boldsymbol {K}}_{\perp } \otimes \boldsymbol{{e}}_z + \boldsymbol{{e}}_z \otimes {\sf\boldsymbol {K}}_{\perp } +{\textsf{K}}_{zz} \boldsymbol{{e}}_z \otimes \boldsymbol{{e}}_z$
, the non-dimensional components of the fluid flux (2.3) are
The stress balances representing conservation of linear momentum (2.9) are
where the PK1 stress tensor is given by
The elastic stress tensor (2.7) is written as
where the functions
![]() $a$
and
$a$
and
![]() $b$
are defined, for convenience, as
$b$
are defined, for convenience, as
The deformation gradient tensor (2.1) is given by
The appearance of
![]() $\mathcal{E}$
,
$\mathcal{E}$
,
![]() $\epsilon$
and
$\epsilon$
and
![]() $\delta$
in the deformation gradient tensor leads to distinct asymptotic regimes that are defined by the relative sizes of these parameters. Finally, the incompressibility condition is given by (2.4).
$\delta$
in the deformation gradient tensor leads to distinct asymptotic regimes that are defined by the relative sizes of these parameters. Finally, the incompressibility condition is given by (2.4).
4.2. Plate model
In the plate, the displacements are scaled according to
![]() $\boldsymbol{{u}}_{\parallel } \sim \delta \mathcal{E} H_f^0$
,
$\boldsymbol{{u}}_{\parallel } \sim \delta \mathcal{E} H_f^0$
,
![]() $\bar{\boldsymbol{{u}}}_{\parallel } \sim \delta \mathcal{E} H_f^0$
and
$\bar{\boldsymbol{{u}}}_{\parallel } \sim \delta \mathcal{E} H_f^0$
and
![]() $w \sim \mathcal{E} H_f^0$
. The mean in-plane strains and stresses are scaled as
$w \sim \mathcal{E} H_f^0$
. The mean in-plane strains and stresses are scaled as
![]() $\bar{{\sf\boldsymbol {E}}}_{\parallel } \sim \delta \epsilon \mathcal{E}$
and
$\bar{{\sf\boldsymbol {E}}}_{\parallel } \sim \delta \epsilon \mathcal{E}$
and
![]() $\bar{{\sf\boldsymbol S}}_{\parallel } \sim \delta \epsilon \mathcal{E} H_p E_p$
. The tractions are scaled as
$\bar{{\sf\boldsymbol S}}_{\parallel } \sim \delta \epsilon \mathcal{E} H_p E_p$
. The tractions are scaled as
![]() $\boldsymbol{\tau }_{\parallel } \sim \epsilon E_f$
and
$\boldsymbol{\tau }_{\parallel } \sim \epsilon E_f$
and
![]() $\tau _{z} \sim \epsilon ^2 E_f$
; see Section 3.
$\tau _{z} \sim \epsilon ^2 E_f$
; see Section 3.
The rescaled FvK equation (3.1) are then given by
where
![]() $\mathcal{B} = 1/[12(1-\nu _b^2)]$
is a non-dimensional bending modulus. The rescaled mean stresses and strains, obtained from (3.1c) and (3.1d), are
$\mathcal{B} = 1/[12(1-\nu _b^2)]$
is a non-dimensional bending modulus. The rescaled mean stresses and strains, obtained from (3.1c) and (3.1d), are
By scaling
![]() $Z \sim H_p$
in the plate, the leading-order contribution to the in-plane displacement (3.2) is given by
$Z \sim H_p$
in the plate, the leading-order contribution to the in-plane displacement (3.2) is given by
4.3. Boundary conditions
In the context of the film model, in which
![]() $H_f^0$
has been used to non-dimensionalise the vertical coordinate
$H_f^0$
has been used to non-dimensionalise the vertical coordinate
![]() $Z$
, the plate has a non-dimensional thickness of
$Z$
, the plate has a non-dimensional thickness of
![]() $\mathcal{H} = \delta \epsilon ^{-1}$
. The upper surface of the plate is therefore located at
$\mathcal{H} = \delta \epsilon ^{-1}$
. The upper surface of the plate is therefore located at
![]() $Z = \mathcal{H}/ 2$
; the free surface of the film is located at
$Z = \mathcal{H}/ 2$
; the free surface of the film is located at
![]() $Z = H_f(\boldsymbol{{X}}_{\parallel }) + \mathcal{H}/2$
.
$Z = H_f(\boldsymbol{{X}}_{\parallel }) + \mathcal{H}/2$
.
The boundary conditions at the free surface of the film, obtained from (2.12) to (2.13), are given by
where the Péclet number is defined as
![]() $\textrm{Pe} = V_e^0 H_f^0 \mu _f/ (\epsilon ^2 k_0 E_f)$
, where
$\textrm{Pe} = V_e^0 H_f^0 \mu _f/ (\epsilon ^2 k_0 E_f)$
, where
![]() $V_e^0$
is a characteristic evaporative flux. Moreover,
$V_e^0$
is a characteristic evaporative flux. Moreover,
![]() $\mathcal{V} = V_e/ V_e^0$
denotes the composition-dependent non-dimensional evaporative flux and
$\mathcal{V} = V_e/ V_e^0$
denotes the composition-dependent non-dimensional evaporative flux and
![]() $\mathcal{N} = (1 + \epsilon ^2 |\nabla _{\parallel } H_f|^2)^{1/2}$
. At the upper plate surface,
$\mathcal{N} = (1 + \epsilon ^2 |\nabla _{\parallel } H_f|^2)^{1/2}$
. At the upper plate surface,
![]() $Z = \mathcal{H}/ 2$
, the no-flux condition on the fluid (2.16) can be written as
$Z = \mathcal{H}/ 2$
, the no-flux condition on the fluid (2.16) can be written as
Using (4.9), continuity of displacement (2.14) can be written as
The non-dimensionalised boundary conditions at the clamped and free edges of the plate are identical to those written in Section 3.2. However, the free edges are now located at
![]() $x_1 = 1$
and
$x_1 = 1$
and
![]() $x_2 = \pm \mathcal{W}/2$
, where
$x_2 = \pm \mathcal{W}/2$
, where
![]() $\mathcal{W} = W/ L$
;
$\mathcal{W} = W/ L$
;
![]() $B$
can be replaced with
$B$
can be replaced with
![]() $\mathcal{B}$
, and
$\mathcal{B}$
, and
![]() $H_p$
can be set to one.
$H_p$
can be set to one.
The tractions can be found by evaluating the normal components of the PK1 stress in the film at
![]() $Z = \mathcal{H}/ 2$
to give
$Z = \mathcal{H}/ 2$
to give
![]() $\boldsymbol{\tau }_{\parallel } = {\sf\boldsymbol S}_{\perp } \cdot \boldsymbol{{e}}_z|_{+}$
and
$\boldsymbol{\tau }_{\parallel } = {\sf\boldsymbol S}_{\perp } \cdot \boldsymbol{{e}}_z|_{+}$
and
![]() $\tau _{z} = \textsf{S}_{zz}|_{+}$
. However, equivalent expressions that are more convenient to use can be found by integrating the stress balances (4.3) across the film thickness, resulting in
$\tau _{z} = \textsf{S}_{zz}|_{+}$
. However, equivalent expressions that are more convenient to use can be found by integrating the stress balances (4.3) across the film thickness, resulting in
5. Asymptotic reductions of the coupled film-plate model
The coupled system of equations for the film and the plate can be asymptotically reduced by taking the limit
![]() $\epsilon \to 0$
. Substantial simplifications occur through a decoupling of the models. In particular, the equations for the film can be solved independently of those for the plate. The problem for the film also simplifies through a decoupling of the mechanical and fluid-transport problems. This decoupling occurs because the deformation gradient tensor, to leading order, is simply
$\epsilon \to 0$
. Substantial simplifications occur through a decoupling of the models. In particular, the equations for the film can be solved independently of those for the plate. The problem for the film also simplifies through a decoupling of the mechanical and fluid-transport problems. This decoupling occurs because the deformation gradient tensor, to leading order, is simply
![]() ${\sf\boldsymbol F} =\textrm{diag}(1, 1, J)$
. Thus, the mechanical problem can be readily solved in terms of
${\sf\boldsymbol F} =\textrm{diag}(1, 1, J)$
. Thus, the mechanical problem can be readily solved in terms of
![]() $J = 1 + \Phi - \phi _0$
and used to formulate a closed-form problem for
$J = 1 + \Phi - \phi _0$
and used to formulate a closed-form problem for
![]() $\Phi$
. Using the asymptotically reduced model in practice therefore involves three steps:
$\Phi$
. Using the asymptotically reduced model in practice therefore involves three steps:
-
1. Solve a reduced model for the nominal fluid fraction
 $\Phi$
and compute the local volumetric contraction
$\Phi$
and compute the local volumetric contraction
 $J$
.
$J$
. -
2. Compute the tractions, which can be expressed in terms of
 $J$
and
$J$
and
 $\nabla _{\parallel } w$
, and substitute them into the FvK equations.
$\nabla _{\parallel } w$
, and substitute them into the FvK equations. -
3. Solve the FvK equations for the plate displacements.
Despite the simplified pathway to obtaining a solution, there are several asymptotic regimes in both the mechanical and fluid-transport problems for the film that must be delicately handled. These regimes arise from the various sizes that
![]() $\mathcal{E}$
and
$\mathcal{E}$
and
![]() $\textrm{Pe}$
can take. The former alters the structure of the mechanical problem whereas the latter alters the fluid-transport problem. In terms of the mechanical problem, we consider three cases that can be summarised as follows:
$\textrm{Pe}$
can take. The former alters the structure of the mechanical problem whereas the latter alters the fluid-transport problem. In terms of the mechanical problem, we consider three cases that can be summarised as follows:
-
 $\delta = O(\epsilon )$
with
$\delta = O(\epsilon )$
with
 $\mathcal{E} = O(1)$
: the deformation of the film is driven by a combination of volumetric contraction and plate bending. Both the in-plane and vertical tractions drive bending.
$\mathcal{E} = O(1)$
: the deformation of the film is driven by a combination of volumetric contraction and plate bending. Both the in-plane and vertical tractions drive bending. -
 $\delta \gg \epsilon$
with
$\delta \gg \epsilon$
with
 $\mathcal{E} = O(1)$
: in-plane film deformation is dominated by plate bending. The vertical film deformation driven by volumetric contraction and plate bending. Only the in-plane traction drives bending.
$\mathcal{E} = O(1)$
: in-plane film deformation is dominated by plate bending. The vertical film deformation driven by volumetric contraction and plate bending. Only the in-plane traction drives bending. -
 $\delta \gg \epsilon$
with
$\delta \gg \epsilon$
with
 $\mathcal{E} = O(\delta \epsilon ^{-1})$
: the deformation of the film is dominated by plate bending. Both the in-plane and vertical traction drive bending.
$\mathcal{E} = O(\delta \epsilon ^{-1})$
: the deformation of the film is dominated by plate bending. Both the in-plane and vertical traction drive bending.
In terms of the drying dynamics, there are three cases to consider:
-
 $\textrm{Pe} = O(1)$
: the nominal fluid fraction is uniform in the vertical direction. The flow of fluid predominantly occurs in the in-plane directions. The case
$\textrm{Pe} = O(1)$
: the nominal fluid fraction is uniform in the vertical direction. The flow of fluid predominantly occurs in the in-plane directions. The case
 $\textrm{Pe} \ll 1$
is a sub-limit in which the film remains homogeneous during drying; that is, the fluid fraction is spatially uniform.
$\textrm{Pe} \ll 1$
is a sub-limit in which the film remains homogeneous during drying; that is, the fluid fraction is spatially uniform. -
 $\textrm{Pe} = O(\epsilon ^{-1})$
: the nominal fluid fraction is uniform in the vertical direction. Fluid flow is two-dimensional, with the in-plane and vertical flux components having similar orders of magnitude.
$\textrm{Pe} = O(\epsilon ^{-1})$
: the nominal fluid fraction is uniform in the vertical direction. Fluid flow is two-dimensional, with the in-plane and vertical flux components having similar orders of magnitude. -
 $\textrm{Pe} = O(\epsilon ^{-2})$
: the nominal fluid fraction is non-uniform in the vertical direction. Fluid flow mainly occurs in the vertical direction.
$\textrm{Pe} = O(\epsilon ^{-2})$
: the nominal fluid fraction is non-uniform in the vertical direction. Fluid flow mainly occurs in the vertical direction.
In Section 5.1, asymptotic solutions to the mechanical problems are detailed for the three cases described above. In Section 5.2, the fluid-transport problem is asymptotically reduced according to the size of the Péclet number.
5.1. Reduction of the mechanical problems
Asymptotic expansions are used to solve the governing equations for the film mechanics. The goal is to obtain expressions for the traction. As the plate model has already been reduced, we do not asymptotically expand the solutions to the FvK equations. Instead, we comment on which terms can be neglected depending on the sizes of
![]() $\delta$
and
$\delta$
and
![]() $\mathcal{E}$
relative to
$\mathcal{E}$
relative to
![]() $\epsilon$
.
$\epsilon$
.
5.1.1. Films and plates of similar thicknesses
We first consider the distinguished limit in which the film and the plate have similar thicknesses by letting
![]() $\delta = \delta _0 \epsilon$
, where
$\delta = \delta _0 \epsilon$
, where
![]() $\delta _0 = O(1)$
as
$\delta _0 = O(1)$
as
![]() $\epsilon \to 0$
. To ensure that the FvK limit remains valid, we also assume that
$\epsilon \to 0$
. To ensure that the FvK limit remains valid, we also assume that
![]() $\mathcal{E} = O(1)$
as
$\mathcal{E} = O(1)$
as
![]() $\epsilon \to 0$
. With this choice of
$\epsilon \to 0$
. With this choice of
![]() $\delta$
, the deformation gradient tensor for the film (4.7) can be asymptotically expanded as
$\delta$
, the deformation gradient tensor for the film (4.7) can be asymptotically expanded as
![]() ${\sf\boldsymbol F} = {\sf\boldsymbol F}^{(0)} + \epsilon {\sf\boldsymbol F}^{(1)} + O(\epsilon ^2)$
, where
${\sf\boldsymbol F} = {\sf\boldsymbol F}^{(0)} + \epsilon {\sf\boldsymbol F}^{(1)} + O(\epsilon ^2)$
, where
 \begin{align} {\sf\boldsymbol F}^{(1)} &= \mathcal{E} \left(\delta _0 \frac{\partial \boldsymbol{{u}}_{\parallel }^{(0)}}{\partial Z}\otimes \boldsymbol{{e}}_z + \boldsymbol{{e}}_z \otimes \nabla _{\parallel } u_z^{(0)}\right) +{\textsf{F}}_{zz}^{(1)} \boldsymbol{{e}}_z \otimes \boldsymbol{{e}}_z. \end{align}
\begin{align} {\sf\boldsymbol F}^{(1)} &= \mathcal{E} \left(\delta _0 \frac{\partial \boldsymbol{{u}}_{\parallel }^{(0)}}{\partial Z}\otimes \boldsymbol{{e}}_z + \boldsymbol{{e}}_z \otimes \nabla _{\parallel } u_z^{(0)}\right) +{\textsf{F}}_{zz}^{(1)} \boldsymbol{{e}}_z \otimes \boldsymbol{{e}}_z. \end{align}
Importantly, the leading-order contribution to
![]() ${\sf\boldsymbol F}$
is diagonal and can be expressed as
${\sf\boldsymbol F}$
is diagonal and can be expressed as
![]() ${\sf\boldsymbol F}^{(0)} = \textrm{diag}(1,1, J^{(0)})$
, where the local contraction ratio is given by
${\sf\boldsymbol F}^{(0)} = \textrm{diag}(1,1, J^{(0)})$
, where the local contraction ratio is given by
![]() $J^{(0)} = 1 + \Phi ^{(0)} - \phi _0$
from the incompressibility condition (2.4). Thus, removal of fluid from the pore space drives a uniaxial contraction of the solid matrix along the vertical direction.
$J^{(0)} = 1 + \Phi ^{(0)} - \phi _0$
from the incompressibility condition (2.4). Thus, removal of fluid from the pore space drives a uniaxial contraction of the solid matrix along the vertical direction.
The components of the PK1 stress tensor for the film are expanded as
![]() ${\sf\boldsymbol S}_{\parallel } = {\sf\boldsymbol S}_{\parallel }^{(0)} + O(\epsilon )$
,
${\sf\boldsymbol S}_{\parallel } = {\sf\boldsymbol S}_{\parallel }^{(0)} + O(\epsilon )$
,
![]() ${\sf\boldsymbol S}_{\perp } = {\sf\boldsymbol S}_{\perp }^{(1)} + O(\epsilon )$
,
${\sf\boldsymbol S}_{\perp } = {\sf\boldsymbol S}_{\perp }^{(1)} + O(\epsilon )$
,
![]() $\textsf{S}_{z \alpha } = \textsf{S}_{z \alpha }^{(1)} + O(\epsilon )$
and
$\textsf{S}_{z \alpha } = \textsf{S}_{z \alpha }^{(1)} + O(\epsilon )$
and
![]() $\textsf{S}_{zz} = \textsf{S}_{zz}^{(2)} + O(\epsilon )$
. Non-zero superscripts are used when a component has already been scaled by a power of
$\textsf{S}_{zz} = \textsf{S}_{zz}^{(2)} + O(\epsilon )$
. Non-zero superscripts are used when a component has already been scaled by a power of
![]() $\epsilon$
when non-dimensionalising the model. The elastic stress tensor and the pressure are written as
$\epsilon$
when non-dimensionalising the model. The elastic stress tensor and the pressure are written as
![]() $\boldsymbol{\mathsf{\Sigma }} = \boldsymbol{\mathsf{\Sigma }}^{(0)} + \epsilon \boldsymbol{\mathsf{\Sigma }}^{(1)} + O(\epsilon ^2)$
and
$\boldsymbol{\mathsf{\Sigma }} = \boldsymbol{\mathsf{\Sigma }}^{(0)} + \epsilon \boldsymbol{\mathsf{\Sigma }}^{(1)} + O(\epsilon ^2)$
and
![]() $p = p^{(0)} + O(\epsilon )$
. From (5.1a) and (4.5), we can deduce that the leading-order contribution to the elastic stress tensor is diagonal and given by
$p = p^{(0)} + O(\epsilon )$
. From (5.1a) and (4.5), we can deduce that the leading-order contribution to the elastic stress tensor is diagonal and given by
![]() $\boldsymbol{\mathsf{\Sigma }}^{(0)} = \boldsymbol{\mathsf{\Sigma }}_{\parallel }^{(0)} + \boldsymbol{\mathsf{\Sigma }}_{zz}^{(0)} \boldsymbol{{e}}_z \otimes \boldsymbol{{e}}_z$
, where
$\boldsymbol{\mathsf{\Sigma }}^{(0)} = \boldsymbol{\mathsf{\Sigma }}_{\parallel }^{(0)} + \boldsymbol{\mathsf{\Sigma }}_{zz}^{(0)} \boldsymbol{{e}}_z \otimes \boldsymbol{{e}}_z$
, where
In addition, by considering the
![]() $O(1)$
contributions of the PK1 stress tensor (4.4), we see that
$O(1)$
contributions of the PK1 stress tensor (4.4), we see that
Therefore, by substituting (5.2) into (5.3), we can deduce that the pressure and the in-plane PK1 stress are given by
Since
![]() $J^{(0)} \lt 1$
, the pressure will be negative. In dimensional terms, this means the fluid pressure will be below atmospheric pressure (which has been set to zero). The in-plane elastic stresses will be compressive, while the total (PK1) in-plane stresses will be tensile. For convenience, we define
$J^{(0)} \lt 1$
, the pressure will be negative. In dimensional terms, this means the fluid pressure will be below atmospheric pressure (which has been set to zero). The in-plane elastic stresses will be compressive, while the total (PK1) in-plane stresses will be tensile. For convenience, we define
so that the in-plane PK1 stress tensor can be written as
![]() ${\sf\boldsymbol S}_{\parallel }^{(0)} = \textsf{S}_{\parallel }(J^{(0)}) {\sf\boldsymbol I}_{\parallel }$
. From the
${\sf\boldsymbol S}_{\parallel }^{(0)} = \textsf{S}_{\parallel }(J^{(0)}) {\sf\boldsymbol I}_{\parallel }$
. From the
![]() $O(\epsilon )$
contributions to the PK1 stress tensor (4.4), we find, after simplification, that
$O(\epsilon )$
contributions to the PK1 stress tensor (4.4), we find, after simplification, that
 \begin{align} {\sf\boldsymbol S}_{\perp }^{(1)} = \mathcal{E} b(\nu _f) \left(\delta _0 \frac{\partial \boldsymbol{{u}}_{\parallel }^{(0)}}{\partial Z} + J^{(0)} \nabla _{\parallel } u_z^{(0)}\right), \end{align}
\begin{align} {\sf\boldsymbol S}_{\perp }^{(1)} = \mathcal{E} b(\nu _f) \left(\delta _0 \frac{\partial \boldsymbol{{u}}_{\parallel }^{(0)}}{\partial Z} + J^{(0)} \nabla _{\parallel } u_z^{(0)}\right), \end{align}
 \begin{align} \textsf{S}_{z \alpha }^{(1)} \boldsymbol{{e}}_\alpha = \mathcal{E} b(\nu _f) \left(\delta _0 J^{(0)} \frac{\partial \boldsymbol{{u}}_{\parallel }^{(0)}}{\partial Z} + \nabla _{\parallel }u_z^{(0)}\right). \end{align}
\begin{align} \textsf{S}_{z \alpha }^{(1)} \boldsymbol{{e}}_\alpha = \mathcal{E} b(\nu _f) \left(\delta _0 J^{(0)} \frac{\partial \boldsymbol{{u}}_{\parallel }^{(0)}}{\partial Z} + \nabla _{\parallel }u_z^{(0)}\right). \end{align}
Equation (5.6a) will enable the in-plane displacement to be determined, whereas (5.6b) will enable the vertical traction to be computed via (4.13b).
The shear stress
![]() ${\sf\boldsymbol S}_{\perp }^{(1)}$
in the film can be determined by integrating the in-plane stress balance (4.3a) and imposing the stress-free boundary condition (4.10b) to obtain, after simplification,
${\sf\boldsymbol S}_{\perp }^{(1)}$
in the film can be determined by integrating the in-plane stress balance (4.3a) and imposing the stress-free boundary condition (4.10b) to obtain, after simplification,
A differential equation for the vertical component of the film displacement
![]() $u_z^{(0)}$
can be obtained by calculating
$u_z^{(0)}$
can be obtained by calculating
![]() $J^{(0)} = \det {\sf\boldsymbol F}^{(0)}$
using (5.1a) to obtain
$J^{(0)} = \det {\sf\boldsymbol F}^{(0)}$
using (5.1a) to obtain
Having determined
![]() ${\sf\boldsymbol S}_{\perp }^{(1)}$
and
${\sf\boldsymbol S}_{\perp }^{(1)}$
and
![]() $\partial u_z^{(0)}/\partial Z$
, we can use (5.6a) to formulate a differential equation for
$\partial u_z^{(0)}/\partial Z$
, we can use (5.6a) to formulate a differential equation for
![]() $\boldsymbol{{u}}_{\parallel }^{(0)}$
. After solving (5.6a) and (5.8) and imposing continuity of displacement (4.12), we find that the film displacements can be written as
$\boldsymbol{{u}}_{\parallel }^{(0)}$
. After solving (5.6a) and (5.8) and imposing continuity of displacement (4.12), we find that the film displacements can be written as
 \begin{align} \boldsymbol{{u}}_{\parallel }^{(0)} &= \bar{\boldsymbol{{u}}}_{\parallel } - (1/ 2)\nabla _{\parallel }w \nonumber \\ & \quad + (\delta _0 \mathcal{E} b(\nu _f))^{-1}\Bigg \{ \int _{\mathcal{H}/2}^{Z}\bigg [{\sf\boldsymbol S}_{\perp }^{(1)} - \mathcal{E} b(\nu _f) \nabla _{\parallel } w - b(\nu _f) J^{(0)} \int _{\mathcal{H}/2}^{Z} \nabla _{\parallel } J^{(0)}\,\textrm{d} Z'\bigg ]\,\textrm{d} Z \Bigg \},\\[-9pt]\nonumber \end{align}
\begin{align} \boldsymbol{{u}}_{\parallel }^{(0)} &= \bar{\boldsymbol{{u}}}_{\parallel } - (1/ 2)\nabla _{\parallel }w \nonumber \\ & \quad + (\delta _0 \mathcal{E} b(\nu _f))^{-1}\Bigg \{ \int _{\mathcal{H}/2}^{Z}\bigg [{\sf\boldsymbol S}_{\perp }^{(1)} - \mathcal{E} b(\nu _f) \nabla _{\parallel } w - b(\nu _f) J^{(0)} \int _{\mathcal{H}/2}^{Z} \nabla _{\parallel } J^{(0)}\,\textrm{d} Z'\bigg ]\,\textrm{d} Z \Bigg \},\\[-9pt]\nonumber \end{align}
The Eulerian film thickness can be obtained from (5.9b) as
We are now in a position to calculate the tractions. Substituting (5.4b) into (4.13a) and using (5.5) leads to an expression for the in-plane traction given by
The vertical traction can be obtained by first substituting the expressions for the displacements (5.9) into (5.6b) and then inserting the result into (4.13b) to find
 \begin{align} \tau _{z} &= \nabla _{\parallel }^2 \int _{\mathcal{H}/2}^{H_f + \mathcal{H}/2} J^{(0)} \left (\int _{Z}^{H_f + \mathcal{H}/2}{\textsf{S}_{\parallel }(J^{(0)})}\,\textrm{d} Z'\right )\,\textrm{d} Z \nonumber \\[4pt] &- \nabla _{\parallel } \cdot \int _{\mathcal{H}/ 2}^{H_f + \mathcal{H}/ 2}\left (\int _{Z}^{H_f + \mathcal{H}/2}{\textsf{S}_{\parallel }(J^{(0)})}\, \textrm{d} Z'\right )\nabla _{\parallel } J^{(0)}\,\textrm{d} Z \nonumber \\[4pt] &+ \nabla _{\parallel } \cdot \int _{\mathcal{H}/ 2}^{H_f + \mathcal{H}/ 2}{\textsf{S}_{\parallel }(J^{(0)})} \left (\int _{\mathcal{H}/2}^{Z} \nabla _{\parallel } J^{(0)}\, \textrm{d} Z'\right )\, \textrm{d} Z\ \nonumber \\[4pt] &+ \nabla _{\parallel } \cdot \int _{\mathcal{H}/2}^{H_f + \mathcal{H}/2} \mathcal{E}{\textsf{S}_{\parallel }(J^{(0)})} \nabla _{\parallel } w\, \textrm{d} Z. \end{align}
\begin{align} \tau _{z} &= \nabla _{\parallel }^2 \int _{\mathcal{H}/2}^{H_f + \mathcal{H}/2} J^{(0)} \left (\int _{Z}^{H_f + \mathcal{H}/2}{\textsf{S}_{\parallel }(J^{(0)})}\,\textrm{d} Z'\right )\,\textrm{d} Z \nonumber \\[4pt] &- \nabla _{\parallel } \cdot \int _{\mathcal{H}/ 2}^{H_f + \mathcal{H}/ 2}\left (\int _{Z}^{H_f + \mathcal{H}/2}{\textsf{S}_{\parallel }(J^{(0)})}\, \textrm{d} Z'\right )\nabla _{\parallel } J^{(0)}\,\textrm{d} Z \nonumber \\[4pt] &+ \nabla _{\parallel } \cdot \int _{\mathcal{H}/ 2}^{H_f + \mathcal{H}/ 2}{\textsf{S}_{\parallel }(J^{(0)})} \left (\int _{\mathcal{H}/2}^{Z} \nabla _{\parallel } J^{(0)}\, \textrm{d} Z'\right )\, \textrm{d} Z\ \nonumber \\[4pt] &+ \nabla _{\parallel } \cdot \int _{\mathcal{H}/2}^{H_f + \mathcal{H}/2} \mathcal{E}{\textsf{S}_{\parallel }(J^{(0)})} \nabla _{\parallel } w\, \textrm{d} Z. \end{align}
At this point, the leading-order mechanical problem for the film has been solved in terms
![]() $J^{(0)} = 1 + \Phi ^{(0)} - \phi _0$
. Thus, all that remains is to solve the transport problem for the nominal solvent fraction
$J^{(0)} = 1 + \Phi ^{(0)} - \phi _0$
. Thus, all that remains is to solve the transport problem for the nominal solvent fraction
![]() $\Phi ^{(0)}$
.
$\Phi ^{(0)}$
.
The expressions for the traction (5.11) can be inserted into the FvK equation (4.8). In the distinguished limit
![]() $\delta = O(\epsilon )$
with
$\delta = O(\epsilon )$
with
![]() $\mathcal{E} = O(1)$
as
$\mathcal{E} = O(1)$
as
![]() $\epsilon \to 0$
, the full set of FvK equations must be solved; no further simplifications to the plate model are possible. In particular, both the in-plane and vertical tractions drive plate bending despite the differences in their orders of magnitude.
$\epsilon \to 0$
, the full set of FvK equations must be solved; no further simplifications to the plate model are possible. In particular, both the in-plane and vertical tractions drive plate bending despite the differences in their orders of magnitude.
5.1.2. Soft films on thick plates
We now consider the limit in which the film is thin relative to the plate,
![]() $\epsilon \ll \delta$
. We further assume that the film is soft so that
$\epsilon \ll \delta$
. We further assume that the film is soft so that
![]() $\mathcal{E} = O(1)$
. In this case, the deflection of the plate will be proportional to the film thickness. The film displacements are expanded as
$\mathcal{E} = O(1)$
. In this case, the deflection of the plate will be proportional to the film thickness. The film displacements are expanded as
![]() $\boldsymbol{{u}}_{\parallel } = \boldsymbol{{u}}_{\parallel }^{(0)} + o(1)$
and
$\boldsymbol{{u}}_{\parallel } = \boldsymbol{{u}}_{\parallel }^{(0)} + o(1)$
and
![]() $u_z = u_z^{(0)} + o(1)$
. The deformation gradient tensor
$u_z = u_z^{(0)} + o(1)$
. The deformation gradient tensor
![]() ${\sf\boldsymbol F}$
remains diagonal to leading order; see (4.7). Therefore, many of the results obtained in Section 5.1.1 for the case
${\sf\boldsymbol F}$
remains diagonal to leading order; see (4.7). Therefore, many of the results obtained in Section 5.1.1 for the case
![]() $\delta = O(\epsilon )$
still apply. In particular, the leading-order contributions to pressure, in-plane stresses, shear stresses and vertical displacement are given by (5.4a), (5.4b), (5.7), and (5.9b), respectively. The main difference occurs in the form of the in-plane displacement, which can be found from examining the
$\delta = O(\epsilon )$
still apply. In particular, the leading-order contributions to pressure, in-plane stresses, shear stresses and vertical displacement are given by (5.4a), (5.4b), (5.7), and (5.9b), respectively. The main difference occurs in the form of the in-plane displacement, which can be found from examining the
![]() $\alpha z$
component of the stress-strain relation (4.4), which reads as
$\alpha z$
component of the stress-strain relation (4.4), which reads as
where
![]() $J^{(0)} = 1 + \mathcal{E} \partial u_z^{(0)}/\partial Z = 1 + \Phi ^{(0)} - \phi _0$
. The leading-order contributions to (5.12), which are
$J^{(0)} = 1 + \mathcal{E} \partial u_z^{(0)}/\partial Z = 1 + \Phi ^{(0)} - \phi _0$
. The leading-order contributions to (5.12), which are
![]() $O(\delta )$
in size, imply that
$O(\delta )$
in size, imply that
![]() $\partial u_\alpha ^{(0)}/\partial Z = 0$
. Solving this equation and imposing continuity of in-plane displacements (4.12a) then shows that
$\partial u_\alpha ^{(0)}/\partial Z = 0$
. Solving this equation and imposing continuity of in-plane displacements (4.12a) then shows that
![]() $\boldsymbol{{u}}_{\parallel }^{(0)} = \bar{\boldsymbol{{u}}}_{\parallel } - (1/2) \nabla _{\parallel } w$
. Therefore, the in-plane displacement of the film simply matches that of the upper plate surface. In-plane deformation due to volumetric contraction is a higher-order effect.
$\boldsymbol{{u}}_{\parallel }^{(0)} = \bar{\boldsymbol{{u}}}_{\parallel } - (1/2) \nabla _{\parallel } w$
. Therefore, the in-plane displacement of the film simply matches that of the upper plate surface. In-plane deformation due to volumetric contraction is a higher-order effect.
The leading-order problem for the plate can be obtained by taking
![]() $\epsilon \to 0$
with
$\epsilon \to 0$
with
![]() $\epsilon \ll \delta$
and
$\epsilon \ll \delta$
and
![]() $\mathcal{E} = O(1)$
in the FvK equations given by (4.8). The vertical traction
$\mathcal{E} = O(1)$
in the FvK equations given by (4.8). The vertical traction
![]() $\tau _{z}$
drops out of (4.8a) and is not required. Thus, plate bending is dominated by the in-plane traction
$\tau _{z}$
drops out of (4.8a) and is not required. Thus, plate bending is dominated by the in-plane traction
![]() $\boldsymbol{\tau }_{\parallel }$
, which can be obtained from (5.11a). The nonlinear terms from
$\boldsymbol{\tau }_{\parallel }$
, which can be obtained from (5.11a). The nonlinear terms from
![]() $\nabla _{\parallel } \cdot (\bar{{\sf\boldsymbol S}}_{\parallel } \nabla _{\parallel } w)$
also drop out of (4.8a); thus, the vertical plate displacement satisfies a linear plate equation. The mean in-plane plate displacements
$\nabla _{\parallel } \cdot (\bar{{\sf\boldsymbol S}}_{\parallel } \nabla _{\parallel } w)$
also drop out of (4.8a); thus, the vertical plate displacement satisfies a linear plate equation. The mean in-plane plate displacements
![]() $\bar{\boldsymbol{{u}}}_{\parallel }$
can be obtained by solving (4.8b)–(4.8d) after neglecting the nonlinear terms in the strain tensor (4.8d).
$\bar{\boldsymbol{{u}}}_{\parallel }$
can be obtained by solving (4.8b)–(4.8d) after neglecting the nonlinear terms in the strain tensor (4.8d).
5.1.3. Stiff films on thick plates
The final case to consider is when the film is thin relative to the plate,
![]() $\epsilon \ll \delta$
, and stiff, so that
$\epsilon \ll \delta$
, and stiff, so that
![]() $\mathcal{E} = O(\delta \epsilon ^{-1})$
. We therefore write the effective film stiffness as
$\mathcal{E} = O(\delta \epsilon ^{-1})$
. We therefore write the effective film stiffness as
![]() $\mathcal{E} = \delta \epsilon ^{-1} \mathcal{E}_1$
. The deformation gradient tensor for the film (4.7) is given by
$\mathcal{E} = \delta \epsilon ^{-1} \mathcal{E}_1$
. The deformation gradient tensor for the film (4.7) is given by
The requirement that
![]() ${\sf\boldsymbol F}$
is invertible implies that the large
${\sf\boldsymbol F}$
is invertible implies that the large
![]() $O(\delta \epsilon ^{-1})$
term in (5.13) must be smaller in magnitude; consequently, the vertical displacement must have the expansion
$O(\delta \epsilon ^{-1})$
term in (5.13) must be smaller in magnitude; consequently, the vertical displacement must have the expansion
The expansion for the in-plane film displacement can be found using a similar argument to that in Section 5.1.2, leading to
By imposing continuity of displacement (4.12), we conclude that
![]() $\boldsymbol{{u}}_{\parallel }^{(0)} = \bar{\boldsymbol{{u}}}_{\parallel } - (1/2) \nabla _{\parallel } w$
and
$\boldsymbol{{u}}_{\parallel }^{(0)} = \bar{\boldsymbol{{u}}}_{\parallel } - (1/2) \nabla _{\parallel } w$
and
![]() $u_z^{(0)} = w$
. Thus, the leading-order film displacement matches the plate displacement, i.e. the film simply bends with the plate. Boundary conditions for
$u_z^{(0)} = w$
. Thus, the leading-order film displacement matches the plate displacement, i.e. the film simply bends with the plate. Boundary conditions for
![]() $\tilde{\boldsymbol{{u}}}_{\parallel }$
and
$\tilde{\boldsymbol{{u}}}_{\parallel }$
and
![]() $\tilde{u}_z$
could be obtained by calculating a higher-order solution to the plate model and imposing continuity of displacement; however, we do not do this here. The deformation gradient tensor for the film therefore reduces to
$\tilde{u}_z$
could be obtained by calculating a higher-order solution to the plate model and imposing continuity of displacement; however, we do not do this here. The deformation gradient tensor for the film therefore reduces to
Although
![]() ${\sf\boldsymbol F}$
is diagonal to leading order, the
${\sf\boldsymbol F}$
is diagonal to leading order, the
![]() $O(\delta )$
corrections result in substantially different film mechanics compared to when the film is soft (
$O(\delta )$
corrections result in substantially different film mechanics compared to when the film is soft (
![]() $\mathcal{E} = O(1)$
). To see this, the deformation gradient tensor (5.16) can be substituted into the stress-strain relation (4.4). Collecting the
$\mathcal{E} = O(1)$
). To see this, the deformation gradient tensor (5.16) can be substituted into the stress-strain relation (4.4). Collecting the
![]() $O(\delta )$
contributions to the
$O(\delta )$
contributions to the
![]() $\alpha z$
and
$\alpha z$
and
![]() $z \alpha$
components leads to the following equations, respectively,
$z \alpha$
components leads to the following equations, respectively,
where
![]() $J^{(0)} = 1 + \mathcal{E}_1 \partial \tilde{u}_z/\partial Z$
. Solving (5.17) shows that
$J^{(0)} = 1 + \mathcal{E}_1 \partial \tilde{u}_z/\partial Z$
. Solving (5.17) shows that
![]() $\nabla _{\parallel } w = \textbf{0}$
, which implies that the plate remains flat. This unphysical result stems from the assumption that the shear stresses
$\nabla _{\parallel } w = \textbf{0}$
, which implies that the plate remains flat. This unphysical result stems from the assumption that the shear stresses
![]() $\textsf{S}_{\alpha z}$
and
$\textsf{S}_{\alpha z}$
and
![]() $\textsf{S}_{z \alpha }$
in the film have the same order of magnitude, which would be the case in linear elasticity. Thus, a resolution can be found by elevating the asymptotic order of
$\textsf{S}_{z \alpha }$
in the film have the same order of magnitude, which would be the case in linear elasticity. Thus, a resolution can be found by elevating the asymptotic order of
![]() $\textsf{S}_{z \alpha }$
and writing
$\textsf{S}_{z \alpha }$
and writing
![]() $\textsf{S}_{z \alpha } = \delta \epsilon ^{-1} \tilde{\textsf{S}}_{z \alpha }$
. From the vertical stress balance (4.3b), we must also elevate the order of
$\textsf{S}_{z \alpha } = \delta \epsilon ^{-1} \tilde{\textsf{S}}_{z \alpha }$
. From the vertical stress balance (4.3b), we must also elevate the order of
![]() $\textsf{S}_{zz}$
by writing
$\textsf{S}_{zz}$
by writing
![]() $\textsf{S}_{zz} = \delta \epsilon ^{-1} \tilde{\textsf{S}}_{zz}$
. Importantly, the elevated order of the vertical stress implies that the non-dimensional vertical traction must also be rescaled according to
$\textsf{S}_{zz} = \delta \epsilon ^{-1} \tilde{\textsf{S}}_{zz}$
. Importantly, the elevated order of the vertical stress implies that the non-dimensional vertical traction must also be rescaled according to
![]() $\tau _{z} = \delta \epsilon ^{-1} \tilde{\tau }_{z}$
. In terms of dimensional quantities, these rescalings imply that
$\tau _{z} = \delta \epsilon ^{-1} \tilde{\tau }_{z}$
. In terms of dimensional quantities, these rescalings imply that
![]() $\textsf{S}_{z \alpha } \sim \delta E_f$
,
$\textsf{S}_{z \alpha } \sim \delta E_f$
,
![]() $\textsf{S}_{zz} \sim \epsilon \delta E_f$
, and
$\textsf{S}_{zz} \sim \epsilon \delta E_f$
, and
![]() $\tau _{z} \sim \epsilon \delta E_f$
.
$\tau _{z} \sim \epsilon \delta E_f$
.
With these rescalings, we proceed by expanding
![]() ${\sf\boldsymbol S}_{\perp } = {\sf\boldsymbol S}_{\perp }^{(1)} + o(1)$
and
${\sf\boldsymbol S}_{\perp } = {\sf\boldsymbol S}_{\perp }^{(1)} + o(1)$
and
![]() $\tilde{\textsf{S}}_{z \alpha }$
as
$\tilde{\textsf{S}}_{z \alpha }$
as
![]() $\tilde{\textsf{S}}_{z \alpha } = \tilde{\textsf{S}}_{z \alpha }^{(1,1)} + o(1)$
. The
$\tilde{\textsf{S}}_{z \alpha } = \tilde{\textsf{S}}_{z \alpha }^{(1,1)} + o(1)$
. The
![]() $\alpha z$
component of the stress-strain relation still leads to (5.17a); however, the
$\alpha z$
component of the stress-strain relation still leads to (5.17a); however, the
![]() $z \alpha$
component now gives
$z \alpha$
component now gives
which replaces (5.17b). The second equality arises from using (5.17a) and the definition of
![]() $\textsf{S}_{\parallel }$
in (5.5). The vertical traction can now be obtained by substituting (5.18) into (4.13b) to find that
$\textsf{S}_{\parallel }$
in (5.5). The vertical traction can now be obtained by substituting (5.18) into (4.13b) to find that
Despite the elevated asymptotic order of the vertical stress
![]() $\textsf{S}_{zz}$
, the
$\textsf{S}_{zz}$
, the
![]() $zz$
component of the stress-strain relation (4.4) leads to an expression for the pressure that is identical to (5.4a). Consequently, the in-plane stresses and traction are given by (5.4b) and (5.11a), respectively.
$zz$
component of the stress-strain relation (4.4) leads to an expression for the pressure that is identical to (5.4a). Consequently, the in-plane stresses and traction are given by (5.4b) and (5.11a), respectively.
In the regime of stiff films on thick plates,
![]() $\epsilon \ll \delta$
with
$\epsilon \ll \delta$
with
![]() $\mathcal{E} = O(\delta \epsilon ^{-1})$
, the full set of FvK equations given by (4.8) must be solved. The small
$\mathcal{E} = O(\delta \epsilon ^{-1})$
, the full set of FvK equations given by (4.8) must be solved. The small
![]() $O(\epsilon \delta ^{-1})$
prefactor of
$O(\epsilon \delta ^{-1})$
prefactor of
![]() $\tau _{z}$
in (4.8a) is exactly offset by the large
$\tau _{z}$
in (4.8a) is exactly offset by the large
![]() $O(\delta \epsilon ^{-1})$
magnitude of
$O(\delta \epsilon ^{-1})$
magnitude of
![]() $\tau _{z}$
. Consequently, the vertical traction must be considered despite the film being much thinner than the plate.
$\tau _{z}$
. Consequently, the vertical traction must be considered despite the film being much thinner than the plate.
5.2. Film drying
Having solved the mechanical problem in the film, the fluid-transport problem is asymptotically reduced by taking the limit
![]() $\epsilon \to 0$
. The goal is to derive a hierarchy of evolution equations for the nominal solvent fraction that capture different drying regimes depending on the magnitude of the Péclet number,
$\epsilon \to 0$
. The goal is to derive a hierarchy of evolution equations for the nominal solvent fraction that capture different drying regimes depending on the magnitude of the Péclet number,
![]() $\textrm{Pe}$
.
$\textrm{Pe}$
.
Physically, the different drying regimes arise from differences in the relative rates at which fluid is removed from the pore space by evaporation and replenished by bulk transport. When
![]() $\textrm{Pe} = O(1)$
, the time scales of evaporation and in-plane fluid transport are commensurate. If
$\textrm{Pe} = O(1)$
, the time scales of evaporation and in-plane fluid transport are commensurate. If
![]() $\textrm{Pe} \ll 1$
, evaporation is slow and a homogeneous drying process can be expected. When
$\textrm{Pe} \ll 1$
, evaporation is slow and a homogeneous drying process can be expected. When
![]() $\textrm{Pe} \gg 1$
, evaporation is fast relative to in-plane transport and a highly non-uniform film composition is likely to arise.
$\textrm{Pe} \gg 1$
, evaporation is fast relative to in-plane transport and a highly non-uniform film composition is likely to arise.
In reducing the fluid-transport problem, we work within the distinguished limit of
![]() $\delta = O(\epsilon )$
as
$\delta = O(\epsilon )$
as
![]() $\epsilon \to 0$
by assuming the film and plate have comparable thicknesses. In this case, the deformation gradient tensor has the asymptotic expansion
$\epsilon \to 0$
by assuming the film and plate have comparable thicknesses. In this case, the deformation gradient tensor has the asymptotic expansion
![]() ${\sf\boldsymbol F} = \textrm{diag}(1, 1, J) + O(\epsilon )$
. Thus, the off-diagonal components of the permeability tensor are small, specifically,
${\sf\boldsymbol F} = \textrm{diag}(1, 1, J) + O(\epsilon )$
. Thus, the off-diagonal components of the permeability tensor are small, specifically,
![]() ${\sf\boldsymbol {K}}_{\perp } = O(\epsilon )$
. We therefore expand the pressure, nominal fluid fraction, and components of the permeability tensor as
${\sf\boldsymbol {K}}_{\perp } = O(\epsilon )$
. We therefore expand the pressure, nominal fluid fraction, and components of the permeability tensor as
![]() $p = p^{(0)} + O(\epsilon )$
,
$p = p^{(0)} + O(\epsilon )$
,
![]() $\Phi = \Phi ^{(0)} + O(\epsilon )$
,
$\Phi = \Phi ^{(0)} + O(\epsilon )$
,
![]() ${\sf\boldsymbol {K}}_{\parallel } = {\sf\boldsymbol {K}}_{\parallel }^{(0)} + O(\epsilon )$
,
${\sf\boldsymbol {K}}_{\parallel } = {\sf\boldsymbol {K}}_{\parallel }^{(0)} + O(\epsilon )$
,
![]() ${\sf\boldsymbol {K}}_{\perp } = \epsilon {\sf\boldsymbol {K}}_{\perp }^{(1)} + O(\epsilon ^2)$
, and
${\sf\boldsymbol {K}}_{\perp } = \epsilon {\sf\boldsymbol {K}}_{\perp }^{(1)} + O(\epsilon ^2)$
, and
![]() ${\textsf{K}}_{zz} ={\textsf{K}}_{zz}^{(0)} + O(\epsilon )$
. The expansions of the flux will depend on the size of
${\textsf{K}}_{zz} ={\textsf{K}}_{zz}^{(0)} + O(\epsilon )$
. The expansions of the flux will depend on the size of
![]() $\textrm{Pe}$
.
$\textrm{Pe}$
.
Although the reduction of the fluid-transport problem will be carried out in the limit that
![]() $\delta = O(\epsilon )$
, the results also apply when the film is thin relative to the plate and
$\delta = O(\epsilon )$
, the results also apply when the film is thin relative to the plate and
![]() $\delta \gg \epsilon$
.
$\delta \gg \epsilon$
.
5.2.1. Slow evaporation:
 $\textrm{Pe} = O(1)$
$\textrm{Pe} = O(1)$
We first consider the drying problem when the evaporation is slow, as characterised by
![]() $\textrm{Pe} = O(1)$
as
$\textrm{Pe} = O(1)$
as
![]() $\epsilon \to 0$
. The components of the flux are expanded as
$\epsilon \to 0$
. The components of the flux are expanded as
![]() $\boldsymbol{{Q}}_\parallel = \boldsymbol{{Q}}_\parallel ^{(0)} + O(\epsilon )$
and
$\boldsymbol{{Q}}_\parallel = \boldsymbol{{Q}}_\parallel ^{(0)} + O(\epsilon )$
and
![]() $Q_z = Q_z^{(0)} + O(\epsilon )$
. Collecting the
$Q_z = Q_z^{(0)} + O(\epsilon )$
. Collecting the
![]() $O(\epsilon ^{-2})$
terms in (4.2b) lead to the conclusion that the pressure
$O(\epsilon ^{-2})$
terms in (4.2b) lead to the conclusion that the pressure
![]() $p^{(0)}$
, and hence
$p^{(0)}$
, and hence
![]() $J^{(0)}$
and
$J^{(0)}$
and
![]() $\Phi ^{(0)}$
, are independent of
$\Phi ^{(0)}$
, are independent of
![]() $Z$
. Therefore, the film composition is uniform along the vertical direction. The
$Z$
. Therefore, the film composition is uniform along the vertical direction. The
![]() $O(1)$
terms in (4.2a) provide an expression for the in-plane flux,
$O(1)$
terms in (4.2a) provide an expression for the in-plane flux,
![]() $\boldsymbol{{Q}}_\parallel ^{(0)} = -{\sf\boldsymbol {K}}_{\parallel }^{(0)} \nabla _{\parallel } p^{(0)}$
, where
$\boldsymbol{{Q}}_\parallel ^{(0)} = -{\sf\boldsymbol {K}}_{\parallel }^{(0)} \nabla _{\parallel } p^{(0)}$
, where
![]() ${\sf\boldsymbol {K}}_{\parallel }^{(0)} = k(\phi ^{(0)}) J^{(0)} {\sf\boldsymbol I}_{\parallel }$
. The Eulerian fluid fraction is given by
${\sf\boldsymbol {K}}_{\parallel }^{(0)} = k(\phi ^{(0)}) J^{(0)} {\sf\boldsymbol I}_{\parallel }$
. The Eulerian fluid fraction is given by
![]() $\phi ^{(0)} = \Phi ^{(0)}/ J^{(0)}$
.
$\phi ^{(0)} = \Phi ^{(0)}/ J^{(0)}$
.
By integrating the solvent conservation equation (4.1) from
![]() $Z = \mathcal{H}/2$
to
$Z = \mathcal{H}/2$
to
![]() $Z = H_f(\boldsymbol{{X}}_{\parallel }) + \mathcal{H}/2$
and using the boundary conditions (4.10a) and (4.11), we find that the nominal solvent fraction evolves according to
$Z = H_f(\boldsymbol{{X}}_{\parallel }) + \mathcal{H}/2$
and using the boundary conditions (4.10a) and (4.11), we find that the nominal solvent fraction evolves according to
where
![]() $J^{(0)} = 1 + \Phi ^{(0)} - \phi _0$
. Upon substituting the expression for the pressure
$J^{(0)} = 1 + \Phi ^{(0)} - \phi _0$
. Upon substituting the expression for the pressure
![]() $p^{(0)}$
given by (5.4a) into (5.20), a nonlinear diffusion equation for
$p^{(0)}$
given by (5.4a) into (5.20), a nonlinear diffusion equation for
![]() $\Phi ^{(0)}$
is obtained. Equation (5.20) can be solved with the boundary conditions
$\Phi ^{(0)}$
is obtained. Equation (5.20) can be solved with the boundary conditions
![]() $\boldsymbol{{Q}}_\parallel ^{(0)} \cdot \boldsymbol{{N}} = 0$
at the contact line,
$\boldsymbol{{Q}}_\parallel ^{(0)} \cdot \boldsymbol{{N}} = 0$
at the contact line,
![]() $X_1=0$
,
$X_1=0$
,
![]() $X_1 = 1$
and
$X_1 = 1$
and
![]() $X_2 = \pm \mathcal{W}/2$
, along with the initial condition
$X_2 = \pm \mathcal{W}/2$
, along with the initial condition
![]() $\Phi ^{(0)} = \phi _0$
.
$\Phi ^{(0)} = \phi _0$
.
Upon solving for
![]() $\Phi ^{(0)}$
and computing
$\Phi ^{(0)}$
and computing
![]() $J^{(0)}$
, the Eulerian film thickness can be obtained from (5.10) as
$J^{(0)}$
, the Eulerian film thickness can be obtained from (5.10) as
![]() $h_f = J^{(0)} H_f$
. Moreover, the traction can be determined from (5.11) as
$h_f = J^{(0)} H_f$
. Moreover, the traction can be determined from (5.11) as
where
![]() $\textsf{S}_{\parallel } = \textsf{S}_{\parallel }(J^{(0)})$
is given by (5.5). In the thin-film regime
$\textsf{S}_{\parallel } = \textsf{S}_{\parallel }(J^{(0)})$
is given by (5.5). In the thin-film regime
![]() $\delta \gg \epsilon$
with
$\delta \gg \epsilon$
with
![]() $\mathcal{E} = O(1)$
, the in-plane traction is given by (5.21a) and the vertical traction (5.21b) is not required. When
$\mathcal{E} = O(1)$
, the in-plane traction is given by (5.21a) and the vertical traction (5.21b) is not required. When
![]() $\delta \gg \epsilon$
with
$\delta \gg \epsilon$
with
![]() $\mathcal{E} = O(\delta \epsilon ^{-1})$
, the in-plane traction is given by (5.21a) and the vertical traction is
$\mathcal{E} = O(\delta \epsilon ^{-1})$
, the in-plane traction is given by (5.21a) and the vertical traction is
If evaporation is very slow,
![]() $\textrm{Pe} \ll 1$
, then time can be rescaled as
$\textrm{Pe} \ll 1$
, then time can be rescaled as
![]() $t \sim \textrm{Pe}^{-1}$
. The leading-order (in
$t \sim \textrm{Pe}^{-1}$
. The leading-order (in
![]() $\textrm{Pe}$
) part of (5.20) then implies that
$\textrm{Pe}$
) part of (5.20) then implies that
![]() $p^{(0)}$
and hence
$p^{(0)}$
and hence
![]() $\Phi ^{(0)}$
are uniform in space. Integrating (5.20) over the plate surface leads to a simple differential equation for the nominal volume fraction, which can be expressed in terms of the original non-dimensional time as
$\Phi ^{(0)}$
are uniform in space. Integrating (5.20) over the plate surface leads to a simple differential equation for the nominal volume fraction, which can be expressed in terms of the original non-dimensional time as
where
![]() $V_0$
is the initial volume of the film. By taking
$V_0$
is the initial volume of the film. By taking
![]() $J^{(0)}$
and hence
$J^{(0)}$
and hence
![]() $\textsf{S}_{\parallel }$
to be constant in (5.21a), the in-plane traction reduces to
$\textsf{S}_{\parallel }$
to be constant in (5.21a), the in-plane traction reduces to
![]() $\boldsymbol{\tau }_{\parallel } = \textsf{S}_{\parallel } \nabla _{\parallel } H_f$
. Given that
$\boldsymbol{\tau }_{\parallel } = \textsf{S}_{\parallel } \nabla _{\parallel } H_f$
. Given that
![]() $\textsf{S}_{\parallel } \gt 0$
, the direction of the traction follows the gradient of the film thickness. Near the contact line, where
$\textsf{S}_{\parallel } \gt 0$
, the direction of the traction follows the gradient of the film thickness. Near the contact line, where
![]() $H_f$
tends to zero, the film will always pull the plate inwards, that is, towards the centre of the plate.
$H_f$
tends to zero, the film will always pull the plate inwards, that is, towards the centre of the plate.
5.2.2. Moderate evaporation:
 $\textrm{Pe} = O(\epsilon ^{-1})$
$\textrm{Pe} = O(\epsilon ^{-1})$
The limit of moderate evaporation is characterised by
![]() $\textrm{Pe} = O(\epsilon ^{-1})$
. Thus, we write
$\textrm{Pe} = O(\epsilon ^{-1})$
. Thus, we write
![]() $\textrm{Pe} = \epsilon ^{-1} \textrm{Pe}_0$
. In order to obtain a balance in the boundary condition (4.10a), we must rescale the vertical component of the flux as
$\textrm{Pe} = \epsilon ^{-1} \textrm{Pe}_0$
. In order to obtain a balance in the boundary condition (4.10a), we must rescale the vertical component of the flux as
![]() $Q_z = \epsilon ^{-1} \tilde{Q}_z$
. Both flux components now have the same order of magnitude. Despite the elevated asymptotic order of
$Q_z = \epsilon ^{-1} \tilde{Q}_z$
. Both flux components now have the same order of magnitude. Despite the elevated asymptotic order of
![]() $Q_z$
, the vertical component of Darcy’s law (4.2b) implies that
$Q_z$
, the vertical component of Darcy’s law (4.2b) implies that
![]() $p^{(0)}$
,
$p^{(0)}$
,
![]() $J^{(0)}$
and
$J^{(0)}$
and
![]() $\Phi ^{(0)}$
are still independent of
$\Phi ^{(0)}$
are still independent of
![]() $Z$
. Balancing terms in the conservation law for the nominal fluid fraction (4.1) requires rescaling time as
$Z$
. Balancing terms in the conservation law for the nominal fluid fraction (4.1) requires rescaling time as
![]() $t = \epsilon \tilde{t}$
. Integrating the
$t = \epsilon \tilde{t}$
. Integrating the
![]() $O(\epsilon ^{-1})$
terms in the conservation law across the film thickness leads to
$O(\epsilon ^{-1})$
terms in the conservation law across the film thickness leads to
Equation (5.24) can be treated as an ordinary differential equation for
![]() $\Phi ^{(0)}$
, with the in-plane coordinates
$\Phi ^{(0)}$
, with the in-plane coordinates
![]() $\boldsymbol{{X}}_{\parallel }$
acting as parameters, and solved with the initial condition
$\boldsymbol{{X}}_{\parallel }$
acting as parameters, and solved with the initial condition
![]() $\Phi ^{(0)} = \phi _0$
at
$\Phi ^{(0)} = \phi _0$
at
![]() $\tilde{t} = 0$
. The expressions for the traction that are provided in Section 5.2.1 also apply to this drying regime.
$\tilde{t} = 0$
. The expressions for the traction that are provided in Section 5.2.1 also apply to this drying regime.
The reduced transport problem defined by (5.24) does not capture the in-plane components of the fluid flux. However, near the contact line, where
![]() $H_f$
is small, (5.24) predicts that the nominal fluid fraction will undergo a rapid decrease. Consequently, large in-plane gradients in the fluid fraction are expected near the contact line, and these will locally amplify the in-plane flux. From an asymptotics perspective, near the contact line, the order of the in-plane flux must be elevated, resulting in additional terms that must be considered in the reduced model. The dynamics near the contact line can therefore be resolved by carrying out a boundary-layer analysis using matched asymptotic expansions. However, we do not resolve these boundary layers because they are unimportant in terms of plate bending; see Section 6.2 for more details.
$H_f$
is small, (5.24) predicts that the nominal fluid fraction will undergo a rapid decrease. Consequently, large in-plane gradients in the fluid fraction are expected near the contact line, and these will locally amplify the in-plane flux. From an asymptotics perspective, near the contact line, the order of the in-plane flux must be elevated, resulting in additional terms that must be considered in the reduced model. The dynamics near the contact line can therefore be resolved by carrying out a boundary-layer analysis using matched asymptotic expansions. However, we do not resolve these boundary layers because they are unimportant in terms of plate bending; see Section 6.2 for more details.
5.2.3. Fast evaporation:
 $\textrm{Pe} = O(\epsilon ^{-2})$
$\textrm{Pe} = O(\epsilon ^{-2})$
The limit of fast evaporation occurs when
![]() $\textrm{Pe} = O(\epsilon ^{-2})$
. Thus, we write
$\textrm{Pe} = O(\epsilon ^{-2})$
. Thus, we write
![]() $\textrm{Pe} = \epsilon ^{-2} \textrm{Pe}_1$
. By following the same strategy as in Section 5.2.2, we deduce that capturing the dynamics requires rescaling time as
$\textrm{Pe} = \epsilon ^{-2} \textrm{Pe}_1$
. By following the same strategy as in Section 5.2.2, we deduce that capturing the dynamics requires rescaling time as
![]() $t = \epsilon ^2 \hat{t}$
and the vertical component of the flux as
$t = \epsilon ^2 \hat{t}$
and the vertical component of the flux as
![]() $Q_z = \epsilon ^{-2} \hat{Q}_z$
. By writing
$Q_z = \epsilon ^{-2} \hat{Q}_z$
. By writing
![]() $\hat{Q}_z = \hat{Q}_z^{({-}2)} + O(\epsilon )$
and equating the
$\hat{Q}_z = \hat{Q}_z^{({-}2)} + O(\epsilon )$
and equating the
![]() $O(\epsilon ^{-2})$
components of (4.2b), we find that
$O(\epsilon ^{-2})$
components of (4.2b), we find that
![]() $\hat{Q}_z^{({-}2)} = -{\textsf{K}}_{zz}^{(0)} \partial _Z p^{(0)}$
, with
$\hat{Q}_z^{({-}2)} = -{\textsf{K}}_{zz}^{(0)} \partial _Z p^{(0)}$
, with
![]() ${\textsf{K}}_{zz}^{(0)} = k(\phi ^{(0)})/ J^{(0)}$
. Therefore, the rate of evaporation is now sufficiently large that vertical gradients will occur in the pressure
${\textsf{K}}_{zz}^{(0)} = k(\phi ^{(0)})/ J^{(0)}$
. Therefore, the rate of evaporation is now sufficiently large that vertical gradients will occur in the pressure
![]() $p^{(0)}$
, the volumetric contraction ratio
$p^{(0)}$
, the volumetric contraction ratio
![]() $J^{(0)}$
, and the nominal fluid fraction
$J^{(0)}$
, and the nominal fluid fraction
![]() $\Phi ^{(0)}$
. Equating the
$\Phi ^{(0)}$
. Equating the
![]() $O(\epsilon ^{-2})$
contributions of the conservation law (4.1) leads to a nonlinear diffusion equation for the fluid fraction given by
$O(\epsilon ^{-2})$
contributions of the conservation law (4.1) leads to a nonlinear diffusion equation for the fluid fraction given by
The boundary conditions and initial for (5.25) are
Again, the in-plane coordinates
![]() $\boldsymbol{{X}}_{\parallel }$
play the role of parameters. After solving for
$\boldsymbol{{X}}_{\parallel }$
play the role of parameters. After solving for
![]() $\Phi ^{(0)}$
and hence
$\Phi ^{(0)}$
and hence
![]() $J^{(0)}$
, the tractions can be evaluated by computing the integrals in (5.11a) and (5.11b) or (5.19).
$J^{(0)}$
, the tractions can be evaluated by computing the integrals in (5.11a) and (5.11b) or (5.19).
The reduced transport problem (5.25) does not capture in-plane fluid transport. However, in contrast to the case
![]() $\textrm{Pe} = O(\epsilon ^{-1})$
, the contributions from the in-plane fluid flux are always asymptotically smaller than those from the large vertical flux. Therefore, there is no need to resolve the dynamics near the contact line using a separate boundary-layer analysis.
$\textrm{Pe} = O(\epsilon ^{-1})$
, the contributions from the in-plane fluid flux are always asymptotically smaller than those from the large vertical flux. Therefore, there is no need to resolve the dynamics near the contact line using a separate boundary-layer analysis.
6. Validation and parametric studies
The asymptotic reductions are validated by comparing them against finite element (FE) solutions of the fully coupled film-plate model proposed in Section 2. The FE method is implemented in Python with FEniCS [Reference Alnæs, Blechta and Hake1, Reference Logg, Mardal and Wells28]. The multiphenics [Reference Ballarin and Rozza2] package is used to couple the film and plate problems. The traction
![]() $\boldsymbol{\tau }$
is treated as a Lagrange multiplier that enables the continuity of displacement at the film-plate interface to be imposed. The film and plate displacements are represented using P2 elements. The pressure and nominal fluid fraction are represented using P1 elements. Finally, DGT1 elements are used for the traction. Time is discretised using a fully implicit Euler method with a fixed time step. The film and plate problems are simultaneously solved as a monolithic nonlinear system. We employ the PETSc SNES nonlinear solver, using MUMPS to solve the linear systems during each Newton iteration.
$\boldsymbol{\tau }$
is treated as a Lagrange multiplier that enables the continuity of displacement at the film-plate interface to be imposed. The film and plate displacements are represented using P2 elements. The pressure and nominal fluid fraction are represented using P1 elements. Finally, DGT1 elements are used for the traction. Time is discretised using a fully implicit Euler method with a fixed time step. The film and plate problems are simultaneously solved as a monolithic nonlinear system. We employ the PETSc SNES nonlinear solver, using MUMPS to solve the linear systems during each Newton iteration.
The FE simulations are carried out in a two-dimensional Cartesian geometry under the assumption of plane strain (
![]() $\mathcal{W} \gg 1$
). In this case, the plate reduces to a beam and the FvK equations (4.8) simplify considerably. The case of plane stress, valid for plates with small widths (
$\mathcal{W} \gg 1$
). In this case, the plate reduces to a beam and the FvK equations (4.8) simplify considerably. The case of plane stress, valid for plates with small widths (
![]() $\mathcal{W} \ll 1$
), can be considered by replacing
$\mathcal{W} \ll 1$
), can be considered by replacing
![]() $\mathcal{B}$
with
$\mathcal{B}$
with
![]() $(1 - \nu _p^2) \mathcal{B}$
in the expressions below. The film is assumed to have a parabolic initial profile that can be written in dimensional form as
$(1 - \nu _p^2) \mathcal{B}$
in the expressions below. The film is assumed to have a parabolic initial profile that can be written in dimensional form as
![]() $H_f(X) = 4 \epsilon X (1 - X/ L)$
, where we define
$H_f(X) = 4 \epsilon X (1 - X/ L)$
, where we define
![]() $X \equiv X_1$
for simplicity. The plate is assumed to be made of steel with a Poisson’s ratio of
$X \equiv X_1$
for simplicity. The plate is assumed to be made of steel with a Poisson’s ratio of
![]() $\nu _p = 0.27$
. The Poisson’s ratio of the film is set to
$\nu _p = 0.27$
. The Poisson’s ratio of the film is set to
![]() $\nu _f = 0.2$
, corresponding to a porous matrix formed from a dried colloidal dispersion [Reference Style and Peppin37].
$\nu _f = 0.2$
, corresponding to a porous matrix formed from a dried colloidal dispersion [Reference Style and Peppin37].
Snapshots from a typical FE simulation are shown in Figure 2. The Eulerian fluid fraction in the film
![]() $\phi = \Phi/ J$
is plotted as a heat map. It has been assumed that the film and plate have the same thickness,
$\phi = \Phi/ J$
is plotted as a heat map. It has been assumed that the film and plate have the same thickness,
![]() $\epsilon = \delta = 0.1$
. The Péclet number has been set to
$\epsilon = \delta = 0.1$
. The Péclet number has been set to
![]() $\textrm{Pe} = 100$
. The effective film stiffness has been set to
$\textrm{Pe} = 100$
. The effective film stiffness has been set to
![]() $\mathcal{E} = 3$
. The other parameters are discussed in Section 6.2. Due to Péclet number being
$\mathcal{E} = 3$
. The other parameters are discussed in Section 6.2. Due to Péclet number being
![]() $O(\epsilon ^{-2})$
in size, film drying is highly non-uniform. Drying first occurs at the contact line, where the film is the thinnest, and then proceeds inwards. Due to the high rate of evaporation, fluid that is removed from the pore space near the free surface cannot be replenished by fluid in the bulk; hence, vertical gradients in the composition arise. Despite drying initially being confined to the contact line, the plate undergoes an appreciable deflection for small times. The deflection then monotonically increases as the film approaches its homogeneous steady state.
$O(\epsilon ^{-2})$
in size, film drying is highly non-uniform. Drying first occurs at the contact line, where the film is the thinnest, and then proceeds inwards. Due to the high rate of evaporation, fluid that is removed from the pore space near the free surface cannot be replenished by fluid in the bulk; hence, vertical gradients in the composition arise. Despite drying initially being confined to the contact line, the plate undergoes an appreciable deflection for small times. The deflection then monotonically increases as the film approaches its homogeneous steady state.

Figure 2. Finite element simulations of the film-plate model presented in Sec. 2. The heat map represents the Eulerian fluid fraction (porosity) of the film,
![]() $\phi = \Phi / J$
. Simulation snapshots are shown at times (a)
$\phi = \Phi / J$
. Simulation snapshots are shown at times (a)
![]() $t = 0$
, (b)
$t = 0$
, (b)
![]() $t = 0.005$
, (c)
$t = 0.005$
, (c)
![]() $t = 0.010$
, (d)
$t = 0.010$
, (d)
![]() $t = 0.015$
, (e)
$t = 0.015$
, (e)
![]() $t = 0.020$
, and (f)
$t = 0.020$
, and (f)
![]() $t = 0.025$
. The parameter values are
$t = 0.025$
. The parameter values are
![]() $\epsilon = \delta = 0.1$
,
$\epsilon = \delta = 0.1$
,
![]() $\textrm{Pe} = 100$
,
$\textrm{Pe} = 100$
,
![]() $\varepsilon = 3$
with
$\varepsilon = 3$
with
![]() $\phi_0 = 0.68$
, and
$\phi_0 = 0.68$
, and
![]() $k(\phi) \equiv 1$
. The non-dimensional evaporative flux is
$k(\phi) \equiv 1$
. The non-dimensional evaporative flux is
![]() $\mathcal{V}(\phi) = \phi - \phi_\infty$
, where
$\mathcal{V}(\phi) = \phi - \phi_\infty$
, where
![]() $\phi_\infty = 0.36$
.
$\phi_\infty = 0.36$
.
6.1. Comparison of the steady states
Calculating the steady states of the film-plate system enables the accuracy of the asymptotic solutions of the mechanical problem to be established. In particular, the steady states satisfy a purely mechanical problem and can be obtained without solving the fluid-transport problem. Thus, in this section, it is assumed that the film has dried to a homogeneous steady state with uniform contraction ratio
![]() $J \lt 1$
. In this case, the poroelastic model for the film developed in Section 2.3 reduces to the equilibrium equations of incompressible nonlinear elasticity,
$J \lt 1$
. In this case, the poroelastic model for the film developed in Section 2.3 reduces to the equilibrium equations of incompressible nonlinear elasticity,
![]() $\nabla \cdot {\sf\boldsymbol S} = \textbf{0}$
with
$\nabla \cdot {\sf\boldsymbol S} = \textbf{0}$
with
![]() $\det {\sf\boldsymbol F} = J$
, where
$\det {\sf\boldsymbol F} = J$
, where
![]() $J$
is now treated as a prescribed constant.
$J$
is now treated as a prescribed constant.
When the full problem is posed in two Cartesian dimensions under the assumption of plane strain, the FvK equations (4.8) become one-dimensional. Moreover, when
![]() $J$
is uniform in the vertical direction so that the expressions for the tractions in (5.21) apply, then the mean in-plane plate stress can be obtained from (4.8b) as
$J$
is uniform in the vertical direction so that the expressions for the tractions in (5.21) apply, then the mean in-plane plate stress can be obtained from (4.8b) as
![]() $\bar{\textsf{S}}_{11} = -H_f \textsf{S}_{\parallel }(J)$
, where
$\bar{\textsf{S}}_{11} = -H_f \textsf{S}_{\parallel }(J)$
, where
![]() $\textsf{S}_{\parallel }(J)$
is given by (5.5). Inserting this result along with the tractions (5.21) into (4.8a) leads to cancellations that allow two integrations to be performed. After imposing the boundary conditions at the free edge
$\textsf{S}_{\parallel }(J)$
is given by (5.5). Inserting this result along with the tractions (5.21) into (4.8a) leads to cancellations that allow two integrations to be performed. After imposing the boundary conditions at the free edge
![]() $X = 1$
, the equation for the vertical plate displacement (4.8a) simplifies to
$X = 1$
, the equation for the vertical plate displacement (4.8a) simplifies to
The boundary conditions for (6.1) are
![]() $w(0) = 0$
and
$w(0) = 0$
and
![]() $\partial _X w(0) = 0$
. The first term on the right-hand side of (6.1) captures the influence of the in-plane traction, whereas the second term captures the vertical traction. When
$\partial _X w(0) = 0$
. The first term on the right-hand side of (6.1) captures the influence of the in-plane traction, whereas the second term captures the vertical traction. When
![]() $J$
is a constant, (6.1) can be solved to find
$J$
is a constant, (6.1) can be solved to find
Equation (6.1) and its solution (6.2) apply to all of the mechanical regimes considered in Section 5.1; however, for asymptotic consistency, the terms that are proportional to
![]() $\epsilon \delta ^{-1}$
should be dropped when
$\epsilon \delta ^{-1}$
should be dropped when
![]() $\epsilon \ll \delta$
.
$\epsilon \ll \delta$
.
We first compare asymptotic and FE solutions when the film and plate have similar thicknesses. In particular, we set
![]() $\delta = \epsilon$
and
$\delta = \epsilon$
and
![]() $\mathcal{E} = 1$
. A comparison of the deflection of the end of the plate,
$\mathcal{E} = 1$
. A comparison of the deflection of the end of the plate,
![]() $w(X = 1)$
, shows that the asymptotic and FE solutions are in good agreement across a wide range of
$w(X = 1)$
, shows that the asymptotic and FE solutions are in good agreement across a wide range of
![]() $J$
values, especially when
$J$
values, especially when
![]() $\epsilon = \delta \leq 0.05$
; see Figure 3(a). The deflection is seen to increase as
$\epsilon = \delta \leq 0.05$
; see Figure 3(a). The deflection is seen to increase as
![]() $J$
is decreased from one, corresponding to greater volumetric contraction of the film. However, the deflection reaches a maximum at
$J$
is decreased from one, corresponding to greater volumetric contraction of the film. However, the deflection reaches a maximum at
![]() $J \simeq 0.30$
, after which it decreases with further decreases in
$J \simeq 0.30$
, after which it decreases with further decreases in
![]() $J$
. The non-monotonic behaviour results from a competition between the in-plane stress in the film
$J$
. The non-monotonic behaviour results from a competition between the in-plane stress in the film
![]() $\textsf{S}_{\parallel }$
and the contribution to (6.1) from the vertical traction. The former increases as
$\textsf{S}_{\parallel }$
and the contribution to (6.1) from the vertical traction. The former increases as
![]() $J$
decreases, whereas the latter decreases.
$J$
decreases, whereas the latter decreases.

Figure 3. Steady-state solutions of the vertical plate displacement when the film and plate have similar thicknesses,
![]() $\delta = O(\epsilon)$
with
$\delta = O(\epsilon)$
with
![]() $\mathcal{E} = O(1)$
. Asymptotic solutions are shown as lines and obtained from (6.2); finite element solutions are shown as symbols. (a) The deflection at the end of the plate as a function of the imposed (uniform) contraction ratio J in the film. (b) The vertical displacement of the plate as a function of space when
$\mathcal{E} = O(1)$
. Asymptotic solutions are shown as lines and obtained from (6.2); finite element solutions are shown as symbols. (a) The deflection at the end of the plate as a function of the imposed (uniform) contraction ratio J in the film. (b) The vertical displacement of the plate as a function of space when
![]() $J = 0.2$
.
$J = 0.2$
.
Profiles of the vertical plate displacement are found to compare favourably in Figure 3(b). As expected, the plate deflection monotonically increases as the distance from the wall increases.
To validate the asymptotic reduction of the mechanical problem when the film is thin relative to the plate, we set
![]() $\epsilon = 0.01$
and
$\epsilon = 0.01$
and
![]() $\delta = \epsilon ^{1/2} = 0.1$
. Solutions are computed when
$\delta = \epsilon ^{1/2} = 0.1$
. Solutions are computed when
![]() $\mathcal{E} = 1$
and
$\mathcal{E} = 1$
and
![]() $\mathcal{E} = \delta \epsilon ^{-1} = 10$
across a range of
$\mathcal{E} = \delta \epsilon ^{-1} = 10$
across a range of
![]() $J$
values. By computing the deflection at the end of the plate, we again find excellent agreement between the asymptotic and FE solutions; see Figure 4(a). The strong agreement when
$J$
values. By computing the deflection at the end of the plate, we again find excellent agreement between the asymptotic and FE solutions; see Figure 4(a). The strong agreement when
![]() $\mathcal{E} = 10$
is remarkable given that the film undergoes extremely large deformations, with the vertical displacement being much greater than the film thickness.
$\mathcal{E} = 10$
is remarkable given that the film undergoes extremely large deformations, with the vertical displacement being much greater than the film thickness.

Figure 4. Steady-state solutions when the film is thin relative to the plate,
![]() $\epsilon \ll \delta$
. Asymptotic solutions are shown as lines; finite element solutions are shown as symbols. (a) The deflection at the end of the plate as a function of the imposed (uniform) contraction ratio J in the film. The asymptotic solution for w is obtained from (6.2) with
$\epsilon \ll \delta$
. Asymptotic solutions are shown as lines; finite element solutions are shown as symbols. (a) The deflection at the end of the plate as a function of the imposed (uniform) contraction ratio J in the film. The asymptotic solution for w is obtained from (6.2) with
![]() $\epsilon \delta^{-1} = 0$
. (b) The vertical traction
$\epsilon \delta^{-1} = 0$
. (b) The vertical traction
![]() $\tau_z$
as a function of space. The asymptotic solutions for the traction are given by (5.21b) when
$\tau_z$
as a function of space. The asymptotic solutions for the traction are given by (5.21b) when
![]() $\mathcal{E} = 1$
and (5.22) when
$\mathcal{E} = 1$
and (5.22) when
![]() $\mathcal{E} = 10$
.
$\mathcal{E} = 10$
.
A distinguishing feature of the thin-film regime (
![]() $\epsilon \ll \delta$
) is that the asymptotic order of the vertical traction increases when the non-dimensional stiffness
$\epsilon \ll \delta$
) is that the asymptotic order of the vertical traction increases when the non-dimensional stiffness
![]() $\mathcal{E}$
increases. To observe this increase, the vertical traction is computed from the FE and asymptotic solutions by fixing
$\mathcal{E}$
increases. To observe this increase, the vertical traction is computed from the FE and asymptotic solutions by fixing
![]() $\epsilon = 0.01$
,
$\epsilon = 0.01$
,
![]() $\delta = 0.1$
, and
$\delta = 0.1$
, and
![]() $J = 0.2$
while considering
$J = 0.2$
while considering
![]() $\mathcal{E} = 1$
and
$\mathcal{E} = 1$
and
![]() $\mathcal{E} = 10$
. When
$\mathcal{E} = 10$
. When
![]() $J$
is independent of
$J$
is independent of
![]() $Z$
, the asymptotic solution for the vertical traction is obtained from (5.21b) when
$Z$
, the asymptotic solution for the vertical traction is obtained from (5.21b) when
![]() $\mathcal{E} = 1$
and (5.22) when
$\mathcal{E} = 1$
and (5.22) when
![]() $\mathcal{E} = 10$
. The solutions for the traction are plotted as a function of space in Figure 4(b). There is clearly a large difference in the magnitude of the traction in the two cases, with the traction remaining
$\mathcal{E} = 10$
. The solutions for the traction are plotted as a function of space in Figure 4(b). There is clearly a large difference in the magnitude of the traction in the two cases, with the traction remaining
![]() $O(1)$
in size when
$O(1)$
in size when
![]() $\mathcal{E} = 1$
and becoming
$\mathcal{E} = 1$
and becoming
![]() $O(\delta \epsilon ^{-1})$
in size when
$O(\delta \epsilon ^{-1})$
in size when
![]() $\mathcal{E} = 10$
. Again, excellent agreement between the asymptotic and FE solutions is found.
$\mathcal{E} = 10$
. Again, excellent agreement between the asymptotic and FE solutions is found.
6.2. Dynamic simulations
Time-dependent simulations are used to explore the dynamics of drying and bending. The non-dimensional evaporative flux is written in terms of a simple phenomenological law given by
![]() $\mathcal{V}(\phi ) = \phi - \phi _\infty$
. The parameter
$\mathcal{V}(\phi ) = \phi - \phi _\infty$
. The parameter
![]() $\phi _\infty$
can have different interpretations depending on the modelling context. For instance,
$\phi _\infty$
can have different interpretations depending on the modelling context. For instance,
![]() $\phi _\infty$
can represent a constant amount of fluid vapour in the surrounding environment. In any case, with this model for
$\phi _\infty$
can represent a constant amount of fluid vapour in the surrounding environment. In any case, with this model for
![]() $\mathcal{V}$
, the film will dry until its porosity (fluid fraction) reaches
$\mathcal{V}$
, the film will dry until its porosity (fluid fraction) reaches
![]() $\phi _\infty$
. For simplicity, we set the scalar permeability of the film,
$\phi _\infty$
. For simplicity, we set the scalar permeability of the film,
![]() $k(\phi )$
, to be a constant. Hennessy et al. [Reference Hennessy, Craster and Matar17] showed that a porosity-dependent permeability can lead to drying fronts propagating into the bulk of the film from the contact line. These fronts separate wet and completely dry solid and hence require the porosity to become very small. By taking
$k(\phi )$
, to be a constant. Hennessy et al. [Reference Hennessy, Craster and Matar17] showed that a porosity-dependent permeability can lead to drying fronts propagating into the bulk of the film from the contact line. These fronts separate wet and completely dry solid and hence require the porosity to become very small. By taking
![]() $\phi _\infty$
to be sufficiently large, the formation of drying fronts will be suppressed and the role of a porosity-dependent permeability will be negligible.
$\phi _\infty$
to be sufficiently large, the formation of drying fronts will be suppressed and the role of a porosity-dependent permeability will be negligible.
Our time-dependent simulations are based on the work of Bouchaudy and Salmon [Reference Bouchaudy and Salmon4], who measured drying-induced stresses in poroelastic discs formed from nanoparticle suspensions. Gelation was estimated to occur at a solid fraction of 0.32. Hence, we take
![]() $\phi _0 = 1 - 0.32 = 0.68$
. We imagine that
$\phi _0 = 1 - 0.32 = 0.68$
. We imagine that
![]() $1 - \phi _\infty$
represents the closest packing fraction of the colloidal dispersion. For a poroelastic film composed of monodisperse nanoparticles,
$1 - \phi _\infty$
represents the closest packing fraction of the colloidal dispersion. For a poroelastic film composed of monodisperse nanoparticles,
![]() $\phi _\infty \simeq 1 - 0.64 = 0.36$
. The drying that occurs after the closest packing fraction is reached can lead to pore invasion by air [Reference Lilin and Bischofberger27], a phenomenon that our model does not capture. For this set of parameters, the film will shed half of its volume during drying, which can be seen by calculating
$\phi _\infty \simeq 1 - 0.64 = 0.36$
. The drying that occurs after the closest packing fraction is reached can lead to pore invasion by air [Reference Lilin and Bischofberger27], a phenomenon that our model does not capture. For this set of parameters, the film will shed half of its volume during drying, which can be seen by calculating
![]() $J = (1 - \phi _0)/ (1 - \phi _\infty ) = 0.5$
.
$J = (1 - \phi _0)/ (1 - \phi _\infty ) = 0.5$
.
6.2.1. Films drying on plates with similar thickness
The first set of time-dependent simulations captures the dynamics when the film and plate have similar thicknesses,
![]() $\delta = O(\epsilon )$
with
$\delta = O(\epsilon )$
with
![]() $\mathcal{E} = O(1)$
. The evaporation is assumed to be slow,
$\mathcal{E} = O(1)$
. The evaporation is assumed to be slow,
![]() $\textrm{Pe} = O(1)$
, or moderate,
$\textrm{Pe} = O(1)$
, or moderate,
![]() $\textrm{Pe} = O(\epsilon ^{-1})$
. We set
$\textrm{Pe} = O(\epsilon ^{-1})$
. We set
![]() $\delta = \epsilon = 0.01$
with
$\delta = \epsilon = 0.01$
with
![]() $\mathcal{E} = 1$
, and consider
$\mathcal{E} = 1$
, and consider
![]() $\textrm{Pe} = 1$
or
$\textrm{Pe} = 1$
or
![]() $\textrm{Pe} = 100$
. For both of these cases, the asymptotic solution to the plate displacement can be obtained from (6.1). The asymptotic solutions for the in-plane film stress,
$\textrm{Pe} = 100$
. For both of these cases, the asymptotic solution to the plate displacement can be obtained from (6.1). The asymptotic solutions for the in-plane film stress,
![]() $\textsf{S}_{\parallel }$
, and local contraction ratio,
$\textsf{S}_{\parallel }$
, and local contraction ratio,
![]() $J$
, can be obtained by numerically solving (5.20) when
$J$
, can be obtained by numerically solving (5.20) when
![]() $\textrm{Pe} = O(1)$
and (5.24) when
$\textrm{Pe} = O(1)$
and (5.24) when
![]() $\textrm{Pe} = O(\epsilon ^{-1})$
.
$\textrm{Pe} = O(\epsilon ^{-1})$
.
When evaporation is slow,
![]() $\textrm{Pe} = 1$
, the Eulerian fluid fraction (porosity) of the film remains relatively uniform during drying. That is, the in-plane composition gradients, in addition to the vertical composition gradients, are weak. The weak in-plane gradients can be seen in Figure 5(a), where the fluid fraction at the bottom of the film (
$\textrm{Pe} = 1$
, the Eulerian fluid fraction (porosity) of the film remains relatively uniform during drying. That is, the in-plane composition gradients, in addition to the vertical composition gradients, are weak. The weak in-plane gradients can be seen in Figure 5(a), where the fluid fraction at the bottom of the film (
![]() $Z = 0$
) is plotted as a function of the in-plane coordinate
$Z = 0$
) is plotted as a function of the in-plane coordinate
![]() $X$
at various times. Black lines represent numerical solutions of the asymptotically reduced transport problem defined by (5.20); circles represent the FE solution. The uniform loss of fluid across the film induces a homogeneous contraction of the film that predominately occurs in the vertical direction. The in-plane stresses in the film,
$X$
at various times. Black lines represent numerical solutions of the asymptotically reduced transport problem defined by (5.20); circles represent the FE solution. The uniform loss of fluid across the film induces a homogeneous contraction of the film that predominately occurs in the vertical direction. The in-plane stresses in the film,
![]() $\textsf{S}_{\parallel }$
, will also be approximately homogeneous. Since the initial film profile is quadratic, the in-plane traction is expected to vary linearly in space, which can be deduced from (5.21a) and is shown in Figure 5(b). The evolution of the vertical traction is more complicated, as seen from Figure 5(c). The vertical traction is typically positive near the contact line, implying the film pulls upwards on the plate. However, near the centre of the plate, the traction becomes negative, implying the film pushes downwards. The vertical displacement of the plate is shown in Figure 5(d); the inset depicts the time evolution of the deflection at the end of the plate,
$\textsf{S}_{\parallel }$
, will also be approximately homogeneous. Since the initial film profile is quadratic, the in-plane traction is expected to vary linearly in space, which can be deduced from (5.21a) and is shown in Figure 5(b). The evolution of the vertical traction is more complicated, as seen from Figure 5(c). The vertical traction is typically positive near the contact line, implying the film pulls upwards on the plate. However, near the centre of the plate, the traction becomes negative, implying the film pushes downwards. The vertical displacement of the plate is shown in Figure 5(d); the inset depicts the time evolution of the deflection at the end of the plate,
![]() $w(1,t)$
. The plate deflection monotonically increases in space and time. The deflection at the end of the beam initially grows linearly with time and then saturates as the film approaches its steady state. The initial linear increase in the beam deflection is a result of the evaporation rate being approximately constant for small times, with an evaporative flux given by
$w(1,t)$
. The plate deflection monotonically increases in space and time. The deflection at the end of the beam initially grows linearly with time and then saturates as the film approaches its steady state. The initial linear increase in the beam deflection is a result of the evaporation rate being approximately constant for small times, with an evaporative flux given by
![]() $\mathcal{V} \sim \phi _0 - \phi _\infty$
. In all of the panels of Figure 5, excellent agreement between the asymptotic and FE solutions can be seen.
$\mathcal{V} \sim \phi _0 - \phi _\infty$
. In all of the panels of Figure 5, excellent agreement between the asymptotic and FE solutions can be seen.

Figure 5. Drying dynamics for small evaporation rates,
![]() $\textrm{Pe} = O(1)$
, when the film and plate have similar thicknesses,
$\textrm{Pe} = O(1)$
, when the film and plate have similar thicknesses,
![]() $\delta = O(\epsilon)$
. Asymptotic solutions are shown as lines; finite element solutions are shown as circles. (a) The Eulerian fluid fraction at the bottom of the film. (b) and (c) The in-plane and vertical traction. (d) The vertical plate displacement. The inset shows the evolution of the deflection of the end of the plate. Solutions are shown at times
$\delta = O(\epsilon)$
. Asymptotic solutions are shown as lines; finite element solutions are shown as circles. (a) The Eulerian fluid fraction at the bottom of the film. (b) and (c) The in-plane and vertical traction. (d) The vertical plate displacement. The inset shows the evolution of the deflection of the end of the plate. Solutions are shown at times
![]() $t = 0.1$
, 0.4, 0.7, 1, and 3. The arrows show the direction of increasing time. The parameter values are
$t = 0.1$
, 0.4, 0.7, 1, and 3. The arrows show the direction of increasing time. The parameter values are
![]() $\epsilon = \delta = 0.01$
,
$\epsilon = \delta = 0.01$
,
![]() $\textrm{Pe} = 1$
, and
$\textrm{Pe} = 1$
, and
![]() $\mathcal{E} = 1$
.
$\mathcal{E} = 1$
.
Increasing the Péclet number to
![]() $\textrm{Pe} = 100$
, corresponding to moderate evaporation, leads to a non-uniform drying process with significant in-plane gradients; see Figure 6. The film rapidly dries near the contact line, as seen in Figure 6(a), which leads to a localisation of both the in-plane and vertical components of the traction; see Figure 6(b) and (c), respectively. Despite the strongly non-uniform tractions, the evolution of the plate deflection, shown in Figure 6(d), is remarkably similar to the case when
$\textrm{Pe} = 100$
, corresponding to moderate evaporation, leads to a non-uniform drying process with significant in-plane gradients; see Figure 6. The film rapidly dries near the contact line, as seen in Figure 6(a), which leads to a localisation of both the in-plane and vertical components of the traction; see Figure 6(b) and (c), respectively. Despite the strongly non-uniform tractions, the evolution of the plate deflection, shown in Figure 6(d), is remarkably similar to the case when
![]() $\textrm{Pe} = O(1)$
. A more in-depth comparison of the plate deflection for different evaporation rates will be provided in Section 6.3. The asymptotic solutions (lines) are in good agreement with the FE simulations (circles). The largest discrepancy occurs in the fluid fraction near the contact line; see Figure 6(a). The asymptotically reduced model (5.24) does not capture the influence of in-plane pressure gradients, which provide a mechanism to replenish the fluid that evaporates at the contact line. Hence, the asymptotically reduced model leads to faster drying compared to the FE solutions. Despite the asymptotically reduced model not correctly capturing the dynamics near the contact line, it is still able to provide a highly accurate prediction of the plate deflection; see Figure 6(d).
$\textrm{Pe} = O(1)$
. A more in-depth comparison of the plate deflection for different evaporation rates will be provided in Section 6.3. The asymptotic solutions (lines) are in good agreement with the FE simulations (circles). The largest discrepancy occurs in the fluid fraction near the contact line; see Figure 6(a). The asymptotically reduced model (5.24) does not capture the influence of in-plane pressure gradients, which provide a mechanism to replenish the fluid that evaporates at the contact line. Hence, the asymptotically reduced model leads to faster drying compared to the FE solutions. Despite the asymptotically reduced model not correctly capturing the dynamics near the contact line, it is still able to provide a highly accurate prediction of the plate deflection; see Figure 6(d).

Figure 6. Drying dynamics for moderate evaporation rates,
![]() $\textrm{Pe} = O(\epsilon^{-1})$
, when the film and plate have similar thicknesses,
$\textrm{Pe} = O(\epsilon^{-1})$
, when the film and plate have similar thicknesses,
![]() $\delta = O(\epsilon)$
. Asymptotic solutions are shown as lines; finite element solutions are shown as circles. (a) The Eulerian fluid fraction at the bottom of the film. (b) and (c) The in-plane and vertical traction. (d) The vertical plate displacement. The inset shows the evolution of the deflection of the end of the plate. Solutions are shown at times
$\delta = O(\epsilon)$
. Asymptotic solutions are shown as lines; finite element solutions are shown as circles. (a) The Eulerian fluid fraction at the bottom of the film. (b) and (c) The in-plane and vertical traction. (d) The vertical plate displacement. The inset shows the evolution of the deflection of the end of the plate. Solutions are shown at times
![]() $t = 0.001$
, 0.005, 0.01, 0.02, and 0.05. The arrows show the direction of increasing time. The parameter values are
$t = 0.001$
, 0.005, 0.01, 0.02, and 0.05. The arrows show the direction of increasing time. The parameter values are
![]() $\epsilon = \delta = 0.01$
,
$\epsilon = \delta = 0.01$
,
![]() $\textrm{Pe} = 100$
, and
$\textrm{Pe} = 100$
, and
![]() $\mathcal{E} = 1$
.
$\mathcal{E} = 1$
.
6.2.2. Films drying on thick plates
The final comparison that we make between the asymptotic and FE solutions considers the case of films that are thin relative to the plate,
![]() $\epsilon \ll \delta$
. Moreover, the film is assumed to be soft,
$\epsilon \ll \delta$
. Moreover, the film is assumed to be soft,
![]() $\mathcal{E} = O(1)$
, and evaporation is fast,
$\mathcal{E} = O(1)$
, and evaporation is fast,
![]() $\textrm{Pe} = O(\epsilon ^{-2})$
. In particular, we set
$\textrm{Pe} = O(\epsilon ^{-2})$
. In particular, we set
![]() $\epsilon = 10^{-2}$
,
$\epsilon = 10^{-2}$
,
![]() $\delta = \epsilon ^{1/2} = 10^{-1}$
,
$\delta = \epsilon ^{1/2} = 10^{-1}$
,
![]() $\mathcal{E} = 1$
, and
$\mathcal{E} = 1$
, and
![]() $\textrm{Pe} = 5\,\epsilon ^{-2} = 5\times 10^{4}$
. In this regime, the vertical displacement of the plate can be obtained by solving
$\textrm{Pe} = 5\,\epsilon ^{-2} = 5\times 10^{4}$
. In this regime, the vertical displacement of the plate can be obtained by solving
subject to
![]() $w(0,t) = 0$
and
$w(0,t) = 0$
and
![]() $\partial _X w(0,t) = 0$
, where
$\partial _X w(0,t) = 0$
, where
![]() $\langle \textsf{S}_{\parallel } \rangle$
denotes the vertically averaged in-plane film stress. The contraction ratio
$\langle \textsf{S}_{\parallel } \rangle$
denotes the vertically averaged in-plane film stress. The contraction ratio
![]() $J$
and the in-plane film stress
$J$
and the in-plane film stress
![]() $\textsf{S}_{\parallel }$
can be obtained by numerically solving (5.25).
$\textsf{S}_{\parallel }$
can be obtained by numerically solving (5.25).
The evolution of the fluid fraction at the bottom of the film and the plate deflection are shown in Figures 7(a) and (b), respectively. Qualitatively, the solutions appear very similar to the
![]() $\textrm{Pe} = O(\epsilon ^{-1})$
case shown in Figure 6. There is a rapid depletion of fluid near the contact line, which leads to large in-plane gradients. However, a key difference is that vertical composition gradients occur when
$\textrm{Pe} = O(\epsilon ^{-1})$
case shown in Figure 6. There is a rapid depletion of fluid near the contact line, which leads to large in-plane gradients. However, a key difference is that vertical composition gradients occur when
![]() $\textrm{Pe} = O(\epsilon ^{-2})$
, which can be seen in Figure 7(c). As expected, the fluid fraction is the greatest at the bottom of the film and the smallest at the free surface. Consequently, the in-plane film stress
$\textrm{Pe} = O(\epsilon ^{-2})$
, which can be seen in Figure 7(c). As expected, the fluid fraction is the greatest at the bottom of the film and the smallest at the free surface. Consequently, the in-plane film stress
![]() $\textsf{S}_{\parallel }$
monotonically increases with
$\textsf{S}_{\parallel }$
monotonically increases with
![]() $Z$
, as shown in Figure 7(d).
$Z$
, as shown in Figure 7(d).

Figure 7. Drying dynamics for large evaporation rates,
![]() $\textrm{Pe} = O(\epsilon^{-2})$
, when the film is much thinner than the plate,
$\textrm{Pe} = O(\epsilon^{-2})$
, when the film is much thinner than the plate,
![]() $\epsilon \ll \delta$
. Asymptotic solutions are shown as lines; finite element solutions are shown as circles. (a) The Eulerian fluid fraction at the bottom of the film. (b) The vertical plate displacement. The inset shows the evolution of the deflection of the end of the plate. (c) and (d) The Eulerian fluid fraction and in-plane film stress at the centre of the film. Solutions are shown at times
$\epsilon \ll \delta$
. Asymptotic solutions are shown as lines; finite element solutions are shown as circles. (a) The Eulerian fluid fraction at the bottom of the film. (b) The vertical plate displacement. The inset shows the evolution of the deflection of the end of the plate. (c) and (d) The Eulerian fluid fraction and in-plane film stress at the centre of the film. Solutions are shown at times
![]() $t = 2 \times 10^{-6}$
,
$t = 2 \times 10^{-6}$
,
![]() $10^{-5}$
,
$10^{-5}$
,
![]() $2 \times 10^{-5}$
,
$2 \times 10^{-5}$
,
![]() $4 \times 10^{-5}$
, and
$4 \times 10^{-5}$
, and
![]() $10^{-4}$
. The arrows show the direction of increasing time. The parameter values are
$10^{-4}$
. The arrows show the direction of increasing time. The parameter values are
![]() $\epsilon = 0.01$
,
$\epsilon = 0.01$
,
![]() $\delta = 0.1$
,
$\delta = 0.1$
,
![]() $\textrm{Pe} = 5 \times 10^{4}$
, and
$\textrm{Pe} = 5 \times 10^{4}$
, and
![]() $\mathcal{E} = 1$
.
$\mathcal{E} = 1$
.
The asymptotically reduced model for the fluid-transport problem (5.25) provides an excellent approximation to the FE solutions of the nominal fluid fraction and the in-plane film stress; see Figures 7(a), (c), and (d). In particular, the fluid fraction near the contact line is well captured. The reduced model for the plate deflection provides a close approximation to the FE solution, as shown in Figure 7(b). Since the reduced model does not account for the vertical traction when
![]() $\epsilon \ll \delta$
and
$\epsilon \ll \delta$
and
![]() $\mathcal{E} = O(1)$
, the deflection is slightly smaller than that obtained using the FE method.
$\mathcal{E} = O(1)$
, the deflection is slightly smaller than that obtained using the FE method.
We have also compared the asymptotic and FE solutions when
![]() $\mathcal{E}$
is increased to
$\mathcal{E}$
is increased to
![]() $\mathcal{E} = \delta \epsilon ^{-1} = 10$
, keeping the other parameters the same (not shown). The solutions are virtually the same as those in Figure 7. The agreement between the fluid fraction and in-plane stresses remains excellent. However, there is much stronger agreement in the plate deflection. This is because the asymptotically reduced model for the plate now captures terms associated with the in-plane (plate) stress and the vertical traction. However, these terms serendipitously cancel out so that (6.3) still applies.
$\mathcal{E} = \delta \epsilon ^{-1} = 10$
, keeping the other parameters the same (not shown). The solutions are virtually the same as those in Figure 7. The agreement between the fluid fraction and in-plane stresses remains excellent. However, there is much stronger agreement in the plate deflection. This is because the asymptotically reduced model for the plate now captures terms associated with the in-plane (plate) stress and the vertical traction. However, these terms serendipitously cancel out so that (6.3) still applies.
6.3. Impact of the evaporation rate on bending
The insets of Figures 5(d) and 6(d) show that the deflection of the plate can undergo similar evolutions despite the evaporation rate differing by two orders of magnitude. We now explore the dependence of the deflection on the evaporation rate in more detail. The asymptotically reduced models for the fluid-transport problem are numerically solved when
![]() $\textrm{Pe} \ll 1$
,
$\textrm{Pe} \ll 1$
,
![]() $\textrm{Pe} = 1$
,
$\textrm{Pe} = 1$
,
![]() $\textrm{Pe} = \epsilon ^{-1}$
and
$\textrm{Pe} = \epsilon ^{-1}$
and
![]() $\textrm{Pe} = \epsilon ^{-2}$
. The equations for the reduced models are given by (5.23), (5.20), (5.24), and (5.25), respectively. The plate deflection is then computed by assuming that the film is thin and solving (6.3). In doing so, we take
$\textrm{Pe} = \epsilon ^{-2}$
. The equations for the reduced models are given by (5.23), (5.20), (5.24), and (5.25), respectively. The plate deflection is then computed by assuming that the film is thin and solving (6.3). In doing so, we take
![]() $\mathcal{E} = 1$
.
$\mathcal{E} = 1$
.
By plotting the deflection at the end of the beam as a function of
![]() $\textrm{Pe}\, t$
, we find that the curves obtained from different values of
$\textrm{Pe}\, t$
, we find that the curves obtained from different values of
![]() $\textrm{Pe}$
nearly overlap; see Figure 8(a). Thus, once the time scale of evaporation is accounted for, the evolution of the beam deflection is relatively insensitive to the evaporation rate for this range of Péclet numbers. The small differences between the curves shown in Figure 8(a) could be attributed to two physical mechanisms. The first is that larger Péclet numbers lead to non-uniform in-plane tractions that become increasingly localised at the contact line. The second is that a larger Péclet number will lead to a more rapid depletion of fluid from the free surface, which, in turn, will reduce the evaporative flux
$\textrm{Pe}$
nearly overlap; see Figure 8(a). Thus, once the time scale of evaporation is accounted for, the evolution of the beam deflection is relatively insensitive to the evaporation rate for this range of Péclet numbers. The small differences between the curves shown in Figure 8(a) could be attributed to two physical mechanisms. The first is that larger Péclet numbers lead to non-uniform in-plane tractions that become increasingly localised at the contact line. The second is that a larger Péclet number will lead to a more rapid depletion of fluid from the free surface, which, in turn, will reduce the evaporative flux
![]() $\mathcal{V}(\phi )$
and hence the rate of deflection. The first mechanism can be ruled out by noticing that the curves in Figure 8(a) do overlap for
$\mathcal{V}(\phi )$
and hence the rate of deflection. The first mechanism can be ruled out by noticing that the curves in Figure 8(a) do overlap for
![]() $\textrm{Pe}\, t \lt 0.5$
. However, the in-plane tractions during this time are very different, as shown in Figure 8(b) when
$\textrm{Pe}\, t \lt 0.5$
. However, the in-plane tractions during this time are very different, as shown in Figure 8(b) when
![]() $\textrm{Pe} = 1$
and
$\textrm{Pe} = 1$
and
![]() $\textrm{Pe} = \epsilon ^{-2}$
. Thus, the differences in the curves can be attributed to the depletion of fluid near the film surface as
$\textrm{Pe} = \epsilon ^{-2}$
. Thus, the differences in the curves can be attributed to the depletion of fluid near the film surface as
![]() $\textrm{Pe}$
increases.
$\textrm{Pe}$
increases.

Figure 8. (a) Asymptotic solutions for plate deflection plotted in terms of
![]() $\textrm{Pe}\, t$
for five different drying regimes. (b) Asymptotic solutions for the in-plane traction when
$\textrm{Pe}\, t$
for five different drying regimes. (b) Asymptotic solutions for the in-plane traction when
![]() $\textrm{Pe} = 1$
(top) and
$\textrm{Pe} = 1$
(top) and
![]() $\textrm{Pe} = \epsilon ^{-2}$
(bottom). The solutions are shown when
$\textrm{Pe} = \epsilon ^{-2}$
(bottom). The solutions are shown when
![]() $\textrm{Pe}\, t = 0.1$
,
$\textrm{Pe}\, t = 0.1$
,
![]() $0.3$
and
$0.3$
and
![]() $0.6$
. The arrows show the direction of increasing time. See text for full details.
$0.6$
. The arrows show the direction of increasing time. See text for full details.
To further demonstrate the impact of fluid depletion at the free surface on the rate of deflection, we consider an extreme case and numerically solve (5.25) when
![]() $\textrm{Pe}_1 = 100$
, corresponding to
$\textrm{Pe}_1 = 100$
, corresponding to
![]() $\textrm{Pe} \gg O(\epsilon ^{-2})$
. In this case, a compositional boundary layer of width
$\textrm{Pe} \gg O(\epsilon ^{-2})$
. In this case, a compositional boundary layer of width
![]() $O(\textrm{Pe}_1^{-1})$
develops at the free surface, where the Eulerian fluid fraction decreases to approximately
$O(\textrm{Pe}_1^{-1})$
develops at the free surface, where the Eulerian fluid fraction decreases to approximately
![]() $\phi _\infty$
. As a result, the evaporation flux
$\phi _\infty$
. As a result, the evaporation flux
![]() $\mathcal{V}(\phi )$
undergoes a considerable decrease. When the plate deflection is obtained from (6.3) and plotted in terms of
$\mathcal{V}(\phi )$
undergoes a considerable decrease. When the plate deflection is obtained from (6.3) and plotted in terms of
![]() $\textrm{Pe}\,t$
, the corresponding curve is markedly different from those obtained from smaller Péclet numbers; see Figure 8(a). When
$\textrm{Pe}\,t$
, the corresponding curve is markedly different from those obtained from smaller Péclet numbers; see Figure 8(a). When
![]() $\textrm{Pe} = O(\epsilon ^{-2})$
or smaller, the deflection initially grows linearly with time. However, when
$\textrm{Pe} = O(\epsilon ^{-2})$
or smaller, the deflection initially grows linearly with time. However, when
![]() $\textrm{Pe} \gg O(\epsilon ^{-2})$
, the kinetics are qualitatively different and the deflection grows approximately with
$\textrm{Pe} \gg O(\epsilon ^{-2})$
, the kinetics are qualitatively different and the deflection grows approximately with
![]() $t^{1/2}$
.
$t^{1/2}$
.
7. Discussion and conclusion
Stoney’s equation relating the in-plane film stress,
![]() $\textsf{S}_{\parallel }$
, to the radius of curvature of the cantilever beam,
$\textsf{S}_{\parallel }$
, to the radius of curvature of the cantilever beam,
![]() $R$
, can be written in dimensional form as
$R$
, can be written in dimensional form as
where
![]() $H_f^0$
denotes the constant film thickness. To fairly compare against the one-dimensional models derived in Section 6, we must consider the thin-film limit
$H_f^0$
denotes the constant film thickness. To fairly compare against the one-dimensional models derived in Section 6, we must consider the thin-film limit
![]() $\epsilon \ll \delta$
. By re-dimensionalising (6.3) and using
$\epsilon \ll \delta$
. By re-dimensionalising (6.3) and using
![]() $\partial ^2 w/ \partial X^2 \sim 1/ R$
, we obtain
$\partial ^2 w/ \partial X^2 \sim 1/ R$
, we obtain
where
![]() $\bar{E}_p = E_p/ (1 - \nu _p^2)$
. Thus, the equations presented here are consistent with Stoney’s. The differing factor of
$\bar{E}_p = E_p/ (1 - \nu _p^2)$
. Thus, the equations presented here are consistent with Stoney’s. The differing factor of
![]() $1 - \nu _p^2$
can be attributed to Stoney working under the assumption of plane stress, whereas (6.3) has been obtained under the assumption of plane strain. The agreement between Stoney’s result and our own suggests that Stoney’s choice of neutral axis is not incorrect after all, as was suggested by Chiu [Reference Chiu6]. That being said, Stoney’s derivation is based on the assumption that bending is driven by the in-plane film traction, whereas the asymptotic analysis reveals that the vertical traction can be just as relevant when the film is thin and sufficiently stiff. However, when reducing the plate model to a beam model, the terms associated with the vertical traction cancel out. Although Stoney did not recognise the importance of the vertical traction, their formula remains correct due to this serendipitous cancellation. A direct comparison of (7.1) and (7.2) shows that the in-plane stress in Stoney’s formula should be interpreted as the mean stress across the film thickness. However, given that significant in-plane stress gradients can also arise during drying, it would be more accurate to interpret Stoney’s
$1 - \nu _p^2$
can be attributed to Stoney working under the assumption of plane stress, whereas (6.3) has been obtained under the assumption of plane strain. The agreement between Stoney’s result and our own suggests that Stoney’s choice of neutral axis is not incorrect after all, as was suggested by Chiu [Reference Chiu6]. That being said, Stoney’s derivation is based on the assumption that bending is driven by the in-plane film traction, whereas the asymptotic analysis reveals that the vertical traction can be just as relevant when the film is thin and sufficiently stiff. However, when reducing the plate model to a beam model, the terms associated with the vertical traction cancel out. Although Stoney did not recognise the importance of the vertical traction, their formula remains correct due to this serendipitous cancellation. A direct comparison of (7.1) and (7.2) shows that the in-plane stress in Stoney’s formula should be interpreted as the mean stress across the film thickness. However, given that significant in-plane stress gradients can also arise during drying, it would be more accurate to interpret Stoney’s
![]() $\textsf{S}_{\parallel }$
as the mean stress across and along the film.
$\textsf{S}_{\parallel }$
as the mean stress across and along the film.
Tomar et al. [Reference Tomar, Shahin and Tirumkudulu39] conducted cantilever experiments using drops of polymer solutions. By analysing their data using an equation that is similar to (7.1), they found that the film stress increases like
![]() $t$
for thin drops and like
$t$
for thin drops and like
![]() $t^{1/2}$
for thicker drops. These observations are consistent with the results in Section 6.3, in which the small-time evolution of the beam deflection is seen to change from
$t^{1/2}$
for thicker drops. These observations are consistent with the results in Section 6.3, in which the small-time evolution of the beam deflection is seen to change from
![]() $t$
to
$t$
to
![]() $t^{1/2}$
as the Péclet number,
$t^{1/2}$
as the Péclet number,
![]() $\textrm{Pe} = V_e^0 H_f^0 \mu _f/ (\epsilon ^2 k_0 E_f)$
increases. For a given polymer solution, the aspect ratio
$\textrm{Pe} = V_e^0 H_f^0 \mu _f/ (\epsilon ^2 k_0 E_f)$
increases. For a given polymer solution, the aspect ratio
![]() $\epsilon$
of the drop will be fixed and determined by the equilibrium contact angle. Thus, increasing the drop thickness is equivalent to increasing the Péclet number.
$\epsilon$
of the drop will be fixed and determined by the equilibrium contact angle. Thus, increasing the drop thickness is equivalent to increasing the Péclet number.
Using asymptotic methods, we have systematically derived a hierarchy of simplified models of the cantilever experiment. Our models extend Stoney-like formulae by accounting for the time dependence of the drying process and the generation of non-uniform in-plane and transverse stresses in the film. Fitting the time-dependent solutions to experimental data could lead to new insights into the solid mechanics of drying films and enable difficult-to-measure quantities, such as the Young’s modulus of the film, to be inferred.
Due to the complex rheology of drying films, a number of extensions to this work are possible. For instance, the Young’s modulus of a colloidal mixture can increase by several orders of magnitude during drying [Reference Bouchaudy and Salmon4]. As a result, the system will pass through many of the asymptotic regimes that we have identified. Matched asymptotic expansions could be used to obtain a reduced drying model that spans all of regimes and captures the evolution of the material properties of the film. The asymptotic analysis could also be adapted to films with viscoelastic or elasto-viscoplastic rheologies and applied to other contexts in which the film undergoes thermal expansion, growth or swelling. Finally, the asymptotic framework that we have laid out could also be applied to drying-induced delamination of thin films.
Acknowledgements
We thank Ludovic Pauchard for many insightful discussions about drying colloidal films and the cantilever experiment.
Conflicts of interest
The authors declare that they have no conflicts of interest.
A. Derivation of the plate model
The purpose of this appendix is to derive (i) the modified FvK equations for a thin plate subject to a non-uniform in-plane traction on its upper surface and (ii) the corresponding boundary conditions at the free edges of the plate. We consider rectangular plates of length
![]() $L$
, width
$L$
, width
![]() $W = O(L)$
and height
$W = O(L)$
and height
![]() $H_p$
. In the reference state, the domain of the plate can be written in terms of Lagrangian coordinates as
$H_p$
. In the reference state, the domain of the plate can be written in terms of Lagrangian coordinates as
![]() $0 \leq X_1 \leq L$
,
$0 \leq X_1 \leq L$
,
![]() $-W/2 \leq X_2 \leq W/2$
and
$-W/2 \leq X_2 \leq W/2$
and
![]() $-H_p/2 \leq Z \leq H_p/2$
. The plate is assumed to be clamped at the
$-H_p/2 \leq Z \leq H_p/2$
. The plate is assumed to be clamped at the
![]() $X_1 = 0$
boundary and free at the
$X_1 = 0$
boundary and free at the
![]() $X_1 = L$
and
$X_1 = L$
and
![]() $X_2 = \pm W/ 2$
boundaries.
$X_2 = \pm W/ 2$
boundaries.
A.1. Derivation of the modified FvK equations
The derivation of the modified FvK equations begins by considering the equations of nonlinear elasticity in the reference configuration, which we summarise here. Conservation of linear momentum is given by
where
![]() ${\sf\boldsymbol S}$
is the first Piola–Kirchhoff (PK1) stress tensor. For convenience, we define the in-plane and shear components of the PK1 stress tensor as
${\sf\boldsymbol S}$
is the first Piola–Kirchhoff (PK1) stress tensor. For convenience, we define the in-plane and shear components of the PK1 stress tensor as
![]() ${\sf\boldsymbol S}_{\parallel } ={\textsf{S}}_{\alpha \beta } \boldsymbol{{e}}_\alpha \otimes \boldsymbol{{e}}_\beta$
and
${\sf\boldsymbol S}_{\parallel } ={\textsf{S}}_{\alpha \beta } \boldsymbol{{e}}_\alpha \otimes \boldsymbol{{e}}_\beta$
and
![]() ${\sf\boldsymbol S}_{\perp } = \textsf{S}_{\alpha z} \boldsymbol{{e}}_\alpha$
, respectively. Conservation of angular momentum implies that the Cauchy stress tensor
${\sf\boldsymbol S}_{\perp } = \textsf{S}_{\alpha z} \boldsymbol{{e}}_\alpha$
, respectively. Conservation of angular momentum implies that the Cauchy stress tensor
![]() ${\sf\boldsymbol T} = J^{-1} {\sf\boldsymbol S} {\sf\boldsymbol F}^T$
is symmetric, which leads to the relation
${\sf\boldsymbol T} = J^{-1} {\sf\boldsymbol S} {\sf\boldsymbol F}^T$
is symmetric, which leads to the relation
The deformation gradient tensor is related to the displacement
![]() $\boldsymbol{{u}}(\boldsymbol{{X}},t) = \boldsymbol{{x}}(\boldsymbol{{X}},t) - \boldsymbol{{X}}$
by
$\boldsymbol{{u}}(\boldsymbol{{X}},t) = \boldsymbol{{x}}(\boldsymbol{{X}},t) - \boldsymbol{{X}}$
by
The mechanical response of the plate is described using the Saint-Venant–Kirchhoff constitutive relation given by
where
![]() $\nu _p$
and
$\nu _p$
and
![]() $E_p$
are the Poisson’s ratio and Young’s modulus of the plate, respectively;
$E_p$
are the Poisson’s ratio and Young’s modulus of the plate, respectively;
![]() ${\sf\boldsymbol {P}}$
is the second Piola–Kirchhoff stress tensor; and
${\sf\boldsymbol {P}}$
is the second Piola–Kirchhoff stress tensor; and
![]() ${\sf\boldsymbol {E}} = (1/2) ({\sf\boldsymbol F}^T {\sf\boldsymbol F} - {\sf\boldsymbol I})$
is the strain tensor.
${\sf\boldsymbol {E}} = (1/2) ({\sf\boldsymbol F}^T {\sf\boldsymbol F} - {\sf\boldsymbol I})$
is the strain tensor.
We assume that the upper surface of the plate, located at
![]() $Z = H_p/ 2$
, experiences a traction given by
$Z = H_p/ 2$
, experiences a traction given by
![]() $\boldsymbol{\tau } = \boldsymbol{\tau }_{\parallel } + \tau _{z} \boldsymbol{{e}}_z$
. The bottom surface of the plate, located at
$\boldsymbol{\tau } = \boldsymbol{\tau }_{\parallel } + \tau _{z} \boldsymbol{{e}}_z$
. The bottom surface of the plate, located at
![]() $Z = -H_p/ 2$
is assumed to be stress-free. Therefore, the following boundary conditions are imposed:
$Z = -H_p/ 2$
is assumed to be stress-free. Therefore, the following boundary conditions are imposed:
The boundary conditions at the edges of the plate will be discussed in Appendix A.2; they are not required in the derivation of the bulk equations.
The equations are non-dimensionalised following Howell et al. [Reference Howell, Kozyreff and Ockendon19]. We let
![]() $\boldsymbol{{X}}_{\parallel } \sim L$
,
$\boldsymbol{{X}}_{\parallel } \sim L$
,
![]() $Z \sim H_p$
, and define
$Z \sim H_p$
, and define
![]() $\delta = H_p/ L \ll 1$
. The displacements, components of the (PK1) stress tensor, and traction vector are scaled according to
$\delta = H_p/ L \ll 1$
. The displacements, components of the (PK1) stress tensor, and traction vector are scaled according to
![]() $\boldsymbol{{u}}_{\parallel } \sim \delta H_p$
,
$\boldsymbol{{u}}_{\parallel } \sim \delta H_p$
,
![]() $u_z \sim H_p$
,
$u_z \sim H_p$
,
![]() ${\sf\boldsymbol S}_{\parallel } \sim \delta ^2 E_p$
,
${\sf\boldsymbol S}_{\parallel } \sim \delta ^2 E_p$
,
![]() ${\sf\boldsymbol S}_{\perp } \sim \delta ^3 E_p$
,
${\sf\boldsymbol S}_{\perp } \sim \delta ^3 E_p$
,
![]() $\textsf{S}_{z \alpha } \sim \delta ^3 E_p$
,
$\textsf{S}_{z \alpha } \sim \delta ^3 E_p$
,
![]() $\textsf{S}_{zz} \sim \delta ^4 E_p$
,
$\textsf{S}_{zz} \sim \delta ^4 E_p$
,
![]() $\boldsymbol{\tau }_{\parallel } \sim \delta ^3 E_p$
and
$\boldsymbol{\tau }_{\parallel } \sim \delta ^3 E_p$
and
![]() $\tau _{z} \sim \delta ^4 E_p$
. Although this scaling differs from that of Section 3, it can be derived in the same way, and it simplifies the notation used in the subsequent calculations.
$\tau _{z} \sim \delta ^4 E_p$
. Although this scaling differs from that of Section 3, it can be derived in the same way, and it simplifies the notation used in the subsequent calculations.
The displacements and (PK1) stress tensor are expanded in powers of
![]() $\delta$
as
$\delta$
as
To streamline the derivation and reduce the algebra, the first two contributions to the vertical displacement
![]() $u_z$
are taken to be independent of the vertical coordinate
$u_z$
are taken to be independent of the vertical coordinate
![]() $Z$
. Using the steps outlined below, it is straightforward to retain the
$Z$
. Using the steps outlined below, it is straightforward to retain the
![]() $Z$
dependence and then show that
$Z$
dependence and then show that
![]() $\partial w/\partial Z = \partial u_z^{(1)}/\partial Z = 0$
. By taking into consideration how the components of the stress tensor have been scaled, we can deduce that
$\partial w/\partial Z = \partial u_z^{(1)}/\partial Z = 0$
. By taking into consideration how the components of the stress tensor have been scaled, we can deduce that
The boundary conditions on the upper and lower surfaces of the plate (A.5) become
The deformation gradient tensor (A.3) can be written as
![]() ${\sf\boldsymbol F} = {\sf\boldsymbol F}^{(0)} + \delta {\sf\boldsymbol F}^{(1)} + \delta ^2 {\sf\boldsymbol F}^{(2)} + O\!\left(\delta ^3\right)$
, where
${\sf\boldsymbol F} = {\sf\boldsymbol F}^{(0)} + \delta {\sf\boldsymbol F}^{(1)} + \delta ^2 {\sf\boldsymbol F}^{(2)} + O\!\left(\delta ^3\right)$
, where
Using these expansions in (A.2) gives
which has been simplified using (A.9a). The
![]() $O(1)$
contributions imply that the in-plane components of the stress tensor are symmetric, i.e.
$O(1)$
contributions imply that the in-plane components of the stress tensor are symmetric, i.e.
![]() ${\sf\boldsymbol S}_{\parallel }^{(0)} = \left({\sf\boldsymbol S}_{\parallel }^{(0)}\right)^T$
. The
${\sf\boldsymbol S}_{\parallel }^{(0)} = \left({\sf\boldsymbol S}_{\parallel }^{(0)}\right)^T$
. The
![]() $O(\delta )$
contributions lead to the equation
$O(\delta )$
contributions lead to the equation
By right-multiplying with the basis vector
![]() $\boldsymbol{{e}}_z$
and using (A.7b) and (A.9b), we find that
$\boldsymbol{{e}}_z$
and using (A.7b) and (A.9b), we find that
We now examine the leading-order contributions to the balance of linear momentum (A.1). After making use of (A.12), these can be written as
By integrating both equations in (A.13) from
![]() $Z = -1/2$
to
$Z = -1/2$
to
![]() $Z = 1/2$
and using the boundary conditions (A.8), we obtain
$Z = 1/2$
and using the boundary conditions (A.8), we obtain
where the mean in-plane and transverse shear stresses are given by
In order to complete the derivation, expressions for
![]() ${\sf\boldsymbol S}_{\parallel }^{(0)}$
and
${\sf\boldsymbol S}_{\parallel }^{(0)}$
and
![]() ${\sf\boldsymbol S}_{\perp }^{(1)}$
are required. These are found by expanding the stress-strain relation given by (A.4). Before doing so, it is useful to examine the strain tensor, which has the asymptotic form
${\sf\boldsymbol S}_{\perp }^{(1)}$
are required. These are found by expanding the stress-strain relation given by (A.4). Before doing so, it is useful to examine the strain tensor, which has the asymptotic form
![]() ${\sf\boldsymbol {E}} = \delta {\sf\boldsymbol {E}}^{(1)} + \delta ^2 {\sf\boldsymbol {E}}^{(2)} + O\!\left(\delta ^3\right)$
, where
${\sf\boldsymbol {E}} = \delta {\sf\boldsymbol {E}}^{(1)} + \delta ^2 {\sf\boldsymbol {E}}^{(2)} + O\!\left(\delta ^3\right)$
, where
![]() ${\sf\boldsymbol {E}}^{(1)} = \textrm{sym} \!\left({\sf\boldsymbol F}^{(1)}\right)$
,
${\sf\boldsymbol {E}}^{(1)} = \textrm{sym} \!\left({\sf\boldsymbol F}^{(1)}\right)$
,
![]() ${\sf\boldsymbol {E}}^{(2)} = \textrm{sym}\!\left({\sf\boldsymbol F}^{(2)}\right) + (1/2)\left({\sf\boldsymbol F}^{(1)}\right)^T {\sf\boldsymbol F}^{(1)}$
and
${\sf\boldsymbol {E}}^{(2)} = \textrm{sym}\!\left({\sf\boldsymbol F}^{(2)}\right) + (1/2)\left({\sf\boldsymbol F}^{(1)}\right)^T {\sf\boldsymbol F}^{(1)}$
and
![]() $\textrm{sym}({\cdot})$
denotes the symmetric part of a tensor, e.g.
$\textrm{sym}({\cdot})$
denotes the symmetric part of a tensor, e.g.
![]() $\textrm{sym}({\sf\boldsymbol F}) = (1/2)({\sf\boldsymbol F} + {\sf\boldsymbol F}^T)$
. By using (A.9b) and (A.9c), we can write the contributions to the strain tensor as
$\textrm{sym}({\sf\boldsymbol F}) = (1/2)({\sf\boldsymbol F} + {\sf\boldsymbol F}^T)$
. By using (A.9b) and (A.9c), we can write the contributions to the strain tensor as
 \begin{align} {\sf\boldsymbol {E}}^{(1)} &= \textrm{sym}\left(\frac{\partial \boldsymbol{{u}}_{\parallel }^{(0)}}{\partial Z}\otimes \boldsymbol{{e}}_z + \boldsymbol{{e}}_z \otimes \nabla _{\parallel } w\right),\qquad\qquad\qquad\qquad \end{align}
\begin{align} {\sf\boldsymbol {E}}^{(1)} &= \textrm{sym}\left(\frac{\partial \boldsymbol{{u}}_{\parallel }^{(0)}}{\partial Z}\otimes \boldsymbol{{e}}_z + \boldsymbol{{e}}_z \otimes \nabla _{\parallel } w\right),\qquad\qquad\qquad\qquad \end{align}
 \begin{align} {\sf\boldsymbol {E}}^{(2)} &= \textrm{sym}\left({\sf\boldsymbol F}^{(2)}\right) + \frac{1}{2}\left(\frac{\partial \boldsymbol{{u}}_{\parallel }^{(0)}}{\partial Z} \cdot \frac{\partial \boldsymbol{{u}}_{\parallel }^{(0)}}{\partial Z} \boldsymbol{{e}}_z \otimes \boldsymbol{{e}}_z + \nabla _{\parallel } w \otimes \nabla _{\parallel } w\right). \end{align}
\begin{align} {\sf\boldsymbol {E}}^{(2)} &= \textrm{sym}\left({\sf\boldsymbol F}^{(2)}\right) + \frac{1}{2}\left(\frac{\partial \boldsymbol{{u}}_{\parallel }^{(0)}}{\partial Z} \cdot \frac{\partial \boldsymbol{{u}}_{\parallel }^{(0)}}{\partial Z} \boldsymbol{{e}}_z \otimes \boldsymbol{{e}}_z + \nabla _{\parallel } w \otimes \nabla _{\parallel } w\right). \end{align}
Since
![]() ${\sf\boldsymbol {P}}$
is linear in the strain tensor
${\sf\boldsymbol {P}}$
is linear in the strain tensor
![]() ${\sf\boldsymbol {E}}$
, it follows that
${\sf\boldsymbol {E}}$
, it follows that
![]() ${\sf\boldsymbol {P}}$
can be expanded as
${\sf\boldsymbol {P}}$
can be expanded as
![]() ${\sf\boldsymbol {P}} = \delta {\sf\boldsymbol {P}}^{(1)} + \delta ^2 {\sf\boldsymbol {P}}^{(2)}+ O\!\left(\delta ^3\right)$
. Therefore, from (A.4), we have that
${\sf\boldsymbol {P}} = \delta {\sf\boldsymbol {P}}^{(1)} + \delta ^2 {\sf\boldsymbol {P}}^{(2)}+ O\!\left(\delta ^3\right)$
. Therefore, from (A.4), we have that
The
![]() $O(\delta )$
contributions to (A.18) imply that
$O(\delta )$
contributions to (A.18) imply that
![]() ${\sf\boldsymbol {P}}^{(1)} = 0$
and hence
${\sf\boldsymbol {P}}^{(1)} = 0$
and hence
![]() ${\sf\boldsymbol {E}}^{(1)} = 0$
. Thus, setting
${\sf\boldsymbol {E}}^{(1)} = 0$
. Thus, setting
![]() ${\sf\boldsymbol {E}}^{(1)} = 0$
in (A.16) leads to a differential equation for
${\sf\boldsymbol {E}}^{(1)} = 0$
in (A.16) leads to a differential equation for
![]() $\boldsymbol{{u}}_{\parallel }^{(0)}$
, which can be solved to find
$\boldsymbol{{u}}_{\parallel }^{(0)}$
, which can be solved to find
where
![]() $\bar{\boldsymbol{{u}}}_{\parallel }$
is a ‘constant’ of integration. This constant is chosen to coincide with the mean horizontal displacement in the beam, defined by
$\bar{\boldsymbol{{u}}}_{\parallel }$
is a ‘constant’ of integration. This constant is chosen to coincide with the mean horizontal displacement in the beam, defined by
Substituting (A.19) into (A.17) and using (A.9c) leads to
 \begin{align} {\sf\boldsymbol {E}}^{(2)} = \frac{1}{2}\left (\nabla _{\parallel } \bar{\boldsymbol{{u}}}_{\parallel } + \left(\nabla _{\parallel } \bar{\boldsymbol{{u}}}_{\parallel }\right)^T\right ) - Z {\sf\boldsymbol {H}} &+ \textrm{sym}\left (\frac{\partial \boldsymbol{{u}}_{\parallel }^{(1)}}{\partial Z}\otimes \boldsymbol{{e}}_z + \boldsymbol{{e}}_z \otimes \nabla _{\parallel } u_z^{(1)}\right ) \nonumber + \frac{\partial u_z^{(2)}}{\partial Z}\boldsymbol{{e}}_z \otimes \boldsymbol{{e}}_z \\ &+ \frac{1}{2}\left (|\nabla _{\parallel } w|^2 \boldsymbol{{e}}_z \otimes \boldsymbol{{e}}_z + \nabla _{\parallel } w \otimes \nabla _{\parallel } w\right ), \end{align}
\begin{align} {\sf\boldsymbol {E}}^{(2)} = \frac{1}{2}\left (\nabla _{\parallel } \bar{\boldsymbol{{u}}}_{\parallel } + \left(\nabla _{\parallel } \bar{\boldsymbol{{u}}}_{\parallel }\right)^T\right ) - Z {\sf\boldsymbol {H}} &+ \textrm{sym}\left (\frac{\partial \boldsymbol{{u}}_{\parallel }^{(1)}}{\partial Z}\otimes \boldsymbol{{e}}_z + \boldsymbol{{e}}_z \otimes \nabla _{\parallel } u_z^{(1)}\right ) \nonumber + \frac{\partial u_z^{(2)}}{\partial Z}\boldsymbol{{e}}_z \otimes \boldsymbol{{e}}_z \\ &+ \frac{1}{2}\left (|\nabla _{\parallel } w|^2 \boldsymbol{{e}}_z \otimes \boldsymbol{{e}}_z + \nabla _{\parallel } w \otimes \nabla _{\parallel } w\right ), \end{align}
where
![]() ${\sf\boldsymbol {H}} ={\nabla _{\parallel } \otimes \nabla _{\parallel } w}$
is a symmetric tensor corresponding to the Hessian of
${\sf\boldsymbol {H}} ={\nabla _{\parallel } \otimes \nabla _{\parallel } w}$
is a symmetric tensor corresponding to the Hessian of
![]() $w$
. The trace of (A.21) is given by
$w$
. The trace of (A.21) is given by
The
![]() $O\!\left(\delta ^2\right)$
contributions to (A.18) imply that
$O\!\left(\delta ^2\right)$
contributions to (A.18) imply that
It is now possible to eliminate
![]() $u_z^{(2)}$
from the problem by left- and right-multiplying with
$u_z^{(2)}$
from the problem by left- and right-multiplying with
![]() $\boldsymbol{{e}}_z$
and using
$\boldsymbol{{e}}_z$
and using
![]() $\boldsymbol{{e}}_z \cdot {\sf\boldsymbol S}_{\parallel }^{(0)} \cdot \boldsymbol{{e}}_z = 0$
,
$\boldsymbol{{e}}_z \cdot {\sf\boldsymbol S}_{\parallel }^{(0)} \cdot \boldsymbol{{e}}_z = 0$
,
![]() $\boldsymbol{{e}}_z \cdot {\sf\boldsymbol {E}}^{(2)} \cdot \boldsymbol{{e}}_z = \partial u_z^{(2)}/\partial z + (1/2) |\nabla _{\parallel } w|^2$
and (A.22) to obtain
$\boldsymbol{{e}}_z \cdot {\sf\boldsymbol {E}}^{(2)} \cdot \boldsymbol{{e}}_z = \partial u_z^{(2)}/\partial z + (1/2) |\nabla _{\parallel } w|^2$
and (A.22) to obtain
By substituting (A.24) into (A.21) and simplifying, the in-plane strain is found to be given by
Moreover, after some algebra it can be shown that
Hence, the in-plane component of (A.23) can be written as
where the in-plane strain is given by (A.25). By integrating over the thickness of the plate, the mean in-plane stress and strain are given by
which may be combined with (A.14a) to determine a system of equations for the mean in-plane displacements
![]() $\bar{\boldsymbol{{u}}}_{\parallel }$
.
$\bar{\boldsymbol{{u}}}_{\parallel }$
.
We are now in a position to compute
![]() ${\sf\boldsymbol S}_{\perp }^{(1)}$
and hence determine a problem for
${\sf\boldsymbol S}_{\perp }^{(1)}$
and hence determine a problem for
![]() $w$
. We first note that the in-plane stress tensor (A.27) can be written as
$w$
. We first note that the in-plane stress tensor (A.27) can be written as
where
![]() ${\sf\boldsymbol {A}}$
is a symmetric tensor that is proportional to the bending moments about the plane
${\sf\boldsymbol {A}}$
is a symmetric tensor that is proportional to the bending moments about the plane
![]() $Z = 0$
. Substituting (A.29) into (A.13a) and using (A.14a) leads to
$Z = 0$
. Substituting (A.29) into (A.13a) and using (A.14a) leads to
Integrating and imposing
![]() ${\sf\boldsymbol S}_{\perp }^{(1)} = 0$
at
${\sf\boldsymbol S}_{\perp }^{(1)} = 0$
at
![]() $Z = -1/2$
gives
$Z = -1/2$
gives
from which it follows that the mean transverse shear stress is
Substituting (A.32) into (A.14b) and simplifying leads to
which completes the main steps of the derivation. Dropping the superscripts
![]() $(0)$
and
$(0)$
and
![]() $(2)$
in (A.14a), (A.19), (A.28), and (A.33) and then re-dimensionalising leads to modified FvK equations presented in Section 3.
$(2)$
in (A.14a), (A.19), (A.28), and (A.33) and then re-dimensionalising leads to modified FvK equations presented in Section 3.
A.2. Derivation of the boundary conditions at a free edge
The boundary conditions at the free edges of the plate can be determined from a boundary-layer analysis of the three-dimensional equations of nonlinear elasticity, i.e. (A.1)–(A.5). We use the non-dimensionalisation discussed in Appendix A.1 so that the domain of the plate is defined by
![]() $0 \leq X_1 \leq 1$
,
$0 \leq X_1 \leq 1$
,
![]() $-\mathcal{W}/2 \leq X_2 \leq \mathcal{W}/2$
, and
$-\mathcal{W}/2 \leq X_2 \leq \mathcal{W}/2$
, and
![]() $-1/2 \leq Z \leq 1/2$
, where
$-1/2 \leq Z \leq 1/2$
, where
![]() $\mathcal{W} = W/ L = O(1)$
represents the ratio of the width to the length of the plate. We will analyse the boundary layer at
$\mathcal{W} = W/ L = O(1)$
represents the ratio of the width to the length of the plate. We will analyse the boundary layer at
![]() $X_1 = 1$
in detail and then generalise the results to the boundaries at
$X_1 = 1$
in detail and then generalise the results to the boundaries at
![]() $X_2 = \pm \mathcal{W}/ 2$
. The derivation presented here is based on Howell et al. [Reference Howell, Kozyreff and Ockendon19, Chap. 6.4] but is extended to the case of nonlinear elasticity and accounts for in-plane (longitudinal) tractions on the upper surface of the plate.
$X_2 = \pm \mathcal{W}/ 2$
. The derivation presented here is based on Howell et al. [Reference Howell, Kozyreff and Ockendon19, Chap. 6.4] but is extended to the case of nonlinear elasticity and accounts for in-plane (longitudinal) tractions on the upper surface of the plate.
The analysis begins by writing
![]() $X_1 = 1 + \delta \xi$
and rescaling the (non-dimensionalised) transverse shear and normal components of the stress as
$X_1 = 1 + \delta \xi$
and rescaling the (non-dimensionalised) transverse shear and normal components of the stress as
![]() $\textsf{S}_{\alpha z} = \delta ^{-1}\tilde{\textsf{S}}_{\alpha z}$
,
$\textsf{S}_{\alpha z} = \delta ^{-1}\tilde{\textsf{S}}_{\alpha z}$
,
![]() $\textsf{S}_{z \alpha } = \delta ^{-1} \tilde{\textsf{S}}_{z \alpha }$
, and
$\textsf{S}_{z \alpha } = \delta ^{-1} \tilde{\textsf{S}}_{z \alpha }$
, and
![]() $\textsf{S}_{zz} = \delta ^{-2} \tilde{\textsf{S}}_{zz}$
. Tildes are used to denote dependent variables in the boundary layer. This rescaling means that all components of the stress tensor
$\textsf{S}_{zz} = \delta ^{-2} \tilde{\textsf{S}}_{zz}$
. Tildes are used to denote dependent variables in the boundary layer. This rescaling means that all components of the stress tensor
![]() $\tilde{{\sf\boldsymbol S}}$
have the same order of magnitude in the boundary layer, in contrast to the bulk. With this rescaling, the conservation of linear momentum (A.1) becomes
$\tilde{{\sf\boldsymbol S}}$
have the same order of magnitude in the boundary layer, in contrast to the bulk. With this rescaling, the conservation of linear momentum (A.1) becomes
Conservation of angular momentum (A.2) implies that
The stress-strain relation (A.4) can be written as
The boundary conditions along the upper and lower surfaces of the plate (A.5) are given by
The edge of the plate is taken to be stress-free; therefore, we impose
The displacements and the stress tensor are asymptotically expanded in powers of
![]() $\delta$
as
$\delta$
as
The deformation gradient tensor has the asymptotic form
![]() $\tilde{{\sf\boldsymbol F}} = \tilde{{\sf\boldsymbol F}}^{(0)} + O(\delta )$
, where
$\tilde{{\sf\boldsymbol F}} = \tilde{{\sf\boldsymbol F}}^{(0)} + O(\delta )$
, where
From the
![]() $O(1)$
contributions to (A.36), we can deduce that
$O(1)$
contributions to (A.36), we can deduce that
![]() $\tilde{{\sf\boldsymbol {E}}}^{(0)} = (1/2)\left[\left(\tilde{{\sf\boldsymbol F}}^{(0)}\right)^T\tilde{{\sf\boldsymbol F}}^{(0)} - {\sf\boldsymbol I}\right] = \boldsymbol{\mathsf{0}}$
, and hence,
$\tilde{{\sf\boldsymbol {E}}}^{(0)} = (1/2)\left[\left(\tilde{{\sf\boldsymbol F}}^{(0)}\right)^T\tilde{{\sf\boldsymbol F}}^{(0)} - {\sf\boldsymbol I}\right] = \boldsymbol{\mathsf{0}}$
, and hence,
![]() $\tilde{{\sf\boldsymbol F}}^{(0)} = {\sf\boldsymbol I}$
. Consequently, the leading-order contribution to the vertical displacement is independent of
$\tilde{{\sf\boldsymbol F}}^{(0)} = {\sf\boldsymbol I}$
. Consequently, the leading-order contribution to the vertical displacement is independent of
![]() $\xi$
and
$\xi$
and
![]() $Z$
; by matching to the outer solution as
$Z$
; by matching to the outer solution as
![]() $\xi \to -\infty$
, we obtain
$\xi \to -\infty$
, we obtain
![]() $\tilde{u}_z^{(0)} = w(1,X_2,t)$
. Importantly, the
$\tilde{u}_z^{(0)} = w(1,X_2,t)$
. Importantly, the
![]() $O(1)$
contributions to (A.35) imply that the stress tensor is symmetric to leading order
$O(1)$
contributions to (A.35) imply that the stress tensor is symmetric to leading order
a result that will be of considerable use in the subsequent analysis. The boundary conditions at the upper and lower surfaces can be expanded as
The stress-free conditions at the edge of the plate are
Having simplified the kinematics and the form of the stress tensor, we are now in a position to derive the boundary conditions for the modified FvK equations. We start by considering the
![]() $O(1)$
contributions to (A.34), which can be written as
$O(1)$
contributions to (A.34), which can be written as
Integrating (A.44a) and (A.44b) from
![]() $Z = -1/2$
to
$Z = -1/2$
to
![]() $Z = 1/2$
and using the boundary conditions (A.42a) and (A.42c) yields
$Z = 1/2$
and using the boundary conditions (A.42a) and (A.42c) yields
By integrating with respect to
![]() $\xi$
and using the boundary condition (A.43a), we deduce that
$\xi$
and using the boundary condition (A.43a), we deduce that
for all
![]() $\xi$
. Thus, taking the limit as
$\xi$
. Thus, taking the limit as
![]() $\xi \to -\infty$
and using the matching condition
$\xi \to -\infty$
and using the matching condition
furnishes two stress-free boundary conditions for (A.14a) given by
By applying a similar procedure to (A.44c) and using the symmetry of the stress tensor, we find that
We now multiply (A.44a) by
![]() $Z$
and integrate across the thickness of the plate to obtain, after using (A.42a), (A.42c) and (A.49),
$Z$
and integrate across the thickness of the plate to obtain, after using (A.42a), (A.42c) and (A.49),
By integrating (A.50) over the boundary layer and using the matching condition (A.47) along with (A.29) and the stress-free condition (A.43a), we find that
which provides one of the two boundary conditions for (A.33). By multiplying (A.44b) by
![]() $Z$
and repeating the process, we find that
$Z$
and repeating the process, we find that
To obtain the second boundary condition for (A.33), we consider the
![]() $O(\delta )$
contributions to (A.34c):
$O(\delta )$
contributions to (A.34c):
Integrating (A.53) across the thickness of the plate and over the boundary layer, and using the boundary conditions (A.42b), (A.42d) and (A.43a) gives
To proceed, the integrands on both sides of (A.54) are rewritten using the symmetry of the stress tensor,
![]() $\tilde{\textsf{S}}_{\alpha z}^{(0)} = \tilde{\textsf{S}}_{z \alpha }^{(0)}$
. Then, (A.52) is substituted into the right-hand side to obtain
$\tilde{\textsf{S}}_{\alpha z}^{(0)} = \tilde{\textsf{S}}_{z \alpha }^{(0)}$
. Then, (A.52) is substituted into the right-hand side to obtain
The boundary term evaluated at
![]() $\xi = 0$
can be set to zero using the stress-free condition (A.43a). The remaining terms associated with the far field can be matched with the outer solution using the matching conditions
$\xi = 0$
can be set to zero using the stress-free condition (A.43a). The remaining terms associated with the far field can be matched with the outer solution using the matching conditions
Thus, (A.55) can be written as
which provides the second and final boundary condition for (A.33).
To summarise, the non-dimensional boundary conditions at the free edge located at
![]() $X_1 = 1$
are given by
$X_1 = 1$
are given by
The final two boundary conditions can be written in terms of the vertical displacement
![]() $w$
using the definition of
$w$
using the definition of
![]() ${\sf\boldsymbol {A}}$
in (A.29) to obtain
${\sf\boldsymbol {A}}$
in (A.29) to obtain
By generalising the results, the boundary conditions at the free edges at
![]() $X_2 = \pm \mathcal{W}/2$
are given by
$X_2 = \pm \mathcal{W}/2$
are given by
The boundary conditions given in Section 3.2 can be obtained from these by dropping the
![]() $(0)$
superscript and re-dimensionalisation.
$(0)$
superscript and re-dimensionalisation.