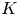1. Introduction
A (separated) orbispace [Reference HaefligerHae90, Reference BehrendBeh14] is a topological stack ![]() $X$ which admits a cover by open substacks of the form
$X$ which admits a cover by open substacks of the form ![]() $Y/\Gamma$ (where
$Y/\Gamma$ (where ![]() $\Gamma \curvearrowright Y$ is a continuous action of a finite group on a topological space) and whose diagonal
$\Gamma \curvearrowright Y$ is a continuous action of a finite group on a topological space) and whose diagonal ![]() $X\to X\times X$ is proper (see § 3 for background on topological stacks). Familiar examples of orbispaces include orbifolds, graphs of groups, complexes of groups, and (the analytifications of) separated Deligne–Mumford algebraic stacks over
$X\to X\times X$ is proper (see § 3 for background on topological stacks). Familiar examples of orbispaces include orbifolds, graphs of groups, complexes of groups, and (the analytifications of) separated Deligne–Mumford algebraic stacks over ![]() $\mathbb {C}$.
$\mathbb {C}$.
An interesting question to ask about a given orbispace ![]() $X$ is whether there exists a global presentation
$X$ is whether there exists a global presentation ![]() $X=Y/G$ for
$X=Y/G$ for ![]() $G$ a compact Lie group; let us call such an orbispace a global quotient. There are a number of known conditions which imply an orbispace is a global quotient. If
$G$ a compact Lie group; let us call such an orbispace a global quotient. There are a number of known conditions which imply an orbispace is a global quotient. If ![]() $X=Y/\Gamma$ for a (possibly infinite) discrete group
$X=Y/\Gamma$ for a (possibly infinite) discrete group ![]() $\Gamma$, then
$\Gamma$, then ![]() $X$ is a global quotient by Lück and Oliver [Reference Lück and OliverLO01, Corollary 2.7]. Every (paracompact) smooth effective
$X$ is a global quotient by Lück and Oliver [Reference Lück and OliverLO01, Corollary 2.7]. Every (paracompact) smooth effective ![]() $n$-dimensional orbifold is a global quotient (of its orthonormal frame bundle by
$n$-dimensional orbifold is a global quotient (of its orthonormal frame bundle by ![]() $O(n)$), and it is an old question whether every (not necessarily effective) smooth orbifold is a global quotient. A sufficient criterion for an orbifold to be a global quotient was given by Henriques and Metzler [Reference Henriques and MetzlerHM04]. Henriques [Reference HenriquesHen05] conjectured that every compact orbispace is a global quotient, however other experts have expressed skepticism that such a general result would be true [Reference SiebertSie98, § 6.4]. The analogous question for algebraic stacks has been studied by Edidin et al. [Reference Edidin, Hassett, Kresch and VistoliEHKV01] and Totaro [Reference TotaroTot04]. It is a result of Kresch and Vistoli [Reference Kresch and VistoliKV04, Theorem 2], [Reference KreschKre09, Theorem 4.4] (using a result of Gabber [Reference de JongdJ03], [Reference Colliot-Thélène and SkorobogatovCTS21, Chapter 4]) that smooth separated Deligne–Mumford stacks over
$O(n)$), and it is an old question whether every (not necessarily effective) smooth orbifold is a global quotient. A sufficient criterion for an orbifold to be a global quotient was given by Henriques and Metzler [Reference Henriques and MetzlerHM04]. Henriques [Reference HenriquesHen05] conjectured that every compact orbispace is a global quotient, however other experts have expressed skepticism that such a general result would be true [Reference SiebertSie98, § 6.4]. The analogous question for algebraic stacks has been studied by Edidin et al. [Reference Edidin, Hassett, Kresch and VistoliEHKV01] and Totaro [Reference TotaroTot04]. It is a result of Kresch and Vistoli [Reference Kresch and VistoliKV04, Theorem 2], [Reference KreschKre09, Theorem 4.4] (using a result of Gabber [Reference de JongdJ03], [Reference Colliot-Thélène and SkorobogatovCTS21, Chapter 4]) that smooth separated Deligne–Mumford stacks over ![]() $\mathbb {C}$ with quasi-projective coarse moduli space are global quotients.
$\mathbb {C}$ with quasi-projective coarse moduli space are global quotients.
Our main result implies that all orbispaces satisfying very mild hypotheses are global quotients. In particular, all compact orbispaces are global quotients.
Theorem 1.1 Let ![]() $X$ be an orbispace, with isotropy groups of bounded order, whose coarse space
$X$ be an orbispace, with isotropy groups of bounded order, whose coarse space ![]() $|X|$ is coarsely finite-dimensional (every open cover has a locally finite refinement with finite-dimensional nerve). Then there exists a complex vector bundle
$|X|$ is coarsely finite-dimensional (every open cover has a locally finite refinement with finite-dimensional nerve). Then there exists a complex vector bundle ![]() $V$ of rank
$V$ of rank ![]() $n>0$ over
$n>0$ over ![]() $X$, whose fiber over every
$X$, whose fiber over every ![]() $x\in X$ is isomorphic to a direct sum of copies of the regular representation of the isotropy group
$x\in X$ is isomorphic to a direct sum of copies of the regular representation of the isotropy group ![]() $G_x$. We may take
$G_x$. We may take ![]() $n=n(d,m)$ if
$n=n(d,m)$ if ![]() $|X|$ is
$|X|$ is ![]() $d$-dimensional (every open cover has a locally finite refinement with nerve of dimension
$d$-dimensional (every open cover has a locally finite refinement with nerve of dimension ![]() $\leqslant d$) and has isotropy groups of order
$\leqslant d$) and has isotropy groups of order ![]() $\leqslant m$.
$\leqslant m$.
(Note that the ‘real’ and ‘complex’ versions of Theorem 1.1 are equivalent, by tensoring from ![]() $\mathbb {R}$ to
$\mathbb {R}$ to ![]() $\mathbb {C}$ and by forgetting from
$\mathbb {C}$ and by forgetting from ![]() $\mathbb {C}$ to
$\mathbb {C}$ to ![]() $\mathbb {R}$.)
$\mathbb {R}$.)
The proof of Theorem 1.1 is split into two parts. In § 2, we prove Theorem 1.1 for any orbispace presented by a simplicial complex of groups; this special case carries the essential topological content of the result. Due to one particular step in this proof, we have no explicit bound on the rank ![]() $n(d,m)$ of the vector bundles proven to exist. In § 4, we deduce Theorem 1.1 in general by showing that every paracompact orbispace admits a representable map to a simplicial complex of groups. This result (Proposition 4.9) is likely of independent interest; it is the analogue of mapping a paracompact Hausdorff space to the nerve of an open covering using a partition of unity (it is, thus, worthy of note that its proof is not trivial).
$n(d,m)$ of the vector bundles proven to exist. In § 4, we deduce Theorem 1.1 in general by showing that every paracompact orbispace admits a representable map to a simplicial complex of groups. This result (Proposition 4.9) is likely of independent interest; it is the analogue of mapping a paracompact Hausdorff space to the nerve of an open covering using a partition of unity (it is, thus, worthy of note that its proof is not trivial).
The following immediate corollaries of Theorem 1.1 are derived in § 5.
Corollary 1.2 For ![]() $X$ as in Theorem 1.1, we have
$X$ as in Theorem 1.1, we have ![]() $X=P/U(n)$ for a space
$X=P/U(n)$ for a space ![]() $P$.
$P$.
Corollary 1.3 Every paracompact smooth orbifold ![]() $X$ of dimension
$X$ of dimension ![]() $\leqslant d$ with isotropy groups of order
$\leqslant d$ with isotropy groups of order ![]() $\leqslant m$ is the quotient
$\leqslant m$ is the quotient ![]() $X=P/U(n)$ of a smooth manifold
$X=P/U(n)$ of a smooth manifold ![]() $P$ by a smooth action of the compact Lie group
$P$ by a smooth action of the compact Lie group ![]() $U(n)$, where
$U(n)$, where ![]() $n=n(d,m)$.
$n=n(d,m)$.
It seems that Theorem 1.1 does not help resolve the question of whether every separated Deligne–Mumford stack of finite type over ![]() $\mathbb {C}$ is a global quotient; the question of whether the vector bundles produced by Theorem 1.1 on its analytification are algebraic (or even analytic) seems difficult.
$\mathbb {C}$ is a global quotient; the question of whether the vector bundles produced by Theorem 1.1 on its analytification are algebraic (or even analytic) seems difficult.
In § 6, we prove the following corollary of Theorem 1.1, to which the titular phrase ‘having enough vector bundles’ refers.
Corollary 1.4 Let ![]() $X\to Y$ be a representable map of orbispaces satisfying the hypothesis of Theorem 1.1. Every vector bundle on
$X\to Y$ be a representable map of orbispaces satisfying the hypothesis of Theorem 1.1. Every vector bundle on ![]() $X$ of bounded rank embeds into the pullback of a vector bundle of bounded rank on
$X$ of bounded rank embeds into the pullback of a vector bundle of bounded rank on ![]() $Y$.
$Y$.
It is well known that Corollary 1.4 is the key statement needed to show that the ![]() $K$-theory of finite rank vector bundles on orbispaces satisfies excision and exactness and is, thus, a cohomology theory (see [Reference Lück and OliverLO01, § 3] and [Reference HenriquesHen05, § 6.3]). We elaborate on this assertion in § 6, using the suggestive reformulation of Corollary 1.4 as the statement that pullback of vector bundles is cofinal. The
$K$-theory of finite rank vector bundles on orbispaces satisfies excision and exactness and is, thus, a cohomology theory (see [Reference Lück and OliverLO01, § 3] and [Reference HenriquesHen05, § 6.3]). We elaborate on this assertion in § 6, using the suggestive reformulation of Corollary 1.4 as the statement that pullback of vector bundles is cofinal. The ![]() $K$-theory of finite-rank vector bundles should agree (for reasonable orbispaces) with the other standard models of
$K$-theory of finite-rank vector bundles should agree (for reasonable orbispaces) with the other standard models of ![]() $K$-theory for orbispaces, such as using bundles of Fredholm operators [Reference SegalSeg70, Reference MatumotoMat71, Reference AtiyahAti69, Reference Atiyah and SingerAS69] or using orthogonal spectra [Reference SchwedeSch18, §§ 6.3–6.4] (compare with Remark 1.6).
$K$-theory for orbispaces, such as using bundles of Fredholm operators [Reference SegalSeg70, Reference MatumotoMat71, Reference AtiyahAti69, Reference Atiyah and SingerAS69] or using orthogonal spectra [Reference SchwedeSch18, §§ 6.3–6.4] (compare with Remark 1.6).
Remark 1.5 Another known (to experts) consequence of Corollary 1.4 (which we do not explain in detail) is that every paracompact quasi-smooth derived smooth orbifold with tangent and obstruction spaces of dimension ![]() $\leqslant d$ and isotropy groups of order
$\leqslant d$ and isotropy groups of order ![]() $\leqslant m$ is the derived zero set of a smooth section of a vector bundle of rank
$\leqslant m$ is the derived zero set of a smooth section of a vector bundle of rank ![]() $\leqslant n$ over a smooth orbifold of dimension
$\leqslant n$ over a smooth orbifold of dimension ![]() $\leqslant n=n(d,m)$. (‘Quasi-smooth’ means locally isomorphic to the derived zero set of a smooth section of a smooth vector bundle over a smooth orbifold.)
$\leqslant n=n(d,m)$. (‘Quasi-smooth’ means locally isomorphic to the derived zero set of a smooth section of a smooth vector bundle over a smooth orbifold.)
Remark 1.6 Combined work of Schwede [Reference SchwedeSch20] and Gepner and Henriques [Reference Henriques and GepnerHG07] established an equivalence between orthogonal spaces up to global equivalence (with respect to the ‘global family’ of all finite groups) and certain categories of ‘cellular’ topological stacks (which include, but are more general than, what we call orbispaces here). The vector bundles produced by Theorem 1.1 allow for a concrete description of the functor from orbispaces to orthogonal spaces (compare [Reference SchwedeSch18, Definition 1.1.27]). Let ![]() $X$ be an orbispace, and let
$X$ be an orbispace, and let ![]() $E$ be any faithful vector bundle over
$E$ be any faithful vector bundle over ![]() $X$ (meaning the fibers of
$X$ (meaning the fibers of ![]() $E$ are faithful representations of the isotropy groups of
$E$ are faithful representations of the isotropy groups of ![]() $X$). The orthogonal space corresponding to
$X$). The orthogonal space corresponding to ![]() $X$ is given by
$X$ is given by
where ![]() $\operatorname {Emb}_X(E,\underline {V})$ denotes the total space of the bundle of embeddings of
$\operatorname {Emb}_X(E,\underline {V})$ denotes the total space of the bundle of embeddings of ![]() $E$ into
$E$ into ![]() $V$ (note that
$V$ (note that ![]() $\operatorname {Emb}_X(E,\underline {V})$ is a space because
$\operatorname {Emb}_X(E,\underline {V})$ is a space because ![]() $E$ is faithful).
$E$ is faithful).
Schwede [Reference SchwedeSch18] also associates to every orthogonal spectrum a cohomology theory on orthogonal spaces, hence on orbispaces. Given an orthogonal spectrum ![]() $A$ and an orbispace
$A$ and an orbispace ![]() $X$ which admits faithful vector bundles, the degree-zero
$X$ which admits faithful vector bundles, the degree-zero ![]() $A$-cohomology of
$A$-cohomology of ![]() $X$ is (in view of the above) given by the direct limit over vector bundles
$X$ is (in view of the above) given by the direct limit over vector bundles ![]() $E$ over
$E$ over ![]() $X$ of the set of homotopy classes of sections of the fibration
$X$ of the set of homotopy classes of sections of the fibration ![]() $\Omega ^EA(E)\to X$. More generally, we may consider the mapping spectrum
$\Omega ^EA(E)\to X$. More generally, we may consider the mapping spectrum ![]() $F(X,A)$ defined by
$F(X,A)$ defined by
whose stable homotopy groups are the ![]() $A$-cohomology groups of
$A$-cohomology groups of ![]() $X$. If
$X$. If ![]() $A$ is a global
$A$ is a global ![]() $\Omega$-spectrum [Reference SchwedeSch18, Definition 4.3.8], then this direct limit is achieved at any faithful
$\Omega$-spectrum [Reference SchwedeSch18, Definition 4.3.8], then this direct limit is achieved at any faithful ![]() $E$, and the above definition of
$E$, and the above definition of ![]() $F(X,A)$ is an
$F(X,A)$ is an ![]() $\Omega$-spectrum. Let us also propose a possible definition of the
$\Omega$-spectrum. Let us also propose a possible definition of the ![]() $A$-homology groups of
$A$-homology groups of ![]() $X$ as the stable homotopy groups of the spectrum
$X$ as the stable homotopy groups of the spectrum
where ![]() $|\cdot |$ indicates taking the coarse space of the total space of
$|\cdot |$ indicates taking the coarse space of the total space of ![]() $\Omega ^EA(E\oplus \mathbb {R}^n)$ over
$\Omega ^EA(E\oplus \mathbb {R}^n)$ over ![]() $X$.
$X$.
Remark 1.7 It is natural to ask to what extent Theorem 1.1 may be generalized to the case of ‘Lie orbispaces’ (topological stacks locally modelled on ![]() $Y/G$ for
$Y/G$ for ![]() $G$ a compact Lie group). The naive generalization is simply false: there are purely ineffective Lie orbispaces with isotropy group
$G$ a compact Lie group). The naive generalization is simply false: there are purely ineffective Lie orbispaces with isotropy group ![]() $S^1$ and coarse space
$S^1$ and coarse space ![]() $S^3$ which have no finite rank faithful vector bundles [Reference TotaroTot04, § 2]. It is, however, reasonable to conjecture that the proof of Theorem 1.1 could be generalized to prove that the existence of enough vector bundles on a Lie orbispace is a purely cohomological question.
$S^3$ which have no finite rank faithful vector bundles [Reference TotaroTot04, § 2]. It is, however, reasonable to conjecture that the proof of Theorem 1.1 could be generalized to prove that the existence of enough vector bundles on a Lie orbispace is a purely cohomological question.
2. The main construction
This section is devoted to proving Theorem 1.1 for orbispaces which are presented by a simplicial complex of groups. This special case (stated as Theorem 2.13) carries the essential topological content of Theorem 1.1. For general background on orbispaces and topological stacks, we refer the reader to § 3.
We begin by describing the basic idea of the proof, which we then implement in detail. Our orbispace ![]() $X$ comes with a filtration by skeleta
$X$ comes with a filtration by skeleta
where ![]() $X_k$ is obtained from
$X_k$ is obtained from ![]() $X_{k-1}$ by attaching cells of the form
$X_{k-1}$ by attaching cells of the form ![]() $(D^k,\partial D^k)\times \mathbb {B} G$ for finite groups
$(D^k,\partial D^k)\times \mathbb {B} G$ for finite groups ![]() $G$ (here
$G$ (here ![]() $\mathbb {B} G=*/G$ is the orbispace quotient). We construct the desired vector bundle by induction on skeleta.
$\mathbb {B} G=*/G$ is the orbispace quotient). We construct the desired vector bundle by induction on skeleta.
A direct implementation of this strategy runs immediately into the following obstruction. A (complex) vector bundle ![]() $V$ on
$V$ on ![]() $\partial D^k\times \mathbb {B} G$ decomposes canonically as
$\partial D^k\times \mathbb {B} G$ decomposes canonically as ![]() $V=\bigoplus _{\rho \in \hat G}V_\rho \otimes \rho$ for vector bundles
$V=\bigoplus _{\rho \in \hat G}V_\rho \otimes \rho$ for vector bundles ![]() $V_\rho$ on
$V_\rho$ on ![]() $\partial D^k$ indexed by the complex irreducible representations
$\partial D^k$ indexed by the complex irreducible representations ![]() $\rho$ of
$\rho$ of ![]() $G$. Thus,
$G$. Thus, ![]() $V$ is classified by an element of
$V$ is classified by an element of ![]() $\prod _{\rho \in \hat G}\pi _{k-1}(\coprod _nBU(n))$, which vanishes if and only if
$\prod _{\rho \in \hat G}\pi _{k-1}(\coprod _nBU(n))$, which vanishes if and only if ![]() $V$ extends to
$V$ extends to ![]() $D^k\times \mathbb {B} G$. We seek to detect these obstructions using Chern characters. According to Bott periodicity, the homotopy groups of
$D^k\times \mathbb {B} G$. We seek to detect these obstructions using Chern characters. According to Bott periodicity, the homotopy groups of ![]() $BU$ are given by
$BU$ are given by
 \[ \pi_i(BU)=\begin{cases}\mathbb{Z} & i\text{ even,}\\0 & i\text{ odd,}\end{cases} \]
\[ \pi_i(BU)=\begin{cases}\mathbb{Z} & i\text{ even,}\\0 & i\text{ odd,}\end{cases} \]
and the Chern character of a generator of ![]() $\pi _{2i}(BU)$ is nonzero. Now the Chern character of
$\pi _{2i}(BU)$ is nonzero. Now the Chern character of ![]() $V=\bigoplus _{\rho \in \hat G}V_\rho \otimes \rho$ is given by
$V=\bigoplus _{\rho \in \hat G}V_\rho \otimes \rho$ is given by ![]() $\operatorname {ch}(V)=\sum _{\rho \in \hat G}\operatorname {ch}(V_\rho )\dim \rho$, so triviality of
$\operatorname {ch}(V)=\sum _{\rho \in \hat G}\operatorname {ch}(V_\rho )\dim \rho$, so triviality of ![]() $\operatorname {ch}(V)$ does not imply triviality of each
$\operatorname {ch}(V)$ does not imply triviality of each ![]() $\operatorname {ch}(V_\rho )$ or of the aforementioned obstructions to extending
$\operatorname {ch}(V_\rho )$ or of the aforementioned obstructions to extending ![]() $V$.
$V$.
To capture the information we need about ![]() $V$, we consider the more refined characteristic class which we call the inertial Chern character Footnote 1
$V$, we consider the more refined characteristic class which we call the inertial Chern character Footnote 1 ![]() $\operatorname {ch}^I$ (studied previously by Adem and Ruan [Reference Adem and RuanAR03]), which is a cohomology class on the inertia stack
$\operatorname {ch}^I$ (studied previously by Adem and Ruan [Reference Adem and RuanAR03]), which is a cohomology class on the inertia stack
In local coordinates ![]() $X=Y/G$, we have
$X=Y/G$, we have ![]() $IX=\bigl (\bigsqcup _{g\in G}Y^g\bigr )/G$. In such coordinates, the inertial Chern character is defined by recalling the Chern–Weil description of the usual Chern character
$IX=\bigl (\bigsqcup _{g\in G}Y^g\bigr )/G$. In such coordinates, the inertial Chern character is defined by recalling the Chern–Weil description of the usual Chern character ![]() $\operatorname {ch}(V)=\operatorname {tr}\exp (\Omega /(-2\pi i))$, for
$\operatorname {ch}(V)=\operatorname {tr}\exp (\Omega /(-2\pi i))$, for ![]() $\Omega$ the curvature of a hermitian connection on
$\Omega$ the curvature of a hermitian connection on ![]() $V$, and writing
$V$, and writing
Now the inertia stack of ![]() $\partial D^k\times \mathbb {B} G$ is
$\partial D^k\times \mathbb {B} G$ is ![]() $\partial D^k\times G/G$ (quotient by the conjugation action), and the inertial Chern character of
$\partial D^k\times G/G$ (quotient by the conjugation action), and the inertial Chern character of ![]() $V=\bigoplus _{\rho \in \hat G}V_\rho \otimes \rho$ is given by
$V=\bigoplus _{\rho \in \hat G}V_\rho \otimes \rho$ is given by ![]() $\operatorname {ch}^I(V)=\sum _{\rho \in \hat G}\operatorname {ch}(V_\rho )\chi _\rho$. Thus, if
$\operatorname {ch}^I(V)=\sum _{\rho \in \hat G}\operatorname {ch}(V_\rho )\chi _\rho$. Thus, if ![]() $\operatorname {ch}^I(V)$ is trivial, then so is each
$\operatorname {ch}^I(V)$ is trivial, then so is each ![]() $\operatorname {ch}(V_\rho )$ by linear independence of characters, and hence
$\operatorname {ch}(V_\rho )$ by linear independence of characters, and hence ![]() $V$ extends to
$V$ extends to ![]() $D^k\times \mathbb {B} G$ as desired.
$D^k\times \mathbb {B} G$ as desired.
We are thus led to consider the modified problem of constructing a vector bundle on ![]() $X$ with the desired fibers and with trivial inertial Chern character. It suffices to show that if
$X$ with the desired fibers and with trivial inertial Chern character. It suffices to show that if ![]() $X_{k-1}$ admits such a vector bundle, then so does
$X_{k-1}$ admits such a vector bundle, then so does ![]() $X_k$. The vanishing of
$X_k$. The vanishing of ![]() $\operatorname {ch}^I(V)\in H^*(IX_{k-1})$ guarantees that the obstructions to extending
$\operatorname {ch}^I(V)\in H^*(IX_{k-1})$ guarantees that the obstructions to extending ![]() $V$ to
$V$ to ![]() $X_k$ vanish, by the above discussion. It thus remains to show that this extension can be taken to have trivial inertial Chern character. The inertial Chern character of any extension is an element of
$X_k$ vanish, by the above discussion. It thus remains to show that this extension can be taken to have trivial inertial Chern character. The inertial Chern character of any extension is an element of ![]() $\ker (H^*(IX_k)\to H^*(IX_{k-1}))$. By the long exact sequence
$\ker (H^*(IX_k)\to H^*(IX_{k-1}))$. By the long exact sequence
it is thus in the image of ![]() $H^*(IX_k,IX_{k-1})$. The inertial Chern character is an even degree class, so we may assume that
$H^*(IX_k,IX_{k-1})$. The inertial Chern character is an even degree class, so we may assume that ![]() $k$ is even. By modifying how we extend
$k$ is even. By modifying how we extend ![]() $V$ from
$V$ from ![]() $X_{k-1}$ to
$X_{k-1}$ to ![]() $X_k$ by an element of
$X_k$ by an element of ![]() $\prod _{\rho \in \hat G}\pi _k(BU)$ over a given
$\prod _{\rho \in \hat G}\pi _k(BU)$ over a given ![]() $k$-simplex, we can shift its inertial Chern character by any integral linear combination of characters in
$k$-simplex, we can shift its inertial Chern character by any integral linear combination of characters in ![]() $\operatorname {Hom}(G/G,\mathbb {C})\subseteq H^*(IX_k,IX_{k-1})$ (for
$\operatorname {Hom}(G/G,\mathbb {C})\subseteq H^*(IX_k,IX_{k-1})$ (for ![]() $G$ the isotropy group of that given
$G$ the isotropy group of that given ![]() $k$-simplex). By replacing
$k$-simplex). By replacing ![]() $V$ with
$V$ with ![]() $V^{\oplus a}$, we can multiply its inertial Chern character by any positive integer
$V^{\oplus a}$, we can multiply its inertial Chern character by any positive integer ![]() $a$. A combination of these two operations suffice to kill the inertial Chern character, provided that it is
$a$. A combination of these two operations suffice to kill the inertial Chern character, provided that it is ![]() $\chi$-rational (rational with respect to a certain
$\chi$-rational (rational with respect to a certain ![]() $\mathbb {Q}$-structure on
$\mathbb {Q}$-structure on ![]() $H^*(IX)$ differing from the usual one). This rationality is not at all obvious given the transcendental definition we give of the inertial Chern character, but it is true, and thus the proof is complete.
$H^*(IX)$ differing from the usual one). This rationality is not at all obvious given the transcendental definition we give of the inertial Chern character, but it is true, and thus the proof is complete.
The remainder of this section is devoted to making the above outline precise. We begin by recalling the definition of a simplicial complex of groups (see also Haefliger [Reference HaefligerHae91], Corson [Reference CorsonCor92], or Bridson and Haefliger [Reference Bridson and HaefligerBH99]).
Definition 2.1 A simplicial complex of groups is a pair ![]() $(Z,G)$ consisting of a simplicial complex
$(Z,G)$ consisting of a simplicial complex ![]() $Z$ together with the following data.
$Z$ together with the following data.
• For every simplex
 $\sigma \subseteq Z$, a group
$\sigma \subseteq Z$, a group  $G_\sigma$.
$G_\sigma$.• For every pair of simplices
 $\sigma \subseteq \tau$, an injective group homomorphism
$\sigma \subseteq \tau$, an injective group homomorphism  $G_\tau \hookrightarrow G_\sigma$.
$G_\tau \hookrightarrow G_\sigma$.• For every triple of simplices
 $\rho \subseteq \sigma \subseteq \tau$, an element of
$\rho \subseteq \sigma \subseteq \tau$, an element of  $G_\rho$ conjugating the inclusion
$G_\rho$ conjugating the inclusion  $G_\tau \hookrightarrow G_\rho$ to the composition of inclusions
$G_\tau \hookrightarrow G_\rho$ to the composition of inclusions  $G_\tau \hookrightarrow G_\sigma \hookrightarrow G_\rho$.
$G_\tau \hookrightarrow G_\sigma \hookrightarrow G_\rho$.• For every quadruple of simplices
 $\pi \subseteq \rho \subseteq \sigma \subseteq \tau$, the resulting product of elements of
$\pi \subseteq \rho \subseteq \sigma \subseteq \tau$, the resulting product of elements of  $G_\pi$ conjugating
$G_\pi$ conjugating  $G_\tau \hookrightarrow G_\pi$ to
$G_\tau \hookrightarrow G_\pi$ to  $G_\tau \hookrightarrow G_\rho \hookrightarrow G_\pi$ to
$G_\tau \hookrightarrow G_\rho \hookrightarrow G_\pi$ to  $G_\tau \hookrightarrow G_\sigma \hookrightarrow G_\rho \hookrightarrow G_\pi$ to
$G_\tau \hookrightarrow G_\sigma \hookrightarrow G_\rho \hookrightarrow G_\pi$ to  $G_\tau \hookrightarrow G_\sigma \hookrightarrow G_\pi$ and back to
$G_\tau \hookrightarrow G_\sigma \hookrightarrow G_\pi$ and back to  $G_\tau \hookrightarrow G_\pi$ must be the identity element of
$G_\tau \hookrightarrow G_\pi$ must be the identity element of  $G_\pi$.
$G_\pi$.
Injectivity of each map ![]() $G_\tau \hookrightarrow G_\sigma$ will ensure that the geometric realization of
$G_\tau \hookrightarrow G_\sigma$ will ensure that the geometric realization of ![]() $(Z,G)$ is an orbispace, rather than some sort of more exotic topological stack.
$(Z,G)$ is an orbispace, rather than some sort of more exotic topological stack.
A simplicial complex of groups ![]() $(Z,G)$ presents an orbispace
$(Z,G)$ presents an orbispace ![]() $\|(Z,G)\|$ called its geometric realization. A precise definition of this geometric realization is given in § 4. For now, it will suffice to know that the coarse space of
$\|(Z,G)\|$ called its geometric realization. A precise definition of this geometric realization is given in § 4. For now, it will suffice to know that the coarse space of ![]() $\|(Z,G)\|$ is (the geometric realization of)
$\|(Z,G)\|$ is (the geometric realization of) ![]() $Z$ itself, and that over the open star
$Z$ itself, and that over the open star ![]() $\operatorname {st}(\sigma )\subseteq Z$ of a simplex
$\operatorname {st}(\sigma )\subseteq Z$ of a simplex ![]() $\sigma \subseteq Z$, the geometric realization
$\sigma \subseteq Z$, the geometric realization ![]() $\|(Z,G)\|$ is given by the orbispace quotient
$\|(Z,G)\|$ is given by the orbispace quotient
 \[ \biggl(\bigsqcup_{\tau\supseteq\sigma}\tau\times(G_\tau\setminus G_\sigma)\biggr)\biggm/G_\sigma, \]
\[ \biggl(\bigsqcup_{\tau\supseteq\sigma}\tau\times(G_\tau\setminus G_\sigma)\biggr)\biggm/G_\sigma, \]
where the pieces for ![]() $\tau \supseteq \tau '\supseteq \sigma$ are glued together via the map
$\tau \supseteq \tau '\supseteq \sigma$ are glued together via the map ![]() $G_\tau \setminus G_\sigma \to G_{\tau '}\setminus G_\sigma$ induced by the map
$G_\tau \setminus G_\sigma \to G_{\tau '}\setminus G_\sigma$ induced by the map ![]() $G_\tau \to G_{\tau '}$ and the element of
$G_\tau \to G_{\tau '}$ and the element of ![]() $G_\sigma$ conjugating the composition
$G_\sigma$ conjugating the composition ![]() $G_\tau \to G_{\tau '}\to G_\sigma$ to the map
$G_\tau \to G_{\tau '}\to G_\sigma$ to the map ![]() $G_\tau \to G_\sigma$.
$G_\tau \to G_\sigma$.
We often abuse terminology and say ‘simplicial complex of groups’ when we really mean its geometric realization. Thus, we refer to ![]() $X=\|(Z,G)\|$ as a simplicial complex of groups. Its coarse space
$X=\|(Z,G)\|$ as a simplicial complex of groups. Its coarse space ![]() $|X|$ is the geometric realization of
$|X|$ is the geometric realization of ![]() $Z$.
$Z$.
To apply the methods of differential topology to a given simplicial complex of groups, we fix a family of (germs of) smooth retractions ![]() $\tau \to \sigma$ for every pair of simplices
$\tau \to \sigma$ for every pair of simplices ![]() $\sigma \subseteq \tau$ such that the maps
$\sigma \subseteq \tau$ such that the maps ![]() $\tau \to \sigma \to \rho$ and
$\tau \to \sigma \to \rho$ and ![]() $\tau \to \rho$ agree for
$\tau \to \rho$ agree for ![]() $\rho \subseteq \sigma \subseteq \tau$ (such a family of smooth retractions may be constructed by induction). Given this data, objects of differential topology on
$\rho \subseteq \sigma \subseteq \tau$ (such a family of smooth retractions may be constructed by induction). Given this data, objects of differential topology on ![]() $\tau$ (functions, differential forms, bundles, connections, etc.) are required to be pulled back under
$\tau$ (functions, differential forms, bundles, connections, etc.) are required to be pulled back under ![]() $\tau \to \sigma$ in a(n unspecified) neighborhood of every
$\tau \to \sigma$ in a(n unspecified) neighborhood of every ![]() $\sigma \subseteq \tau$. For bundles, this requirement consists of the data of a compatible family of isomorphisms with the pullback bundles (one could equivalently consider only vector bundles built out of transition functions which satisfy the given pullback conditions).
$\sigma \subseteq \tau$. For bundles, this requirement consists of the data of a compatible family of isomorphisms with the pullback bundles (one could equivalently consider only vector bundles built out of transition functions which satisfy the given pullback conditions).
In particular, the de Rham complex ![]() $\Omega ^*(X)$ of a simplicial complex of groups
$\Omega ^*(X)$ of a simplicial complex of groups ![]() $X$ is defined, and it coincides with the de Rham complex of its coarse space
$X$ is defined, and it coincides with the de Rham complex of its coarse space ![]() $\Omega ^*(|X|)$. There is a natural map
$\Omega ^*(|X|)$. There is a natural map ![]() $\Omega ^*(|X|)\to C^*(|X|;\mathbb {R})=C^*(X;\mathbb {R})$ from the de Rham complex to the simplicial cochain complex over
$\Omega ^*(|X|)\to C^*(|X|;\mathbb {R})=C^*(X;\mathbb {R})$ from the de Rham complex to the simplicial cochain complex over ![]() $\mathbb {R}$, given by integrating differential forms over oriented simplices. It is a standard fact that this map is a quasi-isomorphism (proof: filter
$\mathbb {R}$, given by integrating differential forms over oriented simplices. It is a standard fact that this map is a quasi-isomorphism (proof: filter ![]() $X$ by skeleta and invoke the five lemma to reduce to showing that
$X$ by skeleta and invoke the five lemma to reduce to showing that ![]() $\Omega ^*(\Delta ^k,\partial \Delta ^k)\to C^*(\Delta ^k,\partial \Delta ^k;\mathbb {R})$ is a quasi-isomorphism, which follows from the Poincaré lemma).
$\Omega ^*(\Delta ^k,\partial \Delta ^k)\to C^*(\Delta ^k,\partial \Delta ^k;\mathbb {R})$ is a quasi-isomorphism, which follows from the Poincaré lemma).
Definition 2.2 (Chern character)
Let ![]() $X$ be a simplicial complex of groups, and let
$X$ be a simplicial complex of groups, and let ![]() $V\to X$ be a complex vector bundle. Given a hermitian metric
$V\to X$ be a complex vector bundle. Given a hermitian metric ![]() $\mu$ and hermitian connection
$\mu$ and hermitian connection ![]() $\theta$ on
$\theta$ on ![]() $V$, the curvature of
$V$, the curvature of ![]() $\theta$ is a
$\theta$ is a ![]() $2$-form
$2$-form ![]() $\Omega (V,\theta )$ valued in
$\Omega (V,\theta )$ valued in ![]() $\mathfrak u(V,\mu )\subseteq \mathfrak {gl}(V)=\operatorname {End}(V)$, and the Chern character form
$\mathfrak u(V,\mu )\subseteq \mathfrak {gl}(V)=\operatorname {End}(V)$, and the Chern character form
is closed. Its class in cohomology ![]() $\operatorname {ch}(V)\in H^\mathrm {even}(X;\mathbb {R})$ is called the Chern character of
$\operatorname {ch}(V)\in H^\mathrm {even}(X;\mathbb {R})$ is called the Chern character of ![]() $V$. This class is independent of
$V$. This class is independent of ![]() $\mu$ and
$\mu$ and ![]() $\theta$ by an interpolation argument (interpolate on
$\theta$ by an interpolation argument (interpolate on ![]() $X\times [0,1]$ between any two metric/connection pairs on
$X\times [0,1]$ between any two metric/connection pairs on ![]() $X\times 0$ and
$X\times 0$ and ![]() $X\times 1$, and use the fact that
$X\times 1$, and use the fact that ![]() $H^*(X\times [0,1])=H^*(X)$).
$H^*(X\times [0,1])=H^*(X)$).
For any stack ![]() $X$, its inertia stack is the stack
$X$, its inertia stack is the stack
When ![]() $X=Y/G$, we have
$X=Y/G$, we have ![]() $IX=\bigl (\bigsqcup _{g\in G}Y^g\bigr )/G$. In particular, the local description of the geometric realization of a simplicial complex of groups provides a local description of its inertia stack as well. In fact, if
$IX=\bigl (\bigsqcup _{g\in G}Y^g\bigr )/G$. In particular, the local description of the geometric realization of a simplicial complex of groups provides a local description of its inertia stack as well. In fact, if ![]() $X$ is a simplicial complex of groups then so is
$X$ is a simplicial complex of groups then so is ![]() $IX$: a simplex of
$IX$: a simplex of ![]() $IX$ is a pair
$IX$ is a pair ![]() $(\sigma,[g])$ where
$(\sigma,[g])$ where ![]() $\sigma \subseteq X$ is a simplex and
$\sigma \subseteq X$ is a simplex and ![]() $[g]\subseteq G_\sigma$ is a conjugacy class, and
$[g]\subseteq G_\sigma$ is a conjugacy class, and ![]() $G_{(\sigma,[g])}$ is the centralizer of any element of the conjugacy class
$G_{(\sigma,[g])}$ is the centralizer of any element of the conjugacy class ![]() $[g]\subseteq G_\sigma$, etc.
$[g]\subseteq G_\sigma$, etc.
Definition 2.3 (Inertial Chern character)
Let ![]() $X$ be a simplicial complex of groups, and let
$X$ be a simplicial complex of groups, and let ![]() $V\to X$ be a complex vector bundle. The inertial Chern character
$V\to X$ be a complex vector bundle. The inertial Chern character ![]() $\operatorname {ch}^I(V)\in H^\mathrm {even}(IX;\mathbb {C})$ is represented by the closed form
$\operatorname {ch}^I(V)\in H^\mathrm {even}(IX;\mathbb {C})$ is represented by the closed form
for any choice of hermitian metric and connection ![]() $\theta$ on
$\theta$ on ![]() $V$. Closedness can be seen by splitting the pullback of
$V$. Closedness can be seen by splitting the pullback of ![]() $V$ to
$V$ to ![]() $IX$ into isotypic pieces for the action of the cyclic group generated by
$IX$ into isotypic pieces for the action of the cyclic group generated by ![]() $g$ and observing that the contribution of each such piece is a (usual) Chern character form. Independence of the metric and connection follows from the same interpolation argument as before.
$g$ and observing that the contribution of each such piece is a (usual) Chern character form. Independence of the metric and connection follows from the same interpolation argument as before.
Example 2.4 If ![]() $X=\mathbb {B} G$, a vector bundle over
$X=\mathbb {B} G$, a vector bundle over ![]() $X$ is simply a representation of
$X$ is simply a representation of ![]() $G$, the inertia stack
$G$, the inertia stack ![]() $IX=G/G$ is the stack quotient of the conjugation action of
$IX=G/G$ is the stack quotient of the conjugation action of ![]() $G$ on itself, and the inertial Chern character
$G$ on itself, and the inertial Chern character ![]() $\operatorname {ch}^I(V):G/G\to \mathbb {C}$ is the character
$\operatorname {ch}^I(V):G/G\to \mathbb {C}$ is the character ![]() $g\mapsto \operatorname {tr}(g|V)$ of
$g\mapsto \operatorname {tr}(g|V)$ of ![]() $V$ regarded as a representation of
$V$ regarded as a representation of ![]() $G$.
$G$.
Example 2.5 If ![]() $X=Y\times \mathbb {B} G$ for a smooth manifold
$X=Y\times \mathbb {B} G$ for a smooth manifold ![]() $Y$ and
$Y$ and ![]() $V=\bigoplus _{\rho \in \hat G}V_\rho \otimes \rho$, then
$V=\bigoplus _{\rho \in \hat G}V_\rho \otimes \rho$, then ![]() $IX=Y\times (G/G)$ and the inertial Chern character
$IX=Y\times (G/G)$ and the inertial Chern character ![]() $\operatorname {ch}^I(V):G/G\to H^*(Y;\mathbb {C})$ is given by
$\operatorname {ch}^I(V):G/G\to H^*(Y;\mathbb {C})$ is given by ![]() $\operatorname {ch}^I(V)=\sum _\rho \operatorname {ch}(V_\rho )\chi _\rho$. As the characters
$\operatorname {ch}^I(V)=\sum _\rho \operatorname {ch}(V_\rho )\chi _\rho$. As the characters ![]() $\chi _\rho$ of the irreducible representations
$\chi _\rho$ of the irreducible representations ![]() $\rho$ of
$\rho$ of ![]() $G$ form a basis for the space of maps
$G$ form a basis for the space of maps ![]() $G/G\to \mathbb {C}$, we see that for
$G/G\to \mathbb {C}$, we see that for ![]() $X=Y\times \mathbb {B} G$, the inertial Chern character determines (and is determined by) the Chern characters of each of the associated bundles
$X=Y\times \mathbb {B} G$, the inertial Chern character determines (and is determined by) the Chern characters of each of the associated bundles ![]() $V_\rho$.
$V_\rho$.
Example 2.6 The degree-zero part of the inertial Chern character ![]() $\operatorname {ch}_0^I(V)\in H^0(IX;\mathbb {C})$ records the characters of the fibers of
$\operatorname {ch}_0^I(V)\in H^0(IX;\mathbb {C})$ records the characters of the fibers of ![]() $V$, regarded as representations of the isotropy groups
$V$, regarded as representations of the isotropy groups ![]() $G_x$ of the points of
$G_x$ of the points of ![]() $X$.
$X$.
Despite admitting the aforementioned transcendental definition in terms of differential forms, the (usual) Chern character ![]() $\operatorname {ch}(V)\in H^*(X;\mathbb {R})$ is well known be rational, i.e. it lies in the subspace
$\operatorname {ch}(V)\in H^*(X;\mathbb {R})$ is well known be rational, i.e. it lies in the subspace ![]() $H^*(X;\mathbb {Q})\subseteq H^*(X;\mathbb {R})$. The inertial Chern character does not always lie in the subspace
$H^*(X;\mathbb {Q})\subseteq H^*(X;\mathbb {R})$. The inertial Chern character does not always lie in the subspace ![]() $H^*(IX;\mathbb {Q})\subseteq H^*(IX;\mathbb {C})$, rather it is rational with respect to a different
$H^*(IX;\mathbb {Q})\subseteq H^*(IX;\mathbb {C})$, rather it is rational with respect to a different ![]() $\mathbb {Q}$-structure, which we now introduce.
$\mathbb {Q}$-structure, which we now introduce.
Definition 2.7 ( $\chi$-integral cohomology of
$\chi$-integral cohomology of  $IX$)
$IX$)
Regard the simplicial cochain group ![]() $C^*(IX;\mathbb {C})$ as the group of simplicial cochains on
$C^*(IX;\mathbb {C})$ as the group of simplicial cochains on ![]() $X$ with coefficients in
$X$ with coefficients in ![]() $\operatorname {Hom}(G_x/G_x,\mathbb {C})$. In this description, let us replace
$\operatorname {Hom}(G_x/G_x,\mathbb {C})$. In this description, let us replace ![]() $\operatorname {Hom}(G_x/G_x,\mathbb {C})$ with its subspace of integral (respectively, rational) linear combinations of characters of
$\operatorname {Hom}(G_x/G_x,\mathbb {C})$ with its subspace of integral (respectively, rational) linear combinations of characters of ![]() $G_x$. Equivalently, we consider the complex of simplicial cochains on
$G_x$. Equivalently, we consider the complex of simplicial cochains on ![]() $IX$ which act on
$IX$ which act on ![]() $\sigma \times (G_\sigma /G_\sigma )\subseteq IX$ (for any simplex
$\sigma \times (G_\sigma /G_\sigma )\subseteq IX$ (for any simplex ![]() $\sigma \subseteq X$) by an integral (respectively, rational) linear combination of characters of
$\sigma \subseteq X$) by an integral (respectively, rational) linear combination of characters of ![]() $G_\sigma$. We denote the resulting cohomology groups by
$G_\sigma$. We denote the resulting cohomology groups by ![]() $H^*(IX;\mathbb {Z}_\chi )$ (respectively,
$H^*(IX;\mathbb {Z}_\chi )$ (respectively, ![]() $H^*(IX;\mathbb {Q}_\chi )$), which are evidently functorial in
$H^*(IX;\mathbb {Q}_\chi )$), which are evidently functorial in ![]() $X$. We say that an element of
$X$. We say that an element of ![]() $H^*(IX;\mathbb {C})$ is
$H^*(IX;\mathbb {C})$ is ![]() $\chi$-integral (respectively,
$\chi$-integral (respectively, ![]() $\chi$-rational) to mean that it lies in the image of
$\chi$-rational) to mean that it lies in the image of ![]() $H^*(IX;\mathbb {Z}_\chi )$ (respectively, in the subspace
$H^*(IX;\mathbb {Z}_\chi )$ (respectively, in the subspace ![]() $H^*(IX;\mathbb {Q}_\chi )$).
$H^*(IX;\mathbb {Q}_\chi )$).
Example 2.8 If ![]() $X=Y\times \mathbb {B} G$, then
$X=Y\times \mathbb {B} G$, then ![]() $IX=Y\times (G/G)$ and
$IX=Y\times (G/G)$ and ![]() $H^*(IX;\mathbb {Z}_\chi )=H^*(X;\mathbb {Z}[\hat G])$. Thus,
$H^*(IX;\mathbb {Z}_\chi )=H^*(X;\mathbb {Z}[\hat G])$. Thus, ![]() $\operatorname {ch}^I(V)=\sum _\rho \operatorname {ch}(V_\rho )\chi _\rho$ is
$\operatorname {ch}^I(V)=\sum _\rho \operatorname {ch}(V_\rho )\chi _\rho$ is ![]() $\chi$-rational because each
$\chi$-rational because each ![]() $\operatorname {ch}(V_\rho )$ is rational.
$\operatorname {ch}(V_\rho )$ is rational.
As the coefficient systems on ![]() $X$ appearing in Definition 2.7 are finite free modules over
$X$ appearing in Definition 2.7 are finite free modules over ![]() $\mathbb {Z}$, we may dualize to define homology groups
$\mathbb {Z}$, we may dualize to define homology groups ![]() $H_*(IX;\mathbb {Z}_\chi )$ as well.
$H_*(IX;\mathbb {Z}_\chi )$ as well.
Lemma 2.9 There are canonical isomorphisms
and a canonical short exact sequence
Proof. The complex ![]() $C_*(IX;\mathbb {Z}_\chi )$ is degreewise free, and the complexes
$C_*(IX;\mathbb {Z}_\chi )$ is degreewise free, and the complexes ![]() $C^*(IX;\mathbb {Z}_\chi )$,
$C^*(IX;\mathbb {Z}_\chi )$, ![]() $C^*(IX;\mathbb {Q}_\chi )$, and
$C^*(IX;\mathbb {Q}_\chi )$, and ![]() $C^*(IX;\mathbb {C})$ are obtained from it by applying the functors
$C^*(IX;\mathbb {C})$ are obtained from it by applying the functors ![]() $\operatorname {Hom}(-,\mathbb {Z})$,
$\operatorname {Hom}(-,\mathbb {Z})$, ![]() $\operatorname {Hom}(-,\mathbb {Q})$, and
$\operatorname {Hom}(-,\mathbb {Q})$, and ![]() $\operatorname {Hom}(-,\mathbb {C})$, respectively.
$\operatorname {Hom}(-,\mathbb {C})$, respectively.
Proposition 2.10 ( $\chi$-rationality of
$\chi$-rationality of  $\operatorname {ch}^I$)
$\operatorname {ch}^I$)
Let ![]() $X$ be a simplicial complex of groups of order
$X$ be a simplicial complex of groups of order ![]() $\leqslant m$. The inertial Chern character of any vector bundle
$\leqslant m$. The inertial Chern character of any vector bundle ![]() $V/X$ is
$V/X$ is ![]() $\chi$-rational. In fact, there exists a positive integer
$\chi$-rational. In fact, there exists a positive integer ![]() $N=N(m,d,\dim V)$ such that
$N=N(m,d,\dim V)$ such that ![]() $N\cdot \operatorname {ch}^I_d(V)$ is
$N\cdot \operatorname {ch}^I_d(V)$ is ![]() $\chi$-integral.
$\chi$-integral.
It is worth remarking that the proof we give does not provide an explicit expression for ![]() $N(m,d,n)$ other than for
$N(m,d,n)$ other than for ![]() $n=1$.
$n=1$.
Proof. We first show that the inertial Chern character of any line bundle ![]() $L/X$ is
$L/X$ is ![]() $\chi$-rational. We have
$\chi$-rational. We have ![]() $\operatorname {tr}(ab)=\operatorname {tr}(a)\operatorname {tr}(b)$ for endomorphisms
$\operatorname {tr}(ab)=\operatorname {tr}(a)\operatorname {tr}(b)$ for endomorphisms ![]() $a,b$ of
$a,b$ of ![]() $\mathbb {C}$, so the inertial Chern character of a line bundle
$\mathbb {C}$, so the inertial Chern character of a line bundle ![]() $L$ splits as the product
$L$ splits as the product
where ![]() $\operatorname {ch}_0^I(L)\in H^0(IX;\mathbb {Z}_\chi )$ is the fiberwise character of
$\operatorname {ch}_0^I(L)\in H^0(IX;\mathbb {Z}_\chi )$ is the fiberwise character of ![]() $L$ and
$L$ and ![]() $\operatorname {ch}_1(L)\in H^2(X;\mathbb {C})$ is the Chern character in degree one. It thus suffices to show that
$\operatorname {ch}_1(L)\in H^2(X;\mathbb {C})$ is the Chern character in degree one. It thus suffices to show that ![]() $\operatorname {ch}_1(L)$ is rational. We have
$\operatorname {ch}_1(L)$ is rational. We have ![]() $k\operatorname {ch}_1(L)=\operatorname {ch}_1(L^{\otimes k})$, so it suffices to show that
$k\operatorname {ch}_1(L)=\operatorname {ch}_1(L^{\otimes k})$, so it suffices to show that ![]() $\operatorname {ch}_1(L^{\otimes k})$ is integral for some positive integer
$\operatorname {ch}_1(L^{\otimes k})$ is integral for some positive integer ![]() $k$. As all isotropy groups of
$k$. As all isotropy groups of ![]() $X$ have order
$X$ have order ![]() $\leqslant m$, the tensor power
$\leqslant m$, the tensor power ![]() $L^{\otimes m!}$ descends to a line bundle
$L^{\otimes m!}$ descends to a line bundle ![]() $M$ on the coarse space. As
$M$ on the coarse space. As ![]() $M$ is an ordinary line bundle over a space (rather than an orbispace), its first Chern class
$M$ is an ordinary line bundle over a space (rather than an orbispace), its first Chern class ![]() $c_1(M)=\operatorname {ch}_1(M)$ is integral. We have thus shown that
$c_1(M)=\operatorname {ch}_1(M)$ is integral. We have thus shown that ![]() $\operatorname {ch}^I(L)$ is
$\operatorname {ch}^I(L)$ is ![]() $\chi$-rational (in fact, we have shown that
$\chi$-rational (in fact, we have shown that ![]() $d!(m!)^d\operatorname {ch}^I_d(L)$ is
$d!(m!)^d\operatorname {ch}^I_d(L)$ is ![]() $\chi$-integral).
$\chi$-integral).
To treat the case of vector bundles of dimension greater than one, we use the splitting principle. Given a vector bundle ![]() $V/X$ with hermitian metric, let
$V/X$ with hermitian metric, let ![]() $\mathbb {F}(V)\to X$ denote the fibration whose fiber over
$\mathbb {F}(V)\to X$ denote the fibration whose fiber over ![]() $x\in X$ is the space of decompositions of
$x\in X$ is the space of decompositions of ![]() $V_x$ into ordered orthogonal one-dimensional subspaces. In other words,
$V_x$ into ordered orthogonal one-dimensional subspaces. In other words, ![]() $\mathbb {F}(V)=P/U(1)^n$ where
$\mathbb {F}(V)=P/U(1)^n$ where ![]() $P\to X$ is the principal
$P\to X$ is the principal ![]() $U(n)$-bundle associated to
$U(n)$-bundle associated to ![]() $V/X$ with its chosen metric. We claim that the pullback map
$V/X$ with its chosen metric. We claim that the pullback map
is injective. The fiber of ![]() $I\mathbb {F}(V)\to IX$ over a given point
$I\mathbb {F}(V)\to IX$ over a given point ![]() $(x,g)\in IX$ is the space of
$(x,g)\in IX$ is the space of ![]() $g$-invariant ordered decompositions of
$g$-invariant ordered decompositions of ![]() $V_x$ into one-dimensional subspaces. As the group generated by
$V_x$ into one-dimensional subspaces. As the group generated by ![]() $g$ is abelian, its irreducible representations are one-dimensional, and hence there are plenty of such decompositions which are
$g$ is abelian, its irreducible representations are one-dimensional, and hence there are plenty of such decompositions which are ![]() $g$-invariant, namely when each one-dimensional subspace is contained in some
$g$-invariant, namely when each one-dimensional subspace is contained in some ![]() $g$-isotypic piece of
$g$-isotypic piece of ![]() $V_x$. Thus,
$V_x$. Thus, ![]() $I\mathbb {F}(V)\to IX$ is a disjoint union of iterated projective space bundles, from which the desired injectivity statement follows (for any projective space bundle
$I\mathbb {F}(V)\to IX$ is a disjoint union of iterated projective space bundles, from which the desired injectivity statement follows (for any projective space bundle ![]() $\mathbb {P}(W)\to Z$ over an orbispace
$\mathbb {P}(W)\to Z$ over an orbispace ![]() $Z$, the pullback map
$Z$, the pullback map ![]() $H^*(Z)\to H^*(\mathbb {P}(W))$ is split by the map
$H^*(Z)\to H^*(\mathbb {P}(W))$ is split by the map ![]() $\alpha \mapsto \int (c_1(L)^{\dim W-1}\cup \alpha )$ where
$\alpha \mapsto \int (c_1(L)^{\dim W-1}\cup \alpha )$ where ![]() $L/\mathbb {P}(W)$ denotes the tautological line bundle and
$L/\mathbb {P}(W)$ denotes the tautological line bundle and ![]() $\int :H^{*+2(\dim W-1)}(\mathbb {P}(W))\to H^*(Z)$ denotes fiberwise integration).
$\int :H^{*+2(\dim W-1)}(\mathbb {P}(W))\to H^*(Z)$ denotes fiberwise integration).
As ![]() $H^*(IX;\mathbb {C})\to H^*(I\mathbb {F}(V);\mathbb {C})$ is injective and
$H^*(IX;\mathbb {C})\to H^*(I\mathbb {F}(V);\mathbb {C})$ is injective and ![]() $\operatorname {Hom}_\mathbb {Z}(-,\mathbb {C})$ is exact, we conclude from Lemma 2.9 that
$\operatorname {Hom}_\mathbb {Z}(-,\mathbb {C})$ is exact, we conclude from Lemma 2.9 that ![]() $\operatorname {Hom}(H_*(IX;\mathbb {Z}_\chi )/H_*(I\mathbb {F}(V);\mathbb {Z}_\chi ),\mathbb {C})=0$, and hence that the domain is torsion. From this and Lemma 2.9 again, it follows that a class in
$\operatorname {Hom}(H_*(IX;\mathbb {Z}_\chi )/H_*(I\mathbb {F}(V);\mathbb {Z}_\chi ),\mathbb {C})=0$, and hence that the domain is torsion. From this and Lemma 2.9 again, it follows that a class in ![]() $H^*(IX;\mathbb {C})$ is
$H^*(IX;\mathbb {C})$ is ![]() $\chi$-rational if and only if its pullback to
$\chi$-rational if and only if its pullback to ![]() $H^*(I\mathbb {F}(V);\mathbb {C})$ is
$H^*(I\mathbb {F}(V);\mathbb {C})$ is ![]() $\chi$-rational. Now consider the pullback of
$\chi$-rational. Now consider the pullback of ![]() $V$ to
$V$ to ![]() $\mathbb {F}(V)$. This pullback splits as a direct sum of line bundles, so because the inertial Chern character is additive under direct sum, we conclude that the pullback of
$\mathbb {F}(V)$. This pullback splits as a direct sum of line bundles, so because the inertial Chern character is additive under direct sum, we conclude that the pullback of ![]() $\operatorname {ch}^I(V)$ to
$\operatorname {ch}^I(V)$ to ![]() $I\mathbb {F}(V)$ is
$I\mathbb {F}(V)$ is ![]() $\chi$-rational, and hence that
$\chi$-rational, and hence that ![]() $\operatorname {ch}^I(V)$ is itself
$\operatorname {ch}^I(V)$ is itself ![]() $\chi$-rational.
$\chi$-rational.
It remains to produce an integer ![]() $N=N(m,d,n)$ such that
$N=N(m,d,n)$ such that ![]() $N\cdot \operatorname {ch}^I_d(V)$ is
$N\cdot \operatorname {ch}^I_d(V)$ is ![]() $\chi$-integral for
$\chi$-integral for ![]() $\dim V=n$. We claim that there exists a finite orbi-complex
$\dim V=n$. We claim that there exists a finite orbi-complex ![]() $\mathbb {B}_{m,d}U(n)$ carrying a principal
$\mathbb {B}_{m,d}U(n)$ carrying a principal ![]() $U(n)$-bundle
$U(n)$-bundle
with the property that every principal ![]() $U(n)$-bundle over a simplicial complex of groups
$U(n)$-bundle over a simplicial complex of groups ![]() $X$ of dimension
$X$ of dimension ![]() $\leqslant d$ and isotropy
$\leqslant d$ and isotropy ![]() $\leqslant m$ is a pullback of
$\leqslant m$ is a pullback of ![]() $\mathbb {E}_{m,d}U(n)\to \mathbb {B}_{m,d}U(n)$. As the inertial Chern character of
$\mathbb {E}_{m,d}U(n)\to \mathbb {B}_{m,d}U(n)$. As the inertial Chern character of ![]() $\mathbb {E}_{m,d}U(n)\to \mathbb {B}_{m,d}U(n)$ is
$\mathbb {E}_{m,d}U(n)\to \mathbb {B}_{m,d}U(n)$ is ![]() $\chi$-rational and
$\chi$-rational and ![]() $\mathbb {B}_{m,d}U(n)$ is finite, there exists an integer
$\mathbb {B}_{m,d}U(n)$ is finite, there exists an integer ![]() $N=N(m,d,n)$ such that
$N=N(m,d,n)$ such that ![]() $N$ times this inertial Chern character is
$N$ times this inertial Chern character is ![]() $\chi$-integral in cohomological degree
$\chi$-integral in cohomological degree ![]() $d$. By pullback, the same integer
$d$. By pullback, the same integer ![]() $N$ works for any vector bundle of rank
$N$ works for any vector bundle of rank ![]() $n$ over a simplicial complex of groups of order
$n$ over a simplicial complex of groups of order ![]() $\leqslant m$. Note that this argument gives no explicit bound on the integer
$\leqslant m$. Note that this argument gives no explicit bound on the integer ![]() $N$.
$N$.
It remains to construct ![]() $\mathbb {E}_{m,d}U(n)\to \mathbb {B}_{m,d}U(n)$. We seek
$\mathbb {E}_{m,d}U(n)\to \mathbb {B}_{m,d}U(n)$. We seek ![]() $U(n)$-spaces
$U(n)$-spaces ![]() $\mathbb {E}_{m,d}U(n)$ such that
$\mathbb {E}_{m,d}U(n)$ such that
 \begin{align*} \mathbb{E}_{m,-1}U(n)&=\varnothing,\\ \mathbb{E}_{m,d}U(n)&=\mathbb{E}_{m,d-1}U(n)\cup\biggl(\,\begin{matrix}\text{finitely many cells of the}\hfill\\\text{form }(D^d,\partial D^d)\times U(n)/G\hfill\end{matrix}\,\biggr),\\ \pi_r((\mathbb{E}_{m,d}U(n))^G)&=0\quad\text{for }r< d, \end{align*}
\begin{align*} \mathbb{E}_{m,-1}U(n)&=\varnothing,\\ \mathbb{E}_{m,d}U(n)&=\mathbb{E}_{m,d-1}U(n)\cup\biggl(\,\begin{matrix}\text{finitely many cells of the}\hfill\\\text{form }(D^d,\partial D^d)\times U(n)/G\hfill\end{matrix}\,\biggr),\\ \pi_r((\mathbb{E}_{m,d}U(n))^G)&=0\quad\text{for }r< d, \end{align*}
where ![]() $G\subseteq U(n)$ ranges over all finite subgroups of
$G\subseteq U(n)$ ranges over all finite subgroups of ![]() $U(n)$ of order
$U(n)$ of order ![]() $\leqslant m$. Note that there are finitely many conjugacy classes of such subgroups, and it suffices to consider just one representative of each conjugacy class. To show that
$\leqslant m$. Note that there are finitely many conjugacy classes of such subgroups, and it suffices to consider just one representative of each conjugacy class. To show that ![]() $\mathbb {E}_{m,d}U(n)$ exists given
$\mathbb {E}_{m,d}U(n)$ exists given ![]() $\mathbb {E}_{m,d-1}U(n)$, argue as follows. We have
$\mathbb {E}_{m,d-1}U(n)$, argue as follows. We have ![]() $\pi _{d-1}((\mathbb {E}_{m,d-1}U(n))^G)=H_{d-1}((\mathbb {E}_{m,d-1}U(n))^G)$ by Hurewicz, and the latter group is finitely generated because
$\pi _{d-1}((\mathbb {E}_{m,d-1}U(n))^G)=H_{d-1}((\mathbb {E}_{m,d-1}U(n))^G)$ by Hurewicz, and the latter group is finitely generated because ![]() $\mathbb {E}_{m,d-1}U(n)$ is made up of finitely many cells. We define
$\mathbb {E}_{m,d-1}U(n)$ is made up of finitely many cells. We define ![]() $\mathbb {E}_{m,d}U(n)$ by attaching cells
$\mathbb {E}_{m,d}U(n)$ by attaching cells ![]() $(D^d,\partial D^d)\times U(n)/G$ along a choice of finitely many generators of
$(D^d,\partial D^d)\times U(n)/G$ along a choice of finitely many generators of ![]() $\pi _{d-1}((\mathbb {E}_{m,d-1}U(n))^G)$, for each of the finitely many subgroups
$\pi _{d-1}((\mathbb {E}_{m,d-1}U(n))^G)$, for each of the finitely many subgroups ![]() $G\subseteq U(n)$ on our fixed set of representatives. Note that
$G\subseteq U(n)$ on our fixed set of representatives. Note that ![]() $(D^d\times U(n)/H)^G=D^d\times \{a\in U(n)\,|\,a^{-1}Ga\subseteq H\}$, so any map
$(D^d\times U(n)/H)^G=D^d\times \{a\in U(n)\,|\,a^{-1}Ga\subseteq H\}$, so any map ![]() $S^r\to (\mathbb {E}_{m,d}U(n))^G$ for
$S^r\to (\mathbb {E}_{m,d}U(n))^G$ for ![]() $r< d$ can be homotoped to land inside
$r< d$ can be homotoped to land inside ![]() $(\mathbb {E}_{m,d-1}U(n))^G$. It follows that the homotopy groups of
$(\mathbb {E}_{m,d-1}U(n))^G$. It follows that the homotopy groups of ![]() $(\mathbb {E}_{m,d}U(n))^G$ satisfy the desired vanishing property.
$(\mathbb {E}_{m,d}U(n))^G$ satisfy the desired vanishing property.
Let us show that any principal ![]() $U(n)$-bundle
$U(n)$-bundle ![]() $P\to X$ is pulled back from
$P\to X$ is pulled back from ![]() $\mathbb {E}_{m,d}U(n)\to \mathbb {B}_{m,d}U(n)$ when
$\mathbb {E}_{m,d}U(n)\to \mathbb {B}_{m,d}U(n)$ when ![]() $\dim X\leqslant d$ with isotropy groups of order
$\dim X\leqslant d$ with isotropy groups of order ![]() $\leqslant m$. That is, we should construct an equivariant map
$\leqslant m$. That is, we should construct an equivariant map ![]() $P\to \mathbb {E}_{m,d}U(n)$ (note that since the target is a space, this is the same as an equivariant map from the coarse space
$P\to \mathbb {E}_{m,d}U(n)$ (note that since the target is a space, this is the same as an equivariant map from the coarse space ![]() $|P|$). By induction on the cells of
$|P|$). By induction on the cells of ![]() $X$, it suffices to solve the extension problem for equivariant maps from
$X$, it suffices to solve the extension problem for equivariant maps from ![]() $(D^r,\partial D^r)\times U(n)/G$ to
$(D^r,\partial D^r)\times U(n)/G$ to ![]() $\mathbb {E}_{m,d}U(n)$ for
$\mathbb {E}_{m,d}U(n)$ for ![]() $r\leqslant d$ and
$r\leqslant d$ and ![]() $|G|\leqslant m$. This is equivalent to the extension problem for maps
$|G|\leqslant m$. This is equivalent to the extension problem for maps ![]() $(D^r,\partial D^r)\to (\mathbb {E}_{m,d}U(n))^G$, whose positive solution for
$(D^r,\partial D^r)\to (\mathbb {E}_{m,d}U(n))^G$, whose positive solution for ![]() $r\leqslant d$ is one of the defining properties of
$r\leqslant d$ is one of the defining properties of ![]() $\mathbb {E}_{m,d}U(n)$.
$\mathbb {E}_{m,d}U(n)$.
Example 2.11 A previous version of this text claimed a version of Proposition 2.10 with ![]() $N$ independent of
$N$ independent of ![]() $m$. This stronger result is false; here is a counterexample. Begin with
$m$. This stronger result is false; here is a counterexample. Begin with ![]() $\mathbb {B}(\mathbb {Z}/m)$ with a line bundle given by multiplication by
$\mathbb {B}(\mathbb {Z}/m)$ with a line bundle given by multiplication by ![]() $e^{2\pi i/m}$ on
$e^{2\pi i/m}$ on ![]() $\mathbb {C}$. Glue on a disk
$\mathbb {C}$. Glue on a disk ![]() $D^2$ using an attaching map
$D^2$ using an attaching map ![]() $\partial D^2=S^1\to \mathbb {B}(\mathbb {Z}/m)$ to a generator of
$\partial D^2=S^1\to \mathbb {B}(\mathbb {Z}/m)$ to a generator of ![]() $\mathbb {Z}/m$. The line bundle extends because all complex line bundles on a circle are trivial. The inertial Chern character of this line bundle has denominator
$\mathbb {Z}/m$. The line bundle extends because all complex line bundles on a circle are trivial. The inertial Chern character of this line bundle has denominator ![]() $m$.
$m$.
Lemma 2.12 (Bott)
The image of the Chern character map
is precisely ![]() $H^{2n}(S^{2n};\mathbb {Z})$.
$H^{2n}(S^{2n};\mathbb {Z})$.
Proof. This is an immediate corollary of Bott periodicity; for completeness, we include the proof from [Reference MathewMat11]. Let ![]() $\eta /S^2$ denote the line bundle with
$\eta /S^2$ denote the line bundle with ![]() $c_1(\eta )=1$, and let
$c_1(\eta )=1$, and let ![]() $1$ denote the trivial line bundle. According to Bott periodicity, multiplication with
$1$ denote the trivial line bundle. According to Bott periodicity, multiplication with ![]() $\eta -1\in \tilde K^0(S^2)$ defines an isomorphism
$\eta -1\in \tilde K^0(S^2)$ defines an isomorphism ![]() $\tilde K^0(X)\to \tilde K^0(\Sigma ^2X)$. In particular,
$\tilde K^0(X)\to \tilde K^0(\Sigma ^2X)$. In particular, ![]() $(\eta -1)^{\otimes n}\in \tilde K^0(S^{2n})$ is a free generator. Multiplicativity of the Chern character gives
$(\eta -1)^{\otimes n}\in \tilde K^0(S^{2n})$ is a free generator. Multiplicativity of the Chern character gives ![]() $\operatorname {ch}_n((\eta -1)^{\otimes n})=\operatorname {ch}_1(\eta -1)^n=1^n=1$.
$\operatorname {ch}_n((\eta -1)^{\otimes n})=\operatorname {ch}_1(\eta -1)^n=1^n=1$.
We now have all the ingredients we need to prove the main result of this section, namely Theorem 1.1 for simplicial complexes of groups.
Theorem 2.13 Let ![]() $X$ be a
$X$ be a ![]() $d$-dimensional simplicial complex of groups of order
$d$-dimensional simplicial complex of groups of order ![]() $\leqslant m$. There exists a complex vector bundle
$\leqslant m$. There exists a complex vector bundle ![]() $V$ of rank
$V$ of rank ![]() $n=n(d,m)>0$ over
$n=n(d,m)>0$ over ![]() $X$, whose fiber over
$X$, whose fiber over ![]() $x\in X$ is isomorphic to a direct sum of copies of the regular representation of
$x\in X$ is isomorphic to a direct sum of copies of the regular representation of ![]() $G_x$.
$G_x$.
Proof. The condition on the fibers of ![]() $V$ amounts to the assertion that
$V$ amounts to the assertion that ![]() $\operatorname {ch}^I_0(V)=n\chi _1$ where
$\operatorname {ch}^I_0(V)=n\chi _1$ where ![]() $\chi _1\in H^0(IX;\mathbb {Q}_\chi )$ denotes ‘the characteristic function of the identity’ as a function
$\chi _1\in H^0(IX;\mathbb {Q}_\chi )$ denotes ‘the characteristic function of the identity’ as a function ![]() $G_x/G_x\to \mathbb {C}$. We construct
$G_x/G_x\to \mathbb {C}$. We construct ![]() $V$ satisfying
$V$ satisfying
(meaning all higher inertial Chern characters vanish). Certainly such a vector bundle exists over the ![]() $0$-skeleton
$0$-skeleton ![]() $X_0$ of
$X_0$ of ![]() $X$, with rank
$X$, with rank ![]() $m!$, because all isotropy groups have order
$m!$, because all isotropy groups have order ![]() $\leqslant m$. It therefore suffices to show that any such vector bundle on
$\leqslant m$. It therefore suffices to show that any such vector bundle on ![]() $X_{k-1}$ extends to
$X_{k-1}$ extends to ![]() $X_k$.
$X_k$.
To extend ![]() $V$ as a vector bundle from
$V$ as a vector bundle from ![]() $X_{k-1}$ to
$X_{k-1}$ to ![]() $X_k$ amounts to doing an extension from
$X_k$ amounts to doing an extension from ![]() $\partial D^k\times \mathbb {B} G$ to
$\partial D^k\times \mathbb {B} G$ to ![]() $D^k\times \mathbb {B} G$ for each
$D^k\times \mathbb {B} G$ for each ![]() $k$-simplex. The obstruction to doing this lies in
$k$-simplex. The obstruction to doing this lies in ![]() $\prod _{\rho \in \hat G}\pi _{k-1}(BU(n_\rho ))$, where
$\prod _{\rho \in \hat G}\pi _{k-1}(BU(n_\rho ))$, where ![]() $n_\rho =(\dim V)(\dim \rho )/|G|$. The map
$n_\rho =(\dim V)(\dim \rho )/|G|$. The map ![]() $BU(n_\rho )\to BU$ is an isomorphism on
$BU(n_\rho )\to BU$ is an isomorphism on ![]() $\pi _{k-1}$ provided
$\pi _{k-1}$ provided ![]() $k-1<2n_\rho +2$, which is guaranteed by taking say
$k-1<2n_\rho +2$, which is guaranteed by taking say ![]() $\dim V>dm$. The Chern character detects
$\dim V>dm$. The Chern character detects ![]() $\pi _*(BU)$ by Lemma 2.12, so vanishing of the inertial Chern character and linear independence of characters means that these obstructions all vanish. Thus,
$\pi _*(BU)$ by Lemma 2.12, so vanishing of the inertial Chern character and linear independence of characters means that these obstructions all vanish. Thus, ![]() $V$ extends to
$V$ extends to ![]() $X_k$.
$X_k$.
It remains to show that the extension of ![]() $V$ to
$V$ to ![]() $X_k$ can be taken to have trivial inertial Chern character. The space of extensions over a given
$X_k$ can be taken to have trivial inertial Chern character. The space of extensions over a given ![]() $k$-simplex is a torsor for
$k$-simplex is a torsor for ![]() $\prod _{\rho \in \hat G}\pi _k(BU(n_\rho ))$, which is again
$\prod _{\rho \in \hat G}\pi _k(BU(n_\rho ))$, which is again ![]() $\prod _{\rho \in \hat G}\pi _k(BU)$ once we take
$\prod _{\rho \in \hat G}\pi _k(BU)$ once we take ![]() $\dim V>dm$. We use this freedom to ensure that the inertial Chern character of
$\dim V>dm$. We use this freedom to ensure that the inertial Chern character of ![]() $V$ on
$V$ on ![]() $X_k$ vanishes. Consider the long exact sequence
$X_k$ vanishes. Consider the long exact sequence
As the inertial Chern character in ![]() $H^*(IX_k;\mathbb {Q}_\chi )$ maps to zero in
$H^*(IX_k;\mathbb {Q}_\chi )$ maps to zero in ![]() $H^*(IX_{k-1};\mathbb {Q}_\chi )$, it is in the image of
$H^*(IX_{k-1};\mathbb {Q}_\chi )$, it is in the image of ![]() $H^*(IX_k,IX_{k-1};\mathbb {Q}_\chi )$. In particular, it may be nonzero only in degree
$H^*(IX_k,IX_{k-1};\mathbb {Q}_\chi )$. In particular, it may be nonzero only in degree ![]() $k$. Let us now replace
$k$. Let us now replace ![]() $V$ with
$V$ with ![]() $V^{\oplus a}$ (which multiplies its inertial Chern character by
$V^{\oplus a}$ (which multiplies its inertial Chern character by ![]() $a$) for an appropriate positive integer
$a$) for an appropriate positive integer ![]() $a$ so that by Proposition 2.10 its inertial Chern character is
$a$ so that by Proposition 2.10 its inertial Chern character is ![]() $\chi$-integral. Modifying our bundle by an element of (the product over the
$\chi$-integral. Modifying our bundle by an element of (the product over the ![]() $k$-simplices of)
$k$-simplices of) ![]() $\prod _{\rho \in \hat G}\pi _k(BU)$ shifts its inertial Chern character by anything in
$\prod _{\rho \in \hat G}\pi _k(BU)$ shifts its inertial Chern character by anything in ![]() $H^k(IX_k,IX_{k-1};\mathbb {Z}_\chi )$ by Lemma 2.12. We are done because
$H^k(IX_k,IX_{k-1};\mathbb {Z}_\chi )$ by Lemma 2.12. We are done because ![]() $H^k(IX_k,IX_{k-1};\mathbb {Z}_\chi )\to H^k(IX_k;\mathbb {Z}_\chi )$ is surjective by the long exact sequence.
$H^k(IX_k,IX_{k-1};\mathbb {Z}_\chi )\to H^k(IX_k;\mathbb {Z}_\chi )$ is surjective by the long exact sequence.
Remark 2.14 One may interpret the proof of Theorem 2.13 in homotopy theoretic terms as follows. Vector bundles are classified by maps to a classifying space ![]() $\mathbb {B} U(n)$, and because
$\mathbb {B} U(n)$, and because ![]() $\mathbb {B} U(n)$ is not contractible, the extension problem for vector bundles has nontrivial obstructions. Vector bundles with rationally trivialized inertial Chern character are classified by maps to the total space of a fibration over
$\mathbb {B} U(n)$ is not contractible, the extension problem for vector bundles has nontrivial obstructions. Vector bundles with rationally trivialized inertial Chern character are classified by maps to the total space of a fibration over ![]() $\mathbb {B} U(n)$ whose fiber classifies odd-dimensional rational cohomology classes on the inertia stack. Our observation that the obstructions to this new problem are torsion is essentially the observation that this total space is rationally contractible. The definition of this fibration over
$\mathbb {B} U(n)$ whose fiber classifies odd-dimensional rational cohomology classes on the inertia stack. Our observation that the obstructions to this new problem are torsion is essentially the observation that this total space is rationally contractible. The definition of this fibration over ![]() $\mathbb {B} U(n)$ depends on the additivity of the Chern character (note that
$\mathbb {B} U(n)$ depends on the additivity of the Chern character (note that ![]() $\mathbb {E} U(n)\to \mathbb {B} U(n)$ is not suitable for this argument because
$\mathbb {E} U(n)\to \mathbb {B} U(n)$ is not suitable for this argument because ![]() $\mathbb {E} U(n)$ is a space, hence every bundle pulled back from
$\mathbb {E} U(n)$ is a space, hence every bundle pulled back from ![]() $\mathbb {E} U(n)$ has trivial isotropy representations). It may prove interesting to interpret this argument within Schwede's framework of global homotopy theory [Reference SchwedeSch18].
$\mathbb {E} U(n)$ has trivial isotropy representations). It may prove interesting to interpret this argument within Schwede's framework of global homotopy theory [Reference SchwedeSch18].
3. Topological stacks
We review some basic facts about stacks (on the category of topological spaces), we give a precise definition of what we mean by an ‘orbispace’, and we establish some of their basic properties. For further background, the reader may wish to consult Noohi [Reference NoohiNoo05], Gepner and Henriques [Reference Henriques and GepnerHG07], Behrend [Reference BehrendBeh14], Metzler [Reference MetzlerMet03], Behrend and Noohi [Reference Behrend and NoohiBN06], Heinloth [Reference HeinlothHei05], or Laumon and Moret-Bailly [Reference Laumon and Moret-BaillyLMB00].
Let ![]() $\mathsf {Top}$ denote the category of topological spaces and continuous maps, and let
$\mathsf {Top}$ denote the category of topological spaces and continuous maps, and let ![]() $\mathsf {Grpd}$ denote the 2-category of (essentially) small groupoids. A stack is a functor
$\mathsf {Grpd}$ denote the 2-category of (essentially) small groupoids. A stack is a functor ![]() $F:\mathsf {Top}^\mathsf {op}\to \mathsf {Grpd}$ which satisfies descent, i.e. such that for every topological space
$F:\mathsf {Top}^\mathsf {op}\to \mathsf {Grpd}$ which satisfies descent, i.e. such that for every topological space ![]() $U$ and every open cover
$U$ and every open cover ![]() $\{U_i\to U\}_i$, the natural functor
$\{U_i\to U\}_i$, the natural functor

is an equivalence. Stacks form a 2-category, with morphisms given by natural transformations of functors. The 2-category of stacks is complete, meaning all (small) limits exist; furthermore, these limits may be calculated pointwise in the sense that ![]() $(\lim _\alpha F_\alpha )(U)=\lim _\alpha (F_\alpha (U))$. Note that, as we are working in a 2-categorical context, all functors are 2-functors, all diagrams are 2-diagrams, all limits are 2-limits, etc. (though we usually omit the prefix ‘2-’).
$(\lim _\alpha F_\alpha )(U)=\lim _\alpha (F_\alpha (U))$. Note that, as we are working in a 2-categorical context, all functors are 2-functors, all diagrams are 2-diagrams, all limits are 2-limits, etc. (though we usually omit the prefix ‘2-’).
The Yoneda lemma implies that the Yoneda functor ![]() $X\mapsto \operatorname {Hom}(-,X)$ embeds the category of topological spaces fully faithfully into the 2-category of stacks, and moreover that the natural map from
$X\mapsto \operatorname {Hom}(-,X)$ embeds the category of topological spaces fully faithfully into the 2-category of stacks, and moreover that the natural map from ![]() $F(X)$ to the groupoid of maps of stacks
$F(X)$ to the groupoid of maps of stacks ![]() $\operatorname {Hom}(-,X)\to F(-)$ is an equivalence. The category of topological spaces is complete, and the Yoneda embedding is continuous (commutes with limits). Hence, we make no distinction between a topological space
$\operatorname {Hom}(-,X)\to F(-)$ is an equivalence. The category of topological spaces is complete, and the Yoneda embedding is continuous (commutes with limits). Hence, we make no distinction between a topological space ![]() $X$ and the associated stack
$X$ and the associated stack ![]() $\operatorname {Hom}(-,X)$ of maps to
$\operatorname {Hom}(-,X)$ of maps to ![]() $X$, nor between objects of
$X$, nor between objects of ![]() $F(X)$ and maps
$F(X)$ and maps ![]() $\operatorname {Hom}(-,X)\to F(-)$ (which we simply write as
$\operatorname {Hom}(-,X)\to F(-)$ (which we simply write as ![]() $X\to F$).
$X\to F$).
Every stack ![]() $X$ has a coarse space
$X$ has a coarse space ![]() $|X|$ (a topological space) which is initial in the category of maps from
$|X|$ (a topological space) which is initial in the category of maps from ![]() $X$ to topological spaces. Concretely, the points of
$X$ to topological spaces. Concretely, the points of ![]() $|X|$ are the isomorphism classes of maps
$|X|$ are the isomorphism classes of maps ![]() $*\to X$, and a subset
$*\to X$, and a subset ![]() $U\subseteq |X|$ is open if and only if for every map
$U\subseteq |X|$ is open if and only if for every map ![]() $Y\to X$ from a topological space
$Y\to X$ from a topological space ![]() $Y$, the inverse image of
$Y$, the inverse image of ![]() $U$ is an open subset of
$U$ is an open subset of ![]() $Y$.
$Y$.
A stack is called representable if and only if it is in the essential image of the Yoneda embedding (i.e. it is isomorphic to a topological space). A morphism of stacks ![]() $F\to G$ is called representable if and only if for every map
$F\to G$ is called representable if and only if for every map ![]() $X\to G$ from a topological space
$X\to G$ from a topological space ![]() $X$, the fiber product
$X$, the fiber product ![]() $F\times _GX$ is representable.
$F\times _GX$ is representable.
For any property ![]() $\mathcal {P}$ of morphisms of topological spaces which is preserved under pullback, a representable morphism of stacks
$\mathcal {P}$ of morphisms of topological spaces which is preserved under pullback, a representable morphism of stacks ![]() $F\to G$ is said to have property
$F\to G$ is said to have property ![]() $\mathcal {P}$ if and only if the pullback
$\mathcal {P}$ if and only if the pullback ![]() $F\times _GX\to X$ has
$F\times _GX\to X$ has ![]() $\mathcal {P}$ for every map
$\mathcal {P}$ for every map ![]() $X\to G$ from a topological space
$X\to G$ from a topological space ![]() $X$. The following are examples of properties
$X$. The following are examples of properties ![]() $\mathcal {P}$ of morphisms
$\mathcal {P}$ of morphisms ![]() $f:X\to Y$ which are preserved under pullback:
$f:X\to Y$ which are preserved under pullback:
•
 $f$ is injective;
$f$ is injective;•
 $f$ is surjective;
$f$ is surjective;•
 $f$ is open, meaning that the image of any open set is open. In contrast, the property of being closed, meaning that the image of any closed set is closed, is not preserved under pullback;
$f$ is open, meaning that the image of any open set is open. In contrast, the property of being closed, meaning that the image of any closed set is closed, is not preserved under pullback;•
 $f$ is an embedding, meaning that it is a homeomorphism onto its image;
$f$ is an embedding, meaning that it is a homeomorphism onto its image;•
 $f$ is a closed embedding;
$f$ is a closed embedding;•
 $f$ is étale, meaning that for every
$f$ is étale, meaning that for every  $x\in X$ there exists an open neighborhood
$x\in X$ there exists an open neighborhood  $x\in U\subseteq X$ such that
$x\in U\subseteq X$ such that  $f|_U:U\to Y$ is an open embedding;
$f|_U:U\to Y$ is an open embedding;•
 $f$ is separated, meaning that for every distinct pair
$f$ is separated, meaning that for every distinct pair  $x_1,x_2\in X$ with
$x_1,x_2\in X$ with  $f(x_1)=f(x_2)$, there exist open neighborhoods
$f(x_1)=f(x_2)$, there exist open neighborhoods  $x_i\in U_i\subseteq X$ which are disjoint
$x_i\in U_i\subseteq X$ which are disjoint  $U_1\cap U_2=\varnothing$ (this is equivalent to the relative diagonal
$U_1\cap U_2=\varnothing$ (this is equivalent to the relative diagonal  $X\to X\times _YX$ being a closed embedding);
$X\to X\times _YX$ being a closed embedding);•
 $f$ is universally closed, meaning that
$f$ is universally closed, meaning that  $X\times _YZ\to Z$ is closed for every
$X\times _YZ\to Z$ is closed for every  $Z\to Y$; this is equivalent to the assertion that for every
$Z\to Y$; this is equivalent to the assertion that for every  $y\in Y$ and every collection of open sets
$y\in Y$ and every collection of open sets  $\{U_i\subseteq X\}_i$ covering
$\{U_i\subseteq X\}_i$ covering  $f^{-1}(y)$, there exists a finite subcollection which covers
$f^{-1}(y)$, there exists a finite subcollection which covers  $f^{-1}(V)$ for some open neighborhood
$f^{-1}(V)$ for some open neighborhood  $y\in V\subseteq Y$ (one proof of this equivalence goes via yet a third equivalent condition, namely that every net
$y\in V\subseteq Y$ (one proof of this equivalence goes via yet a third equivalent condition, namely that every net  $\{x_\alpha \in X\}_\alpha$ with
$\{x_\alpha \in X\}_\alpha$ with  $f(x_\alpha )\to y$ has a subnet converging to some
$f(x_\alpha )\to y$ has a subnet converging to some  $x\in f^{-1}(y)$);
$x\in f^{-1}(y)$);•
 $f$ is proper, meaning that it is separated and universally closed;
$f$ is proper, meaning that it is separated and universally closed;•
 $f$admits local sections, meaning that there is an open cover
$f$admits local sections, meaning that there is an open cover  $\{U_i\subseteq Y\}_i$ such that every restriction
$\{U_i\subseteq Y\}_i$ such that every restriction  $f|_{f^{-1}(U_i)}:f^{-1}(U_i)\to U_i$ admits a section;
$f|_{f^{-1}(U_i)}:f^{-1}(U_i)\to U_i$ admits a section;•
 $f$ is a finite covering space, meaning that there is an open cover
$f$ is a finite covering space, meaning that there is an open cover  $\{U_i\subseteq Y\}_i$ such that every restriction
$\{U_i\subseteq Y\}_i$ such that every restriction  $f|_{f^{-1}(U_i)}:f^{-1}(U_i)\to U_i$ is isomorphic to
$f|_{f^{-1}(U_i)}:f^{-1}(U_i)\to U_i$ is isomorphic to  $U_i^{\sqcup n_i}\to U_i$ for some integer
$U_i^{\sqcup n_i}\to U_i$ for some integer  $n_i\geqslant 0$.
$n_i\geqslant 0$.
Each of these properties ![]() $\mathcal {P}$ is also closed under composition, and thus also under fiber products, meaning that for maps
$\mathcal {P}$ is also closed under composition, and thus also under fiber products, meaning that for maps ![]() $X\to X'$ and
$X\to X'$ and ![]() $Y\to Y'$ over
$Y\to Y'$ over ![]() $Z$, if both
$Z$, if both ![]() $X\to X'$ and
$X\to X'$ and ![]() $Y\to Y'$ have
$Y\to Y'$ have ![]() $\mathcal {P}$, then
$\mathcal {P}$, then ![]() $X\times _ZY\to X'\times _ZY'$ also has
$X\times _ZY\to X'\times _ZY'$ also has ![]() $\mathcal {P}$ (indeed,
$\mathcal {P}$ (indeed, ![]() $X\times _ZY\to X\times _ZY'$ is a pullback of
$X\times _ZY\to X\times _ZY'$ is a pullback of ![]() $Y\to Y'$).
$Y\to Y'$).
For any stack ![]() $X$, open (respectively, closed) embeddings
$X$, open (respectively, closed) embeddings ![]() $Y\hookrightarrow X$ are in natural bijection with open (respectively, closed) subsets of
$Y\hookrightarrow X$ are in natural bijection with open (respectively, closed) subsets of ![]() $|X|$.
$|X|$.
To check that a given map of spaces satisfies one of the properties ![]() $\mathcal {P}$ above, it is often helpful to make use of the fact that these
$\mathcal {P}$ above, it is often helpful to make use of the fact that these ![]() $\mathcal {P}$ are all local on the target, meaning that for every open cover
$\mathcal {P}$ are all local on the target, meaning that for every open cover ![]() $\{U_i\subseteq Y\}_i$, if
$\{U_i\subseteq Y\}_i$, if ![]() $X\times _YU_i\to U_i$ has
$X\times _YU_i\to U_i$ has ![]() $\mathcal {P}$ for every
$\mathcal {P}$ for every ![]() $i$, then so does
$i$, then so does ![]() $X\to Y$. This leads to the following generalization for maps of stacks: if
$X\to Y$. This leads to the following generalization for maps of stacks: if ![]() $F\to G$ is a representable morphism of stacks and
$F\to G$ is a representable morphism of stacks and ![]() $G'\to G$ is a representable morphism of stacks admitting local sections, then
$G'\to G$ is a representable morphism of stacks admitting local sections, then ![]() $F\to G$ has
$F\to G$ has ![]() $\mathcal {P}$ if and only if
$\mathcal {P}$ if and only if ![]() $F\times _GG'\to G'$ has
$F\times _GG'\to G'$ has ![]() $\mathcal {P}$. In fact, in this statement we need not assume that
$\mathcal {P}$. In fact, in this statement we need not assume that ![]() $G'\to G$ is representable, just that it admit local sections in the generalized sense that for every map
$G'\to G$ is representable, just that it admit local sections in the generalized sense that for every map ![]() $X\to G$ from a topological space
$X\to G$ from a topological space ![]() $X$, there exists an open cover
$X$, there exists an open cover ![]() $\{U_i\subseteq X\}_i$ such that each
$\{U_i\subseteq X\}_i$ such that each ![]() $G'\times _GU_i\to U_i$ admits a section. We thus say that ‘
$G'\times _GU_i\to U_i$ admits a section. We thus say that ‘![]() $\mathcal {P}$ descends along maps admitting local sections’. The same descent property holds for representability itself.
$\mathcal {P}$ descends along maps admitting local sections’. The same descent property holds for representability itself.
Lemma 3.1 (Representability descends under maps admitting local sections)
Let ![]() $F\to G$ be a map of stacks, and let
$F\to G$ be a map of stacks, and let ![]() $G'\to G$ be a map of stacks admitting local sections. If
$G'\to G$ be a map of stacks admitting local sections. If ![]() $F\times _GG'\to G'$ is representable, then so is
$F\times _GG'\to G'$ is representable, then so is ![]() $F\to G$.
$F\to G$.
Proof. By replacing ![]() $F\to G$ and
$F\to G$ and ![]() $G'\to G$ with their pullbacks under
$G'\to G$ with their pullbacks under ![]() $U\to G$ for a topological space
$U\to G$ for a topological space ![]() $U$, we may assume without loss of generality that
$U$, we may assume without loss of generality that ![]() $G$ is representable. As
$G$ is representable. As ![]() $G'\to G$ admits local sections, we may replace
$G'\to G$ admits local sections, we may replace ![]() $G'\to G$ with the composition
$G'\to G$ with the composition ![]() $\bigsqcup _iU_i\to G'\to G$ where
$\bigsqcup _iU_i\to G'\to G$ where ![]() $\{U_i\subseteq G\}_i$ is an open cover. Now each
$\{U_i\subseteq G\}_i$ is an open cover. Now each ![]() $F\times _GU_i$ is representable by assumption, and gluing these spaces together on their common overlaps
$F\times _GU_i$ is representable by assumption, and gluing these spaces together on their common overlaps ![]() $F\times _G(U_i\cap U_j)$ gives a topological space representing
$F\times _G(U_i\cap U_j)$ gives a topological space representing ![]() $F$.
$F$.
A complex vector bundle over a stack ![]() $X$ is a representable map
$X$ is a representable map ![]() $V\to X$ together with maps
$V\to X$ together with maps ![]() $V\times _XV\to V$ and
$V\times _XV\to V$ and ![]() $\mathbb {C}\times V\to V$ (both over
$\mathbb {C}\times V\to V$ (both over ![]() $X$) such that for every map
$X$) such that for every map ![]() $U\to X$ from a topological space
$U\to X$ from a topological space ![]() $U$, there exists an open cover
$U$, there exists an open cover ![]() $\{U_i\subseteq U\}_i$ and integers
$\{U_i\subseteq U\}_i$ and integers ![]() $n_i\geqslant 0$ such that
$n_i\geqslant 0$ such that ![]() $V\times _XU_i\to U_i$ is isomorphic to
$V\times _XU_i\to U_i$ is isomorphic to ![]() $\mathbb {C}^{n_i}\times U_i\to U_i$ equipped with its fiberwise addition and scaling maps. A pullback of a complex vector bundle is naturally a complex vector bundle.
$\mathbb {C}^{n_i}\times U_i\to U_i$ equipped with its fiberwise addition and scaling maps. A pullback of a complex vector bundle is naturally a complex vector bundle.
The class of so called topological stacks (those which admit a presentation via a topological groupoid) are somewhat better behaved than general stacks. A topological groupoid ![]() $M\rightrightarrows O$ consists of a pair of topological spaces
$M\rightrightarrows O$ consists of a pair of topological spaces ![]() $O$ (‘objects’) and
$O$ (‘objects’) and ![]() $M$ (‘morphisms’), two maps
$M$ (‘morphisms’), two maps ![]() $M\rightrightarrows O$ (‘source’ and ‘target’), a map
$M\rightrightarrows O$ (‘source’ and ‘target’), a map ![]() $O\to M$ (‘identity’), an involution
$O\to M$ (‘identity’), an involution ![]() $M\to M$ (‘inverse’), and a map
$M\to M$ (‘inverse’), and a map ![]() $M\times _OM\to M$ (‘composition’) satisfying the axioms of a groupoid. A topological groupoid
$M\times _OM\to M$ (‘composition’) satisfying the axioms of a groupoid. A topological groupoid ![]() $M\rightrightarrows O$ presents a stack
$M\rightrightarrows O$ presents a stack ![]() $[M\rightrightarrows O]$ defined as follows. An object of
$[M\rightrightarrows O]$ defined as follows. An object of ![]() $[M\rightrightarrows O](X)$ is an open cover
$[M\rightrightarrows O](X)$ is an open cover ![]() $\{U_i\subseteq X\}_i$ together with maps
$\{U_i\subseteq X\}_i$ together with maps ![]() $U_i\to O$ and
$U_i\to O$ and ![]() $U_i\cap U_j\to M$ satisfying a compatibility condition, and an isomorphism in
$U_i\cap U_j\to M$ satisfying a compatibility condition, and an isomorphism in ![]() $[M\rightrightarrows O](X)$ consists of maps
$[M\rightrightarrows O](X)$ consists of maps ![]() $U_i\cap U_{i'}'\to M$ satisfying a compatibility condition. There is a natural map
$U_i\cap U_{i'}'\to M$ satisfying a compatibility condition. There is a natural map ![]() $O\to [M\rightrightarrows O]$ (take the trivial open cover
$O\to [M\rightrightarrows O]$ (take the trivial open cover ![]() $\{X\subseteq X\}$) and the fiber product
$\{X\subseteq X\}$) and the fiber product ![]() $O\times _{[M\rightrightarrows O]}O$ is naturally identified with
$O\times _{[M\rightrightarrows O]}O$ is naturally identified with ![]() $M$. The morphism
$M$. The morphism ![]() $O\to [M\rightrightarrows O]$ admits local sections (by definition), so because
$O\to [M\rightrightarrows O]$ admits local sections (by definition), so because ![]() $O\times _{[M\rightrightarrows O]}O\to O$ is representable, it follows by descent that
$O\times _{[M\rightrightarrows O]}O\to O$ is representable, it follows by descent that ![]() $O\to [M\rightrightarrows O]$ is representable. Conversely, a representable map
$O\to [M\rightrightarrows O]$ is representable. Conversely, a representable map ![]() $U\to X$ admitting local sections from a topological space
$U\to X$ admitting local sections from a topological space ![]() $U$ to a stack
$U$ to a stack ![]() $X$ determines a topological groupoid
$X$ determines a topological groupoid ![]() $U\times _XU\rightrightarrows U$ presenting
$U\times _XU\rightrightarrows U$ presenting ![]() $X$. Indeed, the fiber product
$X$. Indeed, the fiber product ![]() $U\times _XU$ is representable (because
$U\times _XU$ is representable (because ![]() $U$ and
$U$ and ![]() $U\to X$ are), it admits two maps to
$U\to X$ are), it admits two maps to ![]() $U$ (the two projections), an involution (exchanging the two factors), and a composition map
$U$ (the two projections), an involution (exchanging the two factors), and a composition map ![]() $(U\times _XU)\times _U(U\times _XU)=U\times _XU\times _XU\to U\times _XU$ (forgetting the middle factor), and one can check using the stack property that the natural map
$(U\times _XU)\times _U(U\times _XU)=U\times _XU\times _XU\to U\times _XU$ (forgetting the middle factor), and one can check using the stack property that the natural map ![]() $[U\times _XU\rightrightarrows U]\to X$ is an equivalence. A stack
$[U\times _XU\rightrightarrows U]\to X$ is an equivalence. A stack ![]() $X$ for which there exists a representable map
$X$ for which there exists a representable map ![]() $U\to X$ admitting local sections from a space
$U\to X$ admitting local sections from a space ![]() $U$ is called topological, and such
$U$ is called topological, and such ![]() $U\to X$ is called an atlas for
$U\to X$ is called an atlas for ![]() $X$.
$X$.
For a topological stack ![]() $X$ with atlas
$X$ with atlas ![]() $U\to X$, for any property
$U\to X$, for any property ![]() $\mathcal {P}$ which descends along maps admitting local sections, the map
$\mathcal {P}$ which descends along maps admitting local sections, the map ![]() $U\to X$ has
$U\to X$ has ![]() $\mathcal {P}$ if and only if both maps
$\mathcal {P}$ if and only if both maps ![]() $U\times _XU\to U$ have
$U\times _XU\to U$ have ![]() $\mathcal {P}$, and the diagonal
$\mathcal {P}$, and the diagonal ![]() $X\to X\times X$ has
$X\to X\times X$ has ![]() $\mathcal {P}$ if and only if the map
$\mathcal {P}$ if and only if the map ![]() $U\times _XU\to U\times U$ has
$U\times _XU\to U\times U$ has ![]() $\mathcal {P}$. In particular, for any topological stack
$\mathcal {P}$. In particular, for any topological stack ![]() $X$, the diagonal
$X$, the diagonal ![]() $X\to X\times X$ is representable, and thus every map
$X\to X\times X$ is representable, and thus every map ![]() $Z\to X$ from a topological space
$Z\to X$ from a topological space ![]() $Z$ is representable. More generally, for any map of topological stacks
$Z$ is representable. More generally, for any map of topological stacks ![]() $X\to Y$, the relative diagonal
$X\to Y$, the relative diagonal ![]() $X\to X\times _YX$ is representable (by descent from its pullback
$X\to X\times _YX$ is representable (by descent from its pullback ![]() $V\times _XV\to V\times _YV$ for an atlas
$V\times _XV\to V\times _YV$ for an atlas ![]() $V\to X$). If
$V\to X$). If ![]() $X\to Y$ is representable and
$X\to Y$ is representable and ![]() $Y$ is topological, then so is
$Y$ is topological, then so is ![]() $X$ (if
$X$ (if ![]() $U\to Y$ is an atlas for
$U\to Y$ is an atlas for ![]() $Y$, then its pullback
$Y$, then its pullback ![]() $V=U\times _YX\to X$ is an atlas for
$V=U\times _YX\to X$ is an atlas for ![]() $X$), and the relative diagonal
$X$), and the relative diagonal ![]() $X\to X\times _YX$ has
$X\to X\times _YX$ has ![]() $\mathcal {P}$ if and only if the relative diagonal
$\mathcal {P}$ if and only if the relative diagonal ![]() $V\to V\times _UV$ of atlases has
$V\to V\times _UV$ of atlases has ![]() $\mathcal {P}$ (the latter is the pullback of the former under the map
$\mathcal {P}$ (the latter is the pullback of the former under the map ![]() $V\times _UV\to X\times _YX$, which is representable and admits local sections because it is a pullback of
$V\times _UV\to X\times _YX$, which is representable and admits local sections because it is a pullback of ![]() $U\to Y$).
$U\to Y$).
For a topological space ![]() $V$, a topological group
$V$, a topological group ![]() $G$, and a continuous group action
$G$, and a continuous group action ![]() $G\curvearrowright V$, we may consider the action groupoid
$G\curvearrowright V$, we may consider the action groupoid ![]() $G\times V\rightrightarrows V$ with source and target maps
$G\times V\rightrightarrows V$ with source and target maps ![]() $(g,x)\mapsto x$ and
$(g,x)\mapsto x$ and ![]() $(g,x)\mapsto gx$. The stack associated to this groupoid is denoted
$(g,x)\mapsto gx$. The stack associated to this groupoid is denoted ![]() $V/G$ and is called the stack quotient of the action
$V/G$ and is called the stack quotient of the action ![]() $G\curvearrowright V$. If
$G\curvearrowright V$. If ![]() $G$ is discrete, the two maps
$G$ is discrete, the two maps ![]() $G\times V\to V$ are étale, so
$G\times V\to V$ are étale, so ![]() $V\to V/G$ is étale. If
$V\to V/G$ is étale. If ![]() $G$ is compact and
$G$ is compact and ![]() $V$ is Hausdorff, the map
$V$ is Hausdorff, the map ![]() $G\times V\to V\times V$ is universally closed (factor as
$G\times V\to V\times V$ is universally closed (factor as ![]() $G\times V\to G\times V\times V$ which is a closed embedding because
$G\times V\to G\times V\times V$ which is a closed embedding because ![]() $V$ is Hausdorff and
$V$ is Hausdorff and ![]() $G\times V\times V\to V\times V$ which is universally closed because
$G\times V\times V\to V\times V$ which is universally closed because ![]() $G$ is compact), so
$G$ is compact), so ![]() $V/G$ has universally closed diagonal. If
$V/G$ has universally closed diagonal. If ![]() $G$ is Hausdorff, then the map
$G$ is Hausdorff, then the map ![]() $G\times V\to V\times V$ is separated, so
$G\times V\to V\times V$ is separated, so ![]() $V/G$ has separated diagonal. Thus, if
$V/G$ has separated diagonal. Thus, if ![]() $G$ is compact Hausdorff and
$G$ is compact Hausdorff and ![]() $V$ is Hausdorff, then
$V$ is Hausdorff, then ![]() $V/G$ has proper diagonal.
$V/G$ has proper diagonal.
A groupoid presentation of a topological stack ![]() $X$ also gives a description of its coarse space
$X$ also gives a description of its coarse space ![]() $|X|$ as follows. For an atlas
$|X|$ as follows. For an atlas ![]() $U\to X$, consider the equivalence relation
$U\to X$, consider the equivalence relation ![]() $\sim _X$ on
$\sim _X$ on ![]() $U$ given by the image of
$U$ given by the image of ![]() $U\times _XU\to U\times U$. There is a map
$U\times _XU\to U\times U$. There is a map ![]() $X\to U/{\sim _X}$ (which is tautological once we regard
$X\to U/{\sim _X}$ (which is tautological once we regard ![]() $X$ as
$X$ as ![]() $[U\times _XU\rightrightarrows U]$), inducing a map
$[U\times _XU\rightrightarrows U]$), inducing a map ![]() $|X|\to U/{\sim _X}$, which is a bijection, essentially by definition. As an open substack of
$|X|\to U/{\sim _X}$, which is a bijection, essentially by definition. As an open substack of ![]() $X$ pulls back to an open subset of
$X$ pulls back to an open subset of ![]() $U$ invariant under
$U$ invariant under ![]() $\sim _X$, it follows that
$\sim _X$, it follows that ![]() $|X|\xrightarrow \sim U/{\sim _X}$ is open and is, thus, a homeomorphism. In particular, it follows that the coarse space
$|X|\xrightarrow \sim U/{\sim _X}$ is open and is, thus, a homeomorphism. In particular, it follows that the coarse space ![]() $\big |V/G\big |$ of the stack quotient
$\big |V/G\big |$ of the stack quotient ![]() $V/G$ is the usual topological quotient of
$V/G$ is the usual topological quotient of ![]() $V$ by
$V$ by ![]() $G$.
$G$.
An action ![]() $G\curvearrowright V$ is called locally trivial if and only if
$G\curvearrowright V$ is called locally trivial if and only if ![]() $V$ admits a cover by
$V$ admits a cover by ![]() $G$-invariant open sets
$G$-invariant open sets ![]() $\{G\times Z_i\subseteq V\}_i$ where
$\{G\times Z_i\subseteq V\}_i$ where ![]() $G\curvearrowright G\times Z_i$ acts by left multiplication on
$G\curvearrowright G\times Z_i$ acts by left multiplication on ![]() $G$ and trivially on
$G$ and trivially on ![]() $Z_i$. If
$Z_i$. If ![]() $G\curvearrowright V$ is locally trivial, then the natural map from the stack quotient to the topological quotient
$G\curvearrowright V$ is locally trivial, then the natural map from the stack quotient to the topological quotient ![]() $V/G\to |V/G|$ is an equivalence. Indeed, this assertion is local on
$V/G\to |V/G|$ is an equivalence. Indeed, this assertion is local on ![]() $|V/G|$, so it suffices to consider the case of
$|V/G|$, so it suffices to consider the case of ![]() $G\curvearrowright G\times Z$, where it holds by inspection.
$G\curvearrowright G\times Z$, where it holds by inspection.
Definition 3.2 A (separated) orbispace is a stack ![]() $X$ for which there exists a representable étale surjection
$X$ for which there exists a representable étale surjection ![]() $U\to X$ from a topological space
$U\to X$ from a topological space ![]() $U$ (an ‘étale atlas’), and the diagonal
$U$ (an ‘étale atlas’), and the diagonal ![]() $X\to X\times X$ is proper.
$X\to X\times X$ is proper.
Proposition 3.3 A stack ![]() $X$ is an orbispace if and only if
$X$ is an orbispace if and only if ![]() $|X|$ is Hausdorff and there exists an open cover
$|X|$ is Hausdorff and there exists an open cover ![]() $\{V_i/G_i\subseteq X\}_i$ where
$\{V_i/G_i\subseteq X\}_i$ where ![]() $G_i$ are finite discrete groups acting on Hausdorff spaces
$G_i$ are finite discrete groups acting on Hausdorff spaces ![]() $V_i$.
$V_i$.
(Similar results include [Reference BehrendBeh14, Theorem 1.108] and [Reference NoohiNoo05, Proposition 14.10].)
Proof. Let ![]() $X$ be an orbispace, and let us show that there is an open cover
$X$ be an orbispace, and let us show that there is an open cover ![]() $\{V_i/G_i\subseteq X\}_i$. Fix an étale atlas
$\{V_i/G_i\subseteq X\}_i$. Fix an étale atlas ![]() $U\to X$, and let
$U\to X$, and let ![]() $u\in U$. The automorphism group
$u\in U$. The automorphism group ![]() $G_u:=\{u\}\times _X\{u\}\subseteq U\times _XU$ is finite and discrete because
$G_u:=\{u\}\times _X\{u\}\subseteq U\times _XU$ is finite and discrete because ![]() $X\to X\times X$ is proper. As the two projections
$X\to X\times X$ is proper. As the two projections ![]() $U\times _XU\rightrightarrows U$ are étale, for every
$U\times _XU\rightrightarrows U$ are étale, for every ![]() $g\in G$ there exists an open neighborhood
$g\in G$ there exists an open neighborhood ![]() $g\in U_g\subseteq U\times _XU$ such that each projection restricted to
$g\in U_g\subseteq U\times _XU$ such that each projection restricted to ![]() $U_g$ is an open embedding (this gives another proof that
$U_g$ is an open embedding (this gives another proof that ![]() $G$ has the discrete topology). As
$G$ has the discrete topology). As ![]() $G$ is finite and
$G$ is finite and ![]() $U\times _XU\to U\times U$ is separated, we may take these
$U\times _XU\to U\times U$ is separated, we may take these ![]() $U_g$ to be disjoint. Now the complement of
$U_g$ to be disjoint. Now the complement of ![]() $\bigsqcup _gU_g$ is closed and disjoint from
$\bigsqcup _gU_g$ is closed and disjoint from ![]() $G$, so it projects to a closed (by properness) subset of
$G$, so it projects to a closed (by properness) subset of ![]() $U\times U$ disjoint from
$U\times U$ disjoint from ![]() $(u,u)$. Hence, there is an open neighborhood
$(u,u)$. Hence, there is an open neighborhood ![]() $u\in V\subseteq U$ such that
$u\in V\subseteq U$ such that ![]() $V\times _XV\subseteq \bigsqcup _gU_g$. Thus,
$V\times _XV\subseteq \bigsqcup _gU_g$. Thus, ![]() $V\times _XV$ is a disjoint union of pieces indexed by
$V\times _XV$ is a disjoint union of pieces indexed by ![]() $G$, and each piece maps homeomorphically to
$G$, and each piece maps homeomorphically to ![]() $V$ under each projection. By further shrinking
$V$ under each projection. By further shrinking ![]() $V$, we may assume that the map
$V$, we may assume that the map ![]() $V\times _XV\to G$ respects composition (this is possible because composition is continuous). It follows that
$V\times _XV\to G$ respects composition (this is possible because composition is continuous). It follows that ![]() $V\times _XV\rightrightarrows V$ is an action groupoid
$V\times _XV\rightrightarrows V$ is an action groupoid ![]() $G\times V\rightrightarrows V$ for an action
$G\times V\rightrightarrows V$ for an action ![]() $G\curvearrowright V$. As
$G\curvearrowright V$. As ![]() $V=\{1\}\times V\hookrightarrow G\times V=V\times _XV\to V\times V$ expresses the diagonal of
$V=\{1\}\times V\hookrightarrow G\times V=V\times _XV\to V\times V$ expresses the diagonal of ![]() $V$ as a composition of proper maps, we conclude that
$V$ as a composition of proper maps, we conclude that ![]() $V$ is Hausdorff. Now the map of groupoids
$V$ is Hausdorff. Now the map of groupoids ![]() $(G\times V\rightrightarrows V)=(V\times _XV\rightrightarrows V)\to (U\times _XU\rightrightarrows U)$ induces a map of stacks
$(G\times V\rightrightarrows V)=(V\times _XV\rightrightarrows V)\to (U\times _XU\rightrightarrows U)$ induces a map of stacks ![]() $V/G\to X$. To see that this is an open embedding, let
$V/G\to X$. To see that this is an open embedding, let ![]() $V^+\subseteq U$ denote the orbit of
$V^+\subseteq U$ denote the orbit of ![]() $V$ under the morphisms
$V$ under the morphisms ![]() $U\times _XU\rightrightarrows U$. As the projections
$U\times _XU\rightrightarrows U$. As the projections ![]() $U\times _XU\rightrightarrows U$ are étale, it follows that
$U\times _XU\rightrightarrows U$ are étale, it follows that ![]() $V^+\subseteq U$ is open, and hence
$V^+\subseteq U$ is open, and hence ![]() $[V^+\times _XV^+\rightrightarrows V^+]\to [U\times _XU\rightrightarrows U]$ is an open embedding of stacks; denote this open substack by
$[V^+\times _XV^+\rightrightarrows V^+]\to [U\times _XU\rightrightarrows U]$ is an open embedding of stacks; denote this open substack by ![]() $Z\subseteq X$, so
$Z\subseteq X$, so ![]() $V\to Z$ is an étale atlas. Thus, the topological groupoid
$V\to Z$ is an étale atlas. Thus, the topological groupoid ![]() $V\times _XV=V\times _ZV\rightrightarrows V$ presents
$V\times _XV=V\times _ZV\rightrightarrows V$ presents ![]() $Z$, so
$Z$, so ![]() $V/G\to X$ is an open embedding as desired.
$V/G\to X$ is an open embedding as desired.
Let us now show that for any orbispace ![]() $X$, its coarse space
$X$, its coarse space ![]() $|X|$ is Hausdorff. We saw earlier that
$|X|$ is Hausdorff. We saw earlier that ![]() $|X|$ is the quotient of
$|X|$ is the quotient of ![]() $U$ by the image of
$U$ by the image of ![]() $U\times _XU\to U\times U$ (which is an equivalence relation). This equivalence relation is closed because
$U\times _XU\to U\times U$ (which is an equivalence relation). This equivalence relation is closed because ![]() $U\times _XU\to U\times U$ is proper, so
$U\times _XU\to U\times U$ is proper, so ![]() $|X|$ is Hausdorff provided the quotient map
$|X|$ is Hausdorff provided the quotient map ![]() $U\to |X|$ is open. Now openness of
$U\to |X|$ is open. Now openness of ![]() $U\to |X|$ does not depend on which atlas
$U\to |X|$ does not depend on which atlas ![]() $U\to X$ we take: there are étale maps
$U\to X$ we take: there are étale maps ![]() $U\leftarrow U\times _XU'\to U'$ over
$U\leftarrow U\times _XU'\to U'$ over ![]() $|X|$, which means that
$|X|$, which means that ![]() $U\to |X|$ is open if and only if
$U\to |X|$ is open if and only if ![]() $U'\to |X|$ is open. Moreover, openness of
$U'\to |X|$ is open. Moreover, openness of ![]() $U\to |X|$ can be checked locally on
$U\to |X|$ can be checked locally on ![]() $|X|$, so we may assume without loss of generality that
$|X|$, so we may assume without loss of generality that ![]() $X=V/G$. Hence, it is enough to note that the quotient map
$X=V/G$. Hence, it is enough to note that the quotient map ![]() $V\to |V/G|$ (induced by the canonical étale atlas
$V\to |V/G|$ (induced by the canonical étale atlas ![]() $V\to V/G$) is open. Thus,
$V\to V/G$) is open. Thus, ![]() $|X|$ is Hausdorff.
$|X|$ is Hausdorff.
Finally, let us show that if ![]() $|X|$ is Hausdorff and there is an open cover
$|X|$ is Hausdorff and there is an open cover ![]() $\{V_i/G_i\subseteq X\}_i$, then
$\{V_i/G_i\subseteq X\}_i$, then ![]() $X$ is an orbispace. The maps
$X$ is an orbispace. The maps ![]() $V_i\to V_i/G_i$ are representable étale, so
$V_i\to V_i/G_i$ are representable étale, so ![]() $U:=\bigsqcup _iV_i\to X$ is an étale atlas. To show that the diagonal
$U:=\bigsqcup _iV_i\to X$ is an étale atlas. To show that the diagonal ![]() $X\to X\times X$ is proper, it is equivalent to show that
$X\to X\times X$ is proper, it is equivalent to show that ![]() $U\times _XU\to U\times U$ is proper. This reduces to showing that
$U\times _XU\to U\times U$ is proper. This reduces to showing that ![]() $V\times _XV'\to V\times V'$ is proper for any pair
$V\times _XV'\to V\times V'$ is proper for any pair ![]() $V/G\hookrightarrow X\hookleftarrow V'/G'$. As
$V/G\hookrightarrow X\hookleftarrow V'/G'$. As ![]() $|X|$ is Hausdorff, the map
$|X|$ is Hausdorff, the map ![]() $V\times _{|X|}V'\to V\times V'$ a closed embedding (as it is a pullback of the diagonal of
$V\times _{|X|}V'\to V\times V'$ a closed embedding (as it is a pullback of the diagonal of ![]() $|X|$), so it follows that
$|X|$), so it follows that ![]() $V\times _XV'\to V\times V'$ is proper if and only if
$V\times _XV'\to V\times V'$ is proper if and only if ![]() $V\times _XV'\to V\times _{|X|}V'$ is proper. Now for the purposes of studying the latter map
$V\times _XV'\to V\times _{|X|}V'$ is proper. Now for the purposes of studying the latter map ![]() $V\times _XV'\to V\times _{|X|}V'$, we may as well shrink
$V\times _XV'\to V\times _{|X|}V'$, we may as well shrink ![]() $V$,
$V$, ![]() $V'$, and
$V'$, and ![]() $X$ so that
$X$ so that ![]() $V/G=X=V'/G'$. Now the diagonal of
$V/G=X=V'/G'$. Now the diagonal of ![]() $V/G=V'/G'=X$ is proper, hence so is
$V/G=V'/G'=X$ is proper, hence so is ![]() $V\times _XV'\to V\times V'$.
$V\times _XV'\to V\times V'$.
Corollary 3.4 Every orbispace ![]() $X$ has an étale atlas
$X$ has an étale atlas ![]() $U\to X$ with
$U\to X$ with ![]() $U$ Hausdorff; equivalently, every étale atlas
$U$ Hausdorff; equivalently, every étale atlas ![]() $U\to X$ has
$U\to X$ has ![]() $U$ locally Hausdorff.
$U$ locally Hausdorff.
Proof. By Proposition 3.3 there is an open cover ![]() $\{V_i/G_i\subseteq X\}_i$ with
$\{V_i/G_i\subseteq X\}_i$ with ![]() $V_i$ Hausdorff, so
$V_i$ Hausdorff, so ![]() $U:=\bigsqcup _iV_i\to X$ is an étale atlas with
$U:=\bigsqcup _iV_i\to X$ is an étale atlas with ![]() $U$ Hausdorff. Now for any two étale atlases
$U$ Hausdorff. Now for any two étale atlases ![]() $U,U'\to X$, consideration of the surjective étale maps
$U,U'\to X$, consideration of the surjective étale maps ![]() $U\leftarrow U\times _XU'\to U'$ shows that
$U\leftarrow U\times _XU'\to U'$ shows that ![]() $U$ is locally Hausdorff if and only if
$U$ is locally Hausdorff if and only if ![]() $U'$ is locally Hausdorff. Given any étale atlas
$U'$ is locally Hausdorff. Given any étale atlas ![]() $U\to X$ with
$U\to X$ with ![]() $U$ locally Hausdorff and any open cover
$U$ locally Hausdorff and any open cover ![]() $\{U_i\subseteq U\}_i$ with
$\{U_i\subseteq U\}_i$ with ![]() $U_i$ Hausdorff, the disjoint union
$U_i$ Hausdorff, the disjoint union ![]() $U':=\bigsqcup _iU_i\to X$ is an étale atlas with
$U':=\bigsqcup _iU_i\to X$ is an étale atlas with ![]() $U'$ Hausdorff.
$U'$ Hausdorff.
Corollary 3.5 For any étale atlas ![]() $U\to X$ on an orbispace, there exists an open cover
$U\to X$ on an orbispace, there exists an open cover ![]() $\{V_i/G_i\subseteq X\}_i$ as in Proposition 3.3 such that each map
$\{V_i/G_i\subseteq X\}_i$ as in Proposition 3.3 such that each map ![]() $V_i\to X$ factors through an open embedding
$V_i\to X$ factors through an open embedding ![]() $V_i\to U$.
$V_i\to U$.
Proof. Let ![]() $U\to X$ be given and fix any open cover
$U\to X$ be given and fix any open cover ![]() $\{V_i/G_i\subseteq X\}_i$ as in Proposition 3.3. As
$\{V_i/G_i\subseteq X\}_i$ as in Proposition 3.3. As ![]() $U\times _XV_i\to V_i$ is étale, it admits local sections, and hence by replacing each
$U\times _XV_i\to V_i$ is étale, it admits local sections, and hence by replacing each ![]() $V_i$ with an open cover of itself, we may assume that each projection
$V_i$ with an open cover of itself, we may assume that each projection ![]() $U\times _XV_i\to V_i$ admits a section (which is thus an open embedding). Now the resulting maps
$U\times _XV_i\to V_i$ admits a section (which is thus an open embedding). Now the resulting maps ![]() $V_i\to U$ are étale by the factorization
$V_i\to U$ are étale by the factorization ![]() $V_i\to U\times _XV_i\to U$, so by again replacing each
$V_i\to U\times _XV_i\to U$, so by again replacing each ![]() $V_i$ with an open cover, we may assume they are open embeddings.
$V_i$ with an open cover, we may assume they are open embeddings.
Alternatively, we could note that the open cover ![]() $\{V_i/G_i\subseteq X\}_i$ produced by the proof of Proposition 3.3 is in fact of the desired form.
$\{V_i/G_i\subseteq X\}_i$ produced by the proof of Proposition 3.3 is in fact of the desired form.
Corollary 3.6 A map of orbispaces ![]() $X\to Y$ is representable if and only if it is injective on isotropy groups. In particular, an orbispace
$X\to Y$ is representable if and only if it is injective on isotropy groups. In particular, an orbispace ![]() $X$ is a space if and only if it has trivial isotropy.
$X$ is a space if and only if it has trivial isotropy.
Proof. Any representable morphism of stacks is injective on isotropy groups (just test against points). Thus, we are left with showing that a map of orbispaces ![]() $X\to Y$ which is injective on isotropy groups is representable.
$X\to Y$ which is injective on isotropy groups is representable.
As representability descends under maps admitting local sections, it suffices to show that the fiber product ![]() $X'=X\times _YY'$ is representable for some étale atlas
$X'=X\times _YY'$ is representable for some étale atlas ![]() $Y'\to Y$. Note that
$Y'\to Y$. Note that ![]() $X'$ has trivial isotropy because
$X'$ has trivial isotropy because ![]() $Y'$ has trivial isotropy and
$Y'$ has trivial isotropy and ![]() $X'\to Y'$ is injective on isotropy groups (being a pullback of
$X'\to Y'$ is injective on isotropy groups (being a pullback of ![]() $X\to Y$).
$X\to Y$).
We claim that ![]() $X'$ is an orbispace, provided we take
$X'$ is an orbispace, provided we take ![]() $Y'$ to be Hausdorff (which we can by Corollary 3.4). The pullback of an étale atlas
$Y'$ to be Hausdorff (which we can by Corollary 3.4). The pullback of an étale atlas ![]() $U\to X$ is an étale atlas
$U\to X$ is an étale atlas ![]() $U'\to X'$ (because
$U'\to X'$ (because ![]() $X'\to X$ is representable, being a pullback of
$X'\to X$ is representable, being a pullback of ![]() $Y'\to Y$). The diagonal of
$Y'\to Y$). The diagonal of ![]() $X'$ is the composition
$X'$ is the composition ![]() $X'\to X'\times _XX'\to X'\times X'$. The second map
$X'\to X'\times _XX'\to X'\times X'$. The second map ![]() $X'\times _XX'\to X'\times X'$ is proper as it is a pullback of
$X'\times _XX'\to X'\times X'$ is proper as it is a pullback of ![]() $X\to X\times X$. To analyze the first map
$X\to X\times X$. To analyze the first map ![]() $X'\to X'\times _XX'$, note that it pulls back to
$X'\to X'\times _XX'$, note that it pulls back to ![]() $U'\to U'\times _UU'$ under the map
$U'\to U'\times _UU'$ under the map ![]() $U'\times _UU'\to X'\times _XX'$ which admits local sections (being a pullback of
$U'\times _UU'\to X'\times _XX'$ which admits local sections (being a pullback of ![]() $U\to X$). As
$U\to X$). As ![]() $Y\to Y\times Y$ is separated, its pullback
$Y\to Y\times Y$ is separated, its pullback ![]() $Y'\times _YY'\to Y'\times Y'$ is also separated, which implies each projection
$Y'\times _YY'\to Y'\times Y'$ is also separated, which implies each projection ![]() $Y'\times _YY'\rightrightarrows Y'$ is separated because
$Y'\times _YY'\rightrightarrows Y'$ is separated because ![]() $Y'$ is Hausdorff, which implies
$Y'$ is Hausdorff, which implies ![]() $Y'\to Y$ is separated. Hence, its pullback
$Y'\to Y$ is separated. Hence, its pullback ![]() $U'\to U$ is separated, so
$U'\to U$ is separated, so ![]() $U'\to U'\times _UU'$ is a closed embedding, hence proper. Thus,
$U'\to U'\times _UU'$ is a closed embedding, hence proper. Thus, ![]() $X'\to X'\times _XX'$ is proper, and we conclude that
$X'\to X'\times _XX'$ is proper, and we conclude that ![]() $X'$ is an orbispace.
$X'$ is an orbispace.
We are thus reduced to showing that an orbispace ![]() $Z$ with trivial isotropy is a space. By Proposition 3.3, we know that
$Z$ with trivial isotropy is a space. By Proposition 3.3, we know that ![]() $Z$ is given locally by
$Z$ is given locally by ![]() $V/G$ for
$V/G$ for ![]() $V$ Hausdorff and
$V$ Hausdorff and ![]() $G$ finite discrete acting freely (because
$G$ finite discrete acting freely (because ![]() $Z$ has trivial isotropy). Free actions
$Z$ has trivial isotropy). Free actions ![]() $G\curvearrowright V$ with
$G\curvearrowright V$ with ![]() $V$ Hausdorff and
$V$ Hausdorff and ![]() $G$ finite are locally trivial, so we conclude that the map
$G$ finite are locally trivial, so we conclude that the map ![]() $Z\to |Z|$ is an equivalence. Alternatively, we could note that the chart
$Z\to |Z|$ is an equivalence. Alternatively, we could note that the chart ![]() $V/G$ near a given
$V/G$ near a given ![]() $x\in X$ constructed in the proof of Proposition 3.3 in fact satisfies
$x\in X$ constructed in the proof of Proposition 3.3 in fact satisfies ![]() $G=G_x$ by definition.
$G=G_x$ by definition.
4. Coverings and nerves
We show how Theorem 2.13 implies Theorem 1.1. It is enough to show that a given orbispace admits a representable map to a simplicial complex of groups; this is Proposition 4.9. This simplicial complex of groups is basically just the nerve of a suitable open cover, however its construction is somewhat more delicate than one might initially expect.
A sieve on a topological space ![]() $X$ is a subset
$X$ is a subset ![]() $S\subseteq 2^X$ consisting of open sets such that
$S\subseteq 2^X$ consisting of open sets such that ![]() $U'\subseteq U\in S$ implies
$U'\subseteq U\in S$ implies ![]() $U'\in S$. A covering sieve on
$U'\in S$. A covering sieve on ![]() $X$ is a sieve
$X$ is a sieve ![]() $S$ such that
$S$ such that ![]() $\bigcup _{U\in S}U=X$. An open cover
$\bigcup _{U\in S}U=X$. An open cover ![]() $\{U_i\subseteq X\}_i$ is said to generate the covering sieve on
$\{U_i\subseteq X\}_i$ is said to generate the covering sieve on ![]() $X$ consisting of those open sets which are contained in some
$X$ consisting of those open sets which are contained in some ![]() $U_i$.
$U_i$.
Definition 4.1 A connection sieve on a map of spaces ![]() $f:X\to Y$ is a covering sieve
$f:X\to Y$ is a covering sieve ![]() $S$ on
$S$ on ![]() $X$ such that (1) for
$X$ such that (1) for ![]() $U\in S$, the composition
$U\in S$, the composition ![]() $U\to X\to Y$ is an open embedding, and (2) for
$U\to X\to Y$ is an open embedding, and (2) for ![]() $U,V\in S$ with
$U,V\in S$ with ![]() $f(U)=f(V)$, either
$f(U)=f(V)$, either ![]() $U=V$ or
$U=V$ or ![]() $U\cap V=\varnothing$.
$U\cap V=\varnothing$.
Note that for sieves satisfying condition (1), condition (2) is equivalent to condition (2![]() $'$) for
$'$) for ![]() $U,V\in S$ either
$U,V\in S$ either ![]() $U\cap V=\varnothing$ or
$U\cap V=\varnothing$ or ![]() $f(U\cap V)=f(U)\cap f(V)$. If
$f(U\cap V)=f(U)\cap f(V)$. If ![]() $S'\subseteq S$ is an inclusion of covering sieves and
$S'\subseteq S$ is an inclusion of covering sieves and ![]() $S$ is a connection sieve on
$S$ is a connection sieve on ![]() $X\to Y$, then so is
$X\to Y$, then so is ![]() $S'$. In particular, if
$S'$. In particular, if ![]() $S$ and
$S$ and ![]() $S'$ are connection sieves on
$S'$ are connection sieves on ![]() $X\to Y$, then so is
$X\to Y$, then so is ![]() $S\cap S'$. To check that an open cover
$S\cap S'$. To check that an open cover ![]() $\{U_i\subseteq X\}_i$ generates a connection sieve, it is enough to check axioms (1) and (2
$\{U_i\subseteq X\}_i$ generates a connection sieve, it is enough to check axioms (1) and (2![]() $'$) for the open sets
$'$) for the open sets ![]() $U_i$.
$U_i$.
Definition 4.2 A map ![]() $X\to Y$ is called strongly étale if and only if it admits a connection sieve.
$X\to Y$ is called strongly étale if and only if it admits a connection sieve.
Open embeddings are strongly étale, and strongly étale maps are separated and étale (however, the converse is false by Example 4.3). Being strongly étale is preserved under pullback (take the connection sieve generated by the pullback of the original connection sieve), and the class of strongly étale maps is closed under composition (a connection sieve ![]() $S_{X/Z}$ for a composition
$S_{X/Z}$ for a composition ![]() $X\to Y\to Z$ is given by those elements of a fixed connection sieve
$X\to Y\to Z$ is given by those elements of a fixed connection sieve ![]() $S_{X/Y}$ for
$S_{X/Y}$ for ![]() $X\to Y$ whose image lies in a fixed connection sieve
$X\to Y$ whose image lies in a fixed connection sieve ![]() $S_{Y/Z}$ for
$S_{Y/Z}$ for ![]() $Y\to Z$). A disjoint union
$Y\to Z$). A disjoint union ![]() $\bigsqcup _iX_i\to \bigsqcup _iY_i$ of strongly étale maps
$\bigsqcup _iX_i\to \bigsqcup _iY_i$ of strongly étale maps ![]() $X_i\to Y_i$ is strongly étale (take disjoint union of connection sieves), and the projection
$X_i\to Y_i$ is strongly étale (take disjoint union of connection sieves), and the projection ![]() $A\times Y\to Y$ is strongly étale for any discrete space
$A\times Y\to Y$ is strongly étale for any discrete space ![]() $A$. Being strongly étale is not local on the target, as shown by the following example.
$A$. Being strongly étale is not local on the target, as shown by the following example.
Example 4.3 Let us construct a finite covering space which is not strongly étale. Let ![]() $Z=\{1,\frac 12,\frac 14,\frac 18,\ldots \}\cup \{0\}\subseteq \mathbb {R}$ with the subspace topology. Every double cover of
$Z=\{1,\frac 12,\frac 14,\frac 18,\ldots \}\cup \{0\}\subseteq \mathbb {R}$ with the subspace topology. Every double cover of ![]() $Z$ or
$Z$ or ![]() $Z\setminus 0$ is trivial. A given double cover of
$Z\setminus 0$ is trivial. A given double cover of ![]() $Z\setminus 0$ has, however, many distinct extensions to
$Z\setminus 0$ has, however, many distinct extensions to ![]() $Z$, indexed by functions
$Z$, indexed by functions ![]() $Z\setminus 0\to \mathbb {Z}/2$ modulo those functions which extend continuously to zero.
$Z\setminus 0\to \mathbb {Z}/2$ modulo those functions which extend continuously to zero.
Now suppose given a double cover of ![]() $Z$ together with a connection sieve on it. The restriction of this data to
$Z$ together with a connection sieve on it. The restriction of this data to ![]() $Z\setminus 0$ remembers the extension of the double cover to
$Z\setminus 0$ remembers the extension of the double cover to ![]() $Z$ (use the elements of the connection sieve projecting to open sets of the form
$Z$ (use the elements of the connection sieve projecting to open sets of the form ![]() $Z\cap (0,\varepsilon )$).
$Z\cap (0,\varepsilon )$).
Let ![]() $\tilde {Z}^+_\alpha \to Z^+$ denote the double cover obtained by gluing two copies of
$\tilde {Z}^+_\alpha \to Z^+$ denote the double cover obtained by gluing two copies of ![]() $Z\sqcup Z\to Z$ over
$Z\sqcup Z\to Z$ over ![]() $Z\setminus 0$ via some map
$Z\setminus 0$ via some map ![]() $\alpha :Z\setminus 0\to \mathbb {Z}/2$. If
$\alpha :Z\setminus 0\to \mathbb {Z}/2$. If ![]() $\tilde {Z}^+_\alpha \to Z^+$ is strongly étale, then we can take any connection sieve on it, restrict to the common
$\tilde {Z}^+_\alpha \to Z^+$ is strongly étale, then we can take any connection sieve on it, restrict to the common ![]() $Z\setminus 0\subseteq Z^+$, and deduce that the two extensions of the double cover of
$Z\setminus 0\subseteq Z^+$, and deduce that the two extensions of the double cover of ![]() $Z\setminus 0$ to
$Z\setminus 0$ to ![]() $Z$ coincide, in other words that
$Z$ coincide, in other words that ![]() $\alpha$ extends continuously to zero. Hence, the double cover
$\alpha$ extends continuously to zero. Hence, the double cover ![]() $\tilde {Z}^+_\alpha \to Z^+$ is strongly étale if and only if
$\tilde {Z}^+_\alpha \to Z^+$ is strongly étale if and only if ![]() $\alpha$ extends continuously to zero.
$\alpha$ extends continuously to zero.
Recall that a topological space is called paracompact if and only if every open cover admits a locally finite refinement [Reference DieudonnéDie44]. If ![]() $X$ is paracompact and Hausdorff, then there exists a partition of unity subordinate to any given locally finite open cover
$X$ is paracompact and Hausdorff, then there exists a partition of unity subordinate to any given locally finite open cover ![]() $\{U_i\subseteq X\}_i$, namely functions
$\{U_i\subseteq X\}_i$, namely functions ![]() $f_i:X\to \mathbb {R}_{\geqslant 0}$ with
$f_i:X\to \mathbb {R}_{\geqslant 0}$ with ![]() $\operatorname {supp} f_i\subseteq U_i$ such that
$\operatorname {supp} f_i\subseteq U_i$ such that ![]() $\sum _if_i\equiv 1$ (recall that the support
$\sum _if_i\equiv 1$ (recall that the support ![]() $\operatorname {supp} f$ of a function
$\operatorname {supp} f$ of a function ![]() $f:X\to \mathbb {R}_{\geqslant 0}$ is, by definition, the complement of the largest open set over which
$f:X\to \mathbb {R}_{\geqslant 0}$ is, by definition, the complement of the largest open set over which ![]() $f$ vanishes identically).
$f$ vanishes identically).
Lemma 4.4 If ![]() $Y$ is paracompact Hausdorff, then a map
$Y$ is paracompact Hausdorff, then a map ![]() $X\to Y$ is strongly étale if and only if there exists an open cover
$X\to Y$ is strongly étale if and only if there exists an open cover ![]() $\{U_i\subseteq Y\}_i$ such that each map
$\{U_i\subseteq Y\}_i$ such that each map ![]() $X\times _YU_i\to U_i$ is strongly étale.
$X\times _YU_i\to U_i$ is strongly étale.
Proof. Fix an open cover ![]() $\{U_i\subseteq Y\}_i$ and connection sieves
$\{U_i\subseteq Y\}_i$ and connection sieves ![]() $S_i$ on
$S_i$ on ![]() $X\times _YU_i\to U_i$. As
$X\times _YU_i\to U_i$. As ![]() $Y$ is paracompact, we may assume that our open cover
$Y$ is paracompact, we may assume that our open cover ![]() $\{U_i\subseteq Y\}_i$ is locally finite. Using a partition of unity subordinate to this open cover, we may find another open cover
$\{U_i\subseteq Y\}_i$ is locally finite. Using a partition of unity subordinate to this open cover, we may find another open cover ![]() $\{V_I\subseteq Y\}_I$ indexed by nonempty finite subsets
$\{V_I\subseteq Y\}_I$ indexed by nonempty finite subsets ![]() $I$ of the original index set, such that
$I$ of the original index set, such that ![]() $V_I\subseteq \bigcap _{i\in I}U_i$ and
$V_I\subseteq \bigcap _{i\in I}U_i$ and ![]() $V_I\cap V_J=\varnothing$ unless
$V_I\cap V_J=\varnothing$ unless ![]() $I\subseteq J$ or
$I\subseteq J$ or ![]() $J\subseteq I$ (explicitly, we may take
$J\subseteq I$ (explicitly, we may take ![]() $V_I$ to be the locus where
$V_I$ to be the locus where ![]() $\min _{i\in I}f_i>\max _{i\notin I}f_i$). We may now define a connection sieve on
$\min _{i\in I}f_i>\max _{i\notin I}f_i$). We may now define a connection sieve on ![]() $X\to Y$ as the union over
$X\to Y$ as the union over ![]() $I$ of
$I$ of ![]() $2^{X\times _YV_I}\cap \bigcap _{i\in I}S_i$.
$2^{X\times _YV_I}\cap \bigcap _{i\in I}S_i$.
An orbispace will be called paracompact (respectively, coarsely finite-dimensional, ![]() $d$-dimensional) if and only if its coarse space is.
$d$-dimensional) if and only if its coarse space is.
Proposition 4.5 Every paracompact orbispace ![]() $X$ has an étale atlas
$X$ has an étale atlas ![]() $U\to X$ for which the projections
$U\to X$ for which the projections ![]() $U\times _XU\rightrightarrows U$ are strongly étale. In fact, there exists such
$U\times _XU\rightrightarrows U$ are strongly étale. In fact, there exists such ![]() $U$ of the form
$U$ of the form ![]() $U=\bigsqcup _iV_i$ for an open cover
$U=\bigsqcup _iV_i$ for an open cover ![]() $\{V_i/G_i\subseteq X\}_i$ as in Proposition 3.3.
$\{V_i/G_i\subseteq X\}_i$ as in Proposition 3.3.
Proof. Fix an open cover ![]() $\{V_i/G_i\hookrightarrow X\}_i$ as in Proposition 3.3. As
$\{V_i/G_i\hookrightarrow X\}_i$ as in Proposition 3.3. As ![]() $|X|$ is paracompact, we may shrink the spaces
$|X|$ is paracompact, we may shrink the spaces ![]() $V_i$ (
$V_i$ (![]() $G_i$-equivariantly) so as to ensure that the associated open cover
$G_i$-equivariantly) so as to ensure that the associated open cover ![]() $\{\big |V_i/G_i\big |\subseteq |X|\}_i$ of coarse spaces is locally finite. Choose a partition of unity
$\{\big |V_i/G_i\big |\subseteq |X|\}_i$ of coarse spaces is locally finite. Choose a partition of unity ![]() $\{f_i:|X|\to \mathbb {R}_{\geqslant 0}\}_i$ subordinate to the open cover
$\{f_i:|X|\to \mathbb {R}_{\geqslant 0}\}_i$ subordinate to the open cover ![]() $\{\big |V_i/G_i\big |\subseteq |X|\}_i$. Let
$\{\big |V_i/G_i\big |\subseteq |X|\}_i$. Let ![]() $V_i^0\subseteq V_i$ denote the open subset where
$V_i^0\subseteq V_i$ denote the open subset where ![]() $f_i>0$. We show that the étale atlas
$f_i>0$. We show that the étale atlas ![]() $U:=\bigsqcup _iV_i^0$ has the desired property.
$U:=\bigsqcup _iV_i^0$ has the desired property.
It suffices to show that for any pair of open embeddings ![]() $V/G\hookrightarrow X\hookleftarrow W/H$ and pair of functions
$V/G\hookrightarrow X\hookleftarrow W/H$ and pair of functions ![]() $f_V,f_W:|X|\to \mathbb {R}_{\geqslant 0}$ supported inside
$f_V,f_W:|X|\to \mathbb {R}_{\geqslant 0}$ supported inside ![]() $|V/G|$ and
$|V/G|$ and ![]() $|W/H|$, respectively, the projection
$|W/H|$, respectively, the projection ![]() $W^0\times _XV^0\to V^0$ is strongly étale. We begin by considering the map
$W^0\times _XV^0\to V^0$ is strongly étale. We begin by considering the map ![]() $W\times _XV\to V$, which is a finite covering space over its open image
$W\times _XV\to V$, which is a finite covering space over its open image ![]() $W/H\times _XV\subseteq V$ (by pullback from
$W/H\times _XV\subseteq V$ (by pullback from ![]() $W\to W/H$, which is a finite covering space by descent from its pullback
$W\to W/H$, which is a finite covering space by descent from its pullback ![]() $H\times W\to W$). Thus, every point of
$H\times W\to W$). Thus, every point of ![]() $W/H\times _XV$ has a neighborhood over which
$W/H\times _XV$ has a neighborhood over which ![]() $W\times _XV\to V$ is strongly étale. Even better, because
$W\times _XV\to V$ is strongly étale. Even better, because ![]() $V$ is Hausdorff and
$V$ is Hausdorff and ![]() $G$ is finite, each
$G$ is finite, each ![]() $G$-orbit inside
$G$-orbit inside ![]() $W/H\times _XV$ has a neighborhood over which
$W/H\times _XV$ has a neighborhood over which ![]() $W\times _XV\to V$ is strongly étale. In other words, each point of
$W\times _XV\to V$ is strongly étale. In other words, each point of ![]() $|W/H|\cap |V/G|\subseteq |X|$ has a neighborhood over which
$|W/H|\cap |V/G|\subseteq |X|$ has a neighborhood over which ![]() $W\times _XV\to V$ is strongly étale.
$W\times _XV\to V$ is strongly étale.
Now because ![]() $|X|$ is paracompact, there exists a locally finite open cover of
$|X|$ is paracompact, there exists a locally finite open cover of ![]() $|X|$ by
$|X|$ by ![]() $|X|\setminus (\operatorname {supp} f_V\cup \operatorname {supp} f_W)$ together with open subsets
$|X|\setminus (\operatorname {supp} f_V\cup \operatorname {supp} f_W)$ together with open subsets ![]() $\{A_i\subseteq |W/H|\cap |V/G|\}_i$ over which
$\{A_i\subseteq |W/H|\cap |V/G|\}_i$ over which ![]() $W\times _XV\to V$ is strongly étale. Fix a partition of unity
$W\times _XV\to V$ is strongly étale. Fix a partition of unity ![]() $g:|X|\to \mathbb {R}_{\geqslant 0}$ supported inside
$g:|X|\to \mathbb {R}_{\geqslant 0}$ supported inside ![]() $|X|\setminus (\operatorname {supp} f_V\cup \operatorname {supp} f_W)$ and
$|X|\setminus (\operatorname {supp} f_V\cup \operatorname {supp} f_W)$ and ![]() $\{g_i:|X|\to \mathbb {R}_{\geqslant 0}\}$ supported inside
$\{g_i:|X|\to \mathbb {R}_{\geqslant 0}\}$ supported inside ![]() $A_i$, that is
$A_i$, that is ![]() $g+\sum _ig_i\equiv 1$. Now the patching procedure for connection sieves from the proof of Lemma 4.4 shows that
$g+\sum _ig_i\equiv 1$. Now the patching procedure for connection sieves from the proof of Lemma 4.4 shows that ![]() $W\times _XV\to V$ is strongly étale over the complement of
$W\times _XV\to V$ is strongly étale over the complement of ![]() $\operatorname {supp} g$. In particular, it follows by restriction that
$\operatorname {supp} g$. In particular, it follows by restriction that ![]() $W^0\times _XV^0\to V^0$ is strongly étale.
$W^0\times _XV^0\to V^0$ is strongly étale.
A simplicial complex is a pair ![]() $X=(V,S)$ consisting of a set
$X=(V,S)$ consisting of a set ![]() $V$ (‘vertices’) and a set
$V$ (‘vertices’) and a set ![]() $S\subseteq 2^V\setminus \{\varnothing \}$ (‘simplices’) of finite subsets of
$S\subseteq 2^V\setminus \{\varnothing \}$ (‘simplices’) of finite subsets of ![]() $V$ such that
$V$ such that ![]() $S$ contains all singletons and
$S$ contains all singletons and ![]() $\varnothing \ne A\subseteq B\in S$ implies
$\varnothing \ne A\subseteq B\in S$ implies ![]() $A\in S$. The star
$A\in S$. The star ![]() $\operatorname {st}(X,\sigma )\subseteq X$ of a simplex
$\operatorname {st}(X,\sigma )\subseteq X$ of a simplex ![]() $\sigma$ in a simplicial complex
$\sigma$ in a simplicial complex ![]() $X$ is the subcomplex consisting of all simplices
$X$ is the subcomplex consisting of all simplices ![]() $\tau \subseteq X$ with
$\tau \subseteq X$ with ![]() $\sigma \cup \tau \in S(X)$.
$\sigma \cup \tau \in S(X)$.
A map of simplicial complexes ![]() $X\to Y$ is a map of vertex sets
$X\to Y$ is a map of vertex sets ![]() $V(X)\to V(Y)$ which maps simplices to simplices (the image of an element of
$V(X)\to V(Y)$ which maps simplices to simplices (the image of an element of ![]() $S(X)$ is an element of
$S(X)$ is an element of ![]() $S(Y)$). A map of simplicial complexes is called injective if and only if the map on vertex sets (hence, also the map on simplices) is injective. A map of simplicial complexes
$S(Y)$). A map of simplicial complexes is called injective if and only if the map on vertex sets (hence, also the map on simplices) is injective. A map of simplicial complexes ![]() $f:X\to Y$ is called étale (respectively, locally injective) if and only if the induced maps on stars
$f:X\to Y$ is called étale (respectively, locally injective) if and only if the induced maps on stars ![]() $\operatorname {st}(X,\sigma )\to \operatorname {st}(Y,f(\sigma ))$ are isomorphisms (respectively, injective). We call a map of simplicial complexes
$\operatorname {st}(X,\sigma )\to \operatorname {st}(Y,f(\sigma ))$ are isomorphisms (respectively, injective). We call a map of simplicial complexes ![]() $X\to Y$ sufficiently étale if and only if every simplex
$X\to Y$ sufficiently étale if and only if every simplex ![]() $\sigma \subseteq Y$ (equivalently, every vertex) is the image of a simplex
$\sigma \subseteq Y$ (equivalently, every vertex) is the image of a simplex ![]() $\tau \subseteq X$ at which
$\tau \subseteq X$ at which ![]() $X\to Y$ is étale (this is a useful weakening of the condition of being surjective and étale, which in the context of simplicial complexes is too strong).
$X\to Y$ is étale (this is a useful weakening of the condition of being surjective and étale, which in the context of simplicial complexes is too strong).
The geometric realization ![]() $\|X\|$ of a simplicial complex
$\|X\|$ of a simplicial complex ![]() $X$ is the set of tuples
$X$ is the set of tuples ![]() $t\in \mathbb {R}_{\geqslant 0}^{V(X)}$ with
$t\in \mathbb {R}_{\geqslant 0}^{V(X)}$ with ![]() $\sum _vt_v=1$ such that
$\sum _vt_v=1$ such that ![]() $\{v:t_v>0\}\in S(X)$, topologized by declaring that the realization of the complete simplex on
$\{v:t_v>0\}\in S(X)$, topologized by declaring that the realization of the complete simplex on ![]() $k+1$ vertices has the usual topology and that a realization
$k+1$ vertices has the usual topology and that a realization ![]() $\|X\|$ is given the strongest topology for which (the realization of) every map from a complete simplex to
$\|X\|$ is given the strongest topology for which (the realization of) every map from a complete simplex to ![]() $X$ is continuous. The geometric realization of an étale map of simplicial complexes is an étale map of spaces.
$X$ is continuous. The geometric realization of an étale map of simplicial complexes is an étale map of spaces.
A locally injective simplicial complex groupoid ![]() $M\rightrightarrows O$ consists of simplicial complexes
$M\rightrightarrows O$ consists of simplicial complexes ![]() $O$ and
$O$ and ![]() $M$ together with structure maps satisfying the axioms of a groupoid, where both maps
$M$ together with structure maps satisfying the axioms of a groupoid, where both maps ![]() $M\rightrightarrows O$ are locally injective. Local injectivity of the two maps
$M\rightrightarrows O$ are locally injective. Local injectivity of the two maps ![]() $M\rightrightarrows O$ implies that the natural map
$M\rightrightarrows O$ implies that the natural map ![]() $\big \|M\times _OM\big \|\xrightarrow \sim \|M\|\times _{\|O\|}\|M\|$ is a homeomorphism, and thus the geometric realization
$\big \|M\times _OM\big \|\xrightarrow \sim \|M\|\times _{\|O\|}\|M\|$ is a homeomorphism, and thus the geometric realization ![]() $\|M\|\rightrightarrows \|O\|$ is a topological groupoid. If
$\|M\|\rightrightarrows \|O\|$ is a topological groupoid. If ![]() $\partial O\subseteq O$ denotes the subcomplex consisting of those simplices
$\partial O\subseteq O$ denotes the subcomplex consisting of those simplices ![]() $\sigma \subseteq O$ for which it is not the case that the first projection
$\sigma \subseteq O$ for which it is not the case that the first projection ![]() $M\to O$ is étale at every simplex
$M\to O$ is étale at every simplex ![]() $\tau \subseteq M$ mapped to
$\tau \subseteq M$ mapped to ![]() $\sigma$ under the second projection, then the natural map
$\sigma$ under the second projection, then the natural map ![]() $\|O\|\setminus \|\partial O\|\to [\|M\|\rightrightarrows \|O\|]$ is étale. A locally injective simplicial complex groupoid
$\|O\|\setminus \|\partial O\|\to [\|M\|\rightrightarrows \|O\|]$ is étale. A locally injective simplicial complex groupoid ![]() $M\rightrightarrows O$ is called sufficiently étale if and only if this map is surjective (equivalently, every vertex of
$M\rightrightarrows O$ is called sufficiently étale if and only if this map is surjective (equivalently, every vertex of ![]() $O$ is
$O$ is ![]() $M$-isomorphic to one not in
$M$-isomorphic to one not in ![]() $\partial O$).
$\partial O$).
The abstract simplex category ![]() $\mathsf {Simp}$ has objects finite totally ordered sets and has morphisms weakly order-preserving maps; every object of
$\mathsf {Simp}$ has objects finite totally ordered sets and has morphisms weakly order-preserving maps; every object of ![]() $\mathsf {Simp}$ is isomorphic to
$\mathsf {Simp}$ is isomorphic to ![]() $[n]:=\{0<\cdots < n\}$ for a unique integer
$[n]:=\{0<\cdots < n\}$ for a unique integer ![]() $n\geqslant 0$. A simplicial object in a category
$n\geqslant 0$. A simplicial object in a category ![]() $\mathsf {C}$ is a functor
$\mathsf {C}$ is a functor ![]() $\mathsf {Simp}^\mathsf {op}\to \mathsf {C}$, and the category of simplicial objects in
$\mathsf {Simp}^\mathsf {op}\to \mathsf {C}$, and the category of simplicial objects in ![]() $\mathsf {C}$ is denoted
$\mathsf {C}$ is denoted ![]() $\mathsf {s}\mathsf {C}$. If
$\mathsf {s}\mathsf {C}$. If ![]() $\mathsf {C}$ is complete (respectively, cocomplete), then so is
$\mathsf {C}$ is complete (respectively, cocomplete), then so is ![]() $\mathsf {s}\mathsf {C}$, and limits (respectively, colimits) are calculated pointwise.
$\mathsf {s}\mathsf {C}$, and limits (respectively, colimits) are calculated pointwise.
We consider only simplicial sets (objects of the category ![]() $\mathsf {s}\mathsf {Set}$) and simplicial groupoids (objects of the category
$\mathsf {s}\mathsf {Set}$) and simplicial groupoids (objects of the category ![]() $\mathsf {s}\mathsf {Grpd}$). A simplicial set (or groupoid) will be denoted
$\mathsf {s}\mathsf {Grpd}$). A simplicial set (or groupoid) will be denoted ![]() $X_\bullet$, where
$X_\bullet$, where ![]() $X_n$ is its set (or groupoid) of
$X_n$ is its set (or groupoid) of ![]() $n$-simplices. We denote by
$n$-simplices. We denote by ![]() $\Delta ^n_\bullet \in \mathsf {s}\mathsf {Set}$ the standard
$\Delta ^n_\bullet \in \mathsf {s}\mathsf {Set}$ the standard ![]() $n$-simplex, given by
$n$-simplex, given by ![]() $[m]\mapsto \operatorname {Hom}([m],[n])$. The Yoneda lemma implies that
$[m]\mapsto \operatorname {Hom}([m],[n])$. The Yoneda lemma implies that ![]() $X_n=\operatorname {Hom}(\Delta ^n_\bullet,X_\bullet )$.
$X_n=\operatorname {Hom}(\Delta ^n_\bullet,X_\bullet )$.
A map of simplicial sets ![]() $X_\bullet \to Y_\bullet$ is called injective if and only if it is so levelwise (i.e. every
$X_\bullet \to Y_\bullet$ is called injective if and only if it is so levelwise (i.e. every ![]() $X_n\to Y_n$ is injective). A map
$X_n\to Y_n$ is injective). A map ![]() $X_\bullet \to Y_\bullet$ is called étale (respectively, locally injective) if and only if for every map
$X_\bullet \to Y_\bullet$ is called étale (respectively, locally injective) if and only if for every map ![]() $[n]\to [m]$ in
$[n]\to [m]$ in ![]() $\mathsf {Simp}$, the induced map
$\mathsf {Simp}$, the induced map ![]() $X_m\xrightarrow \sim Y_m\times _{Y_n}X_n$ is a bijection (respectively, injective) (it is equivalent to impose this condition only for
$X_m\xrightarrow \sim Y_m\times _{Y_n}X_n$ is a bijection (respectively, injective) (it is equivalent to impose this condition only for ![]() $n=0$). A map
$n=0$). A map ![]() $X_\bullet \to Y_\bullet$ is called étale (respectively, locally injective) at a given
$X_\bullet \to Y_\bullet$ is called étale (respectively, locally injective) at a given ![]() $n$-simplex
$n$-simplex ![]() $\sigma$ of
$\sigma$ of ![]() $X_\bullet$ if and only if
$X_\bullet$ if and only if ![]() $X_m\xrightarrow \sim Y_m\times _{Y_n}\{\sigma \}$ is a bijection (respectively, injective) (this condition at a given
$X_m\xrightarrow \sim Y_m\times _{Y_n}\{\sigma \}$ is a bijection (respectively, injective) (this condition at a given ![]() $\sigma$ implies the same at any preimage of
$\sigma$ implies the same at any preimage of ![]() $\sigma$ under any structure map of
$\sigma$ under any structure map of ![]() $X_\bullet$). A map
$X_\bullet$). A map ![]() $X_\bullet \to Y_\bullet$ is called sufficiently étale if and only if the
$X_\bullet \to Y_\bullet$ is called sufficiently étale if and only if the ![]() $n$-simplices of
$n$-simplices of ![]() $X_\bullet$ at which the map is étale surject onto the
$X_\bullet$ at which the map is étale surject onto the ![]() $n$-simplices of
$n$-simplices of ![]() $Y_\bullet$ (it is equivalent to impose this condition only for
$Y_\bullet$ (it is equivalent to impose this condition only for ![]() $n=0$). These notions generalize to maps of simplicial groupoids by replacing ‘injectivity’ and ‘surjectivity’ for maps of sets with ‘full faithfulness’ and ‘essential surjectivity’ for functors of groupoids. These properties are all preserved under pullback and closed under composition.
$n=0$). These notions generalize to maps of simplicial groupoids by replacing ‘injectivity’ and ‘surjectivity’ for maps of sets with ‘full faithfulness’ and ‘essential surjectivity’ for functors of groupoids. These properties are all preserved under pullback and closed under composition.
The geometric realization ![]() $\|X_\bullet \|$ of a simplicial set
$\|X_\bullet \|$ of a simplicial set ![]() $X_\bullet$ is the colimit of
$X_\bullet$ is the colimit of ![]() $\Delta ^n$ over all maps
$\Delta ^n$ over all maps ![]() $\Delta ^n_\bullet \to X_\bullet$. Geometric realization is cocontinuous, and the natural map
$\Delta ^n_\bullet \to X_\bullet$. Geometric realization is cocontinuous, and the natural map ![]() $\|\lim _\alpha (X_\bullet )_\alpha \|\to \lim _\alpha \|(X_\bullet )_\alpha \|$ is bijective, however it need not be a homeomorphism even for finite limits (for example, the case of binary products is discussed in [Reference MayMay67, Theorem 14.3, Remark 14.4] and [Reference WhiteheadWhi49, Reference MilnorMil56, Reference Brooke-TaylorBT17]). The map
$\|\lim _\alpha (X_\bullet )_\alpha \|\to \lim _\alpha \|(X_\bullet )_\alpha \|$ is bijective, however it need not be a homeomorphism even for finite limits (for example, the case of binary products is discussed in [Reference MayMay67, Theorem 14.3, Remark 14.4] and [Reference WhiteheadWhi49, Reference MilnorMil56, Reference Brooke-TaylorBT17]). The map ![]() $\|X_\bullet \times _{Y_\bullet }Z_\bullet \|\to \|X_\bullet \| \times _{\|Y_\bullet \|}\|Z_\bullet \|$ is a homeomorphism if at least one of the maps
$\|X_\bullet \times _{Y_\bullet }Z_\bullet \|\to \|X_\bullet \| \times _{\|Y_\bullet \|}\|Z_\bullet \|$ is a homeomorphism if at least one of the maps ![]() $X_\bullet \to Y_\bullet$ and
$X_\bullet \to Y_\bullet$ and ![]() $Z_\bullet \to Y_\bullet$ is locally injective. Thus, a locally injective simplicial set groupoid
$Z_\bullet \to Y_\bullet$ is locally injective. Thus, a locally injective simplicial set groupoid ![]() $M_\bullet \rightrightarrows O_\bullet$ determines a topological groupoid
$M_\bullet \rightrightarrows O_\bullet$ determines a topological groupoid ![]() $\|M_\bullet \|\rightrightarrows \|O_\bullet \|$.
$\|M_\bullet \|\rightrightarrows \|O_\bullet \|$.
Let us now introduce the geometric realization ![]() $\|X_\bullet \|$ of any simplicial groupoid
$\|X_\bullet \|$ of any simplicial groupoid ![]() $X_\bullet$ which is étale, meaning that it admits a locally injective sufficiently étale map
$X_\bullet$ which is étale, meaning that it admits a locally injective sufficiently étale map ![]() $U_\bullet \to X_\bullet$ from a simplicial set
$U_\bullet \to X_\bullet$ from a simplicial set ![]() $U_\bullet$. For any simplicial groupoid
$U_\bullet$. For any simplicial groupoid ![]() $X_\bullet$ and any locally injective map
$X_\bullet$ and any locally injective map ![]() $U_\bullet \to X_\bullet$, the pair of simplicial sets
$U_\bullet \to X_\bullet$, the pair of simplicial sets ![]() $U_\bullet \times _{X_\bullet }U_\bullet \rightrightarrows U_\bullet$ forms a locally injective simplicial set groupoid, whose geometric realization
$U_\bullet \times _{X_\bullet }U_\bullet \rightrightarrows U_\bullet$ forms a locally injective simplicial set groupoid, whose geometric realization ![]() $\|U_\bullet \times _{X_\bullet }U_\bullet \|\rightrightarrows \|U_\bullet \|$ thus defines a topological stack. The geometric realization of
$\|U_\bullet \times _{X_\bullet }U_\bullet \|\rightrightarrows \|U_\bullet \|$ thus defines a topological stack. The geometric realization of ![]() $X_\bullet$ is defined as this topological stack
$X_\bullet$ is defined as this topological stack ![]() $[\|U_\bullet \times _{X_\bullet }U_\bullet \|\rightrightarrows \|U_\bullet \|]$ associated to any locally injective sufficiently étale map
$[\|U_\bullet \times _{X_\bullet }U_\bullet \|\rightrightarrows \|U_\bullet \|]$ associated to any locally injective sufficiently étale map ![]() $U_\bullet \to X_\bullet$.
$U_\bullet \to X_\bullet$.
Lemma 4.6 The geometric realization of an étale simplicial groupoid ![]() $X_\bullet$ is well defined.
$X_\bullet$ is well defined.
Proof. Let ![]() $U_\bullet,U'_\bullet \to X_\bullet$ be locally injective and sufficiently étale. Let
$U_\bullet,U'_\bullet \to X_\bullet$ be locally injective and sufficiently étale. Let ![]() $U''_\bullet :=U_\bullet \times _{X_\bullet }U_\bullet '\to X_\bullet$, and consider the map of simplicial set groupoids
$U''_\bullet :=U_\bullet \times _{X_\bullet }U_\bullet '\to X_\bullet$, and consider the map of simplicial set groupoids ![]() $(U''_\bullet \times _{X_\bullet }U''_\bullet \rightrightarrows U''_\bullet )\to (U_\bullet \times _{X_\bullet }U_\bullet \rightrightarrows U_\bullet )$. As
$(U''_\bullet \times _{X_\bullet }U''_\bullet \rightrightarrows U''_\bullet )\to (U_\bullet \times _{X_\bullet }U_\bullet \rightrightarrows U_\bullet )$. As ![]() $U''_\bullet \to U_\bullet$ is locally injective and sufficiently étale, it follows that this map induces an isomorphism of topological stacks, and the same applies to
$U''_\bullet \to U_\bullet$ is locally injective and sufficiently étale, it follows that this map induces an isomorphism of topological stacks, and the same applies to ![]() $U'_\bullet$ in place of
$U'_\bullet$ in place of ![]() $U_\bullet$.
$U_\bullet$.
Lemma 4.7 The geometric realization ![]() $\|X_\bullet \|$ of an étale simplicial groupoid
$\|X_\bullet \|$ of an étale simplicial groupoid ![]() $X_\bullet$ with finite isotropy is an orbispace.
$X_\bullet$ with finite isotropy is an orbispace.
Proof. All geometric realizations are Hausdorff, so ![]() $\|U_\bullet \times _{X_\bullet }U_\bullet \|\to \|U_\bullet \|\times \|U_\bullet \|$ is separated, hence
$\|U_\bullet \times _{X_\bullet }U_\bullet \|\to \|U_\bullet \|\times \|U_\bullet \|$ is separated, hence ![]() $\|X_\bullet \|$ has separated diagonal. As
$\|X_\bullet \|$ has separated diagonal. As ![]() $X_\bullet$ has finite isotropy, the map
$X_\bullet$ has finite isotropy, the map ![]() $U_\bullet \times _{X_\bullet }U_\bullet \to U_\bullet \times U_\bullet$ has finite fibers, which combined with local injectivity of
$U_\bullet \times _{X_\bullet }U_\bullet \to U_\bullet \times U_\bullet$ has finite fibers, which combined with local injectivity of ![]() $U_\bullet \times _{X_\bullet }U_\bullet \rightrightarrows U_\bullet$ implies that
$U_\bullet \times _{X_\bullet }U_\bullet \rightrightarrows U_\bullet$ implies that ![]() $\|U_\bullet \times _{X_\bullet }U_\bullet \|\to \|U_\bullet \|\times \|U_\bullet \|$ is universally closed, hence
$\|U_\bullet \times _{X_\bullet }U_\bullet \|\to \|U_\bullet \|\times \|U_\bullet \|$ is universally closed, hence ![]() $\|X_\bullet \|$ has universally closed diagonal. We have thus shown that
$\|X_\bullet \|$ has universally closed diagonal. We have thus shown that ![]() $\|X_\bullet \|$ has proper diagonal.
$\|X_\bullet \|$ has proper diagonal.
To construct an étale atlas for ![]() $\|X_\bullet \|$, let
$\|X_\bullet \|$, let ![]() $\partial U_\bullet \subseteq U_\bullet$ denote the simplicial subset consisting of those simplices of
$\partial U_\bullet \subseteq U_\bullet$ denote the simplicial subset consisting of those simplices of ![]() $U_\bullet$ at which
$U_\bullet$ at which ![]() $U_\bullet \to X_\bullet$ is not étale. Then
$U_\bullet \to X_\bullet$ is not étale. Then ![]() $\|U_\bullet \|\setminus \|\partial U_\bullet \|\to \|X_\bullet \|$ is étale. To see that it is surjective, it suffices to show that
$\|U_\bullet \|\setminus \|\partial U_\bullet \|\to \|X_\bullet \|$ is étale. To see that it is surjective, it suffices to show that ![]() $\|U_\bullet \times _{X_\bullet }U_\bullet \|\setminus \|U_\bullet \times _{X_\bullet }\partial U_\bullet \|\to \|U_\bullet \|$ is surjective (note that surjectivity descends under surjective maps such as
$\|U_\bullet \times _{X_\bullet }U_\bullet \|\setminus \|U_\bullet \times _{X_\bullet }\partial U_\bullet \|\to \|U_\bullet \|$ is surjective (note that surjectivity descends under surjective maps such as ![]() $\|U_\bullet \|\to \|X_\bullet \|$), and this follows because
$\|U_\bullet \|\to \|X_\bullet \|$), and this follows because ![]() $U_\bullet \to X_\bullet$ is sufficiently étale.
$U_\bullet \to X_\bullet$ is sufficiently étale.
A simplicial complex ![]() $X$ gives rise to a simplicial set
$X$ gives rise to a simplicial set ![]() $b_\bullet X$ (its barycentric subdivision) whose
$b_\bullet X$ (its barycentric subdivision) whose ![]() $n$-simplices are chains of simplices
$n$-simplices are chains of simplices ![]() $\sigma _0\subseteq \cdots \subseteq \sigma _n\subseteq X$ (in other words,
$\sigma _0\subseteq \cdots \subseteq \sigma _n\subseteq X$ (in other words, ![]() $b_\bullet X$ is the nerve of
$b_\bullet X$ is the nerve of ![]() $S(X)$). Barycentric subdivision preserves injectivity, local injectivity, étale, and sufficiently étale. There is a natural identification of geometric realizations
$S(X)$). Barycentric subdivision preserves injectivity, local injectivity, étale, and sufficiently étale. There is a natural identification of geometric realizations ![]() $\|X\|=\|b_\bullet X\|$. Moreover, for a locally injective sufficiently étale simplicial complex groupoid
$\|X\|=\|b_\bullet X\|$. Moreover, for a locally injective sufficiently étale simplicial complex groupoid ![]() $M\rightrightarrows O$, there is a natural identification
$M\rightrightarrows O$, there is a natural identification ![]() $[\|M\|\rightrightarrows \|O\|]=\|[b_\bullet M\rightrightarrows b_\bullet O]\|$ (the simplicial groupoid
$[\|M\|\rightrightarrows \|O\|]=\|[b_\bullet M\rightrightarrows b_\bullet O]\|$ (the simplicial groupoid ![]() $[b_\bullet M\rightrightarrows b_\bullet O]$ is étale because
$[b_\bullet M\rightrightarrows b_\bullet O]$ is étale because ![]() $M\rightrightarrows O$ is sufficiently étale).
$M\rightrightarrows O$ is sufficiently étale).
A simplicial complex of groups ![]() $(Z,G)$ also admits a barycentric subdivision
$(Z,G)$ also admits a barycentric subdivision ![]() $b_\bullet (Z,G)$ which is a simplicial groupoid. In fact, we define
$b_\bullet (Z,G)$ which is a simplicial groupoid. In fact, we define ![]() $b_\bullet (Z,G)$ for any simplicial complex
$b_\bullet (Z,G)$ for any simplicial complex ![]() $Z$ equipped with a functor
$Z$ equipped with a functor ![]() $G:S(Z)^\mathsf {op}\to \mathsf {Grpd}$ from the face poset to groupoids (a simplicial complex of groups
$G:S(Z)^\mathsf {op}\to \mathsf {Grpd}$ from the face poset to groupoids (a simplicial complex of groups ![]() $(Z,G)$ determines such a functor which sends
$(Z,G)$ determines such a functor which sends ![]() $\sigma$ to
$\sigma$ to ![]() $\mathbb {B} G_\sigma$). The groupoid of
$\mathbb {B} G_\sigma$). The groupoid of ![]() $n$-simplices in the barycentric subdivision
$n$-simplices in the barycentric subdivision ![]() $b_\bullet (Z,G)$ is now defined as the groupoid of functors from the category
$b_\bullet (Z,G)$ is now defined as the groupoid of functors from the category ![]() $0\to \cdots \to n$ to the category whose objects are pairs
$0\to \cdots \to n$ to the category whose objects are pairs ![]() $\sigma \in S(Z)$ and
$\sigma \in S(Z)$ and ![]() $o\in G_\sigma$ and whose morphisms are inclusions
$o\in G_\sigma$ and whose morphisms are inclusions ![]() $\sigma _1\subseteq \sigma _2$ covered by maps
$\sigma _1\subseteq \sigma _2$ covered by maps ![]() $o_1\to o_2|_{\sigma _1}$. The barycentric subdivision of a simplicial complex of groups is étale, as can be seen as follows. For any
$o_1\to o_2|_{\sigma _1}$. The barycentric subdivision of a simplicial complex of groups is étale, as can be seen as follows. For any ![]() $\sigma \subseteq Z$ and
$\sigma \subseteq Z$ and ![]() $o\in G_\sigma$, we consider the functor
$o\in G_\sigma$, we consider the functor ![]() $S(\operatorname {st}(Z,\sigma ))^\mathsf {op}\to \mathsf {Grpd}$ given by
$S(\operatorname {st}(Z,\sigma ))^\mathsf {op}\to \mathsf {Grpd}$ given by ![]() $\tau \mapsto G_{\sigma \cup \tau }\times _{G_\sigma }\{o\}$. Applying the nerve construction from just above to this functor, we obtain a simplicial set mapping to
$\tau \mapsto G_{\sigma \cup \tau }\times _{G_\sigma }\{o\}$. Applying the nerve construction from just above to this functor, we obtain a simplicial set mapping to ![]() $b_\bullet (Z,G)$, which is the required locally injective map which is étale over
$b_\bullet (Z,G)$, which is the required locally injective map which is étale over ![]() $(\sigma,o)\in b_0(Z,G)$. An essentially equivalent discussion (albeit without barycentrically subdividing) appears in [Reference Bridson and HaefligerBH99, 12.24–12.25]. As
$(\sigma,o)\in b_0(Z,G)$. An essentially equivalent discussion (albeit without barycentrically subdividing) appears in [Reference Bridson and HaefligerBH99, 12.24–12.25]. As ![]() $b_\bullet (Z,G)$ is étale, it has a geometric realization
$b_\bullet (Z,G)$ is étale, it has a geometric realization ![]() $\|b_\bullet (Z,G)\|$ which we also write as
$\|b_\bullet (Z,G)\|$ which we also write as ![]() $\|(Z,G)\|$. When
$\|(Z,G)\|$. When ![]() $G$ are finite groups (or, more generally, groupoids with finite isotropy), then the geometric realization
$G$ are finite groups (or, more generally, groupoids with finite isotropy), then the geometric realization ![]() $\|(Z,G)\|$ is an orbispace by Lemma 4.7, and this is what we have been calling the orbispace presented by the simplicial complex of finite groups
$\|(Z,G)\|$ is an orbispace by Lemma 4.7, and this is what we have been calling the orbispace presented by the simplicial complex of finite groups ![]() $(Z,G)$.
$(Z,G)$.
Lemma 4.8 Let ![]() $M\rightrightarrows O$ be a locally injective simplicial complex groupoid with the following properties.
$M\rightrightarrows O$ be a locally injective simplicial complex groupoid with the following properties.
• The vertices of every simplex of
 $O$ are pairwise non-isomorphic via
$O$ are pairwise non-isomorphic via  $M$.
$M$.• If simplices
 $\sigma$ and
$\sigma$ and  $\sigma '$ of
$\sigma '$ of  $O$ have vertex sets which are isomorphic via
$O$ have vertex sets which are isomorphic via  $M$, then
$M$, then  $\sigma$ and
$\sigma$ and  $\sigma '$ are themselves isomorphic via
$\sigma '$ are themselves isomorphic via  $M$.
$M$.
Then there is a simplicial complex of groups giving rise to the same simplicial groupoid as ![]() $M\rightrightarrows O$.
$M\rightrightarrows O$.
Proof. The hypotheses imply that there is a simplicial complex ![]() $Z$ whose vertices are the isomorphism classes in the vertex groupoid
$Z$ whose vertices are the isomorphism classes in the vertex groupoid ![]() $V(M)\rightrightarrows O(M)$, and whose simplices are the
$V(M)\rightrightarrows O(M)$, and whose simplices are the ![]() $M$-isomorphism classes of simplices of
$M$-isomorphism classes of simplices of ![]() $O$. Now
$O$. Now ![]() $M\rightrightarrows O$ defines a functor
$M\rightrightarrows O$ defines a functor ![]() $G:S(Z)^\mathsf {op}\to \mathsf {Grpd}$, and there is a natural isomorphism between
$G:S(Z)^\mathsf {op}\to \mathsf {Grpd}$, and there is a natural isomorphism between ![]() $b_\bullet (Z,G)$ and the simplicial groupoid
$b_\bullet (Z,G)$ and the simplicial groupoid ![]() $[b_\bullet M\rightrightarrows b_\bullet O]$. By definition, all the groupoids
$[b_\bullet M\rightrightarrows b_\bullet O]$. By definition, all the groupoids ![]() $G_\sigma$ have a single isomorphism class, and all the functors
$G_\sigma$ have a single isomorphism class, and all the functors ![]() $G_\tau \to G_\sigma$ are faithful (this follows from local injectivity of
$G_\tau \to G_\sigma$ are faithful (this follows from local injectivity of ![]() $M\rightrightarrows O$). Choosing (independently) a base object of each
$M\rightrightarrows O$). Choosing (independently) a base object of each ![]() $G_\sigma$ shows
$G_\sigma$ shows ![]() $(Z,G)$ comes from a simplicial complex of groups.
$(Z,G)$ comes from a simplicial complex of groups.
The nerve ![]() $N(X,\{U_i\}_i)$ of a collection of open sets
$N(X,\{U_i\}_i)$ of a collection of open sets ![]() $\{U_i\subseteq X\}_i$ is the simplicial complex whose vertices
$\{U_i\subseteq X\}_i$ is the simplicial complex whose vertices ![]() $V$ are the indices
$V$ are the indices ![]() $i$ with
$i$ with ![]() $U_i\ne \varnothing$, and in which a collection
$U_i\ne \varnothing$, and in which a collection ![]() $I$ of indices spans a simplex (i.e.
$I$ of indices spans a simplex (i.e. ![]() $I\in S$) if and only if
$I\in S$) if and only if ![]() $\bigcap _{i\in I}U_i\ne \varnothing$. A partition of unity
$\bigcap _{i\in I}U_i\ne \varnothing$. A partition of unity ![]() $\{f_i:X\to \mathbb {R}_{\geqslant 0}\}_i$ subordinate to a locally finite open cover
$\{f_i:X\to \mathbb {R}_{\geqslant 0}\}_i$ subordinate to a locally finite open cover ![]() $\{U_i\subseteq X\}_i$ defines a map from
$\{U_i\subseteq X\}_i$ defines a map from ![]() $X$ to the geometric realization
$X$ to the geometric realization ![]() $\|N(X,\{U_i\}_i)\|$ of the nerve of the open cover.
$\|N(X,\{U_i\}_i)\|$ of the nerve of the open cover.
Proposition 4.9 For any paracompact orbispace ![]() $X$, there exists a simplicial complex of groups
$X$, there exists a simplicial complex of groups ![]() $(Z,G)$ and a map
$(Z,G)$ and a map ![]() $X\to \|(Z,G)\|$ which is injective on isotropy groups. Moreover, we may take
$X\to \|(Z,G)\|$ which is injective on isotropy groups. Moreover, we may take ![]() $Z$ to be locally finite, and we may take the groups
$Z$ to be locally finite, and we may take the groups ![]() $G_z$ for vertices
$G_z$ for vertices ![]() $z\in Z$ to be isotropy groups of points of
$z\in Z$ to be isotropy groups of points of ![]() $X$. If
$X$. If ![]() $X$ is coarsely finite-dimensional (respectively,
$X$ is coarsely finite-dimensional (respectively, ![]() $d$-dimensional), then
$d$-dimensional), then ![]() $Z$ may be taken to be finite-dimensional (respectively,
$Z$ may be taken to be finite-dimensional (respectively, ![]() $d$-dimensional).
$d$-dimensional).
Proof. We begin with an open cover ![]() $\{V_i/G_i\subseteq X\}_i$ with the properties guaranteed by Proposition 4.5, and we set
$\{V_i/G_i\subseteq X\}_i$ with the properties guaranteed by Proposition 4.5, and we set ![]() $U:=\bigsqcup _iV_i$. As
$U:=\bigsqcup _iV_i$. As ![]() $|X|$ is paracompact, by
$|X|$ is paracompact, by ![]() $G_i$-equivariantly shrinking the spaces
$G_i$-equivariantly shrinking the spaces ![]() $V_i$, we may assume that the associated open cover
$V_i$, we may assume that the associated open cover ![]() $\{|V_i/G_i|\subseteq |X|\}_i$ of coarse spaces is locally finite. We fix a covering sieve
$\{|V_i/G_i|\subseteq |X|\}_i$ of coarse spaces is locally finite. We fix a covering sieve ![]() $S$ on
$S$ on ![]() $U\times _XU$ which is invariant under the ‘exchange’ (i.e. ‘inverse’) involution of
$U\times _XU$ which is invariant under the ‘exchange’ (i.e. ‘inverse’) involution of ![]() $U\times _XU$ and is a connection sieve for both projections
$U\times _XU$ and is a connection sieve for both projections ![]() $U\times _XU\rightrightarrows U$. We also fix a partition of unity
$U\times _XU\rightrightarrows U$. We also fix a partition of unity ![]() $\{f_i:|X|\to \mathbb {R}_{\geqslant 0}\}_i$ subordinate to the open cover
$\{f_i:|X|\to \mathbb {R}_{\geqslant 0}\}_i$ subordinate to the open cover ![]() $\{|V_i/G_i|\subseteq |X|\}_i$.
$\{|V_i/G_i|\subseteq |X|\}_i$.
Denote by ![]() $o(x)\subseteq U$ and
$o(x)\subseteq U$ and ![]() $o_i(x)\subseteq V_i$ the fibers over
$o_i(x)\subseteq V_i$ the fibers over ![]() $x\in |X|$, so
$x\in |X|$, so ![]() $o(x)=\bigsqcup _io_i(x)$; similarly define
$o(x)=\bigsqcup _io_i(x)$; similarly define ![]() $m(x)\subseteq U\times _XU$ and
$m(x)\subseteq U\times _XU$ and ![]() $m_{ij}(x)\subseteq V_i\times _XV_j$ with
$m_{ij}(x)\subseteq V_i\times _XV_j$ with ![]() $m(x)=\bigsqcup _{i,j}m_{ij}(x)$. These sets are finite because the
$m(x)=\bigsqcup _{i,j}m_{ij}(x)$. These sets are finite because the ![]() $G_i$ are finite and
$G_i$ are finite and ![]() $\{|V_i/G_i|\subseteq |X|\}_i$ is locally finite. Furthermore, they have the discrete topology, because
$\{|V_i/G_i|\subseteq |X|\}_i$ is locally finite. Furthermore, they have the discrete topology, because ![]() $U$ is Hausdorff and
$U$ is Hausdorff and ![]() $U\times _XU$ is Hausdorff (because
$U\times _XU$ is Hausdorff (because ![]() $U$ is Hausdorff and
$U$ is Hausdorff and ![]() $X\to X\times X$ is separated).
$X\to X\times X$ is separated).
The Hausdorff property implies that the inclusions ![]() $o_i(x)\subseteq V_i$ and
$o_i(x)\subseteq V_i$ and ![]() $m_{ij}(x)\subseteq V_i\times _XV_j$ admit retractions defined in some open neighborhood. Now the inverse images of small open neighborhoods
$m_{ij}(x)\subseteq V_i\times _XV_j$ admit retractions defined in some open neighborhood. Now the inverse images of small open neighborhoods ![]() $x\in |Z_x|\subseteq |X|$ (i.e. open substacks
$x\in |Z_x|\subseteq |X|$ (i.e. open substacks ![]() $Z_x\subseteq X$) form a basis of neighborhoods of
$Z_x\subseteq X$) form a basis of neighborhoods of ![]() $o_i(x)$ and
$o_i(x)$ and ![]() $m_{ij}(x)$, so for sufficiently small
$m_{ij}(x)$, so for sufficiently small ![]() $Z_x$, these inverse images are naturally disjoint unions
$Z_x$, these inverse images are naturally disjoint unions ![]() $U_x=\bigsqcup _{o\in o(x)}U_o$ and
$U_x=\bigsqcup _{o\in o(x)}U_o$ and ![]() $U_x\times _XU_x=\bigsqcup _{m\in m(x)}U_m$. Note that this applies only inside
$U_x\times _XU_x=\bigsqcup _{m\in m(x)}U_m$. Note that this applies only inside ![]() $V_i$ and
$V_i$ and ![]() $V_i\times _XV_j$ for which
$V_i\times _XV_j$ for which ![]() $o_i(x)$ and
$o_i(x)$ and ![]() $m_{ij}(x)$ are nonempty: the full inverse image of
$m_{ij}(x)$ are nonempty: the full inverse image of ![]() $Z_x$ inside
$Z_x$ inside ![]() $U$ may intersect other
$U$ may intersect other ![]() $V_i$ nontrivially. By shrinking
$V_i$ nontrivially. By shrinking ![]() $Z_x$ further, we may ensure that the retraction
$Z_x$ further, we may ensure that the retraction ![]() $(U_x\times _XU_x\rightrightarrows U_x)\to (m(x)\rightrightarrows o(x))$ is a map of groupoids. For later purposes, let us also take
$(U_x\times _XU_x\rightrightarrows U_x)\to (m(x)\rightrightarrows o(x))$ is a map of groupoids. For later purposes, let us also take ![]() $Z_x$ small enough so that:
$Z_x$ small enough so that:
• if
 $x\in |V_i/G_i|$, then
$x\in |V_i/G_i|$, then  $|Z_x|\subseteq |V_i/G_i|$;
$|Z_x|\subseteq |V_i/G_i|$;• if
 $x\notin \operatorname {supp} f_i$, then
$x\notin \operatorname {supp} f_i$, then  $|Z_x|\cap \operatorname {supp} f_i=\varnothing$;
$|Z_x|\cap \operatorname {supp} f_i=\varnothing$;• if
 $f_i(x)>0$, then
$f_i(x)>0$, then  $f_i>0$ over all of
$f_i>0$ over all of  $|Z_x|$.
$|Z_x|$.
Each of these conditions can be ensured on its own, and because the open cover ![]() $\{|V_i/G_i|\subseteq |X|\}_i$ is locally finite, we can ensure all at once.
$\{|V_i/G_i|\subseteq |X|\}_i$ is locally finite, we can ensure all at once.
We also shrink ![]() $Z_x$ so as to ensure that each
$Z_x$ so as to ensure that each ![]() $U_m\in S$ (our chosen connection sieve), which has the following implication: given
$U_m\in S$ (our chosen connection sieve), which has the following implication: given ![]() $o,o'\in U$ with
$o,o'\in U$ with ![]() $U_o\cap U_{o'}\ne \varnothing$, the relation
$U_o\cap U_{o'}\ne \varnothing$, the relation ![]() $U_m\cap U_{m'}\ne \varnothing$ is a partial bijection between lifts
$U_m\cap U_{m'}\ne \varnothing$ is a partial bijection between lifts ![]() $m,m'\in U\times _XU$ of
$m,m'\in U\times _XU$ of ![]() $o$ and
$o$ and ![]() $o'$. Furthermore, the domain of this bijection is as large as possible: for
$o'$. Furthermore, the domain of this bijection is as large as possible: for ![]() $U_o\cap U_{o'}\ne \varnothing$ (so
$U_o\cap U_{o'}\ne \varnothing$ (so ![]() $o\in o_i(x)$ and
$o\in o_i(x)$ and ![]() $o'\in o_i(x')$ for some
$o'\in o_i(x')$ for some ![]() $i$) with
$i$) with ![]() $x,x'\in |V_j/G_j|$, we get a full bijection between the inverse images of
$x,x'\in |V_j/G_j|$, we get a full bijection between the inverse images of ![]() $o$ and
$o$ and ![]() $o'$ inside
$o'$ inside ![]() $m_{ij}(x)$ and
$m_{ij}(x)$ and ![]() $m_{ij}(x')$ (this follows because the projection
$m_{ij}(x')$ (this follows because the projection ![]() $V_i\times _XV_j\to V_i$ is a finite covering space of degree
$V_i\times _XV_j\to V_i$ is a finite covering space of degree ![]() $|G_j|$ over
$|G_j|$ over ![]() $U_o\cup U_{o'}$).
$U_o\cup U_{o'}$).
We now consider the nerves ![]() $N(U,\{U_o\}_{o\in U})$ and
$N(U,\{U_o\}_{o\in U})$ and ![]() $N(U\times _XU,\{U_m\}_{m\in U\times _XU})$. Note that for simplices in these nerves, namely subsets
$N(U\times _XU,\{U_m\}_{m\in U\times _XU})$. Note that for simplices in these nerves, namely subsets ![]() $O\subseteq U$ or
$O\subseteq U$ or ![]() $M\subseteq U\times _XU$ with
$M\subseteq U\times _XU$ with ![]() $\bigcap _{o\in O}U_o\ne \varnothing$ or
$\bigcap _{o\in O}U_o\ne \varnothing$ or ![]() $\bigcap _{m\in M}U_m\ne \varnothing$, the maps
$\bigcap _{m\in M}U_m\ne \varnothing$, the maps ![]() $O\to |X|$ or
$O\to |X|$ or ![]() $M\to |X|$ are injective. The natural maps on index sets
$M\to |X|$ are injective. The natural maps on index sets ![]() $U\times _XU\rightrightarrows U$ determine maps of nerves
$U\times _XU\rightrightarrows U$ determine maps of nerves
These maps are locally injective; indeed, local injectivity means that for every ![]() $o,o'\in U$ with
$o,o'\in U$ with ![]() $U_o\cap U_{o'}\ne \varnothing$ and every
$U_o\cap U_{o'}\ne \varnothing$ and every ![]() $m\in U\times _XU$ projecting to
$m\in U\times _XU$ projecting to ![]() $o$, there is at most one lift
$o$, there is at most one lift ![]() $m'\in U\times _XU$ of
$m'\in U\times _XU$ of ![]() $o'$ with
$o'$ with ![]() $U_m\cap U_{m'}\ne \varnothing$, and this is a direct consequence of our assumption that every
$U_m\cap U_{m'}\ne \varnothing$, and this is a direct consequence of our assumption that every ![]() $U_m\in S$. Let us now argue that there is a natural composition map
$U_m\in S$. Let us now argue that there is a natural composition map
More precisely, we claim that for nonempty finite subsets ![]() $M\subseteq U\times _XU$ with
$M\subseteq U\times _XU$ with ![]() $\bigcap _{m\in M}U_m\ne \varnothing$ and
$\bigcap _{m\in M}U_m\ne \varnothing$ and ![]() $M'\subseteq U\times _XU$ with
$M'\subseteq U\times _XU$ with ![]() $\bigcap _{m\in M'}U_m\ne \varnothing$ projecting to
$\bigcap _{m\in M'}U_m\ne \varnothing$ projecting to ![]() $O\subseteq U$ (under the first and second projections, respectively), the subset
$O\subseteq U$ (under the first and second projections, respectively), the subset ![]() $M''\subseteq U\times _XU$ defined by applying the composition map
$M''\subseteq U\times _XU$ defined by applying the composition map ![]() $(U\times _XU)\times _U(U\times _XU)\to U\times _XU$ to
$(U\times _XU)\times _U(U\times _XU)\to U\times _XU$ to ![]() $M$ and
$M$ and ![]() $M'$ also satisfies
$M'$ also satisfies ![]() $\bigcap _{m\in M''}U_m\ne \varnothing$. This claim follows from the property that every
$\bigcap _{m\in M''}U_m\ne \varnothing$. This claim follows from the property that every ![]() $U_m\in S$ (indeed, this property implies that
$U_m\in S$ (indeed, this property implies that ![]() $\bigcap _{m\in M}U_m\xrightarrow \sim \bigcap _{o\in O}U_o\xleftarrow \sim \bigcap _{m\in M'}U_m$). We have thus defined a locally injective simplicial complex groupoid
$\bigcap _{m\in M}U_m\xrightarrow \sim \bigcap _{o\in O}U_o\xleftarrow \sim \bigcap _{m\in M'}U_m$). We have thus defined a locally injective simplicial complex groupoid
We now show that this locally injective simplicial complex groupoid is sufficiently étale. Every isomorphism class of vertex (equivalently, every ![]() $x\in |X|$ with
$x\in |X|$ with ![]() $|Z_x|\ne \varnothing$) has a representative
$|Z_x|\ne \varnothing$) has a representative ![]() $o\in V_i\subseteq U$ with
$o\in V_i\subseteq U$ with ![]() $f_i(o)=f_i(x)>0$. To show that these representatives are étale, let
$f_i(o)=f_i(x)>0$. To show that these representatives are étale, let ![]() $m\in U\times _XU$ be a morphism with source
$m\in U\times _XU$ be a morphism with source ![]() $o$ and target
$o$ and target ![]() $o'$, and let
$o'$, and let ![]() $U_{o'}\cap U_{o''}\ne \varnothing$. We must show that there is a bijection between morphisms
$U_{o'}\cap U_{o''}\ne \varnothing$. We must show that there is a bijection between morphisms ![]() $o\to o'$ and
$o\to o'$ and ![]() $o\to o''$. The morphisms in question all have source inside
$o\to o''$. The morphisms in question all have source inside ![]() $V_i$, so we really can consider just
$V_i$, so we really can consider just ![]() $V_i\times U$ for the present purpose. Now the bulleted conditions on
$V_i\times U$ for the present purpose. Now the bulleted conditions on ![]() $|Z_x|$ from above imply that because
$|Z_x|$ from above imply that because ![]() $U_{o'}\cap U_{o''}\ne \varnothing$ and
$U_{o'}\cap U_{o''}\ne \varnothing$ and ![]() $f_i(o')>0$, we have
$f_i(o')>0$, we have ![]() $U_{o'}\cup U_{o''}\subseteq |V_i/G_i|\subseteq |X|$. Thus, over
$U_{o'}\cup U_{o''}\subseteq |V_i/G_i|\subseteq |X|$. Thus, over ![]() $U_{o'}\cap U_{o''}$ the map
$U_{o'}\cap U_{o''}$ the map ![]() $V_i\times _XU\to U$ is a finite covering space of degree
$V_i\times _XU\to U$ is a finite covering space of degree ![]() $|G_i|$. Thus, all points have the same number of lifts, so it follows that the connection sieve property gives us a bijection between lifts.
$|G_i|$. Thus, all points have the same number of lifts, so it follows that the connection sieve property gives us a bijection between lifts.
We have already seen above that our sufficiently étale locally injective simplicial complex groupoid satisfies the first hypothesis of Lemma 4.8, and the second hypothesis follows from the partial bijection property derived above from the connection sieve. Thus, by Lemma 4.8, there is a simplicial complex of groups ![]() $(Z,G)$ giving rise to the same simplicial groupoid
$(Z,G)$ giving rise to the same simplicial groupoid ![]() $b_\bullet (Z,G)=[b_\bullet M\rightrightarrows b_\bullet O]$ and thus (because
$b_\bullet (Z,G)=[b_\bullet M\rightrightarrows b_\bullet O]$ and thus (because ![]() $M\rightrightarrows O$ is sufficiently étale) to the same geometric realization
$M\rightrightarrows O$ is sufficiently étale) to the same geometric realization ![]() $\|(Z,G)\|=[\|M\|\rightrightarrows \|O\|]$. The groups
$\|(Z,G)\|=[\|M\|\rightrightarrows \|O\|]$. The groups ![]() $G_z$ associated to vertices
$G_z$ associated to vertices ![]() $z\in Z$ are, by definition, isotropy groups of the vertex groupoid
$z\in Z$ are, by definition, isotropy groups of the vertex groupoid ![]() $V(M)\rightrightarrows V(O)$, which are, by definition, isotropy groups of points of
$V(M)\rightrightarrows V(O)$, which are, by definition, isotropy groups of points of ![]() $X$.
$X$.
To conclude, it remains to define a map ![]() $X\to \|(Z,G)\|$ which is injective on isotropy groups. To define this map, we shrink the
$X\to \|(Z,G)\|$ which is injective on isotropy groups. To define this map, we shrink the ![]() $Z_x$ so that the open cover
$Z_x$ so that the open cover ![]() $\{|Z_x|\subseteq |X|\}_{x\in |X|}$ is locally finite, and choose a partition of unity
$\{|Z_x|\subseteq |X|\}_{x\in |X|}$ is locally finite, and choose a partition of unity ![]() $\{g_x:|X|\to \mathbb {R}_{\geqslant 0}\}_{x\in |X|}$ subordinate to the open cover
$\{g_x:|X|\to \mathbb {R}_{\geqslant 0}\}_{x\in |X|}$ subordinate to the open cover ![]() $\{|Z_x|\subseteq |X|\}_{x\in |X|}$. These maps
$\{|Z_x|\subseteq |X|\}_{x\in |X|}$. These maps ![]() $g_x$ lift to maps
$g_x$ lift to maps ![]() $g_o:U\to \mathbb {R}_{\geqslant 0}$ supported inside
$g_o:U\to \mathbb {R}_{\geqslant 0}$ supported inside ![]() $U_o$ and
$U_o$ and ![]() $g_m:U\times _XU\to \mathbb {R}_{\geqslant 0}$ supported inside
$g_m:U\times _XU\to \mathbb {R}_{\geqslant 0}$ supported inside ![]() $U_m$. The collection of these lifts defines a map of topological groupoids
$U_m$. The collection of these lifts defines a map of topological groupoids
where ![]() $U^0$ is the disjoint union of the open loci
$U^0$ is the disjoint union of the open loci ![]() $V_i^0\subseteq V_i$ where
$V_i^0\subseteq V_i$ where ![]() $f_i>0$ (the maps
$f_i>0$ (the maps ![]() $g_o$ and
$g_o$ and ![]() $g_m$ do not define a map over all of
$g_m$ do not define a map over all of ![]() $U\times _XU\rightrightarrows U$ due to the fact that
$U\times _XU\rightrightarrows U$ due to the fact that ![]() $U_x=\bigsqcup _{o\in o(x)}U_o$ and
$U_x=\bigsqcup _{o\in o(x)}U_o$ and ![]() $U_x\times _XU_x=\bigsqcup _{m\in m(x)}U_m$ may not be the full inverse images of
$U_x\times _XU_x=\bigsqcup _{m\in m(x)}U_m$ may not be the full inverse images of ![]() $Z_x$ inside
$Z_x$ inside ![]() $U$ and
$U$ and ![]() $U\times _XU$). It remains to check that this map is injective on isotropy groups; in other words, for
$U\times _XU$). It remains to check that this map is injective on isotropy groups; in other words, for ![]() $o,o'\in U^0$ we must show that the map
$o,o'\in U^0$ we must show that the map ![]() $\{o\}\times _X\{o'\}\to \|N(U\times _XU,\{U_m\}_{m\in U\times _XU})\|$ is injective. Distinct elements of
$\{o\}\times _X\{o'\}\to \|N(U\times _XU,\{U_m\}_{m\in U\times _XU})\|$ is injective. Distinct elements of ![]() $\{o\}\times _X\{o'\}$ are, in particular, distinct lifts of
$\{o\}\times _X\{o'\}$ are, in particular, distinct lifts of ![]() $o$, which therefore cannot lie in any common
$o$, which therefore cannot lie in any common ![]() $U_m$ because
$U_m$ because ![]() $U_m\to U$ is injective, so we see that the map is indeed injective on isotropy groups.
$U_m\to U$ is injective, so we see that the map is indeed injective on isotropy groups.
Proof of Theorem 1.1 Apply Proposition 4.9 to find a simplicial complex of finite groups ![]() $(Z,G)$ and a map
$(Z,G)$ and a map ![]() $X\to \|(Z,G)\|$ which is injective on isotropy groups. Now Theorem 2.13 applies to
$X\to \|(Z,G)\|$ which is injective on isotropy groups. Now Theorem 2.13 applies to ![]() $\|(Z,G)\|$ to give a vector bundle
$\|(Z,G)\|$ to give a vector bundle ![]() $V\to \|(Z,G)\|$, and the pullback of this bundle to
$V\to \|(Z,G)\|$, and the pullback of this bundle to ![]() $X$ satisfies the desired property because
$X$ satisfies the desired property because ![]() $X\to \|(Z,G)\|$ is injective on isotropy groups.
$X\to \|(Z,G)\|$ is injective on isotropy groups.
5. From vector bundles to principal bundles
We derive Corollaries 1.2 and 1.3 from Theorem 1.1.
A hermitian inner product on a complex vector bundle ![]() $V\to X$ is a map
$V\to X$ is a map ![]() $h:V\times _XV\to \mathbb {C}$ satisfying
$h:V\times _XV\to \mathbb {C}$ satisfying ![]() $h(v,w)=\overline {h(w,v)}$,
$h(v,w)=\overline {h(w,v)}$, ![]() $h(v,\alpha w)=\alpha h(v,w)$ for
$h(v,\alpha w)=\alpha h(v,w)$ for ![]() $\alpha \in \mathbb {C}$, and
$\alpha \in \mathbb {C}$, and ![]() $h(v,v)>0$ for
$h(v,v)>0$ for ![]() $v\ne 0$ (meaning, these conditions are imposed on the fiber
$v\ne 0$ (meaning, these conditions are imposed on the fiber ![]() $h_x:V_x\times V_x\to \mathbb {C}$ over each map
$h_x:V_x\times V_x\to \mathbb {C}$ over each map ![]() $*\xrightarrow xX$).
$*\xrightarrow xX$).
Lemma 5.1 A complex vector bundle over a paracompact orbispace ![]() $X$ admits a hermitian inner product.
$X$ admits a hermitian inner product.
Proof. Begin with an étale atlas ![]() $\bigsqcup _iU_i\to X$ such that the pullback of
$\bigsqcup _iU_i\to X$ such that the pullback of ![]() $V$ to every
$V$ to every ![]() $U_i$ is trivial. By Corollary 3.5, we may refine this cover further so that each map
$U_i$ is trivial. By Corollary 3.5, we may refine this cover further so that each map ![]() $U_i\to X$ is the composition of
$U_i\to X$ is the composition of ![]() $U_i\to U_i/G_i$ with an open embedding
$U_i\to U_i/G_i$ with an open embedding ![]() $U_i/G_i\hookrightarrow X$. The pullback of
$U_i/G_i\hookrightarrow X$. The pullback of ![]() $V$ to each
$V$ to each ![]() $U_i$ is trivial, hence admits a hermitian inner product; by averaging, we may make it
$U_i$ is trivial, hence admits a hermitian inner product; by averaging, we may make it ![]() $G_i$-invariant thus giving a hermitian inner product
$G_i$-invariant thus giving a hermitian inner product ![]() $h_i$ on the restriction of
$h_i$ on the restriction of ![]() $V$ to each
$V$ to each ![]() $U_i/G_i\subseteq X$. As
$U_i/G_i\subseteq X$. As ![]() $|X|$ is paracompact, there is a partition of unity
$|X|$ is paracompact, there is a partition of unity ![]() $\varphi _i$ subordinate to this open cover of
$\varphi _i$ subordinate to this open cover of ![]() $|X|$, and hence
$|X|$, and hence ![]() $\sum _i\varphi _ih_i$ is the desired hermitian inner product on
$\sum _i\varphi _ih_i$ is the desired hermitian inner product on ![]() $V$.
$V$.
Corollary 5.2 Every short exact sequence of vector bundles over a paracompact orbispace splits.
Given a rank ![]() $n$ complex vector bundle
$n$ complex vector bundle ![]() $V\to X$ with hermitian inner product, the associated frame bundle
$V\to X$ with hermitian inner product, the associated frame bundle ![]() $P\to X$ is defined by declaring that a map
$P\to X$ is defined by declaring that a map ![]() $U\to P$ (
$U\to P$ (![]() $U$ a topological space) is a map
$U$ a topological space) is a map ![]() $U\to X$ together with an isomorphism
$U\to X$ together with an isomorphism ![]() $\mathbb {C}^n\times U\to V\times _XU$ under which the pullback of
$\mathbb {C}^n\times U\to V\times _XU$ under which the pullback of ![]() $h$ is the standard hermitian inner product on
$h$ is the standard hermitian inner product on ![]() $\mathbb {C}^n$. There is an action of
$\mathbb {C}^n$. There is an action of ![]() $U(n)$ on
$U(n)$ on ![]() $P$ (by precomposition with automorphisms of
$P$ (by precomposition with automorphisms of ![]() $\mathbb {C}^n$ respecting its hermitian inner product), giving
$\mathbb {C}^n$ respecting its hermitian inner product), giving ![]() $P$ the structure of a principal bundle over
$P$ the structure of a principal bundle over ![]() $X$, meaning that for every map
$X$, meaning that for every map ![]() $U\to X$ from a topological space, there is an open cover
$U\to X$ from a topological space, there is an open cover ![]() $\{U_i\subseteq U\}_i$ such that
$\{U_i\subseteq U\}_i$ such that ![]() $P\times _XU_i\to U_i$ is isomorphic to
$P\times _XU_i\to U_i$ is isomorphic to ![]() $U(n)\times U_i\to U_i$ with
$U(n)\times U_i\to U_i$ with ![]() $U(n)$ acting by left multiplication on the first factor.
$U(n)$ acting by left multiplication on the first factor.
Proof of Corollary 1.2 Let ![]() $V\to X$ be the rank
$V\to X$ be the rank ![]() $n$ complex vector bundle produced by Theorem 1.1. By Lemma 5.1, there exists a hermitian inner product on
$n$ complex vector bundle produced by Theorem 1.1. By Lemma 5.1, there exists a hermitian inner product on ![]() $V$. The total space
$V$. The total space ![]() $P$ of the associated principal bundle
$P$ of the associated principal bundle ![]() $P\to X$ has trivial isotropy because the isotropy groups of
$P\to X$ has trivial isotropy because the isotropy groups of ![]() $X$ act faithfully on the fibers of
$X$ act faithfully on the fibers of ![]() $V$.
$V$.
We claim that ![]() $P$ is a Hausdorff topological space. By Corollary 3.6, it is enough to show that
$P$ is a Hausdorff topological space. By Corollary 3.6, it is enough to show that ![]() $P$ is an orbispace. As
$P$ is an orbispace. As ![]() $P\to X$ is representable, the pullback of an étale atlas for
$P\to X$ is representable, the pullback of an étale atlas for ![]() $X$ is an étale atlas for
$X$ is an étale atlas for ![]() $P$. The diagonal of
$P$. The diagonal of ![]() $P$ may be expressed as the composition
$P$ may be expressed as the composition ![]() $P\to P\times _XP\to P\times P$. The second map
$P\to P\times _XP\to P\times P$. The second map ![]() $P\times _XP\to P\times P$ is proper, being a pullback of the diagonal of
$P\times _XP\to P\times P$ is proper, being a pullback of the diagonal of ![]() $X$. To check that the first map
$X$. To check that the first map ![]() $P\to P\times _XP$ is proper, it suffices by descent to show that its pullback under an étale atlas
$P\to P\times _XP$ is proper, it suffices by descent to show that its pullback under an étale atlas ![]() $U\to X$ is proper. This pullback is proper because
$U\to X$ is proper. This pullback is proper because ![]() $P\times _XU\to U$ is a principal
$P\times _XU\to U$ is a principal ![]() $U(n)$ bundle (of topological spaces). We have thus shown that
$U(n)$ bundle (of topological spaces). We have thus shown that ![]() $P$ is a topological space.
$P$ is a topological space.
The map ![]() $P\to X$ is representable and admits local sections (by definition), so the topological groupoid
$P\to X$ is representable and admits local sections (by definition), so the topological groupoid ![]() $P\times _XP\rightrightarrows P$ presents the stack
$P\times _XP\rightrightarrows P$ presents the stack ![]() $X$. It can be seen by inspection that
$X$. It can be seen by inspection that ![]() $P\times _XP\rightrightarrows P$ is the action groupoid of the
$P\times _XP\rightrightarrows P$ is the action groupoid of the ![]() $U(n)$ action on
$U(n)$ action on ![]() $P$.
$P$.
Let ![]() $\mathsf {Sm}$ denote the category of topological spaces equipped with a maximal atlas of charts from open sets of
$\mathsf {Sm}$ denote the category of topological spaces equipped with a maximal atlas of charts from open sets of ![]() $\bigsqcup _{n\geqslant 0}\mathbb {R}^n$ with smooth transition maps (a smooth manifold an object of
$\bigsqcup _{n\geqslant 0}\mathbb {R}^n$ with smooth transition maps (a smooth manifold an object of ![]() $\mathsf {Sm}$ whose underlying topological space is Hausdorff). A smooth structure on a stack
$\mathsf {Sm}$ whose underlying topological space is Hausdorff). A smooth structure on a stack ![]() $F:\mathsf {Top}^\mathsf {op}\to \mathsf {Grpd}$ is a substack
$F:\mathsf {Top}^\mathsf {op}\to \mathsf {Grpd}$ is a substack ![]() $F^\mathrm {sm}$ of the pullback of
$F^\mathrm {sm}$ of the pullback of ![]() $F$ under the forgetful functor
$F$ under the forgetful functor ![]() $\mathsf {Sm}\to \mathsf {Top}$ (meaning that
$\mathsf {Sm}\to \mathsf {Top}$ (meaning that ![]() $F^\mathrm {sm}(U)$ is a full subcategory of
$F^\mathrm {sm}(U)$ is a full subcategory of ![]() $F(U)$ for
$F(U)$ for ![]() $U\in \mathsf {Sm}$); maps
$U\in \mathsf {Sm}$); maps ![]() $U\to F$ lying in (the essential image of)
$U\to F$ lying in (the essential image of) ![]() $F^\mathrm {sm}$ are then called smooth. Given a map of stacks
$F^\mathrm {sm}$ are then called smooth. Given a map of stacks ![]() $F\to G$ and a smooth structure on
$F\to G$ and a smooth structure on ![]() $G$, we may consider the pullback smooth structure on
$G$, we may consider the pullback smooth structure on ![]() $F$, defined as those maps
$F$, defined as those maps ![]() $U\to F$ whose composition with
$U\to F$ whose composition with ![]() $F\to G$ is smooth. A map of stacks equipped with smooth structures
$F\to G$ is smooth. A map of stacks equipped with smooth structures ![]() $(F,F^\mathrm {sm})\to (G,G^\mathrm {sm})$ is called smooth if and only if the composition of any smooth map
$(F,F^\mathrm {sm})\to (G,G^\mathrm {sm})$ is called smooth if and only if the composition of any smooth map ![]() $U\to F$ with
$U\to F$ with ![]() $F\to G$ is a smooth map
$F\to G$ is a smooth map ![]() $U\to G$ (equivalently,
$U\to G$ (equivalently, ![]() $F^\mathrm {sm}$ is contained inside the pullback of
$F^\mathrm {sm}$ is contained inside the pullback of ![]() $G^\mathrm {sm}$). Stacks with smooth structures form a 2-category just like stacks. This category is complete, and limits
$G^\mathrm {sm}$). Stacks with smooth structures form a 2-category just like stacks. This category is complete, and limits ![]() $\lim _\alpha (F_\alpha,F_\alpha ^\mathrm {sm})$ are calculated by taking the limit of the underlying stacks
$\lim _\alpha (F_\alpha,F_\alpha ^\mathrm {sm})$ are calculated by taking the limit of the underlying stacks ![]() $\lim _\alpha F_\alpha$ and declaring a map
$\lim _\alpha F_\alpha$ and declaring a map ![]() $U\to \lim _\alpha F_\alpha$ to be smooth if and only if every induced map
$U\to \lim _\alpha F_\alpha$ to be smooth if and only if every induced map ![]() $U\to F_\alpha$ is smooth. The category
$U\to F_\alpha$ is smooth. The category ![]() $\mathsf {Sm}$ embeds fully faithfully into the category of stacks with smooth structures, by sending
$\mathsf {Sm}$ embeds fully faithfully into the category of stacks with smooth structures, by sending ![]() $X\in \mathsf {Sm}$ to the Yoneda functor of its underlying topological space, equipped with the smooth structure consisting of those maps
$X\in \mathsf {Sm}$ to the Yoneda functor of its underlying topological space, equipped with the smooth structure consisting of those maps ![]() $U\to X$ which are morphisms in
$U\to X$ which are morphisms in ![]() $\mathsf {Sm}$.
$\mathsf {Sm}$.
Definition 5.3 A smooth orbifold ![]() $X$ is an orbispace equipped with a smooth structure such that for every (equivalently, some) étale atlas
$X$ is an orbispace equipped with a smooth structure such that for every (equivalently, some) étale atlas ![]() $U\to X$, we have
$U\to X$, we have ![]() $U\in \mathsf {Sm}$ when
$U\in \mathsf {Sm}$ when ![]() $U$ is equipped with the pullback of the smooth structure on
$U$ is equipped with the pullback of the smooth structure on ![]() $X$.
$X$.
By Proposition 3.3, a stack ![]() $X$ with a smooth structure is a smooth orbifold if and only if
$X$ with a smooth structure is a smooth orbifold if and only if ![]() $|X|$ is Hausdorff and there is an open cover of
$|X|$ is Hausdorff and there is an open cover of ![]() $X$ by
$X$ by ![]() $V_i/G_i$ for smooth manifolds
$V_i/G_i$ for smooth manifolds ![]() $V_i$ equipped with smooth actions of finite groups
$V_i$ equipped with smooth actions of finite groups ![]() $G_i$.
$G_i$.
Proof of Corollary 1.3 Let ![]() $V\to X$ be the complex vector bundle produced by Theorem 1.1. It suffices to define a smooth structure on
$V\to X$ be the complex vector bundle produced by Theorem 1.1. It suffices to define a smooth structure on ![]() $V$, because then we may follow the arguments of Lemma 5.1 and Corollary 1.2 in the smooth category.
$V$, because then we may follow the arguments of Lemma 5.1 and Corollary 1.2 in the smooth category.
We begin by arguing that a complex vector bundle ![]() $V$ over a smooth orbifold
$V$ over a smooth orbifold ![]() $X$ has a smooth structure in a neighborhood of any given point of
$X$ has a smooth structure in a neighborhood of any given point of ![]() $|X|$. We may thus assume that
$|X|$. We may thus assume that ![]() $X=U/G$ for a smooth manifold
$X=U/G$ for a smooth manifold ![]() $U$ acted on smoothly by a finite group
$U$ acted on smoothly by a finite group ![]() $G$, and that the pullback of
$G$, and that the pullback of ![]() $V$ to
$V$ to ![]() $U$ is trivial. By shrinking this chart further (and adjusting
$U$ is trivial. By shrinking this chart further (and adjusting ![]() $G$), we may assume that our given point of
$G$), we may assume that our given point of ![]() $|X|$ corresponds to a point
$|X|$ corresponds to a point ![]() $u\in U$ fixed by
$u\in U$ fixed by ![]() $G$. Choose any trivialization
$G$. Choose any trivialization ![]() $V_u\times U\to V\times _XU$ where
$V_u\times U\to V\times _XU$ where ![]() $V_u$ denotes the fiber over
$V_u$ denotes the fiber over ![]() $u$. By averaging, we may make this map
$u$. By averaging, we may make this map ![]() $G$ equivariant, and it remains an isomorphism in a neighborhood of
$G$ equivariant, and it remains an isomorphism in a neighborhood of ![]() $u$. We thus obtain a trivialization of
$u$. We thus obtain a trivialization of ![]() $V\times _XU$ near
$V\times _XU$ near ![]() $u$ in which the action of
$u$ in which the action of ![]() $G$ is constant (independent of the
$G$ is constant (independent of the ![]() $U$ coordinate). The standard smooth structure in this trivialization is thus, in particular, invariant under the action of
$U$ coordinate). The standard smooth structure in this trivialization is thus, in particular, invariant under the action of ![]() $G$, giving the desired smooth structure on
$G$, giving the desired smooth structure on ![]() $V$ near our given point of
$V$ near our given point of ![]() $|X|$.
$|X|$.
Having shown the existence of smooth structures locally, we now show how to patch them together. To show that there exists a smooth structure on ![]() $V$ over all of
$V$ over all of ![]() $X$, it suffices to show that for open subsets
$X$, it suffices to show that for open subsets ![]() $A,B\subseteq |X|$ and smooth structures on
$A,B\subseteq |X|$ and smooth structures on ![]() $V|_A$ and
$V|_A$ and ![]() $V|_B$, there exists a smooth structure on
$V|_B$, there exists a smooth structure on ![]() $V|_{A\cup B}$ restricting to the given smooth structure on
$V|_{A\cup B}$ restricting to the given smooth structure on ![]() $V|_A$ (indeed, this allows us to patch together smooth structures over arbitrary unions of open sets, by choosing a well ordering and adding one open set at a time). To prove this pairwise patching statement, it suffices to show that an isomorphism of smooth vector bundles may be approximated by a smooth isomorphism (then apply this to the identity map on
$V|_A$ (indeed, this allows us to patch together smooth structures over arbitrary unions of open sets, by choosing a well ordering and adding one open set at a time). To prove this pairwise patching statement, it suffices to show that an isomorphism of smooth vector bundles may be approximated by a smooth isomorphism (then apply this to the identity map on ![]() $V|_{A\cap B}$ equipped with the restrictions of the two given smooth structures). As
$V|_{A\cap B}$ equipped with the restrictions of the two given smooth structures). As ![]() $|X|$ is locally the quotient of Euclidean space by a finite group action, it is locally metrizable; because it is paracompact and Hausdorff, it is thus metrizable. Thus, every open subset of
$|X|$ is locally the quotient of Euclidean space by a finite group action, it is locally metrizable; because it is paracompact and Hausdorff, it is thus metrizable. Thus, every open subset of ![]() $|X|$ is metrizable, hence paracompact. We may now conclude with a smooth partition of unity argument.
$|X|$ is metrizable, hence paracompact. We may now conclude with a smooth partition of unity argument.
6.  $K$-theory of orbispaces
$K$-theory of orbispaces
We derive Corollary 1.4 from Theorem 1.1. We then derive from Corollary 1.4 some basic properties of the ![]() $K$-theory of finite-rank vector bundles on orbispaces (some of this derivation is borrowed, with various technical differences, from [Reference Lück and OliverLO01, § 3] and [Reference SegalSeg68]). In what follows, ‘vector bundle’ can be taken to mean either real vector bundle or complex vector bundle (always of finite rank).
$K$-theory of finite-rank vector bundles on orbispaces (some of this derivation is borrowed, with various technical differences, from [Reference Lück and OliverLO01, § 3] and [Reference SegalSeg68]). In what follows, ‘vector bundle’ can be taken to mean either real vector bundle or complex vector bundle (always of finite rank).
Proof of Corollary 1.4 Denote our given map by ![]() $f:X\to Y$, and let
$f:X\to Y$, and let ![]() $E$ be the given vector bundle on
$E$ be the given vector bundle on ![]() $X$. Let
$X$. Let ![]() $F$ be any vector bundle on
$F$ be any vector bundle on ![]() $Y$ satisfying the conclusion of Theorem 1.1.
$Y$ satisfying the conclusion of Theorem 1.1.
We first consider the local situation on ![]() $X$. Fix
$X$. Fix ![]() $x\in X$, and let
$x\in X$, and let ![]() $U/G\hookrightarrow X$ be an open embedding sending
$U/G\hookrightarrow X$ be an open embedding sending ![]() $u\in U$ fixed by
$u\in U$ fixed by ![]() $G$ to
$G$ to ![]() $x\in X$ and inducing an isomorphism
$x\in X$ and inducing an isomorphism ![]() $G\xrightarrow \sim G_x$ (such an open embedding exists by the proof of Proposition 3.3). By shrinking
$G\xrightarrow \sim G_x$ (such an open embedding exists by the proof of Proposition 3.3). By shrinking ![]() $U$, we may ensure that the pullbacks of
$U$, we may ensure that the pullbacks of ![]() $E$ and
$E$ and ![]() $F$ to
$F$ to ![]() $U$ are trivial. Choose any map on
$U$ are trivial. Choose any map on ![]() $U$ from the pullback of
$U$ from the pullback of ![]() $E$ to the pullback of
$E$ to the pullback of ![]() $F^{\oplus N}$ (some integer
$F^{\oplus N}$ (some integer ![]() $N<\infty$) which is injective and
$N<\infty$) which is injective and ![]() $G$-equivariant at
$G$-equivariant at ![]() $u$, and average it to make it equivariant everywhere. This produces over
$u$, and average it to make it equivariant everywhere. This produces over ![]() $U/G$ a map from
$U/G$ a map from ![]() $E$ to
$E$ to ![]() $f^*F^{\oplus N}$ which is injective at
$f^*F^{\oplus N}$ which is injective at ![]() $x$. Now because
$x$. Now because ![]() $|X|$ is paracompact Hausdorff, hence normal, there exists a continuous function
$|X|$ is paracompact Hausdorff, hence normal, there exists a continuous function ![]() $\varphi :|X|\to [0,1]$ supported inside
$\varphi :|X|\to [0,1]$ supported inside ![]() $|U/G|$ with
$|U/G|$ with ![]() $\varphi (x)=1$. Multiplying by this function yields a map
$\varphi (x)=1$. Multiplying by this function yields a map ![]() $E\to f^*F^{\oplus N}$ defined on all of
$E\to f^*F^{\oplus N}$ defined on all of ![]() $X$ which is injective at
$X$ which is injective at ![]() $x$. Note that the integer
$x$. Note that the integer ![]() $N$ may be taken independent of
$N$ may be taken independent of ![]() $x$ because the rank of
$x$ because the rank of ![]() $E$ is bounded.
$E$ is bounded.
We now combine the above maps to give an everywhere injective map ![]() $E\to f^*F^{\oplus M}$ as follows. Fix an open cover
$E\to f^*F^{\oplus M}$ as follows. Fix an open cover ![]() $|X|=\bigcup _iU_i$ and maps
$|X|=\bigcup _iU_i$ and maps ![]() $f_i:E\to f^*F^{\oplus N}$ defined over all of
$f_i:E\to f^*F^{\oplus N}$ defined over all of ![]() $X$ which are injective over
$X$ which are injective over ![]() $U_i$. As
$U_i$. As ![]() $|X|$ is coarsely finite-dimensional, we may refine this open cover so that it is locally finite and has nerve of dimension
$|X|$ is coarsely finite-dimensional, we may refine this open cover so that it is locally finite and has nerve of dimension ![]() $\leqslant d$ for some integer
$\leqslant d$ for some integer ![]() $d<\infty$. As in the proof of Lemma 4.4, there is yet another open cover of
$d<\infty$. As in the proof of Lemma 4.4, there is yet another open cover of ![]() $|X|$ by open sets
$|X|$ by open sets ![]() $V_I$ indexed by the nonempty subsets
$V_I$ indexed by the nonempty subsets ![]() $I$ of the index set of the
$I$ of the index set of the ![]() $U_i$, such that
$U_i$, such that ![]() $V_I\subseteq \bigcap _{i\in I}U_i$ and
$V_I\subseteq \bigcap _{i\in I}U_i$ and ![]() $V_I\cap V_J=\varnothing$ unless
$V_I\cap V_J=\varnothing$ unless ![]() $I\subseteq J$ or
$I\subseteq J$ or ![]() $J\subseteq I$. Note that these conditions imply that
$J\subseteq I$. Note that these conditions imply that ![]() $V_I=\varnothing$ unless
$V_I=\varnothing$ unless ![]() $|I|\leqslant d+1$ and that
$|I|\leqslant d+1$ and that ![]() $V_I\cap V_J=\varnothing$ if
$V_I\cap V_J=\varnothing$ if ![]() $|I|=|J|$ and
$|I|=|J|$ and ![]() $I\ne J$. Now let
$I\ne J$. Now let ![]() $\sum _I\varphi _I\equiv 1$ be a partition of unity subordinate to the open cover
$\sum _I\varphi _I\equiv 1$ be a partition of unity subordinate to the open cover ![]() $|X|=\bigcup _IV_I$. We may now define our desired everywhere injective map
$|X|=\bigcup _IV_I$. We may now define our desired everywhere injective map ![]() $E\to f^*F^{\oplus (d+1)N}$ (so
$E\to f^*F^{\oplus (d+1)N}$ (so ![]() $M=(d+1)N$) by the formula
$M=(d+1)N$) by the formula ![]() $\sum _I\alpha _{|I|}\varphi _If_{i(I)}$, where
$\sum _I\alpha _{|I|}\varphi _If_{i(I)}$, where ![]() $i(I)$ is any choice of index in the set
$i(I)$ is any choice of index in the set ![]() $I$, and
$I$, and ![]() $\alpha _r:F^{\oplus N}\hookrightarrow (F^{\oplus N})^{\oplus (d+1)}=F^{\oplus (d+1)N}$ is the inclusion of the
$\alpha _r:F^{\oplus N}\hookrightarrow (F^{\oplus N})^{\oplus (d+1)}=F^{\oplus (d+1)N}$ is the inclusion of the ![]() $r$th direct summand.
$r$th direct summand.
We have thus constructed an injection ![]() $E\to f^*F^{\oplus M}$ over
$E\to f^*F^{\oplus M}$ over ![]() $X$.
$X$.
Definition 6.1 For any stack ![]() $X$, denote by
$X$, denote by ![]() $\operatorname {Vect}(X)$ the set of isomorphism classes of vector bundles on
$\operatorname {Vect}(X)$ the set of isomorphism classes of vector bundles on ![]() $X$ of bounded rank.
$X$ of bounded rank.
Direct sum of vector bundles equips ![]() $\operatorname {Vect}(X)$ with the structure of an abelian monoid. A map of stacks
$\operatorname {Vect}(X)$ with the structure of an abelian monoid. A map of stacks ![]() $X\to Y$ induces a pullback map
$X\to Y$ induces a pullback map ![]() $\operatorname {Vect}(Y)\to \operatorname {Vect}(X)$.
$\operatorname {Vect}(Y)\to \operatorname {Vect}(X)$.
The reason we restrict attention to vector bundles of bounded rank is so that we may appeal to Corollary 1.4. A counterexample of Lück and Oliver [Reference Lück and OliverLO01, Example 3.11] shows that the ![]() $K$-theory of vector bundles of unbounded rank fails to be a cohomology theory on (possibly infinite) simplicial complexes of groups, whereas we show that the
$K$-theory of vector bundles of unbounded rank fails to be a cohomology theory on (possibly infinite) simplicial complexes of groups, whereas we show that the ![]() $K$-theory of vector bundles of bounded rank is a cohomology theory for such.
$K$-theory of vector bundles of bounded rank is a cohomology theory for such.
For an abelian monoid ![]() $M$, its group completion
$M$, its group completion ![]() $M[-M]$ is the quotient of the free abelian group on the underlying set of
$M[-M]$ is the quotient of the free abelian group on the underlying set of ![]() $M$ by the subgroup generated by
$M$ by the subgroup generated by ![]() $[a]+[b]-[a+b]$ for
$[a]+[b]-[a+b]$ for ![]() $a,b\in M$. The map
$a,b\in M$. The map ![]() $M\to M[-M]$ is universal (initial) among maps from
$M\to M[-M]$ is universal (initial) among maps from ![]() $M$ to an abelian group.
$M$ to an abelian group.
Definition 6.2 We define ![]() $K^0(X)$ as the group completion of
$K^0(X)$ as the group completion of ![]() $\operatorname {Vect}(X)$ for any stack
$\operatorname {Vect}(X)$ for any stack ![]() $X$.
$X$.
A map of stacks ![]() $X\to Y$ induces a pullback map
$X\to Y$ induces a pullback map ![]() $K^0(Y)\to K^0(X)$. The functor
$K^0(Y)\to K^0(X)$. The functor ![]() $K^0$ is finitely additive, in the sense that
$K^0$ is finitely additive, in the sense that ![]() $K^0(\varnothing )=0$ and the natural map
$K^0(\varnothing )=0$ and the natural map ![]() $K^0(X\sqcup Y)\to K^0(X)\oplus K^0(Y)$ is an isomorphism. In the present context of vector bundles of bounded rank, additivity does not hold for general infinite disjoint unions.
$K^0(X\sqcup Y)\to K^0(X)\oplus K^0(Y)$ is an isomorphism. In the present context of vector bundles of bounded rank, additivity does not hold for general infinite disjoint unions.
Eventually, we will restrict attention to the ![]() $K$-theory of orbispaces satisfying the hypothesis of Theorem 1.1. However, we impose such hypotheses gradually, as they become relevant.
$K$-theory of orbispaces satisfying the hypothesis of Theorem 1.1. However, we impose such hypotheses gradually, as they become relevant.
To show that ![]() $K$-theory is homotopy invariant, the following is the key assertion.
$K$-theory is homotopy invariant, the following is the key assertion.
Lemma 6.3 For any paracompact orbispace ![]() $X$, every vector bundle on
$X$, every vector bundle on ![]() $X\times [0,1]$ is pulled back from
$X\times [0,1]$ is pulled back from ![]() $X$.
$X$.
Proof. Let a vector bundle ![]() $V$ over
$V$ over ![]() $X\times [0,1]$ be given.
$X\times [0,1]$ be given.
We first discuss the local structure around a given point ![]() $x\in X$. Fix an open embedding
$x\in X$. Fix an open embedding ![]() $Y/G\hookrightarrow X$ and a lift
$Y/G\hookrightarrow X$ and a lift ![]() $y\in Y$ of
$y\in Y$ of ![]() $x$ fixed by
$x$ fixed by ![]() $G$. We consider the pullback bundle
$G$. We consider the pullback bundle ![]() $V|_{Y\times [0,1]}$ on
$V|_{Y\times [0,1]}$ on ![]() $Y\times [0,1]$, which is a
$Y\times [0,1]$, which is a ![]() $G$-equivariant vector bundle. For each
$G$-equivariant vector bundle. For each ![]() $t\in [0,1]$, there exist open neighborhoods
$t\in [0,1]$, there exist open neighborhoods ![]() $t\in T\subseteq [0,1]$ and
$t\in T\subseteq [0,1]$ and ![]() $y\in U\subseteq Y$ such that
$y\in U\subseteq Y$ such that ![]() $V|_{U\times T}$ is trivial. By the compactness of
$V|_{U\times T}$ is trivial. By the compactness of ![]() $[0,1]$, we may assume
$[0,1]$, we may assume ![]() $U$ is independent of
$U$ is independent of ![]() $t$. Replacing
$t$. Replacing ![]() $Y$ with
$Y$ with ![]() $U$, we may assume that for each
$U$, we may assume that for each ![]() $t\in [0,1]$ there exists an open neighborhood
$t\in [0,1]$ there exists an open neighborhood ![]() $t\in T\subseteq [0,1]$ such that
$t\in T\subseteq [0,1]$ such that ![]() $V|_{Y\times T}$ is trivial. A trivialization induces a map
$V|_{Y\times T}$ is trivial. A trivialization induces a map ![]() $V|_{Y\times T}\to p_T^*V|_{\{y\}\times T}$ which is the identity over
$V|_{Y\times T}\to p_T^*V|_{\{y\}\times T}$ which is the identity over ![]() $\{y\}\times T$. Averaging makes this map
$\{y\}\times T$. Averaging makes this map ![]() $G$-equivariant, so it descends to a map
$G$-equivariant, so it descends to a map ![]() $V|_{Y/G\times T}\to p_T^*V|_{\{y\}/G\times T}$ which is still the identity over
$V|_{Y/G\times T}\to p_T^*V|_{\{y\}/G\times T}$ which is still the identity over ![]() $\{y\}\times T$. It is thus an isomorphism over some
$\{y\}\times T$. It is thus an isomorphism over some ![]() $U\times T'$; another compactness argument and shrinking of
$U\times T'$; another compactness argument and shrinking of ![]() $Y$ ensures that we have a collection of isomorphisms
$Y$ ensures that we have a collection of isomorphisms ![]() $V|_{Y/G\times T}\to p_T^*V|_{\{y\}/G\times T}$ which are the identity over
$V|_{Y/G\times T}\to p_T^*V|_{\{y\}/G\times T}$ which are the identity over ![]() $\{y\}\times T$. Patching these together via a partition of unity on
$\{y\}\times T$. Patching these together via a partition of unity on ![]() $[0,1]$ and further shrinking
$[0,1]$ and further shrinking ![]() $Y$ produces an isomorphism
$Y$ produces an isomorphism
which is the identity over ![]() $\{y\}\times [0,1]$. Any vector bundle over
$\{y\}\times [0,1]$. Any vector bundle over ![]() $\mathbb {B} G\times [0,1]$ is pulled back from
$\mathbb {B} G\times [0,1]$ is pulled back from ![]() $\mathbb {B} G$, and hence we conclude that
$\mathbb {B} G$, and hence we conclude that ![]() $V|_{Y/G\times [0,1]}$ is pulled back from
$V|_{Y/G\times [0,1]}$ is pulled back from ![]() $Y/G$, for some neighborhood
$Y/G$, for some neighborhood ![]() $Y/G$ of
$Y/G$ of ![]() $x\in X$.
$x\in X$.
We now globalize. Begin with an open cover ![]() $|X|=\bigcup _iU_i$ and over each
$|X|=\bigcup _iU_i$ and over each ![]() $U_i$ an isomorphism
$U_i$ an isomorphism ![]() $\xi _i:V|_{U_i\times [0,1]}\to (p_X^*V|_{X\times \{0\}})|_{U_i\times [0,1]}$ which is the identity over
$\xi _i:V|_{U_i\times [0,1]}\to (p_X^*V|_{X\times \{0\}})|_{U_i\times [0,1]}$ which is the identity over ![]() $U_i\times \{0\}$. Note that for any
$U_i\times \{0\}$. Note that for any ![]() $x\in U_i$ and any
$x\in U_i$ and any ![]() $t,t'\in [0,1]$, the map
$t,t'\in [0,1]$, the map ![]() $\xi _i$ determines an isomorphism
$\xi _i$ determines an isomorphism
which is the specialization of an isomorphism between the pullbacks of ![]() $V$ under the two projections
$V$ under the two projections ![]() $X\times [0,1]^2\to X\times [0,1]$. Using this observation, we may now patch together the
$X\times [0,1]^2\to X\times [0,1]$. Using this observation, we may now patch together the ![]() $\xi _i$ into an isomorphism
$\xi _i$ into an isomorphism ![]() $V\to p_X^*V|_{X\times \{0\}}$ as follows. Fix a partition of unity
$V\to p_X^*V|_{X\times \{0\}}$ as follows. Fix a partition of unity ![]() $\varphi _i:|X|\to \mathbb {R}_{\geqslant 0}$ subordinate to the open cover
$\varphi _i:|X|\to \mathbb {R}_{\geqslant 0}$ subordinate to the open cover ![]() $|X|=\bigcup _iU_i$, and fix an arbitrary total ordering of the index set of the open cover. For
$|X|=\bigcup _iU_i$, and fix an arbitrary total ordering of the index set of the open cover. For ![]() $(x,t)\in X\times [0,1]$, let
$(x,t)\in X\times [0,1]$, let ![]() $i=1,\ldots,k$ denote the indices of the open sets
$i=1,\ldots,k$ denote the indices of the open sets ![]() $U_i$ containing
$U_i$ containing ![]() $x$, ordered as in the fixed total order, and consider the composition of isomorphisms
$x$, ordered as in the fixed total order, and consider the composition of isomorphisms
This fiberwise description now translates into the desired isomorphism of vector bundles ![]() $V\to p_X^*|_{X\times \{0\}}$.
$V\to p_X^*|_{X\times \{0\}}$.
Two maps ![]() $X\to Y$ will be called homotopic if and only if there exists a map
$X\to Y$ will be called homotopic if and only if there exists a map ![]() $X\times [0,1]\to Y$ whose restrictions to
$X\times [0,1]\to Y$ whose restrictions to ![]() $X\times \{0\}$ and
$X\times \{0\}$ and ![]() $X\times \{1\}$ are the two given maps. A map
$X\times \{1\}$ are the two given maps. A map ![]() $X\to Y$ is called a homotopy equivalence if and only if there exists a map
$X\to Y$ is called a homotopy equivalence if and only if there exists a map ![]() $Y\to X$ such that the compositions
$Y\to X$ such that the compositions ![]() $X\to Y\to X$ and
$X\to Y\to X$ and ![]() $Y\to X\to Y$ are homotopic to the respective identity maps.
$Y\to X\to Y$ are homotopic to the respective identity maps.
Corollary 6.4 (Homotopy invariance)
If ![]() $X$ is a paracompact orbispace, then homotopic maps
$X$ is a paracompact orbispace, then homotopic maps ![]() $X\to Y$ induce the same map
$X\to Y$ induce the same map ![]() $K^0(Y)\to K^0(X)$.
$K^0(Y)\to K^0(X)$.
For any map of abelian monoids ![]() $M'\to M$, the quotient
$M'\to M$, the quotient ![]() $M/M'$ is, as a set, the quotient of
$M/M'$ is, as a set, the quotient of ![]() $M$ by the equivalence relation
$M$ by the equivalence relation ![]() $x\sim _{M'}y$ if and only if there exist
$x\sim _{M'}y$ if and only if there exist ![]() $a,b\in M'$ with
$a,b\in M'$ with ![]() $x+a=y+b$, equipped with the descent of the monoid operation from
$x+a=y+b$, equipped with the descent of the monoid operation from ![]() $M$. The map
$M$. The map ![]() $M\to M/M'$ is initial among maps from
$M\to M/M'$ is initial among maps from ![]() $M$ to an abelian monoid sending
$M$ to an abelian monoid sending ![]() $M'$ to zero. If (the image inside
$M'$ to zero. If (the image inside ![]() $M$ of)
$M$ of) ![]() $M'$ is an abelian group, then the kernel of the quotient map
$M'$ is an abelian group, then the kernel of the quotient map ![]() $M\to M/M'$ is precisely
$M\to M/M'$ is precisely ![]() $M'$. The group completion
$M'$. The group completion ![]() $M[-M]$ is the quotient of
$M[-M]$ is the quotient of ![]() $M\times M$ by the diagonal submonoid
$M\times M$ by the diagonal submonoid ![]() $M$.
$M$.
Definition 6.5 For any map of stacks ![]() $f:Y\to X$, the relative
$f:Y\to X$, the relative ![]() $K$-theory
$K$-theory ![]() $K^0(X,Y)$ is defined as follows. We consider the set
$K^0(X,Y)$ is defined as follows. We consider the set ![]() $\operatorname {Tri}(X,Y)$ of isomorphism classes of triples
$\operatorname {Tri}(X,Y)$ of isomorphism classes of triples ![]() $(E_0,E_1,i)$ where
$(E_0,E_1,i)$ where ![]() $E_0,E_1$ are vector bundles on
$E_0,E_1$ are vector bundles on ![]() $X$ of bounded rank and
$X$ of bounded rank and ![]() $i:f^*E_0\to f^*E_1$ is an isomorphism between their pullbacks to
$i:f^*E_0\to f^*E_1$ is an isomorphism between their pullbacks to ![]() $Y$. Now
$Y$. Now ![]() $\operatorname {Tri}(X,Y)$ is an abelian monoid under direct sum, and it contains
$\operatorname {Tri}(X,Y)$ is an abelian monoid under direct sum, and it contains ![]() $\operatorname {Vect}(X)$ as the submonoid of triples of the form
$\operatorname {Vect}(X)$ as the submonoid of triples of the form ![]() $(E,E,f^*\operatorname {id}_E)$. The relative
$(E,E,f^*\operatorname {id}_E)$. The relative ![]() $K$-theory is the quotient
$K$-theory is the quotient
Note that a priori ![]() $K^0(X,Y)$ is merely an abelian monoid, not an abelian group.
$K^0(X,Y)$ is merely an abelian monoid, not an abelian group.
A map ![]() $(Y\to X)\to (Y'\to X')$ (i.e. a commutative square) induces a map
$(Y\to X)\to (Y'\to X')$ (i.e. a commutative square) induces a map ![]() $K^0(X',Y')\to K^0(X,Y)$. There is a natural map
$K^0(X',Y')\to K^0(X,Y)$. There is a natural map ![]() $K^0(X,Y)\to K^0(X)$ given by sending
$K^0(X,Y)\to K^0(X)$ given by sending ![]() $(E_0,E_1,i)$ to the formal difference
$(E_0,E_1,i)$ to the formal difference ![]() $[E_0]-[E_1]$, and the composition
$[E_0]-[E_1]$, and the composition ![]() $K^0(X,Y)\to K^0(X)\to K^0(Y)$ is zero. The map
$K^0(X,Y)\to K^0(X)\to K^0(Y)$ is zero. The map ![]() $K^0(X,\varnothing )\to K^0(X)$ is an isomorphism (because
$K^0(X,\varnothing )\to K^0(X)$ is an isomorphism (because ![]() $\operatorname {Tri}(X,\varnothing )$ is simply
$\operatorname {Tri}(X,\varnothing )$ is simply ![]() $\operatorname {Vect}(X)\times \operatorname {Vect}(X)$).
$\operatorname {Vect}(X)\times \operatorname {Vect}(X)$).
A pair ![]() $(X,A)$ shall mean that
$(X,A)$ shall mean that ![]() $A$ is a closed substack of
$A$ is a closed substack of ![]() $X$. A map of pairs
$X$. A map of pairs ![]() $(X,A)\to (Y,B)$ means a map
$(X,A)\to (Y,B)$ means a map ![]() $X\to Y$ sending
$X\to Y$ sending ![]() $A$ inside
$A$ inside ![]() $B$. Note that paracompactness, coarse finite-dimensionality, being an orbispace, and the hypothesis of Theorem 1.1 all pass to closed substacks.
$B$. Note that paracompactness, coarse finite-dimensionality, being an orbispace, and the hypothesis of Theorem 1.1 all pass to closed substacks.
Remark 6.6 Even for very nice orbispace pairs ![]() $(X,A)$, we cannot in general form the quotient
$(X,A)$, we cannot in general form the quotient ![]() $X/A$ in a reasonable way. For example, for an orbispace
$X/A$ in a reasonable way. For example, for an orbispace ![]() $X$, if we could reasonably define
$X$, if we could reasonably define ![]() $(X\times [0,1])/(X\times \{0\})$ as an orbispace, it would follow that
$(X\times [0,1])/(X\times \{0\})$ as an orbispace, it would follow that ![]() $X$ is (globally) the quotient of a topological space by a finite group action (a very special property).
$X$ is (globally) the quotient of a topological space by a finite group action (a very special property).
For any pair ![]() $(X,A)$, let
$(X,A)$, let ![]() $\operatorname {cyl}(X,A)$ denote the pair
$\operatorname {cyl}(X,A)$ denote the pair ![]() $((X\times \{0\})\cup (A\times [0,1]),A\times \{1\})$. Here
$((X\times \{0\})\cup (A\times [0,1]),A\times \{1\})$. Here ![]() $(X\times \{0\})\cup (A\times [0,1])$ denotes the union of closed substacks of
$(X\times \{0\})\cup (A\times [0,1])$ denotes the union of closed substacks of ![]() $X\times [0,1]$ (recall that closed substacks of a stack
$X\times [0,1]$ (recall that closed substacks of a stack ![]() $Z$ are in bijective correspondence with closed subsets of
$Z$ are in bijective correspondence with closed subsets of ![]() $|Z|$, so by union of closed substacks we mean union of subsets of
$|Z|$, so by union of closed substacks we mean union of subsets of ![]() $|Z|$). There is a natural map of pairs
$|Z|$). There is a natural map of pairs ![]() $\operatorname {cyl}(X,A)\to (X,A)$. A map of pairs
$\operatorname {cyl}(X,A)\to (X,A)$. A map of pairs ![]() $f:(X,A)\to (X',A')$ induces a map
$f:(X,A)\to (X',A')$ induces a map ![]() $\operatorname {cyl}(f):\operatorname {cyl}(X,A)\to \operatorname {cyl}(X',A')$.
$\operatorname {cyl}(f):\operatorname {cyl}(X,A)\to \operatorname {cyl}(X',A')$.
Lemma 6.7 For any pair ![]() $(X,A)$ where
$(X,A)$ where ![]() $A$ is a paracompact orbispace,
$A$ is a paracompact orbispace, ![]() $K^0(\operatorname {cyl}(X,A))$ is an abelian group.
$K^0(\operatorname {cyl}(X,A))$ is an abelian group.
Proof. Let ![]() $(E_0,E_1,i:E_0|_{A\times \{1\}}\to E_1|_{A\times \{1\}})$ be a triple representing an arbitrary element of
$(E_0,E_1,i:E_0|_{A\times \{1\}}\to E_1|_{A\times \{1\}})$ be a triple representing an arbitrary element of ![]() $K^0(\operatorname {cyl}(X,A))$. We claim that the triple
$K^0(\operatorname {cyl}(X,A))$. We claim that the triple ![]() $(E_1,E_0,-i)$ is an inverse to it. It suffices to show that
$(E_1,E_0,-i)$ is an inverse to it. It suffices to show that
are isomorphic. In other words, it suffices to show that ![]() $(\begin {smallmatrix}0 & -i\\i & \hfill 0\end {smallmatrix})$ is the restriction to
$(\begin {smallmatrix}0 & -i\\i & \hfill 0\end {smallmatrix})$ is the restriction to ![]() $A\times \{1\}$ of an automorphism of
$A\times \{1\}$ of an automorphism of ![]() $E_0\oplus E_1$. By Lemma 6.3, there exist isomorphisms
$E_0\oplus E_1$. By Lemma 6.3, there exist isomorphisms ![]() $E_i|_{A\times [0,1]}=p_A^*(E_i|_{A\times \{1\}})$. In such coordinates, the desired automorphism of
$E_i|_{A\times [0,1]}=p_A^*(E_i|_{A\times \{1\}})$. In such coordinates, the desired automorphism of ![]() $E_0\oplus E_1$ may be given by
$E_0\oplus E_1$ may be given by
on ![]() $A\times [0,1]$ and the identity on
$A\times [0,1]$ and the identity on ![]() $X\times \{0\}$ (note that to specify a map of vector bundles over a stack, it suffices to specify its restriction to each member of a finite cover by closed substacks, subject to the requirement that these restrictions agree on their pairwise overlaps).
$X\times \{0\}$ (note that to specify a map of vector bundles over a stack, it suffices to specify its restriction to each member of a finite cover by closed substacks, subject to the requirement that these restrictions agree on their pairwise overlaps).
Lemma 6.8 For any pair ![]() $(X,A)$ where
$(X,A)$ where ![]() $A$ is a paracompact orbispace, the map
$A$ is a paracompact orbispace, the map ![]() $K^0(X,A)\to K^0(\operatorname {cyl}(X,A))$ is surjective.
$K^0(X,A)\to K^0(\operatorname {cyl}(X,A))$ is surjective.
Proof. We claim that every vector bundle on ![]() $(X\times \{0\})\cup (A\times [0,1])$ is pulled back from
$(X\times \{0\})\cup (A\times [0,1])$ is pulled back from ![]() $X$. Let
$X$. Let ![]() $E$ be a vector bundle on
$E$ be a vector bundle on ![]() $\operatorname {cyl}(X,A)$, let
$\operatorname {cyl}(X,A)$, let ![]() $F$ denote its restriction to
$F$ denote its restriction to ![]() $X=X\times \{0\}$, and let us show that
$X=X\times \{0\}$, and let us show that ![]() $E=p_X^*F$. The identity map is an identification of
$E=p_X^*F$. The identity map is an identification of ![]() $E$ and
$E$ and ![]() $p_X^*F$ over
$p_X^*F$ over ![]() $X\times \{0\}$, and by Lemma 6.3 there is an identification of
$X\times \{0\}$, and by Lemma 6.3 there is an identification of ![]() $E$ and
$E$ and ![]() $p_X^*F$ over
$p_X^*F$ over ![]() $A\times [0,1]$ which agrees with the identity over
$A\times [0,1]$ which agrees with the identity over ![]() $A\times \{0\}$. These isomorphisms
$A\times \{0\}$. These isomorphisms ![]() $E\to p_X^*F$ thus patch together to define the desired isomorphism.
$E\to p_X^*F$ thus patch together to define the desired isomorphism.
As every vector bundle on ![]() $(X\times \{0\})\cup (A\times [0,1])$ is pulled back from
$(X\times \{0\})\cup (A\times [0,1])$ is pulled back from ![]() $X$, it follows that
$X$, it follows that ![]() $\operatorname {Tri}(X,A)\to \operatorname {Tri}(\operatorname {cyl}(X,A))$ is surjective, so we are done.
$\operatorname {Tri}(X,A)\to \operatorname {Tri}(\operatorname {cyl}(X,A))$ is surjective, so we are done.
Lemma 6.9 For every vector bundle ![]() $E$ over an orbispace
$E$ over an orbispace ![]() $X$, there exists an open cover
$X$, there exists an open cover ![]() $X=\bigcup _iZ_i/G_i$ such that the restriction of
$X=\bigcup _iZ_i/G_i$ such that the restriction of ![]() $E$ to each
$E$ to each ![]() $Z_i/G_i$ is pulled back from
$Z_i/G_i$ is pulled back from ![]() $*/G_i$ (equivalently, the pullback of
$*/G_i$ (equivalently, the pullback of ![]() $E$ to
$E$ to ![]() $Z_i$ is
$Z_i$ is ![]() $G_i$-equivariantly trivial).
$G_i$-equivariantly trivial).
Proof. Every point ![]() $x\in X$ has an open neighborhood of the form
$x\in X$ has an open neighborhood of the form ![]() $Z/G$ by Proposition 3.3. Choose a lift
$Z/G$ by Proposition 3.3. Choose a lift ![]() $z\in Z$ of
$z\in Z$ of ![]() $x$, and by shrinking
$x$, and by shrinking ![]() $Z$ and replacing
$Z$ and replacing ![]() $G$ with the stabilizer of
$G$ with the stabilizer of ![]() $z$, assume that
$z$, assume that ![]() $G$ fixes
$G$ fixes ![]() $z$. Choose a map from
$z$. Choose a map from ![]() $E|_Z$ to the trivial bundle
$E|_Z$ to the trivial bundle ![]() $E_z\times Z$ which is the identity at
$E_z\times Z$ which is the identity at ![]() $z$, average this map to make it
$z$, average this map to make it ![]() $G$-equivariant, and shrink
$G$-equivariant, and shrink ![]() $Z$ so that this map is an isomorphism over all of
$Z$ so that this map is an isomorphism over all of ![]() $Z$.
$Z$.
Lemma 6.10 Let ![]() $G\curvearrowright Z$ be a finite group action on a Hausdorff topological space. If
$G\curvearrowright Z$ be a finite group action on a Hausdorff topological space. If ![]() $Z/G$ is paracompact, then so is
$Z/G$ is paracompact, then so is ![]() $Z$.
$Z$.
Proof. Let an open covering ![]() $Z=\bigcup _\alpha V_\alpha$ be given. For every
$Z=\bigcup _\alpha V_\alpha$ be given. For every ![]() $z\in Z$, there exists an open neighborhood
$z\in Z$, there exists an open neighborhood ![]() $U$ of
$U$ of ![]() $z$ which is
$z$ which is ![]() $G_z$-invariant and whose
$G_z$-invariant and whose ![]() $G/G_z$-translates are disjoint and each contained in some (possibly different)
$G/G_z$-translates are disjoint and each contained in some (possibly different) ![]() $V_\alpha$. The images of such
$V_\alpha$. The images of such ![]() $U$ in
$U$ in ![]() $Z/G$ form an open covering of
$Z/G$ form an open covering of ![]() $Z/G$. Refining this to a locally finite covering and taking inverse images in
$Z/G$. Refining this to a locally finite covering and taking inverse images in ![]() $Z$ gives the desired locally finite refinement of the original covering.
$Z$ gives the desired locally finite refinement of the original covering.
Lemma 6.11 Let ![]() $X$ be a paracompact orbispace, let
$X$ be a paracompact orbispace, let ![]() $E$ be a vector bundle over
$E$ be a vector bundle over ![]() $X$, and let
$X$, and let ![]() $Y\subseteq X$ be a closed substack. Every section of
$Y\subseteq X$ be a closed substack. Every section of ![]() $E|_Y$ extends to a section of
$E|_Y$ extends to a section of ![]() $E$.
$E$.
Proof. Fix an open cover ![]() $X=\bigcup _iZ_i/G_i$ such that the pullback of
$X=\bigcup _iZ_i/G_i$ such that the pullback of ![]() $E$ to each
$E$ to each ![]() $Z_i$ is trivialized
$Z_i$ is trivialized ![]() $G_i$-equivariantly (Lemma 6.9). Let
$G_i$-equivariantly (Lemma 6.9). Let ![]() $\varphi _i:|X|\to [0,1]$ be a partition of unity subordinate to this covering. Now
$\varphi _i:|X|\to [0,1]$ be a partition of unity subordinate to this covering. Now ![]() $\operatorname {supp}\varphi _i$ is a closed subset of a paracompact Hausdorff space, hence paracompact Hausdorff; its inverse image inside
$\operatorname {supp}\varphi _i$ is a closed subset of a paracompact Hausdorff space, hence paracompact Hausdorff; its inverse image inside ![]() $Z_i$ is, thus, paracompact Hausdorff by Lemma 6.10 (recall
$Z_i$ is, thus, paracompact Hausdorff by Lemma 6.10 (recall ![]() $Z_i$ is Hausdorff). Thus, by the Tietze extension theorem, our given section on
$Z_i$ is Hausdorff). Thus, by the Tietze extension theorem, our given section on ![]() $Z_i\times _X(Y\cap \operatorname {supp}\varphi _i)$ extends to
$Z_i\times _X(Y\cap \operatorname {supp}\varphi _i)$ extends to ![]() $Z_i\times _X\operatorname {supp}\varphi _i$. We can make it
$Z_i\times _X\operatorname {supp}\varphi _i$. We can make it ![]() $G_i$-equivariant by averaging, so our given section on
$G_i$-equivariant by averaging, so our given section on ![]() $Y\cap \operatorname {supp}\varphi _i$ extends to
$Y\cap \operatorname {supp}\varphi _i$ extends to ![]() $\operatorname {supp}\varphi _i$. Now
$\operatorname {supp}\varphi _i$. Now ![]() $(\operatorname {supp}\varphi _i)^\circ$ is an open cover of
$(\operatorname {supp}\varphi _i)^\circ$ is an open cover of ![]() $X$, so pick another partition of unity
$X$, so pick another partition of unity ![]() $\psi _i$ subordinate to this cover, and use it to patch together the extended sections on each
$\psi _i$ subordinate to this cover, and use it to patch together the extended sections on each ![]() $\operatorname {supp}\varphi _i$.
$\operatorname {supp}\varphi _i$.
Lemma 6.12 For any paracompact orbispace pair ![]() $(X,A)$, the map
$(X,A)$, the map ![]() $K^0(X,A)\to K^0(\operatorname {cyl}(X,A))$ is an isomorphism.
$K^0(X,A)\to K^0(\operatorname {cyl}(X,A))$ is an isomorphism.
Proof. We know from the proof of Lemma 6.8 that every vector bundle on ![]() $(X\times \{0\})\cup (A\times [0,1])$ is pulled back from
$(X\times \{0\})\cup (A\times [0,1])$ is pulled back from ![]() $X$. Given this fact, it suffices to show that the pullback map
$X$. Given this fact, it suffices to show that the pullback map ![]() $\operatorname {Tri}(X,A)\to \operatorname {Tri}(\operatorname {cyl}(X,A))$ is injective. Thus, suppose that we are given two triples
$\operatorname {Tri}(X,A)\to \operatorname {Tri}(\operatorname {cyl}(X,A))$ is injective. Thus, suppose that we are given two triples ![]() $(E_0,E_1,i:E_0|_A\to E_1|_A)$ and
$(E_0,E_1,i:E_0|_A\to E_1|_A)$ and ![]() $(E_0',E_1',i':E_0'|_A\to E_1'|_A)$ whose pullbacks to
$(E_0',E_1',i':E_0'|_A\to E_1'|_A)$ whose pullbacks to ![]() $\operatorname {cyl}(X,A)$ coincide, meaning that there are isomorphisms
$\operatorname {cyl}(X,A)$ coincide, meaning that there are isomorphisms ![]() $\alpha _i:p_X^*E_i\to p_X^*E_i'$ on
$\alpha _i:p_X^*E_i\to p_X^*E_i'$ on ![]() $(X\times \{0\})\cup (A\times [0,1])$ intertwining
$(X\times \{0\})\cup (A\times [0,1])$ intertwining ![]() $i$ and
$i$ and ![]() $i'$ over
$i'$ over ![]() $A\times \{1\}$. Now these maps
$A\times \{1\}$. Now these maps ![]() $\alpha _i$ extend to all of
$\alpha _i$ extend to all of ![]() $X\times [0,1]$ by Lemma 6.11, and these extended maps are isomorphisms over open neighborhood of
$X\times [0,1]$ by Lemma 6.11, and these extended maps are isomorphisms over open neighborhood of ![]() $(X\times \{0\})\cup (A\times [0,1])$. As
$(X\times \{0\})\cup (A\times [0,1])$. As ![]() $X\times [0,1]\to X$ is universally closed (being a pullback of
$X\times [0,1]\to X$ is universally closed (being a pullback of ![]() $[0,1]\to *$), this neighborhood contains
$[0,1]\to *$), this neighborhood contains ![]() $U\times [0,1]$ for some open neighborhood
$U\times [0,1]$ for some open neighborhood ![]() $U$ of
$U$ of ![]() $A\subseteq X$. Now a paracompact Hausdorff space is normal, so by Urysohn's lemma there exists a continuous function
$A\subseteq X$. Now a paracompact Hausdorff space is normal, so by Urysohn's lemma there exists a continuous function ![]() $\varphi :|X|\to [0,1]$ supported inside
$\varphi :|X|\to [0,1]$ supported inside ![]() $U$ which is identically
$U$ which is identically ![]() $1$ on
$1$ on ![]() $A$. Pulling back
$A$. Pulling back ![]() $\alpha _i$ under the graph of
$\alpha _i$ under the graph of ![]() $\varphi$ defines isomorphisms
$\varphi$ defines isomorphisms ![]() $E_i\to E_i'$ whose restrictions to
$E_i\to E_i'$ whose restrictions to ![]() $A$ intertwine
$A$ intertwine ![]() $i$ and
$i$ and ![]() $i'$, showing that the original triples on
$i'$, showing that the original triples on ![]() $(X,A)$ are isomorphic.
$(X,A)$ are isomorphic.
Proposition 6.13 (Relative homotopy invariance)
For any map of paracompact orbispace pairs ![]() $(X,A)\to (X',A')$ whose constituent maps
$(X,A)\to (X',A')$ whose constituent maps ![]() $X\to X'$ and
$X\to X'$ and ![]() $A\to A'$ are individually homotopy equivalences, the map
$A\to A'$ are individually homotopy equivalences, the map ![]() $K^0(X',A')\to K^0(X,A)$ is an isomorphism.
$K^0(X',A')\to K^0(X,A)$ is an isomorphism.
Proof. We begin by showing that the two maps ![]() $K^0(X\times [0,1],A\times [0,1])\to K^0(X,A)$ (pullback under
$K^0(X\times [0,1],A\times [0,1])\to K^0(X,A)$ (pullback under ![]() $\times \{0\}$ and
$\times \{0\}$ and ![]() $\times \{1\}$) coincide (from which it follows that homotopic maps of pairs induce the same map on relative
$\times \{1\}$) coincide (from which it follows that homotopic maps of pairs induce the same map on relative ![]() $K^0$). As vector bundles on
$K^0$). As vector bundles on ![]() $X\times [0,1]$ are pulled back from
$X\times [0,1]$ are pulled back from ![]() $X$ by Proposition 6.3, this amounts to showing that triples
$X$ by Proposition 6.3, this amounts to showing that triples ![]() $(E_0,E_1,i),(E_0,E_1,j)\in \operatorname {Tri}(X,A)$ represent the same element of
$(E_0,E_1,i),(E_0,E_1,j)\in \operatorname {Tri}(X,A)$ represent the same element of ![]() $K^0(X,A)$ if
$K^0(X,A)$ if ![]() $i$ and
$i$ and ![]() $j$ are homotopic. The construction from the proof of Lemma 6.7 shows that the homotopy between
$j$ are homotopic. The construction from the proof of Lemma 6.7 shows that the homotopy between ![]() $i^{-1}\circ j$ and the identity gives rise to an isomorphism between the pullbacks of these triples to
$i^{-1}\circ j$ and the identity gives rise to an isomorphism between the pullbacks of these triples to ![]() $\operatorname {cyl}(X,A)$, which is enough by Lemma 6.12.
$\operatorname {cyl}(X,A)$, which is enough by Lemma 6.12.
As homotopic maps of pairs induce the same map on relative ![]() $K^0$, it follows that homotopy equivalences of pairs induce isomorphisms on relative
$K^0$, it follows that homotopy equivalences of pairs induce isomorphisms on relative ![]() $K^0$. In light of Lemma 6.12, it thus suffices to show that a map of pairs
$K^0$. In light of Lemma 6.12, it thus suffices to show that a map of pairs ![]() $(X,A)\to (X',A')$ whose constituent maps
$(X,A)\to (X',A')$ whose constituent maps ![]() $X\to X'$ and
$X\to X'$ and ![]() $A\to A'$ are individually homotopy equivalences induces a homotopy equivalence of pairs
$A\to A'$ are individually homotopy equivalences induces a homotopy equivalence of pairs ![]() $\operatorname {cyl}(X,A)\to \operatorname {cyl}(X',A')$. This is well known: given
$\operatorname {cyl}(X,A)\to \operatorname {cyl}(X',A')$. This is well known: given ![]() $(f,g):(X,A)\to (X',A')$, let
$(f,g):(X,A)\to (X',A')$, let ![]() $p:X'\to X$ and
$p:X'\to X$ and ![]() $q:A'\to A$ be homotopy inverses to
$q:A'\to A$ be homotopy inverses to ![]() $f$ and
$f$ and ![]() $g$. To define a map
$g$. To define a map ![]() $\operatorname {cyl}(X',A')\to \operatorname {cyl}(X,A)$ which is
$\operatorname {cyl}(X',A')\to \operatorname {cyl}(X,A)$ which is ![]() $p$ on
$p$ on ![]() $X'\times \{0\}$ and
$X'\times \{0\}$ and ![]() $q$ on
$q$ on ![]() $A'\times \{1\}$, we need a homotopy between the two maps
$A'\times \{1\}$, we need a homotopy between the two maps ![]() $p|_{A'},q:A'\to X$. A distinguished homotopy class of such homotopies is furnished by composing further with the homotopy equivalence
$p|_{A'},q:A'\to X$. A distinguished homotopy class of such homotopies is furnished by composing further with the homotopy equivalence ![]() $f:X\to X'$ and fixing homotopies between
$f:X\to X'$ and fixing homotopies between ![]() $f\circ p$ and
$f\circ p$ and ![]() $\operatorname {id}_{X'}$ and between
$\operatorname {id}_{X'}$ and between ![]() $f|_A\circ q=g\circ q$ and
$f|_A\circ q=g\circ q$ and ![]() $\operatorname {id}_{A'}$. One then checks that this map
$\operatorname {id}_{A'}$. One then checks that this map ![]() $\operatorname {cyl}(X',A')\to \operatorname {cyl}(X,A)$ is a homotopy inverse to the map
$\operatorname {cyl}(X',A')\to \operatorname {cyl}(X,A)$ is a homotopy inverse to the map ![]() $\operatorname {cyl}(X,A)\to \operatorname {cyl}(X',A')$.
$\operatorname {cyl}(X,A)\to \operatorname {cyl}(X',A')$.
Lemma 6.14 Let ![]() $X$ be a paracompact orbispace. Every vector bundle
$X$ be a paracompact orbispace. Every vector bundle ![]() $E$ over a closed substack
$E$ over a closed substack ![]() $Y\subseteq X$ is the restriction of a vector bundle over some open substack
$Y\subseteq X$ is the restriction of a vector bundle over some open substack ![]() $U\subseteq X$ containing
$U\subseteq X$ containing ![]() $Y$.
$Y$.
Proof. Fix a locally finite open cover ![]() $X=\bigcup _iZ_i/G_i$ such that the pullback of
$X=\bigcup _iZ_i/G_i$ such that the pullback of ![]() $E$ to each
$E$ to each ![]() $(Z_i)_Y:=Z_i\times _XY\subseteq Z_i$ is trivialized
$(Z_i)_Y:=Z_i\times _XY\subseteq Z_i$ is trivialized ![]() $G_i$-equivariantly (Lemma 6.9). Such trivializations evidently extend
$G_i$-equivariantly (Lemma 6.9). Such trivializations evidently extend ![]() $E|_{Y\cap (Z_i/G_i)}$ to
$E|_{Y\cap (Z_i/G_i)}$ to ![]() $Z_i/G_i$. We patch together these extensions
$Z_i/G_i$. We patch together these extensions ![]() $E_i$ on
$E_i$ on ![]() $Z_i/G_i$ as follows.
$Z_i/G_i$ as follows.
Choose closed substacks ![]() $K_i\subseteq X$ with
$K_i\subseteq X$ with ![]() $K_i\subseteq Z_i/G_i$ and whose interiors cover
$K_i\subseteq Z_i/G_i$ and whose interiors cover ![]() $X$. We thus have a collection of transition functions
$X$. We thus have a collection of transition functions ![]() $\alpha _{ij}:K_i\cap K_j\cap Y\to \operatorname {Hom}(E_i,E_j)$ satisfying
$\alpha _{ij}:K_i\cap K_j\cap Y\to \operatorname {Hom}(E_i,E_j)$ satisfying ![]() $\alpha _{ii}=\operatorname {id}$ and
$\alpha _{ii}=\operatorname {id}$ and ![]() $\alpha _{ij}\alpha _{jk}\alpha _{ki}=\operatorname {id}$ over
$\alpha _{ij}\alpha _{jk}\alpha _{ki}=\operatorname {id}$ over ![]() $K_i\cap K_j\cap K_k\cap Y$. We now execute the following operation for every pair
$K_i\cap K_j\cap K_k\cap Y$. We now execute the following operation for every pair ![]() $(i,j)$ inductively according to an arbitrary well-ordering of such pairs. For
$(i,j)$ inductively according to an arbitrary well-ordering of such pairs. For ![]() $i=j$, do nothing. For
$i=j$, do nothing. For ![]() $i\ne j$, choose an extension of
$i\ne j$, choose an extension of ![]() $\alpha _{ij}$ from
$\alpha _{ij}$ from ![]() $K_i\cap K_j\cap Y$ to
$K_i\cap K_j\cap Y$ to ![]() $K_i\cap K_j$ using Lemma 6.11. This extension remains an isomorphism in a neighborhood of
$K_i\cap K_j$ using Lemma 6.11. This extension remains an isomorphism in a neighborhood of ![]() $K_i\cap K_j\cap Y$. As (the coarse space of)
$K_i\cap K_j\cap Y$. As (the coarse space of) ![]() $K_i\cap K_j$ is paracompact Hausdorff, hence normal, we may choose a closed substack
$K_i\cap K_j$ is paracompact Hausdorff, hence normal, we may choose a closed substack ![]() $A\subseteq K_i\cap K_j$ whose interior contains
$A\subseteq K_i\cap K_j$ whose interior contains ![]() $K_i\cap K_j\cap Y$ and over which the extension of
$K_i\cap K_j\cap Y$ and over which the extension of ![]() $\alpha _{ij}$ is an isomorphism. Now this new
$\alpha _{ij}$ is an isomorphism. Now this new ![]() $\alpha _{ij}$ over
$\alpha _{ij}$ over ![]() $A$ gives unique extensions of the remaining
$A$ gives unique extensions of the remaining ![]() $\alpha _{k\ell }$ to
$\alpha _{k\ell }$ to ![]() $K_k\cap K_\ell \cap (Y\cup A)$ such that the cocycle condition is satisfied. We now replace
$K_k\cap K_\ell \cap (Y\cup A)$ such that the cocycle condition is satisfied. We now replace ![]() $Y$ with
$Y$ with ![]() $Y\cup A$ and go on to the next pair of indices. Note that because our cover
$Y\cup A$ and go on to the next pair of indices. Note that because our cover ![]() $X=\bigcup _iZ_i/G_i$ is locally finite, the set
$X=\bigcup _iZ_i/G_i$ is locally finite, the set ![]() $Y$ remains closed even after possibly infinitely many steps.
$Y$ remains closed even after possibly infinitely many steps.
After processing every pair ![]() $(i,j)$, our extended transition functions define a vector bundle on a closed substack
$(i,j)$, our extended transition functions define a vector bundle on a closed substack ![]() $\bar Y\subseteq X$ whose restriction to
$\bar Y\subseteq X$ whose restriction to ![]() $Y\subseteq \bar Y$ is
$Y\subseteq \bar Y$ is ![]() $E$, and by construction
$E$, and by construction ![]() $Y$ is contained in the interior of
$Y$ is contained in the interior of ![]() $\bar Y$.
$\bar Y$.
We now come to the exactness and excision properties of ![]() $K$-theory, where we finally make use of Corollary 1.4.
$K$-theory, where we finally make use of Corollary 1.4.
For the proof of exactness, we make use of the following notion. Let us call a map of abelian monoids ![]() $f:M\to N$ cofinal if and only if for every
$f:M\to N$ cofinal if and only if for every ![]() $n\in N$ there exist
$n\in N$ there exist ![]() $m\in M$ and
$m\in M$ and ![]() $n'\in N$ with
$n'\in N$ with ![]() $f(m)=n+n'$. The quotient
$f(m)=n+n'$. The quotient ![]() $M/M'$ is an abelian group if and only if
$M/M'$ is an abelian group if and only if ![]() $M'\to M$ is cofinal. The conclusion of Corollary 1.4 for a map
$M'\to M$ is cofinal. The conclusion of Corollary 1.4 for a map ![]() $Y\to X$ is that the pullback map
$Y\to X$ is that the pullback map ![]() $\operatorname {Vect}(X)\to \operatorname {Vect}(Y)$ is cofinal (recalling from Corollary 5.2 that every inclusion of vector bundles over a paracompact orbispace is split).
$\operatorname {Vect}(X)\to \operatorname {Vect}(Y)$ is cofinal (recalling from Corollary 5.2 that every inclusion of vector bundles over a paracompact orbispace is split).
Proposition 6.15 (Exactness)
Let ![]() $X$ be an orbispace satisfying the hypothesis of Theorem 1.1, let
$X$ be an orbispace satisfying the hypothesis of Theorem 1.1, let ![]() $A\subseteq X\supseteq Y$ be closed substacks, let
$A\subseteq X\supseteq Y$ be closed substacks, let ![]() $B:=A\cap Y$ be their intersection, and let
$B:=A\cap Y$ be their intersection, and let ![]() $A\cup _BY\subseteq X$ be their union. The following sequence is exact:
$A\cup _BY\subseteq X$ be their union. The following sequence is exact:
Proof. The sequence
is exact in the sense that the image of the first map coincides with the inverse image of ![]() $\operatorname {Vect}(Y)$ under the second map. Indeed, given a triple
$\operatorname {Vect}(Y)$ under the second map. Indeed, given a triple ![]() $(E_0,E_1,i)\in \operatorname {Tri}(X,A)$ for which
$(E_0,E_1,i)\in \operatorname {Tri}(X,A)$ for which ![]() $i|_B$ extends to
$i|_B$ extends to ![]() $Y$, we may glue this extension to
$Y$, we may glue this extension to ![]() $i$ over
$i$ over ![]() $B$ to lift
$B$ to lift ![]() $(E_0,E_1,i)$ from
$(E_0,E_1,i)$ from ![]() $\operatorname {Tri}(X,A)$ to
$\operatorname {Tri}(X,A)$ to ![]() $\operatorname {Tri}(X,A\cup _BY)$. Quotienting this sequence by
$\operatorname {Tri}(X,A\cup _BY)$. Quotienting this sequence by ![]() $\operatorname {Vect}(X)$, we conclude that
$\operatorname {Vect}(X)$, we conclude that
is exact. Now ![]() $\operatorname {Vect}(X)\to \operatorname {Vect}(Y)$ is cofinal by Corollary 1.4, so
$\operatorname {Vect}(X)\to \operatorname {Vect}(Y)$ is cofinal by Corollary 1.4, so ![]() $\operatorname {Vect}(Y)/\operatorname {Vect}(X)$ is an abelian group, so the kernel of the map from
$\operatorname {Vect}(Y)/\operatorname {Vect}(X)$ is an abelian group, so the kernel of the map from ![]() $\operatorname {Tri}(Y,B)/\operatorname {Vect}(X)$ to its quotient by
$\operatorname {Tri}(Y,B)/\operatorname {Vect}(X)$ to its quotient by ![]() $\operatorname {Vect}(Y)/\operatorname {Vect}(X)$ is precisely
$\operatorname {Vect}(Y)/\operatorname {Vect}(X)$ is precisely ![]() $\operatorname {Vect}(Y)/\operatorname {Vect}(X)$. This quotient is simply
$\operatorname {Vect}(Y)/\operatorname {Vect}(X)$. This quotient is simply ![]() $\operatorname {Tri}(Y,B)/\operatorname {Vect}(Y)=K^0(Y,B)$, so we are done.
$\operatorname {Tri}(Y,B)/\operatorname {Vect}(Y)=K^0(Y,B)$, so we are done.
For the proof of excision, we make use of the following alternative description of relative ![]() $K$-theory in terms of direct limits. Let
$K$-theory in terms of direct limits. Let ![]() $\widehat {\operatorname {Vect}}(X)$ denote the category whose objects are vector bundles on
$\widehat {\operatorname {Vect}}(X)$ denote the category whose objects are vector bundles on ![]() $X$ of bounded rank and whose morphisms are homotopy classes of injective maps. The category
$X$ of bounded rank and whose morphisms are homotopy classes of injective maps. The category ![]() $\widehat {\operatorname {Vect}}(X)$ is filtered, meaning that (1) it is nonempty, (2) for every pair of objects
$\widehat {\operatorname {Vect}}(X)$ is filtered, meaning that (1) it is nonempty, (2) for every pair of objects ![]() $x,y$, there exist morphisms
$x,y$, there exist morphisms ![]() $x\to z\leftarrow y$, and (3) for every pair of morphisms
$x\to z\leftarrow y$, and (3) for every pair of morphisms ![]() $x\rightrightarrows y$ there exists a morphism
$x\rightrightarrows y$ there exists a morphism ![]() $y\to z$ such that the two compositions
$y\to z$ such that the two compositions ![]() $x\to z$ coincide. Indeed, (1) we have the zero vector bundle, (2) given vector bundles
$x\to z$ coincide. Indeed, (1) we have the zero vector bundle, (2) given vector bundles ![]() $E$ and
$E$ and ![]() $F$, they both admit a morphism to
$F$, they both admit a morphism to ![]() $E\oplus F$, and (3) given two injections
$E\oplus F$, and (3) given two injections ![]() $E\hookrightarrow F$, they become homotopic after composing with the inclusion
$E\hookrightarrow F$, they become homotopic after composing with the inclusion ![]() $F\hookrightarrow F\oplus E$.
$F\hookrightarrow F\oplus E$.
For any map of stacks ![]() $f:Y\to X$ and any vector bundle
$f:Y\to X$ and any vector bundle ![]() $F$ on
$F$ on ![]() $Y$, let
$Y$, let ![]() $\operatorname {Vect}(X,F)$ denote the set of isomorphism classes of pairs
$\operatorname {Vect}(X,F)$ denote the set of isomorphism classes of pairs ![]() $(V,i)$ consisting of a vector bundle
$(V,i)$ consisting of a vector bundle ![]() $V$ on
$V$ on ![]() $X$ of bounded rank and an isomorphism
$X$ of bounded rank and an isomorphism ![]() $i:f^*V\xrightarrow \sim F$. If
$i:f^*V\xrightarrow \sim F$. If ![]() $X$ is a paracompact orbispace,
$X$ is a paracompact orbispace, ![]() $\operatorname {Vect}(X,f^*E)$ forms a directed system over
$\operatorname {Vect}(X,f^*E)$ forms a directed system over ![]() $E\in \widehat {\operatorname {Vect}}(X)$. Indeed, given an inclusion
$E\in \widehat {\operatorname {Vect}}(X)$. Indeed, given an inclusion ![]() $E\hookrightarrow E'$, there is a natural map
$E\hookrightarrow E'$, there is a natural map ![]() $\operatorname {Vect}(X,f^*E)\xrightarrow {{}\oplus (E'/E)}\operatorname {Vect}(X,f^*E')$ because the inclusion
$\operatorname {Vect}(X,f^*E)\xrightarrow {{}\oplus (E'/E)}\operatorname {Vect}(X,f^*E')$ because the inclusion ![]() $E\hookrightarrow E'$ has a(n automatically unique up to homotopy) splitting by Corollary 5.2. For such
$E\hookrightarrow E'$ has a(n automatically unique up to homotopy) splitting by Corollary 5.2. For such ![]() $X$, we claim that
$X$, we claim that ![]() $K^0(X,Y)$ may be expressed as the direct limit
$K^0(X,Y)$ may be expressed as the direct limit
Elements of the direct limit above are, by definition, equivalence classes of triples ![]() $(E,V,i)\in \operatorname {Tri}(X,Y)$. Two triples
$(E,V,i)\in \operatorname {Tri}(X,Y)$. Two triples ![]() $(E,V,i)$ and
$(E,V,i)$ and ![]() $(E',V',i')$ are equivalent in the above direct limit if and only if they become isomorphic after pushing both to a common
$(E',V',i')$ are equivalent in the above direct limit if and only if they become isomorphic after pushing both to a common ![]() $E\hookrightarrow E''\hookleftarrow E'$, which is the same as saying
$E\hookrightarrow E''\hookleftarrow E'$, which is the same as saying ![]() $(E,V,i)$ and
$(E,V,i)$ and ![]() $(E',V',i')$ are isomorphic after adding elements of
$(E',V',i')$ are isomorphic after adding elements of ![]() $\operatorname {Vect}(X)$.
$\operatorname {Vect}(X)$.
Recall that a functor ![]() $F$ between filtered categories is called cofinal if and only if (1) for every
$F$ between filtered categories is called cofinal if and only if (1) for every ![]() $x$ in the target there exists a morphism
$x$ in the target there exists a morphism ![]() $x\to F(y)$, and (2) for every two morphisms
$x\to F(y)$, and (2) for every two morphisms ![]() $x\rightrightarrows F(y)$, there exists a morphism
$x\rightrightarrows F(y)$, there exists a morphism ![]() $y\to z$ such that the compositions
$y\to z$ such that the compositions ![]() $x\to F(z)$ coincide. The significance of cofinality is that pulling back under a cofinal functor induces an isomorphism on direct limits:
$x\to F(z)$ coincide. The significance of cofinality is that pulling back under a cofinal functor induces an isomorphism on direct limits:
is an isomorphism for any cofinal functor ![]() $F:\mathsf {C}\to \mathsf {D}$ between filtered categories
$F:\mathsf {C}\to \mathsf {D}$ between filtered categories ![]() $\mathsf {C}$ and
$\mathsf {C}$ and ![]() $\mathsf {D}$ and any directed system of sets
$\mathsf {D}$ and any directed system of sets ![]() $A$ over
$A$ over ![]() $\mathsf {D}$.
$\mathsf {D}$.
The conclusion of Corollary 1.4 for ![]() $f:Y\to X$ is equivalent to the assertion that the pullback functor
$f:Y\to X$ is equivalent to the assertion that the pullback functor ![]() $f^*:\widehat {\operatorname {Vect}}(X)\to \widehat {\operatorname {Vect}}(Y)$ is cofinal. Indeed,
$f^*:\widehat {\operatorname {Vect}}(X)\to \widehat {\operatorname {Vect}}(Y)$ is cofinal. Indeed, ![]() $f^*$ always satisfies condition (2) because any two inclusions
$f^*$ always satisfies condition (2) because any two inclusions ![]() $E\hookrightarrow f^*F$ become homotopic upon postcomposing with
$E\hookrightarrow f^*F$ become homotopic upon postcomposing with ![]() $f^*(F\hookrightarrow F\oplus F)$, and condition (1) is precisely the conclusion of Corollary 1.4.
$f^*(F\hookrightarrow F\oplus F)$, and condition (1) is precisely the conclusion of Corollary 1.4.
Proposition 6.16 (Excision)
Let ![]() $X'\to X$ be a representable map of orbispaces satisfying the hypothesis of Theorem 1.1. Let
$X'\to X$ be a representable map of orbispaces satisfying the hypothesis of Theorem 1.1. Let ![]() $Y\to X$ be arbitrary, and let
$Y\to X$ be arbitrary, and let ![]() $Y'\to X'$ denote its pullback along
$Y'\to X'$ denote its pullback along ![]() $X'\to X$. If there is an open cover
$X'\to X$. If there is an open cover ![]() $X=U\cup V$ such that
$X=U\cup V$ such that ![]() $Y\to X$ is an isomorphism over
$Y\to X$ is an isomorphism over ![]() $U$ and
$U$ and ![]() $X'\to X$ is an isomorphism over
$X'\to X$ is an isomorphism over ![]() $V$, then the natural map
$V$, then the natural map ![]() $K^0(X,Y)\to K^0(X',Y')$ is an isomorphism.
$K^0(X,Y)\to K^0(X',Y')$ is an isomorphism.
Proof. We may write the map in question in terms of direct limits as
By Corollary 1.4, we may replace the second direct limit with the corresponding direct limit over ![]() $\widehat {\operatorname {Vect}}(X)$. It thus suffices to show that the pullback map
$\widehat {\operatorname {Vect}}(X)$. It thus suffices to show that the pullback map ![]() $\operatorname {Vect}(X,f^*E)\to \operatorname {Vect}(X',(f')^*E')$ is an isomorphism for every vector bundle
$\operatorname {Vect}(X,f^*E)\to \operatorname {Vect}(X',(f')^*E')$ is an isomorphism for every vector bundle ![]() $E$ on
$E$ on ![]() $X$ of bounded rank with
$X$ of bounded rank with ![]() $E':=E\times _XX'$. Since
$E':=E\times _XX'$. Since ![]() $Y\to X$ is an isomorphism over
$Y\to X$ is an isomorphism over ![]() $U$ and
$U$ and ![]() $X=U\cup V$, this coincides with the map
$X=U\cup V$, this coincides with the map ![]() $\operatorname {Vect}(V,f^*E|_V)\to \operatorname {Vect}(V\times _XX',(f')^*E|_V)$, which is a bijection since
$\operatorname {Vect}(V,f^*E|_V)\to \operatorname {Vect}(V\times _XX',(f')^*E|_V)$, which is a bijection since ![]() $X'\to X$ is an isomorphism over
$X'\to X$ is an isomorphism over ![]() $V$.
$V$.
Given the significance of the hypothesis of Theorem 1.1, it is essential to show that this property is preserved under various natural operations.
Lemma 6.17 For any topological stack ![]() $X$ and any locally compact Hausdorff space
$X$ and any locally compact Hausdorff space ![]() $R$, the natural map
$R$, the natural map ![]() $|X\times R|\to |X|\times R$ is an isomorphism.
$|X\times R|\to |X|\times R$ is an isomorphism.
Proof. For any atlas ![]() $U\to X$, the induced map
$U\to X$, the induced map ![]() $U\to |X|$ is a topological quotient map, meaning it is surjective and a subset of the target is open if and only if its inverse image in the source is open. Topological quotient maps are preserved by taking product with a locally compact Hausdorff space [Reference WhiteheadWhi48, Lemma 4], so
$U\to |X|$ is a topological quotient map, meaning it is surjective and a subset of the target is open if and only if its inverse image in the source is open. Topological quotient maps are preserved by taking product with a locally compact Hausdorff space [Reference WhiteheadWhi48, Lemma 4], so ![]() $U\times R\to |X|\times R$ is also a topological quotient map. As
$U\times R\to |X|\times R$ is also a topological quotient map. As ![]() $U\times R\to X\times R$ is also an atlas, the map
$U\times R\to X\times R$ is also an atlas, the map ![]() $U\times R\to |X\times R|$ is also a topological quotient map. Now
$U\times R\to |X\times R|$ is also a topological quotient map. Now ![]() $|X\times R|\to |X|\times R$ is a bijection, so we are done.
$|X\times R|\to |X|\times R$ is a bijection, so we are done.
Lemma 6.18 If a topological space ![]() $X$ is coarsely finite-dimensional, then so is
$X$ is coarsely finite-dimensional, then so is ![]() $X\times R$ for any closed subset
$X\times R$ for any closed subset ![]() $R\subseteq \mathbb {R}^n$.
$R\subseteq \mathbb {R}^n$.
Proof. We begin with the case ![]() $R=[0,1]$. Let a cover
$R=[0,1]$. Let a cover ![]() $X\times [0,1]=\bigcup _\alpha U_\alpha$ be given. For every
$X\times [0,1]=\bigcup _\alpha U_\alpha$ be given. For every ![]() $x\in X$ and
$x\in X$ and ![]() $t\in [0,1]$, there exists a pair of open neighborhoods
$t\in [0,1]$, there exists a pair of open neighborhoods ![]() $x\in V\subseteq X$ and
$x\in V\subseteq X$ and ![]() $t\in W\subseteq [0,1]$ such that
$t\in W\subseteq [0,1]$ such that ![]() $V\times W$ is contained in some
$V\times W$ is contained in some ![]() $U_\alpha$. Fixing
$U_\alpha$. Fixing ![]() $x\in X$ and using compactness of
$x\in X$ and using compactness of ![]() $[0,1]$, we see that there are finitely many such
$[0,1]$, we see that there are finitely many such ![]() $V_i\times W_i$ covering
$V_i\times W_i$ covering ![]() $\{x\}\times [0,1]$. Hence, there exists an open neighborhood
$\{x\}\times [0,1]$. Hence, there exists an open neighborhood ![]() $x\in V\subseteq X$ and an
$x\in V\subseteq X$ and an ![]() $\varepsilon >0$ such that
$\varepsilon >0$ such that ![]() $V\times ((t-\varepsilon,t+\varepsilon )\cap [0,1])$ is contained in some
$V\times ((t-\varepsilon,t+\varepsilon )\cap [0,1])$ is contained in some ![]() $U_\alpha$ for every
$U_\alpha$ for every ![]() $t\in [0,1]$. We consider the collection of all such pairs
$t\in [0,1]$. We consider the collection of all such pairs ![]() $(V,\varepsilon )$. As
$(V,\varepsilon )$. As ![]() $X$ is coarsely finite-dimensional, there is a collection of such pairs
$X$ is coarsely finite-dimensional, there is a collection of such pairs ![]() $(V_\alpha,\varepsilon _\alpha )$ such that the nerve of the covering
$(V_\alpha,\varepsilon _\alpha )$ such that the nerve of the covering ![]() $X=\bigcup _\alpha V_\alpha$ is finite-dimensional. Now cover
$X=\bigcup _\alpha V_\alpha$ is finite-dimensional. Now cover ![]() $X\times [0,1]$ by
$X\times [0,1]$ by ![]() $V_\alpha \times ([0,1]\cap \varepsilon _\alpha \cdot (k,k+2))$ for integers
$V_\alpha \times ([0,1]\cap \varepsilon _\alpha \cdot (k,k+2))$ for integers ![]() $k$.
$k$.
Next, we consider the case ![]() $R=\mathbb {R}$. Let a cover of
$R=\mathbb {R}$. Let a cover of ![]() $X\times \mathbb {R}$ be given. The intersection of this cover with
$X\times \mathbb {R}$ be given. The intersection of this cover with ![]() $X\times [n,n+2]$ has a refinement with finite-dimensional nerve by the case
$X\times [n,n+2]$ has a refinement with finite-dimensional nerve by the case ![]() $R=[0,1]$. Consider this refinement intersected with
$R=[0,1]$. Consider this refinement intersected with ![]() $X\times (n,n+2)$, and take union over all integers
$X\times (n,n+2)$, and take union over all integers ![]() $n$ to obtain a refinement of the original cover of
$n$ to obtain a refinement of the original cover of ![]() $X\times \mathbb {R}$ with finite-dimensional nerve.
$X\times \mathbb {R}$ with finite-dimensional nerve.
Finally, by induction, we obtain the case ![]() $R=\mathbb {R}^n$, and the general case follows because coarse finite-dimensionality passes to closed subsets.
$R=\mathbb {R}^n$, and the general case follows because coarse finite-dimensionality passes to closed subsets.
Corollary 6.19 If ![]() $X$ satisfies the hypothesis of Theorem 1.1, then so does
$X$ satisfies the hypothesis of Theorem 1.1, then so does ![]() $X\times R$ for any closed subset
$X\times R$ for any closed subset ![]() $R\subseteq \mathbb {R}^n$.
$R\subseteq \mathbb {R}^n$.
Let us now recall the Puppe sequence, which produces from Propositions 6.15 and 6.16 a long exact sequence. Let ![]() $(X,A)$ be any pair of orbispaces satisfying the hypothesis of Theorem 1.1. Let
$(X,A)$ be any pair of orbispaces satisfying the hypothesis of Theorem 1.1. Let ![]() $I:=[0,1]$. We now have maps of pairs
$I:=[0,1]$. We now have maps of pairs
 \begin{align*} &(A,\varnothing)\to(X,\varnothing)\to(X,A)\\ &(A\times I,A\times\partial I)\to(X\times I,X\times\partial I)\to(X\times I,(X\times\partial I)\cup(A\times I))\\ &(A\times I^2,A\times\partial I^2)\to(X\times I^2,X\times\partial I^2)\to(X\times I^2,(X\times\partial I^2)\cup(A\times I^2))\\ &\qquad\vdots \end{align*}
\begin{align*} &(A,\varnothing)\to(X,\varnothing)\to(X,A)\\ &(A\times I,A\times\partial I)\to(X\times I,X\times\partial I)\to(X\times I,(X\times\partial I)\cup(A\times I))\\ &(A\times I^2,A\times\partial I^2)\to(X\times I^2,X\times\partial I^2)\to(X\times I^2,(X\times\partial I^2)\cup(A\times I^2))\\ &\qquad\vdots \end{align*}
(note that these pairs satisfy the hypothesis of Theorem 1.1 by Corollary 6.19). We also have maps ![]() $(X\times I^k,(X\times \partial I^k)\cup (A\times I^k))\to (A\times I^{k+1},A\times \partial I^{k+1})$ up to inverting maps inducing isomorphisms on
$(X\times I^k,(X\times \partial I^k)\cup (A\times I^k))\to (A\times I^{k+1},A\times \partial I^{k+1})$ up to inverting maps inducing isomorphisms on ![]() $K^0$. Namely, these ‘connecting maps’ are given by
$K^0$. Namely, these ‘connecting maps’ are given by
 \begin{align*} &(X\times I^k\times I,(X\times\partial I^k\times I)\cup(A\times I^k\times\{1\}))\\ &\qquad\qquad\downarrow\\ &(X\times I^k\times I,(X\times\partial I^k\times I)\cup(A\times I^k\times\{1\})\cup(X\times I^k\times\{0\})) \end{align*}
\begin{align*} &(X\times I^k\times I,(X\times\partial I^k\times I)\cup(A\times I^k\times\{1\}))\\ &\qquad\qquad\downarrow\\ &(X\times I^k\times I,(X\times\partial I^k\times I)\cup(A\times I^k\times\{1\})\cup(X\times I^k\times\{0\})) \end{align*}
where we note that the domain admits a natural map to ![]() $(X\times I^k,(X\times \partial I^k)\cup (A\times I^k))$ (which induces an isomorphism on
$(X\times I^k,(X\times \partial I^k)\cup (A\times I^k))$ (which induces an isomorphism on ![]() $K^0$ by Proposition 6.13) and the target a natural map from
$K^0$ by Proposition 6.13) and the target a natural map from ![]() $(A\times I^{k+1},A\times \partial I^{k+1})$. To see that this second map also induces an isomorphism on
$(A\times I^{k+1},A\times \partial I^{k+1})$. To see that this second map also induces an isomorphism on ![]() $K^0$, factor it as
$K^0$, factor it as
 \begin{align*} (A\times I^k\times I&,(A\times\partial I^k\times I)\cup(A\times I^k\times\{1\})\cup(A\times I^k\times\{0\}))\\ &\qquad\downarrow\\ ((X\times I^k\times\{0\})\cup(A\times I^k\times I)&,(A\times\partial I^k\times I)\cup(A\times I^k\times\{1\})\cup(X\times I^k\times\{0\}))\\ &\qquad\downarrow\\ ((X\times I^k\times I)&,(X\times\partial I^k\times I)\cup(A\times I^k\times\{1\})\cup(X\times I^k\times\{0\})) \end{align*}
\begin{align*} (A\times I^k\times I&,(A\times\partial I^k\times I)\cup(A\times I^k\times\{1\})\cup(A\times I^k\times\{0\}))\\ &\qquad\downarrow\\ ((X\times I^k\times\{0\})\cup(A\times I^k\times I)&,(A\times\partial I^k\times I)\cup(A\times I^k\times\{1\})\cup(X\times I^k\times\{0\}))\\ &\qquad\downarrow\\ ((X\times I^k\times I)&,(X\times\partial I^k\times I)\cup(A\times I^k\times\{1\})\cup(X\times I^k\times\{0\})) \end{align*}
and observe that the first map is an isomorphism by excision Proposition 6.16 (and some manipulation involving adding ![]() $A\times I^k\times [0,\frac 12]$ to the second space of both pairs, which does not change their homotopy type but makes it possibly to apply Proposition 6.16) and the second map is an isomorphism by Proposition 6.13 (a homotopy inverse to
$A\times I^k\times [0,\frac 12]$ to the second space of both pairs, which does not change their homotopy type but makes it possibly to apply Proposition 6.16) and the second map is an isomorphism by Proposition 6.13 (a homotopy inverse to ![]() $(X\times I^k\times \{0\})\cup (A\times I^k\times I)\to X\times I^k\times I$ is given by projection to
$(X\times I^k\times \{0\})\cup (A\times I^k\times I)\to X\times I^k\times I$ is given by projection to ![]() $X\times I^k\times \{0\}$, and the second terms are both homotopy equivalent to
$X\times I^k\times \{0\}$, and the second terms are both homotopy equivalent to ![]() $(X\times D^k)\cup (A\times S^k)$).
$(X\times D^k)\cup (A\times S^k)$).
Definition 6.20 For any pair ![]() $(X,A)$, we defineFootnote 2
$(X,A)$, we defineFootnote 2
 \begin{align*} K^{-n}(X):&=K^0(X\times I^n,X\times\partial I^n),\\ K^{-n}(X,A):&=K^0(X\times I^n,(X\times\partial I^n)\cup(A\times I^n)). \end{align*}
\begin{align*} K^{-n}(X):&=K^0(X\times I^n,X\times\partial I^n),\\ K^{-n}(X,A):&=K^0(X\times I^n,(X\times\partial I^n)\cup(A\times I^n)). \end{align*} Given this definition, we can write the Puppe sequence above in a more familiar form. Namely, for ![]() $X$ an orbispace satisfying the hypothesis of Theorem 1.1, we have a sequence of the form
$X$ an orbispace satisfying the hypothesis of Theorem 1.1, we have a sequence of the form
functorial in the pair ![]() $(X,A)$.
$(X,A)$.
Proposition 6.21 (Long exact sequence)
The sequence above is exact.
Proof. Each of the following three triples satisfies the hypotheses of Proposition 6.15:
 \begin{align*} &(A\times I^k,A\times\partial I^k)\to(X\times I^k,X\times\partial I^k)\to(X\times I^k,(X\times\partial I^k)\cup(A\times I^k)),\\ &(X\times I^k,X\times\partial I^k)\xrightarrow{\times\{0\}}(X\times I^k\times I,(X\times\partial I^k\times I)\cup(A\times I^k\times\{1\}))\\ &\qquad\qquad\qquad\qquad\quad\to(X\times I^k\times I,(X\times\partial I^k\times I)\cup(A\times I^k\times\{1\})\cup(X\times I^k\times\{0\})),\\ &(X\times I^k\times[{\textstyle\frac 12},1],(X\times\partial I^k\times[{\textstyle\frac 12},1])\cup(A\times I^k\times\{1\}))\\ &\qquad\qquad\to(X\times I^k\times I,(X\times\partial I^k\times I)\cup(X\times I^k\times\{0\})\cup(A\times I^k\times\{1\}))\\ &\qquad\qquad\to(X\times I^k\times I,(X\times\partial I^k\times I)\cup(X\times I^k\times\{0\})\cup(X\times I^k\times[{\textstyle\frac 12},1])) \end{align*}
\begin{align*} &(A\times I^k,A\times\partial I^k)\to(X\times I^k,X\times\partial I^k)\to(X\times I^k,(X\times\partial I^k)\cup(A\times I^k)),\\ &(X\times I^k,X\times\partial I^k)\xrightarrow{\times\{0\}}(X\times I^k\times I,(X\times\partial I^k\times I)\cup(A\times I^k\times\{1\}))\\ &\qquad\qquad\qquad\qquad\quad\to(X\times I^k\times I,(X\times\partial I^k\times I)\cup(A\times I^k\times\{1\})\cup(X\times I^k\times\{0\})),\\ &(X\times I^k\times[{\textstyle\frac 12},1],(X\times\partial I^k\times[{\textstyle\frac 12},1])\cup(A\times I^k\times\{1\}))\\ &\qquad\qquad\to(X\times I^k\times I,(X\times\partial I^k\times I)\cup(X\times I^k\times\{0\})\cup(A\times I^k\times\{1\}))\\ &\qquad\qquad\to(X\times I^k\times I,(X\times\partial I^k\times I)\cup(X\times I^k\times\{0\})\cup(X\times I^k\times[{\textstyle\frac 12},1])) \end{align*}
and the last pair is homotopy equivalent to ![]() $(X\times I^k\times [0,\frac 12],(X\times \partial I^k\times [0,\frac 12])\cup (X\times I^k\times \{0\})\cup (X\times I^k\times \{\frac 12\}))$.
$(X\times I^k\times [0,\frac 12],(X\times \partial I^k\times [0,\frac 12])\cup (X\times I^k\times \{0\})\cup (X\times I^k\times \{\frac 12\}))$.
We now define a multiplicative structure on ![]() $K$-theory. There is a natural map
$K$-theory. There is a natural map ![]() $K^0(X)\otimes K^0(Y)\to K^0(X\times Y)$ sending
$K^0(X)\otimes K^0(Y)\to K^0(X\times Y)$ sending ![]() $[E]\otimes [F]$ to
$[E]\otimes [F]$ to ![]() $[E\boxtimes F]$. To define the tensor product map on relative
$[E\boxtimes F]$. To define the tensor product map on relative ![]() $K$-theory, we consider the following alternative model based on chain complexes.
$K$-theory, we consider the following alternative model based on chain complexes.
Definition 6.22 Let ![]() $(X,A)$ be a pair. Consider bounded complexes of vector bundles on
$(X,A)$ be a pair. Consider bounded complexes of vector bundles on ![]() $X$ which are exact over
$X$ which are exact over ![]() $A$. Let us call two such complexes homotopic if and only if they are the restrictions to
$A$. Let us call two such complexes homotopic if and only if they are the restrictions to ![]() $\times \{0\}$ and
$\times \{0\}$ and ![]() $\times \{1\}$ of a complex on
$\times \{1\}$ of a complex on ![]() $X\times [0,1]$ acyclic over
$X\times [0,1]$ acyclic over ![]() $A\times [0,1]$ (homotopy is an equivalence relation). Denote the set of homotopy classes of such complexes by
$A\times [0,1]$ (homotopy is an equivalence relation). Denote the set of homotopy classes of such complexes by ![]() $\operatorname {Kom}(X,A)$, which is an abelian monoid under direct sum, and define
$\operatorname {Kom}(X,A)$, which is an abelian monoid under direct sum, and define
This quotient is an abelian group: indeed, the sum of a complex and its shift is homotopic to the mapping cone of the identity map.
Proposition 6.23 There is a natural isomorphism ![]() $K^0(X,A)=K^0_\mathrm {kom}(X,A)$ for paracompact orbispace pairs
$K^0(X,A)=K^0_\mathrm {kom}(X,A)$ for paracompact orbispace pairs ![]() $(X,A)$.
$(X,A)$.
Proof. There is a natural map ![]() $K^0(X,A)\to K^0_\mathrm {kom}(X,A)$ defined as follows. Given a triple
$K^0(X,A)\to K^0_\mathrm {kom}(X,A)$ defined as follows. Given a triple ![]() $(E_0,E_1,i)\in \operatorname {Tri}(X,A)$, extend the isomorphism
$(E_0,E_1,i)\in \operatorname {Tri}(X,A)$, extend the isomorphism ![]() $i$ to a neighborhood of
$i$ to a neighborhood of ![]() $A$ using Lemma 6.11, and multiply by a cutoff function supported inside this neighborhood to obtain a globally defined map
$A$ using Lemma 6.11, and multiply by a cutoff function supported inside this neighborhood to obtain a globally defined map ![]() $d:E_0\to E_1$ which is an isomorphism over
$d:E_0\to E_1$ which is an isomorphism over ![]() $A$. This complex is well defined up to homotopy, so we have defined a map
$A$. This complex is well defined up to homotopy, so we have defined a map ![]() $\operatorname {Tri}(X,A)\to \operatorname {Kom}(X,A)$. This map evidently sends
$\operatorname {Tri}(X,A)\to \operatorname {Kom}(X,A)$. This map evidently sends ![]() $\operatorname {Vect}(X)$ to (the image of)
$\operatorname {Vect}(X)$ to (the image of) ![]() $\operatorname {Kom}(X,X)$, so it defines a map
$\operatorname {Kom}(X,X)$, so it defines a map ![]() $K^0(X,A)\to K^0_\mathrm {kom}(X,A)$ as desired.
$K^0(X,A)\to K^0_\mathrm {kom}(X,A)$ as desired.
We may also define a natural map ![]() $K^0_\mathrm {kom}(X,A)\to K^0(X,A)$ as follows. Given a complex
$K^0_\mathrm {kom}(X,A)\to K^0(X,A)$ as follows. Given a complex ![]() $(E_\bullet,d)$, choose a metric on each
$(E_\bullet,d)$, choose a metric on each ![]() $E_i$ using Lemma 5.1, and note that the map
$E_i$ using Lemma 5.1, and note that the map ![]() $d+d^*:E_\mathrm {even}:=\bigoplus _{i\text { even}}E_i\to \bigoplus _{i\text { odd}}E_i=:E_\mathrm {odd}$ is an isomorphism wherever
$d+d^*:E_\mathrm {even}:=\bigoplus _{i\text { even}}E_i\to \bigoplus _{i\text { odd}}E_i=:E_\mathrm {odd}$ is an isomorphism wherever ![]() $d$ is exact. As all metrics are homotopic and
$d$ is exact. As all metrics are homotopic and ![]() $K^0(X,A)$ is homotopy invariant by Proposition 6.13, sending
$K^0(X,A)$ is homotopy invariant by Proposition 6.13, sending ![]() $(E_\bullet,d)$ to the triple
$(E_\bullet,d)$ to the triple ![]() $(E_\mathrm {even},E_\mathrm {odd},(d+d^*)|_A)$ gives a well-defined map
$(E_\mathrm {even},E_\mathrm {odd},(d+d^*)|_A)$ gives a well-defined map ![]() $K^0_\mathrm {kom}(X,A)\to K^0(X,A)$. The composition
$K^0_\mathrm {kom}(X,A)\to K^0(X,A)$. The composition ![]() $K^0(X,A)\to K^0_\mathrm {kom}(X,A)\to K^0(X,A)$ is evidently the identity.
$K^0(X,A)\to K^0_\mathrm {kom}(X,A)\to K^0(X,A)$ is evidently the identity.
To finish, it suffices to show that ![]() $K^0(X,A)\to K^0_\mathrm {kom}(X,A)$ is surjective. Equivalently, we are to show that every element of
$K^0(X,A)\to K^0_\mathrm {kom}(X,A)$ is surjective. Equivalently, we are to show that every element of ![]() $K^0_\mathrm {kom}(X,A)$ is represented by a complex concentrated in degrees
$K^0_\mathrm {kom}(X,A)$ is represented by a complex concentrated in degrees ![]() $[0\;\;1]$. To do this, we use the following ‘folding’ operation. Given a complex concentrated in degrees
$[0\;\;1]$. To do this, we use the following ‘folding’ operation. Given a complex concentrated in degrees ![]() $[s\;\;r]$, the differential
$[s\;\;r]$, the differential ![]() $d_r:E_r\to E_{r-1}$ is injective over
$d_r:E_r\to E_{r-1}$ is injective over ![]() $A$, hence over an open neighborhood
$A$, hence over an open neighborhood ![]() $U$ of
$U$ of ![]() $A$ inside
$A$ inside ![]() $X$. If
$X$. If ![]() $d_r$ is, in fact, everywhere injective, then we may choose a metric on
$d_r$ is, in fact, everywhere injective, then we may choose a metric on ![]() $E_{r-1}$ and split it as
$E_{r-1}$ and split it as ![]() $\operatorname {im}(E_r)\oplus \operatorname {im}(E_r)^\perp$, showing that the subcomplex
$\operatorname {im}(E_r)\oplus \operatorname {im}(E_r)^\perp$, showing that the subcomplex ![]() $E_r\to \operatorname {im}(E_r)$ is a direct summand, so our complex represents the same class in
$E_r\to \operatorname {im}(E_r)$ is a direct summand, so our complex represents the same class in ![]() $K^0_\mathrm {kom}$ as one concentrated in degrees
$K^0_\mathrm {kom}$ as one concentrated in degrees ![]() $[s\;\; r-1]$. Now consider the general case where
$[s\;\; r-1]$. Now consider the general case where ![]() $d_r$ is not assumed everywhere injective. By replacing our given complex by its direct sum with the mapping cone of the identity map
$d_r$ is not assumed everywhere injective. By replacing our given complex by its direct sum with the mapping cone of the identity map ![]() $E_r\to E_r$ concentrated in degrees
$E_r\to E_r$ concentrated in degrees ![]() $[r-2\;\; r-1]$, we may assume that there exists an injection
$[r-2\;\; r-1]$, we may assume that there exists an injection ![]() $i:E_r\to E_{r-1}$ which agrees with
$i:E_r\to E_{r-1}$ which agrees with ![]() $d_r$ over a neighborhood
$d_r$ over a neighborhood ![]() $U$ of
$U$ of ![]() $A$. Now multiply
$A$. Now multiply ![]() $d$ by a cutoff function
$d$ by a cutoff function ![]() $\varphi$ supported inside
$\varphi$ supported inside ![]() $U$ and positive on
$U$ and positive on ![]() $A$ (this is homotopic to the original differential), and take the convex interpolation between
$A$ (this is homotopic to the original differential), and take the convex interpolation between ![]() $\varphi d_r$ and
$\varphi d_r$ and ![]() $i$ as a further homotopy. This ensures that the differential
$i$ as a further homotopy. This ensures that the differential ![]() $E_r\to E_{r-1}$ is everywhere injective, so our complex represents the same class in
$E_r\to E_{r-1}$ is everywhere injective, so our complex represents the same class in ![]() $K^0_\mathrm {kom}$ as one concentrated in degrees
$K^0_\mathrm {kom}$ as one concentrated in degrees ![]() $[\min (s,r-2)\;\; r-1]$. The dual operation shows that any complex concentrated in degrees
$[\min (s,r-2)\;\; r-1]$. The dual operation shows that any complex concentrated in degrees ![]() $[s\;\; r]$ represents the same class in
$[s\;\; r]$ represents the same class in ![]() $K^0_\mathrm {kom}$ as one concentrated in degrees
$K^0_\mathrm {kom}$ as one concentrated in degrees ![]() $[s+1\;\; \max (s+2,r)]$. Combining these two operations, we can put anything in degrees
$[s+1\;\; \max (s+2,r)]$. Combining these two operations, we can put anything in degrees ![]() $[0\; 1]$.
$[0\; 1]$.
Tensor product at the level of ![]() $K^0_\mathrm {kom}$ evidently defines commutative and associative maps
$K^0_\mathrm {kom}$ evidently defines commutative and associative maps
for paracompact orbispace pairs ![]() $(X,A)$ and
$(X,A)$ and ![]() $(Y,B)$ for which
$(Y,B)$ for which ![]() $X\times Y$ is paracompact. These induce, by inspection, associative and graded commutative maps
$X\times Y$ is paracompact. These induce, by inspection, associative and graded commutative maps
under the same hypotheses (note that a paracompact space times a compact space is paracompact).
We conclude with a discussion of Bott periodicity. So far, our discussion has applied equally to complex vector bundles as to real vector bundles, however we now restrict to complex vector bundles. The Bott element ![]() $\beta \in K^{-2}(*)=K^0(D^2,\partial D^2)$ is represented by the complex of vector bundles
$\beta \in K^{-2}(*)=K^0(D^2,\partial D^2)$ is represented by the complex of vector bundles ![]() $\underline{\mathbb {C}}\xrightarrow {\cdot z}\underline{\mathbb {C}}$ on
$\underline{\mathbb {C}}\xrightarrow {\cdot z}\underline{\mathbb {C}}$ on ![]() $\mathbb {C}$ (which contains
$\mathbb {C}$ (which contains ![]() $D^2$ as the unit disk).
$D^2$ as the unit disk).
Proposition 6.24 For any finite simplicial complex of groups ![]() $X$ with subcomplex
$X$ with subcomplex ![]() $A$, multiplication by the Bott element
$A$, multiplication by the Bott element ![]() $K^{-k}(X,A)\to K^{-k-2}(X,A)$ is an isomorphism for all
$K^{-k}(X,A)\to K^{-k-2}(X,A)$ is an isomorphism for all ![]() ${k\geqslant 0}$.
${k\geqslant 0}$.
Proof. By the long exact sequence, excision, the five lemma, and finite additivity, we are reduced to the case of ![]() $(D^i,\partial D^i)\times \mathbb {B} G$. By the definition of
$(D^i,\partial D^i)\times \mathbb {B} G$. By the definition of ![]() $K^{-n}$, we are further reduced to the case of
$K^{-n}$, we are further reduced to the case of ![]() $K^0$, namely to showing that multiplication by the Bott element
$K^0$, namely to showing that multiplication by the Bott element
is an isomorphism for all ![]() $k\geqslant 0$, which is well known (see [Reference Atiyah and BottAB64], [Reference AtiyahAti68, Theorem 4.3], and [Reference SegalSeg68, § 3]).
$k\geqslant 0$, which is well known (see [Reference Atiyah and BottAB64], [Reference AtiyahAti68, Theorem 4.3], and [Reference SegalSeg68, § 3]).
In fact, this argument shows more generally that for any complex line bundle ![]() $L$ over a finite simplicial complex of groups
$L$ over a finite simplicial complex of groups ![]() $X$, pullback followed by multiplication with the relative Bott class in
$X$, pullback followed by multiplication with the relative Bott class in ![]() $K^0(L,\infty )$ (represented by the complex
$K^0(L,\infty )$ (represented by the complex ![]() $\underline{\mathbb {C}}\xrightarrow {\cdot p}L$ on
$\underline{\mathbb {C}}\xrightarrow {\cdot p}L$ on ![]() $L$) defines an isomorphism
$L$) defines an isomorphism ![]() $K^{-k}(X)\to K^{-k}(L,\infty )$ (and, yet more generally, that pullback and multiplication with the Koszul complex defines an isomorphism
$K^{-k}(X)\to K^{-k}(L,\infty )$ (and, yet more generally, that pullback and multiplication with the Koszul complex defines an isomorphism ![]() $K^{-k}(X)\to K^{-k}(E,\infty )$ for any complex vector bundle
$K^{-k}(X)\to K^{-k}(E,\infty )$ for any complex vector bundle ![]() $E$).
$E$).
Definition 6.25 The periodic ![]() $K$-theory of a pair
$K$-theory of a pair ![]() $(X,A)$ is the direct limit
$(X,A)$ is the direct limit
over multiplication by ![]() $\beta$. Whereas
$\beta$. Whereas ![]() $K^*$ is defined only in nonpositive degrees,
$K^*$ is defined only in nonpositive degrees, ![]() $K^*_\mathrm {per}$ is defined in all degrees.
$K^*_\mathrm {per}$ is defined in all degrees.
As direct limits are exact, ![]() $K^*_\mathrm {per}$ is, similarly to
$K^*_\mathrm {per}$ is, similarly to ![]() $K^*$, a cohomology theory for orbispace pairs satisfying the hypothesis of Theorem 1.1. When the natural map
$K^*$, a cohomology theory for orbispace pairs satisfying the hypothesis of Theorem 1.1. When the natural map ![]() $K^*\to K^*_\mathrm {per}$ is an isomorphism,
$K^*\to K^*_\mathrm {per}$ is an isomorphism, ![]() $K^*_\mathrm {per}$ provides a natural extension of
$K^*_\mathrm {per}$ provides a natural extension of ![]() $K^*$ from nonpositive degrees to all degrees.
$K^*$ from nonpositive degrees to all degrees.
Corollary 6.26 For any finite simplicial complex of groups ![]() $X$ with subcomplex
$X$ with subcomplex ![]() $A$, the natural map
$A$, the natural map ![]() $K^*(X,A)\to K^*_\mathrm {per}(X,A)$ is an isomorphism in nonpositive degrees.
$K^*(X,A)\to K^*_\mathrm {per}(X,A)$ is an isomorphism in nonpositive degrees.
Acknowledgements
I would like to thank André Henriques for discussions about orbispaces and topological stacks, David Treumann for conversations about the algebraic case, and the referees for their remarks. I also thank the Department of Mathematics at Cambridge University for their hospitality during the time when this paper was conceived.