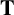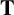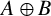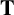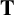ON ENDOMORPHISMS OF EXTENSIONS IN TANNAKIAN CATEGORIES

Abstract

We prove analogues of Schur’s lemma for endomorphisms of extensions in Tannakian categories. More precisely, let $\mathbf {T}$ be a neutral Tannakian category over a field of characteristic zero. Let E be an extension of A by B in $\mathbf {T}$. We consider conditions under which every endomorphism of E that stabilises B induces a scalar map on $A\oplus B$. We give a result in this direction in the general setting of arbitrary $\mathbf {T}$ and E, and then a stronger result when $\mathbf {T}$ is filtered and the associated graded objects to A and B satisfy some conditions. We also discuss the sharpness of the results.

1 Introduction

Throughout the paper, all Tannakian categories are neutral. We will freely use the language of Tannakian categories (see [3] for further details).

Let K be a field of characteristic zero and $\mathbf {T}$ a Tannakian category over K. Given any object X of $\mathbf {T}$ , let $\mathrm{End}_{\mathbf {T}}(X)$ be the endomorphism algebra of X. Given a subobject Y of X, denote the subalgebra of $\mathrm{End}_{\mathbf {T}}(X)$ consisting of the endomorphisms that restrict to an endomorphism of Y (that is, those mapping Y to Y) by $\mathrm{End}_{\mathbf {T}}(X;Y)$ .

Let A and B be nonzero objects of $\mathbf {T}$ . Fix an extension of A by B:

(1.1)

In this note, we prove some analogues of Schur’s lemma for $\mathrm{End}_{\mathbf {T}}(E;B)$ .

The extension (1.1) induces a homomorphism of algebras

(1.2) $$ \begin{align} \Omega: \mathrm{End}_{\mathbf{T}}(E;B) \rightarrow \mathrm{End}_{\mathbf{T}}(B)\times \mathrm{End}_{\mathbf{T}}(A), \quad \phi\mapsto(\phi_B,\phi_A), \end{align} $$

where given $\phi \in \mathrm{End}_{\mathbf {T}}(E;B)$ , its image $(\phi _B,\phi _A)$ is characterised by the commutativity of

(1.3)

The image of $\Omega $ always contains the diagonal copy of K in $\mathrm{End}_{\mathbf {T}}(B)\times \mathrm{End}_{\mathbf {T}}(A)$ (as the image of scalar endomorphisms of E). Roughly speaking, it is natural to expect that the further away (1.1) is from splitting, the smaller the image of $\Omega $ should be. We shall prove two results in this spirit. The first is the following theorem.

Theorem 1.1. Let ${\mathfrak {u}}(E)$ be the Lie algebra of the kernel of the homomorphism from the Tannakian group of E to the Tannakian group of $A\oplus B$ , naturally considered as a subobject of the internal Hom object $\mathrm{Hom}(A,B)$ (see Section 2 for details). Assume that ${\mathfrak {u}}(E)=\mathrm{Hom}(A,B)$ . Then the image of $\Omega $ is equal to the diagonal copy of K.

Hardouin [8, 9] (in the case where A and B are semisimple) and the author and Kumar Murty [5] (for arbitrary possibly nonsemisimple A and B) give a characterisation of the subobject ${\mathfrak {u}}(E)$ of $\mathrm{Hom}(A,B)$ . A summary of this characterisation is recalled in Section 2. It follows from this characterisation that the condition ${\mathfrak {u}}(E)=\mathrm{Hom}(A,B)$ , which we refer to as the maximality of ${\mathfrak {u}}(E)$ , implies that the extension class

(where $\mathrm{Ext}^1_{\mathbf {T}}$ is the $\mathrm{Ext}^1$ group in $\mathbf {T}$ and

is the unit object) corresponding to (1.1) under the canonical isomorphism

is totally nonsplit, that is, for any proper subobject C of $\mathrm{Hom}(A,B)$ , the pushforward of $\mathcal {E}$ along the quotient $\mathrm{Hom}(A,B)\rightarrow \mathrm{Hom}(A,B)/C$ is nonsplit. (Equivalently, an extension

is totally nonsplit if the only subobject of Y that is mapped onto

is Y.)

In the case where A and B are semisimple, the maximality of ${\mathfrak {u}}(E)$ is equivalent to the total nonsplitting of $\mathcal {E}$ . However, in general, the two conditions are not equivalent, as the examples in Section 5 illustrate. The second result of the paper asserts that in some important settings, one can relax the hypothesis of Theorem 1.1 from assuming maximality of ${\mathfrak {u}}(E)$ to assuming total nonsplitting of $\mathcal {E}$ .

A Tannakian category $\mathbf {T}$ is said to be filtered if it is equipped with a filtration $W_\bullet $ satisfying similar properties to the weight filtration on mixed Hodge structures, that is, $W_\bullet $ is indexed by ${\mathbb Z}$ , functorial, exact, increasing, finite on every object and respects the tensor structure. This means that for every integer n, we have an exact linear functor $W_n:\mathbf {T}\rightarrow \mathbf {T}$ such that for every object X of $\mathbf {T}$ ,

$$ \begin{align*} W_{n-1}X \ &\subset \ W_nX \quad (\mbox{for all } n),\\ W_nX \ &= \ 0 \quad (\mbox{for all } n\ll0),\\ W_nX \ &= \ X \quad (\mbox{for all } n\gg 0), \end{align*} $$

and such that the inclusions $W_nX\subset X$ for various X give a morphism of functors from $W_n$ to the identity. Compatibility with the tensor structure means that for all objects X and Y and every n,

$$ \begin{align*} W_n(X\otimes Y) = \sum\limits_{p+q=n}W_p(X)\otimes W_q(Y). \end{align*} $$

We will refer to $W_\bullet $ as the weight filtration. By the weights of an object X, we mean the integers n such that $W_nX/W_{n-1}X$ is not zero. The associated grading of X is defined to be $Gr^W X:=\bigoplus _n W_nX/W_{n-1}X$ . The prototype examples of filtered Tannakian categories are various Tannakian categories of mixed motives and the category of mixed Hodge structures.

We can now state the second result of the paper.

Theorem 1.2. Suppose that $\mathbf {T}$ is a filtered Tannakian category with the weight filtration denoted by $W_\bullet $ . Suppose moreover that condition (i) or (ii) below holds:

1. (i) the associated graded $Gr^W E$ is semisimple and there are no nonzero morphisms $Gr^W A\rightarrow Gr^W B$ ;

2. (ii) the sets of weights of A and B are disjoint.

Then if $\mathcal {E}$ (defined as above) is totally nonsplit, the image of $\Omega $ will be equal to the diagonal copy of K.

In any reasonable category of mixed motives, $Gr^WE$ is always semisimple. In the category of mixed Hodge structures, $Gr^WE$ is semisimple if E is graded polarisable. Of course, it is only useful to include condition (ii) as a separate condition in the statement if $Gr^WE$ is not known to be semisimple.

Theorem 1.2 is used crucially in [4], where we give a classification result for mixed motives with maximal unipotent radicals of motivic Galois groups and a given associated grading with respect to the weight filtration. Note that the assertion of Theorem 1.2 can be equivalently replaced by

$$ \begin{align*} \mathrm{End}_{\mathbf{T}}(E;B)\cong K, \end{align*} $$

that is, every element of $\mathrm{End}_{\mathbf {T}}(E;B)$ is a scalar endomorphisms of E. Indeed, the kernel of $\Omega $ is canonically isomorphic to $\mathrm{Hom}_{\mathbf {T}}(A,B)$ , where $\mathrm{Hom}_{\mathbf {T}}$ is the Hom group in $\mathbf {T}$ . Since the functor that sends an object X to $Gr^WX$ is faithful, under condition (i) or (ii) of Theorem 1.2, $\mathrm{Hom}_{\mathbf {T}}(A,B)$ will be zero.

Below, we first recall the characterisation of ${\mathfrak {u}}(E)$ mentioned above and then prove Theorems 1.1 and 1.2. The final section of the note includes some further remarks. In particular, we give an example that shows that in the general setting of Theorem 1.1, one cannot relax the maximality condition to total nonsplitting. Also, we discuss an example involving 1-motives that shows that in the setting where $\mathbf {T}$ is filtered and the sets of weights of A and B are disjoint, the total nonsplitting of $\mathcal {E}$ does not imply maximality of ${\mathfrak {u}}(E)$ , so that in this setting, the second theorem is indeed stronger than the first one. We also discuss a generalisation of Theorem 1.2 (see Section 5).

2 Recollections on Tannakian groups of extensions

To simplify the notation, we fix a choice of fibre functor and identify $\mathbf {T}$ with the category of finite dimensional (algebraic) representations of an affine group scheme $\mathcal {G}$ over K (with $\mathcal {G}$ = the Tannakian group of $\mathbf {T}$ with respect to the fibre functor). We will use the same symbol for an object of $\mathbf {T}$ and its underlying vector space. For any object X of $\mathbf {T}$ and any $g\in \mathcal {G}$ , we denote the image of g in $\mathrm{GL}(X)$ by $g_X$ . The image of $\mathcal {G}$ in $\mathrm{GL}(X)$ is denoted by $\mathcal {G}(X)$ ; this is the Tannakian group of the Tannakian subcategory $\langle X\rangle $ generated by X. (Recall that $\langle X\rangle $ is the smallest full Tannakian subcategory of $\mathbf {T}$ that contains X and is closed under taking subquotients.)

We should point out that even though we think of $\mathbf {T}$ as the category of representations of $\mathcal {G}$ , all the objects in $\mathbf {T}$ that appear in the following text (in particular, the object ${\mathfrak {u}}(E)$ introduced below) will be intrinsic to the Tannakian category $\mathbf {T}$ . For this reason, we often prefer to use the terms object and subobject ( $=$ object and subobject in $\mathbf {T}$ ) instead of the terms $\mathcal {G}$ -representation and $\mathcal {G}$ -subrepresentation.

As they were in Section 1, the Ext and Hom groups in $\mathbf {T}$ are denoted by $\mathrm{Ext}_{\mathbf {T}}$ and $\mathrm{Hom}_{\mathbf {T}}$ . We use the notation $\mathrm{Hom}$ and $\mathrm{End}$ (without any decorations) to refer to the Hom and End groups in the category of vector spaces. As we have adopted the convention of denoting an object of $\mathbf {T}$ and its underlying vector space by the same symbol, for any objects X and Y of $\mathbf {T}$ , the notation $\mathrm{Hom}(X,Y)$ will refer to both the internal Hom (which is an object of $\mathbf {T}$ ) and the Hom space in the category of vector spaces between the underlying vector spaces. This should not lead to confusion as the relevant interpretation will be clear from the context.

Given a vector space X and a subspace Y of X, denote the subalgebra of $\mathrm{End}(X)$ consisting of linear maps on X which map Y to Y by $\mathrm{End}(X;Y)$ . Similarly, the subgroup of $\mathrm{GL}(X)$ consisting of the elements which map Y to itself is denoted by $\mathrm{GL}(X;Y)$ . Given an object X of any category, the identity map on X is denoted by $\mathrm{Id}_X$ . We will sometimes simply write $\mathrm{Id}$ if X is clear from the context.

Fix objects A, B and E of $\mathbf {T}$ and the exact sequence (1.1). Let $\mathcal {U}(E)$ be the kernel of the natural map

(2.1) $$ \begin{align} \mathcal{G}(E) \ \twoheadrightarrow \ \mathcal{G}(B\oplus A). \end{align} $$

Choosing a section of $E\twoheadrightarrow B$ in the category of vector spaces to identify

$$ \begin{align*} E = B\oplus A \end{align*} $$

as vector spaces, we have an embedding

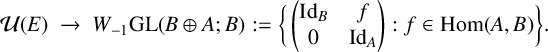$$ \begin{align*} \mathcal{U}(E) \ \rightarrow \ W_{-1}\mathrm{GL}(B\oplus A;B):=\bigg\{\begin{pmatrix} \mathrm{Id}_B & f \\ 0 &\mathrm{Id}_A\end{pmatrix}: f\in \mathrm{Hom}(A,B)\bigg\}. \end{align*} $$

The group $W_{-1}\mathrm{GL}(B\oplus A;B)$ is unipotent and abelian, and hence so is $\mathcal {U}(E)$ . Since $W_{-1}\mathrm{GL}(B\oplus A;B)$ is abelian, the embedding above is actually canonical, that is, it does not depend on the choice of the section of $E \twoheadrightarrow A$ used to identify $E=B\oplus A$ .

Let ${\mathfrak {u}}(E)$ be the Lie algebra of $\mathcal {U}(E)$ . Then ${\mathfrak {u}}(E)$ can be identified as a subspace of $\mathrm{Hom}(A,B)$ with the exponential map ${\mathfrak {u}}(E) \rightarrow \mathcal {U}(E)$ simply sending

$$ \begin{align*} f\in {\mathfrak{u}}(E)\subset \mathrm{Hom}(A,B) \quad \mathrm{to} \quad \begin{pmatrix} \mathrm{Id} & f \\ 0 &\mathrm{Id}\end{pmatrix}. \end{align*} $$

Through the adjoint representation of $\mathcal {G}(E)$ on ${\mathfrak {u}}(E)$ , the Lie algebra ${\mathfrak {u}}(E)$ is naturally equipped with a $\mathcal {G}$ -action. The inclusion ${\mathfrak {u}}(E)\subset \mathrm{Hom}(A,B)$ is compatible with the $\mathcal {G}$ -actions, making ${\mathfrak {u}}(E)$ a subobject of the internal Hom, $\mathrm{Hom}(A,B)$ (see [5, Section 3.1], for instance). This subobject has a nice description, which we recall now.

As in Section 1, let

be the element corresponding to the class of (1.1) under the canonical isomorphism

For any subobject $C\subset \mathrm{Hom}(A,B)$ , the pushforward of $\mathcal {E}$ along the quotient map

$$ \begin{align*}\mathrm{Hom}(A,B)\rightarrow \mathrm{Hom}(A,B)/C\end{align*} $$

is denoted by $\mathcal {E}/C$ . The following characterisation of ${\mathfrak {u}}(E)$ was proved in [5].

Theorem 2.1 ([5, Theorem 3.3.1]; see also [6, Lemma 3.4.3]).

Given any subobject C of $\mathrm{Hom}(A,B)$ , we have ${\mathfrak {u}}(E)\subset C$ if and only if the pushforward

is in the image of the natural injection

where $\mathrm{Ext}^1_{\langle A\oplus B\rangle }$ is the $\mathrm{Ext}^1$ group in the Tannakian subcategory $\langle A\oplus B\rangle $ of $\mathbf {T}$ generated by $A\oplus B$ . (Thus, ${\mathfrak {u}}(E)$ is the smallest subobject of $\mathrm{Hom}(A,B)$ with this property.)

In the case where A and B are semisimple, this was earlier proved by Bertrand [2] in the setting of D-modules and by Hardouin [8, 9] in the setting of arbitrary Tannakian categories. In this case, the statement simplifies to the following theorem.

Theorem 2.2 [9, Theorem 2].

Suppose A and B are semisimple. Let $\mathcal {E}$ be as above. Then given any subobject C of $\mathrm{Hom}(A,B)$ , we have ${\mathfrak {u}}(E)\subset C$ if and only if the pushforward $\mathcal {E}/C$ splits.

In the general case (where A or B may not be semisimple), by Theorem 2.1, if C is any subobject of $\mathrm{Hom}(A,B)$ such that $\mathcal {E}/C$ splits, then C contains ${\mathfrak {u}}(E)$ . The pushforward $\mathcal {E}/{\mathfrak {u}}(E)$ however may not split (see the examples in Section 5).

We also recall an explicit description of $\mathcal {E}$ (see [5, Section 3.2] for details). Let

$$ \begin{align*} \mathrm{Hom}(A,E)^\dagger := \bigg\{f\in \mathrm{Hom}(A,E): \begin{array}{ll} \mathrm{the\ composition}\ {A\xrightarrow{f}E\twoheadrightarrow A}\\ \mathrm{is\ a\ scalar\ multiple\ of}\ {\mathrm{Id}_A}\end{array}\!\!\bigg\}. \end{align*} $$

It is easy to see that this is a subobject of $\mathrm{Hom}(A,E)$ . The element $\mathcal {E}$ is the class of the extension

(2.2)

Here, the injective map is simply the obvious embedding, sending $f\in \mathrm{Hom}(A,B)$ to

$$ \begin{align*} A\xrightarrow{f} B \hookrightarrow E. \end{align*} $$

The surjective map in (2.2) is the map that sends $f\in \mathrm{Hom}(A,E)^\dagger $ to $a\in K$ , where

$$ \begin{align*} A\xrightarrow{f}E\twoheadrightarrow A \end{align*} $$

is $a\cdot \mathrm{Id}_A$ .

3 Proofs of Theorems 1.1 and 1.2 for $A=\mathbb{1}$

The goal of this section is to prove Theorems 1.1 and 1.2 in the case where ; the general case will be deduced from this in the next section. In this case, identifying , the extension $\mathcal {E}$ is simply given by (1.1). Theorem 2.1 asserts that ${\mathfrak {u}}(E)$ is the smallest subobject of B such that $\mathcal {E}/{\mathfrak {u}}(E)$ is an extension of by $B/{\mathfrak {u}}(E)$ in the subcategory $\langle B\rangle $ . If B is semisimple, ${\mathfrak {u}}(E)$ is the smallest subobject of B such that $\mathcal {E}/{\mathfrak {u}}(E)$ splits.

We first establish a lemma.

Lemma 3.1. Assume . Let $\lambda : E\rightarrow B_0$ be a morphism from E to an object $B_0$ , such that $B_0$ belongs to the subcategory $\langle B\rangle $ . Then ${\mathfrak {u}}(E)\subset B\cap \ker (\lambda )$ .

Proof. Set $B':=B\cap \ker (\lambda )$ . Consider the commutative diagram

(3.1)

where the maps are inclusions and quotient maps. The rows and columns are exact.

Case I. Suppose $\ker (\lambda )\not \subset B$ , so that $B'$ is a proper subobject of $\ker (\lambda )$ . Being a nonzero subobject of the unit object, $\ker (\lambda )/B'$ must be isomorphic to . Thus, $\mathcal {E}$ (the second row) is the pushforward of an extension of by $B'$ (the first row). It follows that $\mathcal {E}/B'$ splits and ${\mathfrak {u}}(E)\subset B'$ by Theorem 2.1.

Case II. Suppose $\ker (\lambda )\subset B$ , so that $B'=\ker (\lambda )$ . Then the third row of the diagram is the pushforward $\mathcal {E}/B'$ . By assumption, $E/\ker (\lambda )$ is in the subcategory generated by B. Again ${\mathfrak {u}}(E)\subset B'$ by Theorem 2.1.

We can now establish Theorems 1.1 and 1.2 in the case that . Let $\phi \in \mathrm{End}_{\mathbf {T}}(E;B)$ . Then (= the induced map on by $\phi $ ) is equal to for some $a\in K$ . The endomorphism $\lambda :=\phi -a \cdot \mathrm{Id}_E$ of E then factors through B, that is, it is the composition with the inclusion $B\hookrightarrow E$ of a morphism $E\rightarrow B$ , which we also denote by $\lambda $ .

To obtain Theorem 1.1, apply the previous lemma to $\lambda $ . We get ${\mathfrak {u}}(E)\subset B\cap \ker (\lambda )$ . The assumption that ${\mathfrak {u}}(E)=B$ gives $B\subset \ker (\lambda )$ , that is, $\phi =a\cdot \mathrm{Id}$ on B, as desired.

We now turn our attention to Theorem 1.2. Thus, we assume that $\mathbf {T}$ is a filtered Tannakian category and that either (i) $Gr^WE$ is semisimple and

or (ii) 0 is not a weight of B (note that

is pure of weight 0). Both conditions guarantee that the kernel of $\lambda : E\rightarrow B$ cannot be contained in B. Indeed, this follows simply by weight considerations if item (ii) holds. On the other hand, if item (i) holds, after applying the associated graded functor, the sequence (1.1) splits. Choosing a section for the sequence (which will be unique because

vanishes), if $\ker (\lambda )\subset B$ , we have a diagram

(with obvious maps and the row being exact). We thus get a nonzero morphism

.

Thus, $B':=B\cap \ker (\lambda )$ is a proper subobject of $\ker (\lambda )$ . Considering the diagram (3.1) with $B'$ and $\lambda :E\rightarrow B$ as described, the extension $\mathcal {E}$ is the pushforward of the top row along the inclusion $B'\hookrightarrow B$ , so that $\mathcal {E}/B'$ splits. If $\mathcal {E}$ is totally nonsplit, we get $B'=B$ and $B\subset \ker (\lambda )$ . Thus, we have also established Theorem 1.2 when .

4 Proofs of Theorems 1.1 and 1.2 for arbitrary A

We now assume that A is arbitrary. The extension $\mathcal {E}$ is now given by (2.2). Assume the hypotheses of Theorems 1.1 or 1.2 for the extension given in (1.1). Then the hypotheses also hold for the extension given in (2.2), that is, if (2.2) is taken as our original (1.1). To see this for Theorem 1.1, note that in view of Theorem 2.1, we have ${\mathfrak {u}}(E)\subset {\mathfrak {u}}(\mathrm{Hom}(A,E)^\dagger )$ , as the subcategory $\langle \mathrm{Hom}(A,B)\rangle $ is contained in $\langle A\oplus B\rangle $ ; to see it for Theorem 1.2, note that

Thus, by the special case already proved, the image of the map

(4.1)

induced by (2.2) is the diagonal copy of K. Hence, the general case of the results will be established if we prove the following lemma.

Lemma 4.1. Suppose the image of (4.1) is the diagonal copy of K. Then so is the image of (1.2).

Proof. Let $\phi \in \mathrm{End}_{\mathbf {T}}(E;B)$ . We will show that $(\phi _B,\phi _A)$ is in the diagonal copy of K. Adding a suitable scalar multiple of $\mathrm{Id}_E$ to $\phi $ if necessary, we may assume that $\phi $ is an automorphism (recall that K is of characteristic zero). Let $\phi ^\dagger \in \mathrm{End}(\mathrm{Hom}(A,E))$ be the map that sends any $f\in \mathrm{Hom}(A,E)$ to the composition

$$ \begin{align*} A\xrightarrow{\phi_A^{-1}} A \xrightarrow{~f~} E \xrightarrow{~\phi~} E. \end{align*} $$

Since $\phi _A$ and $\phi $ are morphisms in $\mathbf {T}$ , so is $\phi ^\dagger $ . Since B is stable under $\phi $ , the map $\phi ^\dagger $ stabilises $\mathrm{Hom}(A,B)$ . Moreover, if f is in $\mathrm{Hom}(A,E)^\dagger $ with $f\pmod {B}=\mathrm{Id}_A$ , then we have a commutative diagram

so that $\phi ^\dagger (f)$ is also in $\mathrm{Hom}(A,E)^\dagger $ with $\phi ^\dagger (f) \pmod {B} $ being the identity map on A. We conclude that:

1. (i) $\phi ^\dagger $ restricts to an element of $\mathrm{End}_{\mathbf {T}}(\mathrm{Hom}(A,E)^\dagger ;\mathrm{Hom}(A,B))$ and

2. (ii) denoting this restriction also by $\phi ^\dagger $ , we have (where is the map induced on by $\phi ^\dagger \in \mathrm{End}_{\mathbf {T}}(\mathrm{Hom}(A,E)^\dagger )$ ).

Since the image of (4.1) is the diagonal copy of K, it follows that the restriction of $\phi ^\dagger $ to $\mathrm{Hom}(A,B)$ is also the identity map. That is, for every linear map $f: A\rightarrow B$ ,

$$ \begin{align*} \phi_Bf\phi_A^{-1} = f. \end{align*} $$

Since A and B are nonzero, by elementary linear algebra, $\phi _A$ and $\phi _B$ are both scalar maps and they are given by multiplication with the same element of K.

5 Further remarks

5.1 Sharpness of Theorem 1.1

If (1.1) is an arbitrary extension in a general Tannakian category $\mathbf {T}$ (with no extra assumptions on (1.1) or $\mathbf {T}$ ), total nonsplitting of $\mathcal {E}$ (= the extension of by $\mathrm{Hom}(A,B)$ corresponding to (1.1) under the canonical isomorphism) does not guarantee that the image of $\Omega $ is K. Thus, the hypothesis of maximality of ${\mathfrak {u}}(E)$ in Theorem 1.1 cannot be relaxed to total nonsplitting.

For example, given any field K of characteristic zero, let $\mathbf {T}$ be the category of finite dimensional algebraic representations of the subgroup $\mathcal {G}$ of $\mathrm{GL}_3$ (over K) consisting of all the matrices of the form

$$ \begin{align*} \begin{pmatrix} 1&a&b\\ &1&a\\ &&1 \end{pmatrix}, \end{align*} $$

where the missing entries are zero. Let B be $K^2$ with the action of $\mathcal {G}$ given by left multiplication by the top left $2\times 2$ submatrix, and let E be $K^3$ with the canonical action of $\mathcal {G}$ through left multiplication. We have an embedding $B\hookrightarrow E$ given by $(x_1,x_2)\mapsto (x_1,x_2,0)$ , fitting into a short exact sequence

with the map

being projection onto the third coordinate. It is easy to see that the extension above is totally nonsplit. However, E has an endomorphism

$$ \begin{align*} \phi: (x_1,x_2,x_3)\mapsto (x_2,x_3,0) \end{align*} $$

which stabilises B but its restriction to B is not a scalar multiple of the identity.

It is worth mentioning that here, by Theorem 1.1, ${\mathfrak {u}}(E)$ is not maximal, so this example also shows that, in general, total nonsplitting of $\mathcal {E}$ does not imply that ${\mathfrak {u}}(E)$ must be maximal (in particular, in general, $\mathcal {E}/{\mathfrak {u}}(E)$ does not have to split). See the next subsection for a more interesting example that also illustrates this.

5.2 Sharpness of Theorem 1.2

Assume that $\mathbf {T}$ is filtered, and that A and B have disjoint sets of weights. Then total nonsplitting of $\mathcal {E}$ still does not imply maximality of ${\mathfrak {u}}(E)$ , so that Theorem 1.2 is indeed stronger than Theorem 1.1 in this setting. The example in [6, Section 6.10] using the work of Jacquinot and Ribet [10] on deficient points on semiabelian varieties illustrates this. If we take $\mathbf {T}$ to be the category of mixed Hodge structures, E to be the 1-motive denoted by M in [6, Section 6.10], and $B=W_{-1}M$ and , then the sequence (1.1) (given by the natural inclusion and quotient maps) is totally nonsplit, the weights of A and B are disjoint, and ${\mathfrak {u}}(E)$ (which is the same as ${\mathfrak {u}}_{-1}(M)$ in [6, Section 6.10]) is not maximal. In fact, ${\mathfrak {u}}(E)=0$ (see [6]).

Continuing to work in the category of mixed Hodge structures, here we include a somewhat simpler example which avoids using deficient points. Let J be a simple complex abelian variety of positive dimension. Let N be a nonsplit extension of

by $H_1(J)$ . Then

is a nonsplit extension of $H^1(J)(1)$ by ${\mathbb Q}(1)$ , which after a choice of polarisation can be thought of as a nonsplit extension of $H_1(J)$ by ${\mathbb Q}(1)$ . Since the $\mathrm{Ext}^2$ groups vanish in the category of mixed Hodge structures (see [1], for example), there is an object E fitting into the diagram

in which the rows and columns are exact and the top row and the right column are our nonsplit extensions. (See [7, Lemma 9.3.8] or [6, Lemma 6.4.1].)

Take the first vertical extension of the diagram to play the role of our (1.1); it will also be our $\mathcal {E}$ . Then $\mathcal {E}$ is totally nonsplit, as ${\mathbb Q}(1)$ is the unique maximal proper subobject of and the pushforward $\mathcal {E}/{\mathbb Q}(1)$ (= the right column) is nonsplit. However, $\mathcal {E}/{\mathbb Q}(1)$ is an extension in the subcategory generated by , hence by Theorem 2.1, we have ${\mathfrak {u}}(E)\subset {\mathbb Q}(1)$ . In particular, ${\mathfrak {u}}(E)$ is not maximal.

5.3 Generalisation of Theorem 1.2

In the proof of the case of Theorem 1.2, the only place where the filtration on $\mathbf {T}$ and condition (i) or (ii) played a part is when we concluded that the kernel of $\lambda :E\rightarrow B$ (with $\lambda $ as in the proof) is not contained in B. Combining this remark with Lemma 4.1, we obtain the following generalisation of Theorem 1.2.

Theorem 5.1. Let (1.1) be an extension in any Tannakian category $\mathbf {T}$ over a field of characteristic 0. Suppose that the kernel of any morphism

(5.1) $$ \begin{align} \mathrm{Hom}(A,E)^\dagger \rightarrow \mathrm{Hom}(A,B) \end{align} $$

is not contained in $\mathrm{Hom}(A,B)$ . Then if $\mathcal {E}$ (that is, the extension of by $\mathrm{Hom}(A,B)$ corresponding to (1.1), as before) is totally nonsplit, the image of $\Omega $ will be the diagonal copy of K.

In particular, this can be applied in the following situation. Suppose $\mathcal {R}$ is a reductive subgroup of the group $\mathcal {G}(E)$ (= the Tannakian group of $\langle E\rangle $ ). Every object of $\langle E\rangle $ can also be considered as an $\mathcal {R}$ -representation. In the (semisimple) category of $\mathcal {R}$ -representations, we can choose a splitting of $\mathcal {E}$ to decompose

Suppose that there are no nonzero $\mathcal {R}$ -equivariant maps $A\rightarrow B$ , or equivalently

Then the kernel of any morphism (5.1) in $\mathbf {T}$ cannot be contained in $\mathrm{Hom}(A,B)$ , and hence the image of $\Omega $ will be the diagonal copy of K. In fact, since $\mathrm{Hom}_{\mathbf {T}}(A,B)$ is zero, we get $\mathrm{End}_{\mathbf {T}}(E;B)\cong K$ .

Note that this scenario directly generalises the situation of Theorem 1.2. If $\mathbf {T}$ is filtered, taking $\mathcal {R}$ to be $\mathcal {G}(Gr^WE)$ embedded in $\mathcal {G}(E)$ via the section of $\mathcal {G}(E)\twoheadrightarrow \mathcal {G}(Gr^WE)$ induced by $Gr^W: \langle E\rangle \rightarrow \langle Gr^WE\rangle $ , we recover case (i) of Theorem 1.2. Taking $\mathcal {R}$ to be the multiplicative group $\mathbb {G}_m$ embedded in $\mathcal {G}(E)$ through a (possibly noncentral) cocharacter $\mathbb {G}_m \rightarrow \mathcal {G}(E)$ that induces the weight grading on the associated graded objects, we recover case (ii) of the result.

5.4 Final remark

We have

$$ \begin{align*} \ker(\Omega) = \mathrm{Hom}_{\mathbf{T}}(A,B), \end{align*} $$

where $\mathrm{Hom}_{\mathbf {T}}(A,B)$ is considered as a subset of $\mathrm{End}_{\mathbf {T}}(E)$ via

$$ \begin{align*} (A\xrightarrow{~f~}B) \ \ \mapsto \ \ (E\twoheadrightarrow A \xrightarrow{~f~}B \hookrightarrow E). \end{align*} $$

Whenever ${\text {Im}}(\Omega )=K$ , the natural embedding of K into $\mathrm{End}_{\mathbf {T}}(E;B)$ as the space of scalar maps provides a section for the short exact sequence

This gives an isomorphism

$$ \begin{align*} \mathrm{End}_{\mathbf{T}}(E;B) \cong K\oplus \mathrm{Hom}_{\mathbf{T}}(A,B). \end{align*} $$

The isomorphism is initially of vector spaces only, but transferring the multiplication on $\mathrm{End}_{\mathbf {T}}(E;B)$ to the right-hand side, it becomes an isomorphism of algebras. The multiplication on the right is given by

$$ \begin{align*} (a,f)(a',f') = (aa', af'+a'f) \end{align*} $$

and the embedding of K is through the first factor. In particular, $\mathrm{End}_{\mathbf {T}}(E;B)$ is commutative if ${\text {Im}}(\Omega )=K$ .