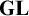COMPLETENESS OF THE GÖDEL–LÖB PROVABILITY LOGIC FOR THE FILTER SEQUENCE OF NORMAL MEASURES

Abstract

Assuming the existence of suitable large cardinals, we show it is consistent that the Provability logic $\mathbf {GL}$ is complete with respect to the filter sequence of normal measures. This result answers a question of Andreas Blass from 1990 and a related question of Beklemishev and Joosten.

1 Introduction

The Gödel–Löb provability logic $\mathbf {GL}$ deals with the study of modality $\Box $ interpreted as the provability predicate in any formal theory T that can describe the arithmetic of natural numbers, such as Peano arithmetic; $\Box \varphi $ is read as $\varphi $ is provable in T. It is proved by Segerberg [16] that $\mathbf {GL}$ is sound and complete with respect to the class of all transitive and conversely well-founded Kripke frames. In fact, it is adequate to consider frames that are finite transitive irreflexive trees. Afterward, Esakia [11] perceived that the modal operator $\lozenge $ , interpreted as consistency in T, has the same behavior as the derivative operator in topological scattered spaces. Then he proved that $\mathbf {GL}$ is (strongly) complete with respect to the class of all scattered spaces.

In 1990, Blass [10] improved Esakia’s result. Instead of topological description, he interpreted modal operators over filters associated with specific uncountable cardinals, which is a most natural viewpoint in set theory. He showed the soundness of $\mathbf {GL}$ concerning some natural classes of filters. Then he studied the completeness of $\mathbf {GL}$ for two classes of these filters: end-segment filters and closed unbounded (club) filters. He proved that (in $ZFC$ ) $\mathbf {GL}$ is complete concerning the end-segment filters. His first completeness result implies the completeness of $\mathbf {GL}$ with respect to any ordinal $\alpha \geq \omega ^{\omega }$ equipped with the interval (order) topology. This result was independently proved by Abashidze [1]. Investigating the class of club filter, Blass proved the completeness of $\mathbf {GL}$ by assuming the Gödel’s axiom of constructibility or, more precisely, Jensen’s square principle $\Box _{\kappa }$ for all uncountable cardinals $\kappa < \aleph _{\omega }$ . Building on some deep results of Harrington and Shelah [13], he also showed that the incompleteness of $\mathbf {GL}$ for club filters is equiconsistent with the existence of a Mahlo cardinal.

Abashidze–Blass theorem launches a new line of research for investigating the completeness of provability logic $\mathbf {GL}$ and also its polymodal extensions $\mathbf {GLP}$ with respect to the natural topologies on ordinals (see, e.g., [4, 5, 6]).

In this paper, we answer a question of Blass [10] by showing that the provability logic $\mathbf {GL}$ consistently can be complete with respect to the filter sequence of normal measures. For each ordinal $\eta $ let

$$ \begin{align*} \mathcal{M}_{\eta}=\bigcap \{\mathcal{U}: \mathcal{U} \text{ is a normal measure on } \eta \}. \end{align*} $$

Note that $\mathcal {M}_{\eta }$ is proper iff $\eta $ is a measurable cardinal, in which case $\mathcal {M}_{\eta }$ is a normal $\kappa $ -complete filter on $\eta $ . Also, it is easily seen that $X \subseteq \eta $ has positive measure with respect to $\mathcal {M}_{\eta }$ iff for at least one normal measure $\mathcal {U}$ on $\eta $ we have $X \in \mathcal {U}$ .

We prove the following theorem.

Theorem 1.1. Assume there are infinitely many strong cardinals. Then there exists a generic extension of the canonical core model in which the provability logic $\mathbf {GL}$ is complete with respect to the filter sequence $\langle \mathcal {M}_{\eta }: \eta \in On \rangle $ .

Remark 1.2. As it is shown in [10], some large cardinals are needed to get the result; indeed the consistency of the statement implies the existence of inner models for measurable cardinals $\kappa $ with $o(\kappa ) \geq n,$ for all $n<\omega .$

As a corollary, we obtain the following, which answers Question 16 from [7].

Corollary 1.3. Assuming the existence of infinitely many strong cardinals $\langle \kappa _n: n<\omega \rangle $ , it is consistent that $\mathbf {GL}$ is complete with respect to the ordinal space $(\alpha , \tau _{M})$ , where $\alpha \geq \sup _{n<\omega }\kappa _n$ and $\tau _M$ is the topology corresponding to the filter sequence of normal measures $\vec {\mathcal {M}}_{\kappa }$ (see Section 4).

The paper is organized as follows. In Section 2 we collect some definitions and facts from provability logic and set theory, and then in Section 3 we complete the proof of Theorem 1.1. In Section 4, we discuss the problem of strong completeness of $\mathbf {GL}$ with respect to the filter sequence of normal measures and conclude with some remarks.

2 Some preliminaries

2.1 Preliminaries from provability logic

Let $\mathbb {P}$ be a set of propositional variables. The syntax of modal logic is obtained by adding the modal operator $\Box $ to propositional logic. So if $\varphi $ is a formula, then $\Box \varphi $ is a formula. As usual, $\lozenge $ is used as a shorthand for $\neg \Box \neg $ and $\bot $ for the logical constant “false.”

The system $\mathbf {GL}$ is defined by the following axioms schemata and rules:

• • propositional tautologies,

• • K. $\Box (\varphi \rightarrow \psi ) \rightarrow (\Box \varphi \rightarrow \Box \psi )$ ,

• • Löb. $\Box (\Box \varphi \rightarrow \varphi ) \rightarrow \Box \varphi $ ,

• • MP. $\vdash \varphi ,\ \vdash \varphi \rightarrow \psi \Rightarrow \vdash \psi $ ,

• • Nec. $\vdash \varphi \Rightarrow \Box \varphi $ .

A Kripke frame is a pair $\mathfrak {F}=(W,R)$ where W is a non-empty set and $R\subseteq W\times W$ is an accessibility relation. A Kripke model is a triple $\mathfrak {M}=(W,R,\nu )$ where $\nu $ is a valuation function which assigns to each $p\in \mathbb {P}$ a subset of W. The valuation function $\nu $ is extended to all formulas as follows:

$$ \begin{align*} \nu(\neg\varphi)&= W - \nu(\varphi),\\ \nu(\varphi \wedge \psi) &= \nu(\varphi)\cap \nu(\psi),\\ \nu(\Box\varphi)&= \{w\in W\ |\ (\forall v\in W)\ wRv\rightarrow v\in \nu(\varphi)\}. \end{align*} $$

A formula $\varphi $ is valid in $\mathfrak {M}$ if $\nu (\varphi )=W$ ; also, it is valid in $\mathfrak {F}$ if it is valid in every model based on $\mathfrak {F}$ .

Proposition 2.1 (Segerberg [16]).

$\mathbf {GL}$ is complete with respect to the class of all finite transitive irreflexive trees.

The Kripke completeness of $\mathbf {GL}$ can facilitate the method of proving the other completeness results. To be more precise, for a given class of structures, instead of proving the completeness directly, one can find a way to transform the validity from this class to the class of Kripke frames. This idea is also used by Blass to give a sufficient condition for the completeness of $\mathbf {GL}$ with respect to any family of filters. To this end, a particular class of trees named $\mathbf {K}_n$ is considered in [10] as a crossing point between these two classes.

For each fixed natural number n, the nodes of $\mathbf {K}_n$ consist of all finite sequences of pairs $\langle (i_1,j_1), \dots ,(i_k,j_k)\rangle $ where $n>i_1>\dots > i_k\geq 0$ and $j_1,\dots ,j_k\in \omega $ are arbitrary. The order of $\mathbf {K}_n$ , denoted by $\lhd $ , is the end extension order; thus, t extends s iff $s \lhd t$ . So the root of $\mathbf {K}_n$ is the empty sequence $\langle \rangle $ , and the height of the tree is n. Also, each node with height $0<i \leq n$ has infinitely many immediate successors of height j for each $j<i$ .

It is easy to see that each finite transitive tree $(W,R)$ with height n is a bounded morphic image of $\mathbf {K}_n$ . That is, there is an onto function f from the nodes of $\mathbf {K}_n$ to W such that for any $s,t\in \mathbf {K}_n$ and $w\in W$ we have:

• • $s \lhd t$ implies $f(s)R f(t)$ .

• • If $f(s)R w$ , then there is $t\in \mathbf {K}_n$ such that $s \lhd t$ and $f(t)=w$ .

It is easy to see that the validity of formulas is preserved under bounded morphic images. So, by Proposition 2.1, we have:

• • If $\mathbf {GL}\vdash \varphi $ , then $\varphi $ is valid in $\mathbf {K}_n$ for every n.

Suppose that $\vec {\mathcal {F}}=\langle \mathcal {F}_{\alpha }: \alpha \in On \rangle $ is a family of filters where $\mathcal {F}_{\alpha }$ is a filter on $\alpha $ , for each $\alpha \in On$ . A valuation $\nu $ on this family is a function which assigns a class of ordinals to each $p\in \mathbb {P}$ . Then the valuation function $\nu $ is extended to all formulas by the standard rules for Boolean connectives and the following for $\Box $ operator:

$$ \begin{align*} \nu(\Box\varphi)&= \{\alpha\ |\ \nu(\varphi)\in \mathcal{F}_{\alpha}\}. \end{align*} $$

Then for the dual operator $\lozenge $ we have

$$ \begin{align*} \nu(\lozenge\varphi)=\{\alpha\ |\ \nu(\varphi) \text{ has positive measure w.r.t } \mathcal{F}_{\alpha}\}. \end{align*} $$

A formula $\varphi $ is $\vec {\mathcal {F}}$ -valid if for every valuation $\nu $ on $\vec {\mathcal {F}}$ we have $\nu (\varphi )=On$ .

In this paper, we are interested in the filter sequence of normal measures $\vec {\mathcal {M}}=\langle \mathcal {M}_{\alpha }: \alpha \in On \rangle ,$ where for each $\alpha $ , $\mathcal {M}_{\alpha }$ is the intersection of all normal measures on $\alpha $ .

Note that in $\vec {\mathcal {M}}$ , the formula $\lozenge \top $ determines the class of all measurable cardinals; reciprocally, $\Box \bot $ defines the class of all non-measurable ordinals. Furthermore, $\lozenge ^n \top $ is true at an ordinal $\alpha $ if and only if $\alpha $ is a measurable cardinal with Mitchell order $\geq n$ (see Definition 2.7).

By showing that for any $\alpha $ and A if $A\in \mathcal {M}_{\alpha }$ , then $\{\beta <\alpha : A\cap \beta \in \mathcal {M}_{\beta }\}\in \mathcal {M}_{\alpha }$ ; Blass proved the following soundness theorem.

Proposition 2.2 [10, Theorem 2].

$\mathbf {GL}$ is sound with respect to the class of normal filters $\vec {\mathcal {M}}$ .

From the soundness result, one can indicate some properties of measurable cardinals. For example, Blass showed that the validity of the Löb formula implies that any measurable cardinal $\kappa $ has a normal measure containing $\{\alpha <\kappa : \alpha \text { is not measurable}\}$ . Also, if A has a positive measure with respect to $\mathcal {M}_{\kappa }$ , then so does the set $\{\alpha \in A : \alpha \text { has no normal filter containing } A\}$ . More generally, one can see that the validity of $\lozenge ^{n+1}\top \rightarrow \lozenge (\lozenge ^m\top \wedge \Box ^{m+1}\bot )$ for each $m<n$ implies that any measurable cardinal $\kappa $ with $o(\kappa )\geq n$ has a normal measure containing $\{\alpha <\kappa : o(\alpha )=m\}$ , where $o(\alpha )$ is the Mitchell order of $\alpha $ (see Definition 2.7).

The following lemma gives a sufficient condition to convert a Kripke interpretation of a given formula into a filter interpretation (see the proof of Theorem 3 in [10] for information on how this conversion is defined). So, the main part of the proof of Theorem 1.1 is to show that the following lemma holds for a family of normal filter sequences; the proof is given in Section 3. Then the completeness of $\mathbf {GL}$ with respect to these filters is obtained by Proposition 2.1.

Lemma 2.3 (Blass [10]).

Let $\vec {\mathcal {F}}=\langle \mathcal {F}_{\alpha }: \alpha \in On \rangle $ be a family of filters $\mathcal {F}_{\alpha }$ on $\alpha .$ Suppose that for each $n<\omega $ there exists a function $\Gamma : \mathbf {K}_n \to \mathcal {P}(On)$ satisfying the following conditions $:$

1. (1) $\Gamma (\langle \rangle )$ in non-empty.

2. (2) If $s \neq t$ are in $\mathbf {K}_n $ , then $\Gamma (s) \cap \Gamma (t)$ is empty.

3. (3) If $s \lhd t$ are in $\mathbf {K}_n $ and $\alpha \in \Gamma (s)$ , then $\Gamma (t) \cap \alpha $ has positive measure with respect to $\mathcal {F}_{\alpha }$ .

4. (4) If $s \in \mathbf {K}_n $ and $\alpha \in \Gamma (s),$ then $\bigcup _{s \lhd t}\Gamma (t) \cap \alpha \in \mathcal {F}_{\alpha }$ .

Then every $\vec {\mathcal {F}}$ -valid modal formula is provable in $\mathbf {GL}$ .

2.2 Preliminaries from set theory

In this subsection we recall some definitions and facts about measurable cardinals and their Mitchell order structure.

Definition 2.4. An uncountable cardinal $\kappa $ is a measurable cardinal if there exists a $\kappa $ -complete non-principal ultrafilter on $\kappa .$

One can show that any measurable cardinal $\kappa $ carries a normal measure, i.e., a $\kappa $ -complete non-principal ultrafilter $\mathcal {U}$ on $\kappa $ which is normal:

$$\begin{align*}\forall \xi < \kappa, A_{\xi} \in \mathcal{U} \Rightarrow \bigtriangleup_{\xi<\kappa}A_{\xi}=\{\alpha < \kappa: \forall\xi<\alpha,~\alpha \in A_{\xi} \}\in \mathcal{U}. \end{align*}$$

Given a normal measure $\mathcal {U}$ on $\kappa $ we can perform the ultrapower $\text {Ult}(V, \mathcal {U})$ and the ultrapower embedding $j: V \to \text {Ult}(V, \mathcal {U})$ which is defined by $j(x) = [c_x]_{\mathcal {U}}$ , where $c_x: \kappa \to V$ is the constant function x. By Łoś theorem, j is easily seen to be an elementary embedding. On the other hand, $\text {Ult}(V, \mathcal {U})$ is well-founded, and hence it is isomorphic to a unique transitive inner model $M_{\mathcal {U}}$ via a unique isomorphism $\pi : \text {Ult}(V, \mathcal {U}) \simeq M_{\mathcal {U}}$ . Then $j_{\mathcal {U}}: V \to M_{\mathcal {U}}$ , defined by $j_{\mathcal {U}}=\pi \circ j$ defines an elementary embedding from the universe V into an inner model $M_{\mathcal {U}}$ with critical point $\kappa $ (i.e., $j_{\mathcal {U}} \restriction \kappa =\text {id}\restriction \kappa $ and $j_{\mathcal {U}}(\kappa )> \kappa $ ).

Conversely, given a non-trivial elementary embedding $j: V \to M$ from V into an inner model M with critical point $\kappa ,$ one can form the normal measure

$$\begin{align*}\mathcal{U}=\{ X \subseteq \kappa: \kappa \in j(X) \} \end{align*}$$

on $\kappa $ and then j factors through $j_{\mathcal {U}}$ in the sense that $j=k \circ j_{\mathcal {U}}$ , where $k: M_{\mathcal U} \to M$ is defined as $k([f]_{\mathcal U})=j(f)(\kappa )$ .

Definition 2.5.

1. (a) Suppose $\lambda \geq \kappa $ are uncountable cardinals. Then $\kappa $ is $\lambda $ -strong if there exists a non-trivial elementary embedding $j: V \to M$ from V into some inner model M with critical point $\kappa $ such that $^{\kappa }M \subseteq M$ , $V_{\lambda } \subseteq M$ and $j(\kappa )> \lambda $ .

2. (b) A cardinal $\kappa $ is strong if it is $\lambda $ -strong for all $\lambda \geq \kappa .$

We now define an order on normal measures introduced by Mitchell.

Definition 2.6 (Mitchell [15]).

Suppose $\kappa $ is a measurable cardinal and $\mathcal {U}, \mathcal {W}$ are normal measures on it. Then $\mathcal {W} \lhd \mathcal {U}$ if and only if $\mathcal {W} \in \text {Ult}(V, \mathcal {U}).$

In [15], Mitchell proved that $\lhd $ is a well-founded order now known as the Mitchell ordering. Thus, given any normal measure $\mathcal {U}$ on $\kappa ,$ we can define its Mitchell order as

$$\begin{align*}o(\mathcal{U})=\sup\{o(\mathcal{W})+1: \mathcal{W} \lhd \mathcal{U} \}. \end{align*}$$

The Mitchell order of $\kappa $ is also defined as

$$\begin{align*}o(\kappa)=\sup\{o(\mathcal{U})+1: \mathcal{U} \text{~is a normal measure on~}\kappa \}. \end{align*}$$

Definition 2.7. Suppose $\kappa $ is a measurable cardinal. Then

$$\begin{align*}\lhd(\kappa)= (\{ \mathcal{U}: \mathcal{U} \text{~is a normal measure on~}\kappa \}, \lhd). \end{align*}$$

The structure of $\lhd (\kappa )$ is widely studied in set theory, we refer to [8, 9] for most recent results. We will need the following, which plays an essential role in the proof of Theorem 1.1.

Theorem 2.8 (Ben-Neria [8]).

Let $V=L[E]$ be a core model. Suppose there is a strong cardinal $\kappa $ and infinitely many measurable cardinals above it. Let $(\mathbf {S}, <)$ be a countable well-founded order of rank at most $\omega .$ Then there exists a generic extension $V^*$ of V in which $\lhd (\kappa )^{V^*} \simeq (\mathbf {S}, <)$ .

Let us recall that a forcing notion $(\mathbb {Q}, \leq , \leq ^*)$ satisfies the Prikry property if $\leq ^* \subseteq \leq $ and for each $p \in \mathbb {Q}$ and each sentence $\sigma $ in the forcing language of $(\mathbb {Q}, \leq )$ , there exists $q \leq ^* p$ such that q decides $\sigma $ . The key point is that in general $(\mathbb {Q}, \leq )$ lacks to be even $\aleph _1$ -distributive, but if $(\mathbb {Q}, \leq , \leq ^*)$ satisfies the Prikry property and $(\mathbb {Q}, \leq ^*)$ is $\kappa $ -closed, then forcing with $(\mathbb {Q}, \leq )$ does not add new bounded subsets to $\kappa .$ We may note that Ben-Neria’s forcing of the above theorem can be considered as a Prikry type forcing notion $(\mathbb {Q}, \leq , \leq ^*)$ , and furthermore, given any $\theta < \kappa $ , we can manage the forcing so that $(\mathbb {Q}, \leq ^*)$ is $\theta $ -closed, in particular it does not add any new bounded subsets to $\theta $ .

The following is an immediate corollary of the above theorem, whose proof requires familiarity with Prikry type forcing notions and their iterations (see [12] for more information). ¹

It is worth mentioning that the usual iteration of Prikry type forcing notions, say, for example, finite support iteration, fails to preserve cardinals. To give a motivation of why this happens, let $\langle \kappa _n: n<\omega \rangle $ be an increasing sequence of measurable cardinals and let $\kappa =\sup _{n<\omega }\kappa _n$ . For each $n< \omega $ , let $\mathcal U_n$ be a normal measure on $\kappa _n$ and let $\mathbb {P}_n$ be the corresponding Prikry forcing. Thus a condition in $\mathbb {P}_n$ is a pair $(s, A),$ where $s \in [\kappa _n]^{<\omega }, A \in \mathcal U_n$ , and $\max (s) < \min (A)$ . Given another condition $(t, B)$ , we say $(t, B) \leq (s, A)$ iff $s \unlhd t, B \subseteq A$ , and $t \setminus s \subseteq A.$ The direct extension order is defined as $(t, B) \leq ^* (s, A)$ iff $(t, B) \leq (s, A)$ and $s=t$ . Forcing with $\mathbb {P}_n$ adds an $\omega $ -sequence $C_n \subseteq \kappa _n$ , which is cofinal in $\kappa _n$ , called the Prikry sequence. Now let $\mathbb {P}$ be the finite support product of $\mathbb {P}_n$ ’s. ² Thus a condition in $\mathbb {P}$ is a sequence $p= \langle p_n: n<\omega \rangle $ , where each $p_n \in \mathbb {P}_n$ , and for all but finitely many $n, p_n=(\emptyset , \kappa _n)=1_{\mathbb {P}_n}$ . We claim that forcing with $\mathbb {P}$ collapses $\kappa $ into $\omega $ . To see this, let G be $\mathbb {P}$ -generic over V, and for each n, let $C_n$ be the Prikry sequence added by it thorough $\kappa _n.$ Define $f: \omega \rightarrow \kappa $ by $f(n)=\min (C_n)$ . Given any $\alpha < \kappa ,$ it is easy to see that the set

$$ \begin{align*} D_{\alpha}=\{p= \langle p_n: n<\omega\rangle \in \mathbb{P}: \exists n \big( \kappa_n> \alpha,~ p_n=(\{\alpha\}, \kappa_n \setminus (\alpha+1)) \big) \} \end{align*} $$

is dense in $\mathbb {P}$ . But if $p \in D_{\alpha }$ is as above, then $p \Vdash _{\mathbb {P}}$ “ .” It follows that $\text {range}(f)=\kappa $ , and thus $\kappa $ is collapsed.

However, there are other ways to iterate Prikry type forcing notions that avoid the above problem; the most known methods are the Magidor iteration (full support iteration) and Gitik iteration (Easton support iteration). Such kinds of iterations satisfy the Prikry property, and by using this fact, one can show that the resulting forcing behaves nicely.

Theorem 2.9. Let $V=L[E]$ be a core model. ³ Suppose there is an $\omega $ -sequence $\langle \kappa _n: n<\omega \rangle $ of strong cardinals and suppose $\langle (\mathbf {S}_n, <_n): n<\omega \rangle $ is a sequence of countable well-founded orders, each of rank at most $\omega .$ Then there exists a generic extension $V^*$ of V in which for each $n<\omega $ , $\lhd (\kappa _n)^{V^*} \simeq (\mathbf {S}_n, <_n)$ .

Proof Recall from the above that Ben-Neria’s forcing of Theorem 2.8 is a Prikry type forcing notion $(\mathbb {Q}, \leq , \leq ^*)$ . Now let $\langle \kappa _n: n<\omega \rangle $ and $\langle (\mathbf {S}_n, <_n): n<\omega \rangle $ be as above. For each $n<\omega $ , let $\langle \lambda ^n_i: i \leq \omega \rangle $ be the first $\omega +1$ measurable cardinals above $\kappa _n$ . ⁴ Then, for each n, $\lambda ^n_{\omega } < \kappa _{n+1}$ . Let

be the Magidor iteration of Prikry type forcing notions, where for each $n<\omega $ ,

is defined in $V^{\mathbb {P}_n}$ such that:

1. (1) $|\mathbb {Q}_n| < \kappa _{n+1}$ .

2. (2) $(\mathbb {Q}_n, \leq ^*_{\mathbb {Q}_n})$ is $\lambda ^{n-1}_{\omega }$ -closed, in particular it adds no new bounded subsets to $\lambda ^{n-1}_{\omega }$ .

3. (3) $\lhd (\kappa _n)^{V^{\mathbb {P}_{n+1}}} \simeq (\mathbf {S}_n, <_n)$ .

This is possible by Theorem 2.8 (and its proof) and the fact that by (1), all cardinals $\kappa _m,$ for $m>n$ , remain strong in the extension by $\mathbb {P}_{n+1}$ . Then $V^*=V^{\mathbb {P}_{\omega }}$ is the required model.

3 Completeness of $\mathbf {GL}$ with respect to the normal filter sequence

In this section we prove Theorem 1.1. Let $L[E]$ be the canonical extender model and suppose in it there is an $\omega $ -sequence $\langle \kappa _n: 0<n<\omega \rangle $ of strong cardinals. By Theorem 2.9, we can extend $L[E]$ to a generic extension V in which the structure of the Mitchell order of $\kappa _n$ , $\lhd (\kappa _n)$ , is isomorphic to $\mathbf {S}_n,$ where $\mathbf {S}_n= \mathbf {K}_n \setminus \{ \langle \rangle \}$ , ordered by $t < s$ iff t end extends s.

We show that in V, the provability logic $\mathbf {GL}$ is complete with respect to the normal filter sequence. Set $\kappa =\sup _{n<\omega }\kappa _n$ . By Lemma 2.3, it suffices to show that for each $n<\omega $ there exists a function $\Gamma : \mathbf {K}_n \to \mathcal {P}(\kappa )$ satisfying the following conditions:

1. (†)₁ $\Gamma (\langle \rangle )$ is non-empty.

2. (†)₂ If $s \neq t$ are in $\mathbf {K}_n$ , then $\Gamma (s) \cap \Gamma (t)$ is empty.

3. (†)₃ If $s \lhd t$ are in $\mathbf {K}_n$ and $\eta \in \Gamma (s)$ , then $\Gamma (t) \cap \eta $ has positive measure with respect to $\mathcal {M}_{\eta }$ , i.e., $\Gamma (t) \cap \eta $ belongs to at least one normal measure on $\eta $ .

4. (†)₄ If $s \in \mathbf {K}_n$ is not maximal and $\eta \in \Gamma (s),$ then $\bigcup _{s \lhd t}\Gamma (t) \cap \eta \in \mathcal {M}_{\eta }$ .

Let us first suppose that $n=1$ . Let $\mathbf {S}=\mathbf {S}_1$ and $\eta =\kappa _1$ . Then $\mathbf {S}=\{\langle (0, \ell )\rangle : \ell <\omega \}$ , and in V, $\eta $ has exactly $\omega $ -many normal measures $\mathcal {U}(0, \ell ), \ell <\omega ,$ all of Mitchell order $0$ . Pick sets $A_{0, \ell } \in \mathcal {U}(0, \ell ),$ so that for all $\ell \neq \ell ', A_{0, \ell } \cap A_{0, \ell '}=\emptyset .$

Define $\Gamma : \mathbf {K}_1 \to \mathcal {P}(\kappa )$ by

$$ \begin{align*} \Gamma(s)= \left\{ \begin{array}{l} \{ \eta \}, \hspace{1.6cm} \text{ if } s= \langle \rangle,\\ A_{0, \ell}, \hspace{1.5cm} \text{ if } s=\langle (0,\ell) \rangle. \end{array} \right. \end{align*} $$

It is clear that $\Gamma $ is as required.

Now suppose that $n \geq 2$ . Let $\mathbf {S}=\mathbf {S}_n$ and $\eta =\kappa _n$ . Thus, in V, $\lhd (\eta )\simeq \mathbf {S}.$ Let

$$\begin{align*}\lhd(\eta) = \{\mathcal{U}(s): s \in \mathbf{S} \}, \end{align*}$$

where for each $s, t \in \mathbf {S}$ ,

$$\begin{align*}t < s \iff \mathcal{U}(t) \lhd \mathcal{U}(s). \end{align*}$$

For ⁵ each $s \in \mathbf {S}$ , let $j_s: V \to M_s \simeq \text {Ult}(V, \mathcal {U}(s))$ be the canonical ultrapower embedding. Note that for each $X \subseteq \eta ,$ we have

$$\begin{align*}X \in \mathcal{U}(s) \iff \eta \in j_s(X). \end{align*}$$

Pick the sets $A_{s}$ for $s \in \mathbf {S}$ such that:

• $(\beth )_1 \ A_{s} \in \mathcal {U}(s).$

• $(\beth )_2$ For all $s \neq t$ in $\mathbf {S}, A_s \cap A_t=\emptyset .$

For $t < s$ in $\mathbf {S}$ , let $g_t^s: \eta \to V$ represent $\mathcal {U}(t)$ in the ultrapower by $\mathcal {U}(s)$ , i.e., $\mathcal {U}(t)=[g_t^s]_{\mathcal {U}(s)}$ . The next lemma is proved in [15].

Lemma 3.1. Suppose $t< s$ are in $\mathbf {S}$ and $X \subseteq \eta .$ Then

$$\begin{align*}X \in \mathcal{U}(t) \iff \{\nu \in A_s: X \cap \nu \in g_t^s(\nu) \} \in \mathcal{U}(s). \end{align*}$$

Proof We give a proof for completeness. Let $X \subseteq \eta $ and set $Y= \{\nu \in A_s: X \cap \nu \in g_t^s(\nu ) \}.$ Then $j_s(X) \cap \eta =X$ and $j_s(g_t^s)(\eta )=\mathcal {U}(t)$ ; hence,

$$\begin{align*}Y \in \mathcal{U}(s) \iff \eta \in j_s(Y) \iff j_s(X) \cap \eta \in j_s(g_t^s)(\eta) \iff X \in \mathcal{U}(t), \end{align*}$$

which gives the result.

The proof of the next lemma follows the ideas of [14].

Lemma 3.2. Suppose $u< t< s$ are in $\mathbf {S}$ . Then

$$\begin{align*}A^1_{s, t, u}=\{ \nu \in A_s: g_u^s(\nu) \lhd g_t^s(\nu) \text{~are normal measures on~}\nu\} \in \mathcal{U}(s). \end{align*}$$

Proof As $j_s(g_u^s)(\eta )=\mathcal {U}(s)$ and $j_s(g_t^s)(\eta )=\mathcal {U}(t)$ , we have

$$\begin{align*}A^1_{s, t, u} \in \mathcal{U}(s) \iff \eta \in j_s(Y) \iff M_s \models \mathcal{U}(s) \lhd \mathcal{U}(t) \text{ are normal measures on } \eta, \end{align*}$$

which gives the required result.

Suppose $u< t< s$ are in $\mathbf {S}$ and $g_u^s(\nu ) \lhd g_t^s(\nu ).$ Then $g_u^s(\nu )$ has a representative function which presents it in the ultrapower by $g_t^s(\nu )$ . The next lemma shows that there is already a canonical such representation.

Lemma 3.3. Suppose $u< t< s$ are in $\mathbf {S}$ . Then

$$\begin{align*}A^2_{s, t, u}=\{ \nu \in A_s: g_u^s(\nu) =[g_u^t \restriction \nu]_{g_t^s(\nu)} \} \in \mathcal{U}(s). \end{align*}$$

Proof As in the proof of Lemma 3.2, we have

$$\begin{align*}A^2_{s, t, u} \in \mathcal{U}(s) \iff M_s \models \mathcal{U}(u)= [j_s(g_u^t)\restriction \eta]_{\mathcal{U}(t)}. \end{align*}$$

On the other hand, $j_s(g_u^t)\restriction \eta =g_u^t$ and hence $[j_s(g_u^t)\restriction \eta ]_{\mathcal {U}(t)}=[g_u^t]_{\mathcal {U}(t)}$ , from which the result follows.

For $u<t<s$ in $\mathbf {S}$ , let $A_{s,t, u}=A^1_{s, t, u} \cap A^2_{s, t, u}$ . The next lemma is an immediate corollary of the above two lemmas.

Lemma 3.4. Suppose $s \in \mathbf {S}$ . Then

$$\begin{align*}B_s= \bigcap_{u<t<s}A_{s, t, u} \in \mathcal{U}(s). \end{align*}$$

For each $s \in \mathbf {S},$ set

$$\begin{align*}\mathbf{S}/(<s) = \{ t \in \mathbf{S}: t< s \}. \end{align*}$$

Lemma 3.5.

1. (a) Suppose $s \in \mathbf {S}$ is a minimal node. Then

   $$\begin{align*}C_{s}=\{\nu \in B_s: \nu \text{~is an inaccessible non-measurable cardinal~} \} \in \mathcal{U}(s). \end{align*}$$

2. (b) Suppose $s \in \mathbf {S}$ is not minimal. Then

   $$\begin{align*}C_s=\{\nu \in B_s: \lhd(\nu) \simeq \mathbf{S}/(<s) \} \in \mathcal{U}(s). \end{align*}$$

   Furthermore, for each $\nu \in C_s,$

   $$\begin{align*}\lhd(\nu) = \{ g_t^s(\nu): t < s \}. \end{align*}$$

Proof (a) Clearly, $\{\nu \in B_s: \nu \text {~is an inaccessible cardinal~} \} \in \mathcal {U}(s).$ Now suppose by contradiction, $Y=\{\nu \in B_s: \nu \text {~is a measurable cardinal~} \} \in \mathcal {U}(s).$ For each $\nu \in Y$ pick some normal measure $\mathcal {W}_{\nu }$ on $\nu $ and set $\mathcal {W}=[\mathcal {W}_{\nu }: \nu \in Y]_{\mathcal {U}(s)}.$ Then $\mathcal {W}$ is a normal measure on $\nu $ and $\mathcal {W} \lhd \mathcal {U}(s)$ . This contradicts our choice of the Mitchell order structure of $\lhd (\eta )$ .

(b) We show that

$$\begin{align*}\{ \nu \in B_s: \lhd(\nu) = \{ g_t^s(\nu): t < s \} \} \in \mathcal{U}(s). \end{align*}$$

Suppose not. Then there exists a measure one set $Y \in \mathcal {U}(s)$ such that for each $\nu \in Y,$ there exists a normal measure $\mathcal {W}_{\nu }$ on $\nu $ such that $\mathcal {W}_{\nu } \notin \{ g_t^s(\nu ): t < s \}.$ Set $\mathcal {W}=[\mathcal {W}_{\nu }: \nu \in Y]_{\mathcal {U}(s)}.$ Then $\mathcal {W} \lhd \mathcal {U}_s$ is a normal measure on $\nu $ and $\mathcal {W} \neq \mathcal {U}(t)$ for all $t<s$ . This contradicts our choice of the Mitchell order structure of $\lhd (\eta )$ below $\mathcal {U}(s)$ .

Using Lemma 3.1, and by shrinking the sets $C_s, s \in \mathbf {S}$ , we may assume that:

• $(\beth )_3$ For all $t<s$ in $\mathbf {S}$ and all $\nu \in C_s,$ $C_t \cap \nu \in g_t^s(\nu ).$

Define $\Gamma : \mathbf {K}_n \to \mathcal {P}(\kappa )$ by

$$ \begin{align*} \Gamma(s)= \left\{ \begin{array}{l} \{\eta\}, \hspace{1.6cm} \text{ if } s=\langle \rangle,\\ C_s, \hspace{1.75cm} \text{ if }s \neq \langle \rangle.\\ \end{array} \right. \end{align*} $$

Lemma 3.6. $\Gamma $ satisfies the requirements $(\dagger )_1$ – $(\dagger )_4.$

Proof Clearly clause $(\dagger )_1$ is satisfied as $\eta \in \Gamma (\langle \rangle )$ and clause $(\dagger )_2$ follows from $(\beth )_2$ and the fact that $C_s \subseteq A_s,$ for each $s \in \mathbf {S}$ .

To show that clause $(\dagger )_3$ is satisfied, let $s \lhd t$ be in $\mathbf {K}_n$ and $\nu \in \Gamma (s)$ . If $s=\langle \rangle ,$ then $\nu =\eta $ and we have $\Gamma (t) =C_t \in \mathcal {U}(t)$ , in particular, $\Gamma (t)$ has positive measure with respect to $\mathcal {M}_{\eta }.$ If $s \neq \langle \rangle ,$ then by $(\beth )_3$ , $\Gamma (t) \cap \nu =C_t \cap \nu \in g_t^s(\nu )$ , and by Lemma 3.2, $g_t^s(\nu )$ is a normal measure on $\nu $ . Thus $\Gamma (t) \cap \nu $ has positive measure with respect to $\mathcal {M}_{\nu }$ , as required.

Finally to see that clause $(\dagger )_4$ is satisfied, let $s \in \mathbf {K}_n$ be a non-maximal element and let $\nu \in \Gamma (s)$ . First suppose that $s=\langle \rangle .$ Then $\nu =\eta $ , and:

• $(\eta )_1$ The only normal measures on $\eta $ are $\mathcal {U}(t), t \in \mathbf {S}$ .

• $(\eta )_2$ For all $t \in \mathbf {S}, C_t \in \mathcal {U}(t)$ .

It immediately follows that

$$\begin{align*}\bigcup_{\langle \rangle \lhd t} \Gamma(t)= \bigcup_{\langle \rangle \lhd t} C_t \in \bigcap_{t \in \mathbf{S}} \mathcal{U}(t)=\mathcal{M}_{\eta}. \end{align*}$$

Now suppose that $s \neq \langle \rangle .$ Then:

• $(\nu )_1$ By Lemma 3.5(b), the only normal measures on $\nu $ are $g_t^s(\nu )$ where $t \rhd s$ .

• $(\nu )_2$ By $(\beth )_3$ , for all $s \lhd t, C_t \cap \nu \in g_t^s(\nu )$ .

Thus,

$$\begin{align*}\bigcup_{s \lhd t} \Gamma(t) \cap \nu= \bigcup_{s \lhd t} C_t \cap \nu \in \bigcap_{s \lhd t} g_t^s(\nu)=\mathcal{M}_{\nu}.\\[-40pt] \end{align*}$$

Theorem 1.1 follows.

4 Concluding remarks

Although $\mathbf {GL}$ is not strongly complete with respect to Kripke semantics, interpreting $\lozenge $ as the derivative operator makes $\mathbf {GL}$ strongly complete over scattered spaces, specifically with respect to any ordinal $\alpha> \omega ^{\omega }$ equipped with the interval topology. However, $\mathbf {GL}$ is not strongly complete concerning filter sequence of normal measures. To see this, consider the set $\Sigma =\{\lozenge p_0\}\cup \{\Box (p_i\rightarrow \lozenge p_{i+1})\ |\ i<\omega \}$ and suppose that there is a valuation $\nu $ on $\vec {\mathcal {M}}$ such that $\kappa $ satisfies $\Sigma $ . Thus, $\nu (p_i\rightarrow \lozenge p_{i+1})\in \mathcal {M}_{\kappa }$ , for each $i<\omega $ . The truth of $\lozenge p_0$ and $\Box p_0\rightarrow \lozenge p_1$ in $\kappa $ implies that there is a normal measure $\mathcal {U}_0$ on $\kappa $ such that $\nu (p_0),\nu (\lozenge p_1)\in \mathcal {U}_0$ . Let $o(\mathcal {U}_0)=\alpha _0$ . Then there exists a normal measure $\mathcal {U}_1$ such that $\nu (p_1), \nu (\lozenge p_2)\in \mathcal {U}_1$ and $o(\mathcal {U}_1)<o(\mathcal {U}_0)$ . By induction, we can see that for each i, there is a normal measure $\mathcal {U}_i$ such that $\nu (p_i), \nu (\lozenge p_{i+1})\in \mathcal {U}_i$ and $o(\mathcal {U}_i)=\alpha _i<\alpha _{i-1}$ . This gives a strictly decreasing sequence $\langle \alpha _i: i<\omega \rangle $ of ordinals, which is a contradiction. Furthermore, in [2, Corollary 2.7], it is generally shown that $\mathbf {GL}$ is not strongly complete with respect to topologies on ordinals based on countably complete filters, such as club filters and measurable filters.

Note that we can consider a filter sequence of normal measures $\vec {\mathcal {M}_{\kappa }}$ , the restriction of $\vec {\mathcal {M}}$ to any cardinal $\kappa $ , as a topological space with a unique topology $\tau _{M}$ generated by the following sets:

• • If $\alpha <\kappa $ is not a measurable cardinal, then $\alpha $ is an isolated point.

• • If $U\subseteq [0,\kappa ]$ , then $U\in \tau $ iff for any measurable cardinal $\alpha \in U$ there is $X\in \mathcal {M}_{\alpha }$ such that $X\subseteq U$ .

For any $A\subseteq [0,\kappa ]$ , the set of limit points of A, denoted by $d(A)$ , is the set of all ordinals $\alpha $ such that $A\cap \alpha $ has positive measure with respect to $\mathcal {M}_{\alpha }$ . Let $o(\alpha )=0$ if $\alpha $ is not measurable, then for any ordinal $\alpha \leq \kappa $ we have $\rho (\alpha )=o(\alpha )$ , where $\rho $ is the derivative topological rank of the space $\vec {\mathcal {M}_{\kappa }}$ , i.e., the least ordinal $\xi $ such that $\alpha \notin d^{\xi +1}(\vec {\mathcal {M}_{\kappa }})$ . Therefore, Corollary 1.3 is obtained from Theorem 1.1 for the space $(\kappa ,\tau _{M})$ for sufficient large cardinal $\kappa $ .

In [3] it is proved that for any given scattered space $\mathfrak {X}=(X,\tau )$ of sufficiently large derivative rank, $\mathbf {GL}$ is strongly complete with respect to $\mathfrak {X}_{+\lambda }=(X,\tau _{+\lambda })$ where $\tau _{+\lambda }$ is a finer topology named Icard topology. In particular, for filter sequence of normal measures and for $\lambda =1$ , it is consistent that $\mathbf {GL}$ is strongly complete with respect to $(\kappa ,\tau _{M+1})$ whenever $\kappa $ is a measurable cardinal with $o(\kappa )\geq \omega ^{\omega }+1$ and $\tau _{M+1}$ is the generalized Icard topology, i.e., the least topology extending $\tau _{M}$ by adding all sets of the form $\{\alpha <\kappa : \zeta <\rho (\alpha )\leq \xi \}$ for all $-1\leq \zeta <\xi \leq o(\kappa )$ . However, the strong completeness of [3] is based on the assumption that the set of propositional variables $\mathbb {P}$ is countable, and it remains open to find a natural topological space $\mathfrak {X}$ with respect to which $\mathbf {GL}$ is strongly complete based on uncountable language.

As it is shown in [10], the incompleteness of $\mathbf {GL}$ with respect to club filters is equiconsistent with the existence of a Mahlo cardinal. However, the following question remains open.

Question 4.1. What is the exact consistency strength of “ $\mathbf {GL}$ is complete with respect to the filter sequence of normal measures $?$ ”

As it is stated by Blass, for $\mathbf {GL}$ to be complete with respect to normal filters, we need the existence of measurable cardinals of all finite Mitchell orders, so the existence of some large cardinals is needed. Our proof is based on a result from Ben-Neria [8], Theorem 2.8, although it seems that the assumption he has used is more than what we need, for now, this is the best possible result. On the other hand, in order to make the article comprehensible to readers who are not familiar with the advanced concepts of set theory, we used a different and slightly stronger assumption than Ben-Neria’s. Note that we do not need our cardinals to be strong, but it suffices to be $\lambda $ -strong for a suitable $\lambda $ . Also, as it is stated by Donder (see [10]), the existence of large cardinals alone is not sufficient for our proof; for example, $\mathbf {GL}$ is incomplete in the known canonical core models for strong cardinals, as in such models, for measurable cardinals $\kappa $ of Mitchell order $1$ , $\mathcal {M}_{\kappa }$ is an ultrafilter, and this prevents $\mathbf {GL}$ from being complete.