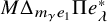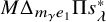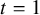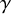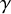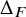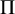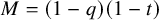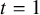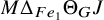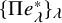Delta and Theta Operator Expansions

Abstract

We give an elementary symmetric function expansion for the expressions $M\Delta _{m_\gamma e_1}\Pi e_\lambda ^{\ast }$ and $M\Delta _{m_\gamma e_1}\Pi s_\lambda ^{\ast }$ when $t=1$ in terms of what we call $\gamma $-parking functions and lattice $\gamma $-parking functions. Here, $\Delta _F$ and $\Pi $ are certain eigenoperators of the modified Macdonald basis and $M=(1-q)(1-t)$. Our main results, in turn, give an elementary basis expansion at $t=1$ for symmetric functions of the form $M \Delta _{Fe_1} \Theta _{G} J$ whenever F is expanded in terms of monomials, G is expanded in terms of the elementary basis, and J is expanded in terms of the modified elementary basis $\{\Pi e_\lambda ^\ast \}_\lambda $. Even the most special cases of this general Delta and Theta operator expression are significant; we highlight a few of these special cases. We end by giving an e-positivity conjecture for when t is not specialized, proposing that our objects can also give the elementary basis expansion in the unspecialized symmetric function.

1 Introduction

Delta and Theta operators, denoted by $\Delta _F$ and $\Theta _F$ for a choice of symmetric function F, are fundamental symmetric function operators in the theory of Macdonald polynomials. Since their introduction, these operators have been shown to have incredible properties and connections to other areas of interest. In introducing a brief history of these operators, we will point out some of these connections. For definitions of the symmetric functions discussed here, we refer the reader to Section 3. Often, this area of study has three aspects. There is the symmetric function side, the representation theoretical side, and a combinatorial description. By giving Schur function expansions of the symmetric function side, one is able to give the multiplicities of irreducible representations in the representation theoretical side via the Frobenius map, which sends irreducible characters of the symmetric group to Schur functions: Let $A^{\lambda }$ denote Young’s irreducible representation of the symmetric group $S_n$ indexed by the partition $\lambda \vdash n$ . For any graded module

$$ \begin{align*} V = \bigoplus_{\alpha} V_{\alpha} & & \text{ with } & & V_\alpha \simeq \bigoplus_{\lambda \vdash n} n^{\alpha}_\lambda A^\lambda, \end{align*} $$

the graded Frobenius characteristic produces the symmetric function

$$\begin{align*}\mathcal{F}(V) = \sum_{\lambda \vdash n} s_\lambda \sum_{\alpha} n_\lambda^\alpha Q^\alpha. \end{align*}$$

On the other hand, when the combinatorial expansion of a symmetric function is Schur positive, it predicts the existence of a representation theoretical side. As we will describe here, when dealing with Macdonald polynomials, the representations associated to these expansions are often natural and important for a variety of areas of study.

As proved in [Hai02] and conjectured in [GH96], $\Delta _{e_n} e_n$ gives the bigraded Frobenius characteristic for the space of $S_n$ coinvariants of the polynomial ring with two sets of commuting variables. More precisely, if $Y_n = y_1,\dots , y_n$ and $Z_n = z_1,\dots , z_n$ are two sets of commuting variables, then $\sigma \in S_n$ acts diagonally on the space of polynomials in $Y_n,Z_n$ by sending $y_i \mapsto y_{\sigma _i}$ and $z_i \mapsto z_{\sigma _i}$ . The space of diagonal coinvariants is given by the quotient

$$\begin{align*}\mathcal{R}^{(2,0)} = \frac{\mathbb{C}[Y_n,Z_n]}{(\mathbb{C}[Y_n,Z_n]^{S_n}_+)}, \end{align*}$$

where $(\mathbb {C}[Y_n,Z_n]^{S_n}_+)$ is the ideal generated by $S_n$ -invariants with no constant term. This space is $\mathbb {N}^2$ graded, and we can record the grading by setting $Q^{(r,s)} = q^r t^s.$ Then Haiman’s theorem states that

$$\begin{align*}\Delta_{e_n} e_n = \mathcal{F} (\mathcal{R}^{(2,0)}). \end{align*}$$

The symmetric function $\Delta _{e_n} e_n$ is most often denoted $\nabla e_n$ , where $\nabla $ is the Bergeron-Garsia nabla operator defined in [BG99]. Haiman proves this equality through algebraic geometrical means, realizing this ring through the Hilbert scheme of points on the plane. Hogancamp showed that the hook Schur functions in this symmetric function give the triply graded Khovanov-Rozansky homology for $(n,n+1)$ -torus knots. There is a more general statement involving $(n,nm \pm 1)$ torus knots, though we will not go into detail [Hog17].

On the combinatorial side, there is the Shuffle theorem, conjectured in [HHL⁺05b] and proved by Carlsson and Mellit [CM18]. This conjecture stated that $\nabla e_n$ can be written as a sum over labeled Dyck paths. Carlsson and Mellit in fact prove the compositional refinement conjectured in [HMZ12] via the identity $\nabla e_n = \sum _{\alpha \vDash n} \nabla C_\alpha $ . Their methods introduced a Dyck path algebra. Mellit expanded this idea in order to prove the related Rational Shuffle theorem [Mel21], and then showed that the triply graded Khovanov-Rozansky homology for $(m,n)$ -torus knots can be realized through the elliptic Hall or Schiffmann algebra [Mel22]. On symmetric functions, this algebra can be generated by using the operators of multiplication by $e_1$ and $\Delta _{e_1}$ . Theta operators can also be viewed as elements of this algebra.

The Delta conjecture [HRW18] gives a similar combinatorial description to the symmetric function $\Delta ^{\prime}_{e_{n-k-1}} e_n$ . Soon after, Zabrocki [Zab19] gave a corresponding $S_n$ -module for this symmetric function, stating that if we introduce a new set of anticommuting variables $T_n = \tau _1,\dots , \tau _n$ , and set

$$\begin{align*}\mathcal{R}^{(2,1)} = \frac{\mathbb{C}[Y_n,Z_n, T_n]}{(\mathbb{C}[Y_n,Z_n,T_n]^{S_n}_+)}, \end{align*}$$

then $\sum _{k} u^{k} \Delta _{e_{n-k-1}}' e_n$ gives $\mathcal {F}(\mathcal {R}^{(2,1)} )$ , the triply graded Frobenius characteristic for the space of $S_n$ coinvariants in two sets of commuting variables and one set of anticommuting variables. The methods used by Carlsson and Mellit in the proof of the shuffle theorem relied on the compositional refinement of the statement; however, the symmetric function $\Delta ^{\prime}_{e_{n-k-1}} C_\alpha $ is not combinatorial. Theta operators were then introduced in [DIVW21] in order to give a compositional refinement of the Delta conjecture, using that $\Delta _{e_{n-k-1}}' e_n = \Theta _{e_k} \nabla e_{n-k}$ and the fact that $\Theta _{e_k} \nabla C_\alpha $ is indeed combinatorial. This refinement ultimately led to a proof of the compositional Delta theorem [DM22]. Most recently, the extended Delta conjecture was also proved in [BHM⁺23], giving the combinatorial description for $\Delta _{h_a} \Delta _{e_{k-1}}' e_n$ . This is realized through a connection to $GL_m$ characters and the $LLT$ polynomials of [LLT97].

If we introduce yet another set of anticommuting variables and let $\mathcal {R}^{(2,2)}$ be the $S_n$ coinvariants with two sets of commuting and two sets of anticommuting variables, then it was also conjectured in [DIVW21] that

(1.1) $$ \begin{align} \mathcal{F}(\mathcal{R}^{(2,2)}) = \sum_{r,s \geq 0} u^r v^s \Theta_{e_r} \Theta_{e_ s} \nabla e_{n-r-s}, \end{align} $$

meaning the Frobenius characteristic of $\mathcal {R}^{(2,2)}$ is given via Theta operators. The purely fermionic case $\mathcal {R}^{(0,2)}$ , involving only the portion with anticommuting variables (obtained by setting $q=t=0$ in (1.1)) has recently been proved in [IRR23]. For the $\mathcal {R}^{(1,1)}$ case (found by setting $t=u=0$ in (1.1)), the graded dimension of the coinvariant space with one set of commuting variables and one set of anticommuting variables has been shown in [RW23] to agree with the conjectured formula.

Theta operators have shown remarkable positivity properties. In [DILB⁺22], the authors give a conjectural formula for $\Theta _{e_\lambda } e_1$ when $q=1$ , in terms of tiered trees, known as Theta Tree Conjecture. When $\lambda $ has two parts, via [DILB⁺22, Theorem 7.2], this expression directly relates to the (conjectured) Frobenius characteristic of $\mathcal {R}^{(2,2)}$ ; when $\lambda = 1^n$ , it was shown to be the generating function for the Kac polynomial of certain quivers, adding yet another geometrical meaning to symmetric functions arising in the study of Macdonald polynomials and its related operators. In the same work, the authors also give a very similar formula for $M \Delta _{e_1} \Pi e_\lambda ^\ast $ , which is an expression that arises naturally when working with Theta operators; the analogous statement is known as the Symmetric Theta Tree Conjecture, and the combinatorial objects involved exhibit nicer symmetries.

This conjecture leads us to the study of the expression , and, in the same fashion as the Extended Delta Conjecture, to the more general expression $\Delta _{m_\gamma } \operatorname {\mathrm {\Xi }} e_\lambda $ (and $\Delta _{m_\gamma } \operatorname {\mathrm {\Xi }} s_\lambda $ ). In this work, we show a positive e-expansion for these symmetric functions when $t=1$ . One can hope that, exploiting the many symmetric function identities involving Theta operators [DR23], these results can directly relate to the aforementioned conjectures.

If a symmetric function is positive in some basis, then setting $t=1$ (or $q=1$ ) leaves the ungraded multiplicities intact. Therefore, giving an expansion at $t=1$ would predict the combinatorial objects enumerated by these symmetric functions without the specialization. Even more, we find that certain symmetric functions are not Schur positive, yet become positive in the elementary basis when $t=1$ . And even more surprising, we have Conjecture 13.1, which predicts that the expression $\Delta _{m_\gamma } \operatorname {\mathrm {\Xi }} s_\lambda $ is e-positive after substituting $q=1+u$ (rather than substituting $t=1$ ).

The main strategy of our work is to expand the symmetric function, when $t=1$ , as a series in q. One of the amazing aspects of this method, found in [HR18], is the use of the combinatorial formula for forgotten symmetric functions and their principal evaluation. The terms in the series are sums of certain signed combinatorial objects. After applying a weight-preserving, sign-reversing involution, we are able to get a finite number of positive fixed points, which bijectively correspond to some set of labeled polyominoes. The end result is found by adjusting the polyomino picture to get an expansion in terms of what we call $\gamma $ -parking functions:

Theorem 1.1. For any two partitions $\lambda $ and $\gamma $ , there is a family of labeled polyominoes ${\mathrm { {PF}}}^{\gamma }_{\lambda }$ , called $\gamma $ -parking functions of content $\lambda $ , and a statistic $\operatorname {\mathrm {area}}$ giving

(1.2) $$ \begin{align} \left. \Delta_{m_\gamma} \operatorname{\mathrm{\Xi}} e_{\lambda} \right\rvert_{t=1} = \sum_{p \in {\mathrm{ {PF}}}^{\gamma}_{\lambda} } q^{\operatorname{\mathrm{area}}(p)} e_{\eta(p)}. \end{align} $$

This gives a combinatorial expansion for $\operatorname {\mathrm {\Xi }} e_\lambda \rvert _{t=1}$ that is different from the one given in [DILB⁺22] in terms of tiered trees, and leaves the interesting problem of finding a correspondence between the two, which would be enough to bijectively prove the Symmetric Theta Conjecture.

Using the same methods that prove Theorem 1.1, we also show

Theorem 1.2. For any two partitions $\lambda $ and $\gamma $ , there is a family of labeled polyominoes ${\mathrm { {LPF}}}^{\gamma }_{\lambda }$ , called lattice $\gamma $ -parking functions of content $\lambda $ , and a statistic $\operatorname {\mathrm {area}}$ giving

(1.3) $$ \begin{align} \left. \Delta_{m_\gamma} \operatorname{\mathrm{\Xi}} s_{\lambda} \right\rvert_{t=1} = \sum_{p \in {\mathrm{ {LPF}}}^{\gamma}_{\lambda'} } q^{\operatorname{\mathrm{area}}(p)} e_{\eta(p)}. \end{align} $$

It is now natural to ask whether this expression also has an interpretation in terms of tiered trees, and if there are further generalizations of these identities.

2 Combinatorial definitions

In this section, we aim to introduce the combinatorial objects that will give us the symmetric function expansions we are interested in.

2.1 Words

Definition 2.1. A word of length r is an element $w = (w_1, \dots , w_r) \in \mathbb {N}^r$ . We denote the length by and the size by .

Let w be a word of length r. We let $m_i(w)$ be the number of indices j, such that $w_j = i$ , that is, $m_i(w)$ is the multiplicity of i in w; we denote the multiplicity type of w as $m(w) = 0^{m_0(w)}1^{m_1(w)} 2^{m_2(w)} \cdots $ . If $w \in \mathbb {N}^r_+$ (it has no $0$ entries), then we call it a composition and write $w \vDash \lvert w \rvert $ . There is a class of words that is of special interest to us.

Definition 2.2. A lattice word is a word $w = (w_1, \dots , w_r) \in \mathbb {N}_+^r$ , such that, for all $1 \leq i, j \leq r$ , we have

$$\begin{align*}m_{j+1}(w_1,\dots,w_i) \leq m_j(w_{1},\dots, w_{i}), \end{align*}$$

that is, a word, such that every prefix has at least as many $1$ s as $2$ s, at least as many $2$ s as $3$ s, and so on.

Denote by $R(w)$ the set of all words $\alpha = (\alpha _1, \dots , \alpha _r)$ whose entries can be rearranged to give w, or $m(\alpha ) = m(w)$ . If $\alpha _1 \geq \alpha _2 \geq \cdots \geq \alpha _r> 0$ , then $\alpha $ is a partition, written $\alpha \vdash \lvert \alpha \rvert $ . It will be convenient to write a sequence of words $\vec {w}= (w^1,\dots , w^r)$ , with $w^i \in \mathbb {N}^{r_i}$ , as a vector. The type of $\vec {w}$ , denoted by $m(\vec {w})$ , is the multiplicity type of the concatenation $w^1 \cdots w^r = (w^1_1, w^1_2, \dots , w^2_1, w^2_2, \dots , \dots ).$

Definition 2.3. We define the sets of word vectors of length $\beta $ and content $\alpha $ , composition vectors of size $\beta $ rearranging to $\alpha $ , and partition vectors of size $\beta $ rearranging to $\alpha $ as

The first is the set of sequences of words where the collective multiplicity of i is $\alpha _i$ and sequence j has length $\beta _j$ . If $\ell (\alpha ) < \lvert \beta \rvert $ , then it is impossible to do this without allowing $0$ entries, of which there must be $|\beta |-\ell (\alpha )$ . The second set is the sequence of compositions whose sizes are determined by $\beta $ and whose parts collectively rearrange to $\alpha $ ; and the last set is the set of sequences of partitions whose sizes are determined by $\beta $ and whose collective union of parts rearranges to $\alpha $ .

Example 2.4. For $\alpha = (1,1,2,1,3,1)$ , $\beta = (3,1,5)$ , we have $((1,2,5), (3), (4,3,5,5,6)) \in {\mathrm { {WV}}}(\alpha , \beta )$ , $((2,1), (1), (1,3,1)) \in \operatorname {\mathrm {CR}}(\alpha , \beta )$ , $((2,1), (1), (3,1,1)) \in \operatorname {\mathrm {PR}}(\alpha , \beta )$ .

Definition 2.5. We define the descent set of a word w as , and the ascent set as . We have the following statistics.

Note that $\operatorname {\mathrm {revmaj}}$ and $\operatorname {\mathrm {revcomaj}}$ are actually the $\operatorname {\mathrm {maj}}$ and $\operatorname {\mathrm {comaj}}$ of the reverse word, hence the name.

2.2 $\gamma $ -Dyck paths

We need to recall this classical definition.

Definition 2.6. A parallelogram polyomino of size $m \times n$ is a pair of lattice paths $(P,Q)$ from $(0,0)$ to $(m,n)$ , consisting of unit North and East steps, such that P (the top path) lies always strictly above Q (the bottom path), except on the endpoints.

Definition 2.7. The area of a parallelogram polyomino of size $m \times n$ is defined as

Since the two paths P and Q do not touch between the endpoints, $m+n-1$ is the minimal number of unit cells between them. An example is given in Figure 1.

Figure 1 A parallelogram polyomino with area $20$ .

We can now introduce our new objects.

Definition 2.8. Let $\gamma \vdash m$ . A $\gamma $ -Dyck path of size n is a parallelogram polyomino of size $(m + n + 1) \times n$ , such that the bottom path does not have two consecutive North steps, and if $\alpha _i$ is the number of East steps of the bottom path on the line $x = i-1$ , then $(\alpha _1 - 1, \alpha _2, \dots , \alpha _n)$ rearranges to .

In other words, we start from a “staircase” path with two East steps on the x-axis and one East step on each other line $x=i$ for $1 \leq i < n$ , and we insert on each of these lines a number of East steps given by the parts of $\gamma $ , in some order.

Remark 2.9. Notice that $\varnothing $ -Dyck paths are essentially the same thing as classical Dyck paths. Indeed, $\gamma = \varnothing $ implies $m=0$ , so the polyomino is of size $(n+1) \times n$ and the bottom path is the staircase as mentioned above. This given, the requirement that the two paths do not touch is exactly asking that the top path lies always weakly above the diagonal $x=y$ (see Figure 2 for an example). The importance of this fact will be apparent in Section 12.2.

Figure 2 A $\varnothing $ -Dyck path.

Figure 3 The set of $(2)$ -parking functions of height $2$ .

Definition 2.10. A labeled $\gamma $ -Dyck path, is a $\gamma $ -Dyck path in which each North step of the top path is assigned a positive integer label, such that consecutive North steps are assigned strictly increasing labels. A labeled $\gamma $ -Dyck path will be denoted as a triple $p = (P,Q,w)$ , where P is the top path, Q is the bottom path, and w is the word formed by the labels when read from bottom to top. The content of a labeled $\gamma $ -Dyck path is the weak composition $\alpha \vDash _w n$ whose parts $\alpha _i$ give the number of i’s appearing in the labeling (or $m(w) =0^{n-\ell (\alpha )}1^{\alpha _1}2^{\alpha _2}\dots $ ). A $\gamma $ -parking function is a labeled $\gamma $ -Dyck path of content $1^n$ . For our convenience, we will also refer to labeled $\gamma $ -Dyck paths of content $\alpha $ as $\gamma $ -parking functions of content $\alpha $ , and denote them by ${\mathrm { {PF}}}_\alpha ^\gamma $ (see Figure 2 for examples of $\gamma $ -parking functions).

Definition 2.11. A lattice $\gamma $ -Dyck path is a labeled $\gamma $ -Dyck path in which the sequence of labels, read bottom to top, is a lattice word. Notice that the content of a lattice word is necessarily a partition. As  above, for our convenience, we will also refer to lattice $\gamma $ -Dyck paths with content $\lambda $ as lattice $\gamma $ -parking functions with content $\lambda $ , and denote them by ${\mathrm { {LPF}}}_\lambda ^\gamma $ .

Definition 2.12. The e-composition $\eta (p)$ of a labeled $\gamma $ -Dyck path $p = (P,Q,w)$ is defined as follows: Let $\overline {P}$ be the path obtained from P by removing the first East step after the $i^{\textit {h}}$ North step for every $i \not \in \operatorname {\mathrm {Asc}}(w)$ ; $\eta (p)$ is the composition whose parts are the lengths of the maximal sequences of consecutive North steps appearing in $\overline {P}$ , from the bottom to the top (see Figure 4 for an example).

Figure 4 The e-composition of a labeled $\gamma $ -Dyck path. In this case, $\eta (p) = (4,2,1)$ .

3 Symmetric function preliminaries

The standard reference for Macdonald polynomials is Macdonald’s book [Mac95]. For some reference on modified Macdonald polynomials, plethystic substitution, and Delta operators, we have [Hag08] and [BGHT99]. As a reference for Theta operators, we have [DIVW21] and [DR23].

We represent partitions by their Young diagram. For a partition $\mu $ and a cell $c \in \mu $ , we let $a(c)$ , $l(c)$ , $a'(c)$ , and $l'(c)$ denote the arm, leg, coarm, and coleg of the cell. This gives the number of cells in $\mu $ strictly to the right, above, to the left, and below of c, respectively (see Figure 5 for an example).

Figure 5 Limbs and colimbs of a cell in a partition.

From here on, we set . For any partition $\mu $ , we define the constants

Recall the ordinary Hall scalar product gives the orthogonality relation

(3.1)

where, for any proposition A, $\chi (A) = 1$ if A is true, and $0$ otherwise. The $\ast $ -scalar product may be given by setting for any two symmetric functions F and G,

(3.2)

where $\omega $ is the algebra isomorphism on symmetric functions defined by . Note that $\omega $ is also an isometry and an involution.

The modified Macdonald basis is orthogonal with respect to the $\ast $ -scalar product, that is,

(3.3) $$ \begin{align} \langle \operatorname{\mathrm{\widetilde{H}}}_\lambda , \operatorname{\mathrm{\widetilde{H}}}_\mu \rangle_\ast = w_\mu \chi(\lambda = \mu). \end{align} $$

We recall the definition of Delta operators, which are eigenoperators of the modified Macdonald basis indexed by symmetric functions [BGHT99].

Definition 3.1. For $F \in \Lambda $ , we define the operator $\Delta _{F} \colon \Lambda \rightarrow \Lambda $ by setting on the Macdonald basis and extending by linearity. We then define .

We now introduce the q-Pochhammer symbol.

Definition 3.2. For $r \in \mathbb {N}$ , we define the q-Pochhammer symbol as

and for $\mu $ a partition, we set

Remark 3.3. When $t=1$ , the modified Macdonald basis specializes as

$$\begin{align*}\operatorname{\mathrm{\widetilde{H}}}_\mu[X;q,1] = (q;q)_\mu h_\mu \left[ \frac{X}{1-q} \right]; \end{align*}$$

this means that, on the space of symmetric functions with coefficients in $\mathbb {Q}(q)$ (rather than $\mathbb {Q}(q,t)$ ), the operator $\widetilde {\Delta }_F$ can be defined by setting

$$\begin{align*}\widetilde{\Delta}_F h_\mu\left[ \frac{X}{1-q} \right] = F\left[ \sum_{i=1}^{\ell(\mu)} [\mu_i]_q \right] h_\mu \left[ \frac{X}{1-q} \right]. \end{align*}$$

This specialization will be useful later.

We now define the Theta operators.

Definition 3.4 [DIVW21, (28)].

For any homogeneous symmetric function $F \in \Lambda $ , we define the Theta operators $\Theta _F \colon \Lambda \rightarrow \Lambda $ as follows. For any homogeneous symmetric function $G \in \Lambda $ , we set

We will often use the common shorthand

Also notice that, from the definition, one has $\Theta _F + \Theta _G = \Theta _{F+G}$ and $\Theta _{F} \Theta _G = \Theta _{FG}.$

In [DILB⁺22], the authors give a (conjectural) combinatorial formula for $\Theta _{e_\lambda } e_1$ (when $t=1$ ) in terms of rooted tiered trees, and then a very similar formula for $M \Delta _{e_1} \Pi e_\lambda ^{\ast }[X]$ (also when $t=1$ ) in terms of $0$ -rooted tiered trees, which have nicer symmetries. The expression $M \Delta _{e_1} \Pi e_\lambda ^{\ast }[X]$ seems to have surprising positivity properties and pops up in various symmetric function identities (cf. [BHIR23]). For this reason, it is convenient to define the following.

Definition 3.5. We define the linear operator $\operatorname {\mathrm {\Xi }} \colon \Lambda \rightarrow \Lambda $ as

In the remainder of this work, we will show another combinatorial expansion for $\operatorname {\mathrm {\Xi }} e_\lambda \rvert _{t=1}$ , different from the one in [DILB⁺22]. We will actually prove a more general result, namely, an expansion for $\widetilde {\Delta }_{m_\gamma } \operatorname {\mathrm {\Xi }} e_{\lambda }$ , which has the remarkable property of being e-positive. Without the specialization $t=1$ , the expression $\operatorname {\mathrm {\Xi }} e_\lambda $ is conjecturally Schur positive, but that fails in general when $\gamma \neq \varnothing $ , making the global e-positivity when $t=1$ even more remarkable.

4 Preliminary manipulations and specializations

In this section, we go through some algebraic manipulations, in order to give a combinatorial meaning to the symmetric function $\widetilde {\Delta }_{m_\gamma } \operatorname {\mathrm {\Xi }} e_{\lambda }$ .

Lemma 4.1. For $\lambda \vdash n$ and $\gamma $ any partition, we have

$$\begin{align*}\Delta_{m_\gamma} \operatorname{\mathrm{\Xi}} e_\lambda = \sum_{\mu \vdash n} m_\gamma[B_\mu] \frac{ M B_\mu \Pi_\mu}{w_\mu} \langle h_{\lambda}, \operatorname{\mathrm{\widetilde{H}}}_\mu \rangle \operatorname{\mathrm{\widetilde{H}}}_\mu. \end{align*}$$

Proof. By (3.3) and (3.2), we have

$$\begin{align*}e_{\lambda}^\ast = \sum_{\mu \vdash n} \frac{\operatorname{\mathrm{\widetilde{H}}}_\mu}{w_\mu} \langle e_{\lambda}^\ast, \operatorname{\mathrm{\widetilde{H}}}_\mu \rangle_\ast = \sum_{\mu \vdash n} \frac{\operatorname{\mathrm{\widetilde{H}}}_\mu}{w_\mu} \langle h_{\lambda}, \operatorname{\mathrm{\widetilde{H}}}_\mu \rangle. \end{align*}$$

Now by Definition 3.5 and Definition 3.1, we have

$$\begin{align*}\Delta_{m_\gamma} \operatorname{\mathrm{\Xi}} e_\lambda = \Delta_{m_\gamma} M \Delta_{e_1} \Pi e_{\lambda}^\ast = \sum_{\mu \vdash n} m_\gamma[B_\mu] \frac{ M B_\mu \Pi_\mu}{w_\mu} \langle h_{\lambda}, \operatorname{\mathrm{\widetilde{H}}}_\mu \rangle\operatorname{\mathrm{\widetilde{H}}}_\mu, \end{align*}$$

as desired.

We will break up these summation terms by analyzing each of the three factors, specializing t to $1$ for each one individually.

Lemma 4.2. For $\mu \vdash n$ , we have

$$\begin{align*}\left. \frac{M B_\mu \Pi_\mu}{w_\mu} \right\rvert_{t=1} = (-1)^{n-\ell(\mu)} (q;q)_\mu^{-1} \sum_{\alpha \in R(\mu)} (1-q^{\alpha_1}). \end{align*}$$

Proof. It follows immediately from the definition that $B_\mu \rvert _{t=1} = \sum _{i=1}^{\ell (\mu )} [\mu _i]_q$ . Let

$$\begin{align*}A_1 = \frac{ (1-q) \prod_{ \substack{ c \in \mu \\ a'(c) \neq 0}} (1-q^{a'(c)}t^{l'(c)})} {\prod_{\substack {c \in \mu \\ a(c) \neq 0}} (q^{a(c)} -t^{l(c)+1}) \prod_{c \in \mu} (t^{l(c)} -q^{a(c)+1}) } \end{align*}$$

and

$$\begin{align*}A_0 = \frac{(1-t) \prod_{ \substack{ c \in \mu \\ a'(c) = 0}} (1-q^{a'(c)}t^{l'(c)})}{\prod_{\substack{c\in \mu \\ a(c) = 0}} (q^{a(c)} -t^{l(c)+1}) }. \end{align*}$$

We have that $M \Pi _\mu / w_\mu = A_1 \cdot A_0$ , where $A_1$ collects the terms that do not vanish when $t=1$ , and $A_0$ collects the terms that evaluate to $0$ when $t=1$ .

Now, evaluating $A_1$ , we get

$$\begin{align*}A_1 \rvert_{t=1} = \frac{(1-q) \prod_{\substack{c \in \mu \\ a'(c) \neq 0}} (1-q^{a'(c)})} {\prod_{\substack {c \in \mu \\ a(c) \neq 0}} (q^{a(c)} -1) \prod \limits_{c \in \mu} (1 -q^{a(c)+1})}, \end{align*}$$

and since

$$ \begin{align*} \frac{ \prod_{\substack{c \in \mu \\ a'(c) \neq 0}} (1-q^{a'(c)}) } { \prod_{\substack {c \in \mu \\ a(c) \neq 0}} (q^{a(c)} -1) } = (-1)^{n-\ell(\mu)} && \text{ and } && \prod_{c \in \mu} (1 -q^{a(c)+1}) = (q;q)_\mu, \end{align*} $$

we have

$$\begin{align*}A_1 \rvert_{t=1} = (-1)^{n-\ell(\mu)} \frac{(1-q)}{(q;q)_\mu}. \end{align*}$$

To evaluate $A_0$ , notice first that

$$\begin{align*}A_0 = \frac{(1-t) \prod_{\substack{c \in \mu \\ a'(c) = 0}} (1-t^{l'(c)}) }{\prod_{\substack{c \in \mu \\ a(c) = 0}} (1 -t^{l(c)+1}) } = \frac{(1-t) (t;t)_{\ell(\mu)-1}}{(t;t)_{m_1(\mu)} \cdots (t;t)_{m_n(\mu)}} = \frac{1}{[\ell(\mu)]_t} {\genfrac{[}{]}{0pt}{}{{\ell(\mu)}}{{m_1(\mu), \dots, m_n(\mu)}}}_t, \end{align*}$$

where $m_i(\mu )$ is the multiplicity of i in $\mu $ . When we set $t=1$ , we get the usual cyclic multinomial.

Putting the pieces together, we get

$$\begin{align*}\left. \frac{M B_\mu \Pi_\mu}{w_\mu} \right\rvert_{t=1} = \frac{(-1)^{n-\ell(\mu)}}{\ell(\mu)} \binom{\ell(\mu)}{ m_1(\mu), \dots, m_n(\mu)} \frac{(1-q)}{(q;q)_\mu} \sum_{i=1}^{\ell(\mu)} [\mu_i]_q. \end{align*}$$

Now we can interpret this product combinatorially. First, note that

$$\begin{align*}(1-q) \sum_{i=1}^{\ell(\mu)} [\mu_i]_q = \sum_{i=1}^{\ell(\mu)} (1-q ^{\mu_i}), \end{align*}$$

and that

$$\begin{align*}\binom{\ell(\mu) }{ m_1(\mu),\dots, m_n(\mu)} = \# R(\mu) \end{align*}$$

is the number of rearrangements $\alpha =(\alpha _1,\dots , \alpha _{\ell }) \in \operatorname {\mathrm {R}}(\mu )$ of the parts of $\mu $ . Therefore,

$$\begin{align*}\# R(\mu) \cdot \sum_{i=1}^{\ell(\mu)} (1-q^{\mu_i}) = \sum_{\alpha \in \operatorname{\mathrm{R}}(\mu)} \sum_{i=1}^{\ell(\mu)}( 1-q^{\alpha_i}). \end{align*}$$

This corresponds to selecting a rearrangement $\alpha $ of $\mu $ then selecting some i from $1$ to $\ell (\mu )$ . Equivalently, we can first select a rearrangement r, take $1-q^{\alpha _1}$ , then circularly rearrange $\alpha $ , keeping this selection of $1-q^{\alpha _1}$ . Since there are $\ell (\mu )$ circular rearrangements, we have that

$$\begin{align*}\frac{\# R(\mu)}{\ell(\mu)} \sum_{i=1}^{\ell(\mu)} (1-q^{\mu_i}) = \sum_{\alpha \in R(\mu)} (1-q^{\alpha_1}) \end{align*}$$

and so we can conclude that

$$\begin{align*}\left. \frac{MB_\mu \Pi_\mu}{w_\mu} \right\rvert_{t=1} = (-1)^{n-\ell(\mu)}(q;q)_{\mu}^{-1}\sum_{\alpha \in R(\mu)} (1-q^{\alpha_1}), \end{align*}$$

as desired.

Lemma 4.3. For $\lambda ,\mu \vdash n$ , we have

$$\begin{align*}\left. \langle \operatorname{\mathrm{\widetilde{H}}}_\mu, h_\lambda \rangle \right\rvert_{t=1} = \sum_{\vec{w} \in {\mathrm{ {WV}}}(\lambda, \mu)} q^{\operatorname{\mathrm{revmaj}}(\vec{w})}. \end{align*}$$

Proof. We recall the classical result (see [Sta99] and [Hag08]) that

$$ \begin{align*} (q;q)_n h_n\left[\frac{X}{1-q} \right] & = \sum_{w= (w_1,\dots,w_n) \in \mathbb{N}_+^n} q^{\operatorname{\mathrm{maj}}(w)} x_{w_1} \cdots x_{w_n} \\ & = \sum_{w= (w_1,\dots,w_n) \in \mathbb{N}_+^n} q^{\operatorname{\mathrm{comaj}}(w)} x_{w_1} \cdots x_{w_n} \\ & = \sum_{w= (w_1,\dots,w_n) \in \mathbb{N}_+^n} q^{\operatorname{\mathrm{revmaj}}(w)} x_{w_1} \cdots x_{w_n}. \end{align*} $$

For our purposes, we need the last of these equalities, involving the reverse major index. Recall that $\langle h_\lambda , m_\mu \rangle = \chi (\lambda =\mu )$ . Since the homogeneous basis is multiplicative, this means that

$$\begin{align*}\left\langle {(q;q)}_\mu h_\mu \left[ \frac{X}{1-q} \right] , h_\lambda \right\rangle = \left\langle \prod_{i=1}^{\ell(\mu)} \sum_{w \in \mathbb{N}_+^{\mu_i}} q^{\operatorname{\mathrm{revmaj}}(w)} x_{w_1} \cdots x_{w_{\mu_i}}, h_\lambda \right\rangle = \sum_{ \vec{w} \in {\mathrm{ {WV}}}(\lambda, \mu)} q^{\operatorname{\mathrm{revmaj}}(\vec{w})}, \end{align*}$$

where $\operatorname {\mathrm {revmaj}}(\vec {w})= \operatorname {\mathrm {revmaj}}(w^1)+\cdots + \operatorname {\mathrm {revmaj}}(w^n)$ . Now by Remark 3.3, we have

$$\begin{align*}\left. \langle \operatorname{\mathrm{\widetilde{H}}}_\mu, h_\lambda \rangle \right\rvert_{t=1} = \sum_{\vec{w} \in {\mathrm{ {WV}}}(\lambda, \mu)} q^{\operatorname{\mathrm{revmaj}}(\vec{w})}, \end{align*}$$

as desired.

Let us recall the Cauchy identity.

Proposition 4.4 (Cauchy identity).

For any two expressions $X,Y$ , and any two dual bases $\{u_\lambda \}_\lambda $ , $\{v_\lambda \}$ under the Hall scalar product, we have

$$\begin{align*}h_{n}[XY] = \sum_{\lambda \vdash n} u_{\lambda}[X] v_\lambda[Y]. \end{align*}$$

We now get to the final term of our product.

Lemma 4.5. For $\mu \vdash n$ , we have

$$\begin{align*}\operatorname{\mathrm{\widetilde{H}}}_\mu[X;q,1] = {(q;q)_\mu} \sum_{\eta \vdash n} e_\eta[X] \sum_{ \vec{\nu} \in \operatorname{\mathrm{PR}}(\eta,\mu)} f_{\vec{\nu}}\left[ \frac{1}{1-q} \right]. \end{align*}$$

Proof. Recall that (see Remark 3.3)

$$\begin{align*}\operatorname{\mathrm{\widetilde{H}}}_\mu[X;q,1] = {(q;q)_\mu} h_\mu \left[ \frac{X}{1-q} \right]. \end{align*}$$

Now by Proposition 4.4, using the fact that the elementary symmetric functions and forgotten symmetric functions are dual, we have

(4.1) $$ \begin{align} h_{n} \left[ \frac{X}{1-q} \right] = \sum_{\lambda \vdash n} e_\lambda[X] f_\lambda \left[ \frac{1}{1-q} \right]. \end{align} $$

Applying (4.1) to each factor in $h_\mu [X/(1-q)]$ and collecting $e_\eta $ terms, we obtain

$$\begin{align*}\operatorname{\mathrm{\widetilde{H}}}_\mu[X;q,1] = {(q;q)_\mu} \sum_{\eta \vdash n} e_\eta[X] \sum_{ \vec{\nu} \in \operatorname{\mathrm{PR}}(\eta,\mu)} f_{\vec{\nu}}\left[ \frac{1}{1-q} \right], \end{align*}$$

where $f_{\vec {\nu }} = f_{\nu ^1} f_{\nu ^2} \cdots f_{\nu ^{\ell (\mu )}}$ .

Putting everything together, we get the following.

Proposition 4.6. For any $\lambda \vdash n$ and $\gamma $ any partition, we have

$$\begin{align*}\widetilde{\Delta}_{m_\gamma} \operatorname{\mathrm{\Xi}} e_{\lambda} = \sum_{\eta \vdash n} D_{\lambda, \eta}^{\gamma}(q) e_\eta, \end{align*}$$

where

$$\begin{align*}D^{\gamma}_{\lambda, \eta} = \sum_{\beta \vDash n} \sum_{\vec{w} \in {\mathrm{ {WV}}}(\lambda, \beta)} \sum_{\vec{\nu} \in \operatorname{\mathrm{PR}}(\eta,\beta)} q^{\operatorname{\mathrm{revmaj}}(\vec{w})} m_\gamma\left[ \sum_i [\beta_i]_q \right] (-1)^{n-\ell(\beta)} (1-q^{\beta_1}) f_{\vec{\nu}}\left[ \frac{1}{1-q} \right]. \end{align*}$$

Proof. By combining Lemma 4.1, 4.2, 4.3, and 4.5, we get the expansion

$$ \begin{align*} {\widetilde{\Delta}}_{m_{\gamma}} \operatorname{\mathrm{\Xi}} e_{\lambda} & = \sum_{\eta \vdash n} e_{\eta} \sum_{\mu \vdash n} (-1)^{n-\ell(\mu)} \sum_{\beta \in \operatorname{\mathrm{R}} (\mu)} (1-q^{\beta_1}) m_{\gamma} \left[\sum_i [\beta_i]_q \right] \\ & \quad \times \sum_{\vec{w} \in {\mathrm{ {WV}}} (\lambda, \mu)} q^{\operatorname{\mathrm{revmaj}}(\vec{w})} \sum_{\vec{\nu} \in \operatorname{\mathrm{PR}}(\eta,\mu)} f_{\vec{\nu}} \left[\frac{1}{1-q}\right]. \end{align*} $$

Now, instead of summing over all $\mu $ then summing over all compositions $\beta \in R(\mu )$ that rearrange to $\mu $ , we can instead just sum over all compositions $\beta $ , and the thesis follows.

Corollary 4.7. For any $\lambda \vdash n$ , we have

$$\begin{align*}\left. \operatorname{\mathrm{\Xi}} e_{\lambda} \right\rvert_{t=1} = \sum_{\eta \vdash n} \sum_{\beta \vDash n} \sum_{\vec{w} \in {\mathrm{ {WV}}} (\lambda, \beta)} \sum_{\vec{\nu} \in \operatorname{\mathrm{PR}}(\eta,\beta)} q^{\operatorname{\mathrm{revmaj}}(\vec{w})} (-1)^{n-\ell(\beta)} (1-q^{\beta_1}) f_{\vec{\nu}} \left[ \frac{1}{1-q} \right] e_{\eta}. \end{align*}$$

Proof. Just set $\gamma = \varnothing $ in Proposition 4.6.

5 Forgotten symmetric functions

For $\mu \vdash n$ of length $\ell $ , the combinatorial formula for the forgotten symmetric function $f_\mu $ [ER91] is given by

$$\begin{align*}f_\mu\left[ X \right] = (-1)^{n-\ell} \sum_{ \alpha \in \operatorname{\mathrm{R}}(\mu)} \sum_{i_1 \leq \cdots \leq i_{\ell}} x_{i_1}^{\alpha_1} \cdots x_{i_\ell}^{a_\ell}. \end{align*}$$

Now, substituting $X = (1-q)^{-1}$ , we get the expansion

(5.1) $$ \begin{align} f_\mu\left[ \frac{1}{1-q}\right] = (-1)^{n-\ell} \sum_{ \alpha \in \operatorname{\mathrm{R}}(\mu)} \sum_{0 \leq i_1 \leq \cdots \leq i_{\ell}} \left( q^{i_1} \right)^{\alpha_1} \cdots \left( q^{i_\ell} \right)^{a_\ell}. \end{align} $$

Definition 5.1. Let $\mu \vdash n$ . A column-composition tableau of type $\mu $ is a pair $C = (\alpha , c)$ , where $\alpha \in \operatorname {\mathrm {R}}(\mu )$ is a composition that rearranges to $\mu $ , and $c = (c_1 \leq c_2 \leq \dots \leq c_n)$ is a sequence, such that

$$\begin{align*}c_i < c_{i+1} \implies i \in \{\alpha_1,\alpha_1+\alpha_2, \dots, \alpha_1+\cdots + \alpha_{\ell-1}\}. \end{align*}$$

We denote by $\operatorname {\mathrm {CC}}_\mu $ the set of column-composition tableaux of type $\mu $ , and by $\overline {\operatorname {\mathrm {CC}}}_\mu $ the subset of those, such that $c_1 = 0$ . For $C \in \operatorname {\mathrm {CC}}_\mu $ , we define the length of C as $\ell (C) = \lvert \mu \rvert $ and size of C as $\lvert C \rvert = c_1 + c_2 + \dots + c_n$ . We will write $c_i(C)$ for $c_i$ when we need to specify the column-composition tableau.

We can depict the elements of $\operatorname {\mathrm {CC}}_\mu $ as follows.

1. 1. First, draw a row of size $\lvert \mu \rvert $ which we call the base, and then depict the composition $\alpha \in \operatorname {\mathrm {R}}(\mu )$ by separating the columns of the base with vertical bars; for instance, when $\mu = (3,2,2,2,1,1,1)$ and $\alpha = (2,1,2,1,2,1,3)$ , we draw the base as

   

2. 2. Next, draw $c_i$ cells above the $i^{\textit {h}}$ column of the base; in continuing our example, if $c = (0,0,0,1,1,1,1,1,3,3,3,3)$ , we draw it as

   

Let us define the q-enumerators

which are power series in q. Then, by construction, we have the following.

Proposition 5.2. For any partition $\mu $ , we have

$$ \begin{align*} f_{\mu}\left[ \frac{1}{1-q} \right] = (-1)^{|\mu| - \ell(\mu)} {\mathbf{CC}}_\mu & & \text{ and } & & (1-q)^{\lvert \mu \rvert} f_{\mu}\left[ \frac{1}{1-q} \right] = (-1)^{|\mu| - \ell(\mu)} \overline{{\mathbf{CC}}}_\mu. \end{align*} $$

Proof. In Equation (5.1), each term in the principal evaluation of $f_\mu $ is given by selecting a rearrangement $\alpha $ of $\mu $ , and choosing $i_1\leq \cdots \leq i_{\ell (\mu )}$ . This uniquely determines an element $(\alpha ,c) \in \operatorname {\mathrm {CC}}_\mu $ , where the first $\alpha _1$ columns $c_1,\dots , c_{\alpha _1}$ are of size $i_1$ , the next $\alpha _2$ columns $c_{\alpha _1+1},\dots , c_{\alpha _1 + \alpha _2}$ are of size $i_2$ , and so on. Since then

$$\begin{align*}\sum_{i=1}^{|\mu|} c_i = \sum_{j=1}^{\ell(\mu)} \alpha_j i_j, \end{align*}$$

we see that $q^{\lvert (\alpha ,c) \rvert }$ equals the term in Equation (5.1) corresponding to choosing $\alpha $ and $i_1\leq \cdots \leq i_{\ell (\mu )}$ .

The second equality follows from the fact that if $(\alpha ,c) \in CC_\mu $ , then so is $(\alpha ,c+1^n)$ , where $c+1^n = (c_1+1,\dots ,c_n+1)$ . This defines an injective map, and we have

$$\begin{align*}q^{ \lvert \mu \rvert} {\mathbf{CC}}_\mu = \sum_{ \substack{ C \in \operatorname{\mathrm{CC}}_\mu \\ c_1(C)>0 }} q^{\lvert C \rvert}. \end{align*}$$

Therefore

$$\begin{align*}{\mathbf{CC}}_\mu -q^{\lvert \mu \rvert} {\mathbf{CC}}_\mu = \sum_{ \substack{ C \in \operatorname{\mathrm{CC}}_\mu \\ c_1 = 0} }q^{\lvert C \rvert}, \end{align*}$$

which gives the last equality in the proposition.

We conclude this section with the following results.

Lemma 5.3. For any $\vec {\nu } \in \operatorname {\mathrm {PR}}(\eta ,\beta )$ , we have

$$\begin{align*}(-1)^{n-\ell(\beta)} (1-q^{\beta_1}) f_{\vec{\nu}} \left[ \frac{1}{1-q} \right] = (-1)^{\ell(\eta) - \ell(\beta)} \overline{{\mathbf{CC}}}_{\nu^1} {{\mathbf{CC}}}_{\nu^2} \cdots {{\mathbf{CC}}}_{\nu^{\ell(\beta)}}. \end{align*}$$

Proof. Using Proposition 5.2, we can replace each $f_\nu [1/(1-q)]$ with ${\mathbf {CC}}_\nu $ . Since $\nu _1 \vdash \beta _1$ , we can also replace $(1-q^{\beta _1}) {\mathbf {CC}}_{\nu _1}$ with $\overline {{\mathbf {CC}}}_{\nu ^1}$ . Finally, since $\ell (\nu ^1) + \cdots + \ell (\nu ^{\ell (\beta )}) = \ell (\eta )$ , we have

$$\begin{align*}(-1)^{n - \ell(\beta)} (-1)^{\ell(\nu^1) - \lvert \nu^1 \rvert} \cdots (-1)^{\ell(\nu^{\ell(\beta)}) - \lvert \nu^{\ell(\beta)} \rvert} = (-1)^{\ell(\eta)- \ell(\beta)}, \end{align*}$$

and the thesis follows.

Proposition 5.4. For $\eta , \lambda \vdash n$ and $\gamma $ any partition, we have

$$\begin{align*}D^{\gamma}_{\lambda, \eta} = \sum_{\beta \vDash n} \sum_{\vec{w} \in {\mathrm{ {WV}}}(\lambda, \beta)} \sum_{\vec{\nu} \in \operatorname{\mathrm{PR}}(\eta,\beta)} q^{\operatorname{\mathrm{revmaj}}(\vec{w})} m_\gamma\left[ \sum_i [\beta_i]_q \right] (-1)^{\ell(\eta) - \ell(\beta)} \overline{{\mathbf{CC}}}_{\nu^1} {{\mathbf{CC}}}_{\nu^2} \cdots {{\mathbf{CC}}}_{\nu^{\ell(\beta)}}. \end{align*}$$

Proof. It follows immediately from Proposition 4.6 and Lemma 5.3.

6 Combinatorial expansions

Recall that we are trying to compute the coefficient in the expansion $\widetilde {\Delta }_{m_\gamma } \operatorname {\mathrm {\Xi }} e_\lambda = \sum _{\eta } D^\gamma _{\lambda ,\eta } e_\eta $ , using the formula in Proposition 5.4. We interpret the terms showing up there by labeling a sequence of column-composition tableaux.

Definition 6.1. A labeled column-composition tableaux is a triple $(C, w, l)$ , where C is a column-composition tableau, $w \in \mathbb {N}_+^{\ell (C)}$ , and $l \in \mathbb {N}^{\ell (C)}$ .

Definition 6.2. Let $\lambda , \eta \vdash n$ , and $\gamma \vdash m$ , such that $\ell (\gamma ) \leq n$ . A sequence of labeled column-composition tableaux of type $\lambda , \eta , \gamma $ is a tuple of labeled column-composition tableaux $(C^i, w^i, l^i)_{1 \leq i \leq r}$ , such that, for $\beta = (\beta _1, \dots , \beta _r)$ , $\beta _i = \ell (C^i)$ , we have:

1. 1. $C^1 \in \overline {\operatorname {\mathrm {CC}}_{\nu ^1}}$ and $C^i \in \operatorname {\mathrm {CC}}_{\nu ^i}$ for $i>1$ , for some $\vec {\nu } \in \operatorname {\mathrm {PR}}(\eta , \beta )$ ;

2. 2. $\vec {w} = (w^1, \dots , w^r) \in {\mathrm { {WV}}}(\lambda , \beta )$ ;

3. 3. $\vec {l} = (l^1, \dots , l^r) \in {\mathrm { {WV}}}(m(\gamma ), \beta )$ .

In other words, a sequence of labeled column-composition tableaux of type $\lambda , \eta , \gamma $ , is a tuple of column-composition tableaux of sizes $\beta _1, \dots , \beta _r$ , such that $c_1(C^1) = 0$ , so that to each tableau we associate a partition $\nu ^i \vdash \beta _i$ and two words $w^i, l^i$ , such that $\vec {\nu }$ rearranges to $\eta $ , the global content of $\vec {w}$ is given by $\lambda $ , and the letters of l are the parts of $\gamma $ followed by an appropriate number of trailing zeros.

We denote by ${\mathrm { {LC}}}_{\lambda ,\eta }^\gamma $ the set of sequences of column-composition tableaux of type $\lambda , \eta , \gamma $ . For $T = (T_i)_{1 \leq i \leq r} \in {\mathrm { {LC}}}_{\lambda ,\eta }^\gamma $ , we set $w(T_i) = w^i$ and $l(T_i) = l^i$ .

Definition 6.3. For $T = (T_i)_{1 \leq i \leq r} \in {\mathrm { {LC}}}_{\lambda ,\eta }^\gamma $ , with $T_i = (C^i, w^i, l^i)$ , let $\nu ^i$ be the type of $C^i$ , let , and let

We define

Notice that, for every letter in $w^i$ or $l^i$ , its contribution to the weight only depends on the letter itself and the number of letters to its right. Also notice that the sign is given by the parity of the number of vertical bars in $C^i$ . Finally, we define

Example 6.4. We are now going through an example in full detail. Let $\lambda =(3,2,2,2)$ , $\eta =(3,2,1,1,1,1)$ , $\gamma =(4,3,2,2,1)$ , so $\lvert \lambda \rvert = \lvert \eta \rvert = 9$ and $\ell (\gamma ) = 5 \leq 9$ . For our convenience, we add four trailing zeros to $\gamma $ , so $\gamma = (4,3,2,2,1,0,0,0,0)$ .

To build an element of ${\mathrm { {LC}}}_{\lambda ,\eta }^\gamma $ , first choose $\beta \vDash 9$ , such that some permutation of $\eta $ refines $\beta $ , say $\beta = (3,1,5)$ . Next, select $\nu ^i \vdash \beta _i$ , say $\nu ^1 = (2,1)$ , $\nu ^2 = (1)$ , $\nu ^3 = (3,1,1)$ , so that the union of parts is $\eta $ . Then, pick $C^1 \in \overline {\operatorname {\mathrm {CC}}}_{\nu ^1}$ and $C^i \in \operatorname {\mathrm {CC}}_{\nu ^i}$ for $i> 1$ ; say, for example

(note that $c_1(C^1)=0$ ). Since $\lambda = (3,2,2,2)$ , we have $m(\lambda ) = (1,1,1,2,2,3,3,4,4)$ . Pick any permutation of it and split it into parts of lengths given by the sizes of the parts of $\beta $ , say, for example $\vec {w} = ((2,1,2),(4),(3,4,1,3,1))$ . Write these words into the bases of the tableaux. We get

Finally, pick any permutation of the parts of $\gamma $ , and, again, split it into parts of lengths given by the sizes of the parts of $\beta $ , say $\vec {l} = ((0,2,0),(1),(2,0,4,3,0))$ . Write it underneath the bases of the tableaux. We get

which is an element of ${\mathrm { {LC}}}_{(3,2,2,2),(3,2,1,1,1,1)}^{(4,3,2,2,1)}$ We now want to compute the weight and the sign of this sequence. Since there are three vertical bars, we have that the sign is given by $(-1)^3$ .

We can compute the weight of this sequence of labeled column-composition tableaux in three steps. First count the number of cells above the base rows: there are $2$ , $1$ , and $5+4=9$ cells, respectively, so the total weight given by the cells is $12$ .

The weight corresponding to the labels in the base is found by taking the reverse major index of each individual base. We compute this by taking

$$\begin{align*}\sum_{ w^i_j < w^i_{j+1}} \# \{ \text{cells in the same base and on the right of}\ w^i_j \}. \end{align*}$$

In the above example, we have that $w^1 = (2,1,2)$ has an ascent in position $2$ , and there is one cell to its right. Therefore, $\operatorname {\mathrm {revmaj}}(w^1) = 1$ . Since $w^2$ has length $1$ , it has no ascents. Finally, $w^3 = (3,4,1,3,1)$ has an ascent in position $1$ and one in position $3$ . There are four cells to the right of the label in position $2$ , and two cells to the right of the last ascent. Therefore, $\operatorname {\mathrm {revmaj}}(w^3) = 4+2$ , and the total contribution given by $\vec {w}$ is $7$ .

The last step is to calculate the contribution of labels underneath the base rows. For this, we will say a label $l^i_j$ has $\beta _i-j$ cells on its right, since these are the number of cells in its base row to the right of the label. We take

$$\begin{align*}\sum_{i,j} l^i_j \times \# \{ \text{cells in the same base and on the right of}\ l^i_j \}. \end{align*}$$

The first nonzero label from the left is a $2$ in the second column of $T_1$ . There is one cell to its right, meaning this label contributes by $2 \cdot 1$ to the weight. The next nonzero label is a $1$ , but there are no cells to its right, so its contribution is $1 \cdot 0 = 0$ . Similarly, $T_2$ has size $1$ , so its contribution is also $0$ . Finally, in $T_3$ , the first label $2$ has four cells to its right (so it contributes $2 \cdot 4$ ). The next label is a $4$ and it has two cells to its right (so it contributes $4 \cdot 2$ ). The last nonzero label is a $3$ and it has one cell to its right (so it contributes $3 \cdot 1$ ). Therefore, the labels under the base rows collectively contribute a factor of $q^{2+8+8+3}$ to the weight. Putting everything together, we have

$$ \begin{align*} \operatorname{\mathrm{weight}}(T) = (2+1+9) + (1+0+4+2) + (2+8+8+3) = 40 \end{align*} $$

and $\operatorname {\mathrm {sign}}(T) = (-1)^3 = -1$ .

The following proposition is an immediate consequence of our construction.

Proposition 6.5. For $\eta , \lambda \vdash n$ and $\gamma $ any partition, we have

$$\begin{align*}D^\gamma_{\lambda, \eta} = \sum_{T \in {\mathrm{ {LC}}}_{\lambda, \eta}^\gamma} q^{\operatorname{\mathrm{weight}}(T)} \operatorname{\mathrm{sign}}(T). \end{align*}$$

Proof. Recall that, by Proposition 5.4, we have

$$\begin{align*}D^{\gamma}_{\lambda, \eta} = \sum_{\beta \vDash n} \sum_{\vec{w} \in {\mathrm{ {WV}}}(\lambda, \beta)} \sum_{\vec{\nu} \in \operatorname{\mathrm{PR}}(\eta,\beta)} q^{\operatorname{\mathrm{revmaj}}(\vec{w})} m_\gamma\left[ \sum_i [\beta_i]_q \right] (-1)^{\ell(\eta) - \ell(\beta)} \overline{{\mathbf{CC}}}_{\nu^1} {{\mathbf{CC}}}_{\nu^2} \cdots {{\mathbf{CC}}}_{\nu^{\ell(\beta)}}. \end{align*}$$

Fix now a composition $\beta \vDash n$ , such that some permutation of $\eta $ refines $\beta $ , a word vector $\vec {w} \in {\mathrm { {WV}}}(\lambda , \beta )$ , and a partition vector $\vec {\nu } \in \operatorname {\mathrm {PR}}(\eta ,\beta )$ . We want to study the summand

(6.1) $$ \begin{align} q^{\operatorname{\mathrm{revmaj}}(\vec{w})} m_\gamma\left[ \sum_i [\beta_i]_q \right] (-1)^{\ell(\eta)-\ell(\beta)} \overline{{\mathbf{CC}}}_{\nu^1} {\mathbf{CC}}_{\nu^2} \cdots {\mathbf{CC}}_{\nu^{\ell(\beta)}}. \end{align} $$

From the combinatorial formula for the monomial symmetric functions, we have

(6.2) $$ \begin{align} m_\gamma\left[ [\beta_1]_q + \cdots + [\beta_{\ell(\beta)}]_q \right] = \sum_{\vec{l} \in {\mathrm{ {WV}}}(m(\gamma),\beta)} q^{u(l^1)+\cdots + u (l^{\ell(\beta)})}. \end{align} $$

Substituting (6.2) in (6.1), we get

$$\begin{align*}\sum_{\vec{l} \in {\mathrm{ {WV}}}(m(\gamma),\beta)} (-1)^{\ell(\eta)-\ell(\beta)} q^{u(l^1)+\cdots + u (l^{\ell(\beta)})} q^{\operatorname{\mathrm{revmaj}}(\vec{w})} \overline{{\mathbf{CC}}}_{\nu^1} {\mathbf{CC}}_{\nu^2} \cdots {\mathbf{CC}}_{\nu^{\ell(\beta)}}, \end{align*}$$

and now every monomial in this expansion corresponds to a choice of $\vec {l} \in {\mathrm { {WV}}}(m(\gamma ),\beta )$ , $C^1 \in \overline {\operatorname {\mathrm {CC}}}_{\nu ^1}$ , and $C^i \in \operatorname {\mathrm {CC}}_{\nu ^i}$ for $i>1$ , giving the term

$$ \begin{align*} (-1)^{\ell(\eta)-\ell(\beta)} q^{\operatorname{\mathrm{revmaj}}(\vec{w})} & q^{u(l^1)+\cdots + u (l^{\ell(\beta)})} q^{\lvert C^1 \rvert + \cdots + \lvert C^{\ell(\beta)} \rvert} = \prod_{i=1}^{\ell(\beta)} (-1)^{\ell(\nu^i)-1} q^{\operatorname{\mathrm{revmaj}}(w^i) + u(l^i) + \lvert C^i \rvert}. \end{align*} $$

For each summand, let now $T \in {\mathrm { {LC}}}^{\gamma }_{\lambda ,\eta }$ be defined as $T_i = (C^i,w^i,l^i)$ ; this correspondence is bijective, and we have $\operatorname {\mathrm {sign}}(T) = \prod _{i=1}^{\ell (\beta )} (-1)^{\ell (\nu ^i)-1}$ and

$$\begin{align*}\operatorname{\mathrm{weight}}(T) = \sum_{i=1}^{\ell(\beta)} \operatorname{\mathrm{revmaj}}(w^i) + u(l^i) + \lvert C^i \rvert. \end{align*}$$

The thesis now follows.

7 A weight-preserving, sign-reversing involution

Our goal is to now give a positive expansion for the coefficients $D_{\lambda ,\eta }^\gamma (q)$ . To achieve this result, we will define a weight-preserving, sign-reversing involution $\psi \colon {\mathrm { {LC}}}_{\lambda ,\eta }^\gamma \rightarrow {\mathrm { {LC}}}_{\lambda ,\eta }^\gamma $ whose fixed points $U^{\gamma }_{\lambda , \eta }$ give

$$\begin{align*}D_{\lambda,\eta}^\gamma (q) = \sum_{T \in U_{\lambda,\eta}^\gamma} q^{\operatorname{\mathrm{weight}}(T)}. \end{align*}$$

To construct $\psi $ , we need to introduce a split map. Suppose $S = (C, w, l)$ is one of the possible labeled column-composition tableaux appearing in a sequence $T \in {\mathrm { {LC}}}_{\lambda ,\eta }^\gamma $ . Let $C = (\alpha , c)$ , and recall that this means that the vertical bars appearing in C are in positions $\alpha _1, \alpha _1 + \alpha _2, \dots , \alpha _1 + \dots + \alpha _{\ell -1}$ . Let $d = \# \{ 1 \leq i \leq \alpha _1 \mid w_i < w_{i+1} \}$ , that is, $d = \operatorname {\mathrm {asc}}(w_1, \dots , w_{\alpha _1+1})$ (we don’t count the last position if $\alpha $ has just one part).

The idea is the following. If S has at least one bar, that is, $\alpha \neq (\alpha _1)$ , then we set ${\mathrm { {split}}}(S) = (S_1, S_2)$ , where $S_1$ is the portion of S occurring before the first vertical bar, and $S_2$ is obtained from the portion of S after the first vertical bar by adding $d + \lvert l^1 \rvert $ cells to each column, $\lvert l^1 \rvert $ being the sum of the labels in l appearing before the first bar (see Example 7.2 for a pictorial realization). More formally, we have the following definition.

Definition 7.1. Suppose that S has at least one bar, that is, $\alpha \neq (\alpha _1)$ . Then we say that S can split, and define , with

$$ \begin{align*} S_1 & = ((\alpha_1, (c_1, \dots, c_{\alpha_1})), w^1, l^1), \\ S_2 & = (((\alpha_2, \dots, \alpha_\ell), (c_{\alpha_1+1} + d + \lvert l^1 \rvert, \dots, c_{\lvert \alpha \rvert} + d + \lvert l^1 \rvert)), w^2, l^2), \end{align*} $$

where we define

$$ \begin{align*} & w^1 = (w_1, \dots, w_{\alpha_1}), \qquad \qquad \qquad & & w^2 = (w_{\alpha_1 + 1}, \dots, w_{\lvert \alpha \rvert}), \\ & l^1 = (l_1, \dots, l_{\alpha_1}), \qquad \qquad \qquad & & l^2 = (l_{\alpha_1 + 1}, \dots, l_{\lvert \alpha \rvert}). \end{align*} $$

Example 7.2. Let $S ((\alpha , c), w, l)$ , $\alpha =(3,1,1)$ , $c=(1,1,1,1,2)$ , $w=(7,4,7,7,5)$ , $l=(0,0,2,0,3)$ . We split it after $\alpha _1 = 3$ cells. We have one ascent in $(7,4,7,7)$ , so $d=1$ , and we have $\lvert l^1 \rvert = 0+0+2 = 2$ , so we add three cells to each column in $S_2$ , and get

(7.1)

Proposition 7.3. The map ${\mathrm { {split}}}$ is weight-preserving: if ${\mathrm { {split}}}(S) = (S_1, S_2)$ , then $\operatorname {\mathrm {weight}}(S) = \operatorname {\mathrm {weight}}(S_1) + \operatorname {\mathrm {weight}}(S_2)$ .

Proof. Suppose ${\mathrm { {split}}}(S) = (S_1, S_2)$ . Let $S = (C, w, l)$ , $C = (\alpha , c)$ with $\alpha _1 = v$ , and let $\ell (C) = n$ . Let us denote $S_1 = (C^1, w^1, l^1)$ and $S_2 = (C^2, w^2, l^2)$ .

By definition, the weight has three components, one coming from the total size, one coming from the $\operatorname {\mathrm {revmaj}}$ of the word w, and one coming from the labels l.

Let $d = \operatorname {\mathrm {asc}}(w_1, \dots , w_{v+1})$ . By definition of ${\mathrm { {split}}}$ , the number of cells above $S_1$ stays the same, while the number of cells above $S_2$ increases by $\ell (C_2) (d + \lvert l^1 \rvert ) = (n-v) (d + \lvert l^1 \rvert )$ , so the first component of the total weight increases by the same amount.

By definition of $\operatorname {\mathrm {revmaj}}$ , we have

$$ \begin{align*} \operatorname{\mathrm{revmaj}}(w) & = \sum_{i \in \operatorname{\mathrm{Asc}}(w)} (n-i) \\ & = \sum_{i \in \operatorname{\mathrm{Asc}}(w^1)} (n-i) + \sum_{i \in \operatorname{\mathrm{Asc}}(w^2)} (n-(v+i)) + \chi(w_v < w_{v+1}) (n-v) \\& = \sum_{i \in \operatorname{\mathrm{Asc}}(w^1)} (n-v+v-i) + \sum_{i \in \operatorname{\mathrm{Asc}}(w^2)} (n-v-i) + \chi(w_v < w_{v+1})(n-v) \\ & = (n-v) \cdot d + \operatorname{\mathrm{revmaj}}(w^1) + \operatorname{\mathrm{revmaj}}(w^2), \end{align*} $$

so the second component of the total weight decreases by $(n-v) \cdot d$ .

Finally, by definition of u, we have

$$ \begin{align*} u(w) & = \sum_{i=1}^n l_i \cdot (n-i) = \sum_{i=1}^v l_i \cdot (n-i) + \sum_{i=v+1}^n l_i \cdot (n-i) \\ & = \sum_{i=1}^v l_i \cdot (n-v+v-i) + \sum_{i=1}^{n-v} l_i \cdot (n-v-i) = (n-v) \lvert l^1 \rvert + u(l^1) + u(l^2), \end{align*} $$

so the third component of the total weight decreases by $ (n-v) \lvert l^1 \rvert $ .

All these changes cancel out and so the weight is preserved, as desired.

Definition 7.4. Given two labeled column-composition tableaux $S_1$ , $S_2$ , we define

that is, the number of ascents in the word of $S_1$ followed by the first letter of $S_2$ .

Lemma 7.5. Let $S_1, S_2$ be two labeled column-composition tableaux. There exists S, such that ${\mathrm { {split}}}(S) = (S_1, S_2)$ if and only if

(7.2) $$ \begin{align} c_1(S_2) \geq c_\ell(S_1) + \operatorname{\mathrm{asc}}(S_1;S_2) + \lvert l(S_1) \rvert .\end{align} $$

If such S exists, then it is unique; we say that $S_1$ can join $S_2$ and set ${\mathrm { {join}}}(S_1, S_2) = S$ .

Proof. If such S exists, then (7.2) holds by construction. Suppose that (7.2) holds. Then we can define S as the labeled column composition tableau obtained by decreasing the size of each column of $S_2$ by $\operatorname {\mathrm {asc}}(S_1; S_2) + \lvert l(S_1) \rvert $ and then concatenating it to $S_1$ , also concatenating their words. Equation (7.2) ensures that the result is still a column-composition tableau.

It is now immediate that ${\mathrm { {split}}}(S) = (S_1, S_2)$ and that such S is unique.

The following lemma is crucial to ensure that our sign-reversing, weight-preserving bijection is well-defined.

Lemma 7.6. Let $S_1$ , S be labeled column-composition tableaux, and let ${\mathrm { {split}}}(S) = (S_2, S_3)$ . Then $S_1$ can join $S_2$ if and only if it can join S.

Proof. Since $c_1(S_2) = c_1(S)$ , then (7.2) holds for $S_1$ and $S_2$ if and only if it holds for $S_1$ and S.

We can now define our bijection as follows.

Definition 7.7. Given $T = (T_1,\dots , T_r) \in {\mathrm { {LC}}}_{\lambda ,\eta }^\gamma $ , define $\psi (T)$ by the following process:

1. 1. if $r=0$ , then ;

2. 2. if $T_1$ can split, then ;

3. 3. if $T_1$ cannot split and $T_1$ can join $T_2$ , then ;

4. 4. otherwise, we inductively define .

Theorem 7.8. Let

$$ \begin{align*} U_{\lambda,\eta}^\gamma = \Big\{ T \in {\mathrm{ {LC}}}_{\lambda,\eta}^\gamma \mid T & \text{ has no vertical bars, and for all}\ i \\ & c_1(T_{i+1}) < c_{\ell(T_i)} (T_i) + \operatorname{\mathrm{asc}}(T_i;T_{i+1}) + \lvert l(T_i) \rvert \Big\}. \end{align*} $$

Then

$$\begin{align*}D_{\lambda,\eta}^\gamma (q) = \sum_{T \in U_{\lambda,\eta}} q^{\operatorname{\mathrm{weight}}(T)}. \end{align*}$$

Proof. Since we are using the split map and its inverse, Proposition 7.3 ensures that $\psi $ is weight-preserving. Furthermore, ${\mathrm { {split}}}$ and ${\mathrm { {join}}}$ either remove or add a single vertical bar, so $\psi $ is sign-reversing.

We have to make sure that $\psi $ is an involution. Let $T = (T_1, \dots , T_r) \in {\mathrm { {LC}}}_{\lambda ,\eta }^\gamma $ . If $\psi (T) = T$ , then clearly, $\psi ^2(T) = T$ .

Suppose that $\psi (T) = (T_1, \dots , T_{i-1}, {\mathrm { {split}}}(T_i), T_{i+1}, \dots , T_r)$ . Let ${\mathrm { {split}}}(T_i) = (S_1, S_2)$ . By construction, $T_1, \dots , T_{i-1}$ cannot split, and $T_j$ cannot join $T_{j+1}$ for $j < i$ . By Lemma 7.6, since $T_{i-1}$ cannot join $T_i$ , it also cannot join $S_1$ . By construction, $S_1$ and $S_2$ can join, so $\psi ^2(T) = T$ .

Suppose instead that $\psi (T) = (T_1, \dots , T_{i-1}, {\mathrm { {join}}}(T_i, T_{i+1}), T_{i+2}, \dots , T_r)$ . We have that, by construction, $T_1, \dots , T_{i-1}$ cannot split, and $T_j$ cannot join $T_{j+1}$ for $j < i$ . By Lemma 7.6, since $T_{i-1}$ cannot join $T_i$ , it also cannot join ${\mathrm { {join}}}(T_i, T_{i+1})$ . By construction, ${\mathrm { {join}}}(T_i, T_{i+1})$ can split, so again, $\psi ^2(T) = T$ and $\psi $ is an involution.

The set of fixed points is the set of labeled column composition whose parts cannot split or be joined, and the conditions for that to hold are exactly the conditions given in the definition of $U^{\gamma }_{\lambda ,\eta }$ .

Example 7.9. We can read the type of the element in Figure 6 as follows. Since the rows have lengths $3,1,4,1$ , respectively, we know that $\eta = (4,3,1,1)$ . Since the words in the base rows are $(2,4,3),(1),(3,1,1,2),(2)$ , which have multiplicities given by $1^3 2^3 3^2 4^1$ , we have $\lambda = (3,3,2,1).$ Lastly, the labels underneath the rows rearrange to $(3,2,2,2,1,1,0,0,0)$ , meaning $\gamma = (3,2,2,2,1,1).$

Figure 6 A fixed point of $\psi $ .

8 A bijection to ascent polyominoes

In this section, we define an intermediate family of objects that will turn out handy to describe our bijection between the fixed points of $\psi $ and $\gamma $ -parking functions, namely, ascent labeled polyominoes.

Definition 8.1. An $m \times n$ ascent labeled parallelogram polyomino is a triple $(P,Q,w)$ , such that $(P,Q)$ is an $m \times n$ parallelogram polyomino (as in Definition 2.6), and $w \in \mathbb {N}^n$ is such that if Q has no East steps on the line $y = i-1$ (or has only one East step if $i=1$ , since the first step of Q must be East), then $w_i \geq w_{i+1}$ .

Definition 8.2. Let $(P, Q, w)$ be an ascent labeled parallelogram polyomino. Let $\lambda \vDash n$ be the content of w (that is, $m(w) = 1^{\lambda _1} 2^{\lambda _2}\cdots $ ), and let $\eta \vdash n$ be the partition whose block sizes are the lengths of the maximal streaks of North steps in P, in some order. Let

and let $\gamma $ be the partition obtained by rearranging $(\beta _1, \dots , \beta _n)$ and removing zeros.

We define ${\mathrm { {type}}}(P, Q, w) = (\lambda , \eta , \gamma )$ , and call ${\mathcal {P}}_{\lambda , \eta }^\gamma $ the set of ascent labeled polyominoes of type $(\lambda , \eta , \gamma )$ . Note that the height is fixed by the type but the width isn’t, as it depends on the number of ascents in w.

We will now give a bijection $\varphi \colon U^{\gamma }_{\lambda ,\eta } \rightarrow {\mathcal {P}}^\gamma _{\lambda ,\eta }$ from the set of fixed points of $\psi $ of given type, and ascent labeled parallelogram polyominoes of the same type.

In order to describe the bijection, for $T = (T_1, \dots , T_r)\in U^{\gamma }_{\lambda ,\eta }$ , we need to define a triple $\varphi (T) = (P(T),Q(T),w(T))$ corresponding to the polyomino and its labels.

Definition 8.3. Let $T = (T_1, \dots , T_r)\in U^{\gamma }_{\lambda ,\eta }$ , with $T_i = (C^i, w^i, l^i)$ . First, we define (the concatenation).

Next, let $l(T) = l^1 \cdots l^r$ and let $r_i(T) = l(T)_i + \chi (i \in \operatorname {\mathrm {Asc}}(w))$ . We define

that is, the path with $r_i(T)$ East step on the line $y=i-1$ , plus $1$ if $i=1$ .

Finally, let $s_i(T) = c_{\ell (T_i)}(T_i) + \operatorname {\mathrm {asc}}(T_i; T_{i+1}) + \lvert l^i \rvert - c_1(T_{i+1})$ , which is guaranteed to be positive by the fact that T is a fixed point of $\psi $ . We set

Example 8.4. We demonstrate the bijection for the sequence of labeled column composition tableaux $T \in U^{(3,2,2,2,1)}_{(3,3,1,1),(4,3,1,1)}$ appearing in Figure 6. We have $w = w(T) = (2,4,3,1,3,1,1,2,2)$ and $l = l(T) = (0,2,0,2,2,1,1,0,3)$ .

We have $\operatorname {\mathrm {Asc}}(w) = \{1, 4, 7\}$ , so we get

$$\begin{align*}Q(T) = E E^{0+1} N E^{2+0} N E^{0+0} N E^{2+1} N E^{2+0} N E^{1+0} N E^{1+1} N E^{0+0} N E^{3+0} N. \end{align*}$$

Finally, we have $s_1(T) = 0 + 1 + 2 - 2 = 1$ , $s_2(T) = 2 + 1 + 2 - 0 = 5$ , $s_3(T) = 0 + 1 + 4 - 2 = 3$ , and $s_4(T) = 2 + 0 + 3 - 0 = 5$ , so we end up with

$$\begin{align*}P(T) = N^3 E^1 N^1 E^5 N^4 E^3 N^1 E^5 E. \end{align*}$$

We refer to Figure 7 for the image of T under $\varphi $ . The North steps of $P(T)$ are labeled with the word w written from bottom to top. The North segments are also distinguished in our picture with a red line on its left. We see that the vertical segments of $P(T)$ have lengths $3,1,4,1$ , which rearranges to $\eta = (4,3,1,1)$ . The green segments highlight the horizontal segments of $Q(T)$ (ignoring the first, mandatory East step), and along each horizontal line, we have lengths $(1,2,0,3,2,1,2,0,3)$ . Since $\operatorname {\mathrm {Asc}}(w) = \{1,4,7\}$ , we subtract term by term to see that

$$\begin{align*}(1,2,0,3,2,1,2,0,3) - (1,0,0,1,0,0,1,0,0)= (0,2,0,2,2,1,1,0,3) \end{align*}$$

has nonzero parts that rearrange to $\gamma = (3,2,2,2,1,1)$ , as expected.

Figure 7 The image $\varphi (T)$ of the fixed point in Figure 6.

Theorem 8.5. The map $\varphi (T) = (P(T),Q(T),w(T))$ is a bijection between $U_{\lambda ,\eta }^\gamma $ and ${\mathcal {P}}_{\lambda ,\eta }^\gamma $ , such that $\operatorname {\mathrm {weight}}(T) = \operatorname {\mathrm {area}}(\varphi (T))$ , that is, $\varphi $ is weight-preserving.

Proof. We describe the inverse $\varphi ^{-1}$ instead. Starting with $S = (P,Q,w) \in {\mathcal {P}}_{\lambda , \eta }^\gamma $ , for each maximal vertical segment in P, draw the maximal rectangle contained in S that has that streak as one of the sides and whose perimeter does not contain any East step in Q. Then slide all of the labels in these vertical segments to the opposite side of the maximal rectangle (see Step 2 of Figure 8).

Figure 8 A pictorial description of $\varphi ^{-1}$ .

To construct $(T_1,\dots , T_{\ell (\lambda )})$ , we can determine the tableaux by looking at the rectangles: if $T_i = (C^i, w^i, l^i)$ , then $C^i$ is the column-composition tableau obtained by rotating the rectangle delimited by the $i^{\textit {h}}$ vertical segment in S; $w^i$ is the sequence of labels appearing in the rectangle, read from bottom to top; if $l = l^1 \cdots l^{\ell (\lambda )}$ , then $l_j + \chi (j \in \operatorname {\mathrm {Asc}}(w))$ is the number of cells of S in the $j^{\textit {h}}$ row that are outside the maximal rectangle and whose bottom segment is an East step of Q (since the condition on P forces $l_j \geq 0$ , so if $j \in \operatorname {\mathrm {Asc}}(w)$ , then there must be at least one such cell). This is better seen by rotating S by $90$ degrees clockwise (as in Figure 8, Step 3). Let us call this rotated picture $S'$ .

We should note that since $(P,Q,w)$ gives a parallelogram polyomino, the $i+1^{\textit {h}}$ vertical segment in P occurs strictly right of the $i^{\textit {h}}$ vertical segment and also strictly left of Q. Using the translation to $T = \varphi ^{-1}(S)$ , this is equivalent to say that

$$\begin{align*}c_1(T_{i+1}) < c_{\ell(T_i)}(T_{i}) + \sum_{j =1}^{\ell(T_i)} \chi(j \in \operatorname{\mathrm{Asc}}(w^i w^{i+1})) + \sum_{j=1}^{\ell(T_i)} l_i \end{align*}$$

or rather

$$\begin{align*}c_1(T_{i+1}) < c_{\ell(T_i)}(T_{i}) + \operatorname{\mathrm{asc}}(T_i;T_{i+1}) + \lvert l(T_i)\rvert. \end{align*}$$

Since the defining property making P a path above Q with respect to w converts directly to the defining relation for elements $T \in U_{\lambda ,\eta }^\gamma $ , then $\varphi $ is a bijection.

We are now going to show that $\varphi $ is weight-preserving. First, draw a path along the cells of $S'$ starting from the top left cell, and moving East if there are labels directly East, and moving South otherwise (see Figure 9). Now the area can be computed by counting the number of unit cells with no dashed line through it, those cells covering the minimal area, we remove as normalization. The area above the dashed line equals the weight contribution in the $T_i$ given by the cells above the base row.

Figure 9 $\varphi $ is weight-preserving.

The cells below the dashed line will be counted in the following way: In $S'$ , directly South of the label $w_j$ , there are by construction $l_j + \chi (j \in \operatorname {\mathrm {Asc}}(w))$ cells which are adjacent to the path on the left. Each of these cells have the same number of cells weakly East of them, namely, the number of cells between $w_j$ and the next base row. The number of cells in these rows is then

$$\begin{align*}(l_j + \chi(j \in \operatorname{\mathrm{Asc}}(w))) \times \# \{ \text{cells in the same base and on the right of}\ w_j \}. \end{align*}$$

Taking the sum over all j, we get the number of cells below the dashed line. But now the second and the third factor contributing to $\operatorname {\mathrm {weight}}(T)$ are exactly

$$\begin{align*}\sum_{j \in \operatorname{\mathrm{Asc}}(w)} \# \{ \text{cells in the same base and on the right of}\ w_j \} \end{align*}$$

and

$$\begin{align*}\sum_j l_j \times \# \{ \text{cells in the same base and on the right of}\ w_j \} \end{align*}$$

(as we described in Example 6.4).

Finally, it is immediate to see that the number of cells on the dashed blue line is exactly $m+n-1$ . So, by Definition 2.7, indeed, $\operatorname {\mathrm {weight}}(T) = \operatorname {\mathrm {area}}(\varphi (T))$ , as desired.

In the end, we get the following result.

Theorem 8.6.

$$\begin{align*}\left. \Delta_{m_\gamma} \operatorname{\mathrm{\Xi}} e_\lambda \right\rvert_{t=1} =\sum_{\eta \vdash n } e_\eta \sum_{S \in {\mathcal{P}}^{\gamma}_{\lambda,\eta} } q^{\operatorname{\mathrm{area}}(S)}. \end{align*}$$

Proof. It follows immediately from Theorem 7.8 and Theorem 8.5.

9 $\gamma $ -Parking Functions

In this section, we complete the construction by giving a weight-preserving bijection between ${\mathcal {P}}_{\lambda ,\eta }^\gamma $ and the set

of $\gamma $ -parking function with content $\lambda $ and e-composition $\eta $ , part of which, we have already seen in Definition 2.12.

It is slightly easier to describe the inverse, so that is what we will do.

Definition 9.1. Let $p = (P, Q, w)$ be a labeled $\gamma $ -Dyck path. We define $\iota (p) = (\overline {P}, \overline {Q}, w)$ , where $\overline {P}$ and $\overline {Q}$ are the paths obtained from P and Q, respectively, by removing, for every $i \not \in \operatorname {\mathrm {Asc}}(w)$ , the first East step of P on the line $y=i$ and the first East step of Q on the line $y=i-1$ .

See Figure 10 for an example.

Theorem 9.2. The map $\iota $ defines a bijection between ${\mathrm { {PF}}}_{\lambda , \eta }^\gamma $ and ${\mathcal {P}}_{\lambda ,\eta }^\gamma $ , such that $\operatorname {\mathrm {area}}(p) = \operatorname {\mathrm {area}}(\iota (p))$ .

Proof. First, notice that $i \not \in \operatorname {\mathrm {Asc}}(w)$ means that $w_i \geq w_{i+1}$ , and so there must be an East step of P on the line $y=i$ , as the labeling is strictly increasing along columns; then, notice that by definition, we have at least an East step of Q on each line; finally, since the first East step of P on the line $y = i$ must necessarily be strictly on the left of the first East step of Q on the line $y=i-1$ , then $(\overline {P}, \overline {Q})$ is still a parallelogram polyomino.

Now, since Q has at least one East step on each line (two on the line $y=0$ ), and we are only removing steps on lines $y=i-1$ , where $i \not \in \operatorname {\mathrm {Asc}}(w)$ , then $\overline {Q}$ is guaranteed to have at least one East step on each line $y=i-1$ , where $i \in \operatorname {\mathrm {Asc}}(w)$ (two on the line $y=0$ if $1 \in \operatorname {\mathrm {Asc}}(w)$ ). This means that $\iota (p)$ is an ascent labeled polyomino.

By construction, the word is the same and so the content is also the same; by Definition 2.12, the e-composition of p is exactly given by the lengths of the maximal vertical segments of $\overline {P}$ , and by Definition 8.2, the last component of the type must be $\gamma $ . It follows that $\iota (p) \in {\mathcal {P}}_{\lambda ,\eta }^\gamma $ .

Since the algorithm that defines $\iota $ is invertible, the map is bijective. Finally, notice that the number of cells in the $i^{\textit {h}}$ row decreases by one if $i \not \in \operatorname {\mathrm {Asc}}(w)$ and stays the same if $i \in \operatorname {\mathrm {Asc}}(w)$ , so we lose $\ell (w) - \operatorname {\mathrm {asc}}(w)$ cells; on the other hand, the width of the polyomino also decreases by $\ell (w) - \operatorname {\mathrm {asc}}(w)$ , so the area stays the same.

Figure 10 A pictorial description of $\iota $ for a $\varnothing $ -parking function.

As a corollary, we get the desired e-expansion.

Theorem 9.3.

$$\begin{align*}\left. \Delta_{m_\gamma} \operatorname{\mathrm{\Xi}} e_\lambda \right\rvert_{t=1} = \sum_{p \in {\mathrm{ {PF}}}^{\gamma}_{\lambda} } q^{\operatorname{\mathrm{area}}(p)} e_{\eta(p)}. \end{align*}$$

Proof. It follows immediately from Theorem 8.6 and Theorem 9.2.

Example 9.4. Looking at Figure 3, we have the e-expansion

$$ \begin{align*} \left. \Delta_{m_2} \operatorname{\mathrm{\Xi}} e_{11} \right\rvert_{t=1} & = e_{11} + e_2 + q e_2 + e_{11} + e_{11} + qe_{11} + qe_{11} + q^2 e_{11} + q^2 e_2 + q^3 e_2 \\ & = (q^3+q^2+q+1) e_2 + (q^2+2q+3) e_{11}, \end{align*} $$

which is indeed correct.

10 Using different labelings

Our construction generalizes to a broader framework, in which we use a different family of labelings and a different statistic on words. If these new labelings satisfy certain properties, then the construction we just described still holds and allows us to give a combinatorial expansion of different families of symmetric functions.

To this end, let us analyze the construction of an element $T \in {\mathrm { {LC}}}^{\gamma }_{\lambda ,\eta }$ and the computation of its statistic. Let $\vec {w}(T) = (w^1,\dots , w^r) \in {\mathrm { {WV}}}(\lambda , \beta )$ with $\beta \in R(\eta )$ , and let $w(T) = w^1 \cdots w^r$ be the concatenation, that is, the word in the base rows of T read from left to right. The key property of $\operatorname {\mathrm {revmaj}}$ we use in Proposition 7.3 and Lemma 7.6 is that it is computed by taking a subset of letters of $w(T)$ and summing the number of letters to the right of, and in the same base as, each letter in the subset. But these two results do not depend on the subset itself. In the end, we can give the following definition.

Definition 10.1. Let W be any set of words, and let $\rho \colon W \rightarrow \mathbb {N}$ be any statistic on W. We say that $\rho $ looks right if

$$\begin{align*}\rho(w) = \sum_{i \in S(w)} (\ell(w)-i) \end{align*}$$

for any subset-picking function $S \colon W \rightarrow 2^{\mathbb {N}}$ , such that $S(w) \subseteq \{1,\dots , \ell (w)\}$ .

Notice that S completely determines $\rho $ , meaning that for any subset-picking function S, the statistic looks right. We can extend the definition to vectors as follows.

Definition 10.2. Let $WV$ be any set of word vectors, and let $\vec {\rho } \colon WV \rightarrow \mathbb {N}$ be any statistic on $WV$ . We say that $\vec {\rho }$ looks right if, for $\vec {w} = (w^1, \dots , w^r) \in WV$ , we have

$$\begin{align*}\vec{\rho}(\vec{w}) = \sum_{i=1}^r \rho(w^i), \end{align*}$$

where $\rho $ is a statistic that is defined on all the entries of word vectors in $WV$ and that looks right. With an abuse of notation, we write $\rho $ for $\vec {\rho }$ .

Let $W \subseteq \mathbb {N}^n$ , let ${\mathrm { {LC}}}_{n,\eta }^\gamma = \bigcup _{\lambda \vDash _w n} {\mathrm { {LC}}}_{\lambda ,\eta }^\gamma $ (i.e., there is no restriction on the word, as we are taking the union over all the weak compositions), and let

Let $\rho $ be any statistic defined on the set of subwords of words in W that looks right. For $T \in {\mathrm { {LC}}}_{W, \eta }^\gamma $ , with the same notation as in Definition 6.3, let

For any composition $\beta $ , let ${\mathrm { {WV}}}(\beta ) = \bigcup _{\lambda \vDash _w n} {\mathrm { {WV}}}(\lambda , \beta )$ , that is, the set of word vectors $\vec {w} = (w^1, \dots , w^{\ell (\beta )})$ , such that $\ell (w^i) = \beta _i$ . We define

which is the subset of such vectors that concatenate to a word in W. Note that $\rho $ extends to $W(\beta )$ so that it looks right.

Let

We have the following analogue of Theorem 7.8.

Theorem 10.3. Let

where . Then

$$\begin{align*}D^{\gamma}_{W,\eta}(q) = \sum_{T \in U_{W,\eta}^\gamma} q^{\operatorname{\mathrm{weight}}(T)}. \end{align*}$$

Proof. The same argument as in Proposition 7.3 and Lemma 7.6 holds if we replace $\operatorname {\mathrm {asc}}$ with any statistic that looks right. In this case, we replaced $\operatorname {\mathrm {asc}}$ with $\rho $ , which looks right by hypothesis, so the statement holds.

Definitions 8.1 and 8.2 generalize as follows.

Definition 10.4. Let W be a set of words of length n, and let S be a subset-picking function on W. An S-labeled parallelogram polyomino is a triple $(P,Q,w)$ , where $w \in W$ , and $(P,Q)$ is a parallelogram polyomino, such that if Q has no East steps on the line $y = i-1$ (or has only one East step if $i=1$ , since the first step of Q must be East), then $i \not \in S(w)$ .

Definition 10.5. Let $(P, Q, w)$ be an S-labeled parallelogram polyomino. Let $\eta \vdash n$ be the partition whose block sizes are the lengths of the maximal streaks of North steps in P, in some order. Let

and let $\gamma $ be the partition obtained by rearranging $(\beta _1, \dots , \beta _n)$ and removing zeros.

We define ${\mathrm { {type}}}(P, Q, w) = (W, \eta , \gamma )$ , and call ${\mathcal {P}}_{W, \eta }^\gamma $ the set of S-labeled polyominoes of type $(W, \eta , \gamma )$ . Once again, the width depends on the cardinality of $S(w)$ and it’s not constant through the set.

Finally, using the same argument as in Theorem 8.5, with the statistic $\rho $ (that looks right) corresponding to S, we have the following.

Theorem 10.6.

$$\begin{align*}D_{W,\eta}^{\gamma}(q) = \sum_{P \in {\mathcal{P}}_{W,\eta}^{\gamma} } q^{\operatorname{\mathrm{area}}(P)}. \end{align*}$$

In particular, for $S = \operatorname {\mathrm {Des}}$ , our labeled polyominoes $(P,Q,w)$ enumerated by $D_{\lambda ,\eta }^{\gamma }$ can be interpreted in two different ways: in one, the path Q has forced East steps at the descents of w, in the other, it has forced East steps at the ascents of w. Both are valid combinatorial interpretations.

Finally, the map $\iota $ from Definition 9.1 also generalizes, by replacing the condition $i \not \in \operatorname {\mathrm {Asc}}(w)$ with $i \not \in S(w)$ . Of course, the set of $\gamma $ -Dyck paths we get in the end will not necessarily have strictly increasing columns, but rather the condition that if $w_i, w_{i+1}$ are in the same column, then $i \in S(w)$ .

11 Applications to Schur functions

We can now use the idea of choosing different labelings to get similar results for other instances of $\widetilde {\Delta }_{m_\gamma } \operatorname {\mathrm {\Xi }} F$ . One interesting case that our technique can handle is when F is a Schur function (rather than an elementary symmetric function). We now find an e-expansion for $\widetilde {\Delta }_{m_\gamma } \operatorname {\mathrm {\Xi }} s_{\lambda }$ .

The idea is to mimic what we did in Section 4. We have the expansion

$$\begin{align*}s_{\lambda}^\ast = \sum_{\mu \vdash n} \frac{\operatorname{\mathrm{\widetilde{H}}}_\mu}{w_\mu} \langle s_{\lambda}^\ast , \operatorname{\mathrm{\widetilde{H}}}_\mu \rangle_\ast = \sum_{\mu \vdash n} \frac{\operatorname{\mathrm{\widetilde{H}}}_\mu}{w_\mu} \langle s_{\lambda'} , \operatorname{\mathrm{\widetilde{H}}}_\mu \rangle, \end{align*}$$

where, again, in the last step, we went from the $\ast $ -scalar product to the ordinary Hall scalar product.

We can handle the term $\langle s_{\lambda '} , \operatorname {\mathrm {\widetilde {H}}}_\mu \rangle $ by using the specialization at $t=1$ of the Macdonald polynomials [Mac95, Hag08, HHL05a]. Combining [Hag08, Equations (2.26), (2.30)] and specializing $t=1$ , we get the formula

$$\begin{align*}\left. \langle s_{\lambda} , \operatorname{\mathrm{\widetilde{H}}}_\mu \rangle \right\rvert_{t=1} = \tilde{K}_{\lambda, \mu}(q,1) = \sum_{T \in {\mathrm{ {SYT}}}(\lambda)} q^{\operatorname{\mathrm{comaj}}(T, \mu)}, \end{align*}$$

where ${\mathrm { {SYT}}}(\lambda )$ is the set of standard Young tableaux of shape $\lambda $ , and $\operatorname {\mathrm {comaj}}(T, \mu )$ is computed as follows: first, partition the entries of T in blocks according to $\mu $ , that is, one block containing the entries going from $1$ to $\mu _1$ , one block containing the entries going from $\mu _1 + 1$ to $\mu _1 + \mu _2$ , and so on; then, for $1 \leq j \leq \lvert \lambda \rvert $ , check if j and $j+1$ are in the same block, say the $i^{\textit {h}}$ block, and check if $j+1$ occurs in a row above j in T; if they do, add $\mu _1 + \dots + \mu _i - j$ to $\operatorname {\mathrm {comaj}}(T, \mu )$ .

We want to convert this statement into one about words. Recall that a lattice word $w = (w_1,\dots , w_n)$ is a word, such that for every i and j,

$$\begin{align*}m_{j+1}(w_1,\dots,w_i) \leq m_j(w_{1},\dots, w_{i}). \end{align*}$$

This means that when read from the left, the number of j’s encountered is, at every moment, greater than or equal to the number of $j+1$ ’s. If $m_j (w) = \lambda _j$ , then we say w has content $\lambda $ , and write $w \in {\mathrm { {LW}}}(\lambda )$ . Notice that, since w is a lattice word, then $\lambda $ must be a partition. The following result is classical, but we add a proof for completeness.

Lemma 11.1. For any partition $\lambda $ , there is a bijection between lattice words with content $\lambda $ and standard Young tableaux of shape $\lambda $ .

Proof. Given a lattice word $w \in {\mathrm { {LW}}}(\lambda )$ , let T be the standard Young tableau obtained by putting i in the $w_i^{\textit {h}}$ row. Since w has content $\lambda $ , then T has shape $\lambda $ , and since w is a lattice word, then T is indeed a standard Young tableau. It is clear that this construction is reversible and hence bijective (see Figure 11 for an example).

If a tableau T is the image of a lattice word w via this bijection, we say that w encodes T.

Figure 11 The standard Young tableau of shape $(4,3,2)$ encoded by the lattice word $112132132$ .

For any composition $\beta $ , recall that ${\mathrm { {WV}}}(\beta )$ is the set of word vectors $\vec {w} = (w^1, \dots , w^{\ell (\beta )})$ , such that $\ell (w^i) = \beta _i$ . We define

which is the subset of vectors that concatenate to a lattice word with content $\lambda $ . Recall that

$$\begin{align*}\operatorname{\mathrm{revmaj}}(\vec{w}) = \sum_{i=1}^{\ell(\beta)} \operatorname{\mathrm{revmaj}}(w^i). \end{align*}$$

We have the following.

Lemma 11.2. If $w \in {\mathrm { {LW}}}(\lambda )$ encodes $T \in {\mathrm { {SYT}}}(\lambda )$ , for $\vec {w} \in {\mathrm { {LW}}}(\lambda , \beta )$ that concatenates to w, we have

$$\begin{align*}\operatorname{\mathrm{revmaj}}(\vec{w}) = \operatorname{\mathrm{comaj}}(T, \beta). \end{align*}$$

Proof. Let $1 \leq i \leq \ell (\beta )$ , let , and let

that is, the set $\operatorname {\mathrm {Asc}}(w^i)$ relabeled so that its entries give the positions of the ascents in w rather than in $w^i$ . By definition,

$$\begin{align*}\operatorname{\mathrm{revmaj}}(w^i) = \sum_{r \in \operatorname{\mathrm{Asc}}(w^i)} (\beta_i - r) = \sum_{j \in \operatorname{\mathrm{Asc}}_{\beta,i}(w)} (\Sigma_i(\beta) - j). \end{align*}$$

If $j \in \operatorname {\mathrm {Asc}}_{\beta ,i}(w)$ , then necessarily $j+1 \leq \Sigma _i(\beta )$ (because $w_j$ must occur within $w^i$ ), so j and $j+1$ belong to the same block of T according to $\beta $ ; moreover, we have $w_j < w_{j+1}$ , so $j+1$ occurs in a row above j in T. This means that the contribution of j to $\operatorname {\mathrm {comaj}}(T, \beta )$ is exactly $\Sigma _{i}(\beta ) - j$ , so taking the sum over all j, we get

$$\begin{align*}\operatorname{\mathrm{revmaj}}(\vec{w}) = \operatorname{\mathrm{comaj}}(T, \beta) \end{align*}$$

as desired.

It is important to remark that

$$\begin{align*}\operatorname{\mathrm{\widetilde{H}}}_\mu[X;q,1] = (q;q)_\mu h_\mu \left[ \frac{1}{1-q} \right], \end{align*}$$

which is a multiplicative basis. This means that, when evaluating $t=1$ , the order of the parts of $\mu $ doesn’t matter and we can use compositions rather than partitions, the combinatorial argument being exactly the same. Putting everything together, we have the following expansion.

Proposition 11.3.

$$\begin{align*}\left\langle s_{\lambda} , (q;q)_\beta h_\beta \left[ \frac{1}{1-q} \right] \right\rangle = \sum_{\vec{w} \in {\mathrm{ {LW}}}(\lambda, \beta)} \operatorname{\mathrm{revmaj}}(\vec{w}). \end{align*}$$

Using this expansion, the same argument we used in Section 4 to prove Proposition 4.6 leads us to the following.

Proposition 11.4. For any $\lambda \vdash n$ and $\gamma \vdash m$ , we have

$$\begin{align*}\widetilde{\Delta}_{m_\gamma} \operatorname{\mathrm{\Xi}} s_{\lambda} = \sum_{\eta \vdash n } e_\eta ~C^{\gamma}_{s_\lambda,\eta}(q), \end{align*}$$

where

$$ \begin{align*} C^{\gamma}_{s_\lambda, \eta} = \sum_{\beta \vDash n} \sum_{\vec{w} \in {\mathrm{ {LW}}}(\lambda', \beta)} \sum_{\vec{\nu} \in \operatorname{\mathrm{PR}}(\eta,\beta)} & q^{\operatorname{\mathrm{revmaj}}(\vec{w})} m_\gamma\left[ \sum_i [\beta_i]_q \right] (-1)^{n-\ell(\beta)} (1-q^{\beta_1}) f_{\vec{\nu}}\left[ \frac{1}{1-q} \right]. \end{align*} $$

Since our statistic is still $\operatorname {\mathrm {revmaj}}$ , we still have $S(w) = \operatorname {\mathrm {Asc}}(w)$ , so we can repeat the whole construction starting from lattice words instead, and get lattice $\gamma $ -Dyck paths. In the end, we get the following.

Theorem 11.5.

$$\begin{align*}\widetilde{\Delta}_{m_\gamma} \operatorname{\mathrm{\Xi}} s_{\lambda} = \sum_{p \in {\mathrm{ {LPF}}}^{\gamma}_{\lambda'} } q^{\operatorname{\mathrm{area}}(p)} e_{\eta(p)}. \end{align*}$$

Example 11.6. For $\lambda = (2,1)$ and $\gamma = (1)$ , we have

$$\begin{align*}\widetilde{\Delta}_{m_\gamma} \operatorname{\mathrm{\Xi}} s_{\lambda} = (q+2) e_{111} + (q^3+4q^2+6q+4) e_{21} + (q^4+2q^3+2q^2+q) e_3. \end{align*}$$

The corresponding combinatorial expansion is shown in Figure 12, and we indeed see that they coincide.

Figure 12 The e-expansion for $\widetilde {\Delta }_{m_1} \operatorname {\mathrm {\Xi }} s_{21}$ .

12 Special cases

Our construction yields a lot of special cases that are of interest and that find matches in the literature. In this section, we aim to go through some of them.

12.1 The extended Delta theorem when $t=1$

From the fundamental fact that $\operatorname {\mathrm {\Xi }} e_n = e_n$ , as a corollary of our construction, we obtain a special case of the results in [HR18], [Rom17], and [Rom19]. Here, the polyominoes in ${\mathcal {P}}^{\gamma }_{(n),\eta }$ are precisely the set of parallelogram polyominoes whose top path has vertical segments whose lengths rearrange to $\eta $ , and whose bottom path has horizontal segments (ignoring the first step of the path), whose lengths rearrange to $\gamma $ . There is only one word labeling the polyominoes, consisting of only $1$ ’s. There are no descents or ascents in this word. Our bijection to $\gamma $ -parking functions produces a pair of paths $(P',Q')$ , where $P'$ has no consecutive North steps, and the bottom path has lengths rearranging to $\gamma + 1^n$ .

The same result can be used to derive the $t=1$ case of the Extended Delta Theorem ([HRW18, DM22, BHM⁺23]). In fact, there is an explicit bijection between appropriate families of our objects and the objects appearing in the theorem; it states the following.

Theorem 12.1 (Extended Delta Theorem).

For $m, n, k \in \mathbb {N}$ , we have the monomial expansion

$$\begin{align*}\Delta_{h_m e_{n-k}} e_n = \sum_{p \in \operatorname{\mathrm{LD}}(n,m)^{\ast k}} q^{\operatorname{\mathrm{dinv}}(p)} t^{\operatorname{\mathrm{area}}(p)} x^p. \end{align*}$$

Here, $\operatorname {\mathrm {LD}}(n,m)^{\ast k}$ is the set of labeled Dyck paths of size $m+n$ , with m zero labels (that cannot be in the first column) and k decorated double rises (i.e., North steps preceded by North steps; the first step also counts as a double rise); $\operatorname {\mathrm {dinv}}(p)$ is the number of diagonal inversions of the path (that we do not define); $\operatorname {\mathrm {area}}(p)$ is the number of whole squares between the path and the main diagonal in rows that do not contain decorations; and $x^p$ is the product of the variables indexed by labels of the path, where $x_0 = 1$ . For our purposes, it will be more convenient to consider paths with decorated double falls (i.e., East steps followed by East steps; the last step also counts as a double fall), which is clearly equivalent.

Note that the symmetric function is also symmetric in q and t, so we can set $q=1, t=q$ , and since the area does not depend on the labels, this gives us an e-expansion of the symmetric function when $t=1$ . We are going to show that this expansion coincides with ours. Since the content of the labeling is $(n)$ , it is more convenient to use ascent polyominoes, rather than $\gamma $ -parking functions, and disregard the labeling altogether.

Indeed, $h_m e_{n-k}$ is monomial-positive: the coefficient of $m_\gamma $ is the number of ways one can fill $\ell (\gamma )$ ordered boxes with m green balls and $n-k$ blue balls, such that the $i^{\textit {h}}$ box contains $\gamma _i$ balls in total and no box contains two or more green balls. In our language, this means that the e-expansion of $\Delta _{h_m e_{n-k}} e_n$ will be given by all the $\gamma $ -parking functions of content $(n)$ , such that the bottom path is obtained by starting with $EN^n$ , then inserting $n-k$ East steps in different rows colored green, and then inserting m more blue East steps in any possible way.

The bijection we give is essentially a combination of [DIVW22, Theorem 6.17] (see also [DIVW19, Theorem 6.1]) and [Rom17, Theorem 2], disregarding the labels. We will not give a rigorous proof, but we will go through an example in detail, and the generalization follows.

Example 12.2. Let $n=7$ , $k=4$ , and $m=3$ .

Step 1. We start with the bottom path $EN^7$ , we add $n-k=3$ East steps in different rows (in green in the picture), and then we add $m=3$ East steps anywhere (in blue in the picture). To compute the area, we ignore the cells that touch the bottom path; the cells that do contribute are shaded.

Step 2. For each blue step (the ones coming from $h_m$ ), we insert a North step in the bottom path right before it, and insert a North step in the top path in the column one unit to the left. We mark the North steps added to the top path with a “ $\bullet $ ” symbol, to denote that they will be the “empty” valleys in the final picture. We highlight these steps in red. Notice that the area does not change in the process, as the number of shaded cells in each column does not change.

Step 3. For each pair of consecutive North steps in the bottom path, we insert an East step in between them, and an East step in the top path in the same column, on the right side of the already present East step. We mark these extra East steps with a “ $\ast $ ” symbol. We do the same in the first row if there is no green step there. By construction, in the top path, these added steps have another East step to the left. We do not shade the area in the newly introduced column. We won’t need the previous colors anymore, so we highlight again in red these new steps.

Step 4. Now, we move the “ $\ast $ ” symbols one column to the left, and we move all the shaded cells that end up under a “ $\ast $ ” one column to the right. Then, we draw the diagonal $y=x$ .

Step 5. The part of the top path going from $(0,0)$ to $(m+n,m+n)$ is now a Dyck path. By construction, it has m marked valleys and $n-k$ decorated double falls (i.e., pairs of consecutive East steps). The area of the path is the number of whole cells between the path and the diagonal that are not in columns containing a “ $\ast $ ,” which are exactly the shaded cells. The lengths of the vertical segments, ignoring the parts containing a marked valley, are also preserved. It follows that this procedure yields a bijection that preserves both the $\operatorname {\mathrm {area}}$ and the e-composition, as desired.

12.2 The parking function case

When $\lambda = 1^n$ and $\gamma = \varnothing $ , then elements in ${\mathrm { {PF}}}^\varnothing _{1^n}$ are constructed by selecting a $\varnothing $ -Dyck path and writing the numbers $1, \dots , n$ along the North segments of the top path so that the columns are increasing. This is precisely the set of parking functions in the classical sense.

Figure 13 shows an element of ${\mathrm { {PF}}}_8 = {\mathrm { {PF}}}_{(1^8)}^\varnothing $ (the parking functions of size $8$ ), drawn in the style of our $\varnothing $ -parking functions. Its area is $10$ .

Figure 13 A parking function of size $8$ .

Indeed, we have

$$\begin{align*}\operatorname{\mathrm{\Xi}} e_{1^n} \vert_{t=1} = \sum_{p \in {\mathrm{ {PF}}}_n} q^{\operatorname{\mathrm{area}}(p)} e_{\eta(p)}, \end{align*}$$

which suggests that the combinatorial description given in [DILB⁺22, Conjecture 6.4] should hold. In fact, it is known that spanning trees on the complete graph on $\{0, 1, \dots , n\}\ K_{n+1}$ , rooted at $0$ , q-weighted with $\kappa $ -inversions, are in bijection with parking functions of size n, q-weighed with the area. To prove the conjecture, one should show that the e-expansion (or, likely easier, the m-expansion) is preserved by the bijection.

We actually have that [DILB⁺22, Conjecture 6.1], which is very close to this statement, is actually solved for the symmetric function $\Theta _{e_{1^n}} e_1$ (evaluated at $t=1$ ), of which it provides a monomial expansion. At the moment, the relation between the e-expansion we just provided and the monomial expansion of [DILB⁺22, Theorem 4.5] remains unclear.

13 Concluding remarks

We conclude this paper with a few remarks and a discussion on possible future directions.

13.1 Combinatorial expansions

We should remark that our identities have multiple consequences. For one, for any F which has a positive expansion in terms of the monomial basis, we have found that $\widetilde {\Delta }_F \operatorname {\mathrm {\Xi }} e_{\lambda }$ and $\widetilde {\Delta }_{F} \operatorname {\mathrm {\Xi }} s_\lambda $ are e-positive, and their expansion can be given in terms of $\gamma $ -parking functions.

When F equals $s_\mu $ , $e_\mu $ , $h_\mu $ or $(-1)^{\lvert \mu \rvert -\ell (\mu )} f_\mu $ , we can get a set of combinatorial objects by labeling the bottom path of $\gamma $ -parking functions (as is done in [Rom19, HR18, Rom17] and in Example 12.2). Furthermore, if G expands positively in terms of the Schur basis, then we have also found that $\widetilde {\Delta }_{F} \operatorname {\mathrm {\Xi }} G$ is e-positive. We can similarly get expansions for these symmetric functions in terms of lattice $\gamma $ -parking functions.

13.2 e-positivity

Many of these symmetric functions become e-positive after the substitution $q=1+u$ (without substituting $t=1$ ). For instance, $\Delta _{m_\gamma } \operatorname {\mathrm {\Xi }} e_n$ seems to exhibit this e-positivity phenomenon.

Conjecture 13.1. If F is monomial positive, and G is Schur positive, then

$$\begin{align*}\Delta_F \operatorname{\mathrm{\Xi}} G \Big|_{q \rightarrow 1+u} \end{align*}$$

is e-positive, that is, the coefficients of the e-expansion are polynomials in $\mathbb {N}[u,t]$ .

In particular, if G is e-positive, the same result holds.

The case $\gamma = (k)$ and $G = e_n$ follows from the proof of the Delta theorem and the e-positivity on vertical strip $LLT$ polynomials proved in [D’A20].

If this conjecture is true, then our combinatorial objects would also give the combinatorial expansions for these symmetric functions. To be more precise, these symmetric functions would enumerate the number of $\gamma $ -parking functions (or lattice $\gamma $ -parking functions) where some subset of its area cells are chosen. It remains to find a t statistic that would give the entire symmetric function.

Conjecture 13.2. There exists a statistic $\mathsf {tstat}$ from pairs $(p,S)$ with $p \in {\mathrm { {PF}}}^{\gamma }_{\lambda }$ and $S \subseteq \operatorname {\mathrm {Area}}(p)$ subset of the area cells of p, such that

$$\begin{align*}\left. \Delta_{m_\gamma} \operatorname{\mathrm{\Xi}} e_{\lambda} \right\rvert_{q \rightarrow 1+u} = \sum_{p \in {\mathrm{ {PF}}}^{\gamma}_{\lambda} } \sum_{S \subseteq \operatorname{\mathrm{Area}}(p)} u^{\# S} t^{\mathsf{tstat}(p,S)} e_{\eta(p)}. \end{align*}$$

13.3 G-parking functions, labeled Dyck paths, tiered trees

It might be possible to apply the construction of the previous subsection in a much broader context. Indeed, we have a statistic-preserving map between $\varnothing $ -Dyck paths with content $\alpha $ and some subset of $\alpha $ -tiered trees rooted at $0$ (as in [DILB⁺22, Conjecture 6.4]), which we can obtain using results about G-parking functions [BTW87, Dha90] (see also [PYY17]) for appropriate multipartite graphs.

This connection may give a proof of [DILB⁺22, Conjecture 6.4], provided that one finds a way to translate the e-expansion into the monomial expansion. It is also possible that investigating this further would lead to the discovery of a bistatistic on rooted tiered trees that describes the symmetric function in full (without the need to specialize $t=1$ ).

13.4 The two-part case

When $\lambda = (n,m)$ and $\gamma = \varnothing $ , our objects are exactly the so-called two-car parking functions, that is, labeled Dyck paths of size $m+n$ with n labels equal to $1$ and m labels equal to $2$ . By [DIVW22, Theorem 3.11], we know that these objects are in fact in bijection with (unlabeled) parallelogram polyominoes of size $(m+1) \times (n+1)$ , and the bijection preserves the area.

In light of the statement in the previous subsection, this is not surprising, as we know that parallelogram polyominoes are in bijection with (unlabeled) $(n,1,m)$ -tiered rooted trees [DILB⁺22, Proposition 7.4]. In fact, the bijection is given for labeled objects; as before, this potentially allows us to get a monomial expansion, but this does not seem to coincide with the e-expansion provided by our theorems. As for the more general case of the previous subsection, this matter is worth investigating.

It might be worth noting that (unlabeled) parallelogram polyominoes are also in bijection with Dyck words in the alphabet $\{ 0 \leq \overline {0} \leq 1 \leq \overline {1} \leq 2 \leq \dots \}$ , starting with either $0$ or $\overline {0}$ , with m nonbarred letters and n barred letters, with an $\operatorname {\mathrm {area}}$ statistic given by the sum of the letters.