1. Introduction
Traditionally the protective capacity of mountain forests has been quantified assuming that avalanches do not start in dense forest stands (Reference De QuervainDe Quervain, 1978; Reference Gubler and RychetnikGubler and Rychetnik, 1991; Neweseley and others, 2000; Reference Gruber and BarteltGruber and Bartelt, 2007). Forests act to stabilize the snow cover and prevent destructive avalanches from releasing. They serve as a natural defense against avalanches where meteorological conditions and the terrain enable trees to grow.
The ability of forests to stop avalanches that start above the timberline is limited. Observations show that trees cannot withstand the dynamic forces of large, fast-moving avalanches (De Reference De QuervainQuervain, 1978; Reference MargrethMargreth, 2004) (Fig. 1). The energy required to break and uproot trees and entrain the woody debris is small in comparison to the overall flow energy of the avalanche (Reference Bartelt and StöckliBartelt and Stöckli, 2001). The braking effect of forests is small for extreme avalanches. Avalanche experts therefore often neglect forests, assuming either extremely large avalanches (that easily destroy the forest) or that the forest has been removed by previous events (Reference Christen, Bartelt and KowalskiChristen and others, 2010a). Consequently, avalanche dynamics calculations typically ignore forests completely or prescribe only minor changes to the flow friction (Reference Gruber and BarteltGruber and Bartelt, 2007).

Fig. 1. Uprooted trees in Val Prada, Switzerland, in winter 2009. The avalanche destroyed the whole forest and does not seem to be stopped or even decelerated by the forest. (Photograph: S. Margreth, SLF.)
Modeling how mountain forests stop small-to-medium avalanches has recently become a critical question in avalanche hazard mitigation (Reference CastellerCasteller and others, 2008; Reference Anderson and ClungAnderson and McClung, 2012). (According to the European avalanche classification scale, release volumes are defined to be <1000 m3 for small avalanches and between 1000 and 10 000 m3 for medium avalanches (EAWS, 2013).) Frequent (not extreme) avalanches are often the primary hazard for roads, railways and ski-runs, particularly in climates where wet snow avalanches are common (Reference Gruber and BarteltGruber and Bartelt, 2007). Local authorities must deal with the risk of small-to-medium avalanches hitting infrastructure, and therefore people, numerous times during a winter season. Forests can stop these avalanches and are an important protective measure (Reference Teich, Bartelt, Regamy and BebiTeich and others, 2012a).
There is thus an urgent need to quantify the braking effect of forests on small-to-medium avalanches (Reference Bebi, Kulakowski and RixenBebi and others, 2009; Reference Teich and BebiTeich and Bebi, 2009; Reference Takeuchi, Torita, Nishimura and HirashimaTakeuchi and others, 2011; Reference Teich, Bartelt, Regamy and BebiTeich and others, 2012a). In this case, trees remain standing after avalanche impact. They withstand dynamic forces and thus work as effective obstacles to decelerate the flow. The effect is similar to avalanche dams (Reference Faug, Naaim, Bertrand, Lachamp and Naaim-BouvetFaug and others, 2003, 2008, 2010; Reference Faug, Naaim, Bertrand, Lachamp and Naaim-BouvetNaaim and others, 2003, 2004); however, the working mechanism differs because the forest is not a single, rigid man-made defense structure, but a natural and inhomogeneous array of slender obstacles (trees, tree groups). If the trees are not broken or uprooted, forest structure (stem density, gaps, crown coverage, age and lowlying vegetation) is of crucial importance.
The existing forest avalanche data contain much material with valuable observational content, especially regarding the effect of different forest structures in hindering avalanche formation (Reference Schneebeli, Meyer-Grass and ArmstrongSchneebeli and Meyer-Grass, 1993; Reference Viglietti, Letey, Motta, Maggioni and FreppazViglietti and others, 2010). However, information on forest structure and avalanche flow (e.g. velocity, flow heights and deposition patterns) is limited and concentrated on the extreme avalanche case (Reference Bartelt and StöckliBartelt and Stöckli, 2001; Reference CastellerCasteller and others, 2008; Reference Christen, Bartelt and KowalskiChristen and others, 2010a; Reference Takeuchi, Torita, Nishimura and HirashimaTakeuchi and others, 2011). A first step to model avalanche flow in forests is to understand how forests stop avalanche snow. To this end, we recorded data from five forest avalanches near Davos, Switzerland, and one within the Bavarian Prealps, Germany (Section 2), in winter 2011/12. One other Bavarian case study during winter 2008/09 completes our dataset. In these events, the avalanche paths were partially or completely covered by forest. The focus of this data collection was to document release areas and fracture depths, snow conditions, forest structure, flow perimeter and deposition patterns. The events were special, in that we collected data on forests that were not destroyed by avalanches. Of particular importance was to quantify the mass deposition behind trees.
Based on the observations, we develop an avalanche/forest interaction function (detrainment function) to be used within the framework of a depth-averaged avalanche dynamics model (Reference Christen, Kowalski and BarteltChristen and others, 2010b). Our goal is to simulate the observed events. We assume that the trees stop the granular snow flow by a combination of processes: impact followed by jamming, resulting in a sudden and local dissipation of flow energy behind trees or tree groups. We address avalanche/forest interactions by specifying snow detrainment rates, rather than using higher friction values to represent the highly nonlinear braking effect of trees. The friction approach has been applied by several authors for extreme avalanches within the framework of Voellmy-type models (Reference VoellmyVoellmy, 1955; Reference Bartelt and StöckliBartelt and Stöckli, 2001; Reference Christen, Bartelt and KowalskiChristen and others, 2010a). This approach is justifiable for extreme avalanches, where the braking effects are small and occur over longer flow distances. For the small-avalanche case, Voellmy-type relations represent the avalanche/forest interaction poorly (Reference Teich, Vasella, Bartelt, Bebi, Feistl and Grêt-RegamyTeich and others, 2012b). The detrainment function is parameterized by a single coefficient representing forest structure. This coefficient determines the braking power of the forest. Both the friction and detrainment approaches have the same goal: to explain the deceleration and quantify the amount of mass stopped by the forest. The detrainment approach, however, is more direct, in the sense that we extract mass from the avalanche volume, removing momentum directly from the flow, rather than indirectly by friction coefficients. Furthermore, it is easier to calibrate, as the detrainment function provides users with the total mass per unit area stopped in the forest. Therefore we are able to compare calculated deposition volumes with observations and measurements of the seven case studies and to demonstrate the potential and limitations of the detrainment approach.
2. Observations
2.1. Documented avalanches
Field campaigns in the Swiss and German Alps were performed to investigate how avalanche mass is stopped by forests. The stopped mass can be estimated by calculating the difference between the volume of the initial release area and the deposition zone, and by determining the volume of deposited snow behind trees. As we assume forest structure has a crucial impact on the mass balance and the runout distance, we also gathered information on stem density and vegetation cover. Although single small trees and low branches were sometimes destroyed when hit by the avalanches, we focused on small-to-medium avalanches flowing through the forest where the trees acted as obstacles. This was the main selection criterion for the observation of an event. Such events are rarely documented by forest managers. Field studies have to be conducted before changing weather conditions (snowfall or melting) affect the deposits. Spotting such avalanches and reaching the tracks quickly, when they are accessible, is generally challenging.
In the 2008/09 and 2011/12 winters, data on seven avalanche events were collected: five in the region of Davos (ID-I to ID-V) and two in the region of Spitzingsee, Germany (ID-VI and ID-VII). The observed avalanche sites cover a wide range of terrain, snow and forest characteristics (Table 1), with altitude levels ranging between 1000 m a.s.l. (runout, Hagenberg, ID-VII) and 2100 m a.s.l. (release area, Dischma, ID-IV). The differences in altitude from release to runout vary from 50 m (Junkerboden, ID-I) to 450 m (Dischma, ID-IV). The smallest release volume was calculated to be ~320 m3 (Junkerboden, ID-I), whereas the largest release area covers ~7400 m2, with a release volume of 5190 m3 (Monstein, ID-V). Different terrain features in the avalanche track, such as gullies and flat slopes, could be distinguished. Slope angles vary from 508 steep release areas to flat runout zones. As the avalanche deposits could generally not be reached before the weather conditions changed, we classified snow characteristics according to qualitative criteria, such as dry, moist and wet, based on meteorological data from the nearest weather station. The meteorological conditions prior to the event, and therefore the causes of the avalanches, differed, resulting in wet snow avalanches (e.g. Filisur, ID-I) as well as dry snow avalanches (e.g. Brecherspitz, ID-VII). Forests penetrated by the avalanches we studied consist mainly of conifers with varying stand densities and age. For modeling we distinguished between a canopy density of >50% for dense forests and <50% for open forests. Canopy density was determined by analyzing orthoimages (from 2011 with 25 cm grid resolution) of each event (Reference Bebi, Kienast and SchönenbergerBebi and others, 2001).
Table 1. Characteristics of forest avalanches documented during the 2008/09 and 2011/12 winters


Fig. 2. Avalanche track near Filisur, Switzerland (ID-III). Note the main avalanche channel in the foreground with little snow on the ground, in comparison with the dense forest in the background.
It was essential to document the exact shapes of the release and deposition areas, to allow comparison with simulation results (Section 3). We used a handheld differential global navigation satellite system (dGNSS) device whenever possible, so we could map the runout areas precisely. Sometimes, due to safety reasons or lack of accessibility, the release area could not be reached. In these cases we used images of the release area from the opposite slope or from a helicopter, and matched these with maps of the area. For the two events near Filisur, Switzerland, we performed a terrain analysis with a spatial resolution of 2 m. Terrain features, such as gullies, ridges and slope angle, were taken into account to identify probable release areas. The GIS analysis is only accurate up to a scale of several meters, whereas the error of measurements with the dGNSS device is in the range of a few centimeters.
We collected information about the deposition patterns of avalanche snow within the forest, which allowed us to quantify the stopped mass. Photographs were taken, which document the significant amount of avalanche snow that remained behind the trees. Not only are considerable amounts of avalanche snow stopped by tree trunks, but also by root plates of upturned trees, low-lying branches and dead woody debris. Depositions in forests were mainly concentrated at the outer edges of the avalanche tracks, where the flow velocities were small (Fig. 2). We observed differences in deposited snow amounts due to slope angle, snow temperature (wet, moist or dry), stand density and age of trees (Section 2.2).
2.2. Deposition volume behind trees
In all the case studies (ID-I to ID-VII) we observed wedge-like depositions behind single trees, as well as tree groups (Fig. 3). Wedge-shaped depositions have been observed behind obstacles in chute experiments with granular materials (Reference Gray, Tai and NoelleGray and others, 2003). Deposition wedges have also been observed behind pressure-measurement pylons at the Swiss Vallée de la Sionne (Reference Sovilla, Kern and SchaerSovilla and others, 2010) and Italian Seehore (Reference Bovet, Chiaia, Frigo, Ubertini, Viola, de Miranda and CastellazziBovet and others, 2011) avalanche test sites. Although the deposition wedges had different dimensions, depending on the snow properties and tree-stand characteristics, a general geometry could be determined (Fig. 3). Typically, the upper and lower width of the wedge at the base (ground), d u and d l, are the same, d u = d l = d. The base width, d, is determined by the base width of the obstacle: (1) the stem diameter (Fig. 3a) or (2) the total width of a dense group of trees (Fig. 3b). Small trees with low-lying branches have base widths much greater than the stem diameter (Fig. 3c), because additional snow can be stopped by the branches. For single-tree impacts, the width of the upper wedge surface at the tree was sometimes smaller than the stem diameter, resulting in a pyramid-shaped wedge (Fig. 3a). The angle δ defines the top wedge angle of the pyramid (Fig. 3a). In general, the exterior side planes were parallel to the primary flow direction of the avalanche; the planes are nearly vertical, especially close to the tree. For large stem diameters, the trees’ sides are often rubbed clean of snow, indicating snow is stopped behind the tree, while the avalanche continues to move forward. This suggests that strong velocity gradients can develop when the avalanche flows within the forest. Shear planes, similar to those found in levee formation in runout zones (Reference Christen, Kowalski and BarteltBartelt and others, 2012b), were observed in case studies ID-II, ID-III and ID-V (Fig. 2). For most cases, the upper surface of the wedges was close to horizontal, i.e. angle γ was equal to the slope angle of the terrain (Fig. 3a). The wedges were sometimes tilted towards the slope, especially if the snow was wet (Fig. 3b and c). Settling and melting affected the depositions while we were getting to the tracks.

Fig. 3. Typical deposition structure of avalanche snow behind trees. The second column depicts the deposition pattern from above; in the third column the approximated deposition volume is illustrated. (a) Deposited snow behind a single trunk of ~100 cm diameter in relatively flat terrain (20˚). (b) Deposited snow behind a group of trees. (c) Deposited snow behind a small tree (~4 m high) in steep terrain (34˚); note the effect of branches close to the ground. The horizontal wedge length, l, and the slope-parallel wedge length, a, depend on the wedge height, hw, and on angle γ.
The observations allow us to quantify the volume, W, of snow captured behind one tree or group of trees. The wedge volume for the single-stem case (Fig. 3a) is

and for the tree-group case (Fig. 3b) it is

where h w is the wedge height and l is the horizontal wedge length.
Equation (2) can also be used for a single tree with low-lying branches (Fig. 3c). We provide calculated volumes of the wedges depicted in Figure 3. The dimensions of the wedges are provided in Table 2. Note that for cases b (tree groups) and c (low-lying branches) the detrained volumes are much larger than for the single-tree case.
The volume equations (Eqns (1) and (2)) allow us to derive a first approximation of the mean deposition height for different stem densities (Fig. 4). The mean deposition height, h d, depends strongly on the deposition widths and therefore on the forest structure (Table 3). Assuming a dense forest (400 trees per hectare), with average stem diameters of d = 1 m (for simplicity) on a slope of 30˚ with a top wedge angle of δ = 60˚ (from measurements), we find a rather small mean deposition height: only 2 cm averaged over the entire forest area struck by the avalanche. We emphasize that the stem diameter is measured at the ground, according to our observations. The snow that can be stopped by the forest can increase by a factor of >10 when wide, wedge-shaped deposits are created behind groups of trees. For example, when d = 4 m for a forest with the same stem density but trees grouped together, the mean deposition height is 18 cm. Here we assume that a tree group contains three trees (Fig. 3b). This result reveals the importance not only of the stem diameter, but also the forest structure.

Fig. 4. The goal of the forest model is to calculate the mean deposition height, h d. Wedge formation behind isolated tree stands is not predicted. The total deposited mass, M d, should, however, be equal to the observations. W is the volume of snow captured behind a single tree or tree group.

Fig. 5. The model domain and definition of primary variables: A r is the release area and A f the forest area. U and V are the velocities in x – and y –direction, respectively. The gravitational acceleration in the x –, y – and z –directions is denoted gx, gy and gz , respectively. S is the resistance acting in the opposite direction to the velocity, V.
Generally, we assume mean deposition heights of a few to 50 cm as reasonable amounts of snow being stopped by forests, 1 cm < h d < 50 cm.
3. Modeling
3.1. Avalanche modeling
We applied the numerical avalanche dynamics program, RAMMS (Rapid Mass Movements), to simulate the observed avalanche events and to perform simulations on an ideal parabola-shaped avalanche track (Reference Christen, Kowalski and BarteltChristen and others, 2010b). We describe the mountain profile in a horizontal X, Y coordinate system. The elevation of the mountain profile, Z (X, Y), is defined for each coordinate pair (X, Y). The geographic coordinates are used to construct a local surface-based coordinate system (x, y, z). The unknown field variables are the avalanche flow height, h (x, y, t), and the mean avalanche velocities, U (x, y, t) and V (x, y, t), in the x – and y –directions, V = (U, V)T (Fig. 5). Avalanche flow is modeled using depth-averaged mass- and momentum-balance equations (Reference Christen, Kowalski and BarteltChristen and others, 2010b):

The force components associated with the gravitational acceleration, g, in the x- and y-directions are denoted G = (Gx, Gy )T and are given by

with
The corresponding resistances in the x – and y –directions are denoted Sx and Sy ; S = (Sx, Sy )T.
Table 2. Observed wedge dimensions and calculated volumes of the depositions in Figure 3. Cases b and c (group of trees and small trees with underlying branches) catch more mass than case a (single trunk)

Table 3. Deposited snow and corresponding mean deposition height, h d, for angle γ = 30˚ (approximately equal to the slope angle of the terrain), wedge height h w = 2 m, top wedge angle, δ = 60˚. The tree diameter, d, is 1 m for a single tree, 2 m for a tree with branches reaching to the ground and 4 m for a group of three trees. For single trees we used Eqn (1) to calculate the volume, and for trees with branches and groups of trees we used Eqn (2). We assume a snow density of ρ = 300 kg m−3, an avalanche length of 50 m and a velocity of 10 m s−1 to calculate K according to Eqn (14)

The field variables are a function of time, t, and thus we solve the equations from avalanche release (t = 0) to avalanche deposition.
Let A
r(x, y) be the location of the avalanche release zone; this can be a forest opening or a region located above the timberline. The region A
f defines the forest. There can be multiple forest areas (Fig. 5). Mass uptake from the snow cover and snow detrainment from the avalanche (stopped mass) is specified by the volumetric mass flux, ![]() (x, y, t), defined per unit area. However, as we assume no mass uptake in forested areas, we did not account for entrainment in this study. We therefore define
(x, y, t), defined per unit area. However, as we assume no mass uptake in forested areas, we did not account for entrainment in this study. We therefore define ![]() as the detrainment rate. This provides the mean deposition height, h
d, of stopped snow mass in the forested area, Af.
as the detrainment rate. This provides the mean deposition height, h
d, of stopped snow mass in the forested area, Af.
An additional depth-averaged energy equation accounting for the kinetic energy, R(x, y, t), associated with particle velocity fluctuations, is included in the RAMMS model (Reference Teich, Bartelt, Regamy and BebiBartelt and others, 2012a):
Parameter α controls the production of random fluctuation energy, R, from the frictional work rate of the mean flow, Ẇ f = S • V. Therefore, for α > 0, we have more collisional, disperse flows; αS corresponds to the granular stresses caused by fluctuating particle motion that is not transformed into heat, which could be considered as a turbulent Reynolds stress, by analogy with conventional fluids. Parameter β determines the dissipation of fluctuation energy by different mechanisms (collisions, plastic deformation, abrasion, fragmentation). The inclusion of the random kinetic energy in the model formulation is helpful when calculating the distribution of cold, dry avalanche deposits in the runout zone, as well as the motion of small avalanches, which can stop on steep slopes (Reference Teich, Bartelt, Regamy and BebiBartelt and others, 2012a).

Fig. 6. Schematic illustration of the mass flux before and after the interaction with forests of different densities. Snow gets deposited behind trees most effectively if groups of trees enable jamming. Higher K –values are applied for the denser forest.
We use the well-known Voellmy Ansatz (Reference VoellmyVoellmy, 1955; Reference SalmSalm, 1993) to model flow resistance. The Voellmy approach splits the total basal friction into a velocity-independent dry-Coulomb term, which is proportional to the normal stress (friction coefficient, μ) and a velocity-dependent ‘viscous’ or ‘turbulent’ friction (friction coefficient, ξ).
and
However, the constitutive parameters, μ and ξ, are functions of the mean fluctuation energy, Rh (J m−2) (Reference Teich, Bartelt, Regamy and BebiBartelt and others, 2012a).
We use
where R 0 is the activation energy per unit area (J m−2) controlling the onset of the fluidized regime (Reference Teich, Bartelt, Regamy and BebiBartelt and others, 2012a). The activation energy depends on the avalanche size (more activation energy is required to overcome the overburden pressures of thick dense avalanche cores) and cohesional properties of the flowing snow (more energy is required to break the bonds of cohesive snow). An estimate for the activation energy, R 0, is the sum of the mean overburden pressure and the cohesion. Parameter μ 0 is the static Coulomb friction parameter and ξ 0 the speed-dependent friction parameter before fluidization. When α = 0, we have the standard Voellmy–Salm (VS) model with constant friction parameters, μ and ξ. For more information concerning the numerical implementation, see Christen and others (2010b), and for the role of fluctuations in avalanche flow see Bartelt and others (2012a).
3.2. Modeling avalanche flow in forests
The region A f(x, y) defines the location of the forest in the model domain. The elements in this domain are assigned forest properties, depending on forest density, age and undergrowth. It is not possible to calculate each wedge-shaped deposition pattern behind individual trees or tree stands, as we assume average forest values per computational element (e.g. tree density) (Fig. 6). Therefore, no information is needed on the position of individual trees. The forest model simulates the mean deposition height, h d, which, when multiplied by the element area, should accurately represent the total deposited volume observed at that location in the case studies (Fig. 4). Isolated trees are not considered to be part of A f when they stop too little snow to have an effect on the overall flow behavior of the avalanche.
In general, there are two possible ways to model the braking effect of forests: (1) the friction approach and (2) the detrainment approach (Fig. 7).
Friction approach
In the friction approach, modified friction parameters, μ f and ξ f, are assigned to the forest domain, A f, to model the enhanced braking effect. For example, in the current version of RAMMS, coefficientf is assumed to be 400 m s−2 (significantly smaller than the open-terrain value of 2000 m s-2); coefficient is only slightly increased (Reference Gruber and BarteltGruber and Bartelt, 2007). These values are based on energy arguments in which different failure modes (tree overturning, trunk fracture, entrainment of woody debris) extract flow energy from the avalanche (Reference Bartelt and StöckliBartelt and Stöckli, 2001). The fundamental assumption in this approach is that the avalanche is both large enough and fast enough to induce tree failure. This approach is presently employed to model all avalanche flows in forests, independent of the avalanche size. The modified μ and ξ values are based on mechanical processes, such as tree overturning or trunk fracturing. As we assume that the trees do not break, the friction parameters, μ f and ξ f, should be related to non-destructive processes, such as jamming.

Fig. 7. Two approaches can be used to model tree interaction with avalanches. The friction approach attempts to find values for S to stop the mass. The detrainment approach determines M d and extracts the corresponding momentum from the flow.
Detrainment approach
Extracting mass that gets caught behind tree stands from the avalanche is an alternative way to model the forest/avalanche interaction. We term this method the detrainment approach, as we postulate that when mass is stopped behind dense tree stands it is instantly subtracted from the flow. The stopping is sudden and caused primarily by material jamming, which is initiated behind dense group structures of trees. The momentum of the stopped mass is removed from the total momentum of the avalanche flow (Fig. 7) (see also Reference Faug, Naaim and BouvetFaug and others, 2004; Reference Faug, Naaim and BouvetNaaim and others, 2004). We assume that the trees do not break and that they act as obstacles causing mass to stop (Fig. 3). This process is difficult to model with Voellmy-type parameters, because the friction coefficients, especially ξ, are designed for avalanche flow in open terrain where the dissipative processes are slow and continual; they are not designed to model tree impact. Instead of attempting to define friction values that slow the avalanche, and therefore allow the avalanche to naturally detrain material (Reference Naaim, Faug and BouvetNaaim and others, 2003), we impose a stress, K (Pa), which instantly detrains mass from the flow. This stress must be in balance with the change in momentum associated with the detrained mass per unit area, M d:
where V is the flow density of the avalanche. We emphasize that the mass, M d, is the average mass per unit area, which might differ from the height of the deposits at the tree. The stress, K, is related to the forest structure and density, but also to properties of the flowing snow. Therefore,
or, in terms of the mean deposition height,
where ρ is the flow density of the avalanche. Parameter K is related to non-destructive processes, such as granular jamming behind tree stands. This assumption is only valid for small and medium avalanches.
4. Results
4.1. Numerical experiment
To begin our analysis, we first carried out a numerical experiment to explore the differences between the friction and detrainment approaches. The numerical experiment enabled us to perform multiple simulations with equal initial conditions and varying forest characterizations. We constructed an ideal, parabola-shaped avalanche track in order to avoid complex terrain features (Fig. 8). The average altitude difference between release area and runout is 380 m. The parabola is characterized by a 300 m long runout area. In width the parabola is flat and therefore the flow is unchanneled. We simulated avalanches with variable starting volumes and α = 0 (standard Voellmy model). We computed the movement of the avalanche with forest (A f ≠ 0) and without forest (A f = 0). We specified a calculation grid size of 1 m.
The release area, fracture depth, snow density and the two friction parameters, μ =μ 0 and ξ = ξ 0, had to be defined. To test the influence of forests on different sizes of avalanches, we specified three release volumes, all with different release areas, but a constant fracture depth of 1 m for all three cases. The resulting release volumes, V0, were ~1000, 5000 and 20000 m3. The flowing snow density was set to ρ = 300 kg m−3. We kept the friction parameters, except for simulations with the friction parameter approach, constant: μ = 0: 26 and ξ = 2000 m s−2. These parameters are valid for frequent avalanches (10 year return period) with release volumes between 5000 and 25000 m3 in unchanneled terrain >1500 m a.s.l., according to the recommended guideline values (Reference Buser and FrutigerBuser and Frutiger, 1980; Reference Salm, Burkard and GublerSalm and others, 1990).

Fig. 8. Simulation of avalanche on parabola-shaped avalanche track. The maximum calculated velocity for a release volume of 20000 m3 is shown.
In our numerical experiment, the forest area covered the whole avalanche path below the release area (Fig. 8). At first we applied the friction approach and employed the μ and ξ values that are used in the current RAMMS version (adding Δμ = 0. 02 to the basic μ value and setting ξ = 400 m s−2), independent of the forest structure (Reference Gruber and BarteltGruber and Bartelt, 2007). Recall that these values are derived for extreme avalanches that destroy the forest. Next we applied the detrainment approach with five different values for parameter K: 10, 20, 50, 100 and 200 Pa. These are reasonable values and are comparable with the calculated K –values of the case studies (Table 3): a K –value of 10 Pa corresponds to an open forest, whereas a K –value of 200 Pa corresponds to a dense forest with tree clusters and low-lying vegetation. As a control, we simulated the avalanches without any forest cover. For these simulations and the detrainment simulations we specified the guideline friction parameters (μ = 0: 26 and ξ = 2000 m s−2) for frequent avalanches.
Profiles of deposition height, velocity and momentum along longitudinal and transverse sections of the avalanche track were analyzed, in order to explore differences in runout length, deposition patterns, velocity distribution and the development of the total momentum of the model avalanches. Although both approaches (friction and detrainment) have the same goal – to stop flowing mass – our findings reveal crucial differences.
Runout shortening was observed in the forest case for both the friction and detrainment approaches in comparison with the simulations without forest (Fig. 9). We display the maximum flow height along the avalanche path for the three different flow volumes. The distance (x –axis of the plots) is measured from the starting zone (x = 0). Simulation results of (1) the detrainment approach for different K –values between K = 10 Pa (K10) and K = 200 Pa (K200), (2) the friction approach (μ, ξ approach) and (3) the case without forest are shown in Figure 9. The numerical results reveal that the runout of small avalanches (1000 m3; Fig. 9c) is barely influenced by changing the friction parameters. Conversely the detrainment approach leads to a significant runout shortening, dependent on the magnitude of parameter K. The runout of larger avalanches (20 000 m3; Fig. 9a) is not significantly shortened when applying the detrainment approach, in contrast to the friction approach. This finding suggests that the immediate stopping and removal of flow mass because of trees has a greater influence on small avalanches than on larger avalanches.

Fig. 9. Profiles of maximum flow height for simulations of avalanches with different release volumes: (a) ~20000 m3; (b) ~5000 m3; (c) ~1000 m3. The simulations were conducted with the VS model of RAMMS on a parabolic slope using both the friction and detrainment approaches. Five different values for the detrainment coefficient, K (Pa), were tested (K10, K20, K50, K100, K200). Note the significant runout shortening for smaller avalanches using the detrainment approach, in contrast to the runout shortening for larger avalanches using the friction approach. The spikes in height at 400 m distance from release, when simulating with the friction approach and without forest for 5000 m3 and 1000 m3, originate from the pile-up of snow at the transition between sloped and flat (0˚) terrain. This spike is missing when using the detrainment approach because the snow is already deposited on the track.
Figure 10 depicts different deposition patterns on the avalanche track with V0 ≈ 20 000 m3 release volume. Most of the avalanche mass reached the flat part of the avalanche track when using either the friction approach or the detrainment approach. The results are similar for the case with no forest area. We investigated deposition heights at profile elevations Z = 30 and 60 m above zero (Fig. 8). At these altitude levels the slope angles of the track are 27˚ and 36˚, respectively. Generally higher deposition heights were observed when applying the detrainment approach than for simulations with the friction approach. In fact, the friction approach even resulted in smaller deposition heights than for simulations without forest (because of the longer simulation times). Note the steep increase of the deposition heights at the edges of the avalanche when applying the detrainment approach, indicating that more mass is deposited at the slower-moving sides of the avalanche, as observed in the field studies. The removal of snow at the slow-moving avalanche edges results in a narrower track width, especially at lower elevations.

Fig. 10. Cross section of the deposition heights of avalanches with friction and detrainment approaches for the parabola experiment. The release volume V 0 ≈ 20000 m3; profiles are taken 30 and 60 m above zero. Note the slow, continual increase of the deposition heights at the avalanche edges when using the friction approach, in comparison with the detrainment approach. The detrainment removes mass faster at the edges, leading to smaller avalanche flow widths at lower elevations. This agrees with the field observations.
The development of the total momentum of the avalanche over time is illustrated in Figure 11. For all approaches (friction, detrainment and no forest) we observe an increase in momentum until the avalanche reaches the forest, i.e. the avalanche accelerates. After it penetrates the forest the momentum decreases. With the friction approach the decrease of momentum starts earlier (4 s) than for the detrainment approach (6–7 s) or without forest on the avalanche track (7 s). The momentum of all avalanches will decrease because the avalanche track is flattening. Although the highest decrease in momentum is reached only after 5 s with the friction approach, the detrainment approach is more effective at lower slope angles. Furthermore, more mass is removed at the tail and the avalanche edges, where the velocities are small. Thus, although the maximum decrease in momentum is reached later (10–11 s) with the detrainment approach, more mass is stopped. From 7 s onwards, the decrease in momentum is higher with the detrainment approach, leading to earlier stopping of the avalanche. The detrainment approach exploits the velocity distribution between the head and tail (and sides) of the avalanche.
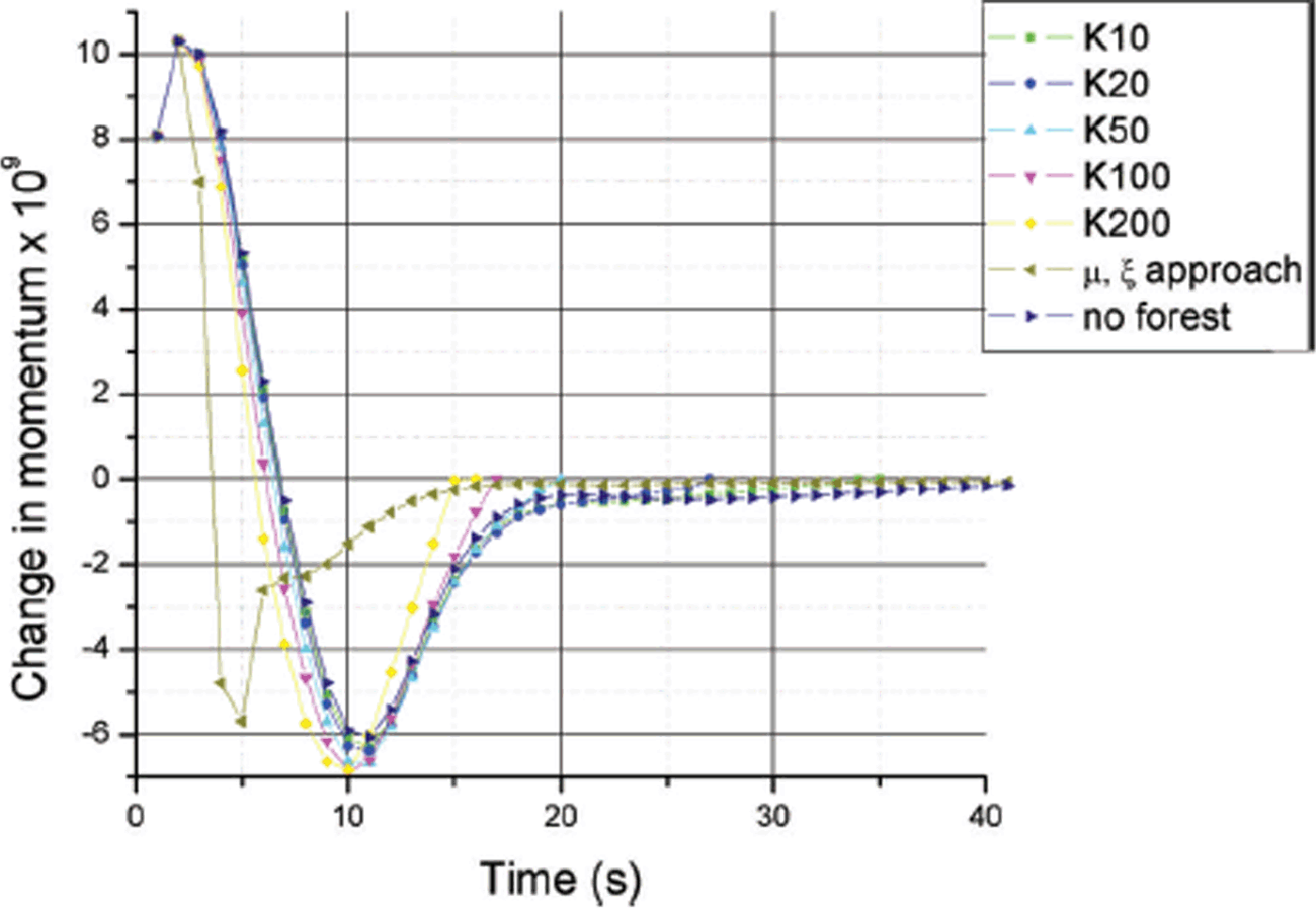
Fig. 11. Development of the total momentum in time of a small avalanche (V 0 ≈ 1000 m3). The plot depicts the change in momentum illustrating the braking process. Detrainment (K10, K20, K50, K100, K200) and friction (μ, ξ) approaches are compared with the case with no forest.
4.2. Simulations of documented avalanches with α = 0
We back-calculated the seven forest avalanche events described in Section 2 with the VS model (α = 0). As in the numerical experiment, the forested region, A f, was characterized by either differing friction parameters or by extracting mass with the detrainment function.
For each particular case study, the input parameters (release area, A r, forest area, A f, fracture height, h 0, and the μ and ξ values for non-forested regions) were identical for all simulations. We varied only the forest friction parameters or detrainment coefficients, K. Release areas and fracture heights were specified according to the observations of the field studies or, when it was impossible to enter the release zone, by applying a terrain analysis (Section 2). The open-terrain μ and ξ values were defined by the automatic procedure within RAMMS. This feature accounts for terrain features (e.g. gullies and flat slopes) as well as altitude level, return period and avalanche size, based on calibrations (Reference Buser and FrutigerBuser and Frutiger, 1980; Reference Gruber and BarteltGruber and Bartelt, 2007).
Accurate, high-precision digital elevation models were necessary to simulate the observed avalanches. Resolutions of 1 m grid size were available for the avalanches released in Germany (ID-VI, ID-VII) and a resolution of 2 m for Switzerland (ID-I, ID-II, ID-III, ID-IV, ID-V).
The forest areas, A f, were specified using orthophoto-graphs taken from fixed-wing, airborne flyovers. For the friction approach we set ξ = 400 m s−2 and added Δμ = 0: 02 to the previously defined μ values; for the detrainment approach we did not change the friction parameters, but removed mass according to the detrainment function. Forest structure and densities were not accounted for when simulating avalanches with the friction approach; we defined dense and open forest structures by varying parameter K when using the detrainment approach (Section 3.2). We selected the following values, according to the field observations:
-
K = 30 Pa (K30) for dense forest stands with some group structures of trees and few low-lying branches that induce jamming;
-
K = 10 Pa (K10) for open-forest structures or older forests, characterized by few branches, root plates or dead wood, which serve as low-lying obstacles.

Fig. 12. Comparison of the simulation results of the seven observed avalanches (ID-I to ID-VII). Deposition heights (up to 50 cm) are shown for (a) the μ, ξ approach and (b) the detrainment approach. The observed runout areas measured with differential GPS (ID-IV and ID-VII) and photographs (ID-VI) are outlined in red. The runout for all case studies is overestimated when using the friction approach. The detrainment approach overestimates two cases significantly (ID-I, ID-V), overestimates two cases slightly (ID-II, ID-IV), matches the runout length in two cases (ID-III, ID-VII) and slightly underestimates one case (ID-VI).
The avalanches were simulated until the final deposition patterns were reached. They were considered stopped when they flowed with <5% of the maximum momentum reached by the avalanches (Reference Christen, Kowalski and BarteltChristen and others, 2010b).
We focused our analysis on the runout distance and deposition structure of the avalanches. Both these characteristics differed significantly between simulations with the detrainment and the friction approach, as illustrated in Figure 12. The spatial distribution of deposition heights is presented for the seven avalanches (ID-I to ID-VII), for both approaches (a – friction, b – detrainment).
Three findings are valid for the seven simulated avalanches:
-
The runout of simulations with the friction approach always exceeded the runout of the detrainment approach. Many times the avalanches reached the valley bottom when using the friction approach, unhindered by the forests.
-
The friction approach always overestimated the runout compared with the observations. This is plausible, because the friction parameters are valid for extreme avalanches, but highlights the difficulties of calibrating forest friction parameters for all avalanche sizes.
-
More snow was deposited on the avalanche tracks when applying the detrainment approach, which caused avalanches to stop on steep slopes in several cases (ID-II, ID-III, ID-VI, ID-VII).
Furthermore, three characteristic deposition patterns could be distinguished for calculations with the detrainment approach:
-
Avalanche runout distances and areas were considerably overestimated in two cases (ID-I, ID-V). For avalanche ID-I at Junkerboden the very small release volume (V 0 = 318 m3) might serve as an explanation. Runouts of small avalanches tend to be overestimated when using the standard VS model (Reference Maggioni, Freppaz, Christen, Bartelt and ZaniniMaggioni and others, 2012). However, the very small release volume can only partly explain the difference, because the avalanche near Monstein (ID-V) had the largest release volume of the documented cases (Table 1). In the Monstein case study, we had no direct measurements of the release zone dimensions (we used photographs), and therefore we might have overestimated the release zone volume. We subsequently reduced the release zone volume and obtained the correct runout distance. This result highlights the problem of selecting the release zone dimensions correctly.
-
The calculation result of the avalanche at Hagenberg (IDVI) was unique: the detrainment approach underestimated the runout distance. This simulation result is different from that for the other avalanches, which provided reasonable approximations to the observed runout distances. The avalanche released during cold weather conditions with dry, cohesionless snow flowing around the trees and therefore reaching the road. The under-prediction can be attributed to the lack of jamming of snow granules between tree stands. Therefore, we specifically simulated this avalanche assuming α ≠ 0, accounting for the fluidization of the flow, and obtained better results (Section 4.3).
-
Simulations of the other four avalanches (ID-II, ID-III, IDIV, ID-VII) produced reasonable deposition patterns (the friction approach greatly overestimated the runout distances and areas). In all of these case studies, wedge-shaped depositions were observed behind the vegetation (Table 4). Jammed snow mass behind tree groups appears to be the dominant stopping mechanism in all of these cases. An interesting feature of the deposition structure observed in the field campaign of avalanche ID-III could be simulated: the main depositions are concentrated on both sides of the primary flow channel, with almost no snow in the channel itself, which resembles the observations (Fig. 2). The main avalanche channel was unforested and mass was stopped at the forest edges.
Table 4. Calculated avalanche characteristics of the seven case studies: mean velocity, mean flow height, detrained volume and mean deposition height, h d. Possible range of deposition widths, d, calculated according to Eqns (1) and (2). From the observations we found the wedge height, h w, to be approximately three times as high as the flow depths. The stem densities are taken from observations; however, we assume tree-stand clusters consisting of three trees. Note the calculated widths, d, are in the range of observed widths. The photographs show typical deposition structures of the six avalanches documented in winter 2011/12

4.3. Simulations with α ≠ 0
We simulated case study ID-VI (Hagenberg) accounting for particle velocity fluctuations (α ≠ 0). The advantage of this model extension is the simplified selection of the friction parameters. They are initially constant over the whole avalanche path and change according to the generation and decay of the energy associated with particle velocity fluctuations. Therefore, defining different pairs of μ and ξ values for different terrain features, altitude levels and return periods is unnecessary. The flow parameters should only account for snow characteristics, and not depend on avalanche size or altitude levels.
For μ 0 we chose a value of 0.55. This value can be approximated as the tangent of the angle of repose of avalanche deposits (measurable at the sides and front of avalanche depositions; Reference Platzer, Bartelt and KernPlatzer and others, 2007). In addition this value corresponds to the steepest slope angle at which snow avalanche deposits are found. It matches the tangent of 29˚, the approximate minimum angle which allows slab avalanches to release (Reference McClung and SchaererMcClung and Schaerer, 2006). The value also corresponds to the initial Coulomb friction values measured when a fracture slab begins to release before fragmentation (Reference Van Herwijnen and HeierliVan Herwijnen and Heierli, 2009). The value of was set constant to 500 m s−2 (Reference VoellmyVoellmy, 1955). Therefore it is between 300 and 700 m s−2, the possible range calculated by Bartelt and others (2012a), who ascertained this value using measured velocities at the avalanche tail when R = 0.

Fig. 13. Comparison of the modeling results of the avalanche at Hagenberg (ID-VI). The results of the friction approach are shown in the first column (a1, a2); the detrainment approach with VS (α = 0) in the second column (b1, b2). The detrainment approach with α ≠ 0 is shown in the third column (c1, c2). The deposition heights are presented in the upper row; the maximum velocities are presented in the lower row. Note the similar shape of the deposition areas calculated with the detrainment approach. The real avalanche reached the road and covered it with several meters of snow, but did not flow further into the forest below.
We determined the activation energy, R 0 (kPa), by summing the mean normal stress, N, and cohesion, c:
using a flow density of 250 kg m−3 and a mean flow height of h = 0: 8 m (Table 4). As the flow was dry and cold, we assumed the flow to be cohesionless and c ≈ 0.
We took a value of α = 0. 05 for the generation of random kinetic energy, less than Bartelt and others (2012a) used for their calculations, as we assume soft snow. The decay, β, was defined according to snow characteristics, β = 0: 7 (Reference Buser and BarteltBuser and Bartelt, 2009). We defined the forested regions, A f, identical to simulations with the VS model (α = 0) with K –values of 10 and 30 Pa, depending on the forest structure.
We show the results of the simulations of avalanche IDVI to highlight the differences and similarities of modeling avalanches in forested terrain with α = 0 and α ≠ 0 with the detrainment approach. This avalanche was unique in the way that the runout distance was underestimated when choosing α = 0. Figure 13 depicts the calculation results of deposition heights and velocities for the friction and the detrainment approaches with α = 0 and α ≠ 0. Generally, the deposition areas of the detrainment approach (Fig. 13b1, c1) are comparable, whereas the friction approach provides the user with an avalanche reaching the valley floor (Fig. 13a1). With the detrainment approach and α = 0, snow is lost on the steep slope, stopping the avalanche before reaching the road. For α ≠ 0, the avalanche overflows the road, in agreement with the observations. These significant differences can be illustrated using the calculated velocity profiles (Fig. 13b2, c2). The fluctuation energy for dry snow (characterized by β = 0: 7) causes higher velocities for α ≠ 0 and therefore less snow is deposited, leading to a longer runout.
5. Discussion And Conclusion
The inclusion of forest effects in avalanche dynamics simulations is an important feature for avalanche hazard analysis, especially for frequent, small-to-medium avalanches. Forests play a crucial protective role by shortening the runout distance of such avalanches. In this paper we have compared two different approaches to quantify this role. The first is to increase the friction parameters (Reference Bartelt and StöckliBartelt and Stöckli, 2001; Reference Gruber and BarteltGruber and Bartelt, 2007); the second is to directly extract mass and its momentum from the flow that has been stopped by the trees. The rate of mass extraction is parameterized by a single coefficient, K, which depends on forest structure. The extraction is the result of higher friction, so the methods are equivalent, but they lead to different parameterizations of the braking process. However, the detrainment approach is more direct and appears to account for physical processes, such as snow jamming between trees, that are not embodied in the Voellmy friction model.
We systematically tested both approaches on an ideal, parabola-shaped slope to gauge the model performance. We found that runout shortening due to detrainment depends on release volume: the smaller the release volume, the larger the decrease in runout length. This result implies that the stopping of equal mass will have a greater effect on smaller avalanches, which qualitatively agrees with observations. There is almost no effect of detrainment on larger avalanches, which also agrees with observations. Additionally we investigated the deposition patterns across the avalanche track and their dependence on velocity. More snow is deposited in steep terrain when applying the detrainment approach. This result also corresponds to the field observations: avalanches did not reach the valley floor because of snow being continuously detrained in the forest, even on steep slopes. Interestingly, our analysis of the development of the total momentum of the avalanche revealed that the deceleration and stopping of the flow is triggered later but more efficiently.
To demonstrate the applicability of the detrainment approach to real avalanche events we simulated seven case studies. We found that the simulated mean deposition heights correspond to the observed wedge heights. This calculation requires knowing the forest structure, as it involves averaging spatially inhomogeneous deposition patterns behind trees. This, coupled with a comparison of the observed runouts and lateral extension of the avalanches, is presently the only method we can apply to ascertain model performance. However, it also indicates that the parameter, K, can be calibrated by performing more mass-balance studies in forests. These studies must involve documenting the overall mass balance of an event and relating these data to the observed deposition patterns and forest structure. The values of K can therefore be improved with future fieldwork, but data from past events can also be employed for this purpose (Reference Teich, Bartelt, Regamy and BebiTeich and others, 2012a). Forest type, stem density, surface roughness and vertical structure of the forest seem to be crucial parameters to be considered (Reference Teich, Fischer, Feistl, Bebi, Christen and Grêt-RegamyTeich and others, 2013).
Runout shortening was reproduced in the simulations, and a good agreement with the observed flow widths was found in four of the seven case studies. Three cases could not be reproduced with K –values of 10 and 30 Pa that we assume to correspond to the observed forest structure. In one case (ID-I), the starting volume was <500 m3 and the avalanche consisted of large, moist snow granules. The simulated avalanche ran too far for K < 200 Pa. This could be an indication that the model scale is not fine enough to represent forest features, terrain roughness or snow characteristics in this particular case. The size limits of depth-averaged models must clearly be established in future work (Reference Maggioni, Freppaz, Christen, Bartelt and ZaniniMaggioni and others, 2012). A second simulation (ID-V) also ran too far for K < 100 Pa, but could be accurately simulated if the release volume was decreased. In this case, the release volume and location were determined by photographs taken from the counter-slope, 1 km distant. Our conclusion is that accurate release zone measurements, as always, are required. Again, we are confronted with documenting small release areas in inaccessible terrain. The third avalanche that could not be simulated adequately (ID-VI) could, however, be reproduced using the Voellmy extension (α > 0). This suggests that the fluidization of the avalanche in dry/cold conditions is important, stressing the idea that jamming effects cannot develop easily in low-density flows with large granular fluctuations.
The detrainment approach, based on momentum extraction, always performed better than the friction approach, based on modified friction coefficients. Nonetheless, the application of the detrainment approach has two fundamental difficulties that must be addressed in future investigations.
First, the detrainment approach is only valid for small-to-medium avalanches where the forest is not destroyed and the trees act as obstacles. This is not always the case and, ideally, the model should determine when the trees in the forest break. This is not an easy task, as the breaking mode can vary from tree fracture to root upheaval and tree overturning. Furthermore, when the trees and other woody debris are entrained in the flow, they can become entangled in tree stands, leading to a complex flow state that is difficult, if not impossible, to model. Whether the entangled mass is stopped or gains more momentum, destroying still more forest, remains an open question. The application of the model is therefore restricted to a specific flow case.
Second, the model results are sensitive to the selection of the starting mass and snow characteristics. Although it is possible to back-calculate documented avalanches, the predictive capacity of the model remains limited. This is a general problem in the simulation of small and medium avalanches, which depends strongly on the size and location of the release zone, entrainment processes, snow properties and terrain features (which might be modified by avalanche deposits). Because of the strong variability of the initial and boundary conditions, as well as material properties, avalanche simulations that include forest effects should only be applied to selected problems (e.g. to determine the general cost effectiveness of silvicultural measures or to determine the vulnerability of specific objects for well-defined starting and boundary conditions).
Our results are, however, promising and will be strengthened by collecting more and specific data during future field studies. We plan to map the entire deposition area, quantifying mass piles behind individual tree clusters. The exact structure of each tree group (location in forest, relative tree composition, tree diameter, branch density, tree spacing, low-lying vegetation) will be documented and correlated with the stopped mass. This will help to calibrate the K parameter, by linking structural features of the forest to mean deposition heights. Granulometry studies are needed in the deposition wedges to relate the jamming process to snow properties. To underpin the fieldwork, small-scale granular chute experiments will be conducted to investigate how detrainment in forest-like structures modifies momentum and energy fluxes of avalanches.
Acknowledgements
We thank Armin Fischer, Jochen Veitinger and Irene Vassella for help with data collection and evaluation. We also thank Bernhard Zenke, who made the close cooperation with the Bavarian Avalanche Service possible. This research was funded by the Bavarian Environment Agency.



















