1. Introduction
Servitization is a transformation process where the value proposition of the manufacturing industries is characterized by a marketable combination of products and services, often described as a product-service system (PSS) (Mont Reference Mont2002; Isaksson, Larsson & Rönnbäck Reference Isaksson, Larsson and Rönnbäck2009). While PSS solutions entail a promising potential, the development of PSS is argued to ingrain many complexity aspects (Sarancic et al. Reference Sarancic, Pigosso, Colli and McAloone2022). These aspects impose many uncertainties during the design phase, leading to opportunities and risks (McManus & Hastings Reference McManus and Hastings2005; Rhodes & Ross Reference Rhodes and Ross2010; Gaspar, Hagen & Erikstad Reference Gaspar, Hagen and Erikstad2016). Tangible products shall be designed to go together with services and the supporting infrastructure and network of actors in the search for higher value compared to traditional product offerings. To maximize value creation, manufacturers often decide to retain the ownership of the product, making it worthwhile to keep it functional as long as it generates through-life profits. When designing PSS with a long lifecycle and a high cost of investment, additional uncertainties are introduced from a multidimensional stakeholder value expectation perspective (Rondini, Bertoni & Pezzotta Reference Rondini, Bertoni and Pezzotta2020) and contextual perspective, including changing technologies, environment, markets and legislation (Pirola et al. Reference Pirola, Boucher, Wiesner and Pezzotta2020).
In such cases, the development team’s capability to make rational decisions concerning the long-term value proposition shrinks significantly (Eckert, Isaksson & Earl Reference Eckert, Isaksson and Earl2019). Various uncertainties in design decision-making make it cumbersome to identify and assess design-related variables that enhance engineers’ understanding of the value sustainment of the PSS along its lifecycle. Engineers are asked to develop “value-robust” (Ross, Rhodes & Hastings Reference Ross, Rhodes and Hastings2008) solutions balancing technical features, service solutions, customer expectations and variable influencing contexts. One of the design strategies to deal with uncertainties is translating them into opportunities and risks and defining measurable attributes that characterize the interaction with those uncertainties (McManus & Hastings Reference McManus and Hastings2005). Systems engineering (SE) literature proposes the concept of “changeability” as one of such measurable attributes that enable systems to achieve value robustness in the face of uncertainty (Ross et al. Reference Ross, Rhodes and Hastings2008). Changeability is the system’s ability “to alter its operations or form, and consequently possibly its function, at an acceptable level of resources” (de Weck, Ross & Rhodes Reference de Weck, Ross and Rhodes2012, p. 6). Thus, changeability enables the system to incur an internal change as a response to external changes under the implied constraints such as cost or time to ensure achieving the expected value during operation.
While the theme of dealing with multiple uncertainties has been discussed since the inception of PSS (Mont Reference Mont2002), changeability is still poorly addressed in the literature. There are several approaches, frameworks, methods and tools (Bertoni et al. Reference Bertoni, Bertoni, Panarotto, Johansson and Larsson2016; Qu et al. Reference Qu, Yu, Chen, Chu and Tian2016; Bocken et al. Reference Bocken, Strupeit, Whalen and Nußholz2019; Braga, Toledo & González Reference Braga, Toledo and González2020; Fernandes et al. Reference Fernandes, Pigosso, McAloone and Rozenfeld2020) that cater to different purposes, such as design, evaluation and operation of the PSS. Although some design methods could be extended to manage changeability, there is no comprehensive outlook on dealing with uncertainties by incorporating changeability to develop a value-robust PSS. One facet is the missing clearer description of complexities in and around the PSS that introduce uncertainty in decision-making concerning value robustness. The other facet is the lack of guidance concerning different methods for incorporating changeability and how those can be extended for PSS. Upon this premise, the research presented in this paper is driven by the following research questions:
-
• What complexity aspects introduce uncertainties in design decision-making, prompting the development of a changeable PSS?
-
• What is the state-of-the-art in incorporating changeability for value robustness, and how can those be applied in the case of PSS?
To address such questions, the paper aims to synthesize and analyze the results of an integrative literature review performed in the field of SE and PSS design. The study outlines various complexity aspects and their link to uncertainty from a PSS perspective and presents the state-of-the-art for achieving value robustness via changeability incorporation. Finally, the findings are synthesized toward the perspective of a framework for value-robust PSS design via changeability incorporation.
2. Research scope and method
2.1. Research scope
A typical lifecycle of a PSS consists of several stages, broadly categorized into three periods: Beginning-of-Life (BOL), Middle-of-Life (MOL) and End-of-Life (EOL) (Pezzotta, Cavalieri & Gaiardelli Reference Pezzotta, Cavalieri and Gaiardelli2012). To delimit the area of contribution, this paper primarily focused on the MOL of a PSS and its implication in design decision-making. Based on Machchhar et al. (Reference Machchhar, Toller, Bertoni and Bertoni2022), MOL comprises the use and reuse of the PSS, where the expected value is met by the PSS being operational along with all the activities associated with “change” that keep the PSS operational, such as reconfiguration, maintenance, repair, and so forth.
Uncertainty is inevitable in developing complex systems and can be defined in many ways (Earl, Eckert & Johnson Reference Earl, Eckert and Johnson2004; de Weck, Eckert & Clarkson Reference de Weck, Eckert and Clarkson2007; Grenyer et al. Reference Grenyer, Erkoyuncu, Zhao and Roy2021). While this topic is elaborated further in Section 3, throughout this work, uncertainty is predominantly used as a broad term encompassing risks and opportunities from various sources (McManus & Hastings Reference McManus and Hastings2005). At times, uncertainty may also be referred to as internal or external to denote the source (de Weck et al. Reference de Weck, Eckert and Clarkson2007). Technical measures included in the system to mitigate the risks or exploit the opportunities ensure value sustainment during operation. For example, temperature and humidity variation uncertainty causes a risk of performance degradation in electronic components. Protective coatings, redundancy, active thermal control, and so forth, are technical measures that mitigate the risk. The outcome is the development of a value-robust system.
Changeability is one of the technical measures that enables systems to achieve value robustness in the face of uncertainty. Changeability is the transition of a system to an altered state within a cost threshold set subjectively (Ross et al. Reference Ross, Rhodes and Hastings2008; de Weck et al. Reference de Weck, Ross and Rhodes2012). Thus, changeability enables the system to incur an internal change as a response to external change under the implied constraints such as cost or time to ensure achieving the expected value during operation. Popular examples of changeability exercised during the operational phase are the Hubble Space Telescope’s servicing mission (NASA 2023). In total, it went through five service missions to replace batteries, gyroscopes, electronic boxes, and so forth, for increased life and enhanced capabilities.
This review mainly focuses on ilities within the change-type set, such as changeability, flexibility, adaptability, and so forth. The necessity of change-type ilities is often realized when a change is expected in the requirements and contexts during the operational phase (Rhodes & Ross Reference Rhodes and Ross2010). Such a perspective distinguishes changeability from other ilities, such as reliability or resilience, where the requirements are constant, and efforts are geared toward absorbing the effects of the changing contexts (Saleh, Mark & Jordan Reference Saleh, Mark and Jordan2009; Mekdeci et al. Reference Mekdeci, Ross, Rhodes and Hastings2015). Similarly, changeability differs from versatility, where the system is designed primarily to satisfy changing requirements (de Weck et al. Reference de Weck, Ross and Rhodes2012; Rehn et al. Reference Rehn, Garcia Agis, Erikstad and de Neufville2018). This distinction is illustrated in Figure 1, where the focus of this review on changeability is highlighted in blue. The blurry boundary of this distinction emphasizes the overlap amongst these ilities in the literature.

Figure 1. The focus of this integrative review, is highlighted in blue.
The adopted definitions of change-type ilities and value robustness have been summarized in Table 1, based on de Weck et al. (Reference de Weck, Ross and Rhodes2012). Changeability is an umbrella term where flexibility and adaptability imply a change in the agent’s correspondence. Thus, changeability will be widely used in this paper.
Table 1. Definition of ilities, from de Weck et al. (Reference de Weck, Ross and Rhodes2012, p. 6)

The term “system” may be subject to different interpretations by different communities. For consistency in this paper, the term “system” always refers to the solution developed by the development team. It could be a mix of products, services or infrastructure in PSS literature or the system (of interest), including System-of-Systems (SoS) in SE literature.
The notion of “value” and its assessment play a significant role in the development process of PSS (Vasantha, Roy & Corney Reference Vasantha, Roy and Corney2016). Thus, defining what value means becomes crucial as it serves as an appraisal metric for different baseline PSS concepts and change options. In this work, the definition proposed by Rondini et al. (Reference Rondini, Bertoni and Pezzotta2020) is adopted, where value is measured in terms of benefits for multiple stakeholders under applicable constraints such as cost. This viewpoint aligns with the notion of value usually adopted in SE literature; for instance, value is expressed as a ratio of utility and costs (Ross et al. Reference Ross, Rhodes and Hastings2008).
2.2. Research method
The findings presented in this paper are based on an integrative literature review (Torraco Reference Torraco2016) aiming to synthesize existing literature to enable new perspectives to emerge. As an integrative review, the intent is not to describe an overview of a specific research domain but to reconceptualize the findings into new theoretical frameworks. The review process follows the guidelines for integrative reviews presented in Torraco (Reference Torraco2016), including conceptualizing, organizing and writing phases.
The conceptualization phase consisted of motivating the purpose, scope and research questions. For finding relevant papers, due to the inherent vastness of the research streams and the use of different terminologies in different research domains, bibliographies of a few literature reviews (Saleh et al. Reference Saleh, Mark and Jordan2009; Cardin Reference Cardin2013; Martins, Marques & Cruz Reference Martins, Marques and Cruz2015) and dissertations (Ranjbar-Bourani Reference Ranjbar-Bourani2015; Rehn Reference Rehn2018) served as a base. Further, keywords like changeability, flexibility, adaptability, upgradability, scalability and value robustness were iteratively combined with framework, design, develop, establish, method, tool and approach. The search was performed in SCOPUS and Google Scholar within the boundaries of PSS and SE. The following criteria were used for the selection of papers:
-
• The study should be related to the manufacturing industry and cannot be purely a service.
-
• The study should report an approach, framework, method, tool or some form of support for incorporating changeability to achieve value robustness.
-
• The study should express some kind of uncertainty that can affect the system’s value.
Backward snowballing was mainly used due to the breadth of the focus as per the guidelines presented by Wohlin (Reference Wohlin2014). The review focuses on publications grounded in engineering design and development of products and services, deliberately excluding contributions in the field of business modeling and development and entrepreneurship.
The organization phase included arranging the selected pool of papers in temporal, methodological or thematic structure. As presented by Torraco (Reference Torraco2016), temporal structures are more appropriate for understanding the evolution of a topic over time, methodological structures are helpful when the purpose of the review is to contrast different methodologies, and thematic structure clusters the studies around the main concepts, eventually providing a framework for a unified idea. Thematic structuring is mainly used to analyze the selected studies in-depth. A methodological structuring has also been partially utilized to cluster these methods based on similarities in the techniques.
The writing phase mainly consisted of presenting the findings. To provide guidance for the reading, Figure 2 summarizes the overall structure of this paper. Section 3 covers relevant aspects of theory, encompassing themes such as complexity, uncertainty and changeability. The findings from the integrative review are divided into Sections 4 and 5.

Figure 2. Structure of the review, where the numbers before the texts indicate the Section number.
Section 4 describes the complexity aspects that lead to uncertainty in design decision-making. These include:
-
• Structural complexity – relates to physical components, their relationship and their interaction.
-
• Behavioral complexity – relates to the system’s operation to achieve the expected value.
-
• Contextual complexity – relates to the influence of external factors on the system’s value.
-
• Temporal complexity – relates to contextual drifts as a function of time.
-
• Perceptual complexity – relates to the value perceived by different stakeholders.
Section 5 presents a thematic critique of various methods oriented toward changeability incorporation for achieving value robustness. These include:
-
• Changeability identification – concerns finding options to be embedded in the system to exercise change during operation.
-
• Changeability quantification – concerns measuring the level of changeability of a system that can be based on the identified options.
-
• Changeability valuation – concerns assessing the worth of changeability in systems.
Based on these findings, Section 6 discusses the results, describing:
-
• Complexity aspects from a PSS perspective – positions these complexity aspects from a PSS perspective.
-
• Incorporating changeability from a PSS perspective – highlights the major challenges in integrating changeability for achieving value robustness in PSS.
-
• Value-robust PSS design via changeability incorporation: A reference framework – synthesizes the findings toward the perspective of a framework.
3. Theoretical overview: complexity, uncertainty and changeability
A complex system is “a system with numerous components and interconnections, interactions or interdependencies that are difficult to describe, understand, predict, manage, design and/or change” (Magee & de Weck Reference Magee and de Weck2004, p. 2). In a complex system, complexity can be defined as the quantity of information necessary to define a system, understand the interdependencies and predict future scenarios (Gaspar et al. Reference Gaspar, Rhodes, Ross and Ove Erikstad2012). Such complex systems usually face many operational challenges and changes (Rhodes & Ross Reference Rhodes and Ross2010). SE literature proposes “development control” (Kossiakoff & Sweet Reference Kossiakoff and Sweet2003) as one of the inclusion and exclusion criteria concerning the system boundary to distinguish the system from the context. As per this criterion, elements within the development team’s control to design or modify lie within the system boundary. Such a boundary definition enables a consistent characterization of internal and external changes. External changes are usually changes in the requirements or contexts that affect the value expectation of the system. Internal changes are usually a response to external changes for sustaining value. Changes in the requirements can be changes in the performance expectations from the system by various stakeholders over time. Changes in the context may be endogenous to the system, such as component failure due to defects, or exogenous to the system, such as an increase in fuel price (Mekdeci et al. Reference Mekdeci, Ross, Rhodes and Hastings2012).
The possibility of external changes during the operational phase introduces many uncertainties in the design decision-making process (Ross et al. Reference Ross, Rhodes and Hastings2008; Gaspar et al. Reference Gaspar, Rhodes, Ross and Ove Erikstad2012; Allaverdi & Browning Reference Allaverdi and Browning2020). In this case, uncertainty can be defined as “things that are not known, or known only imprecisely” (McManus & Hastings Reference McManus and Hastings2005, p. 2). Uncertainties can stem from any of the four (un)known-(un)known risk quadrants that represent different combinations of known and unknown factors (Earl et al. Reference Earl, Eckert and Johnson2004; Marshall et al. Reference Marshall, Ojiako, Wang, Lin and Chipulu2019). Known uncertainties are foreseen events and can be anticipated atleast stochastically. Unknown uncertainties refer to unforeseen events and are challenging to predict. Uncertainties can also be classified as internal and external based on the sources (de Weck et al. Reference de Weck, Eckert and Clarkson2007). Internal uncertainties are directly related to the solution being developed and, thus, under the development team’s control. External uncertainties are beyond the system boundary and, hence, difficult to influence. Besides, the uncertainties can be epistemic or aleatoric in nature (Grenyer et al. Reference Grenyer, Erkoyuncu, Zhao and Roy2021). Epistemic uncertainty is caused by a lack of knowledge or information that can be addressed by proper actions, while aleatoric uncertainty is linked to the randomness of phenomena; hence, it cannot be decreased. Once the uncertainties are identified, their inclusion in the design problem requires an appropriate formulation technique. Mathematical modeling of uncertainties has received considerable attention in the literature (de Weck et al. Reference de Weck, Eckert and Clarkson2007; Cardin Reference Cardin2013; Grenyer et al. Reference Grenyer, Erkoyuncu, Zhao and Roy2021). These include formal as well as practical approaches utilizing Bayesian theory, Dempster-Shafer theory, Possibility theory, Probability theory, diffusion model, lattice model, scenario planning, case-based reasoning, expert opinion, and so forth. The key challenge is the aggregation of uncertainties from various sources to represent a unified problem to determine the overall impact (Richter, Sadek & Steven Reference Richter, Sadek and Steven2010; Grenyer et al. Reference Grenyer, Erkoyuncu, Zhao and Roy2021).
Technical approaches to exploit the opportunities or mitigate the risks result in outcomes as systems having measurable attributes to deal with certain uncertainties (McManus & Hastings Reference McManus and Hastings2005). One such attribute is changeability, which enables the system to incur an internal change in response to external change under implied constraints such as cost or time to ensure the value expectation is achieved during operation (Fricke & Schulz Reference Fricke and Schulz2005). Ross et al. (Reference Ross, Rhodes and Hastings2008) underlined three essential facets for a system to change: (1) the change agent, (2) the change mechanism and (3) the change effect. The agent is the enabler of a change in the system. An emphasis on external enablers makes the system flexible, while focusing on internal enablers makes the system adaptable. Although both these attributes enhance the given system’s changeability. The mechanism is the path that the system takes to reach the desired state under the applicable constraints. The effect is the change in the initial and final state of the system in terms of form or function and, hence, in the system’s operation. In PSS, changeability is not limited to the tangible counterpart but applies to the entire domain of elements such as products, services and infrastructure (Machchhar & Bertoni Reference Machchhar and Bertoni2022).
For a value-centric design of PSS, value-driven design (VDD) (Collopy & Hollingsworth Reference Collopy and Hollingsworth2011) emerges as one of the prominent frameworks that enable assessment of products and services from a multidisciplinary perspective (Bertoni et al. Reference Bertoni, Bertoni, Panarotto, Johansson and Larsson2016). In the field of SE, VDD was originally proposed as a framework supporting the development team in making decisions based on value rather than requirements fulfillment (Collopy & Hollingsworth Reference Collopy and Hollingsworth2011). Thus, it serves as an appraisal metric for different baseline PSS concepts and options (Bertoni et al. Reference Bertoni, Bertoni, Panarotto, Johansson and Larsson2016). Several value-creation opportunities exist in the operational stage of the PSS in the form of maintenance, exchange services, updates, and so forth. (Matschewsky, Lindahl & Sakao Reference Matschewsky, Lindahl and Sakao2020). Value can be created in various spatial and temporal settings, where understanding the impact of changing requirements and contexts as a function of time becomes critical for making design decisions. In such cases, VDD is based on the use of a “value function” that may adopt a quantitative form, such as net present value (NPV) (Rese, Karger & Strotmann Reference Rese, Karger and Strotmann2009), or a more qualitative form, such as “Early Value Oriented design exploration with KnowledgE maturity” (EVOKE) (Bertoni, Bertoni & Ola Reference Bertoni, Bertoni and Ola2018), “engineering value assessment” (EVA) (Rondini et al. Reference Rondini, Bertoni and Pezzotta2020) and so on. However, much of the research efforts have been directed toward customization of the PSS that caters to different needs, for instance (Hara, Sakao & Fukushima Reference Hara, Sakao and Fukushima2019; Papazoglou, Elgammal & Krämer Reference Papazoglou, Elgammal and Krämer2020), rather than quantifying and evaluating the changeability of the PSS to counter uncertainties. Sakao, Hara & Fukushima (Reference Sakao, Hara and Fukushima2020) presented a method for a family design of PSS for effective customization; however, the target was commonality and modularity. A quantitative investigation of how and when incorporating changeability becomes viable is largely missing.
4. Findings: complexity aspects in design decision-making
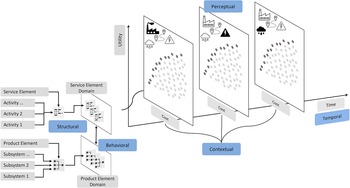
Complexity in engineering design has been addressed from several perspectives in the literature. A primary distinction between internal and external complexity in engineering is based on the system boundary (Heydari & Herder Reference Heydari, Herder, Maier, Oehmen and Vermaas2020). Classifying the uncertainties as internal and external originates from this typology of complexity (de Weck et al. Reference de Weck, Eckert and Clarkson2007). Earl et al. (Reference Earl, Eckert and Johnson2004) highlight four dimensions of complexity, including products, processes, users and organization, further stating that combining these dimensions can result in even higher complexity. However, they argue that external uncertainties arise from the context in which the system operates, making room for an additional dimension of contextual complexity. Expanding upon this viewpoint, Sinha & de Weck (Reference Sinha and de Weck2014) highlight structural, dynamic and organizational complexity, where organization complexity refers to how the evolving structure of an organization affects the system. Notably, these classifications collectively fall within the realm of internal complexity. Rhodes & Ross (Reference Rhodes and Ross2010) considered external complexity alongside internal complexity and distinguished complexity into five engineering aspects: structural, behavioral, contextual, temporal and perceptual. Some complexity perspectives do not require highlighting a distinct boundary. For instance, Mourtzis et al. (Reference Mourtzis, Fotia, Boli and Pittaro2018) considered quantity, variant and content as the three components of complexity without considering system boundaries.
As per Heydari & Herder (Reference Heydari, Herder, Maier, Oehmen and Vermaas2020), however, considering internal and external complexities go hand-in-hand since an imbalance can lead to the system being under-engineered or over-engineered. Therefore, it is essential to factor in contextual aspects when addressing uncertainties, including a perceptual dimension of complexity, which holds particular relevance in the realm of PSS (Bertoni, Bertoni & Isaksson Reference Bertoni, Bertoni and Isaksson2013; Matschewsky et al. Reference Matschewsky, Lindahl and Sakao2020; Rondini et al. Reference Rondini, Bertoni and Pezzotta2020). Thus, this paper adopts the five complexity aspects introduced by Rhodes & Ross (Reference Rhodes and Ross2010) as a foundational framework for discussing complexity in the case of PSS. Furthermore, this approach tends to overlook organizational dynamics, emphasizing the system itself more, and has been applied to an industrial case (Gaspar et al. Reference Gaspar, Rhodes, Ross and Ove Erikstad2012). These five complexity aspects introduce uncertainty in design decision-making (Rhodes & Ross Reference Rhodes and Ross2010). Structural and behavioral complexities ingrain internal uncertainties, while contextual and temporal complexities ingrain external uncertainties. Furthermore, uncertainties grow exponentially from structural to perceptual complexity, although there is no strict prerequisite that certain complexity aspects must precede the successor (Gaspar et al. Reference Gaspar, Hagen and Erikstad2016).
4.1. Structural complexity
Structural complexity arises when the system comprises many interconnected components, often challenging to describe or understand. The notion of structural complexity strongly relates to the architecture of the system. It includes three aspects: the contributions from a sheer number of components, the pair-wise connections between those components and the topology of connections amongst those components (Sinha & Suh Reference Sinha and Suh2018). Hence, simpler architectures can reduce structural complexity. Considering the interconnected components as the vertical dimension, the horizontal dimension is increasing complexity due to variety. Over the years, manufacturing industries have increasingly embraced the mass customization paradigm to develop platform-based or family solutions tailored to individual customer needs (Sakao et al. Reference Sakao, Hara and Fukushima2020). In such platform-based solutions, a higher level of integrity and compatibility is required between the hardware and software, and the tailored solution is usually a subset of this platform. From a product perspective, complexity can be attributed to the need to develop, manage and maintain many variants (Sinha & Suh Reference Sinha and Suh2018). From a service perspective, the complexity arises based on the supply chain characteristics and the “servitization” level of the manufacturing industry (Brax Saara et al. Reference Brax Saara, Anu, Juliana and Chris2017). Thus, summating the horizontal and vertical dimensions of structural complexity from a unified PSS perspective, structural complexity is a function of both product- and service-oriented elements. In such a context, researchers have argued that the literature has not yet reached a standard structural architecture definition for PSS, that is, the primary constituent elements that need to be designed to achieve a function in PSS (Tukker Reference Tukker2015).
Several measures have been proposed in the literature to manage structural complexity. These range from count-based measures (Braha & Maimon Reference Braha and Maimon1998), information transfer efficiency measures (Lindemann, Maurer & Braun Reference Lindemann, Maurer and Braun2008), composite measures based on connectivity (Sinha & de Weck Reference Sinha and de Weck2014), and so forth. One of the prominent usages of such metrics is balancing the inter- and intra-modular complexity while enhancing the system’s modularity and keeping the overall complexity level lower, as shown in Sinha & Suh (Reference Sinha and Suh2018). The principles of modularization have also been extended to the PSS domain, where a PSS instance is composed of product and service modules combined into a solution under relevant constraints (Song & Sakao Reference Song and Sakao2017). Modularity during the design phase can be seen as a construction kit that allows for breaking down structural complexity, workload distribution and selection of the most appropriate subsystems to configure systems (Albers et al. Reference Albers, Bursac, Scherer, Birk, Powelske and Muschik2019). During the operational stage, modularity can be seen as a means for easing the addition or exchange of modules supporting modification, maintenance and upgradation of the system (Aziz et al. Reference Aziz, Wahab, Ramli and Azhari2016). However, by reducing external connections, modularity may amplify inter-modular complexity and its variance by complicating internal relationships (Sinha & Suh Reference Sinha and Suh2018). In such cases, swapping modules makes changes in a system less cost-effective. Thus, increasing component commonality does not necessarily imply higher changeability due to a higher associated module switching cost.
4.2. Behavioral complexity
Behavioral complexity relates to the evaluation of a system’s response to stimuli. These stimuli can be internal or external factors based on the system boundary. Behavioral complexity is limited to considering internal factors for fixed external factors. Such a limitation enables its distinction from contextual complexity, where the external factors are also variable. In complex systems, the variability in response to a stimulus is high due to many components, interactions and inherent dynamics. Thus, the prospects of systems having unforeseeable behavior are significant, leading to uncertainty in design decision-making (Rhodes & Ross Reference Rhodes and Ross2010). Behavioral complexity shall not be interpreted as physiological-behavioral complexity but complexity that emerges from form-to-function mapping and primarily concerns a system’s evaluability given the external factors. On handling a ship design problem, Gaspar et al. (Reference Gaspar, Rhodes, Ross and Ove Erikstad2012) explained the challenge in performance analysis of the ship concerning propulsion, maneuverability, stability and seakeeping due to the complex mathematical formulations that are often difficult to solve. Especially during the early design stage, assessing such functions relies on empirical formulation, expert opinions or surrogate modeling, leading to uncertainty in design decision-making. Another aspect is the computational cost as a curse of dimensionality, explained with a wheel loader example by Frank, Kleinert & Filla (Reference Frank, Kleinert and Filla2018). For the same simulation model of the wheel loader, the calculation time grew exponentially with a rising level of discretization. Approximation methods to reach a viable solution may introduce uncertainty as well. Uncertainty may also arise from the probabilistic performance of a configured variant derived from platforms. Jiao (Reference Jiao2012) showed how changes in adding, swapping or removing subsystems combined with process variations can result in performance degradation of the vibration motors in cell phones.
The challenges highlighted above mainly stem from the product aspect. However, developing PSS requires a coherent analysis of the product- and service-oriented elements, leading to higher behavioral complexity. Mourtzis et al. (Reference Mourtzis, Fotia, Boli and Pittaro2018) proposed a vector-based complexity metric that enables the development to identify the options that yield a higher complexity in the overall solution, along with the possibility of identifying the dominant complexity contributor. With a laser machine example, it is further shown that adding the same services to different products or services to the same product yields additional complexity, signifying that the interplay between the products and services is crucial in the design stages. Several other operational and training factors, such as delivering spares and maintenance, maintenance location, software support, trainer availability, trainer suitability, and so forth, can lead to higher complexity and uncertainty in design decision-making (Erkoyuncu, Durugbo & Roy Reference Erkoyuncu, Durugbo and Roy2013). Lately, the product element of the PSS has been evolving to include SoS, requiring a thorough evaluation of how well the constituent systems fit in SoS (Fakhfakh et al. Reference Fakhfakh, Jankovic, Hein, Chazal and Dauron2021). This evolution poses an additional challenge to decision-makers as the engineering design phase transitions from emphasizing performance to effectiveness. An SoS problem adds the constituent system connectivity dimension to the existing configuration and control simulation (Mekdeci et al. Reference Mekdeci, Ross, Rhodes and Hastings2015). Distinct regimes of desired behavioral properties emerge with the connectivity dimension, raising the uncertainty level in design decision-making.
4.3. Contextual complexity
Contextual complexity focuses on understanding the influence of external stimuli on the system. External stimuli include considerations of all aspects beyond the development team’s control, such as requirements and contexts. Consideration of context in system design has been a field of research for many decades. For instance, Belk (Reference Belk1975) considered context as situational characteristics, arguing that the situation (or context) and the object (or system) as a stimulus cumulatively influence the response of the system used by a person. Building on it, Green et al. (Reference Green, Tan, Linsey, Seepersad and Wood2005) stated that these situational factors consist of the customer context, usage context and market context, arguing that the preferences of opting for a specific system hugely depend on the context. Since then, the context seems to have broadened to include a vast range of factors such as technology, market, environment, expectations, competitors, regulations, fashions, and so forth (de Weck et al. Reference de Weck, Eckert and Clarkson2007). External factors are typically independent of internal factors, and thus, both must be brought together in an integrated model to represent all the associated complexities at a given instance (de Weck et al. Reference de Weck, Eckert and Clarkson2007). The critical challenge concerning the external factors is to view the context and the requirements as circumstances that are likely to change (Rhodes & Ross Reference Rhodes and Ross2010; Gaspar et al. Reference Gaspar, Rhodes, Ross and Ove Erikstad2012). Hence, the “epoch” in “Epoch-Era analysis” consists of periods with fixed requirements and context that enable the selection of designs that have the highest utility at acceptable resource expenditure based on the tradespace exploration process (Ross & Hastings Reference Ross and Hastings2005; Ross et al. Reference Ross, McManus, Rhodes, Hastings and Long2009). Performing tradespace exploration on multiple epochs enables the selection of the most valuable designs under different conditions. Researchers have also shown that the choice probability of a solution depends on the usage context attributes (He et al. Reference He, Chen, Hoyle and Yannou2012). These usage context attributes are argued to be a function of task definition along with physical and social surroundings, indicating that the considerations of requirements and contexts are coupled problems. The philosophy of changing requirements and contexts has also been extended to support developing a family of products using set-based design thinking principles, where platform-based solutions are developed to custom fit different users by analyzing several usage intentions and anticipations (Yannou et al. Reference Yannou, Yvars, Hoyle and Chen2013).
Gaspar et al. (Reference Gaspar, Hagen and Erikstad2016) argued that contextual complexity is often difficult to grasp, and thus, it brings considerable uncertainty to decision-making. This viewpoint is preserved in PSS design, where many researchers have actively acknowledged the context and its influence on the lifecycle of the PSS (Richter et al. Reference Richter, Sadek and Steven2010; Li et al. Reference Li, Wang, Chen and Zheng2021). Focusing on the operational phase, Machchhar et al. (Reference Machchhar, Toller, Bertoni and Bertoni2022) considered the operational scenario as an “umbrella” consisting of the PSS attributes and all the contextual possibilities that are worthwhile for grasping a comprehensive overview of value creation possibilities. The environment, humans, infrastructure and network were considered interacting elements that introduce uncertainties in the operation of the PSS. A similar perspective is shared by Zhang et al. (Reference Zhang, Qin, Li, Zou and Ding2020), who argued that understanding the influences of external factors in the form of environment, humans and cyberspace is the key to developing successful PSS. More recently, Wang et al. (Reference Wang, Mitake, Tsutsui, Alfarisi and Shimomura2022) built a taxonomy of six classes of perturbations from a systematic literature review to support the development teams in scoping the perturbations during the design phase. These classes include behavioral, resource, competence, environmental, organizational and social perturbations. While some classes relate more to perceptual complexity, these classes provide a meaningful theoretical supplement for mapping various contextual complexities that lead to uncertainty in design decision-making.
4.4. Temporal complexity
Fundamentally, temporal complexity incorporates a time perspective to contextual complexity. In contrast to contextual complexity, where a scenario of different external factors is analyzed, temporal complexity concerns the system subjected to a drift of these external factors (Rhodes & Ross Reference Rhodes and Ross2010; Gaspar et al. Reference Gaspar, Hagen and Erikstad2016). This drift implies that the development team must formulate a way to anticipate changes in external factors sequentially. Thus, a path-dependent arrangement of these external factors is vital in developing a value-robust system. Path dependency mainly concerns the irreversibility of decisions made at the stage gates of external changes (Caputo & Cardin Reference Caputo and Cardin2021). For example, the decision to expand a system to meet demand higher than expectations may not be easily reverted if the market falls in the future. The lack of capabilities in the development team to effectively estimate the implications of sequential changes in the external factors results in a higher level of uncertainty during design decision-making.
Concerning PSS, while many value-creation opportunities exist in the operational phase, discerning the value-creation opportunities that should be leveraged and those that should be left untouched is a challenging task with many uncertainties (Matschewsky et al. Reference Matschewsky, Lindahl and Sakao2020; Gaiardelli et al. Reference Gaiardelli, Pezzotta, Rondini, Romero, Jarrahi, Bertoni, Wiesner, Wuest, Larsson, Zaki, Jussen, Boucher, Bigdeli and Cavalieri2021). The situation worsens as manufacturing industries shift toward a servitized business model, where a longer functional span of the PSS in the operation stage is prominent (Alcayaga, Wiener & Hansen Reference Alcayaga, Wiener and Hansen2019). PSS becomes a capital investment for the provider in use- or result-oriented business models, and the economic breakeven and the eventual profit are gained by approaches such as renting, leasing, pay-per-unit, and so forth. If the user is considered a change in the context of the PSS, these business models intrinsically experience the drift of external factors. The perturbation taxonomy presented by Wang et al. (Reference Wang, Mitake, Tsutsui, Alfarisi and Shimomura2022) can be leveraged here by adding time dependence. SE literature proposes passive and active ways of maintaining the expected value during operation (Ross et al. Reference Ross, McManus, Rhodes, Hastings and Long2009). Passive value robustness implies that the system is largely indifferent to several external factors and their drift. Active value robustness means that the system’s value characterized by change-type abilities can be maintained by changing internally to externally. While preserved, this viewpoint seems to be scattered in PSS literature. den Hollander, Bakker & Hultink (Reference den Hollander, Bakker and Hultink2017) argued that designing PSS for a longer lifespan involves product integrity and recycling. Product integrity is the ability to remain identical over time, implying passive robustness. On the other hand, Aziz et al. (Reference Aziz, Wahab, Ramli and Azhari2016) considered changeable modules as a crucial part of the PSS lifecycle that enables superior customer satisfaction and longer operational life, reflecting active value robustness. However, the critical challenge in resolving temporal complexity is to involve many relevant external factors across the operational phase, understand contextual drifts and extract actionable information to support design decisions (Curry & Ross Reference Curry and Ross2015; Bertoni & Bertoni Reference Bertoni and Bertoni2019).
4.5. Perceptual complexity
The essence of perceptual complexity is the dynamics of value expectations from the system through time. The cognitive and subjective aspects in human decision-making are a few essential considerations, usually supplemented with efforts toward mitigating differences in opinion in multi-stakeholder setups (Rhodes & Ross Reference Rhodes and Ross2010; Gaspar et al. Reference Gaspar, Hagen and Erikstad2016). Practical data compilation and communication measures are needed to support decision-making in the design phases. Different techniques have been applied across research domains to address perceptual complexity. For example, Bertoni et al. (Reference Bertoni, Bertoni and Isaksson2013) used color-coded CAD models to enhance the awareness of stakeholders concerning a particular component of PSS, Curry & Ross (Reference Curry and Ross2015) used interactive tradespaces for visualizing complex simulation data and assisting design decision-making, He et al. (Reference He, Wang, Zhou, Li, Makridis, Williams, Lu and Xu2020) used parallel coordinates plots for mapping Pareto-optimal solutions and choosing a compromised solution, Toller et al. (Reference Toller, Machchhar, Bertoni, Bertoni and Sorgini2022) used network graphs for understanding the complexities associated with linking value and data to bring consensus amongst the stakeholders regarding the importance of operational data, and so forth. Idrissov, Škec & Maier (Reference Idrissov, Škec and Maier2020) listed several such techniques and related them to the addressed feature of a system. In what follows, it is pointed out that an appropriate choice of visualization technique is necessary to facilitate design decision-making meaningfully. For example, tables are better suited for specific information, while graphs are better suited to show trends. With the emergence of gaming engines, Extended reality (XR) platforms have become increasingly popular among researchers and practitioners to address perceptual limitations (Davila Delgado et al. Reference Davila Delgado, Oyedele, Demian and Beach2020). XR serves as a collaboration platform, empowering various stakeholders to participate in the development process and promoting collaboration and discussions to mitigate the differences in opinion (Kostis & Ritala Reference Kostis and Ritala2020).
For PSS, perceptual complexity can be articulated around comprehending product, service and relationship-based values in PSS (Kowalkowski & Kindström Reference Kowalkowski and Kindström2009). At such an intersection of tangible and intangible dimensions of value, objectifying value is crucial for the development team to rationalize their choices (Bertoni & Bertoni Reference Bertoni and Bertoni2019). One common challenge in value perception is the models’ uncertainty and the output’s reliability. In such situations, the perception of value hinges on experienced judgments, and the development team actively avoids extreme values even though they may be superior (Bertoni & Bertoni Reference Bertoni and Bertoni2019). Thus, it can be argued that perceptual complexity increases with lesser confidence in the underlying models, that is, when there is a lot of structural, behavioral, contextual and temporal uncertainty. Hence, this paper proposes that perceptual complexity does not have an independent stance but is a function of all the previously mentioned complexities. Higher levels of accumulated uncertainties due to previously mentioned complexities result in higher perceptual complexity.
5. Findings: incorporating changeability for value robustness
Suitable measures must address the uncertainties stemming from the complexity aspects to achieve the expected value along the operational phase (Erkoyuncu et al. Reference Erkoyuncu, Roy, Shehab and Cheruvu2011). Building on the principle of “design for changeability” (Fricke & Schulz Reference Fricke and Schulz2005), a value-robust system must change easily under events that affect the expected value. Different methods for integrating changeability during the design phases have been proposed in the literature. Three separate streams for incorporating changeability can be highlighted based on the literature review: identification, quantification and valuation. Changeability identification signifies finding options to be embedded in the system to exercise change during operation. Changeability quantification implies measuring the level of changeability of a system that can be based on the identified options. Changeability valuation suggests assessing the worth of changeability in systems. The system and the change options are nomenclated differently in the literature, such as a set, portfolio, platform and so forth. Here on, the term “changeable” is used to denote a system embedded with change options, such as changeable PSS. The following sections highlight the central idea of these three streams, predominantly from SE literature.
5.1. Changeability identification
As mentioned above, the options must be identified for a system to change its state. Based on real options theory, real options can be defined as the “right, but not the obligation to do something for a certain cost within or at a specific period of time” (Wang & De Neufville Reference Wang and De Neufville2005, p. 15). The term “real” in real options implies that the options pertain to physical assets, not financial investments such as stocks or bonds. An analysis of such real options aims at evaluating decisions under uncertainty, where decisions imply choosing a change option for a system.
5.1.1. Real options “on” and “in” systems
There are two types of change options applicable to a system: real options “on” systems and real options “in” systems (Wang & De Neufville Reference Wang and De Neufville2005). Real options “on” systems include deferring, staged deployment, altering operations by expanding or contracting, abandoning, switching operations and combining two or more of the options above (Trigeorgis Reference Trigeorgis1996). Deferring implies waiting until favorable conditions arise, staged deployment implies the cautious deployment of assets over time instead of all at once, altering operations implies scaling the output by expanding or contracting operations, abandoning implies halting the operation entirely and selling the assets to recover part of the value, and switching implies targeting different markets. Real options “in” systems are options created by changing some aspect within the system (Wang & De Neufville Reference Wang and De Neufville2005). Real options “in” systems can be exercised to achieve the same or different objectives in response to changing requirements or contexts. A spare tire in a vehicle is an example of real options “in” system, where the user has the right to change the tire but is not obliged to change it. Usually, a unified view of real options “on” and “in” systems is adopted to select the most feasible option for exercising a change in the system (Wang & De Neufville Reference Wang and De Neufville2005; Mikaelian et al. Reference Mikaelian, Rhodes, Nightingale and Hastings2012). However, choosing an option can also be seen as a combinatorial problem of “in” and “on” options (Mikaelian et al. Reference Mikaelian, Rhodes, Nightingale and Hastings2012; Cardin Reference Cardin2013). Specifically, the options can be structured sequentially or parallelly, forming a compound choice. An illustration of a sequential “on” and “on” compound is the staged deployment of assets that allow for an initial deployment and an option to expand later. Compounding “on” and “in” options is particularly relevant for exercising change in SoS. For example, in a fleet of high mobility multipurpose wheeled vehicles, a real option “in” comprised of swapping the armor, while the real option “on” included swapping and reallocating the vehicles entirely (Sapol & Szajnfarber Reference Sapol and Szajnfarber2022).
5.1.2. Change propagation analysis
Real options “on” systems are generic options attributed to a system while considering it as a blackbox. However, real options “in” systems require a deeper understanding of the interconnection and dependencies within the system, as change can propagate. Performing change propagation analysis (CPA) enables the development team to understand how change spreads through and affects the system, further supporting the system to be designed to minimize the risks associated with change propagation (Clarkson, Simons & Eckert Reference Clarkson, Simons and Eckert2004). CPA entails a four-step process: mapping system and subsystem interdependencies, populating the models, analyzing change propagation and visualizing the results (Brahma & Wynn Reference Brahma and Wynn2023). Mapping interdependencies involves bringing attention to the direct and indirect connections among different components within the system. From a product-centric perspective, tools based on the Design Structure Matrix (DSM) (Eppinger et al. Reference Eppinger, Whitney, Smith and Gebala1994) have been dominantly used, such as Multiple-domain Matrix (MDM) (Ahmad, Wynn & Clarkson Reference Ahmad, Wynn and Clarkson2013) or Engineering System Matrix (ESM) (Bartolomei et al. Reference Bartolomei, Hastings, de Neufville and Rhodes2012). From a process-centric perspective, the interdependencies are better captured by flow diagrams, such as workflow networks (Wynn, Caldwell & John Clarkson Reference Wynn, Caldwell and John Clarkson2014) or network diagrams (Ma, Jiang & Liu Reference Ma, Jiang and Liu2016). Especially from a service perspective, blueprints are more prominently used to provide correlations among intangible aspects (Geum & Park Reference Geum and Park2011; Fargnoli, Haber & Sakao Reference Fargnoli, Haber and Sakao2019; Kim Reference Kim2020). Such representations can be directly used to understand the implications of a single change (Cardin Reference Cardin2013). However, the core of CPA is to embed changeability into the system, rendering it more resilient and indifferent to changes. The data required to populate the propagation model can be generated by analysis, workshops, expert opinions or historical change data (Clarkson et al. Reference Clarkson, Simons and Eckert2004; Brahma & Wynn Reference Brahma and Wynn2023). Once the model is populated, it can be analyzed via several techniques such as network analysis, Monte Carlo, manual tracing, and so forth, and the results can be visualized (Brahma & Wynn Reference Brahma and Wynn2023). For instance, the change prediction method (Clarkson et al. Reference Clarkson, Simons and Eckert2004) is a classical network analysis method that highlights the combined likelihood and impact of change to estimate the risk associated with a specific change option. This method has also been expanded to include multiple uncertainties from a multidisciplinary perspective (Koh, Caldwell & Clarkson Reference Koh, Caldwell and Clarkson2013).
5.1.3. The concept of margins
Measures resulting from performing CPA, such as the change propagation index (CPI) (Suh, de Weck & Chang Reference Suh, de Weck and Chang2007; Giffin et al. Reference Giffin, de Weck, Bounova, Keller, Eckert and Clarkson2009), quantify the degree of change propagation caused by a change in the system. Through a normalized CPI, system elements can be identified as change multipliers (CPI is a positive value), change carriers (CPI is equal to zero) and change absorbers (CPI is a negative value). Change multipliers are seen as intervention points by the development team to enhance the changeability of the system (Giffin et al. Reference Giffin, de Weck, Bounova, Keller, Eckert and Clarkson2009; Masood, Kern & John Clarkson Reference Masood, Kern and John Clarkson2021). Allocating margins is an overarching concept that deals with such interventions (Brahma et al. Reference Brahma, Ferguson, Eckert and Isaksson2023). Margins can be defined as the absolute difference between the requirements or the constraints on a parameter value and its actual capability (Eckert et al. Reference Eckert, Isaksson and Earl2019). They are included in systems to achieve different purposes, such as enhancing safety and reliability, ensuring future rework, mitigating the impact of changing specifications, and so forth (Brahma et al. Reference Brahma, Ferguson, Eckert and Isaksson2023). Margins can be subdivided into buffer and excess, where the buffer addresses uncertainties and the excess represents the surplus (Eckert et al. Reference Eckert, Isaksson and Earl2019). Buffers are deliberately added to manage uncertainties, while excess is an undesirable by-product of a local optimization process or added due to using off-the-shelf parts (Brahma & Wynn Reference Brahma and Wynn2020). A rigorously optimized system will have no excess margin in its components (Eckert et al. Reference Eckert, Isaksson and Earl2019). Tilstra et al. (Reference Tilstra, Backlund, Seepersad and Wood2015) identified the circumstances when margins can enhance the system’s changeability, eventually aiding the development team in managing known and unknown certainties. In the frame of exercising a change option, margins facilitate change. For example, change absorbers, as additional resilient objects (Panarotto et al. Reference Panarotto, Giordano, Chiarello, Brahma, Fernández and Fantoni2023), are special kinds of margins incorporated to mitigate change propagation. Such objects are typically called “enablers” when exercising a change option (Cardin Reference Cardin2013; Allaverdi & Browning Reference Allaverdi and Browning2020). Enablers need not necessarily be components; they can also be attributes, such as modularity, that support changeability. Thus, minimization of accumulated CPI (Ma et al. Reference Ma, Jiang and Liu2016) or iterating the process until a satisfactorily modularized system architecture is achieved (Koh et al. Reference Koh, Förg, Kreimeyer and Lienkamp2015) can be other strategies to enhance changeability and identify viable change options.
5.1.4. Explicit mapping
Approaches that require an accurate description of system dependencies entail an exhaustive effort to build this representation. Explicitly evaluating design variables and mapping their responses for different requirements and contexts in a tradespace could be worthwhile from a practical stance. This mapping gives insight into how each variable performs when an objective changes, enabling the development team to identify the most valuable variables to achieve value robustness. For example, Ross et al. (Reference Ross, McManus, Rhodes, Hastings and Long2009) discretized the range of design variables for designing a Satellite Radar System and mapped them on a tradespace for changing requirements and contexts. Such a mapping enhances the identification of worthwhile change options as uncertainty unfolds. When the design point does not appear on the Pareto front, it indicates that a margin is allocated to that variable (Eckert et al. Reference Eckert, Isaksson and Earl2019).
5.2. Changeability quantification
In the face of uncertainty, maximizing the number of available change options in the prospects of including the capability to exercise the most suitable option when and if needed could be worthwhile. Since options inherit investment and switch costs, the problem transcends to finding a cost-effective level of changeability in the face of uncertainty (Fricke & Schulz Reference Fricke and Schulz2005). It must be noted that changeability is an active way of achieving value robustness, and it could be worthwhile in systems significantly affected by external factors. To illustrate, the Pareto Trace metric and its extensions, like effective Normalized Pareto Trace and effective fuzzy Normalized Pareto Trace, highlight the designs that perform superiorly in multiple epochs. Since these designs are passively value-robust, changeability may not be advantageous in such systems. Thus, a homogenous outlook on active and passive measures of value robustness is often necessary to find a cost-effective level of changeability (Viscito, Chattopadhyay & Ross Reference Viscito, Chattopadhyay and Ross2009).
Changeability quantification is necessary to decide upon a suitable level of changeability in a given system. CPA reveals which components have a higher influence on other components and vice versa, thus guiding decisions on which components must be prioritized for modularization (Koh et al. Reference Koh, Förg, Kreimeyer and Lienkamp2015). However, these measures do not enlist real options for exercising change, and thus, they are not suitable for changeability quantification. Enumeration-based quantification can enlist all real options for exercising change at the given changeability level, where each enumerated option can be identified via CPA. Range, cost and time are the three significant dimensions for characterizing a system’s changeability, resulting in top-down, bottom-up and vector-based approaches. A higher quantification value implies a higher level of changeability in the system.
5.2.1. Top-down changeability metric
In top-down approaches, range is the primary objective, and changeability quantification can be based on the tradespace mapping. For instance, changeability can be quantified as a measure between two extreme points on a Pareto front, where the quantification equation is transformed into a double summation for more than two objectives (Olewnik & Lewis Reference Olewnik and Lewis2006). In contrast to the Pareto front, Ross et al. (Reference Ross, Rhodes and Hastings2008) proposed a metric for changeability quantification called Filtered Outdegree that relies on a complete enumeration of the tradespace. The term “Filtered” implies constraints such as cost or time. The term “Outdegree” means counting the number of conceivable states a system can achieve or the number of unique paths the system can adopt to achieve a desired state change. This distinction is necessary since counting paths will always be higher than counting end states. Ross et al. (Reference Ross, Rhodes and Hastings2008) used Filtered Outdegree based on the enumeration of paths in a tradespace network based on the transition rules, while Rehn et al. (Reference Rehn, Pettersen, Garcia, Brett, Erikstad, Asbjørnslett, Ross and Rhodes2019) used Filtered Outdegree based on the enumeration of end states. Building on the Filtered Outdegree metric, Niese & Singer (Reference Niese and Singer2014) proposed a Temporal Outdegree metric resembling time-dependent system changeability. Rehn et al. (Reference Rehn, Pettersen, Garcia, Brett, Erikstad, Asbjørnslett, Ross and Rhodes2019) proposed the Relative Filtered Outdegree metric that represents the fraction of conceivable states a system can achieve under given constraints, a normalized equivalence of the Filtered Outdegree metric. Using cost as the filtering constraint is not a prerequisite for changeability quantification. Zhang, Grossmann & Lima (Reference Zhang, Grossmann and Lima2016) quantified changeability as a function of variable space with a constraint of feasible steady-state operation. This metric is conceptually similar to Filtered Outdegree, where variable space can be the tradespace, and violation in steady-state operation can be penalized by costs. Differently, Mikaelian et al. (Reference Mikaelian, Rhodes, Nightingale and Hastings2012) proposed a Disjunctive Normal Form metric as a logical formula that consists of disjunctions of conjunctions. The disjunctive normal form essentially isolates the logical ORs from the logical ANDs, thus allowing the identification of options explicit from obligations. The total number of disjunctive normal form clauses quantifies changeability for the selected design.
5.2.2. Bottom-up changeability metric
In bottom-up approaches, cost or time are the primary objectives, where changeability quantification is based on reducing switch cost or time for the given performance threshold. Špačková, Dittes & Straub (Reference Špačková, Dittes and Straub2015) proposed a changeability quantification metric ranging from 0 to 1 based on the expected cost saving for performing a change. Along similar lines, Rehn et al. (Reference Rehn, Pettersen, Garcia, Brett, Erikstad, Asbjørnslett, Ross and Rhodes2019) proposed a normalized metric that denotes the anticipated reduction in the switching cost. A similar time-based metric was also proposed, where the reduction in time is measured instead for a given change. An explicit design variable called “design for changeability” as an “enabler” is incorporated to factor in the investment costs related to integrating elements that facilitate changeability within a system. In their offshore construction vessel example, a design for changeability variable was structural reinforcement that supports an additional load. While this reduces the switch cost during operation, it has undesirable consequences on investment costs.
5.2.3. Vector-based changeability metric
More recently, Torres-Rincón, Sánchez-Silva & Bastidas-Arteaga (Reference Torres-Rincón, Sánchez-Silva and Bastidas-Arteaga2021) combined the range and cost to support capturing the complex nature of changeability. In their work, changeability is quantified as a vector of two components; one represents the transition space, while the other represents the cost space. Thus, a system may increase its changeability by increasing the number of state transitions or reducing the cost of transitions. Such a vector-based changeability quantification allows a head-to-head comparison of two systems with the same changeability level, where one is superior in the extent of options available for change, while the other is superior in cost expenditure for a given change.
5.3. Changeability valuation
Changeability valuation is the process of assessing the worth of changeability in systems. This process implies reinforcing a set of change options within the system that cumulatively achieves higher value during the operational phase. To represent the uncertainties in the design problem, a decision must be made regarding the most suitable method to model uncertainty, such as continuous or discretized events (de Weck et al. Reference de Weck, Eckert and Clarkson2007). Subsequently, several scenarios are generated to capture possible outcomes while considering computational limitations. Several methods have been proposed in the literature to value changeability under the generated scenarios. The following discussion on changeability valuation is inspired by the summaries of valuation methods (Wang & De Neufville Reference Wang and De Neufville2005; Cardin Reference Cardin2013; Martins et al. Reference Martins, Marques and Cruz2015), and it further aims to extend their synopsis with novel contributions.
An essential prerequisite for valuing the changeability of a system is to define an appraisal metric, and the theory of VDD can be leveraged here. The value function can be defined in terms of NPV or surplus value (Cardin Reference Cardin2013) to allow discounted cash flow analysis (Cardin Reference Cardin2013). If estimating the monetary worth of a system and options is not feasible, the utility (Ross et al. Reference Ross, Rhodes and Hastings2008, Reference Ross, McManus, Rhodes, Hastings and Long2009) or benefits (Rondini et al. Reference Rondini, Bertoni and Pezzotta2020) function can be utilized. Especially from the PSS literature, many such qualitative ranking approaches emerge that could be used for valuing changeability. These include choice modeling (He et al. Reference He, Chen, Hoyle and Yannou2012), usage coverage parametrization (Yannou et al. Reference Yannou, Yvars, Hoyle and Chen2013), EVOKE (Bertoni et al. Reference Bertoni, Bertoni and Ola2018), EVA (Rondini et al. Reference Rondini, Bertoni and Pezzotta2020), and so forth. Particularly for operational scenario analysis, for instance, discrete-event simulation, agent-based simulation or hybrid approaches may also be adopted (Douglas, Mazzuchi & Sarkani Reference Douglas, Mazzuchi and Sarkani2020; Panarotto, Borgue & Isaksson Reference Panarotto, Borgue and Isaksson2020). A rigorous discussion of these methods is beyond the scope of this paper. The choice ultimately depends on the nature of the design problem and the measure suitable for the development team. Upon setting the appraisal metrics, the valuation methods support comparing a changeable system consisting of embedded options to an unchangeable system.
5.3.1. Standard real options analysis
Formerly, changeability was valued via real options analysis (ROA), which adopts the concept of options from the finance literature. For a continuous problem, the famous Black–Scholes formula (Black & Scholes Reference Black and Scholes1973) is used to price an option that confers the system’s right but not the obligation to exercise it to appreciate value. For discrete-time problems, lattice analysis such as binomial lattice (Cox, Ross & Rubinstein Reference Cox, Ross and Rubinstein1979) is usually adopted. These lattices may not necessarily be binomial; they can be trinomial or even multinomial., but path recombination is possible. Backtracking techniques such as dynamic programming fold back time to the current state to value options. Decision Analysis is a method that relies on decision trees but does not consider path recombination (Babajide, de Neufville & Cardin Reference Babajide, de Neufville and Cardin2009). Analogous to lattice analysis, however, backtracking with dynamic programming enables maximization of performance along the lifecycle. Since paths are not recombined, it allows the evaluation in the context of path dependency and/or evaluating drastic changes at the cost of computational complexity. Cumulative distribution graphs denoting the Value-At-Risk and Value-At-Gain highlight the value of changeability in a visual manner.
Overall, ROA does not apply well in engineering settings, explained elaboratively by (Wang & De Neufville Reference Wang and De Neufville2005; Cardin, de Neufville & Geltner Reference Cardin, de Neufville and Geltner2015). In summary, defining a market price for the assets is difficult. The no-arbitrage assumption is problematic for real options “in” systems since the markets are not complete and efficient. The buying and selling by arbitrageurs can affect the demand and supply of real options, affecting their price. The Geometric Brownian motion model for pricing has the property of growing forever. Due to continuous inflation, this ever-growing property works for financial options but not for real options. Besides, ROA requires knowledge of advanced mathematics, making it less intuitive for cross-functional teams. Especially from a lattice analysis perspective, the assumption of path independence during recombination does not reflect the true nature of physical systems. A decision to expand may not be reverted easily. Also, backtracking approaches are usually intractable for complex systems since they require an exhaustive search in all directions. To address these challenges, approaches that better support the valuation of changeability in an engineering context have been proposed and explained in the following sections.
5.3.2. Network-based methods
Network-based methods assume a system represented as a network embedded with change options and switch costs. For instance, the Time-Expanded Decision Networks method (Silver & de Weck Reference Silver and de Weck2007; Mirshekarian Reference Mirshekarian2015) configures a baseline design with embedded options associated with the switching cost using a static network. These static networks are then used to find the shortest paths through the lifecycle based on the decision to exercise a change option. The uncertainties are modeled in the form of discretized events to enable the selection of the most viable change option. Along similar lines, Epoch-Era analysis utilizes a network-based representation of a changeable system outlined by Filtered Outdegree. Subsequently, tradespace exploration enables comparing and selecting the most viable design options for sustaining value (Ross et al. Reference Ross, Rhodes and Hastings2008, Reference Ross, McManus, Rhodes, Hastings and Long2009). Epoch-Era analysis visually structures diverse expectations and contextual possibilities, emphasizing subjectivity for consideration of uncertainty. An Era comprises several epochs representing a fraction or full lifespan of the system to understand the short-term and long-term impacts of dynamic requirements and contexts. Extensions of Epoch-Era analysis, such as Multi-Epoch Analysis and Multi-Era Analysis, map the system’s performance across multiple epochs and eras to determine the design variables most sensitive to external factors (Ross et al. Reference Ross, McManus, Rhodes, Hastings and Long2009; Curry & Ross Reference Curry and Ross2015). An optimal threshold of Relative Filtered Outdegree can be derived from Epoch-Era analysis, as shown by Rehn et al. (Reference Rehn, Pettersen, Garcia, Brett, Erikstad, Asbjørnslett, Ross and Rhodes2019). Finding effective change decisions and options relies on optimal path-finding algorithms. Thus, analyzing all possible ways the system can change to sustain value in multiple eras may require exhaustive effort.
5.3.3. Optimization-based methods
Some changeability valuation methods can be collectively grouped under optimization-based approaches. These methods typically use evolutionary optimization algorithms for ranking promising options to be embedded in the system and finding a set of conditions denoting when the change option shall be exercised. These methods may also be referred to as robust optimization (Caputo & Cardin Reference Caputo and Cardin2021) since the optimization problem involves finding a pair comprising the option and the decisions that maximize value. In the evolutionary real options framework, Zhang & Babovic (Reference Zhang and Babovic2011) used an evolutionary algorithm to assess change options and the exercising decision by fine-tuning the exercising condition thresholds. Similarly, Jiao (Reference Jiao2012) used genetic algorithms to value changeability in product platforms. Their approach relied on finding an optimal set of change options that satisfy some equilibrium constraints. Song & Sakao (Reference Song and Sakao2017) combined rough TOPSIS with multi-objective optimization using a genetic algorithm to select suitable modules that eventually represent a design concept. Xia et al. (Reference Xia, Cardin, Ranjbar-Bourani and Caunhye2015) used Simulated Annealing to screen the design alternatives that effectively perform better under uncertainty. More recently, Varl, Duhovnik & Tavčar (Reference Varl, Duhovnik and Tavčar2022) proposed developing an expert system that can generate a custom platform embedded with options to deal with uncertainty using optimization principles. In many of these approaches, Monte Carlo simulation seems a popular choice to include uncertainty in the design problem, although a historic data-driven approach (Jiao Reference Jiao2012) is also utilized. Global and local sensitivity analysis may be performed to highlight the design variables that are most and least significant for sustaining value (Sapol & Szajnfarber Reference Sapol and Szajnfarber2022). Approximation methods such as surrogate modeling and sampling methods such as Design of Experiments may be utilized to reduce computational burden (Cardin Reference Cardin2013).
5.3.4. Decision rule-based methods
A separate class of methods uses heuristic-based decision rules to value changeability in the face of uncertainty. These decision rules mainly express an appropriate condition to exercise one of the available change options (Cardin et al. Reference Cardin, Xie, Ng, Wang and Hu2017). An example of such a decision rule is, if the demand decreases below a certain threshold, then exercise the reduction in the size option. Decision rules can be “on” systems as well as “in” systems, and thus, a complex system may entail many decision rules to be explored and analyzed depending on the characteristics of a given system and involved uncertainties. At a broad level, they include condition-go (if-then-else statements), constant, and linear rules (Cardin et al. Reference Cardin, Xie, Ng, Wang and Hu2017). Decision rules are evaluated at specific timestamps, and thus, the problem involves solving to find the most suitable values for decision rules and the most suitable options. Such problems can be solved via multistage stochastic programming (Cardin et al. Reference Cardin, Xie, Ng, Wang and Hu2017; Torres-Rincón et al. Reference Torres-Rincón, Sánchez-Silva and Bastidas-Arteaga2021; Sánchez-Silva & Calderón-Guevara Reference Sánchez-Silva and Calderón-Guevara2022). Multistage stochastic programming is a generalized form of two-staged stochastic programming that allows for representing a wider range of uncertainties. From a conceptual standpoint, this is quite similar to the optimization-based methods elucidated earlier. However, a notable distinction is the presence of decision rules that are practical and intuitive to use as uncertainties are resolved, as opposed to relying on an algorithm attempt to deduce the rules autonomously. Sánchez-Silva & Calderón-Guevara (Reference Sánchez-Silva and Calderón-Guevara2022) mapped a Pareto of expected NPV and its variance to highlight the risk and returns of each change decision. Such a mapping supports the development team in visually identifying the suitable change decision. Furthermore, it is shown to have results that align with standard ROA techniques (Cardin et al. Reference Cardin, Xie, Ng, Wang and Hu2017). However, this approach faces limitations due to its computational complexity, and problem decomposition techniques may be required to alleviate it to some extent (Cardin et al. Reference Cardin, Xie, Ng, Wang and Hu2017; Torres-Rincón et al. Reference Torres-Rincón, Sánchez-Silva and Bastidas-Arteaga2021). The Design Catalog approach (Cardin et al. Reference Cardin, de Neufville and Geltner2015) partly solves the complexity issue by using a factorial analysis technique to generate a catalog of options to be embedded in the system that performs better overall at the cost of loss in resolution. Some researchers have adopted an explorative approach, where Monte Carlo simulation evaluates several decision rules via iterations (Gamba Reference Gamba2002; Panarotto et al. Reference Panarotto, Borgue and Isaksson2020; Sapol & Szajnfarber Reference Sapol and Szajnfarber2022). Monte Carlo simulation samples the uncertainties and generates several representative future scenarios. Changeability is then valued via increased expected performance across the generated samples by exercising the available change options. The simulations must be repeated if the development team updates the uncertainty measures or the decision rules.
5.3.5. Markov-decision process-based methods
A Markov-decision process (MDP) models the decision-making process, where the system’s current state is enough to predict the next state. It is a way to represent the settings in which the system takes successive decisions. An MDP is formulated as a tuple
![]() $ \left(s,a,{P}_a,{R}_a\right) $
, where
$ \left(s,a,{P}_a,{R}_a\right) $
, where
![]() $ s $
represents the current state of the system,
$ s $
represents the current state of the system,
![]() $ a $
represents the action the system takes while following a policy,
$ a $
represents the action the system takes while following a policy,
![]() $ {P}_a\left(s,{s}^{\prime}\right) $
represents the probability that the action
$ {P}_a\left(s,{s}^{\prime}\right) $
represents the probability that the action
![]() $ a $
will transition the system from state
$ a $
will transition the system from state
![]() $ s $
to state
$ s $
to state
![]() $ {s}^{\prime } $
, and
$ {s}^{\prime } $
, and
![]() $ {R}_a\left(s,{s}^{\prime}\right) $
is the expected reward on transitioning from state
$ {R}_a\left(s,{s}^{\prime}\right) $
is the expected reward on transitioning from state
![]() $ s $
to state
$ s $
to state
![]() $ {s}^{\prime } $
at the given timestamp
$ {s}^{\prime } $
at the given timestamp
![]() $ t $
. Decision rules and MDP formulation have a lot of synergy. For instance, in a conditional-go decision rule, the “if” is analogous to the system’s current state, and the “then” is the suggestion of an action. Thus, MDP enables the development of policies for a complex system to operate in uncertain conditions. Niese & Singer (Reference Niese and Singer2014) formulated an MDP to identify an effective change strategy for a given system. Value iterations output a decision matrix that maximizes the cumulative reward for the system during its lifecycle as the uncertainties unfold. However, MDPs are well-suited for low-dimensional problems. The decision matrices can scale exponentially as the system’s complexity increases, making the evaluation of policies intractable. Deep reinforcement learning is an approximation technique based on the MDP that can mitigate these dimensionality issues (Caputo & Cardin Reference Caputo and Cardin2021). In reinforcement learning, an agent interacts with its so-called environments, takes some actions, transitions to the next state and gains rewards for choosing that action. These iterations are repeated to train the agent to select the most optimum action during operation. The term “deep” implies using neural networks for this approximation. Caputo & Cardin (Reference Caputo and Cardin2021) used deep reinforcement learning on a waste-to-energy system example and showed better valuation performance than decision rules. This approach opens the possibility of investigating the potential of many different deep reinforcement learning algorithms for changeability valuation.
$ t $
. Decision rules and MDP formulation have a lot of synergy. For instance, in a conditional-go decision rule, the “if” is analogous to the system’s current state, and the “then” is the suggestion of an action. Thus, MDP enables the development of policies for a complex system to operate in uncertain conditions. Niese & Singer (Reference Niese and Singer2014) formulated an MDP to identify an effective change strategy for a given system. Value iterations output a decision matrix that maximizes the cumulative reward for the system during its lifecycle as the uncertainties unfold. However, MDPs are well-suited for low-dimensional problems. The decision matrices can scale exponentially as the system’s complexity increases, making the evaluation of policies intractable. Deep reinforcement learning is an approximation technique based on the MDP that can mitigate these dimensionality issues (Caputo & Cardin Reference Caputo and Cardin2021). In reinforcement learning, an agent interacts with its so-called environments, takes some actions, transitions to the next state and gains rewards for choosing that action. These iterations are repeated to train the agent to select the most optimum action during operation. The term “deep” implies using neural networks for this approximation. Caputo & Cardin (Reference Caputo and Cardin2021) used deep reinforcement learning on a waste-to-energy system example and showed better valuation performance than decision rules. This approach opens the possibility of investigating the potential of many different deep reinforcement learning algorithms for changeability valuation.
6. Discussion
The following discussion positions the findings of the integrative review for PSS with the aspiration of guiding the development team more systematically in design decision-making concerning value robustness.
6.1. Complexity aspects from a PSS perspective
The five complexity aspects described previously mainly support the development team in identifying the sources of uncertainties during the design stage. Such an identification can be seen as a prerequisite for modeling them mathematically. Figure 3 positions these complexity aspects from a PSS perspective.

Figure 3. Positioning the five complexity aspects from a PSS perspective.
From a product perspective, structural complexity relates to many interconnected components, often challenging to describe or understand. Another aspect is the increasing complexity due to variety. From a service perspective, the structural complexity is mainly associated with the supply chain characteristics that depend on the manufacturing firm’s servitization level. Behavioral complexity concerns the reaction to stimuli of a system, although limited to the consideration of internal factors. The product element, consisting of many subsystems, and the service element, composed of many activities, constitute behavioral complexity because of their interactions and inherent dynamics. Such an interplay leads to higher prospects of the PSS having unforeseeable behavior. Contextual complexity refers to the circumstances in which the system exists. It is the system-context interactions (Machchhar et al. Reference Machchhar, Toller, Bertoni and Bertoni2022) that create value for various stakeholders based on the requirements. Mapping these interactions for design problems results in tradespaces that enable the selection of the best compromise. Figure 3 shows the mapping of many design options in terms of utility and cost. Contextual complexity concerns the formulation of the utility function and the completeness of this mapping. Temporal complexity imposes a path dependency on contextual complexity. The challenge transcends from explicitly analyzing the impact of external factors to studying the effects of external factors in a sequence. Finally, perceptual complexity refers to the cognitive and subjective limitation of the development team to understand the value of the PSS. As stated before, perceptual complexity is a function of structural, behavioral, contextual and temporal complexities. Efforts toward mitigating the risks associated with uncertainties promote a lesser perceptual complexity.
6.2. Incorporating changeability from a PSS perspective
In PSS, complexity may arise from the tangible aspects, including products and infrastructure, as well as the intangible aspects, including all the associated services. The PSS complexity metric (Mourtzis et al. Reference Mourtzis, Fotia, Boli and Pittaro2018) shows how customization variants of services can raise the overall complexity of the PSS. This phenomenon indicates that understanding the orientation of the PSS complexity is necessary since the same product with different service offerings can lead to uncertainty in design decision-making. Thus, researchers have stressed the need to formulate accurate requirements and understand the interplay between product and service modules during the design phase to ensure the PSS achieves the expected value for all stakeholders (Fargnoli et al. Reference Fargnoli, Haber and Sakao2019; Hara et al. Reference Hara, Sakao and Fukushima2019). Such an analysis provides a more concrete basis for tailoring the PSS for different stakeholder needs based on use cases (Haber & Fargnoli Reference Haber and Fargnoli2021). However, the dynamism of changing requirements and contexts during the operational phase makes it difficult to identify and manage different external factors that affect the value of the PSS (Gaiardelli et al. Reference Gaiardelli, Pezzotta, Rondini, Romero, Jarrahi, Bertoni, Wiesner, Wuest, Larsson, Zaki, Jussen, Boucher, Bigdeli and Cavalieri2021; Wang et al. Reference Wang, Mitake, Tsutsui, Alfarisi and Shimomura2022). In such a case, incorporating changeability can be an effective strategy to achieve value robustness, but defining the extent of changeability in PSS can be difficult. The challenges, especially relevant to early stage decision-making in PSS, have been highlighted below:
-
• Structural and behavioral aspects: A unified view of the PSS configuration and control variables under the influencing context is required for a practical performance tradeoff for the desired objectives. This view implies that the mapping of configuration and control variables must be discretized at the desired level of resolution for decision-making with reasonable reliability. Such a unified view is necessary for trading off control policy changes with configurational changes as they are relatively easier. Also, the confinement of design space due to the higher degree of unbounded states in the PSS must be motivated.
-
• Contextual and temporal aspects: The mapping of configuration and control variables needs to consider the evolution of external factors. These factors shall include the applicable business model characteristics that impose different expectations and contextual possibilities. An appropriate mix of continuous and discrete modeling techniques must be selected to represent uncertainties; for instance, market trends are better modeled with a continuous variable, while expectations could be better modeled in a discrete form. Based on the finite horizon of simulation, operational strategies that provide insights into selecting the most feasible option and time to exercise change need to be formulated.
-
• Perceptual aspect: The notion of value in PSS is poised with subjectivity due to multiple stakeholders involved in decision-making. This multidimensionality of value makes simplifying value into a monetary metric largely unfeasible in the early stages. The aggregation of different objectives into such a singular function is a challenging task. Furthermore, the value may be defined only within a given epoch. As the contexts change, so does the expectation of what constitutes to be valuable. Absolute numbers of these scalar metrics may not be directly comparable for different scenarios.
-
• Incorporating changeability: Changeability in PSS is not limited to just the tangible counterpart but applies to the entire domain of components, including product, service and infrastructure. This wider extent of application poses a significant challenge to the development team regarding choosing the most suitable blend of elements for exercising change. Additionally, changes in software and digital services are relatively easier and quicker but challenging to build predictive models and simulate.
A synopsis of incorporating changeability as a response to the uncertainties stemming from the complexity aspect has been presented in Figure 4. A systematic outlook of uncertainty recognition is required, considering the internal factors comprising structural and behavioral complexities and the external factors comprising contextual and temporal complexities. Changeability identification, quantification and valuation constitute to be the three pillars for incorporating changeability in PSS. The resultant PSS can range from inadequately changeable, which does not have sufficient options for exercising change, to excessively changeable PSS, which is overengineered with too many change options. The goal is to develop a cost-effectively changeable PSS that sustains the expected value during operation, leading to perceptual complexity in design decision-making. The arrows in Figure 4 indicate that this process of incorporating changeability in PSS is iterative. A holistic confluence of changeability identification, quantification and valuation is necessary to integrate changeability in PSS. However, selecting specific methods to be employed at each step largely depends on the design problem and the development team’s preferences.

Figure 4. Incorporating changeability to respond to the uncertainties stemming from the five complexity aspects.
Concerning changeability identification, the goal is to identify change options and their implications on the system, given the system architecture. CPA emerges as a prominent method to facilitate this analysis, but it relies on a comprehensive system representation to denote all the linkages and interdependencies. From a PSS perspective, the representation must include product and service elements. A recent study showed how these elements can be unified via aggregating and clustering (Gan et al. Reference Gan, Steffan, Grunow and Akkerman2022). Explicit mapping of configuration and control variables with respect to the competing objectives in tradespaces allows the identification of the most crucial states of the system to achieve value robustness. However, it does not indicate the impact of the system transitioning from one state to another. CPA can incorporate a more rigorous cost dimension to altering a system’s state and determine the aspects of the PSS that require redesign to either enhance the range of change options or mitigate the switch costs.
Concerning changeability quantification, top-down and bottom-up metrics are commonly used in the literature. The vector-based metric is simply a unified view of both these metrics. Regardless of the metric employed, the changeability quantification is a basis for comparing different changeability levels within the PSS. The investment cost must also include the cost of enablers that enhance the system’s ability to transition into numerous states or facilitate changes at a reduced cost or time expenditure. These enablers can be modular interfaces to ease swapping subsystems, reinforcement for enhanced payload and interoperability to plug in different ecosystems. The key difference between the top-down and bottom-up metrics is the information that can be readily extracted (Rehn et al. Reference Rehn, Pettersen, Garcia, Brett, Erikstad, Asbjørnslett, Ross and Rhodes2019). Bottom-up metrics can be useful in investigating the impact of a specific change enabler in the PSS in terms of reduction in switching cost. Such investigations can support the development team in valuing change enablers based on overall cost reduction. Conversely, the top-down metrics offer a comprehensive perspective that enables the development team to comprehend the PSS’s capacity to handle uncertainties across a broader spectrum. For instance, the development team can gain insight into the addition to the operational space coverage for an increased cost threshold. To summarize, the superiority of one metric over another cannot be asserted, but instead, it is acknowledged that the suitability of these metrics varies based on the needs of the development team.
Concerning changeability valuation, a combinatorial problem is generally solved to find an optimal strategy to exercise change and an optimal set of change options. As explained previously, standard ROA methods are not suitable in engineering settings. Optimization-based methods support finding near-optimal solutions for combinatorial problems when the design space is large. However, Monte Carlo simulation, a commonly used uncertainty propagation technique in optimization-based methods, is highly sensitive to the input, and many variables can make the sampling computationally demanding. Network-based methods that require explicit modeling of uncertainties solve this issue by giving the development team more control in shaping future alternatives. For example, based on the scenario planning technique (de Weck et al. Reference de Weck, Eckert and Clarkson2007), Epoch-Era analysis allows sequential ordering of the epochs into eras, including variational factors particularly relevant to the design problem. These eras can also support the development team in evaluating the strategy for exercising change. Such freedom could be precious in a PSS with many potential perturbations (Wang et al. Reference Wang, Mitake, Tsutsui, Alfarisi and Shimomura2022), although constructing representative scenarios can be time-consuming and challenging. Epoch-era analysis does not support the development team in discerning the optimal change exercising conditions that would yield the most significant enhancement in value. Decision rule-based methods address this issue by mapping change exercising conditions to observed uncertainty (Cardin et al. Reference Cardin, Xie, Ng, Wang and Hu2017). This mapping grants the development team a reasonable understanding of the change option that should be exercised as uncertainties are progressively resolved. Overall, multistage stochastic programming is relatively advanced from a mathematical perspective, making it challenging to implement, especially in the early design stages. Also, decision rules are statically determined at the beginning of the time horizon, and adjustments can be difficult in a dynamic fashion. Since the formulation of decision rules relies on the opinions and expertise of the development team, they could be limited to human cognition of the problem. In a recent effort, reinforcement learning has been proposed as a means to address this issue, aiming at discovering novel change strategies along with an optimal set of options through the analysis of empirical data (Caputo & Cardin Reference Caputo and Cardin2021). While it requires an exhaustive amount of empirical data, it must be highlighted that the change strategies could be an overfit for the design problem and may not be entirely generalizable.
6.3. Value-robust PSS design via changeability incorporation: a reference framework
In summary, incorporating changeability in PSS requires the following considerations:
-
• Define a baseline design that corresponds to an unchangeable PSS for comparison.
-
• Identify change options from a configuration and control perspective that can be integrated to represent a changeable PSS collectively.
-
• Measure the changeability level of the PSS.
-
• Describe and represent the sources of internal and external uncertainties in the design problem.
-
• Define an appraisal metric for measuring value.
-
• Formulate an operational strategy to represent the change decisions.
-
• Following this strategy, determine the optimal timing for exercising change.
Drawing upon the discussion above, it is apparent that incorporating changeability methods within the PSS domain requires a certain degree of adaptation. This adaptation starts with defining a baseline design many researchers have assumed to be pre-existing. To this end, the PSS design methodologies can be leveraged to define a concept representing a total solution (Qu et al. Reference Qu, Yu, Chen, Chu and Tian2016; Braga et al. Reference Braga, Toledo and González2020; Fernandes et al. Reference Fernandes, Pigosso, McAloone and Rozenfeld2020). Such a concept can consist of product, service and infrastructural elements depending on the system boundary. For changeability incorporation, a reference framework has been illustrated in Figure 5. This framework shall not be seen as the standard technique but as one of the many potential ways changeability can be incorporated in PSS.

Figure 5. Value-robust PSS design via changeability incorporation: A reference framework.
For a concrete grip on generating future alternatives, using Epoch-Era is deemed to be most suitable in the case of a PSS since it facilitates a more comprehensive collaboration within the development team to shape future alternatives. While it is a discrete-time model, the resolution of this discretization can be adjusted to suit the detail of the simulation. The identification of uncertainty factors can be resolved in three types of epochs, as illustrated in Gaspar et al. (Reference Gaspar, Hagen and Erikstad2016). These include positive epochs (green in Figure 5), neutral epochs (gray in Figure 5) and negative epochs (orange in Figure 5). Furthermore, the shade of these colors indicates the intensity of change in that epoch. The sequential ordering of epochs into eras ingrains path dependency in the design problem necessary to manage the irreversibility of exercised change. Numerous eras need to be simulated to gain confidence in the performance of changeable PSS over the operational phase.
Changeability identification and quantification support the development team in highlighting the available change options at the given timestamp. Filtered Outdegree is proposed for changeability quantification, as shown in Figure 5, based on enumeration in a tradespace. Tradespaces are versatile to include the configuration and control variables essential to changeability incorporation. These tradespaces shall be expanded to have all the elements within the development boundary, including products, services and infrastructural elements. The decision to adopt either a top-down or a bottom-up quantification metric is left to the information sought by the development team. Changeability identification implies finding the impact of adopting a transition path. To treat propagation explicitly in tangible and intangible aspects of the PSS, an MDM-based approach is proposed to highlight the dependencies from the product perspective, and blueprints are proposed to highlight the dependencies from the service perspective, as shown in Figure 5. An ESM includes product and service dependencies in a unified view, making it challenging to populate and manage, especially in the early design stages. Normalization and clustering, such as the Clustered Decision Matrix (Gan et al. Reference Gan, Steffan, Grunow and Akkerman2022), can be implemented to comprehend interactions and trade-offs systematically.
Upon selecting a suitable valuation metric (Rese et al. Reference Rese, Karger and Strotmann2009; Cardin Reference Cardin2013; Bertoni et al. Reference Bertoni, Bertoni and Ola2018; Rondini et al. Reference Rondini, Bertoni and Pezzotta2020), change can be exercised based on identifying the most feasible option at each epoch in an era. The black circles with numbers in Figure 5 indicate various timestamps when a decision for change was evaluated. A combination of network and optimization-based methods is proposed for the following reasons. Decision rule-based methods need prior knowledge for deciding the change exercising conditions. Optimization algorithms can decipher the conditions for exercising change. Also, since the uncertainties are modeled in terms of epochs, Epoch-Era analysis is relevant for valuing changeability requiring network-based representation of the PSS.
Overall, the problem is split into two parts, one comprising the positive and the other comprising negative epochs. Neutral epochs generally do not require exercising a change option. Splitting the problem is usually beneficial from tractability and comprehensibility perspectives, similar to how Cardin et al. (Reference Cardin, Xie, Ng, Wang and Hu2017) discretized the problem into many subproblems. A change option is generally exercised if the value can be appreciated, but this may not always be true due to path dependencies. While the depiction of value appreciation is linear, the process could be non-linear. For example, the state transition of the PSS from timestamp 2 to 3 in a negative epoch is exemplified in Figure 5 (marked in blue). Consequently, the value of the PSS is appreciated from 3′ to 3. Following this process at every epoch in the era repeatedly, incorporating changeability is worthwhile if the value of changeable PSS (denoted by
![]() $ {v}_c $
in Figure 5) is greater than the value of the unchangeable PSS (denoted by
$ {v}_c $
in Figure 5) is greater than the value of the unchangeable PSS (denoted by
![]() $ {v}_u $
in Figure 5), cumulatively for all timestamps
$ {v}_u $
in Figure 5), cumulatively for all timestamps
![]() $ t $
. Additionally, the goal is to maximize the variance of value with respect to time (denoted by
$ t $
. Additionally, the goal is to maximize the variance of value with respect to time (denoted by
![]() $ \max .\mathit{\operatorname{var}}\left({v}_c(t)\right) $
in Figure 5) for all positive epochs and minimize the variance of value with respect to time (denoted by
$ \max .\mathit{\operatorname{var}}\left({v}_c(t)\right) $
in Figure 5) for all positive epochs and minimize the variance of value with respect to time (denoted by
![]() $ \min .\mathit{\operatorname{var}}\left({v}_c(t)\right) $
in Figure 5) for all negative epochs, explicitly. Iterative analysis can reveal optimal exercising conditions and the changeability level of the PSS to achieve value robustness.
$ \min .\mathit{\operatorname{var}}\left({v}_c(t)\right) $
in Figure 5) for all negative epochs, explicitly. Iterative analysis can reveal optimal exercising conditions and the changeability level of the PSS to achieve value robustness.
7. Conclusion
The changing market dynamics, the journey toward servitization, stricter legislation, and the recent technological advancements are pushing the manufacturing industries beyond their comfort zone, forcing them to deal with many uncertainties during the design stages. In such a case, the development of PSS requires a closer integration of multidisciplinary domains along with mechanisms to exploit the opportunities or mitigate the risks associated with the uncertainties. Thus, it is stressed that considering changeability can be a worthwhile dimension for developing value-robust PSS. Positioned at the boundary of PSS and SE literature, this paper presented a descriptive outline of the complexity aspects in design decision-making and the state-of-the-art in incorporating changeability for value-robust design. Concerning the two research questions, the contributions are summarized as follows:
-
• What complexity aspects introduce uncertainties in design decision-making, prompting the development of a changeable PSS? – Figure 3 highlights the synopsis of the first research question, thereby positioning the five complexity aspects from a PSS perspective. These include structural, behavioral, contextual, temporal and perceptual aspects that introduce uncertainty in design decision-making. Structural and behavioral complexity aspects relate to internal factors, while contextual and temporal complexity aspects relate to external factors. Further, it is argued that perceptual complexity is a function of the other four complexity aspects.
-
• What is the state-of-the-art in incorporating changeability for value robustness, and how can those be applied in the case of PSS? – Figure 4 summarizes the answer to the second research question by presenting the state-of-the-art in changeability incorporation based on the three identified research streams: changeability identification, quantification and valuation. Each of these streams caters to different design problems. Thus, a suitable blend of methods must be selected to incorporate changeability during design decision-making based on the objective and available resources.
With the intent to present the current literature from a different standpoint, Figure 5 outlines a reference framework to support the development team in incorporating changeability for value-robust PSS design, especially during the early design stages. This framework shall be seen as a guiding instrument for future case study applications.
The study outlined in this paper is subject to certain limitations that may influence the resultant findings. The first is the screening process and filtration bias. As the papers have been reviewed qualitatively, it was impossible to avoid subjectivity. However, the authors made an effort to mitigate such effects through critical discussion. Besides, the maturity of the research field, resulting in a substantial number of publications, along with the inconsistency in the use of keywords, may have collectively resulted in the exclusion of some relevant studies in this integrative review. A larger share of papers emerging from the snowballing process is a confirmation of this phenomenon. However, the authors believe that the work presented in this paper captures the central idea of incorporating changeability to reasonable depth, thereby providing a grounded basis for achieving stable results and conclusions.
Acknowledgements
The work was partially performed in the frame of the TRUST-SOS and ASPECT projects funded by the Swedish Innovation Agency (VINNOVA) through the FFI Fossil-free mobile work machine initiative.