Resonant excitation of terahertz surface magnetoplasmons by optical rectification over a rippled surface of n-type indium antimonide

Abstract

We analysed the excitation of a surface magnetoplasmon wave by the mode conversion of a p-polarized laser beam over a rippled semiconductor (n-type)-free space interface. The pump surface magnetoplasmon wave exerts a ponderomotive force on the free electrons in the semiconductor, imparting a linear oscillatory velocity at the laser modulation frequency to them. This linear oscillatory velocity couples with the modulated electron density to produce a current density, which develops a resonant surface magnetoplasmon wave in the terahertz region. The amplitude of the terahertz surface magnetoplasmon wave can be tuneable with an external magnetic field and the semiconductor's temperature.

1. Introduction

Electromagnetic radiation with a frequency ranging from $0.3$ to $10\times 10^{12}$ Hz refers to terahertz (THz) gap (Shumyatsky & Alfano 2011). Recently, THz has attracted a lot of interest because its frequency application can be used in spectroscopy (Afsah-Hejri et al. 2019; Spies et al. 2020), communication (Yang et al. 2020; Ghazialsharif et al. 2023; Katyba et al. 2023), imaging in medical diagnostics (Peng et al. 2020; Zhang et al. 2020; Wang 2021), sensing (Islam et al. 2022; Lai et al. 2023; Tan et al. 2023), detection (Lewis 2019), etc. Terahertz radiation can be generated by a variety of techniques and processes, such as laser–plasma interaction (Malik & Singh 2020; Manendra et al. 2020), electron beam–plasma interaction (Yang et al. 2022; Gupta, Gurjar & Jain 2023), photoconductivity antenna (Isgandarov et al. 2021; Lu et al. 2022; Sandeep & Malik 2023), electron beam or laser interaction with a semiconductor or metal (Liu et al. 2007; Davidson et al. 2020; Dong et al. 2021), nonlinear mixing of lasers (Kumar, Rajouria & KK 2013; Kumar et al. 2017, 2023; Srivastav & Panwar 2022), optical rectification (Lee et al. 2000; Yeh et al. 2007; Aoki, Savolainen & Havenith 2017) and second and third harmonic generation (Beer et al. 2022; Gour et al. 2022) etc. Kumar et al. (2021) investigated THz radiation generation by beating of two laser pulses of finite spot size in a rippled density plasma. Kumar et al. (2021) studied excitation of THz radiation by nonlinear mixing of two continuous wave-laser beams in an axially modulated magnetized plasma. Jang et al. (2020) observed experimentally the excitation of multicycle and narrowband THz radiation by optical rectification of femtosecond laser pulses in $\text {LiNbO}_{3}$ crystal. Voevodin et al. (2022) experimentally demonstrated THz generation by optical rectification of 780 nm femtosecond laser pulses on $\text {ZnGeP}_{2}$ and $\text {ZnGeP}_{2}:\text {Sc}$ crystals and reported that the $\text {ZnGeP}_{2}:\text {Sc}$ crystal was more efficient for optical rectification. Wang et al. (2022) observed THz radiation generation by optical rectification from a liquid crystal using an 800 nm femtosecond laser and reported that the polarization of the femtosecond laser and the liquid crystal's orientation affected the THz amplitude. Kumar, Singh & Sharma (2016b) reported strong THz radiation generation by optical rectification of a super-Gaussian laser beam in rippled plasma. Singh et al. (2017a) discussed the generation of THz radiation from a shaped laser pulse by optical rectification in rippled plasma with an axial magnetic field. Singh et al. (2017b) examined the strong THz radiation generation of hyperbolic-secant laser pulses by optical rectification in magnetized (transversely) rippled plasma. Bhasin & Tripathi (2009) theoretically investigated the THz radiation generation of an x-mode laser in magnetized rippled plasma by optical rectification. Bhasin & Tripathi (2010) reported the resonant excitation of THz surface plasma waves (SPWs) by optical rectification of the SPW modulated amplitude on a rippled metal surface.

The electron density in metals is of the order of ${\approx }10^{28}\,\text {m}^{-3}$ and the corresponding plasma frequency is $10^{15}$ Hz, which lies in the visible region (Deepika et al. 2015; Sharma, Ghotra & Kant 2018). In a semiconductor (n-type), the electron density is ${\approx }10^{23}\,\text {m}^{-3}$ and the relative plasma frequency is of the order of $10^{12}$ Hz, which lies in THz region (Kumar, Kumar & Tripathi 2016a; Gupta 2021; Srivastav & Panwar 2023). The plasma frequency and dispersion relation of SPWs can be tuned with temperature and an external magnetic field, respectively. Srivastav & Panwar (2023) explored the effect of a magnetic field over the excitation of a THz surface magnetoplasmon (SMP) wave on n-type indium antimonide (n-InSb) by beating the laser and its second harmonic frequencies.

In the present paper, we investigated the excitation of THz SMPs by optical rectification of the modulated amplitude of the SMP wave on a rippled surface of a semiconductor (n-InSb) in the presence of an external magnetic field (see figure 1). The excitation of the SMPs can be achieved by an amplitude modulated laser (p-polarized) obliquely incident at an angle on the interface between a semiconductor and free space. This can be achieved in either the attenuated total reflection configuration or by directly impinging the laser on a semiconductor surface with a ripple of specific wavenumber $q$, where $q$ is the difference between the SMPs’ wavenumber and the component of the laser wave vector along the semiconductor surface. A modulated amplitude of the SMP wave exerts a ponderomotive force on the free electrons of the semiconductor (n-InSb). The ponderomotive force imparts an oscillatory velocity to the free electrons at the modulation frequency. This oscillatory velocity couples with the modulated electron density to produce a nonlinear current density at the modulation frequency, and resonantly excites the THz SMP wave at the modulation frequency. In Sec.II, we discussed the temperature-dependent dispersion relation of THz SMPs. Sec.III represents the linear response of THz SMPs at the modulation frequency. Sec.IV represents the excitation process of the THz SMP field. Results and discussion are in Sec.V and the conclusion in Sec.VI.

Figure 1. Schematic of linear mode conversion of an amplitude modulated laser into a SMP wave and the excitation of THz SMP radiation by the latter at the modulation frequency.

2. Temperature-dependent dispersion relation of terahertz surface magnetoplasmon

Assume that $x=0$ represents the interface between a rippled semiconductor (n-type) ($x\leq 0$) and free space ($x>0$) with the electron density perturbation $n = (n_0/2)(1+\cos q z)$ (Srivastav & Panwar 2023), where $q a\geq 1$, $a$ and $q$ are the amplitude and ripple wavenumber, respectively. Apply the magnetic field $B_{0}\hat {y}$ to the semiconductor (n-type) (cf. figure 1). The effective mass $m_{e}^{\ast }$ of free electrons inside a semiconductor (n-type) is $0.014 m_{e}$. The effective permittivities $\overline {\bar {\epsilon }}$ of the semiconductor (n-type) components are presented by $\varepsilon _{{\rm eff}} = (\epsilon _{x x}^{2} + \epsilon _{x z}^{2})/ (\epsilon _{x x})$, $\epsilon _{x x} = \epsilon _{z z} = \epsilon _r-(\epsilon _r{\omega _{p}^2 (\omega + {\rm i}\nu )})/\omega ((\omega + {\rm i}\nu )^2 - \omega ^2_{{\rm ce}})$, $\epsilon _{x z} =-\epsilon _{ z x} =-{\rm i} {\epsilon _r \omega _{{\rm ce}}\omega _{p}^2}/\omega ((\omega + {\rm i}\nu )^2 - \omega ^2_{{\rm ce}})$, $\omega _{{\rm ce}} = e B_{0}/m_{e}^{\ast }$ is the electron cyclotron frequency, e is electron charge, $\omega _{p}=\sqrt {(n_{0} e^{2})/(m_{e}^{\ast } \epsilon _{0}\epsilon _{r})}$ is the electron plasma frequency, $\nu$ is the collision frequency of electrons and the temperature-dependent electron density $n_{0}= 5.76\times 10^{20}\,\text {T}^{3/2}\exp (-0.26/2\text {k}_{\text {B}}\text {T})$ of n-InSb (Srivastav & Panwar 2023), where $\text {k}_{\text {B}}$ and $\text {T}$ are the Boltzmann constant and temperature, respectively.

The electric field of the SMP wave is given as

(2.1)\begin{equation} \boldsymbol{E} = A \exp({- {\rm i} (\omega t - k_z z)}) \begin{cases} (\hat{z} + \beta_{1} \hat{x}) \exp({- \alpha_{1} x}), & \text{for free space}\ x > 0 \\ (\hat{z} + \beta_{2} \hat{x}) \exp({\alpha_{2} x}), & \text{for n-InSb}\ x \leq 0, \end{cases}\end{equation}

where $A=A_{0}(1+\mu \cos \varOmega (t-z/v_{g}))$, $\beta _{1} = -({\rm i} k_{z}/ \alpha _{1})$, $\beta _{2} = ( {\epsilon _{x z} \alpha _{2}+ \epsilon _{x x} {\rm i} k_{z}}) /( -\epsilon _{x x} \alpha _{2} + \epsilon _{x z} {\rm i} k_{z} )$, $\alpha _{2}^2 = k_z^2 -(\omega ^2/c^2) (({\epsilon ^2_{x z} + \epsilon ^2_{x x}})/{\epsilon _{x x}})$, $\alpha _{1}^2 = k_z^2 -(\omega ^2/c^2)$, $\epsilon _{{\rm eff}} = ({\epsilon ^2_{x z} + \epsilon ^2_{x x}})/{\epsilon _{x x}}$ and $v_{g}$ is the group velocity of the SMP wave.

It adheres to the dispersion relation (Srivastav & Panwar 2023) as

(2.2)\begin{equation} \alpha_{2}=\alpha_{1} \epsilon_{{\rm eff}}+\frac{{\rm i} k_{z} \epsilon_{xz}}{\epsilon_{xx}}.\end{equation}

Srivastav & Panwar (2022, 2023) reported the dispersion curve of SMPs for different values of the normalized electron cyclotron frequency $\omega _{{\rm ce}}/\omega _{p}$. It shows that the dispersion curve of SMPs shifts away from the dispersion curve of electromagnetic waves in free space for increases in the normalized electron cyclotron frequency.

The dispersion curve of SMPs and electromagnetic waves is shown in figure 2 for different semiconductor temperatures $T=310$ K (orange dot dashed line), $T=300$ K (magenta dotted line), $T=290$ K (red dashed line) and $T=280$ K (green double dot dashed line) at the normalized electron cyclotron frequency $\omega _{{\rm ce}}/\omega _{p} = 0.05$. Dispersion curve of SMPs shifts towards a lower normalized THz frequency as the semiconductor (n-InSb) temperature increases. The cutoff frequency of the dispersion curve also shifts to a lower normalized THz frequency with increases in the semiconductor's temperature.

Figure 2. The $\omega /\omega _{p}$ variation with $k_{z}c/\omega _{p}$ for temperature $T=310$ K (orange dot dashed line), $T=300$ K (magenta dotted line), $T=290$ K (red dashed line) and $T=280$ K (green double dot dashed line) at normalized electron cyclotron frequency $\omega _{{\rm ce}}/\omega _{p} = 0.05$.

3. Linear response of terahertz surface magnetoplasmons

The SMP wave imparts a linear oscillatory velocity to the free electrons of the semiconductors as

(3.1)\begin{equation} v_{\omega}^x = \frac{e}{m_e^{{\ast}}} \tilde{v}_{\omega}^x A \exp({{\alpha }_2 x}) \exp({- {\rm i} (\omega t - k_z z)}) ,\end{equation}

and

(3.2)\begin{equation} v_{\omega}^z = \frac{e}{m_e^{{\ast}}} \tilde{v}_{\omega}^z A \exp({{\alpha }_2 x}) \exp({- {\rm i} (\omega t - k_z z)}) ,\end{equation}

where $\tilde {v}_{\omega }^x = ( \omega _{{\rm ce}} - {\rm i} (\omega + {\rm i} \nu ) {\beta _2} ) / ((\omega + {\rm i} \nu )^2 - \omega _{{\rm ce}}^2)$ and $\tilde {v}_{\omega }^z = - ( \omega _{{\rm ce}} {\beta _2} + {\rm i} (\omega + {\rm i} \nu ) ) / ((\omega + {\rm i} \nu )^2 - \omega _{{\rm ce}}^2)$.

The SMP wave exerts a ponderomotive force $\boldsymbol {F}_p = - (m_e^{\ast }/4) (\boldsymbol {v}_s \boldsymbol {\cdot } \boldsymbol {\nabla } \boldsymbol {v}_s^{\ast } + \boldsymbol {v}_s^{\ast } \boldsymbol {\cdot } \boldsymbol {\nabla } \boldsymbol {v}_s) - (e/4) (\boldsymbol {v}_s \times \boldsymbol {B}_s^{\ast } + \boldsymbol {v}_s^{\ast } \times \boldsymbol {B}_s)$ on the free electrons and it is represented as

(3.3)\begin{equation} \boldsymbol{F}_p = \frac{1}{4} \frac{e^2}{m_e^{{\ast}}} A^2 \exp({(\alpha_2 + \alpha^{{\ast}}_2) x}) (- F_{P x} \hat{x} + F_{P z} \hat{z}),\end{equation}

where

(3.4)\begin{align} F_{P x} & = (\tilde{v}_{\omega}^x \alpha^{{\ast}}_2 \tilde{v}^{{\ast} x}_{\omega} - \tilde{v}_{\omega}^z {\rm i} k_z \tilde{v}^{{\ast} x}_{\omega}) + ( {{\tilde{v}^{{\ast} x}_{\omega}} } \alpha_2 \tilde{v}_{\omega}^x {{+ \tilde{v}^{{\ast} z}_{\omega}} } {\rm i} k_z \tilde{v}_{\omega}^x) \nonumber\\ & \quad + \frac{1}{{\rm i} \omega} (\tilde{v}_{\omega}^{{\ast} z} (\alpha_2 - {\rm i} k_z {\beta_2}) + \tilde{v}_{\omega}^z (\alpha^{{\ast}}_2 + {\rm i} k_z \beta_2^{{\ast}})), \end{align}

and

(3.5)\begin{align} F_{P z} & = \frac{1}{{\rm i} \omega} (\tilde{v}_{\omega}^{{\ast} x} (\alpha_2 - {\rm i} k_z {\beta_2}) + \tilde{v}_{\omega}^x (\alpha^{{\ast}}_2 + {\rm i} k_z \beta_2^{{\ast}})) - ((\tilde{v}_{\omega}^x \alpha^{{\ast}}_2 \tilde{v}^{{\ast} z}_{\omega} \nonumber\\ & \quad - \tilde{v}_{\omega}^z {\rm i} k_z \tilde{v}^{{\ast} z}_{\omega}) + ({{\tilde{v}^{{\ast} x}_{\omega}} } \alpha_2 \tilde{v}_{\omega}^z {{+ \tilde{v}^{{\ast} z}_{\omega}} } {\rm i} k_z \tilde{v}_{\omega}^z)). \end{align}

The ponderomotive force at modulation frequency $\varOmega$ can be written as

(3.6)\begin{equation} F_{p \varOmega}^x ={-} \frac{e^2}{m_e^{{\ast}}} A_0^2 \mu F_{P x} \exp({(\alpha_2 + \alpha^{{\ast}}_2) x}) {\exp\left({- {\rm i} \varOmega \left(t - \frac{z}{v_g} \right)}\right)}.\end{equation}

Now, the oscillatory velocity components of the free electrons at modulation frequency $\varOmega$ are given as

(3.7)\begin{equation} v_{\varOmega}^x = \tilde{v}_{\varOmega}^x \frac{e^2}{(m^{{\ast}}_e)^{2}} A_0^2 \mu \exp({(\alpha_2 + \alpha^{{\ast}}_2) x}) {\exp\left({- {\rm i} \varOmega \left( t - \frac{z}{v_g} \right)}\right)},\end{equation}

and

(3.8)\begin{equation} v_{\varOmega}^z = \tilde{v}_{\varOmega}^z \frac{e^2}{(m^{{\ast}}_e)^{2}} A_0^2 \mu \exp({(\alpha_2 + \alpha^{{\ast}}_2) x}) {\exp\left({- {\rm i} \varOmega \left( t - \frac{z}{v_g} \right)}\right)},\end{equation}

where $\tilde {v}_{\varOmega }^x = ({\rm i} (\varOmega + {\rm i} \nu ) F_{P x}) / ((\varOmega + {\rm i} \nu )^2 - \omega _{{\rm ce}}^2)$ and $\tilde {v}_{\varOmega }^z = (\omega _{{\rm ce}} F_{P x}) / ((\varOmega + {\rm i} \nu )^2 - \omega _{{\rm ce}}^2)$.

The oscillatory velocity couples with the modulated electron density to produce current density $\boldsymbol {J}_{\varOmega }$ at modulation frequency $\varOmega$ and it is given as

(3.9)\begin{align} \boldsymbol{J}_{\varOmega} & ={-} \frac{1}{2} n_0 (- \tilde{v}_{\varOmega}^x \hat{x} + \tilde{v}_{\varOmega}^z \hat{z}) \frac{e^3}{(m^{{\ast}}_e)^{2}} A_0^2 \mu h \delta (x) \exp({(\alpha_2 + \alpha^{{\ast}}_2) x}) \nonumber\\ & \quad \times\exp({- {\rm i} \varOmega t}) \exp\left({{\rm i} \left( \frac{\varOmega}{v_g} + q \right) z}\right). \end{align}

4. Excitation process of terahertz surface magnetoplasmon field

By using Maxwell's equation, the $\varOmega$ modulation frequency SMP wave field can be expressed as

(4.1)\begin{equation} \boldsymbol{\nabla} \times \boldsymbol{E}_{s} = {\rm i} \varOmega\boldsymbol{B}_{s},\end{equation}

and

(4.2)\begin{equation} \boldsymbol{\nabla} \times \boldsymbol{B}_{s} = \boldsymbol{J}_{\varOmega} - {\rm i} \varOmega \epsilon_0 \epsilon_{{\rm eff}}^{\varOmega} \boldsymbol{E}_{s},\end{equation}

where $\varepsilon _{{\rm eff}}^{\varOmega } = ((\epsilon _{x x}^{\varOmega })^{2} + (\epsilon _{x z}^{\varOmega })^{2})/ (\epsilon _{x x}^{\varOmega })$, $\epsilon _{x x}^{\varOmega } = \epsilon _{z z}^{\varOmega } = \epsilon _r-(\epsilon _r{\omega _{p}^2 (\varOmega + {\rm i} \nu )})/\varOmega ( (\varOmega + {\rm i}\nu )^2 - \omega ^2_{{\rm ce}} )$, $\epsilon _{ x z}^{\varOmega } =-\epsilon _{ z x}^{\varOmega } =-{\rm i} {\epsilon _r \omega _{{\rm ce}}\omega _{p}^2}/\varOmega ((\varOmega + {\rm i}\nu )^2 - \omega ^2_{{\rm ce}}) \text { for}\ x \leq 0$ and $\varepsilon _{{\rm eff}}^{\varOmega } = 1 \text { for}\ x > 0$, and $s$ represents the SMPs.

The wave equation may be written as

(4.3)\begin{equation} \nabla^2 \boldsymbol{E}_{s} - \boldsymbol{\nabla} (\boldsymbol{\nabla} \boldsymbol{\cdot} \boldsymbol{E}_{s}) - \frac{\omega^2}{c^2} \left(\overline{\bar{\epsilon}} \boldsymbol{E}_{s} \right) ={-}\mu_{0} {\rm i} \varOmega \boldsymbol J_{\varOmega}.\end{equation}

Here, $\overline {\bar {\epsilon }}$ is an n-type semiconductor effective permittivity at frequency $\varOmega$. When the right-hand side term of (4.2) is zero, that is $\boldsymbol {J}_{\varOmega }$ is absent, then the SMP eigenmode structure with

(4.4)\begin{equation} \boldsymbol{E}_{s} = \boldsymbol{E}_{s,0}, \boldsymbol{B}_{s} = \boldsymbol{B}_{s,0},\end{equation}

where $\boldsymbol {E}_{s,0}$ and $\boldsymbol {B}_{s,0}$ is given as

(4.5)\begin{equation} \boldsymbol{\nabla} \times \boldsymbol{E}_{s,0} = {\rm i} \varOmega\boldsymbol{B}_{s,0},\end{equation}

and

(4.6)\begin{equation} \boldsymbol{\nabla} \times \boldsymbol{B}_{s,0} ={-} {\rm i}\varOmega \epsilon_0 \epsilon_{{\rm eff}}^{\varOmega} \boldsymbol{E}_{s,0}.\end{equation}

The SMP electric field can be represented as

(4.7)\begin{equation} \boldsymbol{E}_{s,0} = \exp({- {\rm i} (\varOmega t - k_z^{\varOmega} z)}) \begin{cases} (\hat{z} + \beta_{1}^{\varOmega} \hat{x}) \exp({- \alpha_{1}^{\varOmega} x}), & \text{for free space}\ x > 0 \\ (\hat{z} + \beta_{2}^{\varOmega} \hat{x}) \exp({\alpha_{2}^{\varOmega} x}), & \text{for n-InSb}\ x \leq 0 \end{cases},\end{equation}

where $\beta _{1}^{\varOmega } \!=\! -({\rm i} k_{z}^{\varOmega }/ \alpha _{1}^{\varOmega })$, $\beta _{2}^{\varOmega } \!=\! ( {\epsilon _{x z}^{\varOmega } \alpha _{2}^{\varOmega }+ \epsilon _{x x}^{\varOmega } {\rm i} k_{z}^{\varOmega }})/({ -\epsilon _{x x}^{\varOmega } \alpha _{2}^{\varOmega } + \epsilon _{x z}^{\varOmega } {\rm i} k_{z}^{\varOmega } })$, $(\alpha _{2}k_z^{\varOmega })^2 = (k_z^{\varOmega })^2 -(\varOmega ^2/c^2) \epsilon _{{\rm eff}}^{\varOmega }$, $(\alpha _{1}^{\varOmega })^2 = (k_z^{\varOmega })^2 -(\varOmega ^2/c^2)$, $k_{z}^{\varOmega } = q + \varOmega /v_{g}$ and $q$ provides the extra wave-number for the phase matching condition.

Figure 3 represents the variation of normalized ripple wavenumber $qc/\omega _{p}$ with normalized electron cyclotron frequency $\omega _{{\rm ce}}/\omega _{p}$ for the three values of THz frequency $\omega = 0.5$ THz (green line), $\omega = 1.0$ THz (blue dashed line) and $\omega = 1.5$ THz (red dot dashed line). Normalized ripple wavenumber $qc/\omega _{p}$ increases with an increase in the normalized electron cyclotron frequency $\omega _{{\rm ce}}/\omega _{p}$ at $\omega _{p} = 2.7$ THz. Also, it increases with a decrease in the THz frequency.

Figure 3. Variation of normalized ripple wavenumber $q$ with normalized electron cyclotron frequency $\omega _{{\rm ce}}/\omega _{p}$ for THz frequency $\omega = 0.5$ THz (green line), $\omega = 1.0$ THz (blue dashed line) and $\omega = 1.5$ THz (red dot dashed line).

If the current density $\boldsymbol {J}_{\varOmega }$ is present, then the electric and magnetic fields of the THz SMP wave can be expressed as

(4.8a,b)\begin{equation} \boldsymbol{E}_{s} = a(t) \boldsymbol{E}_{s,0},\quad \boldsymbol{B}_{s} = b(t) \boldsymbol{B}_{s,0}.\end{equation}

Solving (4.1) and (4.2) with (4.8a,b), and using (4.4), we get

(4.9)\begin{equation} (a - b) {\rm i} \varOmega \epsilon_0 \epsilon_{{\rm eff}}^{\varOmega} {\boldsymbol{E}_{s,0}} = \boldsymbol{J}_{\varOmega} + {\boldsymbol{E}_{s,0}} \frac{\partial a }{\partial t} \epsilon_0 \epsilon_{{\rm eff}},\end{equation}

and

(4.10)\begin{equation} b - a = \frac{1}{{\rm i} \varOmega} \frac{\partial b (t)}{\partial t}.\end{equation}

Using (4.10) in (4.9) and taking $\partial a /\partial t \approx \partial b /\partial t$, we get

(4.11)\begin{equation} \frac{\partial a}{\partial t} {\boldsymbol{E}_{s,0}} ={-} \frac{1}{2 \epsilon_0 \epsilon_{{\rm eff}}^{\varOmega}} \boldsymbol{J}_{\varOmega}.\end{equation}

Multiplying (4.11) by $\boldsymbol {E}_{s,0}^{\ast }\,{{\rm d}x}$ and integrating $- \infty$ to $\infty$, we obtain

(4.12)\begin{equation} \frac{\partial a }{\partial t} ={-} \frac{1}{2 \epsilon_0 \epsilon_{{\rm eff}}^{\varOmega}} \frac{I_2}{I_1},\end{equation}

where $I_{1} = \int ^{\infty }_{- \infty } \boldsymbol {E}_{s,0} \boldsymbol {\cdot } \boldsymbol {E}_{s,0}^{\ast }\,{{\rm d}x}$ and $I_{2} = \int ^{\infty }_{- \infty } \boldsymbol {J}_{\varOmega } \boldsymbol {\cdot } \boldsymbol {E}_{s,0}^{\ast }\,{{\rm d}x}$.

Solving the (4.12), one may obtain

(4.13)\begin{equation} \frac{\partial a }{\partial t} = \frac{A_0^{2} \mu h}{2 \epsilon_{{\rm eff}}^{\varOmega}} \frac{n_0 e^3}{\epsilon_0 (m_e^{{\ast}})^{2}} \frac{( - \tilde{v}_{\varOmega}^x ({\beta^{\varOmega}_2})^{{\ast}} + \tilde{v}_{\varOmega}^z )}{\left( \dfrac{1 + \beta^2_2}{\alpha^{\varOmega}_2} + \dfrac{1 + \beta^2_1}{\alpha^{\varOmega}_1} \right)}.\end{equation}

Letting $\partial /\partial t = - {\rm i} \varOmega$, we obtain

(4.14)\begin{equation} \left|\frac{a}{A_{0}}\right| = \left|{\rm i} \frac{A_0 e h \mu \omega^2_{p}}{2 \varOmega \epsilon_{{\rm eff}}^{\varOmega} m_e^{{\ast}}} \frac{(- \tilde{v}_{\varOmega}^x ({\beta^{\varOmega}_2})^{{\ast}} + \tilde{v}_{\varOmega}^z )}{\left( \dfrac{1 + \beta^2_2}{\alpha^{\varOmega}_2} + \dfrac{1 + \beta^2_1}{\alpha^{\varOmega}_1} \right)}\right|.\end{equation}

The amplitude ratio of THz SMPs to the SMP pump ($a/A_{0}$) is represented by (4.14). It shows that $a/A_{0}$ is directly proportional to the amplitude $A_{0}$ and modulation index $\mu$ of the SMP wave. The amplitude ratio of THz SMPs ($a/A_{0}$) also depends upon the electron cyclotron frequency $\omega _{{\rm ce}}$ (external magnetic field $B_{0} \hat {y}$) and n-type semiconductor temperature. The following parameter modulation index $\mu = 0.3$, ripple height ${h} = 50\,\mathrm {\mu }$m, effective mass of free electrons $m_{e}^{\ast } = 0.014 m_{e}$, $\epsilon _{r} = 15.68$ are used for the numerical study of the THz SMP wave.

5. Results and discussion

The amplitude ratio of THz SMP ($a/A_{0}$) variation with normalized THz frequency $\omega /\omega _{p}$ is plotted in figure 4 for normalized electron cyclotron frequency $\omega _{{\rm ce}}/\omega _{p} = 0$ (green line), $\omega _{{\rm ce}}/\omega _{p} = 0.05$ (red dashed line), $\omega _{{\rm ce}}/\omega _{p} = 0.1$ (blue dot-dashed line) and $\omega _{{\rm ce}}/\omega _{p} = 0.15$ (yellow dotted line) at $\mu = 0.3$, $n_{0} = 1.96 \times 10^{22}\,\text {m}^{-3}$, $\epsilon _{r} = 15.68$ and ripple height ${h} = 50\,\mathrm {\mu }$m. The amplitude ratio of THz SMPs increases with an increase in normalized electron cyclotron frequency $\omega _{{\rm ce}}/\omega$ and decreases with normalized THz frequency $\omega /\omega _{p}$. Figure 5 represents the variation of the amplitude ratio of THz SMPs ($a/A_{0}$) with normalized THz frequency $\omega /\omega _{p}$ for temperature $T = 280\,\text {K}$ (yellow dotted line), $T = 290\,\text {K}$ (green dot dashed line), $T = 30\,\text {K}$ (red dashed line) and $T = 310\,\text {K}$ (blue line) at normalized electron cyclotron frequency $\omega _{{\rm ce}}/\omega _{p} = 0.1$. The amplitude ratio of THz SMPs increases with a decrease in normalized THz frequency $\omega /\omega _{p}$ and a decrease in n-type semiconductor temperature.

Figure 4. The amplitude ratio of THz SMP wave $|a/A_{0}|$ with respect to normalized THz frequency $\omega /\omega _{p}$ for normalized electron cyclotron frequency $\omega _{{\rm ce}}/\omega _{p} = 0$ (green line), $\omega _{{\rm ce}}/\omega _{p} = 0.05$ (red dashed line), $\omega _{{\rm ce}}/\omega _{p} = 0.1$ (blue dot-dashed line) and $\omega _{{\rm ce}}/\omega _{p} = 0.15$ (yellow dotted line). Other parameters $\mu = 0.3$, $n_{0} = 1.96 \times 10^{22}\,\text {m}^{-3}$, $\epsilon _{r} = 15.68$ and ${h} = 50\,\mathrm {\mu }$m .

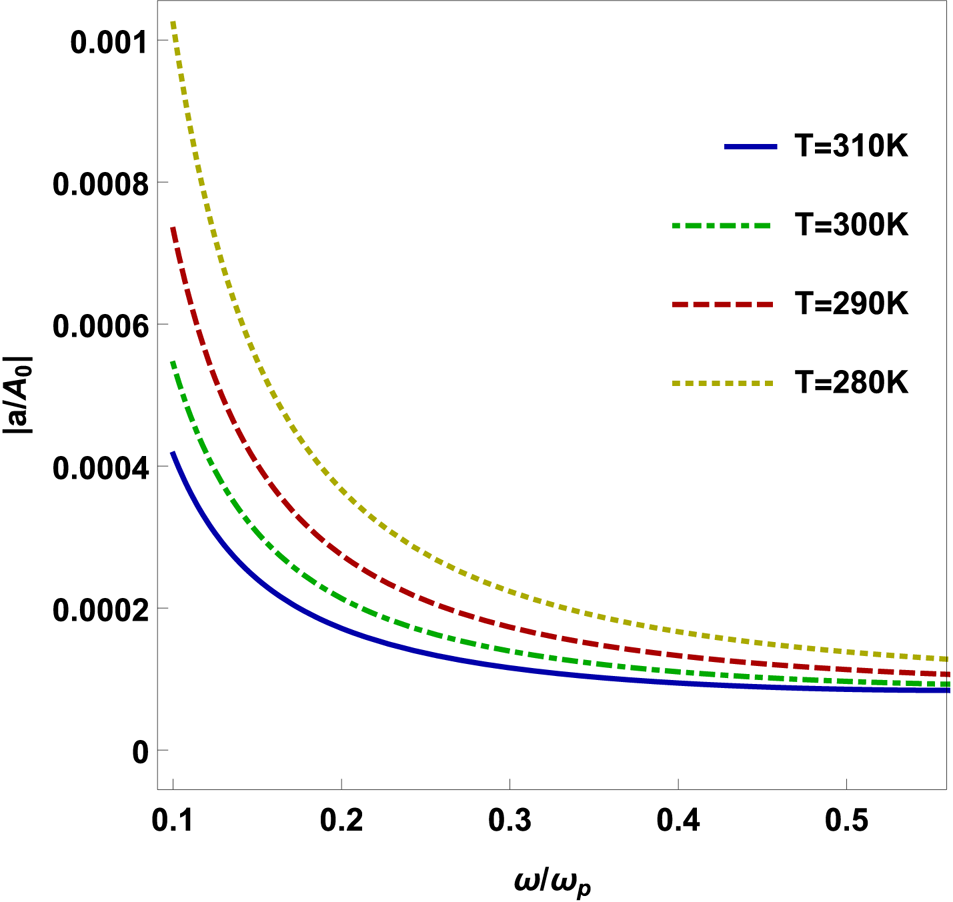
Figure 5. The amplitude ratio of THz SMP wave $|a/A_{0}|$ with respect to normalized THz frequency $\omega _{{\rm ce}}/\omega$ for temperature $T = 280\,\text {K}$ (yellow dotted line), $T = 290\,\text {K}$ (green dot dashed line), $T = 300\,\text {K}$ (red dashed line) and $T = 310\,\text {K}$ (blue line) at normalized electron cyclotron frequency $\omega _{{\rm ce}}/\omega _{p} = 0.05$ and other parameters $\mu = 0.3$, $\epsilon _{r} = 15.68$ and ${h} = 50\,\mathrm {\mu }$m.

6. Conclusion

In this paper, we propose the theoretical analysis of resonant excitation of THz SMPs by optical rectification of the modulated amplitude of SMPs in a magnetized rippled semiconductor (n-type). The current density generates THz SMPs at modulation frequency $\varOmega$ because of the ponderomotive force. Here, the ripple wavenumber gives an extra wavenumber for resonant excitation of the THz SMP wave. The THz SMP wave amplitude reaches its maximum value in the resonance condition and decreases in the non-resonant condition. It is observed that the THz SMP amplitude ratio rises as the normalized electron cyclotron frequency (external magnetic field) rises for normalized THz frequency. THz SMP amplitude ratio rises with a decrease in the normalized THz frequency. Further, it rises with a drop in semiconductor (n-type) temperature. This study could be used for THz devices for the excitation of THz waves at a desired THz frequency by changing the applied magnetic field and the semiconductor's temperature.