Published online by Cambridge University Press: 19 September 2024
This study presents an analysis of the optical variability of the blazar 1E 1458.8+2249 on diverse timescales using multi-band observations, including observations in the optical BVRI bands carried out with the T60 and T100 telescopes from 2020 to 2023 and ZTF gri data from 2018 to 2023. On seven nights, we searched for intraday variability using the power-enhanced F-test and the nested ANOVA test, but no significant variability was found. The long-term light curve shows a variability behaviour in the optical BVRI bands with amplitudes of 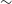 $\sim$100% and in the gri bands with amplitudes of
$\sim$100% and in the gri bands with amplitudes of 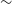 $\sim$120%, including short-term variability of up to
$\sim$120%, including short-term variability of up to  $\sim$1.1 mag. Correlation analysis revealed a strong correlation between the optical multi-band emissions without any time lag. From 62 nightly spectral energy distributions, we obtained spectral indices between 0.826 and 1.360, with an average of
$\sim$1.1 mag. Correlation analysis revealed a strong correlation between the optical multi-band emissions without any time lag. From 62 nightly spectral energy distributions, we obtained spectral indices between 0.826 and 1.360, with an average of  $1.128\pm0.063$. The relationships of both spectral indices and colour with respect to brightness indicate a mild BWB trend throughout the observation period, both intraday and long-term. We also performed a periodicity search using the weighted wavelet Z-transform and Lomb–Scargle methods. A recurrent optical emission pattern with a quasi-periodicity of
$1.128\pm0.063$. The relationships of both spectral indices and colour with respect to brightness indicate a mild BWB trend throughout the observation period, both intraday and long-term. We also performed a periodicity search using the weighted wavelet Z-transform and Lomb–Scargle methods. A recurrent optical emission pattern with a quasi-periodicity of  $\sim$340 days is detected in the combined V- and R-band light curves. The observational results indicate that the blazar 1E 1458.8+2249 has a complex variability, while emphasising the need for future observations to unravel its underlying mechanisms.
$\sim$340 days is detected in the combined V- and R-band light curves. The observational results indicate that the blazar 1E 1458.8+2249 has a complex variability, while emphasising the need for future observations to unravel its underlying mechanisms.