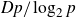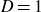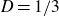1. Introduction
The study of the number of conjugacy classes k(G) of a finite group G has been a central theme in group theory since the work of Burnside, Frobenius and Landau around 1900. Since then, much effort has been made on the determination of finite groups with a small number of conjugacy classes (see [
Reference Vera–López and Sangroniz28
] and the references there). In a different direction, R. Brauer [
Reference Brauer2
] gave the first explicit lower bound for k(G) in terms of
![]() $|G|$
and, in one of the problems in his celebrated collection of open problems, asked for substantially better bounds. This was essentially solved by L. Pyber in 1992 [
Reference Pyber26
], but there have been a number of improvements on Pyber’s bound since then (see [
Reference Baumeister, Maróti and Tong–Viet1
,
Reference Keller18
] and the references there).
$|G|$
and, in one of the problems in his celebrated collection of open problems, asked for substantially better bounds. This was essentially solved by L. Pyber in 1992 [
Reference Pyber26
], but there have been a number of improvements on Pyber’s bound since then (see [
Reference Baumeister, Maróti and Tong–Viet1
,
Reference Keller18
] and the references there).
A variation of Brauer’s problem was considered by L. Héthelyi and B. Külshammer in 2000 [
Reference Héthelyi and Külshammer9
]. They proved that if G is a finite solvable group and p divides
![]() $|G|$
, then
$|G|$
, then
![]() $k(G)\geq2\sqrt{p-1}$
(and this bound is best possible). This has originated a lot of, still ongoing, research. They conjectured that this inequality should hold for an arbitrary group G and even that
$k(G)\geq2\sqrt{p-1}$
(and this bound is best possible). This has originated a lot of, still ongoing, research. They conjectured that this inequality should hold for an arbitrary group G and even that
![]() $k(B)\geq2\sqrt{p-1}$
when B is a Brauer p-block of G of positive defect. The Héthelyi–Külshammer bound was finally extended to arbitrary finite groups by A. Maróti in [
Reference Maróti22
]. Later, Maróti and G. Malle proved that even the number of irreducible characters of degree not divisible by p of a finite group G is
$k(B)\geq2\sqrt{p-1}$
when B is a Brauer p-block of G of positive defect. The Héthelyi–Külshammer bound was finally extended to arbitrary finite groups by A. Maróti in [
Reference Maróti22
]. Later, Maróti and G. Malle proved that even the number of irreducible characters of degree not divisible by p of a finite group G is
![]() $|{{\textrm{Irr}}}_{p'}(G)|\geq2\sqrt{p-1}$
. (See [
Reference Hung, Malle and Maróti11
] for a recent strengthening of this result involving fields of values.) The block-version still remains open, but the principal block case has been very recently solved by N. N. Hung and A. A. Schaeffer Fry. In [
Reference Hung and Schaeffer Fry12
], they prove that if
$|{{\textrm{Irr}}}_{p'}(G)|\geq2\sqrt{p-1}$
. (See [
Reference Hung, Malle and Maróti11
] for a recent strengthening of this result involving fields of values.) The block-version still remains open, but the principal block case has been very recently solved by N. N. Hung and A. A. Schaeffer Fry. In [
Reference Hung and Schaeffer Fry12
], they prove that if
![]() $B_0$
is the principal p-block of a finite group G, then the number of irreducible characters in
$B_0$
is the principal p-block of a finite group G, then the number of irreducible characters in
![]() $B_0$
is
$B_0$
is
![]() $k(B_0)\geq2\sqrt{p-1}$
. Even more, Hung, Schaeffer Fry and C. Vallejo have proven in [
Reference Hung, Schaeffer Fry and Vallejo13
] that the number of height zero irreducible characters in the principal p-block is
$k(B_0)\geq2\sqrt{p-1}$
. Even more, Hung, Schaeffer Fry and C. Vallejo have proven in [
Reference Hung, Schaeffer Fry and Vallejo13
] that the number of height zero irreducible characters in the principal p-block is
![]() $k_0(B_0)\geq2\sqrt{p-1}$
.
$k_0(B_0)\geq2\sqrt{p-1}$
.
On the other hand, R. Guralnick and G. Robinson [
Reference Guralnick and Robinson7
] have proved that if
![]() $\textbf{F}(G)$
is the Fitting subgroup of a group G of even order, p divides
$\textbf{F}(G)$
is the Fitting subgroup of a group G of even order, p divides
![]() $|G:\textbf{F}(G)|$
and
$|G:\textbf{F}(G)|$
and
![]() $t\in G$
is an involution, then
$t\in G$
is an involution, then
![]() $p\leq|\textbf{C}_G(t)|+1$
. This bound is best possible, as shown by the groups
$p\leq|\textbf{C}_G(t)|+1$
. This bound is best possible, as shown by the groups
![]() $\textrm{SL}_2(p-1)$
for
$\textrm{SL}_2(p-1)$
for
![]() $p\geq5$
a Fermat prime. We have observed that for these groups
$p\geq5$
a Fermat prime. We have observed that for these groups
![]() $k(\textrm{SL}_2(p-1))=|\textbf{C}_G(t)|+1$
, and this leads us to the question of whether
$k(\textrm{SL}_2(p-1))=|\textbf{C}_G(t)|+1$
, and this leads us to the question of whether
![]() $k(G)\geq p$
when p is a prime that divides
$k(G)\geq p$
when p is a prime that divides
![]() $|G:\textbf{F}(G)|$
. This is false, as
$|G:\textbf{F}(G)|$
. This is false, as
![]() $k(\textrm{PSL}_2(p))=(p+5)/2$
for any prime
$k(\textrm{PSL}_2(p))=(p+5)/2$
for any prime
![]() $p>3$
. Even more, if we assume that there are infinitely many Mersenne primes (as is expected), then the best bound that we can hope for is of the order of
$p>3$
. Even more, if we assume that there are infinitely many Mersenne primes (as is expected), then the best bound that we can hope for is of the order of
![]() $p/\log p$
, where
$p/\log p$
, where
![]() $\log$
(here and thoroughout the paper) means
$\log$
(here and thoroughout the paper) means
![]() $\log_2$
. In order to see this, let q be a prime such that
$\log_2$
. In order to see this, let q be a prime such that
![]() $p=2^q-1$
is a Mersenne prime and consider the affine semi-linear group
$p=2^q-1$
is a Mersenne prime and consider the affine semi-linear group
![]() $G=A\Gamma(2^q)$
. Then it is easy to see that p divides
$G=A\Gamma(2^q)$
. Then it is easy to see that p divides
![]() $|G:\textbf{F}(G)|$
and
$|G:\textbf{F}(G)|$
and
Our main result shows that indeed there exists a bound of this order of magnitude.
Theorem A.
There exists a constant D such that if G is a finite group and p divides
![]() $|G:\textbf{F}(G)|$
, then
$|G:\textbf{F}(G)|$
, then
Furthermore, if G is solvable, we can take
![]() $D=1/3$
.
$D=1/3$
.
Note that the hypothesis p divides
![]() $|G:\textbf{F}(G)|$
is redundant for non-p-solvable groups. In this case, we show that there are even better bounds.
$|G:\textbf{F}(G)|$
is redundant for non-p-solvable groups. In this case, we show that there are even better bounds.
Theorem B.
Let p be a prime. Then there exists
![]() $C>0$
such that if G is a non-p-solvable group, then
$C>0$
such that if G is a non-p-solvable group, then
![]() $k(G)\geq Cp$
.
$k(G)\geq Cp$
.
These theorems leave open the following questions.
Conjecture C. Let p be a prime and let G be a finite group. If p divides
![]() $|G:\textbf{F}(G)|$
, then
$|G:\textbf{F}(G)|$
, then
![]() $k(G)\geq p/\log p$
.
$k(G)\geq p/\log p$
.
Conjecture D. Let p be a prime and let G be a non-p-solvable group. Then
![]() $k(G)\geq (p+5)/2$
.
$k(G)\geq (p+5)/2$
.
Note that this would be a substantial improvement on the Héthelyi–Külshammer bound for non-p-solvable groups.
We remark that the straightforward versions of the main results in this paper for the number of irreducible characters of p
′-degree or for the number of characters in a block do not hold. For instance, the bound
![]() $|{{\textrm{Irr}}}_{p'}(G)|\geq2\sqrt{p-1}$
cannot be improved even if we assume that p divides
$|{{\textrm{Irr}}}_{p'}(G)|\geq2\sqrt{p-1}$
cannot be improved even if we assume that p divides
![]() $|G:\textbf{F}(G)|$
. This distinguishes our results from [
Reference Héthelyi and Külshammer9
,
Reference Maróti22
] and shows that our results are tighter, in the sense that it is not possible to replace k(G) by usually smaller invariants like
$|G:\textbf{F}(G)|$
. This distinguishes our results from [
Reference Héthelyi and Külshammer9
,
Reference Maróti22
] and shows that our results are tighter, in the sense that it is not possible to replace k(G) by usually smaller invariants like
![]() $|{{\textrm{Irr}}}_{p'}(G)|$
or k(B). Nevertheless, we think that they could also admit a block version and a version for the number of p
′-degree irreducible characters. This will be discussed in the last section of the paper.
$|{{\textrm{Irr}}}_{p'}(G)|$
or k(B). Nevertheless, we think that they could also admit a block version and a version for the number of p
′-degree irreducible characters. This will be discussed in the last section of the paper.
2. Preliminaries
All groups in this paper will be finite. Our notation is standard and follows [
Reference Isaacs16
,
Reference Manz and Wolf20
]. If N is a normal subgroup of a group G, then
![]() ${{\textrm{Irr}}}(G|N)$
is the set of irreducible characters of G whose kernel does not contain N. If a group G acts on an abelian group V, then we write n(G,V) to denote the number of orbits of G on V.
${{\textrm{Irr}}}(G|N)$
is the set of irreducible characters of G whose kernel does not contain N. If a group G acts on an abelian group V, then we write n(G,V) to denote the number of orbits of G on V.
In this section, we collect some results that will be used several times in the proofs of the main theorems. We start by recalling several results on the number of conjugacy classes that will be used without further explicit mention.
Lemma 2·1.
Let G be a finite group and let
![]() $N\trianglelefteq G$
. Then:
$N\trianglelefteq G$
. Then:
-
(i)
 $k(G)\geq k(G/N)$
;
$k(G)\geq k(G/N)$
; -
(ii)
 $k(G)\leq k(G/N)k(N)$
;
$k(G)\leq k(G/N)k(N)$
; -
(iii) If N is abelian and
 $C=\textbf{C}_G(N)$
then
$C=\textbf{C}_G(N)$
then
 $k(G)\geq k(G/C)+(|N|-1)/|G:C|$
.
$k(G)\geq k(G/C)+(|N|-1)/|G:C|$
.
Proof. Parts (i) and (ii) are well known (see, for instance, [
Reference Gallagher6
] for (ii)). We prove (iii). Note that
![]() $|{{\textrm{Irr}}}(G|N)|\geq (|N|-1)/|G:C|$
. Hence,
$|{{\textrm{Irr}}}(G|N)|\geq (|N|-1)/|G:C|$
. Hence,
as wanted.
The following result, which is a combination of the main results of [ Reference Héthelyi and Külshammer10 , Reference Maróti and Simion23 ], will allow us to consider just groups with Sylow p-subgroups of order p.
Theorem 2·2.
There exists a constant c such that for any group G whose order is divisible by the square of a prime p, we have
![]() $k(G)\geq cp$
. Furthermore, if G is solvable, then we can take
$k(G)\geq cp$
. Furthermore, if G is solvable, then we can take
![]() $c=49/60$
.
$c=49/60$
.
We definitely cannot take
![]() $c=49/60$
when G is a non-solvable p-solvable group, as [
Reference Héthelyi and Külshammer9
, Examples (iv), p· 671] shows. This is one of the reasons why our constant D in Theorem A is not explicit for non-solvable p-solvable groups.
$c=49/60$
when G is a non-solvable p-solvable group, as [
Reference Héthelyi and Külshammer9
, Examples (iv), p· 671] shows. This is one of the reasons why our constant D in Theorem A is not explicit for non-solvable p-solvable groups.
The following theorem of Seager [ Reference Seager27 ] will be another fundamental result to get our explicit bound in the solvable case.
Theorem 2·3.
Let p be a prime and let G be a solvable primitive subgroup of
![]() $\mathrm{GL}_n(p)$
. If G is not permutation isomorphic to a subgroup of
$\mathrm{GL}_n(p)$
. If G is not permutation isomorphic to a subgroup of
![]() $\Gamma(p^n)$
, then the number of orbits of G on the natural module V is
$\Gamma(p^n)$
, then the number of orbits of G on the natural module V is
except possibly when
![]() $p^n=17^4, 19^4, 7^6, 5^8, 7^8, 13^8, 7^9, 3^6$
and
$p^n=17^4, 19^4, 7^6, 5^8, 7^8, 13^8, 7^9, 3^6$
and
![]() $5^{16}$
.
$5^{16}$
.
Another fundamental tool will be Zsigmondy’s prime theorem (see [
Reference Huppert and Blackburn15
, IX, 8·3]). Recall that if
![]() $a>1$
and n are integers, a prime p is called a Zsigmondy prime divisor for
$a>1$
and n are integers, a prime p is called a Zsigmondy prime divisor for
![]() $a^n-1$
if p divides
$a^n-1$
if p divides
![]() $a^n-1$
but p does not divide
$a^n-1$
but p does not divide
![]() $a^j-1$
for
$a^j-1$
for
![]() $j<n$
. (This is dependent upon a and n, and not just
$j<n$
. (This is dependent upon a and n, and not just
![]() $a^n-1$
.)
$a^n-1$
.)
Theorem 2·4.
Let
![]() $a>1$
and n be positive integers. Then there exists a Zsigmondy prime divisor for
$a>1$
and n be positive integers. Then there exists a Zsigmondy prime divisor for
![]() $a^n-1$
unless
$a^n-1$
unless
![]() $(a,n)=(2,6)$
or
$(a,n)=(2,6)$
or
![]() $(a,n)=(2^k-1,2)$
for some positive integer k.
$(a,n)=(2^k-1,2)$
for some positive integer k.
We will also use several times the following consequence of the Fong–Swan theorem, that could be useful for other purposes.
Lemma 2·5.
Let G be a solvable group, and let V be a faithful irreducible G-module over the field with q elements, where q is a prime. Then
![]() $|V|\geq q^d$
, where d is the smallest dimension of a faithful complex representation of G.
$|V|\geq q^d$
, where d is the smallest dimension of a faithful complex representation of G.
Proof. Let F be an algebraically closed field in characteristic q. Write
![]() $|V|=q^n$
. Let
$|V|=q^n$
. Let
![]() $\mathcal{X}$
be the
$\mathcal{X}$
be the
![]() $\textrm{GF}(q)$
-representation associated to V and let
$\textrm{GF}(q)$
-representation associated to V and let
![]() $\mathcal{X}^F$
be the representation
$\mathcal{X}^F$
be the representation
![]() $\mathcal{X}$
viewed as an F-representation. By [
Reference Isaacs16
, Theorem 9·21],
$\mathcal{X}$
viewed as an F-representation. By [
Reference Isaacs16
, Theorem 9·21],
![]() $\mathcal{X}^F$
decomposes as a sum of pairwise different irreducible F-representations. Therefore, if
$\mathcal{X}^F$
decomposes as a sum of pairwise different irreducible F-representations. Therefore, if
![]() $\varphi$
is the (faithful) q-Brauer character associated to
$\varphi$
is the (faithful) q-Brauer character associated to
![]() $\mathcal{X}^F$
we have that
$\mathcal{X}^F$
we have that
![]() $\varphi(1)=n$
and
$\varphi(1)=n$
and
![]() $\varphi$
is a sum of pairwise different irreducible q-Brauer characters. By the Fong–Swan theorem ([
Reference Navarro24
, Theorem 10·1]) all these irreducible Brauer characters can be lifted to complex irreducible characters. Therefore,
$\varphi$
is a sum of pairwise different irreducible q-Brauer characters. By the Fong–Swan theorem ([
Reference Navarro24
, Theorem 10·1]) all these irreducible Brauer characters can be lifted to complex irreducible characters. Therefore,
![]() $\varphi=\chi^{\circ}$
for some faithful complex character
$\varphi=\chi^{\circ}$
for some faithful complex character
![]() $\chi$
. The result follows.
$\chi$
. The result follows.
We will need the following calculus exercise together with [ Reference Héthelyi and Külshammer9 ] in the proof of the solvable case of Theorem A.
Lemma 2·6.
If
![]() $2\leq x<1800$
, then
$2\leq x<1800$
, then
![]() $2\sqrt{x-1}>x/(2\log x)$
. If
$2\sqrt{x-1}>x/(2\log x)$
. If
![]() $2<x\leq 4936$
then
$2<x\leq 4936$
then
![]() $2\sqrt{x-1}>0.3492x/\log x$
.
$2\sqrt{x-1}>0.3492x/\log x$
.
3. Proof of Theorem B
In this short section, we prove Theorem B. It is an easy consequence of results of Fulman and Guralnick on the number of conjugacy classes of simple groups of Lie type (and the classification of finite simple groups).
Proof of Theorem B. By Theorem 2·2, we may assume that
![]() $|G|_p=p$
. Let
$|G|_p=p$
. Let
![]() $M/N=S$
be the chief factor of G whose order is divisible by p. Arguing by induction, we may assume that
$M/N=S$
be the chief factor of G whose order is divisible by p. Arguing by induction, we may assume that
![]() $N=1$
and
$N=1$
and
![]() $\textbf{C}_G(M)=1$
. Therefore, M is the unique minimal normal subgroup of G, so G is an almost simple group with socle S. Using the CFSG, we may assume that S is of Lie type of rank r over a field of size q, for some integers r and q (because there are finitely many sporadic groups, so we can ignore them and it is easy to see that if S is an alternating group, then the number of conjugacy classes of G is at least the largest prime divisor of
$\textbf{C}_G(M)=1$
. Therefore, M is the unique minimal normal subgroup of G, so G is an almost simple group with socle S. Using the CFSG, we may assume that S is of Lie type of rank r over a field of size q, for some integers r and q (because there are finitely many sporadic groups, so we can ignore them and it is easy to see that if S is an alternating group, then the number of conjugacy classes of G is at least the largest prime divisor of
![]() $|S|$
).
$|S|$
).
Now, it follows from [
Reference Fulman and Guralnick5
] that
![]() $k(G)\geq q^r/|M(S)|$
, where M(S) is the Schur multiplier of G. The result follows from inspection of [
Reference Hering8
, table 2].
$k(G)\geq q^r/|M(S)|$
, where M(S) is the Schur multiplier of G. The result follows from inspection of [
Reference Hering8
, table 2].
4. p-solvable groups
In this section, we prove the first part of Theorem A. We start with a particular case.
Lemma 4·1.
Let G be a finite group with a unique minimal normal subgroup N. Suppose that
![]() $|G|_p=p$
and
$|G|_p=p$
and
![]() $N=S\times\cdots\times S$
, where S is a non-abelian simple p′-group. Then
$N=S\times\cdots\times S$
, where S is a non-abelian simple p′-group. Then
![]() $k(G)> Cp$
, where C is the constant that appears in Theorem B.
$k(G)> Cp$
, where C is the constant that appears in Theorem B.
Proof. We know that G is isomorphic to a subgroup of
![]() ${{\textrm{Aut}}}(N)={{\textrm{Aut}}}(S)\wr\textsf{S}_n$
, where n is the number of direct factors isomorphic to S that appear in N. Let
${{\textrm{Aut}}}(N)={{\textrm{Aut}}}(S)\wr\textsf{S}_n$
, where n is the number of direct factors isomorphic to S that appear in N. Let
![]() $M=G\cap{{\textrm{Aut}}}(S)^n$
. We distinguish two cases.
$M=G\cap{{\textrm{Aut}}}(S)^n$
. We distinguish two cases.
Suppose first that p divides
![]() $|G/M|$
. Since
$|G/M|$
. Since
![]() $G/M$
is isomorphic to a subgroup of
$G/M$
is isomorphic to a subgroup of
![]() $\textsf{S}_n$
, we deduce that
$\textsf{S}_n$
, we deduce that
![]() $n\geq p$
. Hence if we fix any
$n\geq p$
. Hence if we fix any
![]() $1\neq x\in S$
, we have that
$1\neq x\in S$
, we have that
![]() $(x,1,\dots,1), (x,x,1,\dots,1),\dots,(x,\dots,x)\in N$
are representatives of at least p different conjugacy classes of G. The result follows in this case.
$(x,1,\dots,1), (x,x,1,\dots,1),\dots,(x,\dots,x)\in N$
are representatives of at least p different conjugacy classes of G. The result follows in this case.
Now, we may assume that p divides
![]() $|M/N|$
. This implies that p divides
$|M/N|$
. This implies that p divides
![]() $|{{\textrm{Out}}}(S)|$
. Since p does not divide
$|{{\textrm{Out}}}(S)|$
. Since p does not divide
![]() $|S|$
, it follows from the classification of finite simple groups that S is a group of Lie type over the field with
$|S|$
, it follows from the classification of finite simple groups that S is a group of Lie type over the field with
![]() $q^a$
elements for some prime q and some positive integer a that is divisible by p. By the order formulae of the simple groups of Lie type (see [
Reference Conway, Curtis, Norton, Parker and Wilson3
]),
$q^a$
elements for some prime q and some positive integer a that is divisible by p. By the order formulae of the simple groups of Lie type (see [
Reference Conway, Curtis, Norton, Parker and Wilson3
]),
![]() $q^a-1$
divides
$q^a-1$
divides
![]() $|S|$
. If l is a Zsigmondy prime divisor for
$|S|$
. If l is a Zsigmondy prime divisor for
![]() $q^a-1$
, then q has order a modulo l, so
$q^a-1$
, then q has order a modulo l, so
![]() $l\equiv 1\pmod{a}$
. In particular,
$l\equiv 1\pmod{a}$
. In particular,
![]() $l\geq a+1>p$
. Applying Theorem B with the prime l, we deduce that there exists a constant C such that
$l\geq a+1>p$
. Applying Theorem B with the prime l, we deduce that there exists a constant C such that
![]() $k(G)\geq Cl>Cp$
, as wanted.
$k(G)\geq Cl>Cp$
, as wanted.
Next, we handle the critical case.
Theorem 4·2. There exists a universal constant A such that the following holds. Let p be a prime and G a group such that the Sylow p-subgroup of G is normal in G and cyclic of order p. Let V be a faithful G-module over GF(q) where q is a prime different from p. Then
Proof. We first define a constant A that will do the job. Let
![]() $\beta$
be as in [
Reference Keller18
, Theorem B]. Moreover let
$\beta$
be as in [
Reference Keller18
, Theorem B]. Moreover let
![]() $\delta_0=1/\delta$
, where
$\delta_0=1/\delta$
, where
![]() $\delta$
is the constant one gets from [
Reference Baumeister, Maróti and Tong–Viet1
, Theorem 2·1] if one chooses
$\delta$
is the constant one gets from [
Reference Baumeister, Maróti and Tong–Viet1
, Theorem 2·1] if one chooses
![]() $\epsilon =1$
there. Now choose
$\epsilon =1$
there. Now choose
![]() $A>0$
sufficiently small such that it satisfies the following conditions:
$A>0$
sufficiently small such that it satisfies the following conditions:
First note that there is nothing to prove if
![]() $A p/\log p\leq 1$
, so we may assume that
$A p/\log p\leq 1$
, so we may assume that
![]() $p/\log p\geq 1/A$
and thus
$p/\log p\geq 1/A$
and thus
![]() $p>1/A$
. Since the function
$p>1/A$
. Since the function
![]() $f(x)=x/(\log x)^4$
is strictly increasing for
$f(x)=x/(\log x)^4$
is strictly increasing for
![]() $x>e^4$
, we see that with (ii) and (iii) we obtain
$x>e^4$
, we see that with (ii) and (iii) we obtain
Hence for any real number
![]() $a_0$
with
$a_0$
with
![]() $a_0\geq \log(p)$
we get the inequality
$a_0\geq \log(p)$
we get the inequality
which can easily be seen to be equivalent to
Now let GV be a counterexample of minimal order. Let P be the Sylow p-subgroup of G and observe that since P is normal and cyclic we see that
![]() $V_P=[P,V]\oplus C_V(P)$
, and P acts frobeniusly on [P, V]. By induction we may assume that
$V_P=[P,V]\oplus C_V(P)$
, and P acts frobeniusly on [P, V]. By induction we may assume that
![]() $V=[P,V]$
, and so P acts frobeniusly on V. Now if
$V=[P,V]$
, and so P acts frobeniusly on V. Now if
![]() $0<V_1<V$
is a G-module, then G also acts on
$0<V_1<V$
is a G-module, then G also acts on
![]() $V/V_1$
and P acts frobeniusly on
$V/V_1$
and P acts frobeniusly on
![]() $V/V_1$
, and so by induction we are done again. Hence no such
$V/V_1$
, and so by induction we are done again. Hence no such
![]() $V_1$
exists, and hence V is irreducible as G-module.
$V_1$
exists, and hence V is irreducible as G-module.
Write
![]() $M=\textbf{C}_G(P)$
and note that
$M=\textbf{C}_G(P)$
and note that
![]() $M=K\times P$
for a Hall p
′-subgroup K of M. Then
$M=K\times P$
for a Hall p
′-subgroup K of M. Then
![]() $G/M$
is isomorphic to a subgroup of Aut(P), and hence if we write
$G/M$
is isomorphic to a subgroup of Aut(P), and hence if we write
![]() $a=|G/M|$
, then a divides
$a=|G/M|$
, then a divides
![]() $p-1$
, and
$p-1$
, and
![]() $G/M$
is cyclic of order a. Now we see that
$G/M$
is cyclic of order a. Now we see that
Also, if
![]() $g\in G$
is such that
$g\in G$
is such that
![]() $G/M=\langle gM\rangle$
, then
$G/M=\langle gM\rangle$
, then
![]() $P\langle g\rangle$
is a subgroup U of G which has a factor group that is a Frobenius group of order ap. So if
$P\langle g\rangle$
is a subgroup U of G which has a factor group that is a Frobenius group of order ap. So if
![]() $0<V_0<V$
is an irreducible U-submodule of V, then by Lemma 2·5 we have
$0<V_0<V$
is an irreducible U-submodule of V, then by Lemma 2·5 we have
![]() $|V|\geq |V_0|\geq q^a\geq 2^a$
.
$|V|\geq |V_0|\geq q^a\geq 2^a$
.
Now let S be the solvable radical of G. Then SV is a solvable group with trivial Frattini subgroup, and hence by [
Reference Keller18
, Theorem B] with
![]() $\beta$
as introduced above we have that
$\beta$
as introduced above we have that
Furthermore,
![]() $G/S$
is a group with trivial solvable radical, and so by [
Reference Baumeister, Maróti and Tong–Viet1
, Theorem 2·1] with
$G/S$
is a group with trivial solvable radical, and so by [
Reference Baumeister, Maróti and Tong–Viet1
, Theorem 2·1] with
![]() $\delta_0>0$
as introduced above we get
$\delta_0>0$
as introduced above we get
Furthermore, note that
![]() $k(K)\leq a$
, because if
$k(K)\leq a$
, because if
![]() $k(K)>a$
, then
$k(K)>a$
, then
and then
contradicting GV being a counterexample. Now since
![]() $P\leq S$
, we see that
$P\leq S$
, we see that
and hence
![]() $k(MS/S)\leq k(K)\leq a$
. Since
$k(MS/S)\leq k(K)\leq a$
. Since
![]() $|G:M|=a$
, we then conclude that
$|G:M|=a$
, we then conclude that
With this we get
Putting (1) and (2) together, we obtain
Note that by (0) we may assume that
![]() $a\geq \log p$
. Therefore by
$a\geq \log p$
. Therefore by
![]() $(*)$
we know that
$(*)$
we know that
![]() $\beta a -16\delta_0(\log a)^4\geq (\beta/2) a$
. Therefore by (3) we get
$\beta a -16\delta_0(\log a)^4\geq (\beta/2) a$
. Therefore by (3) we get
Hence
![]() $a\leq (2/\beta)\log p$
, and thus (0) yields
$a\leq (2/\beta)\log p$
, and thus (0) yields
But now by (i) we see that
which is the final contradiction to GV being a counterexample. The proof is complete.
Now, we can complete the proof of the first part of Theorem A. We refer the reader to [ Reference Isaacs17 , 9A] for the definition and basic properties of the generalised Fitting subgroup.
Theorem 4·3.
There exists a constant C such that if G is a finite group such that p divides
![]() $|G:\textbf{F}(G)|$
then
$|G:\textbf{F}(G)|$
then
![]() $k(G)\geq Cp/\log p$
.
$k(G)\geq Cp/\log p$
.
Proof. By Theorem B, we may assume that G is p-solvable. By Theorem 2·2, we may assume that
![]() $|G|_p=p$
. We argue by induction on
$|G|_p=p$
. We argue by induction on
![]() $|G|$
. By [
Reference Huppert14
, III·4·2(d)], we know that
$|G|$
. By [
Reference Huppert14
, III·4·2(d)], we know that
![]() $\textbf{F}(G/\Phi(G))=\textbf{F}(G)/\Phi(G)$
. Hence, p divides
$\textbf{F}(G/\Phi(G))=\textbf{F}(G)/\Phi(G)$
. Hence, p divides
![]() $|G/\Phi(G):\textbf{F}(G/\Phi(G))|$
. Since
$|G/\Phi(G):\textbf{F}(G/\Phi(G))|$
. Since
![]() $k(G)\geq k(G/\Phi(G))$
, we may assume that
$k(G)\geq k(G/\Phi(G))$
, we may assume that
![]() $\Phi(G)=1$
. Note that this implies that the Frattini subgroup of any subnormal subgroup of G is trivial and in particular any component of G is simple. Hence
$\Phi(G)=1$
. Note that this implies that the Frattini subgroup of any subnormal subgroup of G is trivial and in particular any component of G is simple. Hence
![]() $\textbf{E}(G)$
is a direct product of (non-abelian) simple p
′-groups. Furthermore,
$\textbf{E}(G)$
is a direct product of (non-abelian) simple p
′-groups. Furthermore,
![]() $\textbf{F}(G)$
is a direct product of elementary abelian minimal normal subgroups of G, by [
Reference Huppert14
, III·4·5].
$\textbf{F}(G)$
is a direct product of elementary abelian minimal normal subgroups of G, by [
Reference Huppert14
, III·4·5].
Hence the generalised Fitting subgroup
![]() $\textbf{F}^*(G)=\textbf{E}(G)\textbf{F}(G)$
is the direct product of the minimal normal subgroups of G, i.e., coincides with the socle of G. Note also that p does not divide
$\textbf{F}^*(G)=\textbf{E}(G)\textbf{F}(G)$
is the direct product of the minimal normal subgroups of G, i.e., coincides with the socle of G. Note also that p does not divide
![]() $|\textbf{F}^*(G)|$
. Write
$|\textbf{F}^*(G)|$
. Write
![]() $\textbf{F}^*(G)=V_1\times\cdots\times V_t$
, where
$\textbf{F}^*(G)=V_1\times\cdots\times V_t$
, where
![]() $V_1,\dots, V_t$
are minimal normal subgroups of G.
$V_1,\dots, V_t$
are minimal normal subgroups of G.
Since
![]() $\textbf{C}_G(\textbf{F}^*(G))\leq\textbf{F}^*(G)$
, we deduce that
$\textbf{C}_G(\textbf{F}^*(G))\leq\textbf{F}^*(G)$
, we deduce that
![]() $\textbf{C}_G(\textbf{F}^*(G))=\textbf{F}(G)$
. Write
$\textbf{C}_G(\textbf{F}^*(G))=\textbf{F}(G)$
. Write
![]() $C_i=\textbf{C}_G(V_i)$
for every i. Note that
$C_i=\textbf{C}_G(V_i)$
for every i. Note that
![]() $\textbf{C}_G(\textbf{F}^*(G))=\bigcap_{i=1}^t C_i$
so
$\textbf{C}_G(\textbf{F}^*(G))=\bigcap_{i=1}^t C_i$
so
![]() $G/\textbf{F}(G)$
is isomorphic to a subgroup of the direct product
$G/\textbf{F}(G)$
is isomorphic to a subgroup of the direct product
![]() $G/C_1\times\cdots\times G/C_t$
. Since p divides
$G/C_1\times\cdots\times G/C_t$
. Since p divides
![]() $|G/\textbf{F}(G)|$
, there exists j such that p divides
$|G/\textbf{F}(G)|$
, there exists j such that p divides
![]() $|G/C_j|$
. Write
$|G/C_j|$
. Write
![]() $V=V_j$
and
$V=V_j$
and
![]() $C=C_j$
. Note that since p divides
$C=C_j$
. Note that since p divides
![]() $|G/C|$
, p does not divide
$|G/C|$
, p does not divide
![]() $|C|$
.
$|C|$
.
Suppose first that V is abelian. Using [
Reference Huppert14
, III·4·4], we deduce that there exists
![]() $H\leq G$
such that
$H\leq G$
such that
![]() $G=HV$
and
$G=HV$
and
![]() $H\cap V=1$
. Let
$H\cap V=1$
. Let
![]() $D=\textbf{C}_H(V)$
, which is a normal p
′-subgroup of G. Hence
$D=\textbf{C}_H(V)$
, which is a normal p
′-subgroup of G. Hence
![]() $VD/D$
is the unique minimal normal subgroup of
$VD/D$
is the unique minimal normal subgroup of
![]() $G/D$
and
$G/D$
and
![]() $H/D$
acts faithfully on
$H/D$
acts faithfully on
![]() $VD/D$
. Since
$VD/D$
. Since
![]() $k(G)\geq k(G/D)$
and the hypotheses hold for
$k(G)\geq k(G/D)$
and the hypotheses hold for
![]() $G/D$
, we may assume that
$G/D$
, we may assume that
![]() $D=1$
. Hence, V is the unique minimal normal subgroup of G and
$D=1$
. Hence, V is the unique minimal normal subgroup of G and
![]() $\textbf{F}(G)=V$
. By induction, again, we may assume that p divides
$\textbf{F}(G)=V$
. By induction, again, we may assume that p divides
![]() $|\textbf{F}_2(G):\textbf{F}(G)|$
, so H has a normal Sylow p-subgroup. Now, the result follows from Theorem 4·2.
$|\textbf{F}_2(G):\textbf{F}(G)|$
, so H has a normal Sylow p-subgroup. Now, the result follows from Theorem 4·2.
Hence, we may assume that V is not abelian. In this case,
![]() $VC/C$
is the unique minimal normal subgroup of
$VC/C$
is the unique minimal normal subgroup of
![]() $G/C$
and we are in the situation of Lemma 4·1. The theorem follows.
$G/C$
and we are in the situation of Lemma 4·1. The theorem follows.
5. Solvable Groups: Imprimitive Case
In this and the next section, we work to provide the explicit and reasonable constant in the solvable case of Theorem A. The problem is reduced to studying the action of a group on a finite faithful irreducible module. Our first result handles the imprimitive case.
Theorem 5·1. There exists a universal constant D such that the following holds. Let p be a prime and H a solvable group such that the Sylow p-subgroup of H is normal in H and cyclic of order p. Let V be a faithful irreducible H-module over GF(q) where q is a prime different from p, and suppose that V is not quasi-primitive (in particular, it is imprimitive). Then
One can choose
![]() $D=0.3492$
. Moreover, if
$D=0.3492$
. Moreover, if
![]() $p>11000$
, then one can even choose
$p>11000$
, then one can even choose
![]() $D=1/2$
.
$D=1/2$
.
Proof. Let
![]() $0<D\leq 1/2$
be arbitrary. We will see that the proof will work with this D except for one critical case. In that one case the argument will only work under the additional assumption
$0<D\leq 1/2$
be arbitrary. We will see that the proof will work with this D except for one critical case. In that one case the argument will only work under the additional assumption
![]() $p>11000$
, and for arbitrary p it will only work if
$p>11000$
, and for arbitrary p it will only work if
![]() $D\leq 0.3492$
.
$D\leq 0.3492$
.
First note that by Lemma 2·6 and [
Reference Héthelyi and Külshammer9
], we may assume that
![]() $2\sqrt{p-1}\leq Dp/\log_2(p)$
, that is,
$2\sqrt{p-1}\leq Dp/\log_2(p)$
, that is,
![]() $D \geq (2\sqrt{p-1}\log_2(p))/p$
. If
$D \geq (2\sqrt{p-1}\log_2(p))/p$
. If
![]() $D=1/2$
, this forces
$D=1/2$
, this forces
![]() $p>1800$
, and if
$p>1800$
, and if
![]() $D=0.34924$
, this forces
$D=0.34924$
, this forces
![]() $p>4936$
.
$p>4936$
.
Let HV be a counterexample of minimal order.
Now let
![]() $N\unlhd H$
be maximal such that
$N\unlhd H$
be maximal such that
![]() $V_N$
is not homogeneous, and then by Clifford’s theorem we know that
$V_N$
is not homogeneous, and then by Clifford’s theorem we know that
![]() $V_N=\oplus_{i=1}^n V_i$
for some
$V_N=\oplus_{i=1}^n V_i$
for some
![]() $n>1$
and homogeneous components
$n>1$
and homogeneous components
![]() $V_i$
, and
$V_i$
, and
![]() $H/N$
permutes the
$H/N$
permutes the
![]() $V_i$
(
$V_i$
(
![]() $i=1,\dots ,n$
) faithfully and primitively.
$i=1,\dots ,n$
) faithfully and primitively.
Next, let P be the Sylow p-subgroup of H and observe that since P is normal and cyclic, it acts frobeniusly on V. We claim that
![]() $P\leq N$
. If not, then P would permute the
$P\leq N$
. If not, then P would permute the
![]() $V_i$
nontrivially, and we could without loss assume that
$V_i$
nontrivially, and we could without loss assume that
![]() $\{V_1, \dots , V_p\}$
would be an orbit of P in this action. But then if x is a generator of P and
$\{V_1, \dots , V_p\}$
would be an orbit of P in this action. But then if x is a generator of P and
![]() $0\ne v_1\in V_1$
, then
$0\ne v_1\in V_1$
, then
![]() $\scriptstyle{\sum\limits_{i=0}^{p-1}v_1^{x^i}}$
would clearly be a nonzero element of V which is fixed by x and thus P, contradicting P acting frobeniusly on V. This proves our claim that
$\scriptstyle{\sum\limits_{i=0}^{p-1}v_1^{x^i}}$
would clearly be a nonzero element of V which is fixed by x and thus P, contradicting P acting frobeniusly on V. This proves our claim that
![]() $P\leq N$
.
$P\leq N$
.
We study the action of N on V.
We claim that N has at least
![]() $p^{n-1}/(p-1)$
distinct orbits on V. (*)
$p^{n-1}/(p-1)$
distinct orbits on V. (*)
To see this, we let
![]() $0\ne v_1\in V_1$
. Let
$0\ne v_1\in V_1$
. Let
![]() $g_i\in H$
(
$g_i\in H$
(
![]() $i=1, \dots , n$
) such that
$i=1, \dots , n$
) such that
![]() $V_1^{g_i}=V_i$
for all i; clearly we may assume that
$V_1^{g_i}=V_i$
for all i; clearly we may assume that
![]() $g_1=1$
. Put
$g_1=1$
. Put
![]() $v_i=v_1^{g_i}\in V_i$
for all i. Then
$v_i=v_1^{g_i}\in V_i$
for all i. Then
obviously is an N-invariant subset of V. For
![]() $j=1,\dots n$
we define
$j=1,\dots n$
we define
 \[T_j:=\sum\limits_{i=1}^j v_i^N\]
\[T_j:=\sum\limits_{i=1}^j v_i^N\]
so that
![]() $T_n=T$
. Write
$T_n=T$
. Write
![]() $M=\textbf{C}_N(P)$
and note that
$M=\textbf{C}_N(P)$
and note that
![]() $M=K\times P$
for a Hall p
′-subgroup K of M. To establish our claim (*), we prove the following.
$M=K\times P$
for a Hall p
′-subgroup K of M. To establish our claim (*), we prove the following.
Let
![]() $j\in\{1,\dots , n\}$
. Then M has at least
$j\in\{1,\dots , n\}$
. Then M has at least
![]() $p^{j-1}$
orbits on
$p^{j-1}$
orbits on
![]() $T_j$
. (**)
$T_j$
. (**)
We prove this by induction on j. If
![]() $j=1$
, then the assertion is trivial. So let
$j=1$
, then the assertion is trivial. So let
![]() $1<j\leq n$
and suppose that M has at least
$1<j\leq n$
and suppose that M has at least
![]() $p^{j-2}$
orbits on
$p^{j-2}$
orbits on
![]() $T_{j-1}$
. Now let
$T_{j-1}$
. Now let
![]() $y\in T_{j-1}$
be in one of these orbits. Since P is normal in H and acts frobeniusly on V, we conclude that p does not divide the order of
$y\in T_{j-1}$
be in one of these orbits. Since P is normal in H and acts frobeniusly on V, we conclude that p does not divide the order of
![]() $\textbf{C}_M(y)$
; that is,
$\textbf{C}_M(y)$
; that is,
![]() $\textbf{C}_M(y)=\textbf{C}_K(y)$
. Since M is p-nilpotent and P acts frobeniusly on V, the N-orbit
$\textbf{C}_M(y)=\textbf{C}_K(y)$
. Since M is p-nilpotent and P acts frobeniusly on V, the N-orbit
![]() $v_j^N\subseteq V_j$
decomposes into at least p distinct
$v_j^N\subseteq V_j$
decomposes into at least p distinct
![]() $\textbf{C}_M(y)$
-orbits (since the sizes of the
$\textbf{C}_M(y)$
-orbits (since the sizes of the
![]() $\textbf{C}_M(y)$
-orbits are not divisible by p, but
$\textbf{C}_M(y)$
-orbits are not divisible by p, but
![]() $|v_j^M|$
is divisible by p, and P will always join p of the
$|v_j^M|$
is divisible by p, and P will always join p of the
![]() $\textbf{C}_M(y)$
-orbits to a single
$\textbf{C}_M(y)$
-orbits to a single
![]() $\textbf{C}_M(y)\times P$
-orbit). If
$\textbf{C}_M(y)\times P$
-orbit). If
![]() $w_i\in v_j^N$
(
$w_i\in v_j^N$
(
![]() $i=1, \dots , p$
) are representatives of such p distinct
$i=1, \dots , p$
) are representatives of such p distinct
![]() $\textbf{C}_M(y)$
-orbits, then we see that the
$\textbf{C}_M(y)$
-orbits, then we see that the
![]() $y+w_i\in T_j$
(
$y+w_i\in T_j$
(
![]() $i=1, \dots , p$
) are representatives of p distinct M-orbits. Since y was chosen from an arbitrary M-orbit on
$i=1, \dots , p$
) are representatives of p distinct M-orbits. Since y was chosen from an arbitrary M-orbit on
![]() $T_{j-1}$
, and since furthermore clearly any
$T_{j-1}$
, and since furthermore clearly any
![]() $y_1+w_i$
and
$y_1+w_i$
and
![]() $y_2+w_j$
(for any
$y_2+w_j$
(for any
![]() $i,j\in\{1,\dots ,p\}$
lie in different M-orbits if
$i,j\in\{1,\dots ,p\}$
lie in different M-orbits if
![]() $y_1$
and
$y_1$
and
![]() $y_2$
lie in different M-orbits on
$y_2$
lie in different M-orbits on
![]() $T_{j-1}$
, it follows that M has at least
$T_{j-1}$
, it follows that M has at least
![]() $p^{j-2}\cdot p=p^{j-1}$
distinct orbits on
$p^{j-2}\cdot p=p^{j-1}$
distinct orbits on
![]() $T_j$
. Thus (**) is proved.
$T_j$
. Thus (**) is proved.
Now
![]() $|N/M|=|\textbf{N}_N(P)/\textbf{C}_N(P)|$
divides
$|N/M|=|\textbf{N}_N(P)/\textbf{C}_N(P)|$
divides
![]() $p-1$
, and so by (**) for
$p-1$
, and so by (**) for
![]() $j=n$
it follows that N has at least
$j=n$
it follows that N has at least
![]() $p^{n-1}/(p-1)$
orbits on V, establishing (*).
$p^{n-1}/(p-1)$
orbits on V, establishing (*).
Now by a result of Dixon [
Reference Dixon4
] we know that
![]() $|H/N|\leq 24^{(n-1)/3}$
, and since
$|H/N|\leq 24^{(n-1)/3}$
, and since
![]() $H/N$
permutes the N-orbits on V, and the H-orbits on V are clearly conjugacy classes of HV, with (*) we obtain
$H/N$
permutes the N-orbits on V, and the H-orbits on V are clearly conjugacy classes of HV, with (*) we obtain
 \[k(HV)\geq \frac{n(N,V)}{|H/N|}\geq \frac{ \frac{p^{n-1}}{p-1} }{24^{(n-1)/3}}=\frac{1}{p-1}\ \left(\frac{p}{2\sqrt[3]{3}}\right)^{n-1}.\ \ \ \ \ (+)\]
\[k(HV)\geq \frac{n(N,V)}{|H/N|}\geq \frac{ \frac{p^{n-1}}{p-1} }{24^{(n-1)/3}}=\frac{1}{p-1}\ \left(\frac{p}{2\sqrt[3]{3}}\right)^{n-1}.\ \ \ \ \ (+)\]
This implies that if
then
![]() $k(HV)\geq p$
, contradiction, and we are done.
$k(HV)\geq p$
, contradiction, and we are done.
Hence as
![]() $p>1000$
, p will satisfy (***) unless
$p>1000$
, p will satisfy (***) unless
![]() $n\leq 3$
. Since we are done if (***) holds, we may assume that
$n\leq 3$
. Since we are done if (***) holds, we may assume that
![]() $n\leq 3$
, i.e.,
$n\leq 3$
, i.e.,
![]() $n=2$
or
$n=2$
or
![]() $n=3$
.
$n=3$
.
First suppose that
![]() $n=3$
. Then by
$n=3$
. Then by
![]() $(+)$
we get that
$(+)$
we get that
![]() $k(HV)\geq {p}/{4\sqrt[3]{9}}\geq {Dp}/{\log_2(p)}$
. So we are done when
$k(HV)\geq {p}/{4\sqrt[3]{9}}\geq {Dp}/{\log_2(p)}$
. So we are done when
![]() $n=3$
.
$n=3$
.
So let finally
![]() $n=2$
. Then
$n=2$
. Then
![]() $|H/N|=2$
. Recall that
$|H/N|=2$
. Recall that
![]() $M=K\times P$
for a Hall p
′-subgroup K of M.
$M=K\times P$
for a Hall p
′-subgroup K of M.
We first want to show that M acts irreducibly on
![]() $V_1$
. To do so, assume that
$V_1$
. To do so, assume that
![]() $V_1=X_1\oplus X_2$
for nontrivial M-modules
$V_1=X_1\oplus X_2$
for nontrivial M-modules
![]() $X_1$
and
$X_1$
and
![]() $X_2$
. Then we also have
$X_2$
. Then we also have
![]() $V_2=Y_1\oplus Y_2$
for nontrivial M-modules
$V_2=Y_1\oplus Y_2$
for nontrivial M-modules
![]() $Y_1$
and
$Y_1$
and
![]() $Y_2$
. Arguing just as in the proof of (**), we let
$Y_2$
. Arguing just as in the proof of (**), we let
![]() $0\ne x_1\in X_1$
, so that each M-orbit on
$0\ne x_1\in X_1$
, so that each M-orbit on
![]() $X_2$
splits in at least p nontrivial
$X_2$
splits in at least p nontrivial
![]() $\textbf{C}_M(x_1)$
-orbits. If
$\textbf{C}_M(x_1)$
-orbits. If
![]() $x_2$
is in one of these orbits, then each M-orbit on
$x_2$
is in one of these orbits, then each M-orbit on
![]() $Y_1$
splits in at least p nontrivial
$Y_1$
splits in at least p nontrivial
![]() $\textbf{C}_M(x_1+x_2)$
-orbits. If
$\textbf{C}_M(x_1+x_2)$
-orbits. If
![]() $y_1$
is in one of these orbits, then each M-orbit on
$y_1$
is in one of these orbits, then each M-orbit on
![]() $Y_2$
splits in at least p nontrivial
$Y_2$
splits in at least p nontrivial
![]() $\textbf{C}_M(x_1+x_2+y_1)$
-orbits. This shows that M has at least
$\textbf{C}_M(x_1+x_2+y_1)$
-orbits. This shows that M has at least
![]() $p^3$
nontrivial orbits on V. Thus
$p^3$
nontrivial orbits on V. Thus
 \begin{eqnarray*}k(HV)\ &\geq\ & \frac{k(MV)}{|HV:MV|}\ \geq \ \frac{n(M,V)}{|H:M|}\ \\&\geq\ &\frac{p^3}{2(p-1)}\ \geq\ p,\\\end{eqnarray*}
\begin{eqnarray*}k(HV)\ &\geq\ & \frac{k(MV)}{|HV:MV|}\ \geq \ \frac{n(M,V)}{|H:M|}\ \\&\geq\ &\frac{p^3}{2(p-1)}\ \geq\ p,\\\end{eqnarray*}
contradicting HV being a counterexample. So indeed M acts irreducibly on
![]() $V_1$
(and also on
$V_1$
(and also on
![]() $V_2$
).
$V_2$
).
Next we claim that M acts primitively on
![]() $V_1$
. To see this, assume to the contrary that
$V_1$
. To see this, assume to the contrary that
![]() $V_1=W_1\oplus \dots\oplus W_l$
is the sum of
$V_1=W_1\oplus \dots\oplus W_l$
is the sum of
![]() $l\geq 2$
subspaces
$l\geq 2$
subspaces
![]() $W_i$
(
$W_i$
(
![]() $i=1,\dots l$
) which are transitively permuted by M. Let
$i=1,\dots l$
) which are transitively permuted by M. Let
![]() $L\unlhd M$
be the kernel of this permutation action. Then likewise
$L\unlhd M$
be the kernel of this permutation action. Then likewise
![]() $V_2=W_{l+1}\oplus \dots\oplus W_{2l}$
is the sum of l subspaces
$V_2=W_{l+1}\oplus \dots\oplus W_{2l}$
is the sum of l subspaces
![]() $W_i$
(
$W_i$
(
![]() $i=l+1,\dots ,2l$
) which are transitively permuted by
$i=l+1,\dots ,2l$
) which are transitively permuted by
![]() $M/L$
. Now if P is not a subgroup of L, then P permutes the
$M/L$
. Now if P is not a subgroup of L, then P permutes the
![]() $W_i$
with orbits of length p. Hence
$W_i$
with orbits of length p. Hence
![]() $l\geq p$
and we may assume that
$l\geq p$
and we may assume that
![]() $\{W_1,\dots , W_p\}$
is a P-orbit. But then taking
$\{W_1,\dots , W_p\}$
is a P-orbit. But then taking
![]() $0\ne w_1\in W_1$
and adding up the elements in
$0\ne w_1\in W_1$
and adding up the elements in
![]() $w_1^P$
we easily find a nonzero fixed point of P on
$w_1^P$
we easily find a nonzero fixed point of P on
![]() $W_1\oplus\dots\oplus W_p$
, contradicting P acting frobeniusly on V. Thus indeed
$W_1\oplus\dots\oplus W_p$
, contradicting P acting frobeniusly on V. Thus indeed
![]() $P\leq L$
.
$P\leq L$
.
We can now argue as for M above to see that L has at least
![]() $p^{2l-1}$
nontrivial orbits on V. Using Dixon’s result again, we know that
$p^{2l-1}$
nontrivial orbits on V. Using Dixon’s result again, we know that
![]() $|M/L|\leq 24^{(2l-1)/3}\leq 3^{2l-1}$
so that we get
$|M/L|\leq 24^{(2l-1)/3}\leq 3^{2l-1}$
so that we get
 \begin{eqnarray*}k(HV)\ &\geq\ & \frac{k(LV)}{|HV:LV|}\ \geq \ \frac{n(L,V)}{|H:L|}\ \\&\geq\ &\frac{p^{2l-1}}{|H:N| |N:M| |M:L|}\ \geq\ \frac{p^{2l-1}}{2(p-1) 3^{2l-1}},\\\end{eqnarray*}
\begin{eqnarray*}k(HV)\ &\geq\ & \frac{k(LV)}{|HV:LV|}\ \geq \ \frac{n(L,V)}{|H:L|}\ \\&\geq\ &\frac{p^{2l-1}}{|H:N| |N:M| |M:L|}\ \geq\ \frac{p^{2l-1}}{2(p-1) 3^{2l-1}},\\\end{eqnarray*}
where the first inequality follows from the well-known fact that the number of conjugacy classes in a subgroup is bounded by its index times the number of conjugacy classes in the whole group [
Reference Gallagher6
]. Now since
![]() $p>1000$
and
$p>1000$
and
![]() $l\geq 2$
, we further get
$l\geq 2$
, we further get
contradicting HV being a counterexample. This shows that
![]() $V_1$
(and thus also
$V_1$
(and thus also
![]() $V_2$
) is primitive as an M-module. Then clearly V is also primitive as an N-module.
$V_2$
) is primitive as an M-module. Then clearly V is also primitive as an N-module.
We keep writing
![]() $|V_1|=q^m$
and apply Seager’s result (Theorem 2·3) to the action of
$|V_1|=q^m$
and apply Seager’s result (Theorem 2·3) to the action of
![]() $N/\textbf{C}_N(V_1)$
on
$N/\textbf{C}_N(V_1)$
on
![]() $V_1$
. This yields that we have one of the following situations:
$V_1$
. This yields that we have one of the following situations:
-
(1)
 $N/\textbf{C}_N(V_1)$
is permutation isomorphic to a subgroup of
$N/\textbf{C}_N(V_1)$
is permutation isomorphic to a subgroup of
 $\Gamma(q^m)$
;
$\Gamma(q^m)$
; -
(2) If r is the number of orbits of N on
 $V_1$
, then
$V_1$
, then
 $r>(q^{m/2}/12m) +1$
; or
$r>(q^{m/2}/12m) +1$
; or -
(3)
 $q^m\in\{17^4, 19^4, 7^6, 5^8, 7^8, 13^8, 7^9, 3^{16}, 5^{16}\}$
.
$q^m\in\{17^4, 19^4, 7^6, 5^8, 7^8, 13^8, 7^9, 3^{16}, 5^{16}\}$
.
Let
![]() $W\leq V$
be an irreducible P-module. Since
$W\leq V$
be an irreducible P-module. Since
![]() $V_P$
is homogenous, then there is a
$V_P$
is homogenous, then there is a
![]() $t\in\mathbb{N}$
such that
$t\in\mathbb{N}$
such that
![]() $ V_P$
is a direct sum of t copies of W. Now we have
$ V_P$
is a direct sum of t copies of W. Now we have
![]() $q^m=|V|=|W|^t$
, so if we write
$q^m=|V|=|W|^t$
, so if we write
![]() $|W|=q^s$
, then we see that
$|W|=q^s$
, then we see that
![]() $m=st$
.
$m=st$
.
Note that if
![]() $s=1$
, then by [
Reference Manz and Wolf20
, Theorem 2·1] we have that (1) holds; so if (1) does not hold, then we know that
$s=1$
, then by [
Reference Manz and Wolf20
, Theorem 2·1] we have that (1) holds; so if (1) does not hold, then we know that
![]() $s\geq 2$
.
$s\geq 2$
.
We first assume that (2) holds, but (1) does not hold. As just observed, then
![]() $s\geq 2$
. Moreover, from (2) we get
$s\geq 2$
. Moreover, from (2) we get
Now if
![]() $v_1\in V_1$
, then
$v_1\in V_1$
, then
![]() $\textbf{C}_N(v_1)\leq N$
also has at least r distinct orbits on
$\textbf{C}_N(v_1)\leq N$
also has at least r distinct orbits on
![]() $V_2$
, and this shows that each orbit of N on
$V_2$
, and this shows that each orbit of N on
![]() $V_1$
gives rise to at least r orbits of N on V which all have a representative that has
$V_1$
gives rise to at least r orbits of N on V which all have a representative that has
![]() $v_1$
as their
$v_1$
as their
![]() $V_1$
-component. Then we have
$V_1$
-component. Then we have
![]() $n(N,V)\geq r^2$
, and with the above and the fact that
$n(N,V)\geq r^2$
, and with the above and the fact that
![]() $s=\log_q|W|$
we see that
$s=\log_q|W|$
we see that
Now since
![]() $|W|>|P|=p>1000$
, we see that the function
$|W|>|P|=p>1000$
, we see that the function
![]() $f(x)= |W|^x/x^2$
is increasing for
$f(x)= |W|^x/x^2$
is increasing for
![]() $x\geq 2$
, and hence
$x\geq 2$
, and hence
![]() $|W|^t/t^2\geq |W|^2/2^2=|W|2t/4$
, and thus
$|W|^t/t^2\geq |W|^2/2^2=|W|2t/4$
, and thus
 \begin{eqnarray*}n(N,V)\ &\geq\ &\frac{|W|^{2}}{576(\log_q|W|)^2} \ \geq\ \frac{|W|^{2}}{576(\log_2|W|)^2}\ \\\ &=\ & \frac{D|W|}{(\log_2|W|)}\cdot \frac{|W|}{576D\log_2|W|}\ \geq\ \frac{Dp}{\log_2p}\cdot \frac{p}{576D\log_2p}.\end{eqnarray*}
\begin{eqnarray*}n(N,V)\ &\geq\ &\frac{|W|^{2}}{576(\log_q|W|)^2} \ \geq\ \frac{|W|^{2}}{576(\log_2|W|)^2}\ \\\ &=\ & \frac{D|W|}{(\log_2|W|)}\cdot \frac{|W|}{576D\log_2|W|}\ \geq\ \frac{Dp}{\log_2p}\cdot \frac{p}{576D\log_2p}.\end{eqnarray*}
Since clearly
![]() $k(HV)\geq n(N,V)/|H/N|=n(N,V)/2$
, we see that we are done if
$k(HV)\geq n(N,V)/|H/N|=n(N,V)/2$
, we see that we are done if
![]() ${p}/{576D(\log_2p)}\geq 2$
. This happens if and only if
${p}/{576D(\log_2p)}\geq 2$
. This happens if and only if
Now first note that if
![]() $p>11000$
and
$p>11000$
and
![]() $D=1/2$
, then this is the case (we actually could choose D slightly larger here) and we are done.
$D=1/2$
, then this is the case (we actually could choose D slightly larger here) and we are done.
In general, however, with our lower bound on D from the beginning of the proof we obtain
This is the critical case mentioned at the beginning of the proof and is thus the one which determines D. The optimal D is reached when we have equality here, so we have to find p such that the left hand side is equal to the right-hand side. With the help of a calculator one easily finds that this happens exactly when
![]() $p = 4936.0274$
, and then the value of D equals 0.3492276. Therefore if
$p = 4936.0274$
, and then the value of D equals 0.3492276. Therefore if
![]() $D=0.3942$
, then we are done in this situation as well.
$D=0.3942$
, then we are done in this situation as well.
Next we assume that (3) holds, but (1) does not hold. As observed above, since (1) does not hold, we have
![]() $s\geq 2$
. Hence
$s\geq 2$
. Hence
![]() $|W|\leq q^{m/2}$
and actually
$|W|\leq q^{m/2}$
and actually
![]() $|W|= q^{m/s}$
. Since
$|W|= q^{m/s}$
. Since
![]() $p=|P|$
divides
$p=|P|$
divides
![]() $|W|-1$
and since (3) holds (and since
$|W|-1$
and since (3) holds (and since
![]() $a-1$
divides
$a-1$
divides
![]() $a^b-1$
for any positive integers a, b), we see that p is a prime divisor of one of the following numbers:
$a^b-1$
for any positive integers a, b), we see that p is a prime divisor of one of the following numbers:
![]() $17^2-1, 19^2-1, 7^2-1, 7^3-1, 5^4-1, 5^2-1, 7^4-1, 7^2-1, 11^4-1, 11^2-1,13^4-1, 7^3-1, 3^8-1, 3^4-1, 3^2-1, 5^8-1, 5^4-1, 5^2-1$
. But recall from the very beginning that
$17^2-1, 19^2-1, 7^2-1, 7^3-1, 5^4-1, 5^2-1, 7^4-1, 7^2-1, 11^4-1, 11^2-1,13^4-1, 7^3-1, 3^8-1, 3^4-1, 3^2-1, 5^8-1, 5^4-1, 5^2-1$
. But recall from the very beginning that
![]() $p>1000$
, and none of the numbers listed has a prime divisor this large. This is a contradiction.
$p>1000$
, and none of the numbers listed has a prime divisor this large. This is a contradiction.
It remains to consider the case that (1) holds. Then N is isomorphic to a subgroup of
![]() $\Gamma(q^m)\times\Gamma(q^m)$
. Recall that
$\Gamma(q^m)\times\Gamma(q^m)$
. Recall that
![]() $\Gamma(q^m)$
is of order
$\Gamma(q^m)$
is of order
![]() $(q^m-1)m$
and has a normal cyclic subgroup
$(q^m-1)m$
and has a normal cyclic subgroup
![]() $\Gamma_0(q^m)$
. Write
$\Gamma_0(q^m)$
. Write
![]() $N_0=N\cap (\Gamma_0(q^m)\times\Gamma_0(q^m))$
, so that
$N_0=N\cap (\Gamma_0(q^m)\times\Gamma_0(q^m))$
, so that
![]() $N_0/\textbf{C}_{N_0}(V_i)$
acts frobeniusly on
$N_0/\textbf{C}_{N_0}(V_i)$
acts frobeniusly on
![]() $V_i$
(
$V_i$
(
![]() $i=1,2$
). Furthermore, we have
$i=1,2$
). Furthermore, we have
![]() $|N/N_0|\leq m^2$
.
$|N/N_0|\leq m^2$
.
Let s be as above, that is,
![]() $V_1$
viewed as a P-module, is the direct sum of s copies of an irreducible P-module W. First suppose that
$V_1$
viewed as a P-module, is the direct sum of s copies of an irreducible P-module W. First suppose that
![]() $s\geq 2$
. Writing again n(N,V) for the number of orbits of N on V, we have
$s\geq 2$
. Writing again n(N,V) for the number of orbits of N on V, we have
Since
![]() $k(HV)\geq k(NV)/2$
, then we are done if
$k(HV)\geq k(NV)/2$
, then we are done if
![]() . Therefore we now assume that
. Therefore we now assume that
![]() or, equivalently,
or, equivalently,
![]() $|N_0|>(1/2D)((\log_2 p)/p)(q^m/m)^2$
.
$|N_0|>(1/2D)((\log_2 p)/p)(q^m/m)^2$
.
Now since p divides
![]() $|W|-1$
and
$|W|-1$
and
![]() $s\geq 2$
, it follows that
$s\geq 2$
, it follows that
![]() $p\leq |V_1|^{1/2}=q^{m/2}$
and
$p\leq |V_1|^{1/2}=q^{m/2}$
and
![]() $p^2\leq q^m$
. Therefore we argue as follows.
$p^2\leq q^m$
. Therefore we argue as follows.
 \begin{eqnarray*}k(HV) &\geq & \frac{k(NV)}{2}\ \geq \frac{k(N)}{2}\geq \frac{\frac{k(N_0)}{|N/N_0|}}{2} = \frac{|N_0|}{2|N/N_0|}\geq \frac{|N_0|}{2m^2}\\[6pt]&\geq &\frac{(1/2D)((\log_2 p)/p)(q^m/m)^2}{2m^2} = \frac{1}{4D}\frac{\log_2 p}{p}\left(\frac{q^m}{m^2}\right)^2\\\end{eqnarray*}
\begin{eqnarray*}k(HV) &\geq & \frac{k(NV)}{2}\ \geq \frac{k(N)}{2}\geq \frac{\frac{k(N_0)}{|N/N_0|}}{2} = \frac{|N_0|}{2|N/N_0|}\geq \frac{|N_0|}{2m^2}\\[6pt]&\geq &\frac{(1/2D)((\log_2 p)/p)(q^m/m)^2}{2m^2} = \frac{1}{4D}\frac{\log_2 p}{p}\left(\frac{q^m}{m^2}\right)^2\\\end{eqnarray*}
 \begin{eqnarray*}& \geq & \frac{1}{4D}\frac{\log_2 p}{p}\left(\frac{q^m}{(\log_2 q^m)^2}\right)^2\geq\frac{1}{4D}\frac{\log_2 p}{p}\left(\frac{p^2}{(\log_2 p^2)^2}\right)^2\\&\geq & \frac{1}{64D}\frac{\log_2 p}{p}\left(\frac{p}{\log_2 p}\right)^4=\frac{1}{64D}\left(\frac{p}{\log_2 p}\right)^3= \frac{Dp}{\log_2 p}\ \cdot\ \frac{1}{64D^2}\left(\frac{p}{\log_2 p}\right)^2.\end{eqnarray*}
\begin{eqnarray*}& \geq & \frac{1}{4D}\frac{\log_2 p}{p}\left(\frac{q^m}{(\log_2 q^m)^2}\right)^2\geq\frac{1}{4D}\frac{\log_2 p}{p}\left(\frac{p^2}{(\log_2 p^2)^2}\right)^2\\&\geq & \frac{1}{64D}\frac{\log_2 p}{p}\left(\frac{p}{\log_2 p}\right)^4=\frac{1}{64D}\left(\frac{p}{\log_2 p}\right)^3= \frac{Dp}{\log_2 p}\ \cdot\ \frac{1}{64D^2}\left(\frac{p}{\log_2 p}\right)^2.\end{eqnarray*}
Now since
![]() $p>1000$
, it is easy to see that the last factor
$p>1000$
, it is easy to see that the last factor
![]() ${1}/{64D^2}\left({p}/{\log_2 p}\right)^2$
is greater than 1, and so we have the desired contradiction to HV being a counterexample and are done.
${1}/{64D^2}\left({p}/{\log_2 p}\right)^2$
is greater than 1, and so we have the desired contradiction to HV being a counterexample and are done.
So let finally
![]() $s=1$
. We argue somewhat similarly to the case that
$s=1$
. We argue somewhat similarly to the case that
![]() $s\geq 2$
, but need some more detailed structural information first. Since
$s\geq 2$
, but need some more detailed structural information first. Since
![]() $s=1$
, we know that
$s=1$
, we know that
![]() $V_1$
is irreducible as a P-module. By [
Reference Manz and Wolf20
, Example 2·7] we know that p is a Zsigmondy prime divisor of
$V_1$
is irreducible as a P-module. By [
Reference Manz and Wolf20
, Example 2·7] we know that p is a Zsigmondy prime divisor of
![]() $q^m-1$
. Since P acts faithfully (actually, frobeniusly) on
$q^m-1$
. Since P acts faithfully (actually, frobeniusly) on
![]() $V_1$
and
$V_1$
and
![]() $V_2$
, with [
Reference Manz and Wolf20
, Lemma 6·5(c)] we conclude that
$V_2$
, with [
Reference Manz and Wolf20
, Lemma 6·5(c)] we conclude that
![]() $\textbf{C}_N(P)=N_0$
. In particular,
$\textbf{C}_N(P)=N_0$
. In particular,
![]() $N/N_0$
is isomorphic to a subgroup of
$N/N_0$
is isomorphic to a subgroup of
![]() ${{\textrm{Aut}}}(P)$
, and thus
${{\textrm{Aut}}}(P)$
, and thus
![]() $N/N_0$
is cyclic. On the other hand, since N is isomorphic to a subgroup of
$N/N_0$
is cyclic. On the other hand, since N is isomorphic to a subgroup of
![]() $\Gamma(q^m)\times\Gamma(q^m)$
, we see that
$\Gamma(q^m)\times\Gamma(q^m)$
, we see that
![]() $N/N_0$
is isomorphic to a subgroup of a homocyclic group of type (m,m), so in particular the exponent of
$N/N_0$
is isomorphic to a subgroup of a homocyclic group of type (m,m), so in particular the exponent of
![]() $N/N_0$
is bounded above by m. Altogether it follows that
$N/N_0$
is bounded above by m. Altogether it follows that
![]() $|N/N_0|\leq m$
.
$|N/N_0|\leq m$
.
Now
Since
![]() $k(HV)\geq k(NV)/2$
, then we are done if
$k(HV)\geq k(NV)/2$
, then we are done if
![]() $\frac{1}{|N_0|}\frac{q^{2m}}{m} \geq \frac{2Dp}{\log_2p}$
. Therefore we now assume that
$\frac{1}{|N_0|}\frac{q^{2m}}{m} \geq \frac{2Dp}{\log_2p}$
. Therefore we now assume that
![]() or, equivalently,
or, equivalently,
![]() $|N_0|>(1/2D)((\log_2 p)/p)(q^{2m}/m)$
.
$|N_0|>(1/2D)((\log_2 p)/p)(q^{2m}/m)$
.
As clearly
![]() $p<|V_1|=q^m$
, we can argue as follows.
$p<|V_1|=q^m$
, we can argue as follows.
 \begin{eqnarray*}k(HV) &\geq & \frac{k(NV)}{2}\ \geq \frac{k(N)}{2}\geq \frac{\frac{k(N_0)}{|N/N_0|}}{2} = \frac{|N_0|}{2|N/N_0|}\geq \frac{|N_0|}{2m}\\&\geq &\frac{(1/2D)((\log_2 p)/p)(q^{2m}/m)}{2m} \geq \frac{1}{4D}\frac{\log_2 p}{p}\left(\frac{q^m}{m}\right)^2 \geq \frac{1}{4D}\frac{\log_2 p}{p}\left(\frac{q^m}{\log_2 q^m}\right)^2\\&\geq &\frac{1}{4D}\frac{\log_2 p}{p}\left(\frac{p}{\log_2 p}\right)^2 = \frac{1}{4D}\frac{p}{\log_2 p}=\frac{Dp}{\log_2 p}\cdot \frac{1}{4D^2}.\end{eqnarray*}
\begin{eqnarray*}k(HV) &\geq & \frac{k(NV)}{2}\ \geq \frac{k(N)}{2}\geq \frac{\frac{k(N_0)}{|N/N_0|}}{2} = \frac{|N_0|}{2|N/N_0|}\geq \frac{|N_0|}{2m}\\&\geq &\frac{(1/2D)((\log_2 p)/p)(q^{2m}/m)}{2m} \geq \frac{1}{4D}\frac{\log_2 p}{p}\left(\frac{q^m}{m}\right)^2 \geq \frac{1}{4D}\frac{\log_2 p}{p}\left(\frac{q^m}{\log_2 q^m}\right)^2\\&\geq &\frac{1}{4D}\frac{\log_2 p}{p}\left(\frac{p}{\log_2 p}\right)^2 = \frac{1}{4D}\frac{p}{\log_2 p}=\frac{Dp}{\log_2 p}\cdot \frac{1}{4D^2}.\end{eqnarray*}
Hence we are done if
![]() ${1}/{4D^2}\geq 1$
or, equivalently,
${1}/{4D^2}\geq 1$
or, equivalently,
![]() $D\leq 1/2$
. Fortunately, this is the case, and the proof is complete.
$D\leq 1/2$
. Fortunately, this is the case, and the proof is complete.
6. Solvable Groups: Primitive Case
Next, we consider the primitive case.
Theorem 6·1. Let p be a prime and H a solvable group such that the Sylow p-subgroup of H is normal in H and cyclic of order p. Let V be a faithful irreducible H-module over GF(q) where q is a prime different from p, and suppose that V is primitive. Then
Proof. By Lemma 2·6 and [
Reference Héthelyi and Külshammer9
], we may assume that
![]() $p>1800$
. Let P be the normal Sylow p-subgroup of H. Let
$p>1800$
. Let P be the normal Sylow p-subgroup of H. Let
![]() $C=\textbf{C}_H(P)$
and put
$C=\textbf{C}_H(P)$
and put
![]() $n=|H:C|$
. Since
$n=|H:C|$
. Since
![]() $H/C$
is isomorphic to a subgroup of
$H/C$
is isomorphic to a subgroup of
![]() ${{\textrm{Aut}}}(P)$
, we deduce that
${{\textrm{Aut}}}(P)$
, we deduce that
![]() $H/C$
is cyclic and n divides
$H/C$
is cyclic and n divides
![]() $p-1$
. If
$p-1$
. If
![]() $\lambda\in{{\textrm{Irr}}}(P)$
is nonprincipal, then
$\lambda\in{{\textrm{Irr}}}(P)$
is nonprincipal, then
![]() $I_H(\lambda)=C$
. By Clifford’s correspondence [
Reference Isaacs16
, Theorem 6·11], any faithful complex representation of H has dimension at least
$I_H(\lambda)=C$
. By Clifford’s correspondence [
Reference Isaacs16
, Theorem 6·11], any faithful complex representation of H has dimension at least
![]() $|H:I_H(\lambda)|=n$
. Furthermore, note that
$|H:I_H(\lambda)|=n$
. Furthermore, note that
![]() $C=P\times U$
, where U is a Hall p
′-complement of C. By Gallagher’s theorem [
Reference Isaacs16
, Corollary 6·17] and Clifford’s correspondence, there are k(U) irreducible characters of H lying over
$C=P\times U$
, where U is a Hall p
′-complement of C. By Gallagher’s theorem [
Reference Isaacs16
, Corollary 6·17] and Clifford’s correspondence, there are k(U) irreducible characters of H lying over
![]() $\lambda$
. We conclude that H has exactly
$\lambda$
. We conclude that H has exactly
![]() $(p-1)k(U)/n$
irreducible characters lying over nonprincipal irreducible characters of P. Since
$(p-1)k(U)/n$
irreducible characters lying over nonprincipal irreducible characters of P. Since
![]() $H/C$
is abelian, we conclude that
$H/C$
is abelian, we conclude that
In particular, the result follows if either
![]() $n\leq2\log p$
or
$n\leq2\log p$
or
![]() $n\geq p/2\log p$
, so we may assume that
$n\geq p/2\log p$
, so we may assume that
![]() $2\log p<n<p/2\log p$
.
$2\log p<n<p/2\log p$
.
Since V is a faithful irreducible module in characteristic q, using Lemma 2·5 we deduce that
Suppose that
![]() $2\log p<n\leq 4\log p$
. Then
$2\log p<n\leq 4\log p$
. Then
In particular
![]() $k(H)\geq p/4\log p$
. Also, the result follows if
$k(H)\geq p/4\log p$
. Also, the result follows if
![]() $k(U)\geq 2$
, so we may assume that
$k(U)\geq 2$
, so we may assume that
![]() $U=1$
. Thus
$U=1$
. Thus
so
Since
the result follows in this case too.
Hence, we may assume that
![]() $4\log p<n<p/2\log p$
. Recall that by hypothesis V is a primitive H-module. (Note that we have not used this hypothesis in the remaining cases.) If H is not isomorphic to a subgroup of
$4\log p<n<p/2\log p$
. Recall that by hypothesis V is a primitive H-module. (Note that we have not used this hypothesis in the remaining cases.) If H is not isomorphic to a subgroup of
![]() $\Gamma(V)$
, then Theorem 2·3 implies that the number of nontrivial orbits of H on V is
$\Gamma(V)$
, then Theorem 2·3 implies that the number of nontrivial orbits of H on V is
![]() $n(H,V)\geq q^{n/2}/12n$
except for when
$n(H,V)\geq q^{n/2}/12n$
except for when
![]() $|V|=17^4, 19^4, 7^6, 5^8, 7^8, 13^8, 7^9, 3^6$
or
$|V|=17^4, 19^4, 7^6, 5^8, 7^8, 13^8, 7^9, 3^6$
or
![]() $5^{16}$
. Thus, in the nonexceptional cases, we have
$5^{16}$
. Thus, in the nonexceptional cases, we have
Note that the third summand is
![]() $\geq p^2/12(p/2\log p)\geq p\log p/6>p/2\log p$
since
$\geq p^2/12(p/2\log p)\geq p\log p/6>p/2\log p$
since
![]() $p>1800$
. The result also follows.
$p>1800$
. The result also follows.
Now, we consider the exceptional cases. In all of them
![]() $|V|\leq q^{16}$
. On the other hand, we know that
$|V|\leq q^{16}$
. On the other hand, we know that
![]() $|V|\geq q^n$
. We conclude that
$|V|\geq q^n$
. We conclude that
![]() $n\leq 16$
. Using (6·1) and the fact that
$n\leq 16$
. Using (6·1) and the fact that
![]() $p> 1800$
, we have that
$p> 1800$
, we have that
and the result follows.
Finally, assume that H is isomorphic to a subgroup of
![]() $\Gamma(V)=CN$
with
$\Gamma(V)=CN$
with
![]() $N=\textrm{GF}(q^m)^{\times}$
and C is the Galois group of
$N=\textrm{GF}(q^m)^{\times}$
and C is the Galois group of
![]() $\textrm{GF}(q^m)/\textrm{GF}(q)$
. Thus
$\textrm{GF}(q^m)/\textrm{GF}(q)$
. Thus
![]() $D=N\cap H$
is a normal subgroup of H of order a divisor of
$D=N\cap H$
is a normal subgroup of H of order a divisor of
![]() $q^m-1$
. Write
$q^m-1$
. Write
![]() $|D|=pf$
. Note that
$|D|=pf$
. Note that
![]() $H/D$
is cyclic of order e, for some divisor e of m. As before,
$H/D$
is cyclic of order e, for some divisor e of m. As before,
Thus, we may assume that
![]() $e\leq p/(2\log p)$
. If
$e\leq p/(2\log p)$
. If
![]() $e\leq 2f\log p$
, then the second summand is
$e\leq 2f\log p$
, then the second summand is
![]() $\geq p/(2\log p)$
and we are done. Since
$\geq p/(2\log p)$
and we are done. Since
![]() $2f\log p<e\leq p/(2\log p)$
, we deduce that
$2f\log p<e\leq p/(2\log p)$
, we deduce that
![]() $f<p/(2\log p)^2$
. It follows that
$f<p/(2\log p)^2$
. It follows that
On the other hand, since
![]() $m\geq e\geq n>4\log p$
,
$m\geq e\geq n>4\log p$
,
Hence, the number of orbits of H on V is at least
![]() $p^{4}/|H|>p$
, and we are done in this case too. This completes the proof.
$p^{4}/|H|>p$
, and we are done in this case too. This completes the proof.
The following is a slightly strengthened version of the second part of Theorem A.
Theorem 6·2.
If G be a solvable group and p divides
![]() $|G:\textbf{F}(G)|$
, then
$|G:\textbf{F}(G)|$
, then
Furthermore, if
![]() $p>11000$
then
$p>11000$
then
Proof. If
![]() $p^2$
divides
$p^2$
divides
![]() $|G|$
, it follows from Theorem 2.2, that
$|G|$
, it follows from Theorem 2.2, that
![]() $k(G)\geq (49p+1)/60\geq p/(2\log p)$
. Hence, we may assume that
$k(G)\geq (49p+1)/60\geq p/(2\log p)$
. Hence, we may assume that
![]() $|G|_p=p$
. Since
$|G|_p=p$
. Since
![]() $k(G)\geq k(G/N)$
for any
$k(G)\geq k(G/N)$
for any
![]() $N\trianglelefteq G$
, we may assume that p divides
$N\trianglelefteq G$
, we may assume that p divides
![]() $|\textbf{F}_2(G):\textbf{F}(G)|$
. By the same reason, we may also assume that
$|\textbf{F}_2(G):\textbf{F}(G)|$
. By the same reason, we may also assume that
![]() $\Phi(G)=1$
so that
$\Phi(G)=1$
so that
![]() $\textbf{F}(G)$
is elementary abelian. By Gaschütz’s theorem [
Reference Huppert14
, III·4·2, III·4·4. and III·4·5], there exists
$\textbf{F}(G)$
is elementary abelian. By Gaschütz’s theorem [
Reference Huppert14
, III·4·2, III·4·4. and III·4·5], there exists
![]() $H\leq G$
such that
$H\leq G$
such that
![]() $G=H\textbf{F}(G)$
and the action of H on
$G=H\textbf{F}(G)$
and the action of H on
![]() $\textbf{F}(G)$
is completely reducible. Write
$\textbf{F}(G)$
is completely reducible. Write
![]() $\textbf{F}(G)=V_1\oplus\cdots\oplus V_t$
as a direct sum of irreducible H-modules. For every i, let
$\textbf{F}(G)=V_1\oplus\cdots\oplus V_t$
as a direct sum of irreducible H-modules. For every i, let
![]() $C_i=\textbf{C}_H(V_i)$
and note that
$C_i=\textbf{C}_H(V_i)$
and note that
![]() $k(G)\geq k((H/C_i)V_i)$
. Thus, we may assume that
$k(G)\geq k((H/C_i)V_i)$
. Thus, we may assume that
![]() $G=HV$
, where
$G=HV$
, where
![]() $V=\textbf{F}(G)$
is a faithful irreducible H-module in characteristic q, for some prime
$V=\textbf{F}(G)$
is a faithful irreducible H-module in characteristic q, for some prime
![]() $q\neq p$
. Now the result follows from Theorem 5·1 and 6·1.
$q\neq p$
. Now the result follows from Theorem 5·1 and 6·1.
It seems that with additional work it might be possible to get
![]() $D=1$
in Theorem 5·1 when p is large enough. However, it is not clear how to improve the constant in Theorem 6·1 even when p is very large.
$D=1$
in Theorem 5·1 when p is large enough. However, it is not clear how to improve the constant in Theorem 6·1 even when p is very large.
We conclude by remarking that, on the other hand, the stronger bound in Theorem 6·2 also holds for small primes. In fact, even Conjectures C and D hold when p is small enough. More precisely, using [
Reference Vera–López and Sangroniz28–Reference Vera–López and Vera–López30
] we have checked that these conjectures hold when
![]() $k(G)\leq14$
. It follows that Conjecture D holds when
$k(G)\leq14$
. It follows that Conjecture D holds when
![]() $p<29$
, Conjecture C holds when
$p<29$
, Conjecture C holds when
![]() $p<100$
and the stronger bound in Theorem 6·2 holds when
$p<100$
and the stronger bound in Theorem 6·2 holds when
![]() $p<230$
.
$p<230$
.
7. Blocks and Characters of p ′-Degree
As we have mentioned in the Introduction, the Hethélyi–Külshammer problem on the number of conjugacy classes has interesting connections with representation theory. For instance, they already pointed out that the inequality
![]() $k(G)\geq2\sqrt{p-1}$
holds for every finite group if it holds for p-solvable groups and the Alperin–McKay conjecture is true for every finite group (McKay’s conjecture is enough; see [
Reference Khukhro, Moretó and Zarrin19
] for this and related questions). The straightforward versions of the results in this paper for p
′-degree irreducible characters and Brauer p-blocks are not true. Recall from [
Reference Héthelyi and Külshammer9
] that the groups
$k(G)\geq2\sqrt{p-1}$
holds for every finite group if it holds for p-solvable groups and the Alperin–McKay conjecture is true for every finite group (McKay’s conjecture is enough; see [
Reference Khukhro, Moretó and Zarrin19
] for this and related questions). The straightforward versions of the results in this paper for p
′-degree irreducible characters and Brauer p-blocks are not true. Recall from [
Reference Héthelyi and Külshammer9
] that the groups
![]() $H_p=\textsf{C}_{\sqrt{p-1}}\ltimes\textsf{C}_p$
where p is a prime such that
$H_p=\textsf{C}_{\sqrt{p-1}}\ltimes\textsf{C}_p$
where p is a prime such that
![]() $p-1$
is a square have
$p-1$
is a square have
![]() $2\sqrt{p-1}$
conjugacy classes. Let
$2\sqrt{p-1}$
conjugacy classes. Let
![]() $V_p$
be a faithful irreducible
$V_p$
be a faithful irreducible
![]() $H_p$
-module over
$H_p$
-module over
![]() $\textrm{GF}(q)$
, where
$\textrm{GF}(q)$
, where
![]() $q\neq p$
is prime, and let
$q\neq p$
is prime, and let
![]() $G_p=H_p\ltimes V_p$
. Then
$G_p=H_p\ltimes V_p$
. Then
![]() ${{\textrm{Irr}}}_{p'}(G_p)={{\textrm{Irr}}}(H_p)$
so
${{\textrm{Irr}}}_{p'}(G_p)={{\textrm{Irr}}}(H_p)$
so
and there is no hope to get a better lower bound for the number of p
′-degree irreducible characters of a finite group G such that p divides
![]() $|G:\textbf{F}(G)|$
than the one in [
Reference Malle and Maróti21
]. Similarly, if
$|G:\textbf{F}(G)|$
than the one in [
Reference Malle and Maróti21
]. Similarly, if
![]() $B_0(G_p)$
is the principal p-block of
$B_0(G_p)$
is the principal p-block of
![]() $G_p$
, then
$G_p$
, then
![]() $k(B_0(G_p))=k(H_p)=2\sqrt{p-1}$
. However, the following natural versions could have an affirmative answer.
$k(B_0(G_p))=k(H_p)=2\sqrt{p-1}$
. However, the following natural versions could have an affirmative answer.
Question 7·1. Is it true that if G is a finite group such that
and p divides
![]() $|G:\textbf{F}(G)|$
then
$|G:\textbf{F}(G)|$
then
![]() $k(G)\geq p/\log p$
?
$k(G)\geq p/\log p$
?
The subgroup
![]() $\bigcap_{\chi\in{{\textrm{Irr}}}_{p'}(G)}\textrm{Ker}\chi$
is known to have interesting properties. For instance, by a theorem of Y. Berkovich [
Reference Navarro25
, Theorem 7·7] it has a normal p-complement.
$\bigcap_{\chi\in{{\textrm{Irr}}}_{p'}(G)}\textrm{Ker}\chi$
is known to have interesting properties. For instance, by a theorem of Y. Berkovich [
Reference Navarro25
, Theorem 7·7] it has a normal p-complement.
Question 7·2.
Is it true that if B is a faithful Brauer p-block of positive defect of a finite group G and p divides
![]() $|G:\textbf{F}(G)|$
then
$|G:\textbf{F}(G)|$
then
![]() $k(B)\geq p/\log p$
?
$k(B)\geq p/\log p$
?
It would be interesting to see if the proposed bounds in these questions are of the right order of magnitude. In other words, does there exist a universal constant
![]() $c>0$
such that k(G) (respectively k(B)) is at least
$c>0$
such that k(G) (respectively k(B)) is at least
![]() $cp/\log p$
?
$cp/\log p$
?
Acknowledgements
We thank R. Guralnick for helping us understand the results in [Reference Dixon4]. We also thank the referee for their very careful reading of the paper. Parts of this work were written while both authors were attending the conference “Counting conjectures and beyond” at the Isaac Newton Institute for Mathematical Sciences in Cambridge. We thank the Institute for their financial support via the EPSRC grant no EP/R014604/1. The research of the second author is supported by Ministerio de Ciencia e Innovación (Grant PID2019-103854GB-I00 funded by MCIN/AEI/ 10.13039/501100011033) and Generalitat Valenciana CIAICO/2021/163.